钢结构基本原理习题参考解答第六章
钢结构基本原理(沈祖炎)课后习题答案完全版之欧阳治创编

第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅ 非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610yf E ε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386yc f E εε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+= 卸载后残余应变:0.05869c c Eσεε=-= 可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构习题答案第6章

钢结构习题答案第6章第6章钢结构习题答案钢结构是一种广泛应用于建筑和工程领域的结构材料。
它具有高强度、耐腐蚀、抗震等优点,因此被广泛应用于大型建筑、桥梁、塔楼等工程中。
然而,钢结构的设计和施工并不简单,需要经过严格的计算和分析。
本文将针对钢结构的第6章习题提供详细的解答,帮助读者更好地理解和掌握钢结构的相关知识。
1. 问题:一根长度为10m的钢梁,截面为矩形,宽度为200mm,高度为400mm。
如果梁的材料为Q345B,弹性模量为200GPa,计算梁的弯矩和最大应力。
解答:首先计算梁的惯性矩I,根据矩形截面的公式I=(1/12)bh^3,代入宽度和高度的数值,得到I=(1/12)×0.2×0.4^3=0.00533m^4。
然后计算梁的弯矩M,根据梁的长度和材料的弹性模量,使用弯矩公式M=EI/R,其中E为弹性模量,I为惯性矩,R为曲率半径。
曲率半径可以通过梁的长度和挠度计算得到,挠度可以通过梁的受力和材料的弹性模量计算得到。
假设梁的受力为F,根据受力平衡,可以得到F=mg,其中m为梁的质量,g为重力加速度。
将质量和重力加速度的数值代入,得到F=780N。
根据梁的受力和挠度的关系,可以得到挠度δ=F×L^3/(48EI),将受力、长度、弹性模量和惯性矩的数值代入,得到挠度δ=0.00026m。
最后,根据挠度和曲率半径的关系,可以得到曲率半径R=δ/(2L^2),将挠度和长度的数值代入,得到曲率半径R=0.0000013m。
将弹性模量、惯性矩和曲率半径的数值代入弯矩公式,可以得到弯矩M=200GPa×0.00533m^4/0.0000013m=820000N·m。
最大应力可以通过弯矩和截面惯性矩的关系计算得到,最大应力σ=M×h/2I,将弯矩、高度和惯性矩的数值代入,得到最大应力σ=820000N·m×0.4m/(2×0.00533m^4)=307MPa。
《钢结构基本原理》作业解答

《钢结构基本原理》作业解答[判断题]18、在格构式柱中,缀条可能受拉,也可能受压,但设计时缀条应按拉杆来进行设计。
参考答案:错误[论述题]14、工字形截面绕强轴的塑性发展系数与绕弱轴的塑性发展系数哪个大?为什么?15、对于轴压构件,有时也常采用格构式截面(1)请说明什么情况下比较适合采用格构式截面?(2)采用格构式截面时,为什么采用换算长细比来计算虚轴的稳定承载力?(3)在已知双肢格构柱截面形式的条件下,如何计算换算长细比和验算绕虚轴的稳定性?(4)对于双肢缀条柱,除了上一问的验算外还需验算哪些内容?答:14、答:绕弱轴的塑性发展系数大;绕强轴受弯,翼?发生屈服以后截面继续发生塑性发展的潜力不大。
16、答:(1)A 、柱的计算长度较大 B 、柱所承受的轴向荷载较大 C 、对柱的刚度要求较严格,这样情况下截面强度富余,由稳定控制做实腹式浪费材料,所以采用格构式。
(2)构件在微弯的临界平衡状态外,将在截面上产生剪力,从而产生剪切变形。
对于实腹式构件而言,剪力由腹板承担,而腹板的剪切刚度又很大,所以剪切变形小可以忽略不计,但是对于由缀材组成的格构式截面,剪力由缀材承担变形较大不能忽略。
考虑剪切变形的影响,构件的临界承载力降低了,规范用增大长细比的方法考虑这种影响,所以绕虚轴失稳时,采用换算长细比。
1227A A x ox +=λλ(3)缀条柱 (4)还需验算:A 、格构柱的净截面强度;B 、格构柱绕实轴的稳定性 C 、格构柱绕两个轴的长细比是否需要满足刚度要求 D 、单肢的稳定 E 、缀条的稳定 F 、缀条与柱肢连接的强度验算.论述题]13、某焊接工字形截面柱,截面几何尺寸如图所示。
柱的上、下端均为铰接,柱高4。
2m,承受的轴心压力设计值为1000kN ,钢材为Q235,翼缘为火焰切割边,焊条为E43系列,手工焊。
试验算该柱的整体稳定性。
参考资料: f=215N/mm 2【论述题]12、分析图示实腹轴心受压柱头的传力路线,写出焊缝①、②的计算表达式。
(完整版)钢结构基本原理课后习题与答案完全版
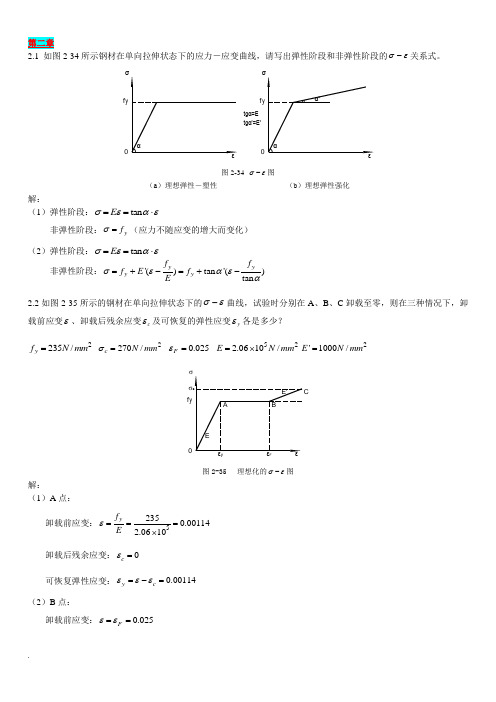
2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化) (2)弹性阶段:tan E σεαε==⋅ 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσ图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===⨯卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε==卸载后残余应变:0.02386y c f Eεε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点: 卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构基本基础原理课后习题集与标准答案完全版

-/第二章2.1如图2-34所示钢材在单向拉伸状态下的应力一应变曲线,请写出弹性阶段和非弹性阶段的解:(1)A 点:卸载后残余应变:关系式。
解:(1) 弹性阶段:非弹性阶段:(2)弹性阶段: 非弹性阶段:(b )理想弹性强化tan(应力不随应变的增大而变化)tan E'(y―)f y tan '(tan2.2如图2-35所示的钢材在单向拉伸状态下的 曲线,试验时分别在载前应变、卸载后残余应变c 及可恢复的弹性应变y 各是多少?f y 235N/mm 2270N/mm 20.025 E52 2.06 105N/mm 2A 、B 、C 卸载至零,则在三种情况下,卸2E' 1000N/mm 2卸载前应变: fy E235 52.06 1050.00114可恢复弹性应c 0.00114图图图2-35 理想化的(2)B 点:卸载前应变: 0.025卸载后残余应变:可恢复弹性应变:2.3试述钢材在单轴反复应力作用下,钢材的曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材曲线与反复应力大小和作用时间关系:当构件反复力|| f y时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材曲线基本无变化;当| | f y时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢材曲线会相对更高而更短。
另外,载一定作用力下,作用时间越快,钢材强度会提高、而变形能力减弱,钢材曲线也会更高而更短。
钢材疲劳强度与反复力大小和作用时间关系:反复应力大小对钢材疲劳强度的影响以应力比或应力幅(焊接结构)来量度。
一般来说,应力比或应力幅越大,疲劳强度越低;而作用时间越长(指次数多),疲劳强度也越低。
2.4试述导致钢材发生脆性破坏的各种原因。
答:(1)钢材的化学成分,如碳、硫、磷等有害元素成分过多;(2)钢材生成过程中造成的缺陷,如夹层、偏析等;(3)钢材在加工、使用过程中的各种影响,如时效、冷作硬化以及焊接应力等影响;(4)钢材工作温度影响,可能会引起蓝脆或冷脆;(5)不合理的结构细部设计影响,如应力集中等;(6)结构或构件受力性质,如双向或三向同号应力场;(7)结构或构件所受荷载性质,如受反复动力荷载作用。
钢结构设计原理习题及答案

第一章 绪论1.填空题(1)某构件当其可靠指标β减小时,相应失效概率将随之 。
(2)承载能力极限状态为结构或构件达到 或达到不适于继续承载的变形时的极限状态。
(3)在对结构或构件进行 极限状态验算时,应采用永久荷载和可变荷载的标准值。
2.选择题(1)在结构设计中,失效概率P f 与可靠指标β的关系为 。
A. P f 越大,β越大,结构可靠性越差B. P f 越大,β越小,结构可靠性越差C. P f 越大,β越小,结构越可靠D. P f 越大,β越大,结构越可靠(2)按承载力极限状态设计钢结构时,应考虑 。
A. 荷载效应的基本组合B. 荷载效应的标准组合C. 荷载效应的基本组合,必要时尚应考虑荷载效应的偶然组合D. 荷载效应的频遇组合3.简答题(1)钢结构和其他建筑材料结构相比的特点。
(2)钢结构的设计方法。
第二章 钢结构的材料1.(1)假定钢材为理想的弹塑性体,是指屈服点以前材料为 性的。
(2)伸长率10δ和伸长率5δ,分别为标距长l = 和l = 的试件拉断后的 。
(3)如果钢材具有 性能,那么钢结构在一般情况下就不会因偶然或局部超载而发生突然断裂。
α是钢材的指标。
(4)k2.填空题选择题(1)钢材的设计强度是根据确定的。
A. 比例极限B. 弹性极限C. 屈服点D. 极限强度(2)钢结构设计中钢材的设计强度为。
A. 强度标准值B. 钢材屈服点C. 强度极限值D. 钢材的强度标准值除以抗力分项系数(3)钢材是理想的体。
A. 弹性B. 塑性C. 弹塑性D. 非弹性(4)钢结构中使用钢材的塑性指标,目前最主要用表示。
A. 流幅B. 冲击韧性C. 可焊性D. 伸长率(5)钢材的伸长率δ用来反映材料的。
A. 承载能力B. 弹性变形能力C. 塑性变形能力D. 抗冲击荷载能力(6)建筑钢材的伸长率与标准拉伸试件标距间长度的伸长值有关。
A. 达到屈服应力时B. 达到极限应力时C. 试件塑性变形后D. 试件断裂后(7)钢材的三项主要力学性能为。
钢结构基本原理(第二版)习题参考解答第六章

6.1 工字形焊接组合截面简支梁,其上密铺刚性板可以阻止弯曲平面外变形。
梁上均布荷载(包括梁自重)4/q kN m =,跨中已有一集中荷载090F kN =,现需在距右端4m 处设一集中荷载1F 。
问根据边缘屈服准则,1F 最大可达多少。
设各集中荷载的作用位置距梁顶面为120mm ,分布长度为120mm 。
钢材的设计强度取为2300/N mm 。
另在所有的已知荷载和所有未知荷载中,都已包含有关荷载的分项系数。
图6-34 题6.1解:(1)计算截面特性2250122800812400A mm =⨯⨯+⨯=339411250824(2508)800 1.33101212x I mm =⨯⨯-⨯-⨯=⨯ 633.229102x x I W mm h==⨯ 32501240640082001858000m S mm =⨯⨯+⨯⨯= 31250124061218000S mm =⨯⨯=(2)计算0F 、1F 两集中力对应截面弯矩()210111412901263422843F M F kN m =⨯⨯+⨯⨯+⨯=+⋅ ()1118128248489012824424333F M F kN m =⨯-⨯⨯+⨯⨯⨯+⨯=+⋅ 令10M M >,则当1147F kN >,使弯矩最大值出现在1F 作用截面。
(3)梁截面能承受的最大弯矩63.22910300968.7x M W f kN m ==⨯⨯=⋅令0M M =得:1313.35F kN =;令1M M =得:1271.76F kN =故可假定在1F 作用截面处达到最大弯矩。
(4)a .弯曲正应力61max 68(244)1033003.22910x x F M W σ+⨯==≤⨯ ① b.剪应力1F 作用截面处的剪力1111122412449053()2233V F F kN ⎛⎫=⨯⨯-⨯+⨯+=+ ⎪⎝⎭311max 925310185800031.33108m x F V S I t τ⎛⎫+⨯⨯ ⎪⎝⎭==≤⨯⨯ ② c.局部承压应力 在右侧支座处:()312244510330081205122120c F σ⎛⎫++⨯ ⎪⎝⎭=≤⨯+⨯+⨯ ③ 1F 集中力作用处:()311030081205122120c F σ⨯=≤⨯+⨯+⨯ ④ d.折算应力1F 作用截面右侧处存在很大的弯矩,剪力和局部承压应力,计算腹板与翼缘交界处的分享应力与折算应力。
钢结构习题答案第六章

最大弯矩设计值: M max =
1 1 ( g + q )l 2 = × 56.4 × 5.52 = 213.26KN ⋅ m 8 8
最大剪力设计值: Vmax =
1 1 ( g + q)l = × 56.4 × 5.5 = 155.1KN 2 2
①截面选择: 由 Wnx ≥
(2)当采用工字型截面时:
4 2 5 g k l 4 ( 5n + 2n + 1) p k l 3 νT = + 384 EI x 384n3 EI x
③腹板局部承压计算:由于在支座反力作用处设置了支承加劲肋,因而不必验算腹板的局部承压强度。
④刚度:梁跨中的最大绕度为:
4
νQ
(5n =
(5 × 54 + 2 × 52 +1) 5 × 3.06 × 18000 + × 119.61× 103 × 180003 3 1 18000 5 = × = 22.3mm ≤ [ν T ] = = 45mm 3 4 384 206 × 10 × 1097352 × 10 400
《钢结构》第六章
习题答案
1 解: (1)荷载统计: 图1 由板传给次梁的荷载(先不考虑工字梁的自重) : 则:次梁上的线荷载标准值为: 可变荷载效应控制的组合:
g k = 2.0 × 3 = 6KN / m, qk = 4.5 × 3 = 13.5KN / m
g k + q k = 6 + 13.5 = 19.5KN / m
主梁的自重: g k = 1.1× 7850 × 354 × 10 = 3.06KN/m (1.1 表示考虑加劲肋等的重量而采用的构造系数)
-6
1 M max = 2047.032 + 1.2 × × 3.06 × 182 = 2195.748KN ⋅ m 8 ;
钢结构第六章作业参考答案

习题 6.1 有一两端铰接长度为4m 的偏心受压柱,用Q235的HN400x200x8x13做成,压力的设计值为490KN ,两端偏心距相同,皆为20cm 。
试验算其承载力。
解:(1)截面的几何特性A = 84.12 cm 2 I X = 23700cm 4 I y = 1740cm 4 i x = 16.8cm i y = 4.54cm w x = 1190cm 3 (2) 验算强度 N= 490kN M= N x e 0 =490x0.2=98kN ∙mAnN+ X Mx r Wnx = 324901084.1210⨯⨯ + 6398101.05119010⨯⨯⨯ = 58.25+78.43=136.68N/mm 2 < f =215 N/mm 2 (3) 验算弯矩作用平面内的稳定 λx = x xl i =40016.8= 23.8< [λ] =150 查附表4.2(b 类截面) ϕx = 0.958'Ex N = 22X1.1EAπλ = 2220600084121.123.8π⨯⨯⨯ = 2744.86kN mx β=1.0 x ANϕ +mx X 1x 'Mxr W (10.8)ExNN β- =3490100.9588412⨯⨯+631.098104901.05119010(10.8)2744.86⨯⨯⨯⨯-=152.30N/mm 2 < f =215 N/mm 2可见平面内不失稳。
(4)验算弯矩作用平面外的稳定 λy = 4004.54=88.1 查附表4.2 (b 类截面) ϕy = 0.634ϕb = 1.07 -2y 44000λ = 1.07-288.144000=0.894 tx β=1.0 , η=1.0y A N ϕ + b 1tx x x M W βηϕ = 3490100.6348412⨯⨯ + 631.098101.00.894119010⨯⨯⨯⨯⨯ =184 N/ mm 2< f = 215 N/mm 2 平面外不失稳。
钢结构基本原理课后习题与答案完全版电子教案

钢结构基本原理课后习题与答案完全版2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
tgα'=E'f y 0f y 0tgα=E图2-34 σε-图(a )理想弹性-塑性 (b )理想弹性强化解:(1)弹性阶段:tan E σεαε==⋅非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==⋅非弹性阶段:'()tan '()tan yyy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f y 0σF图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f E ε===⨯卸载后残余应变:0c ε= 可恢复弹性应变:0.00114y c εεε=-=(2)B 点:卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-= 可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变:0.05869c c E σεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
钢结构设计原理(北方民族大学)知到章节答案智慧树2023年

钢结构设计原理(北方民族大学)知到章节测试答案智慧树2023年最新第一章测试1.钢结构计算中,实际内力和力学计算结果最符合的原因是()参考答案:钢材材质均匀2.下述破坏属于正常使用极限状态的是()参考答案:构件在荷载作用下产生较大变形而影响作3.结构的重要性系数是根据结构的( )分别取 1.1、1.0、0.9。
参考答案:安全等级的一、二、三级4.在构件发生断裂破坏前,有明显先兆的情况是()的典型特征。
参考答案:塑性破坏5.下列关于荷载分项系数的论述( )不正确。
参考答案:不分场合均取为1.26.验算型钢梁正常使用极限状态的变形时,用荷载( )。
参考答案:标准值7.钢结构设计中按荷载设计值计算的有 ( )参考答案:局部稳定;强度;整体稳定8.承载能力极限状态包括构件和连接的强度破坏、疲劳破坏和因过度变形而不适于继续承载的状态。
参考答案:对9.承载能力极限状态包括影响结构、构件和非结构构件正常使用或外观的变形,影响正常使用的振动,影响正常使用或耐久性能的局部破坏。
参考答案:错10.焊接结构的疲劳强度的大小与()关系不大。
参考答案:应力循环次数第二章测试1.反映钢材在塑性变形和断裂过程中吸收能量的能力的指标为()参考答案:韧性2.钢中含碳量越高()参考答案:强度越高3.结构钢的屈服强度 ( ) :参考答案:随着厚度增大而降低,而且随质量等级从A到D逐级提高4.在钢的化学元素中,下列哪一种元素的有害作用主要是使钢在低温时韧性降低并容易发生脆性破坏( )参考答案:磷5.碳的含量对钢材性能的影响很大,一般情况下随着含碳量的增高,钢材的塑性和韧性逐渐增高。
参考答案:错6.碳含量在0.12%-0.20%范围内碳素钢,可焊性最好。
参考答案:对7.钢材越厚压缩比越小,因此厚度大的钢材不但强度较高,而且塑性、冲击韧性和焊接性能也较好。
参考答案:错8.钢材具有两种性质完全不同的破坏形式,即塑性破坏和脆性破坏。
参考答案:对9.能够较显著的提高钢材的强度而不过多降低塑性和韧性的弱脱氧剂是( )参考答案:锰10.钢材中硫的含量超过规定标准,()。
钢结构基本原理(沈祖炎)课后习题答案完全版
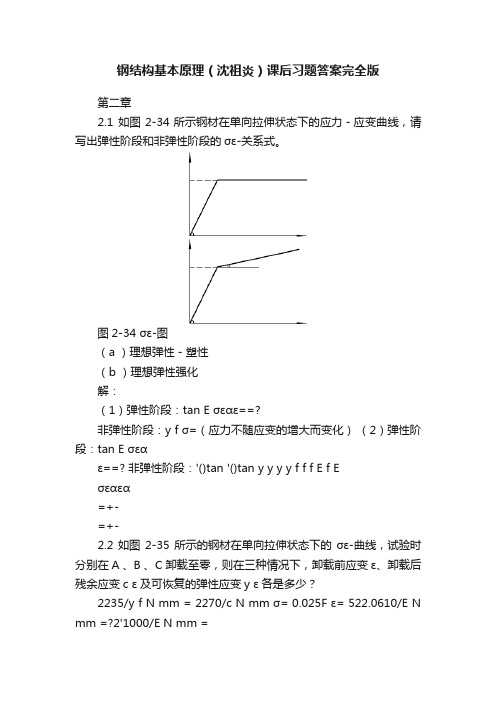
钢结构基本原理(沈祖炎)课后习题答案完全版第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式。
图2-34 σε-图(a )理想弹性-塑性(b )理想弹性强化解:(1)弹性阶段:tan E σεαε==?非弹性阶段:y f σ=(应力不随应变的增大而变化)(2)弹性阶段:tan E σεαε==? 非弹性阶段:'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少?2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =?2'1000/E N mm =图2-35 理想化的σε-图解:(1)A 点:卸载前应变:52350.001142.0610y f Eε===?卸载后残余应变:0c ε=可恢复弹性应变:0.00114y c εεε=-=tgα'=E'f y 0f y 0tgα=E σf yCσF卸载前应变:0.025F εε== 卸载后残余应变:0.02386y c f E εε=-=可恢复弹性应变:0.00114y c εεε=-=(3)C 点:卸载前应变:0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变:0.05869cc Eσεε=-=可恢复弹性应变:0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。
答:钢材σε-曲线与反复应力大小和作用时间关系:当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化;当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载-卸载连续进行,钢材σε-曲线也基本无变化;若加载-卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。
(完整版)钢结构设计原理习题集及答案

式中N——轴心拉力或轴心压力
An——构件的净截面面积
n——在节点或拼接处,构件一端连接的高强度螺栓数目;
n1——所计算截面上高强度螺栓数目;
f——钢材的抗拉或抗压强度设计值。
上式括号内数值小于1,这表明所计算截面上的轴心力N已有一定程度的减少。对比普通螺栓受剪连接构件开孔截面的净截面强度的计算公式:
钢结构设计原理习题集及答案(2011-09-28 10:53:54)
标签:a格极限状态焊缝构件承载力教育分类:试卷题库
钢结构设计原理习题集及答案
第一章绪论
练习题
一、简答题
1.简述钢结构的特点和应用范围。
答:特点:(1)承载能力大;(2)稳妥可靠;(3)便于工业化生产,施工周期短;(4)密闭性好;耐热但不耐火;(5)耐腐蚀性差;(6)容易产生噪音
综上所述,无论是从焊条等焊接材料的消耗和焊接速度、焊接残余应力,或是从焊缝的相对强度,角焊缝都以选用小焊脚尺寸为宜。因此,当焊件的焊接长度较富余,在满足最大焊缝长度的要求下,采用小而长比大强度螺栓的较普通螺栓的小?
答:摩擦型高强度螺栓的受剪连接传力特点不同于普通螺栓。后者是靠螺栓自身受剪和孔壁承压传力,而前者则是靠被连接板叠间的摩擦力传力。一般可认为摩擦力均匀分布于螺栓孔四周,故孔前传力约为0.5。因此,构件开孔截面的净截面强度的计算公式为:
应用范围:(1)承受荷载很大或跨度大,高度大的结构;(2)承受动力荷载作用或经常移动的结构;(3)经常拆装的拼装式结构;(4)对密闭性要求高的结构;(5)高温车间或需承受一定高温的结构;(6)轻型结构
(完整版)钢结构基础第六章答案

钢结构基础第六章答案6.1 工字形焊接组合截面简支梁,其上密铺刚性板可以阻止弯曲平面外变形。
梁上均布荷载(包括梁自重),跨中已有一集中荷载,现需在距右端4处4/q kN m =090F kN =m 设一集中荷载。
问根据边缘屈服准则,最大可达多少。
设各集中荷载的作用位置距梁1F 1F 顶面为120mm ,分布长度为120mm 。
钢材的设计强度取为。
另在所有的已知2300/N mm 图6-34 题6.1解:(1)计算截面特性2250122800812400A mm =⨯⨯+⨯= 339411250824(2508)800 1.33101212x I mm =⨯⨯-⨯-⨯=⨯633.229102x x IW mm h ==⨯ 32501240640082001858000m S mm =⨯⨯+⨯⨯=31250124061218000S mm =⨯⨯=(2)计算、两集中力对应截面弯矩0F 1F ()210111412901263422843F M F kN m =⨯⨯+⨯⨯+⨯=+⋅()1118128248489012824424333F M F kN m =⨯-⨯⨯+⨯⨯⨯+⨯=+⋅令,则当,使弯矩最大值出现在作用截面。
10M M >1147F kN >1F (3)梁截面能承受的最大弯矩63.22910300968.7x M W f kN m==⨯⨯=⋅令得:;令得:0M M =1313.35F kN =1M M =1271.76F kN =故可假定在作用截面处达到最大弯矩。
1F (4)a .弯曲正应力①61max68(244)1033003.22910x x F M W σ+⨯==≤⨯b.剪应力作用截面处的剪力1F 1111122412449053()2233V F F kN ⎛⎫=⨯⨯-⨯+⨯+=+ ⎪⎝⎭ ②311max925310185800031.33108m x F V S I t τ⎛⎫+⨯⨯ ⎪⎝⎭==≤⨯⨯c.局部承压应力在右侧支座处: ③()312244510330081205122120c F σ⎛⎫++⨯⎪⎝⎭=≤⨯+⨯+⨯集中力作用处: ④1F ()311030081205122120c F σ⨯=≤⨯+⨯+⨯d.折算应力作用截面右侧处存在很大的弯矩,剪力和局部承压应力,计算腹板与翼缘交界处的分享1F 应力与折算应力。
钢结构习题5-6章参考答案

第5章 受弯构件14. 一简支梁,梁跨为7m,焊接组合工字形对称截面150mm 450mm 18mm 12mm ×××(图5-57),梁上作用有均布恒载(标准值,未含梁自重)17.1kN/m ,均布活荷载6.8kN/m ,距梁端2.5m 处,尚有集中恒荷载标准值60kN ,支承长度200mm ,荷载作用面距离钢梁顶面为120mm ,钢材抗拉强度设计值为2215N/mm ,抗剪强度设计值为2125N/mm ,荷载分项系数对恒载取1.2,对活载取1.4。
试验算钢梁截面是否满足强度要求(不考虑疲劳)。
解:截面积2A=1501824141210368mm ××+×=334150450138414323046144mm 1212××=−=x I3x W 1440000mm 2==xI h梁自重 32-67850kg/m 10368mm 10=81.4kg/m=0.814kN/m ××简支梁承受的均布恒载荷载标准值k (0.814+17.1)kN/m=17.9kN/m q =均布线荷载设计值y 1.217.9+1.4 6.8=31kN/m q =××集中荷载设计值y 1.26072kN p =×=(1)验算该简支梁的抗弯强度按y xx nx y ny+γW γW M M f ≤计算,取y 0M =。
集中恒荷载作用处有2x 317 4.512.572 2.531 2.5290.1kN m 272M ×=×+××−××=⋅ 跨中处2x 317 4.513.572 3.531 3.5721279.9kN m 272M ×=×+××−××−×=⋅受压翼缘的宽厚比:w 1b-t b 15012= 3.8t 2t 36−==取x 1.05γ=截面模量6y 22xx nx y ny 290.110+192.3N/mm 215N/mm 1.051440000γγ×==<=×M M f W W (满足) (2)验算抗剪强度 支座处剪力最大且317 4.572108.546.3154.8kN 27V ×=+×=+= 320715018(2079)20712840294mm 2S =××++××=322v w 154.810840294=33.5N/mm 125N/mm 32304614412VS f It τ××==<=×(满足) (3)局部承压强度集中力沿腹板平面作用于梁上翼缘,该荷载作用处未加加劲肋,应验算该处腹板计算高度上边缘的局部承压强度。
