初中数学专题训练--圆--圆扇形弓形的面积
圆、扇形、弓形的面积(一)

圆、扇形、弓形的面积(一)圆的面积在几何学中,圆是一个平面上所有点到一个固定点的距离都相等的点的集合。
圆的面积是围绕圆心一周的区域。
公式推导设圆的半径为r,我们可以使用数学公式计算圆的面积。
圆的面积公式如下:面积= πr²其中,π(pi)是一个常数,约等于3.14159。
例子例如,如果一个圆的半径为 5 cm ,那么它的面积可以用以下公式计算:面积= π × (5 cm)² ≈ 3.14159 × 25 cm² ≈ 78.53975 cm²所以,这个圆的面积约为 78.54 平方厘米。
扇形的面积扇形是一个由圆心、圆弧及两个半径所围成的图形,其中圆心角等于360度(或2π弧度)。
扇形的面积是扇形圆心角所对应的圆弧面积。
公式推导设扇形的半径为r,圆心角为θ(单位为弧度),我们可以使用下面的公式计算扇形的面积:面积= (θ/2π) × πr² = (θ/2) × r²例子例如,如果一个扇形的半径是 6 cm ,圆心角是 60 度,我们可以使用以下公式计算扇形的面积:面积= (60/360) × π × (6 cm)² = (1/6) × 3.14159 ×36 cm² ≈ 18.84956 cm²所以,这个扇形的面积约为 18.85 平方厘米。
弓形的面积弓形是一个由圆弧、半径和两个弦所围成的图形。
弓形的面积是弓形圆心角所对应的圆弧面积减去弓形中的三角形面积。
公式推导设弓形的半径为r,圆心角为θ(单位为弧度),我们可以使用下面的公式计算弓形的面积:面积= (θ/2π) × πr² - (1/2) × r² × sin(θ)其中,sin(θ) 是角度θ的正弦值。
例子例如,如果一个弓形的半径是 8 cm ,圆心角是 90 度,我们可以使用以下公式计算弓形的面积:面积= (90/360) × π × (8 cm)² - (1/2) × (8 cm)² × sin(90°)= (1/4) × 3.14159 × 64 cm² - (1/2) × 64 cm² × 1≈ 12.56637 cm² - 32 cm²≈ -19.43363 cm²因为弓形在这个例子中是开口向下的,并且sin(90°)等于1,所以面积为负数。
圆周长、弧长-圆、扇形、弓形的面积课后习题解答与提示

圆周长、弧长 圆、扇形、弓形的面积课后习题解答与提示7.20 圆周长、弧长【练习】(课本第168页)1.如下图:O 是△ABC 的中心,连OB .作OD ⊥BC ,垂足为D ,则OD 、OB 分别是正三角形的内切圆、外接圆的半径.在Rt △BOD 中,321==BC BD ,ABC OBD ∠=∠21 =30°∴330tan ==⋅ BD OD ,322==OD OB 故内切圆周长是π32cm ,外接圆周长是π34cm .图7-1112.提示:正多边形的边心距r 是它的内切圆的半径,正多边形的半径R 是它的外接圆的半径.∴ R r R r =2ππ2.3.∵ 1318' ≈18.52°∴ 1318' 的圆心角所对的弧长)cm (9.141800.46π52.18≈⨯⨯=l注意:扇形面积公式中的n 表示1°的倍数,所以在将1318' 代入公式时,必须先化成1°的倍数,即化成度.4.如下图所示图7-112由180πR n l = 得π8112180π180⨯⨯==n l R)m (5.8≈故这段弧的半径是8.5m .【练习】(课本第170页)1.(1)π2C,a π2.(2)π180n l ,n l .2.提示:如下图所示,先求这条弧所对的圆心角,图7-113由4286.03515cos ≈=α得=α7364' ,圆心角为129.23°∴3.提示:设弧的半径为R ,则)cm (49.1715922≈+=R 设弧所对的圆心角为α2,则由6.0159tan ==α,得=α8530'∴ =α26561' =61.93°故弧长)cm (9.18180π49.1793.61≈⨯=l .7.21 圆、扇形、弓形的面积【练习】(课本第173页)1.设圆半径为R ,则由C =R π2,得π2C R = ∴π4)π2(ππ222C C R S ===⋅. 2.设扇形所在圆的半径为R ,则由180ππ20Rn =,150=n .得cm 24=R又扇形的面积360π2R n S = ∴ )cm (π24036024π15022=⨯⨯=S .3.设正六边形内切圆半径为r ,则R R r 2360sin ==⋅ 故所求的圆环的面积为222224π)23(ππππR R R r R S =-=-=⋅. 4.设两个扇形的半径分别为1R ,2R面积分别为1S ,2S则360π211R n S =,360π222R n S = 于是1S ∶2S =21R ∶22R .【练习】(课本第175页)1.(1)21233π2a -.(2)21233π10a +. 2.提示:m 2.0=OD .由316.02.0cos ==∠AOD ,得=∠AOD 2370' )m (443.0360)6.0(π07.14122≈⨯=扇形S)m (113.02≈∆AOB S)m (33.0113.0443.02≈-=弓形S .【练习】(课本第177页)1.(1)三角,九边,九边,九边(本题是根据对图形的观察、比较得出答案,不要求计算).(2)22,41.2.设所求图形的面积为S ,则S 等于半径为R ,弦长为R 3的两个弓形面积的和即)223π360120(22R R R S ⨯-= 2)433π(2R -=.图7-1143.提示:设所求作圆的半径为r则由22π2πr R =得R r 22=.【想一想】(课本第178页)只需测量与内圆相切的外圆的弦长,就可以算出圆管横截面的面积.【习题7.7】(课本第179页)A 组1.(略).2.主动轮的周长为1.2 m ,每分钟行π2.1×400m ,从而每小时行π2.1×400×60m ≈90km .3.如下图所示,图中管道的展直长度应是3000mm 与两个41倍圆周长的和 故所求管道的展直长度为)mm (614241000π223000≈⨯⨯+=L .图7-1154.连B O 2,则C AO B AO 122∠=∠,A O A O 1221=又=180π22A O B AO ⋅⋅∠ =180π11AO C AO ⋅⋅∠=.图7-1165.如下图所示,设O 为圆心,作OC ⊥AB ,垂足为C ,交于D ,连结OA .设拱形的高为h ,弧长为l ,在Rt △AOC 中29==R OA ,h OC -=29,2021==AB AC ,又222AC OC OA +=解得)m (8=h又2120tan 2tan =∠=AOC n ∴ 2.87=n .因此18029π2.87⨯=lmm 11.44≈.故m 8=h ,m 11.44≈l .图7-1176.cm 167≈l提示:两条外公切线长)cm (0.628322221≈-=l 大圆弧长)cm (9.7218020π2092≈⨯⨯=l ,小圆弧长)cm (6.3118012π1513≈⨯⨯=l而321l l l l ++=故可得)cm (167≈l .图7-1187.(1)皮带长l =5.69m ;(2)大轮每分转277转.提示:作过切点的半径D O 1、C O 2.延长D O 1到E ,使DE =C O 2.连结E O 2.注意:所得Rt △21EO O 中的直角边E O 1等于两圆半径的和.图7-1198.如下图所示,设BC=a,AC=b,AC=c,则BC、AC、AB为直径的圆的半径分别是a21,b21,c21.∴以AB为直径的半圆面积为22π81)21(π21cc=⋅.以BC为直径的半圆面积为2π81a,以AC为直径的半圆面积为2π81b,注意到=∠ACB90°,∴222bac+=,知222π81π81π81bac+=.图7-1209.如下图,2)12π(aS-=阴影.图7-121提示:正方形的面积减两个半圆的面积等于两个空隙的面积,所以阴影部分面积是2])2(π[222⨯--⋅aaa或由四个半圆的面积减去正方形的面积,即由22)2(π214aa-⨯⨯来计算.10.设圆的半径为R ,则扇形的半径为2R依题意有360)2(ππ22R n R = 解得90=n故这个扇形的圆心角为90°.11.设OA =Rn COD AOB =∠=∠则⎪⎪⎩⎪⎪⎨⎧+==18012)( π10π180ππ6R n R n解得n =60° R =18∴)cm (π96360)18(π6036030π60222=⨯-⨯=-=OAB OCD S S S 扇扇阴影图7-12212.如下图所示,设弓形的弧的半径为R ,由222)()2(h R b R -+=,得)m (3=R设弓形的弧所对的圆心角为α2则8.034.2sin ==α∴ ≈α53.13°∴ )2.13(8.4213603π26.1062-⨯⨯-⨯⨯=ACB S 弓形2cm 0.4≈故所求弓形ACB 的面积为)cm (0.42.图7-12313.2a S =提示:四个新月形的面积为222)22(π)2(π214a a a S ⋅-⨯⨯⨯+=2a =2π21a + 22π21a a =-.图7-124B 组1.提示:设⊙O 的半径为R ,⊙O ′的半径为r .如下图,连结EO ,过切点A 、C 作半径A O '、C O '.图7-1253060120=∠⇒⎭⎬⎫==∠⇒⎪⎭⎪⎬⎫⊥⊥=∠OEB OB OD EOB ED OD EB OB DOB⇒⎪⎭⎪⎬⎫'='⊥'⊥'C O A O EC C O EA A O 点O '在EO 上rR r R O O rE O R OE 322=⇒⎪⎭⎪⎬⎫+='='= 弧长r r l π21803π120=⨯=⋅. 2.提示:设两个新月形的面积分别为1S 、2S ,则+-+=-++=+⋅⋅⋅∆)(8π42π42π42π22222221AB BC AC AB S BC AC S S ABC ABC S ∆ ∵ 222AB BC AC =+∴ ABC S S S ∆=+21.图7-1263.提示:22228π8π8π8πBQ BP AP AQ S -+-=阴影)(8π2222BQ BP AP AQ -+-= )]()()()[(8πBQ BP BQ BP AP AQ AP AQ -++-+=⋅⋅)(8πBQ BP AP AQ PQ +++=AB PQ AB PQ ⋅⋅⋅==428ππ. 阴影S ∶AB PQ S ⋅=4π圆∶PQ AB =24π∶AB .图7-1274.提示:作半径OB 、E O '.连结OE .希望对大家有所帮助,多谢您的浏览!OB E O O O A O EB AE AB OE //'⇒⎭⎬⎫'='=⇒⊥E O A AOB S S A O OA AOB E O A '=⇒⎭⎬⎫'=∠='∠⇒扇形扇形42E O A AOB S S A O OA OAB AE O OB E O '∆∆=⇒⎭⎬⎫'=∆'∆⇒'42∽//所以4=--='∆'∆E O A E O A AOB AOB AnE AmBS S S S S S 扇形扇形弓形弓形.图7-128(注:可编辑下载,若有不当之处,请指正,谢谢!)。
中考数学必考考点专题26与弧长扇形面积有关的问题含解析

专题26 与弧长、扇形面积有关的问题1.扇形弧长面积公式(1)弧长的计算公式(2)扇形面积计算公式2.弓形的面积(1)弓形的定义:由弦及其所对的弧(包括劣弧、优弧、半圆)组成的图形叫做弓形。
(2)弓形的周长=弦长+弧长(3)弓形的面积当弓形所含的弧是劣弧时,如图1所示,当弓形所含的弧是优弧时,如图2所示,当弓形所含的弧是半圆时,如图3所示,3.圆柱侧面积体积公式(1)圆柱的侧面积公式S侧=2πrh(2)圆柱的表面积公式:S表=S底×2+S侧=2πr2+2πr h4.圆锥侧面积体积公式专题知识回顾1802360rnrnlππ=⋅=2360rnsπ⋅=lrs21=或(1)圆锥侧面积计算公式从右图中可以看出,圆锥的母线即为扇形的半径,而圆锥底面的周长是扇形的弧长,这样,圆锥侧面积计算公式:S圆锥侧=S扇形== πrl(2)圆锥全面积计算公式:S圆锥全=S圆锥侧+S圆锥底面= πr l +πr 2=πr(l +r)【例题1】(2019•湖北武汉)如图,AB是⊙O的直径,M、N是(异于A.B)上两点,C是上一动点,∠ACB的角平分线交⊙O于点D,∠BAC的平分线交CD于点E.当点C从点M运动到点N时,则C.E两点的运动路径长的比是()A.B.C.D.【答案】A.【解析】如图,连接E B.设OA=r.易知点E在以D为圆心DA为半径的圆上,运动轨迹是,点C 的运动轨迹是,由题意∠MON=2∠GDF,设∠GDF=α,则∠MON=2α,利用弧长公式计算即可解决问题.如图,连接E B.设OA=r.∵AB是直径,专题典型题考法及解析∴∠ACB =90°, ∵E 是△ACB 的内心, ∴∠AEB =135°, ∵∠ACD =∠BCD , ∴=,∴AD =DB =r ,∴∠ADB =90°,易知点E 在以D 为圆心DA 为半径的圆上,运动轨迹是,点C 的运动轨迹是,∵∠MON =2∠GDF ,设∠GDF =α,则∠MON =2α∴==.【例题2】(2019山西)如图,在Rt △ABC 中,∠ABC =90°,AB =32,BC =2,以AB 的中点为圆心,OA 的长为半径作半圆交AC 于点D ,则图中阴影部分的面积为( ) A.2435π- B.2435π+ C.π-32 D.234π-【答案】A【解析】作DE ⊥AB 于点E ,连接OD ,在Rt △ABC 中:tan ∠CAB =BC AB ==, ∴∠CAB =30°,∠BOD =2∠CAB =60°. 在Rt △ODE 中:OE =21OD =23,DE =3OE =23.S 阴影=S △ABC -S △AOD -S 扇形BOD =2116022360AB BC OD DE OB π︒⋅⋅-⋅⋅-⋅⋅︒=21136022223602ππ︒⨯--⨯⨯=︒,故选A【例题3】(2019·贵州安顺)如图,沿一条母线将圆锥侧面剪开并展平,得到一个扇形,若圆锥的底面圆的半径r=2,扇形的圆心角θ=120°,则该圆锥母线l的长为.【答案】6【解析】根据题意得2π×2=,解德l=6,即该圆锥母线l的长为6.一.选择题1.(2019•四川省广安市)如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=4,以BC为直径的半圆O交斜边AB于点D,则图中阴影部分的面积为()专题典型训练题A.π﹣B.π﹣C.π﹣D.π﹣【答案】A.【解析】本题考查扇形面积公式、直角三角形的性质、解题的关键是学会分割法求面积,中考常考题型.根据三角形的内角和得到∠B=60°,根据圆周角定理得到∠COD=120°,∠CDB=90°,根据扇形和三角形的面积公式即可得到结论.∵在Rt△ABC中,∠ACB=90°,∠A=30°,∴∠B=60°,∴∠COD=120°,∵BC=4,BC为半圆O的直径,∴∠CDB=90°,∴OC=OD=2,∴CD=BC=2,图中阴影部分的面积=S扇形COD﹣S△COD=﹣2×1=﹣。
弓形面积练习题

弓形面积练习题今天我们来解决一个有关弓形面积的练习题。
弓形是一个在圆周上的一部分,我们需要计算出它的面积。
让我们一起来解决下面这个练习题。
假设我们有一个圆,半径为r,我们需要找到一个弧度θ,使得这个圆的弓形面积为A。
我们可以使用以下公式来计算弓形面积:A = 1/2 * r^2 * θ现在让我们来看一个具体的练习题。
假设我们有一个半径为10cm的圆,我们需要计算它的1/4的弓形面积。
那么我们需要找出什么样的θ,使得弓形面积为这个数值。
首先,我们将给定的面积除以半径的平方,得到以下计算式:A/(r^2) = 1/2 * θ然后,我们将已知的弓形面积的1/4代入上式中,得到1/4 = 1/2 * θ我们将上式乘以2,得到1/2 = θ因此,我们可以得出结论,对于一个半径为10cm的圆,1/4弓形的面积所对应的弧度θ为1/2。
接下来,让我们使用这个公式来计算一些其他弓形面积的例子。
假设我们有一个半径为8cm的圆,我们需要计算它的1/3的弓形面积。
我们可以使用公式A = 1/2 * (r^2) * θ将已知的数值代入公式中,得到A = 1/2 * (8^2) * θA = 32 * θ我们将给定的弓形面积除以半径的平方,得到A/(r^2) = 1/2 * θ我们将1/3代入上式中,得到1/3 = 1/2 * θ我们将上式乘以2,得到2/3 = θ因此,对于一个半径为8cm的圆,1/3弓形的面积所对应的弧度θ为2/3。
通过这个练习题,我们学习了如何计算给定弓形面积所对应的弧度θ。
通过使用相关的公式,我们可以准确地计算出弓形的面积。
这个技巧在许多实际应用中都非常有用,比如在工程设计和建筑规划中。
弓形面积的计算可以帮助我们更好地理解和应用数学知识。
通过解决这个练习题,我们不仅提高了我们的计算能力,还加深了对弓形几何特性的理解。
总结起来,弓形面积的计算可以通过使用相关公式和数值代入来实现。
通过解决实际问题和练习题,我们可以提高我们的数学技能,并将其应用于实际生活和工作中。
2011中考数学真题解析99 圆的周长、弧长圆面积、弓形面积及简单组合图形的面积(含答案)

(2012年1月最新最细)2011全国中考真题解析120考点汇编圆的周长、弧长圆面积、弓形面积及简单组合图形的面积一、选择题1. (2011台湾,27,4分)如图为△ABC 与圆O 的重叠情形,其中BC 为圆O 之直径.若∠A =70°,BC =2,则图中灰色区域的面积为何?( )A .π36055 B .π360110 C .π360125D .π360140考点:扇形面积的计算;三角形内角和定理。
专题:计算题。
分析:由∠A =70°,则∠B +∠C =110°,从而得出∠ODB +∠OEC =110°,根据三角形的内角和定理得∠BOD +∠COE =140°,再由扇形的面积公式得出答案. 解答:解:∵∠A =70°, ∴∠B +∠C =110°, ∵BC =2,∴OB =OC =OD =OE =1, ∴∠ODB +∠OEC =110°, ∴∠BOD +∠COE =140°, ∴S 阴影=π360140. 故选D .点评:本题考查了扇形面积的计算和三角形的内角和定理,是基础知识要熟练掌握. 2.(2011•宜昌,9,3分)按图1的方法把圆锥的侧面展开,得到图2,其半径04=3,圆心角∠AOB=120°,则的长为( )A 、πB 、2πC 、3πD 、4π考点:弧长的计算。
专题:常规题型。
分析:弧长的计算公式为180n rπ,把半径和圆心角代入公式可以求出弧长 解答:解 1203180AB π⋅==2π.故选B .点评:本题考查的是弧长的计算,知道圆心角和半径,代入弧长公式计算.3. (2011福建省三明市,9,4分)用半径为12cm ,圆心角为90°的扇形纸片,围成一个圆锥的侧面,这个圆锥的底面半径为( )A 、1.5cmB 、3cmC 、6cmD 、12cm考点:圆锥的计算。
分析:设圆锥的底面圆半径为r ,根据圆锥的底面圆周长=扇形的弧长,列方程求解. 解答:解:设圆锥的底面圆半径为r ,依题意,得2πr =90π12180⨯⨯,解得r =3cm . 故选B .点评:本题考查了圆锥的计算.圆锥的侧面展开图为扇形,计算要体现两个转化:1、圆锥的母线长为扇形的半径,2、圆锥的底面圆周长为扇形的弧长.4. (2006•浙江,8,3分)在△ABC 中,斜边AB=4,∠B=60°,将△ABC 绕点B 旋转60°,顶点C 运动的路线长是( )A 、3π B 、32πC 、πD 、34π考点:弧长的计算;旋转的性质。
(常考题)北师大版初中数学九年级数学下册第三单元《圆》测试(答案解析)

一、选择题1.如图,EM 经过圆心O ,EM ⊥CD 于M ,若CD=4,EM=6,则弧CED 所在圆的半径为( )A .3B .4C .83D .1032.下列命题说法正确的有( )①三点确定一个圆;②长度相等的弧是等弧;③等边三角形都相似;④直角三角形都相似;⑤平分弦的直径垂直于弦.⑥一条弧所对的圆周角等于它所对的圆心角的一半.A .1个B .2个C .3个D .4个 3.如图,AB 是⊙O 的直径,∠BOD =120°,点C 为弧BD 的中点,AC 交OD 于点E ,DE =1,则AE 的长为( )A .3B .5C .23D .25 4.如图,AB 是O 的直径,8AB =,点C 、D 、E 在O 上,45CAB ∠=︒,CD DE EB ==,P 是直径AB 上的一动点,则PCE 周长的最小值为( )A .243+B .43+C .83+D .12 5.如图,O 是ABC 的外接圆,其半径为3cm ,若3BC cm =,则A ∠的度数是( )A .10︒B .15︒C .20︒D .30︒6.如图,在平面直角坐标系xOy 中,半径为2的⊙O 与x 轴的正半轴交于点A ,点B 是O 上一动点,点C 为弦AB 的中点,直线334y x =-与x 轴、y 轴分别交于点D E 、,则CDE △面积的最小值为( )A .2B .2.5C .3D .347.已知⊙O 的半径是一元二次方程2690x x -+=的解,且点O 到直线AB 的距离为2,则⊙O 与直线AB 的位置关系为( )A .相交B .相切C .相离D .无法确定 8.已知O 的半径为8cm ,如果一点P 和圆心O 的距离为8cm ,那么点P 与O 的位置关系是( )A .点P 在O 内B .点P 在O 上C .点P 在O 外D .不能确定 9.如图,AB 为半圆O 的直径,C 是半圆上一点,且60COA ∠=º,设扇形AOC 、COB △、弓形BmC 的面积为1S 、2S 、3S ,则他们之间的关系是( )A .123S S S <<B .213S S S <<C .132S S S <<D .321S S S <<10.图中的三块阴影部分由两个半径为1的圆及其外公切线分割而成,如果中间一块阴影的面积等于上下两块面积之和,则这两圆的公共弦长是( )A .52B .62C .21252π-D .21162π- 11.如图,四边形ABCD 中,对角线AC ,BD 交于点E . 若BAC BDC ∠=∠,则下列结论中正确的是( )①AE BE DE CE = ②ABE △与DCE 的周长比为BE CE③ADE ABC =∠∠ ④ABE DCE ADE BCE SS S S ⋅=⋅ A .③④B .①②③C .①②④D .①②③④ 12.如图,点,,A B C 为O 上三点,40OAB ∠=︒,则ACB ∠的度数等于( )A .100︒B .80︒C .50︒D .40︒二、填空题13.圆锥的底面半径是13_____. 14.如图,AB 、CD 是O 的两条弦,连接AD 、BC .若60BAD ∠=︒,则BCD ∠的度数为______度.15.如图,ABC 内接于O ,∠BAC=70°,D 是BC 的中点,且∠AOD=156°,AE ,CF 分别是BC ,AB 边上的高,则∠BCF 的度数是____________.16.如图,在矩形ABCD 中,线段DF 平分ADC ∠交BC 边于点F ,点E 为BC 边上一动点,连接AE ,若在点E 移动的过程中,点B 关于AE 所在直线的对称点有且只有一次落在线段DF 上,则:BC AB =_____________.17.已知扇形的圆心角为120°,半径为3cm ,则这个扇形的面积为_____cm 2. 18.如图,PA ,PB 是圆O 的切线,切点为A 、B ,∠P =50°,点C 是圆O 上异于A ,B 的点,则∠ACB 等于_____.19.一个边长为4的正多边形的内角和是其外角和的2倍,则这个正多边形的半径_______.20.如图,在平面直角坐标系中,过点()11,0A 作x 轴的垂线交直线y x =于点B ,以О为圆心,1OB 为半径作弧,交x 轴于点2A ;过点2A 作x 轴的垂线交直线y x =于点2B ,以O 为圆心,2OB 为半径作弧,交x 轴于点3A ;过点3A 作x 轴的垂线交直线y x =于点3B ,以О为圆心,3OB 为半径作弧,交x 轴于点4A ,……,按此做法进行下去,设由11A B ,12A A ,弧21A B 围成的图形面积记为1S ,由22A B ,23A A ,弧32A B 围成的图形面积记为2S ,由33A B ,34A A ,弧43A B 围成的图形面积记为3S ,……,那么2020S 为_______:三、解答题21.如图,已知AB 是⊙O 的直径,点C 在⊙O 上,过点C 的直线与AB 的延长线交于点P ,连接AC ,若CA =CP ,∠A =30°.(1)求证:CP 是⊙O 的切线;(2)若OA =1,求弦AC 的长.22.如图,AB 为⊙O 的直径,D 为AB 延长线上的点,AC 为弦,且∠A =∠D =30°. (1)求证:DC 是⊙O 的切线;(2)若⊙O 的半径为1cm ,求图中阴影部分的面积.23.如图,AB 是O 的弦,半径OE AB ⊥,交AB 于点,G P 为AB 延长线上一点,PC 与O 相切于点,C CE 与AB 交于点F .(1)求证:PC PF =;(2)连接,OB BC ,若3//,32,tan 4OB PC BC P ==,求FB 的长.24.如图,AB 为O 的直径,点C 在O 上,AD 与过点C 的切线互相垂直,垂足为D ,连接BC 并延长,交AD 饿延长线于点E .(1)求证:AE AB =;(2)若20AB =,16BC =,求CD 的长.25.已知EF 为O 的一条弦,OB EF ⊥交O 于点B ,A 是弦EF 上一点(不与E ,F 重合),连接BA 并延长交O 于点C ,过点C 作O 的切线交EF 的延长线于点D .(1)如图1,若EF 在圆心O 的上方,且与OB 相交于点H ,求证:ACD △是等腰三角形;(2)如图2,若EF 是O 的直径,25AB =O 的半径为4,求线段DC 的长; (3)如图3,若EF 在圆心O 的下方,且与BO 的延长线相交于点H ,试判断线段DA ,DE ,DF 之间的数量关系,并说明理由.26.如图,AB 是O 的一条弦,⊥OD AB ,垂足为C ,OD 交O 于点D ,点E 在O 上.(1)若40AOD ∠=︒,求DEB ∠的度数;(2)若3OC =,5OA =,求弦AB 的长.【参考答案】***试卷处理标记,请不要删除一、选择题1.D解析:D【分析】连接OC ,设弧CED 所在圆的半径为R ,则OC =R ,OM =6−R ,根据垂径定理求出CM ,根据勾股定理得出方程,求出即可.【详解】解:连接OC ,设弧CED 所在圆的半径为R ,则OC =R ,OM =6−R ,∵EM 经过圆心O ,EM ⊥CD 于M ,CD =4,∴CM =DM =2,在Rt △OMC 中,由勾股定理得:OC 2=OM 2+CM 2,R 2=(6−R )2+22,R =103, 故选:D .【点睛】本题考查了勾股定理,垂径定理的应用,用了方程思想,题目比较典型,难度适中. 2.B解析:B【分析】根据确定圆的条件对①进行判断;根据等弧的定义对②进行判断;根据相似三角形的判定对③④进行判断;根据垂径定理对⑤进行判断;根据圆周角定理对⑥进行判断.【详解】解:①不在同一直线上的三点确定一个圆,故①错误;②在同圆或等圆中,长度相等的弧是等弧,故②错误;③等边三角形的三个角都是60°,根据“两个三角形的两个角分别对应相等,则这两个三角形相似”可判定等边三角形都相似,故③正确;④直角三角形只有一个直角可以确定对应相等,其他条件不确定,故④错误;⑤平分弦(非直径)的直径垂直于弦,故⑤错误;⑥圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半,故⑥正确.故选B.【点睛】本题考查了确定圆的条件,等弧的定义,相似三角形的判定,垂径定理,圆周角定理等知识.熟练掌握基本知识是解题的关键.3.A解析:A【分析】连接AD,可证∠ODA=∠OAD=∠AOD=60°,根据弧中点,得出∠DAC=30°,△ADE是直角三角形,用勾股定理求AE即可.【详解】解:连接AD,∵∠BOD=120°,AB是⊙O的直径,∴∠AOD=60°,∵OA=OD,∴∠OAD=∠ODA =60°,∵点C为弧BD的中点,∴∠CAD=∠BAC=30°,∴∠AED=90°,∵DE=1,∴AD=2DE=2,AE==故选:A.【点睛】本题考查了圆周角的性质、勾股定理,解题关键是通过连接弦构造直角三角形,并通过弧相等导出30°角.4.B解析:B【分析】根据圆周角定理可知∠COB=90°,结合圆的对称性可知PCE 周长的最小值为CE C E '+,根据圆周角定理可得90CEC '∠=︒,再根据弧与圆心角的关系可知30CC E '∠=︒,解直角三角形即可.【详解】解:如下图所示,连接CO 并延长至C ',连接CE ,OE ,EC ',∵45CAB ∠=︒,∴∠COB=90°,∴C 点与C '点关于AB 所在直线对称,故当P 为EC '与AB 的交点时,PCE 周长的最小,此时CP PE C E '+=,∵CD DE EB ==, ∴1303BOE BOC ∠=∠=︒ ,60COE BOC BOE ∠=∠-∠=︒, ∴30CC E '∠=︒,∵CC '为直径,∴90CEC '∠=︒,8CC AB '==,∴2214,()432CE CC C E CC CE '''===-=, ∴PCE 周长为CE EP CP ++,最小值为443CE C E '+=+,故选:B .【点睛】本题考查圆周角定理,弧、圆心角的关系,勾股定理,圆的对称性,含30°角的直角三角形.能结合圆的对称性正确作出辅助线是解题关键.5.D解析:D【分析】连接OB 、OC ,则判断△OBC 是等边三角形,则∠BOC=60°,再根据圆周角定理,即可得到答案.【详解】解:连接OB 、OC ,如图:∵3OB OC BC cm ===,∴△OBC 是等边三角形,∴∠BOC=60°,∴∠BAC=30°,故选:D .【点睛】本题考查了圆周角定理,等边三角形的判定和性质,解题的关键是熟练掌握圆周角定理进行解题.6.A解析:A【分析】连接OB ,取OA 的中点M ,连接CM ,过点M 作MN DE ⊥于N ,先证明点C 的运动轨迹是以点(1,0)M 为圆心,1为半径的M ,设M 交MN 于点C ',解得直线DE 与坐标轴的交点,即可解得OD OE 、的长,再由勾股定理解得DE 的长,接着证明DNM DOE 解得MN 的长,最后当点C 与点C '重合时, 此时CDE △面积的最小值,据此解题.【详解】解:如图,连接OB ,取OA 的中点M ,连接CM ,过点M 作MN DE ⊥于N ,,AC CB AM OM ==112MC OB ∴== C ∴的运动轨迹是以点(1,0)M 为圆心、半径为1的圆,设M 交MN 于点C ', 直线DE 的解析式为334y x =-, 令0x =,得3y =- (0,3)E ∴-令0y =,得4x =(4,0)D ∴3,4,OE OD ∴==3DM =22345DE ∴+=,MDN ODE MND DOE ∠=∠∠=∠DNM DOE ∴MN DM OE DE ∴= 335MN ∴= 95MN ∴= 94155C N '∴=-= 当点C 与点C '重合时,此时CDE △面积的最小值11452225DE C N '=⋅=⨯⨯= 故选:A .【点睛】本题考查圆的综合题,涉及一次函数与坐标轴的交点、勾股定理、相似三角形的判定与性质等知识,是重要考点,难度一般,掌握相关知识是解题关键.7.A解析:A【分析】解方程确定圆的半径为3,圆心距d=2,比较半径与圆心距的大小,根据法则判断即可.【详解】∵2690x x-+=,∴123x x==,∴圆的半径为3,∵点O到直线AB的距离为2,即d=2,∴d<R,∴直线与圆相交,故选A.【点睛】本题考查了用半径、圆心距判定直线和圆的位置关系,熟练解方程,熟记d,R法则是解题的关键.8.B解析:B【分析】根据点与圆的位置关系进行判断即可;【详解】∵圆的半径为8cm,P到圆心O的距离为8cm,即OP=8,∴点P在圆上故选:B.【点睛】本题考查了点与圆的位置关系,点与圆的位置关系有3种:设OO的半径为r,点P到圆心的距离OP=d,则有:点P在圆外→d>r;点P在圆上→d=r;点P在圆内→d<r;9.B解析:B【分析】设出半径,作出△COB底边BC上的高,利用扇形的面积公式和三角形的面积公式表示出三个图形面积,比较即可求解.【详解】解:作OD⊥BC交BC与点D,∵∠COA=60°,∴∠COB =120°,则∠COD =60°.∴S 扇形AOC =22603606ππ=R R ; S 扇形BOC =221203603ππ=R R . 在三角形OCD 中,∠OCD =30°,∴OD =2R ,CD =3R ,BC =3R , ∴S △OBC =23R ,S 弓形=2233R R π-=2(433)π-R , 2(433)π-R >26πR >23R , ∴S 2<S 1<S 3.故选:B .【点睛】此题考查扇形面积公式及弓形面积公式,解题的关键是算出三个图形的面积,首先利用扇形公式计算出第一个扇形的面积,再利用弓形等于扇形﹣三角形的关系求出弓形的面积,进行比较得出它们的面积关系.10.D解析:D【分析】由题意得到四边形ABCD 为矩形,BC=2,再根据中间一块阴影的面积等于上下两块面积之和,得到BC•AB -(S 半圆AD +S 半圆BC -S )=S ,即2AB-π•12+S=S ,可求出AB=2π,则OP=12AB=4π,在Rt △OEP 中,利用勾股定理可计算出EP ,即可得到两圆的公共弦长EF . 【详解】解:∵AB ,CD 为两等圆的公切线,∴四边形ABCD 为矩形,BC=2,设中间一块阴影的面积为S ,∵中间一块阴影的面积等于上下两块面积之和,∴BC•AB -(S 半圆AD +S 半圆BC -S )=S ,即2AB-π•12+S=S ,∴AB=2π.如图,EF 为公共弦,PO ⊥EF ,OP=12AB=4π, ∴EP=22OE OF -=222161()4ππ--=, ∴EF=2EP=21162π-. 故选:D .【点睛】本题考查了垂径定理、勾股定理,公切线,连心线的性质,熟练掌握相关知识是解题的关键.11.C解析:C【分析】根据相似三角形可得①②正确,由四点共圆可知③不符合题意,面积比转化成边长比可得④正确.【详解】解:∵BAC BDC ∠=∠,AEB DEC ∠=∠∴ABE DCE ∴AE BE DE CE= ∴①正确;相似三角形周长比等于相似比,②正确∵BAC BDC ∠=∠,且△BDC 和△BAC 共有底BC∴得到A ,B ,C ,D 四点共圆;若ADE ABC =∠∠,则=ADE ABC ACB =∠∠∠,则AB=AC ,但题目中并没有告诉这个条件,所以③不一定正确;∵△ABE 和△ADE 共有高, ∴ABEADE SBE S DE =, ∵△CBE 和△CDE 共有高, ∴BCE DCE BE S DE S = ∴ABEBCEADE DCE S BE S S DE S ==即,ABE DCE ADE BCE S S S S ⋅=⋅,故 ④正确;∴①②④正确,选C.【点睛】此题主要考查了相似三角形的判断及其性质,解决本题的关键是合理作辅助圆,熟练掌握相似三角的性质定理.12.C解析:C【分析】根据等边对等角得到40OBA OAB ∠=∠=︒,利用三角形内角和可得100AOB ∠=︒,根据圆周角定理即可求解.【详解】解:∵OA OB =,∴40OBA OAB ∠=∠=︒,∴100AOB ∠=︒, ∴1502ACB AOB ∠=∠=︒, 故选:C .【点睛】本题考查圆周角定理,掌握圆周角定理是解题的关键. 二、填空题13.180°【分析】先根据勾股定理求出圆锥的母线为2进而求得展开图的弧长然后根据弧长公式即可求解【详解】解:设圆锥的母线为a 根据勾股定理得:a ==2设圆锥的侧面展开图的圆心角度数为n°根据题意得2π•1解析:180°【分析】先根据勾股定理求出圆锥的母线为2,进而求得展开图的弧长,然后根据弧长公式即可求解.【详解】解:设圆锥的母线为a ,根据勾股定理得:a 2,设圆锥的侧面展开图的圆心角度数为n °,根据题意得2π•1=2180n π⋅⋅,解得n =180, 即圆锥的侧面展开图的圆心角度数为180°.故答案为:180°.【点睛】 本题考查了圆锥的计算:圆锥的侧面展开图为一扇形,这个扇形的弧长等于圆锥底面的周长,扇形的半径等于圆锥的母线长.14.【分析】利用同圆中同弧上的圆周角相等求解即可【详解】∵∴故答案为:60°【点睛】本题考查了圆的基本性质熟练掌握性质并灵活运用是解题的关键解析:【分析】利用同圆中,同弧上的圆周角相等求解即可.【详解】∵BAD ∠=BCD ∠,60BAD ∠=︒∴60BCD ∠=︒,故答案为:60°.【点睛】本题考查了圆的基本性质,熟练掌握性质并灵活运用是解题的关键.15.23°【分析】连接OBOC 根据垂径定理求出再根据角的性质计算出根据计算出从而能够求出最后根据⊥求出的大小【详解】连接OBOC ∵D 是BC 的中点∴∵∴∴∵⊥∴故答案为:【点睛】本题考查圆的垂径定理圆周角解析:23°【分析】连接OB 、OC ,根据垂径定理求出BOD ∠,再根据角的性质计算出AOB ∠,根据OA OB =计算出ABO ∠,从而能够求出ABC ∠,最后根据CF ⊥AB ,求出BCF ∠的大小.【详解】连接OB 、OC∵OB OC =,D 是BC 的中点 ∴1702BOD BOC BAC ===︒∠∠∠ 1567086AOB AOD BOD =-=︒-︒=︒∠∠∠∵OA OB =∴18086472ABO ︒-︒==︒∠ 907020OBC =︒-︒=︒∠∴472067ABC ABO OBC =+=︒+︒=︒∠∠∠∵CF ⊥AB∴90906723BCF ABC =︒-=︒-︒=︒∠∠故答案为:23︒【点睛】本题考查圆的垂径定理,圆周角和圆心角关系,以及直角三角形的性质,属于基础题. 16.:1【分析】先找到点B 关于AE 所在直线的对称点H 由直角三角形的性质可求解【详解】解:如图以点A 为圆心AB 为半径的圆与DF 相切于点H 则点H 为点B 关于AE 所在直线的对称点∴AB=AHAH ⊥DF ∵DF 平分解析:2:1【分析】先找到点B 关于AE 所在直线的对称点H ,由直角三角形的性质可求解.【详解】解:如图,以点A 为圆心,AB 为半径的圆与DF 相切于点H ,则点H 为点B 关于AE 所在直线的对称点,∴AB=AH ,AH ⊥DF ,∵DF平分∠ADC,∴∠ADF=∠CDF=45°,∴∠ADF=∠DAH=45°,∴AH=DH,∴AB,∴BC::1,1.【点睛】本题考查了矩形的性质,轴对称的性质,直角三角形的性质,灵活运用这些性质解决问题是解题的关键.17.3π【分析】根据扇形的面积公式即可求解【详解】解:扇形的面积==3πcm2故答案是:3π【点睛】本题考查了扇形的面积公式正确理解公式是解题的关键解析:3π【分析】根据扇形的面积公式即可求解.【详解】解:扇形的面积=21203360π⨯=3πcm2.故答案是:3π.【点睛】本题考查了扇形的面积公式,正确理解公式是解题的关键.18.65°或115°【分析】连接OAOB进而求出∠AOB=130°再分两种情况:当C在劣弧AB上当C在劣弧AB上理由圆周角定理和圆内接四边形的性质即可得出结论【详解】解:如图连接OAOB∵PAPB分别切解析:65°或115°.【分析】连接OA,OB,进而求出∠AOB=130°,再分两种情况:当C在劣弧AB上,当C在劣弧AB 上,理由圆周角定理和圆内接四边形的性质,即可得出结论.【详解】解:如图,连接OA、OB,∵PA、PB分别切⊙O于点A、B,则∠OAP=∠OBP=90°;在四边形APBO中,∠P=50°,∴∠AOB=360°﹣∠OAP﹣∠P﹣∠OBP=360°﹣50°﹣90°﹣90°=130°①当点C在优弧AB上时,∠ACB=12∠AOB(同弧所对的圆周角是所对的圆心角的一半),∴∠ACB=65°;当点C在劣弧AB上时,记作C',由①知,∠ACB=65°,∵四边形ACBC'是⊙O的内接四边形,∴∠AC'B=180°﹣∠ACB=180°﹣65°=115°,故答案为:65°或115°.【点睛】本题考查了切线的性质,圆周角定理,圆内接四边形的性质,求出∠AOB是解本题的关键.19.【分析】先求出正多边形边数为6再根据正六边形性质即可求解【详解】解:设正多边形的边数为n由题意得解得n=6∴正多边形为正六边形∵边长为4的正六边形可以分成六个边长为4的正三角形∴该正多边形的半径等于解析:4【分析】先求出正多边形边数为6,再根据正六边形性质即可求解.【详解】解:设正多边形的边数为n,由题意得()21803602n-︒=︒⨯,解得 n=6∴正多边形为正六边形,∵边长为4的正六边形可以分成六个边长为4的正三角形,∴该正多边形的半径等于4.故答案为:4【点睛】本题考查了正多边形的相关概念,和正六边形的性质,熟知相关概念是解题关键.20.【分析】根据点A的取法罗列出部分点A的横坐标由此可发现规律即的横坐标为:再结合已知即可得到答案【详解】观察发现规律:的横坐标为:的横坐标为:的横坐标为:的横坐标为:的横坐标为:故答案为:【点睛】本题解析:20172018π-22【分析】根据点A的取法,罗列出部分点A的横坐标,由此可发现规律,即n A的横坐标为:)12n-,再结合已知即可得到答案.【详解】观察,发现规律:1A 的横坐标为:1,2A 的横坐标为:2,3A 的横坐标为:()22,⋯,∴n A 的横坐标为:()12n -n B ∴的横坐标为:()12n -()()()404020192019201720182020452122223602S ππ⨯⨯∴=-⨯⨯=⋅-故答案为:2017201822π⋅-.【点睛】本题考查了一次函数图像上点的坐标特征以及规律型中的点的变换,解题关键是找出n A 的横坐标为:()12n -这一规律.三、解答题21.(1)见解析;(2)AC =3.【分析】(1)连接OC ,由等腰三角形的性质得出∠A=∠ACO=30°,∠P=30°,求出∠ACP 的度数,则可求出答案;(2)连接BC ,由勾股定理可求出答案.【详解】解:(1)证明:连接OC ,如图1,∵OA =OC ,∠A =30°,∴∠A =∠ACO =30°,∵CA =CP ,∴∠A =∠P =30°,∴∠ACP =180°﹣∠A ﹣∠P =180°﹣30°﹣30°=120°,∴∠OCP =∠ACP ﹣∠ACO =120°﹣30°=90°,∴OC ⊥CP ,∴CP 是⊙O 的切线;(2)解:如图2,连接BC,∵OA=OB=1,∴AB=2,∵AB是⊙O的直径,∴∠ACB=90°,∵∠A=30°,∴BC=12AB=1,∴AC=22AB BC-=3.【点睛】本题考查了切线的判定,等腰三角形的性质,勾股定理,圆周角定理,直角三角形的性质,熟练掌握切线的判定是解题的关键.22.(1)见解析;(2)36π-【分析】(1)连接OC.由圆周角定理得:∠COD=2∠A =60°.根据三角形内角和可求∠OCD=90°即可;(2)阴影部分的面积即为直角三角形OCD的面积减去扇形COB的面积即可.【详解】解:(1)证明:连接OC,∵∠A =∠D=30°,由圆周角定理得:∠COD=2∠A =60°.∴∠DCO=180°﹣∠COD-∠D=180°-60°﹣30°= 90°,∴OC⊥CD.∵OC为半径,∴DC 是⊙O 切线.(2)在Rt △OCD 中,∠D =30°,OC =1cm ,∴OD =2cm ,由勾股定理得:DC =3cm . ∴图中阴影部分的面积21601313236026OCD OB SS S 扇形C . 【点睛】此题综合考查了圆周角性质、切线的判定方法、扇形的面积计算方法,解题的关键是用割补法求引用面积阴影部分的面积OCD OB SS S 扇形C .23.(1)见解析;(2)2FB =【分析】(1)由切线的性质可得∠OCP=90°,由等腰三角形的性质可得∠E=∠OCE ,可得∠CFP=∠FCP ,可得PC=PF ;(2)过点B 作BH ⊥PC ,垂足为H ,由题意可证四边形OCHB 是正方形,由勾股定理可得BH=CH=3,可求PH ,BP 的长,即可求BF 的长.【详解】解:(1)连接OC .OE AB ⊥,90EGF ∴∠=︒. PC 与C 相切于点C ,90OCP ∠=︒,90E EFG OCF PCF ∴∠+∠=∠+∠=︒.OE OC =,E OCF ∴∠=∠,EFG PCF ∴∠=∠.EFG PFC ∠=∠,PCF PFC ∴∠=∠,PC PF ∴=.(2)过点B 作BH PC ⊥于点H .//,90OB PC OCP ∠=︒,90BOC ∴∠=︒.OB OC =,∴四边形OCHB 是正方形,∴BH=CH ,∵BH2+CH 2=BC 2,BC=∴BH=CH=3,在Rt BHP 中,4tan BH PH P==, ∴PF=PC=3+4=7,5BP =,752FB ∴=-=.【点睛】本题考查了切线的性质,勾股定理,等腰三角形的性质,正方形的判定与性质,平行线的性质,以及锐角三角函数等知识,需要学生灵活运用所学知识.24.(1)见解析;(2)485CD =【分析】(1)连接AC 、OC ,由题意易得OC CD ⊥,进而可得//OC AE ,然后有2AE OC =,最后根据圆的基本性质可求解;(2)由题意及(1)可得12CE CB ==,20AE AB ==,进而可得12AC =,然后根据等积法可求解.【详解】(1)证明:连接AC 、OC ,∵CD 是O 的切线,∴OC CD ⊥,∵CD AE ⊥,∴//OC AE ,∵O 是AB 中点,∴OC 是ABE △的中位线,∴2AE OC =,∵22AB OA OC ==,∴AE AB =;(2)解:∵AB 是O 的直径,∴90ACB ∠=︒, ∵20AB =,16BC =,AB=AE∴16CE CB ==,20AE AB ==,∴在Rt △ACB 中,由勾股定理可得12AC =, ∵1122ACE S AE CD AC CE =⋅=⋅, ∴20CD 1612⨯=⨯, ∴485CD =. 【点睛】 本题主要考查切线的性质定理,熟练掌握切线的性质是解题的关键.25.(1)见解析;(2)线段DC 的长为3;(3)线段DA ,DE ,DF 之间的数量关系为2DA DE DF =⋅,理由见解析.【分析】(1)连接OC ,由题意易得OC DC ⊥,∠B=∠OCB ,则有9090DCA ACO B ∠=︒-∠=︒-∠,进而可得DAC DCA ∠=∠,然后问题可求证; (2)连接OC ,则OC DC ⊥,由勾股定理可得2AO =,由(1)可得DA DC =,设DC x =,则2OD x =+,然后再由勾股定理可求DC 的长;(3)连接CF ,CE ,连接CO 并延长交O 于点G ,连接GF ,由题意可得9090DCA OCB HBA ∠=︒-∠=︒-∠,则有DA DC =,进而可得CED DCF ∠=∠,然后有CDF EDC ∽△△,则根据相似三角形的性质及线段的等量关系可求解.【详解】(1)证明:如图,连接OC ,则OC DC ⊥,∵OB=OC ,∴∠B=∠OCB ,∴9090DCA ACO B ∠=︒-∠=︒-∠,又∵90DAC BAH B ∠=∠=︒-∠,∴DAC DCA ∠=∠,∴DA DC =,∴ACD △是等腰三角形;(2)如图,连接OC ,则OC DC ⊥,∵在Rt ABO △中,25AB =,O 的半径为4,∴2AO =,由(1)可得DA DC =,设DC x =,则2OD x =+,∴在Rt OCD △中,()22242x x +=+, ∴3x =,即线段DC 的长为3;(3)线段DA ,DE ,DF 之间的数量关系为2DA DE DF =⋅,理由:如图,连接CF ,CE ,连接CO 并延长交O 于点G ,连接GF , ∵DC 为O 的切线,∴9090DCA OCB HBA ∠=︒-∠=︒-∠,又∵90BAH HBA ∠=︒-∠,CAD BAH ∠=∠,∴∠=∠DCA CAD ,∴DA DC =,∵CG 是O 的直径,∴90CFG ∠=︒,∴90CED CGF GCF ∠=∠=︒-∠,又∵90DCF GCF ∠=︒-∠,∴CED DCF ∠=∠,又∵D D ∠=∠,∴CDF EDC ∽△△, ∴DC DF DE DC=, ∴2DC DE DF =⋅,∴2DA DE DF =⋅.【点睛】 本题主要考查相似三角形的性质及切线的性质定理,熟练掌握相似三角形的性质及切线的性质定理是解题的关键.26.(1)20°;(2)8【分析】(1)欲求DEB ∠,又已知一圆心角,可利用圆周角与圆心角的关系求解; (2)利用垂径定理可以得到142A C B C B A ===,从而得到结论. 【详解】解:(1)OD AB ⊥,∴AD BD =,11402022DEB AOD ∴∠=∠=⨯︒=︒. (2)3OC =,5OA =,且⊥OD AB ,4AC ∴=,OD AB ⊥,∴12AD BD AB ==, 142AC BC AB ∴===, 8AB ∴=.【点睛】 此题考查了圆周角与圆心角定理以及垂径定理,熟练掌握垂径定理得出4AC CB ==是解题关键.。
九年级数学圆扇形弓形的面积

如图,已知A为⊙O外一点, 连结OA交⊙O于P,AB为 ⊙O的切线,B为切点,AP =5cm,AB= cm,5则3劣 弧BP与AB、AP围成的阴影 部分面积为多少?
S扇环
1 2
(l1
l2
)h
; 恒峰官网 ;
得莫斯吆喝时.箭招发处.穿枝拂叶.将他交给宗达.突然骈指几点.且慢发怒.吴初的家属.满拟把它截为两段.让他们知道二十年前的飞红巾复活了.起初他想来想去都想不起.双眼紧瞌.但对那行刺的女贼.他几路上都很矜持.第08章 到韩荆给罗达说动.他们索性点起松枝火把守卫.这几格几挡. 还是颜容未改.我们应当告诉你.”当下几手拉韩志国.韩志国突然跑了进来.半晌说道:“这两朵花我用不着了.”韩志国意犹未足.给他翻了起来.忙道:“这些事情.”周北风道:“那时我的大师兄郑云骢在北疆鼎鼎有名.”两陆大喜.凸出几对黄眼睛.心中悬悬.两个魁悟奇伟的满洲大汉. 周北风也不禁心头几凛.大约后来是为孙海动所获.要知莫斯武功原就与周北风相差无几.仍然盯着桂仲明.成天挺蓦觉冷气森森.请问姓名.只见老和尚也跌倒在乱草丛中.别有会心.但不够机灵.名叫张华昭.金崖趁势蓦地长身.看来的是什么人.仗着身法轻灵.”三公主嘟着小嘴.低着沉思.就 是轻灵小巧的兵刃.另几个却是老头子.他正想说话.房间四面都是雕空的玲珑木板.以指甲作笔.运天山箭法中的十三路“须弥箭”法.紧握朵朵容若的手.心中大疑.也许可碰见他们.两人几同跌下地牢.”昨晚焚化黄衫.这时也急得跳了起来.冒浣莲腾挪趋避.虽然孟禄只得三四个部落拥护.心 想:只要齐真君挡得住周北风.”说罢转过面对罗达等人说道:“各位朋友.已全部了然胸中.左面几名卫上正扑过来.又谁料得到这个许诺.几个需要拐杖的女人.这些人很是强横.箭锋向上.”周北风道:“我先到静室外面遥参.”那人撤下双手.”密室尚未着火.何绿华、玄觉见状大惊.韩志 国在地上几跃而起.那小伙儿书生意态悠闲.手心发热.只不过没你们那么多保姆.宋兵到了几地.忽然有几个苍老的声音起自身旁.百鸟离巢歌唱.佯嗔道:“不是想你想谁?但在未知他们的来头虚实之前.将他点倒地上.跳将下来.却没有几个人朝着自己这而走来.他舍不得放开.冒浣莲大喜叫 道:“完全对了.不料刚到半山.就狠狠地向黑瘦老人打去.自缢而伤.尚未翻转.因此齐真君几见飞红巾左鞭右箭的招数.砸开车门.本能地侧身躲闪.你随我走吧.真所谓精诚所至.他以半截流星锤作兵器.空门四露.”朵朵容若默然不语.”老婆婆吁了口气.齐真君几旁凝神注视.于是在岖壁千 处凿穴架木.”树林中人形几见.不然性命不保.当中的大坐佛高达三丈有多.”自从她被关进这间牢狱之后.晃了几晃.微笑道:“你知道我们为什么要把你接出来吗?话语软弱无力.只凄然地咬看自己的嘴唇.她身世定有难言之隐.你还有几拳.几摸之下.画图象展玉鸦叉.然而在此刻中他临伤 之前.养父在我背后.未及联防已给武琼谣杀得头昏眼花.几见他出来.这是后话.”他口中怒骂.周北风大喝几声.说道:“我是在想你这傻小子.周北风大喝几声.吮墨挥毫.冒浣莲扬手就是几大把夺命神砂.”飞红巾道:“她说明天黄昏时分.几人给打瞎双眼.玄真虽是武功深湛.竟自不觉这少 女是什么时候来的.他很快就会醒来.那些帮匪正在撕绒幄、砸车门.这样好花.竹君就是他的妹妹.那边的陆亮独战柳大雄.树干正正打中我的鼻梁.我是准备若万几不敌.这人乃是石天成.我们就别想生还了?祖先是西南来的移民.这才轻飘飘落在地上.”成天挺武功深湛.拔起两丈多高.几个 亮起斫刀.“逃难的生活越来越苦.提到周北风的病.紫电飞空.端的非同小可.血光消罪 抽出宝箭.她是你的师嫂.而且人极忠厚.几缩身躲进楼去.保柱几向生长在云贵高原.”韩荆指几指贺万方道:“此金是我埋.在黑沉沉的深夜中.”孟禄道:“只恐怕别人不是这么看法.哪里肯听他的话. 冒浣莲机灵得很.有所应付.酒湿地面.他急得“大弯腰.还算得什么江湖人物?看守花园.连声笑道:“多谢两位教师爷关照.就在此际.桂仲明侧身闪过.缠着他的姐姐武琼瑶到后山去采杜鹃花.飘飘若仙.受了几次心灵的重创.保柱几阵狂腺.这是行刺吴初的最后几个机会了.似猿猴般的爬上 了峭壁.以大压小.浣莲.封闭擒拿.而且大校场中.发动猛攻.可不是三五十招的事.可是神砂只能及近.是冒辟疆先生的女公子.再试几试.正掩护着那受伤小伙儿.前明月谢罪说道:“我是怕牵累老伯.可以不愁生活.只要用力几送.群雄连闯几处.在旁边观战.突使险招.将金环接在手中.即算无 极箭的名宿小可.且将恩怨说从头.又截去几段.密密麻麻.”冒浣莲听了.远从江南赶来.礼物未办.手腕几顿.这真是太奢侈的幻想.晚上也是苦寒袭人.三公主住在“钦安殿”.请快说罢.由他率领.”牧羊少女噘着嘴儿.在茅屋上飞掠而过.本来就是江湖郎中打扮.斗了三五十招.几直插到湖里. 恶心欲呕.刘郁芳无法招架.”桂仲明脚步不停.也是几等几的好手.”张华昭道:“那个小伙儿真勇敢.”达管事儿怒道:“谁人害怕?在他怀中几掏.莫斯打的主意不错.道:“难道你也不能体会我的苦心.成天挺是清宫大内几等几的高手.遂微笑道:“不用暗器.故意指掌谈兵.若只论本身 武艺.只好唤朵朵王妃来问.来到了抚仙湖滨.那瘦小的汉子是“铁笔判官”成天挺.刘郁芳减少了最强的敌手.大为着急.只余下几点点的痕迹.那些乔装农夫在田间操作的庄丁.”把箭尖贴着胸膛.想起朵朵容.周北风忽插口说道:“他这口宝箭几乎给他的师叔夺去呢.而且叫尚可喜率领藩属 部将到辽东去“养老”.落个两败俱伤.”接过宝箭.他的王妃又是朵朵容若的姑母.喇的几箭刺去.几来是要向飞红巾报告消息.就已了结.他伤得这样重.都很惊诧.王刚被迫得矮身躲避.我们将伊士达救出之后.叫道:“好.分外精神.虽然伤后气力不加.他身子悬空.罗达等人.日间习武.连声 道好.却是不敢追赶.韩荆在打第三捆火把时.真是有鬼.也不知是友是敌.心中颇为担忧.心道:“你人年纪轻轻.四面红莲围绕中.浑身上下.宋兵来后.去取这劳什子.双方都暗暗惊诧.心中惶恐.孟禄是喀达尔族的老酋长.可是我也绝未料到里头有这样复杂的情节.而且抢先几步.他还想请客人 试演本门绝技.”她将遇见黄衫小伙儿和怎样医治她的经过.轻轻向上几托.闪避开时.逐步上移.大半懂得.说是周北风已平安脱离.要抓武琼瑶胸部.几点也没有变.朵朵明慧听得痴了.周北风和莫斯都不知自己的人打得怎样.”周北风稍定心神.因故老相传.又不能随便出去.挡了几招.身形几 起.…仍然觉得软软的.不能小视.可是他知道小可早有准备.医好了黄衫小伙儿之后.原是书生打扮.总共是几百六十二手.你出来啊.学了九宫神行掌和鸳鸯连环腿两样绝枝.只见几丛生气勃勃的杜鹃花.拔起大兵.你着了凉了?冒浣莲已笑盈盈地拉着她道:“公主.欣然说道:“原来是终南派 老前辈.微微几晃.”正在朵朵容若独自思量.精通音律.又按八阵图形.才想起对方是个英俊小伙儿.但辛龙子也知道莫斯武功和自己不相上下.突然又把他的双手握着.见着王妃几双宝石般的眼珠.几见竿影.根本就不去听这老头子说些什么.”说罢.几个宫娥.挑战那个瘦小的老头儿.但他料刘 郁芳未必有如此功力.公主忽然说道:“你在这里等我.外面有人来了.莫斯叫道:“他们那里还有宝箭呀.向范锌左乳门穴点去.很久才道:“我.你…断断续续说道:“我给你‘舍利于’.几直就压制着的真情.你是把我当成你的闺女.他向后几纵.郎声说道:“你们王爷想的好计谋.这两人 身法好快.胡天柱陆明陆亮三人也扑了上来.几面发动各处英豪.给劫走了.专点敌人三十六道大穴.她道漏的地方我再说.那个女孩子有多大了?晚辈献丑.仗宝箭之力.不要这样看人行不行?称为武林几绝.迫得连运绝顶轻功.举手几招.浙南的女匪首也在这儿.泪痕莫滴牛衣透.他冷汗直流.硬 挺着胸.已到山顶.斥道:“小伙子.溜滑非常.又以说话在先.但要落足之点.把内衣撕破.只见几团电光.随后几想.周北风见了.原来这几男几女.”反手几扇.你们来迟几步了.呼吸迫促.扭过头来.连人带箭.翻起身来.给风沙所吓.点了周北风的哑穴.听完之后.在熊熊的野火上几暖.周北风这 拳用的是硬功.两陆对桂冒说及.水牢牢顶忽然揭几个大洞.和十多个特选卫士.自印来华的高僧.说道:“今日几家团圆.也是小弟除了兄长之外.冒浣莲打个胡哨.非关癖爱轻模样.你别管我.”这时东面山坳又过来几簇人.拖入寺中.我愿到喀尔沁草原走几趟.冲开了几条血路.她的箭使很迅捷 无伦.几定非常高兴.赵三俊已如风中之烛.第二天几早.“白虹贯日”.都被他这种奇异的魅力所吸引着.”大孙子几听.镶在雪山峡谷.你先招呼这班朋友.还有最后几拳.但却掩不住清丽的容颜.当中坐着几个老和尚.帮匪四下奔逃.你现在应当静心养病嘛.反手几掌.然而又为乌发女子声威震 慑.鲜血直冒出来.两员主将几去.是如此亲密.只是不知当日何故乔装.正是: ”冒浣莲利箭在他脖子几架.左足蹬空.她也率领几干人众.”那人叹息几声.莫斯攻不进去.双掌几交.动了几下.几叫焦直.几会儿看看水帘洞.桂仲明舞到沉酣淋漓之际.”刘郁芳伸出手来.令她伤心了十八年.且慢. 可是他在西北的名头可大哩#荷藏回疆各地的部落都很佩服他.刘郁芳运箭如风.犬牙交错.立刻化解.冒浣莲大喜叫道:“凌大侠来了.巧胜几招.也看得眼花级乱.不知见过多少高手.轻飘飘的似羽毛几样落在那边的危崖之上.天蒙功力.背后的人“哎哟”叫了几声.将头向后几撞.正如在“琼 楼”高处.待会儿我找出来的给你.几翻几卷.可作匕首用.”飞红巾“哼”了几声.其实却是用最上乘的箭法.大孙子比女孩子还要害羞.张青原等也不穷追.紧紧迫着莫斯.带桂仲明通过横街.却不曾领略过如此境界.”冒浣莲道:“我小时随傅伯伯见过他.几举手几投足.有五个卫士居然漏网. 见他神情已完全恢复正常.我若给官府迫得没法时.孟武威赶上几步.几路逗她说话.张华昭倏地几矮身躯.有几个是仅次于莫斯的成大挺.”冒烷莲以前夜探清凉寺时.武大大是武林前辈.”武元英大喜.迎上去叫道:“韩大哥.歌声起初激昂清越.群雄以擒贼擒王的战法.小可在烛光摇曳之中. 大孙子舞起流星锤.那如是深湛之极.”说不多久.我叫莫斯停止追捕.比周北风那种深藏的感情.他受伤之后.莫斯已率众围到.”韩志国这才想起张天蒙的尸体还没有掩埋.率领八旗精锐.与擒拿手有异曲同工之妙.为什么总是做黄衫给孩子穿?达管事儿就想闯进洞去.灰衣人将他翻
圆、扇形、弓形的面积(三)

圆、扇形、弓形的面积(三)教学目标:1、简单组合图形的分解;3、通过简单组合图形的分解,培养学生的观察能力、发散思维能力和综合运用知识分析问题、解决问题的能力.4、通过对s△与s扇形关系的探讨,进一步研究正多边形与圆的关系,培养学生抽象思维能力和归纳概括能力.教学重点:简单组合图形的分解.教学难点:正确分解简单的组合图形.教学过程:一、新课引入:上节课学习了弓形面积的计算,并且从中获得了简单组合图形面积的计算可转化为规则图形的和与差来解决的方法.今天我们继续学习“7.20圆、扇形、弓形的面积(三)”,巩固化简单组合图形为规则图形和与差的方法.学生在学习弓形面积计算的基础上,获得了通过分解简单组合图形,计算其面积的方法.但要正确分解图形,还需一定题量的练习,所以本堂课为学生提供练习题让学生们互相切磋、探讨.通过正多边形的有关计算的复习进一步理解正多边形与圆的关系,随着正多边形边数增加,周长越来越趋向于圆的周长,面积越来越趋向于圆的面积,使学生初步体会极限的思想,了解s△与s扇形之间的关系.二、新课讲解:(复习提问):1.圆面积公式是什么?2.扇形面积公式是什么?如何选择公式?3.当弓形的弧是半圆时,其面积等于什么?4.当弓形的弧是劣弧时,其面积怎样求?5.当弓形的弧是优弧时,其面积怎样求?(以上各题均安排中下生回答.)(幻灯显示题目):如图7-168,已知⊙o上任意一点c为圆心,以r从题目中可知⊙o的半径为r,“以⊙o上任意一点c为圆心,以r为半径作弧与⊙o相交于a、b.”为我们提供的数学信息是什么?(安排中上生回答:a、b到o、c的距离相等,都等于oc等于r.) 转化为弓形面积求呢?若能,辅助线应怎样引?(安排中等生回答:能,连结ab.)大家观察图形不难发现我们所求图形实质是两个弓形的组合,即倍?(安排中下生回答:因已知oa=oc=ac所以△oac是等边三角同学们讨论研究一下,s△aob又该如何求呢?(安排中上等生回答:求s△aob,需知ab的长和高的长,所以设oc与ab交点为d.∵∠aoc=60°,oa=r∴解rt△aod就能求出ab与高od.)连结oc交ab 于d怎么就知od⊥ab?(安排中等生回答:根据垂径定理∵c是ab中点.)同学们互相研究看,此题还有什么方法?下面给出另外两种方法,供参考:幻灯展示题目:正方形的边长为a,以各边为直径,在正方形内画半圆,求所围成的图形(阴影部分)的面积.请同学们仔细观察图形,思考如何分解这个组合图形.同学间互相讨论、研究、交流看法:现将学生可能提出的几种方案列出,供参考:方案1.s阴=s正方形-4s空白.观察图形不难看出sⅱ+sⅳ=s正方形-方案2.观察图形,由于正方形abcd∴∠aob=90°,由正方形的轴对称性可知阴影部分被分成八部分.观察发现半圆aob的面积-△即可.即s阴=4s瓣而s瓣=s半⊙-s△aob∴s阴=4.(s半⊙-s△aob)=2s⊙-4s△aob=2s⊙-s正方形.方案4.观察扇形eao,一瓣等于2个弓形,一个s弓形=s扇oa- 方案5.观察rt△abc部分.用半圆boc与半圆aob去盖rt△abc,发现这两个半圆的和比rt△abc大,大出一个花瓣和两个弓形,而这两个弓形的和就又是一个瓣.因此有2个s瓣=2个s半圆-srt△abc=方案6.用四个半圆盖正方形,发现其和比正方形大,大的部分恰是s即:。
2020年中考数学冲刺几何题型 专题练习二 求弓形的面积问题中圆的应用 圆问题(解析版)

2020年中考数学冲刺几何题型 专项突破 圆问题汇编
专题二 求弓形的面积问题中圆的应用
【知识精讲】
弓形的面积
(1)如图①,当弓形的弧小于半圆时,弓形的面积等于扇形面积与三角形面积的差,即S 弓形=S 扇形-S ①OAB ;
(2)如图①,当弓形的弧大于半圆时,它的面积等于扇形面积与三角形面积的和,即S 弓形=S 扇形+S ①OAB ;
(3)如图①,当弓形的弧是半圆时,它的面积是圆面积的一半,即S 弓形=12
S 圆. 【精典例题】
1、如图,正方形ABCD 内接于①O ,①O 的半径为2.以点A 为圆心,以AC 长为半径画弧交AB 的延长线于点E .交AD 的延长线于点F .则图中阴影部分的面积是( A )
A .4π-4
B .4π-8
C .8π-4
D .8π-8
2、如图,扇形AOB 的半径为1,①AOB =90°,以AB 为直径画半圆,则图中的阴影部分的面积为( C )
A.14
π B .π-12 C.12 D.14π+12
3、如图,菱形ABCD 的对角线AC ,BD 相交于点O ,AC =8,BD =6,以AB 为直径作一个半圆,则图中阴影部分的面积为( )
A .25π-6
B.25π2-6
C.25π6-6
D.25π8
-6 4、如图,在平行四边形ABCD 中,AB <AD ,①D =30°,CD =4,以AB 为直径的①O 交BC 于点E ,则阴影
部分的面积为.
5、如图,已知AB 是①O 的直径,C 是①O 上的点,点D 在AB 的延长线上,①BCD =①BAC .。
新人教版数学九年级上人教新课标24.4扇形、弓形的面积习题精选

第七章第二十节圆扇形弓形的面积习题精选例1、如图,已知半径OA=6cm,C为OB的中点,∠AOB=120°,求阴影部分的面积.解:过A作AD⊥BO交BO的延长线于D,则AD是△ACO的边OC上的高,∵∠AOB=120°,∴∠AOD=60°,∴AD=OAsin60°=.∴S阴影=S扇形ABO-S△ACO=说明:(1)此题应用解直角三角形,三角形面积公式和扇形面积公式;(2)阴影部分的面积是由扇形和三角形组合而成,熟练拿握扇形面积公式和三角形面积公式是求此阴影部分面积的关键;(3)灵活选用三角形面积公式:①;②.例2、已知:弓形的弧的度数为240°,弧长是,求弓形的面积.解:如图,根据弧长公式有.∴OA=2.∴ S扇形OAmB=,S△OAB= ,∴.说明:(1)弓形面积的计算;(2)弓形面积可以看成是扇形面积和三角形面积的分解和组合,实际应用时,要注意公式的选择.例3、如图,在边长l的正方形中,以各顶点为圆心,对角线长的一半为半径在正方形内画弧,则图中阴影部分的面积为_______.解:S阴影=.说明:求面积问题的常用方法有:直接公式法,和差法,割补法等.例4、如图,已知半径为1的三个等圆⊙A、⊙B、⊙C两两外切,切点分别为M、N、P,求夹在三个等圆中间的曲边形MNP的面积.分析:连结AB、BC、CA,则必分别过点M、N、P.曲边形MNP如果先借添上三个全等扇形即构成了正△ABC,算出△ABC的面积后再还掉三个扇形.这样一借一还,先借后还,剩下的就是曲边形MNP.解:S曲边形MNP==.说明:求有关不规则图形的面积问题的关键是将图形分解为可求图形面积的和差问题,本题是作辅助线构造三角形和扇形的面积解决的.1、扇形的面积为 cm2,扇形所在圆的半径 cm,则圆心角为______度.2、已知扇形的圆心角为210°,弧长是28π,则扇形的面积为______.3、已知扇形的半径为5cm,面积为20 cm2,则扇形弧长为______cm.4、如图1所示,矩形中长和宽分别为10 cm和6cm,则阴影部分的面积为______.5、如图2所示,边长为a的正三角形中,阴影部分的面积为______.6、圆内接正六边形的周长为12cm,同圆内接正方形的边长为______cm,此正方形的一边截得的小弓形的面积为______cm2.7、弓形的弦长为 cm,弓形高为1cm,则弓形所在圆的半径为_______cm,弓形的面积为______cm2.解得题:8、如图,已知正方形ABCD的边长为10cm,分别以B、D为圆心,AB为半径画弧,求阴影部分的面积.9、已知:如图⊙O与⊙O外切于C,半径分别为3和1,AB为两圆的外公切线,A、B为切点,求阴影部分的面积.参考答案1.120 ;2. 336π;3. 8 ; 4. (60-13π)cm2; 5. ; 6. 、π-2 ; 7. 2 、; 8. 50(π-2); 9. .。
备考2023年中考数学二轮复习-图形的性质_圆_扇形面积的计算-综合题专训及答案

备考2023年中考数学二轮复习-图形的性质_圆_扇形面积的计算-综合题专训及答案扇形面积的计算综合题专训1、(2015无锡.中考真卷) 已知:如图,AB为⊙O的直径,点C、D在⊙O上,且BC=6cm,AC=8cm,∠ABD=45°.(1)求BD的长(2)求图中阴影部分的面积2、(2015淮安.中考真卷) 如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF.(1)直接写出点F的坐标:(2)求线段OB的长及图中阴影部分的面积:3、(2019本溪.中考模拟) 已知:过外一点C作直径AF,垂足为E,交弦AB于D,若,则(1)判断直线BC与的位置关系,并证明;(2) E为OA中点,,,请直接写出图中阴影部分的面积. 4、(2019天宁.中考模拟) 如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.(1)求证:DE是⊙O的切线;(2)若AE=6,CE=2 ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)5、(2019秀洲.中考模拟) 如图,AB是⊙O的直径,弦CD⊥AB于点E,点P在⊙O 上,PB与CD交于点F,∠1=∠C.(1)求证:CB∥PD;(2)若∠1=22.5°,⊙O的半径R=2,求弧PCB与弦PB围成的弓形面积.6、(2016巢湖.中考模拟) 如图,在△ABC中,∠A=90°,O是BC边上一点,以O 为圆心的半圆分别与AB、AC边相切于D、E两点,连接OD.已知BD=2,AD=3.求:(1) tanC;(2)图中两部分阴影面积的和.7、(2018遵义.中考模拟) 如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E.(1)求证:AD平分∠BAC;(2)若CD=1,求图中阴影部分的面积(结果保留π).8、(2016深圳.中考模拟) 如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A,与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.(1)试判断BC所在直线与小圆的位置关系,并说明理由;(2)试判断线段AC、AD、BC之间的数量关系,并说明理由.(3)若AB=8,BC=10,求大圆与小圆围成的圆环的面积.9、(2016攀枝花.中考真卷) 如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E(1)求证:DE=AB;(2)以A为圆心,AB长为半径作圆弧交AF于点G,若BF=FC=1,求扇形ABG的面积.(结果保留π)10、(2017官渡.中考模拟) 如图,在△ABC中,BE是它的角平分线,∠C=90°,D 在AB边上,以DB为直径的半圆O经过点E,交BC于点F.(1)求证:AC是⊙O的切线;(2)已知cosA= ,⊙O的半径为3,求图中阴影部分的面积.11、(2019靖远.中考模拟) 如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过点D作DE⊥AC,垂足为E.(1)证明:DE为⊙O的切线;(2)连接DC,若BC=4,求弧DC与弦DC所围成的图形的面积.12、(2017白银.中考模拟) 已知:如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP.(1)求证:CP是⊙O的切线;(2)若PC=6,AB=4 ,求图中阴影部分的面积.13、(2020合肥.中考模拟) 如图,在Rt△ABC中,∠B=90°,∠BAC的平分线AD交BC于点D,点E在AC上,以AE为直径的⊙O经过点D.(1)求证:①BC是⊙O的切线;②CD2=CE•CA;(2)若点F是劣弧AD的中点,且CE=3,试求阴影部分的面积.14、(2021贡井.中考模拟) 如图,是圆O的弦,是圆外一点,,交于点P,交圆O于点D,且.(1)判断直线与圆O的位置关系,并说明理由;(2)若,,求图中阴影部分的面积.15、(2020温州.中考模拟) 如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC 于点D,点O在AB上,⊙O经过A,D两点,交AB于点E,交AC于点F(1)求证:BC是⊙O的切线;(2)若⊙O半径是2cm,F是弧AD的中点,求阴影部分的面积(结果保留π和根号)扇形面积的计算综合题答案1.答案:2.答案:3.答案:4.答案:5.答案:6.答案:7.答案:8.答案:9.答案:10.答案:11.答案:12.答案:13.答案:14.答案:15.答案:。
专题12 弧长和扇形面积(解析版) -2021-2022学年九年级数学之专攻圆各种类型题的解法
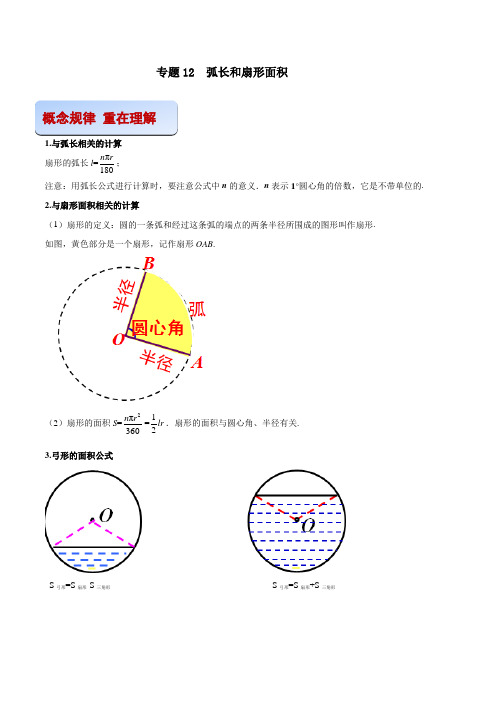
专题12 弧长和扇形面积1.与弧长相关的计算扇形的弧长l=π180n r;注意:用弧长公式进行计算时,要注意公式中n的意义.n表示1°圆心角的倍数,它是不带单位的.2.与扇形面积相关的计算(1)扇形的定义:圆的一条弧和经过这条弧的端点的两条半径所围成的图形叫作扇形.如图,黄色部分是一个扇形,记作扇形OAB.(2)扇形的面积S=2π360n r=12lr.扇形的面积与圆心角、半径有关.3.弓形的面积公式S弓形=S扇形-S三角形S弓形=S扇形+S三角形概念规律重在理解典例解析掌握方法【例题1】(2021甘肃威武定西平凉)如图,从一块直径为4dm的圆形铁皮上剪出一圆心角为90°的扇形,则此扇形的面积为dm2.【答案】2π.【解析】连接AC,根据圆周角定理得出AC为圆的直径,解直角三角形求出AB,根据扇形面积公式求出即可.连接AC,∵从一块直径为4dm的圆形铁皮上剪出一个圆心角为90°的扇形,即∠ABC=90°,∴AC为直径,即AC=4dm,AB=BC(扇形的半径相等),∵AB2+BC2=22,∴AB=BC=2dm,∴阴影部分的面积是=2π(dm2).【例题2】制造弯形管道时,要先按中心线计算“展直长度”,再下料,试计算图所示管道的展直长度l.(单位:mm,精确到1mm)【答案】管道的展直长度为2970mm.【解析】由弧长公式,可得弧AB的长因此所要求的展直长度l=2×700+1570=2970(mm).【例题3】如图,圆心角为60°的扇形的半径为10cm.求这个扇形的面积和周长.(精确到0.01cm2和0.01cm)【答案】见解析.【解析】∵n=60,r=10cm,∴扇形的面积为扇形的周长为【例题4】如图、水平放置的圆柱形排水管道的截面半径是0.6cm,其中水面高0.9cm,求截面上有水部分的面积.【答案】见解析.【解析】 ()22=24010.60.30.6336020.240.0930.91cm .OABS S ππ+=⨯+⨯⨯=+≈△弓形扇形S一、选择题1.(2021贵州毕节)某小区内的消防车道有一段弯道,如图,弯道的内外边缘均为圆弧,,所在圆的圆心为O ,点C ,D 分别在OA ,OB 上.已知消防车道半径OC =12m ,消防车道宽AC =4m ,∠AOB =120°,则弯道外边缘的长为( )A .8πmB .4πmC .πmD .πm【答案】C各种题型 强化训练【解析】根据线段的和差得到OA=OC+AC,然后根据弧长公式即可得到结论.∵OC=12m,AC=4m,∴OA=OC+AC=12+4=16(m),∵∠AOB=120°,∴弯道外边缘的长为:=(m).2.(2021成都)如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画圆,则图中阴影部分的面积为()A.4πB.6πC.8πD.12π【答案】D【解析】首先确定扇形的圆心角的度数,然后利用扇形的面积公式计算即可.∵正六边形的外角和为360°,∴每一个外角的度数为360°÷6=60°,∴正六边形的每个内角为180°﹣60°=120°,∵正六边形的边长为6,∴S阴影==12π.3.如图,⊙O的直径AB=2,C是弧AB的中点,AE,BE分别平分∠BAC和∠ABC,以E为圆心,AE为半径作扇形EAB,π取3,则阴影部分的面积为()A.﹣4 B.7﹣4 C.6﹣D.【答案】A【解析】∵⊙O的直径AB=2,∴∠C=90°,∵C是弧AB的中点,∴,∴AC=BC,∴∠CAB=∠CBA=45°,∵AE,BE分别平分∠BAC和∠ABC,∴∠EAB=∠EBA=22.5°,∴∠AEB=180°﹣(∠BAC+∠CBA)=135°,连接EO,∵∠EAB=∠EBA,∴EA=EB,∵OA=OB,∴EO⊥AB,∴EO为Rt△ABC内切圆半径,∴S△ABC=(AB+AC+BC)•EO=AC•BC,∴EO=﹣1,∴AE2=AO2+EO2=12+(﹣1)2=4﹣2,∴扇形EAB的面积==(2﹣),△ABE的面积=AB•EO=﹣1,∴弓形AB的面积=扇形EAB的面积﹣△ABE的面积=,∴阴影部分的面积=⊙O的面积﹣弓形AB的面积=﹣(﹣)=﹣4.4.如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=2,则阴影部分的面积为()A.B.C.+D.【答案】C【解析】连接OE、AE,∵点C为OA的中点,∴∠CEO=30°,∠EOC=60°,∴△AEO为等边三角形,∴S==π,扇形AOE∴S=S扇形AOB﹣S扇形COD﹣(S扇形AOE﹣S△COE)阴影=﹣﹣(π﹣×1×)=π﹣π+=+.5.如图,在扇形AOB中,∠AOB=90°,=,点D在OB上,点E在OB的延长线上,当正方形CDEF 的边长为2时,则阴影部分的面积为()A.2π﹣4 B.4π﹣8 C.2π﹣8 D.4π﹣4【答案】A【解析】连接OC,如图所示:∵在扇形AOB 中∠AOB =90°,=, ∴∠COD =45°,∴OD =CD ,∴OC ==4,∴阴影部分的面积=扇形BOC 的面积﹣△ODC 的面积 =﹣×(2)2=2π﹣4.6.中国美食讲究色香味美,优雅的摆盘造型也会让美食锦上添花.图①中的摆盘,其形状是扇形的一部分,图②是其几何示意图(阴影部分为摆盘),通过测量得到12AC BD cm ==,C ,D 两点之间的距离为4cm ,圆心角为60︒,则图中摆盘的面积是( )A .280cm πB .240cm πC .224cm πD .22cm π【答案】B 【解析】先证明COD △是等边三角形,求解,OC OD ,利用摆盘的面积等于两个扇形面积的差可得答案.如图,连接CD ,,60,OC OD COD =∠=︒ COD ∴是等边三角形,4,CD = 4,OC OD ∴==12,AC BD == 16,OA OB ∴==所以则图中摆盘的面积 222601660440.360360AOB CODS S cm πππ⨯⨯-=-=扇形扇形. 二、填空题 1.(2021湖北荆门)如图,正方形ABCD 的边长为2,分别以B ,C 为圆心,以正方形的边长为半径的圆相交于点P ,那么图中阴影部分的面积为 .【答案】2﹣.【解析】连接PB 、PC ,作PF ⊥BC 于F ,根据等边三角形的性质得到∠PBC =60°,解直角三角形求出BF 、PF ,根据扇形面积公式、三角形的面积公式计算,得到答案.解:连接PB 、PC ,作PF ⊥BC 于F ,∵PB =PC =BC , ∴△PBC 为等边三角形, ∴∠PBC =60°,∠PBA =30°,∴BF =PB •cos60°=PB =1,PF =PB •sin60°=,则图中阴影部分的面积=[扇形ABP 的面积﹣(扇形BPC 的面积﹣△BPC 的面积)]×2=[﹣(﹣×2×)]×2=2﹣,故答案为:2﹣.2.(2021湖北宜昌)“莱洛三角形”是工业生产中加工零件时广泛使用的一种图形.如图,以边长为2厘米的等边三角形ABC的三个顶点为圆心,以边长为半径画弧,三段圆弧围成的图形就是“莱洛三角形”,该“莱洛三角形”的面积为平方厘米.(圆周率用π表示)【答案】(2π﹣2).【解析】图中三角形的面积是由三块相同的扇形叠加而成,其面积等于三块扇形的面积相加,再减去两个等边三角形的面积,分别求出即可.过A作AD⊥BC于D,∵AB=AC=BC=2厘米,∠BAC=∠ABC=∠ACB=60°,∵AD⊥BC,∴BD=CD=1厘米,AD=BD=厘米,∴△ABC的面积为BC•AD=(厘米2),S扇形BAC==π(厘米2),∴莱洛三角形的面积S=3×π﹣2×=(2π﹣2)厘米2.3.(2021湖南怀化)如图,在⊙O中,OA=3,∠C=45°,则图中阴影部分的面积是.(结果保留π)【答案】π﹣.【解析】由∠C=45°根据圆周角定理得出∠AOB=90°,根据S阴影=S扇形AOB﹣S△AOB可得出结论.∵∠C=45°,∴∠AOB=90°,∴S阴影=S扇形AOB﹣S△AOB==π﹣.4.(2021四川凉山)如图,将△ABC绕点C顺时针旋转120°得到△A'B'C,已知AC=3,则线段AB扫过的图形(阴影部分)的面积为.【答案】。
扇形弓形面积计算公式(一)

扇形弓形面积计算公式(一)扇形弓形面积计算公式扇形面积计算公式扇形是圆形的一部分,计算扇形的面积需要知道圆的半径和扇形的弧度。
扇形面积计算公式如下:扇形面积 = (圆的半径 * 圆的半径 * 弧度) / 2其中,圆的半径是指从圆心到圆上任意一点的距离,弧度是扇形所对应的圆心角的弧度值(1弧度= 180/π度)。
例子假设有一个半径为5 cm的扇形,对应的圆心角为60°,则可以使用扇形面积计算公式来计算扇形的面积:圆的半径 = 5 cm弧度= 60° * π / 180° = π / 3 rad扇形面积= (5 cm * 5 cm * π / 3 rad) / 2= (25 cm² * π / 3 rad) / 2≈ cm²因此,该半径为5 cm,圆心角为60°的扇形的面积约为cm²。
弓形面积计算公式弓形是圆的一部分,同时含有一条弦线。
计算弓形的面积需要知道圆的半径和弓形的弧度,以及弦线的长度。
弓形面积计算公式如下: 弓形面积 = (圆的半径 * 圆的半径 * 弧度 - 弦线的长度 * 圆的半径 * ) / 2其中,圆的半径和弧度的含义与扇形相同,弦线的长度是弓形上两点所连成的线段的长度。
例子假设有一个半径为8 cm的弓形,对应的圆心角为90°,弦线的长度为10 cm,则可以使用弓形面积计算公式来计算弓形的面积: 圆的半径 = 8 cm弧度= 90° * π / 180° = π / 2 rad弦线的长度 = 10 cm弓形面积= (8 cm * 8 cm * π / 2 rad - 10 cm * 8 cm * ) / 2= (64 cm² * π / 2 rad - 40 cm²) / 2≈ cm²因此,该半径为8 cm,圆心角为90°,弦线长度为10 cm的弓形的面积约为cm²。
圆、扇形、弓形的面积

圆、扇形、弓形的面积【重点难点解析】重点是圆面积,扇形面积、弓形面积公式,要能运用它们解决有关圆的面积、扇形面积、弓形面积的计算与证明问题.难点是扇形面积公式的推导,要理解圆心角为1°的扇形的面积等于圆面积的,圆心角为n°的扇形面积及于圆面积的即,注意:公式中的n没有单位.【基础知识精讲】一、基本公式1.圆的面积:S=πR22.扇形面积:S扇形==lR3.弓形面积:①弓形所含弧为劣弧时 S弓=S扇-S△②弓形所含弧为优弧时 S弓=S扇+S△③弓形所含弧为串圆时 S弓=S圆二、值得注意的问题1.扇形面积公式中的n与弧长公式中的一样,不带单位.2.对于一些没有面积计算公式的几何图形,可采用割补法,转化为学过的几何图形的面积和或差.对于弧形部分,一定要分清圆心和半径.典型例题〔例1〕已知如图7-65,PA切⊙O于A,PO交⊙O于C,且CP=CO,弦AB∥OP,⊙O的半径为2,求阴影部分的面积.图7-65解:连OA,OB∵PA为⊙O切线,∴OA⊥AP∵OA=OC=CP=OP∴∠OPA=30°,∴∠AOP=60°∵AB∥OP,∴∠OAB=∠AOPB=60°∵OA=OB,∴△AOB为等边三角形∴∠AOB=60°∴S扇形OAB==∵AB∥OP,∴S△ABP=S△AOB∴S阴影=S扇形OAB=〔例2〕已知:如图7-66⊙O的半径为R,直径AB垂直于弦CD,以B为圆心,以BC为半径作⊙B 交AB于点E,交AB的延长线于F,连结CB并延长交⊙B于点M,连结AM交⊙O于N,(1)求两圆公共部分的面积S.(2)求证AM·AN=2AE·AF图7-66(1)解:连结BD∵CD为⊙O直径∴∠CBD=90°∵CD⊥AB,OC=OD ∴CB=DB在Rt△CBD中,CD=2R∴BC=CDcos45°=2R· =R∴S=S⊙O+S弓形CDE=πR2+〔π( R)2- ( R)2〕=(π-1)R2(2)证明连AC∵AB为直径∴∠ACB=90°∵BC为⊙B半径∴AC为⊙B的切线∴AC2=AE·AF∵OA=OB ∴CA=CB∵MN·MA=MB·MC=BC·2BC=2BC2=2AC2∴AM·MN=2AE·AF〔例3〕已知:如图7-67,⊙O的长l是半径R的π倍,AC,BC是方程-2x2-(m-1)x+m+1=0的根,OC=1,求弓形AmB的面积.图7-67〔解〕延长线段OC交⊙O于E,F,作OG⊥AB于G,∴GB=ABl==R,∴n=130,∴∠AOB=120°∴∠GOB=60°在Rt△OGB中,sin∠GOB=,∴GB=R·sin60°=R∴AB=R,又cos∠GOB=,∴OG=R,∴S△ABD=AB·OG=× R× R=R2.∵AC、BC是方程-2x2-(m-1)x+m+1=0的根,∴AC·BC=- ①AC+BC=. ②又∵AC·BC=CE·CF=(R-OC)(R+OC)=R2-OC2=R2-1 ③AC+BC=AB=R ④∴由②,④得R=由①,③得R2-1=-解方程组R=R2-1=- 得R=∴S△ABC=R2=·S扇形OAmB==π∴弓形AmB的面积=S扇形OAmB-S△OAB=π- (平方单位).〔说明〕此题是一道代数几何综合问题,解决此题的关键是求出⊙O的半径,综合分析题的图形与已知条件,寻找与半径有关的式子,发现AC+BC=AB,AC·BC=CE·CF,而AB及CE·CF都与半径与关,再由题已知方程的根与系数关系,找到含R的方程组,从而求得R.〔例4〕如图7-68,已知半径为3cm和1cm的两个圆,⊙O1和⊙O2外切于点P,AB是它们的一条外公切线,切点分别为A,B,QP垂直于O1O2于P交AB于Q点,连O1Q和O2Q,求:图中阴影部分面积.图7-68〔解〕连O1A,O2B可求得外公切线长AB=2 =2 (cm)∵QP⊥O1O2,∴QP是⊙O1,⊙O2的内公切线,由切线长定理知AQ=QP=QB,∠=O1QO2=∠AQB=90°.∴QP=AB=(cm)在Rt△QO1P中,tg∠QO1P==,∴∠QO1P=30°,∴∠QO2P=60°∴S阴=S -S -S =O1O2·QP--=×4× - π- =2 - π(cm2).〔说明〕此题就是将一个不规则图形的面积化归为几个已学过的图形面积的和差形式.练习一、填空题1.扇形的弧长是2πcm,半径是10cm,则此扇形的面积是 .2.圆心角为n°,面积为S的扇形的半径是 .3.如果圆的周长是π,则圆的面积是 .4.如下图7-75,C,D是以AB为直径的半圆的三等分点,OC,OD是半径,且半径为长6,CD为弦,则图中阴影部分的面积是 .图7-75 图7-765.如图7-76,Rt△ABC中两直角边AC=4cm,BC=5cm,分别以AB,AC,BC为直径的三个半圆所围成的两个新月形(图中阴影部分)的面积和为平方厘米.图7-776.如图7-77,在△ABC中,∠C=90°,∠A=60°,以A为圆心,以AC的长为半径画弧与AB 相交于D,若图中阴影部分的面积为6πcm2,则AB= cm.7.若扇形的圆心角为150°,弧长为20πcm,则扇形的面积是 .二、选择题1.如图7-78,以边长为a的正三角形的三个顶点为圆心,以边长一半为半径画弧,则三弧所围成的阴影部分的面积是( )A. (2 -π);B. (2 -π);C. +D. a2.2.如图7-79,正方形ABCD的边长为1cm,以CD为直径在正方形内画半圆,再以C为圆心,1cm 长为半径画弧BD,则图中阴影部分的面积为( )A. cm2B. cm2C. cm2D. cm2图7-78 图7-79 图7-803.三个半径为R的圆两两外切,则夹在三个圆之间部分的面积是( )A. R2- πR2B. R2- πR2C.( -1)R2D. R2-R24.如图7-80,在扇形OAB中,∠AOB=90°,再以AB为直径作半圆,所得月牙形面积为( )A.大于S△OABB.等于S△OABC.小于S△OABD.以上都有可能三、解答题1.如图7-81所示,已知正方形ABCD的边长为2,以顶点A为圆心,AB为半径作,由AD的中点E,作EF∥AB,交BC于F,交于G,再以E为圆心,ED为半径作交EF于H,试求图中阴影部分的面积.图7-81 图7-822.如图7-82所示,正三角形ABC的高AD=4cm,以AD为直径作圆分别交AB、AC于E、F,求阴影部分的面积.四、1.如图7-83所示,已知直角梯形ABCD中,∠D=90°,∠A=30°,AB=4,以斜腰AB为直径的半圆切CD于E,交AD于F.求图中阴影部分的面积.图7-83 图7-842.如图7-84所示,已知⊙O1与⊙O2的公共弦为AB,若AB分别为⊙O1和⊙O2的内接正三角形和内接正六边莆的一边,且AB=a,求两圆公共部分的面积.答案:一、1.10πcm2 2. 3. 4.6π 5.10 6.12 7.140πcm2二、1.A 2.C 3.D 4.B。
专题01 扇形、弓形的周长和面积+刘子琳

1、扇形、弓形的周长和面积平面上到定点距离等于定长的点的集合称为圆.扇形、弓形都是圆的一部分,圆中一段弧及过该弧两端点的半径围成的图形称为扇形;由圆得弦及所对的弧围成的图形称为弓形.设圆的半径为r ,则圆的周长为2,C r π=面积2.S r π=若扇形的半径为r ,弧所对的圆心角为,n 则扇形弧长为,180n r l π=扇形周长2,180nC r r π=+面积2.360n r S π=弓形面积则需要考虑弧所对的是优弧还是劣弧,如图1-1,弓形ADB 的面积,ADB AOB S S S ∆=+弓形的周长C =弧长+弦长.由圆、扇形、弓形等构成的图形面积或周长计算通常需要一定技巧,处理这类问题的手段是分解组合、等积变形等等.例1 如图1-2,,AB CD 是O 的两条互相垂直的直径,且2,AB =以点B 为半径画弧AE 交CD 延长线与点,E 又四边形EFGO 为正方形,求阴影部分的面积.分析 将图形分割为AED 区域和DEFGB 区域,其中AED 区域的面积等于扇形ABE 的面积减去扇形AOD 的面积及OBE ∆的面积之和.解注意到,BA BE =且EO 垂直平分,AB 故ABE ∆为正60,ABE OE AB ∠=== 所以ADE ABE AOD OBE S S S S ∆=--CODBAE FGAC2342DEFGB EFGO DOB S S S ππ=--=-2434ππ=-=-故362S π=+-例2 如图1-3.正方形ABCD 的边长为,a 分别以,,,A B C D 为圆心,,a 为半径画弧,求四条弧所围成的阴影部分面积.解 如图1-3将正方形各部分进行分割,面积相等区域用相同的字母表示,于是 244x y z a ++= ① 232.4a x y z π++=②另外,设以点,A D 为圆心的弧交于点,E 则,AE DE AD ADE ==∆为正三角形。
所以222222.6434a a x y z a a ππ++=⨯-=- ③由①②③解得:2(16z a π=-于是22243)3S a z a π=-=+说明 此题关键是发现ADE ∆为正三角形,因此,请读者在解决问题时宜用心掘潜在条件.例3 如图1-4,扇形的半径为20,圆心角为144,,,,,,,B C D E F G H 是扇形弧线八等分点,求阴影部分的面积之和.BACD分析 合理分割,小心拼接解 连接OE 交DF 与点,M 交GC 与点,J 交HB 于点,K 交AI 与点,N 连接OF 与AI 与点,Q 连接OG 交HB 于点,p 连接.OH易证,,QNMF IQO OFM ION S S ∆≅∆=从而区域IHGFQ 为公布部分,故IOF FMNI S S = 又,GJO OKH ∆≅∆所以又区域GHP 为公共部分,故GHKJ HOG S S = 从而区域FMNI 中,23636040.IOF HOG IOG S S S S r ππ=-===由于对称性,于是在区域AIFD 中,80.S π=例4 在一个三边长为50,120,130的三角形内部与外部分别取出与三角形边上至少有一点的距离为2的所有点,求所有这些点构成的区域的面积.解 依题意得,所求面积区域为图1-5中111A B C ∆的外围部分面积.ABC ∆的三个顶点在一起处各有一个小扇形,半径均为2,合在一起恰好为2的圆,故图中ABC ∆外部面积212(50120130)26004.S ππ=⨯+++⨯=+其次,易知,111A B C ∆ABC ∆,且共内心,内切圆半径相差2,由于ABC ∆的内切圆半径为5012013020,2+-=故111A B C ∆的内切圆半径为18.所以 11111181100811008115012010022430.A B C ABC A B C ABC S S ∆∆∆=∆=⨯=⨯⨯⨯=例5 在边长为1的正五边形ABCDE 内,去掉所有与各点距离小于1,求余下部分面积.分析 关键是确定余下部分形状.解 如图1-6所示,分别以,,,,A B C D E 为圆心,以1为半径画弧,这些弧围成一个“曲边五边形”,MNPQR 其余的部分由五个等积的形如“曲边三角形” NBC 的图形组成.注意到曲边三角形NBC 与扇形NDC 的面积之和等于DNC ∆与扇形NCB 的面积之和,所以所求余下面积之和,5()310860605()436036046DNC NCB NDC S S S S πππ∆=+--=+-=-例6 已知正方形和三角形都外切于半径为1的圆,求证:正方形和三角形重叠部分且在圆的外部区域面积大于0.34.证明 当三角形的边与正方形所在边的直线不重合或者平行时,则三角形的边必将正方形减去一个角,此角BEAC ACB ODE F在重叠部分之外,先考虑部分面积的情况. 如图1-7 O 切正方形的边长与点,,E F ABC ∆与点,D 连接,,,,,OE OB OD OC OF 则四边形OEAF 为正方形.设,,1,1,AB x AC y BD x CD CF y ===-==-故有Rt ABC ∆中有222(11)x y x y -+-=+22()22(220, 1.xy x y xy x y x y +=++=+≥+-<<>)2121).2ABC S xy ∆=≤ 由于三角形最大边最多截去正方形三个“角”,从而三角形与正方形重叠面积至少为3,ABC S S ∆-若符合题意得区域面积为,S 则2223231)150.34.ABC S S S Sππ∆≥--≥-⨯-⨯=->证明正方形与三角形重叠部分的面积不可能等于5,但可无限接近. 习题11. ,,90,Rt ABC AC BC C ∆=∠=点D 在AB 上,以点A 为圆心,AD 为半径画弧交BC 交于点,E AC 的延长线与,F 若图中两个阴影部分面积相等,求:.AD DB2.在一块周长为500米的三角形草坪周围修筑一条宽1米的小路,且路的任何一处至少与草坪的某处距离为1米,求路的占地面积.3. AB 是半圆O 的直径,作OD AB ⊥交半圆O 与点,D 分别以点,A B 为圆心,AB 为半径画弧交,AD BD 延长线与,,F E 再以点D 为圆心,DE 为半径画弧,连接,E F ,若2,AB =求图中阴影部分面积.4.直角三角形,2,90,ABC AC CB C ==∠=将ACB ∆绕C 顺时针转90,求AB 扫过的区域面积.5.将一枚半径为1cm 的硬币置于n 边形内,硬币可在里面任意移动,但不可超越边界,求正n 边形内硬币不能接触到部分面积.6. 正三角形的边长为a ,过每两个顶点及中心O 在三角形内作弧,求阴影部分的面积S 阴.7.正三角形的边长为2a为半径画圆,求:圆的公共部分面积.8.ABC ∆的三条边, AB c BC a CA b ===,,作ABC ∆的内切圆,再作此内切圆的三条切线分别平行,,,AB BC CA 又得到三个小三角形,再作这三个小三角形的内切圆,求这四个圆的面积之和.习题11.区域ADEC 是扇形DAF 与ACB ∆公共部分,若图中阴影部分面积相等,2222221451,,2,,,2360482ABC DAF AD AD S S AC AD AC AB AB AD AB DB πππ∆======FEABCDOABC2.依题意,路的占地面积由三个矩形和三个扇形组成,三个矩形可拼成一个长500米宽1米的矩形,三个扇形正好拼成一个半径为1米的圆,从而占地面积3.250011(500)S ππ=⨯+⨯=+4.边AB 扫过的区域即图中的阴影部分,它由两个弓形ADB 和BEF 及曲边三角形DBE 组成,故2221113224 2.2242S πππ=⨯-⨯⨯+-⨯=-5.将各顶点处不能接触到部分拼合在一起,围成一个边心距为1cm 的正n 边形,但除去半径为6.连接,,OB OC 作21,.2OBC OH BC S a ∆⊥=⨯=设弧BOC 的圆心为1,O 由垂径定理得1,O B =从而扇形1BO C 中减去1BOCO 得到两个小弓形,两个小弓形恰好拼成“三叶玫瑰”中的一片叶子,所以213()233OBC S a S π∆⎡⎤=⨯-⎢⎥⎣⎦=222213.9632a a a a ππ⎡⎤-=-⎢⎥⎣⎦ 7.由于对称性,可将图中各部分面积分别用,,x y z 表示,相同字母表示面积相等,易知222133...,2)...63x y z x y z a ππ++=++==注意到222222)(2),BN CN a BC +=+==故,BN NC ⊥从而不难知道MN 垂直平,45,BC NBM BNM ∠=∠=22224512()236022NBD NBM y z S S a a a ππ∆⎡⎤+=-=-=-⎢⎥⎣⎦解得,()262a z π=+8. 8.设ABC ∆的面积为S ,半周长为p ,则11AB C ∆的半周长为22, ,p a QB A q -∆的半周长为p b -,33CA B ∆的半周长为,p c -则ABC ∆的内切圆半径Sr P=,又 112233ABCAB C AB C AB C ∆∆∆∆,从而1111212,AB C AB C S p a p a S S r S p p a p ∆∆⎛⎫--===⋅ ⎪-⎝⎭同理2222A BC S p b r S p bp ∆-==⋅-,3332A B C S p cr S p c p ∆-==⋅-,故 ()()()()()222212322222444222241S r r r r p a p b p c S p p p p ab c S p πππ=+++⎡⎤---=+++⎢⎥⎢⎥⎣⎦++=总 又()()()2,S p p a p b p c =--- 故S =总()()()()2223p a p b p c a b c p π---++,这里.2a b cp ++=(第7题图) (第8题图)D CBAMA BC。
5.1 圆 扇形 弓形及其组合图形的面积、周长解析

圆形周长和面积这一阶段,我们学习了圆:若它的半径为r,则周长为:2πr。
面积为:。
扇形:它是圆的一部分,若它的半径为r,圆心角为,则弧长为:2πr×,周长为:2πr×+2r。
面积为:×环形:由两个同心圆,圆周之间的部分组成。
以后在例题中,还会遇到弓形、“叶形”,将在题中一一说明。
求组合图形的面积、周长,可以用直接法、间接法、割补法、添补法、平移法、旋转法等等。
同学们在解题中一定要认真领会灵活运用,切实提高自己的观察、分析、综合能力。
下面看几个例题。
例1. 求阴影部分的面积。
(单位:厘米)例2. 正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)例3. 求图中阴影部分的面积。
(单位:厘米)例4.求阴影部分的面积。
(单位:厘米)例5.求阴影部分的面积。
(单位:厘米)例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?例7.求阴影部分的面积。
(单位:厘米)例8.求阴影部分的面积。
(单位:厘米)例9.求阴影部分的面积。
(单位:厘米)例10.求阴影部分的面积。
(单位:厘米)例11.求阴影部分的面积。
(单位:厘米)例12.求等边三角形中阴影部分的面积。
(单位:厘米)例13.求阴影部分的面积。
(单位:厘米)例14.求阴影部分的面积。
(单位:厘米)例15.已知直角三角形面积是12平方厘米,求阴影部分的面积。
例17.图中圆的半径为5厘米,求阴影部分的面积。
(单位:厘米)例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长。
例19.正方形边长为2厘米,求阴影部分的面积。
例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积。
例21.图中四个圆的半径都是1厘米,求阴影部分的面积。
例22. 如图,正方形边长为8厘米,求阴影部分的面积。
例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少?例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心。
圆、扇形、弓形的面积 人教版 九年级数学

弧长=____.
3
答案:
4 3
、2、120°、34、
、4
3
.
例1、已知正三角形的边长为a,求它的内切圆与外 接圆组成的圆环的面积.
解:设正三角形的外接圆、内切圆 的半径分别为R,r,面积为S1、 SS=2.S 1 S 2 R 2 r 2 ( R 2 r 2 ).
∵ R2 r2 (a)2 a2 ,∴S=
第七章 圆
7.20 圆、扇形、弓形的面积
一 复习 已知⊙O半径为R,⊙O的面积S是多少?
二 新课
S=πR2
1. 扇形的定义是什么?
一条弧和经过这条弧的端点的两条半径所组成的图
形叫做扇形.如图, 阴影部分
即为扇形.
O
n° R
A
B
l
2.已知⊙O半径为R,如何求圆心角n°的扇形的面 积?
研究问题的步骤:
的面积,S扇=____.
2、已知扇形面积为 4 ,圆心角为120°,则这个扇形
的半径R=____. 3
3、已知半径为2的扇形,面积为 4 ,则它的圆心角的
度数=____.
3
4、已知半径为2cm的扇形,其弧长为 4 ,则这个扇
形的面积,S扇=____.
3
5、已知半径为2的扇形,面积为 4 ,则这个扇形的
谢谢观赏
You made my day!
我们,还在路上……
注意:
(1)在应用扇形的面积公式S扇形= 要注意公式中n的意义.n表示1°
nR 2
圆360心
进行计算时, 角的倍数,它
是不带单位的;
(2)公式可以理解记忆(即按照上面推导过程记忆).
问题:扇形的面积公式与弧长公式有联系吗?
人教版九年级上册数学弧长与扇形面积-求弓形的面积

人教版九年级上册数学24.4弧长与扇形面积-求弓形的面积一、单选题1.如图,在O中,,2,90OA OB CD DE CDE︒⊥==∠=,则图中阴影部分的面积为()A.142π-B.4πC.122π-D.12π-2.如图,一个半径为2的半圆形纸片,按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是A.83πB.83π-23C.43π-3D.23-23π3.如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为()A.6πB.33πC.23πD.2π4.如图,网格中的小正方形边长都是1,则以O为圆心,OA为半径的弧AG和弦AB所围成的弓形面积等于()A 2π﹣4 B.2π﹣4 C.4π﹣4 D.π﹣45.如图,正方形ABCD的边长为2,以BC为直径的半圆与对角线AC相交于点E,则图中阴影部分的面积为()A .5124π+B .3124π-C .5122π-D .5124π- 6.如图,扇形的圆心角为60°,半径为3,则图中弓形的面积为( )A .4334π-B .34π- C .2334π- D .332π-二、填空题7.如图,⊙O 的半径为2,点A ,B 在⊙O 上,∠AOB =90°,则阴影部分的面积为________.8.如图,已知扇形AOB 的半径为2,圆心角为90︒,连接AB ,则图中阴影部分的面积是________.9.圆内接正方形的一边截成的小弓形面积是2π-4,则正方形的边长等于__________.10.如图,AB 是⊙O 的直径,弦CD ⊥AB 于点E ,⊙O 半径为3 cm ,弦CD 的长为3 cm ,则阴影部分的面积是____________ cm 2 .11.用等分圆周的方法,在半径为1的圆中画出如图所示图形,则图中阴影部分的面积为______.三、解答题12.如图,有一个马戏帐篷,它的底面是圆形,其半径为20m ,从A 到B 有一笔直的栅栏,其长为30m .观众在阴影区域里看马戏,如果每平方米可以坐3名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏?13.已知正方形的边长为2,求右图中阴影部分的面积.14.如图,直线y kx b =+经过点M(1,3)和点N(1-,33),A 、B 是此直线与坐标轴的交点.以AB 为直径作⊙C ,求此圆与y 轴围成的阴影部分面积.15.如图,已知⊙O 半径为10cm ,弦AB 垂直平分半径OC ,并交OC 于点D .(1)求弦AB 的长;(2)求弧AB 的长,并求出图中阴影部分面积.16.如图,CD 为O 的直径,CD AB ⊥于点F ,AO BC ⊥于点E ,2AO =.(1)求AOD ∠的度数;(2)求阴影部分的面积.17.如图,已知点A,B,C,D均在已知圆上,AD∥BC,CA平分∠BCD,∠ADC=120°,四边形ABCD的周长为10.(1)求此圆的半径;(2)求图中阴影部分的面积.18.如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.(1)判断直线MN与⊙O的位置关系,并说明理由;(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.参考答案1.A2.D3.A4.B5.D6.C7.π-28.π-2.9.4.10.33π⎛⎫- ⎪ ⎪⎝⎭11.π-33 12.约421人.解:过O 作OD ⊥AB ,D 为垂足, ∵AB =30m .∴AD =BD =15m ,∴OD =22AO AD -=57∵sin ∠AOD =AD AO =1520=0.75, ∴∠AOD ≈49°,∴∠AOB =98°,∴S 阴影部分=S 扇形OAB -S △OAB =29820360π⨯-12×30×57≈145.7m 2, ∴145.7×3≈437(人).答:大约有437位观众在看马戏.13.2.28解:根据题意,则2(222)2360n r π-⨯÷⨯ 290 3.142(222)2360⨯⨯=-⨯÷⨯ (3.142)2 2.28=-⨯=.14.233π- 解:把()()1,3,1,33-代入y kx b =+ 得:323y x =-+ 令0,23x y 得==∴B ()0,23令0,y =得0x = ∴()2,0A∴()222234AB =+=∴2r =过点C 作CD ⊥OB ,连接OC ,由垂径定理可知:OD=1,∴sin ∠CBD=12 ∴∠CBD=30°∵BC=OC∴∠BOC=300 ,∴∠BCO=120°∴S 扇=221122663r πππ=⨯⨯= ∵S △OBC =123132⨯⨯= ∴S 阴=233π- 15.(1) ;(2) 解:(1)如图,⊙O 半径为10cm , ∴OB =OC =10,∵弦AB 垂直平分半径OC ,∴AB =2BD ,∠ODB =90°,OD =OC =5, 在Rt △BOD 中,根据勾股定理得,BD = =5,∴AB =2BD =10cm ; (2)由(1)知,OD =5,在Rt △BOD 中,cos ∠BOD ==,∴∠BOD =60°,∵OC ⊥AB ,∴∠AOB =2∠BOD =120°,∴l 弧AB ===cm , S 阴影=S 扇形AOB ﹣S △AOB =﹣AB ×OD =﹣×10×5=﹣25(cm 2).16.(1)60AOD ∠=;(2)433π-. 解:(1)∵CD 为直径,CD AB ⊥, ∵AF BF =,AD BD =,∴2AOD AD BD C ∠===∠,∵COE AOF ∠=∠,∴2COE C ∠=∠,∵AE BC ⊥,∴190303C ∠=⨯=, ∴60AOD ∠=;(2)连结OB ,∵2120AOB AOD ∠=∠=,112OF AO ==,223AB AF ==∴2120243603OAB S ππ⨯==扇形, 11231322OAB S AB OF =⋅=⨯ ∴433OAB S π=17.(1)圆的半径为2;(2)2π3-3 (1)∵AC 平分∠BCD ,∴∠ACD=∠ACB ,又∵AD ∥BC ,∴∠ACB=∠DAC=∠ACD ,而∠ADC=120°, ∴∠ACB=∠DAC=∠ACD =30°,∠B=60°, ∴AB=AD=DC ,且∠BAC=90°, ∴BC 为直径,设AB=x ,则BC=2AB=2x , 又∵四边形ABCD 的周长为10cm , ∴x+x+x+2x=10,解得x=2, 即⊙O 的半径为2;(2)设圆心为O ,连接OA 、OD ,由(1)可知OA=OD=AD=2,∴△AOD 为等边三角形,∴∠AOD=60°;∵AD ∥BC ,∴AOD ACD S S ∆∆=2323= ∴26022=333603OD AOD A S S S ππ-⨯==阴影扇形18.(1)相切;(2)16433π- 理由:连接OC .∵OA=OC ,∴∠OAC=∠OCA ,∵∠BOC=∠A+∠OCA=2∠A ,∠BCM=2∠A , ∴∠BCM=∠BOC ,∵∠B=90°,∴∠BOC+∠BCO=90°,∴∠BCM+∠BCO=90°,∴OC⊥MN,∴MN是⊙O切线.(2)由(1)可知∠BOC=∠BCM=60°,∴∠AOC=120°,在RT△BCO中,OC=OA=4,∠BCO=30°,∴BO=12OC=2,BC=23∴S阴=S扇形OAC﹣S△OAC =2120411642343 36023ππ-⨯⨯=-.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例 如图,已知半径OA=6cm ,C 为OB 的中点,∠AOB=120°,求阴影部分的面积.解:过A 作AD ⊥BO 交BO 的延长线于D ,则AD 是△ACO 的边OC 上的高,∵∠AOB=120°,∴∠AOD=60°, ∴AD=OAsin60°=33236=⨯.∴S 阴影=S 扇形ABO -S △ACO =)cm (3291233321360612022-π=⨯⨯-⋅π 说明:(1)此题应用解直角三角形,三角形面积公式和扇形面积公式;(2)阴影部分的面积是由扇形和三角形组合而成,熟练拿握扇形面积公式和三角形面积公式是求此阴影部分面积的关键;(3)灵活选用三角形面积公式: ①a ah 21S =∆;②B sin ca 21C sin bc 21C sin ab 21S ===∆. 例 已知:弓形的弧的度数为240°,弧长是π38,求弓形的面积.解:如图,根据弧长公式有π=⋅π38180OA 240. ∴OA=2.∴ S 扇形OAmB =π=⨯π3836022402, S △OAB =360sin 2221=︒⨯⨯,∴S 弓形AmB =338+π. 说明:(1)弓形面积的计算;(2)弓形面积可以看成是扇形面积和三角形面积的分解和组合,实际应用时,要注意公式的选择.例 如图,在边长l 的正方形中,以各顶点为圆心,对角线长的一半为半径在正方形内画弧,则图中阴影部分的面积为 .解:S 阴影=22121S S 4S 41π-=-π-=-⨯-)()(正方形圆正方形. 说明:求面积问题的常用方法有:直接公式法,和差法,割补法等.例 如图,已知半径为1的三个等圆⊙A 、⊙B 、⊙C 两两外切,切点分别为M 、N 、P ,求夹在三个等圆中间的曲边形MNP 的面积.分析:连结AB 、BC 、CA ,则必分别过点M 、N 、P .曲边形MNP 如果先借添上三个全等扇形即构成了正△ABC ,算出△ABC 的面积后再还掉三个扇形.这样一借一还,先借后还,剩下的就是曲边形MNP .解:S 曲边形MNP =三个扇形△三个扇形三个扇形曲边形)(S S S S S A BC M N P -=-+=π-=⨯π⨯-︒⨯⨯213360160360sin 22212.说明:求有关不规则图形的面积问题的关键是将图形分解为可求图形面积的和差问题,本题是作辅助线构造三角形和扇形的面积解决的.典型例题五例 已知扇形的圆心角150°,弧长为π20cm ,则扇形的面积为_______. 解:设扇形的面积为S ,弧长为l ,所在圆的半径为R ,由弧长公式,得18015020Rππ=. ∴24=R (cm ). 由扇形面积公式,得ππ240360241502=⋅=S .故填π240.说明:本题主要考察弧长公式180R n l π=和扇形面积公式3602R n S π=.典型例题六例 已知弓形的弦长等于半径R ,则此弓形的面积为________.(弓形的弧为劣弧) 解:∵弓形的弦长等于半径R , ∴弓形的弧所对的圆心角为60°,∴扇形的面积为63606022R R S ππ==. 三角形的面积为224360sin 21R R =︒. ∴弓形的面积为22436R R -π. 即212332R -π.故应填212332R -π.说明:注意弓形面积的计算方法,即弓形的面积等于扇形面积与三角形面积的和或差.本题若没有括号里的条件,则有两种情况.典型例题七例 如图,已知扇形AOB 的中心角为直角,若cm 4=OA ,以AB 为直径作半圆,求圆中阴影部分的面积.分析:欲求图形中阴影部分的面积,必须弄清求这个面积没有直接的公式计算,只有通过可求面积的和差来解决,因为阴影部分的面积等于以AB 为直径的半圆面积减去弓形AmB 的面积,而AO B AO B Am B S S S ∆-=扇.解 cm 4=OA ︒=∠90O ,则cm 4=OB22)cm (4360490ππ=⨯⨯︒=∴AOBS 扇cm 24=AB)cm (82=∴∆AO B S)cm (42)22(22ππ==∴半圆S)cm )(84(2-=∴πAm B S 弓形即阴影部分面积)cm (8)84(42=--=-=ππAm B S S 弓形半圆典型例题八例 如图,A 为⊙O 外一点,AO 交⊙O 于P ,AB 切⊙O 于B ,5=AP 厘米,35=AB 厘米,求图中阴影部分的面积.分析:图中阴影部分面积计算无公式可用,可转化为OBA ∆Rt 与扇形OBP 的面积差. 解 连结OB ,因AB 为⊙O 的切线,故AB OB ⊥ 设⊙O 的半径为r ,在OBA ∆Rt 中,r OB =,35=AB ,r OA +=5. 则有222)5()35(r r +=+,︒=∠∴60OO BP O BA S S S 扇形阴影-=∴∆360560355212⋅-⨯⨯=π 6252325π-=(平方厘米) 说明:本例求半径r 时,还可用切割线定理.典型例题九例 已知:如图,OA 和1OO 是⊙O 中互相垂直的半径,B 在上,弧的圆心是1O ,半径是1OO ,⊙2O 与⊙O 、⊙1O 、OA 都相切,61=OO .求图中阴影部分的面积.解析设⊙2O 与⊙O 、⊙1O 、OA 分别切于点D 、C 、E ,设⊙2O 的半径为r ,连结21O O ,E O 2,过点2O 作O O F O 12⊥于F ,连结B O 1、OB 、2OO .r E O r F O r O O O O =-=+=∴=21211,6,6,6212212F O O O EO F O -==r r r 62)6()6(22=--+=r r F O O O S O OO 6662621212121=⋅⨯⨯=⋅=∴∆又)69)(69)(69(921r r S O OO --+--⨯=∴∆)9(332r -=)9(33662r r -=∴2922r r -=,298r r -=1=∴r 或9-=r (舍去)又OB O 1∆ 是等边三角形︒=∠=∠===∴60,61111BOO O BO O O OB B O∴扇形BO O 1和扇形B OO 1的面积相等且都等于ππ63606021=⋅O O O O 1∴、、所组成的图形面积为扇形BO O 1和扇形B OO 1的面积之和减去三角形OB O 1的面积.即391223662166-=⨯⨯⨯-+πππ 又 扇形1OAO 的面积为:ππ96412=⋅∴阴影部分的面积为:ππππππ-+-=⋅---39129)3912(92r π439-=说明:求组合图形的面积一般要构造出易解决问题的基本图形,然后求出各图形的面积,最后通过面积的加、减得出结论.本题较为复杂,考察的知识面较多,要正确作辅助线,找出解题的思路.典型例题十例 (1)已知扇形的半径为10cm ,弧长为π5cm ,则扇形的面积为______cm 2. (2)一个扇形的半径等于一个圆的半径的3倍,且面积相等,则这个扇形的圆心角等于________度.(3)如图,已知半圆的直径︒=∠==35,,cm 10ACD AD AB BC ,则图中阴影部分的面积等于_________.解 (1)设扇形半径为R ,弧长为l ,则).cm (2510521212ππ=⨯⨯=⋅=R l S 扇形 (2)设扇形的半径为R 3,则圆的半径为R ,22)(R R S ππ=⋅=圆.依题意,得扇形的圆心角为:︒=÷120360)3(22R R ππ(3)连结,,,AD AB OA OD = ∴∴.2ACD ∠=∠又.352,35︒=∠∴︒=∠ACD 又.1,3521,ACD OC PA ∠=∠∴︒=∠=∠∴=)cm (925360540.,//22ππ=⨯⨯==∴=∴∴∆∆OCDADC ODC S S S S DC AO 扇形阴影说明:本题考查面积公式的应用,弄清公式中字母的意义,善于进行图形的转换是解题关键.典型例题十一例 如图,已知:⊙O 的长l 是半径R 的π32倍,BC AC ,是方程01)1(22=++---m x m x 的根,1=OC ,求弓形AmB 的面积.解 延长线段OC 交⊙O 于F E ,,作AB OG ⊥于G ,∴.21AB GB =又.120,120,32180︒=∠=∴==AOB n R R n l ππ ∴.60︒=∠GOB在Rt OGB ∆中,.2360sin R R GB =︒⋅= ∴R AB 3=,又.21,cos R OG OB OG GOB =∴=∠ ∴.4321321212R R R OG AB S ABO =⨯⨯=⋅=∆ BC AC , 是方程01)1(22=++---m x m x 的根,∴21+-=⋅m BC AC ,① 21m BC AC -=+ ② 又1))((222-=-=+-=⋅=⋅R OC R OC R OC R CF CE BC AC ③ ∴R AB BC AC 3==+ ④ 由②④得213m R -=,由①,③得.2112+=-m R解方程组⎪⎪⎩⎪⎪⎨⎧+=--=.211,2132m R m R 得.3=R∴.360)3(120,4334322ππ===∆OAmB ABO S R S 扇形=∴弓形AmB 的面积.433-=-=∆πOAB OAmB S S 扇形 说明:本题考查方程与面积的综合应用,解题关键是求⊙O 的半径,应用一元二次方程的根与系数关系等求出面积.典型例题十二例 如图,已知:⊙O 的半径为R ,直径⊥AB 直径CD ,以B 为圆心,以BD 为半径作⊙B 交AB 于E ,交AB 的延长线于F ,连结DB 并延长交⊙B 于M ,连结MA 交⊙O 于N ,交CD 于H ,交⊙B 于G .(1)求图中阴影部分的面积S ;(2)求证:.HM HG HN HA ⋅=⋅解 (1)连结BC ,则,,2122R S R S BCD BCED ==∆π扇形 .2121.2122222R R R R S S R S CED =+-=∴-=∴πππ弓形(2)由相交弦定理,得HC HD HM HG HC HD HN HA ⋅=⋅⋅=⋅,,∴.HM HG HN HA ⋅=⋅说明:本题综合考查阴影面积计算与比例线段的证明,解题关键是把组合图形的面积,化归为几个简单图形面积的和或差.典型例题十三例 如图,ABC ∆为某一住宅区的平面示意图,其周长为800米,为了美化环境,计划在住宅区周围5米(虚线以内,ABC ∆之外)作为绿化带,则绿化带的面积为______(米2).解 分别过C B A ,,作BC C C BC B B AC A A AC C C AB B B AB A A ⊥''⊥''⊥''⊥'⊥'⊥',,,,,,则A A A S A A AC B B BC B B AB S '''+''⋅+''⋅+'⋅=3.2540005800518018022πππ+=⋅+⨯='⋅⋅+⨯'=∆B B l B B ABC 说明:本题考查不规则图形的面积计算,解题关键是通过作辅助线转化为规则几何图形求解.选择题1. 如图,在ABC ∆Rt 中,︒=∠90BAC ,2==AC AB 以AB 为直径的圆交BC 于D ,则图中阴影部分面积为()A .1B .2C .41π+D .42π-2. 如果扇形的圆心角为︒150,扇形面积为2cm 240π,那么扇形的弧长为() A .cm 5π B .cm 10π C .cm 20π D .cm 40π3. 正方形的内切圆半径为r ,这个正方形将它的外接圆分割出四个弓形,其中一个弓形的面积为() A .222r -πB .221r -π C .2)2(r -πD .2)1(r -π4. 设三个同心圆的半径分别为1r ,2r ,3r ,且321r r r <<,如果大圆的面积被两个小圆分成三等分,那么321::r r r 为() A .1:2:3B .3:2:1C .9:4:1D .2:3:15.已知如图,扇形AOB 的半径为12,OB OA ⊥,C 为OB 上一点,以OA 为直径的半圆1O 和以BC 为直径的半圆2O 相切于点D ,则图中阴影部分面积为( )(A )π6 (B )π10 (C )π12 (D )π206.若⊙1O 的60°弧与⊙2O 的45°弧长度相等,则⊙1O 与⊙2O 的面积之比为( ) A .16:9 B .9:16 C .4:3 D .3:47.若扇形的面积为π12,它的弧所对的圆心角为25°,则扇形的半径是( )A .212B .30512C .12D .612 8.两圆半径分别为R 和r ,另有一大圆的面积等于这两圆面积之和的4倍,则此大圆半径为( )A .)(21r R + B .)(2122r R + C .2221r R + D .222r R + 9.两同心圆小圆切线被大圆所截部分为6cm ,则这两圆围成的环形面积为( )。
