中考典型例题解析
中考英语——名词典型例题解析

中考英语——名词典型例题剖析1.--- How far is your home from school?--- About _____ walk.A. five minute’sB. five minutesB. five minutes’ D. five minute剖析:表示“步行多长时间”用名词所有格;受five 修饰, minute 用复数形式;以 s 结尾的名词,其所有格只加“-”,应选 B。
2.This is _____ bedroom. It’ s nice and clean.A. Lily ’ s and Lucy’sB. Lily and Lucy’sC. Lily’ s and LucyD. Lily and Lucy剖析: bedroom 是单数形式,由此推断两人共用一间卧室。
表示两人共同拥有某物,只需要最后一个名词用所有格,应选B。
’ s sports time. Most _____ students in Class 1 are playing football on the playground.A. boyB. boysC. boy ’sD. boys ’剖析:名词作定语修饰以后的复数名词,平时用单数形式,应选 A 。
4.--- Can I help you?--- Yes, please. I need a pair of _____.A. shoesB. T-shirtsC. sweatersD. bags剖析: a pair of 后接成双成对的物品,应选 A 。
5.Our school has fifty-six _____teachers.A. womanB. womenC. woman’sD. women’s剖析:名词作定语修饰复数名词,平时用单数形式;但 woman 作定语,要与以后名词保持数的一致;teachers为复数形式,故用复数形式women 作定语,应选 B。
中考典型例题解析(2)

中考典型例题解析(2)1.(06年威海中考)小小诊室你值班张华的哥哥最近常感到头晕、疲劳、精神不振、面色苍白,他到了医院做了血常规化验。
下面是化验报告单,请仔细分析并回答问题:(1)请你根据报告单上的信息,判断张华的哥哥可能患了。
A.青光眼 B.贫血 C.阑尾炎(2)判断的依据是:与参考值相比过少。
(根据血细胞的数量分析)。
(3)你应该建议他多吃含较多的食物。
A.钙 B.铁 C.锌2.(潍坊06年中考)根据右图和提供的资料,回答问题:很早以前,我国劳动人民就学会了用桑叶喂蚕、蚕沙(蚕粪)养鱼、塘泥肥桑的方法,创造了“桑基鱼塘”生态农业。
随着科学技术的进步,“桑基鱼塘”也得到了不断的发展,人们改变以蚕沙直接下鱼塘的老办法,将蚕沙、人畜粪便、秸秆、杂草、树叶等投入沼气池内发酵,制成沼气作燃料,然后再用沼气渣喂鱼。
这样,就把传统的“桑、蚕、鱼”农业结构,变成了“桑、蚕、气、鱼”的新型农业结构。
(1)在该生态系统中,桑与蚕是关系。
(2)在利用蚕沙、人畜粪便、秸秆、杂草、树叶等物质生产沼气的过程中,发挥作用的生物主要是。
(3)鱼进行生命活动所需要的能量最终来自。
(4)该生态系统中,物质经多次重复利用,提高了率。
(5)DDT是一种很难分解的有毒物质,如果DDT进入该生态系统,体内DDT含量最高的生物应是。
解题解析:解答这类题目分三步 1. 从中寻找有关生物学信息;2. 筛选有关有用的生物学信息;3. 结合题目要求和问题解答,提高生物知识的运用能力典题演练3.(06年岳阳中考)据今年新华社报导,北京某县全年发生35起“煤气”(主要成份是CO气体)中毒事件,死亡116人。
中毒事件的发生大多是由于人们在通风不良的房间内,使用煤炉燃煤而引起的。
造成中毒的原因是C0易与血红蛋白结合,从而使人缺_____________窒息死亡。
4.下表是某学生奶粉袋上的产品说明及部分营养成分表产品说明表部分营养成分表(每100克含量]根据以上材料和相关生物知识解答下列问题:(6分)(1)奶粉中可由消化道直接吸收的营养成分有,这些营养成分吸收的主要场所是。
2022年中考数学复习专题三半角模型及其例题解析

专题03 半角模型半角模型:是指有公共顶点,锐角等于较大的角的一半,且较大的角的两边相等(不等),通过旋转,可将角进行等量转化,构造全等(相似)的三角形的几何模型。
主要解法:一、经典之旋转法。
二、创新之翻折法。
三、常规之补短法。
熟练掌握:正方形的10个结论。
学会变通:矩形通过截或补变成正方形。
含60°角的菱形除旋转外,还可以借助对角线,构成等边三角形,利用三边相等,构造全等。
模型总讲:如图,已知在正方形ABCD 中,∠EAF =45°,连接BD 与AM ,AN 分别交于E 、F 两点。
1. BE+DF=EF ;2. △CEF 的周长等于正方形的边长的2倍。
3. S △ABE +S △ADF =S △AEF4. 点A 到MN 的距离等于正方形的边长;即AH=AD5. MN 2=MB 2+DN 2;6. 点A,M,F,D 四点共圆。
点A,B,E,N 四点共圆. 点M,E,F,N四点共圆。
点N,F,C,E,M 五点共圆。
7. 证明△AFM 和△AEN 为等腰直角三角形。
8.MN EF=√229. S △AMF =2S △AEF 10. 5组相似△HMN ∼△DFN(图9) △HMN ∼△BME(图10) △AMN ∼△BNA(图11) △AMN ∼△DMA(图12) △ AMN∽△ AFE证明如下: 结论1(图1)将△ABE 逆时针旋转90°,与△ADE'重合. 则AE=AE', ∠BAE=∠DAE’,易得 ∠EAF=∠E'AF=45° 又∵ AF=AF∴△EAF ≌ △E'AF (SAS )(图2) ∴EF=E'F=DE'+DF ∴BE+DF=EF(结论1成立) 结论2 由结论1可得:AO HN M EBCD FAE'OEBCD F图1C △CEF =CE+CF+EF= CE+CF+BE+DF=BC+CD=2BC即△CEF 的周长等于正方形的边长的2倍。
24道中考物理电功电功率典型例题解析

典型例题解析例1 一盏灯标有“36Y 40W”字样,将这盏灯接到某电路中,通过它的电流是1A,此时,这盏灯的电功率是精析 考查额定电压,额定功率的概念.已知:灯的额定电压弘=36,额定功率A=40W,实际电流A=h\. 求:P t .(实际电功率)解先判定灯是否正常发光p 40W灯正常发光时:A= —= ------------ ^1. 1A所以灯不能正常发光,且"•应VE ・斤不变 灯的实际功率:R = I ;R= (1A) "X32.4Q=32.4W答案灯的功率为32. 4W思考有的同学际功率,采用下面做法:E=%=36VX1V = 36W你能看出其中的问题吗?例2某导体接到6V 电压下,它消耗的功率是6W ;将改接到3V 的电压下,这个导体的功率是W. 巳知仏=6V A=6W 实际仏=3Y求:实际A分析一个导体,在额定电压下,电阻为斤,同样一个导体,电压改变,电阻仍为忆同样一个导体,电压改变,电阻仍为电功率的习题,往往从求解电阻入手.解法1导体电阻电压变了,导体消耗的功率改变解法2导体电阻不变U'根据:R=—PP E P L P E Uj(6V)2 =6Q ・R 6QP L = Z ・ P E = U( —)~X6W=1.5W6V 先求出灯的电阻斤=鱼P E小结 从解法2看出,电阻一定时,电压是原来的倍,功率是原来的“77.倍.因为片陆〃是原来的倍,/也是原来的"/?”倍,所以尸是原来的倍.答案功率是1.5W例3 (市中考试題)电能表是测量的仪表.1 kWh 的电能可供标有“220V 40W”的灯泡正常工作 h. 精析 电能表是日常生活中常用的仪表.考查能否灵活利用^Pt 进行计算.正确选择合适的单位,可以简化计算.解 电能表是测量电功的仪表.題目给出:AlkWh Q40W=0.04kWL 「 VV 1 kWh时间:t= — = -------------- =25h P 0.04kW如果选用国际单位,则计算要麻烦得多.答案电功,25例4 (市中考试题)一个“12V 6W”的小灯泡,如果接在36V 电源上,为使其正常发光,需串联一个一 Q 的电阻,该电阻消耗的功率是 ___________________ W.精析 在串联电路中,利用电流、电压等特点,计算电阻和电功率.已知:额定A=6W,仏=12V,总电压£«=36V求:R 、必解 灯的额定电压是12V,直接将其接在36V 的电源上,灯将烧毁:这时应将一个电阻和灯串联;一使灯正常发光. 画出灯与斤串联的电路草图2-3-1.并标出已知量和未知量・=36V-图 2—3—1只要求出通过斤的电流和斤两端的电压.就可以求出未知量.流过灯的电流和流过斤的电流相等:答案 48 Q, 12W例5 (市中考试題)电阻斤和灯泡£串联接到电压为10V 的电路中,C10Q,电路接通后,100s 电阻斤上电流 做的功为10J,已知灯Z 的额定功率为10W,灯的电阻不变.求:灯的额定电压.解 画出灯£和电阻只串联的电路草图2-3-2,并标明已知量和未知量.串联电路,通过厶和斤电流相等,设为/・贝寸瓯=IRt-------------- =—A=0. 1A lOQxlOOs 10 斤两端电压:^=Z J ?=O. 1AX1OQ = 1V 灯厂两端电压:〃=/一丛=1OV —1V=9V7=12Jft=6W图 2—3—2灯电阻用¥=議灯额定电压:U E = = V10Wx90Q =30Vp i ow误解 有的同学在算完电流后,直接用:&=旦=—— =1OOV\是错误的.因为此时灯并不是正常发光,电路中的电流不是几当然,有的同学把«=9V 算为灯的额定电压,也是错误的.答案灯额定电压为30V例6 (市中考试题)有两个灯泡,厶标有"6V 3W”字样,厶没有标记,测得厶的电阻为6Q,把它们串联起来 接入某一电路,两个灯泡均能正常发光,那么该电路两端的电压和£2的电功率分别是 ( )A. 12 V 3WB. 12 V 1.5WC. 9 V 3W D ・ 9 V 1.5W解 画出厶和厶串联的电路草图2-3-3,标明已知量和未知量.厶正常发光时,〃=6V, P.=3W 电路中电流:P 、 3W 7= — =--------- =0. 5A U x 6V图 2—3—3此时Z 也正常发光,厶两端电压:鸟=/=0.5AX6Q=3V几=丛=0・ 5AX3V = 1.5W*$ +丛=6V + 3V=9Y答案D例7有一盏小灯泡,当它与5Q 电阻串联后接15V 电源上,灯恰好正常发光,这时灯的功率是10W. 求:小灯泡正常发光时的电阻和小灯泡的额定电压的可能值.已知:斤=5QA=10WU=15V 求:U E (额定)分析 画出分析电路图2—3—4.—U = 15V —图 2—3—4从图中看,所给物理量无对应关系,解法1心和斤串联,设灯两端电压为仏I E =L可以采用方程求解. P 匸】0W lh七P 卜:_U-U EU E R10W _ 15V-t/£可=5C整理得加一15丛+50 = 0(员一 10)(仏一5) =0 仏=iov 或 a=5v灯电盼詈二需FOQ 或,)=£/=(W =25QP E 1OW解法2丘和斤串联:U=臥AU=^-+IR 15Y=12空+/X5Q 5/-15/+10=0Z-3/+2=0(1-2) (Z-l) =0 解得:/=2A 或/=]AP 卜 10W Ri= —r = ------- ? =2. 5 Q I 1 (2A)2答案 灯正常发光,当丛=10V 时,灯电阻为10Q ;当&=5V 时,灯电阻为2.5Q例8 (市区中考试題)将分别标有"6Y 9W"和"6V 3W”的两个灯泡厶、厶串联接在12V 电源上,则()A.两灯都能正常发光B.灯厶可能被烧毁C.两灯都比正常发光时暗D.灯厶比灯厶亮 精析考查学生能否根据实际电压和额定电压的关系,判断灯的发光情况. 解先求出两盏灯的电阻灯厶的电阻:用=牛二籌w灯厶的电阻:"詈嗥=12Q或用=牛=竺.I 1(1A)2 = 10Q求出灯两端的实际电压orV R\、底串联/ _ & _ 4G _ 1U R. + R2 4Q + 12Q 4UJ =-lf=-X 12V=3V4 4厶两端电压厶『=U-UC =12V-3V=9V 比较实际电压和额定电压W V0;,圧<lk两灯都不能正常发光;灯厶可能会被烧毁答案B例9 (市东城区中考试题)家庭电路中正在使用的两白炽灯,若甲灯比乙灯亮,则()A.甲灯灯丝电阻一定比乙灯的大B.甲灯两端的电压一定比乙灯的大C.通过甲灯的电量一定比乙灯的多D.甲灯的实际功率一定比乙灯的大精析考查家庭电路中灯的连接方式,并由灯的亮度判断电阻的大小.分析家庭电路・灯的连接方式是并联・甲、乙两灯两端电压相同.甲灯比乙灯亮,说明甲灯实际功率比乙灯大.D 选项正确.甲灯比乙灯亮,在并联电路中,RYRu〃相同,1^>1乙电量Q=It.若两灯同时使用,因为E相同,则C选项正确. 答案c、D例10如图2—3—5,电源电压和电灯厶的电阻均保持不变.当开关S闭合后,在变阻器的滑片"从中点向下滑精析考查学生识别电路的能力.能否根据欧姆定律分析电路中电流变化,灯的亮度变化.分析电路是由灯和变阻器并联而成.测的是干路电流测的是流过变阻器的电流测的是电路两端电压当变阻器的滑片戶由中点向b端移动时,变阻器的电阻增大,通过变阻器电流减小,示数变小,D选项正确. 并联电路,〃一定,灯电阻不变,则流过灯的电流不变,灯的亮度不变.示数变小.答案D例11如图2—3—6,电源电压不变,开关S由断开到闭合,电流表两次示数之比为2 : 7,则电阻用:R产电功率*:£,电功率P\:P\' =_.,电功率P\: R=_精析分析S闭合前后,电路中电阻的连接关系.写出只/、氏斤之间的关系,利用公式求解.解S断开,只有用,示数为用两端电压为伉流过用的电流为八S闭合,R\、凡并联,示数为厶+ 12,水两端电压不变为£流过用的电流不变为G心功率为/V・动的过程中,下列说确的是(A.电压表的示数变大C.电流表儿的示数不变)B.电灯£的亮度变暗D.电流表九的示数变小亠竺」p; 2 1P 】_I\U—2P (人+QW 7答案 R\ :金=5 : 2, A : £=2 : 5, A : /V =1 : 1. A : P=2 : 7例12如图2-3-7 (a),当变阻器滑片从A 点滑到B 点时,凡两端的电压比为2 : 3,变阻器两端电压比UZ =4 : 3.(电源电压不变)求:L :几忆:弘Pd 几:凡RJR.、图 2—3—7精析 画出电路变化前后对应的两个电路:如图2-3-7 (b) (c)所示.已知:解 R 、 乞=厶Rfl U BRi(b)(c)O 讥_F_(2」P ;心 F 3 9匕 _ /'心 _ 4 2 _ 8, ■ 八、■ ■ ■P R /,心 9 1 9图(b ): U=h (用+丘)图(c ): U=h (M+处) 1 I 2Z7相等:必=一乩」■=二代入2 £ 3L (用+忆)=/”(用+丄他)2 2 (用+忆)=3 (用+丄忆)2 乞=丄心2另解:图(b ) 图(c ) U=W + 伽3 3••• R =-L\9 U尸二叽〃不变2 43 3••• 〃; +仏=二併+二伤2 41 1—4= 一仏2 4 £L = 1 J 2R\、忆串「•心“飞答案 h : A=2 : 3,忆:&=2 : U ”: R =4 : 9, P A :必=8 : 9,用:笊=1 : 2例13如2—3—8 (a ),已知水:金=2: 3,当$闭合,S 、$断开时,用的功率为A,电路中电流为/;当S 、金闭合,$断开时,用的功率为/r ,电路中电流为r. r •(电源电压不变)求:a : &、A :*',/: v精析画出变化前后电路图(b )和(c ) (a) 图 2—3—8PC 已知: R 、_2 乩 3 R 、 a----------Ria---------- y rU ------------- -(c)P\ /-F > —Pl 1解图(b)中用、凡串,学=学=3u, R、 3R - & _疔_(2 2_ 4 p/ t/2U2 5 25瓦~图(c)中用两端电压为U图(b):U=I IR\ + RJ2昔)〃不变/ (用+底)=『(一竺一)R} +尺2I(24-3)=1'(士上)2+ 3£= _6_7_ 25答案6{ : U>=2 : 3, R : R' =4 :25, /:I' =6 : 25例14如果将两个定值电阻水和丘以某种形式连接起来,接入电路中,则电阻水消耗的电功率为12W.如果将这两个电阻以另一种形式连接起来接入原电路中,测得该电路的总电流为9A,此时电阻用上消耗的电功率为108W.(电源电压不变)求:(1)电阻用和用的阻值;(2)电阻金上两次电功率的比值.精析先判断电阻用、用的两次连接方式.因为总电压不变,由PS和凡一定,判断出:L\<L\f所以第一次用、凤串联,第二次并联.求:R\、R、A、Pi解画出分析电路图2-3-9 (a)(b)图2—3一9一U2同一电阻用,根据P=——RV R\、矗串=r =9AIJ =3A(/, )2 仲广R?=2 /?】=6 Q⑵求2p 2关键求出凡两端电压比(SY = Z/)如图(a) U\ + lh= U £L =L如图(b) R 、、 金并联, R.R 、从图(a)可知:^- = 1八 2 U. L^= 27F -3由图(a)和(b)UJ同一电阻凡:A- = L \ 4 (S )2答案用= 3Q,用=6Q, PC PJ 例15甲灯标有9V,乙灯标有3W, 2_ 4 9 =4 : 9 已知电阻斤甲〉斤?•,若把两灯以某种方式连接到某电源上,两灯均正常发光, 若把两灯以另一种方式连接到另一电源上,乙灯仍能正常发光,甲灯的实际功率与它的额定功率比P/ :戶甲=4:9求:(1)甲灯的额定功率/\;(2) 乙灯的额定电压〃乙;(3) 两灯电阻斤b 和斤乙.精析 注意两次电路总电压不同,所以不能像例4那样判断电路连接方式已知:^\=9V,戶乙=3W, RQR 乙,PJ :戶甲=4:9求:P 甲、U 乙、R v y R J设第一次斤甲、斤7•并联,此时两灯均能正常发光,说明:6\ = 6>=9Vu/R - 「二 P/.第二次斤(9V)2 =- ------- =27 Q 3W 斤乙串联,乙灯仍正常发光,说明〃乙'=仇=9\「 而斤甲不变时,2 ?1/ =一 〃甲= _X9V=6V33 R 冲、&乙串联心 _ _ 6V _ 2 心 U ; * 3得R 与题意不符.由上判定:电路第一次串联,第二次并联,画出分析示意图2-3-10 (a)和(b).解 由图G)和(b)得:/不变 ^=^=K_=i f F 山922 If = _ 叭=—X9V=6V3 3 UV =6^=6V由图(b)乙灯正常发光由图(a) R 卑、7? 7.串=0. 5A"甲=7> D 甲=0. 5AX9V=4. 5W答案 甲灯额定功率4.5W,乙灯额定电压6V,甲灯电阻10Q,乙灯电阻6Q例16 (市1997年中考试题)如图2-3-11 (a)所示电路中,灯厶的电阻忆的丄(不考虑灯丝随温度的变化).电 2源电压为10V,并保持不变.,为开关.当闭合S,断开S 时,灯厶正常发光,电阻凡消耗的电功率为2W,电压 表示数弘 当闭合久 断开S 时,电阻爪消耗的电功率为丄W,电压表示数为丄乩4 2R _"中ZT 甲 -- 9V O.5A = 180求(1)灯厶的额定功率;(2)电阻凡的阻值.Rs£ZZH匚 L? /?4 Si—口 f Rx2WR\ R^2R R A(c)f ・・4(a)—10V —(b)图 2—3—11已知:用=丄忌 U= 10V A=2W 0 =-L\Px =」W2 2 4求:(1) P\ (厶额定功率);(2) R\解 画出变化前后电路分析图2-3-11 (b )和(c ). 先求出两次电路(”和(C )中电流比/: r/ _U\ _ U\ 2V U ;1R\不变人77•可可b)-(3-4图 R 一/?由U=I (用+凤)由图(c> u=r (水+用+用) 〃不变,将&=2心和R\=2凡代入 /(用+2尺)=r (用+2用+用) 2 (用+2AO = (3用+ 丘)& _3心1得 R\: RJ.用=3 : 6 : 1由图(c) R\、R-丘串,且 U=UC +£ +/=10V 囚:出:R=R 、:用:R 、=3 : 6 : 1仏=丄*丄X1OY = 1V10 104屮十A 丄W4由图(b —串£=碁=|3 A=_X2W=3W2答案厶额定功率为3W,凡为4Q例17 (市1998年中考试题)如图2-3-12所示,电路两端电压保持不变,当只闭合开关$时,通过电阻丘 的电流是厶;当只闭合开关$时,通过电阻底的电流是心 电阻金消耗的功率是20W,厶:厶=3: 2,当只闭合开关S 时,电阻凤消耗的功率是15W ・求:(1)只闭合S 时,用消耗的功率;(2)只闭合9时,用消耗的功率. 已知:厶:72=3 : 2,七=20W, E=15W 如图2—3—13 (a)当只闭合,时,R\、Rz 串,如图2—3—13 (b);当只闭合$时,R\、Rz 、忆串,如图 2—3—13 (c).解图(a) U= IR 图(b) U=l2 (用 + 用)0•不变,—=—人 23用=2 (心+丘)& _ 2R 2 1图(b) R\、凡串丄=”=一P 2 1PJ =2P 2=2X20W=40W 如图(a)和(b)-」Pl /.2 2 2 4 同一电阻用•—=—=(—)=—R I ;3 94/^=_X40W=90W9r2 U 2如图(b) R = 12 R 尸( ---------- )R 、(1)如图(c) P\ = I ;R 、=⑴三⑵ 需将T 代入宀融+9曲(0-3 用)‘=0精析只闭合开关S,只有乩(2)图 2—3—12 R\ /i(a)(c)用=3 R-又I R\=2 R:.& _2• ■-------------R3 3如图(c),串联电路H5- = — = - PC = - X 15W=10WP、R、33答案图(a)中,凡功率为90W,图(c)中,岳功率为10W例18 (市东城区中考试题)小明设计了一个电加热器,有加热状态和保温状态,如图2-3-14,发热体川〃是一根阻值500Q的电阻丝,C、〃是电阻丝上的两点,S'是一个温度控制控制开关.当开关$闭合,开关S接通C 点时,电阻丝每分钟放出的热量是Q;当C闭合,S接通〃点时,电阻丝每分钟放出的热量是@;当F断开时,电阻丝每分钟放出的热量是此时测得G 〃两点间的电压是33Y.C DA ------- ----------------------- Bf ----- y ---------- )图2—3—14(1)按大小排列出Q、Q和Q的顺序是:> >(2)将上述热量由大到小的顺序排列,其比值是20 : 10 : 3,求电源电压〃和电热器处于保温状态时,每分钟放出的热疑.精析对于联系实际的问题,首先把它和所学的物理知识对应起来,本题用到的是焦耳定律的知识.U2从图中看出,不论使用哪一段电阻丝,电压均为电热丝放热公式:0= ——t・R(1)可以将段电阻分成三部分:U1第一次,£闭合,S接G使用的是电阻丝伪段,电阻为斤伽电阻丝lining热4=——tR(JBU1第一次,£闭合,S接〃,使用的是电阻丝励段,电阻为乩力电阻丝lmin放热Q=——tR DBU1第三次,S'断开,电阻丝lmin放热Q=—— tR AB*•*RdV R购:.Q>Q»Q\开关位于〃,是加热状态,断开S',电阻为爲,是保温状态.(2)已知血=500Q Q》=33V, Q : Q : @=20 : 10 : 3t —定,Qi —R 【)B _ P.\B — 20G £1 尬 3 R.\B3 3/.— X— X500Q=75Q2020 七一定,〃一定,0 _ 险 _ 10 aR"33 3•*•— R.w= — X 500 Q = 150 Q10 10必=150Q —75Q=75QU CD 33V1= ------- = -------- =0. 44A ・R C D 75QU= /局=0. 44X500Q= 220V保温时$电阻为R.w 、t — 1 min =60s答案(1) Q>Q>Q\、电源电压220V,保温:@ = 5808J例19 (市海滨区中考试题)图2-3-15是一个电热毯示意电路图.凡是电热毯中的电阻丝,/?是与电热毯与电 阻丝串联的电阻.电热毯上标有“220V 100W"字样,S 是控制电热毯处于加热状态或保温状态的开关.图 2—3—15(1) 用学过的公式推理说明开关S 断开时,电热毯是处于加热状态还是保温状态?(2) 若要求在保温时电流通过电阻丝风每分钟有60J 的电能转化为能,电阻斤的阻值是多大?解 (1)根据公式*力?丘一定,七一定时,电热毯功率大时,处于加热状态・2(J 2s 闭合时r 发热功率*心爲必①2 US 断开时,R‘ o=/7? o=( -------------- 厂风R + Ro比较①②两式得岛>用・S 闭合,电热毯处于加热状态. S 断开,电热毯处于保温状态・Q\=U 2 R.X Bx 片空空500 Q X 60s = 5808J保温时:电阻凡两端电压为&・60Jx484Q =22V.60$电路中电流,化二兰—心484Q 22U R U _U° 220V-22V/?= —= ------------- ------ - -------- =4356 07 7丄A22答案(1)闭合S,电热毯处于加热状态(2)斤=4356Q例20 (市中考试題)图2-3-16,是供电设备向居民楼用户输电的示意图,为保证居民楼的用户所有用电器都能正常工作,居民楼的输入导线间的电压必须保证为220V,当居民楼消耗的功率为44 kW的时候r•••••••••・:•■:•:供电: :A•:K :••\设希!j川尹:•:■: ....... J: ........ J图2—3—16(1)通过输电线的电流为多少安?(2)若输电线的总电阻为0.1Q,供电设备的输出电压是多少伏?(3)居民楼由于家用电器的增加,将向供电部分申请"增容”,即増加用电功率.当居民的用电器的额定功率由44 kW增加到88kW,所有用电器均在正常工作时,输电线路损失的功率比''增容'‘前增加了多少?(4)若要求减小输电线损失的功率,用学过的公式及知识说明应采取的措施.精析将实际问题转化为电路图.画出图2—3—17解(1)已知仏=220V/^=44Kw=4. 4X10W7 (/■4.4X104W= -------------- =220220V(2) U=%HR宀&=220AX0. 1Q+22OV=24OV 已知:Q=60J f=l min=60 sQ=(3)r - p == 8-8xl°W=400220VPJ =『仏=(400A) XO. 1Q=16OOOW增容前:Pd 仇=(200A) XO. 1Q=4OOOW\P F PY -/>^=16000W-4000W= 12000W(4)分析:在弘,几一定时,/不能减少,使P^=IR线减小的方法,应减小斤线.•••导线电阻与材料、长度、横截面积有关长度一定,可换用电阻率小的导线或适当增加线的横截面积,这样可以减小电阻.答案(1) 220A (2) 240V (3) 12000 W例21已知两个小灯泡厶、厶的额定电压均为〃额,在额定电压下通过厶的电流厶是通过厶电流厶的2倍,若把灯厶.厶串联后接到电压为〃的电源上,则 ( )Li U图2—3—18•& _ 人_ 1•・------ ------尺2 U额217串联电路:—u? R2 23 1选项儿U= - Un &=7叭丛=〃盯厶正常发光2 2选项B:EH%、所以厶、厶都不能正常发光选项C:W, lh=%、Z烧毁,导致厶不能正常发光选项D:只要U\ = LG,也就要烧毁,所以厶总不能正常发光答案A、D例22将标有"6V 3W”的灯泡厶和标"4V 4W”的灯泡厶串联起来接入电路,欲使其中一盏灯能够正常发光,电源电压应是 ( )A. 12V B・ 8V C・ 10V D・ 16V精析求出两盏灯的电阻,分析加在灯上的实际电压是"大于”"等于”还是“小于”弘、(厶I为额定电压)画出电路示意图2—3—19,并标出灯的电阻.图2—3—19解灯厶和厶电阻:^C£ = (6V);=12QP 、 3WU=H +M =6V+2V=8V ・B 选项符合题意 若厶正常发光,日应=丛=4V ・若厶上电压,H =3 Ui f =12V f ••• R =2lk :.灯厶烧毀,因此电源电压不能取12V + 4V=16V.答案B.例23将一个阻值是4 Q 的电热器放进质量是0. 5kg 的冷水中,通过电热器的电流是5A,且电热器放出的热量全 部被水吸收,则7 min 可使水温升高多少度?精析利用焦耳定律和热学中物体吸放热的公式求解. 已知:J ?=4Q /=5A t=l min=420s,刃=0. 5kg 求:(t — to )4.2X 104J(t — to) = — ■ — ----------7 ----------------------- =20 C cm4.2xlO 3J/(kg-°C)xO.5kg答案2or例24 (省中考试題)某电热饮水器上有乩〃两根电热丝,将两根电热丝串联接在电源上,20 min 可将饮水器 中的水加热至沸腾;若将M 单独接到同一电源上,同样使初温和质量相同的水加热至沸腾,需要8 min ;若将〃单独接 在同样电源上,使初温和质量相同的水加热至沸腾,需要多长时间?(不计热损失)精析电热丝串联或单独使用,都接在同样电源上,放出的热量可用Q=*t 计算三种情况水吸热相同,Q 尸Q 头 三次电热丝放出的热量相等.Q 亠RAR A + R B _ 20 min _ 5 R A8 min 2• R\ _ 2 • -------------- •R B 3 又u 2 u 1(4V)24W=4 Q 3 4Q T凡"串联乞一&一皿u 2若厶正常发光, 则刃应=_ /3W 应=/=6V =2V,厶比正常发光暗0b = I2Rt= (5A) JX4Q X420S=4.2X10J——=—— &R B R AR R 3ta=—— X — X8mni= 12min心 2答案12 min。
中考数学试卷典型例题解析

例题1:一元二次方程的应用题题目:某工厂生产一批产品,若每天生产80件,则生产完这批产品需要10天;若每天生产100件,则生产完这批产品需要8天。
问:这批产品共有多少件?解析:设这批产品共有x件。
根据题意,我们可以列出以下方程:80 × 10 = x100 × 8 = x解这个方程组,我们可以得到:x = 800答案:这批产品共有800件。
例题2:几何证明题题目:已知:在三角形ABC中,AB=AC,点D是BC边上的一个点,AD⊥BC。
证明:∠B=∠C。
解析:证明:由于AB=AC,根据等腰三角形的性质,我们有∠ABC=∠ACB。
又因为AD⊥BC,所以∠ADB=∠ADC=90°。
在直角三角形ADB和ADC中,∠BAD=∠CAD,所以三角形ADB和ADC是相似的。
根据相似三角形的性质,我们有:∠B/∠A = ∠C/∠A由于∠A是公共角,可以约去,得到:∠B = ∠C答案:证明完成,∠B=∠C。
例题3:函数问题题目:已知函数f(x) = 2x - 3,求函数f(x)在x=2时的函数值。
解析:要求函数f(x)在x=2时的函数值,我们只需将x=2代入函数f(x)中。
f(2) = 2 × 2 - 3f(2) = 4 - 3f(2) = 1答案:函数f(x)在x=2时的函数值为1。
例题4:代数式求值题目:已知a+b=5,ab=6,求(a+b)^2的值。
解析:首先,我们知道(a+b)^2可以展开为a^2 + 2ab + b^2。
由题意,a+b=5,ab=6,代入上式,得:(a+b)^2 = a^2 + 2ab + b^2(a+b)^2 = (a+b)^2 + 2ab(a+b)^2 = 5^2 + 2×6(a+b)^2 = 25 + 12(a+b)^2 = 37答案:(a+b)^2的值为37。
通过以上例题解析,我们可以看到中考数学试卷中的典型题目涉及了代数、几何、函数等多个知识点,考生需要掌握扎实的数学基础和解题技巧。
中考化学复习---《元素物质分类》典型例题讲解

中考化学复习---《元素物质分类》典型例题讲解题型一物质分类【经典例题】【2021湖北荆州】下列物质属于纯净物的是()A. 空气B. 牛奶C. 84消毒液D. 蒸馏水【答案】D【解析】根据分析,空气、牛奶、84消毒液均是由多种物质混合而成的物质,属于混合物;而蒸馏水中只含有水一种物质,是纯净物;故选择D。
【解题技巧】在熟悉混合物、纯净物、单质、化合物、氧化物等概念的基础上能从宏观和微观两个方面来判断纯净物和混合物,还要从社会实践中了解生活中常见物质的组成。
【经典例题】【2021湖南常德】分类是化学研究中常用的方法。
下列物质分类正确的是()A. 碱:烧碱、纯碱、氢氧化钾B. 氧化物:五氧化二磷、氧化铝、过氧化氢C. 混合物:空气、石油、亚硝酸钠D. 人体中的微量元素:钙、铁、硒、碘【答案】B【解析】A、烧碱是氢氧化钠的俗称,氢氧化钠、氢氧化钾都是电离时产生的阴离子都是氢氧根离子的化合物,属于碱,纯碱是碳酸钠的俗称,是由钠离子和碳酸根离子构成的化合物,属于盐,不符合题意;B、五氧化二磷是由P、O两种元素组成的化合物,属于氧化物;氧化铝是由Al、O两种元素组成的化合物,属于氧化物,过氧化氢是由H、O元素组成的化合物,属于氧化物,符合题意;C、空气是由氮气、氧气等混合而成,属于混合物;石油是由汽油、柴油等混合而成,属于混合物;亚硝酸钠是由同种物质组成,属于纯净物,不符合题意;D、钙元素属于常量元素,铁、碘、硒属于微量元素,不符合题意。
故选B。
【解题技巧】本考点考查了物质的分类,要加强记忆混合物、纯净物、单质、化合物、氧化物、酸、碱、盐等基本概念,并能够区分应用。
本考点的基础性比较强,主要出现在选择题和填空题中。
1、【2021贵州铜仁】生活中的下列物质前者属于纯净物,后者属于单质的是()A. 水泥、镁B. 食盐、干冰C. 硫酸亚铁、金刚石D. 空气、H2【答案】C【解析】A、水泥是由多种物质组成,属于混合物;镁只含有镁元素,属于单质,此选项错误;B、食盐中含有氯化钠、氯化镁等物质,属于混合物;干冰是固态二氧化碳,二氧化碳是由碳元素和氧元素组成的化合物,不属于单质,此选项错误;C、硫酸亚铁是由一种物质组成的,属于纯净物;金刚石是由碳原子直接构成的物质,由同种元素组成的纯净物,属于单质,此选择正确;D、空气中含有氮气、氧气等多种气体,属于混合物;氢气是氢元素组成的纯净物,属于单质,此选项错误。
中考数学 二元一次方程组8种典型例题详解,一次解决应用题

中考数学二元一次方程组8种典型例题详解,一次解决应用题1.列方程组解应用题的基本思想列方程组解应用题,是把“未知”转换成“已知”的重要方法,它的关键是把已知量和未知量联系起来,找出题目中的等量关系。
一般来说,有几个未知量就必须列出几个方程,所列方程必须满足:①方程两边表示的是同类量;②同类量的单位要统一;③方程两边的数要相等。
2.列二元一次方程组解应用题的一般步骤设:用两个字母表示问题中的两个未知数;列:列出方程组(分析题意,找出两个等量关系,根据等量关系列出方程组);解:解方程组,求出未知数的值;答:写出答案。
3.要点诠释(1)“设”、“答”两步,都要写清单位名称;(2)一般来说,设几个未知数就应该列出几个方程并组成方程组。
1.和差倍数问题知识梳理和差问题是已知两个数的和或这两个数的差,以及这两个数之间的倍数关系,求这两个数各是多少。
典型例题:【思路点拨】由甲乙两人2分钟共打了240个字可以得到第一个等量关系式2(x+y)=240,再由甲每分钟比乙多打10个字可以得到第二个等量关系式x-y=10,组成方程组求解即可。
变式拓展:【思路点拨】由甲组学生人数是乙组的3倍可以得到第一个等量关系式x=3y,由乙组的学生人数比甲组的3倍少40人可以得到第二个等量关系式3x-y=40,组成方程组求解即可。
2.产品配套问题知识梳理总人数等于生产各个产品的人数之和;各个产品数量之间的比例符合整体要求。
典型例题:【思路点拨】本题的第一个等量关系比较容易得出:生产螺钉和螺母的工人共有22名;第二个等量关系的得出要弄清螺钉与螺母是如何配套的,即螺母的数量是螺钉的数量的2倍(注意:别把2倍的关系写反)。
变式拓展:【思路点拨】根据共有170名学生可得出第一个等量关系x+y=170,根据每个树坑对应一棵树可得第二个等量关系3x=7y,组成方程组求解即可。
3.工作量问题知识梳理我们在解决工程问题时通常把工作总量看成1;工作量=工作效率×工作时间;总工作量=每个个体工作量之和;工作效率=工作量÷工作时间(即单位时间的工作量);工作效率=1÷完成工作的总时间。
一元二次方程典型例题及中考精讲(答案)

例题精讲:1. 已知(m -1)x |m |+1+3x -2=0是关于x 的一元二次方程,求m 的值.2. 用配方法解一元二次方程2x 2+1=3 x .3. 解方程x 2-2x -2=0.4. 若a 是关于x 的方程x 2+bx +a =0的根,且a ≠0,则由此可得求得下列代数式的值恒为常数的是( c ) A .ab B . b aC .a +bD .a -b 5. 物鲁木齐农牧区校舍改造工程初见成效,农牧区最漂亮的房子是校舍,2005年市政府对农牧区校舍改造的投入资金是5786万元,2007年校舍改造的投入资金是8050.9万元,若设这两年投入农牧区校舍改造资金的年平均增长率为x ,则根据题意列方程得 5786(1+x )2=8058.96. 如果(2m +2n +1)(2m +2n -1)=63,那么m +n 的值是 ±4 .7. (x +2)(x +3)(x -4)(x -5)=44. (解析(x 2-2x -8)(x 2-2x -15)-44=0原方程的根是1211x x ==3411x x =+=-)。
8. 说明:无论x 取何值,代数式x 2-6x +10的值大于0;再求出当x 取何值时,代数式x2-6x +10的值最小,最小值是多少. x =3时,(x 2-6x +10)最小=1.9. 若实数m ,n ,p 满足m -n =8,mn +p 2+16=0,则m +n +p 的值为 0 (消去m)。
10. 构造法:3x 2+11x +10=0(两边同时乘以3).125, 2.3x x =-=- 11. 特殊解法: 解方程(x -1994)(x -1995)=1996×1997.( x 1=3991,x 2=-2.) 12. 建模思想:经过两年的连续治理,某城市的大气环境有了明显改善,其每年每平方公里的降尘量从50吨下降到40.5吨,则平均每年下降的百分率是 10% .13. 某商店如果将进货价8元的商品按每件10元出售,每天可销售200件,现采用提高售价,减少进货量的方法增加利润,已知这种商品每涨0.5元,其销售量就可以减少10元,问应将售价定为多少时,才能使所赚利润最大,并求出最大利润.(14元 120元).14. 每件商品的成本是120元,在试销阶段发现每件售价(元)与产品的日销售量(件)始终存在下表中的数量关系,但每天的盈利(元)却不一样。
(2020编)中考语文备考:语法和修辞 典型例题解析-推荐

典型中考真题巧剖析(修辞·语法)一·修辞1.【2018 年山西省中考】4.读语段,找出表述有误的一项()(2 分)人生有一首诗,当我们拥有它的时候,往往并没有读懂它;而当我们能够读懂它的时候,它却早已远去。
这首诗的名字叫青春。
青春是那么美好,在这段不可复制的旅途当中,我们拥有独一无二的记忆。
(▲)它是迷茫的、孤独的、不安的,还是欢腾的、炽热的、激越的,它(▲)是最闪亮的日子。
雨果曾经说,谁虚度了年华,青春就将褪色。
是的,青春是用奋斗的,不是用挥霍的。
只有这样,当有一天我们回首时路,和那个站在最绚烂的骄阳下曾经青春的自己告别的时候,我们才可能说,谢谢你,再见。
A.结尾处“谢谢你,再见”中的“你”指的是“那个站在最绚烂的骄阳下曾经青春的自己”。
B.“青春是那么美好,在这段不可复制的旅途当中,我们拥有独一无二的记忆。
”这句话中的“那么美好”和“独一无二”两个短语结构一致。
C.文中括号内可填入的关联词依次是“不管”“都”。
D.“人生有一首诗,当我们拥有它的时候,往往并没有读懂它;而当我们能够读懂它的时候,它却早已远去。
这首诗的名字叫青春”这里运用了比喻的修辞手法,生动形象,耐人寻味。
【答案】 B【解析】B 项“那么美好”和“独一无二”两个短语结构一致,表述错误。
“那么美好”和“独一无二”分别是偏正短语和并列短语。
D 项,把青春比作一首诗,生动形象。
正确此题综合考查了代词的指代内容、短语的类型、关联词的正确使用和比喻的修辞手法,考查的覆盖面较广,不失为一道好题。
2.【2018 年江西省中考】5.下列句子没有使用修辞手法的一项是A.性情开朗活泼,劳动手脚勤快,这种年轻女子在昆明附近村子中多的是。
B.清国留学生头顶盘着大辫子,顶得学生制帽的顶上高高耸起,形成一座富士山。
C.他总结失败的教训,把失败接起,焊上去,作为登山用的尼龙绳子和金属梯子。
D.老信客在黑暗中睁着眼,迷迷乱乱地回想着一个个码头,一条条船只,一个个面影。
中考说明文典型例题(完整版)

说明文典型例题解题思路一、【题型类别】说明文中特殊题型(表达效果类)解题思路:(1)这是说明文中类似记叙文的考点,关注句子本身就可以。
(2)看出句子形式上的特点,如修辞等。
(3)读出句子用这种形式上的特点想强调什么内容。
(4)整句话读完,看看解说的意思有没有完整。
例题:宝山二模《人类的身高为何不会永远上长》16.“于是,这些巨人便会被自己的体重压得举步维艰,甚至筋骨断裂,哪里还谈得上拔山举鼎,力扫千军呢?”该句的表达效果是:__________________________。
答案:运用反问的修辞手法,强调了巨人根本无法拔山举鼎,力扫千军。
突出了巨人被自己的体重压迫的程度极深。
二、【题型类别】说明文的过渡句1、解题思路:(1)看一下有没有承接上文的作用(某一事物的特点,现象)(2)引出下文2、例题:青浦区二模卷《深坑酒店》深坑酒店的主体建筑依悬崖建造,整体是向内凹的弧形,因此它使用的钢结构构件全是弯的,施工变形大,定位也困难。
为此,工程师们_____________;然后,______________;最后____________。
(1):配合以精准的全站仪定位控制,将这些“七扭八歪”的构件调教的服服帖帖(2):经过了大量的模拟计算分析,精准地控制了结构在安装过程中产生的应力和形变量(3):将施工划分成了十个流水段,通过巧妙的控制安装和浇筑顺序,利用中心找平衡答案:(2)(3)(1)三、【题型类别】说明文某材料能否删去/是否多余解题思路:(1)概括某材料在文中的意思(2)运用了什么说明方法(3)……地说明了……(4)在文中有什么作用例题:普陀区二模卷《了解再生纸》17.有人认为第6段两处划线句语意重复,可删除其中一句。
请你谈谈看法。
“每回收1吨废纸,可以用来制造再生纸0.85吨,相当于少用木材3立方米,化工原料0.3吨”“每利用1吨废纸,可节省电力600度,标准煤1.2吨,水100立方米”答案: 不重复。
中考数学100道典型例题详解

实际应用:数的运算在实际问题 中的应用广泛,如购物问题、行 程问题等,考生需学会将实际问 题转化为数学问题求解。
02
几何部分
三角形与四边形
总结词:中考数学中,三角形与四边形 是常见的几何题型,主要考察学生的基 础几何知识和推理能力。
勾股定理的应用:主要考察勾股定理的 基本性质和逆定理,以及在实际问题中 的应用。
特殊四边形的性质与判定:主要考察平 行四边形、矩形、菱形和正方形的性质 和判定方法。
详细描述
三角形全等的判定:主要考察全等三角 形的基本性质和判定方法,如边角边、 角边角、角角边等。
圆
详细描述
总结词:圆是中考数学中较为重 要的几何题型,主要考察学生的 空间想象能力和逻辑推理能力。
圆的性质:主要考察圆的基本性 质和定理,如直径所对的圆周角 为直角、圆的内接四边形等。
方程组的解法,注重解题步骤和书写规范。 • 不等式的性质:掌握不等式的性质,包括不等式的两边同时加上或减去
同一个数,不等号的方向不变;不等式的两边同时乘以或除以同一个正 数,不等号的方向不变;不等式的两边同时乘以或除以同一个负数,不 等号的方向改变。 • 实际应用:方程与不等式在实际问题中的应用广泛,如行程问题、工程 问题、利润问题等,考生需学会构建数学模型,将实际问题转化为数学 问题求解。
02
详细描述
03
图形的平移、旋转和对称:主要考察图形的平移、旋转和对称的基本 性质和变换方法。
04
作图题:主要考察学生的实际操作能力,如作图题中要求画出一个符 合条件的图形或给出条件让学生作出相应的图形等。
03
统计与概率部分
统计初步
平均数
理解平均数的概念,掌握求平 均数的方法,理解加权平均数
中考数学试题解析之最短路径问题
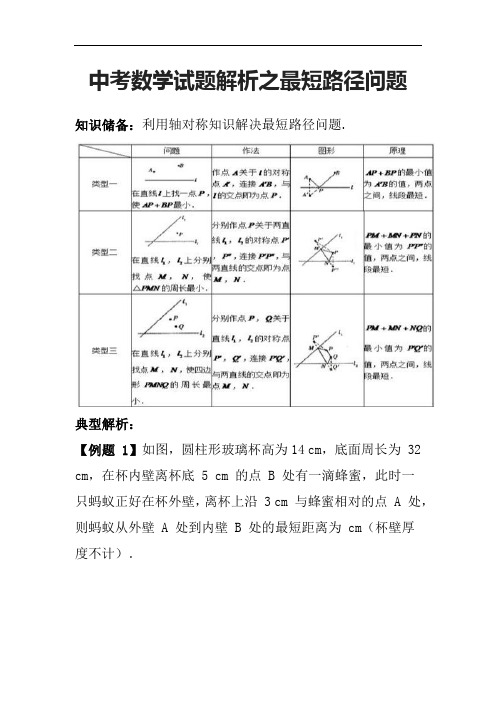
中考数学试题解析之最短路径问题知识储备:利用轴对称知识解决最短路径问题.典型解析:【例题 1】如图,圆柱形玻璃杯高为14 cm,底面周长为 32 cm,在杯内壁离杯底 5 cm 的点 B 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿 3 cm 与蜂蜜相对的点 A 处,则蚂蚁从外壁 A 处到内壁 B 处的最短距离为 cm(杯壁厚度不计).【答案】20.【分析】解:如图,将杯子侧面展开,作点 A 关于 EF 的对称点A′,连接A′B,则A′B 即为最短距离,A′B = √(A′D²+BD²)=20(cm).当蚂蚁在一个几何体的表面上爬行时,通常情况下都会考虑将其展开成一个平面,运用勾股定理计算其最短路程,也就是运用“化曲为平” 或“化折为直” 的思想来解决问题.【例题 2】如图,∠AOB = 60°,点 P 是∠AOB 内的定点且OP = √3,若点 M、N 分别是射线OA、OB 上异于点 O 的动点,则△PMN 周长的最小值是()A.3√6/2B.3√3/2C.6D.3【答案】D.【分析】解:如图作 P 点分别关于 OA、OB 的对称点 C、D,连接 CD 分别交 OA、OB 于 M、N,则 MP = MC,NP = ND,OP = OD = OC = √3,∠BOP = ∠BOD,∠AOP = ∠AOC,∴ PN + PM + MN = ND + MN + NC = DC,∠COD = ∠BOP + ∠BOD + ∠AOP + ∠AOC = 2∠AOB = 120°,∴ 此时△PMN 周长最小,作OH⊥CD 于 H,则 CH = DH,∵ ∠OCH = 30°,∴ OH = 1/2OC = √3/2,CH = √3OH= 3/2,∴ CD = 2CH = 3.【例题 3】如图,⊙M 的半径为 2,圆心 M 的坐标为(3,4),点 P 是⊙M 上的任意一点,PA⊥PB,且 PA、PB 与 x 轴分别交于 A、B 两点,若点 A、点 B 关于原点 O 对称,则AB 的最小值为()A.3B.4C.6D.8【答案】C.【分析】解:∵ PA⊥PB,∴ ∠APB = 90°,∵ AO=BO,∴ AB = 2PO,若要使 AB 取得最小值,则 PO 需取得最小值,连接 OM,交⊙M 于点P′,当点 P 位于P′ 位时,OP′ 取得最小值,过点 M 作MQ⊥x 轴于点 Q,则 OQ = 3、MQ = 4,∴ OM = 5,又∵ MP′ = 2,∴ OP′ = 3,∴ AB = 2OP′ = 6.【例题 4】如图,点 P 是边长为 1 的菱形 ABCD 对角线 AC 上的一个动点,点 M、N 分别是 AB、BC 边上的中点,则 MP + PN 的最小值是()A.1/2B.1C.√2D.2【答案】B.【分析】解:如图,作点 M 关于 AC 的对称点M′,连接M′N 交 AC 于 P,此时 MP + NP 有最小值,最小值为M′N 的长.∵ 菱形 ABCD 关于 AC 对称,M 是 AB 边上的中点,∴ M′ 是 AD 的中点,又∵ N 是 BC 边上的中点,∴ AM′∥BN,AM′=BN,∴ 四边形ABNM′ 是平行四边形,∴ M′N = AB = 1,∴ MP + NP = M′N =1,即 MP + NP 的最小值为 1.。
尺规作图(中考典型题例)

AA
CD
C
尺规作图----中考典型题例
P
【典型例题】如图,⊙O与直线l相离,请用尺规
在⊙O上找一点P,使其到直线l的距离最长。
O
(保留作图痕迹,不写作法)
C
l
【规范解答】解:如图,所得点P即为求作的点。
尺规作图----中考典型题例
【典型例题】如图,已知△ABC,请用尺规作图法,
A
在BC边上求作点D,使得点D到边AB和AC的距离相等。
N B
A
M C
尺规作图----中考典型题例
【典型例题】如图,在△ABC中,请用尺规在边 AB上作一点D,使∠ADC=2∠B. (保留作图痕迹,不写作法)
B 【规范解答】解:如图,所得点D即为求作的点。
A D
C
尺规作图----中考典型题例
【典型例题】如图,点B在AD上,点C在AD外,连接 AC,BC. 请用尺规作图法,过点B作直线BP,使BP∥AC。 (保留作图痕迹,不写作法)
AA
E
F
【规范解答】解:如图,菱形AEDF即为求作图形。 B B
DD CC
尺规作图----中考典型题例
【典型例题】如图,点D为△ABC的边AB的中点。
请用尺规在AC上找一点E,
使������△������������������
=
������ ������
������△������������������。
【规范解答】解:如图,所得直线BP即为求作。
A
C
P
B
D
尺规作图----中考典型题例
【典型例题】如图,在△ABC中,请用尺规作图法, 在AC上求作一点D,使△ABC∽△BDC。 (保留作图痕迹,不写作法)
中考数学压轴题----《解决实际问题规律》例题讲解

中考数学压轴题----《解决实际问题规律》例题讲解【典例1】(2020•广西)如图,某校礼堂的座位分为四个区域,前区一共有8排,其中第1排共有20个座位(含左、右区域),往后每排增加两个座位,前区最后一排与后区各排的座位数相同,后区一共有10排,则该礼堂的座位总数是.【答案】556个【解答】解:因为前区一共有8排,其中第1排共有20个座位(含左、右区域),往后每排增加两个座位,所以前区最后一排座位数为:20+2(8﹣1)=34,所以前区座位数为:(20+34)×8÷2=216,因为前区最后一排与后区各排的座位数相同,后区一共有10排,所以后区的座位数为:10×34=340,所以该礼堂的座位总数是216+340=556个.故答案为:556个.【变式1-1】(2022•玉林)如图的电子装置中,红黑两枚跳棋开始放置在边长为2的正六边形ABCDEF的顶点A处.两枚跳棋跳动规则是:红跳棋按顺时针方向1秒钟跳1个顶点,黑跳棋按逆时针方向3秒钟跳1个顶点,两枚跳棋同时跳动,经过2022秒钟后,两枚跳棋之间的距离是()A.4B.2C.2D.0【答案】B【解答】解:∵红跳棋从A点按顺时针方向1秒钟跳1个顶点,∴红跳棋每过6秒返回到A点,2022÷6=337,∴经过2022秒钟后,红跳棋跳回到A点,∵黑跳棋从A点按逆时针方向3秒钟跳1个顶点,∴黑跳棋每过18秒返回到A点,2022÷18=112•6,∴经过2022秒钟后,黑跳棋跳到E点,连接AE,过点F作FM⊥AE,由题意可得:AF=AE=2,∠AFE=120°,∴∠FAE=30°,在Rt△AFM中,AM=AF=,∴AE=2AM=2,∴经过2022秒钟后,两枚跳棋之间的距离是2.故选:B.【变式1-2】(2022•德阳)古希腊的毕达哥拉斯学派对整数进行了深入的研究,尤其注意形与数的关系,“多边形数”也称为“形数”,就是形与数的结合物.用点排成的图形如下:其中:图①的点数叫做三角形数,从上至下第一个三角形数是1,第二个三角形数是1+2=3,第三个三角形数是1+2+3=6,……图②的点数叫做正方形数,从上至下第一个正方形数是1,第二个正方形数是1+3=4,第三个正方形数是1+3+5=9,…………由此类推,图④中第五个正六边形数是.【答案】45【解答】解:图①的点数叫做三角形数,从上至下第一个三角形数是1,第二个三角形数是1+2=3,第三个三角形数是1+2+3=6,……图②的点数叫做正方形数,从上至下第一个正方形数是1,第二个正方形数是1+3=4,第三个正方形数是1+3+5=9,……图③的点数叫做五边形数,从上至下第一个五边形数是1,第二个五边形数是1+4=5,第三个五边形数是1+4+7=12,……由此类推,图④中第五个正六边形数是1+5+9+13+17=45.故答案为:45.本课结束。
中考数学复习----一次方程(组)应用典型例题与考点归纳

中考数学复习----一次方程(组)应用典型例题与考点归纳典型例题讲解1.(2022·山东泰安)泰安某茶叶店经销泰山女儿茶,第一次购进了A 种茶30盒,B 种茶20盒,共花费6000元;第二次购进时,两种茶每盒的价格都提高了20%,该店又购进了A 种茶20盒,B 种茶15盒,共花费5100元.求第一次购进的A 、B 两种茶每盒的价格.【答案】A 种茶每盒100元,B 种茶每盒150元【分析】设第一次购进A 种茶每盒x 元,B 种茶每盒y 元,根据第一次购进了A 种茶30盒,B 种茶20盒,共花费6000元;第二次购进时,两种茶每盒的价格都提高了20%,该店又购进了A 种茶20盒,B 种茶15盒,共花费5100元列出方程组求解即可.【详解】解:设第一次购进A 种茶每盒x 元,B 种茶每盒y 元,根据题意,得30206000,1.220 1.2155100.x y x y +=⎧⎨⨯+⨯=⎩解,得100,150.x y =⎧⎨=⎩∴A 种茶每盒100元,B 种茶每盒150元.【点睛】本题主要考查了二元一次方程组的实际应用,正确设出未知数列出方程组求解是解题的关键.2.(2022·湖南常德)小强的爸爸平常开车从家中到小强奶奶家,匀速行驶需要4小时,某天,他们以平常的速度行驶了12的路程时遇到了暴雨,立即将车速减少了20千米/小时,到达奶奶家时共用了5小时,问小强家到他奶奶家的距离是多少千米?【答案】240千米【分析】平常速度行驶了12的路程用时为2小时,后续减速后用了3小时,用遇到暴雨前行驶路程加上遇到暴雨后行驶路程等于总路程这个等量关系列出方程求解即可.【详解】解:设小强家到他奶奶家的距离是x 千米,则平时每小时行驶4x 千米,减速后每小时行驶204x ⎛⎫− ⎪⎝⎭千米,由题可知:遇到暴雨前用时2小时,遇到暴雨后用时5-2=3小时, 则可得:232044x x x ⎛⎫⨯+−= ⎪⎝⎭,解得:240x =, 答:小强家到他奶奶家的距离是240千米.【点睛】本题考查了一元一次方程应用中的行程问题,直接设未知数法,找到准确的等量关系,列出方程正确求解是解题的关键.3.(2021·重庆中考真题)重庆小面是重庆美食的名片之一,深受外地游客和本地民众欢迎.某面馆向食客推出经典特色重庆小面,顾客可到店食用(简称“堂食”小面),也可购买搭配佐料的袋装生面(简称“生食”小面).已知3份“堂食”小面和2份“生食”小面的总售价为31元,4份“堂食”小面和1份“生食”小面的总售价为33元.(1)求每份“堂食”小面和“生食”小面的价格分别是多少元?(2)该面馆在4月共卖出“堂食”小面4500份,“生食”小面2500份,为回馈广大食客,该面馆从5月1日起每份“堂食”小面的价格保持不变,每份“生食”小面的价格降低3a%4.统计5月的销量和销售额发现:“堂食”小面的销量与4月相同,“生食”小面的销量在4月的基础上增加5%2a ,这两种小面的总销售额在4月的基础上增加5%11a .求a 的值. 【答案】(1)每份“堂食”小面价格是7元,“生食”小面的价格是5元.(2)a 的值为8.【分析】(1)设每份“堂食”小面和“生食”小面的价格分别是x 、y 元,根据题意列出二元一次方程组,解方程组即可;(2)根据题意列出一元二次方程,解方程即可.【详解】解:(1)设每份“堂食”小面和“生食”小面的价格分别是x 、y 元,根据题意列方程组得,3231433x y x y +=⎧⎨+=⎩, 解得,75x y =⎧⎨=⎩, 答:每份“堂食”小面价格是7元,“生食”小面的价格是5元.(2)根据题意得,535450072500(1%)5(1%)(4500725005)(1%)2411a a a ⨯++⨯−=⨯+⨯+, 解得,10a =(舍去),28a =,答:a 的值为8.【点睛】本题考查了二元一次方程组的应用和一元二次方程的应用,解题关键是找准题目中的等量关系,列出方程,熟练运用相关知识解方程.4.(2020•安徽)某超市有线上和线下两种销售方式.与2019年4月份相比,该超市2020年4月份销售总额增长10%,其中线上销售额增长43%,线下销售额增长4%.(1)设2019年4月份的销售总额为a 元,线上销售额为x 元,请用含a ,x 的代数式表示2020年4月份的线下销售额(直接在表格中填写结果);(2)求2020年4月份线上销售额与当月销售总额的比值.【分析】(1)由线下销售额的增长率,即可用含a ,x 的代数式表示出2020年4月份的线下销售额;(2)根据2020年4月份的销售总额=线上销售额+线下销售额,即可得出关于x 的一元一次方程,解之即可得出x 的值(用含a 的代数式表示),再将其代入1.43x 1.1a 中即可求出结论. 【解析】(1)∵与2019年4月份相比,该超市2020年4月份线下销售额增长4%,∴该超市2020年4月份线下销售额为1.04(a ﹣x )元.故答案为:1.04(a ﹣x ).(2)依题意,得:1.1a =1.43x+1.04(a ﹣x ),解得:x =213,∴1.43x1.1a =1.43⋅213a1.1a =0.22a1.1a =0.2.答:2020年4月份线上销售额与当月销售总额的比值为0.2.5.(2020•江西)放学后,小贤和小艺来到学校附近的地摊上购买一种特殊型号的笔芯和卡通笔记本,这种笔芯每盒10支,如果整盒买比单支买每支可优惠0.5元.小贤要买3支笔芯,2本笔记本需花费19元;小艺要买7支笔芯,1本笔记本需花费26元.(1)求笔记本的单价和单独购买一支笔芯的价格;(2)小贤和小艺都还想再买一件单价为3元的小工艺品,但如果他们各自为要买的文具付款后,只有小贤还剩2元钱.他们要怎样做才能既买到各自的文具,又都买到小工艺品,请通过运算说明.【分析】(1)设笔记本的单价为x 元,单独购买一支笔芯的价格为y 元,根据“小贤要买3支笔芯,2本笔记本需花费19元;小艺要买7支笔芯,1本笔记本需花费26元”,即可得出关于x ,y 的二元一次方程组,解之即可得出结论;(2)先求两人带的总钱数,再求出两人合在一起买文具所需费用,由二者的差大于2个小工艺品所需钱数,可找出:他们合在一起购买,才能既买到各自的文具,又都买到小工艺品.【解析】(1)设笔记本的单价为x 元,单独购买一支笔芯的价格为y 元,依题意,得:{2x +3y =19x +7y =26, 解得:{x =5y =3. 答:笔记本的单价为5元,单独购买一支笔芯的价格为3元.(2)小贤和小艺带的总钱数为19+2+26=47(元).两人合在一起购买所需费用为5×(2+1)+(3﹣0.5)×10=40(元).∵47﹣40=7(元),3×2=6(元),7>6,∴他们合在一起购买,才能既买到各自的文具,又都买到小工艺品.6.(2020•重庆)“中国人的饭碗必须牢牢掌握在咱们自己手中”.为优选品种,提高产量,某农业科技小组对A ,B 两个小麦品种进行种植对比实验研究.去年A ,B 两个品种各种植了10亩.收获后A ,B 两个品种的售价均为2.4元/kg ,且B 的平均亩产量比A 的平均亩产量高100kg ,A ,B 两个品种全部售出后总收入为21600元.(1)请求出A ,B 两个品种去年平均亩产量分别是多少?(2)今年,科技小组加大了小麦种植的科研力度,在A ,B 种植亩数不变的情况下,预计A ,B 两个品种平均亩产量将在去年的基础上分别增加a%和2a%.由于B 品种深受市场的欢迎,预计每千克价格将在去年的基础上上涨a%,而A 品种的售价不变.A ,B 两个品种全部售出后总收入将在去年的基础上增加209a%.求a 的值.【分析】(1)设A 、B 两个品种去年平均亩产量分别是x 千克和y 千克;根据题意列方程组即可得到结论;(2)根据题意列方程即可得到结论.【解析】(1)设A 、B 两个品种去年平均亩产量分别是x 千克和y 千克;根据题意得,{y −x =10010×2.4(x +y)=21600, 解得:{x =400y =500, 答:A 、B 两个品种去年平均亩产量分别是400千克和500千克;(2)2.4×400×10(1+a%)+2.4(1+a%)×500×10(1+2a%)=21600(1+209a%), 解得:a =10,答:a 的值为10. 一次方(组)程应用考点归纳1.列方程(组)解应用题的一般步骤(1)审题;(2)设出未知数;(3)列出含未知数的等式——方程;(4)解方程(组);(5)检验结果;(6)作答(不要忽略未知数的单位名称).2.一次方程(组)常见的应用题型(1)销售打折问题:利润=售价-成本价;利润率=利润成本×100%;售价=标价×折扣;销售额=售价×数量.(2)储蓄利息问题:利息=本金×利率×期数;本息和=本金+利息=本金×(1+利率×期数);贷款利息=贷款额×利率×期数.(3)工程问题:工作量=工作效率×工作时间.(4)行程问题:路程=速度×时间.(5)相遇问题:全路程=甲走的路程+乙走的路程.(6)追及问题(同地不同时出发):前者走的路程=追者走的路程.(7)追及问题(同时不同地出发):前者走的路程+两地间距离=追者走的路程.(8)水中航行问题:顺水速度=静水速度+水流速度;逆水速度=静水速度-水流速度.。
24年初中中考数学典型例题解析-数形结合

24年初中中考数学典型例题解析-数形结合1.如图,在边长为3的正方形ABCD中,30∠=︒CDE,DE CF⊥,则BF的长是______.【分析】根据题意,证得()ASA△≌△DCE CBF,从而BF CE=,在Rt CDE△中,30∠=︒CDE,3CD=,根据含30︒直角三角形边的关系与勾股定理可得CE=得到答案.【详解】解:在正方形ABCD中,BC CD=,90B DCE∠=∠=︒,DE CF⊥,90CDE DCF∴∠+∠=︒,90DCE DCF BCF∠=︒=∠+∠,∴CDE BCF∠=∠,在DCE△和CBFV中,90B DCEBC CDCDE BCF∠=∠=︒⎧⎪=⎨⎪∠=∠⎩,()ASA△△≌DCE CBF∴,∴BF CE=,在Rt CDE△中,30∠=︒CDE,3CD=,在含30︒直角三角形中:①由30︒所对的直角边是斜边的一半可设CE x=,则2DE x=;②由勾股定理得到CD==;从而可得CE===,【点睛】本题考查正方形背景下求线段长,涉及正方形性质、全等三角形的判定与性质、含30︒直角三角形、勾股定理等知识,熟练掌握全等三角形的判定与性质是解题的关键.2.如图,在ABC 中,70CAB ∠=︒,将ABC 绕点A 逆时针旋转到AB C '' 的位置,使得CC AB '∥,划BAB '∠的度数是()A.35︒B.40︒C.50︒D.70︒【答案】B 【分析】根据平行线的性质,结合旋转性质,由等腰三角形性质及三角形内角和定理求解即可得到答案.【详解】解:∵70CC AB CAB '∠=︒,∥,∴70C CA CAB '∠=∠=︒,∵将ABC 绕点A 逆时针旋转到AB C '' 的位置,∴70C AB CAB AC AC '''∠=∠=︒=,,∴由等腰三角形性质可得70AC C C CA ''∠=∠=︒,∴由三角形内角和定理得到180707040C AC '∠=︒-︒-︒=︒,BAB CAB CAB ''∠=∠- ,CAC C AB CAB ''''∠=∠-,∴40BAB C AC ''∠=∠=︒,即旋转角的度数是40︒,故选:B .【点睛】本题考查旋转性质求角度,涉及平行线的性质、旋转性质、等腰三角形的判定与性质及三角形内角和定理,熟练掌握旋转性质,数形结合,是解决问题的关键.3.将图绕其中心旋转某一角度后会与原图形重合,这个角不能是()A.90︒B.120︒C.180︒D.270︒【答案】B 【分析】将图按照对角线分成四个相同的基本图形,利用旋转的性质求解即可得到答案.【详解】解:如图所示:正方形对角线将图形分成四个完全一样的基本图形,可看作由这个基本图形旋转90︒所组成,∴将图绕其中心最小旋转角90︒后会与原图形重合,∴该图形绕其中心旋转90︒的正整数倍后会与原图形重合,从而确定这个角不能是120︒,故选:B .【点睛】本题考查图形旋转,分析出图中的基本图形是解决问题的关键.4.用不同的方式表示同一图形的面积可以解决线段长度之间关系的有关问题,这种方法称为等面积法,这是一种重要的数学方法,请你用等面积法来探究下列三个问题:(1)如图1是著名的“赵爽弦图”,由四个全等的直角三角形拼成,请用它验证勾股定理222c a b =+.(2)如图2,在Rt ABC △中,90ACB CD ∠=︒,是AB 边上的高,43AC BC ==,,求CD 的长度;(3)如图1,若大正方形的面积是13,小正方形的面积是1,求()2a b +的值()a b <.【答案】【小问1】见解析【小问2】125【小问3】25【分析】(1)如图1所示,大正方形的面积等于四个全等的直角三角形面积与小正方形面积和,用代数式表示出各部分面积按要求列等式化简即可得证;(2)利用勾股定理得到5AB =,根据等面积法列式求解即可得到125AC BC CD AB ⋅==;(3)由(1)的结论,结合完全平方公式变形,代值求解即可得到答案.【小问1详解】解:如图1所示:大正方形的面积等于四个全等的直角三角形面积与小正方形面积和,2S c = 大正方形;()2S b a =-小正方形;12S ab =直角三角形;()22142c b a ab ∴=-+⨯,即222c a b =+;【小问2详解】解:如图2所示:在Rt ABC △中,90ACB ∠=︒,43AC BC ==,,∴由勾股定理可得5AB ==,CD 是AB 边上的高,∴由等面积法可得1122ABC S AC BC AB CD =⋅=⋅△, 43AC BC ==,,5AB =,∴125AC BC CD AB ⋅==;【小问3详解】解:∵大正方形的面积是13,小正方形的面积是1,()a b <,如图1所示:∴()22131c b a -==,,∴()22221b a a b ab +--==,由(1)知222c a b =+,∴22113112ab c =-=-=,∴()222222131225a b a b ab c ab +++=+=+==,即()2a b +的值为25.【点睛】本题考查等面积法解决问题,涉及勾股定理证明、等面积法求线段长、以及完全平方公式与勾股定理综合,熟练掌握等面积法求解是解决问题的关键.5.下列图形不是轴对称图形的是()A. B. C.D.【答案】C【分析】根据轴对称图形定义:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合的图形,逐项验证即可得到答案.【详解】解:A 、该图形是轴对称图形,不符合题意;B 、该图形是轴对称图形,不符合题意;C 、该图形不是轴对称图形,符合题意;D 、该图形是轴对称图形,不符合题意;故选:C .【点睛】本题考查轴对称图形的定义与判断,熟练掌握轴对称图形的定义是解题关键.6.一个由小立方块搭成的几何体,从正面、左面、上面看到的形状如图所示,这个几何体是由()个小立方块搭成的.A.4B.5C.6D.7【答案】B 【分析】从上面看到的图确定底层小立方块个数及形状;从正面看到的图确定行列小立方块的个数及形状;从左面看到的图确定行列小立方块的个数及形状,综合起来即可得到答案.【详解】解:从上面看到的图确定最底层由4个小立方块组成;从正面看到的图及从左面看到的图确定前行只有1个小立方块、第二层有1个小立方块;综上所述,这个几何体由5个小立方块搭成,故选:B .【点睛】本题考查从三个方面看组合体,借助空间想象能力,由三个方面看到的平面图还原成立体图形是解决问题的关键.7.完成下面的证明.如图,己知AD BC ⊥于点D ,EF BC ⊥于点F ,12∠=∠,求证:AB DG ∥.证:AD BC ⊥ 于点D ,EF BC ⊥于点F (_________)90ADB EFB ∴∠=∠=︒(垂直的定义)AD EF ∴∥(__________________)1∴∠=_________(两直线平行,同位角相等)12∠=∠ (已知)2∴∠=_________(__________________)AB DG ∴∥(内错角相等,两直线平行)【答案】已知,同位角相等,两直线平行,BAD ∠,BAD ∠,等量代换【分析】根据平行线的判定与性质,按照题中证明过程求解即可得到答案.【详解】证:AD BC ⊥ 于点D ,EF BC ⊥于点F (已知)90ADB EFB ∴∠=∠=︒(垂直的定义)AD EF ∴∥(同位角相等,两直线平行)1∴∠=BAD ∠(两直线平行,同位角相等)12∠=∠ (已知)2∴∠=BAD ∠(等量代换)AB DG ∴∥(内错角相等,两直线平行),故答案为:已知,同位角相等,两直线平行,BAD ∠,BAD ∠,等量代换.【点睛】本题考查平行线的判定与性质,读懂题意,按照题中证明过程求解是解决问题的关键.8.如图,四边形ABCD 是长方形,8BC =,6CD =,将ABE 沿BE 折叠,使点A 恰好落在对角线BD 上F 处,求DE 的长.【答案】5DE =【分析】由四边形ABCD 为矩形,得到BAD ∠为直角,由折叠得到EF BD ⊥,AE EF =,AB BF =,利用勾股定理求出BD 的长,由BD BF -求出DF 的长,在Rt DEF △中,设EF x =,表示出ED ,利用勾股定理列出关于x 的方程,求出方程的解得到x 的值,即可确定出DE 的长.【详解】解: 四边形ABCD 是长方形,8BC =,6CD =,90A ∴∠=︒,6AB CD ==,8BC AD ==,将ABE 沿BE 折叠可得,90EFB A ∠=∠=︒,AE EF =,6BF AB ==,在Rt △ABD 中,90A ∠=︒,6AB =,8AD =,则由勾股定理得10BD ==,即1064FD BD BF =-=-=,设EF AE x ==,则有8ED x =-,在Rt DEF △中,90EFD ∠=︒,则由勾股定理得222DE EF FD =+,即()22284x x -=+,解得3x =,835DE AD AE ∴=-=-=.【点睛】本题考查了翻折变换,矩形的性质,勾股定理,解方程等知识,熟练掌握相关几何定理及性质是解本题的关键.9.有足够多的长方形和正方形卡片(如图1),分别记为1号,2号,3号卡片.(1)如果选取4张3号卡片,拼成如图2所示的一个正方形,请用2种不同的方法表示阴影部分的面积(用含m ,n 的式子表示).方法1:__________________________________________________.方法2:__________________________________________________.(2)若320a b ab +-+-=,求2()a b -的值.(3)如图3,选取1张1号卡片,2张2号卡片,3张3号卡片,可拼成一个长方形(无缝隙不重叠),根据图形的面积关系,因式分解:2232m mn n ++=.【答案】【小问1】2()m n -;2()4m n mn+-【小问2】1【小问3】(2)()m n m n ++【分析】(1)从“整体”和“部分”两个方面分别表示阴影部分的面积即可;(2)根据非负数的定义可得6a b +=,4ab =,再根据22()()4a b a b ab -=+-进行计算即可;(3)求出所拼成的长方形的长、宽以及总面积即可.【小问1详解】解:方法1:图2中阴影部分是边长为()m n -,因此面积为2()m n -;方法2:图2阴影部分也可以看作从边长为()m n +的正方形减去4个长为m ,宽为n 的长方形面积,因此有2()4m n mn +-;【小问2详解】解:∵320a b ab +-+-=,30a b +-≥,20ab -≥,30a b ∴+-=,20ab -=,即3a b +=,2ab =,22()()4a b a b ab∴-=+-98=-1=;【小问3详解】解:如图所示:1张1号,2张2号,3张3号卡片的总面积为2223m n mn ++,而1张1号,2张2号,3张3号卡片可以拼成长为(2)m n +,宽为()m n +的长方形,∴2223(2)()m n mn m n m n ++=++,故答案为:(2)()m n m n ++.【点睛】本题考查了完全平方公式,数形结合,掌握完全平方公式的结构特征是关键.10.如图,在平行四边形ABCD 中,对角线AC BD ,相交于点O ,点E F ,在AC 上,点G H ,在BD 上.(1)若6050ADC CAD ∠=︒∠=︒,,求BAC ∠和BCD ∠的度数;(2)若四边形EHFG 是平行四边形,求证:AE CF =.【答案】【小问1】70120BAC BCD ∠=︒∠=︒,【小问2】证明见解析【分析】(1)根据三角形内角和定理得到70ACD ∠=︒,由平行四边形性质得AD BC AB CD ,∥∥,再由平行线性质即可得到答案;(2)根据平行四边形对角线相互平分即可得证.【小问1详解】解:∵6050ADC CAD ∠=︒∠=︒,,∴在ACD △中,由三角形内角和定理可得18070ACD ADC CAD ∠=︒-∠-∠=︒,∵四边形ABCD 是平行四边形,∴AD BC AB CD ,∥∥,∴5070BCA CAD BAC ACD ∠=∠=︒∠=∠=︒,,∴120BCD BCA ACD ∠=∠+∠=︒;【小问2详解】证明:∵四边形EHFG 是平行四边形,∴OE OF =,四边形ABCD 是平行四边形,∴OA OC =,∴OA OE OC OF -=-,即AE CF =.【点睛】本题考查平行四边形综合,熟练掌握平行四边形性质是解决问题的关键.。
中考英语——形容词典型例题解析

中考英语一一形容词典型例题解析()1. --- Is there _________ i n today ' s newspaper?---No. I thi nk everyth ing in it is bori ng.A. interesting anythingB. somebody interestingC. i nteresti ng somethi ngD. anything in terest ing解析:anything用于疑问句,表示“某事”,排除B与C;形容词修饰复合不定代词置于其后,排除A和C,故选D。
()2. No moun tai n in the world is as ______ as Qomola ngmaA. highB. higherC. highestD. tall解析:as+形容词原级+as译为“和...... 一样”故选A。
()3. Their classroom is as ______ a s ours.A. cleanerB. cleanC. the cleanestD. much cleaner解析:“ as+形容词原级+as”是固定结构,意思是“和.... 一样”,四个选项中,只有clean是原级,故选B。
()4. I think that you need to eat ______ sweets and more fruit.A. fewB. fewerC. littleD. less解析:由题中的“ and more”可推断,设空处对应比较级;修饰可数名词并表示肯定意义,用fewer,故选Bo()5. Which subject do you like ______ , En glish or math?A. wellB. betterC. bestD. good解析:表示两者间的比较,用比较级,故选Bo()6. As we know, the Yangtze River is one of ______ rivers in the world.A. I ongB. l on gerC. Ion gestD. the Ion gest解析:“ one of+最高级+复数名词”是固定结构,表示“最…… 的…… 之一”,故选()7. Life is _____ the un expected. Whatever we do, try our best.A. full ofB. proud ofC. in stead ofD. because of解析:BCD项与句意不符;be full of 充满符合句意,故选A()8. The cake tastes _____ and it is really delicious.A. wellB. badlyC. goodD. bad解析:由“确实可口”推断,蛋糕尝起来“好”,排除B和D; well作形容词译为身体好,故排除,描述事物品质好选Co()9. My father caught a big fish this morning, but I caught a _____ one. I feel great!A. smallerB. biggestC. biggerD. big解析:由最后一句“我感觉特别棒”推断,“我抓的鱼比父亲抓的更大”,故选Co()10. --- How s it going?--Pretty good. All my new classmates ____ me.A. are angry withB. are friendly toC. are hard onD. are sorry for解析:由“相当好”推断,“新同学对我友好”;be friendly to 表示“对.....友好”,故选B。
中考典型例题解析(316)

2011年中考典型例题解析例1(2011·山东临沂)如图1所示,一闹钟静止在水平桌面上,则()A.闹钟受到的重力和桌面对闹钟的支持力是一对平衡力B.闹钟受到的重力和闹钟对桌面的压力是一对平衡力C.闹钟受到的重力和闹钟受到的支持力是一对相互作用力D.闹钟受到的重力和闹钟对桌面的压力是一对相互作用力解析:根据题意,要分析闹钟所受的平衡力,首先确定四个选项中所描述的力是否是闹钟的受力,然后根据二力平衡条件进行判断,选出符合要求的选项。
B选项中的闹钟对桌面的压力不作用在闹钟上,所以不符合平衡力的条件;C中闹钟受到的重力和闹钟受到的支持力是一对平衡力,不是相互作用力;D中重力和闹钟对桌面的压力方向都是向下的也不是一对相互作用力。
故选A。
点评:正确理解二力平衡的条件是解题关键,平衡力的成立条件:同物、同线、等值、反向,难度中等。
例2(2011·浙江温州)如图2是投掷实心球的场景。
下列情况中实心球受到平衡力作用的是()A.实心球在空中上升B.实心球从空中下落C.实心球在地上越滚越慢 D.实心球停在地面上解析:若实心球受到平衡力作用应处于静止状态或匀速直线运动。
实心球在空中上升和从空中下落时做曲线运动,在地上越滚时做减速运动,以上三种情况都没有受到平衡力作用。
点评:本题考查的是平衡状态的判断,难度中等。
例3(2011·浙江绍兴市)如图3,木块竖立在小车上,随小车一起以相同的速度向右作匀速直线运动。
下列分析正确的是()A.木块没有受到小车的摩擦力B.木块运动速度越大,惯性也越大C.木块对小车的压力与小车对木块的支持力是一对平衡力D.当小车受到阻力突然停止运动时,如果木块与小车接触面光滑,木块将向右倾倒解析:因为木块竖立在小车上且随小车一起向右做匀速直线运动,说木块受到的平衡力,即木块受到竖直向上的支持力和竖直向下的重力是一对平衡力,水平方向上不受力的作用,答案A项正确,B.C项错误;当小车受到阻力突然停止运动时,如果木块与小车接触面光滑,此时木块由于惯性继续以原来的速度向前运动,D项错误。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考典型试题解析
1、人类与几种类人猿进化特点上的比较如下表所示,请据表回答下列问题:
⑴表中数据表明,人类与类人猿在进化关系上有着亲缘关系。
⑵根据细胞中染色体分析,亲缘关系最近的生物是猩猩、黑猩猩和大猩猩。
⑶你认为与人类有着最近的亲缘关系的类人猿是黑猩猩,你的判断依据是染色体数、血清免疫实验记录与人类最接近。
2、根据探究鼠妇选择生活环境的行为实验回答下列问题:
⑴本实验探究的是 光照条件 的不同对鼠妇选择生活环境的影响。
⑵本实验为什么要用10只而不是1只鼠妇?
排除偶然因素的影响。
⑶为什么要计算全班的平均值?
减少实验误差。
3、某同学的父母是双眼皮,而他本人则
是单眼皮,这是怎么回事呢?下列
图解可以解释。
(1)右图能说明,人的眼睑是由一对
基因控制的,而成对的基因往往
有显性、隐性之分。
(2)在形成生殖细胞时,位于成对染
色体上的成对基因要随染色体的分离
而分别进入两个生殖细胞中去。
(3)该同学父母分别会产生哪几种类型
的精子或卵细胞?A 、a 。
(4)该单眼皮同学正是图中哪种类型
的受精卵发育而来的?aa 。
(5)该同学父母再生一个小孩是单眼皮的机率是多少?25%。
4、小强午饭只吃了馒头、白菜、豆腐,请同学们用自己所学的知识,分析下列问题:
(1) 这顿午饭,能为他提供的几类营养物质是糖类、蛋白质、脂肪、维生
素、水、无机盐。
(2) 小强咀嚼馒头是有甜味,这是因为口腔内的唾液淀粉酶将淀粉分解成
麦芽糖。
(3) 午饭中可被直接吸收的营养物质是水、无机盐、维生素。
(4) 含有多种消化酶的消化液存在于消化道的小肠器官。
5、给你提供西瓜种子和其它必要的实验器材,请设计实验探究种子萌发与光的关系。
⑴实验目的:探究西瓜种子萌发与光照的关系
⑵实验方法:分组对照实验
⑶实验步骤:
①取两个大小一样的锥形瓶,分别记为A、B,瓶中垫数层餐巾纸,并加水使餐巾纸湿润。
然后将西瓜种子等分为两份,一份放入A中,一分放入B中(其它条件如温度、空气等都相同且适于种子萌发)。
②将 A放在有光环境中,将B放在无光环境中(其它条件相同)。
③观察记录瓶中种子萌发情况。
⑷若实验结果出现如下三种情况之一,请说明实验结论。
①A和B中的种子同样萌发,说明西瓜种子萌发与光照无关。
②A中种子萌发,B中种子不萌发,说明西瓜种子萌发需要光。
③A中种子不萌发,B中种子萌发,说明西瓜种子萌发不能有光。
6、
下图是某生态系统的食物网,回答有关问题:(6分)
(1)此食物网属于草原生态系统。
(2)图中生产者是草,从营养方式来看,它是自养生物。
(3)图中所有动物可统称为消费者。
其中,兔与草、鹰与鼠
是吃与被吃(或捕食)的关系。
(4)生态系统中,细菌、真菌等能将动物、植物的遗体分解成
无机物,因此叫做分解者。
7、
请对显微镜的结构和使用回答:(可填序号)(3分)
(1)正确的显微镜操作步骤是③②①⑤④⑥⑦⑧.(填序号)
①对光②装镜头③放置④升镜筒⑤降镜筒
⑥低倍镜观察⑦细准焦螺旋⑧寻找物像
(2)如果目镜上标有5×,物镜上标有40×,则显微镜观察到的物体被放大的倍数是200倍。
(3)若想观察到较多的细胞,应使用的物镜是低倍物镜。
对光时使用的物镜是低倍物镜。
8、下图是某地区男性每天吸烟数量与肺癌发病率的关系,请据图作答:
1)根据上图,你能得出哪些结论?(至少写出二点)
如:①每天吸烟数量与肺癌发病率成正比例的关系,吸烟数量越多,发病率越高;
②吸非过滤嘴的烟比过滤嘴的烟引起肺
癌发病率要高
9、右图中一只蚊子在
叮咬了甲的血液后,又吸食
了乙的血液,若甲的血液中
含有丝虫病的幼虫——微丝
蚴,乙被蚊子叮咬后患上丝
虫病,请回答下列问题:
(1)甲是_________________。
(2)乙在患病前是______________,患病后是
____________________。
(3)微丝蚴是_________________________。
(4)蚊子是___________________________。
(1)传染源(2)易感人群传染源(3)
病原体(4)传播
途径
10、下表是医院为两个体检者所作的尿常规化验单(表中“-”表示少或无,“+”表示较多,“++”表示很多),根据化验单上的数据,回答下列问题。
数据显示,尿液正常的是体检者 检者 ;可能患肾小球肾炎的是体检者 。
B 、A 、A。
