相似三角形常见模型总结
相似三角形典型模型及其例题

.\1:相像三角形模型一:相像三角形判断的基本模型(一) A 字型、反 A 字型(斜 A 字型)AADD E EB C B C(平行)(不平行)(二) 8 字型、反 8 字型AA BBO JC DC D(蝴蝶型)(平行)(不平行)(三)母子型AADDB C C(四)一线三等角型:三等角型相像三角形是以等腰三角形(等腰梯形)或许等边三角形为背景,一个与等腰三角形的底角相等的极点在底边所在的直线上,角的两边分别与等腰三角形的两边订交以下图:.\(五)一线三直角型:三直角相像能够看着是“一线三等角”中当角为直角时的特例,三直角型相像往常是以矩形或许正方形形为背景,或许在一条直线上有一个极点在该直线上挪动或许旋转的直角,几种常有的基本图形以下:当题目的条件中只有一个或许两个直角时,就要考虑经过增添协助线结构完好的三直角型相像,这常常是好多压轴题的打破口,从而将三角型的条件进行转变。
(六)双垂型:ADC二:相像三角形判断的变化模型旋转型:由 A 字型旋转获得AD EB C8 字型拓展AE FGB C 共享性一线三等角的变形.\一线三直角的变形2:相像三角形典型例题( 1)母子型相像三角形例 1:如图,梯形ABCD 中, AD ∥ BC,对角线 AC、 BD 交于点 O, BE∥ CD 交 CA 延伸线于E.求证: OC2OA OE .例 2:已知:如图,△ABC中,点E在中线AD上,D EB ABC .求证:( 1)DB2DE DA ;(2)DCE DAC .BDEA C例 3:已知:如图,等腰△ABC中,AB=AC,AD⊥ BC于D,CG∥ AB,BG分别交AD、AC于E、F.求证: BE2EF EG .1、如图,已知AD 为△ABC 的角均分线, EF 为 AD 的垂直均分线.求证:FD 2FB FC .2、已知: AD 是 Rt△ABC 中∠ A 的均分线,∠ C=90°,EF 是 AD 的垂直均分线交AD 于 M ,EF、BC 的延.\长线交于一点N。
相似三角形常见模型(总结材料)

第一部分 相似三角形模型分析一、相似三角形判定的基本模型认识(一)A 字型、反A 字型(斜A 字型)ABCDE(平行)CBA DE(不平行)(二)8字型、反8字型J OADBCAB CD(蝴蝶型)(平行) (不平行) (三)母子型ABCDCAD(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(五)一线三直角型:(六)双垂型:CAD二、相似三角形判定的变化模型旋转型:由A 字型旋转得到。
8字型拓展CB EDA共享性GABCEF一线三等角的变形一线三直角的变形第二部分 相似三角形典型例题讲解母子型相似三角形例1:如图,梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点O ,BE ∥CD 交CA 延长线于E . 求证:OE OA OC ⋅=2.例2:已知:如图,△ABC 中,点E 在中线AD 上, ABC DEB ∠=∠.求证:(1)DA DE DB ⋅=2; (2)DAC DCE ∠=∠.例3:已知:如图,等腰△ABC 中,AB =AC ,AD ⊥BC 于D ,CG ∥AB ,BG 分别交AD 、AC 于E 、F . 求证:EG EF BE ⋅=2.相关练习:1、如图,已知AD 为△ABC 的角平分线,EF 为AD 的垂直平分线.求证:FC FB FD ⋅=2.AC D E B2、已知:AD 是Rt △ABC 中∠A 的平分线,∠C=90°,EF 是AD 的垂直平分线交AD 于M ,EF 、BC 的延长线交于一点N 。
求证:(1)△AME ∽△NMD; (2)ND 2=NC ·NB3、已知:如图,在△ABC 中,∠ACB=90°,CD ⊥AB 于D ,E 是AC 上一点,CF ⊥BE 于F 。
求证:EB ·DF=AE ·DB4.在∆ABC 中,AB=AC ,高AD 与BE 交于H ,EF BC ⊥,垂足为F ,延长AD 到G ,使DG=EF ,M 是AH 的中点。
相似三角形模型总结以及例题

相似三角形模型总结以及例题
相似三角形模型是同一个三角形被两次放大或缩小的一种模型,具有
以下特点:
1. 比较定理:三条边的比值相等,两个三角形都是一样的形状,只有
大小不同。
2. 角平分线定理:若两个三角形相似,则其中一角被平分线分割,得
到的两条边构成另一个三角形,且两个三角形也是相似的。
3. 中位线定理:若两个三角形相似,则其中一角的一边被中线分割,
形成的两个三角形,也是相似的。
理解相似三角形模型,最重要的是理解它的边和角之间的关系。
例题:若两个三角形的边比例是2:3:4和8:24:32,则它们是否相似?
答案:是的,它们是相似的。
由比较定理可知,若两个三角形的边比
例满足x:ax:ax^2关系,则它们是相似的,而2:3:4 = 8:24:32,满足
x:ax:ax^2关系,所以它们是相似的。
中考数学几何专项——相似模型(相似三角形)

中考数学几何专项——相似模型(相似三角形)相似模型相似模型一:A字型特征:DE∥BC模型结论:根据A字型相似模型,可以得出以下结论:C∠B=∠XXXAC²=AD×AB相似模型二:X型特征:AC∥BD模型结论:根据X型相似模型,可以得出以下结论:AO×OB=OC×ODBOC∽△DOACAOC∽△DOB相似模型三:旋转相似特征:成比例线,段共端点模型结论:根据旋转相似模型,可以得出以下结论:BEF∽△BCDDEF∽△DABAEB∽△DEC相似模型四:三平行模型特征:AB∥EF∥CD模型结论:根据三平行模型,可以得出以下结论:ABE∽△CDF相似模型五:半角模型特征:90度,45度;120度,60度模型结论:根据半角模型,可以得出以下结论:ABN∽△MAN∽△MCAABD∽△CAE∽△CBA相似模型六:三角形内接矩形模型特征:矩形EFGH或正方形EFGH内接与三角形模型结论:根据三角形内接矩形模型,可以得出以下结论:ABC∽△EFH相似模型七:十字模型特征:正方形HDGB模型结论:根据十字模型,可以得出以下结论:若AF=BE,则AF⊥BE,且为长方形若AF⊥BE,则AF=BEBDBC平行四边形,且△GME∽△HNF,△MED≌△BFA。
下面给出几个几何问题。
1.在△ABC中,AB=AC,且有以下七个结论:①D为AC中点;②AE⊥BD;③BE:EC=2:1;④∠ADB=∠CDE;⑤∠AEB=∠CED;⑥∠BMC=135°;⑦BM:MC=2:1.求AC和CD的比值。
2.在平行四边形ABCD中,AB∥CD,线段BC,AD相交于点F,点E是线段AF上一点且满足∠BEF=∠C,其中AF=6,DF=3,CF=2,求AE的长度。
3.在Rt△ABD中,过点D作CD⊥BD,垂足为D,连接XXX于点E,过点E作EF⊥BD于点F,若AB=15,CD=10,求4.在□ABCD中,E为BC的中点,连接AE,AC,分别交BD于M,N,求5.在平行四边形ABCD中,AB∥CD,AD,BC相交于点E,过E作EF∥AB交BD于点F。
相似三角形典型模型及例题

1:相似三角形模型一:相似三角形判定的根本模型〔一〕 A 字型、反 A 字型〔斜 A 字型〕〔平行〕〔不平行〕〔二〕 8 字型、反 8 字型AA BBO JC DC D〔蝴蝶型〕〔平行〕〔不平行〕〔三〕母子型〔四〕一线三等角型:三等角型相似三角形是以等腰三角形〔等腰梯形〕或者等边三角形为背景,一个与等腰三角形的底角相等的顶点在底边所在的直线上,角的两边分别与等腰三角形的两边相交如下图:〔五〕一线三直角型:三直角相似可以看着是“一线三等角〞中当角为直角时的特例,三直角型相似通常是以矩形或者正方形形为背景,或者在一条直线上有一个顶点在该直线上移动或者旋转的直角,几种常见的根本图形如下:当题目的条件中只有一个或者两个直角时,就要考虑通过添加辅助线构造完整的三直角型相似,这往往是很多压轴题的突破口,进而将三角型的条件进行转化。
〔六〕双垂型:二:相似三角形判定的变化模型旋转型:由 A 字型旋转得到8 字型拓展AE FGB C共享性一线三等角的变形一线三直角的变形2:相似三角形典型例题〔 1〕母子型相似三角形例 1:如图,梯形ABCD 中, AD ∥ BC,对角线 AC、 BD 交于点 O, BE∥ CD 交 CA 延长线于 E.求证: OC 2OA OE.例 2::如图,△ABC 中,点 E 在中线 AD 上 ,DEBABC .求证:〔 1〕DB2DE DA ;〔2〕 DCE DAC .BDEA C例 3::如图,等腰△ABC 中, AB= AC,AD⊥ BC 于 D, CG∥ AB, BG 分别交 AD 、 AC 于 E、 F.求证: BE 2EF EG .1、如图,AD 为△ABC 的角平分线, EF 为 AD 的垂直平分线.求证:FD2FB FC.2、: AD 是 Rt△ABC 中∠ A 的平分线,∠ C=90°,EF 是 AD 的垂直平分线交AD 于 M ,EF、BC 的延长线交于一点 N。
专题07 相似三角形的五种模型(老师版)

专题07 相似三角形的五种模型相似三角形考查范围广,综合性强,其模型种类多,其中有关一线三垂直模型在前面的专题已经很详细的讲解,这里就不在重复。
模型一、A 字型A 字型(平行) 反A 字型(不平行)例.如图,在中,点分别在上,且.(1)求证:;(2)若点在上,与交于点,求证:.【答案】见解析【详解】解:(1)在△AEF 和△ABC 中,∵,,∴△AEF ∽△ABC ;(2)∵△AEF ∽△ABC ,∴∠AEF =∠ABC ,∴EF ∥BC ,∴△AEG ∽△ABD ,△AGF ∽△ADC ,∴,,∴.【变式训练1】已知:如图,点D ,F 在△ABC 边AC 上,点E 在边BC 上,且DE ∥AB ,CD 2=CF •CA .(1)求证:EF ∥BD ;(2)如果AC •CF =BC •CE ,求证:BD 2=DE •BA .ABC ∆,E F ,AB AC AE ABAF AC=AEF ABC ∆∆:D BC AD EF G EG FGBD CD=EAF BAC ∠=∠AE ABAF AC=EG AG BD AD =FG AGCD AD =EG FG BD CD=【答案】见解析【解析】证明:(1)∵DE∥AB,∴CDAC =CECB,∵CD2=CF•CA.∴CDAC =CFCD,∴CFCD=CECB,∴EF∥BD;(2)∵EF∥BD,∴∠CEF=∠CBD,∵AC•CF=BC•CE,∴ACBC =CECF,且∠C=∠C,∴△CEF∽△CAB,∴∠CEF=∠A,∴∠DBE=∠A,∵DE∥AB,∴∠EDB=∠DBA,且∠DBE=∠A,∴△BAD∽△DBE,∴BABD =BDDE∴BD2=BA•DE【变式训练2】如图所示,在△ABC中,DE∥BC,AD=5,BD=10,AE=3.(1)求CE的长.(2)在△ABC中,点D,E,Q分别是AB,AC,BC上,且DE∥BC,AQ交DE于点P.小明认为DPBQ =PEQC,你认为小明的结论正确吗?请说明你的理由.【答案】(1)6;(2)见解析【解析】(1)由DE∥BC,∴△ADE∽△ABC,∴ADAD+BD=AEAE+EC,∵AD=5,BD=10,AE=3,∴CE=6.(2)结论正确,理由如下,在△ABQ中,由于DP∥BQ,∴△ADP∽△ABQ,∴DPBQ =APAQ,同理可得:EPCQ=APAQ,∴DPBQ=EPCQ【变式训练3】如图,在中,,,,平分,交边于点,过点作的平行线,交边于点.(1)求线段的长;(2)取线段的中点,联结,交线段于点,延长线段交边于点,求的值.【答案】(1)4;(2)【解析】解:(1)∵平分,,∴.在中,,,,∴.在中,,,,∴.∴.∵,∴∴.∴.(3)∵点是线段的中点,∴.∵,∴∴.∴.∵,∴∴∴.模型二、8字型与反8字型相似Rt ABC∆90ACB∠=︒60BAC∠=︒6AC=AD BAC∠BC D D CA AB E DE AD MBM DE F BM AC GEFDF23EFDF=AD BAC∠60BAC∠=︒30DAC∠=︒Rt ACD∆90ACD∠=︒30DAC∠=︒6AC=CD=Rt ACB∆90ACB∠=︒60BAC∠=︒6AC=BC=BD BC CD=-=//DE CA BDE BCAV V∽23DE BDCA BC==4DE=M ADDM AM=//DE CA DFM AGM△∽△DF DMAG AM=DF AG=//DE CA BEF BAG△∽△23EF BE BDAG BA BC===23EFDF=例.如图,已知在△ABC 中,BE 平分∠ABC 交AC 于E ,点D 在BE 延长线上,且BA •BC =BD •BE .(1)求证:△ABD ∽△EBC ;(2)求证:AD 2=BD •DE .【答案】见解析【解答】证明:(1)∵BE 平分∠ABC ,∴∠ABD =∠EBC ,∵BA •BC =BD •BE .即ABBC =BDBE ,∴△ABD ∽△EBC ;(2)∵△ABD ∽△EBC ,∴∠BAD =∠BEC ,∠ADB =∠BCE ,∵∠AED =∠BEC ,∴∠BAD =∠AED ,∴△ADE ∽△BEC ,∴△AED ∽△ABD ,∴ADBD =DEAD ,即AD 2=BD •DE .【变式训练1】如图,AD 与BC 交于点O ,EF 过点O ,交AB 与点E ,交CD 与点F ,BO =1,CO =3,AO =32,DO =92.(1)求证:∠A =∠D .(2)若AE =BE ,求证:CF =DF .【答案】【解析】证明:(1)∵BO =1,CO =3,AO =32,DO =92.∴OBOC =AODO ,∵∠AOB =∠COD ,∴△OAB ∽△ODC ,∴∠A =∠D .(2)∵∠A =∠D ,∴AB ∥CD ,∴AEDF =OEOF ,BECF =OEOF ,∴AEDF =BECF .∵AE =BE ,∴CF =DF .【变式训练2】如图,AG ∥BD ,AF :FB =1:2,BC :CD =2:1,求GEED 的值【答案】32【解析】∵AG ∥BD ,∴△AFG ∽△BFD ,∴AGBD =AFBF =12,∵BCCD =2,∴CD =13BD ,∴AGCD =32,∵AG ∥BD ,∴△AEG ∽△CED ,∴GEED =AGCD =32.【变式训练3】如图,四边形ABCD 和四边形ACED 都是平行四边形,点R 为DE 的中点,BR 分别交AC 、CD 于点P 、Q .(1)求证:△PCQ ∽△RDQ ;(2)求BP :PQ :QR 的值.【答案】(1)见解析;(2)【解析】解:(1)∵,∴.又∵.∴.(2)∵四边形和四边形都是平行四边形,∴,.∴,.又∵点是中点,∴.由(1)知,∴,∴.又∵,∴.模型三、AX 型(A 字型及X 字型两者相结合)例.如图,△ABC 中,D .E 分别是AB 、AC 上的点,且BD =2AD ,CE =2AE .(1)求证:△ADE ∽△ABC ;(2)若DF =2,求FC 的长度.【答案】见解析【解答】(1)证明:∵BD =2AD ,CE =2AE ,∴ADAB =AEAC =13,又∵∠DAE =∠BAC ,∴△ADE ∽△ABC ;:3:1:2BP PQ QR =PC DR ∥PCQ RDQ ∠=∠PQC RQD ∠=∠PCQ RDQ △∽△ABCD ACED BC AD CE ==//AC DE PB PR =12PC RE =R DE DR RE =PCQ RDQ △∽△12PQ PC PC QR DR RE ===2QR PQ =3BP PR PQ QR PQ ==+=::3:1:2BP PQ QR =(2)解:∵△ADE ∽△ABC ,∴DE BC =AD AB =13,∠ADE =∠ABC ,∴DE ∥BC ,∴△DEF ∽△CBF ,∴DFCF =DECB ,即2CF =13,∴FC =6.【变式训练1】如图,在菱形ABCD 中,∠ADE 、∠CDF 分别交BC 、AB 于点E 、F ,DF 交对角线AC 于点M ,且∠ADE =∠CDF .(1)求证:CE =AF ;(2)连接ME,若=,AF =2,求的长.【解析】解:(1)∵四边形ABCD 是菱形,∴AD =CD ,∠DAF =∠DCE ,又∵∠ADE =∠CDF ,∴∠ADE ﹣∠EDF =∠CDF ﹣∠EDF ,∴∠ADF =∠CDE ,在△ADF和△CDE 中,,∴△ADF ≌△CDE ,∴CE =AF .(2)∵四边形ABCD 是菱形,∴AB =BC ,由(1)得:CE =AF =2,∴BE =BF ,设BE =BF =x ,∵=,AF =2,∴,解得x ,∴BE =BF ,∵=,且CE =AF ,∴==,∵∠CMD =∠AMF ,∠DCM =∠AMF ,∴△AMF ∽△CMD ,∴,∴,且∠ACB =∠ACB,∴△ABC ~△MEC, ∴∠CAB =∠CME=∠ACB ,∴ME=CE=2.【变式训练2】如图,已知AB ∥CD ,AC 与BD 相交于点E ,点F 在线段BC 上,AB CD =12,BF CF =12.(1)求证:AB ∥EF ;(2)求S △ABE :S △EBC :S △ECD .【答案】见解析【解析】(1)证明:∵AB ∥CD ,∴ABCD =BEED =12,CE BE CDCEME ADF CDF AD CD DAF DCE ∠=∠⎧⎪=⎨⎪∠=∠⎩CE BE CD CE 222x x +=11CE BE CD CE CE BE CD CE CDAFCD CMAF AM=CD CM CEAF AM BE==∵BF CF =12,∴BE ED =BFFC ,∴EF ∥CD ,∴AB ∥EF .(2)设△ABE 的面积为m .∵AB ∥CD ,∴△ABE ∽△CDE ,∴S △ABES △EDC =(ABCD )2=14,∴S △CDE =4m ,∵AECE =ABCD =12,∴S △BEC =2m ,∴S △ABE :S △EBC :S △ECD =m :2m :4m =1:2:4.【变式训练3】如图:AD ∥EG ∥BC ,EG 交DB 于点F ,已知AD =6,BC =8,AE =6,EF =2.(1)求EB 的长;(2)求FG 的长.【答案】见解析【解答】解:(1)∵EG ∥AD ,∴△BAD ∽△BEF ,∴BEBA =EFAD ,即BE BE+6=26,∴EB =3.(2)∵EG ∥∥BC ,∴△AEG ∽△ABC ,∴EGBC =AEAB ,即EG8=66+3,∴EG =163,∴FG =EG ﹣EF=103.模型四、共边角模型(子母型)例.在中,,垂足为,求的长【答案】4【解析】∵,∴,∴,∵,∴,∴,Rt ABC V 90,ACB CD AB ∠=︒⊥,8,2D AD DB ==CD CD AB ⊥90ADC CDB ∠=∠=︒90ACD A ∠+∠=︒90ACB ∠=︒90ACD BCD ∠+∠=︒A BCD ∠=∠∴,∴,∴,∴.【变式训练1】如图,矩形ABCD 中,F 是DC 上一点,BF ⊥AC ,垂足为E ,ADAB =12,△CEF 的面积为S 1,△AEB 的面积为S 2,则S 1S 2的值等于( )A .116B .15C .14D .125【解答】解:∵ADAB =12,∴设AD =BC =a ,则AB =CD =2a ,∴AC =5a ,∵BF ⊥AC ,∴△CBE ∽△CAB ,△AEB ∽△ABC ,∴BC 2=CE •CA ,AB 2=AE •AC ∴a 2=CE •5a ,4a 2=AE •5a ,∴CE =5a5,AE=45a5,∴CE AE =14,∵△CEF ∽△AEB ,∴S 1S 2=(CEAE )2=116,故选:A .【变式训练2】如图,在△ABC 中,∠ACB =90°,CD 是AB 边上的高.如果BD =4,CD =6,那么BC :AC 是( )A .3:2B .2:3C .3:13D .2:13.【答案】B【解答】解:∵∠ACB =90°,CD 是AB 边上的高,∴∠ADC =∠CDB =∠ACB =90°,∵∠A +∠B =90°,∠A +∠ACD =90°,∴∠ACD =∠B ,∴△ACD ∽△CBD ,∴ACBC =CDBD =64=32∴BCAC =23,故选:B .【变式训练3】如图,在△ABC 中,AB=AC ,点P 、D 分别是BC 、AC 边上的点,且∠APD=∠B,(1)求证:AC•CD=CP •BP ;(2)若AB=10,BC=12,当PD ∥AB 时,求BP 的长.【答案】见解析【解析】(1)∵AB=AC ,∴∠B=∠C .∵∠APD=∠B ,∴∠APD=∠B=∠C .∵∠APC=∠BAP+∠B ,∠APC=∠APD+∠DPC ,∴∠BAP=∠DPC ,∴△ABP ∽△PCD ,∴,∴AB•CD=CP•BP .∵AB=AC ,∴AC•CD=CP•BP ;ADC CDB V V ∽CD ADBD CD=28216CD AD BD =⋅=⨯=4CD =BP ABCD CP=(2)∵PD ∥AB ,∴∠APD=∠BAP .∵∠APD=∠C ,∴∠BAP=∠C .∵∠B=∠B ,∴△BAP ∽△BCA,∴.∵AB=10,BC=12,∴,∴BP=.模型五、手拉手模型例.如图,在△ABC 与△ADE 中,∠ACB =∠AED =90°,∠ABC =∠ADE ,连接BD 、CE ,若AC :BC =3:4,则BD :CE 为( )A .5:3B .4:3C .5:2D .2:3【答案】A【解析】∵∠ACB =∠AED =90°,∠ABC =∠ADE ,∴△ABC ∽△ADE ,∴∠BAC =∠DAE ,ACAB =AEAD ,∵∠BAC +∠BAE =∠DAE +∠BAE ,即∠CAE =∠BAD ,∵ACAB =AEAD ,∴△ACE ∽△ABD ,∴BDCE =AB AC ,∵AC :BC =3:4,∠ACB =∠AED =90°,∴AC :BC :AB =3:4:5,∴BD :CE =5:3,选A .【变式训练1】如图,△ABC ∽△ADE ,∠BAC =∠DAE =90°,AB 与DE 交于点O ,AB =4,AC =3,F 是DE 的中点,连接BD ,BF ,若点E 是射线CB 上的动点,下列结论:①△AOD ∽△FOB ,②△BOD ∽△EOA ,③∠FDB +∠FBE =90°,④BF =56AE ,其中正确的是( )A .①②B .③④C .②③D .②③④【答案】D【解析】∵△ABC ∽△ADE ,∴∠ADO =∠OBE ,∵∠AOD =∠BOE ,∴△AOD ∽△EOB ,∴ODOB =OAOE ,∴ODOA =OBOE ,∵∠BOD =∠AOE ,∴△BOD ∽△EOA ,故②正确,BA BPBC BA=101210BP =253∵△AOD ∽△EOB ,△BOD ∽△EOA ,∴∠ADO =∠EBO ,∠AEO =∠DBO ,∵∠ADO +∠AEO =90°,∴∠DBE =∠DBO +∠EBO =90°,∵DF =EF ,∴FD =FB =FE ,∴∠FDB =∠FBD ,∴∠FDB +∠FBE =∠FBD +∠FBE =90°,故③正确,在R t △ABC 中,∵AB =4,AC =3,∴BC =32+42=5,∵△ABC ∽△ADE ,∴DEAE =BCAC =53,∵BF =12DE ,∴2BFAE =53,∴BF =56AE ,故④正确,∵∠ADO =∠OBE ,∴∠ADO ≠∠OBF ,∴无法判断△AOD ∽△FOB ,故①错误.选D .【变式训练2】已知:如图,在△ABC 中,点D 、E 分别在边BC 、AC 上,点F 在DE 的延长线上,AD =AF ,AE •CE =DE •EF .(1)求证:△ADE ∽△ACD ;(2)如果AE •BD =EF •AF ,求证:AB =AC .【答案】见解析【解析】证明:(1)∵AD =AF ,∴∠ADF =∠F ,∵AE •CE =DE •EF ,∴AEDE =EFCE ,又∵∠AEF =∠DEC ,∴△AEF ∽△DEC ,∴∠F =∠C ,∴∠ADF =∠C ,又∵∠DAE =∠CAD ,∴△ADE ∽△ACD .(3)∵AE •BD =EF •AF ,∴AEAF =EFBD ,∵AD =AF ,∴AEAD =EFBD ,∵∠AEF =∠EAD +∠ADE ,∠ADB =∠EAD +∠C ,∴∠AEF =∠ADB ,∴△AEF ∽△ADB ,∴∠F =∠B ,∴∠C =∠B ,∴AB =AC .【变式训练3】已知,ABC 中,AB =AC ,∠BAC =2α°,点D 为BC 边中点,连接AD ,点E 为线段AD 上一动点,把线段CE 绕点E 顺时针旋转2α°得到线段EF ,连接FG ,FD .(1)如图1,当∠BAC =60°时,请直接写出的值;(2)如图2,当∠BAC =90°时,(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请写出正确的结论,并说明理由;V BFAE【答案】(1)1;(2)不成立,,理由见解析;(3)E为AD中点时,的最小值=sinα【解析】(1)连接BF,∵AB=AC,∠BAC=60°,∴△ABC为等边三角形,∵线段CE绕点E顺时针旋转60°得到线段EF,∴EC=EF,∠CEF=60°,∴△EFC都是等边三角形,∴AC=BC,EC=CF,∠ACB=∠ECF=60°,∴∠ACE=∠BCF,∴△ACE≌△BCF(SAS),∴AE=BF,∴=1.(2)不成立,结论:.证明:连接BF,∵AB=AC,D是BC中点,∴AD⊥BC,∴∠ADC=90°,∴∠BAC=∠CEF=90°,∴△ABC和△CEF为等腰直角三角形,∴∠ACB=∠ECF=45°,∴∠ACE=∠BCF,∴=,∴△ACE∽△BCF,∴∠CBF=∠CAE=α,∴==.课后训练1.如图,在中,、分别是边、的中点,、分别交于点、,则图中阴影部分图形的面积与的面积之比为 A.B.C.D.【解答】B【解析】,是的中点,,,即,同理可得,,,,、分别是边、的中点,,,,AEBFDFDCBFAEAEBFACBCCECFAEBFACBCABCDY E F BC CD AE AF BD G HABCDY()7:127:2413:3613:72//BE AD E B∽∴∆∆BEG DAG∴BG12==BEDG DA13=BG BD13=DH BD13∴=GH BD1136四边形∆∆∴==AGH ABD ABCDS S SE F BC CD//∴EF BD12=EF BD∽∴∆∆CEF CBD,,图中阴影部分图形的面积,即图中阴影部分图形的面积与的面积之比为.2.如图,△ABC 中,D 为BC 中点,E 为AD 的中点,BE 的延长线交AC 于F ,则AF FC 为( ) A .1:5B .1:4C .1:3D .1:2【答案】D【解析】过D 作BF 的平行线,交AC 边于G ,如下图所示:∵D 为BC 中点,DG ∥BF ,∴∠CGD =∠CFB ,又∵∠C =∠C ,∴△CDG ∽△CBF∴CG CF =CD CB =12,即:CG =12CF =FG又E 为AD 的中点,BE 的延长线交AC 于F ,DG ∥BF同理可得:△AEF ∽△ADG ,∴AE AD =AF AG =12,即:AF =12AG =FG∴AF =FG =GC ,∴AF FC =AF 2AF =12=1:2,选D .3.如图平行四边形,为中点,延长至,使,连结交于点,则 .【答案】2:9【解析】如图,连接∵四边形是平行四边形,,,为中点,,,,,,,∴211()24∆∆==CEF CBD S S 1148四边形∆∆∴==CEF BCD ABCD S S S ∴1176824四边形四边形⎛⎫=+= ⎪⎝⎭ABCD ABCD S S Y ABCD 7:24=ABCD F BC AD E :1:3DE AD =EF DC G :DEG BGC S S ∆∆=BGABCD //∴AD BC =AD BC ∴∠=∠E CFG F BC 1122∴==FC BC AD :1:3= DE AD :1:3∴=DE BC :2:3∴=DE CF ∠=∠ E CFG ∠=∠DGE CGF ∽∴∆DGE CGF :4:9∆∆∴=DEG CFG S S为中点,,.4.如图,等边三角形ABC 中,AB =3,点D 是CB 延长线上一点,且BD =1,点E 在直线AC 上,当∠BAD =∠CDE 时,AE 的长为 .【分析】分两种情形分别画出图形,利用相似三角形的性质解决问题即可.【解析】∵△ABC 是等边三角形,∴∠ABC =∠ACB =60°,AC =BC =AB =3,∴∠ABD =120°,①当点E 在边AC 上时.作EF ∥AB 交BC 于F ,如图1所示:则△EFC 是等边三角形.∴∠CFE =60°,EF =CF =CE ,∴∠BFE =120°=∠ABD ,∵∠BAD =∠CDE ,∴△ABD ∽△DFE ,∴AB BD =DF EF ,即31=DF EF ,∴DF =3EF ,∴DF =3CF ,∴CD =4CF ,∵BC =3,BD =1,∴CD =BC +BD =4,∴CF =1,∴CE =1,∴AE =AC ﹣CE =2;②点E 在AC 的延长线上时.如图2所示:∵∠ABD =∠DCE =120°,∠BAD =CDE ,∴△ABD ∽△DCE ,∴AB CD =BD CE ,即34=1CE ,解得:CE =43,∴AE =AC +CE =3+43=133;综上所述,当∠BAD =∠CDE 时,AE 的长为2或133;5.如图,在△ABC 中,点D ,E 分别在边AB ,AC 上,∠AED =∠B ,线段AG 分别交线段DE ,BC 于点F ,G ,且AD AC =DF CG .(1)求证:△ADF ∽△ACG ;(2)若AD AC =37,求AF FG的值. F BC 2∆∆∴=BGC CFG S S :4:182:9∆∆∴==DEG BGC S S【解答】(1)证明:∵∠AED =∠B ,∠DAE =∠CAB ,∴△AED ∽△ABC ,∴∠ADF =∠C ,又∵AD AC =DF CG ,∴△ADF ∽△ACG ;(2)解:∵△ADF ∽△ACG ,∴AD AC =AF AG ,∵AD AC =37,∴AF AG =37,∴AF FG =34.6.如图,在平行四边形ABCD 中,点E 在边BC 上,连结AE 并延长,交对角线BD 于点F 、DC 的延长线于点G .如果CE BE =23,求FE EG 的值.【解答】解:∵四边形ABCD 为平行四边形,∴AD ∥BC ,AD =BC .∵AD ∥BE ,∴△BEF ∽△DAF ,∴EF AF =BE DA .又∵BC =BE +CE ,CE BE =23,∴BE =35BC =35DA ,∴EF =35AF ,∴AE =3+53EF =83EF .∵CE ∥AD ,△CEG ∽DAG ,∴GE GA =CE DA =22+3,∴GE =25GA ,∴GE =25−2AE =23×83EF =169EF ,∴FE EG =916.7.已知中,,(如图).以线段为边向外作等边三角形,点是线段的中点,连接并延长交线段于点.(1)求证:四边形为平行四边形;(2)连接,交于点.①若,求的长;②作,垂足为,求证:.【解析】(1)∵是等边三角形 ∴,在中,∴∵点是线段的中点∴∴是等边三角形∴,∴∴∴∴四边形为平行四边形;(2)①如图,连接,交于点 ∵∴∴Rt ABC V 90ACB ∠=︒30CAB ∠=︒AB ABD E AB CE AD F BCFD CD AB M 6AB =BM MN AC ⊥N 111BC AD MN+=ABD △AD AB BD ==60BAD ABD D ∠=∠=∠=︒Rt ABC V 30CAB ∠=︒60ABC ∠=︒E AB 12CE BE AE AB ===BCE V 60CEB CBE ABC ∠=∠=∠=︒BC CE =60ABD CEB ∠=∠=︒//CF BD606060180CBD D CBE ABD D ∠+∠=∠+∠+∠=︒+︒+︒=︒//BC FD BCFD CD AB M //BC FD BCM ADM ~V V BM BC AM AD=∵,∴ ∵∴;②如图,作,垂足为∵,,∴∴,∴,∴ ∴.8.如图,在平行四边形中,过点作,垂足为,连接,为线段上一点,且.(1)求证:;(2)若,,,求的长.【答案】(1)见解析;(2)AE【详解】(1)证明:四边形是平行四边形,,,,;,,,;(2)解:∵四边形是平行四边形,,,.,,.在中,,,,9.如图1,在矩形中,于点.(1)求证:;(2)如图2,若点是边上一点,且.求证:.【答案】(1)见解析;(1)见解析12BC CE AB ==AB AD =12BM BC AM AD ==6AB BM AM =+=123BM AB ==MN AC ⊥N90ACB ∠=︒306090CAD BAC BAD ∠=∠+∠=︒+︒=︒MN AC⊥////BC MN DA AMN ABC V :V C CMN DA ~V V MN AN BC AC =MN CN DA CA=1MN MN AN CN AN CN AC BC DA AC CA AC AC ++=+===111BC AD MN+=ABCD A AE BC ⊥E DE F DE AFE B ∠=∠ADF DEC ∆∆∽8AB =AD =AF =AE ABCD //∴AD BC //AB CD ∴∠=∠ADF CED 180∠+∠=︒B C 180∠+∠=︒ AFE AFD ∠=∠AFE B ∴∠=∠AFD C ∽∴∆∆ADF DEC ABCD 8∴==DC AB ∽∆∆ ADF DEC ∴=AD AFDE DC =12∴=DE // AD BC ⊥AE BC ∴⊥AE AD Rt ADE ∆90∠=︒EAD 12=DE =AD ∴===AE ABCD AE BD ⊥E BE BC AE CD =g g P AD PE EC ⊥AE AB DE AP =g g【详解】证明:∵在矩形中,,,,,,,,,,,;(2)证明:,,,,,,,,,,.10.已知,正方形中,点是边延长线上一点,连接,过点作,垂足为点,与交于点.(1)如图1,求证:;(2)如图2,连接,若,的值.【答案】(1)见解析;(2)【详解】(1)四边形是正方形,,,又,,又,,,在和中,,,;(2)过点作,设,,如图2所示:ABCD =AB CD =AD BC 90∠=︒BAD ⊥ AE BD 90∴∠=∠=︒AEB AED ∴∠+∠=∠+∠BAE ABE BAE EAD ∴∠=∠ABE DAE ∽∴∆∆ABE DAE ∴=AB BE AD AE ∴=CD BE BC AE∴=g g BE BC AE CD ⊥ AE BD ⊥PE EC 90∴∠=∠=︒AED PEC ∴∠=∠AEP DEC 90∠+∠=︒ EAD ADE 90∠+∠=︒ADE CDE ∴∠=∠EAP EDC ∽∴∆∆AEP DEC ∴=AE AP DE CD= AB CD ∴=g g AE AB DE AP ABCD E BC DE B BF DE ⊥F BF CD G CG CE =BD BE =DG =cos DBG ∠cos ∠=DBG ABCD ∴=BC DC 90∠=∠=︒BCG DCE ⊥ BF DE 90∴∠=︒GFD 180∠+∠+∠=︒ GBC BGC GCB 180∠+∠+∠=︒GFD FDG DGF ∠=∠BGC DGF ∆BGC ∆DEC ∠=∠⎧⎪=⎨⎪∠=∠⎩BCG DCE BC DCCBG CDE ()∴∆≅∆BGC DEC ASA ∴=CG CE G ⊥GH BD =CE x =HD y,,又,,,,,,解得:,在中,由勾股定理得:,同理可得:,又,,在中,由勾股定理得:,= CG CE ∴=CG x =+ BE BC CE =+DC DG GC =BC DC =BE =DG ∴=+x x =x ∴=BC Rt BCD ∆6===BD 2=HD =+ BD BH HD 624∴=-=BH Rt HBG ∆===BG cos ∴∠===BH DBG BG。
相似三角形六大证明技巧

相似三角形的判定方法总结:1. 平行于三角形一边的直线与其他两边相交,所构成的三角形与原三角形相似.2. 三边成比例的两个三角形相似.〔SSS 〕3. 两边成比例且夹角相等的两个三角形相似. (SAS)4. 两角分别相等的两个三角形相似.(AA)5.斜边和一条直角边成比例的两个直角三角形相似(HL) 相似三角形的模型方法总结: “反A 〞型与“反X 〞型.示意图结论E D CB A反A 型:如图,△ABC ,∠ADE =∠C ,如此△ADE ∽△ACB 〔AA 〕,∴AE ·AC =AD ·AB.假如连CD 、BE ,进而能证明△ACD ∽△ABE (SAS)O DCBA反X 型:如图,角∠BAO =∠CDO ,如此△AOB ∽△DOC 〔AA 〕,∴OA ·OC =OD ·OB . 假如连AD ,BC ,进而能证明△AOD ∽△BOC .“类射影〞与射影模型示意图结论A BCD类射影:如图,△ABC ,∠ABD =∠C ,如此△ABD ∽△ACB 〔AA 〕,∴2AB =AD ·AC.CABH射影定理如图,∠ACB =90°,CH ⊥AB 于H ,如此222,,AC AH AB BC BH BA HC HA HB =⋅=⋅=⋅“旋转相似〞与“一线三等角〞示意图结论相似三角形6大证明技巧相似三角形证明方法ABCDE旋转相似:如图,△ABC ∽△ADE ,如此AB ADAC AE=,∠BAC =∠DAE ,∴∠BAD =∠CAE ,∴△BAD ∽△CAE 〔SAS 〕CBAED一线三等角:如图,∠A =∠C =∠DBE ,如此△DAB ∽△BCE 〔AA 〕巩固练习 反A 型与反X 型△ABC 中,∠AEF=∠ACB ,求证:〔1〕AE AB AF AC ⋅=⋅〔2〕∠BEO=∠CFO ,∠EBO=∠FCO 〔3〕∠OEF=∠OBC ,∠OFE=∠OCBOF ECBA类射影如图,2AB AC AD =⋅,求证:BD ABBC AC= A BCD射影定理△ABC ,∠ACB =90°,CH ⊥AB 于H ,求证:2AC AH AB =⋅,2BC BH BA =⋅,2HC HA HB =⋅比例式的证明方法通过前面的学习,我们知道,比例线段的证明,离不开“平行线模型〞〔A 型,X 型,线束型〕,也离不开上述的6种“相似模型〞. 但是,王教师认为,“模型〞只是工具,怎样选择工具,怎样使用工具,怎样用好工具,取决于我们如何思考问题. 合理的思维方法,能让模型成为解题的利刃,让复杂的问题变简单。
相似三角形的基本模型归纳总结

相似三角形的基本模型归纳总结
相似三角形是指拥有相似的形状但大小不同的三角形。
在相似三角形中,对应角度相等,而对应边长之间存在比例关系。
以下是一些基本的相似三角形模型:
1. 比例模型:在两个相似三角形中,对应边长之比相等。
例如,若∆ABC与∆DEF相似,则有AB/DE = BC/EF = AC/DF。
2. 三角形高度模型:在两个相似三角形中,对应高度之比等于对应边长之比。
例如,若∆ABC与∆DEF相似,则有h_1/h_2 = AB/DE = BC/EF = AC/DF,其中h_1和h_2分别为∆ABC和
∆DEF的高度。
3. 角平分线模型:在两个相似三角形中,对应角的平分线所延伸的比例相等。
例如,若∆ABC与∆DEF相似,角A和角D相等,则有BD/CE = AB/DE = AC/DF。
4. 底角模型:在两个相似三角形中,底角对应相等。
例如,若∆ABC与∆DEF相似,并且∠A = ∠D,则有∠B = ∠E和∠C
= ∠F。
5. 周长模型:在两个相似三角形中,对应边长之比等于相似三角形的周长比。
例如,若∆ABC与∆DEF相似,则有
(A+B+C)/(D+E+F) = AB/DE = BC/EF = AC/DF。
这些是常见的相似三角形模型,可以根据具体问题选择适合的模型进行求解。
但需要注意的是,在相似三角形中,只有形状
相似,而边长比例相等,因此,对于三角形中角度的求解通常更加重要。
中考中相似三角形的常见模型及典型例题

(1)A字、8字; (3)角平分线; (5)一线三等角; (7)内接矩形;
2.基本辅助线:
(2)反A、反8; (4)旋转型; (6)线束模型; (8)相似比与面积比。
(1)作平行线构造A字、8字; (2)作垂线构造直角三角形相似
3.基本问题类型:
(1)证明相似;
(2)求线段长;
(1)若点P在线段CB上,且BP=6,求线段CQ的长; (2)若BP=x,CQ=y,求y与x的关系式,并求出自变量x的取值范围。
例 9 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CD,
AD与BE相交于点F. (1)求证:△ABD≌△BCE; (2)求证:△ABE∽△FAE;
(3)当AF=7,DF=1时,求BD的长。
(量得BN=70cm)
C
C
DME
DME
A PN F
B
A PN F
B
1.如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80 毫米,要把它加工成正方形零件,使正方形的一边在BC上,其 余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?
A
A
M
EN
H
KG
∟
B Q DPC
B
E
DF C
E
AB AC BC
B
C (2)公共边平方=共线边之积:AC 2 AE • AB
反A字 型 【模型2】反“A”字型&反“8”字型
(Ⅱ)DE拉下来经过点C,又称之为母子型,为相似常考模型:
A
A
E
B
C
AC2 AED • BC
AC2 CD • CB
AD2 BD • CD
相似三角形常见模型(总结)1

相似三角形第一部分 相似三角形模型分析一、相似三角形判定的基本模型认识(一)A 字型、反A 字型(斜A 字型)BDE(平行)BDE(不平行)(二)8字型、反8字型J OADBCAB CD(蝴蝶型)(平行) (不平行) (三)母子型BDD(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(五)一线三直角型:(六)双垂型:ADC 二、相似三角形判定的变化模型旋转型:由A字型旋转得到。
8字型拓展CB EDA共享性GABEF一线三等角的变形一线三直角的变形第二部分相似三角形典型例题讲解母子型相似三角形例1:如图,梯形ABCD中,AD∥BC,对角线AC、BD交于点O,BE∥CD交CA延长线于E.求证:OEOAOC⋅=2.例2:已知:如图,△ABC中,点E在中线AD上, ABCDEB∠=∠.求证:(1)DADEDB⋅=2;(2)DACDCE∠=∠.例3:已知:如图,等腰△ABC中,AB=AC,AD⊥BC于D,CG∥AB,BG分别交AD、AC于E、F.求证:EGEFBE⋅=2.相关练习:1、如图,已知AD为△ABC的角平分线,EF为AD的垂直平分线.求证:FCFBFD⋅=2.A CDEBGMF EHDCBA2、已知:AD 是Rt △ABC 中∠A 的平分线,∠C=90°,EF 是AD 的垂直平分线交AD 于M ,EF 、BC 的延长线交于一点N 。
求证:(1)△AME ∽△NMD; (2)ND 2=NC ·NB3、已知:如图,在△ABC 中,∠ACB=90°,CD ⊥AB 于D ,E 是AC 上一点,CF ⊥BE 于F 。
求证:EB ·DF=AE ·DB4.在∆ABC 中,AB=AC ,高AD 与BE 交于H ,EF BC ⊥,垂足为F ,延长AD 到G ,使DG=EF ,M 是AH 的中点。
求证:∠=︒GBM 905.(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)已知:如图,在Rt △ABC 中,∠C =90°,BC =2,AC =4,P 是斜边AB 上的一个动点,PD ⊥AB ,交边AC 于点D (点D 与点A 、C 都不重合),E 是射线DC 上一点,且∠EPD =∠A .设A 、P 两点的距离为x ,△BEP 的面积为y .(1)求证:AE =2PE ;(2)求y 关于x 的函数解析式,并写出它的定义域; (3)当△BEP 与△ABC 相似时,求△BEP 的面积.双垂型1、如图,在△ABC 中,∠A=60°,BD 、CE 分别是AC 、AB 上的高 求证:(1)△ABD ∽△ACE ;(2)△ADE ∽△ABC ;(3)BC=2ED2、如图,已知锐角△ABC ,AD 、CE 分别是BC 、AB 边上的高,△ABC 和△BDE 的面积分别是27和3,DE=62,求:点B 到直线AC 的距离。
相似三角形中的 基本模型 (共21张PPT)

连接BE并延长BE交CD的延长线于点F,交AC于点G.
(1)若FD=2,
ED BC
1 3
,求线段DC的长.
ቤተ መጻሕፍቲ ባይዱ
(2)求证:
EF BF
GE GB
.
(2)求证 EF GB BF GE .
AD AE ED AC AB BC
模型二:相交线型
例3 如图,要判断△ADE与△ACB相似,添加一个条件,不正
确的是:(C )
A. ∠ADE=∠C C. AE DE
AB CB
B. ∠AED=∠B D. AE AD
AB AC
模型二:相交线型
例4 如图,EC和BD相交于点A,且∠D=∠C, 则△EDA∽ △ BCA ; AD: AC = AE :AB
△BDC∽△CDA △BDC∽△BCA △CDA∽△BCA
练习4 如图,四边形ABCD中,AD∥BC,∠B=90°,E为
AB上一点,分别以ED、EC为折痕将两个角(∠A、∠B)
向内折起,点A、B恰好落在CD边的点F处,AD=3,BC=5,
则EF的长为
.
练习5. 如图,四边形ABCD中,AD∥BC,点E是边AD的中点,
解:∵四边形ABCD是平行四边形
∴BC∥AD,BC=AD
∴△EDF∽△CBF ∴DF:BF=DE:BC 又∵ DE:BC= DE:AD= 2:5 ∴DF:BF=2:5 而BF=15 cm
∴DF=6 cm
A B
ED F
C
模型二:相交线型
△AED∽△ACB AE AD ED AC AB CB
△AED∽△ABC
例4 如图,△ABC中,∠A=∠DBC,BC=3 ,CD=2,
9
则AC= 2 .
相似三角形的九大模型

相似三角形的九大模型1.在三角形ABC中,已知2.在三角形ABC中,CD为边AB上的高,正方形EFGH 的四个顶点分别在三角形ABC上,证明:111+EF^2=AB^2+BC^2+AC^2.3.在矩形ABCD中,AB=2,BC=3,点E、F、G、H分别在矩形ABCD的各边上,且EF∥HG∥AC,EH∥FG∥BD,则四边形EFGH的周长是10.4.在三角形ABC中,M是AC的中点,E是AB上一点,且BE=3AE,求BC的值。
5.在三角形ABC中,D、E分别为边AB、AC上的点,且∠ADE=∠ACB。
证明:AD×AB=AE×AC。
如果三角形ABC的面积为m,DE=3,BC=5,求三角形ADE的面积。
6.在三角形ABC中,点D、E分别在边AB、AC上,DE、BC的延长线相交于点F,且EF×DF=BF×CF。
证明:AD×AB=AE×AC。
当AB=12,AC=9,AE=8时,求BD的长与△ADE的面积。
7.将三角形纸片△ABC按如图所示的方式折叠,使点C落在AB边上的点D,折痕为EF。
已知AB=AC=3,BC=4,若以点B、D、F为顶点的三角形与△ABC相似,那么CF的长度是2/7.8.将三角形ABC纸片按如图所示的方式折叠,使点B落在边AC上,记为点B',折痕为EF。
已知AB=AC=6,BC=8.求△ABC的周长。
若以点B'、F、C为顶点的三角形与△XXX 相似,求BF的长。
9.在三角形ABC中,AB=6,BC=8.点D以每秒1个单位长度的速度由B向A运动,同时点E以每秒2个单位长度的速度由C向B运动,当点E停止运动时,点D也随之停止。
设运动时间为t秒,当以B、D、E为顶点的三角形与△ABC相似时,求t的值。
10.在锐角三角形ABC中,AG⊥BC于点G,点D、E分别在XXX、AB上,XXX⊥DE于点F,且∠EAF=∠GAC。
证明:△ADE∽△ABC。
模型05 相似三角形中的常见五种基本模型(解析版)

模型探究相似三角形考查范围广,综合性强,其模型种类多,其中有关一线三垂直模型在前面的专题已经很详细的讲解,这里就不在重复.模型一、A字型相似模型A字型(平行)反A字型(不平行)模型二、8字型与反8字型相似模型模型三、AX型相似模型(A字型及X字型两者相结合)模型四、共边角相似模型(子母型)模型五、手拉手相似模型例题精讲考点一、A字相似模型【例1】.如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是()A.B.C.D.解:A、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;B、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错误;C、两三角形的对应边不成比例,故两三角形不相似,故本选项正确.D、两三角形对应边成比例且夹角相等,故两三角形相似,故本选项错误;故选:C.变式训练【变式1-1】.如图,在△ABC中,DE∥BC,AH⊥BC于点H,与DE交于点G.若,则=.解:∵,∴,∵DE∥BC,∴△ADE∽△ABC,∴,故答案为.【变式1-2】.如图,在△ABC中,M是AC的中点,E是AB上一点,AE=AB,连接EM并延长,交BC的延长线于D,则=__________.解:如图,过C点作CP∥AB,交DE于P,∵PC∥AE,∴△AEM∽△CPM,∴=,∵M是AC的中点,∴AM=CM,∴PC=AE,∵AE=AB,∴CP=AB,∴CP=BE,∵CP∥BE,∴△DCP∽△DBE,∴==,∴BD=3CD,∴BC=2CD,即=2.【变式1-3】.如图,在△ABC中,点D在边AB上,AD=9,BD=7.AC=12.△ABC的角平分线AE交CD于点F.(1)求证:△ACD∽△ABC;(2)若AF=8,求AE的长度.解:(1)∵AD=9,BD=7,AC=12,∴AB=AD+BD=16,∵==,==,∴=,∵∠BAC=∠CAD,∴△ACD∽△ABC;(2)由(1)可知,△ACD∽△ABC,∴∠ABE=∠ACF,∵AE平分∠BAC,∴∠BAE=∠CAF,∴△ABE∽△ACF,∴=,即=,∴AE==.考点二、8字与反8字相似模型【例2】.如图,AG∥BD,AF:FB=1:2,BC:CD=2:1,求的值解:∵AG∥BD,∴△AFG∽△BFD,∴=,∵,∴CD=BD,∴,∵AG∥BD,∴△AEG∽△CED,∴.变式训练【变式2-1】.如图,AB∥CD,AE∥FD,AE、FD分别交BC于点G、H,则下列结论中错误的是()A.B.C.D.解:A、∵AB∥CD,∴=,故本选项不符合题目要求;B、∵AE∥DF,∴△CEG∞△CDH,∴=,∴=,∵AB∥CD,∴=,∴=,∴=,∴=,故本选项不符合题目要求;∵AB∥CD,AE∥DF,∴四边形AEDF是平行四边形,∴AF=DE,∵AE∥DF,∴,∴=,故本选项不符合题目要求;D、∵AE∥DF,∴△BFH∞△BAG,∴,故本选项符合题目要求;故选:D.【变式2-2】.如图,在平行四边形ABCD中,E为边AD的中点,连接AC,BE交于点F.若△AEF的面积为2,则△ABC的面积为()A.8B.10C.12D.14解:如图,∵四边形ABCD是平行四边形,∵EA∥BC,∴△AEF∽△CBF,∵AE=DE=AD,CB=AD,∴====,∴AF=AC,EF=BF,=S△ABC,∴S△ABF=S△ABF=×S△ABC=S△ABC,∴S△AEF=2,∵S△AEF=6S△AEF=6×2=12,故选:C.∴S△ABC【变式2-3】.如图,锐角三角形ABC中,∠A=60°,BE⊥AC于E,CD⊥AB于D,则DE:BC=1:2.解:如图,∵在△ADC中,∠A=60°,CD⊥AB于点D,∴∠ACD=30°,∴=.又∵在△ABE中,∠A=60°,BE⊥AC于E,∴∠ABE=30°,∴=,∴=.又∵∠A=∠A,∴△ADE∽△ACB,∴DE:BC=AD:AC=1:2.故答案是:1:2.考点三、AX型相似模型(A字型及X字型两者相结合)【例3】.如图,在△ABC中,点D和E分别是边AB和AC的中点,连接DE,DC与BE交于点O,若△DOE的面积为1,则△ABC的面积为()A.6B.9C.12D.13.5解:∵点D和E分别是边AB和AC的中点,∴O点为△ABC的重心,∴OB=2OE,=2S△DOE=2×1=2,∴S△BOD=3,∴S△BDE∵AD=BD,=2S△BDE=6,∴S△ABE∵AE=CE,=2S△ABE=2×6=12.故选C.∴S△ABC变式训练【变式3-1】.如图,DE是△ABC的中位线,F为DE中点,连接AF并延长交BC于点G,=1,则S△ABC=24.若S△EFG解:方法一:∵DE是△ABC的中位线,∴D、E分别为AB、BC的中点,如图过D作DM∥BC交AG于点M,∵DM∥BC,∴∠DMF=∠EGF,∵点F为DE的中点,∴DF=EF,在△DMF和△EGF中,,∴△DMF≌△EGF(AAS),=S△EGF=1,GF=FM,DM=GE,∴S△DMF∵点D为AB的中点,且DM∥BC,∴AM=MG,∴FM=AM,=2S△DMF=2,∴S△ADM∵DM为△ABG的中位线,∴=,=4S△ADM=4×2=8,∴S△ABG=S△ABG﹣S△ADM=8﹣2=6,∴S梯形DMGB=S梯形DMGB=6,∴S△BDE∵DE是△ABC的中位线,=4S△BDE=4×6=24,∴S△ABC方法二:连接AE,∵DE是△ABC的中位线,∴DE∥AC,DE=AC,∵F是DE的中点,∴=,∴==,=1,∵S△EFG=16,∴S△ACG∵EF∥AC,∴==,∴==,=S△ACG=4,∴S△AEG=S△ACG﹣S△AEG=12,∴S△ACE=2S△ACE=24,故答案为:24.∴S△ABC【变式3-2】.如图:AD∥EG∥BC,EG交DB于点F,已知AD=6,BC=8,AE=6,EF =2.(1)求EB的长;(2)求FG的长.解:(1)∵EG∥AD,∴△BAD∽△BEF,∴=,即=,∴EB=3.(2)∵EG∥∥BC,∴△AEG∽△ABC,∴=,即=,∴EG=,∴FG=EG﹣EF=.【变式3-3】.如图,已知AB∥CD,AC与BD相交于点E,点F在线段BC上,,.(1)求证:AB∥EF;:S△EBC:S△ECD.(2)求S△ABE(1)证明:∵AB∥CD,∴==,∵,∴=,∴EF∥CD,∴AB∥EF.(2)解:设△ABE的面积为m.∵AB∥CD,∴△ABE∽△CDE,∴=()2=,=4m,∴S△CDE∵==,=2m,∴S△BEC:S△EBC:S△ECD=m:2m:4m=1:2:4.∴S△ABE模型四、子母型相似模型【例4】.如图,点C,D在线段AB上,△PCD是等边三角形,且∠APB=120°,求证:(1)△ACP∽△PDB,(2)CD2=AC•BD.证明:(1)∵△PCD是等边三角形,∴∠PCD=∠PDC=∠CPD=60°,∴∠ACP=∠PDB=120°,∵∠APB=120°,∴∠APC+∠BPD=60°,∵∠CAP+∠APC=60°∴∠BPD=∠CAP,∴△ACP∽△PDB;(2)由(1)得△ACP∽△PDB,∴,∵△PCD是等边三角形,∴PC=PD=CD,∴,∴CD2=AC•BD.变式训练【变式4-1】.如图,点P在△ABC的边AC上,要判断△ABP∽△ACB,添加一个条件,不正确的是()A.∠ABP=∠C B.∠APB=∠ABC C.D.解:在△ABP和△ACB中,∠BAP=∠CAB,∴当∠ABP=∠C时,满足两组角对应相等,可判断△ABP∽△ACB,故A正确;当∠APB=∠ABC时,满足两组角对应相等,可判断△ABP∽△ACB,故B正确;当时,满足两边对应成比例且夹角相等,可判断△ABP∽△ACB,故C正确;当时,其夹角不相等,则不能判断△ABP∽△ACB,故D不正确;故选:D.【变式4-2】.如图,在△ABC中,点D在AC边上,连接BD,若∠ABC+∠BDC=180°,AD=2,CD=4,则AB的长为()A.3B.4C.D.2解:∵∠ABC+∠BDC=180°,∠ADB+∠BDC=180°,∴∠ADB=∠ABC,∵∠A=∠A,∴△ABC∽△ADB,∴,∵AD=2,CD=4,∴,∴AB2=12,∴AB=2或﹣2(不合题意,舍去),故选:D.【变式4-3】.如图,边长为4的正方形,内切圆记为圆O,P为圆O上一动点,则PA+PB的最小值为2.解:设⊙O半径为r,OP=r=BC=2,OB=r=2,取OB的中点I,连接PI,∴OI=IB=,∵,,∴,∠O是公共角,∴△BOP∽△POI,∴,∴PI=PB,∴AP+PB=AP+PI,∴当A、P、I在一条直线上时,AP+PB最小,作IE⊥AB于E,∵∠ABO=45°,∴IE=BE=BI=1,∴AE=AB﹣BE=3,∴AI==,∴AP+PB最小值=AI=,∵PA+PB=(PA+PB),∴PA+PB的最小值是AI==2.故答案是2.模型五、手拉手相似模型【例5】.如图,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为.解:连接OA、OD,∵△ABC与△DEF均为等边三角形,O为BC、EF的中点,∴AO⊥BC,DO⊥EF,∠EDO=30°,∠BAO=30°,∴OD:OE=OA:OB=:1,∵∠DOE+∠EOA=∠BOA+∠EOA即∠DOA=∠EOB,∴△DOA∽△EOB,∴OD:OE=OA:OB=AD:BE=:1=,故答案为:.变式训练【变式5-1】.如图,在△ABC与△ADE中,∠BAC=∠DAE,∠ABC=∠ADE.求证:(1)△BAC∽△DAE;(2)△BAD∽△CAE.证明:(1)∵∠BAC=∠DAE,∠ABC=∠ADE.∴△BAC∽△DAE;(2)∵△BAC∽△DAE,∴,∴,∵∠BAC=∠DAE,∴∠BAD=∠CAE,∴△BAD∽△CAE.【变式5-2】.如图,点D是△ABC内一点,且∠BDC=90°,AB=2,AC=,∠BAD=∠CBD=30°,AD=.解:如图,过点A作AB的垂线,过点D作AD的垂线,两垂线交于点M,连接BM,∵∠BAD=30°,∴∠DAM=60°,∴∠AMD=30°,∴∠AMD=∠DBC,又∵∠ADM=∠BDC=90°,∴△BDC∽△MDA,∴,又∠BDC=∠MDA,∴∠BDC+∠CDM=∠ADM+∠CDM,即∠BDM=∠CDA,∴△BDM∽△CDA,∴=,∵AC=,∴BM=3,在Rt△ABM中,AM===,∴AD=AM=.【变式5-3】.如图,在四边形ABCD中,AE⊥BC,垂足为E,∠BAE=∠ADC,BE=CE=2,CD=5,AD=kAB(k为常数),则BD的长为.(用含k的式子表示)解:如图中,∵AE⊥BC,BE=EC,∴AB=AC,将△ABD绕点A逆时针旋转得到△ACG,连接DG.则BD=CG,∵∠BAD=∠CAG,∴∠BAC=∠DAG,∵AB=AC,AD=AG,∴∠ABC=∠ACB=∠ADG=∠AGD,∴△ABC∽△ADG,∵AD=kAB,∴DG=kBC=4k,∵∠BAE+∠ABC=90°,∠BAE=∠ADC,∴∠ADG+∠ADC=90°,∴∠GDC=90°,∴CG==.∴BD=CG=,故答案为:.实战演练1.如图,已知DE∥BC,EF∥AB,则下列比例式中错误的是()A.=B.C.D.解:A、∵EF∥AB,∴=,∵DE∥BC,∴=,∴=,故A正确,B、易知△ADE∽△EFC,∴=,∴=,故B正确.C、∵△CEF∽△CAB,∴=,∴=,故C正确.D、∵DE∥BC,∴=,显然DE≠CF,故D错误.故选:D.2.如图,梯形ABCD中,AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为()A.2:3B.2:5C.4:9D.:解:∵AD∥BC,∴∠ACB=∠DAC又∵∠B=∠ACD=90°,∴△CBA∽△ACD===,∵=()2=∴△ABC与△DCA的面积比为4:9.故选:C.3.如图,菱形ABCD中,E点在BC上,F点在CD上,G点、H点在AD上,且AE∥HC ∥GF.若AH=8,HG=5,GD=4,则下列选项中的线段,何者长度最长?()A.CF B.FD C.BE D.EC解:∵AH=8,HG=5,GD=4,∴AD=8+5+4=17,∵四边形ABCD为菱形,∴BC=CD=AD=17,∵AE∥HC,AD∥BC,∴四边形AECH为平行四边形,∴CE=AH=8,∴BE=BC﹣CE=17﹣8=9,∵HC∥GF,∴=,即=,解得:DF=,∴FC=17﹣=,∵>9>8>,∴CF长度最长,故选:A.4.如图,在△ABC中,BC=6,E,F分别是AB,AC的中点,动点P在射线EF上,BP 交CE于点D,∠CBP的平分线交CE于点Q,当CQ=CE时,EP+BP的值为()A.6B.9C.12D.18解:如图,延长BQ交射线EF于M,∵E、F分别是AB、AC的中点,∴EF∥BC,∴∠M=∠CBM,∵BQ是∠CBP的平分线,∴∠PBM=∠CBM,∴∠M=∠PBM,∴BP=PM,∴EP+BP=EP+PM=EM,∵CQ=CE,∴EQ=2CQ,由EF∥BC得,△MEQ∽△BCQ,∴=2,∴EM=2BC=2×6=12,即EP+BP=12.故选:C.5.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,AB=2,AD=2,将△ABC绕点C顺时针方向旋转后得△A′B′C,当A′B′恰好经过点D时,△B′CD为等腰三角形,若BB′=2,则AA′等于()A.B.2C.D.解:过D作DE⊥BC于E,则BE=AD=2,DE=2,设B′C=BC=x,则DC=x,∴DC2=DE2+EC2,即2x2=28+(x﹣2)2,解得:x=4(负值舍去),∴BC=4,AC=,∵将△ABC绕点C顺时针方向旋转后得△A′B′C,∴∠DB′C=∠ABC=90°,B′C=BC,A′C=AC,∠A′CA=∠B′CB,∴∴△A′CA∽△B′CB,∴,即∴AA′=,故选:A.6.如图,已知,△ABC中边AB上一点P,且∠ACP=∠B,AC=4,AP=2,则BP=6.解:∵∠A=∠A,∠ACP=∠B,∴△ACP∽△ABC,∴AC2=AP•AB,即AB=AC2÷AP=16÷2=8,∴BP=AB﹣AP=6.7.如图,在▱ABCD中,AC、BD相交于点O,点E是OA的中点,联结BE并延长交AD 于点F,如果△AEF的面积是4,那么△BCE的面积是36.解:∵在▱ABCD中,AO=AC,∵点E是OA的中点,∴AE=CE,∵AD∥BC,∴△AFE∽△CBE,∴==,=4,=()2=,∵S△AEF=36,故答案为36.∴S△BCE8.如图,在△ABC中,点G为ABC的重心,过点G作DE∥AC分别交边AB、BC于点D、E,过点D作DF∥BC交AC于点F,如果DF=4,那么BE的长为8.解:连接BG并延长交AC于H,∵G为ABC的重心,∴=2,∵DE∥AC,DF∥BC,∴四边形DECF是平行四边形,∴CE=DF=4,∵GE∥CH,∴△BEG∽△CBH,∴=2,∴BE=8,故答案为:8.9.如图,已知Rt△ABC中,两条直角边AB=3,BC=4,将Rt△ABC绕直角顶点B旋转一定的角度得到Rt△DBE,并且点A落在DE边上,则sin∠ABE=.解:∵将Rt△ABC绕直角顶点B旋转一定的角度得到Rt△DBE,∴BD=AB,BC=BE,∠ABD=∠CBE,∠DEB=∠ACB,∴∠D=∠BAC=∠BAD=(180°﹣∠ABD),∴∠BEC=(180°﹣∠CBE),∴∠D=∠BEC,∵∠ABC=∠DBE=90°,∴∠DEB+∠BEC=90°,∴∠AEC=90°,∵∠AGB=∠EGC,∴∠ACE=∠ABE,∵在Rt△ABC中,AB=3,BC=4,∴AC=DE=5,过B作BH⊥DE于H,则DH=AH,BD2=DH•DE,∴DH==,∴AD=,∴AE=DE﹣AD=,∴sin∠ABE=sin∠ACE===,故答案为:.10.如图,在Rt△ABC中,∠ACB=90°,∠BAC=60°,AC=6,AD平分∠BAC,交边BC于点D,过点D作CA的平行线,交边AB于点E.(1)求线段DE的长;(2)取线段AD的中点M,联结BM,交线段DE于点F,延长线段BM交边AC于点G,求的值.解:(1)∵AD平分∠BAC,∠BAC=60°,∴∠DAC=30°,在Rt△ACD中,∠ACD=90°,∠DAC=30°,AC=6,∴CD=2,在Rt△ACB中,∠ACB=90°,∠BAC=60°,AC=6,∴BC=6,∴BD=BC﹣CD=4,∵DE∥CA,∴,∴DE=4;(2)如图,∵点M是线段AD的中点,∴DM=AM,∵DE∥CA,∴,∴DF=AG,∵DE∥CA,∴,∴,∵BD=4,BC=6,DF=AG,∴.11.如图,在菱形ABCD中,∠ADE、∠CDF分别交BC、AB于点E、F,DF交对角线AC 于点M,且∠ADE=∠CDF.(1)求证:CE=AF;(2)连接ME,若=,AF=2,求ME的长.解:(1)∵四边形ABCD是菱形,∴AD=CD,∠DAF=∠DCE,又∵∠ADE=∠CDF,∴∠ADE﹣∠EDF=∠CDF﹣∠EDF,∴∠ADF=∠CDE,在△ADF和△CDE中,,∴△ADF≌△CDE,∴CE=AF.(2)∵四边形ABCD是菱形,∴AB=BC,由(1)得:CE=AF=2,∴BE=BF,设BE=BF=x,∵=,AF=2,∴,解得x=,∴BE=BF=,∵=,且CE=AF,∴==,∵∠CMD=∠AMF,∠DCM=∠AMF,∴△AMF∽△CMD,∴,∴=,且∠ACB=∠ACB∴△ABC∽△MEC∴∠CAB=∠CME=∠ACB∴ME=CE=212.[问题背景](1)如图①,已知△ABC∽△ADE,求证:△ABD∽△ACE.[尝试应用](2)如图②,在△ABC和△ADE中,∠BAC=∠DAE=90°∠ABC=∠ADE=30°,AC与DE相交于点F,点D在BC边上,=,①填空:=1;②求的值.(1)证明:如图①,∵△ABC∽△ADE,∴∠BAC=∠DAE,=,∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,=,∴∠BAD=∠CAE,∴△ABD∽△ACE.(2)解:①如图②,∵∠DAE=90°,∠ADE=30°,∴DE=2AE,∴AD===AE,∵=,∴AD=BD,∴AE=BD,∴=1,故答案为:1.②如图②,连接CE,∵∠BAC=∠DAE=90°,∠ABC=∠ADE,∴△BAC∽△CAE,∴=,∴=,∵∠BAD=∠CAE=90°﹣∠CAD,∴△BAD∽△CAE,∴∠ABC=∠ACE,∴∠ADE=∠ACE,∵∠AFD=∠EFC,∴△AFD∽△EFC,∴=,由①得AD=AE,AD=BD,∴==,∴BD=CE,∴AD=×CE=3CE,∴=3,∴=3,∴的值是3.13.如图,在正方形ABCD中,AB=4,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于点M、N,连接EN、EF.(1)求证:△ABN∽△MBE;(2)求证:BM2+ND2=MN2;(3)①求△CEF的周长;②若点G、F分别是EF、CD的中点,连接NG,则NG的长为.(1)证明:如图1,∵四边形ABCD是正方形,∴AB=AD,∠BAD=∠ABC=90°,∴∠ABD=∠ADB=45°,∴∠ABN=∠MBE=45°,∠BME=∠ABD+∠BAM=45°+∠BAM,∵∠EAF=45°,∴∠BAN=∠EAF+∠BAM=45°+∠BAM,∴∠BAN=∠BME,∴△ABN∽△MBE.(2)证明:如图1,将△ADN绕点A顺时针旋转90°得到△ABH,连接MH,∴∠BAH=∠DAN,AH=AN,HB=ND,∵∠MAN=∠EAF=45°,∴∠MAH=∠BAH+∠BAM=∠DAN+∠BAM=45°,∴∠MAH=∠MAN,∵AM=AM,∴△MAH≌△MAN(SAS),∴MH=MN,∵∠ABH=∠ADN=45°,∴∠MBH=∠ABD+∠ABH=90°,∴BM2+HB2=MH2,∴BM2+ND2=MN2.(3)解:①如图2,将△ADF绕点A顺时针旋转90°得到△ABK,∴AK=AF,∠BAK=∠DAF,BK=DF,∠ABK=∠ADF=90°,∴∠ABK+∠ABE=180°,∴点K、点B、点E在同一条直线上,∵∠EAK=∠BAE+∠BAK=∠BAE+∠DAF=45°,∴∠EAK=∠EAFM,∵AE=AE,∴△EAK≌△EAF(SAS),∴EK=EF,∴BE+DF=BE+BK=EK=EF,∵CB=CD=AB=4,∴CE+EF+CF=CE+BE+DF+CF=CB+CD=4+4=8,∴△CEF的周长是8.②如图2,∵F是CD的中点,∴CF=DF=CD=2,∵∠C=90°,∴CF2+EF2=CE2,∵EF=BE+DF=BE+2,CE=CB﹣BE=4﹣BE,∴22+(4﹣BE)2=(BE+2)2,解得BE=,∴EF=+2=,∵∠MBE=∠MAN=45°,∠BME=∠AMN,∴△BME∽△AMN,∴=,∴=,∴∠AMB=∠NME,∴△AMB∽△NME,∴∠NEM=∠ABM=45°,∴∠ENF=∠MAN+∠NEM=90°,∵G是EF的中点,∴NG=EF=×=,故答案为:.14.问题背景如图(1),已知△ABC∽△ADE,求证:△ABD∽△ACE;尝试应用如图(2),在△ABC和△ADE中,∠BAC=∠DAE=90°,∠ABC=∠ADE=30°,AC与DE相交于点F,点D在BC边上,=,求的值;拓展创新如图(3),D是△ABC内一点,∠BAD=∠CBD=30°,∠BDC=90°,AB =4,AC=2,直接写出AD的长.问题背景证明:∵△ABC∽△ADE,∴,∠BAC=∠DAE,∴∠BAD=∠CAE,,∴△ABD∽△ACE;尝试应用解:如图1,连接EC,∵∠BAC=∠DAE=90°,∠ABC=∠ADE=30°,∴△ABC∽△ADE,由(1)知△ABD∽△ACE,∴,∠ACE=∠ABD=∠ADE,在Rt△ADE中,∠ADE=30°,∴,∴=3.∵∠ADF=∠ECF,∠AFD=∠EFC,∴△ADF∽△ECF,∴=3.拓展创新解:如图2,过点A作AB的垂线,过点D作AD的垂线,两垂线交于点M,连接BM,∵∠BAD=30°,∴∠DAM=60°,∴∠AMD=30°,∴∠AMD=∠DBC,又∵∠ADM=∠BDC=90°,∴△BDC∽△MDA,∴,又∠BDC=∠MDA,∴∠BDC+∠CDM=∠ADM+∠CDM,即∠BDM=∠CDA,∴△BDM∽△CDA,∴,∵AC=2,∴BM=2=6,∴在Rt△ABM中,AM===2,∴AD=.15.如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:(1)①猜想如图1中线段BG、线段DE的数量关系BG=DE及所在直线的位置关系BG⊥DE;②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2,如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断;(2)将原题中正方形改为矩形(如图4﹣6),且AB=a,BC=b,CE=ka,CG=kb(a≠b,k>0),则线段BG、线段DE的数量关系=及所在直线的位置关系BG ⊥DE;(3)在第(2)题图5中,连接DG、BE,且a=4,b=3,k=,直接写出BE2+DG2的值为.解:(1)①猜想:BG ⊥DE ,BG =DE ;故答案为:BG =DE ,BG ⊥DE ;②结论成立.理由:如图2中,∵四边形ABCD 和四边形CEFG 是正方形,∴BC =DC ,CG =CE ,∠BCD =∠ECG =90°,∴∠BCG =∠DCE ,∴△BCG ≌△DCE (SAS ),∴BG =DE ,∠CBG =∠CDE ,又∵∠CBG +∠BHC =90°,∴∠CDE +∠DHG =90°,∴BG ⊥DE .(2)∵AB =a ,BC =b ,CE =ka ,CG =kb ,∴==,又∵∠BCG =∠DCE ,∴△BCG ∽△DCE ,∴∠CBG =∠CDE ,==,又∵∠CBG +∠BHC =90°,∴∠CDE +∠DHG =90°,∴BG⊥DE.故答案为:=,BG⊥DE.(3)连接BE、DG.根据题意,得AB=4,BC=3,CE=2,CG=1.5,∵BG⊥DE,∠BCD=∠ECG=90°∴BE2+DG2=BO2+OE2+DO2+OG2=BC2+CD2+CE2+CG2=9+16+2.25+4=.。
相似三角形典型模型及例题

1:相似三角形模型一:相似三角形判定的基本模型 (一)A 字型、反A 字型(斜A 字型)(平行)(不平行)(二)8字型、反8字型JOADBCAB CD(蝴蝶型)(平行)(不平行)(三)母子型(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景,一个与等腰三角形的底角相等的顶点在底边所在的直线上,角的两边分别与等腰三角形的两边相交如图所示:(五)一线三直角型:三直角相似可以看着是“一线三等角”中当角为直角时的特例,三直角型相似通常是以矩形或者正方形形为背景,或者在一条直线上有一个顶点在该直线上移动或者旋转的直角,几种常见的基本图形如下:当题目的条件中只有一个或者两个直角时,就要考虑通过添加辅助线构造完整的三直角型相似,这往往是很多压轴题的突破口,进而将三角型的条件进行转化。
(六)双垂型:二:相似三角形判定的变化模型旋转型:由A 字型旋转得到8字型拓展共享性GABC EF一线三等角的变形一线三直角的变形2:相似三角形典型例题(1)母子型相似三角形例1:如图,梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点O ,BE ∥CD 交CA 延长线于E . 求证:OE OA OC ⋅=2.例2:已知:如图,△ABC 中,点E 在中线AD 上,ABC DEB ∠=∠. 求证:(1)DA DE DB ⋅=2;(2)DAC DCE ∠=∠.例3:已知:如图,等腰△ABC 中,AB =AC ,AD ⊥BC 于D ,CG ∥AB ,BG 分别交AD 、AC 于E 、F . 求证:EG EF BE ⋅=2.1、如图,已知AD 为△ABC 的角平分线,EF 为AD 的垂直平分线.求证:FC FB FD ⋅=2.2、已知:AD 是Rt △ABC 中∠A 的平分线,∠C=90°,EF 是AD 的垂直平分线交AD 于M ,EF 、BC 的延长线交于一点N 。
求证:(1)△AME ∽△NMD;(2)ND 2=NC·NB3、已知:如图,在△ABC 中,∠ACB=90°,CD ⊥AB 于D ,E 是AC 上一点,CF ⊥BE 于F 。
(完整版)相似三角形模型分析大全(非常全面-经典)
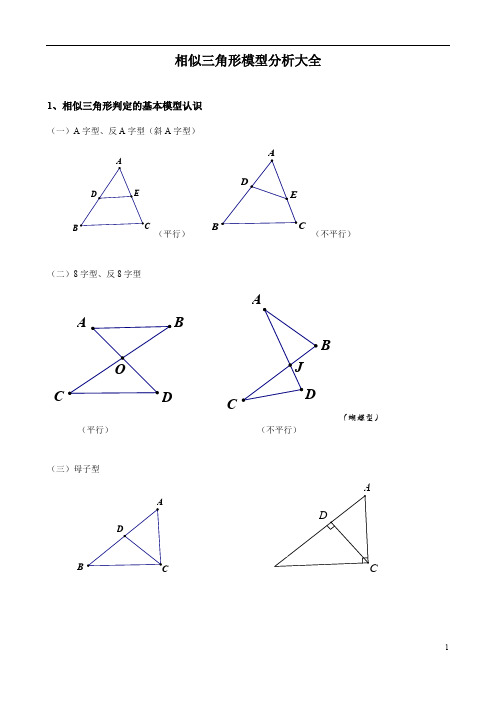
相似三角形模型分析大全1、相似三角形判定的基本模型认识(一)A字型、反A字型(斜A字型)B(平行)B(不平行)(二)8字型、反8字型BCBC(蝴蝶型)(平行)(不平行)(三)母子型B(四)一线三等角型:三等角型相似三角形是以等腰三角形(等腰梯形)或者等边三角形为背景(五)一线三直角型:(6)双垂型:2、相似三角形判定的变化模型旋转型:由A 字型旋转得到。
8字型拓展B一线三等角的变形一线三直角的变形第二部分 相似三角形典型例题讲解母子型相似三角形例1:如图,梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点O ,BE ∥CD 交CA 延长线于E .求证:.OE OA OC ⋅=2例2:已知:如图,△ABC 中,点E 在中线AD 上, .ABC DEB ∠=∠求证:(1); (2).DA DE DB ⋅=2DAC DCE ∠=∠ACDEB例3:已知:如图,等腰△ABC 中,AB =AC ,AD ⊥BC 于D ,CG ∥AB ,BG 分别交AD 、AC 于E 、F .求证:.EG EF BE ⋅=2相关练习:1、如图,已知AD 为△ABC 的角平分线,EF 为AD 的垂直平分线.求证:.FC FB FD ⋅=22、已知:AD 是Rt△ABC 中∠A 的平分线,∠C=90°,EF 是AD 的垂直平分线交AD 于M ,EF 、BC 的延长线交于一点N 。
求证:(1)△AME∽△NMD; (2)ND =NC·NB23、已知:如图,在△ABC中,∠ACB=90°,CD⊥AB于D,E是AC上一点,CF⊥BE于F。
求证:EB·DF=AE·DB⊥,垂足为F,延长AD到G,使DG=EF,M是AH的中点。
4.在∆ABC中,AB=AC,高AD与BE交于H,EF BCGBM90求证:∠=︒5.(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)已知:如图,在Rt△ABC 中,∠C =90°,BC =2,AC =4,P 是斜边AB 上的一个动点,PD ⊥AB ,交边AC于点D (点D 与点A 、C 都不重合),E 是射线DC 上一点,且∠EPD =∠A .设A 、P 两点的距离为x ,△BEP 的面积为y .(1)求证:AE =2PE ;(2)求y 关于x 的函数解析式,并写出它的定义域;(3)当△BEP 与△ABC 相似时,求△BEP 的面积.双垂型1、如图,在△ABC 中,∠A=60°,BD 、CE 分别是AC 、AB 上的高A(第25题图)求证:(1)△ABD∽△ACE;(2)△ADE∽△ABC;(3)BC=2ED2、如图,已知锐角△ABC ,AD 、CE 分别是BC 、AB 边上的高,△ABC 和△BDE 的面积分别是27和3,DE=6,求:点B 到直线AC 的距离。
相似三角形的九大模型

相似三角形的九大模型相似三角形是几何学中一类重要的图形,它具有一些独特的性质和模型。
这些模型可以用来解决各种实际问题,从简单的长度关系到复杂的空间结构。
本文将介绍相似三角形的九大模型,并给出相应的例子和应用场景。
相似三角形是指两个三角形形状相同,大小成比例。
相似三角形的对应边成比例,对应角相等。
相似三角形还有一些其他的性质,例如,相似三角形的中线、角平分线、高的比等于它们的相似比。
平行线模型:两个三角形分别在两条平行线上,它们的对应边平行且成比例。
这种模型经常用于解决一些与长度和角度相关的问题。
共顶点模型:两个三角形有一个共同的顶点,且它们的对应边成比例。
这种模型常用于证明两个三角形相似,以及求解一些角度问题。
角平分线模型:一个三角形的角平分线将这个三角形分成两个小的相似三角形。
这种模型可以用于证明两个三角形相似,以及求解一些角度问题。
平行四边形模型:一个平行四边形被它的两条对角线分成四个小的相似三角形。
这种模型可以用于解决一些与面积和长度相关的问题。
位似模型:一个相似变换将一个三角形映射到另一个三角形,这种变换称为位似变换。
这种模型可以用于解决一些与长度、角度和面积相关的问题。
旋转模型:一个三角形绕着它的一个顶点旋转一定的角度后得到另一个三角形,这两个三角形是相似的。
这种模型可以用于解决一些与角度和长度相关的问题。
镜像模型:一个三角形沿一条直线翻折后得到另一个三角形,这两个三角形是相似的。
这种模型可以用于解决一些与长度和角度相关的问题。
传递模型:如果一个三角形与另一个三角形相似,那么这个三角形的每一个部分都与另一个三角形的对应部分相似。
这种模型可以用于解决一些与长度和角度相关的问题。
扩展模型:如果一个三角形与另一个三角形相似,那么这个三角形的每一个部分都与另一个三角形的对应部分成比例。
这种模型可以用于解决一些与长度和角度相关的问题。
相似三角形的九创作者是几何学中一类重要的模型,它们具有广泛的应用价值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一部分相似三角形模型分析一、相似三角形判定的基本模型认识(一)A字型、反A字型(斜A字型)(平行)B(不平行)(二)8字型、反8字型BCBC(蝴蝶型)(平行)(不平行)(三)母子型(四)一线三等角型:(五)一线三直角型:(六)双垂型:二、相似三角形判定的变化模型旋转型:由A 字型旋转得到。
8字型拓展CB EDA共享性GABCEF一线三等角的变形一线三直角的变形第二部分 相似三角形典型例题讲解母子型相似三角形例1:如图,梯形ABCD 中,AD ∥BC ,对角线AC 、BD 交于点O ,BE ∥CD 交CA 延长线于E . 求证:OE OA OC ⋅=2.例2:已知:如图,△ABC 中,点E 在中线AD 上, ABC DEB ∠=∠.求证:(1)DA DE DB ⋅=2; (2)DAC DCE ∠=∠.例3:已知:如图,等腰△ABC 中,AB =AC ,AD ⊥BC 于D ,CG ∥AB ,BG 分别交AD 、AC 于E 、F .求证:EG EF BE ⋅=2.相关练习:1、如图,已知AD 为△ABC 的角平分线,EF 为AD 的垂直平分线.求证:FC FB FD ⋅=2.2、已知:AD 是Rt △ABC 中∠A 的平分线,∠C=90°,EF 是AD 的垂直平分线交AD 于M ,EF 、BC 的延长线交于一点N 。
求证:(1)△AME ∽△NMD; (2)ND 2=NC ·NB3、已知:如图,在△ABC 中,∠ACB=90°,CD ⊥AB 于D ,E 是AC 上一点,CF ⊥BE 于F 。
求证:EB ·DF=AE ·DB4.在∆ABC 中,AB=AC ,高AD 与BE 交于H ,EF BC ⊥,垂足为F ,延长AD 到G ,使DG=EF ,M 是AH的中点。
求证:∠=︒GBM 905.(本题满分14分,第(1)小题满分4分,第(2)、(3)小题满分各5分)已知:如图,在Rt △ABC 中,∠C =90°,BC =2,AC =4,P 是斜边AB 上的一个动点,PD ⊥AB ,交边AC 于点D (点D 与点A 、C 都不重合),E 是射线DC上一点,且∠EPD =∠A .设A 、P 两点的距离为x ,△BEP 的面积为y .(1)求证:AE =2PE ;(2)求y 关于x 的函数解析式,并写出它的定义域;(3)当△BEP 与△ABC 相似时,求△BEP 的面积.双垂型1、如图,在△ABC 中,∠A=60°,BD 、CE 分别是AC 、AB 上的求证:(1)△ABD ∽△ACE ;(2)△ADE ∽△ABC ;(3)BC=2ED2、如图,已知锐角△ABC ,AD 、CE 分别是BC 、AB 边上的高,△和3,DE=62,求:点B 到直线AC 的距离。
共享型相似三角形1、△ABC 是等边三角形,D 、B 、C 、E 在一条直线上,∠DAE=︒120,已知BD=1,CE=3,,求等边三角形的边长.ACD ED2、已知:如图,在Rt△ABC 中,AB =AC ,∠DAE =45°.求证:(1)△ABE ∽△ACD ; (2)CD BE BC ⋅=22.一线三等角型相似三角形例1:如图,等边△ABC 中,边长为6,D 是BC 上动点,∠EDF =60°(1)求证:△BDE ∽△CFD(2)当BD =1,FC =3时,求BE例2:(1)在ABC ∆中,5==AC AB ,8=BC ,点P 、Q 分别在射线CB 、AC 上(点P 不与点C 、点B 重合),且保持ABC APQ ∠=∠.①若点P 在线段CB 上(如图),且6=BP ,求线段CQ 的长;②若x BP =,y CQ =,求y 与x 之间的函数关系式,并写出函数的定义域;(2)正方形ABCD 的边长为5(如下图),点P 、Q 分别在直线..CB 、DC 点B 重合),且保持︒=∠90APQ .当1=CQ 时,求出线段BP例3:已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且AD=5,AB =DC =2.(1)如图8,P 为AD 上的一点,满足∠BPC =∠A .①求证;△ABP ∽△DPC②求AP 的长.(2)如果点P 在AD 边上移动(点P 与点A 、D 不重合),且满足∠BPE =∠A ,PE 交直线BC 于点E ,同时交直线DC 于点Q ,那么①当点Q 在线段DC 的延长线上时,设AP =x ,CQ =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当CE =1时,写出AP 的长.例4:如图,在梯形ABCD 中,AD ∥BC ,6AB CD BC ===,3AD =.点M 为边BC 的中点,以M 为顶点作EMF B ∠=∠,射线ME 交腰AB 于点E ,射线MF 交腰CD 于点F ,联结EF .(1)求证:△MEF ∽△BEM ;(2)若△BEM 是以BM 为腰的等腰三角形,求EF 的长;(3)若EF CD ⊥,求BE 的长.相关练习:C1、如图,在△ABC 中,8==AC AB ,10=BC ,D 是BC 边上的一个动点,点E 在AC 边上,且C ADE ∠=∠.(1) 求证:△ABD ∽△DCE ;(2) 如果x BD =,y AE =,求y 与x 的函数解析式,并写出自变量x 的定义域;(3) 当点D 是BC 的中点时,试说明△ADE 是什么三角形,并说明理由.2、如图,已知在△ABC 中, AB =AC =6,BC =5,D 是AB 上一点,BD =2,E 是BC 上一动点,联结DE ,并作DEF B ∠=∠,射线EF 交线段AC 于F .(1)求证:△DBE ∽△ECF ; (2)当F 是线段AC 中点时,求线段BE 的长;(3)联结DF ,如果△DEF 与△DBE 相似,求FC 的长.3、已知在梯形ABCD 中,AD ∥BC ,AD <BC ,且BC =6,AB =DC =4,点E 是AB 的中点.(1)如图,P 为BC 上的一点,且BP =2.求证:△BEP ∽△CPD ;(2)如果点P 在BC 边上移动(点P 与点B 、C 不重合),且满足∠EPF =∠C ,PF 交直线CD于点F ,同时交直线AD 于点M ,那么①当点F 在线段CD 的延长线上时,设BP =x ,DF =y ,求y 关于x 的函数解析式,并写出函数的定义域;②当BEP DMF S S ∆∆=49时,求BP 的长. BC4、如图,已知边长为3的等边ABC ∆,点F 在边BC 上,1CF =,点E 是射线BA 上一动点,以线段EF 为边向右侧作等边EFG ∆,直线,EG FG 交直线AC 于点,M N ,(1)写出图中与BEF ∆相似的三角形;(2)证明其中一对三角形相似;(3)设,BE x MN y ==,求y 与x 之间的函数关系式,并写出自变量x 的取值范围; (4)若1AE =,试求GMN ∆的面积.例1、已知矩形ABCD 中,CD=2,AD=3,点P 是AD 上的一个动点,且和点A,D 不重合,过点P 作CP PE ⊥,交边AB 于点E,设y AE x PD ==,,求y 关于x 的函数关系式,并写出x 的取值范围。
例2、在ABC ∆中,O BC AC C ,3,4,90===∠o 是AB 上的一点,且52=AB AO ,点P 是AC 上的一个动点,OP PQ ⊥交线段BC 于点Q ,(不与点B,C 重合),设y CQ x AP ==,,试求y 关于x 的函数关系,并写出定义域。
【练习1】BC 的在直角ABC ∆中,43tan ,5,90===∠B AB C o ,点D 是中点,点E 是AB 边上的动点,DE DF ⊥交射线AC 于点F(1)、求AC 和BC 的长B(2)、当BC EF //时,求BE 的长。
(3)、连结EF,当DEF ∆和ABC ∆相似时,求BE 的长。
【练习2】在直角三角形ABC 中,D BC AB C ,,90==∠o 是AB 边上的一点,E 是在AC 边上的一个动点,(与A,C 不重合),DF DE DF ,⊥与射线BC 相交于点F.(1)、当点D 是边AB 的中点时,求证:DF DE =(2)、当m DBAD=,求DF DE 的值(3)、当21,6===DB AD BC AC ,设y BF x AE ==,,求y 关于x 的函数关系式,并写出定义域 【 练习4】]如图,在ABC ∆中,90C ∠=︒,6AC =,3tan 4B =,D 是BC 边的中点,E 为AB 边上的一个动点,作90DEF ∠=︒,EF 交射线BC 于点F .设BE x =,BED ∆的面积为y .(1)求y 关于x 的函数关系式,并写出自变量x 的取值范围;(2)如果以B 、E 、F 为顶点的三角形与BED ∆相似,求BED ∆的面积.【 练习5】、(2015年黄浦一模25)如图,在梯形ABCD 中,CD AB , 34tan ,4,2===C AD AB ,P DAB ADC ,900=∠=∠是腰BC 上一个动点(不含点B 、C ),作AP PQ ⊥交CD 于点Q .(图1)(1)求BC 的长与梯形ABCD 的面积;(2)当DQ PQ =时,求BP 的长;(图2)(3)设y CQ x BP ==,,试求y 关于x 的函数解析式,并写出定义域.(图1) (图2)。
