霍普金森杆实验技术简介
霍普金森杆实验技术经验简介

霍普金森杆实验技术简介1.材料动态力学性能实验简史在各类工程技术、军事技术和科学研究等广泛领域的一系列实际问题中,甚至就在日常生活中,人们都会遇到各种各样的爆炸/冲击载荷问题,并且可以观察到,物体在爆炸/冲击载荷下的力学响应往往与静载荷下的有显着不同。
了解材料在冲击加载条件下的力学响应必将大大有助于这些材料的工程应用和工程设计。
此外,数值模拟已在工程设计中发挥着重要作用,而进行数值模拟的ns)量,即比应变率的提高,材料的屈服极限提高,强度极限提高,延伸率降低,以及屈服滞后和断裂滞后等现象变得明显起来等等。
因此,除了上述的介质质点的惯性作用外,物体在爆炸/冲击载荷下力学响应之所以不同于静载荷下的另一个重要原因,是材料本身在高应变率下的动态力学性能与静态力学性能的不同,即由于材料本构关系对应变率的相关性。
从热力学的角度来说,静态下的应力-应变过程接近于等温过程,相应的应力应变曲线可近似视为等温曲线;而高应变率下的动态应力-应变过程则接近于绝热过程,因而是一个伴有温度变化的热-力学耦合过程,相应的应力应变曲线可近似视为绝热曲线。
这样,如果将一个结构物在爆炸/冲击载荷下的动态响应与静态响应相区别的话,则实际上既包含了介质质点的惯性效应,也包含着材料本构关系的应变率效应。
然而从19世纪开始人们才逐步认识到了材料在动载下的力学性能与其在静载下的力学性能不同。
ThomasYoung是分析弹性冲击效应的先驱,他(1807)提出了弹性波的概念,指出杆受轴向冲击力以及梁受横向冲击力时可从能量进行分析而得出定量的结果。
J.Hopkinson1872完成了第一个动态演示实验(如图1所示),铁丝受冲击而被拉断的位置不是冲击端A,而是固定端B;并且冲击拉断的控制因素是落重的高度,即取决于撞击速度,而与落重质量的大小基本无关。
Pochhammer,1876;Chree,1886Rayleigh,Lord1887分别研究了一维杆中的横向惯性运动。
霍普金森杆实验原理

霍普金森杆实验原理
嘿,朋友们!今天咱来唠唠霍普金森杆实验原理。
你说这霍普金森杆实验啊,就像是一场奇妙的力量较量!想象一下,有一根杆子,它可不普通,它能帮我们搞清楚材料在瞬间受力时的表现。
这杆子就像一个超级裁判,能准确地判断出材料的“实力”。
当我们给材料施加一个快速的冲击力时,霍普金森杆就开始它的工作啦。
它会把这个冲击力分成两部分,一部分往前跑,一部分往后跑。
这多有意思啊,就好像是把力量给“分家”了。
然后呢,通过测量这前后跑的力量和其他数据,我们就能知道材料到底有多“强壮”,能不能经得住这样的折腾。
这就好像我们看一个人能不能扛起很重的东西一样,一试便知。
你说这是不是很神奇?而且这个实验原理在很多领域都大有用处呢!比如说在工程上,我们要建大桥、造高楼,就得知道那些建筑材料能不能扛得住各种力的作用。
要是材料不行,那可不得了,大桥可能会塌,高楼可能会倒,那得多危险啊!
还有在材料研发方面,通过霍普金森杆实验,科学家们可以不断改进材料,让它们变得更厉害。
就像我们不断锻炼让自己变得更强壮一样。
再想想,要是没有这个实验原理,我们对材料的了解岂不是少了很多?那我们的生活可能都会受到影响呢!所以说啊,这个霍普金森杆实验原理可真是太重要啦!
它就像是一个默默无闻的英雄,在背后为我们的科技发展和生活保障贡献着力量。
我们得好好珍惜它,好好利用它,让它为我们创造更美好的世界呀!你们说是不是呢?。
霍普金森压杆试验-sillyoranger解析

简述“霍普金斯”杆测量材料动态应力应变曲线的原理;选用一种大型软件对其进行计算模拟,并对模拟结果进行分析。
答:选用ABAQUS大型有限元软件一、“霍普金斯”压杆理论:Hopkinson压杆技术源于1914年B.Hopkinson测试压力脉冲的试验工作,后来R.M.Davies对它进行了改进。
1949年,H.Kolsky在这些基础上建立了进行材料单轴动态压缩性能试验的试验方法,测试了高应变率下金属材料的力学性能,这个方法称为分离式Hopkinson压杆(或Kolsky杆)技术。
其原理是将试样夹持于两个细长弹性杆(入射杆与透射杆)之间,由圆柱形子弹以一定的速度撞击入射弹性杆的另一端,产生压应力脉冲并沿着入射弹性杆向试样方向传播。
当应力波传到入射杆与试样的界面时,一部分反射回入射杆,另一部分对试样加载并传向透射杆,通过贴在入射杆与透射杆上的应变片可记录入射脉冲,反射脉冲及透射脉冲,由一维应力波理论可以确定试样上的应力、应变率、应变随时间的变化,以及应力、应变曲线。
5O多年来,此技术广泛用在高变形速率下材料力学性能的测试。
研究人员也对Hopkinson压杆试验方法进行了系统深入的研究,使该技术不断地改善和发展。
J.Harding 等在1960年将用于单轴压缩试验的Hopkinson压杆推广到了单轴拉伸试验,在此基础上,1983年又提出至今被广泛使用的Hopkinson拉杆试验方法。
W.E.Backer等、J.D.Campbell 等、J.Dully等又提出了Hopkinson扭杆技术,可对于试样施加高应变速率的纯扭转载荷。
为提高试验精度,前人在应力波的弥散效应、三维效应、应力波分离、试样中的瞬态平衡对试验结果的影响等方面做了大量工作。
分离式Hopkinson压杆实验的示意图如下:图8-1 分离式Hopkinson压杆示意图上图表示了压杆、试件和测试仪器等的位置安排。
压杆由高强度合金钢制成。
压杆与试件的接触面需要加工得很平并且保持平行。
霍普金森压杆实验在爆破中的应用

霍普金森压杆实验在爆破中的应用
霍普金森压杆实验是一种利用金属杆的压缩性进行测量的实验,在近年来的矿山爆破领域中被广泛应用。
本文将围绕这个实验展开,详细阐述它在爆破中的应用。
第一步:测量工程爆破预处理
在进行矿山爆破前,需要对爆破前的地质结构和岩石强度进行测量和评估,以此为基础设计爆破方案。
这其中有一个关键步骤就是测量地下岩体的应力状态,其中之一的测量方法便是通过霍普金森压杆实验来评估地质条件和确定安全距离。
第二步:构建压杆实验基础
在进行霍普金森压杆实验之前,需要先构建出实验基础,通常为混凝土块或固定架。
而实验基础的建造需要严格的工程施工规范和技术手段,以保证实验数据的准确性和可靠性。
第三步:插入压杆进行测量
在构建好实验基础后,需要将压杆插入基础中。
在此过程中,需要对压杆进行校准和测试,以确保压力传感器和测量仪器的准确性和可靠性。
压杆通常包括一个测量传感器和一个压力传感器,可以测量岩石的应力和应变状态。
第四步:应力状态测量
在应力状态测量阶段,需要进行岩体应力状态的测量和记录,包括岩石的承载能力和破坏状态。
通过这些数据,可以评估矿山爆破方案的合理性和安全性,并制定相关的爆破方案或调整现有方案。
总结起来,霍普金森压杆实验是一种可靠的测量方法,在矿山爆破预处理阶段和实施过程中都有着重要的应用。
这一方法能够帮助工程师、科学家和矿山工人对地形、地质、地下建筑物和其他关键因素进行测量,并在需要时调整设计方案,以提高爆破的效率和安全性。
霍普金森杆实验技术读书札记

《霍普金森杆实验技术》读书札记目录一、内容综述 (1)二、霍普金森杆实验技术基本原理 (2)2.1 理解霍普金森杆 (3)2.2 实验设备与材料 (4)2.3 实验原理与方法 (5)三、霍普金森杆实验技术应用 (6)3.1 材料试验 (8)3.2 结构试验 (9)3.3 冲击试验 (10)四、实验设计与实施 (12)4.1 实验设计原则 (13)4.2 实验操作流程 (14)五、实验结果与分析 (15)5.1 数据处理与分析方法 (16)5.2 实验结果讨论 (17)六、结论与展望 (18)一、内容综述《霍普金森杆实验技术》系统地介绍了霍普金森杆实验技术的原理、方法、应用及最新发展。
霍普金森杆实验技术,作为一种独特的材料试验手段,自19世纪末由英国科学家亨利霍普金森提出以来,已历经一个多世纪的发展,成为材料科学、力学领域的重要研究工具。
本书首先概述了霍普金森杆实验技术的历史背景与发展历程,从最初的实验构想,到后来的理论完善与实验方法的不断创新,霍普金森杆实验技术已成为材料科学领域的研究热点。
书中详细介绍了实验的基本原理、实验设备、数据处理方法以及在不同领域(如材料加工、岩石力学、爆炸力学等)的应用。
在实验设备方面,本书详细描述了霍普金森杆实验系统的组成,包括发射系统、加载系统、测量系统和控制系统。
这些设备的设计巧妙,能够模拟材料在高速压缩下的力学行为,为研究者提供了深入了解材料特性的窗口。
在数据处理方法上,本书介绍了多种先进的数值分析方法,如有限元分析、颗粒流模拟等,这些方法能够有效地处理实验数据,揭示材料的内部结构与性能。
通过与实验结果的对比验证,这些数值分析方法为霍普金森杆实验技术的准确性提供了有力支持。
本书还探讨了霍普金森杆实验技术在材料科学领域的重要性,以及它在其他学科领域的潜在应用价值。
随着科技的进步,霍普金森杆实验技术将继续在材料科学领域发挥其独特的作用,推动相关学科的发展。
《霍普金森杆实验技术》一书为我们提供了一个全面了解霍普金森杆实验技术的平台。
基于光学检测方法的霍普金森压杆技术综述

基于光学检测方法的霍普金森压杆技术综述分离式霍普金森压杆技术是一种被广泛应用于测量材料在高应变率范围内动态力学性能的一种行之有效的实验手段。
传统的霍普金森压杆测量方法主要是利用粘贴在入射杆和透射杆上的应变片实现对被测材料动态力学性能测量的目的,但是这种应变片式的霍普金森压杆技术中仍存在一些固有的问题和不足。
为了获得更高效、精确的实验数据,基于光学检测方法的霍普金森压杆测量技术应运而生。
它具有非接触性、高度可重复性、测量结果更加可靠和准确等优点。
文章首先简要回顾了传统分离式霍普金森压杆技术的起源与发展,以及测量装置和测量原理。
在此基础上,重点介绍了三种基于光学检测方法的分离式霍普金森技术,并简要说明了各个测量方法的特点。
标签:光学检测;霍普金森压杆;动态特性;光干涉Abstract:The split Hopkinson pressure bar(SHPB)technology is an effective experimental method for measuring the dynamic mechanical properties of materials at high strain rates. The traditional Hopkinson pressure bar measurement method mainly uses strain gauges attached to the incident rod and transmission rod to achieve the purpose of measuring the dynamic mechanical properties of the material under test. However,there are still some inherent problems and shortcomings in this strain gauge Hopkinson pressure bar technology. In order to obtain more efficient and accurate experimental data,Hopkinson pressure bar measurement technology based on optical detection method came into being. It has the advantages of non-contact,high repeatability,more reliable and accurate measurement results. This paper traces the origin and development of the traditional split Hopkinson pressure bar technology,and the measuring device and the measuring principle are briefly reviewed. On this basis,three separate Hopkinson techniques based on optical detection are introduced,and the characteristics of each measurement method are briefly described.Keywords:optical inspection (OI);Hopkinson pressure bar (HPB);dynamic characteristics;optical interference1 概述在军事和民用领域中的许多方面,类似于高速碰撞和爆炸等冲击加载形式的力学现象十分常见[1-2]。
分离式霍普金森压杆推导

分离式霍普金森压杆推导一、引言霍普金森压杆实验是材料科学中一个非常重要的实验手段,它被广泛应用于测量材料的弹性模量、屈服强度等重要物理性质。
然而,传统的霍普金森压杆实验存在一些局限性和不足,例如,对于某些特殊材料或者复杂材料的测量精度不高。
因此,本文将探讨一种新型的分离式霍普金森压杆,并对其原理、设计和应用进行详细介绍。
二、霍普金森压杆简介霍普金森压杆实验是一种动态力学实验方法,它通过在试样上施加周期性变化的应力或应变,测量试样的响应,从而得到材料的弹性模量、屈服强度等物理性质。
该实验方法具有简单易操作、测量精度高等优点,被广泛应用于材料科学、物理学等领域。
三、分离式霍普金森压杆的提出传统的霍普金森压杆实验存在一些不足之处,例如,对于某些具有非线性行为的材料,其测量结果可能存在较大的误差。
此外,传统的霍普金森压杆实验对于试样的尺寸和形状有一定的限制,对于某些特殊形状的试样,其适用性较差。
为了解决这些问题,本文提出了一种分离式霍普金森压杆,它可以更加准确地测量材料的性能,并且能够适应更复杂或更特殊的材料。
四、分离式霍普金森压杆的模型建立分离式霍普金森压杆的设计和构建过程如下:首先选择合适的材料和尺寸,然后根据实验要求确定加载条件。
在设计和构建过程中,需要遵循一定的理论基础和实践依据,以确保实验结果的准确性和可靠性。
与传统的霍普金森压杆相比,分离式霍普金森压杆具有更高的测量精度和更广泛的适用性。
五、材料性能的影响材料的性能对分离式霍普金森压杆实验结果有着重要的影响。
例如,材料的弹性模量、屈服强度、韧性等性质都会影响实验结果。
为了获得准确的实验结果,需要对这些因素进行深入分析和研究。
六、边界条件与加载条件在分离式霍普金森压杆实验中,边界条件和加载条件对实验结果也有着重要的影响。
例如,实验温度、应变率、应力状态等都会影响试样的响应和实验结果。
因此,在实验过程中需要严格控制这些因素,以获得准确的实验结果。
霍普金森杆实验介绍

霍普金森杆实验技术介绍传统的液压伺服系统上准静态实验的应变率通常在1s -1以下,对于更高的应变率,需要采用其他实验手段。
高应变率实验和准静态实验的根本不同点在于,随着应变率的增加,惯性效应即应力波效应明显增强。
分离式霍普金森压杆(Split Hopkinson Pressure Bars ,SHPB )实验技术是研究材料在中高应变率下(102~104S -1)力学性能的主要实验方法。
美国ASM 协会出版的ASM 手册第八卷Material Testing and Evaluation 一书中系统的介绍了分离式霍普金森杆及其相关实验技术,可是并没有建立详细的通用实验标准。
分离式霍普金森杆实验技术主要基于两个基本假定:一维应力波假定;试样中应力应变沿试样长度均匀分布假定(均匀性假定)。
典型的分离式霍普金森杆实验装置由压(拉)杆系统、测量系统、数据采集系统和数据处理系统组成,其中压(拉)杆系统是实验装置的最重要部分。
霍普金森压杆图1 分离式霍普金森压杆实验装置简图图2 试样连接部分简图霍普金森压杆主要由撞击杆、输入杆、吸收杆和试样组成,实验装置简图如图1所示。
其实验原理主要通过使用应变片对入射杆中的入射波、反射杆以及透射杆中的透射脉冲进行测量,然后根据一维应力波理论导出实验的应力-应变关系。
如图2所示,设试样与入射杆相连接端面为面Ⅰ,试样与透射杆相连接端面为面Ⅱ。
在实验过程中面Ⅰ和面Ⅱ上的位移分别为U 1和U 2,则根据线弹性波的线性叠加原理,有()100ti r U c d εετ=-⎰ ()100ti U c d ετ=⎰式中:c 0为压杆中的弹性波速; 、 、 分别为入射波、反射波和透射波独立传播式所对应的杆中的应变。
设试样的长度为L 0,横截面积为A 0。
则试样中的平均应变为:()012000t i r t c U U d L L εεεετ-==--⎰试样的平均平均应变率为: ()00i r t c L εεεε=-- 根据力的平衡性,试样的平均应力为:()02i r t AE A σεεε=++ 其中A 和E 分别为杆的横截面积和弹性模量。
霍普金森压杆实验报告
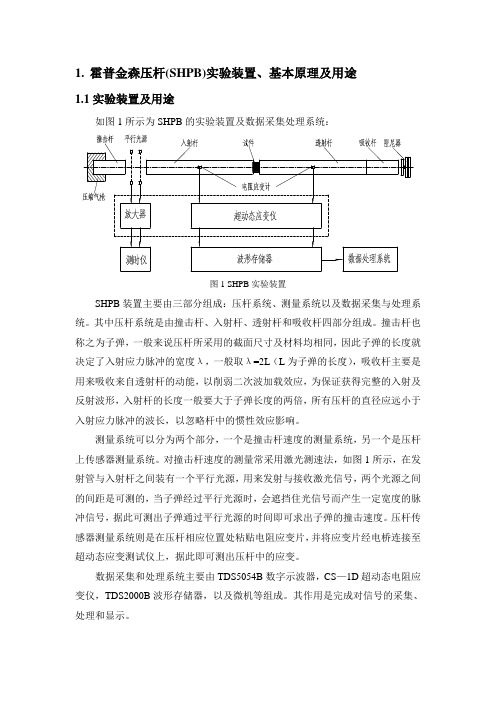
(Байду номын сангаас)
νⅠ = ν2 = ν i +ν r = −c(ε i − ε r )
′ = ν t = −cε t νⅡ = ν 2
(t= ε )
νⅡ −νⅠ
l0 c l0
=
t
c (ε i − ε r − ε t ) l0 − ε r − ε t )dt
ε= (t )
∫ (ε
0
i
(2)
由 (1) 、 (2) 式进而可得试件材料的应力应变关系。根据均匀假定,可得
1. 霍普金森压杆(SHPB)实验装置、基本原理及用途
1.1 实验装置及用途
如图 1 所示为 SHPB 的实验装置及数据采集处理系统:
图 1 SHPB 实验装置
SHPB 装置主要由三部分组成:压杆系统、测量系统以及数据采集与处理系 统。其中压杆系统是由撞击杆、入射杆、透射杆和吸收杆四部分组成。撞击杆也 称之为子弹, 一般来说压杆所采用的截面尺寸及材料均相同,因此子弹的长度就 决定了入射应力脉冲的宽度λ,一般取λ=2L(L 为子弹的长度) ,吸收杆主要是 用来吸收来自透射杆的动能, 以削弱二次波加载效应,为保证获得完整的入射及 反射波形, 入射杆的长度一般要大于子弹长度的两倍,所有压杆的直径应远小于 入射应力脉冲的波长,以忽略杆中的惯性效应影响。 测量系统可以分为两个部分,一个是撞击杆速度的测量系统,另一个是压杆 上传感器测量系统。对撞击杆速度的测量常采用激光测速法,如图 1 所示,在发 射管与入射杆之间装有一个平行光源,用来发射与接收激光信号,两个光源之间 的间距是可测的, 当子弹经过平行光源时,会遮挡住光信号而产生一定宽度的脉 冲信号, 据此可测出子弹通过平行光源的时间即可求出子弹的撞击速度。压杆传 感器测量系统则是在压杆相应位置处粘贴电阻应变片, 并将应变片经电桥连接至 超动态应变测试仪上,据此即可测出压杆中的应变。 数据采集和处理系统主要由 TDS5054B 数字示波器,CS—1D 超动态电阻应 变仪,TDS2000B 波形存储器,以及微机等组成。其作用是完成对信号的采集、 处理和显示。
霍普金森杆冲击力学试验

霍普金森杆冲击力学试验霍普金森杆冲击力学试验,说到这个名字,听起来是不是有点儿高大上?其实啊,这玩意儿看起来复杂,做起来却能让你大开眼界,瞬间明白很多物理现象是怎么回事儿。
你要是觉得这种名字过于学术,那你就当它是“冲击测试”也行,简单来说,就是模拟物体在快速碰撞时的力学行为。
想象一下,你在滑板上玩得开心,然后突然撞上了个障碍物,啪的一声,你的身体瞬间停住,滑板却飞了好远。
这一瞬间发生了什么?冲击力有多大?如果再碰到不同的材料,力的变化会怎样?霍普金森杆就是用来解决这些问题的。
这个试验其实挺有意思的,它可以帮助我们了解材料在突然遭遇外力时的反应,不管是金属、塑料还是橡胶,甚至是你手机屏幕上的玻璃,都能用这个方法测试。
当我们说“冲击”时,脑袋里可能会想起什么赛车撞车啊,或者乒乓球拍打球那一瞬间的反应,但你要知道,这种瞬间的碰撞背后可隐藏着复杂的物理学原理。
霍普金森杆试验的核心就是通过撞击测试来研究材料如何吸收和传递这些突然的外力。
它的原理,简单点说,就是通过两根杆子、一个待测试的样品以及一些传感器来完成的。
试验的操作原理就像你在玩一个简单的“打击游戏”。
我们有一个很重的锤子,或者说是一个冲击源,它会猛烈地撞击到材料的表面。
而这时,冲击力会通过材料传递给接下来的几根钢杆。
等到这一力量传到材料的另一端,就能通过传感器测量这些变化,搞清楚材料在受到撞击时是如何变形的,力传递的速度是怎样的,以及它到底能承受多大的冲击力而不崩溃。
嘿,听起来有点像科幻电影里的实验室场景,是不是?而且啊,霍普金森杆试验的一个好处就是可以在极短的时间内完成。
你想想,物体一旦遭受冲击,瞬间发生的变化是非常剧烈的,如果要测量这些变化,光凭肉眼是不行的。
而通过霍普金森杆,我们就能精准地捕捉到冲击的全过程,所有的细节都不放过!通过这么快速、精准的实验数据,我们就可以知道,某个物体究竟在冲击力下能撑多久,是“顶住了”还是“断了”。
在许多高科技领域,尤其是航空航天、军事装备、汽车碰撞测试等,这种试验可说是“救命稻草”。
霍普金森压杆实验报告

1.1 实验装置及用途
如图 1 所示为 SHPB 的实验装置及数据采集处理系统:
图 1 SHPB 实验装置
SHPB 装置主要由三部分组成:压杆系统、测量系统以及数据采集与处理系 统。其中压杆系统是由撞击杆、入射杆、透射杆和吸收杆四部分组成。撞击杆也 称之为子弹, 一般来说压杆所采用的截面尺寸及材料均相同,因此子弹的长度就 决定了入射应力脉冲的宽度λ,一般取λ=2L(L 为子弹的长度) ,吸收杆主要是 用来吸收来自透射杆的动能, 以削弱二次波加载效应,为保证获得完整的入射及 反射波形, 入射杆的长度一般要大于子弹长度的两倍,所有压杆的直径应远小于 入射应力脉冲的波长,以忽略杆中的惯性效应影响。 测量系统可以分为两个部分,一个是撞击杆速度的测量系统,另一个是压杆 上传感器测量系统。对撞击杆速度的测量常采用激光测速法,如图 1 所示,在发 射管与入射杆之间装有一个平行光源,用来发射与接收激光信号,两个光源之间 的间距是可测的, 当子弹经过平行光源时,会遮挡住光信号而产生一定宽度的脉 冲信号, 据此可测出子弹通过平行光源的时间即可求出子弹的撞击速度。压杆传 感器测量系统则是在压杆相应位置处粘贴电阻应变片, 并将应变片经电桥连接至 超动态应变测试仪上,据此即可测出压杆中的应变。 数据采集和处理系统主要由 TDS5054B 数字示波器,CS—1D 超动态电阻应 变仪,TDS2000B 波形存储器,以及微机等组成。其作用是完成对信号的采集、 处理和显示。
图 6 透射波波形
万试屋 – 材料测试仪器方法资源小站/test_house
2.5 试件应力-应变曲线
工程应力曲线:
图 7 试样的工程应力曲线
工程应变曲线:
图 8 试样的工程应变曲线
霍普金森杆试验报告

霍普金森压杆(SHPB)试验报告一、SHPB试验目的及用途1、了解霍普金森压杆(SHPB)测试的试验原理,掌握试验的基本操作步骤;2、霍普金森压杆(SHPB)测试技术主要用来测试材料在高应变率下的力学性能。
此试验主要通过霍普金森压杆(SHPB)测试技术,来测试泡沫铝(37mm×21mm)的力学性能,获取应力-应变曲线。
二、SHPB试验装置及其示意图1—发射气枪2—撞击杆3—激光发射器4—激光接收器5—电阻应变片6—入射杆7—试件8—透射杆9—吸收杆10—缓冲装置11—超动态应变仪12—波形存贮器13—数据处理系统三、试验原理1、三种波形的获取过程通过发射气枪作用,赋予撞击杆一定的初速度,此初速度可以由激光发射器和接收器测出间隔时间,然后计算得出。
撞击杆以此速度撞击入射杆,输入入射波脉冲,随着入射波的传播,在试件表面产生反射和穿透。
入射、反射、透射脉冲均可以通过电阻应变片测出,进而通过超动态应变仪传递到波形存贮器进行保存三种波形,从而利用入射、反射和透射脉冲来推导出试件中的应力、应变和应变率。
2、应力应变曲线获取的原理利用这些脉冲信号来获得材料在高应变率下的应力-应变曲线原理如下:图SHPB系统加载示意图上图是SHPB系统加载过程的示意图,Iε、Rε、Tε分别表示的是应变片测量到的入射、反射和透射信号。
1、2分别是试件的两个端面,S A是试件的横截面积,L是试件的长度,A和E分别是压杆的横截面积和弹性模量。
根据一维应力波理论,试件的两个端面的位移1u和2u可分别表示为1010t u C dt ε=⎰ (1) 2020tu C dt ε=⎰ (2)式中,1ε、2ε分别是试件两个端面的应变,0C 是压杆的弹性波速。
由于入射波到达杆与试样接触端是立刻会有反射波产生,因此入射杆与试件接触面上的应变1ε既包括了向右传播的应变脉冲I ε,又包括向左传播的反射应变脉冲R ε,即:1I R εεε=+ (3)因此界面1上的位移1u 就可以表示为:100()t I R u C dt εε=-⎰ (4)而界面2处的位移2u 只与透射脉冲T ε有关,故有:200t T u C dt ε=⎰ (5)这里的应变均是压应变。
霍普金森杆实验技术简介

霍普金森杆实验技术简介1.材料动态力学性能实验简史在各类工程技术、军事技术和科学研究等广泛领域的一系列实际问题中,甚至就在日常生活中,人们都会遇到各种各样的爆炸/冲击载荷问题,并且可以观察到,物体在爆炸/冲击载荷下的力学响应往往与静载荷下的有显著不同。
了解材料在冲击加载条件下的力学响应必将大大有助于这些材料的工程应用和工程设计。
此外,数值模拟已在工程设计中发挥着重要作用,而进行数值模拟的前提是必须首先建立一个基于材料在各种应变率下(尤其是在动态应变率下)的精确应力-应变曲线基础上的本构模型。
所以,获得一套材料在高应变率下的应力—应变曲线则成为首要任务。
尽管人们已经研制了多种动态实验技术,但是,与准静态实验相比,进行有效并准确的高应变率下的动态实验依然是一个很大的挑战。
因此,为得到有效并准确的材料的应变率相关的应力—应变曲线,研制高效的、精确的高应变率实验装置是非常重要的。
首先,人们知道,固体力学的静力学理论所研究的是处于静力平衡状态下的固体介质,以忽略介质微元体的惯性作用为前提。
这只是在载荷强度随时间不发生显著变化的时候,才是允许和正确的。
而爆炸/冲击裁荷以载荷作用的短历时为其特征,在以毫秒(ms)、微秒(?s)甚至纳秒(ns)计的短暂时间尺度上发生了运动参量(位移、速度、加速度)的显著变化。
在这样的动载荷条件,介质的微元体处于随时间迅速变化着的动态过程中,这是一个动力学问题。
对此必须计及介质微元体的惯性,从而就导致了对应力波传播的研究。
一切固体材料都具有惯性和可变形性,当受到随时间变化着的外载荷的作用时,它的运动过程总是一个应力波传播、反射和相互作用的过程。
在忽略了介质惯性的可变形固体的静力学问题中,只是允许忽略或没有必要去研究这一在达到静力平衡前的应力波的传播和相互作用的过程,而着眼于研究达到应力平衡后的结果而已。
在忽略了介质可变形性的刚体力学问题中,则相当于应力波传播速度趋于无限大,因而不必再予以考虑。
霍普金森杆实验技术简介

霍普金森杆实验技术简介1.材料动态力学性能实验简史在各类工程技术、军事技术和科学研究等广泛领域的一系列实际问题中,甚至就在日常生活中,人们都会遇到各种各样的爆炸/冲击载荷问题,并且可以观察到,物体在爆炸/冲击载荷下的力学响应往往与静载荷下的有显着不同。
了解材料在冲击加载条件下的力学响应必将大大有助于这些材料的工程应用和工程设计。
此外,数值模拟已在工程设计中发挥着重要作用,而进行数值模拟的前提是必须首先建立一个基于材料在各种应变率下(尤其是在动态应变率下)的精确应力-应变曲线基础上的本构模型。
所以,获得一套材料在高应变率下的应力—应变曲线则成为首要任务。
尽管人们已经研制了多种动态实验技术,但是,与准静态实验相比,进行有效并准确的高应变率下的动态实验依然是一个很大的挑战。
因此,为得到有效并准确的材料的应变率相关的应力—应变曲线,研制高效的、精确的高应变率实验装置是非常重要的。
首先,人们知道,固体力学的静力学理论所研究的是处于静力平衡状态下的固体介质,以忽略介质微元体的惯性作用为前提。
这只是在载荷强度随时间不发生显着变化的时候,才是允许和正确的。
而爆炸/冲击裁荷以载荷作用的短历时为其特征,在以毫秒(ms)、微秒(?s)甚至纳秒(ns)计的短暂时间尺度上发生了运动参量(位移、速度、加速度)的显着变化。
在这样的动载荷条件,介质的微元体处于随时间迅速变化着的动态过程中,这是一个动力学问题。
对此必须计及介质微元体的惯性,从而就导致了对应力波传播的研究。
一切固体材料都具有惯性和可变形性,当受到随时间变化着的外载荷的作用时,它的运动过程总是一个应力波传播、反射和相互作用的过程。
在忽略了介质惯性的可变形固体的静力学问题中,只是允许忽略或没有必要去研究这一在达到静力平衡前的应力波的传播和相互作用的过程,而着眼于研究达到应力平衡后的结果而已。
在忽略了介质可变形性的刚体力学问题中,则相当于应力波传播速度趋于无限大,因而不必再予以考虑。
霍普金森杆试验报告

11—超动态应变仪 12—波形存贮器 13—数据处理系统霍普金森压杆 (SHPB) 试验报告一、 SHPB 试验目的及用途1、了解霍普金森压杆 (SHPB) 测试的试验原理, 掌握试验的 基本操作步骤;2、霍普金森压杆 (SHPB) 测试技术主要用来测试材料在高应 变率下的力学性能。
此试验主要通过霍普金森压杆 (SHPB) 测试 技术,来测试泡沫铝 (37mm ×21mm) 的力学性能, 获取应力 -应变 曲线。
二、 SHPB 试验装置及其示意图1 —发射气枪 2—撞击杆 3 —激光发射器 4—激光接收器 5 —电阻应变片 6—入射杆7—试件8—透射杆9—吸收杆10—缓冲装置三、试验原理1、三种波形的获取过程通过发射气枪作用,赋予撞击杆一定的初速度,此初速度可以由激光发射器和接收器测出间隔时间,然后计算得出。
撞击杆以此速度撞击入射杆,输入入射波脉冲,随着入射波的传播,在试件表面产生反射和穿透。
入射、反射、透射脉冲均可以通过电阻应变片测出,进而通过超动态应变仪传递到波形存贮器进行保存三种波形,从而利用入射、反射和透射脉冲来推导出试件中的应力、应变和应变率。
2、应力应变曲线获取的原理利用这些脉冲信号来获得材料在高应变率下的应力-应变曲线原理如下:1 2上图是SHPB 系统加载过程的示意图,I、R、T分别表示的是应变片测量到的入射、反射和透射信号。
1、2 分别是试件的两个端面,A S是试件的横截面积,L是试件的长度,A和E 分别是压杆的横截面积和弹性模量。
根据一维应力波理论,试件的两个端面的位移u1和u2可分别表示为(7)(8)tu 1 0C 0 1d t(1) tu 2 0C 0 2d t(2)式中, 1、 2分别是试件两个端面的应变, C 0是压杆的弹性 波速。
由于入射波到达杆与试样接触端是立刻会有反射波产生, 因此入射杆与试件接触面上的应变 1既包括了向右传播的应变脉冲 I,又包括向左传播的反射应变脉冲即:(3)因此界面 1 上的位移 u 1就可以表示为:而界面 2 处的位移 u 2只与透射脉冲 T有关,故有:5)这里的应变均是压应变。
霍普金森杆实验技术经验简介

精心整理霍普金森杆实验技术简介1.材料动态力学性能实验简史在各类工程技术、军事技术和科学研究等广泛领域的一系列实际问题中,甚至就在日常生活中,人们都会遇到各种各样的爆炸/冲击载荷问题,并且可以观察到,物体在爆炸/冲击载荷下的力学响应往往与静载荷下的有显著不同。
了解材料在冲击加载条件下的力学响应必将大大有助于这些材料的工程应用和工程设计。
此外,数值模拟已在工程设计中发挥着重要作用,而进行数值模拟的前提是必须首先建立一个基于材料在各种应变率下(尤其是在动态应变率下)的精确应力-应变曲线基础研制高首先,而爆炸/)计的只是甚进行的等等)因此,除了上述的介质质点的惯性作用外,物体在爆炸/冲击载荷下力学响应之所以不同于静载荷下的另一个重要原因,是材料本身在高应变率下的动态力学性能与静态力学性能的不同,即由于材料本构关系对应变率的相关性。
从热力学的角度来说,静态下的应力-应变过程接近于等温过程,相应的应力应变曲线可近似视为等温曲线;而高应变率下的动态应力-应变过程则接近于绝热过程,因而是一个伴有温度变化的热-力学耦合过程,相应的应力应变曲线可近似视为绝热曲线。
这样,如果将一个结构物在爆炸/冲击载荷下的动态响应与静态响应相区别的话,则实际上既包含了介质质点的惯性效应,也包含着材料本构关系的应变率效应。
然而从19世纪开始人们才逐步认识到了材料在动载下的力学性能与其在静载下的力学性能不同。
ThomasYoung 是分析弹性冲击效应的先驱,他(1807)提出了弹性波的概念,指出杆受轴向冲击力以及梁受横向冲击力时可从能量进行分析而得出定量的结果。
J.Hopkinson1872完成了第一个动态演示实验(如图1所示),铁丝受冲击而被拉断的位置不是冲击端A,而是固定端B;并且冲击拉断的控制因素是落重的高度,即取决于撞击速度,而与落重质量的大小基本无关。
Pochhammer,1876;Chree,1886Rayleigh,Lord1887分别研究了一维杆中的横向惯性运动。
关于霍普金森杆高温动态实验技术的简单总结

s (t )
பைடு நூலகம்A0 I R T 2 AS
(1)
通过其一维弹性应力应变关 系及弹性波理论别得到:
S (t )
V1 V2 VI VR VT LS LS
(2)
V1 VI VR C0 I R (4)
S (t ) S (t )dt
由实验下获得的不同温度下的弹性模量 [19]拟合出模量随温度线性变化的曲线
拟合出一个杆模量随温度变化的经验公式:
E(T ) 1.0 / (c3 / T 3 c2 / T 2 c1 / T 1 c0 )
(2)
由公式(1)、(2)我们可以得到不同实 验温度下弹性模量随距离x的变化规律E(x)
关于霍普金森杆高温动态 实验技术的简单总结
汇报人:武强
主要内容
一、基本理论
二、高温实验方法及数据处理 三、高温实验中应该注意到的问题
四、项目进展
材料在冲击加载 条件下动态力学行为 的研究是许多涉及冲 击加载问题的工程设 计的基础,此外,由 于数值模拟在爆炸、 碰撞等工程问题的研 究中扮演者越来越重 要的角色,所以确定 材料在高应变率和大 应变等极端条件下的 力学行为,对于这些 材料在如此环境下的 应用有着重要的意义。
S (t )
2C0 t 0 R (t )dt ls
(11)
公式9-11即为常用的二波法
经典的SHPB实验技术可以有 效测量材料高应变率下的动态力 学行为,但由于科学技术的进步, 当前工程材料的工作环境不仅仅 涉及涉高应变率、大变形等极端 条件, 同时还涉及高温、高升温 率等条件,例如航空航天材料、 核反应堆材料、弹靶材料等, 因 此, 高温下材料的动态力学性能 称为人们非常关心的一个问题。 而经典的SHPB实验技术无法满足 测量要求。
国内霍普金森杆发展

国内Hopkinson压杆实验技术概况在国内,SHPB实验技术的提出最早始于力学所。
文革前,当时在力学所的王礼立教授就已开始了这方面的文献调研和筹建,后因他本人调离而中断。
文革结束,力学所的段祝平教授重新开始了这项工作,并建起了我国第一套SHPB实验装置。
中科大的朱兆祥教授和刚从兰州调入科大的王礼立教授也开始了这方面的工作,并得到了力学所郑哲敏院士和段祝平教授的大力支持,当时科大的胡时胜教授还在力学所SHPB实验室学习了一个多月。
几乎在同一期间,太原理工大学杨桂通教授等也建起了国内第一套SHB扭杆。
另外,与材料动态力学性能关系最密切的兵器工业部52所的羡梦梅研究员在兵器行业率先建了一套SHPB实验装置,之后,调到53所的她又建起了另一套SHPB实验装置。
北理工则分别有两个系(7系的张宝坪教授和8系的杨宝明教授)也有了SHPB实验室。
在这期间,还有一些高校和科研部门先后建立了SHPB实验室,开展了材料动态力学性能方面的研究,并在国内外有了一定影响。
他们是北京大学、宁波大学材力中心、中南工业大学、南京理工大学、西北工业大学和九院的一所和四所等。
最近这几年,形势的需要和科研投入的增加,国防科技大学等更多高校和科研单位建起了SHPB实验室。
目前,在国内拥有SHPB实验装置的单位应该有三四十家之多。
在国内,SHPB最初的研究对象主要是集中在金属和高聚物材料,其一是,铝合金、钛合金以及短纤维高聚物是当时航天部门十分关注的材料,其二是,这两类材料的可变形量大、材质也均匀,实验技术相对来说最为容易。
因此人们利用SHPB实验装置测量了这些材料的动态应力-应变曲线,同时又开展了细微观察机理分析,讨论钛合金等金属材料热塑失稳引起的绝热剪切破坏,讨论短纤维对高聚物材料的增强机理等。
除此之外,人们还利用SHPB实验装置研究岩石等脆性材料的动态力学性能,尽管这方面的SHPB实验技术还存在着一系列问题。
此外,还有研究骨头等生物材料的动态力学性能,利用SHPB的改进型测量材料的冲击拉伸强度和动态断裂韧性等材料常数。
霍普金森杆原理

霍普金森杆原理霍普金森杆原理,又称霍普金森效应,是指在一定条件下,一根细长的杆子在一端受到外力作用时,会在另一端产生一定的位移。
这一原理被广泛应用于工程和科学领域,对于理解杆的力学性质和结构设计具有重要意义。
首先,我们来了解一下霍普金森杆原理的基本概念。
在一根细长的杆子上,当一端受到外力作用时,由于杆子的材料特性,外力将会沿着杆子传递,最终在杆的另一端产生位移。
这种现象可以用一系列的力学公式和理论来描述和解释,其中包括杨氏模量、剪切模量等材料力学参数的影响。
其次,我们需要了解霍普金森杆原理的应用范围。
在工程实践中,霍普金森杆原理被广泛运用于桥梁、建筑、机械等领域。
例如,在桥梁设计中,我们需要考虑桥梁的受力情况和变形情况,而霍普金森杆原理可以帮助我们分析和预测桥梁在受力情况下的变形情况,从而指导工程设计和施工。
此外,霍普金森杆原理还可以应用于科学研究中。
在物理学和材料科学领域,研究人员可以通过对杆的受力和变形情况进行实验和分析,来探索材料的性能和力学特性,为新材料的研发和应用提供理论依据和技术支持。
除此之外,霍普金森杆原理还可以在日常生活中找到应用。
比如,我们在搬运长条物体时,就需要考虑霍普金森杆原理对物体的受力和变形情况的影响,以避免因受力不当而导致的意外损坏或伤害。
总的来说,霍普金森杆原理作为材料力学和结构工程中的重要原理,对于理解和分析杆的受力和变形具有重要意义。
通过对霍普金森杆原理的研究和应用,我们可以更好地设计和使用杆结构,提高工程质量和安全性,推动科学技术的发展和进步。
希望本文对大家对霍普金森杆原理有所帮助,谢谢阅读!。
道生科技—霍普金森杆简介

道生科技—霍普金森杆简介一、总体结构综述:霍普金森多功能压杆设备主要由储气设备、发射系统、杆系与子弹、量测系统、中心支撑部件、基础导轨、缓冲装置和辅助设备等组成。
霍普金森多功能压杆设备是建立在统一高精度基准之下的一套专用设备。
¢4mm—¢16mm SHPB实验装置1、发射系统:由储气室、发射体、汽缸、活塞、联接体、支承座、多种可更换炮管、反后座支架等组成。
压力最高可达 5.8MPa ,炮管内径可实现为Φ 120、Φ 100、Φ 80、Φ 75、Φ 50、Φ37、Φ20、Φ14.5、Φ 12、Φ8、Φ 6、Φ 4等多种规格,长度最长为5.5m 。
2、杆系与子弹:超高强度钢,热处理,直径规格同上,最大长度5.5m 。
超硬铝合金,规格同上,最大长度5.5m 。
3、中心支撑部件:由基座、三向精密锁紧定位机构、高精度轴承、压盖、手动机构等构成。
主要特点在统一基准导轨下可使不同直径杆系沿轴向运动为滚动摩擦。
夹持直径连续可调,滑动轻快,杆件同轴调整方便快捷。
基础导轨:由多根经过导轨磨床精密磨削加工,并经过人工时效+自然失效的高精度导轨,地脚调节装置等连接组成的一条整体导轨。
导轨在安装好后,形成两个基准:一个是侧面基准,一个是水平基准,可使发射装置、杆系、支撑部件等在同一基准下工作,大大提高调试工作效率。
整体基准直线度可控制在 0.04/m 以内。
¢20mm—¢37mm SHPB实验装置二、系统特点:1、多功能性:由一套压杆系统,可以将炮管换成需要试验的炮管,可实现多种规格杆件试验。
调整方便快捷,为用户节省大笔费用。
2、统一基准性:由专有技术拼合成的组合式高精度导轨,可任意接长或缩短,具有侧向和平面高精度统一基准,可使发射系统、杆件在同一基准下任一位置调试安装,极大节约调试时间,操作方便,实验重复精度高。
3、标准模块化:无论发射系统、中心支撑装置,还是导轨,全部采用标准模块化结构。
不同的试验设备,都可以通过数量增减而达到试验要求。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
霍普金森杆实验技术简介1.材料动态力学性能实验简史在各类工程技术、军事技术和科学研究等广泛领域的一系列实际问题中,甚至就在日常生活中,人们都会遇到各种各样的爆炸/冲击载荷问题,并且可以观察到,物体在爆炸/冲击载荷下的力学响应往往与静载荷下的有显著不同。
了解材料在冲击加载条件下的力学响应必将大大有助于这些材料的工程应用和工程设计。
此外,数值模拟已在工程设计中发挥着重要作用,而进行数值模拟的前提是必须首先建立一个基于材料在各种应变率下(尤其是在动态应变率下)的精确应力-应变曲线基础上的本构模型。
所以,获得一套材料在高应变率下的应力—应变曲线则成为首要任务。
尽管人们已经研制了多种动态实验技术,但是,与准静态实验相比,进行有效并准确的高应变率下的动态实验依然是一个很大的挑战。
因此,为得到有效并准确的材料的应变率相关的应力—应变曲线,研制高效的、精确的高应变率实验装置是非常重要的。
首先,人们知道,固体力学的静力学理论所研究的是处于静力平衡状态下的固体介质,以忽略介质微元体的惯性作用为前提。
这只是在载荷强度随时间不发生显著变化的时候,才是允许和正确的。
而爆炸/冲击裁荷以载荷作用的短历时为其特征,在以毫秒(ms)、微秒(?s)甚至纳秒(ns)计的短暂时间尺度上发生了运动参量(位移、速度、加速度)的显著变化。
在这样的动载荷条件,介质的微元体处于随时间迅速变化着的动态过程中,这是一个动力学问题。
对此必须计及介质微元体的惯性,从而就导致了对应力波传播的研究。
一切固体材料都具有惯性和可变形性,当受到随时间变化着的外载荷的作用时,它的运动过程总是一个应力波传播、反射和相互作用的过程。
在忽略了介质惯性的可变形固体的静力学问题中,只是允许忽略或没有必要去研究这一在达到静力平衡前的应力波的传播和相互作用的过程,而着眼于研究达到应力平衡后的结果而已。
在忽略了介质可变形性的刚体力学问题中,则相当于应力波传播速度趋于无限大,因而不必再予以考虑。
对于爆炸/冲击载荷条件下的可变形固体,由于在与应力波传过物体特征长度所需时间相比是同量级或更低量级的时间尺度上,载荷已经发生了显著变化,甚至已作用完毕,而这种条件下可变形固体的运动过程常常正是我们关心所在,因此就必须考虑应力波的传播过程。
其次,强冲击载荷所具有的在短暂时间尺度上发生载荷显著变化的特点,必定同时意味着高加载率或高应变率。
一般常规静态试验中的应变率为10-5~10-1 s-1量级.而在必须计及应力波传播的冲击试验中的应变率则为102~104 s-1,甚至可高达107s-1,即比静态试验中的高多个量级。
大量实验表明,在不同应变率下,材料的力学行为往往是不同的。
从材料变形机理来说,除了理想弹性变形可看作瞬态响应外,各种类型的非弹性变形和断裂都是以有限速率发展、进行的非瞬态响应(如位错的运动过程,应力引起的扩散过程,损伤的演化过程,裂纹的扩展和传播过程等等),因而材料的力学性能本质上是与应变率相关的。
通常表现为:随着应变率的提高,材料的屈服极限提高,强度极限提高,延伸率降低,以及屈服滞后和断裂滞后等现象变得明显起来等等。
因此,除了上述的介质质点的惯性作用外,物体在爆炸/冲击载荷下力学响应之所以不同于静载荷下的另一个重要原因,是材料本身在高应变率下的动态力学性能与静态力学性能的不同,即由于材料本构关系对应变率的相关性。
从热力学的角度来说,静态下的应力-应变过程接近于等温过程,相应的应力应变曲线可近似视为等温曲线;而高应变率下的动态应力-应变过程则接近于绝热过程,因而是一个伴有温度变化的热-力学耦合过程,相应的应力应变曲线可近似视为绝热曲线。
这样,如果将一个结构物在爆炸/冲击载荷下的动态响应与静态响应相区别的话,则实际上既包含了介质质点的惯性效应,也包含着材料本构关系的应变率效应。
然而从19世纪开始人们才逐步认识到了材料在动载下的力学性能与其在静载下的力学性能不同。
Thomas Young是分析弹性冲击效应的先驱,他(1807)提出了弹性波的概念,指出杆受轴向冲击力以及梁受横向冲击力时可从能量进行分析而得出定量的结果。
J. Hopkinson 1872完成了第一个动态演示实验(如图1所示),铁丝受冲击而被拉断的位置不是冲击端A,而是固定端B;并且冲击拉断的控制因素是落重的高度,即取决于撞击速度,而与落重质量的大小基本无关。
Pochhammer, 1876; Chree, 1886 Rayleigh,Lord 1887分别研究了一维杆中的横向惯性运动。
1897年Dunn 设计了第一台高应变率试验。
1914年,B.Hopkinson想出了一个巧妙的方法,用以测定和研究炸药爆炸或子弹射击杆端时的压力~时间关系。
所采用的装置被称为Hopkinson压杆(Pressure Bar),有时缩写为HPB。
二战之前,很少有人研究动态压缩加载问题,只是G..I. Taylor 在三十年代末想出了一个方法来测量材料的动态压缩强度。
Taylor 方法主要是假设材料是刚性——理想塑性,运用一维波传播的基本概念,用一个圆柱撞击刚性靶,然后测出其变形,最后得到材料动态压缩屈服应力。
1948年Davies 分析了Hopkinson杆中的应力波传播并发明了用电容方法测量杆中的应力脉冲。
Kolsky(1949)把Hopkinson压杆首先变成分离式并用以研究材料在高应变率下的动态力学行为及其数学模型—材料动态本构关系,成功地发展了分离式Hopkinson压杆(简称SHPB,有时也称Kolsky杆)技术。
50年代,人们用实验检验了St. Venant原理,这样便可以用贴在杆表面的应变片来测量杆中的应变脉冲。
在动态实验设备方面还先后发展了落锤和轻气炮。
落锤装置主要由一个落锤和一个大质量的基础组成。
它可以完成中等应变率的压缩实验。
它的一个突出缺点是在这种实验中既不能实验恒定载荷,也不能实现恒应变率。
利用轻气炮可以进行平板正撞实验和斜板撞击实验,可以研究一维应变状态和高应变率下的材料动态性能,方便研究一维纵波(压力波)和一维横波(剪切波)在试件材料中的传播特性以及材料在这两种应力波作用下的变形和破坏规律。
其缺点是设备复杂,运行成本高。
2.分离式霍普金森杆实验技术的产生2.1 1872年J. Hopkinson铁丝冲击拉伸试验1872年J. Hopkinson 完成了弹性波研究方面的一个著名实验?——一端固定的铁丝冲击拉伸实验。
图1是其实验装置草图。
铁丝上端固定,下端接一托盘,一空心质量块套在该铁丝上,由上向下运动,当其运动到铁丝的下端,被托盘接住,形成对铁丝的冲击拉伸。
J. Hopkinson 研究了杆(丝)中应力波传播的理论,得到了不同加载条件下铁丝断裂强度的实验结果。
J Hopkinson通过变化落体的质量和速度来研究铁丝究竟加载端(下端)还是在反射端(上端)断裂。
结果表明能冲断下端铁丝的冲击速度的一半就足以冲断上端铁丝,冲击拉断的主要控制因素是落体的高度,即取决于撞击速度,而不是落体的质量。
这项研究从理论和实验两方面增强了人们对波在杆中传播规律及其在界面透、反射规律的理解。
2.2 1914年B. Hopkinson在霍普金森压杆方面的杰出工作1905年B. Hopkinson继续他父亲J. Hopkinson的研究工作。
他加长了铁丝的长度,给出了波在其中传播的分析表达式。
进而他设计了一个实验,用一接触块和弹道计(摆)来测量铁丝的瞬间伸长,通过多次试验就可以准确确定铁丝的伸长量。
这个试验为后来的霍普金森压杆的研制奠定了基础。
1914年,B. Hopkinson完成了霍普金森压杆的实验设计,并用以测定和研究了炸药爆炸或子弹射击杆端时的压力~时间关系。
Hopkinson 观察到“如果用来复枪(rifle)发射一子弹撞击一圆柱形钢杆的端部,则在撞击期间,有一确定的压力作用在杆的端部,形成一个压力脉冲。
这个撞击引起的压力脉冲沿着杆传播,在自由端发生反射产生一个拉伸脉冲。
”他还指出如何用一与压杆(主杆)材料相同,直径相同的短杆捕捉入射波的动量,而飞离主杆。
如图2所示,飞片(短杆)的动量由弹道摆测得,而留在杆内的动量则可由杆的摆动振幅来确定。
显然,当飞片长(厚度)度等于或大于压力脉冲长度的一半时,压力脉冲的动量将全部陷入飞片中,从而当飞片飞离时,杆将保持静止。
因此,变化飞片的长度,求得其飞离时而杆能保持静止的最小长度l0,就可求得压力脉冲的长度?=2l0,或压力脉冲的持续时间?=?/C0=2l0/C0。
这种测量压力脉冲的方式迅速在一战中得到了广泛的应用。
2.3 1948年Davies在霍普金森压杆压力波形检测与分析方面的杰出工作在霍普金森压杆发明后三十多年中,这项实验技术并没有得到更多的关注。
直到1948年Davies首次用平行板电容器和圆柱形电容器测量压杆的轴向位移和径向位移(图3所示),这项实验技术才又取得了关键性进展。
除了测量压杆的轴向和径向位移之外, Davies还首次详尽讨论了霍普金森压杆的一些局限性,如弥散问题。
另外原始的霍普金森压杆还存在两个主要缺陷:(1)压杆与飞片之间的粘附力的存在限制了对最小压力值的精确测量;(2)无法得到压力时间曲线(历史)。
Davies指出杆端的质点速度和位移之间的关系,通过测量位移时间关系,可发计算出杆中的压力时间关系。
Davies强调了几个重要的问题:(1)杆材料是均匀的,杆中所受应力均不超过材料的比例极限;(2)杆的直径是均匀的;(3)撞击端可以被一短的硬的砧垫保护;(4)少许油脂粘住砧垫;(5)所用杆长范围为2至22英尺;(6)通常情况下杆直径为0.5~1.5英寸。
(7)杆中纵波速度由振动技术测得。
由圆柱形电容器测得的向位移,由平行板电容器测得杆端的轴向位移,由它们分别计算出杆中的轴向和径向压力时间曲线。
2.4 1949年Kolsky在分离式霍普金森压杆方面的奠基性工作1949年,即在Davies发表关于霍普金森压杆的重要文章后一年,Kolsky发表了他关于分离式霍普金森压杆的奠基性文章。
他将霍普金森压杆实验中的飞片加厚(加长),并称之为扩展杆(extension bar)(现称为透射杆或输出杆)。
并用它首次研究了几种材料(聚乙烯、橡胶、有机玻璃、铜、铅)的动态力学性能。
他将被试材料制成圆形薄片试件,置于压杆与扩展杆之间,压力脉冲在试件界面上发生透、反射,他也采用Davies测量杆轴向、径向位移的方法,用平行板电容器和圆柱形电容器测量杆的轴向和径向位移。
图4是分离式霍普金森压杆草图。
它的主要部分与Davies的霍普金森压杆相类似只是多了一根扩展杆,其长度分别为4英寸,6英寸,8英寸。
试件置于压杆与扩展杆之间,用一黄铜轴套帮助将压杆、试件和扩展杆联接在一起。
