电子线路 非线性部分 (第四版)第一章 习题解答
电子线路非线性部分习题解答

电子线路非线性部分习题解答第一章(1-20)第三章(3-5、3-6、3-7、3-8、3-9、3-18、3-22)3-5 试判断下图所示交流通路中,哪些可能产生振荡,哪些不能产生振荡。
若能产生振荡,则说明属于哪种振荡电路。
解:(a) 不振。
同名端接反,不满足正反馈;(b) 能振。
变压器耦合反馈振荡器;(c) 不振。
不满足三点式振荡电路的组成法则;(d) 能振。
但L2C2回路呈感性,ωosc < ω2,L1C1回路呈容性,ωosc > ω1,组成电感三点式振荡电路。
(e) 能振。
计入结电容C b'e,组成电容三点式振荡电路。
(f) 能振。
但L1C1回路呈容性,ωosc > ω1,L2C2回路呈感性,ωosc > ω2,组成电容三点式振荡电路。
3-6 试画出下图所示各振荡器的交流通路,并判断哪些电路可能产生振荡,哪些电路不能产生振荡。
图中,C B、C C、C E、C D为交流旁路电容或隔直流电容,L C为高频扼流圈,偏置电阻R B1、R B2、R G不计。
解:画出的交流通路如图所示。
(a)不振,不满足三点式振荡电路组成法则。
(b) 可振,为电容三点式振荡电路。
(c) 不振,不满足三点式振荡电路组成法则。
(d) 可振,为电容三点式振荡电路,发射结电容C b'e为回路电容之一。
(e) 可振,为电感三点式振荡电路。
(f) 不振,不满足三点式振荡电路组成法则。
3-7 如图所示电路为三回路振荡器的交流通路,图中f01、f02、f03分别为三回路的谐振频率,试写出它们之间能满足相位平衡条件的两种关系式,并画出振荡器电路(发射极交流接地)。
解:(1) L2C2、L1C1若呈感性,f osc < f01、f02,L3C3 呈容性,f osc > f03,所以f03 < f osc < f01、f02。
(2) L2C2、L1C1若呈容性,f osc > f01、f02,L3C3 呈感性,f osc < f03,所以f03 > f osc > f01、f02。
电路分析基础(第四版)课后答案第1章

目录 Contents
• 电路分析的基本概念 • 电路分析的基本定律 • 电路分析的基本方法 • 电路分析的应用
01
电路分析的基本概念
电路的定义和组成
总结词
电路是由若干个元件按照一定的方式连接起来,用于实现电能或信号传输的闭 合部分组成。电源是提供电能的设备,负载是消 耗电能的设备,中间环节则包括导线和开关等用于连接电源和负载的元件。
详细描述
电流是指单位时间内通过导体横截面的电荷量,电压是指电场力将单位正电荷从一点移动到另一点所做的功,功 率是指单位时间内完成的电功或电能消耗,能量则是指电荷在电场中由于电场力作用而具有的势能。这些物理量 在电路分析中具有重要的作用。
02
电路分析的基本定律
欧姆定律
总结词
欧姆定律是电路分析中最基本的定律之一,它描述了电路中 电压、电流和电阻之间的关系。
电路元件的分类
总结词
电路元件可以分为线性元件和非线性元件两大类。
详细描述
线性元件的电压和电流关系可以用线性方程表示,而非线性元件的电压和电流关 系则不能用线性方程表示。常见的线性元件包括电阻、电容和电感,而非线性元 件有二极管、晶体管等。
电路的基本物理量
总结词
电路的基本物理量包括电流、电压、功率和能量等。
详细描述
网孔电流法是以网孔电流为未知量,根据基尔霍夫定律列出节点电流方程和回路电压方程,求解各网 孔电流的方法。该方法适用于具有多个网孔的电路,特别是网孔较多的复杂电路。
04
电路分析的应用
电阻电路的分析
总结词
电阻电路是最基本的电路类型,其分析方法 主要包括欧姆定律、基尔霍夫定律等。
详细描述
(完整word版)郑州大学电子线路非线性部分复习总结
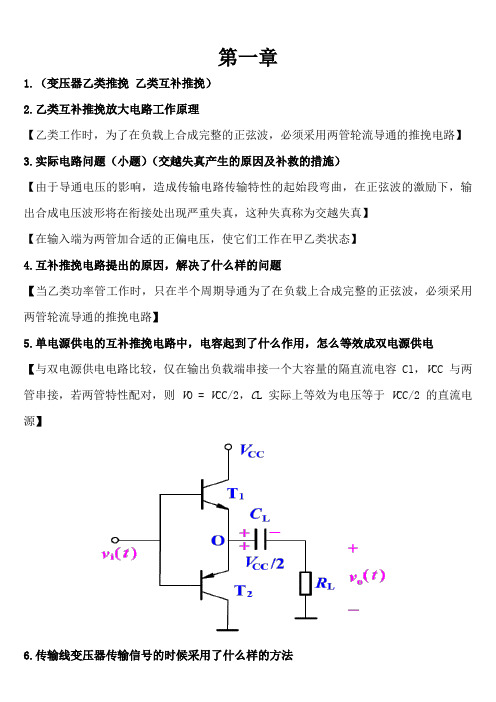
第一章1.(变压器乙类推挽乙类互补推挽)2.乙类互补推挽放大电路工作原理【乙类工作时,为了在负载上合成完整的正弦波,必须采用两管轮流导通的推挽电路】3.实际电路问题(小题)(交越失真产生的原因及补救的措施)【由于导通电压的影响,造成传输电路传输特性的起始段弯曲,在正弦波的激励下,输出合成电压波形将在衔接处出现严重失真,这种失真称为交越失真】【在输入端为两管加合适的正偏电压,使它们工作在甲乙类状态】4.互补推挽电路提出的原因,解决了什么样的问题【当乙类功率管工作时,只在半个周期导通为了在负载上合成完整的正弦波,必须采用两管轮流导通的推挽电路】5.单电源供电的互补推挽电路中,电容起到了什么作用,怎么等效成双电源供电【与双电源供电电路比较,仅在输出负载端串接一个大容量的隔直流电容Cl,V CC 与两管串接,若两管特性配对,则V O = V CC/2,C L 实际上等效为电压等于V CC/2 的直流电源】6.传输线变压器传输信号的时候采用了什么样的方法【传输线变压器,低频依靠变压器磁耦合方式传输信号,高频依靠传输线电磁能交换方式传输信号,所以高频受限于传输线长度,低频受限于初级绕组电感量】7.整流器的作用【整流器:电网提供的50Hz交流电—直流电。
整流电路的功能是将电力网提供的交流电压变换为直流电压】8.计算:利用传输线变压器,端电压相等,两端电流大小相等方向相反这样的准则计算传输线变压构成的阻抗变换器的阻抗比第二章丙类谐振功率放大器1.电路结构【Z L ——外接负载,呈阻抗性,用C L 与R L 串联等效电路表示L r 和C r ——匹配网络,与Z L 组成并联谐振回路调节C r 使回路谐振在输入信号频率V BB——基极偏置电压,设置在功率管的截止区,以实现丙类工作】2.偏置条件【基极偏置电压,是静态工作点设置在功率管的截止区,以实现丙类(导通小于半个周期)工作】3.工作原理【输入完整正余弦波形,ib和ic为脉冲波形,要求输出为同频率正余弦电压,所以在输入、输出端要有谐振回路,使ib和ic电流变为基波电压,实现无失真输出】4.谐振回路的作用【选频:利用谐振回路的选频作用,可将失真的集电极电流脉冲变换为不失真的输出余弦电压阻抗匹配:调节 Lr 和 Cr , 谐振回路将含有电抗分量的外接负载变换为谐振电阻Re ,实现阻抗匹配】5.直流供电【因为丙类功率谐振放大器是放大高频信号,对于高频信号的直流供电来说,应该引入高频扼流圈和滤波电容,进行高低频信号隔离,提高稳定性】6.谐振功率放大器工作状态【欠压、临界和过压状态(波形形貌)】7.谐振功率放大器外部特性【负载特性放大特性(可以构成线性放大器,作为线性功放和振幅限幅器)调制特性(运用到基极、集电极调制电路,实现调幅作用)】1.正弦波振荡器【反馈振荡器、负阻振荡器】2.反馈振荡器结构组成【由主网络和反馈网络构成的闭合环路】3.闭合环路成为反馈振荡器的三个条件【(1) 起振条件——保证接通电源后从无到有地建立起振荡(2) 平衡条件——保证进入平衡状态后能输出等幅持续振荡(3) 稳定条件——保证平衡状态不因外界不稳定因素影响而受到破坏】4.三点式正弦波振荡器组成法则【交流通路中三极管的三个电极与谐振回路的三个引出端点相连接,其中,与发射极相接的为两个同性质电抗,而另一个(接在集电极与基极间)为异质电抗】5.判断能否产生正弦振荡的方法【(1)是否可能振荡——首先看电路供电是否正确;二是看是否满足相位平衡条件(2)是否起振——看是否满足振幅起振条件(3)是否产生正弦波——看是否有正弦选频网络】6.3.2.3例题(不看例2)7.对于各个类型的振荡电路的优势【晶体振荡器优势:将石英谐振器作为振荡器谐振回路,就会有很高的回路标准性,因此有很高的频率稳定度】8.实现负阻振荡器利用的是什么【平均负增量电导】9.平均负增量电导在正弦波振荡器当中实现的作用【当正弦电压振幅增加时,相应的负阻器件向外电路提供的基波功率增长趋缓。
电路分析基础(第四版)课后答案第1章ppt课件

1.8 求图示各电路中的电压U。 题解1.8图
解 图(a):U=1×3-2=1 V 图(b): 在图示电路中设电压U1的参考方向, 如题解1.8
图(b)所示。 应用电阻串并联等效及分压关系式, 得电压
(24)//3 U1(24)//3196V
所以
U2 44U13 264V
图(c): 在图示电路中设电流I1、 I2的参考方向, 如题解 1.8图(c)所示。 由电阻串联等效及欧姆定律, 得电流
1.11 图示直流电路, 图中电压表、 电流表均是理想的, 并已知电压表读数为30 V。
(1) (2) 电压源Us产生的功率Ps为多少?
题解1.11图
解 用短路线将图示电路中两处接地点连在一起,并设 a、 b点, 电流I、 I1、 I2参考方向, 如题解 1.11图所示。 由图可见, 电流表所在支路的10 kΩ电阻同与电压表相并的 30 kΩ电阻是串联关系。 因电压表读数是30 V, 所以
图(b): 在图示电路中设节点a及电流I1、I2、I3、I4的参 考方向,如题解1.10图(b)所示。 应用电阻串并联等效, 得
电流
I1[4//44]5/1/6//6153A
由3个相等电阻并联分流, 得
I2I313I11331A
再由2个电阻并联分流, 得电流
I44 44I31 210.5A
对节点a应用KCL, I=I2+I4=1+0.5=1.5 A
图(c)电路中, 设电流I1、 I2、 I3如题解1.7图(c)所示。 应用电阻串并联等效, 得电流
I13//61 22 1//613A 再应用电阻并联分流公式, 得
I23 66I13 232A
61 I3126I1331A
对节点a应用KCL, I=I2-I3=2-1=1 A
电路第四版课后习题答案

电路第四版课后习题答案第一章:电路基础1. 确定电路中各元件的电压和电流。
- 根据基尔霍夫电压定律和电流定律,我们可以列出方程组来求解未知的电压和电流值。
2. 计算电路的等效电阻。
- 使用串联和并联电阻的计算公式,可以求出电路的等效电阻。
3. 应用欧姆定律解决实际问题。
- 根据欧姆定律 \( V = IR \),可以计算出电路中的电压或电流。
第二章:直流电路分析1. 使用节点电压法分析电路。
- 选择一个参考节点,然后对其他节点应用基尔霍夫电流定律,列出方程组并求解。
2. 使用网孔电流法分析电路。
- 选择电路中的网孔,对每个网孔应用基尔霍夫电压定律,列出方程组并求解。
3. 应用叠加定理解决复杂电路问题。
- 将复杂电路分解为简单的子电路,然后应用叠加定理计算总的电压或电流。
第三章:交流电路分析1. 计算交流电路的瞬时值、有效值和平均值。
- 根据交流信号的表达式,可以计算出不同参数。
2. 使用相量法分析交流电路。
- 将交流信号转换为复数形式,然后使用复数运算来简化电路分析。
3. 计算RLC串联电路的频率响应。
- 根据电路的阻抗,可以分析电路在不同频率下的响应。
第四章:半导体器件1. 分析二极管电路。
- 根据二极管的伏安特性,可以分析电路中的电流和电压。
2. 使用晶体管放大电路。
- 分析晶体管的共发射极、共基极和共集电极放大电路,并计算放大倍数。
3. 应用场效应管进行电路设计。
- 根据场效应管的特性,设计满足特定要求的电路。
第五章:数字逻辑电路1. 理解逻辑门的工作原理。
- 描述不同逻辑门(如与门、或门、非门等)的逻辑功能和电路实现。
2. 使用布尔代数简化逻辑表达式。
- 应用布尔代数的规则来简化复杂的逻辑表达式。
3. 设计组合逻辑电路。
- 根据给定的逻辑功能,设计出相应的组合逻辑电路。
第六章:模拟集成电路1. 分析运算放大器电路。
- 根据运算放大器的特性,分析电路的增益、输入和输出关系。
2. 设计滤波器电路。
电子线路_非线性部分(第四版)谢嘉奎_绪论第一章_标准

优点: 增益高,选择性好。 直接高放接收机:解调前仅包括高放,无混频器、本 机振荡、中频放大器等,增益低,选择性差。
17
6.其他通信系统
① 调频无线通信系统,发射机和接收机都包括上述各
模块,区别主要在于调制器和解调器上。
实现调制的模块——频率调制器;
Po 一定,C 越高,PD 越小 PC 小, 既可选 PCM
小的管子,以降低费用,也节省能源。
③ 失真小。
31
尽管功率增益也是重要的性能指标,但安全、高效和 小失真更重要,前者可以通过增加前置级祢补。
二、功率管的运用特点
1.功率管的运用状态 根据功率管在一个信号周期内导通时间的不同,功率管 运用状态可分为甲类、乙类、甲乙类、丙类等多种。
非线性电路:对信号进行处理时,使用了器件特性的 非线性部分,利用器件的非线性完成振荡、频率变换等功 能。
器件特性与使用条件密切相关,例如:
2
小信号条件下,输入信号小,在一定条件下电路可用 线性等效电路表示,例如各种小信号放大器(《线性电子线 路》)中,器件的特性归属线性电子线路。
大信号条件下,输入信号大,必涉及器件的非线性部 分,例如功率放大器。故不能用线性等效电路表示电子器 件的特征,而必须用非线性电路的分析方法。所以,功放 归属非线性电子线路。
18
(2)本课程讨论的内容——三类电路 ① 功率放大电路——在输入信号作用下,可将直流 电源提供的部分功率转换为按输入信号规律变化的输出信 号功率,并使输出信号的功率大于输入信号的功率。
② 振荡电路——可在不加输入信号的情况下,稳定 地产生特定频率或特定频率范围的正弦波振荡信号。
③ 波形变换和频率变换电路——能在输入信号作用 下产生与之波形和频谱不同的输出信号。包括:调制电路、 解调电路、混频电路和倍频电路。
高频电子线路第1章习题参考答案__第四版

高频电子线路习题参考解答
1-3 无线通信为什么要进行凋制?如何进行调制? 答: 因为基带调制信号都是频率比较低的信号,为了达到较高的 发射效率和接收效率,减小天线的尺寸,可以通过调制,把 调制信号的频谱搬移到高频载波附近;另外,由于调制后的 信号是高频信号,所以也提高了信道利用率,实现了信道复 用。 调制方式有模拟调调制和数字调制。在模拟调制中,用调 制信号去控制高频载波的某个参数。在调幅方式中,AM普通 调幅、抑制载波的双边带调幅(DSB)、单边带调幅 (SSB)、残留单边带调幅(VSSB);在调频方式中,有调 频(FM)和调相(PM)。 在数字调制中,一般有频率键控(FSK)、幅度键控 (ASK)、相位键控(PSK)等调制方法。 5
3
高频电子线路习题参考解答
1-2 无线通信为什么要用高频信号?“高频”信号指的 是什么? 答: 高频信号指的是适合天线发射、传播和接收的射频信 号。 采用高频信号的原因主要是: (1)频率越高,可利用的频带宽度就越宽,信道容量就 越大,而且可以减小或避免频道间的干扰; (2)高频信号更适合电线辐射和接收,因为只有天线尺 寸大小可以与信号波长相比拟时,才有较高的辐射效率和接 收效率,这样,可以采用较小的信号功率,传播较远的距离, 也可获得较高的接收灵敏度。
高频电子线路习题ห้องสมุดไป่ตู้考解答
1-4 无线电信号的频段或波段是如何划分的?各个频段的传 播特性和应用情况如何?
6
高频电子线路习题参考解答
第1章习题参考答案 1-1 1-2 1-3 1-4
1
高频电子线路习题参考解答
1-1 画出无线通信收发信机的原理框图,并说出各部分的功 用。 答:
话 筒 音频 放大器 调制器 变频器 激励放大 输出功 率放大
非线性电路-习题解

率放大器例1-1图例1-1为变压器耦合甲类功率放大器。
图中,R T1为变压器初级线圈的直流电阻,例1-2变压器的匝比为n=4。
调节R b,使电路不失真的输出功率最大。
(1)求静态集电极电流。
(2)若忽略晶体管的饱和压降,负载得到的最大交流输出功率是多少?(3)若调节电位器使R b减小,同时增大输出信号,输出波形将如何变化?解:(1)R L在初级的反射电阻为R L'=n2R L=42×8Ω=128Ω总的交流负载电阻为R L"=R L'+R T1=138Ω为了使输出功率最大,静态工作点应设在交流负载线的中点。
若忽略R T1的直流负载作用,则应使(2)晶体管的最大输出功率为负载得到的输出功率为(3)R B减小,I CQ将增大,交流负载线将向上平行移动。
若增大输出信号,输出波形将产生饱和失真,其负峰值大于电源电压V CC,输出电压的波形如右图所示。
例1-2 某晶体管收音机的功率输出级电路如图例1-2所示。
(1)若R T2=0,Tr2传输效率ηT=80%,R E短路,T1、T2的V CE(sat)≈0,试求负载能得到的最大输出功率P Lmax ;(2)在输出最大功率时,求电源供给的峰值电流和平均电流;(3)校核采用3AX22是否满足要求?(晶体管手册3Ax22的P CM=125mW,V(BR)CEO≥18V,I CM=100mA变压器初级的耗损电阻为2R T1,所以忽略R E的负载效应,晶体管的交流负载为R=R L'+R T1=72+18Ω=90Ω。
负载得到的最大输出功率为每管的功耗为最大集电极电流为I cm=66.7mA<I CM=100mA最高反向电压V CEmax≈2V CC=12V<V(BR)CEO=18V采用3AX22可以满足要求。
例1-3 图例1-3为某收音机的输出电路。
(1)说出电路名称;(2)简述C2、C3、R4、R5的作用;(3)已知V CC=24V,电路的最大输出功率P0max=6.25w,估算对称功放管T2、T3的饱和压降;(4)若V CE(sat)≈0,求极限运用时,电路的输出功率P0max,每个功率管的最大管耗P cmax,最大集电极峰值电流I cm,流过电源的平均电流。
非线线性电子线路答案(1_2)

I DSS 2 U1 (1 − cos ϕ ) 2 2 UP
4β n 2 = 2 2 (1 − cos120 ) 2 2 = 7.2mA I D1 = I Pα1 (120 ) = 3.457mA I D1 3.457 Gm1 = = = 1.728mS 17 U1 2 University
of Science and Technology of China
①
⋅ I 0 ( x)
iE = I ES ⋅ e
I E 0 = I ES ⋅ e
I E 0 = 1.886mA
uo (t ) = −9 + 2 I E 0 I 0 ( x)
α I1 ( x)
② I E1 2 I1 ( x) = IE0 I 0 ( x)
R cos wt = −9 + 5.267 cos wt
2
University of Science and Technology of China
1.2 (2) )
解: i = 5u + u 2 − 0.5u 2 (mA)
UQ = 3.5V ,u = UQ + 0.8cosωt (V )
IQ =5UQ +UQ2 −0.5UQ3 =8.3mA IQ 8.3mA GQ =U = 3.5V =2.375mS
IC3 =αIE3 =1.25mA u0 =VCC + IC3Rcos wt =10 +3.125cos3×10 t(v)
7
1 THD = QT
In (x) 3n 2 ∑[ I (x) n2 −9] = 4.2% n=1 3
n≠3
9
∞
University of Science and Technology of China
非线性电子线路(谢嘉奎第四版_部分)答案

⾮线性电⼦线路(谢嘉奎第四版_部分)答案声明:由不动脑筋⽽直接抄取答案的⾏为引发的后果⾃负,与本⼈⽆任何关联,愿好⾃为之。
解释权归本⼈所有。
1-2 ⼀功率管,它的最⼤输出功率是否仅受其极限参数限制?为什么?解:否。
还受功率管⼯作状态的影响,在极限参数中,P CM 还受功率管所处环境温度、散热条件等影响。
1-3 ⼀功率放⼤器要求输出功率P。
= 1000 W,当集电极效率ηC由40%提⾼到70‰时,试问直流电源提供的直流功率P D和功率管耗散功率P C各减⼩多少?解:当ηC1 = 40%时,P D1 = P o/ηC = 2500 W,P C1 = P D1P o=1500 W当ηC2 = 70%时,P D2 = P o/ηC =1428.57 W,P C2 = P D2P o = 428.57 W可见,随着效率升⾼,P D下降,(P D1 P D2) = 1071.43 WPC下降,(P C1 P C2) = 1071.43 W1-6 如图所⽰为低频功率晶体管3DD325的输出特性曲线,由它接成的放⼤器如图1-2-1(a)所⽰,已知V CC = 5 V,试求下列条件下的P L、P D、ηC(运⽤图解法):(1)R L= 10Ω,Q点在负载线中点,充分激励;(2)R L = 5 Ω,I BQ同(1)值,I cm = I CQ;(3)R L = 5Ω,Q点在负载线中点,激励同(1)值;(4)R L = 5 Ω,Q点在负载线中点,充分激励。
解:(1) R L = 10 Ω时,作负载线(由V CE = V CC I C R L),取Q在放⼤区负载线中点,充分激励,由图得V CEQ1 = 2.6V,ICQ1= 220mA,I BQ1 = I bm = 2.4mA因为V cm = V CEQ1V CE(sat) = (2.6 0.2)V = 2.4 V,I cm = I CQ1 = 220 mA所以mW26421cmcmL==IVP,P D= V CC I CQ1 =ICRL作负载线,I BQ同(1)值,即I BQ2 =2.4mA,得Q2点,V CEQ2 =3.8V,I CQ2 = 260mA这时,V cm = V CC V CEQ2 = 1.2 V,I cm = I CQ2 = 260 mA所以mW15621cmcmL==IVP,P D = V CC I CQ2 = 1.3 W,ηC = P L/ P D = 12%(3)当R L = 5 Ω,Q在放⼤区内的中点,激励同(1),由图Q3点,V CEQ3 = 2.75V,I CQ3= 460mA,I BQ3 = 4.6mA, I bm = 2.4mA 相应的v CEmin= 1.55V,i Cmax= 700mA。
电工电子第四版答案(最新)

第1章思考题与习题解答1-3 I 1的实际方向向下,I 2的实际方向向左,I 3的实际方向向上;U 1的实际方向下正上负,U 2的实际方向向右正左负,U 3的实际方向下正上负;W 360111-==I U P 释放功率 W 210222=-=I U P 吸收功率 W 150333==I U P 吸收功率1-4 (a )W 162A V 8=⨯=P(b )W 123A V 4-=⨯-=P (c )W 51A V 5=⨯=P (d )W 183A V 6-=⨯-=P 1-6 V 600==RI U W 1802==RI P 1-7 []900kWh kWh 30)(3100)10100(3=⨯⨯⨯⨯==-Pt W1-8 (a )A 1A 268=-=I V 2V )12(bc -=⨯-=U (b )8V V )152512(S =⨯++-⨯+U 4V S =U 1-9 (a )V 1V 2V 3ab =-=U(b )1)V 2(V 5⨯+-=R Ω=7R1-10 (a )A 2)A 221(=+=I电压源功率:W 42)W 2(US -=⨯-=P 电流源功率:W 21)W 2(IS =⨯=P电阻功率:W 2W 222R =⎥⎦⎤⎢⎣⎡=P(b )1V V )211(=⨯+-=U电压源功率:W 22)W 1(US -=⨯-=P电流源功率:[]W 2W 2)1(2)W (IS -=⨯--=⨯-=U P 电阻功率:[]W 4W 122R =⨯=P 1-11 0521=-+I I I0645=--I I I 0236=-+I I I0134=--I I I0S11144S455=-++-U I R I R U I R 0S44433S366=+--+U I R I R U I R05566S222=--+-I R I R U I R 其他回路电压方程略1-12 5V 2)V 756366(-=⨯-+⨯+=U 1-13 0321=-+I I I0S13311=-+U I R I R0S23322=-+U I R I R将已知数据代入方程,得:A 121=I ,A 42-=I ,A 83=I 以b 点位参考点, 0b =V0V 1233a ==I R V 0V 18S1c ==U V 0V 8S2d ==U V 0V 10d c cd =-=V V U以d 点位参考点, 0d =V0V 422a =-=I R V 0V 8S2b -=-=U V 0V 10S2S1c =-=U U V 0V 10d c cd =-=V V U第2章思考题与习题解答2-1 (a )图中四个电阻并联,Ω=2R(b )图中两个2Ω电阻并联后与3Ω电阻串联,然后与4Ω电阻并联,再与6Ω电阻串联,最后与 8Ω电阻并联,Ω=4R 2-2 开关打开A 91.2A 2624)2(6)2(410=++++⨯+=I开关闭合A 94.2A 2222646410=+⨯++⨯=I2-3 (a )(b )6V(c2-4 将电路进行等效变换,可求出电流。
电路分析基础第四版课后习题第一章第二章第三章第四章答案
+ 42V
−
i1
18Ω
i2 3Ω
i3
gu
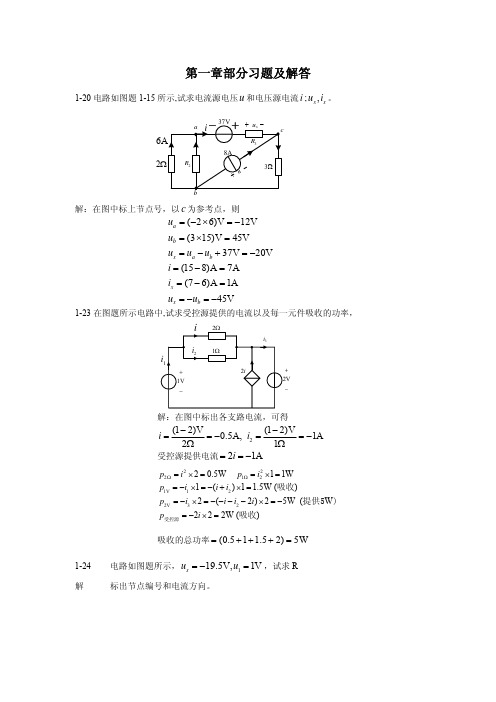
2−5
解
设网孔电流为 i1, i2 , i3 ,则 i3 = −guA = −0.1uA ,所以只要列出两个网孔方程
27i1 −18i2 = 42 −18i1 + 21i2 − 3(−0.1uA ) = 20
因 uA = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20
⎪⎩i3 = 4A
第二章部分习题及解答
2-1 试用网孔电流法求图题所示电路中的电流 i 和电压 uab 。
4Ω
1Ω
i2
+
7V
−
i1
2Ω
i3 i
+ 3V
−
解
设网孔电流为 i1, i2 ,i3 ,列网孔方程
⎪⎨⎧3−ii11
− i2 − 2i3 = 7 + 8i2 − 3i3 = 9
⎪⎩−2i1 − 3i2 + 5i3 = −12
解得
i1 = 4.26A uA = (9× 4.26)V = 38.34V i3 = −0.1uA = −3.83A
2-8 含 CCVS 电路如图题 2-6 所示,试求受控源功率。
1Ω i3
5Ω
+
i 4Ω
+
50V i1 −
20Ω i2
15i −
2−6
解
标出网孔电流及方向,
⎧⎪⎨2−52i01i−1 +202i42i−2 −5i43 i=3
50 = −15i
⎪⎩−5i1 − 4i2 +10i3 = 0
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2
电子线路(非线性部分)习题完全答案(谢嘉奎第四版)

电子线路(非线性部分)1-2 一功率管,它的最大输出功率是否仅受其极限参数限制?为什么?解:否。
还受功率管工作状态的影响,在极限参数中,P CM 还受功率管所处环境温度、散热条件等影响。
第二章2-1 为什么谐振功率放大器能工作于丙类,而电阻性负载功率放大器不能工作于丙类?解:因为谐振功放的输出负载为并联谐振回路,该回路具有选频特性,可从输出的余弦脉冲电流中选出基波分量,并在并联谐振回路上形成不失真的基波余弦电压,而电阻性输出负载不具备上述功能。
2-2 放大器工作于丙类比工作于甲、乙类有何优点?为什么?丙类工作的放大器适宜于放大哪些信号?解:(1)丙类工作,管子导通时间短,瞬时功耗小,效率高。
(2) 丙类工作的放大器输出负载为并联谐振回路,具有选频滤波特性,保证了输出信号的不失真。
为此,丙类放大器只适宜于放大载波信号和高频窄带信号。
2-4 试证如图所示丁类谐振功率放大器的输出功率2)sat (CE CC L2o )2(π2V V R P -=,集电极效率CC)sat (CE CC C 2V V V -=η。
已知V CC = 18 V ,V CE(sat) = 0.5 V ,R L = 50 Ω,试求放大器的P D 、P o 和ηC 值。
解:(1) v A 为方波,按傅里叶级数展开,其中基波分量电压振幅。
)2(π2)sat (CE CC cm V V V -=通过每管的电流为半个余弦波,余弦波幅度,)2(π2)sat (CE CC LL cm cm V V R R V I -==其中平均分量电流平均值 cm C0π1I I =所以 2)sat (CE CC L2cm cm o )2(π221V V R I V P -== )2(π2)sat (CE CC CC L2C0CC D V V V R I V P -==CC)sat (CE CC D o C 2/V V V P P -==η(2) W 24.1)2(π2)sat (CE CC CC L2D =-=V V V R P W 17.1)2(π22)sat (CE CC L2o =-=V V R P %36.94/D o C ==P P η2-5 谐振功率放大器原理电路和功率管输出特性曲线如图所示,已知V CC = 12 V ,V BB = 0.5 V ,V cm = 11 V ,V bm = 0.24 V 。
电子线路1课后习题答案

《电子线路(I )》 董尚斌编 课后习题(1到7章)第1章1—1 本征半导体与杂质半导体有什么区别?解:本征半导体是纯净的,没有掺杂的半导体,本征半导体的导电性能较差,在温度为0K 时,半导体中没有载流子,它相当于绝缘体。
在室温的情况下,由本征激发产生自由电子—空穴对,并达到某一热平衡值,本征载流子浓度kTE i g eT A n 22300-=与温度有关。
杂质半导体是在本征硅或本征锗中掺入杂质得到的,若掺入5价元素的杂质可得到N 型半导体,N 半导体中的多子为自由电子,少子为空穴,由于掺入微量的杂质其导电性能得到了极大的改善,其电导率是本征半导体的好几个数量级。
在杂质半导体中,多子的浓度取决于杂质的浓度,而少子的浓度与2i n 或正比,即与温度有很大的关系。
若掺入3价元素的杂质可得到P 型半导体。
1—2 试解释空穴的作用,它与正离子有什么不同?解:空穴的导电实际上是价电子导电,在半导体中把它用空穴来表示,它带正电是运载电流的基本粒子,在半导体中,施主杂质电离后,它为半导体提供了一个自由电子,自身带正电,成为正离子,但由于它被固定在晶格中,是不能移动的。
1—3 半导体中的漂移电流与扩散电流的区别是什么? 解:漂移电流是在电场力的作用下载流子定向运动而形成的电流,扩散电流是由于浓度差而引起的载流子的定向运动而形成的电流1-4 在PN 结两端加反向偏压时,为什么反向电流几乎与反向电压无关?解:PN 结加反偏电压,外加电场与内电场方向相同,PN 结变宽,外加电压全部降落在PN 结上,而不能作用于P 区和N 区将少数载流子吸引过来.漂移大于扩散,由于在P 区及N 区中少子的浓度一定,因而反向电流与反偏电压无关。
1—5 将一个二极管看作一个电阻,它和一般由导体构成的电阻有何区别?解:将二极管看作一个电阻,其明显的特点是非线性特性.而一般由导体构成的电阻,在有限的电压、电流范围内,基本上是线性的.(1) 二极管的正反向电阻,其数值相差悬殊。
完整版电路分析基础课后习题第一章答案第四版李瀚荪

I 1接住图1 -34所示电路中电流表A的读数随时间变化的况如图中所示.试确定th、2s及35时的电流i・图1-34【分析】当电流由•・+”*«入电流表时•指针正向《转・电淺为正值;当电沆从“一”靖耳入电a表时・指针反向«转,电流为仓值•同时ffl中所求电流°的参考方向如®中箭头所示a表的接法所反映的电流*考方向与图中箭头参考方向相尺9锣因图中以箭头所示电流i的参考方向是从电流表负端到正端•所以t = 15 时.1 =— 1A:/ = 2s 时U = 0八;t = 3s 时u = 1A»⑴若元件A 吸收功杓譽::⑵若元件“吸收功率[阿求;⑶若元件C 吸收功率T°W,柑C, ⑷试求元件D 吸收的功率'W 叶 ⑸若无件E 提供的功率为RW •求丁⑹若元件F 提供的功率为TOW ,* “F.⑺若元件G 捷供的功率为lOmW •求心 就求云件H 提供的功率•赞由功率的定义知准取关联参考方向呗吸收功率曲提供如顾取轶 参考方向时,相反•(l)pA = «AM = inW. (3)A' = =一 lOWi⑷fc = »简=(10 X 1()7X 2 X lOT)W = (20 X 10 ")w砒⑴删卿义若钳艸梯处 -电何而訐也 論况如图',一,— ⑵⑶以上沟系指正 ,-3各元件'♦ “ - (I) 图皿,卄i 若参为方向假定为f ,切“\•娜汎动加必i M 皿Lb,两者不吻合M 电流应记为 “阳电谎实际豊b :血⑴⑵的答案均狈改变符号• -:动的删电亦则⑴、I 1-36所辰 lOV ⑵_ E --気♦(5)F幼(6图 1-36MA =( IO/1)V = lOVT 晋)AiAic =— lA (2)他==_ low.H 黑峡⑵缈岬 囂黑爲案阿郵 • 20羊考万I2mAD*10inV* (4)/cc♦ lOV - ⑶i oG♦ lOV* ⑺2mAH+ 2V - (8)It 关联參易方向•功率为正友发出功率・«吸收功率为伽=-处=-2Oxui*W ・(5)元件縄供功*为low •取关联参考方向,W 吸收功率为/> - W — low 所 W rE=-lA (6>元件为关联参考方向,P N W 为元件吸收功率,P — « **— WW所以圳=(-1O/1)V 1OV(7)元件为关联參考方向"=«为元件ft 牧功率"h W 所以 1/, N (— 10/l0)rnA = _ ImA⑻P H --““5 N (-2X2X lCr*)W —4mWI 4某兀件电” £«和电讯J 的波形如图1-37所不,Kfth 为关联♦号方向・试赫出值尤件 吸收功率洌门的披形,幷计算该无件从f - 0至『=25MM 所吸收的(feH.ffl 1 37❻ 111 f 尤件地关联•号方向・11为吸收功*・所以^^门-所议吸收能»Wfp ⑺击0・,5时图I 39⑺所示俗点•已知W 和心的渡够如图5山2所眉求⑷ 的渡形图■ lOmW・以流人节点的电潦为正•按黑所标示的电潦方向删KW 伽T 旧肿 go 翊创■如图卜39((0所示•冉与为渡形相加•得訂液形如图1-393所不.注教电路中•对任何电淹、电压都満足KgKg<4(f) •曲人廉形如图I :怡所爪.图 1-41> jA > h + 2 — 3 = 0 ii = lA b 点, i — h 亠 5 = 0 I* = 4A c A :i, + 7 — 5 二 0 1:二一2A dA< n + 4 — h =0 fi — — 6A t Aln — h — 2 L 0n —— 4A(3) W 据KVI.计算《八“一和s •ui - 6 = 2 u - 8Vu> — 6 — 12 八 0“ 1«V图 172;<1)由方程①町知.元件1、2、3所庄支路为回路•出左正右负t 正F 负•山力程 :町知•兀件仏2・6、5姐成冋路•址左正右负•段左负右正宀上正尸负・⑺由尸支路必涉及任何方程中•所以其参苇极件•并不能由已知的两个方删岀•呃 文支路4的參号ft 性为左正右负・血+ “9 •⑷ 0 I 7图丨42!蝕賂屮电丿农"的鬱芍极性已选定・£A 电賂的W 卜KVI.力用为U, U : — U K 0U 、“ 心 0< 1)I X N I 迄f(i.« »«收《*的・号极性》 (2>|6金艸遇 4确疋⑷的參写极性? ⑶人朮址“ lov.u. -.V.w - W ・试備疋W 余备咆压.0 --------“・ u> lit loV10V«u.I ----- LLJ ----•-CLHr-EP'd/b〜人h◊.“ * 上;RMHMKM- ZrW4〜■(>* U I Ut1 i\卜中t^ffH i 就町Hid 宜M 全电”"1I • 咯為岔也< «M♦弓〃剛.KCR 卜列箝}略电A H .2A.h■ V. '门野 3A2»电■•定MM 对編宦并木知电■銅《・疋"命电A 々V A 思■我电* ■电JI 書•第疋几卜电AlttM 定«^>^电就0—2 “林 —I -o.^W , 3AM ・9U0.WK( I 丿祐• *门八 .\. - »- ?A.i : - - ■, -^ - SA.浚电»右 >B AWR^KCL 方S皿",二■"HHUMUP•所以不足必帕必须全少M«bUI 电・»第任忆♦■!£・ICV.M :八“.m 史冒沽电廿"宦其“压'"■“a#• N11 - 6'・ .-V.u. 3V* - :、••♦ -~3\l@ 试«出电压g4««lu -"I ':V.U Mr W Ml<dl< VL I w^«MIIRVL 方W■斗 % ♦6I♦ ■~电略如图1・44所示•已知ii =2A ・U =3A 心=lOV.g 吸收的功拿•+由KCL 得由KVL 得h + h 十 i ,H ° 12 = (—2+ 3)A j lA/— U1 + “2 十卿=°n J 均=5V I HI +U , =0 \ui =均一旳=5V元件1是非关联参考方向,Pl — «> • i] = <-l0X2)W=-20W. 元件2是关联参考方向=血.*1 =(-5X2)W = 10W.元件3是非关联参考方向,R =—呛・八=[-5X(-3)]W= 15W. 元件4是失联参考方向宀=-W* 5 W(-5XnW =-5W ・J.n 电路如图1-45所示・(1)H(a)中已知« = 7cos(2r)V,求n(2) ffl(b)中已知 « = (5 + 4e~*)Vu = (lb + 12e-**)A.?)t R»<3) ffl(c)中已知 M = 3cofi(2CV,求 5£1 电阻的功 粉⑷图(a)中已知电压《的波形图1-7中的如•求《的波形•O-o-4门CZZ3 ----- 0 O-U +(«)(b)图P45(c)锣(l )i =背=⑵〉A… M 5+4严=±n ⑵尺=厂3(5 + 4严) 3^*3+ “I ■+M 60― 巧』 ■■方向卜效•则在聊时老3 \加"r;寫:%F'电2;績妙“"诃 1-型,'I SA, 7A 丄.叮:丫爲宀乳>十屮用W 叫yS I IhL|・}絡电!<・马〃向・剧丫; K 「lvr? n '-M7A4 -24 -们V「 ■ 2V■ r ・• HVJ • J(P CVfg 畑3毗利柚靳20gpflftJ * / * li t r 1■* r I6V\nI)•1 ;“・ bI ar(4UbrM4Xh= 5X6=livft4. 2A ・+ uw 36. 2\6X f, =25. 2V剛功亨/>s - “5152. 04 Wu^h ♦ uur 4 “b “ ++ (—十 M)r.时RN*购协电点电说K 「L 方.A bII Jr — ||*»电"电》1»,"按4出KVT 方K152. (MW(WU3ii + 切一“ 0~1 0 (> 1 -,二>0 0 1 10 10 2・J 1A ・*电■析1(的功♦之10为 电 UH 功“*"4 =(4 + 4+16》W ,24W呦电M 住功平:「;;;;;;⑴.2>W = 24W图1・49侈叭旳和⑹中标出节点编号和电流参考方飢 财0")猗示电路:N 土 = 1A ・= 3X6S+ I2V030Ally=2V=2 X is -293(«2 0 d1 n40d (b)c + 3 I<! - 2A-1AB1-50 ® y'先定文电路中各支魔电踣mu 将中闾柿支路祀为一 z 点•利用3 "5 ♦ f —6 K 0I - 1A —I — 15 —— 14 A俗点处 1» — 3A侨以4 3 X 18 12 Z II - <54 4 36W 9OV1 17 I 汕件{电ft 中•代爭作用便13.6 ■ Wf 电于由淡冷转移判悴壳•"转棒中 衣3•⑸的化林点求懺电催的电*堆事少?S 毎电了帯价肌他•4 转移的总电荷»Q rx N - 1.6OX 10 '• X 15.6X 10** - 2. 496(' W 昱型。
电子线路1第一章习题解答

2
解: (1) N a
3 10
14
n N
14
d
p
14
n 2 10
2
p p 10
n
np n i n 10
2
14
n 5 . 76 10
26
0
26
14 14 2 n 10 10 4 5 . 76 10 2 14 3 p 1 . 05 10 cm
VD2:VAB2=VA-VB2=15V-(-10V) =25V
二极管接入以后,因VD2承受的正向电压较VD1 高,优先导通;使A点的电位
VA =VB2 +VD2(on) =-10V +0.7V=-9.3V。
D1因承受电压而截止。
故 VO=VA=-9.3V
1-28 图题1-28所示电路中稳压管的稳压 值为6V,稳定电流为10mA,额定功率为 200mW,试问 (1)当电源电压在18V至30V范围内变化 时,输出Vo=?,稳压管是否安全? (2)若将电源电压改为5V,Vo=? (3)要使稳压管起稳压作用,电源电压 的大小应满足什么条件?
则有 或
杂 本
238 10
5
本 杂
4 . 23 10
8
1-21 在室温(300K)情况下,若二极管 的反向饱和电流为1nA,问它的正向电流 为0.5mA时应加多大的电压。设二极管的 指数模型为,其中m=1,VT=26mV。
解: 由
vD v
I I s (e
VT
1 ) 5 10
5 . 76 10
12
cm
3
p n
电子线路1课后习题答案精品PPT课件

解:
习题2.4在图2-4所示电路中,已知管子
的 100,VBE(on) 0.7V , ICQ 2.17mA,
信号源 vs 0.1sin wt(V ), Rs 10k
设 rbb 0, rce 不计,
试求三极管各极电压和电 流值
iB、iC、 vBE、vCE
图2- 4
解:
(1)
I BQ
82
3
(1
0.3V
150) 2.2K
6.5A
ICQ IBQ 0.98mA
VEE VCC (RC Re ) ICQ VCEQ
VCEQ VCC VEE (RC Re ) ICQ
12 5.6 2.2 0.98 3V 7.3V
求Av ——微变等效电路 交流通路
微变等效电路
(2)当RL=2KΩ时,不产生削波失真的最大输出电 压动态范围是多少?
解:(1)估算IB
基极电流
IB
VCC
VCEQ Rb
6 0.6 270
20μA
画出直流负载线(MN)
VCE
VCC
IC RC
VCiEC
0, VCE 0, iC
VCC VCC / RC
由图中Q点得:
IBQ = 20μA ICQ = 2mA VCEQ = 2V
习题2.11 已知图示共射放大电路中锗三
极管的 150,VCES 0.2V
试用微变等效电路法,求:
1.Av; 2.Ri 和Ro; 3.最大不失真输 出电压幅值;
4.最大输入电压 幅值和此时基极 电流交流分量幅 值。
解:求静态工作点
直流通路
由直流通路可得:
I BQ
VEE VBE
Rb (1 )RE
电子线路1第一章习题解答PPT课件

np ni2 n2 1014 n 5.761026 0
n 1014
1014 2 4 5.761026
2
5.761012 cm3
p 1.051014 cm3
p n P型锗
(2) Na Nd 1015
pnni 2.41103 c m 3
本征半导体
(3)同理
n 9.9 1015 cm3 p 5.82 1010 cm3 n p P型锗
第一章 习题
1-18 在300K下,一个锗晶体中的施主原子数等于 2×1014cm-3,受主原子数等于3×1014cm-3。 试求这块晶体中的自由电子与空穴浓度。由此判断 它是N型还是P型锗?亦即,它的电功能主要是由 电子还是由空穴来体现?
[提示] 若Na=受主原子(负离子)浓度, N d=施主原子(正离子)浓度,
则根据电中性原理,可得 NanNdp
又 np ni2
(300K下,锗的n i=2.4×1013cm-3) 由上二式可求出n、p之值。 2)若 Na=N d=1015cm-3,重做上述内容。 3)若 N d=1016cm-3,Na=1014cm-3,重做上述 内容。
解:(1) NanNdp
31014 n 21014 p p 1014 n
2.25 106 cm 3
p0 n0 N型半导体
(2) T 500K时,
3 -Eg0
ni AT2e2kT 3.491014cm3 ni Nd
本征半导体
1-20 若在每105个硅原子中掺杂一个施主 原子,试计算在T=300K时自由电子和空 穴热平衡浓度值,掺杂前后半导体的电导 率之比。
I1
10V 5K
2mA
流过R2电流:
I2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-2 一功率管,它的最大输出功率是否仅受其极限参数限制?为什么?解:否。
还受功率管工作状态的影响,在极限参数中,P CM 还受功率管所处环境温度、散热条件等影响。
1-3 一功率放大器要求输出功率P 。
= 1000 W ,当集电极效率ηC 由40%提高到70‰时,试问直流电源提供的直流功率P D 和功率管耗散功率P C 各减小多少?解:当ηC1 = 40% 时,P D1 = P o /ηC = 2500 W ,P C1 = P D1 - P o =1500 W当ηC2 = 70% 时,P D2 = P o /ηC =1428.57 W ,P C2 = P D2 - P o = 428.57 W 可见,随着效率升高,P D 下降,(P D1 - P D2) = 1071.43 WP C 下降,(P C1 - P C2) = 1071.43 W1- 如图所示为低频功率晶体管3DD325的输出特性曲线,由它接成的放大器如图1-2-1(a )所示,已知V CC = 5 V ,试求下列条件下的P L 、P D 、ηC (运用图解法):(1)R L = 10Ω,Q 点在负载线中点,充分激励;(2)R L = 5 Ω,I BQ 同(1)值,I cm = I CQ ;(3)R L = 5Ω,Q 点在负载线中点,激励同(1)值;(4)R L = 5 Ω,Q 点在负载线中点,充分激励。
解:(1) R L = 10 Ω 时,作负载线(由V CE = V CC - I C R L ),取Q 在放大区负载线中点,充分激励,由图得V CEQ1 = 2.6V ,I CQ1 = 220mA ,I BQ1 = I bm = 2.4mA因为V cm = V CEQ1-V CE(sat) = (2.6 - 0.2) V = 2.4 V ,I cm = I CQ1 = 220 mA所以mW 26421cm cm L ==I V P ,P D = V CC I CQ1 =1.1 W ,ηC = P L / P D = 24%(2) 当 R L = 5 Ω 时,由V CE = V CC - I C R L作负载线,I BQ 同(1)值,即I BQ2 = 2.4mA ,得Q 2点,V CEQ2 = 3.8V ,I CQ2 = 260mA这时,V cm = V CC -V CEQ2 = 1.2 V ,I cm = I CQ2 = 260 mA所以 mW 15621cm cm L ==I V P ,P D = V CC I CQ2 = 1.3 W ,ηC = P L / P D = 12%(3) 当 R L = 5 Ω,Q 在放大区内的中点,激励同(1),由图Q 3点,V CEQ3 = 2.75V ,I CQ3= 460mA ,I BQ3 = 4.6mA , I bm = 2.4mA 相应的v CEmin = 1.55V ,i Cmax = 700mA 。
因为V cm = V CEQ3 - v CEmin = 1.2 V ,I cm = i Cmax - I CQ3 = 240 mA所以mW 14421cm cm L ==I V P ,P D = V CC I CQ3 = 2.3 W ,ηC = P L / P D = 6.26%(4当 R L = 5 Ω,充分激励时,I cm = I CQ3 = 460 mA ,V cm = V CC -V CEQ3 = 2.25 V所以 mW 5.51721cm cm L ==I V P ,P D = V CC I CQ3 = 2.3 W ,ηC = P L / P D = 22.5%1-7 如图所示为三种甲类功率放大器的输出电路,采用相同的功率管及V CC 值。
设V CE(sat) = 0,I CEO = 0,变压器是理想无耗的,试在同一输出特性曲线上作出各电路的交、直流负载线,并求这三种放大器的最大输出功率之比)c max(L )b max(L )a max(L ::P P P 。
解:(1 ○1 直流负载线方程 v CE = V CC - i C R C ,负载线CD ,当i C = I CQ 时,V CEQ = V CC - I CQ R C 。
○2 交流负载线中点过Q ,斜率为(-1/L R '),C C L L 21//R R R R ==',根据交流负载线 AB 得I cm = I CQ ,V cm = V CEQ = I cm LR ' 代入V CEQ 方程中 V cm = V CC - I cm R C = V CC - I CQ R C = V CC - 2I cm LR '= V CC - 2V cm 解得LCC cmCC cm 3131R V I V V '==, 即L2CC L CC CC )a m ax(L 181313121R V R V V P '='⨯⨯= L2CCcmCC CQ CC D 31R V I V I V P '===所以 61D)a max(L C ==P P η (2) 交流负载相同,均为CF ,为获最大输出功率,Q 处于交流负载线的中点,故V cm = V CEQ = V CC /2,L CC CQ cm 2R VI I ==所以 ;L 2CCcm cm )b max(L 8121R V I V P ==L2CC CQ CC D 2R V I V P ==41D)b max(L C(b)==P P η (3) 因为直流负载电阻为零,故直流负载线为CG ,交流负载线斜率为(-1/LR ')的直线MN ,当Q C 处于中点时,得V cm = V CEQ = V CC ,L CC CQ cm R VI I '==,L 2CCcm cm )c max(L 2121R V I V P '==,L 2CC CQ CC D R V I V P '== 所以21D )c max(L C(c)==P P η 所以36:9:421:81:181::)c m ax(L )b m ax(L )a m ax(L ==P P P 6:3:221:41:61::C(c)C(b)C(a)==ηηη1-8 如图(a )所示为变压器耦合甲类功率放大电路,图(b )所示为功率管的理想化输出特性曲线。
已知R L = 8 Ω,设变压器是理想的,R E 上的直流压降可忽略,试运用图解法:(1)V CC = 15 V ,L R ' = 50 Ω,在负载匹配时,求相应的n 、P Lmax 、ηC ;(2)保持(1)中V CC .I bm 不变,将I CQ 增加一倍,求P L 值;(3)保持(1)中I CQ 、LR '、I bm 不变,将V CC 增加一倍,求P L 值;(4)在(3)条件中,将I bm 增加一倍,试分析工作状态。
解:(1) 因为V CC = 15 V ,LR '= 50 Ω,负载匹配时,A 3.0LCCcm CQ1='==R V I I 由此得知Q 1的坐标为Q 1(15V ,0.3A),Q 1点处于交流负载线AB 的中点,其在坐标轴上的截距为A (32 V ,0),B (0,0.6A)。
由图可见I cm = I CQ1=0.3A ,V cm = V CC = 15 V此时,W 25.221cm cm Lm ax ==I V P ,W 5.4CQ CC D ==I V P%505.425.2D max L C ===P P η,5.2850L L =='=R R n (2) LR '是否变化没说明,故分两种情况讨论 ○1当L R '不变时,因为I CQ 增加一倍,因此,L R '已不是匹配值,其交流负载线平行移动,为一条过Q 2点的直线EF(LR '不变,斜率不变,I CQ 增加,Q 点升高) 此时,由于V CC 、I bm 、LR '都不变,其P Lmax 亦不变,为2.25 W (I bm 不变,I cm 不变,V cm 不变)但 P D = V CC ⨯ I CQ = 9 W ηC = P Lmax / P D = 25%○2当L R '改变时,且L R '< 50 Ω,交流负载线以Q 2为中心顺时针转动,但由于V CC 、I bm 、I cm 不变,因而LR '↓ → P L ↓ ηC ↓ 当LR '> 50 Ω,交流负载线以Q 2为中心逆时针转动,但由于激励不变,输出将出现饱和失真。
(3) V CC = 30 V ,交流负载线平移到EF ,静态工作点为Q 3,因为I bm 不变,所以V cm 不变,I cm 不变,因此P L 不变,P L = 2.25 W ,但V CC = 30 V ,所以P D = V CC ⨯ I CQ = 9 W ηC = P L / P D = 25%(4) I bm = 6 mA ,以Q 3点为静态工作点,出现截止失真。
1-9 单管甲类变压器耦合和乙类变压器耦合推挽功率放大器采用相同的功率管3DD303、相同的电源电压V CC 和负载R L ,且甲类放大器的L R '等于匹配值,设V CE(sat) = 0, I CEO= 0,R E 忽略不计。
(1)已知V CC = 30 V ,放大器的i Cmax = 2 A ,R L = 8 Ω,输入充分激励,试作交流负载线,并比较两放大器的P omax 、 P Cmax 、ηC 、L R '、n ;(2)功率管的极限参数P CM = 30 W ,I CM = 3 A ,V (BR)CEO = 60 V ,试求充分利用功率管时两放大器的最大输出功率P omax 。
解:(1) 见表 甲类乙类交流负载线P omax W 15212121Cm ax CC cm cm ==i V I V W 30212121Cm ax CC cm cm ==i V I V P Cmax2P omax = 30 W0.2P omax = 6 W(单管)ηC50%78.5%LR ' Ω=302/omax 2CC P VΩ=152/omax 2cm P Vn 94.1830L L =='R R 37.1815L L =='R R (2)见表 甲类 乙类P omaxW 15W 302121CM m ax o =⨯=≤'P P W 5.22A 3V 608181CM (BR)CEO omax=⨯⨯=≤''I V P所以W 15m ax o om ax='=P PW 45A 3V 604141CM(BR)CEO max o =⨯⨯=≤'I V PW 150W 3055CM omax =⨯=≤''P P 所以W 45m ax o om ax ='=P P1-14 如图所示为两级功放电路,其中,T l 、T 2工作于乙类,试指出T 4、R 2、R 3的作用。
