初三数学几何地动点问题专题

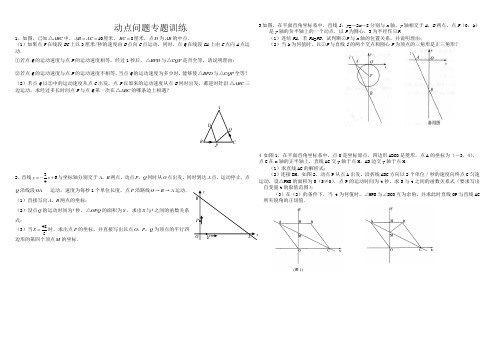
动点问题专题训练1、如图，已知ABC==厘米，8BC=厘米，点D为AB的中点．AB AC△中，10（1）如果点P在线段BC上以3厘米/秒的速度由B点向C点运动，同时，点Q 在线段CA上由C点向A点运动．①若点Q的运动速度与点P的运动速度相等，经过1秒后，BPD△与Array CQP△是否全等，请说明理由；②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使BPD△全等？△与CQP（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿ABC△三边运动，求经过多长时间点P与点Q第一次在ABC△的哪条边上相遇？2、直线364y x=-+与坐标轴分别交于A B、两点，动点P Q、同时从O点出发，同时到达A点，运动停止．点Q沿线段OA运动，速度为每秒1个单位长度，点P沿路线O→B→A运动．（1）直接写出A B、两点的坐标；（2）设点Q的运动时间为t秒，OPQ△的面积为S，求出S 与t之间的函数关系式；（3）当485S=时，求出点P的坐标，并直接写出以点O P Q、、为顶点的平行四边形的第四个顶点M的坐标．3如图，在平面直角坐标系中，直线l：y=－2x－8分别与x轴，y轴相交于A，B两点，点P（0，k）是y轴的负半轴上的一个动点，以P为圆心，3为半径作⊙P.（1）连结PA，若PA=PB，试判断⊙P与x轴的位置关系，并说明理由；（2）当k为何值时，以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形？4 如图1，在平面直角坐标系中，点O是坐标原点，四边形ABCO是菱形，点A 的坐标为（－3，4），点C在x轴的正半轴上，直线AC交y轴于点M，AB边交y轴于点H．（1）求直线AC的解析式；（2）连接BM，如图2，动点P从点A出发，沿折线ABC方向以2个单位／秒的速度向终点C匀速运动，设△PMB的面积为S（S≠0），点P的运动时间为t 秒，求S与t之间的函数关系式（要求写出自变量t的取值范围）；（3）在（2）的条件下，当 t为何值时，∠MPB与∠BCO互为余角，并求此时直线OP与直线AC所夹锐角的正切值．5在Rt △ABC 中，∠C =90°，AC = 3，AB = 5．点P 从点C 出发沿CA 以每秒1个单位长的速度向点A 匀速运动，到达点A 后立刻以原来的速度沿AC 返回；点Q 从点A 出发沿AB 以每秒1个单位长的速度向点B 匀速运动．伴随着P 、Q 的运动，DE 保持垂直平分PQ ，且交PQ 于点D ，交折线QB -BC -CP 于点E ．点P 、Q 同时出发，当点Q 到达点B 时停止运动，点P 也随之停止．设点P 、Q 运动的时间是t 秒（t ＞0）．（1）当t = 2时，AP = ，点Q 到AC 的距离是 ；（2）在点P 从C 向A 运动的过程中，求△APQ 的面积S 与t 的函数关系式；（不必写出t 的取值范围）（3）在点E 从B 向C 运动的过程中，四边形QBED 能否成为直角梯形？若能，求t 的值．若不能，请说明理由； （4）当DE 经过点C 时，请直接．．写出t 的值．图166如图，在Rt ABC △中，9060ACB B ∠=∠=°，°，2BC =．点O 是AC 的中点，过点O 的直线l 从与AC 重合的位置开始，绕点O 作逆时针旋转，交AB 边于点D ．过点C 作CE AB ∥交直线l 于点E ，设直线l 的旋转角为α．（1）①当α= 度时，四边形EDBC 是等腰梯形，此时AD 的长为 ；②当α= 度时，四边形EDBC 是直角梯形，此时AD 的长为 ；（2）当90α=°时，判断四边形EDBC 是否为菱形，并说明理由．（备用图）7如图，在梯形ABCD中，3545 AD BC AD DC AB B====︒∥，，，．动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动；动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动．设运动的时间为t秒．（1）求BC的长．（2）当MN AB∥时，求t的值．（3）试探究：t为何值时，MNC△为等腰三角形．C M8如图1，在等腰梯形ABCD 中，AD BC ∥，E 是AB 的中点，过点E 作EF BC ∥交CD 于点F ．46AB BC ==，，60B =︒∠. （1）求点E 到BC 的距离；（2）点P 为线段EF 上的一个动点，过P 作PM EF ⊥交BC 于点M ，过M 作MN AB ∥交折线ADC 于点N ，连结PN ，设EP x =. ①当点N 在线段AD 上时（如图2），PMN △的形状是否发生改变？若不变，求出PMN △的周长；若改变，请说明理由； ②当点N 在线段DC 上时（如图3），是否存在点P ，使PMN △为等腰三角形？若存在，请求出所有满足要求的x 的值；若不存在，请说明理由.A D E BF C图4（备用）ADE BF C图5（备用）A D E BF C图1 图2A DEBF C PN M 图3A D EBFCPN M（第25题）9如图①，正方形ABCD中，点A、B的坐标分别为（0，10），（8，4），点C在第一象限．动点P在正方形ABCD的边上，从点A出发沿A→B→C→D匀速运动，同时动点Q以相同速度在x轴正半轴上运动，当P点到达D点时，两点同时停止运动，设运动的时间为t秒．(1)当P点在边AB上运动时，点Q的横坐标x（长度单位）关于运动时间t（秒）的函数图象如图②所示，请写出点Q开始运动时的坐标及点P运动速度；(2)求正方形边长及顶点C的坐标；(3)在（1）中当t为何值时，△OPQ的面积最大，并求此时P点的坐标；(4)如果点P、Q保持原速度不变，当点P沿A→B→C→D匀速运动时，OP与PQ能否相等，若能，写出所有符合条件的t的值；若不能，请说明理由．10数学课上，张老师出示了问题：如图1，四边形ABCD是正方形，点E是边BC的中点．90AEF∠=，且EF交正方形外角DCG∠的平行线CF于点F，求证：AE=EF．经过思考，小明展示了一种正确的解题思路：取AB的中点M，连接ME，则AM=EC，易证AME ECF△≌△，所以AE EF=．在此基础上，同学们作了进一步的研究：（1）小颖提出：如图2，如果把“点E是边BC的中点”改为“点E是边BC 上（除B，C外）的任意一点”，其它条件不变，那么结论“AE=EF”仍然成立，你认为小颖的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由；（2）小华提出：如图3，点E是BC的延长线上（除C点外）的任意一点，其他条件不变，结论“AE=EF”仍然成立．你认为小华的观点正确吗？如果正确，写出证明过程；如果不正确，请说明理由．A DFG B图1 A DFGB图2A DFGEB图311已知一个直角三角形纸片OAB ，其中9024AOB OA OB ∠===°，，．如图，将该纸片放置在平面直角坐标系中，折叠该纸片，折痕与边OB 交于点C ，与边AB 交于点D ．（Ⅰ）若折叠后使点B 与点A 重合，求点C 的坐标；（Ⅱ）若折叠后点B 落在边OA 上的点为B '，设OB x '=，OC y =，试写出y 关于x 的函数解析式，并确定y 的取值范围；（Ⅲ）若折叠后点B 落在边OA 上的点为B '，且使B D OB '∥，求此时点C 的坐标．12问题解决 如图（1），将正方形纸片ABCD 折叠，使点B 落在CD 边上一点E （不与点C ，D 重合），压平后得到折痕MN ．当12CE CD =时，求AMBN 的值．类比归纳在图（1）中，若13CE CD =，则AM BN 的值等于 ；若14CE CD =，则AMBN 的值等于 ；若1CE CD n=（n 为整数），则AMBN 的值等于 ．（用含n 的式子表示） 联系拓广 如图（2），将矩形纸片ABCD 折叠，使点B 落在CD 边上一点E （不与点C D，重合），压平后得到折痕MN ，设()111AB CE m BC m CD n=>=，，则AMBN 的值等于 ．（用含m n ，的式子表示）方法指导： 为了求得AM BN 的值，可先求BN 、AM 的长，不妨设：AB =2 图（2） AB C D EF M 图（1） AB C D E FM N1.解：（1）①∵1t =秒， ∴313BP CQ ==⨯=厘米，∵10AB =厘米，点D 为AB 的中点， ∴5BD =厘米．又∵8PC BC BP BC =-=，厘米， ∴835PC =-=厘米， ∴PC BD =． 又∵AB AC =， ∴B C ∠=∠，∴BPD CQP △≌△． ························· （4分） ②∵P Q v v ≠， ∴BP CQ ≠，又∵BPD CQP △≌△，B C ∠=∠，则45BP PC CQ BD ====，， ∴点P ，点Q 运动的时间433BP t ==秒， ∴515443Q CQ v t===厘米/秒． ····················· （7分） （2）设经过x 秒后点P 与点Q 第一次相遇， 由题意，得1532104x x =+⨯， 解得803x =秒． ∴点P 共运动了803803⨯=厘米． ∵8022824=⨯+，∴点P 、点Q 在AB 边上相遇， ∴经过803秒点P 与点Q 第一次在边AB 上相遇． ············· （12分） 2.解（1）A （8，0）B （0，6） ···· 1分 （2）86OA OB ==， 10AB ∴=点Q 由O 到A 的时间是881=（秒） ∴点P 的速度是61028+=（单位/秒） 1分 当P 在线段OB 上运动（或03t ≤≤）时，2OQ t OP t ==，2S t = ·································· 1分当P 在线段BA 上运动（或38t <≤）时，6102162OQ t AP t t ==+-=-，, 如图，作PD OA ⊥于点D ，由PD AP BO AB =，得4865tPD -=， ········· 1分 21324255S OQ PD t t ∴=⨯=-+ ······················ 1分（自变量取值范围写对给1分，否则不给分．）（3）82455P ⎛⎫ ⎪⎝⎭， ······························ 1分12382412241224555555I M M 2⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，，，，， ················ 3分3.解：（1）⊙P 与x 轴相切.∵直线y =－2x －8与x 轴交于A （4，0），与y 轴交于B （0，－8）， ∴OA =4，OB =8. 由题意，OP =－k ， ∴PB =PA =8+k .在Rt △AOP 中，k 2+42=(8+k )2， ∴k =－3，∴OP 等于⊙P 的半径， ∴⊙P 与x 轴相切.（2）设⊙P 与直线l 交于C ，D 两点，连结PC ，PD 当圆心P在线段OB 上时,作PE ⊥CD 于E .∵△PCD 为正三角形，∴DE =12CD =32，PD =3，∴PE . ∵∠AOB =∠PEB =90°， ∠ABO =∠PBE ， ∴△AOB ∽△PEB ，∴2,AO PE AB PB PB =，∴PB =∴8PO BO PB =-=∴8)P -，∴8k =-.当圆心P 在线段OB 延长线上时,同理可得P (0,－8)，∴k =－8，∴当k －8或k =－8时，以⊙P 与直线l 的两个交点和圆心P 为顶点的三角形是正三角形.4.5.解：（1）1，85；（2）作QF⊥AC于点F，如图3， AQ = CP= t，∴3AP t=-．由△AQF∽△ABC，4BC==，得45QF t =．∴45QF t =． ∴14(3)25S t t =-⋅， 即22655S t t =-+．（3）能．①当DE ∥QB 时，如图4．∵DE ⊥PQ ，∴PQ ⊥QB ，四边形QBED 是直角梯形． 此时∠AQP =90°．由△APQ ∽△ABC ，得AQ APAC AB=， 即335t t -=． 解得98t =． ②如图5，当PQ ∥BC 时，DE ⊥BC ，四边形QBED 是直角梯形．此时∠APQ =90°． 由△AQP ∽△ABC ，得AQ APAB AC=， 即353t t -=． 解得158t =．（4）52t =或4514t =． ①点P 由C 向A 运动，DE 经过点C ．连接QC ，作QG ⊥BC 于点G ，如图6．PC t =，222QC QG CG =+2234[(5)][4(5)]55t t =-+--．由22PC QC =，得22234[(5)][4(5)]55t t t =-+--，解得52t =．②点P 由A 向C 运动，DE 经过点C ，如图7．22234(6)[(5)][4(5)]55t t t -=-+--，4514t =】6.解（1）①30，1；②60，1.5；（2）当∠α=900时，四边形EDBC 是菱形. ∵∠α=∠ACB=900，∴BC //ED .∵CE //AB , ∴四边形EDBC 是平行四边形. ……………………6分 在Rt △ABC 中，∠ACB =900，∠B =600,BC =2,∴∠A =300.∴AB =4,AC . ∴AO =12AC ……………………8分 P图4图5在Rt △AOD 中，∠A =300，∴AD =2. ∴BD =2. ∴BD =BC .又∵四边形EDBC 是平行四边形，∴四边形EDBC 是菱形 ……………………10分7.解：（1）如图①，过A 、D 分别作AK BC ⊥于K ，DH BC ⊥于H ，则四边形ADHK 是矩形∴3KH AD ==．·························· 1分 在Rt ABK △中，sin 454AK AB =︒== 2cos 454242BK AB =︒== ·················· 2分 在Rt CDH △中，由勾股定理得，3HC ==∴43310BC BK KH HC =++=++= ··············· 3分（2）如图②，过D 作DG AB ∥交BC 于G 点，则四边形ADGB 是平行四边形∵MN AB ∥ ∴MN DG ∥ ∴3BG AD == ∴1037GC =-= ························· 4分 由题意知，当M 、N 运动到t 秒时，102CN t CM t ==-，． ∵DG MN ∥∴NMC DGC =∠∠ 又C C =∠∠∴MNC GDC △∽△∴CN CMCD CG = ··························· 5分 即10257t t -= 解得，5017t = ··························· 6分（3）分三种情况讨论：（图①） A D C B K H （图②） A D C B G M N①当NC MC =时，如图③，即102t t =- ∴103t =····························· 7分②当MN NC =时，如图④，过N 作NE MC ⊥于E 解法一：由等腰三角形三线合一性质得()11102522EC MC t t ==-=- 在Rt CEN △中，5cos EC tc NC t -==又在Rt DHC △中，3cos 5CH c CD ==∴535t t -=解得258t = ···························· 8分解法二：∵90C C DHC NEC =∠=∠=︒∠∠， ∴NEC DHC △∽△∴NC ECDC HC =即553t t -= ∴258t = ····························· 8分③当MN MC =时，如图⑤，过M 作MF CN ⊥于F 点.1122FC NC t ==解法一：（方法同②中解法一）132cos 1025tFC C MC t ===- 解得6017t =解法二：∵90C C MFC DHC =∠=∠=︒∠∠， ∴MFC DHC △∽△ ∴FC MCHC DC= A DCB M N （图③） （图④） A D CB M NH E（图⑤）A DCBH N MF即1102235tt-=∴6017t =综上所述，当103t =、258t =或6017t =时，MNC △为等腰三角形 ···· 9分8.解（1）如图1，过点E 作EG BC ⊥于点G ． ······ 1分∵E 为AB 的中点，∴122BE AB ==．在Rt EBG △中，60B =︒∠，∴30BEG =︒∠． ··· 2分∴112BG BE EG ====， 即点E 到BC··········· 3分 （2）①当点N 在线段AD 上运动时，PMN △的形状不发生改变．∵PM EF EG EF ⊥⊥，，∴PM EG ∥． ∵EF BC ∥，∴EP GM =，PM EG ==同理4MN AB ==． ·························· 4分 如图2，过点P 作PH MN ⊥于H ，∵MN AB ∥， ∴6030NMC B PMH ==︒=︒∠∠，∠．∴12PH PM == ∴3cos302MH PM =︒=．则35422NH MN MH =-=-=．在Rt PNH △中，PN === ∴PMN △的周长=4PM PN MN ++=． ············ 6分 ②当点N 在线段DC 上运动时，PMN △的形状发生改变，但MNC △恒为等边三角形．当PM PN =时，如图3，作PR MN ⊥于R ，则MR NR =．类似①，32MR =． ∴23MN MR ==．··························· 7分 ∵MNC △是等边三角形，∴3MC MN ==．此时，6132x EP GM BC BG MC ===--=--=． ··········· 8分图1A DE BF C G图2A D EBF CPNMG H当MP MN =时，如图4，这时MC MN MP ===此时，615x EP GM ===-=-当NP NM =时，如图5，30NPM PMN ==︒∠∠． 则120PMN =︒∠，又60MNC =︒∠， ∴180PNM MNC +=︒∠∠．因此点P 与F 重合，PMC △为直角三角形． ∴tan301MC PM =︒=．此时，6114x EP GM ===--=．综上所述，当2x =或4或(5时，PMN △为等腰三角形． ······ 10分 9解：（1）Q （1，0） ··························· 1分 点P 运动速度每秒钟1个单位长度． ····················· 2分 （2） 过点B 作BF ⊥y 轴于点F ，BE ⊥x 轴于点E ，则BF ＝8，4OF BE ==． ∴1046AF =-=．在Rt △AFB中，10AB == 3分 过点C 作CG ⊥x 轴于点G ，与FB 的延长线交于点H ． ∵90,ABC AB BC ∠=︒= ∴△ABF ≌△BCH ． ∴6,8BH AF CH BF ====． ∴8614,8412OG FH CG ==+==+=．∴所求C 点的坐标为（14，12）． 4分 （3） 过点P 作PM ⊥y 轴于点M ，PN ⊥x 轴于点N ， 则△APM ∽△ABF ．∴AP AM MP AB AF BF ==． 1068t AM MP∴==． ∴3455AM t PM t ==，． ∴3410,55PN OM t ON PM t ==-==．设△OPQ 的面积为S （平方单位）∴213473(10)(1)5251010S t t t t =⨯-+=+-（0≤t ≤10） ·············· 5分说明:未注明自变量的取值范围不扣分．∵310a =-<0 ∴当474710362()10t =-=⨯-时， △OPQ 的面积最大． ········ 6分 图3A D E BFCPN M 图4A D EBF CPM N 图5A D EBF （P ）CMN GGRG此时P 的坐标为（9415，5310） ． ······················ 7分 （4） 当 53t =或29513t =时， OP 与PQ 相等． ················ 9分10.解：（1）正确． ··············· （1分） 证明：在AB 上取一点M ，使AM EC =，连接ME ． （2分）BM BE ∴=．45BME ∴∠=°，135AME ∴∠=°．CF 是外角平分线，45DCF ∴∠=°，135ECF ∴∠=°．AME ECF ∴∠=∠．90AEB BAE ∠+∠=°，90AEB CEF ∠+∠=°， ∴BAE CEF ∠=∠．AME BCF ∴△≌△（ASA ）． ······················ （5分） AE EF ∴=． ···························· （6分） （2）正确． ················· （7分） 证明：在BA 的延长线上取一点N ．使AN CE =，连接NE ． ·········· （8分） BN BE ∴=． 45N PCE ∴∠=∠=°． 四边形ABCD 是正方形， AD BE ∴∥．DAE BEA ∴∠=∠．NAE CEF ∴∠=∠．ANE ECF ∴△≌△（ASA ）． ······················ （10分） AE EF ∴=． （11分）11.解（Ⅰ）如图①，折叠后点B 与点A 重合， 则ACD BCD △≌△.设点C 的坐标为()()00m m >，. 则4BC OB OC m =-=-. 于是4AC BC m ==-.在Rt AOC △中，由勾股定理，得222AC OC OA =+， 即()22242m m -=+，解得32m =. ∴点C 的坐标为302⎛⎫⎪⎝⎭，. ·························· 4分（Ⅱ）如图②，折叠后点B 落在OA 边上的点为B ', 则B CD BCD '△≌△.AD F C G B M A D F C G B N由题设OB x OC y '==，， 则4B C BC OB OC y '==-=-，在Rt B OC '△中，由勾股定理，得222B C OC OB ''=+.()2224y y x ∴-=+，即2128y x =-+······························ 6分 由点B '在边OA 上，有02x ≤≤，∴ 解析式2128y x =-+()02x ≤≤为所求.∴ 当02x ≤≤时，y 随x 的增大而减小，y ∴的取值范围为322y ≤≤.······················ 7分 （Ⅲ）如图③，折叠后点B 落在OA 边上的点为B ''，且B D OB ''∥. 则OCB CB D ''''∠=∠. 又CBD CB D OCB CBD ''''∠=∠∴∠=∠，，有CB BA ''∥. Rt Rt COB BOA ''∴△∽△. 有OB OC OA OB''=，得2OC OB ''=. ····················· 9分 在Rt B OC ''△中，设()00OB x x ''=>，则02OC x =. 由（Ⅱ）的结论，得2001228x x =-+，解得000808x x x =-±>∴=-+，∴点C的坐标为()016. ······················ 10分12解：方法一：如图（1-1），连接BM EM BE ，，．由题设，得四边形ABNM 和四边形FENM 关于直线MN 对称．∴MN 垂直平分BE ．∴BM EM BN EN ==，． ··········· 1分 ∵四边形ABCD 是正方形，∴902A D C AB BC CD DA ∠=∠=∠=====°,．N 图（1-1）A BC EF M∵112CE CE DE CD =∴==，．设BN x =，则NE x =，2NC x =-．在Rt CNE △中，222NE CN CE =+．∴()22221x x =-+．解得54x =，即54BN =． ············ 3分在Rt ABM △和在Rt DEM △中，222AM AB BM +=， 222DM DE EM +=，∴2222AM AB DM DE +=+． ···················5分设AM y =，则2DM y =-，∴()2222221y y +=-+．解得14y =，即14AM =． ······················6分 ∴15AM BN =．··························· 7分 方法二：同方法一，54BN =． ····················3分如图（1－2），过点N 做NG CD ∥，交AD 于点G ，连接BE ．∵AD BC ∥，∴四边形GDCN 是平行四边形． ∴NG CD BC ==． 同理，四边形ABNG 也是平行四边形．∴54AG BN ==． ∵90MN BE EBC BNM ⊥∴∠+∠=，°． 90NG BC MNG BNM EBC MNG ⊥∴∠+∠=∴∠=∠，°，． 在BCE △与NGM △中90E B C M N G B C N G C N G M ∠=∠⎧⎪=⎨⎪∠=∠=⎩，，°．∴BCE NGM EC MG =△≌△，． ······· ５分∵114AM AG MG AM =--=5，=．4 ················ 6分 ∴15AM BN =． ·························· 7分 类比归纳N 图（1-2）A B C DE FM G25（或410）；917； ()2211n n -+ ····················· 10分 联系拓广2222211n m n n m -++ ···························· 12分。