第六章 SPSS的方差分析
第6章SPSS的方差分析课件

方差分析的三种变异
方差分析的三种变异
三种变异之间的关系
方差分析的基本思想
• 明确观测变量和控制变量 • 剖析观测变量的方差 • 比较观测变量总离差平方和各部分的比例
方差分析的应用条件
各样本是相互独立的随机样本; 各样本来自正态总体; 各处理组总体方差相等,即方差齐性或齐同。
二、单因素方差分析
练习
• 完成上例,并利用得到的数据进行分 析
方差分析
提纲
1 方差分析概述 2 单因素方差分析 3 多因素方差分析
协方差分析
4
一、方差分析概述
在实际中常常要了解各种因素对产品的性能、产量等的 影响.例如在化工生产中,有原料成分、催化剂、反应温度、 压力、溶液浓度、反应时间等因素(factor). 有些因素是可以控制的,可控因素所处的不同状态称为 因素的水平(level)。 方差分析正是从观测变量的方差入手,研究诸多控制变 量中哪些变量是对观测变量有显著影响的变量。对观测 变量有显著影响的各个控制变量其不同水平以及各水平 的交互搭配是如何影响观测变量的。
步骤
• 1)分析→比较均值→单因素AVONA • 2因子”框
进一步:方差齐性检验
目的:对控制变量不同水平下各观测变量总体的 方差是否相等进行分析。 实现方法:同两独立样本t检验中的方差检验
进一步:多重比较检验
目的:进一步确定控制变量的不同水平对观测变 量的影响程度如何,其中哪个水平的作用明显区 别于其他水平,哪个水平的作用是不显著的,等 等。 原假设:相应两水平下观测变量总体的均值不存 在显著差异。
目的:用来研究一个控制变量的不同水平是否对 观测变量产生了显著影响。
应用举例
某企业在制定某商品的广告策略时,对不同 广告形式在不同地区的广告效果进行了评估 。 以商品销售额为观测变量,广告形式和地区 为控制变量,利用单因素方差分析分别对广 告形式、地区对销售额的影响进行分析。
spss第六章作业
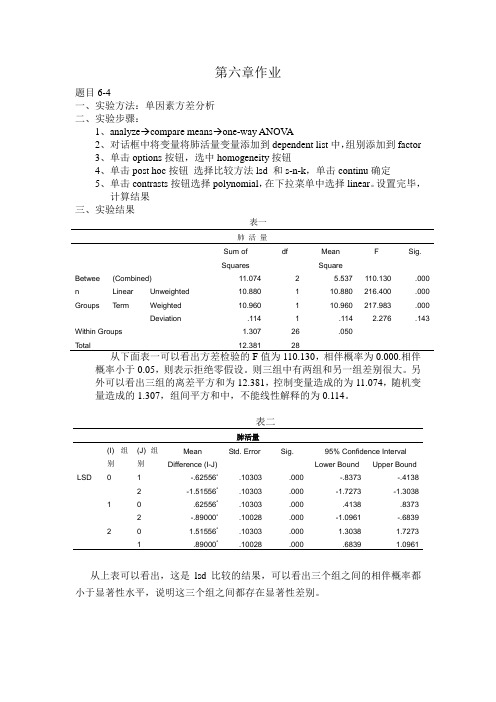
第六章作业题目6-4一、实验方法:单因素方差分析二、实验步骤:1、analyze→compare means→one-way ANOV A2、对话框中将变量将肺活量变量添加到dependent list中,组别添加到factor3、单击options按钮,选中homogeneity按钮4、单击post hoc按钮选择比较方法lsd 和s-n-k,单击continu确定5、单击contrasts按钮选择polynomial,在下拉菜单中选择linear。
设置完毕,计算结果三、实验结果表一肺活量Sum of Squares df MeanSquareF Sig.Betwee n Groups (Combined) 11.074 2 5.537 110.130 .000 LinearTermUnweighted 10.880 1 10.880 216.400 .000Weighted 10.960 1 10.960 217.983 .000Deviation .114 1 .114 2.276 .143Within Groups 1.307 26 .050Total 12.381 28从下面表一可以看出方差检验的F值为110.130,相伴概率为0.000.相伴概率小于0.05,则表示拒绝零假设。
则三组中有两组和另一组差别很大。
另外可以看出三组的离差平方和为12.381,控制变量造成的为11.074,随机变量造成的1.307,组间平方和中,不能线性解释的为0.114。
表二肺活量(I) 组别(J) 组别MeanDifference (I-J)Std. Error Sig. 95% Confidence IntervalLower Bound Upper BoundLSD 0 1 -.62556*.10303 .000 -.8373 -.41382 -1.51556*.10303 .000 -1.7273 -1.30381 0 .62556*.10303 .000 .4138 .83732 -.89000*.10028 .000 -1.0961 -.68392 0 1.51556*.10303 .000 1.3038 1.72731 .89000*.10028 .000 .6839 1.0961从上表可以看出,这是lsd比较的结果,可以看出三个组之间的相伴概率都小于显著性水平,说明这三个组之间都存在显著性差别。
第6章方差分析

• 结果解读5
➢ S-N-K检验结果将无统计学意义的比较组列在同 一列中。即样本均数显示在同一列时,表示两组 总体均数差别无统计学意义。
➢单因素方差分析 完全随机设计的单因素方差分析 多个样本均数间的多重比较 ➢多因素方差分析 随机区组设计的方差分析 交叉设计的方差分析 拉丁方设计的方差分析 析因设计的方差分析 正交设计的方差分析 重复测量资料的方差分析 协方差分析
区组 I组
II组
III组
1
3.6
3.0
0.4
2
4.5
2.3
1.7
3
4.2
2.4
2.3
4
4.4
1.1
4.5
5
3.7
4.0
3.6
6
5.6
3.7
1.3
7
7.0
2.7
3.2
8
4.1
1.9
3.0
9
5.0
2.6
2.1
10
4.5
1.3
2.5
IV组 3.3 1.2 0.0
2.7 3.0 3.2 0.6 1.4 1.2 2.1
• 第五步:点击模型。在单变量:模型对话框中,选 定“设定”后,将“患者编号”、“阶段”、“药 物”移入右模型框。
第六步:设置两两比较。将“药物”选入两两 比较检验。勾上LSD、S-N-K、Dunnett。
• 第七步:设置选项。勾上“描述统计”。
第八步:完成,解读结果 • 结果解读1
阶段F=0.313, p=0.583;(药物顺序与疗效无关) 药物间F=0.522, p=0.479;(功效相当) 患者间F=2.537,p=0.027。
第六章 方差分析
SPSS基础第六章

第四节 有交互作用的双因素方差分析
spss基础
第四节 有交互作用的双因素方差分析
spss基础
第四节 有交互作用的双因素方差分析
spss基础
第四节 有交互作用的双因素方差分析
spss基础
第四节 有交互作用的双因素方差分析
§6.4.1 有交互作用的双因素方差分析的概念 如果对一个问题我们考虑A、B两个因素,因素A有m个水平记为:a1.a2,…,am;因素B有n个水平,记为b1,b2,…,bn;我们称之为双因素方差分析问题。如果两个因素的各个水平交节点上仅作一次试验,称之为无交互作用的双因素方差分析;如果两因素的各个水平交节点上进行重复多次试验,则称之为有交互作用的双因素方差分析。 有交互作用的双因素方差分析的原假设是一个组,有HA、HB和HAB。 HA:µa1=µa2=…=µam HB:µb1=µb2=…=µbn HAB:µab11=µab12=…=µabmn
spss基础
第四节 有交互作用的双因素方差分析
spss基础
第四节 有交互作用的双因素方差分析
spss基础
第四节 有交互作用的双因素方差分析
spss基础
第四节 有交互作用的双因素方差分析
spss基础
作 业
spss基础
第二节 单因素方差分析
§6.2.1 软件操作
spss基础
第二节 单因素方差分析
spss基础
第二节 单因素方差分析
spss基础
第二节 单因素方差分析
spss基础
第二节 单因素方差分析
spss基础
第二节 单因素方差分析
§6.2.2 实例 【例6-1】学生被随机分成4组,接受4种不同的计算机辅导教学方 案:①每天辅导10分钟; ②每天辅导20分钟; ③每天辅导30分钟; ④每天辅导60分钟; 一段时间之后,测试成绩如下表。问:四种方法的效果是否存在 显著差异? 表6-1 接受4种不同计算机辅助教学方案学生的成绩
《SPSS的方差分析》课件

数据来源与格式
详细描述
介绍如何新建数据文件,以及如何导入不同格式的数据文件,如Excel、CSV等。同时说明数据的基本 格式和要求。
SPSS数据的基本操作与整理
总结词
数据清洗与整理技巧
VS
详细描述
介绍SPSS中常见的数据清洗和整理操作 ,如缺失值处理、异常值检测与处理、数 据排序与分组等。同时提供实际操作案例 和技巧。
03
对于非数值型数据或分类数据,需要进行 转换或处理,较为繁琐。
04
对于大规模数据集,计算量大,需要较长 时间才能得出结果。
方差分析的未来发展方向
结合机器学习算法
01
利用机器学习算法对方差分析进行优化,提高分析的效率和准
确性。
拓展到多因素分析
02
将方差分析拓展到多因素分析领域,对方差分析进行更深入的
06
总结与展望
方差分析的优缺点总结
01
优点
02
适用于多组数据的比较,能够快速准确地判断各组 之间的差异。
03
可用于不同类型的数据,如计数数据、计量数据等 ,具有广泛的适用性。
方差分析的优缺点总结
• 能够考虑多种影响因素,进行多因素分析 。
方差分析的优缺点总结
01
缺点
02
对数据的要求较高,需要满足一定的假设 条件,如正态分布、方差齐性等。
双因素方差分析
总结词
用于比较两个分类变量各自所划分的不同组 之间的总体均值是否存在显著差异。
详细描述
双因素方差分析是单因素方差分析的扩展, 用于比较两个分类变量各自所划分的不同组
之间的总体均值是否存在显著差异。在 SPSS中,可以通过“分析”菜单中的“一 般线性模型”选项进行双因素方差分析。
SPSS方差分析

1 -2
方差分析概述
(二)分析目的: 方差分析是从数据间的差异入手,分析哪些因素 是影响数据差异的众多因素中的主要因素;
影响因素的交互作用
例如: 影响移动话费大小的因素(客户年龄、性别、职业、 收入、类型等) 影响学生成绩高低的因素(区域、性别、班级等)
1 - 25
单因素方差分析中的多重比较
(三)实现方式
post hoc选项
(四)应用举例 哪两个班级的高等数学成绩显著不同
LSD *表示在0.05的显著性水平下I和J水平之间ห้องสมุดไป่ตู้均值
存在显著差异.
哪两种类型的客户移动话费有显著差异
Games-Howell法
1 - 26
单因素方差分析中的先验对比
(二)实现方式 Contrasts选项, polynomial框
(三)应用举例 不同客户类型对移动话费的影响呈线性变化趋势吗?
1 - 29
多因素方差分析
(一)目的
测试若干个控制因素的不同水平的交叉变化是否 给观察变量带来了显著影响. 例如:
小城市 中等城市 大城市 特大城市
小型 XX,XX, XX,XX, 广告 XX,XX XX,XX
观测变量的数据差异= 控制因素造成+随机因素造成 当控制因素对实验结果有显著影响时,和随机因
素共同作用必然使观测变量产生显著变动;反之, 观测变量的变动较小,将归结为随机性造成的(这 里指抽样误差造成的).
1 -6
方差分析概述
300,300,300 钻卡 200,200,200 金卡 100,100,100 银卡
dependent list 框 (3)选择一个变量作为控制变量到factor框
spss之统计挖掘第6章 方差分析

5.“两两比较”
6.“保存”
▪ 单击“保存”按钮,弹出图6-18所示的“单变 量:保存”对话框
7.“选项”
▪ 单击“选项”按钮,弹出图6-19所示的“单变 量:选项”对话框。
析因设计方差分析
▪ 例6.3 A、B两种药物联合应用对红细胞增加数 的影响,数据见表6-8。数据库见6-3.sav。
▪ 1.操作步骤
▪ (4)单击“选项”按钮,将“因子与因子交互 ”列表中的“组别”移入右侧“显示均值”框 ,同时勾选“比较主效应”复选框;“输出” 列表中选择“描述统计”和“方差齐性检验” ,单击“继续”按钮,返回主对话框,单击“ 确定”按钮运行。
▪ 2.主要结果解读
▪ 图6-33所示给出两组的例数、均值和标准差; 图6-34所示为两组治疗后血压的Levene方差齐 性检验,本例F=0.049,P=0.826>0.05,因此 方差齐性,符合方差分析条件要求;图6-35所 示为协方差分析结果,可见组别因素F=0.820, P=0.373,组别因素(即两种药物)对降压效果 没有差别;而治疗前血压因素的F=6.463, P=0.017,说明治疗前血压确实对治疗后血压有 影响。
▪ (1)单击“分析”|“一般线性模型”|“单变 量”命令。
▪ (2)将“治疗后血压”放入“因变量”框;将 分组变量“组别”放入“固定因子”框;将“ 治疗前血压”放入“协变量”框。
▪ (3)单击“模型”按钮,在弹出框中将“因子 与协变量”列表中的“组别”和“治疗前血压 ”放入右侧“模型”列表。“构建项”中类型 选择“主效应”。其他默认,单击继续返回。
▪ 实例详解
▪ 例6.1:比较三个不同电池生产企业生产电池的 寿命,见例6-1.sav。此例企业为因素,不同厂 家为水平,本例为单因素3水平设计。
方差分析的SPSS过程PPT课件

均数估计
41
点击“OK”,运行结果
2024/10/16
42
➢结果输出
2024/10/16
43
有效数据例数统计
2024/10/16
44
分组统计描 述(均数、 标准差)
2024/10/16
45
方差分析表
平方 和
自由 度
均方
F值 P值
2024/10/16
46
均数估计
均数
标准误
3.16
3.26
3.82
3.28
2024/10/16
19
t检验法的不足
t 检验法适用于单样本及两样本平均数间的差异显著性检验 ⑴ 检验过程烦琐
本例中用t 检验法要进行 3次两两平均数的差异显著性检验 若有k个处理,则要作 k(k-1)/2次类似的检验
⑵无统一的试验误差,误差估计的精确性和检验的灵敏性低 ⑶推断的可靠性低,检验的 I 型错误率大
• 另一种情况是处理因素确实有作用。组间均方是 由于误差与不同处理共同导致的结果,即各样本 来自不同总体。那么,组间均方会远远大于组内 均方。MS组间>>MS组内。
• MS组间/MS组内比值构成F分布。用F值与其临界 值比较,推断各样本是否来自相同的总体。
2024/10/16
5ቤተ መጻሕፍቲ ባይዱ
多重比较检验问题
多重比较是通过对总体均值之间的配对比较来进一步 检验到底哪些均值之间存在差异。
方此差43案224分02平 ..4例均 28/析1方 0将/1数 6和数((xQ据i i按))区组和处153理531657组4...3843两.802个方向进行17分3594组.55.5,6540属46..于20 无重2复247数44.97据.94的9 双向34
SPSS实验报告

第六章方差分析一实验目的1.理解方差分析的概念、原理及作用;2.掌握用 SPSS 进行单因素、双因素及协方差分析的方法;3.结合参考资料了解方差分析的其它方法及作用。
二方差分析的原理方差分析的基本原理是认为不同处理组的均值间的差别基本来源有两个:(1)随机误差,如测量误差造成的差异或个体间的差异,称为组内差异,用变量在各组的均值与该组内变量值之偏差平方和的总和表示,记作w SS ,组内自由度w df ;(2)实验条件,即不同的处理造成的差异,称为组间差异。
用变量在各组的均值与总均值之偏差的总平方和表示,记作b SS ,组间自由度b df 。
三实验过程1. 某农场为了比较4种不同品种的小麦产量的差异,选择土壤条件基本相同的土地,分成16块,将每一个品种在4块试验田上试种,测得小表亩产量(kg)的数据如表6.17所示(数据文件为data6-4.sav),试问不同品种的小麦的平均产量在显著性水平0.05和0.01下有无显著性差异。
(数据来源:《SPSS实用统计分析》郝黎仁,中国水利水电出版社)表6.17实验步骤:第1步分析:由于有一个因素(小麦),而且是4种饲料。
故不能用独立样本T 检验(仅适用两组数据),这里可用单因素方差分析;第2步数据的组织:分成两列,一列是试验田的产量(output),另一列是小麦品种(breed)(A、B、C、D);第3步方差相等的齐性检验:由于方差分析的前提是各个水平下(这里是不同品种的小麦产量)的总体服从方差相等的正态分布。
其中正态分布的要求并不是很严格,但对于方差相等的要求是比较严格的。
因此必须对方差相等的前提进行检验。
从SPSS的数据管理窗口中选择analyze—compare means—One-Way ANOVA,将小麦产量(output)选入dependent list框中,将品种(breed)选入factor框中,点开Options,选中Homogeneity of variance test(方差齐性检验),点开post hoc multiple comparisons,将significance level的值在两次实验时分别设置为0.01和0.05。
第六章 SPSS方差分析讲解

SPSS单因素方差分析的基本操作步骤: (1)选择菜单:【分析】-【比较均值】-【单因素ANOVA】 (2)选择观测变量到【因变量列表】 (3)选择控制变量到【因子】(自变量)。
ANOVA(广告形式对销售额的单因素的方差分析结果)
43.4732
61.3689 53.7135 57.7044 57.5944 57.2863 44.0597
61.0268
78.1311 80.2865 70.5456 76.4056 81.2137 63.6903
40.00
51.00 42.00 52.00 50.00 44.00 37.00
70.00
常用的几个检验统计量 (1)LSD方法(Least Significant Difference) LSD方法称为最小显著性差异法。其字面就体现了其检 验敏感性高的特点,即水平间的均值只要存在一定程度的微 小差异就可能被检验出来。它利用全部观测变量值,而非仅 使用某两组的数据。 LSD方法使用于各总体方差相等的情况,但它并没有对 范一类错误的概率问题加以有效控制。 (2)Bonferroni方法 Bonferroni方法与LSD方法基本相同。不同的是Bonferroni对 范一类错误的概率进行了控制。
如果控制变量各水平下的观测变量总体的分布出现了显著 差异,则认为观测变量值发生了明显的波动,意味着控制变 量的不同水平对观测变量产生了显著影响;反之,如果控制 变量值没有发生明显波动,意味着控制变量的不同水平对观 测变量没有产生显著影响。
方差分析对观测变量各总体的分布还有以下两个基本假设前提: 观测变量各总体应服从正态分布。(不是非常严格)
第六章SPSS的方差分析-精品文档

多因素方差分析的基本思想
SPSS
概念
多因素方差分析用来研究两个及两个以 上控制变量是否对观测变量产生显著影响。 它不仅能分析多个因素对观测变量的独立 影响,更能够分析多个控制因素的交互作 用能否对观测变量的分布产生显著影响, 进而找到有利于观测变量的最优组合。
基本思想 SPSS
确定观测变量和若干个控制变量 剖析观测变量的方差 比较观测变量总离差平方和和各部分所占
S-N-K方法 SPSS
• 用于进行所有各组均值间的配对比较,且 用于水平观测值个数相等的情况。用逐步 过程进行其次子集的均值配对比较。在该 过程中各组均值按从小到大的顺序排列, 最先比较最极端的差异。
方差不相等时的一些多重比较方法
SPSS
• Tamhane,sT2方法:表示用T检验进行配 对比较检验
对销售额有显著差异。
SPSS
方法二 分析
比较均值
均值
SPSS
SPSS
SPSS
单因素 方差分 析一定 要选上
SPSS
单因素方差分析的进一步分析
SPSS
进一步 分析
SPSS
方差相等时的一些多重比较方法
SPSS
LSD方法
即最小显著性差异法。用T检验完成组间成对 均值的比较。检验的敏感度较高,即使是 各个水平间的均值存在细微差别也有可能 被检验出来,但此方法对第一类弃真错误 不进行控制和调整
i1 j1 k1
S S T S S A S S B S S C S S A B S S B C S S A B C S S E
多因素方差分析的数学模型
SPSS
• 设控制变量A有k个水平,B有r个水平,每 个交叉水平下均有l个样本,则在控制变量
SPSS新手简明教程(6)

第六章方差分析第一节Simple Factorial过程6.1.1 主要功能6.1.2 实例操作第二节General Factorial过程6.2.1 主要功能6.2.2 实例操作第三节Multivarite过程6.3.1 主要功能6.3.2 实例操作方差分析是R.A.Fister发明的,用于两个及两个以上样本均数差别的显著性检验。
由于各种因素的影响,研究所得的数据呈现波动状,造成波动的原因可分成两类,一是不可控的随机因素,另一是研究中施加的对结果形成影响的可控因素。
方差分析的基本思想是:通过分析研究中不同来源的变异对总变异的贡献大小,从而确定可控因素对研究结果影响力的大小。
方差分析主要用于:1、均数差别的显著性检验,2、分离各有关因素并估计其对总变异的作用,3、分析因素间的交互作用,4、方差齐性检验。
第一节 Simple Factorial过程6.1.1 主要功能调用此过程可对资料进行方差分析或协方差分析。
在方差分析中可按用户需要作单因素方差分析(其结果将与第五章第四节相同)或多因素方差分析(包括医学中常用的配伍组方差分析);当观察因素中存在有很难或无法人为控制的因素时,则可对之加以指定以便进行协方差分析。
返回目录返回全书目录6.1.2 实例操作[例6-1]下表为运动员与大学生的身高(cm)与肺活量(cm3)的数据,考虑到身高与肺活量有关,而一般运动员的身高高于大学生,为进一步分析肺活量的差异是否由于体育锻炼所致,试作控制身高变量的协方差分析。
6.1.2.1 数据准备激活数据管理窗口,定义变量名:组变量为group(运动员=1,大学生=2),身高为x,肺活量为y,按顺序输入相应数值,建立数据库,结果见图6.1。
图6.1 原始数据的输入6.1.2.2 统计分析激活Statistics 菜单选ANOV A Models中的Simple Factorial...项,弹出Simple Factorial ANOV A对话框(图6.2)。
SPSS_第6章 方差分析

-12.3756
15.7090
-31.0423
-2.9577
-15.7090
12.3756
-32.7090
-4.6244
2.9577
31.0423
4.6244
32.7090
40
结果2
英语
Subset for alpha = .05
Student-Newman-Keul sa
g rou p 2 1 3 Si g.
Std. Deviation 13.70280 12.42176 6.96898 13.79175
Std. Error 5.59414 5.07116 2.84507 3.25075
95% Confidence Interval for M ea n
Lower Bound Upper Bound
58.7865
75 70
74
80 72
72
77 66
68
68 72
71
75 70
71
75 70
Xt =72
4
从上表可知,三种不同实验教材的教学效果不完全 一致,表现在三个不同实验处理组的平均数之间存 在差异;同时,同一实验组内部的5名样本的反应变 量也存在差异。
5
我们可以将三个实验组的所有15名样本分数的差异 分为两部分:实验组间的差异(称为组间差异)和 实验组内的差异(称为组内差异)。
18.66667* 6.58815
*. The mean difference is significant at the .05 level.
Si g. .804 .021 .804 .013 .021 .013
95% Confidence Interval
第6章spss方差分析(共39张PPT)

因sp为he当ric一ity个)I因n,变c否l量则u被应d重校e复正i测n。量te几r次c,ep从t而i同n一m个体o的d几e次l 观-在察结模果间型存在中相关包,这括样就截不满距足独。立若性的能要求确,但定要求回满足协方差矩阵的球形性( 归线不通过原点,则不选此项。 01,说明模型有统计学意义。
控制因素,可多 个
随机因素,不是 必需
协变量-用于去除该变量对因变量 的影响 ,协方差分析用
5
异方差时,将选入变量用加权最小二乘 法估计模型参数,协方差分析用
【Model按钮】:
Full factorial 全模型,包括所有因素的主效应、交互效应、协变 量主效应等。是系统默认的模型。
Custom 自定义模型。用户可以选择实验中感兴趣的效应 。
6
Factors&covariate-框中所列出的是主对话框中所选的因素:包 括固定因素(标F)、随机因素(标R)、协变量因素(标C) 。本例中只含有固定因素。
Build terms:针对所选因素选择不同的效应。 Interaction 指定任意的交互效应; Main effects 指定主效应; All 2-way 指定所有2维交互效应; All 3-way 指定所有3维交互效应; All 4-way 指定所有4维交互效应 All 5-way 指定所有5维交互效应。
Error 误差。其偏差平方和反应的是组内差异。也称组内偏差平方 和。
Total 是偏差平方和,在数值上等于截距+主效应+交互效应+误差
偏差平方和。 Corrected Total 校正总和。其偏差平方和等于校正模型与误差之偏 差平方和之总和。
22
SPSS数据分析与应用 第6章实训案例

SPSS数据分析与应用第6章实训案例本章介绍《SPSS数据分析与应用第6章实训案例》的背景和目的。
这个案例是为了帮助读者更好地理解和应用SPSS数据分析工具而设计的。
在本章中,我们将介绍一个具体的实训案例,包括案例的背景、数据的来源以及需要进行的数据分析任务。
通过这个案例,读者将研究如何使用SPSS软件进行数据分析,并掌握常用的数据分析方法和技巧。
在这一章节中,我们将详细介绍实际操作SPSS软件的步骤,包括数据导入、数据清洗、变量设置、数据分析等。
每个步骤都会给出详细的说明和示例,以帮助读者顺利完成实训案例。
在这一章节中,我们将展示实际进行数据分析后得到的结果,并进行对结果的解读和分析。
读者将通过实验结果的展示和分析,更好地理解数据分析方法和结果的含义。
在这个章节中,我们将对整个实训案例进行总结,并给出一些拓展的内容,包括其他可能的数据分析方法和应用场景。
读者将通过这个章节更好地巩固所学的知识,并拓展自己的数据分析能力。
这个章节将给出实训案例的参考答案,供读者参考和对比。
读者可以通过对比答案,进一步检查自己的数据分析能力和理解程度。
通过研究本章内容,读者将能够熟练使用SPSS软件进行数据分析,掌握常用的数据分析方法和技巧,并能够将数据分析应用于实际问题中。
本章介绍了《SPSS数据分析与应用第6章实训案例》中涉及的数据集和问题。
以下是详细描述:该案例涉及的数据集为某医院的病人信息和医疗费用数据集。
主要问题是研究不同因素对病人的医疗费用的影响。
在数据集中,每个病人都有一些基本信息,如年龄、性别、是否吸烟等。
此外,还有每个病人的医疗费用数据,包括住院费、手术费、药费等。
研究问题主要包括以下几个方面:病人的基本信息对医疗费用的影响:通过分析年龄、性别、是否吸烟等因素与医疗费用之间的关系,研究这些基本信息对医疗费用的影响程度。
不同费用项之间的关系:通过探究住院费、手术费、药费等不同费用项之间的相关性,了解各项费用之间的关系,为进一步分析提供依据。
SPSS第6单元多因素方差分析

数学 99.00 88.00 99.00 89.00 94.00 90.00 79.00 56.00 89.00 99.00 70.00 89.00 55.00 50.00 67.00 67.00 56.00 56.00
组别 0 0 0 0 0 0 2 2 2 2 2 2 1 1 1 1 1 1
SPSS应用
图5-9 “Univariate: Options”对话框 (一)
SPSS应用
图5-10 “Univariate:
Post Hoc Multiple Comparisons for Observed Means”对话框
SPSS应用
SPSS应用
图5-11 “Univariate:Model”对话框
SPSS应用
图5-12 “Univariate:Profile Plots”对话框
SPSS应用
图5-13 “Univariate:Contrasts”对话框
5.3.3 结果和讨论
SPSS应用
(1)SPSS输出结果文件中的第一部分如 下两表所示。
SPSS应用
(2)输出的结果文件中第二部分如下表所示
SPSS应用
多因素方差分析(Univariate)是检验两 个或两个以上因素变量(自变量)的不同水平 是否给一个(或几个相互独立的)因变量造成 了显著的差异或变化的分析方法。
SPSS应用
多因素方差分析包含一个因变量,至少两个 自变量(因素)每个因素把被试区分为至少 两个实验水平,因变量必须是连续型变量。 多因素设计的方差分析过程通常分两步,首 先对因素主效应和交互效应进行综合检验,如 果效应显著,然后再作进一步检验。
性别 male female male male female male male female male male female male female male female male female male
SPSS操作—方差分析

SPSS操作—方差分析
一、概念
方差分析(ANOVA)法是统计学中一种用于检验三个或以上水平的均数差异的统计方法。
方差分析从表面上看是利用方差的大小,在一定的概率和显著水平下,比较多组数据的均值差异,确定数据的显著性。
一般来说,它用来检验有多自变量时的均数差异,其中包括一个或多个因素,每个因素又有两个或者多个水平。
二、SPSS操作步骤
1、打开SPSS软件,点击“文件”,选择“新建”,在弹出的界面中选择“数据集”,点击“确定”,新建一个数据集。
2、将所要分析的数据输入到数据集中,在“变量视图”中定义响应变量和自变量,并设置其变量类型,完成数据的输入。
3、点击“分析”,选择“统计”,在弹出的界面中选择“参数检验”,点击“F检验”,然后在窗口中选择因变量和自变量,完成基本的参数设置,点击“确定”,弹出方差分析窗口,点击“确定”,即可开始运行方差分析。
4、方差分析运行完毕后,在输出窗口中可以看到结果,包括方差分析汇总表和方差分析的结果等信息。
5、方差分析的结果主要包括拟合度指数、F值、绝对值、样本量、概率值、单组比较、多组比较等内容,在这里。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(一)单因素方差分析的基本步骤
提出原假设:自变量不同水平下因变量各总体 的均值无显著差异。 选择检验统计量:F统计量。 计算检验统计量的观测值和概率P值。 给出显著性水平,并作出决策。
(二)单因素方差分析的应用举例
案例: 某企业在制定某商品的广告策略时,收集了 该商品在不同地区采用不同广告形式促销后的 销售额数据,希望对广告形式和地区是否对商 品销售额产生影响进行分析。
五种功能各有不同,可根据数据的特征选用其中的一个过程。
第六章 SPSS的方差分析
与多选题分析
本章内容
单因素方差分析
多选题分析
方差分析概述
概念:方差分析是从因变量的方差入手,研究 诸多自变量中哪些变量是对因变量有显著影响 的变量,对因变量有显著影响的各个自变量其 不同水平以及各水平的交互搭配是如何影响因 变量的。 方差分析就其内容来说,是分析或检验总体间 的均值是否有所不同。但就其检验的方法或手 段来说则是通过方差进行的。
案例:总体上讲,不同广告形式对产品的销售 额有显著影响,那么究竟哪种广告形式的作用 显著?
第二节 多选题分析
(一)简介
多选题在录入时通常是需要分解的。因此它录 入时是多个变量。其分解有两种方法,即二分 法(01编码),分类法(直接编码录入)。 多选题分析的思路: 分多个变量录入后,分析时先合并为一个集合, 再进行频次和交互分析。
方差分析的基本思想
方差分析认为因变量的变化受两类因素的影响: 第一,自变量不同水平所产生的影响; 第二,随机变量所产生的影响。这里的随机变量 指那些人为很难控制的因素,主要指试验过程 中的抽样误差。 (如果自变量的不同水平对因变量产生了显著影 响,那么它和随机变量共同作用必然使得因变 量值有显著变动;反之,则认为因变量的变化 是由抽样误差造成的。
步骤:
按Analyze Compared Means One-Way Anova顺序单 击。打开 One-Way Anova主对话框.
结果分析
广告形式对销售额的单因素方差分析结果:因 变量销售额的总离差平方和为26169.306;如 果仅考虑广告形式单个因素的影响,则销售额 总变差中,不同广告形式可解释的变差为 5866.083,抽样误差引起的变差为20303.222, F统计量的值为13.483,对应的概率P值近似 为0。如果显著性水平为0.05,则概率P值小于 显著性水平,因此因拒绝原假设,认为不同广 告形式对销售额产生了显著影响。
二分法
1、数据结构如下
二分法的特点是,题目有几个选项,SPSS数据文件 中就有相应的几个变量以之对应。选项选中为1,不 选中为0(也可以自己定义)。
分类法
2 分类法,数据结构如下
分类法的话,就是把选项序号依次输入到 SPSS里面就可以了。变量个数等于同时选中 的选项个数的最大值。
例:择业中考虑的主要因素(多选)
方差分析的条件
各个总体中因变量都服从正态分布; 在各个总体中因变量的方差都相等; 各个因变量值之间是相互独立的。ຫໍສະໝຸດ 第一节单因素方差分析
当一个变量为定类变量,另一变量为定距 变量时,两变量间是否有关,通常以分组 平均数比较的方法来考察。即按照定类变 量的不同取值来分组,看每个分组的定距 变量的平均数是否有差异。不同组间的平 均数差异越小,两个变量间的关系越弱; 相反,平均数差异越大,变量间关系越强。
假设检验在统计方法中的地位
统计方法
描述统计
推断统计
参数估计
假设检验
两总体均值比较的概念
目的
研究样本与总体之间的差异。 因为在所有数值特征中,均值是反映总体一般水平的最重要特征,因此可以通过 比较样本均值与总体均值之间的差异来判断统计分析的质量。
方法
应用统计学方法解决上述问题称为“差异的显著性检验”。 参数检验:若已知总体为正态分布,所进行差异的显著性检验。 非参数检验:若未知总体分布,所进行差异的显著性检验。
1.经济收入 2.专业对口 3.发展前途 4.地理区位 5.个人爱好 6.风险大小 7.劳动强度 8.社会福利 9.其他
有13个样本中分别选择了:
上机作业
1.熟练掌握单因方差的操作,熟悉 其基本参数的设置,正确解读分析 结果。 2.了解多选题分析的操作。
SPSS软件中Compare Means相关的五种功能
两个总体均值的比较(Mean): 单样本T检验(One-Samples T Test): 独立样本T检验(Independent-Samples T Test): 配对样本T检验(Paired-Samples T Test): 单因素方差分析(One-Way ANOVA):
(二)操作步骤
1.定义变量集
依次按 AnalyzeMu ltiple ResponseD efine Sets, 打开变量集 对话框。
案例
Q假设有5个被访者,分别选择了 A1 B 1,2 C 1,2,3 D 2,3
(三)单因素方差分析的进一步分析
方差齐性检验:是对自变量不同水
平下各因变量总体方差是否相等进 行分析。 案例:不同广告形式、不同地区下 销售额总体的方差是否相同,是否 满足单因素方差分析的前提要求, 是首先应检验的问题。
多重比较检验:单因素方差分析的基本分析只 能判断自变量是否对因变量产生了显著影响。 如果产生了显著影响,进一步还应确定自变量 的不同水平对因变量的影响程度如何,其中哪 个水平的作用明显区别于其他水平等。 例如:如果确定了不同施肥量对农作物的产量 有显著影响,那么还需要了解10公斤、20公斤、 30公斤肥料对农作物产量的影响幅度是否有差 异,哪种施肥量水平最有利于提高产量等等。
