2019-2020学年北京市海淀区八年级(上)期末数学试卷 及答案解析
北京市海淀区第一学期八年级数学期末试卷及答案(含答案)(优选)

海淀区八年级第一学期期末练习数 学(分数:100分 时间:90分钟)一、选择题:(本题共36分,每小题3分)在下列各题的四个备选答案中,只有一个是正确的. 请将正确选项前的字母填在表格中相应的位置.1.下列图形中,不是..轴对称图形的是(A ) (B ) (C ) (D ) 2.下列运算中正确的是(A )xy y x 532=+ (B )428x x x =÷ (C )3632)(y x y x = (D )62322x x x =⋅3.在平面直角坐标系xOy 中,点P (-3,5)关于x 轴的对称点的坐标是(A ) (3,5) (B )(3,-5) (C )(5,-3) (D )(-3,-5)4x 的取值范围是 (A )x ≠-32 (B )x <-32 (C )x ≥-32 (D )x ≥23-5.下列各式中,从左到右的变形是因式分解的是(A )3353()5x y x y +-=+- (B )2(1)(1)1x x x +-=- (C )2221(1)x x x ++=+ (D )xy x y x x -=-2)( 6.下列三个长度的线段能组成直角三角形的是(A )1 (B )1 (C )2,4,6 (D )5,5,6 7.计算)123(2- ,结果为 (A )6 (B )6- (C )66- (D )66-8.下列各式中,正确的是 (A )212+=+a b a b (B )22++=a b a b (C ) a b a b c c-++=- (D )22)2(422--=-+a a a a9.若x m +与2x -的乘积中不含x 的一次项,则实数m 的值为 (A )2- (B )2 (C )0 (D )110.如图,在△ABC 和△CDE 中,若︒=∠=∠90CED ACB ,AB=CD ,BC=DE ,则下列结论中不正..确.的是 (A )△ABC ≌ △CDE (B )CE=AC(C )AB ⊥CD (D )E 为BC 中点11如果大正方形的面积是25,(A 12.当x (A )1314151617,则APF ∠18CD =1,CE =3,则BC =_____.19.在平面直角坐标系xOy 中,点A 、点B 的坐标分别为(-6,0)、(0,8).若△ABC 是以∠BAC 为顶角的等腰三角形,点C 在x 轴上,则点C 的坐标为 .20.如图,分别以正方形ABCD 的四条边为边,向其内部作等边三角形,得到△ABE 、△BCF 、△CDG 、△DAH ,连接EF 、FG 、GH 、HE .若AB =2,则四边形EFGH 的面积为 .三、解答题:(本题共14分,第21题5分,第22题9分)21.计算: 101()(2)2π--++1.22.(1)解方程:xx x 211=--.(2))先化简,再求值:2)4442(22+÷-+--+x xx x x x x ,其中2=x .四、解答题:(本题共9分,第23题4分,第24题5分)23.如图,点F 、C 在BE 上,BF CE =,AB DE =,∠B =∠E . 求证: ∠A =∠D .24. 列方程(组)解应用题:上图为地铁调价后的计价图. 调价后,小明、小伟从家到学校乘地铁分别需4元和3元.由于刷卡坐地铁有优惠,因此,他们平均每次实付3.6元和2.9元.已知小明从家到学校乘地铁的里程比小伟从家到学校乘地铁的里程多5千米,且小明每千米享受的优惠金额是小伟的2倍,求小明和小伟从家到学校乘地铁的里程分别是多少千米?五、解答题:(本题共17分,第25题5分,第26题6分,第27题6分) 25.已知:如图,△ABC ,射线AM 平分BAC ∠.(1)尺规作图(不写作法,保留作图痕迹)作BC 的中垂线,与AM 相交于点G ,连接BG 、CG .(2)在(1)的条件下,∠BAC 和∠BGC 的等量关系为 ,证明你的结论..27.阅读:如图1,在△ABC 中,3180A B ∠+∠=︒,4BC =,5AC =,求AB 的长. 小明的思路:如图2,作BE AC ⊥于点E ,在AC 的延长线上取点D ,使得DE AE =,连接BD ,易得A D ∠=∠,△ABD 为等腰三角形.由3180A ABC ∠+∠=︒和180A ABC BCA ∠+∠+∠=︒,易得2BCA A ∠=∠,△BCD 为等腰三角形.依据已知条件可得AE 和AB 的长.图1 图2解决下列问题:(1)图2中, AE = ,AB = ;(2)在△ABC 中,A ∠、B ∠、C ∠的对边分别为a 、b 、c .①如图3,当32180A B ∠+∠=︒时,用含a 、c 的式子表示b ;(要求写解答过程) ②当34180A B ∠+∠=︒,2b =,3c =时,可得a = .图3数 学 答 案一、 选择题:(本题共36分,每小题3分)13.1; 14.26425b a ; 15.<; 16.3(2)(2)a a a +-; 17. 74︒; 18.4; 19.(16,0)-,(4,0); 20.8-21 22.(∴ (2 =2x x⋅+-----------------3分 =2x. -----------------4分当x ==分四、解答题:(本题共9分,第23题4分,第24题5分)23.证明:∵BF CE =,∴BC EF =. -----------------1分 在△ABC 和△DEF 中,,,,AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DEF . -----------------3分 ∴A D ∠=∠. -----------------4分24.解:设小明从家到学校乘地铁的里程为x 千米.4 3.62(3 2.9)5x x --=-. -----------------3分解方程,得 10x =.-----------------4分经检验,10x =为原分式方程的解,且符合题意.∴55x -=.答:小明和小伟从家到学校乘地铁的里程分别是10千米和5千米. ------------5分五、解答题:(本题共17分,第25题5分,第26题6分,第27题6分)25.解:(1)(注:不写结论不扣分)-----------------1分(2) 180BAC BGC ∠+∠=︒ . -----------------2分证明:过点G 作GE AB ⊥于点E ,GF AC ⊥交AC 的延长线于点F .∵点G 在∠BAC 平分线上, ∴GE GF =.∵点G 在BC 的中垂线上,∴GB GC =. 在Rt △GBE 和Rt △GCF 中,,,GE GF GB GC ==⎧⎨⎩∴△GBE ≌△GCF . ---------------4分 ∴12∠=∠. ∴BGC EGF ∠=∠.∵360AEG AFG BAC EGF ∠+∠+∠+∠=︒,90AEG AFG ∠=∠=︒,∴180BAC EGF ∠+∠=︒. ∴180BAC BGC ∠+∠=︒.-----------------5分 26. 解:(1)4x =;-----------------1分 (2) 112x =,22x =;-----------------3分(3)∵22322321n n x n x +-+=+-,∴223212221n n x n x +--+=+-. ∵223(1)(3)n n n n +-=-+,(1)(3)22n n n -++=+,12x x <, ∴1211x n -=-,2213x n -=+. ∴12n x =,222nx =+.-----------------5分 ∴212122x x -=.-----------------6分 27.(1)9AE =,6AB =;-----------------2分(2∴∴∴∵∴∵∴∵∴∴∴∴②3a =.-----------------6分 (注:本卷中许多问题解法不唯一,请老师根据评分标准酌情给分)。
北京市各区2019-2020学年上学期八年级期末数学试卷精选汇编:几何综合专题(含答案)
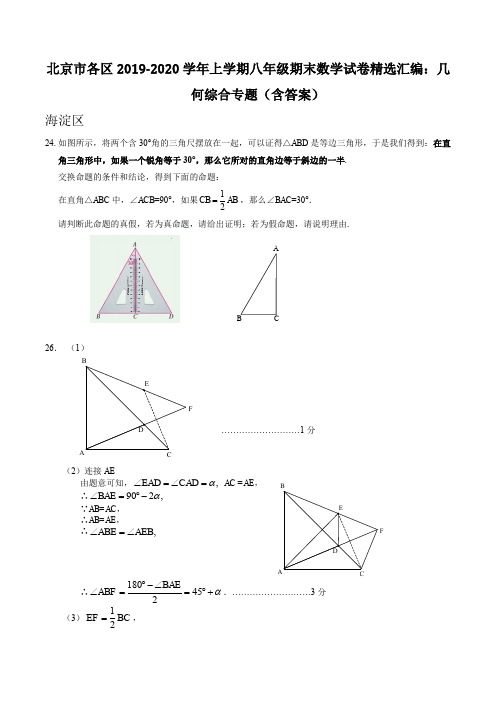
FFA北京市各区2019-2020学年上学期八年级期末数学试卷精选汇编:几何综合专题(含答案)海淀区24.如图所示,将两个含30°角的三角尺摆放在一起,可以证得△ABD 是等边三角形,于是我们得到:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半. 交换命题的条件和结论,得到下面的命题: 在直角△ABC 中,∠ACB =90°,如果12CB AB =,那么∠BAC =30°. 请判断此命题的真假,若为真命题,请给出证明;若为假命题,请说明理由.26. (1)………………………1分(2)连接AE由题意可知,,EAD CAD α∠=∠= AC =AE , ∴902,BAE α∠=︒- ∵AB=AC ,∴AB=AE , ∴,ABE AEB ∠=∠∴180452BAEABF α︒-∠∠==︒+.………………………3分(3)12EF BC =, CA证明:由(2)可知45,AEB ABE α∠=∠=︒+ ∴.CBF α∠= ………………………4分 ∵点C 关于直线AD 的对称点为点E , ∴135,ACF AEF α∠=∠=︒- ∴90,BCF α∠=︒-∵90,CBF BCF ∠+∠=︒ ………………………5分 ∴△BCF 是直角三角形.∵△ACE 是等边三角形, ∴30.α=︒∴30CBF ∠=︒ ∴1.2EF CF BC ==………………………6分东城区23.在三角形纸片ABC 中,∠B =90°,∠A =30°,AC =4,点E 在AC 上,AE =3.将三角形纸片按图1方式折叠,使点A 的对应点A '落在AB 的延长线上,折痕为ED ,A E '交BC 于点F. (1)求∠CFE 的度数;(2)如图2,,继续将纸片沿BF 折叠,点A '的对应点为A '',A F ''交DE 于点G .求线段DG 的长.图1图224. 如图,△ABC .(1)尺规作图:过点C 作AB 的垂线交AB 于点O .不写作法,保留作图痕迹; (2)分别以直线AB ,OC 为x 轴,y 轴建立平面直角坐标系,使点B ,C 均在正半轴上.若AB=7.5,OC =4.5,∠A =45°,写出点B 关于y 轴的对称点D 的坐标; (3)在(2)的条件下,求△ACD 的面积.23.解:(1)∵∠A =30°,∴∠A '=30°. ……………………1分∵∠A BF '=90°,∴∠A FB '=60°. ……………………2分 ∵∠CFE =∠A FB ', ∴∠CFE =60°. ……………………3分(2)∵点A 与点A '关于直线DE 对称, ∴DE ⊥AA '. ∵∠A =30°,AE =3, ∴1322DE AE == . ……………………4分 由(1)知,∠CFE =60°,∠C =60°,∴△CFE 是等边三角形.∴EF =CE =AC -AE =1. ……………………5分 同理,△EFG 也是等边三角形,∴12DG DE EG =-=DG =DE -EG =.……………………6分24.解:(1)……………………………………………………………………………………2分(2)D (-3,0); ……………………4分 (3)13927==2228ACD S ⨯⨯△.……………………6分 密云区25.已知如图,点A 、点B 在直线l 异侧,以点A 为圆心,AB 长为半径作弧交直线l 于C 、D 两点.分别以C 、D 为圆心,AB 长为半径作弧,两弧在l 下方交于点E,连结AE. (1)根据题意,利用直尺和圆规补全图形; (2)证明:l 垂直平分AE.lAB25.(1)图2A………………2分(2)证明:AC=AD=AB,CE=ED=AB,∴AC=CE,AD=DE又CD=CD∴△ACD ≌△ECD………………4分∴∠ACD=∠ECD∵AC=CE ∴l 垂直平分AE.………………6分门头沟区24.如图,在△ABC 中,AC 的垂直平分线交AC 于点D , 交BC 延长线交于点E ,连接AE ,如果∠B =50°,∠BAC =21°,求∠CAE 的度数.24.解答题(本小题满分5分) ∵AC 的垂直平分线交AC 于点D ∴EA =EC ……………………………………… 1分 ∴∠E AC =∠ECA ………………………… 2分∵∠B =50°,∠BAC =21°∴∠ECA=∠B+∠BAC=71°………………… 4分∴∠E AC =71° ………………… 5分27. 如图,在△ABC 中,AB=AC ,点M 在△ABC 内,AM 平分∠BAC .点D 与点M 在AC 所在直线的两侧,AD ⊥AB ,AD= BC ,点E 在AC 边上,CE=AM ,连接MD 、BE . (1) 补全图形;(2) 请判断MD 与BE 的数量关系,并进行证明;(3) 点M 在何处时,BM+BE 会有最小值,画出图形确定点M 的位置;如果AB =5,BC = 6,求出BM+BE的最小值.BBB27.解答题(本小题满分7分) 解:(1)补全图形正确 ………………………………………………………1分 (2)MD =BE ………………………………………………………2分证明:延长AM 交BC 于点F (如图2). ∵ AM 平分∠BAC , ∴ ∠BAM =∠CAM .∵ AD ⊥AB , ∴ ∠MAD +∠BAM =90°. ∴ ∠MAD +∠CAM =90°∵ AB=AC ,AM 平分∠BAC ,∴ AF ⊥BC .∴ ∠C +∠CAM =90°.∴ ∠MAD =∠C . ………………………………3分 又∵ AM= CE ,AD= BC ,∴ △AMD ≌△CEB . …………………………………………… 4分 ∴ MD =BE . …………………………………………… 5分(3) 点M 的位置如图 …………………………………………… 6分∵ AB=5,BC = 6, ∴ AD = BC=6,.∴BD ==∴ BM+BE……………… 7分朝阳区26.如图,△ABC 是等边三角形,△ADC 与△ABC 关于直线AC 对称,AE 与CD 垂直交BC 的延长线于点E ,∠EAF=45º,且AF 与AB 在AE 的两侧,EF ⊥AF . (1)依题意补全图形.(2)①在AE 上找一点P ,使点P 到点B ,点C 的距离和最短;②求证:点D 到AF ,EF 的距离相等.26.(1)补全图形,如图………………………..2分(2与AE 的交点.B B…………..4分②证明:连接DE ,DF .∵△ABC ,△ADC 是等边三角形,∴AC =AD ,∠ACB =∠CAD =60°. ∵AE ⊥CD , ∴∠CAE =21∠CAD =30°. ∴∠CEA =∠ACB -∠CAE =30°. ∴∠CAE =∠CEA. ∴CA =CE . ∴CD 垂直平分AE . ∴DA =DE .∵EF ⊥AF ,∠EAF =45°, ∴∠FEA =45°. ∴∠FEA =∠EAF . ∴F A =FE .∴△F AD ≌△FED .∴∠AFD =∠EFD .点D 到AF ,EF 的距离相等. ……………..7分顺义区27.在平面内,给定∠AOB =60°,及OB 边上一点C ,如图所示.到射线OA ,OB 距离相等的所有点组成图形G ,线段OC 的垂直平分线交图形G 于点D ,连接CD .(1)依题意补全图形;直接写出∠DCO 的度数;(2)过点D 作OD 的垂线,交OA 于点E ,OB 于点F .求证:CF =DE .O27.(5分)F EDCBA(1)画图………………………………… 2分30°………………………………… 3分(2) 证明:∵OD 是∠AOB 的平分线,∠AOB =60°, ∴∠1 =∠2=30°,又∵点D 在OC 的垂直平分线上, ∴CD =OD ,∴∠3 =∠2=30°, ∵EF ⊥OD ,∴∠EDO =∠FDO =90°, ∴∠DFO =60°,∴∠4 =30°,∠4 =∠3, ∴CF =DF ,又∵△OED ≌△OFD ,……………………………………4分 ∴DE =DF ,∴CF =DE .…………………………………………………5分昌平区27.如图,将△ABC 分别沿 AB ,AC 翻折得到△ABD 和△AEC ,线段 BD 与AE交于点 F ,连接BE .(1)如果∠ABC =16º,∠ACB =30°,求∠DAE 的度数; (2)如果BD ⊥CE ,求∠CAB 的度数.27. 解:(1)∵△ABC 沿AC 、AB 翻折得到△AEC 和△ABD , ∴△AEC ≌△ABC ,△ABD ≌△ABC.∴∠2=∠1=30°, ∠4=∠3=16°. …………1分 ∠EAC =∠BAD =∠BAC =180°-30°--16°=134°. ……2分∵∠DAC =360°-∠BAD -∠BAC ,O54321F EDCBA∴∠DAC=360°-134°-134°=92°. ………………3分∴∠DAE=∠EAC -∠DAC=134°-92°=42°. …………4分(2)∵BD ⊥CE ,∴∠5=90°. . …………………………………………………………………… 5分∴∠DBC+∠ECB=90°.∵∠1=∠2,∠3=∠4,∴∠DBC+∠ECB=2∠3+2∠1=90°.∴∠3+∠1=45°. . …………………………………………… 6分 在△ABC 中,∠CAB =180°-(∠3+∠1)=180°-45°=135°. …… 7分平谷区27. 已知:在△ABC 中,∠ABC =45°,BD ⊥AC 于点D ,过点C 作CE ⊥AB 于点E ,交BD 于点F .(1)依题意补全图形; (2)求证:∠ABD =∠ACE (3)求证:EF =AE27. (1) 依题意补全图形………………………………………………… 1 (2)证明:∵CE ⊥AB ,BD ⊥AC∴∠BEC=∠BDC=90°………………………2 ∴∠ABD+∠EFB=90°∠ACE+∠CFD=90° ∵∠EFB=∠CFD∴∠ABD=∠ACE (3)(3)∵∠BEC=90°,∠ABC=45° ∴ BE=EC (4)在△BEF 和△AEC 中 ⎪⎩⎪⎨⎧∠∠=∠=∠ACE =ABD ECBE AEC BEC∴BEF ∆≌AEC ∆)(ASA (5)∴EF =AE燕山地区27.阅读下面材料:学习了三角形全等的判定方法(即“SAS ”“ASA ”“AAS ”“SSS ”)和直角三角形全等的判定方法(即“HL ”)后,明明继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行探究明明将命题用符号语言表示为:在△ABC 和△DEF 中,AC=DF ,BC=EF ,∠B =∠E . 明明的探究方法是把∠B 分为“直角、钝角、锐角”三种情况进行探究.(1) 当∠B 是直角时,如图甲,△ABC 和△DEF 中,AC=DF ,BC=EF ,∠B =∠E =90°, 根据“HL ”定理,可以知道Rt △ABC ≌ Rt △DEF.(2)当∠B 是锐角时,如图乙,BC=EF ,∠B =∠E ﹤90°,在射线EM 上有点D,使DF=AC,画出符合条件的点D ,则△ABC 和△DEF 的关系是 ;A. 全等B. 不全等C.不一定全等(3)当∠B 是钝角时,如图丙,在△ABC 和△DEF 中,AC=DF ,BC=EF ,∠B =∠E ﹥90°.过点C 作AB 边的垂线交AB 延长线于点M;同理过点F 作DE 边的垂线交DE 延长线于N ,根据“ASA ”,可以知道△CBM ≌△FEN,请补全图丙,进而证出△ABC ≌△DEF.A27.(2)画出点D 正确,选C ………………… 2分 (3)补全图 ………………… 3分证明:由△CBM ≌△FEN得,CM=FN,BD=EN 又在Rt △CMA 和Rt △FND 中⎩⎨⎧==FN CM DF AC ∴△CMA ≌△FND ∴AM=DN∴AB=DE ……………… 4分 又在△ABC 和△DEF 中 ⎪⎩⎪⎨⎧===DE AB EF BC DFAC ∴△ABC ≌△DEF ……………… 5分房山区26.(1)证明:∵AB AD =,=60A ∠︒,∴△ABD 是等边三角形.∴60ADB ∠=︒. …….………..……….1分∵CE ∥AB ,∴60CED A ∠=∠=︒. …….………..……….2分 ∴CED ADB ∠=∠. (2)解:连接AC 交BD 于点O ,∵AB AD =,BC DC =, ∴AC 垂直平分BD . ∴30BAO DAO ∠=∠=︒. ∵△ABD 是等边三角形,8AB = ∴8AD BD AB ===,∴4BO OD ==. ………….………..……….3分 ∵CE ∥AB , ∴ACE BAO ∠=∠.∴6AE CE ==, 2DE AD AE =-=.O F EDBA∵60CED ADB ∠=∠=︒.∴60EFD ∠=︒.∴△EDF 是等边三角形.∴2EF DF DE ===,∴4CF CE EF =-=,2OF OD DF =-=.在Rt △COF 中,∴OC ==. …….………..……….4分 在Rt △BOC 中,∴BC ===. …….………..……….5分 大兴区26. 解:∵AD 是△ABC 的高∴90ADB ADC ∠=∠= ………………………… 1分∵45ABC ∠=∴45DBA ABC ∠=∠=o∴BD =AD ………………………… 2分∵BE 是△ABC 的高∴90BEC ∠=∴90EBC C ∠+∠=∵90ADC ∠=∴90DAC C ∠+∠=∴EBC DAC ∠=∠ ………………………… 3分在△BDF 和△ADC 中,EBC DAC BD ADBDF ADC ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BDF ≌△ADC . ………………………… 4分∴DF =CD . ………………………… 5分∵CD =4∴DF =4 ………………………… 6分27.解:(1)EBA ………………………… 2分(2)∵将线段CD 绕点C 逆时针旋转90°得到线段CE ,∴90DCE ∠=,CD =CE∵ ∠ACB =90°∴ACD BCE ∠=∠ ………………………… 3分在△ACD 和△BCE 中,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩∴△ACD ≌△BCE ………………………… 5分∴CBE A ∠=∠ ………………………………………… 6分 ∵90,ACB AC BC ∠==o∴45A ∠=o∴45CBE ∠=o∵90DCE ∠=,CD =CE∴45CED ∠=……………………………………………………… 7分 在△BCE 中, BCE ACD α∠=∠=.∴90DEB ∠=-α…………………………………………………… 8分 石景山区通州区。
北京市海淀区2018-2019学年八年级上期末数学试卷含答案解析

北京市海淀区2019-2019学年八年级第一学期期末考试数学试题2019.1一、选择题(本题共36分,每小题3分)在下列各题的四个备选答案中,只有一个..符合题意.请将正确选项前的字母填在表格中相应的位置. 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案1.下列标志是轴对称图形的是A B C D【考点】轴对称与轴对称图形 【试题解析】根据轴对称图形的定义可观察得知B 为轴对称图形.故选B . 【答案】B2.PM2.5是指大气中直径小于或等于2.5微米的颗粒物,2.5微米等于0.000 002 5米,把数字0.000 002 5用科学记数法表示为A .62.510⨯B .60.2510-⨯C .62510-⨯D .62.510-⨯ 【考点】科学记数法和近似数、有效数字 【试题解析】根据题意得0.000 002 5=.故选D . 【答案】D 3.使分式23x -有意义的x 的取值范围是 A .3x ≠ B .3x > C .3x < D .3x = 【考点】分式的概念 【试题解析】由于分式的分母不能为0,否则无意义,所以.故选A .【答案】A4.下列计算中,正确的是A .238()a a =B .842a a a ÷=C .325a a a +=D .235a a a ⋅= 【考点】幂的运算 【试题解析】同底数幂相乘,底数不变,指数相加。
所以D 选项正确.故选D . 【答案】D5.如图,△ABC ≌△DCB ,若AC =7,BE =5,则DE 的长为A .2B .3C .4D .5 【考点】全等三角形的性质 【试题解析】由于△ABC ≌△DCB ,根据全等三角形的性质可得BD=AC=7,又因为BE =5,所以DE=BD-BE=2.故选A . 【答案】A6.在平面直角坐标系中,已知点A (2,m )和点B (n ,-3)关 于x 轴对称,则m n +的值是A .-1B .1C .5D .-5 【考点】平面直角坐标系及点的坐标 【试题解析】由于A 、B 两点关于x 轴对称,所以横坐标相同,纵坐标互为相反数,得m=3,n=2.故选C . 【答案】C7.工人师傅常用角尺平分一个任意角.做法如下:如图,∠AOB 是一个任意角,在边OA ,OB 上分别取OM =ON ,移动角尺,使角尺两边相同..的刻度分别与点M ,N 重合,过角尺顶点C 作射线OC .由此作法便可得△MOC ≌△NOC ,其依据是A .SSSB .SASC .ASAD .AAS 【考点】全等三角形的判定 【试题解析】根据题意得在△MOC 和△NOC 中,∴△MOC ≌△NOC (SSS ).故选A .【答案】A8.下列各式中,计算正确的是A .2(21)21x x x -=-B .23193x x x +=-- C .22(2)4a a +=+ D . 2(2)(3)6x x x x +-=+-【考点】整式的运算因式分解 【试题解析】 根据题意得B 选项.故选B .【答案】B9.若1a b +=,则222a b b -+的值为A .4B .3C .1D .0 【考点】因式分解整式的运算 【试题解析】 根据题意得.故选C .【答案】C10.如图,在△ABC 中,AB =AC ,∠A =40°,AB 的垂直平分线MN 交AC 于D 点,则∠DBC 的度数是A .20°B .30°C .40°D .50° 【考点】线段的垂直平分线 【试题解析】根据题意得∵AB =AC ,∠A =40°∴∠ABC=70°,又∵AB 的垂直平分线MN 交AC 于 D 点,∴∠ABD=40°,∴∠DBC=30°.故选B . 【答案】B 11.若分式61a +的值为正整数,则整数a 的值有 A .3个 B .4个 C .6个 D .8个 【考点】分式的基本性质 【试题解析】 根据题意得的值为正整数,∴a+1必定是可以整除6正整数,∴a+1=1,2,3或6,a=0,1,2,或5.故选B . 【答案】B12.如图,等腰三角形ABC 的底边BC 长为4,面积是16,腰AC 的垂直平分线EF 分别交AC ,AB 边于E ,F 点.若点D 为BC 边 的中点,点M 为线段EF 上一动点,则△CDM 周长的最小值为 A .6 B .8C .10D .12【考点】一元二次方程的根与系数的关系 【试题解析】根据题意得CD=2,等腰三角形ABC 的高AD=8,∵EF 垂直平分AC ,所以连接AM 可得AM=CM ,∴△CDM 周长=CD+DM+CM=CD+DM+AM ,当AM 与DM 在同一直线上时最短,即为高AD=8,∴△CDM 周长的最小值为=2+8=10.故选C .【答案】C二、填空题(本题共24分,每小题3分) 13.当x = 时,分式1xx -值为0. 【考点】分式的概念 【试题解析】根据题意得分式分母不能为0 ,所以分式的分子为0时,即x=0时,分式值为0.【答案】14.分解因式:24x y y-=.【考点】因式分解【试题解析】根据题意得.【答案】15.计算:233xy⎛⎫-=⎪⎝⎭.【考点】分式的运算【试题解析】根据题意得.【答案】16.如果等腰三角形的两边长分别为3和7,那么它的周长为.【考点】等腰三角形【试题解析】根据题意得等腰三角形的另一边可能为7或3,由于三角形的三边关系(两边之和大于第三边,两边之差小于第三边)可知,另一边为3不成立,所以另一边只能为7.所以周长为7+7+3=17【答案】1717.如图,DE⊥AB,∠A=25°,∠D=45°,则∠ACB的度数为.【考点】三角形的性质及其分类【试题解析】根据题意得DE⊥AB,∠A=25°,∴∠AFE==∠DFC=65°,∵∠D=45°,∴∠ACD=70°,∠ACB=110°.【答案】110°18.等式222()a b a b+=+成立的条件为.【考点】整式乘法【试题解析】根据题意得.∵,∴.【答案】19.如图,在△ABC中,BD是边AC上的高,CE平分∠ACB,交BD于点E,DE=2,BC=5,则△BCE的面积为.【考点】三角形中的角平分线、中线、高线三角形的面积【试题解析】根据题意得DE=2,如图,过E作BC的垂线交于F,∵CE平分∠ACB,∴EF=ED=2(角平分线的性质),又∵BC =5,∴△BCE 的面积=。
北京市海淀区第一学期八年级数学期末试卷及答案(含答案)-优质版

海淀区八年级第一学期期末练习数 学(分数:100分 时间:90分钟)一、选择题:(本题共36分,每小题3分)在下列各题的四个备选答案中,只有一个是正确的. 请将正确选项前的字母填在表格中相应的位置.1.下列图形中,不是..轴对称图形的是(A ) (B ) (C ) (D ) 2.下列运算中正确的是(A )xy y x 532=+ (B )428x x x =÷ (C )3632)(y x y x = (D )62322x x x =⋅3.在平面直角坐标系xOy 中,点P (-3,5)关于x 轴的对称点的坐标是(A ) (3,5) (B )(3,-5) (C )(5,-3) (D )(-3,-5)4x 的取值范围是 (A )x ≠-32 (B )x <-32 (C )x ≥-32 (D )x ≥23-5.下列各式中,从左到右的变形是因式分解的是(A )3353()5x y x y +-=+- (B )2(1)(1)1x x x +-=- (C )2221(1)x x x ++=+ (D )xy x y x x -=-2)( 6.下列三个长度的线段能组成直角三角形的是(A )1 (B )1(C )2,4,6 (D )5,5,6 7.计算)123(2- ,结果为 (A )6 (B )6-(C )66- (D )66-8.下列各式中,正确的是 (A )212+=+a b a b (B )22++=a b a b(C ) a b a b c c-++=- (D )22)2(422--=-+a a a a 9.若x m +与2x -的乘积中不含x 的一次项,则实数m 的值为 (A )2- (B )2 (C )0 (D )110.如图,在△ABC 和△CDE 中,若︒=∠=∠90CED ACB ,AB=CD ,BC=DE ,则下列结论中不正确...的是(A )△ABC ≌ △CDE (B )CE=AC (C )AB ⊥CD (D )E 为BC 中点11.如图,由四个全等的直角三角形与一个小正方形拼成一个大正方形. 如果大正方形的面积是25,小正方形的面积是1,直角三角形的两条直角边的长分别是a 和b ,那么2()a b +的值为 (A )49 (B )25 (C )13 (D )1 12.当x 分别取2014-、2013-、2012-、….、2-、1-、0、1、12、13、…、12012、12013、12014时,计算分式2211x x -+的值,再将所得结果相加,其和等于(A )1- (B )1 (C )0 (D ) 2014二、填空题:(本题共24分,每小题3分)13.若实数x y 、20y +=,则x y +的值为 .14.计算:2325b a ⎛⎫- ⎪⎝⎭= .15.比较大小:.16.分解因式:3312a a -= .17.如图,△ABC ≌△DEF ,点F 在BC 边上,AB 与EF 相交于点P .若37DEF ∠=︒,PB=PF ,则APF ∠= °.18.如图,△ABC 是等边三角形,点D 为 AC 边上一点,以BD 为边作等边△BDE, 连接CE .若CD =1,CE =3,则BC =_____.19.在平面直角坐标系xOy 中,点A 、点B 的坐标分别为(-6,0)、(0,8).若△ABC 是以∠BAC 为顶角的等腰三角形,点C 在x 轴上,则点C 的坐标为 .20.如图,分别以正方形ABCD 的四条边为边,向其内部作等边三角形,得到△ABE 、△BCF 、△CDG 、△DAH ,连接EF 、FG 、GH 、HE .若AB =2,则四边形EFGH 的面积为 .三、解答题:(本题共14分,第21题5分,第22题9分)21.计算:101()(2)2π--++1.22.(1)解方程:xx x 211=--.(2))先化简,再求值:2)4442(22+÷-+--+x xx x x x x ,其中2=x .四、解答题:(本题共9分,第23题4分,第24题5分)23.如图,点F 、C 在BE 上,BF CE =,AB DE =,∠B =∠E . 求证: ∠A =∠D .24. 列方程(组)解应用题:上图为地铁调价后的计价图. 调价后,小明、小伟从家到学校乘地铁分别需4元和3元.由于刷卡坐地铁有优惠,因此,他们平均每次实付3.6元和2.9元.已知小明从家到学校乘地铁的里程比小伟从家到学校乘地铁的里程多5千米,且小明每千米享受的优惠金额是小伟的2倍,求小明和小伟从家到学校乘地铁的里程分别是多少千米?五、解答题:(本题共17分,第25题5分,第26题6分,第27题6分) 25.已知:如图,△ABC ,射线AM 平分BAC ∠.(1)尺规作图(不写作法,保留作图痕迹)作BC 的中垂线,与AM 相交于点G ,连接BG 、CG .(2)在(1)的条件下,∠BAC 和∠BGC 的等量关系为 ,证明你的结论.26.阅读:对于两个不等的非零实数a 、b ,若分式()()x a x b x--的值为零,则x a =或x b =.又因为2()()()()x a x b x a b x ab ab x a b x x x ---++==+-+,所以关于x 的方程abx a b x+=+有两个解,分别为1x a =,2x b =.应用上面的结论解答下列问题: (1)方程86x x+=的两个解中较大的一个为 ; (2)关于x 的方程42m n m mn nx mnx mn-+-+=的两个解分别为1x 、2x (12x x <),若1x 与2x 互为倒数,则1_____x =,2______x =;(3)关于x 的方程22322321n n x n x +-+=+-的两个解分别为1x 、2x (12x x <),求2122x x -的值.27.阅读:如图1,在△ABC 中,3180A B ∠+∠=︒,4BC =,5AC =,求AB 的长. 小明的思路:如图2,作BE AC ⊥于点E ,在AC 的延长线上取点D ,使得DE AE =,连接BD ,易得A D ∠=∠,△ABD 为等腰三角形.由3180A ABC ∠+∠=︒和180A ABC BCA ∠+∠+∠=︒,易得2BCA A ∠=∠,△BCD 为等腰三角形.依据已知条件可得AE 和AB 的长.图1 图2解决下列问题:(1)图2中, AE = ,AB = ; (2)在△ABC 中,A ∠、B ∠、C ∠的对边分别为a 、b 、c .①如图3,当32180A B ∠+∠=︒时,用含a 、c 的式子表示b ;(要求写解答过程) ②当34180A B ∠+∠=︒,2b =,3c =时,可得a = .图3数 学 答 案一、 选择题:(本题共36分,每小题3分)二、填空题:(本题共24分,每小题3分)13.1; 14.26425b a ; 15.<; 16.3(2)(2)a a a +-; 17. 74︒; 18.4; 19.(16,0)-,(4,0); 20.8-三、解答题:(本题共14分,第21题5分,第22题9分)21101()(2)2π--++1.解:原式=211------------------4分=分 22.(1)解方程:211x x x-=-. 解:方程两边同时乘以(1)x x -,得2(1)2(1)x x x x --=-. -----------------1分解方程,得2=x . -----------------3分 经检验,2=x 是原方程的解.∴ 原方程的解为2=x . -----------------4分(2)先化简,再求值:2244()242x x x xx x x -+-÷+-+,其中x = 解:原式=2(2)2(2)(2)2x x xx x x x ⎡⎤--÷⎢⎥++-+⎣⎦-----------------2分 =22()22x x x x x x-+-⋅++ =222x x x+⋅+-----------------3分 =2x. -----------------4分当x ==分四、解答题:(本题共9分,第23题4分,第24题5分)23.证明:∵BF CE =,∴BC EF =. -----------------1分 在△ABC 和△DEF 中,,,,AB DE B E BC EF =⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DEF . -----------------3分 ∴A D ∠=∠. -----------------4分 24.解:设小明从家到学校乘地铁的里程为x 千米.4 3.62(3 2.9)5x x --=-. -----------------3分 解方程,得 10x =.-----------------4分经检验,10x =为原分式方程的解,且符合题意.∴55x -=.答:小明和小伟从家到学校乘地铁的里程分别是10千米和5千米. ------------5分五、解答题:(本题共17分,第25题5分,第26题6分,第27题6分)25.解:(1)(注:不写结论不扣分)-----------------1分(2) 180BAC BGC ∠+∠=︒ . -----------------2分证明:过点G 作GE AB ⊥于点E ,GF AC ⊥交AC 的延长线于点F .∵点G 在∠BAC 平分线上, ∴GE GF =.∵点G 在BC 的中垂线上,∴GB GC =. 在Rt △GBE 和Rt △GCF 中,,,GE GF GB GC ==⎧⎨⎩∴△GBE ≌△GCF . ---------------4分 ∴12∠=∠. ∴BGC EGF ∠=∠.∵360AEG AFG BAC EGF ∠+∠+∠+∠=︒,90AEG AFG ∠=∠=︒,∴180BAC EGF ∠+∠=︒. ∴180BAC BGC ∠+∠=︒.-----------------5分 26. 解:(1)4x =;-----------------1分 (2) 112x =,22x =;-----------------3分 (3)∵22322321n n x n x +-+=+-,∴223212221n n x n x +--+=+-. ∵223(1)(3)n n n n +-=-+,(1)(3)22n n n -++=+,12x x <, ∴1211x n -=-,2213x n -=+. ∴12n x =,222nx =+.-----------------5分 ∴212122x x -=.-----------------6分 27.(1)92AE =,6AB =;-----------------2分(2)①作BE AC ⊥交AC 延长线于点E ,在AE 延长线上取点D ,使得DE AE =,连接BD .∴BE 为AD 的中垂线. ∴AB =BD =c .∴A D ∠=∠.-----------------3分 ∵180A D ABD ∠+∠+∠=︒, ∴21180DBC A ∠+∠+∠=︒. ∵321180A ∠+∠=︒, ∴1DBC A ∠=∠+∠.∵31A ∠=∠+∠,∴3DBC ∠=∠. ∴CD =BD =c . -----------------4分 ∴AE =2b c +, 2c bCE -=. 在△BEC 中,90BEC ∠=︒,222BE BC CE =-. 在△BEA 中,90BEA ∠=︒,222BE AB AE =-. ∴2222AB AE BC CE -=-. ∴2222()()22b c c b c a +--=-.∴22c abc-=.-------------5分②a=.-----------------6分(注:本卷中许多问题解法不唯一,请老师根据评分标准酌情给分)。
海淀区202020学年初二期末数学试题及答案(word版)

海淀区八年级第一学期期末调研2020.01数 学学校 班级 姓名 成绩一、 选择题(本大题共30分,每小题3分)第1~10题符合题意的选项均只有一个,请将你的答案填写在下面的表格中.1.斐波那契螺旋线也称为“黄金螺旋线”,是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线图案.下列斐波那契螺旋线图案中属于轴对称图形的是A .B .C .D .2.2019年被称为“5G 元年”.据媒体报道,5G 网络的理论下载速度为1.25GB/s ,这就意味着我们下载一张2.5M 的照片只需要0.002s ,将0.002用科学记数法表示为 A .2210-⨯B .3210-⨯C .20.210-⨯D .30.210-⨯3.下列运算结果为6a 的是 A .32a a ⋅B .93a a -C .()32aD .183a a ÷4.在下列因式分解的过程中,分解因式正确的是A .()22242x x x ++=+ B .24(4)(4)x x x -=+-C .()22442x x x -+=-D .()2242x x +=+5.如图,经过直线AB 外一点C 作这条直线的垂线,作法如下: (1)任意取一点K ,使点K 和点C 在AB 的两旁.(2)以点C 为圆心,CK 长为半径作弧,交AB 于点D 和E . (3)分别以点D 和点E 为圆心,大于12DE 的长为半径作弧,两弧相交于点F . (4)作直线CF .则直线CF 就是所求作的垂线.根据以上尺规作图过程,若将这些点作为三角形的顶点,其中不一定...是等腰三角形的为 A .△CDFB .△CDKC .△CDED .△DEF6.有两块总面积相等的场地,左边场地为正方形,由四部分构成,各部分的面积数据如图所示.右边场地为长方形,长为()2a b +,则宽为A .12B .1C .()12a b +D .a b + 7.如图,在△ABC 中,AB =AC ,D 是BC 边上的动点(点D 与B ,C 不重合),△ABD 和△ACD 的面积分别表示为S 1和S 2,下列条件不能..说明AD 是△ABC 角平分线的是A .BD =CDB .∠ADB =∠ADC C .S 1=S 2D .AD =12BC 8.如图,左边为参加2019年国庆70周年阅兵的武警摩托车礼宾护卫队,如果将每位队员看成一个点,队形可近似看成由右边所示的若干个正方形拼成的图形,其中与△ABC 全等的三角形是 A .△AEGB .△ADFC .△DFGD .△CEGDCBA2(a+b )aba 2ab b 29.若4ab =-,其中a b >,以下分式中一定比ba大的是 A .22b a B .2b aC .2a -D .+2b a10.已知长方形ABCD 可以按图示方式分成九部分,在a ,b 变化的过程中, 下面说法正确的有①图中存在三部分的周长之和恰好等于长方形ABCD 的周长②长方形ABCD 的长宽之比可能为2③当长方形ABCD 为正方形时,九部分都为正方形 ④当长方形ABCD 的周长为60时,它的面积可能为100 A .①② B .①③ C .②③④ D .①③④二、填空题(本大题共16分,每小题2分)11.请写出一个只含有字母x 的分式,当x =3时分式的值为0,你写的分式是 .12.计算:()()3422a a a ⋅-÷=.13.如图,要测量池塘两岸相对的两点A ,B 的距离,可以在池塘外取AB 的垂线BF 上的两点C ,D ,使BC =CD ,再画出BF 的垂线DE ,使E 与A ,C 在一条直线上.若想知道两点A ,B 的距离,只需要测量出线段 即可.14.如图,已知空间站A 与星球B 距离为a ,信号飞船C 在星球B 附近沿圆形轨道行驶,B ,C 之间的距离为b .数据S 表示bb aab aCDBA BABCF G DE飞船C 与空间站A 的实时距离,那么S 的最大值是 . 15.平面直角坐标系xOy 中,点A (4,3),点B (3,0),点C (5,3),点E 在x 轴上.当CE=AB 时,点E 的坐标为 .16.北京大兴国际机场于2019年9月25日正式投入运营.小贝和小京分别从草桥和北京站出发赶往机场乘坐飞机,出行方式及所经过的站点与路程如下表所示:由于地面交通拥堵,地铁的平均速度约为公交平均速度的两倍,于是小贝比小京少用了半小时到达机场.若设公交的平均速度为x 公里/时,根据题意可列方程: .17.如图,△ABC 中,AD 平分∠BAC ,CD ⊥AD ,若∠ABC 与∠ACD 互补,CD =5,则BC 的长为 .18.如图,已知MON ∠,在边ON 上顺次取点1P ,3P ,5P …,在边OM 上顺次取点2P ,4P ,6P …,使得112233445===OP PP P P P P P P =…,得到等腰△12OPP ,△123P P P ,△234P P P ,△345P P P …BP 5P 4P 3P 2P 1ONM(1)若MON ∠=30°,可以得到的最后一个等腰三角形是 ; (2)若按照上述方式操作,得到的最后一个等腰三角形是△345P P P ,则MON ∠的度数α的取值范围是 .三、解答题(本大题共54分,第19题8分,20~22题每题5分,第23~26每题6分,第27题7分) 19.(1)计算:()18613333π-⎛⎫--÷+ ⎪⎝⎭(2)因式分解:22312x y -20.如图,已知AB=AC ,E 为AB 上一点,ED ∥AC ,ED=AE . 求证:BD=CD .21.已知2220a ab b -+=,求代数式()()()422a a b a b a b --+-的值.A22.如图,AB⊥AC,AB=AC,过点B,C分别向射线AD作垂线,垂足分别为E,F. (1)依题意补全图形;(2)求证:BE=EF+FC.23.已知+2x a b=-,222+y ab a b-=.(1)用x表示y;(2)求代数式44()2xxx y x-⋅++的值.CBAD24.如图所示,将两个含30°角的三角尺摆放在一起,可以证得△ABD 是等边三角形,于是我们得到:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.交换命题的条件和结论,得到下面的命题: 在直角△ABC 中,∠ACB =90°,如果12CB AB,那么∠BAC =30°. 请判断此命题的真假,若为真命题,请给出证明;若为假命题,请说明理由.CB A25.对于代数式,不同的表达形式能表现出它的不同性质.例如代数式245A x x =-+,若将其写成()221A x =-+的形式,就能看出不论字母x 取何值,它都表示正数;若将它写成()2=12(1)2A x x ---+的形式,就能与代数式B=222x x -+建立联系.下面我们改变x 的值,研究一下A ,B 两个代数式取值的规律:(1)完成上表; (2)观察表格可以发现:若x =m 时,222=B x x n =-+,则x =m +1时,245A x x n =-+=.我们把这种现象称为代数式A 参照代数式B 取值延后,此时延后值为1.①若代数式D 参照代数式B 取值延后,相应的延后值为2,求代数式D ;②已知代数式210ax x b -+参照代数式234x x c -+取值延后,请直接写出b -c 的值:_____________.ACB26.如图,在△ABC 中,AB=AC ,∠BAC =90°,点D 是边BC 上的动点,连接AD ,点C 关于直线AD 的对称点为点E ,射线BE 与射线AD 交于点F . (1)在图1中,依题意补全图形;(2)记DAC α∠=(45α<︒),求ABF ∠的大小;(用含α的式子表示) (3)若△ACE 是等边三角形,猜想EF 和BC 的数量关系,并证明.图1 备用图CA27.在平面直角坐标系xOy 中,直线l 为一、三象限角平分线.点P 关于y 轴的对称点称为P 的一次反射点,记作1P ;1P 关于直线l 的对称点称为点P 的二次反射点,记作2P .例如,点(2,5)-的一次反射点为(2,5),二次反射点为(5,2).根据定义,回答下列问题:(1)点(2,5)的一次反射点为_____________,二次反射点为_______________; (2)当点A 在第一象限时,点(3,1)M ,(3,1)N -,(1,3)Q --中可以是点A 的二次反射点的是______________;(3)若点A 在第二象限,点1A ,2A 分别是点A 的一次、二次反射点,△12OA A 为等边三角形,求射线OA 与x 轴所夹锐角的度数.附加问题:(本问3分,可计入总分,但全卷总分不超过100分)若点A 在y 轴左侧,点1A ,2A 分别是点A 的一次、二次反射点,△12AA A 是等腰直角三角形,请直接写出点A 在平面直角坐标系xOy 中的位置.海淀区八年级第一学期期末调研(数学)参考答案二、 选择题(本大题共30分,每小题3分)第1~10题符合题意的选项均只有一个,请将你的答案填写在下面的表格中.二、填空题(本大题共16分,每小题2分) 11.3x x-(答案不唯一) 12. 58a 13.DE 14.a b + 15.(4,0)或(6,0)16.5443122x x -= 17. 1018. (1)△123PP P ;(2)1822.5α︒≤<︒ 三、解答题(本大题共54分,第19题8分,20~22题每题5分,第23~26每题6分,第27题7分)19.(1)解:原式2133=-+ ………………………3分193=-+5=- ………………………4分(2)解:原式223(4)x y =- ………………………2分3(2)(2)x y x y =+- ………………………4分20.证明:∵ED ∥AC ,∴∠EDA =∠DAC , ………………………1分 ∵ED=AE ,∴∠EAD =∠EDA . ………………………2分 ∴∠EAD =∠DAC . ………………………3分在△ADB 和△ADC 中, ,,,AB AC DAB DAC AD AD =⎧⎪∠=∠⎨⎪=⎩∴△ADB ≌△ADC (SAS ). ………………………4分 ∴BD=CD . ………………………5分21. 解: ∵2220a ab b -+=,∴2()0a b -=. ………………………1分 ∴a b =.…………………3分…………………4分∴原式=()0b b a -= . …………………5分22.(1)………………………1分 (2)证明:∵AB ⊥AC ,BE ⊥AD ,CF ⊥AD ,∴∠BAE +∠CAF =90°,∠BAE +∠B =90°,∠CF A =∠AEB =90°.………………………2分∴∠CAF =∠B . ………………………3分()()()2222422(4)(4)a ab a b a b a ab a b b ab--+-=---=-FEDCBA222244244=(2)2(2)(2)4(2)22422221x x x y x x x x x x x x x x x x x x x x x -=⋅++-⋅+++-+=⋅+++-=++++=+=在△ABE 和△CAF 中, ,,,B CAF AEB CFA AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABE ≌△CAF (AAS ). ………………………4分 ∴BE=AF ,AE=CF . ∵AF=AE+EF ,∴BE=EF+CF . ………………………5分23.解:(1)∵+2x a b =-,222+y ab a b -=,∴+2a b x =+,2222+()y a ab b a b =+=+. ………………………1分 ∴2(2)y x =+. ………………………2分(2)由题意可知:原式 ………………………3分………………………4分………………………5分………………………6分24. 解:此命题是真命题. ………………………1分证明:延长BC 至点D ,使得CD=BC , ………………………2分∵∠ACB =90°,CD=BC∴AC 是线段BD 的垂直平分线,FC F∴AB=AD . ………………………3分∵12CB AB =,∴BD=AB .∴△ABD 是等边三角形. ………………………4分 ∴∠BAD =60°. ………………………5分 ∵AC BD ⊥ ∴12BAC BAD ∠=∠=30°. ………………………6分25.解(1)2;2,1,2. ………………………2分(2)①∵代数式D 参照代数式B 取值延后,相应的延后值为2,∴22(2)2(2)2610D x x x x =---+=-+. …………………4分② 7 ………………………6分26. (1)………………………1分 (2)连接AE由题意可知,,EAD CAD α∠=∠= AC =AE , ∴902,BAE α∠=︒-∵AB=AC , ∴AB=AE , ∴,ABE AEB ∠=∠∴180452BAEABF α︒-∠∠==︒+.………………………3分(3)12EF BC =, DCB A证明:由(2)可知45,AEB ABE α∠=∠=︒+ ∴.CBF α∠= ………………………4分 ∵点C 关于直线AD 的对称点为点E , ∴135,ACF AEF α∠=∠=︒- ∴90,BCF α∠=︒-∵90,CBF BCF ∠+∠=︒ ………………………5分 ∴△BCF 是直角三角形.∵△ACE 是等边三角形, ∴30.α=︒∴30CBF ∠=︒ ∴1.2EF CF BC ==………………………6分27. 解:(1)(2,5)-,(5,2)-; ………………………2分(2)N 点; ………………………3分(3)∵点A 在第二象限,∴点12,A A 均在第一象限.∵△12OA A 为等边三角形,12,A A 关于OB 对称,∴1230AOB A OB ∠=∠=︒ 分类讨论:①若点1A 位于直线l 的上方,如图1所示,此时115,AOC AOC ∠=∠=︒ 因此射线OA 与x 轴所夹锐角为75︒; ………………………5分 ②若点1A 位于直线l 的上下方,如图2所示,此时175,AOC AOC ∠=∠=︒ 因此射线OA 与x 轴所夹锐角为15︒; ………………………7分综上所述,射线OA 与x 轴所夹锐角为75︒或15︒.图1 图2附加题:x 轴负半轴或第三象限的角平分线 …………2分(不含点O ).…………3分说明:附加题得分可计入总分,但全卷总分不超过100分。
北京市海淀区2019-2020八年级上学期期末数学试卷 及答案解析

北京市海淀区2019-2020八年级上学期期末数学试卷一、选择题(本大题共10小题,共30.0分)1.下列图案是轴对称图形的是().A. B.C. D.2.用科学记数法表示−0.0000031,结果是()A. −3.1×10−4B. 3.1×10−6C. −0.31×10−5D. −3.1×10−63.下列运算的结果为a6的是()A. a3+a3B. (a3)3C. a3⋅a3D. a12÷a24.下列分解因式正确的是()A. x2−4=(x−4)(x+4)B. 2x3−2xy2=2x(x+y)(x−y)C. x2+y2=(x+y)2D. x2−2x+1=x(x−2)+15.如图,在△ABC中,AB=AC.在AB、AC上分别截取AP,AQ,使AP=AQ.再分别以点P,Q为圆心,以大于12PQ的长为半径作弧,两弧在∠BAC内交于点R,作射线AR,交BC于点D.若BC=6,则BD的长为()A. 2B. 3C. 4D.56.一个长方形的面积为2x2y−4xy3+3xy,长为2xy,则这个长方形的宽为()A. x−2y2+32B. x−y3+32C. x−2y+3D. xy−2y+327.如图,AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,则有下列结论:(1)△ADE≌△ADF;(2)△BDE≌△CDF;(3)△ABD≌△ACD;(4)AE=AF;(5)DE=DF;(6)BD=CD;(7)∠ADE=∠ADF,错误的个数有()A. 1个B. 2个C. 3个D. 4个8.如图,在正方形ABCD中,点E、F在边BC、CD上,且CE=CF.则图中全等的三角形的对数为()A. 6B. 7C. 8D. 99.分式1a+1+1a(a+1)的计算结果是().A. 1a+1B. aa+1C. 1aD. a+1a10.一个大长方形ABCD按如图方式分割成九个四边形,且只有标号为①和②的两个正好为正方形,其余均为长方形.若已知小正方形①的周长为12,小长方形③的周长为2m,小长方形④的周长为2n,且3(m+n)+mn=61,这个大长方形ABCD的面积()A. 60B. 70C. 80D. 90二、填空题(本大题共8小题,共16.0分)11.如果分式x(x−2)x−2的值为0,则x的值是______.12.计算(−x2)2⋅(2xy2)2=______ .13.如图,要测量河两岸相对两点A、B间的距离,在河岸BM上截取BC=CD,作DE⊥BD交AC的延长线于点E,垂足为点D,测得ED=3,CD=4,则A、B两点间的距离等于______.14.两点之间________叫做这两点之间的距离.15.在平面直角坐标系xOy中,如果AB//y轴,点A的坐标为(−3,4),A、B两点的距离为5,那么点B的坐标为____________。
2019-2020学年北京北京八年级上数学期末试卷

2019-2020学年北京北京八年级上数学期末试卷一、解答题 1. 若分式−2x+9x−1值为正整数,则x 的值为________.2. 已知c a+b =a b+c =13,则bc+a =________ .3. 若x ,y 为变量,m ,n 为参数,则关于y 的一元一次方程(n −1)x m−2+(m −2)y m+n−5=8的解为________.4. 若x 2−3x +1=0,则3x 2−233x +8+4x 2+1=________ .5. 若关于x 的方程4x+3x−5−mx+35−x=1无解,则m 的值为________.6. 如果关于x ,y 的方程组{ax −5y =62x +3y =b 有无穷多组解,请比较a 和b 的大小关系:________(填写a >b,a =b,a <b 中的一个)7. 若关于x 的一元一次不等式组{2(x −3)≥3(x −1)mx ≥x +1的解为x ≤−5,则m 的值为________.8. 有两个行向量(行矩阵):A =(1−k ,+2k)和B =(x −y ,x +y),无论k 取何值,总能保证A ×B T =2成立,则x 的值为________.9. 已知关于x ,y 的方程组{2ax −y =2a +5x +y =2a +4的解为正整数(解得x ,y 均为正整数),且a 为整数,则a =________ .10. 若x 满足2+2x 2+1x≥0,则x 的取值范围是________.11. 已知ba +ab =3,则a 4+a 2b 2+b 4a 4+a 3b+ab 3+b 4的值为________.12. 求(20112−2017)(20112+4019)2008×2010×2014=________.13. 已知行列式满足以下关系:|a 2−21|≤|34b 2|≤|1−33a |,则a +4b 的绝对值的最大值是________.14. 若x 满足|x −3|−|x +1|<2,则x 的取值范围是________.15. 若将关于x 的分式2x 2+3x+1x 4−x,化成部分分式为A x +B x−1+Cx+Dx 2+x+1,则A +B +C +D =________.16. 已知a ,b ,c 均不为0,且3a−2b 2a−b =b−5c b−2c =−c+3a c−a,则ab =________.17. 已知x ,y 满足(3−213)×(x y )=(3k −13k +1)和(2 1)×(x y )=3,则k 的值为________.18. 已知a ,b 满足a ≠−2, b ≠−2,设M =aa+2+bb+2,N =1a+2+1b+2,则下面叙述正确的有________ . ①ab =1时,M <2N ;②ab =2时,M =2N ;③a +b =0时,M ⋅N ≤0;④ab =2且a +b >0时,MN >1.19. 已知关于x 的不等式{5(x −1)≤3x +7x +7<2x +3k 只有3个整数解,则k 的取值范围是________.20. 对于数x ,符号[x ] 表示不超过x 的最大整数,暨[x ]≤x <[x ]+1.若关于x 的方程[x+2|a|5]=4有正整数解,则a 的取值范围是________.21. 解方程或不等式(1)解关于x 的方程:|x −|2x +1||=3.(2)解关于x 的方程:x+3x+1+x 2+3x−2x 2+4x+3−2x+7x+3=0.(3)请用克莱姆法则求解方程:{2x +3y =73x +2y =9.(4)解关于x ,y 的方程组:{2x −y =bx −2ay =2b +2.(5)解关于x,y,z 的方程组:{ 1x −2y +2z =31x +1y +1z =51x +3y +1z =7(6)将行列式|a −1a(a −1)ab −1b(b −1)b c −1c (c −1)c|因式分解.(7)解关于x 的不等式组:{|2x +4|≤2ax −a ≤x +2.22. 在通信系统中,传输的过程一般需要进行加密.一种加密方法是发送方将原有的信息X 左乘一个加密矩阵A ,作为加密后的信息S 发送出去,暨S =AX .接收方在接收到信息S 后只需要再左乘一个解密矩阵B ,便可得到X ,暨BS =X .(1)现已知X 和S 都是3×1的列向量(列矩阵),加密矩阵A 如下所示,请尝试去解密矩阵B . A =(132313231)(2)在发射端可以对X 进行多重加密,暨在X 左边乘上多个矩阵作为加密后的信息S .例如:三重加密时S =ABCX ,其中,A ,B ,C 均为可逆的加密方阵.为了对多重加密进行解密,也可以采取相同的方式,在解密端对S 左乘一个矩阵D ,使得DS =X ,根据矩阵逆的定义和性质,D 应该为ABC 的逆矩阵,暨D =(ABC )−1,求证:(ABC )−1=C −1B −1A −1.23. 并行计算是计算机科学中最漂亮的工具之一.它的基本原理是:将一个复杂的问题,分成若干个简单的子问题,将这些子问题放在多台计算机上同时进行运算.相比于在一台计算机上完成所有运算,并行运算的运算时间会被大大缩减(多台计算机并行运算的总时间为最后一台计算机完成计算的时间).并行计算被广泛运用到当今时代的“云计算”场景中.下面举例说明云计算中是如何进行两个n ×n 的矩阵A 和B 的乘法运算的,A 和B 如下所示: A =(a 11⋅a 1n ⋮⋱⋮a n1⋯a nn ),B =(b 11⋅b 1n⋮⋱⋮b n1⋯b nn) 如果使用一台计算机直接计算A ×B ,需要进行很多次的乘法运算和很多次的加法运算.但如果把矩阵A 和B都拆成更小的矩阵放在多台计算机上进行运算则能节省很多时间,例如,将矩阵A 拆成一个个行向量(行矩阵),矩阵B 拆成一个个列向量(列矩阵),则可以把矩阵的乘法A ×B 看成n ×n 次独立的行向量乘以列向量的运算.把这些行向量乘以列向量的运算平均分配到k 台计算机中运算,则每台计算机最多只用进行[n×n k]+1次行向量乘以列向量的运算,其中[n×n k]表示取n×n k的整数部分.假如一台计算机计算一次加法运算所需要的时间t 1=1×10−9秒,计算一次乘法运算需要的时间是t 1=3×10−9秒.如果n =104 ,则(1)完成一次行向量乘以列向量所耗费的时间是多少秒?(2)如果是用一台计算机,完成A ×B 运算耗费的总时间是多少秒?(3)如果要求A ×B 在1秒之内完成运算,则至少需要几台计算机?24. 卷积神经网络(Convolutionai Neural Networks ,CNN)是一类包含卷积计算且具有深度结构的前馈神经网络,是深度学习(Deep Learning )的代表算法之一,也是人工智能时代开启的标志性算法,已经被广泛应用于图像处理(Image Processing )和行为认知(Acting Recognition )等场景中.图(a)是一个在图像处理中的卷积神经网络使用案例.图像在计算机中一般用矩阵进行储存,矩阵中的每一个元素值暨代表图像中对应点颜色的深浅.将图像反复经过卷积神经网络中的两种运算:卷积(Convolution)和池化(Pooling),便可得到最后的输出结果,用来判断图像中的物体是否属于哪一类.如图30(a)中,经过卷积神经网络,计算机可以自动判断图像是一条狗.本题是关于池化过程的应用题.池化是卷积神经网络的一个重要过程,其核心思想是用一个数值(记为s )来代替矩阵.例如:对于如下所示的一个3×3的矩阵A ,在池化过程中可以使用a 11来代替矩阵A .池化用矩阵的乘法就可以实现,如下所示: A =[a 11a 12a 13a 21a 22a 23a 31a 32a 33] a 11=[100][a 11a 12a 13a 21a 22a 23a 31a 32a 33][100] 若B 是一个行向量(行矩阵):(b 11,b 12,b 13),请尝试只用矩阵的乘法求B 中所有元素的平均值.进一步的,希望用A 中所有元素的平均值,来进行池化过程,请只使用矩阵的乘法实现求A 中所有元素的平均值的池化过程.(可以引入新的矩阵,但是不能使用加法、求逆等乘法之外的其他运算)25. 本题是关于卷积过程的应用题.为了能够更好地引入卷积,我们首先引入矩阵的内积运算(记作⊙),用来表示两个矩阵所有对应项的乘积的和.对于两个n ×n 的矩阵A 和B ,如下所示:内积运算定义如下:A ⊙B =a 11b 11+a 12b 12+⋯a 1n b 1n +a 21b 21+⋯+a nn b nn =∑∑a ij nj=1n i=1b ij 图(b )是一个更为简单的两个2×2的矩阵内积运算过程如下:(1)对于任意两个3×3 的矩阵A 和B ,若A 是单位阵(只有对角线元素为1,其他元素均为0),B 的主对角线上所有元素均为1,其他元素均不为0.求A ⊙B .(2)求证:对于任意三个3×3 内矩阵A 、B 、C ,均有(A +B )⊙C =A ⊙C +B ⊙C .卷积运算可以在内积运算基础上进行定义.对于一个m ×m 的矩阵A 和一个n ×n 的矩阵B (m ≤n );A 与B 的卷积运算记作A ∗B .定义如下:图(c )是一个更为直观的2×2矩阵与一个4×4矩阵进行卷积的例子:(3)已知两个矩阵A =(1001),B =(123242136763426731),求A ∗B .参考答案与试题解析2019-2020学年北京北京八年级上数学期末试卷一、解答题1.【答案】此题暂无答案【考点】分使的凝【解析】此题暂无解析【解答】此题暂无解答2.【答案】此题暂无答案【考点】列代明式织值【解析】此题暂无解析【解答】此题暂无解答3.【答案】此题暂无答案【考点】一元一表方磁的定义【解析】此题暂无解析【解答】此题暂无解答4.【答案】此题暂无答案【考点】分式因化简优值列较洗式源值情法的优势【解析】此题暂无解析【解答】此题暂无解答5.【答案】此题暂无答案【考点】分式明程稀解【解析】此题暂无解析【解答】此题暂无解答6.【答案】此题暂无答案【考点】二元一都接程组的解【解析】此题暂无解析【解答】此题暂无解答7.【答案】此题暂无答案【考点】解一元表次镜等式组【解析】此题暂无解析【解答】此题暂无解答8.【答案】此题暂无答案【考点】整式较混合轻算【解析】此题暂无解析【解答】此题暂无解答9.【答案】此题暂无答案【考点】二元一都接程组的解【解析】此题暂无解析【解答】此题暂无解答10.【答案】此题暂无答案【考点】解一元因次不丙式【解析】此题暂无解析【解答】此题暂无解答11.【答案】此题暂无答案【考点】列代明式织值【解析】此题暂无解析【解答】此题暂无解答12.【答案】此题暂无答案【考点】列较洗式源值情法的优势【解析】此题暂无解析【解答】此题暂无解答13.【答案】此题暂无答案【考点】绝对值【解析】此题暂无解析【解答】此题暂无解答14.【答案】此题暂无答案【考点】绝对值【解析】此题暂无解析【解答】此题暂无解答15.【答案】此题暂无答案【考点】分式因混合似算【解析】此题暂无解析【解答】此题暂无解答16.【答案】此题暂无答案【考点】列较洗式源值情法的优势【解析】此题暂无解析【解答】此题暂无解答17.【答案】此题暂无答案【考点】二元一因方程似应用【解析】此题暂无解析【解答】此题暂无解答18.【答案】此题暂无答案【考点】有理数三混合运臂列较洗式源值情法的优势【解析】此题暂无解析【解答】此题暂无解答19.【答案】此题暂无答案【考点】一元三次实等另组每整数解【解析】此题暂无解析【解答】此题暂无解答20.【答案】此题暂无答案【考点】方射的加【解析】此题暂无解析【解答】此题暂无解答21.【答案】此题暂无答案【考点】解一使以次方程解于姆方程二元一都接程组的解二元一都接程组的解解三元体次序程组因水都解解一元表次镜等式组【解析】此题暂无解析【解答】此题暂无解答22.【答案】此题暂无答案【考点】规律型:因字斯变化类有理数三混合运臂【解析】此题暂无解析【解答】此题暂无解答23.【答案】此题暂无答案【考点】列使数种有理数三混合运臂一元体次拉程的言亿——其他问题【解析】此题暂无解析【解答】此题暂无解答24.【答案】此题暂无答案【考点】有理数三混合运臂【解析】此题暂无解析【解答】此题暂无解答25.【答案】此题暂无答案【考点】定射新从号代明综约【解析】此题暂无解析【解答】此题暂无解答。
2020-2021学年北京市海淀区初二数学第一学期期末试卷及解析

2020-2021学年北京市海淀区初二数学第一学期期末试卷一、选择题(本大题共24分,每小题3分)第1~8题符合题意的选项均只有一个,请将你的答案填写在下面的表格中.1.(3分)下列四个图分别是四届冬奥会图标中的一部分,其中是轴对称图形的为( )A .B .C .D .2.(3分)0.0000003用科学记数法表示为( ) A .6310-⨯B .7310-⨯C .60.310-⨯D .70.310-⨯3.(3分)下列计算正确的是( ) A .236a a a ⋅=B .236()a a =C .33(2)2a a =D .1025a a a ÷=4.(3分)下列等式中,从左到右的变形是因式分解的是( ) A .2(2)2x x x x -=- B .22(1)21x x x +=++ C .24(2)(2)x x x -=+-D .22(1)x x x+=+5.(3分)如图,菊花1角硬币为外圆内正九边形的边缘异形币,则该正九边形的一个内角大小为()A .135︒B .140︒C .144︒D .150︒6.(3分)小聪在用直尺和圆规作一个角等于已知角时,具体过程是这样的: 已知:AOB ∠.求作:AO B ∠''',使AO B AOB ∠'''=∠.作法:(1)如图,以点O 为圆心,任意长为半径画弧,分别交OA ,OB 于点C ,D ; (2)画一条射线O A '',以点O '为圆心,OC 长为半径画弧,交O A ''于点C '; (3)以点C '为圆心,CD 长为半径画弧,与第(2)步中所画的弧相交于点D '; (4)过点D '画射线O B '',则AO B AOB ∠'''=∠.小聪作法正确的理由是( )A .由SSS 可得△O C D OCD '''≅∆,进而可证AOB AOB ∠'''=∠ B .由SAS 可得△OCD OCD '''≅∆,进而可证AO B AOB ∠'''=∠ C .由ASA 可得△O C D OCD '''≅∆,进而可证AO B AOB ∠'''=∠D .由“等边对等角”可得AO B AOB ∠'''=∠7.(3分)如果2a b -=,那么代数式22(2)a b a b a a b+-⋅-的值是( ) A .2 B .2- C .12 D .12-8.(3分)在ABC ∆中,AB AC ≠,线段AD ,AE ,AF 分别是ABC ∆的高,中线,角平分线,则点D ,E ,F 的位置关系为( )A .点D 总在点E ,F 之间B .点E 总在点D ,F 之间C .点F 总在点D ,E 之间D .三者的位置关系不确定二、填空题(本大题共24分,每小题3分) 9.(3分)使式子32x -有意义的x 取值范围是 . 10.(3分)计算:2(32)a a a +÷= .11.(3分)如图,在ABC ∆中,90ABC ∠=︒,60ACB ∠=︒,BD AC ⊥,垂足为D .若6AB =,则BD 的长为 .12.(3分)如图,AB BC ⊥,AD DC ⊥,垂足分别为B ,D .只需添加一个条件即可证明ABC ADC ∆≅∆,这个条件可以是 .(写出一个即可)13.(3分)某中学要举行校庆活动,现计划在教学楼之间的广场上搭建舞台. 已知广场中心有一座边长为b 的正方形的花坛.学生会提出两个方案:方案一:如图1,围绕花坛搭建外围为正方形的“回”字形舞台(阴影部分),舞台的面积记为1S ; 方案二:如图2,在花坛的三面搭建“凹”字形舞台(阴影部分),舞台的面积记为2S ; 具体数据如图所示,则1S 2S .(填“>”,“ <”或“=” )14.(3分)如图,AB AC =,40A ∠=︒,AB 的垂直平分线MN 交AC 于点D .则DBC ∠的大小为 .15.(3分)在平面直角坐标系xOy 中,点A 的坐标为(0,3),点B 与点A 关于x 轴对称,点C 在x 轴上,若ABC ∆为等腰直角三角形,则点C 的坐标为 .16.(3分)图1是小明骑自行车的某个瞬间的侧面示意图,将小明右侧髋关节和车座看作一个整体抽象为A 点,将膝盖抽象为B 点,将脚跟、脚掌、踏板看作一个整体抽象为C 点,将自行车中轴位置记为D 点(注:自行车中轴是连接左右两个踏板,使两个踏板绕其旋转的部件),在骑行过程中,点A ,D 的位置不变,B ,C 为动点.图2是抽象出来的点和线.若40AB BC cm ==,16CD cm =,小明在骑车前,需调整车座高度,保证在骑行过程中脚总可以踩到踏板,则AD 最长为 cm .三、解答题(本大题共52分,第17题8分,第18~21题每题5分,第22题6分,第23题5分,第24题6分,第25题7分)17.(8分)(1)计算:2201()2(2)2π--+--;(2)分解因式:22363x xy y -+.18.(5分)已知2310x x --=,求代数式(25)(25)2(1)x x x x +-+-的值.19.(5分)如图,C 是AB 的中点,//CD BE ,CD BE =,连接AD ,CE .求证:AD CE =.20.(5分)《几何原本》是一部集前人思想和欧几里得个人创造性于一体的不朽之作,把人们公认的一些事实列成定义、公理和公设,用它们来研究各种几何图形的性质,从而建立了一套从定义、公理和公设出发,论证命题得到定理的几何学论证方法.在其第一卷中记载了这样一个命题:“在任意三角形中,大边对大角.”请补全上述命题的证明.已知:如图,在ABC ∆中,AC AB >. 求证: .证明:如图,由于AC AB=,连接BD.(在图中补全图形)>,故在AC边上截取AD AB=,AD AB∴∠=∠.()(填推理的依据)ABD∠是BCDADB∆的外角,ADB C DBC∴∠=∠+∠.()(填推理的依据)∴∠>∠.ADB C∴∠>∠.ABD CABC ABD DBC∠=∠+∠,∴∠>∠.ABC ABD∴∠>∠.ABC C21.(5分)列方程解应用题开展“光盘行动”,拒绝“舌尖上的浪费”,已成为一种时尚.某学校食堂为了激励同学们做到光盘不浪费,提出如果学生每餐做到光盘不浪费,那么餐后奖励香蕉或橘子一份.近日,学校食堂花了2800元和2500元分别采购了香蕉和橘子,采购的香蕉比橘子多150千克,香蕉每千克的价格比橘子每千克的价格低30%,求橘子每千克的价格.22.(6分)如图,在ABC∠=︒,AB AC⊥,=,D是AC边上一点,连接BD,EC AC ∆中,90BAC且AE BD=,AE与BC交于点F.(1)求证:CE AD=;(2)当AD CF∠.=时,求证:BD平分ABC23.(5分)小明在学习有关整式的知识时,发现一个有趣的现象:对于关于x的多项式223-+,由x x于2223(1)2x x x -+=-+,所以当1x -取任意一对互为相反数的数时,多项式223x x -+的值是相等的.例如,当11x -=±,即2x =或0时,223x x -+的值均为3;当12x -=±,即3x =或1-时,223x x -+的值均为6.于是小明给出一个定义:对于关于x 的多项式,若当x t -取任意一对互为相反数的数时,该多项式的值相等,就称该多项式关于x t =对称.例如223x x -+关于1x =对称.请结合小明的思考过程,运用此定义解决下列问题: (1)多项式246x x -+关于x = 对称;(2)若关于x 的多项式223x bx ++关于3x =对称,求b 的值; (3)整式22(816)(44)x x x x ++-+关于x = 对称.24.(6分)已知ABC ∆是等边三角形,点D 在射线BC 上(与点B ,C 不重合),点D 关于直线AC 的对称点为点E ,连接AD ,AE ,CE ,DE .(1)如图1,当点D 为线段BC 的中点时,求证:ADE ∆是等边三角形;(2)当点D 在线段BC 的延长线上时,连接BE ,F 为线段BE 的中点,连接CF .根据题意在图2中补全图形,用等式表示线段AD 与CF 的数量关系,并证明.25.(7分)在平面直角坐标系xOy 中,直线l 为过点(,0)M m 且与x 轴垂直的直线.对某图形上的点(,)P a b 作如下变换:当||b m 时,作出点P 关于直线l 的对称点1P ,称为Ⅰ()m 变换;当||b m <时,作出点P 关于x 轴的对称点2P ,称为Ⅱ()m 变换.若某个图形上既有点作了Ⅰ()m 变换,又有点作了Ⅱ()m 变换,我们就称该图形为m -双变换图形.例如,已知(1,3)A ,(2,1)B -,如图1所示,当2m =时,点A 应作Ⅰ(2)变换,变换后1A 的坐标是(3,3);点B 作Ⅱ(2)变换,变换后1B 的坐标是(2,1). 请解决下面的问题: (1)当0m =时,①已知点P 的坐标是(1,1)-,则点P 作相应变换后的点的坐标是 ;②若点(,)P a b作相应变换后的点的坐标为(1,2)-,求点P的坐标;(2)已知点(1,5)D-,C-,(4,2)①若线段CD是m-双变换图形,则m的取值范围是;②已知点(,)E m m在第一象限,若CDE∆及其内部(点E除外)组成的图形是m-双变换图形,且变换后所得图形记为G,直接写出所有图形G所覆盖的区域的面积.参考答案与试题解析一、选择题(本大题共24分,每小题3分)第1~8题符合题意的选项均只有一个,请将你的答案填写在下面的表格中.1.【解答】解:A 、不是轴对称图形,故本选项不合题意;B 、不是轴对称图形,故本选项不合题意;C 、不是轴对称图形,故本选项不合题意;D 、是轴对称图形,故本选项符合题意.故选:D .2.【解答】解:0.0000003用科学记数法表示为:7310-⨯. 故选:B .3.【解答】解:A 、235a a a ⋅=,故本选项不合题意;B 、236()a a =,故本选项符合题意;C 、33(2)8a a =,故本选项不合题意;D 、1028a a a ÷=,故本选项不合题意;故选:B .4.【解答】解:A 、是整式的乘法,不是因式分解,故此选项不符合题意;B 、是整式的乘法,不是因式分解,故此选项不符合题意;C 、把一个多项式转化成几个整式乘积的形式,是因式分解,故此选项符合题意;D 、没把一个多项式转化成几个整式乘积的形式,不是因式分解,故此选项不符合题意.故选:C .5.【解答】解:该正九边形内角和180(92)1260=︒⨯-=︒, 则每个内角的度数12609140=︒÷=︒. 故选:B .6.【解答】解:由作图得OD OC OD OC =='=',CD C D ='', 则根据“SSS ”可判断△C O D COD '''≅∆. 故选:A .7.【解答】解:原式222a b ab a a a b+-=⋅-2()a b aa a b-=⋅- a b =-,当2a b -=时,原式2=. 故选:A .8.【解答】解:假设AB AC <,如图所示,延长AE 至点H ,使EH AE =,连接CH , 在AEB ∆和HEC ∆中, AE HE AEB HEC BE CE =⎧⎪∠=∠⎨⎪=⎩, ()AEB HEC SAS ∴∆≅∆, AB CH ∴=,BAE H ∠=∠, AB AC <, CH AC ∴<, CAH H ∴∠<∠, CAH BAE ∴∠<∠,∴点F 总在点D ,E 之间,故选:C .二、填空题(本大题共24分,每小题3分) 9.【解答】解:要使式子32x -有意义,得 20x -≠.解得2x ≠, 故答案为:2x ≠.10.【解答】解:2(32)a a a +÷ 232a a a a =÷+÷ 32a =+.故答案为:32a +.11.【解答】解:在ABC ∆中,90ABC ∠=︒,60ACB ∠=︒, 90906030BAC ACB ∴∠=︒-∠=︒-︒=︒, BD AC ⊥, 90ADB ∴∠=︒, 6AB =,116322BD AB ∴==⨯=, 故答案为:3.12.【解答】解:若添加AB AD =,且AC AC =,由“HL ”可证Rt ABC Rt ADC ∆≅∆; 若添加BC CD =,且AC AC =,由“HL ”可证Rt ABC Rt ADC ∆≅∆; 若添加BAC DAC ∠=∠,且AC AC =,由“AAS ”可证Rt ABC Rt ADC ∆≅∆; 若添加BCA DCA ∠=∠,且AC AC =,由“AAS ”可证Rt ABC Rt ADC ∆≅∆; 故答案为:AB AD =或BC CD =或BAC DAC ∠=∠或ACB ACD ∠=∠(答案不唯一). 13.【解答】解:方案一:如图1,221S a b =-,方案二:如图2,22222222()()()()222a aS a b b b a b a b b a b b a b =-++-=---=--=-,22222222212(2)20S S a b a b a b a b b -=---=--+=>, 12S S ∴>.故答案为:>. 14.【解答】解:AB AC =,70ABC ACB ∴∠=∠=︒, MN 的垂直平分AB ,DA DB ∴=,40A ABD ∴∠=∠=︒,704030DBC ABC ABD ∴∠=∠-∠=︒-︒=︒.故答案为:30︒.15.【解答】解:点A 的坐标为(0,3),点B 与点A 关于x 轴对称,∴点(0,3)B -,3OA OB ∴==,又90ACB ∠=︒,AC BC =,3OC OA OB ∴===,∴点(3,0)C 或(3,0)-,故答案为:(3,0)或(3,0)-.16.【解答】解:在骑行过程中脚总可以踩到踏板,∴当AB BC AD CD +=+时,AD 最长,则,AD 最长为40401664()AB BC CD cm +-=+-=,故答案为:64.三、解答题(本大题共52分,第17题8分,第18~21题每题5分,第22题6分,第23题5分,第24题6分,第25题7分)17.【解答】解:(1)原式11144=+- 112=- 12=-; (2)原式223(2)x xy y =-+23()x y =-.18.【解答】解:原式222425226225x x x x x =-+-=--,2310x x --=,231x x ∴-=.∴原式22(3)25212523x x =--=⨯-=-.19.【解答】证明:C 是AB 的中点,AC CB ∴=,//CD BE ,ACD B ∴∠=∠.在ACD ∆和CBE ∆中,AC CB ACD B CD BE =⎧⎪∠=∠⎨⎪=⎩,()ACD CBE SAS ∴∆≅∆,AD CE ∴=.20.【解答】已知:如图,在ABC ∆中,AC AB >.求证:ABC C ∠>∠.证明:如图,由于AC AB >,故在AC 边上截取AD AB =,连接BD .(在图中补全图形).AD AB =,ABD ADB ∴∠=∠(等边对等角), ADB ∠是BCD ∆的外角,ADB C DBC ∴∠=∠+∠.(三角形的外角等于与它不相邻的两个内角的和), ADB C ∴∠>∠,ABD C ∴∠>∠,ABC ABD DBC ∠=∠+∠,ABC ABD ∴∠>∠,ABC C ∴∠>∠.故答案为:ABC C ∠>∠,ADB ,等边对等角,三角形的一个外角等于与它不相邻的两个内角的和.21.【解答】解:设橘子每千克的价格为x 元,则香蕉每千克的价格为70%x 元. 根据题意,得2800250015070%x x-=, 解得10x =,检验:当10x =时,70%0x ≠.所以原分式方程的解为10x =且符合题意. 答:橘子每千克的价格为10元.22.【解答】证明:(1)EC AC ⊥,90BAC ∠=︒, 90ACE BAC ∴∠=∠=︒, 在Rt CAE ∆与Rt ABD ∆中,AE BD CA AB =⎧⎨=⎩, Rt CAE Rt ABD(HL)∴∆≅∆,CE AD ∴=.(2)由(1)得Rt CAE Rt ABD ∆≅∆,EAC ABD ∴∠=∠,E ADB ∠=∠.由(1)得CE AD =,AD CF =,CE CF ∴=.CFE E ∴∠=∠,CFE AFB ∠=∠,AFB E ∴∠=∠.E ADB ∠=∠,AFB ADB ∴∠=∠,AGB EAC ADB ∠=∠+∠,AGB DBC AFB ∠=∠+∠, EAC DBC ∴∠=∠.EAC DBA ∠=∠,DBA DBC ∴∠=∠,BD ∴平分ABC ∠.23.【解答】解:(1)2246(2)2x x x -+=-+, 则多项式关于2x =对称,故答案为:2;(2)22223()3x bx x b b ++=++-,∴关于x 的多项式223x bx ++关于x b =-对称, 3b ∴-=,3b ∴=-;(3)原式22(4)(2)x x =+-2[(4)(2)]x x =+-22(28)x x =+-22[(1)9]x =+-2[(13)(13)]x x =+++-22(4)(2)x x =+-,当4x =-和2时,原式0=,∴关于1x =-对称,故答案为:1-.24.【解答】(1)证明:点D ,E 关于直线AC 对称, AD AE ∴=,DAC EAC ∠=∠,ABC ∆是等边三角形,AB AC ∴=,60BAC ∠=︒.点D 为线段BC 的中点, ∴11603022DAC BAC ∠=∠=⨯︒=︒. 30DAC EAC ∴∠=∠=︒.60DAE ∴∠=︒.AD AE =,ADE ∴∆是等边三角形;(2)解:补全图形如图所示,线段AD 与CF 的数量关系:2AD CF =.证明:延长CF 到点G ,使GF CF =,连接BG . F 为线段BE 的中点,BF EF ∴=.在BFG ∆和EFC ∆中,,,,GF CF BFG EFC BF EF =⎧⎪∠=∠⎨⎪=⎩()BFG EFC SAS ∴∆≅∆,GB CE ∴=,G FCE ∠=∠.//BG CE ∴.ABC ∆是等边三角形,AC BC ∴=,60ACB ∠=︒.120ACD ∴∠=︒.点D ,E 关于直线AC 对称,CD CE ∴=,120ACD ACE ∠=∠=︒.CD BG ∴=,60BCE ∠=︒,//BG CE .180BCE CBG ∴∠+∠=︒,120CBG ∴∠=︒,ACD CBG ∴∠=∠,在ACD ∆和CBG ∆中,,,,AC CB ACD CBG CD BG =⎧⎪∠=∠⎨⎪=⎩()ACD CBG SAS ∴∆≅∆.AD CG ∴=,2AD CF ∴=.25.【解答】解:(1)①0m =,1||m >, (1,1)∴-相应变换后的点的坐标是(1,1),故答案为:(1,1).②0m =,∴直线l 为y 轴.若0b ,则(,)P a b 作(0)I 变换,变换后的点为(,)a b -, ∴1,2.a b -=-⎧⎨=⎩ ∴1,2.a b =⎧⎨=⎩且符合题意.(1,2)P ∴.若0b <,则(,)P a b 作(0)II 变换,变换后的点为(,)a b -, ∴1,2.a b =-⎧⎨-=⎩∴1,2.a b =-⎧⎨=-⎩且符合题意. (1,2)P ∴--.综上,(1,2)P 或(1,2)P --.(2)①线段CD 是m -双变换图形,(1,5)C -,(4,2)D -, 52m ∴-<-或25m <.故答案为:52m -<-或25m <.②如图2中,由题意,满足条件的图形是平行四边形CDMN ,变换后所有图形G 所覆盖的区域的面积226336CDMN S =⨯=⨯⨯=平行四边形.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019-2020学年北京市海淀区八年级(上)期末数学试卷一、选择题(本大题共10小题,共30.0分)1. 若分式76−x 有意义,则x 的取值范围是( ) A. x =6 B. x ≠6 C. x <6 D. x >62. 已知分式x−1x+1的值是0,则x 的值是( )A. −1B. 0C. 1D. ±13. 下列等式从左到右的变形是因式分解的是( )A. −6a 3b 2=2a 2b ⋅(−3ab)B. 9a 2−4b 2=(3a +2b)(3a −2b)C. ma −mb +c =m(a −b)+cD. (a +b)2=a 2+2ab +b 2 4. 把分式13x+1612x−14的分子与分母各项系数化为整数,得到的正确结果是( )A. 3x+24x−3B. 4x+26x−3C. 2x+12x−1D. 4x+16x−3 5. 下列运算正确的是( )A. (a −b)(b −a)=b 2−a 2B. −3x 2y ⋅2xy 2=−6x 2y 2C. (−t −1)2=t 2−2t +1D. (−10)10÷109=106. 如图,△ABC 中,∠A =70°,点O 是AB 、AC 垂直平分线的交点,则∠BCO 的度数是( )A. 10°B. 20°C. 30°D.40° 7. 二次根式√3、√75、√2a 3、√a 2+1、√8ab 中,最简二次根式有( )A. 1个B. 2个C. 3个D. 4个8. 一个大长方形ABCD 按如图方式分割成九个四边形,且只有标号为①和②的两个正好为正方形,其余均为长方形.若已知小正方形①的周长为12,小长方形③的周长为2m ,小长方形④的周长为2n ,且3(m +n)+mn =61,这个大长方形ABCD 的面积( )A. 60B. 70C. 80D. 909.化简x2x−1+x1−x的结果是()A. x+1B. x−1C. −xD. x10.如图,从一个大正方形中裁去面积为30cm2和48cm2的两个小正方形,则余下部分的面积为()A. 78 cm2B. (4√3+√30)2cm2C. 12√10cm2D. 24√10cm2二、填空题(本大题共8小题,共24.0分)11.若二次根式√a−5有意义,则a的取值范围为______ .12.化简:3−x9−6x+x213.某种细胞的直径是0.00000095米,将0.00000095米用科学记数法表示为______.14.(3x−2y)(______)=4y2−9x2.15.若x2−2x−2的值为0,则3x2−6x的值是_________.16.若36x2+kx+16是一个完全平方式,则k的值为______.17.如图,在△ABC中,∠C=90°,AD平分∠CAB交BC于D,DE⊥AB于E,且AB=10cm,AC=8cm,BC=6cm,则△DEB的周长______.18.对于实数x,我们规定[x]表示不大于x的最大整数,例如[1.2]=1,[3]=3,则[−√5]=______.三、计算题(本大题共2小题,共13.0分)19.(1)计算:√9−(π−3)0−(−13)−1;(2)化简:(a−b)2+b(2a+b).20.先化简,再求值:2xx+1−2x−4x2−1÷x−2x2−2x+1,其中x=−13.四、解答题(本大题共6小题,共33.0分)21.解方程:16x2−4+1x+2=x+2x−222.如图,D是△ABC的边AB上一点,E是AC的中点,过点C作CF//AB,交DE的延长线于点F.若CF=6.BD=2,求AB的长.23.列方程解应用题2018年10月23日上午,港珠澳大桥开通仪式在广东珠海举行.国家主席习近平出席仪式并宣布大桥正式开通.港珠澳大桥跨越零丁洋,东接香港,西接广东珠海和澳门,总长约55公里,是粤港澳三地首次合作共建的超大型跨海交通工程,也是中国第一例集桥、双人工岛、隧道为一体的跨海通道.据统计,港珠澳大桥开通后的首个周日经大桥往来三地的车流量超过3000辆次,客流量则接近7.8万人次.当天,甲乙两辆巴士均从香港国际机场附近的香港口岸人工岛出发,开往珠海洪湾.甲巴士出发11分钟后乙巴士才出发,结果两车同时到达,已知两辆巴士的速度比是5:6,求两车的平均速度各是多少?24.已知代数式(x+2x2−2x −x−1x2−4x+4)÷x−4x.(1)化简这个代数式;(2)“当x=0时,该代数式的值为1”,这个说法正确吗?请说明理由.425.已知a,b,c是△ABC的三边长,化简:√(a+b+c)2−√(b+c−a)2+√(c−b−a)2.26.如图1,在平面直角坐标系中,直线AB分别交x轴、y轴于点A(a,0)点B(0,b),且a、b满足a2+4a+4+|2a+b|=0(1)a=______;b=______.(2)点P在直线AB的右侧,且∠APB=45°①若点P在x轴上,则点P的坐标为______;②若△ABP为直角三角形,求点P的坐标;(2)如图2,在(2)的条件下,点P在第四象限,∠BAP=90°,AP与y轴交于点M,BP与x轴交于点N,连接MN,求证:MP平分△BMN的一个外角.-------- 答案与解析 --------1.答案:B有意义,解析:解:∵分式76−x∴6−x≠0,解得:x≠6.故选:B.直接利用分式有意义的条件进而分析得出答案.此题主要考查了分式有意义的条件,正确把握分式的定义是解题关键.2.答案:C解析:本题主要考查了分式值为零的条件是分子等于零且分母不等于零.根据分式的值为零的条件可得x−1=0且x+1≠0,再解方程即可.解:由题意得:x−1=0,且x+1≠0,解得x=1,故选C.3.答案:B解析:解:A、−6a3b2=2a2b⋅(−3ab),不符合因式分解的定义;B、9a2−4b2=(3a+2b)(3a−2b),是因式分解,符合题意;C、ma−mb+c=m(a−b)+c,不符合因式分解的定义;D、(a+b)2=a2+2ab+b2,不符合因式分解的定义.故选:B.直接利用因式分解的定义和公式法分解因式分析得出答案.此题主要考查了因式分解,正确把握因式分解的定义是解题关键.4.答案:B解析:此题考查分式的基本性质,关键是根据分式的分子分母乘以一个式子分式的值不变解答. 解:13x+1612x−14=(13x+16)×12(12x−14)×12=4x+26x−3. 故选B .5.答案:D解析:解:A 、(a −b)(b −a)=−(a −b)2=−a 2+2ab −b 2,故本选项错误;B 、−3x 2y ⋅2xy 2=−6x 3y 3,故本选项错误;C 、(−t −1)2=t 2+2t +1,故本选项错误;D 、(−10)10÷109=1010÷109=10,故本选项正确;故选:D .根据完全平方公式判断A 、C ;根据单项式乘单项式的法则判断B ;根据乘方的意义以及同底数幂的除法法则判断D .此题考查了整式的混合运算,熟练掌握运算法则以及乘法公式是解本题的关键.6.答案:B解析:本题考查的是线段的垂直平分线的性质,线段的垂直平分线上的点到线段的两个端点的距离相等.连接OA 、OB ,根据三角形内角和定理求出∠ABC +∠ACB =110°,根据线段的垂直平分线的性质得到OA =OB ,OA =OC ,根据等腰三角形的性质计算即可.解:连接OA 、OB ,∵∠BAC =70°,∴∠ABC +∠ACB =110°,∵O 是AB ,AC 垂直平分线的交点,∴OA =OB ,OA =OC ,∴∠OAB =∠OBA ,∠OCA =∠OAC ,OB =OC ,∴∠OBA+∠OCA=70°,∴∠OBC+∠OCB=110°−70°=40°,∵OB=OC,∴∠BCO=∠CBO=20°.故选B.7.答案:B解析:本题考查的是最简二次根式的概念,最简二次根式的概念:(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式.根据最简二次根式的概念进行判断即可.解:√3是最简二次根公式,√75=5√3不是最简二次根式,√2a3=a√2a不是最简二次根式,√a2+1是最简二次根式,√8ab=2√2ab不是最简二次根式.∴最简二次根式有2个.故选B.8.答案:B解析:本题考查了矩形的性质,正方形的性质,先求得小正方形①的边长为3,小长方形③的长与宽的和为m,小长方形④的长与宽的和为n,设小正方形②的边长为x,则则大长方形ABCD的面积= (m−x+3+x)(x+3+n−x)=3(m+n)+mn+9,再根据3(m+n)+mn=61,即可求得答案.解:∵小正方形①的周长为12,∴小正方形①的边长为3,∵小长方形③的周长为2m,∴小长方形③的长与宽的和为m,∵小长方形④的周长为2n,∴小长方形④的长与宽的和为n,设小正方形②的边长为x,则大长方形ABCD的面积=(m−x+3+x)(x+3+n−x),=(m+3)(n+3),=3(m+n)+mn+9,∵3(m+n)+mn=61,∴大长方形ABCD的面积=70,故选B.9.答案:D解析:解:x2x−1+x1−x=x2x−1−xx−1=x2−xx−1=x(x−1)x−1=x,故选:D.将分母化为同分母,通分,再将分子因式分解,约分.本题考查了分式的加减运算.分式的加减运算中,如果是同分母分式,那么分母不变,把分子直接相加减即可;如果是异分母分式,则必须先通分,把异分母分式化为同分母分式,然后再相加减.10.答案:D解析:此题主要考查了二次根式的应用,正确求出阴影部分面积是解题关键.根据题意求出阴影部分的面积进而得出答案.解:∵从一个大正方形中裁去面积为30cm2和48cm2的两个小正方形,∴大正方形的边长是√30+√48=√30+4√3,∴留下部分(即阴影部分)的面积是(√30+4√3)2−30−48=8√90=24√10(cm2).故选D.11.答案:a≥5解析:根据二次根式的被开方数是非负数即可求解.考查了二次根式的意义和性质.概念:式子√a(a≥0)叫二次根式.性质:二次根式中的被开方数必须是非负数,否则二次根式无意义.解:依题意,得a−5≥0,解得a≥5.故答案是:a≥5.12.答案:13−x解析:本题主要考查了分式的约分及因式分解,解题的关键是正确的因式分解.先利用完全平方公式进行因式分解,再约分求解即可.解:3−x9−6x+x2=3−x(3−x)2=13−x.故答案为13−x.13.答案:9.5×10−7解析:解:将0.00000095米用科学记数法表示为9.5×10−7,故答案为:9.5×10−7.绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10−n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.本题考查用科学记数法表示较小的数,一般形式为a×10−n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.14.答案:−3x−2y解析:此题考查了平方差公式,熟练掌握平方差公式是解本题的关键.原式利用平方差公式的结构特征判断即可.解:因为(3x−2y)(−3x−2y)=4y2−9x2.故答案为:−3x−2y.15.答案:6解析:本题考查的是求代数式的值,根据题意得到x2−2x=2,然后3x2−6x变形得到3(x2−2x),利用整体代入法代入计算即可.解:∵x2−2x−2=0,∴x2−2x=2,∴3x2−6x=3(x2−2x)=3×2=6.故答案为6.16.答案:±48解析:此题考查了完全平方式,熟练掌握完全平方公式是解本题的关键.根据完全平方公式的特征判断即可得到k的值.解:∵(6x±4)2=36x2±48x+16,∴在36x2+kx+16中,k=±48.故答案为:±4817.答案:8cm解析:本题考查了角平分线上的点到角的两边距离相等的性质,三角形全等的判定与性质,三角形的周长,熟记性质并确定出三角形的周长的表示是解题的关键.根据角平分线上的点到角的两边距离相等可得CD=DE,然后利用“HL”证明Rt△ACD和Rt△AED全等,根据全等三角形对应边相等可得AE=AC,然后求出BE,再根据三角形的周长的定义求解即可.解:∵∠C=90°,AD平分∠CAB交BC于D,DE⊥AB,∴CD=DE,在Rt△ACD和Rt△AED中,{AD=AFDCD=CE,∴Rt△ACD≌Rt△AED(HL),∴AC=AE,∴BE=AB−AE=AB−AC=10−8=2(cm),∴△DEB的周长=BD+DE+BE=BD+CD+BE=BC+BE=6+2=8(cm).故答案为8cm.18.答案:−3解析:解:∵[1.2]=1,[3]=3,−3<−√5<−2,∴[−√5]=−3.故答案为:−3.直接利用[x]表示不大于x的最大整数,再结合−3<−√5<−2,进而得出答案.此题主要考查了估算无理数大小,正确得出−3<−√5<−2是解题关键.19.答案:解:(1)原式=3−1−(−3)=3−1+3=5;(2)原式=a2−2ab+b2+2ab+b2=a2+2b2.解析:此题考查了实数的运算,以及整式的混合运算,熟练掌握运算法则是解本题的关键.(1)原式第一项利用算术平方根定义计算,第二项利用零指数幂法则计算,最后一项利用负整数指数幂法则计算即可得到结果;(2)原式利用完全平方公式,单项式乘以多项式法则计算,去括号合并即可得到结果.20.答案:解:原式=2xx+1−2(x−2)(x+1)(x−1)⋅(x−1)2x−2=2xx+1−2(x−1)x+1=2x−2x+2x+1=2x+1,当x =−13时,原式=2−13+1=3.解析:先根据分式的混合运算顺序和运算法则化简原式,再将x 的值代入计算可得.本题主要考查分式的化简求值,解题的关键是熟练掌握分式的混合运算顺序和运算法则. 21.答案:解:去分母得:16+x −2=(x +2)2,整理方程得,x 2+3x −10=0,解得:x 1=−5,x 2=2,经检验x =−5是原方程的解,x =2是增根(舍去),∴原方程的解是x =−5.解析:分式方程去分母转化为整式方程,求出整式方程的解得到x 的值,经检验即可得到分式方程的解.此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.22.答案:解:∵CF//AB ,∴∠A =∠FCE ,∠ADE =∠F ,∵E 是AC 的中点,∴AE =CE ,在△ADE 和△FCE 中{∠ADE =∠F ∠A =∠FCE AE =EC∴△ADE≌△CFE(AAS),∴AD =CF ,∵CF =6,BD =2,∴AB =BD +AD =BD +CF =2+6=8.解析:根据平行线的性质得出∠A =∠FCE ,∠ADE =∠F ,又AE =CE ,根据全等三角形的判定得出△ADE≌△CFE ,根据全等三角形的性质得出AD =CF ,即可求出答案.本题考查了全等三角形的性质和判定,平行线的性质的应用,能求出△ADE≌△FCE是解此题的关键,注意:全等三角形的判定定理有:SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.23.答案:解:设甲巴士速度为5x km/ℎ,乙巴士速度为6x km/ℎ,根据题意,列方程得55 5x =556x+1160解得x=10经检验:x=10是原方程解,且符合题意∴5x=506x=60答:甲巴士速度为50 km/ℎ,乙巴士速度为60 km/ℎ.解析:设甲巴士速度为5x km/ℎ,乙巴士速度为6x km/ℎ,根据题意列出方程解答即可.本题考查分式方程的应用,分析题意,找到合适的等量关系是解决问题的关键.24.答案:(1)1(x−2)2;(2)不正确,理由见解析.解析:[分析](1)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果;(2)将x=0代入验证即可.[详解]解:(1)原式=[x+2x(x−2)−x−1(x−2)2]⋅xx−4=(x+2)(x−2)−x(x−1)x(x−2)2⋅xx−4=x−4x(x−2)2⋅xx−4=1(x−2)2;(2)不正确,∵当x=0时,代数式x+2x2−2x ,x−4x中的分母x2−2x,x都等于0,该代数式无意义,∴所以这个说法不正确.[点睛]本题考查了分式的化简求值以及分式有意义的条件,熟练掌握分式混合运算的运算顺序以及运算法则是解本题的关键.25.答案:解:∵a,b,c是△ABC的三边长,∴a+b+c>0,b+c−a>0,c−b−a<0.∴原式=(a+b+c)−(b+c−a)−(c−b−a)=3a+b−c.解析:本题主要考查了二次根式的性质与三角形的综合,关键是熟练掌握三角形的三边关系及二次根式的性质.先根据三角形的三边关系得出被开方数的符号,然后利用二次根式的性质进行化简即可.26.答案:(1)−2,4 ;(2)①(4,0);②由(1)知a=−2,b=4,∴A(−2,0),B(0,4),∴OA=2,OB=4,∵△ABP是直角三角形,且∠APB=45°,∴只有∠ABP=90°或∠BAP=90°,如图3,Ⅰ、当∠ABP=90°时,∵∠APB=∠BAP=45°,∴AB=PB,过点P作PC⊥OB于C,∴∠BPC+∠CBP=90°,∵∠CBP+∠ABO=90°,∴∠ABO=∠BPC,在△AOB和△BCP中,{∠AOB=∠BCP=90°∠ABO=∠BPCAB=PB,∴△AOB≌△BCP(AAS),∴PC=OB=4,BC=OA=2,∴OC=OB−BC=2,∴P(4,2),Ⅱ、当∠BAP=90°时,过点P′作P′D⊥OA于D,同Ⅰ的方法得,△ADP′≌△BOA,∴DP′=OA=2,AD=OB=4,∴OD=AD−OA=2,∴P′(2,−2);即:满足条件的点P(4,2)或(2,−2);(3)如图2,由(2)知点P(2,−2),∵A(−2,0),∴直线AP的解析式为y=−12x−1,∴M(0,−1),∴BM=5,同理:直线BP的解析式为y=−3x+4,∴N(43,0),∴MN=53,过点P作PH//AB交x轴于H,∵∠BAP=90°,∴∠BAO+∠PAH=90°,∴∠BAO+∠ABM=90°,∴∠ABM=∠PAH,在△ABM和△PAH中,{∠ABM=∠PAHAB=AP∠BAM=∠APH=90°,∴△ABM≌△PAH(ASA),∴∠AMB=∠PHA,AH=BM=5,∴∠PMG=∠PHA,OH=AH−OA=3,∴H(3,0),∴NH=3−43=53=MN,∵P(2,−2),M(0,−1),H(3,0),∴PM=√5,PH=√5,∴PM=PH,∴△PNM≌△PNH(SSS),∴∠AHP=∠PMN,∴∠PMG=∠PMN,即:MP是△BMN的一个外角的平分线.解析:解:(1)∵a2+4a+4+|2a+b|=0,∴(a+2)2+|2a+b|=0,∴a=−2,b=4,故答案为:−2,4;(2)见答案;(3)见答案.(1)利用非负数的和等于0,即可建立方程组求出a,b;(2)①利用等腰直角三角形的性质即可得出结论;②分两种情况,利用等腰三角形的性质,及全等三角形的性质求出PC,BC,即可得出结论;(3)先判断出∠PMG=∠AHP,再SSS判断出△PMN≌△PHN,得出∠AHP=∠PMN,即可得出结论.此题是三角形综合题,主要考查了非负性,等腰直角三角形的性质,全等三角形的判定和性质,待定系数法,构造全等三角形是解本题的关键.。
