3 习题三 稳恒电流的磁场
吉林大学大学物理练习册稳恒电流的磁场作业

取半径为 r ~ r+dr 的细圆环
dq 2rdr
dI
2
2rdr rdr
O Rr
B1 B2 r 1 R
dI
2
dB dr
B1 B2
2r dB
2dI
r
dr
R r
2
I
dr
2r
2
0
(
2 R
r
)
2
5. 两条无穷长的平行直导线距2a,分别载有大小相等方 向相反的电流I。空间任一点P到两导线的垂直距离分别为 x1和x2,求P点的磁感应强度B。
(2)当φ= / 2 时,线圈所受的力矩最大。
5.半径为R细圆环均匀带电,电荷线密度为λ。
若圆环以角速度ω绕过环心且垂直于 环面转轴作
匀速转动,则环心处的磁感应强度B 的大小
为
0 / 2
。 I nq 2R
2
B
0 I
2R
0 /
2
6. 一均匀带电圆环,带电量为+q,其半径为R,
置于均匀磁场 中B, 的B方向与圆环所在平面成
和洛仑兹力
B.只有库仑力和洛仑兹力
C.只有三种中某一种
5.载流为I、磁矩为Pm的线圈,置于磁感应强度 为B的均匀磁场中。若Pm与B方向相同,则通过线 圈的磁通量Ф与线圈所受的磁力矩M的大小为
A. IBPm , M 0
B. BPm , M 0
I
C. IBPm , M BPm
D.
BPm I
b 2 x 2
b
F3
0I1I2 dl L 2 x
ba
0 I1I 2
dx
0 I1I 2
ba ln
b 2 cos45 x 2 cos45 b
大学物理学

磁场中的磁介质一.选择题1.关于稳恒电流磁场的磁场强度H,下列几种说法中哪个是正确的? (A)H仅与传导电流有关.(B)若闭合曲线内没有包围传导电流,则曲线上各点的H必为零.(C)若闭合曲线上各点H均为零,则该曲线所包围传导电流的代数和为零.(D)以闭合曲线L为边缘的任意曲面的H通量均相等.[] 2.磁介质有三种,用相对磁导率μr 表征它们各自的特性时, (A)顺磁质μr >0,抗磁质μr <0,铁磁质μr >>1. (B)顺磁质μr >1,抗磁质μr =1,铁磁质μr >>1. (C)顺磁质μr >1,抗磁质μr <1,铁磁质μr >>1.(D)顺磁质μr <0,抗磁质μr <1,铁磁质μr >0.[]3.用细导线均匀密绕成长为l 、半径为a (l>>a )、总匝数为N 的螺线管,管内充满相对磁导率为μr 的均匀磁介质.若线圈中载有稳恒电流I ,则管中任意一点的(A)磁感强度大小为B =μ0μr NI .(B)磁感强度大小为B =μr NI/l . (C)磁场强度大小为H =μ0NI/l .(D)磁场强度大小为H =NI/l .[]4.如图所示的一细螺绕环,它由表面绝缘的导线在铁环上密绕而成,每厘米绕10匝.当导线中的电流I 为2.0A 时,测得铁环内的磁感应强度的大小B 为1.0T ,则可求得铁环的相对磁导率μr 为(真空磁导率μ0=4×10-7T ·m ·A -1)(A)7.96×102(B)3.98×102(C)1.99×102(D)63.3[]5.附图中,M 、P 、O 为由软磁材料制成的棒,三者在同一平面内,当K 闭合后,MO图1-4(A)M 的左端出现N 极.(B)P 的左端出现N 极. (C)O 的右端出现N 极.(D)P 的右端出现N 极.[]二.填空题1.一个绕有500匝导线的平均周长50cm 的细环,载有0.3A 电流时,铁芯的相对磁导率为600.(1)铁芯中的磁感强度B 为__________________________. (2)铁芯中的磁场强度H 为____________________________.(μ0=4×10-7T·m·A -1)2.长直电缆由一个圆柱导体和一共轴圆筒状导体组成,两导体中有等值反向均匀电流I 通过,其间充满磁导率为μr 的均匀磁介质.介质中离中心轴距离为r 的某点处的磁场强度的大小H =____________,磁感强度的大小B =__________。
第十一章稳恒电流的磁场(一)作业解答

一、利用毕奥—萨法尔定律计算磁感应强度毕奥—萨法尔定律:304r rl Id B d⨯=πμ1.有限长载流直导线的磁场)cos (cos 4210ααπμ-=a I B ,无限长载流直导线a IB πμ20=半无限长载流直导线a IB πμ40=,直导线延长线上0=B2. 圆环电流的磁场232220)(2x R IR B +=μ,圆环中心R I B 20μ=,圆弧中心πθμ220∙=R I B电荷转动形成的电流:πωωπ22q q T q I === 【 】基础训练1、载流的圆形线圈(半径a 1 )与正方形线圈(边长a 通有相同电流I .如图若两个线圈的中心O 1 、O 2处的磁感强度大小相同,则半径a 1与边长a 2之比a 1∶a 2为 (A) 1∶1 (B) π2∶1 (C) π2∶4 (D) π2∶8【 】基础训练3、有一无限长通电流的扁平铜片,宽度为a ,厚度不计,电流I 在铜片上均匀分布,在铜片外与铜片共面,离铜片右边缘为b 处的P 点的磁感强度B的大小为(A))(20b a I+πμ. (B)b b a aI +πln20μ.(C) b b a b I +πln 20μ. (D) )2(0b a I+πμ. 解法:【 】自测提高2、通有电流I 的无限长直导线有如图三种形状,则P ,Q ,O 各点磁感强度的大小B P ,B Q ,B O 间的关系为 (A) B P > B Q > B O . (B) B Q > B P > B O . B Q > B O > B P . (D) B O > B Q > B P . 解法:根据直线电流的磁场公式和圆弧电流产生磁场公式可得【 】自测提高7、边长为a 的正方形的四个角上固定有四个电荷均为q 的点电荷.此正方形以角速度ω 绕AC 轴旋转时,在中心O 点产生的磁感强度大小为B 1;此正方形同样以角速度ω 绕过O 点垂直于正方形平面的轴旋转时,在O 点产生的磁感应强度的大小为B 2,则B 1与B 2间的关系为 (A) B 1 = B 2. (B) B 1 = 2B 2. (C) B 1 = 21B 2. (D) B 1 = B 2 /4. 解法:设正方形边长为a ω 相同,所以每个点电荷随着正方形旋转时形成的等效电流相同, 为当正方形绕AC 轴旋转时,一个点电荷在O 旋转产生电流,在O 点产生的总磁感小为O 点产生的磁感应强度的大小为基础训练12、一长直载流导线,沿空间直角坐标Oy 轴放置,电流沿y 正向.在原点O 处取一电流元l Id ,则该电流元在(a ,0,0)点处的磁感强度的大小为 ,方向为 。
《大学物理》习题册题目及答案第12单元稳恒电流的磁场

第12单元 稳恒电流的磁场 第七章 静电场和恒定磁场的性质(三)磁感应强度序号序号 学号学号 姓名姓名 专业、班级专业、班级一 选择题[ C ]1.一磁场的磁感应强度为B ai bj ck =++(T ),则通过一半径为R ,开口向z 正方向的半球壳表面的磁通量的大小是:向的半球壳表面的磁通量的大小是: (A) Wb 2a R p(B) Wb 2b R p (C) Wb 2c R p (D) Wb 2abc R p[ B ]2. ]2. 若要使半径为若要使半径为4×103-m 的裸铜线表面的磁感应强度为7.07.0××105- T T,则铜线中需,则铜线中需要通过的电流为要通过的电流为((μ0=4π×107-T ·m ·A 1-)(A) 0.14A (B) 1.4A (C) 14A (D) 28A[ B ]3. [ B ]3. 一载有电流一载有电流I 的细导线分别均匀密绕在半径为R 和r 的长直圆筒上形成两个螺线管(R=2r)(R=2r),,两螺线管单位长度上的匝数相等,两螺线管中的磁感应强度大小R B 和r B 应满足: (A) R B =2r B(B) R B =rB (C) 2R B =r B (D) R B R=4r B[ D ]4.如图,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感应强度B 沿图中闭合路径L 的积分l B d ×ò等于等于(A)I 0m(B)I 031m (C) I041m(D)I032m[ D ]5. [ D ]5. 有一由有一由N 匝细导线绕成的平面正三角形线圈,边长为a ,通有电流I ,置于均匀外磁场外磁场 B 中,当线圈平面的法向与外磁场同向时,该线圈所受的磁力矩mM(A) 2/32IB Na (B) 4/32IB Na (C) 0260sin 3IB Na (D) 0abcdI L1201I 2I 1R 2R二 填空题1.1.一无限长载流直导线,通有电流一无限长载流直导线,通有电流I ,弯成如图形状,设各线段皆在纸面内,则P 点磁感应强度强度 B B 的大小为aIp m 830。
大学物理习题课-稳恒电流的稳恒磁场-2011.6.10

1 5
r r 向上, M垂直 B, 向上,
一根无限长的直圆柱形铜导线, 例5. 一根无限长的直圆柱形铜导线,外包一层相对磁导率为 µr的圆筒形磁介质,导线半径为 R1,磁介质的外半径为 R2。 的圆筒形磁介质, 导线内有电流通过, 磁介质内、 导线内有电流通过 , 求 : 磁介质内 、 外的磁场强度和磁感应 强度的分布
大学物理习题课
恒定电流的稳恒磁场
•
电流 电流密度 电动势
电流强度 电流密度
v v j = qnv
(S )
∆q dq I = lim = ∆t →0 ∆ t dt
v r 对任意曲面S: 对任意曲面 : I = ∫∫ j ⋅ dS
r I 是 j 的通量
v v dqin 电流的连续性方程 ∫∫S j ⋅ dS = − dt v v 电流稳恒条件 ∫∫ j ⋅ dS = 0
I
v × B 1
p -e 3r
用补偿法求p处的磁感应强度: 用补偿法求 处的磁感应强度: 处的磁感应强度
v v 根据 ∫ B⋅ dl = µ0 ∑Ii
L
v v
v • B2
δ
o`
v
得: B = 1
µ0δ r
6
B2 =
µ0δr
88
41µ0δr ∴B = B − B2 = 1 264
v v v v v fm = qv× B = −ev× B
计算得 方向: B = 5.0×10−16 (T) 方向:垂直于纸面向里
例2:空气中有一半径为 的“无限长”直圆柱金属导体,竖直 :空气中有一半径为r的 无限长”直圆柱金属导体, 的圆柱空洞, 线oo`为中心轴线 ,在圆柱体内挖一个直径为 r 的圆柱空洞, 为中心轴线 空洞侧面与oo`相切,在未挖洞部分通以均匀分布的电流I,方 空洞侧面与 相切,在未挖洞部分通以均匀分布的电流 , 相切 向沿oo`向下,如图所示。在距轴线 处有一电子 电量为-e) 处有一电子( 向沿 向下,如图所示。在距轴线3r处有一电子(电量为 ) 向下 o 沿平行于oo`轴方向 在中心轴线oo` 轴方向, 沿平行于 轴方向,在中心轴线 r/2
《稳恒电流的磁场》选择题解答与分析

由毕奥-萨伐尔定律 d B 0 I d l r /(4r 3 ) ,知答案(B)正确。
a d
b I dl
c
选择(A)给出下面的分析:
dq ˆ r 4 0 r 2 0 I d l r 电流元磁场公式: d B 4r 3
点电荷电场公式: d E
比较 d B d B x iˆ d B y ˆ j, d B x
0 I d ly 4r 3
0 I d l
4 ( x y
2 2 3 z2 ) 2
y.
对于所有错误选择,给出下面的资料:
0 I d l r 毕奥-萨伐尔定律: d B ,涉及矢量的叉乘,其基本运算公式: 4r 3 ˆ ˆ ˆa ˆ ˆ ˆ 设: a a1i 2 j a 3 k , b b1i b2 j b3k
对所有错误的选择,进入下一题: 1.1 在阴极射线管的上方放置一根载流直导线,导线平行于射 线管轴线,电流方向如图所示,阴极射线向什么方向偏转?当 电流 I 反向后,结果又将如何?
I
参考解答: 电流产生的磁场在射线管内是指向纸面内的,由 F ev B 知,阴极射线(即电 子束)将向下偏转.当电流反方向时,阴极射线将向上偏转. 进入下一题:
3. 关于磁感应强度方向的定义,以下说法,正确的是 (A) 能把磁场作用于运动电荷的力的方向,定义为磁感应强度的方向. (B) 不能把磁场作用于运动电荷的力的方向,定义为磁感应强度的方向. 答案:(B) 参考解答: 因为磁力的方向还随电荷运动速度方向而不同,因而在磁场中同一点运动电荷受 力的方向是不确定的.
6
B
3. 如图,一条任意形状的载流导线位于均匀磁场中,试证明 导线 a 到 b 之间的一段上所受的安培力等于载同一电流的直 导线 ab 所受的安培力. 参考解答: 证:由安培定律
稳恒磁场及答案
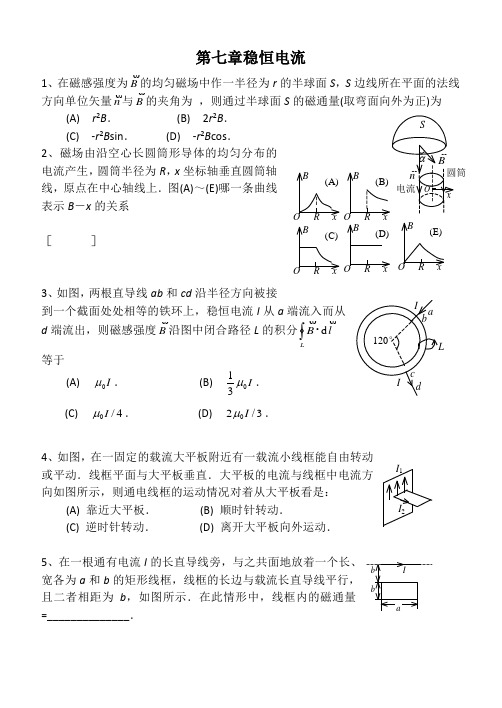
第七章稳恒电流1、在磁感强度为B的均匀磁场中作一半径为r 的半球面S ,S 边线所在平面的法线方向单位矢量n 与B的夹角为 ,则通过半球面S 的磁通量(取弯面向外为正)为 (A) r 2B . . (B) 2r 2B . (C) -r 2B sin . (D) -r 2B cos .2、磁场由沿空心长圆筒形导体的均匀分布的电流产生,圆筒半径为R ,x 坐标轴垂直圆筒轴线,原点在中心轴线上.图(A)~(E)哪一条曲线表示B -x 的关系[ ]3、如图,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感强度B沿图中闭合路径L 的积分 LlB d 等于(A) I 0 . (B) I 031. (C) 4/0I . (D) 3/20I .4、如图,在一固定的载流大平板附近有一载流小线框能自由转动或平动.线框平面与大平板垂直.大平板的电流与线框中电流方向如图所示,则通电线框的运动情况对着从大平板看是: (A) 靠近大平板. (B) 顺时针转动. (C) 逆时针转动. (D) 离开大平板向外运动.5、在一根通有电流I 的长直导线旁,与之共面地放着一个长、宽各为a 和b 的矩形线框,线框的长边与载流长直导线平行,且二者相距为b ,如图所示.在此情形中,线框内的磁通量 =______________.n B SOB x O R (A) BxO R (B)Bx O R (D) Bx O R (C)BxO R (E)x电流 圆筒II ab c d120°I 1I 2b baI6、如图所示,在真空中有一半圆形闭合线圈,半径为a ,流过稳恒电流I ,则圆心O 处的电流元l I d 所受的安培力Fd 的大小为____,方向________.7、有一根质量为m ,长为l 的直导线,放在磁感强度为 B的均匀磁场中B 的方向在水平面内,导线中电流方向如图所示,当导线所受磁力与重力平衡时,导线中电流I =___________________.8、如图所示,一无限长载流平板宽度为a ,线电流密度(即沿x 方向单位长度上的电流)为,求与平板共面且距平板一边为b的任意点P 的磁感强度.9、一根同轴线由半径为R 1的长导线和套在它外面的内半径为R 2、外半径为R 3的同轴导体圆筒组成.中间充满磁导率为的各向同性均匀非铁磁绝缘材料,如图.传导电流I 沿导线向上流去,由圆筒向下流回,在它们的截面上电流都是均匀分布的.求同轴线内外的磁感强度大小B 的分布.答案:一 选择题1、D2、A3、D4、B5、2ln 20Ia6、a l I 4/d 20 垂直电流元背向半圆弧(即向左)7、)/(lB mgIlI dIBI8、解:利用无限长载流直导线的公式求解. (1) 取离P 点为x 宽度为d x 的无限长载流细条,它的电流x i d d(2) 这载流长条在P 点产生的磁感应强度x i B 2d d 0 xx2d 0 方向垂直纸面向里.(3) 所有载流长条在P 点产生的磁感强度的方向都相同,所以载流平板在P 点产生的磁感强度B B dba bxdx x20b b a x ln 20 方向垂直纸面向里.9、解:由安培环路定理: i I l Hd 0< r <R 1区域: 212/2R Ir rH 212R Ir H, 2102R Ir BR 1< r <R 2区域: I rH 2r I H 2, rIB 2R 2< r <R 3区域: )()(22223222R R R r I I rH )1(22223222R R R r r IH )1(2222322200R R R r r IH B r >R 3区域: H = 0,B = 0x d x PO x。
大学物理稳恒磁场习题及答案
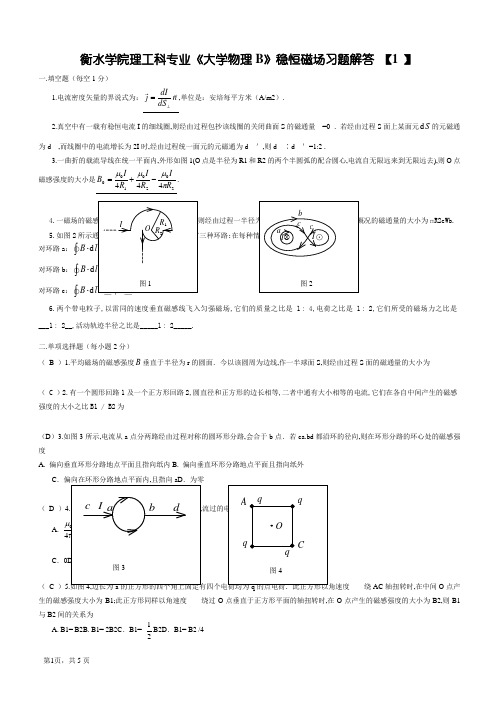
衡水学院理工科专业《大学物理B 》稳恒磁场习题解答 【1 】一.填空题(每空1分)1.电流密度矢量的界说式为:dIj n dS ⊥=,单位是:安培每平方米(A/m2). 2.真空中有一载有稳恒电流I 的细线圈,则经由过程包抄该线圈的关闭曲面S 的磁通量=0 .若经由过程S 面上某面元d S 的元磁通为d,而线圈中的电流增长为2I 时,经由过程统一面元的元磁通为d ',则d ∶d '=1:2 .3.一曲折的载流导线在统一平面内,外形如图1(O 点是半径为R1和R2的两个半圆弧的配合圆心,电流自无限远来到无限远去),则O 点磁感强度的大小是2020100444R IR IR IB πμμμ-+=.4.一磁场的磁感强度为k c j b i a B++= (SI),则经由过程一半径为R,启齿向z 轴正偏向的半球壳概况的磁通量的大小为πR2cWb. 5.如图2所示通有电流I 的两根长直导线旁绕有三种环路;在每种情形下,等于: 对环路a :d B ⋅⎰=____μ0I__;对环路b :d B ⋅⎰=___0____; 对环路c :d B ⋅⎰=__2μ0I__.6.两个带电粒子,以雷同的速度垂直磁感线飞入匀强磁场,它们的质量之比是1∶4,电荷之比是1∶2,它们所受的磁场力之比是___1∶2__,活动轨迹半径之比是_____1∶2_____. 二.单项选择题(每小题2分)( B )1.平均磁场的磁感强度B 垂直于半径为r 的圆面.今以该圆周为边线,作一半球面S,则经由过程S 面的磁通量的大小为( C )2.有一个圆形回路1及一个正方形回路2,圆直径和正方形的边长相等,二者中通有大小相等的电流,它们在各自中间产生的磁感强度的大小之比B1 / B2为(D )3.如图3所示,电流从a 点分两路经由过程对称的圆环形分路,会合于b 点.若ca.bd 都沿环的径向,则在环形分路的环心处的磁感强度A. 偏向垂直环形分路地点平面且指向纸内B. 偏向垂直环形分路地点平面且指向纸外C .偏向在环形分路地点平面内,且指向aD .为零( D )4.在真空中有一根半径为R 的半圆形细导线流过的电流为I,则圆心处的磁感强度为 A.R 140πμ B. R120πμ C .0D .R 140μ ( C )5.如图4,边长为a 的正方形的四个角上固定有四个电荷均为q 的点电荷.此正方形以角速度绕AC 轴扭转时,在中间O 点产生的磁感强度大小为B1;此正方形同样以角速度绕过O 点垂直于正方形平面的轴扭转时,在O 点产生的磁感强度的大小为B2,则B1与B2间的关系为A. B1= B2B. B1= 2B2C .B1=21B2D .B1= B2 /4O IR 1 R 2图1b⊗ ⊙ cI I c a图2c I db a图3A CqqqqO图4(B )6.有一半径为R 的单匝圆线圈,通以电流I,若将该导线弯成匝数N = 2的平面圆线圈,导线长度不变,并通以同样的电流,则线圈中间的磁感强度和线圈的磁矩分离是本来的 (A) 4倍和1/8. (B) 4倍和1/2. (C) 2倍和1/4.(D) 2倍和1/2. 三.断定题(每小题1分,请在括号里打上√或×)( × )1.电源的电动势是将负电荷从电源的负极经由过程电源内部移到电源正极时,非静电力作的功. ( √ )2.磁通量m SB dS φ=⋅⎰的单位为韦伯.( × )3.电流产生的磁场和磁铁产生的磁场性质是有区此外. ( × )4.电动势用正.负来暗示偏向,它是矢量.( √ )5.磁场是一种特别形态的物资,具有能量.动量和电磁质量等物资的根本属性. ( × )6.知足0m SB dS φ=⋅=⎰的面积上的磁感应强度都为零.四.简答题(每小题5分)1.在统一磁感应线上,各点B 的数值是否都相等?为何不把感化于活动电荷的磁力偏向界说为磁感应强度B的偏向?答:在统一磁感应线上,各点B 数值一般不相等.(2分)因为磁场感化于活动电荷的磁力偏向不但与磁感应强度B 的偏向有关,并且与电荷速度偏向有关,即磁力偏向其实不是独一由磁场决议的,所以不把磁力偏向界说为B 的偏向.(3分)2.写出法拉第电磁感应定律的数学表达式,解释该表达式的物理意义. 答:法拉第电磁感应定律的数学表达式r lS BE dl dS t∂⋅=-⋅∂⎰⎰(2分) 物理意义:(1)感生电场是由变更的磁场激发的;(1分)(2)感生电场r E 与Bt∂∂组成左手螺旋关系;(1分)(3)右侧的积分面积S 为左侧积分路径L 包抄的面积.(1分)五.盘算题(每题10分,写出公式.代入数值.盘算成果.)1.如图5所示,AB.CD 为长直导线,BC 为圆心在O 点的一段圆弧形导线,其半径为R.若通以电流I,求O 点的磁感应强度. 解:如图所示,O 点磁场由AB .C B.CD 三部分电流产生.个中AB 产生01=B(1分)CD 产生RIB 1202μ=,(2分)偏向垂直向里(1分)CD 段产生)231(2)60sin 90(sin 24003-πμ=-πμ=︒︒R I R I B ,(2分)偏向⊥向里(1分)∴)6231(203210ππμ+-=++=R I B B B B ,(2分)偏向⊥向里.(1分) 2.如图6所示.半径为R 的平均带电圆盘,面电荷密度为σ.当盘以角速度ω绕个中间轴OO '扭转时,求盘心O 点的B 值.解法一:当带电盘绕O 轴迁移转变时,电荷在活动,因而产生磁场.可将圆盘算作很多齐心圆环的组合,而每一个带电圆环迁移转变时相当图5于一圆电流.以O 为圆心,r 为半径,宽为dr 的圆环,此环上电量rdr ds dq πσσ2⋅==(2分)此环迁移转变时,其等效电流rdr dq dI ωσπω=⋅=2(3分) 此电流在环心O 处产生的磁感应强度大小2200drrdIdB ωσμμ==(2分)其偏向沿轴线,是以全部圆盘在盘心O 处产生的磁感应强度大小是R dr dBB Rωσμωσμ0002121==⎰⎰(3分) 解法二:依据活动电荷的磁场公式304r rv q B ⨯=πμ,(2分)求解,在圆盘上取一半径为r,宽为dr 的圆环,电量rdr dq πσ2=,ωr v =(2分)dr rdr r r dq r dB 22440020σωμπσπωμπωμ=⋅==(3分)偏向垂直于盘面向上,同样RqRdr dB B Rπωμωσμσωμ2220000====⎰⎰(3分) 3.图7所示,在一长直载流导线旁有一长为L 导线ab,其上载电流分离为I1和I2,a 端到直导线距离为d 求当导线ab 与长直导线垂直,求ab 受力.解:取如图8所示坐标系直导线在距其为x 处,产生的磁场xI B πμ210=(2分) 其偏向垂直低面向里,电流之I2dx 受安培力大小为dx xI I Bdx I df πμ22102==(3分) df 偏向垂直向上,且各电流之受力偏向雷同,(2分)故,ab 受力为012012ln22d L LdI I I I d Lf df dx x dμμππ++===⎰⎰(3分) 4.一长直导线通有电流120A I =,旁边放一导线ab,个中通有电流210A I =,且两者共面,如图8所示.求导线ab 所受感化力对O 点的力矩.解:如图9所示,在ab 上取r d ,它受力ab F ⊥d 向上,(2分)大小为rI rI F πμ2d d 102=(2分) F d 对O 点力矩F r M⨯=d (2分)图6I 1I2dL图7Md 偏向垂直纸面向外,大小为r I I F r M d 2d d 210πμ==(2分) ⎰⎰-⨯===ba bar II M M 6210106.3d 2d πμm N ⋅(2分)5.两平行长直导线相距d=40cm,每根导线载有I1=I2=20A 如图10所示.求: ⑴两导线地点平面内与该两导线等距的一点A 处的磁感应强度; ⑵经由过程图中斜线所示面积的磁通量.(r1=r3=10cm,l=25cm)解: (1)图中的A 点的磁场122222O O A I I B d d μμππ=+⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭()512124010O O OI I I I T d d dμμμπππ-=+=+=⨯(4分) (2)在正方形中距中间x 处,取一窄条ds ldx =,则经由过程ds 的磁通量m d B ldx φ=()1222O O I I ldxx d z μμππ⎛⎫=+ ⎪ ⎪-⎝⎭ 122O l I I dx x d x μπ⎛⎫=+ ⎪-⎝⎭(3分)31122d r O m m r l I I d dx x d x μφφπ-⎛⎫==+ ⎪-⎝⎭⎰⎰311213ln ln 2O l d r d r I I r r μπ⎛⎫--=+ ⎪⎝⎭ ()121ln 2O l d n I I r μπ⎛⎫-=+ ⎪⎝⎭6111ln 2.210O l d r I wb r μπ--==⨯(3分) 6.已知磁感应强度B=2.0Wb ·m -2的平均磁场, 偏向沿X 轴正偏向,如图11所示,试求:(1) 经由过程abcd 面的磁通量; (2) 经由过程图中befc 面的磁通量; (3)经由过程图中aefd 面的磁通量. 解:(1)经由过程abcd 面的磁通量mabcd abcd B S φ= 2.00.40.3=⨯⨯ 0.24wb =(4分)(2)经由过程ebfc 面的磁通量,因为B 线擦过此面 故0mbdfc φ=(3分)(3)经由过程aefd 面的磁通量图110.24 maefd mabcd wbφφ==(3分)。
《大学物理》习题册题目及答案第12单元 稳恒电流的磁场

第12单元 稳恒电流的磁场第七章 静电场和恒定磁场的性质(三)磁感应强度序号 学号 姓名 专业、班级一 选择题[ C ]1.一磁场的磁感应强度为B ai bj ck =++(T ),则通过一半径为R ,开口向z 正方向的半球壳表面的磁通量的大小是: (A) Wb 2a R π(B) Wb 2b R π (C) Wb 2c R π(D) Wb 2abc R π[ B ]2. 若要使半径为4×103-m 的裸铜线表面的磁感应强度为7.0×105- T ,则铜线中需要通过的电流为(μ0=4π×107-T ·m ·A1-)(A) 0.14A (B) 1.4A (C) 14A (D) 28A[ B ]3. 一载有电流I 的细导线分别均匀密绕在半径为R 和r 的长直圆筒上形成两个螺线管(R=2r),两螺线管单位长度上的匝数相等,两螺线管中的磁感应强度大小R B 和r B 应满足: (A) R B =2r B(B) R B =rB (C) 2R B =r B (D) R B R=4r B[ D ]4.如图,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I 从a 端流入而从d 端流出,则磁感应强度B沿图中闭合路径L 的积分l B d ⋅⎰等于(A)I 0μ(B)I 031μ (C) I 041μ(D)I 032μ[ D ]5. 有一由N 匝细导线绕成的平面正三角形线圈,边长为a ,通有电流I ,置于均匀外磁场 B 中,当线圈平面的法向与外磁场同向时,该线圈所受的磁力矩mM(A) 2/32IB Na (B) 4/32IB Na (C) 0260sin 3IB Na (D) 0二 填空题1.一无限长载流直导线,通有电流I ,弯成如图形状,设各线段皆在纸面内,则P 点磁感应强度 B 的大小为aIπμ830。
3.半径为0.5cm 的无限长直圆柱形导体上,沿轴线方向均匀地流着I=3A 的电流,作一个半径r=5cm 、长l=5cm 且与电流同轴的圆柱形闭合曲面S ,则该曲面上的磁感应强度 B 沿曲面的⎰=⋅Sd s B _______0_________________________。
(完整版)大学物理电磁场练习题含答案

(完整版)⼤学物理电磁场练习题含答案前⾯是答案和后⾯是题⽬,⼤家认真对对. 三、稳恒磁场答案1-5 CADBC 6-8 CBC 三、稳恒磁场习题1. 有⼀个圆形回路1及⼀个正⽅形回路2,圆直径和正⽅形的边长相等,⼆者中通有⼤⼩相等的电流,它们在各⾃中⼼产⽣的磁感强度的⼤⼩之⽐B 1 / B 2为 (A) 0.90. (B) 1.00.(C) 1.11. (D) 1.22.[]2.边长为l 的正⽅形线圈中通有电流I ,此线圈在A 点(见图)产⽣的磁感强度B 为(A) l I π420µ. (B) l Iπ220µ.(C)l Iπ02µ. (D) 以上均不对.[]3.通有电流I 的⽆限长直导线有如图三种形状,则P ,Q ,O 各点磁感强度的⼤⼩B P ,B Q ,B O 间的关系为:(A) B P > B Q > B O . (B) B Q > B P > B O .(C) B Q > B O > B P . (D) B O > B Q > B P .[]4.⽆限长载流空⼼圆柱导体的内外半径分别为a 、b ,电流在导体截⾯上均匀分布,则空间各处的B ?的⼤⼩与场点到圆柱中⼼轴线的距离r 的关系定性地如图所⽰.正确的图是[]5.电流I 由长直导线1沿平⾏bc 边⽅向经a 点流⼊由电阻均匀的导线构成的正三⾓形线框,再由b 点沿垂直ac 边⽅向流出,经长直导线2返回电源(如图).若载流直导线1、2和三⾓形框中的电流在框中⼼O 点产⽣的磁感强度分别⽤1B ?、2B ?和3B表⽰,则O 点的磁感强度⼤⼩(A) B = 0,因为B 1 = B 2 = B 3 = 0.(B) B = 0,因为虽然B 1≠ 0、B 2≠ 0,但021=+B B ??,B 3 = 0.(C) B ≠ 0,因为虽然B 2 = 0、B 3= 0,但B 1≠ 0.(D) B ≠ 0,因为虽然021≠+B B ?,但B 3≠ 0.[]6.电流由长直导线1沿半径⽅向经a 点流⼊⼀电阻均匀的圆环,再由b 点沿切向从圆环流出,经长导线2返回电源(如图).已知直导线上电流强度为I ,圆环的半径为R ,且a 、b 与圆⼼O 三点在同⼀直线上.设直电流1、2及圆环电流分别在O 点产⽣的磁感强度为1B ?、2B ?及3B,则O 点的磁感强度的⼤⼩(A) B = 0,因为B 1 = B 2 = B 3 = 0.(B) B = 0,因为021=+B B ?,B 3= 0.(C) B ≠ 0,因为虽然B 1 = B 3 = 0,但B 2≠ 0. (D) B ≠ 0,因为虽然B 1 = B 2 = 0,但B 3≠ 0.(E) B ≠ 0,因为虽然B 2 = B 3 = 0,但B 1≠ 0.[] v7.电流由长直导线1沿切向经a 点流⼊⼀个电阻均匀的圆环,再由b 点沿切向从圆环流出,经长直导线2返回电源(如图).已知直导线上电流强度为I ,圆环的半径为R ,且a 、b 和圆⼼O 在同⼀直线上.设长直载流导线1、2和圆环中的电流分别在O 点产⽣的磁感强度为1B ?、2B ?、3B,则圆⼼处磁感强度的⼤⼩(A) B = 0,因为B 1 = B 2 = B 3 = 0.(B) B = 0,因为虽然B 1≠ 0、B 2≠ 0,但021=+B B ??,B 3 = 0.(C) B ≠ 0,因为B 1≠ 0、B 2≠ 0,B 3≠ 0.(D) B ≠ 0,因为虽然B 3= 0,但021≠+B B ??.[]8.a R r OO ′I在半径为R 的长直⾦属圆柱体内部挖去⼀个半径为r 的长直圆柱体,两柱体轴线平⾏,其间距为a ,如图.今在此导体上通以电流I ,电流在截⾯上均匀分布,则空⼼部分轴线上O ′点的磁感强度的⼤⼩为(A) 2202R a a I ?πµ (B)22202R r a a I -?πµ(C) 22202r R a a I-?πµ (D) )(222220a r Ra a I -πµ []参考解:导体中电流密度)(/22r R I J -π=.设想在导体的挖空部分同时有电流密度为J 和-J 的流向相反的电流.这样,空⼼部分轴线上的磁感强度可以看成是电流密度为J 的实⼼圆柱体在挖空部分轴线上的磁感强度1B ?和占据挖空部分的电流密度-J 的实⼼圆柱在轴线上的磁感强度2B ?的⽮量和.由安培环路定理可以求得02=B , )(222201r R a Ia B -π=µ 所以挖空部分轴线上⼀点的磁感强度的⼤⼩就等于)(22201r R IaB -π=µ 9. πR 2c3分10.221R B π-3分11. 6.67×10-7 T 3分7.20×10-7 A ·m 2 2分12. 减⼩ 2分在2/R x <区域减⼩;在2/R x >区域增⼤.(x 为离圆⼼的距离) 3分13. 0 1分I 0µ- 2分14. 4×10-6 T 2分 5 A 2分15. I0µ 1分 0 2分2I0µ 2分16. 解:①电⼦绕原⼦核运动的向⼼⼒是库仑⼒提供的.即∶ 02202041a m a e v =πε,由此得 002a m e επ=v 2分②电⼦单位时间绕原⼦核的周数即频率000142a m a e a ενππ=π=v 2分由于电⼦的运动所形成的圆电流00214a m a e e i ενππ== 因为电⼦带负电,电流i 的流向与 v ?⽅向相反 2分③i 在圆⼼处产⽣的磁感强度002a i B µ=00202018a m a eεµππ= 其⽅向垂直纸⾯向外 2分17.1 234 R ROI a β2解:将导线分成1、2、3、4四部份,各部分在O 点产⽣的磁感强度设为B 1、B 2、B 3、B 4.根据叠加原理O 点的磁感强度为:4321B B B B B +++= ∵ 1B ?、4B ?均为0,故32B B B ?+= 2分)2(4102R I B µ= ⽅向? 2分 242)sin (sin 401203R I a I B π=-π=µββµ)2/(0R I π=µ ⽅向 ? 2分其中 2/R a =, 2/2)4/sin(sin 2=π=β 2/2)4/sin(sin 1-=π-=β∴ R I R I B π+=2800µµ)141(20π+=R I µ ⽅向 ? 2分 18. 解:电流元1d l I ?在O 点产⽣1d B ?的⽅向为↓(-z ⽅向) 电流元2d l I ?在O 点产⽣2d B ?的⽅向为?(-x ⽅向) 电流元3d l I ?在O 点产⽣3d B ?的⽅向为? (-x ⽅向) 3分kR I i R IB π-+ππ-=4)1(400µµ 2分 19. 解:设x 为假想平⾯⾥⾯的⼀边与对称中⼼轴线距离,++==Rx RRxrl B r l B S B d d d 21Φ, 2分d S = l d r2012R IrB π=µ (导线内) 2分r I B π=202µ (导线外) 2分)(42220x R R Il -π=µΦR R x Il +π+ln20µ 2分令 d Φ / d x = 0,得Φ最⼤时 Rx )15(21-= 2分20. 解:洛伦兹⼒的⼤⼩ B q f v = 1分对质⼦:1211/R m B q v v = 1分对电⼦: 2222/R m B q v v = 1分∵ 21q q = 1分∴ 2121//m m R R = 1分21.解:电⼦在磁场中作半径为)/(eB m R v =的圆周运动. 2分连接⼊射和出射点的线段将是圆周的⼀条弦,如图所⽰.所以⼊射和出射点间的距离为:)/(3360sin 2eB m R R l v ==?= 3分2解:在任⼀根导线上(例如导线2)取⼀线元d l ,该线元距O 点为l .该处的磁感强度为θµsin 20l I B π=2分⽅向垂直于纸⾯向⾥. 1分电流元I d l 受到的磁⼒为 B l I F=d d 2分其⼤⼩θµsin 2d d d 20l lI l IB F π== 2分⽅向垂直于导线2,如图所⽰.该⼒对O 点的⼒矩为 1分θµsin 2d d d 20π==lI F l M 2分任⼀段单位长度导线所受磁⼒对O 点的⼒矩+π==120d sin 2d l l l I M M θµθµsin 220π=I 2分导线2所受⼒矩⽅向垂直图⾯向上,导线1所受⼒矩⽅向与此相反.23. (C) 24. (B)25. 解: ===l NI nI H /200 A/m3分===H H B r µµµ0 1.06 T 2分26. 解: B = Φ /S=2.0×10-2 T 2分===l NI nI H /32 A/m 2分 ==H B /µ 6.25×10-4 T ·m/A 2分=-=1/0µµχm 496 2分9. ⼀磁场的磁感强度为k c j b i a B ?++= (SI),则通过⼀半径为R ,开⼝向z 轴正⽅向的半球壳表⾯的磁通量的⼤⼩为____________Wb .10.在匀强磁场B ?中,取⼀半径为R 的圆,圆⾯的法线n ?与B ?成60°⾓,如图所⽰,则通过以该圆周为边线的如图所⽰的任意曲⾯S 的磁通量==Sm S B ?d Φ_______________________.11. ⼀质点带有电荷q =8.0×10-10 C ,以速度v =3.0×105 m ·s -1在半径为R =6.00×10-3 m 的圆周上,作匀速圆周运动.该带电质点在轨道中⼼所产⽣的磁感强度B =__________________,该带电质点轨道运动的磁矩p m =___________________.(µ0 =4π×10-7 H ·m -1)12. 载有⼀定电流的圆线圈在周围空间产⽣的磁场与圆线圈半径R 有关,当圆线圈半径增⼤时,(1) 圆线圈中⼼点(即圆⼼)的磁场__________________________.(2) 圆线圈轴线上各点的磁场________如图,平⾏的⽆限长直载流导线A 和B ,电流强度均为I ,垂直纸⾯向外,两根载流导线之间相距为a ,则(1) AB 中点(P 点)的磁感强度=p B ?_____________.(2) 磁感强度B ?沿图中环路L 的线积分 =??L l B ??d ______________________.14. ⼀条⽆限长直导线载有10 A 的电流.在离它 0.5 m 远的地⽅它产⽣的磁感强度B 为______________________.⼀条长直载流导线,在离它 1 cm 处产⽣的磁感强度是10-4 T ,它所载的电流为__________________________.两根长直导线通有电流I ,图⽰有三种环路;在每种情况下,??lB ?____________________________________(对环路a ).____________________________________(对环路b ).____________________________________(对环路c ).设氢原⼦基态的电⼦轨道半径为a 0,求由于电⼦的轨道运动(如图)在原⼦核处(圆⼼处)产⽣的磁感强度的⼤⼩和⽅向.17.⼀根⽆限长导线弯成如图形状,设各线段都在同⼀平⾯内(纸⾯内),其中第⼆段是半径为R 的四分之⼀圆弧,其余为直线.导线中通有电流I ,求图中O 点处的磁感强度.18.z y xR 1 321d l I ?2d l I ?3d l I ?O如图,1、3为半⽆限长直载流导线,它们与半圆形载流导线2相连.导线1在xOy平⾯内,导线2、3在Oyz 平⾯内.试指出电流元1d l I ?、2d l I ?、3d l I ?在O 点产⽣的Bd 的⽅向,并写出此载流导线在O 点总磁感强度(包括⼤⼩与⽅向).19.⼀根半径为R 的长直导线载有电流I ,作⼀宽为R 、长为l 的假想平⾯S ,如图所⽰。
大学物理《稳恒电流的磁场》习题答案

第14章 稳恒电流的磁场 参考答案一、选择题1(B),2(A),3(D),4(C),5(B),6(D),7(B),8(C),9(D),10(A) 二、填空题(1). 最大磁力矩,磁矩 ; (2). πR 2c ; (3). )4/(0a I μ; (4).RIπ40μ ;(5). μ0i ,沿轴线方向朝右. ; (6). )2/(210R rI πμ, 0 ; (7). 4 ; (8).B I R2,沿y 轴正向; (9). ωλB R 3π,在图面中向上; (10). 正,负.三 计算题1. 将通有电流I 的导线在同一平面内弯成如图所示的形状,求D 点的磁感强度B的大小.解:其中3/4圆环在D 处的场 )8/(301a I B μ=AB 段在D 处的磁感强度 )221()]4/([02⋅π=b I B μBC 段在D 处的磁感强度)221()]4/([03⋅π=b I B μ1B、2B 、3B 方向相同,可知D 处总的B 为)223(40baI B +ππ=μ2. 半径为R 的导体球壳表面流有沿同一绕向均匀分布的面电流,通过垂直于电流方向的每单位长度的电流为K .求球心处的磁感强度大小.解:如图θd d d KR s K I ==2/32220])cos ()sin [(2)sin (d d θθθμR R R I B +=32302d sin R KR θθμ=θθμd sin 2120K =⎰π=020d sin 21θθμK B ⎰π-=00d )2cos 1(41θθμK π=K 041μ3. 如图两共轴线圈,半径分别为R 1、R 2,电流为I 1、I 2.电流的方向相反,求轴线上相距中点O 为x 处的P 点的磁感强度. 解:取x 轴向右,那么有2/322112101])([2x b R I R B ++=μ 沿x 轴正方向 2/322222202])([2x b R I R B -+=μ 沿x 轴负方向21B B B -=[2μ=2/32211210])([x b R I R ++μ]])([2/32222220x b R I R -+-μ若B > 0,则B方向为沿x 轴正方向.若B < 0,则B的方向为沿x 轴负方向.4.一无限长圆柱形铜导体(磁导率μ0),半径为R ,通有均匀分布的电流I .今取一矩形平面S (长为1 m ,宽为2 R ),位置如右图中画斜线部分所示,求通过该矩形平面的磁通量.解:在圆柱体内部与导体中心轴线相距为r 处的磁感强度的大小,由安培环路定 律可得: )(220R r rRIB ≤π=μ因而,穿过导体内画斜线部分平面的磁通Φ1为⎰⎰⋅==S B S B d d 1 Φr r RI Rd 2020⎰π=μπ=40Iμ在圆形导体外,与导体中心轴线相距r 处的磁感强度大小为)(20R r rIB >π=μ因而,穿过导体外画斜线部分平面的磁通Φ2为⎰⋅=S Bd 2Φr r I R Rd 220⎰π=μ2ln 20π=I μ穿过整个矩形平面的磁通量 21ΦΦΦ+=π=40I μ2ln 20π+I μ5. 一半径为 4.0 cm 的圆环放在磁场中,磁场的方向对环而言是对称发散的,如图所示.圆环所在处的磁感强度的大小为0.10 T ,磁场的方向与环面法向成60°角.求当圆环中通有电流I =15.8 A 时,圆环所受磁力的大小和方向.1 m解:将电流元I d l 处的B分解为平行线圈平面的B 1和垂直线圈平面的B 2两分量,则 ︒=60sin 1B B ; ︒=60cos 2B B分别讨论线圈在B 1磁场和B 2磁场中所受的合力F 1与F 2.电流元受B 1的作用力l IB lB I F d 60sin 90sin d d 11︒=︒=方向平行圆环轴线.因为线圈上每一电流元受力方向相同,所以合力⎰=11d F F ⎰π︒=Rl IB 20d 60sin R IB π⋅︒=260sin = 0.34 N ,方向垂直环面向上.电流元受B 2的作用力l IB lB I F d 60cos 90sin d d 22︒=︒= 方向指向线圈平面中心. 由于轴对称,d F 2对整个线圈的合力为零,即02=F . 所以圆环所受合力 34.01==F FN , 方向垂直环面向上.6. 如图所示线框,铜线横截面积S = 2.0 mm 2,其中OA 和DO '两段保持水平不动,ABCD 段是边长为a 的正方形的三边,它可绕OO '轴无摩擦转动.整个导线放在匀强磁场B中,B 的方向竖直向上.已知铜的密度ρ = 8.9×103 kg/m 3,当铜线中的电流I =10 A 时,导线处于平衡状态,AB段和CD 段与竖直方向的夹角α =15°.求磁感强度B的大小.解:在平衡的情况下,必须满足线框的重力矩与线框所受的磁力矩平衡(对OO '轴而言). 重力矩 αραρs i n s i n 2121gSa a a gS a M +⋅=αρsin 22g Sa =B 2d l磁力矩ααcos )21sin(222B Ia BIa M =-π=平衡时 21M M = 所以 αρsin 22g Sa αcos 2B Ia = 31035.9/tg 2-⨯≈=I g S B αρT7. 半径为R 的半圆线圈ACD 通有电流I 2,置于电流为I 1的无限长直线电流的磁场中,直线电流I 1恰过半圆的直径,两导线相互绝缘.求半圆线圈受到长直线电流I 1的磁力.解:长直导线在周围空间产生的磁场分布为 )2/(10r I B π=μ取xOy 坐标系如图,则在半圆线圈所在处各点产生的磁感强度大小为:θμsin 210R I B π=, 方向垂直纸面向里,式中θ 为场点至圆心的联线与y 轴的夹角.半圆线圈上d l 段线电流所受的力为:l B I B l I F d d d 22=⨯= θθμd sin 2210R R I I π=θsin d d F F y =. 根据对称性知: F y =0d =⎰y F θcos d d F F x = ,⎰π=0x x dF F ππ=2210I I μ2210I I μ=∴半圆线圈受I 1的磁力的大小为: 2210I I F μ=,方向:垂直I 1向右.I 2I 1A DC8. 如图所示.一块半导体样品的体积为a ×b ×c .沿c 方向有电流I ,沿厚度a 边方向加有均匀外磁场B (B的方向和样品中电流密度方向垂直).实验得出的数据为 a =0.10 cm 、b =0.35 cm 、c =1.0 cm 、I =1.0 mA 、B =3.0×10-1 T ,沿b 边两侧的电势差U =6.65 mV ,上表面电势高.(1) 问这半导体是p 型(正电荷导电)还是n 型(负电荷导电)?(2) 求载流子浓度n 0 (即单位体积内参加导电的带电粒子数).解:(1) 根椐洛伦兹力公式:若为正电荷导电,则正电荷堆积在上表面,霍耳电场的方向由上指向下,故上表面电势高,可知是p 型半导体。
稳恒电流和稳恒磁场习题解答

第十一章 稳恒电流和稳恒磁场一 选择题1. 边长为l 的正方形线圈中通有电流I ,此线圈在A 点(如图)产生的磁感应强度B 的大小为( )A. lI μπ420 B.lIμπ20 C .lI μπ20 D. 0解:设线圈四个端点为ABCD ,则AB 、AD 线段在A 点产生的磁感应强度为零,BC 、CD 在A 点产生的磁感应强度由)cos (cos π4210θθμ-=dIB ,可得 lI lIB BC π82)2πcos 4π(cosπ400μμ=-=,方向垂直纸面向里 lI lIB CD π82)2πcos 4π(cosπ400μμ=-=,方向垂直纸面向里合磁感应强度 lIB B B CD BC π420μ=+= 所以选(A )2. 如图所示,有两根载有相同电流的无限长直导线,分别通过x 1=1、x 2=3的点,且平行于y 轴,则磁感应强度B 等于零的地方是:( )选择题2选择题1A.x=2的直线上B.在x>2的区域C.在x<1的区域D.不在x、y平面上解:本题选(A)3. 图中,六根无限长导线互相绝缘,通过电流均为I,区域Ⅰ、Ⅱ、Ⅲ、Ⅳ均为相等的正方形,哪一个区域指向纸内的磁通量最大( )A. Ⅰ区域B. Ⅱ区域 C.Ⅲ区域D.Ⅳ区域 E.最大不止一个解:本题选(B)4. 如图,在一圆形电流I所在的平面内,选取一个同心圆形闭合回路L,则由安培环路定理可知:()A.∮L B·d l=0,且环路上任意一点B=0B.∮L B·d l=0,且环路上任意一点B≠0ⅠⅡ选择题3选择题4C. ∮L B ·d l ≠0,且环路上任意一点B ≠0D.∮L B ·d l ≠0,且环路上任意一点B =常量解:本题选(B )5. 无限长直圆柱体,半径为R ,沿轴向均匀流有电流,设圆柱体内(r <R )的磁感应强度为B i ,圆柱体外(r >R )的磁感应强度为B e ,则有:( )A.B t 、B e 均与r 成正比 B. B i 、B e 均与r成反比C. B i 与r 成反比,B e 与r 成正比D. B i 与r 成正比,B e 与r 成反比解:导体横截面上的电流密度2πRI J =,以圆柱体轴线为圆心,半径为r 的同心圆作为安培环路,当r <R ,20ππ2r J r B i ⋅=⋅μ,20π2RIrB i μ=r <R ,I r B e ⋅=⋅0π2μ, rIB e π20μ=所以选(D )6. 有三个质量相同的质点a 、b 、c ,带有等量的正电荷,它们从相同的高度自由下× × × ×abc落,在下落过程中带电质点b 、c 分别进入如图所示的匀强电场与匀强磁场中,设它们落到同一水平面的动能分别为E a 、E b 、E c ,则( )A.E a <E b =E c B. E a =E b =E cC. E b >E a =E cD. E b >E c >E a解:由于洛伦兹力不做功,当它们落到同一水平面上时,对a 、c 只有重力做功, 则E a =E c ,在此过程中,对b 不仅有重力做功,电场力也要做正功,所以E b >E a =E c所以选(C )7. 图为四个带电粒子在O 点沿相同方向垂直于磁力线射入均匀磁场后的偏转轨迹的照片,磁场方向垂直纸面向外,四个粒子的质量相等,电量大小也相等,则其中动能最大的带负电的粒子的轨迹是:( )A.Oa B. ObC. Oc D . Od解:根据B F ⨯=v q ,从图示位置出发,带负电粒子要向下偏选择题7cdbaBO转,所以只有Oc 、Od 满足条件,又带电粒子偏转半径Bqm R v =,22k 22qB m E R =∴,质量相同、带电量也相等的粒子,动能大的偏转半径大,所以选Oc 轨迹所以选(C )8. 如图,一矩形样品,放在一均匀磁场中,当样品中的电流I 沿X 轴正向流过时,实验测得样品A 、A 两侧的电势差V A V A >0,设此样品的载流子带负电荷,则磁场方向为:( )A . 沿X 轴正方向B .沿X 轴负方向C .沿Z 轴正方向D .沿Z 轴负方向 解:本题选(C )9. 长直电流I 2与圆形电流I 1共面,并与其一直径相重合如图(但两者间绝缘),设长直电流不动,则圆形电流将:( )选择题8图XA. 绕I 2旋转B. 向左运动C. 向右运动D. 向上运动E. 不动解:圆形电流左半圆和右半圆受到长直电流安培力的方向均向右,所以圆形电流将向右运动所以选(C )二 填空题1. 成直角的无限长直导线,流有电流I =10A ,在直角决定的平面内,距两段导线的距离都是a =20cm 处的磁感应强度B = 。
大学物理磁场习题

时刻,穿过回路的磁通量 BS 常数
p
由法拉第电磁感应定律 d
dt
可知: 0 op直线 po半圆
vB
R
op直线 po半圆 2RvB
o
Up>U0
由上述结果可知,在均匀磁场中,任意闭合导体回路平动所产生的动生电动势为零;
任意曲线形导体上的动生电动势就等于其两端所连直线形导体上的动生电动势。
大学物理
习题讨论、探索发现
稳恒电流的静磁场 磁场中的磁介质 电磁场 探索与发现
1
1. 如图所示,半径为R的木球上绕有密集的细导线,线圈平面彼此平行, 且以单层线圈覆盖住半个球面,设线圈的总匝数为N,通过线圈的电流为 I,求球心O处的磁感应强度。
解:设单位弧长上电流线圈匝数为n,则
n N 2N
2R / 4 R 沿弧长取dl,d I Indl, dl Rd, d I 2N R d I
10
d dt
0l1I (t) 2
ln
al2 aຫໍສະໝຸດ vl2 a(a l2)
由法拉第电磁感应定律得
d dt
0l1 I 0 2
ln
a l2 a
vl2 a(a
l2
)
e
t
显然,它是大于零的,表明感应电动势在线框内
取顺时针方向,可以通过楞次定律进行验证。
I (t) I0et
l1 v
a
l2
0 I 0 2
Br
0 I 2r
0 2
r
方向与矢径r垂直.
同理,密度为- 的电流在P点产生的磁感应强度为
Br
R
r
P
r
Br
O1
b a
O2
Br
大学物理习题答案稳恒电流的磁场

第十章 稳恒电流的磁场1、四条相互平行的无限长直载流导线,电流强度均为I ,如图放置,若正方形每边长为2a ,求正方形中心O 点的磁感应强度的大小和方向。
解:43210B B B B B r r r r r +++=无限长载流直导线产生的磁感应强度 rI2B 0πμ=由图中的矢量分析可得a 2I a 2I22B B 0042πμ=πμ=+a I45cos a2I 2B 0000πμ=⋅πμ= 方向水平向左2、把一根无限长直导线弯成图 (a)、(b) 所示形状,通以电流I ,分别求出O 点的磁感应强度B 的大小和方向。
解:(a )(b )均可看成由两个半无限长载流直导线1、3和圆弧2组成,且磁感应强度在O 点的方向相同 (a )方向垂直纸面向外。
)38(R16I43R 4I R 4I R 4I B 00000π+πμ=π⋅πμ+πμ+πμ=(b )由于O 点在电流1、3的延长线上,所以0B B 31==r r方向垂直纸面向外。
R8I323R I 4B B 0020μ=π⋅πμ==14(a ) I(b )3、真空中有一边长为l 的正三角形导体框架,另有互相平行并与三角形的bc 边平行的长直导线1和2分别在a 点和b 点与三角形导体框架相连 (如图) 。
已知直导线中的电流为I ,求正三角形中心点O 处的磁感应强度B 。
解:三角形高为 l l360sin h .0==4 它在 θθπμ=θ=d sin R 2Isin dB dB 20x θθπμ−=θ−=d cos R2I cos dB dB 20yRI d sin R2I dB B 20200x x πμ=∫θθπμ∫==π0d cos R2I dB B 020y y =∫∫θθπμ−==π)T (1037.6100.10.5104RI B B 522720x P −−−×=××π××π=πμ==∴轴正方向。
第四章习题 稳恒电流的磁场

第四章习题稳恒电流的磁场第四章稳恒电流的磁场一、判断题1、在安培定律的表达式中,若r21?0,则aF21??。
2、真空中两个电流元之间的相互作用力满足牛顿第三定律。
意一点都不受力,则该空间不存在磁场。
4、对于横截面为正方形的长螺线管,其内部的磁感应强度仍可用?0nI 表示。
5、安培环路定理反映了磁场的有旋性。
?3、设想用一电流元作为检测磁场的工具,若沿某一方向,给定的电流元I0dl放在空间任?6、对于长度为L的载流导线来说,可以直接用安培定理求得空间各点的B。
7、当霍耳系数不同的导体中通以相同的电流,并处在相同的磁场中,导体受到的安培力是相同的。
8、载流导体静止在磁场中于在磁场运动所受到的安培力是相同的。
9、安培环路定理中的磁感应强度只是由闭合环路内的电流激发的。
10、在没有电流的空间区域里,如果磁感应线是一些平行直线,则该空间区域里的磁场一定均匀。
??CB?dl??0I二、选择题1、把一电流元依次放置在无限长的栽流直导线附近的两点A和B,如果A点和B点到导线的距离相等,电流元所受到的磁力大小(A)一定相等(B)一定不相等(C)不一定相等(D)A、B、C都不正确2、半径为R的圆电流在其环绕的圆内产生的磁场分布是:(A)均匀的(B)中心处比边缘处强(C)边缘处比中心处强(D)距中心1/2处最强。
3、在均匀磁场中放置两个面积相等而且通有相同电流的线圈,一个是三角形,另一个是矩形,则两者所受到的(A)磁力相等,最大磁力矩相等(B)磁力不相等,最大磁力矩相等(C)磁力相等,最大磁力矩不相等(D)磁力不相等,最大磁力矩不相等4、一长方形的通电闭合导线回路,电流强度为I,其四条边分别为ab、bc、cd、da如图所示,设B1、B2、B3及B4分别是以上各边中电流单独产生的磁场的磁感应强度,下列各式中正确的是:(A)?(B)?C1B1?dl??0IB1?dl?0C2(C)?B1?B1?dl?0(D)?C1??c?B?B12?B3?B4?dl??0I??I和I设电流IB21单独产生的磁场为1,电流I2单独产生的磁5、两个载流回路,电流分别为1?场为B2,下列各式中正确的是:(A)?C2B1?dl??0?I1?I2??(B)(C)C1B2?dl??0I212 ??B?B??dlC1??0?I1?I2?(D)6、半径为R的均匀导体球壳,内部沿球的直线方向有一载流直导线,电线I从A流向B后,再沿球面返回A点,如图所示下述说法中正确的是:??B?B??dlC212??0?I1?I2??(A)在AB线上的磁感应强度B?0 ?(B)球外的磁感应强度B?0 ?(C)只是在AB线上球内的部分感应强度B?0 ?(D)只是在球心上的感应强度B?07、如图所示,在载流螺线管的外面环绕闭合路径一周积分(A)0(B)?0nI ?LB?dl等于?0nI(C)2 (D)?0I LI8、一电量为q的点电荷在均匀磁场中运动,下列说法正确的是(A)只要速度大小相同,所受的洛伦兹力就相同。
稳恒电流的磁场总结

1. 体电流密度矢量:()i i iJ v nqv q v ρ=∑或或2.SI J ds =⎰⎰3. 毕奥-萨伐尔定律:34Idl r dB rμπ⨯=34LI r B dl rμπ⨯=⎰4. 有限长载流导线的磁感应强度()021cos cos 4I B zμββπ=- !!!注意:1β与2β分别为载流导线初末两端与场点的连线与电流反方向的夹角。
zP 1无限长载流导线的磁感应强度 02IB zμπ= !!!例2 求载流线圈在其轴线上的磁感应强度分布。
假设线圈半径为R,载有的电流强度为I。
l载流线圈在轴线上的磁场例3 求载流密绕长直螺线管内轴线上的磁感应强度分布,设螺线管半径为R,通有电流I,单位长线圈匝数为n。
密绕长直螺线管内的磁场密绕长直螺线管内的磁场分布例1 在氢原子中,按经典理论,电子以恒速6v=⨯绕2.210m/s核作半径为11=⨯的圆周运动。
求运动的电子在r-5.310m轨道中心所产生的磁感应强度与磁矩。
()e-(1)磁力线的特点:(a)磁力线是一些与电流相套链的闭合曲线。
长直载流导线周围的磁场载流线圈周围的磁场螺线管周围的磁场电流与磁力线的方向互成右手螺旋关系(b ) 磁力线上任意一点的切线方向,代表该点的磁感应强度矢量B的方向。
(c ) 磁力线彼此永不相交。
(d ) 磁场中任意一点磁感应强度的大小 0d l i md s n n B s s ⊥∆→⊥⊥∆==∆垂直通过s ⊥∆的磁力线根数为n ∆B的大小与磁力线的疏密程度成正比。
密集处,B 变大;反之,稀疏处,B变小。
如前图,12B B。
长直载流导线周围磁场的环路积分例1 半径为R 的无限长圆柱形导线,通有稳恒电流I ,设I 在导线内均匀分布,求空间各点的磁感应强度B。
例2 求无限长直密绕螺线管内外的磁感应强度分布。
设螺线管内通有电流I,单位长线圈匝数为n。
L1无限长直载流螺线管的磁场例 3 如图所示,在xy 平面内沿x 轴方向的面电流密度为i αα= ,求空间各处的磁感应强度分布。
稳恒电流的磁场习题详解

r习题三一、选择题1.如图3-1所示,两根长直载流导线垂直纸面放置,电流I 1 =1A ,方向垂直纸面向外;电流I 2 =2A ,方向垂直纸面向内,则P 点的磁感应强度B 的方向与x 轴的夹角为[ ](A )30˚; (B )60˚; (C )120˚; (D )210˚。
答案:A解:如图,电流I 1,I 2在P 点产生的磁场大小分别为1212,222I IB B d d ππ==,又由题意知12B B =;再由图中几何关系容易得出,B 与x 轴的夹角为30º。
2.如图3-2所示,一半径为R 的载流圆柱体,电流I 均匀流过截面。
设柱体内(r < R )的磁感应强度为B 1,柱体外(r > R )的磁感应强度为B 2,则 [ ](A )B 1、B 2都与r 成正比; (B )B 1、B 2都与r 成反比;(C )B 1与r 成反比,B 2与r 成正比; (D )B 1与r 成正比,B 2与r 成反比。
答案:D解:无限长均匀载流圆柱体,其内部磁场与截面半径成正比,而外部场等效于电流集中于其轴线上的直线电流磁场,所以外部磁场与半径成反比。
3.关于稳恒电流磁场的磁场强度H ,下列几种说法中正确的是 [ ] (A )H 仅与传导电流有关。
(B )若闭合曲线内没有包围传导电流,则曲线上各点的H 必为零。
(C )若闭合曲线上各点H 均为零,则该曲线所包围传导电流的代数和为零。
(D )以闭合曲线L为边缘的任意曲面的H 通量均相等。
答案:C解:若闭合曲线上各点H 均为零,则沿着闭合曲线H环流也为零,根据安培环路定理,则该曲线所包围传导电流的代数和为零。
4.一无限长直圆筒,半径为R ,表面带有一层均匀电荷,面密度为σ,在外力矩的作用下,这圆筒从t=0时刻开始以匀角加速度α绕轴转动,在t 时刻圆筒内离轴为r 处的磁感应强度B 的大小为 []图2I 1I(A )0; (B )0R t μσα; (C )0R t r μσα; (D )0rt Rμσα。
稳恒电流与稳恒磁场课件

x
dBx x
r dB
·16 ·
Ch a p t e r 10. 稳恒电流与稳恒磁场 §10. 2 磁场的描述 毕奥-萨伐尔定律 运动电荷的磁场
B 0 I sin
4 r2
dl 0 IR sin
2 r2
L
B
Bx
0
2
(R2
IR2 x2 )3/ 2
B
方向: 沿 +x 方向。
Id l r dB dB
ne 2
m
E eˆ i
ne2
m
E
v2
令:
c
ne2
m
称作电导率(conductivity),Ω-1·m-1
j c E ( 欧姆定律的微分形式 )
·6 ·
Ch a p t e r 10. 稳恒电流与稳恒磁场
§10. 1 稳恒电流
如图让稳恒电流垂直通过某段导体截面 S。
j
cE
c
V l
I
j dS
jSc
S l
V
S
E
V I
令:R
1
c
l S
l S
( 即电阻 )
l
I j
S
I
V R
或 V IR ( 欧姆定律 )
j
eˆ n S
·7 ·
说明
Ch a p t e r 10. 稳恒电流与稳恒磁场
§10. 1 稳恒电流
☻V = IR 仅适用于 R 为常量的情形。对于非线性:
微分电阻:
R
dV dI
☻电阻随温度 t 变化较明显:
☻载流圆线圈内磁感 线
ox
dBx x
的绕向与线圈中的电
流构成右手关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1页共4页 习题三 稳恒电流的磁场 习题册-下-3
学院 班 序号___________姓名
习题三(第十九章)
一、选择题
1.如图3-1所示,两根长直载流导线垂直纸面放置,电流I 1 =1A ,方向垂直纸面向外;电流I 2 =2A ,方向垂直纸面向内,则P 点的磁
感应强度B
的方向与x 轴的夹角为 [ ]
(A )30˚; (B )60˚; (C )120˚; (D )210˚。
2.如图3-2所示,一半径为R 的载流圆柱体,电流I 均匀流过截面。
设柱体内(r < R )的
磁感应强度为B 1,柱体外(r > R )的磁感应强度为B 2,则 [ ]
(A )B 1、B 2都与r 成正比; (B )B 1、B 2都与r 成反比;
(C )B 1与r 成反比,B 2与r 成正比; (D )B 1与r 成正比,B 2与r 成反比。
3.如图所示,实线为载流导线,通以电流I ,A 、B 各伸延到无限远处,在园心O 处是磁感应强度为:( ) A .R I R I 4200μπμ+; B .R I
R I 8400μπμ+;
C .R I R I 8200μπμ+
; D .R
I
R I 4400μπμ+
4.一无限长直圆筒,半径为R ,表面带有一层均匀电荷,面密度为σ,在外力矩的作用下,这圆筒从t=0时刻开始以匀角加速度α绕轴转动,在t 时刻圆筒内离轴为r 处的磁感应强度B
的大小为 [ ]
(A )0; (B )0R t μσα; (C )0R t r μσα; (D )0r
t R
μσ。
图3-1
2
I 1
I
5.能否用安培环路定律,直接求出下列各种截面的长直载流导线各自所产生的磁感应强度B 。
(1)圆形截面;(2)半圆形截面;(3)正方形截面 [ ]
(A )第(1)种可以,第(2)(3)种不行; (B )第(1)(2)种可以,第(3)种不行; (C )第(1)(3)种可以,第(2)种不行; (D )第(1)(2)(3)种都可以。
二、填空题
1.如图3-3所示,一无限长扁平铜片,宽度为a ,厚度不计,电流I 在铜片上均匀分布。
求
铜片外与铜片共面、离铜片右边缘为b 处的P 点的磁感应强度B
的大小 。
2.在真空中,电流I 由长直导线1沿垂直bc 边方向经a 点流入一电阻均匀分布的正三角形线框,再由b 点沿平行ac 边方向流出,经长直导线2返回电源,如图3-4所示。
三角形框每边长为l ,则在该正三角框中心O 点处磁感应强度的大小B = 。
3.在一根通有电流I 的长直导线旁,与之共面地放着一个长、宽各为a 和b 的矩形线框,线框的长边与载流长直导线平行,且二者相距为b ,如图3-5所示。
在此情形中,线框内的磁通量 Φ=______________。
4.电子在磁感应强度为 B
的均匀磁场中沿半径为R 的圆周运动,电子运动所形成的等效
圆电流I =______________;等效圆电流的磁矩m P =______________。
(已知电子电量的大小为e ,电子的质量为m )。
5.如图3-6所示,无限长直导线在P 处弯成半径为R 的圆,当通以电流I 时,则在圆心O 点的磁感强度大小等于 ;方向 。
2图3-4
图3-3 P 图3-6
三、计算题 1.如图3-7所示,载流圆线圈通有电流为I ,求载流圆线圈轴线上某点P 的磁感应强度。
2.一个塑料圆盘,半径为R ,电荷q 均匀分布于表面,圆盘绕通过圆心垂直盘面的轴转动,角速度为ω。
求圆盘中心处的磁感应强度。
x
图3-8
3.如图3-9所示,真空中一无限长圆柱形铜导体,磁导率为0μ,半径为R ,I 均匀分布,求通过S (阴影区)的磁通量。
4.如图3-10所示,一半径R 的非导体球面均匀带电,面密度为σ,若该球以通过球心的直
径为轴用角速度ω旋转,求球心处的磁感应强度的大小和方向。
图3-10。
