摄影测量程序汇总(后方交会+前方交会+单模型光束法平差)
摄影测量解析基础(后方交会前方交会)

06
结果输出
输出目标点的三维坐标数据。
前方交会方法的优缺点分析
优点 不需要地面控制点,可以在未知环境中进行测量。
可以快速获取大范围的三维空间信息。
前方交会方法的优缺点分析
• 适用于动态目标和快速测量场景。
前方交会方法的优缺点分析
01
缺点
02
03
04
对光照条件敏感,光照变化会 影响测量精度。
对摄影图像的质量要求较高, 需要清晰、分辨率高的图像。
随着科技的不断发展,摄影测量技术也在不断进步和完善,其在各个领域的应用 也日益广泛和深入。
摄影测量的历史与发展
01
摄影测量起源于19世纪中叶,当时人 们开始使用胶片相机进行地形测量。 随着技术的发展,数字相机逐渐取代 了胶片相机,使得摄影测量更加便捷 和高效。
02
近年来,随着计算机技术和人工智能 的飞速发展,摄影测量技术也取得了 重大突破。例如,无人机技术的兴起 使得摄影测量更加灵活、快速和安全 ;计算机视觉和深度学习技术的应用 则提高了影像解析的自动化和智能化 水平。
在复杂地形和遮挡严重的环境 中,前方交会方法可能会失效
。
05 实际应用案例
Hale Waihona Puke 后方交会方法应用案例总结词
通过已知的摄影站和地面控制点,解算出摄影中心和地面点的空间坐标。
详细描述
后方交会方法常用于地图更新、地籍测量和城市三维建模等领域。例如,在城市三维建模中,利用后方交会方法 可以快速准确地获取建筑物表面的空间坐标,为构建真实感强的城市三维模型提供数据支持。
图像获取
获取至少两幅不同角度的摄影图像。
01
02
像片处理
对图像进行预处理,包括图像校正、去噪等 操作。
5摄影测量解析基础(后方交会+前方交会)

内定向通常采用多项式变换公式。假设框标在以像主点为原点的像平
面坐标系中的理论坐标为(x,y),在量测坐标系(车架坐标系、扫描 坐标系)的量测坐标为(I,J),则常用的多项式变换公式有:
线性正形变换公式
x a 0 a1I a 2 J y a3 a 2I a1J x a 0 a1I a 2 J y a3 a 2I a1J x a0 a1I a2 J a3IJ y b0 b1I b2 J b3IJ
S (XS、YS、ZS)
c b Z
a
C B
Y
A
X
2、空间后方交会基本关系式 ——共线方程式
a1 X X S b1 Y YS c1 Z Z S xf a3 X X S b3 Y YS c3 Z Z S
a2 X X S b2 Y YS c2 Z Z S yf a3 X X S b3 Y YS c3 Z Z S
0 h1 v1 ( X B dX B ) HA 0 0 h2 v 2 ( X B dX B ) ( X C dX C ) 0 ( X C dX C ) HA h3 v 3 h v 0 0 ( X C dX C ) ( X D dX D ) 4 4 0 h5 v 5 ( X D dX D ) H A
路线长度 Si / km
h1 A h3
B h2
1
2 3 4 5
5.835
3.782 9.640 7.384 2.270
3.5
2.7 4.0 3.0 2.5
C h5
Байду номын сангаасD h4
摄影测量-空间前交、后交【精选文档】

空间后交—前交程序设计(实验报告)姓名:班级:学号:时间:空间后交-前交程序设计一、实验目的用 C 、VB或MATLAB语言编写空间后方交会-空间前方交会程序⑴提交实习报告:程序框图、程序源代码、计算结果、体会⑵计算结果:像点坐标、地面坐标、单位权中误差、外方位元素及其精度二、实验数据f=150。
000mm,x0=0,y0=0三、实验思路1。
利用空间后方交会求左右像片的外方位元素(1).获取m(于像片中选取两点,于地面摄影测量坐标系中选取同点,分别计算距离,距离比值即为m),x,y,f,X,Y,Z(2).确定未知数初始值Xs,Ys,Zs,q,w,k(3).计算旋转矩阵R(4).逐点计算像点坐标的近似值(x),(y)(5)。
组成误差方程式(6)。
组成法方程式(7).解求外方位元素(8)。
检查是否收敛,即将求得的外方位元素的改正数与规定限差比较,小于限差即终止;否则用新的近似值重复步骤(3)-(7)2。
利用求出的外方位元素进行空间前交,求出待定点地面坐标(1).用各自像片的角元素计算出左、右像片的方向余弦值,组成旋转矩阵R1,R2(2)。
根据左、右像片的外方位元素,计算摄影基线分量Bx,By,Bz(3)。
计算像点的像空间辅助坐标(X1,Y1,Z1)和(X2,Y2,Z2)(4).计算点投影系数N1和N2(5)。
计算未知点的地面摄影测量坐标四、实验过程⑴程序框图函数AandL%求间接平差时需要的系数%%%已知%a=像点坐标x,b=像点坐标y,f内方位元素主距%φ=q,ψ=w,κ=k%像空间坐标系X,Y,Z%地面摄影测量坐标系Xs,Ys,Zsfunction [A1,L1,A2,L2]=AandL(a,b,f,q,w,k,X,Y,Z,Xs,Ys,Zs) %%%%%%%%%%%选择矩阵元素a1=cos(q)*cos(k)—sin(q)*sin(w)*sin(k);a2=-cos(q)*sin(k)—sin(q)*sin(w)*cos(k);a3=-sin(q)*cos(w);b1=cos(w)*sin(k);b2=cos(w)*cos(k);b3=—sin(w);c1=sin(q)*cos(k)+cos(q)*sin(w)*sin(k);c2=—sin(q)*sin(k)+cos(q)*sin(w)*cos(k);c3=cos(q)*cos(w);%%%%%%%共线方程的分子分母X_=a1*(X—Xs)+b1*(Y-Ys)+c1*(Z-Zs);Y_=a2*(X-Xs)+b2*(Y—Ys)+c2*(Z-Zs);Z_=a3*(X—Xs)+b3*(Y—Ys)+c3*(Z-Zs);%%%%%%%近似值x=-f*X_/Z_;y=-f*Y_/Z_;%%%%%%%A组成L组成a11=1/Z_*(a1*f+a3*x);a12=1/Z_*(b1*f+b3*x);a13=1/Z_*(c1*f+c3*x);a21=1/Z_*(a2*f+a3*y);a22=1/Z_*(b2*f+b3*y);a23=1/Z_*(c2*f+c3*y);a14=y*sin(w)-(x/f*(x*cos(k)—y*sin(k))+f*cos(k))*cos(w);a15=-f*sin(k)—x/f*(x*sin(k)+y*cos(k));a16=y;a24=—x*sin(w)-(y/f*(x*cos(k)-y*sin(k))—f*sin(k))*cos(w);a25=-f*cos(k)-y/f*(x*sin(k)+y*cos(k));a26=-x;lx=a—x;ly=b-y;%%%%%%%%%组成一个矩阵,并返回A1=[a11,a12,a13,a14,a15,a16];A2=[a21,a22,a23,a24,a25,a26];L1=lx;L2=ly;函数deg2dms%%%%%%%%角度转度分秒function y=deg2dms(x)a=floor(x);b=floor((x-a)*60);c=(x-a—b/60)*3600;y=a+(b/100)+(c/10000);函数dms2deg%%%%%度分秒转度function y=dms2deg(x)a=floor(x);b=floor((x-a)*100);c=(x-a—b/100)*10000;y=a+b/60+c/3600;函数ok%%%%%%%%%%%%%%目的是为了保证各取的值的有效值%%xy为n*1,a为1*nfunction result=ok(xy,a)format short gi=size(xy,1);for n=1:io=xy(n)—floor(xy(n,1));o=round(o*(10^a(n)))/(10^a(n));xy(n,1)=floor(xy(n,1))+o;endformat long gresult=xy;函数rad2dmsxy%%%%求度分秒表现形式的三个外方位元素,三个角度function xydms=rad2dmsxy(xy)[a,b,c,d,e,f]=testvar(xy);d=deg2dms(rad2deg(d));e=deg2dms(rad2deg(e));f=deg2dms(rad2deg(f));xydms=[a,b,c,d,e,f]';函数spacehoujiao%%%%%%%空间后交%%% f%%输入p(2*n,1)%%像点坐标x,y,X,Y,Z,均为(n,1)function [xy,m,R]=spacehoujiao(p,x,y,f,X,Y,Z)format long;%%%%%权的矢量化,这是等精度时的,如果非,将函数参数改为PP=diag(p);%%求nj=size(X,2);%%初始化Xs=0;Ys=0;Zs=0;for n=1:jXs=Xs+X(n);Ys=Ys+Y(n);Zs=Zs+Z(n);endSx=sqrt((x(2)-x(1))^2+(y(2)—y(1))^2);%%%%两像点之间距离Sd=sqrt((X(2)-X(1))^2+(Y(2)-Y(1))^2);%%%%两地面控制点之间距离m=Sd/Sx; %%%%图像比例系数Xs=Xs/j;Ys=Ys/j;Zs=m*f+Zs/j;m0=0;q=0;w=0;k=0;i=0;a=rand(2*j,6);l=rand(2*j,1);%%%%for n=1:j[a(2*n—1,:),l(2*n—1,1),a(2*n,:),l(2*n,1)]=AandL(x(n),y(n),f,q,w,k,X(n),Y(n),Z(n),Xs,Ys,Zs);enddet=inv(a’*P*a)*transpose(a)*P*l;%%%%%%%%%循环体while 1%%%%%%%%%%%%%%%%[dXs,dYs,dZs,dq,dw,dk]=testvar(det);detXs=abs(dXs);detYs=abs(dYs);detZs=abs(dZs);detq=abs(dq);detw=abs(dw);detk=abs(dk);%%%%%%%%%if ((detXs<0。
摄影测量学部分课后习题答案

精心整理第一章1.摄影测量学:摄影测量是从非接触成像系统,通过记录、量测、分析与表达等处理,获取地球及其环境和其他物体的几何、属性等可靠信息的工艺、科学与技术。
1.2摄影测量学的任务:地形测量领域:各种比例尺的地形图、专题图、特种地图、正射影像地图、景观图;建立各种数据库;提供地理信息系统和土地信息系统所需要的基础数据。
非地形测量领域:生物医学、公安侦破、古文物、古建筑、建筑物变形监测2.摄影测量的三个发展阶段及其特点:模拟摄影测量阶段:(1)使用的影像资料为硬拷贝像片。
(2)利用光学机械模拟装置,实现了复杂的摄影测量解算。
(3)得到的是(或说主要是)模拟产品。
(4)摄影测量科技的发展可以说6)(44)它是3.1.3.答:1.左右的面。
4.L 于4.对于8.1.9.因素:13. 答:摄影测量中常用的坐标系有两大类。
一类是用于描述像点的位置,称为像方空间坐标系;另—类是用于描述地面点的位置.称为物方空间坐标系。
(1).像方空间坐标系①像平面坐标系像平面坐标系用以表示像点在像平面上的位置,通常采用右手坐标系,y x ,轴的选择按需要而定.在解析和数字摄影测量中,常根据框标来确定像平面坐标系,称为像框标坐标系。
②像空间坐标系,为了便于进行空间坐标的变换,需要建立起描述像点在像空间位置的坐标系,即像空间坐标系。
以摄影中心S 为坐标原点,y x ,轴与像平面坐标系的y x ,轴平行,z 轴与主光轴重合,形成像空间右手直角坐标系xyz S -③像空间辅助坐标系,像点的像空间坐标可直接以像平面坐标求得,但这种坐标的待点是每张像片的像空间坐标系不统一,这给计算带来困难。
为此,需要建立一种相对统一的坐标系.称为像空间辅助坐标系,用XYZ S -表示。
此坐标系的原点仍选在摄影中心S 坐标轴系的选择视需要而定。
(2)物方空间坐标系①摄影测量坐标系,将像空间辅助坐标系XYZ S -沿着Z 轴反方向平移至地面点P ,得到的坐标系p p p Z Y X P -称为摄影测量坐标系②地面测量坐标系,地面测量坐标系通常指地图投影坐标系,也就是国家测图所采用的高斯—克吕格︒3带或︒6带投影的平面直角坐标系和高程系,两者组成的空间直角坐标系是左手系,用t t t Z Y X T -表示。
摄影测量重点总结

摄影测量重点总结1、摄影测量中常用的坐标系有像平面直角坐标系、像空间直角坐标系、像空间辅助坐标系、地面摄影测量坐标系、地面测量坐标系。
2、解求单张像片的外方位元素最少需要3个平高地面控制点。
3、gps辅助空中三角测量的促进作用就是大量增加甚至全然免去地面控制点,缩为图周期,提升生产效率,降低生产成本。
4、两个空间直角坐标系间的坐标变换最少需要2个平高和1个高程地面控制点。
5、摄影测量的发展经历了模拟摄影测量、解析摄影测量和数字摄影测量三个阶段。
6、恢复立体像对左右像片的相互位置关系依据的是共面条件方程。
7、法方程消元的通式为=8、表示航摄像片的外方位角元素可以采用以y轴为主轴的?-ω-κ、以x轴为主轴的ω'-?'-κ'以z轴为主轴的a-a?k三种转角系统。
9、航摄像片是所覆盖地物的中心投影。
10、摄影测量加密按数学模型可以分成航带法、单一制模型法和光束法三种方法。
摄影测量加密按黄赤范围可以分成单模型法、航带法和区域网法三种方法。
11、从航摄像片上量测的像点坐标可能带有摄影材料变形、摄影机物镜畸变、大气折光误差和地球曲率误差四种系统误差。
12、要将地物点在摄影测量坐标系中的模型坐标转换到地面摄影测量坐标系,最少需要2个平高和1个高程地面控制点。
13、带状法方程系数矩阵的带宽是指法方程系数矩阵中主对角线元素起沿某一行到最远处的非零元素间所包含的未知数个数。
14、人眼观察两幅影像能产生立体视觉的基本条件是在不同摄站获取的具有一定重叠的两幅影像、观察时每只眼睛只能看一张像片、两幅影像的摄影比例尺尽量一致和两幅影像上相同地物的连线与眼基线尽量平行。
15、中心投影的共线条件方程抒发了摄影中心、像是点和对应地物点三点坐落于同一直线的几何关系,利用其解求单张像片6个外方位元素的方法称作单片空间后方交会,最少须要3个上恩地面控制点。
16、摄影测量中,为了恢复立体像对两张像片之间的相互位置关系,可以根据左右像片上的同名像点位于同一核面的几何条件,采用相对定向方法来实现,最少需要量测5对同名像点。
双像解析摄影测量三种方法的比较-学习心得

双像解析摄影测量三种⽅法的⽐较-学习⼼得双像解析摄影测量三种⽅法的⽐较为了加强印象,还是要做做笔记的,那继续做电⼦笔记吧双像解析摄影测量三种⽅法的⽐较:后⽅交会-前⽅交会⽅法;相对定向-绝对定向法;⼀步定向法后⽅交会-前⽅交会法主要步骤:⾸先进⾏后⽅交会,利⽤单张影像上3个以上已知控制点分别计算像⽚外⽅位元素,再通过前⽅交会计算出地⾯⽬标的物⽅坐标。
该⽅法的缺点在于每张影像上都必须有3个以上控制点,并且前⽅交会求取的地⾯点坐标的精度取决于后⽅交会所解算外⽅位元素的精度(前⽅交会过程没有充分利⽤多余条件进⾏平差计算)。
因此,该⽅法往往在已知影像的外⽅位元素、需确定少量的待定点坐标时采⽤。
相对定向-绝对定向法主要步骤:⾸先利⽤两张影像重叠区内5对以上同名点,按照共⾯条件⽅程解算相对定向元素,并计算同名点模型坐标,同时要求⾄少2个平⾼点1个⾼程点位于像⽚重叠区内以计算控制点模型坐标。
然后利⽤控制点模型坐标和对应地⾯坐标根据三维相似变换⽅程解算出绝对定向元素。
最后根据绝对定向元素求取⽬标的物⽅坐标。
(计算公式⽐较多,⽤这种⽅法的解算结果不能严格表达⼀幅图像的外⽅位元素)该⽅法的缺点在于需要已知重叠区内最少5对同名点。
同样地,绝对定向的精度取决于相对定向精度。
因此常⽤于航带法解析三⾓测量的应⽤。
⼀步定向法主要步骤:利⽤已有控制点地⾯坐标、像⽚上对应像点坐标,根据共线条件⽅程⼀步解算出像⽚外⽅位元素和⽬标的地⾯坐标。
该⽅法⼀步完成,精度完全由控制点和像点坐标量测精度决定,理论上⽐以上两种⽅法精度⾼。
但该⽅法相较以上两种⽅法,求解过程较复杂。
(待定点的坐标是完全按最⼩⼆乘法原理解求出来的,该⽅法常⽤于光线束法解析空中三⾓测量中的应⽤。
)下⾯简单介绍⼀种影像定位的⽅法:有理函数模型(RFM)有理函数模型可以直接建⽴起像点和空间坐标之间的关系,不需要内外⽅位元素,回避成像的⼏何过程,可以⼴泛⽤于线阵影像的处理中。
摄影测量后方交会

单张相片后方交会目录●作业任务 (3)●解算原理 (3)●具体过程 (4)●算法描述及程序流程 (4)●计算结果 (7)●结果分析 (8)●心得体会及建议 (8)●参考文献 (9)一,作业任务已知摄影机主距f=153.24mm,四对点的像点坐标与相应地面坐标列入下表:表1-1计算近似垂直摄影情况下后方交会解。
二,解算原理【关键词1】中心投影构像方程在摄影测量学中,最重要的方程就是中心投影构像方程(图2-1)。
这个方程将地面点在地面摄影测量坐标系中的坐标(物方坐标)和地面点对应像点的像平面坐标联系起来。
在解析摄影测量与数字摄影测量中是极其有用的。
在以后将要学习到的双像摄影测量光束法、解析测图仪原理及数字影像纠正等都要用到该式。
图2-1在上述公式中:x和y分别为以像主点为原点的像点坐标,相应地面点坐标为X,Y,Z,相片主距f以及外方位元素Xs,Ys,Zs,ψ,ω,κ。
而在此次作业中,就是已知四个地面控制点的坐标以及其对应的像点坐标,通过间接平差原理来求解此张航片的外方位元素。
【关键词2】间接平差在一个平差问题中,当所选的独立参数X的个数等于必要观测值t时,可将每个观测值表达成这t个参数的函数,组成观测方程,然后依据最小二乘原理求解,这种以观测方程为函数模型的平差方法,就是间接平差方法间接平差的函数模型为:随机模型为:平差准则为:VtPV=min【关键词3】单像空间后方交会利用至少三个已知地面控制点的坐标A(Xa,Ya,Za)、B(Xb,Yb,Zb)、Z(Xc,Yc,Zc),与其影像上对应的三个像点的影像坐标a(xa,ya)、b(xb,yb)、c(xc,yc),根据共线方程,反求该像点的外方位元素Xs,Ys,Zs,ψ,ω,κ。
这种解算方法是以单张像片为基础,亦称单像空间后方交会。
在此次作业中,就是已知四个控制点在地面摄影测量坐标系中的坐标和对应的像点坐标。
由此可以列出8个误差方程,存在两个多余观测数,则n=2。
简述单像空间后方交会的程序设计步骤

简述单像空间后方交会的程序设计步骤摘要:一、单像空间后方交会概念阐述二、单像空间后方交会程序设计目的三、单像空间后方交会程序设计步骤1.数据准备2.建立中心投影几何模型3.求解像片外方位元素4.评定精度四、实验意义及能力培养正文:单像空间后方交会是一种基于摄影测量原理的算法,通过计算影像的外方位元素,实现对影像的定位和测量。
在已知地面上若干点的地面坐标和对应像点的像片坐标的情况下,利用共线条件方程求解像片外方位元素。
以下详细介绍单像空间后方交会的程序设计步骤:一、单像空间后方交会概念阐述单像空间后方交会是指在影像覆盖范围内,根据一定数量的分布合理的地面控制点(已知其像点和地面点的坐标),利用共线条件方程求解像片外方位元素的过程。
它是摄影测量中一种基础的算法,为后续复杂算法的演进提供了基础。
二、单像空间后方交会程序设计目的单像空间后方交会程序设计的目的是让学生深入理解单片空间后方交会的原理,通过上机调试程序加强动手能力的培养,通过对实验结果的分析,增强学生综合运用所学知识解决实际问题的能力。
三、单像空间后方交会程序设计步骤1.数据准备:已知航摄仪的内方位元素,摄影比例尺,以及地面控制点的地面坐标和对应像点的像片坐标。
2.建立中心投影几何模型:根据针孔相机模型,建立中心投影的几何模型,包括物空间坐标系、像空间坐标系和摄影坐标系。
3.求解像片外方位元素:利用共线条件方程,通过最小二乘平差方法求解像片的外方位元素。
4.评定精度:根据实验数据,评定求解得到的像片外方位元素的精度。
四、实验意义及能力培养单像空间后方交会实验有助于学生掌握摄影测量基本原理,了解单像空间后方交会的计算过程,提高动手实践能力。
通过实验,学生可以深入理解线性代数和微分学在摄影测量中的应用,为后续学习提供更扎实的基础。
此外,实验还可以培养学生的解决问题的能力和综合运用所学知识的能力,为未来从事相关领域工作打下坚实基础。
综上所述,单像空间后方交会是一种重要的摄影测量方法,通过程序设计实现对影像的定位和测量。
摄影测量学 空间前方后方交会

地球科学与环境工程学院实验报告书一实习任务在LPS中采集4个控制点及两个检查点的像平面坐标及其对应物方坐标;编写空间后方前方交会的程序,利用该程序计算出相片的外方位元素,并且利用内外方位元素解算出两个检查点的物方坐标,并与LPS工作站上的对应坐标相比较。
二实验原理前方交会数学模型及公式后方交会数学模型,公式计算时使用迭代计算附源代码三实验思路及步骤利用后方交会得出两张像片各自的外方位元素1)获取已知数据:从摄影资料中插曲像片比例尺、平均航高、内方位元素以及控制点的地面摄影测量坐标及对应的像点坐标。
2)确定未知数的初始值:在竖直摄影的情况下,胶原素的初始值为0,线元素其中Zs=m*f+∑Z 41,Xs=∑X 41,Ys=∑Z 41。
3) 计算旋转矩阵R 。
4) 逐点计算像点坐标的近似值:利用共线方程。
5) 组成误差方程并法化。
6) 解求外方位元素。
7) 检查计算是否收敛。
利用解求出的外方位元素进行前方交会1) 用各自像片的角元素计算出左右像片的旋转矩阵R1和R2。
2) 根据左右像片的外方位元素计算摄影基线分量Bx,By ,Bz 。
3) 逐点计算像点的空间辅助坐标。
4) 计算投影系数。
5) 计算未知点的地面摄影测量坐标。
6) 重复以上步骤完成所有点的地面坐标的计算。
四 程序框图后方交会程序框图五计算成果由四个地面控制点求出相片外方位元素的解航向倾角:-0.00398694旁向倾角:0.00211388相片旋角:-0.067578两检查点物方坐标分别为:2001 160.561 2127.272 2002 2031.232 2185.930Point ID rX rY rZ2001 -0.8600 -2.8281 1683.90242002 1.4830 -0.0987 2.31812001 670969.5900 114812.4019 1883.9024 22002 671410.2130 123166.4213 1986.0801 2误差:2001 +0.000231 -0.000729 +0.0010822002 -0.000196 -0.000238 +0.000374六心得体会通过本次实习,对于LPS有了更深的了解,操作上也更加熟练,同时在翻译操作手册的工程中,对本专业设计到的某些词汇有了初步的掌握在编写后方交会的程序过程中,对空间后方-前方交会的算法认识的更加深刻,对迭代计算的步骤也更加熟悉。
摄影测量工作流程概述

摄影测量工作流程概述摄影测量是一项通过使用摄影测量仪器和相关技术手段,进行测量、记录和分析物体或地貌特征的空间位置和形状的科学方法。
它在地理信息系统、城市规划、工程测量等领域具有广泛的应用。
本文将概述摄影测量的工作流程,并介绍其中的关键步骤和技术。
摄影测量的工作流程可以大致分为预处理、影像测量和数据处理三个主要阶段。
首先,在预处理阶段,在摄影测量之前,需要进行场地勘测并确定控制点的位置。
控制点是指在摄像机坐标系统中已知坐标的地面点,它们用于将摄像机坐标与地面坐标系统建立联系。
勘测人员使用全球定位系统(GPS)等工具进行控制点的测量,确保摄影测量的精度和准确性。
在影像测量阶段,摄影测量仪器的选择和相机设置非常重要。
通常使用航空相机或无人机搭载相机进行摄影测量。
航空相机由航空器上方的固定平台携带,可以在高空对大面积地区进行拍摄。
而无人机则可以小范围、低高度地进行拍摄,得到更高分辨率的影像。
在实际操作中,需要根据具体任务需求选择相机和摄影参数,如焦距、拍摄模式和遥控设置等。
摄影测量的核心过程是影像测量,也就是测量影像中的地面特征。
影像测量可以分为两个方面,即外业测量和内业测量。
外业测量是指在野外利用观测设备对拍摄的影像进行测量,确定控制点和获取物体特征的三维坐标信息。
内业测量则是在办公室环境下,根据外业测量获得的数据,利用相关软件进行影像解算和地物三维重建。
内业测量是影像测量的重要环节,主要包括内方位元素的解算、像控测量和空间后方交会等。
数据处理是摄影测量的最后一个环节,它将外业测量和内业测量所得到的数据进行整合和分析。
在数据处理阶段,需要进行数据的校正、配准和融合,以得到一幅高精度的地理信息图。
数据处理的过程中,需要使用数字摄影测量软件、图像处理工具和地理信息系统等。
这些工具可以对图片进行处理、配准、测量、投影等操作,从而提供更准确、可靠的测量结果,并帮助用户进行后续的地理信息分析和规划工作。
摄影测量的工作流程可以说是一个科学而严谨的过程,它需要测量人员具备扎实的地理、数学和影像解算等方面的知识,并运用适当的仪器和软件工具。
摄影测量学教案(第10讲后方交会).doc
三、概述
1、 单像空间后方交会 利用地面控制点及其在像片上的像点,确定一张像片外方位元素的方法。 2、单像空间后方交会的基本方法 a. 角锥体法
S
c a b
角锥体法介绍大 体思路
b. 利用共线条件方程解算像片的外方位元素
x f y f
a1 ( X X S ) b1 ( Y YS ) c1 ( Z Z S ) a3 ( X X S ) b3 ( Y YS ) c3 ( Z Z S ) a2 ( X X S ) b2 ( Y YS ) c2 ( Z Z S ) a3 ( X X S ) b3 ( Y YS ) c3 ( Z Z S )
a1 ( X X S ) b1 ( Y YS ) c1 ( Z Z S ) a3 ( X X S ) b3 ( Y YS ) c3 ( Z Z S ) a2 ( X X S ) b2 ( Y YS ) c2 ( Z Z S ) a3 ( X X S ) b3 ( Y YS ) c3 ( Z Z S )
lx x x计
ly y y计
(7)
而 Z 和 x计 , y 计 分别按如下方法计算:
X a1 Y b1 c1 Z
《摄影测量与遥感》知识点课件-16 后方交会-前方交会解算地面点坐标

4.交会过程回顾
首先由后方交会,利用地面至少三个控制点恢复像片的空 间位置和姿态,即求得了左右像片的十二个参数。解决 了共线方程的参数问题。
再次是前方交会过程,相邻像片的两组共线方程参数解决 后,再量测同名点的像平面坐标即可构建四个方程,理 论上四个方程解三个未知数,就可以将这个同名点对应 的地面坐标反算出来。
再次是前方交会过程相邻像片的两组共线方程参数解决后再量测同名点的像平面坐标即可构建四个方程理论上四个方程解三个未知数就可以将这个同名点对应的地面坐标反算出来
主讲人:孙宝明
课程导入
1、双像解析摄影测量中,先求解每张像片的外方位元素, 能否求解出地面点坐标呢?
1.后方交会-前方交会方法
确定一张航摄像片(或摄影光束)在地面坐标系统中的 方位,需要六个外方位元素
2.后方交会
z y x s(Xs, Ys, Zs)
Z a
bc
根据影像覆盖范围内一定数 量的分布合理的地面控制 点(已知其像点和地面点 的坐标),利用共线条件 方程求解像片外方位元素 的过程就是单像空间后方 交会。
Y
A
C
BXLeabharlann 2.后方交会已知值 x0 , y0 , f , X, Y, Z 观测值 x,y
左片:Xs1、Ys1、Zs1、φ1、ω1、κ1; 右片:Xs2、Ys2、Zs2、φ2、ω2、κ2。
恢复立体像对中两张像片的12个外方位元素即能恢复其 绝对位置和姿态,重建被摄地面的绝对立体模型。
1.后方交会-前方交会方法
首先根据影像覆盖范围内一定数量的分布合理的地 面控制点,利用共线条件方程求解像片外方位元素,恢 复相邻两张相片的绝对位置;再由立体像对中两张像片 的内、外方位元素和像点坐标来确定相应地面点在物方 空间坐标系中坐标的方法就是后方交会-前方交会方法。
五上、数字摄影测量学单片空间后方交会

总误差方程
法方程
V Ax L
x (AT A) 1 (AT L)
X s Ys V1 A1 l1 Z V2 A2 l2 s V , A , L , x , Vn An ln T T li xi ( xi ) yi ( yi ) , Vi v xi v yi a11 a12 a13 a14 a15 a16 Ai a21 a22 a23 a24 a25 a26
已知点必须多余点, 数据处理方法采用 最小二乘法!
这是所有测量的一个统一的基本原则! 摄影测量也不例外。
二、误差方程与法方程
已知值 x0 , y0 , f ,m, X, Y, Z 观测值 x , y 相应改正数 vx,vy 未知数 Xs, Ys, Zs, , , 泰勒级数展开
四、空间后方交会的精度
求解各未知数的精度可以通过法方程系数矩阵 求逆的方法,解出相应的权倒数 Qii
mi m0 Qii 按下式计算第i未知数的中误差:
式中,m0为单位权中误差,计算公式 为: m [VV ] 0 2n 6 ,其中n为控制点的点数。
空间后方交会用到的已知点越多,空间后方交会 的精度越高,此外空点的分布也空间后方交会计算 的精度。空间后方交会使用的控制点应当避免位于 一个圆柱面上,否则,会出现解不唯一的情况。
偏导数 1
x f X Z 2 ( Z X) X s Z X s X s f 2 ( a1Z a3 X ) Z 1 X (a1 f f a3 ) Z Z 1 (a1 f a3 x) Z
偏导数 2
x f X Z 2 ( Z X) Z
简述单像空间后方交会的程序设计步骤

简述单像空间后方交会的程序设计步骤
单像空间后方交会是一种用于测量摄影点在三维空间中位置的方法。
以下是简述的程序设计步骤:
1.读取摄影测量数据:首先,从摄影测量设备(如相机)中读取图像和相关的内参数据,包括相机的焦距、像点大小等。
2.图像处理:对读取的图像进行预处理。
可能需要进行去畸变操作,校正图像的畸变。
3.特征提取:从图像中提取关键点或特征点。
这些特征点可以是角点、边缘、斑点等。
提取出的特征点用于后方交会计算。
4.求解相机位姿:使用特征点的像素坐标和已知内参数,通过解非线性方程组的方法,计算相机在三维空间中的位姿(即相机的位置和方向)。
5.求解三维点坐标:对于每个特征点,使用单像模型,将像素坐标投影到相机坐标系中。
然后,通过解线性方程组的方法,计算特征点在三维空间中的坐标。
6.误差检测与优化:计算测量误差,并进行误差检测。
可以使用一些优化算法,如最小二乘法,来优化相机位姿和三维点坐标。
7.输出测量结果:将计算得到的三维点坐标输出,可以是数字格式或者可视化结果。
以上是单像空间后方交会的基本程序设计步骤。
每个步骤可能会有不同的具体实现,根据具体的应用场景和需求进行设计和调整。
摄影测量学基础试题 (2)

一、名词解释1摄影测量学 2航向重叠3单像空间后方交会 4相对航高5解析空中三角测量 6外方位元素7核面 8绝对定向元素二、问答题1.写出中心投影的共线方程式并说明式中各参数的含义。
2.指出采用“后方交会+前方交会”和“相对定向+绝对定向”两种方法计算地面点坐标的基本步骤。
3.简述利用光束法(一步定向法)求解物点坐标的基本思想。
4.简述解析绝对定向的基本过程。
5.简述相对定向的基本过程。
6.试述航带网法解析空中三角测量的基本步骤。
二、填空1摄影测量的基本问题,就是将_________转换为__________。
2人眼产生天然立体视觉的原因是由于_________的存在。
3相对定向完成的标志是__________。
三、简答题1两种常用的相对定向元素系统的特点及相对定向元素。
2倾斜位移的特性。
3单航带法相对定向后,为何要进行比例尺归化?怎样进行?4独立模型法区域网平差基本思想。
5何谓正形变换?有何特点?四、论述题1空间后方交会的计算步骤。
2有三条航线,每条航线六张像片组成一个区域,采用光束法区域网平差。
(1)写出整体平差的误差方程式的一般式。
(2)将像片进行合理编号,并计算带宽,内存容量。
(3)请画出改化法方程系数阵结构简图。
参考答案:一、1是对研究的对象进行摄影,根据所获得的构想信息,从几何方面和物理方面加以分析研究,从而对所摄影的对象本质提供各种资料的一门学科。
2供测图用的航测相片沿飞行方向上相邻像片的重叠。
3知道像片的内方位元素,以及三个地面点坐标和量测出的相应像点的坐标,就可以根据共线方程求出六个外方位元素的方法。
4摄影瞬间航摄飞机相对于某一索取基准面的高度。
5将中心投影转换成正射投影时,经过投影变换来消除相片倾斜所引起的像点位移,使它相当于水平相片的构象,并符合所规定的比例尺的变换过程。
6是将建立的投影光束,单元模型或航带模型以及区域模型的数字模型,根据少数地面控制点,按最小二乘法原理进行平差计算,并求加密点地面坐标的方法。
摄影测量程序汇总(后方交会+前方交会+单模型光束法平差)

程序运行环境为Visual Studio2010.运行前请先将坐标数据放在debug 下。
1.单像空间后方交会C语言程序:#include <stdio.h>#include <math.h>#include <iostream>double *readdata();void savedata(int hang,double *data,double *xishuarray,double *faxishu,double *l,int i,double xs,double ys,double zs,double fai,double oumiga,double kapa);void transpose(double *m1,double *m2,int m,int n);void inverse(double *a,int n);void multi(double *mat1,double * mat2,double * result,int a,int b,int c);void inverse(double *a,int n)/*正定矩阵求逆*/{int i,j,k;for(k=0;k<n;k++){for(i=0;i<n;i++){if(i!=k)*(a+i*n+k)=-*(a+i*n+k)/(*(a+k*n+k));}*(a+k*n+k)=1/(*(a+k*n+k));for(i=0;i<n;i++){if(i!=k){for(j=0;j<n;j++){if(j!=k)*(a+i*n+j)+=*(a+k*n+j)* *(a+i*n+k);}}}for(j=0;j<n;j++){if(j!=k)*(a+k*n+j)*=*(a+k*n+k);}}}void transpose(double *m1,double *m2,int m,int n) //矩阵转置{ int i,j;for(i=0;i<m;i++)for(j=0;j<n;j++)m2[j*m+i]=m1[i*n+j];return;}void multi(double *mat1,double *mat2,double * result,int a,int b,int c) { int i,j,k;for(i=0;i<a;i++){for(j=0;j<c;j++){result[i*c+j]=0;for(k=0;k<b;k++)result[i*c+j]+=mat1[i*b+k]*mat2[k*c+j];}}return;}double *readdata(){FILE *fp;int i,j;int number;char datacatolog[100];//scanf("%s",datacatolog);if ((fp=fopen("控制点坐标.txt","r"))==NULL){printf("读取数据出错!\n");return false;}fscanf(fp,"%d",&number);double *cordata=new double[number*5];for (i=0;i<number;i++){for (j=0;j<5;j++){fscanf(fp,"%lf",cordata+i*5+j);}}printf("控制点坐标数据读取成功!\n");return cordata;}void savedata(int hang,double *data,double *xishuarray,double *faxishu,double *l,int i,double xs,double ys,double zs,double fai,double oumiga,double kapa){FILE *fp;char *file1="结算数据.txt";fp=fopen(file1,"w");fprintf(fp,"---------原始坐标数据为--------:\n");for (int i=0;i<hang;i++){for (int j=0;j<5;j++){fprintf(fp,"%7.4lf ",data[i*5+j]);}fprintf(fp,"\n");}fprintf(fp,"--------------------------------\n");fprintf(fp,"---------误差方程系数阵为:--------:\n");for (int i=0;i<hang*2;i++){for (int j=0;j<6;j++){fprintf(fp,"%7.4lf ",xishuarray[i*5+j]);}fprintf(fp,"\n");}fprintf(fp,"--------------------------------\n");fprintf(fp,"---------法方程系数阵为:--------:\n");for (int i=0;i<6;i++){for (int j=0;j<6;j++){fprintf(fp,"%7.5lf ",faxishu[i*5+j]);}fprintf(fp,"\n");}fprintf(fp,"--------------------------------\n");fprintf(fp,"---------误差方程常数项为:--------:\n");for (int i=0;i<hang*2;i++){fprintf(fp,"%lf ",l[i]);fprintf(fp,"\n");}fprintf(fp,"--------------------------------\n");fprintf(fp,"---------迭代次数为:--------:\n");fprintf(fp,"%d\n",i);fprintf(fp,"--------------------------------\n");fprintf(fp,"-----------外方位元素为:---------\n");fprintf(fp," Xs= %lf, Ys=%lf, Zs=%lf\n",xs,ys,zs);fprintf(fp," fai= %lf, oumiga=%lf, kapa=%lf\n",fai,oumiga,kapa);fprintf(fp,"--------------------------------\n");fclose(fp);return;}void main(){int i,j;int ii,jj;int diedainumber=0;double x0=0.0,y0=0.0,f=0.0;double m=50000; //估算比例尺double fai=0,oumiga=0,kapa=0,Xs=0,Ys=0,Zs=0;double R[3][3]={0.0};double X=0.0,Y=0.0,Z=0.0,L[8][1]={0.0},A[8][6]={0.0};double correct[6][1]={0.0},AT[6][8]={0.0},ATA[6][6]={0.0},ATL[6][1]={0.0};int row; //row用于存放坐标行数double *controlpoint;controlpoint=readdata();row=sizeof(controlpoint);for (i=0;i<row;i++){for (j=0;j<5;j++){printf("%3.3lf ",controlpoint[i*5+j]);}printf("\n");}/*----------内方位元素----------*/printf("请输入像片的内方位元素(mm):\n");printf("x0=");x0/=1000.0;scanf("%lf",&x0); //double类型数据要用%lfprintf("y0=");y0/=1000.0;scanf("%lf",&y0);printf("f=");scanf("%lf",&f);f=f/1000.0;/*------------------------------*///-------确定未知数初始值------for(int i=0;i<row;i++){Xs=Xs+controlpoint[i*5+2];Ys=Ys+controlpoint[i*5+3];Zs=Zs+controlpoint[i*5+4];}Xs/=row;Ys/=row;Zs=Zs/row+m*f;//-----------------------------do{diedainumber++;//---------组成旋转矩阵--------R[0][0]=cos(fai)*cos(kapa)-sin(fai)*sin(oumiga)*sin(kapa);R[0][1]=-cos(fai)*sin(kapa)-sin(fai)*sin(oumiga)*cos(kapa);R[0][2]=-sin(fai)*cos(oumiga);R[1][0]=cos(oumiga)*sin(kapa);R[1][1]=cos(oumiga)*cos(kapa);R[1][2]=-sin(oumiga);R[2][0]=sin(fai)*cos(kapa)+cos(fai)*sin(oumiga)*sin(kapa);R[2][1]=-sin(fai)*sin(kapa)+cos(fai)*sin(oumiga)*cos(kapa);R[2][2]=cos(fai)*cos(oumiga);//-----------------------------//计算系数阵和常数项for(int i=0,k=0,j=0;i<=3;i++,k++,j++){X=R[0][0]*(controlpoint[i*5+2]-Xs)+R[1][0]*(controlpoint[i*5+3]-Ys)+R[2][0]*(co ntrolpoint[i*5+4]-Zs);Y=R[0][1]*(controlpoint[i*5+2]-Xs)+R[1][1]*(controlpoint[i*5+3]-Ys)+R[2][1]*(con trolpoint[i*5+4]-Zs);Z=R[0][2]*(controlpoint[i*5+2]-Xs)+R[1][2]*(controlpoint[i*5+3]-Ys)+R[2][2]*(controlpoint[i*5+4]-Zs);L[j][0]=controlpoint[i*5+0]-(x0-f*X/Z);L[j+1][0]=controlpoint[i*5+1]-(y0-f*Y/Z);j++;A[k][0]=(R[0][0]*f+R[0][2]*(controlpoint[i*5+0]-x0))/Z;A[k][1]=(R[1][0]*f+R[1][2]*(controlpoint[i*5+0]-x0))/Z;A[k][2]=(R[2][0]*f+R[2][2]*(controlpoint[i*5+0]-x0))/Z;A[k][3]=(controlpoint[i*5+1]-y0)*sin(oumiga)-((controlpoint[i*5+0]-x0)*((control point[i*5+0]-x0)*cos(kapa)-(controlpoint[i*5+1]-y0)*sin(kapa))/f+f*cos(kapa))*cos(o umiga);A[k][4]=-f*sin(kapa)-(controlpoint[i*5+0]-x0)*((controlpoint[i*5+0]-x0)*sin(kapa) +(controlpoint[i*5+1]-y0)*cos(kapa))/f;A[k][5]=controlpoint[i*5+1]-y0;A[k+1][0]=(R[0][1]*f+R[0][2]*(controlpoint[i*5+1]-y0))/Z;A[k+1][1]=(R[1][1]*f+R[1][2]*(controlpoint[i*5+1]-y0))/Z;A[k+1][2]=(R[2][1]*f+R[2][2]*(controlpoint[i*5+1]-y0))/Z;A[k+1][3]=-(controlpoint[i*5+0]-x0)*sin(oumiga)-((controlpoint[i*5+1]-y0)*((cont rolpoint[i*5+0]-x0)*cos(kapa)-(controlpoint[i*5+1]-y0)*sin(kapa))/f-f*sin(kapa))*cos( oumiga);A[k+1][4]=-f*cos(kapa)-(controlpoint[i*5+1]-y0)*((controlpoint[i*5+0]-x0)*sin(ka pa)+(controlpoint[i*5+1]-y0)*cos(kapa))/f;A[k+1][5]=-(controlpoint[i*5+0]-x0);k++;}transpose(A[0],AT[0],8,6);multi(AT[0],A[0],ATA[0],6,8,6);inverse(ATA[0],6);multi(AT[0],L[0],ATL[0],6,8,1);multi(ATA[0],ATL[0],correct[0],6,6,1);Xs=Xs+correct[0][0];Ys=Ys+correct[1][0];Zs=Zs+correct[2][0];fai=fai+correct[3][0];oumiga=oumiga+correct[4][0];kapa=kapa+correct[5][0];}while(correct[3][0]>=6.0/206265.0||correct[4][0]>=6.0/206265.0||correct[5][0] >=6.0/206265.0);printf("迭代次数为:%d\n",diedainumber);printf("---------误差方程系数为:--------\n");for (i=0;i<8;i++){for (j=0;j<6;j++){printf("%4.4lf ",A[i][j]);}printf("\n");}printf("--------------------------------\n");printf("求解得到的外方位元素为:\n");printf(" Xs= %lf\n",Xs);printf(" Ys= %lf\n",Ys);printf(" Zs= %lf\n",Zs);printf(" fai= %lf\n",fai);printf(" oumiga= %lf\n",oumiga);printf(" kapa= %lf\n",kapa);savedata(row,controlpoint,A[0],ATA[0],L[0],diedainumber,Xs,Ys,Zs,fai,oumiga,kap a);printf("-----------------解算结束!--------------\n");system("pause");}解算结果:已知左右像片外方位元素,给出像点坐标:C语言代码:#include <stdio.h>#include <iostream>#include <math.h>double *readdata();void savedata(int hang,double *data);double *readdata(){FILE *fp;int i,j,k;int number;char datacatolog[100];char leftdata[300];//scanf("%s",datacatolog);if ((fp=fopen("像点坐标数据.txt","r"))==NULL){printf("读取数据出错!\n");system("pause");exit(0);}fscanf(fp,"%d",&number);double *c=new double[number*4];for (k=0;k<2;k++){fread(&leftdata,14,1,fp);for (i=0;i<number;i++){for (j=0;j<2;j++){fscanf(fp,"%lf",c+k*2+i*4+j);}}}fclose(fp);return c;}void savedata(int hang,double *data){FILE *fp;char *file1="地面点坐标数据.txt";fp=fopen(file1,"w");fprintf(fp,"---------像点对应地面点坐标为--------:\n");fprintf(fp,"\n");for (int i=0;i<hang;i++){fprintf(fp,"第%d点:",i+1);for (int j=0;j<3;j++){fprintf(fp,"%7.4lf ",data[i*3+j]);}fprintf(fp,"\n\n");}fprintf(fp,"-----------------------------------------");fclose(fp);return;}void main(){double *imagepoint;int row;int i,j;imagepoint=readdata();row=sizeof(imagepoint);//--------------------------------------------double f=24;f/=1000;doublefai1=-0.0061,oumiga1=0.0327,kapa1=0.1711,Ys1=397367.171,Xs1=3445820.098,Zs1=1486.212;doublefai2=0.0063,oumiga2=0.0178,kapa2=0.1489,Ys2=397367.234,Xs2=3445959.266,Zs2=1490.096;// printf("请输入左像片的外方位元素:\n");//printf("Xs1= ");//scanf("%lf",&Xs1);//printf("Ys1= ");//scanf("%lf",&Ys1);//printf("Zs1= ");//scanf("%lf",&Zs1);//printf("fai1= ");//scanf("%lf",&fai1);//printf("oumiga1= ");//scanf("%lf",&oumiga1);//printf("kapa1= ");//scanf("%lf",&kapa1);//printf("请输入右像片的外方位元素:\n");//printf("Xs2= ");//scanf("%lf",&Xs2);//printf("Ys2= ");//scanf("%lf",&Ys2);//printf("Zs2= ");//scanf("%lf",&Zs2);//printf("fai2= ");//scanf("%lf",&fai2);//printf("oumiga2= ");//scanf("%lf",&oumiga2);//printf("kapa2= ");//scanf("%lf",&kapa2);double Bx=Xs2-Xs1,By=Ys2-Ys1,Bz=Zs2-Zs1;double N1=0,N2=0;double X1=0,Y1=0,Z1=0,X2=0,Y2=0,Z2=0;double R1[3][3]={0.0};double R2[3][3]={0.0};double GEOdata[4][3]={0.0};for (i=0;i<row;i++){//---------组成左影像旋转矩阵--------R1[0][0]=cos(fai1)*cos(kapa1)-sin(fai1)*sin(oumiga1)*sin(kapa1);R1[0][1]=-cos(fai1)*sin(kapa1)-sin(fai1)*sin(oumiga1)*cos(kapa1);R1[0][2]=-sin(fai1)*cos(oumiga1);R1[1][0]=cos(oumiga1)*sin(kapa1);R1[1][1]=cos(oumiga1)*cos(kapa1);R1[1][2]=-sin(oumiga1);R1[2][0]=sin(fai1)*cos(kapa1)+cos(fai1)*sin(oumiga1)*sin(kapa1);R1[2][1]=-sin(fai1)*sin(kapa1)+cos(fai1)*sin(oumiga1)*cos(kapa1);R1[2][2]=cos(fai1)*cos(oumiga1);//-----------------------------------//---------组成右影像旋转矩阵--------R2[0][0]=cos(fai2)*cos(kapa2)-sin(fai2)*sin(oumiga2)*sin(kapa2);R2[0][1]=-cos(fai2)*sin(kapa2)-sin(fai2)*sin(oumiga2)*cos(kapa2);R2[0][2]=-sin(fai2)*cos(oumiga2);R2[1][0]=cos(oumiga2)*sin(kapa2);R2[1][1]=cos(oumiga2)*cos(kapa2);R2[1][2]=-sin(oumiga2);R2[2][0]=sin(fai2)*cos(kapa2)+cos(fai2)*sin(oumiga2)*sin(kapa2);R2[2][1]=-sin(fai2)*sin(kapa2)+cos(fai2)*sin(oumiga2)*cos(kapa2);R2[2][2]=cos(fai2)*cos(oumiga2);//-------------像空辅系坐标-------------X1=R1[0][0]*imagepoint[i*4+0]+R1[0][1]*imagepoint[i*4+1]-R1[0][2]*f;Y1=R1[1][0]*imagepoint[i*4+0]+R1[1][1]*imagepoint[i*4+1]-R1[1][2]*f;Z1=R1[2][0]*imagepoint[i*4+0]+R1[2][1]*imagepoint[i*4+1]-R1[2][2]*f;X2=R2[0][0]*imagepoint[i*4+2]+R2[0][1]*imagepoint[i*4+3]-R2[0][2]*f;Y2=R2[1][0]*imagepoint[i*4+2]+R2[1][1]*imagepoint[i*4+3]-R2[1][2]*f;Z2=R2[2][0]*imagepoint[i*4+2]+R2[2][1]*imagepoint[i*4+3]-R2[2][2]*f;//--------------------------------------//------------点投影系数-------------N1=(Bx*Z2-Bz*X2)/(X1*Z2-Z1*X2);N2=(Bx*Z1-Bz*X1)/(X1*Z2-Z1*X2);//-----------------------------------//------------计算地面点坐标------------GEOdata[i][0]=Xs1+N1*X1;GEOdata[i][1]=Ys1+By+N2*Y2;GEOdata[i][2]=Zs1+N1*Z1;//--------------------------------------}//--------------------------------------------for (i=0;i<4;i++){printf("第%d个地面点坐标:",i+1);for (j=0;j<3;j++){printf("%lf ",GEOdata[i][j]);}printf("\n\n");}savedata(row,GEOdata[0]);system("pause");}测试结果:3.单模型光束法严密平差缺少已知数据进行验证,因此如果有已知数据请代入已知数据进行验证。
摄影测量学部分课后习题答案

摄影测量学部分课后习题答案两者组成的空间直角坐标系是左手系,用t t t Z Y X T -表示。
③地面摄影测量坐标系,由于摄影测量坐标系采用的是右手系,而地面测量坐标系采用的是左手系,这给由摄影测量坐标到地面测量坐标的转换带来了困难。
为此,在摄影测量坐标系与地面测量坐标系之间建立一种过渡性的坐标系,称为地面摄影测量坐标系,用tp tp tp Z Y X D -表示,其坐标原点在测区内的其一地面点上。
18. 摄影测量中常用的坐标系有哪两大类?用来表示像点的像方坐标系和用来描述地面点的物方坐标系分别有哪些,如何定义的?各有什么关系?(1)像方坐标系,用于描述像点的位置,表示缘点的平面和空间坐标1.像平面坐标系:是以主点为原点的右手平面坐标系,用O-xy 表示,又常用框标连线 交点不重合,须平移,框表坐标系中x0,y0,化算为x-x0,y-y02.像空间坐标系:进行像点空间坐标变换,描述像点在像空间位置的坐标系从摄影中心S 为原点,x ,y 轴与像平面坐标系x ,y 轴平行,z 轴与光轴重合。
形成像空间右手直角坐标系S-XYZ ,每张像片的像空间坐标系而建立的坐标系,3.像空间辅助坐标系: 用S-UVW 表示,原点为S ,坐标轴依情况而定a.取u 、v 、w 分别平行地面摄影测量坐标系D-XYZ.b.以每个像片对的左片摄影中心为原点.c.摄影基本为u 轴,以摄影基线及左片光轴构成的平面作为uw 平面,过原点且垂直于uw 平面的轴为v 构成右手直角坐标系(2)物方坐标系,用于描述地面在物方空间的位置1.地面测量坐标系: 高斯-克吕格6°带或3°带投影的平面直角坐标与定义的从某一基准面量起的高程组合而成的空间左手直角坐标系,用T-XtYtZt 。
2.地面摄影测量坐标系: 过渡像空间辅助坐标系的右手系换算到地面测量坐标系左手系的坐标系,用D-XYZ 表示,原点为测区骱某一地面点上,X 轴与航向一致,Y 轴与X 轴正交,Z 轴沿铅垂方向,构成右手直角系。
单像空间摄影测量前方交会法度模范代码(vc++)[最新]
![单像空间摄影测量前方交会法度模范代码(vc++)[最新]](https://img.taocdn.com/s3/m/235bb5ee7d1cfad6195f312b3169a4517723e59a.png)
往链点点通共享资源,了解更多请登录单像空间后方交会程序西南交通大学土木工程学院测绘工程张慧鑫学号:20030593输入文件形式如下:C++源程序如下:#include <iostream>#include <fstream>#include <cmath>#include <string>#include <iomanip>using namespace std;const int n=6;void inverse (double c[n][n]);template<typename T1,typename T2>void transpose (T1*mat1,T2*mat2,int a,int b); template<typename T1,typename T2>void multi(T1*mat1,T2 * mat2,T2 * result,int a,int b,int c);template<typename T>void input (T*mat,int a,int b);template<typename T>void output(T*mat,char*s,int a,int b);int main(){ofstream outFile;cout.precision(5);double x0=0.0, y0=0.0; double fk=0.15324; //内方位元素double m=39689; //估算比例尺double B[4][5]={0.0},R[3][3],XG[6][1],AT[6][8],ATA[6][6],ATL[6][1];input (B,4,5); //从文件中读取控制点的影像坐标和地面坐标,存入数组B double Xs=0.0, Ys=0.0, Zs=0.0,Q=0.0,W=0.0,K=0.0;double X,Y,Z,L[8][1],A[8][6];//确定未知数的出始值for(int i=0;i<4;i++){Xs=Xs+B[i][2];Ys=Ys+B[i][3];Zs=Zs+B[i][4];}Xs=Xs/4; Ys=Ys/4; Zs=Zs/4+m*fk;int f=0;do//迭代计算{f++;//组成旋转矩阵R[0][0]=cos(Q)*cos(K)-sin(Q)*sin(W)*sin(K);R[0][1]=-cos(Q)*sin(K)-sin(Q)*sin(W)*cos(K);R[0][2]=-sin(Q)*cos(W);R[1][0]=cos(W)*sin(K);R[1][1]=cos(W)*cos(K);R[1][2]=-sin(W);R[2][0]=sin(Q)*cos(K)+cos(Q)*sin(W)*sin(K);R[2][1]=-sin(Q)*sin(K)+cos(Q)*sin(W)*cos(K);R[2][2]=cos(Q)*cos(W);//计算系数阵和常数项for(int i=0,k=0,j=0;i<=3;i++,k++,j++){X=R[0][0]*(B[i][2]-Xs)+R[1][0]*(B[i][3]-Ys)+R[2][0]*(B[i][4]-Zs);Y=R[0][1]*(B[i][2]-Xs)+R[1][1]*(B[i][3]-Ys)+R[2][1]*(B[i][4]-Zs);Z=R[0][2]*(B[i][2]-Xs)+R[1][2]*(B[i][3]-Ys)+R[2][2]*(B[i][4]-Zs);L[j][0]=B[i][0]-(x0-fk*X/Z);L[j+1][0]=B[i][1]-(y0-fk*Y/Z);j++;A[k][0]=(R[0][0]*fk+R[0][2]*(B[i][0]-x0))/Z;A[k][1]=(R[1][0]*fk+R[1][2]*(B[i][0]-x0))/Z;A[k][2]=(R[2][0]*fk+R[2][2]*(B[i][0]-x0))/Z;A[k][3]=(B[i][1]-y0)*sin(W)-((B[i][0]-x0)*((B[i][0]-x0)*cos(K)-(B[i][1]-y0)*sin(K))/fk+fk*cos(K))*cos(W);A[k][4]=-fk*sin(K)-(B[i][0]-x0)*((B[i][0]-x0)*sin(K)+(B[i][1]-y0)*cos(K))/ fk;A[k][5]=B[i][1]-y0;A[k+1][0]=(R[0][1]*fk+R[0][2]*(B[i][1]-y0))/Z;A[k+1][1]=(R[1][1]*fk+R[1][2]*(B[i][1]-y0))/Z;A[k+1][2]=(R[2][1]*fk+R[2][2]*(B[i][1]-y0))/Z;A[k+1][3]=-(B[i][0]-x0)*sin(W)-((B[i][1]-y0)*((B[i][0]-x0)*cos(K)-(B[i][1] -y0)*sin(K))/fk-fk*sin(K))*cos(W);A[k+1][4]=-fk*cos(K)-(B[i][1]-y0)*((B[i][0]-x0)*sin(K)+(B[i][1]-y0)*cos(K ))/fk;A[k+1][5]=-(B[i][0]-x0);k++;}transpose(A,AT,6,8);multi(AT,A,A TA,6,8,6);inverse(ATA);multi(AT,L,ATL,6,8,1);multi(A TA,ATL,XG,6,6,1);Xs=Xs+XG[0][0]; Ys=Ys+XG[1][0]; Zs=Zs+XG[2][0];Q=Q+XG[3][0]; W=W+XG[4][0]; K=K+XG[5][0];}while(XG[3][0]>=6.0/206265.0||XG[4][0]>=6.0/206265.0||XG[5][0]>=6.0/2062 65.0);cout<<"迭代次数为:"<<f<<endl;//精度评定double AXG[8][1],V[8][1],VT[1][8],VTV[1][1],m0,D[6][6];multi(A,XG,AXG,8,6,1);for( i=0;i<8;i++) //计算改正数V[i][0]=AXG[i][0]-L[i][0];transpose (V,VT,1,8);multi(VT,V,VTV,1,8,1);m0=VTV[0][0]/2;for(i=0;i<6;i++)for(int j=0;j<6;j++)D[i][j]=m0*ATA[i][j];//屏幕输出误差方程系数阵、常数项、改正数output(A,"误差方程系数阵A为:",8,6);output(L,"常数项L为:",8,1);output(XG,"改正数为:",6,1);outFile.open("aim.txt",ios::app); //打开并添加aim.txt文件outFile.precision(10);//以文件的形式输出像片外方位元素、旋转矩阵、方差阵outFile<<"一、像片的外方位元素为:"<<endl<<endl;outFile<<setw(10)<<"Xs="<<Xs<<setw(10)<<"Ys="<<Ys<<setw(10)<<"Zs="<<Zs<<endl;outFile<<setw(20)<<"航向倾角为:"<<Q<<setw(10)<<"旁向倾角为:"<<W<<setw(10)<<"像片旋角为:"<<K<<endl;outFile<<endl<<"二、旋转矩阵R为:"<<endl<<endl;for( i=0;i<3;i++){for(int j=0;j<3;j++)outFile<<setw(25)<<R[i][j]<<setw(25);outFile<<endl;}outFile<<endl;outFile<<setw(0)<<"三、精度评定结果为:"<<endl;outFile.precision(5);for(i=0;i<6;i++){for(int j=0;j<6;j++)outFile<<setw(14)<<D[i][j]<<setw(14);outFile<<endl;}outFile.close();return 0;}template<typename T1,typename T2>void transpose(T1*mat1,T2*mat2,int a,int b) { int i,j;for(i=0;i<b;i++)for(j=0;j<a;j++)mat2[j][i]=mat1[i][j];return;}template<typename T1,typename T2>void multi(T1*mat1,T2 * mat2,T2 * result,int a,int b,int c){ int i,j,k;for(i=0;i<a;i++){for(j=0;j<c;j++){result[i][j]=0;for(k=0;k<b;k++)result[i][j]+=mat1[i][k]*mat2[k][j];}}return;}template <typename T>void input (T*mat,int a,int b){ ifstream inFile;inFile.open("控制点坐标.txt");while(!inFile.eof()){for (int i=0;i<a;i++)for(int j=0;j<b;j++)inFile>>mat[i][j];}inFile.close();return;}template<typename T>void output(T*mat,char*s,int a,int b) { cout<<setw(15)<<s<<endl;for(int i=0;i<a;i++){for(int j=0;j<b;j++)cout<<setw(13)<<mat[i][j];cout<<endl;}return;}void inverse(double c[n][n]){ int i,j,h,k;double p;double q[n][12];for(i=0;i<n;i++)//构造高斯矩阵for(j=0;j<n;j++)q[i][j]=c[i][j];for(i=0;i<n;i++)for(j=n;j<12;j++){if(i+6==j)q[i][j]=1;elseq[i][j]=0;}for(h=k=0;k<n-1;k++,h++)//消去对角线以下的数据for(i=k+1;i<n;i++){if(q[i][h]==0)continue;p=q[k][h]/q[i][h];for(j=0;j<12;j++){ q[i][j]*=p;q[i][j]-=q[k][j];}}for(h=k=n-1;k>0;k--,h--) // 消去对角线以上的数据for(i=k-1;i>=0;i--){if(q[i][h]==0)continue;p=q[k][h]/q[i][h];for(j=0;j<12;j++){q[i][j]*=p;q[i][j]-=q[k][j];}}for(i=0;i<n;i++)//将对角线上数据化为1{ p=1.0/q[i][i];for(j=0;j<12;j++)q[i][j]*=p;}for(i=0;i<n;i++) //提取逆矩阵for(j=0;j<n;j++)c[i][j]=q[i][j+6];}程序的结果输出如下:(包括文本输出结果和荧屏输出中间数据)。
摄影测量实验报告(空间后方交会—前方交会)
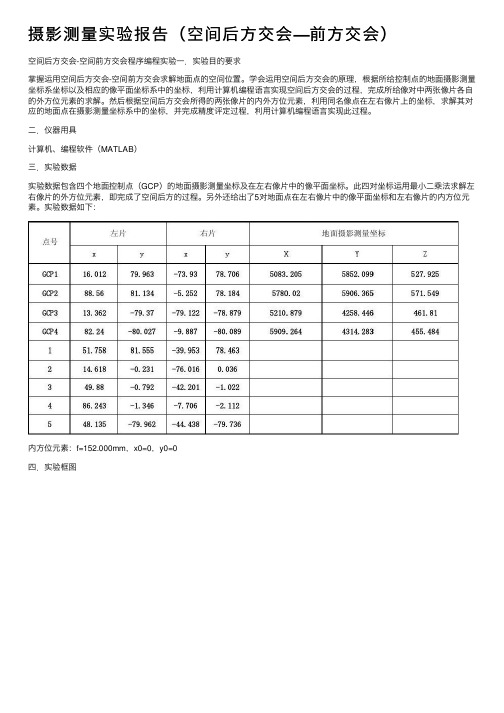
摄影测量实验报告(空间后⽅交会—前⽅交会)空间后⽅交会-空间前⽅交会程序编程实验⼀.实验⽬的要求掌握运⽤空间后⽅交会-空间前⽅交会求解地⾯点的空间位置。
学会运⽤空间后⽅交会的原理,根据所给控制点的地⾯摄影测量坐标系坐标以及相应的像平⾯坐标系中的坐标,利⽤计算机编程语⾔实现空间后⽅交会的过程,完成所给像对中两张像⽚各⾃的外⽅位元素的求解。
然后根据空间后⽅交会所得的两张像⽚的内外⽅位元素,利⽤同名像点在左右像⽚上的坐标,求解其对应的地⾯点在摄影测量坐标系中的坐标,并完成精度评定过程,利⽤计算机编程语⾔实现此过程。
⼆.仪器⽤具计算机、编程软件(MATLAB)三.实验数据实验数据包含四个地⾯控制点(GCP)的地⾯摄影测量坐标及在左右像⽚中的像平⾯坐标。
此四对坐标运⽤最⼩⼆乘法求解左右像⽚的外⽅位元素,即完成了空间后⽅的过程。
另外还给出了5对地⾯点在左右像⽚中的像平⾯坐标和左右像⽚的内⽅位元素。
实验数据如下:内⽅位元素:f=152.000mm,x0=0,y0=0四.实验框图此过程完成空间后⽅交会求解像⽚的外⽅位元素,其中改正数⼩于限差(0.00003,相当于0.1’的⾓度值)为⽌。
在这个过程中采⽤迭代的⽅法,是外⽅位元素逐渐收敛于理论值,每次迭代所得的改正数都应加到上⼀次的初始值之中。
确定Xs,Ys,Zs的初始值时,对于左⽚可取地⾯左边两个GCP的坐标的平均值作为左⽚Xs 和Ys的初始值,取右边两个GCP 的坐标平均值作为右⽚Xs 和Ys的初始值。
Zs可取地⾯所有GCP的Z坐标的平均值再加上航⾼。
空间前⽅交会的数学模型为:五.实验源代码function Main_KJQHFJH()global R g1 g2 m G a c b1 b2;m=10000;a=5;c=4;feval(@shuru); %调⽤shuru()shurujcp()函数完成像点及feval(@shurujcp); %CCP有关数据的输⼊XYZ=feval(@MQZqianfangjh); %调⽤MQZqianfangjh()函数完成空间前⽅、%%%%%% 单位权中误差%%%% %后⽅交会计算解得外⽅位元素global V1 V2; %由于以上三个函数定义在外部⽂件中故需VV=[]; %⽤feval()完成调⽤过程for i=1:2*cVV(i)=V1(i);VV(2*i+1)=V2(i);endm0=sqrt(VV*(VV')/(2*c-6));输⼊GCP像点坐标及地⾯摄影测量坐标系坐标的函数和输⼊所求点像点坐标函数:function shurujcp()global c m;m=input('摄影⽐例尺:'); %输⼊GCP像点坐标数据函数并分别将其c=input('GCP的总数='); % 存⼊到不同的矩阵之中disp('GCP左⽚像框标坐标:');global g1;g1=zeros(c,2);i=1;while i<=cm=input('x=');n=input('y=');g1(i,1)=m;g1(i,2)=n;i=i+1;enddisp('GCP右⽚像框标坐标:');global g2;g2=zeros(c,2);i=1;while i<=cm=input('x=');n=input('y=');g2(i,1)=m;g2(i,2)=n;i=i+1;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function shuru()global a;a=input('计算总像对点数='); %完成想计算所需的像平⾯坐标global b1; %坐标输⼊,存⼊不同的矩阵中b1=zeros(a,2); disp('左⽚像点坐标:')i=1;while i<=am=input('x=');n=input('y=');b1(i,1)=m;b1(i,2)=n;i=i+1;end%%b2=zeros(a,2);disp('右⽚像点坐标:')i=1;while i<=am=input('x=');n=input('y=');b2(i,1)=m;b2(i,2)=n;i=i+1;end%%global c;c=input('GCP的总数=');disp('GCP摄影测量系坐标:')global G;G=zeros(3,c);i=1;while i<=cm=input('X=');n=input('Y=');v=input('Z=');G(i,1)=m;G(i,2)=n;G(i,3)=v;i=i+1;end %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%空间前⽅交会和后⽅交会函数:function XYZ=MQZqianfangjh()global R1 R2 a f b1 b2 Ra Rb;global X1 X2;R1=Ra;R2=Rb;R1=zeros(3,3);R2=zeros(3,3);global g1 g2 G V1 V2 V WF c QXX QXX1 QXX2;xs0=(G(1,1)+G(3,1))/2;ys0=(G(1,2)+G(3,2))/2;[Xs1,Ys1,Zs1,q1,w1,k1 R]=houfangjh(g1,xs0,ys0); %对左⽚调⽤后⽅交会函数R1=R;V1=V;WF1=WF;save '左⽚外⽅位元素为.txt' WF -ascii %将计算所得的外⽅位元素存⼊到.txt% ⽂件中for i=1:cg1(i,1)=g1(i,1)+V1(2*i-1);g1(i,2)=g1(i,2)+V1(2*i);endsave '左⽚像点坐标.txt' g1 -asciixs0=(G(2,1)+G(4,1))/2;ys0=(G(2,2)+G(4,2))/2;[Xs2,Ys2,Zs2,q2,w2,k2 R]=houfangjh(g2,xs0,ys0); %对右⽚调⽤后⽅交会函数R2=R; V2=V;WF2=WF;QXX2=QXX;save '右⽚外⽅位元素为.txt' WF –ascii %将计算所得的外⽅位元素存⼊到.txt% ⽂件中for i=1:cg2(i,1)=g2(i,1)+V2(2*i-1);g2(i,2)=g2(i,2)+V2(2*i);endsave '右⽚像点坐标.txt' g2 -asciiX1=zeros(a,3);X2=zeros(a,3);xx=zeros(3,1);xxx=zeros(3,1);for i=1:ass=[b1(i,1);b1(i,2);-f];dd=[b2(i,1);b2(i,2);-f];xx=R1*ss;X1(i,:)=xx';xxx=R2*dd;X2(i,:)=xxx';endglobal Xs1 Xs2 Ys1 Ys2 Zs1 Zs2;BX=Xs2-Xs1;BY=Ys2-Ys1;BZ=Zs2-Zs1;global N1 N2;N1=zeros(1,a);N2=zeros(1,a);for i=1:aN1(1,i)=(BX*X2(i,3)-BZ*X2(i,1))/(X1(i,1)*X2(i,3)-X2(i,1)*X1(i,3));N2(1,i)=(BX*X1(i,3)-BZ*X1(i,1))/(X1(i,1)*X2(i,3)-X2(i,1)*X1(i,3));end %计算投影系数,并计算五点的三维坐标global XYZ;XYZ=zeros(a,3);for i=1:aXYZ(i,1)=Xs1+N1(1,i)*X1(i,1);XYZ(i,2)=((Ys1+N1(1,i)*X1(i,2))+(Ys2+N2(1,i)*X2(i,2)))/2;enddisp('左⽚外⽅位元素为:Xs Ys Zs ψωκ');disp(WF1);disp('左⽚外⽅位元素协因素阵为:');disp(QXX1);disp('左⽚像点坐标为:')disp(g1)disp('右⽚外⽅位元素为:Xs Ys Zs ψωκ');disp(WF2);disp('右⽚外⽅位元素协因素阵为:')disp(QXX2)disp('右⽚像点坐标为:')disp(g2)disp('计算所得点摄影测量坐标(X,Y,Z)为:');disp(XYZ);save 'XYZ.txt' XYZ -ascii %将计算所得结果保存到XYZ.txt⽂件中%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% function [Xs,Ys,Zs,q,w,k R]=houfangjh(g1,Xs0,Ys0) %计算像⽚外⽅位元素%%%%%%%%%%global f G m c b1 b2;f=0.152;Xs=Xs0;Ys=Ys0;Zs=m*f+G(1,3);q=0;w=0;k=0;while 1 %实现⼀个永真循环,是改正数⼩于限差以后跳出循环a1=cos(q)*cos(k)-sin(q)*sin(w)*sin(k);a2=-cos(q)*sin(k)-sin(q)*sin(w)*cos(k);a3=-sin(q)*cos(w);b1_=cos(w)*sin(k);b2_=cos(w)*cos(k);b3=-sin(w);c1=sin(q)*cos(k)+cos(q)*sin(w)*sin(k);c2=-sin(q)*sin(k)+cos(q)*sin(w)*cos(k);c3=cos(q)*cos(w);R=[a1,a2,a3;b1_,b2_,b3;c1,c2,c3];for i=1:caX(i)=a1*(G(i,1)-Xs)+b1_*(G(i,2)-Ys)+c1*(G(i,3)-Zs);aY(i)=a2*(G(i,1)-Xs)+b2_*(G(i,2)-Ys)+c2*(G(i,3)-Zs);aZ(i)=a3*(G(i,1)-Xs)+b3*(G(i,2)-Ys)+c3*(G(i,3)-Zs);endxj=[];yj=[];for i=1:cxj(i)=-f*aX(i)/aZ(i);yj(i)=-f*aY(i)/aZ(i);enda11=[];a12=[];a13=[];a14=[];a15=[];a16=[];a21=[];a22=[];a23=[];a24=[];a25=[];a26=[];for i=1:ca11(i)=(a1*f+a3*g1(i,1))/aZ(i);a12(i)=(b1_*f+b3*g1(i,1))/aZ(i);a13(i)=(c1*f+c3*g1(i,1) )/aZ(i);a21(i)=(a2*f+a3*g1(i,2))/aZ(i);a22(i)=(b2_*f+b3*g1(i,2))/aZ(i);a23(i)=(c2*f+c3*g1(i,2) )/aZ(i);a14(i)=g1(i,2)*sin(w)-(g1(i,1)*(g1(i,1)*cos(k)-g1(i,2)*sin(k))/f+f*cos(k))*cos(w);a15(i)=-f*sin(k)-g1(i,1)*(g1(i,1)*sin(k)+g1(i,2)*cos(k))/f;a16(i)=g1(i,2);a24(i)=-g1(i,1)*sin(w)-(g1(i,2)*(g1(i,1)*cos(k)-g1(i,2)*sin(k))/f-f*sin(k))*cos(w);a25(i)=-f*cos(k)-g1(i,2)*(g1(i,1)*sin(k)+g1(i,2)*cos(k))/f;a26(i)=-g1(i,1);endlx=[];ly=[];for i=1:clx(i)=g1(i,1)-xj(i);ly(i)=g1(i,2)-yj(i);endA=zeros(2*c,6);for i=1:cA(2*i-1,1)=a11(i);A(2*i-1,2)=a12(i);A(2*i-1,3)=a13(i);A(2*i-1,4)=a14(i);A(2*i-1,5)=a15 (i);A(2*i-1,6)=a16(i); A(2*i,1)=a21(i); A(2*i,2)=a22(i); A(2*i,3)=a23(i); A(2*i,4)=a24(i); A(2*i,5)=a25(i); A(2*i,6)=a26(i);endL=zeros(2*c,1);for i=1:cL(2*i-1,1)=lx(i);endX=inv((A')*A)*(A')*L;Xs=Xs+X(1,1);Ys=Ys+X(2,1);Zs=Zs+X(3,1);q=q+X(4,1);w=w+X(5,1);k=k+X(6,1);Xabs=abs(X);aaa=max(Xabs);if aaa<0.00003 %当改正数中绝对值最⼤的改正数⼩于限差0.00003 break; %后跳出循环,计算结果已经收敛endendglobal V;V=L';global WF QXX;WF(1)=Xs;WF(2)=Ys;WF(3)=Zs;WF(4)=q;WF(5)=w;WF(6)=k;QXX=A'*A;六.实验结果左⽚外⽅位元素Xs,Ys,Zs,ψ、ω、κ、为:5.0001950e+003 5.0007250e+003 2.0201583e+003 -7.2888190e-005 2.8193877e-002 9.5130388e-002左⽚外⽅位元素协因素阵为:4.0166895e-008 -3.7263703e-010 1.3218695e-008 7.0720033e-005 1.0001730e-007 -2.5748604e-006-3.7263703e-010 4.0032797e-008 2.6568407e-009 -2.1103715e-007 7.7772275e-005 1.9993587e-0051.3218695e-0082.6568407e-009 1.7931301e-0083.1008915e-005 6.6697659e-006 5.6403374e-0077.0720033e-005 -2.1103715e-007 3.1008915e-005 1.3087511e-001 1.0148977e-003 -1.9981396e-003 1.0001730e-007 7.7772275e-005 6.6697659e-006 1.0148977e-003 1.5539404e-001 3.0264331e-002-2.5748604e-006 1.9993587e-005 5.6403374e-007 -1.9981396e-003 3.0264331e-002 4.0721943e-002左⽚外⽅位元素Xs,Ys,Zs,ψ、ω、κ、为:5.8967023e+003 5.0687355e+003 2.0506347e+003 1.4337709e-002 4.6257617e-0021.1037952e-001右⽚外⽅位元素协因素阵为:3.9305329e-0084.9400147e-010 -1.0339207e-008 6.8065940e-005 -4.2504770e-007 1.8461496e-0064.9400147e-010 3.9051893e-008 3.3958896e-011 -3.9945442e-008 7.6312421e-005 -1.6453951e-005-1.0339207e-008 3.3958896e-011 1.5155886e-008 -2.3705097e-005 3.5940467e-007 -7.3527082e-007 6.8065940e-005 -3.9945442e-008 -2.3705097e-005 1.2229164e-001 -2.3449223e-003 4.8281474e-003-4.2504770e-007 7.6312421e-005 3.5940467e-007 -2.3449223e-003 1.5233230e-001 -2.5374659e-0022.5374659e-0023.6794789e-002GCP在左⽚和右⽚改正后的坐标(x,y)为:1.6019582e-002 7.9954660e-002 -7.3934212e-002 7.8699356e-0028.8559633e-002 8.1141190e-002 -5.2455612e-003 7.8187184e-0021.3352398e-002 -7.9378247e-002 -7.9125440e-002 -7.8877760e-0028.2242309e-002 -8.0017749e-002 -9.8858970e-003 -8.0086832e-002单位权中误差为:±1.515610577029578e-005所求地⾯点的三维坐标(X, Y, Z)为:5.4310348e+003 5.8851463e+003 5.4831646e+0025.1473645e+003 5.0555934e+003 4.8499600e+0025.4957931e+003 5.0826911e+003 5.0668967e+0025.8442434e+003 5.1098033e+003 5.3025650e+0025.5603279e+003 4.2870779e+003 4.6536459e+002七.⼼得体会经过三周的努⼒,这个当初看来艰巨的任务终于在我的不懈努⼒下圆满的完成了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
程序运行环境为Visual Studio2010.运行前请先将坐标数据放在debug 下。
1.单像空间后方交会C语言程序:#include <stdio.h>#include <math.h>#include <iostream>double *readdata();void savedata(int hang,double *data,double *xishuarray,double *faxishu,double *l,int i,double xs,double ys,double zs,double fai,double oumiga,double kapa);void transpose(double *m1,double *m2,int m,int n);void inverse(double *a,int n);void multi(double *mat1,double * mat2,double * result,int a,int b,int c);void inverse(double *a,int n)/*正定矩阵求逆*/{int i,j,k;for(k=0;k<n;k++){for(i=0;i<n;i++){if(i!=k)*(a+i*n+k)=-*(a+i*n+k)/(*(a+k*n+k));}*(a+k*n+k)=1/(*(a+k*n+k));for(i=0;i<n;i++){if(i!=k){for(j=0;j<n;j++){if(j!=k)*(a+i*n+j)+=*(a+k*n+j)* *(a+i*n+k);}}}for(j=0;j<n;j++){if(j!=k)*(a+k*n+j)*=*(a+k*n+k);}}}void transpose(double *m1,double *m2,int m,int n) //矩阵转置{ int i,j;for(i=0;i<m;i++)for(j=0;j<n;j++)m2[j*m+i]=m1[i*n+j];return;}void multi(double *mat1,double *mat2,double * result,int a,int b,int c) { int i,j,k;for(i=0;i<a;i++){for(j=0;j<c;j++){result[i*c+j]=0;for(k=0;k<b;k++)result[i*c+j]+=mat1[i*b+k]*mat2[k*c+j];}}return;}double *readdata(){FILE *fp;int i,j;int number;char datacatolog[100];//scanf("%s",datacatolog);if ((fp=fopen("控制点坐标.txt","r"))==NULL){printf("读取数据出错!\n");return false;}fscanf(fp,"%d",&number);double *cordata=new double[number*5];for (i=0;i<number;i++){for (j=0;j<5;j++){fscanf(fp,"%lf",cordata+i*5+j);}}printf("控制点坐标数据读取成功!\n");return cordata;}void savedata(int hang,double *data,double *xishuarray,double *faxishu,double *l,int i,double xs,double ys,double zs,double fai,double oumiga,double kapa){FILE *fp;char *file1="结算数据.txt";fp=fopen(file1,"w");fprintf(fp,"---------原始坐标数据为--------:\n");for (int i=0;i<hang;i++){for (int j=0;j<5;j++){fprintf(fp,"%7.4lf ",data[i*5+j]);}fprintf(fp,"\n");}fprintf(fp,"--------------------------------\n");fprintf(fp,"---------误差方程系数阵为:--------:\n");for (int i=0;i<hang*2;i++){for (int j=0;j<6;j++){fprintf(fp,"%7.4lf ",xishuarray[i*5+j]);}fprintf(fp,"\n");}fprintf(fp,"--------------------------------\n");fprintf(fp,"---------法方程系数阵为:--------:\n");for (int i=0;i<6;i++){for (int j=0;j<6;j++){fprintf(fp,"%7.5lf ",faxishu[i*5+j]);}fprintf(fp,"\n");}fprintf(fp,"--------------------------------\n");fprintf(fp,"---------误差方程常数项为:--------:\n");for (int i=0;i<hang*2;i++){fprintf(fp,"%lf ",l[i]);fprintf(fp,"\n");}fprintf(fp,"--------------------------------\n");fprintf(fp,"---------迭代次数为:--------:\n");fprintf(fp,"%d\n",i);fprintf(fp,"--------------------------------\n");fprintf(fp,"-----------外方位元素为:---------\n");fprintf(fp," Xs= %lf, Ys=%lf, Zs=%lf\n",xs,ys,zs);fprintf(fp," fai= %lf, oumiga=%lf, kapa=%lf\n",fai,oumiga,kapa);fprintf(fp,"--------------------------------\n");fclose(fp);return;}void main(){int i,j;int ii,jj;int diedainumber=0;double x0=0.0,y0=0.0,f=0.0;double m=50000; //估算比例尺double fai=0,oumiga=0,kapa=0,Xs=0,Ys=0,Zs=0;double R[3][3]={0.0};double X=0.0,Y=0.0,Z=0.0,L[8][1]={0.0},A[8][6]={0.0};double correct[6][1]={0.0},AT[6][8]={0.0},ATA[6][6]={0.0},ATL[6][1]={0.0};int row; //row用于存放坐标行数double *controlpoint;controlpoint=readdata();row=sizeof(controlpoint);for (i=0;i<row;i++){for (j=0;j<5;j++){printf("%3.3lf ",controlpoint[i*5+j]);}printf("\n");}/*----------内方位元素----------*/printf("请输入像片的内方位元素(mm):\n");printf("x0=");x0/=1000.0;scanf("%lf",&x0); //double类型数据要用%lfprintf("y0=");y0/=1000.0;scanf("%lf",&y0);printf("f=");scanf("%lf",&f);f=f/1000.0;/*------------------------------*///-------确定未知数初始值------for(int i=0;i<row;i++){Xs=Xs+controlpoint[i*5+2];Ys=Ys+controlpoint[i*5+3];Zs=Zs+controlpoint[i*5+4];}Xs/=row;Ys/=row;Zs=Zs/row+m*f;//-----------------------------do{diedainumber++;//---------组成旋转矩阵--------R[0][0]=cos(fai)*cos(kapa)-sin(fai)*sin(oumiga)*sin(kapa);R[0][1]=-cos(fai)*sin(kapa)-sin(fai)*sin(oumiga)*cos(kapa);R[0][2]=-sin(fai)*cos(oumiga);R[1][0]=cos(oumiga)*sin(kapa);R[1][1]=cos(oumiga)*cos(kapa);R[1][2]=-sin(oumiga);R[2][0]=sin(fai)*cos(kapa)+cos(fai)*sin(oumiga)*sin(kapa);R[2][1]=-sin(fai)*sin(kapa)+cos(fai)*sin(oumiga)*cos(kapa);R[2][2]=cos(fai)*cos(oumiga);//-----------------------------//计算系数阵和常数项for(int i=0,k=0,j=0;i<=3;i++,k++,j++){X=R[0][0]*(controlpoint[i*5+2]-Xs)+R[1][0]*(controlpoint[i*5+3]-Ys)+R[2][0]*(co ntrolpoint[i*5+4]-Zs);Y=R[0][1]*(controlpoint[i*5+2]-Xs)+R[1][1]*(controlpoint[i*5+3]-Ys)+R[2][1]*(con trolpoint[i*5+4]-Zs);Z=R[0][2]*(controlpoint[i*5+2]-Xs)+R[1][2]*(controlpoint[i*5+3]-Ys)+R[2][2]*(controlpoint[i*5+4]-Zs);L[j][0]=controlpoint[i*5+0]-(x0-f*X/Z);L[j+1][0]=controlpoint[i*5+1]-(y0-f*Y/Z);j++;A[k][0]=(R[0][0]*f+R[0][2]*(controlpoint[i*5+0]-x0))/Z;A[k][1]=(R[1][0]*f+R[1][2]*(controlpoint[i*5+0]-x0))/Z;A[k][2]=(R[2][0]*f+R[2][2]*(controlpoint[i*5+0]-x0))/Z;A[k][3]=(controlpoint[i*5+1]-y0)*sin(oumiga)-((controlpoint[i*5+0]-x0)*((control point[i*5+0]-x0)*cos(kapa)-(controlpoint[i*5+1]-y0)*sin(kapa))/f+f*cos(kapa))*cos(o umiga);A[k][4]=-f*sin(kapa)-(controlpoint[i*5+0]-x0)*((controlpoint[i*5+0]-x0)*sin(kapa) +(controlpoint[i*5+1]-y0)*cos(kapa))/f;A[k][5]=controlpoint[i*5+1]-y0;A[k+1][0]=(R[0][1]*f+R[0][2]*(controlpoint[i*5+1]-y0))/Z;A[k+1][1]=(R[1][1]*f+R[1][2]*(controlpoint[i*5+1]-y0))/Z;A[k+1][2]=(R[2][1]*f+R[2][2]*(controlpoint[i*5+1]-y0))/Z;A[k+1][3]=-(controlpoint[i*5+0]-x0)*sin(oumiga)-((controlpoint[i*5+1]-y0)*((cont rolpoint[i*5+0]-x0)*cos(kapa)-(controlpoint[i*5+1]-y0)*sin(kapa))/f-f*sin(kapa))*cos( oumiga);A[k+1][4]=-f*cos(kapa)-(controlpoint[i*5+1]-y0)*((controlpoint[i*5+0]-x0)*sin(ka pa)+(controlpoint[i*5+1]-y0)*cos(kapa))/f;A[k+1][5]=-(controlpoint[i*5+0]-x0);k++;}transpose(A[0],AT[0],8,6);multi(AT[0],A[0],ATA[0],6,8,6);inverse(ATA[0],6);multi(AT[0],L[0],ATL[0],6,8,1);multi(ATA[0],ATL[0],correct[0],6,6,1);Xs=Xs+correct[0][0];Ys=Ys+correct[1][0];Zs=Zs+correct[2][0];fai=fai+correct[3][0];oumiga=oumiga+correct[4][0];kapa=kapa+correct[5][0];}while(correct[3][0]>=6.0/206265.0||correct[4][0]>=6.0/206265.0||correct[5][0] >=6.0/206265.0);printf("迭代次数为:%d\n",diedainumber);printf("---------误差方程系数为:--------\n");for (i=0;i<8;i++){for (j=0;j<6;j++){printf("%4.4lf ",A[i][j]);}printf("\n");}printf("--------------------------------\n");printf("求解得到的外方位元素为:\n");printf(" Xs= %lf\n",Xs);printf(" Ys= %lf\n",Ys);printf(" Zs= %lf\n",Zs);printf(" fai= %lf\n",fai);printf(" oumiga= %lf\n",oumiga);printf(" kapa= %lf\n",kapa);savedata(row,controlpoint,A[0],ATA[0],L[0],diedainumber,Xs,Ys,Zs,fai,oumiga,kap a);printf("-----------------解算结束!--------------\n");system("pause");}解算结果:已知左右像片外方位元素,给出像点坐标:C语言代码:#include <stdio.h>#include <iostream>#include <math.h>double *readdata();void savedata(int hang,double *data);double *readdata(){FILE *fp;int i,j,k;int number;char datacatolog[100];char leftdata[300];//scanf("%s",datacatolog);if ((fp=fopen("像点坐标数据.txt","r"))==NULL){printf("读取数据出错!\n");system("pause");exit(0);}fscanf(fp,"%d",&number);double *c=new double[number*4];for (k=0;k<2;k++){fread(&leftdata,14,1,fp);for (i=0;i<number;i++){for (j=0;j<2;j++){fscanf(fp,"%lf",c+k*2+i*4+j);}}}fclose(fp);return c;}void savedata(int hang,double *data){FILE *fp;char *file1="地面点坐标数据.txt";fp=fopen(file1,"w");fprintf(fp,"---------像点对应地面点坐标为--------:\n");fprintf(fp,"\n");for (int i=0;i<hang;i++){fprintf(fp,"第%d点:",i+1);for (int j=0;j<3;j++){fprintf(fp,"%7.4lf ",data[i*3+j]);}fprintf(fp,"\n\n");}fprintf(fp,"-----------------------------------------");fclose(fp);return;}void main(){double *imagepoint;int row;int i,j;imagepoint=readdata();row=sizeof(imagepoint);//--------------------------------------------double f=24;f/=1000;doublefai1=-0.0061,oumiga1=0.0327,kapa1=0.1711,Ys1=397367.171,Xs1=3445820.098,Zs1=1486.212;doublefai2=0.0063,oumiga2=0.0178,kapa2=0.1489,Ys2=397367.234,Xs2=3445959.266,Zs2=1490.096;// printf("请输入左像片的外方位元素:\n");//printf("Xs1= ");//scanf("%lf",&Xs1);//printf("Ys1= ");//scanf("%lf",&Ys1);//printf("Zs1= ");//scanf("%lf",&Zs1);//printf("fai1= ");//scanf("%lf",&fai1);//printf("oumiga1= ");//scanf("%lf",&oumiga1);//printf("kapa1= ");//scanf("%lf",&kapa1);//printf("请输入右像片的外方位元素:\n");//printf("Xs2= ");//scanf("%lf",&Xs2);//printf("Ys2= ");//scanf("%lf",&Ys2);//printf("Zs2= ");//scanf("%lf",&Zs2);//printf("fai2= ");//scanf("%lf",&fai2);//printf("oumiga2= ");//scanf("%lf",&oumiga2);//printf("kapa2= ");//scanf("%lf",&kapa2);double Bx=Xs2-Xs1,By=Ys2-Ys1,Bz=Zs2-Zs1;double N1=0,N2=0;double X1=0,Y1=0,Z1=0,X2=0,Y2=0,Z2=0;double R1[3][3]={0.0};double R2[3][3]={0.0};double GEOdata[4][3]={0.0};for (i=0;i<row;i++){//---------组成左影像旋转矩阵--------R1[0][0]=cos(fai1)*cos(kapa1)-sin(fai1)*sin(oumiga1)*sin(kapa1);R1[0][1]=-cos(fai1)*sin(kapa1)-sin(fai1)*sin(oumiga1)*cos(kapa1);R1[0][2]=-sin(fai1)*cos(oumiga1);R1[1][0]=cos(oumiga1)*sin(kapa1);R1[1][1]=cos(oumiga1)*cos(kapa1);R1[1][2]=-sin(oumiga1);R1[2][0]=sin(fai1)*cos(kapa1)+cos(fai1)*sin(oumiga1)*sin(kapa1);R1[2][1]=-sin(fai1)*sin(kapa1)+cos(fai1)*sin(oumiga1)*cos(kapa1);R1[2][2]=cos(fai1)*cos(oumiga1);//-----------------------------------//---------组成右影像旋转矩阵--------R2[0][0]=cos(fai2)*cos(kapa2)-sin(fai2)*sin(oumiga2)*sin(kapa2);R2[0][1]=-cos(fai2)*sin(kapa2)-sin(fai2)*sin(oumiga2)*cos(kapa2);R2[0][2]=-sin(fai2)*cos(oumiga2);R2[1][0]=cos(oumiga2)*sin(kapa2);R2[1][1]=cos(oumiga2)*cos(kapa2);R2[1][2]=-sin(oumiga2);R2[2][0]=sin(fai2)*cos(kapa2)+cos(fai2)*sin(oumiga2)*sin(kapa2);R2[2][1]=-sin(fai2)*sin(kapa2)+cos(fai2)*sin(oumiga2)*cos(kapa2);R2[2][2]=cos(fai2)*cos(oumiga2);//-------------像空辅系坐标-------------X1=R1[0][0]*imagepoint[i*4+0]+R1[0][1]*imagepoint[i*4+1]-R1[0][2]*f;Y1=R1[1][0]*imagepoint[i*4+0]+R1[1][1]*imagepoint[i*4+1]-R1[1][2]*f;Z1=R1[2][0]*imagepoint[i*4+0]+R1[2][1]*imagepoint[i*4+1]-R1[2][2]*f;X2=R2[0][0]*imagepoint[i*4+2]+R2[0][1]*imagepoint[i*4+3]-R2[0][2]*f;Y2=R2[1][0]*imagepoint[i*4+2]+R2[1][1]*imagepoint[i*4+3]-R2[1][2]*f;Z2=R2[2][0]*imagepoint[i*4+2]+R2[2][1]*imagepoint[i*4+3]-R2[2][2]*f;//--------------------------------------//------------点投影系数-------------N1=(Bx*Z2-Bz*X2)/(X1*Z2-Z1*X2);N2=(Bx*Z1-Bz*X1)/(X1*Z2-Z1*X2);//-----------------------------------//------------计算地面点坐标------------GEOdata[i][0]=Xs1+N1*X1;GEOdata[i][1]=Ys1+By+N2*Y2;GEOdata[i][2]=Zs1+N1*Z1;//--------------------------------------}//--------------------------------------------for (i=0;i<4;i++){printf("第%d个地面点坐标:",i+1);for (j=0;j<3;j++){printf("%lf ",GEOdata[i][j]);}printf("\n\n");}savedata(row,GEOdata[0]);system("pause");}测试结果:3.单模型光束法严密平差缺少已知数据进行验证,因此如果有已知数据请代入已知数据进行验证。
