北理工自控实验三
北理工自动控制理论实验报告

北理工自动控制理论实验报告摘要:本实验主要研究和探索自动控制理论在北理工的应用。
通过实验验证控制系统在不同环境下的稳定与准确性,并针对实验结果进行分析和总结。
引言:自动控制理论是近年来快速发展的学科之一,广泛应用于工业自动化系统、航空航天、交通运输等领域。
在北理工学习自动控制理论的过程中,本实验通过搭建实验系统,验证了自动控制理论的实际应用。
实验目的:1.验证控制系统的稳定性;2.检测不同环境下控制系统的输出准确性;3.分析控制系统参数的优化方法。
实验原理:本实验使用PID控制器来实现对控制系统的控制。
PID控制器是一种常见且广泛应用的控制方式,具有简单且高效的优点。
PID控制器的原理是根据系统测量值与期望值的误差计算出一个综合的控制值,通过反馈作用对系统进行调整。
其中,P项(比例项)、I项(积分项)和D项(微分项)表示了系统的偏差、系统稳定性和系统响应速度。
实验装置:实验所需的装置包括一台控制系统、传感器和执行器。
控制系统通过传感器获取反馈信号,将其与期望值进行比较,并通过执行器调节控制系统的输出。
实验步骤:1.搭建实验系统,包括控制器、传感器和执行器;2.设定期望值,将期望值输入控制系统;3.设置控制器参数,并将其与控制系统连接;4.开始实验,记录系统的输出值;5.对实验结果进行分析和总结。
实验结果:实验中记录了不同环境下控制系统的输出值,并与期望值进行比较。
结果表明,控制系统在不同环境下都能保持稳定,且输出值与期望值的误差在可接受范围内。
通过分析实验结果,总结出了一些优化控制系统参数的方法,如调整P、I、D参数的比例,根据实际需求对系统进行调整等。
结论:本实验通过对自动控制理论的实际应用进行研究和探索,验证了控制系统在不同环境下的稳定性和准确性。
实验结果表明,自动控制理论在北理工的应用具有较高的实效性和可行性。
本实验的结果对进一步优化控制系统参数和提高系统稳定性具有一定的指导意义。
[1]张三.自动控制理论与应用[M].北京:XXXX。
北理工 自动化 微机原理实验一

微型计算机原理与接口技术软件实验报告(一)班级:学号:姓名:2012.11一、实验题目1、学习并掌握IDE86集成开发环境的使用;2、参考书例4-8,以单步形式观察程序的执行过程;3、修改该程序,求出10个数中的最大值和最小值。
以单步形式观察如何求出最大值、最小值。
二、实验目的1、熟悉IDE86集成开发环境的使用。
2、通过编程、上机调试,进一步理解汇编语言的设计思路与执行过程。
3、锻炼动手编程,独立思考的能力。
三、实验内容3.1题目2设计思路及流程图3.1.1设计思路为实现求和的功能,首先将十个数存入内存中,设定AX为计算结果存储单元,CX为计数器,随后建立循环,将每个数依次加到AX上,直至CX=O,最后将AX中存储的结果移动到SUM存储单元中,结束程序。
3.1.2程序流程图题目2的程序流程图如图1所示:图1题目2的程序流程图3.2题目3设计思路及流程图3.2.1设计思路为实现求取最大值最小值的功能,首先将十个数存入内存中,设定CX为计数器,将第一个数分别存入到MAX与M1N储存单元中,随后建立循环,将每个数依次与MAX(MIN)相比较,如果有大于(小于)MAX(MIN)中的,移入相应存储单元,直至CX=0。
最后将MAX和MIN中存储的数据打印在屏幕上,返回DoS系统,结束程序。
3.2.2程序流程图题目3的程序流程图如图2所示:图2题目3的程序流程图4.1题目2源程序DATA SEGMENT ;定义数据段TAB1E DB12H,23H,34h,45h,56h ;10个加数DB67H,78H z89H z9AH z0FDHSUM DW?DATA ENDSCODE SEGMENT ;定义代码段ASSUMECS:CoDE,DS:DATA,ES:DATASTART: MOVAX z DATAMOVDS,AX ;初始化DSMOVES,AX ;初始化ES1EASUAB1E ;SI指向TAB1EMOVCX,10 ;循环计数器XORAX z AX ;AX为中间结果NEXT: ADDA1z[SI] ;把一个数加到A1中ADCAH z O ;若有进位,则加到AH中INCSI ;指向下一个数1OOPNEXT ;若未加完,继续循环MOVSUM Z AX ;若结束,存结果于SUMH1T ;结束CODE ENDS ;代码段结束END START ;汇编结束DATA SEGMENT ;定义数据段TAB1E DB12H,23H,34h,45h,56h;十个待比较数DB67H,78H,89H,9AH,0FDHMAX DB?MIN DB?A DB,MaxOS ;屏幕提示字符串B DBoDH,0AH「Min:,SDATA ENDSCODE SEGMENT;定义代码段ASSUMECS:CoDE,DS:DATA,ES:DATASTART: MOVAX z DATAMOVDS,A× ;初始化DSMOVES,AX ;初始化ES1EASIJAB1E ;SI指向TAB1EMOVCX z IO ;循环计数器XORAX z AX ;清空AXC1D ;清方向标志DF1ODSB ;A1存入一个8位数MOVMAX z A1 ;将该数送MAXMOVMIN Z A1 ;将该数送MINDECCX ;计数器减一NEXT: 1ODSB ;取下一个数CMPA1Z MAX ;与MAX比较JA1ARGERCMPA1Z MIN JBSMA11ERJMPGOON1ARGER:M0VMAX,A1JMPGOONSM A11ER:MOVMIN z A1GO ON:1OOPNEXT1EADX,AMOVAH z09HINT21HMOVA1z MAXCA11DISP1AY1EADX,BMOVAH z09HINT21HMOVA1z MINCA11DISP1AYMOVAH z4CHINT21H DISP1AYPROCPUSHBXPUSHCX ;若大于转1ARGER;否则与MIN比较;若小于转SMA11ER ;否则转GOON;A1的值存入MAX;转到GOON;A1的值存入MIN;CX-1,若CXWO转NEXT ;获取A的首地址;调用字符串显示功能;MAX值存入A1;调用显示子程序;获取B的首地址;调用字符串显示功能;MIN值存入A1;调用显示子程序;调用返回DoS功能;十六进制显示子程序;保持BX内容;保持CX内容MOVBH z A1MOV CH,2 ;设置循环计数器ROT: MOV C1,4 ;移位次数RO1 BX z C1MOV A1B1AND A1z OFH ;清空A1高四位ADD A1,30H ;0-9转换ASCII码CMP A1z3AHJ1 PRITADD A1,7H ;A-F转换ASCII码PRIT: MOV D1,A1MOV AH,2 ;调用字符显不功能INT 21HDEC CH ;计数器-1JNZ ROT ;CHW0,继续循环POPCX 丁恢复CX内容POPBX 丁恢复BX内容RET ;返回D ISP1AYENDPCODEENDS ;代码段结束END START ;结束五、实验运行结果5.1题目2运行结果前五个数运算结束后寄存器状态:图3 其中ax 值为图4前五个数计算后AX 的值故此时前五个数之和为0104Ho 前八个数运算结束后寄存器状态:×0000图6前八个数计算后AX 的值故此时前八个数之和为026CH o 全部运算结束后,ax 的值为:图7计算结束后AX 的值故十个数的和为0403H 。
北京理工大学单片机实验报告

北京理工大学实验选修课程《单片机原理与应用》课程实验报告姓名:学号:**********专业:信息工程班级:05111003实验一 P1口基本实验一、实验目的1.掌握如何建立项目,并用Keil C51软件调试程序。
二、实验内容1. P1口基本实验P1口做输出口,接八只发光二极管(如图1-1),编写程序,使发光二极管从左到右依次单个点亮,再从右至左依次单个点亮,以此循环。
各发光二极管的阳极通过保护电阻接到+5V 的电源上,阴极接到接线端口上,因此使其点亮应使相应接线端口为低电平。
三、实验原理1. P1口实验原理P1口为准双向口,P1口的每一位都能独立地定义为输入位或输出位。
作为输入位时,必须向锁存器相应位写入“1”。
2. 延时原理及计算方法常用的延时程序有两种方法,一种是用定时器中断来实现,另一种是用指令循环来实现。
用C 语言编写的延时子程序,计算延时时间时需转化为汇编语言。
针对不同的编译环境,C51编译后生成的代码不同。
针对本实验系统,若延时时间大于255ms,用C51实现可大致写出如下:unsigned int i;unsigned char j;while(i--){ for(j=0;j<60;j++){;}}若延时时间不大于255ms ,可将循环变量(i,j )定义为unsigned char ,并将内循环体中参数改为75。
四、实验代码#include<reg51.h>unsigned char L; /*L 传递亮灭的数值*/或 unsigned int i, ms; unsigned char j; for(i=0;i<ms;i++) { for(j=0;j<60;j++) {;} }delay(unsigned int ms) /*延时子程序*/{unsigned char j;unsigned int i;for(i=0;i<ms;i++){for(j=0;j<60;j++) /*内循环空操作*/{;}}}void display() /*显示输出子程序*/{P1=~L; /*LED共阳极,L取反输出*/delay(1000); /*延时1秒*/}main(){unsigned char i;L=0xFF; /*全亮*/display();L=0x00; /*全灭*/display();while(1) /*进入死循环,重复执行程序*/{L=0x01; /*LED1亮*/display();for(i=0;i<8;i++) /*LED右移8次点亮*/{L=L<<1; /*L左移1位*/display();}L=0x80; /*LED8亮*/display();for(i=0;i<8;i++) /*LED左移8次点亮*/{L=L>>1; /*L右移1位*/display();}}}五、实验心得通过这次实验我们熟悉了专用的调试环境,并练习了编写代码、编译链接、烧写程序、调试运行等一系列的实验步骤,对C51单片机有了一个初步的直观认识。
北理工:自动控制实验实验报告汇总

北理工:自动控制实验实验报告汇总控制理论基础实验(基于MATLAB)控制理论基础实验班级:05611001 学号:1120211327 姓名:付予实验时间:周五下午7、8节指导教师:范哲意1控制理论基础实验(基于MATLAB)实验一:控制系统的模型建立一、实验目的1. 掌握利用MATLAB 建立控制系统模型的方法。
2. 掌握系统的各种模型表述及相互之间的转换关系。
3. 学习和掌握系统模型连接的等效变换。
二、实验原理1.系统模型的MATLAB描述 1)传递函数(TF)模型 2)零极点增益(ZPK)模型 3)状态空间(SS)模型 4)三种模型之间的转换2. 系统模型的连接在实际应用中,整个控制系统是由多个单一的模型组合而成,基本的组合方式有串联连接、并联连接和反馈连接。
三、实验内容1. 已知控制系统的传递函数如下2s2?18s?40G(s)?3 2S?5s?8s?6试用MATLAB 建立系统的传递函数模型、零极点增益模型及系统的状态空间方程模型,并绘制系统零极点图。
实验代码: >> num=[2,18,40]; >> den=[1,5,8,6];>> gtf=tf(num,den) >> gzpk=zpk(gtf)2控制理论基础实验(基于MATLAB)>> gss=ss(gtf) >> pzmap(gzpk)实验结果:传递函数模型: gtf =x1 -5 -2 -1.5 x2 4 0 0 >> grid on2 s^2 + 18 s + 40 --------------------- s^3 + 5 s^2 + 8 s + 6零极点增益模型: gzpk =2 (s+5) (s+4) -------------------- (s+3) (s^2 + 2s + 2)状态空间方程模型: gss = a =x1 x2 x3零极点图形:x3 0 1 0 b = u1 x1 4 x2 0 x3 0 c =x1 x2 x3 y1 0.5 1.125 2.5 d = u1 y1 0 3控制理论基础实验(基于MATLAB)2.已知控制系统的状态空间方程如下?0100??0??0010??0??x???ux???0001??0? ????-1-2-3-4???1?y??10200?x试用MATLAB 建立系统的传递函数模型、零极点增益模型及系统的状态空间方程模型,并绘制系统零极点图。
北理工大学计算机实验三 字符编码与信息交换

北理工大学计算机实验三字符编码与信息交换----d6624366-6eab-11ec-b02a-7cb59b590d7d北理工大学计算机实验三字符编码与信息交换实验报告实验名称:学生编号姓名班级实验时间年月日实验报告表3-1西文字符显示过程编码记录表输入字符5a,<ASCII码(十进制数)536560内存信息(二进制)0011010101000000111100显示字体码(十六进制)0FE008000800000008001400000060018实验报告表3-2汉字显示过程代码记录表编码类型汉字输入法汉字输入码机内码(十六进制)国标码(十六进制)区位码(十六进制)字形码(十六进制)输入字符1:“字”全拼输入zid7d6h5756373600080000000600000001c0000000c0000000c0000400800c07fffffe0c00001 c0c0000101c000020380001c01输入字符2:“形状”双输入XD0BEH503E301E0000000000000000000000000002000100000703C1FFF803018300600018300C 001830183018001830100018302000018304000FFC000000038000000700000000000000000000 0000000000000000E7FFFFFFF0000600000000600000000600000000600000000600000000fe000000FC0000001C0000018308040183201E0183701C3FFFFFFFFF8380010060018300C00183 08030003030400030318060303202203000E0630301C060300380403000000E0630300C0080308 01C060300380403000C008030801001C3000FFFFFFFF380010060018300C008030000C000实验报告表3-3不同字体的字体代码“字”的字形码字体(十六进制表示)宋体00080000000600000001c0000000c0000000c0000400800c二“形”的字形码(十六进制表示)0000000000000000000020210000703c1fff80300183006007fffffe0c00001c0c0000101c0000 20380001c001ffffc0000003800000070000000c000000180000006000000060040000600e7fff ffff00006000000060000000600000006000000060000000600000006000000060000000600000 3fe000000fc0000001c000018300c001830180018301000183020001830400018308040183201e 0183701c3ffff83801830060018300c001830180018303000303040003031806030320210303000e0603001c0603003804030060040300c0080303801003060030030c00000030000000c000黑体00080000000600000001c0000000c0000000000000000000000020210000703c三0000c0000400800c07fffffe0c00001c0c0000101c000020380001c001ffffc000000380000007 0000000c000000180000006000000060040000600e7fffffff0000600000006000隶书1FF8030001830060018300C00183018001830100018302000018304000018308040183201E0183 701C3FF83801830060018300C0018301800183030003030400030318060320224。
北京理工大学自动化学院810自控2009-2013年真题详细 回忆版

2009年北理810 真题回忆2010年北京理工大学自动控制原理(810)真题(回忆版)2010年试卷总共九道大题,没有选择填空题,除六七题外,每道大题均在3问到5问之间一、二阶系统分析题目给出了一个二阶系统(带框图需要自己求传递函数)的单位阶跃响应的曲线图,让求其峰值,超调量等,这题不难,只需想到其阶跃响应应该是单位阶跃响应的积分,然后在所给曲线上找到与该图像与X轴的交点,这就是峰值时间,积分面积就是峰值,但是给出的数很怪,很影响人的情绪让人一看就不想做的那种,不过总体说来这应该算是试卷上最简单的题之一了,要分析加计算估计20分钟----25分钟。
二、系统框图分析给了一个框图,第一问让化简,它只是让证明,结果已经给了就是用平常的框图化简方法与Mason公式,我之前做了大量的框图化简的题,结果还是没证出来,应该有难度的,大家可以参考一下东北大学09年的那个框图化简题,应该有这个难度,就是知道框图但是很巧妙化Mason图很容易画错的那种,框图化简也不好弄,第二三四问然后赋予了第一问中的G(s)比较麻烦的式子,让你证明这个那个,比如说该系统对所有的某个参数都稳定啦之类,不难,思路你都会,很麻烦,一遍做对很不简单,要完整做完至少至少30分钟(如果你计算能力超强,写字很清晰的话)。
三、状态空间方法第一问还是证明,很麻烦,类似06年第二题,不过T矩阵让你自己取,然后他还给你了一个取矩阵的方法,也是很麻烦,不过如若你线性代数学得好的话,你可以根据给的那个方法一眼抽出该矩阵怎么取,不过计算量超大的,那个变换后的A矩阵,应该是T的逆乘A乘T,这里面T是4*4矩阵,A是含t的约旦标准型,结果可以从试卷这边写到那边,这一问做出来,至少20分钟,后面还有三问,判断可控客观性什么的,这个简单,但通篇做出来,至少30分钟吧。
四、根轨迹方法:用了第一题还是第二个题的框图来着,忘了,让画根轨迹,非最小相位环节的,两个复数零点两个开环零点,光求那个分离点,四个分母通分化简嘛,何况还是复数的,每个通分后都是三项,求出分离点就二十分钟没了,何况还要求什么入射角出射角什么的,第一问保守35分钟,第二问第三问没心情做了,当时一看时间过去一大半了,铁定做不完了,让证明对所有什么都稳定之类,当时脑子糊糊,没啥思路,应该要转个弯的。
北理工控制考研书目

北理工控制考研书目
(实用版)
目录
1.北京理工大学控制考研的书目列表
2.每本书的主要内容和重点
3.如何有效地利用这些书目进行复习
正文
对于准备北京理工大学控制考研的同学来说,了解并掌握考试所需的书目是至关重要的。
以下是一些主要的控制考研书目:
1.《自动控制原理》
2.《现代控制理论》
3.《控制理论》
4.《工业过程控制》
5.《检测与仪表》
《自动控制原理》是一本经典的控制理论教材,主要介绍了自动控制的基本原理和方法。
这本书的重点内容包括:控制系统的数学模型、时间域分析、频域分析、非线性控制系统等内容。
《现代控制理论》则从更深的层次探讨了控制理论,包括状态空间模型、线性二次型调节器、模型预测控制等。
《控制理论》这本书则从数学的角度,介绍了控制的基本理论,包括矩阵论、最优控制等。
《工业过程控制》主要介绍了工业过程中的控制方法和技术,包括PID 控制、自适应控制等。
《检测与仪表》则从工程实践的角度,介绍了检测仪表的原理和使用
方法。
要如何有效地利用这些书目进行复习呢?首先,要理解每本书的主要内容和重点,然后制定一个详细的复习计划。
在复习过程中,要将理论知识与实际应用结合起来,多做一些例题和习题,以提高自己的解题能力。
同时,也要关注历年的考试真题,以便更好地了解考试的题型和难度。
北理工自动控制理论实验报告

Gzpk = 2 (s+5) (s+4) -------------------(s+3) (s^2 + 2s + 2) Continuous-time zero/pole/gain model.
Gss = A= x1 x2 x3 B= x1 x2 x3 C= y1 D= u1 y1 0 Continuous-time state-space model. 系统零极点图 x1 x2 0.5 1.125 x3 2.5 u1 4 0 0 x1 -5 4 0 x2 x3 -2 -1.5 0 0 1 0
系统模型的连接
在实际应用中,整个控制系统是由多个单一的模型组合而成,基本的组合方式有串联连
接、并联连接和反馈连接。图 1-2 分别为串联连接、并联连接和反馈连接的结构框图和等效总 传递函数。
(a)串联系统
(b)并联系统
(c)反馈连接 在 MATLAB 中可以直接使用“*”运算符实现串联连接,使用“+”运算符实现并联连接。反馈系 统传递函数求解可以通过命令 feedback 实现,调用格式如下: T = feedback(G,H), T = feedback(G,H,sign) 其中,G 为前向传递函数,H 为反馈传递函数;当 sign = +1 时,GH 为正反馈系统传递函 数;当 sign = -1 时,GH 为负反馈系统传递函数;默认值是负反馈系统。
传递函数因式分解后可以写成:
式中 z1,z2,…,zm 称为传递函数的零点;P1,P2,…,Pn 称为传递函数的极点;k 为传递系数(系统增益) 。 在 MATLAB 中,直接用[z,p,k]矢量组表示系统,其中 z,p,k 分别表示系统的零极点及其 增益,即:z=[z1,z2,…,zm];p=[p1,p2,…,pn];k=[k]; 调用 zpk 函数可以创建 ZPK 对象模型,调用格式如下: Gzpk = zpk(z,p,k) 同样,MATLAB 提供了 zpkdata 命令用来提取系统的零极点及其增益,调用格式如下: [z,p,k] = zpkdata(Gzpk) 返回 cell 类型的零极点及增益 [z,p,k] = zpkdata (Gzpk,’v’) 返回向量形式的零极点及增益 函数 pzmap 用来求取系统的零极点或绘制系统得零极点图,调用格式如下:pzmap(G) 在 复平面内绘出系统模型的零极点图。 [p,z] = pzmap(G) 返回的系统零极点,不作图。 3) 状态空间(SS)模型
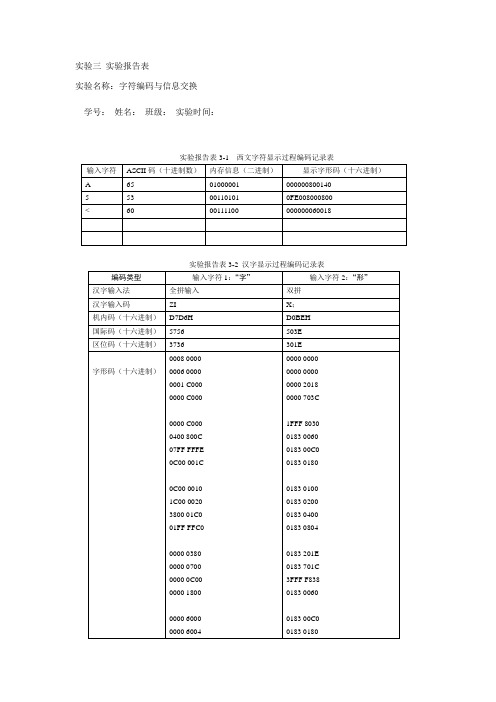
(完整word版)北京理工大学计算机实验三报告表
0000 C000
0000 C000
0400 800C
07FF FFFE
0C00 001C
0C00 0010
1C00 0020
3800 01C0
01FF FFC0
0000 0380
0000 0700
0000 0C00
0000 1800
0000 6000
0000 6004
0000 600E
0303 2007
0303 000E
0603 001C
0603 0038
0403 0060
0403 00C0
0803 0380
1003 0600
3003 0C00
0000 3000
0000 C000
实验报告表3-3不同字体的字型码
字体
“字”的字型码
(十六进制表示)
“形”的字型码
(十六进制表示)
宋体
0008 0000
0400 800C
07FF FFFE
0C00 001C
0C00 0010
1C00 0020
3800 01C0
01FF FFC0
0000 0380
0000 0700
0000 0C00
0000 1800
0000 6000
0000 6004
0000 600E
7FFF FFFF
0000 6000
0000 6000
7FFF FFFF
0000 6000
0000 6000
0000 6000
0000 6000
0000 6000
0000 6000
0000 6000
0000 6000
北理工自控实验三

实验3 根轨迹分析一、实验目的1. 学习和掌握利用MATLAB 绘制根轨迹图的方法。
2. 学习和掌握利用系统根轨迹图分析系统的性能。
二、实验原理1. 根轨迹分析的 MATLAB 实现根轨迹是指系统某一参数变化时,闭环特征根在s 平面上运动的轨迹。
在MATLAB 中,提供了用于根轨迹分析的专门函数。
1)rlocus 函数该函数的使用方法如下:rlocus(sys) 绘制单输入单输出LTI 系统的根轨迹图。
rlocus(sys,k) 使用用户指定的根轨迹增益k 来绘制系统的根轨迹图。
[r,k] = rlocus(sys) 返回根轨迹增益值和闭环极点值,不绘制根轨迹图 2)rlocfind 函数该函数的使用方法如下:[k,poles]=rlocfind(sys) 计算鼠标选取点处的根轨迹增益值和闭环极点值,可在图形窗口根轨迹图中显示出十字光标,当用户选择其中一点时,相应的增益值和极点值记录在k 和poles 中。
[k,poles]=rlocfind(sys,p) 计算最靠近给定闭环极点p 处的根轨迹增益。
3)sgrid 函数该函数的使用方法如下:sgrid 可在连续系统根轨迹或零极点图上绘制出栅格线,栅格线由等阻尼系数和等自然频率线构成。
sgrid(’new’) 先清除当前的图形,然后绘制出栅格线,并将坐标轴属性设置成hold on 。
sgrid(z,Wn) 指定阻尼系数z 和自然频率Wn 。
sgrid(z,Wn,’new’) 指定阻尼系数z 和自然频率Wn ,在绘制栅格线之前清除当前的图形并将坐标轴属性设置成hold on 。
三、实验内容1. 已知系统开环传递函数为(s 5)(s)(s 1)(s 3)(s 12)K G +=+++(1)使用MATLAB 绘制系统的根轨迹图。
(2)求根轨迹的两条分支离开实轴时的K 值,并确定该K 值对应的所有闭环极点。
(3)以区间[-40,-5]之间的值替代s = −12处的极点,重新绘制根轨迹图,观察其对根轨迹图的影响。
北理自控实验报告共21页文档

控制理论基础实验姓名:班级:学号:专业:控制理论基础实验 ______________________________________________________________ 1实验一控制系统的模型建立 _____________________________________________________ 2实验二控制系统的暂态特性分析 ________________________________________________ 10实验三根轨迹分析 ____________________________________________________________ 13实验四系统的频率特性分析 ____________________________________________________ 19实验一 控制系统的模型建立一、实验目的1.掌握利用matlab 建立控制系统模型的方法2.掌握系统的各种模型表述及相互之间的转换关系3.学习和掌握系统模型连接的等效转换二、实验原理1.系统模型的matlab 综述系统的模型描述了系统的输入、输出变量以及内部各变量之间的关系,主要有系统传递函数(TF )模型、零极点增益(ZPK )模型和状态空间(ss )模型传递函数①传递函数模型传递函数是描述线性定常系统输入-输出关系的一种最常用得数学模型,其表达式一般为 在matlab 中,直接使用分子分母多项式的行向量表示系统,即调用tf 函数可以建立传递函数TF 对象模型,调用格式如下:gtf=tf (num ,den )②零极点增益模型传递函数因式分解后可以写成式中,12,,...m z z z 称为传递函数的零点,12,,...m p p p 称为传递函数的极点,k 为传递系数(系统增益)在matlab 中,直接用[z,p,k]矢量组表示系统,其中z ,p ,k 分别表示系统的零极点及其增益,即:z=[12,,...m z z z ] p=[12,,...m p p p ] k=[k]调用zpk 函数可以创建zpk 对象模型,调用格式如下:gzpk=zpk(z,p,k)pzmap(g)在复平面内绘出系统模型的零极点图③状态空间(ss)模型由状态变量描述的系统模型称为状态空间模型,由状态方程和输出方程组成:其中x为n维状态向量,u为r维输入向量,y为m维输出向量,A为n×n方阵,称为系统矩阵,B为n×r矩阵,称为输入矩阵或控制矩阵,C为m×n矩阵,称为输出矩阵,D为m×r 矩阵,称为直接传输矩阵在matlab中,直接用矩阵组[A,B,C,D]表示系统,调用ss函数可以创建zpk对象模型,调用格式如下:gss=ss(A,B,C,D)④三种模型之间的转换Matlab实现方法如下:TF模型→ZPK模型:zpk(sys)或tf2zp(num,den)TF模型→SS模型:ss(sys)或tf2ss(num,den)ZPK模型→TF模型:tf(sys)或zp2tf(z,p,k)ZPK模型→SS模型:ss(sys)或zp2ss(z,p,k)SS模型→TF模型:tf(sys)或ss2tf(A,B,C,D)SS模型→ZPK模型:zpk(sys)或ss2zp(A,B,C,D)2.系统模型的连接串联系统G(s)=G1(s)G2(s)并联系统G(s)=G1(s)+G2(s)反馈连接T(s)=G(s)/(1+G(s)H(s))U(s) Y(s)G(s)=(s )(s )⊕ G(s)=(s )+((b) 并联系统⊕反馈连接图1-1串联、并联和反馈连接在matlab 中可以直接使用“*”运算符实现串联连接,使用“+”运算符实现并联连接,反馈系统传递函数求解可以通过命令feetback 实现,调用格式如下:T=feedback (G ,H )T=feedback (G ,H ,sign )其中,G 为前向传递函数,H 为反馈传递函数,当sign=+1时,GH 为正反馈系统传递函数;当sign=-1时,GH 为负反馈系统传递函数,默认值是负反馈系统。
北理工自控原理实验三 三阶系统的稳定性和瞬态响应

由表格看出,惯性时间常数T1和T2的增大,均会导致系统临界稳定时的K值减小。在超调量相同( 相同)的衰减振荡中,T1和T2的增大,将导致增益K减小。
五,思考题
1,改变被测系统的电路参数,从而改变闭环系统的极点,观察对比前后响应曲线,分析各级点对系统过渡过程的影响?
4、了解和掌握利用MATLAB的开环根轨迹求解系统的性能指标的方法。
二,实验结果数据
一型三阶系统的模拟电路图如下:
I型三阶系统的开环传递函数为
G(s)=
闭环传递函数(单位反馈)为
积分时间常数Ti=R1*C1=1S,惯性时间常数T1=R3*C2=0.1S,
K1=R3/C2=1,T2=R4*C3=0.5S,K=R4/R=500KΩ/R
自动Байду номын сангаас制理论实验
——三阶系统的稳定性和瞬态响应
姓名
学号:
班级:
实验日期:
一、实验目的
1、了解和掌握典型三阶系统模拟电路的构成方法及I型三阶系统的传递函数表达式。
2、了解和掌握求解高阶闭环系统临界稳定增益K的多种方法(劳斯稳定判据法、代数求解法、MATLAB根轨迹求解法)。
3、观察和分析I型三阶系统在阶跃信号输入时,系统的稳定、临界稳定及不稳定三种瞬态响应。
(3)当可变电阻分别为R=30 kΩ,此时系统不稳定,发散振荡。
输出波形如下:
三,数据分析
用matlab画出G(S)= 的根轨迹
根轨迹与虚轴交点是s=4.45j和-4.45j,此时的根轨迹增益K=11.9813
(1)当0<K<12时,由于K=R4/R,随着R的增大,K值减小,则根轨迹越来越远离虚轴。此时由于 ,当远离虚轴时,易知 增大,即 。由于Ts= , 增大,故Ts减小。即随着R的增大,调节时间变小。
北京理工大学 控制理论基础实验报告

控制理论基础实验1.控制系统的模型建立2.控制系统的暂态特性分析3.根轨迹分析4.系统的频率特性分析一、实验目的实验一1.掌握利用MATLAB建立控制系统模型的方法。
2.掌握系统的各种模型表述及相互之间的转换关系。
3.学习和掌握系统模型连接的等效变化。
实验二1.学习和掌握利用MATLAB进行系统时域响应求解和仿真的方法。
2.考察二阶系统的时间响应,研究二阶系统参数对系统暂态特性的影响。
实验三1.学习和掌握利用MATLAB绘制根轨迹图的方法2.学习和掌握利用系统根轨迹图分析系统的性能。
实验四1.学习和掌握利用MATLAB绘制系统Nyquist图和Bode图的方法。
2.学习和掌握利用系统的频率特性分析系统的性能。
二、实验原理1)传递函数模型(TF)gtf=tf(num,den)2)零极点增益模型(ZPK)Gzpk=zpk(z,p,k)3)状态空间模型(SS)Gss=ss(a,b,c,d)4)三种模型之间的转换TF→ZPK:z pk(sys)TF→SS:ss(sys)ZPK→TF:t f(sys)ZPK→SS:s s(sys)SS→TF:tf(sys)SS→ZPK:z pk(sys)5)绘制系统零极点图Pzmap(gzpk);Grid on;6)系统模型的串联G(s)=G1(s)*G2(s)7)系统模型的并联G(s)=G1(s)+G2(s)8)系统模型的反馈连接T=feedback(G,H)T=feedback(G,H,sign)9)绘制阶跃响应step(sys)step(sys,T)10)线性时不变系统仿真工具ltiview11)绘制系统根轨迹图rlocus(sys)rlocus(sys,k)[r,k]=rlocus(sys)12)计算鼠标选择点处根轨迹增益值和闭环极点值[k,poles]=rlocfind(sys)13)在连续系统根轨迹或零极点图上绘制出栅格线sgrid(‘new’)sgrid(z,Wn)14)绘制系统的Nyquist图nyquist(SYS)nyquist(sys,w)15)绘制系统的Bode图bode(sys)bode(sys,w)16)从频率响应数据中计算幅度裕度,相位裕度及对应角频率margin(sys)[mag,phase]=bode(sys,w)三、实验结果实验一1)零极点图2)零极点图3)总串联函数Transfer function:10 s^6 + 170 s^5 + 1065 s^4 + 3150 s^3 + 4580 s^2 + 2980 s + 525---------------------------------------------------------------------------------------------------------------------- s^9 + 24 s^8 + 226 s^7 + 1084 s^6 + 2905 s^5 + 4516 s^4 + 4044 s^3 + 1936 s^2 + 384 s 4)闭环传递函数Transfer function:2.25 s^2 + 7.5 s + 6-------------------------------------------------------0.25 s^4 + 1.25 s^3 + 2 s^2 + 5.5 s + 65)闭环传递函数Transfer function:20 s^3 + 160 s^2 + 400 s + 320-------------------------------------------------------------------------s^6 + 10 s^5 + 35 s^4 + 44 s^3 + 82 s^2 + 116 s - 48%1num=[2 18 40]; den=[1 5 8 6]; gtf=tf(num,den) gzpk=zpk(gtf) gss=ss(gtf) pzmap(gzpk);grid on%2a=[0 1 0 00 0 1 00 0 0 1-1 -2 -3 -4];b=[0 0 0 0]’;c=[10 2 0 0];d=0;gss=ss(a,b,c,d); gtf=tf(gss); gzpk=zpk(gss); pzmap(gzpk)grid on%3g1a=[2 6 5]; g1b=[1 4 5 2];g2a=[1 4 1];g2b=[1 9 8 0];g3z=[-3 -7];g3p=[-1 -4 -6];g3k=5;g1tf=tf(g1a,g1b);g2tf=tf(g2a,g2b);g3zpk=zpk(g3z,g3p,g3k);g3tf=tf(g3zpk);g=g1tf*g2tf*g3tf%4g1=tf([1],[1 1]);g2=tf(1,[0.5 1]);g3=g2;g4=tf(3,[1 0]);g=feedback((g1+g2)*g4,g3)%5g1=tf(10,[1 1]);g2=tf(2,[1 1 0]);g3=tf([1 3],[1 2]);g4=tf([5 0],[1 6 8]);g=feedback(g1*(feedback(g2, g3,1)),g4)实验二12(1)t d=0.272 t r=0.371 t p=0.787 t s=1.19ϭ=9%(2)(3)(4)ξ变大,延迟时间,上升时间,峰值时间,调整时间均越来越长,超调量开始时减小,然后保持不变。
北理工自控实验报告
本科实验报告实验名称:控制理论基础实验课程名称:控制理论基础实验时间:任课教师:实验地点:实验教师:实验类型:□原理验证□综合设计□自主创新学生姓名:学号/班级:组号:学院:同组搭档:专业:成绩:实验1 控制系统的模型建立一、实验目的1、掌握利用MATLAB 建立控制系统模型的方法。
2、掌握系统的各种模型表述及相互之间的转换关系。
3、学习和掌握系统模型连接的等效变换。
二、实验原理1、系统模型的 MATLAB描述系统的模型描述了系统的输入、输出变量以及内部各变量之间的关系,表征一个系统的模型有很多种,如微分方程、传递函数模型、状态空间模型等。
这里主要介绍系统传递函数(TF)模型、零极点增益(ZPK)模型和状态空间(SS)模型的MATLAB 描述方法。
1)传递函数(TF)模型传递函数是描述线性定常系统输入-输出关系的一种最常用的数学模型,其表达式一般为在MATLAB 中,直接使用分子分母多项式的行向量表示系统,即num = [bm, bm-1, … b1, b0];den = [an, an-1, … a1, a0];调用tf 函数可以建立传递函数TF 对象模型,调用格式如下:Gtf = tf(num,den);Tfdata 函数可以从TF 对象模型中提取分子分母多项式,调用格式如下:[num,den] = tfdata(Gtf) 返回cell 类型的分子分母多项式系数;[num,den] = tfdata(Gtf,'v') 返回向量形式的分子分母多项式系数;2)零极点增益(ZPK)模型传递函数因式分解后可以写成式中, z1 , z2, …,z m称为传递函数的零点, p1,p2,…,p n称为传递函数的极点,k 为传递系数(系统增益)。
在MATLAB 中,直接用[z,p,k]矢量组表示系统,其中z,p,k 分别表示系统的零极点及其增益,即:z=[z1,z2,…,zm];p=[p1,p2,…,pn];k=[k];调用zpk 函数可以创建ZPK 对象模型,调用格式如下:Gzpk = zpk(z,p,k)同样,MATLAB 提供了zpkdata 命令用来提取系统的零极点及其增益,调用格式如下:[z,p,k] = zpkdata(Gzpk) 返回cell 类型的零极点及增益;[z,p,k] = zpkdata(Gzpk,’v’) 返回向量形式的零极点及增益;函数pzmap 可用于求取系统的零极点或绘制系统得零极点图,调用格式如下:pzmap(G) 在复平面内绘出系统模型的零极点图。
北京理工大学自动控制matlab实验报告概要

软件工具在控制系统分析和综合中的应用实验MATLAB 班级:01811001学号:1120100209姓名:戚煜华一、试验目的:1.了解MATLAB这种强大的数学软件的基本特点和语言特点。
2.掌握控制系统在MATLAB中的描述。
3.学会用MATLAB的Control工具箱中提供的仿真函数,例如连续时间系统在阶跃输入激励下的仿真函数step(),脉冲激励下的仿真函数impulse()等。
4掌握典型一阶、二阶系统中参数的变化对阶跃响应曲线的影响;5掌握使用MATLAB绘制控制系统的根轨迹图,并了解附加开环零、极点对闭环根轨迹的影响。
6.学会使用MATLAB绘制系统频率特性曲线—乃氏图和伯德图,并利用MATLAB 求出系统的稳定裕度。
7.掌握系统串联校正后,开环指标及时域响应指标的变化规律。
二、试验设备:一台装有MATLAB软件的电脑三、试验内容:1为例,令T=0.1,1,10,绘制其单位阶跃响应曲线,并?(Gs) 2.以传函1Ts?总结给出惯性时间常数对阶跃响应影响的结论。
时的单位阶跃响应曲线T=0.1T=1时的单位阶跃响应曲线T=10时的单位阶跃响应曲线结论:惯性时间常数T越大,上升时间、调节时间和延迟时间越长。
2?分,,,,为对象,令,n?s)=1=030.2.0.5以传函1G1.5(??n???nn22?2ss?分别绘制阶跃响应曲线,进行,,,别绘制阶跃响应曲线。
令101=0.1=0.7??n对二阶阶跃响应的影响分析。
、??n :,=0=1??n时,分析:=1?n?,零阻尼,响应为无阻尼等幅振荡;=0??的增大,振荡幅值减小,响应速度变慢,超调量和,欠阻尼,随着0.5=0.2减小;?,临界阻尼,响应变慢,超调和振荡消失;=1?,过阻尼,系统没有超调,且过渡时间较长。
=1.5??以后,系统没有了超越大,振荡幅值越小,过渡时间越长;综上所述,>=1?对二阶系统的影响是改变系统的振荡幅值和过渡时调和振荡。
北理工:自动控制实验实验报告汇总

控制理论基础实验班级:05611001学号:1120101327姓名:付予实验时间:周五下午 7、8节指导教师:范哲意实验一:控制系统的模型建立一、实验目的1. 掌握利用MATLAB 建立控制系统模型的方法。
2. 掌握系统的各种模型表述及相互之间的转换关系。
3. 学习和掌握系统模型连接的等效变换。
二、实验原理1. 系统模型的MATLAB描述1)传递函数(TF)模型2)零极点增益(ZPK)模型3)状态空间(SS)模型4)三种模型之间的转换2. 系统模型的连接在实际应用中,整个控制系统是由多个单一的模型组合而成,基本的组合方式有串联连接、并联连接和反馈连接。
三、实验内容1.已知控制系统的传递函数如下22s 18s 40G(s)3 2S 5s 8s 6试用MATLAB建立系统的传递函数模型、零极点增益模型及系统的状态空间方程模型, 并绘制系统零极点图。
实验代码:>> num=[2,18,40];>> den=[1,5,8,6];>> gtf=tf(num,den)>> gzpk=zpk(gtf)实验结果:传递函数模型:gtf =2 s A2 + 18 s + 40s A3 + 5 sA2 + 8 s + 6零极点增益模型:gzpk =2 (s+5) (s+4)(s+3) (sA2 + 2s + 2)状态空间方程模型:gss = >> gss=ss(gtf)>> pzmap(gzpk)>> grid ona =x1x2x3 x1-5-2 1.5x2400x3010b =u1x14x20x3c =x1x2x3 y10.5 1.125 2.5u1=y1 0零极点图形:Pole-Zero Ntato2•已知控制系统的状态空间方程如下0 10 0 0 0 0 10 0 xx u0 0 0 1 0-1 -2 -3 -4 1y 10 2 0 0x试用MATLAB 建立系统的传递函数模型、零极点增益模型及系统的状态空间方程模型,并绘制系统零极点图。
北理工自动控制实验报告,DOC

本科实验报告实验名称:控制理论基础实验)模型、1)传递函数(TF)模型传递函数是描述线性定常系统输入-输出关系的一种最常用的数学模型,其表达式一般为在MATLAB中,直接使用分子分母多项式的行向量表示系统,即num=[bm,bm-1,…b1,b]den=[an,an-1,…a1,a0]调用tf函数可以建立传递函数TF对象模型,调用格式如下:Gtf=tf(num,den)Tfdata函数可以从TF对象模型中提取分子分母多项式,调用格式如下:[num,den]=tfdata(Gtf)返回cell类型的分子分母多项式系数[num,den]=tfdata(Gtf,'v')返回向量形式的分子分母多项式系数2)零极点增益(ZPK)模型传递函数因式分解后可以写成式中,称为传递函数的零点,?称为传递函的极点,k为传递系数(系统增益)。
在即:z=[p=[调用返回向量形式的零极点及增益函数返回的系统零极点,不作图。
3矩阵;B为n×r矩阵,称为输入矩阵或控制矩阵;C为m×n矩阵,称为输出矩阵;D为m×r矩阵,称为直接传输矩阵。
在MATLAB中,直接用矩阵组[A,B,C,D]表示系统,调用ss函数可以创建ZPK对象模型,调用格式如下:Gss=ss(A,B,C,D)同样,MATLAB提供了ssdata命令用来提取系统的A、B、C、D矩阵,调用格式如下:[A,B,C,D]=ssdata(Gss)。
它返回系统模型的A、B、C、D矩阵。
4)三种模型之间的转换上述三种模型之间可以互相转换,MATLAB实现方法如下TF模型→ZPK模型:zpk(SYS)或tf2zp(num,den)TF模型→SS模型:ss(SYS)或tf2ss(num,den)ZPK模型→TF模型:tf(SYS)或zp2tf(z,p,k)ZPK模型→SS模型:ss(SYS)或zp2ss(z,p,k)SS模型→TF模型:tf(SYS)或ss2tf(A,B,C,D)SS模型→ZPK模型:zpk(SYS)或ss2zp(A,B,C,D)2.系统模型的连接在实际应用中,整个控制系统是由多个单一的模型组合而成,基本的组合方式有串联连接、并联连接和反馈连接。
北京理工大学自动控制理论实验报告三

自动控制理论实验报告(三)——二阶开环及闭环系统的频率特性曲线班级:姓名:学号:一、实验目的1.了解和掌握Ⅰ型二阶闭环系统中的对数幅频特性)(ωL 和相频特性)(ωϕ,实频特性Re(ω)和虚频特性Im(ω)的计算。
2.了解和掌握欠阻尼Ⅰ型二阶闭环系统中的自然频率ωn 、阻尼比ξ对谐振频率ωr 和谐振峰值L(ωr )的影响及ωr 和L(ωr ) 的计算。
3.了解阻尼比ξ对开环参数幅值穿越频率ωc 和相位裕度γ的影响及幅值穿越频率ωc 和相位裕度γ的计算。
4.了解和掌握Ⅰ型二阶闭环系统对数幅频曲线、相频曲线和幅相曲线的构造及绘制方法。
二、实验原理及说明被测系统的结构图如图:图中被测系统的闭环传递函数φ(S)=)()(S R S C =)()(1)(S H S G S G + 以角频率ω为参数的闭环系统对数幅频特性和相频特性为L(ω)=20lg|φ(j ω)| φ(ω)= ∠φ(j ω)本实验以二阶闭环系统模拟电路为例,令积分时间常数为Ti ,惯性时间常数为T ,开环增益为K ,可得:自然频率:TiTK=n ω 阻尼比:KTTi21=ξ谐振频率:221ξωω-=n r 谐振峰值:2121lg20)(ξξω-=r L频率特性测试电路如图,其中惯性环节的R 用可变电阻取代。
其中输入“数/模转换OUT ”,输出“数/模转换IN ”。
计算欠阻尼二阶闭环系统中的幅值穿越频率ωc 、相位裕度γ: 幅值穿越频率:24241ξξωω-+⨯=n c相位裕度:424122arctan)(180ξξξωϕγ++-=+=cγ值越小,Mp%越大,振荡越厉害;γ值越大,Mp%小,调节时间ts 越长,因此为使二阶闭环系统不致于振荡太厉害及调节时间太长,一般希望:30°≤γ≤70°本实验以二阶闭环系统频率特性曲线为例,得:ωc =14.186 γ=34.93°二阶闭环系统模拟电路的各环节参数:积分环节的积分时间常数T i =R 1C 1=1s ,惯性环节的惯性时间常数 T=R 3C 2=0.1s ,开环增益K=R 3/R 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验3 根轨迹分析
一、实验目的
1. 学习和掌握利用MATLAB 绘制根轨迹图的方法。
2. 学习和掌握利用系统根轨迹图分析系统的性能。
二、实验原理
1. 根轨迹分析的 MATLAB 实现
根轨迹是指系统某一参数变化时,闭环特征根在s 平面上运动的轨迹。
在MATLAB 中,提供了用于根轨迹分析的专门函数。
1)rlocus 函数
该函数的使用方法如下:
rlocus(sys) 绘制单输入单输出LTI 系统的根轨迹图。
rlocus(sys,k) 使用用户指定的根轨迹增益k 来绘制系统的根轨迹图。
[r,k] = rlocus(sys) 返回根轨迹增益值和闭环极点值,不绘制根轨迹图 2)rlocfind 函数
该函数的使用方法如下:
[k,poles]=rlocfind(sys) 计算鼠标选取点处的根轨迹增益值和闭环极点值,可在图形窗口根轨迹图中显示出十字光标,当用户选择其中一点时,相应的增益值和极点值记录在k 和poles 中。
[k,poles]=rlocfind(sys,p) 计算最靠近给定闭环极点p 处的根轨迹增益。
3)sgrid 函数
该函数的使用方法如下:
sgrid 可在连续系统根轨迹或零极点图上绘制出栅格线,栅格线由等阻尼系数和等自然频率线构成。
sgrid(’new’) 先清除当前的图形,然后绘制出栅格线,并将坐标轴属性设置成hold on 。
sgrid(z,Wn) 指定阻尼系数z 和自然频率Wn 。
sgrid(z,Wn,’new’) 指定阻尼系数z 和自然频率Wn ,在绘制栅格线之前清除当前的图形并将坐标轴属性设置成hold on 。
三、实验内容
1. 已知系统开环传递函数为
(s 5)
(s)(s 1)(s 3)(s 12)
K G +=
+++
(1)使用MATLAB 绘制系统的根轨迹图。
(2)求根轨迹的两条分支离开实轴时的K 值,并确定该K 值对应的所有闭环极点。
(3)以区间[-40,-5]之间的值替代s = −12处的极点,重新绘制根轨迹图,观察其对根轨迹图的影响。
(1)实验代码: z=[-5];
p=[-1 -3 -12];
k=[1];
G=zpk(z,p,k); rlocus(G);
[k,poles]=rlocfind(G); 实验结果:
(2)
-14
-12-10-8-6-4-202
-30-20
-10
10
20
30
Root Locus
Real Axis (seconds -1)
I m a g i n a r y A x i s (s e c o n d s -1
)
K=3.38 P1=-2.12 P2=-12
(3)实验代码:
z=[-5];
for i=-40:1:-5 p=[-1 -3 i]; k=[1];
sys=zpk(z,p,k); rlocus(sys) hold on; end
实验结果:
随着s 的变大,根轨迹中分离点逐渐靠近s=-1,并且对于s=-5会有包围逐渐的变成不包围。
会使的根轨迹中的汇合点逐渐靠近s=-5,最后会消失,消失的同时会使对于s=-5变成不包围。
2. 已知系统开环传递函数为
2(s 8)
(s)(s 2)(s 8s 32)
K G s +=+++
(1)使用MATLAB 绘制系统的根轨迹图。
(2)计算两条分支进入右半平面和两条分支复数极点出发在实轴相交处的K 值。
(3)以区间[-20,-1]之间的值替代零点的位置,重新绘制根轨迹图,观察其对根轨迹图的影响。
(1)与(2)实验代码:
z=[-8];
p=[0,-2,-4+4*j,-4-4*j];
k=[1];
sys=zpk(z,p,k);
rlocus(sys)
实验结果:
进入右半平面的K值:K1=50.8 两条分支复数极点出发在实轴相交处K 值:K2=2.07*103
(3)实验代码:
p=[0,-2,-4+4*j,-4-4*j];
for i=-20:2:-1
z=[i];
k=[1];
sys=zpk(z,p,k);
rlocus(sys)
hold on;
end
实验结果:
随着零点的变大,使得根轨迹的汇合点逐渐的向原点靠近。
3. 已知单位负反馈系统的开环传递函数为
2
(s)(s 4s 5)
K G s =
++
(1)使用MATLAB 绘制系统的根轨迹图。
(2)分析使系统稳定的K 值范围和使系统无超调的K 值范围,并通过观察系统的单位阶跃响应曲线加以验证。
(1)实验代码: num=[1];
den=[1 4 5 0]; G=tf(num,den);
rlocus(G); 实验结果:
-6
-5
-4
-3
-2
-1
1
-4
-3
-2-10
12
3
4Root Locus
Real Axis (seconds -1)
I m a g i n a r y A x i s (s e c o n d s -1)
(2)
根轨迹进入右半平面的时候与虚轴的交点对应的K值为K=20,所以当K=20的时候,系统是临界稳定的。
所以当0<k<20的时候系统是稳定的。
根轨迹在实轴上的分离点所对应的K值是K=2。
所以当K=2的时候,系统是
x=,当0<k<=2阻尼比是大于等于1的,所以是有两个重实根,所以阻尼比1
过阻尼振荡,不会产生超调。
验证实验代码:
den=[1 4 5 0];
t=0:0.1:50;
for k1=20:5:50
num1=[k1];
G1=tf(num1,den);
sys1=feedback(G1,1);
step(sys1,t);
hold on;
end
den=[1 4 5 0];
t=0:0.1:50;
for k2=1:2:20
num2=[k2];
G2=tf(num2,den);
sys2=feedback(G2,1);
step(sys2,t);
hold on;
end
den=[1 4 5 0];
t=0:0.1:50;
for k3=0.1:0.1:1
num3=[k3];
G3=tf(num3,den); sys3=feedback(G3,1); step(sys3,t);
hold on;
end
分析:
K>19,系统不稳定
K>1,系统有超调
K<1,系统无超调
四、实验心得
在这次实验中,实验的是开环系统的特征方程的特征根随开环放大系数的变化而变化。
针对不同的开环放大系数对于系统的性能的影响。
在实验的时候对于《自动控制原理》这门理论课上的一些系统的知识不是很熟悉和理解,所以在做实验的时候就有一些犯糊涂。
尤其是对于根的理解。
对于出现共轭复根的时候是对应的什么阻尼比,这样的阻尼比会使系统的的根是怎样的。
对于分离点和汇合点,我们是可以从根轨迹上直接的找出来。
分离点和汇合点是系统的阻尼比为1,也就是系统产生震荡,处于临界稳定的状态。
所以我们在根轨迹上找出无超调的最大的开环放大系数的点。
对于系统稳定性的判断,则是需要理论上的临界稳定的知识储备。
系统的极点全部在频域的左半平面,那么系统就是稳定,那么特征方程的特征根在虚轴上,那么此时的开环放大系数就是使系统处于系统临界稳定的K值。
所以在根轨迹与虚轴的交点就是我们需要的临界状态。
并且通过对于零点和极点的位置改变来观察对于系统的根轨迹的影响。
通过图像生动形象的展示出极点和零点的影响。
通过实验,自己更好的掌握了根轨迹的画法,并且能够很好的利用根轨迹去分析系统的动态性能指标和稳定指标。
通过根轨迹去很好的理解系统,分析系统和掌握系统的特点。
