数学奥林匹克初中训练模拟试题附答案(一)
初中数学奥林匹克竞赛题4套带详解

初中数学奥林匹克竞赛题4套带详解初中数学奥林匹克竞赛是挑战数学天赋和才能的绝佳场所。
这种竞赛是为那些对数字和逻辑有天赋和兴趣的人所设计的。
无论是追求数学事业,还是成为一名数学家,初中数学奥林匹克竞赛都是一个巨大的机会,可以开阔思维和向高级数学的道路迈进。
本文所述的四套初中数学奥林匹克竞赛题带有详细解析,可供所有有兴趣的人参考学习。
第一套试题:平方和试题:假设我们有两个正整数 a 和 b。
如果我们写一个等式 a²+ b² = 130, 请问这个方程有多少对正整数解?解析:通过对题目的分析,我们发现 a 和 b 都是小于等于 11 的正整数,因为如果是大于 11,它们的平方数之和会大于 130。
我们可以用双重循环解决这个问题:```ans = 0for a in range(1, 12):for b in range(1, 12):if a * a + b * b == 130:ans += 1print(ans)```第二套试题:比率试题:如果 3 个大苹果的重量等于 4 个小苹果的重量,又知道3 个小苹果重量等于 2 个中等苹果的重量,那么问:如果要将 20 个中等苹果与其中 $x$ 个大苹果混合,让它们的重量相等,求出$x$ 的值。
解析:我们可以用比率法解决这个题目。
首先,根据第一个给出的条件,我们有:```3a = 4b```其中,$a$ 是大苹果的重量,$b$ 是小苹果的重量。
然后,根据第二个条件,我们可以得到:```3b = 2c```其中,$c$ 是中等苹果的重量。
现在我们只需要将 $a$ 和$c$ 的比率相等,即:```a / c = 20x / (20 - x)```通过简单的代数运算,我们可以得到:```60x = 80(20 - x)x = 16```因此,我们需要加入 $16$ 个大苹果。
第三套试题:平均值试题:32 个正整数的平均值为20,当其中一个数字被改变后,平均数变为 19.875。
初中数学奥林匹克竞赛题包括答案.docx

初中数学奥林匹克竞赛题及答案奥数题一一、选择题(每题 1 分,共 10 分)1.如果 a,b 都代表有理数,并且a+b=0 ,那么 ( ) A.a,b 都是 0B.a,b 之一是 0C.a,b 互为相反数D. a,b 互为倒数答案: C解析:令 a=2 , b= - 2,满足 2+( - 2)=0 ,由此 a、b 互为相反数。
2.下面的说法中正确的是( )A.单项式与单项式的和是单项式B.单项式与单项式的和是多项式C.多项式与多项式的和是多项式D.整式与整式的和是整式答案: D3都是单项式.两个单项式33A。
两个单项式解析: x2, x x , x2之和为 x +x 2是多项式,排除x2, 2x2之和为3x2是单项式,排除 B。
两个多项式x3+x2 与 x3-x2之和为2x3 是个单项式,排除 C,因此选 D。
3.下面说法中不正确的是( )A.有最小的自然数B.没有最小的正有理数Word资料C.没有最大的负整数D.没有最大的非负数答案: C解析:最大的负整数是-1 ,故 C 错误。
4.如果 a,b 代表有理数,并且a+b 的值大于 a- b 的值,那么( ) A.a,b 同号B.a,b 异号C.a>0D. b> 0答案: D5.大于-π并且不是自然数的整数有( )A.2 个B.3 个C.4 个D.无数个答案: C解析:在数轴上容易看出:在-π右边0的左边(包括0 在)的整数只有-3,- 2,-1 ,0 共 4 个.选 C。
6.有四种说法:甲.正数的平方不一定大于它本身;乙.正数的立方不一定大于它本身;丙.负数的平方不一定大于它本身;丁.负数的立方不一定大于它本身。
Word资料这四种说法中,不正确的说法的个数是( )A.0 个B.1 个C.2 个D. 3 个答案: B解析:负数的平方是正数,所以一定大于它本身,故 C 错误。
7.a 代表有理数,那么, a 和- a 的大小关系是( )A.a 大于- aB.a 小于- aC.a 大于- a 或 a 小于- aD. a 不一定大于- a答案: D解析:令 a=0 ,马上可以排除A、 B、 C,应选 D。
数学奥林匹克初中训练题_16_ (1)

( D) 无数Leabharlann 2. 若 2 x - 6y + xy + kx + 6 能分解为两 个一次因 式的积 , 则 整数 k 的值 有 ( ) 个. (A) 1 ( B) 2 ( C) 3 ( D) 4 3. 一名学生在用某自然数代入下面的某 个二次函数 f k ( x ) ( k = 1, 2, 3, 4) 时, 得到了 一个完全平方数 . 则他用的函数是 ( (A) f 1 ( x ) = x + 5x + 7 ( B) f 2 ( x ) = x + 7x + 10 ( C) f 3 ( x ) = x + 9x + 18 ( D) f 4 ( x ) = x + 11x + 2 4. 若正六边形 T 1 内接于 P O , 正六边形 T 2 外 切 于 P O, 则 T 1 与 T 2 的 面 积 比 为 ( ). (A) 2B3 ( B) 3B4 ( C) 4B5 ( D) 5B6 5. 设 a 、 b、 c、 d、 e 为互异正奇数. 若方程
2009 年第 1 期
3
参考答案
第一试
一、 1. D. 点 1、 2、 3 分数轴为四个区间: ( - ] , 1] , ( 1, 2] , ( 2, 3] , ( 3, + ] ) . 在每种情况下去掉绝对值符号, 共得到解 1 [ x [ 2, x = 5, 其中的有理数有无数多个. 2. B. 利用判别式或待定系数法得 k= ? 7. 3. D. 当 x 为自然数时, 有 2 2 2 ( x + 2) < x + 5x + 7< ( x + 3) , 2 2 2 ( x + 3) < x + 7x + 10< ( x + 4) , 2 2 2 ( x + 4) < x + 9x + 18< ( x + 5) . 也就 是当 x 取 自然 数时 , 函数 f 1 ( x ) 、 f 2 ( x) 、 f 3 ( x ) 都介于两个相邻的平方数之间, 故不可能是平方数. 因此 , 可能取值平方数的 2 只能是 f 4 ( x ) = x + 11x + 2. 另外 , 当 x = 23 时 , f 4 ( 23) = 784= 28 . 4. B. 如图 3, 将 T 1 、 T2 分 别看成由顶角为 120b 的 等腰 三 角形 拼 组 而成 , 则 T 1 中含有 18 个 等腰 三角形, T 2 中含有 24 个 等腰 三角 形 . 故 其 面 积 比为 18B24= 3B4.
初中数学奥林匹克模拟试卷1-10套

数学奥林匹克模拟试卷(一)一、选择题:1、已知311=-=-b b a a ,且3>+b a ,则33a b b a -的值是( )。
(A )521(B )1321(C )533(D )13332、如果二次函数()522++++=k x k x y 的图象与x 轴的两个不同交点的横坐标是正的,那么k 值应为( )(A )4>k 或5.-<k (B )45-<<-k (C )4.-≥k 或5-≤k (D )45-≤≤-k3、如图,∆ABC 为锐角三角形,BE ⊥AC 于F ,则ABCAEF S S ∆∆:的值为( )(A )A sin (B )A cos (C )A 2sin (D )A 2cos 4、方程1997111=+y x 的正整数解的组数为( ) (A )1(B )2(C )3(D )大于等于45、P 为∆ABC 内一点,PA 、PB 、PC 把∆ABC 的面积分成三等分,则P 点是∆ABC 的( )(A )内心(B )外心(C )垂心(D )重心6、抛物线122++=bx x y 与直线ab ax y 22+=的图象至多有一个交点,则的最大值是( )(A )1(B )23(C )22(D )0 二、填空题:1、已知四个实数的乘积为1,其中任意一个数与其余三个数的积的和都等于1000,则此四数的和是_________。
2、如果c yz b xz a xy ===,,,而且它们都不等于0,则222z y x ++=_________。
3、若抛物线()242+++=a x ax y 全在x 轴的上方,a 的范围是_________。
4、如图,在图形ABCD 中,AB ∥CD ,∠A=900,E 为BC 重点,GE ⊥BC 于,交DA 延长线于G ,DC=17cm ,AB=25cm ,BC=10cm ,则CE=_________。
AB CEFABC E DG三、解答题:1、已知∠ACE=∠CDE=900,点B 在CE 上,CA=CB=CD ,过点A 、C 、D 三点的圆交AB 于F ,求证:F 是∆CDE 的内心。
数学奥林匹克初中训练题1

3 + 2 + 3 + 6x y 2模拟训练数学奥林匹克初中训练题(1)第 一 试一、选择题(每小题 7 分 ,共 42 分)a = .2. 当 x = 29 - 3时 ,代数式x 4 + 5 x 3 - 3 x 2- 8 x + 91. 设 = + + z ,且 x 、y 、z 为有理数. 则 xyz = () . (A ) 3 (B ) 5 (C ) 7 (D )13 4 6 12 182. 设二次函数 f ( x ) = ax 2+ ax + 1 的图像开口向下 ,且满足 f ( f ( 1) ) = f ( 3) . 则 2 a 的值为( ) .(A ) - 3(B ) - 5(C ) - 7(D ) - 93. 方程| xy | + | x + y | = 1 的整数解的组数 为 ( ) .(A ) 2 (B ) 4 (C ) 6 (D ) 8 4. a 、b 是方程 x 2+ ( m - 5) x + 7 = 0 的两个根. 则 ( a 2 + ma + 7) ( b 2+ mb + 7) = ( ) .的值是 .3. 给定两组数 , A 组为 : 1 , 2 , , 100 ; B 组为 : 12 ,22 , ,1002. 对于 A 组中的数 x ,若有 B 组中的数 y ,使 x + y 也是 B 组中的数 , 则称 x 为“关联数”. 那么 , A 组中这样的关联 数 有 个 .4. 已知 △ABC 的三边长分别为 AB =2a 2+ 576 , BC =a 2+ 14 a + 625 , AC =a 2 - 14 a + 625 ,其中 a > 7. 则 △ABC 的面积为 .第 二 试一、(20 分) 解方程 :(A ) 365 (B ) 245 (C ) 210 (D ) 175 5. 如图 1 , Rt △ABC(12x + 5) 2( 6 x - 1) (x + 1) = 55 .2的斜边 BC = 4 , ∠ABC = 30°,以 AB 、AC 为直径分别作圆. 则这两圆的公共部分面积为( ) 图 1二、( 25 分) 如图 2 , 四边形 ABCD 中 ,∠ACB = ∠ADB = 90°, 自对角线 AC 、BD 的交点 N 作 NM ⊥AB 于点 M ,线段 AC 、MD 交于点 E , BD 、MC (A ) 2π + 3 (B ) 5π -2 3 交于点 F , P 是线 3 2 6 3 (C )5π - 3(D )2π- 3段 EF 上的任意 一点. 证明 : 点 P 6 3 到线段 CD 的距6. 从 1 ,2 , ,13 中取出 k 个不同的数 ,使这 k 个数中任两个数之差既不等于 5 ,也不等于 8. 则 k 的最大值为() . (A ) 5 (B ) 6 (C ) 7 (D ) 8二、填空题(每小题 7 分 ,共 28 分) 1. 若整系数一元二次方程x 2+ ( a + 3) x + 2 a + 3 = 0有一正根 x 1 和一负根 x 2 ,且| x 1 | < | x 2 | ,则离等于点P 到线图2段MC 、MD 的距离之和.三、(25 分) 矩形玻璃台板碎裂成一些小玻璃片,每块碎片都是凸多边形,将其重新粘合成原矩形后,有交结点30 个,其中20 个点在原矩形的周界上( 包括原矩形的四个顶点),其余10 个点在矩形内部. 在矩形的内部yz 即 2× × × × ×2007 年第 1 期 3有 45 条粘缝 ( 两个结点之间的线段算是一条粘缝 ,如图 3 所示) .试求该矩形台板 所碎裂成的各种类型 图 3 (指三角形、四边形、五 图 4图 5边形等) 的块数.说明 :若凸多边形的周界上有 n 个点 , 就将其看成 n 边形 ,例如 ,图 3 中的多边形ABCDE 要看成五边形.参 考 答 案第 一 试1. A.两边平方得将这 13 个数按照相邻两数的差为 5 或 8 排列于一个圆周上(如图 5) . 若取出的数多于 6 个 ,则必有 2 个数在圆周上相邻. 另一方面 ,可以取出适合条件的 6 个数 (任取圆周上不相邻的 6 个数即可) ,因此 , k 的最大值为 6.二 、1. - 2.因方程的两根不等 ,故Δ > 0 ,即( a + 3) 2 > 4 (2 a + 3) .解得 a > 3 或 a < - 1.又由题设条件知 ,方程的两根和与积皆负 ,即3 + 2 + 3 + 6 = x + y + z + 2 + 2+ 2xz .- ( a + 3) < 0 ,2 a + 3 < 0.根据有理数 x 、y 、z 的对称性 ,可考虑方程组x + y + z = 3 ,从而 , a > - 3 , a < -3, - 3 < a < - 23 . 2 2 xy = 2 , 2 yz = 3 , 2xz = 6 .解得 x = 1 , y = 1, z = 3 . 此 时 , xyz = 3 .而 a 为整数 ,则 a = - 2.2. 7 29 - 32.因 x =29 - 3是方程 x 2 + 3 x - 5 = 0 的根 ,则 2 2 4 2. B.注意到f (1) = 2 a + 1 , f (3) = 12 a + 1 , f ( f (1) ) = a (2 a + 1) 2+ a (2 a + 1) + 1.x 4 + 5 x 3 - 3 x 2 - 8 x + 9= ( x 2 + 3 x - 5) ( x 2 + 2 x - 4) + 14 x - 11= 14 x - 11 = 14 29 - 3- 11 = 7 2 3. 73.- 32.由 f ( f (1) ) = f (3) , 得(2 a + 1) 2+ (2 a + 1) = 12.所以 ,2 a + 1 = 3 或 - 4. 因 a < 0 , 故 2 a = - 5.3. C.因 x 、y 为整数 ,则| xy | 、| x + y | 为非负整数. 于是 ,| xy | 、| x + y | 中一个为 0 ,一个为 1. 分情形考虑得 6 组解.4. D.由 ab = 7 , a 2 + ma + 7 = 5 a , b 2 + mb + 7 = 5 b , 所以 , ( a 2 + ma + 7) ( b 2 + mb + 7) = 25 ab = 175.5. C.记两圆公共部分的面积为 S . 如图 4 ,易知S = S 扇形EAD + S 扇形FAD - S 四边形A EDF= π 12 + π ( 3) 2 - 1 2 3 = 5π - 3 . 36266. B.记 x + y = a 2 , y = b 2 , 则 1 ≤b < a ≤100.而 x = a 2 - b 2 = ( a + b ) ( a - b ) ≤100 , 因 a + b 、a -b 同奇偶 ,故 a + b ≥( a - b ) + 2.(1) 若 a - b = 1 ,则 a + b 为奇数 ,且 3 ≤a + b ≤ 99. 于是 , a + b 可取 3 ,5 ,7 ,,99 ,共 49 个值 ,这时 ,相应的 x 也可取这 49 个值.(2) 若 a - b = 2 ,则 a + b 为偶数 ,且 4 ≤a + b ≤ 50. 于是 , a + b 可取 4 ,6 ,8 , ,50 ,共 24 个值 ,这时 ,相应的 x 可取 8 ,12 ,16 , ,100 这 24 个值.其他情况下所得的 x 值均属于以上情形. 若 a - b = 奇数 ,则 a + b = 奇数. 而 x = a 2 - b 2 ≥a + b ≥3 ,归入(1) . 若 a - b = 偶数 ,则 a + b = 偶数.而 x = ( a - b ) ( a + b ) 为 4 的倍数 ,且 a - b ≥2 ,a +b ≥4 ,故 x ≥8 ,归入(2) .xy 29121 1 因此 ,这种 x 共有 49 + 24 = 73 个.4. 168.注意到AB 2 = (2 a ) 2+ 482, BC 2 = ( a + 7) 2+ 242, AC 2 = ( a - 7) 2+ 242.如图 6 , 以 AB 为斜边 , 向 △ABC 一 侧 作 直 角如图 7 ,设 PH ⊥MC 于点 H , PG ⊥MD 于点 G ,PT ⊥CD 于点 T ;过点 P 作 XY ∥MC ,交 MD 于点 X ,交 AC 于点 Y ;过点 Y 作 YZ ∥CD ,交 MD 于点 Z ,交PT 于点 R ; 再作 YH 1 ⊥MC 于点 H 1 , YT 1 ⊥CD 于点 T 1 . 由平行线及角平分线的性质得PH = YH 1 = YT 1 = RT .为证 PT = PG + PH ,只须证 PR = PG .由平行线的比例性质得 EP = EY = EZ.△ABD ,使因此 , ZP ∥DF .EFECEDBD = 2 a , AD = 48 ,图 6∠ADB = 90°.在 BD 上取点 E ,使 B E = a + 7 , ED = a - 7 ,又取 AD 的中点 F ,作矩形 EDFC 1 .因 BC 2= B E 2 + EC 2 = ( a + 7) 2+ 242= BC 2 ,AC 2 = C F 2 + A F 2 = ( a - 7) 2 + 242= AC 2 ,由于 △XYZ 与 △MCD 的对应边分别平行 , 且DF 平分 ∠MDC ,故 ZP 是 ∠XZY 的平分线.从而 , PR = PG . 因此 ,所证结论成立.三、设全部碎片中 , 共有三角形 a 3 个 , 四边形a 4 个 , , k 边形 a k 个 ( a 3 , a 4 , , a k 为非负整数) . 记这些多边形的内角和为 S 角 ,于是 ,11S 角 = a 3 ×π+ a 4 ×2π+ + a k ( k - 2)π. 故点 C 与点 C 1 重合.而 S △ABD = 48 a , S △CBD = 24 a , S △ACD = 24 ( a - 7) , 则 S △ABC = S △ABD - S △CBD - S △ACD = 168.第 二 试一、将原方程变形得(12 x + 5) 2 (12 x - 2) (12 x + 12) = 660.令 12 x + 5 = t , 则 t 2 ( t - 7) ( t + 7) = 660 , 即t 4 - 49 t 2 = 660.解得 t 2 = 60 或 t 2 = - 11 (舍去) . 另一方面 ,矩形内部有 10 个结点 ,对于每个点 ,围绕它的多边形顶角和为 2π,10 个内结点共获得 10 ×2π弧度 ;矩形边界上(不含 4 个顶点) 共有 16 个结点 ,在每个这种结点处 ,各多边形的顶角在此汇合成一个平角 ,16 个这种结点共获得 16π弧度 ;而原矩形的 4 个顶点处 ,共获得多边形碎片的 2π弧度. 因此 ,S 角 = 20π+ 16π+ 2π= 38π.于是 , a 3 + 2 a 4 + + ( k - 2) a k = 38. ①记这些多边形的边数和为 S 边 . 由于每个 n 边形有 n 条边 ,则S 边 = 3 a 3 + 4 a 4 ++ ka k .由此得 t = ±2,即有 12 x + 5 = ±2 15 .另一方面 ,在矩形内部的 45 条粘缝 ,每条都是 因此 ,原方程的根为 x 1 ,2 =- 5 ±2 15.二、如图 7 ,易知 A 、B 、C 、D 四点共圆 , B 、C 、N 、M 四点共圆 ,因此 , ∠ACD = ∠ABD = ∠MCN .故 AC 平分 ∠DCM . 同理 , BD 平分 ∠CDM .图 7两个多边形的公共边 ,故都计算了两次 ;矩形周界上的 20 条线段各被计算了一次 ,因此 ,S 边 = 2 ×45 + 20 = 110.于是 ,3 a 3 + 4 a 4 + + ka k = 110.② ②- ① 得 2 ( a 3 + a 4 ++ a k ) = 72.故 a 3 + a 4 + + a k = 36.③①- ③ 得a 4 + 2 a 5 + 3 a 6 ++ ( k - 3) a k = 2.因所有 a i ∈N ,故a 6 = a 7 == a k = 0 , a 4 + 2 a 5 = 2.所以 ,或者 a 4 = 2 , a 5 = 0 ;或者 a 4 = 0 , a 5 = 1. 综上 ,本题的解共有两种情况 , 即全部碎片共36 块 ,其中 ,或含有 34 个三角形 ,2 个四边形 ; 或含有 35 个三角形 ,1 个五边形.(陶平生 提供)15。
2025年全国中学生数学奥林匹克竞赛(预赛)模拟卷(全国高中数学联赛一试)(解析版)

2025年全国中学生数学奥林匹克竞赛(预赛)暨2025年全国高中数学联合竞赛 一试全真模拟试题1参考答案及评分标准说明:1.评阅试卷时,请依据本评分标准.填空题只设8分和0分两档;其他各题的评阅,请严格按照本评分标准的评分档次给分,不得增加其他中间档次.2. 如果考生的解答方法和本解答不同,只要思路合理、步骤正确,在评卷时可参考本评分标准适当划分档次评分,解答题中第9小题4分为一个档次,第10、11小题5分为一个档次,不得增加其他中间档次.一、填空题:本大题共8小题,每小题8分,满分64分.1.已知函数()sin()f x x 是定义在R 上的偶函数,则cos(2) 的值为 . 答案:0.解:由于()sin()f x x 是偶函数,故()2k kZ ,所以 cos(2)cos cos sin 02k k. 2.若关于z 的复系数一元二次方程2i 0()z z R 的一个根为11z =,则另一个根2z .答案:i 12. 解:由题意得201i 1 ,解得i 12.因此12i 12i z z ,所以2i 12z . 3.设数列{}n a 的通项公式为2[log ]n a n n ,其中[]x 表示不超过x 的最大整数,则{}n a 的前32项和为 .答案:631.解:事实上,22[log ][log ]n a n n n n .而当1n 时,2[log ]0n ;当2,3n 时,2[log ]1n ;当4,5,6,7n 时,2[log ]2n ;当8,9,,15n 时,2[log ]3n ;当16,17,,31n 时,2[log ]4n ;当32n 时,2[log ]5n ,因此{}n a 的前32项和为321232102142831645631S .4.已知向量,a b的最小值为 .答案:2.解:设向量,a b的夹角为 ,其中(0,) ,则. 令254()((1,1))1x f x x x ,则222(2)(21)()(1)x x f x x .因此()f x 在11,2 单调递减,1,12单调递增,所以()f x 的最小值为142f .2,此时1cos 2 . 5.在梯形ABCD 中,,2260A D C A B B ,M 为CD 边点Q (异于的中点,动点P 在BC 边上,ABP 与CMP 的外接圆交于点P ),则BQ 的最小值为 .1.解:由熟知的结论,,,ABP CMP AME 的外接圆有唯一公共点,该公共点即为题中的点Q ,故点Q 在AME 的外接圆上,如图所示.而AME 是直角三角形,故其外接圆半径1R AD .在ABD中,由余弦定理,BD ,所以BQ1,此时P 在线段BC 上,且CP .6.已知双曲线 的两条渐近线互相垂直,过 的右焦点F 且斜率为3的直线与 交于,A B 两点,与 的渐近线交于,C D 两点.若||5AB ,则||CD .答案:.7.已知某圆台的侧面是一个圆环被圆心角为90 的扇形所截得的扇环,且圆台的侧面积为2 ,则该圆台体积的取值范围是 .答案:.解:设圆台上底面为圆1O ,半径为1R ,下底面为圆2O ,半径为2R ,圆台母线为l .由圆台的侧面积为2 可得21(222)π2lR R ,故212l R R ①.由侧面展开是圆心角为90 的扇形所截得的扇环,可得 11122222l R l l R,故2144l R R ②.因此圆台的高21)h R R ,圆台的体积2222121212211(()3)V R R h R R R R R R .结合①②可得222112R R.由于210R R,故21R R.令21x R R ,则12124124x R x x R x,进而可得3134V x x .令31()34f x x x x ,则43()304f x x .因此()f x在 上单调递增,故()f x f .所以V ,即圆台体积的取值范围是 . 8.用 表示11元集合{1,2,3,,10,2024}A 的三元子集的全体.对 中任意一个三元子集{,,}()T x y z x y z ,定义()m T y ,则()T m T的值为 .答案:990.解:不妨将集合A 视为{}1,2,3,,10,11 (这是因为,将“2024”改成“11”不影响每个()()m T T 的值).对每个T ,定义*{12|}T t t T ,则*T ,且*)12()(T m T m . 由于当T 遍历 的所有三元子集时,*T 也遍历 的所有三元子集,所以**311()666C 990()()(2)T T T T m T m T m T m T .二、解答题:本大题共3小题,满分56分,解答应写出文字说明、证明过程或演算步骤.9.(本题满分16分)已知,,0a b c ,二次函数2()f x ax bx c 存在零点,求a b cb c a的最小值.解:令,b c m n a a ,则,0m n 且1a b c mn b c a m n.由题意得240b ac ,即24m n,故m .考虑11()f m m m n,则()f m在) 上单调递增.所以()a b c f m n f n n b c a,当n m 时等号成立.因此a b c b c a. 10.(本题满分20分)在ABC 中,,30AB AC BAC .在AB 边上取五等分点12345,,,,T T T T T (12345,,,,,,A T T T T T B 顺次排列).记(1,2,3,4)k k BT C k ,求31141tan tan tan tan tan tan k k k A B 的值.解:在AB 延长线上任取一点D ,记05,A DBC B ,则所求式子即为410tan tan kk k.为方便,记05,T A T B .作CH AB 于点H ,则tan (04)k k CH k T H(这里及以下,有向线段的方向约定为AB方向).注意到,30AB AC BAC ,有111112tan tan 555k k k k k k AC T H T H T T ABCH CHCH CH , 故115tan tan (tan tan (04))2k k k k k .进而4411500055tan tan (ta )n tan (tan tan 22)k k k kk k575tan tan (252126211.(本题满分20分)已知A 是抛物线22(0)y px p 上一点(异于原点),斜率为1k 的直线1l 与抛物线恰有一个公共点A (1l 与x 轴不平行),斜率为2k 的直线2l 与抛物线交于,B C两点.若ABC 是正三角形,求12k k 的取值范围.解:设(,),(,),(,)A A B B C C A x y B x y C x y .设直线):(A A AB y y t x x −=−,代入抛物线22y px 得2220A A y p y y p x t t ,故2B A p y y t. 设直线):(A A AC y y s x x ,同理可得2C A py y s. 由AB AC 知2222111)(1()B A C A y y y y t s. 不妨设,,A B C 是绕着ABC 的重心逆时针排列的,则由3BAC知s t ,代入化简得)2A A p t y t p y t.结合t 0t 时B A y y 与C A y y 同号可知A py , 又22B C B C B C y y p k x x y y,进而121112B C AA y y k p k y t s y ,代入化简得1211k k0,t . 因此121111,,00,227k k.当t时,易知AC x 轴,B 位于坐标原点,此时12122B C A y y k k y.而0,t 均不符合题意.k k 的取值范围是1(1,0)0,7.因此,12。
初中数学奥林匹克竞赛模拟试卷(八年级)

初中数学奥林匹克竞赛模拟试卷(八年级)全国初中数学奥林匹克竞赛试卷(八年级)一、选择题1、已知三点A(2,3),B(5,4),C(-4,1)依次连接这三点,则三点在同一直线上。
解析:AB的解析式为y= 3x+3,当x= -4时,y=1,即点C在直线AB上,∴选D。
2、边长为整数,周长为20的三角形个数是8个。
解析:设三角形的三边为a、b、c且a≥b≥c,a+b+c=20,a≥7,又b+c>a,2a<20a<10,又7≤a≤9,可列出(a、b、c)有:(9,9,2)(9,8,3)(9,7,4)(9,6,5)(8,8,4)(8,7,5)(8,6,6)(7,7,6)共八组,选C。
3、N=++,则N的个位数字是9.解析:的个位数字为3,的个位数字为9,的个位数字为7,∴N的各位数字为9,选C。
4、P为正方形ABCD内一点,若解析:过P作BP’⊥BP,且使BP’=BP,连P’A。
易得△P’AB≌△PBC,则P’A=PC,设PA=k,则PB=2k,PC=P’A=3k,连PP’,则Rt△PBP’中,∠P’PB=45°且PP’=22k,在△P’AP中有:P’A2=P’P2+PA2,∴∠P’PA=90°,∴∠APB=135°选B。
5、在函数y= -x(a为常数)的图象上有三点:(-1,y1)(-4,y2)(2,y3),则函数值y1,y2,y3的大小关系是y3<y1<y2.解析:-(a2+1)<0,∴在每个象限,y随x的增大而增大,因此y1<y2.又∵(-1,y1)在第二象限,而(2,y3)在第四象限,∴y3<y1,选C。
6、已知a+b+c≠0,且c=a=b。
解析:由c=a=b,可得a=b=c,代入a+b+c≠0中,得3a≠0,∴a≠0,选D。
初中数学竞赛数学奥林匹克初中训练题(1)(含解答)

数学奥林匹克初中训练题(1)第 一 试一、选择题:(每小题7分,共42分)1.已知33333a b c abca b c++-=++,则22()()()()a b b c a b b c -+-+--的值为( ) (A)1 (B)2 (C)3 (D)42.规定”Δ”为有序实数对的运算,如果(,)a b Δ(,)(,).c d ac bd ad bc =++如果对任意实数,a b 都有(,)a b Δ(,)(,),x y a b =则(,)x y 为( )(A)(0,1) (B)(1,0) (C)(1,0)- (D)(0,1)- 3.在ΔABC 中,211a b c=+,则∠A( ) (A)一定是锐角 (B)一定是直角 (C)一定是钝角 (D)非上述答案4.下列五个命题:①若直角三角形的两条边长为3与4,则第三边长是5;②2;a =③若点(,)P a b 在第三象限,则点1(,1)P a b --+在第一象限;④连结对角线垂直且相等的四边形各边中点的四边形是正方形;⑤两边及其第三边上的中线对应相等的两个三角形全等.其中正确的命题的个数是( )(A)2个 (B)3个 (C)4个 (D)5个5.设P 为等腰Rt ΔABC 斜边AB 上或其延长线上一点,22S AP BP =+,那么( )(A)22S CP < (B)22S CP = (C)22S CP > (D)不确定 6.满足方程222()x y x y xy +=++的所有正整数解有( )(A)一组 (B)二组 (C)三组 (D)四组 二、填空题:(每小题7分,共28分)1.一辆客车,一辆货车和一辆小轿车在同一条直线上朝同一方向行驶,在某一时刻,货车在中,客车在前,小轿车在后,且它们的距离相等.走了10分钟,小轿车追上了货车;又走了5分钟,小轿车追上了客车.问再过 分钟,货车追上了客车.2.若多项式2228171642070P a ab b a b =-+--+,那么P 的最小值是 .3.如图, ∠AOB=30O, ∠AOB 内有一定点P,且OP=10.在OA 上有一点Q,OB 上有一点R.若ΔPQR 周长最小,则最小周长是 .4.已知二次函数2(1)y ax a =≥的图象上两点A,B 的横坐标分别为1,2-,O 是坐标原点,如果ΔAOB 是直角三角形,则ΔAOB 的周长为 .B第 二 试一、(20分)已知实数,,a b c 满足不等式,a b c b c a ≥+≥+,c a b ≥+,求a b c ++的值.二、(25分)如图2,点D 在ΔABC 的边BC 上,且与B,C 不重合,过点D 作AC 的平行线DE 交AB 于E,作AB 的平行线DF 交AC 于点F.又知BC=5. (1) 设ΔABC 的面积为S.若四边形AEFD 的面积为25S .求BD 长. (2)若,AC =且DF 经过ΔABC 的重心G,求E,F 两点的距离.三、(25分)已知定理:”若三个大于3的质数,,a b c 满足关系式25a b c +=,则a b c ++是整数n 的倍数.”试问:上述定理中整数n 的最大可能值是多少?并证明你的结论.。
七年级数学奥林匹克竞赛题(一)解析

初中一年级奥赛训练题(一)及解析一、选择题(每题1分,共10分)1.如果a,b都代表有理数,并且a+b=0,那么( C)A.a,b都是0 B.a,b之一是0C.a,b互为相反数D.a,b互为倒数2.下面的说法中正确的是( D)A.单项式与单项式的和是单项式B.单项式与单项式的和是多项式C.多项式与多项式的和是多项式D.整式与整式的和是整式3.下面说法中不正确的是( C)A. 有最小的自然数B.没有最小的正有理数C.没有最大的负整数D.没有最大的非负数4.如果a,b代表有理数,并且a+b的值大于a-b的值,那么( D) A.a,b同号B.a,b异号C.a>0 D.b>05.大于-π并且不是自然数的整数有( B)A.2个B.3个C.4个D.无数个6.有四种说法:甲.正数的平方不一定大于它本身;乙.正数的立方不一定大于它本身;丙.负数的平方不一定大于它本身;丁.负数的立方不一定大于它本身。
这四种说法中,不正确的说法的个数是( B)A.0个B.1个C.2个D.3个解析:负数的平方是正数,所以一定大于它本身,故丙错误。
7.a代表有理数,那么a和-a的大小关系是( D)A.a大于-a B.a小于-aC.a大于-a或a小于-a D.a不一定大于-a解析:令a=0,马上可以排除A、B、C,应选D。
8.在解方程的过程中,为了使得到的方程和原方程同解,可以在原方程的两边( D)A.乘以同一个数B.乘以同一个整式C.加上同一个代数式D.都加上1解析:对方程同解变形,要求方程两边同乘不等于0的数,所以排除A。
我们考察方程x-2=0,易知其根为x=2.若该方程两边同乘以一个整式x-1,得(x-1)(x -2)=0,其根为x=1及x=2,不与原方程同解,排除B。
同理应排除C.事实上方程两边同时加上一个常数,新方程与原方程同解,D所加常数为1,因此选D.9.杯子中有大半杯水,第二天较第一天减少了10%,第三天又较第二天增加了10%,那么,第三天杯中的水量与第一天杯中的水量相比的结果是( C) A.一样多B.多了C.少了D.多少都可能解析:设杯中原有水量为a,依题意可得,第二天杯中水量为(1-10%)a=0.9a;第三天杯中水量为0.9a(1+10%)=0.9×1.1a;第三天杯中水量与第一天杯中水量之比为0.99∶1,所以第三天杯中水量比第一天杯中水量少了,选C。
初中数学奥数题综合模拟试卷及答案

初中数学奥数题综合模拟试卷及答案初中数学奥数题:综合模拟试卷及答案篇一:初中数学模拟试题及答案初四数学试题一、选择题:本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,请将第i卷选择题所选选项填入下表,第1~3小题每题3分,第4~12小题每题4分,错选、不选或选出的答案超过一个,均记零分.1.例如图,数轴的单位长度为1,如果点a,b则表示的数的绝对值成正比,那么点a则表示的数是(a)-4(b)-2(c)0(d)42.以下排序恰当的就是(a)(-p2q)3=-p5q3(b)(12a2b3c)÷(6ab2)=2ab2-(c)3m÷(3m-1)=m-3m2(d)(x2-4x)x1=x-43.长方体的主视图、俯视图如图所示,则其左视图面积为(a)3(b)4(c)12(d)164.未知m=??221,则存有3??(a)5<m<6(b)4<m<5(c)-5<m<-4(d)-6<m<-55.下列命题中,假命题是(a)平行四边形就是中心对称图形(b)三角形三边的垂直平分线相交于一点,这点到三角形三个顶点的距离相等(c)对于直观的随机样本,可以用样本的方差回去估算总体的方差(d)若x2=y2,则x=y6.如图,将周长为8的△abc沿bc方向平移1个单位得到△def,则四边形abfd的周长为(a)6(b)8(c)10(d)127.如图,b处在a处的南偏西45°方向,c处在a处的南偏东15°方向,c处在b处的北偏东80°方向,则∠acb等于(a)40°(b)75°(c)85°(d)140°8.未知一组数据:1,3,5,5,6,则这组与数据的方差就是(a)16(b)5(c)4(d)3.29.如图,在直角坐标系中,矩形oabc的顶点o在坐标原点,边oa在x轴上,oc在y轴上,如果矩形oa′b′c′与矩形oabc关于点o位似,且矩形oa′b′c′的面积等于矩形oabc面积的1,那么点b′的坐4(-∠abc线段点标是(a)(-2,3)(b)(2,-3)c)(3,-2)或(-2,3)(d)2,3)或(2,-3)10.如图,△abc是等边三角形,p是的平分线bd上一点,pe⊥ab于点e,bp的垂直平分线交bc于点f,垂足为q.若bf=2,则pe的长为(a)23(b)3(c)2(d)311.例如图,在rt△abo中,斜边ab=1.若oc∥ba,∠aoc=36°,则(a)点b到ao的距离为sin54°(b)点b到ao的距离为tan36°(c)点a到oc 的距离为sin36°sin54°(d)点a到oc的距离为cos36°sin54°12.如图,点a是反比例函数y?23(x>0)的图象上任意一点,ab∥x轴交反比例函数y??的xx图象于点b,以ab为边作□abcd,其中c,d在x轴上,则s□abcd为(a)5(b)4(c)3(d)2二、填空题:本题共5小题,满分20分,13.水解因式:3m3-18m2n+27mn2=.14.例如图,在菱形abcd中,点e,f分别就是bd,cd的中点,ef=6cm,那么存有ab=15.如果代数式x2+3x+2可以则表示为(x-1)2+a(x-1)+b的形式,则a+b的值是.16.当阔为3cm的刻度尺的一边与圆切线时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为cm.17.二次函数y=-(x-2)2+9的图象与x4轴围整数利用说道一个变成的半封闭区域内(包含边界),斜、纵坐标都就是的点有个.(提示信息:必要时可以.三、答疑题:本大题共7小题,共55分后.答疑必须写下必要的文字清、证明过程或编程语言步骤.18.(本题满分6分后)x?x2?x?x化简分式?,并从-1≤x<3中选出?2??2x1x1x2x1你认为合适的整数x代入求值.19.(本题满分6分后)如图,在△abc中,ab=ac,ad是高,am是△abc外角∠cae的平分线.(1)用尺规作图方法,并作∠adc的平分线dn;(留存作图痕迹,不文学创作法和证明)(2)设dn与am处设点f,推论△adf的形状,并详述理由.20.(本题满分8分)关于x的一元二次方程x2+3x+m-1=0的两个实数根分别为x1,x2.(1)谋m的值域范围.(2)若2(x1+x2)+x1x2+10=0,谋m的值.21.(本题满分8分)某校八年级为介绍学生课堂讲话情况,随机提取该年级部分学生,对他们某天在课堂上讲话的次数展开了统计数据,其结果如下表中,并绘制了如图所示的两幅不完备的统计图,未知b,e两组发言人数的比为5:2,恳请融合图中有关数据提问以下问题:(1)求出样本容量,并补全直方图;(2)该年级共计学生500人,恳请估算全年级在这天里讲话次数不少于12的人数;(3)已知a组发言的学生中恰有1位女生,e组发言的学生中有2位男生,现从a组与e组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.22.(本题满分9分)某学校为了提升办学条件,计划添置一批电子白板和一批笔记本电脑,经投标,出售1块电子白板比卖3台笔记本电脑多3000元,出售4块电子白板和5台笔记本电脑共需80000元.(1)求购买1块电子白板和一台笔记本电脑各需多少元?(2)根据该校实际情况,须要出售电子白板和笔记本电脑的总数为40,建议出售的总费用不少于300000元,并且出售笔记本电脑的台数不少于出售电子白板数量的3倍,该校存有哪几种出售方案?(3)上面的哪种购买方案最省钱?按最省钱方案购买需要多少钱?23.(本题满分9分)例如图,梯形abcd就是全等梯形,且ad∥bc,o就是腰cd的中点,以cd短为直径作圆,交bc于e,过e作eh⊥ab于h.(1)澄清:oe∥ab;1cd,澄清:ab就是⊙o的切线;2bh(3)在(2)的条件下,若be=4bh,谋的值.ce(2)若eh=24.(本题满分9分)例如图,顶点为p(4,-4)的二次函数图象经过原点(0,0),点a在该图象上,oa缴其对称轴l于点m,点m,n关于点p等距,相连接an,on.(1)求该二次函数的关系式.(2)若点a的座标就是(6,-3),谋△ano的面积.(3)当点a在对称轴l右侧的二次函数图象上运动,请解答下列问题:①证明:∠anm=∠onm.②恳请从∠ona、∠nao中挑选出一个推论其若想为直角,并详细表明理由.一、选择题1.与无理数最吻合的整数就是a.1b.22.以下运算恰当的就是c.3d.4篇二:2021年初中奥数题及答案2021年初中奥数题及答案初中奥数题试题一一、选择题(每题1分,共10分)1.如果a,b都代表有理数,并且a+b=0,那么()a.a,b都就是0b.a,b之一就是0c.a,b互为相反数d.a,b互为倒数答案:c解析:令a=2,b=-2,满足2+(-2)=0,由此a、b互为相反数。
数学初中竞赛函数最值专题训练(含答案) (1)

数学初中竞赛函数最值专题训练一.选择题1.当三个非负实数x、y、z满足关系式x+3y+2z=3与3x+3y+z=4时,M=3x﹣2y+4z的最小值和最大值分别是()A.B.C.D.2.正实数a,b,c,d满足a+b+c+d=1,设p=+++,则()A.p>5 B.p=5C.p<5 D.p与5的大小关系不确定3.已知y=+(x,y均为实数),则y的最大值与最小值的差为()A.2﹣1 B.4﹣2C.3﹣2D.2﹣2 4.设x≥0,y≥0,2x+y=6,则u=4x2+3xy+y2﹣6x﹣3y的最小值是()A.B.18 C.20 D.不存在5.代数式的最小值是()A.0 B.C.D.6.设x是实数,y=|x﹣1|+|x+1|.下列四个结论:Ⅰ.y没有最小值;Ⅱ.只有一个x使y取到最小值;Ⅲ.有有限多个x(不止一个)使y取到最大值;Ⅳ.有无穷多个x使y取到最小值.其中正确的是()A.ⅠB.ⅡC.ⅢD.Ⅳ7.方程|x﹣1|+|y﹣1|=1确定的曲线所围成的图形面积为()A.4 B.3 C.2 D.18.如果a,b,c是正实数且满足abc=1,则代数式(a+1)(b+1)(c+1)的最小值是()A.64 B.8C.8 D.二.填空题9.代数式的最小值为.10.a,b是正数,并且抛物线y=x2+ax+2b和y=x2+2bx+a都与x轴有公共点,则a2+b2的最小值是.11.当|x|≤4时,函数y=|x﹣1|+|x﹣2|+|x﹣3|的最大值减去最小值的差是:.12.若a,c,d都是整数,b是正整数,且a+b=c,b+c=d,c+d=a,则a+b+c+d的最大值是.13.函数f(x)=λx2+(λ﹣3)x+1对于任意实数x都有f(x)≤f(λ),则函数f(x)的最大值是.14.代数式的最小值是.15.函数y=|x﹣1|+|x﹣2|+…+|x﹣10|,当x在实数范围内取值时,y的最小值是.16.a、b、c是非负实数,并且满足3a+2b+c=5,2a+b﹣3c=1.设m=3a+b﹣7c,记x为m的最小值,y为m的最大值.则xy=.三.解答题17.当﹣1≤x≤2时,函数y=2x2﹣4ax+a2+2a+2有最小值2.求a所有可能取的值.18.已知非负实数x,y,z满足,记W=3x+4y+5z.求W的最大值与最小值.19.附加题:某城镇沿环形路有五所小学,依次为一小、二小、三小、四小、五小,它们分别有电脑15,7,11,3,14台,现在为使各校电脑台数相等,各调几台给邻校:一小给二小,二小给三小,三小给四小,四小给五小,五小给一小.若甲小给乙小﹣3台,则乙小给甲小3台,要使电脑移动的总台数最小,应做怎样安排?20.阅读材料:若a,b都是非负实数,则a+b≥.当且仅当a=b时,“=”成立.证明:∵()2≥0,∴a﹣+b≥0.∴a+b≥.当且仅当a=b时,“=”成立.举例应用:已知x>0,求函数y=2x+的最小值.解:y=2x+≥=4.当且仅当2x=,即x=1时,“=”成立.当x=1时,函数取得最小值,y最小=4.问题解决:汽车的经济时速是指汽车最省油的行驶速度.某种汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油(+)升.若该汽车以每小时x公里的速度匀速行驶,1小时的耗油量为y升.(1)求y关于x的函数关系式(写出自变量x的取值范围);(2)求该汽车的经济时速及经济时速的百公里耗油量(结果保留小数点后一位).21.设x1、x2、x3、x4、x5均为正整数,且x1+x2+x3+x4+x5≤x1x2x3x4x5.试求x5的最大值.22.某环形道路上顺时针排列着4所中学:A1,A2,A3,A4,它们顺次有彩电15台,8台,5台,12台.为使各校的彩电数相同,允许一些中学向相邻中学调出彩电.问怎样调配才能使调出的彩电台数最小?并求调出彩电的最小总台数.23.已知:实数x,y,z满足:x+y+z=0,xy+yz+zx=﹣3,求z的最大值.参考答案一.选择题1.解:由得:,代入M的表达式中得,M=3x﹣2y+4z=3x﹣(1﹣x)+4(2x﹣1)=﹣,又因x、y、z均为非负实数,所以,即≤x≤1,当x=时,M有最小值为﹣,当x=1时,M有最大值为7.故选:B.2.解:∵a,b,c,d均为正数,且a+b+c+d=1,∴必有0<a,b,c,d<1∵p=+++,事实上我们在xOy坐标系中作出函数f(x)=的图象,显然可以发现其图象一定在点(0,1)和(1,2)这两点连线的上方,而这两点连线的方程为y=x+1,∴可以发现在(0,1)上恒有>x+1,当然这样只是画图所得,未必准确,∴还要严格证明,证之如下:上式两边平方得:3x+1>x2+2x+1,∴x2﹣x≤x(x﹣1)<0,而此时x∈(0,1),可见上式显然成立.所以我们有:>a+1,>b+1,>c+1,>d+1,以上四式相加得p=+++>a+b+c+d+4=5,即有P>5.故选:A.3.解:∵y=+,∴y2=4+2=4+2×,∵1≤x≤5,当x=3时,y的最大值为2,当x=1或5时,y的最小值为2,故当x=1或5时,y取得最小值2,当x取1与5中间值3时,y取得最大值2,故y的最大值与最小值的差为2﹣2,故选:D.4.解:由已知得:y=6﹣2x,代入u=4x2+3xy+y2﹣6x﹣3y,整理得:u=2x2﹣6x+18,而x≥0,y=6﹣2x≥0,则0≤x≤3,u=2(x﹣)2+,当x=0或x=3时,u取得最大值,u max=18,当x=时,u取得最小值,u min=.故选:A.5.解:由题意得:,解得x≥0,又∵、、都是随x的增大而增大,∴当x=0时,代数式取得最小值,此时式()min=+=1+.故选:B.6.解:从数轴上可知,区间[﹣1,1]上的任一点x到点1与点﹣1的距离之和均为2;区间[﹣1,1]之外的点x到点1与点﹣1的距离之和均大于2.所以函数y=|x﹣1|+|x+1|当﹣1≤x≤1时,取得最小值2.Ⅰ、y在区间[﹣1,1]上取得最小值2;故本选项错误;Ⅱ、y在区间[﹣1,1]上的任一点x到点1与点﹣1的距离之和均为2;故本选项错误;Ⅲ、y在区间[﹣1,1]之外的点x到点1与点﹣1的距离之和均大于2,且无限大,所以y在区间[﹣1,1]之外的点没有最大值;故本选项错误;Ⅳ、y在区间[﹣1,1]上的任一点x到点1与点﹣1的距离之和均为最小值2,所以有无穷多个x使y取到最小值.故本选项正确;故选:D.7.解:先考虑简单的情况:当|x|+|y|=1时:当x>0,y>0时,x+y=1,当x>0,y<0时,x﹣y=1,当x<0,y>0时,y﹣x=1,当x<0,y<0时,x+y=﹣1,∴四条直线与坐标轴的交点分别为(0,1),(1,0),(﹣1,0),(0,﹣1),∴正方形边长为:=,∴正方形面积为:×=2.∵|x﹣1|+|y﹣1|=1的在坐标系内的图象只不过是将|x|+|y|=1的图象向右又向上移动了一个单位,图象的形状并未改变,∴其面积依然为2.故选:C.8.解:要使(a+1)(b+1)(c+1)取得最小值,则三个因式都应取得最小值,∵m+n≥2,当且仅当m=n时取得最小值,故可得①当a=1时,a+1取得最小值2;②当b=1时,b+1取得最小值2;③当c=1时,c+1取得最小值2;又∵a=1,b=1,c=1可能满足条件abc=1,∴代数式(a+1)(b+1)(c+1)的最小值=2×2×2=8.故选:C.二.填空题(共8小题)9.解:求代数式,即+的最小值,实际上就是求x轴上一点到(0,﹣2)以及(12,3)两点的和的最小值,而两点间的距离是线段最短,所以,点到(0,﹣2)到点(12,3)的距离即为所求,即=13.故答案为:13.10.解:由题设知a2﹣8b≥0,4b2﹣4a≥0.则a4≥64b2≥64a,∵a,b是正数,∴a3≥64,∴a≥4,b2≥a≥4.∴a2+b2≥20.又∵当a=4,b=2时,抛物线y=x2+ax+2b和y=x2+2bx+a都与x 轴有公共点,∴a2+b2的最小值是20.故答案为:20.11.解:∵|x|≤4,∴,∴当x=﹣4时,y取最大值18,当x=2时,y取最小值2.则最大值与最小值的差是18﹣2=16.故答案为:16.12.解:∵a+b=c,①b+c=d,②c+d=a,③由①+③,得(a+b)+(c+d)=a+c,∴b+d=0,④b+c=d;⑤由④+⑤,得∴2b+c=b+d=0,∴c=﹣2b;⑥由①⑥,得∴a=c﹣b=﹣3b,⑦由④⑥⑦,得∴a+b+c+d=(a+c)+(b+d)=a+c=﹣5b;∵b是正整数,∴b≥1,∴a+b+c+d≤﹣5,∴a+b+c+d的最大值是﹣5.故答案为:﹣5.13.解:由题意得,f(x)有最大值,则可得λ<0,又∵f(x)=λ(x+)2+1﹣,∴f(x)的最大值为1﹣,又∵f(x)≤f(λ),∴f(λ)=λ3+(λ﹣3)λ+1=1﹣,解得:λ=1(舍去)或λ=﹣,将λ=﹣,代入可得f(x)的最大值为.故答案为:.14.解:若代数式有意义,则,解得:x≥2,∵,,是增函数,∴当x=2时,代数式的值最小,即=2+1+0=3.故答案为3.15.解:设y1=|x﹣1|+|x﹣10|,则y1可以看作数轴上点x到点1与10的距离和,即可得当x==5.5时,y1取最小值,同理:设y2=|x﹣2|+|x﹣9|,y3=|x﹣3|+|x﹣8|,y4=|x﹣4|+|x﹣7|,y5=|x﹣5|+|x﹣6|,∴当x=5.5时,y2,y3,y4,y5取最小值,∴当x=5.5时,函数y=|x﹣1|+|x﹣2|+…+|x﹣10|取最小值,最小值为:y=|5.5﹣1|+|5.5﹣2|+…+|5.5﹣10|=4.5+3.5+2.5+1.5+…+0.5+0.5+1.5+2.5+3.5+4.5=25.故答案为:25.16.解:由3a+2b+c=5,2a+b﹣3c=1得⇒,∴可得a=7c﹣3,b=7﹣11c,由a、b、c是非负数得:⇒≤c≤,又m=3a+b﹣7c=3c﹣2,故﹣≤m≤﹣,于是可得x=﹣,y=﹣,故xy=﹣×(﹣)=.三.解答题(共7小题)17.解:y=2x2﹣4ax+a2+2a+2图象的对称轴为:x=a,①当﹣1≤a≤2时,函数在x=a处取得最小值2,故﹣a2+2a+2=2,即a2﹣2a=0,解得:a=0或2,②当a<﹣1时,函数在x=﹣1处取得最小值2,代入函数式得2+4a+a2+2a+2=2,即:a2﹣6a+2=0,解得:a=﹣3±,取a=﹣3﹣,③当a>2时,函数在x=2处取得最小值2,代入函数式得:8﹣8a+a2+2a+2=2,即a2﹣6a+8=0,解得:a=2或4,取a=4.故a所有可能的值为:﹣3﹣,0,2,4.18.解:设=k,则x=2k+1,y=﹣3k+2,z=4k+3,∵x,y,z均为非负实数,∴,解得﹣≤k≤,于是W=3x+4y+5z=3(2k+1)﹣4(3k﹣2)+5(4k+3)=14k+26,∴﹣×14+26≤14k+26≤×14+26,即19≤W≤.∴W的最大值是35,最小值是19.19.解:如图,用A、B、C、D、E分别表示这五所小学的位置,并设A向B调x1台电脑,B向C调x2台电脑,…,E向A调x5台电脑,依题意有:7+x1﹣x2=11+x2﹣x3=3+x3﹣x4=14+x4﹣x5=15+x5﹣x1=50÷5=10,所以,x2=x1﹣3,x3=x1﹣2,x4=x1﹣9,x5=x1﹣5,设调动的电脑的总台数为y,则y=|x1|+|x1﹣3|+|x1﹣2|+|x1﹣9|+|x1﹣5|,这样,这个实际问题就转化为求y的最小值问题,并由上面所得结论知:当x1==3时,y的最小值为|3|+|3﹣3|+|3﹣2|+|3﹣9|+|3﹣5|=12,即调动的总台数为12.因为x1=3时,x2=0,x3=1,x4=﹣6,x5=﹣2,故一小就向二小调3台电脑,二小不调出,三小向四小调一台电脑,五小向四小调6台电脑,一小向五小调2台电脑.20.解:(1)∵汽车在每小时70~110公里之间行驶时(含70公里和110公里),每公里耗油(+)升.∴y=x×(+)=(70≤x≤110);(2)根据材料得:当时有最小值,解得:x=90∴该汽车的经济时速为90千米/小时;当x=90时百公里耗油量为100×(+)≈11.1升.21.解:由于x1、x2、x3、x4、x5在式中对称,故不妨设x1≤x2≤x3≤x4≤x5,并令S=x1+x2+x3+x4+x5≤x1x2x3x4x5.则S≤5x5,即t=x1x2x3x4≤5;那么t为1或2或3或4或5,而a,b,c,d则为t的约数.①当t=5时,由于t=1×5,故令x1=x2=x3=1,x4=5,代入S 可得x5=2,与x4≤x5相矛盾,故x5=2不合题意;②同理,当t=1或4时均不合题意.当t=3时,x5=3,符合题意;③当t=2时,由于t=1×2,令x1=x2=x3=1,x4=2,代入S可得x5=5,符合题意;综上所述,故x5的最大值为5.22.解:设A1中学调给A2彩电x1台(若x1<0,则认为是A2,向A1调出|x1|台),A2中学调给A3彩电x2台,A3调给A4x3台,A4调给A1x4台.∵共有40台彩电,平均每校10台,∴15﹣x1+x4=10,8﹣x2+x1=10,5﹣x3+x2=10,12﹣x4+x3=10,∴x4=x1﹣5,x1=x2+2,x2=x3+5,x3=x4﹣2,x3=(x1﹣5)﹣2=x1﹣7,x2=(x1﹣7)+5=x1﹣2.本题即求y=|x1|+|x2|+|x3|+|x4|=|x1|+|x1﹣2|+|x1﹣7|+|x1﹣5|的最小值,其中x1是满足﹣8≤x1≤15的整数.设x1=x,并考虑定义在﹣8≤x≤15上的函数:y=|x|+|x﹣2|+|x ﹣7|+|x﹣5|,当2≤x≤5时,y取最小值10,即当x1=2,3,4,5时,|x1|+|x1﹣2|+|x1﹣7|+|x1﹣5|取到最小值10.从而调出彩电的最小台数为10,调配方案有如下4种:23.解:∵x+y+z=0,∴x+y=﹣z,①∵xy+yz+zx=﹣3,∴xy=﹣3﹣(yz+zx)=﹣3﹣z(x+y)=﹣3﹣z(﹣z),即xy=﹣3+z2,②由①②及韦达定理知:xy是一元二次方程w2+zw+(﹣3+z2)=0的两实根,则判别式△=z2﹣4(﹣3+z2)≥0,化简得:z2≤4,∴﹣2≤z≤2,∴z的最大值是2.。
数学奥林匹克初中训练题
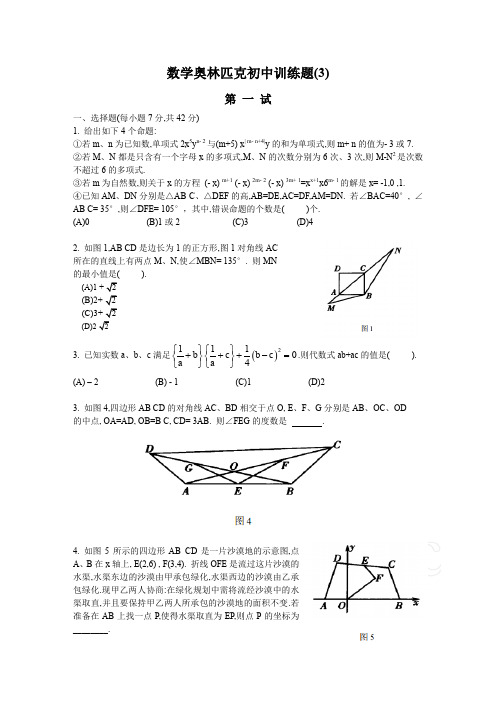
数学奥林匹克初中训练题(3)第 一 试一、选择题(每小题7分,共42分)1. 给出如下4个命题:①若m 、n 为已知数,单项式2x 5y n- 2与(m+5) x | m- n+4|y 的和为单项式,则m+ n 的值为- 3或7. ②若M 、N 都是只含有一个字母x 的多项式,M 、N 的次数分别为6次、3次,则M-N 2是次数不超过6的多项式.③若m 为自然数,则关于x 的方程 (- x) m+1 (- x) 2m- 2 (- x) 3m+ 1=x x+1x6m- 1的解是x= -1,0 ,1. ④已知AM 、DN 分别是△AB C 、△DEF 的高,AB=DE,AC=DF,AM=DN. 若∠BAC=40°, ∠AB C= 35°,则∠DFE= 105°,其中,错误命题的个数是( )个.(A)0 (B)1或2 (C)3 (D)42. 如图1,AB CD 是边长为1的正方形,图1对角线AC所在的直线上有两点M 、N,使∠MBN= 135°. 则MN的最小值是( ).3. 已知实数a 、b 、c 满足()211104b c b c a a ⎧⎫⎧⎫+++-=⎨⎬⎨⎬⎩⎭⎩⎭.则代数式ab+ac 的值是( ). (A) – 2 (B) - 1 (C)1 (D)23. 如图4,四边形AB CD 的对角线AC 、BD 相交于点O, E 、F 、G 分别是AB 、OC 、OD 的中点, OA=AD, OB=B C, CD= 3AB. 则∠FEG 的度数是.4. 如图5所示的四边形AB CD 是一片沙漠地的示意图,点A 、B 在x 轴上, E(2,6) , F(3,4). 折线OFE 是流过这片沙漠的水渠,水渠东边的沙漠由甲承包绿化,水渠西边的沙漠由乙承包绿化.现甲乙两人协商:在绿化规划中需将流经沙漠中的水渠取直,并且要保持甲乙两人所承包的沙漠地的面积不变.若准备在AB 上找一点P,使得水渠取直为EP,则点P 的坐标为________.。
初中奥林匹克数学竞赛训练题(7套)

数学奥林匹克初中训练题第 一 试一. 选择题.(每小题7分,共42分)( )1.已知33333a b c abc a b c++-=++,则22()()()()a b b c a b b c -+-+--的值为: (A)1 (B)2 (C)3 (D)4( )2.规定”Δ”为有序实数对的运算,如果(,)a b Δ(,)(,).c d ac bd ad bc =++如果对任意实数,a b 都有(,)a b Δ(,)(,),x y a b =则(,)x y 为:(A)(0,1) (B)(1,0) (C)(1,0)- (D)(0,1)-( )3.在ΔABC 中,211a b c=+,则∠A: (A)一定是锐角 (B)一定是直角 (C)一定是钝角 (D)非上述答案( )4.下列五个命题:①若直角三角形的两条边长为3与4,则第三边长是5;②2;a =③若点(,)P a b 在第三象限,则点1(,1)P a b --+在第一象限;④连结对角线垂直且相等的四边形各边中点的四边形是正方形;⑤两边及其第三边上的中线对应相等的两个三角形全等.其中正确的命题的个数是:(A)2个 (B)3个 (C)4个 (D)5个( )5.设P 为等腰Rt ΔABC 斜边AB 上或其延长线上一点,22S AP BP =+,那么:(A)22S CP (B)22S CP = (C)22S CP (D)不确定( )6.满足方程222()x y x y xy +=++的所有正整数解有:(A)一组 (B)二组 (C)三组 (D)四组二. 填空题.(每小题7分,共28分)1.一辆客车,一辆货车和一辆小轿车在同一条直线上朝同一方向行驶,在某一时刻,货车在中,客车在前,小轿车在后,且它们的距离相等.走了10分钟,小轿车追上了货车;又走了5分钟,小轿车追上了客车.问再过分钟,货车追上了客车.2.若多项式2228171642070P a ab b a b =-+--+,那么P 的最小值是 .3.如图1, ∠AOB=30O , ∠AOB 内有一定点P ,且OP=10.在OA 上有一点Q,OB 上有一点R.若ΔPQR 周长最小,则最小周长是 .4.已知二次函数2(1)y ax a =≥的图象上两点A,B 的横坐标分别为1,2-,O 是坐标原点,如果ΔAOB 是直角三角形,则ΔAOB 的周长为 .第 二 试一.(20分)已知实数,,a b c 满足不等式,a b c b c a ≥+≥+,c a b ≥+,求a b c ++的值.二.(25分)如图2,点D 在ΔABC 的边B 小 C 上,且与B,C 不重合,过点D 作AC 的平行线DE 交AB 于E,作AB 的平行线DF 交AC 于点F.又知BC=5.(1) 设ΔABC 的面积为S.若四边形AEFD 的面积为25S .求BD 长.(2) 若,AC =且DF 经过ΔABC 的重心G,求E,F 两点的距离.三.(25分)已知定理:”若三个大于3的质数,,a b c 满足关系式25a b c +=,则a b c ++是整数n 的倍数.”试问:上述定理中整数n 的最大可能值是多少?并证明你的结论。
初中数学竞赛专项训练(1)及答案

初中数学(实数)竞赛专项训练(1)一、选择题1、如果自然数a 是一个完全平方数,那么与a 之差最小且比a 大的一个完全平方数是( ) A. a +1B. a 2+1C. a 2+2a+1D. a+2a +12、在全体实数中引进一种新运算*,其规定如下:①对任意实数a 、b 有a *b=(a +b )(b -1)②对任意实数a 有a *2=a *a 。
当x =2时,[3*(x *2)]-2*x +1的值为 ( )A. 34B. 16C. 12D. 63、已知n 是奇数,m 是偶数,方程⎩⎨⎧=+=+m y x n y 28112004有整数解x 0、y 0。
则 ( )A. x 0、y 0均为偶数B. x 0、y 0均为奇数C. x 0是偶数y 0是奇数D. x 0是奇数y 0是偶数4、设a 、b 、c 、d 都是非零实数,则四个数-ab 、ac 、bd 、cd ( )A. 都是正数B. 都是负数C. 两正两负D. 一正三负或一负三正5、满足等式2003200320032003=+--+xy x y x y y x 的正整数对的个数是( ) A. 1B. 2C. 3D. 46、已知p 、q 均为质数,且满足5p 2+3q=59,由以p +3、1-p +q 、2p +q -4为边长的三角形是( )A. 锐角三角形B. 直角三角形C. 钝角三角形D. 等腰三角形7、一个六位数,如果它的前三位数码与后三位数码完全相同,顺序也相同,由此六位数可以被( )整除。
A. 111B. 1000C. 1001D. 11118、在1、2、3……100个自然数中,能被2、3、4整除的数的个数共( )个 A. 4 B. 6 C. 8 D. 16二、填空题 1、若20011198********⋯⋯++=S ,则S 的整数部分是____________________2、M 是个位数字不为零的两位数,将M 的个位数字与十位数字互换后,得另一个两位数N ,若M -N 恰是某正整数的立方,则这样的数共___个。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学奥林匹克初中训练题附答案(一)
第一试
一、选择题(每小题7分,共42分)
1.如图,已知在Rt △ABC 中,AB=35,一个边长为12的正方形CDEF 内
接于△ABC.则△ABC 的周长为( ).
(A)35 (B)40 (C)81 (D)84
2.设n=9+99+…+99…9(99个9).则n 的十进制表示中,数码1有( )个. (A)50 (B)90 (C)99 (D)100
3.已知f(x)=x 2+6ax-a ,y=f(x)的图像与x 轴有两个不同的交点(x 1,0),(x 2,0),且
)
x -6a -)(1x -6a -(13
)
x )(1x (1a
2121-
++=8a-3.则a 的值是( ).
(A)1 (B)2 (C)0或2
1 (D)2
1
4.若不等式ax 2+7x-1>2x+5对-1≤a≤1恒成立,则x 的取值范围是( ). (A)2≤x≤3 (B)2<x<3 (C)-1≤x≤1 (D)-1<x<1
5.在Rt △ABC 中,∠B=60°,∠C=90°,AB=1,分别以AB 、BC 、CA 为边长向△ABC 外作等边△ABR 、等边△BCP 、等边△CAQ ,联结QR 交AB 于点T.则△PRT 的面积等于( ). (A)
32
39 (B)
4
3 (C)
2
1 (D)
3
3
6.在3×5的棋盘上,一枚棋子每次可以沿水平或者垂直方向移动一小格,但不可以沿任何斜对角线移动.从某些待定的格子开始,要求棋子经过全部的小正方格恰好一次,但不必回到原来出发的小方格上.在这15个小方格中,有( )个可以是这枚棋子出发的小方格. (A)6 (B)8 (C)9 (D)10
二、填空题(每小题7分,共28分)
1.正方形ABCD 的边长为5,E 为边BC 上一点,使得BE=3,P 是对角线BD 上的一点,使得PE+PC 的值最小.则PB= .
2.设a 、b 、c 为整数,且对一切实数x ,(x-a)(x-8)+1=(x-b)(x-c) 恒成立.则a+b+c 的值
为 .
3.如图,在以O 为圆心的两个同心圆图2中,MN 为大圆的直径,交
小圆于点P 、Q ,大圆的弦MC 交小圆于点A 、B.若OM=2,OP= 1,MA=AB=BC ,则△MBQ 的面积为 .
4.从1, 2,…, 2 006中,至少要取出 个奇数,才能保证其中必定存在两个数,它们的和为2 008.
第二试
一、(20分)实数x 、y 、z 、w 满足x≥y≥z≥w≥0,且5x+4y+3z+6w=100.求x+y+z+w 的最大值和最小值.
二、(25分)如图,在Rt △ABC 中,∠B=90°,它的内切圆分别与边BC 、CA 、AB 相切于点D 、E 、F ,联结AD 与内切圆相交于另一点P ,联结PC 、PE 、PF.已知PC ⊥PF.求证:
(1)EP/DE=PD/DC;(2)△EPD 是等腰三角形.
三、(25分)在]2008
2008[
],2008
2
[
],2008
1
[2
2
2
中,有多少个不同的整数(其中,[x]表示不大于x
的最大整数)?
数学奥林匹克初中训练题参考答案
第一试 一、1.D. 设BC=a ,AC=b.则
a 2+
b 2=352=1 225.①又Rt △AFE ∽Rt △ACB ,则FE/CB=AF/AC ,. 故12(a+b)=ab.
由式①、②得(a+b)2=1 225+24(a+b).解得a+b=49(a+b=-25舍去).所以,周长为84. 2.C.
因为n=(10-1)+(100-1)+…+(100…0(99个0)-1)=11…1(99个1)0-99=11…1(97个1)011, 所以,n 的十进制表示中,数码1有97+2=99(个). 3.D.
由Δ=36a 2+4a>0,得a>0或a<-1/9.由题意可设f(x)=x 2+6ax-a=(x-x 1)(x-x 2). 则(1+x 1)(1+x 2)=f(-1)=1-7a , (1-6a-x 1)(1-6a-x 2)=f(1-6a)=1-7a. 所以,
7a
-13-a =8a-3.
解得a=1/2或a=0(舍去). 4.B.
由题意知,不等式ax 2+7x-1>2x+对-1≤a≤1恒成立,即关于a 的不等x 2a+5x-6>0对-1≤a≤1恒成立.令g(a)=x 2a+5x-6.则g(-1)=-x 2+5x-6>0,g(1)=x 2+5x-6>0.解得2<x<3. 5.A.
如图,联结PQ.由题设得BC=1/2 ,AC=3 /2,∠QAT=90°, ∠QCP=150°,P 、B 、R 三点共线. 因为S △AQT =
2
1 AT·AQ=
2
1 AT·AC=
4
3AT ,
而S △ART /S △ARB =AT/AB ,所以,S △ART =
4
3AT=S △AQT.从而,QT=RT.
于是,S △PRT =
2
1 S △PQR =
2
1 (S △ABC +S △ABR +S △BCP +S △CAQ +S △CPQ -S △AQR )=
32
39.
6.B.
如图5,将3×5的棋盘黑白染色.图5中有8个黑色小方格和7个白色小方格,棋子每次移动都是黑白交替的,则7个白格不能作为出点.另一方面,如图6的8个黑格中的任一个都可以作为出发点.
二、1.15
2 /8.因为PE+PC=PE+PA ,所以,当A 、P 、E 三点共线时,PE+PA 最小.
如图,建立直角坐标系,设B 为坐标原点,BA 为x 轴.则l BD :y=x , l AE :3x+5y=15.所以,P(15/8,15/8).故PB=15 2 /8.
2.20或28.
因x 2-(8+a)x+8a+1=x 2-(b+c)x+bc 恒成立,所以,8+a=b+c ,8a+1=bc. 消去a 可得bc-8(b+c)=-63,即(b-8)(c-8)=1.
因为b 、c 都是整数,所以,b-8=c-8=1或b-8=c-8=-1. 从而,a+b+c=20或28. 3.3
15/8.
设MA=x.
由MA·MB=MP·MQ ,得x·2x=1×3.解得x=
2
3.
联结CN.在Rt △MCN 中,MC=3x=3
2
3,MN=4.
所以,NC=
2
5,S △MCN =
4
153.
又S △MQB /S △MCN =1/2,则S △MQB =8
153.
4.503.
从1,2,…,2 006中选出两个奇数,和为2 008的共有如下501组: 3+2 005,5+2 003,…,1 003+1 005.
由于1与其中的任意一个奇数的和都不会等于2 008,因此,至少要取出503个奇数,才能
保证其中一定有两个数,它们的和为2 008. 第二试
一、设z=w+a ,y=w+a+b ,x=w+a+b+c.则a 、b 、c≥0,且x+y+z+w=4w+3a+2b+c. 故100=5(w+a+b+c)+4(w+a+b)+3(w+a)+6w=18w+12a+9b+5c=4(4w+3a+2b+c)+(2w+b+c) ≥4(x+y+z+w). 因此,x+y+z+w≤25.
当x=y=z=25/3,w=0时,上式等号成立.故x+y+z+w 的最大值为25. 又100=18w+12a+9b+5c=5(4w+3a+2b+c)-(2w+3a+b)≤5(x+y+z+w), 则 x+y+z+w≥20.
当x=20,y=z=w=0时,上式等号成立.故x+y+z+w 的最小值为20. 二、(1)如图,联结DF.则△BDF 是等腰直角三角形.于是,
∠FPD=∠FDB=45°.故∠DPC=45°.
又因为∠PDC=∠PFD ,所以,△PFD ∽△PDC. 从而,PF/FD=PD/DC.①
由∠AFP=∠ADF ,∠AEP=∠ADE , 得△AFP ∽△ADF ,△AEP ∽△ADE. 于是,EP/DE=AP/AE=AP/AF=FP/DF. 故由式①得EP/DE=PD/DC.
(2)因为∠EPD=∠EDC ,结合式②得△EPD’∽△EDC.所以,△EPD 也是等腰三角形. 三、设f(n)=
008
2n
2
.
当n=2,3,…,1 004时,有f(n)-f(n-1)=008
21-2n <1.
而f(1)=0,f(1 004)=1 0042/2 008=502,
以,从0到502的整数都能取到.当n=1 005,1 006,…,2 008时,有f(n)-f(n-1)= 008
21-2n >1.
而f(1 005)=1 0052/2 008=(1 004+1)2/2 008=502+1+1/2 008>503, 故]2008
2008[
],2008
2
[
],2008
1
[
2
2
2
是互不同的整数.从而,在]2008
2008[
],2008
2
[
],2008
1
[
2
2
2
中,共
有503+1 004=1 507个不同的整数.。
