魔方阵实现方法(全)
魔方阵算法及C语言实现

魔方阵算法及C语言实现1 魔方阵概念魔方阵是指由1,2,3……n2填充的,每一行、每一列、对角线之和均相等的方阵,阶数n = 3,4,5…。
魔方阵也称为幻方阵。
例如三阶魔方阵为:魔方阵有什么的规律呢?魔方阵分为奇幻方和偶幻方。
而偶幻方又分为是4的倍数(如4,8,12……)和不是4的倍数(如6,10,14……)两种。
下面分别进行介绍。
2 奇魔方的算法2.1 奇魔方的规律与算法奇魔方(阶数n = 2 * m + 1,m =1,2,3……)规律如下:1.数字1位于方阵中的第一行中间一列;2.数字a(1 < a ≤ n2)所在行数比a-1行数少1,若a-1的行数为1,则a的行数为n;3.数字a(1 < a ≤ n2)所在列数比a-1列数大1,若a-1的列数为n,则a的列数为1;4.如果a-1是n的倍数,则a(1 < a ≤ n2)的行数比a-1行数大1,列数与a-1相同。
2.2 奇魔方算法的C语言实现1 #include <stdio.h> 2// Author: / 3// N为魔方阶数 4#define N 115 6int main()7{8int a[N][N]; 9int i;10 int col,row;1112 col = (N-1)/2;13 row = 0;1415a[row][col] = 1;1617for(i = 2; i <= N*N; i++)18 {19if((i-1)%N == 0 )20 {21 row++;22 }23else24 {25// if row = 0, then row = N-1, or row = row - 126 row--;27 row = (row+N)%N;2829// if col = N, then col = 0, or col = col + 130 col ++;31 col %= N;32 }33 a[row][col] = i;34 }35for(row = 0;row<N;row++)36 {37for(col = 0;col < N; col ++)38{39 printf("%6d",a[row][col]);40 }41printf("\n");42 }43return0;44 }3 偶魔方的算法偶魔方的情况比较特殊,分为阶数n = 4 * m(m =1,2,3……)的情况和阶数n = 4 * m + 2(m = 1,2,3……)情况两种。
魔方阵

问题3.1、n –魔方阵一、提出问题所谓“n – 魔方阵”是指由1至n 这n 个不同整数构成的魔方阵,其魔方常数为n ( n + 1 ) / 2。
例如,5 – 魔方阵和7 – 魔方阵如图3 – 1所示。
易知,这两个魔方阵的魔方常数分别为15和28。
3215415432432152154354321 ,4321765176543254321762176543654321732176547654321 图3 – 1 5 – 魔方阵和7 – 魔方阵n – 魔方阵的数字排列很有规律,若用人工的方法给出并不困难。
现在要求给出:能让计算机自动输出n (≥ 3)为奇数时形如图3 – 1所示的n – 魔方阵的算法。
二、简单分析n – 魔方阵较我们之后将要讨论的奇、偶数阶魔方阵,要简单许多。
观察后不难发现:1.要填入的n 个数字在阵列的每一行和每一列都要出现且仅出现一次,且各行(列)中的数字顺序相同,这里的顺序是指循环顺序,其中数字1接在数字n 的后面。
2.从阵列的行来看,每一行的第一个数字与它上一行正中间的数字相同。
通过对“n – 魔方阵”的分析,下面几个基本问题必须得到解决:◆ 如何确定阵列第一行各个数字?◆ 在填入其他行的数字时如何保证数字原有的顺序不改变同时每一行的第一个数字正好是其上一行正中间的数字?三、设计准备假设我们要构建的是一个n – 魔方阵,为此定义一个有n 行n 列的二维数组。
1.确定阵列第一行各个数字这里我们处理的方法很简单,即可以利用循环方法顺序地在二维数组第一行中填写1,2,3,…,n 这n 个自然数即可。
2.填入其他行的数字,并保证数字原有的顺序不改变同时每一行的第一个数字正好是其上一行正中间的数字要解决这个问题,需借助一个有n + 1单元的一维数组,并对该数组进行若干次“循环左移”处理。
所谓做一次“循环左移”,即指在一维数组中,将第1个数填入第n + 1个单元,第2个数填入第1个单元,……,第n个数填入第n– 1 个单元,最后再将第n + 1个单元中的数填入第n个单元。
11阶立方体魔方阵的制作及原理(精)

11 階立方體魔方陣的製作及原理摘要:在這篇報告中,我們將0~1330中每一個正整數,先將每一個數都連續除以11兩次,再把每一個數的餘數以及商,分別取出來,再將每一個數都表示成a×112+b×11+c,其中a、b、c都是0~10的正整數,再將這些數轉化成座標形式(a、b、c),再利用等差數列的觀念,從原點分別向X軸、Y軸、Z軸增加一定的座標量,希望11 階立方體陣中,每一個平面上它們的橫線、直線、對角線,及立方體的四條對角線,他們的x座標、y座標及z座標0~10均只出現一次,如此一來,將這些座標換算回所對的數,會出現每一個面的直線、橫線、對角線及方體中四條對角線上面的數字總和相等的結果。
研究動機:在上學期學習「數量關係」,曾經提到一種以相同大小增加或減少的數列,老師提到可以用這種觀念來解釋平面上的魔方陣.在「有趣的魔方陣」這本書中,我們又看到了有關於魔方的各種製作方法及各式各樣的變形魔方,其中所介紹的立體方陣引起了我們的興趣,但是我們發現書本所記的立體方陣都只提到2階,3階或者12面體的立體方陣(見圖)的製作及結果,但是這本書的介紹僅限於此,並沒有再提到任何立體方陣的敘述,所以我們就想到了一個問題:”能不能用類似的手法創造一個與正方形魔方類似的立體方陣?”,也就是在它的格子中填入一些數字,使它裡面的每一面橫、直、對角線的總和均相等且立方體內的四條對角線總和也與前述相等,基於這項原因經過多次的實驗及推理觀察,我們將對11階的立方體進行觀察研究。
研究目的:發展一個製作11階立方體魔方的方法,使它能滿足研究動機中的結論,並推測是否還有其他立體方陣存在。
研究方法:根據85年度嘉義中小學科展作品「奇數階的製作及原理」我們以11階的平面魔方陣為例,重新觀察它的製作過程,現在我們的問題是:”將0-120的每一個正整數填入(如圖)11×11的正方形空格中,使它的直、橫、及對角線總和均相等”,面對這個問題,我們先將0-120的每個數都除以11,找出商及餘數,並表示成座標得到詳細結果如下:0÷11=0 ……0(0,0)1÷11=0……1(0,1)2÷11=0……2(0,2)3÷11=0 ……3(0,3)4÷11=0……4(0,4)5÷11=0……5(0,5)6÷11=0 ……6(0,6)7÷11=0……7(0,7)8÷11=0……8(0,8)9÷11=0 ……9(0,9)10÷11=0……10(0,10)11÷11=1……0(1,0)12÷11=1 ……1(1,1)13÷11=1……2(1,2)14÷11=1……3(1,3)15÷11=1 ……4(1,4)16÷11=1……5(1,5)17÷11=1……6(1,6)18÷11=1 ……7(1,7)19÷11=1……8(1,8)20÷11=1……9(1,9)21÷11=1 ……10(1,10)22÷11=2……0(2,0)23÷11=2……1(2,1)24÷11=2 ……2(2,2)25÷11=2……3(2,3)26÷11=2……4(2,4)27÷11=2 ……5(2,5)28÷11=2……6(2,6)29÷11=2……7(2,7)30÷11=2 ……8(2,8)31÷11=2……9(2,9)32÷11=2……10(2,10)33÷11=3 ……0(3,0)34÷11=3……1(3,1)35÷11=3……2(3,2)36÷11=3 ……3(3,3)37÷11=3……4(3,4)38÷11=3……5(3,5)39÷11=3 ……6(3,6)40÷11=3……7(3,7)41÷11=3……3(3,8)42÷11=3 ……9(3,9)43÷11=3……10(3,10)44÷11=4……0(4,0)45÷11=4 ……1(4,1)46÷11=4……2(4,2)47÷11=4……3(4,3)48÷11=4 ……4(4,4)49÷11=4……5(4,5)50÷11=4……6(4,6)51÷11=4 ……7(4,7)52÷11=4……8(4,8)53÷11=4……9(4,9)54÷11=4 ……10(4,10)55÷11=5……0(5,0)56÷11=5……1(5,1)57÷11=5 ……2(5,2)58÷11=5……3(5,3)59÷11=5……4(5,4)60÷11=5 ……5(5,5)61÷11=5……6(5,6)62÷11=5……7(5,7)63÷11=5 ……8(5,8)64÷11=5……9(5,9)65÷11=5……10(5,10)66÷11=6 ……0(6,0)67÷11=6……1(6,1)68÷11=6……2(6,2)69÷11=6 ……3(6,3)70÷11=6……4(6,4)71÷11=6……5(6,5)72÷11=6 ……6(6,6)73÷11=6……7(6,7)74÷11=6……8(6,8)75÷11=6 ……9(6,9)76÷11=6……10(6,10)77÷11=7……0(7,0)78÷11=7 ……1(7,1)79÷11=7……2(7,2)80÷11=7……3(7,3)81÷11=7 ……4(7,4)82÷11=7……5(7,5)83÷11=7……6(7,6)84÷11=7 ……7(7,7)85÷11=7……8(7,8)86÷11=7……9(7,9)87÷11=7 ……10(7,10)88÷11=8……0(8,0)89÷11=8……1(8,1)90÷11=8 ……2(8,2)91÷11=8……3(8,3)92÷11=8……4(8,4)93÷11=8 ……5(8,5)94÷11=8……6(8,6)95÷11=8……7(8,7)96÷11=8 ……8(8,8)97÷11=8……9(8,9)98÷11=8……10(8,10)99÷11=9 ……0(9,0)100÷11=9……1(9,1)101÷11=9……2(9,2)102÷11=9 ……3(9,3)103÷11=9……4(9,4)104÷11=9……5(9,5)105÷11=9 ……6(9,6)106÷11=9……7(9,7)107÷11=9……8(9,8)108÷11=9 ……9(9,9)109÷11=9……10(9,10)110÷11=10……0(10,0)111÷11=10 ……1(10,1)112÷11=10……2(10,2)113÷11=10……3(10,3)114÷11=10 ……4(10,4)115÷11=10……5(10,5)116÷11=10……6(10,6)117÷11=10 ……7(10,7)118÷11=10……8(10,8)119÷11=10……9(10,9)120÷11=10 ……10(10,10)現在我們想將這些數對填入空格中,而且我們希望能讓我們的橫、直、對角線的x座標及y座標總和均相等,我們所利用的方法如下:從左下角開始填入(0,0)分別向下每跳一格加上(1,1) ,(2,3)我們可先得到如下圖結果:因為(6,9)再加(2,3)得到(8,12),我們將12除以11取其餘數一可得座標(8,1)再將其向填入空格中,其餘的座標填法均如上所述,所以我們將所有座標填入後所得到下圖結果(見圖3)觀察上述結果,因為橫、直、對角線他們的x座標及y座標均從0-10出現一次,所以我們可以推測將座標還原成原先代表的數字能夠得到我們要的結論,還原的結果如下:上述方法的優點是:1.我們將原本相當多且複雜的數轉換成座標後,每一個座標所要考慮的對象都變少了(只要考慮0~10)2.因為從(0,0)向x軸、向y軸增加一定的座標。
10种魔方还原方法

10种魔方还原方法《10种魔方还原方法》你是不是看到魔方就觉得很神奇,但自己动手还原却毫无头绪?别担心,这篇文章就是来帮你解决这个问题的。
在这里,你将学到10种魔方还原的方法,让你从魔方小白逐渐变成魔方高手。
一、层先法:从底层开始构建层先法是一种很基础也很容易理解的魔方还原方法。
核心思路就是一层一层地还原魔方。
1. 底层十字这一步就像是给魔方搭建一个稳固的地基。
我们的目的是在魔方的底层拼出一个白色的十字。
操作方法:先找到白色的中心块,然后把带有白色棱块的一面旋转到和中心块相对应的颜色面旁边,通过转动底层或者中层,将白色棱块移动到底层正确的位置。
就好比盖房子要先确定好框架的横竖结构一样。
小贴士:注意观察棱块的颜色,不要搞错方向,不然后续会很麻烦。
2. 底层角块归位这一步是让底层的角块回到正确的位置,使得底层完整。
解释:这就像是在地基上添砖加瓦,让底层更加稳固。
操作:找到带有白色的角块,把它移动到顶层,然后通过调整角块的位置,让它的另外两种颜色和相邻面的中心块颜色一致,最后旋转底层,将角块归位。
比如你要把一块拼图放到正确的位置,需要不断调整它的方向。
注意事项:在移动角块的过程中,可能会破坏之前做好的底层十字,要小心操作。
3. 中层棱块归位这一步主要是把中层的棱块还原。
作用:中层是连接底层和顶层的关键部分,这一步就像搭建房子的中层结构。
操作:先找到一个没有在中层正确位置的棱块,把它所在的面旋转到顶层,然后通过公式(如“远切回回,接孩子放学”的口诀对应的操作)将棱块移动到中层正确的位置。
这就像火车要在铁轨上准确地行驶到指定的站点。
小贴士:要熟悉公式的操作,多练习才能熟练掌握。
4. 顶层十字目标是在魔方的顶层拼出一个黄色的十字。
意义:这是还原顶层的第一步,是一个重要的标志性阶段。
操作:如果顶层已经有黄色棱块,就通过转动顶层将它们调整成十字形状;如果没有,就需要通过特定的公式(如F R U R' U' F')来让黄色棱块出现在顶层并形成十字。
三阶魔方中级教程
—
三阶魔方共有4325亿亿种排列方式,如何把打乱的魔术方块复原是个有趣而又困难的问题,玩魔方实在是奥妙无穷、乐趣无比。
复原魔方需要一双灵巧的手,一个好魔方,
敏锐的空间想象力和高效顺手的转动程序,需要你的信心、决心、耐心、细心、恒心、上进心!魔方可以使你的聪明才智得到尽情的发挥,使你的信心能力得到充分的展示!
通过训练,一秒钟可以转动4-8
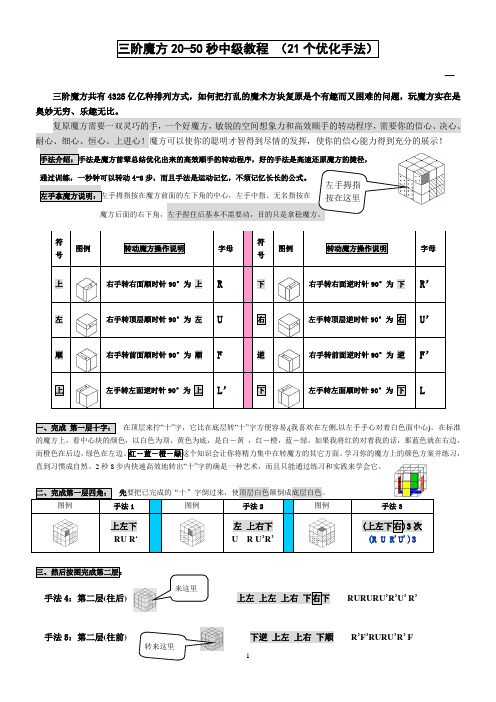
在顶层来拧“十”字,它比在底层转“十”字方便容易,(我喜欢在左侧,以左手手心对着白色面中心)。
在标准的魔方上,看中心块的颜色,以白色为顶,黄色为底,是白-黄 ,红-橙,蓝-绿,如果我将红的对着我的话,那蓝色就在右边,而橙色在后边,学习你的魔方上的颜色方案并练习,直到习惯成自然。
2秒8步内快速高效地转出“十”字的确是一种艺术,而且只能通过练习和实践来学会它。
手法3
手法4:第二层(往后) RURURU ’R ’U ’ R ’
手法5:第二层(往前) 下逆 上左 上右 下顺 R ’F ’RURU ’R ’ F
第一层十字(2秒8步)→→第一层四底角(4个手法)→→第二层四中棱(4个手法)→第三层顶面十字(1个手法)→→第三层十字反色(1个手法)→→第三层换位(2个手法)第一层十字后总共最多用12个手法完成!20-50秒快速还原三阶魔方!。
奇数阶魔方算法及实现方法+数据结构

课程设计封面题目:奇数阶魔方的算法与实现课程:数据结构学院:信息工程学院专业:物联网工程班级:12普本物联网学号:1201141009姓名:李冰洋指导教师:叶茂功任务书书写说明:1完成期限:自2014 年6 月5 日至2014 年6 月18 日共2 周2. 计划答辩时间:2014年 6 月22 日黄河科技学院本科课程设计任务书信息工程学院计算机科学系物联网工程专业2008 级12普本物联网班学生李冰洋学号1201141009 指导教师叶茂功课程名称:数据结构完成期限:自2014 年6 月 5 日至2014 年 6 月18 日共 2 周课程设计题目奇数阶魔方的算法与实现课程设计内容与基本要求一、内容本次课程设计内容主要是利用二维数组输出正确的n阶魔方矩阵。
二、要求(1)通过实际项目的分析、设计、编码、测试等工作,掌握用C语言来开发和维护软件。
(2)按要求编写课程设计报告书,能正确编写分析、设计、编码、测试等技术文档和用户三、参考文献1.王红梅.数据结构.清华大学出版社2.王红梅.数据结构学习辅导与实验指导.清华大学出版社3.严蔚敏,吴伟民.数据结构(C语言版).清华大学出版社4.叶茂功,代文征.数据结构项目化教程.国防工业出版社四、注意事项1.提交课程设计代码与课程设计说明书;2.材料的书写符合《黄河科技学院毕业设计指导规范手册》。
计划答辩时间:2014 年 6 月31 日专业(教研室)审批意见:审批人(签字):目录1摘要 (1)2课程设计目的 (2)3课程设计内容 (2)4程序执行流程图 (3)5程序源代码 (4)6运行结果 (9)7结束语.............................................。
(11)摘要VC++6.0是一种基于C语言的数据库设计、创建和管理的软件,利用它可以对各种事务管理工作中的大量数据进行有效的管理并满足数据检索的需要。
本系统就是根据现阶段的需要,通过VC++6.0开发一个员工管理系统来实现对员工的信息的查找、高效的管理和维护。
魔方阵算法(精品)

到D中。然后按下列方法交换:
a、将A和D的第一列对应位置的元素(出各自的中间一行外)进行交换;
b、将A和D的中间一列的中间一行的元素进行交换;
c、如果(U+1)/2>2,则将A和D中左边的第二列开始到第(U-1)/2列为止,对应行的数
魔方阵算法(精品)
魔方阵算法2008-11-22 17:12幻方问题分为奇幻方和偶幻方。奇幻方和偶幻方方阵的布阵规律不同,而偶幻方又分为
是4的倍数(如4,8,12,16,20等)和不是4的倍数(如6,10,14,18等)两种。现在
就幻方的三种情形的布阵规律分别加以介绍。
1、奇幻方 N=2*M+1(M=1,2,3,……)的布阵规律
2、①偶幻方N=4*(M=1,2,3,……)的布阵规律
先将1至N*N由小到大的顺序,从第一行开是依序填入N*N的方阵中,然后将N*N的方阵以4
行4列划分为若干个4*4的小方阵,再将所有4*4小方阵的两个对角线上的数字划掉,之后
将所有被划掉的数字重新由大到小的进行排列,然后再将这些数字按排列顺序由N*N方阵
(第二种解释)
a,将1填入第一行中间;
b,将每个数填在前一个数的右上方。
c,若该位置超出最上行,则改填在最下行的对应位置;
d,若该位置超出最右列,则该填在最左列的对应行位置;
e,若某元素填在第一行最右列,下右上角已填了其他数据,则下一个数填在该数同列的下一行位置。
第二步:將中央部分半數的列,所有數字左右翻轉。
第三步:將中央部分半數的行,所有數字上下翻轉。
实验报告魔方阵程序(3篇)

第1篇一、实验目的1. 熟悉Python编程语言的基本语法和常用数据结构。
2. 学习使用嵌套循环实现复杂数据结构的构建。
3. 掌握随机数生成和排序算法在程序中的应用。
4. 提高编程能力和问题解决能力。
二、实验环境1. 操作系统:Windows 102. 编程语言:Python3.83. 开发工具:PyCharm三、实验内容本实验旨在设计一个魔方阵程序,实现以下功能:1. 生成一个nn的魔方阵。
2. 魔方阵中,每一行的数字之和等于n。
3. 魔方阵中,每一列的数字之和等于n。
4. 魔方阵中,对角线的数字之和等于n。
四、实验步骤1. 导入所需的库```pythonimport random```2. 定义一个函数,用于生成nn的魔方阵```pythondef generate_magic_square(n):初始化一个nn的二维数组,用于存储魔方阵的数字 magic_square = [[0] n for _ in range(n)]num = 1 用于存储当前要填充的数字i, j = 0, n // 2 初始化起始位置while num <= n n:将数字num填充到当前位置magic_square[i][j] = numnum += 1判断下一个位置new_i, new_j = (i - 1) % n, (j + 1) % n 如果当前位置已被填充,则移动到新位置if magic_square[new_i][new_j] != 0:i, j = (i + 1) % n, jelse:i, j = new_i, new_jreturn magic_square```3. 定义一个函数,用于检查魔方阵是否正确```pythondef check_magic_square(magic_square, n):检查每一行的数字之和是否等于nfor i in range(n):if sum(magic_square[i]) != n:return False检查每一列的数字之和是否等于nfor j in range(n):if sum(magic_square[i][j] for i in range(n)) != n:return False检查对角线的数字之和是否等于nif sum(magic_square[i][i] for i in range(n)) != n or sum(magic_square[i][n - i - 1] for i in range(n)) != n:return Falsereturn True```4. 主函数```pythondef main():n = int(input("请输入魔方阵的阶数:"))magic_square = generate_magic_square(n)if check_magic_square(magic_square, n):for row in magic_square:print(' '.join(map(str, row)))else:print("生成的魔方阵不正确!")```5. 运行程序```pythonif __name__ == "__main__":main()```五、实验结果当输入阶数n为5时,程序输出如下魔方阵:```1 2 3 4 512 13 14 15 1011 16 17 18 196 7 8 9 205 4 3 2 1```六、实验总结通过本次实验,我们成功设计并实现了一个魔方阵程序。
C语言实现魔方阵

C语言实现魔方阵魔方阵(Magic Square)是一个古老且有趣的数学问题,它是一个正方形矩阵,其中每行、每列以及对角线上的元素之和都相等。
例如,下面是一个3阶魔方阵:```816357492```实现魔方阵的算法有多种,下面我们将介绍一种基于C语言的实现方法。
首先,我们需要设计一个函数来检查生成的矩阵是否是魔方阵。
这个函数的输入是一个二维数组和魔方阵的阶数,输出是一个布尔值,表示输入的矩阵是否是魔方阵。
下面是这个函数的实现:```c#include <stdbool.h>bool checkMagicSquare(int **matrix, int n)int sum = n * (n * n + 1) / 2;//检查每行的和for (int i = 0; i < n; i++)for (int j = 0; j < n; j++) rowSum += matrix[i][j];}if (rowSum != sum)return false;}}//检查每列的和for (int i = 0; i < n; i++) int colSum = 0;for (int j = 0; j < n; j++) colSum += matrix[j][i];}if (colSum != sum)return false;}}//检查主对角线的和for (int i = 0; i < n; i++)diagSum += matrix[i][i];}if (diagSum != sum)return false;}//检查副对角线的和int antiDiagSum = 0;for (int i = 0; i < n; i++) antiDiagSum += matrix[i][n - 1 - i]; }if (antiDiagSum != sum)return false;}return true;```接下来,我们使用一个递归函数来生成魔方阵。
魔方全解(比较简单的几种解法)

三阶魔方、魔方构造1 •魔方共六个面,每个面有一种颜色,若以红面为正面,绿面为底面,则橙面为背面,蓝面为顶面,白面为左面,黄面为右面。
2•三阶魔方由3X3X3=27块小正方体构成,其中一块在内部色,叫做角块。
3 •只要魔方任意三块小正方体连成一线,就能旋转。
4 •三阶魔方中心块的位置不会改变。
5 •魔方还原的前提是有一个被转乱的魔方、转向表示为了方便表示魔方的转向,使用以下字母。
(箭头所指为前面)1 • 一层旋转F (Front )F将魔力刖面一层顺时针旋转90度。
Fi将魔方前面一层逆时针旋转90度。
B(Back)B将魔方后面一层顺时针旋转90度。
Bi将魔方后面一层逆时针旋转90度。
L Li R RiU Ui D Di没有颜色;6块只有一种颜色,叫做中心块;12块有两种颜色,叫做边块;8块有三种颜中心块边块L (Left)L将魔力左面一层顺时针旋转90度。
Li将魔方左面一层逆时针旋转90度。
R(Right)R将魔方右面一层顺时针旋转90度。
Ri将魔方右面一层逆时针旋转90度。
U(Up)U将魔方上面一层顺时针旋转90度。
Ui将魔方上面一层逆时针旋转90度。
D(Down )D将魔方下面一层顺时针旋转90度。
Di将魔方下面一层逆时针旋转90度。
2. 中间层旋转M(riR)M将魔方左面第二层顺时针旋转90度。
M MiMi将魔方左面第二层逆时针旋转90度。
E (diD )E将魔方上面第二层顺时针旋转90度。
Ei将魔方上面第二层逆时针旋转90度。
S (fiF )S将魔方后面第二层顺时针旋转90度。
Si将魔方后面第二层逆时针旋转90度。
E Ei S Sif将魔方前面两层顺时针旋转90度。
fi将魔方前面两层逆时针旋转90度。
b b将魔方后面两层顺时针旋转90度。
bi将魔方后面两层逆时针旋转90度。
lI将魔方左面两层顺时针旋转90度。
li将魔方左面两层逆时针旋转90度。
rr将魔方右面两层顺时针旋转90度。
ri将魔方右面两层逆时针旋转90度。
魔方全解(比较简单的几种解法)

魔方全解(比较简单的几种解法)LT三阶魔方一、魔方构造1.魔方共六个面,每个面有一种颜色,若以红面为正面,绿面为底面,则橙面为背面,蓝面为顶面,白面为左面,黄面为右面。
2.三阶魔方由3×3×3=27块小正方体构成,其中一块在内部,没有颜色;6块只有一种颜色,叫做中心块;12块有两种颜色,叫做边块;8块有三种颜色,叫做角块。
3.只要魔方任意三块小正方体连成一线,就能旋转。
4.三阶魔方中心块的位置不会改变。
5.魔方还原的前提是有一个被转乱的魔方。
二、转向表示为了方便表示魔方的转向,使用以下字母。
(箭头所指为前面)1.一层旋转F (Front ) 中心块边块F 将魔方前面一层顺时针旋转90度。
Fi 将魔方前面一层逆时针旋转90度。
B (Back )B 将魔方后面一层顺时针旋转90度。
Bi 将魔方后面一层逆时针旋转90度。
L (Left )L 将魔方左面一层顺时针旋转90度。
Li 将魔方左面一层逆时针旋转90度。
R (Right )R 将魔方右面一层顺时针旋转90度。
Ri 将魔方右面一层逆时针旋转90度。
U (Up )U 将魔方上面一层顺时针旋转90度。
Ui 将魔方上面一层逆时针旋转90度。
D (Down )D 将魔方下面一层顺时针旋转90度。
Di 将魔方下面一层逆时针旋转90度。
2.中间层旋转F Fi B BiL Li R Ri U Ui D Di·通常,单个字母表示顺时针旋转,加i或ˊ表示逆时针旋转。
·双写转向或在转向后加2表示在这个方向上旋转180度。
·()×n表示重复括号内的步骤n次。
三、魔方还原1.一面(一层)还原1)还原一面边块①选择好一种颜色的中间块作为要还原的一面,将其作为前面,记住它的背面中间块颜色。
②先恢复一个色块,以这个色块为准,旋转前面使上、下、左、右四面中心块正位。
③旋转后面一层或第二层使其出现下面情况,逐个恢复色块,直到前面形成十字。
三阶魔方教程图解(彩版可编辑打印)

三阶魔方入门教程前言我们常见的魔方是3x3x3的三阶魔方,是一个正6 面体,有6种颜色,由26块组成,有8个角块;12个棱块;6个中心块(和中心轴支架相连)见下图:(图1)学习魔方首先就要搞清它的以上结构,知道角块只能和角块换位,棱块只能和棱块换位,中心块不能移动。
魔方的标准色:国际魔方标准色为:上黄-下白,前蓝-后绿,左橙-右红。
(见图2)注:(这里以白色为底面,因为以后的教程都将以白色为底面,为了方便教学,请都统一以白色为准)。
(图2)认识公式(图3)(图4)公式说明:实际上就是以上下左右前后的英文的单词的头一个大写字母表示(图5)(图6)(图7)(图8)步骤一、完成一层首先要做的是区分一层和一面:很多初学者对于“一面”与“一层”缺乏清楚的认识,所以在这里特别解释一下。
所谓一层,就是在完成一面(如图2的白色面)的基础上,白色面的四条边,每条边的侧面只有一种颜色,图(2).如图(1)中心块是蓝色,则它所在面的角和棱全都是蓝色,是图(2)的反方向图(3)和(4)则是仅仅是一面的状态,而不是一层!(1)(2)(3)(4)注:图(2)和(4)分别是图(1)和(3)的底面状态想完成魔方,基础是最重要的,就像建筑一样,魔方也如此,基础是最重要的。
由于上文提到过中心块的固定性,这一性质,在魔方上实质起着定位的作用,简单的说就是中心块的颜色就代表它所在的面的颜色。
一、十字(就是快速法中的CROSS)第一种情况如图所示:(橙色下面颜色为白色,为方便观察,特意翻出颜色)公式为R2第二种情况如图所示:(白色下面颜色为橙色,为方便观察,特意翻出颜色)橙白块要移到上右的位置,现在橙白块在目标位置的下面。
但其橙色片没有和橙色的中心块贴在一起。
为此我们先做D’F’即把橙色粘在一起,接着R 还原到顶层,,F 是把蓝白橙还原到正确的位置(上面的F’使蓝白块向左移了九十度)。
公式为D’F’R F图解:当然,架十字不只只有上面两种情况,现我们在分析下其它的一些情况吧!如下图:橙白块的位置己对好,但颜色反了,我就先做R2化成第二种情况,然后用还原第二种情况的公式即可!上面两种情况都为前右的块要移到上后的位置。
c语言程序设计第五版课后答案谭浩强第六章习题答案

c语⾔程序设计第五版课后答案谭浩强第六章习题答案第六章:利⽤数组处理批量数据1. ⽤筛选法求100之内的素数【答案解析】素数:约数为1和该数本⾝的数字称为素数,即质数筛选法:⼜称为筛法。
先把N个⾃然数按次序排列起来。
1不是质数,也不是合数,要划去。
第⼆个数2是质数留下来,⽽把2后⾯所有能被2整除的数都划去。
2后⾯第⼀个没划去的数是3,把3留下,再把3后⾯所有能被3整除的数都划去。
3后⾯第⼀个没划去的数是5,把5留下,再把5后⾯所有能被5整除的数都划去。
这样⼀直做下去,就会把不超过N 的全部合数都筛掉,留下的就是不超过N的全部质数。
因为希腊⼈是把数写在涂腊的板上,每要划去⼀个数,就在上⾯记以⼩点,寻求质数的⼯作完毕后,这许多⼩点就像⼀个筛⼦,所以就把埃拉托斯特尼的⽅法叫做“埃拉托斯特尼筛”,简称“筛法”。
(另⼀种解释是当时的数写在纸草上,每要划去⼀个数,就把这个数挖去,寻求质数的⼯作完毕后,这许多⼩洞就像⼀个筛⼦。
)【代码实现】//⽤筛选法求100以内的素数#include<stdio.h>int main(){int i, j, k = 0;// 将数组汇总每个元素设置为:1~100int a[100];for (i = 0; i < 100; i++)a[i] = i+1;// 因为1不是素数,把a[0]⽤0标记// 最后⼀个位置数字是100,100不是素数,因此循环可以少循环⼀次a[0] = 0;for (i = 0; i < 99; i++){// ⽤a[i]位置的数字去模i位置之后的所有数据// 如果能够整除则⼀定不是素数,该位置数据⽤0填充for (j = i + 1; j < 100; j++){if (a[i] != 0 && a[j] != 0){//把不是素数的都赋值为0if (a[j] % a[i] == 0)a[j] = 0;}}}printf(" 筛选法求出100以内的素数为:\n");for (i = 0; i < 100; i++){//数组中不为0的数即为素数if (a[i] != 0)printf("%3d", a[i]);}printf("\n");return 0;}【运⾏结果】2. ⽤选择法对10个整数排序【答案解析】选择排序原理:总共两个循环,外循环控制选择的趟数,内循环控制具体选择的⽅式。
魔方7步复原指南

魔方七步复原指南魔方是一个好玩的益智玩具,挑战你的智力,启发你的创意。
扭动魔方不同的颜色方块,都会出现意想不到的新挑战。
本文介绍的方法可以在七步内帮助您复原一个魔方。
魔方小故事:魔方是由匈牙利建筑及设计学教授ErnoRubik在1974发明的,之后在一年内魔方成为世界上空前产销的益智玩具。
现在魔方仍是销量最佳的益智玩具。
在电脑的帮助下,多数打乱了的3阶(即3×3×3)魔方可以在17次内归位。
到目前为止,没有一个难解的情况,要拧20多次才能把魔方复原。
有人可以把任何打乱了的魔方,在45次就可以归位,有人甚至在1分钟左右的时间以用盲拧的方法使其归位。
在学习魔方复原之前,掌握魔方的一些基本常识会有利于我们下面的学习。
阅读本文时建议你手里拿一个魔方。
首先你要熟悉魔方的不同部分和色块:棱(边,12个)、角(8个)和中心点(6个)。
棱的颜色有2种,角的颜色有3种,而中心点的色块只有1种颜色。
中心点的色块是固定在玩具内部的装置上,所以位置是不会改变的。
例如,红色中央色块永远都在橙色中央色块的对面。
魔方的每一面都可以用字母表示,如下图所示:F —Front ,前面,你正对的一面。
B —Back ,后面,背对你(看不到)的那一面。
R —Right ,右侧面L —Left ,左侧面U —Up ,顶层,上面D —Down ,底层,下面归位方法中会用字母来说明要拧动的层(面)及方向,单个字母表示顺时针拧90度,字母加了后缀i 后表示将该面逆时针拧90度。
如U 表示将顶层顺时针转90度,Ui 表示将顶层逆时针转90度。
下面介绍将一任意打乱的3阶魔方归位的详细步骤:第一步,顶层做十字。
要做出十字,要先使同色的棱块逐一归位(要求与其所在的侧面中心块的颜色相同),同时不能把已归位的棱块打乱,这个你基本上可以无师自通地完成。
有时棱块位置正确,但颜色相反。
如果颜色错误(相反)的棱块在顶层的右方,用Ri →U →Fi →Ui 的次序转动就可以将它正确归R BU FDL位又不影响其它已归位的棱块。
最全面的魔方还原步骤(带图解及公式)

三阶魔方玩法教程下图是本教程介绍的三阶魔方入门的玩法(层先法)复原的基本步骤示意图:第一步:底棱归位(又称底部架十字,底层四个棱块正确复原的过程)注:(本教程以白色为底面,为了方便交流与学习,请统一把白色作为底面)。
魔方底层架十字可以无师自通,只是我们这一步要复原的四个棱块的相对位置顺序要注意,由于我们以白色中心块做底层,按照我们现在的主流魔方的贴纸的帖法(上黄下白,前蓝后緑,左橙右红),如果我们先复原了白蓝这个棱块,那我们在保持白色中心块在底部的情况下,白红的棱块就一点要放在白蓝棱块的右边,白橙棱块放在白蓝棱块的左边,白緑棱块放在白蓝棱块的对面,由于魔方的中心块不会发生变化,所以在原的过程中,我们是以中心块为参照物的,第一步我们在复原白蓝、白红、白绿、白橙这四个棱块的时候,我们可以先把白色面旋转到顶层,和黄色中心块同一个平面,然后再把他对应的另一个颜色(蓝或红或緑或橙)经过旋转最上层,使之和对应的中心块的颜色同色,这样我们再旋转180度,对应的棱块就正确复原到底部了。
注意:图1-1的情况是没有正确归位的情况,需要调整白蓝和白红两个棱块的位置,才是正确的完成了底棱归位。
第二步:底角归位(复原魔方第一层四个角块)魔方的四个底角正确归位以后一定会出现倒T字型,如图2所示,如果不是这样肯定是底面角块没有正确归位(位置错了,重新来过)。
底角归位也可无师自通,有兴致的朋友可以自己琢磨一些技巧和完成这一步。
有难度的朋友可参考我下面介绍的一种技巧来完成,我们先看图2-1和图2-2,首先我们先确定目标块的位置是在他要正确归位的正上面的位置,然后我们再看白色的面朝向何方,就很快的能快速判断出来是下图几种情况中的哪一种了。
复原基本思想:先将目标角块调至顶层侧面,再转动能与之相连形成顺色整体的面,使目标角与底棱连成一个(1×1×2)的归位整体,再转至正确的位置。
因此,下列的五个实例并没有必要死记。
C语言魔方阵的三种实现方法

C语⾔魔⽅阵的三种实现⽅法⽬录魔⽅阵:1.奇数阶魔⽅阵2.偶数阶魔⽅阵(n=4K)3.偶数阶魔⽅阵(n=4K+2)魔⽅阵:把1到n*n排成n⾏n列⽅阵,使⽅阵中的每⼀⾏、每⼀列以及对⾓线上的数之和都相同,即为n阶魔⽅阵。
根据魔⽅阵的规律,我将它分为三种情况。
1.奇数阶魔⽅阵规律:第⼀个数放在第⼀⾏的中间,下⼀个数放在上⼀个数的上⼀⾏下⼀列,若该位置已经有了数字即放在上个数的下⾯⼀⾏的相同列⽤C语⾔编程如下:⽰例:n=5;#include<stdio.h>#include<stdlib.h>#include<assert.h>void Magic1(){#define ROW 5#define COL ROWassert(ROW % 2 != 0); //判断n是否为奇数int arr[ROW][COL] = { 0 }; //定义⼆维数组int currow = 0;int curcol = COL / 2;arr[currow][curcol] = 1;for (int i = 2; i <= ROW * COL; i++){if (arr[(currow - 1 + ROW) % ROW][(curcol + 1) % COL] == 0) //按照规律赋值{currow = (currow - 1 + ROW) % ROW;curcol = (curcol + 1) % COL;}else{currow = (currow + 1) % ROW;}arr[currow][curcol] = i;}for (int i = 0; i < ROW; i++) //打印魔⽅阵{for (int j = 0; j < COL; j++){printf("%-3d", arr[i][j]);}printf("\n");}}int main(){Magic1();return 0;}结果:2.偶数阶魔⽅阵(n=4K)规律:按数字从⼩到⼤,即1,2,3……n顺序对魔⽅阵从左到右,从上到下进⾏填充;将魔⽅阵分成若⼲个4×4⼦⽅阵(如:8阶魔⽅阵可分成四个4×4⼦⽅阵),将⼦⽅阵对⾓线上的元素取出;将取出的元素按从⼤到⼩的顺序依次填充到n×n⽅阵的空缺处。
求魔方阵的十种算法

求魔方阵的十种算法魔方阵,古代又称“纵横图”,是指组成元素为自然数1、2…n的平方的n×n的方阵,其中每个元素值都不相等,且每行、每列以及主、副对角线上各n个元素之和都相等。
如3×3的魔方阵:8 1 63 5 74 9 2魔方阵的排列规律如下:(1)将1放在第一行中间一列;(2)从2开始直到n×n止各数依次按下列规则存放;每一个数存放的行比前一个数的行数减1,列数加1(例如上面的三阶魔方阵,5在4的上一行后一列);(3)如果上一个数的行数为1,则下一个数的行数为n(指最下一行);例如1在第一行,则2应放在最下一行,列数同样加1;(4)当上一个数的列数为n时,下一个数的列数应为1,行数减去1。
例如2在第3行最后一列,则3应放在第二行第一列;(5)如果按上面规则确定的位置上已有数,或上一个数是第一行第n列时,则把下一个数放在上一个数的下面。
例如按上面的规定,4应该放在第1行第2列,但该位置已经被占据,所以4就放在3的下面;1居上行正中央依次右上切莫忘上出框时往下写右出框时左边放右上有数下边写右上出框也一样一、魔方阵的简介1.何谓矩阵?矩阵就是由方程组的系数及常数所构成的方阵。
把用在解线性方程组上既方便,又直观。
2.何谓n阶方阵?若一个矩阵是由n个横列与n个纵行所构成,共有个小方格,则称这个方阵是一个n阶方阵。
3.何谓魔方阵?4 9 2 3 5 7 8 1 6定义:由n*n个数字所组成的n阶方阵,具有各对角线,各横列与纵行的数字和都相等的性质,称为魔方阵。
而这个相等的和称为魔术数字。
若填入的数字是从1到n*n,称此种魔方阵为n阶正规魔方阵。
4.最早的魔方阵相传古时为了帮助治水专家大禹统治天下,由水中浮出两只庞大动物背上各负有一图,只有大禹才可指挥其中之由龙马负出的为河图,出自黄河;另一由理龟负出的洛书出自洛河。
洛书5.最早的四阶魔方阵最早的四阶方阵刻在印度一所庙宇石上,年代大约是十一世纪。
三阶魔方速成教程

三阶魔方还原方法魔方还原方法魔方解法快速解法首先,我们要了解一下魔方的结构和相关术语:先简单了解一下魔方的结构。
魔方是由26个“块”组成,我们把它们分为三类:含有三个颜色的块是“角块”,处于魔方的八个角,魔方上共8个。
含有二个颜色的块是“棱块”,处于角块和中心块之间,共12个。
只有一个颜色的块是“中心块”,处于魔方每个面的中心,共6个。
魔方各种不同类别的“块”之间不能互移,即魔方的角块无法移动到棱块或中心块的位置,魔方的棱块也无法移动到角块或中心块的位置,中心块也一样。
此外,这26个块没有任何两个块的颜色是相同的,每个块都不同。
我们称的还原六面,其实也可以说是在还原26个“块”,科学的还原方法主要是以块为单位进行还原,以块还原层,以层还原整个魔方,而不是平常一般人所认为的一面一面的还原。
我们把魔方分为三层,本教程是以一层一层的还原,最终还原整个魔方。
其中,第一层的还原共涉及四个角块和四个棱块,需要一块一块的还原,我们先从4个棱块开始,然后再还原4个角块即可完成第一层。
第二层的还原只涉及四个棱块的还原, 也是需要一块一块的还原,还原4个棱块,即可还原第二层.第三层的还原共涉及到四个角块和四个棱块,也是需要一块一块的还原,但是这层的步骤比较多一点,可是还是比较容易学会的.先还原四个棱块,再还原四个角块就可以转好第三层了,这样魔方就还原好了.当然在我们的还原方法中要用到一些公式,先说明一下公式中各个代表意义(如下图):了解了公式中各种符号的意义,那么我现现在就开始学习吧(记不住不要紧,可以到上图中去查一下,是了.第一步:先还原第一层还原十字棱:如果你做丌出来,没关系,可以看下面的具体步骤,大胆的去转吧,你会成功的,这个很简单:如果还是不能调出一个十字架出来,那么看下面的一些可能出现的情况以及解决办法。
这些方法可转好所需棱块,并且丌打乱其他3个已做好的棱块。
如果你在调第2或第3个的棱块就已经碰到不会做,那么也可以参照以下这次转法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a[i][j]=0; /*先令所有元素都为0*/
}
j=(N-1)/2; /*判断j的位置*/
a[0][j]=1; /*将1放在第一行中间一列*/
for(k=2;k<=N*N;k++) /*再从2开始处理*/
{
i=i-1; /*存放的行比前一个数的行数减1*/
j=j+1; /*存放的列比前一个数的列数加1*/
if((i<0)&&(j==N)) /*前一个数是第一行第N列时,把下一个数放在上一个数的下面*/
{
i=i+2;
j=j-1;
}
else
{
if(i<0) /*当行数减到第一行,返回到最后一行*/
i=N-1;
if(j>N-1) /*当列数加到最后一行,返回到第一行*/
j=0;
}
if(a[i][j]==0) /*如果该元素为0,继续执行程序*/
首先,在左上角的方阵中做记号,每行每列,各取一半打上记号。
然后,将其向其余3个方阵中映像。接着,从左上角格子开始,按从左到右,从上到下的次序将1到n*n的值往方阵中填写,但遇到作了标记的格子时跳过。再从右下角格子开始,按从右到左,从下到上的次序将1到n*n的值往方阵中填写,但遇到已填过值的格子时跳过,既可以构成一个魔方阵。
{
swap(&Array[i][j],&Array[n-1-i][n-1-j]);
}
else if(i%2==0&&Array[i][j]%2==1)/*奇行换奇*/
{
swap(&Array[i][j],&Array[n-1-i][n-1-j]);
}
}
else
{
if(i%2==1&&Array[i][j]%2==1)/*偶行换奇*/
(1)当n为奇数时,即n=2*m+1时,算法为:
首先,把1填在第一行的正中间。
其次,若数k填在第i行第j列的格子中,那么k+1应填在它的左上方,即i-1,j-1;如果左上方没有格子,若i-1=0,那么k+1填在第n行第j-1列的格子中;若j-1=0,那么k+1填在第i-1行第n列的格子中;若i-1=0,j-1=0,那么k+1填在第n行第n列的格子中。
int tempArray2[MAX_INDEX];
a=n/2;
b=a+1;
m=n%4;
switch(m)
{
case 0:
case 2:
/*穿心对调*/
for(i=0;i<n;i++)
for(j=0;j<n/2;j++)
{
if(i<n/2)
{
if(i%2==1&&Array[i][j]%2==0)/*偶行换偶*/
{
swap(&Array[i][j],&Array[n-1-i][n-1-j]);
}
else if(i%2==0&&Array[i][j]%2==0)/*奇行换偶*/
{
swap(&Array[i][j],&Array[n-1-i][n-1-j]);
}
}
}
/*End穿心对调*/
if(m==2)
{
for(i=0;i<n/2;i++)
}
}
else if(i>n/2)
{
if(i%2==1&&Array[i][j]%2==0)/*偶行换偶*/
{
swap(&Array[i][j],&Array[n-1-i][n-1-j]);
}
else if(i%2==0&&Array[i][j]%2==0)/*奇行换奇*/
{
swap(&Array[i][j],&Array[n-1-i][n-1-j]);
{
if((i!=0)&&(i!=a-1)&&(i!=b-1)&&(i!=n-1))
{
swap(&Array[i][a-1],&Array[n-1-i][a-1]);
swap(&Array[b-1][i],&Array[b-1][n-1-i]);
}
}
swap(&Array[0][a-1],&Array[0][b-1]);
a[j] = pivot;
QuickSort(a, l, j-1); /*对左段排序*/
QuickSort(a, j+1, r); /*对右段排序*/
}
void Huanf(int Array[][MAX_INDEX],int n)
{
int i,j;
int a,b,m;
int tempArray1[MAX_INDEX];
a[i][j]=k;
else /*如果该元素不为0,就说明要填的数的位置已经被占,则该数放在上一个数的下面*/
{
i=i+2;
j=j-1;
a[i][j]=k;
}
}
for(i=0;i<N;i++) /*输出数组*/
{
for(j=0;j<N;j++)
printf("%5d",a[i][j]);
printf("\n\n");
{
i=i+2;
j=j-1;
}
else if(i<0) /*当行数减到第一行,返回到最后一行*/
i=N-1;
else if(j>N-1) /*当列数加到最后一行,返回到第一行*/
j=0;
else if(!a[i][j]){ /*如果该元素为0,继续执行程序*/
a[i][j]=k++;
i=i-1;
j=j+1;方法源自:/*这个是我找到的功能最强大的求魔方阵的程序,奇、偶阵都可以求,可以多次测试,最大阶可以自己设定(我测试的最大设定值是507,此时可以运行到506阶,不过也可以设定到508,但是这时真正运行的时候却达不到506阶)*/
#include <stdio.h>
#include <stdlib.h>
}
else /*如果该元素不为0,就说明要填的数的位置已经被占,则该数放在上一个数的下面*/
{
i=i+2;
j=j-1;
}
}
for(i=0;i<N;i++) /*输出数组*/
{
for(j=0;j<N;j++)
printf("%5d",a[i][j]);
printf("\n\n");
}
}
方法三:
/*此程序是在网上找到的c程序设计习题7.7的答案,只能算奇数阵,可以算到15阶*/
方法一;
/*此程序使我按照上面介绍的魔方阵的规律编写的,不过只能求奇数魔方阵,经过测试可以算到508阶*/
#define N 7
#include<stdio.h>
void main()
{
int a[N][N],i,j,k;
for(i=0;i<N;i++) /*先处理第一行*/
for(j=0;j<N;j++)
{
Array[i][i]=tempArray2[i];
}
}
}
/*End穿心对调*/
/*重排米字*/
for(i=0;i<n;i++)
{
tempArray1[i]=Array[i][i];
tempArray2[i]=Array[a][i];
}
QuickSort(tempArray1,0,n-1);
QuickSort(tempArray2,0,n-1);
for(i=0;i<n;i++)
}
}
方法二:
/*这个是网友qfyzy提供的,可以算到99阶*/
#define N 7
#include<stdio.h>
void main()
{
int a[N][N]={0},i=0,j,k; /*先令所有元素都为0*/
j=(N-1)/2;
i=0;
for(k=1;k<=N*N;) /*开始处理*/
{
if((i<0)&&(j==N)) /*前一个数是第一行第N列时,把下一个数放在上一个数的下面*/
具体实现时:
左上角和右下角的n/2*n/2的小矩阵,偶行偶列,奇行奇列赋值为0,其余赋值为1;右上角和左上角的n/2*n/2的小矩阵,偶行奇列,奇行偶列赋值为0,其余赋值为1。然后,从左上角格子开始,按从左到右,从上到下的次序将1到n*n的值往方阵中赋,但遇到值为0时跳过;再从右下角格子开始,按从右到左,从下到上的次序将1到n*n的值往方阵中赋,但遇到值为1时跳过。
swap(&Array[a-1][0],&Array[b-1][0]);
swap(&Array[2][0],&Array[2][n-1]);
swap(&Array[0][2],&Array[n-1][2]);
}
break;
case 1:
case 3:
/*穿心对调*/
for(i=0;i<n;i++)
