1、计算距离权重
权重计算公式大全

权重计算公式大全
权重计算公式是根据具体情况和需求而定的,不同情况下可能会有不同的权重计算公式。
下面列举几种常见的权重计算公式:
1.线性加权计算:
权重计算公式:W = w1 * x1 + w2 * x2 + ... + wn * xn
其中,W表示总权重,wi表示第i个指标的权重,xi表示第i个指标的值。
2.比例加权计算:
权重计算公式:W = (w1 * x1) / (w1 * x1 + w2 * x2 + ... + wn * xn)
其中,W表示总权重,wi表示第i个指标的权重,xi表示第i个指标的值。
3.熵权法计算:
权重计算公式:W = (-1/ln(n)) * (p1 * ln(p1) + p2 * ln(p2) + ... + pn * ln(pn))
其中,W表示总权重,pi表示第i个指标的权重,n表示指标的个数。
4.主成分分析法计算:
权重计算公式:W = ai1 * x1 + ai2 * x2 + ... + ain * xn
其中,W表示总权重,aij表示第i个指标在第j个主成分上的权重,xi表示第i个指标的值。
以上只是几种常见的权重计算公式,在实际应用中还可以根据需求进行适当的拓展和改进。
例如,在机器学习中常用的梯度下降算法中,会根据误差函数来计算不同参数的权重,以更新模型的参数。
在推荐系统中,可以使用基于用户行为等因素的协同过滤算法来计算不同推荐项的权重。
总之,权重计算公式的选择和设计需要根据具体情况和需求来确定,并且这些公式也可以进行适当的拓展和改进,以满足实际应用的需求。
g1序关系法计算权重

G1序关系法计算权重
G1序关系分析法是一种确定权重的方法,其基本步骤如下:
1.首先,对评价指标进行定性排序,确定序关系。
2.然后,对相邻的两两指标之间的重要程度进行比较并定量赋
值。
相邻指标之间的重要程度可以用rk=ωk−1/ωk来表示,其中ωk为第k个指标的权重。
3.根据排序结果和定量赋值,可以计算出每个指标的权重。
需要注意的是,在使用G1序关系分析法时,需要先确定评价指标之间的序关系,即根据它们的重要程度进行排序。
然后,根据排序结果和相邻指标之间的重要程度进行比较并定量赋值。
最后,根据排序结果和定量赋值计算出每个指标的权重。
G1序关系分析法具有简便、直观的特点,且对同一层次中的元素没有数量限制,便于广泛应用。
是距离空间但不是赋范空间的例子

是距离空间但不是赋范空间的例子1. 距离空间但不是赋范空间的例子:有限维距离空间在数学中,有限维距离空间是指其维数有限且满足距离公理的空间。
具体来说,有限维距离空间是指具有有限维度的向量空间,其中定义了一个满足距离公理的度量。
距离公理包括非负性、同一性、对称性和三角不等式等性质。
有限维距离空间在实际问题中具有广泛的应用,例如在计算机图形学中,用于表示和处理二维或三维图像。
2. 距离空间但不是赋范空间的例子:离散距离空间离散距离空间是指其元素之间的距离只能取0或1的距离空间。
具体来说,离散距离空间是一个集合,其中的元素之间的距离要么为0,要么为1。
这种距离空间在离散数学和计算机科学中被广泛应用,例如在图论中,可以用离散距离空间来描述图中的节点之间的距离。
3. 距离空间但不是赋范空间的例子:带权距离空间带权距离空间是指其元素之间的距离通过权重进行调整的距离空间。
具体来说,带权距离空间是一个集合,其中的元素之间的距离根据权重进行加权。
这种距离空间在现实生活中有诸多应用,例如在交通规划中,可以使用带权距离空间来表示不同道路之间的距离,其中权重可以表示道路的拥堵程度或者行驶时间。
4. 距离空间但不是赋范空间的例子:离散度量空间离散度量空间是指其元素之间的距离满足度量公理的距离空间,但不满足赋范公理。
具体来说,离散度量空间是一个集合,其中的元素之间的距离满足非负性、同一性和三角不等式等性质,但不满足缩放性和三角不等式的等式性质。
离散度量空间在计算机科学和离散数学中有广泛应用,例如在聚类算法中,可以使用离散度量空间来度量样本之间的相似度。
5. 距离空间但不是赋范空间的例子:有限距离空间有限距离空间是指其元素之间的距离取值范围是有限的距离空间。
具体来说,有限距离空间是一个集合,其中的元素之间的距离有上界存在。
这种距离空间在实际问题中有广泛应用,例如在机器学习中,可以使用有限距离空间来度量样本之间的相似度。
6. 距离空间但不是赋范空间的例子:离散拓扑空间离散拓扑空间是指其元素之间的距离定义了一个离散拓扑的空间。
使用筹码衰减系数计算筹码分布的公式(一)

使用筹码衰减系数计算筹码分布的公式(一)使用筹码衰减系数计算筹码分布的公式引言在计算筹码的分布时,采用筹码衰减系数是十分常见的方法。
筹码衰减系数可以根据一定的规则来计算筹码在不同区间的分布情况。
本文将介绍两种常见的筹码衰减系数计算公式,并通过示例来解释说明。
一、线性衰减公式线性衰减公式是最简单直观的计算筹码分布的方法。
该公式根据筹码所在区间与目标区间的距离,确定筹码的权重。
公式:权重 = 1 - 衰减系数 * (筹码所在区间与目标区间的距离)示例:假设我们有一个目标区间为[0, 100]的筹码分布。
现在,我们有一枚筹码处于区间[50, 150],衰减系数为。
根据线性衰减公式计算得到该筹码的权重为:权重 = 1 - * (150 - 100) =即该筹码的权重为。
二、指数衰减公式指数衰减公式是一种较为复杂但更加灵活的筹码分布计算方法。
该公式根据筹码所在区间与目标区间的距离,以指数形式衰减筹码的权重。
公式:权重 = 衰减系数 ^ (筹码所在区间与目标区间的距离)示例:假设我们仍然有一个目标区间为[0, 100]的筹码分布,现在我们有一枚筹码处于区间[50, 150],衰减系数为。
根据指数衰减公式计算得到该筹码的权重为:权重 = ^ (150 - 100) =即该筹码的权重为。
总结通过以上两种公式的示例计算,我们可以看到筹码衰减系数对于计算筹码的分布起到了很大的作用。
线性衰减公式简单直观,适用于一些较为简单的情况。
而指数衰减公式更加灵活,可以根据需求进行调整,适用于更多种情况的筹码分布计算。
使用筹码衰减系数计算筹码分布的公式可以帮助我们更好地了解筹码的分布情况,对于一些筹码分布相关的问题提供了有效的解决方案。
权重计算公式大全

权重计算公式大全权重计算公式是用于计算不同变量或因素的重要性或影响力的数学公式。
它们常用于各种领域的分析和决策,例如金融、统计学、机器学习等。
以下是一些常见的权重计算公式:1.简单加权平均公式(Simple Weighted Average):权重计算公式:WA = (w1 * x1 + w2 * x2 + ... + wn * xn) / (w1 + w2 + ... + wn)其中,WA表示加权平均值,wi表示第i个变量的权重,xi表示第i个变量的值。
2.实际投资收益率(Realized Rate of Return):权重计算公式:RRR = (w1 * r1 + w2 * r2 + ... + wn * rn)其中,RRR表示实际投资收益率,wi表示第i个投资资产的权重,ri表示第i个投资资产的实际收益率。
3.对数收益率加权公式(Logarithmic Rate of Return):权重计算公式:LRR = exp(w1 * ln(1 + r1) + w2 * ln(1 + r2) + ... + wn * ln(1 + rn)) - 1其中,LRR表示对数收益率加权值,wi表示第i个投资资产的权重,ri表示第i个投资资产的对数收益率。
4.主成分分析(Principal Component Analysis):权重计算公式:PCi = (λi / Σλ) * Φi其中,PCi表示第i个主成分的权重,λi表示第i个主成分的特征值,Σλ表示所有主成分的特征值之和,Φi表示第i个主成分的特征向量。
5.回归系数(Regression Coefficients):权重计算公式:y = b0 + b1 * x1 + b2 * x2 + ... + bn * xn 其中,yi表示因变量的值,xi表示自变量的值,bi表示第i个自变量的回归系数。
这些公式只是权重计算的一些常见方法。
在实际应用中,根据具体问题和数据的不同,可能会有各种不同的权重计算公式和方法。
地理距离权重矩阵

地理距离权重矩阵
地理距离权重矩阵是一种用于统计分析和空间数据分析的方法。
它是基于地理距离的计算方法,可以帮助研究人员分析空间数据的空
间相关性。
在这种方法中,研究人员首先根据地理位置信息计算每个
地理单元之间的距离,然后使用这些距离值来构建一个距离权重矩阵。
距离权重矩阵通常包含一个矩阵,其中每个地理单元与其他地理
单元之间的距离表示为一个值。
这些值可以是直线距离、驾驶距离、
行车时间、飞行时间等。
研究人员在使用距离权重矩阵时,通常会使
用不同的权重值,以考虑不同距离级别之间的相对重要性。
通过使用地理距离权重矩阵,研究人员可以更好地理解空间数据
之间的关系。
它可以用于分析空间相关性、聚类分析、地理模式分析
等应用领域。
一图看遍9种距离度量,图文并茂,详述应用场景!

⼀图看遍9种距离度量,图⽂并茂,详述应⽤场景!距离度量在CV 、NLP以及数据分析等领域都有众多的应⽤。
最常见的距离度量有欧式距离和余弦距离,本⽂将会分享九种距离,分析其优缺点以及相应的应⽤常见,如果对你有所帮助,在看完之后,可以分享给你朋友圈的好兄弟,好姐妹们,共同成长进步!有图有真相许多算法,⽆论是监督或⾮监督,都使⽤距离度量。
这些度量,如欧⼏⾥得距离或余弦相似度,经常可以在k-NN、UMAP、HDBSCAN等算法中找到。
理解距离度量⽐你可能⽐你想象中更加重要。
以k-NN为例,这是⼀种经常⽤于监督学习的技术。
作为默认值,它通常使⽤欧⼏⾥得距离。
它本⾝就是⼀个很⼤的距离。
但是,如果你的数据是⾼维的呢?那么欧⼏⾥得距离还有效吗?或者,如果你的数据包含地理空间信息呢?也许haversine距离是更好的选择!知道何时使⽤哪种距离度量可以帮助您从⼀个糟糕的分类器变成⼀个精确的模型。
在本⽂中,我们将介绍许多距离度量⽅法,并探讨如何以及何时最好地使⽤它们。
最重要的是,我将讨论它们的缺点,以便您能够意识到何时应该避开某些措施。
注意:对于⼤多数距离度量,很长的详细的⽂件可以并且已经写在它们的⽤例、优点和缺点上。
我会尽我所能去弥补,但可能会达不到!因此,本⽂是这些措施的总体概述。
1、Euclidean Distance我们从最常见的距离度量开始,即欧⼏⾥得距离。
它是⼀种距离度量,最好解释为连接两点的线段的长度。
这个公式相当简单,因为距离是从这些点的笛卡尔坐标⽤勾股定理计算出来的。
缺点尽管欧⼏⾥德距离是⼀种常见的距离度量,但它不是尺度不变的,这意味着计算的距离可能是倾斜的,这取决于特征的单位。
通常,在使⽤这个距离度量之前,需要对数据进⾏标准化(normalize)。
此外,随着数据维度的增加,欧⼏⾥得距离就变得不那么有⽤了。
这与维数的'诅咒'有关,它与⾼维空间并不像我们直观地期望的那样,在2维或3维空间中发挥作⽤的概念有关。
反距离加权插值法原理(一)

反距离加权插值法原理(一)反距离加权插值法原理介绍反距离加权插值法是一种常用的空间插值方法,用于根据已知离散点数据估计未知位置的值。
该方法利用距离权重来确定每个已知点对未知点的贡献程度,进而进行插值计算。
原理反距离加权插值法的原理可以概括为以下几个步骤:1.计算未知点与所有已知点之间的距离。
2.根据距离计算每个已知点的权重。
一般情况下,离未知点越近的已知点权重越高,距离的增大会导致权重递减。
3.根据已知点的权重和值,通过加权平均计算未知点的估计值。
加权平均的计算公式为:插值公式,其中,w表示权重,z表示已知点的值。
算法步骤根据原理,可以得到反距离加权插值法的具体算法步骤:1.输入已知点坐标和值,以及待插值点的坐标。
2.根据欧氏距离计算待插值点与已知点之间的距离。
3.根据距离计算权重。
常用的权重计算方式为反距离的倒数,即:权重计算公式,其中,d表示待插值点与已知点的距离,p表示距离的指数(调节权重衰减的速度)。
4.根据权重和已知点的值,计算待插值点的估计值。
参数调节反距离加权插值法中,有两个重要的参数可以进行调节,即距离的指数p和权重的归一化。
调节这些参数可以对插值结果产生影响,不同的参数组合可能得到不同的结果。
•距离的指数p:调节权重的衰减速度。
当p较小时,距离较远的已知点对插值点的影响仍较大,而当p较大时,距离较远的已知点对插值点的影响衰减较快。
•权重的归一化:将所有权重除以它们的总和,以确保权重之和为1。
归一化可以消除由于距离和权重的变化而引起的估计值变化。
应用领域反距离加权插值法常被应用于以下领域:•地理信息系统(GIS)中的空间插值。
•气象领域中的气象站点值的插值。
•地质领域中的岩矿样点值的推断。
总结反距离加权插值法是一种常用的空间插值方法,适用于根据已知离散点数据估计未知位置的值。
它利用距离权重来确定每个已知点对未知点的贡献程度,并通过加权平均计算插值值。
参数调节可以影响插值结果,需要根据具体情况选择合适的参数。
一种三维城市模型多纹理自动合并方法

一种三维城市模型多纹理自动合并方法摘要:本文提出了一种自动合并多纹理三维城市模型的方法。
通过利用三维城市模型中的地面切片和纹理信息,将城市模型进行多层分区处理。
基于分区信息,提出了一种纹理映射方法用于合并相邻分区的纹理信息。
通过对模型进行实验分析和性能测试,证明了该方法在纹理合并效果和运行速度上都比现有方法有所提升。
关键词:三维城市模型;多纹理;自动合并;多层分区;纹理映射1.引言随着计算机技术的不断进步,三维城市模型已经被广泛应用于城市规划、游戏开发、虚拟漫游等领域。
纹理是三维城市模型的一个重要组成部分。
目前,市面上的三维城市模型多数是基于单一纹理贴图,而对于真实的城市场景来说,单一纹理贴图往往不能满足需求。
在一个城市中,建筑、道路、广场等不同区域的纹理风格和细节都存在差异,需要采用多种纹理。
多纹理的使用会对模型的渲染速度产生很大的影响,严重影响用户的体验。
如何高效地合并多个纹理是一个重要的研究问题。
现有的多纹理合并方法大多是基于纹理相似性的,并严重依赖于人工干预。
Mueller 等[1] 提出了一种基于图像分割的纹理合并方法,对于相似区域的纹理进行合并。
对于一些细节纹理如窗户、门板等,这些方法却很难自动识别。
Gao等[2] 提出了一种基于局部统计信息的纹理合并方法,但是计算量很大,实用性不高。
有必要研究一种自动合并多纹理的新方法,用于提高纹理合并的效果和速度。
2.多层分区在本文提出的方法中,城市模型首先被分为不同的区域,在每个区域中确定初始的纹理。
分区的过程可以简化为如下几个步骤:(1)将整个建筑区域按照固定大小的地面切片进行分割。
(2)然后,根据每个区域中的信息,将区域继续进行分割,直到满足分割条件。
(3)对每个分区进行纹理的初始化,确定初始纹理。
下面,我们详细说明如何进行多层分区。
2.1 地面切片在城市模型中,地面是相对平整的,可以将其进行切片处理。
本文中,我们采用矩形地面切片进行区域分割。
一种高效的自适应双边滤波方法

121在当今时代,图像处理因数码设备的普及而成为信息领域的热门研究方向,主要致力于解决人们在获取图像时所附带的噪声而降低图像质量的问题[1]。
而双边滤波就是一个能在去除图像噪声的同时能较好地保留图像边缘细节的滤波方法。
传统的双边滤波方法通过手动设置滤波参数的方法进行滤波,但仅凭经验人工设定参数的方法不能保证设定参数的合理性,且存在一定的随机性,于是有必要设计一种自适应双边滤波器[2]。
文献[3]中提出了一种新的自适应双边滤波方法,但是该方法在对强噪声点的处理时通过强制增大空域标准差的方法减弱噪声影响,造成全局式的去噪,导致图像模糊。
对于上述问题,本文提出了一种自适应双边滤波方法,使用中值滤波方法对强噪声进行处理,保证在滤除强噪声时不会损害原始图像。
1 改进型双边滤波算法1.1 双边滤波算法原理双边滤波是一种非线性滤波器,它可以达到保持边缘、降噪平滑的效果。
双边滤波的两个权重概念就是空间域与像素范围域。
以下是双边滤波的基本公式。
ω(i,j,k,l)=exp(--) (1)I D (i,j)=(2)双边滤波的核函数是空间域核与像素范围域核的综合结果:在图像的平坦区域,像素值变化很小,对应的像素范围域权重接近于1,此时空间域权重起主要作用,相当于进行高斯模糊;在图像的边缘区域,像素值变化很大,像素范围域权重变大,从而保持了边缘的信息。
在上面的式(1)中,σr 和σd 是平滑参数,他们的值随机给定,I(i,j)和I(k,l)是任意点(i,j)和(k,l)的像素值。
最后,w(i,j,k,l)是权重值。
括号里的第一个算式是求空间上任意一点到周边的点的距离的权重,第二个算式则是算任意一点和给定窗口内其他点的像素权重。
式(2)表示的是去掉噪声后的图像,w为空间域权值和灰度域权值的乘积。
1.2 自适应双边滤波算法首先,先读取视频图像的序列,然后将序列值赋给一个输入变量,确定取出的块的大小。
空域方差随机给出,然后通过整个图像分块的for循环先计算出任意点的像素值,之后再使用一个单个块中的for循环计算块中所有像素值的方差,再由开方获得标准差,这也是像素域方差值。
权重的确定方法汇总

一、指标权重的确定1.综述目前关于属性权重的确定方法很多,根据计算权重时原始数据的来源不同,可以将这些方法分为三类:主观赋权法、客观赋权法、组合赋权法。
主观赋权法是根据决策者(专家)主观上对各属性的重视程度来确定属性权重的方法,其原始数据由专家根据经验主观判断而得到。
常用的主观赋权法有专家调查法(Delphi法)、层次分析法(AHP )[106-108]、二项系数法、环比评分法、最小平方法等。
本文选用的是利用人的经验知识的有序二元比较量化法。
主观赋权法是人们研究较早、较为成熟的方法,主观赋权法的优点是专家可以根据实际的决策问题和专家自身的知识经验合理地确定各属性权重的排序,不至于出现属性权重与属性实际重要程度相悖的情况。
但决策或评价结果具有较强的主观随意性,客观性较差,同时增加了对决策分析者的负担,应用中有很大局限性。
鉴于主观赋权法的各种不足之处,人们又提出了客观赋权法,其原始数据由各属性在决策方案中的实际数据形成,其基本思想是:属性权重应当是各属性在属性集中的变异程度和对其它属性的影响程度的度量,赋权的原始信息应当直接来源于客观环境,处理信息的过程应当是深入探讨各属性间的相互联系及影响,再根据各属性的联系程度或各属性所提供的信息量大小来决定属性权重。
如果某属性对所有决策方案而言均无差异(即各决策方案的该属性值相同),则该属性对方案的鉴别及排序不起作用,其权重应为0;若某属性对所有决策方案的属性值有较大差异,这样的属性对方案的鉴别及排序将起重要作用,应给予较大权重.总之,各属性权重的大小应根据该属性下各方案属性值差异的大小来确定,差异越大,则该属性的权重越大,反之则越小。
常用的客观赋权法[109-110]有:主成份分析法、熵值法[111-112]、离差及均方差法、多目标规划法等。
其中熵值法用得较多,这种赋权法所使用的数据是决策矩阵,所确定的属性权重反映了属性值的离散程度。
客观赋权法主要是根据原始数据之间的关系来确定权重,因此权重的客观性强,且不增加决策者的负担,方法具有较强的数学理论依据。
混凝土平均运距计算公式(一)

混凝土平均运距计算公式(一)混凝土平均运距在建筑工程中,混凝土的运输是一个重要的环节,其中一个重要指标就是混凝土的平均运距。
混凝土平均运距指的是将混凝土从搅拌站运送到施工现场的平均距离。
下面列举了与混凝土平均运距相关的计算公式。
1. 混凝土平均运距计算公式公式1:平均运距 = (搅拌站到运输点距离1 + 运输点1到运输点2的距离+ … + 运输点n到施工现场的距离)/ 运输次数这个公式计算了混凝土从搅拌站到施工现场的整体平均运距,包括了多个运输点和运输次数。
公式2:平均运距= ∑(运输距离i * 运输次数i) / ∑运输次数i 这个公式是公式1的推导形式,它考虑到了不同运输距离的运输次数对平均运距的影响。
公式3:平均运距= ∑(混凝土体积i * 运输距离i)/ ∑混凝土体积i 这个公式将混凝土的体积纳入考虑,计算了混凝土的平均运距与体积的关系。
2. 示例解释假设有一个施工工地,需要运送混凝土到该工地进行浇筑。
搅拌站距离工地1000米,有两个运输点,分别距离搅拌站200米和500米,最后运送到工地的距离为300米。
现有的搅拌车共运送了5次混凝土,每次运送体积分别为10立方米、15立方米、12立方米、20立方米和18立方米。
例子1:使用公式1计算平均运距平均运距 = (1000 + 200 + 500 + 300)/ 5 = 400米例子2:使用公式2计算平均运距平均运距 =(2001 + 5001 + 800*3)/(1+1+3)= 625米例子3:使用公式3计算平均运距平均运距 = (10200 + 15500 + 12800 + 20300 + 18*300)/(10+15+12+20+18) = 米通过以上计算示例可以看出,不同的计算方法得出的平均运距结果可能有所差异,取决于运输距离和运输次数的权重分配方式以及是否考虑混凝土的体积因素。
在实际工程中,建议根据具体情况选择合适的计算公式,以准确评估混凝土的平均运距。
交叉中值例题

1 现在你有一项任务,为一个食品供应公司在市中心商业区选择一个新店面位置,在xy 坐标系中,潜在顾客位置为:1=(4,4),2=(12,4),3=(2,7),4=(11,11),5=(7,14)。
需求的期望权重为:w1=4,w2=3,w3=2,w4=4,w5=1。
(1)用交叉中值法并结合城市距离进行计算,推荐一个食品供应店面地址,使得所有顾客到达新店面的总距离最短。
(7分)(2)将1)中的结果作为一个初始解迭代一次,采用精确重心法用欧几米德距离重新进行优化,推荐一个新的最优位置。
(8分)解:(1) 中值w*=4+3+2+4+1/2=7.X轴方向坐标点3,1,5,4,2坐标依次为2,4,7,11,12。
从左到右中值点位于5,从右到左中值点位于4。
则x方向最优坐标为5-4之间。
Y轴方向坐标点1,2,3,4,5,坐标依次为4,4,7,11,14。
从上到下中值点位于2,从下到上中值点位于3。
则y方向最优坐标为2,3。
综合,横坐标在7-11之间,纵坐标在4-7之间所有点都是最优解。
(2) 选取(7,4)作为初始解。
进行迭代需求点1 2 3 4 5位置(x s(i-1) ,y s(i-1)) (4,4) (12,4) (2,7) (11,11) (7,14) 权重w i 4 3 2 4 1距离d is(i-1)3 5 5.83 8.06 10w i\ d is(i-1) 1.33 0.6 0.34 0.50 0.1w i x i \d is(i-1)5.35 7.2 0.68 5.5 0.7w i y i \d is(i-1)5.35 2.4 2.38 5.5 1.4x si=6.77y si=5.93。
一组数据 某个点到平均值的距离的平方

数据分析是当今社会中非常重要的一项工作。
在进行数据分析时,经常需要计算数据集中每个数据点到平均值的距离的平方。
这个距离的平方代表了数据点与平均值之间的偏离程度。
本文将从数学和实际应用的角度,深入探讨一组数据中某个点到平均值的距离的平方的意义和计算方法。
二、数学原理在进行数据分析时,经常会遇到一组数字,我们可以将这些数字表示为一个集合{x1,x2,...,xn},其中n表示数据的个数。
我们可以用数学公式表示这组数据的平均值μ为:μ = (x1 + x2 + ... + xn) / n那么某个数据点xi到平均值的距离的平方可以表示为:(xi - μ)^2这个平方是表示数据点xi到平均值μ的偏离程度的一个重要指标。
三、计算方法我们可以通过以下步骤计算一组数据中某个数据点到平均值的距离的平方:1. 计算数据的平均值μ,将每个数据点分别减去平均值,得到xi - μ2. 将这个差值再进行平方运算,得到(xi - μ)^2。
3. 对每个数据点都按照上述方法进行计算,最终得到每个数据点到平均值的距离的平方。
四、实际应用数据分析是应用广泛的一项工作,某个点到平均值的距离的平方也常常在实际工作中被使用到。
1. 在统计学中,这个距离的平方被用来计算方差,方差是衡量数据分散程度的重要指标。
方差越大,数据点到平均值的距离的平方平均值也越大,说明数据的波动程度较大。
2. 在财务分析中,某个点到平均值的距离的平方可以用来评估投资风险。
如果某个投资的收益率偏离平均值较大,那么其风险也会相对较高。
3. 在科学研究中,这个距离的平方可以用来比较实验数据与理论模型的拟合程度。
数据点到平均值的距离的平方越小,说明实验数据与理论模型的拟合程度越高。
五、总结通过本文的介绍,我们深入了解了一组数据中某个点到平均值的距离的平方。
这个距离的平方可以帮助我们更准确地了解数据的分散程度和偏离程度,对于数据分析和实际应用都具有重要意义。
希望本文的内容能够为读者带来有益的启发,并在实际工作中得到应用。
idw反距离权重法

idw反距离权重法idw反距离权重法是一种用于空间插值的方法,它通过对离目标点较近的观测值加上较大的权重,而对离目标点较远的观测值加上较小的权重,从而对尚未被观测的空间位置进行预测。
下面我们将详细介绍idw反距离权重法的具体流程。
第一步:设定邻域半径。
邻域半径是指在预测任意空间位置的值时,所考虑的已知样本点应该取多远的范围。
通常情况下,邻域半径的大小可以通过试验和比较选定合适的值。
第二步:在邻域范围内确定工作部位。
对于目标点所对应的邻域范围内的已知样本点,需要计算它们与目标点之间的距离。
第三步:根据距离计算权重。
通常根据距离的倒数函数计算权重,也就是越接近目标点的样本点,其距离越小,其所带的影响力就越大,相应的权重也更大,而距离越远的样本点所带的影响力就越小。
第四步:对已知样点进行加权平均。
对于已知样点,按照其在目标点邻域范围内对应的权重,对它们所对应的值进行加权平均。
第五步:返回预测值。
将加权平均值作为该预测点的预测值输出。
需要注意的是,idw反距离权重法虽然在空间插值中的操作简单易行,但并不一定适用于所有的样本,它的主要限制因素在于行业标准是基于idw反距离权重法进行空间插值,而在实践中部分样本点距离过远或过近,或者分布不均匀,都可能造成分析和预测偏差。
因此,在实践中,我们需要综合考虑许多合适的方法,从而能够有效地进行空间插值。
总之,idw反距离权重法作为一种常见的空间插值方法,对于许多空间预测问题,尤其对于较规则的采样网格,依旧是一种相对精确的方法。
在实际操作中,需要根据具体情况综合应用,从而得到准确而可信的结果。
一种高程数据平滑处理算法

一种高程数据平滑处理算法
高程数据平滑处理算法是指通过对高程数据进行一系列运算和处理,使之呈现一定的平滑特性。
平滑处理可以减小高程数据中的噪声以及异常值,使结果更加准确和可靠。
下面介绍一种常用的高程数据平滑处理算法-加权平均法。
加权平均法是一种基于邻域统计的平滑处理算法,其思想是通过计算相邻数据点的加权平均值来平滑目标点的高程值。
具体步骤如下:
1. 设置平滑算法的参数-邻域大小和权重。
2. 对于每个目标点,选取邻域内的数据点作为其周围数据。
3. 计算邻域内数据点的权重,常用的权重计算方法有距离加权和角度加权。
距离加权法根据目标点与邻域内点之间的距离计算权重,距离越远的点权重越小;角度加权法根据目标点与邻域内点的夹角计算权重,夹角越大的点权重越小。
4. 根据邻域内数据点的权重,计算目标点的加权平均值。
具体计算方法为将每个邻域内数据点的高程值乘以对应权重,并求和后再除以所有权重之和。
5. 对于所有目标点,重复上述步骤,计算每个点的加权平均值。
最终得到平滑后的高程数据。
加权平均法的优点是简单高效,适用于不同类型的高程数据。
通过调整邻域大小和权重,可以灵活地控制平滑程度。
但也存在一些缺点,例如容易平滑掉尖峰和局部特征,对于大范围的异常值和噪声处理效果较差。
除了加权平均法,还有其他一些高程数据平滑处理算法,如中值滤波法、高斯滤波法等。
不同的算法适用于不同的数据情况,选择合适的平滑算法可以提高数据的质量和可用性。
Geoda计算莫兰指数
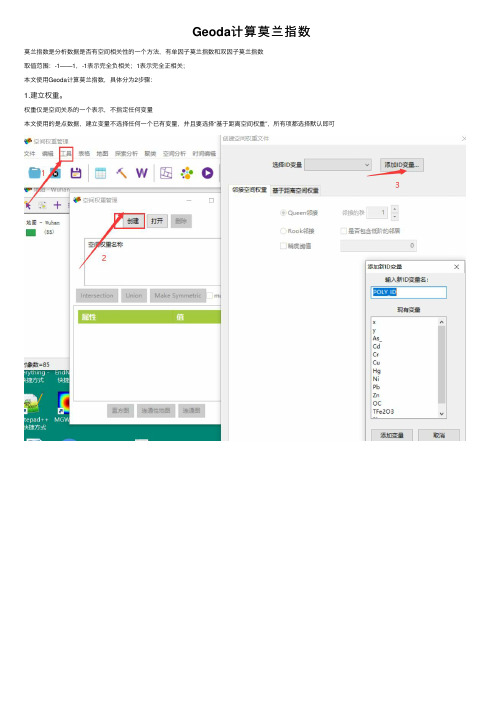
Geoda计算莫兰指数
莫兰指数是分析数据是否有空间相关性的⼀个⽅法,有单因⼦莫兰指数和双因⼦莫兰指数
取值范围:-1——1,-1表⽰完全负相关;1表⽰完全正相关;
本⽂使⽤Geoda计算莫兰指数,具体分为2步骤:
1.建⽴权重。
权重仅是空间关系的⼀个表⽰,不指定任何变量
本⽂使⽤的是点数据,建⽴变量不选择任何⼀个已有变量,并且要选择“基于距离空间权重”,所有项都选择默认即可
2. 计算莫兰指数
单变量莫兰指数,双变量莫兰指数,
选择合适的space-method即可
第⼀个是单变量莫兰指数,第⼆个是双变量莫兰指数,可运⾏多次求解均值、⽅差⼀类的统计值
下⾯计算局部双变量莫兰指数,可以看出high-high分布、high-low分布、low-high分布、low-low分布、不显著5类最后的红框是运⾏多次的统计数据
3. 另外,Geoda还可以直接回归等操作,具体可在⼦菜单中的尝试。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
end
%B算出来的单位是度。
换算成距离的话,需要再乘以Pi/180再乘以6378.2,单位为千米。
(此处将地球当做一个球体,半径为6378.2千米)
C=B*pi/180*6378.2; %C即为地点间地理距离矩阵,单位为千米
D=1./C %D的元素为距离的倒数。即距离数值越小,倒数后构成的权重越大;反之亦然
A(i,j)=Z(i,1)-U(j,1); %A中的元素即为2003年对应两个省区市之间人均实际GDP的差值
end
end
B=abs(A);%取A元素的绝对值。因为空间权重矩阵考虑的是距离,不是差值大小
C=1./B;
C(C==inf)=0;
%以下行标准化
D=sum(C,2); %计算各行之和
T=xlsread('Book4.xlsx','A3:K32');%读取表格数据
X=T(:,2);%读取30各地区的纬度
Y=T(:,3);%读取30个地区的经度
A=[X Y];%维度和经度并排放,构成一个大矩阵
for i=1:30;%
for j=1:30;%
B(i,j)=distance(A(i,1),A(i,2),A(j,1),A(j,2)); %根据经纬度计算地点间的距离,主要应用distance函数
%主要思想是:通过上一个matlab程序获得行标准化后的地理距离W,现在获得行标准化后的人均实际GDP经济距离矩阵,再将二者相乘再行标准化。
%与一些文章的细节处理不大一样。但我觉得本处理更合理些,因为多了几次行标准化,避免了地理距离和经济距离量级不一样造成的较大影响。
%注意:地理距离不变,但经济距离(很多人使用人均实际GDP的差额表示)是每年都改变的,所以有几年就有几个Wes
E=repmat(D,1,30); %主要应用repmat函数
We=C./E; %We即为行标准化后的经济距离权重矩阵
Wes1=W.Leabharlann We;%地理距离倒数 点乘经济距离倒数
%以下再行标准化
F=sum(Wes1,2);
G=repmat(F,1,30);
Wes=Wes1./G
D(D==inf)=0 %当矩阵元素为无限大时,将其变为0
E=sum(D,2) %计算各行之和
F=repmat(E,1,30) %主要应用repmat函数(平铺函数),一行30列,每个元素都是E
W=D./F %W即为行标准化后的地理距离空间权重矩阵
计算经济地理距离空间权重矩阵
%以下为计算经济地理距离空间权重矩阵 Wes的matlab程序。
%{
选中下面一行,按F9(F9是matlab运行选中程序的快捷键),新建某年(例2002年)30个省(市,区)的人均实际GDPx列向量
Z=T(:,6) %将2002年30个省(市,区)的人均实际GDP放入Z
U=Z; %U与Z是一样的,这样做是为了后面计算经济距离
for i=1:30
for j=1:30
