海明码校验
写出8位二进制数01101010b的海明校验码

写出8位二进制数01101010b的海明校验
码
海明码(Hamming(Code)是一种错误检测和纠正的编码技术,它通过添加冗余位来检测和纠正数据传输中的错误。
海明码中的校验位的数量取决于要纠正的错误数量,常见的有海明码(7,4)和海明码(8,4)等。
现在给定一个(8(位二进制数(`01101010b`,要计算海明校验码,可以按照海明码(8,4)的方式进行。
这里的((8,4)(指的是(8(位数据中有(4(个数据位和(4(个校验位。
首先,将原始数据位从左到右编号为(D1,(D2,(D3,(D4,(P1,(P2,(P3,(P4 P(代表校验位)。
然后计算校验位的值,使得每个校验位控制特定的数据位。
海明码的校验位的位置是(1、2、4、8。
现在计算每个校验位的值:
P1(控制的数据位是(1,(3,(5,(7。
计算方法为:P1(=(D1(⊕(D3(⊕(D5(⊕(D7(=(0(⊕(1(⊕(1(⊕(0(=(0
P2(控制的数据位是(2,(3,(6,(7。
计算方法为:P2(=(D2(⊕(D3(⊕(D6(⊕(D7(=(1(⊕(1(⊕(0(⊕(0(=(0
P3(控制的数据位是(4,(5,(6,(7。
计算方法为:P3(=(D4(⊕(D5(⊕(D6(⊕(D7(=(1(⊕(0(⊕(0(⊕(0(=(1
P4(控制的数据位是(8。
计算方法为:P4(=(D1(⊕(D2(⊕(D3(⊕(D4(⊕(D5(⊕(D6(⊕(D7(=(0(⊕(1(⊕(1(⊕(1(⊕(1(⊕(0(⊕(0(=(0所以,计算得到的海明校验码是(`0010b`。
1/ 1。
说明海明码校验的工作机制

说明海明码校验的工作机制海明码校验的工作机制。
海明码校验是一种常用的错误检测和纠正技术,它可以帮助我们在数据传输过程中检测和纠正错误,确保数据的完整性和准确性。
海明码校验是由美国数学家理查德·W·海明提出的,它利用了一些数学原理和算法来实现对数据的检验和纠正。
在本文中,我们将详细介绍海明码校验的工作机制,包括海明码的生成和校验过程,以及它的应用场景和优缺点。
海明码的生成过程。
海明码是一种特殊的纠错码,它可以通过一些简单的数学运算来生成。
海明码的生成过程包括以下几个步骤:1. 数据分组,首先,需要将要传输的数据分成若干个数据块,每个数据块包含若干个比特(0或1)。
2. 添加校验位,对于每个数据块,需要添加一些校验位来实现错误检测和纠正。
校验位的数量取决于数据块的大小和需要实现的纠错能力。
3. 计算校验位,校验位的计算是通过一些数学运算来实现的,通常是利用异或操作和位移操作来计算。
校验位的值是通过对数据块中的比特进行运算得到的。
4. 合并数据块,将数据块和对应的校验位合并成一个完整的海明码。
海明码的校验过程。
一旦生成了海明码,就可以在数据传输过程中使用它来进行校验。
海明码的校验过程包括以下几个步骤:1. 数据传输,将生成的海明码发送给接收方进行数据传输。
2. 接收数据,接收方接收到海明码后,需要对其进行解码,得到原始的数据块和校验位。
3. 计算校验位,接收方利用接收到的海明码中的数据块和校验位,重新计算校验位的值。
4. 检测错误,接收方将重新计算得到的校验位和接收到的校验位进行比较,如果两者不一致,则说明数据传输过程中出现了错误。
5. 纠正错误,如果检测到错误,接收方可以利用海明码中的校验位来纠正错误,通常是通过一些数学运算来实现的。
海明码的应用场景。
海明码校验在计算机网络、通信系统、存储系统等领域都有广泛的应用。
它可以帮助我们在数据传输过程中检测和纠正错误,确保数据的完整性和准确性。
海明码校验方法

海明码校验方法
海明码校验那可老厉害了!先说说步骤呗,得先确定要校验的数据位数,这就像你要盖房子得先知道要盖多大面积似的。
然后根据数据位数计算出需要多少个校验位,哇塞,这可不能马虎,就跟挑队友一样得选合适的。
接着把数据和校验位放在合适的位置,这就好比摆棋子,得摆对地方。
最后进行校验,看看有没有错误,这就像考试检查答案一样,可重要了呢!注意事项也不少,得仔细计算校验位,不然一步错步步错,那可就悲催了。
而且放置数据和校验位的时候不能搞错位置,不然就白忙活了。
那安全性和稳定性咋样呢?嘿,这海明码校验就像一个忠诚的卫士,守护着数据的安全。
只要正确使用,就能大大提高数据的准确性和可靠性,不用担心数据出错,多棒啊!
应用场景可多了去了。
在数据传输中,它能确保数据完整无误地到达目的地,就像快递小哥把包裹安全送到你手上一样。
在存储数据的时候,也能防止数据被损坏,就像给宝贝找了个安全的保险箱。
优势也很明显啊,能快速检测出错误,还能定位错误的位置,这就像有个超级侦探,一下子就能找到问题所在。
比如说在网络通信中,海明码校验就发挥了大作用。
如果没有它,数据在传输过程中可能就会出错,那可就麻烦了。
有了它,就能保证数据的准确性,让通信更加顺畅。
海明码校验真的超棒,是数据安全的好帮手,你还能不试试?。
海明码校验和纠错原理详细

海明码校验和纠错原理详细海明纠错码当计算机存储或移动数据时,可能会产⽣数据位错误,这时可以利⽤汉明码来检测并纠错,简单的说,汉明码是⼀个错误校验码码集,由Bell实验室的R.W.Hamming发明,因此定名为汉明码。
海明码(Hamming Code)是⼀个可以有多个校验位,具有检测并纠正⼀位错误的纠错码,所以它也仅⽤于通信特性较好的环境中,如以太局域⽹中,因为如果通道特性不好的情况下,出现的错通常也不是⼀位。
海明码的检错、纠错基本思想是将有效信息按某种规律分成若⼲组,每组安排⼀个校验位进⾏奇偶性测试,然后产⽣多位检测信息,并从中得出具体的出错位置,最后通过对错误位取反来将其纠正。
要采⽤海明码纠错,需要按以下⼏个步骤。
1计算校验位数2 确定校验码位置3 确定校验码4 实现校验和纠错1. 计算校验位数它是这样的规定的:假设⽤N表⽰添加了校验码位后整个信息的⼆进制位数,⽤K代表其中有效信息位数,r表⽰添加的校验码位,它们之间的关系应满⾜:N=K+r≤2r-1。
如K=5,则要求2r-r≥5+1=6,根据计算可以得知r的最⼩值为4,也就是要校验5位信息码,则要插⼊4位校验码。
如果信息码是8位,则要求2r-r≥8+1=9,根据计算可以得知r的最⼩值也为4。
根据经验总结,得出信息码和校验码位数之间的关系如表5-1所⽰。
2.确定校验码位置上⼀步我们确定了对应信息中要插⼊的校验码位数,但这还不够,因为这些校验码不是直接附加在信息码的前⾯、后⾯或中间的,⽽是分开插⼊到不同的位置。
但不⽤担⼼,校验码的位置很容易确定的,那就是校验码必须是在2n次⽅位置,如第1、2、4、8、16、32,……位(对应20、21、22、23、24、25,……,是从最左边的位数起的),这样⼀来就知道了信息码的分布位置,也就是⾮2n次⽅位置,如第3、5、6、7、9、10、11、12、13,……位(是从最左边的位数起的)。
举⼀个例⼦,假设现有⼀个8位信息码,即b1、b2、b3、b4、b5、b6、b7、b8,由表5-1得知,它需要插⼊4位校验码,即p1、p2、p3、p4,也就是整个经过编码后的数据码(称之为“码字”)共有12位。
海明校验

①海明校验的基本思想将有效信息按某种规律分成若干组,每组安排一个校验位,做奇偶测试,就能提供多位检错信息,以指出最大可能是哪位出错,从而将其纠正。
实质上,海明校验是一种多重校验。
②海明校验的特点它不仅具有检测错误的能力,同时还具有给出错误所在准确位置的能力。
一.校验位的位数校验位的位数与有效信息的长度有关设:N--为校验码的位数K--是有效信息位r--校验位(分成r组作奇偶校验,能产生r位检错信息)海明码应满足N=K+r≤2r-1 若r=3 则N=K+r≤7 所以K≤4二.分组原则`在海明码中,位号数(1、2、3、……、n)为2的权值的那些位,即:1(20)、2(21)、4(22)、8(23)、…2r-1位,作为奇偶校验位并记作: P1、P2、P3 、P4、…Pr,余下各位则为有效信息位。
例如:N=11 K=7 r=4 相应海明码可示意为位号 1 2 3 4 5 6 7 8 9 10 11P占位P1 P2 × P3 × × × P4 ×××其中×均为有效信息,海明码中的每一位分别被P1P2P3P4… Pr 中的一至若干位所校验,其规律是:第i位由校验位位号之和等于i的那些校验位所校验如:海明码的位号为3,它被P1P2(位号分别为1,2)所校验海明码的位号为5,它被P1P3(位号分别为1,4)所校验归并起来: 形成了4个小组,每个小组一个校验位,校验位的取值,仍采用奇偶校验方式确定。
如表2·6 、表2·7所示:三.编码、查错、纠错原理以4位有效信息(b1、b2、b3、b4)和3位校验位(P1、P2、P3)为例: K=4 r=3海明序号1 2 3 4 5 6 7海明码P1 P2 b1 P3 b2 b3 b4根据表2-8可以看到(1)每个小组只有一位校验位,第一组是P1、第二组是P2、第三组是P3。
(2)每个校验位校验着它本身和它后面的一些确定位。
海明码校验例题

海明码校验例题以下是一个海明码校验的例题:假设发送方想要发送一个8位的二进制数01011011,并使用海明码进行校验。
可以使用4个海明码位来校验8位的数据,即增加4个校验位。
要求校验位的位置为1,2,4和8。
首先,确定校验位的位置,对于8位的数据,在第1,2,4和8位的位置增加校验位(用P表示),则得到以下数据:P1 P2 0 P4 1 0 1 1 P8接下来,计算校验位的值。
校验位的值是使得数据中包含的1的个数是偶数个的位的值为0,奇数个的位的值为1。
对于P1,计算P1的值时需要考虑与P1相关的位,即包括P1在内的第1,3,5,7和9位:P1 = (P3 + P5 + P7 + P9) mod 2= (0 + 0 + 1 + 1) mod 2= 0对于P2,计算P2的值时需要考虑与P2相关的位,即包括P2在内的第2,3,6和7位:P2 = (P3 + P6 + P7) mod 2= (0 + 0 + 1) mod 2= 1对于P4,计算P4的值时需要考虑与P4相关的位,即包括P4在内的第4,5和6位:P4 = (P5 + P6) mod 2= (1 + 0) mod 2= 1对于P8,计算P8的值时需要考虑与P8相关的位,即包括P8在内的第8位:P8 = (P9) mod 2= (1) mod 2= 1将计算得到的校验位值插入对应的位置,得到校验码:P1 P2 0 P4 1 0 1 1 P80 1 0 1 0 1 1 1发送方将校验码10101111发送给接收方,接收方根据校验码进行校验,通过计算校验位的值,可以检测出是否存在错误。
如果接收方收到的校验码中的某些位发生了错误,那么校验位的计算结果将不会匹配,接收方可以根据不匹配的校验位推断出错误发生的位置并进行纠正。
希望这个例题能帮助你理解海明码的校验过程。
海明校验码

例如:欲传递信息为b4b3b2b1(n=4),根据 2k≥n+k+1,可求出配置成海明码需增添检测位 k=3,且它们位置的安排如下:
二进制序号 1 2 3 4 5 6 7
ห้องสมุดไป่ตู้名称
C1 C2 b4 C4 b3 b2 b1
如果按照配偶原则来配置海明码,则
C1 应使1,3,5,7位中的“1”的个数为偶数;
1234567
正确的海明码 0 1 0 0 1 0 1
接收到的海明码 0 1 0 0 1 1 1
则新的检测位为:
P4=4⊕5⊕6⊕7,即P4=0⊕1⊕1⊕1=1
P2=2⊕3⊕6⊕7,即P2=1⊕0⊕1⊕1=1
P1=1⊕3⊕5⊕7,即P1=0⊕0⊕1⊕1=0
• 由此可见,传送结果P4、P2均不呈偶数, 显然出了差错。那么,错位在哪一位呢? 极为有意思的是,P4、P2、P1所构成的二 进制值恰恰是出错的位置,即P4P2P1=110, 表示第六位出错。发现错误后,计算机便 自动地将错误的第六位“1”纠正为“0”。
P1=1⊕3⊕5⊕7,即P1=C1⊕b4⊕b3⊕b1 P2=2⊕3⊕6⊕7,即P2=C2⊕b4⊕b2⊕b1 P4=4⊕5⊕6⊕7,即P4=C4⊕b3⊕b2⊕b1
设已知传送的正确海明码(按配偶原则配置)为 0100101,若传送后接收到的海明码为0100111, 其出错位可按下述步骤进行:
令:
二进制序号
• 又如,若收到按偶配置的海明码为1100101, 则经检测得:
P4=4⊕5⊕6⊕7,即P4=0⊕1⊕0⊕1=0 P2=2⊕3⊕6⊕7,即P2=1⊕0⊕0⊕1=0 P1=1⊕3⊕5⊕7,即P1=1⊕0⊕1⊕1=1 • 所以,出错位为:P4P2P1=001,即第一位。 可是第一位不是欲传送的信息位,而是检 测位,在一般情况下,可以不予纠正。
4位数据海明校验码的生成与纠错

数据在传输或存储过程中常常会出现错误,为了保证数据的完整性和准确性,通常会采用校验码来进行数据校验和纠错。
海明码是一种常用的校验码之一,它能够在一定程度上实现数据的纠错和校验。
本文将详细介绍4位数据海明校验码的生成与纠错原理及方法。
一、海明码的基本原理海明码是由美国数学家理查德·海明提出的一种能够检测和纠正数据中出现的错误的编码方式。
它通过向数据中添加校验位来实现对数据进行校验和纠错。
海明码的基本原理可以概括为以下几点:1. 通过向数据中添加冗余位来实现纠错功能。
2. 通过对数据进行位的异或运算来计算校验位。
3. 通过校验位的比较来检测错误位并进行纠错。
二、4位数据海明校验码的生成方法在生成4位数据海明校验码时,需要依据原始数据的位数来确定校验位的数量。
对于4位数据,通常采用2位校验位。
而具体的生成方法如下:1. 将4位原始数据表示成二维矩阵形式。
2. 根据原始数据矩阵的每一列,计算出校验位的值。
3. 将校验位添加到原始数据矩阵中。
4. 根据生成的数据矩阵,计算出校验位的值并添加到数据中。
三、4位数据海明校验码的纠错方法当使用4位数据海明校验码进行数据传输或存储时,若出现错误,需要通过校验位来检测错误位并进行纠错。
纠错方法如下:1. 对接收到的数据进行校验,计算出校验位的值。
2. 将计算得到的校验位的值与接收到的校验位的值进行比较。
3. 根据比较结果确定错误位的位置,并将其进行纠正。
四、4位数据海明校验码的应用场景4位数据海明校验码主要应用于对数据进行短距离传输和存储过程中。
其应用场景包括但不限于以下几种情况:1. 在计算机内存中对数据进行校验和纠错。
2. 在通信传输过程中对数据进行校验和纠错。
3. 在存储介质中对数据进行校验和纠错。
4. 在传感器数据采集过程中对数据进行校验和纠错。
五、4位数据海明校验码的优缺点4位数据海明校验码作为一种常见的纠错码,具有一定的优点和缺点。
主要表现在以下几个方面:优点:1. 能够有效检测和纠正数据中出现的错误。
海明码校验例题

海明码校验例题摘要:1.海明码的概念与原理2.海明码的校验方法3.海明码的例题解析正文:一、海明码的概念与原理海明码是一种用于数据传输时检测和纠正错误的编码方法,由美国数学家海明在1950 年提出。
海明码的主要原理是利用冗余信息来实现数据的校验和修复。
在数据传输过程中,通过增加一定的冗余信息,使得接收方能够检测到传输中出现的错误,并根据冗余信息对错误进行修复。
二、海明码的校验方法海明码的校验方法主要有两种:奇偶校验和CRC 校验。
1.奇偶校验:通过在数据位之间插入奇数或偶数个校验位,使得整个编码后的数据包中1 的个数为奇数或偶数。
接收方在接收到数据后,统计1 的个数,如果与发送方一致,则认为数据传输正确;如果不一致,则说明数据传输出现错误。
2.CRC 校验:CRC(Cyclic Redundancy Check)校验是一种基于循环冗余的校验方法。
在数据传输过程中,发送方计算待发送数据的CRC 值,并将其附加在数据后面。
接收方收到数据后,也对数据进行CRC 计算,然后将接收到的CRC 值与计算得到的CRC 值进行比较。
如果两者相同,则认为数据传输正确;如果不同,则说明数据传输出现错误。
三、海明码的例题解析假设我们有一个数据传输系统,需要传输一个4 位的数据包,为了保证数据的正确性,我们希望在传输过程中能够检测到并纠正单个比特的错误。
为了实现这一目标,我们可以使用海明码进行编码。
具体编码过程如下:1.在数据位之间插入3 个校验位,使得整个数据包中1 的个数为奇数。
这样,在传输过程中,如果出现单个比特的错误,总1 的个数将变为偶数。
2.接收方在接收到数据后,统计1 的个数。
如果1 的个数为奇数,则认为数据传输正确;如果为偶数,则说明数据传输出现错误。
3.如果检测到错误,接收方可以根据校验位信息对错误进行修复。
例如,通过奇偶校验,我们可以知道错误发生在哪个比特位置,并据此对错误进行纠正。
综上所述,海明码是一种有效的数据校验和修复方法。
海明码数据位和校验位关系

海明码数据位和校验位关系什么是海明码海明码(Hamming Code)是一种用于检测和纠正错误的线性二进制码。
它由理查德·W·海明(Richard W. Hamming)于1950年提出,被广泛应用于计算机存储和通信系统中。
在计算机存储和通信中,数据传输过程中可能会发生错误。
为了保证数据的准确性,需要使用一种纠错编码来检测并纠正这些错误。
海明码就是一种常用的纠错编码方式。
海明码的原理海明码通过在待传输的数据中添加冗余位来实现错误检测和纠正。
冗余位被称为校验位,它们的值由数据位决定。
假设待传输的数据有m个比特(bit),则需要添加r个校验位,使总共有n=m+r个比特。
其中,r满足以下不等式:2^r ≥ m + r + 1根据以上不等式可以求得最小满足条件的r值。
对于每一个校验位,它的位置是2^i-1(i从1开始),即第1、2、4、8…个位置上都是校验位。
对于每一个校验位来说,它所涵盖的数据比特取决于它的位置。
假设第i个校验位涵盖的数据比特为D1, D2, …, Dk,则该校验位的值为:Ci = D1 ⊕ D2 ⊕ … ⊕ Dk其中,⊕表示异或运算。
这样,每个校验位都可以检测到特定位置上的错误。
海明码的编码过程海明码的编码过程可以分为以下几个步骤:1.确定待传输数据的长度m和校验位的数量r,并计算总共需要传输的比特数n。
2.根据待传输数据,确定每个校验位所涵盖的数据比特。
3.计算每个校验位的值,并将其添加到待传输数据中对应位置。
4.将编码后的数据进行传输。
下面以一个具体例子来说明海明码的编码过程。
假设待传输数据为1010,通过计算可以确定需要添加两个校验位。
因此,总共需要传输4+2=6个比特。
数据比特P1 P2 D1 P3 D2 D31 0 1其中,P1覆盖了D1、D2、D3,P2覆盖了D1、D2,P3覆盖了D1、D3。
计算P1的值:P1 = D1 ⊕ D2 ⊕ D3 = 1 ⊕ 0 ⊕ 1 = 0计算P2的值:P2 = D1 ⊕ D2 = 1 ⊕ 0 = 1计算P3的值:P3 = D1 ⊕ D3 = 1 ⊕ 1 = 0将校验位的值添加到待传输数据中,得到编码后的数据:101010。
海明码校验公式

海明码校验公式海明码校验公式,这可真是个让人又爱又恨的家伙!咱们先来说说海明码到底是啥。
想象一下,你给朋友寄了封信,可又担心路上这信会不会被弄破了、弄乱了。
海明码就像是给这封信加的一个特殊标记,能让接收的人一下子就知道这信有没有出问题。
那海明码校验公式呢,就是算出这个特殊标记的办法。
比如说,咱们要传一个数据,像“10110”这样的。
这时候,就得用海明码校验公式来搞点“小动作”啦。
咱们先得确定需要多少个校验位。
这就好比你要给一个箱子打包,得先知道要多少绳子才够。
假设数据位有 m 位,校验位有 r 位,那满足 2^r >= m + r + 1 这个式子,就能算出 r 的值。
比如说,数据位是 5 位,那 2^r >= 5 + r + 1 ,算一算,r 至少得 3 。
然后呢,把这些校验位放在特定的位置上。
这就像把宝贝放在特定的抽屉里,可不能乱放。
比如第 1 个校验位在 1 号位,第 2 个在 2 号位,第 3 个在 4 号位,依次类推。
再接下来,就是根据公式计算校验位的值。
这一步就有点像做数学题啦,得认真仔细。
我记得有一次给学生们讲这个的时候,有个小家伙一脸懵地看着我,说:“老师,这也太难懂啦!”我笑着跟他说:“别着急,咱们一步步来。
”我带着他们一步一步地计算,看着他们从一开始的迷茫,到后来渐渐明白,那种成就感真是没得说。
海明码校验公式虽然有点复杂,但只要咱们耐心点儿,多练几遍,就能掌握它。
就像学骑自行车,一开始可能摇摇晃晃,但多练几次,就能稳稳当当地上路啦。
总之,海明码校验公式虽然看着有点吓人,但只要咱们用心去学,它也能被咱们拿下!希望大家都能跟这个家伙成为好朋友,让数据传输更可靠,更准确!。
海明校验码(靠谱的解释)

海明校验码(靠谱的解释)
【定义】
海明码(Hamming Code)是利⽤奇偶性来检错和纠错的校验⽅法。
海明码的构成⽅法是在数据位之间的确定位置插⼊k个校验位,通过扩⼤吗距来实现检错和纠错。
对于数据位m的数据,加⼊k位的校验码,它应满⾜:
2^k>m+k+1
【例⼦】
设数据为01101001,试采⽤校验位求其偶校验⽅式的海明码。
(1)确定数据位D和校验位P在海明码中的位置:
由海明码编码规则可知:
p i在海明码的第2i-1
⽐如P4=2^(4-1)=8,所以位于第8位
(2)确定校验关系
这个难点在于如何确定校验位组。
举⼀个例⼦来说:H3=D0,海明码下标为3,我们必须⽤已知的校验位所对应的海明码下标(P1,P2,P3,P4,它们的海明码下标分别是1,2,4,8)来表⽰3,这⾥3就可以等于1+2。
H5为什么是1+4⽽不是2+3呢?因为H3不是校验位,是数据位。
⽐如P1 的校验位为表格中红⾊标记出来所对应的海明码的位数
故:P1校验:P1,D0,D1,D3,D4,D6
P1=D0⊕D1⊕D3⊕D4⊕D6=1⊕0⊕1⊕0⊕1=1
⊕符号:代表异或,相同则为0,不同则为1。
只要仔细⼀定可以计算正确。
P2、P3、P4的海明码计算也是如此,关键是要找出正确的校验位组,所以海明校验码:011001001101。
计算机组成原理--海明码的编码和校验方法(易懂)

计算机组成原理--海明码的编码和校验⽅法(易懂)海明码(也叫汉明码)具有⼀位纠错能⼒。
本⽂以1010110这个⼆进制数为例解释海明码的编码和校验⽅法。
编码 确定校验码的位数x 设数据有n位,校验码有x位。
则校验码⼀共有2x种取值⽅式。
其中需要⼀种取值⽅式表⽰数据正确,剩下2x-1种取值⽅式表⽰有⼀位数据出错。
因为编码后的⼆进制串有n+x位,因此x应该满⾜2x-1 ≥ n+x 使不等式成⽴的x的最⼩值就是校验码的位数。
在本例中,n=7,解得x=4。
确定校验码的位置 校验码在⼆进制串中的位置为2的整数幂。
剩下的位置为数据。
如图所⽰。
位置1234567891011内容x1x21x3010x4110 求出校验位的值 以求x2的值为例。
为了直观,将表格中的位置⽤⼆进制表⽰。
位置00010010001101000101011001111000100110101011内容x1x21x3010x4110 为了求出x2,要使所有位置的第⼆位是1的数据(即形如**1*的位置的数据)的异或值为0。
即x2^1^1^0^1^0 = 0。
因此x2 = 1。
同理可得x1 = 0, x3 = 1, x4 = 0。
位置00010010001101000101011001111000100110101011内容01110100110 因此1010110的海明码为01110100110。
校验 假设位置为1011的数据由0变成了1,校验过程为: 将所有位置形如***1, **1*, *1**, 1***的数据分别异或。
***1: 0^1^0^0^1^1 = 1 **1*: 1^1^1^0^1^1 = 1 *1**: 1^0^1^0 = 0 1***: 0^1^1^1 = 1 以上四组中,如果⼀组异或值为1,说明该组中有数据出错了。
***1 **1* 1***的异或都为1,说明出错数据的位置为1011。
海明码简单分析确定校验位个数海明码的码组长度需要符合:2^r – 1 (r代表校验位个数)为什么是这个公式呢?因为:只有这样才能保证校验位⾜够覆盖整个需要校验的码组。
海明校验码原理

海明校验码原理
海明校验码是用来检测和纠正二进制数据传输中的错误的编码方式,其实现原理如下:
1. 数据转换:首先需要将要传输的数据转换成二进制码形式。
2. 生成海明码:根据生成规则生成海明校验码。
生成海明码的步骤如下:
- 确定校验位数:根据要传输的数据确定校验位的个数。
- 确定校验位的位置:将二进制数据码按一定规则排列,将二进制数据码的每一位(包括校验位)都与校验位位置有关联。
- 生成校验位:根据规则算出校验位的值,将其填入海明校验码的相应位置。
- 得到海明码:将数据码和校验位合并成海明码。
3. 传输:以海明码的形式进行传输。
4. 检测和纠正错误:接收方收到海明码时,先对码中的每个二进制数进行校验,以检测是否存在错误。
如果存在错误,可以根据海明码的规则进行修正。
如果存在多个错误,则无法进行修正。
海明校验码是一种比较简单有效的纠错码,但是其校验能力有限,无法纠正大量的错误。
海明校验码的设计原理

海明校验码的设计原理今天来聊聊海明校验码的设计原理。
你知道吗?我们生活中有很多时候都需要检查信息有没有出错,就好比我们去超市买东西,售货员要核对商品价格扫码有没有扫错,这就像是一种简单的校验过程。
在计算机的数据世界里,也有一个类似的超级校验器,那就是海明校验码。
海明校验码的原理其实还挺巧妙的。
想象一下,我们在一个仓库里放了很多箱子(数据位),这些箱子排得很整齐。
海明校验码就像给这些箱子安排了一些管理员(校验位)。
这些管理员的位置是有规定的,他们可不是随便站在某个地方。
比如说,第1个校验位(管理员)负责查看特定几个箱子的数据有没有问题,第3个校验位(管理员)又负责另外一组不同的箱子。
我一开始也不明白,为什么要这么复杂地安排这些管理员(校验位)呢?其实这里面是有数学规律的。
海明码设计的时候是让校验位按照2的幂次方的位置来分布的,就像1、2、4、8、16……这样的位置。
为什么这样呢?这就要说到它的校验方法了。
打个比方吧,校验位就像是一个个探测器。
当数据出错的时候,这些探测器会根据自己负责的那些箱子(数据位)发现异常,然后通过一些特定的运算,就能准确地找到是哪个箱子(位)的数据出现了错误。
比如说,假如发现是1号、3号探测器报警了,就说明是特定的某个数据位出现了问题。
这里的1号、3号探测器是按照海明码的规则设定好负责对应的一些数据位的。
海明校验码在实际的计算机存储和数据传输中非常有用。
比如说在硬盘存储数据的时候,数据可能因为电磁干扰或者其他硬件问题产生错误。
海明校验码就能在数据被读取的时候,快速地检查数据是否正确,如果错了就加以纠正。
不过要注意的是,海明校验码也不是万能的。
存在一种万分之一或者百万分之一的特殊情况,几个地方同时出错,就可能会让校验码判断失误。
虽然这种情况非常少,但也是我们在使用的时候需要知道的局限性。
我学习这个原理花了不少时间,一开始真的是一头雾水,但是静下心来慢慢研究这个数据位和校验位之间的关系,就像解开一团复杂的毛线球一样。
海明码距离及检错纠错问题和CRC校验

海明码距离及检错纠错问题和CRC校验海明校验码两个长度相等的字符串的海明距离是在相同位置上不同的字符的个数,也就是将⼀个字符串替换成另⼀个字符串需要的替换的次数。
海明距离与检错和纠错的关系:1.海明距离为d+1的编码能检测出d位差错。
因为在距离为d+1的检验码中,只改变d位的值,不可能产⽣另⼀个合法码。
如奇偶校验码,海明距离为2,能查出单个错。
2.海明距离为2d+1的编码,能纠正d位差错。
因为此时,如果⼀个码字有d位发⽣差错,它仍然距离原来的码字距离最近,可以直接恢复为该码。
(奇偶校验码,海明距离为2,可以检出单个错)纠正单⽐特错的冗余位下界,m为数据位数,r为校验位数 (m+R+1)≤2^r1.每⼀个码字从左到右编号,最左边为第1位2.校验位和数据位凡编号为2的乘幂的位是校验位,如1、2、4、8、16、……。
其余是数据位,如3、5、6、7、9、……。
3.每⼀个校验位设置根据:包括⾃⼰在内的⼀些位的集合的奇偶值(奇数或偶数)。
海明码纠错过程(只纠错1位)⾸先将差错计数器置“0”。
当海明码数据到达接收端后,接收端逐个检查各个校验位的奇偶性。
如发现某⼀校验位和它所检测的集合的奇偶性不正确,就将该检验位的编号加到差错计数器中。
待所有校验位核对完毕:若差错计数器仍为“0”值,则说明该码字接收⽆误。
⾮“0”值,差错计数器的值为出错位的编号,将该位求反就可得到正确结果。
循环冗余检错码CRC可以检测到所有长度⼩于等于r的突发错误⼴泛⽤于各种⽹络,⼏乎所有的局域⽹使⽤CRC编码时发送⽅和接收⽅必须预先商定⼀个⽣成多项式G(x),假设有⼀个m为的帧M(x),使⽤G(x)⽣成的帧的步骤如下:假设G(x)的阶为r,那么M(x)在末尾添加r个0,得到 m+r位的位模式。
利⽤模2出发,⽤G(x)去除 ,得到对应的余数(总是⼩于等于r位)。
利⽤减去(模2减法)第2步中得到的余数,得到的位模式就是即将被传输的带校验和的帧⼩结:Sender在数据帧的低端加上r个零,对应多项式为XrM(x)采⽤模2除法,⽤G(x)去除XrM(x),得余数采⽤模2减法,⽤XrM(x)减去余数,得到带CRC校验和的帧Receiver⽤收到的幀去除以G(x)为零:⽆错误产⽣。
《海明码校验》课件

在传输过程中,可能发生位错误,如1011010。
编码
根据海明码规则,将数据编码为1101010。
校验和纠正
接收端利用校验位和冗余位检测并纠正错误, 得到正确的数据1101。
海明码校验的应用领域
1 通信领域
海明码广泛应用于数据通信和网络传输,保 证数据的准确性和完整性。
2 存储技术
海明码被用于存储设备中,检测和纠正存储 介质中的位错误,保护数据的可靠性。
3 数字电路
海明码在数字电路设计中有重要作用,用于 检测和纠正硬件中的错误。
4 计算机科学
海明码被广泛应用于计算机科学领域,如数 据校验和纠错算法等。
总结和展望
海明码校验是一种有效的错误检测和纠正技术,可应用于多个领域。未来, 随着技术的发展,海明码校验将在数据传输和存储中发挥更广泛的作用。
数据完整性
通过校验位,可以确定数据是否在传输过程中发生了改变,确保数据完整性。
海明码的定义和原理
海明码是一种线性错误检测和纠正码,通过引入冗余位来检测和纠正传输中的错误。
二进制编码
奇偶校验
海明码使用二进制编码表示信息, 每个编码位代表一个数据位或校 验位。
海明码利用奇偶校验的原理,在 编码中添加冗余位来检测和纠正 错误。
《海明码校验》PPT课件
海明码校验(Hamming Code)是一种常见的错误检测和纠正技术,具有广 泛应用。本课件将分享海明码校验的定义、原理、校验过程、算法、实例以 及应用领域。
常见的错误和校验位的作用
常见错误
数据传输过程中常会发生位错误、插入错误或删除错误,影响信息的准确性。
校验位作用
校验位用于检测和纠正传输中发生的错误,提高数据的可靠性。
计算及校验海明码的3个举例

计算及校验海明码的3个举例海明码具有检错纠错能⼒,⽤于传输质量较好的信道,因为出错太多检测不出来。
m位数据需要满⾜具有r位校验码m+r ≤ 2r-1校验位放在2n位置上,如??1? 111? 1111 111? 111...校验码依次在20、 21、 22、 23、 24位置上,有的是从后往前写的,结果不影响,知道怎么算就⾏。
例1,计算1011的海明码及检验1. 算校验位原数据1011, 有4位数据位,需满⾜4+r≤2r-1这个公式,求得r=3,表明有3个检验位,以下⽤a、b、c、...来代替得到ab1c0112. 算校验位值令发送⽅和接受⽅都采⽤偶检验的⽅法,也就是保证1的个数为偶数。
采⽤奇检验结果也⼀样,但收发双⽅⼀定要⽤相同的检验⽅法。
a b 1 c 0 1 1第⼀位检验位a的计算⽅法:从a开始检验⼀位,跳过⼀位,即20位,利⽤偶检验确定a。
第⼆位检验位b的计算⽅法:从b开始检验两位,跳过两位,即21位,利⽤偶检验确定b。
第三位检验位c的计算⽅法:从c开始检验四位,跳过四位,即22位,利⽤偶检验确定c。
a b 1 c 0 1 1a 1 0 1 偶检验确定a=0a b 1 c 0 1 1b 1 1 1 偶检验确定b=1a b 1 c 0 1 1后⾯没有了,所以就是c 0 1 偶检验确定c=0代⼊abc得海明码0110 0113. 检验传输海明码,若在信道上受到⼲扰,导致⼀位编码出现异常由0110 011→0111 011根据确定检验位的值来检验,第n组检验2n位,跳过2n位,分别把每组的数据异或,得出错位置。
这⾥的异或也就是相当于偶检验的过程,1的个数为偶数G就为0。
0 1 1 1 0 1 1G1=0⊕1⊕0⊕1=00 1 1 1 0 1 1G2=1⊕1⊕1⊕1=00 1 1 1 0 1 1G3=1⊕0⊕1⊕1=1由于发送端采⽤的是偶检验那么G3G2G1=000可说明传送中没有出错,G3G2G1=100转化为⼗进制说明海明码第4位出错,将第四位纠错后变成0110 011例2,计算0111 011的海明码及检验1. 算校验位m=7,根据m+r ≤ 2r-1求得r=4a b 0 c 1 1 1 d 0 1 12. 算校验位值令发送⽅和接受⽅都采⽤偶检验的⽅法,也就是保证1的个数为偶数。
海明码校验
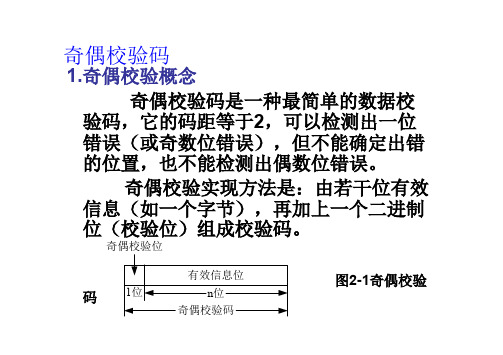
海明校验码
• 位置4检查4,5,6,7,12: • 0 1 1 ? 0 0 1 _ 1 0 1 0. 奇数个1,因
此位置4设为1,即: 0 1 1 1 0 0 1 _ 1 0 1 0 • 位置8检查8,9,10,11,12: • 0 1 1 1 0 0 1 ? 1 0 1 0. 偶数个1,因
有效信息(8位) 奇校验码(9位) 偶校验码(9位)
00000000
100000001010100
101010100
01111111
001111111
101111111
11111111
111111111
011111111
2.简单奇偶校验(续)
⑴ 校验位形成
当要把一个字节的代码D7~D0写入 主存时,就同时将它们送往奇偶校验逻辑 电路,该电路产生的“奇形成”信号就是校 验位。它将与8位代码一起作为奇校验码 写入主存。
3.交叉奇偶校验
计算机在进行大量字节(数据块)传 送时,不仅每一个字节有一个奇偶校验 位做横向校验,而且全部字节的同一位 也设置一个奇偶校验位做纵向校验,这 种横向、纵向同时校验的方法称为交叉 校验。
第1字节 1 1 0 0 1 0 1 1 → 1 第2字节 0 1 0 1 1 1 0 0 → 0 第3字节 1 0 0 1 1 0 1 0 → 0 第4字节 1 0 0 1 0 1 0 1 → 0
奇偶校验码
1.奇偶校验概念
奇偶校验码是一种最简单的数据校 验码,它的码距等于2,可以检测出一位 错误(或奇数位错误),但不能确定出错 的位置,也不能检测出偶数位错误。
奇偶校验实现方法是:由若干位有效 信息(如一个字节),再加上一个二进制 位(校验位)组成校验码。
海明码校验特征

海明码校验特征海明码是一种纠错码,用于检测和纠正数据传输或存储过程中出现的错误。
它是由理查德·海明于1950年提出的,因此得名。
海明码的基本原理是在数据位之间插入校验位,使得当数据位发生错误时,可以通过校验位来检测和纠正错误。
海明码的校验特征主要有以下几点:1. 纠错能力:海明码具有纠错能力,可以检测和纠正单个比特的错误。
具体来说,对于长度为n的数据块,海明码可以纠正其中任意s个比特的错误,同时检测出t个比特的错误,其中s+t ≤n。
这种纠错能力的实现是通过在数据位之间插入校验位来实现的。
2. 校验位的数量:海明码的校验位数量取决于数据块的长度和纠错能力的要求。
一般来说,数据块的长度越大,需要插入的校验位越多。
同时,要求纠错能力越强,需要插入的校验位也越多。
3. 校验位的位置:海明码的校验位是按照一定的规则插入到数据位之间的。
具体来说,对于长度为n的数据块,海明码的校验位是从第2个数据位开始,每隔r个数据位插入一个校验位,直到插入了r个校验位为止。
其中,r是一个正整数,表示校验位之间的距离。
4. 校验位的计算:海明码的校验位是通过一定的计算规则得到的。
具体来说,对于长度为n的数据块,每个校验位都是通过对一定数量的数据位进行异或运算得到的。
这些数据位的选择是根据校验位的位置和纠错能力的要求来确定的。
5. 纠错过程:当接收到传输或存储的数据块时,首先对其中的校验位进行计算,得到一个校验值。
然后,将这个校验值与接收到的校验位进行比较,如果两者相等,则说明数据块没有错误;如果不相等,则说明数据块中存在错误。
接下来,根据校验值和错误位数的要求,可以确定错误的具体位置,并进行纠正。
6. 编码过程:当需要对数据块进行编码时,首先将数据块分成若干个分组,每个分组包含一定数量的数据位和校验位。
然后,对每个分组进行编码,得到编码后的数据块。
最后,将所有编码后的数据块进行合并,得到最终的编码结果。
7. 解码过程:当需要对编码后的数据块进行解码时,首先对数据块进行拆分,得到每个分组的编码结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
海明校验码
• 例1.已知:信息码为:" 1 1 0 0 1 1 0 0 " (r=4代表冗余位数,即校验码位数) • 求:海明码码字。
海明校验码
采用偶校验,如果全部校验的位置中 有奇数个1,把该奇偶校验位置为1;如果 全部校验的位置中有偶数个1,把该奇偶 校验位置为0.
海明校验码
• 举例说明: • 一个字节的数据:10011010 • 构造数据字(Data Word),对应的校验 位留空_ _ 1 _ 0 0 1 _ 1 0 1 0 • 计算每个校验位的奇偶性 ( ?代表要设置 的比特位):
奇偶校验位的形成及校验电路
奇形成 偶校验 奇校验 偶形成 出错 出错 A
=1 1
B
1 =1
=1
=1
=1
=1Βιβλιοθήκη D7 D6D5 D 4
=1
D 3 D2
=1
D1 D0 D校
图2-2 奇偶校验位的形成及校验电路
2.简单奇偶校验(续) ⑵校验检测 读出时,将读出的9位代码(8位信 息位和1位校验位)同时送入奇偶校验电 路检测。若读出代码无错,则“奇校验出 错”=0;若读出代码中的某一位上出现 错误,则“奇校验出错”=1,从而指示 这个9位代码中一定有某一位出现了错误, 但具体的错误位置是不能确定的。
海明校验码
• 位置4检查4,5,6,7,12: • 0 1 1 ? 0 0 1 _ 1 0 1 0. 奇数个1,因 此位置4设为1,即: 0 1 1 1 0 0 1 _ 1 0 1 0 • 位置8检查8,9,10,11,12: • 0 1 1 1 0 0 1 ? 1 0 1 0. 偶数个1,因 此位置8设为0,即: 0 1 1 1 0 0 1 0 1 0 1 0 • 因此码字为: 011100101010.
海明校验码
• 位置1检查1,3,5,7,9,11: • ? _ 1 _ 0 0 1 _ 1 0 1 0. 偶数个1,因 此位置1设为0,即: 0 _ 1 _ 0 0 1 _ 1 0 1 0 • 位置2检查2,3,6,7,10,11: • 0 ? 1 _ 0 0 1 _ 1 0 1 0. 奇数个1,因 此位置2设为1,即: 0 1 1 _ 0 0 1 _ 1 0 1 0
海明校验码
• 3、每个奇偶校验位的值代表了代码字中部分数 据位的奇偶性,其所在位置决定了要校验和跳 过的比特位顺序。 • 位置1:校验1位,跳过1位,校验1位,跳 过1位(1,3,5,7,9,11,13,15,…) • 位置2:校验2位,跳过2位,校验2位,跳 过2位 (2,3,6,7,10,11,14,15,…) • 位置4:校验4位,跳过4位,校验4位,跳 过4位 (4,5,6,7,12,13,14,15,20,21,22,23,…) • 位置8:校验8位,跳过8位,校验8位,跳 过8位(8-15,24-31,40-47,…) • …
有效信息(8位) 奇校验码(9位) 偶校验码(9位)
00000000
01010100 01111111 11111111
100000000
001010100 001111111 111111111
000000000
101010100 101111111 011111111
2.简单奇偶校验(续) ⑴ 校验位形成 当要把一个字节的代码D7~D0写入 主存时,就同时将它们送往奇偶校验逻辑 电路,该电路产生的“奇形成”信号就是 校验位。它将与8位代码一起作为奇校验 码写入主存。 若D7~D0中有偶数个“1”,则“奇 形成”=1, 若D7~D0中有奇数个“1”,则“奇 形成”=0。
3.交叉奇偶校验(续) 交叉校验可以发现两位同时出错的 情况,假设第2字节的A6、A4两位均出错, 横向校验位无法检出错误,但是第A6、 A4位所在列的纵向校验位会显示出错,这 与前述的简单奇偶校验相比要保险多了。
海明校验码
海明码是一种可以纠正一位差错的编 码。它是利用在信息位为k位,增加r位冗 余位,构成一个n=k+r位的码字,然后用r 个监督关系式产生的r个校正因子来区分 无错和在码字中的n个不同位置的一位错。 它必需满足以下关系式: 2r ≥ k+r+1 或 2r ≥ n+1
奇偶校验规律 校验位的取值(0或1)将使整个校 验码中“1”的个数为奇数或偶数,所以有 两种可供选择的校验规律: 奇校验──整个校验码(有效信息位 和校验位)中“1”的个数为奇数。 偶校验──整个校验码中“1”的个数 为偶数。
2.简单奇偶校验 简单奇偶校验仅实现横向的奇偶校验, 下表给出几个字节的奇偶校验码的编码结 果。最高一位为校验位,其余8位为信息 位。在实际应用中,多采用奇校验,因为 奇校验中不存在全“0”代码,在某些场合 下更便于判别。
海明校验码
• 海明码(Hamming Code )编码的关键是使 用多余的奇偶校验位来识别一位错误。 • 码字(Code Word) 按如下方法构建: • 1、把所有2的幂次方的数据位标记为 奇偶校验位(编号为1, 2, 4, 8, 16, 32, 64等 的位置) • 2、其他数据位用于待编码数据. (编 号为3, 5, 6, 7, 9, 10, 11, 12, 13, 14, 15, 17等的位置)
海明校验码
上例中构建了一个码字 011100101010, 假定实际接收到的数据 011100101110. 则接收方可以计算出哪一位出错并对其进 行更正。方法就是验证每一个校验位。记 下所有出错的校验位,可以发现校验位2 和8的数据不正确. 错误校验位 2 + 8 = 10, 则位置10的数据出错。一般说来,对所有 校验位进行检查, 将所有出错的校验位置 相加, 得到的就是错误信息所在的位置.
3.交叉奇偶校验 计算机在进行大量字节(数据块)传 送时,不仅每一个字节有一个奇偶校验 位做横向校验,而且全部字节的同一位 也设置一个奇偶校验位做纵向校验,这 种横向、纵向同时校验的方法称为交叉 校验。 第1字节 1 1 0 0 1 0 1 1 → 1 第2字节 0 1 0 1 1 1 0 0 → 0 第3字节 1 0 0 1 1 0 1 0 → 0 第4字节 1 0 0 1 0 1 0 1 → 0 ↓ ↓↓↓↓ ↓ ↓↓ 1 0 0 1 1 0 0 0
