2.4 弦切角的性质 课件(人教A选修4-1)(2)
合集下载
2.4 弦切角的性质 教学课件(人教A版选修4-1)
知能达标演练
课后习题解答
【考题2】 (2012·辽宁高考)如图，⊙O和⊙O′相交于A，B两点， 过A作两圆的切线分别交两圆于 C， D两点，连结 DB并延长交 ⊙O于点E.
证明
(1)AC·BD＝AD·AB； (2)AC＝AE.
课前探究学习
课堂讲练互动
知能达标演练
课后习题解答
证明
(1)由 AC 与圆 O′相切于点 A， 得∠CAB＝∠ADB；
课前探究学习 课堂讲练互动 知能达标演练 课后习题解答
反思感悟
(1)弦切角是很重要的与圆相交的角．其主要功能是协
调与圆相关的各种角，如圆心角、圆周角等，是连接圆与三角形
全等、三角形相似及与圆相关的各种直线位置关系的桥梁．
(2)弦切角定理经常作为工具，进行三角形相似的证明，然后利用 三角形相似进一步确定相应边之间的关系，在圆中证明比例式或 等积式，常常需要借助于三角形相似处理． (3)弦切角定理有时还与圆周角定理等知识综合运用，它们不但在
课前探究学习
课堂讲练互动
知能达标演练
课后习题解答
解
如图所示，连接 BD.
∵AC 为⊙O 的切线，∴∠ADE＝∠ABD. ∵∠A＝∠A，∴△ADE∽△ABD， AD BD BD 2 DE 1 ∴ AE ＝DE，即DE＝1，∴BD＝2. DE 1 ∵BE 为⊙O 的直径，∴∠BDE＝90° ，∴tan∠ABD＝BD＝2. ∵∠F＋∠BEF＝90° ，∠ABD＋∠BEF＝90° ， 1 ∴∠ABD＝∠F，∴tan∠F＝tan∠ABD＝ . 2
②一边和圆相切(一边所在直线为圆的切线)；
③一边和圆相交(一边为圆的过切点的弦)． 三者缺一不可，例如图中，∠CAD很像弦切角，但它不是弦切 角，因为 AD 与圆相交， ∠ BAE 也不一定是弦切角，只有已知 AE切圆于点A，才能确定它是弦切角．
2017-2018学年高中数学选修4-1课件人教A版2.4弦切角的性质(共30张PPT)
������������ ∥ ������������⇒∠������������������ = ∠������������������ ������������切☉������于点������⇒∠������������������ = ∠������
探究一
探究二
探究三
思维辨析
当堂检测
反思感悟比例式(或乘积式)的证明方法 1.证明乘积式成立,往往与相似三角形有关.若存在切线,常要寻 找弦切角,确定三角形相似的条件,有时需要添加辅助线创造条件. 2.直接证明比例式或乘积式有困难时,可考虑把它分解成两个比 例式的形式.
解析:∵PA是圆O的切线,∴∠BAP=∠BCA.
������������ 又∠BAC=∠APB,∴△BAP∽△BCA,∴������������
=
∴AB2=PB· CB=7×5=35,故 AB=√35.
答案:√35
������������ , ������������
探究一
探究二
探究三
思维辨析
当堂检测
2.与弦切角定理有关的结论 (1)弦切角的度数等于它所夹的弧的度数的一半. (2)弦切角的度数等于它所夹的弧所对的圆心角度数的一半. (3)如果两个弦切角所夹的弧相等,那么这两个弦切角也相等.
【做一做2】 如图,正三角形ABC内接于圆O,CP是圆O的切线,则 ∠ACP=( )
A.90° B.30°C.60° D.75° 解析:因为△ABC是正三角形,所以∠B=60°.又因为CP是圆O的切 线,所以∠ACP=∠B=60°. 答案:C
四
弦切角的性质
学 习 目 标 1.理解弦切角的概念. 2.掌握弦切角定理,并能运 用定理解决问题.
思 维 脉 络 弦切角的性质 概念 弦切角定理—应用
弦切角的性质 课件
弦切角的性质
1．弦切角的定义 顶点在圆上，一边和圆相交、另一边和圆相切的角叫 做弦切角． 温馨提示 弦切角具备的三个条件：(1)顶点在圆上 (顶点为切线的切点)；(2)一边和圆相切(一边所在的直线 为圆的切线)；(3)一边和圆相交(一边为圆的过切点的弦)．
2．弦切角的性质定理 弦切角等于它所夹的弧所对的圆周角．
类型 2 利用定理求线段的长度、证明线段相等
[典例 2] 如图所示，P 是⊙O 外一点，PA 是切线， A 为切点，割线 PBC 与⊙O 相交与点 B，C，PC＝2PA， D 为 PC 的中点，AD 与延长线交⊙O 于点 E.
证明：BE＝EC.
证明：连接 AB，AC(如图)．
由题设知 PA＝PD. 故∠PAD＝∠PDA. 因为∠PDA＝∠DAC＋∠DCA， ∠PAD＝∠BAD＋解题的第一步是要准确找到 弦切角．弦切角的特点是：(1)顶点在圆上；(2)一边是圆 的弦；(3)一边与圆相切．第二步是要准确地找到弦切角 所夹的弧，再看这段弧所对的圆周角或圆心角．再结合弦 切角定理、圆周角定理进行推理证明．
2．利用弦切角解决与角有关的问题的步骤：(1)根据 图形及弦切角的定义找出与题目有关的弦切角；(2)利用 弦切角定理找出与其相等的角；(3)综合运用相关的知识 进行角的求解．
∠DCA＝∠PAB， 所以∠DAC＝∠BAD，从而B︵E＝E︵C， 因此 BE＝EC.
归纳升华 1．利用弦切角定理证明线段相等的技巧． 利用弦切角定理证明线段相等时，常常通过弦切角定 理获得角相等，然后再转化为线段相等的关系，从而解决 问题．
2．比例式(或等积式)的证明方法． 证明比例式(或等积式)成立，往往与相似三角形有 关，若存在切线，常要寻找弦切角．确定三角形相似，有 时需要添加辅助线创造条件．
1．弦切角的定义 顶点在圆上，一边和圆相交、另一边和圆相切的角叫 做弦切角． 温馨提示 弦切角具备的三个条件：(1)顶点在圆上 (顶点为切线的切点)；(2)一边和圆相切(一边所在的直线 为圆的切线)；(3)一边和圆相交(一边为圆的过切点的弦)．
2．弦切角的性质定理 弦切角等于它所夹的弧所对的圆周角．
类型 2 利用定理求线段的长度、证明线段相等
[典例 2] 如图所示，P 是⊙O 外一点，PA 是切线， A 为切点，割线 PBC 与⊙O 相交与点 B，C，PC＝2PA， D 为 PC 的中点，AD 与延长线交⊙O 于点 E.
证明：BE＝EC.
证明：连接 AB，AC(如图)．
由题设知 PA＝PD. 故∠PAD＝∠PDA. 因为∠PDA＝∠DAC＋∠DCA， ∠PAD＝∠BAD＋解题的第一步是要准确找到 弦切角．弦切角的特点是：(1)顶点在圆上；(2)一边是圆 的弦；(3)一边与圆相切．第二步是要准确地找到弦切角 所夹的弧，再看这段弧所对的圆周角或圆心角．再结合弦 切角定理、圆周角定理进行推理证明．
2．利用弦切角解决与角有关的问题的步骤：(1)根据 图形及弦切角的定义找出与题目有关的弦切角；(2)利用 弦切角定理找出与其相等的角；(3)综合运用相关的知识 进行角的求解．
∠DCA＝∠PAB， 所以∠DAC＝∠BAD，从而B︵E＝E︵C， 因此 BE＝EC.
归纳升华 1．利用弦切角定理证明线段相等的技巧． 利用弦切角定理证明线段相等时，常常通过弦切角定 理获得角相等，然后再转化为线段相等的关系，从而解决 问题．
2．比例式(或等积式)的证明方法． 证明比例式(或等积式)成立，往往与相似三角形有 关，若存在切线，常要寻找弦切角．确定三角形相似，有 时需要添加辅助线创造条件．
2.4 弦切角的性质 课件(人教A选修4-1)(2)
[读教材·填要点] 1．弦切角 顶点在圆上，一边和圆 相交 ，另一边和圆 相切 的角叫
弦切角．
2．弦切角定理 弦切角等于 它所夹的弧所对的圆周角 ．
[小问题·大思维] 1．一边和圆相交，另一边和圆相切的角是弦切角吗？ 提示：不一定．弦切角必须同时具备三点： ①顶点在圆上；②一边和圆相交；③一边和圆相切． 2．弦切角与它所夹的弧所对的圆心角之间有什么关系？
∴∠DAC＝∠CAB.
法二： 如图， 延长 BO 交⊙O 于 E， 连接 AE，则∠CAE＝90° . 又∵AD⊥CE，∴∠DAC＝∠E. ∵AB 是⊙O 的切线， ∴∠CAB＝∠E. ∴∠DAC＝∠CAB.
法三：如图，连接OA. ∵AB切⊙O于A，∴OA⊥AB.
∴∠CAB与∠OAC互余．
又∵AD⊥OB， ∴∠DAC与∠ACO互余． ∵OA＝OC，∴∠OAC＝∠ACO. ∴∠DAC＝∠CAB.
[考题印证] (2012· 辽宁高考)如图，⊙O和⊙O′相交于A，B两点， 过A作两圆的切线分别交两圆于C，D两点，连结DB并延长
交⊙O于点E.证明：
(1)AC· BD＝AD· AB； (2)AC＝AE.
[命题立意]
本题主要考查弦切角定理，考查学生综合
运用所学知识，分析问题并解决问题的能力．
证明：(1)由 AC 与⊙O′相切于 A， 得∠CAB＝∠ADB， 同理∠ACB＝∠DAB， 所以△ACB∽△DAB. AC AB 从而AD＝BD， 即 AC· BD＝AD· AB. (2)由 AD 与⊙O 相切于 A，得∠AED＝∠BAD， 又∠ADE＝∠BDA，得 AE AD △EAD∽△ABD.从而AB＝BD， 即 AE· BD＝AD· AB. 结合(1)的结论，AC＝AE.
解决此类问题的关键是把握弦切角的三个要素：
弦切角．
2．弦切角定理 弦切角等于 它所夹的弧所对的圆周角 ．
[小问题·大思维] 1．一边和圆相交，另一边和圆相切的角是弦切角吗？ 提示：不一定．弦切角必须同时具备三点： ①顶点在圆上；②一边和圆相交；③一边和圆相切． 2．弦切角与它所夹的弧所对的圆心角之间有什么关系？
∴∠DAC＝∠CAB.
法二： 如图， 延长 BO 交⊙O 于 E， 连接 AE，则∠CAE＝90° . 又∵AD⊥CE，∴∠DAC＝∠E. ∵AB 是⊙O 的切线， ∴∠CAB＝∠E. ∴∠DAC＝∠CAB.
法三：如图，连接OA. ∵AB切⊙O于A，∴OA⊥AB.
∴∠CAB与∠OAC互余．
又∵AD⊥OB， ∴∠DAC与∠ACO互余． ∵OA＝OC，∴∠OAC＝∠ACO. ∴∠DAC＝∠CAB.
[考题印证] (2012· 辽宁高考)如图，⊙O和⊙O′相交于A，B两点， 过A作两圆的切线分别交两圆于C，D两点，连结DB并延长
交⊙O于点E.证明：
(1)AC· BD＝AD· AB； (2)AC＝AE.
[命题立意]
本题主要考查弦切角定理，考查学生综合
运用所学知识，分析问题并解决问题的能力．
证明：(1)由 AC 与⊙O′相切于 A， 得∠CAB＝∠ADB， 同理∠ACB＝∠DAB， 所以△ACB∽△DAB. AC AB 从而AD＝BD， 即 AC· BD＝AD· AB. (2)由 AD 与⊙O 相切于 A，得∠AED＝∠BAD， 又∠ADE＝∠BDA，得 AE AD △EAD∽△ABD.从而AB＝BD， 即 AE· BD＝AD· AB. 结合(1)的结论，AC＝AE.
解决此类问题的关键是把握弦切角的三个要素：
人教版高中数学选修四教学课件-弦切角的性质
在圆上”和“另一边和圆相切”两个条件.
题型一 题型二 题型三
题型一
平行问题
【例1】 如图,AD是△ABC中∠BAC的平分线,☉O经过点A且与 BC切于点D,与AB,AC分别相交于点E,F.求证:EF∥BC.
分析:连接DF,于是∠FDC=∠DAC,根据AD是∠BAC的平分线,有 ∠BAD=∠DAC,而∠BAD与∠EFD对着同一段弧,由此得到∠EFD与 ∠FDC的相等关系,根据内错角相等,可以断定两条直线平行.
题型一 题型二 题型三
证明:连接BD,如图.
∵AD是∠BAC的平分线, ∴∠BAD=∠CAD.
又∠BCD=∠BAD, ∠CBD=∠CAD,
∴∠BCD=∠CBD. ∴BD=CD.
题型一 题型二 题型三
又BE为☉O的切线,
∴∠EBD=∠BCD.
在△BED和△CEB中, ∠EBD=∠ECB,∠BED=∠CEB,
题型一 题型二 题型三
题型二 线段成比例问题
【例2】 已知△ABC内接于☉O,∠BAC的平分线交☉O于点D,CD
的延长线交过点B的切线于点E.
求证:
������������2 ������������2
=
������������������������.
分析:直接证明此等式有一定的难度,可以考虑把它分解成两个 比例式的形式,借助相似三角形的性质得出结论.
又
BD=CD,∴
������������ 2 ������������ 2
=
������������.
������������
反思已知直线与圆相切,证明线段成比得到角相等,再通过三角形相似得到成比例线段.
题型一 题型二 题型三
【变式训练2】 如图,AB为☉O的直径,弦CD∥AB,AE切☉O于点A,
题型一 题型二 题型三
题型一
平行问题
【例1】 如图,AD是△ABC中∠BAC的平分线,☉O经过点A且与 BC切于点D,与AB,AC分别相交于点E,F.求证:EF∥BC.
分析:连接DF,于是∠FDC=∠DAC,根据AD是∠BAC的平分线,有 ∠BAD=∠DAC,而∠BAD与∠EFD对着同一段弧,由此得到∠EFD与 ∠FDC的相等关系,根据内错角相等,可以断定两条直线平行.
题型一 题型二 题型三
证明:连接BD,如图.
∵AD是∠BAC的平分线, ∴∠BAD=∠CAD.
又∠BCD=∠BAD, ∠CBD=∠CAD,
∴∠BCD=∠CBD. ∴BD=CD.
题型一 题型二 题型三
又BE为☉O的切线,
∴∠EBD=∠BCD.
在△BED和△CEB中, ∠EBD=∠ECB,∠BED=∠CEB,
题型一 题型二 题型三
题型二 线段成比例问题
【例2】 已知△ABC内接于☉O,∠BAC的平分线交☉O于点D,CD
的延长线交过点B的切线于点E.
求证:
������������2 ������������2
=
������������������������.
分析:直接证明此等式有一定的难度,可以考虑把它分解成两个 比例式的形式,借助相似三角形的性质得出结论.
又
BD=CD,∴
������������ 2 ������������ 2
=
������������.
������������
反思已知直线与圆相切,证明线段成比得到角相等,再通过三角形相似得到成比例线段.
题型一 题型二 题型三
【变式训练2】 如图,AB为☉O的直径,弦CD∥AB,AE切☉O于点A,
高二数学人教A版选修4-1课件：2.4 弦切角的性质
1.如图,圆 O 的直径 AB=6,C 为圆周上一点,BC=3,过点 C 作圆的切线
l,过 A 作 l 的垂线 AD,垂足为 D,则线段 CD 的长为
.
解析:∵直线 l 是圆 O 的切线, ∴∠ACD=∠ABC, ∠BCE=∠BAC. 又 AB 是直径,∴AC⊥BC. ∵BC=3,AB=6,
∴∠ABC=60°.∴AC=3 3.
证明:连接 DF,如图所示,
∵AD 是∠BAC 的平分线,∴∠BAD=∠DAC. ∵∠EFD=∠BAD,∴∠EFD=∠DAC. ∵BC 切☉O 于 D,∴∠FDC=∠DAC. ∴∠EFD=∠FDC.∴EF∥BC. 当已知条件中出现圆的切线时,借助于弦切角定理,常用角的关系 证明两条直线平行:(1)内错角相等,两条直线平行;(2)同位角相等,两条 直线平行;(3)同旁内角互补,两条直线平行等.证题时可以根据图形与已 知合理地选择.
☉O,AD⊥AC,∠C=32°,∠B=110°,则∠BAD=
.
错解:∵AD⊥AC, ∴∠BAD 是弦切角. ∴∠BAD=∠C.
又∠C=32°,∴∠BAD=32°.
错因分析:错解中,误认为∠BAD 是弦切角,其实不然,虽然 AD⊥AC,但 AD 不是切线.
正解:∵∠C+∠B+∠BAC=180°, ∴∠BAC=180°-∠C-∠B=38°.
∴∠ACE=∠ABC.
∴∠ACE=∠BCD.
(2)∵∠ECB=∠CDB,∠EBC=∠BCD, ∴△BDC∽△ECB.∴BBCE = CBDC, 即 BC2=BE×CD.
5.如图,AB 是半圆 O 的直径,C 是圆周上一点(异于点 A,B),过点 C 作 圆 O 的切线 l,过点 A 作直线 l 的垂线 AD,垂足为点 D.AD 交半圆于 点 E.求证:CB=CE.
人教A版-高中数学选修4-1-第二讲--四-弦切角的性质-课件(共25张PPT)品质课件PPT
在△PAB中, ∠APB=180-∠PAB-∠ABP
A
O P
由弦切角定理,得 ∠PAB=∠ACB=∠ABP,
C B
∴ ∠APB=180-2∠ACB
在Rt△ABC中,∠BAC=90-∠ACB
∴ ∠APB=2∠BAC
•
长风破浪会有时，直挂云帆济沧海。努力，终会有所收获，功夫不负有心人。以铜为镜，可以正衣冠；以古为镜，可以知兴替；以人为镜，可以明得失。前进
∠BAC=∠CAP+∠PAB=90+∠PAB
E
而∠PAB=∠PCB
∴∠BCE=∠BAC
C
综合 (1) (2) (3), 题意即证.
O
A
P
B
观察
如上三个图,图中每个角的共同特点是什么？
知识要 点
弦切角定义：
顶点在圆上，一边和圆相交、另一 边和圆相切的角 .
归纳
C
E EC
E C
OB
O
O
A
A
B
A B
人就会从卑微中站起来，带着封存梦想去拥抱蓝天。成功需要成本，时间也是一种成本，对时间的珍惜就是对成本的节约。人只要不失去方向，就不会失去自
决定今天的你，所以，过去的懒惰，决定你今天的一败涂地。让我记起容易，但让我忘记我怕我是做不到。不要跟一个人和他议论同一个圈子里的人，不管你
想象困难做出的反应，不是逃避或绕开它们，而是面对它们，同它们打交道，以一种进取的和明智的方式同它们奋斗。他不爱你，你为他挡一百颗子弹也没用
志坚强，只有刚强的人，才有神圣的意志，凡是战斗的人，才能取得胜利。卓越的人的一大优点是：在不利和艰难的遭遇里百折不挠。疼痛的强度，同自然赋
刚度成正比。能够岿然不动，坚持正见，度过难关的人是不多的。钢是在烈火和急剧冷却里锻炼出来的，所以才能坚硬和什么也不怕。我们的一代也是这样的
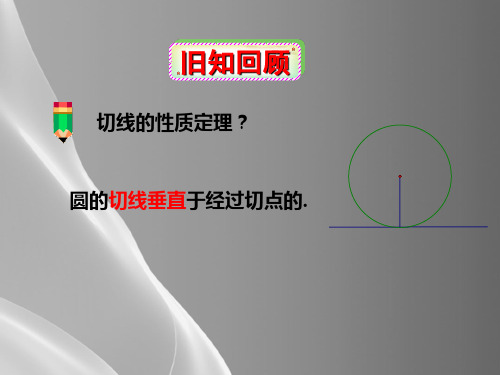
A
O P
由弦切角定理,得 ∠PAB=∠ACB=∠ABP,
C B
∴ ∠APB=180-2∠ACB
在Rt△ABC中,∠BAC=90-∠ACB
∴ ∠APB=2∠BAC
•
长风破浪会有时，直挂云帆济沧海。努力，终会有所收获，功夫不负有心人。以铜为镜，可以正衣冠；以古为镜，可以知兴替；以人为镜，可以明得失。前进
∠BAC=∠CAP+∠PAB=90+∠PAB
E
而∠PAB=∠PCB
∴∠BCE=∠BAC
C
综合 (1) (2) (3), 题意即证.
O
A
P
B
观察
如上三个图,图中每个角的共同特点是什么？
知识要 点
弦切角定义：
顶点在圆上，一边和圆相交、另一 边和圆相切的角 .
归纳
C
E EC
E C
OB
O
O
A
A
B
A B
人就会从卑微中站起来，带着封存梦想去拥抱蓝天。成功需要成本，时间也是一种成本，对时间的珍惜就是对成本的节约。人只要不失去方向，就不会失去自
决定今天的你，所以，过去的懒惰，决定你今天的一败涂地。让我记起容易，但让我忘记我怕我是做不到。不要跟一个人和他议论同一个圈子里的人，不管你
想象困难做出的反应，不是逃避或绕开它们，而是面对它们，同它们打交道，以一种进取的和明智的方式同它们奋斗。他不爱你，你为他挡一百颗子弹也没用
志坚强，只有刚强的人，才有神圣的意志，凡是战斗的人，才能取得胜利。卓越的人的一大优点是：在不利和艰难的遭遇里百折不挠。疼痛的强度，同自然赋
刚度成正比。能够岿然不动，坚持正见，度过难关的人是不多的。钢是在烈火和急剧冷却里锻炼出来的，所以才能坚硬和什么也不怕。我们的一代也是这样的
《2.4弦切角的性质》课件1-优质公开课-人教A版选修4-1精品
第二讲
直线与圆的位置关系
2.4 弦切角的性质
1．理解弦切角的定义． 2．掌握弦切角的性质定理，并能应用它们进行简 单的计算和证明．
相交 、另一边和 1．弦切角的定义：顶点在圆上，一边和圆__________ 相切 的角叫做弦切角． 圆________
2．弦切角的性质定理： _______________________________________________________. 弦切角等于它所夹的弧所对的圆周角 3． 在⊙O 的直径 CB 延长线上取一点 A，AP 与⊙O 相切于点 P，
例3
证明：如图，连接 BD.
►变式训练
答案：∠C＝∠CAB
1．直线与圆相切是一种重要的、特殊的位置关系，在与弦切角 相关的证明题目中，重点是用好弦切角的定义和定理． 2．同学们要能在图形中准确地识别弦切角，并能正确应用弦切 角定理及其推论． 它给我们提供了证明角相等的又一个重要依据， 常 常与圆周角、圆心角性质联合应用来证明、求解． 3．利用弦切角性质来证明两个角相等，再利用三角形相似证比 例中项，是一种较常见的题型．
⇒△ACE∽△ABC⇒ ∠CAE＝∠CAB
⇒∠ACD＝∠B
AC AE 2 ＝ ⇒ AC ＝AB· AE. AB AC 点评： 此题主要是利用弦切角的性质去证明两个角相等， 再利用 三角形相似证比例中项，这样的类型题较常见．
►变式训练
1． PC 与⊙O 相切于 C 点， 割线 PAB 过圆心 O， 则 PC2 是 PA· PB 的________倍．
3 , 且∠APB＝30° ，AP＝ 3，则 CP＝________.
题型1
比例式证明
例1 已知 MN 是⊙O 的切线，点 A 为切点，MN 平行于弦 CD，弦
直线与圆的位置关系
2.4 弦切角的性质
1．理解弦切角的定义． 2．掌握弦切角的性质定理，并能应用它们进行简 单的计算和证明．
相交 、另一边和 1．弦切角的定义：顶点在圆上，一边和圆__________ 相切 的角叫做弦切角． 圆________
2．弦切角的性质定理： _______________________________________________________. 弦切角等于它所夹的弧所对的圆周角 3． 在⊙O 的直径 CB 延长线上取一点 A，AP 与⊙O 相切于点 P，
例3
证明：如图，连接 BD.
►变式训练
答案：∠C＝∠CAB
1．直线与圆相切是一种重要的、特殊的位置关系，在与弦切角 相关的证明题目中，重点是用好弦切角的定义和定理． 2．同学们要能在图形中准确地识别弦切角，并能正确应用弦切 角定理及其推论． 它给我们提供了证明角相等的又一个重要依据， 常 常与圆周角、圆心角性质联合应用来证明、求解． 3．利用弦切角性质来证明两个角相等，再利用三角形相似证比 例中项，是一种较常见的题型．
⇒△ACE∽△ABC⇒ ∠CAE＝∠CAB
⇒∠ACD＝∠B
AC AE 2 ＝ ⇒ AC ＝AB· AE. AB AC 点评： 此题主要是利用弦切角的性质去证明两个角相等， 再利用 三角形相似证比例中项，这样的类型题较常见．
►变式训练
1． PC 与⊙O 相切于 C 点， 割线 PAB 过圆心 O， 则 PC2 是 PA· PB 的________倍．
3 , 且∠APB＝30° ，AP＝ 3，则 CP＝________.
题型1
比例式证明
例1 已知 MN 是⊙O 的切线，点 A 为切点，MN 平行于弦 CD，弦
人教版数学高二A版选修4-1第二讲四 弦切角的性质
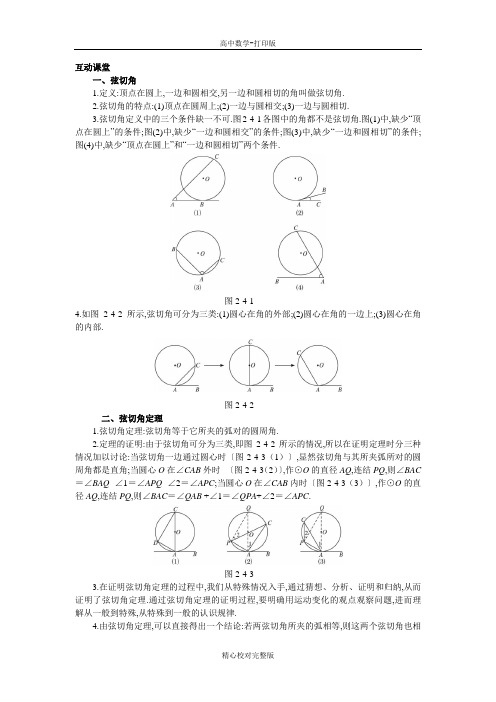
互动课堂一、弦切角1.定义:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.2.弦切角的特点:(1)顶点在圆周上;(2)一边与圆相交;(3)一边与圆相切.3.弦切角定义中的三个条件缺一不可.图2-4-1各图中的角都不是弦切角.图(1)中,缺少“顶点在圆上”的条件;图(2)中,缺少“一边和圆相交”的条件;图(3)中,缺少“一边和圆相切”的条件;图(4)中,缺少“顶点在圆上”和“一边和圆相切”两个条件.图2-4-14.如图2-4-2所示,弦切角可分为三类:(1)圆心在角的外部;(2)圆心在角的一边上;(3)圆心在角的内部.图2-4-2二、弦切角定理1.弦切角定理:弦切角等于它所夹的弧对的圆周角.2.定理的证明:由于弦切角可分为三类,即图2-4-2所示的情况,所以在证明定理时分三种情况加以讨论:当弦切角一边通过圆心时〔图2-4-3（1）〕,显然弦切角与其所夹弧所对的圆周角都是直角;当圆心O在∠CAB外时〔图2-4-3（2）〕,作⊙O的直径AQ,连结PQ,则∠BAC ＝∠BAQ -∠1＝∠APQ -∠2＝∠APC;当圆心O在∠CAB内时〔图2-4-3（3）〕,作⊙O的直径AQ,连结PQ,则∠BAC＝∠QAB +∠1＝∠QPA+∠2＝∠APC.图2-4-33.在证明弦切角定理的过程中,我们从特殊情况入手,通过猜想、分析、证明和归纳,从而证明了弦切角定理.通过弦切角定理的证明过程,要明确用运动变化的观点观察问题,进而理解从一般到特殊,从特殊到一般的认识规律.4.由弦切角定理,可以直接得出一个结论:若两弦切角所夹的弧相等,则这两个弦切角也相等,我们把这一结论称为弦切角定理的推论,它也是角的变换的依据.5.弦切角定理也可以表述为弦切角的度数等于它所夹的弧的度数的一半.这就建立了弦切角与弧的数量之间的关系,它为直接依据弧进行角的转换确立了基础.三、刨根问底问题到目前为止,对于圆中有关的角我们已学过圆心角、圆周角、弦切角,它们各自有定义、定理及和它所对的弧的度数关系,这三种角在证明题和计算题中经常用到,它们相互之间有哪些联系和区别？探究:我们可用下表来分析它们的联系与区别.名称圆心角圆周角弦切角定义顶点在圆心的角顶点在圆上,两边和圆相交顶点在圆上,一边和圆相交,另一边和圆相切图形有关定理①圆心角的度数等于它所对的弧的度数②在同圆或等圆中相等的圆心角所对的弧相等,所对的弦相等,所对弦的弦心距相等同弧所对的圆周角等于它所对的圆心角的一半弦切角等于它所夹弧所对的圆周角有关推论四者关系定理的推论圆周角定理的推论①②③弦切角定理的推论角与弧的关系∠AOB的度数=AB的度数∠ACB的度数=21的度数∠ACB的度数=21的度数活学巧用【例1】如图2-4-4,AD是⊙O的切线,AC是⊙O的弦,过C作AD的垂线,垂足为B,CB与⊙O 相交于点E,AE平分∠CAB,且AE =2,求△ABC各边的长.图2-4-4思路解析:∠BAE为弦切角,于是∠BAE=∠C,再由AE平分∠CAB和△ABC是直角三角形可得∠C的度数,进而解直角三角形即可.解:∵AD为⊙O的切线,∴∠BAE=∠C.∵AE平分∠CAB,∴∠BAC=2∠BAE.又∵∠C+∠BAC =90°,∴∠BAE =∠C =30°.则有BE =1,AB =3,BC =3,AC =23.【例2】如图2-4-5,AD 是△ABC 中∠BAC 的平分线,经过点A 的⊙O 与BC 切于点D ,与AB 、AC 分别相交于E 、F .求证:EF ∥BC .图2-4-5思路解析:连结DF,构造弦切角,于是∠FDC =∠DAC ,根据AD 是△ABC 中∠BAC 的平分线有∠BAD =∠DAC ,而∠BAD 与∠EFD 对着同一段弧,所以相等,由此建立∠EFD 与∠FDC 的相等关系,根据内错角相等,可以断定两直线平行. 证明:连结DF .∵AD 是∠BAC 的平分线,∴∠BAD =∠DAC.∵∠EFD =∠BAD ,∴∠EFD =∠DAC . ∵⊙O 切BC 于D ,∴∠FDC =∠DAC . ∴∠EFD =∠FDC . ∴EF ∥BC .【例3】如图2-4-6,△ABC 内接于⊙O ,AB =AC ,直线XY 切⊙O 于点C ,弦BD ∥XY ,AC 、BD 相交于点E .（1）求证:△ABE ≌△ACD ;（2）若AB =6 cm,BC=4 cm,求AE 的长.图2-4-6思路解析:第（1）问中的全等已经具备了AB =AC ,再利用弦切角定理与圆周角定理可以得角的相等关系;对于（2）,则利用△BCE ∽△ACB 建立比例式,解方程获得AE 的长. （1）证明:∵XY 是⊙O 的切线,∴∠1=∠2.∵BD ∥XY ,∴∠1=∠3. ∴∠2=∠3.∵∠3=∠4,∴∠2=∠4. ∵∠ABD =∠ACD , 又∵AB =AC ,∴△ABE ≌△ACD .（2）解:∵∠3 =∠2,∠BCE =∠ACB , ∴△BCE ∽△ACB . ∴AC BC =CBCE. ∴AC ·CE = BC 2, 即AC ·(AC -AE )=BC 2.∵AB =AC =6,BC =4, ∴6(6-AE )=16. ∴)(310cm AE. 【例4】 如图2-4-7,AB 和AC 与⊙O 相切于B 、C ,P 是⊙O 上一点,且PE ⊥AB 于E ,PD ⊥BC于D ,PF ⊥AC 于F.求证:PD 2= PE ·PF .图2-4-7思路解析:由结论先想到证△PDE ∽△PFD ,但这两个三角形相似的条件不够,注意到图中有切线AB 、AC ,构造弦切角. 证明:连结PB 、PC .∵AB 切⊙O 于B,则∠PBE =∠PCD . 又∵PE ⊥AB ,PD ⊥BC , ∴∠PEB =∠PDC =90°. ∴△PBE ∽△PCD . ∴PD PE =PCPB. ∵AC 切⊙O 于C , ∴∠PCF =∠PBD . 又∵PF ⊥AC ,PD ⊥BC , ∴∠PFC =∠PDB =90°. ∴△PBD ∽△PCF.∴PF PD =PC PB. ∴PD PE =PFPD . ∴PD 2 =PE ·PF .。
高中数学2.4弦切角的性质课件新人教A版选修4-1
思考 1 你对弦切角是怎样理解的?
提示:弦切角的特点 :(1)顶点在圆上 ;(2)一边与圆相交;(3)另一边与圆相 切. 弦切角定义中的三个条件缺一不可.如图①②③④中的角都不是弦切 角.图①中,缺少“顶点在圆上 ”的条件; 图②中,缺少“一边和圆相交”的条件; 图③中,缺少“一边和圆相切”的条件 ;图④中,缺少 “顶点在圆上”和 “另一边 和圆相切”两个条件.
2 =
=
������������ . ������������
又 BD=CD,∴
������������ . ������������
点评 已知直线与圆相切,证明线段成比例时,常先利用弦切角定
理和圆周角定理获得角相等,再通过三角形相似得到成比例线段.
探究一
探究二
探究三
探究三 易错辨析
易错点:忽视弦切角的一边是切2° ,∠ B=110° ,则∠ BAD= .
角与弧 的关系
∠AOB 的度数 =AB的度数
∠ACB 的度数= AB
2
1
∠ACB 的度数= AC的度数
2
1
的度数
探究一
探究二
探究三
探究一 弦切角定理
在使用弦切角定理时,关键是要弄清哪个角是弦切角,这样才能正确解 决问题.
探究一
探究二
探究三
【典型例题 1】 如图,AD 是☉ O 的切线,AC 是☉ O 的弦,过 C 作 AD 的 垂线,垂足为 B,CB 与☉O 相交于点 E,AE 平分∠CAB,且 AE=2,求△ABC 各 边的长.
四
弦切角的性质
课程目标 1.理解弦切角的概念,会判断弦切角. 2.掌握弦切角定理的内容,并能利用它解决有关 问题.
学习脉络
2.4 弦切角的性质 课件(人教A选修4-1)
Rt△CAE∽Rt△CBD CE CD → ＝ → 结论 Rt△CBF∽Rt△CAD CD CF
[证明]
连接CA、CB.
∵PA、PB是⊙O的切线， ∴∠CAP＝∠CBA， ∠CBP＝∠CAB. 又CD⊥AB，CE⊥PA，CF⊥PB， ∴Rt△CAE∽Rt△CBD， Rt△CBF∽Rt△CAD， CA CE CB CF ∴CB＝CD，CA＝CD， CE CD ∴CD＝ CF，即CD2＝CE· CF.
5．如图，AD是△ABC的角平分线，
经过于点E、F， 连接DF，EF. (1)求证：EF∥BC； (2)求证：DF2＝AF· BE.
证明：(1)∵⊙O切BC于D，
∴∠CAD＝∠CDF.
∵AD是△ABC的角平分线， ∴∠BAD＝∠CAD. 又∵∠BAD＝∠EFD， ∴∠EFD＝∠CDF. ∴EF∥BC.
证明乘积式成立，往往与相似三角形有关，若
存在切线，常要寻找弦切角，确定三角形相似的条
件，有时需要添加辅助线创造条件．
4．如图，已知MN是⊙O的切线，A为切点，MN平行于弦 CD，弦AB交CD于E.求证：AC2＝AE· AB.
证明：连接BC. MN∥CD⇒∠MAC＝∠ACD MN切⊙O于A⇒∠MAC＝∠B ⇒∠ACD＝∠B ⇒△ACE∽△ABC ∠CAE＝∠CAB AC AE ⇒AB＝AC⇒AC2＝AB· AE.
1. 弦切角定理
(1)文字语言叙述： 弦切角等于它 所夹的弧 所对的圆周角． (2)图形语言叙述： 如图，AB与⊙O切于A点，则∠BAC＝ ∠D .
[说明]
弦切角的度数等于它所夹弧度数的一半，
圆周角的度数等于它所对的弧的度数的一半，圆心
角的度数等于它所对弧的度数．
[例 1]
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
[研一题]
[例3] 如图，梯形ABCD内接于
⊙O，DC∥AB，AB＝AC，过A点作
⊙O的切线与CD的延长线交于E.求证：
AD2＝ED· EC. 分析：本题考查弦切角定理，圆内接四边形、相似三 角形等知识的综合应用，解答本题可转化为证明△EAD∽ △ECA.
证明：AE切⊙O于点A， ∴∠EAC＝∠B(弦切角定理)， ∵AB＝AC，∴∠ACB＝∠B， ∴∠EAC＝∠ACB， ∴AE∥BC，又∵DC∥AB， ∴四边形ABCE是平形四边形，∴∠E＝∠B. ∵梯形ABCD内接于⊙O， ∴∠ADE＝∠B，∴∠ADE＝∠E， ∴AD＝AE. ∵EA切⊙O于A，∴∠EAD＝∠ACE， 又∵∠E＝∠E，∴△EDA∽△EAC， ∴EA2＝ED· EC， ∴AD2＝ED· EC.
点击下图进入“创新演练”
∴∠EFB＝90°.
连接BC，则∠ECB＝90°， ∴E、F、B、C四点共圆．
∴AE· AC＝AF· AB.①
同理A、D、E、F四点共圆． ∴BE· BD＝BF· AB.②
将①、②两式相加得
AF· AB＋BF· AB＝AE· AC＋BE· BD＝AB2.
弦切角定理在几何证明中有广泛的应用，高考中 常与三角形相似、圆的切线等问题结合考查.2012年辽 宁高考以解答题的形式将弦切角定理与相似三角形的 判定及应用相结合考查，是高考命题的一个新亮点．
法四：如图，过C作⊙O的切线交AB于G
∵AB是⊙O的切线， ∠CAG＝∠ACG， 又∵OC⊥CG，AD⊥OB， ∴CG∥AD.
∴∠ACG＝∠DAC，即∠DAC＝∠CAB.
[悟一法] (1)由弦切角定理可直接得到角相等，在与弦切角
有关的几何问题中，往往还需要借助其它几何知识来
综合解答，由弦切角得到的角相等只是推理论证中的 一个条件． (2)借助弦切角定理和圆的其他性质(如等弧所对的 弦相等)以及三角形有关知识我们可以得到特殊三角形
[悟一法]
充分利用圆周角定理、圆内接四边形的性质、平行 四边形性质定理、弦切角定理等结论，架设与三角形有 关问题的桥梁，证明三角形相似是解决此类问题的有效
途径．
[通一类] 3．AB是圆O的直径，过A、B作两弦AC和BD相交于E，求 证：AB2＝AE· AC＋BE· BD. 证明：如图，AB是圆的直径． AC与BD相交于E，作EF⊥AB，F为垂足．
[读教材·填要点] 1．弦切角 顶点在圆上，一边和圆 相交 ，另一边和圆 相切 的角叫
弦切角．
2．弦切角定理 弦切角等于 它所夹的弧所对的圆周角 ．
[小问题·大思维] 1．一边和圆相交，另一边和圆相切的角是弦切角吗？ 提示：不一定．弦切角必须同时具备三点： ①顶点在圆上；②一边和圆相交；③一边和圆相切． 2．弦切角与它所夹的弧所对的圆心角之间有什么关系？
[通一类] 1．如图，NA与⊙O切于点A，AB和AD是 ⊙O的弦，AC为直径，试指出图中有 哪几个弦切角？
解：弦切角分三类：如题图：
(1)圆心在角的外部； (2)圆心在角的一边上； (3)圆心在角的内部． 即∠BAN、∠CAN、∠DAN为弦切角.
[研一题] [例2] 已知：AB切⊙O于A，OB交⊙O于C，AD⊥
[考题印证] (2012· 辽宁高考)如图，⊙O和⊙O′相交于A，B两点， 过A作两圆的切线分别交两圆于C，D两点，连结DB并延长
交⊙O于点E.证明：
(1)AC· BD＝AD· AB； (2)AC＝AE.
[命题立意]
本题主要考查弦切角定理，考查学生综合
运用所学知识，分析问题并解决问题的能力．
证明：(1)由 AC 与⊙O′相切于 A， 得∠CAB＝∠ADB， 同理∠ACB＝∠DAB， 所以△ACB∽△DAB. AC AB 从而AD＝BD， 即 AC· BD＝AD· AB. (2)由 AD 与⊙O 相切于 A，得∠AED＝∠BAD， 又∠ADE＝∠BDA，得 AE AD △EAD∽△ABD.从而AB＝BD， 即 AE· BD＝AD· AB. 结合(1)的结论，AC＝AE.
OB于D.求证：∠DAC＝∠CAB. 分析：本题考查弦切角定理的应用．解答本题需要
根据题意画出图形，然后利用相关定理解决．
证明：法一：如图，延长 AD 交⊙O 于 E，AB 切⊙O 于 A， ∵CD⊥AE， ∴ ＝ CE . AC
又∵∠DAC 的度数等于 CE 度数的一
半，
AC ∠CAB 的度数等于 度数的一半，
或全等三角形，从而证得线段相等．
[通一类] 2.如图，AB是半圆O的直径，C是圆 周上一点(异于A、B)，过C作圆O 的切线l，过A作直线l的垂线AD， 垂足为D，AD交半圆于点E.求证：
CB＝CE.
证明：法一：连接BE.
因为AB是半圆O的直径，E为圆周上一点， 所以∠AEB＝90°， 即BE⊥AD. 又因为AD⊥l，所以BE∥l. 所以∠DCE＝∠CEB. 因为直线l是圆O的切线，
所以∠DCE＝∠CBE.
所以∠CBE＝∠CEB. 所以CE＝CB.
法二：连接AC、BE，在DC延长线上取一点F. 因为AB是半圆O的直径，C为圆周上一点， 所以∠ACB＝90°，即∠BCF＋∠ACD＝90°. 又因为AD⊥l，所以∠DAC＋∠ACD＝90°.
所以∠BCF＝∠DAC.
又因为直线l是圆O的切线，所以∠CEB＝∠BCF. 又∠DAC＝∠CBE，所以∠CBE＝∠CEB. 所以CE＝CB.
提示：弦切角等题] [例1] 如图，AB、CB分别切⊙O于D、
E，试写出图中所有的弦切角． 分析：本题考查弦切角的定义．解答本 题需要明确构成弦切角的三个条件，然后依
据定义作出判断．
解：由弦切角的定义可知， ∠ADE、∠BDE、∠BED、∠CED都是弦切角．
[悟一法]
∴∠DAC＝∠CAB.
法二： 如图， 延长 BO 交⊙O 于 E， 连接 AE，则∠CAE＝90° . 又∵AD⊥CE，∴∠DAC＝∠E. ∵AB 是⊙O 的切线， ∴∠CAB＝∠E. ∴∠DAC＝∠CAB.
法三：如图，连接OA. ∵AB切⊙O于A，∴OA⊥AB.
∴∠CAB与∠OAC互余．
又∵AD⊥OB， ∴∠DAC与∠ACO互余． ∵OA＝OC，∴∠OAC＝∠ACO. ∴∠DAC＝∠CAB.
解决此类问题的关键是把握弦切角的三个要素：
(1)顶点在圆上(顶点为圆切线的切点)；
(2)一边和圆相切(一边所在直线为圆的切线)；
(3)一边和圆相交(一边为圆的过切点的弦)．
三者缺一不可，例如上图中，∠CAD很像弦切角， 但它不是弦切角，因为AD与圆相交，∠BAE也不一定是 弦切角，只有已知AE切圆于点A，才能确定它是弦切角．