图形思维导图
图形的思维导图五年级

A
底面
人顶点
属幕 高 圆柱 侧面 i高
o
AB
直线
射线
6
A
0:底面
底面
球
长方体 面 正方体 棱 顶点
校长
6
顶角
圆柱
圆锥
长方体
正方体
c
660° 602
等边三角形
腰腰
6底角 底角△
等腰三角形
高
A底
三角形的底和高
比萨斜塔 基本
立体
图形
图形
图形的认识
三角形
平面
线 线段 A
B
角的意
边B
直径(d)
线的位
置关系
相交与
平行
形的关系
圆
A
,D
长方形
高
正方形
平行四边形 上底
B 底c
ab
平行四边那
四边形
梯形
长方形
等 直
正方形
形 梯形
底滑 梯形腰高 腰
底角
下底
在工保上,"Im3"的土,沙.
石干均同你"1方"。
B
o 义及表
角 示方法
1
顶角 边
A
O
A
角的 B
分类
BB
0
锐角
A
O
A
直角
钝角
角的
性质
B 6 A@
AB
平角
周角
两点间 的距离
角的大小是由两条边张开的程
度决定的,与边的长短无关
连接两点之间的线段的长度,叫
做两点间的距离,简称距离
长方
平行四边
ms
m
北师大二年级数学下册第六单元:认识图形知识点思维导图

定义
由一个点和从这个点引出的两条 直直的线所组成的图形叫角。
各部分名称
认识角
角的大 小比较
将两个角的顶点和一条边重合, 张口大的角就大。
角的分类
判断角 的方法
用三角板上的直角比一比。
长方形 与正方形
长方形 的特征
长方形的对边相等, 四个角都是直角。
正方形 的特征
正方形的四条边都相等
平行四边 形的特征
对边相等,对角相等,容易变形。
欣赏与设计
用我们学过的长方形 、正方形、三角形、 平行四边形等能够设 计出很多美丽的图案
。பைடு நூலகம்
丰富的图形世界思维导图
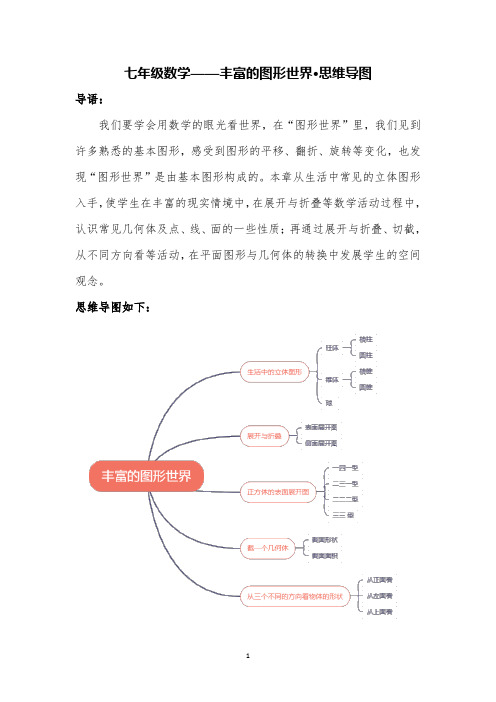
七年级数学——丰富的图形世界·思维导图导语:我们要学会用数学的眼光看世界,在“图形世界”里,我们见到许多熟悉的基本图形,感受到图形的平移、翻折、旋转等变化,也发现“图形世界”是由基本图形构成的。
本章从生活中常见的立体图形入手,使学生在丰富的现实情境中,在展开与折叠等数学活动过程中,认识常见几何体及点、线、面的一些性质;再通过展开与折叠、切截,从不同方向看等活动,在平面图形与几何体的转换中发展学生的空间观念。
思维导图如下:一、立体图形的表面展开图:几何体的表面展开图在中考中主要涉及两个方面的内容:一是考查几何体的侧面展开图,以圆锥和圆柱等几何体为主,二是考查几何体的表面展开图,以柱体为主要考查对象;其中难点为利用正方体的表面展开图,找对应面。
例题1解析:利用空间想象或通过动手操作,将展开图还原成立体图形,看能否构成正方体。
A,B,D选项的展开图都能折叠成一个正方体,C选项的展开图中含有“凹”的图形,不能折叠成一个正方体。
故选C。
二、截一个几何体:当用一个平面去截一个几何体时:首先要明确该截面是个平面图形,然后看截面与几何体哪些面相交;其次通过确定交线的条数来判断截面的边数,最后判断该平面图形的形状。
判断立体图形截面的形状是这类问题的重点和难点。
例题2解析:(1)截面与底面平行,可以得到圆形截面;(2)截面沿圆柱的高线切割,可得到长方形截面;(3)截面与底面平行,可以得到三角形截面.综上所述,截面的形状分别是圆形、长方形、三角形.三、从不同方向看物体:从不同方向看物体,主要指的是从正面、左面、上面看到的图形,最为常见的是由小正方体组成的图形从不同方向看到的图形,或根据从三个方向看到的图形判断小正方体的个数。
例题3。
小学数学《图形与几何》思维导图

“图形与几何”知识体系思维导图
图形与几何
图形的认识
图形的测量
方向与位置
图形的运动
知识体系
认识规律
基本内容
立体图形的认识
平面图形的认识 线段、射线、直线 周长
面积
体积
长方形、正方形
平行四边形、三角形、梯形
【不确定+相对】前后、左右、上下
【确定+相对】东、西、南、北
【确定+精准】数对 图形的变换
平移
旋转
轴对称
点
方向 角度 相似
投影
角的初步认识
三角形的认识
四边形的认识
圆的认识
长方体、正方体、圆柱、圆锥 学科逻辑:点→线→面→体 认识逻辑:体→面→线→点 立体→平面→立体 整体→局部 外部→内部
形状、名称、特征、性质
构成要素:顶点、边、角 方向
距离 对称轴
长方形的周长
圆的周长 圆的面积
长方体、圆柱、圆锥。
立体图形思维导图

立体图形思维导图立体图形思维导图是一种用于表达和展示复杂概念的有力工具。
在这个导图中,立体图形的形式被巧妙地运用,使得观者可以更加直观地理解信息之间的关联和层次。
导图的结构立体图形思维导图通常由多个层次组成,每个层次包含一些相关的概念或信息。
这些层次可以根据内容的逻辑关系,分为主要思路和次要思路,形成一个有机的整体结构。
导图的优势立体图形思维导图相比传统的平面导图,具有以下优势:•视觉冲击力:立体图形更能够吸引观者的注意,让信息更有吸引力。
•空间展示:立体图形提供了一个立体的展示空间,使得观者可以更好地理解信息之间的空间关系。
•思维拓展:通过立体图形的形式展示信息,可以激发观者的思维,帮助他们更好地理解和应用所呈现的概念。
制作立体图形思维导图的步骤步骤一:确定主题首先要确定导图的主题或中心概念,以确保整个导图内容的一致性和逻辑性。
步骤二:绘制基本框架在确定主题后,可以开始绘制导图的基本框架,包括主要思路和次要思路的层次结构。
步骤三:填充内容填充导图的内容时,需将相关概念或信息按照逻辑顺序和层次性填入各个层次中,确保信息的完整性和连贯性。
步骤四:添加立体效果通过添加合适的立体效果,使得导图更具立体感和视觉冲击力,提升信息传达的效果。
应用范围立体图形思维导图可以应用于各种领域,如教育、商业、科研等。
在教育领域,可以用于展示复杂概念,帮助学生更好地理解知识;在商业领域,可以用于制定战略计划或产品规划;在科研领域,可以用于展现研究成果和数据。
结语立体图形思维导图作为一种全新的信息展示工具,对于提升信息传达效果和拓展思维具有重要作用。
希望通过本文的介绍,能够让更多人了解并应用立体图形思维导图,为信息传达和思维拓展带来新的可能性。
常见的平面图形图示平面图形分类思维导图几何图形知识体系图

平面图形:
有些几何图形(如线段、角、三角形、长方形、圆等)的各个部分都在同一平面内,它们是平面图形。
如直线、射线、角、三角形、平行四边形、长方形(正方形)、梯形和圆都是几何图形,这些图形所表示的各个部分都在同一平面内,称为平面图形。
例如:有一组对边平行的四边形一定是平面图形。
(两条平行线确定一个平面)
平面图形的大小,叫做它们的面积
点的形成是线,线的形成是面,面的形成是体。
平面图形:有些几何图形(如线段、角、三角形、长方形、圆等)的各个部分都在同一平面内,它们是平面图形。
常见的平面图形图示:
从左到右依次为:长方形、正方形、三角形、圆、椭圆、
菱形、五边形、六边形。
平面图形分类:
几何图形知识体系图:
平面图形有哪些
基本的平面图形:直线、射线、长方形、正方形、三角形、平行四边形、梯形、圆形等等。
平面图形是几何图形的一种。
平面几何图形可分为以下几类:1.圆形:包括正圆、椭圆等;2.多边形:三角形、四边形等;3.弓形:优弧弓、抛物线弓等;4.多弧形:月牙形、太极形、葫芦形等。
什么是平面图形
平面图形是几何图形的一种,指所有点都在同一平面内的图形,如直线、三角形、平形四边形等都是基本的平面图形。
平面图形是平面几何研究的对象。
几何图形,即从实物中抽象出的各种图形,可帮助人们有效的刻画错综复杂的世界。
生活中到处都有几何图形,我们所看见的一切都是由点、线、面等基本几何图形组成的。
几何源于西文西方的测地术,解决点线面体之间的关系。
无穷尽的丰富变化使几何图案本身拥有无穷魅力。
小学数学几何图形概念、公式大全-思维导图

上次和孩子一起做了小学数学几何图形的思维导图,今天把这个导图彻底完善了下,把所有的计算公式都加进去了,整个导图画下来,等于把这些几何图形知识全部复习了一遍,同时找到不同几何图形之间的关联,加深了孩子的记忆。
里面还有些图形孩子目前还没学到,我在填充的时候,着重给孩子讲解了公式的由来,实在讲不出来的,就直接写上公式了,等于给孩子预习,也方便孩子以后的复习。
下面直接上图。
一、基本图形在认识线和角的基础上,主要回顾了计量单位以及换算。
线段的长度单位:千米:km、米:m、分米:dm、厘米:cm、毫米:mm换算:1千米=1000米、1米=10分米、1分米=10厘米、1厘米=10毫米、1米=100厘米、1米=1000毫米角的计量单位:(°)二、平面图形平面图形在认识三角形、四边形、圆的基础上,主要是回顾计量单位、周长、面积计算公式,还有些图形对应的性质。
面积的计量单位:1、周长:围成一个图形的所有边长的总和就是这个图形的周长周长的计量单位和换算和线段一样2、面积:物体的表面或围成的平面图形的大小,叫做它们的面积面积的计量单位:平方千米、公顷、平方米、平方分米、平方厘米单位换算:1平方千米=100公顷、1公顷=10000平方米、1平方米=100平方分米、1平方分米=100平方厘米长方形:周长:长方形周长=(长+宽)× 2面积:长方形面积=长×宽正方形:正方形周长= 边长× 4正方形面积= 边长×边长长方形和正方形的周长和面积公式,孩子都记得比较熟悉,所以直接列出来。
平行四边形:平行四边形的周长是四条边相加,但对边相等,所以只要是两条边相加×2就可以了。
面积:平行四边形的面积是通过剪切和平移,转化成一个长方形来计算,最后演变结果是:平行四边形面积=底×高。
即:S=ah梯形:周长比较好计算,四边相加即可。
梯形的面积演变过程,因为两个一样的梯形可以拼成一个平行四边形,所以梯形的面积就是:梯形面积=(上底+下底)×高÷2。
几何图形初步思维导图初一

几何图形初步思维导图知识点梳理背诵1.我们把实物中抽象的各种图形统称为几何图形。
2.有些几何图形(如长方体.正方体.圆柱.圆锥.球等)的各部分不都在同一平面内,它们是立体图形。
3.有些几何图形(如线段.角.三角形.长方形.圆等)的各部分都在同一平面内,它们是平面图形。
4.将由平面图形围成的立体图形表面适当剪开,可以展开成平面图形,这样的平面图形称为相应立体图形的展开图。
5.几何体简称为体。
6.包围着体的是面,面有平的面和曲的面两种。
7.面与面相交的地方形成线,线和线相交的地方是点。
8.点动成面,面动成线,线动成体。
9.经过两点有一条直线,并且只有一条直线。
简述为:两点确定一条直线(公理)。
10.当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做它们的交点。
11.点M把线段AB分成相等的两条线段AM和MB,点M叫做线段AB的中点。
12.经过比较,我们可以得到一个关于线段的基本事实:两点的所有连线中,线段最短。
简单说成:两点之间,线段最短。
(公理)13.连接两点间的线段的长度,叫做这两点的距离。
14.角∠也是一种基本的几何图形。
15.把一个周角360等分,每一份就是1度的角,记作1°;把一度的角60等分,每一份叫做1分的角,记作1′;把1分的角60等分,每一份叫做1秒的角,记作1″。
16.从一个角的顶点出发,把这个角分成相等的两个角的射线,叫做这个角的平分线。
17.如果两个角的和等于90°(直角),就是说这两个叫互为余角,即其中的每一个角是另一个角的余角。
18.如果两个角的和等于180°(平角),就说这两个角互为补角,即其中一个角是另一个角的补角。
19.等角的补角相等,等角的余角相等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
II
重心的加方法 迈重心\移动的考法I 识^:图形穴稳定(大头朝上)
云的涯 交占 交点的形成过程 I b 直卿直线 •建曲线和曲线 I 直线和曲线 -交点的位宣 两面之问 两面之间也可 i°sy :囹形不稳定(恿觉国形要掉下来了) n 内制线段之间的交点
内外线段Z 间的交点 中心对称
重心
元羡
结构
a 阴影移动 我
w
笔画数
对称性(議体/微软稚黑;
第一笔] 一笔亘(毛笔悴》
开枚封用
o® 空司数(日月田目)
图形推理
黑+黒二?白+白黑+白二?白+黒二?
阴影
£0数量/面积考法 | 0童加
-
交点] II 点-
中心对称]
元索券婆(注意uii ) 空体和祁分
汉宁
d白宜性
価主向性
4目经段等咲性
7
1仝可数莹| 飞别.有到召形内祁画统,考虑内那交点数、内都裁段数、空⑤数
空习的老成过程宜践和直埃所形战的空瓦宜裟和白茨馬形辰的空目
歪乏之可相交
■(❺凹凸性
'|
有交面位畳
I边数査三:达数少的鬲形在/我者达戴歹的鬲形亡上
—r4性质孫庄:白馥臣形在上或者直我関形在上
判断方法:做任意苑点之间的连践,有任意一点出现往零彩外部,迂个理形就是凹边彩-|盲交面面积大小(以1/2)为准
4是否尋夫r
面积分割等大
I等大面积的数量■I
等大面积的位E ■I n面积克裁
4 空目数和外部吳段数之w的关系。
