有限差分法及matlab实现
完整word版,一维扩散方程有限差分法matlab

Fpg一维扩散方程の有限差分法——计算物理实验作业七 陈万物理学 2013 级 题目:编程求解一维扩散方程の解uD 2u 2 (0 x a 0 ,0 t t max ) tx u(x,t) |t 0 e x ua 1ub 1 nc 1(x 0)a 2ub 2 uc 2( x a 0 )n取 a 1 1,b 1 1, c 1 0, a 2 1, b 21, c 2 0, a 0 1.0,t max 。
输出 t=1,2,...,10 时辰の x 和 u(x), 并与解析解 u=exp(x+0.1t)作比较。
主程序:% 一维扩散方程の有限差分法 clear,clc;%定义初始常量a1 = 1; b1 = 1; c1 = 0; a2 = 1;b2 =-1; c2 = 0;a0 = 1.0; t_max = 10; D = 0.1; h = 0.1; tao = 0.1;%调用扩散方程子函数求解u = diffuse_equation(a0,t_max,h,tao,D,a1,b1,c1,a2,b2,c2);子程序 1:function output = diffuse_equation(a0,t_max,h,tao,D,a1,b1,c1,a2,b2,c2)% 一维扩散方程の有限差分法,采用隐式六点差分格式 (Crank-Nicolson)% a0: x の最大值% t:_max: t の最大值% h: 空间步长% tao: 时间步长% D :扩散系数% a1,b1,c1是( x=0)界线条件の系数; a2,b2,c2是( x=a0)界线条件の系数x = 0:h:a0;n = length(x);t = 0:tao:t_max;k = length(t);P = tao * D/h^2;P1=1/P+1;P2 = 1/P- 1;u = zeros(k,n);%初始条件u(1,:) = exp(x);%求 A 矩阵の对角元素dd = zeros(1,n);d(1,1) = b1*P1+h*a1;d(2:(n-1),1) = 2*P1;d(n,1) = b2*P1+h*a2;%求 A 矩阵の对角元素下边一行元素ee= -ones(1,n-1);e(1,n-1) = -b2;%求 A 矩阵の对角元素上边一行元素ff= -ones(1,n-1);f(1,1) = -b1;R = zeros(k,n);%求 R%追赶法求解for i = 2:kR(i,1) = (b1*P2-h*a1)*u(i -1,1)+b1*u(i -1,2)+2*h*c1;for j = 2:n-1R(i,j) = u(i -1,j-1)+2*P2*u(i -1,j)+u(i -1,j+1);endR(i,n) = b2*u(i -1,n-1)+( b2*P2-h*a2)*u(i -1,n)+2*h*c2;M = chase(e,d,f,R(i,:));u(i,:) = M';plot(x,u(i,:)); axis([0 a0 0 t_max]); pause(0.1)endoutput = u;%绘图比较解析解和有限差分解[X,T] = meshgrid(x,t);Z = exp(X+0.1*T);surf(X,T,Z),xlabel( 'x'),ylabel('t'),zlabel('u'),title( '解析解 '); figuresurf(X,T,u),xlabel('x'),ylabel('t'),zlabel('u'),title( '有限差分解 ');子程序 2:function M = chase(a,b,c,f)%追赶法求解三对角矩阵方程, Ax=f%a 是对角线下边一行の元素%b 是对角线元素%c 是对角线上边一行の元素%M 是求得の结果,以列向量形式保存n = length(b);beta = ones(1,n-1);y = ones(1,n);M = ones(n,1);for i = (n-1):(-1):1a(i+1) = a(i);end%将 a 矩阵和 n 对应beta(1) = c(1)/b(1);for i = 2:(n-1)beta(i) = c(i)/( b(i) -a(i)*beta(i -1) );endy(1) = f(1)/b(1);for i = 2:ny(i) = (f(i) -a(i)*y(i -1))/(b(i) - a(i)*beta(i-1));endM(n) = y(n);for i = (n-1):(-1):1M(i) = y(i) -beta(i)*M(i+1);endend结果:比较解析两图,结果令人满意。
有限差分法Matlab实现课件

CATALOGUE
有限差分法在解决实际问题中的应用
在求解微分方程中的应用
生物种群模型
传染病模型 化学反应动力学
在求解偏微分方程中的应用
热传导方程 波动方程 弹性力学问题
在图像处理中的应用
图像去噪
图像增强
图像重建
CATALOGUE
Matlab实现的代码示例及解析
一维有限差分法的代码示例及解析
隐式差分法
02
03
边界条件处理
基于一维偏微分方程的隐式差分 法,将连续的函数离散化,用差 分方程近似代替原方程。
对于一维有限差分法,需要特别 处理边界条件,以保证求解的精 度和稳定性。
二维有限差分法的Matlab实现
规则网格 不规则网格 边界条件处理
三维有限差分法的Matlab实现
三维规则网格 三维不规则网格 边界条件处理
Matlab语言简介
Matlab发展史
Matlab的特点
Matlab编程语法
变量与数据类型
01
控制结构
02
函数与脚本
03
Matlab的数据类型
数值型 单元数组
结构体
字符型 逻辑型
CATALOGUE
有限差分法的Matlab实现
一维有限差分法的Matlab实现
01
显式差分法
基于一维偏微分方程的显式差分 法,将连续的函数离散化,用差 分方程近似代替原方程。
有限差分法matlab 实现
contents
目录
• 有限差分法概述 • Matlab编程基础 • 有限差分法的Matlab实现 • 有限差分法在解决实际问题中的应用 • Matlab实现的代码示例及解析
CATALOGUE
matlab有限差分法

matlab有限差分法一、前言Matlab是一种广泛应用于科学计算和工程领域的计算机软件,它具有简单易学、功能强大、易于编程等优点。
有限差分法(Finite Difference Method)是一种常用的数值解法,它将微分方程转化为差分方程,通过对差分方程进行离散化求解,得到微分方程的数值解。
本文将介绍如何使用Matlab实现有限差分法。
二、有限差分法基础1. 有限差分法原理有限差分法是一种通过将微分方程转化为离散形式来求解微分方程的数值方法。
其基本思想是将求解区域进行网格划分,然后在每个网格点上进行逼近。
假设要求解一个二阶常微分方程:$$y''(x)=f(x,y(x),y'(x))$$则可以将其转化为离散形式:$$\frac{y_{i+1}-2y_i+y_{i-1}}{h^2}=f(x_i,y_i,y'_i)$$其中$h$为网格步长,$y_i$表示在$x_i$处的函数值。
2. 一维情况下的有限差分法对于一维情况下的常微分方程:$$\frac{d^2 y}{dx^2}=f(x,y,y')$$可以使用中心差分法进行离散化:$$\frac{y_{i+1}-2y_i+y_{i-1}}{h^2}=f(x_i,y_i,y'_i)$$这个方程可以写成矩阵形式:$$A\vec{y}=\vec{b}$$其中$A$为系数矩阵,$\vec{y}$为函数值向量,$\vec{b}$为右端项向量。
三、Matlab实现有限差分法1. 一维情况下的有限差分法假设要求解的方程为:$$\frac{d^2 y}{dx^2}=-\sin(x)$$首先需要确定求解区域和网格步长。
在本例中,我们将求解区域设为$[0,2\pi]$,网格步长$h=0.01$。
则可以通过以下代码生成网格:```matlabx = 0:0.01:2*pi;```接下来需要构造系数矩阵和右端项向量。
根据上面的公式,系数矩阵应该是一个三对角矩阵,可以通过以下代码生成:```matlabn = length(x)-2;A = spdiags([-ones(n,1), 2*ones(n,1), -ones(n,1)], [-1 0 1], n, n); ```其中`spdiags`函数用于生成一个稀疏矩阵。
matlab 时域有限差分法

matlab 时域有限差分法
时域有限差分法是一种常用的数值求解偏微分方程的方法,也被广泛应用于地球物理、电磁学、声学等领域。
Matlab是一种常用的科学计算软件,其强大的矩阵计算功能和丰富的可视化工具,使其成为时域有限差分法求解偏微分方程的理想工具。
本文将介绍如何使用Matlab实现时域有限差分法,包括离散化、边界条件、数值求解等方面的内容。
同时,还将介绍如何利用Matlab的可视化工具,对时域有限差分法的结果进行可视化展示。
通过本文的学习,读者可以掌握时域有限差分法的基本原理和实现方法,为进一步开展相关领域的研究和应用奠定基础。
- 1 -。
一维热传导方程数值解法及matlab实现分离变量法和有限差分法

一维热传导方程数值解法及matlab实现分离变量法和有限差分法一维热传导方程的Matlab解法:分离变量法和有限差分法。
问题描述:本实验旨在利用分离变量法和有限差分法解决热传导方程问题,并使用Matlab进行建模,构建图形,研究不同情况下采用何种方法从更深层次上理解热量分布与时间、空间分布关系。
实验原理:分离变量法:利用分离变量法,将热传导方程分解为两个方程,分别只包含变量x和变量t,然后将它们相乘并求和,得到一个无穷级数的解。
通过截取该级数的前n项,可以得到近似解。
有限差分法:利用有限差分法,将空间和时间分别离散化,将偏导数用差分代替,得到一个差分方程组。
通过迭代求解该方程组,可以得到近似解。
分离变量法实验:采用Matlab编写代码,利用分离变量法求解热传导方程。
首先设定x和t的范围,然后计算无穷级数的前n项,并将其绘制成三维图形。
代码如下:matlabx = 0:0.1*pi:pi;y = 0:0.04:1;x。
t] = meshgrid(x。
y);s = 0;m = length(j);for i = 1:ms = s + (200*(1-(-1)^i))/(i*pi)*(sin(i*x).*exp(-i^2*t));endsurf(x。
t。
s);xlabel('x')。
XXX('t')。
zlabel('T');title('分离变量法(无穷)');axis([0 pi 0 1 0 100]);得到的三维热传导图形如下:有限差分法实验:采用Matlab编写代码,利用有限差分法求解热传导方程。
首先初始化一个矩阵,用于存储时间t和变量x。
然后计算稳定性系数S,并根据边界条件和初始条件,迭代求解差分方程组,并将其绘制成三维图形。
代码如下:matlabu = zeros(10.25);s = (1/25)/(pi/10)^2;fprintf('稳定性系数S为:\n');disp(s);for i = 2:9u(i。
有限差分法求解偏微分方程MATLAB

南京理工大学课程考核论文课程名称:高等数值分析论文题目:有限差分法求解偏微分方程*名:**学号: 1成绩:有限差分法求解偏微分方程一、主要内容1.有限差分法求解偏微分方程,偏微分方程如一般形式的一维抛物线型方程:22(,)()u uf x t t xαα∂∂-=∂∂其中为常数具体求解的偏微分方程如下:22001(,0)sin()(0,)(1,)00u u x t x u x x u t u t t π⎧∂∂-=≤≤⎪∂∂⎪⎪⎪=⎨⎪⎪==≥⎪⎪⎩2.推导五种差分格式、截断误差并分析其稳定性;3.编写MATLAB 程序实现五种差分格式对偏微分方程的求解及误差分析;4.结论及完成本次实验报告的感想。
二、推导几种差分格式的过程:有限差分法(finite-difference methods )是一种数值方法通过有限个微分方程近似求导从而寻求微分方程的近似解。
有限差分法的基本思想是把连续的定解区域用有限个离散点构成的网格来代替;把连续定解区域上的连续变量的函数用在网格上定义的离散变量函数来近似;把原方程和定解条件中的微商用差商来近似,积分用积分和来近似,于是原微分方程和定解条件就近似地代之以代数方程组,即有限差分方程组,解此方程组就可以得到原问题在离散点上的近似解。
推导差分方程的过程中需要用到的泰勒展开公式如下:()2100000000()()()()()()()......()(())1!2!!n n n f x f x f x f x f x x x x x x x o x x n +'''=+-+-++-+- (2-1)求解区域的网格划分步长参数如下:11k k k kt t x x h τ++-=⎧⎨-=⎩ (2-2) 2.1 古典显格式2.1.1 古典显格式的推导由泰勒展开公式将(,)u x t 对时间展开得 2,(,)(,)()()(())i i k i k k k uu x t u x t t t o t t t∂=+-+-∂ (2-3) 当1k t t +=时有21,112,(,)(,)()()(())(,)()()i k i k i k k k k k i k i k uu x t u x t t t o t t tuu x t o tττ+++∂=+-+-∂∂=+⋅+∂ (2-4)得到对时间的一阶偏导数1,(,)(,)()=()i k i k i k u x t u x t uo t ττ+-∂+∂ (2-5) 由泰勒展开公式将(,)u x t 对位置展开得223,,21(,)(,)()()()()(())2!k i k i k i i k i i u uu x t u x t x x x x o x x x x∂∂=+-+-+-∂∂ (2-6)当11i i x x x x +-==和时,代入式(2-6)得2231,1,1122231,1,1121(,)(,)()()()()(())2!1(,)(,)()()()()(())2!i k i k i k i i i k i i i i i k i k i k i i i k i i i iu uu x t u x t x x x x o x x x x u u u x t u x t x x x x o x x x x ++++----⎧∂∂=+-+-+-⎪⎪∂∂⎨∂∂⎪=+-+-+-⎪∂∂⎩(2-7) 因为1k k x x h +-=,代入上式得2231,,22231,,21(,)(,)()()()2!1(,)(,)()()()2!i k i k i k i k i k i k i k i ku uu x t u x t h h o h x xu u u x t u x t h h o h x x +-⎧∂∂=+⋅+⋅+⎪⎪∂∂⎨∂∂⎪=-⋅+⋅+⎪∂∂⎩ (2-8) 得到对位置的二阶偏导数2211,22(,)2(,)(,)()()i k i k i k i k u x t u x t u x t u o h x h+--+∂=+∂ (2-9) 将式(2-5)、(2-9)代入一般形式的抛物线型偏微分方程得21112(,)(,)(,)2(,)(,)(,)()i k i k i k i k i k i k u x t u x t u x t u x t u x t f x t o h h αττ++---+⎡⎤-=++⎢⎥⎣⎦(2-10)为了方便我们可以将式(2-10)写成11122k kk k k k i i i i i i u u u u u f h ατ++-⎡⎤--+-=⎢⎥⎣⎦(2-11) ()11122k k k k k k i i i i i i u u uu u f h τατ++----+= (2-12)最后得到古典显格式的差分格式为()111(12)k k k k k i i i i i u ra u r u u f ατ++-=-+++ (2-13)2r h τ=其中,古典显格式的差分格式的截断误差是2()o h τ+。
有限差分 matlab

有限差分 MATLAB简介有限差分方法(Finite Difference Method)是一种常用的数值计算方法,用于求解偏微分方程或者常微分方程的数值近似解。
MATLAB是一个功能强大的数值计算软件,可以很方便地实现有限差分方法。
本文将介绍有限差分方法在MATLAB中的应用。
首先,我们将简要介绍有限差分方法的原理和基本思想。
然后,我们将通过一个具体的例子来演示如何使用MATLAB进行有限差分计算。
最后,我们将总结本文内容,并提供一些相关资源供读者进一步深入学习。
有限差分方法原理有限差分方法是一种基于离散化思想的数值计算方法。
它通过将求解区域划分为网格点,并利用离散点上函数值之间的差商逼近导数来近似求解微分方程。
对于一维问题,我们可以将求解区域划分为等距离的网格点,记作x0, x1,x2, …, xn。
每个网格点上函数值记作u0, u1, u2, …, un。
我们希望通过已知边界条件和微分方程来求解其他未知函数值。
有限差分法的基本思想是使用差商逼近导数。
例如,对于一阶导数,我们可以使用前向差分、后向差分或者中心差分来逼近。
其中,前向差分定义为:f'(x) ≈ (f(x+h) - f(x)) / h后向差分定义为:f'(x) ≈ (f(x) - f(x-h)) / h中心差分定义为:f'(x) ≈ (f(x+h) - f(x-h)) / (2h)类似地,我们可以使用更高阶的有限差分来逼近更高阶的导数。
对于二维问题,我们可以将求解区域划分为二维网格点,并在每个网格点上计算函数值。
然后,我们可以使用类似的方法来逼近偏导数。
MATLAB实现在MATLAB中,我们可以很方便地使用矩阵运算和向量化操作来实现有限差分方法。
首先,我们需要定义求解区域和网格点。
假设我们要求解一个一维问题,在区间[0, 1]上进行离散化。
我们可以通过指定网格点个数n和步长h来确定网格点坐标:n = 100; % 网格点个数h = 1/n; % 步长x = linspace(0, 1, n+1); % 网格点坐标接下来,我们需要定义边界条件和微分方程。
有限差分法解决电场边值问题

ϕ =0
o
x
a
具体要求: 具体要求: (1) 编写一个计算机程序(Matlab):以步距 编写一个计算机程序( 以步距h=a/40的正方形网格离散化场域, 的正方形网格离散化场域, ) 以步距 的正方形网格离散化场域 的数值解。 然后应用有限差分法求电位ϕ的数值解。 (2)求相邻两次迭代值的指定的最大允许误差小于 -5的迭代收敛解和迭代次 求相邻两次迭代值的指定的最大允许误差小于10 求相邻两次迭代值的指定的最大允许误差小于 分别用简单迭代法、高斯-赛德尔迭代法和逐次超松弛法 赛德尔迭代法和逐次超松弛法)。 数(分别用简单迭代法、高斯 赛德尔迭代法和逐次超松弛法)。 (3) 对逐次超松弛法,分别取α为n个不同的值和最佳值α0,求电位ϕ的数值解, 对逐次超松弛法, 的数值解, 个不同的值和最佳值 以此分析加速收敛因子的作用。 以此分析加速收敛因子的作用。从迭代收敛时的迭代次数和最终数值解这两 方面总结自已的看法。 方面总结自已的看法。 (4)用计算机描绘等位线分布。 用计算机描绘等位线分布。 用计算机描绘等位线分布
y
u=0 u=0 u=100 u=0
y y
u=0 u=0 0 u=0 u=100
0
x
hy x i行
行 hx=5 列 hy=3
j列 hx x
y 高斯-赛德尔迭代法 高斯 赛德尔迭代法 1 ϕi(,kj+1) = (ϕi(+k1), j + ϕi(,kj)+1 + ϕi(−k1+1j) + ϕi(,kj+1) ) , −1 4 u=0
简单迭代法
ϕ
( k +1) i, j
1 (k ) k = (ϕ i −1, j + ϕ i(,kj)−1 + ϕ i(+1), j + ϕ i(,kj)+1 ) 4
斯托克斯第一问题的有限差分法的MATLAB实现

斯托克斯第一问题的有限差分法的MATLAB实现作者:***来源:《现代信息科技》2023年第20期摘要:斯托克斯方程是流體力学中描述粘性牛顿流体运动的方程组,在航空航天、流体力学、化工工程、生物工程等与流体有关的所有领域都有着非常重要的作用和广泛的应用。
有限差分方法通过离散物理问题,从而以代数方程式的形式来求解出误差较小的近似数值解。
文章给出斯托克斯第一问题使用有限差分法和MATLAB矩阵运算的计算方法,通过对网格进行二维剖分细化,借用计算机的强大算力得出稳定性条件下的速度曲线,并使用相关算例进一步确定扩散数的阈值。
关键词:有限差分法;斯托克斯问题;MATLAB中图分类号:TP391 文献标识码:A 文章编号:2096-4706(2023)20-0058-04MATLAB Implementation of the Finite Difference Method for Stokes First ProblemCHEN Geng(North Minzu University, Yinchuan 750030, China)Abstract: The Stokes equations are a set of equations describing the motion of viscous Newtonian fluids in fluid mechanics and have a very important role and wide application in all fields related to fluids such as aerospace, fluid mechanics, chemical engineering and bioengineering. The finite difference method solves approximate numerical solutions with small errors in algebraic equation form by discretizing the physical problem. This paper gives a computational approach to the Stokes first problem using the finite difference method and MATLAB matrix operations to derive the velocity profile under stability conditions by refining the grid with a two-dimensional profile,borrowing the power of computer arithmetic, and using relevant arithmetic examples to further determine the threshold value of the diffusion number.Keywords: finite difference method; Stokes problem; MATLAB0 引言随着科技的进步和计算机技术的快速发展,在自然科学和工程计算领域诞生了许多实际问题,人们发现这些问题可以通过微分方程恰当地表示出来[1]。
matlab有限差分法

matlab有限差分法有限差分法是一种数值计算方法,用于求解偏微分方程的近似解。
它的基本思想是在定义的网格上近似偏微分方程中的导数,然后将偏微分方程转化为代数方程组,通过求解代数方程组得到近似解。
因此,有限差分法是一种离散化方法。
在有限差分法中,我们需要定义一个网格来离散化要求解的空间,例如我们可以将一个矩形区域分成相等小的正方形网格。
我们还需要定义一个时间网格,用来离散化所求解的时间区间,例如将整个时间区间分成相等的小时间段。
通过将空间和时间分别进行离散化,我们就得到了有限差分法的两个主要元素:网格和时间步长。
在有限差分法中,我们需要用数值来近似地表示空间函数和时间函数。
离散化后的空间和时间函数在网格点处的取值称为网格点数值。
通过近似表示空间和时间函数,我们将物理问题转化为了一个大量的代数问题。
有限差分法的主要思想是使用中心差分公式来计算导数值。
中心差分公式是指:将导数近似为相邻两个网格点之间的差,然后取其平均值,即可得到一个数值。
对于一个二维的偏微分方程,我们可以使用五点差分公式(即中心差分公式的扩展)来计算数值解。
五点差分公式是指:在一个网格点上,使用该点周围四个相邻网格点的取值来计算该点导数值。
通过对每一个网格点应用五点差分公式,我们可以构造出一个代数方程组,通过求解该方程组,我们可以得到偏微分方程的数值解。
有限差分法有很多优点,例如易于实现、计算速度快、稳定性好、适用于不规则区域和边界等。
但有限差分法也有一些缺点,例如精度受限、局限性大、实现复杂等。
总之,有限差分法是求解偏微分方程的重要数值方法,它在科学和工程计算中得到了广泛的应用。
通过对其原理和实现细节的深入学习,我们可以更好地理解它的优点和局限性,从而更加适用于不同实际问题的数值计算。
有限差分法matlab研究现状

有限差分法matlab研究现状有限差分法(Finite Difference Method,FDM)是一种广泛应用于物理学、工程学和计算机科学中的数值方法。
在有限差分法中,将实际问题转化为数学模型,通过离散化求解模型,得到离散的数值解。
MATLAB是功能强大的数学软件,广泛应用于各个领域的的数值计算。
在有限差分法的研究中,MATLAB是一个必不可少的工具。
以下是一些关于有限差分法在MATLAB中的研究现状。
1. 有限差分法在物理学中的应用有限差分法在物理学中的应用非常广泛,包括力学、热力学、电磁学和波动光学等领域。
其中,有限差分法在力学中的应用最为普遍,包括牛顿运动定律、万有引力定律、弹性碰撞等。
在热力学中,有限差分法可以用于求解热传导、热扩散和热膨胀等问题。
在电磁学中,有限差分法可以用于求解电场、磁场和电磁波等问题。
在波动光学中,有限差分法可以用于求解波动方程和光传播问题。
2. 有限差分法在工程学中的应用有限差分法在工程学中的应用也非常广泛,包括材料科学、机械工程、电子工程、土木工程和水利工程等领域。
其中,有限差分法在材料科学中的应用包括材料强度计算、材料变形计算和材料性能分析等。
在机械工程中,有限差分法可以用于求解机械系统的运动学、动力学和热力学等问题。
在电子工程中,有限差分法可以用于求解电路的欧姆定律、电磁场分析和信号处理等问题。
在土木工程中,有限差分法可以用于求解建筑物的位移、应力和变形等问题。
在水利工程中,有限差分法可以用于求解水力学和波浪力学等问题。
3. 有限差分法在计算机科学中的应用有限差分法在计算机科学中的应用也非常广泛,包括算法设计、数据结构、计算机图形学和人工智能等领域。
其中,有限差分法在算法设计中的应用包括快速排序、归并排序、堆排序和遗传算法等。
在数据结构中,有限差分法可以用于求解树、图和线性结构等。
在计算机图形学中,有限差分法可以用于求解三维图形的几何形状、纹理和材质等。
有限差分法及matlab实现

U i1, j , k U i−1, j , k U i , j 1, kU i , j −1, kU i , j , k1 U i , j , k−1 = 6U i , j , k ρ ----- (1) ⋯ ∂ x 2 ∂ x2 6 ∂ x3 ∂ U 1 ∂2 U 1 ∂3 U U i , j 1, k =U i , j ,k ⋯ ∂ y 2 ∂ y2 6 ∂ y3 ∂ U 1 ∂2 U 1 ∂ 3 U U i , j , k1 =U i , j ,k ⋯ ∂ z 2 ∂ z2 6 ∂ z3 ∂ U 1 ∂2 U 1 ∂3 U U i−1, j , k =U i , j , k− − ⋯ ∂ x 2 ∂ x2 6 ∂ x3 ∂ U 1 ∂2 U 1 ∂3 U U i , j 1, k =U i , j , k− − ⋯ ∂ y 2 ∂ y2 6 ∂ y3 ∂ U 1 ∂2 U 1 ∂ 3 U U i , j , k1 =U i , j , k− − ⋯ ∂ z 2 ∂ z2 6 ∂ z3 U i1, j , k =U i , j ,k
= 6U i , j , k ρ
这就是泊松方程的有限差分形式,以下估计该方程的精度: 由泰勒公式,易知有以下结果:
∂U 1 ∂2 U 2 1 ∂3 U 3 h h h ⋯ ∂x 2 ∂ x2 6 ∂ x3 ∂U 1 ∂ 2 U 2 1 ∂3 U 3 U x , y k, z =U x , y , z k k k ⋯ ∂y 2 ∂ y2 6 ∂ y3 2 3 ∂U 1∂ U 2 1∂ U 3 U x , y , z l =U x , y , z l l l ⋯ ∂z 2 ∂ z2 6 ∂ z3 U x h , y , z =U x , y , z
有限差分法解决平面弹性问题的matlab建模仿真

有限差分法解决平面弹性问题的matlab建模仿真用有限差分法解决弹性平面问题的建模与仿真的报告建模与仿真的目的 :解决弹性平面问题——偏心拉伸应力问题,并与实验数值理论解相比较。
建模与仿真的基本原理:有限差分法建模与仿真的方法途径:经过理论推导出所求变量所满足的关系,通过Matlab 软件进行数学建模,将物理语言和数学语言转化成计算机语言,进行计算。
应用软件进行绘图,将抽象的数学表示法转化成直观的形象具体的图像,进行展示,使人们对该建模所研究的问题有更清晰而感性的认识。
报告论文结构:(一)基本原理介绍(差分法)(二)偏心拉伸问题的理论推导(三)建模与仿真的具体方法(应用Matlab 软件)(四)结果展示(五)建模程序特点介绍(六)与实验结果、理论结果的对比(七)前进展望与程序改进(八)任务分工*************************************************************** ****************一、基本原理——有限差分法的介绍有限差分法使用差分方程代替微分方程,从而把基本方程微分方程限组和边界条件求解化为代数方程组的求解。
在将偏微分方程和相应的边界条件转换成有限差分方程之前,我们先将函数的导数改用差分表示,从而导出常用的差分公式。
二、关于偏心拉伸应力问题的理论推导对于边界外一行的结点,我们适当的选择一个基点A ,使得φA =0,(δφ/δx)A =0,(δφ/δy)A =0 ,这样我们可以通过推导得到边界点满足的方程:(δφ/δy)B =∫X B A ds (δφ/δx)B =?∫Y B A ds φB =∫(y B ?y)X B A ds+∫(x ?x B )Y BA ds 而对于边界外一圈的虚结点,有公式:φ13=φ9+2h x (δφ/δx)A φ14=φ10+2h y (δφ/δx)B因而我们可以用内点和边界点表示出边界外一圈虚点,由此平面上的任意点的应力函数都可以用平面上其他十二个点的应力函数表示,列出这些方程,由外及内,依次解出各点的应力函数。
用matlab求解超越方程的方法

用matlab求解超越方程的方法Matlab作为一款强大的数学软件,可以帮助我们比较轻松地解决超越方程,提供了一个快速、灵活且可靠的求解超越方程的方法。
Matlab是一种流行的计算机软件,它拥有强大的数值分析能力。
它经常用来求解复杂的函数方程,特别是有关超越方程的计算。
本文介绍使用Matlab求解超越方程的几种方法:一、用数值方法求解1、采用有限差分法(Finite Difference Method)Finite Difference Method(FDM)是以在离散的网格上对变量的数值求解来实现的。
FDM可以有效的求解多维、非线性的超越方程。
通过在网格上求解多次,可以找出方程的根。
2、采用拉格朗日插值法(Lagrange Interpolation)Lagrange Interpolation是一种数学插值方法,可以有效地解决超越方程中多维非线性方程组。
其运算速度快、精度高,且可以有效求解实际问题中出现的复杂超越方程。
二、用几何方法求解1、采用图像法(Graphics Method)使用图像法可以可视化超越方程。
当然,由于超越方程具有多个变量,因此采用图像法进行求解的难度较大。
但由于图像简单明了,它仍然是一种有效的计算方法。
2、采用微分几何(Differential Geometry)Differential Geometry是一种在曲面上进行计算的数学方法。
它有助于求解超越方程,尤其是表达形式为系统多元不等式的超越方程。
总结:Matlab是一种强大的计算软件,可以用来求解超越方程。
它有许多方法可以用于求解超越方程,包括:用数值方法求解、用几何方法求解等。
它能帮助我们解决复杂的科学问题,因此得到了广泛的应用。
有限差分法的Matlab程序

有限差分法的Matlab程序(椭圆型方程)function FD_PDE(fun,gun,a,b,c,d)% 用有限差分法求解矩形域上的Poisson方程tol=10^(-6); % 误差界N=1000; % 最大迭代次数n=20; % x轴方向的网格数m=20; % y轴方向的网格数h=(b-a)/n; % x轴方向的步长l=(d-c)/m; % y轴方向的步长for i=1:n-1x(i)=a+i*h;end % 定义网格点坐标for j=1:m-1y(j)=c+j*l;end % 定义网格点坐标u=zeros(n-1,m-1); %对u赋初值% 下面定义几个参数r=h^2/l^2;s=2*(1+r);k=1;% 应用Gauss-Seidel法求解差分方程while k<=N% 对靠近上边界的网格点进行处理% 对左上角的网格点进行处理z=(-h^2*fun(x(1),y(m-1))+gun(a,y(m-1))+r*gun(x(1),d)+r*u(1,m-2)+u(2,m-1))/s;norm=abs(z-u(1,m-1));u(1,m-1)=z;% 对靠近上边界的除第一点和最后点外网格点进行处理for i=2:n-2z=(-h^2*fun(x(i),y(m-1))+r*gun(x(i),d)+r*u(i,m-2)+u(i+1,m-1)+u(i-1,m-1))/s;if abs(u(i,m-1)-z)>norm;norm=abs(u(i,m-1)-z);endu(i,m-1)=z;end% 对右上角的网格点进行处理z=(-h^2*fun(x(n-1),y(m-1))+gun(b,y(m-1))+r*gun(x(n-1),d)+r*u(n-1,m-2)+u(n-2,m-1))/s;if abs(u(n-1,m-1)-z)>normnorm=abs(u(n-1,m-1)-z);endu(n-1,m-1)=z;% 对不靠近上下边界的网格点进行处理for j=m-2:-1:2% 对靠近左边界的网格点进行处理z=(-h^2*fun(x(1),y(j))+gun(a,y(j))+r*u(1,j+1)+r*u(1,j-1)+u(2,j))/s;if abs(u(1,j)-z)>normnorm=abs(u(1,j)-z);endu(1,j)=z;% 对不靠近左右边界的网格点进行处理for i=2:n-2z=(-h^2*fun(x(i),y(j))+u(i-1,j)+r*u(i,j+1)+r*u(i,j-1)+u(i+1,j))/s;if abs(u(i,j)-z)>normnorm=abs(u(i,j)-z);endu(i,j)=z;end% 对靠近右边界的网格点进行处理z=(-h^2*fun(x(n-1),y(j))+gun(b,y(j))+r*u(n-1,j+1)+r*u(n-1,j-1)+u(n-2,j))/s;if abs(u(n-1,j)-z)>normnorm=abs(u(n-1,j)-z);endu(n-1,j)=z;end% 对靠近下边界的网格点进行处理% 对左下角的网格点进行处理z=(-h^2*fun(x(1),y(1))+gun(a,y(1))+r*gun(x(1),c)+r*u(1,2)+u(2,1))/s;if abs(u(1,1)-z)>normnorm=abs(u(1,1)-z);endu(1,1)=z;% 对靠近下边界的除第一点和最后点外网格点进行处理for i=2:n-2z=(-h^2*fun(x(i),y(1))+r*gun(x(i),c)+r*u(i,2)+u(i+1,1)+u(i-1,1))/s;if abs(u(i,1)-z)>normnorm=abs(u(i,1)-z);endu(i,1)=z;end% 对右下角的网格点进行处理z=(-h^2*fun(x(n-1),y(1))+gun(b,y(1))+r*gun(x(n-1),c)+r*u(n-1,2)+u(n-2,1))/s; if abs(u(n-1,1)-z)>normnorm=abs(u(n-1,1)-z);endu(n-1,1)=z;% 结果输出if norm<=tolfid = fopen('FDresult.txt', 'wt');fprintf(fid,'\n********用有限差分法求解矩形域上Poisson方程的输出结果********\n\n');fprintf(fid,'迭代次数: %d次\n\n',k);fprintf(fid,' x的值 y的值 u的值 u的真实值 |u-u(x,y)|\n');for i=1:n-1for j=1:m-1fprintf(fid, '%8.3f %8.3f %14.8f %14.8f %14.8f\n',[x(i),y(j),u(i,j),gun(x(i),y(j)),abs(u(i,j)-gun(x(i),y(j)))]);endendfclose(fid);break; % 用来结束while循环endk=k+1;endif k==N+1fid = fopen('FDresult.txt', 'wt');fprintf(fid,'超过最大迭代次数,求解失败!');fclose(fid);endclc[a1 a2 a3 a4] = textread('F:\aa.txt','%f %f %f %f');a = [a1 a2 a3];a=a';b=a4';[pa,mina,maxa,pb,minb,maxb]=premnmx(a,b);net =newrb(pa,pb,0,1.3,24,2);an =sim(net,pa);E = an - pb;m =sse(E)n = mse(E)[f1 f2 f3 f4]= textread('F:\bb.txt','%f %f %f %f');f = [f1 f2 f3];f=f';pf = tramnmx(f,mina,maxa);an2 = sim(net,pf);g =postmnmx(an2,minb,maxb);g= g';E2 = g- f4; mm =sse(E2) nn = mse(E2)欢迎您的下载,资料仅供参考!致力为企业和个人提供合同协议,策划案计划书,学习资料等等打造全网一站式需求。
用有限差分法和Matlab计算二维热加工温度场分析
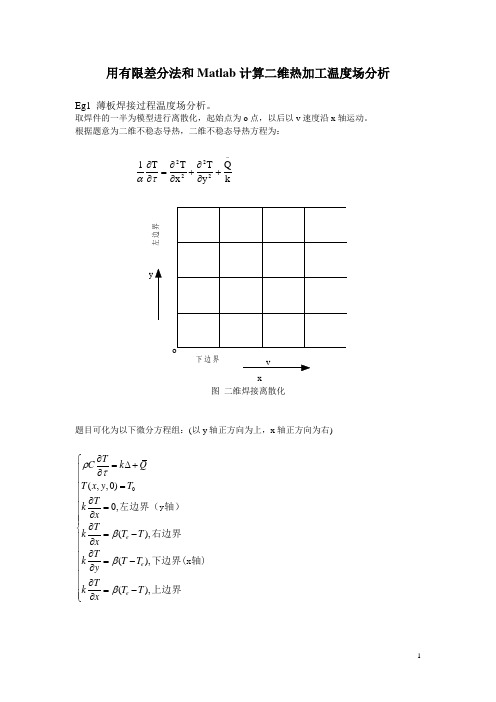
用有限差分法和Matlab 计算二维热加工温度场分析Eg1 薄板焊接过程温度场分析。
取焊件的一半为模型进行离散化,起始点为o 点,以后以v 速度沿x 轴运动。
根据题意为二维不稳态导热,二维不稳态导热方程为:k Qy T x T T 12222-+∂∂+∂∂=∂∂ταyx 左边界下边界图 二维焊接离散化题目可化为以下微分方程组:(以y 轴正方向为上,x 轴正方向为右)(,,0)0,(),(),(),e e e TC k QT x y TTk xT k T T x Tk T T y Tk T T x ρτβββ∂⎧=∆+⎪∂⎪=⎪⎪∂=⎪∂⎪⎪∂⎨=-⎪∂⎪∂⎪=-⎪∂⎪∂⎪=-⎪∂⎩左边界(y 轴)右边界下边界(x 轴)上边界需要的参数(均已cm,cal,g 为单位,所以不必换算):参数数值 备注 ρ7.82 g/cm 3 密度 v0.4 cm/s 焊接速度 h1cm 板厚度 Qm 4000 cal/cm 3 热源分布密度 β0.0008cal/cm 2·s ·℃ 换热系数 Te ,T 020℃ 周边介质温度,初始温度 k 0.1 cal/c m ·s ·℃ 导热系数用PDE Tool 解题步骤如下:1. 区域设置单击工具,在窗口拉出一个矩形,双击矩形区域,在Object Dialog 对话框输入Left 为0,Bottom 为0,Width 为2,Height 为2。
与默认的坐标相比,图形小的看不见,所以要调整坐标显示比例。
方法:选择Options->Axes Limits,把X ,Y 轴的自动选项打开。
设置Options->Application 为Heat Transfer (设置程序应用热传输模型)2. 设置边界条件单击,使边界变红色,然后分别双击每段边界,打开Boundary Conditions 对话框,设置边界条件(根据边界条件)。
matlab在有限差分法数值计算中的应用

matlab在有限差分法数值计算中的应用1.前言有限差分法是一种常用的数值计算方法,常用于求解偏微分方程。
Matlab是一种非常强大的数值计算软件,也被广泛应用于各种科学计算中。
本文将围绕有限差分法在Matlab中的应用进行讨论。
2.有限差分法有限差分法是一种数值计算方法,通常用于求解偏微分方程。
其基本思想是将偏微分方程中的导数用差分的形式进行近似。
这样就可以把偏微分方程转化为差分方程,进而用数值方法求解。
在有限差分法中,将求解区域离散化为网格,并在网格上通过差分近似来求解偏微分方程。
有限差分法的基本思想是将导数转化为差分形式。
由于导数的定义是极限形式的,因此我们可以通过极限的概念来推导差分近似。
例如,对于函数$f(x)$,它在$x=a$处的导数为$f'(a)$,则可以表示为:$$f'(a)=\lim_{h\to0}\frac{f(a+h)-f(a)}{h}$$如果我们取一个无穷小的$h$,则可以得到:$$f'(a)\approx\frac{f(a+h)-f(a)}{h}$$这就是一个一阶中心差分近似。
同样,我们还可以用其他的差分形式来表示导数。
有限差分法的核心就是建立差分方程。
在建立差分方程时,我们需要先将求解区域离散化为网格,然后在每个网格点上建立差分方程。
通常情况下,差分方程和原始的偏微分方程形式相同,只是将偏导数用差分近似来替代。
例如,对于泊松方程:$$\frac{\partial^2\phi}{\partialx^2}+\frac{\partial^2\phi}{\partial y^2}=f(x,y)$$我们可以将其离散化为网格上的差分方程:$$\frac{\phi_{i-1,j}-2\phi_{i,j}+\phi_{i+1,j}}{\Deltax^2}+\frac{\phi_{i,j-1}-2\phi_{i,j}+\phi_{i,j+1}}{\Deltay^2}=f_{i,j}$$其中,$\Delta x$和$\Delta y$表示网格的大小,$\phi_{i,j}$表示在网格点$(x_i,y_j)$处的解,$f_{i,j}$表示在网格点$(x_i,y_j)$处的源项。
一维导热方程有限差分法matlab实现

第五次作业(前三题写在作业纸上)一、用有限差分方法求解一维非定常热传导方程,初始条件和边界条件见说明.pdf 文件,热扩散系数α=const ,22T T t xα∂∂=∂∂ 1. 用Tylaor 展开法推导出FTCS 格式的差分方程2. 讨论该方程的相容性和稳定性,并说明稳定性要求对求解差分方程的影响。
3. 说明该方程的类型和定解条件,如何在程序中实现这些定解条件。
4. 编写M 文件求解上述方程,并用适当的文字对程序做出说明。
(部分由网络搜索得到,添加,修改后得到。
)function rechuandaopde%以下所用数据,除了t 的范围我根据题目要求取到了20000,其余均从pdf 中得来 a=0.00001;%a 的取值xspan=[0 1];%x 的取值范围tspan=[0 20000];%t 的取值范围ngrid=[100 10];%分割的份数,前面的是t 轴的,后面的是x 轴的f=@(x)0;%初值g1=@(t)100;%边界条件一g2=@(t)100;%边界条件二[T,x,t]=pdesolution(a,f,g1,g2,xspan,tspan,ngrid);%计算所调用的函数[x,t]=meshgrid(x,t);mesh(x,t,T);%画图,并且把坐标轴名称改为x ,t ,Txlabel('x')ylabel('t')zlabel('T')T%输出温度矩阵dt=tspan(2)/ngrid(1);%t 步长h3000=3000/dt;h9000=9000/dt;h15000=15000/dt;%3000,9000,15000下,温度分别在T矩阵的哪些行T3000=T(h3000,:)T9000=T(h9000,:)T15000=T(h15000,:)%输出三个时间下的温度分布%不再对三个时间下的温度-长度曲线画图,其图像就是三维图的截面%稳定性讨论,傅里叶级数法dx=xspan(2)/ngrid(2);%x步长sta=4*a*dt/(dx^2)*(sin(pi/2))^2;if sta>0,sta<2fprintf('\n%s\n','有稳定性')elsefprintf('\n%s\n','没有稳定性')errorend%真实值计算[xe,te,Te]=truesolution(a,f,g1,g2,xspan,tspan,ngrid);[xe,te]=meshgrid(xe,te);mesh(xe,te,Te);%画图,并且把坐标轴名称改为xe,te,Texlabel('xe')ylabel('te')zlabel('Te')Te%输出温度矩阵%误差计算jmax=1/dx+1;%网格点数[rms]=wuchajisuan(T,Te,jmax)rms%输出误差function [rms]=wuchajisuan(T,Te,jmax)for j=1:jmaxrms=((T(j)-Te(j))^2/jmax)^(1/2)endfunction[Ue,xe,te]=truesolution(a,f,g1,g2,xspan,tspan,ngrid)n=ngrid(1);%t份数m=ngrid(2);%x份数Ue=zeros(ngrid);xe=linspace(xspan(1),xspan(2),m);%画网格te=linspace(tspan(1),tspan(2),n);%画网格for j=2:nfor i=2:m-1for g=1:m-1Ue(j,i)=100-(400/(2*g-1)/pi)*sin((2*g-1)*pi*xe(j))*exp(-a*(2*g-1)^2*pi^2*te(i)) endendendfunction [U,x,t]=pdesolution(a,f,g1,g2,xspan,tspan,ngrid)n=ngrid(1);%t份数m=ngrid(2);%x份数h=range(xspan)/(m-1);%x网格长度x=linspace(xspan(1),xspan(2),m);%画网格k=range(tspan)/(n-1); %t网格长度t=linspace(tspan(1),tspan(2),n);%画网格U=zeros(ngrid);U(:,1)=g1(t);%边界条件U(:,m)=g2(t);U(1,:)=f(x);%初值条件%差分计算for j=2:nfor i=2:m -1U(j,i)=(1-2*a*k/h^2)*U(j -1,i)+a*k/h^2*U(j -1,i -1)+a*k/h^2*U(j -1,i+1);endend5. 将温度随时间变化情况用曲线表示x t T6. 给出3000、9000、15000三个时刻的温度分布情况,对温度随时间变化规律做说明。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
迭代解法 :
程序如下:
lx=17;ly=11; v1=zeros(ly,lx); for j=2:lx-1 v1(ly,j)=100; end v2=v1;maxt=1;t=0; k=0; while(maxt>1e-6) k=k+1 maxt=0; for i=2:ly-1 for j=2:lx-1; v2(i,j)=(v1(i,j+1)+v1(i+1,j)+v1(i-1,j)+v1(i,j-1))/4; % 进行迭代计算 t=abs(v2(i,j)-v1(i,j)); if(t>maxt) maxt=t;end end end v1=v2; end k=419 % 输出迭代次数 % 定义矩阵维数 % 建立一个矩阵 % 设置边界条件
有限差分法解静电场的边值问题的算法实现及相关问题讨论:
王宁远
中国科学技术大学 09 级物理 2 班 E-mail wny@
摘要: 本文用 MATLAB 实现了有限差分法解静电场边值问题的算法,将偏微分方程的问题化为线性方程 组问题,并使用了迭代法进行线性方程组的数值解。讨论了从几个角度去优化迭代法的措施。并运用这 样的方法解决了文[1]的闪电模拟问题,,使用了更优化的算法对重新进行了计算,并一定程度上改进了 模型,讨论了几个与文[1]所持的不同的观点。
计算出的矩阵:
绘图:
subplot(1,2,1),mesh(v2) axis([0,17,0,11,0,100]) subplot(1,2,2),contour(v2,32)
有限差分法求出的电势的分布图像:
在这个例子中,我们对网格的划分并不细致(17×11),但却要去计算一个 135 阶方阵的逆,算法的 时间复杂度和空间复杂度都比较大,而且对于边界条件较复杂的情况,这样的矩阵会使得程序的编写十 分不便,由于我们给出的差分公式本身就是近似公式,求出该方程的精确解没有实际意义,我们只需要 一个符合精度要求的近似解即可,我们所以我们应该考虑一个效率更高的,更容易实现的算法,那么可 以考虑使用迭代法。
%精度要求,达到精度要求跳出循环
1.3 算法改进
提前使用新值:因为在上述程序中,我们的扫描赋值方式是一行一行扫描,在对 v2(i,j)赋值时,它 周围四个点其中有 2 个已经被扫描过了,即已经获得了新的数值,这个数值应该更优,所以我们尽量使 用新算出的数值进行迭代,其中: 只要把上述代码中
v2(i,j)=(v1(i,j+1)+v1(i+1,j)+v1(i-1,j)+v1(i,j-1))/4
此即拉普拉斯方程的有限差分形式。
----- (2)式
这里,我们通过有限差分的方法,把偏微分方程在三阶精度下简化为形式易于计算的代数方程。从而使 之易于在计算机上实现。
注:有时我们需要解二维静电场,则方程退化为:
U i1, j U i−1, j U i , j 1 U i , j −1 =4U i , j
由一个简单的例子出发先讨论: 矩形截面由四块导体板围成,其中一块有 100v,其他三块全部接地(电 势 为 0),求解 平 面 各处 电 势 :
解: 基于有限差分法,我们得到的差分形式事实上是线性方程组。 由于边界上的点电势已经作为已知条件所固定。所以实际上的未知数只有 15×9=135 个,而对于 每一个未知数(每一个点),我们都可以写出一个方程(每个点的电势等于它旁边四个点的电势的平均 值), 从物理意义上考虑,方程确实是独立的,所以方程是可解的,我们那么考虑构造一个 135 阶的方阵,只 要求出其逆就可以了。
矩阵(数组)是计算机中重要的数据结构,为了方便用矩阵去存储数据,我们网格去划分空间,从而不 仅使方程化为简单的有限差分形式,而且这样的数据类型在 计算机中易于储存和运算。那么 h=k=l=1,并且令 f(x,y,z)=u(x,y,z) 就有
U i1, j , k U i−1, j , k U i , j 1, kU i , j −1, kU i , j , k1 U i , j , k−1
h
dx
用有限的 h 代替,使得
f ' x ≈
△y △x
差分的种类:
f x h − f x f x − f x −h f x h − f x −h 或者 或者 h 2h h f x h − f x f x − f x −h − h h f x h f x −h −2f x 二阶差分: = h h2 设 U x , y , z 为空间电势的函数 。
一阶差分: 泊松方程:
∇2 U = ρ
使用二阶差分代替泊松方程中的拉普拉斯算符,有:
∇ U=
2
f x h, y , z f x −h , y , z −2f x , y , z ∂2 U ∂2 U ∂2 U =∑ 2 2 2 ∂x ∂y ∂z h2
∑
表示分别对三个变元求差分之和,以下相同
= 6U i , j , k ρ
这就是泊松方程的有限差分形式,以下估计该方程的精度: 由泰勒公式,易知有以下结果:
∂U 1 ∂2 U 2 1 ∂3 U 3 h h h ⋯ ∂x 2 ∂ x2 6 ∂ x3 ∂U 1 ∂ 2 U 2 1 ∂3 U 3 U x , y k, z =U x , y , z k k k ⋯ ∂y 2 ∂ y2 6 ∂ y3 2 3 ∂U 1∂ U 2 1∂ U 3 U x , y , z l =U x , y , z l l l ⋯ ∂z 2 ∂ z2 6 ∂ z3 U x h , y , z =U x , y , z
上述六式相加
2
3
U i1, j , k U i−1, j , k U i , j 1, kU i , j −1, kU i , j , k1 U i , j , k−1 2 2 2 ∂ U ∂ U ∂ U ⋯ = 6U i , j , k ∂ x2 ∂ y 2 ∂ z 2 2 代入 ∇ U = ρ U i1, j , k U i−1, j , k U i , j 1, kU i , j −1, kU i , j , k1 U i , j , k−1 = 6U i , j , k∇ 2 U ⋯=6U i , j ,k ρ ⋯
即
∂2 U ∂2 U ∂ x2 ∂ y2 ∂2 U ∂2 U ∂ x2 ∂ y2
U i1, j U i−1, j U i , j 1 U i , j −1 =4U i , j
1 M 语言本身带有矩阵的数据类型,且 MATLAB 具有高效的数值计算功能。所以我 们选择通过 MATLAB 的 M 语言去实现这种算法。 (可以看出,三维情况与二维情况没有本质的区别,所以在一下的一系列讨论中,我们为方便起见都只考 虑二维情况。)
for i=2:14 a(i,i-1)=-0.25;a(i,i+1)=-0.25; a(i,i+15)=-0.25; end for i=122:134 a(i,i-1)=-0.25;a(i,i+1)=-0.25; a(i,i-15)=-0.25; end for i=1:7 for j=2:14; a(15*i+j,15*i+j-1)=-0.25; a(15*i+j,15*i+j+1)=-0.25; a(15*i+j,15*i+j+15)=-0.25; a(15*i+j,15*i+j-15)=-0.25; end end b=a^(-1); c=zeros(135,1); for i=121:135 c(i,1)=25;end d=b*c;s=zeros(11,17);for i=2:16 s(11,i)=100; end for i=1:9 for j=1:15; s(i+1,j+1)=d(15*(i-1)+j,1); end
正文: 经典场的边值问题在数学上表达为泊松方程和拉普拉斯方程,但解偏微分方程往往是困难的。幸而 很多时候对于具体问题我们需要的不是解析解,而是数值解,所以可以考虑用连续变量离散化的方法求 出数值解,在足够的精度上进行逼进,这就引出了有限差分法。
1.1 有限差分法:
有限差分法: 微分: f ' x = f x h − f x h 0 = dy
若考虑离散的点:
∂U 1 ∂ U 1 ∂ U ⋯ ∂ x 2 ∂ x2 6 ∂ x3 ∂ U 1 ∂2 U 1 ∂3 U U i , j 1, k =U i , j ,k ⋯ ∂ y 2 ∂ y2 6 ∂ y3 ∂ U 1 ∂2 U 1 ∂ 3 U U i , j , k1 =U i , j ,k ⋯ ∂ z 2 ∂ z2 6 ∂ z3 ∂ U 1 ∂2 U 1 ∂3 U U i−1, j , k =U i , j , k− − ⋯ ∂ x 2 ∂ x2 6 ∂ x3 ∂ U 1 ∂2 U 1 ∂3 U U i , j 1, k =U i , j , k− − ⋯ ∂ y 2 ∂ y2 6 ∂ y3 ∂ U 1 ∂2 U 1 ∂ 3 U U i , j , k1 =U i , j , k− − ⋯ ∂ z 2 ∂ z2 6 ∂ z3 U i1, j , k =U i , j ,k
由于所有的奇次项被抵消,所以方程:
U i1, j , k U i−1, j , k U i , j 1, kU i , j −1, kU i , j , k1 U i , j , k−1 = 6U i , j , k ρ ----- (1) 式
的精度为三阶,四阶及更高阶项被略去。 若满足 ∇ U =0 有
2
U i1, j , k U i−1, j , k U i , j 1, kU i , j −1, kU i , j , k1 U i , j , k−1
