杨辉三角的规律以及推导公式word版本
杨辉三角的规律以及推导公式

杨辉三角的规律以及定理李博洋摘要杨辉三角中的一些规律关键词杨辉三角幂二项式引言杨辉是我国南宋末年的一位杰出的数学家。
在他所着的《详解九章算法》一书中,画了一张表示二项式展开后的系数构成的三角图形,称做“开方做法本源”,现在简称为“杨辉三角”,它是世界的一大重要研究成果。
我们则来对“杨辉三角”的规律进行探讨和研究。
内容1二项式定理与杨辉三角与杨辉三角联系最紧密的是二项式乘方展开式的系数规律,即。
杨辉三角我们首先从一个二次多项式(a+b)2的展开式来探讨。
由上式得出:(a+b)2=a2+2ab+b2此代数式的系数为:121则(a+b)3的展开式是什么呢?答案为:a3+3a2b+3ab2+b3由此可发现,此代数式的系数为:1331但似乎没有什么规律,所以让我们再来看看(a+b)4的展开式。
展开式为:a4+4a3b+6a2b2+4ab3+b4由此又可发现,代数式的系数为:14641似乎发现了一些规律,就可以发现以下呈三角形的数列:1(110)11(111)121(112)1331(113)14641(114)15101051(115)1615201561(116)因此可得出二项式定理的公式为:(a+b)n=C(n,0)a^n*b^0+C(n,1)a^(n-1)*b^1+...+C(n,r)a^(n-r)*b^r...+C(n,n)a^0*b^n 因此,二项式定理与杨辉三角形是一对天然的数形趣遇,它把带进了。
求二项式展开式系数的问题,实际上是一种组合数的计算问题。
用系数来计算,称为“式算”;用杨辉三角形来计算,称作“图算”。
2杨辉三角的幂的关系首先我们把杨辉三角的每一行分别相加,如下:1(1)11(1+1=2)121(1+2+1=4)1331(1+3+3+1=8)14641(1+4+6+4+1=16)15101051(1+5+10+10+5+1=32)1615201561(1+6+15+20+15+6+1=64)……相加得到的数是1,2,4,8,16,32,64,…刚好是2的0,1,2,3,4,5,6,…次幂,即杨辉三角第n行中n个数之和等于2的n-1次幂3杨辉三角中斜行和水平行之间的关系(1)1(2)n=111(3)n=2121(4)n=31331(5)n=414641(6)n=515101051n=61615201561把斜行(1)中第7行之前的数字相加得1+1+1+1+1+1+1=6把斜行(2)中第7行之前的数字相加得1+2+3+4+5=15把斜行(3)中第7行之前的数字相加得1+3+6+10=20把斜行(4)中第7行之前的数字相加得1+4+10=15把斜行(5)中第7行之前的数字相加得1+5=6把斜行(6)中第7行之前的数字相加得1将上面得到的数字与杨辉三角中的第7行中的数字对比,我们发现它们是完全相同的。
杨辉三角的规律公式

杨辉三角的规律公式杨辉三角,又称帕斯卡三角,是古代数学中一种重要的图形。
它的构造方法非常简单:从第一行开始,每一行的两端都是1,其余的数是上一行相邻两个数的和。
下面我们将深入探讨杨辉三角的规律和公式。
1. 杨辉三角的构造让我们以一个简单的示例来说明杨辉三角的构造过程。
首先是第一行的唯一元素1。
然后,每一行的两端都是1,如下所示:11 1接着,根据规则,我们可以继续构造出下一行:11 11 2 1依此类推,我们可以继续构造出更多行,形成完整的杨辉三角。
2. 杨辉三角的规律杨辉三角不仅仅是一种几何图形,它还蕴含着许多有趣的规律。
其中最引人注目的规律之一就是每一行的数字都遵循一定的数学公式。
首先,每一行的数字个数是递增的,从1开始逐渐增加;其次,除了两端的数字是1之外,其他数字都是其上一行相邻两个数字之和。
这一规律可以用数学公式表示如下:考虑第n行的第k个数字,我们记为T(n, k)。
根据规律,有:T(n, k) = T(n-1, k-1) + T(n-1, k)当k等于1或n时,T(n, k)为1。
这个公式描述了杨辉三角中每个数字的生成过程。
3. 应用与拓展杨辉三角虽然看似简单,却有着丰富的应用。
在数学领域,它与组合数学和多项式有着密切的联系;在计算机科学领域,它则与动态规划等算法密切相关。
此外,杨辉三角还有不少拓展和变体。
例如,帕斯卡梯形(Pascal’s Trapezium)就是杨辉三角的一个拓展形式,每一行的元素都是由对应的斜线上的元素之和得到。
结语杨辉三角作为古代数学的经典之作,展现了数学中的奇妙规律和美丽结构。
通过对其规律和公式的探究,我们可以更深入地理解其内在的数学之美。
愿每一个探索者在这个数学的世界里都能发现属于自己的精彩之处!。
杨辉三角的系数规律公式

杨辉三角的系数规律公式杨辉三角,这玩意儿在数学里可有着独特的魅力。
咱们先来说说啥是杨辉三角。
它就是一个像三角形一样的数字排列组合。
从最上面的“1”开始,然后下面每行的数字都是由上一行相邻两个数字相加得到的。
比如说,最上面那行是 1,第二行就是 1 1 ,第三行就是 1 2 1 ,第四行就是 1 3 3 1 ,就这么一直排下去。
那杨辉三角的系数规律公式是啥呢?其实就是二项式定理的系数嘛。
咱们就拿(a + b)² = a² + 2ab + b²来说,这里的系数 1 2 1 正好就是杨辉三角第三行的数字。
再比如(a + b)³ = a³ + 3a²b + 3ab² + b³,系数 1 3 3 1 就是杨辉三角第四行的数字。
我还记得我之前给学生们讲这个的时候,有个小同学瞪着大眼睛,一脸懵地问我:“老师,这有啥用啊?”我笑着跟他说:“孩子,这用处可大了去了。
就比如说咱们算组合数的时候,杨辉三角就能帮上大忙。
”这杨辉三角里的数字排列可是有很多有趣的规律。
比如说每行数字的和是 2 的幂次方。
像第二行 1 1 ,和是 2;第三行 1 2 1 ,和是 4;第四行 1 3 3 1 ,和是 8 ,就这么一直下去。
还有呢,杨辉三角是左右对称的,就像照镜子一样。
而且每行中间的数字最大。
咱们在解题的时候,杨辉三角能让复杂的计算变得简单明了。
比如有个题目让咱们算从 10 个不同的球里选 3 个的组合数,要是直接去算,那可麻烦了。
但要是咱们对照着杨辉三角,一下就能找到对应的系数,轻松得出答案。
我之前碰到过一个实际问题,就是在安排座位的时候。
教室里有 5排座位,每排要安排不同数量的学生,而且要求总的安排方式要尽可能多。
这时候我就想到了杨辉三角,通过分析其中的规律,很快就找到了最优的安排方案。
总之,杨辉三角的系数规律公式虽然看起来有点神秘,但只要咱们认真去琢磨,就能发现它在数学世界里就像一把神奇的钥匙,能打开很多难题的大门,让咱们在数学的海洋里畅游得更畅快!所以啊,同学们,可别小看了这杨辉三角,好好研究它,能让你们的数学更上一层楼!。
杨辉三角的规律以及推导公式

杨辉三角的规律以及定理1二项式定理与杨辉三角杨辉三角我们首先从一个二次多项式(a+b)2的展开式来探讨。
由上式得出:(a+b)2=a2+2ab+b2此代数式的系数为: 1 2 1则(a+b)3的展开式是什么呢?答案为:a3+3a2b+3ab2+b3由此可发现,此代数式的系数为: 1 3 3 1 但似乎没有什么规律,所以让我们再来看看(a+b)4的展开式。
展开式为:a4+4a3b+6a2b2+4ab3+b4由此又可发现,代数式的系数为:1 4 6 4 1 似乎发现了一些规律,就可以发现以下呈三角形的数列:1 (110)1 1 (111)1 2 1 (112)1 3 3 1 (113)1 4 6 4 1 (114)1 5 10 10 5 1 (115)1 6 15 20 15 6 1 (116)杨辉三角形的系数分别为:1,(1,1),(1,2,1),(1,3,3,1),(1,4,6,4,1)(1,5,10,10,5,1),(1,6,15,20,15,6,1),(1,7,21,35,35,21,7,1)所以:(a+b)7=a7+7a6b+21a5b2+35a4b3+35a3b4+21a2b5+7ab6+b7。
由上式可以看出,(a+b)n等于a的次数依次下降n、n-1、n-2…n-n,b的次数依次上升,0、1、2…n次方。
系数是杨辉三角里的系数。
2杨辉三角的幂的关系首先我们把杨辉三角的每一行分别相加,如下:1 ( 1 )1 1 ( 1+1=2 )1 2 1 (1+2+1=4 )1 3 3 1 (1+3+3+1=8 )1 4 6 4 1 (1+4+6+4+1=16 )1 5 10 10 5 1 (1+5+10+10+5+1=32 )1 6 15 20 15 6 1 (1+6+15+20+15+6+1=64 )……相加得到的数是1,2,4,8,16,32,64,…刚好是2的0,1,2,3,4,5,6,…n次幂,即杨辉三角第n 行中n个数之和等于2的n-1次幂3 杨辉三角中斜行和水平行之间的关系(1)1 (2) n=11 1 (3) n=21 2 1 (4) n=31 3 3 1 (5) n=41 4 6 4 1 (6) n=51 5 10 10 5 1 n=61 6 15 20 15 6 1把斜行(1)中第7行之前的数字相加得1+1+1+1+1+1+1=6把斜行(2)中第7行之前的数字相加得1+2+3+4+5=15把斜行(3)中第7行之前的数字相加得1+3+6+10=20把斜行(4)中第7行之前的数字相加得1+4+10=15把斜行(5)中第7行之前的数字相加得1+5=6把斜行(6)中第7行之前的数字相加得1将上面得到的数字与杨辉三角中的第7行中的数字对比,我们发现它们是完全相同的。
杨辉三角系数的规律公式

杨辉三角系数的规律公式杨辉三角,这可是数学世界里一个相当有趣的存在!咱先来说说杨辉三角到底是啥。
简单来讲,它就是一个三角形的数阵。
从最上面的 1 开始,然后每行的数字都是由上一行相邻两个数字相加得到的。
就像搭积木一样,一层一层地往下搭。
杨辉三角里藏着好多神奇的规律和公式呢。
比如说,它的每行数字之和是 2 的幂次方。
你看,第一行是 1,和是 1,也就是 2 的 0 次方;第二行是 1 1,和是 2,就是 2 的 1 次方;第三行是 1 2 1,和是 4,正好是 2 的 2 次方。
以此类推,是不是很神奇?还有啊,杨辉三角里的二项式系数也有规律。
比如 (a + b) 的 n 次方展开式的系数,就可以在杨辉三角的第 n + 1 行找到。
这就像是一个神秘的密码本,只要你懂得解读,就能轻松找到答案。
我记得有一次,我在给学生们讲杨辉三角的时候,有个小调皮鬼一直说不明白,还跟我较劲。
我就指着黑板上的杨辉三角问他:“你看这一行的数字,1 3 3 1,这是不是和 (a + b)³的展开式系数一模一样?”他眨眨眼睛,还是一脸迷茫。
我又耐心地给他解释:“(a + b)³ = a³ + 3a²b + 3ab² + b³,系数不就是 1 3 3 1 嘛。
”他挠挠头,突然恍然大悟,大声说:“老师,我懂啦!”那一刻,我心里别提多有成就感了。
再说说杨辉三角的对称性。
它就像一面镜子,左右对称得完美无缺。
从中间画一条线,两边的数字完全一样。
这种对称美,在数学里可不少见,就像大自然中的蝴蝶,两边的翅膀也是对称的。
而且杨辉三角里还有一个很有趣的规律,就是相邻两行数字之间的关系。
比如第 n 行的数字乘以 n 再除以 n + 1 ,就可以得到第 n + 1 行的数字。
这就像是一个神奇的魔法,让数字们按照一定的规则变化着。
杨辉三角的规律和公式可不仅仅是为了好玩,它们在数学的很多领域都有重要的应用。
杨辉三角的规律公式(a b)的n次方

杨辉三角的规律公式(a b)的n次方好的,以下是为您生成的文章:在咱们数学的奇妙世界里,有一个超级有趣的东西,那就是杨辉三角。
这玩意儿可藏着不少的规律和公式呢,特别是当我们碰到形如 (a + b)^n 这样的式子时,它就能大显身手啦。
先来说说杨辉三角长啥样。
它就是一个三角形形状的数字排列,从最上面的 1 开始,然后下面的每一行数字都是由上一行相邻两个数字相加得到的。
就拿简单的几行来说,第一行是1,第二行是1 1,第三行是1 2 1,第四行是 1 3 3 1,第五行是 1 4 6 4 1 ,是不是有点意思?我记得有一次给学生们讲杨辉三角的时候,有个小家伙特别积极,瞪着大眼睛一直盯着黑板上的数字,嘴里还念念有词。
我就问他:“你是不是发现啥秘密啦?”他兴奋地说:“老师,我发现每行数字的个数都比行数多 1 个!”我笑着给他点了个赞,这孩子观察得还挺仔细。
那杨辉三角和 (a + b)^n 到底有啥关系呢?其实啊,杨辉三角中的每一行数字,就是 (a + b)^n 展开式的系数。
比如说 (a + b)^2 = a^2 + 2ab + b^2 ,系数是 1 2 1,正好就是杨辉三角的第三行。
再比如 (a + b)^3 =a^3 + 3a^2b + 3ab^2 + b^3 ,系数 1 3 3 1 就是杨辉三角的第四行。
而且啊,杨辉三角还有一个特别好玩的性质。
就是它的每行数字,左右都是对称的。
就像照镜子一样,是不是很神奇?咱们再深入一点,假如要求 (a + b)^5 的展开式,咱们不用费劲去一个一个乘,直接看杨辉三角的第六行,1 5 10 10 5 1 ,那展开式就是a^5 + 5a^4b + 10a^3b^2 + 10a^2b^3 + 5ab^4 + b^5 。
在实际解题的时候,杨辉三角可帮了大忙。
有一次考试,就有一道题是让求(a + b)^4 的展开式,很多同学都傻眼了,不知道从哪儿下手。
但是平时认真研究过杨辉三角的同学,很快就写出了答案,轻松拿到了分数。
杨辉三角的递推公式

杨辉三角的递推公式杨辉三角,这可是数学世界里一个相当有趣的存在!咱们先来说说啥是杨辉三角。
它是一个三角形的数阵,每行数字左右对称,由 1 开始逐渐变大,然后再逐渐变小,最后回到 1 。
就像一个排列整齐的数字大军,非常有规律。
那杨辉三角的递推公式是啥呢?其实就是通过前面一行的数字来计算得出下一行的数字。
具体来说,如果我们把杨辉三角的第 n 行第 m 个数记为 C(n,m) ,那么递推公式就是:C(n,m) = C(n - 1,m - 1) + C(n - 1,m) 。
这个公式看起来有点复杂,但咱们一点点来理解。
我记得之前给学生们讲这个的时候,有个小同学瞪着大眼睛问我:“老师,这有啥用啊?”我笑了笑,给他举了个例子。
比如说咱们要算从 5 个不同的水果里选 2 个的组合数,这时候杨辉三角的递推公式就能派上用场啦。
咱们先找到第 5 行,然后找到第 2 个数,就能得出答案。
咱们再深入点讲讲这个递推公式的妙处。
它就像是一个神奇的魔法咒语,能让我们在数字的世界里畅游。
通过不断地运用这个公式,我们可以快速地填满整个杨辉三角,就像在拼图游戏中一块一块地拼凑出完整的画面。
想象一下,我们就像是数字世界的建筑师,用这个递推公式一砖一瓦地搭建起杨辉三角这座宏伟的数字大厦。
每一行、每一个数字都在我们的掌控之中,那种感觉简直太棒了!而且啊,杨辉三角的递推公式可不只是在数学课本里才有意义。
在实际生活中,它也能帮我们解决很多问题呢。
比如说在概率计算中,它可以帮助我们算出各种可能性的数量;在编码理论中,它能优化信息的存储和传输。
还记得有一次,我和几个朋友一起玩猜数字的游戏。
游戏规则是我心里想一个数字,然后他们通过提问来猜出这个数字。
我就突然想到了杨辉三角的递推公式,我把数字的范围想象成杨辉三角的行数,然后根据他们的提问,用类似递推的方式缩小范围,最后他们费了好大劲才猜中。
这让我更加深刻地体会到了杨辉三角递推公式的巧妙之处。
总之,杨辉三角的递推公式虽然看起来有点神秘,但只要我们用心去理解、去运用,就能发现它就像一把万能钥匙,能打开数学世界里一扇又一扇神奇的大门。
杨辉三角的规律以及推导公式doc资料

杨辉三角的规律以及定理李博洋摘要杨辉三角中的一些规律关键词杨辉三角幂二项式引言杨辉是我国南宋末年的一位杰出的数学家。
在他所著的《详解九章算法》一书中,画了一张表示二项式展开后的系数构成的三角图形,称做“开方做法本源”,现在简称为“杨辉三角”,它是世界的一大重要研究成果。
我们则来对“杨辉三角”的规律进行探讨和研究。
内容1二项式定理与杨辉三角杨辉三角我们首先从一个二次多项式(a+b)2的展开式来探讨。
由上式得出:(a+b)2=a2+2ab+b2此代数式的系数为: 1 2 1则(a+b)3的展开式是什么呢?答案为:a3+3a2b+3ab2+b3由此可发现,此代数式的系数为: 1 3 3 1 但似乎没有什么规律,所以让我们再来看看(a+b)4的展开式。
展开式为:a4+4a3b+6a2b2+4ab3+b4由此又可发现,代数式的系数为:1 4 6 4 1 似乎发现了一些规律,就可以发现以下呈三角形的数列:1 (110)1 1 (111)1 2 1 (112)1 3 3 1 (113)1 4 6 4 1 (114)1 5 10 10 5 1 (115)1 6 15 20 15 6 1 (116)因此可得出二项式定理的公式为:(a+b)n=C(n,0)a^n*b^0+C(n,1)a^(n-1)*b^1+...+C(n,r)a^(n-r)*b^r...+ C(n,n)a^0*b^n因此,二项式定理与杨辉三角形是一对天然的数形趣遇,它把数形结合带进了计算数学。
求二项式展开式系数的问题,实际上是一种组合数的计算问题。
用系数通项公式来计算,称为“式算”;用杨辉三角形来计算,称作“图算”。
2杨辉三角的幂的关系首先我们把杨辉三角的每一行分别相加,如下:1 ( 1 )1 1 ( 1+1=2 )1 2 1 (1+2+1=4 )1 3 3 1 (1+3+3+1=8 )1 4 6 4 1 (1+4+6+4+1=16 )1 5 10 10 5 1 (1+5+10+10+5+1=32 )1 6 15 20 15 6 1 (1+6+15+20+15+6+1=64 )……相加得到的数是1,2,4,8,16,32,64,…刚好是2的0,1,2,3,4,5,6,…次幂,即杨辉三角第n行中n个数之和等于2的n-1次幂3 杨辉三角中斜行和水平行之间的关系(1)1 (2) n=11 1 (3) n=21 2 1 (4) n=31 3 3 1 (5) n=41 4 6 4 1 (6) n=51 5 10 10 5 1 n=61 6 15 20 15 6 1把斜行(1)中第7行之前的数字相加得1+1+1+1+1+1+1=6把斜行(2)中第7行之前的数字相加得1+2+3+4+5=15把斜行(3)中第7行之前的数字相加得1+3+6+10=20把斜行(4)中第7行之前的数字相加得1+4+10=15把斜行(5)中第7行之前的数字相加得1+5=6把斜行(6)中第7行之前的数字相加得1将上面得到的数字与杨辉三角中的第7行中的数字对比,我们发现它们是完全相同的。
杨辉三角解题公式

杨辉三角解题公式
杨辉三角(也被称为帕斯卡三角)是一个数字三角形,它的第n行(从1开始计数)包含n 个数,其生成规则如下:
1. 第一行只包含一个数字:1。
2. 从第二行开始,每一行的首尾数字都是1。
3. 从第二行开始,每个内部数字都是上一行中与其相邻的两个数字之和。
杨辉三角的前几行如下所示:
```
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
```
为了计算杨辉三角中的特定行和位置的数字,你可以使用组合公式(组合数)来计算。
第n 行的第k个数字可以表示为组合数C(n-1, k-1),其中C(n, k)表示从n个元素中选择k个元素的组合数。
组合数C(n, k)的计算公式为:
C(n, k) = n! / (k! * (n - k)!)
其中,n表示总共的元素数,k表示要选择的元素数,"!"表示阶乘。
例如,如果你想要计算杨辉三角的第5行(从0开始计数)的第2个数字,你可以使用组合数公式:
C(4, 1) = 4! / (1! * (4 - 1)!) = 4! / (1! * 3!) = (4 * 3 * 2 * 1) / (1 * 3 * 2 * 1) = 4
因此,第5行的第2个数字为4。
这个方法可以用来计算杨辉三角中的任何数字,只需替换n和k为你想要的行数和位置即可。
杨辉三角
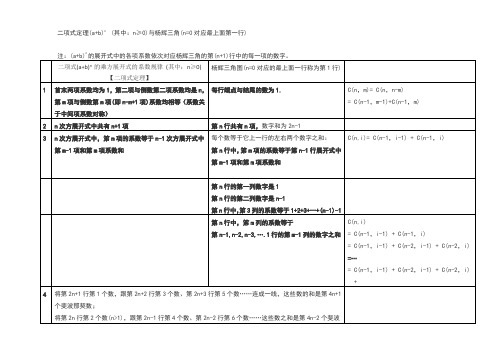
与杨辉三角联系最紧密的是二项式乘方展开式的系数规律,即二项式定理。
例如在杨辉三角中,第3行的三个数恰好对应着两数和的平方的展开式的每一项的系数(性质 8),第4行的四个数恰好依次对应两数和的立方的展开式的每一项的系数,即,以此类推。
又因为性质5:第n行的m个数可表示为C(n-1,m-1),即为从n-1个不同元素中取m-1个元素的组合数。
因此可得出二项式定理的公式为:因此,二项式定理与杨辉三角形是一对天然的数形趣遇,它把数形结合带进了计算数学。
求二项式展开式系数的问题,实际上是一种组合数的计算问题。
用系数通项公式来计算,称为“式算”;用杨辉三角形来计算,称作“图算”[3]。
杨辉三角数在杨辉三角中的出现次数由1开始,正整数在杨辉三角形出现的次数为∞,1, 2, 2, 2, 3, 2, 2, 2, 4, 2, 2, 2, 2, 4, ... (OEIS:A003016)。
最小而又大于1的数在贾宪三角形至少出现n次的数为2, 3, 6, 10, 120, 120, 3003, 3003, ... (OEIS:A062527)除了1之外,所有正整数都出现有限次,只有2出现刚好一次,6,20,70等出现三次;出现两次和四次的数很多,还未能找到出现刚好五次的数。
120,210,1540等出现刚好六次。
(OEIS:A098565)因为丢番图方程有无穷个解,所以出现至少六次的数有无穷个多。
解为,其中F n表示第n个斐波那契数(F1=F2=1)。
3003是第一个出现八次的数。
这也是多项式(a+b) n打开括号后的各个项的n次项系数的规律即为0 (a+b) 0 (0 nCr 0)1 (a+b) 1 (1 nCr 0) (1 nCr 1)2 (a+b)2 (2 nCr 0) (2 nCr 1) (2 nCr 2)3 (a+b)3 (3 nCr 0) (3 nCr 1) (3 nCr 2) (3 nCr 3). ... ... ... ... ...杨辉三角最本质的特征是,它的两条斜边都是由数字1组成的,而其余的数则是等于它肩上的两个数之和。
杨辉三角的规律以及推导公式

精心整理杨辉三角的规律以及定理1二项式定理与杨辉三角杨辉三角我们首先从一个二次多项式(a+b)2的展开式来探讨。
222则为:11(11)(1,5,10,10,5,1),(1,6,15,20,15,6,1),(1,7,21,35,35,21,7,1)所以:(a+b)7=a7+7a6b+21a5b2+35a4b3+35a3b4+21a2b5+7ab6+b7。
由上式可以看出,(a+b)n等于a的次数依次下降n、n-1、n-2…n-n,b的次数依次上升,0、1、2…n次方。
系数是杨辉三角里的系数。
2杨辉三角的幂的关系首先我们把杨辉三角的每一行分别相加,如下:1(1)11(1+1=2)121(1+2+1=4)1331(1+3+3+1=8)6,…n31615201561把斜行(1)中第7行之前的数字相加得1+1+1+1+1+1+1=6把斜行(2)中第7行之前的数字相加得1+2+3+4+5=15把斜行(3)中第7行之前的数字相加得1+3+6+10=20把斜行(4)中第7行之前的数字相加得1+4+10=15把斜行(5)中第7行之前的数字相加得1+5=6把斜行(6)中第7行之前的数字相加得1将上面得到的数字与杨辉三角中的第7行中的数字对比,我们发现它们是完全相同的。
n(3)中第2、每行数字左右对称,由1开始逐渐变大。
3、第n行的数字有n+1项。
4、第n行数字和为2(n-1)。
(2的(n-1)次方)5 (a+b)n的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。
[1]6、第n行的第m个数和第n-m个数相等,即C(n,m)=C(n,n-m),这是组合数性质。
杨辉三角的规律以及推导公式

精心整理杨辉三角的规律以及定理李博洋摘要杨辉三角中的一些规律展开式为:a4+4a3b+6a2b2+4ab3+b4由此又可发现,代数式的系数为:14641似乎发现了一些规律,就可以发现以下呈三角形的数列:1(110)11(111)121(112)1331(113)14641(114)15101051(115)1615201561(116)因此可得出二项式定理的公式为:(a+b)n=C(n,0)a^n*b^0+C(n,1)a^(n-1)*b^1+...+C(n,r)a^(n-r)*b^r...+C(n,n)a^0*b^n。
2相加得到的数是1,2,4,8,16,32,64,…刚好是2的0,1,2,3,4,5,6,…次幂,即杨辉三角第n行中n个数之和等于2的n-1次幂3杨辉三角中斜行和水平行之间的关系(1)1(2)n=111(3)n=2121(4)n=31331(5)n=414641(6)n=515101051n=61615201561由上面可得:杨辉三角中n行中的第i个数是i-1中前n-1个数之和,即第n 行的数分别为1、(1)中第n行之前的数字之和、(2)中第n行之前的数字之和、(3)中第n行之前的数字之和、(4)中第n行之前的数字之和、…、(n-3)中第n行之前的数字之和、1。
总结杨辉三角对于我们好理解的规律,如下六点:杨辉,字谦光,南宋时期杭州人。
在他1261年所着的《详解九章算法》一书中,辑录了如上所示的三角形数表,称之为“开方作法本源”图,并说明此表引自11世纪前半贾宪的《释锁算术》,并绘画了“古法七乘方图”。
故此,杨辉三角又被称为“贾宪三角”。
在我国古老的文明中,人们发现了很多有趣的规律,而杨辉三角就是其中一个。
杨辉三角的规律以及推导公式杨辉三角规律

杨辉三角的规律以及推导公式杨辉三角规律下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!杨辉三角的规律及推导公式引言杨辉三角是中国古代数学宝库中的一颗璀璨明珠,它展现了一种神奇的数学规律,被广泛应用于代数、组合数学、概率论等领域。
杨辉三角的规律以及推导公式

杨辉三角的规律以及推导公式文件编码(GHTU-UITID-GGBKT-POIU-WUUI-8968)杨辉三角的规律以及定理1二项式定理与杨辉三角与杨辉三角联系最紧密的是二项式乘方展开式的系数规律,即。
杨辉三角我们首先从一个二次多项式(a+b)2的展开式来探讨。
由上式得出:(a+b)2=a2+2ab+b2此代数式的系数为:121则(a+b)3的展开式是什么呢?答案为:a3+3a2b+3ab2+b3由此可发现,此代数式的系数为:1331但似乎没有什么规律,所以让我们再来看看(a+b)4的展开式。
展开式为:a4+4a3b+6a2b2+4ab3+b4由此又可发现,代数式的系数为:14641似乎发现了一些规律,就可以发现以下呈三角形的数列:1(110)11(111)121(112)1331(113)14641(114)15101051(115)1615201561(116)杨辉三角形的系数分别为:1,(1,1),(1,2,1),(1,3,3,1),(1,4,6,4,1)(1,5,10,10,5,1),(1,6,15,20,15,6,1),(1,7,21,35,35,21,7,1)所以:(a+b)7=a7+7a6b+21a5b2+35a4b3+35a3b4+21a2b5+7ab6+b7。
由上式可以看出,(a+b)n等于a的次数依次下降n、n-1、n-2…n-n,b的次数依次上升,0、1、2…n次方。
系数是杨辉三角里的系数。
2杨辉三角的幂的关系首先我们把杨辉三角的每一行分别相加,如下:1(1)11(1+1=2)121(1+2+1=4)1331(1+3+3+1=8)14641(1+4+6+4+1=16)15101051(1+5+10+10+5+1=32)1615201561(1+6+15+20+15+6+1=64)……相加得到的数是1,2,4,8,16,32,64,…刚好是2的0,1,2,3,4,5,6,…n 次幂,即杨辉三角第n行中n个数之和等于2的n-1次幂3杨辉三角中斜行和水平行之间的关系(1)1(2)n=111(3)n=2121(4)n=31331(5)n=414641(6)n=515101051n=61615201561把斜行(1)中第7行之前的数字相加得1+1+1+1+1+1+1=6把斜行(2)中第7行之前的数字相加得1+2+3+4+5=15把斜行(3)中第7行之前的数字相加得1+3+6+10=20把斜行(4)中第7行之前的数字相加得1+4+10=15把斜行(5)中第7行之前的数字相加得1+5=6把斜行(6)中第7行之前的数字相加得1将上面得到的数字与杨辉三角中的第7行中的数字对比,我们发现它们是完全相同的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
杨辉三角的规律以及定理
李博洋
摘要杨辉三角中的一些规律
关键词杨辉三角幂二项式
引言
杨辉是我国南宋末年的一位杰出的数学家。
在他所著的《详解九章算法》一书中,画了一张表示二项式展开后的系数构成的三角图形,称做“开方做法本源”,现在简称为“杨辉三角”,它是世界的一大重要研究成果。
我们则来对“杨辉三角”的规律进行探讨和研究。
内容
1二项式定理与杨辉三角
杨辉三角我们首先从一个二次多项式(a+b)2的展开式来探讨。
由上式得出:(a+b)2=a2+2ab+b2此代数式的系数为: 1 2 1
则(a+b)3的展开式是什么呢?答案为:a3+3a2b+3ab2+b3由此可发现,此代数式的系数为: 1 3 3 1 但似乎没有什么规律,所以让我们再来看看(a+b)4的展开式。
展开式为:a4+4a3b+6a2b2+4ab3+b4由此又可发现,代数式的系数为:
1 4 6 4 1 似乎发现了一些规律,就可以发现以下呈三角形的数列:
1 (110)
1 1 (111)
1 2 1 (112)
1 3 3 1 (113)
1 4 6 4 1 (114)
1 5 10 10 5 1 (115)
1 6 15 20 15 6 1 (116)
因此可得出二项式定理的公式为:
(a+b)n=C(n,0)a^n*b^0+C(n,1)a^(n-1)*b^1+...+C(n,r)a^(n-r)*b^r...+ C(n,n)a^0*b^n
因此,二项式定理与杨辉三角形是一对天然的数形趣遇,它把数形结合带进了计算数学。
求二项式展开式系数的问题,实际上是一种组合数的计算问题。
用系数通项公式来计算,称为“式算”;用杨辉三角形来计算,称作“图算”。
2杨辉三角的幂的关系
首先我们把杨辉三角的每一行分别相加,如下:
1 ( 1 )
1 1 ( 1+1=
2 )
1 2 1 (1+2+1=4 )
1 3 3 1 (1+3+3+1=8 )
1 4 6 4 1 (1+4+6+4+1=16 )
1 5 10 10 5 1 (1+5+10+10+5+1=3
2 )
1 6 15 20 15 6 1 (1+6+15+20+15+6+1=64 )
……
相加得到的数是1,2,4,8,16,32,64,…刚好是2的0,1,2,3,4,5,6,…次幂,即杨辉三角第n行中n个数之和等于2的n-1次幂
3 杨辉三角中斜行和水平行之间的关系
(1)
1 (2) n=1
1 1 (3) n=2
1 2 1 (4) n=3
1 3 3 1 (5) n=4
1 4 6 4 1 (6) n=5
1 5 10 10 5 1 n=6
1 6 15 20 15 6 1
把斜行(1)中第7行之前的数字相加得1+1+1+1+1+1+1=6
把斜行(2)中第7行之前的数字相加得1+2+3+4+5=15
把斜行(3)中第7行之前的数字相加得1+3+6+10=20
把斜行(4)中第7行之前的数字相加得1+4+10=15
把斜行(5)中第7行之前的数字相加得1+5=6
把斜行(6)中第7行之前的数字相加得1
将上面得到的数字与杨辉三角中的第7行中的数字对比,我们发现它们是完全相同的。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
由上面可得:杨辉三角中n行中的第i个数是i-1中前n-1个数之和,即第n行的数分别为1、(1)中第n行之前的数字之和、(2)中第n行之前的数字之和、(3)中第n行之前的数字之和、(4)中第n行之前的数字之和、…、(n-3)中第n行之前的数字之和、1。
总结杨辉三角对于我们好理解的规律,如下六点:
1、
每个数等于它上方两数之和。
2、
每行数字左右对称,由1开始逐渐变大。
3、
第n行的数字有n+1项。
4、
第n行数字和为2^(n-1)。
(2的(n-1)次方)
5
(a+b)^n的展开式中的各项系数依次对应杨辉三角的第(n+1)行中的每一项。
[1]
6、
第n行的第m个数和第n-m个数相等,即C(n,m)=C(n,n-m),这是组合数性质
上面的式子是什么意思?首先c i n+1中的n+1,i的意思是从n+1个相同物体中选出i 个物体有多少种选法。
杨辉,字谦光,南宋时期杭州人。
在他1261年所著的《详解九章算法》一书中,辑录了如上所示的三角形数表,称之为“开方作法本源”图,并说明此表引自11世纪前半贾宪的《释锁算术》,并绘画了“古法七乘方图”。
故此,杨辉三角又被称为“贾宪三角”。
在我国古老的文明中,人们发现了很多有趣的规律,而杨辉三角就是其中一个。
