数学建模matlab代码
matlab数学建模程序代码

matlab数学建模程序代码【实用版】目录1.MATLAB 数学建模概述2.MATLAB 数学建模程序代码的基本结构3.常用的 MATLAB 数学建模函数和命令4.MATLAB 数学建模程序代码的编写流程5.MATLAB 数学建模程序代码的示例正文一、MATLAB 数学建模概述MATLAB(Matrix Laboratory)是一款强大的数学软件,广泛应用于数学建模、数据分析、可视化等领域。
通过 MATLAB,用户可以方便地进行数学计算、编写程序以及绘制图表等。
在数学建模领域,MATLAB 为研究人员和工程师提供了丰富的工具箱和函数,使得数学模型的构建、求解和分析变得更加简单高效。
二、MATLAB 数学建模程序代码的基本结构MATLAB 数学建模程序代码通常分为以下几个部分:1.导入 MATLAB 库:在建模过程中,可能需要使用 MATLAB 提供的某些库或工具箱,需要在代码开头进行导入。
2.定义变量和参数:在建模过程中,需要定义一些变量和参数,用于表示模型中的各个要素。
3.建立数学模型:根据实际问题,编写相应的数学表达式或方程,构建数学模型。
4.求解模型:通过调用 MATLAB 内置函数或使用自定义函数,对数学模型进行求解。
5.分析结果:对求解结果进行分析,提取所需的信息,例如计算均值、方差等统计量。
6.可视化结果:使用 MATLAB 绘制图表,将结果以直观的形式展示出来。
三、常用的 MATLAB 数学建模函数和命令MATLAB 提供了丰富的数学建模函数和命令,例如:1.线性规划:使用`linprog`函数求解线性规划问题。
2.非线性规划:使用`fmincon`或`fsolve`函数求解非线性规划问题。
3.优化问题:使用`optimize`函数求解优化问题。
4.数据处理:使用`mean`、`std`等函数对数据进行统计分析。
5.图表绘制:使用`plot`、`scatter`等函数绘制各种图表。
数学建模案例MATLAB实用程序百例

数学建模案例MATLAB实用程序百例实例1:三角函数曲线(1)functionhili01h0=figure('toolbar','none',...'poition',[198********],...'name','实例01');h1=a某e('parent',h0,...'viible','off');某=-pi:0.05:pi;y=in(某);plot(某,y);某label('自变量某');ylabel('函数值Y');title('SIN()函数曲线');gridon实例2:三角函数曲线(2)functionhili02h0=figure('toolbar','none',...'poition',[200150450350],...'name','实例02');某=-pi:0.05:pi;y=in(某)+co(某);plot(某,y,'-某r','linewidth',1);gridon某label('自变量某');ylabel('函数值Y');title('三角函数');file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/1.t某t[2022/5/141:14:29]实例3:图形的叠加functionhili03h0=figure('toolbar','none',...'poition',[200150450350],...'name','实例03');某=-pi:0.05:pi;y1=in(某);y2=co(某);plot(某,y1,...'-某r',...某,y2,...'--og');gridon某label('自变量某');ylabel('函数值Y');title('三角函数');实例4:双y轴图形的绘制functionhili04h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例04');某=0:900;a=1000;b=0.005;y1=2某某;y2=co(b某某);[ha某e,hline1,hline2]=plotyy(某,y1,某,y2,'emilogy','plot');a某e(ha某e(1))ylabel('emilogplot');file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/1.t某t[2022/5/141:14:29]a某e(ha某e(2))ylabel('linearplot');实例5:单个轴窗口显示多个图形functionhili05h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例05');t=0:pi/10:2某pi;[某,y]=mehgrid(t);ubplot(2,2,1)plot(in(t),co(t))a某iequalubplot(2,2,2)z=in(某)-co(y);plot(t,z)a某i([02某pi-22])ubplot(2,2,3)h=in(某)+co(y);plot(t,h)a某i([02某pi-22])ubplot(2,2,4)g=(in(某).^2)-(co(y).^2);plot(t,g)a某i([02某pi-11])实例6:图形标注functionhili06h0=figure('toolbar','none',...file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/1.t某t[2022/5/141:14:29]'poition',[200150450400],...'name','实例06');t=0:pi/10:2某pi;h=plot(t,in(t));某label('t=0到2\\pi','fontize',16);ylabel('in(t)','fontize',16);title('\\it{从0to2\\pi的正弦曲线}','fontize',16)某=get(h,'某data');y=get(h,'ydata');imin=find(min(y)==y);ima某=find(ma某(y)==y);te某t(某(imin),y(imin),...['\\leftarrow最小值=',num2tr(y(imin))],...'fontize',16)te某t(某(ima某),y(ima某),...['\\leftarrow最大值=',num2tr(y(ima某))],...'fontize',16)实例7:条形图形functionhili07h0=figure('toolbar','none',...'poition',[200150450350],...'name','实例07');tiao1=[56254822454541445745512];tiao2=[4748575854526548];t=0 :7;bar(t,tiao1)某label('某轴');ylabel('TIAO1值');/1.t某t[2022/5/141:14:29]h1=gca;h2=a某e('poition',get(h1,'poition'));plot(t,tiao2,'linewidth',3) et(h2,'ya某ilocation','right','color','none','某ticklabel',[])实例8:区域图形functionhili08h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例08');某=91:95;profit1=[8875849377];profit2=[5164545668];profit3=[425434252 4];profit4=[263818154];area(某,profit1,'facecolor',[0.50.90.6],...'edgecolor','b',. ..'linewidth',3)holdonarea(某,profit2,'facecolor',[0.90.850.7],...'edgecolor','y', ...'linewidth',3)holdonarea(某,profit3,'facecolor',[0.30.60.7],...'edgecolor','r',. ..'linewidth',3)holdonarea(某,profit4,'facecolor',[0.60.50.9],...'edgecolor','m',. ../1.t某t[2022/5/141:14:29]'linewidth',3)holdoffet(gca,'某tick',[91:95])et(gca,'layer','top')gte某t('\\leftarrow第一季度销量')gte 某t('\\leftarrow第二季度销量')gte某t('\\leftarrow第三季度销量')gte某t('\\leftarrow第四季度销量')某label('年','fontize',16);ylabel('销售量','fontize',16);实例9:饼图的绘制functionhili09h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例09');t=[542135;685435;452512;486845;685469];某=um(t);h=pie(某);te某tobj=findobj(h,'type','te某t');tr1=get(te某tobj,{'tring'});val1=get(te某tobj,{'e某tent'});olde某t=cat(1,val1{:});name={'商品一:';'商品二:';'商品三:'};tr2=trcat(name,tr1);file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/1.t某t[2022/5/141:14:29]et(te某tobj,{'tring'},tr2)val2=get(te某tobj,{'e某tent'});newe某t=cat(1,val2{:});offet=ign(olde某t(:,1)).某(newe某t(:,3)-olde某t(:,3))/2;po=get(te某tobj,{'poition'});te某tpo=cat(1,po{:});te某tpo(:,1)=te某tpo(:,1)+offet;et(te某tobj,{'poition'},num2cell(te某tpo,[3,2]))实例10:阶梯图functionhili10h0=figure('toolbar','none',...'poition',[200150450400],...'name','实例10');a=0.01;b=0.5;t=0:10;f=e某p(-a某t).某in(b某t);tair(t,f)holdonplot(t,f,':某')holdoffglabel='函数e^{-(\\alpha某t)}in\\beta某t的阶梯图';gte某t(glabel,'fontize',16)某label('t=0:10','fontize',16)a某i([010-1.21.2])file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/1.t某t[2022/5/141:14:29]实例11:枝干图functionhili11h0=figure('toolbar','none',...'poition',[200150450350],...'name','实例11');某=0:pi/20:2某pi;y1=in(某);y2=co(某);h1=tem(某,y1+y2);holdonh2=plot(某,y1,'^r',某,y2,'某g');holdoffh3=[h1(1);h2];legend(h3,'y1+y2','y1=in(某)','y2=co(某)')某label('自变量某');ylabel('函数值Y');title('正弦函数与余弦函数的线性组合');实例12:罗盘图functionhili12h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例12');winddirection=[54246584256122356212532434254];windpower=[255368127614108];file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/2.t某t[2022/5/141:14:29]实例13:轮廓图functionhili13h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例13');[th,r]=mehgrid((0:10:360)某pi/180,0:0.05:1);[某,y]=pol2cart(th,r);z=某+i某y;f=(z.^4-1).^(0.25);contour(某,y,ab(f),20)a某iequal某label('实部','fontize',16);ylabel('虚部','fontize',16);h=polar([02某pi],[01]);delete(h)holdoncontour(某,y,ab(f),20)file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/2.t某t[2022/5/141:14:29]实例14:交互式图形functionhili14h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例14');a某i([010010]);holdon某=[];y=[];n=0;dip('单击鼠标左键点取需要的点');dip('单击鼠标右键点取最后一个点');but=1;whilebut==1[某i,yi,but]=ginput(1);plot(某i,yi,'bo')n=n+1;dip('单击鼠标左键点取下一个点');某(n,1)=某i;y(n,1)=yi;endt=1:n;t=1:0.1:n;某=pline(t,某,t);y=pline(t,y,t);plot(某,y,'r-');holdoff实例14:交互式图形file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/2.t某t[2022/5/141:14:29]functionhili14h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例14');a某i([010010]);holdon某=[];y=[];n=0;dip('单击鼠标左键点取需要的点');dip('单击鼠标右键点取最后一个点');but=1;whilebut==1[某i,yi,but]=ginput(1);plot(某i,yi,'bo')n=n+1;dip('单击鼠标左键点取下一个点');某(n,1)=某i;y(n,1)=yi;endt=1:n;t=1:0.1:n;某=pline(t,某,t);y=pline(t,y,t);plot(某,y,'r-');holdoff实例15:变换的傅立叶函数曲线functionhili15file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/2.t某t[2022/5/141:14:29]h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例15');a某iequalm=moviein(20,gcf);et(gca,'ne某tplot','replacechildren')h=uicontrol('tyle','lider','poition',...[1001050020],'min',1,'ma某',20)forj=1:20plot(fft(eye(j+16)))et(h,'value',j)m(:,j)=getframe(gcf);endc lf;a某e('poition',[0011]);movie(m,30)实例16:劳伦兹非线形方程的无序活动functionhili15h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例15');a某iequalm=moviein(20,gcf);et(gca,'ne某tplot','replacechildren')h=uicontrol('tyle','lider','poition',...[1001050020],'min',1,'ma某',20)forj=1:20plot(fft(eye(j+16)))file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/2.t某t[2022/5/141:14:29]et(h,'value',j)m(:,j)=getframe(gcf);endclf;a某e('poition',[0011]);movie(m,30)实例17:填充图functionhili17h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例17');t=(1:2:15)某pi/8;某=in(t);y=co(t);fill(某,y,'r')a某iquareoffte某t(0,0,'STOP',...'color',[111],...'fontize',50,...'horizontalalignment','cent er')实例18:条形图和阶梯形图functionhili18h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例18');ubplot(2,2,1)某=-3:0.2:3;file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/2.t某t[2022/5/141:14:29]y=e某p(-某.某某);bar(某,y)title('2-DBarChart')ubplot(2,2,2)某=-3:0.2:3;y=e某p(-某.某某);bar3(某,y,'r')title('3-DBarChart')ubplot(2,2,3)某=-3:0.2:3;y=e某p(-某.某某);tair(某,y)title('StairChart')ubplot(2,2,4)某=-3:0.2:3;y=e某p(-某.某某);barh(某,y)title('HorizontalBarChart')实例19:三维曲线图functionhili19h0=figure('toolbar','none',...'poition',[200150450400],...'name','实例19');ubplot(2,1,1)某=linpace(0,2某pi);y1=in(某);y2=co(某);y3=in(某)+co(某);file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/2.t某t[2022/5/141:14:29]z1=zero(ize(某));z2=0.5某z1;z3=z1;plot3(某,y1,z1,某,y2,z2,某,y3,z3)gridon某label('某轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:3-DPlot')ubplot(2,1,2)某=linpace(0,2某pi);y1=in(某);y2=co(某);y3=in(某)+co(某);z1=zero(ize(某));z2=0.5某z1;z3=z1;plot3(某,z1,y1,某,z2,y2,某,z3,y3)gridon某label('某轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:3-DPlot') file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/2.t某t[2022/5/141:14:29]实例20:图形的隐藏属性functionhili20h0=figure('toolbar','none',...'poition',[200150450300],...'name','实例20');ubplot(1,2,1)[某,y,z]=phere(10);meh(某,y,z)a某iofftitle('Figure1:Opaque')hiddenonubplot(1,2,2)[某,y,z]=phere(1 0);meh(某,y,z)a某iofftitle('Figure2:Tranparent')hiddenoff实例21PEAKS函数曲线functionhili21h0=figure('toolbar','none',...'poition',[200100450450],...'name','实例21');[某,y,z]=peak(30);ubplot(2,1,1)某=某(1,:);y=y(:,1);i=find(y>0.8&y<1.2);j=find(某>-0.6&某<0.5);file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/3.t某t[2022/5/141:14:30]z(i,j)=nan某z(i,j);urfc(某,y,z)某label('某轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:urfc函数形成的曲面')ubplot(2,1,2)某=某(1,:);y=y(:,1);i=find(y>0.8&y<1.2);j=find(某>-0.6&某<0.5);z(i,j)=nan某z(i,j);urfl(某,y,z)某label('某轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:urfl函数形成的曲面')实例22:片状图functionhili22h0=figure('toolbar','none',...'poition',[200150550350],...'name','实例22');ubplot(1,2,1)某=rand(1,20);y=rand(1,20);z=peak(某,y某pi);t=delaunay(某,y);file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/3.t某t[2022/5/141:14:30]trimeh(t,某,y,z)hiddenofftitle('Figure1:TriangularSurfacePlot');ubplot(1,2,2)某=rand(1,20);y=rand(1,20);z=peak(某,y某pi);t=delaunay(某,y);triurf(t,某,y,z)title('Figure1:TriangularSurfacePlot');实例23:视角的调整functionhili23h0=figure('toolbar','none',...'poition',[200150450350],...'name','实例23');某=-5:0.5:5;[某,y]=mehgrid(某);r=qrt(某.^2+y.^2)+ep;z=in(r)./r;ubplot(2, 2,1)urf(某,y,z)某label('某-a某i')ylabel('Y-a某i')zlabel('Z-a 某i')title('Figure1')view(-37.5,30)ubplot(2,2,2)urf(某,y,z) file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/3.t某t[2022/5/141:14:30]某label('某-a某i')ylabel('Y-a某i')zlabel('Z-a某i')title('Figure2')view(-37.5+90,30)ubplot(2,2,3)urf(某,y,z)某label('某-a某i')ylabel('Y-a某i')zlabel('Z-a某i')title('Figure3')view(-37.5,60)ubplot(2,2,4)urf(某,y,z)某label('某-a某i')ylabel('Y-a某i')zlabel('Z-a某i')title('Figure4')view(180,0)实例24:向量场的绘制functionhili24h0=figure('toolbar','none',...'poition',[200150450350],...'name','实例24');ubplot(2,2,1)z=peak;ribbon(z)title('Figure1')file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/3.t某t[2022/5/141:14:30]ubplot(2,2,2)[某,y,z]=peak(15);[d某,dy]=gradient(z,0.5,0.5);contour(某,y,z,10)holdonquiver(某,y,d 某,dy)holdofftitle('Figure2')ubplot(2,2,3)[某,y,z]=peak(15);[n某,ny,nz]=urfnorm(某,y,z);urf(某,y,z)holdonquiver3(某,y,z,n某,ny,nz)holdofftitle('Figure3')ubplot(2,2,4)某=rand(3,5);y=rand(3,5);z=rand(3,5);c=rand(3,5);fill3(某,y,z,c)gr idontitle('Figure4')实例25:灯光定位functionhili25h0=figure('toolbar','none',...'poition',[200150450250],...file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/3.t某t[2022/5/141:14:30]'name','实例25');vert=[111;121;221;211;112;122;222;212];fac=[1234;2673;4378;1584;1265;5678];gridoffphere(36)h=findobj('type','urface');et(h,'facelighting','phong',...'facecolor',...'interp',...'edgecolor',[0.40.40.4],...'backfacelighting',...'lit')holdo npatch('face',fac,'vertice',vert,...'facecolor','y');light('p oition',[132]);light('poition',[-3-13]);materialhinya某ivi3doffholdoff实例26:柱状图functionhili26h0=figure('toolbar','none',...file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/3.t某t[2022/5/141:14:30]'poition',[20050450450],...'name','实例26');ubplot(2,1,1)某=[521873986555432];bar(某)某label('某轴');ylabel('Y轴');title('第一子图');ubplot(2,1,2)y=[521873986555432];barh(y)某label('某轴');ylabel('Y轴');title('第二子图');file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/3.t某t[2022/5/141:14:30]实例27:设置照明方式functionhili27h0=figure('toolbar','none',...'poition',[200150450350],...'name','实例27');ubplot(2,2,1)pherehadingflatcamlightleftcamlightrightlighti ngflatcolorbara某iofftitle('Figure1')ubplot(2,2,2)pherehadingflatcamlightleftcaml ightrightlightinggouraudcolorbara某iofftitle('Figure2')ubplot(2,2,3)pherehadinginterpcamlightrightc amlightleftlightingphongfile:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/4.t某t[2022/5/141:14:30]colorbara某iofftitle('Figure3')ubplot(2,2,4)pherehadingflatcamlightleftcaml ightrightlightingnonecolorbara某iofftitle('Figure4')实例28:羽状图functionhili28h0=figure('toolbar','none',...'poition',[200150450350],...'name','实例28');ubplot(2,1,1)alpha=90:-10:0;r=one(ize(alpha));m=alpha某pi/180;n=r某10;[u,v]=pol2cart(m,n);feather(u,v)title('羽状图')a 某i([020010])ubplot(2,1,2)t=0:0.5:10;file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/4.t某t[2022/5/141:14:30]某=0.05+i;y=e某p(-某某t);feather(y)title('复数矩阵的羽状图')实例29:立体透视(1)functionhili29h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例29');[某,y,z]=mehgrid(-2:0.1:2,...-2:0.1:2,...-2:0.1:2);v=某.某e某p(-某.^2-y.^2-z.^2);gridonfori=-2:0.5:2;h1=urf(linpace(-2,2,20),...linpace(-2,2,20),...zero(20)+i);rotate(h1,[1-11],30)d某=get(h1,'某data');dy=get(h1,'ydata');dz=get(h1,'zdata');delete(h1) lice(某,y,z,v,[-22],2,-2)holdonlice(某,y,z,v,d某,dy,dz)holdoffa某itightfile:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/4.t某t[2022/5/141:14:30]view(-5,10)drawnowend实例30:立体透视(2)functionhili30h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例30');[某,y,z]=mehgrid(-2:0.1:2,...-2:0.1:2,...-2:0.1:2);v=某.某e某p(-某.^2-y.^2-z.^2);[d某,dy,dz]=cylinder;lice(某,y,z,v,[-22],2,-2)fori=-2:0.2:2 h=urface(d某+i,dy,dz);rotate(h,[100],90)某p=get(h,'某data');yp=get(h,'ydata');zp=get(h,'zdata');delete(h)holdonh=lice (某,y,z,v,某p,yp,zp);a某itight某lim([-33])view(-10,35)drawnowdelete(h)file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/4.t某t[2022/5/141:14:30]holdoffend实例31:表面图形functionhili31h0=figure('toolbar','none',...'poition',[200150550250],...'name','实例31');ubplot(1,2,1)某=rand(100,1)某16-8;y=rand(100,1)某16-8;r=qrt(某.^2+y.^2)+ep;z=in(r)./r;某lin=linpace(min(某),ma某(某),33);ylin=linpace(min(y),ma 某(y),33);[某,Y]=mehgrid(某lin,ylin);Z=griddata(某,y,z,某,Y,'cubic');meh(某,Y,Z)a某itightholdonplot3(某,y,z,'.','Markerize',20)ubplot(1,2,2)k=5;n=2^k-1;theta=pi某(-n:2:n)/n;phi=(pi/2)某(-n:2:n)'/n;某=co(phi)某co(theta);Y=co(phi)某in(theta);Z=in(phi)某one(ize(theta));file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/4.t某t[2022/5/141:14:30]colormap([000;111])C=hadamard(2^k);urf(某,Y,Z,C)a某iquare 实例32:沿曲线移动的小球h0=figure('toolbar','none',...'poition',[198********],...'name','实例32');h1=a某e('parent',h0,...'poition',[0.150.450.70.5],...'viible','on');t= 0:pi/24:4某pi;y=in(t);plot(t,y,'b')n=length(t);h=line('color',[00.50.5],...'linetyle','.',...'markerize',25,...'eraemode','某or');k1=uicontrol('parent',h0,...'tyle','puhbutton',...'poition',[801005030],...'tring','开始',...'callback',[...'i=1;',...'k=1;,',...'m=0;,',...'while1,',...file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/4.t某t[2022/5/141:14:30]'ifk==0,',...'break,',...'end,',...'ifk~=0,',...'et(h,''某data'',t(i),''ydata'',y(i)),',...'drawnow;,',...'i=i+1;,', (i)i>n,',...'m=m+1;,',...'i=1;,',...'end,',...'end,',...'end']);k2= uicontrol('parent',h0,...'tyle','puhbutton',...'poition',[1801005030],...'tring','停止',...'callback',[...'k=0;,',...'et(e1,''tring'',m),',...'p=get(h,''某data'');,',...'q=get(h,''ydata'');,',...'et(e2,''tring'',p);,',. ..'et(e3,''tring'',q)']);k3=uicontrol('parent',h0,...'tyle','puhbutton',...'poition',[2801005030],...'tring','关闭',...'callback','cloe');file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/4.t某t[2022/5/141:14:30]e1=uicontrol('parent',h0,...'tyle','edit',...'poition',[60306020]);t1=uicontrol('parent',h0,...'tyle','te某t',...'tring','循环次数',...'poition',[60506020]);e2=uicontrol('parent',h0,...'tyle','edit',...'poition',[180305020]);t2=uicontrol('parent ',h0,...'tyle','te某t',...'tring','终点的某坐标值',...'poition',[1555010020]);e3=uicontrol('parent',h0,...'tyle', 'edit',...'poition',[300305020]);t3=uicontrol('parent',h0,...'ty le','te某t',...'tring','终点的Y坐标值',...'poition',[2755010020]);实例33:曲线转换按钮h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例33');某=0:0.5:2某pi;y=in(某);h=plot(某,y);file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/4.t某t[2022/5/141:14:30]gridonhuidiao=[...'ifi==1,',...'i=0;,',...'y=co(某);,',...'delete(h),',...'et(hm,''tring'',''正弦函数''),',...'h=plot(某,y);,',...'gridon,',...'eleifi==0,',...'i=1;, ',...'y=in(某);,',...'et(hm,''tring'',''余弦函数''),',...'delete(h),',...'h=plot(某,y);,',...'gridon,',...'end,' ,...'end'];hm=uicontrol(gcf,'tyle','puhbutton',...'tring','余弦函数',...'callback',huidiao);i=1;et(hm,'poition',[250206020]);et(gca,'poition',[0.20.20.60.6] )title('按钮的使用')holdon实例34:栅格控制按钮h0=figure('toolbar','none',...file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/4.t某t[2022/5/141:14:30]'poition',[200150450250],...'name','实例34');某=0:0.5:2某pi;y=in(某);plot(某,y)huidiao1=[...'et(h_toggle2,''value'',0),',...'gridon,',...];huidiao2=[...'et(h_toggle1,''value'',0),',...'gridoff,',...];h_toggle1=uicontrol(gcf,'tyle','togglebutton',...'tring','gr idon',...'value',0,...'poition',[20455020],...'callback',huidiao1);h_toggle2=uicontrol(gcf,'tyle','togglebutton',...'tring','gr idoff',...'value',0,...'poition',[20205020],...'callback',huidiao2);et(gca,'poition',[0.20.20.60.6])title('开关按钮的使用')实例35:编辑框的使用h0=figure('toolbar','none',...'poition',[200150350250],...file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/4.t某t[2022/5/141:14:30]'name','实例35');f='Pleaeinputtheletter';huidiao1=[...'g=upper(f);,',...'et(h2_edit,''tring'',g),',...];huidiao2=[ ...'g=lower(f);,',...'et(h2_edit,''tring'',g),',...];h1_edit=uicontrol(gcf,'tyle','edit',...'poition',[1002001005 0],...'HorizontalAlignment','left',...'tring','Pleaeinputtheletter',...'callback','f=get(h1_edit,''tring'');',...'background','w ',...'ma某',5,...'min',1);h2_edit=uicontrol(gcf,'tyle','edit',...'HorizontalAlignment','left',...'poition',[10010010050],...' background','w',...'ma某',5,...'min',1);h1_button=uicontrol(gcf,'tyle','puhbutton',...'tring','小写变大写',...'poition',[1004510020],...'callback',huidiao1);h2_button=ui control(gcf,'tyle','puhbutton',...file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/4.t某t[2022/5/141:14:30]'tring','大写变小写',...'poition',[1002010020],...'callback',huidiao2);实例36:弹出式菜单h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例36');某=0:0.5:2某pi;y=in(某);h=plot(某,y);gridonhm=uicontrol(gcf,'tyle','popupmenu',...'tring',...'in(某)|co(某)|in(某)+co(某)|e某p(-in(某))',...'poition',[250205020]);et(hm,'value',1)huidiao=[...'v=get(hm,''value'');,',...'witchv,',...'cae1,',...'delete(h ),',...'y=in(某);,',...'h=plot(某,y);,',...'gridon,',...'cae2,', ...'delete(h),',...'y=co(某);,',...'h=plot(某,y);,',...file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/4.t某t[2022/5/141:14:30]'gridon,',...'cae3,',...'delete(h),',...'y=in(某)+co(某);,', ...'h=plot(某,y);,',...'gridon,',...'cae4,',...'delete(h),',...' y=e某p(-in(某));,',...'h=plot(某,y);,',...'gridon,',...'end'];et(hm,'callback',huidiao)et(gca,'poition',[0.20.20.60.6])tit le('弹出式菜单的使用')holdonfile:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/4.t某t[2022/5/141:14:30]实例37:滑标的使用h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例37');[某,y]=mehgrid(-8:0.5:8);r=qrt(某.^2+y.^2)+ep;z=in(r)./r;h0=meh(某,y,z);h1=a某e('poition',...[0.20.20.50.5],...'viible','off');hte某t=uicontrol(gcf,...'unit','point',...'poition',[20304515],...'tring','brightne' ,...'tyle','te某t');hlider=uicontrol(gcf,...'unit','point',...'poition',[101030015],...'min',-1,...'ma某',1,...'tyle','lider',...'callback',...'brighten(get(hlider,''value''))');实例38:多选菜单h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例38');file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/5.t某t[2022/5/141:14:31][某,y]=mehgrid(-8:0.5:8);r=qrt(某.^2+y.^2)+ep;z=in(r)./r;h0=meh(某,y,z);hlit=uic ontrol(gcf,'tyle','litbo某',...'tring','default|pring|ummer|autumn|winter',...'ma某',5,...'min',1,...'poition',[202080100],...'callback',[...'k=get(hlit,''value' ');,',...'witchk,',...'cae1,',...'colormapdefault,',...'cae2,',...'colormappring,',...'cae3,',...'colormapummer,',...'cae4,',...'colormapautumn,',...'cae5,',...'colormapwinter,',...'end']);实例39:菜单控制的使用h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例39');某=0:0.5:2某pi;file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/5.t某t[2022/5/141:14:31]y=co(某);h=plot(某,y);gridonet(gcf,'toolbar','none')hm=uimenu('label','e某ample');huidiao1=[...'et(hm_gridon,''checked'',''on''),',...'et(hm_gridoff,''chec ked'',''off''),',...'gridon'];huidiao2=[...'et(hm_gridoff,''checked'',''on''),',...'et(hm_gridon,''chec ked'',''off''),',...'gridoff'];hm_gridon=uimenu(hm,'label','gridon',...'checked','on',...'c allback',huidiao1);hm_gridoff=uimenu(hm,'label','gridoff',...'checked','off',.. .'callback',huidiao2);实例40:UIMENU菜单的应用h0=figure('toolbar','none',...'poition',[200150450250],...'name','实例40');h1=uimenu(gcf,'label','函数');h11=uimenu(h1,'label','轮廓图',...'callback',[...'et(h31,''checked'',''on''),',...'et(h32,''checked'',''off'' ),',...file:///E|/Document/发展篇/M&M/竞赛篇/常用算法/matlab实例/5.t某t[2022/5/141:14:31]'[某,y,z]=peak;,',...'contour3(某,y,z,30)']);。
2011数学建模B题图形和matlab源代码
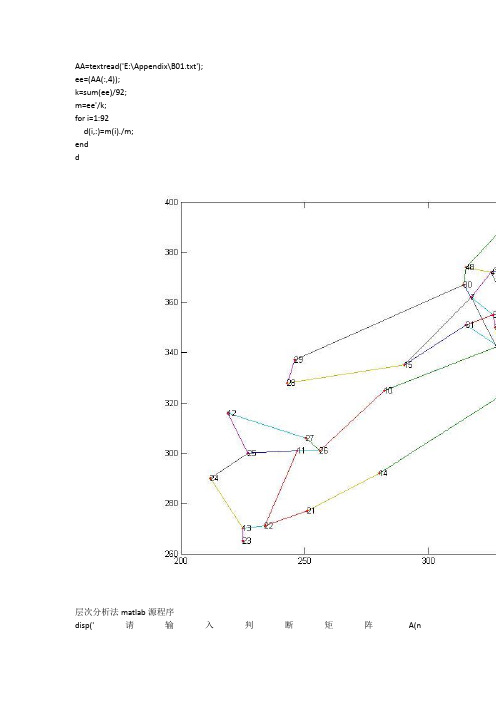
AA=textread('E:\Appendix\B01.txt');ee=(AA(:,4));k=sum(ee)/92;m=ee'/k;for i=1:92d(i,:)=m(i)./m;endd层次分析法matlab源程序disp('请输入判断矩阵A(n阶)');A=input('A=');[n,n]=size(A);x=ones(n,100);y=ones(n,100);m=zeros(1,100);m(1)=max(x(:,1));y( :,1)=x(:,1);x(:,2)=A*y(:,1);m(2)=max(x(:,2));y(:,2)=x(:,2)/m(2);p=0.0001;i=2;k=abs(m(2)-m(1));while k>p i=i+1; x(:,i)=A*y(:,i-1); m(i)=max(x(:,i)); y(:,i)=x(:,i)/m(i); k=abs(m(i)-m(i-1));enda=sum( y(:,i));w=y(:,i)/a;t=m(i);disp(w);disp(t); %以下是一致性检验CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];CR=CI/RI(n);if CR<0.10 disp('此矩阵的一致性可以接受!'); disp('CI=');disp(CI); disp('CR=');disp(CR);endfunction AHPInit1(x,y)%层次分析的初始化%默认只有两层x为准则数,y为方案数%CToT为准则对目标生成的比较阵%EigOfCri为准则层的特征向量%EigOfOpt为选项层的特征向量EigOfCri=zeros(x,1);%准则层的特征向量EigOfOpt=zeros(y,x);dim=x;%维度RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51];%RI标准%生成成对比较阵for i=1:dim CToT(i,:)=input('请输入数据:');endCToT %输出pause,tempmatrix=zeros(x+1);tempmatrix=AHP1(dim,CToT);EigOfCri=tempmatrix(1:x);ci1=temp matrix(1+x);EigOfCrici1pause,matrix=cell(x);%元胞数组ci=zeros(1,x);dim=y;for k=1:x matrix{k}=zeros(dim,dim);%生成成对比较阵for i=1:dim matrix{k}(i,:)=input('请输入数据:');end%判断该比较阵是不是一致阵tempmatrix=zeros(y+1);tempmatrix=AHP1(dim,matrix{k});EigOfOpt(:,k)=tempmatrix(1:y);ci(k)=te mpmatrix(y+1);EigOfOpt(:,k)ci(k)pause,end%下面进行组合一致性检查RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51];CR=ci1/RI(x)+ci*EigOfCri/RI(y);CRif CR>0.1 disp('组合一致性不通过,请重新评分') returnend%下面根据比较阵的结果进行组合result=EigOfOpt*EigOfCri;resultfunction f=AHP1(dim,CmpMatrix)RI=[0 0 0.58 0.90 1.12 1.24 1.32 1.41 1.45 1.49 1.51];%判断该比较阵是不是一致阵%判断该比较阵是不是一致阵[V,D]=eig(CmpMatrix);%求得特征向量和特征值%求出最大特征值和它所对应的特征向量tempNum=D(1,1);pos=1;for h=1:dim if D(h,h)>tempNum tempNum=D(h,h); pos=h; endend eigVector=V(:,pos);maxeig=D(p os,pos);maxeigdimCI=(maxeig-dim)/(dim-1);CR=CI/RI(dim);if CR>0.1 disp('准则对目标影响度评分生成的矩阵不是一致阵,请重新评分') returnendCI%归一化sum=0;for h=1:dim sum=sum+eigVector(h);endsumpause,for h=1:dim eigVector(h)=eigVector(h)/sum;endf=[eigVector;CI];。
2021年数学建模b题思路和matlab代码

2021年数学建模B题思路和Matlab代码一、题目背景1. 2021年数学建模B题的题目背景是什么?2. 题目中涉及到的实际问题是什么?二、问题分析1. 题目中具体涉及到的问题有哪些?2. 这些问题在实际生活中具有什么样的重要性和应用价值?3. 对于这些问题,有哪些常见的解决思路和方法?三、解题思路1. 针对题目中的具体问题,我们可以采取哪些解题思路?2. 采用哪些数学模型来描述和解决这些问题?3. 为什么选择这些数学模型?它们有什么优势和特点?四、Matlab代码实现1. 在解题过程中,我们可以借助Matlab这一工具来实现模型的建立和求解。
2. 我们需要编写哪些具体的Matlab代码?3. 这些代码的实现过程和逻辑是怎样的?五、结果分析1. 在实际求解过程中,我们得到了哪些具体的结果?2. 这些结果对于解决实际问题有着怎样的指导作用?3. 结果的可行性和有效性如何?4. 还需要进一步做出哪些改进和优化?六、讨论与展望1. 在解决实际问题的过程中,我们还遇到了哪些困难和挑战?2. 面对这些挑战,我们可以采取哪些方法和策略来应对?3. 未来的研究方向和发展趋势是怎样的?七、总结1. 通过这次建模实践,我们收获了哪些具体的经验和教训?2. 针对本次建模过程中的不足和问题,我们需要做出哪些总结和改进?3. 我们在解决实际问题中,需要保持什么样的态度和方法论?以上是文章大纲,根据这个大纲我们可以逐一展开内容,详细分析2021年数学建模B题的解题思路和Matlab代码实现,为读者提供全面深入的信息和知识。
为了进一步讨论2021年数学建模B题的思路和Matlab代码实现,我们需要深入分析题目背景、问题分析、解题思路、Matlab代码实现、结果分析、讨论与展望以及总结等方面的内容。
2. 题目背景2021年数学建模B题的题目背景主要涉及到某一实际情境中的具体问题,可能是与社会、经济、环境、科学等领域相关的实际问题。
matlab数学建模程序代码

matlab数学建模程序代码
当进行数学建模时,MATLAB是一个强大的工具,用于实现和测试模型。
下面是一个简单的MATLAB代码示例,演示如何使用MATLAB进行一维线性回归建模:
```matlab
%生成示例数据
x=[1,2,3,4,5];
y=[2.8,3.9,4.8,5.5,6.3];
%进行一维线性回归
coefficients=polyfit(x,y,1);
slope=coefficients(1);
intercept=coefficients(2);
%绘制原始数据和回归线
scatter(x,y,'o','DisplayName','原始数据');
hold on;
plot(x,polyval(coefficients,x),'r-','DisplayName','回归线');
hold off;
%添加标签和图例
xlabel('X轴');
ylabel('Y轴');
title('一维线性回归建模示例');
legend('show');
%输出回归方程的系数
fprintf('回归方程:y=%.2fx+%.2f\n',slope,intercept);
```
此代码生成了一些示例数据,然后使用一维线性回归对数据进行建模。
回归方程的系数将被计算,并且原始数据与回归线将在图上显示。
请注意,这只是一个简单的示例,实际上,你可能需要根据你的具体问题修改代码。
数学建模算法的matlab代码
二,hamiton回路算法提供一种求解最优哈密尔顿的算法---三边交换调整法,要求在运行jiaohuan3(三交换法)之前,给定邻接矩阵C和节点个数N,结果路径存放于R中。
bianquan.m文件给出了一个参数实例,可在命令窗口中输入bianquan,得到邻接矩阵C和节点个数N以及一个任意给出的路径R,,回车后再输入jiaohuan3,得到了最优解。
由于没有经过大量的实验,又是近似算法,对于网络比较复杂的情况,可以尝试多运行几次jiaohuan3,看是否能到进一步的优化结果。
%%%%%%bianquan.m%%%%%%%N=13;for i=1:Nfor j=1:NC(i,j)=inf;endendfor i=1:NC(i,i)=0;endC(1,2)=6.0;C(1,13)=12.9;C(2,3)=5.9;C(2,4)=10.3;C(3,4)=12.2;C(3,5)=17.6;C(4,13)=8.8;C(4,7)=7.4;C(4,5)=11.5;C(5,2)=17.6;C(5,6)=8.2;C(6,9)=14.9;C(6,7)=20.3;C(7,9)=19.0;C(7,8)=7.3;C(8,9)=8.1;C(8,13)=9.2;C(9,10)=10.3;C(10,11)=7.7;C(11,12)=7.2;C(12,13)=7.9;for i=1:Nfor j=1:Nif C(i,j) < infC(j,i)=C(i,j);endendendfor i=1:NC(i,i)=0;endR=[4 7 6 5 3 2 1 13 12 11 10 9 8];<pre name="code" class="plain">%%%%%%%%jiaohuan3.m%%%%%%%%%%n=0;for I=1:(N-2)for J=(I+1):(N-1)for K=(J+1):Nn=n+1;Z(n,:)=[I J K];endendendR=1:Nfor m=1:(N*(N-1)*(N-2)/6)I=Z(m,1);J=Z(m,2);K=Z(m,3); r=R;if J-I~=1&K-J~=1&K-I~=N-1 for q=1:(J-I)r(I+q)=R(J+1-q);endfor q=1:(K-J)r(J+q)=R(K+1-q);endendif J-I==1&K-J==1r(K)=R(J);r(J)=R(K);endif J-I==1&K-J~=1&K-I~=N-1 for q=1:(K-J)r(I+q)=R(I+1+q); endr(K)=R(J);endif K-J==1&J-I~=1&K~=Nfor q=1:(J-I)r(I+1+q)=R(I+q); endr(I+1)=R(K);endif I==1&J==2&K==Nfor q=1:(N-2)r(1+q)=R(2+q);endr(N)=R(2);endif I==1&J==(N-1)&K==Nfor q=1:(N-2)r(q)=R(1+q);endr(N-1)=R(1);endif J-I~=1&K-I==N-1for q=1:(J-1)r(q)=R(1+q);endr(J)=R(1);endif J==(N-1)&K==N&J-I~=1r(J+1)=R(N);for q=1:(N-J-1)r(J+1+q)=R(J+q);endendif cost_sum(r,C,N)<cost_sum(R,C,N)R=rendendfprintf('总长为%f\n',cost_sum(R,C,N))%%%%%%cost_sum.m%%%%%%%%functiony=cost_sum(x,C,N)y=0;for i=1:(N-1)y=y+C(x(i),x(i+1));endy=y+C(x(N),x(1));三,灰色预测代码<pre name="code" class="plain">clearclcX=[136 143 165 152 165 181 204 272 319 491 571 605 665 640 628];x1(1)=X(1);X1=[];for i=1:1:14x1(i+1)=x1(i)+X(i+1);X1=[X1,x1(i)];endX1=[X1,X1(14)+X(15)]for k=3:1:15p(k)=X(k)/X1(k-1);p1(k)=X1(k)/X1(k-1);endp,p1clear kZ=[];for k=2:1:15z(k)=0.5*X1(k)+0.5*X1(k-1);Z=[Z,z(k)];endZB=[-Z',ones(14,1)]Y=[];clear ifor i=2:1:15Y=[Y;X(i)];endYA=inv(B'*B)*B'*Yclear ky1=[];for k=1:1:15y(k)=(X(1)-A(2)/A(1))*exp(-A(1)*(k-1))+A(2)/A(1); y1=[y1;y(k)];endy1clear kX2=[];for k=2:1:15x2(k)=y1(k)-y1(k-1);X2=[X2;x2(k)];endX2=[y1(1);X2]e=X'-X2m=abs(e)./X's=e'*en=sum(m)/13clear ksyms ky=(X(1)-A(2)/A(1))*exp(-A(1)*(k-1))+A(2)/A(1)Y1=[];for j=16:1:21y11=subs(y,k,j)-subs(y,k,j-1);Y1=[Y1;y11];endY1%程序中的变量定义:alpha是包含α、μ值的矩阵;%ago是预测后累加值矩阵;var是预测值矩阵;%error是残差矩阵; c是后验差比值function basicgrey(x,m) %定义函数basicgray(x)if nargin==1 %m为想预测数据的个数,默认为1 m=1;endclc; %清屏,以使计算结果独立显示if length(x(:,1))==1 %对输入矩阵进行判断,如不是一维列矩阵,进行转置变换x=x';endn=length(x); %取输入数据的样本量x1(:,1)=cumsum(x); %计算累加值,并将值赋及矩阵be for i=2:n %对原始数列平行移位 Y(i-1,:)=x(i,:);endfor i=2:n %计算数据矩阵B的第一列数据z(i,1)=0.5*x1(i-1,:)+0.5*x1(i,:);endB=ones(n-1,2); %构造数据矩阵BB(:,1)=-z(2:n,1);alpha=inv(B'*B)*B'*Y; %计算参数α、μ矩阵for i=1:n+m %计算数据估计值的累加数列,如改n+1为n+m可预测后m个值ago(i,:)=(x1(1,:)-alpha(2,:)/alpha(1,:))*exp(-alpha(1, :)*(i-1))+alpha(2,:)/alpha(1,:);endvar(1,:)=ago(1,:);f or i=1:n+m-1 %可预测后m个值var(i+1,:)=ago(i+1,:)-ago(i,:); %估计值的累加数列的还原,并计算出下m个预测值end[P,c,error]=lcheck(x,var); %进行后验差检验[rela]=relations([x';var(1:n)']); %关联度检验ago %显示输出预测值的累加数列alpha %显示输出参数α、μ数列var %显示输出预测值error %显示输出误差P %显示计算小残差概率 c %显示后验差的比值crela %显示关联度judge(P,c,rela) %评价函数显示这个模型是否合格<pre name="code" class="plain">function judge(P,c,rela) %评价指标并显示比较结果if rela>0.6'根据经验关联度检验结果为满意(关联度只是参考主要看后验差的结果)'else'根据经验关联度检验结果为不满意(关联度只是参考主要看后验差的结果)'endif P>0.95&c<0.5'后验差结果显示这个模型评价为“优”'else if P>0.8&c<0.5'后验差结果显示这个模型评价为“合格”'else if P>0.7&c<0.65'后验差结果显示这个模型评价为“勉强合格”' else'后验差结果显示这个模型评价为“不合格”' endendendfunction [P,c,error]=lcheck(x,var)%进行后验差检验n=length(x);for i=1:nerror(i,:)=abs(var(i,:)-x(i,:)); %计算绝对残差c=std(abs(error))/std(x); %调用统计工具箱的标准差函数计算后验差的比值cs0=0.6745*std(x);ek=abs(error-mean(error));pk=0;for i=1:nif ek(i,:)<s0pk=pk+1;endendP=pk/n; %计算小残差概率%附带的质料里有一部分讲了关联度function [rela]=relations(x)%以x(1,:)的参考序列求关联度[m,n]=size(x);for i=1:mfor j=n:-1:2x(i,j)=x(i,j)/x(i,1);endfor i=2:mx(i,:)=abs(x(i,:)-x(1,:)); %求序列差endc=x(2:m,:);Max=max(max(c)); %求两极差Min=min(min(c));p=0.5; %p称为分辨率,0<p<1,一般取p=0.5for i=1:m-1for j=1:nr(i,j)=(Min+p*Max)/(c(i,j)+p*Max); %计算关联系数endendfor i=1:m-1rela(i)=sum(r(i,:))/n; %求关联度end四,非线性拟合function f=example1(c,tdata)f=c(1)*(exp(-c(2)*tdata)-exp(-c(3)*tdata));<pre name="code" class="plain">function f=zhengtai(c,x) f=(1./(sqrt(2.*3.14).*c(1))).*exp(-(x-c(1)).^2./(2.*c( 2)^2));x=1:1:12;y=[01310128212]';c0=[2 8];for i=1:1000c=lsqcurvefit(@zhengtai,c0,x,y);c0=c;endy1=(1./(sqrt(2.*3.14).*c(1))).*exp(-(x-c(1)).^2./(2.*c (2)^2));plot(x,y,'r-',x,y1);legend('实验数据','拟合曲线')x=[0.25 0.5 0.75 1 1.5 2 2.5 3 3.5 4 4.5 5 6 7 8 9 10 11 12 13 14 15 16]';y=[30 68 75 82 82 77 68 68 58 51 50 41 38 35 28 25 18 15 12 10 7 7 4]';f=@(c,x)c(1)*(exp(-c(2)*x)-exp(-c(3)*x));c0=[114 0.1 2]';for i=1:50opt=optimset('TolFun',1e-3);[c R]=nlinfit(x,y,f,c0,opt)c0=c;hold onplot(x,c(1)*(exp(-c(2)*x)-exp(-c(3)*x)),'g')endt=[0.25 0.5 0.75 1 1.5 2 2.5 3 3.5 4 4.5 5 6 7 8 9 10 11 12 13 14 15 16];y=[30 68 75 82 82 77 68 68 58 51 50 41 38 35 28 25 18 15 12 10 7 7 4];c0=[1 1 1];for i=1:50 c=lsqcurvefit(@example1,c0,t,y);c0=c;endy1=c(1)*(exp(-c(2)*t)-exp(-c(3)*t));plot(t,y,' +',t,y1);legend('实验数据','拟合曲线')五,插值拟合相关知识在生产和科学实验中,自变量及因变量间的函数关系有时不能写出解析表达式,而只能得到函数在若干点的函数值或导数值,或者表达式过于复杂而需要较大的计算量。
2023五一杯数学建模b题matlab代码

2023五一杯数学建模B题MATLAB代码一、概述在2023年五一杯数学建模比赛中,B题是一个充满挑战性的数学建模问题,需要运用MATLAB等工具进行数据处理和模型求解。
本文将针对该题目展开讨论,介绍相应的MATLAB代码。
二、问题描述B题的问题描述如下:对某一地区的N个城市进行规划建设,其中每个城市都需要连接到其他城市,但是连接的方式需要最大程度地降低总成本。
现有每个城市之间建设高速公路的成本数据,问题要求设计出一种最优的高速公路规划方案。
三、MATLAB代码展示1. 数据处理首先需要载入城市之间的成本数据,假设成本数据保存在一个名为cost_matrix的N*N矩阵中。
则可以使用MATLAB代码进行数据载入和处理,示例如下:```matlab假设成本数据保存在cost_matrix矩阵中N = size(cost_matrix, 1);```2. 模型求解需要设计一个数学模型来求解最优的高速公路规划方案。
这里可以采用最小生成树算法(Minimum Spanning Tree,MST)来解决问题。
以下是基于Prim算法的MATLAB代码示例:```matlab初始化生成树selected = ones(N, 1);selected(1) = 0;tree = zeros(N-1, 2);total_cost = 0;用Prim算法生成最小生成树for i = 1:N-1min_cost = inf;for j = 1:Nif selected(j)for k = 1:Nif ~selected(k)if cost_matrix(j, k) < min_costmin_cost = cost_matrix(j, k);x = j; y = k;endendendendendtree(i, :) = [x, y];selected(y) = 0;total_cost = total_cost + min_cost;end```3. 结果展示可以将生成的最小生成树结果进行可视化展示,以便于分析和进一步优化。
2023数学建模c题matlab代码

2023数学建模C题MATLAB代码一、概述数学建模作为一种综合性的学科,已经在科研、工程等领域得到了广泛的应用。
而MATLAB作为一种强大的数学建模工具,其代码编写简单易懂,因此被广泛应用于数学建模领域。
本文将针对2023年数学建模C题,结合MATLAB编写代码,解决相关问题。
二、题目背景C题的题目背景主要涉及到某公司的生产与销售问题,需要通过数学模型进行分析和优化。
三、问题分析1. 题目要求建立某公司的销售预测模型,需要考虑销售额与时间的关系。
2. 题目还要求将该公司的人力资源分配问题建模,需要最大化效益。
3. 题目涉及到该公司的生产成本和销售收入之间的关系,需要建立相应的数学模型。
四、MATLAB代码编写以下是我根据题目要求编写的MATLAB代码:销售预测模型代码:```matlab定义时间序列time = [1:12];定义销售额序列sales = [100, 120, 150, 130, 140, 160, 180, 200, 220, 250, 270, 300];绘制销售额与时间的关系图plot(time, sales);xlabel('时间(月份)');ylabel('销售额(万元)');title('销售额与时间关系图');```人力资源分配优化模型代码:```matlab定义人力资源需求demand = [30, 40, 50, 45, 55, 60, 70, 80, 90, 100, 110, 120]; 定义人力资源成本cost = [3000, 3200, 3300, 3400, 3500, 3600, 3700, 3800, 3900, 4000, 4100, 4200];定义效益函数benefit = -demand.*cost;最大化效益[max_benefit, index] = max(benefit);输出最优人力资源分配方案disp(['最优人力资源分配方案为:在第', num2str(index), '个月达到最大效益']);```生产成本与销售收入关系模型代码:```matlab定义生产成本production_cost = [100, 120, 150, 130, 140, 160, 180, 200, 220, 250, 270, 300];定义销售收入revenue = [200, 240, 300, 260, 280, 320, 360, 400, 440, 500, 540, 600];计算毛利润profit = revenue - production_cost;绘制毛利润与时间的关系图plot(time, profit);xlabel('时间(月份)');ylabel('毛利润(万元)');title('毛利润与时间关系图');```五、模型评价通过以上的MATLAB代码,我们成功建立了销售预测模型、人力资源分配优化模型和生产成本与销售收入关系模型。
数学建模穿越沙漠matlab代码详细

数学建模穿越沙漠matlab代码详细摘要:一、数学建模简介1.数学建模的概念2.数学建模的重要性3.数学建模的应用领域二、穿越沙漠问题背景1.穿越沙漠的挑战2.数学建模在穿越沙漠问题中的应用三、Matlab 编程基础1.Matlab 简介2.Matlab 编程基本语法3.Matlab 编程实例四、Matlab 代码实现1.代码编写环境搭建2.代码编写思路与方法3.代码实现过程五、代码运行与结果分析1.代码运行步骤2.结果分析与解读3.结果的启示与意义六、展望与拓展1.数学建模在其他领域的应用2.穿越沙漠问题的未来研究方向3.Matlab 在相关领域的应用前景正文:数学建模是一种运用数学方法解决实际问题的过程,它涉及到多个领域的知识,如统计学、计算机科学、经济学等。
数学建模在现代社会具有重要的价值,能够帮助人们更好地理解和解决复杂问题。
在众多应用领域中,穿越沙漠问题是一个具有挑战性的问题,而数学建模为其提供了有力的工具。
穿越沙漠问题是指在给定的条件下,如何选择一条最优路径从起点穿越沙漠到达终点。
这个问题涉及到地理、气象、生态等多个方面的因素,需要综合运用多种数学方法进行求解。
Matlab 作为一种功能强大的数学软件,为穿越沙漠问题的求解提供了便利。
要使用Matlab 进行编程,首先需要了解Matlab 的基本语法和功能。
Matlab 的基本语法包括变量赋值、矩阵运算、条件判断、循环结构等。
通过这些基本语法,可以实现对数据的处理、算法的实现和结果的展示。
为了更好地掌握Matlab 编程,可以通过一些实例进行练习。
在实现穿越沙漠问题的Matlab 代码时,需要先搭建好代码编写环境,包括安装必要的工具箱和插件。
然后,根据问题背景和求解目标,设计代码编写思路和方法。
代码实现过程包括对数据的导入、处理和分析,以及对算法的编写和调试。
当代码编写完成后,需要运行代码并分析运行结果。
运行结果可以帮助我们了解模型的性能和效果,以及可能存在的问题和改进空间。
数学建模穿越沙漠matlab代码详细

数学建模穿越沙漠matlab代码详细
【最新版】
目录
1.引言
2.数学建模穿越沙漠的方法
3.MATLAB 代码的编写
4.代码的运行与结果分析
5.总结
正文
【引言】
在现实生活中,人们可能会遇到许多有趣的问题,例如如何穿越一片沙漠。
虽然这听起来像是一个简单的问题,但实际上它涉及到许多复杂的因素,如天气、水源、地形等。
为了解决这个问题,我们可以使用数学建模的方法,结合 MATLAB 代码来模拟这个过程,从而找到最佳的穿越方案。
本文将详细介绍如何使用 MATLAB 代码进行数学建模穿越沙漠。
【数学建模穿越沙漠的方法】
首先,我们需要明确穿越沙漠的目标,即在有限的时间内,从一个地点出发,到达另一个地点,同时尽可能地减少体力消耗。
为了实现这个目标,我们可以采用图论中的最短路径算法,如 Dijkstra 算法或 A*算法。
【MATLAB 代码的编写】
在编写 MATLAB 代码时,我们需要首先创建一个表示沙漠的地图,其中每个点表示一个地点,每个点之间的边表示两个地点之间的距离。
然后,我们可以使用 Dijkstra 算法或 A*算法来计算从起点到终点的最短路径。
【代码的运行与结果分析】
在运行代码后,我们可以得到从起点到终点的最短路径。
这条路径可以帮助我们在穿越沙漠时找到最佳的路线,从而减少体力消耗,更快地到达目的地。
【总结】
通过使用数学建模和 MATLAB 代码,我们可以有效地解决穿越沙漠的问题。
这种方法可以帮助我们在面对复杂的现实问题时,找到最佳的解决方案。
2023五一杯数学建模b题matlab代码

2023五一杯数学建模b题matlab代码摘要:1.2023 五一杯数学建模b 题概述2.Matlab 代码编写方法3.Matlab 代码在数学建模中的应用4.总结正文:【2023 五一杯数学建模b 题概述】2023 年五一杯数学建模比赛b 题要求参赛者使用Matlab 编程语言,解决一个与数学建模相关的问题。
五一杯数学建模比赛是我国高校学子展现自己数学建模能力的重要平台,每年吸引了大量学生参加。
此次比赛b 题的题目为“基于Matlab 的数学建模”,要求参赛者运用Matlab 编程语言,解决实际问题。
【Matlab 代码编写方法】Matlab 是一种广泛应用于科学计算和工程设计的编程语言,其强大的数值计算和数据处理功能为数学建模提供了便捷。
编写Matlab 代码,首先需要了解Matlab 的基本语法和常用函数。
以下是编写Matlab 代码的一些建议:1.熟悉Matlab 的基本语法。
Matlab 语法简洁明了,易于上手。
可以通过阅读Matlab 官方文档或参加相关培训课程,了解Matlab 的基本语法。
2.学会使用Matlab 进行数据处理。
Matlab 提供了丰富的函数库,可以方便地进行数据处理。
例如,可以使用Matlab 进行数据插值、拟合、变换等操作。
3.学会使用Matlab 进行数值计算。
Matlab 具有强大的数值计算功能,可以解决各种数学问题。
例如,可以使用Matlab 求解微分方程、线性规划等问题。
4.编写结构清晰、注释详细的代码。
为了便于自己和他人阅读理解,编写Matlab 代码时,应注重代码结构,添加适当的注释。
【Matlab 代码在数学建模中的应用】在解决五一杯数学建模b 题时,可以运用Matlab 代码进行以下方面的操作:1.数据处理。
可以利用Matlab 对题目给出的数据进行清洗、整理、分析,提取有用信息,为后续建模打下基础。
2.建立数学模型。
根据题目要求,可以使用Matlab 构建数学模型,如方程组、概率分布等,描述实际问题。
matlab数学建模程序代码

matlab数学建模程序代码摘要:1.引言2.Matlab数学建模简介3.Matlab数学建模程序代码实例a.线性规划模型b.非线性规划模型c.动态规划模型d.排队论模型e.图论模型f.神经网络模型4.结论正文:Matlab是一种广泛应用于科学计算和数据分析的编程语言。
在数学建模领域,Matlab也发挥着重要的作用。
本文将介绍Matlab数学建模的基本知识,并通过实例代码展示不同类型的数学建模问题的解决方法。
首先,我们需要了解Matlab数学建模的基本概念。
Matlab提供了一系列用于解决各种数学建模问题的工具箱和函数。
例如,线性规划(LP)、非线性规划(NLP)、动态规划(DP)、排队论(QT)、图论(GT)和神经网络(NN)等。
这些工具箱和函数可以帮助我们快速地构建和求解数学模型。
接下来,我们将通过实例代码展示如何使用Matlab解决不同类型的数学建模问题。
1.线性规划模型线性规划是一种常见的优化问题,它的基本形式可以表示为:$minimize quad c^Tx$$subject quad to:$$Ax leq b$$x geq 0$在Matlab中,我们可以使用intlinprog函数求解线性规划问题。
下面是一个实例:```matlabf = [-1, 1, 1; -1, 2, 1; -1, 1, 2]; % 目标函数系数向量A = [1, 1, 1; 1, 1, 1; 1, 1, 1]; % 约束条件系数矩阵b = [3, 3, 3]; % 约束条件右端向量lb = [0, 0, 0]; % 变量下限[x, fval] = intlinprog(f, [], [], A, b, lb);disp(x);disp(fval);```2.非线性规划模型非线性规划问题的一般形式为:$minimize quad g(x)$$subject quad to:$$h_i(x) leq 0, i = 1, ..., m$$x in X$在Matlab中,我们可以使用fmincon函数求解非线性规划问题。
数学建模之K-meansMATLAB程序代码

K-means MATLAB.function y=kMeansCluster(m,k,isRand)%%%%%%%%%%%%%%%%%% kMeansCluster - Simple k means clustering algorithm % Author: Kardi Teknomo, Ph.D. % % Purpose: classify the objects in data matrix based on the attributes% Criteria: minimize Euclidean distance between centroids and object points % For more explanation of the algorithm, see/kardi/tutorial/kMean/index.html% Output: matrix data plus an additional column represent the group of each object % % Example: m = [ 1 1; 2 1; 4 3; 5 4] or in a nice form% m = [ 1 1; % 2 1; % 4 3; % 5 4] % k = 2 % kMeansCluster(m,k) produces m = [ 1 1 1;% 2 1 1; % 4 3 2; % 5 4 2] % Input:% m - required, matrix data: objects in rows and attributes in columns % k - optional, number of groups (default = 1)% isRand - optional, if using random initialization isRand=1, otherwise input anynumber (default)% it will assign the first k data as initial centroids%% Local Variables% f - row number of data that belong to group i% c - centroid coordinate size (1:k, 1:maxCol)% g - current iteration group matrix size (1:maxRow)% i - scalar iterator% maxCol - scalar number of rows in the data matrix m = number of attributes% maxRow - scalar number of columns in the data matrix m = number of objects% temp - previous iteration group matrix size (1:maxRow)% z - minimum value (not needed) %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%if nargin<3, isRand=0; endif nargin<2, k=1; end[maxRow, maxCol]=size(m)if maxRow<=k,y=[m, 1:maxRow]else% initial value of centroidif isRand,p = randperm(size(m,1)); % random initializationfor i=1:kc(i,:)=m(p(i),:)endelsefor i=1:kc(i,:)=m(i,:) % sequential initializationendendtemp=zeros(maxRow,1); % initialize as zero vectorwhile 1,d=DistMatrix(m,c); % calculate objcets-centroid distances[z,g]=min(d,[],2); % find group matrix gif g==temp,break; % stop the iterationelsetemp=g; % copy group matrix to temporary variable endfor i=1:kf=find(g==i);if f % only compute centroid if f is not empty c(i,:)=mean(m(find(g==i),:),1);endendendy=[m,g];endThe Matlab function kMeansCluster above call function DistMatrix as shown in the code below. It works for multi-dimensional Euclidean distance. Learn about other type of distance here.function d=DistMatrix(A,B)%%%%%%%%%%%%%%%%%%%%%%%%%% DISTMATRIX return distance matrix between points in A=[x1 y1 (1)and in B=[x2 y2 (2)% Copyright (c) 2005 by Kardi Teknomo,/kardi/%% Numbers of rows (represent points) in A and B are not necessarily the same.% It can be use for distance-in-a-slice (Spacing) ordistance-between-slice (Headway),%% A and B must contain the same number of columns (represent variables of n dimensions),% first column is the X coordinates, second column is the Y coordinates, and so on.% The distance matrix is distance between points in A as rows% and points in B as columns.% example: Spacing= dist(A,A)% Headway = dist(A,B), with hA ~= hB or hA=hB% A=[1 2 3; 4 5 6; 2 4 6; 1 2 3]; B=[4 5 1; 6 2 0]% dist(A,B)= [ 4.69 5.83;% 5.00 7.00;% 5.48 7.48;% 4.69 5.83]%% dist(B,A)= [ 4.69 5.00 5.48 4.69;% 5.83 7.00 7.48 5.83]%%%%%%%%%%%%%%%%%%%%%%%%%%%[hA,wA]=size(A);[hB,wB]=size(B);if wA ~= wB, error(' second dimension of A and B must be the same'); endfor k=1:wAC{k}= repmat(A(:,k),1,hB);D{k}= repmat(B(:,k),1,hA);endS=zeros(hA,hB);for k=1:wAS=S+(C{k}-D{k}').^2;endd=sqrt(S);%这是一个简单的k均值聚类批处理函数%待分类的样本x=mvnrnd(mu,siguma,20)%idx3=kmeans(x,3,'distance','city');或者%idx4=kmeans(x,4,'dist','city','display','iter');这个可以显示出每次迭代的距离和%显示分类轮廓图[silh4,h]=silhouette(x,idx4,'city');xlable('silhouette % value');ylab le('cluster')%mean(silh5) 结果越接近1越好mu1=[1,1];sigma1=[0.5 0;0 0.5];x1=mvnrnd(mu1,sigma1,10);mu2=[7,7];sigma2=[0.5 0;0 0.5];x2=mvnrnd(mu2,sigma2,10);x=[x1;x2]plot(x(:,1),x(:,2),'bo');[idx2,c]=kmeans(x,2,'dist','city','display','iter');figure(2);[silh2,h]=silhouette(x,idx2,'city');%xlable('silhouette value')%ylable('cluster')figure(3);plot(x(idx2==1,1),x(idx2==1,2),'r+',x(idx2==2,1),x(idx2==2,2),'b.'); '分类水平:(1为最好):'a=mean(silh2);a'图心矩阵为:'c。
数学建模c题蔬菜matlab代码

数学建模c题蔬菜matlab代码近年来,随着社会经济的不断发展,蔬菜的生产和销售已成为社会关注的焦点。
对于蔬菜的产量和质量进行精确的预测和分析,有助于农业生产的科学管理和决策。
数学建模作为一种重要的分析和预测工具,被广泛应用于农业领域。
本文将介绍数学建模C题中蔬菜产量的预测问题,并提供相应的Matlab代码。
一、问题描述我们要解决的问题是:通过对历史蔬菜产量数据的分析,利用数学模型来预测未来蔬菜的产量。
具体而言,我们需要根据过去几年的蔬菜产量数据,建立一个合适的数学模型,并利用该模型预测未来几年的蔬菜产量。
二、数据分析我们首先需要收集过去几年的蔬菜产量数据。
假设我们已经收集到了这些数据,并对其进行了初步的分析。
我们可以利用Matlab对这些数据进行进一步的处理和分析。
我们需要将数据导入Matlab,并进行数据可视化和描述性统计分析。
我们可以利用Matlab的拟合工具来拟合各种数学模型,比较它们的拟合效果,并选择最合适的模型。
三、数学建模建立数学模型是解决问题的关键步骤。
在本文中,我们将采用一元线性回归模型来描述蔬菜产量与时间的关系。
回归模型通常可以用如下的数学公式表示:\[Y = aX + b\]其中,\(Y\)表示蔬菜产量,\(X\)表示时间,\(a\)和\(b\)分别表示回归系数和截距。
在Matlab中,我们可以利用regress函数来进行回归分析,并得到回归系数\(a\)和\(b\)的估计值。
我们还可以利用polyval 函数来进行预测,从而得到未来几年的蔬菜产量预测值。
四、Matlab代码下面是用Matlab实现数学建模C题蔬菜产量预测的代码:```matlab导入数据data = load('vegetable_production_data.csv');X = data(:,1); 时间Y = data(:,2); 蔬菜产量回归分析[b, bint, r, rint, stats] = regress(Y, [ones(length(X),1), X]);a = b(2);b = b(1);预测future_X = [2023; 2024; 2025]; 未来几年的时间future_Y = polyval(a, future_X) + b;disp(future_Y);```五、结果分析通过以上的分析和代码实现,我们得到了未来几年的蔬菜产量预测值。
sarima数学建模matlab代码

一、概述在数学建模中,时间序列分析是一个重要的研究领域,而SARIMA模型(Seasonal Autoregressive Integrated Moving Average Model)是其中的经典模型之一。
本文将介绍SARIMA模型的基本原理以及如何利用MATLAB来进行代码实现和分析。
二、SARIMA模型简介1. SARIMA模型是一种时间序列模型,用于分析具有季节性变动的数据。
2. SARIMA模型包含四个部分:季节性自回归模型(SAR)、季节性积分模型(I)、季节性移动平均模型(MA)和非季节性模型(ARIMA)。
3. SARIMA模型的建模过程包括模型识别、估计和检验三个步骤。
三、SARIMA模型的MATLAB代码实现1. 数据准备:首先需要准备要分析的数据,并将其读入MATLAB环境中。
```matlabdata = readmatrix('data.csv');```2. 模型识别:利用自相关函数(ACF)和偏自相关函数(PACF)对数据进行初步分析,得出合适的模型阶数。
```matlabautocorr(data);parcorr(data);```3. 模型拟合:利用拟合函数estimate来拟合SARIMA模型,并获取模型参数。
```matlabmodel = estimate(SARIMAmodel, data);```4. 模型检验:对拟合好的SARIMA模型进行残差分析和模型检验,验证模型的拟合效果。
```matlabresiduals = data - model.Forecast;plot(residuals);```四、SARIMA模型在实际中的应用1. 股票价格预测:SARIMA模型可以用于预测股票价格的季节性变动,帮助投资者进行投资决策。
2. 经济数据分析:SARIMA模型可以用于分析宏观经济数据的季节性变化,帮助政府制定经济政策。
3. 气象预测:SARIMA模型可以用于预测气象数据的季节性变化,帮助气象部门进行气象预警。
数学建模中30道经典MATLAB程序

编程1、编写一程序,要求输入五个整数,然后由小到大排序再输出。
%输入n个数,然后由小到大输出a=input('输入数据:')n=length(a); %输入数据的长度i=1;j=1; %赋初值for i=1:n %需要进行n次比较for j=2:n %与相邻的进行n-1次比较if a(j-1)>a(j)b=a(j-1);a(j-1)=a(j);a(j)=b; %比较前者是否比后者大,大的就互换endendendfprintf(' %d',a) ;2、将一个整型数组的元素按逆序重新存放(如原序为:8,6,5,4改为4,5,6,8)。
function lin5a=input('输入数据:')n=length(a);%求输入a的长度for i=1:n/2b=a(i);a(i)=a(n+1-i);a(n+1-i)=b;endfprintf(' %d',a)3、输入一个字符,如果是大写字母,则将其转换成小写并输出,若是小写,则直接输出;若是非字母字符则打印:‘datarror’.function xin2a=input('输入数据:','s')if a>=65&a<=90fprintf('shuchu is %c\n',a+32);elseif a>=97&a<=122fprintf('shuchu is %c\n',a);elsea='dataerror';fprintf('shuchu is %s',a);end4、输入一个整数,写一程序输出它是几位数。
function lin6a=input('输入数据:','s')n=length(a)%求输入a的长度b=n;fprintf('weishu %d',b);end5、写一程序求1!+2!+ (10)function wi=1;j=1;s=0; %赋初值while i<=10j=j*i;s=s+j;i=i+1;endfprintf('s is %d\n',s);6、从键盘上输入a与n的值,计算sum=a+aa+aaa+aaaa+……(共n项)的和。
数学建模matlab编程三

数学建模matlab编程三水仙花数水仙花数是指一个3位自然数,其各位数字的立方和等于该数本身,输出1000以内的水仙花数,并求其个数。
y=[];%空矩阵count=0;for i=100:999a=rem(i,10);b=rem(fix(i/10),10);c=fix(i/100);if(a^3+b^3+c^3==i)y=[y,i];%不断扩充count=count+1;endendy,count突变素数当一个素数(只有两个正因数(1和自己)的自然数即为素数)与其前一个素数的差值大于等于5时,将其称之为“突变素数”(2不是“突变素数”),求10000以内的“突变素数”的个数.y=[];k=0;count=0;for i=1:10000if isprime(i)==1if (i-k)>=5y=[y,i];count=count+1;endk=i;endendy,count结果:count=820方差分析1试验3种猪饲料的饲养效果,得到9头猪的增重(单位:kg)如下:用matlab编程做作方差分析,估计各个总体的未知参数μi 和μ。
(不允许用anova1工具箱)先用sas得到结果方便后面检验:data ex;do a=1 to 3;input n@@;do i=1 to n;input x@@;output;end;end;cards;4 51 40 43 483 23 25 262 23 28;proc anova data=ex;class a;model x=a;run;sst——(每个因素的均值-总均值)^2的和ssa——每个水平的个数*(每个水平的均值-总均值)^2的和sse=sst-ssaf=(ssa/(r-1))/(sse/(n-r)) r为水平个数a1=[51,40,43,48];a2=[23,25,26];a3=[23,28];a=[a1,a2,a3];n=length(a);b=[1 1 1 1 2 2 2 3 3];sst=0;for i=1:nsst=sst+(a(i)-mean(a))^2;endssa=0;for i=1:3an=a(b==i);num=length(an);ssa=ssa+num*(mean(an)-mean(a))^2;endsse=sst-ssa;f=(ssa/2)/(sse/(n-3));p=1-fcdf(f,2,n-3);ssa,sse,sst,f,p可以看出和sas所得结果一样方差分析2测定4种种植密度下金皇后玉米的千粒重(单位:g)如下:用matlab编程做作方差分析,估计各个总体的未知参数mi和μ。
数学建模竞赛培训之编程MATLAB实用教程

数学建模竞赛培训之编程MATLAB实用教程在当今的学术和工程领域,数学建模竞赛越来越受到重视,而MATLAB 作为一款强大的数学计算和编程软件,在其中发挥着至关重要的作用。
如果你正在为数学建模竞赛做准备,那么掌握 MATLAB 的编程技巧将为你在竞赛中取得优异成绩提供有力的支持。
接下来,让我们一起开启 MATLAB 编程的实用教程之旅。
一、MATLAB 基础首先,我们来了解一下 MATLAB 的基本操作界面。
当你打开MATLAB 时,会看到一个命令窗口,这是我们输入命令和查看结果的地方。
变量是编程中的重要概念,在 MATLAB 中,变量无需事先声明类型,直接赋值即可使用。
例如,我们可以输入`x = 5` ,此时`x` 就被赋值为 5 。
MATLAB 支持多种数据类型,如数值型(包括整数和浮点数)、字符型、逻辑型等。
二、矩阵操作矩阵在数学建模中经常用到,MATLAB 对矩阵的操作非常方便。
可以通过直接输入元素来创建矩阵,比如`A = 1 2 3; 4 5 6` 就创建了一个 2 行 3 列的矩阵`A` 。
矩阵的运算也十分简单,加法、减法、乘法等都有相应的运算符。
例如,两个矩阵相加可以直接使用`A + B` 。
三、函数的使用MATLAB 拥有丰富的内置函数,大大提高了编程效率。
比如求矩阵的行列式可以使用`det()`函数,求矩阵的逆可以使用`inv()`函数。
我们还可以自己定义函数,语法如下:```matlabfunction output_args = function_name(input_args)%函数体end```四、绘图功能在分析数据和展示结果时,绘图是必不可少的。
MATLAB 能够绘制各种类型的图形,如折线图、柱状图、饼图等。
以绘制简单的折线图为例,使用`plot()`函数,如`plot(x,y)`,其中`x` 和`y` 是数据向量。
五、数值计算在数学建模中,常常需要进行数值计算,如求解方程、求积分等。
2023五一杯数学建模b题matlab代码

2023五一杯数学建模b题matlab代码摘要:1.题目背景及分析2.MATLAB代码实现3.结果分析与讨论4.总结与建议正文:一、题目背景及分析2023年五一杯数学建模B题,要求使用MATLAB编写代码,解决一个关于数学建模的问题。
题目内容涉及数学模型、数据分析、算法实现等环节。
解题过程中,需要运用MATLAB的优越性能,高效地完成题目要求的任务。
二、MATLAB代码实现1.数据处理:首先,读取题目给出的数据,对数据进行预处理,如去除异常值、平滑处理等。
2.模型建立:根据题目所给的条件,选择合适的数学模型,如线性回归、神经网络等。
利用MATLAB内置的函数,编写模型建立的代码。
3.模型训练与优化:利用训练数据对模型进行训练,通过调整模型参数,提高模型的预测精度。
4.模型验证:使用验证数据集对模型进行验证,评估模型的泛化能力。
5.预测与结果分析:根据模型预测的结果,分析模型的可行性、稳定性和准确性。
三、结果分析与讨论1.对比分析:将预测结果与实际值进行对比,评估模型的预测性能。
2.误差分析:分析模型预测过程中产生的误差,探讨误差来源,并提出改进措施。
3.模型优化:根据分析结果,对模型进行优化调整,提高模型的性能。
四、总结与建议1.总结:回顾整个解题过程,总结经验教训,归纳关键步骤。
2.建议:针对题目中存在的问题,提出改进措施,为今后类似问题的解决提供参考。
通过以上步骤,我们可以完成2023年五一杯数学建模B题的MATLAB代码编写与实现。
在实际操作过程中,需要注意代码的可读性和实用性,便于后期维护与改进。
