电路第八章答案(简)
电力电子技术第四版课后题答案第八章

电力电子技术第四版课后题答案第八章第8章组合变流电路1. 什么是组合变流电路?答:组合变流电路是将某几种基本的变流电路(AC/DC、DC/DC、AC/AC、DC/DC)组合起来,以实现一定新功能的变流电路。
2. 试阐明图8-1间接交流变流电路的工作原理,并说明该电路有何局限性。
答:间接交流变流电路是先将交流电整流为直流电,在将直流电逆变为交流电,图8-1所示的是不能再生反馈电力的电压型间接交流变流电路。
该电路中整流部分采用的是不可控整流,它和电容器之间的直流电压和直流电流极性不变,只能由电源向直流电路输送功率,而不能由直流电路向电源反馈电力,这是它的一个局限。
图中逆变电路的能量是可以双向流动的,若负载能量反馈到中间直流电路,导致电容电压升高。
由于该能量无法反馈回交流电源,故电容只能承担少量的反馈能量,这是它的另一个局限。
3. 试分析图8-2间接交流变流电路的工作原理,并说明其局限性。
答:图8-2是带有泵升电压限制电路的电压型间接交流变流电路,它是在图8-1的基础上,在中间直流电容两端并联一个由电力晶体管V0和能耗电阻R0组成的泵升电压限制电路。
当泵升电压超过一定数值时,使V0导通,把从负载反馈的能量消耗在R0上。
其局限性是当负载为交流电动机,并且要求电动机频繁快速加减速时,电路中消耗的能量较多,能耗电阻R0也需要较大功率,反馈的能量都消耗在电阻上,不能得到利用。
4. 试说明图8-3间接交流变流电路是如何实现负载能量回馈的。
答:图8-3为利用可控变流器实现再生反馈的电压型间接交流变流电路,它增加了一套变流电路,使其工作于有源逆变状态。
当负载回馈能量时,中间直流电压上升,使不可控整流电路停止工作,可控变流器工作于有源逆变状态,中间直流电压极性不变,而电流反向,通过可控变流器将电能反馈回电网。
5. 何为双PWM电路?其优点是什么?答:双PWM电路中,整流电路和逆变电路都采用PWM控制,可以使电路的输入输出电流均为正弦波,输入功率因数高,中间直流电路的电压可调。
《电路第五版课后习题答案

答案及解析115答案第一章电路模型和电路定律【题1】:由U A B 5 V 可得:IA C 2.5 A:U DB 0 :U S 125. V。
【题2】:D。
【题3】:300;-100。
【题4】:D。
【题5】: a i i 1 i 2 ; b u u1 u2 ; c u u S i i S R S ; d i iS1RSu u S 。
【题6】:3;-5;-8。
【题7】:D。
【题8】:PU S 1 50 W ;P U S 2 6 W ;P U S3 0 ;P I S 1 15 W ;P I S2 14 W ;P I S 3 15 W 。
【题9】:C。
【题10】:3;-3。
【题11】:-5;-13。
【题12】:4(吸收);25。
【题13】:0.4。
1【题14】:3 I 1 2 3 ;IA 。
3【题15】:I 4 3 A;I 2 3 A;I 3 1A;I 5 4 A。
【题16】:I 7 A;U 35 V;X 元件吸收的功率为P U I 245 W。
【题17】:由图可得U E B 4 V;流过 2 电阻的电流I E B 2 A;由回路ADEBCA 列KVL 得U A C 2 3I ;又由节点 D 列KCL 得I C D 4 I ;由回路CDEC 列KVL 解得;I 3 ;代入上式,得U A C 7 V。
【题18】:P1 P2 2 II212222 ;故I I122;I 1 I 2 ;⑴KCL:43I I ;I 11 12858A;U I 1 I 1 V 或 1.6 V;或I 1 I2 。
S 2 15⑵KCL:43I I ;I1 121 8 A;U S 24V。
第二章电阻电路的等效变换【题1】:[解答]I9 47 3ab 9 4 8.5 V;A =0 .5 A ;U II 1 U 6ab . A ;P 6 1.2 5 W = 7 .5 W ;吸1 252收功率7.5W。
【题2】:[解答]【题3】:[解答] C。
天津理工电路习题及答案 第八章 相量法

第八章 相量法8.1 学习指导8.1.1 学习要点(1)正弦量及其三要素。
(2)相位差的概念。
(3)相量的概念及其性质。
(4)KCL 、KVL 的相量形式。
(5)R 、L 、C 元件VAR 的相量形式。
8.1.2内容概述1.正弦量1)正弦量的时域表达式(以i 为例):)t cos(I i m ψω+= ①2)正弦量的三要素、有效值的定义 (1)角频率、频率、周期(要素之一) 角频率:dt)t (d ψωω+=,即正弦量单位时间内变化的电角度,单位:rad /s(弧度/秒)。
频率:f —单位时间内正弦量变化的周波数,单位:Z H周期:T —正弦波变化一次所需要的时间,即一个完整周波在时间轴上的宽度,单位:s 、ms 、s μω、f 、T 之间的关系:f 2πω=T1f = 或 f 1T =(2)最大值、有效值(要素之二)式①中:m I —最大值;I —有效值。
有效值的定义:若i 为周期性电流函数(不一定是正弦量),则i 有效值的定义式为 ⎰=T2dt i T1I上式可写成:含义是:对同一电阻R ,在周期T 内,i 通过R 时产生的热量与恒定电流I 通过R 时产生的热量相等。
正弦量:I 2I m =对电压等量有效值的定义式在形式上与电流i 的定义式相同。
(3)相位角、初相角(要素之三)相位角: ψω+t ,单位:rad 或(o )(弧度或度)。
初相角:ψ,单位:rad 或(o )(弧度或度)。
注意:正弦量的一个周期对应的相位角为2πrad 或360o 3)相位差相位差是正弦稳态电路中的一个重要概念,设两个正弦量分别为 )t cos(f f 1m 11ψω+= )t cos(f f 2m 22ψω+= 则1f 与2f 之间的相位差定义为)t (112ψωϕ+=-)t (2ψω+=21ψψ- ② 设πϕπ≤≤-12则:(1)当12ϕ>0时,称1f 越前(超前) 2f (12ϕ角),或2f 滞后1f (12ϕ角)。
电路基础第8章部分习题答案

0
Yb
=
⎢ ⎢
⎢
0
⎢
1
⎥
0
R3
0
0
0⎥ ⎥,
0
01 R4
0
⎥ 0⎥
⎥
⎢
⎢
0
⎢
1
⎥
0
00
0⎥
R5
⎥
⎢
⎢
0
⎢⎣
1⎥
0
000 ⎥
R6 ⎥⎦
⎡ ⎢ ⎢
L2 jω(L2L1 −
M
2)
+
1 R3
+
1 R6
⎢ Yn = ⎢
⎢
−
M
jω(L2L1 − M 2 )
⎢
⎢
0
⎣
−
M
jω(L2L1 − M 2 )
L1
+1
jω(L2L1 − M 2 ) R4
⎡1 0 1 0 0 1⎤ 8.28 A = ⎢⎢0 1 0 1 0 0⎥⎥ ,
⎢⎣0 0 0 −1 1 0⎥⎦
⎡
L2
⎢ ⎢
jω(L2L1 − M 2 )
−
M
jω(L2L1 − M 2 )
0
0
0
0
⎤ ⎥
⎥
⎢⎢− ⎢
M jω(L2L1 −
M
2
)
L1 jω(L2L1 − M 2 )
0
0
0
0
⎥ ⎥
⎥
⎢
⎢
(2) 5 2 cos(ωt +143.1° ) ;
(3) 3 2 cos(ωt + 90° ) ;
(4) 220 2 cos(ωt + 60o )
电路与电子技术基础第八章习题答案

习题八8-1 什么是反馈?如何判断反馈的极性?答:电路加入反馈以后,反馈信号削弱原来输入信号,使放大倍数下降的反馈称为负反馈。
判断负反馈多采用瞬时极性法,即将反馈网络与放大电路断开,然后假定输入有一个增量变化,再看反馈信号的变化是导致净输入增加还是减小,若使得净输入减小就是负反馈,否则是正反馈。
8-2 如何判断电压反馈和电流反馈?如何判断串联反馈和并联反馈?答:判断电压反馈还是电流反馈是从输出端去看,若反馈与输出位于三极管的同一个极是电压反馈,否则是电流反馈。
判断串联、并联反馈是从输入端来看,若反馈信号是以电压形式串联在输入回路中,并且与输入信号叠加在一起决定净输入,则是串联反馈;并联反馈则是并接在输入回路中,且是以电流的形式与输入信号进行叠加以决定净输入的大小。
8-3 为了使反馈效果好,对信号源内阻R s和负载电阻R L有何要求?答:为了使反馈得效果更好对信号源的内阻R s的要求是越小越好,而对R L的要求则是越大越好。
8-4 对下面的要求,如何引入反馈(1)要求稳定静态工作点;(2)要求输出电流基本不变,且输入电阻提高;(3)要求电路的输入端向信号源索取的电流较小;(4)要求降低输出电阻;(5)要求增大输入电阻。
答:(1)要稳定静态工作点,必须引入直流负反馈;(2)要求输出电流基本不变,且输入电阻提高,应该引入电流串联负反馈;(3)要求电路的输入端向信号源索取的电流较小就应该使输入电阻增大,增大输入电阻的方法是引入串联负反馈;(4)要求降低输出电阻应该引入的反馈是电压负反馈;(5)要求增大输入电阻可以通过引入串联负反馈来实现。
8-5 电路如题图8-1所示。
判断电路引入了什么性质的反馈(包括局部反馈和级间反馈:正、负、电流、电压、串联、并联、直流、交流)。
答:对于图(a),R3将输出电流采样,以电压的形式反馈到输入回路中,且不仅对直流进行反馈也对交流进行反馈,并根据瞬时极性法可以知道是负反馈,故该电路是一直流/交流、电流、串联负反馈。
逻辑电路习题解答
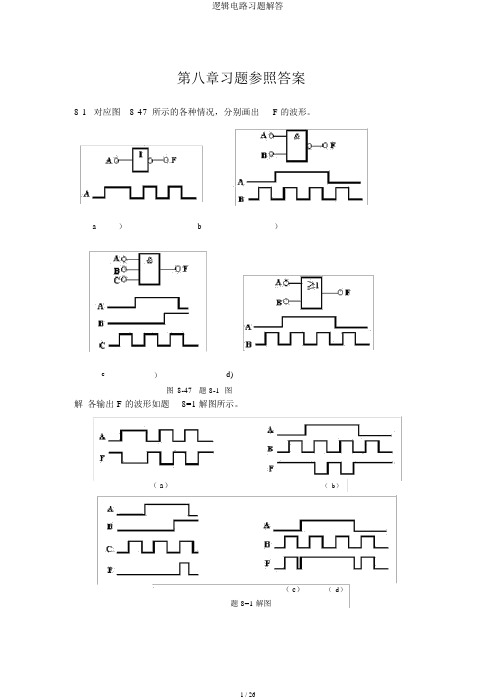
第八章习题参照答案8-1对应图8-47所示的各种情况,分别画出 F 的波形。
a)b)c)d)图8-47题 8-1图解各输出 F 的波形如题8=1 解图所示。
( a)(b)( c)(d)题 8=1 解图8-2 若是“与”门的两个输入端中, A 为信号输入端, B 为控制端。
设 A 的信号波形如图 8-48 所示,当控制端 B=1 和 B=0 两种状态时,试画出输出波形。
若是是“与非”门、“或”门、“或非”门则又如何?分别画出输出波形,最后总结上述四种门电路的控制作用。
图 8-48题8-2图解各种门电路的输出波形如图5- 4 所示。
与门与非门或门或非门图 5-4 习题 5- 2 的解图它们的控制作用分别为:(1)与门:控制端 B 为高电平时,输出为 A 信号;控制端 B 为低电平时,输出为低电平。
( 2)与非门:控制端 B 为高电平时,输出为 A 信号;控制端 B 为低电平时,输出为高电平。
( 3)或门:控制端 B 为高电平时,输出为高电平;控制端 B 为低电平时,输出为 A 信号。
( 4)或非门:控制端 B 为高电平时,输出为低电平;控制端 B 为低电平时,输出为A信号。
8-3 对应图 8-49 所示的电路及输入信号波形,分别画出 F 、 F 、 F 、 F 的波形。
1234a)b)c)d)e)图 8-49题8-3图解各电路的输出波形题8-3 解图所示。
( a)( b)( c)( d)题 8-3 解图8-4化简以下逻辑函数(方法不限)1) F AB A C C D D2) F A(C D CD) B CD A CD ACD3) F( A B)D(A B BD) C A CBD D 4) F AB CD A CDE BDE AC D EF A B A C C D D解 1)A B A C C D(屡次利用吸取率)A B A C DB AC DF A (CD CD) B CD A CD A CDA CD A CD BCD ACD A CD2)(合并同类项)CD CD BCDCD CDF A (CD CD) B CD A CD A CD或CD CD BCD A CD CDCDF(A B )D(A B BD) C A CBD D3)A B D A B C BD C A CBD DAB D A B C BD C A CBD再利用卡诺图,如题8-4 解图( a)所示。
电路 第四版 答案(第八章)

第八章 相量法求解电路的正弦稳态响应,在数学上是求非齐次微分方程的特解。
引用相量法使求解微分方程特解的运算变为复数的代数运运算,从儿大大简化了正弦稳态响应的数学运算。
所谓相量法,就是电压、电流用相量表示,RLC 元件用阻抗或导纳表示,画出电路的相量模型,利用KCL,KVL 和欧姆定律的相量形式列写出未知电压、电流相量的代数方程加以求解,因此,应用相量法应熟练掌握:(1)正弦信号的相量表示;(2)KCL,KVL 的相量表示;(3)RLC 元件伏安关系式的相量形式;(4)复数的运算。
这就是用相量分析电路的理论根据。
8-1 将下列复数化为极坐标形式:(1)551j F --=;(2)342j F +-=;(3)40203j F +=; (4)104j F =;(5)35-=F ;(6)20.978.26j F +=。
解:(1)a j F =--=551θ∠ 25)5()5(22=-+-=a 13555arctan-=--=θ(因1F 在第三象限) 故1F 的极坐标形式为 135251-∠=F(2) 13.1435)43arctan(3)4(34222∠=-∠+-=+-=j F (2F 在第二象限) (3) 43.6372.44)2040arctan(40204020223∠=∠+=+=j F (4) 9010104∠==j F (5) 180335∠=-=F(6) 19.7361.9)78.220.9arctan(20.978.220.978.2226∠=∠+=+=j F注:一个复数可以用代数型表示,也可以用极坐标型或指数型表示,即θθj ae a ja a F =∠=+=21,它们相互转换的关系为:2221a a a += 12arctan a a =θ和 θcos 1a a = θsin 2a a =需要指出的,在转换过程中要注意F 在复平面上所在的象限,它关系到θ的取值及实部1a 和虚部2a 的正负。
第八章习题解答

习题八答案1. 试比较多谐振荡器、单稳态触发器、施密特触发器的工作特点,并说明每种电路的主要用途。
答:多谐振荡器是一种自激振荡电路,不需要外加输入信号,它没有稳定状态,只有两个暂稳态。
暂稳态间的相互转换完全靠电路本身电容的充电和放电自动完成。
改变外接R 、C 定时元件数值的大小,可调节振荡频率。
施密特触发器具有回差特性,它有两个稳定状态,有两个不同的触发电平。
施密特触发器可将任意波形变换成矩形脉冲,输出脉冲宽度取决于输入信号的波形和回差电压的大小。
单稳态触发器有一个稳定状态和一个暂稳态。
输入信号起到触发电路进入暂稳态的作用,其输出脉冲的宽度取决于电路本身 R 、C 定时元件的数值。
改变 R 、C 定时元件的数值可调节输出脉冲的宽度。
多谐振荡器是常用的矩形脉冲产生电路。
施密特触发器和单稳态触发器是两种常用的整形电路。
施密特触发器可用来进行整形、幅度鉴别、构成多谐振荡器等。
单稳态触发器常用于脉冲的延时、定时和整形等。
2.在图8.2所示555集成定时器中,输出电压uo 为高电平UOH、低电平UOL及保持原来状态不变的输入信号条件各是什么?假定UCO端已通过0.01μF 接地,u D 端悬空。
答:当1=R 时, TR U <3V CC ,则C 2输出低电平, 1=Q ,OH o U u =。
当1=R 时, TH U >32V CC ,TR U >3V CC ,则C 1输出低电平、C 2输出高电平,1=Q 、0=Q ,OL o U u =。
当1=R 时, TH U <32V CC,TR U >3V CC ,则C 1C 2输出均为高电平,基本RS 触发器保持原来状态不变,因此o u 保持原来状态不变。
3.在图8.3所示多谐振荡器中,欲降低电路振荡频率,试说明下面列举的各种方法中,哪些是正确的,为什么?1) 加大R 1的阻值; 2) 加大R 2的阻值; 3) 减小C 的容量。
答:根据式(8-2)()ln221121C R R T f +==可知,1)2)两种方法是正确的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8-3 图中各电路换路前原已达稳态,试求i L (0)、u C (0)、+
+
0 0
dt
du dt
di C L 和。
;
解:S S (a) (); (); C L U U u i R ++=
=0033 S ; ;C L du U di dt RC dt +
+
==0003 (c) ()A; ()V;
,
.A s .
L C C L
i u du di dt
dt
+++
+
====0005017045/
8-5 (1) 求图(a)电路中的i (0);
(2) 求图(b)电路中的u (0); (3) 求图(c)电路中的u C (0)、
+
0 dt
du C 。
,
:
解:() ().A;i +=10333
() ()V;() ()V,V s .C
C u du
u dt
+++
==-=020*******/
8-6 时将开关换路。
试求t
0时的u (t )及i (t ) 。
解:..(b) ()V, ().mA , ;t t u t e i t e t --==-≥11111111306670
U S
R R R
C L .
i
S (t =0) (a)
4 (t =0)
S
3
1 u C !
10F
i L 2H
5A 12V (c)
S
20
i
(t =0) 100sin(t /3)V
u C (0-)
… =20V
(a)
4cos2t A 2
(t =0) S 2
2H
u
《
(b)
10 u
S 2H
(t =0) ?
u C 0.1F
10e t V (c)
9V
3k S
" 6k
3k
u 2F (t =0)
i (b)
¥
15V
10
(t =0) 10 10
10 1H
i S '
(c)
(c) (). A , ().V, .t t i t e u t e t --==-≥5505250
8-8 电路如图所示,i L (t )2A ,求i L (t )及u (t ),t 0。
解:(a) () A ,()V, ;L t
t
i t e
u t e
t --==-≥222160
(b) () A , ()V, .L t t i t e u t e t --==≥5050260
8-9 换路前图示电路已达稳态,试求i (t ),t 0。
解: ().()A , .t t i t e e t --=-≥50010000240
.
8-11 试求图示各电路的零状
态响应u C (t ),t 0。
解:.(a) ()().V, ;C t
u t e
t -=-=≥333333910240
.(b) ()()V, .C t u t e t -=-≥011210
{
8-13 电路如图所示,开关S 在t 0时闭合,求t 15s 时u a 及各电阻中的
电流。
设S 闭合前电容上无电荷。
解:
a (s).V,
(s).mA ,(s).mA ,(s).mA .
u i i i =-=-==121539347152022154191156213μμμμ
(
8-17 图示电路在开关S 闭合前已处于稳态,在t
0时S 闭合,试求t
0的u L (t )。
解:.()V, .L t u t e t -=≥75150
4H 3
@
u
i L
i L …
1
u
2 2i L '
100
S (t =0)
20
F 100
150
60V i i L
i C 12V
(t =0) 8
6
2 …
10F
S 2A 4
—
2 i 1
S (t =0)
i 1 4 1F
(b)
+200V 60k a
-300V
40k
6k i 》 S (t 0) 1000pF
i 1 i 2
20
100V S
(t 0) 2H ' u L
5 20 50V
[
8-20 图示电路中,已知t 0时开关S 在“1”的位置,且电路已达稳定状态。
现于t 0
时刻将S 扳到“2”的位置。
(1) 试用三要素法求t 0的响应u C (t ); (2) 求u C (t )经过零值的时刻t 0 . 解:(1) .()V, ;C t
u t e
t -=-+≥0210200
() ().sec.C u t t =⇒=203466由
△8-22 解:()e V, .t C u t t -⨯=+≥4
41010300
8-23 图示电路中,t 0时开关S 在a 点,且电路已达稳态。
现于t 0时刻将S 扳到b
点。
求t 0u (t ) . 解:().V, .C t
u t e
t -=->33050
△8-25 图示电路原已达稳态,t = 0时将开关S 闭合。
(1) 试用三要素法求换路后的u C (t ),并绘出其波形; (2) 从已求得的响应u C (t 中分解出零输入响应和零状态响应。
?
解:
zi zs e
V, ;
e V; (e )V, .
t
C t t C C u t u u t ---=+≥==-≥100010001000100150025010010
8-32 图示电路中,开关在t =0时闭合,且设t =0时的电路已处于稳态,在t =100ms
时又打开,求u ab (t ),并绘出波形图。
解:ab i) .s , ().V ; t t u t e -<<=+250001120675
10V
0.5F
10
u C
(
2A
S 1 2 (t 0)
; cos2t V 6
(t 0) S
1
12
1
F a ) 3V
u (t )
u C , V &
10
t , s
40
1A 100Ω
150Ω
50Ω
(
10F S (t =0)
+ C
- $ 2k Ω5μF
300V
2k Ω
3k Ω 1k Ω
S
u C , V 0 100 t ,
s
250
3
0 :
t (s)
u (V)
.(.)ab ii) .s , ().V.t t u t e -->=-5710101150386
'
8-41 试判断图示两电路的过渡过
程的阻尼状态。
解:(a) 02
.02==C
L R ,临界阻尼;
(b) 02
.02 04.05.002.0=>Ω=-=C
L i i i R ,过阻尼;
8-55. 写出图示网络标准形式的状态方程。
解:
S C C L L du u
dt u di i
dt ⎡⎤⎡⎤⎡⎤-⎡⎤
⎢⎥⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎢⎥⎣⎦⎣⎦⎣⎦3102020136525
25
8-56写出图示电路的状态方程。
解: S C C L L du u
dt u di i dt ⎡⎤⎡⎤⎡⎤⎡⎤
⎢⎥--⎢⎥⎢⎥⎢⎥=+⎢⎥⎢⎥⎢⎥⎢⎥--⎢⎥⎣⎦⎣⎦
⎣⎦⎣⎦1114
431630
8-57 写出图示电路的状态方程和以u 0为输出量的
输出方程。
解:S C C L L L L du u dt C C di R u i dt L L L di R i dt L L ⎡⎤⎡⎤--⎢⎥⎢⎥⎡⎤⎡⎤
⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥=-+-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥-⎢⎥⎣⎦⎣⎦
11
11112222
21
100110010
u ab , V t , ms
0 4
100 : 120
150 + U S -
1H 0.01F ¥ S (t =0)
(a)
+
U S
-
1H 0.01F S ^ (t =0)(b)
i
4
1F +
u C -
5u 1 1H i L
+ u S - +u 1- 6
R 1 i L 2 + u S -
i L 1 R 2 L 1 L 2
C + u C
- + u 0 -
+ u S
- i L !
5H
3
2
4F +C -
输出方程为:[][][]S 2120 0 00u i i u R u L L C +⎥⎥⎥⎦
⎤
⎢⎢⎢⎣⎡=。
