信息光学 ppt课件
合集下载
信息光学 ppt课件

都可以用同样的数学方法——傅里叶分析和“系统” 理论来描写各自有关的系统. 采用相同的数学方法的 根本原因不只是由于两门学科都对“信息”感兴趣, 而更在于通讯系统和成像系统都具有某些相同的基本 性质.
许多电子学网络和成像装置都具有线性和不变性. 任何具有这两种性质的网络或装置(电子学的、光学的 或其他),在数学上都很容易用频谱分析方法来描述.
一门新的学科——信息光学从传统的经典波动 光学中脱颖而出.
信息光学又称傅里叶光学,它是应用光学、计 算机和信息科学相结合而发展起来的一门新的光学 学科,是信息科学的一个重要组成部分,也是现代 光学的核心.
光信息科学与技术的基础是傅里叶光学(通常 称之为信息光学).
信息光学的特点:引用通信和信息理论中的普 遍概念和思想阐述光学现象,使光学和通信信息理 论相结合,光学和信息科学相互渗透.
计算速度
要求达 1015 次/秒
关于现代机器人
2003年2月23日报道
❖ 日本 研制的 世界第一个机器人
能行走,能认识10个人 会握手、挥手、跟在人后面走
结论 电子系统速度慢,现代机器人比不上 人
光子技术的 优越性
响应 速度快
对比
光传播速度 30万km /s ( 3*108 m/s )
光开关速度:飞秒 (fs) 10-15 s
信息光学中采用傅里叶分析和线性系统理论分析 光波的传播、衍射和成像现象,将光学系统看成是 收集和传输信息的系统,把光学现象用通信和信息 理论进行阐述,因而信息光学是信息科学的一个重 要部分.
在光学工程、光学仪器检测、模式识别、图像处 理、显示、传感器、通信、数据处理和成像系统等 领域有许多应用.
2) 光学信息及其特点
• 20世纪以前的光学 古典光学
许多电子学网络和成像装置都具有线性和不变性. 任何具有这两种性质的网络或装置(电子学的、光学的 或其他),在数学上都很容易用频谱分析方法来描述.
一门新的学科——信息光学从传统的经典波动 光学中脱颖而出.
信息光学又称傅里叶光学,它是应用光学、计 算机和信息科学相结合而发展起来的一门新的光学 学科,是信息科学的一个重要组成部分,也是现代 光学的核心.
光信息科学与技术的基础是傅里叶光学(通常 称之为信息光学).
信息光学的特点:引用通信和信息理论中的普 遍概念和思想阐述光学现象,使光学和通信信息理 论相结合,光学和信息科学相互渗透.
计算速度
要求达 1015 次/秒
关于现代机器人
2003年2月23日报道
❖ 日本 研制的 世界第一个机器人
能行走,能认识10个人 会握手、挥手、跟在人后面走
结论 电子系统速度慢,现代机器人比不上 人
光子技术的 优越性
响应 速度快
对比
光传播速度 30万km /s ( 3*108 m/s )
光开关速度:飞秒 (fs) 10-15 s
信息光学中采用傅里叶分析和线性系统理论分析 光波的传播、衍射和成像现象,将光学系统看成是 收集和传输信息的系统,把光学现象用通信和信息 理论进行阐述,因而信息光学是信息科学的一个重 要部分.
在光学工程、光学仪器检测、模式识别、图像处 理、显示、传感器、通信、数据处理和成像系统等 领域有许多应用.
2) 光学信息及其特点
• 20世纪以前的光学 古典光学
光学信息处理全套课件

2、已知函数
f x rectx 2 rectx 2 求下列函数,
并作出函数图形。 (1)
f x 1 (2) f xsgnx
3、已知连续函数 f x ,若 x0 b 0 ,利用
函数可筛选出函数在 x x0 b 的值,试写出运算式。
4、利用梳状函数与矩形函数的卷积表示线光栅的透过率。
假定光栅常数为 ,缝宽为 ,缝数为 。
x, y x y
1.1.2 脉冲响应和叠加积分(1)
• 函数作为基元函数的情况。根据 函数的筛选性质(A.7,或
《积分变换》P16中1.12式),任何输入函数都可以表达为
f x1, y f , x , y dd
• 积分就是“相加 ”,筛选性质表明任意函数都可以表示为无穷多的
函数的和,每个 函数的“大小”被输入函数“调制”。
2 2
27
傅里叶级数的三角形式和指数形式之间关系
• 根据欧拉公式,三角形式的傅里叶级数可以写成
g x
1 a0
a
n
e
j
2nf
0
x
n1
e j 2nf0x 2
bn e j2nf0x
e j 2nf0x 2j
•令
1 a0
an n1
jbn 2
e j 2nf0x
an
coskxdx 0 (k 1,2,3,...)
sin kxdx 0 (k 1,2,3,...)
sin kxsin lxdx 0 (k l, k,l 1,2,3,...)
coskxcoslxdx 0 (k l, k,l 1,2,3,...)
22
周期函数展开为傅里叶级数
• 第1章的主要内容是二维线性系统分析 ,抽样定理 • 第2章关于标量衍射理论,由傅里叶分析与综合导出近
《信息光学第二章》课件

干涉条纹:干涉现象产生的 明暗相间的条纹
光的干涉:光波在传播过程 中相互叠加,形成干涉现象
干涉原理:光的相位差、频 率和振幅对干涉条纹的影响
光的衍射和衍射系统
傅里叶光学基础
傅里叶光学是研究光的传播、干涉、衍射等现象的学科 傅里叶光学的基本原理包括光的波动性、干涉、衍射等 傅里叶光学的应用包括光学成像、光学通信、光学测量等 傅里叶光学的发展对现代光学和光电子学产生了深远影响
量子信息光学:研究量子信息处理和传 输
生物光子学:研究生物系统中的光子学 现象和应用
光子晶体:研究光子晶体的制备和应用
光学成像:研究光学成像技术和应用
光子学:研究光子学器件和系统的设计、 制造和应用
光学通信:研究光学通信技术和应用
信息光学的发展展望
光学技术在信息领域的应用越来 越广泛
光学技术在通信、传感、成像等 领域的发展趋势
1960年代,信息光学理论得到快速发展
1990年代,信息光学在光学通信、光学成像等 领域得到进一步发展
1970年代,信息光学在通信、雷达等领域得到 广泛应用
2000年代,信息光学在光学通信、光学成像等领域得 到广泛应用,并开始向生物医学、环境监测等领域拓展
信息光学的基本原理
光的干涉和干涉系统
干涉系统:由两个或多个光源 组成的系统,可以产生干涉现 象
光学技术在生物医学、环境监测 等领域的应用前景
光学技术在量子信息、人工智能 等领域的发展潜力
感谢您的耐心观看
汇报人:
添加副标题
信息光学第二章
汇报人:
目录
CONTENTS
01 添加目录标题
02 信息光学的基本概 念
03 信息光学的基本原 理
信息光学课件

电磁场与麦克斯韦方程
电磁场的基本概念
电磁场是由电场和磁场组成的, 它们之间存在相互作用。
麦克斯韦方程
描述了电磁场变化的四个基本方程 ,包括电场的散射方程、磁场的散 射方程、电场的波动方程和磁场的 波动方程。
电磁场的能量守恒
电磁场在空间中传播时,其能量不 会消失也不会凭空产生,即电磁场 的能量守恒。
将光学传感技术应用于物联网领域,实现智能化 、远程化和自动化的监测和控制。
3
光学传感器的集成与小型化
通过集成和优化光学器件,实现光学传感器的微 型化和便携化,满足不同应用场景的需求。
05 信息光学实验与实践教学 环节设计
实验内容与目标设定
实验内容
信息光学实验包括干涉、衍射、光学 信息处理等基本实验,以及一些综合 性和创新性实验。
信息光学课件
目录
CONTENTS
• 信息光学概述 • 信息光学基础理论 • 信息光学器件与系统 • 信息光学前沿技术与发展趋势 • 信息光学实验与实践教学环节设计 • 信息光学课程评价与总结反思环节设计
01 信息光学概述
信息光学定义与特点
信息光学定义
信息光学是一门研究光学信息的 获取、传输、处理、存储和显示 的科学。
傅里叶变换与信息光学
傅里叶变换
是一种将时域信号转换为频域信号的数学工具,常用于信号处理 和图像处理等领域。
信息光学的基本概念
信息光学是一门研究光波在空间和时间上传递、处理和存储信息的 科学。
信息光学的应用
信息光学在通信、生物医学成像、军事等领域有着广泛的应用,如 光纤通信、光学显微镜、光学雷达等。
03 信息光学器件与系统
光学器件分类与特点
主动光学器件
信息光学ppt课件

Introduction 4、应用范围的扩展
Information Optics
精选ppt
School of Physics & Material Science
Introduction
光电子 技术
光电子成为信息产业的主角
• 许多学科分支和方向
已形成大规模的产业
全世界光学和光(电)子学技术产业规模
• 空间尺度:百亿光年 单原子尺度,介观尺度
研究方向
天文光学
纳米光学
• 时间尺度:天文时间
原子反应时间(10-15 秒)
研究方向 静态光学
瞬态光学
如超快速现象
纳秒、 皮秒、飞秒
Information Optics
精选ppt
School of Physics & Material Science
Introduction
2、应用功能的扩展 光学工程 —— 综合技术学科
现代精密仪器:
多功能、高效率
光、机、电、算、材 一体化
光学
光
技术手段:自动化、 数字化、智能化
精密机械
机
材
材料
电子
Information Optics
电
算
计算机
精选ppt
School of Physics & Material Science
Introduction
Introduction
享受光 享受光学
光学科学与技术的成果已深深渗透到我们 的生活中.
--王大珩
Information Optics
精选ppt
School of Physics & Material Science
信息光学第七章-光学全息ppt课件
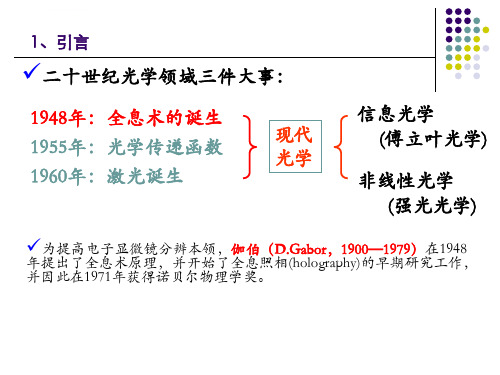
引入一相干参考波,该参考波在H上产生 的复振幅分布为
R x,yr0x,yejrx,y
那么,两波相遇叠加的总光场是
U x ,y O x ,y R x ,y
对应的强度分布为
I x , y U x , y 2 O x , y 2 R x , y 2 O x , y R * x , y O * x , y R x , y
➢用共轭参考波照明
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
2、波前记录与再现
✓用相干光波照射全息图,假定它在全息图平面上的复振幅分布为C(x,y),
全息图的透射光场分布为 U t x , y C t x , y C t b C O 2 C O R * C O * R U 1 U 2 U 3 U 4
4、基元全息图分析
✓全息图可看作是很多基元全息图的线性组合,了解基元全息图的结构和
作用对于深入理解整个全息图的记录和再现机理非常有益。 空域方法是把物体看作一些相干点源的集合,物光波前是所有点源发出的 球面波的线性叠加。每一个点源发出的球面波与参考波干涉,记录的基元 全息图称为基元波带片; 频域方法是把物光波看作由很多不同方向传播的平面波分量的线性叠加, 每一个平面波分量与参考平面波干涉而记录的基元全息图称为基元光栅。
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
1、引言
✓全息发展简史
➢ 1948年 Dennis Gabor 提出 “波前重现” 理论
目的:改善电子显微镜的分辨率 光源:汞灯 效果:因光源相干性差,效果很不明显
R x,yr0x,yejrx,y
那么,两波相遇叠加的总光场是
U x ,y O x ,y R x ,y
对应的强度分布为
I x , y U x , y 2 O x , y 2 R x , y 2 O x , y R * x , y O * x , y R x , y
➢用共轭参考波照明
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
2、波前记录与再现
✓用相干光波照射全息图,假定它在全息图平面上的复振幅分布为C(x,y),
全息图的透射光场分布为 U t x , y C t x , y C t b C O 2 C O R * C O * R U 1 U 2 U 3 U 4
4、基元全息图分析
✓全息图可看作是很多基元全息图的线性组合,了解基元全息图的结构和
作用对于深入理解整个全息图的记录和再现机理非常有益。 空域方法是把物体看作一些相干点源的集合,物光波前是所有点源发出的 球面波的线性叠加。每一个点源发出的球面波与参考波干涉,记录的基元 全息图称为基元波带片; 频域方法是把物光波看作由很多不同方向传播的平面波分量的线性叠加, 每一个平面波分量与参考平面波干涉而记录的基元全息图称为基元光栅。
火灾袭来时要迅速疏散逃生,不可蜂 拥而出 或留恋 财物, 要当机 立断, 披上浸 湿的衣 服或裹 上湿毛 毯、湿 被褥勇 敢地冲 出去
1、引言
✓全息发展简史
➢ 1948年 Dennis Gabor 提出 “波前重现” 理论
目的:改善电子显微镜的分辨率 光源:汞灯 效果:因光源相干性差,效果很不明显
傅立叶光学(信息光学)_课件
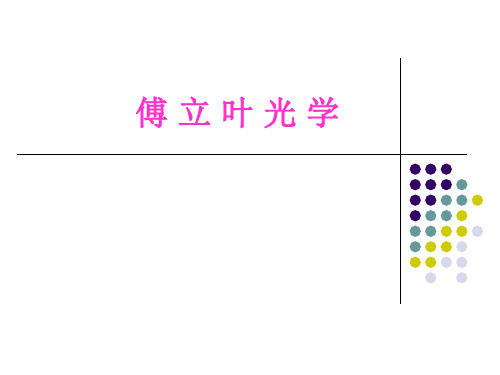
1 x>0 Step(x)= ½ x=0
0 x<0
step(x)
1
0
step(x-x0),间断点移到x0处
x
二、符号函数:描述某孔径一半宽有 的位相差
1 x>0 Sgn(x)= 0 x=0
-1 x<0
Sgn(x)=2step(x)-1
sgn(x)
1
x
0
1
三、矩形函数(门函数):表示狭缝、矩孔的透过
傅立叶光学
第一章 绪论 第二章 线性系统与Fourier分析 第三章 光波的标量衍射理论 第四章 透镜的Fourier变换性质 第五章 光学成像系统的频率响应 第七章 光学全息 第八章 空间滤波与光学信息处理
第一章 绪论
一、“信息光学”的含义 信息光学=数学工具(级数、积分)+经典光学 (光波的传播、干涉、衍射、成像、光学信息的记 录与再现、光学信号的处理)
2、光学中的线性叠加原理uv uuv uuv 波的迭加原理:矢量:E E1( p) E2( p) L
n
相干光场:复振幅:U(p)=Ui ( p) i 1
n
非相干光场:光强:I ( p) Ii ( p) i 1
3、利用系统的特性来求输入/输出关系 “三步法则”: 第一步:将复杂输入分解为简单输入函数之和 第二步:分别求出简单函数的输出 第三步:将简单函数输出加起来
2.1 线性系统的基本概念 一、系统:同类事物按一定关系所组
成的整体
特征(性):不管内部结构,只是全体与外 部的关系,是整体行为,综 合行为
二、物理系统:由一个或多个物理装
置所组成的系统
1、概念:考虑与外形的信息交换 2、内容:输入/输出关系 3、特点:系统的外特性 4、作用:对输入信号变换作用——运算作用
0 x<0
step(x)
1
0
step(x-x0),间断点移到x0处
x
二、符号函数:描述某孔径一半宽有 的位相差
1 x>0 Sgn(x)= 0 x=0
-1 x<0
Sgn(x)=2step(x)-1
sgn(x)
1
x
0
1
三、矩形函数(门函数):表示狭缝、矩孔的透过
傅立叶光学
第一章 绪论 第二章 线性系统与Fourier分析 第三章 光波的标量衍射理论 第四章 透镜的Fourier变换性质 第五章 光学成像系统的频率响应 第七章 光学全息 第八章 空间滤波与光学信息处理
第一章 绪论
一、“信息光学”的含义 信息光学=数学工具(级数、积分)+经典光学 (光波的传播、干涉、衍射、成像、光学信息的记 录与再现、光学信号的处理)
2、光学中的线性叠加原理uv uuv uuv 波的迭加原理:矢量:E E1( p) E2( p) L
n
相干光场:复振幅:U(p)=Ui ( p) i 1
n
非相干光场:光强:I ( p) Ii ( p) i 1
3、利用系统的特性来求输入/输出关系 “三步法则”: 第一步:将复杂输入分解为简单输入函数之和 第二步:分别求出简单函数的输出 第三步:将简单函数输出加起来
2.1 线性系统的基本概念 一、系统:同类事物按一定关系所组
成的整体
特征(性):不管内部结构,只是全体与外 部的关系,是整体行为,综 合行为
二、物理系统:由一个或多个物理装
置所组成的系统
1、概念:考虑与外形的信息交换 2、内容:输入/输出关系 3、特点:系统的外特性 4、作用:对输入信号变换作用——运算作用
信息光学第一章ppt

例: f(x)={
x, 0
0<x<1 其它
求 f (-2x+4)
解1: f(-2x+4)= f[-2(x-2)],包含折叠、压缩、平移
先折叠
再压缩
f(x)
f(-x)
f(-2x)
0 1 x -1 0 x
-1/2 0 x
最后平移
f[-2(x-2)]
0 3/2 x
11
解2: 根据已知条件有
f
(2x
4)
x a/2
其它
应用:单缝透过率、门函数、时间脉冲波形.
标准型:
1 x 1/ 2
rect(x)
0
else
15
y
0
x0
a
x
rect ( x x0 ) a
16
17
18
2 sinc函数 应用:单缝或矩形孔的夫琅和费衍射的振幅分布
强度分布为sinc函数平方
注意归一化和非归一 化的两种表达方法。
xa / 2
原函数f(x)在某点x的值卷积后用某一段(x-a/2, x+a/2) 的积分值来表示, 等价于这段区间的平均值。
50
卷积的运算性质
交换律:f (x) h(x) h(x) f (x) 分配律:[aw(x) bv(x)] h(x) aw(x) h(x) bv(x) h(x) 分配律体现了卷积的线性特性。 结合律:[v(x) w(x)] h(x) v(x) [w(x) h(x)] 可分离变量特性: 如果参与卷积的两个函数是可分离的, 其 二维卷积也是可分离的。(极坐标和直角坐标)
1 a
1 a
当a 0时, (ax)dx lim m (ax)dx lim am (ax)d ax
《信息光学》课件

信息光学的发展历程
19世纪末至20世纪初
光学显微镜和望远镜等光学仪器的发明和应用,为信息光学的发展 奠定了基础。
20世纪中叶
随着激光技术的出现和发展,信息光学开始进入快速发展阶段。
20世纪末至今
随着计算机技术和光电子技术的不断进步,信息光学在通信、数据 存储、生物医学等领域得到了广泛应用。
信息光学的基本原理
02
信息光学的基本技术
光学全息技术
光学全息技术是一种利用光的干涉和衍射原理来记录和再现 三维物体的技术。通过将物体发出的光波与参考光波干涉, 将干涉图样记录在全息介质上,然后使用合适的照明光波进 行再现,即可得到物体的三维图像。
全息技术可以用于制作全息图、全息显示、全息干涉计量和 全息光学元件等。在科学研究、工业检测、医疗诊断和军事 领域等方面有广泛应用。
光学信息处理技术
光学信息处理技术是指利用光的干涉、衍射和折射等光学现象来进行信息处理的 技术。这种技术具有高速、大容量、并行处理等优点,可以用于图像处理、信号 处理、模式识别和计算机科学等领域。
常见的光学信息处理技术包括傅里叶变换光学、光学图像处理、光学计算和光学 神经网络等。
光学计算技术
光学计算技术是指利用光学方法来实现计算的技术。这种 技术利用了光的并行性和快速性,可以实现高速、高精度 和大容量的计算。
运行,为人工智能领域的发展提供新的动力。
信息光学在未来的应用前景
下一代光通信网络
随着5G、6G等通信技术的发展,信息光学将在构建下一代光通信 网络中发挥关键作用,实现超高速、超大规模的数据传输。
智能感知与物联网
光学传感器和光通信技术将在智能感知和物联网领域发挥重要作用 ,实现更高效、更智能的物联网应用。
《信息光学》课件

第二章:光学矩阵理论
光学矩阵是描述光学元件的传输特性的数学工具。学习光学矩阵的定义、表示方法、性质和计算方法,以及如 何通过光学矩阵推导光学元件的传输特性。
第三章:信息光学器件
光波导器件
光波导器件是利用光波导的特性来传输和处理信息的器件,包括光纤和光波导芯片。
光栅器件
光栅器件利用光栅结构的衍射特性来处理信息,例如光栅衍射和光栅激光器。
结束语
感谢大家的聆听与支持!在未来,信息光学将在通信、计算、存储等领域有 更广泛的应用,让我们Байду номын сангаас起探索信息光学的无限可能。
闪烁光记录器
闪烁光记录器是一种使用光固体材料记录和存储信息的高密度光存储设备。
第四章:信息光学应用
光学通信
光学通信是利用光信 号传输信息的通信方 式,具有高速、大容 量和低损耗的优势。
光存储
光存储技术利用光的 特性进行信息的高密 度存储,如光盘和固 态存储器。
光量子计算
光量子计算利用光的 量子特性进行高速并 行计算,被认为是未 来计算科学的重要方 向。
《信息光学》PPT课件
欢迎大家来到《信息光学》PPT课件!本课程将带领您探索信息光学的世界, 学习信息光学的概念、原理和应用,为您展示信息光学的魅力。
第一章:信息光学概述
信息光学是研究光与信息传输、处理和存储的学科,涉及广泛的应用领域。了解信息光学的定义、研究内容以 及与其他学科的关系,将打开信息光学的大门。
光晶体管
光晶体管是一种利用 光调控电流和电压的 器件,具有高速、低 功耗和可重构性。
第五章:信息光学前沿研究
1
研究热点
了解当前信息光学领域的研究热点,如全息影像、量子信息和高速光通信等。
信息光学PPT课件

平行于yo轴的狭缝在像面上产生的相干线扩散函数为相干传递
函数沿方向的逆变换
L xiF 1 {H ,0}
在衍射受限系统中相干传递函数可以用孔经函数表达
L xi F 1 { P ( d i ,0 )}
无论孔径形状如何,在一个方向的截面总是一个矩形。因此 L(xi)将
呈sinc20函21/3数/9 变化。
3.3.2相干线扩散函数和边缘扩散函数
传递函数测量方法
a. 测量系统的点扩散函数,再通过傅里叶变换得到传递函数。 b. 输入大量不同本征函数到系统,并确定每个本征函数
所受到的衰减和相移。 c. 由线扩散函数确定传递函数
2021/3/9
授课:XXX
1
1.线扩散函数与边缘扩散函数的概念
在相干光照明时,一个点物在像面上造成的强度分布即为点 扩散函数h(xi,yi)。位于轴上的物点产生的像是圆对称的。通过一 条过中心的狭缝观察像斑,得到强度分布曲线h(xi)作为沿xi的点 扩散函数。
Exi
xi Ld
即
Lxi
dExi
dxi
2021/3/9
授课:XXX
4
边缘扩散函数的另一种表述
系统输入一阶跃函数,如直边或刀口形成的光分布。系统 的输出叫阶跃响应或边缘扩散函数。
E(xi ) step(xi )h(xi, yi)
h(,)step(xi )dd
h(,
)dstep(xi
)d
L
step(xi
)d
xi Ld
2021/3/9
授课:XXX
L(xi) h(xi,5 )d
1. 相干线扩散函数和边缘扩散函数
相干照明下,狭缝在像面上产生的复振幅分布就是相干线扩 散函数。由
Chap4-3——信息光学课件PPT

exp j
k 2f
1
d0 f
(
x
2 f
y
2 f
)
fx
xf
f
1
exp
jk
(
x
2 f
y
2 f
)
2 f
fy
yf
f
exp
jk
(
x
2 f
y
2 f
2d
)
exp
jk
(
x
2 f
2f
y
2 f
)
fx
xf d
,
fy
yf d
fx
xf
f
,
fy
yf
f
照明光源
?
(5)?
的像面
§4-2 透镜的傅里叶变换性质
§4-2 透镜的傅里叶变换性质: 小结
Summary
照明光源 位置
轴上无穷远 点源
同上
同上
同上
同上 轴上有限远
点源
物平面 位置 透镜前,与透 镜距离为d0 特例: d0= f 特例d0= 0
物体紧靠透镜
透镜后, 后 焦面前d处
特例: d= f
透镜后
谱面 位置
二次位相 因子
频谱缩放 比例
后焦面 后焦面 后焦面 后焦面 后焦面
lL 2d0
0
M
l
d0
f
则衍射波完全能通过透镜, A,B点能准确反映t的频谱值.
A
O z
B
若 tan
tan M
lL 2d0
则衍射波完全不能通过透镜, A,B 处频谱值消失
若< <M, 则A,B点的复振幅不能准确反映相应的频谱值.
信息光学第08章ppt

光密度也称为黑度,等于透射率的倒数的对数,即
1 D lg T
在线性吸收条件下 D 2 L lg e 0.869 L 光密度的测量通常采用平行光束,分别测出入射光强和透射光强,相除后取 对数即可得光密度之值。
6. E D 曲线
通常用 E D 曲线描述照片光密度与曝光量对数之间的关系曲线来表示 其曝光特性,称为 E D曲线。下图所示的是负片的典型曲线,显然它是非 线性的,但当曝光量小于ET时,光密度与曝光量无关,并且等于一个极小 值,称为灰雾。在曲线的趾部,密度开始随曝光量的增加而增加,其后是一 个密度与曝光量的对数成线性关系的区域,该区域的直线斜率称为胶片的值。 在线性区,密度与曝光量的关系可以表示为
1962年苏联科学家丹尼苏克(U. Denisyuk)提出了反射全息图 的方法,第一次用普通的白炽灯照明全息图观察全息像。由于脉冲 红宝石激光器可辐射持续时间很短(短到几个纳秒)的强脉冲激光, 这样,人们开始用激光脉冲全息记录运动的物体,如飞行子弹、喷 射微粒、飞虫等,该方法后来开创了激光脉冲全息人物肖像的应用。 1965年,鲍威尔(R. L. Powell)、斯泰特森(K. A. Stetson)提出全息 干涉术,物体施加应力前后经两次全息曝光,再现的全息像上的等 高线显示物体变形的状况,这在材料的无损检测、流场分析等方面 得到应用。1968年,本顿(S. A. Benton)发了彩虹全息术,这一发 明可用白光观察全息图,看到记录物体的彩虹图,这是全息术的重 要进展。 由于激光再现的全息图失去了色调信息,人们开始致力于研究 第三代全息图。第三代全息图是利用激光记录和白光再现的全息 图,例如反射全息、像全息、彩虹全息及模压全息等,在—定的条 件下赋予全息图以鲜艳的色彩。
8.1.5 基本术语
1 D lg T
在线性吸收条件下 D 2 L lg e 0.869 L 光密度的测量通常采用平行光束,分别测出入射光强和透射光强,相除后取 对数即可得光密度之值。
6. E D 曲线
通常用 E D 曲线描述照片光密度与曝光量对数之间的关系曲线来表示 其曝光特性,称为 E D曲线。下图所示的是负片的典型曲线,显然它是非 线性的,但当曝光量小于ET时,光密度与曝光量无关,并且等于一个极小 值,称为灰雾。在曲线的趾部,密度开始随曝光量的增加而增加,其后是一 个密度与曝光量的对数成线性关系的区域,该区域的直线斜率称为胶片的值。 在线性区,密度与曝光量的关系可以表示为
1962年苏联科学家丹尼苏克(U. Denisyuk)提出了反射全息图 的方法,第一次用普通的白炽灯照明全息图观察全息像。由于脉冲 红宝石激光器可辐射持续时间很短(短到几个纳秒)的强脉冲激光, 这样,人们开始用激光脉冲全息记录运动的物体,如飞行子弹、喷 射微粒、飞虫等,该方法后来开创了激光脉冲全息人物肖像的应用。 1965年,鲍威尔(R. L. Powell)、斯泰特森(K. A. Stetson)提出全息 干涉术,物体施加应力前后经两次全息曝光,再现的全息像上的等 高线显示物体变形的状况,这在材料的无损检测、流场分析等方面 得到应用。1968年,本顿(S. A. Benton)发了彩虹全息术,这一发 明可用白光观察全息图,看到记录物体的彩虹图,这是全息术的重 要进展。 由于激光再现的全息图失去了色调信息,人们开始致力于研究 第三代全息图。第三代全息图是利用激光记录和白光再现的全息 图,例如反射全息、像全息、彩虹全息及模压全息等,在—定的条 件下赋予全息图以鲜艳的色彩。
8.1.5 基本术语
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
*d1combxd1
rectxb1
=m=-rectx1
-amdrectxb1
Ffx=asincafx•com bdfx*bsincbfx
=a dbm = -sincad msincbfxm d
讨论
1.狭缝滤波器只让零级谱通过,这时有m=0
FfxH fx=a d bsin cbfx
于是,在输出平面上的像场分布为
故改变滤波函数就能改变物图像的空间频谱结构。
其他的空间滤波系统
点光源 点光源 点光源
P2面上给出的物 频谱不是物函数 准确的傅里叶变 换,带有位相因 子。
五、空间滤波的傅里叶分析
现将一维光栅置于4f 系统输入面,采用傅里叶分析方 法分析空间滤波过程。一维光栅的透过率为:
其频谱为:
f
x1=rectxa1
讨论:
输出平面上的像场分布为:
gx3=F 1FfxHfx
=darectxb3
dasincdarect
x3 b
ei2xd3
-i2x3
e d
=darect
x3 b
12sincdacos2dx3
受到余弦函数的调制, 频率是1/d。
出现同周期结构,像的 对比度降低了。
讨论
3.双缝滤波器,仅允许±2级谱通过 m=±2
二、阿贝二次成像理论
像面
物
面
频谱面
图6.1.1 阿贝二次成像理论示意图
阿贝认为透镜的成像过程可分为两步: (1)物波在透镜后焦面形成频谱;分解 (2)这些频谱成为新的次波源,由他们发出的次波在 像平面上干涉叠加形成物的像。 合成
阿贝二次成像理论 的真正价值:
提供了一种新的频 谱语言来描述信息,用 改变频谱的手段来改造 信息。
空间滤波发展简史
阿贝二次成像理论(1873) 泽尼克相衬显微术(1935) 杜费《傅里叶变换及其在光学中的应用》出版(1946) 艾里斯等人经典论文“光学过程的傅里叶处理方
法”(1952)、“光学与通信理论”(1953)、“光学中 的空间滤波”(1956)相继发表 范德·拉格特提出复数空间滤波的概念(1964) 从而使光学信息处理进入了一个广泛应用的新阶段。
gxቤተ መጻሕፍቲ ባይዱ=F1FfxHfx
=darectxb3
像平面上未出现强度起伏。
讨论
2.狭缝增宽到只允许0级和±1级谱通过m=0,±1
F fx H fx = a d b s in c b fx s in c d a s in c b fx d 1 s in c d a s in c b fx d 1
第6章 空间滤波
Spatial Filtering
1 空间滤波的基本原理 2 空间滤波器的结构类型和应用举例
6.1空间滤波的基本原理
一 空间滤波的意义
光学信息处理:用光学方法实现对输入信息实施 某种运算或变换,已达到对感兴趣的信息进行提取、 编码、存储、增强、识别和恢复等目的。
空间滤波:指在光学系统的傅里叶频谱面上放置 适当的滤波器,以改变光波的频谱结构,使其像按照 人们要求得到预期的改善。据此,发展了光学信息处 理技术。
H *fx ,fy= H * λ x f 2,λ y f 2 = Fh *-x 1 ,-y 1
则在输出面上产生的光场(在反射坐标下)为:
gx 3 ,y 3 F - 1G fx ,fyH *fx ,fy g x 3 ,y 3 h x 3 ,y 3
I x 3 ,y 3 g x 3 ,y 3 h x 3 ,y 3 2
F f x H f x = a d b s in c 2 d a s in c b f x d 2 s in c b f x d 2
讨论:
在输出平面上的像场分布为:
gx3=F1FfxHfx
=2dasinc2darectxb3cos2dx23
率值越来越高。且较小的物结构对应较高的空间频率。
三、空间频谱分析系统
(2)方向特性: 物的线状结构与其
功率谱扩展方向正交, 且物图像中线状结构越 密集,则其功率谱延伸 越远;反之亦然。
图6.1.4 线状结构 (a)和频谱的方向特性(b)
(3)对称特性: 光学图像(实函数)的频谱具有厄米特函数特性:
F f x ,f y= F * - f x , - f y F f x ,f y2 = F - f x , - f y2
即频谱面上的功率谱呈中心对称分布。
四、空间频率滤波系统——4f 系统
空间频率滤波系统是相干光学信息处理中一种最简单的处 理方式,它利用了透镜的傅里叶变换特性,把透镜作为一个频 谱分析仪,并在其频谱面上通过插入适当的滤波器,借以改变 物的频谱,从而使物图像得到改善。
为了验证此理论, 阿贝(1873年)、波特 (1905年)分别成功地做了 实验:阿贝-波特实验
图6.1.2 阿贝-波特实验原理图
三、空间频谱分析系统
图6.1.3 频谱分析系统光路图
频谱面上的功率谱分布具有特征:
(1)频率特性:
fx
=
x2 λf
,
fy
=
y2 λf
中心的空间频率值为零,由中心点向外其空间频
则在输出面上产生的光场(在反射坐标下)为:
g x 3 ,y 3 F - 1G fx ,fyH fx ,fy g x 3 ,y 3 * h x 3 ,y 3
I x 3 ,y 3 g x 3 ,y 3 * h x 3 ,y 3 2
四、空间频率滤波系统——4f 系统
(2)若在频谱面上插上滤波器: 匹配滤波器
像的结构为余弦振幅光 栅,但其周期为无周期 的一半,则频率是2/d。
讨论:
4.小圆屏滤波器,仅挡掉零级频谱而允许其余频谱全 部通过。
F fx H fx= F fx a d b s in c b fx
4f 系统
点 源
准直 物平面
频谱面
像面
四、空间频率滤波系统——4f 系统
设输入物的复振幅透过率为g (x1 , y1),则它在频 谱面上的频谱函数为:
G fx,fy= F g x 1 ,y 1
四、空间频率滤波系统——4f 系统
GH
(1)若在频谱面上插上滤波器:
滤波器的脉冲响应函数
H fx,fy= H λ x f 2,λ y f 2 = Fh x 1 ,y 1
