博弈论 第 三 章 完全信息动态博弈
第3讲 完全信息动态博弈

最优化的一阶条件意味着: s(q1) (a q1 c) =1 2 2
第3讲 完全信息动态博弈
假定q1 a c。这实际上是库诺特模型中企业2的反应函数,不同的 是,这里,s(q1)是当企业1选择q1时企业2的实际选择,而在库诺 2 特模型中,R2 q1)是企业2对于假设的q1的最优反应。 ( 因为企业1预测到企业2将根据s(q1)选择q 2,企业1在第一阶段的问 2 题是: max 1 = q1,s(q1)=q1 a q1 s(q1) c) ( 2 2
第3讲 完全信息动态博弈
• 这个例子也说明,在博弈中,拥有信息优势可能 使参与人处于劣势,而这在单人决策中是不可能 的。企业2在斯坦克尔伯格博弈中的利润之所以低 于库诺特博弈中的利润,是因为它在决策之前就 知道了企业1的产量。即使企业1先行动,但如果 企业2在决策之前不能观测到企业1的产量,我们 就回到了库诺特均衡,因为此时,企业1的先动优 势就不存在了。
第3讲 完全信息动态博弈
* 1 回忆一下,在上一讲得到的库诺特模型的纳什均衡是q1 =q* = (a c), 2 3 3 比较这两个结果,发现斯坦克尔伯格均衡的总产量 (a c)大于库诺特 4 2 的总产量 (a c)。但是,企业1的斯坦克尔伯格均衡产量大于库诺特 3
均衡产量,而企业2的斯坦克尔伯格均衡产量小于库诺特均衡产量。 因为企业1本来可以选择库诺特均衡产量但它没有选择,说明企业1在斯坦 克尔伯格博弈中的利润大于库诺特博弈中的利润,而总产量上升意味着 总利润下降了从而企业2的利润一定下降了。这就是所谓的“先动优势”。
第3讲 完全信息动态博弈
• 宏观经济政策的动态一致性 宏观经济学上与子博弈精炼纳什均衡相对应的概 念是政府政策的动态一致性(dynamic consistency 或time consistency)。政府政策 的动态一致性指的是,一个政策不仅在制定阶段 应该是最优的(从政府的角度),而且在指定之 后的执行阶段也应该是最优的,假设没有任何新 的信息出现。如果一个政策只是在制定阶段是最 优的,而在执行阶段并不是最优的,这个政策就 是动态不一致的。说它是动态不一致的,是因为
北京大学博弈论课件第3章-完全信息动态博弈

和“进入”。因此,从初始节点处引出两条线段,在两条线段旁分别标识“不进 入”和“进入”。 ❖ 当潜在进入者选择结束后,达到在位者的节点。 ❖ 在位者有两个选择:“斗争”和“默许”。 ❖ 因此,从在位者的节点处引出两条线段,在两条线段旁分别标识“斗争”和“默 许”。
❖ 博弈树中每个节点都独立构成一个信息集,没有虚线连接两个或多个博弈树节点。 ❖ 求解完全且完美信息动态博弈的重要方法之一是:逆向归纳法。 ❖ 可以通过“海盗分宝博弈”这个生动有趣的故事对“逆向归纳法”进行一个直观
介绍。
一、海盗分宝博弈
❖ 1.海盗分宝博弈的规则 ❖ 五个海盗首先进行抽签,确定决策顺序。 ❖ 五个海盗按照决策顺序依次提出对 100 个金币的分配方案。 ❖ 第一个海盗提出一个分配方案,如超过半数的海盗(包括提出分配方案的海盗)
2021/8/1
POWERPOINT TEMPLATE POWERPOINT TEMPLATE POWERPOINT TEMPLATE POWERPOINT TEMPLATE POWERPOINT TEMPLATE POWERPOINT TEMPLATE
第三章 POWERPOINT TEMPLATE
❖ 在完全信息动态博弈中,博弈参与者的行动存在先后顺序。 ❖ 可以用博弈树表示完全信息动态博弈。 ❖ 可以通过逆向归纳法求解完全信息动态博弈的子博弈精炼纳什
均衡,剔除不可置信的威胁。
第一节 完全信息动态博弈概述
❖ 一、完全信息动态博弈的定义 在完全信息静态博弈中,博弈参与者同时采取行动。但在完全信息动 态博弈中,博弈参与者的行动存在先后顺序。从信息角度上,完全信息 动态博弈与完全信息静态博弈类似,博弈参与者对博弈结构、博弈顺序、 双方收益等信息都具备完全了解。
第三章信息经济学的研究方法—博弈论

第一节 概述-人生处处皆博弈
人生是永不停歇的博弈过程,博弈意 略达到合意的结果。
作为博弈者,最佳策略是最大限度地 利用游戏规则,最大化自己的利益;
作为社会最佳策略,是通过规则使社 会整体福利增加。
一、博弈论的定义
博弈论(game theory,又译为对策论,游戏论)
定义:研究决策主体的行为在直接相互作用时,人们如 何进行决策、以及这种决策如何达到均衡。
五、博弈论与信息经济学
博弈论是给定信息结构求均衡结果,它实际上是一种均衡理论, 我们最终要找的是一个均衡的结果,博弈论是方法论导向的, 它实际上是一种解决问题的方法。它是一个实证的方法。
信息经济学是给定信息结构求契约的安排。它实际上是一种契 约设计理论,它是问题导向的。它是一个规范的方法。
石匠的决策与拳击手的决策的区别
一、博弈论的定义
2、理性人假设 理性人是指一个很好定义的偏好,在面临给定的约束条件下
最大化自己的偏好。
博弈论说起来有些绕嘴,但理解起来很好理解,那就是 每个对弈者在决定采取哪种行动时,不但要根据自身的利益 和目的行事,而且要考虑到他的决策行为对其他人可能的影 响,通过选择最佳行动计划,来寻求收益或效用的最大化。
(一)囚徒困境
假定: (1)每个局中人都知道博弈规则和博弈结果的支付
矩阵; (2)每个局中人都是理性的(个人理性和个人最优
决策); (3)不能“串通”
(一)囚徒困境——纳什均衡
囚徒A
坦白
坦白 囚徒 B
-8,-8
抵赖 -10,0
抵赖 0,-10 -1,-1
-8大于-10 0大于-1
(坦白,坦白)是纳什均衡
第三章 信息经济学的研究方法 ——博弈论
博弈论 第 三 章 完全信息动态博弈讲解

房地产开发博弈
开发
A hA(1) 不开发
h表示信息集
N hN(1)
需求大
需求小
N hN(2)
需求大
需求小
B hB(1)
开发
不开发
B hB(2)
B hB(3)
开发
不开发 开发 不开发 开发
B hB(4)
不开发
(4,4)
(8,0) (-3,-3)
(1,0) (0,8) (0,0) (0,1) 单 位:百万元
定 义 一 个 展 开 式 博 弈 的 子 博 弈G 由 一 个 决 策 结x 和 所 有 该 决 策 结 的 后继结T(x)( 包 括终点结0 组 成, 它 满 足 下 列 条 件:⑴x 是 一 个 单 点 信 息 结即h(x)={x};⑵对于所有的 x′∈T(x),如果x″∈h(x′),则x″∈T(x)。
(3)
N
1/3
2/3
1
Y1
z1
1
x1
w1
(2,6) (5,6)
2
2
a2 (9,0)
b2 (0,3)
a2 (9,5)
b2 (0,3)
3.3 子 博 弈 与 子 博 弈 完 美
Nash 均衡在原则上适用所有的博弈,但对于预 测 参与人的行为来说,Nash均衡可能并不是 一个 合理的预测, 如房地产博弈:
A
开发
不开 发
A
开发
不开发
B
B
B
B
开发 不开发 开发 不开发 开发 不开发 开发
不开发
有了信息集的概念, 展开式表示也可以用来表 示静态博弈, 如“囚徒的困境 ”博弈可以表 示为:
1
坦白
2
最新博弈论-完全信息动态博弈3

在重复博弈的每个阶段博弈中,参与人可同时 行动,也可不同时行动。在后一情形中,每一 阶段博弈本身就是一个动态博弈。
影响重复博弈均衡结果的主要因素:
博弈的重复次数:参与人可能为了长期利益 而牺牲眼前利益从而选择不同的均衡策略。
信息的完备性:当一个参与人的支付函数不 为其他人所知时,该参与人可能有积极性建立 一个好的声誉以换取长远利益(声誉模型)。
预期
若参与人均有这样的预期,若第一阶段出现合作 (M1,M2),则第二阶段预期的纳什均衡是(R1, R2),若第一阶段出现其他结果,则第二阶段预期 的纳什均衡是(L1,L2)。 考虑策略:参与人1(2)在第一阶段首先选择M1 (M2);在第二阶段,若第一阶段的博弈结果是 (M1,M2),则第二阶段选择合作的纳什均衡策略 R1( R2),否则选择惩罚的纳什均衡策略L1 (L2)。 该策略是一个子博弈精炼纳什均衡。
连锁店悖论
首先考虑第100个市场,在博弈最后阶段,斗争已没有 任何意义,在位者将默许,进入者将选择进入。
再考虑第99个市场,因为不论在位者选择什么行动, 第100个市场的均衡结果不受影响,在位者的最优选择 仍然是默许。
如此一直倒推回去,得到该博弈的唯一的子博弈精炼 纳什均衡是在位者在每一个市场上都选择默许,进入 者在每一个市场上选择进入。
阶段
参 与 人
L1 M1
1 R1
L2 1,1 0,5 0,0
L2 4,4 3,8 3,3
参与人2
M2 5,0 4,4 0,0 参与人2
M2 8,3 7,7 3,3
R2 0,0 0,0 3,3
R2 3,3 3,3 6,6
参与人有动机实施惩罚的例子
L2
M2
R2
P2
完全信息动态博弈

-3 1
-3, 0,
-3 0
1, 0,
0 1
1, 0,
0 0
这里有3个纯战略Nash均衡,分别是 {开发,{不开发,开发}} (均衡结果:A
14
开发,B不开发) {开发,{不开发,不开发}} {不开发,{开发,开发}} 在每一个均衡,给定对方的战略,自己 的战略是最优的(效用最大) 均衡结果是(开,不开) , (开,不开) , (不开,开) 。注意均衡与均衡结果不同。 一般定义:扩展式博弈的战略 令 H i 为第 i 个参与人的信息集的集合,
1
选择什么行动, 而不是简单的, 与环境无关的 行动选择。 为了说明,我们考虑房地产开发博弈的 例子。有两个开发商A和B,互为竞争对手,决 定是否进行房地产开发。但他们不是同时行 动,且后行动者可以观察到先行动者的行动。 假定博弈的行动顺序如下: (1)开发商A先行 动,选择开发或不开发; (2)在A决策后,自 然选择市场需求大小; (3) 开发商B在观察到A 的决策和市场需求(自然的行动)后,决定开 发或不开发。 如图是房地产开发博弈的博弈树。
4
路径: (path)从初始结到终点结,由结 和枝所组成的系列。 扩展式 (extensive form) 是对博弈的一种描述,满足以下条件: (1)由结和枝组成的整体结构,由单个 起始结开始到终点结, 中间无闭合的圈。 即没 有以下结构
11
1
(所有前列结全排序) (2)必须说明每个结点属于某个参与人。 (3)在自然选择的结上,有自然选择不同 枝的概率。 (4)有划分每个参与人的结的信息集。 (每个信息集是决策结集合的一个子集, 满足 (a)每个决策结都是同一个参与人的决
11
1
U 2 L R L R 1 D
第三讲 完全信息动态博弈
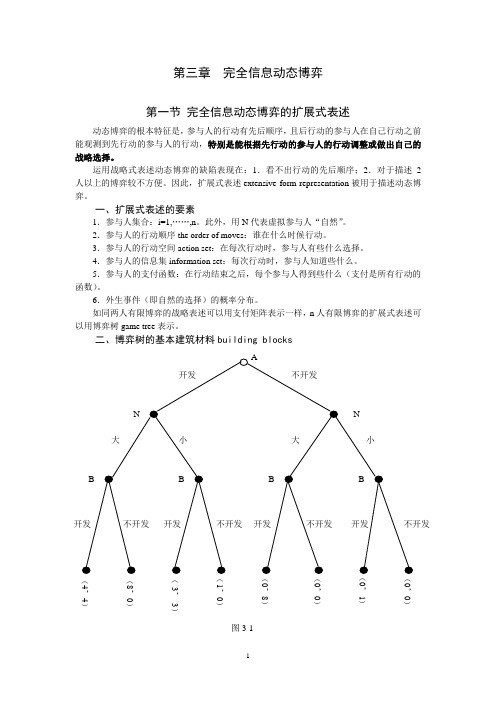
第三章完全信息动态博弈第一节完全信息动态博弈的扩展式表述动态博弈的根本特征是,参与人的行动有先后顺序,且后行动的参与人在自己行动之前能观测到先行动的参与人的行动,特别是能根据先行动的参与人的行动调整或做出自己的战略选择。
运用战略式表述动态博弈的缺陷表现在:1.看不出行动的先后顺序;2.对于描述2人以上的博弈较不方便。
因此,扩展式表述extensive form representation被用于描述动态博弈。
一、扩展式表述的要素1.参与人集合:i=1,……,n。
此外,用N代表虚拟参与人“自然”。
2.参与人的行动顺序the order of moves:谁在什么时候行动。
3.参与人的行动空间action set:在每次行动时,参与人有些什么选择。
4.参与人的信息集information set:每次行动时,参与人知道些什么。
5.参与人的支付函数:在行动结束之后,每个参与人得到些什么(支付是所有行动的函数)。
6.外生事件(即自然的选择)的概率分布。
如同两人有限博弈的战略表述可以用支付矩阵表示一样,n人有限博弈的扩展式表述可以用博弈树game tree表示。
二、博弈树的基本建筑材料building blocks(4,4)(8,)(-3,-3)1,),8),),1),)图3-1(一)结nodes1.结的分类(1)决策结decision nodes:参与人采取行动的时点。
包括:起点结——initial nodes非起点结——(2)终点结terminal nodes:博弈行动路径的终点。
2.结的顺序关系precedence relation用X表示所有结的集合,x∈X表示某个特定的结。
x≺x"表示“x在x"之前”≺3.前列集the set of predecessors和后续集the set of successors定义P(x)为在x之前的所有结的集合,简称为x的前列集;定义T(x)为x之后的所有结的集合,简称为x的后续集。
经济博弈论_谢识予_2_完全信息动态博弈0.1

单结信息集:只包含一个决策结的信息集 完美(Perfect)信息:博弈树的所有信息都是单结的。 ——博弈中没有任何参与人同时行动,且后行动者能观察到先 行动者的行动,且所有参与人观察到N的行动)
1 动态博弈的扩展式表述
静态博弈用扩展式表述 A
坦白 抵赖 坦白
Q:何为完 全信息? B
抵赖
囚 徒 困 境 博 弈
-3,-3 -4,-3
-3,-3 0,0
1,-2 -4,-3 割耳
1,-2 0,0 (-3,-3) (1,-2) 默认 割耳 (-4,-3) (0,0)
三个NE: (不画,{割耳,默认}) (画,{默认,割耳}) (画,{默认,默认})
画 小孩 不画
父亲
父亲
默认
4 NE的缺陷——不可置信的威胁
换句话说,与抽烟有关决策不是单人在中性环境中 的决定,而是一种博弈。“今日卡门”和不同偏好的卡 门自己,即“未来卡门”间的博弈。
5 逆向归纳法
继续抽 未来的 卡门 不抽 今天的卡门
-1,1
1,-1
0,0 两个“卡门”如何行事? 未来卡门如何行事? 考虑到未来卡门的未来行动,今日卡门今日如何行事?
2 动态博弈中的策略
博弈树中参与人在结点上所选择的单个行动—— 一步/招 (move)
美中军事博弈
但是,参与人可以制定一个行动计划,将每个决策结上 的选择都事先规定好,即使这个决策点实际上不会出 美国 现。——策略
中国 中国
策略: 人不犯我、我不犯人; 人若犯我、我必犯人
不犯人
(-2,-2) (2,-4) (3,-5) (0,0)
4 NE的缺陷——不可置信的威胁
博弈论——完全信息动态博弈

博弈论——完全信息动态博弈2 完全信息的动态博弈2.1完全和完美信息的动态博弈动态博弈(dynamic game):参与⼈在不同的时间选择⾏动。
完全信息动态博弈指的是各博弈⽅先后⾏动,后⾏动者知道先⾏动者的具体⾏动是什么且各博弈⽅对博弈中各种策略组合下所有参与⼈相应的得益都完全了解的博弈静态博弈习惯⽤战略式(Strategic form representation)表述,动态博弈习惯⽤扩展式(Extensive form representation)表述。
战略式表述的三要素:参与⼈集合、每个参与⼈的战略集合、由战略组合决定的每个参与⼈的⽀付。
扩展式表述的要素包括:参与⼈集合、参与⼈的⾏动顺序、参与⼈的⾏动空间、参与⼈的信息集、参与⼈的⽀付函数、外⽣事件(⾃然的选择)的概率分布。
n⼈有限战略博弈的扩展式表述⽤博弈树来表⽰1(1,2) (0,3)①结:包括决策结和终点结。
决策结是参与⼈采取⾏动的时点,终点结是博弈⾏动路径的终点。
第⼀个⾏动选择对应的决策结为“初始结”,⽤空⼼圆表⽰,其它决策结⽤实⼼圆表⽰。
X表⽰结的集合,x X表⽰某个特定的结。
z表⽰终点结,Z表⽰终点结集合。
表⽰结之间的顺序关系,x x′表⽰x在x′之前。
x之前所有结的集合称为x的前列集,x之后所有结的集合称为x的后续集。
以下两种情况不允许:前者违背了传递性和反对称性;后者违背了前列节必须是全排序的。
在以上两个假设之下,每个终点结都完全决定了博弈树的某个路径。
②枝:博弈树上,枝是从⼀个决策结到其直接后续结的连线,每⼀个枝代表参与⼈的⼀个⾏动选择。
在每⼀个枝旁标注该具体⾏动的代号。
⼀般地,每个决策结下有多个枝,给出每次⾏动时参与⼈的⾏动空间,即此时有哪些⾏动可供选择。
③信息集(information sets):博弈树中某⼀决策者在某⼀⾏动阶段具有相同信息的所有决策结集合称为⼀个信息集。
博弈树上的所有决策结分割成不同的信息集。
每⼀个信息集是决策结集合的⼀个⼦集(信息集是由决策结构成的集合),该⼦集包括所有满⾜下列条件的决策结:(1)每⼀个决策结都是同⼀个参与⼈的决策结。
博弈论与信息经济学讲义5
• • •
一 博弈扩展式表述 二 子博弈精练纳什均衡
扩展式表述博弈的纳什均衡
子博弈精练纳什均衡 用逆向归纳法求子搏弈精练纳什均衡
•
•
承诺行动与子搏弈精练纳什均衡
逆向归纳法与子搏弈精练纳什均衡的存在问题
三 应用举例
博弈的划分
博弈的划分: 从参与人行动的先后顺序:静态博弈和动态博弈
静态博弈:参与人同时选择行动或非同时行动但后 行动者并不知道前行动者采取了什么具体行动;
不开发
B
开发
x
不开发
B
开发
x’
不开发
(-3,-3)
(1,0) (0,1)
(0,0)
扩展式 A
开发
不开发
纳什均衡与均衡结果:
存在三个纯战略纳什均衡: (不开发,(开发,开发)), (开发,(不开发,开发), (开发,(不开发,不开发)) 两个均衡结果: (开发,不开发) (不开发,开发)
• • • • •
一 博弈扩展式表述 二 子博弈精练纳什均衡
扩展式表述博弈的纳什均衡 子博弈精练纳什均衡 用逆向归纳法求子搏弈精练纳什均衡 承诺行动与子搏弈精练纳什均衡 逆向归纳法与子搏弈精练纳什均衡的存在问题
三 应用举例
战略的表述
战略:参与人在给定信息集的情况下选择行动的规则, 它规定参与人在什么情况下选择什么行动,是参与人 的“相机行动方案”。
开发
若A先行动,B在知道A的行动后行动,则A 有一个信息集,两个可选择的行动,战略 空间为:(开发,不开发); B有两个信息集,四个可选择的行动,B有 四个纯战略: 开发策略:不论A开发不开发,我开发; 追随策略:A开发我开发,A不开发我不开 发; 对抗策略:A开发我不开发,A不开发我开 发; 不开发策略不论A开发不开发我不开发, 简写为: (开发,开发),(开发,不开发), (不开发,开发),(不开发,不开发), 括号内的第一个元素对应A选择“开发”时 B的选择,第二个元素对应A选择“不开发” 时B的选择。
信息经济学第三章博弈论

目录
• 博弈论基本概念 • 完全信息静态博弈 • 完全信息动态博弈 • 不完全信息静态博弈 • 不完全信息动态博弈 • 博弈论在信息经济学中应用
01
博弈论基本概念
博弈论定义与特点
博弈论是研究决策过程中参与者之间 相互作用和影响的理论。
博弈论的特点包括:参与者之间的相 互影响、策略的选择和收益的分配。
混合策略在静态博弈中应用
混合策略定义
在静态博弈中,参与人选择以一定的概率分布随机选择不同策略的 行为。
应用场景
当参与人无法确定对手的策略选择时,采用混合策略可以增加对手 的不确定性,从而提高自身的期望收益。
示例
在石头、剪刀、布游戏中,每个参与人随机选择出拳的策略就是一 种混合策略的应用。
信号传递机制在静态博弈中作用
如环保税、碳交易制度等。
案例:拍卖、招标等经济活动中的博弈论应用
拍卖中的博弈论
拍卖是一种典型的博弈论应用场景,通过竞价机制实现资源的有效配 置。常见的拍卖方式有英式拍卖、荷兰式拍卖、密封拍卖等。
招标中的博弈论
招标是一种采购方式,通过竞争机制引导供应商提供优质的商品和服务。招标 过程中需要考虑价格、质量、信誉等多个因素,博弈论可以帮助制定有效的招 标策略。
机制设计原理及其在信息经济学中应用
机制设计原理
01
通过设计合理的规则和制度,引导参与者的行为,实现资源的
有效配置和社会福利最大化。
信息经济学中的应用
02
在信息不对称的情况下,通过机制设计实现信息的有效传递和
资源的优化配置,如价格机制、竞争机制等。
激励机制设计
03
通过设计合理的激励机制,引导参与者的行为符合社会目标,
经济博弈论(第三章)

第三章完全信息动态博弈上一章介绍了完全信息静态博弈,本章在前面的基础上探讨完全信息动态博弈。
现实社会经济活动的决策大多数是有先后顺序的行为而不是同时选择的行为,而且后行者能够看到先行者的决策内容,在先行者的决策结果之后再定夺自己的策略。
这样的经济行为比比皆是,如商业活动中的讨价还价,拍卖活动中的轮流竞价,资本市场上的收购兼并和反收购兼并都是如此。
依次选择与一次性同时选择有很大的差异,因此这种决策问题构成的博弈也是从时间序列上有别于静态博弈的,我们称之为“动态博弈”(Dynamic Games)。
例如下象棋通常需要两个参与人,我们定义为红方和黑方,红方先走,黑方后走,这是一个典型的完全信息动态博弈。
动态博弈由于添加了时间因素,因而更加贴近现实。
根据博弈方是否相互了解得益情况,可分为“完全信息动态博弈”和“不完全信息动态博弈”,根据是否所有博弈方都对自己选择前的博弈过程完全了解,可分为“完美信息动态博弈”和“不完美信息动态博弈”。
在本章中,我们首先对博弈的扩展式表达给出完整的定义,为动态博弈的分析奠定基础;其次,我们从扩展式表述博弈的纳什均衡分析逐步深入到子博弈精炼纳什均衡,为动态博弈的分析提供可行的方法,接下来介绍两种完全信息动态博弈经典模型;最后,分析具有无穷次的重复博弈,推导出无名氏定理。
3.1 博弈的扩展式表述在动态博弈中,博弈方的行动是有先后次序的,且后行动者在自己行动之前能够观测到先行动者的行动,每个博弈方的一次选择行为常称为一个“阶段”(Stage )。
动态博弈中也可能存在几个博弈方同时选择的情况,这时博弈方的同时选择构成一个阶段。
一个动态博弈至少有两个阶段,因此动态博弈有时也称为“多阶段博弈”(Multistage Games )。
此外,也有把动态博弈称为“序列博弈”(Sequential Games )的,这也是由动态博弈中的次序特征引出来的。
设有一个商人要从A 地向B 地运输一批货物。
exfd经济博弈论3—完全且完美信息动态博弈

动态博弈中博弈方的策略是他们自己预先设定
的,在各个博弈阶段针对各种情况的相应行为 选择的计划。
这些策略实际上并没有强制力,而且实施起来 有一个过程,因此只要符合博弈方自己的利益, 他们完全可以在博弈过程中改变计划。我们称 这种问题为动态博弈中的“相机选择 (Contingent Play)”。
(-1,0) (0,4)
法律保障不足的开金矿博弈 ——分钱打官司都不可信
稳定。为什么会出现这种情
况呢?
其实,该博弈中 (不借-不打,不分)和(借-打,分)都是纳什
均衡。但后者不可信,不可能实现或稳定。
上述纳什均衡不稳定的原因,主要在于如果甲在第二阶段选择了 “不分”而不是“分”,乙策略中设定的第三阶段“打”是不可 信的,不可能真正实施,理由是该行为对乙自身也是不利的,追 求自身利益最大化的乙的理性不允许他这么做。甲只要稍作分析 就可以掌握乙的这个弱点,因此不可能理睬乙策略中的“打”官 司威胁,在第二阶段不会选择“分”。反过来,乙也不会愚蠢到 想靠一个明显不可信的威胁撑腰,冒险将资金借给甲,因此他在 第一阶段也不可能“借”。
第三章 完全且完美信息动态博弈
本章讨论动态博弈(Dynamic Games),所
有博弈方都对博弈过程和得益完全了解的完全 且完美信息动态博弈。这类博弈也是现实中常
见的基本博弈类型。由于动态博弈中博弈方的 选择、行为有先后次序,因此在表示方法、利 益关系、分析方法和均衡概念等方面,都与静 态博弈有很大区别。本章对动态博弈的概念和 分析方法,特别是子博弈完美均衡和逆推归纳 法作系统介绍,并介绍各种经典的动态博弈模 型。
所以,在一个动态博弈中,博弈的结果包括双
方(或多方)采用的策略组合,实现的博弈路 径和各博弈方的得益。
经典:博弈论-完全信息动态博弈

2、博弈的扩展式表述的要素
博弈的扩展式表述包含以下要素: (1) 参与人集合:i=1,2,…,n。此外,用N代表虚拟
参与人——自然。 (2) 行动顺序:谁在什么时候行动。 (3) 参与人的行动空间: (4) 参与人的信息集: (5) 参与人的策略集: (6) 参与人的支付函数: (7)外生事件的概率分布。
博弈的收益矩阵
(1)高需求
开发 开发商A 不开发
(2)低需求
开发 开发商A 不开发
开发商B
开发
不开发
2, 2
4, 0
0, 4
0, 0
开发商B
开发
不开发
-1, -1
1, 0
0, 1
0, 0
博弈分类
按开发商博弈的先后顺序分: 静态博弈:两个开发商同时决策,或后决策者不
能观察到先行动者的行动。 动态博弈:博弈有先后顺序,且后决策者能观察
完全信息动态博弈图示:N A B
开发 (2,2)
高需求
○
A
N
低需求
开发 不开发 开发 不开发
不开发 (4,0)
开发 (0,4) B 不开发 (0,0)
开发 (-1,-1) 不开发 (1,0)
开发 (0,1) 不开发 (0,0)
(4)不完全信息动态情形:ANB
开发商A不清楚市场的需求状态,决定是否开发; 开发商B 在观察到市场需求和A的决策后决定是否开发。
到先行动者的行动后再行动。 按开发商是否知道市场需求状态分:
完全信息博弈:若两个开发商都知道市场需求状 态(高需求或低需求)。
不完全信息博弈:由自然决定市场的需求状态, 两开发商不知道。 共同知识:在市场各种可能状态和各开发商不同策 略组合下的得益矩阵是双方的共同知识。
3 完全且完美信息动态博弈 博弈论

3.2 子博弈完美纳什均衡
3.2.1 子博弈
某个动态博弈从其 某个阶段开始的后 续阶段,可以自成 一个博弈。
条件:有初始信息集
和进行博弈所需要的 全部信息。
乙
借
不借
甲
分
(2,2) 打
(1,0) 不分
乙
不打
(1,0)
(0,4)
3.2.2 逆推归纳法
从动态博弈的最后一个阶段或最后一 个子博弈开始,逐步向前倒推以求解 动态博弈的方法。
3 完全且完美信息动态博弈
开金矿
甲欲开采价值4万元的金矿,缺1万资金。甲向 乙借1万,许诺采到金后对半分成。乙是否该借 钱给甲呢?
分析: 乙借不借依赖于甲守不守信 甲为不可信承诺 乙选不借
3 完全且完美信息动态博弈
3.1 动态博弈的表示法和特点 3.2 子博弈完美纳什均衡 3.3 几个经典的动态博弈模型
法律制度应满足两方面的要求
一是对人们正当权益保护力度足够大 二是对侵害他人利益者有足够的震慑
IBM公司的可信威胁
IBM公司曾经对市场公开承诺,对一些刚刚推向市场的新型电脑将在 二、三年后以很低的价格销售。这似乎不可思议,因为既然二、三 年后会降价,许多人就可能推迟购买,这将降低IBM的销量。但实际 上,IBM公司这样做是为了阻止其他电脑公司模仿它的产品。
不开发
子博弈完美开纳发什商均B 衡:
(开发,{不开开发 发,开发不}开)发 开发
(-3,-3)
(1,0) (0,1)
开发商B
不开发 (0,0)
A的策略集合:{开发,不开发} B的策略集合:{{开发,开发},{开发,不开发}
{不开发,开发},{不开发,不开发}}
均衡路径equilibrium path
博弈论 3

扩展式表述博弈的纳什均衡
什么是参与人 的战略? A
开发
• 若A先行动,B在知道A的行 动后行动,则A有一个信息 集,两个可选择的行动,战 略空间为:(开发,不开发); • B有两个信息集,四个可选 择的行动,B有四个纯战略:
不开发
B
开发
x
不开发
B
开发
(-3,-3)
(1,0) (0,1)
• 简写为:(开发,开发), 不开发 (开发,不开发),(不开 发,开发),(不开发,不 开发),括号内的第一个元 (0,0) 素对应A选择“开发”时B的 选择,第二个元素对应A选 择“不开发”时B的选择。
• 逆推归纳法是求完美信息动态博弈子博弈完美纳 什均衡的基本方法。
用逆向归纳法求-子博弈精练纳什均衡
给定博弈达到最后一个 决策结,该决策结上行动 的参与人有一个最优选择, 这个最优选择即该决策结 开始的子博弈的纳什均衡 1
完美信息(perfect information)与 不完美信息(imperfect information)
不完美信息:2不能区 分1是采用了L还是S
L L L 1 S 2 S (1,1) 2 S L (2,2) 1 S (-1,-1) (-1,-1) 2 S (1,1)
L
2 S L
(2,2)
(-1,-1) (-1,-1)
A
开发 不开发
B
开发
x
不开发
B
开发
x’
不开发
(-3,-3)
(1,0) (0,1)
(0,0)
(不开发,(开发,开发)),(开发,(不开发,开发),(开发,(不开发,不开发))
如果A选择开发,B的最优选择是不开发,如果A选择不开发,B的最优选 择是开发,A预测到自己的选择对B的影响,因此开发是A的最优选择。A选择 开发,B选择不开发。我们把这种均衡称为“子博弈精练纳什均衡”
第3章 博弈论与信息经济学--完全信息动态博弈

二、子博弈精炼纳什均衡
第三,由于不考虑自己选择对别人选择的影响,纳 均衡允许了不可置信威胁的存在。如“市场阻挠博 弈”中,如果进入者者真的进入,在位者的最优行 动显然是默许而不是斗争,因为默许带来50的利润, 斗争则将预期的利润化为乌有。所以,斗争是一种 不可置信的威胁,
©&® by H. Q. Feng, CUFE 21/58
二、子博弈精炼纳什均衡
泽尔腾的“子博弈精炼纳什均衡”
一个纳什均衡称为精炼纳什均衡,当且仅当参与 人的战略在每一个子博弈中都构成纳什均衡。
就是说,组成精炼纳什均衡的战略必须在每一个 子博弈中都是最优的。
©&® by H. Q. Feng, CUFE
就是说,如果在位企业摆出一副“你进入我斗争”的 架势,那么进入企业不应该被这种威胁所吓倒。因 为它是不可置信的。但是,纳什均衡概念承认了这 种不可置信的威胁,所以(不进入,斗争)便成为 一个纳什均衡。
©&® by H. Q. Feng, CUFE 18/58
子博弈精炼纳什均衡-不可置信威胁
美国普林斯顿大学古尔教授1997年在《经济学透视》里发表文 章,提出一个例子说明威胁的可信性问题: 两兄弟老是为玩具吵架,哥哥老是要抢弟弟的玩具,不耐烦 的父亲宣布政策:好好去玩,不要吵我,不管你们谁向我告 状,我都把你们两个关起来,关起来比没有玩具更可怕。现 在,哥哥又把弟弟的玩具抢去玩了,弟弟没有办法,只好说: 快把玩具还我,不然我就要去告诉爸爸。哥哥想,你真要告 诉爸爸,我是要倒霉的,可是你不告状不过没有玩具玩,而 告了状却要被关禁闭,告状会使你的境遇变得更坏,所以你 不会告状,因此哥哥对弟弟的警告置之不理。 的确,如果弟弟是会算计自己利益的理性人,在这样的环境下, 还是不告状的好。可见,弟弟是理性人,他的告状威胁是不可 置信的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A
开发
不开 发
A
开发
不开发
B
B
B
B
开发 不开发 开发 不开发 开发 不开发 开发
不开发
有了信息集的概念, 展开式表示也可以用来表 示静态博弈, 如“囚徒的困境 ”博弈可以表 示为:
1
坦白
2
不坦白
2
坦白
不坦白 坦白
不坦白
(-5,-5)
(0,-8) (-8,0)
(-1,-1)
或者:
2
坦白
不坦白
1
1
坦白
1
C
D
现在重新考虑上述房地产开发博弈,以解释信 息集的概念,其中开发商B是在知道A的选择 和自然的选择之后决策的。
如果B在决策时并不知道自然的选择,则有博
弈树:
开发
A
hA
不开发
N
N
大(1/2)
hB B
小(1/2)
B
大(1/2)
B
小(1/2)
B h′B
开发
不开发 开发 不开发 开发 不开发 开发 不开发
黑
N
[0.5]
红 [0.5]
<1> 1
<1> 1
加注r <1/3>
y2 2 <1/4>
摊牌f
摊牌F
<2/3> <0>
(-1,1) (1,-1)
加注R <1>
x2 2 <3/4>
放弃P
对抗M
放弃P
对抗M
(1,-1)
(-2,2)
(1,-1)
(2,-2)
摊 牌 博 弈 的 策 略 空 间 分 别 为:
S1={(R,F)×(r,f)}={Rr,Rf,Fr,Ff},S2={M,P}
混合策略的子博弈完美Nash均衡可类似定 义。 简单地说: 子博弈完美Nash均衡要 求均衡策略 的行为规则在每一个信息集 上都是最优的(包括均衡路径和非均衡路 径)。
定 义 展开型博弈的一个策略组合称为子 博弈 完美Nash均衡,如果对于该博弈 的每一个子 博弈,该策略组合都是 Nash均衡。
定 义 一 个 展 开 式 博 弈 的 子 博 弈G 由 一 个 决 策 结x 和 所 有 该 决 策 结 的 后继结T(x)( 包 括终点结0 组 成, 它 满 足 下 列 条 件:⑴x 是 一 个 单 点 信 息 结即h(x)={x};⑵对于所有的 x′∈T(x),如果x″∈h(x′),则x″∈T(x)。
参 与 人1
B 1,0
3,1
(3,1)
展 开 型 博 弈:
T
2
L
R
1 B 2
l
(2,2) 可以表示成:
(4,0) (1,0)
参 与 人2
Ll
lr
Rl
T 2,2 2,2 4,0
参 与 人1
B 1,0 3,1 1,0
r (3,1)
Rr 4,0 3,1
同样地,展开型博弈也可以用策略式来表示:
例 摊牌博弈
(3)
N
1/3
2/3
1
Y1
z1
1
x1
w1
(2,6) (5,6)
2
2
a2 (9,0)
b2 (0,3)
a2 (9,5)
b2 (0,3)
3.3 子 博 弈 与 子 博 弈 完 美
Nash 均衡在原则上适用所有的博弈,但对于预 测 参与人的行为来说,Nash均衡可能并不是 一个 合理的预测, 如房地产博弈:
(0,0)
上述博弈树给出了有限博弈的几乎所有信息。
博 弈 树 必 须 满 足 下 列 规 则:
(1) 每一个结(node)至多有一个其他结直接位 于 它的前面;
(2) 在博弈中没有一条路径可以使决策集与自身 相连;
(3) 每一个结是唯一初始结的后续结, 即博弈树 必须有初始结;
(4) 每个博弈树“正好”只有一个初始结(多于 一个 可以用“ 自 然”连接。
集包含不止一个结, 假设x与x′∈h(x),则恰 好拥有信息h(x)并正在选择自己行动的参与 人其实对自己究竟是处于x还界x′是不确定的。
要 求: 如 果x′∈h(x), 则x与x′ 应 该由同 一 个参与人采取行动,且可以选择的策略空 间 相同:A(x)=A(x′), 由此可以将信息集h上 的 行动集记 为A(h)。
Ff 0,0
0,0
该博弈有唯一的Nash均衡(σ1,σ2)=(1/3(Rr)+2/2(Rf), 2/3(M)+1/3(P)),它与信念体系一起构成序贯均衡。
习题
1.写出下列博弈的策略型表示:
(1)
(2)
1
U
D
U
1 D
2
L
R
2
L
R
(2,1) (0,0) (-1,1) (3,2)
2
2
L
RL
R
(2,1) (0,0) (-1,1) (3,2)
可表示为策略型
参 与 人2
M
P
Rr 0,0
1,-1
注:u1(Rf,M)= 2×1/2+(-1)×1/2=0,5
u2((Rf,M)= -2×1/2+1×1/2=-0.5
Rf 0.5,-0.5
参 与 人1
Fr –0.5,0.5
0,6 1,-1
其中R(r)表示加注;F(f)表 示摊牌;M表示对抗;P表示 放弃。
另一种情况就则B知道自然的选择,但不知道A的
选择,这时博弈树如下:
A
开发
不开发
N
N
大
小
大
小
B
B
B
B
开发
不开发 开发
不开发 开发
不开发 开发
不开发
(-5,-5)
(0,-8) (-3,-3)
(1,0) (0,8) (0,0) (0,1)
(0,0)
上述房地产开发博弈还有另一种表示:
N
大(1/2)
小(1/2)
不坦白
坦白
不坦白
(-5,-5)
(0,-8) (-8,0)
(-1,-1)
注 意: 得 益 向 量 的 次 序 与 参 与 人 决 策 的 顺 序 一 致。
同样地,展开型博弈也可以用策略式来表示, 如
展开型博弈:
1
T
B
2
L
R
2
L
R
(2,2)
(4,0) ((1,0)
可以表示为:
参 与 人2
L
R
T 2,2 4,0
如果博弈树的所有信息集都是单结的, 则称该 博弈为完美(perfect)息 博弈。(无虚线连接), 而完全(complete)信息博弈是指得益函数和纯 策略空间均为博弈各方的共同知识。完全信息 可以是完美的也可以是不完美的。
3.2 展开型博弈的策略与均衡
一、 行 为 策 略
在策略型博弈中, 参与人的策略是进行博 弈的计划( 或打算)的详细集合, 而在展 开型博弈中 参与人的策略必须确定在该 参与人的每一个决 策集上 所 采 取 的 行 动,又 结 与 信 息 集 紧 密 相 连, 对 于 参 与 人i,基于信息hi的行动的
hi∈Hi
例
上 2 h2(1)
左
右
h1(2)
1
1
1 h1(1) 下
2 h2(2)
左
右
h1(3)
1
1
A
B
A
B
C
D
C
D
参与人2有两个策略集,相应地也有两个信息集 A(h2(1))=A(h2(2))={左,右}
其中H2={h2(1),h2(2)};参与人2的纯策略空间为: S2=(A(h2(1)),Ah2(2))={(左,右)×(左,右)}
(path), 达到s相应的终点结。 有一个事 实非常重要:s中有些信息集在博弈 树 的这条路径上,我们称这些信息集是s的 路 径(path), 当然也可能存在s中某些信 息集不在 此路径上。
定义了纯策略的得益函数后,我们就可以定义 展
开型博弈的Nash 均衡;
定义 策略组合s*=(s1*,…si*,…sn*)是展开型 博弈的
注意:行为策略是在A(hi)上随机化,而混合策 略则是在Si( 即A(hi) 的乘积 空 间)上的随机化
定 理 (Kuhn,1953) 在完美回忆博弈中,混合 策略与行为策略是等价的。
完美回忆指没有参与人会忘记以前知道的信息。
例 下列展开型博弈不具备完美回忆:
A 2
L
R
1
B
2
L
R
1
C
D
1
CD
1
C
D
⑷ 当参与人作出他们的行动决策时,他所 观测到 或他所了解到的信息,即他在此时 获得的信息 集合;
⑸ 参与人的得益(支付或效用), 它们是已 知行动的函数;
⑹ 在任何外生事件的概率分布。
例 房地产开发博弈
有两个房地产开发商(分别为参与人1,记为 A和参与人2,记为B) 在某地开发房地产, 但该 地的房地产需求状况是不确定的, 假定该博弈 的行动顺序如下:(1) 开发商1先行动, 选择开 发或不开发;(2)在1决策后,“ 自然”选择需求 的大小;(3)开发商2在 观测到1的决策和市场 的需求后, 再决定开发 或不开发。( 如 下 图)
A
开
不
B
开
不
B
开
不
(-3,-3)
(1,0)
的 策 略 式 表 示 为:
(0,1)
(0,0)
参 与 人B
( 开, 开) ( 开, 不) ( 不, 开) ( 不, 不)
