泡利不相容原理
泡利不相容原理与洪特规则

泡利不相容原理与洪特规则泡利不相容原理与洪特规则是量子力学中两个重要的原则,它们对于电子在原子轨道中的排布和原子结构的稳定性起着关键作用。
泡利不相容原理由奥地利物理学家波尔斯·泡利于1925年提出,它指出相同的自旋量子数的两个电子不能在同一个原子轨道中同时存在。
这一原理保证了原子的稳定性,避免了电子之间的相互斥力过大,从而使原子结构能够保持相对稳定。
而洪特规则则是由美国物理学家罗伯特·洪特在1923年提出的,它总结了电子在原子轨道中填充的顺序规律,有助于理解原子的能级分布和化学性质。
泡利不相容原理与洪特规则的提出,彻底改变了人们对原子结构的认识。
在泡利不相容原理的指导下,我们可以确定原子中各个电子的排布方式,从而进一步推导出原子的化学性质和化学键的形成。
洪特规则则为我们提供了一个简单而有序的填充电子的方式,帮助我们理解原子中电子的能级分布和轨道角动量的排布规律。
这两个原理的相互配合,为我们解释原子结构和化学键提供了有力的理论支持。
泡利不相容原理的核心概念是电子的自旋量子数,它决定了电子的自旋状态以及电子之间的排斥能。
根据泡利不相容原理,相同自旋量子数的两个电子无法同时处于同一个原子轨道中,这意味着在一个原子轨道中最多只能容纳两个电子,并且这两个电子的自旋量子数必须相反。
这一原理的提出,解决了之前无法解释原子结构和化学性质的难题,为后来量子力学的发展奠定了基础。
洪特规则则为我们提供了填充电子的顺序规律。
根据洪特规则,电子在填充原子轨道时会优先填充能量较低的轨道,而不同轨道的填充顺序遵循一定的规律。
具体来说,s轨道先于p轨道填充,p轨道又先于d轨道填充,最后才是f轨道。
在每个轨道内,电子的填充顺序则遵循洪特规则中的“两电子自旋相反”的原则。
这一规律简洁而有序,帮助我们理解原子各能级之间的排布规律,以及不同能级之间的能级间隔。
泡利不相容原理与洪特规则的结合,使得我们能够更加深入地理解原子结构和化学键的形成。
泡利不相容原理证明

泡利不相容原理证明泡利不相容原理是量子力学中的一个重要概念,它解释了为什么相同类型的费米子无法存在于相同的量子态中。
费米子是一类具有半整数自旋的粒子,如电子、质子和中子等。
泡利不相容原理的证明可以通过考虑多粒子波函数的对称性来进行。
根据泡利不相容原理,任意两个相同类型的费米子不能处于完全相同的量子态中,也就是说它们的波函数在空间和自旋两个方面不能完全相同。
首先,考虑两个相同类型的费米子,我们可以将它们的波函数表示为:Ψ(1,2) = Φ(1)Φ(2)其中,Φ(1)和Φ(2)分别是第一个和第二个粒子的波函数。
由于费米子的自旋是半整数,因此它们的自旋波函数必须是反对称的。
也就是说,当交换两个粒子的标签时,波函数需要发生符号变化。
我们可以用符号来表示波函数的对称性。
如果波函数对于每一对交换的粒子都保持不变,那么波函数是对称的;如果波函数在每一对交换的粒子上发生了符号变化,那么波函数是反对称的。
对于费米子,其波函数必须是反对称的。
现在考虑两个相同类型的费米子,我们可以交换它们的标签,即交换粒子1和粒子2。
根据波函数的反对称性,我们得到:Ψ(2,1) = -Ψ(1,2)两个波函数的差异可以通过将它们相加和相减来揭示:Ψ(1,2) + Ψ(2,1) = 0Ψ(1,2) - Ψ(2,1) = 2Ψ(1,2)根据量子力学的原理,波函数的模的平方表示找到一个粒子在某个量子态的概率。
如果两个波函数的和为零,那么在这个量子态下的概率为零,也就是说两个粒子不能同时处于相同的量子态中。
由此可见,泡利不相容原理限制了相同类型的费米子处于相同的量子态中。
这一概念对于理解原子和分子的电子结构以及凝聚态物理中的电子行为非常重要。
泡利不相容原理 库珀对

泡利不相容原理库珀对
泡利不相容原理是量子力学中的一个基本原理,由奥地利物理学家沃纳·泡利于1925年提出。
这个原理主要描述了原子中电子的排布规律,指出在一个原子中,不可能有两个电子具有完全相同的四个量子数(主量子数、角量子数、磁量子数和自旋量子数)。
这一原理对于我们理解原子结构和原子光谱现象具有重要意义。
在原子物理中,泡利不相容原理的应用非常广泛。
例如,它解释了为什么原子中的电子会按照特定的能级分布,这是因为每个能级只能容纳一个电子。
此外,泡利不相容原理还解释了原子光谱线的复杂性,这是因为电子在能级之间跃迁时,会吸收或释放特定能量的光子。
与此同时,库珀对是另一种重要的量子现象。
1954年,美国物理学家约翰·库珀提出了库珀对的概念。
库珀对是指在超导体中,两个电子通过交换声子(晶格振动)产生的有效吸引力而成对。
在超导体中,库珀对的存在使得电子能够克服原子核的库仑排斥力,从而形成稳定的电子对。
这一现象是超导现象的基础,对于解释超导体的高温超导和高压超导具有重要意义。
泡利不相容原理与库珀对之间存在着密切的联系。
在超导体中,泡利不相容原理使得电子能够按照特定的规律排列,形成稳定的库珀对。
这种排列有助于提高超导体的临界温度,从而使超导现象更加显著。
此外,库珀对在超导体中的形成过程也受到泡利不相容原理的调控。
在现代科学研究中,泡利不相容原理和库珀对的重要性不言而喻。
它们为我们在原子物理、超导物理等领域的研究提供了基本理论依据。
泡利不相容定律(3篇)

第1篇一、引言在微观世界的探索中,科学家们发现了一系列神奇的现象。
其中,泡利不相容定律是量子力学中一个非常重要的原理,它揭示了微观粒子之间的一种特殊关系。
本文将详细阐述泡利不相容定律的内涵、起源、应用以及在我国科研领域的重要性。
二、泡利不相容定律的内涵泡利不相容定律,又称为泡利原理,是奥地利物理学家沃尔夫冈·泡利于1925年提出的。
该定律指出:在同一个原子中,不可能有两个电子的四个量子数完全相同。
这四个量子数分别是主量子数(n)、角量子数(l)、磁量子数(m)和自旋量子数(s)。
1. 主量子数(n):表示电子所处的能级,取值为正整数(1、2、3...)。
2. 角量子数(l):表示电子在原子轨道中的角动量大小,取值范围为0到n-1。
3. 磁量子数(m):表示电子在特定角动量状态下的磁矩方向,取值范围为-l到l。
4. 自旋量子数(s):表示电子自旋的取向,取值为+1/2或-1/2。
泡利不相容定律意味着,在同一个原子中,两个电子的四个量子数不能同时取相同值。
这保证了电子在原子中的稳定分布,为原子的化学性质提供了基础。
三、泡利不相容定律的起源泡利不相容定律的发现源于对原子结构的探索。
在20世纪初,科学家们发现,通过改变原子核的电荷数,可以产生不同元素。
然而,当时的原子模型无法解释元素周期表中的周期性规律。
泡利在研究电子在原子中的分布时,发现了这一神奇的现象,并提出了泡利不相容定律。
四、泡利不相容定律的应用泡利不相容定律在物理学、化学、材料科学等领域具有广泛的应用。
1. 物理学:泡利不相容定律是量子力学的基本原理之一,为研究原子、分子、固体等微观世界的性质提供了理论基础。
2. 化学:泡利不相容定律解释了元素周期表中元素的周期性规律,为化学元素的研究提供了重要依据。
3. 材料科学:泡利不相容定律在研究材料电子结构、导电性等方面具有重要意义。
五、泡利不相容定律在我国科研领域的重要性泡利不相容定律作为量子力学的基本原理之一,在我国科研领域具有重要地位。
1945年诺贝尔物理学奖──泡利不相容原理

1945年诺贝尔物理学奖──泡利不相容原理1945年诺贝尔物理学奖授予美国新泽西州普林斯顿大学的奥地利物理学家泡利(Wolfgamg Pauli,1900—1958),以表彰他发现了所谓泡利原理的不相容原理。
不相容原理是量子理论中的重要原理,是1925年1月由泡利提出的。
这一原理可以表述为:对于完全确定的量子态来说,每一量子态中不可能存在多于一个的粒子。
泡利后来用量子力学理论处理了h/4π自旋问题,引入了二分量波函数的概念和所谓的泡利自旋矩阵。
通过泡利等人对量子场的研究,人们认识到只有自旋为半整数的粒子(即费米子)才受不相容原理的限制,从而确立了自旋统计关系。
关于不相容原理的发现,泡利在他的诺贝尔奖演说中讲到,不相容原理发现的历史可以追溯到他在慕尼黑的学生时代。
在维也纳读中学时,他就掌握了经典物理学和相对论的知识。
在慕尼黑大学经索末菲引导接触到从经典的思想方法看来有些离奇的原子结构理论。
他和所有习惯于经典思想方法的物理学家一样,当第一次接触到玻尔的量子理论的基本假设时不免受到冲击。
他一方面接受了玻尔的原子理论;一方面了解索末菲企图用光谱定律的解释来克服使用动力学模型所遇到的困难。
泡利对这两种理论都不满意。
反常塞曼效应的解释问题,使物理学家倍感苦恼,泡利也不例外。
据说当时有一位友人看见泡利在哥本哈根的大街上闲逛,就问他为什么不高兴。
泡利回答说:“当一个人正在想到反常塞曼效应时,他怎么高兴得起来啊!”。
按照玻尔的想法,当分析原子的结构时,应该首先从内层开始。
可以设想有一个带正电荷Ze的原子核,在其周围是若干电子,这些电子一个接着一个被原子核俘获,直到它俘获了Z个电子而形成中性原子时为止。
最先被俘获的电子占据能量最低的量子轨道,这就是玻尔所谓的“组建原则”。
泡利不满意的原因在于他认为原子光谱的根源在于价电子的运动,不应该从原子实的结构去找。
泡利仔细研究了碱金属光谱的双重结构,引入了“经典不能描述的双重值”概念,在这基础上概括成一个重要结论,即原子中不能有两个电子具有相同的四个量子数。
泡利不相容原理与洪特规则

泡利不相容原理与洪特规则是量子力学中非常重要的概念,它们对于理解原子和分子的结构以及化学反应起着至关重要的作用。
泡利不相容原理是由意大利物理学家泡利于1925年提出的,它说明了相同自旋的两个费米子(如电子)不能同时处于同一量子态。
这一原理的提出,对于解释元素的电子排布以及化学键的形成都具有重要意义。
与泡利不相容原理相似的是洪特规则,它是由美国化学家洪特提出的,用于描述原子的电子排布规律。
洪特规则指出电子会优先填充能量较低的轨道,然后才会填充能量较高的轨道,这一规则帮助我们理解元素的电子排布及其性质。
在本文中,我们将深入探讨泡利不相容原理与洪特规则的本质、应用以及相关领域的研究进展。
泡利不相容原理和洪特规则的提出,彰显了量子力学在化学领域的重要性。
在传统的经典力学中,电子的轨道可以是任意填充的,而在量子力学中,由于波函数的对称性,相同自旋的两个费米子无法处于同一态。
这一原理的提出,极大地改变了我们对于原子结构和元素性质的认识。
借助泡利不相容原理,我们可以解释为什么每个电子壳层中有特定数量的电子,以及为什么元素会表现出不同的化学性质。
洪特规则则进一步完善了我们对于电子排布的认识,指导着化学家们设计新的材料和化合物。
泡利不相容原理和洪特规则的研究不仅仅停留在理论层面,更多的是在实际应用中得到体现。
例如,在材料科学领域,研究人员可以通过控制电子的排布来设计出具有特定性质的新材料。
另外,在化学反应的研究中,泡利不相容原理和洪特规则也起着关键的作用。
通过这些规则,人们可以预测某种化学反应中可能产生的产物,从而指导实验的进行。
可以说,泡利不相容原理和洪特规则是化学、物理领域不可或缺的基础知识。
泡利不相容原理和洪特规则所揭示的电子排布规律,也为我们提供了一种新的思维方式。
通过理解这些规则,我们可以更好地理解原子和分子的结构,从而为材料设计、催化剂开发以及环境保护等领域提供新的思路。
值得一提的是,随着技术的不断进步,人们对于泡利不相容原理和洪特规则的理解也在不断深入。
泡利不相容原理能量最低原理洪特规则

泡利不相容原理能量最低原理洪特规则泡利不相容原理是由奥地利物理学家沃尔夫冈·泡利于1925年提出的。
该原理主要描述的是在原子或分子中,不能有两个或两个以上的粒子(如电子)处于完全相同的量子状态。
根据泡利不相容原理,每个电子必须具有唯一的一组量子数,包括主量子数、角量子数、磁量子数和自旋量子数。
这意味着即使在同一原子中,两个电子也必须具有至少一个不同的量子数。
泡利不相容原理限制了电子的排布方式,使得原子和分子中的电子结构变得稳定和有序。
能量最低原理是在量子力学中的一个基本概念,它指出在任何系统中,自然趋向于取得能量最低的状态。
在原子和分子中,能量最低原理指出原子中的电子会按照一定规则填充能级。
电子首先填充较低能量的能级,然后逐渐向较高能量的能级填充。
这个填充顺序是根据洪特规则来确定的。
洪特规则是由洪特(Hund)于1925年提出的。
根据洪特规则,当填充原子中的电子时,电子首先会填充处于不同能级的轨道。
然后,在同一能级的轨道上填充电子时,电子趋向于尽可能地保持自旋方向相同,以最小化电子之间的相互排斥。
这种电子填充方式称为“单电子占据”或“零自旋规则”。
根据洪特规则,这一填充顺序能够使得原子和分子结构更加稳定和有序。
这三个原理为我们提供了理解原子和分子的结构以及元素周期表中特殊性质的重要理论基础。
泡利不相容原理限制了电子在原子和分子中的状态,使得不同元素和化合物具有不同的基本特性。
能量最低原理和洪特规则则解释了电子在原子和分子中的填充顺序,进一步揭示了原子和分子结构以及它们之间相互作用的基本规律。
这些原理不仅对于理解原子和分子的性质和行为有重要意义,也在化学、材料科学和纳米科学等领域中具有广泛应用。
泡利不相容原理
L l(l 1)
n一定时 有n种取值 l 越小能量越低 4
3.磁量子数 ml 0,1,2… l 引起磁场中能级的分裂
Lz ml
4.自旋磁量子数
ms
1 2
产生精细结构
Sz ms
5
需要说明的是 自旋量子数 s = 1/2 只有一个值 自旋角动量也只有一个值
S s(s 1) 3 2
不变 不必总提及 可不计入
原子中核外电子的排布要遵守 泡利不相容原理 能量最低原理
6
四个量子数小结
名称
取值
主量子数 n 1,2,
l 0,1,2,n 1
角量子数 L ll 1
磁量子数
自旋磁量 子数
ml 0,1, l
Lz ml
ms
1 2
SZ 2
物理意 义
高能级: 能量较高的能级 低能级: 能量较低的能级
基能级: 能量最低的能级
(相应的状态称基态) 激发能级: 能量高于基能
级的其它所有能级(相应 状态称激发态)
n
6
5 4 激发态 3
2
基态 1
3
一、原子中电子的四个量子数 描述原子中电子的运动状态 需要一组量子数( n,l,ml,ms )
1.主量子数 n = 1, 2, 3, 决定能量的主要因素
n=1 n=2
n=3
1
l
2 3d 1 3p 0 3s
1 2p 0 2s
0 1s
10
•一个支壳层内电子 可有(2l+1)× 2种量子态
∴ 主量子数为n的壳层
内可容纳的电子数为
Zn
n1
泡利不相容原理和洪特规则

泡利不相容原理和洪特规则
泡利不相容原理(Pauli Exclusion Principle)和洪特规则(Hund's Rule)是量子力学中描述原子内电子行为的两个基本原理。
泡利不相容原理指出,在费米子(具有半整数自旋的粒子,如电子、质子和中子)组成的系统中,不能有两个或两个以上的粒子同时处于完全相同的量子态。
在原子中,这表现为不能有两个或两个以上的电子具有完全相同的四个量子数,即每个电子都有一个独特的自旋方向和轨道。
这一原理确保了电子在原子中的稳定分布,是元素周期表形成的基础。
洪特规则则是在等价轨道(即具有相同能量和电子云形状的轨道)上排布的电子将尽可能分占不同的轨道,且自旋方向相同。
这一规则有助于降低整个原子的能量,使体系更加稳定。
后来量子力学证明,电子这样排布可使能量最低,所以洪特规则可以包括在能量最低原理中,作为能量最低原理的一个补充。
总的来说,泡利不相容原理和洪特规则共同决定了原子内电子的排布方式,从而影响了元素的化学性质和物理性质。
全同粒子和泡利不相容原理的关系

全同粒子和泡利不相容原理的关系引言:全同粒子和泡利不相容原理是量子力学中两个重要的概念。
全同粒子指的是具有相同内部属性(如质量、电荷、自旋等)的粒子,而泡利不相容原理则规定了这些全同粒子在量子态中的行为。
本文将探讨全同粒子和泡利不相容原理之间的关系,并解释其在物理学中的重要性。
一、全同粒子的定义和性质全同粒子是指在物理性质上完全相同的粒子,它们无法通过任何实验手段来区分。
例如,所有的电子都是全同粒子,它们具有相同的电荷和质量。
全同粒子之间不存在任何区别,它们之间的交换不会改变系统的性质。
二、泡利不相容原理的概念泡利不相容原理是由奥地利物理学家泡利于1925年提出的。
该原理规定,在一个量子态中,不允许有两个全同费米子(具有半整数自旋的粒子)处于相同的量子态,即不允许多个全同费米子同时处于系统的同一个量子态。
这意味着费米子的态空间是排斥的,每个量子态最多只能容纳一个费米子。
三、全同粒子和泡利不相容原理的关系全同粒子和泡利不相容原理之间存在着密切的关系。
泡利不相容原理实际上是对全同粒子的一种限制。
由于全同粒子之间无法区分,如果允许多个全同费米子同时处于相同的量子态,那么在描述系统的波函数中就无法正确地反映全同粒子的统计性质。
因此,泡利不相容原理保证了全同费米子在量子态中的正确描述。
四、泡利不相容原理的应用泡利不相容原理在物理学中有着广泛的应用。
首先,它解释了为什么原子中的电子能够按照能级填充,即为什么电子不能全部处于最低能级。
根据泡利不相容原理,每个能级最多只能容纳两个全同费米子,因此电子在填充能级时必须按照一定的顺序进行。
这就解释了为什么原子中的电子分布会呈现出规律性。
泡利不相容原理还解释了为什么物质会表现出不同的化学性质。
由于泡利不相容原理的存在,不同原子中的电子组态不同,导致它们的化学性质也不同。
例如,氢原子中只有一个电子,因此它只能形成一种化学键;氧原子中有六个电子,因此它可以形成多种化学键。
泡利不相容原理名词解释

泡利不相容原理名词解释泡利不相容原理,是指在同一晶体中,不能有两种不同的原子。
1、泡利不相容原理的含义是:当两种晶体所处的环境不同时,由于它们原子间相互作用的差别,使得他们的熔沸点不同,从而产生“熔解度”的差异。
因此,对于同一个物质,如果把它们放到同一个容器里加热,结果一个物质先熔化,一个物质却后熔化。
这个熔化现象被称为“泡利不相容原理”。
例如,我们常用的食盐和白糖在100 ℃时的溶解度很小,而在高于100 ℃时,则可以任意比例地互溶。
除了高于100 ℃以外,两者还可以任意比例互溶。
如果把这两种固体加热到150 ℃,这两种固体就会互溶。
但是在水的溶液里,则不会发生这样的情况。
只有在低于100 ℃时,它们才会互溶。
2、同素异形体、异素异形体、准同素异形体、多晶型、准晶型的定义:晶体中质点的大小和形状等结构因素都完全相同,只是由于微量的杂质原子或分子混入,使得整个晶体变得不完整,出现缺陷或空隙。
所以,这种晶体中质点的排列和形态具有部分不同的性质,这些性质统称为同素异形体。
例如金刚石和石墨都是由碳元素组成的。
虽然它们的化学组成相同,但由于微量杂质原子的混入,使得它们的原子排列和形态结构发生了变化。
金刚石的原子排列呈片状,而石墨的原子排列呈鳞片状,即所谓片状石墨。
又如三氧化二铝晶体与硅酸钠晶体是相同的物质,但前者为正三面体,而后者为六角形柱体。
所以前者为同素异形体,后者为同质多象体。
3、晶胞和晶格:晶胞和晶格可用来描述单质分子的集合,通过观察晶胞内质点排列的规律,可以推测原子或离子的排列顺序。
每个晶胞是一个空间几何图形,它包括棱、面、顶点等。
在相邻两个晶胞中,顶点在同一条棱上,且棱长相等。
每个晶胞中都包含相同数目的质点,所以整个晶胞体积也是相等的。
因此,晶胞是一个有限空间几何体。
通常,晶胞的边长与最长的棱长之比,即晶胞的体积,等于这条棱的正投影面积与这个晶胞棱长之比,即棱长之比。
晶胞的表示方法是:用符号c表示晶胞;用符号c表示棱的正投影面积;用符号l 表示棱长;用符号l表示棱长的平方;用符号d表示体积。
泡利不相容原理证明

泡利不相容原理证明泡利不相容原理是量子力学中的一个重要原理,它描述了在同一量子态下,两个或多个相同类型的费米子(包括电子、质子、中子等)不能具有完全相同的量子状态。
这意味着两个费米子不能同时处于相同的能级和自旋状态。
泡利不相容原理的证明可以从波函数的对称性入手。
根据费米子的统计特性,其波函数必须满足反对称性,即对于两个费米子的波函数ψ(x1, x2)来说,交换两个粒子的位置后,波函数会发生变号,即ψ(x2, x1) = -ψ(x1, x2)。
这种反对称性导致了泡利不相容原理的成立。
假设存在两个完全相同的费米子,其波函数为ψ(x1, x2)。
根据反对称性,交换两个粒子的位置后,波函数应该变为-ψ(x1, x2)。
然而,由于费米子是完全相同的,交换两个粒子的位置并不会改变其波函数,也就是说,ψ(x1, x2) = -ψ(x1, x2)。
这个等式只有在波函数为零的情况下才能成立,也就是说,两个费米子不能处于相同的量子态。
泡利不相容原理的应用非常广泛。
最常见的例子是电子在原子中的排布。
根据泡利不相容原理,每个能级最多只能容纳两个电子,且它们的自旋方向必须相反。
这就解释了为什么原子中电子的能级是分裂的,以及为什么原子中的电子不会全部堆积在最低能级。
除了原子结构外,泡利不相容原理还解释了其他许多物理现象,例如金属中的电子行为、超导体中的电子配对等。
它的发现对于理解物质的基本性质和开发新的材料具有重要意义。
总之,泡利不相容原理是量子力学的基本原理之一,它要求同一量子态下的费米子具有不同的量子状态。
这一原理通过波函数的反对称性得到证明,对于解释原子结构和其他物理现象有着重要的意义。
下列正确的是 泡利不相容原理

下列正确的是泡利不相容原理
泡利不相容原理是量子力学中的一个重要原理,它规定相同自
旋的费米子(如电子、质子等)不能占据同一个量子态。
这个原理
是由物理学家恩里科·费米和维尔纳·海森堡在20世纪提出的,被
称为泡利不相容原理,它是量子力学中的基本原理之一。
从微观粒子的角度来看,泡利不相容原理解释了为什么原子内
的电子不能全部处于最低能级,而必须占据不同的能级。
这一原理
对于解释原子结构和化学键的形成都有着重要的意义。
从宏观角度来看,泡利不相容原理也解释了为什么物质呈现出
了多样性和复杂性。
如果泡利不相容原理不存在,所有的费米子都
会聚集在能级最低的状态,这将导致物质的性质变得非常单一和简单,而泡利不相容原理的存在使得物质能够表现出多样性和复杂性。
另外,泡利不相容原理也为我们解释了核子构成原子核的方式,以及为核子之间的相互作用提供了理论基础。
在核物理领域,泡利
不相容原理也有着重要的应用。
总的来说,泡利不相容原理是量子力学中的一个基本原理,它
对我们理解微观世界和宏观世界的物质行为都具有重要的意义。
通过这一原理,我们能够更好地理解原子结构、化学反应以及物质的多样性和复杂性。
高中泡利不相容原理

高中泡利不相容原理引言高中化学中,泡利不相容原理是我们经常听到的一个概念。
它是由奥地利物理学家泡利在1925年提出的。
这一原理深刻地解释了原子中电子的排布规律,并对化学反应和物质性质产生了重要影响。
本文将全面、详细、完整且深入地探讨泡利不相容原理的相关知识。
二级标题1:泡利不相容原理的概念泡利不相容原理是指一个原子中的电子在同一量子态下,无法具有相同的四个量子数。
这四个量子数分别是主量子数n、角量子数l、磁量子数m以及自旋量子数ms。
根据泡利不相容原理,每个电子必须在至少一个量子数上与其他电子不同,以确保电子的自旋方向不同。
二级标题2:泡利不相容原理的原理和意义泡利不相容原理的背后有两个重要原理:波函数对称性和波函数反对称性。
对于相同的自旋态(自旋量子数相同),波函数必须是反对称的;对于不同的自旋态(自旋量子数不同),波函数必须是对称的。
这两个原理保证了泡利不相容原理的有效性。
泡利不相容原理的意义在于决定了电子在原子中的排布方式。
根据泡利不相容原理,每个电子需要占据一个不同的量子态,这导致了各个原子轨道填充电子的顺序和规律。
这种排布方式决定了原子的化学性质,如反应活性、价电子数等。
二级标题3:分子轨道理论与泡利不相容原理分子轨道理论是基于泡利不相容原理的理论体系。
它根据原子轨道的线性组合,描述了分子中电子排布和能级结构的特点。
分子轨道理论认为,相邻原子轨道的线性组合会产生成键轨道和反键轨道,其中成键轨道具有较低的能量而反键轨道具有较高的能量。
根据泡利不相容原理,每个分子轨道最多只能容纳两个电子,且自旋量子数相反。
这意味着成键轨道中的两个电子自旋方向相反,而反键轨道中的两个电子自旋方向也相反。
这种电子分布方式决定了分子的化学性质,如键能、分子形状等。
三级标题1:泡利不相容原理与原子轨道能级填充规律根据泡利不相容原理,我们可以了解到原子轨道能级的填充规律。
主量子数越大的能级越远离原子核,能级的能量也越高。
什么是泡利不相容原理

泡利不相容原理
泡利不相容原理(Pauli exclusion principle)是由奥地利物理学家沃尔夫冈·泡利(Wolfgang Pauli)在1925年提出的物理学原理。
泡利不相容原理指出,在同一个量子系统中,两个或多个具有自旋的费米子(如电子、质子、中子等)不能同时处于相同的量子态。
具体而言,对于自旋为1/2的费米子,即遵循费米-狄拉克统计的粒子,它们的自旋态不能完全相同。
这意味着在一个原子中的电子排布规则中,每个电子的量子态必须不同,至少有一个量子数不同,例如自旋朝上和自旋朝下。
这导致了电子排布在原子中的不同能级,形成了原子的电子壳层结构。
泡利不相容原理的重要性在于它解释了为什么原子、分子和凝聚态物质中的电子能够遵循一定的排布规则,并且决定了元素周期表的结构。
该原理对于理解和描述原子结构、化学键合以及材料的电子性质等方面都具有重要的意义。
泡利不相容原理怎么用

泡利不相容原理怎么用Paley's Principle of Imperfection:No Perfect System Can Accommodate all Desires.泡利不相容原理是由美国物理学家、哈佛大学教授Erwin博士提出来的,他在1920年所出版的《热力学行为学》一书中提出了这一概念。
这一理论表明,没有任何一种生态系统能够完全相容,任何系统的改变会直接影响该系统的整体结构或稳定性。
也就是说,给予系统做出某一项改变就会带来必然的影响,而这种影响将会引起另外的变化,这些变化会进一步引发一系列变化,最终导致某些相容性被迫破坏。
一、泡利不相容原理定义泡利不相容原理指出,当人们将一种新制度、新科技或新实践引入一个系统时,这种变化必将影响另外一种系统,或者说不同的系统之间存在着不完全的相容性。
换句话说,所有的系统实际上都相互依存,所以人们在实施一项计划时,必须要考虑其他系统可能会遭受的影响,而这种影响往往会导致实施计划遭受挫折。
二、泡利不相容原理之使用1、商业活动泡利不相容原理通常被用于商业活动和行为。
企业或组织在介入新的行业或市场时,需要充分考虑这个市场对其他系统的影响,以及它是如何影响到未来的结果。
例如,一家公司如果决定自行发展一种新的技术的时候,它应该考虑新技术的可行性,也应该考虑该技术如何影响到它的既有产品线。
2、沙盒游戏设计游戏设计者可以利用泡利不相容原理来处理游戏的规则、物品、配置以及游戏的整体编剧。
当引入新的游戏元素进入游戏时,必须考虑该元素如何影响游戏当前要求玩家完成的游戏内容以及未来玩家可能经历的游戏过程,从而确保游戏继续有效和稳定。
3、政治议程当一个国家要讨论一个政治议程或社会改革时,泡利不相容原理对政策制定者来说也是一本重要的参考书。
他们在引入新政策或法律元素时,必须考虑可能带来的潜在影响,并且重视这些影响可能会随时发生的可能性。
在设计新政策时,必须考虑如何防止不合理的变化,并帮助社会实现正能量发展。
泡利不相容

泡利不相容泡利不相容原理也叫泡利原理和不相容原理。
科学实验告诉我们,一个原子中不可能有两个电子的电子层、电子子层和轨道的空间延伸方向和自旋状态完全相同。
这个原理叫做泡利不相容原理。
泡利不相容原理是微观粒子运动的基本定律之一。
它指出,在费米子系统中,没有两个或两个以上的粒子可以处于同一状态。
需要四个量子数才能完全确定一个电子在原子中的状态,所以泡利不相容原理用原子来表示:没有两个或两个以上的电子可以有相同的四个量子数,这成为解释元素周期表将电子排列在原子核外形成周期性的标准之一。
由来在奥地利维也纳出生的沃尔冈夫·泡利(Wolfgang Pauli 1900一1958),是20世纪卓越的理论物理学家,19岁时就因撰写相对论方面的综述文章而获得了很高的声誉.25岁时,为了对原子光谱中的反常塞曼效应做出解释提出了“泡利不相容原理”。
泡利原理:电子在原子核外运动状态是相当复杂的。
一个电子的运动状态取决于它所处的电子层、电子亚层、轨道的空间伸展方向和自旋状况。
由于不同电子层具有不同的能量,而每个电子层中不同亚层的能量也不同。
为了表示原子中各电子层和亚层电子能量的差异,把原子中不同电子层亚层的电子按能量高低排成顺序,像台阶一样,称能级。
例如,1S能级,2s能级,2p能级等等。
可是对于那些核外电子较多的元素的原子来说.情况比较复杂。
多电子原子的各个电子之间存在着斥力,在研究某个外层电子的运动状态时,必须同时考虑到核对它的吸引力及其它电子对它的排斥力。
由于其他电子的存在。
往往会削弱原子核对外层电子的吸引力,使多电子原子中电子的能级交错排列。
实验也告诉我们,一个原子中不可能有两个电子具有相同的电子层、电子子层和轨道的空间延伸方向和自旋状态。
这个原理叫做泡利不相容原理。
如氢原子的两个电子,都在第一层(K层),电子云形状是球形对称、只有一种完全相同伸展的方向,自旋方向必然相反。
核外电子排布遵循泡利不相容原理、能量最低原理和洪特规则。
原子物理学基石之一:泡利不相容原理

原子物理学基石之一:泡利不相容原理1925年,比海森堡发现量子力学稍早一点,奥地利物理学家泡利发现了一个重要原理,即泡利不相容原理。
这个原理非常重要,没有它,我们就很难解释原子结构,当然也很难解释分子结构。
那么,泡利不相容原理说的是什么呢?这个原理说,两个电子不可能处于同一个量子态中。
推而广之,任何一个电子只能处于不同的状态中。
怎么理解这个说法呢?在泡利发现这个原理时,海森堡的量子力学还没有建立,与海森堡量子力学等价的薛定谔波动力学更没有建立,所以,泡利那时用的是玻尔的轨道概念。
在玻尔的轨道概念中,我们可以这样理解泡利的原理:假设一个原子里有两个电子,那么,一个轨道上最多容纳两个电子。
可是,在旧量子论中,一个轨道就是电子的一个状态,那么,泡利为什么会说一个轨道电子的状态可以容纳两个电子呢?这是因为上堂课中提到的电子自旋。
一个轨道上,电子可以有两种状态:自旋向上或者自旋向下。
也就是说,如果两个电子同时在这个轨道上,那么,一个电子的自旋是向上的,另一个电子的自旋是向下的。
这样,这两个电子其实处于不同的状态。
有趣的是,泡利写他的论文时,物理学家们还没有发现电子的自旋。
就在泡利发表他的原理的同一年,另外两个物理学家在泡利论文的启发下,发现了电子的自旋。
故事听起来有点绕,但这就是历史的真相。
现在的量子力学早已抛弃了轨道的概念。
代替轨道的是量子态,用薛定谔发现的概念来说,一个量子态就是一个波。
泡利不相容原理可以这样说:在一个波态中,可以允许有两个电子,其中一个电子自旋向上,一个电子自旋向下。
如果我们将电子态比喻成云彩,泡利发现的这个原理可以这么说:两个电子不可能处于同一朵云彩中,当然,这朵云彩还含有电子的自旋状态。
泡利不相容原理十分重要,它解释了原子的刚性:由于电子的“云彩”具有排他性,因此电子的“云彩”和现实生活中的云彩不同,不可能融合在一起。
后来,有物理学家用泡利不相容原理解释为什么物质不会一直不断地缩小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12
13
各壳层可容纳的电子数
Nl n
l
0123 4 5 spdf g h
6 i
Nn
1K 2L 3M 4N 5O 6P 7Q
2
2
26
8
2 6 10
18
2 6 10 14
32
2 6 10 14 18
50
2 6 10 14 18 22
72
2 6 10 14 18 22 26 98
14
泡利
Wolfgang Pauli 奥地利人 1900-1958
同一个量子态
9
2.各壳层可容纳的电子数
•同一个n 组成一个壳层 对应于n = 1, 2, 3,…的各壳层 分别记做 K, L, M, N, O, P…
•相同 n, l 组成一个支壳层 对应于l = 0, 1, 2, 3,…的各支壳层 分别记做 s, p, d, f, g, h…
10
n 3
Ze K L M 2
例: 钠原子有11个核外电子,钠原子基态的电子组态为
1s2 2s2 2 p6 3s
1s2 2s2 2 p6
这10原子称原子实。原子实以外 的电子称为价电子,可以被激发
n≥3的激发态的钠原子电子组态为
(1s2 2s2 2 p6 3p) (1s2 2s2 2 p6 3d) (1s2 2s2 2 p6 4s) 等等
物理意 义
电子能量的主体
确定的能级 角动量的可 能取值 对总能量有一定 影响
“轨道”角动量在磁场中 可能的取向 能级分裂
谱线精细结构
8
二、泡利不相容原理
1.泡利不相容原理 一个原子内不可能有两个或两个以上的
电子具有完全相同的状态 或说 一个原子内不可能有四个量子数完全
相同的电子 或说 不可能有两个或两个以上的电子处于
n一定时 有n种取值 l 越小能量越低 5
3.磁量子数 ml 0,1,2… l 引起磁场中能级的分裂
Lz ml
4.自旋磁量子数
ms
1 2
产生精细结构
Sz ms
6
需要说明的是 自旋量子数 s = 1/2 只有一个值 自旋角动量也只有一个值
S s(s 1) 3 2
论的结果相同
3
玻尔理论的一条能级对 2 应于电子的一种轨道
量子力学的一条能级
1
则对应于电子的一种状态
每个状态用量子数 n , l , ml , ms 描述
3
能级: 粒子的内部能量值
高能级: 能量较高的能级 低能级: 能量较低的能级
基能级: 能量最低的能级
(相应的状态称基态) 激发能级: 能量高于基能
20
不变 不必总提及 可不计入
原子中核外电子的排布要遵守 泡利不相容原理 能量最低原理
7
四个量子数小结
名称
取值
主量子数 n 1,2,
l 0,1,2, n 1
角量子数 L ll 1
磁量子数
自旋磁量 子数
ml 0,1, l
Lz ml
ms
1 2
SZ
2
n=1 n=2
n=3
1
l
2 3d 1 3p 0 3s
1 2p 0 2s
0 1s
11
•一个支壳层内电子 可有(2l+1)× 2种量子态
∴ 主量子数为n的壳层
内可容纳的电子数为
Zn
n1
(2l
1) 2
2n2
l0
泡利原理是一个极为重要的自然规律是理 解原子结构和元素周期表的重要理论基础。
统中,不可能有两个电子具有相同的状态——
4对量子数 n、l、m、m s 至少有一对不同。
2、能量最小原理:基态原子中电子先填
满能量小的壳层。
例题:氯原子有
17个电子,写出 基态原子组态。
1s22s22p63s23p5
n l 2(2l+1)
10 2
1s2
20 2
2s2
16
2p6
30 2
3s2
15
3p5 19
获1945年诺贝尔 物理学奖
15
三、能量最低原理
“电子优先占据最低能态
”
n
3
Ze K L M 2
n=1
n=2
n=3
1
l
2 3d 1 3p 0 3s
1 2p 0 2s
0 1s
16
17
能 量
主量子数
电子能量水平随主量子数和次量子数的变化情况
18
四、原子的电子组态符号
Hale Waihona Puke 分配原则1、泡利不相容原理:一个多电子原子系
级的其它所有能级(相应 状态称激发态)
n
6
5 4 激发态 3
2
基态 1
4
一、原子中电子的四个量子数 描述原子中电子的运动状态 需要一组量子数( n,l,ml,ms )
1.主量子数 n = 1, 2, 3, 决定能量的主要因素
2.角(轨道)量子数 l = 0,1,2…(n-1) 对能量有一定影响
L l(l 1)
孤立原子的能级
围绕原子核旋转的电子能量不能任意取值,只能取特定 的离散值(离散轨道),这种现象称为电子能量的量子化。
原子核 电子
低能级
高能级 电子优先抢占低能级
1
E
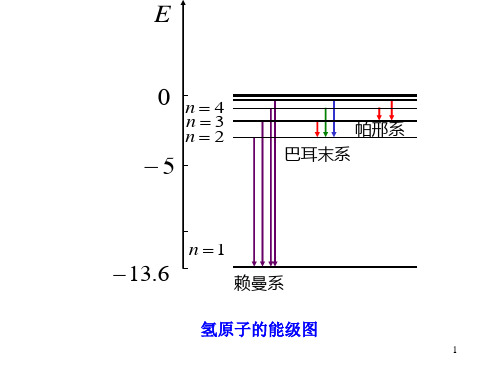
0 n4
n3 n2
5
帕邢系 巴耳末系
n 1
13.6
赖曼系
氢原子的能级图
2
n
由量子力学得出的氢 原子能级图和玻尔理
65 4
