均值比较检验和方差分析
均值检验方差分析课件

通过均值检验和方差分析,可以研究消费者行为、消费习惯、消费 心理等方面的差异和变化。
产业组织
在产业组织研究中,均值检验和方差分析可用于研究企业规模、市 场结构、企业绩效等方面的差异和变化。
04
均值检验与方差分析的注意事项
数据正态性的检验
总结词
在进行均值检验和方差分析之前,需要检验数据是否符合正态分布。正态分布是许多统计方法的前提假设,如果 数据不满足正态分布,可能导致分析结果不准确。
详细描述
为了控制第一类错误的概率,可以采用适当 的统计方法进行多重比较校正。例如,在方 差分析后,可以使用多重比较校正的方法( 如Tukey's HSD、Scheffé's method)来比 较各组之间的差异,以减少假阳性错误。此 外,还可以根据实际研究目的和数据情况选
择其他适当的统计方法进行多重比较。
适用场景
比较不同组别或不同时间点的平均值
例如比较不同班级的平均成绩、不同月份的平均销售额等。
检验总体均值的假设
例如检验某产品的平均质量是否符合标准。
计算方法
01
02
03
04
计算各组的平均值。
计算标准误差或标准差。
使用t检验或z检验等方法比较 平均值。
根据p值判断是否拒绝原假设 ,即各组平均值相等。
05
均值检验与方差分析的软件实现
SPSS软件实现
描述性统计
SPSS提供了丰富的描述性统计功能,如均值、中位数、众数、标准 差等,用于初步了解数据分布情况。
均值检验
SPSS中的“比较均值”功能可以比较两组或多组数据的均值,通过 T检验或非参数检验等方法,判断组间差异是否具有统计学显著性 。
方差分析
假设检验的方法选择

假设检验的方法选择在进行假设检验时,我们需要选择适合的方法来判断样本数据是否支持或拒绝其中一种假设。
下面将介绍一些常用的方法选择原则和方法:1.比较均值的方法比较均值的常用方法有t检验和方差分析。
当只涉及两个样本时,可以使用t检验。
当涉及多个样本时,可以使用方差分析。
需要注意的是,t检验和方差分析都要求样本数据符合正态分布。
2.比较比例的方法比较两个或多个比例的常用方法有Z检验和卡方检验。
当样本量较大时,可以使用Z检验。
当样本量较小时,可以使用卡方检验。
3.相关性的方法相关性的常用方法有相关系数检验和秩和检验。
相关系数检验适用于两个连续变量之间的相关性检验。
秩和检验适用于一个连续变量和一个分类变量之间的相关性检验。
4.拟合优度的方法拟合优度的常用方法是卡方检验。
拟合优度检验用于检验观察频数与理论频数之间的差异是否显著。
5.分类问题的方法对于分类问题,常用的方法有Fisher精确检验、G独立性检验和McNemar检验。
Fisher精确检验适用于二分类问题,G独立性检验适用于多分类问题,McNemar检验适用于配对分类问题。
6.多重比较的方法多重比较的常用方法有Bonferroni校正、Tukey HSD和Scheffe方法。
这些方法可以避免因多次比较而带来的类型I错误的增加。
在选择方法时,我们需要考虑以下几个因素:1.数据的类型:根据问题的性质和数据类型选择合适的方法进行假设检验。
2.假设的类型:根据研究问题和假设的类型选择相应的方法。
例如,比较均值问题使用t检验,比较比例问题使用Z检验等。
3.样本量:对于样本量较大的情况,我们可以使用正态分布近似方法进行假设检验。
对于样本量较小的情况,我们可以使用非参数方法进行假设检验。
4.数据的分布:假设检验通常基于数据分布的假设,所以需要先对数据的分布进行检验。
如果数据不符合正态分布,可以尝试进行转换或使用非参数方法。
5.类型I错误和类型II错误:在选择方法时,需要考虑希望控制的错误率。
SPSS软件中常用统计分析方法

SPSS软件中常用统计分析方法:均值比较与检验方差分析(参数检验)非参数检验相关分析回归分析聚类分析与判别分析因子分析与对应分析时间序列分析生存分析尺度分析(心理学)多响应变量分析常用统计图形条形图、线图和面积图圆图高低图帕累托图控制图箱图和误差条图散点图直方图P-P和Q-Q图序列图时间序列图审计抽样所谓审计抽样,是指注册会计师在实施审计程序时,从审计对象总体中选取一定数量的样本进行测试,并根据测试结果,推断审计对象总体特征的一种方法。
目录审计抽样,是指注册会计师对某类交易或账户余额中低于百分之百的项目实施审计程序,使所有抽样单元都有被选取的机会。
审计抽样,是指内部审计人员在内部审计活动中,采用适当的抽样方法从被审查和评价的审计总体中抽取一定数量有代表性的样本进行测试,以样本审查结果推断总体特征并作出相应结论的过程。
1、抽样审计不同于详细审计。
详细审计是指百分百地审计对象总体中的全部项目,并根据审计结果形成审计意见。
而抽样审计是从审计对象总体根据统计原理选取部分样本进行审计,并根据样本推断总体并发表审计意见。
2、审计抽样不能等同于抽查。
抽查作为一种技术,可以用于审前调查、确定审计重点、取得审计证据,在使用中无严格要求。
而审计抽样作为一种审计方法,需运用统计原理,并严格按规定的程序和抽样方法的要求实施。
3、抽样审计一般可用于逆查、顺查、函证等审计程序,也可用于符合性测试和实质性测试;但审计师在进行询问、观察、分析性复核时则不宜运用审计抽样。
(1)统计抽样和非统计抽样。
审计抽样统计抽样和非统计抽样的相同点:A、都需合理运用专业判断;B、都可以提供审计所要求的充分、适当的证据;C、都存在某种程度的抽样风险和非抽样风险。
统计抽样和非统计抽样的根本区别:统计抽样时利用概率法则来量化控制抽样风险;非统计抽样中,注册会计师全凭主观标准和个人经验确定样本规模和评价样本结果。
只要设计得当,非统计抽样也可达到统计抽样一样的效果。
均值比较检验和方差分析详解演示文稿

均值比较检验和方差分析详解演示文稿一、均值比较检验1.两个样本的均值比较:用于比较两个样本的均值是否存在显著差异。
常用的假设检验方法有t检验和z检验。
2.多个样本的均值比较:用于比较两个以上样本的均值是否存在显著差异。
常用的假设检验方法有方差分析。
针对不同的研究问题和样本特征,我们可以选择不同的假设检验方法进行均值比较。
二、方差分析方差分析是一种统计学中常用的分析方法,用于检验两个以上样本均值之间是否存在显著差异。
方差分析基于方差的分解原理,将总体方差分解为组内变异和组间变异,并通过统计检验来确定组间变异是否显著。
方差分析包括单因素方差分析和多因素方差分析两种形式。
1.单因素方差分析:适用于只有一个自变量(因素)的情况,用于比较不同水平的因素是否对观测变量有显著影响。
单因素方差分析有一元方差分析和重复测量方差分析两种形式。
2.多因素方差分析:适用于有两个或两个以上自变量(因素)的情况,用于比较多个自变量的主效应及其交互效应对观测变量的影响。
常用的多因素方差分析方法有二元方差分析和三元方差分析。
方差分析的基本思想是通过比较组间方差和组内方差的大小关系来判断样本均值之间是否有显著差异。
在进行方差分析前,需要先对数据的正态性、方差齐性进行检验,以确定方差分析是否适用。
三、均值比较检验和方差分析的步骤进行均值比较检验和方差分析的步骤如下:1.确定研究问题和样本特征:明确需要比较的样本均值或不同因素对样本均值的影响。
2.数据收集和整理:收集相应的样本数据,并进行数据清洗和整理。
3.正态性检验:对样本数据进行正态性检验,以确定是否满足方差分析的正态性假设。
4.方差齐性检验:对样本数据进行方差齐性检验,以确定是否满足方差分析的方差齐性假设。
5.假设检验:根据样本特征和研究问题,选择适当的假设检验方法进行分析。
对于均值比较检验,常用的方法有t检验和z检验;对于方差分析,常用的方法有一元方差分析和多元方差分析。
6.结果解释和报告:根据显著性检验结果,给出结论并解释研究结果。
方差分析中均值比较的方法

方差分析中均值比较的方法最近看文献时,多数实验结果用到方差分析,但选的方法不同,主要有LSD,SNK-q,TukeyHSD法等,从百度广库里找了一篇文章,大概介绍这几种方法,具体公式不列了,软件都可以计算。
这几种方法主要用于方差分析后,对均数间进行两两比较。
均数间的两两比较根据研究设计的不同分为两种类型:一种常见于探索性研究,在研究设计阶段并不明确哪些组别之间的对比是更为关注的,也不明确哪些组别问的关系已有定论、无需再探究,经方差分析结果提示“ 概括而言各组均数不相同”后,对每一对样本均数都进行比较,从中寻找有统计学意义的差异:另一种是在设计阶段根据研究目的或专业知识所决定的某些均数问的比较.常见于证实性研究中多个处理组与对照组、施加处理后的不同时间点与处理前比较。
最初的设计方案不同.对应选择的检验方法也不同.下面分述两种不同设计均数两两比较的方法选择。
1. 事先计划好的某对或某几对均数间的比较:适用于证实性研究。
在设计时就设定了要比较的组别,其他组别间不必作比较。
常用的方法有: Dunnett-t 检验、LSD-t 检验(Fisher ’s least significant dif ference t test) 。
这两种方法不管方差分析的结果如何——即便对于 P稍大于检验水平α进行所关心组别间的比较。
1.1 LSD-t检验即最小显著法,是Fisher于1935年提出的,多用于检验某一对或某几对在专业上有特殊探索价值的均数间的两两比较,并且在多组均数的方差分析没有推翻无效假设H0时也可以应用。
该方法实质上就是 t检验,检验水准无需作任何修正,只是在标准误的计算上充分利用了样本信息,为所有的均数统一估计出一个更为稳健的标准误,因此它一般用于事先就已经明确所要实施对比的具体组别的多重比较。
由于该方法本质思想与 t 检验相同,所以只适用于两个相互独立的样本均数的比较。
LSD法单次比较的检验水准仍为α ,因此可以认为该方法是最为灵敏的两两比较方法.另一方面,由于LSD法侧重于减少第Ⅱ类错误,势必导致此法在突出组间差异的同时,有增大I类错误的倾向。
方差分析中均值比较的方法

方差分析中均值比较的方法方差分析是统计学中常用的一种假设检验方法,用于比较多个样本均值是否有显著差异。
它通过分析不同组之间的方差来判断均值是否有显著差异,即通过计算组间的均方和组内的均方来进行比较。
方差分析有两种基本类型:单因素方差分析和多因素方差分析。
1.单因素方差分析:单因素方差分析主要是比较一个因素对于结果的影响,只有一个自变量。
在进行单因素方差分析时,首先需要确定因变量的类型是连续型还是离散型。
对于连续型的因变量,通常使用单因子方差分析方法;对于离散型的因变量,可以使用卡方检验等方法。
(1)单因素方差分析有三个基本要素:因变量、自变量和一个或多个水平。
因变量是研究对象,自变量是影响因子,水平是不同的取值类型。
(2)计算组间方差和组内方差。
组间方差是因变量的总方差被解释的部分,组内方差是因变量的多余差异(误差)。
方差的比例是判断均值是否有显著差异的依据。
(3)计算F值。
F值是组间均方除以组内均方。
F值越大,表示组间差异越大,样本均值差异的可靠性越高,有显著差异的可能性越大。
(4)根据F分布表和显著性水平(通常为0.05),确定拒绝域。
如果计算得到的F值大于F分布表中的临界值,就拒绝原假设,即认为组间均值存在显著差异。
2.多因素方差分析:多因素方差分析是在单因素方差分析的基础上,增加了一个或多个自变量,用来研究多个因素对于结果的影响以及交互作用。
多因素方差分析可以更全面地研究各因素的影响,并考虑因素之间的关系。
(1)主效应。
主效应用来检验各个自变量对于因变量的影响是否显著。
计算各个因素的F值和显著性水平。
(2)交互效应。
交互效应是指两个或多个因素之间的相互作用导致的影响,即一些因素对于因变量的影响在其他因素不同水平下是否有显著差异。
计算交互效应的F值和显著性水平。
(3)解释方差。
计算组间方差、组内方差、主效应方差和交互效应方差的比例来判断各个因素的影响程度。
注意事项:1.在进行方差分析之前,需要进行方差齐性和正态性检验,确保数据符合方差分析的前提条件。
第5章SPSS均值比较T检验和方差分析

第5章SPSS均值比较T检验和方差分析第5章主要介绍了SPSS软件中进行均值比较的方法,包括t检验和方差分析。
本文将详细介绍SPSS中进行均值比较的步骤,以及如何解读结果。
5.1t检验t检验是一种用于比较两个样本均值差异的统计方法。
在SPSS中,进行t检验的步骤如下:1.打开SPSS软件,并导入需要进行t检验的数据集。
2.选择“分析”菜单,在下拉菜单中选择“比较均值”选项,再选择“独立样本t检验”选项。
3.在弹出的对话框中,将需要比较的变量移动到“因子”框中,将“分组变量”移动到“因子”框中,并选择需要进行的假设检验类型。
4.点击“确定”按钮,等待计算结果。
5.在输出窗口中,可以查看计算结果,包括均值、标准差、样本量、t值和p值等。
通常,我们关注的是p值,如果p值小于0.05,则认为差异显著。
例如,我们想比较男性和女性的体重是否有显著差异。
我们将体重作为因变量,性别作为自变量,进行t检验。
在计算结果中,如果p值小于0.05,则可以认为男女性别对体重有显著影响。
5.2方差分析方差分析是一种用于比较三个或更多个样本均值是否存在差异的统计方法。
在SPSS中,进行方差分析的步骤如下:1.打开SPSS软件,并导入需要进行方差分析的数据集。
2.选择“分析”菜单,在下拉菜单中选择“比较均值”选项,再选择“单因素方差分析”选项。
3.在弹出的对话框中,将需要比较的变量移动到“因子”框中,将“分组变量”移动到“因子”框中,并选择需要进行的假设检验类型。
4.点击“确定”按钮,等待计算结果。
5.在输出窗口中,可以查看计算结果,包括均值、标准差、样本量、F值和p值等。
通常,我们关注的是p值,如果p值小于0.05,则认为差异显著。
例如,我们想比较不同药物对治疗效果的影响。
我们将药物作为因变量,治疗效果作为自变量,进行方差分析。
在计算结果中,如果p值小于0.05,则可以认为不同药物对治疗效果有显著影响。
通过以上步骤,我们可以在SPSS中进行均值比较、t检验和方差分析。
均值检验方差分析
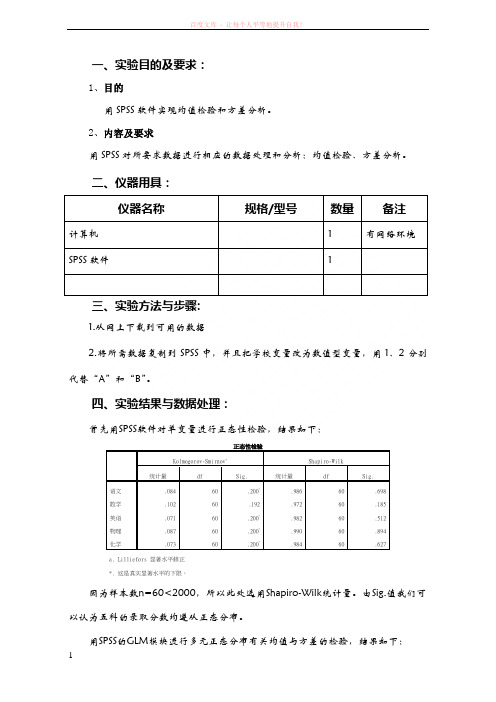
一、实验目的及要求:1、目的用SPSS软件实现均值检验和方差分析。
2、内容及要求用SPSS对所要求数据进行相应的数据处理和分析:均值检验、方差分析。
二、仪器用具:仪器名称规格/型号数量备注计算机 1 有网络环境SPSS软件1三、实验方法与步骤:1.从网上下载到可用的数据2.将所需数据复制到SPSS中,并且把学校变量改为数值型变量,用1、2分别代替“A”和“B”。
四、实验结果与数据处理:首先用SPSS软件对单变量进行正态性检验,结果如下:正态性检验Kolmogorov-Smirnov a Shapiro-Wilk统计量df Sig. 统计量df Sig.语文.084 60 .200*.986 60 .698数学.102 60 .192 .972 60 .185英语.071 60 .200*.982 60 .512物理.087 60 .200*.990 60 .894化学.073 60 .200*.984 60 .627a. Lilliefors 显著水平修正*. 这是真实显著水平的下限。
因为样本数n=60<2000,所以此处选用Shapiro-Wilk统计量。
由Sig.值我们可以认为五科的录取分数均遵从正态分布。
用SPSS的GLM模块进行多元正态分布有关均值与方差的检验,结果如下:第一张主体间因子表展示了样本数据分别来自两个学校的个数。
第二张多变量检验表给出了几个统计量,由Sig.值可以看出,无论从哪个统计量来看,两个学校的录取分数都是有显著差别的。
由于模型通过了显著性检验,意味着两所学校的录取分数线是不同的。
主体间因子N学校A 30B 30多变量检验b效应值 F 假设df误差dfSig.截距Pillai 的跟踪.99916790.281a5.0054.000.000Wilks的Lambda.00116790.281a5.0054.000.000Hotelling的跟踪1554.65616790.281a5.0054.000.000Roy的最大根1554.65616790.281a5.0054.000.000学校Pillai 的跟踪.85161.672a5.0054.000.000Wilks的Lambda.14961.672a5.0054.000.000Hotelling的跟踪5.7161.672a5.0054.000.000Roy 的最大根5.7161.672a5.0054.000.000a. 精确统计量b. 设计 : 截距 + 学校主体间效应的检验源因变量III型平方和df均方 FSig.校正模型语文1050.017a1 1050.01748.251.000数学1470.150b1 1470.15086.034.000英语1135.350c1 1135.35039.831.000物理1859.267d1 1859.26783.392.000化学1560.600e1 1560.60041.652.000截距语文372408.8171 372408.81717113.201.000数学376833.751 376833.7522052.626.000英语388010.4171 388010.41713612.479.000物理389781.601 389781.6017482.600.000化学383360.2671 383360.26710231.722.000学校语文1050.0171 1050.01748.251.000数学1470.1501 1470.15086.034.000英语1135.3501 1135.35039.831.000物理1859.2671 1859.26783.392.000化学1560.6001 1560.60041.652.000误差语文1262.16758 21.761数学991.1058 17.088英语1653.23358 28.504物理1293.13358 22.295化学2173.13358 37.468总计语文374721.0060数学379295.0060英语390799.0060物理392934.0060化学387094.0060校正的总计语文2312.18359数学2461.25059英语2788.58359物理3152.40059化学3733.73359a. R 方 = .454(调整 R 方 = .445)b. R 方 = .597(调整 R 方 = .590)c. R 方 = .407(调整 R 方 = .397)d. R 方 = .590(调整 R 方 = .583)e. R 方 = .418(调整 R 方 = .408)由上面主体间效应的检验表可知五科分数的Sig.值均为0.000说明两个学校本科录取分数在五门课上都存在显著差别。
方差分析多个总体均值比较的统计方法

方差分析多个总体均值比较的统计方法方差分析(analysis of variance, ANOVA)是一种通过对样本数据的方差进行分析,来比较多个总体均值是否存在显著差异的统计方法。
方差分析可以用于比较三个或三个以上总体均值之间的差异,是一种常用的多样本比较方法。
本文将介绍方差分析的基本原理、假设检验与实施步骤。
一、方差分析的基本原理方差分析的基本原理是通过比较组内变异和组间变异的大小,来判断多个总体均值是否存在显著差异。
方差分析假设总体服从正态分布,且各总体具有相同的方差。
方差分析将总体均值的差异分解成组内差异和组间差异,并通过计算F值来进行假设检验。
二、方差分析的假设检验在进行方差分析时,我们需要建立空假设(H0)和备择假设(Ha),并通过计算统计量进行假设检验。
常见的方差分析假设如下:H0:各总体均值相等,即μ1 = μ2 = μ3 = ... = μk;Ha:至少存在两个总体均值不相等。
在进行假设检验时,我们需要计算F统计量。
F统计量的计算公式如下:F = 组间均方(MSB) / 组内均方(MSW)其中,组间均方(MSB)等于组间平方和(SSB)除以自由度(k-1);组内均方(MSW)等于组内平方和(SSW)除以自由度(n-k)。
三、方差分析的实施步骤以下是进行方差分析的一般步骤:1. 收集数据:根据研究目的,选择合适的样本进行数据收集,确保数据的准确性和可靠性。
2. 计算数据:根据实际情况,计算各组的样本均值、平方和以及总体均值等统计量。
3. 计算平方和:根据计算的样本数据,计算组内平方和(SSW)和组间平方和(SSB)。
4. 计算均方和F统计量:根据计算的平方和,计算组内均方(MSW)、组间均方(MSB)和F统计量。
5. 判断显著性:将计算得到的F值与临界值进行比较,如果F值大于临界值,则拒绝空假设,认为存在至少两个总体均值不相等。
6. 结果解释:如果拒绝空假设,可以进一步进行事后检验(post-hoc tests)来确定具体哪些组之间存在显著差异。
均值比较与方差分析
均值比较的上机实现Means过程单一样本T检验两独立样本T检验两配对样本T检验1 Means过程统计学上的定义和计算公式定义:Means过程是按照用户指定条件,对样本进行分组计算均数和标准差,如按性别计算各组的均数和标准差。
Means过程的计算公式为研究问题比较不同性别同学的数学成绩平均值和方差。
数据如表2-1所示。
实现步骤图2-1 在菜单中选择“Means”命令图2-2 Means对话框图2-3 “Means:Options”对话框结果和讨论2 单一样本T检验统计学上的定义和计算公式定义:SPSS单样本T检验是检验某个变量的总体均值和某指定值之间是否存在显著差异。
统计的前提样本总体服从正态分布。
也就是说单样本本身无法比较,进行的是其均数与已知总体均数间的比较。
计算公式如下。
单样本T检验的零假设为H0总体均值和指定检验值之间不存在显著差异。
采用T检验方法,按照下面公式计算T统计量:SPSS中实现过程研究问题分析某班级学生的高考数学成绩和全国的平均成绩70之间是否存在显著性差异。
数据如表2-1所示。
实现步骤图2-4 “One-Sample T Test”设置框图2-5 “One-Sample T Test:OPtions”对话框结果和讨论3 两独立样本T检验统计学上的定义和计算公式定义:所谓独立样本是指两个样本之间彼此独立没有任何关联,两个独立样本各自接受相同的测量,研究者的主要目的是了解两个样本之间是否有显著差异存在。
这个检验的前提如下。
∙两个样本应是互相独立的,即从一总体中抽取一批样本对从另一总体中抽取一批样本没有任何影响,两组样本个案数目可以不同,个案顺序可以随意调整。
∙样本来自的两个总体应该服从正态分布。
两独立样本T检验的零假设H0为两总体均值之间不存在显著差异。
在具体的计算中需要通过两步来完成:第一,利用F检验判断两总体的方差是否相同;第二,根据第一步的结果,决定T统计量和自由度计算公式,进而对T检验的结论作出判断。
(整理)实习四均值比较方差分析.

实习四均值比较和方差分析一均值比较与方差分析的概念统计分析常常采取抽样研究的方法。
即从总体中随机抽取一定数量的样本进行研究来推论总体的特性。
由于总体中的每个个体间均存在差异,即使严格遵守随机抽样原则也会由于多抽到一些数值较大或较小的个体致使样本统计量与总体参数之间有所不同。
由此可以得出这样的认识:均值不相等的两个样本不一定来自均值不同的总体。
能否用样本均数估计总体均数,两个变量均数接近的样本是否来自均值相同的总体?换句话说,两个样本某变量均值不同,其差异是否具有统计意义,能否说明总体差异?这是各种研究工作中经常提出的问题。
这就要进行均值比较。
对来自正态总体的两个样本进行均值比较常使用T检验的方法。
T检验要求两个被比较的样本来自正态总体。
两个样本方差相等与不等时使用的计算t值的公式不同。
进行方差齐次性检验使用F检验。
对应的零假设是:两组样本方差相等。
p值小于0.05说明在该水平上否定原假设,方差不齐;否则两组方差无显著性差异。
F值的计算公式是:F=S12(较大)/S22(较小)方差分析(ANOVA)又称“变异数分析”或“F检验”,是R.A.Fisher发明的,用于两个及两个以上样本均数差别的显著性检验。
二实习目的和原理假设检验的目的:推断两个总体均数是否相等均值过程单一样本T检验(One-Sample T Test)独立样本T检验(Independent-Sample T Test)配对样本T检验(Paired-Sample T Test)方差分析(One-Way ANOVA)附正态分布的检验数据要求(t检验适用范围):使用T检验法对两个独立样本的均值进行比较,除要求这两个样本都来自正态总体或近似正态分布(包括偏态转换),还要对两个正态总体的方差是否相等加以区分,即需要确定两个正态总体是否具有方差齐性。
t检验适用于可比性资料,即除了欲比较的因素外,其它所有可影响的因素应相似。
假设检验的注意事项1 假设检验的P值不能反映总体均数差别的大小。
方差分析中均值比较的方法

方差分析中均值比较的方法最近看文献时,多数实验结果用到方差分析,但选的方法不同,主要有LSD,SNK-q,TukeyHSD法等,从百度广库里找了一篇文章,大概介绍这几种方法,具体公式不列了,软件都可以计算。
这几种方法主要用于方差分析后,对均数间进行两两比较。
均数间的两两比较根据研究设计的不同分为两种类型:一种常见于探索性研究,在研究设计阶段并不明确哪些组别之间的对比是更为关注的,也不明确哪些组别问的关系已有定论、无需再探究,经方差分析结果提示“ 概括而言各组均数不相同”后,对每一对样本均数都进行比较,从中寻找有统计学意义的差异:另一种是在设计阶段根据研究目的或专业知识所决定的某些均数问的比较.常见于证实性研究中多个处理组与对照组、施加处理后的不同时间点与处理前比较。
最初的设计方案不同.对应选择的检验方法也不同.下面分述两种不同设计均数两两比较的方法选择。
1. 事先计划好的某对或某几对均数间的比较:适用于证实性研究。
在设计时就设定了要比较的组别,其他组别间不必作比较。
常用的方法有: Dunnett-t 检验、LSD-t 检验(Fisher ’s least significant dif ference t test) 。
这两种方法不管方差分析的结果如何——即便对于 P稍大于检验水平α进行所关心组别间的比较。
1.1 LSD-t检验即最小显著法,是Fisher于1935年提出的,多用于检验某一对或某几对在专业上有特殊探索价值的均数间的两两比较,并且在多组均数的方差分析没有推翻无效假设H0时也可以应用。
该方法实质上就是 t检验,检验水准无需作任何修正,只是在标准误的计算上充分利用了样本信息,为所有的均数统一估计出一个更为稳健的标准误,因此它一般用于事先就已经明确所要实施对比的具体组别的多重比较。
由于该方法本质思想与 t 检验相同,所以只适用于两个相互独立的样本均数的比较。
LSD法单次比较的检验水准仍为α ,因此可以认为该方法是最为灵敏的两两比较方法.另一方面,由于LSD法侧重于减少第Ⅱ类错误,势必导致此法在突出组间差异的同时,有增大I类错误的倾向。
均值比较与方差分析

均值比较与方差分析
一、均值比较:
均值比较是比较不同组别之间的平均值差异。
常用的方法有独立样本t检验和配对样本t检验。
1.独立样本t检验:
独立样本t检验是用来比较两个独立样本之间的均值是否存在显著差异。
常见的应用场景包括比较两个不同组别的观测值(例如男性和女性的身高差异)或者比较两种不同治疗方法的疗效。
2.配对样本t检验:
配对样本t检验是用来比较同一组个体在不同时间点或者不同条件下的均值差异。
常见的应用场景包括比较同一组人群在接受其中一种治疗前后的效果或者在两种不同测试之间的得分差异。
二、方差分析:
方差分析是比较不同组别之间的方差差异。
常用的方法有单因素方差分析和多因素方差分析。
1.单因素方差分析:
单因素方差分析是用来比较一个因素对于不同组别间的均值差异是否存在显著影响。
例如,研究人员想要知道不同教育程度对于收入的影响,可以将不同教育程度作为一个因素进行方差分析。
2.多因素方差分析:
多因素方差分析是用来同时比较两个或两个以上因素对于不同组别间的均值差异是否存在显著影响。
例如,研究人员想要知道不同教育程度和不同工作经验对于收入的影响,可以同时将教育程度和工作经验作为因素进行方差分析。
在使用这两种方法时,需要确保数据符合一定的假设条件,如正态性和方差齐性。
如果数据不符合这些假设条件,可能需要采取一些数据转换或者使用非参数方法进行分析。
总结来说,均值比较和方差分析是常用的统计分析方法,用于比较不同组别之间的差异。
通过这些方法,我们可以了解不同组别之间是否存在显著差异,帮助我们做出更准确的结论和决策。
spss教程第二章--均值比较检验与方差分析

第二章均值比较检验与方差分析在经济社会问题的研究过程中,常常需要比较现象之间的某些指标有无显著差异,特别当考察的样本容量n比较大时,由随机变量的中心极限定理知,样本均值近似地服从正态分布。
所以,均值的比较检验主要研究关于正态总体的均值有关的假设是否成立的问题。
◆本章主要内容:1、单个总体均值的 t 检验(One-Sample T Test);2、两个独立总体样本均值的 t 检验(Independent-Sample T Test);3、两个有联系总体均值均值的 t 检验(Paired-Sample T Test);4、单因素方差分析(One-Way ANOVA);5、双因素方差分析(General Linear Model Univariate)。
◆假设条件:研究的数据服从正态分布或近似地服从正态分布。
在Analyze菜单中,均值比较检验可以从菜单Compare Means,和General Linear Model得出。
如图2.1所示。
图2.1 均值的比较菜单选择项§2.1 单个总体的t 检验(One-Sample T Test)分析单个总体的 t 检验分析也称为单一样本的 t 检验分析,也就是检验单个变量的均值是否与假定的均数之间存在差异。
如将单个变量的样本均值与假定的常数相比较,通过检验得出预先的假设是否正确的结论。
例1:根据2002年我国不同行业的工资水平(数据库SY-2),检验国有企业的职工平均年工资收入是否等于10000元,假设数据近似地服从正态分布。
首先建立假设:H0:国有企业工资为10000元;H1:国有企业职工工资不等于10000元打开数据库SY-2,检验过程的操作按照下列步骤:1、单击Analyze →Compare Means →One-Sample T Test,打开One-Sample T Test 主对话框,如图2.2所示。
图2.2 一个样本的t检验的主对话框2、从左边框中选中需要检验的变量(国有单位)进入检验框中。
均值分析与方差分析

协方差分析
协方差分析是利用线性回归的方法消除混杂因素的 影响后进行的方差分析,这是实际工作中经常要考 虑的问题。
非饱和模型的SPSS操作
饱和模型的SPSS操作
本章小结
本章介绍了均值分析、方差分析的方法,其中方差分 析由包括单因素方差分析、多因素方差分析、重复度 量和协方差分析。均值分析和方差分析是专业统计分 析中最重要的,同时也是最基础的统计分析方法,在 多元统计中已经得到了广泛的应用,希望读者能认真 学习和掌握。
多因素方差分析
单变量:保存
多因素方差量资料是指对同一受试对象的某项观测指标 进行多次测量所得到的数据。如对病人治疗(后手 术)后一天、三天、一周、两周等多个时间点进行 连续观测;教育研究中观察不同学期学生的成绩变 化情况;心理研究中观察不同时间段个体的心理调 适能力;经济领域中研究市场的动态等。重复测量 设计的数据分析若采用前述的普通方差分析方法, 同样需要满足独立、正态、等方差的前提假设。可 实际情况是:重复测量观测值来自同一受试对象的 不同时间点,不能完全满足以上各项前提假设条件 。
6.协方差分析 7. 本章小结
均值分析
均值分析过程的优势在于所有的描述性统计量均按 因变量的取值分组计算,无需像其他程序那样必须 先运行文件拆分过程。在输出结果中各组的描述指 针被放在一起,也便于相互比较。如果需要,均值 分析过程还可以直接输出方差分析结果,并计算相 应的相关性指针而无需再次运行其他过程,显然要 比先描述再比较要方便得多。
单因素方差分析
单因素ANOVA:对比
单因素方差分析
单因素ANOVA:两两比较
单因素方差分析
单因素ANOVA:选项
多因素方差分析
多因素方差分析用来研究两个及两个以上的控制变 量是否对观察变量产生显著影响。由于讨论多个因 素对个案的影响,因此这种方差分析过程被称为多 因素方差分析。多因素方差分析不仅能够分析多个 因素对观测变量的影响,而且能够分析多个控制因 素的交互作用能否对观测变量的分布产生影响,进 而最终找到利于观测变量的最优组合。
多重均值比较与方差分析前提假设检验

组内离差平方和
kn
SSE
( xij xi )2
i1 j 1
随机因素导致的变差
SST=SSA+SSE
2019/10/8
19
离差平方和的自由度与均方
三个平方和的自由度分别是 SST 的自由度为nk-1,nk为全部观察值的个数 SSA的自由度为k-1,其中k为因素水平的个数 SSE 的自由度为nk-k
(奖金=1) (奖金=2) (奖金=3) (奖金=4)
样本1
x1, s12
样本2
x2, s22
样本3
x3, s32
样本4
x4, s42
H 0 : 1 2 3 4 ??
2019/10/8
4
各个总体的均值相等吗?
f(X)
X
1 2 3 4
f(X)
2019/10/8
2019/10/8
9
ANOVA (analysis of variance)
由于方差分析法是通过比较有关方差的大小而 得到结论的,所以在统计中,常常把运用方差 分析法的活动称为方差分析。
方差分析的内容很广泛,既涉及到实验设计的 模式,又关乎数据分析模型中因素效应的性质。 本章在完全随机试验设计下,讨论固定效应模 型方差分析的基本原理与方法,重点介绍单因 素方差分析。
全部检验过程烦琐,做法不经济 无统一的总体方差估计 ,检验的精度降低 犯第一类错误的概率增大,检验的可靠性降
低
2019/10/8
7
思考
7岁儿童的平均身高为102,现测得某班12名7 岁儿童身高分别为:
97、99、103、100、104、97、105、110、99、 98、103、99
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两个独立样本T检验的零假设 H0为两总体均值之间不存在显 著差异。
在两总体方差未知且不等时,
T统计量计算公式如右:
t
x1 x2
s12 / n1 s22 / n2
s12 s22
f
n1
s12 n1
2
n2
s22 n2
2
n1
n2
两总体方差未知且 相同情况下,T统 计量计算公式:
t x1 x2
s
2 p
/
n1
s2p
/
n2
S
2 p
(n1
1)s12 (n2 1)s22 n1 n2 1
评判标准:
Spss将会根据计算的T值和T分布表,给 出相应的相伴概率值Sig。
如果相伴概率值小于或等于显著水平a, 则拒绝H0,认为两总体均值之间存在显著 差异,相反,相伴概率大于显著水平a,则 不能拒绝H0 ,认为两总体均值之间不存 在显著差异。
结果与讨论
T值为0.566
相伴概率Sig =0.584
Sig>0.05, 因此不能拒绝H0, 可以认为 11名同学的成绩与全国数学平均成绩相 比,没有显著差异。
作业
抽取一个由12名学生组成的随机样本,调查他 们在作业上花费的时间。假设学生作业时间服 从正态分布,老师建议时间不低于36小时,检 验其平均时间是否与老师建议的时间相符?
计算公式:Leabharlann nx1ix1
i 1
n
例1
以下是某个班同学的数学成绩,比较不同性别 同学的数学成绩平均值和方差。
性别 male female
数学 99 79 59 89 79 89 99 88 54 56 23 70 80 67
步骤:
Analyze->Compare Means- >Means
Groups
本例中大于相伴概率0.461,大于显著水 平0.05,不能拒绝方差相等的假设,可 以认为两个学校学生数学成绩方差无显 著差异;
在方差相等时看T检验结果,T检验值等 于相伴概率0.423,大于显著水平0.05,不 能拒绝T检验的零假设,可以认为两个学 校学生数学平均成绩无显著差异。
31
40
26
30
36
38
29
40
38
30
35
38
二、两个独立样本T检验
所谓独立样本是指两个样本之间彼此独 立没有任何关联,两个独立样本各自接 受相同的测量,研究者的主要目的是了 解两个变量之间是否有显著差异存在。
检验的前提: 1、两个样本相互独立 2、样本来自的两个总体服从正态分布
计算步骤
利用F检验判断两总体的方差是否相同。 Spss采用Levene F方法检验两总体方差是否相 同,自动计算F统计量,并根据F分布表给出统 计量对于的相伴概率和显著水平a进行比较, 从而判断方差是否相同。
5.3
7.9
7
5.9
4.9
5.3
4.2
7.1
6.5
5.9
6.7
6.6
4.2
5.9
7.1
5.8
7
5.7
假设两个总体的方差相等,显著水平为 0.05,这两种方法效率是否有显著差异?
D是样本均值与检验值的差。 S.E.Mean:样本均差,或抽样平均误差 S是样本标准差,n为样本数
中心极限定理
如果总体存在有限的平均数和方差时, 不管总体是否属于正态分布,只要当抽 样单位数不断增加,当样本容量大于30 后,即当抽样单位数足够大时,样本平 均数x分布趋近于正态发布。
正态分布
-2u 否决域
-u
x
u
68.27%
2u 否决域
95.45% 接受域
当以全及总体平均数为中心各加减一个抽样平均误差 范围时,此范围的抽样指标占总体所有可能指标的 68.27%。两倍时为95.45%。这个倍数称为概率度
抽样平均误差
样本平均数x的平均数等于总体平均数,样 本平均数分布的方差等于总体方差除以样本 容量。
例2
上题中,数学高考成绩与全国平均成绩 70之间是否存在显著差异?
步骤
Analyze->Compare Means- >One Sample T Test
Test Variables: 数学 Test Values: 70
Option: Confidence Interval: 95% Missing Values: Exclude cases
例3
清华、北大学生的高考数学成绩表
学校 清华 北大
数学 99 88 79 59 54 89 79 56 89 99 23 89 70 50 67 78 89 56
步骤:
Analyze->Compare Means- >Independent- Sample T Test
Test Variables: 数学 Test Values: Source->Define
Dependent List 对话框->数学 Independent List对话框->性别 Option按钮,选择统计项目
第二节 T检验
一、单一样本T检验 二、两个独立样本T检验
一、单一样本T检验
检验某个变量的样本均值与某个指定总体均值之间 是否存在显著差异。
计算公式:
t xx D S.E.Mean s / n
本章内容
第一节 均值比较 第二节 T检验 第三节 方差分析
要点:
均值比较是对同一样本进行分组,对组 与组之间平均水平的比较。
T检验主要运用在两个样本间平均水平的 比较。
方差分析运用于两个以上样本的均数比 较。
第一节 均值比较
一、Means过程
Means过程是按用户指定条件,对样本进 行分组计算均值和标准差。
抽样平均误差
(x X )2 = S
所有样本的个数 n
(S.E.Mean)
T分布
当样本容量小于30,样本平均数分布服 从n-1个自由度的T分布。
SPSS将根据T分布表给出t值对应的相伴 概率值。如果相伴概率值小于或等于用 户设想的显著性水平a,则拒绝H0,认为总 体均值和检验值之间存在显著差异。反 之,总体均值和检验值之间不存在差异。
作业
一家企业生产某种产品,随机抽取50 名工人,分成两个组,每组25名工人, 用A方法生产所需时间:
6.8
5
7.9
5.2
7.6
6.1
6.2
7.1
4.6
6
6.4
6.1
6.6
7.7
6.4
5
5.9
5.2
6.5
7.4
7.1
6.1
5
6.3
7
作业
用B方法生产所需时间:
5.2
6.7
5.7
6.6
8.5
4.2
4.5
