第11章 模糊RBF网络
基于模糊RBF神经网络的智能PID控制

基于模糊RBF神经网络的智能PID控制胥良;郭林;梁亚;杨金龙;张卫芳【摘要】针对常规PID控制参数变化系统效果不佳的缺点,设计一种利用智能控制理论RBF神经网络与模糊控制技术相融合的新型智能PID控制方法[1].该控制方法将系统的输入误差及其变化率进行模糊化后,再利用RBF神经网络算法对PID控制参数进行在线学习、运算和整定[副.MATLAB仿真结果表明,基于上述的PID控制方法能够克服传统PID控制器的局限性,具有较高的控制精度,较好的动态品质及较强的鲁棒性.【期刊名称】《工业仪表与自动化装置》【年(卷),期】2015(000)006【总页数】4页(P67-69,75)【关键词】RBF神经网络;模糊算法;PID控制【作者】胥良;郭林;梁亚;杨金龙;张卫芳【作者单位】黑龙江科技大学电气与控制工程学院,哈尔滨150022;黑龙江科技大学电气与控制工程学院,哈尔滨150022;黑龙江科技大学电气与控制工程学院,哈尔滨150022;黑龙江科技大学电气与控制工程学院,哈尔滨150022;黑龙江科技大学电气与控制工程学院,哈尔滨150022【正文语种】中文【中图分类】TP1830 引言常规PID控制通过调整参数以获得良好的控制效果,但是参数整定值只能在一定局域内得到优化值,全局控制效果不是很理想。
为了解决这一问题,该文将模糊控制理论和神经网络理论与计算机技术结合设计了一种新型智能PID控制器[3]。
1 常规PID控制器常规的PID控制方法采用线性控制,通过将系统初始给定的采样值r(k)和系统实际输出的采样值y(k)作差的操作而得到控制的偏差:PID控制就是分别对系统的偏差e(k)进行比例、积分、微分运算,将所得结果按照一定的规则进行加法运算,从而得到PID控制器的控制输出量u(k),通过控制输出u(k)对系统中的被控对象进行相应的控制。
如图1所示。
图1 PID控制器原理图在离散时间域内,PID控制的控制输出表达式如下:其中:kp为比例系数,该系数的作用是将系统中计算得到的偏差系数进行成比例的反应,使得当系统中突然出现系统偏差的时候控制器能够敏锐地检测到该偏差并对系统对应的部分进行相应的控制处理以达到减小误差的目的;ki为积分系数,该系数的作用主要是用来将系统的无差度进行显著地提高以达到消除静差的目的,静态误差消除速度与该系数可以近似认为正比关系,即ki越小,静态误差的减小速度越快[4]。
基于模糊RBF神经网络的人脸识别系统研究

基于模糊 RBF神经网络的人脸识别系统研究摘要:随着时间的推移,国内社会已经进入到一个快速发展的信息时代、智能时代,其重要表现就是不同的识别系统开始在各个领域内进行运用,人脸识别系统就是其中之一,并且取得了很好的作用和效果。
目前人脸识别系统的研究已经成为了模式识别领域中的一个重点课题,在身份认证、智能监控、信息安全和金融安全等等领域都具有良好的发展前景。
目前人脸识别系统的运用主要具有以下几个芳年,包含安全控制、司法运用等等,后续很有可能发展成为一个巨大的、对人类生活、工作产生深刻影响的产业,需要给予相应的重视。
故此,在本文中主要针对基于模糊RBF神经网络的人脸识别系统进行系统的研究和分析,其主要目的在于促进基于模糊RBF神经网络的人脸识别系统的运用,使得这一系统具有很好的学习能力,提升人脸识别的准确率。
关键词:模糊神经;神经网络;人脸识别;识别系统;研究分析Face recognition system based on Fuzzy RBF neural network, abstract: with the passage of time, the domestic society has entered a rapidly developing information age, intelligent age, the important performance is that different recognition systems start to be used in various fields, and face recognition system is one of them, and has achieved a good effect. At present, the research of face recognition system has become an important topic in the field of pattern recognition, which has a good prospect in the fields of identity authentication, intelligent monitoring, information security and financial security. At present, the application of face recognition system mainly has the following several years, including security control, judicial application and so on, and the follow-up is likelyto develop into a huge industry that has a profound impact on human life and work, it needs to be taken seriously. Therefore, in this paper, we mainly study and analyze the face recognition system based on fuzzy RBF neural network, the main aim is to promote the application of the face recognition system based on fuzzy RBF neural network, so this system has a good learning ability, improve the accuracy of face recognition. Keywords: Fuzzy neural network; neural network; face recognition; recognition system; research and analysis前言:随着时间的推移和时代的不断改革创新,国内的社会经济和科学技术都实现了快速的发展和推进,国民群众的日常工作和生活水平都得到了比较大的提升,但与此同时,时代发展和国民大众对于众多领域提出了更高的要求,包含安全验证、身份认证和人机交互等等。
2019【大学课件】模糊神经网络.ppt

11.4 模糊神经元的一般构造方法
模糊神经元除具有普通神经元 的功能外,还具有处理模糊信息的 能力。按功能可分为以下三种: ① 由IF-THEN规则构造的模糊神经 元(对应类型I) 该规则常用于表示专家知识。 i 表示对应 设 y i 是某规则的输出。 规则输出的推理隶属函数值(如式 (11.6)和式(11.7))。则我们 可以构造如下的神经元:
/sundae_me ng
11.1 模糊神经网络理论概述
模糊逻辑系统易于理解,而神经网络则有极强的自适应 学习能力.随着模糊信息处理技术和神经网络技术研究的不 断深入,如何将模糊技术与神经网络技术进行有机结合,利 用两者的长处,提高整个系统的学习能力和表达能力,是目 前最受人注目的课题之一。模糊神经网络就是在这种背景 下诞生的一门新生技术。 将模糊逻辑与神经网络相结合就构成了模糊神经网络. 虽然这是两个截然不同的领域,但是均是对人类智能的研究. 目前,将模糊逻辑和神经网络相结合的研究主要有以下几种 形式:
i i G F 其中 j(j=1,2…r)和 k(k=1,2…s)是模糊集的标识, 它们用适当的隶属函数来刻画。
X ( x1, x1
xr ) R
Y=(y1 , y2
ys ) R
分别是语言变量的输入和输出,上标i(=1,2…u)表示第i个 规则。
/sundae_me ng
ri xr (11.4)
ij (j=1,2…r, 其中 Fji(j=1,2…r)是一个模糊集, i i=1,2…u)是实值参数。而 y 是第i个规则的系统的输出。
TSK模型考虑的规则的IF部分是模糊的,而THEN部分 是清晰的。它的输出是所有输入变量的线性组合。
/sundae_me ng
RBF网络模型及其预测程序

RBF 神经网络模型径向基函数(RBF Radial Basis Function )神经网络是由J.Moody 和C.Darken 在20世纪80年代末提出的一种神经网络,它是具有单隐层的三层前馈网络。
由于它模拟了人脑中局部调整、相互覆盖接受域(或称感受野-Receptive Field )的神经网络结构,因此,RBF 网络使一种局部逼近网络,已证明它能以任意精度逼近任意连续函数。
(1) 网络结构RBF 网络是一种三层前向网络,由输入到输出的映射是非线性的,而隐含层空间到输出空间的映射是线性的,从而大大加快了学习速度并避免局部极小问题。
RBF 网络结构如下图1所示。
图1 RBF 神经网络结构(2) 被控对象Jacobian 信息的辨识算法在RBF 网络结构中,[]12,,,Tn x x x x = 为网络的输入向量。
设RBF 网络的径向基向量[]12,,,Tm h h h h = ,其中j h 为高斯基函数22exp ,1,2,,2jj j x c h j m b ⎛⎫- ⎪=-= ⎪⎝⎭(1) 其中网络的第j 个节点的中心矢量为12,,1,2,,Tj j j ji jn C c c c c i n ⎡⎤==⎣⎦ 。
设网络的基宽向量为[]12,,,Tm B b b b =j b 为节点j 的基宽度参数,且为大于零的数。
网络的权向量为[]12,,,Tm W w w w ⎡⎤=⎣⎦ (2)辨识网络的输出为()1122m m m y k w h w h w h =+++ (3)辨识器的性能指标函数为my()()()212mJ y k y k =- (4)根据梯度下降法,输出权、节点中心及节点基宽参数的迭代算法如下()()()()j m j w k y k y k h η∆=-()()()()()()112j j j j j w k w k w k w k w k α=-+∆+---()()()()23jj m j jjX C b k y k y k w h bη-∆=-()()()()()112j j j j j b k b k b b k b k α=-+∆+---()()()()2j jiji m jjx c c k y k y k w b η-∆=-()()()()()()112ji ji ji ji ji c k c k c k c k c k α=-+∆+---式中,η为学习速率,α为动量因子。
基于模糊聚类的RBF分类器的设计与实现

基于模糊聚类的RBF分类器的设计与实现
何迎生;段明秀
【期刊名称】《重庆科技学院学报(自然科学版)》
【年(卷),期】2009(011)002
【摘要】提出一种RBF网络设计方法,利用模糊c均值聚类算法确定径向基函数的数目、基函数中心及宽度,输出层权值由线性方程组确定.对uci数据集进行分类仿真实验,证明利用该方法设计的RBF网络分类效果良好.
【总页数】3页(P101-103)
【作者】何迎生;段明秀
【作者单位】吉首大学,吉首,416000;吉首大学,吉首,416000
【正文语种】中文
【中图分类】TP393
【相关文献】
1.基于模糊聚类与RBF网络集成分类器的验证码识别 [J], 宋人杰;刘娟
2.基于RBF核函数支持向量机分类器的多导脑电信号分类识别研究 [J], 张海军;王学军
3.基于改进自适应聚类算法的RBF神经网络分类器设计与实现 [J], 郝晓丽;张靖
4.新的C-RBF神经网络分类器的设计与实现 [J], 黄国宏;刘刚
5.基于迭代模糊聚类算法与K近邻和数据字典的集成TSK模糊分类器 [J], 张雄涛; 蒋云良; 潘兴广; 胡文军; 王士同
因版权原因,仅展示原文概要,查看原文内容请购买。
绝对经典RBF神经网络

平均值与目标值之平均值之间差异。
第6页
函数迫近问题(内插值)
普通函数都可表示成一组基函数线性组合,
RBF网络相当于用隐层单元输出组成一组基函数,
然后用输出层来进行线性组合,以完成迫近功效。
①给定样本数据
P {p1, p2 pi pQ},
②寻找函数,使其满足:ti F ( pi )
各隐节点扩展常数。因为RBF网隐节点数对其泛化能力有
极大影响,所以寻找能确定聚类数目标合理方法,是聚类
方法设计RBF网时需首先处理问题。除聚类算法外,还有
绝对经典RBF神经网络 梯度训练方法、资源分配网络(RAN)等
第16页
一. 自组织中心选取法
1989年,Moody和Darken提出了一个由两个阶段组成混合 学习过程思绪。
Cover定理能够定性地表述为:将复杂模式分类问题非线 性地投射到高维空间将比投射到低维空间更可能是线性可 分
空间转换
低维空间:线性不可分
高维空间:线性可分
绝对经典RBF神经网络
第12页
举例:逻辑运算异或分类
X1 X2
空间变换前
绝对经典RBF神经网络
Φ1(x)
w11
Φ2(x)
w11
Output y
j 1
设第j 个隐节点在第i个样本输出为: ij G( pi p j )
可矩阵表示:W T,若R可逆,则解为 W 1T 依据Micchelli定理可得,假如隐节点激活函数采取
径向基函数,且p1, p2 ,..., pQ 各不相同,则线性方程组
有唯一解。 Q RBF网络输出 F( pi ) wj( pi cj )
% 每一层神经元权值和阈值都与径向基函数位置和宽度相关系,输出层线性神经元将这些径 向基函数权值相加。假如隐含层神经元数目足够,每一层权值和阈值正确,那么径向基函 数网络就完全能够准确迫近任意函数。
基于模糊-RBF神经网络优化的PID控制

假设一个非线性被控对象的数学模型为:
y㈤=业错专邕笋业
(1)采用RBF神经网络优化参数的PIT)控制仿 真
单独采用RBF神经网络优化的PID控制,仿真 的阶跃响应曲线如图3中点划线所示。
(2)采用模糊RBF神经网络优化的PID控制的 仿真
网络的结构取2—5—5—3的形式,输入信号为 指令信号和对象的实际输出,针对每个输入取5个 模糊集进行模糊化,即n=2,N=5,网络学习参数 取≈=0.2,a=0.02。网络的初始权值及隶属函数 参数初值通过实验得到。仿真结果如图3中实线所 示:
网络权值的学习算法如下:
她(女)=口·(删£(^)一一”(女))·逊aAu·砑a,Su·瓦af4
=々‘(删(^)一砌(^))‘挚(J),3(j)
万方数据
墨!塑
塾兰!叁主壅麴二曼塑塑丝旦整垡些堕塑望苎墅
:!!:
圈2模糊RBF神经网络结构
式中,m,为网络输出节点与上一层各节点的连接 权,J=1,2,…N,口为学习速率。如果考虑动量因 子,输出层的权值为:
用模糊控制查询表数据训练的模糊RBF神经 网络能加快RBF网络的学习速度,比单独采用RBF 神经网络对控制器参数的调整更优,尤其是对于非 线性系统的控制,具有更明显的优势。对非线性系 统的仿真结果表明,模糊RBF网络比单独采用RBF 网络有更好的控制效果。
参考文献
[1]闯新,周露等MATLAB神经网络仿真与应用[M].北 京:科学出版社,2003.
fs(J)=IIfdi,j)(N=ⅡNi)
J;1
J-1
(4)输出层
输出层输出,4为k。,岛,幻的整定结果,由三个
节点构成,即:
盥 f4(i)=m·f3=∑∞(i,』)·fs(j)
模糊RBF神经网络PID在汽车定速巡航控制系统应用

模糊RBF神经网络PID在汽车定速巡航控制系统应用张袅娜;李昊林【摘要】结合模糊控制的推理和RBF神经网络的自学习能力,实现对PID控制器参数的实时在线整定.仿真结果表明,该方法可以有效改善汽车巡航系统速度跟随过程中的动态性能和稳定性能.【期刊名称】《长春工业大学学报(自然科学版)》【年(卷),期】2017(038)003【总页数】8页(P237-244)【关键词】巡航;模糊控制;RBF神经网络;PID整定【作者】张袅娜;李昊林【作者单位】长春工业大学电气与电子工程学院, 吉林长春 130012;长春工业大学电气与电子工程学院, 吉林长春 130012【正文语种】中文【中图分类】U463.6汽车巡航控制系统(CCS)对预定车速与实际车速之间的偏差进行有效识别,通过控制器对车辆的节气门进行自动调节,实现行驶车速对预定车速的快速稳定跟随,作为一种高效的辅助驾驶系统,当车辆行驶速度超过某一阈值时,驾驶员即可手动开启车辆的自动巡航驾驶模式。
鉴于自动巡航系统的优势,目前,国内外各汽车研发企业已将自动巡航系统作为高档车型的重要配置,但由于车辆在巡航过程中存在较强的非线性,易受到外界干扰的影响,且车辆行驶工况复杂,因此,实现对汽车巡航控制系统的优化升级已成为未来汽车行业发展的重要方向,得到相关汽车控制方面专家的普遍重视[1-4]。
目前,国内多家科研机构和高校企业都对汽车定速巡航控制有一定研究,如刘文彬[5]通过该方法可以使系统具有较好的精度,响应速度快,系统工作稳定,能够满足汽车巡航系统实际使用要求。
李肖含[6]提出了基于模糊控制的自动巡航控制器,该种控制器可以与传统ACC系统控制方法相比,该控制策略有着响应迅速、达到稳态速度快的优势,这也说明了文中所提出的ACC系统模糊控制策略都有很好的表现。
沈亮[7]提出了汽车巡航系统的模糊PID控制器,经过仿真验证,该方法可以满足对汽车车速的实时控制。
随着自动控制技术的不断发展,人们对汽车巡航系统自动学习能力的需求逐渐增加,模糊PID技术虽可以实现预定车速的稳定跟随,但汽车巡航过程中此技术在动态性能上的不足逐渐显现出来,为了有效解决模糊控制不灵活的问题,文中在模糊PID控制的基础上引入RBF神经网络算法。
基于改进遗传算法的模糊RBF神经网络控制在液压伺服系统中的应用研究

基于改进遗传算法的模糊RBF神经网络控制在液压伺服系统中的应用研究李斌;朱小平;柳润清【摘要】针对电液同服系统普遍存在非线性、时变性和不确定性的情况,提出一种基于改进遗传算法的模糊RBF神经网络控制方法.该方法采用模糊RBF神经网络控制实现对液压伺服系统的自适应模糊控制,并将GA的全局寻优及BP局部寻优相结合,克服了单独应用GA算法或BP算法调节模糊RBF神经网络控制器参数存在的缺陷.仿真结果表明,该方法具有很强的自适应性和鲁棒性.【期刊名称】《机电工程技术》【年(卷),期】2010(039)001【总页数】4页(P66-69)【关键词】液压伺服系统;模糊RBF神经网络;遗传算法;BP算法【作者】李斌;朱小平;柳润清【作者单位】西安石油大学机械工程学院,陕西西安,710065;西安石油大学机械工程学院,陕西西安,710065;西安石油大学机械工程学院,陕西西安,710065【正文语种】中文【中图分类】TP273+.41 引言由于液压伺服系统是结构复杂的机、电、液综合系统,普遍存在非线性、时变性和不确定性,用传统理论设计的控制器不易解决液压伺服系统中存在的这些问题,因此有必要寻找新的控制策略。
常规模糊控制缺乏神经网络所具有的自学习能力,神经网络不具备模糊系统的规则推理机制,将二者结合起来的模糊神经网络,既具有模糊逻辑的强大知识表达推理能力,又具有神经网络的自学习能力。
RBF神经网络具有全局逼近能力,可以以任意精度逼近任意的非线性特性,并且具有拓扑结构紧凑、结构参数可实现分离学习和收敛速度快等特点。
采用RBF设计模糊神经网络的最大优势在于RBF网络与模糊推理过程具有函数等价性,这个等价性将两种不同构造的系统在函数上统一起来,使网络的参数和运算有了明确的物理意义[1]。
通常采用BP算法来训练神经网络的参数,但BP算法收敛速度慢,且不易得到全局最优值。
GA算法提供了一种求解复杂系统优化问题的通用框架,采用多点并行操作机制寻找全局最优解,收敛速度快。
基于模糊RBF神经网络的分数阶滑模控制器优化设计

基于模糊RBF神经网络的分数阶滑模控制器优化设计作者:余潇黄辉先来源:《现代电子技术》2018年第11期摘要:针对神经滑模控制系统中存在的对先验数据依赖性较强的问题,结合RBF神经网络的泛化能力和自学习能力以及模糊推理算法的强适应能力,提出基于模糊RBF神经网络的永磁同步电机分数阶速度控制系统。
模糊推理的引入为神经网络的不确定性提供了有效的指导作用,同时,分数阶微积分算子的引入增加了传统滑模控制器的自由度,从而对该控制器进行了进一步的优化。
仿真结果表明,相比RBF神经滑模控制器,提出的模糊RBF神经分数阶滑模控制器具有更好的控制性能。
关键词:永磁同步电机;滑模控制器; RBF神经网络;分数阶;模糊推理;自由度中图分类号: TN876⁃34; TM461 文献标识码: A 文章编号: 1004⁃373X(2018)11⁃0087⁃04Optimization design of fractional⁃order sliding mode controllerbased on fuzzy RBF neural networkYU Xiao, HUANG Huixian(College of Information Engineering, Xiangtan University, Xiangtan 411105, China)Abstract: Since sliding mode control based on neural network has the problem of strong dependence on prior information, the generalization ability and self⁃learning ability of RBF neural network and strong adaptability of fuzzy reasoning algorithm are combined to propose the fuzzy RBF neural network based fractional order speed control system of permanent magnet synchronous motor (PMSM). The introduction of fuzzy reasoning provides an effective guidance for the uncertainty of the neural network, and the introduction of fractional⁃order calculus operator can increase the degree of freedom of the traditional sliding mode controller, so as to further optimize the controller. The simulation results show that, in comparison with the sliding mode controller based on RBF neural network, the fractional order sliding mode controller based on fuzzy RBF neural network has better control performance.Keywords: PMSM; sliding mode controller; RBF neural network; fractional order;fuzzy inference; degree of freedom永磁同步电机在机器人、数控机床、医疗设备等领域内得到了广泛应用,但受制于系统中的参数变化和负载扰动等因素,电机的转速控制性能受到一定的影响。
RBF网络原理及应用

X1 X2
输入
R1(X)
x1
x2 0 1 0 1 R1(X) 0.3679 0.3679 0.1353 1
y 0 0 0 1 R2(X) 0.3679 0.3679 1 0.1353
∑
R2(X)
径向基神经元
− x − µ1
2
y
输出 x1 1 0 0 1 x2 0 1 0 1
1 0 0 1
a1 1
1 y = b0 + b1 (a0 * x ) + b2 (c0 + c1 * ) x2
0.811 y1 = 0.932 + 0.784* x + x2 ∧ 0.603 0.538 y2 = 1.161 + 0.920* x1 + x2
0.538 1 ∧
求出模型参数可得到如下三个非线性回归模型:
下面以1-9作为训练样本,10-12作为检验样本,采用 RBFNN方法进行预测。结果如下表.
10-12的预测值与实际值比较 10-12的预测值与实际值比较
RBFNN模型在多元非线性回归中的应用 2.2 RBFNN模型在多元非线性回归中的应用
从以上分析可知,用RBFNN方法做非线性回归的 拟合效果和预测效果都比传统回归方法好. 从上面的实例和分析可以得出如下结论: RBFNN法与传统回归方法相比,具有如下的特点: 1)避免数据的分析工作和建模工作,RBFNN能够从观测 样本中发现隐含的复杂结构。 2)能够完成复杂的输入输出非线性映射,理论上对任一 连续函数或映射可由一个三层神经网络实现。
y3 = 1.452 + 0.689* x
∧
0.538 1
0.754 + x2
RBF神经网络概述

RBF 神经网络概述1 RBF 神经网络的基本原理2 RBF 神经网络的网络结构3 RBF 神经网络的优点1 RBF 神经网络的基本原理人工神经网络以其独特的信息处理能力在许多领域得到了成功的应用。
它不仅具有强大的非线性映射能力,而且具有自适应、自学习和容错性等,能够从大量的历史数据中进行聚类和学习,进而找到某些行为变化的规律。
径向基函数(RBF)神经网络是一种新颖有效的前馈式神经网络,它具有最佳逼近和全局最优的性能,同时训练方法快速易行,不存在局部最优问题,这些优点使得RBF 网络在非线性时间序列预测中得到了广泛的应用。
1985年,Powell 提出了多变量插值的径向基函数(Radial-Basis Function, RBF)方法。
1988年,Broomhead 和Lowe 首先将RBF 应用于神经网络设计,构成了径向基函数神经网络,即RBF 神经网络。
用径向基函数(RBF)作为隐单元的“基”构成隐含层空间,对输入矢量进行一次变换,将低维的模式输入数据变换到高维空间内,通过对隐单元输出的加权求和得到输出,这就是RBF 网络的基本思想。
2 RBF 神经网络的网络结构RBF 网络是一种三层前向网络:第一层为输入层,由信号源节点组成。
第二层为隐含层,隐单元的变换函数是一种局部分布的非负非线性函数,他对中心点径向对称且衰减。
隐含层的单元数由所描述问题的需要确定。
第三层为输出层,网络的输出是隐单元输出的线性加权。
RBF 网络的输入空间到隐含层空间的变换是非线性的,而从隐含层空间到输出层空间的变换是线性。
不失一般性,假定输出层只有一个隐单元,令网络的训练样本对为{,}(1,2,...,)n n X d n N =,其中12[,,...,],(1,2,...,)T n n n nM X x x x n N ==为训练样本的输入,(1,2,...,)n d n N =为训练样本的期望输出,对应的实际输出为(1,2,...,)n Y n N =;基函数(,)i X t ϕ为第i 个隐单元的输出12[,,...,,...,](1,2,...,)i i i im iM t t t t t i I ==为基函数的中心; (1,2,...,)i w i I =为第i 个隐单元与输出单元之间的权值。
基于模糊RBF网络补偿的控制输入受限滑模控制

• 8•基于模糊RBF网络补偿的控制输入受限滑模控制沈阳航天新光集团有限公司电源研究室 李忠秋 赵春雨 洪 洋 姜 波【摘要】在运动控制领域,由于执行机构的限制,只能提供有限的控制力矩。
在实际工程中,很容易产生控制输入受限问题。
本文从控制理论的角度出发,针对控制系统存在输入受限的问题,提出了基于模糊系统的RBF网络补偿的控制输入受限的滑模控制方法。
具体而言,采用模糊系统与RBF神经网络相结合逼近输出受限值,并进行了相应的稳定性分析。
仿真结果表明,本文所提出的模糊RBF滑模控制策略能较好地补偿控制输入受限影响,具有较好的跟踪效果。
【关键词】输入受限;模糊系统;RBF网络;滑模控制;逼近1.引言在实际系统中,执行器往往存在饱和现象,当控制饱和发生时,系统跟踪性能下降,该问题在某种程度上将影响控制系统的稳定性和控制性能,甚至使得整个控制系统不稳定。
如何在控制输入限制的条件下实现有效的控制算法设计,是一个很有意义的命题,这就是“控制输入饱和”问题。
近年来针对执行器非线性受限情况的控制系统分析与综合问题受到广泛关注,并且近年来关于该类系统的滑模控制问题也开始受到许多研究者的关注,并取得了一些有意义的研究成果[1-4],然而,值得注意的是,已有的一些研究工作主要是针对线性控制系统,而由于非线性系统的复杂性,导致对于控制输入受限下非线性系统的滑模控制问题的研究工作尚不多见。
目前,处理饱和的方法有Nussbaum 型函数法[5]、小增益控制法[6]、线性反馈调节法[7]、预测控制法[8]和指令滤波器法[9]等。
然而, 文献[5-9]均是针对线性系统或仿射非线性系统,目前关于输入受限非线性系统控制的研究仍然较少。
滑模控制(SMC)因其设计简单,控制精度高,且滑动模态对系统的摄动和外部扰动具有鲁棒性强等优势,已成为当前解决非线性问题的主要方法。
但因控制输入存在符号函数,控制器抖振问题制约了传统滑模控制在工程中的应用。
基于遗传算法的模糊RBF神经网络设计及应用

第31卷 第1期 吉首大学学报(自然科学版)Vol.31 No.1 2010年1月J ournal of J is ho u Uni ver s i t y (Nat ural Sci ence Editio n)J an.2010 文章编号:1007-2985(2010)01-0043-04基于遗传算法的模糊RB F 神经网络设计及应用3段明秀(吉首大学数学与计算机科学学院,湖南吉首 416000)摘 要:提出了一种基于遗传算法的模糊RB F 神经网络学习算法.采用遗传算法对模糊RB F 神经网络需要调整的参数进行优化,再将遗传算法优化的各参数结果作为模糊RB F 神经网络各个参数的初始值,并结合梯度下降法对网络的各参数进行动态调整.在对非线性函数逼近的仿真中,仿真结果验证了优化后的模糊RBF 神经网络具有更高的精度及强鲁棒性.关键词:遗传算法(G A );模糊RBF ;神经网络;函数逼近中图分类号:TP18 文献标识码:A神经网络具有并行计算、分布式信息存储、容错能力强以及具备自适应学习功能等优点,但不适合表达基于规则的知识,模糊控制比较适合于表达模糊或定性知识,其推理方式比较类似于人的思维模式,但缺乏学习和自适应能力.[1]模糊神经网络结合了模糊控制的推理能力强与神经网络学习能力强的特点,更适合非线性复杂系统.有效确定模糊RBF 神经网络的网络结构和参数,是当今的研究热点和难点.模糊RB F 神经网络需要确定的参数主要包括基函数的中心值和宽度、隐含层到输出层的连接权值.目前确定基函数的中心值最常用的方法是使用聚类方法,而隐藏层到输出层的权值采用伪逆法确定,但这种方法使得网络一旦训练完成便无法调整,往往达不到精度要求,而且网络的泛化能力很差;而采用梯度下降法的模糊RB F 神经网络学习算法又存在各层权值的初始值随机给定、网络的训练结果受初始值的影响极大的不利方面,导致网络的训练结果很不稳定[2-3].遗传算法[4]是模仿生物遗传学和自然选择机理,通过人工方式构造的一类优化搜索算法.遗传算法具有搜索范围广、搜索效率高、鲁棒性强的特点,运用遗传算法训练模糊RB F 神经网络无需先验知识,而且对初始参数不敏感,不会陷入局部极小点.笔者提出将模糊RB F 神经网络需要确定的参数看作染色体,利用遗传算法的强搜索能力,求出各参数的最优解或次优解,然后将经遗传算法优化的各参数结果作为模糊RB F 神经网络各个参数的初始值,再采用梯度下降法对网络的各参数进行动态调整,从而提高网络的泛化能力及稳定性.1 模糊RBF 神经网络的原理模糊RB F 神经网络由输入层、模糊化层、模糊推理层及输出层构成[5].(1)输入层.输入层的各个节点直接与输入量的各个分量连接,将输入量传到下一层.该层的每个节3收稿日期:2009-09-07基金项目:湖南省教育厅科学研究项目(09C795)作者简介段明秀(5),女,湖南茶陵人,吉首大学数学与计算机科学学院讲师,硕士,主要从事数据挖掘、神经网络、信息安全研究:197-.点i 表示一个输入变量:f 1(i)=X.X =(x 1,x 2,…,x n )T ,n 为输入向量的维数.(2)模糊化层.该层的作用是将输入划分为模糊集.该层的每个节点代表一个语言变量值,采用一种径向基函数如高斯函数为模糊隶属度函数求取各输入变量属于各语言变量的隶属度函数,c ij 和b ij 分别是第i 个输入变量第j 个模糊集合的隶属函数的均值(中心)和标准差(宽度).f 2(i ,j )=e xp {-(f 1(i )-c ij )2/(b ij )2}.(1)式中:i =1,2,…,n;j =1,2,…,N ;n 为网络第1层输入变量的个数;N 为网络第2层隐藏层节点的个数,即模糊集合的个数;f 2(i ,j)表示第i 个输入属于模糊集j 的隶属度,即概率密度.(3)模糊推理层.模糊推理层通过与模糊化层的连接来完成模糊规则的匹配,各个节点之间实现模糊运算,即通过各个节点的组合得到相应的点火强度.该层的每个节点表示一条模糊规则,完成模糊规则到输出空间的映射,每个节点的输出为该节点所有输入信号的乘积,即f 3(m)=∏N j =1∏ni =1f 2(i ,j),(2)式中m =1,2,…,M.M 为网络第3层的节点数.(4)输出层.f 4(l )=w 3f 3=∑M m =1w (l ,m )f 3(m ),(3)式中l =1,2,…,L.L 为输出层的节点数,w 为输出层节点与第3层各节点的连接权矩阵.2 遗传算法原理遗传算法(G enetic Al gorit hm s ,GA )的思想来源于生物遗传学和适者生存的自然规律,是一种群体操作,该操作以群体中的所有染色体为对象,通过选择、交叉和变异等操作产生新一代群体,直到获得满意的结果.(1)编码.将模糊RB F 神经网络需要进行优化的参数进行二进制编码,称此二进制串为染色体,每个参数用10位二进制表示.(2)选择操作.采用适应度比例方法,也称为赌轮法.该方法中染色体被选择的概率与其适应度成正比,即p i =f i /∑Nj =1f j ,其中f i 为第i 个染色体的适应度,N 为种群大小,p i 为第i 个染色体被选择的概率,具有较大适应值的染色体被选中的概率较大.为了保证搜索的全局最优,在进行交叉操作之前将本代染色体中的最优染色体直接保留到下一代中,其他染色体按照交叉概率和变异概率进行交叉操作和变异操作,以形成新的染色体[6].(3)交叉和变异操作.交叉操作可以提高遗传算法的搜索能力,一般采用2点交叉方式,保留一个最优染色体不进行交叉变异,确保了算法的收敛[7].根据交叉概率PC 选择染色体,交叉位随机选取.变异操作则可以增强遗传算法的局部搜索能力,同时使得遗传算法保持种群的多样性,确保种群能够继续进化.(4)适应度函数的选取.适应度函数应选取能够客观地反映染色体优劣的函数[8].对模糊RB F 神经网络的参数来说,网络输出的精度,即误差的大小可以充分反映染色体的优劣,定义模糊RB F 神经网络的性能指标为误差平方和,即E =12∑L i =1∑n j =1(d ij-o ij )2.(4)其中:d ij 和o ij 为第j 个样本的第i 个输出的期望输出和实际输出;n 为样本的个数;L 为输出层神经元的个数,即输出向量的维数.设计适应度函数为f i =1/E.44吉首大学学报(自然科学版)第31卷3 基于梯度下降法的模糊RB F 神经网络的参数调整模糊RB F 网络的可调参数包括隐层节点的中心、宽度和输出层权值.文中采用梯度下降法进行网络参数学习.隐层节点的中心的更新公式如下所示:c k (n +1)=c k (n )+Δc k (n +1)+η[c k (n )-c k (n -1)],Δc k (n +1)=-γ(d(n +1)-o (n +1))×w k (n +1)× f 3(k )×(x (1)-c (k ))×b (k )-2.(5)基函数宽度的更新公式如下所示:σk (n +1)=σk (n )+Δσk (n +1)+η[σk (n )-σk (n -1)],Δσk (n +1)=γ(d (n +1)-o (n +1))×w k (n +1)× f 3(k)×(x (1)-c(1,k))2×b (k)-3.(6)对输出层节点与上一层各节点的权值W 采用(6)式进行调整:w k (n +1)=w k (n)+Δw k (n +1)+η[w k (n)-w k (n -1)],Δw k (n +1)=-γ(d (n +1)-o (n +1))×f 3(k ).(7)其中:η为学习动量因子;n 为迭代步数;γ为学习速率;d 表示网络的期望输出;o 表示网络的实际输出.3.1算法描述基于遗传算法的模糊RB F 神经网络的学习算法描述如下:(a )依据模糊RB F 神经网络要优化的参数个数设置染色体的二进制串长度,并设置各参数的寻优范围;(b)随机初始化种群;(c )对种群中各个染色体进行译码,并根据网络的性能指标函数计算各个染色体的误差平方和;(d)依据适应度函数即(4)式计算种群中各个染色体的适应值,并对适应值排序,选择适应值最大的染色体作为最优染色体;(e )依据赌轮法计算每个染色体的选择概率.选择适应值较大的染色体来产生新的染色体;(f)设置交叉概率.产生1个随机数,若该数小于交叉概率,则将染色体相应的串进行交叉操作,保留1个最优染色体不进行交叉;(g )设置变异概率.产生1个随机数,若该数小于变异概率,则将染色体进行变异操作,保留1个最优染色体不进行变异;(h )若达到迭代次数则结束,否则转步骤(c );(i)将优化的模糊RB F 网络的各参数作为网络参数的初始值;(j )利用(1)至(3)式计算模糊RB F 神经网络各层节点的输出;(k )计算网络的实际输出与理想输出的差值;(l )利用(5)至(7)式调整模糊RB F 神经网络的各个参数;(m )重复步骤(j )至(l ),直到训练的模糊RB F 神经网络满足结束条件;(n )用测试数据对模糊RB F 神经网络进行验证.3.2仿真实验为了验证算法的有效性及准确性,对文中所设计的基于遗传算法优化的模糊RB F 神经网络用于函数逼近.函数y =si n c (x )的逼近效果如图1所示,图2是逼近过程的误差.从函数的逼近效果可以看出,文中所设计的基于遗传算法优化的模糊RB F 神经网络逼近所得结果基本与原函数一致,而且迭代过程中误差基本为0.4 结语利用遗传算法具有搜索范围广、搜索效率高、鲁棒性强的特点,运用遗传算法优化的模糊RB F 神经网络结构、参数,再采用梯度下降法对优化的网络参数进行动态调整,克服了遗传算法局部寻优能力的不足,54第1期 段明秀:基于遗传算法的模糊RB F 神经网络设计及应用图1 函数Y =si n c(x )的逼近效果 图2 函数Y=sin c(x )的逼近误差从而提高网络的泛化能力及稳定性.仿真结果表明了该算法的有效性.参考文献:[1] 高建英.基于遗传算法设计模糊RB F 神经网络控制器[D ].大连:大连理工大学,2000.[2] 李国勇.智能控制及其MA TLAB 实现[M ].北京:电子工业出版社,2005.[3] 何迎生,彭 华,段明秀.基于交叉验证的改进RB F 分类器设计[J ].微计算机信息,2009,25(6-3):248-250.[4] 王小平,曹立明.遗传算法———理论、应用与软件实现[M ].西安:西安交通大学出版社,2003.[5] 苗卓广,何秀然,魏永志.基于模糊RB F 神经网络整定的航空发动机多变量解耦控制[J ].空军工程大学学报,2009,10(2):10-13.[6] 高静巧,朱伟兴.基于遗传算法的RB F 神经模糊控制器[J ].计算机仿真,2003,20(11):53-54.[7] 陈小平,赵鹤鸣,杨新艳.遗传前馈神经网络在函数逼近中的应用[J ].计算机工程,2008,34(20):24-28.[8] 赵志刚,单晓虹.一种基于遗传算法的RB F 神经网络优化方法[J ].计算机工程,2007,33(6):13-15.Design of Fuzzy RBF N eural N et w or k B ased on G enetic Algor ithm an dits Applicat ionDU AN Mi ng 2xi u(College of Mathematics and Compute r Science ,Jishou Unive rsity ,Jishou 416000,Hunan China)Abstract :A fuzzy RB F ne ural net wor k learni ng algorit hm based on genetic al gori t hm i s propo sed.Thi s al 2gori t hm adopt s genet ic al gorit hm to opti mize t he fuzzy RB F neural network ’s st ruct ure parameter s ,a 2dapt s t he optimizat ion result as t he init ial value of t he f uzzy RB F neural net work ’s st ruct ure pa ramet ers ,and dynamicl y adj ust s t he parameter s using t he gradient decent met hods.Finall y t he al gorit hm is applied t o cl assif y t he dat a a nd function approximation.The sim ulation shows t hat t he f uzzy RB F neural net work has hi gher p reci sion and robust ness.K ey w or ds :genetic algori t hm (GA );f uzzy RB F ;neural net work ;f unct ion approximation(责任编辑 向阳洁)64吉首大学学报(自然科学版)第31卷。
RBF网络
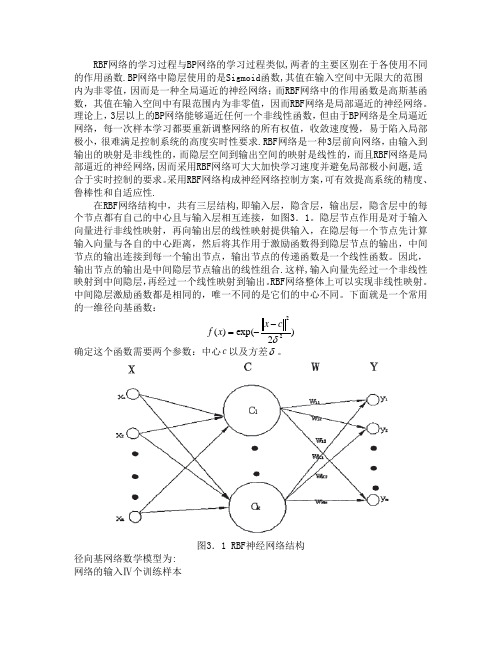
RBF 网络的学习过程与BP 网络的学习过程类似,两者的主要区别在于各使用不同的作用函数.BP 网络中隐层使用的是Sigmoid 函数,其值在输入空间中无限大的范围内为非零值,因而是一种全局逼近的神经网络;而RBF 网络中的作用函数是高斯基函数,其值在输入空间中有限范围内为非零值,因而RBF 网络是局部逼近的神经网络。
理论上,3层以上的BP 网络能够逼近任何一个非线性函数,但由于BP 网络是全局逼近网络,每一次样本学习都要重新调整网络的所有权值,收敛速度慢,易于陷入局部极小,很难满足控制系统的高度实时性要求.RBF 网络是一种3层前向网络,由输入到输出的映射是非线性的,而隐层空间到输出空间的映射是线性的,而且RBF 网络是局部逼近的神经网络,因而采用RBF 网络可大大加快学习速度并避免局部极小问题,适合于实时控制的要求。
采用RBF 网络构成神经网络控制方案,可有效提高系统的精度、鲁棒性和自适应性.在RBF 网络结构中,共有三层结构,即输入层,隐含层,输出层,隐含层中的每个节点都有自己的中心且与输入层相互连接,如图3.1。
隐层节点作用是对于输入向量进行非线性映射,再向输出层的线性映射提供输入,在隐层每一个节点先计算输入向量与各自的中心距离,然后将其作用于激励函数得到隐层节点的输出,中间节点的输出连接到每一个输出节点,输出节点的传递函数是一个线性函数。
因此,输出节点的输出是中间隐层节点输出的线性组合.这样,输入向量先经过一个非线性映射到中间隐层,再经过一个线性映射到输出。
RBF 网络整体上可以实现非线性映射。
中间隐层激励函数都是相同的,唯一不同的是它们的中心不同。
下面就是一个常用的一维径向基函数:)2exp()(22δc x x f --=确定这个函数需要两个参数:中心c 以及方差δ。
图3.1 RBF 神经网络结构径向基网络数学模型为:网络的输入Ⅳ个训练样本{}km k k k x x x X ,....,21=(N k ,...2,1=)网络对应的输出:{}km k k k y y y Y ,...,21= (N k ,...2,1=)网络输出连接权系数构成连接矩阵:}{,,..2,1,,...2,1,,J j I i j i W ===隐层节点个数I,中心点:{i C } I i ,...2,1= 方差i δ网络输入输出之间的关系:221)21exp()(i k i I i ij k kj C X w X y --=∑=δRBF 网络逼近的性能指标函数为:)(k E =2)]([21k kj k X y Y - 3.2 RBF 神经网络的性能改进3.2.1 RBF 神经网络训练数据的预处理1.进行数据预处理的原因对于使用有教师训练算法的前向神经网络,训练样本的质量对网络的性能非常重要.RBF 神经网络是一种局部网络,只有在隐含层节点中心的一定范围内的点才会使网络产生一定的输出。
RBF网络

:学习速率,0 1
(4)k=k+1,转到第(2)步,重复上述过程,直到c(k)的改变量
小于要求的值。
(5)确定扩展常数
d j (k ) min c j ci
i j
j d j
7
② 有教师学习
当 c j 确定后,训练由隐层至输出层间的连接权值,它是线
性方程组,则求连接权值成为线性优化问题,可利用各种线 性优化算法求得,如:LMS算法、最小二乘递推法等。 设有q 组输入/输出样本xq/dq, q=1,2,…,L。 目标函数 L J eq
j
u
wj bj
j 1
m
c j x1
2 j
x1 u
RBF网络结构:N3-6-1,网络的三个输入分别是u(k), y(k), y(k-1)。
18
辨识器性能指标
1 J1 ( y (k ) y L (k )) 2 2
按梯度下降法得RBF的迭代公式
权值 wj (k ) wj (k 1) ( y(k ) yL (k ))bj (wj (k 1) wj (k 2))
m
x cj 2
2 j
2
),
j 1, 2,
,p
输出层:
yi wij b j ( x), i 1, 2, , m
j 1
b1(x)
bp(x)
4
3. RBF网络的训练
1)基函数固定 根据输入样本随机选取基函数的中心点,如果基函数个 数足够多,就能充分反映输入样本的概率分布,网络学习的 结果能很好地逼近非线性函数。
d j (k ) x(k ) c j (k 1) ,1 j p
通俗易懂讲解RBF网络

通俗易懂讲解RBF⽹络AI有道⼀个有情怀的公众号1RBF Network Hypothesis之前我们介绍过,在SVM中引⼊Gaussian Kernel就能在⽆限多维的特征转换中得到⼀条“粗壮”的分界线(或者⾼维分界平⾯、分界超平⾯)。
从结果来看,Gaussian SVM其实就是将⼀些Gaussian函数进⾏线性组合,⽽Gaussian函数的中⼼就位于Support Vectors上,最终得到预测模型gsvm(x)。
Gaussian kernel的另⼀种叫法是Radial Basis Function(RBF) kernel,即径向基函数。
这个名字从何⽽来?⾸先,radial表⽰Gaussian函数计算结果只跟新的点x与中⼼点xn的距离有关,与其它⽆关。
basis function就是指Gaussian函数,最终的矩gsvm(x)就是由这些basis function线性组合⽽成。
从另外⼀个⾓度来看Gaussian SVM。
⾸先,构造⼀个函数gn(x):上式中,指数项表⽰新的点x与xn之间的距离⼤⼩。
距离越近,即权重越⼤,相当于对yn投的票数更多;⽽距离越远,权重越⼩,相当于对yn投的票数更少。
其物理意义是新的点与xn的距离远近决定了gn(x)与yn的接近程度。
如果距离越近,则yn对gn(x)的权重影响越⼤;如果距离越远,则yn对gn(x)的权重影响越⼩。
那么整体来说,gsvm(x)就由所有的SV组成的gn(x)线性组合⽽成,不同gn(x)对应的系数是αn,最后由sign函数做最后的选择。
这个过程很类型我们之前介绍的aggregation中将所有较好的hypothesis线性组合,不同的gn(x)有不同的权重αn。
我们把gn(x)叫做radial hypotheses,Gaussian SVM就是将所有SV对应的radial hypotheses进⾏线性组合(linear aggregation)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模糊RBF神经网络结构
第十一章
MATLAB优化算法案例分析与应用
•11.2.2 基于模糊RBF的网络逼近
模糊RBF神经网络逼近 网络的逼近误差为:
e k y k ym k
输出层的权值学习算法
w k w k 1 w k w k 1 w k 2
2 j
隶属函数参数学习算法为:
cij k cij k 1 cij k cij k 1 cij k 2
b j k b j k 1 b j k b j k 1 b j k 2
0.2
0.4
0.1
0.2
y and ym
0
0 -0.2 -0.4 -0.6 -0.8 -1
dyu
-0.1 -0.2 -0.3 -0.4 -0.5
0
0.2
0.4
0.6
0.8
1 time(s)
1.2
1.4
1.6
1.8
2
0
0.2
ቤተ መጻሕፍቲ ባይዱ0.4
0.6
0.8
1 times
1.2
1.4
1.6
1.8
2
RBF网络辨识结果
RBF网络敏感度Jacobian信息
利用模糊RBF网络逼近下列函数:
y k u k
3
y k 1 1 y k 1
2
% Layer2:fuzzation for i=1:1:2 for j=1:1:5 net2(i,j)=-(f1(i)-c(i,j))^2/b(j)^2; end end for i=1:1:2 for j=1:1:5 f2(i,j)=exp(net2(i,j)); end end % Layer3:fuzzy inference(49 rules) for j=1:1:5 m1(j)=f2(1,j); m2(j)=f2(2,j); end
w k E E e ym e k f3 w e ym w
第十一章
MATLAB优化算法案例分析与应用
•11.2.2 基于模糊RBF的网络逼近
隶属函数参数可通过如下方式调整:
2 2 xi cij E E net j 2 cij j 2 2 cij net j cij bij
第十一章
MATLAB优化算法案例分析与应用
第11章 模糊RBF网络
第十一章
MATLAB优化算法案例分析与应用
•11.1 RBF神经网络
RBF网络的学习过程与BP网络的学习过程类似,两者的主要 区 别 在 于 各 使 用 不 同 的 作 用 函 数 。 BP 网 络 中 隐 层 使 用 的 是 Sigmoid函数,其值在输入空间中无限大的范围内为非零值,因 而是一种全局逼近的神经网络;而 RBF 网络中的作用函数是高 斯基函数,其值在输入空间中有限范围内为非零值,因为 RBF 网络是局部逼近的神经网络。 RBF 网络是一种 3 层前向网络,由输入到输出的映射是非线 性的,而隐层空间到输出空间的映射是线性的,而且 RBF 网络 局部逼近的神经网络,因而采用 RBF 网络大大加快学习速度并 避免局部极小问题,适合于实时控制的要求。采用 RBF 网络构 成神经网络控制方案,可有效提高系统的精度、鲁棒性和自适 应性。
网络的权向量为: RBF网络的输出为:
T
W w1 , w2 , w3 , ……, wn
T
ym k w1h1 w2h2 …… wnhn
RBF网络逼近的性能指标函数为: T 1 E k y k ym k 2 Jacobian 信息 w h y k y k
第十一章
MATLAB优化算法案例分析与应用
•11.2.2 基于模糊RBF的网络逼近
利用模糊RBF网络逼近下列函数:
y k u k
3
y k 1 1 y k 1
2
输入信号为正弦信号:
u k 0.35sin 2 t
网络结构选则输入层2个-模糊化层25个-模糊推理层25个-输出层1个 中心矢量和高斯基宽向量的初值取
for i=1:1:5 for j=1:1:5 ff3(i,j)=m2(i)*m1(j); end end f3=[ff3(1,:),ff3(2,:),ff3(3,:),ff3(4,:),ff3(5,:)]; % Layer4:output f4=w_1'*f3'; ym(k)=f4; e(k)=y(k)-ym(k); d_w=0*w_1; for j=1:1:25 d_w(j)=xite*e(k)*f3(j); end
3 0 2.3 4.5 5 2. C cij 5 2.3 0 2.3 4.5
网络的学习参数取
B b j 3.5 3.5 3.5 3.5 3.5
T
0.4 , 0.07
第十一章
MATLAB优化算法案例分析与应用
•11.2.2 基于模糊RBF的网络逼近
y k u k
3
y k 1 1 y k 1
2
输入信号为正弦信号:
u k 0.35sin 3 t
高斯函数的初始值
C j 0.65, 0.65
T
B 1.35,1.35,1.35,1.35
T
采用时间为0.001s,网络隐层神经元个数取m=4 网络结构为输入层2-隐层4-输出1 网络的学习参数取
•11.2.1 网络结构
如图11-10所示为模糊RBF神经网络结构,该网络由输入 层、模糊化层、模糊推理层和输出层构成。
模糊RBF神经网络结构
第十一章
MATLAB优化算法案例分析与应用
•11.2.1 网络结构
如图11-10所示为模糊RBF神经网络结构,该网络由输入 层、模糊化层、模糊推理层和输出层构成。
0.6
Approaching error
0
Approaching
0.4
-0.2
0.2
-0.4
0
-0.6
-0.2
-0.8
-0.4
0
0.1
0.2
0.3
0.4
0.5 time(s)
0.6
0.7
0.8
0.9
1
-1
0
0.1
0.2
0.3
0.4
0.5 time(s)
0.6
0.7
0.8
0.9
1
模糊RBF网络逼近效果
0.07 , 0.9
第十一章
MATLAB优化算法案例分析与应用
•11.1.2 RBF网络的逼近
采用RBF网络逼近下列对象
y k u k
3
y k 1 1 y k 1
2
for j=1:1:4 h(j)=exp(-norm(x-c(:,j))^2/(2*b(j)*b(j))); 高斯基函数 end ym(k)=w'*h'; em(k)=y(k)-ym(k);
%
第十一章
MATLAB优化算法案例分析与应用
•11.1.2 RBF网络的逼近
采用RBF网络逼近下列对象
y k u k
3
RBF网 络 辨 识 结 果 1 0.8
y k 1 1 y k 1
0.4 0.3
2
RBF网 络 敏 感 度 Jacobian信 息
0.6
第十一章
MATLAB优化算法案例分析与应用
•11.2 模糊RBF网络
在模糊系统中,模糊集、隶属度函数和模糊规则的设计是 建立在经验知识基础上的。这种设计方法存在很大的主观性。 将学习机制引到模糊系统中,使模糊系统能够通过不断学习来 修改和完善隶属函数和模糊规则,是模糊系统的发展方向。
第十一章
MATLAB优化算法案例分析与应用
第十一章
MATLAB优化算法案例分析与应用
•11.1.2 RBF网络的逼近
RBF神经网络逼近 高斯基函数
X C j h j exp 2b 2 j
2
第十一章
MATLAB优化算法案例分析与应用
•11.1.2 RBF网络的逼近
网络的基宽向量为:
B b1 , b2 , b 3 , ……, bn
第十一章
MATLAB优化算法案例分析与应用
•11.1.1 RBF网络结构
RBF网络是一种三层前向网络,由于输入到输出的映射是 非线性的,而隐含层空间到输出空间的映射是线性的,从而 可以大大加快学习速度并避免局部极小问题。多输入单输出 的RBF网络结构如图11-1所示。
图11-1 RBF神经网络结构
for j=1:1:4 d_w(j)=xite*em(k)*h(j); d_b(j)=xite*em(k)*w(j)*h(j)*(b(j)^-3)*norm(x-c(:,j))^2; for i=1:1:2 d_c(i,j)=xite*em(k)*w(j)*h(j)*(x(i)-c(i,j))*(b(j)^-2); end end w=w_1+ d_w+alfa*(w_1-w_2); b=b_1+d_b+alfa*(b_1-b_2); c=c_1+d_c+alfa*(c_1-c_2);
u k
j j u k j u k
m
c 1, j x1 wj wj hj u k b2 j j j h j
第十一章
MATLAB优化算法案例分析与应用
•11.1.2 RBF网络的逼近
