相遇问题与追及问题应用题训练1(四上)
相遇问题应用题1

一. 相遇和追及问题
1.甲、乙两地相距8
2.5千米,小张、小李两人分别以15千米/时和12.5千米/时的速度从甲、乙两地同时出发相向而行,问他们几个小时以后相遇?在距离甲多少千米的地方相遇?
2.A、B两地相距48公里,甲、乙两人分别从A、B两地同时出发相向而行,经过2小时相遇,已知甲的速度比乙的速度每小时快2公里,求甲、乙两人的速度。
3.AB两地间有一条公路长2800米,甲车从A地出发5分钟后,乙车从B地出发,又经过10分钟两车相遇。
已知乙车每分钟行100米,甲车每分钟行多少米
4.甲、乙两人从A、B两地相向而行,甲比乙早出发15分钟,甲、乙速度比为2:3,相遇时甲比乙少走6公里,已知乙走了1小时30分,求甲、乙两人的速度和两地距离。
5. 一条环形跑道长400米,甲骑自行车平均每分钟骑300米,乙跑步,平均每分钟跑250米,两人同时同地同向出发,经过多少分钟两人相遇?
6.两名运动员在湖周围环形道上练习长跑,甲每分钟跑250米,乙每分钟跑200米,两人同时同地同向出发,经过45分钟甲追上乙,如果两人同时同地反向出发,经过多少分钟两人相遇?
7.小强以每小时5公里的速度走16分钟,然后小明以每小时13公里的速度追,则小明从出发到追上小强所需的时间为多少?
8.小丽每天早上要在6:20之前赶到距家1000米的学校上学。
一天,小丽以80米/分的速度出发,5分后,小丽的爸爸发现他忘了带语文书。
于是,爸爸立即以180米/分的速度去追小丽,并且在途中追上了她。
(1)爸爸追上小丽用了多长时间?
(2)追上小丽时,距离学校还有多远?。
小学数学 基本的相遇与追及问题 课件+作业(带答案)

练习5:一辆客车和一辆货车分别从相距1200千米的甲、乙两城出发。客车的速度是货车的2 倍。若两车
同时出发,相向而行,则10小时后两车可以相遇。若两车同时出发,同向而行,经过多长时间,客车可以 从后面追上货车?
相遇路程和:1200千米 相遇时间:10小时
速度和:1200÷10=120(千米/时) 货车速度:120÷(1+2)=40(千米/时)
知识点二:基本追及问题
例题4:一天早晨,小芳以每分钟90米的速度步行去上学。 出发5分钟后,妈妈发现小芳忘记带作业本,
于是以每分钟140米的速度骑车去追小芳。经过多少分钟,妈妈可以追上小芳?
小芳 家
妈妈
分析:
路程差:5×90=450(米) 速度差:140-90=50(米/分钟) 追及时间:450÷50=9(分钟) 答:经过9分钟,妈妈可以追上小芳。
总结:追及时间=路程差÷速度差
练习4:下午放学后,小新从学校出发步行去体育场。小东放学后因为要值日,15分钟后才从学
校出发骑车去体育场。小新的步行速度为每分钟60米,小东的骑车速度为 每分钟160米。经过多少分 钟,小东可以追上小新?
路程差:60×15=900(米) 速度差:160-60=100(米/分钟) 追及时间:900÷100=9(分钟) 答:经过9分钟,小东可以追上小新。
客车前2小时先行驶:80×2=160(千米) 客车和货车共同行驶:460-160=300(千米)
速度和:80+70=150(千米/小时) 相遇时间:300÷150=2(小时)
答:货车行驶2小时后可以与客车相遇。
知识点二:基本追及问题
例题3:甲、乙两列火车从相距150千米的A、B 两地同时出发,同向而行。乙车在前,甲车在后
(word完整版)四年级+相遇问题与追及问题

简单的相遇与追及问题一、学习目标1. 理解相遇与追及的运动模型,掌握相遇与追及这两种情况下路程、时间、速度这三个基本量之间的关系.会利用这个关系来解决一些简单的行程问题.2. 体会数形结合的数学思想方法.二、主要内容1. 行程问题的基本数量关系式:路程=时间×速度;速度=路程÷时间;时间=路程÷速度.2.相遇问题的数量关系式:相遇路程=相遇时间×速度和;速度和=相遇路程÷相遇时间;相遇时间=相遇路程÷速度和.3.追及问题的数量关系式:追及距离=追及时间×速度差;速度差=追及距离÷追及时间;追及时间=追及距离÷速度差.4. 能熟练运用路程、时间、速度这三个基本量的关系,结合图形分析,解决一些简单的行程问题.三、例题选讲例1两辆汽车同时分别从相距500千米的A,B两地出发,相向而行,速度分别为每小时40千米和每小时60千米.求几小时后两车相遇.例2甲车在乙车前200千米,同时出发,速度分别为每小时40千米与60千米.问多少小时后,乙车追上甲车.例3一辆公共汽车和一辆小轿车同时从相距598千米的两地相向而行.公共汽车每小时行40千米,小轿车每小时行52千米,问几小时后两车相距138千米?例4 甲、乙两辆汽车同时从东、西两地相向开出,甲车每小时行56千米,乙车每小时行48千米,两车在离中点32千米处相遇.求东、西两地相距多少千米?例5甲、乙两人同时从相距18千米的两地相向而行,甲每小时行4千米,乙每小时行5千米.甲带着一只狗,每小时走20千米,狗走得比人快,同甲一起出发,碰到乙后,它往甲方向奔走;碰到甲后,它又往乙方向奔走,直到甲、乙两人相遇为止,这只狗一共奔走了多少千米?例6一辆卡车和一辆摩托车同时从A、B两地相对开出,两车在途中距A地60千米处第一次相遇.然后,两车继续前进,卡车到达B地,摩托车到达A地后都立即返回,两车又在途中距B地30千米处第二次相遇.求A、B两地相距多少千米?例7甲、乙、丙三人进行100米赛跑.当甲到达终点时,乙离终点还有20米,丙离终点还有40米.如果甲、乙、丙赛跑的速度都不变,那么当乙到达终点时,丙离终点还有多远?例8小明步行上学,每分行75米,小明离家12分后,爸爸骑单车去追,每分行375米.问爸爸出发多少分后能追上小明?例9解放军某部快艇追击敌舰,追到A岛时,敌舰已逃离该岛15分钟,已测出敌舰每分钟行驶1000米,解放军快艇每分钟行驶1360米,在距离敌舰600米处可开炮射击.问解放军快艇从A岛出发经过多少分钟就可以开炮射击敌舰?例10甲、乙两人在环形跑道上以各自的不变速度跑步,如果两人同时从同地相背而行,乙跑4分钟后两人第一次相遇,已知甲跑一周需6分钟,那么乙跑一周需要多少分钟?例11两名运动员在湖周围环形道上练习长跑,甲每分跑250米,乙每分跑200米,两人同时从两地同向出发,经过45分甲追上乙,如果两人同时同地反向出发,经过多少分两人相遇?例12甲、乙两人在相距90米的直路上来回跑步,甲的速度是每秒3米,乙的速度是每秒2米,如果她们同时分别从直路两端点出发,跑了6分,那么,这段时间内,两人共迎面相遇了多少次?四、练习题1、甲、乙两站相距980千米,两列火车由两站相对开出,快车每小时行50千米,慢车每小时行多少千米,两车经10小时能相遇?2、甲车每小时行60千米,1小时后,乙车紧紧追赶,速度为每小时80千米,几小时后乙车可追上甲车?3、早晨6时,有一列货车和一列客车同时从相距360千米的甲、乙两城相对开出,中途相遇,这期间,货车停车一次60分钟,客车停车两次各30分钟,已知货车每小时行42千米,客车每小时行78千米,问两车在几点钟相遇?4、东、西两镇相距240千米,一辆客车从上午8时从东镇开往西镇,一辆货车在上午9时从西镇开往东镇,到正午12点,两车恰好在两镇间的中点相遇,如果两车都从上午8时由两地相向开出,速度不变,到上午10时,两车还相距多少千米?5、骑单车从甲地到乙地,以每小时10千米的速度行进,下午1点到,以每小时15千米的速度行进,上午11点到.如果希望中午12点到,那么应以怎样的速度行进呢?6、A、B两地相距480千米.甲、乙两车同时从两站相对出发,甲车每小时行35千米,乙车每小时行45千米,一只燕子以每小时行50千米的速度和甲车同时出发向乙车飞去,遇到乙车又折回向甲车返飞去,遇到甲车又返飞向乙车,这样一直飞下去,燕子飞了多少米两车才相遇?7、某人由甲地去乙地,如果他从甲地先骑摩托车行了12小时,再换骑自行车行9小时,恰好到达乙地.如果他从甲地先骑自行车行了21小时,再换骑摩托车行8小时,也恰好到达乙地.问:全程骑摩托车需要多少小时才能到达乙地?8、兄妹两人同时由家上学,哥哥每分钟走90米,妹妹每分钟走60米,哥哥到校门口时,发现忘了带课本,立即沿原路返回去取,行至离校门口180米处与妹妹相遇,他们家离学校多少米?9、兄妹两人在周长300米的圆形水池边玩.从同一地点同时背向饶水池而行.哥哥每分钟走13米,妹妹每分钟走12米.他们第5次相遇时,哥哥共走了多长的路?。
【小学数学】小学数学常考相遇问题、追及问题(附例题、解题思路)

相遇问题【含义】两个运动的物体同时由两地出发相向而行;在途中相遇。
这类应用题叫做相遇问题。
【数量关系】相遇时间=总路程÷(甲速+乙速)总路程=(甲速+乙速)×相遇时间【解题思路和方法】简单的题目可直接利用公式;复杂的题目变通后再利用公式。
例1南京到上海的水路长392千米;同时从两港各开出一艘轮船相对而行;从南京开出的船每小时行28千米;从上海开出的船每小时行21千米;经过几小时两船相遇?解392÷(28+21)=8(小时)答:经过8小时两船相遇。
例2小李和小刘在周长为400米的环形跑道上跑步;小李每秒钟跑5米;小刘每秒钟跑3米;他们从同一地点同时出发;反向而跑;那么;二人从出发到第二次相遇需多长时间?解“第二次相遇”可以理解为二人跑了两圈。
因此总路程为400×2相遇时间=(400×2)÷(5+3)=100(秒)答:二人从出发到第二次相遇需100秒时间。
例3甲乙二人同时从两地骑自行车相向而行;甲每小时行15千米;乙每小时行13千米;两人在距中点3千米处相遇;求两地的距离。
解“两人在距中点3千米处相遇”是正确理解本题题意的关键。
从题中可知甲骑得快;乙骑得慢;甲过了中点3千米;乙距中点3千米;就是说甲比乙多走的路程是(3×2)千米;因此;相遇时间=(3×2)÷(15-13)=3(小时)两地距离=(15+13)×3=84(千米)答:两地距离是84千米。
追及问题【含义】两个运动物体在不同地点同时出发(或者在同一地点而不是同时出发;或者在不同地点又不是同时出发)作同向运动;在后面的;行进速度要快些;在前面的;行进速度较慢些;在一定时间之内;后面的追上前面的物体。
这类应用题就叫做追及问题。
【数量关系】追及时间=追及路程÷(快速-慢速)追及路程=(快速-慢速)×追及时间【解题思路和方法】简单的题目直接利用公式;复杂的题目变通后利用公式。
追及和相遇问题习题(打印)

专题:追及相遇问题2011.11.71、一辆汽车在十字路口等候绿灯,当绿灯亮时,汽车以的加速度开始行驶,恰在此时一辆自行车以的速度匀速驶来,从后面赶过汽车.求:(1)什么时候汽车追上自行车?(2)汽车追上自行车时,汽车的速度是多大?2、一辆值勤的警车停在公路边,当警员发现从他旁边以v=8m/s的速度匀速行驶的货车有违章行为时,决定前去追赶,经2.5s,警车发动起来,以加速度a=2m/s2做匀加速运动(警车的速度可以达到很大),试问:(1)警车要经多长时间才能追上违章的货车?(2)在警车追上货车之前,两车间的最大距离是多少?=10m/s,B车在后,其(选做)3、A、B两列火车,在同一轨道上同向行驶,A车在前,其速度vA速度v=30m/s,因大雾能见度低,B车在距A车时才发现前方有A车,这时B车立即刹B车,但B车要经过900m才能停止.问(1)A车若按原速前进时,通过计算说明两车是否会相撞?(2)若B车在刹车的同时发出信号,A车司机经1.0s收到信号后加速前进,则A车的加速度至少多大才能避免相撞事故?4、2011年7月23日,发生在温州的动车追尾事故造成重大的人员伤亡和经济损失。
有报道称,在紧急关头,D301次列车司机放弃逃生,紧急制动使列车尽量降速,使得列车相撞的冲击力大大降低,他用生命挽救了许多人和许多家庭。
据资料记载进行估算,当时火车以216km/h行进,制动后以180km/h与静止的前车相撞,该动车制动时最大能产生1m/s2的加速度。
司机从发现险情,需0.7s的反应时间,采取措施紧急制动。
根据以上信息,估算列车司机是在距相撞地点多少米处,发现前方静止的列车的?5、猎狗能以最大速度v1=10m/s持续地奔跑,野兔只能以最大速度v2=8m/s的速度持续奔跑。
如图所示,一只野兔在离洞窟s1=200m处的草地上玩耍,猎狗发现野兔后,正以其最大速度直朝野兔追来。
野兔发现猎狗时,与猎狗只相距s2=60m,野兔立即掉头跑向洞窟。
四年级数学上册相遇问题、追及问题、相离问题重难点+练习题【重点精选】全国通用

行程问题知识点1、在行车、行船、行走时,按照速度、时间和距离之间的相依关系,已知其中的两个量,要求第三个量,这类应用题,叫做行程应用题。
也叫行程问题。
2、行程应用题的解题关键是掌握速度、时间、距离之间的数量关系:距离=速度×时间速度=距离÷时间时间=距离÷速度3、按运动方向,行程问题可以分成三类:(1)相向运动问题(相遇问题)(2)同向运动问题(追及问题)(3)背向运动问题(相离问题)应用题1、相向运动问题(1)相向运动问题(相遇问题),是指地点不同、方向相对所形成的一种行程问题。
两个运动物体由于相向运动而相遇。
(2)解答相遇问题的关键,是求出两个运动物体的速度之和。
基本公式有:两地距离=速度和×相遇时间相遇时间=两地距离÷速度和速度和=两地距离÷相遇时间例1、两列火车同时从相距540千米的甲乙两地相向而行,经过3.6小时相遇。
已知客车每小时行80千米,货车每小时行多少千米?例2、两城市相距138千米,甲乙两人骑自行车分别从两城出发,相向而行。
甲每小时行13千米,乙每小时行12千米,乙在行进中因修车候车耽误1小时,然后继续行进,与甲相遇。
求从出发到相遇经过几小时?2、同向运动问题(追及问题)(1)两个运动物体同向而行,一快一慢,慢在前快在后,经过一定时间快的追上慢的,称为追及。
解答追及问题的关键,是求出两个运动物体的速度之差。
(2)基本公式有:追及距离=速度差×追及时间追及时间=追及距离÷速度差速度差=追及距离÷追及时间例1、甲乙两人在相距12千米的AB两地同时出发,同向而行。
甲步行每小时行4千米,乙骑车在后面,每小时速度是甲的3倍。
几小时后乙能追上甲?例2、一个通讯员骑摩托车追赶前面部队乘的汽车。
汽车每小时行48千米,摩托车每小时行60千米。
通讯员出发后2小时追上汽车。
通讯员出发的时候和部队乘的汽车相距多少千米?注意:要求距离差,需要知道速度差和追及时间。
人教版四年级上册数学相遇问题应用题(含答案)

人教版四年级上学期数学相遇问题一、填空题1.一辆汽车的速度是每小时行驶72千米,可以写作( );李亮每分钟步行的速度是65米,可以写作( );一种超音速飞机2秒钟可以飞行800米,它的速度可以写作( )。
2.把下面表格填完整。
根据上面的计算,你发现:时间=( ),速度=( )。
3.一辆轿车4小时行驶360千米,路程和时间的最简整数比是( ),比值是( ),这个比值表示( )。
4.一辆汽车每小时行75千米,它的速度可以写成( ),读作( ),这辆汽车4小时行( )千米。
5.一辆货车从甲地开往乙地再按原路返回甲地,下面是货车与甲地之间距离的变化情况。
(1)甲地到乙地的距离是( )千米。
(2)货车从甲地到乙地的速度与货车从乙地返回甲地的速度的比是( )。
(3)货车在乙地停留了( )分。
二、解答题6.小东和小明赛跑,他们的速度之比为11∶8,结果小东比小明早了6秒到达终点。
请问∶小东花了多长时间跑到终点?7.李伯伯从李庄到县城商场购买电视机。
去的时候每小时行驶48千米,用了5小时,返回时仅用了4小时。
从李庄到县城商场有多远?返回时的速度是多少?8.一辆卡车从工厂出发去某港口送货,每小时行78千米,行了2小时后离全程的中点还差24千米,工厂与港口相距多少千米?9.快、慢两同时分别从甲乙两地相对而行,经过6小时在离中点30千米处两车相遇,相遇后两车仍以原速行驶,快车又用5小时到达乙地。
甲乙两地间的路程是多少千米?10.爸爸骑自行车,经过一段下坡路时,以每秒3.5米的速度开始下坡,以后每秒行驶的路程都比前一秒多4.5米,经过5秒后,爸爸到达坡底。
这段下坡路有多少米?11.为了响应国家绿色出行的号召,甲、乙、丙三人由开车出行改为步行出行。
甲、乙从A地,丙从B 地同时出发,相向而行。
甲每小时行4km,乙每小时行5km,丙每小时行6km,丙遇到乙后12分钟又遇到甲,求A、B两地相距多少千米?12.甲、乙两船在静水中的速度分别是24千米/时和32千米/时。
四年级奥数第11讲相遇问题 第12讲追及问题

第11讲相遇问题练习十一1、两辆摩托车同时从甲、乙两地相对开出,一辆摩托车每小时行62千米,另一辆摩托车每小时行65千米,经过5小时相遇。
甲、乙两地相距多少千米?2、一个圆形跑道的周长是500米,两个学生同时从同地相背而行。
甲每分钟走65米,乙每分钟走60米,经过几分钟才能相遇?3、一列货车和一列客车同时从某站向相反方向开出,货车每小时行38千米,客车每小时行42千米,5小时后两车相距多少千米?4、A、B两城相距420千米,一辆公共汽车和一辆小轿车同时从A、B两地出发,相向而行,经过4小时相遇,已知小轿车的速度是每小时55千米,公共汽车的速度是多少?5、甲、乙两城相距310千米,一列快车从甲城出发开往乙城,每小时行70千米。
快车开出1小时后,慢车从乙城开往甲城,经过2小时后两车相遇,求慢车的速度。
6、甲、乙两城相距340千米,一列慢车从乙城出发开往甲城,每小时行50千米,行了2小时后,一列快车从甲城出发开往乙城,每小时行70千米,慢车共行几小时后与快车相遇?7、小刚家距学校有1120米,早晨他和妹妹小慧同时离家上学,小刚每分钟走80米,小慧每分钟走60米。
哥哥到校门口时,发现忘带作业,立即沿原路回家去取,兄妹俩从出发到相遇共用了几分钟?8、兄妹二人同时离家去上学,哥哥每分钟走90米,妹妹每分钟走70米,哥哥到校门时,发现忘带跳绳,立即沿原路回家去取,行至离学校120米处与妹妹相遇。
他们家离学校有多远?9、甲、乙两辆客车同时从东、西两城相向对开,甲客车每小时行58千米,乙客车每小时行50千米,两车在离中点32千米处相遇。
东、西两城间相距多少千米?10、快车和慢车同时从东、西两地相对开出,已知快车每小时行50千米,经过4小时后,快车已驶过中点32千米,这时与慢车还相距12千米。
慢车的速度是多少?11、A、B两地相距460千米,甲列车从A地开出2小时后,乙列车从B地开出,经4小时与甲列车相遇,已知甲列车比乙列车每小时多行10千米,甲列车的速度是多少?12、南湾小学和北岗小学的学生从相隔18千米的两村同时出发,相向而行。
四年级相遇问题应用题

四年级相遇问题应用题1. 小明和小华从相距500米的两地同时出发,相向而行。
小明每分钟走60米,小华每分钟走70米。
问他们多少分钟后相遇?2. 甲、乙两车从相距400千米的两地同时出发,相对而行。
甲车每小时行60千米,乙车每小时行70千米。
问几小时后两车相遇?3. 小红和小丽在环形跑道上跑步,跑道长400米。
小红每秒跑5米,小丽每秒跑7米。
他们从同一地点出发,同向而行。
问多少秒后他们再次相遇?4. 爸爸和小明同时从家出发去公园,家离公园有800米。
爸爸每分钟走80米,小明每分钟走60米。
他们会在公园的哪个位置相遇?5. 两只小船分别从河的两岸同时出发,相向而行。
一只船每小时行20千米,另一只船每小时行25千米。
河宽120千米,问它们多少小时后相遇?6. 小华和小明从相距300米的两地同时出发,同向而行。
小华每分钟走70米,小明每分钟走60米。
问小华追上小明需要多少分钟?7. 甲、乙两人骑自行车从相距60千米的两地同时出发,相向而行。
甲每小时行15千米,乙每小时行18千米。
问他们相遇时离中点多少千米?8. 小明和小丽同时从两地出发,相向而行。
小明每分钟走50米,小丽每分钟走60米。
他们在距离中点100米的地方相遇。
求两地之间的距离。
9. 小红和小华从相距450米的两地同时出发,相向而行。
小红每分钟走65米,小华每分钟走75米。
问他们相遇时一共走了多少分钟?10. 两列火车从相距500千米的两地同时出发,相对而行。
一列火车每小时行70千米,另一列火车每小时行80千米。
问他们相遇时离出发地多少千米?希望这些题目能帮助四年级的学生更好地理解和练习相遇问题的应用题。
追及和相遇问题(教案与练习)

追及和相遇问题(教案与练习)追击与相遇专题(1).匀加速运动追匀速运动的情况(开始时v1< v2):v1< v2时,两者距离变⼤;v1= v2时,两者距离最⼤;v1>v2时,两者距离变⼩,相遇时满⾜x1= x2+Δx,全程只相遇(即追上)⼀次。
【例1】⼀⼩汽车从静⽌开始以3m/s2的加速度⾏驶,恰有⼀⾃⾏车以6m/s的速度从车边匀速驶过.求:(1)⼩汽车从开动到追上⾃⾏车之前经过多长时间两者相距最远?此时距离是多少?(2)⼩汽车什么时候追上⾃⾏车,此时⼩汽车的速度是多少?(2).匀速运动追匀加速运动的情况(开始时v1> v2):v1> v2时,两者距离变⼩;v1= v2时,①若满⾜x1 x2+Δx,则后者撞上前者(或超越前者),此条件下理论上全程要相遇两次。
【例2】⼀个步⾏者以6m/s的最⼤速率跑步去追赶被红灯阻停的公共汽车,当他距离公共汽车25m 时,绿灯亮了,汽车以1m/s2的加速度匀加速启动前进,问:⼈能否追上汽车?若能追上,则追车过程中⼈共跑了多少距离?若不能追上,⼈和车最近距离为多少?(3).匀减速运动追匀速运动的情况(开始时v1> v2):v1> v2时,两者距离变⼩;v1= v2时,①若满⾜x1 x2+Δx,则后者撞上前者(或超越前者),此条件下理论上全程要相遇两次。
【例3】汽车正以10m/s的速度在平直公路上前进,突然发现正前⽅有⼀辆⾃⾏车以4m/s 的速度做同⽅向的匀速直线运动,汽车⽴即关闭油门做加速度⼤⼩为6 m/s2的匀减速运动,汽车恰好不碰上⾃⾏车。
求关闭油门时汽车离⾃⾏车多远?(4).匀速运动追匀减速运动的情况(开始时v1v2时,两者距离变⼩,相遇时满⾜x1= x2+Δx,全程只相遇⼀次。
注意:若被追赶的物体做匀减速运动,⼀定要注意追上前该物体是否停⽌运动.【例4】当汽车B在汽车A前⽅7m时,A正以v A=4m/s的速度向前做匀速直线运动,⽽汽车B此时速度v B=10m/s,并关闭油门向前做匀减速直线运动,加速度⼤⼩为a=2m/s2。
四年级相遇与追及问题

四年级相遇与追及问题相遇和追及是初中数学中比较基础的运动问题。
相遇问题是指两个人从两个不同的地点出发,在途中相遇的情况。
追及问题是指一个人从后面赶上另一个人的情况。
在解决这些问题时,需要用到速度、时间和路程的关系。
具体来说,对于相遇问题,假设甲从A地到B地,乙从B地到A地。
如果两人同时出发,他们在途中相遇,实质上是甲和乙一起走了A、B之间这段路程。
如果甲的速度为v甲,乙的速度为v乙,相遇的时间为t,则相遇路程为S和=V和t,其中V和=v甲+v乙。
对于追及问题,假设甲走得快,乙走得慢。
在相同的时间(追及时间)内,甲比乙多走了一段路程,也就是追及路程。
如果甲的速度为v甲,乙的速度为v乙,速度差为V差=v甲-v乙,则追及路程为S差=V差t。
需要注意的是,在研究这些问题时,一般都隐含以下两种条件:(1)在整个被研究的运动过程中,两个物体所运行的时间相同;(2)在整个运行过程中,两个物体所走的是同一路径。
举个例子,假设XXX和明明同时从各自的家相对出发,明明每分钟走20米,XXX骑着脚踏车每分钟比明明快42米,经过20分钟后两人相遇。
那么,聪聪家和明明家的距离为S和=(20+42)×20=1640米。
在解决这些问题时,可以选择直接利用公式计算,也可以画图帮助理解。
对于刚刚研究奥数的孩子,需要引导他们认识、理解及应用公式。
已经行驶了82千米(41千米/小时×2小时),此时甲、乙两车相距770-82=688千米。
接下来,甲、乙两车相向而行,速度之和为45+41=86千米/小时。
根据“相遇时间=路程和/速度和”的公式,甲车行驶的时间为688/86=8小时。
因此,甲车行驶8小时后与乙车相遇。
答案】甲车行驶8小时后与乙车相遇。
考点】行程问题【难度】☆☆【题型】解答【解析】先求出XXX出发后,XXX所行的路程:70×5=350(米);再求出XXX返回学校和取运动服所需的时间:2×2=4(分钟);因为XXX比XXX每分钟多走40米,所以追上XXX的时间为350÷40=8.75(分钟),即约9分钟后追上XXX.答案】9分钟已知XXX和XXX同时从学校出发,XXX的速度是XXX的1.6倍,他们向同一个方向走,5分钟后XXX返回学校取运动服,这样用去了5分钟,在学校又耽误了2分钟,XXX一共耽误了12分钟。
四年级奥数——相遇、追及

四年级奥数——行程问题相遇问题1、南北两村相距90千米,甲从南村出发,他要在9分钟内赶到北村,那他每分钟至少要行多少千米?2、王叔叔因急事,以每小时78千米的车速从甲地赶往乙地,3小时后,他发现时间足够,又以每小时62千米的速度行驶了2小时,赶到了乙地,甲乙两地相距多少千米?3、小飞和小华同时从相距5320米的两地相向而行,两人行了40分钟后还相距1520米,问两人再走几分钟才能相遇?4、甲乙两个车队同时从相隔330千米的两地相向而行,甲队每小时行60千米,乙队每小时行50千米,一个人骑摩托车每小时行80千米在两车队中间往返联络,问两车队相遇时,摩托车行驶了多少千米?5、小明骑摩托车、小军骑自行车分别从甲、乙两地同时出发,相向而行,3小时后相遇。
小军从甲地到乙地要12小时,小明从乙地到甲地要几小时?6、甲、乙两车同时从东西两地相对开出,6小时相遇。
如果甲车每小时少行9千米,乙车每小时多行6千米,那么经过6小时后,两车已行路程是剩下路程的19倍。
东西两地相距多少千米?7、A、B两车同时从甲、乙两站相对开出,两车第一次在距甲站50千米处相遇。
相遇后继续前进,各自到达乙、甲两站后立即返回,第二次在距乙站20千米处相遇。
甲、乙两站相距多少千米?追及问题1、甲从A出发,每小时12千米,2小时后,乙也从A地相背而行,每小时16千米,再经过4小时他们同时停下来,这时他们相距多远?2、甲、乙相背而行,甲每小时比乙多行2千米,8小时后两人相隔112千米,求甲、乙各自的速度?3、快车和慢车同时从南北两地相对开出,已知快车每小时行60千米,经过3小时后,快车已驶过中点25千米。
这时与慢车还相距6千米。
慢车每小时行多少千米?4、小华和小亮的家相距410米,两人同时从家中出发,在同一条笔直的路上行走,小华每分钟走65米,小亮每分钟走55米。
3分钟后两人可能相距多少米?5、甲、乙两人绕周长为1000米的环形广场竞走,已知甲每分钟走125米,乙的速度是甲的2倍,现在甲在乙的后面250米,乙追上需要多少分钟?6、甲、乙二人同时从A地到B地,甲每小时行10千米,乙每小时行8千米,甲行至15千米处又回去取东西,因此比乙迟1小时到B地。
追及与相遇问题(含答案)

追及与相遇问题练习(含答案)一、多选题(本大题共5小题,共20.0分)1. 在一个大雾天,一辆小汽车以的速度行驶在平直的公路上,突然发现正前方处有一辆大卡车以的速度同方向匀速行驶,汽车司机立即刹车,忽略司机的反应时间,后卡车也开始刹车,从汽车司机开始刹车时计时,两者的图象如图所示,下列说法正确的是( )A. 小汽车与大卡车一定没有追尾B. 由于在减速时大卡车的加速度大小小于小汽车的加速度大小,导致两车在时追尾C. 两车没有追尾,两车最近距离为D. 两车没有追尾,并且两车都停下时相距2. 两物体均沿轴正方向从静止开始做匀变速直线运动,时刻两物体同时出发,物体的位置随速率平方的变化关系如图甲所示,物体的位置随运动时间的变化关系如图乙所示,则( )A. 物体的加速度大小为B. 时,两物体相距C. 内物体的平均速度大小为D. 两物体相遇时,物体的速度是物体速度的倍3. 甲乙两车在一平直道路上同向运动,其图象如图所示,图中和的面积分别为和,初始时,甲车在乙车前方处( )A. 若,两车不会相遇B. 若,两车相遇次C. 若,两车相遇次D. 若,两车相遇次4. ,两辆汽车从同一地点同时出发沿同一方向做直线运动,它们的速度的平方随位置的变化规律如图所示,下列判断正确的是( )A. 汽车的加速度大小为B. 汽车、在处的速度大小为C. 从开始到汽车停止前,当时、相距最远D. 从开始到汽车停止前,当时、相距最远二、计算题(本大题共5小题,共50.0分)5. 一辆值勤的警车停在公路边,当警员发现从他旁边以的速度匀速直线行驶的货车有违章行为时,决定前去追赶,经过后警车启动,并以的加速度做匀加速直线运动,试问:警车在追赶货车的过程中,两车间的最大距离是多少若警车能达到的最大速度是,达到最大速度后以该速度匀速运动,则警车启动后要多长时间才能追上货车6. 一辆汽车以的速度在平直公路上行驶,制动后要经过才能停下来。
现在该汽车正以的速度在平直公路上行驶,突然发现正前方处停有一辆摩托车,汽车司机经的反应时间后,立即采取制动措施,汽车开始制动的同时摩托车以的加速度加速启动。
行程问题(相遇、追及、流水)习题汇总

⾏程问题(相遇、追及、流⽔)习题汇总四年级上⾏程问题(⼀)我们把研究路程、速度、时间以及这三者之间关系的⼀类问题,总称为⾏程问题.在对⼩学数学的学习中,我们已经接触过⼀些简单的⾏程应⽤题,并且已经了解到:上述三个量之间存在这样的基本关系:路程=速度×时间.因此,在这⼀讲中,我们将在前⾯学习的基础上,主要来研究⾏程问题中较为复杂的⼀类问题——反向运动问题,也即在同⼀道路上的两个运动物体作⽅向相反的运动的问题.它⼜包括相遇问题和相背问题.所谓相遇问题,指的就是上述两个物体以不同的点作为起点作相向运动的问题;所谓相背问题,指的就是这两个运动物体以同⼀点作为起点作背向运动的问题,下⾯,我们来具体看⼏个例⼦.例1 甲、⼄⼆⼈分别从相距30千⽶的两地同时出发相向⽽⾏,甲每⼩时⾛6千⽶,⼄每⼩时⾛4千⽶,问:⼆⼈⼏⼩时后相遇?分析出发时甲、⼄⼆⼈相距30千⽶,以后两⼈的距离每⼩时都缩短6+4=10(千⽶),即两⼈的速度的和(简称速度和),所以30千⽶⾥有⼏个10千⽶就是⼏⼩时相遇.解:30÷(6+4)=30÷10=3(⼩时)答:3⼩时后两⼈相遇.例1是⼀个典型的相遇问题.在相遇问题中有这样⼀个基本数量关系:路程=速度和×时间.例2 ⼀列货车早晨6时从甲地开往⼄地,平均每⼩时⾏45千⽶,⼀列客车从⼄地开往甲地,平均每⼩时⽐货车快15千⽶,已知客车⽐货车迟发2⼩时,中午12时两车同时经过途中某站,然后仍继续前进,问:当客车到达甲地时,货车离⼄地还有多少千⽶?分析货车每⼩时⾏45千⽶,客车每⼩时⽐货车快15千⽶,所以,客车速度为每⼩时(45+15)千⽶;中午12点两车相遇时,货车已⾏了(12—6)⼩时,⽽客车已⾏(12—6-2)⼩时,这样就可求出甲、⼄两地之间的路程.最后,再来求当客车⾏完全程到达甲地时,货车离⼄地的距离.解:①甲、⼄两地之间的距离是:45×(12—6)+(45+15)×(12—6—2)=45×6+60×4=510(千⽶).②客车⾏完全程所需的时间是:510÷(45+15)=510÷60=8.5(⼩时).③客车到甲地时,货车离⼄地的距离:510—45×(8.5+2)=510-472.5=37.5(千⽶).答:客车到甲地时,货车离⼄地还有37.5千⽶.例3 两列⽕车相向⽽⾏,甲车每⼩时⾏36千⽶,⼄车每⼩时⾏54千⽶.两车错车时,甲车上⼀乘客发现:从⼄车车头经过他的车窗时开始到⼄车车尾经过他的车窗共⽤了14秒,求⼄车的车长.分析⾸先应统⼀单位:甲车的速度是每秒钟36000÷3600=10(⽶),⼄车的速度是每秒钟54000÷3600=15(⽶).本题中,甲车的运动实际上可以看作是甲车乘客以每秒钟10⽶的速度在运动,⼄车的运动则可以看作是⼄车车头的运动,因此,我们只需研究下⾯这样⼀个运动过程即可:从⼄车车头经过甲车乘客的车窗这⼀时刻起,⼄车车头和甲车乘客开始作反向运动14秒,每⼀秒钟,⼄车车头与甲车乘客之间的距离都增⼤(10+15)⽶,因此,14秒结束时,车头与乘客之间的距离为(10+15)×14=350(⽶).⼜因为甲车乘客最后看到的是⼄车车尾,所以,⼄车车头与甲车乘客在这段时间内所⾛的路程之和应恰等于⼄车车⾝的长度,即:⼄车车长就等于甲、⼄两车在14秒内所⾛的路程之和.解:(10+15)×14=350(⽶)答:⼄车的车长为350⽶.我们也可以把例3称为⼀个相背运动问题,对于相背问题⽽⾔,相遇问题中的基本关系仍然成⽴.例4 甲、⼄两车同时从A、B两地出发相向⽽⾏,两车在离B地64千⽶处第⼀次相遇.相遇后两车仍以原速继续⾏驶,并且在到达对⽅出发点后,⽴即沿原路返回,途中两车在距A地48千⽶处第⼆次相遇,问两次相遇点相距多少千⽶?分析甲、⼄两车共同⾛完⼀个AB全程时,⼄车⾛了64千⽶,从上图可以看出:它们到第⼆次相遇时共⾛了3个AB全程,因此,我们可以理解为⼄车共⾛了3个64千⽶,再由上图可知:减去⼀个48千⽶后,正好等于⼀个AB全程.解:①AB间的距离是64×3-48=192-48=144(千⽶).②两次相遇点的距离为144—48-64=32(千⽶).答:两次相遇点的距离为32千⽶.例5 甲、⼄⼆⼈从相距100千⽶的A、B两地同时出发相向⽽⾏,甲骑车,⼄步⾏,在⾏⾛过程中,甲的车发⽣故障,修车⽤了1⼩时.在出发4⼩时后,甲、⼄⼆⼈相遇,⼜已知甲的速度为⼄的2倍,且相遇时甲的车已修好,那么,甲、⼄⼆⼈的速度各是多少?分析甲的速度为⼄的2倍,因此,⼄⾛4⼩时的路,甲只要2⼩时就可以了,因此,甲⾛100千⽶所需的时间为(4—1+4÷2)=5⼩时.这样就可求出甲的速度.解:甲的速度为:100÷(4-1+4÷2)=10O÷5=20(千⽶/⼩时).⼄的速度为:20÷2=10(千⽶/⼩时).答:甲的速度为20千⽶/⼩时,⼄的速度为10千⽶/⼩时.例6 某列车通过250⽶长的隧道⽤25秒,通过210⽶长的隧道⽤23秒,若该列车与另⼀列长150⽶.时速为72千⽶的列车相遇,错车⽽过需要⼏秒钟?分析解这类应⽤题,⾸先应明确⼏个概念:列车通过隧道指的是从车头进⼊隧道算起到车尾离开隧道为⽌.因此,这个过程中列车所⾛的路程等于车长加隧道长;两车相遇,错车⽽过指的是从两个列车的车头相遇算起到他们的车尾分开为⽌,这个过程实际上是⼀个以车头的相遇点为起点的相背运动问题,这两个列车在这段时间⾥所⾛的路程之和就等于他们的车长之和.因此,错车时间就等于车长之和除以速度之和.列车通过250⽶的隧道⽤25秒,通过210⽶长的隧道⽤23秒,所以列车⾏驶的路程为(250—210)⽶时,所⽤的时间为(25—23)秒.由此可求得列车的车速为(250—210)÷(25—23)=20(⽶/秒).再根据前⾯的分析可知:列车在25秒内所⾛的路程等于隧道长加上车长,因此,这个列车的车长为20×25—250=250(⽶),从⽽可求出错车时间.解:根据另⼀个列车每⼩时⾛72千⽶,所以,它的速度为:72000÷3600=20(⽶/秒),某列车的速度为:(25O-210)÷(25-23)=40÷2=20(⽶/秒)某列车的车长为:20×25-250=500-250=250(⽶),两列车的错车时间为:(250+150)÷(20+20)=400÷40=10(秒).答:错车时间为10秒.例7 甲、⼄、丙三辆车同时从A地出发到B地去,甲、⼄两车的速度分别为每⼩时60千⽶和48千⽶,有⼀辆迎⾯开来的卡车分别在它们出发后的5⼩时.6⼩时,8⼩时先后与甲、⼄、丙三辆车相遇,求丙车的速度.分析甲车每⼩时⽐⼄车快60-48=12(千⽶).则5⼩时后,甲⽐⼄多⾛的路程为12×5=60(千⽶).也即在卡车与甲相遇时,卡车与⼄的距离为60千⽶,⼜因为卡车与⼄在卡车与甲相遇的6-5=1⼩时后相遇,所以,可求出卡车的速度为60÷1-48=12(千⽶/⼩时)卡车在与甲相遇后,再⾛8-5=3(⼩时)才能与丙相遇,⽽此时丙已⾛了8个⼩时,因此,卡车3⼩时所⾛的路程与丙8⼩时所⾛的路程之和就等于甲5⼩时所⾛的路程.由此,丙的速度也可求得,应为:(60×5-12×3)÷8=33(千⽶/⼩时).解:卡车的速度:(60-48)×5÷(6-5)-48=12(千⽶/⼩时),丙车的速度:(60×5-12×3)÷8=33(千⽶/⼩时),答:丙车的速度为每⼩时33千⽶.注:在本讲中出现的“⽶/秒”、“千⽶/⼩时”等都是速度单位,如5⽶/秒表⽰为每秒钟⾛5⽶.习题六1.甲、⼄两车分别从相距240千⽶的A、B两城同时出发,相向⽽⾏,已知甲车到达B城需4⼩时,⼄车到达A城需6⼩时,问:两车出发后多长时间相遇?2.东、西镇相距45千⽶,甲、⼄⼆⼈分别从两镇同时出发相向⽽⾏,甲⽐⼄每⼩时多⾏1千⽶,5⼩时后两⼈相遇,问两⼈的速度各是多少?3.甲、⼄⼆⼈以均匀的速度分别从A、B两地同时出发,相向⽽⾏,他们第⼀次相遇地点离A地4千⽶,相遇后⼆⼈继续前进,⾛到对⽅出发点后⽴即返回,在距B地3千⽶处第⼆次相遇,求两次相遇地点之间的距离.4.甲、⼄⼆⼈从相距100千⽶的A、B两地出发相向⽽⾏,甲先出发1⼩时.他们⼆⼈在⼄出后的4⼩时相遇,⼜已知甲⽐⼄每⼩时快2千⽶,求甲、⼄⼆⼈的速度.5.⼀列快车和⼀列慢车相向⽽⾏,快车的车长是280⽶,慢车的车长为385⽶,坐在快车上的⼈看见慢车驶过的时间是11秒,那么坐在慢车上的⼈看见快车驶过的时间是多少?6.前进钢铁⼚⽤两辆汽车从距⼯⼚90千⽶的矿⼭运矿⽯,现有甲、⼄两辆汽车,甲车⾃矿⼭,⼄车⾃钢铁⼚同时出发相向⽽⾏,速度分别为每⼩时40千⽶和50千⽶,到达⽬的地后⽴即返回,如此反复运⾏多次,如果不计装卸时间,且两车不作任何停留,则两车在第三次相遇时,距矿⼭多少千⽶?习题六解答1.解:240÷(240÷4+240÷6)=2.4(⼩时).2.解:①甲、⼄的速度和45÷5=9(千⽶/⼩时).②甲的速度:(9+1)÷2=5(千⽶/⼩时).③⼄的速度:9—5=4(千⽶/⼩时).3.解:①A、B两地间的距离:4×3—3=9(千⽶).②两次相遇点的距离:9-4-3=2(千⽶).4.解:①⼄的速度为:[100—2×(4+1)]÷(4×2+1)=10(千⽶/⼩时).②甲的速度为:10+2=12(千⽶/⼩时).提⽰:甲⽐⼄每⼩时快2千⽶,则(4+1)⼩时快2×(4+1)=10(千⽶),因此,相当于⼄⾛100—10=90千⽶的路需(4×2+1)=9(⼩时).5.解:280÷(385÷11)=8(秒).提⽰:在这个过程中,对⽅的车长=两列车的速度和×驶过的时间.⽽速度和不变.6.解:①第三次相遇时两车的路程和为:90+90×2+90×2=450(千⽶).②第三次相遇时,两车所⽤的时间:450÷(40+50)=5(⼩时).③距矿⼭的距离为:40×5—2×90=20(千⽶).四年级下第七讲⾏程问题在本讲中,我们研究两个运动物体作⽅向相同的运动时,路程、速度、时间这三个基本量之间有什么样的关系.例1 下午放学时,弟弟以每分钟40⽶的速度步⾏回家.5分钟后,哥哥以每分钟60⽶的速度也从学校步⾏回家,哥哥出发后,经过⼏分钟可以追上弟弟?(假定从学校到家有⾜够远,即哥哥追上弟弟时,仍没有回到家).分析若经过5分钟,弟弟已到了A地,此时弟弟已⾛了40×5=200(⽶);哥哥每分钟⽐弟弟多⾛20⽶,⼏分钟可以追上这200⽶呢?解:40×5÷(60-40)=200÷20=10(分钟)答:哥哥10分钟可以追上弟弟.我们把类似例1这样的题,称之为追及问题.如果我们把开始时刻前后两物体(或⼈)的距离称为路程差(如例1中的200⽶),从开始时刻到后者追上前者路程差这⼀段路程所⽤的时间称为追及时间,则从例1容易看出:追及问题存在这样的基本关系:路程差=速度差×追及时间.如果已知其中的两个量,那么根据上式就很容易求出第三个量.例2 甲、⼄⼆⼈练习跑步,若甲让⼄先跑10⽶,则甲跑5秒钟可追上⼄;若甲让⼄先跑2秒钟,则甲跑4秒钟就能追上⼄.问:甲、⼄⼆⼈的速度各是多少?分析若甲让⼄先跑10⽶,则10⽶就是甲、⼄⼆⼈的路程差,5秒就是追及时间,据此可求出他们的速度差为10÷5=2(⽶/秒);若甲让⼄先跑2秒,则甲跑4秒可追上⼄,在这个过程中,追及时间为4秒,因此路程差就等于2×4=8(⽶),也即⼄在2秒内跑了8⽶,所以可求出⼄的速度,也可求出甲的速度.综合列式计算如下:解:⼄的速度为:10÷5×4÷2=4(⽶/秒)甲的速度为:10÷5+4=6(⽶/秒)答:甲的速度为6⽶/秒,⼄的速度为4⽶/秒.例3 某⼈沿着⼀条与铁路平⾏的笔直的⼩路由西向东⾏⾛,这时有⼀列长520⽶的⽕车从背后开来,此⼈在⾏进中测出整列⽕车通过的时间为42秒,⽽在这段时间内,他⾏⾛了68⽶,则这列⽕车的速度是多少?分析整列⽕车通过的时间是42秒,这句话的意思是:从⽕车的车头追上⾏⼈时开始计时,直到车尾超过⾏⼈为⽌共⽤42秒,因此,如果我们把⽕车的运动看作是车尾的运动的话,则本题实际上就是⼀个车尾与⼈的追及问题,开始时刻,它们的路程差就等于这列⽕车的车长,追及时间就等于42秒,因此可以求出它们的速度差,从⽽求出⽕车的车速.解:520÷42+68÷42=(520+68)÷42=588÷42=14(⽶/秒)答:⽕车的车速为14⽶/秒.例4 幸福村⼩学有⼀条200⽶长的环形跑道,冬冬和晶晶同时从起跑线起跑,冬冬每秒钟跑6⽶,晶晶每秒钟跑4⽶,问冬冬第⼀次追上晶晶时两⼈各跑了多少⽶,第2次追上晶晶时两⼈各跑了多少圈?分析这是⼀道封闭路线上的追及问题,冬冬与晶晶两⼈同时同地起跑,⽅向⼀致.因此,当冬冬第⼀次追上晶晶时,他⽐晶晶多跑的路程恰是环形跑道的⼀个周长(200⽶),⼜知道了冬冬和晶晶的速度,于是,根据追及问题的基本关系就可求出追及时间以及他们各⾃所⾛的路程.解:①冬冬第⼀次追上晶晶所需要的时间:200÷(6-4)=100(秒)②冬冬第⼀次追上晶晶时他所跑的路程应为:6×100=600(⽶)③晶晶第⼀次被追上时所跑的路程:4×100=400(⽶)④冬冬第⼆次追上晶晶时所跑的圈数:(600×2)÷200=6(圈)⑤晶晶第2次被追上时所跑的圈数:(400×2)÷200=4(圈)答:略.解答封闭路线上的追及问题,关键是要掌握从并⾏到下次追及的路程差恰是⼀圈的长度.例5 军事演习中,“我”海军英雄舰追击“敌”军舰,追到A岛时,“敌”舰已在10分钟前逃离,“敌”舰每分钟⾏驶1000⽶,“我”海军英雄舰每分钟⾏驶1470⽶,在距离“敌”舰600⽶处可开炮射击,问“我”海军英雄舰从A岛出发经过多少分钟可射击敌舰?分析“我”舰追到A岛时,“敌”舰已逃离10分钟了,因此,在A岛时,“我”舰与“敌”舰的距离为10000⽶(=1000×10).⼜因为“我”舰在距离“敌”舰600⽶处即可开炮射击,即“我”舰只要追上“敌”舰9400(=10000⽶-600⽶)即可开炮射击.所以,在这个问题中,不妨把9400当作路程差,根据公式求得追及时间.解:(1000×10-600)÷(1470-1000)=(10000-600)÷470=9400÷470=20(分钟)答:经过20分钟可开炮射击“敌”舰.例6 在⼀条直的公路上,甲、⼄两个地点相距600⽶,张明每⼩时⾏4公⾥,李强每⼩时⾏5公⾥.8点整,张李⼆⼈分别从甲、⼄两地同时出发相向⽽⾏,1分钟后他们都调头反向⽽⾏,再经过3分钟,他们⼜调头相向⽽⾏,依次按照1,3,5,…(连续奇数)分钟数调头⾏⾛,那么张、李⼆⼈相遇时是8点⼏分?分析⽆论相向还是反向,张李⼆⼈每分钟都共⾛4000÷60+5000÷60=150(⽶).如果两⼈⼀直相向⽽⾏,那么从出发经过600÷150=4(分钟)两⼈相遇.显然,按现在的⾛法,在16分钟(=1+3+5+7)之内两⼈不会相遇.在这16分钟之内,他们相向⾛了6分钟(=1+5),反向⾛了10分钟(=3+7),此时两⼈相距600+[150×(3+7-1-5)]=1200⽶,因此,再相向⾏⾛,经过1200÷150=8(分钟)就可以相遇.解:600+150×(3+7-1-5)=1200(⽶)1200÷(4000÷60+5000÷60)=8(分钟)1+3+5+7+8=24(分钟)答:两⼈相遇时是8点24分.例7 ⾃⾏车队出发12分钟后,通信员骑摩托车去追他们,在距出发点9千⽶处追上了⾃⾏车队,然后通信员⽴即返回出发点;随后⼜返回去追⾃⾏车队,再追上时恰好离出发点18千⽶,求⾃⾏车队和摩托车的速度.分析在第⼀次追上⾃⾏车队与第⼆次追上⾃⾏车队之间,摩托车所⾛的路程为(18+9)千⽶,⽽⾃⾏车所⾛的路程为(18-9)千⽶,所以,摩托车的速度是⾃⾏车速度的3倍(=(18+9)÷(18-9));摩托车与⾃⾏车的速度差是⾃⾏车速度的2倍,再根据第⼀次摩托车开始追⾃⾏车队时,车队已出发了12分钟,也即第⼀次追及的路程差等于⾃⾏车在12分钟内所⾛的路程,所以追及时间等于12÷2=6(分钟);联系摩托车在距出发点9千⽶的地⽅追上⾃⾏车队可知:摩托车在6分钟内⾛了9千⽶的路程,于是摩托车和⾃⾏车的速度都可求出了.解:(18+9)÷(18-9)=3(倍)12÷(3-1)=6(分钟)9÷6=1.5(千⽶/分钟)1.5÷3=0.5(千⽶/分钟)答:摩托车与⾃⾏车的速度依次为1.5千⽶/分钟,0.5千⽶/分钟.例8 A、B两地间有条公路,甲从A地出发,步⾏到B地,⼄骑摩托车从B地出发,不停地往返于A、B两地之间,他们同时出发,80分钟后两⼈第⼀次相遇,100分钟后⼄第⼀次追上甲,问:当甲到达B地时,⼄追上甲⼏次?+分析由上图容易看出:在第⼀次相遇与第⼀次追上之间,⼄在100-80=20(分钟)内所⾛的路程恰等于线段FA的长度再加上线段AE的长度,即等于甲在(80+100)分钟内所⾛的路程,因此,⼄的速度是甲的9倍(=180÷20),则BF的长为AF的9倍,所以,甲从A到B,共需⾛80×(1+9)=800(分钟)⼄第⼀次追上甲时,所⽤的时间为100分钟,且与甲的路程差为⼀个AB全程.从第⼀次追上甲时开始,⼄每次追上甲的路程差就是两个AB全程,因此,追及时间也变为200分钟(=100×2),所以,在甲从A到B的800分钟内,⼄共有4次追上甲,即在第100分钟,300分钟,500分钟和700分钟.解:(略).习题七1.解放军某部先遣队,从营地出发,以每⼩时6千⽶的速度向某地前进,6⼩时后,部队有急事,派通讯员骑摩托车以每⼩时78千⽶的速度前去联络,问多少时间后,通讯员能赶上先遣队?2.⼩明以每分钟50⽶的速度从学校步⾏回家,12分钟后⼩强从学校出发骑⾃⾏车去追⼩明,结果在距学校1000⽶处追上⼩明,求⼩强骑⾃⾏车的速度.3.甲、⼄两架飞机同时从⼀个机场起飞,向同⼀⽅向飞⾏,甲机每⼩时⾏300千⽶,⼄机每⼩时⾏340千⽶,飞⾏4⼩时后它们相隔多少千⽶?这时候甲机提⾼速度⽤2⼩时追上⼄机,甲机每⼩时要飞⾏多少千⽶?4.两⼈骑⾃⾏车从同⼀地点出发沿着长900千⽶环形路⾏驶,如果他们反向⽽⾏,那么经过2分钟就相遇,如果同向⽽⾏,那么每经过18分钟快者就追上慢者,求两⼈骑车的速度?5.⼀条环形跑道长400⽶,甲骑⾃⾏车每分钟骑450⽶,⼄跑步每分钟250⽶,两⼈同时从同地同向出发,经过多少分钟两⼈相遇?6.上午8点零8分,⼩明骑⾃⾏车从家⾥出发,8分钟后,爸爸骑摩托车去追他,在离家4千⽶的地⽅追上了他.然后爸爸⽴刻回家,到家后⼜⽴刻回头去追⼩明、再追上他的时候,离家恰好是8千⽶,问这时是⼏点⼏分?习题七解答1.(6×6)÷(78-6)=0.5(⼩时).2.①⼩强需⼏分钟追上⼩明:(1000-12×50)÷50=8(分钟)②⼩强每分钟骑车⾏多少⽶:1000÷8=125(⽶/分).3.①4⼩时后相差多少千⽶?(340-300)×4=160(千⽶)②甲机提⾼速度后每⼩时飞⾏多少千⽶?160÷2+340=420(千⽶).4.900÷2=450(⽶/分)900÷18=50(⽶/分)快车速度:(450+50)÷2=250(⽶/分)慢车速度:(450-50)÷2=200(⽶/分).5.400÷(450-250)=2(分钟).6.从爸爸第⼀次追上⼩明到第⼆次追上这⼀段时间内,⼩明⾛的路程是8-4=4(千⽶),⽽爸爸⾏了4+8=12(千⽶),因此,摩托车与⾃⾏车的速度⽐是12∶4=3∶1.⼩明全程骑车⾏8千⽶,爸爸来回总共⾏4+12=16(千⽶),还因晚出发⽽少⽤8分钟,从上⾯算出的速度⽐得知,⼩明骑车⾏8千⽶,爸爸如同时出发应该骑24千⽶.现在少⽤8分钟,少骑24-16=8(千⽶),因此推算出摩托车的速度是每分钟1千⽶.爸爸总共骑了16千⽶,需16分钟,8+16=24(分钟),这时是8点32分.五年级上第⼋讲流⽔⾏船问题船在江河⾥航⾏时,除了本⾝的前进速度外,还受到流⽔的推送或顶逆,在这种情况下计算船只的航⾏速度、时间和所⾏的路程,叫做流⽔⾏船问题。
追及和相遇问题

△x
x
v自t
1 2
at 2
6t
3 2
t2
x自
当t
6 2 (
3)
2s时
xm
62 4( 3)
6m
2
2
那么,汽车经过多少时间能追上自行车?此时汽车的速度是多
大?汽车运动的位移又是多大?
x
6T
3 2
T
2
0 x汽
T 4s
1 aT 2=24m 2
v汽
aT
12m /
s
方法四:相对运动法
选自行车为参照物,则从开始运动到两车相距最远这段过程中,
v自T
1 2
aT 2
T 2v自 4s a
v汽 aT 12m / s
x汽
1 2
aT 2=24m
方法二:图象法
解:画出自行车和汽车的速度-时间图线,自行车的位移x自等于 其图线与时间轴围成的矩形的面积,而汽车的位移x汽则等于其 图线与时间轴围成的三角形的面积。两车之间的距离则等于图
中矩形的面积与三角形面积的差,不难看出,当t=t0时矩形与三 角形的面积之差最大。
x汽
△x
x自
方法一:公式法
当汽车的速度与自行车的速度
x汽
相等时,两车之间的距离最大。设
经时间t两车之间的距离最大。则
△x
v汽 at v自
t v自 6 s 2s
x自
xm
x自
a
x汽
3
v自t
1 2
at 2
6 2m
1 2
3 22 m
6m
那么,汽车经过多少时间能追上自行车?此时汽车的速度是
多大?汽车运动的位移又是多大?
应用题板块-行程问题之相遇追及(小学四年级奥数题)
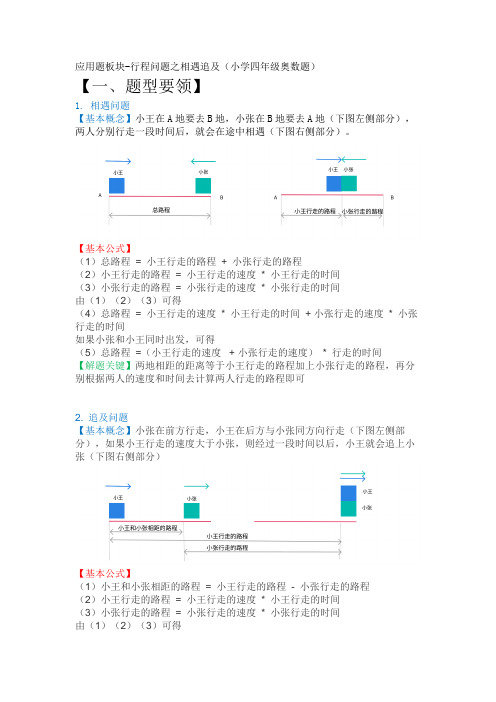
应用题板块-行程问题之相遇追及(小学四年级奥数题)【一、题型要领】1. 相遇问题【基本概念】小王在A地要去B地,小张在B地要去A地(下图左侧部分),两人分别行走一段时间后,就会在途中相遇(下图右侧部分)。
【基本公式】(1)总路程= 小王行走的路程+ 小张行走的路程(2)小王行走的路程= 小王行走的速度* 小王行走的时间(3)小张行走的路程= 小张行走的速度* 小张行走的时间由(1)(2)(3)可得(4)总路程= 小王行走的速度* 小王行走的时间+ 小张行走的速度* 小张行走的时间如果小张和小王同时出发,可得(5)总路程=(小王行走的速度 + 小张行走的速度)* 行走的时间【解题关键】两地相距的距离等于小王行走的路程加上小张行走的路程,再分别根据两人的速度和时间去计算两人行走的路程即可2. 追及问题【基本概念】小张在前方行走,小王在后方与小张同方向行走(下图左侧部分),如果小王行走的速度大于小张,则经过一段时间以后,小王就会追上小张(下图右侧部分)【基本公式】(1)小王和小张相距的路程= 小王行走的路程- 小张行走的路程(2)小王行走的路程= 小王行走的速度* 小王行走的时间(3)小张行走的路程= 小张行走的速度* 小张行走的时间由(1)(2)(3)可得(4)小王和小张相距的路程 = 小王行走的速度* 小王行走的时间- 小张行走的速度* 小张行走的时间如果小张和小王同时出发,可得(5)小王和小张相距的路程 =(小王行走的速度 - 小张行走的速度)* 行走的时间【解题关键】小王和小张相距的距离等于小王行走的路程减去小张行走的路程,再分别根据两人的速度和时间去计算两人行走的路程即可【举一反三】有一类题目是为赶时间,题目描述“为了节省XX时间从原本的速度x变成了之后的速度y”,解题时可以假象成另一个人以原速度提前走了XX 时间,而自身以修改后的速度从原地出发,最终两人同时到达终点,即可用“追及”问题解答【二、重点例题】例题1【题目】小张从甲地到乙地步行需要36分钟,小王骑自行车从乙地到甲地需要12分钟,他们同时出发,几分钟后两人相遇?【分析】走同样长的距离,小张花费的时间是小王花费时间的36 ÷ 12 = 3(倍),因此自行车的速度是步行速度的3倍。
追及与相遇问题练习题

追及与相遇问题练习题一、基础题1. 甲、乙两人同时从同一地点出发,甲以5米/秒的速度向前走,乙以3米/秒的速度向前走。
问甲追上乙需要多长时间?2. 甲、乙两车从相距100公里的两地同时出发,甲车速度为60公里/小时,乙车速度为40公里/小时。
问两车相遇需要多长时间?3. 甲、乙两人同时从相距10公里的两地出发,甲向乙方向走,速度为4公里/小时,乙向甲方向走,速度为6公里/小时。
问两人相遇需要多长时间?4. 甲、乙两人同时从同一地点出发,甲以6米/秒的速度向前走,乙以4米/秒的速度向前走。
问甲比乙多走多少米?5. 甲、乙两车从相距120公里的两地同时出发,甲车速度为70公里/小时,乙车速度为50公里/小时。
问两车相遇时,甲车比乙车多走了多少公里?二、提高题1. 甲、乙、丙三人同时从同一地点出发,甲以5米/秒的速度向前走,乙以4米/秒的速度向前走,丙以3米/秒的速度向前走。
问甲追上丙需要多长时间?2. 甲、乙两车从相距150公里的两地同时出发,甲车速度为80公里/小时,乙车速度为60公里/小时。
两车相遇后,甲车继续前行,乙车掉头返回。
问两车再次相遇需要多长时间?3. 甲、乙两人同时从相距12公里的两地出发,甲向乙方向走,速度为5公里/小时,乙向甲方向走,速度为7公里/小时。
问两人相遇时,各自走了多少公里?4. 甲、乙两人同时从同一地点出发,甲以7米/秒的速度向前走,乙以5米/秒的速度向前走。
问甲追上乙时,两人共走了多少米?5. 甲、乙两车从相距180公里的两地同时出发,甲车速度为90公里/小时,乙车速度为60公里/小时。
问两车相遇时,甲车比乙车多走了多少公里?三、拓展题1. 甲、乙、丙三人同时从同一地点出发,甲以6米/秒的速度向前走,乙以4米/秒的速度向前走,丙以2米/秒的速度向前走。
问甲追上乙和丙分别需要多长时间?2. 甲、乙两车从相距200公里的两地同时出发,甲车速度为100公里/小时,乙车速度为80公里/小时。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
相遇问题与追及问题应用题训练(一)
1、甲、乙两辆汽车同时从两地相对开出,甲车每小时行驶54千米,乙车每小时行驶53千米,经过4小时相遇。
两地相距多少千米
2、两列火车从两地同时相对开出,一列火车每小时行驶100千米,另一列火车每小时行驶125千米。
两列火车在途中先后停车4次,每次15分钟,经过5小时两车相遇。
两地相距多少千米
3、A、B两地相距1340千米,一辆大客车和一辆小汽车分别从A、B两地同时出发,相向而行。
大客车每小时行驶40千米,小汽车每小时行驶52千米。
12小时后两车相距多少千米
4、两城相距1404千米,甲、乙两列火车从两城同时相向行驶。
甲车每小时行驶48千米,乙车每小时比甲车快12千米。
两车开出多长时间后相遇
5、甲、乙两地相距735千米,客车和货车分别从两地同时出发,相向而行。
客车每小时行70千米,它的速度是货车的2倍。
多少小时后两车相遇
6、珠珠和丹丹分别从相距30千米的两地同时出发相向而行,经过3小时相遇。
珠珠每小时走6千米,丹丹每小时走多少千米
7、甲、乙两船同时从相距645千米的两个码头相向出发,8小时后还相距390千米。
甲船每小时行驶15千米,乙船每小时行驶多少千米
8、两列火车从两地相对行驶,甲车每小时行80千米,乙车每小时行70千米。
甲车开出1小时后,乙车才出发,经过2小时两车相遇。
两地间的铁路长多少千米
9、一条公路长385千米,一辆货车和一辆客车分别从这条公路的两端相对出发,货车每小时行驶75千米,开出1小时后客车才开出,客车每小时行80千米。
再过几小时两车相遇
10、两列火车同时从上海站向相反方向的两个城市开出。
一列火车每小时行驶60千米,另一列火车每小时行驶50千米。
经过几小时后两车相距1430千米11、甲每小时行19千米,乙每小时行17千米。
甲从南庄向南行,同时乙从北庄向北行,经过3小时后,两人相隔120千米。
南、北两庄相距多少千米
12、甲队以每小时15千米的速度去驻地正前方120千米外的A镇,与甲队同时同地出发的乙队以每小时9千米的速度前进。
甲队抵达A镇后立刻原路返回,行进几小时后能与乙队相遇。
