六年级奥数期末测试题1
六年级奥数测试卷-1-答案

测试卷11、服装商店用1800元进来一批衬衫,按20%的利润定价,能获利润元。
2、一种商品,按成本的120%定价后打九折出售,结果赚了400元,这种商品的成本是元。
3、某种商品的利润率是20%,如果进货价降低20%,售出价保持不变,那么这时的利润率将是 %。
4、某种商品按定价卖出可得利润96元,如按定价的80%出售,则亏损83.2元。
该商品购入价是元。
5、一件商品随季节变化降价出售。
如果按现价降价10%,仍可获利32元;如果降价20%就要亏损48元。
这件商品的进价为元。
6、某信用社将113400元分为两部分同时贷给甲、乙两人。
一部分以年利率5.58%贷给甲,另一部分以年利率5.76%贷给乙。
甲、乙两人一年后同时交来的利息恰好相等。
甲、乙各贷款元。
7、红红皮鞋店以每双39元购进一批儿童皮鞋,售出价为48元,卖到还剩5双时,除去购进的这批儿童皮鞋的所有开支,还获利93元。
问这批儿童皮鞋一共购进了双。
8、某商品按每个5元利润卖出4个的钱数,与按每个20元利润卖出3个的钱数一样多,问这一商品的每个成本是元。
9、商店用相同的费用购进甲、乙两种不同的糖果,已知甲种糖果每千克18元,乙种糖果每千克12元,如果把这两种糖果混在一起成为什锦糖,那么这种糖每千克的成本是元。
10、某商品按原定价出售,每件利润是成本的20%,后来按原定价的90%出售,结果每天售出的件数比降件前增加了2.5倍,每天经营这种商品的总利润比降价前增加了 %。
11、某物品按定价出售可获6元利润,现按定价的80%出售15个所获得利润与按原价每个减价2.4元出售10个所获利润相等,那么每个物品的成本价是元。
12、果品公司购进苹果5.2万千克,每千克的进价是0.98元,付运费等开支1840元,预计损耗为1%,如果希望全部进货销售后能获利17%,那么每千克苹果零售价应定为元。
测试卷21、张大伯在银行存入3000元钱,定期三年,年利率3.24%,到期后能取得本息共元。
小学六年级奥数题及答案1

小学六年级奥数题及答案1标题:小学六年级奥数题及答案解析(一)在数学的世界里,奥数题是一种既能锻炼思维,又能增加学习兴趣的题型。
以下我们来看一道小学六年级的奥数题。
题目:一个正方形的面积是320平方厘米,将其剪成8个相等的小正方形,求小正方形的面积。
这道题涉及到正方形的面积计算,以及面积的均分。
首先,我们来计算一下这个正方形的边长。
设正方形的边长为a,根据正方形的面积公式,我们可以得到以下等式:a^2 = 320我们将这个等式两边同时开平方根,得到:a = √320由于这是一个正方形,因此边长是等于对角线的,我们可以将其表示为:a = √1600 + √9600的和的平方根这样,我们就得到了正方形的边长。
接下来,我们需要将正方形剪成8个相等的小正方形。
每个小正方形的边长等于原来正方形的边长的1/2,即:b = a/2 = √(1600 + 9600)/2 的平方根这样,我们就可以计算出每个小正方形的面积了:每个小正方形的面积 = b^2 = (√(1600 + 9600)/2 的平方根)的平方所以,每个小正方形的面积为:40平方厘米。
总结来说,解决这道奥数题的关键在于理解并运用正方形的面积公式,以及如何将一个正方形分割成相等的小正方形。
通过这道题,我们可以看到,奥数题的解题过程既锻炼了我们的思维能力,也提高了我们的数学素养。
小学六年级奥数测试题及答案小学六年级奥数测试题及答案小学六年级是学生学习数学的重要阶段,而奥数测试题则是检验学生数学能力的重要手段之一。
下面我们来看一道小学六年级奥数测试题及答案。
题目:一个正方形的边长为4厘米,将其分割成四个小三角形,每个小三角形的面积是多少平方厘米?这道题目是一道几何题,需要学生掌握正方形的性质以及三角形的面积计算方法。
首先,我们可以根据正方形的性质,得出其面积等于边长的平方。
因此,该正方形的面积为16平方厘米。
接下来,我们需要将正方形分割成四个小三角形。
树人学校六年级奥数测试题1

考试试卷
1、1866、1876、1886、1896、2006这五个数的总和是多少?
2、每边长都是12厘米的正方形纸片,正中间挖了一个正方形的洞,成为一个宽度是2厘米的方框,把这五个这样的方框放在桌面上,成为这样的图案,问桌面上被这些方框盖住的面积是多少平方厘米?
3、125的约数有多少个?
4、妈妈让小明给客人沏茶,洗开水壶要用2分钟,烧开水要用15分钟,洗茶壶要用2分钟,洗茶杯要1分钟,那茶叶要用2分钟,小明估算了一下,完成这些工作22分钟,为了给客人早点喝上茶,按你认为最合理的安排,多少分钟就能沏茶了?
5,右边的算式里,四个小纸片个盖住了一个数字,被盖住的四个数字总和是多少?。
六年级奥数试题及答案[1]
![六年级奥数试题及答案[1]](https://img.taocdn.com/s3/m/15b13b00cc17552707220856.png)
1.把33,51,65,77,85,91六个数分为两组,每组三个数,使两组的积相等,则这两组数之差为______.2.有一堆糖果,其中奶糖占45%,再放入16块水果糖后,奶糖就只占25%,那么,这堆糖中有奶糖______块.3.某地区水电站规定,如果每月用电不超过24度,则每度收9分;如果超过24度,则多出度数按每度2角收费.若某月甲比乙多交了9.6角,则甲交了______角______分.4.某人工作一年酬金是1800元和一台全自动洗衣机.他干了7个月,得到490元和一台洗衣机,问这台洗衣机为多少元?5.一个长方体的体积为2009立方厘米,如果长、宽、高均为整数厘米,求几种长方体满足条件?6.2009的平方的约数有多少个?(看清楚是2009的”平方”的约数有多少个。
)7.某人从甲地到乙地,计划8点出发9点到达,在距中点2000米的地方修车10分钟,又提速1/4前进最后提前两分钟到达终点。
求原速度?8.有一项工程,按原计划甲、乙合作120天可以完工,后因特殊原因,甲队的工效提高20%,乙队的工效则下降了20%,因此比计划多用5天完成。
求甲队单独完成全部工程要用多少天?问题补充:是按原工效完成全部工程哦~!9.营业员把一张5元的人民币和一张5角的人民币换成了28张票面为1元和1角的人民币,求换来的这两种人民币各多少张?10.有一元,二元,五元的人民币共50张,总面值为116元,已知一元的比二元的多2张,问三种面值的人民币各多少张?11.有3元,5元和7元的电影票400张,一共价值1920元,其中7元和5元的张数相等,三种价格的电影票各多少张?12.用大、小两种汽车运货,每辆大汽车装18箱,每辆小汽车装12箱,现在有18车货,价值3024元,若每箱便宜2元,则这批货价值2520元,问:大、小汽车各有多少辆?13.一辆卡车运矿石,晴天每天可运20次,雨天每天可运12次,它一共运了112次,平均每天运14次,这几天中有几天是雨天?14.运来一批西瓜,准备分两类卖,大的每千克0.4元,小的每千克0.3元,这样卖这批西瓜共值290元,如果每千克西瓜降价0.05元,这批西瓜只能卖250元,问:有多少千克大西瓜?15.甲、乙二人投飞镖比赛,规定每中一次记10分,脱靶每次倒扣6分,两人各投10次,共得152分,其中甲比乙多得16分,问:两人各中多少次?16.某次数学竞赛共有20条题目,每答对一题得5分,错了一题不仅不得分,而且还要倒扣2分,这次竞赛小明得了86分,问:他答对了几道题?答案:1.(16)把各数因数分解.33=11×3;51=17×3;65=13×5;77=11×7;85=17×5;91=13×7,所以33×85×91=77×51×65故差为91+85+33-77-65-51=16.2.(9块)45%3.27角6分不妨设甲家用电x度,乙家用电y度,因为96既不是20的倍数,也不是9的倍数.所以必然甲家用电大于24度,乙家小于24度.即x>24≥y.由条件得.24×9+20(x-24)=9y+96,20x-9y=360,由9y=20x-360,20|9y,又(9,20)=1,所以|20y.当0≤y≤24时,y=20或0.而y=0即x=18<24,矛盾,故y=20,x=27.甲应交24×9+20×(27-24)=276(分)=27.6(角).4.(1344)设洗衣机x元,则每月应得报酬为:5.2009=1×7×7×41长宽高可以是:2009,1,1;1,7,287;1,41,49;7,7,416.20092有6个不同的约数:1、7、41、49、287、20097.解:设原速度为x千米/时,则甲乙两地相距x千米(60-2)/60=29/30(小时),10/60=1/6(小时)(1)在中点前2000米的地方修车则(0.5x-2)/x+1/6+(0.5x+2)/(1.25x)=29/30解得x=4(2)在中点后2000米的地方修车则(0.5x+2)/x+1/6+(0.5x-2)/(1.25x)=29/30解得x=-4不符题意,舍去答:原速度为4千米/时8.甲+乙=1/1204甲+4乙=1/30(1)1.2甲+0.8乙=1/125 6甲+4乙=1/25(2)(2)-(1)得:1.营业员把一张5元的人民币和一张5角的人民币换成了28张票面为1元和1角的人民币,求换来的这两种人民币各多少张?2.有一元,二元,五元的人民币共50张,总面值为116元,已知一元的比二元的多2张,问三种面值的人民币各多少张?3.有3元,5元和7元的电影票400张,一共价值1920元,其中7元和5元的张数相等,三种价格的电影票各多少张?4.用大、小两种汽车运货,每辆大汽车装18箱,每辆小汽车装12箱,现在有18车货,价值3024元,若每箱便宜2元,则这批货价值2520元,问:大、小汽车各有多少辆?5.一辆卡车运矿石,晴天每天可运20次,雨天每天可运12次,它一共运了112次,平均每天运14次,这几天中有几天是雨天?6.运来一批西瓜,准备分两类卖,大的每千克0.4元,小的每千克0.3元,这样卖这批西瓜共值290元,如果每千克西瓜降价0.05元,这批西瓜只能卖250元,问:有多少千克大西瓜?7.甲、乙二人投飞镖比赛,规定每中一次记10分,脱靶每次倒扣6分,两人各投10次,共得152分,其中甲比乙多得16分,问:两人各中多少次?8.某次数学竞赛共有20条题目,每答对一题得5分,错了一题不仅不得分,而且还要倒扣2分,这次竞赛小明得了86分,问:他答对了几道题?1.解:设有1元的x张,1角的(28-x)张x+0.1(28-x)=5.50.9x=2.7x=328-x=25答:有一元的3张,一角的25张。
六年级奥数:转化单位“1”测试题(4份)[精华]
![六年级奥数:转化单位“1”测试题(4份)[精华]](https://img.taocdn.com/s3/m/53ca3171f4335a8102d276a20029bd64783e62ad.png)
转化单位“1”测试题(一)转化单位“1”测试题(二)1、一根绳子,第一次剪去全长的41,第二次剪去余下的32,两次共剪去全长的几分之几?13、小芳三天看完一本书,第一天看了全书的31,第二天看了余下的43,第二天比第一天多看了20页,这本书共有多少页?14、 运送一批水泥,第一天运了这堆水泥的41,第二天运的是第一天的32,还剩84吨没有运,这堆水泥有多少吨?15、修路队修一条公路,第一天修了这条公路的52,第二天修了余下的31,已知这两天共修路120米,这条公路全长多少米?16、某工厂有三个车间,第一车间的人数占三个车间总人数的20%。
第二车间人数是第三车间的32,已知第一车间比第二车间多30人,三个车间一共有多少人?17、 甲比乙多60%,乙比甲少百分之几?7、学校体育室有篮球、排球和足球,篮球的只数占三种球总数的53,足球的只数是排球的32,足球比篮球少11只,这三种球一共有多少只?8、小张1996年花5000元购得一种股票,这种股票平均每年课增值20%。
如果小张一直持有这种股票,最早在哪一年这些股票的总价值转化单位“1”测试题(三)转化单位“1”测试题(四)会超过10000元?9、加工一批零件,甲先加工了这批零件的31,接着乙加工了余下的65,已知乙加工的个数比甲多160个,这批零件共有多少个?10、饲养场饲养着牛、羊、猪,牛的头数占总头数的31,羊的头数比猪少41,牛比猪少42头。
饲养场有多少头牛?11、实验小学六年级三个班植树,一班植树的棵数占三个班总数的41,二班和三班植树棵数的比是3:4,二班比三班少植树24棵,这三个班各植树多少棵?12、有一批商品,按50%的利润定价,当售出这批服装的80%以后,决定换季减价售出,剩下的商品全部按定价的八折出售,这批商品全部售完后实际可获利百分之几? 13、梨的个数是苹果的43,橘子的个数是梨的321倍,橘子和苹果共有90个,梨有多少个?14、学校美术兴趣组和电脑兴趣组共102人,美术组人数的92和电脑组人数的41相等。
六年级奥数题(一)

一、分数的巧算(一) 年级 班 姓名 得分一、填空题1.计算:=÷-⨯+⨯2582.432.02588.6 . 2.=⨯÷⎪⎭⎫ ⎝⎛++1919989898199800980019001900980980190190989898191919 . 3.1000减去它的一半,再减去余下的三分之一,再减去余下的四分之一,依此下去,直到余下的五百分之一,最后剩下 .4.计算:=⨯+⋅⋅⋅+⨯+⨯+⨯100991431321211 . 5.计算:=+++++++496124811241621311814121 . 6.计算:=+--+3121131211 . 7.计算:=⨯+⨯+⨯655161544151433141 . 8.计算:=++⋅⋅⋅+++++⋅⋅⋅+++199719953991199619943989537425313199719961995199619951994543432321 . 9.计算:=⎪⎭⎫ ⎝⎛-⨯-⎪⎭⎫ ⎝⎛+⨯+⎪⎭⎫ ⎝⎛-⨯761231537615312353123176 . 10.计算:⎪⎭⎫ ⎝⎛+++-⎪⎭⎫ ⎝⎛++++⎪⎭⎫ ⎝⎛+++-⎪⎭⎫ ⎝⎛+++20115110151161121814112191613181614121 = .二、解答题11.尽可能化简427863887116690151. 12.计算:⎪⎭⎫ ⎝⎛+⋅⋅⋅+-+-+⋅⋅⋅+⎪⎭⎫ ⎝⎛-+-+⎪⎭⎫ ⎝⎛+-+⎪⎭⎫ ⎝⎛-+914637281941322314312213211211. 13.计算:1999321132112111+⋅⋅⋅++++⋅⋅⋅++++++. 14.计算: ⎪⎭⎫ ⎝⎛⨯-⨯⎪⎭⎫ ⎝⎛⨯-⨯⋅⋅⋅⨯⎪⎭⎫ ⎝⎛⨯-⨯⎪⎭⎫ ⎝⎛⨯-⨯⎪⎭⎫ ⎝⎛⨯-⨯⎪⎭⎫ ⎝⎛⨯-9997319896317531643153314231.———————————————答 案—————————————————————— 1. 513. 原式()12.48.62582582.42582588.6-+=-⨯+⨯= 51351610258==⨯=. 2. 19915. 原式101191019898191000198001000119001001980100119010101981010119⨯⨯⨯÷⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯= 19981998981998199819⨯⨯⎪⎭⎫ ⎝⎛++= 19915192941998199898193==⨯⨯⨯=.3. 2 1000减去它的一半,余下⎪⎭⎫ ⎝⎛-⨯2111000,再减去余下的31, 余下⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯3112111000,再减去余下的41, 余下⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯4113112111000,…,直到减去余下的五百分之一,最后剩下: ⎪⎭⎫ ⎝⎛-⨯⋅⋅⋅⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯500114113112111000 5004994332211000⨯⋅⋅⋅⨯⨯⨯⨯= 2=4. 10099. 原式⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⋅⋅⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=100199199198141313121211 1009910011=-=. 5. 1615. 原式⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=124162162131131181414121211 ⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+4961248124811241 4961311311811-++-= 163131187161231187⨯+=⎪⎭⎫ ⎝⎛-⨯+=161516187=+=. 6. 542. 原式5425144758745873153116311631==⨯==-+=+--+=.7. 123. 原式655660544550433440⨯⎪⎭⎫ ⎝⎛++⨯⎪⎭⎫ ⎝⎛++⨯⎪⎭⎫ ⎝⎛+= 123150140130=+++++=.8. 21. 原式⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⋅⋅⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⋅⋅⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=19972399219962399052842632419971199619961199551441331221=.9. 1原式=()()()532376123765315376231+⨯+-⨯--⨯ 1111=+-=. 10. 14465. 原式⎪⎭⎫ ⎝⎛+++⨯-⎪⎭⎫ ⎝⎛+++⨯+⎪⎭⎫ ⎝⎛+++⨯-⎪⎭⎫ ⎝⎛+++⨯=413121151413121141413121131413121121 ⎪⎭⎫ ⎝⎛-+-⨯⎪⎭⎫ ⎝⎛+++=514131214131211 1446560131225201611234612=⨯=⎪⎭⎫ ⎝⎛+⨯+++=.11. 分子数字之和等于30,故它可以被3整除,分母奇位上数字之和与偶位上数字之和的差为32-21=11,所以它可以被11整除,把这此因数提出,得:1131138896717338896717=⨯⨯.12.原式=⎪⎭⎫ ⎝⎛+⋅⋅⋅++-⎪⎭⎫ ⎝⎛+⋅⋅⋅+++⎪⎭⎫ ⎝⎛+⋅⋅⋅++-⎪⎭⎫ ⎝⎛+⋅⋅⋅++++4642413732312822211914131211 91828173727164636261555251+⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+++⎪⎭⎫ ⎝⎛+++-⎪⎭⎫ ⎝⎛+⋅⋅⋅+++ 9183761061265512764128731298212109+-+⨯-⨯⨯+⨯⨯-⨯⨯+⨯⨯-⨯=9183763534213281845+-+-+-+-=91837641532730+-+-+= 504533=.13.因为2)1(21+=+⋅⋅⋅++n n n ,所以 原式=200019992432322212⨯+⋅⋅⋅+⨯+⨯+⨯ ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+⋅⋅⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=2000119991413131212112 100099912000112=⎥⎦⎤⎢⎣⎡-=.14.因为()()()()()()()()()11311131111312+---=+--+-=+--K K K K K K K K K ()()()()()()112211222+-+-=+--=K K K K K K K ,所以 原式()()()()()()()()()()()()()()()()()()()()198198298298197197297297151525251414242413132323+-+-⨯+-+-⨯⋅⋅⋅⨯+-+-⨯+-+-⨯+-+-= 99971009698969995647353624251⨯⨯⨯⨯⨯⋅⋅⋅⨯⨯⨯⨯⨯⨯⨯⨯⨯=97259710041=⨯=.一、分数的巧算(二) 年级 班 姓名 得分一、填空题1.计算:13471711613122374⨯+⨯+⨯= . 2.计算:⎪⎭⎫ ⎝⎛⨯+÷⨯⎪⎭⎫ ⎝⎛+-25.1522546.79428.0955= . 3.计算:25114373611125373185444.4⨯+÷+÷= . 4.计算:()()015.06.32065.022.0013.000325.0⨯÷-÷= . 5.计算:⎪⎭⎫ ⎝⎛-⨯⋅⋅⋅⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛+⨯⋅⋅⋅⨯⎪⎭⎫ ⎝⎛+⨯⎪⎭⎫ ⎝⎛+⨯⎪⎭⎫ ⎝⎛+9115113111011611411211= . 6.计算:222345567566345567+⨯⨯+= . 7.计算:322131433141544151655161766171⨯+⨯+⨯+⨯+⨯= . 8.计算:4513612812111511016131+++++++= . 9.计算:()()⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⋅⋅⋅⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⋅⋅⋅⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++293112831133112311311312913029132912291291= . 10.计算:217665544332217665544332212⨯⎪⎭⎫ ⎝⎛++++++⎪⎭⎫ ⎝⎛+++++ ⎪⎭⎫ ⎝⎛++++⨯⎪⎭⎫ ⎝⎛++++++-76655443327665544332211= .二、问答题11.用简便方法计算:421330112091276523-+-+-.12.计算:()1999119981997199919985.19935.1995÷⨯÷-.(得数保留三位小数) 13.计算:⋅⋅⋅+++⋅⋅⋅+++++++++1999219991313233323121222111 1999119992199919981999199919991998++⋅⋅⋅++++. 14.计算:299810001299799912001312000211999111999119981199714131211++++⋅⋅⋅+++++++-+⋅⋅⋅+-+-.———————————————答 案——————————————————————1. 16 原式162874131413122374=⨯=⎪⎭⎫ ⎝⎛++⨯=.2. 90 原式⎪⎭⎫ ⎝⎛⨯+⨯⨯⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛+=45522455378.0942955 ()⎪⎭⎫ ⎝⎛+⨯⨯-=522537458.08 90457210452.7=⨯=⨯⨯=.3. 9. 原式25114373625114373137825114⨯+⨯+⨯= ⎪⎭⎫ ⎝⎛++⨯=37363731378251149377525114=⨯=.4. 1 原式1100131351536325=⨯⨯⨯⨯=.5. 1.1 原式1.110119854321011674523==⨯⋅⋅⋅⨯⨯⨯⨯⋅⋅⋅⨯⨯⨯=6. 1.原式()2223455663455663455672223451566566345567++⨯⨯+=+⨯+⨯+=1567566345566345567=+⨯⨯+=.7. 205. 原式322330433440544550655660766770⨯⎪⎭⎫ ⎝⎛++⨯⎪⎭⎫ ⎝⎛++⨯⎪⎭⎫ ⎝⎛++⨯⎪⎭⎫ ⎝⎛++⨯⎪⎭⎫ ⎝⎛+= 205120130140150160=+++++++++=.8. 54 原式1092542432322⨯+⋅⋅⋅+⨯+⨯+⨯= ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛-+⋅⋅⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=101915141413131212 54101212=⎪⎭⎫ ⎝⎛-=.9. 1. 原式2960285933423313231603059332231130⨯⨯⋅⋅⋅⨯⨯⨯⨯⨯⋅⋅⋅⨯⨯⨯= 13130321605934333229283216059323130=⨯⨯⋅⋅⋅⨯⨯⨯⨯⨯⨯⋅⋅⋅⨯⨯⨯⨯⨯⋅⋅⋅⨯⨯⨯⨯⨯⨯⋅⋅⋅⨯⨯⨯=. 10.21. 令a =+++++766554433221,则 原式⎪⎭⎫ ⎝⎛-⨯+-⨯+=21)1(212a a a a222222=⎪⎭ ⎝-+-+=a a a a .11. 原式767665655454434332322121⨯+-⨯++⨯+-⨯++⨯+-⨯+= ⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+-⎪⎭⎫ ⎝⎛+=71616151514141313121211 76711=-=.12. 原式199919981200019982⨯⎪⎭⎫ ⎝⎛-⨯= 199811998199824000+⨯⎪⎭⎫ ⎝⎛-= ⎪⎭⎫ ⎝⎛+⨯⎪⎭⎫ ⎝⎛-=199811199824000 1998199821998240004000⨯--+= 1998199821998224000⨯-++= 001.4002≈.13. 因为kk k k k k k k k k k k k k k -+⋅⋅⋅+++=+++⋅⋅⋅+-++-+⋅⋅⋅+++)321(212311321 k kk k k =-+=)1(,所以, 原式19990002200019991999321=÷⨯=+⋅⋅⋅+++=. 14. 分子⎪⎭⎫ ⎝⎛+⋅⋅⋅+++⨯-⎪⎭⎫ ⎝⎛+++⋅⋅⋅++++=1998161412121999119981199714131211 ⎪⎭⎫ ⎝⎛+⋅⋅⋅+++-⎪⎭⎫ ⎝⎛+⋅⋅⋅+++=9991312111999131211 199911001110001+⋅⋅⋅++= 分母3998139961200412002120001++⋅⋅⋅+++=⎪⎭ ⎝+⋅⋅⋅++⨯=1999100110002 原式211999110011100012199911001110001=⎪⎭⎫ ⎝⎛+⋅⋅⋅++⨯+⋅⋅⋅++=.二、估计与估算(一)年级 班 姓名 得分 一、填空题1.有若干个小朋友,他们的年龄各不相同.将他们的年龄分别填入下式的□中,都能使不等式成立.这些小朋友最多有 个. 215<43.2.010000000009999999999100099910099109+⋅⋅⋅⋅⋅⋅+++的整数部分是 .3.10971939719297199719⨯+⋅⋅⋅+⨯+⨯+=A ,与A 最接近的整数是 .4.有24个偶数的平均数,如果保留一位小数的得数是15.9,那么保留两位小数的得数是 .5.1995003这个数,最多可以拆成 个不同的自然数相加的和.6.有一列数,第一个数是105,第二个数是85,从第三个数开始,每个数都是它前面两个数的平均数.那么第19个数的整数部分是 .7.有一长3米的线段,第一次把这条线段三等分后去掉中间一部分,第二次再把剩下的两线段中的每一段都三等分后都去掉中间一部分,第三次再把剩下的所有线段的每一段都三等分后都去掉中间一部分.继续这一过程,这样至少连续 次后,才使剩下的所有线段的长度的和小于0.4米.8.已知199711982119811198011+⋅⋅⋅+++=S ,那么S 的整数部分是 .9.1009987654321⨯⋅⋅⋅⨯⨯⨯⨯与101相比较,较大的哪个数是 .10.某工厂有三个车间,共有75人报名参加冬季长跑,其中第一车间人数最多,第三车间人数最少.如果第一车间报名人数是第三车间报名人数的212倍,那么第二车间报名人数是第三车间报名人数的 倍.二、解答题11.已知1006915681467136612651170156914681367126611⨯⨯+⨯+⨯+⨯+⨯⨯+⨯+⨯+⨯+⨯=a ,问a 的整数部分是 .12.四个连续自然数的倒数之和等于2019,求这四个自然数的两两乘积之和.13.用四舍五入的方法计算三个分数的和,得近似值为35.1875≈++cb a ,试求c b a ,,的值.(c b a ,,是三个自然数)14.国际象棋比赛的奖金总数为10000元,发给前五名.每一名的奖金都不一样,名次在前的钱数要比名次在后的钱数多.每份奖金钱数都是100元的整数倍.现在规定,第一名的钱数是第二、第三名两人之和,第二名的钱数是第四、第五名两人之和,那么第三名最多能得多少元?———————————————答 案——————————————————————1. 3.依题意,得320326=<□<10,所以□=7,8,9.2. 9.原式>9999=+⋅⋅⋅++, 原式<10,所以原式的和的整数部分是9.3. 11.()97751010219719=+⋅⋅⋅++⨯=A ,因此与A 最接近的整数是11.4. 15.92设这24个偶数之和为S .由S >15.85×24=380.4和S <15.95×24=382.8,以及S 是偶数,推知S =382,所求数为92.1524382≈÷.5. 1997.若要拆成的不同自然数尽量多,应当从最小的自然数1开始,则2)1(321+=+⋅⋅⋅+++n n n ≤1995003. 所以 )1(+n n ≤3990006当1997=n 时,正好有)1(+n n ≤3990006, 所以最多可以拆成1997个不同自然数的和.6. 91.根据题设条件,这列数依次是105,85,95,90,92.5, 91.25, 91.875, …, 显然,从第六项起后面每个数的整数部分都是91,所以,第19个数的整数部分是91.7. 5.这一过程每进行一次,剩下所有线段的和等于上次剩下的322716323232323=⨯⨯⨯⨯>0.4, 813232323232323=⨯⨯⨯⨯⨯<0.4, 所以至少进行5次.8. 110.分母>11011819801=⨯,分母<11111819981=⨯, 所以110<S <111,即S 的整数部分等于110.9. 101.证9998765432,10099654321⨯⋅⋅⋅⨯⨯⨯=⋅⋅⋅⨯⨯⨯=B A , 则2101100110099999854433221⎪⎭⎫ ⎝⎛==⨯⨯⋅⋅⋅⨯⨯⨯⨯=⨯B A .因为A 的前49项的对应项都小于B , A 的最后一项10099<1, 所以A <B , 再由B A ⨯=⎪⎭⎫⎝⎛2101>A ×A , 推知, 101>A .10. 761或1631.设第二和第三车间报名人数分别为a 和b ,则第一车间b b 25212=⨯,依题意,得 b a b a b 272575+=++=因为b ≤a ≤b 25,所以b 29≤b a 27+≤6b ,即b 29≤75≤6b ,所以2112≤b ≤3216,又b 为偶数,所以b =14或16.(1) 当b =14时, a =26, 761=b a ;(2) 当b =16时, a =19, 1631=b a .11. 1006915661265111512111⨯⎪⎭⎫⎝⎛⨯+⋅⋅⋅+⨯+⨯+⋅⋅⋅+++=a691566126511100151001210011100⨯+⋅⋅⋅+⨯+⨯⨯+⋅⋅⋅+⨯+⨯+=6915661265113115341235111100⨯+⋅⋅⋅+⨯+⨯⨯+⋅⋅⋅+⨯+⨯++=最后一个分数小于1,所以a 的整数部分是101.12. 设这四个连续自然数分别为a ,a +1,a +2, a +3,则 20193121111=++++++a a a a ,所以 31211112019++++++=a a a a <a a a a a 41111=+++, a <1944. 易知a =1,2,4均不合题意,故a =3,这四个自然数为3,4,5,6,其两两乘积之和为:119656454635343=⨯+⨯+⨯+⨯+⨯+⨯.13. 依题意,得 1.345≤875cb a ++<1.355,所以 376.6≤56a +40b +35c <379.4又a ,b ,c 为自然数,因此, 56a +40b +35c =377 ① 或56a +40b +35c =378 ② 或56a +40b +35c =379 ③考虑不定方程①,由奇偶分析,知c 为奇数,所以40b +35c 的个位为5, 因此56a 的个位为2,a 的个位为2或7.又a <5643656379=,故a =2, 因此8b +7c =53,易知b =4, c =3.同法可知不定方程②无解,方程③的解为a =4, b =3, c =1.14. 设第i 名的奖金为100ai 元(i =1,2,3,4,5).依题意,得 1000010010010010010054321=++++a a a a a , 且542321,a a a a a a +=+=,整理 1002332=+a a ① 所以 3223100a a +=<222523a a a =+,故2a >20, 由①易知2a 必为偶数,所以2a ≥22.故 ()23310021a a -=≤()1722310021=⨯-. 即第三名最多能得1700元.二、估计与估算(二)年级 班 姓名 得分 一、填空题1. 将六个分数215,94,12011,451,83,358分成三组,使每组的两个分数的和相等,那么与451分在同一组的那个分数是 .2. 数151311197535232129171551719212321357911131÷的十分位到十万分位的数字为 .3. 满足下式的n 最小等于 . )1(1431321211+⨯+⋅⋅⋅+⨯+⨯+⨯n n >19981949.4. 已知1101011102103101102100101+⋅⋅⋅+++=A ,则A 的整数部分是 .5. 小明计算17个自然数的平均数所得的近似值是31.3,老师指出小明少取了一位有效数字,则老师要求的平均数应该是 .6.有三十个数:,302964.1,,30364.1,30264.1,30164.1,64.1+⋅⋅⋅+++如果取每个数的整数部分,并将这些整数相加,那么其和是 .7.将奇数1,3,5,7,…,由小到大按第n 组有2n -1个奇数进行分组 (1), (3,5,7), (9,11,13,15,17), … 第一组 第二组 第三组 那么1999位于第 组的第 个数.8. 22.103.823.102.824.101.8⨯+⨯+⨯的整数部分是 .9. 数222⨯⋅⋅⋅⨯⨯写成小数时的前两位小数是 .10. 有甲、乙、丙、丁四个同学去林中采蘑菇.平均每人采得的蘑菇的个数的整数部分是一个十位数为3的两位数.又知甲采的数量是乙的54,乙采的数量是丙的23倍.丁比甲多采3个蘑菇.那么,丁采蘑菇 个. 二、解答题11.两个连续自然数的平方之和等于365,又有三个连续自然数的平方之和也等于365.试找出这两个连续自然数和那三个连续自然数.12.如图所示,方格表包括A 行B 列(横向为行,纵向为列),其中依次填写了自然数1至B A ⨯ ,现知20在第3行,41在第5行,103在最后一行,试求A 和B .13.求分数1611514131211++⋅⋅⋅++++=A 的整数部分.14.甲、乙、丙三个班向希望工程捐赠图书.已知甲班1人捐6册,有2人各捐7册,其余人各捐11册;乙班有1人捐6册,3人各捐8册,其余人各捐10册;丙班有2人各捐4册,6人各捐7册,其余人各捐9册.已知甲班捐书总数比乙班多28册,乙班比丙班多101册.各班捐书总数都在400册与550册之间.问:每班各有多少人?———————————————答 案——————————————————————1.94. 注意到451是六个分数中的最小数,因此与451在同一组的分数,必须是这六个分数中的最大数(否则,六个数不能分成三组,每组的两个分数的和相等),因此所求数为94.2. 2,5,9,5,3.设题中所述式子为B A ÷,由于题中所涉及的数太大,不太可能通过直接计算来确定前五位数(否则计算量太大),下面利用估值方法来求:因为2.05313,3.05214>÷>÷<÷<÷B A B A , 所以此数的第一位数字为2.又因为259.052331357,2597.05238.135>÷>÷<÷<÷B A B A , 所以此数的第一、二、三位数字为2,5,9. 又因为,25954.0523212135792<÷<÷B A25953.0523********1>÷>÷B A , 所以此五位数字是2,5,9,5,3.3. 40.原式左端等于111+-n ,可得不等式199********>+-n ,所以19984911<+n , 解得493839>n ,故n 最小等于40.4. 67.⎪⎭⎫ ⎝⎛+⋅⋅⋅+++++⋅⋅⋅+++=11010102101011010010)11321(A⎪⎭⎫ ⎝⎛+⋅⋅⋅++++=1101010210101101001066所以 1016711100106611110106667=⨯+<<⨯+=A 因此, A 的整数部分为67.5. 31.29.设17个自然数的和为S ,由3.3117≈S ,得31.25≤35.3117<S. 所以531.25≤S <532.95,又S 为整数,所以S =532,则29.311753217≈=S6. 49.关键是判断从哪个数开始整数部分是2,因为2-1.64=0.36,我们就知⋅⋅⋅==33.0301031, 故先看3011,3011=⋅⋅⋅66.036.0>,这说明“分界点”是301164.1+,所以前11个数整数部分是1,后19个数整数部分为2,其和为4921911=⨯+.7. 32, 39.第n 组的最后一个奇数为自然数中的第2)12(531n n =-+⋅⋅⋅+++个奇数, 即122-n .设1999位于第n 组,则19991)1(22<--n ≤122-n . 由 223222047199919211312⨯=<<=-⨯1-知n=32. 所以1999在第32组第39312119992=-+个数.8. 29.当两个数的和不变时,两数越接近(即差越小)它们的积越大. 所以24.101.823.102.822.103.8⨯<⨯<⨯,从而30325.18324.101.822.103.823.102.824.101.8=⨯⨯<⨯⨯<⨯+⨯+⨯.52.2969.38)22.123.124.1(822.103.823.102.824.101.8=⨯=++⨯>⨯+⨯+⨯,所以22.103.823.102.824.101.8⨯+⨯+⨯的整数部分是29.9. 0.01注意到35327322=>=,所以6992332132,2132>>,所以01.01001961321322132561010=>=⨯=⨯> 又443818025=<=⨯,所以25132,51328844<<.所以02.0501212513225132221010==⨯<⨯<. 故数222⨯⋅⋅⋅⨯⨯写成小数时的前两位小数是0.01.10. 39.设丙采蘑菇数为x 个,则乙采x 23个,甲采x x 562354=⋅个,丁采⎪⎭⎫⎝⎛+356x 个,四人合采蘑菇数为:310493565623+=++++x x x x x . 依题意,得:30≤⎪⎭⎫⎝⎛+3104941x <40解得 4910117494323⨯=≤492324910157=⨯<x又x 1049必须为整数, x 为10的倍数,因此只能x =30, 从而丁采39356=+x (个).11. 用估值法,先求两个连续自然数,因为5.1822365=÷,所以在两个连续自然数中,一个的平方小于182.5,另一个的平方大于182.5.由132=169,142=196得到,这两个连续自然数是13和14.类似地,3365÷32121=,最接近32121的自然数的平方是112=121,所以这三个连续自然数应是10,11,12.经验证,符合题意.12. 依题意,得2B <20≤3B ,4B <41≤5B ,所以326≤B <10,518≤B <4110,故518≤B <10,因此, B =9.由103在最后一行,得9(A -1)<103≤9A ,所以, 9411≤A <9412,故A =12.13.⎪⎭⎫ ⎝⎛+⋅⋅⋅++++⎪⎭⎫ ⎝⎛++++⎪⎭⎫ ⎝⎛+++=16111110191817151416131211A⎪⎭⎫ ⎝⎛+⋅⋅⋅++++⎪⎭⎫ ⎝⎛++++=16111110191817151412又因为14148171514181421=⨯<+++<⨯= 181816111110191161821=⨯<+⋅⋅⋅+++<⨯= 所以 4112212123=++<<++=A故A 的整数部分是3.14.由题目条件,甲班捐书最多,丙班最小,甲班比丙班多捐28+101=129(册). 因为丙班捐书不少于400册,所以甲班捐书在529~550册之间.甲班人数不少于11349311)776529(=+÷---(人),不多于11251311)776550(=+÷---(人),即甲班人数是50人或51人.如果甲班有50人,则甲班共捐书6+7+7+11×(50-3)=537(册),推知乙班捐书537-28=509(册),乙班有10951410)386509(=+÷⨯--(人),人数是分数,不合题意.所以甲班有51人,甲班共捐书548)351(11776=-⨯+++(册),推知乙班捐有53÷+⨯--(人),-(=548104)38628丙班有49⨯÷+-⨯-(人).-(=548)697212948三、定义新运算(一) 年级 班 姓名 得分一、填空题1.规定a ☉b =ab b a -,则2☉(5☉3)之值为 .2.规定“※”为一种运算,对任意两数a ,b ,有a ※b 32b a +=,若6※x 322=,则x =.3.设a ,b ,c ,d 是自然数,定义bc ad d c b a +>=<,,,.则<><><<,3,2,1,4,4,3,2,13, 4, 1, 2>>=<>1,4,3,2, .4.[A ]表示自然数A 的约数的个数.例如,4有1,2,4三个约数,可以表示成[4]=3.计算:]7[])22[]18([÷+= .5.规定新运算※:a ※b=3a -2b .若x ※(4※1)=7,则x= .6.两个整数a 和b ,a 除以b 的余数记为a ☆b .例如,13☆5=3,5☆13=5,12☆4=0.根据这样定义的运算,(26☆9) ☆4= .7.对于数a ,b ,c ,d 规定d c ab d c b a +->=<2,,,.如果7,5,3,1>=<x , 那么x = .8.规定:6※2=6+66=72,2※3=2+22+222=246,1※4=1+11+111+1111=1234.7※5= .9.规定:符号“△”为选择两数中较大数,“☉”为选择两数中较小数.例如:3△5=5,3☉5=3.那么,[(7☉3)△5]×[5☉(3△7)]= .10.假设式子b a a ⨯#表示经过计算后,a 的值变为原来a 与b 的值的积,而式子b a b -#表示经过计算后,b 的值为原来a 与b 的值的差.设开始时a =2,b =2,依次进行计算b a a ⨯#,b a b -#,b a a ⨯#,b a b -#,则计算结束时,a 与b 的和是 .二、解答题11.设a ,b ,c ,d 是自然数,对每两个数组(a ,b ),(c ,d ),我们定义运算※如下: (a ,b )※(c ,d )= (a+c ,b +d );又定义运算△如下: (a ,b )△(c ,d )= (ac+bd ,ad+bc ).试计算((1,2) ※(3,6))△((5,4)※(1,3)).12.羊和狼在一起时,狼要吃掉羊,所以关于羊及狼,我们规定一种运算,用符号△表示羊△羊=羊;羊△狼=狼;狼△羊=狼;狼△狼=狼.运算意思是羊与羊在一起还是羊,狼与狼在一起还是狼,但是狼与羊在一起便只剩下狼了.小朋友总是希望羊能战胜狼,所以我们规定另一种运算,用符号☆表示为羊☆羊=羊;羊☆狼=羊;狼☆羊=羊;狼☆狼=狼.运算意思是羊与羊在一起还是羊,狼与狼在一起还是狼,由于羊能战胜狼,当狼与羊在一起时,它便被羊赶走而只剩下羊了.对羊或狼,可用上面规定的运算作混合运算,混合运算的法则是从左到右,括号内先算.运算的结果是羊,或是狼.求下式的结果:羊△(狼☆羊)☆羊△(狼△狼).13.22264⨯⨯=222⨯⨯⨯表示成()664=f ;33333243⨯⨯⨯⨯=表示成()5243=g .试求下列的值:(1)()=128f ; (2))()16(g f =; (3)6)27()(=+g f ;(4)如果x , y 分别表示若干个2的数的乘积,试证明:)()()(y f x f y x f +=⋅.14.两个不等的自然数a 和b ,较大的数除以较小的数,余数记为a ☉b ,比如5☉2=1,7☉25=4,6☉8=2.(1)求1991☉2000,(5☉19)☉19,(19☉5)☉5;(2)已知11☉x =2,而x 小于20,求x ;(3)已知(19☉x )☉19=5,而x 小于50,求x .———————————————答 案—————————————————————— 1. 120411. 5☉3=15165335=-,2☉(5☉3)=2☉12041112016121516151621516==-=.2. 8.依题意,6※326x x +=,因此322326=+x ,所以x=8.3. 280.;1421343,2,1,4;1032414,3,2,1=⨯+⨯>=<=⨯+⨯>=<.1443121,4,3,2;1014232,1,4,3=⨯+⨯>=<=⨯+⨯>=< 原式2801014141014,10,14,10=⨯+⨯>==<.4. 5.因为23218⨯=有6)12()11(=+⨯+个约数,所以[18]=6,同样可知[22]=4,[7]=2.原式52)46(=÷+=.5. 9.因为4※1=101243=⨯-⨯,所以x ※(4※1)= x ※10=3x -20.故3x -20=7,解得x =9.6. 0.89226+⨯=,26☆9=8,又428⨯=,故(26☆9)☆4=8☆4=0.7. 6.因为x x x +=+-⨯⨯>=<15312,5,3,1,所以71=+x ,故6=x .8. 86415.7※5=7+77+777+7777+77777=86415.9. 25.原式=[3△5]×[5☉7]=5×5=25.10. 14.第1次计算后,422=⨯=a ;第2次计算后,224=-=b ;第3次计算后,824=⨯=a ;第4次计算后,628=-=b .此时1468=+=+b a .11. (1,2)※(3,6)=(1+3,2+6)=(4,8),(5,4)※(1,3)=(5+1,4+3)=(6,7). 原式=(4,8)△(6,7)=(4×6+8×7,4×7+8×6)=(80,76).12. 原式=羊△羊☆羊△狼=羊☆羊△狼=羊△狼=狼.13. (1)()72)128(7==f f ;(2)()())81(342)16(44g g f f ====;(3)因为()())8(233636)27(633f f g g ===-=-=-,所以6)27()8(=+g f ; (4)令,2,2n m y x ==则n y f m x f ==)(,)(.()())()(222)(y f x f n m f f y x f n m n m +=+==⋅=⋅+.14. (1)1991☉2000=9;由5☉19=4,得(5☉19)☉19=4☉19=3;由19☉5=4,得(19☉5)☉5=4☉5=1.(2)我们不知道11和x 哪个大(注意,x ≠11),即哪个作除数,哪个作被除数,这样就要分两种情况讨论.1) x <11,这时x 除11余2, x 整除11-2=9.又x ≥3(因为x 应大于余数2),所以x =3或9.2) x >11,这时11除x 余2,这说明x 是11的倍数加2,但x <20,所以x =11+2=13.因此(2)的解为x =3,9,13.(3)这个方程比(2)又要复杂一些,但我们可以用同样的方法来解.用y 表示19☉x ,不管19作除数还是被除数,19☉x 都比19小,所以y 应小于19.方程y ☉19=5,说明y 除19余5,所以y 整除19-5=14,由于y ≥6,所以y =7,14.当y =7时,分两种情况解19☉x =7.1)x <19,此时x 除19余7,x 整除19-7=12.由于x ≥8,所以x =12.2) x >19,此时19除x 余7, x 是19的倍数加7,由于x <50,所以x =19+7=26或7219+⨯=x =45.当y =14时,分两种情况解19☉x =14.1) x <19,这时x 除19余14, x 整除19-14=5,但x 大于14,这是不可能的.2)x >19,此时19除x 余14,这就表明x 是19的倍数加14,因为x <50,所以x =19+14=33.总之,方程(19☉x )☉19=5有四个解,x =12,26,33,45.三、定义新运算(二) 年级 班 姓名 得分一、填空题1.规定:a ※b =(b+a )×b ,那么(2※3)※5= .2.如果a △b 表示b a ⨯-)2(,例如3△444)23(=⨯-=,那么,当a △5=30时, a= .3.定义运算“△”如下:对于两个自然数a 和b ,它们的最大公约数与最小公倍数的和记为a △b .例如:4△6=(4,6)+[4,6]=2+12=14.根据上面定义的运算,18△12= .4.已知a ,b 是任意有理数,我们规定: a ⊕b = a +b -1,2-=⊗ab b a ,那么[]=⊗⊕⊕⊗)53()86(4 .5.x 为正数,<x >表示不超过x 的质数的个数,如<5.1>=3,即不超过5.1的质数有2,3,5共3个.那么<<19>+<93>+<4>×<1>×<8>>的值是 .6.如果a ⊙b 表示b a 23-,例如4⊙5=3×4-2×5=2,那么,当x ⊙5比5⊙x 大5时, x = .7.如果1※4=1234,2※3=234,7※2=78,那么4※5= .8.我们规定:符号○表示选择两数中较大数的运算,例如:5○3=3○5=5,符号△表示选择两数中较小数的运算,例如:5△3=3△5=3.请计算:=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛∙∙25.210623799343.03323625.026176.0 .9.规定一种新运算“※”: a ※b =)1()1(++⨯⋅⋅⋅⨯+⨯b a a a .如果(x ※3)※4=421200,那么x = .10.对于任意有理数x , y ,定义一种运算“※”,规定:x ※y=cxy by ax -+,其中的c b a ,,表示已知数,等式右边是通常的加、减、乘运算.又知道1※2=3,2※○ △ △ ○3=4,x ※m=x (m ≠0),则m 的数值是 .二、解答题11.设a ,b 为自然数,定义a △b ab b a -+=22.(1)计算(4△3)+(8△5)的值;(2)计算(2△3)△4;(3)计算(2△5)△(3△4).12.设a ,b 为自然数,定义a ※b 如下:如果a ≥b ,定义a ※b=a -b ,如果a <b ,则定义a ※b= b - a .(1)计算:(3※4)※9;(2)这个运算满足交换律吗?满足结合律吗?也是就是说,下面两式是否成立?①a ※b= b ※a ;②(a ※b )※c= a ※(b ※c ).13.设a ,b 是两个非零的数,定义a ※b ab b a +=. (1)计算(2※3)※4与2※(3※4).(2)如果已知a 是一个自然数,且a ※3=2,试求出a 的值.14.定义运算“⊙”如下:对于两个自然数a 和b ,它们的最大公约数与最小公倍数的差记为a ⊙b . 比如:10和14,最小公倍数为70,最大公约数为2,则10⊙14=70-2=68.(1)求12⊙21,5⊙15;(2)说明,如果c 整除a 和b ,则c 也整除a ⊙b ;如果c 整除a 和a ⊙b ,则c 也整除b ;(3)已知6⊙x =27,求x 的值.———————————————答 案——————————————————————1. 100.因为2※3=(3+2)×3=15,所以(2※3)※5=15※5=(5+15)×5=100.2. 8.依题意,得305)2(=⨯-a ,解得8=a .3. 42.18△12=(18,12)+[18,12]=6+36=42.4. 98.原式]1313[4)]253()186[(4⊕⊗=-⨯⊕-+⊗=982254254]11313[4=-⨯=⊗=-+⊗=5. 11.<19>为不超过19的质数,有2,3,5,7,11,13,17,19共8个.<93>为不超过的质数,共24个,易知<1>=0,所以原式=<<19>+<93>>=<8+24>=<32>=11.6. 6.x ⊙5-5⊙x=(3 x -2×5)-(3×5-2 x )=5 x -25,由5 x -25=5,解得x=6.7. 45678.8. 21. 因为∙6.0○322617=○322617=,0.625△853323=△853323=, ∙3.0△319934=△319934=,106237○10623725.2=○4949=, 所以,原式2149318532=++=.9. 2.令x ※3=y ,则y ※4=421200,又4212002726252413532244⨯⨯⨯=⨯⨯⨯=,所以y=24,即x ※3=24.又24=432323⨯⨯=⨯,故x =2.10. 4.由题设的等式x ※y=cxy by ax -+及x ※m=x (m ≠0),得000=⋅⋅-+⋅m c bm a ,所以bm=0,又m ≠0,故b=0.因此x ※y=ax -cxy.由1※2=3,2※3=4,得⎩⎨⎧=-=-46232c a c a 解得a =5,c =1. 所以x ※y =5x -xy ,令x =1,y=m 得5-m=1,故m =4.11. (1)原式()()62585834342222=⨯-++⨯-+=;(2)原式()323222⨯-+=△4=7△4=37474722=⨯-+;(3)原式()525222⨯-+=△()19434322=⨯-+△132831319131922=⨯-+=.12. (1)原式=(4-3)※9=1※9=9-1=8;(2)因为表示a ※b 表示较大数与较小数的差,显然a ※b= b ※a 成立,即这个运算满是交换律,但一般来说并不满足结合律,例如:(3※4)※9=8,而3※(4※9)=3※(9-4)=3※5=5-3=2.13. (1)按照定义有2※36132332=+=,3※412253443=+=. 于是(2※3)※4613=※4=3127451324241361344613=+=+. 2※(3※4)=2※60012012425252421225122521225=+=+=. (2)由已知得233=+aa ① 若a ≥6,则3a ≥2,从而233>+aa 与①矛盾.因此a ≤5,对a =1,2,3,4,5这5个可能的值,一一代入①式中检查知,只有a =3符合要求.14. (1)为求12⊙21,先求出12与21的最小公倍数和最大公约数分别为84,3,因此12⊙21=84-3=81,同样道理5⊙15=15-5=10.(2)如果c 整除a 和b ,那么c 是a 和b 的公约数,则c 整除a ,b 的最大公约数,显然c 也整除a ,b 最小公倍数,所以c 整除最小公倍数与最大公约的差,即c 整除a ⊙b .如果c 整除a 和a ⊙b ,由c 整除a 推知c 整除a ,b 的最小公倍数,再由c 整除a ⊙b 推知, c 整除a ,b 的最大公约数,而这个最大公约数整除b ,所以 c 整除b .(3)由于运算“⊙”没有直接的表达式,解这个方程有一些困难,我们设法逐步缩小探索范围.因为6与x 的最小公倍数不小于27+1=28,不大于27+6=33,而28到33之间,只有30是6的倍数,可见6和x 的最小公倍数是30,因此它们的最大公约数是30-27=3.由“两个数的最小公倍数与最大公约数的积=这两个数的积”,得到x ⨯=⨯6330.所以15=x .四、工程问题(1)年级 班 姓名 得分 一、填空题1.一项工程,甲、乙两队合作20天完成,乙丙两队合作60天完成,丙丁两队合作30完成,甲丁合作 天完成?2.甲乙两队合作一项工程,计划在24天内完成.如果甲队做6天,乙队做4天,只能做完全工程的20%,两队单独做完全工程各需要 天.3.一条公路,甲队独修24天完成,乙队独修30天完成.甲乙两队合修若干天后,乙队停工休息,甲队继续修了6天完成,乙队修了 天.4.某市举办菊展,新建一个喷水池.单开甲管1小时可将喷水池注满,单开乙管40分钟可将水注满,两管同时齐开5210分钟后,共注水314吨.喷水池能装水吨.5.一项工作,两个师傅和三个徒弟合作需922天完成,如果三个师傅2个徒弟合作需要712天完成,如果一名师傅单独做需 天完成.6.加工一批零件,甲独做需3天完成,乙独做需4天完成,两人同时加工,完成任务时,甲比乙多做24个,这批零件共有 个.7.一项建筑工程,由甲建筑队单独承建要一年半,乙建筑队单独承建要一年零三个月,现在两队合作半年,剩下的由乙队继续完成还要 个月.(假设每月实际工作天数一样)8.甲、乙、丙三人合修一围墙.甲、乙合修6天修好围墙的31,乙、丙合修2天修好余下的41,剩下的三人又合修了5天才完成.共得工资180元,按各人所完成的工作量的多少来合理分配,每人应得 元.9.原计划用24个工人挖一定数量的土方,按计划工作5天后,因为调走6人,于是剩下的工人每天比原定工作量多挖1方土才能如期完成任务,原计划每人每天挖土 方.10.一个水池,底部安有一个常开的排水管,上部安有若干个同样粗细的进水管,当打开4个进水管时,需要5小时才能注满水池,当打开2个进水管时,需要15小时才能注满水池;现在需要在2小时内将水池注满,那么至少要打开 个进水管.二、解答题11.抄一份书稿,甲每天的工作效率等于乙、丙二人每天的工作效率的和;丙每天的工作效率相当于甲、乙二人每天工作效率之和的51;如果三人合抄只需8天就完成了,那么乙一人单独抄需多少天才能完成?12.一项工程,甲独做需10天,乙独做需15天,如果两人合作,甲的工作效率就要降低,只能完成原来的54,乙只能完成原来的109,现在要8天完成这项工程,两人合作天数尽可能少,那么两人要合作多少天?13.一空水池有甲、乙两根进水管和一根排水管.单开甲管需5分钟注满水池,单开乙管需10分钟注满水池,满池水如果单开排水管需6分钟流尽.某次池中没有水,打开甲管若干分钟后,发现排水管未关上,随即关上排水管,同时打开乙管,又过了同样长的时间,水池的1/4注了水.如果继续注满水池,前后一共要花多少时间?14.有一个蓄水池装有9根水管,其中一根为进水管,其余8根为相同的出水管,进水管以均匀的速度不停地向这个蓄水池注水.后来有人想打开出水管,使池内的水全部排光(这时池内已注入一些水).如果把8根出水管全部打开,需3小时把池内的水全部排光;如果仅打开5根出水管,需6小时把池内的水全部排光.问要想在4.5小时内把池内的水全部排光,需同时打开几根出水管?———————————————答 案——————————————————————1. 156********1=⎪⎭⎫ ⎝⎛-+÷(天).2. 乙的工作效率为()()40116244%201=-÷⨯-, 甲的工作效率为601401241=-. 故甲做60天完成,乙做40天完成.3. 1030124162411=⎪⎭⎫ ⎝⎛+÷⎪⎭⎫ ⎝⎛⨯-(天).4. 104016015210314=⎪⎭⎫ ⎝⎛+÷⎪⎭⎫ ⎝⎛÷(吨)5. 一个师傅与一个徒弟工作效率之和为:()60112371219221=+÷⎪⎪⎪⎪⎭⎫⎝⎛+, 故师傅的工作效率是101601127121=⨯-,即一名师傅单独做10天完成.6. 16841311413124=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-⨯⎪⎭⎫ ⎝⎛-÷(个).7. 415161511811=÷⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛+-(月).8. 甲分得的钱为:()3356241311541311311180=+⨯⎭⎬⎫⎩⎨⎧÷⨯⎪⎭⎫ ⎝⎛--÷⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛---⨯(元);丙分得的钱为:()5652631541311311180=+⨯⎭⎬⎫⎩⎨⎧÷-÷⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛---⨯(元);乙分得的钱为:180-33-56=91(元).9. 36)624(=÷-(方).10. 进水管一小时进水量为:()()[]15124541521=-÷⨯-⨯÷; 排水管一小时排水量为:1515120151=÷⎪⎭⎫⎝⎛-⨯.故只开一进水管、一排水管池中无水,多开进水管数为5.71521=÷,取整为8 个,至少要打开9个进水管.11. 24281511811=⎥⎦⎤⎢⎣⎡÷-⎪⎭⎫ ⎝⎛+÷÷(天).12. 设两人要合作x 天,依题意得:()15078101=+-x x ,故x =5(天).13. 设注满池中41的水需x 分钟,故有23,412615126151==⨯⎪⎭⎫ ⎝⎛++⨯⎪⎭⎫ ⎝⎛-x x x .继续注满池中水的43411=-需要251015143=⎪⎭⎫ ⎝⎛+÷(分), 共需时间42523=+(分).14. 将每根进水管每小时的进水量看作单位1,则每根出水管每小时的排水量为2)36()3865(=-÷⨯-⨯,而池中原有水量为186265=⨯-⨯,从而要想在4.5小时内把池中水抽干,需要打开65.4182=÷+(根)出水管.四、工程问题(2)年级 班 姓名 得分一、填空题1.一项工作,甲乙两队合作9天完成,乙丙两队合作12天完成,甲丙两队合作需18天完成,现在三队合作需 天完成.2.某工程先由甲单独做63天,再由乙单独做28天即可完成.如果由甲、乙两人合作,需48天完成.现在甲先单独做42天,然后再由乙来单独完成,那么还需要做 天.3.甲、乙两队合作20天可以完成一项工程.如果两队合作8天后,乙队再独做4天,还剩这项工程的158没有完成.甲、乙两队工作效率之比为: .4.一份稿件,甲单独打字需6小时完成,乙单独打字需10小时完成.现在甲单独打若干小时后,因有事由乙接着打完,共用了7小时,那么甲打字用了 小时.5.有批机器零件,甲单独制作需要218天,比乙单独制作多用了21天,两人合作4天后,剩下210个零件由甲单独去做,自始至终甲共制作了 零件.6.一个水池子,甲、乙两管同时开,5小时灌满,乙、丙两管同时开,4小时灌满,如果乙管先开6小时,还需要甲、丙两管同时开2小时才能注满(这时乙管关闭).那么乙管单独灌满水池需要 小时.7.一个水池,地下水从四壁渗入,每小时渗入该水池的水量是固定的.当这个水池水满时,打开A 管,8小时可将水池排空;打开B 管,10小时可将水池排空;打开C 管,12小时可将水池排空.如果打开A 、B 两管,4小时可将水池排空,那么打开B 、C 两管,将水池排空需要 小时.8.一件工作,如果单独做,甲按规定时间可提前2天完成,乙则要超过规定时间3天才完成.现在,甲乙二人合做2天后,剩下的继续由乙单独做,刚好在规定的日期内完成.若甲乙二人合做,完成这件工作需要 天.9.有一水池,装有甲、乙两个注水管,下面装有丙管放水.池空时,单开甲管5分钟可注满;单开乙管10分钟可注满.水池装满水后,单开丙管15分钟可将水放完.如果在池空时,将甲、乙、丙三管齐开,2分钟后关闭乙管,还要 分钟可以注满水池.10.放满一个水池的水,如果同时开放①、②、③号阀门,7.5小时可以完成;如果同时开放①、③、⑤号阀门,5小时可以完成;如果同时开放①③④号阀门,6小时可以完成;如果同时开放②④⑤号阀门,4小时可以完成.问同时开放这五个阀门, 小时可以放满这个水池.二、解答题11.师徒三人合作承包一项工程,4天能够全部完成.已知师傅单独做所需天数与两个徒弟合作所需天数相等;而师傅与乙徒弟合作所需天数的2倍与甲徒弟单独做完所需的天数相等.那么甲徒弟单独做,完成这项工程需要多少天?乙徒弟单独做,完成这项工程需要多少天?12.甲、乙、丙三人从三月一日开始合作一项工程,甲每天的工作量是乙每天工作量的3倍,乙每天的工作量是丙每天工作量的2倍.三人合作5天完成全工程的31后,甲休3天,乙休2天,丙没有休息,问这项工程是在几月几日完成的?13.一个蓄水池装了一根进水管和三根放水速度一样的出水管.单开一根进水管20分钟可注满空池.单开一根出水管,45分钟可以放完满池水.现有32池的水,如果四管齐开,多少分钟后池水还剩52?14.蓄水池有甲、丙两条进水管,和乙丁两条排水管.要灌满一池水,单开甲管需要3小时,单开丙管需要5小时,要排光一池水,单开乙管需要4小时,单开丁管需要6小时.现在池内有61池水.如果按甲、乙、丙、丁、甲、乙……的顺序,轮流各开一小时,多少时间后水开始溢出水池?———————————————答 案——————————————————————1. 82181121911=⎥⎦⎤⎢⎣⎡÷⎪⎭⎫ ⎝⎛++÷(天).2. 甲乙合做28天,完成任务的1274828=÷, 故甲的工作效率为()84128631271=-÷⎪⎭⎫ ⎝⎛-,乙的工作效率为1121841481=-, 于是乙还需做56112184421=÷⎪⎭⎫ ⎝⎛-(天).3. 乙的工作效率为601482011581=÷⎪⎭⎫⎝⎛⨯--,甲的工作效率为301601201=-, 甲乙工作效率之比为1:2601:301=.4. 5.41016171011=⎪⎭⎫⎝⎛-÷⎪⎭⎫ ⎝⎛⨯-(小时).5. 35702102184421218121811210=+⨯⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⨯⎪⎪⎪⎪⎭⎫ ⎝⎛-+-÷(个).6. 20)46(5141211=⎭⎬⎫⎩⎨⎧-÷⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+⨯-÷(小时).7. B 管每小时排水量为81421=÷(池)水. 每小时渗水量为4011011081=÷⎪⎭⎫⎝⎛-⨯(池).C 管每小时排水量为1201312124011=÷⎪⎭⎫⎝⎛⨯+(池).从而B 、C 两管排一池水,需8.440112013811=⎪⎭⎫ ⎝⎛-+÷(小时).8. 甲与乙工作效率之比为3:2,甲独做要101235=⎪⎭⎫⎝⎛-÷(天),乙独做需10+5=15(天),甲乙合做要61511011=⎪⎭⎫⎝⎛+÷(天).9. 4151512151101511=⎪⎭⎫⎝⎛-÷⎥⎦⎤⎢⎣⎡⨯⎪⎭⎫ ⎝⎛-+-(分钟).10. 434134161515.711=⎥⎦⎤⎢⎣⎡+÷⎪⎭⎫ ⎝⎛-++÷(小时).11. 243412411=⎪⎭⎫⎝⎛÷-÷÷(天).12. 甲的工作效率为4522616151=++⨯,乙的工作效率为13522612151=++⨯, 丙的工作效率为13512611151=++⨯.乙丙三天干了151313511352=⨯⎪⎭⎫ ⎝⎛+,甲丙二天干了1351421351452=⨯⎪⎭⎫ ⎝⎛+. 整个工作剩下13567135********=---.由甲乙丙合干还要9471351135245213567=⎪⎭⎫ ⎝⎛++÷(天), 完成此项工作共需9417947235=+++(天),即3月18日完成.13. 1620134515232=⎪⎭⎫ ⎝⎛-⨯÷⎪⎭⎫ ⎝⎛-(分).14. 按甲、乙、丙、丁顺序各开一小时水池中进水60761514131=-+-.这样5个周期(即20小时)后,池中有水43560761=⨯+,再开甲管注满水池需时4331431=÷⎪⎭⎫ ⎝⎛-(小时),故一共要43204320=+(小时)开始溢出.五、分数应用题(1)年级 班 姓名 得分 一、填空题1.有一个分数,它的分母比分子多4.如果把分子、分母都加上9,得到的分数约分后是97,这个分数是 .2.甲、乙两数是自然数,如果甲数的65恰好是乙数的41.那么甲、乙两数之和的最小值是 .3.商店的书包降价41后,又提价51,最后的价格是8元1角一个,那么最初是元钱一个.4.小萍今年的年龄是妈妈的31,二年前母子年龄相差24岁,四年后小萍的年龄是 .5.甲、乙、丙三人共同加工一批零件.甲比乙多加工零件20个,丙加工零件是乙加工零件的54,甲加工零件是乙丙两人加工零件总数的65.甲、乙、丙各加工零件 个.6.六一班男生的一半和女生的41共16人,女生的一半和男生的41共14人,这个班男、女生各 人.7.在4点多钟时,时钟的时针和分针在一直线上且方向相反,这时是4点 分.8.甲、乙两人各有钱若干元,已知甲的钱数是乙的4倍,当甲花去31后,又花去余下的31,如果这时甲给乙7元钱,甲、乙两人的钱数正好相等.甲原来有_____元钱.9.A 、B 、C 三根木棒插在水池中,(如图)三根捧长度和是360厘米,A 棒有43露出水面外,B 棒有4露出水面外.C 棒有2露出水面外.水池有 厘米深.。
小学六年级数学奥数期末测试卷

小学六年级数学奥数期末测试卷姓名:________一、简便计算(24分)51115612126⨯+⨯15589797⨯+⨯0.9999 1.50.3333 5.5⨯+⨯34.80.755.24⨯+⨯111204510⎛⎫++⨯ ⎪⎝⎭199919891619198********⨯-⨯+2468100++++⋅⋅⋅+1111112612203042+++++二、(第1、2小题5分,其余6分)(1)修路队在一条公路上施工,第一天修了这条公路的14,第二天修了余下的12,已知这两天一共修了1400米,这条公路全长多少米?(2)某火车车速是120千米/小时,现在提速110,现在火车的速度是多少千米?(3)一项工程,甲单独做10小时完成,乙单独做12小时完成,甲、乙合做,几小时完成?(4)一项工程,甲、乙两人合作36天完成,乙丙两人合作45天完成,甲、丙两人合作60天完成,甲、乙、丙单独做各需多少天完成?(5)水池上装有三个水管,单开甲管5小时注满水池,单开乙管8小时注满水池,单开丙管12小时放完一池水,三管齐开需几小时注满水池?(6)有一艘船行驶于90千米的河中,逆行需要10小时,顺行需要6小时,求划速和水速分别是多少?(7)一艘轮船同样的速度往返于甲、乙两个港口,它顺流而下行了6小时,逆流而上行12小时,如果水流速度是每小时4千米,求甲、乙两个港口之间的距离(列方程解答)(8)260克盐水中盐与水的比是5:8,盐有多少克?水有多少克?(9)哥哥和弟弟在长400米的跑道上跑步,他俩同时从同一地点出发,如果背向而行,5分钟相遇,如果同向而行,哥哥10分钟可以追上弟弟,哥哥和弟弟的速度分别是多少米?(10)甲、乙两车分别从A、B两地出发,相向而行,甲、乙两车的速度比4:3,相遇后,甲的速度减少20%,乙速度增加20%,这样,当甲到达B地时,乙离A地还有15千米,求A、B两地相距多少千米?(11)甲班50人,乙班有45人,从甲班调几人到乙班才能使甲乙两班人数比是2:3?(12)甲、乙两个仓库共存粮540吨,已知甲仓库存粮的14等于乙仓库存粮的15,甲、乙两个仓库各存粮多少吨?(13)某商品原价3600元,先降价12%,再提价12%,现价多少元?甲是乙、丙、丁之和的12,乙是甲、丙、丁之和的13,丙是甲、乙、丁之和的14,已知丁是390,求甲、乙、丙、丁四个数之和?(10分)。
六年级奥数题及答案1

六年级奥数题及答案11、如图,长方形ABCD中,E为的AD中点,AF与BE、BD分别交于G、H,OE垂直AD于E,交AF于O,已知AH=5cm,HF=3cm,求AG.2阴影面积:(高等难度)如右图,在以AB为直径的半圆上取一点C,分别以AC和BC为直径在△ABC外作半圆AEC和BFC.当C点在什么位置时,图中两个弯月型(阴影部分)AEC和BFC的面积和最大。
3、巧克力豆:(高等难度)甲、乙、丙三人各有巧克力豆若干粒,要求互相赠送.先由甲给乙、丙,甲给乙、丙的豆数依次等于乙、丙原来各人所有豆数.依同办法,再由乙给甲、丙,所给豆数依次等于甲、丙各人现有的豆数.最后由丙给甲、乙,所给的豆数依次等于甲、乙各人现有的豆数.互赠后每人恰好各有豆32粒,问原来三人各有豆多少粒?4、得奖人数:(高等难度)六年级举行一次数学竞赛,共有若干名同学得奖,其中得一等奖的同学比余下的得奖人数的五分之一少三名,得二等奖的占领奖人数的三分之一,得三等奖的人数比二等奖的人数同学多21名,问得奖人数是多少?粮食问题:(高等难度)5、甲仓有粮80吨,乙仓有粮120吨,如果把乙仓的一部分粮调入甲仓,使乙仓存粮是甲仓的60%,需要从乙仓调入甲仓多少吨粮食?6、分苹果:(高等难度)有一堆苹果平均分给幼儿园大、小班小朋友,每人可得6个,如果只分给大班每人可得10个,问只分给小班时,每人可得几个?、7、巧算:(中等难度)计算:8、四位数:(中等难度)某个四位数有如下特点:①这个数加1之后是15的倍数;②这个数减去3是38的倍数;③把这个数各数位上的数左右倒过来所得的数与原数之和能被10整除,求这个四位数.9跑步狗跑5步的时间马跑3步,马跑4步的距离狗跑7步,现在狗已跑出30米,马开始追它。
问:狗再跑多远,马可以追上它?、10排队有五对夫妇围成一圈,使每一对夫妇的夫妻二人动相邻的排法有()、11路程A,B,C三地的距离(单位:千米)如左下图所示。
六年级奥数题1

六年级奥数题一.填空题(每道3分)1、师徒俩人加工同样多的零件。
当师傅完成了1/2时,徒弟完成了120个。
当师傅完成了任务时,徒弟完成了4/5这批零件共有个。
2、鸡与兔共100只,鸡的腿数比兔的腿数少28条,问鸡与兔各有只。
3、一船以同样速度往返于两地之间,它顺流需要6小时;逆流8小时。
如果水流速度是每小时2千米,则两地间的距离是千米。
4、一个两位数,在它的前面写上3,所组成的三位数比原两位数的7倍多24,则原来的两位数为。
5、如果现在是上午的10点21分,那么在经过28799...99(一共有20个9)分钟之后的时间将是点分。
6、有五对夫妇围成一圈,使每一对夫妇的夫妻二人动相邻的排法有种。
7、有100种赤贫.其中含钙的有68种,含铁的有43种,那么,同时含钙和铁的食品种类的最大值和最小值分别是、。
8、一只布袋中装有大小相同但颜色不同的手套,颜色有黑、红、蓝、黄四种,问最少要摸出只手套才能保证有3副同色的。
9、狗跑5步的时间马跑3步,马跑4步的距离狗跑7步,现在狗已跑出30米,马开始追它。
那么狗再跑米,马可以追上它。
10、慢车车长125米,车速每秒行17米,快车车长140米,车速每秒行22米,慢车在前面行驶,快车从后面追上来,那么,快车从追上慢车的车尾到完全超过慢车需要秒。
二、简答题(每道7分)1.甲乙两个水管单独开,注满一池水,分别需要20小时,16小时.丙水管单独开,排一池水要10小时,若水池没水,同时打开甲乙两水管,5小时后,再打开排水管丙,问水池注满还是要多少小时?2、有一个四位数,个位数字与百位数字的和是12,十位数字与千位数字的和是9,如果个位数字与百位数字互换,千位数字与十位数字互换,新数就比原数增加2376,求原数.3、某盒子内装50只球,其中10只是红色,10只是绿色,10只是黄色,10只是蓝色,其余是白球和黑球,为了确保取出的球中至少包含有7只同色的球,问:最少必须从袋中取出多少只球?4、把1至2005这2005个自然数依次写下来得到一个多位数123456789.....2005,这个多位数除以9余数是多少?5、小华从甲地到乙地,3分之1骑车,3分之2乘车;从乙地返回甲地,5分之3骑车,5分之2乘车,结果慢了半小时.已知,骑车每小时12千米,乘车每小时30千米,问:甲乙两地相距多少千米?6、甲乙两人在河边钓鱼,甲钓了三条,乙钓了两条,正准备吃,有一个人请求跟他们一起吃,于是三人将五条鱼平分了,为了表示感谢,过路人留下10元,甲、乙怎么分?7、秦奋和妈妈的年龄加在一起是40岁,妈妈的年龄是秦奋年龄的4倍,问秦奋和妈妈各是多少岁?8、用白铁皮做罐头盒,每张铁皮可制盒身16个,或制盒底43个,一个盒身和两个盒底配成一个罐头盒,现有150张铁皮,用多少张制盒身,多少张制盒底,才能使盒身与盒底正好配套?9、甲盒中放有180个白色围棋子和181个黑色围棋子,乙盒中放有181个白色围棋子,李平每次任意从甲盒中摸出两个棋子,如果两个棋子同色,他就从乙盒中拿出一个白子放入甲盒;如果两个棋子不同色,他就把黑子放回甲盒。
小学六年级奥数题(1)

A (1)4.互质的两个合数。
它们的最小公倍数是702,这两个数是( , )。
A (1) 7.若(1525-口)×15+44=80,口中应是( )A (1) 10.小明前5次考试的平均成绩为90分,他暗下决心,争取尽快将平均分提高到94分以上,若他每次考试都得100分,那么他至少还要考( )次A (2)2.5、已知A ×150%=B ÷112==C ÷13,那么A 、B 、C 三个数从大到小的排列顺序是( )A 、A>B>CB 、B>A>C C 、C>B>AD 、A>C>BA (2)3.如果数a 除以数b,商是8,那么( )。
A 、a 一定能被b 整除B 、a 能被b 除尽C 、a 一定不能被b 整除D 、a 一定是b 的倍数A (2)1.甲乙两辆汽车同时从两地相向而行,甲车每小时行45千米,乙车每小时行42千米。
两车在距离中点12千米处相遇。
两车同时开出后经过多少小时相遇A (2)2.在一次数学竞赛中,有5位同学成绩分别为98分,86分,78分,89分,94分。
小明的成绩比小明在内的这6位同学的平均成绩比要高7.5分,小明的数学竞赛成绩是多少分A (2)3.一批学生,女生走了15名,这时的男生与女生的人数的比是2:1,此后,男生走了45名,余下的男生与女生的比是1:5,女生原来共有多少名A (3)计算: 1245÷45 –[667+178×(2720−214)] A (3)24.下列判断中正确的有( )个A 、0个B 、1个C 、2个D 、3个①在0.1和0.01之间的小数有9个。
② 三个连续自然数的和必定是3的倍数。
③两个面积相等的三角形,一定能拼成一个平行四边形。
④半圆的周长不等于圆周长的一半。
⑤两个小数,位数多的那个数一定较大。
A (4)4.甲乙两个两位数,甲数是乙数的75%,它们的最小公倍数是48。
【经典】小学奥数-六年级-奥数题及答案一
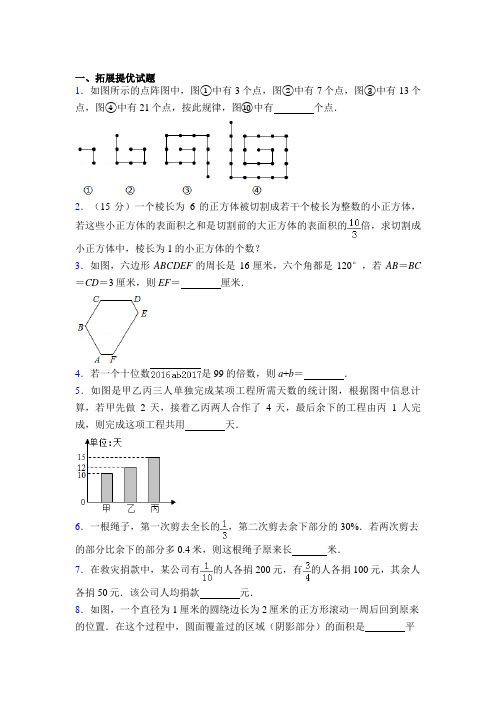
一、拓展提优试题1.如图所示的点阵图中,图①中有3个点,图②中有7个点,图③中有13个点,图④中有21个点,按此规律,图⑩中有个点.2.(15分)一个棱长为6的正方体被切割成若干个棱长为整数的小正方体,若这些小正方体的表面积之和是切割前的大正方体的表面积的倍,求切割成小正方体中,棱长为1的小正方体的个数?3.如图,六边形ABCDEF的周长是16厘米,六个角都是120°,若AB=BC =CD=3厘米,则EF=厘米.4.若一个十位数是99的倍数,则a+b=.5.如图是甲乙丙三人单独完成某项工程所需天数的统计图,根据图中信息计算,若甲先做2天,接着乙丙两人合作了4天,最后余下的工程由丙1人完成,则完成这项工程共用天.6.一根绳子,第一次剪去全长的,第二次剪去余下部分的30%.若两次剪去的部分比余下的部分多0.4米,则这根绳子原来长米.7.在救灾捐款中,某公司有的人各捐200元,有的人各捐100元,其余人各捐50元.该公司人均捐款元.8.如图,一个直径为1厘米的圆绕边长为2厘米的正方形滚动一周后回到原来的位置.在这个过程中,圆面覆盖过的区域(阴影部分)的面积是平方厘米.(π取3)9.若将算式9×8×7×6×5×4×3×2×1中的一些“×”改成“÷”使得最后的计算结果还是自然数,记为N,则N最小是.10.一次智力测试由5道判断对错的题目组成,答对一道得20分,答错或不答得0分.小花在答题时每道题都是随意答“对”或“错”,那么她得60分或60分以上的概率是%.11.快车和慢车同时从甲、乙两地相对开出,快车每小时行33千米,相遇行了全程的,已知慢车行完全程需要8小时,则甲、乙两地相距千米.12.等腰△ABC中,有两个内角的度数比是1:2,则△ABC的内角中,角度最大可以是度.13.已知x是最简真分数,若它的分子加a,化简得;若它的分母加a,化简得,则x=.14.小丽做一份希望杯练习题,第一小时做完了全部的,第二小时做完了余下的,第三小时做完了余下的,这时,余下24道题没有做,则这份练习题共有道.15.将浓度为40%的100克糖水倒入浓度为20%的a克糖水中,得到浓度为25%的糖水,则a=.16.请你想好一个数,将它加上5,其结果乘以2,再减去4,得到的差除以2,再减去你最初想好的那个数,最后的计算结果是.17.2015减去它的,再减去余下的,再减去余下的,…,最后一次减去余下的,最后得到的数是.18.已知两位数与的比是5:6,则=.19.如图,向装有水的圆柱形容器中放入三个半径都是1分米的小球,此时水面没过小球,且水面上升到容器高度的处,则圆柱形容器最多可以装水188.4立方分米.20.如图,一个长方形的长和宽的比是5:3.如果长方形的长减少5厘米,宽增加3厘米,那么这个长方形边长一个正方形.原长方形的面积是平方厘米.21.一个两位数除以一位数,所得的商若是最小的两位数,那么被除数最大是.22.定义新运算“*”:a*b=例如3.5*2=3.5,1*1.2=1.2,7*7=1,则=.23.用底面内半径和高分别是12cm,20cm的空心圆锥和空心圆柱各一个组成如图所示竖放的容器,在这个容器内注入一些细沙,能填满圆锥,还能填部分圆柱,经测量,圆柱部分的沙子高5cm,若将这个容器倒立,则沙子的高度是cm.24.从12点开始,经过分钟,时针与分针第一次成90°角;12点之后,时针与分针第二次成90°角的时刻是.25.有一个温泉游泳池,池底有泉水不断涌出,要想抽干满池的水,10台抽水机需工作8小时,9台抽水机需工作9小时,为了保证游泳池水位不变(池水既不减少,也不增多),则向外抽水的抽水机需台.26.若一个长方体,长是宽的2倍,宽是高的2倍,所有棱长之和是56,则此长方体的体积是.27.图中阴影部分的两段圆弧所对应的圆心分别为点A和点C,AE=4m,点B 是AE的中点,那么阴影部分的周长是m,面积是m2(圆周率π取3).28.某次数学竞赛,甲、乙、丙3人中只有一人获奖,甲说:“我获奖了.”乙说:“我没获奖.”丙说:“甲没有获奖.”他们的话中只有一句是真话,则获奖的是.29.如图,设定E、F分别是△ABC的边AB、AC上的点,线段CE,BF交于点D,若△CDF,△BCD,△BDE的面积分别为3,7,7,则四边形AEDF的面积是.30.12013+22013+32013+42013+52013除以5,余数是.(a2013表示2013个a相乘)31.如图是根据鸡蛋的三个组成部分的质量绘制的扇形统计图,由图可知,蛋壳重量占鸡蛋重量的%,一枚重60克的鸡蛋中,最接近32克的组成部分是.32.如图1是一个正方体的展开图,图2的四个正方体中只有一个是和这个展开图对应的,这个正方体是.(填序号)33.图中的三角形的个数是.34.从1,2,3,4,…,15,16这十六个自然数中,任取出n个数,其中必有这样的两个数:一个是另一个的3倍,则n最小是.35.某工程队修建一条铁路隧道,当完成任务的时,工程队采用新设备,使修建速度提高了20%,同时为了保养新设备,每天工作时间缩短为原来的,结果,前后共用185天完工,由以上条件可推知,如果不采用新设备,完工共需天.36.对任意两个数x,y规定运算“*”的含义是:x*y=(其中m是一个确定的数),如果1*2=1,那么m=,3*12=.37.如图所示的“鱼”形图案中共有个三角形.38.李华在买某一商品的时候,将单价中的某一数字“7”错看成了“1”,准备付款189元,实际应付147元,已知商品的单价及购买的数量都是整数,则这种商品的实际单价是元,李华共买了件.39.如图,已知AB=40cm,图中的曲线是由半径不同的三种半圆弧平滑连接而成,那么阴影部分的面积是cm2.(π取3.14)40.如图,三个同心圆分别被直径AB,CD,EF,GH八等分,那么,图中阴影部分面积与非阴影部分面积之比是.【参考答案】一、拓展提优试题1.解:根据分析得出的规律我们可以得到:图⑩中有3+(4+6+8+10+12+14+16+18+20)=3+(4+20)×9÷2=111;故答案为:111.2.解:大正方体表面积:6×6×6=216,体积是:6×6×6=216,切割后小正方体表面积总和是:216×=720,假设棱长为5的小正方体有1个,那么剩下的小正方体的棱长只能是1,个数是:(63﹣53)÷13=91(个),这时表面积总和是:52×6+12×6×91=696≠720,所以不可能有棱长为5的小正方体.(1)同理,棱长为4的小正方体最多为1个,此时,不可能有棱长为3的小正方体,剩下的只能是切割成棱长为2的小正方体或棱长为1的小正方体,设棱长为2的小正方体有a个,棱长为1的小正方体有b个,则解得:(2)棱长为3的小正方体要少于(6÷3)×(6÷3)×(6÷3)=8个,设棱长为2的小正方体有a个,棱长为1的小正方体有b个,棱长为3的小正方体有c个,化简:由上式可得:b=9c+24,a=,当c=0时,b24=,a=24,当c=1时,b=33,a=19.5,(不合题意舍去)当c=2时,b=42,a=15,当c=3时,b=51,a=10.5,(不合题意舍去)当c=4时,b=60,a=6,当c=5时,b=69,a=28.5,(不合题意舍去)当c=6时,b=78,a=﹣3,(不合题意舍去)当c=7时,a=负数,(不合题意舍去)所以,棱长为1的小正方体的个数只能是:56或24或42或60个.答:棱长为1的小正方体的个数只能是:56或24或42或60个.3.解:如图延长并反向延长AF,BC,DE,分别相交与点G、H、N,因六边形ABCDEF的每个角是120°所以∠G=∠H=∠N=60°所以△GHN,△GAB,△HCD,△EFN都是等边三角形AB=BC=CD=3厘米,△GHN边长是3+3+3=9(厘米)AN=9﹣3=6(厘米)AN=AF+EFDE=六边形ABCDEF的周长﹣AB﹣BC﹣CD﹣(AF+EF)=16﹣3﹣3﹣3﹣6=1(厘米)EF=EN=9﹣3﹣1=5(厘米)答:EF=5厘米.故答案为:5.4.解:根据99的整除特性可知:20+16++20+17=99..a+b=8.5.解:依题意可知:甲乙丙的工作效率分别为:,,;甲乙工作总量为:×2+×4=;丙的工作天数为:(1﹣)=3(天);共工作2+4+3=9故答案为:96.解:第二次剪求的占全长的:(1)×30%==,0.4÷[(1)]=0.4÷[]==0.4×15=6(米);答:这根绳子原来长6米.故答案为:6.7.解:捐50元人数的分率为:1﹣=,(200×+100×+50×)÷1=(20+75+7.5)÷1=102.5(元)答:该公司人均捐款102.5元.故答案为:102.5.8.解:2×1×4+3×12=8+3=11(平方厘米)答:阴影部分的面积是11平方厘米.9.解:根据分析,先分解质因数9=3×3,8=2×2×2,6=2×3,故有:9×8×7×6×5×4×3×2×1=(3×3)×(2×2×2)×7×(3×2)×5×(2×2)×3×2×1,所以可变换为:9×8×7÷6×5÷4÷3×2×1=70,此时N最小,为70,故答案是:70.10.解:有答对一题,两题,三题,四题,五题,全错六种情况,答对三题是60分,四题是80分,五题是100分,她得60分或60分以上的概率是:=50%.答:她得60分或60分以上的概率是50%.故答案为:50%.11.解:1﹣=×8=(小时)×33=(千米)÷=198(千米)答:甲、乙两地相距198千米.故答案为:198.12.解:180°×=180°×=90°答:角度最大可以是 90度.故答案为:90.13.解:设原来的分数x是,则:=则:b=3(c+a)=3c+3a①=则:4c=a+b②①代入②可得:4c=a+3c+3a4c=4a+3c则:c=4a③③代入①可得:b=3c+3a=3×4a+3a=15a所以==即x=.故答案为:.14.解:24÷(1﹣)÷(1﹣)÷(1﹣)=24÷=60(道)答:这份练习题共有 60道.故答案为:60.15.解:依题意可知:根据浓度是十字交叉法可知:浓度差的比等于溶液质量比即1:3=100:a,所以a=300克故答案为:30016.解:设这个数是a,[(a+5)×2﹣4]÷2﹣a=[2a+6]÷2﹣a=a+3﹣a=3,故答案为:3.17.解:2015×(1﹣)×(1﹣)×(1﹣)×…×(1﹣)=2015××××…×=1故答案为:1.18.解:因为(10a+b):(10b+a)=5:6,所以(10a+b)×6=(10b+a)×560a+6b=50b+5a所以55a=44b则a=b,所以b只能为5,则a=4.所以=45.故答案为:45.19.解:×3.14×13×3÷(﹣)=12.56×15=188.4(立方分米)答:圆柱形容器最多可以装水188.4立方分米.故答案为:188.4.20.解:先求出一份的长:(5+3)÷(5﹣3)=8÷2=4(厘米)长是:4×5=20(厘米)宽是:4×3=12(厘米)原来的面积是:20×12=240(平方厘米);答:原来长方形的面积是240平方厘米.故答案为:240.21.解:商是10,除数最大是9,余数最大是8,9×10+8=98;被除数最大是98.故答案为:98.22.解:根据分析可得,,=,=2;故答案为:2.23.解:据分析可知,沙子的高度为:5+20÷3=11(厘米);答:沙子的高度为11厘米.故答案为:11.24.解:分针每分钟走的度数是:360÷60=6(度),时针每分钟走的度数是:6×5÷60=0.5(度),第一成直角用的时间是:90÷(6﹣0.5),=90÷5.5,=16(分钟),第二次成直角用的时间是:270÷(6﹣0.5),=270÷5.5,=49(分钟).这时的时刻是:12时+49分=12时49分.故答案为:16,12时49分.25.解:设1台抽水机1小时抽1份水,每小时新增水:9×9﹣10×8=1;答:向外抽水的抽水机需1台.26.解:长方体的高是:56÷4÷(1+2+4),=14÷7,=2,宽是:2×2=4,长是:4×2=8,体积是:8×4×2=64,答:这个长方体的体积是64.故答案为:64.27.解:阴影部分的周长:4+3×4×2÷4+3×2×2÷4,=4+6+3,=13(米);阴影部分的面积:3×42÷4+3×22÷4﹣2×4,=12+3﹣8,=7(平方米);答:阴影部分的周长是13米,面积是7平方米.故答案为:13、7.28.解:由分析可知:假设甲说的是真话,那乙说的也是真话,所以不成立;假设乙说的是真话,那甲说的也是真话,也不成立;所以只能是丙说的是真话,乙说的是假话,即:乙得奖了;故答案为:乙.29.解:连接AD,因△CDF和△BCD的高相等,所以FD:DB=3:7,所△AFD和△ABD的面积比也是3:7,即可把△AFD的面积看作是3份,△ABD的面积看作是7份,S△BCD=7,S△BDE=7所以CD=DE,S△ACD=S△ADE,S△ACD+S△BDE=S△ABD,S△ACD+S△BDE=7份,S△AFD+S△CDF+S△BDE=7份,3份+3+7=7份,则1份=2.5,S四边形AEDF=10份﹣7=10×2.5﹣7=25﹣7=18答:四边形AEDF的面积是18.故答案为:18.30.解:多个2相乘结果个位数字有一个规律:2、4、8、6每4个2相乘一个循环,多个3相乘结果个位数字有一个规律:3、9、7、1每4个3相乘一个循环,2013÷4=503…1,所以2013个2相乘后个位数字是2,2013个3相乘后个位数字是3,2013个4相乘后个位数字是4,1的任何次方都是1,5的任何次方的个位数字都是5,1+2+3+4+5=15所以12013+22013+32013+42013+52013的个位数字是5,所以除以5的余数是0;故答案为:0.31.解:(1)1﹣32%﹣53%,=1﹣85%,=15%;答:蛋壳重量占鸡蛋重量的15%.(2)蛋黄重量:60×32%=19.2(克),蛋白重量:60×53%=31.8(克),蛋壳重量:60×15%=9(克),所以最接近32克的组成部分是蛋白.答:最接近32克的组成部分是蛋白.故答案为:15,蛋白.32.解:如图.图1是一个正方体的展开图,图2的四个正方体中只有一个是和这个展开图对应的,这个正方体是图2①;故答案为:①33.解:根据题干分析可得:10+10+10+5=35(个),答:一共有35个三角形.故答案为:35.34.解:将有3倍关系的放入一组为:(1,3,9)、(2,6)、(4,12)、(5,15)共有4组,其余7个数每一个数为一组,即将这16个数可分为11组,.则第一组最多取2个即1和9,其余组最多取一个,即最多能取12个数保证没有一个数是另一个的三倍,此时只要再任取一个,即取12+1=13个数必有一个数是另一个数的3倍.所以n最小是13.35.解:设计划用x天完成任务,那么原计划每天的工作效率是,提高后每天的工作效率是×(1+20%)=×=,前面完成工程的所用时间是天,提高工作效率后所用的实际是(185﹣)×天,所以,+(185﹣)××=1,+(185﹣)××﹣=1﹣,(185﹣)××=,(185﹣)×÷=÷,185﹣+=x+,x÷=185÷,x=180,答:工程队原计划180天完成任务.故答案为:180.36.解:①因为:x*y=(其中m是一个确定的数)且1*2=1所以:=18=m+6m+6=8m+6﹣6=8m=2②3*12===故答案为:2,.37.解:由一个三角形组成:14个;由两个三角形组成:8个;由三个三角形组成:8个;由四个三角形组成:4个;由六个三角形组成:1个;总共:14+8+8+4+1=35个.故共有35个三角形.故答案为:35.38.解:189=3×3×3×7=27×7147=3×7×7=21×7正好是27×7=189中把27看成21×7=147所以这种商品的实际单价是21元,卖了7件.故答案为:21,7.39.解:40÷2=20(厘米)20÷2=10(厘米)3.14×202﹣3.14×102÷2×4=1256﹣628=628(平方厘米)答:阴影部分的面积是628平方厘米.故答案为:628.40.解:由图可知,阴影部分的面积是图中最大圆面积的,非阴影部分的面积是图中最大圆面积的,所以图中阴影部分面积与非阴影部分面积之比是::=1:3;答:图中阴影部分面积与非阴影部分面积之比是1:3.故答案为:1:3.。
小学六年级奥数题100道及答案

小学六年级奥数题100道及答案Part 1 warm up1.甲、乙、丙三人行路,甲每分钟走60米,乙每分钟走米,丙每分钟走75米,甲乙从东镇去西镇,丙从西镇去东镇,三人同时出发,丙与乙相遇后,又经过2分钟与甲相遇,求东西两镇间的路程有多少米解:那2分钟是甲和丙相遇,所以距离是(60+75) X2=270米,这距离是乙丙相遇时间里甲乙的路程差所以乙丙相遇时间=270+ () =36分钟,所以路程=36X (60+75) =4860米。
2.小明每天早晨6: 50从家出发,7: 20到校,老师要求他明天提早6分钟到校。
如果小明明天早晨还是6: 50从家出发,那么,每分钟必须比往常多走25米才能按老师的要求准时到校。
问:小明家到学校多远(第六届《小数报》数学竞赛初赛题第1题)解:原来花时间是30分钟,后来提前6分钟,就是路上要花时间为24分钟。
这时每分钟必须多走25米,所以总共多走了 24X25=600米,而这和30分钟时间里,后6分钟走的路程是一样的,所以原来每分钟走600 + 6=100米。
总路程就是二100X30=3000米。
3.小张与小王分别从甲、乙两村同时出发,在两村之间往返行走(到达另一村后就马上返回),他们在离甲村千米处第一次相遇,在离乙村2千米处第二次相遇.问他们两人第四次相遇的地点离乙村多远(相遇指迎面相遇)第二次相遇两人已共同走了甲、乙两村距离的3倍・,因此张走了X3=(千米).从图上可看出,第二次相遇处离乙村2千米.因此,甲、乙两村距离是=(千米).每次要再相遇,两人就要共同再走甲、乙两村距离2倍的路程.第四次相遇时,两人已共同走了两村距离(3+2+2)倍的行程.其中张走了X7=(千米),二十+ (千米).就知道第四次相遇处,离乙村(千米).答:第四次相遇地点离乙村1千米.4.哥哥有12枚5分硬币,妹妹有10枚2分硬币,哥哥给妹妹几枚5分硬币,两人的钱数相等解答:5X12=60(分)2X10=20(分)(60-20)+2=20(分)20 + 5=4(枚)I5.阿香去吃午饭,发现附近的中餐厅有9个,西餐厅有3个,日式餐厅有2个,他准备找一家餐厅吃饭,一共有多少种不同的选择解答:9+3+2=14 (种)6.用400个棋子摆放了 5层空心方阵,最内层每边有几个棋子解答:400+5=80(个)80-8-8=64(个)64+4+1=17(个)7.用棋子摆方阵恰好摆成每边为20的实心方阵,若改为4层空心方阵,最外层每边应放几枚解答:20X20=400(个)400+8X(1+2+3) =448(个)448 + 4=112(个)112・4+1=29(个)8. 一把钥匙只能开一把锁,现有10把钥匙和10把锁,最少要试验多少次就一定能使全部的钥匙和锁相匹配解答:从最不利的情形考虑。
小学六年级数学下册奥数必考题目及参考答案,期末必看

1、某市举行小学数学竞赛,结果不低于80分的人数比80分以下的人数的4倍还多2人,及格的人数比不低于80分的人数多22人,恰是不及格人数的6倍,求参赛的总人数?解:设不低于80分的为A人,则80分以下的人数是(A-2)/4,及格的就是A+22,不及格的就是A+(A-2)/4-(A+22)=(A-90)/4,而6*(A-90)/4=A+22,则A=314,80分以下的人数是(A-2)/4,也即是78,参赛的总人数314+78=3922、电影票原价每张若干元,现在每张降低3元出售,观众增加一半,收入增加五分之一,一张电影票原价多少元?解:设一张电影票价x元(x-3)×(1+1/2)=(1+1/5)x(1+1/5)x这一步是什么意思,为什么这么做(x-3){现在电影票的单价}×(1+1/2){假如原来观众总数为整体1,则现在的观众人数为(1+2/1)}左边算式求出了总收入(1+1/5)x{其实这个算式应该是:1x*(1+5/1)把原观众人数看成整体1,则原来应收入1x元,而现在增加了原来的五分之一,就应该再*(1+5/1),减缩后得到(1+1/5x)}如此计算后得到总收入,使方程左右相等3、甲乙在银行存款共9600元,如果两人分别取出自己存款的40%,再从甲存款中提120元给乙。
这时两人钱相等,求乙的存款答案:取40%后,存款有9600×(1-40%)=5760(元)这时,乙有:5760÷2+120=3000(元)乙原来有:3000÷(1-40%)=5000(元)4、由奶糖和巧克力糖混合成一堆糖,如果增加10颗奶糖后,巧克力糖占总数的60%。
再增加30颗巧克力糖后,巧克力糖占总数的75%,那么原混合糖中有奶糖多少颗?巧克力糖多少颗?答案:加10颗奶糖,巧克力占总数的60%,说明此时奶糖占40%,巧克力是奶糖的60/40=1.5倍再增加30颗巧克力,巧克力占75%,奶糖占25%,巧克力是奶糖的3倍增加了3-1.5=1.5倍,说明30颗占1.5倍奶糖=30/1.5=20颗巧克力=1.5*20=30颗奶糖=20-10=10颗5、小明和小亮各有一些玻璃球,小明说:“你有球的个数比我少1/4!”小亮说:“你要是能给我你的1/6,我就比你多2个了。
小学六年级奥数训练(阶段一)及其答案

小学六年级奥数测试一一、计算题:(每题4分,共20分)1、8-(7.14⨯31-292÷2.5)+∙10. 2、∙∙∙++30.20.10.3、541431321211⨯+⨯+⨯+⨯ 4、4213012011216121+++++5、 =⎪⎭⎫ ⎝⎛++⨯⎪⎭⎫ ⎝⎛++++-⎪⎭⎫ ⎝⎛+++⨯⎪⎭⎫ ⎝⎛+++513121715131211715131215131211二、选择题:(每题4分,共16分) 1、如果12+[++⨯21(75.052□983.0]3)=÷⨯,方框代表的数是( ). A 、9 B 、8 C 、102、规定a △b=1+a b++121,则1△2等于( )A 、1B 、2C 、33、修路队修一条路,第一天修了全长的31,第二天修了余下的31,还剩160米没有修,这条路全长( )米.A 、360B 、288C 、4804、2013201320132013201354321++++除以5,余数是( )。
(其中,2013a 表示2013个a 相乘)A 、3B 、2C 、0三、填空题:(每题5分,共25分)1、计算:777777771234567654321⨯++++++++++++= . 2、将9017化成小数后,第2015位是____ 3、观察下面的数列,找规律并填空:3,8,15,24,35,48, ,80, ,120.4、设a *b=3a -b ×21,求(25*12)*(10*5)5、同学们大扫除擦玻璃,如果每人擦6块,则有10块没人擦;如果每人擦7块,则余1人没玻璃可擦。
则有____人擦玻璃,有玻璃_____块四、解答题:(1-2题每题6分,3,4,5题每题9分,共39分) 1、如果12+22+32+…+n 2=6)1)(12(n n n ++,那么12+22+…+202得多少?2、如果1*5111111111111111=++++,2*42222222222=+++,3*3333333=++,4*2444=+,那么求7*4以及210*2的值。
小学六年级奥数题集锦(1)

小学六年级奥数题集锦1、甲乙两车同时从AB两地相对开出。
甲行驶了全程的5/11,如果甲每小时行驶4.5千米,乙行了5小时。
求AB两地相距多少千米2、一辆客车和一辆货车分别从甲乙两地同时相向开出。
货车的速度是客车的五分之四,货车行了全程的四分之一后,再行28千米与客车相遇。
甲乙两地相距多少千米?3、甲乙两人绕城而行,甲每小时行8千米,乙每小时行6千米。
现在两人同时从同一地点相背出发,乙遇到甲后,再行4小时回到原出发点。
求乙绕城一周所需要的时间?4、甲乙两人同时从A地步行走向B地,当甲走了全程的1\4时,乙离B地还有640米,当甲走余下的5\6时,乙走完全程的7\10,求AB两地距离是多少米?5、甲,乙两辆汽车同时从A,B两地相对开出,相向而行。
甲车每小时行75千米,乙车行完全程需7小时。
两车开出3小时后相距15千米,A,B两地相距多少千米?6、甲,已两人要走完这条路,甲要走30分,已要走20分.现两人同时出发相向而走.走3分后,甲发现有东西没拿,拿东西耽误3分,甲再走几分钟跟已相遇7、甲,乙两辆汽车从A地出发,同向而行,甲每小时走36千米,乙每小时走48千米,若甲车比乙车早出发2小时,则乙车经过多少时间才追上甲车?8、甲乙两人分别从相距36千米的ab两地同时出发,相向而行,甲从a 地出发至1千米时,发现有物品落在a地,便立即返回,拿了物品又立即从a地向b地行进,这样甲、乙两人恰好在a,b两地的中点处相遇,又知甲每小时比乙多走0.5千米,求甲、乙两人的速度9、两列火车同时从相距400千米两地相向而行,客车每小时行60千米,货车小时行40千米,两列火车行驶几小时后,相遇有相距100千米?10、甲每小时行驶9千米,乙每小时行驶7千米。
两者在相距6千米的两地同时向背而行,几小时后相距150千米11、甲乙两车从相距600千米的两地同时相向而行已知甲车每小时行42千米,乙车每小时行58千米两车相遇时乙车行了多少千米?12、两车相向,6小时相遇,后经4小时,客车到达,货车还有188千米,问两地相距?13、甲乙两地相距600千米,客车和货车从两地相向而行,6小时相遇,已知货车的速度是客车的3分之2 ,求二车的速度?14、小兔和小猫分别从相距40千米的A、B两地同时相向而行,经过4小时候相距4千米,再经过多长时间相遇?15、甲、乙两车分别从a b两地开出甲车每小时行50千米乙车每小时行40千米甲车比乙车早1小时到两地相距多少?16、两辆车从甲乙两地同时相对开出,4时相遇。
小学六年级奥数试题(8篇)

小学六年级奥数试题(8篇)小学六年级奥数试题(8篇)在学习和工作的日常里,我们都经常看到试题的身影,试题可以帮助参考者清楚地认识自己的知识掌握程度。
你知道什么样的试题才算得上好试题吗?以下是小编整理的小学六年级奥数试题,仅供参考,欢迎大家阅读。
小学六年级奥数试题11、(鸡兔同笼问题)小丽买回0.8元一本和0.4元一本的练习本共50本,付出人民币32元。
0.8元一本的练习本有多少本?2、(年龄问题)5年前父亲的年龄是儿子的7倍。
15年后父亲的年龄是儿子的二倍,父亲和儿子今年各是多少岁?3、(盈亏问题)王老师发笔记本给学生们,每人6本则剩下41本,每人8本则差29本。
求有多少个学生?有多少个笔记本?4、(还原问题)便民水果店卖芒果,第一次卖掉总数的一半多2个,第二次卖掉剩下的一半多1个,第三次卖掉第二次卖后剩下的一半少1个,这时只剩下11个芒果。
求水果店里原来一共有多少个芒果?5、(置换问题)学校买回6张桌子和6把椅子共用去192元。
已知3张桌子的价钱和5把椅子的价钱相等,每张桌子和每把椅子各是多少元?6、(安排)烤面包的架子上一次最多只能烤两个面包,烤一个面包每面需要2分钟,那么烤三个面包最少需要多少分钟?7、(油和桶问题)一桶油连桶共重18千克,用去油的一半后,连桶还重9.75千克,原有油多少千克?桶重多少千克?8、(和倍)青青农场一共养鸡、鸭、鹅共12100只,鸭的只数是鸡的2倍,鹅的只数是鸭的4倍,问鸡、鸭、鹅各有多少只?9、(鸡兔同笼)实验小学举行数学竞赛,每做对一题得9分,做错一题倒扣3分,共有12道题,小旺得了84分,小旺做错了几道题?10、(相遇问题)甲、乙两人同时从相距20xx米的两地相向而行,甲每分钟行55米,乙每分钟行45米,如果一只狗与甲同时同向而行,每分钟行120米,遇到乙后,立即回头向甲跑去,遇到甲再向乙跑去。
这样不断来回,直到甲和乙相遇为止,狗共行了多少米?小学六年级奥数试题2标有A、B、C、D、E、F、G记号的七盏灯顺次排成一行,每盏灯安装着一个开关,现在A、C、D、G四盏灯亮着,其余三盏灯是灭的。
小学六年级奥数题100道及答案解析(完整版)

小学六年级奥数题100道及答案解析(完整版)1. 一种商品先提价10%,再降价10%,现价与原价相比()A. 提高了B. 降低了C. 不变D. 无法确定答案:B解析:假设原价为100 元,提价10%后价格为100×(1 + 10%) = 110 元,再降价10%,价格为110×(1 - 10%) = 99 元,所以现价比原价降低了。
2. 一个圆的半径扩大3 倍,它的面积扩大()倍。
A. 3B. 6C. 9D. 27答案:C解析:圆的面积= π×半径²,半径扩大3 倍,面积扩大3²= 9 倍。
3. 甲数的2/3 等于乙数的3/4,甲数()乙数。
A. 大于B. 小于C. 等于D. 无法比较答案:A解析:设甲数×2/3 = 乙数×3/4 = 1,可得甲数= 3/2,乙数= 4/3,3/2 > 4/3,所以甲数大于乙数。
4. 把20 克盐放入200 克水中,盐和盐水的比是()A. 1:10B. 1:11C. 10:1D. 11:1答案:B解析:盐20 克,盐水= 20 + 200 = 220 克,盐和盐水的比是20:220 = 1:115. 一个三角形三个内角的度数比是1:2:3,这个三角形是()A. 锐角三角形B. 直角三角形C. 钝角三角形D. 无法确定答案:B解析:三个内角分别为180×1/(1 + 2 + 3) = 30°,180×2/(1 + 2 + 3) = 60°,180×3/(1 + 2 + 3) = 90°,是直角三角形。
6. 要反映某地气温变化情况,应绘制()统计图。
A. 条形B. 折线C. 扇形D. 以上都可以答案:B解析:折线统计图能清晰反映数据的变化情况。
7. 一个圆柱和一个圆锥等底等高,它们的体积相差18 立方厘米,圆锥的体积是()立方厘米。
小学六年级 奥数题及答案100道

小学六年级奥数竞赛100道测试题!附答案解析1、有28位小朋友排成一行.从左边开始数第10位是学豆,从右边开始数他是第几位?2、纽约时间是香港时间减13小时.你与一位在纽约的朋友约定,纽约时间4月1日晚上8时与他通电话,那么在香港你应几月几日几时给他打电话?3、鸡与兔共100只,鸡的腿数比兔的腿数少28条,问鸡与兔各有几只?4、请找出下面哪个图形与其他图形不一样.5、四个房间,每个房间里不少于2人,任何三个房间里的人数不少8人,这四个房间至少有多少人?6、在1998的约数(或因数)中有两位数,其中最大的是哪个数?7、英文测验,小明前三次平均分是88分,要想平均分达到90分,他第四次最少要得几分?8、相传古时候一位老人留在人间很多宝盒,里面装着世界上最宝贵的财富,但是并不是拥有宝盒都可以得到这笔财富,在宝盒的上面设置了密码,只有写出密码的人才会真正拥有这笔财富,聪明的你你能找出密码吗?9、将0, 1, 2, 3, 4, 5, 6, 7, 8, 9这十个数字中,选出六个填在下面方框中,使算式成立,一个方框填一个数字,各个方框数字不相同.□+□□=□□□问算式中的三位数最大是什么数?10、有一个号码是六位数,前四位是2857,后两位记不清,即2857□□但是我记得,它能被11和13整除,请你算出后两位数.11、观察图形的变化,想一想,按图形的变化规律,在带“?”的空格处应画什么样的图形?12、一个三位数的各位数字之和是17.其中十位数字比个位数字大1.如果把这个三位数的百位数字与个位数字对调,得到一个新的三位数,则新的三位数比原三位数大198,求原数.13、一个两位数,在它的前面写上3,所组成的三位数比原两位数的7倍多24,求原来的两位数.14、幼儿园的老师把一些画片分给A, B, C三个班,每人都能分到6张.如果只分给B班,每人能得15张,如果只分给C班,每人能得14张,问只分给A班,每人能得几张?15、两人做一种游戏:轮流报数,报出的数只能是1, 2, 3, 4, 5, 6, 7, 8.把两人报出的数连加起来,谁报数后,加起来的数是123,谁就获胜,让你先报,就一定会赢,那么你第一个数报几?16、四个小动物排座位,一开始,小鼠坐在第1号位子上,小猴坐在第2号,小兔坐在第3号,小猫坐在第4号.以后它们不停地交换位子,第一次上下两排交换.第二次是在第一次交换后左右两列交换,第三次再上下两排交换,第四次再左右两列交换…这样一直换下去.问:第五次交换位子后,小兔坐在第几号位子上?17、狗跑5步的时间马跑3步,马跑4步的距离狗跑7步,现在狗已跑出30米,马开始追它。
六年级下册数学试题奥数阶段测试一全国通用

阶段测试(一)1.简算:(1)3.6×11.1+1.2×66.7(2)7.2×14.5+17×2.8计算:38252.14×7+0.65×-×14+×0.65137133.41.2×8.1+11×91+53.7×1.944.如何简易如何算.22(2)999×274+6274(1)2004-20032(3)9999+1999948贯通融会六年级(年“数学花园探秘”小高组复赛)5.2018计算:7×11×13+27×371000(年全国“数学花园探秘”比赛高年级组)6.20171)1)计算:(63-÷1-63(637.修路队俢一条公路,第一天修了这条公路的2,次日俢了余5下的1,已知这两天共俢米,这条公路全长是多少米?12038.某市有三个工厂,第一个工厂的人数占三个工厂总人数的20%,第二个工厂的人数是第三个工厂人数的2.已知第二3个工厂比第一个工厂多人,三个工厂一共有多少人?300阶段测试(一)49甲、乙两人共做了个部件,此中甲做的部件的5与乙做9.1848的部件的3共个.甲、乙两人各做了多少个部件?123410.比较222和22的大小. 1111111(秋新东方教育科技公司万人测)一件工作,甲独自完11.2017小时,乙独自达成要用小时,两人合作几小时后成要用64还剩下这项工作的1?3(“”)桌上有两堆棋子,第年数学花园探秘小高组复赛12.2018一堆棋子的枚数恰好是第二堆的一半,假如从第二堆中取走枚,那么第二堆棋子的枚数将变为第一堆的一半,那15?么两堆棋子共有多少枚50贯通融会六年级。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
六年级奥数期末测试题
姓名:
一、填空(每题4分,计20分)
1.设P 、q 是两个数,规定:P △q = 4×q +(P+ q )÷2。
求7△(6△4)=( )。
2.在()中填>、<、=。
8888988887( )203
201
3.把16拆成若干个自然数的和,要使乘积最大,应拆成( )。
4.在1---100的自然数中,不含数字0和7的数有( )个。
5. 有一个分数,如果分子加1,这个分数等于2
1
,如果分母加3,这个分数等于3
2
,这个分数是( )。
二、计算(每题5分,计30分) 150×149148+148×149
1
88888×77778+44444×44444
725+342×724 41.2×8.1+11×9.25+53.7×1.9 725×342+383
1×2×3+3×6×9+7×14×21 3.6×11.1+1.2×66.7 1×3×5+3×9×15+7×21×35
三、应用题(每题5分,计50分)
1、把一个正方体削成一个体积最大的圆柱,如果圆柱的侧面积是314cm 2,求正方体的表面积。
2、已知2001年的儿童节是星期五,求2014年的儿童节是星期几?
3、甲桶里的油是乙桶里的油的2倍多40千克,若从两桶里各倒出20千克油,则甲桶的油是乙桶的4倍,甲乙两桶原来各有多少油?
4.甲乙丙三个袋子里共有120个小球,从甲袋中拿出和乙袋同样多小球放入乙袋,再从乙袋中拿出和丙袋同样多的小球放入丙袋,最后从丙袋中拿出和甲袋同样多的小球放入甲袋,此时,三个袋子中的数量相等。
原来三个袋子中甲袋比丙袋多多少个小球?
5.一项工程,甲乙合做,18天可以完成;乙丙合做10天可以完成,甲丙合做15天可以完成。
甲乙丙独做,各需要多少天完成?
6、用浓度为40%和10%的盐水配制浓度为30%的盐水300克,则需要两种盐水各多少?
7、一只袋中有红黄黑三种大小相同、颜色不同的玻璃珠,问至少取出多少个珠子才能保证有两个同色的?
8、在1、2、3、4、5中,任取三个数字组成被3除余2的四位数,这样的四位数一个有多少个?
9、某班48人,从A、B、C、D、E中选一人任班长,A得了28票B、C得票相同,D 得票居第四位,E得票最少,只有3票。
C得了多少票?
10、有一艘船行驶在100千米的河中,逆行需要10小时,顺行需要5小时,求船速和水速?。
