《黄金分割》专题练习
人教版九年级下册数黄金分割同步练习

27.1.2 黄金分割基础训练知识点1 比例中项1.若x是2,18的比例中项,则x=___________.2.若线段a=6 cm,b=3 cm,且c是a,b的比例中项,则线段c的长度为( )A.3错误!未找到引用源。
cmB.±3错误!未找到引用源。
cmC.±18 cmD.18 cm3.如果a∶b=3∶2,且b是a,c的比例中项,那么b∶c等于( )A.4∶3B.3∶2C.2∶3D.3∶44.如图,有三个直角三角形,其中OA=AB=BC=CD=1,则线段OA,OD的比例中项线段的长度为( )A.错误!未找到引用源。
B.错误!未找到引用源。
C.±错误!未找到引用源。
D.错误!未找到引用源。
知识点2 黄金分割5.如果点C是线段AB的黄金分割点(AC>BC),则下列比例式正确的是( )A.AB∶AC=AC∶BCB.AB∶BC=BC∶ACC.AC∶BC=BC∶ABD.AC∶AB=AB∶BC6.若点C为线段AB的黄金分割点,且AC>BC,则①AB=错误!未找到引用源。
AC;②AC=错误!未找到引用源。
AB;③AB∶AC=AC∶CB;④AC≈0.618AB.其中正确的有( )A.1个B.2个C.3个D.4个7.从美学角度来说,人的上身长与下身长之比为黄金比例,可以给人一种协调的美感.某女老师上身长约61.80 cm,下身长约93.00 cm,她要穿约___________cm的高跟鞋才能达到黄金比的美感效果(精确到1 cm).提升训练考查角度1 利用比例性质求解比例中项问题8.已知线段a,b,c满足错误!未找到引用源。
=错误!未找到引用源。
=错误!未找到引用源。
,且a+2b+c=26.(1)求a,b,c的值;(2)若线段x是线段a,b的比例中项,求x.考查角度2 利用黄金分割的定义找黄金分割点(计算法、定义法)9.以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.(1)求MA,DM的长;(2)求证:AM2=AD·DM.(3)根据(2)的结论你能找出图中的一个黄金分割点吗?考查角度3 利用黄金分割的定义证明黄金矩形(计算法、定义法)10.宽与长的比是错误!未找到引用源。
黄金分割(基础篇)(专项练习)-2022-2023学年九年级数学下册基础知识专项讲练(人教版)

专题27.13 黄金分割(基础篇)(专项练习)一、单选题1.大自然巧夺天工,一片树叶也蕴含着“黄金分割”.如图,P为AB的黄金分割点(AP>PB),如果AB的长度为8cm,那么BP的长度是()A.125-C.454D.54 -B.9452.已知点C是线段AB的黄金分割点,且2<,则AC长是()AB=,AC BCA51-B51C.35D3523.把2米的线段进行黄金分割,则分成的较短的线段长为()A.35B51C.15D.354.已知2AB=,点P是线段AB上的黄金分割点,且AP BP>,则AP的长为()A51B51-C35D.3525.下列说法正确的是()A.每条线段有且仅有一个黄金分割点B.黄金分割点分一条线段为两条线段,其中较长的线段约是这条线段的0.618倍C.若点C把线段AB黄金分割,则AC2=AB•BCD.以上说法都不对6.下列说法正确的是()A.每一条线段有且只有一个黄金分割点B.黄金分割点分一条线段为两段,其中较短的一段是这条线段的0.618倍C.若点C把线段AB黄金分割,则AC是AB和BC的比例中项D.黄金分割点分一条线段为两段,其中较短的一段与较长的一段的比值约为0.6187.下列命题正确的是()A.任意两个等腰三角形一定相似B.任意两个正方形一定相似C .如果C 点是线段AB 的黄金分割点,那么51AC AB -=D .相似图形就是位似图形8.如图,线段1AB =,点1P 是线段AB 的黄金分割点(且11AP BP <),点2P 是线段1AP 的黄金分割点(212AP PP <),点3P 是线段3AP 的黄金分割点()323,,AP P P <依此类推,则线段2020AP 的长度是( )A .202051-⎝⎭B .202151-⎝⎭C .202035-⎝⎭D .202135-⎝⎭9.已知点C 把线段AB 分成两条线段AC 、BC ,且AC BC >,下列说法错误的是( ) A .如果AC BCAB AC=,那么线段AB 被点C 黄金分割 B .如果2AC AB BC =⋅,那么线段AB 被点C 黄金分割C .如果线段AB 被点C 黄金分割,那么BC 与AB 的比叫做黄金比D .0.618是黄金比的近似值10.等腰△ABC 中,AB=AC ,△A=36°,D 是AC 上的一点,AD=BD ,则以下结论中正确的有( )△△BCD 是等腰三角形;△点D 是线段AC 的黄金分割点;△△BCD△△ABC ;△BD 平分△ABC . A .1个B .2个C .3个D .4个11.在△ABC 中,△A=36°,AB=AC ,BD 是△ABC 的角平分线,下列结论: △△ABD ,△BCD 都是等腰三角形; △AD=BD=BC ; △BC 2=CD•CA ; △D 是AC 的黄金分割点 其中正确的是( )A .1个B .2个C .3个D .4个二、填空题12.在线段AB 上,点C 把线AB 分成两条线段AC 和BC ,若AC BCAB AC=,则点C 叫做线段AB 的黄金分割点.若点P 是线段MN 的黄金分割点(PM PN >),当1MN =时,PM 的长是__________.13.勾股定理与黄金分割是几何中的双宝,前者好比黄金,后者堪称珠玉,生活中到处可见黄金分割的美.如图是一种贝壳的俯视图,点C 分线段AB 近似于黄金分割,已知AB =10 cm ,AC >BC ,那么AC 的长约为____________cm (结果精确到0.1 cm ). 14.把2米长的线段进行黄金分割,则分成的较长的线段长为__________.15.古希腊时期,51-(称为黄金分割比例),著名的“断臂维纳斯”5 2.236≈,则黄金分割比例约为______________.(精确到0.01)16.已知AB=2,点C 是线段AB 的黄金分割点(AC>BC ),则AC= . 17.把长度为4cm 的线段进行黄金分割,则较长线段的长是__________cm .18.已知线段4AB =,点P 是线段AB 的黄金分割点(AP BP >),那么线段AP =______.(结果保留根号)19.已知线段AB 长为2cm ,P 是AB 的黄金分割点,则较长线段PA = ___;PB =______. 20510.61803398-=…,将这个分割比保留4个有效数字的近似数是 .21.若点C 为线段AB 的黄金分割点,且AC <BC ,若AB =10,则BC =_____. 22.若点P 是线段AB 的黄金分割点,AB=10cm ,则较长线段AP 的长是_____cm .三、解答题23.已知C 、D 是线段AB 上的点,CD =(√5﹣2)AB ,AC =BD ,则C 、D 是黄金分割点吗?为什么?24.已知线段MN = 1,在MN 上有一点A ,如果AN =,求证:点A 是MN 的黄金分割点.25.(1)对于实数a 、b ,定义运算“⊕”如下:2a b a b ⊕=-.若(1)(2)8x x +⊕-=,求: 2(2)(23)x x x -⊕-的值;(2)已知点C 是线段AB 的黄金分割点(AC <BC ),若AB =4,求AC 的长.26.(1)我们知道,将一条线段AB 分割成大小两条线段AP 、PB ,使AP >PB ,点P 把线段AB 分成两条线段AP 和BP ,且=AP BP AB AP ,点P 就是线段AB 的黄金分割点,此时PAAB的值为 (填一个实数):(2)如图,Rt△ABC 中,△B=90°,AB=2BC ,现以C 为圆心、CB 长为半径画弧交边AC 于D ,再以A 为圆心、AD 长为半径画弧交边AB 于E . 求证:点E 是线段AB 的黄金分割点.27.某校要设计一座2m 高的雕像(如图),使雕像的点C (肚脐)为线段AB (全身)的黄金分割点,上部AC (肚脐以上)与下部BC (肚脐以下)的高度比为黄金比.则雕像下部设计的高度应该为______(结果精确到0.001)米. 5 2. 236=,结果精确到0.001).28.在等边三角形ABC中,点D,E分别在BC,AC上,且DC=AE,AD与BE交于点P,连接PC.(1)证明:ΔABE△ΔCAD.(2)若CE=CP,求证△CPD=△PBD.(3)在(2)的条件下,证明:点D是BC的黄金分割点.参考答案1.A【分析】根据黄金分割的定义得到AP 51-AB ,然后把AP 的长度代入可求出AB 的长. 【详解】解:△P 为AB 的黄金分割点(AP >PB ), △AP 51-AB , △AB 的长度为8cm , △AP 51-×8=454(cm ), △BP =AB -AP =8-(454)=125- 故选:A .【点拨】本题考查了黄金分割:把线段AB 分成两条线段AC 和BC (AC >BC ),且使AC 是AB 和BC 的比例中项(即AB :AC =AC :BC ),叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点,其中AC 51-AB . 2.C 【分析】利用黄金分割比的定义即可求解. 【详解】由黄金分割比的定义可知 5151251BC AB --=== △2(51)35AC AB BC =-=-= 故选C【点拨】本题主要考查黄金分割比,掌握黄金分割比是解题的关键. 3.A 【分析】根据黄金分割的定义列式进行计算即可得解. 【详解】解: 较短的线段长=2⨯ (15-1=255 故选A.【点拨】本题考查了黄金分割的概念, 熟记黄金分割的比值5-1是解题的关键.4.A 【分析】根据黄金分割点的定义和AP BP>得出51AP AB-=,代入数据即可得出AP的长度.【详解】解:由于P为线段AB=2的黄金分割点,且AP BP>,则5151251ABAP--===.故选:A.352,51-.5.B【分析】根据黄金分割的定义分别进行解答即可.【详解】A.每条线段有两个黄金分割点,故本选项错误;B.黄金分割点分一条线段为两条线段,其中较长的线段约是这条线段的0.618倍,正确;C.若点C把线段AB黄金分割,则AC2=AB•BC,不正确,有可能BC2=AB•AC.故选B.【点拨】本题考查了黄金分割,熟练掌握黄金分割的定义是解题的关键.6.D【分析】根据比例中项和黄金分割的概念分析各个说法.【详解】解:A、每一条线段有两个黄金分割点,错误;B、黄金分割点分一条线段为两段,其中较长的一段是这条线段的0.618倍,错误;C、若点C把线段AB黄金分割,则AC是AB和BC的比例中项,错误;D、黄金分割点分一条线段为两段,其中较长的一段与这条线段的比值约为0.618,正确;故选D.【点拨】此题考查黄金分割问题,理解比例中项、黄金分割的概念,是解题的关键. 7.B 【分析】根据相似多边形的概念、黄金分割点及位似可直接进行排除选项. 【详解】解:A 、任意两个等腰三角形的底角或顶角相等,则这两个等腰三角形相似,故原命题错误; B 、任意两个正方形一定相似,故原命题正确;C 、如果C 点是线段AB 的黄金分割点(AC >BC ),那么51AC AB -=D 、相似图形不一定是位似图形,故原命题错误; 故选B .【点拨】本题主要考查相似多边形的概念、黄金分割点及位似,熟练掌握相似多边形的概念、黄金分割点及位似是解题的关键. 8.C 【分析】根据把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线51-叫做黄金比进行解答即可. 【详解】解:根据黄金比的比值,151BP -= 则151351AP --==23233535,,AP AP --==⎝⎭⎝⎭…依此类推,则线段2020202035AP -=⎝⎭,故选C .【点拨】本题考查的是黄金分割的知识,理解黄金分割的概念,找出黄金分割中成比例的对应线段是解决问题的关键. 9.C 【解析】【分析】根据黄金分割的定义判断即可.【详解】根据黄金分割的定义可知A、B、D正确;C.如果线段AB被点C黄金分割(AC>BC),那么AC与AB的比叫做黄金比,所以C错误.所以C选项是正确的.【点拨】本题考查了黄金分割的概念:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB 的黄金分割点.注意线段AB的黄金分割点有两个.10.D【详解】△AB=AC,△△ABC=△C=12(180°-△A)=12(180°-36°)=72°,△AD=BD,△△DBA=△A=36°,△△BDC=2△A=72°,△△BDC=△C,△△BCD为等腰三角形,所以△正确;△△DBC=△ABC-△ABD=36°,△△ABD=△DBC,△BD平分△ABC,所以△正确;△△DBC=△A,△BCD=△ACB,△△BCD△△ABC,所以△正确;△BD:AC=CD:BD,而AD=BD,△AD:AC=CD:AD,△点D是线段AC的黄金分割点,所以△正确.故选D.11.D【解析】试题分析:在△ABC,AB=AC,△A=36°,BD平分△ABC交AC于点D,可推出△BCD,△ABD 为等腰三角形,可得AD=BD=BC,利用三角形相似解题.解:如图,△AB=AC,△A=36°,△△ABC=△C=72°,△BD平分△ABC交AC于点D,△△ABD=△CBD=△ABC=36°=△A,△AD=BD,△BDC=△ABD+△A=72°=△C , △BC=BD ,△△ABD ,△BCD 都是等腰三角形,故△正确; △BC=BD=AD ,故△正确; △△A=△CBD ,△C=△C , △△BCD△△ACB , △,即BC 2=CD•AC ,故△正确; △AD=BD=BC ,△AD 2=AC•CD=(AD+CD )•CD , △AD=CD ,△D 是AC 的黄金分割点.故△正确, 故选D .考点:相似三角形的判定与性质;黄金分割. 1251- 【分析】根据若点P 是线段MN 的黄金分割点(PM PN >),则PM MN 51-计算即可. 【详解】当PM >PN 时,51-51-, 51-. 51-是解题的关键. 13.6.2 【分析】黄金分割又称黄金率,是指事物各部分间一定的数学比例关系,即将整体一分为二,较大部分与较小部分之比等于整体与较大部分之比,其比值为1:0.618或1.618:1,即长段为全段的0.618,0.618被公认为最具有审美意义的比例数字.上述比例是最能引起人的美感的比例,因此被称为黄金分割.【详解】由题意知AC :AB =BC :AC ,△AC :AB ≈0.618,△AC =0.618×10cm ≈6.2(结果精确到0.1cm )故答案为6.2.【点拨】本题考查黄金分割,解题关键是掌握黄金分割定理.14.51-米 【解析】【分析】把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分51-叫做黄金比. 【详解】解:△将长度为2米的线段进行黄金分割,△较长的线段=2⨯51-51- 51-米.51-是解的关键. 15.0.62【分析】把黄金分割比例按要求进行计算即可.【详解】解:51-5 2.236≈, 51-≈2.23612-≈0.62, 故答案为:0.62. 【点拨】本题考查了求一个数的近似值,有理数的除法,正确计算是解题的关键. 1651 【解析】51251AC -==17.()252cm .【解析】根据黄金分割的定义得到较长线段的长=×4,然后进行二次根式的运算即可. 解:较长线段的长=×4=(2)cm .故答案为(2)cm . 18.52 【分析】51-计算即可. 【详解】 解:△点P 是线段AB 的黄金分割点(AP>BP ) △51AP 252AB -== 故答案为:252.【点拨】本题考查的知识点是黄金分割,熟记黄金分割点的比值是解题的关键.19.)51cm (35cm 【分析】根据黄金分割的概念得到较长线段51-AB ,则PB=AB -352AB ,然后把AB=2cm 代入计算即可.【详解】解:△P 是AB 的黄金分割点, △较长线段51-AB , △PB=AB -352AB , 而AB=2cm , △PA=)51cm ,PB=(35cm . 故答案为:)51cm ;(35cm .【点拨】本题考查了黄金分割的概念:一个点把一条线段分成两段,其中较长线段是较短线段与整个线段的比例中项,那么就说这条线段被这点黄金分割,这个点叫这条线段的黄金分51-倍. 20.0.6180【解析】根据有效数字的定义,运用四舍五入法保留4个有效数字,需观察第五位有效数字,由于第五位有效数字是,不需往前面进一位.所以0.61803398…≈0.618021.555【分析】根据黄金分割点的定义,知BC 为较长线段;则BC 51-AB ,代入数据即可得出AC 的值.【详解】解:由于C 为线段AB =10的黄金分割点,且AC <BC ,BC 为较长线段;则BC =51-=55. 故答案为:555.【点拨】本题考查黄金分割:把线段AB 分成两条线段AC 和BC (AC >BC ),且使AC 是AB 和BC 的比例中项(即AB :AC=AC :BC ),叫做把线段AB 黄金分割,点C 叫做线段AB 的黄金分割点.其中51-AB≈0.618AB ,并且线段AB 的黄金分割点有两个. 22.555【解析】△P 是线段AB 的黄金分割点,AP >BP ,51-AB , △AB=10cm , △AP=5110555-=. 故答案为555.点睛:若点P 是线段AB 的黄金分割点,且AP>BP ,则AP 2=BP·AB ,即51-AB. 23.C 、D 是黄金分割点.【解析】【分析】 根据题意求出AC 与AB 的关系,计算出AD 与AB 的关系,根据黄金比值进行判断即可.【详解】解:C 、D 是黄金分割点,△AC+CD+BD =AB ,CD =(√5﹣2)AB ,AC =BD ,△AC =3−√52AB , AD =AC+CD =3−√52AB+(√5﹣2)AB =√5−12AB , △D 是AB 的黄金分割点,同理C 也是AB 的黄金分割点.【点拨】本题考查黄金分割,关键是掌握黄金分割的概念和黄金比.24.见解析 【解析】试题分析:先求得AM=√5−12,即可得到AM MN =AN AM =√5−12,结论得证。
《黄金分割》随堂练习

§ 6.2黄金分割姓名班级学号【基础知识】1.一条线段的黄金分割点有()A.1个B.2个C.3个D.无数个2.黄金分割比的准确值是是()3.小明同学发现自己一本书的宽与长之比是黄金比约为0.618.已知这本书的长为20cm,则它的宽约为()A.12.36cm B.13.6cm C.32.386cm D.7.64cm3.已知P为线段AB的黄金分割点,且AP>PB,则()A.AP2+BP2=AB2 B.BP2=AP•AB C.AP2=AB•BP D.AB2=AP•PB4.如图,若点P是线段AB的黄金分割点,AP>BP,AB=2,则AP的长度是()A.B.C.D.5.如图,电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体,若舞台AB长为20m,试计算主持人应走到离A点至少..多少米处是比较得体的位置?(结果精确到0.1m)【能力达标】6.如图,乐器上的一根弦AB=80cm,两个端点A,B固定在乐器板面上,支撑点C是靠近点B的黄金分割点,支撑点D是靠近点A的黄金分割点,则C,D之间的距离为()A.(405﹣40)cm B.(805﹣40)cmC.(120﹣405)cm D.(805﹣160)cm7.我们把宽与长的比值等于黄金比例512的矩形称为黄金矩形.如图,在黄金矩形()ABCD AB BC的边AB上取一点E,使得BE BC,连接DE,则AEAD等于()A.22B.512C.352D.5128.如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AB、宽为AC的矩形面积,则S1与S2的大小关系为()A.S1>S2B.S1=S2C.S1<S2D.不能确定9.在人体躯和身高的比例上,肚脐是理想的黄金分割点,即(下半身长m与身高l)比例越接近0.618越给人以美感,某女士身高165cm,下半身长(脚底到肚脐的高度)与身高的比值是0.60,为尽可能达到匀称的效果,求她应该选择的高跟鞋得高度.(结果保留整数)【拓展提升】10.如图,以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.(1)求AM,DM的长.(2)点M是线段AD的黄金分割点吗?请说明理由.。
4.2黄金分割练习题
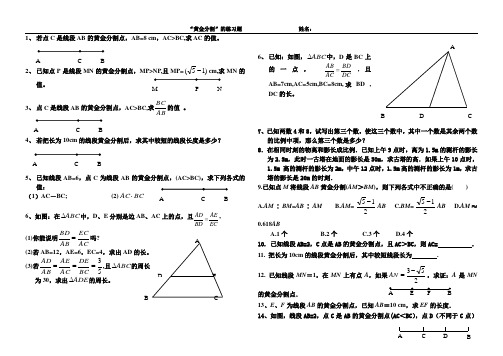
D EB CA1、 若点C 是线段AB 的黄金分割点,AB=8 cm ,AC>BC,求AC 的值。
2、 已知点P 是线段MN 的黄金分割点,MP>NP,且MP=)15(-cm,求MN 的值。
3、 点C 是线段AB 的黄金分割点,AC>BC,求ABBC 的值 。
4、 若把长为10cm 的线段黄金分割后,求其中较短的线段长度是多少?5、 已知线段AB=6,点C 为线段AB 的黄金分割点,(AC>BC),求下列各式的值: (1)AC -BC; (2)BC AC ⋅6、如图:在ABC ∆中,D 、E 分别是边AB 、AC 上的点,且ECAE BDAD =,(1)你能说明AC EC AB BD =吗?(2)若AB=12,AE=6,EC=4,求出AD 的长。
(3)若53===BCDE ACAE ABAD ,且ABC ∆的周长为30,求出ADE ∆的周长。
6、 已知:如图,ABC ∆中,D 是BC 上的一点,DCBD ACAB =,且AB=7cm,AC=5cm,BC=8cm,求BD , DC 的长。
7、已知两数4和8,试写出第三个数,使这三个数中,其中一个数是其余两个数的比例中项,那么第三个数是多少?8.在相同时刻的物高和影长成比例.已知上午9点时,高为1.5m 的测杆的影长为2.5m ,此时一古塔在地面的影长是50m ,求古塔的高.如果上午10点时,1.5m•高的测杆的影长为2m ,中午12点时,1.5m 高的测杆的影长为1m ,求古塔的影长是20m 的时刻.9.已知点M 将线段AB 黄金分割(AM >BM ),则下列各式中不正确的是( ) A.AM ∶BM =AB ∶AM B.AM =215-AB C.BM =215-AB D.AM ≈0.618ABA.1个B.2个C.3个D.4个10. 已知线段AB=2,C 点是AB 的黄金分割点,且AC >BC ,则AC= . 11. 把长为10cm 的线段黄金分割后,其中较短线段长为 .12. 已知线段MN =1,在MN 上有点A ,如果253-=AN ,求证:A 是MN 的黄金分割点.13、E 、F 为线段AB 的黄金分割点,已知AB =10 cm ,求EF 的长度. 14、如图,线段AB=2,点C 是AB 的黄金分割点(AC <BC ),点D (不同于C 点)A CB M P N AC BA CB AC BAB D CAEFBACDB在AB 上,且AB BD AD ⋅=2,求:ACCD 的值。
黄金分割练习题

一、填空题1.若点C 是线段AB 的黄金分割点(BC AC >),则AC:AB=_____,BC:AB___________:=BC AC .如果AB=10cm,则AC=______,BC=_________.若C 是线段AB 的黄金分割点,则____:=BC AC2.若Q P ,是线段AB 上的两个黄金分割点,且452-=PQ ,则____=AB3.若点C 是线段AB 的黄金分割点且AC>BC ,则______,AB BC AC AB==_______. 4.若点C 是线段AB 的黄金分割点(BC AC >),则AB 与AC 的比值是__________,BC 与AC 的比值是_________.5.在线段AB 上取一点P ,使AP :PB=1:3,则AP :AB=______,6.如图,已知3,(1)2ABACBCCEAD AE DE AE ===则:=______,(2)若BD=10cm ,则AD=______;(3)若△ADE 的周长为16cm ,则△ABC 的周长为_______ .二、认真选一选 7.已知y x 23=,那么下列式子成立的是( )A.3x=2yB.xy=6C.32=y xD.32=x y8.把ab=21cd 写成比例式,不正确的写法是( ) A.b d c a 2= B.b d c a =2C.bd c a =2 D.d a b c 2= 9已知线段x,y 满足(x+y )∶(x -y )=3∶1,那么x ∶y 等于( )A.3∶1B.2∶3C.2∶1D.3∶210.若3a=4b ,则(a-b ):(a+b )的值是( ).A .17B .7C .-17D .-710.已知P 是线段AB 上一点,且AP :PB=2:5,则AB :PB 等于( ). A .7:5 B .5:2 C .2:7 D .5:711有以下命题:①如果线段d 是线段a,b,c 的第四比例项,则有d c b a =②如果点C 是线段AB 的中点,那么AC 是AB 、BC 的比例中项 ③如果点C 是线段AB 的黄金分割点,且AC>BC ,那么AC 是AB 与BC 的比例中项 ④如果点C 是线段AB 的黄金分割点,AC>BC ,且AB=2,则 AC=5-1其中正确的判断有( )A.1个B.2个C.3个D.4个A .7:5B .5:2C .2:7D .5:7。
中考数学复习难题训练:黄金分割专题训练

精品基础教育教学资料,仅供参考,需要可下载使用!中考数学复习难题训练:黄金分割专题训练一、选择题1.若P是线段AB的黄金分割点(PA>PB),设AB=1,则PA的长约为()A. 0.191B. 0.382C. 0.5D.0.6182.上海东方明珠电视塔高468m.其上球体位于塔身的黄金分割点,那么它到塔底部的距离大约是()A. 289.2mB. 178.8mC. 110.4mD. 468m3.如果把一条线段分为两部分,使其中较长的一段与整条线段的长度比是黄金比,那么较短一段与较长一段的长度比也是黄金比.由此,假设整条线段长为1,较长的一段为x,可以列出的方程为()A. 1−xx =x1B. 1−x1=1xC. x1−x=1−x1D. 1−xx=x√54.已知点C是线段AB的黄金分割点(AC>BC),AB=4,则线段AC的长是()A. 2√5−2B. 6−2√5C. √5−1D. 3−√55.一条线段的黄金分割点有()个A. 1B. 2C. 3D. 无数个6.在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至点F,使得EF=BE,以AF为边作正方形AFGH,则H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1,矩形BCIH的面积为S2,则S1与S2的大小关系是()A. S1>S2B. S1<S2C. S1=S2D. 不能确定7.已知点C把线段AB分成两条线段AC、BC,且AC>BC,下列说法错误的是()A. 如果ACAB =BCAC,那么线段AB被点C黄金分割B. 如果AC2=AB⋅BC,那么线段AB被点C黄金分割C. 如果线段AB被点C黄金分割,那么BC与AB的比叫做黄金比D. 0.618是黄金比的近似值8.如图,在△ABC中,AB=AC,∠BAC=108°,AD、AE将∠BAC三等分交边BC于点D,点E,则下列结论中错误的是()A. 点D是线段BC的黄金分割点B. 点E是线段BC的黄金分割点C. 点E是线段CD的黄金分割点D. EDBE =√5−12二、填空题9.据有关测定,当气温处于人体正常体温(37℃)的黄金比值时,人体感到最舒适,则这个气温约为_________℃(结果保留整数).10.如果线段AB=10cm,P是线段AB的黄金分割点,那么线段BP=________cm.11.如图是一种贝壳的俯视图,点C分线段AB近似于黄金分割(BC<AC).已知AB=4cm,则BC的长约为________cm.(结果精确到0.1)12.在自然界中,蝴蝶的身长与双翅展开后的长度的比接近于0.618.若双翅展开后的长度约为5.62cm,则其身长约为_______cm(保留两位小数)13.美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.某女模特身高165cm,下半身长x(cm)与身高l(cm)的比值是0.60.为尽可能达到好的效果,她应穿的高跟鞋的高度大约为____.14.在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20cm,则宽约为________(精确到1cm).15.已知点C为线段AB的黄金分割点,且AC>BC,若P点为线段AB上的任意一点,则P点出现在线段AC上的概率为________.三、解答题16.拥有一个完美的身材是很多人的梦想,世界著名的雕像“维纳斯”就被认为是最美的身材。
黄金分割练习题

黄金分割练习题(总3页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--黄金分割比:假设身高160cm,上半身高度为64cm,则妈妈应该穿多高的高跟鞋64÷≈ cm 理想下半身160-64=96 cm 实际下半身-96= cm 高跟鞋高度实践作业:1、帮妈妈计算需要的高跟鞋高度2、寻找生活中的黄金比记录下来。
易错题:1.一个和长方形的周长是36厘米,长和宽的比是4:5,长和宽各是多少厘米2.一个三角形三个内角度数比是1:2:3,这个三角形是什么三角形3.六年级三个班数学平均成绩是87,比为4:5:6,三个班的成绩各是多少24.一项工程,甲队单独做完成要5天完成,乙队单独做要6天完成,甲乙两队工作效率比是多少5.糖与水比是1:50,现有水300千克,需加糖多少千克6.甲,乙两数之和是18,.甲数是乙数的5分之一,求甲乙两数、B两地相距408KM,客车和货车同时从A、B两地相对开出,3小时后相遇,已知客车和货车的速度比是9:8,客车每时比货车每时快多少千米?8.一件商品按20%的利润定价,然后又按8折出售,结果亏了64元,这件商品的成本是多少元?9.将一根384cm的铁丝焊成一个长、宽、高的比是3:2:1的长方体模型。
这个模型的长、宽、高各是多少厘米表面积是多少平方厘米?10.一块长方形土地,周长是160m,长和宽的是5:3,这块长方形土地的面积是多少平方米?311.李老师把2000元钱存入银行,整存整取五年,年利率是%。
到期时,李老师一共能取回多少钱(利息税是5%)12.李明和张华参加赛跑,李明跑到中点时,张华跑了全程的40%,此时两人相距80米,你知道赛程多少米吗?4。
黄金分割 习题精选

黄金分割 习题精选一、请你填一填(1)如图,若点P 是AB 的黄金分割点,则线段A P 、PB 、AB 满足关系式________,即AP 是________与________的比例中项.(2)黄金矩形的宽与长的比大约为________(精确到0.001).(3)如果线段d 是线段a 、b 、c 的第四比例项,其中a =2 cm,b =4 cm,c =5 cm,则d =_____________cm.(4)已知O 点是正方形ABCD 的两条对角线的交点,则AO ∶AB ∶AC =________.(5)、一个主持人站在舞台的黄金分割点处最自然得体,如果舞台AB 长为20米,一个主持人现在站在A 处,则它应至少再走 米才最理想。
(6)已知y x 23=,那么下列式子成立的是( ) A.3x =2y B.xy =6 C.32=y x D.32=x y (7)有以下命题:①如果线段d 是线段a ,b ,c 的第四比例项,则有dc b a = ②如果点C 是线段AB 的中点,那么AC 是AB 、BC 的比例中项③如果点C 是线段AB 的黄金分割点,且AC >BC ,那么AC 是AB 与BC 的比例中项④如果点C 是线段AB 的黄金分割点,AC >BC ,且AB =2,则AC =5-1其中正确的判断有( )A.1个B.2 个C.3个D.4个8、已知P 为线段AB 的黄金分割点,且AP <PB ,则( )A 、PB AB AP ⋅=2; B 、PB AP AB ⋅=2;C 、AB AP PB ⋅=2;D 、222AB BP AP =+ 9、已知P 、Q 是线段AB 的两个黄金分割点,且AB =10cm ,则PQ 长为( )A 、)15(5-B 、)15(5+C 、)25(10-D 、)53(5-二、已知点C 是线段AB 的黄金分割点AC =555 ,且AC >BC ,求线段AB 与BC 的长。
三、好好想一想以长为2的线段AB 为边作正方形ABCD ,取AB 的中点P ,连结PD ,在BA 的延长线上取点F ,使PF =PD ,以AF 为边作正方形AMEF ,点M 在AD 上,如图4—2—2.(1)求AM 、DM 的长.(2)求证:AM 2=AD ·DM .(3)根据(2)的结论你能找出图中的黄金分割点吗?。
10.2 黄金分割(练习)

C B A C B A 10.2 黄金分割概念:点C 把线段AB 分成两条线段AC 和BC ,如果ACBC AB AC =,那么称线段被点C 黄金分割(golden section ),点C 叫做线段AB 的黄金分割点,AC 与AB 的比叫做黄金比,AC ∶AB=215-∶1≈0.618。
注意:(1)如图,AC 是较长线段,则AC ∶AB=215-∶ 1 (2)如图,AC 是较短线段,则BC ∶AB=215-:1 练习:一、选择题:1、如图,点C 把线段AB 分成两条线段AC 和BC,如果AC BC AB AC =,那么下列说法错误的是 ( ) A 、线段AB 被点C 黄金分割 B 、点C 叫做线段AB 的黄金分割点C 、AB 与AC 的比叫做黄金比D 、AC 与AB 的比叫做黄金比2、如果点C 是线段AB 的黄金分割点(AC >BC ), 则 下列比例式正确的是( )A 、BC AC AC AB = B 、AC BC BC AB = C 、AB BC BC AC = D 、BCAB AB AC = 3、如图,点C 是AB 的黄金分割点,那么AC AB 与AC BC的值分别是( ) AB,C , 4、如图的五角星中,AC AB 与BC AC的关系是 ( ) A 、相等 B 、AC AB >BC AC C 、AC AB <BC AC D 、不能确定 5、若P 为线段AB 的黄金分割点且AP>PB,则下列各式成立的是( )A. AB 2=AP·BPB. BP 2=AP· ABC. PA 2=2BA·BPD. AP 2=AB·BP6、点C 为线段AB 的黄金分割点,AC 为较长线段,若AC=1,则AB 等于( ) 253.253.215.215.+-+-D C B A 7、 已知点C 是AB 的黄金分割点(AC >BC),若AB=4cm ,则AC 的长为( )(A)(2 5 –2)cm(B)(6-2 5 )cm(C)( 5–1)cm (D)(3- 5 )cm8、把长为8cm 的线段进行黄金分割,则较长的线段的长为 ( ) A (4.4).8).4)cm B cm C cm D cm -D C BA 1)2)二、填空题:1、一条线段的黄金分割点有个。
黄金分割专项练习题有答案

黄金分割专项练习30题(有答案)1.定义:如图1,点C在线段AB上,若满足AC2=BC?AB,则称点C为线段AB的黄金分割点.如图2,△ABC 中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D.(1)求证:点D是线段AC的黄金分割点;(2)求出线段AD的长.2.如图,用长为40cm的细铁丝围成一个矩形ABCD(AB>AD).(1)若这个矩形的面积等于99cm2,求AB的长度;(2)这个矩形的面积可能等于101cm2吗?若能,求出AB的长度,若不能,说明理由;(3)若这个矩形为黄金矩形(AD与AB之比等于黄金比),求该矩形的面积.(结果保留根号)3.定义:如图1,点C在线段AB上,若满足AC2=BC?AB,则称点C为线段AB的黄金分割点.如图2,△ABC中,AB=AC=2,∠A=36°,BD平分∠ABC交AC于点D.(1)求证:点D是线段AC的黄金分割点;(2)求出线段AD的长.4.作一个等腰三角形,使得腰与底之比为黄金比.(1)尺规作图并保留作图痕迹;(2)写出你的作法;(3)证明:腰与底之比为黄金比.5.(1)已知线段AB的长为2,P是AB的黄金分割点,求AP的长;(2)求作线段AB的黄金分割点P,要求尺规作图,且使AP>PB.6.如图,线段AB的长度为1.(1)线段AB上的点C满足系式AC2=BC?AB,求线段AC的长度;(选做)(2)线段AC上的点D满足关系式AD2=CD?AC,求线段AD的长度;(选做)(3)线段AD上的点E满足关系式AE2=DE?AD,求线段AE的长度;上面各题的结果反映了什么规律?(提示:在每一小题中设x和l)7.如图,在△ABC中,AB=AC,∠A=36°,∠1=∠2,请问点D是不是线段AC的黄金分割点.请说明理由.8.在△ABC中,AB=AC=2,BC=﹣1,∠A=36°,BD平分∠ABC,交于AC于D.试说明点D是线段AC的黄金分割点.9.在数学上称长与宽之比为黄金分割比的矩形为黄金矩形,如在矩形ABCD中,当时,称矩形ABCD为黄金矩形ABCD.请你证明黄金矩形是由一个正方形和一个更小的黄金矩形构成.10.如图,设AB是已知线段,在AB上作正方形ABCD;取AD的中点E,连接EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH.则点H是AB的黄金分割点.为什么说上述的方法作出的点H是这条线段的黄金分割点,你能说出其中的道理吗?请试一试,说一说.11.如图,已知△ABC中,D是AC边上一点,∠A=36°,∠C=72°,∠ADB=108°.求证:(1)AD=BD=BC;(2)点D是线段AC的黄金分割点.12.已知AB=2,点C是AB的黄金分割线,点D在AB上,且AD2=BD?AB,求的值.13.如果一个矩形ABCD(AB<BC)中,≈0.618,那么这个矩形称为黄金矩形,黄金矩形给人以美感.在黄金矩形ABCD内作正方形CDEF,得到一个小矩形ABFE(如图),请问矩形ABFE是否是黄金矩形?请说明你的结论的正确性.14.五角星是我们常见的图形,如图所示,其中,点C,D分别是线段AB的黄金分割点,AB=20cm,求EC+CD的长.15.人的肚脐是人的身高的黄金分割点,一般来讲,当肚脐到脚底的长度与身高的比为0.618时,是比较好看的黄金身段.一个身高1.70m的人,他的肚脐到脚底的长度为多少时才是黄金身段(保留两位小数)?16.如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.(1)求AM,DM的长;(2)点M是AD的黄金分割点吗?为什么?17.如图,点P是线段AB的黄金分割点,且AP>BP,设以AP为边长的正方形面积为S1,以PB为宽和以AB为长的矩形面积为S2,试比较S1与S2的大小.18.如图,在平行四边形ABCD中,E为边AD延长线上的一点,且D为AE的黄金分割点,即,BE交DC于点F,已知,求CF的长.19.图1是一张宽与长之比为的矩形纸片,我们称这样的矩形为黄金矩形.同学们都知道按图2所示的折叠方法进行折叠,折叠后再展开,可以得到一个正方形ABEF和一个矩形EFDC,那么EFDC这个矩形还是黄金矩形吗?若是,请根据图2证明你的结论;若不是,请说明理由.20.(如图1),点P将线段AB分成一条较小线段AP和一条较大线段BP,如果,那么称点P为线段AB的黄金分割点,设=k,则k就是黄金比,并且k≈0.618.(1)以图1中的AP为底,BP为腰得到等腰△APB(如图2),等腰△APB即为黄金三角形,黄金三角形的定义为:满足≈0.618的等腰三角形是黄金三角形;类似地,请你给出黄金矩形的定义:;(2)如图1,设AB=1,请你说明为什么k约为0.618;(3)由线段的黄金分割点联想到图形的“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分(设S1<S2),如果,那么称直线l为该图形的黄金分割线.(如图3),点P是线段AB的黄金分割点,那么直线CP是△ABC的黄金分割线吗?请说明理由;(4)图3中的△ABC的黄金分割线有几条?21.在人体躯干(脚底到肚脐的长度)与身高的比例上,肚脐是理想的黄金分割点,即比例越接近0.618,越给人以美感.张女士原来脚底到肚脐的长度与身高的比为0.60,她的身高为1.60m,她应该选择多高的高跟鞋穿上看起来更美?(精确到十分位)22.已知线段AB,按照如下的方法作图:以AB为边作正方形ABCD,取AD的中点E,连接EB,延长DA到F,使EF=EB,以线段AF为边,作正方形AFGH,那么点H是线段AB的黄金分割点吗?请说明理由.23.如图,用纸折出黄金分割点:裁一张正方的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落到线段EA上,折出点B的新位置B′,因而EB′=EB.类似地,在AB上折出点B″使AB″=AB′.这时B″就是AB的黄金分割点.请你证明这个结论.24.如图,用纸折出黄金分割点:裁一张边长为2的正方形纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置F,因而EF=EB.类似的,在AB上折出点M使AM=AF.则M是AB的黄金分割点吗?若是请你证明,若不是请说明理由.25.如图,在△ABC中,点D在边AB上,且DB=DC=AC,已知∠ACE=108°,BC=2.(1)求∠B的度数;(2)我们把有一个内角等于36°的等腰三角形称为黄金三角形.它的腰长与底边长的比(或者底边长与腰长的比)等于黄金比.①写出图中所有的黄金三角形,选一个说明理由;②求AD的长;③在直线AB或BC上是否存在点P(点A、B除外),使△PDC是黄金三角形?若存在,在备用图中画出点P,简要说明画出点P的方法(不要求证明);若不存在,说明理由.26.宽与长的比是的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小波同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示):第一步:作一个正方形ABCD;第二步:分别取AD,BC的中点M,N,连接MN;第三步:以N为圆心,ND长为半径画弧,交BC的延长线于E;第四步:过E作EF⊥AD,交AD的延长线于F.请你根据以上作法,证明矩形DCEF为黄金矩形.27.在△ABC中,AB=AC,∠A=36°,把像这样的三角形叫做黄金三角形.(1)请你设计三种不同的分法,将黄金三角形ABC分割成三个等腰三角形,使得分割成的三角形中含有两个黄金三角形(画图工具不限,要求画出分割线段;标出能够说明不同分法所得三角形的内角度数,不要求写画法,不要求证明.分别画在图1,图2,图3中)注:两种分法只要有一条分割线段位置不同,就认为是两种不同的分法.(2)如图4中,BF平分∠ABC交AC于F,取AB的中点E,连接EF并延长交BC的延长线于M.试判断CM 与AB之间的数量关系?只需说明结果,不用证明.答:CM与AB之间的数量关系是.28.折纸与证明﹣﹣﹣用纸折出黄金分割点:第一步:如图(1),先将一张正方形纸片ABCD对折,得到折痕EF;再折出矩形BCFE的对角线BF.第二步:如图(2),将AB边折到BF上,得到折痕BG,试说明点G为线段AD的黄金分割点(AG>GD)29.三角形中,顶角等于36°的等腰三角形称为黄金三角形,如图1,在△ABC中,已知:AB=AC,且∠A=36°.(1)在图1中,用尺规作AB的垂直平分线交AC于D,并连接BD(保留作图痕迹,不写作法);(2)△BCD是不是黄金三角形?如果是,请给出证明;如果不是,请说明理由;(3)设,试求k的值;(4)如图2,在△A1B1C1中,已知A1B1=A1C1,∠A1=108°,且A1B1=AB,请直接写出的值.30.如图1,点C将线段AB分成两部分,如果,那么称点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果,那么称直线l为该图形的黄金分割线.(1)研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点(如图2),则直线CD是△ABC的黄金分割线.你认为对吗?为什么?(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?(3)研究小组在进一步探究中发现:过点C任作一条直线交AB于点E,再过点D作直线DF∥CE,交AC于点F,连接EF(如图3),则直线EF也是△ABC的黄金分割线.请你说明理由.(4)如图4,点E是平行四边形ABCD的边AB的黄金分割点,过点E作EF∥AD,交DC于点F,显然直线EF是平行四边形ABCD的黄金分割线.请你画一条平行四边形ABCD的黄金分割线,使它不经过平行四边形ABCD各边黄金分割点.黄金分割专项练习30题参考答案: 1.(1)证明:∵AB=AC=1,∴∠ABC=∠C=(180°﹣∠A)=(180°﹣36°)=72°,∵BD平分∠ABC交AC于点D,∴∠ABD=∠CBD=∠ABC=36°,∴∠BDC=180°﹣36°﹣72°=72°,∴DA=DB,BD=BC,∴AD=BD=BC,易得△BDC∽△ABC,∴BC:AC=CD:BC,即BC2=CD?AC,∴AD2=CD?AC,∴点D是线段AC的黄金分割点;(2)设AD=x,则CD=AC﹣AD=1﹣x,∵AD2=CD?AC,∴x2=1﹣x,解得x1=,x2=,即AD的长为2.解:(1)设AB=xcm,则AD=(20﹣x)cm,根据题意得x(20﹣x)=99,整理得x2﹣20x+99=0,解得x1=9,x2=11,当x=9时,20﹣x=11;当x=11时,20﹣11=9,而AB>AD,所以x=11,即AB的长为11cm;(2)不能.理由如下:设AB=xcm,则AD=(20﹣x)cm,根据题意得x(20﹣x)=101,整理得x2﹣20x+101=0,因为△=202﹣4×101=﹣4<0,所以方程没有实数解,所以这个矩形的面积可能等于101cm2;(3)设AB=xcm,则AD=(20﹣x)cm,根据题意得20﹣x=x,解得x=10(﹣1),则20﹣x=10(3﹣),所以矩形的面积=10(﹣1)?10(3﹣)=(400﹣800)cm2.3.解:(1)∵∠A=36°,AB=AC,∴∠ABC=∠ACB=72°,∵BD平分∠ABC,∴∠CBD=∠ABD=36°,∠BDC=72°,∴AD=BD,BC=BD,∴△ABC∽△BDC,∴=,即=, ∴AD 2=AC?CD .∴点D 是线段AC 的黄金分割点.(2)∵点D 是线段AC 的黄金分割点,∴AD=AC ,∵AC=2,∴AD=﹣14.解:(1)腰与底之比为黄金比为黄金比如图,(2)作法:①画线段AB 作为三角形底边;②取AB 的一半作AB 的垂线AC ,连接BC ,在BC 上取CD=CA .③分别以A 点和B 点为圆心、以BD 为半径划弧,交点为E ;④分别连接EA 、EB ,则△ABE 即是所求的三角形.(3)证明:设AB=2,则AC=1,BC=,AE=BE=BD=BC ﹣CD=﹣1,=. 5.解:(1)由于P 为线段AB=2的黄金分割点,则AP=2×=﹣1,或AP=2﹣(﹣1)=3﹣; (2)如图,点P 是线段AB 的一个黄金分割点.6.解:(1)设AC=x ,则BC=AB ﹣AC=1﹣x ,∵AC 2=BC?AB ,∴x 2=1×(1﹣x ),整理得x 2+x ﹣1=0,解得x 1=,x 2=(舍去),所以线段AC 的长度为; (2)设线段AD 的长度为x ,AC=l ,∵AD 2=CD?AC ,∴x 2=l×(l ﹣x ),∴x 1=,x 2=(舍去),∴线段AD 的长度AC ;(3)同理得到线段AE 的长度AD ; 上面各题的结果反映:若线段AB 分成两条线段AC 和BC (AC >BC ),且使AC 是AB 和BC 的比例中项(即AB :AC=AC :BC ),则C 点为AB 的黄金分割点7.解:D 是AC 的黄金分割点.理由如下:∵在△ABC 中,AB=AC ,∠A=36°,∴∠ABC=∠ACB==72°.∵∠1=∠2,∴∠1=∠2=∠ABC=36°.∴在△BDC中,∠BDC=180°﹣∠2﹣∠C=72°,∴∠C=∠BDC,∴BC=BD.∵∠A=∠1,∴AD=BC.∵△ABC和△BDC中,∠2=∠A,∠C=∠C,∴△ABC∽△BDC,∴,又∵AB=AC,AD=BC=BD,∴,∴AD2=AC?CD,即D是AC的黄金分割点8.证明:∵AB=AC,∠A=36°,∴∠ABC=(180°﹣36°)=72°,∵BD平分∠ABC,交于AC于D,∴∠DBC=×∠ABC=×72°=36°,∴∠A=∠DBC,又∵∠C=∠C,∴△BCD∽△ABC,∴∵AB=AC,∴=,∵AB=AC=2,BC=﹣1,∴(﹣1)2=2×(2﹣AD),解得AD=,AD:AC=():2.∴点D是线段AC的黄金分割点.9.证明:在AB上截取AE=BC,DF=BC,连接EF.∵AE=BC,DF=BC,∴AE=DF=BC=AD,又∵∠ADF=90°,∴四边形AEFD是正方形.BE=,∴,∴矩形BCFE的宽与长的比是黄金分割比,矩形BCFE是黄金矩形.∴黄金矩形是由一个正方形和一个更小的黄金矩形构成.10.解:设正方形ABCD的边长为2,在Rt△AEB中,依题意,得AE=1,AB=2,由勾股定理知EB===,∴AH=AF=EF﹣AE=EB﹣AE=﹣1,HB=AB﹣AH=3﹣;∴AH2=()2=6﹣2,AB?HB=2×(3﹣)=6﹣2,∴AH2=AB?HB,所以点H是线段AB的黄金分割点.11.证明:(1)∵∠A=36°,∠C=72°,∴∠ABC=180°﹣36°﹣72°=72°,∵∠ADB=108°,∴∠ABD=180°﹣36°﹣108°=36°,∴△ADB是等腰三角形,∵∠BDC=180°﹣∠ADC=180°﹣108°=72°,∴△BDC是等腰三角形,∴AD=BD=BC.(2)∵∠DBC=∠A=36°,∠C=∠C,∴△ABC∽△BDC,∴BC:AC=CD:BC,∴BC2=AC?DC,∵BC=AD,∴AD2=AC?DC,∴点D是线段AC的黄金分割点.12.解:∵D在AB上,且AD2=BD?AB,∴点D是AB的黄金分割点而点C是AB的黄金分割点,∴AC=AB=﹣1,AD=AB﹣AB=AB=3﹣或AD=﹣1,AC=3﹣,∴CD=﹣1﹣(3﹣)=2﹣4,∴==或==.13.解:矩形ABFE是黄金矩形.∵AD=BC,DE=AB,∴==﹣1==.∴矩形ABFE是黄金矩形.14.解:∵D为AB的黄金分割点(AD>BD),∴AD=AB=10﹣10,∵EC+CD=AC+CD=AD,∴EC+CD=(10﹣10)cm.15.解:设他的肚脐到脚底的长度为xm时才是黄金身段,根据题意得x:1.70=0.618,即x=1.70×0.618≈1.1(m).答:他的肚脐到脚底的长度为1.1m时才是黄金身段.16.解:(1)在Rt△APD中,AP=1,AD=2,由勾股定理知PD===,∴AM=AF=PF﹣AP=PD﹣AP=﹣1,DM=AD﹣AM=3﹣.故AM的长为﹣1,DM的长为3﹣;(2)点M是AD的黄金分割点.由于=,∴点M是AD的黄金分割点.17.解:∵点P是线段AB的黄金分割点,且AP>BP,∴AP2=BP×AB,又∵S1=AP2,S2=PB×AB,∴S1=S2.18.解:∵四边形ABCD为平行四边形,∴∠CBF=∠AEB,∠BCF=∠BAE,∴△BCF∽△EAB,∴,即,把AD=,AB=+1代入得,=,解得:CF=2.故答案为:2.19.解:矩形EFDC是黄金矩形,证明:∵四边形ABEF是正方形,∴AB=DC=AF,又∵,∴,即点F是线段AD的黄金分割点.∴,∴,∴矩形CDFE是黄金矩形.20.解:(1)满足≈0.618的矩形是黄金矩形;(2)由=k得,BP=1×k=k,从而AP=1﹣k,由得,BP2=AP×AB,即k2=(1﹣k)×1,解得k=,∵k>0,∴k=≈0.618;(3)因为点P是线段AB的黄金分割点,所以,设△ABC的AB上的高为h,则,∴∴直线CP是△ABC的黄金分割线.(4)由(2)知,在BC边上也存在这样的黄金分割点Q,则AQ也是黄金分割线,设AQ与CP交于点W,则过点W的直线均是△ABC的黄金分割线,故黄金分割线有无数条.21.解:根据已知条件得下半身长是160×0.6=96cm,设选择的高跟鞋的高度是xcm,则根据黄金分割的定义得:=0.618,解得:x≈7.5cm.故她应该选择7.5cm左右的高跟鞋穿上看起来更美.22.解:设正方形ABCD的边长为2a,在Rt△AEB中,依题意,得AE=a,AB=2a,由勾股定理知EB==a,∴AH=AF=EF﹣AE=EB﹣AE=(﹣1)a,HB=AB﹣AH=(3﹣)a;∴AH2=(6﹣2)a2,AB?HB=2a×(3﹣)a=(6﹣2)a2,∴AH2=AB?HB,所以点H是线段AB的黄金分割点.23.证明:设正方形ABCD的边长为2,E为BC的中点,∴BE=1∴AE==,又∵B′E=BE=1,∴AB′=AE﹣B′E=﹣1,∴AB″∴点B″是线段AB的黄金分割点.24.证明:∵正方形ABCD的边长为2,E为BC的中点,∴BE=1∴AE==,∵EF=BE=1,∴AF=AE﹣EF=﹣1,∴AM=AF=﹣1,∴AM:AB=(﹣1):2,∴点M是线段AB的黄金分割点.25.解:(1)∵BD=DC=AC.则∠B=∠DCB,∠CDA=∠A.设∠B=x,则∠DCB=x,∠CDA=∠A=2x.又∠BOC=108°,∴∠B+∠A=108°.∴x+2x=108,x=36°.∴∠B=36°;(2)①有三个:△BDC,△ADC,△BAC.∵DB=DC,∠B=36°,∴△DBC是黄金三角形,(或∵CD=CA,∠ACD=180°﹣∠CDA﹣∠A=36°.∴△CDA是黄金三角形.或∵∠ACE=108°,∴∠ACB=72°.又∠A=2x=72°,∴∠A=∠ACB.∴BA=BC.∴△BAC是黄金三角形.②△BAC是黄金三角形,∴,∵BC=2,∴AC=﹣1.∵BA=BC=2,BD=AC=﹣1,∴AD=BA﹣BD=2﹣(﹣1)=3﹣,③存在,有三个符合条件的点P1、P2、P3.ⅰ)以CD为底边的黄金三角形:作CD的垂直平分线分别交直线AB、BC得到点P1、P2.ⅱ)以CD为腰的黄金三角形:以点C为圆心,CD为半径作弧与BC的交点为点P3.26.证明:在正方形ABCD中,取AB=2a,∵N为BC的中点,∴NC=BC=a.在Rt△DNC中,.又∵NE=ND,∴CE=NE﹣NC=(﹣1)a.∴.故矩形DCEF为黄金矩形.27.解:(1)(2)CM=AB(4分)28.证明:如图,连接GF,设正方形ABCD的边长为1,则DF=.在Rt△BCF中,BF==,则A′F=BF﹣BA′=﹣1.设AG=A′G=x,则GD=1﹣x,在Rt△A′GF和Rt△DGF中,有A'F2+A'G2=DF2+DG2,即,解得x=,即点G是AD的黄金分割点(AG>GD).29.解:(1)如图所示;(2)△BCD是黄金三角形.证明如下:∵点D在AB的垂直平分线上,∴AD=BD,∴∠ABD=∠A.∵∠A=36°,AB=AC,∴∠ABC=∠C=72°,∴∠ABD=∠DBC=36°.又∵∠BDC=∠A+∠ABD=72°,∴∠BDC=∠C,∴BD=BC,∴△BCD是黄金三角形.(3)设BC=x,AC=y,由(2)知,AD=BD=BC=x.∵∠DBC=∠A,∠C=∠C,∴△BDC∽△ABC,∴,即,整理,得x2+xy﹣y2=0,解得.因为x、y均为正数,所以.(4).理由:延长BC到E,使CE=AC,连接AE.∵∠A=36°,AB=AC,∴∠ACB=∠B=72°,∴∠ACE=180°﹣72°=108°,∴∠ACE=∠B1A1C1.∵A1B1=AB,∴AC=CE=A1B1=A1C1,∴△ACE≌△B1A1C1,∴AE=B1C1.由(3)知,∴,,∴.30.解:(1)直线CD是△ABC的黄金分割线.理由如下:设△ABC的边AB上的高为h.则,,,∴,.又∵点D为边AB的黄金分割点,∴,∴.故直线CD是△ABC的黄金分割线.(2)∵三角形的中线将三角形分成面积相等的两部分,∴,即,故三角形的中线不可能是该三角形的黄金分割线.(3)∵DF∥CE,∴△DFC和△DFE的公共边DF上的高也相等,∴S△DFC=S△DFE,∴S△ADC=S△ADF+S△DFC=S△ADF+S△DFE=S△AEF,S△BDC=S四边形BEFC.又∵,∴.因此,直线EF也是△ABC的黄金分割线.(7分)(4)画法不惟一,现提供两种画法;画法一:如答图1,取EF的中点G,再过点G作一条直线分别交AB,DC于M,N点,则直线MN就是平行四边形ABCD的黄金分割线.画法二:如答图2,在DF上取一点N,连接EN,再过点F作FM∥NE交AB于点M,连接MN,则直线MN 就是平行四边形ABCD的黄金分割线.(9分)。
黄金分割 同步测试题-最新,经典试题,通用

6.2 黄金分割同步测试题(满分120分;时间:120分钟)真情提示:亲爱的同学,欢迎你参加本次考试,祝你答题成功!题号一二三总分得分一、选择题(本题共计10 小题,每题3 分,共计30分,)1. △ABC中,AC=BC,在边AB上截取AD=AC,连接CD,若点D恰好是线段AB的一个黄金分割点,则∠A的度数是()A.22.5∘B.30∘C.36∘D.45∘2. 如图,已知点P是线段AB的黄金分割点,且PA>PB,若S1表示以PA为边的正方形的面积,S2表示长为AB、宽为PB的矩形的面积,那么S1()S2.A.>B.=C.<D.无法确定3. 如图,点C是线段AB的黄金分割点(AC>BC),下列结论错误的是()A.AC2=BC⋅ABB.BC2=AC⋅ABC.BC AC =√5−12D.ABAC=√5+124. 小明同学发现自己一本书的宽与长之比是黄金比约为0.618.已知这本书的长为20cm,则它的宽约为()A.12.36cmB.13.6cmC.32.386cmD.7.64cm5. 把10cm长的线段进行黄金分割,则较长线段的长(精确到0.01)是()A.3.82cmB.6.18cmC.3.09cmD.7.00cm6. 已知点P是线段AB的一个黄金分割点(AP>PB),则PB:AB的值为()A.3−√52B.√5−12C.1+√52D.3−√547. 如果C是线段AB一点,并且AC>CB,AB=1,那么AC的长度为()时,点C是线段AB的黄金分割点.A.0.618B.1−√52C.√5−12D.3−√528. 如图,已知线段AB=10,点P是线段AB的黄金分割点,那么线段PB的长约为()A.6.18B.0.382C.0.618D.3.829. 若点P是线段AB的黄金分割点,且AP>BP,则下列结论正确的是()A.AP2=BP⋅ABB.BP2=AP⋅ABC.AB2=AP⋅ABD.以上都不对10. 如图,点P是线段AB的黄金分割点,AP>BP,若AB=6,则PB的长是()A.3(√5−1)B.3(√5+1)C.9−3√5D.6−3√5二、填空题(本题共计10 小题,每题3 分,共计30分,)11. 已知,线段AB=6cm,C为线段AB的黄金分割点,则BC=________.12. 如图,在黄金矩形ABCD中,作一个边长为10的正方形ABEF,则EC约为________.13. 线段AB=10cm,点P是它的黄金分割点,且PA>PB,则PA=________.14. 己知:线段MN的长为20厘米,点P是线段MN的黄金分割点,则较长线段MP的长是________厘米.15. 若点B是线段AC的黄金分割点(AB>BC),已知AB=2,则BC=________(精确到0.1).16. 舞台的形状为矩形,宽度AB为12米,如果主持人站立的位置是宽度AB的黄金分割点,那么主持人从台侧点A沿AB走到主持的位置至少需走________米.17. 点P为线段AB的黄金分割点(PA>PB),则关于PA、PB、AB的比例式是________.18. 已知点P是线段AB的黄金分割点,且AB长为10cm,则线段AB被P分成的两线段中较长线段的长为________cm.19. 若线段AB=2cm,点C是线段AB的黄金分割点,且AC<BC,则线段AC的长为________.20. 顶角是36∘的等腰三角形称为黄金三角形,设黄金三角形的底边与腰之比为m.如图,在黄金△ABC中,AB=AC=1,BD平分底角ABC,得到第二个黄金△BCD,CE平分底角BCD,得到第三个黄金△CDE,以此类推,则第2016个黄金三角形的周长为________(用含m的式子表示).三、解答题(本题共计6 小题,共计60分,)21. 已知:如图,△ABC为黄金三角形,即AB=AC,且∠A=36∘,求证:BCAC =√5−12.22. 如图,已知AB=AC,BC=BD=DA.(1)求∠A的度数;(2)求证:点D是AC的黄金分割点;(3)求sin A2的值.23. 如图,在矩形ABCD中,AB=a,AD=b,E、F分别是AD、BC上的点,ABFE是正方形,且AB:AD=ED:EF,判断ABCD是否为黄金矩形(宽比长=(√5−1)比2的矩形叫黄金矩形),并说明理由.24. 如图,四边形ABCD中,AD // BC,AC与BD交于点P,点P是BD的黄金分割点(BP大于PD),已知AD=1,求BC的长.25. 如图,在△ABC中,AB=AC,AC的垂直平分线交AC于点D,交AB于点E,若AE=BC,则点E是线段AB的黄金分割点吗?说明你的理由.26. 在△ABC中,AB=AC,∠A=36∘,把像这样的三角形叫做黄金三角形.(1)请你设计三种不同的分法,将黄金三角形ABC分割成三个等腰三角形,使得分割成的三角形中含有两个黄金三角形(画图工具不限,要求画出分割线段;标出能够说明不同分法所得三角形的内角度数,不要求写画法,不要求证明.分别画在图1,图2,图3中)注:两种分法只要有一条分割线段位置不同,就认为是两种不同的分法.(2)如图4中,BF平分∠ABC交AC于F,取AB的中点E,连接EF并延长交BC的延长线于M.试判断CM与AB之间的数量关系?只需说明结果,不用证明.答:CM与AB之间的数量关系是________.第1组知识梳理一、近义词弓缴弓箭辩斗争辩专心致志一心一意沧沧凉凉清清凉凉空虚空洞挪移挪动旋转转动觉察发觉遮挽遮挡叹息叹气徘徊彷徨痕迹印迹聪明聪慧特别特殊枯萎干枯收成收获依赖依靠锻炼磨炼优雅优美语重心长苦口婆心勃勃生机盎然生机偶然偶尔萦绕萦回舒展伸展歉疚愧疚陶醉沉醉惊心动魄触目惊心姿态姿势机会机遇消受享受机敏机灵薄弱单薄渺小微小二、反义词远近热凉专心致志三心二意沧沧凉凉热热乎乎空虚充实匆匆缓缓徘徊果断蒸融凝结高大矮小笔直弯曲相信怀疑偶尔经常依赖独立优雅粗俗柔软坚硬喧哗安静镇静慌张座无虚席空无一人意想不到不出所料目不转睛左顾右盼不知所措胸有成竹强硬软弱机敏迟钝薄弱强大渺小伟大养尊处优含辛茹苦三、词语积累伶伶俐俐勃勃生机【表示注意力集中的成语】专心致志聚精会神全神贯注目不转睛心无旁骛(wù)【AABB式词语】沧沧凉凉干干净净虚虚实实潇潇洒洒恭恭敬敬沸沸扬扬头涔涔泪潸潸赤裸裸笑哈哈恶狠狠傻乎乎娇滴滴【AABB式词语】轻轻悄悄伶伶俐俐整整齐齐慌慌张张勤勤恳恳迷迷糊糊轰轰烈烈吞吞吐吐【形容时间飞快的词语】白驹过隙日月如梭光阴似箭稍纵即逝日不暇给日月如流【形容珍惜时间的词语】惜时如金争分夺秒时不我待只争朝夕千金一刻闻鸡起舞废寝忘食【表示雨大的词语】狂风暴雨大雨如注大雨滂沱倾盆大雨瓢泼大雨【描写语言的词语】语重心长对答如流滔滔不绝谈笑风生高谈阔论夸夸其谈口若悬河冷嘲热讽【描写树木的词语】树形优美高大笔直优雅自在勃勃生机郁郁葱葱枝繁叶茂旁逸斜出从从容容安安全全飘飘荡荡断断续续浩浩荡荡扭扭捏捏昏昏沉沉【无A无B式词语】无缘无故无边无际无声无息无忧无虑无法无天【AABC式词语】勃勃生机津津有味娓娓动听熠熠生辉【ABAC式词语】不慌不忙大摇大摆一心一意【形容人多的词语】座无虚席门庭若市摩肩接踵人山人海【与想有关的词语】意想不到深思熟虑胡思乱想费尽心机冥思苦想【表示担心害怕的词语】提心吊胆惊慌失措惊魂未定惊恐万状胆战心惊心有余悸惊弓之鸟【一A一B式词语】一文一武一心一意一模一样一张一弛【ABAC式词语】随时随地不慌不忙无影无踪呆头呆脑多才多艺独来独往无缘无故先知先觉【含有反义词的二字词语】左右进退吞吐好坏长短高低明暗深浅高矮强弱快慢正负贵贱软硬多少胜负善恶因果厚薄【含有人体器官的词语】指手画脚口无遮拦撕心裂肺痛心疾首手足无措卑躬屈膝眼明手快心急如焚【表示贬义的词语】养尊处优处心积虑口是心非鼠目寸光贼眉鼠眼钩心斗角【形容团结的词语】团结一致齐心协力同甘共苦同舟共济精诚团结群策群力众志成城患难与共勠(lù)力同心四、词语搭配(游丝样)的痕迹(明显)的痕迹(轻轻悄悄)地挪移(缓慢)地挪移(茫茫然)地旋转 (小心)地旋转(伶伶俐俐)地跨过(灵巧)地跨过(百年)的基业(坚实)的基业(依赖)的心(感恩)的心(巨大)的能量(微弱)的能量(优雅)的乐曲(优美)的乐曲(意想不到)的失误(重大)的失误(惊心动魄)的拼搏(震撼人心)的拼搏(暴风雨般)的掌声(热烈)的掌声(歉疚)地微笑(宽容)地微笑(剧烈)地晃动(猛烈)地晃动(拉)胡琴(打)算盘(拧)螺丝(解)纽扣(研)脂粉(蘸)药末(戴)戒指(掏)耳朵(强硬)的曲线(优美)的曲线五、积累句型第3课桃花心木1.关联词:(1)桃花心木是一种特别的树,树形优美,高大而笔直,从前老家林场种了许多,已长成几丈高的一片树林。
初中数学相似三角形之黄金分割专项练习题(附答案详解)

第二步:如图(2),将AB边折到BF上,得到折痕BG,试说明点G为线段AD的黄金分割点(AG>GD)
18.已知线段AB,按照如下的方法作图:以AB为边作正方形ABCD,取AD的中点E,连接EB,延长DA到F,使EF=EB,以线段AF为边,作正方形AFGH,那么点H是线段AB的黄金分割点吗?请说明理由.
【详解】
解:设MP=x,则PN=1﹣x,根据题意得 ,
解得,x= >1(不合题意,舍去),
又因为题中没强调MP是长的一段还是短的一段,所以MP的长也可以为1﹣ = .
故选:C.
【点睛】
本题考查黄金分割,解题的关键是掌握黄金分割点的概念.
9.B
【解析】
【分析】
根据黄金分割的概念表示出比例式,再结合正方形的面积进行分析计算.
5.A
【解析】
【分析】
利用黄金分割的定义得到PA= AB,然后把AB=4代入计算即可.
【详解】
∵点P是线段AB的黄金分割点(AP>BP),
∴PA= AB= ×4=2 -2.
故选:A.
【点睛】
本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC= AB≈0.618AB,并且线段AB的黄金分割点有两个.
6.B
【解析】
【分析】
把AB当作已知数求出AC,求出BC,再分别求出各个比值,根据结果判断即可.
【详解】
∵AC2=BC•AB,
∴AC2﹣BC•AB=0,
∵AB=AC+BC
最新中考数学复习难题训练:黄金分割专题训练(有答案)

最最中考复习--黄金分割专题训练(一)一、选择题1.若P是线段AB的黄金分割点(PA>PB),设AB=1,则PA的长约为()A. 0.191B. 0.382C. 0.5D. 0.6182.上海东方明珠电视塔高468m.其上球体位于塔身的黄金分割点,那么它到塔底部的距离大约是()A. 289.2mB. 178.8mC. 110.4mD. 468m3.如果把一条线段分为两部分,使其中较长的一段与整条线段的长度比是黄金比,那么较短一段与较长一段的长度比也是黄金比.由此,假设整条线段长为1,较长的一段为x,可以列出的方程为()A. 1−xx =x1B. 1−x1=1xC. x1−x=1−x1D. 1−xx=x√54.已知点C是线段AB的黄金分割点(AC>BC),AB=4,则线段AC的长是()A. 2√5−2B. 6−2√5C. √5−1D. 3−√55.一条线段的黄金分割点有()个A. 1B. 2C. 3D. 无数个6.在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至点F,使得EF=BE,以AF为边作正方形AFGH,则H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1,矩形BCIH的面积为S2,则S1与S2的大小关系是()A. S1>S2B. S1<S2C. S1=S2D. 不能确定7.已知点C把线段AB分成两条线段AC、BC,且AC>BC,下列说法错误的是()A. 如果ACAB =BCAC,那么线段AB被点C黄金分割B. 如果AC2=AB⋅BC,那么线段AB被点C黄金分割第 2 页 共 15 页C. 如果线段AB 被点C 黄金分割,那么BC 与AB 的比叫做黄金比D. 0.618是黄金比的近似值8. 如图,在△ABC 中,AB =AC ,∠BAC =108°,AD 、AE 将∠BAC 三等分交边BC 于点D ,点E ,则下列结论中错误的是( )A. 点D 是线段BC 的黄金分割点B. 点E 是线段BC 的黄金分割点C. 点E 是线段CD 的黄金分割点D. EDBE =√5−12二、填空题9. 据有关测定,当气温处于人体正常体温(37℃)的黄金比值时,人体感到最舒适,则这个气温约为_________℃(结果保留整数).10. 如果线段AB =10cm ,P 是线段AB 的黄金分割点,那么线段BP =________cm . 11. 如图是一种贝壳的俯视图,点C 分线段AB 近似于黄金分割(BC <AC).已知AB =4 cm ,则BC 的长约为________cm.(结果精确到0.1)12. 在自然界中,蝴蝶的身长与双翅展开后的长度的比接近于0.618.若双翅展开后的长度约为5.62 cm ,则其身长约为_______cm(保留两位小数)13. 美是一种感觉,当人体下半身长与身高的比值越接近0.618时,越给人一种美感.某女模特身高165cm ,下半身长x(cm)与身高l(cm)的比值是0.60.为尽可能达到好的效果,她应穿的高跟鞋的高度大约为____.14. 在中华经典美文阅读中,小明同学发现自己的一本书的宽与长之比为黄金比.已知这本书的长为20 cm ,则宽约为 ________ (精确到1 cm).15. 已知点C 为线段AB 的黄金分割点,且AC >BC ,若P 点为线段AB 上的任意一点,则P 点出现在线段AC 上的概率为________.三、解答题16.拥有一个完美的身材是很多人的梦想,世界著名的雕像“维纳斯”就被认为是最美的身材。
专题07-黄金分割-同步学与练-(含解析)数学苏科版九年级下册

专题07黄金分割(2个知识点2种题型1个中考考点)【目录】倍速学习四种方法【方法一】脉络梳理法知识点1.黄金分割(重点)知识点2.黄金矩形(拓展)【方法二】实例探索法题型1.与黄金分割有关的计算题型2.黄金分割的实际应用【方法三】仿真实战法考法:利用黄金分割的概念计算【方法四】成果评定法【学习目标】1.通过建筑、艺术上的实例了解黄金分割、黄金比、黄金分割点、黄金矩形的定义.2.会一条线段的黄金分割点.3.了解黄金分割在生活中的应用,会运用黄金比解决实际问题.【知识导图】【倍速学习五种方法】【方法一】脉络梳理法知识点1.黄金分割(重点)黄金分割:一般地,点C 把线段AB 分成两条线段AC 和BC (如图AC BC >),如果AC BC AB AC=,则称线段AB 被点C 黄金分割,点C 叫线段AB 的黄金分割点,其中0.618AC AB =≈,BC AB =.AB ≈0382,AC 与AB 的比叫做黄金比.(注意:对于线段AB 而言,黄金分割点有两个.)注意!!!一条线段有两个黄金分割点,因此,一般说点P 是线段AB 的黄金分割点时,需加注 AP PB >或AP < BP ,否则在已知AB 的长度求AP (或BP )的长度时,会有两种情况,此时应分情况讨论.【例1】1.已知线段AB 的长度为l ,点P 在线段上,PB AP AP AB=,求线段AP 的长.【变式1】2.(1)点P 是线段AB 的黄金分割点,AP BP >,6AB =厘米,求BP 的长;(2)已知点P 是线段AB 的黄金分割点,1AB =,求AP 的值.【变式2】3.如图,以长为2的线段AB 为边作正方形ABCD ,取AB 的中点P ,连接PD .在BA 的延长线上取点F ,使PF PD =.以AF 为边作正方形AMEF ,点M 在AD 上.(1)求线段AM 、DM 的长;(2)求证:2AM AD DM =⋅;(3)请指出图中的黄金分割点.知识点2.黄金矩形(拓展)【例2】4的矩形叫黄金矩形.如图:如果在一个黄金矩形里面画一个正方形,那么留下的矩形还是黄金矩形吗?请证明你的结论.【变式】.(绵阳)5.黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法.其原理是:如图,将正方形ABCD 的底边BC 取中点E ,以E 为圆心,线段DE 为半径作圆,其与底边BC 的延长线交于点F ,这样就把正方形ABCD 延伸为矩形ABFG ,称其为黄金矩形.若4CF a =,则AB =( ).A .)1a -B .()2aC .)1aD .()2a 【方法二】实例探索法题型1.与黄金分割有关的计算(芦溪县期中)6.已知线段AB 的长度为2,点C 是线段AB 的黄金分割点,则AC 的长度为( )A B C 1或3D 2(瑞安市期末)7.已知P 为线段AB 的黄金分割点,4AB =,AP BP >,则AP 的长为( )A .2B .4C .1D .6-题型2.黄金分割的实际应用(安庆期中)8.大自然巧夺天工,一片小树叶也蕴含着“黄金分割”,如图,P 为AB 的黄金分割点(AP PB >),如果AP 的长度为10cm ,那么AB 的长度是( )A .5B .15-C .5D .15+(沈河区期末)9.如图,冬奥会吉祥物“冰墩墩”意喻敦厚,健康,可爱,活泼,它泛着可爱笑容的嘴巴位于黄金分割点处,若玩偶身高6cm ,则玩偶嘴巴到脚的距离是( )A .3)cmB C D .(9-(天长市期中)10.大自然是美的设计师,即使是一个小小的盆景,经常也会产生最具美感的黄金分割比(黄金分割比约为0.618).如图,点B 为AC 的黄金分割点(AB BC >),若100AC =cm ,则BC 约为( )A .42cmB .38cmC .62cmD .70cm(酒泉期中)11.某品牌汽车为了打造更加精美的外观,特将汽车倒车镜设计为整个车身黄金分割点的位置(如图),若车头与倒车镜的水平距离为1.58米,则该车车身总长约为( )米.A .4.14B .2.56C .6.70D .3.82【方法三】 仿真实战法考法:利用黄金分割的概念计算(黄石)12.关于x 的一元二次方程210x mx +-=,当1m =时,该方程的正根称为黄金分割数.宽与长的比是黄金分割数的矩形叫做黄金矩形,希腊的巴特农神庙采用的就是黄金矩形的设计;我国著名数学家华罗庚的优选法中也应用到了黄金分割数.(1)求黄金分割数;(2)已知实数a ,b 满足:221,24a ma b mb +=-=,且2b a ≠-,求ab 的值;(3)已知两个不相等的实数p ,q 满足:2211p np q q nq p +-=+-=,,求pq n -的值.【方法四】 成果评定法一.选择题(共8小题)(杨浦区期末)13.已知P 是线段AB 的黄金分割点,且AP>BP ,那么下列比例式能成立的是( )A .AB AP AP BP =B .AB BP AP AB =C .BP AB AP BP =D .AB AP =(开化县模拟)14.美是一种感觉,当人体下半身长与身高的比值接近0.618时,越给人一种美感.某女士身高 165cm ,下半身长x 与身高l 的比值是0.60,为尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )A .4cmB .6cmC .8cmD .10cm(会同县期末)15.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”.如图,P 为AB 的黄金分割点()AP PB >,如果AB 的长度为8cm ,那么AP 的长度是( )cm .A .4-B .4C .4+D .4-(八步区期中)16.若线段MN 的长为1cm ,点P 是线段MN 的黄金分割点,MP NP >,则较长的线段MP 的长为( )A .1)cmB .(3CD (鄞州区期中)17.点P ,点Q 是线段AB 的黄金分割点,若2AB =,则PQ 长度是( )A .1B .C .4-D (福鼎市期中)18.在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示以线段AB 为边作正方形ABCD ,取AD 的中点E ,连接BE ,延长DA 至F ,使得EF BE =,以AF 为边作正方形AFGH ,则点H 即是线段AB 的黄金分割点.若记正方形AFGH 的面积为1S ,矩形BCIH 的面积为2S ,则1S 与2S 的比值是( )A B C D .1(盐湖区校级期中)19.如图,正五边形ABCDE 的几条对角线的交点分别为,,,,M N P Q R ,它们分别是所在对角线的黄金分割点.若2AB =,则MN 的长为( )A .3B .3C 1D 1(和平区期末)20.如果一个等腰三角形的顶角为36︒,我们把这样的等腰三角形称为黄金三角形.如图,在ABC 中,1AB AC ==,36A ∠=︒,ABC 看作第一个黄金三角形;作ABC ∠的平分线BD ,交AC 于点D ,BCD △看作第二个黄金三角形;作BCD ∠的平分线CE ,交BD 于点E ,CDE 看作第三个黄金三角形……以此类推,第2024个黄金三角形的腰长是( )A .2023B .2024C .2023D .2024二.填空题(共8小题)(沈北新区校级月考)21.如果点C 是线段AB 的黄金分割点,2cm =AC ,AC BC >,那么AB 的长为 .(平川区校级期末)22.若点P 为线段AB 的黄金分割点,且AP BP <,10BP =,则AP = .(吉安期中)23.如图,线段10cm AB =,点C 是线段AB 的黄金分割点,且AC BC >,设以AC 为边的正方形的面积为1S ,以BC 为一边,AB 长为另一边的矩形BCFG 的面积为21S S , 2S (填:“>”、“=”或“<”).(高港区期中)24.我们把宽与长的比是1):2的矩形叫做黄金矩形,从外形看它最具美感.小明想制作一张“黄金矩形”的贺卡,已知贺卡长为20cm ,那么贺卡的宽为 cm .(结果保留根号).(朝阳一模)25.如图,在某校的2022年新年晚会中,舞台AB 的长为20米,主持人站在点C 处自然得体,已知点C 是线段AB 上靠近点B 的黄金分割点,则此时主持人与点A 的距离为 米.(徐汇区期末)26.已知点P 是线段AB 的黄金分割点()AP BP >,如果2AB =,那么BP 的长是 .(达州)27.如图,乐器上的一根弦80cm AB =,两个端点,A B 固定在乐器板面上,支撑点C 是靠近点B 的黄金分割点,支撑点D 是靠近点A 的黄金分割点,,C D 之间的距离为 .(天府新区期中)28.黄金分割由于其美学性质,受到摄影爱好者和艺术家的喜爱,摄影中有一种拍摄手法叫黄金构图法.其原理是:如图,将正方形ABCD 的底边BC 取中点E ,以E 为圆心,线段DE 为半径作圆,其与底边BC 的延长线交于点F ,这样就把正方形ABCD 延伸为矩形ABFG ,称其为黄金矩形.若4CF a =,则AB = .三.解答题(共5小题)(市南区校级期中)29.如图,点C 是线段AB 的黄金分割点,AC BC >,计算线段AB 的黄金比AC AB 的值.(瑞安市期中)30.(1)已知 4.5a =,2b =,c 是a ,b 的比例中项,求c ;(2)如图,C 是AB 的黄金分割点,且AC BC >,4AB =,求AC 的长.(金安区校级期中)31.已知顶角为36︒的等腰三角形称为黄金三角形(底边与腰的比值为黄金分割比),如图,ABC ,BDC ,DEC 都是黄金三角形,已知36A ∠=︒,1AB =,求DE 的长度.(上城区校级期中)32.如图所示,以长为2的定线段AB 为边作正方形ABCD ,取AB 的中点P ,连接PD ,在BA 的延长线上取点F ,使PF PD =,以AF 为边作正方形AMEF ,点M 在AD 上.(1)求,AM DM 的长;(2)点M 是AD 的黄金分割点吗?为什么?(兰山区期中)33.在设计人体雕像时,使雕像的上部(腰以上)与下部(腰以下)的高度比,等于下部与全部(全身)的高度比,可以增加视觉美感.按此比例,如果雕像的高为2m,那么它的下部应设计多高?参考答案:1.AP=【分析】由题意得点P是线段AB的黄金分割点,再列式计算即可.=,【详解】解: 点P在线段AB上,PB APAP AB∴点P是线段AB的黄金分割点,且AP BP>,PB AP∴==AP AB线段AB的长度为l,AP∴.【点睛】本题考查了黄金分割点的定义,解题的关键是掌握黄金分割的几何含义并熟记其比值.2.(1)(9BP=-厘米;(2)2AP=或1AP=-.【分析】(1)根据条件建立等式AP AB=,求解即可;(2然后建立等式求解.【详解】解:(1)根据黄金分割点定义,且AP BP>,可知AP AB=,此时(BP AB69===-厘米;(2故2AP ABAP=.==或1【点睛】本题考查了黄金分割点,解题的关键是注意黄金分割点和黄金分割的区别,一条线段的黄金分割点有两个,满足黄金分割黄金比的只有一个.3.(1)1DM=AM=-,3(2)见解析(3)见解析【分析】此题综合考查了正方形的性质、勾股定理和黄金分割的概念.(1)要求AM 的长,只需求得AF 的长,又AF PF AP =-,PF PD =,则1,3AM AF DM AD AM ===-=(2)根据(1)所求分别求出2AM AD DM ⋅,的值即可证明结论;(3)根据(1)中的数据得:AM AD M 是AD 的黄金分割点.【详解】(1)解:在Rt APD 中,1,2AP AD ==,由勾股定理知:PD∴1AM AF PF AP PD AP ==-=-=,∴3DM AD AM =-=(2)证明:由(1)得)(2216236AM AD DM ==-⋅=⨯=-∴2AM AD DM =⋅;(3)解:∵AM AD =∴点M 是AD 的黄金分割点.4.是;见解析【分析】本题主要考查了黄金分解的定义,根据黄金矩形的定义去计算宽与长之比即可得出答案.【详解】解:是,证明如下:∵四边形ABEF 是正方形,∴AB AF =,∵四边形ABCD 是矩形 ,∴AB CD =,∴AF CD =,又∵AB AD =∴AF AD =, 即点F 是AD 的黄金分割点,∴AF AD =,∴DF AD AF AD =-=,∴DF AF =,即DFDC=∴矩形CDEF 是黄金矩形.5.D【分析】本题考查了黄金分割,正方形的性质,矩形的性质,解题的关键是掌握A BB F =计算即可.【详解】解:设AB x =,四边形ABCD 是正方形,AB BC x ∴==,矩形ABFG 是黄金矩形,A B B F \=4x x a \=+解得:(2x a =+,经检验:(2x a =+是原方程的根,(2A B a \=+,故选:D .6.C【分析】分AC <BC 、AC >BC 两种情况,根据黄金比值计算即可.【详解】解:当AC <BC 时,∵点C 是线段AB 的黄金分割点,∴1BC AB ==,同理当AC >BC 时,1AC AB ==,∴)213BC AB AC =-=-=故选C .【点睛】本题考查的是黄金分割的概念,把一条线段分成两部分,使其中较长的线段为全线)叫做黄金比.7.A【分析】本题考查了黄金分割的概念.黄金分割的定义,把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值【详解】解: 点P 是线段AB 上的一个黄金分割点,且4AB =,AP BP >,42AP ∴==.故选:A .8.A【分析】本题考查黄金分割的应用;由黄金分割知:AP AB =,由此可求得AB 的长.【详解】解:∵P 为AB 的黄金分割点,∴AP AB =,即105)cm AB ==+,故选:A .9.A【分析】本题考查了黄金分割,熟练掌握黄金分割的定义是解题的关键.根据黄金分割的定义进行列式计算即可解答.【详解】解:由题意得玩偶嘴巴到脚的距离为:()63cm =故选:A .10.B【分析】本题考查黄金分割.根据黄金分割点的定义,列出比例式进行求解即可.熟练掌握黄金分割中的比例关系,是解题的关键.【详解】解:由题意,得:0.618ABAC≈,100AC =cm ,∴61.8cm AB ≈,∴38cm BC AC AB =-≈;故选B .11.A【分析】设整个车身长为AB ,点C 表示倒车镜位置,根据题意,确定BC 的长,继而确定车身长,对照选项判断即可.【详解】如图,设整个车身长为AB ,点C 表示倒车镜位置,根据题意,AC =1.58米,∴BC =1.58÷0.618=2.56米,故车长为1.58+2.56=4.14米,故选:A .【点睛】本题考查了线段的黄金分割点,准确理解黄金分割点的意义并灵活计算是解题的关键.12.(2)2(3)0【分析】(1)依据题意,将1m =代入然后解一元二次方程210x x +-=即可得解;(2)依据题意,将224b m b -=变形为21022b b m ⎛⎫⎛⎫-+⋅--= ⎪ ⎪⎝⎭⎝⎭,从而可以看作a ,2b -是一元二次方程210x mx +-=的两个根,进而可以得解;(3)依据题意,将已知两式相加减后得到,两个关系式,从而求得pq ,进而可以得解.【详解】(1)依据题意,将1m =代入210x mx +-=得210x x +-=,解得x =,∵黄金分割数大于0,∴(2)∵224b m b -=,∴2240b m b --=,则21022b b m ⎛⎫⎛⎫-+⋅--= ⎪ ⎪⎝⎭⎝⎭.又∵2b a ≠-,∴a ,2b-是一元二次方程210x mx +-=的两个根,则12b a ⎛⎫⋅-=- ⎪⎝⎭,∴2ab =.(3)∵21p np q +-=,21q nq p +-=;∴()()2211p np q nq q p +-++-=+;即()()222p q n p q p q +++-=+;∴()()222p q pq n p q p q +-++-=+.又∵()()2211p np q nq q p +--+-=-;∴()()()22p q n p q p q -+-=--;即()()10p q p q n -+++=.∵p ,q 为两个不相等的实数,∴0p q -≠,则10p q n +++=,∴1p q n +=--.又∵()()222p q pq n p q p q +-++-=+,∴()()212121n pq n n n ---+---=--,即0pq n -=.【点睛】本题考查的是一元二次方程根与系数的关系,解题的关键是掌握根与系数的关系,灵活运用所学知识解决问题.13.A【分析】由于点P 是线段AB 的黄金分割点,且AP>BP ,故有AP 2=BP×AB ,那么AB APAP BP=.【详解】∵点P是线段AB的黄金分割点,且AP>BP,∴AP2=BP×AB,即AB APAP BP=,故A正确,B、C错误;BP APAP AB==D错误;故答案为A.【点睛】本题考查了黄金分割的知识,把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项,叫做把线段AB黄金分割.14.C【分析】本题考查了黄金分割的应用.先求得下半身的实际高度,再根据黄金分割的定义求解即可.【详解】根据已知条件得下半身长是1650.6099⨯=,设需要穿的高跟鞋是y,根据黄金分割的定义得:990.618 165yy+=+,解得:8y≈.故选:C.15.B【分析】根据黄金分割的定义得到AP AB,然后把AP的长度代入可求出AB的长.【详解】解:∵P为AB的黄金分割点(AP>PB),∴AP AB,∵AB的长度为8cm,∴AP×8=4(cm).故选:A.【点睛】本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC 是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点,其中AC AB.16.C【分析】本题考查了黄金分割.利用黄金分割的定义进行计算,即可解答.【详解】解: 点P 是线段MN 的黄金分割点,MP NP >,1cm MN =,)cm MP ∴==,故选:C .17.C【分析】本题考查了黄金分割,熟练掌握黄金分割的定义是解答本题的关键.根据黄金分割的定义,得到AQ BP AB AB ==【详解】如图,点P ,点Q 是线段AB 的黄金分割点,若2AB =,∴AQ BP AB AB ==∴1AQ BP ==,∴1124PQ AQ BP AB =+-=---=,故选:C .18.D【分析】根据H 是AB 的黄金分割点求出2AH BH AB =⋅,求出21S AH =,2S BH BC BH AB =⋅=⋅,再得出答案即可.【详解】解:H 是AB 的黄金分割点,2AH BH AB ∴=⋅,21S AH = ,2S BH BC BH AB =⋅=⋅,12S S ∴=,即121S S =,故选:D .【点睛】本题考查了黄金分割,能熟记黄金分割的性质是解此题的关键.19.A【分析】本题主要考查了正多边形的相关性质,平行四边形的性质及判定,首先根据正五边形的相关性质判定四边形ABME 为平行四边形,进而求出BM 的长度,再根据黄金分割点进行计算即可得到MN 的长.黄金分割点等相关内容,熟练掌握黄金分割点的计算方法是解决本题的关键.【详解】解:∵五边形ABCDE 为正五边形∴2AE AB ==,()180521085EAB ABC ︒⨯-∠=∠==︒,∴36AEB ABE ∠=∠=︒同理可得36CBD ∠=︒∴1083672ABD ∠=︒-︒=︒∵10872180EAB ABD ∠+∠=︒+︒=︒∴AE BD同理可证明EC AB ∥∴四边形ABME 为平行四边形∴2EM AB ==,2BM AE ==,同理:2DN =,∵M 、N 为BD 的黄金分割点∴BD =21=+,∴DM BD BM =-=1,∴21)3MN DN DM =-=-=故选:A .20.A【分析】本题考查了黄金三角形,规律型等知识;由黄金三角形的定义得BC AB =,同理求出2CD =,3DE =,可得第1个黄金三角形的腰长为1AB AC ==,第2,第3个黄金三角形的腰长是2,第4个黄金三角形的腰长是3,得出规律第n 个黄金三角形的腰长是1n -,即可得出答案.【详解】解:∵ABC 是第1个黄金三角形,第1个黄金三角形的腰长为1AB AC ==,∴BC AB =,BC AB ∴==,∵BCD △是第2个黄金三角形,∴CD BC =第2,2CD ∴==,∵CDE 是第3个黄金三角形,∴DE CD 第3个黄金三角形的腰长是2,3DE ∴==,∴第4个黄金三角形的腰长是3,…∴第n 个黄金三角形的腰长是1n -,∴第2024个黄金三角形的腰长是202412023-=,故选:A .21.(1cm【分析】本题考查黄金分割.根据黄金分割比“将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,”结合题意AC BC >,且2cm =AC ,即可列出关于线段AC 长的等式,解出AC 即可.【详解】解:∵点C 是线段AB 的一个黄金分割点,且AC BC >,∴AC AB =,∴2AB∴)1cm AC =+.故答案为:(1cm .22.5-+5【分析】本题考查了黄金分割的定义,解题的关键是熟练掌握黄金分割的定义及黄金比值.设AP x =,则10AB x =+,根据黄金分割的定义得到AP BP BP AB =即101010x x =+,解方程即可得到答案.【详解】解:设AP x =,则10AB AP BP x =+=+,∵点P 为线段AB 的黄金分割点,∴AP BP BP AB =,即101010x x =+,∴2101000x x +-=,解得5x =-+或5x =--(舍去),经检验,5x =-+∴5AP =-+故答案为:5-+23.=【分析】根据黄金分割的定义,即可得到答案.【详解】解:∵点C 是线段AB 的黄金分割点,且AC BC >,∴AC BC AB AC=,∴2AC AB BC =⋅,∵212,S AC S AB BC ==×,∴12S S =,故答案为:=.【点睛】本题主要考查黄金分割的定义,记住公式即可.24.)101【分析】本题主要考查的是黄金分割的概念和性质,根据黄金比值求解即可.【详解】解∶ 宽与长的比是1):2-,∵贺卡长为20cm∴贺卡宽为)20101=,故答案为:)101.25.()10##(10-+【分析】本题考查了黄金分割,熟练掌握黄金分割点的定义是解题的关键.由黄金分割点的定义得AC AB =,再代入AB 的长计算即可.【详解】解: 点C 是线段AB 上靠近点B 的黄金分割点,20AB =米,2010)AC ∴===(米),故答案为:10).26.3##3+【分析】本题考出来黄金分割,解一元二次方程组.由题意知,2BP AB AP AP =-=-,由点P 是线段AB 的黄金分割点,可得=AP BP AB AP ,即22AP AP AP -=,整理得2240AP AP -+=,计算求出满足要求的解即可.【详解】解:由题意知,2BP AB AP AP =-=-,∵点P 是线段 AB 的黄金分割点,∴=AP BP AB AP ,即22AP AP AP-=,整理得2240AP AP -+=,解得:1AP =-1AP =-,∴(2213BP AP =-=--=故答案为:327.160)cm-【分析】黄金分割点是指把一条线段分割为两部分,使其中一部分与全长之比等于另一部分,由此即可求解.【详解】解:弦80cm AB =,点C 是靠近点B 的黄金分割点,设BC x =,则80AC x =-,∴8080x -=120x =-点D 是靠近点A 的黄金分割点,设AD y =,则80BD y =-,∴8080y -=120y =-,∴,C D 之间的距离为8080120120160x y --=-++=,故答案为:160)cm .【点睛】本题主要考查线段成比例,掌握线段成比例,黄金分割点的定义是解题的关键.28.()2a【分析】结合题意可得,DE 和EF 是扇形DEF 的边,则DE EF CE CF ==+,根据正方形性质可得BC CD AB ==,90ECD ∠=︒,因为E 是BC 的中点,则12CE BE BC ==;根据勾股定理可得,直角CDE 中,222CD CE DE +=,即DE =CE CF +=AB 的值.【详解】解:依题得:DE EF =,设2AB x =,则正方形ABCD 中,2BC CD AB x ===,90ECD ∠=︒,E 是BC 的中点,12CE BE BC x ∴===,又4CF a = ,4EF CE CF x a DE ∴=+=+=,在直角CDE 中,222CD CE DE +=,即()()22224x x x a +=+2225816x x ax a =++2224x ax a -=()225x a a -=)11x a ∴=,()21x a =,40CF a => ,即0a >,()210x a ∴=<,2x ∴舍去,)()2212AB x a a ∴===+.故答案为:()2a .【点睛】本题考查的知识点是正方形的性质、圆的性质、勾股定理、一元二次方程的解,解题关键是找到DE EF CE CF ==+和222DE CE CD =+两个等量关系式列一元二次方程.29即可解答,熟练掌握黄金分割的定义是解题的关键.【详解】解: 点C 是线段AB 的黄金分割点,AC BC >,∴AC AB =,∴线段AB 的黄金比AC AB .30.(1)c 为3或3-;(2)2AC =【分析】本题主要考查了黄金分割点以及比例中项,正确理解比例中项和黄金分割点的定义是解题的关键.(1)由c 是a ,b 的比例中项,可得29c ab ==,由此求解即可;(2)根据黄金分割点的定义进行求解即可.【详解】解:(1)∵c 是,a b 的比例中项,∴2 4.529c ab ==⨯=∴13c =,23c =-∴c 为3或3-;(2)∵C 是AB 的黄金分割点,且AC BC >,4AB =,∴4 2.AC AB ===31【分析】证明ABC BDC ∽△△,可得2BC AB CD =⨯,从而得到221CD BC AD CD AD AC ==+==①,②,进而得到CD =【详解】解:∵ABC ,BDC ,DEC 都是黄金三角形,∴,,AB AC BD BC AD DE CD ====,36A CBD CDE ∠=∠=∠=︒,∵C C ∠=∠,∴ABC BDC ∽△△,∴AC BC BC CD=,∴2BC AB CD =⨯,∵1AB =,∴221CD BC AD CD AD AC ==+==①,②,∴1AD CD =-③,代入①整理得,()21CD CD =-,解得:CD =∵1CD <,∴CD =,∵DE CD =,∴DE =【点睛】本题考查了相似三角形的判定和性质,黄金三角形的定义,解题的关键是理解黄金三角形的定义.32.(1)AM 1,DM 的长为3(2)点M 是AD 的黄金分割点,理由见解析【分析】(1)要求AM 的长,只需求得AF 的长,又AF PF AP =-,PF PD ===,则1,3AM AF DM AD AM ==-=-=(2)根据(1)中的数据得:AM AD M 是AD 的黄金分割点.【详解】(1)在Rt APD 中,1,2AP AD ==,由勾股定理知∶PD∴1AM AF PF AP PD AP ==-=-=,3DM AD AM =-=故AM 1,DM 的长为3(2)点M 是AD 的黄金分割点.∵AM AD =∴点M 是AD 的黄金分割点.【点睛】此题综合考查了正方形的性质、勾股定理和黄金分割的概念.先求得线段,AM DM 的长,然后求得线段AM 和AD 之间的比,根据黄金分割的概念进行判断.33.1)m【分析】本题考查了黄金分割,解题的关键是设雕像的下部高为x m ,则上部长为(2)m x -,然后根据题意列出方程求解即可.【详解】解:设雕像的下部高为x m ,则题意得:22x x x -=,整理得:2240x x +-=,解得11x =,21x =-(舍去),答:雕像的下部高为1)m -.。
黄金分割专题练习

《黄金分割》专题练习一、选择题1.已知C 是线段AB 的一个黄金分割点,则AC ∶AB 为( )A .215-B .253-C .215+D .215-或253-A .55B .21C .25 D 3.把2米的线段进行黄金分割,则分成的较短的线段长为( )A .53-B .15-C .51+D .3+4.美是一种感觉,本应没有什么客观的标准,但在自然界里,物体形状的比例却提供了在匀称与协调上的一种美感的参考,在数学上,这个比例称为黄金分割。
在人体躯干(由脚底至肚脐的长度)与身高的比例上,肚脐是理想的黄金分割点,也就是说,若此比值越接近,就越给别人一种美的感觉。
如果某女士身高为1.60m ,躯干与身高的比为,为了追求美,她想利用高跟鞋达到这一效果,那么她选的高跟鞋的高度约为( )A .2.5cmB .5.1cmC .7.5cmD .8.2cm 5.如图,在正五边形ABCDE 中,对角线AD 、AC 与EB 分别相交于点M 、N .下列命题:①四边形EDCN 是菱形;②四边形MNCD 是等腰梯形;③△AEN 与△EDM 全等;④△AEM 与△CBN 相似;⑤点M 是线段AD 、BE 、NE 的黄金分割点,其中假命题有( )A .0个B .1个C .2个D .4个二、填空题1.C 是AB 的黄金分割点,则=BCAC 。
2.P 为线段AB =10cm 的黄金分割点,则AP = cm (保留两个有效数字)。
3.当人的肚脐到脚底的距离与身高的比等于黄金分割比时,身材是最完美的。
一位身高为165cm ,肚脐到头顶高度为65cm的女性,应穿鞋跟为 cm的高跟鞋才能使身材最完美(精确到1cm)。
4.如图,节目主持人现站在舞台AB的一端A点,在主持节目时,站在舞台的黄金分割点处可获得最佳美学效果,若舞台AB长20米,主持人要想站在舞台的黄金分割点处,她应走到距A点至少米处,如果向B点再走米,也处在舞台的黄金分割点处(结果精确到0.1米)5.如图,在平行四边形ABCD中,点E是边BC上的黄金分割点,且BE>CE,AE与BD相交于点F.那么BF:FD的值为。
《黄金分割》综合练习【九年级 上学期 数学 北师大 试题】

《黄金分割》综合练习一、选择题1.等边三角形的一边与这边上的高的比是( ) A.3∶2 B.3∶1C.2∶3D.1∶32.下列各组中的四条线段成比例的是( ) A.a =2,b =3,c =2,d =3 B.a =4,b =6,c =5,d =10 C.a =2,b =5,c =23,d =15 D.a =2,b =3,c =4,d =13.已知线段a 、b 、c 、d 满足ab =cd ,把它改写成比例式,错误的是( ) A.a ∶d =c ∶b B.a ∶b =c ∶d C.d ∶a =b ∶cD.a ∶c =d ∶b4.若ac =bd ,则下列各式一定成立的是( ) A.dc b a = B.c cb d d a +=+ C.c d ba =22D.da cd ab = 5.已知点M 将线段AB 黄金分割(AM >BM ),则下列各式中不正确的是( ) A.AM ∶BM =AB ∶AM B.AM =215-AB C.BM =215-AB D.AM ≈0.618AB 二、填空题6.在1∶500000的地图上,A 、B 两地的距离是64 cm ,则这两地间的实际距离是________.7.正方形ABCD 的一边与其对角线的比等于________. 8.若2x -5y =0,则y ∶x =________,xyx +=________.9.若53=-b b a ,则ba=________. 10.若AEACAD AB =,且AB =12,AC =3,AD =5,则AE =________. 三、解答题 11.已知342=+x y x ,求y x .12.在同一时刻物高与影长成比例,如果一古塔在地面上的影长为50 m ,同时高为1.5 m 的测杆的影长为2.5 m ,那么古塔的高是多少?13.在△ABC 中,D 是BC 上一点,若AB =15 cm ,AC =10 cm ,且BD ∶DC =AB ∶AC ,BD -DC =2 cm ,求B C.14.现有三个数1,2,2,请你再添上一个数写出一个比例式,这样的比例式唯一吗?*15.如果一个矩形ABCD (AB <BC )中,215-=BC AB ≈0.618,那么这个矩形称为黄金矩形,黄金矩形给人以美感.在黄金矩形ABCD 内作正方形CDEF ,得到一个小矩形ABFE (如图1),请问矩形ABFE 是否是黄金矩形?请说明你的结论的正确性.图1参考答案一、1.C 2.C 3.B 4.B 5.C 二、6.320 km 7.1∶2 8.2∶557 9.58 10.45 三、11.5312.30 m 13.10 cm14.22,1,2,2成比例;12 2,2也成比例,比例式不惟一15.矩形ABFE 是黄金矩形 由于215-=BC AB ,设AB =(5-1)k ,BC =2k , 所以FC =CD =AB ,BF =BC -FC =BC -AB =2k -(5-1)k =(3-5)k , 所以215)15()53(-=--=k k AB BF ,所以矩形ABFE 是黄金矩形.。
黄金分割专项练习30题(有答案)

黄金分割专项练习30题(有答案)1.定义:如图1,点C在线段AB上,若满足AC2=BC•AB,则称点C为线段AB的黄金分割点.如图2,△ABC 中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D.(1)求证:点D是线段AC的黄金分割点;(2)求出线段AD的长.2.如图,用长为40cm的细铁丝围成一个矩形ABCD(AB>AD).(1)若这个矩形的面积等于99cm2,求AB的长度;(2)这个矩形的面积可能等于101cm2吗?若能,求出AB的长度,若不能,说明理由;(3)若这个矩形为黄金矩形(AD与AB之比等于黄金比),求该矩形的面积.(结果保留根号)3.定义:如图1,点C在线段AB上,若满足AC2=BC•AB,则称点C为线段AB的黄金分割点.如图2,△ABC中,AB=AC=2,∠A=36°,BD平分∠ABC交AC于点D.(1)求证:点D是线段AC的黄金分割点;(2)求出线段AD的长.4.作一个等腰三角形,使得腰与底之比为黄金比.(1)尺规作图并保留作图痕迹;(2)写出你的作法;(3)证明:腰与底之比为黄金比.5.(1)已知线段AB的长为2,P是AB的黄金分割点,求AP的长;(2)求作线段AB的黄金分割点P,要求尺规作图,且使AP>PB.6.如图,线段AB的长度为1.(1)线段AB上的点C满足系式AC2=BC•AB,求线段AC的长度;(选做)(2)线段AC上的点D满足关系式AD2=CD•AC,求线段AD的长度;(选做)(3)线段AD上的点E满足关系式AE2=DE•AD,求线段AE的长度;上面各题的结果反映了什么规律?(提示:在每一小题中设x和l)7.如图,在△ABC中,AB=AC,∠A=36°,∠1=∠2,请问点D是不是线段AC的黄金分割点.请说明理由.8.在△ABC中,AB=AC=2,BC=﹣1,∠A=36°,BD平分∠ABC,交于AC于D.试说明点D是线段AC的黄金分割点.9.在数学上称长与宽之比为黄金分割比的矩形为黄金矩形,如在矩形ABCD中,当时,称矩形ABCD 为黄金矩形ABCD.请你证明黄金矩形是由一个正方形和一个更小的黄金矩形构成.10.如图,设AB是已知线段,在AB上作正方形ABCD;取AD的中点E,连接EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH.则点H是AB的黄金分割点.为什么说上述的方法作出的点H是这条线段的黄金分割点,你能说出其中的道理吗?请试一试,说一说.11.如图,已知△ABC中,D是AC边上一点,∠A=36°,∠C=72°,∠ADB=108°.求证:(1)AD=BD=BC;(2)点D是线段AC的黄金分割点.12.已知AB=2,点C是AB的黄金分割线,点D在AB上,且AD2=BD•AB,求的值.13.如果一个矩形ABCD(AB<BC)中,≈0.618,那么这个矩形称为黄金矩形,黄金矩形给人以美感.在黄金矩形ABCD内作正方形CDEF,得到一个小矩形ABFE(如图),请问矩形ABFE是否是黄金矩形?请说明你的结论的正确性.14.五角星是我们常见的图形,如图所示,其中,点C,D分别是线段AB的黄金分割点,AB=20cm,求EC+CD 的长.15.人的肚脐是人的身高的黄金分割点,一般来讲,当肚脐到脚底的长度与身高的比为0.618时,是比较好看的黄金身段.一个身高1.70m的人,他的肚脐到脚底的长度为多少时才是黄金身段(保留两位小数)?16.如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.(1)求AM,DM的长;(2)点M是AD的黄金分割点吗?为什么?17.如图,点P是线段AB的黄金分割点,且AP>BP,设以AP为边长的正方形面积为S1,以PB为宽和以AB为长的矩形面积为S2,试比较S1与S2的大小.18.如图,在平行四边形ABCD中,E为边AD延长线上的一点,且D为AE的黄金分割点,即,BE交DC于点F,已知,求CF的长.19.图1是一张宽与长之比为的矩形纸片,我们称这样的矩形为黄金矩形.同学们都知道按图2所示的折叠方法进行折叠,折叠后再展开,可以得到一个正方形ABEF和一个矩形EFDC,那么EFDC这个矩形还是黄金矩形吗?若是,请根据图2证明你的结论;若不是,请说明理由.20.(如图1),点P将线段AB分成一条较小线段AP和一条较大线段BP,如果,那么称点P为线段AB的黄金分割点,设=k,则k就是黄金比,并且k≈0.618.(1)以图1中的AP为底,BP为腰得到等腰△APB(如图2),等腰△APB即为黄金三角形,黄金三角形的定义为:满足≈0.618的等腰三角形是黄金三角形;类似地,请你给出黄金矩形的定义:;(2)如图1,设AB=1,请你说明为什么k约为0.618;(3)由线段的黄金分割点联想到图形的“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分(设S1<S2),如果,那么称直线l为该图形的黄金分割线.(如图3),点P是线段AB的黄金分割点,那么直线CP是△ABC的黄金分割线吗?请说明理由;(4)图3中的△ABC的黄金分割线有几条?21.在人体躯干(脚底到肚脐的长度)与身高的比例上,肚脐是理想的黄金分割点,即比例越接近0.618,越给人以美感.张女士原来脚底到肚脐的长度与身高的比为0.60,她的身高为1.60m,她应该选择多高的高跟鞋穿上看起来更美?(精确到十分位)22.已知线段AB,按照如下的方法作图:以AB为边作正方形ABCD,取AD的中点E,连接EB,延长DA到F,使EF=EB,以线段AF为边,作正方形AFGH,那么点H是线段AB的黄金分割点吗?请说明理由.23.如图,用纸折出黄金分割点:裁一张正方的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落到线段EA上,折出点B的新位置B′,因而EB′=EB.类似地,在AB上折出点B″使AB″=AB′.这时B″就是AB的黄金分割点.请你证明这个结论.24.如图,用纸折出黄金分割点:裁一张边长为2的正方形纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置F,因而EF=EB.类似的,在AB上折出点M使AM=AF.则M是AB的黄金分割点吗?若是请你证明,若不是请说明理由.25.如图,在△ABC中,点D在边AB上,且DB=DC=AC,已知∠ACE=108°,BC=2.(1)求∠B的度数;(2)我们把有一个内角等于36°的等腰三角形称为黄金三角形.它的腰长与底边长的比(或者底边长与腰长的比)等于黄金比.①写出图中所有的黄金三角形,选一个说明理由;②求AD的长;③在直线AB或BC上是否存在点P(点A、B除外),使△PDC是黄金三角形?若存在,在备用图中画出点P,简要说明画出点P的方法(不要求证明);若不存在,说明理由.26.宽与长的比是的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小波同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示):第一步:作一个正方形ABCD;第二步:分别取AD,BC的中点M,N,连接MN;第三步:以N为圆心,ND长为半径画弧,交BC的延长线于E;第四步:过E作EF⊥AD,交AD的延长线于F.请你根据以上作法,证明矩形DCEF为黄金矩形.27.在△ABC中,AB=AC,∠A=36°,把像这样的三角形叫做黄金三角形.(1)请你设计三种不同的分法,将黄金三角形ABC分割成三个等腰三角形,使得分割成的三角形中含有两个黄金三角形(画图工具不限,要求画出分割线段;标出能够说明不同分法所得三角形的内角度数,不要求写画法,不要求证明.分别画在图1,图2,图3中)注:两种分法只要有一条分割线段位置不同,就认为是两种不同的分法.(2)如图4中,BF平分∠ABC交AC于F,取AB的中点E,连接EF并延长交BC的延长线于M.试判断CM 与AB之间的数量关系?只需说明结果,不用证明.答:CM与AB之间的数量关系是.28.折纸与证明﹣﹣﹣用纸折出黄金分割点:第一步:如图(1),先将一张正方形纸片ABCD对折,得到折痕EF;再折出矩形BCFE的对角线BF.第二步:如图(2),将AB边折到BF上,得到折痕BG,试说明点G为线段AD的黄金分割点(AG>GD)29.三角形中,顶角等于36°的等腰三角形称为黄金三角形,如图1,在△ABC中,已知:AB=AC,且∠A=36°.(1)在图1中,用尺规作AB的垂直平分线交AC于D,并连接BD(保留作图痕迹,不写作法);(2)△BCD是不是黄金三角形?如果是,请给出证明;如果不是,请说明理由;(3)设,试求k的值;(4)如图2,在△A1B1C1中,已知A1B1=A1C1,∠A1=108°,且A1B1=AB,请直接写出的值.30.如图1,点C将线段AB分成两部分,如果,那么称点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果,那么称直线l为该图形的黄金分割线.(1)研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点(如图2),则直线CD是△ABC的黄金分割线.你认为对吗?为什么?(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?(3)研究小组在进一步探究中发现:过点C任作一条直线交AB于点E,再过点D作直线DF∥CE,交AC于点F,连接EF(如图3),则直线EF也是△ABC的黄金分割线.请你说明理由.(4)如图4,点E是平行四边形ABCD的边AB的黄金分割点,过点E作EF∥AD,交DC于点F,显然直线EF 是平行四边形ABCD的黄金分割线.请你画一条平行四边形ABCD的黄金分割线,使它不经过平行四边形ABCD 各边黄金分割点.黄金分割专项练习30题参考答案:1.(1)证明:∵AB=AC=1,∴∠ABC=∠C=(180°﹣∠A)=(180°﹣36°)=72°,∵BD平分∠ABC交AC于点D,∴∠ABD=∠CBD=∠ABC=36°,∴∠BDC=180°﹣36°﹣72°=72°,∴DA=DB,BD=BC,∴AD=BD=BC,易得△BDC∽△ABC,∴BC:AC=CD:BC,即BC2=CD•AC,∴AD2=CD•AC,∴点D是线段AC的黄金分割点;(2)设AD=x,则CD=AC﹣AD=1﹣x,∵AD2=CD•AC,∴x2=1﹣x,解得x1=,x2=,即AD的长为2.解:(1)设AB=xcm,则AD=(20﹣x)cm,根据题意得x(20﹣x)=99,整理得x2﹣20x+99=0,解得x1=9,x2=11,当x=9时,20﹣x=11;当x=11时,20﹣11=9,而AB>AD,所以x=11,即AB的长为11cm;(2)不能.理由如下:设AB=xcm,则AD=(20﹣x)cm,根据题意得x(20﹣x)=101,整理得x2﹣20x+101=0,因为△=202﹣4×101=﹣4<0,所以方程没有实数解,所以这个矩形的面积可能等于101cm2;(3)设AB=xcm,则AD=(20﹣x)cm,根据题意得20﹣x=x,解得x=10(﹣1),则20﹣x=10(3﹣),所以矩形的面积=10(﹣1)•10(3﹣)=(400﹣800)cm2.3.解:(1)∵∠A=36°,AB=AC,∴∠ABC=∠ACB=72°,∵BD平分∠ABC,∴∠CBD=∠ABD=36°,∠BDC=72°,∴AD=BD,BC=BD,∴△ABC∽△BDC,∴=,即=,∴AD2=AC•CD.∴点D是线段AC的黄金分割点.(2)∵点D是线段AC的黄金分割点,∴AD=AC,∵AC=2,∴AD=﹣14.解:(1)腰与底之比为黄金比为黄金比如图,(2)作法:①画线段AB作为三角形底边;②取AB的一半作AB的垂线AC,连接BC,在BC上取CD=CA.③分别以A点和B点为圆心、以BD为半径划弧,交点为E;④分别连接EA、EB,则△ABE即是所求的三角形.(3)证明:设AB=2,则AC=1,BC=,AE=BE=BD=BC﹣CD=﹣1,=.5.解:(1)由于P为线段AB=2的黄金分割点,则AP=2×=﹣1,或AP=2﹣(﹣1)=3﹣;(2)如图,点P是线段AB的一个黄金分割点.6.解:(1)设AC=x,则BC=AB﹣AC=1﹣x,∵AC2=BC•AB,∴x2=1×(1﹣x),整理得x2+x﹣1=0,解得x1=,x2=(舍去),所以线段AC的长度为;(2)设线段AD的长度为x,AC=l,∵AD2=CD•AC,∴x2=l×(l﹣x),∴x1=,x2=(舍去),∴线段AD的长度AC;(3)同理得到线段AE的长度AD;上面各题的结果反映:若线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),则C点为AB的黄金分割点7.解:D是AC的黄金分割点.理由如下:∵在△ABC中,AB=AC,∠A=36°,∴∠ABC=∠ACB==72°.∵∠1=∠2,∴∠1=∠2=∠ABC=36°.∴在△BDC中,∠BDC=180°﹣∠2﹣∠C=72°,∴∠C=∠BDC,∴BC=BD.∵∠A=∠1,∴AD=BC.∵△ABC和△BDC中,∠2=∠A,∠C=∠C,∴△ABC∽△BDC,∴,又∵AB=AC,AD=BC=BD,∴,∴AD2=AC•CD,即D是AC的黄金分割点8.证明:∵AB=AC,∠A=36°,∴∠ABC=(180°﹣36°)=72°,∵BD平分∠ABC,交于AC于D,∴∠DBC=×∠ABC=×72°=36°,∴∠A=∠DBC,又∵∠C=∠C,∴△BCD∽△ABC,∴∵AB=AC,∴=,∵AB=AC=2,BC=﹣1,∴(﹣1)2=2×(2﹣AD),解得AD=,AD:AC=():2.∴点D是线段AC的黄金分割点.9.证明:在AB上截取AE=BC,DF=BC,连接EF.∵AE=BC,DF=BC,∴AE=DF=BC=AD,又∵∠ADF=90°,∴四边形AEFD是正方形.BE=,∴,∴矩形BCFE的宽与长的比是黄金分割比,矩形BCFE是黄金矩形.∴黄金矩形是由一个正方形和一个更小的黄金矩形构成.10.解:设正方形ABCD的边长为2,在Rt△AEB中,依题意,得AE=1,AB=2,由勾股定理知EB===,∴AH=AF=EF﹣AE=EB﹣AE=﹣1,HB=AB﹣AH=3﹣;∴AH2=()2=6﹣2,AB•HB=2×(3﹣)=6﹣2,∴AH2=AB•HB,所以点H是线段AB的黄金分割点.11.证明:(1)∵∠A=36°,∠C=72°,∴∠ABC=180°﹣36°﹣72°=72°,∵∠ADB=108°,∴∠ABD=180°﹣36°﹣108°=36°,∴△ADB是等腰三角形,∵∠BDC=180°﹣∠ADC=180°﹣108°=72°,∴△BDC是等腰三角形,∴AD=BD=BC.(2)∵∠DBC=∠A=36°,∠C=∠C,∴△ABC∽△BDC,∴BC:AC=CD:BC,∴BC2=AC•DC,∵BC=AD,∴AD2=AC•DC,∴点D是线段AC的黄金分割点.12.解:∵D在AB上,且AD2=BD•AB,∴点D是AB的黄金分割点而点C是AB的黄金分割点,∴AC=AB=﹣1,AD=AB﹣AB=AB=3﹣或AD=﹣1,AC=3﹣,∴CD=﹣1﹣(3﹣)=2﹣4,∴==或==.13.解:矩形ABFE是黄金矩形.∵AD=BC,DE=AB,∴==﹣1==.∴矩形ABFE是黄金矩形.14.解:∵D为AB的黄金分割点(AD>BD),∴AD=AB=10﹣10,∵EC+CD=AC+CD=AD,∴EC+CD=(10﹣10)cm.15.解:设他的肚脐到脚底的长度为xm时才是黄金身段,根据题意得x:1.70=0.618,即x=1.70×0.618≈1.1(m).答:他的肚脐到脚底的长度为1.1m时才是黄金身段.16.解:(1)在Rt△APD中,AP=1,AD=2,由勾股定理知PD===,∴AM=AF=PF﹣AP=PD﹣AP=﹣1,DM=AD﹣AM=3﹣.故AM的长为﹣1,DM的长为3﹣;(2)点M是AD的黄金分割点.由于=,∴点M是AD的黄金分割点.17.解:∵点P是线段AB的黄金分割点,且AP>BP,∴AP2=BP×AB,又∵S1=AP2,S2=PB×AB,∴S1=S2.18.解:∵四边形ABCD为平行四边形,∴∠CBF=∠AEB,∠BCF=∠BAE,∴△BCF∽△EAB,∴,即,把AD=,AB=+1代入得,=,解得:CF=2.故答案为:2.19.解:矩形EFDC是黄金矩形,证明:∵四边形ABEF是正方形,∴AB=DC=AF,又∵,∴,即点F是线段AD的黄金分割点.∴,∴,∴矩形CDFE是黄金矩形.20.解:(1)满足≈0.618的矩形是黄金矩形;(2)由=k得,BP=1×k=k,从而AP=1﹣k,由得,BP2=AP×AB,即k2=(1﹣k)×1,解得k=,∵k>0,∴k=≈0.618;(3)因为点P是线段AB的黄金分割点,所以,设△ABC的AB上的高为h,则,∴∴直线CP是△ABC的黄金分割线.(4)由(2)知,在BC边上也存在这样的黄金分割点Q,则AQ也是黄金分割线,设AQ与CP交于点W,则过点W的直线均是△ABC的黄金分割线,故黄金分割线有无数条.21.解:根据已知条件得下半身长是160×0.6=96cm,设选择的高跟鞋的高度是xcm,则根据黄金分割的定义得:=0.618,解得:x≈7.5cm.故她应该选择7.5cm左右的高跟鞋穿上看起来更美.22.解:设正方形ABCD的边长为2a,在Rt△AEB中,依题意,得AE=a,AB=2a,由勾股定理知EB==a,∴AH=AF=EF﹣AE=EB﹣AE=(﹣1)a,HB=AB﹣AH=(3﹣)a;∴AH2=(6﹣2)a2,AB•HB=2a×(3﹣)a=(6﹣2)a2,∴AH2=AB•HB,所以点H是线段AB的黄金分割点.23.证明:设正方形ABCD的边长为2,E为BC的中点,∴BE=1∴AE==,又∵B′E=BE=1,∴AB′=AE﹣B′E=﹣1,∴AB″∴点B″是线段AB的黄金分割点.24.证明:∵正方形ABCD的边长为2,E为BC的中点,∴BE=1∴AE==,∵EF=BE=1,∴AF=AE﹣EF=﹣1,∴AM=AF=﹣1,∴AM:AB=(﹣1):2,∴点M是线段AB的黄金分割点.25.解:(1)∵BD=DC=AC.则∠B=∠DCB,∠CDA=∠A.设∠B=x,则∠DCB=x,∠CDA=∠A=2x.又∠BOC=108°,∴∠B+∠A=108°.∴x+2x=108,x=36°.∴∠B=36°;(2)①有三个:△BDC,△ADC,△BAC.∵DB=DC,∠B=36°,∴△DBC是黄金三角形,(或∵CD=CA,∠ACD=180°﹣∠CDA﹣∠A=36°.∴△CDA是黄金三角形.或∵∠ACE=108°,∴∠ACB=72°.又∠A=2x=72°,∴∠A=∠ACB.∴BA=BC.∴△BAC是黄金三角形.②△BAC是黄金三角形,∴,∵BC=2,∴AC=﹣1.∵BA=BC=2,BD=AC=﹣1,∴AD=BA﹣BD=2﹣(﹣1)=3﹣,③存在,有三个符合条件的点P1、P2、P3.ⅰ)以CD为底边的黄金三角形:作CD的垂直平分线分别交直线AB、BC得到点P1、P2.ⅱ)以CD为腰的黄金三角形:以点C为圆心,CD为半径作弧与BC的交点为点P3.26.证明:在正方形ABCD中,取AB=2a,∵N为BC的中点,∴NC=BC=a.在Rt△DNC中,.又∵NE=ND,∴CE=NE﹣NC=(﹣1)a.∴.故矩形DCEF为黄金矩形.27.解:(1)(2)CM=AB(4分)28.证明:如图,连接GF,设正方形ABCD的边长为1,则DF=.在Rt△BCF中,BF==,则A′F=BF﹣BA′=﹣1.设AG=A′G=x,则GD=1﹣x,在Rt△A′GF和Rt△DGF中,有A'F2+A'G2=DF2+DG2,即,解得x=,即点G是AD的黄金分割点(AG>GD).29.解:(1)如图所示;(2)△BCD是黄金三角形.证明如下:∵点D在AB的垂直平分线上,∴AD=BD,∴∠ABD=∠A.∵∠A=36°,AB=AC,∴∠ABC=∠C=72°,∴∠ABD=∠DBC=36°.又∵∠BDC=∠A+∠ABD=72°,∴∠BDC=∠C,∴BD=BC,∴△BCD是黄金三角形.(3)设BC=x,AC=y,由(2)知,AD=BD=BC=x.∵∠DBC=∠A,∠C=∠C,∴△BDC∽△ABC,∴,即,整理,得x2+xy﹣y2=0,解得.因为x、y均为正数,所以.(4).理由:延长BC到E,使CE=AC,连接AE.∵∠A=36°,AB=AC,∴∠ACB=∠B=72°,∴∠ACE=180°﹣72°=108°,∴∠ACE=∠B1A1C1.∵A1B1=AB,∴AC=CE=A1B1=A1C1,∴△ACE≌△B1A1C1,∴AE=B1C1.由(3)知,∴,,∴.30.解:(1)直线CD是△ABC的黄金分割线.理由如下:设△ABC的边AB上的高为h.则,,,∴,.又∵点D为边AB的黄金分割点,∴,∴.故直线CD是△ABC的黄金分割线.(2)∵三角形的中线将三角形分成面积相等的两部分,∴,即,故三角形的中线不可能是该三角形的黄金分割线.(3)∵DF∥CE,∴△DFC和△DFE的公共边DF上的高也相等,∴S△DFC=S△DFE,∴S△ADC=S△ADF+S△DFC=S△ADF+S△DFE=S△AEF,S△BDC=S四边形BEFC.又∵,∴.因此,直线EF也是△ABC的黄金分割线.(7分)(4)画法不惟一,现提供两种画法;画法一:如答图1,取EF的中点G,再过点G作一条直线分别交AB,DC于M,N点,则直线MN就是平行四边形ABCD的黄金分割线.画法二:如答图2,在DF上取一点N,连接EN,再过点F作FM∥NE交AB于点M,连接MN,则直线MN就是平行四边形ABCD的黄金分割线.(9分)第21 页共21 页。
黄金分割同步练习及答案 (10)

黄金分割同步练习(典型题汇总)1.点C是线段AB上的一个黄金分割点,且AC>BC,若AB=5cm,则AC=_____,BC=____.2.若点C是线段AB上一点,AB=1,AC=215-,则AC:BC=______.3.如果点P是线段AB的黄金分割点,且AP>PB,则下列结论:①AB2=AP·PB,②AP2=PB·AB,③BP2=AP·AB,④AP:AB=PB:AP,其正确的是______(填序号).4.据有关实验测定,当气温处于人体正常体温(37o C)的黄金比值时,人体感到最舒适.这个气温约为_______ o C (精确到1 o C).5、已知点M将线段AB黄金分割(AM>BM),则下列各式中不正确的是( )A.AM∶BM=AB∶AMB.AM=215-AB C.BM=215-AB D.AM≈0.618AB6、若点C在线段AB上,且AB=1.AC=215-.请说明点C是否是线段AB的黄金分割点.7、如果一个矩形ABCD(AB<BC)中,215-=BCAB≈0.618,那么这个矩形称为黄金矩形,黄金矩形给人以美感.在黄金矩形ABCD内作正方形CDEF,得到一个小矩形ABFE(如图1),请问矩形ABFE是否是黄金矩形?请说明你的结论的正确性.CBA 参考答案1、cm cm 25515,2555--. 2、2:)51(+. 3、②④4、23 o C .5、C .6、因为BCAC =215-,而21542524)15)(53(15532152151-=-=+-=--=---=ACBC ,AC BC AB AC =,故点C 是线段AB 的黄金分割点.7、矩形ABFE 是黄金矩形 由于BCAB =215-,设AB =(5-1)k ,BC =2k ,所以FC =CD =AB ,BF =BC -FC =BC -AB =2k -(5-1)k =(3-5)k , 所以215)15()53(-=--=kk AB BF ,所以矩形ABFE 是黄金矩形.黄金分割同步练习(典型题汇总)一、选择题:1.如图,点C 把线段AB 分成两条线段AC 和BC,如果AC BCAB AC=,那么下列说法错误的是( ) A.线段AB 被点C 黄金分割; B.点C 叫做线段AB 的黄金分割点C.AB 与AC 的比叫做黄金比;D.AC 与AB 的比叫做黄金比2.如图的五角星中,AC AB 与BCAC 的关系是( ) A.相等; B.AC AB >BC AC ; C.AC AB <BCAC; D.不能确定3.一条线段的黄金分割点有( )CBAC BA A.1个 B.2个 C.3个 D.无数个 4.黄金分割比是( )D.0.618 5.如图,点C 是AB 的黄金分割点,那么AC AB 与ACBC的值分别是( ) A.,B.,; C.,; D.12,126.如图,若点C 是AB 的黄金分割点,AB=2,则AC= ( )11 二、填空题:1.点C 把线段AB 分成两条线段AC 和BC,如果_________,那么称线段AB 被点C•黄金分割,点C 叫做线段AB 的________,AC 与AB 的比叫做_________.2.如图,若点C 是AB 的黄金分割点,AB=1,则AC=_______,BC=______.3.已知点C 是AB 的黄金分割点,即AC AB =12,那么ACCB=________.4.如图,点C 是AB 的黄金分割点,AB=4,则AC 2=________.5.宽与长的比等于________的矩形叫做黄金矩形.6.已知黄金矩形的长等于6,则这个黄金矩形的宽等于_________. 三、计算题:1.已知线段AB 长6厘米,点P 是AB 的黄金分割点,且AP>BP,求AP 和BP 的长.2.仿照课本上“做一做”的方法,画出线段AB 的黄金分割点.3.请你在实际生活中搜集一个与黄金分割有关的资料,并与同伴相互交流. 四、已知一个等腰三角形如果腰与底边的比是黄金比,•那么这样的等腰三角形称为黄金三角形.请你设法作出一个黄金三角形.五、已知线段AB=1,C 为AB 的黄金分割点,且AC>BC,求AC-BC 的值.六、如图的五角星中,AD=BC,且C 、D 两点都是AB 的黄金分割点,AB=1,求CD 的长.D CBA七、已知C 、D 是线段AB 上的两点,且不难证明当AB=1时,C 、D 是线段AB 的黄金分割点,试探究当AB 任意长时,C 、D 是否是线段AB 的黄金分割点?为什么?答案:一、1.C 2.A 3.B 4.B 5.B 6.C二、1.AC BCAB AC=;黄金分割点;黄金比 2. 12;32-黄金比三、1.因为点P 是AB 的黄金分割点,且AP>BP,所以AP PB AB AP==12,AP=12×AB=12×2.(1)过点B 作BD ⊥AB 且BD=12AB,连接AD (2)以D 为圆心BD 为半径作圆弧交AD 于E(3)以A 为圆心AE 为半径作圆弧交AB 于C,则C 为AB 的黄金分割点 3.查阅资料四、先做出线段AB,及其黄金分割点C(AC>BC)分别以A 、B 为圆心,AC 为半径作圆弧,交点为P,则△PAB 就是黄金三角形五、根据C 为AB 的黄金分割点,AC>BC 得AC AB,因为AB=1,所以所以AC-BC=12-32-六、根据C 、D 都是AB 的黄金分割点得ACAB =12,BD AB=12因为AB=1,所以AC=12,BD=12,所以因此七、C 、D 是线段AB 的黄金分割点.。
黄金分割专项练习题有答案

黄金分割专项练习30题(有答案)1.定义:如图1,点C在线段AB上,若满足AC2=BC•AB,则称点C为线段AB的黄金分割点.如图2,△ABC 中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D.(1)求证:点D是线段AC的黄金分割点;(2)求出线段AD的长.2.如图,用长为40cm的细铁丝围成一个矩形ABCD(AB>AD).(1)若这个矩形的面积等于99cm2,求AB的长度;(2)这个矩形的面积可能等于101cm2吗?若能,求出AB的长度,若不能,说明理由;(3)若这个矩形为黄金矩形(AD与AB之比等于黄金比),求该矩形的面积.(结果保留根号)3.定义:如图1,点C在线段AB上,若满足AC2=BC•AB,则称点C为线段AB的黄金分割点.如图2,△ABC中,AB=AC=2,∠A=36°,BD平分∠ABC交AC于点D.(1)求证:点D是线段AC的黄金分割点;(2)求出线段AD的长.4.作一个等腰三角形,使得腰与底之比为黄金比.(1)尺规作图并保留作图痕迹;(2)写出你的作法;(3)证明:腰与底之比为黄金比.5.(1)已知线段AB的长为2,P是AB的黄金分割点,求AP的长;(2)求作线段AB的黄金分割点P,要求尺规作图,且使AP>PB.6.如图,线段AB的长度为1.(1)线段AB上的点C满足系式AC2=BC•AB,求线段AC的长度;(选做)(2)线段AC上的点D满足关系式AD2=CD•AC,求线段AD的长度;(选做)(3)线段AD上的点E满足关系式AE2=DE•AD,求线段AE的长度;上面各题的结果反映了什么规律?(提示:在每一小题中设x和l)7.如图,在△ABC中,AB=AC,∠A=36°,∠1=∠2,请问点D是不是线段AC的黄金分割点.请说明理由.8.在△ABC中,AB=AC=2,BC=﹣1,∠A=36°,BD平分∠ABC,交于AC于D.试说明点D是线段AC的黄金分割点.9.在数学上称长与宽之比为黄金分割比的矩形为黄金矩形,如在矩形ABCD中,当时,称矩形ABCD 为黄金矩形ABCD.请你证明黄金矩形是由一个正方形和一个更小的黄金矩形构成.10.如图,设AB是已知线段,在AB上作正方形ABCD;取AD的中点E,连接EB;延长DA至F,使EF=EB;以线段AF为边作正方形AFGH.则点H是AB的黄金分割点.为什么说上述的方法作出的点H是这条线段的黄金分割点,你能说出其中的道理吗?请试一试,说一说.11.如图,已知△ABC中,D是AC边上一点,∠A=36°,∠C=72°,∠ADB=108°.求证:(1)AD=BD=BC;(2)点D是线段AC的黄金分割点.12.已知AB=2,点C是AB的黄金分割线,点D在AB上,且AD2=BD•AB,求的值.13.如果一个矩形ABCD(AB<BC)中,≈0.618,那么这个矩形称为黄金矩形,黄金矩形给人以美感.在黄金矩形ABCD内作正方形CDEF,得到一个小矩形ABFE(如图),请问矩形ABFE是否是黄金矩形?请说明你的结论的正确性.14.五角星是我们常见的图形,如图所示,其中,点C,D分别是线段AB的黄金分割点,AB=20cm,求EC+CD 的长.15.人的肚脐是人的身高的黄金分割点,一般来讲,当肚脐到脚底的长度与身高的比为0.618时,是比较好看的黄金身段.一个身高1.70m的人,他的肚脐到脚底的长度为多少时才是黄金身段(保留两位小数)?16.如图所示,以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上.(1)求AM,DM的长;(2)点M是AD的黄金分割点吗?为什么?17.如图,点P是线段AB的黄金分割点,且AP>BP,设以AP为边长的正方形面积为S1,以PB为宽和以AB为长的矩形面积为S2,试比较S1与S2的大小.18.如图,在平行四边形ABCD中,E为边AD延长线上的一点,且D为AE的黄金分割点,即,BE交DC于点F,已知,求CF的长.19.图1是一张宽与长之比为的矩形纸片,我们称这样的矩形为黄金矩形.同学们都知道按图2所示的折叠方法进行折叠,折叠后再展开,可以得到一个正方形ABEF和一个矩形EFDC,那么EFDC这个矩形还是黄金矩形吗?若是,请根据图2证明你的结论;若不是,请说明理由.20.(如图1),点P将线段AB分成一条较小线段AP和一条较大线段BP,如果,那么称点P为线段AB的黄金分割点,设=k,则k就是黄金比,并且k≈0.618.(1)以图1中的AP为底,BP为腰得到等腰△APB(如图2),等腰△APB即为黄金三角形,黄金三角形的定义为:满足≈0.618的等腰三角形是黄金三角形;类似地,请你给出黄金矩形的定义:;(2)如图1,设AB=1,请你说明为什么k约为0.618;(3)由线段的黄金分割点联想到图形的“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积为S1和面积为S2的两部分(设S1<S2),如果,那么称直线l为该图形的黄金分割线.(如图3),点P是线段AB的黄金分割点,那么直线CP是△AB C的黄金分割线吗?请说明理由;(4)图3中的△ABC的黄金分割线有几条?21.在人体躯干(脚底到肚脐的长度)与身高的比例上,肚脐是理想的黄金分割点,即比例越接近0.618,越给人以美感.张女士原来脚底到肚脐的长度与身高的比为0.60,她的身高为1.60m,她应该选择多高的高跟鞋穿上看起来更美?(精确到十分位)22.已知线段AB,按照如下的方法作图:以AB为边作正方形ABCD,取AD的中点E,连接EB,延长DA到F,使EF=EB,以线段AF为边,作正方形AFGH,那么点H是线段AB的黄金分割点吗?请说明理由.23.如图,用纸折出黄金分割点:裁一张正方的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落到线段EA上,折出点B的新位置B′,因而EB′=EB.类似地,在AB上折出点B″使AB″=AB′.这时B″就是AB的黄金分割点.请你证明这个结论.24.如图,用纸折出黄金分割点:裁一张边长为2的正方形纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置F,因而EF=EB.类似的,在AB上折出点M使AM=AF.则M是AB的黄金分割点吗?若是请你证明,若不是请说明理由.25.如图,在△ABC中,点D在边AB上,且DB=DC=AC,已知∠ACE=108°,BC=2.(1)求∠B的度数;(2)我们把有一个内角等于36°的等腰三角形称为黄金三角形.它的腰长与底边长的比(或者底边长与腰长的比)等于黄金比.①写出图中所有的黄金三角形,选一个说明理由;②求AD的长;③在直线AB或BC上是否存在点P(点A、B除外),使△PDC是黄金三角形?若存在,在备用图中画出点P,简要说明画出点P的方法(不要求证明);若不存在,说明理由.26.宽与长的比是的矩形叫黄金矩形.心理测试表明:黄金矩形令人赏心悦目,它给我们以协调,匀称的美感.现将小波同学在数学活动课中,折叠黄金矩形的方法归纳如下(如图所示):第一步:作一个正方形ABCD;第二步:分别取AD,BC的中点M,N,连接MN;第三步:以N为圆心,ND长为半径画弧,交BC的延长线于E;第四步:过E作EF⊥AD,交AD的延长线于F.请你根据以上作法,证明矩形DCEF为黄金矩形.27.在△ABC中,AB=AC,∠A=36°,把像这样的三角形叫做黄金三角形.(1)请你设计三种不同的分法,将黄金三角形ABC分割成三个等腰三角形,使得分割成的三角形中含有两个黄金三角形(画图工具不限,要求画出分割线段;标出能够说明不同分法所得三角形的内角度数,不要求写画法,不要求证明.分别画在图1,图2,图3中)(2)如图4中,BF平分∠ABC交AC于F,取AB的中点E,连接EF并延长交BC的延长线于M.试判断CM 与AB之间的数量关系?只需说明结果,不用证明.答:CM与AB之间的数量关系是.28.折纸与证明﹣﹣﹣用纸折出黄金分割点:第一步:如图(1),先将一张正方形纸片ABCD对折,得到折痕EF;再折出矩形BCFE的对角线BF.第二步:如图(2),将AB边折到BF上,得到折痕BG,试说明点G为线段AD的黄金分割点(AG>GD)29.三角形中,顶角等于36°的等腰三角形称为黄金三角形,如图1,在△ABC中,已知:AB=AC,且∠A=36°.(1)在图1中,用尺规作AB的垂直平分线交AC于D,并连接BD(保留作图痕迹,不写作法);(2)△BCD是不是黄金三角形?如果是,请给出证明;如果不是,请说明理由;(3)设,试求k的值;(4)如图2,在△A1B1C1中,已知A1B1=A1C1,∠A1=108°,且A1B1=AB,请直接写出的值.30.如图1,点C将线段AB分成两部分,如果,那么称点C为线段AB的黄金分割点.某研究小组在进行课题学习时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成两部分,这两部分的面积分别为S1,S2,如果,那么称直线l为该图形的黄金分割线.(1)研究小组猜想:在△ABC中,若点D为AB边上的黄金分割点(如图2),则直线CD是△ABC的黄金分割线.你认为对吗?为什么?(2)请你说明:三角形的中线是否也是该三角形的黄金分割线?(3)研究小组在进一步探究中发现:过点C任作一条直线交AB于点E,再过点D作直线DF∥CE,交AC于点F,连接EF(如图3),则直线EF也是△ABC的黄金分割线.请你说明理由.(4)如图4,点E是平行四边形ABCD的边AB的黄金分割点,过点E作EF∥AD,交DC于点F,显然直线EF 是平行四边形ABCD的黄金分割线.请你画一条平行四边形ABCD的黄金分割线,使它不经过平行四边形ABCD 各边黄金分割点.黄金分割专项练习30题参考答案:1.(1)证明:∵AB=AC=1,∴∠ABC=∠C=(180°﹣∠A)=(180°﹣36°)=72°,∵BD平分∠ABC交AC于点D,∴∠ABD=∠CBD=∠ABC=36°,∴∠BDC=180°﹣36°﹣72°=72°,∴DA=DB,BD=BC,∴AD=BD=BC,易得△BDC∽△ABC,∴BC:AC=CD:BC,即BC2=CD•AC,∴AD2=CD•AC,∴点D是线段AC的黄金分割点;(2)设AD=x,则CD=AC﹣AD=1﹣x,∵AD2=CD•AC,∴x2=1﹣x,解得x1=,x2=,即AD的长为2.解:(1)设AB=xcm,则AD=(20﹣x)cm,根据题意得x(20﹣x)=99,整理得x2﹣20x+99=0,解得x1=9,x2=11,当x=9时,20﹣x=11;当x=11时,20﹣11=9,而AB>AD,所以x=11,即AB的长为11cm;(2)不能.理由如下:设AB=xcm,则AD=(20﹣x)cm,根据题意得x(20﹣x)=101,整理得x2﹣20x+101=0,因为△=202﹣4×101=﹣4<0,所以方程没有实数解,所以这个矩形的面积可能等于101cm2;(3)设AB=xcm,则AD=(20﹣x)cm,根据题意得20﹣x=x,解得x=10(﹣1),则20﹣x=10(3﹣),所以矩形的面积=10(﹣1)•10(3﹣)=(400﹣800)cm2.∵BD平分∠ABC,∴∠CBD=∠ABD=36°,∠BDC=72°,∴AD=BD,BC=BD,∴△ABC∽△BDC,∴=,即=,∴AD2=AC•CD.∴点D是线段AC的黄金分割点.(2)∵点D是线段AC的黄金分割点,∴AD=AC,∵AC=2,∴AD=﹣14.解:(1)腰与底之比为黄金比为黄金比如图,(2)作法:①画线段AB作为三角形底边;②取AB的一半作AB的垂线AC,连接BC,在BC上取CD=CA.③分别以A点和B点为圆心、以BD为半径划弧,交点为E;④分别连接EA、EB,则△ABE即是所求的三角形.(3)证明:设AB=2,则AC=1,BC=,AE=BE=BD=BC﹣CD=﹣1,=.5.解:(1)由于P为线段AB=2的黄金分割点,则AP=2×=﹣1,或AP=2﹣(﹣1)=3﹣;(2)如图,点P是线段AB的一个黄金分割点.6.解:(1)设AC=x,则BC=AB﹣AC=1﹣x,∵AC2=BC•AB,∴x2=1×(1﹣x),整理得x2+x﹣1=0,解得x1=,x2=(舍去),所以线段AC的长度为;(2)设线段AD的长度为x,AC=l,∵AD2=CD•AC,∴x2=l×(l﹣x),∴x1=,x2=(舍去),∴线段AD的长度AC;(3)同理得到线段AE的长度AD;上面各题的结果反映:若线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),则C点为AB的黄金分割点7.解:D是AC的黄金分割点.理由如下:∵在△ABC中,AB=AC,∠A=36°,∴∠ABC=∠ACB==72°.∵∠1=∠2,∴∠1=∠2=∠ABC=36°.∴在△BDC中,∠BDC=180°﹣∠2﹣∠C=72°,∴∠C=∠BDC,∴BC=BD.∵∠A=∠1,∴AD=BC.∵△ABC和△BDC中,∠2=∠A,∠C=∠C,∴△ABC∽△BDC,∴,又∵AB=AC,AD=BC=BD,∴,∴AD2=AC•CD,即D是AC的黄金分割点8.证明:∵AB=AC,∠A=36°,∴∠ABC=(180°﹣36°)=72°,∵BD平分∠ABC,交于AC于D,∴∠DBC=×∠ABC=×72°=36°,∴∠A=∠DBC,又∵∠C=∠C,∴△BCD∽△ABC,∴∵AB=AC,∴=,∵AB=AC=2,BC=﹣1,∴(﹣1)2=2×(2﹣AD),解得AD=,AD:AC=():2.∴点D是线段AC的黄金分割点.9.证明:在AB上截取AE=BC,DF=BC,连接EF.∵AE=BC,DF=BC,∴AE=DF=BC=AD,又∵∠ADF=90°,∴四边形AEFD是正方形.BE=,∴,∴矩形BCFE的宽与长的比是黄金分割比,矩形BCFE是黄金矩形.∴黄金矩形是由一个正方形和一个更小的黄金矩形构成.10.解:设正方形ABCD的边长为2,在Rt△AEB中,依题意,得AE=1,AB=2,由勾股定理知EB===,∴AH=AF=EF﹣AE=EB﹣AE=﹣1,HB=AB﹣AH=3﹣;∴AH2=()2=6﹣2,AB•HB=2×(3﹣)=6﹣2,∴AH2=AB•HB,所以点H是线段AB的黄金分割点.11.证明:(1)∵∠A=36°,∠C=72°,∴∠ABC=180°﹣36°﹣72°=72°,∵∠ADB=108°,∴∠ABD=180°﹣36°﹣108°=36°,∴△ADB是等腰三角形,∵∠BDC=180°﹣∠ADC=180°﹣108°=72°,∴△BDC是等腰三角形,∴AD=BD=BC.(2)∵∠DBC=∠A=36°,∠C=∠C,∴△ABC∽△BDC,∴BC:AC=CD:BC,∴BC2=AC•DC,∵BC=AD,∴AD2=AC•DC,∴点D是线段AC的黄金分割点.12.解:∵D在AB上,且AD2=BD•AB,∴点D是AB的黄金分割点而点C是AB的黄金分割点,∴AC=AB=﹣1,AD=AB﹣AB=AB=3﹣或AD=﹣1,AC=3﹣,∴CD=﹣1﹣(3﹣)=2﹣4,∴==或==.13.解:矩形ABFE是黄金矩形.∵AD=BC,DE=AB,∴==﹣1==.∴矩形ABFE是黄金矩形.14.解:∵D为AB的黄金分割点(AD>BD),∴AD=AB=10﹣10,∵EC+CD=AC+CD=AD,∴EC+CD=(10﹣10)cm.15.解:设他的肚脐到脚底的长度为xm时才是黄金身段,根据题意得x:1.70=0.618,即x=1.70×0.618≈1.1(m).答:他的肚脐到脚底的长度为1.1m时才是黄金身段.16.解:(1)在Rt△APD中,AP=1,AD=2,由勾股定理知PD===,∴AM=AF=PF﹣AP=PD﹣AP=﹣1,DM=AD﹣AM=3﹣.故AM的长为﹣1,DM的长为3﹣;(2)点M是AD的黄金分割点.由于=,∴点M是AD的黄金分割点.17.解:∵点P是线段AB的黄金分割点,且AP>BP,∴AP2=BP×AB,又∵S1=AP2,S2=PB×AB,∴S1=S2.18.解:∵四边形ABCD为平行四边形,∴∠CBF=∠AEB,∠BCF=∠BAE,∴△BCF∽△EAB,∴,即,把AD=,AB=+1代入得,=,解得:CF=2.故答案为:2.19.解:矩形EFDC是黄金矩形,证明:∵四边形ABEF是正方形,∴AB=DC=AF,又∵,∴,即点F是线段AD的黄金分割点.∴,∴,∴矩形CDFE是黄金矩形.20.解:(1)满足≈0.618的矩形是黄金矩形;(2)由=k得,BP=1×k=k,从而AP=1﹣k,由得,BP2=AP×AB,即k2=(1﹣k)×1,解得k=,∵k>0,∴k=≈0.618;(3)因为点P是线段AB的黄金分割点,所以,设△ABC的AB上的高为h,则,∴∴直线CP是△ABC的黄金分割线.(4)由(2)知,在BC边上也存在这样的黄金分割点Q,则AQ也是黄金分割线,设AQ与CP交于点W,则过点W的直线均是△ABC的黄金分割线,故黄金分割线有无数条.21.解:根据已知条件得下半身长是160×0.6=96cm,设选择的高跟鞋的高度是xcm,则根据黄金分割的定义得:=0.618,解得:x≈7.5cm.故她应该选择7.5cm左右的高跟鞋穿上看起来更美.22.解:设正方形ABCD的边长为2a,在Rt△AEB中,依题意,得AE=a,AB=2a,由勾股定理知EB==a,∴AH=AF=EF﹣AE=EB﹣AE=(﹣1)a,HB=AB﹣AH=(3﹣)a;∴AH2=(6﹣2)a2,AB•HB=2a×(3﹣)a=(6﹣2)a2,∴AH2=AB•HB,所以点H是线段AB的黄金分割点.23.证明:设正方形ABCD的边长为2,E为BC的中点,∴BE=1∴AE==,又∵B′E=BE=1,∴AB′=AE﹣B′E=﹣1,∴AB″∴点B″是线段AB的黄金分割点.24.证明:∵正方形ABCD的边长为2,E为BC的中点,∴BE=1∴AE==,∵EF=BE=1,∴AF=AE﹣EF=﹣1,∴AM=AF=﹣1,∴AM:AB=(﹣1):2,∴点M是线段AB的黄金分割点.25.解:(1)∵BD=DC=AC.则∠B=∠DCB,∠CDA=∠A.设∠B=x,则∠DCB=x,∠CDA=∠A=2x.又∠BOC=108°,∴∠B+∠A=108°.∴x+2x=108,x=36°.∴∠B=36°;(2)①有三个:△BDC,△ADC,△BAC.∵DB=DC,∠B=36°,∴△DBC是黄金三角形,(或∵CD=CA,∠ACD=180°﹣∠CDA﹣∠A=36°.∴△CDA是黄金三角形.或∵∠ACE=108°,∴∠ACB=72°.又∠A=2x=72°,∴∠A=∠ACB.∴BA=BC.∴△BAC是黄金三角形.②△BAC是黄金三角形,∴,∵BC=2,∴AC=﹣1.∵BA=BC=2,BD=AC=﹣1,∴AD=BA﹣BD=2﹣(﹣1)=3﹣,③存在,有三个符合条件的点P1、P2、P3.ⅰ)以CD为底边的黄金三角形:作CD的垂直平分线分别交直线AB、BC得到点P1、P2.ⅱ)以CD为腰的黄金三角形:以点C为圆心,CD为半径作弧与BC的交点为点P3.26.证明:在正方形ABCD中,取AB=2a,∵N为BC的中点,∴NC=BC=a.在Rt△DNC中,.又∵NE=ND,∴CE=NE﹣NC=(﹣1)a.∴.故矩形DCEF为黄金矩形.27.解:(1)(2)CM=AB(4分)28.证明:如图,连接GF,设正方形ABCD的边长为1,则DF=.在R t△BCF中,BF==,则A′F=BF﹣BA′=﹣1.设AG=A′G=x,则GD=1﹣x,在Rt△A′GF和Rt△DGF中,有A'F2+A'G2=DF2+DG2,即,解得x=,即点G是AD的黄金分割点(AG>GD).29.解:(1)如图所示;(2)△BCD是黄金三角形.证明如下:∵点D在AB的垂直平分线上,∴AD=BD,∴∠ABD=∠A.∵∠A=36°,AB=AC,∴∠ABC=∠C=72°,∴∠ABD=∠DBC=36°.又∵∠BDC=∠A+∠ABD=72°,∴∠BDC=∠C,∴BD=BC,∴△BCD是黄金三角形.(3)设BC=x,AC=y,由(2)知,AD=BD=BC=x.∵∠DBC=∠A,∠C=∠C,∴△BDC∽△ABC,∴,即,整理,得x2+xy﹣y2=0,解得.因为x、y均为正数,所以.(4).理由:延长BC到E,使CE=AC,连接AE.∵∠A=36°,AB=AC,∴∠ACB=∠B=72°,∴∠ACE=180°﹣72°=108°,∴∠ACE=∠B1A1C1.∵A1B1=AB,∴AC=CE=A1B1=A1C1,∴△ACE≌△B1A1C1,∴AE=B1C1.由(3)知,∴,,∴.30.解:(1)直线CD是△ABC的黄金分割线.理由如下:设△ABC的边AB上的高为h.则,,,∴,.又∵点D为边AB的黄金分割点,∴,∴.故直线CD是△ABC的黄金分割线.(2)∵三角形的中线将三角形分成面积相等的两部分,∴,即,故三角形的中线不可能是该三角形的黄金分割线.(3)∵DF∥CE,∴△DFC和△DFE的公共边DF上的高也相等,∴S△DFC=S△DFE,∴S△ADC=S△ADF+S△DFC=S△ADF+S△DFE=S△AEF,S△BDC=S四边形BEFC.又∵,∴.因此,直线EF也是△ABC的黄金分割线.(7分)(4)画法不惟一,现提供两种画法;画法一:如答图1,取EF的中点G,再过点G作一条直线分别交AB,DC于M,N点,则直线MN就是平行四边形ABCD的黄金分割线.画法二:如答图2,在DF上取一点N,连接EN,再过点F作FM∥NE交AB于点M,连接MN,则直线MN就是平行四边形ABCD的黄金分割线.(9分)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《黄金分割》专题练习
一、选择题
1.已知C是线段AB的一个黄金分割点,则AC∶AB为()
A.
21
5-
B.
25
3-
C.
21
5+
D.
21
5-
或
25
3-
1.在人体躯干(脚底到肚脐的长度)与身高的比例上,肚脐是理想的
黄金分割点,即比例越接近0.618越给人以
美感。
张女士的身高为1.68米,身体躯干(脚底到肚脐的高度)为1.02米,那么她应选择约多大的高跟鞋看起
来更美。
(精确到十分位)
是ABCD是ABCD 的黄金分割线。
请你画一条ABCD的黄金分割线,使它不经过
图形的黄金分割线。
(1)如图2,在△ABC中,∠A=36°,AB=AC,∠C的平分线交AB于点D,请问点D是否是AB边上的黄金分割点,并证明你的结论;
(2)若△ABC在(1)的条件下,如图3,请问直线CD是不是△ABC的黄金分割线,并证明你的结论;
(3)如图4,在直角梯形ABCD中,∠D=∠C=90°,对角线AC、BD交于点F,延长AB、DC交于点E,连接EF 交梯形上、下底于G、H两点,请问直线GH是不是直角梯形ABCD的黄金分割线,并证明你的结论。
8.已知线段AB,求作线段AB的黄金分割点C,使AC>BC。
《相似形》专题练习答案
一、选择题
1.D
2.D
3.A
4.C
5.B
二、填空题
1.215-或2
15+;
23618.0= 4
561.设张女士应该选择xcm 高的高跟鞋,则
618.0168102=++x
x ,解得x =4.8(cm )。
2.解:设应穿xcm 高的鞋子,
=
3
答:维纳斯女神雕像下部的高度为1.236m 。
618.0≈。
4
56.(1)直线是的黄金分割线。
理由如下:
设ABC △的边AB 上的高为h 。
12ADC S AD h =
△,12BDC S BD h =△,12ABC S AB h =△, 所以,ADC ABC S AD S AB =△△,BDC ADC S BD S AD
=△△。
又因为点D 为边AB 的黄金分割点,所以有
AD BD AB AD
=.因此ADC BDC ABC ADC S S S S =△△△△。
所以,直线CD 是ABC △的黄金分割线。
(2)因为三角形的中线将三角形分成面积相等的两部分,此时1212
s s s ==,即 121
s s s s ≠,所以三角形的中线不可能是该三角形的黄金分割线。
(3)因为DF CE ∥,所以DEC △和FCE △的公共边CE 上的高也相等,
所以有DEC FCE S S =△△。
N 点,则直
DF M ,连接MN ,
就是7
8另一种作法:
⑴经过点B 作BD ⊥AB ,使BD =12
AB ; ⑵连接AD ,在AD 上截取DE =DB 。
⑶在线段AB 上截取AC =AE 。
如图,点C 就是线段AB 的黄金分割点。
A E
B
C D。
