6_10+病态方程组和迭代改善法1
chapter03线性代数方程组迭代解法PPT课件

不完全分解
当矩阵无法进行完全分解时,迭代法可以作为 替代方案进行求解。
数值稳定性
对于某些数值不稳定的问题,迭代法可以提供更稳定的近似解。
迭代解法的优缺点分析
优点
适用于大规模问题,计算量相对较小; 适用于不完全分解和数值不稳定问题; 能够提供近似解,满足工程精度要求。
缺点
需要设定初始解向量或近似解向量; 迭代过程可能不收敛或收敛速度慢; 对于某些问题可能无法得到准确解。
SOR方法案例分析
01
SOR(Successive Over-Relaxation)方法是一种改进
的迭代方法,通过引入松弛因子来加速收敛。
02
SOR方法适用于系数矩阵为稀疏、对称正定的情况,
广泛应用于实际工程问题。
03
SOR方法的收敛速度与松弛因子的选择有关,选择合
适的松弛因子可以加快收敛速度。
Jacobi方法案例分析
松弛方法
松弛方法是另一种改进的迭代 算法,用于求解线性代数方程
组。
该方法通过引入松弛因子来调 整迭代过程中的系数矩阵,以
提高收敛速度和稳定性。
松弛方法适用于系数矩阵为非 对角占优的情况,尤其在处理 稀疏矩阵时具有优势。
总结词:松弛方法是一种适用 于非对角占优矩阵的迭代算法 ,通过调整松弛因子提高收敛 速度和稳定性。
收敛速度与系数矩阵
收敛速度与系数矩阵的特征值和范数有关,不同的迭 代法适用于不同的系数矩阵情况。
加速迭代法
为了提高迭代法的收敛速度,可以采用一些加速技巧, 如预处理技术、共轭梯度法等。
03 几种常见的迭代解法
Gauss-Seidel迭代法
Gauss-Seidel方法是一种迭 代算法,用于求解线性代数
线性方程组解的迭代改进

算法名称:线性方程组解的迭代改进算法描述:假定向量x是线性方程组(1)的精确解,然而并不知道解x,而仅仅知道一些略有误差的解x+δx,其中δx为未知的误差。
当将其乘以矩阵A时,这个有误差的解使乘积与原来的右端项b也存在偏差,即(2)由(2)式减去(1)式得,(3)但由(2)式也可求得δb,将其带入(3)式中得,(4)该方程中整个右端项是已知量,因为x+δx是有待改进的有误差的解。
然后,只需求解(4)式的偏差量δx,将其从有误差的解中减去便得到改进后的解。
这种情况下,已经有了矩阵A的LU分解形式,要求解(4)式,只需计算右端项再进行回代即可。
运行示例:The origin matrix:0.0 3.0 1.0 1.02.0 2.03.0 2.04.0 -3.0 0.0 1.06.0 1.0 -2.0 -5.0--------------------------The matrix (after LU decomposition):6.0 1.0 -2.0 -5.00.0 3.0 1.0 1.00.3333333333333333 0.5555555555555556 3.1111111111111107 3.11111111 111111070.6666666666666666 -1.222222222222222 0.8214285714285714 3.00000000 00000004--------------------------The right vector:0.0-2.0-5.06.0--------------------------The solution vector (before improvement):-0.45238095238095220.428571428571428660.6190476190476184-1.9047619047619044--------------------------The solution vector (after improvement):-0.452380952380952330.42857142857142860.6190476190476188-1.9047619047619049--------------------------代码示例:package com.nc4nr.chapter02.mprove;public class Mprove {// 建议从构造函数看起,Mprove// 4 * 4 coefficient matrix adouble[][] a = {{0.0, 3.0, 1.0, 1.0},{2.0, 2.0, 3.0, 2.0},{4.0, -3.0, 0.0, 1.0},{6.0, 1.0, -2.0, -5.0}};// 4 * 1 coefficient matrix bdouble[][] b = {{0.0},{-2.0},{-5.0},{6.0}};int anrow = 4;int[] indx = new int[anrow];double[][] x = new double[anrow][1]; // 请留意后面的注释double[][] ora = new double[anrow][anrow]; // 拷贝分解前的系数矩阵a,因为a被分解后将被破坏private void ludcmp() {int n = anrow, imax = 0;double[] vv = new double[anrow];for (int i = 0; i < n; i++) {double big = 0.0;for (int j = 0; j < n; j++) {double temp = Math.abs(a[i][j]);if (temp > big) big = temp;}if (big == 0.0) System.out.println("lu: singular matrix");vv[i] = 1.0/big;}for (int j = 0; j < n; j++) {for (int i = 0; i < j; i++) {double sum = a[i][j];for (int k = 0; k < i; k++) sum -= a[i][k]*a[k][j];a[i][j] = sum;}double big = 0.0;for (int i = j; i < n; i++) {double sum = a[i][j];for (int k = 0; k < j; k++) sum -= a[i][k]*a[k][j]; a[i][j] = sum;double dum = Math.abs(vv[i]*sum);if (dum >= big) {big = dum;imax = i;}}if (j != imax) {for (int i = 0; i < n; i++) {double mid = a[imax][i];a[imax][i] = a[j][i];a[j][i] = mid;}vv[imax] = vv[j];}indx[j] = imax;if (j != n-1) {double dum = 1.0/a[j][j];for (int k = j+1; k < n; k++) a[k][j] *= dum;}}}private void lubksb(double[][] alu, int[] idx, double[][] rb) { int n = anrow, ii = 0;for (int i = 0; i < n; i++) {int k = idx[i];double sum = rb[k][0];rb[k][0] = rb[i][0];if (ii != 0)for (int j = 0; j < i; j++) sum -= alu[i][j]*rb[j][0];else if (sum != 0)ii = i+1;rb[i][0] = sum;}for (int i = n-1; i >= 0; i--) {double dum = 1.0/alu[i][i];double sum = rb[i][0];for (int k = i+1; k < n; k++) sum -= alu[i][k]*rb[k][0]; rb[i][0] = dum * sum;}}private void mprove() {int n = anrow;double[][] r = new double[anrow][1];for (int i = 0; i < n; i++) {double sdp = -b[i][0];for (int j = 0; j < n; j++) {sdp += ora[i][j]*x[j][0];}r[i][0] = sdp;}lubksb(a,indx,r);for (int i = 0; i < n; i++) x[i][0] -= r[i][0];}private void output(double[][] m, int nrow, int ncol) { for (int i = 0; i < nrow; i++) {String str = "";for (int j = 0; j < ncol; j++) str += m[i][j] + " "; System.out.println(str);}System.out.println("--------------------------");}public Mprove() {// 拷贝原始系数矩阵a到orafor (int i = 0; i < anrow; i++) {for (int j = 0; j < anrow; j++) {ora[i][j] = a[i][j];}}// 拷贝原始右端项bfor (int i = 0; i < anrow; i++) {x[i][0] = b[i][0];}System.out.println("The origin matrix:");output(ora,anrow,anrow);// 这里将对a进行LU分解,并将分解结果存放到aludcmp();System.out.println("The matrix (after LU decomposition):");output(a,anrow,anrow);System.out.println("The right vector:");output(b,anrow,1);// 这里传入的是LU分解后的矩阵a,x将为带误差的解向量lubksb(a,indx,x);System.out.println("The solution vector (before improvement):"); output(x,anrow,1);// 这里将进行迭代改进xmprove();System.out.println("The solution vector (after improvement):"); output(x,anrow,1);// 本程序没有改变b和ora}public static void main(String[] args) {new Mprove();}}。
对病态方程组的处理方法研究

对病态方程组的处理方法研究蓝醒龙(广西民族大学数学与计算机科学学院03数本2班,530006)摘 要: 对病态线性方程组解法研究是数值计算方法的一个重要研究课题。
本文分析了病态方程组的特点,介绍了几种有效的解法。
关键词: 病态线性方程组;条件数;预处理;迭代Studying The Algorithm For Solving Ill-conditionedSystem Of EquationsAbstract : Studying the algorithm for solving ill-conditioned system of equations is an important issue. This paper analyses the equations characteristic, and introduces several effective algorithms.Key words :ill-conditioned system of equations; condition number; pretreatment; iteration1 问题的提出一个线性方程组 A X b =,若右端向量b 或系数矩阵A 的微小变化就会引起方程组的解发生很大的变化,则称A X b =为病态方程组。
方程组的系数矩阵A 的条件数()1C o n d A AA -=刻画了方程组的性态,若()1C ond A ≥,则称A X b =为“病态”方程组;若()Cond A 相对较小,则称A X b =为“良态”方程组。
良态方程组用GAUSS 消去法和JACOBI 等简单的迭代法就可以得到比较好的计算解,而对于病态方程组,一般的直接法和迭代法会有较大的误差,甚至严重失真。
所以,在解方程组时,有必要先对方程组的性态进行研究,采用相应的算法,才能得到比较精确的计算解。
利用方程组的条件数来判断就是一个很好的办法。
《2024年度病态方程组的RA加速投影法及新型SSOR预处理迭代法研究》范文

《病态方程组的RA加速投影法及新型SSOR预处理迭代法研究》篇一一、引言在科学计算和工程应用中,病态方程组常常出现,其解的稳定性与准确性对实际问题至关重要。
传统的迭代法如高斯-赛德尔法、雅可比法等,在处理病态方程组时往往面临收敛速度慢、解的稳定性差等问题。
因此,研究高效的迭代算法和预处理技术,对于解决病态方程组具有重要意义。
本文将重点研究RA加速投影法和新型SSOR预处理迭代法,以期为病态方程组的求解提供新的思路和方法。
二、RA加速投影法RA加速投影法是一种基于迭代思想的求解病态方程组的方法。
该方法通过引入RA(重启算法)思想,在迭代过程中动态调整迭代方向和步长,从而加快收敛速度。
首先,该方法对原问题进行适当的预处理,将原问题转化为一个易于求解的形式。
然后,利用投影法将解空间投影到某个子空间中,以降低问题的复杂性。
在迭代过程中,通过计算残差向量和投影矩阵的乘积,得到新的迭代方向和步长。
通过不断调整迭代方向和步长,使迭代过程逐渐逼近真实解。
RA加速投影法的优点在于其能够根据问题的特点动态调整迭代方向和步长,从而加快收敛速度。
同时,该方法具有较好的稳定性和鲁棒性,对于病态方程组的求解具有较好的适用性。
三、新型SSOR预处理迭代法SSOR(对称逐点松弛)预处理技术是一种常用的预处理方法,可以有效地改善原问题的条件数,从而提高迭代法的收敛速度。
本文将研究新型的SSOR预处理技术与迭代法相结合的方法。
新型SSOR预处理迭代法首先对原问题进行SSOR预处理,将原问题的系数矩阵转化为一个条件数较小的矩阵。
然后,利用迭代法对预处理后的矩阵进行求解。
在迭代过程中,通过引入适当的松弛因子和松弛策略,使迭代过程更加稳定和快速。
与传统的SSOR预处理技术相比,新型SSOR预处理迭代法具有更高的灵活性和可调性。
通过调整松弛因子和松弛策略,可以更好地适应不同的问题特点,从而提高求解的准确性和效率。
四、RA加速投影法与新型SSOR预处理迭代法的比较与分析RA加速投影法和新型SSOR预处理迭代法都是针对病态方程组求解的有效方法。
病态线性方程组

数值分析
由实际问题建立起来的线 性方程组Ax=b本身存在模 型误差和观测误差,或者 是由计算得到的,存在舍 入误差等。总之,A,b都会 有一定扰动ΔA, Δb, 因此实 际处理的是A+ ΔA或b+ Δb ,我们需要分析A或b的扰 动对解的影响。
数值分析
矩阵的条件数与病态线性方程组
提问:求解Ax=b时,A和b的误差对x有何影响? 1:A非奇异,设精确,b有误差Δb,导致解x有多大 误差?
北京航空航天大学 数学与系统科学学院
Email: numerical_analysis@ Password:beihang 答疑时间:星期三下午2:00-5:00 答疑地点:主216
朱立永
数值分析
第二章 线性方程组的解法
第四讲 病态线性方程组求解
数值分析
Gaussian elimination
• ||A|| ||A^-1||是我们遇到的第二个放大因子;
• cond(A)的具体大小与||∙||有关,但相对大小一致; • cond(A)的大小本质取决于A,与解题的方法无关;
• cond(A)=∞,如果A是奇异的。
数值分析
常用的矩阵条件数
cond ( A ) || A || || A
1
||
cond ( A ) 1 || A ||1 || A
1
||1
cond ( A ) 2 || A ||2 || A
1
||2
数值分析
1 1 2 Hn 例:Hilbert 阵 1 n
1 2 1 3
1 n 1
1 n 1 1 2 n 1
迭代法解方程组课程设计

迭代法解方程组课程设计一、课程目标知识目标:1. 学生能理解迭代法的概念,掌握迭代法解线性方程组的基本原理。
2. 学生能够运用迭代法求解特定类型的线性方程组,并理解其数学背景。
3. 学生了解迭代法的收敛性,并能够判断给定迭代法的收敛速度。
技能目标:1. 学生能够独立进行迭代法的算法设计,完成相关计算,并解决实际问题。
2. 学生通过数学软件或编程语言实践迭代法,提高计算和问题解决能力。
3. 学生通过小组合作,培养沟通和协作能力,共同完成更复杂的迭代法解题任务。
情感态度价值观目标:1. 学生培养对数学科学的兴趣,增强对迭代法在工程和科学计算中应用的认知。
2. 学生在学习过程中,培养耐心、细致的学术态度和勇于尝试的精神。
3. 学生通过解决实际问题,体会数学知识在实际生活中的应用,增强学习的积极性和实践意识。
课程性质分析:本课程为高中数学选修课,适用于已有一定线性代数基础的学生。
课程内容具有较强的逻辑性和实践性,要求学生具备一定的抽象思维能力及数学运算能力。
学生特点分析:高中生逻辑思维能力逐步成熟,具备一定的自主学习与合作探究能力。
学生对新鲜事物充满好奇,喜欢通过实践来验证理论知识。
教学要求:1. 教学中注重理论与实践相结合,提高学生的实际操作能力。
2. 教学过程中鼓励学生提问和分享,提高课堂互动性。
3. 关注学生个体差异,实施差异化教学,确保每位学生都能达到课程目标。
二、教学内容1. 迭代法基本概念:介绍迭代法的定义,迭代法的数学表达,以及迭代法在解线性方程组中的应用。
- 教材章节:第三章第四节“迭代法的基本概念”2. 迭代法的原理与算法:讲解雅可比迭代、高斯-赛德尔迭代等常用迭代法的原理和步骤。
- 教材章节:第三章第五节“迭代法的算法”3. 迭代法的收敛性分析:阐述迭代法的收敛条件,以及如何判断迭代法的收敛性。
- 教材章节:第三章第六节“迭代法的收敛性”4. 迭代法的计算实践:通过数学软件(如MATLAB)或编程语言(如Python)实现迭代法,求解具体线性方程组。
数值分析希尔伯特病态线性方程组

病态线性代数方程组的求解理论的分析表明,求解病态的线性代数方程组是困难的。
考虑方程组Hx = b的求解,其中H为Hilbert矩阵,H=(hij)n⨯n,hij=1,i,j=1,2,...,n i+j-11. 估计Hilbert矩阵2-条件数与阶数的关系;2. 选择问题的不同维数,分别用Gauss消去法,Jacobi迭代,GS迭代和SOR迭代求解,比较结果;3. 讨论病态问题求解的算法。
解:1、取Hilbert矩阵阶数最高分别为n=20和n=100。
采用Hilbert矩阵的2-条件数作为实验的比较对象,画出的曲线如下图所示:lg(cond(Hn))nlg(cond(Hn))~n关系图lg(cond(Hn))n从图中可以看出,在n≤13之前,图像接近直线,在n>13之后,图像趋于平缓,在一定的范围内上下波动。
为了比较图像的线性部分,作出一条直线与已知曲线进行比较。
比较直线的关系式为:lg(cond(Hn))=1.519n-1.833,结果下图所示。
lg(cond(Hn))~n关系图lg(cond(Hn))n从图2中可以看出,当n较小时,lg(cond(Hn))~n之间近似满足线性关系。
当n 继续增大到100时,lg(cond(Hn))~n关系图下图所示:lg(cond(Hn))~n关系图lg(cond(Hn))n从图中可以看出,图像的走势符合在n=20时的猜想,在n大于一定的值之后,图像趋于平缓,且在一定范围内震荡,同时又有一定上升趋势,但上升速度很慢。
2、选择不同的阶数n,设方程组的精确解为xz=(1,1,…,1)T进行计算,用四种方法解x_Guass1、x_Jacobi1、x_GS1、x_SOR1对比表如下表所示。
Gauss消去法求解:选择问题的阶数为3~8时,用Gauss消去法求得的解与精确解一致,当阶数为9~14时,解开始出现偏差,而且n越大,偏差越大。
用迭代法求解:取初始向量为1.2(1,1,…,1)T.无论n为多少阶,用Jacobi迭代方法迭代出现发散的不稳定现象,无法求解;用GS迭代方法迭代不发散,能求得解,但收敛非常缓慢,当迭代次数取得相当大(20000次)时解仍在精确解附近波动;取w=1.5,用SOR迭代方法迭代不发散,能求得解,收敛速度较GS迭代快一些,但仍非常缓慢。
迭代解法全章

向量-矩阵范数旳相容性,得到
|λ| || x ||=||λx|| =|| Ax|| ≤ || A || ||x||
从而,对A旳任何特征值λ均成立 |λ|≤|| A ||
(6.1)
设n阶矩阵A旳n个特征值为λ1,λ2,…λn。称
(
A)
max
1i n
i
为矩阵A旳谱半径,从(6.1)式得知,对矩阵A旳任何一
称(3)为求解(1)旳近似解旳迭代解法,称{x(k)}为(1)近
似解序列,称B为迭代矩阵。
假如 lim x (k ) x* 则有 k x*= Bx*+F
(4)
我们称迭代法(3)收敛,不然为发散。下面分析迭代格 式(3)收敛旳条件.
12/29/2023
19
x(k+1)= Bx(k)+F , k=0 ,1 , … , x*= Bx*+F
及向量
x*
( x1* ,
x2* ,,
x
* n
)T
假如
lim x(k) x* 0
k
则称向量序列 x(k) 收敛于向量 x* 。记作
lim x(k ) x* 或 x(k ) x*
k
向量序列 {x(k)} 收敛于向量 x*,当且仅当它旳每一 种分量序列收敛于x*旳相应分量,即
x(k)
x*
x(k) i
1
求解线性方程组旳数值解除了使用直接解法,迭代解 法也是经常采用旳一种措施,这种措施更有利于编程计 算,本章将简介这种措施。
§1 向量和矩阵旳范数
为了对线性方程组数值解旳精确程度,以及方程组 本身旳性态进行分析,需要对向量和矩阵旳“大小”引 进某种度量,范数就是一种度量尺度,向量和矩阵旳范 数在线性方程组数值措施旳研究中起着主要旳作用。
数值分析实验-病态线性方程组的算法设计
数值分析课程实验报告 实验名称 病态线性方程组的算法设计
班级
学号 姓名 序号
任课教师 评分 一、 实验目的
1、 初步病态线性方程组的判定。
2、 初步了解常规方法在求解病态线性方程组时遇到的困难。
3、 针对病态问题设计求解算法并验证算法的有效性。
二、用文字或图表记录实验过程和结果
1、Hilbert 矩阵如下:
11/21/1/21/31/(1)()1/1/(1)1/(21)n ij n
n H h n n n ⎡⎤⎢⎥+⎢⎥==⎢⎥⎢⎥+-⎣⎦L L M M M L 其中1(1)ij h i j =+-,它是一个对称正定矩阵,并且()n cond H 随着n 的增加迅速增加,利用Matlab 分析如下:
可以发现在阶数不断增大
Hilbert 矩阵的条件数不断增大,
这样使得求解Hilbert 病态方程
变得非常困难,即使A 或b 有微小
扰动时,即使求解过程是精确进
行的(即没有舍入误差),所得的
解相对于原方程的解也会有很大
的相对误差。
这就需要提出病态
线性方程组的求解方法,对于一
般的方程求解常用的有高斯(选
主元)消去算法、高斯—赛德尔迭代。
本试验先使用用列主元高斯消去算法和高斯-赛德尔迭代算法求解线性方程组:
n
H x b = 其中11(,,),(1,2,,)n T n i ij j b b b b h i n ====∑L L 。
2、高斯列主元消去算法
(1)设计流程图:。
数值分析实验报告--实验6--解线性方程组的迭代法

1 / 8数值分析实验六:解线性方程组的迭代法2016113 张威震1 病态线性方程组的求解1.1 问题描述理论的分析表明,求解病态的线性方程组是困难的。
实际情况是否如此,会出现怎样的现象呢?实验内容:考虑方程组Hx=b 的求解,其中系数矩阵H 为Hilbert 矩阵,,,1(),,,1,2,,1i j n n i j H h h i j n i j ⨯===+-这是一个著名的病态问题。
通过首先给定解(例如取为各个分量均为1)再计算出右端b 的办法给出确定的问题。
实验要求:(1)选择问题的维数为6,分别用Gauss 消去法、列主元Gauss 消去法、J 迭代法、GS 迭代法和SOR 迭代法求解方程组,其各自的结果如何?将计算结果与问题的解比较,结论如何?(2)逐步增大问题的维数(至少到100),仍然用上述的方法来解它们,计算的结果如何?计算的结果说明了什么?(3)讨论病态问题求解的算法1.2 算法设计首先编写各种求解方法的函数,Gauss 消去法和列主元高斯消去法使用实验5中编写的函数myGauss.m 即可,Jacobi 迭代法函数文件为myJacobi.m ,GS 迭代法函数文件为myGS.m ,SOR 方法的函数文件为mySOR.m 。
1.3 实验结果1.3.1 不同迭代法球求解方程组的结果比较选择H 为6*6方阵,方程组的精确解为x* = (1, 1, 1, 1, 1, 1)T ,然后用矩阵乘法计算得到b ,再使用Gauss 顺序消去法、Gauss 列主元消去法、Jacobi 迭代法、G-S 迭代法和SOR 方法分别计算得到数值解x1、x2、x3、x4,并计算出各数值解与精确解之间的无穷范数。
Matlab 脚本文件为Experiment6_1.m 。
迭代法的初始解x 0 = (0, 0, 0, 0, 0, 0)T ,收敛准则为||x(k+1)-x(k)||∞<eps=1e-6,SOR方法的松弛因子选择为w=1.3,计算结果如表1。
病态线性方程组的求解

《科学与工程计算》实验报告学号:姓名:一、实验内容:考虑方程组Hx=b 的求解,其中系数矩阵H 为Hilbert 矩阵,nj i j i h h H j i n n j i ,,2,1,,11,)(,, =-+==⨯这是一个著名的病态问题。
通过首先给定解(例如取为各个分量均为1)再计算出右端b 的办法给出确定的问题。
实验要求:(1)选择问题的维数为6,分别用Jacobi 迭代法、GS 迭代法和SOR 迭代法求解方程组,其各自的结果如何?将计算结果与问题的解比较,结论如何?(2)逐步增大问题的维数,仍然用上述的方法来解它们,计算的结果如何?计算的结果说明了什么? (3)讨论病态问题求解的算法。
二、程序设计的基本思想、原理和算法描述:1、 算法 Jacobi 迭代法若A 为稀疏矩阵,只需遍历非零元素GS 迭代法若A 为稀疏矩阵,只需遍历非零元素每步迭代计算量相当于一次矩阵与向量的乘法;不需要保留上一步的迭代解,与Jacobi 迭代法计算量一样。
SOR 迭代法(稠密矩阵)2、 函数组成double max(double array[100]) 求数组中的最大值函数3、 输入/输出设计对于方程组Hx=b 的求解,系数矩阵H 为Hilbert 矩阵,矩阵中的数由下列函数生成。
nj i j i h h H j i n n j i ,,2,1,,11,)(,, =-+==⨯X*取一个特解[1,1,1, (1)b 数组由矩阵的每行元素相加得来。
4、符号名说明double c[100] 用来存储第k+1次和第k 次迭代结果的差值的绝对值 double x[100] 第k+1次迭代结果,储存解数组 double x0[100] 初始向量double r 第k+1次和第k 次迭代结果的差值的绝对值的最大值 double sum 矩阵方程变换后右侧值的和 int k 迭代次数double a[100][100] 存储Hilbert 矩阵 double b[100] 存储b 向量三、源程序及注释:Jacobi 迭代法#include<iostream> #include<math.h> #include <iomanip> #include <stdio.h> using namespace std; int n;double max(double array[100])//求最大值函数 {double a=array[0]; int i;for(i=1; i<n; i++) {if(a<array[i]) a=array[i]; return a; } }double c[100]= {0.0};double x[100]= {0.0}; //第k+1次迭代结果,储存解数组 double x0[100]= {0.0}; //初始向量double r,sum=0; int main(){double s=0;int i,k,j;//k为迭代次数double a[100][100];double b[100]= {0.0};cout<<"请输入维数:"<<endl;cin>>n;cout<<"输出a数组:"<<endl;double max(double array[100]);for(i=0; i<n; i++){for(j=0; j<n; j++){a[i][j]=1.0/(i+j+1);printf("%10.6lf ",a[i][j]);//矩阵中的数精确到六位}cout<<endl;}cout<<"输出b数组:"<<endl;for(i=0; i<n; i++){for(j=0; j<n; j++){b[i]+=a[i][j];//矩阵每行的和}cout<<b[i]<<" ";}cout<<endl;cout<<"输入精度:"<<endl;cin>>s;for(k=1;; k++){for(i=0; i<n; i++){for(j=0; j<n; j++){sum=a[i][j]*x0[j]+sum;}x[i]=x0[i]+((b[i]-sum)/a[i][i]);//雅克比迭代方法计算方式c[i]=fabs(x[i]-x0[i]);//求差值的绝对值x0[i]=x[i];sum=0;r=max(c);if(r<s)//输出迭代次数{for(i=0; i<n; i++)cout<<"x"<<i<<" = "<<x[i]<<setprecision(10)<<endl;cout<<"迭代次数:"<<k<<endl;return 0;}}return 0;}GS迭代法#include<iostream>#include<math.h>#include <iomanip>#include <stdio.h>using namespace std;int n;double max(double array[100])//求最大值函数{double a=array[0];int i;for(i=1;i<n;i++){if(a<array[i])a=array[i];}return a;}main() {double s=0;double max(double array[100]);double c[100]={0.0};double x[100]={0.0};//第k+1次迭代结果,储存解数组double x0[100]={0.0};//初始向量int i,k,j;double r,sum=0;double a[100][100];double b[100]= {0.0};cout<<"请输入维数:"<<endl;cout<<"输出a数组:"<<endl;for(i=0; i<n; i++){for(j=0; j<n; j++){a[i][j]=1.0/(i+j+1);printf("%10.6lf ",a[i][j]);//矩阵中的数精确到六位}cout<<endl;}cout<<"输出b数组:"<<endl;for(i=0; i<n; i++){for(j=0; j<n; j++){b[i]+=a[i][j];//矩阵每行的和}cout<<b[i]<<" ";}cout<<endl;cout<<"输入精度:"<<endl;cin>>s;for(k=1;;k++){for(i=0;i<n;i++){for(j=0;j<n;j++){sum=a[i][j]*x0[j]+sum;}x[i]=x0[i]+((b[i]-sum)/a[i][i]);//gs迭代方法计算方式c[i]=fabs(x[i]-x0[i]);//求差值的绝对值x0[i]=x[i];sum=0;}r=max(c);if(r<s)//输出迭代次数{for(i=0;i<n;i++)cout<<"x"<<i<<" = "<<x[i]<<setprecision(10)<<endl;cout<<"迭代次数:"<<k<<endl;return 0;}}}SOR迭代法#include<iostream>#include<math.h>#include <iomanip>#include <stdio.h>using namespace std;int n;double max(double array[100]){double a=array[0];int i;for(i=1;i<n;i++){if(a<array[i])a=array[i];}return a;}int main() {double s=0,w=0;int i,k,j;//k为迭代次数double max(double array[100]);double c[100]= {0.0}; //double x[100]= {0.0}; //第k+1次迭代结果,储存解数组double x0[100]= {0.0}; //初始向量int i,k,j;double r,sum=0;double a[100][100];double b[100]= {0.0};cout<<"请输入维数:"<<endl;cin>>n;cout<<"输出a数组:"<<endl;for(i=0; i<n; i++){for(j=0; j<n; j++){a[i][j]=1.0/(i+j+1);printf("%10.6lf ",a[i][j]);//cout<<a[i][j]<<" ";}cout<<endl;}cout<<"输出b数组:"<<endl;for(i=0; i<n; i++){for(j=0; j<n; j++){b[i]+=a[i][j];}cout<<b[i]<<" ";}cout<<endl;cout<<"输入精度:"<<endl;cin>>s;cout<<"输入松弛因子:"<<endl;cin>>w;for(k=1;;k++){for(i=0;i<n;i++){for(j=0;j<n;j++){sum=a[i][j]*x0[j]+sum;}x[i]=x0[i]+(w*(b[i]-sum)/a[i][i]);//sor迭代方法的计算公式c[i]=fabs(x[i]-x0[i]);//求差值的绝对值x0[i]=x[i];sum=0;}r=max(c);if(r<s)//输出迭代次数{for(i=0;i<n;i++)cout<<"x"<<i<<" = "<<x[i]<<setprecision(10)<<endl; cout<<"迭代次数:"<<k<<endl;return 0;}}}四、运行输出结果:JacobiGSSOR五、结果比较分析:说明:Hx=b,H矩阵可以由函数hi,j=1/(i+j-1)直接由程序生成,为了设定参考解,我们先设x为分量全1的向量,求出b,然后将H和b作为已知量,求x,与设定的参考解对比。
第六章病态方程解算方法

2、病态性程度的衡量方法 a、特征分析法 法矩阵N有多少个特征值很接近于零,设计矩阵B中就有多少 个复共线性关系。但“很接近于零”是一个很模糊的说法。
通常的判断标准,N的特征值i中,i 0.1时,可以认为不存 在复共线性;0.05 i 0.1时,有弱复共线性;0.01 i 0.05时,有 中等强度复共线性;i 0.01时,有严重的复共线性。
所以:x A A1 b
x
b
2)设A、b均有误差时,解x有多大误差?
即 A Ax x b b
得解的相对误差为:x x
1
A A1 A A1
A
b b
A A
A
定义
矩阵的条件数:对非奇异阵A,称乘积 A A1 为矩阵A的 条件数。它刻画了方程组的解对原始数据的敏感程度。
b、条件数法
K condN N N 1 max
m in
一般认为K 100时没有复共线性;K 1000时存在严重的复共线性,系统 呈病态。这个指标是在对数据中心化标准化的前提下得到的。但在测量
数据处理实际应用中,如GPS快速定位中,条件数大致在1013左右。所以 对上述准则应根据实际情况修正取舍。
设有观测方程(式中观测值向量L的权阵P已经单位化): A x L e
nt t1 n1 n1
A是设计矩阵,e是误差向量。得x的最小二乘最小范数解为 xˆLS A L
A是A的广义逆。 下面对A进行奇异值分解:
(1)当rank( A) p p minn,t时,对A阵可分解为
若A与A
E
均
A
属于R
病态线性方程组的求解
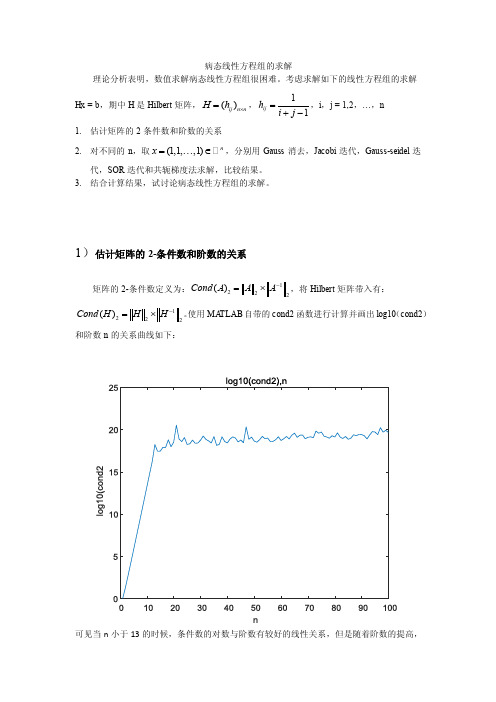
病态线性方程组的求解理论分析表明,数值求解病态线性方程组很困难。
考虑求解如下的线性方程组的求解Hx = b ,期中H 是Hilbert 矩阵,()ij n n H h ⨯=,11ij h i j =+-,i ,j = 1,2,…,n1. 估计矩阵的2条件数和阶数的关系2. 对不同的n ,取(1,1,,1)n x =∈ ,分别用Gauss 消去,Jacobi 迭代,Gauss-seidel 迭代,SOR 迭代和共轭梯度法求解,比较结果。
3. 结合计算结果,试讨论病态线性方程组的求解。
1)估计矩阵的2-条件数和阶数的关系矩阵的2-条件数定义为:1222()Cond A A A-=⨯,将Hilbert 矩阵带入有:1222()Cond H H H -=⨯。
使用MA TLAB 自带的cond2函数进行计算并画出log10(cond2)和阶数n 的关系曲线如下:可见当n 小于13的时候,条件数的对数与阶数有较好的线性关系,但是随着阶数的提高,条件数趋于“稳定”地振荡。
但是事实上,n较大时,H矩阵已经奇异,直接使用cond函数计算结果可能存在不准确性。
原因是对于条件数过大的矩阵使用inv函数求逆矩阵是不可靠的,应该使用invhilb函数进行求逆,并代入定义式中求解,生成的结果如下所示。
线性度较好,可知,Hilbert矩阵的2-条件数会随其阶数n的增加呈指数增大趋势,因此当n 较大时Hilbert矩阵将是严重病态的。
对不同的n,采用各种方法求解方程编写程序,选取n=2,3,5,10,15,20,迭代条件为迭代100000次或者是计算精度达到1e-6,若迭代次数少于设定最大值,表示相邻两次迭代达到精度要求,或者是计算结果超出范围。
X0取零向量,w取1.2,计算结果如下所示:由上可见,当n大于2时,Jacobi法已经不收敛,故其迭代次数已经没有意义。
当n=15时,Gauss消去法已经不收敛。
并且随着阶数的上升,gauss消去法的误差也随之上升。
迭代改善法

设
a11 a21 (1) A= A = a m1 a12 a22 am2 a1n a2n a 列 块. =(a1 a2 n ) (按 分 ) amn
′ xi =cxi +sx j , x′ =sxi +cx j , j ′ xk = xk (k ≠i, j).
23
由 c, s 的取法得
′ xi = xi2 + x2 , x′ =0. j j
24
5.7.3
矩阵的QR分解 分解 矩阵的
设 A∈Rm×n 且为非零矩阵,则存在初等反射阵
H1,H2 , Hs , 使 ,
∞
Ly = Pr , k 即 (用单精度) Udk = y.
/ xk
∞
≤10t 则输出 k, xk , r , 停机 k
改善 xk+1 = xk + dk (用单精度计算)
4
3.
输出迭代改善方法迭代 N0次失败信息
当 Ax = b 不是过分病态时,迭代改善法是比较好的改进 近似解精度的一种方法,当 Ax = b非常病态时,{xk }可能 不收敛. 例11 用迭代改善法解
9
2 nω2 ω
定理25 定理25
设有初等反射阵 H = I 2wwT , 其中
wT w=1 则: ,
(1) H是对称矩阵,即 HT = H. (2) H是正交矩阵,即 H 1 = H. (3) 设 A为对称矩阵,那么 A = H 1AH = HAH 亦是对 1 称矩阵. 证明 只证 H 的正交性,其他都可通过验证得到.
显然, P(i, j,θ ) 具有性质: (1) P 与单位阵 I 只是在 (i, i), (i, j), ( j, i), ( j, j) 位置 元素不一样,其他相同. (2) P 为正交矩阵 (P1 = PT ). (3) P(i, j) A(左乘)只需计算第 i 行与第 j 行元素, 即对 A = (aij )m×n 有
迭代改善法

212 2 1 22 2
9
定理25
设有初等反射阵 H I 2wwT , 其中
wT w 1, 则:
(1) H 是对称矩阵,即 H T H .
(2) H 是正交矩阵,即 H 1 H .
说明 x2 就是 Ax b 的精确解.
2
但在实际计算中,由于有舍入误差,x2 只是方程组的 近似解,重复(6.14),(6.15)的过程,就产生一近似解序列 ,有时可能得到比较好的近似. { xk } 算法5 (迭代改善法) 设 Ax b,其中 A R nn 为非
奇异矩阵,且 Ax b为病态方程组(但不过分病态),用选 主元分解法得到 PA 及计算解 x1 . LU
5.6.2
迭代改善法
设 Ax b,其中 A R nn 为非奇异矩阵,且为病态 方程组(但不过分病态).
本节研究的问题是,当求得方程组的近似解 x1后,
如何对其精度进行改善.
首先用选主元三角分解法实现分解计算
PA LU ,
其中 P为置换阵, L为单位下三角阵, U为上三角阵, 且求得计算解 x1 .
(1) 计算 rk b Axk (用原始 A 及双精度计算)
(2) 求解 LUdk P rk , (3) (4) 如果 d k
即
Ly P rk , (用单精度) Udk y.
/ xk
10t 则输出 k , xk , rk , 停机
改善 xk 1 xk d k (用单精度计算)
i1
n
1/ 2
在计算 时,为了避免上溢或下溢,将 x
d x
,
x
求解线性方程组的迭代解法

可简记为: ( k 1) 1 i 1 ( k ) n xi ( aij x j aij x (jk ) bi ) aii j 1 j i 1 也可写作为:
(i 1,2,, n)
(4 - 3)
x
( k 1)
Bx
(k )
g
(k 0,1,2,, )
(4 - 4)
由此可建立迭代格式:
雅可比(Jacobi)迭代法(续)
(k ) (k ) (k ) x1( k 1) ( a12 x2 a13 x3 a1n xn b1 ) / a11 ( k 1) (k ) (k ) (k ) a23 x3 a2 n xn b2 ) / a22 x2 ( a21 x1 4 2 (k ) (k ) (k ) ( k 1) (k ) x ( a x a x a x a x bn ) / ann n1 1 n2 2 ni i nn 1 n 1 n
1 12 2 1n n 1
(4 - 1)
简记为:
a
j 1
n
ij
x j bi
(i 1,2,, n)
其系数矩阵A非奇异,不妨设aii≠ 0 (1,2,…,n)可将上式 改写为等价方程组: a12 x2 a13 x3 a1n xn b1 ) / a11 x1 ( x ( a x a 23 x3 a 2 n xn b2 ) / a 22 2 21 1 bn ) / a nn xn ( a n1 x1 a n 2 x2 a ni xi a nn 1 xn 1
§1 向量序列与矩阵序列的极限
与求解方程类似,需要讨论的问题是:如何建 立迭代公式,向量序列的收敛条件是什么,若向量 序列{x(k)}收敛,如何进行误差估计?
迭代改善法

例11 用迭代改善法解
1.0303 0.99030
0.99030 0.95285
x1 x2
2.4944 2.3988
(记为Ax b) (这里 10,,t 用55位浮点数运算).
5
解 精确解 x* (1.2240,1(.2舍4入54到)T小数后 第4位).
cond ( A)
A
A1
22000 4000.
如果 需xk要更多的数位,迭代可以继续.
7
5.7 矩阵的正交三角化及应用
8
5.7.1 初等反射阵
定义9
设向量 w R且n w,T w 1
H (w) I 2wwT
为初等反射阵(或称为豪斯霍尔德(Householder)变换).
如果记 w (1,,2则, ,n )T
1 212 212
r1 5.7 107 3.3715 105
d1
x2
r2
0.03220 1.2238 1.18106
0.033502 1.2456 9107
d2 2.285 104 2.365104
x3 (1.2240,1.2454)T , r3 (0.682105 , 0.659105 )T , d3 (0.2717104 , 0.3515104 )T .
i
j
Px (x1, xi, 0, xn )T
其中 xi
xi2
x
2 j
,
arctan(x j / xi ).
证明 取 c cos xi / xi, s .sin x j / xi 由 P(i, j, )x x (x1, x2 , ,, xi, , xj , , xn )T
利用矩阵乘法,显然有
H
方程与方程组的迭代解法PPT课件

a)
0
lim
n
an
lim
n
bn
x
第5页/共68页
求方程 f(x)=0的根的二分法算法
(1) 输入 : 有根区间[a,b]的a,b值及精度控制量 ;
(2) if f (a) f (b) 0 then 返回第1步,重新 输入a, b值else转第3步;
(3)while | a b | 时做
1)令x 1 (a b),计算f (x); 2
例题
• 精确到小数点后五位
x 1.32472 1 105
2
第15页/共68页
例题
• 但如果由
建立迭代公式
仍取
,则有
,
显然结果越来越大, 是发散序列
x x3 1
xk1 xk3 1 k 1, 22.39 {xk }
第16页/共68页
迭代法的收敛性
第28页/共68页
迭代法收敛的阶
当p=1时,称为线性收敛; 当p>1时,称为超线性收敛; 当p=2时,称为平方收敛或二次收敛。 迭代法p 阶收敛的充要条件是:迭代函数(x) 满
足
'( ) ''( ) ( p1) ( ) 0,但 ( p) 0。
第29页/共68页
加速收敛技术
1. 松弛法:适当选取常数(称为松弛因子),令
第39页/共68页
Newton迭代法收敛性
|
xn
|
Ln 1 L
|
x1
x0
|
这是事前估计。选取n,预先估计迭代次数。
第22页/共68页
|
xn
|
L 1 L
|
xn
xn 1
|
基于LU分解的阻尼谱修正迭代法在病态线性方程组中的应用

êê-1.000 0
A18 × 7
=
êêêêêêêêêêêêêêêêêêêêêêêêêêêêêêêê-
1.000 1.000 3.000 5.000 4.000 4.000 1.500 3.000 1.000 5.000
0 0 0 0 0 0 0 0 0 0
ê 1.200 0
êê-3.000 0
ê ê ë
2.000 0 4.000 0 1.000 0 3.000 0 3.500 0 2.000 0 1.000 0 3.000 0 -1.000 0 6.000 0 3.000 0 2.000 0 -4.000 0 1.000 0 3.000 0 1.500 0 5.000 0 2.000 0
5.029 3 -3.012 6 -2.976 0
第 32 卷 第 3 期 2021 年 9 月
广西科技大学学报 JOURNAL OF GUANGXI UNIVERSITY OF SCIENCE AND TECHNOLOGY
Vol.32 No.3 Sep. 2021
基于 LU 分解的阻尼谱修正迭代法在病态 线性方程组中的应用
莫春鹏,覃柏英*
(广西科技大学 理学院,广西 柳州 545006)
ê 1848.116 0ú
7.000 0úú
ê ê
2 153.024 0úú
-3.000 0úú
ê ê
935.775 2úú
1.000 0ú
ê 931.853 1ú
-9.000 0úú
êê-2 763.276 2úú
2.000 6.000
00ûúú
ê ê ë
2
165.484 606.828
50ûúú
6_10+病态方程组和迭代改善法1

§10 病态方程组一、 病态方程组二、 扰动对解的影响三、 矩阵的条件数与病态、良态方程组四、 病态方程组的解法一、 病态方程组引例:方程组 1212570.77101x x x x +=⎧⎨+=⎩的解为x=(0.0,0.1)T . 现考虑项b 有微小的误差(0.69,1.01)T b b b δ→+=,其中(0.01,0.01)T b δ=−, 得到一个扰动方程组1212570.69710 1.01x x x x +=⎧⎨+=⎩其解为ˆ(0.17,0.22)T x =−.此例说明方程组的常数项分量只有微小的变化(||||/||||1/100b b δ∞∞=),但是方程组的解发生了较大的变化(||||/||||17/100x x δ∞∞=),并且这种变化并不是由求解方法带来的,而是方程组本身固有的,也就是说该方程组不是个好的方程组,通常我们称此类方程组为病态方程组。
那么如何知道一个方程组是不是病态方程组呢?显然我们必须建立起常数项以及系数矩阵的扰动对解的影响的估计式,以此对这个问题进行判断。
二、 扰动对解的影响(一) b 扰动对解的影响定理17 (b 扰动对解的影响)(1) Ax=b≠0,x 为精确解,A 为非奇异矩阵;(2) A(x+δx)=b+δb则有1||||||||||||||||||||||||x b A A x b δδ−≤⋅⋅.该定理表明,常数项变化引起的解的变化受因子1||||||||A A −⋅的控制,1||||||||A A −⋅的大小刻画了解对常数项的灵敏程度。
注意:一般说来11||||||||||||A A A A −−⋅≠⋅(二) A 扰动对解的影响定理18 (A 扰动对解的影响)(1) Ax=b≠0,x 为精确解,A 为非奇异矩阵;(2) (A+δA)(x+δx)=b ,且设1||||1/||||A A δ−≤ 则有11||||||||||||||||||||||||||||1||||||||||||A A A x A A x A A A δδδ−−⋅⋅≤−⋅⋅.该定理表明,系数矩阵项变化引起的解的变化也受因子1||||||||A A −⋅的控制, 1||||||||A A −⋅的大小也刻画了解对系数矩阵的灵敏程度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§10 病态方程组
一、 病态方程组
二、 扰动对解的影响
三、 矩阵的条件数与病态、良态方程组
四、 病态方程组的解法
一、 病态方程组
引例:方程组 1212
570.77101x x x x +=⎧⎨+=⎩的解为x=(0.0,0.1)T . 现考虑项b 有微小的误差
(0.69,1.01)T b b b δ→+=,其中(0.01,0.01)T b δ=−, 得到一个扰动方程组
1212570.69710 1.01x x x x +=⎧⎨+=⎩
其解为
ˆ(0.17,0.22)T x =−.
此例说明方程组的常数项分量只有微小的
变化(||||/||||1/100b b δ∞∞=)
,但是方程组的解发生了较大的变化(||||/||||17/100x x δ∞∞=)
,并且这种变化并不是由求解方法带来的,而是方程组本身固有的,也就是说该方程组不是个好的方程组,通常我们称此类方程组为病态方程组。
那么如何知道一个方程组是不是病态方程组呢?显然我们必须建立起常数项以及系数矩阵的扰动对解的影响的估计式,以此对这个问题进行判断。
二、 扰动对解的影响
(一) b 扰动对解的影响
定理17 (b 扰动对解的影响)
(1) Ax=b≠0,x 为精确解,A 为非奇异矩阵;
(2) A(x+δx)=b+δb
则有
1||||||||||||||||||||||||x b A A x b δδ−≤⋅⋅.
该定理表明,常数项变化引起的解的变化受因子
1||||||||A A −⋅的控制,1||||||||A A −⋅的大小刻画了解对常数项的灵敏程度。
注意:一般说来
11||||||||||||A A A A −−⋅≠⋅
(二) A 扰动对解的影响
定理18 (A 扰动对解的影响)
(1) Ax=b≠0,x 为精确解,A 为非奇异矩阵;
(2) (A+δA)(x+δx)=b ,且设
1||||1/||||A A δ−≤ 则有
11||||
||||||||||||||||||||||||1||||||||||||A A A x A A x A A A δδδ−−⋅⋅
≤−⋅⋅.
该定理表明,系数矩阵项变化引起的解的变
化也受因子
1||||||||A A −⋅的控制, 1||||||||A A −⋅的大小也刻画了解对系数矩阵的灵敏程度。
三、 矩阵的条件数与病态、良态方程组
(一) 矩阵的条件数
1.定义
矩阵的条件数:1()||||||||v
v v cond A A A −=⋅, 其中v 为矩阵的算子范数,如1,2,或∞.
2.性质
(1)()1v cond A ≥
(2)()(),0v v cond cA cond A c =≠
(3)
2()cond A = (4)若A 为对称正定矩阵,设其特征值为
120n λλλ≥≥≥>"
则
21()/n cond A λλ=
(5)若A 为正交矩阵,则2()1cond A =
(6)若A 为非奇异矩阵,P 为正交矩阵,则
222()()()cond PA cond AP cond A ==
3.例子:Hilbert 矩阵(病态矩阵的典型例子)
11/21/1/21/31/(1)1/1/(1)1/(21)n n n H n n n ⎡⎤⎢⎥+⎢⎥=⎢⎥⎢⎥+−⎣⎦
""####"
H n 是对称正定矩阵,21()/n n cond H λλ= n 3 5 6 8 2()n cond H 5×1025×10515×10615×109
(三) 病态、良态方程组
矩阵的条件数很大(远远大于1)称为病态方程组,此外称为良态方程组。
注:方程组的病态是方程组本身固有的特性,当方程组的病态程度高时,用普通的数值解法很难求得比较精确的解。
四、 病态方程组的解法
1.判断和发现病态方程组Ax=b
(1) 当A的行列式相对来说很小,或A的某些行(或列)近似线性相关时.
(2) 若用选主元素消去法求解时,出现小主元. (3) 当A的元素数量级相差很大,并且无一定规则时.
(4) A的条件数很大
2. 病态方程组的解法
根本目的:改善矩阵的条件数
(1) 方程组预处理法(变换系数矩阵)
1ˆˆˆ()Ax b PAQ Q x Pb Ax b −=⇔=⇔=
其中,P,Q 为非奇异的矩阵,且应使
ˆ()()()cond A
cond PAQ cond A =< 当A 为对称正定矩阵时,一般选择P,Q 为非奇异的对角矩阵或三角矩阵。
(2)平衡方法
当A的元素数量级相差很大时,首先将A 的行(或列)进行均衡化处理,即对Ax=b的每一行乘以适当的数,使所有行按照某种范数大体均衡。
ˆ
ˆ
=⇔=⇔=
Ax b DAx Db Ax b
其中D为非奇异的对角矩阵。
例子:方程组
44
1211010112x x ⎡⎤
⎡⎤⎡
⎤
=⎢⎥⎢⎥
⎢⎥⎣⎦⎣⎦⎣⎦
解:
4()10cond A ∞≈较大,为病态矩阵 采用平衡方法,将A 化为
4
100ˆ01A DA A −⎡⎤
==⎢⎥⎣⎦
则ˆ()4cond A ∞≈,ˆˆAx b =为良态方程组,用列
主元素消去法,可得其解为x1=x2=1(是较好的近似解)。
