动力学系统时域响应计算的六种方法Matlab源程序(Newmark,Houbolt法,中心差分法)
newmark法程序法计算多自由度体系的动力响应

用matlab 编程实现Newmark -β法计算多自由度体系的动力响应用matlab 编程实现Newmark -β法计算多自由度体系的动力响应一、Newmark -β法的基本原理Newmark-β法是一种逐步积分的方法,避免了任何叠加的应用,能很好的适应非线性的反应分析。
Newmark-β法假定:t u u u ut t t t t t ∆ββ∆∆]}{}){1[(}{}{+++-+= (1-1)2]}{}){21[(}{}{}{t u u t u u u t t t t t t ∆γγ∆∆∆+++-++= (1-2)式中,β和γ是按积分的精度和稳定性要求进行调整的参数。
当β=0.5,γ=0.25时,为常平均加速度法,即假定从t 到t +∆t 时刻的速度不变,取为常数)}{}({21t t t u u ∆++ 。
研究表明,当β≥0.5, γ≥0.25(0.5+β)2时,Newmark-β法是一种无条件稳定的格式。
由式(2-141)和式(2-142)可得到用t t u ∆+}{及t u }{,t u}{ ,t u }{ 表示的t t u ∆+}{ ,t t u ∆+}{ 表达式,即有t t t t t t t u u t u u t u }){121(}{1)}{}({1}{2 ----=++γ∆γ∆γ∆∆(1-3)t t t t t t t u t u u u t u }{21(}){1()}{}({}{ ∆γβγβ∆γβ∆∆-+-+-=++(1-4)考虑t +∆t 时刻的振动微分方程为:t t t t t t t t R u K u C u M ∆∆∆∆++++=++}{}]{[}]{[}]{[ (1-5)将式(2-143)、式(2-144)代入(2-145),得到关于u t +∆t 的方程t t t t R u K ∆∆++=}{}]{[(1-6)式中][][1][][2C t M tK K ∆γβ∆γ++=)}{)12(}){1(}{]([)}){121(}{1}{1]([}{}{2t t t t t t t t u t u u t C u u t u t M R R ∆γβγβ∆γβγ∆γ∆γ∆-+-++-+++=+求解式(2-146)可得t t u ∆+}{,然后由式(2-143)和式(2-144)可解出t t u∆+}{ 和t t u ∆+}{ 。
动力学系统时域响应计算的四种方法Matlab源程序(接上)

Fu=varargin{3};
t=varargin{5};
[n,n]=size(M);[n,m]=size(Fu);
nstep=size(t');
[V,D]=eig(K,M);
[lambda,k]=sort(diag(D)); % Sort the eigenvalues and eigenvalues
% q0,dq0 - Initial conditions
% nummode - the number of extracted modes
% a, b - Parameters for proportional damping [C]=a[M]+b[K]
% Output parameters
error('Incorrect number of input arguments')
else
switch nargin
case 9
%------------------------------------------------------------------------
Modalresponse模态叠加法法Matlab源程序
function varargout=Modalresponse(varargin)
%-------------------------------------------------------------------------
% Solve the eigenvalue problem and normalized the eigenvectors
%-----------------------------------------------------------------------
第5讲利用matlab进行系统的时域分析

1 y[k ] M
M 1Βιβλιοθήκη n 0f [ k n]
f [k ] s[k ] d[k ] (2k )0.9k d[k ]
%program3_3 Signal Smoothing by moving average filter R=51;%length of input signal %generate(-0.5,0.5)uniformly distributed randon numbers d=rand(1,R)-0.5; k=0:R-1; s=2*k.*(0.9.^k); f=s+d; figure(1);plot(k,d, 'r -.', k,s, 'b --', k,f, 'g -'); xlabel('Time indes k');legend('d[k]','s[k]','f[k]'); M=5;b=ones(M,1)/M;a=1; y=filter(b,a,f); figure(2); plot(k,s,'b--',k,y,'r-'); xlabel('Time index k'); legend('s[k]','y[k]');
用lsim求处该系统的零状态响应的数值解
5.2连续时间系统冲击响应和阶跃响应的求解
5.2.1系统的冲击响应的定义 系统的冲击响应的定义为在系统初始状态为零 的条件下,以单位冲击信号激励系统所产生 的输出响应,以符号h(t)表示。由于系统冲击 响应h(t)要求系统在零状态条件下,且输入激 励为单位冲击信号 (t ),因而冲击响应仅取决 于系统的内部结构及其元件参数
newmark法程序法计算多自由度体系的动力响应知识讲解

用matlab 编程实现Newmark -β法计算多自由度体系的动力响应用matlab 编程实现Newmark -β法 计算多自由度体系的动力响应一、Newmark -β法的基本原理Newmark-β法是一种逐步积分的方法,避免了任何叠加的应用,能很好的适应非线性的反应分析。
Newmark-β法假定:t u u u ut t t t t t ∆ββ∆∆]}{}){1[(}{}{+++-+= (1-1)2]}{}){21[(}{}{}{t u u t uu u t t t t t t ∆γγ∆∆∆+++-++= (1-2) 式中,β和γ是按积分的精度和稳定性要求进行调整的参数。
当β=0.5,γ=0.25时,为常平均加速度法,即假定从t 到t +∆t 时刻的速度不变,取为常数)}{}({21t t t u u ∆++ 。
研究表明,当β≥0.5, γ≥0.25(0.5+β)2时,Newmark-β法是一种无条件稳定的格式。
由式(2-141)和式(2-142)可得到用t t u ∆+}{及t u }{,t u}{ ,t u }{ 表示的t t u ∆+}{ ,t t u ∆+}{ 表达式,即有t t t t t t t u u t u u tu}){121(}{1)}{}({1}{2----=++γ∆γ∆γ∆∆ (1-3) t t t t t t t u t uu u t u}{)21(}){1()}{}({}{ ∆γβγβ∆γβ∆∆-+-+-=++ (1-4) 考虑t +∆t 时刻的振动微分方程为:t t t t t t t t R u K u C uM ∆∆∆∆++++=++}{}]{[}]{[}]{[ (1-5) 将式(2-143)、式(2-144) 代入(2-145),得到关于u t +∆t 的方程t t t t R u K ∆∆++=}{}]{[ (1-6)式中][][1][][2C t M tK K ∆γβ∆γ++= )}{)12(}){1(}{]([)}){121(}{1}{1]([}{}{2t t t t t t t t u t uu t C u u t u tM R R ∆γβγβ∆γβγ∆γ∆γ∆-+-++-+++=+求解式(2-146)可得t t u ∆+}{,然后由式(2-143)和式(2-144)可解出t t u∆+}{ 和t t u ∆+}{ 。
3.6 用Matlab进行动态响应分析
3.6 用Matlab 进行动态响应分析利用Matlab 可方便地进行控制系统的时域分析。
若读者对Matlab 的基本功能尚不了解,请先阅读本书的附录部分。
3.6.1绘制响应曲线Matlab 提供了求取线性定常连续系统单位脉冲响应和单位阶跃响应的函数。
分别为impulse ,step 。
对单位斜坡响应,可间接求取。
如果已知闭环传递函数的分子num 与分母den ,则命令impulse (num ,den ),impulse (num ,den ,t )将产生单位脉冲响应曲线。
命令step (num ,den ),step (num ,den ,t )将产生单位阶跃响应曲线。
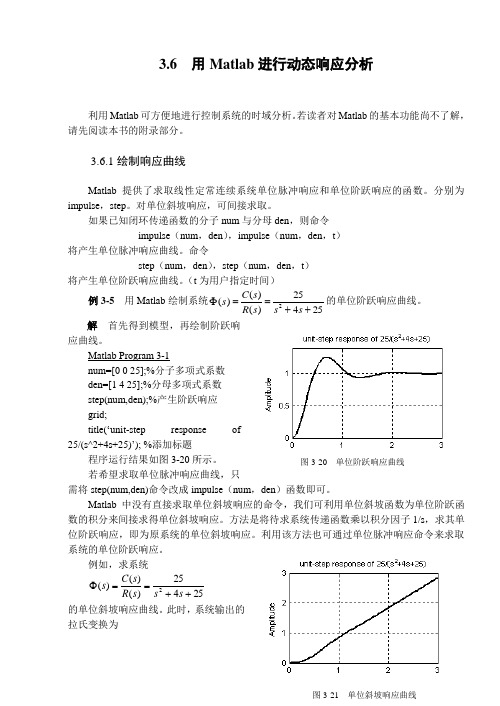
(t 为用户指定时间)例3-5 用Matlab 绘制系统25425)()()(2++==Φs s s R s C s 的单位阶跃响应曲线。
解 首先得到模型,再绘制阶跃响应曲线。
Matlab Program 3-1num=[0 0 25];%分子多项式系数den=[1 4 25];%分母多项式系数step(num,den);%产生阶跃响应grid;title(‘unit-step response of25/(s^2+4s+25)’); %添加标题程序运行结果如图3-20所示。
若希望求取单位脉冲响应曲线,只需将step(num,den)命令改成impulse (num ,den )函数即可。
Matlab 中没有直接求取单位斜坡响应的命令,我们可利用单位斜坡函数为单位阶跃函数的积分来间接求得单位斜坡响应。
方法是将待求系统传递函数乘以积分因子1/s ,求其单位阶跃响应,即为原系统的单位斜坡响应。
利用该方法也可通过单位脉冲响应命令来求取系统的单位阶跃响应。
例如,求系统25425)()()(2++==Φs s s R s C s 的单位斜坡响应曲线。
此时,系统输出的拉氏变换为图3-20 单位阶跃响应曲线图3-21 单位斜坡响应曲线ss s s s s s s C 1)254(25125425)(222⋅++=⋅++= 为此,求该系统单位斜坡响应曲线的程序如下: Matlab Program 3-2num=[0 0 0 25];den=[1 4 25 0];step(num,den,3)gridtitle('unit-step response of 25/(s^2+4s+25)');程序运行结果如图3-21所示。
(最新整理)第八章时域分析MATLAB

可以看出系统特征根中有两个实 部为正值,所以该闭环系统是不 稳定的。
10
例8-3 已知系统开环传递函数为:
Gsss101s0s22 0
试用代数稳定判据判断该闭环系统的稳定性。
解 其MATLAB命令如下:
z=[-2];p=[0,-1,-20];k=100; [num,den]=zp2tf(z,p,k); p=num+den; roots(p)
Gk2=solve('5/(5*s^2+5*s+6)=Gk2/(1+Gk2)','Gk2');
Kp=limit(Gk2,s,0)
运行结果为:
Kv=limit(s*Gk2,s,0)
Kp =5
Ka=limit(s^2*Gk2,s,0)
2021/7/26
Kv =0,Ka =0
14
二、三种典型信号下的稳态误差计算
解 由于在例8-4中已经判断了系统的稳定性,故在这里不再对系
统进行稳定性判断。
(1)单位阶跃响应与其稳态误差 syms s phi; num=5;den=[5,5,6];phi=tf (num, den);
t=[0:0.01:30]';y=step (phi, t);
subplot(1,2,1);plot(t,y);grid
其MATLAB命令如下: num=80;den=[1,2,0]; sys=tf (num, den); closys=feedback(sys,1); step (closys)
2021/7/26
3
二、连续系统单位脉冲响应
MATLAB中用函数命令impulse ( )来求连续系统单位脉冲响 应,其调用格式为:
用matlab编程实现法计算多自由度体系的动力响应

用matlab 编程实现Newmark -β法计算多自由度体系的动力响应姓名:学号: 班级: 专业:用matlab 编程实现Newmark -β法 计算多自由度体系的动力响应一、Newmark -β法的基本原理Newmark-β法就是一种逐步积分的方法,避免了任何叠加的应用,能很好的适应非线性的反应分析。
Newmark-β法假定:t u u u u t t t t t t ∆ββ∆∆]}{}){1[(}{}{+++-+=&&&&&&(1-1)2]}{}){21[(}{}{}{t u u t u u u t t t t t t ∆γγ∆∆∆+++-++=&&&&& (1-2)式中,β与γ就是按积分的精度与稳定性要求进行调整的参数。
当β=0、5,γ=0、25时,为常平均加速度法,即假定从t 到t +∆t 时刻的速度不变,取为常数)}{}({21t t t u u ∆++&&&&。
研究表明,当β≥0、5, γ≥0、25(0、5+β)2时,Newmark-β法就是一种无条件稳定的格式。
由式(2-141)与式(2-142)可得到用t t u ∆+}{及t u }{,t u}{&,t u }{&&表示的t t u ∆+}{&,t t u ∆+}{&&表达式,即有t t t t t t t u u t u u tu }){121(}{1)}{}({1}{2&&&&&----=++γ∆γ∆γ∆∆ (1-3)t t t t t t t u t u u u t u }{)21(}){1()}{}({}{&&&&∆γβγβ∆γβ∆∆-+-+-=++ (1-4)考虑t +∆t 时刻的振动微分方程为:t t t t t t t t R u K u C u M ∆∆∆∆++++=++}{}]{[}]{[}]{[&&& (1-5)将式(2-143)、式(2-144) 代入(2-145),得到关于u t +∆t 的方程t t t t R u K ∆∆++=}{}]{[ (1-6)式中][][1][][2C t M t K K ∆γβ∆γ++=)}{)12(}){1(}{]([)}){121(}{1}{1]([}{}{2t t t t t t t t u t u u t C u u t u tM R R &&&&&&∆γβγβ∆γβγ∆γ∆γ∆-+-++-+++=+求解式(2-146)可得t t u ∆+}{,然后由式(2-143)与式(2-144)可解出t t u∆+}{&与t t u ∆+}{&&。
应用MatLab软件探讨结构动力响应时域和频域数值模拟教学

应用MatLab软件探讨结构动力响应时域和频域数值模拟教学1. 引言结构动力学是工程力学中的重要分支,在现代工程设计中起着至关重要的作用。
传统的结构动力学教学方法主要基于理论推导和实验验证,然而这种教学方法存在时空限制和人力资源限制的问题。
随着计算机技术和数值模拟技术的不断发展,提高结构动力响应数值模拟技能已经成为了现代工程设计的重要课题,MatLab作为一种常用的科学计算软件,因其性能优良、易于使用和广泛应用而备受青睐。
本文借助MatLab软件,通过对结构动力响应的时域和频域数值模拟探究,讨论如何优化结构动力学的教学方法。
2. 时域数值模拟时域数值模拟是研究结构动力响应的常用方法,其原理是通过分析机械系统的运动学和动力学方程,在时域内求解结构响应的变化规律,这种方法对于研究结构响应的时间变化非常有帮助。
MatLab软件作为一种功能强大的科学计算软件,拥有丰富的函数库和数据分析工具,能够支持多种结构动力响应的时域数值模拟。
通过MatLab中的ode45函数,结构动力响应的时域数值模拟可以轻松完成,可以设置不同的初值条件和参数来模拟不同的结构响应情况。
3. 频域数值模拟频域数值模拟是研究结构动力响应的另一种常用方法,其原理是将结构响应在频域内进行分析,分析结构系统在不同频率下的动态响应特性,这种方法对于研究结构响应的频率特性非常有帮助。
MatLab软件作为一种功能强大的科学计算软件,同样能够支持多种结构动力响应的频域数值模拟。
通过MatLab中的FFT函数,结构动力响应的频域分析可以轻松完成,同时还可以使用MatLab的模拟仿真工具Simulink,进行结构动力响应的实时仿真。
4. 结构动力学教学优化通过MatLab软件进行结构动力响应的数值模拟,不仅可以提高学生对结构动力学教学的理解,同时也能够培养学生的计算机仿真技能和科学研究能力。
综合来看,基于MatLab软件进行结构动力学的教学方法能够更好地满足现代工程设计中对结构动力学技能的需求,是一种具有广阔前景的教学改革方法。
应用MatLab软件探讨结构动力响应时域和频域数值模拟教学

应用MatLab软件探讨结构动力响应时域和频域数值模拟教学【摘要】本文探讨了应用MatLab软件进行结构动力响应时域和频域数值模拟教学的相关内容。
在介绍了研究背景、研究意义和研究目的。
接着在详细讨论了MatLab软件在结构动力响应研究中的应用,时域和频域数值模拟教学的探讨,以及通过结构动力响应数值模拟案例分析来展示方法和应用。
最后对教学效果进行了评估。
结论部分总结了MatLab 软件在结构动力响应教学中的价值,并展望了未来的研究方向。
通过本文的研究,可以更好地掌握MatLab软件在结构动力响应领域的应用,提高教学效果和研究水平,促进结构动力学领域的发展。
【关键词】MatLab软件、结构动力响应、时域、频域、数值模拟、教学、案例分析、教学效果评估、教学价值、研究展望、结论总结。
1. 引言1.1 研究背景结构动力学是研究结构在外力作用下的振动特性和响应行为的一门学科,其研究对于评估结构工程的稳定性、安全性和耐久性具有重要意义。
随着科学技术的发展和应用需求的增加,人们对结构动力响应的研究需求也越来越迫切。
结构动力响应的研究不仅有助于优化结构设计和改进结构性能,还可以为减灾防灾和工程管理提供重要参考。
本研究旨在探讨利用MatLab软件进行结构动力响应的时域和频域数值模拟教学,旨在提高学生对结构动力学理论的理解和实践能力,促进结构动力响应研究的发展和应用。
1.2 研究意义结构动力响应是结构工程领域一个重要的研究方向,涉及到结构在外力作用下的振动响应。
结构动力响应的研究对于提高结构的安全性、可靠性及性能具有重要意义。
通过对结构动力响应进行研究,可以更好地了解结构在振动状态下的性能表现,从而为结构设计、改进和维护提供参考。
探讨MatLab软件在结构动力响应研究中的应用具有重要的研究意义。
通过研究MatLab软件在结构动力响应数值模拟教学中的应用,能够提高学生对结构振动与响应的理解,培养学生的实际应用能力,促进结构动力学教育的发展和完善。
基于 MATLAB 实现对结构动力响应的几种算法的验证

基于 MATLAB 实现对结构动力响应的几种算法的验证1. 算例首先,本文给出一算例, 结构在外力谐振荷载 P (t ) = P 0 sin θt 作用下,分别利用理论解法,杜哈梅积分, Wilson-θ 法求出该结构的位移时程反应。
其中:m = 3.5×103 kg , P 0 = 1.0×104 N , k =1.3584515×107 ,ξ=0.05 ,θ=52.3s −1 ,ω=62.3s −1 ,⋅D ω= ω 1-ξ2=62.222 ,初始位移、速度v (0) = 0 ,v (0) = 0 ;2. 算法验证2.1 理论解法运动方程为: mv+cv+kv=0P sin t ϑ由线性代数解出其理论解为:]cos 2)sin -[(]4)-[(t]sin )-(2cos [2]4)-[(t]sin )0()0(cos )0([2222222202222222222t t m P t m P ev v t v e v D DD tD DD t θξωθθθωθωξθωωωθωωξωξωθωξθωθωωξωωξωξω-++-+⋅++++=--由于初始位移v(0) =0 ,v(0) =0 ;则:]cos 2)sin -[(]4)-[(t]sin )-(2cos [2]4)-[(22222222022222222220t t m P t m P e v D DD tθξωθθθωθωξθωωωθωωξωξωθωξθωθξω-++-+⋅+=-v(t ) =-3.115te⋅ 1.05269898×410-⋅[6.230cos62.222t −18.106sin 62.222t]+2.012808757 610-⨯⋅[1146sin 52.3t −325.829cos52.3t]可以用 MA TLAB 进行编程分析,画图位移时程图,详细程序见附录。
2.2Wilson-θ法Wilson-θ法是Wilson 于1966年基于线性加速度法的基础上提出一种无条件收敛的计算方法。
第八章时域分析MATLAB

∞ ∞
I型 II型
0ห้องสมุดไป่ตู้0
Av/K 0
∞ Aa/K
14
5 已知一个单位负反馈系统的闭环传递函数为: s 5s 2 5s 6
(1)试绘制出该系统的单位阶跃响应曲线并求此响应的稳态误差; (2)试绘制出该系统的单位斜坡响应曲线并求此响应的稳态误差; (3)试绘制出该系统的单位加速度响应曲线并求此响应的稳态误差;
17
(3)单位加速度响应与其稳态误差 syms s phi2;num=5;den=[5,5,6,0,0];phi2=tf (num, den);
t=[0:0.01:30]';y=step(phi2,t); subplot(1,2,1);plot(t,y);grid subplot(1,2,2);ess=1/2*t.^2-y;plot(t,ess);grid
19
R(s)
-
E(s)
G(s)
C(s)
p=num+den; roots(p)
可以看出系统特征根的实部全为负值,所以该闭环系统是稳定的。
10
8.3 控制系统稳态误差计算
在这一小节里必须注意:要计算控制系统稳态误差,首先要 确定系统是稳定的! 一、静态误差系数 位置误差系数Kp:
K p lim Gk s
s0 s0
速度误差系数Kv: K v lim s Gk s
s
R s
对于单位阶跃信号有: Rs 1 C s s Rs s 1
s
s
对于单位加速度信号有:
1 1 1 1 Rs 3 C s s Rs s 3 s 2 s s s s
利用MATLAB进行系统的时域分析

利用MATLAB进行系统的时域分析 1.1连续时间系统零状态响应的求解
例:如下图所示的电路系统中,电容器极板上电 荷量与输入电压的关系为
设电感系数为L=1H,电阻R=10Ω,电容器的电容 C=5mF,系统的初始储能为零,若外加电压 是
振幅为10V、频率1Hz的正弦信号,求电容器极板 上的电荷量 。
计算此系统的单位冲激响应和单位阶跃响应的 MATLAB程序如下
程序运行结果如下图(1)和(2)所示。
图(1)单位冲激响应曲线 图(2)单位阶跃响应曲线
信号与系统
解:由已知条件,系统的输入信号为
系统的微分方程为
计算电荷量 的MA.2 利用MATLAB求单位冲激响应和单位阶跃响 应 系统的单位冲激响应:
系统的单位阶跃响应:
其中y为输出响应;sys为由tf,zpk或ss建立的 系统模型;t为仿真时间区段(可选)。
例:若系统的微分方程为
Matlab技术时域分析方法

MatIab技术时域分析方法时域分析是信号处理中的一个重要领域,它主要研究信号在时间域内的变化规律。
MatEb作为最常用的科学计算软件之一,提供了丰富的时域分析工具和函数,便于工程师和科研人员对信号进行分析和处理。
本文将介绍一些常用的MaUab技术时域分析方法,以及它们在实际应用中的一些案例。
一、时域分析的基本概念时域分析是将信号视为时间的函数,对信号在时间域内进行描述和分析。
通过时域分析,我们可以获得信号的幅值、相位、周期性等特性,从而更好地理解和处理信号。
在MatIab中,使用波形图和信号处理工具箱中的函数可以方便地进行时域分析。
二、波形图分析波形图是时域分析的基本工具之一,通过绘制信号在时间轴上的变化来直观地观察信号的特征。
在MaUab中,我们可以使用p1ot函数来画出信号的波形图。
例如,以下代码可以绘制一个简单的正弦信号的波形图:ZmatIabt=0:0.01:1;%时间范围为0到1,采样频率为IooHZf=1;%正弦信号频率为IHZA=I;%正弦信号幅值为1x=A*sin(2*pi*f*t);%生成正弦信号p1ot(t,X);%绘制波形图波形图可以直观地显示信号的频率、幅值、周期等特性,对于初步了解信号非常有帮助。
三、傅里叶变换傅里叶变换是时域分析的重要方法之一,它可以将信号从时域转换到频域。
频域分析可以更好地揭示信号的频率成分和频谱特征,对于滤波、谱估计等应用具有重要意义。
在MaHab中,我们可以使用fft函数进行傅里叶变换。
傅里叶变换的输出是一个复数数组,其中包含信号的频谱信息。
为了更好地显示信号的频谱,我们通常会进行幅度谱和相位谱的分析。
以下是一个简单的例子:'''ma11abFs=1000;%采样频率为IOOOHzt=0:1/Fs:1;%采样点数为1000f=10;%正弦信号频率为IOHzX=sin(2*pi*f*t);%生成正弦信号N=Iength(X);%信号长度X=fft(x);%进行傅里叶变换frequencies=Fs*(0:(N/2))/N;%计算频率轴amp1itude=abs(X(kN∕2+1));%计算幅度谱phase=ang1e(X(kN∕2+1));%计算相位谱subp1ot(2,1,1);p1ot(frequencies,amp1itude);%绘制幅度谱X1abe1CFrequency(Hz)');y1abe1('Amp1itude,);subp1ot(2,1,2);p1ot(frequencies,phase);%绘制相位谱X1abeICFrequency(Hz)');y1abe1('Phase');四、自相关函数和互相关函数自相关函数和互相关函数是时域分析中用于测量信号相似性和信号之间的关系的重要方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
acc(:,1)=inv(mm)*(fd(:,1)-kk*dsp(:,1)-cc*vel(:,1));
dsp0=dsp(:,1)-vel(:,1)*dt+0.5*acc(:,1)*dt^2;
dsp(:,1)=q0; % initial displacement
vel(:,1)=dq0; % initial velocity
dsp(:,it+1)=inv(ekk)*efd; % find the displacement at time t+dt
acc(:,it+1)=(dsp(:,it+1)-dsp(:,it))/(alpha*dt^2)-vel(:,it)/(alpha*dt)...
alpha=0.5; beta=0.5; % select the parameters
acc(:,1)=inv(mm)*(fd(:,1)-kk*dsp(:,1)-cc*vel(:,1)); % compute the initial acceleration (t=0)
cfc=dsp(:,it)*beta/(alpha*dt)+vel(:,it)*(beta/alpha-1)...
+acc(:,it)*(0.5*beta/alpha-1)*dt;
efd=fd(:,it)+mm*cfm+cc*cfc; % compute the effective force vector
-acc(:,it)*(0.5/alpha-1); % find the acceleration at time t+dt
vel(:,it+1)=vel(:,it)+acc(:,it)*(1-beta)*dt+acc(:,it+1)*beta*dt;% find the velocity at time t+dt
Newmark法Matlab源程序
function [acc,vel,dsp]=Newmark_2(kk,cc,mm,fd,nt,dt,q0,dq0)
%输入参数
% kk------刚度矩阵
% mm------质量矩阵
% cc------阻尼矩阵
% q0------初始位移
% dq0------初始速度
% dt------时间步长
% nt------总的计算步数,等于结束时间除以dt
%返回值
% dsp------位移
% vel------速度
% acc------加速度
[sdof,n2]=size(kk);
dsp=zeros(sdof,nt); % displacement matrix
vel=zeros(sdof,nt); % velocity matrix
acc=zeros(sdof,nt); % acceleration matrix
ekk=mm/dt^2+cc/(2*dt);
efd=fd(:,1)-(kk-2*mm/dt^2)*dsp(:,1)-(mm/dt^2-cc/(2*dt))*dsp0;
% mm------质量矩阵
% cc------阻尼矩阵
% q0------初始位移
% dq0------初始速度
% dt------时间步长
% nt------总的计算步数,等于结束时间除以dt
%返回值
% dsp------位移
% vel------速度
% acc------加速度
acc=zeros(sdof,nt); % acceleration matrix
dsp(:,1)=q0; % initial displacement
end
中心差分法Matlab源程序
function [acc,vel,dsp]=central_diff(kk,cc,mm,fd,nt,dt,q0,dq0)
%输入参数
% kk------刚度矩阵
[sdof,n2]=size(kk);
dsp=zeros(sdof,nt); % displacement matrix
vel=zeros(sdof,nt); % velocity matrix
ekk=kk+mm/(alpha*dt^2)+cc*beta% loop for each time step
cfm=dsp(:,it)/(alpha*dt^2)+vel(:,it)/(alpha*dt)+acc(:,it)*(0.5/alpha-1);
