数分精品课程.ppt
小学教育ppt课件教案数字分解与组合速算轻松计算窍门

门
目录
• 课程介绍与目标 • 数字分解基本概念与技巧 • 组合速算原理及应用 • 轻松计算窍门之加减法 • 轻松计算窍门之乘除法 • 轻松计算窍门之分数与小数 • 总结回顾与拓展延伸
01
课程介绍与目标
课程背景与意义
适应新时代教育需求
随着科技的进步,数学教育更加注重培养学生的逻辑思维与创新能力,数字分 解与组合速算作为其中的重要内容,有助于提高学生的计算速度与准确性。
02
数字分解基本概念与技巧
数字分解定义及作用
定义
数字分解是将一个复杂的数字拆 分成若干个简单的数字,以便更 容易进行计算和理解。
作用
数字分解可以帮助学生更好地掌 握数字的结构和规律,提高计算 速度和准确性,培养数感和数学 思维能力。
常见数字分解方法
拆十法
将十几拆成十和几,先计算十 与另一个数的和或差,再与几
相加或数相加或相减。
破十法
将十几拆成十和几,先用十减 去另一个数,再加上几。
平十法
将两个数中较大的一个数拆成 两个数相加或相减,使其中一 部分与另一个数相等,从而简
化计算。
实用数字分解技巧
01
02
03
04
观察数字特点
根据数字的特点和规律,选择 合适的分解方法。
感谢您的观看
THANKS
难度。
分解法
将减数分解成两个较小数的和或 差,再与被减数相减,以简化计
算过程。
互补数法
利用互补数的性质,将减法转化 为加法,从而简化计算。
加减法结合运用实例
加减混合运算
在解决实际问题时,常常需要将加法和减法结合运用。例如,计 算购物总金额和找零钱的问题。
数分选讲讲稿第17讲

青岛大学讲稿讲 授 内 容备 注 第十七讲§4.3 定积分的可积性一、直接用定义证明可积性1lim()()nb i i ai f x J f x dx λξ→=∆==∑⎰:0, 0εδ∀>∃>,使得对[,]a b 的任何分割T,以及在其上的任意选取的点集{}i ξ,只要||||T δ<,就有1()ni i i f x J ξε=∆-<∑.例1 设(), F()f x x 在[,]a b 上连续,且a x b <<时,F ()()x f x '=试用定义直接证明()f x 在[,]a b 上可积,且()()().b af x dx F b F a =-⎰证 对任意分划 01:n T a x x x b =<<<=[]11()()()()nii i F b F a F x F x-=-=-∑111()() [,]nii i i i i i F x x x x ηη--='=-∈∑111()() [,]ni i i i i i i f x x x x ηη--='=-∈∑因为1 01()lim() [,]nb i i i i i ai f x dx f x x x λξξ-→==∆∈∑⎰问题是要证明 01lim ()()()ni i i f x F b F a λξ→=∆=-∑3学时即证: []10,()()nii ii f f x εξη=∀>-∆∑11()() ,[,]ni i i i i i i i f f x x x ξηεξη-=≤-∆<∈∑因为()f x 在[,]a b 上连续,所以()f x 在[,]a b 上一致连续,0, 0εδ∀>∃>,当,[,]x x a b '''∈,且x x δ'''-<时,有()()f x f x b aε'''-<-.因此,当||||T λδ=<时,i i i x ξηλδ-≤∆≤<故11()().nni i i ii i f f x xb a εξηε==-∆≤∆=-∑∑例2 证明:()f x 在[,]a b 上可积的充要条件是:对任何一个使得||||0k k T λ=→的分划序列{}k T 所作的积分和 1()kn i i i f x ξ=∆∑,其极限1lim()kn i i k i f x ξ→∞=∆∑恒存在,并且相同(不妨记为I )证 必要性明显.充分性:(利用反证法)若()f x 在[,]a b 上不可积,则010, 0,kε∃>∀>∃分划kT 及()1[,]k i i i x x ξ-∈,虽然对应的1||||k k T kλ=<,但()01()kn k i i i I f x ξε=-∆≥∑.如此得到一个分划序列{}k T ,虽然0k λ→,但()1lim()kn k ii k i f x I ξ→∞=∆≠∑与已知条件矛盾.二、利用定理证明可积性 定理9.3 (可积准则)函数()f x 在[,]a b 上可积的充要条件是:任给0,ε>总存在相应的一个分划T ,使得()()S T s T ε-<.定理9.3' (可积准则)函数()f x 在[,]a b 上可积的充要条件是:任给0,ε>总存在相应的一个分划T ,使得iiTxωε∆<∑.定理9.16 (可积的充要条件)函数()f x 在[,]a b 上可积的充要条件是:任给正数,εη、总存在某一个分划T ,使得属于T 的所有小区间中,对应于振幅k ωε'≥的那些小区间k '∆的总长.k k x η''∆<∑方法A :若1ni i ω=∑有界,可以利用11nni i i i i x M ωλωλ==∆≤≤∑∑,只要Mελ<即可.方法B :证明, (1,2,,)i i n ωε<= 从而1()n i i i x b a ωε=∆<-∑. 方法C :利用i i i i i i x x x ωωω'''∆=∆+∆∑∑∑ 其中'∑中,,i b aεω<-则i i ix x b aεωε''∆<∆<-∑∑.''∑中,ix ε''∆<Ω∑,则i ii x x ωε''''∆<Ω∆<∑∑. 其中[,][,]sup ()inf ()x a b x a b f x f x ∈∈Ω=-是()f x 在[,]a b 上的全振幅.方法D :利用f g i i ωω≤(其中,f g i i ωω分别表示函数()f x 与()g x 在第i 个小区间上的振幅).从()g x 的可积性,得()f x 的可积性.见参考书 《数学分析》 上册(第三版)华师大数学系编证明单调函数的可积性证明连续函数的可积性如:()f x 在[,]a b 上可积,用方法D 可证()f x 在[,]a b 上可积例3 设()f x 是[,]a b 上的有界变差函数,即()f x 在[,]a b 上的全变差在11sup ()()ni i Ti M f x f x -=⎧⎫=-<+∞⎨⎬⎩⎭∑.试证:()f x 在[,]a b 上可积.证 对任意分划T ,有1ni i M ω=≤∑由方法A ,可证其可积性.例4 设()f x 在[,]a b 上的每一点处的极限存在并且皆为零.试证:()f x 在[,]a b 上可积,且 ()0.ba f x dx =⎰证 设0[,]x a b ∀∈,有0lim ()0x x f x →=.010, 0,x εδ∀>∃>当0000(,)x x x x x δδ∈-+时,有10() ()f x x x ε<≠如此,{}0000(,)[,]x x x x x a b δδ-+∈组成了[,]a b 的一个开覆盖. 由有限覆盖定理,其中存在有限子覆盖{}(,)1,2,,i i ix i x xx i kδδ-+=至此,证明了除有限个点{}12,,,k x x x 外,恒有112() (,,,)k f x x x x x ε<≠ (A ) 下证()f x 的可积性.0, ε∀>令1=4()b a εε-,则(A )式成立. 取{}121max (),(),,(),k M f x f x f x ε> ,作一分划T使含12,,,k x x x 的各小区间之总长.4i x Mε'∆<∑ 则iii ii i x x xωωω'''∆=∆+∆∑∑∑()()ii i i i i Mm x M m x'''=-∆+-∆∑∑122i iMx xε'''≤∆+∆∑∑122()4Mb a Mεεε<+-=其中'∑表示含12,,,kx x x的各小区间的对应项之和.''∑表示其余各项之和.()f x ∴在[,]a b 上可积.既然()f x 在[,]a b 上可积,点i ξ不论怎样选取,积分和的极限相同.因此,每次只要选取i ξ与(A )中的12,,,k x x x 不同.取{}12m in ,,kx x x δδδδ= ,当||||T λδ=<时,11111()()()n n ni i i i i i i i f x f x x b a ξξεε===∆≤∆≤∆=-∑∑∑1lim()=0ni i i f x λξ→=∴∆∑即: ()0.baf x dx =⎰例5 设()f x 在[,]a b 上可微.试证:()f x '在[,]a b 上可积的充要条件是:存在可积函数()g x ,使得()()().xa f x f a g t dt =+⎰ (1)证 必要性 令 ()()g x f x '=,则()g x 在[,]a b 上可积()()()()x x aaf x f a f t dtg t dt '-==⎰⎰充分性 设01: n T a x x x b =<<<= 是[,]a b 的任一分划.记11inf (), sup ()i ii ig g i i x x x x x x m g x M g x --≤≤≤≤== 1,2.i n =则 g g g iiiM m ω=- 1,2.i n =设 1[,]i i x x x -∈为任意一点,1[,]i i x x x x -+∆∈,则由题设()()1()x x xf f x x f xg t dtxxx+∆+∆-==∆∆∆⎰注意到 ()g g i i m g x M ≤≤,所以关于充分性,下面的证法是错误的: 将(1)式两端对x求导,得()()f xg x '=由()g x 的可积性,知()f x '可积. 错误是()g x 未必g gi if m M x∆≤≤∆.令0x ∆→,得1() [,]g g ii i i mf x Mx x x -'≤≤∀∈因此()f x '在1[,]i i x x -上的振幅11sup ()inf()i ii if g g g i iiix x x x x x f x f x Mm ωω--'≤≤≤≤''=-≤-=故 0f g i i i i x x ωω'≤∆≤∆∑∑因为()g x 在[,]a b 上可积,0lim 0g i i x λω→∆=∑可知 0lim 0f i i x λω'→∆=∑所以()f x '在[,]a b 上可积.例6 证明R iem ann 函数()R x 在[0,1]上可积. 例7 ()f x 在[,]a b 上可积的充要条件是:0, ε∀>0,σ∀> ∃分划T,使得振幅i ωε≥的那些小区间1[,]i i x x -的长度之和i i x ωεσ≥∆<∑.(通俗地说,即是振幅不能任意小的那些小区间之总长可任意小)证 必要性 设()f x 在[,]a b 上可积,则0, ε∀>0,σ∀> ∃分划T,使得iixωεσ∆<∑1i i ni iiiii x xxωεωεεωωεσ≥≥=∴∆≤∆≤∆<∑∑∑有.i i x ωεσ≥∆<∑充分性 已知10, ε∀>0,σ∀> ∃分划T ,使得i x ωεσ≥∆<∑连续,从而()()()x ag t dtg x '=⎰未必成立.从而 111i i ni i i i i i i x x x ωεωεωωω=≥<∆=∆+∆∑∑∑111i i i i x x ωεωεε≥<≤Ω∆+∆∑∑1()b a σε<Ω⋅+-其中[,][,]sup ()inf ()x a b x a b f x f x ∈∈Ω=-是()f x 在[,]a b 上的全振幅.当0, ε∀>取1, , 2()2T b a εεεσ==∃-Ω,则有1niii xωε=∆<∑所以,()f x 在[,]a b 上可积.例8 设()y f u =在[,]A B 上连续,()u x ϕ=在[,]a b 上可积.当[,]x a b ∈时,().A x B ϕ≤≤试证:[]()()F x f x ϕ≡在[,]a b 上可积.证 ()f u 在[,]A B 上连续,()f u ∴在[,]A B 上一致连续.0, 0εδ∀>∃>,当,[,], u u A B u u δ''''''∈-<时,有()()<(1)2f u f u ε'''-因此作分划后,在1[,]i i x x -上,若()x ϕ的振幅i ϕωδ< 则[]()()F x f x ϕ≡的振幅F i ωε<.[事实上,这时1,[,],i i x x x x -'''∀∈ 记(), ()u x u x ϕϕ''''''== 则 ()()i u u x x ϕϕϕωδ''''''-=-≤< 从而 ()()()()<.2F x F x f u f u ε''''''-=-1,sup()()2i iF i x x x x F x F x εωε-'''≤≤'''=-≤<]本例题可作为定理用.关键在于对0, ε∀>0,σ∀>找一个分划T ,使得.i i x ωεσ≥∆<∑由此可见,在1[,]i i x x -上,若F i ωε≥,必有i ϕωδ≥ 故(2)Fi i i i x x ϕωεωδ≥≥∆≤∆∑∑如此,0, ε∀>0σ∀>,首先按(1)式找出0,δ>再由()x ϕ在[,]a b 上可积,对0δ>与0,σ> ∃分划T ,使得<i i x ϕωδσ≥∆∑由(2)得F ii i i x x ϕωεωδσ≥≥∆≤∆<∑∑所以,()F x 在[,]a b 上可积.下面讨论可积性与连续性的关系.例9 若()f x 在[,]a b 上的不连续点,可以用有限个总长度任意小的有限个区间所覆盖,则()f x 在[,]a b 上可积.(直接应用定理9.16)例10 若()f x 在[,]a b 上可积,则()f x 连续点在[,]a b 上处处稠密.证 只要证明()f x 在[,]a b 内至少有一个连续点.若找到一个连续点0x ,则()f x 在0[,]a x 、0[,]x b 上可积,在 0[,]a x 、0[,]x b 内有连续点.以此类推,证明了连续点处处稠密.用区间套定理,证明()f x 在[,]a b 内至少有一个连续点. ()f x 在[,]a b 上可积,1lim0.ni i i x λω→=∴∆=∑对11, 2ε=∃分划1T ,使得1() (1)i i x b a ωε∆<-∑如此,至少存在一个小区间1[,]i i x x -,使得其上()f x 的振幅1i ωε<(若不然,11()i i i x x b a ωεε∆≥∆≥-∑∑与(1)式矛盾)将此小区间适当收缩,总可以使得它的长度11()2i i x x b a --<-记缩小后的小区间为11[,]a b ,则11111, (),2a ab b b a b a <<<-<-()f x 在11[,]a b 的振幅 11[,]112fab ωε<=.将11[,]a b 取代上面的[,]a b ,作同样的处理 ,可知对 11, 2ε=2211 [,][,][,]a b a b a b ∃⊂⊂, 1221, a a b b <<<2211211()(),22b a b a b a -<-<-()f x 在22[,]a b 的振幅 22[,]2212fab ωε<=如此无限做下去,可得一区间套1 1122[,][,][,][,]n n a b a b a b a b ⊃⊃⊃⊃⊃2 1 0<()0 ()2n n nb a b a n -<-→→∞且()f x 在[,]n n a b 的振幅 [,]12nn f ab n nωε<=据区间套定理,[,] (1,2,)n n a b n ξ∃∈=lim lim (1,2,)n n n n n n a b a b n ξξ→∞→∞==<<=则()f x 在ξ处连续.事实上0,ε∀>可取n 足够大,使得12nε<从而令 {}min ,n n b a δξξ=-- 则当 x ξδ-<时,[,]n n x a b ∈,有[,]1()()2n n fa b nf x f ξωε-≤<<即 lim ()()x f x f ξξ→=所以()f x 在ξ处连续.例11 证明:若()0f x ≥在[,]a b 上有定义且可积,则 等式 ()0ba f x dx =⎰.成立的充要条件是()f x 在连续点上恒为零.证 必要性(反证法)若0[,]x a b ∈为()f x 的连续点,0()0f x >,则0,δ∃>使得00 ()()0b x ax f x dx f x dx δδ+-≥>⎰⎰矛盾.所以,0()0f x =.充分性 因为 ()f x 在[,]a b 上可积,则()f x 的连续点在 [,]a b 上处处稠密.∀分划01: n T a x x x b =<<<=取i ξ为1[,] (1,2,,)i i x x i n -= 上()f x 的连续点,则()0i f ξ=积分和1()0ni i i f x ξ=∆=∑1()lim()=0nb i i ai f x dx f x λξ→==∆∑⎰.连续函数的局部保号性。
部编三年级上数学《认识几分之一》赵晓霞PPT课件 一等奖新名师优质课获奖比赛公开人教版

PPT课件
把一个长方形平均分成2份,每份是它的二分之一。
PPT课件认识几分之一
四分之一 三分之一 五分之一
1 4
1
3
像这样的数,
都是分数。
1 5
PPT课件
活动二 要求:
每个同学拿出一张你喜欢的图 形纸,先折一折。
然后把它的几分之一用斜线涂 上颜色。
PPT你课件知道涂色部分占整个图形的几分之一吗? 说一说理由。
1 6
PPT课件
生活中处处有数学问题。 善于用数学的眼光去看世 界,就会使自己越来越充 满智慧!
PPT课件
通过今天的学习,你有怎样的收获?
PPT课件
在古代,人们在分东西 时,经常出现不是整数的情 况,于是渐渐产生了分数。
PPT课件
在我国,很早就有了
分数,最初用算筹表示, 比如 1就表示成 。
PPT课件
PPT课件
PPT课件
PPT课件
PPT课件
1 《科学天地》大约占黑板报版面的 2 。
PPT课件
《艺术园地》大约占黑板报版面的
1 4
。
PPT课件
1
1
4
2
PP生T课件 活中的分数
让我们一起走进生活,寻找分数!
1 3
PPT课件
1 4
PPT课件
1 5
PPT课件
1 3
PPT课件
1
1
1
1
3
5
6
4
PPT下课件面的分数能表示各图中的涂色部分吗? 能表示的画“√”,不能表示的画“×”。 说一说理由。
1
( √)
2
1 ( )
3
1
(√ )
4
数分选讲讲稿第讲

(2)式变形为
(3)
问题转化为由方程(1)证明式(3).
方程(1)满足隐函数存在定理的条件,因此(1)式将 定义为 的函数.将(1)式对 求导
即 (4)
由轮换对称 (5)
(6)
(4),(5),(6)平方后相加,约去两端的公因子,得
(7)
(4) +(5) +(6) ,再由(1)得
总之,有
.
例3求 在椭球面 上的点 处的外法线方向的导数.
解法向量
单位法向量
其中 .
因此,
.
例4设 是区间 上的可微函数,在 直角坐标平面内,其图像为曲线 .若二元函数 在包含曲线 的某区域上连续可微(即具有连续的偏导数).且在曲线 上恒为0.求证: 在曲线 上任一给定点处沿该曲线切线方向的导数等于0.
数分选讲讲稿第讲
讲授内容
备注
第三十四讲
§隐函数存在定理
对方程 而言,隐函数存在定理是: 满足
;
及 在 的某邻域内连续,
则方程 在 的邻域里确定了唯一的隐函数.
具体来说,即 ,及函数 ,满足:
i) ;
ii)
其中 ;
iii)满足条件i)、ii)的函数 是唯一的;
iv) 在 内连续.
若附加条件: 在 的邻域内连续,
3)利用梯度与方向导数的关系
若 在点 处可微,则 在 点沿任意方向 的方向导数存在,且
其中 表示 与 的夹角.
例1设
试证: 在 点沿任意方向的方向导数存在,但在 处不可微.
证取任意方向
则
于是
可见在 处沿任意方向的方向导数存在.
不可微性是课本上的例题.
《数字的分解与组合》课件完整版

《数字的分解与组合》课件完整版一、教学内容本节课我们将学习《数学基础》第四章第二节“数字的分解与组合”。
详细内容包括:理解数字的分解与组合概念,掌握基本的数字拆分方法,运用组合原理解决实际问题。
二、教学目标1. 理解数字的分解与组合的概念,并能够灵活运用。
2. 学会基本的数字拆分方法,提高数学逻辑思维能力。
3. 能够运用组合原理解决生活中的实际问题。
三、教学难点与重点教学难点:数字的分解与组合在实际问题中的运用。
教学重点:数字的分解与组合概念的理解,基本拆分方法的掌握。
四、教具与学具准备1. 教具:多媒体课件、黑板、粉笔。
2. 学具:练习本、计算器、草稿纸。
五、教学过程1. 实践情景引入:通过讲解生活中关于数字分解与组合的实例,如购物时找零问题,引导学生思考数字的分解与组合的实用性。
2. 知识讲解:a. 介绍数字的分解与组合概念。
b. 讲解基本的数字拆分方法。
c. 通过例题讲解组合原理的应用。
3. 随堂练习:针对本节课所学的知识点,设计相关练习题,让学生独立完成。
4. 答疑与讨论:针对学生在练习中遇到的问题,进行解答和讨论。
六、板书设计1. 数字分解与组合概念2. 基本数字拆分方法3. 组合原理应用例题七、作业设计1. 作业题目:a. 将数字45分解成两个因数的乘积,并找出所有可能的组合。
b. 某商店举行满100元减30元的促销活动,小明购买商品共花费270元,请问小明实际支付多少钱?c. 运用组合原理,求解从A、B、C、D四个字母中任选两个字母的所有组合。
2. 答案:a. 45=1×45、3×15、5×9,共有6种组合。
b. 小明实际支付240元。
c. 所有可能的组合为:AB、AC、AD、BC、BD、CD。
八、课后反思及拓展延伸1. 数字分解与组合在生活中的其他应用场景。
2. 如何利用分解与组合原理简化计算过程?3. 探索更多组合原理在实际问题中的运用。
重点和难点解析1. 教学难点与重点的确定2. 教学过程中的实践情景引入3. 例题讲解的详细步骤4. 作业设计中的题目难度和答案解析5. 课后反思及拓展延伸的深度和广度一、教学难点与重点的确定1. 数字分解与组合概念的理解:这是基础中的基础,学生需要明确数字分解与组合的定义,为后续学习打下坚实基础。
数学分析课件

连续性
01 02
连续性的定义
连续性是函数的一种性质,它描述了函数在某一点处的变化情况。如果 函数在某一点处的左右极限相等且等于该点的函数值,则函数在该点处 连续。
连续性的性质
连续性具有一些重要的性质,如局部保序性、介值定理等。这些性质在 数学分析中有着广泛的应用。
03
连续性的判定
判定一个函数是否连续,可以通过计算该函数的左右极限并检查它们是
否相等来实现。此外,还可以利用连续性的性质进行判定。
导数
导数的定义
导数是函数的一种性质,它描述了函 数在某一点处的切线斜率。导数的定 义包括函数在某一点的导数和函数在 某区间的导数。
导数的性质
导数的计算
计算导数的方法有很多种,如直接法、 乘积法则、复合函数求导法则等。这 些方法可以帮助我们计算一些复杂的 导数表达式。
电子工程
在电子工程中,数学分析用于信号处理、图像处 理和通信系统设计。
计算机科学
在计算机科学中,数学分析用于算法设计、数据 分析和人工智能等领域。
06 数学分析的习题与解答
CHAPTER
习题的选择与解答
精选习题
选择具有代表性的数学分析题目,涵盖各个知识点,难度适中, 适合学生巩固所学内容。
详细解答
极限的计算方法
计算极限的方法有很多种,如直接代入法、分解因式法、等价无穷小替换法、洛必达法则 等。根据不同的情况选择合适的方法可以简化计算过程。
导数问题
导数的定义
导数描述了函数在某一点处的切线斜率,是函数局部性质的一种体现。导数可以分为一阶导数、二阶导数等,高阶导 数可以用来研究函数的拐点、凸凹性等性质。
03 数学分析的定理与证明
最新精品课程完整课件(第8讲)---数据分类-决策树

属性选择度量
❖ 属性选择度量-划分规则
▪ 划分属性:度量得分高的属性
❖ 流行的属性选择度量
▪ 信息增益(ID3, C4.5)
• 选取时,偏向于多值属性
▪ 增益率(C4.5)
• 偏向不平衡划分
▪ Gini指标( CART, SLIQ, SPRINT)
• 偏向于多值属性 • 类的数量很大时,计算较困难
23
关于数据分类的小结
❖ 所谓分类即是使用某种分类模型,以对象的若干维描述属 性为输入,经过计算输出该对象所属类别的过程
❖ 数据分类的两个关键步骤是
▪ 分类器训练:选定合适的分类模型及参数 ▪ 分类器测试:利用合适的指标检验分类器有效性
❖ 目前已有一些成熟的分类器可供使用
▪ 决策树 ▪ 支持向量机 ▪ 最近邻/k-近邻
❖ 多类分类示例
▪ 油气传输:区分行人走过、汽车碾过、镐刨、电钻等行为 ▪ 文字识别:区分不同的字符(其中汉字识别是一个大类别问题) ▪ 社会网络:区分中心用户、活跃用户、不活跃用户、马甲用户等
6
示例数据集
❖ 数据集包含多个描述属性和一个类别属性
Age
Salary
Class
30
high
c1
25
high
c2
21
low
c2
43
high
c1
18
low
c2
33
low
c1
......
......
......
❖ 一般来说
▪ 描述属性:连续值或离散值
▪ 类别属性:只能是离散值(目标属性连续对应回归问题)
7
分类问题的形式化描述
数据集X {(xi , yi ) | i 1,2,,total}, 其中数据样本xi (i 1,2,, total)用d维特征向量xi (xi1, xi2 ,, xid )表示 xi1, xi2 ,, xid分别对应d个描述属性A1, A2 ,, Ad的具体取值 yi表示数据样本xi的类标号 假设给定数据集包含m个类别,则yi {c1, c2 ,, cm}
【升小衔接一年级数学课程】数的分解与组成21页PPT

61、奢侈是舒适的,否则就不是奢侈 。——CocoCha nel 62、少而好学,如日出之阳;壮而好学 ,如日 中之光 ;志而 好学, 如炳烛 之光。 ——刘 向 63、三军可夺帅也,匹夫不可夺志也。 ——孔 丘 64、人生就是学校。在那里,与其说好 的教师 是幸福 ,不如 说好的 教师是 不幸。 ——海 贝尔 65、接受挑战,就可以享受胜利的喜悦 。——杰纳勒 尔·乔治·S·巴顿
【升小衔接一年级数学课程】数的分 解与组成
6、法律的基础有两个,而且只有两个……公平和实用。——伯克 7、有两种和平的暴力,那就是法律和礼节。——歌德
8、法律就是秩序,有好的法律才有好的秩序。——亚里士多德 9、上帝把法律和公平凑合在一起,可是人类却把它拆开。——查·科尔顿 10、一切法律都是无用的,因为好人用不着它们,而坏人又不会因为它们而变得规矩起来。——
数分课件180
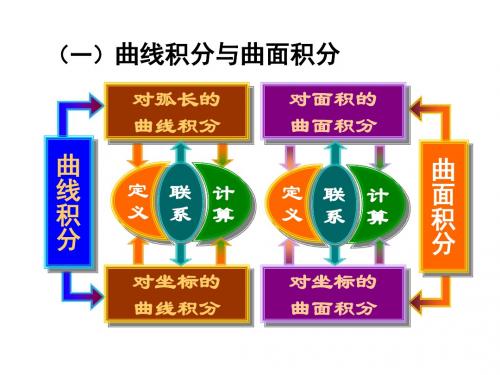
Pdydz Qdzdx Rdxdy
(P cos Q cos Rcos )ds
理论上的联系
1.定积分与不定积分的联系
b
f ( x)dx F (b) F (a) (F( x) f ( x)) a 牛顿--莱布尼茨公式
2.二重积分与曲线积分的联系
D
(
Q x
P y
)dxdy
L
Pdx
Qdy
(沿L的正向)
格林公式
3.三重积分与曲面积分的联系
P Q R
(
x
y
z
)dv
Pdydz
Qdzdx
Rdxdy
高斯公式
4.曲面积分与曲线积分的联系
R Q
P R
Q P
(
y
z
)dydz
二代一定 (与方向有关)
与路径无关的四个等价命题
条 在单连通开区域D 上 P( x, y),Q( x, y) 具有 件 连续的一阶偏导数,则以下四个命题成立.
等 (1) 在D内L Pdx Qdy与路径无关
价 (2) C Pdx Qdy 0,闭曲线C D
命 (3) 在D内存在U( x, y)使du Pdx Qdy 题 (4) 在D内, P Q
f (x, y, z)dV
b
dx
y2
(
x
)
dy
z2( x,y) f ( x, y, z)dz, (dV体元素)
a
y1 ( x )
z1 ( x, y )
数学分析ppt课件

有限覆盖定理
总结词
有限覆盖定理是实数完备性定理中的另一个 重要结论,它涉及到实数集的覆盖问题。
详细描述
有限覆盖定理说明,任意一个开覆盖${(a_n, b_n)}$的实数集都可以被有限个开区间覆盖 。换句话说,对于任意一个实数集$S$,都 存在有限的开区间${(a_1, b_1), (a_2, b_2), ldots, (a_n, b_n)}$,使得$S subseteq cup_{i=1}^{n} (a_i, b_i)$。这个定理在证 明紧空间的性质和实数完备性中起到了关键 作用。
3
实数系中的基本运算
实数系中可以进行加法、减法、乘法和 除法等基本运算,这些运算具有交换律 、结合律、分配律等性质。此外,实数 系中还可以定义绝对值、最大值、最小 值等概念。
极限理论
01
极限的定义
极限是数学分析中的一个基本概念,它描述了当自变量趋向某一值时,
函数值的变化趋势。极限的定义包括数列极限和函数极限两种形式。
详细描述
介绍向量值函数和空间曲线的定义,通过实例说明向量值函 数和空间曲线的性质,并解释其在数学分析中的重要性和应 用。
06
实数完备性定理
区间套定理
总结词
区间套定理是实数完备性定理中的一个 重要组成部分,它描述了闭区间套的性 质。
VS
详细描述
区间套定理指出,如果存在一个闭区间套 ,即一列闭区间${[a_n, b_n]}$,满足 $a_n < b_n$且$a_n < a_{n+1} < b_{n+1} < b_n$(对任意$n$),则该区 间套中至少存在一个实数。这个定理在数 学分析中有着广泛的应用,例如在证明连 续函数的性质和极限理论中。
数分课件17-3

Q dx x
y d
x 1 ( y)
Q( 2 ( y ), y )dy Q( 1 ( y ), y )dy A c c c CBE Q( x , y )dy CAE Q( x , y )dy
o
L
E D
B
x 2 ( y)
C
x
CBE Q( x , y )dy EAC Q( x , y )dy Q( x , y )dy
y型区域
证明依赖于区域的形状
x型区域
单连通 复连通
既 x 又 y型
一般区域
6
证明:
y
x 1 ( y)
1. 若区域 D 既是 x 型 又是 y 型区域,
d
E
y 2 ( x)
D
C y 1 ( x )
B
x 2 ( y)
即平行于坐标轴的直 c 线和 L至多交于两点. o a
2
曲线 AMO :
A(a ,0)
N
y ax x, x从a变到0.
1 A xdy ydx 2 L 1 1 ONA xdy ydx AMO xdy ydx 2 2 1 a 0 1 2 AMO xdy ydx a xdx a . 4 6 2
所以
y
L
xdy ydx xdy ydx L x 2 y 2 l x 2 y 2
2 2 2 r cos r sin d 0 2 r
l
D1
o
r
x
2 2
2 .
17
xdy ydx 例5 计算 , 其中L是以点(1, 0)为中心, 2 2 4x y L R为半径的圆周( R 1), 取逆时针方向.
数的认识分数-PPT演示课件

带分数比较大小,先比较整数部分, 整数部分大的就大,整数部分相同,比较分 数部分,分数部分大的就大。
•12
分数与除法的关系:
两个自然数相除(0除外),它们的 商可以用分数来表示:
被 除 除 数 数 被 除除 数 (数 除 0 ) 数
是1 4 。
9
(4)20分=( )时(填分数)
(5)540平方厘米=( (填分数)
)平方分米
•18
(7)分数单位是 1 的最简真分数有( )。
10
(8)11÷9的商用带分数表示是( )。
(9)把12化成分母是3的假分数是( )。
(10) 3
4
=3÷(
)=( )
12
=( 15 ) 。
(最1小1带)分分数数是单(位是)141 ,的最最小小真假分分数数是是((
) )。
(12)把5米长的一根绳子平均分成3份,每 份是这条绳子的( ),是( )米。 •19
约分
约分------把一个分数化成和它相等,但分子 和分母都比较小的分数.
分子分母只有公因数1的分数叫最简分数。 计算的结果,能约分的要约成最简分数。
约分的方法: 1.用分子分母的公因数(1除外)逐次去除分
如 :24 24 4 6 4
245
2
5
4
6
1 4
•9
假分数与带分数或整数的互化:
整数(0除外)化成假分数,用指定 的数作分母,用分母与整数的乘积作分子。
如 :把7化 成2以 为 分 母 的 假 分 数 。
7
72 2
14 2
带分数化成假分数,用原来的分母作分
幼儿园大班数学分一分5的分解组成说课稿PPT课件

11
一、说教材
说
二、说学情
课
流
三、说活动目标
程
四、说重难点
五、说活动准备
六、说教法学法
七、说活动过程
八、说活动预期
12
四、说重难点
教学重点 让幼儿学习5的分解和组成
教学难点 在此基础上引导幼儿归纳出
分合式中两边数列的关系。
13
一、说教材
本次活动选自大班上册数学《分一分》中5的分
大班数学上册
——5的分解组成
大三班
张红
1
鸡妈妈呀,有5只鸡宝宝,可是慢 慢的鸡宝宝都长大了,他们的房子 住不下了。于是鸡妈妈就给宝宝们 又盖个两间新房子。可是鸡妈妈不 知道该怎么把鸡宝宝们分到房子里
面。
2
一、基本部分——学习5的分解组成
幼儿将鸡宝宝分到两座房子里并根据分的结果在记录 卡上作记录。
7
四、活动延伸
指导幼儿完成书上相关题目
请将左右两边合起来数目是5的两组红豆连在 一起,然后说一说几各几合起来是5
8
用竖线将每排的5朵小花分成两份,每次要分 得不一样,想想怎样分不漏掉,并用数字把结果记 在格子里
9
八、活动预测效果
通过这节课,幼儿能了解5的组成。知道5的4 种分合方法并初步掌握分合规律。幼儿在整个活动中, 能积极的动手操作。在操作中发现知识。达到培养幼 儿对数学活动的兴趣,锻炼幼儿的动手操作能力,发 展幼儿思维的灵活性,培养幼儿分析综合能力。
设计意图:《指南》中指出:幼儿思维发展以具体形象思维为主,
应引导幼儿通过直接感知、亲身体验和实际操作进行科学学习,不 应为追求知识的掌握而对幼儿进行灌输和强化训练。本活动通过创 设情境——抛出问题导入,能激发幼儿的学习兴趣,气氛活跃,而 重点部分的教学采取让幼儿自主探究,动手操作实践的方式,保证 了教学活动效果,本教学活动是环环相扣的,让幼儿在学中玩,玩 中学,使新知识得到巩固和利用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
可微,且 (t) 0. )则曲边梯形的面积为
A | (t) (t) | dt.
数学分析
湖南人文科技学院
例4
求椭圆
x2 a2
y2 b2
1
的面积.
解:
椭圆的参数方程
x
y
a cos t bsin t
由对称性知总面积等于4倍第一象限部分面积.
A 4 2 | bsin t(a cos t) | dt 0
数学分析
湖南人文科技学院
第十章 定 积 分的应用
§1平面图形的面积 §2 由平行截面面积求体积 §3 平面曲线的弧长 §4 旋转曲面的面积
§5 定积分在物理中的应用 §6 定积分的近似计算
小结与习题
数学分析
(一)直角坐标系下的面积公式
湖南人文科技学院
由连续曲线y=f(x)(≥0),直线x=a,x=b及x轴所围成的图形
上的投影为区间[1,9].
故所求面积为
S 3 (2 y 3 y2 )dy 1
32 .
3
(-1,1)
首页
数学分析
湖南人文科技学院
(二)参数函数的面积公式
如果曲边梯形的曲边为参数方程
x y
(t) (t)
(
t
)
其中 y (t) 在[,]上连续, x (t) 在[,]上可微,且
(t) 0, (或 x (t) 在[,]上连续, y (t) 在[,]上
的面积S为
y
y=f(x)
b
S a f ( x)dx
x
oa
b
数学分析
湖南人文科技学院
(2)若函数f(x)在[a,b]上连续,且对任意x[a,b], f(x)≤0,
则由曲线y=f(x),x=a,x=b,y=0所围成的平面图形的面积S为
y
a
b
x
b
S a f ( x)dx
o
y=f(x)
数学分析
湖南人文科技学院
例6 求双纽线 2 a 2 cos 2 所围平面图形的面积.
解 由对称性知总面积等于第一象限部分面积的4倍, 所以
y x
A1
2 a2 cos 2
A 4A1
4
4
0
1 a2 cos 2 d
2
a2.
数学分析
湖南人文科技学院
例7 求心形线
r a(1 cos ), (a 0)
所围平面图形的面积.
1. 3
O
y x2
x
数学分析
湖南人文科技学院
例2
求曲线
y
1 2
x2,y
1 1 x2
, 与直线x=2,x=-2
所围成的图形的面积.
y
y 1 x2
2
1
y 1 1 x2
O 12 x
-1
下页
数学分析
湖南人文科技学院
解: 由对称性,所围图形关于y轴对称,因此只要求第一 象限部分的两倍即可.
S
2
2
|
0
y
4ab 2 sin2 tdt 0
ab.
t
x
O
由摆线x=a(t-sint), x=a(1-cost)(a>0)的一拱与
x轴所围成的平面图形的面积.
解: 摆线的一拱可取t[0,2],故所求面积为
y
A a2 2 (1 cos t )2 dt 0
ta
3 a2 .
O
x
2a
数学分析
三、极坐标系的面积计算
设由曲线r= r()及射线 、 围成一曲边扇形,求其面积. 这里, r()在[, ]上连续,且 r()
面积元素 dA 1[ ( )]2 d
2
曲边扇形的面积
A 1[ ( )]2 d . 2
湖南人文科技学院
d
r r( )
d
o
x
数学分析
湖南人文科技学院
b
S a | f ( x) g( x) | dx
y
y=f(x)
oa
y=g(x) x
b
数学分析
湖南人文科技学院
例1 计算由两条抛物线y2=x,和y=x2所围成的图形的 面积.
解 两曲线的交点 为(0,0),(1,1),选x为积 分变量, x[0,1]
y
x y2
A
1
0 (
x x2 )dx
2 3 x3 1 3 x 2 3 0
1 2
x2
1
1 x
2
| dx
2
11
0
( 1
x2
1 2
x2 )dx
2
21 ( 12
x2
1
1 x
2
)dx
2( 1) 2(7 arctan 2 )
46 6
4
2 arctan 2.
数学分析
湖南人文科技学院
例3 计算抛物线y2x 与直线x2y-3=0所围成的图形
的面积. 解:易求得两曲线的交点为:(1,1),(9,3). 图形在y轴
解 由对称性知
d
A 2 1 a2 (1 cos )2 d 20
a2
(1 2cos cos2 )d
0
a2
23
2 sin
1 4
sin
2
0
3 2
a2 .
湖南人文科技学院
(3)若f(x)和g(x)都在[a,b]上连续,且对任意x[a,b],
g(x)≤ f(x),则由曲线y=f(x), x=a,x=b,y=g(x)所围成的平面
图形的面积S为
f(x) y
b
S a ( f ( x) g( x))dx
g(x)
O
x
数学分析
湖南人文科技学院
(4)若f(x)和g(x)都在[a,b]上连续,则由曲线y=f(x), x=a, x=b,y=g(x)所围成的平面图形的面积S为
(3)若f(x)在[a,b]上连续,则由曲线y=f(x), x=a,x=b,y=0
所围成的平面图形的面积S为
S S1 S2 S3
c1 f ( x)dx
c2 f ( x)dx
b
f (x)dx
a
c1
c2
b
| f ( x) | dx y a
y=f(x)
S1
S3
oa
c1 S2 c2
x b
数学分析
