集合历年高考真题精编WORD版
(完整版)集合历年高考题.docx

圆学子梦想铸金字品牌1.( 2013 ·重庆高考文科·T 1)已知全集U1,2,3,4 ,集合 A1,2 ,B2,3 ,则 C U A B()A .1,3,4 B.3,4 C.3 D.42、( 2013 ·四川高考文科·T 1)设集合A{1,2,3} ,集合 B {2,2} ,则A I B()A. B. {2} C. {2,2} D. {2,1,2,3}3.(2013 ·福建高考文科·T3) 若集合A=1,2,3 ,B= 1,3,4 ,,则A∩B的子集个数为()A.2B.3C.4D.164.( 2013 ·湖北高考文科·T 1)已知全集U{1,2,3,4,5} ,集合A{1,2} , B{2,3,4},则 B C u A ()A. {2} B . {3,4}C. {1,4,5} D . {2,3,4,5}5.( 2013 ·新课标Ⅰ高考文科·T 1)已知集合A{1,2,3,4} , B{ x | x n2 , n A} ,则A∩B=A. {1,4}B. { 2,3}C.{ 9,16}D. {1,2}6.( 2013 ·大纲版全国卷高考文科·T 1)设集合U1,2,3,4,5,集合A1,2 ,e u A()则C U AA.1,2B.3,4,5C.1,2,3,4,5D.7.( 2013 ·湖南高考文科)已知集合 U{2,3,6,8},A{2,3}, B{2,6,8},则(C U A)B________8.设集合A1,2,3 , B4,5, M x | x a b, a A, b B, 则 M 中元素的个数为()A.3B.4C.5D.69. (2013 江·苏高考数学科·T4) 集合 {-1,0,1} 共有个子集 .10.( 2013 ·四川高考理科·T 1)设集合A{ x | x20} ,集合 B { x | x240} ,则AI B()A. {2}B. {2}C. { 2,2}D.11.(2013 浙·江高考文科·T1) 设集合 S={x|x>-2},T={x|- 4≤ x≤ 1},则 S∩ T= ()A.[- 4,+ ∞)B.(- 2,+ ∞ )C.[ -4,1]D.(-2,1]12.( 2013 ·安徽高考文科·T2)已知A= { x|x+1>0 }, B= { -2, -1, 0, 1},则( C 错误!未找到引用源。
(完整版)历年高考真题(集合与函数部分)

历年高考真题(集合与函数部分)1. (2004年高考题)设A 、B 、丨均为非空集合,且满足 A BI ,则下列各式中错误的是 A . (C I A) U B=I 2.(2006年高考题)已知集合M (A )0 (C ) |x|1 x 3| B . (C I A) U (C I B)=I|x|x 3|,N C . A n (C I|x|log 2 x (B ) (D ) B)=1|,|x|0 |x|2D . (C I A) (C I B)= C I BM N3|3|3. (2008年高考题)设集合M{m Z 3 2} N{n n 3},则 M NA . {0,1} B. { 1,0,1} C. {0,1,2} D { 1,0,1,2}4. (2009年高考题)设集合A AIA. B.3,4C. 2,1D.4.5.(2012年高考题)已知集合 A {123,4,5} ,B {(x,y) xA,y A,x yA };,则B 中所含元素的个数为( ) (A) 3 (B)6 2 6、(2013年高考题)已知集合 M {x|(x 1) (A ) {0,1,2} (B ) { 1,0,1,2} (C ) { (C) 4,x R}, 1,0,2,3}( ,N(D) (D)1,0,1,2,3},贝U M I{ {0,1,2,3}7. (2014 年高考题)设集合 M= {0,1,2} , N= x | x 2 3x 2<0 ,则 M N =()A. {1}B. {2}C. {0, 1}D. { 1, 2}8. (2015 年高考题)已知集合 A= {-2, -1 , 0, 2}, B= {x| ( x-1) (x+2)V 0},贝U A A B= (A ) {-1, 0} ( B ) { 0 , 1} (C ) {-1 , 0, 1} ( D ) {0, 1, 2}9. (2008 年高考题)若 x (e 1,1), In x , b 2ln x , c ln x ,则A . a b c B. C. b a c D. b 10. (2005年高考题)若a ln 2 ln3A . a<b<cB . c<b<a 11.(2007年高考题)下列四个数中最大的是 (B ) ln (ln 2) (A) (ln2)2 12、(2013年高考题)设a (A ) c b a (B ) log 36, b c aC . c<a<bD . b<a<c(C ) In 2 (D ) ln213. (2003年高考题)设函数f (x ) A . (- 1, 1)log 510 , c (C ) a log 714 , b (D ) 2 12 x 2, x1,x 0. 0, ,若f (X 。
(完整版)集合有关近年高考题50道及答案解析

【经典例题】【例1】(2009年广东卷文)已知全集U R ,则正确表示集合 M ( 1,0,1)和Nx|x 2 x 0关系的韦恩(Venn )【解析】 由N x|x 2 x 0 ,得N ( 1,0),则N ME B.【例2】(2011广东)已知集合 A (x,y )|x,y 为实数,且x 2的元素个数为 A 、0 B 、1 C 、2 D 、3【答案】C【解析】A 为圆心在原点的单位圆, B 为过原点的直线,故有y 2 1 , B (x,y ) |x,y 为实数,且 y x ,则A I B( )2个交点,故选C.【例3】(2010天津理)设集合A= x||x a| 1,xx||x b| 2,x R .若A B ,则实数a,b 必满足()A 、 |a b| 3 C 、 |a b| 3B 、 |a b| 3 D 、 |a b| 3系的韦恩(Venn )图如图所示,则阴影部分所示的集合的元素共有【答案】D 【解析】A= {x|a-1<x<a+1 } ,B={x|x<b-2 |a-b| 3 或x>b+2),因为A B,所以 a+1 b-2 或 a-1 b+2, 即 a-b -3 或 a-b 3,即【例4】(2009广东卷理)已知全集U R ,集合M {x 2 x 1 2)和 N{xx 2k 1,k 1,2,L )的关R ,B A. 3个 C. 1个 【答案】 B. 2个 D.无穷多个【解析】{x 2 x 1 2)得 1 x 3,则 MN 1,3 ,有2个,选B.【例5】 (2010 天津文)设集合 A x||x-a|<1,x R ,B x|1 x 5,x R .若A B,则实数a 的取值范围A 、 a|0 a 6B 、 a | a 2,或a 4C、 a | a 0,或a 6D、a |2 a 4【答案】C——i ------------ X—冬—【解析】由|x-a|<1得-1<x-a<1,即a-1<x<a+1.如图'T 。
2024全国高考真题数学汇编:集合

2024全国高考真题数学汇编集合一、单选题1.(2024全国高考真题)已知集合{}355,{3,1,0,2,3}A x x B =-<<=--∣,则A B = ()A .{1,0}-B .{2,3}C .{3,1,0}--D .{1,0,2}-2.(2024天津高考真题)集合{}1,2,3,4A =,{}2,3,4,5B =,则A B = ()A .{}1,2,3,4B .{}2,3,4C .{}2,4D .{}13.(2024全国高考真题)若集合{}1,2,3,4,5,9A =,{}1B x x A =+∈,则A B = ()A .{}1,3,4B .{}2,3,4C .{}1,2,3,4D .{}0,1,2,3,4,94.(2024北京高考真题)已知集合{|31}M x x =-<<,{|14}N x x =-≤<,则M N ⋃=()A .{}11x x -≤<B .{}3x x >-C .{}|34x x -<<D .{}4x x <5.(2024全国高考真题)已知集合{}{}1,2,3,4,5,9,A B A ==,则()A A B ⋂=ð()A .{}1,4,9B .{}3,4,9C .{}1,2,3D .{}2,3,5参考答案1.A【分析】化简集合A ,由交集的概念即可得解.【详解】因为{{}|,3,1,0,2,3A x x B =<=--,且注意到12<<,从而A B = {}1,0-.故选:A.2.B【分析】根据集合交集的概念直接求解即可.【详解】因为集合{}1,2,3,4A =,{}2,3,4,5B =,所以{}2,3,4A B = ,故选:B3.C【分析】根据集合B 的定义先算出具体含有的元素,然后根据交集的定义计算.【详解】依题意得,对于集合B 中的元素x ,满足11,2,3,4,5,9x +=,则x 可能的取值为0,1,2,3,4,8,即{0,1,2,3,4,8}B =,于是{1,2,3,4}A B ⋂=.故选:C4.C【分析】直接根据并集含义即可得到答案.【详解】由题意得{}|34M x x N ⋃=-<<.故选:C.5.D【分析】由集合B 的定义求出B ,结合交集与补集运算即可求解.【详解】因为{}{}1,2,3,4,5,9,A B A ==,所以{}1,4,9,16,25,81B =,则{}1,4,9A B = ,(){}2,3,5A A B = ð故选:D。
集合高考真题完整版完整版.doc

(2017.1 )已知集合 A= x|x 2 , B= x|3 2 x 0 ,则
3 A . A I B= x|x 2
B.A I B
3
C.A U B
x|x 2
D .A U B= R
(2016.1 )设集合 A {1,3,5,7} , B { x |2 x 5} ,则 A I B
(A){1,3} ( B) {3,5} ( C){5,7} ( D) {1,7}
( C) (1,3)
( D ) ( 2,3)
(2013.1) 已知集合 A {1,2,3, 4} , B { x | x n2 ,n A} , 则 A I B ( )
(A ){0}
( B ){ -1, ,0} ( C) {0 , 1}
( D){ -1, ,0,1}
(2012.1 )已知集合 A={ x| x2-x- 2<0} , B={ x|- 1<x<1} ,则(
对于考生来说,掌握有效的应试技巧比再做题突击更为有效。
1.草稿纸也要逐题顺序写草稿要整洁,草稿纸使用要便于检查。不要 在一大张纸上乱写乱画,东写一些,西写一些。打草稿也要像解题一 样,一题一题顺着序号往下写。最好在草稿纸题号前注上符号,以确 定检查侧重点。为了便于做完试卷后的复查,草稿纸一般可以折成 4-8 块的小方格, 标注题号以便核查,保留清晰的分析和计算过程。
2.答题要按 先易后难 顺序不要考虑考试难度与结果,可以先用 5 分 钟熟悉试卷,合理安排考试进度,先易后难,先熟后生,排除干扰。 考试中很可能遇到一些没有见过或复习过的难题, 不要 蒙 了。一般 中考试卷的题型难度分布基本上是从易到难排列的,或者交替排列。
3.遇到容易试题不能浮躁遇到容易题,审题要细致。圈点关键字词, 边审题边画草图,明确解题思路。有些考生一旦遇到容易的题目,便 觉得心应手、兴奋异常,往往情绪激动,甚至得意忘形。要避免急于 求成、粗枝大叶, 防止受熟题答案与解题过程的定式思维影响,避免 漏题,错题,丢掉不该丢的分。
专题01 集合-五年(2017-2021)高考数学真题分项详解(新高考地区专用)(原卷版)

专题01 集合【2021年】一、【2021·浙江高考】设集合{}1A x x =≥,{}12B x x =-<<,则AB =( ) A. {}1x x >- B. {}1x x ≥ C. {}11x x -<< D. {}12x x ≤<二、【2021·江苏高考】设集合A ={x|−2<x <4},B ={2,3,4,5},则A ∩B =( ) A. {2}B. {2,3}C. {3,4}D. {2,3,4}【2020年】一、【2020·北京高考】已知集合A ={−1,0,1,2},B ={x|0<x <3},则A ∩B =( )A. {−1,0,1}B. {0,1}C. {−1,1,2}D. {1,2}二、【2020·浙江高考】已知集合P ={x|1<x <4},Q ={x|2<x <3},则P ∩Q =( )A. {x|1<x ≤2}B. {x|2<x <3}C. {x|3≤x <4}D. {x|1<x <4}三、【2020·天津高考】设全集U ={−3,−2,−1,0,1,2,3},集合A ={−1,0,1,2},B ={−3,0,2,3},则A ∩(∁U B)=( )A. {−3,3}B. {0,2}C. {−1,1}D. {−3,−2,−1,1,3 }四、【2020·上海高考】已知集合A ={1,2,4},集合B ={2,4,5},则A ∩B = .【2019年】一、【2019·北京高考(文)】已知集合A ={x|−1<x <2},B ={x|x >1},则A ∪B =( )A. {x|−1<x <1}B. {x|1<x <2}C. {x|x >−1}D. {x|x >1}二、【2019·浙江高考】已知全集U={−1,0,1,2,3},集合A={0,1,2},B={−1,0,1},则(∁U A)∩B=()A. {−1}B. {0,1}C. {−1,2,3}D. {−1,0,1,3}三、【2019·天津高考】设集合A={−1,1,2,3,5},B={2,3,4},C={x∈R|1≤x<3},则(A∩C)∪B=()A. {2}B. {2,3}C. {−1,2,3}D. {1,2,3,4}四、【2019·上海高考】已知集合A={1,2,3,4,5},B={3,5,6},则A∩B=______.【2018年】一、【2018·北京高考】已知集合A={x||x|<2},B={−2,0,1,2},则A∩B=()A. {0,1}B. {−1,0,1}C. {−2,0,1,2}D. {−1,0,1,2}二、【2018·浙江高考】已知全集U={1,2,3,4,5},A={1,3},则∁U A=()A. ⌀B. {1,3}C. {2,4,5}D. {1,2,3,4,5}三、【2018·天津高考(理)】设全集为R,集合A={x|0<x<2},B={x|x≥1},则A∩(∁R B)=()A. {x|0<x≤1}B. {x|0<x<1}C. {x|1≤x<2}D. {x|0<x<2}【2018·天津高考(文)】设集合A={1,2,3,4},B={−1,0,2,3},C={x∈R|−1≤x<2},则(A∪B)∩C=()A. {−1,1}B. {0,1}C. {−1,0,1}D. {2,3,4}四、【2018·上海高考】已知α∈{−2,−1,−12,12,1,2,3},若幂函数f(x)=xα为奇函数,且在(0,+∞)上递减,则α=______.【2017年】一、【2017·北京高考(理)】若集合A={x|−2<x<1},B={x|x<−1或x>3},则A∩B=()A. {x|−2<x<−1}B. {x|−2<x<3}C. {x|−1<x<1}D. {x|1<x<3}【2017·北京高考(文)】已知全集U=R,集合A={x|x<−2或x>2},则∁U A=()A. (−2,2)B. (−∞,−2)∪(2,+∞)C. [−2,2]D. (−∞,−2]∪[2,+∞)二、【2017·浙江高考】已知集合P={x|−1<x<1},Q={x|0<x<2},那么P∪Q=()A. {x|−1<x<2}B. {x|0<x<1}C. {x|−1<x<0}D. {x|1<x<2}三、【2017·天津高考】设集合A={1,2,6},B={2,4},C={x∈R|−1≤x≤5},则(A∪B)∩C=()A. {2}B. {1,2,4}C. {1,2,4,5}D. {x∈R|−1≤x≤5}四、【2017·上海高考】已知集合A={1,2,3,4},集合B={3,4,5},则A∩B=______ .。
高考数学真题汇编---集合

高考数学真题汇编---集合学校:___________姓名:__________班级:___________考号:__________29小题)一.选择题(共1.(2017?北京)已知全集U=R,集合A={ x| x<﹣2 或x>2},则?U A=()A.(﹣2,2)B.(﹣∞,﹣2)∪(2,+∞)C.[ ﹣2,2] D.(﹣∞,﹣2] ∪[ 2,+∞)2+y2=1} ,B={ (x,y)| y=x} ,则A 2.(2017?新课标Ⅲ)已知集合A={(x,y)| x∩B中元素的个数为()A.3 B.2 C.1 D.03.(2017?天津)设集合A={ 1,2,6} ,B={ 2,4} ,C={ x∈R|﹣1≤x≤5} ,则(A ∪B)∩C=()A.{ 2} B.{ 1,2,4} C.{1,2,4,5} D.{x∈R| ﹣1≤x≤5} 4.(2017?新课标Ⅲ)已知集合A={ 1,2,3,4} ,B={ 2,4,6,8},则A∩B中元素的个数为()A.1 B.2 C.3 D.45.(2017?山东)设函数y= 的定义域为A,函数y=ln(1﹣x)的定义域为B,则A∩B=()A.(1,2)B.(1,2] C.(﹣2,1)D.[ ﹣2,1)6.(2017?新课标Ⅰ)已知集合A={ x| x<2} ,B={ x| 3﹣2x>0},则()A.A∩B={ x| x<} B.A∩B=?C.A∪B={ x| x<} D.A∪B=R7.(2017?天津)设集合A={ 1,2,6},B={ 2,4} ,C={ 1,2,3,4},则(A∪B)∩C=()A.{ 2} B.{1,2,4}C.{ 1,2,4,6} D.{ 1,2,3,4,6}8.(2017?山东)设集合M={ x|| x﹣1| <1} ,N={ x| x<2},则M ∩N=()A.(﹣1,1)B.(﹣1,2)C.(0,2)D.(1,2)x<1} ,则()9.(2017?新课标Ⅰ)已知集合A={ x| x<1} ,B={ x|3A.A∩B={ x| x<0} B.A∪B=RC.A∪B={ x| x>1} D.A∩B=?10.(2017?新课标Ⅱ)设集合A={ 1,2,3} ,B={ 2,3,4} ,则A∪B=()A.{ 1,2,3,4} B.{1,2,3} C.{ 2,3,4} D.{ 1,3,4} 11.(2017?北京)若集合A={ x|﹣2<x<1} ,B={ x| x<﹣1或x>3} ,则A∩B=()A.{ x|﹣2<x<﹣1} B.{ x|﹣2<x<3} C.{x|﹣1<x<1} D.{x| 1<x<3} 12.(2017?浙江)已知集合P={ x|﹣1<x<1} ,Q={ x| 0<x<2},那么P∪Q=()A.(﹣1,2)B.(0,1)C.(﹣1,0)D.(1,2)4x+m=0} .若A∩B={ 1} , 13.(2017?新课标Ⅱ)设集合A={ 1,2,4} ,B={ x| x2﹣则B=()A.{ 1,﹣3} B.{ 1,0} C.{ 1,3} D.{ 1,5}14.(2016?新课标Ⅲ)设集合A={ 0,2,4,6,8,10},B={ 4,8},则?A B=()A.{ 4,8} B.{0,2,6}C.{ 0,2,6,10} D.{ 0,2,4,6,8,10}15.(2016?山东)设集合U={ 1,2,3,4,5,6} ,A={ 1,3,5} ,B={ 3,4,5} ,则?U(A∪B)=()A.{ 2,6} B.{ 3,6}C.{ 1,3,4,5} D.{ 1,2,4,6}16.(2016?新课标Ⅰ)设集合A={ 1,3,5,7} ,B={ x| 2≤x≤5},则A∩B=()A.{ 1,3} B.{ 3,5}C.{ 5,7} D.{1,7}17.(2016?浙江)已知全集U={ 1,2,3,4,5,6},集合P={ 1,3,5} ,Q={ 1,2,4} ,则(?U P)∪Q=()A.{ 1} B.{ 3,5}C.{ 1,2,4,6} D.{ 1,2,3,4,5}18.(2016?四川)设集合A={ x| 1≤x≤5},Z 为整数集,则集合A∩Z 中元素的个数是()A.6 B.5 C.4 D.319.(2016?北京)已知集合A={ x|| x| <2},B={﹣1,0,1,2,3},则A∩B=()A.{ 0,1} B.{ 0,1,2} C.{ ﹣1,0,1} D.{ ﹣1,0,1,2} 20.(2016?北京)已知集合A={ x| 2<x<4} ,B={ x| x<3 或x>5} ,则A∩B=()A.{ x| 2<x<5} B.{ x| x<4 或x>5} C.{ x| 2<x<3} D.{x| x<2 或x>5} 2≥4} ,则P∪(?R Q) 21.(2016?浙江)已知集合P={ x∈R| 1≤x≤3} ,Q={ x∈R|x =()A.[ 2,3] B.(﹣2,3] C.[ 1,2)D.(﹣∞,﹣2] ∪[ 1,+∞)x,x∈R},B={ x| x2﹣1<0} ,则A∪B=()22.(2016?山东)设集合A={ y| y=2A.(﹣1,1)B.(0,1)C.(﹣1,+∞)D.(0,+∞)A∩B=() 23.(2016?新课标Ⅱ)已知集合A={ 1,2,3},B={ x| x 2<9} ,则A.{ ﹣2,﹣1,0,1,2,3} B.{﹣2,﹣1,0,1,2}C.{ 1,2,3} D.{1,2}A∩B=2﹣4x+3<0} ,B={ x| 2x﹣3>0} ,则24.(2016?新课标Ⅰ)设集合A={ x| x()A.(﹣3,﹣)B.(﹣3,)C.(1,)D.(,3)25.(2016?新课标Ⅱ)已知集合A={ 1,2,3} ,B={ x| (x+1)(x﹣2)<0,x∈Z} ,则A∪B等于()A.{ 1} B.{ 1,2} C.{0,1,2,3} D.{ ﹣1,0,1,2,3} 26.(2016?新课标Ⅲ)设集合S={ x| (x﹣2)(x﹣3)≥0},T={ x| x>0} ,则S∩T=()A.[ 2,3] B.(﹣∞,2] ∪[ 3,+∞)C.[ 3,+∞)D.(0,2] ∪[ 3,+∞)27.(2016?天津)已知集合A={ 1,2,3,4} ,B={ y| y=3x﹣2,x∈A},则A∩B= ()A.{ 1} B.{ 4} C.{ 1,3} D.{ 1,4}28.(2016?四川)设集合A={ x| ﹣2≤x≤2} ,Z 为整数集,则A∩Z 中元素的个数是()A.3 B.4 C.5 D.629.(2016?天津)已知集合A={ 1,2,3},B={ y| y=2x﹣1,x∈A},则A∩B=()A.{1,3}B.{1,2}C.{2,3}D.{1,2,3}二.填空题(共3小题)2+3}.若A∩B={1},则实数 a 30.(2017?江苏)已知集合A={1,2},B={a,a的值为.31.(2017?上海)已知集合A={1,2,3,4},集合B={3,4,5},则A∩B=.32.(2016?江苏)已知集合A={﹣1,2,3,6},B={x|﹣2<x<3},则A∩B=.编---集合高考数学真题汇参考答案与试题解析29小题)一.选择题(共1.【解答】解:∵集合A={x|x<﹣2或x>2}=(﹣∞,﹣2)∪(2,+∞),全集U=R,∴?U A=[﹣2,2],故选:C.2、【解答】解:由,解得:或,∴A∩B的元素的个数是2个,故选:B.3.【解答】解:∵A={1,2,6},B={2,4},∴A∪B={1,2,4,6},又C={x∈R|﹣1≤x≤5},∴(A∪B)∩C={1,2,4}.故选:B.4.【解答】解:∵集合A={1,2,3,4},B={2,4,6,8},∴A∩B={2,4},∴A∩B中元素的个数为2.故选:B.2≥0,解得:﹣2≤x≤2,则函数y=的定义域[﹣2,5.(解答】解:由4﹣x2],:1﹣x>0,解得:x<1,则函数y=ln(1﹣x)的定义由对数函数的定义域可知域(﹣∞,1),则A∩B=[﹣2,1),故选:D.6【解答】解:∵集合A={x|x<2},B={x|3﹣2x>0}={x|x<},∴A∩B={x|x<},故A正确,B错误;A∪B={x||x<2},故C,D错误;故选:A.7.【解答】解:∵集合A={1,2,6},B={2,4},C={1,2,3,4},∴(A∪B)∩C={1,2,4,6}∩{1,2,3,4}={1,2,4}.故选:B.8.【解答】解:集合M={x||x﹣1|<1}=(0,2),N={x|x<2}=(﹣∞,2),∴M∩N=(0,2),故选:C.9.【解答】解:∵集合A={x|x<1},x<1}={x|x<0},B={x|3∴A∩B={x|x<0},故A正确,D错误;A∪B={x|x<1},故B和C都错误.故选:A.10.【解答】解:∵A={1,2,3},B={2,3,4},∴A∪B={1,2,3,4}故选:A.11【解答】解:∵集合A={x|﹣2<x<1},B={x|x<﹣1或x>3},∴A∩B={x|﹣2<x<﹣1}故选:A.12.【解答】解:集合P={x|﹣1<x<1},Q={x|0<x<2},1,2).1<x<2}=(﹣那么P∪Q={x|﹣故选:A.4x+m=0}. 13.【解答】解:集合A={1,2,4},B={x|x2﹣若A∩B={1},则1∈A且1∈B,4+m=0,解得m=3,可得1﹣4x+3=0}={1,3}.即有B={x|x2﹣故选:C.14.【解答】解:集合A={0,2,4,6,8,10},B={4,8},则?A B={0,2,6,10}.故选:C.15.【解答】解:集合U={1,2,3,4,5,6},A={1,3,5},B={3,4,5},A∪B={1,3,4,5}.则?U(A∪B)={2,6}.故选:A.16【解答】解:集合A={1,3,5,7},B={x|2≤x≤5},则A∩B={3,5}.故选:B.17.【解答】解:?U P={2,4,6},(?U P)∪Q={2,4,6}∪{1,2,4}={1,2,4,6}.故选:C.18.【解答】解:∵集合A={x|1≤x≤5},Z为整数集,则集合 A ∩Z={ 1,2,3,4,5} . ∴集合 A ∩Z 中元素的个数是 5. 故选: B .19.【解答】 解:∵集合 A={ x|| x| <2} ={ x|﹣2<x <2} , B={﹣1,0,1,2,3} , ∴A ∩B={﹣1,0,1} . 故选: C .20.【解答】 解:∵集合 A={ x| 2<x <4} ,B={ x| x <3 或 x >5} , ∴A ∩B={ x| 2<x <3} . 故选: C .2≥ 4} ={ x ∈R | x ≥ 2 或 x ≤﹣2} ,21. 【解答】 解:Q={ x ∈R| x 即有 ?R Q={ x ∈R|﹣2<x <2} , 则 P ∪(?R Q )=(﹣2,3] . 故选: B .x ,x ∈R} =(0,+∞), 22. 【解答】 解:∵ A={ y| y=22﹣1<0} =(﹣1,1),B ={ x| x ∴A ∪B=(0,+∞)∪(﹣1,1)=(﹣1,+∞). 故选:C .2<9} ={ x|﹣3<x <3} , 23【解答】 解:∵集合 A={ 1,2,3} ,B={ x| x∴A ∩B={ 1,2} . 故选: D .2﹣4x+3<0} =(1,3), 24. 【解答】 解:∵集合 A={ x| xB={x|2x﹣3>0}=(,+∞),∴A∩B=(,3),故选:D.25.【解答】解:∵集合A={1,2,3},B={x|(x+1)(x﹣2)<0,x∈Z}={0,1},∴A∪B={0,1,2,3}.故选:C.26.【解答】解:由S中不等式解得:x≤2或x≥3,即S=(﹣∞,2]∪[3,+∞),∵T=(0,+∞),∴S∩T=(0,2]∪[3,+∞),故选:D.27.【解答】解:把x=1,2,3,4分别代入y=3x﹣2得:y=1,4,7,10,即B={1,4,7,10},∵A={1,2,3,4},∴A∩B={1,4},故选:D.28.【解答】解:∵A={x|﹣2≤x≤2},Z为整数集,∴A∩Z={﹣2,﹣1,0,1,2},A∩Z中元素的个数是5,则故选:C.29【解答】解:根据题意,集合A={1,2,3},而B={y|y=2x﹣1,x∈A},则B={1,3,5},则A∩B={1,3},故选:A.二.填空题(共3小题)2+3}.A∩B={1},30.【解答】解:∵集合A={1,2},B={a,a∴a=1或 a2+3=1,当a=1时,A={1,1},B={1,4},成立;2+3=1无解.a综上,a=1.故答案为:1.31.【解答】解:∵集合A={1,2,3,4},集合B={3,4,5},∴A∩B={3,4}.故答案为:{3,4}.32.【解答】解:∵集合A={﹣1,2,3,6},B={x|﹣2<x<3},∴A∩B={﹣1,2},故答案为:{﹣1,2}富不贵只能是土豪,你可以一夜暴富,但是贵气却需要三代以上的培养。
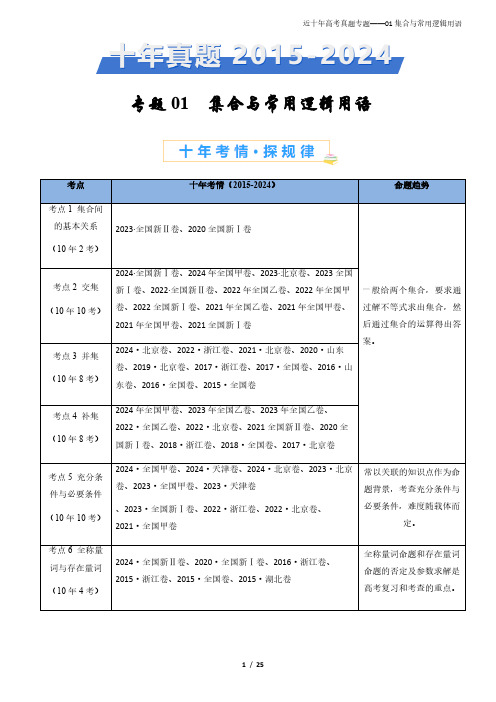
十年(2015-2024)高考真题分项汇编数学专题01集合与常用逻辑用语

专题01集合与常用逻辑用语考点十年考情(2015-2024)命题趋势考点1集合间的基本关系(10年2考)2023·全国新Ⅱ卷、2020全国新Ⅰ卷一般给两个集合,要求通过解不等式求出集合,然后通过集合的运算得出答案。
考点2交集(10年10考)2024·全国新Ⅰ卷、2024年全国甲卷、2023·北京卷、2023全国新Ⅰ卷、2022·全国新Ⅱ卷、2022年全国乙卷、2022年全国甲卷、2022全国新Ⅰ卷、2021年全国乙卷、2021年全国甲卷、2021年全国甲卷、2021全国新Ⅰ卷考点3并集(10年8考)2024·北京卷、2022·浙江卷、2021·北京卷、2020·山东卷、2019·北京卷、2017·浙江卷、2017·全国卷、2016·山东卷、2016·全国卷、2015·全国卷考点4补集(10年8考)2024年全国甲卷、2023年全国乙卷、2023年全国乙卷、2022·全国乙卷、2022·北京卷、2021全国新Ⅱ卷、2020全国新Ⅰ卷、2018·浙江卷、2018·全国卷、2017·北京卷考点5充分条件与必要条件(10年10考)2024·全国甲卷、2024·天津卷、2024·北京卷、2023·北京卷、2023·全国甲卷、2023·天津卷、2023·全国新Ⅰ卷、2022·浙江卷、2022·北京卷、2021·全国甲卷常以关联的知识点作为命题背景,考查充分条件与必要条件,难度随载体而定。
考点6全称量词与存在量词(10年4考)2024·全国新Ⅱ卷、2020·全国新Ⅰ卷、2016·浙江卷、2015·浙江卷、2015·全国卷、2015·湖北卷全称量词命题和存在量词命题的否定及参数求解是高考复习和考查的重点。
高考集合试题及答案

高考集合试题及答案一、选择题1. 集合A={x|x<10},集合B={x|x>5},求A∩B。
A. {x|x<5}B. {x|x>10}C. {x|5<x<10}D. {x|x>=10}答案:C2. 已知集合C={y|y=x^2, x∈R},求C中所有元素的和。
A. 0B. 无法计算C. 正无穷D. 1答案:B二、填空题1. 集合D={1,2,3},集合E={2,3,4},求D∪E。
答案:{1,2,3,4}2. 若集合F={x|0≤x≤1},求F的补集。
答案:{x|x<0或x>1}三、解答题1. 已知集合G={x|x^2-5x+6=0},求G的所有元素。
解:首先解方程x^2-5x+6=0,分解因式得(x-2)(x-3)=0,所以x=2或x=3。
因此,集合G={2,3}。
2. 集合H={x|-3≤x≤3},求H的子集个数。
解:集合H有7个元素,根据子集个数公式2^n(其中n为集合元素个数),H的子集个数为2^7=128。
四、证明题1. 证明:若A⊆B,则A∪B=B。
证明:根据集合并集的定义,A∪B包含所有属于A或B的元素。
由于A⊆B,A中的所有元素也属于B,所以A∪B中的元素与B中的元素完全相同,即A∪B=B。
2. 证明:若A∩B=∅,则A∪B=A+B。
证明:由于A∩B=∅,说明A和B没有共同元素。
因此,A∪B中的元素要么是A的元素,要么是B的元素,这正是A+B的定义,所以A∪B=A+B。
集合—(2018-2022)高考真题汇编

集合—(2018-2022)高考真题汇编一、单选题(共41题;共205分)1.(5分)(2022·浙江)设集合A={1,2},B={2,4,6},则A∪B=()A.{2}B.{1,2}C.{2,4,6}D.{1,2,4,6}【答案】D【解析】【解答】由并集运算,得A∪B={1,2,4,6}.故答案为:D【分析】利用并集运算求解即可.2.(5分)(2022·新高考Ⅱ卷)已知集合A={−1,1,2,4},B={x||x−1|≤1},则A∩B=()A.{−1,2}B.{1,2}C.{1,4}D.{−1,4}【答案】B【解析】【解答】B={x|0≤x≤2},故A∩B={1,2}.故答案为:B【分析】先求出集合B,再根据交集的概念求A∩B即可.3.(5分)(2022·全国乙卷)集合M={2,4,6,8,10},N={x|−1<x<6},则M∩N=()A.{2,4}B.{2,4,6}C.{2,4,6,8}D.{2,4,6,8,10}【答案】A【解析】【解答】因为M={2,4,6,8,10},N={x|−1<x<6},所以M∩N={2,4}. 故选:A【分析】根据集合的交集运算即可求解.4.(5分)(2022·全国甲卷)设全集U={−2,−1,0,1,2,3},集合A={−1,2},B={x∣A.{1,3}B.{0,3}C.{−2,1}D.{−2,0}【答案】D【解析】【解答】解:由题意得,B={x∣x2−4x+3=0}={1,3},所以A∪B={-1,1,2,3} ,所以∁U(A∪B)={−2,0}.故选:D【分析】先求解方程求出集合B,再由集合的并集、补集运算即可得解.5.(5分)(2022·全国甲卷)设集合A={−2,−1,0,1,2},B={x∣0⩽x<52},则A∩B=()A.{0,1,2}B.{−2,−1,0}C.{0,1}D.{1,2}【答案】A【解析】【解答】解:∵A={−2,−1,0,1,2},B={x∣0⩽x<52},∴A∩B={0,1,2}.故选:A【分析】根据集合的交集运算即可解出.6.(5分)(2022·全国乙卷)设全集U={1,2,3,4,5},集合M满足∁U M={1,3},则()A.2∈M B.3∈M C.4∉M D.5∉M【答案】A【解析】【解答】易知M={2,4,5},对比选项即可判断,A正确.故选:A【分析】先写出集合M,即可判断.7.(5分)(2022·北京)已知全集U={x|−3<x<3},集合A={x|−2<x≤1},则C U A=()A.(−2,1]B.(−3,−2)∪[1,3)C.[−2,1)D.(−3,−2]∪(1,3)【解析】【解答】根据题意可得:C U A=(−3,−2]∪(1,3)故答案为:D【分析】直接根据补集的概念计算即可.8.(5分)(2022·新高考Ⅱ卷)若集合M={x∣√x<4},N={x∣3x⩾1},则M∩N=()A.{x∣0≤x<2}B.{x∣13≤x<2}C.{x∣3≤x<16}D.{x∣13≤x<16}【答案】D【解析】【解答】解:由题意得,M={x|0≤x<16},N={x|x≥13},则M∩N= {x∣13≤x<16},故选:D【分析】先由不等式的解法求得集合M,N,再根据交集的运算求得答案.9.(5分)(2021·北京)已知集合A={x|−1<x<1},B={x|0≤x≤2},则A∪B=()A.(−1,2)B.(−1,2]C.[0,1)D.[0,1]【答案】B【解析】【解答】解:根据并集的定义易得A∪B={x|−1<x≤2},故答案为:B【分析】根据并集的定义直接求解即可.10.(5分)(2021·浙江)设集合A={x|x≥1},B={x|−1<x<2},则A∩B=()A.{x|x>−1}B.{x|x≥1}C.{x|−1<x<1}D.{x|1≤x<2}【答案】D【解析】【解答】因为A={x|x≥1},B={x|−1<x<2},所以A∩B={x|1≤x<2}.故答案为:D.【分析】利用数轴,求不等式表示的集合的交集。
十年(2015-2024)高考真题数学分项汇编(全国通用)——专题01 集合与常用逻辑用语
专题01 集合与常用逻辑用语考点01 集合间的基本关系1.(2023·全国新Ⅱ卷·高考真题)设集合A ={0,−a },B ={1,a −2,2a −2},若A ⊆B ,则a =( )A .2B .1C .23 D .1−2.(2020全国新Ⅰ卷·高考真题)已知a ∈R ,若集合M ={1,a },N ={−1,0,1},则“a =0”是“M ⊆N ”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件考点02 交集1.(2024·全国新Ⅰ卷高考真题)已知集合{}355,{3,1,0,2,3}A x x B =−<<=−−∣,则A ∩B =( )A .{−1,0}B .{2,3}C .{−3,−1,0}D .{−1,0,2}2.(2024年全国甲卷高考真题)若集合A ={1,2,3,4,5,9},B ={x |x +1∈A },则A ∩B =( )A .{1,3,4}B .{2,3,4}C .{1,2,3,4}D .{0,1,2,3,4,9}3.(2023·北京·高考真题)已知集合M ={x ∣x +2≥0},N ={x ∣x −1<0},则M ∩N =( )A .{x ∣−2≤x <1}B .{x ∣−2<x ≤1}C .{x ∣x ≥−2}D .{x ∣x <1}4.(2023全国新Ⅰ卷高考真题)已知集合M ={−2,−1,0,1,2},N ={x |x 2−x −6≥0},则M ∩N =()A .{−2,−1,0,1}B .{0,1,2}C .{−2}D .{2}5.(2022·全国新Ⅱ卷高考真题)已知集合A ={−1,1,2,4},B ={x||x −1|≤1},则A ∩B =( )A .{−1,2}B .{1,2}C .{1,4}D .{−1,4}6.(2022年全国乙卷·高考真题)集合M ={2,4,6,8,10},N ={x |−1<x <6},则M ∩N =( )A .{2,4}B .{2,4,6}C .{2,4,6,8}D .{2,4,6,8,10}7.(2022年全国甲卷·高考真题)设集合A ={−2,−1,0,1,2},B ={x ∣0≤x <52},则A ∩B =( )A .{0,1,2}B .{2,1,0}−−C .{0,1}D .{1,2}8.(2022全国新Ⅰ卷·高考真题)若集合M ={x ∣∣√x <4}, N ={x ∣3x ≥1},则M ∩N =( )A .{x |0≤x <2}B .{x |13≤x <2}C .{x |3≤x <16}D .{x |13≤x <16} 9.(2021年全国乙卷·高考真题)已知集合S ={s |s =2n +1,n ∈Z },T ={t |t =4n +1,n ∈Z },则S ∩T =( )A .∅B .SC .TD .Z10.(2021年全国甲卷·高考真题)设集合M ={1,3,5,7,9},N ={x |2x >7},则M ∩N =( )A .{7,9}B .{5,7,9}C .{3,5,7,9}D .{1,3,5,7,9}11.(2021年全国甲卷·高考真题)设集合M ={x |0<x <4},N ={x |13≤x ≤5},则M ∩N =( )A .{x |0<x ≤13}B .{x |13≤x <4} C .{x |4≤x <5} D .{x |0<x ≤5} 12.(2021全国新Ⅰ卷·高考真题)设集合A ={x |−2<x <4},B ={2,3,4,5},则A ∩B =( )A .{}2B .{}2,3C .{3,4}D .{2,3,4} 考点03 并集1.(2024·北京·高考真题)已知集合M ={x |−3<x <1},N ={x |−1≤x <4},则M ∪N =( )A .{x |−1≤x <1}B .{x |x >−3}C .{x|−3<x <4}D .{x |x <4}2.(2022·浙江·高考真题)设集合A ={1,2},B ={2,4,6},则A ∪B =( )A .{2}B .{1,2}C .{2,4,6}D .{1,2,4,6} 3.(2021·北京·高考真题)已知集合A ={x|−1<x <1},B ={x|0≤x ≤2},则A ∪B =( )A .{x|−1<x <2}B .{x|−1<x ≤2}C .{x|0≤x <1}D .{x|0≤x ≤2}4.(2020·山东·高考真题)设集合A ={x |1≤x ≤3},B ={x |2<x <4},则A ∪B =( )A .{x |2<x ≤3}B .{x |2≤x ≤3}C .{x |1≤x <4}D .{x |1<x <4}5.(2019·北京·高考真题)已知集合A ={x |–1<x <2},B ={x |x >1},则A ∪B =A .(–1,1)B .(1,2)C .(–1,+∞)D .(1,+∞)6.(2017·浙江·高考真题)已知集合P ={x |−1<x <1},Q = {x |0<x <2},那么P ∪Q = ( )A .(-1,2)B .(0,1)C .(-1,0)D .(1,2)7.(2017·全国·高考真题)设集合A ={1,2,3},B ={2,3,4},则A ∪B =( )A .{1,2,3,4}B .{1,2,3}C .{2,3,4}D .{1,3,4}8.(2016·山东·高考真题)设集合A ={y |y =2x ,x ∈R },B ={x |x 2−1<0},则A ∪B =( )A .(1,1)−B .(0,1)C .(−1,+∞)D .(0,+∞)9.(2016·全国·高考真题)已知集合A ={1,2,3},B ={x |(x +1)(x −2)<0,x ∈Z },则A ∪B = ( )A .{1}B .{1,2}C .{0,1,2,3}D .{−1,0,1,2,3}10.(2015·全国·高考真题)已知集合A ={x|−1<x <2},B ={x|0<x <3},则A ∪B =( )A .(−1,3)B .(−1,0)C .(0,2)D .(2,3) 考点04 补集1.(2024年全国甲卷·高考真题)已知集合A ={1,2,3,4,5,9},B ={x|√x ∈A},则∁A (A ∩B )=( )A .{1,4,9}B .{3,4,9}C .{1,2,3}D .{2,3,5}2.(2023年全国乙卷·高考真题)设全集{}0,1,2,4,6,8U =,集合{}{}0,4,6,0,1,6M N ==,则U M N ⋃=ð( )A .{0,2,4,6,8}B .{}0,1,4,6,8C .{1,2,4,6,8}D .U3.(2023年全国乙卷·高考真题)设集合U =R ,集合M ={x |x <1},N ={x |−1<x <2},则{x |x ≥2}=( )A .∁U (M ∪N )B .N ∪∁U MC .∁U (M ∩N )D .M ∪∁U N4.(2022·全国乙卷·高考真题)设全集U ={1,2,3,4,5},集合M 满足∁U M ={1,3},则( )A .2∈MB .3M ∈C .4∉MD .5∉M5.(2022·北京·高考真题)已知全集U ={x |−3<x <3},集合A ={x |−2<x ≤1},则∁U A =( )A .(−2,1)B .(−3,−2)∪[1,3]C .[−2,1]D .(−3,−2)∪(1,3)6.(2021全国新Ⅱ卷·高考真题)设集合U ={1,2,3,4,5,6},A ={1,3,6},B ={2,3,4},则A ∩(∁U B )=( )A .{3}B .{1,6}C .{5,6}D .{1,3}7.(2020全国新Ⅰ卷·高考真题)已知全集U ={a,b,c,d },集合M ={a,c },则∁U M 等于( )A .∅B .{a,c }C .{b,d }D .{a,b,c,d }8.(2018·浙江·高考真题)已知全集U ={1,2,3,4,5},A ={1,3},则∁U A =( )A .∅B .{1,3}C .{2,4,5}D .{1,2,3,4,5}9.(2018·全国·高考真题)已知集合A ={x |x 2−x −2>0},则∁R A =A .{x |−1<x <2}B .{x |−1≤x ≤2}C .{x|x <−1}∪{x |x ⟩2}D .{x|x ≤−1}∪{x|x ≥2}10.(2017·北京·高考真题)已知全集U =R ,集合{|22}A x x x =<−>或,则∁U A =A .(−2,2)B .(−∞,−2)∪(2,+∞)C .[−2,2]D .(−∞,−2)∪[2,+∞]考点05 充分条件与必要条件1.(2024·全国甲卷·高考真题)设向量a ⃗=(x +1,x ),b⃗⃗=(x,2),则( ) A .“x =−3”是“a ⃗⊥b⃗⃗”的必要条件 B .“x =−3”是“a ⃗⃗⃗b ⃗⃗”的必要条件 C .“x =0”是“a ⃗⊥b ⃗⃗”的充分条件 D .“x =−1+√3”是“a ⃗⃗⃗b⃗⃗”的充分条件 2.(2024·天津·高考真题)设a,b ∈R ,则“a 3=b 3”是“3a =3b ”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件3.(2024·北京·高考真题)设 a ⃗,b ⃗⃗是向量,则“(a ⃗+b ⃗⃗)·(a ⃗−b⃗⃗)=0”是“a b =−或a b =”的( ). A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.(2023·北京·高考真题)若xy ≠0,则“x +y =0”是“y x +x y =−2”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5.(2023·全国甲卷·高考真题)设甲:22sin sin 1αβ+=,乙:sin α+cos β=0,则( )A .甲是乙的充分条件但不是必要条件B .甲是乙的必要条件但不是充分条件C .甲是乙的充要条件D .甲既不是乙的充分条件也不是乙的必要条件6.(2023·天津·高考真题)已知a,b ∈R ,“a 2=b 2”是“a 2+b 2=2ab ”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件7.(2023·全国新Ⅰ卷·高考真题)记S n 为数列{a n }的前n 项和,设甲:{a n }为等差数列;乙:{S n n}为等差数列,则()A.甲是乙的充分条件但不是必要条件B.甲是乙的必要条件但不是充分条件C.甲是乙的充要条件D.甲既不是乙的充分条件也不是乙的必要条件8.(2022·浙江·高考真题)设x∈R,则“sin x=1”是“cos x=0”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件9.(2022·北京·高考真题)设{a n}是公差不为0的无穷等差数列,则“{a n}为递增数列”是“存在正整数N0,当n>N0时,a n>0”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件10.(2021·全国甲卷·高考真题)等比数列{a n}的公比为q,前n项和为S n,设甲:q>0,乙:{S n}是递增数列,则()A.甲是乙的充分条件但不是必要条件B.甲是乙的必要条件但不是充分条件C.甲是乙的充要条件D.甲既不是乙的充分条件也不是乙的必要条件考点06 全称量词与存在量词1.(2024·全国新Ⅱ卷·高考真题)已知命题p:∀x∈R,|x+1|>1;命题q:∃x>0,x3=x,则()A.p和q都是真命题B.¬p和q都是真命题C.p和¬q都是真命题D.¬p和¬q都是真命题2.(2020·全国新Ⅰ卷·高考真题)下列命题为真命题的是()A.1>0且3>4B.1>2或4>5C.∃x∈R,cos x>1D.∀x∈R,x2≥03.(2016·浙江·高考真题)命题“∀x∈R,∃n∈N∗,使得n≥x2”的否定形式是()A.∀x∈R,∃n∈N∗,使得n<x2B.∀x∈R,∀n∈N∗,使得n<x2C.∃x∈R,∃n∈N∗,使得n<x2D.∃x∈R,∀n∈N∗,使得n<x24.(2015·浙江·高考真题)命题“∀n∈N∗,f(n)∈N∗且f(n)≤n的否定形式是()A.∀n∈N∗,f(n)∉N∗且f(n)>n B.∀n∈N∗,f(n)∉N∗或f(n)>nC.∃n0∈N∗,f(n0)∉N∗且f(n0)>n0D.∃n0∈N∗,f(n0)∉N∗或f(n0)>n05.(2015·全国·高考真题)设命题P:∃n ∈N,n 2>2n ,则¬P 为( )A .∀n ∈N,n 2>2nB .∃n ∈N,n 2≤2nC .∀n ∈N,n 2≤2nD .∃n ∈N,n 2=2n 6.(2015·湖北·高考真题)命题“∃x 0∈(0,+∞),ln x 0=x 0−1”的否定是 ( )A .∃x 0∈(0,+∞),ln x 0≠x 0−1B .∃x 0∉(0,+∞),ln x 0=x 0−1C .∀x ∈(0,+∞),ln x ≠x −1D .∀x ∉(0,+∞),ln x =x −1答案解析考点01 集合间的基本关系1.(2023·全国新Ⅱ卷·高考真题)设集合{}0,A a =−,{}1,2,22B a a =−−,若A B ⊆,则=a ( ).A .2B .1C .23D .1− 【答案】B【分析】根据包含关系分20a −=和220a −=两种情况讨论,运算求解即可.【详解】因为A B ⊆,则有:若20a −=,解得2a =,此时{}0,2A =−,{}1,0,2B =,不符合题意;若220a −=,解得1a =,此时{}0,1A =−,{}1,1,0B =−,符合题意;综上所述:1a =.故选:B.2.(2020全国新Ⅰ卷·高考真题)已知a ∈R ,若集合{}1,M a =,{}1,0,1N =−,则“0a =”是“M N ⊆”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】A【分析】根据充分条件和必要条件的定义即可求解.【详解】当0a =时,集合{}1,0M =,{}1,0,1N =−,可得M N ⊆,满足充分性,若M N ⊆,则0a =或1a =−,不满足必要性,所以“0a =”是“M N ⊆”的充分不必要条件,故选:A.考点02 交集1.(2024·全国新Ⅰ卷高考真题)已知集合{}355,{3,1,0,2,3}A xx B =−<<=−−∣,则A B =( ) A .{1,0}− B .{2,3} C .{3,1,0}−− D .{1,0,2}−【答案】A【分析】化简集合A ,由交集的概念即可得解.【详解】因为{{}|,3,1,0,2,3A x x B =<=−−,且注意到12,从而A B ={}1,0−.故选:A.2.(2024年全国甲卷高考真题)若集合{}1,2,3,4,5,9A =,{}1B x x A =+∈,则A B =() A .{}1,3,4 B .{}2,3,4 C .{}1,2,3,4 D .{}0,1,2,3,4,9【答案】C【分析】根据集合B 的定义先算出具体含有的元素,然后根据交集的定义计算.【详解】依题意得,对于集合B 中的元素x ,满足11,2,3,4,5,9x +=,则x 可能的取值为0,1,2,3,4,8,即{0,1,2,3,4,8}B =,于是{1,2,3,4}A B ⋂=.故选:C3.(2023·北京·高考真题)已知集合{20},{10}M x x N x x =+≥=−<∣∣,则M N ⋂=( )A .{21}x x −≤<∣B .{21}x x −<≤∣C .{2}x x ≥−∣D .{1}x x <∣【答案】A【分析】先化简集合,M N ,然后根据交集的定义计算.【详解】由题意,{20}{|2}M x x x x =+≥=≥−∣,{10}{|1}N x x x x =−<=<∣,根据交集的运算可知,{|21}M N x x =−≤<.故选:A4.(2023全国新Ⅰ卷高考真题)已知集合{}2,1,0,1,2M =−−,{}260N x x x =−−≥,则M N ⋂=( ) A .{}2,1,0,1−−B .{}0,1,2C .{}2−D .{}2【答案】C 【分析】方法一:由一元二次不等式的解法求出集合N ,即可根据交集的运算解出.方法二:将集合M 中的元素逐个代入不等式验证,即可解出. 【详解】方法一:因为{}(][)260,23,N x x x ∞∞=−−≥=−−⋃+,而{}2,1,0,1,2M =−−, 所以M N ⋂={}2−.故选:C .方法二:因为{}2,1,0,1,2M =−−,将2,1,0,1,2−−代入不等式260x x −−≥,只有2−使不等式成立,所以M N ⋂={}2−.故选:C .5.(2022·全国新Ⅱ卷高考真题)已知集合{}{}1,1,2,4,11A B x x =−=−≤,则A B =( )A .{1,2}−B .{1,2}C .{1,4}D .{1,4}− 【答案】B【分析】方法一:求出集合B 后可求A B ⋂.【详解】[方法一]:直接法因为{}|02B x x =≤≤,故{}1,2A B =,故选:B.[方法二]:【最优解】代入排除法 =1x −代入集合{}11B x x =−≤,可得21≤,不满足,排除A 、D ;4x =代入集合{}11B x x =−≤,可得31≤,不满足,排除C. 故选:B.【整体点评】方法一:直接解不等式,利用交集运算求出,是通性通法;方法二:根据选择题特征,利用特殊值代入验证,是该题的最优解.6.(2022年全国乙卷·高考真题)集合{}{}2,4,6,8,10,16M N x x ==−<<,则M N ⋂=( )A .{2,4}B .{2,4,6}C .{2,4,6,8}D .{2,4,6,8,10}【答案】A【分析】根据集合的交集运算即可解出.【详解】因为{}2,4,6,8,10M =,{}|16N x x =−<<,所以{}2,4M N =.故选:A.7.(2022年全国甲卷·高考真题)设集合5{2,1,0,1,2},02A B x x ⎧⎫=−−=≤<⎨⎬⎩⎭∣,则A B =( )A .{}0,1,2B .{2,1,0}−−C .{0,1}D .{1,2}【答案】A【分析】根据集合的交集运算即可解出.【详解】因为{}2,1,0,1,2A =−−,502B x x ⎧⎫=≤<⎨⎬⎩⎭∣,所以{}0,1,2A B =.故选:A.8.(2022全国新Ⅰ卷·高考真题)若集合{4},{31}M x N x x =<=≥∣,则M N ⋂=( )A .{}02x x ≤<B .123x x ⎧⎫≤<⎨⎬⎩⎭ C .{}316x x ≤< D .1163x x ⎧⎫≤<⎨⎬⎩⎭【答案】D【分析】求出集合,M N 后可求M N ⋂. 【详解】1{16},{}3M x x N x x =≤<=≥∣0∣,故1163M N x x ⎧⎫⋂=≤<⎨⎬⎩⎭,故选:D9.(2021年全国乙卷·高考真题)已知集合{}21,S s s n n ==+∈Z ,{}41,T t t n n ==+∈Z ,则S ∩T =() A .∅ B .S C .T D .Z【答案】C【分析】分析可得T S ⊆,由此可得出结论.【详解】任取t T ∈,则()41221t n n =+=⋅+,其中Z n ∈,所以,t S ∈,故T S ⊆,因此,S T T =.故选:C.10.(2021年全国甲卷·高考真题)设集合{}{}1,3,5,7,9,27M N x x ==>,则M N ⋂=( )A .{}7,9B .{}5,7,9C .{}3,5,7,9D .{}1,3,5,7,9【答案】B【分析】求出集合N 后可求M N ⋂. 【详解】7,2N ⎛⎫=+∞ ⎪⎝⎭,故{}5,7,9M N ⋂=, 故选:B.11.(2021年全国甲卷·高考真题)设集合{}104,53M x x N x x ⎧⎫=<<=≤≤⎨⎬⎩⎭,则M N ⋂=( ) A .103x x ⎧⎫<≤⎨⎬⎩⎭ B .143x x ⎧⎫≤<⎨⎬⎩⎭C .{}45x x ≤<D .{}05x x <≤ 【答案】B【分析】根据交集定义运算即可 【详解】因为1{|04},{|5}3M x x N x x =<<=≤≤,所以1|43M N x x ⎧⎫⋂=≤<⎨⎬⎩⎭, 故选:B. 【点睛】本题考查集合的运算,属基础题,在高考中要求不高,掌握集合的交并补的基本概念即可求解. 12.(2021全国新Ⅰ卷·高考真题)设集合{}24A x x =−<<,{}2,3,4,5B =,则A B =( )A .{}2B .{}2,3C .{}3,4D .{}2,3,4【答案】B【分析】利用交集的定义可求A B ⋂.【详解】由题设有{}2,3A B ⋂=,故选:B .1.(2024·北京·高考真题)已知集合{|31}M x x =−<<,{|14}N x x =−≤<,则M N ⋃=( )A .{}11x x −≤<B .{}3x x >−C .{}|34x x −<<D .{}4x x <【答案】C【分析】直接根据并集含义即可得到答案.【详解】由题意得{}|34M x x N ⋃=−<<.故选:C.2.(2022·浙江·高考真题)设集合{1,2},{2,4,6}A B ==,则A B ⋃=( )A .{2}B .{1,2}C .{2,4,6}D .{1,2,4,6}【答案】D【分析】利用并集的定义可得正确的选项.【详解】{}1,2,4,6A B =,故选:D.3.(2021·北京·高考真题)已知集合{}|11A x x =−<<,{}|02B x x =≤≤,则A B ⋃=()A .{}|12x x −<<B .{}|12x x −<≤C .{}|01x x ≤<D .{}|02x x ≤≤【答案】B【分析】结合题意利用并集的定义计算即可.【详解】由题意可得:{}|12A B x x =−<≤.故选:B.4.(2020·山东·高考真题)设集合A ={x |1≤x ≤3},B ={x |2<x <4},则A ∪B =( )A .{x |2<x ≤3}B .{x |2≤x ≤3}C .{x |1≤x <4}D .{x |1<x <4}【答案】C【详解】[1,3](2,4)[1,4)A B ==U U故选:C【点睛】本题考查集合并集,考查基本分析求解能力,属基础题.5.(2019·北京·高考真题)已知集合A ={x |–1<x <2},B ={x |x >1},则A ∪B =A .(–1,1)B .(1,2)C .(–1,+∞)D .(1,+∞) 【答案】C【分析】根据并集的求法直接求出结果.【详解】∵{|12},{|1}A x x B x =−<<=> ,∴(1,)A B =−+∞ ,故选C.【点睛】考查并集的求法,属于基础题.6.(2017·浙江·高考真题)已知集合{}{}x -1<x 1Q=x 0x 2P =<<<,,那么P Q=⋃A .(-1,2)B .(0,1)C .(-1,0)D .(1,2) 【答案】A【详解】利用数轴,取,P Q 所有元素,得P Q ⋃=(1,2)−.【名师点睛】对于集合的交、并、补运算问题,应先把集合化简再计算,常常借助数轴或韦恩图处理. 7.(2017·全国·高考真题)设集合{1,2,3},{2,3,4}A B ==,则A B ⋃=A .{}123,4,,B .{}123,,C .{}234,,D .{}134,, 【答案】A【详解】由题意{1,2,3,4}A B ⋃=,故选A.8.(2016·山东·高考真题)设集合2{|2,},{|10},x A y y x R B x x ==∈=−<则A B ⋃=A .(1,1)−B .(0,1)C .(1,)−+∞D .(0,)+∞【答案】C【详解】A ={y |y =2x ,x ∈R }={y |y >0}.B ={x |x 2-1<0}={x |-1<x <1},∴A ∪B ={x |x >0}∪{x |-1<x <1}={x |x >-1},故选C .A .{1}B .{12},C .{0123},,,D .{10123}−,,,, 【答案】C 【详解】试题分析:集合{}{|12,}0,1B x x x Z =−<<∈=,而{1,2,3}A =,所以{}0,1,2,3A B ⋃=,故选C.【考点】 集合的运算【名师点睛】集合的交、并、补运算问题,应先把集合化简再计算,常常借助数轴或韦恩图进行处理. 10.(2015·全国·高考真题)已知集合{}{}|12,|03,A x x B x x =−<<=<<则A B ⋃=( )A .()1,3−B .()1,0−C .()0,2D .()2,3【答案】A【详解】因为{}|12A x x =−<<,{}|03B x x =<<,所以{}|13.A B x x =−<<故选A.考点04 补集1.(2024年全国甲卷·高考真题)已知集合{}{}1,2,3,4,5,9,A B A ==,则∁A (A ∩B )=( )A .{}1,4,9B .{}3,4,9C .{}1,2,3D .{}2,3,5【答案】D【分析】由集合B 的定义求出B ,结合交集与补集运算即可求解.【详解】因为{}{}1,2,3,4,5,9,A B A ==,所以{}1,4,9,16,25,81B =,则{}1,4,9A B =,(){}2,3,5A A B =ð故选:D2.(2023年全国乙卷·高考真题)设全集{}0,1,2,4,6,8U =,集合{}{}0,4,6,0,1,6M N ==,则M ∪∁U N ()A .{}0,2,4,6,8B .{}0,1,4,6,8C .{}1,2,4,6,8D .U【答案】A【分析】由题意可得∁U N 的值,然后计算M ∪∁U N 即可.【详解】由题意可得∁U N ={2,4,8},则M ∪∁U N ={0,2,4,6,8}.3.(2023年全国乙卷·高考真题)设集合U =R ,集合{}1M x x =<,{}12N x x =−<<,则{}2x x ≥=( )A .∁U (M ∪N )B .N ∪∁U MC .∁U (M ∩N )D .M ∪∁U N【答案】A【分析】由题意逐一考查所给的选项运算结果是否为{}|2x x ≥即可.【详解】由题意可得{}|2M N x x =<,则∁U (M ∪N )={x|x ≥2},选项A 正确;∁U M ={x|x ≥1},则N ∪∁U M ={x|x >−1},选项B 错误;{}|11M N x x =−<<,则∁U (M ∩N )={x|x ≤−1或}1x ≥,选项C 错误;{|1U N x x =≤−ð或}2x ≥,则M ∪∁U N ={|1x x <或}2x ≥,选项D 错误;故选:A.4.(2022·全国乙卷·高考真题)设全集{1,2,3,4,5}U =,集合M 满足∁U M ={1,3},则( )A .2M ∈B .3M ∈C .4M ∉D .5M ∉【答案】A【分析】先写出集合M ,然后逐项验证即可【详解】由题知{2,4,5}M =,对比选项知,A 正确,BCD 错误故选:A5.(2022·北京·高考真题)已知全集{33}U x x =−<<,集合{21}A x x =−<≤,则∁U A =( )A .(2,1]−B .(3,2)[1,3)−−C .[2,1)−D .(3,2](1,3)−−【答案】D【分析】利用补集的定义可得正确的选项.【详解】由补集定义可知:∁U A ={x|−3<x ≤−2或13}x <<,即∁U A =(−3,−2]∪(1,3),故选:D .6.(2021全国新Ⅱ卷·高考真题)设集合{1,2,3,4,5,6},{1,3,6},{2,3,4}U A B ===,则A ∩(∁U B )=()A .{3}B .{1,6}C .{5,6}D .{1,3}【分析】根据交集、补集的定义可求A ∩(∁U B ).【详解】由题设可得∁U B ={1,5,6},故A ∩(∁U B )={1,6},故选:B.7.(2020全国新Ⅰ卷·高考真题)已知全集{},,,U a b c d =,集合{},M a c =,则∁U M 等于( )A .∅B .{},a cC .{},b dD .{},,,a b c d 【答案】C【分析】利用补集概念求解即可.【详解】∁U M ={b,d }.故选:C8.(2018·浙江·高考真题)已知全集{}1,2,3,4,5U =,{}1,3A =,则∁U A =( )A .∅B .{}1,3C .{}2,4,5D .{}1,2,3,4,5 【答案】C【分析】根据补集的定义可得结果.【详解】因为全集{}1,2,3,4,5U =,{}1,3A =,所以根据补集的定义得∁U A ={2,4,5},故选C.【点睛】若集合的元素已知,则求集合的交集、并集、补集时,可根据交集、并集、补集的定义求解.9.(2018·全国·高考真题)已知集合{}220A x x x =−−>,则∁R A = A .{}12x x −<<B .{}12x x −≤≤C .}{}{|12x x x x <−⋃D .}{}{|1|2x x x x ≤−⋃≥ 【答案】B 【详解】分析:首先利用一元二次不等式的解法,求出220x x −−>的解集,从而求得集合A ,之后根据集合补集中元素的特征,求得结果.详解:解不等式220x x −−>得12x x <−>或,所以{}|12A x x x =<−>或,所以可以求得{}R |12C A x x =−≤≤,故选B.二次不等式的解集的形式以及补集中元素的特征,从而求得结果.10.(2017·北京·高考真题)已知全集U =R ,集合{|22}A x x x =<−>或,则∁U A =A .(2,2)−B .(,2)(2,)−∞−+∞C .[2,2]−D .(,2][2,)−∞−+∞【答案】C 【详解】因为{2A x x =<−或2}x >,所以{}22U A x x =−≤≤ð,故选:C .【名师点睛】集合分为有限集合和无限集合,若集合个数比较少时可以用列举法表示;若集合是无限集合就用描述法表示,并注意代表元素是什么.集合的交、并、补运算问题,应先把集合化简再计算,常常借助数轴或Venn 图进行处理. 考点05 充分条件与必要条件1.(2024·全国甲卷·高考真题)设向量()()1,,,2a x x b x =+=,则( )A .“3x =−”是“a b ⊥”的必要条件B .“3x =−”是“//a b ”的必要条件C .“0x =”是“a b ⊥”的充分条件D .“1x =−是“//a b ”的充分条件 【答案】C【分析】根据向量垂直和平行的坐标表示即可得到方程,解出即可.【详解】对A ,当a b ⊥时,则0a b ⋅=,所以(1)20x x x ⋅++=,解得0x =或3−,即必要性不成立,故A 错误;对C ,当0x =时,()()1,0,0,2a b ==,故0a b ⋅=,所以a b ⊥,即充分性成立,故C 正确;对B ,当//a b 时,则22(1)x x +=,解得1x =B 错误;对D ,当1x =−22(1)x x +=,所以//a b 不成立,即充分性不立,故D 错误.故选:C.2.(2024·天津·高考真题)设,a b ∈R ,则“33a b =”是“33a b =”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【分析】说明二者与同一个命题等价,再得到二者等价,即是充分必要条件.【详解】根据立方的性质和指数函数的性质,33a b =和33a b =都当且仅当a b =,所以二者互为充要条件. 故选:C.3.(2024·北京·高考真题)设 a ,b 是向量,则“()()·0a b a b +−=”是“a b =−或a b =”的( ).A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件 【答案】B【分析】根据向量数量积分析可知()()0a b a b +⋅−=等价于a b =,结合充分、必要条件分析判断.【详解】因为()()220a b a b a b +⋅−=−=,可得22a b =,即a b =, 可知()()0a b a b +⋅−=等价于a b =,若a b =或a b =−,可得a b =,即()()0a b a b +⋅−=,可知必要性成立;若()()0a b a b +⋅−=,即a b =,无法得出a b =或a b =−,例如()()1,0,0,1a b ==,满足a b =,但a b ≠且a b ≠−,可知充分性不成立;综上所述,“()()0a b a b +⋅−=”是“a b ≠且a b ≠−”的必要不充分条件.故选:B.4.(2023·北京·高考真题)若0xy ≠,则“0x y +=”是“2y x x y +=−”的( ) A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【答案】C【分析】解法一:由2x y y x +=−化简得到0x y +=即可判断;解法二:证明充分性可由0x y +=得到x y =−,代入x y y x +化简即可,证明必要性可由2x y y x +=−去分母,再用完全平方公式即可;解法三:证明充分性可由x y y x +通分后用配凑法得到完全平方公式,再把0x y +=代入即可,证明必要性可由x y y x+通分后用配凑法得到【详解】解法一:因为0xy ≠,且2x y y x +=−,所以222x y xy +=−,即2220x y xy ++=,即()20x y +=,所以0x y +=.所以“0x y +=”是“2x yy x +=−”的充要条件.解法二:充分性:因为0xy ≠,且0x y +=,所以x y =−, 所以112xy y y y x y y −+=+=−−=−−, 所以充分性成立;必要性:因为0xy ≠,且2x yy x +=−,所以222x y xy +=−,即2220x y xy ++=,即()20x y +=,所以0x y +=. 所以必要性成立.所以“0x y +=”是“2x yy x +=−”的充要条件.解法三:充分性:因为0xy ≠,且0x y +=,所以()2222222222x y xy x y x y x y xy xy xy y x xy xy xy xy +−+++−−+=====−, 所以充分性成立;必要性:因为0xy ≠,且2x y y x +=−,所以()()22222222222x y xy x y x y x y x y xy xy y x xy xy xy xy+−++++−+====−=−, 所以()20x y xy +=,所以()20x y +=,所以0x y +=, 所以必要性成立.所以“0x y +=”是“2x y y x +=−”的充要条件.故选:C5.(2023·全国甲卷·高考真题)设甲:22sin sin 1αβ+=,乙:sin cos 0αβ+=,则( )A .甲是乙的充分条件但不是必要条件B .甲是乙的必要条件但不是充分条件【答案】B【分析】根据充分条件、必要条件的概念及同角三角函数的基本关系得解.【详解】当22sin sin 1αβ+=时,例如π,02αβ==但sin cos 0αβ+≠, 即22sin sin 1αβ+=推不出sin cos 0αβ+=;当sin cos 0αβ+=时,2222sin sin (cos )sin 1αβββ+=−+=,即sin cos 0αβ+=能推出22sin sin 1αβ+=.综上可知,甲是乙的必要不充分条件.故选:B6.(2023·天津·高考真题)已知,R a b ∈,“22a b =”是“222a b ab +=”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分又不必要条件 【答案】B【分析】根据充分、必要性定义判断条件的推出关系,即可得答案.【详解】由22a b =,则a b =±,当0a b =−≠时222a b ab +=不成立,充分性不成立;由222a b ab +=,则2()0a b −=,即a b =,显然22a b =成立,必要性成立;所以22a b =是222a b ab +=的必要不充分条件.故选:B7.(2023·全国新Ⅰ卷·高考真题)记n S 为数列{}n a 的前n 项和,设甲:{}n a 为等差数列;乙:{}n S n 为等差数列,则( )A .甲是乙的充分条件但不是必要条件B .甲是乙的必要条件但不是充分条件C .甲是乙的充要条件D .甲既不是乙的充分条件也不是乙的必要条件【答案】C答.,【详解】方法1,甲:{}n a 为等差数列,设其首项为1a ,公差为d , 则1111(1)1,,222212n n n n S S S n n n d d d S na d a d n a n n n +−−=+=+=+−−=+, 因此{}n S n为等差数列,则甲是乙的充分条件; 反之,乙:{}n S n 为等差数列,即111(1)1(1)(1)n n n n n n S S nS n S na S n n n n n n +++−+−−==+++为常数,设为t , 即1(1)n n na S t n n +−=+,则1(1)n n S na t n n +=−⋅+,有1(1)(1),2n n S n a t n n n −=−−⋅−≥, 两式相减得:1(1)2n n n a na n a tn +=−−−,即12n n a a t +−=,对1n =也成立,因此{}n a 为等差数列,则甲是乙的必要条件,所以甲是乙的充要条件,C 正确.方法2,甲:{}n a 为等差数列,设数列{}n a 的首项1a ,公差为d ,即1(1)2n n n S na d −=+, 则11(1)222n S n d d a d n a n −=+=+−,因此{}n S n 为等差数列,即甲是乙的充分条件; 反之,乙:{}n S n 为等差数列,即11,(1)1n n n S S S D S n D n n n+−==+−+, 即1(1)n S nS n n D =+−,11(1)(1)(2)n S n S n n D −=−+−−,当2n ≥时,上两式相减得:112(1)n n S S S n D −−=+−,当1n =时,上式成立,于是12(1)n a a n D =+−,又111[22(1)]2n n a a a nD a n D D +−=+−+−=为常数,因此{}n a 为等差数列,则甲是乙的必要条件,所以甲是乙的充要条件.故选:C8.(2022·浙江·高考真题)设x ∈R ,则“sin 1x =”是“cos 0x =”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件【答案】A【分析】由三角函数的性质结合充分条件、必要条件的定义即可得解.【详解】因为22sin cos 1x x +=可得:当sin 1x =时,cos 0x =,充分性成立;当cos 0x =时,sin 1x =±,必要性不成立;所以当x ∈R ,sin 1x =是cos 0x =的充分不必要条件.故选:A.9.(2022·北京·高考真题)设{}n a 是公差不为0的无穷等差数列,则“{}n a 为递增数列”是“存在正整数0N ,当0n N >时,0n a >”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】C 【分析】设等差数列{}n a 的公差为d ,则0d ≠,利用等差数列的通项公式结合充分条件、必要条件的定义判断可得出结论.【详解】设等差数列{}n a 的公差为d ,则0d ≠,记[]x 为不超过x 的最大整数.若{}n a 为单调递增数列,则0d >,若10a ≥,则当2n ≥时,10n a a >≥;若10a <,则()11n a a n d +−=,由()110n a a n d =+−>可得11a n d >−,取1011a N d ⎡⎤=−+⎢⎥⎣⎦,则当0n N >时,0n a >, 所以,“{}n a 是递增数列”⇒“存在正整数0N ,当0n N >时,0n a >”;若存在正整数0N ,当0n N >时,0n a >,取N k *∈且0k N >,0k a >,假设0d <,令()0n k a a n k d =+−<可得k a n k d >−,且k a k k d−>, 当1k a n k d ⎡⎤>−+⎢⎥⎣⎦时,0n a <,与题设矛盾,假设不成立,则0d >,即数列{}n a 是递增数列. 所以,“{}n a 是递增数列”⇐“存在正整数0N ,当0n N >时,0n a >”.所以,“{}n a 是递增数列”是“存在正整数0N ,当0n N >时,0n a >”的充分必要条件.故选:C.10.(2021·全国甲卷·高考真题)等比数列{}n a 的公比为q ,前n 项和为n S ,设甲:0q >,乙:{}n S 是递增数列,则( )A .甲是乙的充分条件但不是必要条件B .甲是乙的必要条件但不是充分条件C .甲是乙的充要条件D .甲既不是乙的充分条件也不是乙的必要条件【答案】B【分析】当0q >时,通过举反例说明甲不是乙的充分条件;当{}n S 是递增数列时,必有0n a >成立即可说明0q >成立,则甲是乙的必要条件,即可选出答案.【详解】由题,当数列为2,4,8,−−−时,满足0q >,但是{}n S 不是递增数列,所以甲不是乙的充分条件.若{}n S 是递增数列,则必有0n a >成立,若0q >不成立,则会出现一正一负的情况,是矛盾的,则0q >成立,所以甲是乙的必要条件.故选:B .【点睛】在不成立的情况下,我们可以通过举反例说明,但是在成立的情况下,我们必须要给予其证明过程.考点06 全称量词与存在量词1.(2024·全国新Ⅱ卷·高考真题)已知命题p :x ∀∈R ,|1|1x +>;命题q :0x ∃>,3x x =,则( )A .p 和q 都是真命题B .p ⌝和q 都是真命题C .p 和q ⌝都是真命题D .p ⌝和q ⌝都是真命题【答案】B【分析】对于两个命题而言,可分别取=1x −、1x =,再结合命题及其否定的真假性相反即可得解.【详解】对于p 而言,取=1x −,则有101x +=<,故p 是假命题,p ⌝是真命题,对于q 而言,取1x =,则有3311x x ===,故q 是真命题,q ⌝是假命题,综上,p ⌝和q 都是真命题.故选:B.2.(2020·全国新Ⅰ卷·高考真题)下列命题为真命题的是( )A .10>且34>B .12>或45>C .x R ∃∈,cos 1x >D .x ∀∈R ,20x ≥【答案】D【分析】本题可通过43>、12<、45<、cos 1≤x 、20x ≥得出结果.【详解】A 项:因为43>,所以10>且34>是假命题,A 错误;B 项:根据12<、45<易知B 错误;C 项:由余弦函数性质易知cos 1≤x ,C 错误;D 项:2x 恒大于等于0,D 正确,故选:D.3.(2016·浙江·高考真题)命题“*,x R n N ∀∈∃∈,使得2n x ≥”的否定形式是A .*,x R n N ∀∈∃∈,使得2n x <B .*,x R n N ∀∈∀∈,使得2n x <C .*,x R n N ∃∈∃∈,使得2n x <D .*,x R n N ∃∈∀∈,使得2n x <【答案】D【详解】试题分析:∀的否定是∃,∃的否定是∀,2n x ≥的否定是2n x <.故选D .4.(2015·浙江·高考真题)命题“()**,n N f n N ∀∈∈且()f n n ≤的否定形式是( ) A .()**,n N f n N ∀∈∉且()f n n > B .()**,n N f n N ∀∈∉或()f n n > C .()**00,n N f n N ∃∈∉且()00f n n > D .()**00,n N f n N ∃∈∉或()00f n n >【答案】D【详解】由定义,可知命题“()**,n N f n N ∀∈∈且()f n n ≤的否定形式是()**00,n N f n N ∃∈∉或()00f n n >故选D.考点:命题的否定5.(2015·全国·高考真题)设命题2:,2n P n N n ∃∈>,则P ⌝为A .2,2n n N n ∀∈>B .2,2n n N n ∃∈≤C .2,2n n N n ∀∈≤D .2,2n n N n ∃∈= 【答案】C【详解】由定义,命题的否命题应该为2,2n n N n ∀∈≤,即本题的正确选项为C. 6.(2015·湖北·高考真题)命题“0(0,)x ∃∈+∞,00ln 1x x =−”的否定是A .0(0,)x ∃∈+∞,00ln 1x x ≠−B .0(0,)x ∃∉+∞,00ln 1x x =−C .(0,)x ∀∈+∞,ln 1x x ≠−D .(0,)x ∀∉+∞,ln 1x x =−【答案】C 【详解】由定义可知,命题的否定为:(0,)x ∀∈+∞,ln 1x x ≠−。
高中数学历年集合高考题汇编(专题)

集合与常用逻辑用语一、选择题1.(2010浙江理)(1)设P{x?x4},Q{x?4},则(A) (B) (C) (D)答案 B【解析】,可知B正确,本题主要考察了集合的基本运算,属容易题2.(2010陕西文)1.集合Ax-1≤x≤2,B={xx<1},则A∩B()Axx<1 (B)x-1≤x≤2C x-1≤x≤1D x-1≤x<1答案 D【解析】本题考查集合的基本运算由交集定义得x-1≤x≤2∩{xx<1}x-1≤x<13.(2010辽宁文)(1)已知集合,,则(A) (B)(C) (D)答案 D【解析】选D在集合中,去掉,剩下的元素构成4.(2010辽宁理)1.已知A,B均为集合U1,3,5,7,9的子集,且A ∩B3,B∩A9,则A(A)1,3 B3,7,9 C3,5,9 D3,9答案 D【命题立意】本题考查了集合之间的关系、集合的交集、补集的运算,考查了同学们借助于Venn图解决集合问题的能力。
【解析】因为A∩B3,所以3∈A,又因为B∩A9,所以9∈A,所以选D。
本题也可以用Venn图的方法帮助理解。
6.(2010江西理)2.若集合,,则()A B CD答案 C【解析】考查集合的性质与交集以及绝对值不等式运算。
常见的解法为计算出集合A、B;,,解得。
在应试中可采用特值检验完成。
8.(2010浙江文)(1)设则ABCD答案 D解析:,故答案选D,本题主要考察了集合的基本运算,属容易题9.(2010山东文)(1)已知全集,集合,则ABC. D答案:C11.(2010北京理)(1) 集合,则 A 1,2 B 0,1,2 Cx|0≤x3D x|0≤x≤3答案:B12.(2010天津文)7设集合则实数a的取值范围是A BCD答案 C【解析】本题主要考查绝对值不等式的基本解法与集合交集的运算,属于中等题。
由|x-a|1得-1x-a1,即a-1xa+1.如图由图可知a+1?1或a-1?5,所以a?0或a?6.【温馨提示】不等式型集合的交、并集通常可以利用数轴进行,解题时注意验证区间端点是否符合题意。
专题01 集合-2013-2022十年全国高考数学真题分类汇编(文科,全国通用版)(解析版)

2013-2022十年全国高考数学真题分类汇编专题01 集合一、选择题1.(2022年全国高考甲卷(文)·第1题)设集合5{2,1,0,1,2},02A B xx ⎧⎫=--=≤<⎨⎬⎩⎭∣,则A B =( )A .{}0,1,2B .{2,1,0}--C .{0,1}D .{1,2}【答案】A【解析】因为{}2,1,0,1,2A =--,502B xx ⎧⎫=≤<⎨⎬⎩⎭∣,所以{}0,1,2A B =.故选:A .【题目栏目】集合\集合的基本运算【题目来源】2022年全国高考甲卷(文)·第1题2.(2022年高考全国乙卷(文)·第1题)集合{}{}2,4,6,8,10,16M N x x ==-<<,则M N =( )A .{2,4}B .{2,4,6}C .{2,4,6,8}D .{2,4,6,8,10}【答案】A解析:因为{}2,4,6,8,10M =,{}|16N x x =-<<,所以{}2,4M N =.故选:A .【题目栏目】集合\集合的基本运算【题目来源】2022年高考全国乙卷(文)·第1题3.(2022新高考全国II 卷·第1题)已知集合{}{}1,1,2,4,11A B x x =-=-≤,则AB =( )A .{1,2}-B .{1,2}C .{1,4}D .{1,4}-【答案】B解析: {}|02B x x =≤≤,故{}1,2AB =. 故选 B .【题目栏目】集合\集合的基本运算【题目来源】2022新高考全国II 卷·第1题4.(2022新高考全国I 卷·第1题)若集合{4},{31}M x x N x x =<=≥∣∣,则M N =( )A .{}02x x ≤<B .123xx ⎧⎫≤<⎨⎬⎩⎭C .{}316x x ≤<D .1163xx ⎧⎫≤<⎨⎬⎩⎭【答案】D解析:1{16},{}3M x x N x x =≤<=≥∣0∣,故1163MN x x ⎧⎫=≤<⎨⎬⎩⎭, 故选:D【题目栏目】集合\集合的基本运算【题目来源】2022新高考全国I 卷·第1题5.(2021年新高考全国Ⅱ卷·第2题)设集合{1,2,3,4,5,6},{1,3,6},{2,3,4}U A B ===,则()UAB =( )A .{3}B .{1,6}C .{5,6}D .{1,3}【答案】B解析:由题设可得{}U1,5,6B =,故(){}U 1,6A B⋂=,故选B .【题目栏目】集合\集合的基本运算【题目来源】2021年新高考全国Ⅱ卷·第2题6.(2021年新高考Ⅱ卷·第1题)设集合{}24A x x =-<<,{}2,3,4,5B =,则AB =( )A .{}2B .{}2,3C .{}3,4D .{}2,3,4【答案】B解析:由题设有{}2,3A B ⋂=,故选B .【题目栏目】集合\集合的基本运算【题目来源】2021年新高考Ⅱ卷·第1题7.(2020年新高考I 卷(山东卷)·第1题)设集合A ={x |1≤x ≤3},B ={x |2<x <4},则A ∪B =( )A .{x |2<x ≤3}B .{x |2≤x ≤3}C .{x |1≤x <4}D .{x |1<x <4}【答案】C解析:[1,3](2,4)[1,4)A B ==故选:C【题目栏目】集合\集合的基本运算【题目来源】2020年新高考I 卷(山东卷)·第1题 8.(2020新高考II 卷(海南卷)·第1题)设集合A={2,3,5,7},B ={1,2,3,5,8},则AB=( )A .{1,3,5,7}B .{2,3}C .{2,3,5}D .{1,2,3,5,7,8} 【答案】C解析:因为{2,3,5,7},{1,2,3,5,8}A B == ,所以{2,3,5}A B = ,故选:C【题目栏目】集合\集合的基本运算【题目来源】2020新高考II 卷(海南卷)·第1题9.(2021年高考全国甲卷文科·第1题)设集合{}{}1,3,5,7,9,27M N x x ==>,则M N =( )A .{}7,9B .{}5,7,9C .{}3,5,7,9D .{}1,3,5,7,9【答案】B解析:7,2N ⎛⎫=+∞ ⎪⎝⎭,故{}5,7,9M N ⋂=, 故选:B .【题目栏目】集合\集合的基本运算【题目来源】2021年高考全国甲卷文科·第1题10.(2021年全国高考乙卷文科·第1题)已知全集{}1,2,3,4,5U =,集合{}{}1,2,3,4M N ==,则()U M N ⋃=( )A .{}5B .{}1,2C .{}3,4D .{}1,2,3,4【答案】A解析:由题意可得:{}1,2,3,4M N =,则(){}5UM N =.故选:A .【题目栏目】集合\集合的基本运算【题目来源】2021年全国高考乙卷文科·第1题 11.(2020年高考数学课标Ⅱ卷文科·第1题)已知集合2{|340},{4,1,3,5}A x x x B =--<=-,则A B =( )A .{4,1}-B .{1,5}C .{3,5}D .{1,3}【答案】D【解析】由2340x x --<解得14x -<<, 所以{}|14A x x =-<<, 又因为{}4,1,3,5B =-,所以{}1,3A B =,故选:D .【点睛】本题考查的是有关集合的问题,涉及到的知识点有利用一元二次不等式的解法求集合,集合的交运算,属于基础题目.【题目栏目】集合\集合的基本运算【题目来源】2020年高考数学课标Ⅱ卷文科·第1题 12.(2020年高考数学课标Ⅱ卷文科·第1题)已知集合A ={x ||x |<3,x ∈Z },B ={x ||x |>1,x ∈Z },则A ∩B =( ) A .∅ B .{–3,–2,2,3)C .{–2,0,2}D .{–2,2}【答案】D【解析】因为{}{}3,2,1,0,1,2A x x x Z =<∈=--,{}{1,1B x x x Z x x =>∈=>或}1,x x Z <-∈,所以{}2,2AB =-.故选:D .【点睛】本题考查绝对值不等式的解法,考查集合交集的定义,属于基础题. 【题目栏目】集合\集合的基本运算【题目来源】2020年高考数学课标Ⅱ卷文科·第1题13.(2020年高考数学课标Ⅱ卷文科·第1题)已知集合{}1235711A =,,,,,,{}315|B x x =<<,则A ∩B 中元素的个数为( ) A .2 B .3 C .4 D .5【答案】B【解析】由题意,{5,7,11}A B ⋂=,故A B 中元素的个数为3.故选:B【点晴】本题主要考查集合的交集运算,考查学生对交集定义的理解,是一道容易题. 【题目栏目】集合\集合的基本运算【题目来源】2020年高考数学课标Ⅱ卷文科·第1题14.(2019年高考数学课标Ⅱ卷文科·第1题)已知集合{|1012}A x =-,,,,2{|1}B x x =≤,则A ∩B =( )A .{1,0,1}-B .{0,1}C .{1,1}-D .{0,1,2}【答案】A【解析】因为{1A =-,0,1,2},2{|1}{|11}B x x x x ==-,所以{1,0,1}A B =-,故选:A .【题目栏目】集合\集合的基本运算【题目来源】2019年高考数学课标Ⅱ卷文科·第1题15.(2019年高考数学课标Ⅱ卷文科·第1题)已知集合={|1}A x x >-,{|2}B x x =<,则A B =( )A .()1,-+∞B .(),2-∞C .()1,2-D .φ【答案】C【解析】由题知,{}{}|1|2(1,2)AB x x x x =>-<=-,故选C .【点评】本题主要考查交集运算,容易题,注重了基础知识、基本计算能力的考查.易错点是理解集合的概念及交集概念有误,不能借助数轴解题. 【题目栏目】集合\集合的基本运算【题目来源】2019年高考数学课标Ⅱ卷文科·第1题16.(2019年高考数学课标Ⅱ卷文科·第2题)已知集合{}1,2,3,4,5,6,7U =,{}2,3,4,5A =,{}2,3,6,7B =,则UBA =()( )A .{}1,6B .{}1,7C .{}6,7D .{}1,6,7【答案】C【解析】 }7,6,5,4,3,2,1{=U ,5}43{2,,,=A ,则7}6{1,,=A C U 又 7}63{2,,,=B ,则7}{6,=A C B U . 【题目栏目】集合\集合的基本运算【题目来源】2019年高考数学课标Ⅱ卷文科·第2题17.(2018年高考数学课标Ⅱ卷文科·第1题)已知集合{}|10A x x =-≥,{}012,,B =,则A B =( )A .{}0B .{}1C .{}12,D .{}012,, 【答案】C解析:{}{}|10|1A x x x x =-=≥≥,{}0,1,2B =,故{}1,2A B =.故选C .【题目栏目】集合\集合的基本运算【题目来源】2018年高考数学课标Ⅱ卷文科·第1题 18.(2018年高考数学课标Ⅱ卷文科·第2题)已知集合{}1,3,5,7A =,{}2,3,4,5B =,则A B =( ) A .{}3 B .{}5C .{}3,5D .{}1,2,3,4,5,7【答案】C解析:∵集合{}{}1,3,5,7,2,3,4,5A B ==,∴{}3,5AB =.故选C .【题目栏目】集合\集合的基本运算【题目来源】2018年高考数学课标Ⅱ卷文科·第2题19.(2018年高考数学课标Ⅱ卷文科·第1题)已知集合{0,2}A =,{2,1,0,1,2}B =--,则A B =( )A .{0,2}B .{1,2}C .{0}D .{2,1,0,1,2}--【答案】A解析:因为{0,2}A =,{2,1,0,1,2}B =--,则{0,2}A B =. 【题目栏目】集合\集合的基本运算【题目来源】2018年高考数学课标Ⅱ卷文科·第1题 20.(2017年高考数学课标Ⅱ卷文科·第1题)已知集合,则中元素的个数为( )A .1B .2C .3D .4【答案】 【解析】由题意可得: ,中元素的个数为2,所以选.【考点】集合运算【点评】集合的基本运算的关注点(1)看元素组成.集合是由元素组成的,从研究集合中元素的构成入手是解决集合运算问题的前提.(2)有些集合是可以化简的,先化简再研究其关系并进行运算,可使问题简单明了,易于解决.(3)注意数形结合思想的应用,常用的数形结合形式有数轴、坐标系和Venn 图. 【题目栏目】集合\集合的基本运算【题目来源】2017年高考数学课标Ⅱ卷文科·第1题21.(2017年高考数学课标Ⅱ卷文科·第1题)设集合A=,B=,则=( )1,2,3,42,4,6,8AB ,A B B {}2,4AB =A B B {}123,,{}234,,A BA .B .C .D . 【答案】 A【解析】由题意得.故选A .【考点】集合并集的运算.【点评】掌握集合的基本运算即可. 【题目栏目】集合\集合的基本运算【题目来源】2017年高考数学课标Ⅱ卷文科·第1题22.(2017年高考数学课标Ⅱ卷文科·第1题)已知集合,,则( ) A .B .C .D .【答案】 A【解析】由得,所以,故选A【考点】集合运算【点评】对于集合的交、并、补运算问题,应先把集合化简再计算,常常借助数轴或韦恩图处理【题目栏目】集合\集合的基本运算【题目来源】2017年高考数学课标Ⅱ卷文科·第1题23.(2016年高考数学课标Ⅱ卷文科·第1题)设集合{0,2,4,6,8,10},{4,8}A B ==,则AB =( )A .{48},B .{026},,C .{02610},,,D .{0246810},,,,, 【答案】C 【解析】根据补集的定义,从集合{0,2,4,6,8,10}A =中去掉集合B 中的元素4,8,剩下的四个元素为0,2,6,10,故{0,2,6,10}AC B =,故选C .【题目栏目】集合\集合的基本运算【题目来源】2016年高考数学课标Ⅱ卷文科·第1题24.(2016年高考数学课标Ⅱ卷文科·第1题)已知集合{123}A =,,,2{|9}B x x =<,则A B =( ).A .{210123}--,,,,,B .{21012}--,,,,C .{123},,D .{12},【答案】D 【解析】由29x <得,33x -<<,所以{|33}B x x =-<<,所以{1,2}A B =.【题目栏目】集合\集合的基本运算【题目来源】2016年高考数学课标Ⅱ卷文科·第1题25.(2016年高考数学课标Ⅱ卷文科·第1题)设集合{1,3,5,7}A =,{|25}B x x =≤≤,则A B =( ) A .{}1,3 B .{}3,5C .{}5,7D .{}1,7【答案】B 【解析】集合A 与集合B 公共元素有3,5,故{3,5}A B =,选B .【题目栏目】集合\集合的基本运算【题目来源】2016年高考数学课标Ⅱ卷文科·第1题26.(2015年高考数学课标Ⅱ卷文科·第1题)已知集合{}|12A x x =-<<,{}123,4,,{}123,,{}23,4,{}13,4,{}1,2,3,4AB ={}2A x x =<{}320B x x =->3=2AB x x ⎧⎫<⎨⎬⎩⎭A B =∅3=2A B x x ⎧⎫<⎨⎬⎩⎭=A B R 320x ->32x <33{|2}||22A B x x x x x x ⎧⎫⎧⎫=<<=<⎨⎬⎨⎬⎩⎭⎩⎭{}|03B x x =<<,则A B =( )A .()1,3-B .()1,0-C .()0,2D .()2,3【答案】A 解析:因为{}|12A x x =-<<,{}|03B x x =<<,所以{}|13.A B x x =-<<故选A .考点:本题主要考查不等式基础知识及集合的交集运算. 【题目栏目】集合\集合的基本运算【题目来源】2015年高考数学课标Ⅱ卷文科·第1题27.(2015年高考数学课标Ⅱ卷文科·第1题)已知集合{32,},{6,8,10,12,14}A x x n n B ==+∈=N ,则集合A B 中的元素个数为( )A .5B .4C .3D .2 【答案】D分析:由条件知,当n=2时,3n+2=8,当n=4时,3n+2=14,故A∩B={8,14},故选D . 考点:集合运算【题目栏目】集合\集合的基本运算【题目来源】2015年高考数学课标Ⅱ卷文科·第1题28.(2014年高考数学课标Ⅱ卷文科·第1题)已知集合A={-2,0,2},B={x |220x x --=},则A B =( )A.∅B.{2}C.{0}D.{-2} 【答案】B解析:∵B={x |220x x --=}={-1,2},∴A B ={2}.∴选B . 考点:集合的运算 难度:A备注:常考题.【题目栏目】集合\集合的基本运算【题目来源】2014年高考数学课标Ⅱ卷文科·第1题 29.(2014年高考数学课标Ⅱ卷文科·第1题)已知集合M ={|13}x x -<<,N ={|21}x x -<<,则M ∩N =( ) A .(-2,1)B .(-1,1)C .(1,3)D .(-2,3)【答案】B解析: 在数轴上表示出对应的集合,可得()1,1MN =- ,选B考点:1.集合的基本运算。
集合有关近年高考题50道及答案解析

【经典例题】【例1】(2009年广东卷文)已知全集U R =,则正确表示集合{1,0,1}M =-和{}2|0N x x x =+=关系的韦恩(Venn )图是 ( )【答案】B【解析】 由{}2|0N x x x =+=,得{1,0}N =-,则N M ⊂,选B.【例2】(2011广东)已知集合{(,)|,A x y x y =为实数,且}221,x y +={(,)|,B x y x y =为实数,且},AB y x =则的元素个数为 ( ) A 、0 B 、1 C 、2 D 、3 【答案】C【解析】A 为圆心在原点的单位圆,B 为过原点的直线,故有2个交点,故选C.【例3】(2010天津理)设集合A={}{}|||1,,|||2,.x x a x R B x x b x R -<∈=->∈若A ⊆B ,则实数a,b 必满足( ) A 、||3a b +≤ B 、||3a b +≥ C 、||3a b -≤ D 、||3a b -≥【答案】D【解析】A={x|a-1<x<a+1},B={x|x<b-2或x>b+2},因为A ⊆B,所以a+1≤b-2或a-1≥b+2,即a-b ≤-3或a-b ≥3,即|a-b|≥3【例4】(2009广东卷理)已知全集U R =,集合{212}M x x =-≤-≤和{21,1,2,}N x x k k ==-=的关系的韦恩(Venn )图如图所示,则阴影部分所示的集合的元素共有 ( )A. 3个B. 2个C. 1个D. 无穷多个 【答案】 B【解析】 由{212}M x x =-≤-≤得31≤≤-x ,则{}3,1=⋂N M ,有2个,选B. 【例5】(2010天津文)设集合{}{}A x||x-a|<1,x R ,|15,.A B B x x x R =∈=<<∈⋂=∅若,则实数a 的取值范围是 ( ) A 、{}a |0a 6≤≤ B 、{}|2,a a ≤≥或a 4C 、{}|0,6a a ≤≥或aD 、{}|24a a ≤≤ 【答案】 C【解析】由|x-a|<1得-1<x-a<1,即a-1<x<a+1.如图由图可知a+1≦1或a-1≧5,所以a ≦0或a ≧6.【例6】(2012大纲全国)已知集合{}{}1,3,,1,,A m B m A B A ==⋃=,则m = ( )A 、0或3B 、0或3C 、1或3D 、1或3 【答案】B 【解析】A B A ⋃= B A ∴⊂,{}{}1,3,,1,A m B m ==m A ∴∈,故m m =或3m =,解得0m =或3m =或1m =,又根据集合元素的互异性1m ≠,所以0m =或3m =。
(完整版)集合有关近年高考题50道及答案解析

【经典例题】【例1】(2009年广东卷文)已知全集U R =,则正确表示集合{1,0,1}M =-和{}2|0N x x x =+=关系的韦恩(Venn )图是 ( )【答案】B【解析】 由{}2|0N x x x =+=,得{1,0}N =-,则N M ⊂,选B.【例2】(2011广东)已知集合{(,)|,A x y x y =为实数,且}221,x y +={(,)|,B x y x y =为实数,且},AB y x =则的元素个数为 ( ) A 、0 B 、1 C 、2 D 、3 【答案】C【解析】A 为圆心在原点的单位圆,B 为过原点的直线,故有2个交点,故选C.【例3】(2010天津理)设集合A={}{}|||1,,|||2,.x x a x R B x x b x R -<∈=->∈若A ⊆B ,则实数a,b 必满足( ) A 、||3a b +≤ B 、||3a b +≥ C 、||3a b -≤ D 、||3a b -≥【答案】D【解析】A={x|a-1<x<a+1},B={x|x<b-2或x>b+2},因为A ⊆B,所以a+1≤b-2或a-1≥b+2,即a-b ≤-3或a-b ≥3,即|a-b|≥3【例4】(2009广东卷理)已知全集U R =,集合{212}M x x =-≤-≤和{21,1,2,}N x x k k ==-=的关系的韦恩(Venn )图如图所示,则阴影部分所示的集合的元素共有 ( )A. 3个B. 2个C. 1个D. 无穷多个 【答案】 B【解析】 由{212}M x x =-≤-≤得31≤≤-x ,则{}3,1=⋂N M ,有2个,选B. 【例5】(2010天津文)设集合{}{}A x||x-a|<1,x R ,|15,.A B B x x x R =∈=<<∈⋂=∅若,则实数a 的取值范围是 ( ) A 、{}a |0a 6≤≤ B 、{}|2,a a ≤≥或a 4C 、{}|0,6a a ≤≥或aD 、{}|24a a ≤≤ 【答案】 C【解析】由|x-a|<1得-1<x-a<1,即a-1<x<a+1.如图由图可知a+1≦1或a-1≧5,所以a ≦0或a ≧6.【例6】(2012大纲全国)已知集合{}{}1,3,,1,,A m B m A B A ==⋃=,则m = ( )A 、0或3B 、0或3C 、1或3D 、1或3 【答案】B 【解析】A B A ⋃= B A ∴⊂,{}{}1,3,,1,A m B m ==m A ∴∈,故m m =或3m =,解得0m =或3m =或1m =,又根据集合元素的互异性1m ≠,所以0m =或3m =。
全国卷近五年高考真题汇总---1.集合(理)

J 接生产工艺过程的特点,工业企业的生产可分为大量生产、成批生产和单件生产三种,
X
K可修复废品是指技术上可以修复使用的废品。错
K 可修复废品是指经过修理可以使用,而不管修复费用在经济上是否合算的废品。X
P 品种法只适用于大量大批的单步骤生产的企业。×
Q企业的制造费用一定要通过“制造费用”科目核算。X
(×)
Z在产品品种规格繁多的情况下,应该采用分类法计算产品成本。对
Z 直接生产费用就是直接计人费用。 X
Z 逐步结转分步法也称为计列半成品分步法。√
A 按年度计划分配率分配制造费用, “制造费用”账户月末 ( 可能有月末余额 / 可能有借方余额 / 可能有贷方余额 / 可能无月末余额 ) 。
x ,则A∩B中元
D.0 )
A. A B { x | x 0}
B. A B R
C. A B { x | x 1}
D. A B
【 2017 全国 2,理】 设集合
1,2,4 ,
x x2 4x m 0 。若
1,
则 ()
A. 1, 3
B. 1,0
C. 1,3
D. 1,5
【 2016全国 1,理】设集合 A { x | x2 4x 3 0} , B { x | 2x 3 0} ,则 A B
5 < x<
5 } ,则
( ).
A. A∩B=
B.A∪ B= R
C.B A
D. A B
3 、通过活动,使学生养成博览群书的好
习惯。
B 比率分析法和比较分析法不能测算出各因素的影响程度。√
C 采用约当产量比例法,分配原材料费用与分配加工费用所用的完工率都是一致的。X
C采用直接分配法分配辅助生产费用时,应考虑各辅助生产车间之间相互提供产品或劳务的情况。错
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
集合历年高考真题精编W O R D版IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】高考集合历年真题题型1 集合的基本概念——暂无题型2 集合间的基本关系——暂无题型3 集合的运算1.(2014新课标Ⅰ文1)已知集合{|13}M x x =-<<,{|21}N x x =-<<,则M N =( ) A. (2,1)- B. (1,1)- C. (1,3) D. )3,2(-2.(2014新课标Ⅱ文1)已知集合{}2,0,2A =-,{}2|20B x x x =--=,则AB =( )A.∅B.{}2C.{}0D.{}2- 3(2014江西文2)设全集为R ,集合2{|90},{|15}A x x B x x =-<=-<≤,则()A B =R ( ).A.(3,0)-B.(3,1)--C.(3,1]--D.(3,3)-4(2014辽宁文1)已知全集U =R ,{|0}A x x =≤,{|1}B x x =≥,则集合()U A B =( )A .{|0}x x ≥B .{|1}x x ≤C .{|01}x x ≤≤D .{|01}x x <<5.(2014陕西文1)设集合{}{}2|0|1M x x x N x x x =∈=<∈R R ≥,,,,则M N =( ).A.[]0,1B. ()0,1C.(]0,1 D. [)0,1 6.(2014四川文1)已知集合()(){}120A x x x =+-,集合B 为整数集,则A B =( ).A.{}1,0-B.{}0,1C.{}2,1,0,1--D.{}1,0,1,2-7.(2014北京文1)若集合{}0,1,2,4A =,{}1,2,3B =,则A B =( )A.{}0,1,2,3,4B.{}0,4C.{}1,2D.{}38.(2014大纲文1)设集合{12468}{123567}M N ==,,,,,,,,,,,则M N 中元素的个数为( ).A .2B .3C .5D .79.(2014福建文1)若集合}{}{24,3,P x x Q x x =<=≤≥则P Q 等于( )A.}{34x x <≤B.}{34x x <<C.}{23x x <≤D. }{23x x ≤≤10.(2014广东文1)已知集合{}{}2,3,4,0,2,3,5M N ==,则M N =( ).A.{}0,2B.{}2,3C.{}3,4D. {}3,511.(2014湖北文1)已知全集{}1234567U =,,,,,,,集合{}1356A =,,,,则U A = ( ).A .{}1356,,,B .{}237,,C .{}247,,D . {}257,,12.(2014湖南文2)已知集合{|2}A x x =>,{|13}B x x =<<,则A B =( ).A.{|2}x x >B. {|1}x x >C.{|23}x x <<D. {|13}x x <<13.(2014江苏1)已知集合{}2134A =--,,,,{}123B =-,,,则A B = .14(2014重庆文11)已知集合{3451213}{235813}A B A B ===,,,,,,,,,,则 .15.(2015重庆文1)已知集合{}1,2,3A =,{}1,3B =,则A B =( ).A.{2}B.{1,2}C.{1,3}D. {1,2,3}16.(2015广东文1)若集合{}1,1M =-,{}2,1,0N =-,则M N =( ).A .{}0,1-B .{}0C .{}1D .{}1,1-17.(2015天津文1)已知全集{}1,2,3,4,5,6U =,集合{}2,3,4A =,集合{}1,3,4,6B =, 则集合U A B =( ).A.{}3B. {}2,5C. {}1,4,6D.{}2,3,518.(2015安徽文2)设全集{}1,2,3,4,5,6U =,{}1,2A =,{}2,3,4B =,则()U A B = ( ).A. {}1,2,5,6B. {}1C. {}2D. {}1,2,3,419.(2015全国I 文1)已知集合{32,},{6,8,10,12,14}A x x n n B ==+∈=N ,则集合A B 中元素的个数为( ).A. 5B. 4C. 3D. 220.(2015北京文1)若集合{}52A x x =-<<,{}33B x x =-<<,则A B =( ). A. {}32x x -<< B. {}52x x -<< C. {}33x x -<< D. {}53x x -<<21.(2015全国II 文1)已知集合{|12}A x x =-<<,{}03B x x =<<,则=B A ( ).A. ()13,-B. ()10,-C. ()02,D. ()23,22.(2015山东文1)已知集合{}|24A x x =<<,{}|(1)(3)0B x x x =--<,则 A B =( ).A. (13),B. (14),C. (23),D. (24),23.(2015四川文1) 设集合{}12A x x =-<<,集合{}13B x x =<<,则A B =( ). A. {}13x x -<< B. {}11x x -<< C. {}12x x << D. {}23x x <<24.(2015浙江文1)已知集合{}223P x x x =-,{}24Q x x =<<,则=P Q ( ). A. [)34, B. (]23, C.()12-, D.(]13-,25.(2015湖南文11)已知集合{}1,2,3,4U =,{}1,3A =,{}1,3,4B =,则()U A B = .26.(2015江苏1)已知集合{}1,2,3A =,{}2,4,5B =,则集合A B 中元素的个数为 .27.(2016北京文1)已知集合{}24A x x =<<,{}35B x x x =<>或,则A B =( ). A. {}25x x << B. {}45x x x <>或 C. {}23x x << D.{}25x x x <>或28.(2016全国丙文1)设集合{0,2,4,6,8,10}A =,{4,8}B =,则A B =( ).A.{}4,8B.{}0,2,6C.{}0,2,6,10D.{}0,2,4,6,8,1029.(2016全国甲文1)已知集合{}1,2,3A =,{}2|9B x x =<,则A B =( ).A.{}2,1,0,1,2,3--B.{}2,1,0,1,2--C.{}1,2,3D.{}1,230.(2016山东文1)设集合{123456}{135}{345}U A B ===,,,,,,,,,,,,则()=U A B ( ).A.{2,6}B.{3,6}C.{1,3,4,5}D.{1,2,4,6}31.(2016浙江文1)已知全集{}12,3456U =,,,,,集合{}13,5P =,,{}124Q =,,,则()U P Q =( ).A.{}1B.{}3,5C.{}1,2,4,6D.{}1,2,3,4,532.(2016江苏卷1)已知集合{}1,2,3,6A =-,{}23B x x =-<<,则A B = .33.(2016上海文1)设x ∈R ,则不等式31x -<的解集为 .34.(2017全国1文1)已知集合{}2A x x =<,{}320B x x =->,则( ).A .32AB x x ⎧⎫=<⎨⎬⎩⎭ B .A B =∅C .32A B x x ⎧⎫=<⎨⎬⎩⎭ D .A B =R 35.(2017全国2文1)设集合{}123A =,,,{}234B =,,,则=A B ( ).A. {}123,4,,B. {}123,,C. {}234,,D. {}134,,36(2017全国3文1)已知集合{}1234A =,,,,{}2468B =,,,,则A B 中元素的个数为( ).A .1B .2C .3D .437.(2017北京文1)已知U =R ,集合{|22}A x x x =<->或,则U A =( ).A.(2,2)-B.(,2)(2,)-∞-+∞C.[2,2]-D.(,2][2,)-∞-+∞38.(2017山东文1)设集合{}11M x x =-<,{}2N x x =<,则M N =( ).A. ()1,1-B. ()1,2-C. ()0,2D. ()1,2 39(2017天津文1)设集合{}1,2,6A =,{}2,4B =,{}1,2,3,4C =,则()A B C =( ).A.{}2B.{}1,2,4C.{}1,2,4,6D.{}1,2,3,4,640.(2017浙江1)已知集合{}11P x x =-<<,{}02Q x x =<<,那么P Q =( ).A.()1,2-B.()01,C.()1,0-D.()1,2。
