2018年浙江省舟山市中考数学试卷及解析
2018年浙江省舟山市中考数学试卷含答案解析(Word版)
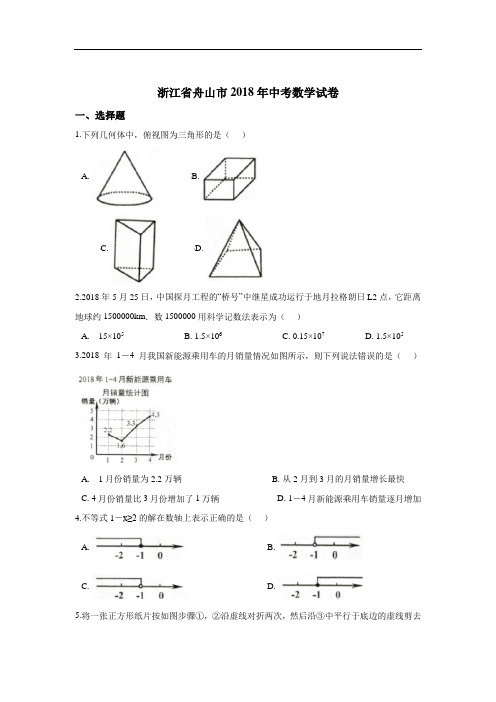
浙江省舟山市2018年中考数学试卷一、选择题1.下列几何体中,俯视图为三角形的是()A. B.C. D.2.2018年5月25日,中国探月工程的“桥号”中继星成功运行于地月拉格朗日L2点,它距离地球约1500000km.数1500000用科学记数法表示为()A. 15×105B. 1.5×106C. 0.15×107D. 1.5×1053.2018年1-4月我国新能源乘用车的月销量情况如图所示,则下列说法错误的是()A. 1月份销量为2.2万辆B. 从2月到3月的月销量增长最快C. 4月份销量比3月份增加了1万辆D. 1-4月新能源乘用车销量逐月增加4.不等式1-x≥2的解在数轴上表示正确的是()A. B.C. D.5.将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是()A. B. C. D.6.用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是()A. 点在圆内B. 点在圆上C. 点在圆心上D. 点在圆上或圆内7.欧几里得的《原本》记载,形如x2+ax=b2的方程的图解法是;画Rt△ABC,使∠ACB=90°,BC= ,AC=b,再在斜边AB上截取BD= 。
则该方程的一个正根是()A.AC的长B.AD的长C.BC的长D.CD的长8.用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是()A. B.C. D.9.如图,点C在反比例函数(x>0)的图象上,过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,则k的值为()A. 1B. 2C. 3 D . 410.某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分,某小组比赛结束后,甲、乙,丙、丁四队分别获得第一,二,三,四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是()A.甲B.甲与丁C.丙D.丙与丁二、填空题11.分解因式m2-3m=________。
2018年舟山市中考数学试题含答案(Word版)

浙江省舟山市2018年中考数学试题卷Ⅰ(选择题)一、选择题(本题有10小题,每题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选,均不得分)1.下列几何体中,俯视图...为三角形的是()A.B.C.D.2.2018年5月25日,中国探月工程的“鹊桥号”中继星成功运行于地月拉格朗日2L点,它距离地球约1500000km.数1500000用科学记数法表示为()A.51510⨯B.61.510⨯C.70.1510⨯D.51.510⨯3.2018年1~4月我国新能源乘用车的月销售情况如图所示,则下列说法错误..的是()A.1月份销售为2.2万辆B.从2月到3月的月销售增长最快C.4月份销售比3月份增加了1万辆D.1~4月新能源乘用车销售逐月增加14.不等式12x-≥的解在数轴上表示正确的是()A.B.C.D.5.将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是()A.B.C.D.6.用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是()A.点在圆内B.点在圆上C.点在圆心上D.点在圆上或圆内7.欧几里得的《原本》记载,形如22x ax b+=的方程的图解法是:画Rt ABC∆,使90ACB∠=,2aBC=,AC b=,再在斜边AB上截取2aBD=.则该方程的一个正根是()A.AC的长B.AD的长C.BC的长D.CD的长8.用尺规在一个平行四边形内作菱形ABCD,下列作法中错误..的是()23A .B .C .D .9.如图,点C 在反比例函数(0)k y x x=>的图象上,过点C 的直线与x 轴,y 轴分别交于点A ,B ,且AB BC =,AOB ∆的面积为1,则k 的值为( )A .1B .2C .3D .410.某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分.某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是( )A .甲B .甲与丁C .丙D .丙与丁卷Ⅱ(非选择题)二、填空题(本题有6小题,每题4分,共24分)11.分解因式:23m m -= .12.如图,直线123////l l l ,直线AC 交1l ,2l ,3l 于点A ,B ,C ;直线DF 交1l ,2l ,3l 于点D ,E ,F .已知13AB AC =,则EF DE= .。
(完整版)2018年浙江省舟山市中考数学试卷及答案解析

2018年浙江省舟山市中考数学试卷一、选择题(本题有10小题,每题3分,共30分。
请选出各题中唯一的正确选项,不选、多选、错选,均不得分)1.(3分)下列几何体中,俯视图为三角形的是()A. B.C.D.2.(3分)2018年5月25日,中国探月工程的“鹊桥号”中继星成功运行于地月拉格朗日L2点,它距离地球约1500000km,数1500000用科学记数法表示为()A.15×105 B.1.5×106C.0.15×107D.1.5×1053.(3分)2018年1~4月我国新能源乘用车的月销量情况如图所示,则下列说法错误的是()A.1月份销量为2.2万辆B.从2月到3月的月销量增长最快C.4月份销量比3月份增加了1万辆D.1~4月新能源乘用车销量逐月增加4.(3分)不等式1﹣x≥2的解在数轴上表示正确的是()A.B.C.D.5.(3分)将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是()A.B.C. D.6.(3分)用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是()A.点在圆内B.点在圆上C.点在圆心上D.点在圆上或圆内7.(3分)欧几里得的《原本》记载,形如x2+ax=b2的方程的图解法是:画Rt △ABC,使∠ACB=90°,BC=,AC=b,再在斜边AB上截取BD=.则该方程的一个正根是()A.AC的长 B.AD的长 C.BC的长D.CD的长8.(3分)用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是()A. B.C.D.9.(3分)如图,点C在反比例函数y=(x>0)的图象上,过点C的直线与x 轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,则k的值为()A.1 B.2 C.3 D.410.(3分)某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分,某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是()A.甲B.甲与丁C.丙D.丙与丁二、填空题(本题有6小题,每题4分,共24分)11.(4分)分解因式:m2﹣3m=.12.(4分)如图,直线l1∥l2∥l3,直线AC交l1,l2,l3于点A,B,C;直线DF 交l1,l2,l3于点D,E,F,已知=,则=.13.(4分)小明和小红玩抛硬币游戏,连续抛两次,小明说:“如果两次都是正面,那么你赢;如果两次是一正一反,则我嬴.”小红赢的概率是,据此判断该游戏(填“公平”或“不公平”).14.(4分)如图,量角器的0度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10cm,点D在量角器上的读数为60°,则该直尺的宽度为cm.15.(4分)甲、乙两个机器人检测零件,甲比乙每小时多检测20个,甲检测300个比乙检测200个所用的时间少10%,若设甲每小时检测x个,则根据题意,可列出方程:.16.(4分)如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F 是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是.三、解答题(本题有8小题,第17~19题每题6分,第20,21题每题8分,第22,23题每题10分,第24题12分,共66分)17.(6分)(1)计算:2(﹣1)+|﹣3|﹣(﹣1)0;(2)化简并求值()•,其中a=1,b=2.18.(6分)用消元法解方程组时,两位同学的解法如下:解法一:由①﹣②,得3x=3.解法二:由②得,3x+(x﹣3y)=2,③把①代入③,得3x+5=2.(1)反思:上述两个解题过程中有无计算错误?若有误,请在错误处打“ד.(2)请选择一种你喜欢的方法,完成解答.19.(6分)已知:在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为点E,F,且DE=DF.求证:△ABC是等边三角形.20.(8分)某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为176mm~185mm的产品为合格),随机各抽取了20个样品进行检测,过程如下:收集数据(单位:mm)甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.整理数据:165.5~170.5170.5~175.5175.5~180.5180.5~185.5185.5~190.5190.5~195.5甲车间245621乙车间12a b20分析数据:车间平均数众数中位数方差甲车间180********.1乙车间180********.6应用数据:(1)计算甲车间样品的合格率.(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.21.(8分)小红帮弟弟荡秋千(如图1),秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图2所示.(1)根据函数的定义,请判断变量h是否为关于t的函数?(2)结合图象回答:①当t=0.7s时,h的值是多少?并说明它的实际意义.②秋千摆动第一个来回需多少时间?22.(10分)如图1,滑动调节式遮阳伞的立柱AC垂直于地面AB,P为立柱上的滑动调节点,伞体的截面示意图为△PDE,F为PD的中点,AC=2.8m,PD=2m,CF=1m,∠DPE=20°,当点P位于初始位置P0时,点D与C重合(图2).根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳.(1)上午10:00时,太阳光线与地面的夹角为65°(图3),为使遮阳效果最佳,点P需从P0上调多少距离?(结果精确到0.1m)(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点P 在(1)的基础上还需上调多少距离?(结果精确到0.1m)(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,≈1.41,≈1.73)23.(10分)已知,点M为二次函数y=﹣(x﹣b)2+4b+1图象的顶点,直线y=mx+5分别交x轴正半轴,y轴于点A,B.(1)判断顶点M是否在直线y=4x+1上,并说明理由.(2)如图1,若二次函数图象也经过点A,B,且mx+5>﹣(x﹣b)2+4b+1,根据图象,写出x的取值范围.(3)如图2,点A坐标为(5,0),点M在△AOB内,若点C(,y1),D(,y2)都在二次函数图象上,试比较y1与y2的大小.24.(12分)我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.(1)概念理解:如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.(2)问题探究:如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求的值.(3)应用拓展:如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.2018年浙江省舟山市中考数学试卷参考答案与试题解析一、选择题(本题有10小题,每题3分,共30分。
2018年浙江省舟山市数学中考试卷含答案解析(Word版)

浙江省舟山市2018年中考数学试卷
、选择题
1•下列几何体中,俯视图为三角形的是()
2.2018年5月25日,中国探月工程的桥号”中继星成功运行于地月拉格朗日
地球约1500000km .数1500000用科学记数法表示为()
5 6 7
A. 15 X10
B. 1.5 10
C. 0.15 10
3.2018年1-4月我国新能源乘用车的月销量情况如图所示,则下列说法错误的是(
)
A. 1月份销量为2.2万辆
C. 4月份销量比3月份增加了1万辆
B.从2月到3月的月销量增长最快
D. 1 —4月新能源乘用车销量逐月增
加
4.不等式1-x的解在数轴上表示正确的是(
B.
汕卅年|7月粥能廉幺用车
L2点,它距离
D. 1.5 05
C.
B.
A.
(I
D.
5.将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去。
2018年浙江省舟山市中考数学试卷及参考答案解析
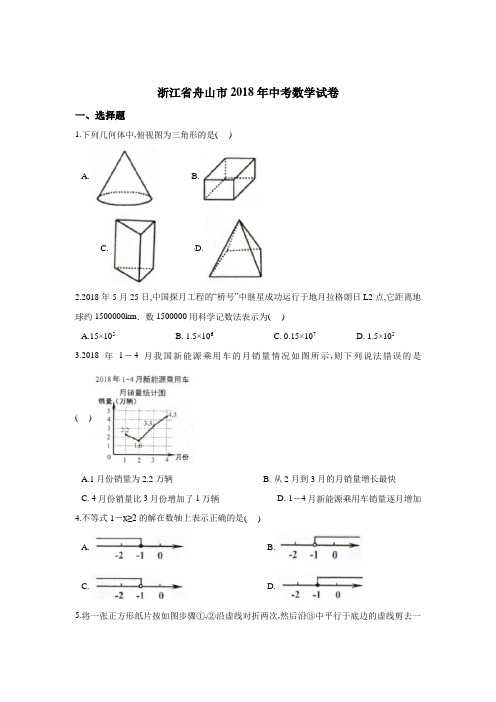
浙江省舟山市2018年中考数学试卷一、选择题1.下列几何体中,俯视图为三角形的是( )A. B.C. D.2.2018年5月25日,中国探月工程的“桥号”中继星成功运行于地月拉格朗日L2点,它距离地球约1500000km.数1500000用科学记数法表示为( )A.15×105B. 1.5×106C. 0.15×107D. 1.5×1053.2018年1-4月我国新能源乘用车的月销量情况如图所示,则下列说法错误的是( )A.1月份销量为2.2万辆B. 从2月到3月的月销量增长最快C. 4月份销量比3月份增加了1万辆D. 1-4月新能源乘用车销量逐月增加4.不等式1-x≥2的解在数轴上表示正确的是( )A. B.C. D.5.将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )A. B. C. D.6.用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是( )A. 点在圆内B. 点在圆上C. 点在圆心上D. 点在圆上或圆内7.欧几里得的《原本》记载,形如x2+ax=b2的方程的图解法是;画Rt△ABC,使∠ACB=90°,BC=,AC=b,再在斜边AB上截取BD=。
则该方程的一个正根是( )A.AC的长B.AD的长C.BC的长D.CD的长8.用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是( )A. B.C. D.9.如图,点C在反比例函数(x>0)的图象上,过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,则k的值为( )A. 1B. 2C. 3 D . 410.某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分,某小组比赛结束后,甲、乙,丙、丁四队分别获得第一,二,三,四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是( )A.甲B.甲与丁C.丙D.丙与丁二、填空题11.分解因式m2-3m=________。
(完整版)2018年浙江省舟山市中考数学试卷及答案解析,推荐文档

21.(8 分)小红帮弟弟荡秋千(如图 1),秋千离地面的高度 h(m)与摆动时
第 5 页(共 31 页)
间 t(s)之间的关系如图 2 所示. (1)根据函数的定义,请判断变量 h 是否为关于 t 的函数? (2)结合图象回答: ①当 t=0.7s 时,h 的值是多少?并说明它的实际意义. ②秋千摆动第一个来回需多少时间?
拉格朗日 L2 点,它距离地球约 1500000km,数 1500000 用科学记数法表示为(
)
A.15×105 B.1.5×106C.0.15×107 D.1.5×105
3.(3 分)2018 年 1~4 月我国新能源乘用车的月销量情况如图所示,则下列说
法错误的是( )
A.1 月份销量为 2.2 万辆 B.从 2 月到 3 月的月销量增长最快 C.4 月份销量比 3 月份增加了 1 万辆 D.1~4 月新能源乘用车销量逐月增加 4.(3 分)不等式 1﹣x≥2 的解在数轴上表示正确的是( )
三、解答题(本题有 8 小题,第 17~19 题每题 6 分,第 20,21 题每题 8 分,第 22,23 题每题 10 分,第 24 题 12 分,共 66 分) 17.(6 分)(1)计算:2( ﹣1)+|﹣3|﹣( ﹣1)0; (2)化简并求值( )• ,其中 a=1,b=2.
18.(6 分)用消元法解方程组
,173,185,169,187,176,180.
乙车间:
186,180,189,183,176,173,178,167,180,175,178,182,180,179
,185,180,184,182,180,183.
整理数据:
165.5~1 170.5~1 175.5~1 180.5~1 185.5~1 190.5~1
2018年舟山市中考数学试卷(解析版)

2018年舟山市中考数学试卷(解析版)一、选择题(本题有10小题,每题3分,共30分)1.(3分)下列几何体中,俯视图为三角形的是()A. B.C.D.2.(3分)2018年5月25日,中国探月工程的“鹊桥号”中继星成功运行于地月拉格朗日L2点,它距离地球约1500000km,数1500000用科学记数法表示为()A.15×105 B.1.5×106C.0.15×107D.1.5×1053.(3分)2018年1~4月我国新能源乘用车的月销量情况如图所示,则下列说法错误的是()A.1月份销量为2.2万辆B.从2月到3月的月销量增长最快C.4月份销量比3月份增加了1万辆D.1~4月新能源乘用车销量逐月增加4.(3分)不等式1﹣x≥2的解在数轴上表示正确的是()A.B.C.D.5.(3分)将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是()A.B.C. D.6.(3分)用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是()A.点在圆内B.点在圆上C.点在圆心上D.点在圆上或圆内7.(3分)欧几里得的《原本》记载,形如x2+ax=b2的方程的图解法是:画Rt△ABC,使∠ACB=90°,BC=,AC=b,再在斜边AB上截取BD=.则该方程的一个正根是()A.AC的长 B.AD的长 C.BC的长D.CD的长8.(3分)用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是()A. B.C.D.9.(3分)如图,点C在反比例函数y=(x>0)的图象上,过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,则k的值为()A.1 B.2 C.3 D.410.(3分)某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分,某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是()A.甲B.甲与丁C.丙D.丙与丁二、填空题(本题有6小题,每题4分,共24分)11.(4分)分解因式:m2﹣3m=.12.(4分)如图,直线l1∥l2∥l3,直线AC交l1,l2,l3于点A,B,C;直线DF交l1,l2,l3于点D,E,F,已知=,则=.13.(4分)小明和小红玩抛硬币游戏,连续抛两次,小明说:“如果两次都是正面,那么你赢;如果两次是一正一反,则我嬴.”小红赢的概率是,据此判断该游戏(填“公平”或“不公平”).14.(4分)如图,量角器的0度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10cm,点D在量角器上的读数为60°,则该直尺的宽度为cm.15.(4分)甲、乙两个机器人检测零件,甲比乙每小时多检测20个,甲检测300个比乙检测200个所用的时间少10%,若设甲每小时检测x个,则根据题意,可列出方程:.16.(4分)如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是.三、解答题(本题有8小题,第17~19题每题6分,第20,21题每题8分,第22,23题每题10分,第24题12分,共66分)17.(6分)(1)计算:2(﹣1)+|﹣3|﹣(﹣1)0;(2)化简并求值()•,其中a=1,b=2.18.(6分)用消元法解方程组时,两位同学的解法如下:解法一:由①﹣②,得3x=3.解法二:由②得,3x+(x﹣3y)=2,③把①代入③,得3x+5=2.(1)反思:上述两个解题过程中有无计算错误?若有误,请在错误处打“ד.(2)请选择一种你喜欢的方法,完成解答.19.(6分)已知:在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为点E,F,且DE=DF.求证:△ABC是等边三角形.20.(8分)某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为176mm~185mm的产品为合格),随机各抽取了20个样品进行检测,过程如下:收集数据(单位:mm)甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.整理数据:165.5~170.5170.5~175.5175.5~180.5180.5~185.5185.5~190.5190.5~195.5甲车间245621乙车间12a b20分析数据:车间平均数众数中位数方差甲车间180********.1乙车间180********.6应用数据:(1)计算甲车间样品的合格率.(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.21.(8分)小红帮弟弟荡秋千(如图1),秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图2所示.(1)根据函数的定义,请判断变量h是否为关于t的函数?(2)结合图象回答:①当t=0.7s时,h的值是多少?并说明它的实际意义.②秋千摆动第一个来回需多少时间?22.(10分)如图1,滑动调节式遮阳伞的立柱AC垂直于地面AB,P为立柱上的滑动调节点,伞体的截面示意图为△PDE,F为PD的中点,AC=2.8m,PD=2m,CF=1m,∠DPE=20°,当点P 位于初始位置P0时,点D与C重合(图2).根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳.(1)上午10:00时,太阳光线与地面的夹角为65°(图3),为使遮阳效果最佳,点P需从P0上调多少距离?(结果精确到0.1m)(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点P在(1)的基础上还需上调多少距离?(结果精确到0.1m)(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,≈1.41,≈1.73)23.(10分)已知,点M为二次函数y=﹣(x﹣b)2+4b+1图象的顶点,直线y=mx+5分别交x 轴正半轴,y轴于点A,B.(1)判断顶点M是否在直线y=4x+1上,并说明理由.(2)如图1,若二次函数图象也经过点A,B,且mx+5>﹣(x﹣b)2+4b+1,根据图象,写出x的取值范围.(3)如图2,点A坐标为(5,0),点M在△AOB内,若点C(,y1),D(,y2)都在二次函数图象上,试比较y1与y2的大小.24.(12分)我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.(1)概念理解:如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.(2)问题探究:如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求的值.(3)应用拓展:如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C 所在直线交l2于点D.求CD的值.答案与解析一、选择题(本题有10小题,每题3分,共30分)1.【解答】解:A、俯视图是圆,故A不符合题意;B、俯视图是矩形,故B不符合题意;C、俯视图是三角形,故C符合题意;D、俯视图是四边形,故D不符合题意;故选:C.2.【解答】解:1500000=1.5×106,故选:B.3.【解答】解:由图可得,1月份销量为2.2万辆,故选项A正确,从2月到3月的月销量增长最快,故选项B正确,4月份销量比3月份增加了4.3﹣3.3=1万辆,故选项C正确,1~2月新能源乘用车销量减少,2~4月新能源乘用车销量逐月增加,故选项D错误,故选:D.4.【解答】解:不等式1﹣x≥2,解得:x≤﹣1,表示在数轴上,如图所示:故选:A.5.【解答】解:由于得到的图形的中间是正方形,且顶点在原来的正方形的对角线上,故选:A.6.【解答】解:反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是:点在圆上或圆内.故选:D.7.【解答】解:欧几里得的《原本》记载,形如x2+ax=b2的方程的图解法是:画Rt△ABC,使∠ACB=90°,BC=,AC=b,再在斜边AB上截取BD=.则该方程的一个正根是AD的长,故选:B.8.【解答】解:A、作图根据由作图可知,AC⊥BD,且平分BD,即对角线平分且垂直的四边形是菱形,正确;B、由作图可知AB=BC,AD=AB,即四边相等的四边形是菱形,正确;C、由作图可知AB=DC,AD=BC,只能得出ABCD是平行四边形,错误;D、由作图可知对角线AC平分对角,可以得出是菱形,正确;故选:C.9.【解答】解:设点A的坐标为(a,0),∵过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,∴点C(﹣a,),∴点B的坐标为(0,),∴=1,解得,k=4,故选:D.10.【解答】解:∵甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,∴甲得分为7分,2胜1平,乙得分5分,1胜2平,丙得分3分,1胜0平,丁得分1分,0胜1平,∵甲、乙都没有输球,∴甲一定与乙平,∵丙得分3分,1胜0平,乙得分5分,1胜2平,∴与乙打平的球队是甲与丁.故选:B.二、填空题(本题有6小题,每题4分,共24分)11.【解答】解:m2﹣3m=m(m﹣3).故答案为:m(m﹣3).12.【解答】解:∵=,∴=2,∵l1∥l2∥l3,∴==2,故答案为:2.【解答】解:所有可能出现的结果如下表所示:正反正(正,正)(正,反)反(反,正)(反,反)因为抛两枚硬币,所有机会均等的结果为:正正,正反,反正,反反,所以出现两个正面的概率为,一正一反的概率为=,因为二者概率不等,所以游戏不公平.故答案为:,不公平.14.【解答】解:连接OC,∵直尺一边与量角器相切于点C,∴OC⊥AD,∵AD=10,∠DOB=60°,∴∠DAO=30°,∴OE=,OA=,∴CE=OC﹣OE=OA﹣OE=,故答案为:15.【解答】解:设设甲每小时检测x个,则乙每小时检测(x﹣20)个,根据题意得,=(1﹣10%),故答案为=×(1﹣10%).16.【解答】解:∵△EFP是直角三角形,且点P在矩形ABCD的边上,∴P是以EF为直径的圆O与矩形ABCD的交点,①当AF=0时,如图1,此时点P有两个,一个与D重合,一个交在边AB上;②当⊙O与AD相切时,设与AD边的切点为P,如图2,此时△EFP是直角三角形,点P只有一个,当⊙O与BC相切时,如图4,连接OP,此时构成三个直角三角形,则OP⊥BC,设AF=x,则BF=P1C=4﹣x,EP1=x﹣1,∵OP∥EC,OE=OF,∴OG=EP1=,∴⊙O的半径为:OF=OP=,在Rt△OGF中,由勾股定理得:OF2=OG2+GF2,∴,解得:x=,∴当1<AF<时,这样的直角三角形恰好有两个,③当AF=4,即F与B重合时,这样的直角三角形恰好有两个,如图5,综上所述,则AF的值是:0或1<AF或4.故答案为:0或1<AF或4.三、解答题(本题有8小题,第17~19题每题6分,第20,21题每题8分,第22,23题每题10分,第24题12分,共66分)17.【解答】解:(1)原式=4﹣2+3﹣1=4;(2)原式=•=a﹣b;当a=1,b=2时,原式=1﹣2=﹣1.18.【解答】解:(1)解法一中的解题过程有错误,由①﹣②,得3x=3“×”,应为由①﹣②,得﹣3x=3;(2)由①﹣②,得﹣3x=3,解得x=﹣1,把x=﹣1代入①,得﹣1﹣3y=5,解得y=﹣2.故原方程组的解是.19.【解答】证明:∵DE⊥AB,DF⊥BC,垂足分别为点E,F,∴∠AED=∠CFD=90°,∵D为AC的中点,∴AD=DC,在Rt△ADE和Rt△CDF中,,∴Rt△ADE≌Rt△CDF,∴∠A=∠C,∴BA=BC,∵AB=AC,∴AB=BC=AC,∴△ABC是等边三角形.20.【解答】解:(1)甲车间样品的合格率为:×100%=55%;(2)∵乙车间样品的合格产品数为:20﹣(1+2+2)=15(个),∴乙车间样品的合格率为:×100%=75%,∴乙车间的合格产品数为:1000×75%=750(个);(3)①乙车间合格率比甲车间高,所以乙车间生产的新产品更好;②甲、乙平均数相等,且均在合格范围内,而乙的方差小于甲的方差,说明乙比较稳定,所以乙车间生产的新产品更好.21.【解答】解:(1)由图象可知,对于每一个摆动时间t,h都有唯一确定的值与其对应,∴变量h是关于t的函数;(2)①由函数图象可知,当t=0.7s时,h=0.5m,它的实际意义是秋千摆动0.7s时,离地面的高度是0.5m;②由图象可知,秋千摆动第一个来回需2.8s.22.【解答】解:(1)如图2中,当P位于初始位置时,CP0=2m,如图3中,上午10:00时,太阳光线与地面的夹角为65°,上调的距离为P0P1.∵∠1=90°,∠CAB=90°,∠ABE=65°,∴∠AP1E=115°,∴∠CP1E=65°,∵∠DP1E=20°,∴∠CP1F=45°,∵CF=P1F=1m,∴∠C=∠CP1F=45°,∴△CP1F是等腰直角三角形,∴P1C=m,∴P0P1=CP0﹣P1C=2﹣≈0.6m,即为使遮阳效果最佳,点P需从P0上调0.6m.(2)如图4中,中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点P调到P2处.∵P2E∥AB,∴∠CP2E=∠CAB=90°,∵∠DP2E=20°,∴∠CP2F=70°,作FG⊥AC于G,则CP2=2CG=1×cos70°≈0.68m,∴P1P2=CP1﹣CP2=﹣0.68≈0.7m,即点P在(1)的基础上还需上调0.7m.23.【解答】解:(1)点M为二次函数y=﹣(x﹣b)2+4b+1图象的顶点,∴M的坐标是(b,4b+1),把x=b代入y=4x+1,得y=4b+1,∴点M在直线y=4x+1上;(2)如图1,直线y=mx+5交y轴于点B,∴B点坐标为(0,5)又B在抛物线上,∴5=﹣(0﹣b)2+4b+1=5,解得b=2,二次函数的解析是为y=﹣(x﹣2)2+9,当y=0时,﹣(x﹣2)2+9=0,解得x1=5,x2=﹣1,∴A(5,0).由图象,得当mx+5>﹣(x﹣b)2+4b+1时,x的取值范围是x<0或x>5;(3)如图2,∵直线y=4x+1与直线AB交于点E,与y轴交于F,A(5,0),B(0,5)得直线AB的解析式为y=﹣x+5,联立EF,AB得方程组,解得,∴点E(,),F(0,1).点M在△AOB内,1<4b+1<∴0<b<.当点C,D关于抛物线的对称轴对称时,b﹣=﹣b,∴b=,且二次函数图象开口向下,顶点M在直线y=4x+1上,综上:①当0<b<时,y1>y2,②当b=时,y1=y2,③当<b<时,y1<y2.24.【解答】解:(1)△ABC是“等高底”三角形;理由:如图1,过A作AD⊥BC于D,则△ADC是直角三角形,∠ADC=90°,∵∠ACB=30°,AC=6,∴AD=AC=3,∴AD=BC=3,即△ABC是“等高底”三角形;(2)如图2,∵△ABC是“等高底”三角形,BC是“等底”,∴AD=BC,∵△ABC关于BC所在直线的对称图形是△A'BC,∴∠ADC=90°,∵点B是△AA′C的重心,∴BC=2BD,设BD=x,则AD=BC=2x,CD=3x,由勾股定理得AC=x,∴==;(3)①当AB=BC时,Ⅰ.如图3,作AE⊥BC于E,DF⊥AC于F,∵“等高底”△ABC的“等底”为BC,l1∥l2,l1与l2之间的距离为2,AB=BC,∴BC=AE=2,AB=2,∴BE=2,即EC=4,∴AC=2,∵△ABC绕点C按顺时针方向旋转45°得到△A'B'C,∴∠DCF=45°,设DF=CF=x,∵l1∥l2,∴∠ACE=∠DAF,∴==,即AF=2x,∴AC=3x=2,∴x=,CD=x=.Ⅱ.如图4,此时△ABC等腰直角三角形,∵△ABC绕点C按顺时针方向旋转45°得到△A'B'C,∴△ACD是等腰直角三角形,∴CD=AC=2.②当AC=BC时,Ⅰ.如图5,此时△ABC是等腰直角三角形,∵△ABC绕点C按顺时针方向旋转45°得到△A'B'C,∴A'C⊥l1,∴CD=AB=BC=2;Ⅱ.如图6,作AE⊥BC于E,则AE=BC,∴AC=BC=AE,∴∠ACE=45°,∴△ABC绕点C按顺时针方向旋转45°,得到△A'B'C时,点A'在直线l1上,∴A'C∥l2,即直线A'C与l2无交点,综上所述,CD的值为,2,2.。
浙江省舟山市2018年中考数学试题含答案

浙江省舟山市2018年中考数学试题卷Ⅰ(选择题)一、选择题(本题有10小题,每题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选,均不得分)1.下列几何体中,俯视图...为三角形的是( )A .B .C .D .2.2018年5月25日,中国探月工程的“鹊桥号”中继星成功运行于地月拉格朗日2L 点,它距离地球约1500000km .数1500000用科学记数法表示为( )A .51510⨯B .61.510⨯C .70.1510⨯D .51.510⨯3.2018年1~4月我国新能源乘用车的月销售情况如图所示,则下列说法错误..的是( )A .1月份销售为2.2万辆B .从2月到3月的月销售增长最快C .4月份销售比3月份增加了1万辆D .1~4月新能源乘用车销售逐月增加4.不等式12x -≥的解在数轴上表示正确的是( )A .B .C .D .5.将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是( )A .B .C .D .6.用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是( ) A .点在圆内 B .点在圆上 C .点在圆心上 D .点在圆上或圆内7.欧几里得的《原本》记载,形如22x ax b +=的方程的图解法是:画Rt ABC ∆,使90ACB ∠=,2a BC =,AC b =,再在斜边AB 上截取2aBD =.则该方程的一个正根是( )A .AC 的长B .AD 的长C .BC 的长D .CD 的长 8.用尺规在一个平行四边形内作菱形ABCD ,下列作法中错误..的是( )A .B .C .D . 9.如图,点C 在反比例函数(0)ky x x=>的图象上,过点C 的直线与x 轴,y 轴分别交于点A ,B ,且AB BC =,AOB ∆的面积为1,则k 的值为( )A .1B .2C .3D .410.某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分.某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是( ) A .甲 B .甲与丁 C .丙 D .丙与丁卷Ⅱ(非选择题)二、填空题(本题有6小题,每题4分,共24分)11.分解因式:23m m -= .12.如图,直线123////l l l ,直线AC 交1l ,2l ,3l 于点A ,B ,C ;直线DF 交1l ,2l ,3l 于点D ,E ,F .已知13AB AC =,则EFDE= .13.小明和小红玩抛硬币游戏,连续抛两次.小明说:“如果两次都是正面,那么你赢;如果两次是一正一反,则我赢.”小红赢的概率是 ,据此判断该游戏 (填“公平”或“不公平”).14.如图,量角器的0度刻度线为AB ,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C ,直尺另一边交量角器于点A ,D ,量得10AD cm =,点D 在量角器上的读数为60,则该直尺的宽度为____________cm .15.甲、乙两个机器人检测零件,甲比乙每小时多检测20个,甲检测300个比乙检测200个所用的时间少10%,若设甲每小时检测x 个,则根据题意,可列出方程: . 16.如图,在矩形ABCD 中,4AB =,2AD =,点E 在CD 上,1DE =,点F 在边AB 上一动点,以EF 为斜边作Rt EFP ∆.若点P 在矩形ABCD 的边上,且这样的直角三角形恰好有两个,则AF 的值是 .三、解答题(本题有8小题,第17~19题每题6分,第20,21题每题8分,第22,23题每题10分,第24题12分,共66分)17.(1)计算:01)31)+--; (2)化简并求值:a b abb a a b ⎛⎫-⋅⎪+⎝⎭,其中1a =,2b =. 18.用消元法解方程组35,43 2.x y x y -=⎧⎨-=⎩①②时,两位同学的解法如下:(1)反思:上述两个解题过程中有无计算错误?若有误,请在错误处打“×”. (2)请选择一种你喜欢的方法,完成解答.19.如图,等边AEF ∆的顶点E ,F 在矩形ABCD 的边BC ,CD 上,且45CEF ∠=.求证:矩形ABCD 是正方形.20.某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为176185mm mm 的产品为合格),随机各抽取了20个样品进行检测,过程如下:收集数据(单位:mm ):甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183. 整理数据:170.5170.5175.5175.5180.5180.5185.5185.5190.5190.5分析数据: 应用数据:别(1)计算甲车间样品的合格率.(2)估计乙车间生产的1000个该款新产品中合格产品有多少个? (3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.21.小红帮弟弟荡秋千(如图1),秋千离地面的高度()h m 与摆动时间()t s 之间的关系如图2所示.(1)根据函数的定义,请判断变量h 是否为关于t 的函数? (2)结合图象回答:①当0.7t s =时,h 的值是多少?并说明它的实际意义. ②秋千摆动第一个来回需多少时间?22.如图1,滑动调节式遮阳伞的立柱AC 垂直于地面AB ,P 为立柱上的滑动调节点,伞体的截面示意图为PDE ∆,F 为PD 中点, 2.8AC m =,2PD m =,1CF m =,20DPE ∠=.当点P 位于初始位置0P 时,点D 与C 重合(图2).根据生活经验,当太阳光线与PE 垂直时,遮阳效果最佳.(1)上午10:00时,太阳光线与地面的夹角为65(图3),为使遮阳效果最佳,点P 需从0P 上调多少距离?(结果精确到0.1m )(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点P 在(1)的基础上还需上调多少距离?(结果精确到0.1m )(参考数据:sin 700.94≈,cos700.34≈,tan 70 2.75≈ 1.41≈ 1.73≈) 23.已知,点M 为二次函数2()41y x b b =--++图象的顶点,直线5y mx =+分别交x 轴正半轴,y 轴于点A ,B .(1)判断顶点M 是否在直线41y x =+上,并说明理由.(2)如图1,若二次函数图象也经过点A ,B ,且25()41m x x b b +>--++,根据图象,写出x 的取值范围.(3)如图2,点A 坐标为(5,0),点M 在AOB ∆内,若点11(,)4C y ,23(,)4D y 都在二次函数图象上,试比较1y 与2y 的大小.24.已知,ABC ∆中,B C ∠=∠,P 是BC 边上一点,作CPE BPF ∠=∠,分别交边AC ,AB 于点E ,F .(1)若CPE C ∠=∠(如图1),求证:PE PF AB +=.(2)若CPE C ∠≠∠,过点B 作CBD CPE ∠=∠,交CA (或CA 的延长线)于点D .试猜想:线段PE ,PF 和BD 之间的数量关系,并就CPE C ∠>∠情形(如图2)说明理由.(3)若点F 与A 重合(如图3),27C ∠=,且PA AE =.①求CPE ∠的度数;②设PB a =,PA b =,AB c =,试证明:22a cb c-=.数学参考答案一、选择题1-5: CBDAA 6-10: DBCDB二、填空题11. (3)m m - 12. 2 13. 14;不公平300200(110%)20x x =⨯-- 16. 0或1113AF <<或4 三、解答题17.(1)原式231=+-=(2)原式22a b aba b ab a b-=⋅=-+. 当1a =,2b =时,原式121=-=-. 18.(1)解法一中的计算有误(标记略). (2)由①-②,得33x -=,解得1x =-, 把1x =-代入①,得135y --=,解得2y =-,所以原方程组的解是12x y =-⎧⎨=-⎩.18.用消元法解方程组35,43 2.x y x y -=⎧⎨-=⎩①②时,两位同学的解法如下:19.(方法一)∵四边形ABCD 是矩形, ∴90B D C ∠=∠=∠=, ∵AEF ∆是等边三角形,∴AE AF =,60AEF AFE ∠=∠=,又45CEF ∠=,∴45CFE CEF ∠=∠=,∴180456075AFD AEB ∠=∠=--=, ∴()AEB AFD AAS ∆≅∆, ∴AB AD =,∴矩形ABCD 是正方形.(方法二)(连结AC ,利用轴对称证明,表述正确也可)20.(1)甲车间样品的合格率为56100%55%20+⨯=. (2)∵乙车间样品的合格产品数为20(122)15-++=(个), ∴乙车间样品的合格率为15100%75%20⨯=. ∴乙车间的合格产品数为100075%750⨯=(个).(3)①从样品合格率看,乙车间合格率比甲车间高,所以乙车间生产的新产品更好. ②从样品的方差看,甲、乙平均数相等,且均在合格范围内,而乙的方差小于甲的方差,说明乙比甲稳定,所以乙车间生产的新产品更好.21.(1)∵对于每一个摆动时间t ,都有一个唯一的h 的值与其对应, ∴变量h 是关于t 的函数.(2)①0.5h m =,它的实际意义是秋千摆动0.7s 时,离地面的高度为0.5m . ②2.8s .22.(1)如图2,当点P 位于初始位置0P 时,02CPm =. 如图3,10:00时,太阳光线与地面的夹角为65,点P 上调至1P 处,190∠=,90CAB ∠=,∴1115APE ∠=, ∴165CPE ∠=. ∵120DPE ∠=,∴145CPF ∠=. ∵11CF PF m ==,∴145C CPF ∠=∠=,∴1CPF ∆为等腰直角三角形,∴1CP =,∴010120.6P P CP CP m =-=≈,即点P 需从0P 上调0.6m .(2)如图4,中午12:00时,太阳光线与PE ,地面都垂直,点P 上调至2P 处, ∴2//P E AB .∵90CAB ∠=,∴290CP E ∠=. ∵220DP E ∠=,∴22270CP F CP E DP E ∠=∠-∠=.∵21CF P F m ==,得2CP F ∆为等腰三角形, ∴270C CP F ∠=∠=.过点F 作2FG CP ⊥于点G , ∴22cos7010.340.34CP P F m =⋅=⨯=, ∴2220.68CP GP m ==,∴12120.680.7PP CP CP m =-≈,即点P 在(1)的基础上还需上调0.7m .23.(1)∵点M 坐标是(,41)b b +,∴把x b =代入41y x =+,得41y b =+,∴点M 在直线41y x =+上.(2)如图1,∵直线5y mx =+与y 轴交于点为B ,∴点B 坐标为(0,5). 又∵(0,5)B 在抛物线上,∴25(0)41b b =--++,解得2b =,∴二次函数的表达式为2(2)9y x =--+,∴当0y =时,得15x =,21x =-,∴(5,0)A .观察图象可得,当25()41mx x b b +>--++时, x 的取值范围为0x <或5x >.(3)如图2,∵直线41y x =+与直线AB 交于点E ,与y 轴交于点F , 而直线AB 表达式为5y x =-+,解方程组415y x y x =+⎧⎨=-+⎩,得45215x y ⎧=⎪⎪⎨⎪=⎪⎩.∴点421(,)55E ,(0,1)F . ∵点M 在AOB ∆内, ∴405b <<. 当点C ,D 关于抛物线对称轴(直线x b =)对称时, 1344b b -=-,∴12b =. 且二次函数图象的开口向下,顶点M 在直线41y x =+上, 综上:①当102b <<时,12y y >; ②当12b =时,12y y =; ③当1425b <<时,12y y <.24.(1)∵B C ∠=∠,CPE BPF ∠=∠,CPE C ∠=∠, ∴B BPF CPE ∠=∠=∠,BPF C ∠=∠,∴PF BF =,//PE AF ,//PF AE ,∴PE AF =.∴PE PF AF BF AB +=+=.(2)猜想:BD PE PF =+,理由如下:过点B 作DC 的平行线交EP 的延长线于点G ,则ABC C CBG ∠=∠=∠,∵CPE BPF ∠=∠,∴BPF CPE BPG ∠=∠=∠,又BP BP =,∴()FBP GBP ASA ∆≅∆,∴PF PG =.∵CBD CPE ∠=∠,∴//PE BD ,∴四边形BGED 是平行四边形,∴BD EG PG PE PE PF ==+=+.(3)①设CPE BPF x ∠=∠=,∵27C ∠=,PA AE =,∴27APE PEA C CPE x ∠=∠=∠+∠=+,又180BPA APE CPE ∠+∠+∠=,即27180x x x +++=, ∴51x =,即51CPE ∠=.②延长BA 至M ,使AM AP =,连结MP ,∵27C ∠=,51BPA CPE ∠=∠=.∴180BAP B BPA ∠=-∠-∠102M MPA ==∠+∠, ∵AM AP =,∴1512M MPA BAP ∠=∠=∠=, ∴M BPA ∠=∠,而B B ∠=∠,∴ABPPBM ∆∆. ∴BP BM AB BP=, ∴2BP AB BM =⋅.∵PB a =,PA AM b ==,AB c =, ∴2()a c b c =+, ∴22a cb c-=.。
浙江省舟山市2018年中考数学试卷含答案

浙江省舟山市2018年中考数学试卷含答案一、选择题1.下列几何体中,俯视图为三角形的是()A. B.C. D.2.2018年5月25日,中国探月工程的“桥号”中继星成功运行于地月拉格朗日L2点,它距离地球约1500000km.数1500000用科学记数法表示为()A. 15×105B. 1.5×106C. 0.15×107D. 1.5×1053.2018年1-4月我国新能源乘用车的月销量情况如图所示,则下列说法错误的是()A. 1月份销量为2.2万辆B. 从2月到3月的月销量增长最快C. 4月份销量比3月份增加了1万辆D. 1-4月新能源乘用车销量逐月增加4.不等式1-x≥2的解在数轴上表示正确的是()A. B.C. D.5.将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是()A. B. C. D.6.用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是()A. 点在圆内B. 点在圆上C. 点在圆心上D. 点在圆上或圆内7.欧几里得的《原本》记载,形如x2+ax=b2的方程的图解法是;画Rt△ABC,使∠ACB=90°,BC= ,AC=b,再在斜边AB上截取BD= 。
则该方程的一个正根是()A.AC的长B.AD的长C.BC的长D.CD的长8.用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是()A. B.C. D.9.如图,点C在反比例函数(x>0)的图象上,过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,则k的值为()A. 1B. 2C. 3D. 410.某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分,某小组比赛结束后,甲、乙,丙、丁四队分别获得第一,二,三,四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是()A.甲B.甲与丁C.丙D.丙与丁二、填空题11.分解因式m2-3m=________。
2018浙江舟山中考数学解析

2018年浙江省初中毕业生学业考试(舟山卷)数学试题卷卷Ⅰ(选择题)一、选择题(本题有10小题,每题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选,均不得分)1.(2018浙江舟山,1,3)下列几何体中,俯视图...为三角形的是()【答案】C 【解析】A选项的俯视图是圆,B选项的俯视图是矩形,C选项的俯视图是三角形,D选项的俯视图是四边形,故正确答案是C.2.(2018浙江舟山,2,3)2018年5月25日,中国探月工程的“鹊桥号”中继星成功运行于地月拉格朗日L2点,它距离地球约1500000km.数1500000用科学记数法表示为()A.15×105 B.1.5×106 C.0.15×107 D.1.5×105【答案】B 【解析】1500000=1.5×106,故正确答案为B.3.(2018浙江舟山,3,3)2018年1~4月我国新能源乘用车的月销量情况如图所示,则下列说法错误..的是()A.1月份销量为2.2万辆. B.从2月到3月的月销量增长最快.C.1~4月份销量比3月份增加了1万辆. D.1~4月新能源乘用车销量逐月增加.2018年1-4月新能源乘用车月销售量统计图【答案】D 【解析】从统计图中看出1月份的销量为2.2万辆,故A 正确;从1月到2月销量减少0.6万辆,从2月到3月销量增加1.7万辆,从3月到4月销量增加1万辆,故B 、C 都正确;1月到2月的销量是减少的,故D 错误;故正确答案为D .4.(2018浙江舟山,4,3) 不等式21≥-x 的解在数轴上表示正确的是()【答案】A 【解析】先解不等式1-x≥2,得x≤﹣1,故正确答案为A .5.(2018浙江舟山,5,3) 将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是()【答案】A 【解析】把剪后的图形展开,本质是作出它的轴对称图形.故正确答案为A .6.(2018浙江舟山,6,3) 用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是()A .点在圆内.B .点在圆上.C .点在圆心上.D .点在圆上或圆内.【答案】D 【解析】点和圆的位置关系有:点在圆上,点在圆内,点在圆外三种,故“点在圆外”不成立,即“点在圆内或圆上”,故正确答案为D7.(2018浙江舟山,7,3) 欧几里得的《原本》记载.形如22b ax x =+的方程的图解法是:画Rt △ABC ,使∠ACB =90°,2a BC =,AC =b ,再在斜边AB 上截取2aBD =.则该方程的一个正根是()A .AC 的长B .AD 的长C .BC 的长D .CD 的长 【答案】B 【解析】利用配方法解方程x 2+ax =b 2,得到222()24aa xb +=+,解得:2a x=,根据勾股定理知道AB =BD =2a,所以根据图形知道AD =AB -BD ,即AD 的长是方程的一个正根,故正确答案为B .8.(2018浙江舟山,8,3)用尺规在一个平行四边形内作菱形ABCD ,下列作法中错误的是()【答案】C 【解析】根据尺规作图以及菱形的判定方法. 9.(2018浙江舟山,9,3) 如图,点C 在反比例函数)0(>=x xky 的图象上,过点C 的直线与x 轴,y 轴分别交于点A 、B ,且AB =BC ,△AOB 的面积为1.则k 的值为()A .1B . 2C .3D . 4【答案】D 【解析】过点C 作CD ⊥x 轴于点D ,连接OC .由CD ∥OB 值,△ABO ∽△ACD ,∴AB AOAC AD=,∵AB =BC ,∴AO =OD ,∵AB =BC ,故S △ABO =S △BOC =1,而AO =OD ,故S △AOC =S △COD =2,根据S △COD =2k,所以k =4,故正确答案为D .10.(2018浙江舟山,10,3) 某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分.某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是() A .甲. B .甲与丁. C .丙. D .丙与丁.【答案】B 【解析】因为一共6场比赛,则四队的分数加起来不超过18分,因为四个队的分数是四个连续的奇数,所以四队分数只能为:1分,3分,5分,7分.故甲队应该2胜1平,乙队1胜2平,丁队1平2负,丙对1胜2负(三平不可能),故正确答案为B .卷Ⅱ(非选择题)二、填空题(本题有6小题,毎题4分.共24分)11.(2018浙江舟山,11,4) 分解因式:=-m m 32.【答案】m (m -3) 【解析】提取公因式得:m 2-3m =m (m -3) .12.(2018浙江舟山,12,4) 如图.直线l 1∥l 2∥l 3.直线AC 交l 1,l 2,l 3于点A 、B 、C ;直线DF 交l 1,l 2,l 3于点D 、E 、F ,已知31=AC AB ,=DEEF. l3l 2l 1F ED CBA 【答案】2 【解析】∵13AB AC =,∴2BC AB =,∵l 1∥l 2∥l 3,∴2EF BCDE AB==.13.(2018浙江舟山,13,4) 小明和小红玩抛硬币游戏,连续抛两次.小明说:“如果两次都是正面、那么你赢;如果两次是一正一反.则我赢.”小红赢的概率是 .据此判断该游戏 .(填“公平”或“不公平”)【答案】14;不公平 【解析】2次抛硬币出现的可能的结果为:(正,正),(正,反),(反,正),(反,反),且每一个结果出现的可能性相同,故P (小红赢)=14,而P (小明赢)=12,所以游戏不公平.14.(2018浙江舟山,14,4) 如图,量角器的O 度刻度线为AB .将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C ,直尺另一边交量角器于点A 、D ,量得AD =10cm ,点D 在量角器上的读数为60°.则该直尺的宽度为 cm .B【解析】根据题意,抽象出数学图形 O根据题意可知:AD =10,∠AOD =120°,由OA =OD ,∴∠DAO =30°,设OE =x ,则OA =2x ,∵OE ⊥AD ,∴AE =DE =5,在Rt △AOE 中,x 2+52=(2x )2,解得:x CE =OE.15.(2018浙江舟山,15,4) 甲、乙两个机器人检测零件,甲比乙每小时多检测20个,甲检测300个比乙检测200个所用的时间少10%.若设甲每小时检测x 个.则根据题意,可列出方程: .【答案】300200(110%)20x x =⨯-- 【解析】本题的等量关系是甲检测300个的时间=乙检测200个所用的时间×(1-10%),甲检测300个零件所花时间为300x ,乙检测200个零件所花时间为20020x - ,故所列方程为300200(110%)20x x =⨯--. 16.(2018浙江舟山,16,4) 如图,在矩形ABCD 中,AB =4,AD =2,点E 在CD 上,DE =1,点F 是边AB 上一动点,以EF 为斜边作Rt △EFP .若点P 在矩形ABCD 的边上,且这样的直角三角形恰好有两个,则AF 的值是 .CDAF【答案】0或1113AF <<或4 【解析】显然当点F 与A 点和B 点重合时,符合题意. 当以EF 为直径的圆与CB 相切,此时存在三个这样的直角三角形,则EF =2OG ,ON =CG =1,设OG 为x ,由勾股定理OE 2=EN 2+ON 2,则x 2=(3-x )2+12,解得:x =53,则BF =13,所以AF =113 ,∴1113AF <<.G D A三、解答题(本题有8小题,第17~19题每题6分.第20,21题每题8分.第22,23题每题10分,第24题12分,共66分)友情提示:做解答题,别忘了写出必要的过程;作图(包括添加辅助线)最后必须用黑色字迹的签字笔或钢笔将线条描黑.17.(2018浙江舟山,17①,3) (1)计算:0)13(3)18(2---+-;【思路分析】3- ,01) ,再进行运算.【解答过程】原式=2+3-1=(2018浙江舟山,17②,3)(2)化简并求值:b a aba b b a +⋅⎪⎭⎫⎝⎛-,其中a=1,b =2; 【思路分析】先算括号,再算乘法.【解答过程】(2)原式=22a b aba b ab a b -⋅=-+;当a=1,b =2时,原式=1-2=-1;18.(2018浙江舟山,18,6) 用消元法解方程组3 5 43 2 x y x y -=⎧⎨-=⎩①②时,两位同学的解法如下:(1)反思:上述两个解题过程中有无计算错误?若有误,请在错误处打“⨯”. (2)请选择一种你喜欢的方法,完成解答.【思路分析】解法一中x -4x =﹣3x ,故解法一有错.【解答过程】(1)解法一中的计算有误(标记略) (2)由①-②,得-3x =3,解得x =﹣1,把x =﹣1代入①,得﹣1﹣3y =5,解得y =﹣2.所以原方程组的解是12x y =-⎧⎨=-⎩.19.(2018浙江舟山,19,6) 如图,等边△AEF 的顶点E ,F 在矩形ABCD 的边BC ,CD 上,且∠CEF =45°.求证:矩形ABCD 是正方形.E BC【思路分析】只要证明△ABE ≌△ADF 即可. 【解答过程】∵四边形ABCD 是矩形, ∴∠B =∠D =∠C =90°, ∵△AEF 是等边三角形,∴AE =AF ,∠AEF =∠AFE =60°, 又∠CEF =45°,∴∠CFE =∠CEF =45°, ∴∠AFD =∠AEB =180°-45°-60°=75°, ∴△ABE ≌△ADF(AAS), ∴AB =AD ,∴矩形ABCD 是正方形.20.(2018浙江舟山,20,8) 某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为176mm~185mm 的产品为合格).随机各抽取了20个祥品迸行检测.过程如下:解法二:由②,得3x +(x -3y )=2, ③ 把①代入③,得3x +5=2.收集数据(单位:mm):甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.应用数据:(1)计算甲车间样品的合格率.(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?(3)结合上述数据信息.请判断哪个车间生产的新产品更好.并说明理由.【思路分析】(1)根据合格产品的尺寸,甲20个样品中合格产品数为11个;(2)根据合格产品的尺寸,乙 20个样品中合格产品数为15个;(3)从平均数和方差来描述;【解答过程】(1)甲车间样品的合格率为56100%55% 20+⨯=.(2)∵乙车间样品的合格产品数为20-(1+2+2)=15(个),∴乙车间样品的合格率为15100%75% 20⨯=.∴乙车间的合格产品数为1000×75%=750(个).(3)①乙车间合格率比甲车间高,所以乙车间生产的新产品更好.②甲、乙平均数相等,且均在合格范围内,而乙的方差小于甲的方差,说明乙比甲稳定,所以乙车间生产的新产品更好.(其他理由,按合理程度分类分层给分.)21.(2018浙江舟山,21,8)小红帮弟弟荡秋千(如图1),秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图2所示.(1)根据函数的定义,请判断变量h是否为关于t的函数?(2)结合图象回答:①当t=0.7s时,h的值是多少?并说明它的实际意义.②秋千摆动第一个来回需多少时间?【思路分析】(1)根据函数的定义进行判断; (2)看图说话;【解答过程】(1)∵对于每一个摆动时间t ,都有一个唯一的h 的值与其对应, ∴变量h 是关于t 的函数.(2)①h =0.5m ,它的实际意义是秋千摆动0.7s 时,离地面的高度为0.5m . ②2.8s .22.(2018浙江舟山,22,10)如图1,滑动调节式遮阳伞的立柱AC 垂直于地面AB ,P 为立柱上的滑动调节点,伞体的截面示意图为△PDE ,F 为PD 中点,AC =2.8m ,PD =2m ,CF =1m ,∠DPE =20°.当点P 位于初始位置P 0时,点D 与C 重合(图2).根据生活经验,当太阳光线与PE 垂直时,遮阳效果最佳. (1)上午10:00时,太阳光线与地面的夹角为60°(图3),为使遮阳效果最佳,点P 需从P 0上调多少距离?(结果精确到0.1m )(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点P 在(1)的基础上还需上调多少距离?(结果精确到0.1m )(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.7523)EDPA CF BEC (D )P (P 0)A F B图1 图2太阳光线AB 太阳光线A图3 图4【思路分析】(1)已知CP 0,只要求出图3中的CP 长即可,故只需解△CPF ; (2)解出图4中的CP 的长,过点F 作FG ⊥CP ;【解答过程】(1)如图2,当点P 位于初始位置P 0时,CP 0=2m . 如图3,10∶ 00时,太阳光线与地面的夹角为65°,点P 上调至P 1处, ∠1=90°,∠CAB =90°,∴∠AP 1E =115°, ∴∠CP 1E =65°, ∵∠DP 1E =20°,∠CP 1F =45°, ∵CF =P 1F =1m, ∴∠C =∠CP 1F =45° ∴△CP 1F 为等腰直角三角形,∴CP 1m ,∴P 0P 1=CP 0-CP 1=2≈0.6m 即点需P 从P 0上调0.6m .(2)如图4,中午12 : 00时,太阳光线与PE ,地面都垂直,点P 上调至P 2处, ∴P 2E ∥AB ∵∠CAB =90°,∴∠CP 2E =90° ∵∠DP 2E =20°∴∠CP 2F =∠CP 2E -∠DP 2E =70°∵CF =P 2F =1m ,得△CP 2F 为等腰三角形, ∴∠C =∠CP 2F =70°过点F 作FG ⊥CP 2于点G ∴GP 2=P 2F·cos70°=1×0.34=0.34m∴CP 2=2GP 2=0.68m∴P 1P 2=CP 1-CP 20.68≈0.7m 即点P 在(1)的基础上还需上调0.7m .P AB太阳光线AB22题图2 22题图3太阳光线A22题图423.(2018浙江舟山,23,10)巳知,点M 为二次函数14)(2++--=b b x y 图象的顶点,直线5+=mx y 分别交x 轴,y 轴于点A 、B .(1)判断顶点M 是否在直线14+=x y 上,并说明理由.(2)如图1,若二次函数图象也经过点A 、B ,且14)(52++-->+b b x mx .根据图象,写出x 的取值范围.(3)如图2,点A 坐标为(5,0),点M 在△AOB 内,若点11(,)4C y ,23(,)4D y 都在二次函数图象上,试比较y 1与y 2的大小.【思路分析】(1)根据二次函数顶点式可以知道M (b ,4b +1),即x =b ,y =4b +1,消去b ,得y =4x +b ;(2)由题意知B (0,5),二次函数过点B ,代入解析式可求得b 的值,求得A 点坐标,再利用函数图象比较大小;(3)先通过点M 在△AOB 内得到b 的取值范围,也就是抛物线的对称轴,再根据抛物线的对称性和增减性解决y 1,y 2大小关系.【解答过程】(1)∵点M 坐标是(b ,4b +1), ∴把x =b 代入y =4x +1,得y =4b +1, ∴点M 在直线y =4x +1上.(2)如图1,∵直线y =mx +5与y 轴交于点B ,∴点B 坐标为(0,5). 又∵B(0,5)在抛物线上,∴5=﹣(0-b)2+4b +1,解得b =2, ∴二次函数的表达式为2(2)9y x =--+,∴当0=y 时,得x 1=5,x 2=﹣1.∴ A(5,0)观察图象可得,当25()41mx x b b +>--++时, x 的取值范围为x <0或x >5.(3)如图2,∵直线y =4x +1与直线AB 交于点E ,与y 轴交于点F , 而直线AB 表达式为y =﹣x +5,解方程组415y x y x =+⎧⎨=-+⎩,得45215x y ⎧=⎪⎪⎨⎪=⎪⎩. ∴点421(,)55E ,F (0,1).点M 在△AOB 内,∴405b <<.当点C 、D 关于抛物线对称轴(直线x =b )对称时,1344b b -=- ,∴12b = .且二次函数图象的开口向下,顶点M 在直线y =4x +1上,综上:①当102b <<时,y 1>y 2;②当12b =时,y 1=y 2;③当1425b <<时,y 1<y 223题图1 23题图224.(2018浙江舟山,24,12)已知,△ABC 中,∠B =∠C ,P 是BC 边上一点,作∠CPE =∠BPF ,分别交边AC ,AB 于点E ,F .CPCP图1图2CP图3(1)若∠CPE =∠C (如图1),求证:PE +PF =AB .(2)若∠CPE≠∠C ,过点B 作∠CBD =∠CPE ,交CA (或CA 的延长线)于点D .试猜想:线段PE ,PF 和BD 之间的数量关系,并就∠CPE >∠C 情形(如图2)说明理由. (3)若点F 与A 重合(如图3),∠C =27°,且PA =AE . ①求∠CPE 的度数;②设PB =a ,PA =b ,AB =c ,试证明:22a cb c-=.【思路分析】(1)等腰三角形的性质及平四的性质即可证明; (2)构造△BPF 的全等形及利用平四的性质;(3)构造△ABP的相似形.【解答过程】(1)∵∠B=∠C,∠CPE=∠BPF,∠CPE=∠C,∴∠B =∠BPF=∠CPE,∠BPF=∠C,∴PF=BF,PE∥AF,PF∥AE,∴PE=AF.∴PE+PF=AF+BF=AB.CP24题图1(2)猜想:BD=PE+PF,理由如下:过点B作DC的平行线交EP的延长线于点G,则∠ABC=∠C=∠CBG,∵∠CPE=∠BPF,∴∠BPF=∠CPE=∠BPG,又BP=BP,∴△FBP≌△GBP(ASA),∴PF=PG.∵∠CBD=∠CPE,∴PE∥BD,∴四边形BGED是平行四边形,∴BD=EG=PG+PE=PE+PF.C24题图2(3)①设∠CPE=∠BPF=x,∵∠C=27°,PA=AE,∴∠APE=∠PEA=∠C+∠CPE=27°+x,又∠BPA+∠APE+∠CPE=180°,即x+x+27°+x=180°,∴x=51°,即∠CPE=51°.②延长BA至M,使AM=AP,连结MP,∵∠C=27°,∠BPA=∠CPE=51°.∴∠BAP=180°-∠B-∠BPA=102°=∠M+∠MPA,∵AM=AP,∴∠M=∠MPA=12∠BAP=51°,∴∠M=∠BPA,而∠B=∠B,∴△ABP∽△PBM.∴BP BMAB BP=, ∴2BP AB BM =⋅.∵PB =a ,PA =AM =b ,AB =c , ∴2()a c b c =+,∴22a cb c-=.CP24题图3。
浙江省舟山市2018年数学中考试题及答案演示教学

组
165.别5 : 170.5 170.5 : 175.5 175.5 : 180.5 180.5 : 185.5 185.5 : 190.5 190.5 : 195.5
频
数
甲
车
2
4
5间乙Fra bibliotek车1
2
a
间
分析数据:
车间
平均数
众数
甲车间
180
185
乙车间
180
180
应用数据:
6
2
1
b
2
0
中位数
方差
180
43.1
的读数为 60o ,则该直尺的宽度为 ____________ cm .
15. 甲、乙两个机器人检测零件,甲比乙每小时多检测
20 个,甲检测 300 个比乙检测 200
个所用的时间少 10% ,若设甲每小时检测 x 个,则根据题意,可列出方程:
.
16. 如图,在矩形 ABCD 中, AB 4 , AD 2 ,点 E 在 CD 上, DE 1 ,点 F 在边 AB
(2)化简并求值: a b ab ,其中 a 1 , b 2 . b a ab
18. 用消元法解方程组
x 3y 5, ①
时,两位同学的解法如下:
4x 3y 2.②
解法一:
由① - ②,得 3x 3 .
解法二:由②,得 3x x 3y 2 ,③ 把①代入③,得 3x 5 2 .
(1)反思:上述两个解题过程中有无计算错误?若有误,请在错误处打“×”
180
22.6
只供学习与交流
此文档仅供收集于网络,如有侵权请联系网站删除
(1)计算甲车间样品的合格率 .
精品解析:2018年浙江省舟山市中考数学试题(原卷版)

数学浙江省舟山市2018中考数学试题一、选择题(本题有10小题,每题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选,均不得分)1. 下列几何体中,俯视图...为三角形的是()A. B. C. D.2. 2018年5月25日,中国探月工程的“鹊桥号”中继星成功运行于地月拉格朗日点,它距离地球约.数1500000用科学记数法表示为()A. B. C. D.3. 2018年1~4月我国新能源乘用车的月销售情况如图所示,则下列说法错误..的是()学&科&网...学&科&网...A. 1月份销售为2.2万辆B. 从2月到3月的月销售增长最快C. 4月份销售比3月份增加了1万辆D. 1~4月新能源乘用车销售逐月增加4. 不等式的解在数轴上表示正确的是()A. B.C. D.5. 将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是()A. B. C. D.6. 用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是()A. 点在圆内B. 点在圆上C. 点在圆心上D. 点在圆上或圆内7. 欧几里得的《原本》记载,形如的方程的图解法是:画,使,,,再在斜边上截取.则该方程的一个正根是()A. 的长B. 的长C. 的长D. 的长8. 用尺规在一个平行四边形内作菱形,下列作法中错误..的是()A. B. C. D.9. 如图,点在反比例函数的图象上,过点的直线与轴,轴分别交于点,,且,的面积为1,则的值为()A. 1B. 2C. 3D. 410. 某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分.某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是()A. 甲B. 甲与丁C. 丙D. 丙与丁二、填空题(本题有6小题,每题4分,共24分)11. 分解因式:________.12. 如图,直线,直线交,,于点,,;直线交,,于点,,.已知,则__________.13. 小明和小红玩抛硬币游戏,连续抛两次.小明说:“如果两次都是正面,那么你赢;如果两次是一正一反,则我赢.”小红赢的概率是__________,据此判断该游戏__________(填“公平”或“不公平”).14. 如图,量角器的0度刻度线为,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点,直尺另一边交量角器于点,,量得,点在量角器上的读数为,则该直尺的宽度为____________.15. 甲、乙两个机器人检测零件,甲比乙每小时多检测20个,甲检测300个比乙检测200个所用的时间少,若设甲每小时检测个,则根据题意,可列出方程:__________.16. 如图,在矩形中,,,点在上,,点在边上一动点,以为斜边作.若点在矩形的边上,且这样的直角三角形恰好有两个,则的值是__________.三、解答题17. (1)计算:;(2)化简并求值:,其中,.18. 用消元法解方程组时,两位同学的解法如下:(1)反思:上述两个解题过程中有无计算错误?若有误,请在错误处打“×”.(2)请选择一种你喜欢的方法,完成解答.19. 如图,等边的顶点,在矩形的边,上,且.求证:矩形是正方形.20. 某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为的产品为合格),随机各抽取了20个样品进行检测,过程如下:收集数据(单位:):甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.整理数据:分析数据:应用数据:(1)计算甲车间样品的合格率.(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.21. 小红帮弟弟荡秋千(如图1),秋千离地面的高度与摆动时间之间的关系如图2所示.(1)根据函数的定义,请判断变量是否为关于的函数?(2)结合图象回答:①当时,的值是多少?并说明它的实际意义.②秋千摆动第一个来回需多少时间?22. 如图1,滑动调节式遮阳伞的立柱垂直于地面,为立柱上的滑动调节点,伞体的截面示意图为,为中点,,,,.当点位于初始位置时,点与重合(图2).根据生活经验,当太阳光线与垂直时,遮阳效果最佳.(1)上午10:00时,太阳光线与地面的夹角为(图3),为使遮阳效果最佳,点需从上调多少距离?(结果精确到)(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点在(1)的基础上还需上调多少距离?(结果精确到)(参考数据:,,,,)23. 已知,点为二次函数图象的顶点,直线分别交轴正半轴,轴于点,.(1)判断顶点是否在直线上,并说明理由.(2)如图1,若二次函数图象也经过点,,且,根据图象,写出的取值范围.(3)如图2,点坐标为,点在内,若点,都在二次函数图象上,试比较与的大小.24. 已知,中,,是边上一点,作,分别交边,于点,.(1)若(如图1),求证:.(2)若,过点作,交(或的延长线)于点.试猜想:线段,和之间的数量关系,并就情形(如图2)说明理由.(3)若点与重合(如图3),,且.①求的度数;②设,,,试证明:.。
浙江省舟山市中考数学真题试卷(解析版)

数学浙江省舟山市2018中考数学试题一、选择题(本题有10小题,每题3分,共30分.请选出各题中唯一的正确选项,不选、多选、错选,均不得分)1.下列几何体中,俯视图...为三角形的是()A. B. C. D.【答案】C【解析】【分析】依次观察四个选项,A中圆锥从正上看,是其在地面投影;B中,长方体从上面看,看到的是上表面;C中,三棱柱从正上看,看到的是上表面;D中四棱锥从正上看,是其在地面投影;据此得出俯视图并进行判断.【解答】A、圆锥俯视图是带圆心的圆,故本选项错误;B、长方体的俯视图均为矩形,故本选项错误;C、三棱柱的俯视图是三角形,故本选项正确.D、四棱锥的俯视图是四边形,故本选项错误;故选C.【点评】本题应用了几何体三视图的知识,从上面向下看,想象出平面投影是解答重点;2.2018年5月25日,中国探月工程的“鹊桥号”中继星成功运行于地月拉格朗日点,它距离地球约.数1500000用科学记数法表示为()A. B. C. D.【答案】B【解析】【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:将1500000用科学记数法表示为:.故选B.【点评】本题考查了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.3.2018年1~4月我国新能源乘用车的月销售情况如图所示,则下列说法错误..的是()A.1月份销售为2.2万辆B.从2月到3月的月销售增长最快C.4月份销售比3月份增加了1万辆D.1~4月新能源乘用车销售逐月增加【答案】D【解析】【分析】观察折线统计图,一一判断即可.【解答】观察图象可知:A.1月份销售为2.2万辆,正确.B.从2月到3月的月销售增长最快,正确.C.,4月份销售比3月份增加了1万辆,正确.D.1~4月新能源乘用车销售先减少后增大.故错误.故选D.【点评】考查折线统计图,解题的关键是看懂图象.4.不等式的解在数轴上表示正确的是()A. B.C. D.【答案】A【解析】【分析】根据解不等式,可得不等式的解集,根据不等式的解集在数轴上的表示方法,可得答案.【解答】在数轴上表示为:故选A.【点评】考查在数轴上表示不等式的解集,解一元一次不等式,解题的关键是解不等式.5.将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是()A.(A)B.(B)C.(C)D.(D)【答案】A【解析】【分析】根据两次折叠都是沿着正方形的对角线折叠,展开后所得图形的顶点一定在正方形的对角线上,根据③的剪法,中间应该是一个正方形.【解答】根据题意,两次折叠都是沿着正方形的对角线折叠的,根据③的剪法,展开后所得图形的顶点一定在正方形的对角线上,而且中间应该是一个正方形.故选A.【点评】关键是要理解折叠的过程,得到关键信息,如本题得到展开后的图形的顶点在正方形的对角线上是解题的关键.6.用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是()A.点在圆内B.点在圆上C.点在圆心上D.点在圆上或圆内【答案】D【解析】【分析】在假设结论不成立时要注意考虑结论的反面所有可能的情况,如果只有一种,那么否定一种就可以了,如果有多种情况,则必须一一否定。
(完整版)浙江省舟山市2018年数学中考试题及答案,推荐文档

C.点在圆心上
D.点在圆上或圆内
7.欧几里得的《原本》记载,形如 x2 ax b2 的方程的图解法是:画 RtABC ,使
ACB 90 , BC a , AC b ,再在斜边 AB 上截取 BD a .则该方程的一个正根
2
2
是( )
A. AC 的长
B. AD 的长
C. BC 的长
D.CD 的长
收集数据(单位: mm ):
甲车间:
168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185 ,169,187,176,180. 乙车间: 186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180 ,184,182,180,183. 整理数据:
8.用尺规在一个平行四边形内作菱形 ABCD ,下列作法中错误的是( )
A.
B.
C.
D.
9.如图,点C 在反比例函数 y k (x 0) 的图象上,过点C 的直线与 x 轴, y 轴分别交于 x
点 A , B ,且 AB BC , AOB 的面积为 1,则 k 的值为( )
A.1
B.2
C.3
cm .
15. 甲、乙两个机器人检测零件,甲比乙每小时多检测 20 个,甲检测 300 个比乙检测 200
个所用的时间少10% ,若设甲每小时检测 x 个,则根据题意,可列出方程:
.
16.如图,在矩形 ABCD 中, AB 4 , AD 2 ,点 E 在 CD 上, DE 1 ,点 F 在边 AB 上一动点,以 EF 为斜边作 RtEFP .若点 P 在矩形 ABCD 的边上,且这样的直角三
浙江省舟山市2018年中考数学试题(解析版)

数学浙江省舟山市2018 中考数学试题一、选择题(此题有10 小题,每题 3 分,共30 分 .请选出各题中独一的正确选项,不选、多项选择、错选,均不得分)1.为三角形的是()以下几何体中,俯视图...A. B. C. D.【答案】C【分析】【剖析】挨次察看四个选项, A 中圆锥从正上看,是其在地面投影; B 中,长方体从上边看,看到的是上表面;C 中,三棱柱从正上看,看到的是上表面; D 中四棱锥从正上看,是其在地面投影;据此得出俯视图并进行判断.【解答】 A 、圆锥俯视图是带圆心的圆,故本选项错误;B、长方体的俯视图均为矩形,故本选项错误;C、三棱柱的俯视图是三角形,故本选项正确;D、四棱锥的俯视图是四边形,故本选项错误;应选 C.【评论】此题应用了几何体三视图的知识,从上边向下看,想象出平面投影是解答要点;2. 2018 年 5 月25 日,中国探月工程的“鹊桥号”中继星成功运转于地月拉格朗日点,它距离地球约.数1500000 用科学记数法表示为()A. B. C. D.【答案】B【分析】【剖析】科学记数法的表示形式为a×10n的形式,此中1≤|a< 10,n 为整数.确立n 的值时,要看把原数变为 a 时,小数点挪动了多少位,n 的绝对值与小数点挪动的位数同样.当原数绝对值> 1 时, n 是正数;当原数的绝对值< 1 时, n 是负数.【解答】解:将1500000 用科学记数法表示为:.应选B.【评论】此题考察了科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,此中1≤|a< 10, n 为整数,表示时要点要正确确立 a 的值以及 n 的值.3. 2018 年 1~ 4 月我国新能源乘用车的月销售状况以下图,则以下说法错误的是()..A. 1 月份销售为 2.2 万辆B.从 2 月到 3 月的月销售增添最快C. 4 月份销售比 3 月份增添了 1 万辆D.1~4 月新能源乘用车销售逐月增添【答案】 D【分析】【剖析】察看折线统计图,一一判断即可.【解答】察看图象可知:A. 1月份销售为 2.2 万辆 ,正确 .B. 从 2 月到 3 月的月销售增添最快,正确 .C., 4 月份销售比 3 月份增添了 1 万辆,正确.D. 1~ 4 月新能源乘用车销售先减少后增大.故错误.应选 D.【评论】考察折线统计图,解题的要点是看懂图象.4. 不等式的解在数轴上表示正确的选项是()A. B.C. D.【答案】 A【分析】【剖析】依据解不等式,可得不等式的解集,依据不等式的解集在数轴上的表示方法,可得答案.【解答】在数轴上表示为:应选 A.【评论】考察在数轴上表示不等式的解集,解一元一次不等式,解题的要点是解不等式.5. 将一张正方形纸片按如图步骤①,②沿虚线对折两次,而后沿③中平行于底边的虚线剪去一个角,睁开摊平后的图形是()A. B. C. D.【答案】 A【分析】【剖析】依据两次折叠都是沿着正方形的对角线折叠, 睁开后所得图形的极点必定在正方形的对角线上 , 依据③的剪法,中间应当是一个正方形.【解答】依据题意,两次折叠都是沿着正方形的对角线折叠的,依据③的剪法,睁开后所得图形的极点必定在正方形的对角线上,并且中间应当是一个正方形.应选 A.【评论】要点是要理解折叠的过程,获取要点信息,如此题获取睁开后的图形的极点在正方形的对角线上是解题的要点.6. 用反证法证明时,假定结论“点在圆外”不建立,那么点与圆的地点关系只好是()A. 点在圆内B.点在圆上C.点在圆心上D.点在圆上或圆内【答案】 D【分析】【剖析】在假定结论不建即刻要注意考虑结论的反面全部可能的状况,假如只有一种,那么否认一种就能够了,假如有多种状况,则一定一一否认.【解答】用反证法证明时,假定结论“点在圆外”不建立,那么点应当在圆内或许圆上.应选 D.【评论】考察反证法以及点和圆的地点关系,解题的要点是掌握点和圆的地点关系.7. 欧几里得的《本来》记录,形如的方程的图解法是:画,使,,,再在斜边上截取.则该方程的一个正根是()A.的长B.的长C.的长D.的长【答案】 B【分析】【剖析】能够利用求根公式求出方程的根,依据勾股定理求出AB 的长,从而求得AD 的长 ,即可发现结论 .【解答】用求根公式求得:∵∴∴AD 的长就是方程的正根.应选 B.【评论】考察解一元二次方程已经勾股定理等,娴熟掌握公式法解一元二次方程是解题的要点.)8. 用尺规在一个平行四边形内作菱形,以下作法中错误的是(..A. B. C. D.【答案】 C【分析】【剖析】依据菱形的判断方法一一进行判断即可.学& 科& 网...学& 科& 网...学& 科& 网...学&科 &网 ...学 &科 & 网...学& 科& 网...学& 科& 网...学& 科& 网...学& 科& 网...B.有一组邻边相等的平行四边形是菱形.C.没法判断是菱形.D.有一组邻边相等的平行四边形是菱形.应选 C.【评论】考察菱形的判断,掌握菱形的判断方法是解题的要点.9. 如图,点在反比率函数的图象上,过点的直线与轴,轴分别交于点,,且,的面积为1,则的值为()A.1B.2C.3D.4【答案】 D【分析】【剖析】过点 C 作轴,设点,则得到点 C 的坐标,依据的面积为1,获取的关系式,即可求出的值.【解答】过点C作轴,设点,则获取点 C 的坐标为:的面积为1,即应选 D.【评论】考察反比率函数图象上点的坐标特点,掌握待定系数法是解题的要点.10. 某届世界杯的小组竞赛规则:四个球队进行单循环竞赛(每两队赛一场),胜一场得 3 分,平一场得 1分,负一场得0 分 .某小组竞赛结束后,甲、乙、丙、丁四队分别获取第一、二、三、四名,各队的总得分恰巧是四个连续奇数,则与乙打平的球队是()A. 甲B. 甲与丁C. 丙D. 丙与丁【答案】 B【分析】【剖析】 4 个队一共要比场竞赛 ,每个队都要进行 3场竞赛 ,各队的总得分恰巧是四个连续奇数,甲、乙、丙、丁四队的得分状况只好是进行剖析即可 .【解答】4 个队一共要比场竞赛 ,每个队都要进行 3 场竞赛 ,各队的总得分恰巧是四个连续奇数,甲、乙、丙、丁四队的得分状况只好是因此 ,甲队胜 2 场,平 1 场,负 0 场.乙队胜 1 场,平 2 场,负0 场 .丙队胜 1 场,平0 场,负 2 场 .丁队胜0 场,平 1 场,负 2 场 .与乙打平的球队是甲与丁,应选 B.【评论】第一确立竞赛总场数,而后依据“各队的总得分恰巧是四个连续的奇数”进行剖析是达成此题的要点 .二、填空题(此题有 6 小题,每题 4 分,共 24 分)11. 分解因式 :________.【答案】【分析】【剖析】用提取公因式法即可获取结果.【解答】原式 =.故答案为:【评论】考察提取公因式法因式分解,解题的要点是找到公因式.12. 如图,直线,直线交,,于点,,;直线交,,于点,,.已知,则__________.【答案】2,能够知道,即可求得.【分析】【剖析】依据【解答】,依据,故答案为: 2.【评论】考察平行线分线段成比率定理,娴熟掌握定理是解题的要点.13. 小明和小红玩抛硬币游戏,连续抛两次.小明说:“假如两次都是正面,那么你赢;假如两次是一正一反,则我赢. ”小红赢的概率是__________ ,据此判断该游戏__________ (填“公正”或“不公平”).【答案】(1).(2). 不公正【分析】【剖析】第一利用列举法列举出可能出现的状况,可能是两正,两反,一正一反、一反一正四种状况,用可能状况数除以状况总数即可得出都是正面向上或许都是反面向上和一正一反的可能性,可能性同样则公正,不然就不公正.【解答】抛两枚硬币可能会是两正,两反,一正一反、一反一正四种状况;小红赢的可能性,即都是正面向上,赢的概率是:小明赢的可能性,即一正一反的可能性是:因此游戏对小红不公正.故答案为:(1).(2). 不公正【评论】考察概率的计算,明确概率的意义是解题的要点,概率等于所讨状况数与总状况数的比.14. 如图,量角器的0 度刻度线为于点,直尺另一边交量角器于点的宽度为 ____________.,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切,,量得,点在量角器上的读数为,则该直尺【答案】【分析】【剖析】连结OC,OD,OC 与 AD径定理有:解直角【解答】连结OC,OD,OC 与 AD 交于点交于点即可 .E,E,依据圆周角定理有依据垂直尺的宽度:故答案为:【评论】考察垂径定理,熟记垂径定理是解题的要点.【答案】【分析】【剖析】若设甲每小时检测个,检测时间为,乙每小时检测个,检测时间为,依据甲检测300 个比乙检测200 个所用的时间少,列出方程即可.【解答】若设甲每小时检测个,检测时间为,乙每小时检测个,检测时间为,依据题意有:.故答案为:【评论】考察分式方程的应用,解题的要点是找出题目中的等量关系.16. 如图,在矩形中,,,点在上,,点在边斜边作 .若点在矩形的边上,且这样的直角三角形恰巧有两个,则上一动点,以的值是为__________.【答案】 0 或或 4【分析】【剖析】在点 F 的运动过程中分别以EF 为直径作圆,察看圆和矩形矩形边的交点个数即可获取结论 .【解答】当点 F 与点 A 重合时,以为斜边恰巧有两个,切合题意 .当点 F从点 A向点 B运动时,当时,共有4个点 P使是以为斜边.当时,有 1个点 P使是以为斜边.当时,有 2个点 P使是以为斜边.当时,有 3个点 P使是以为斜边.当时,有 4个点 P使是以为斜边.当点 F 与点 B 重合时,以为斜边恰巧有两个,切合题意.故答案为: 0或或4【评论】考察圆周角定理,熟记直径所对的圆周角是直角是解题的要点.注意分类议论思想在数学中的应用 .三、解答题17. ( 1)计算:;( 2)化简并求值:,此中,.【答案】( 1)原式;(2)原式=-1【分析】【剖析】( 1)依据实数的运算法例进行运算即可.( 2)依据分式混淆运算的法例进行化简,再把字母的值代入运算即可.【解答】( 1)原式( 2)原式.当,时,原式.【评论】考察实数的混淆运算以及分式的化简求值,掌握运算法例是解题的要点.18. 用消元法解方程组时,两位同学的解法以下:( 1)反省:上述两个解题过程中有无计算错误?如有误,请在错误处打“×”.( 2)请选择一种你喜爱的方法,达成解答.【答案】( 1)解法一中的计算有误;(2)原方程组的解是.【分析】【剖析】依据加减消元法和代入消元法进行判断即可.【解答】( 1)解法一中的计算有误(标志略).( 2)用消元法解方程组时,两位同学的解法以下:由① -②,得,解得,把代入①,得,解得,因此原方程组的解是.【评论】考察加减消元法和代入消元法解二元一次方程组,娴熟掌握两种方法是解题的要点.19.如图,等边的极点,在矩形的边,上,且.求证:矩形是正方形 .【答案】证明看法析.【分析】【剖析】证明【解答】∵四边形∴,∵是等边三角形,∴,又,∴,∴≌是矩形,,,获取,,即可证明矩形是正方形.∴≌,∴,∴矩形是正方形 .【评论】考察正方形的判断,娴熟掌握判断方法是解题的要点.20. 某厂为了查验甲、乙两车间生产的同一款新产品的合格状况(尺寸范围为的产品为合格),随机各抽取了20 个样品进行检测,过程以下:采集数据(单位:):甲车间:168, 175, 180, 185, 172, 189,185, 182, 185,174, 192, 180, 185, 178,173, 185, 169,187, 176, 180.乙车间:186, 180, 189, 183, 176, 173,178, 167, 180,175, 178, 182, 180, 179,185, 180, 184,182, 180, 183.整理数据:剖析数据:车间均匀数众数中位数方差甲车间180********.1乙车间180********.6应用数据:( 1)计算甲车间样品的合格率.( 2)预计乙车间生产的1000 个该款新产品中合格产品有多少个?( 3)联合上述数据信息,请判断哪个车间生产的新产品更好,并说明原因【答案】( 1)甲车间样品的合格率为;(2)乙车间的合格产品数为【分析】【剖析】( 1)用合格产品数除以抽样老是乘以即可确立..750 个;(3)看法析.( 2)用乙车间生产的1000 个该款新产品乘以乙车间样品的合格率即可求解.( 3)能够从合格率,方差等各方面综合剖析.【解答】( 1)甲车间样品的合格率为.( 2)∵乙车间样品的合格产品数为(个),∴乙车间样品的合格率为.∴乙车间的合格产品数为(个) .( 3)①从样品合格率看,乙车间合格率比甲车间高,因此乙车间生产的新产品更好.②从样品的方差看,甲、乙均匀数相等,且均在合格范围内,而乙的方差小于甲的方差,说明乙比甲稳固,因此乙车间生产的新产品更好.【评论】考察用样本预计整体,数据的剖析,方差等,注意方差越小,越稳固.21. 小红帮弟弟荡秋千(如图1),秋千离地面的高度与摇动时间之间的关系如图 2 所示 .( 1)依据函数的定义,请判断变量能否为对于的函数?( 2)联合图象回答:①当时,的值是多少?并说明它的实质意义.②秋千摇动第一个往返需多少时间?【答案】( 1)看法析;(2)①看法析;②.【分析】【剖析】依据函数的定义进行判断即可 .①当时,依据函数的图象即可回答以下问题.②依据图象即可回答 .【解答】( 1)∵对于每一个摇动时间,都有一个独一的的值与其对应,∴变量是对于的函数 .( 2)①,它的实质意义是秋千摇动时,离地面的高度为.②.【评论】此题型旨在考察学生从图象中获守信息、用函数的思想认识、剖析和解决问题的能力.22. 如图 1,滑动调理式遮阳伞的立柱垂直于地面企图为,为中点,,,点与重合(图2) .依据生活经验,当太阳光芒与,为立柱上的滑动调理点,伞体的截面示,.当点位于初始地点垂直时,遮阳成效最正确.时,( 1)上午 10:00 时,太阳光芒与地面的夹角为(图3),为使遮阳成效最正确,点需从上浮多少距离?(结果精准到)( 2)正午 12:00 时,太阳光芒与地面垂直(图4),为使遮阳成效最正确,点在( 1)的基础上还需上浮多少距离?(结果精准到)(参照数据:,,,,)【答案】( 1)点需从上浮;( 2)点在( 1)的基础上还需上浮.【分析】【剖析】( 1)如图 2,当点位于初始地点时,. 10:00时,太阳光芒与地面的夹角为,点上浮至处,.,为等腰直角三角形,,即可求出点需从上浮的距离 .( 2)正午 12:00 时,太阳光芒与,地面都垂直,点上浮至处,过点作于点,,,依据即可求解 .【解答】( 1)如图 2,当点位于初始地点时,.如图 3, 10:00 时,太阳光芒与地面的夹角为,点上浮至处,,,∴,∴.∵,∴.∵,∴,∴为等腰直角三角形,∴,∴,即点需从上浮.( 2)如图 4,正午 12:00 时,太阳光芒与,地面都垂直,点上浮至处,∴.∵,∴.∵,∴.∵,得为等腰三角形,∴.过点作于点,∴,∴,∴,即点在( 1)的基础上还需上浮.【评论】考察等腰三角形的性质,解直角三角形,娴熟运用三角函数是解题的要点.能够数形联合.23. 已知,点为二次函数图象的极点,直线分别交轴正半轴,轴于点,.( 1)判断极点能否在直线上,并说明原因 .( 2)如图1,若二次函数图象也经过点,,且,依据图象,写出的取值范围 .( 3)如图2,点坐标为,点在内,若点,都在二次函数图象上,试比较与的大小.【答案】( 1)点在直线上,原因看法析;( 2)的取值范围为或.( 3)①当时,;②当时,;③当时,.【分析】【剖析】( 1)写出点的坐标,代入直线进行判断即可 .( 2)直线与轴交于点为,求出点坐标,把在抛物线上,代入求得,求出二次函数表达式,从而求得点 A 的坐标,数形联合即可求出时,的取值范围 .( 3)直线与直线交于点,与轴交于点,而直线表达式为,联立方程组,得.点,.分三种状况进行议论.【解答】( 1)∵点坐标是,∴把代入,得,∴点在直线上 .( 2)如图1,∵直线与轴交于点为,∴点坐标为.又∵在抛物线上,∴,解得,∴二次函数的表达式为,∴当时,得,,∴.察看图象可得,当时,的取值范围为或.( 3)如图2,∵直线与直线交于点,与轴交于点,而直线表达式为,解方程组,得.∴点,.∵点在内,∴.当点,对于抛物线对称轴(直线)对称时,,∴.在直线上,且二次函数图象的张口向下,极点综上:①当时,;②当时,;③当时,.【评论】考察一次函数图像上点的坐标特点,不等式,二次函数的性质等,注意数形联合思想和分类议论思想在数学中的应用.24. 已知,中,,是边上一点,作,分别交边,于点,.( 1)若(如图1),求证:.( 2)若,过点作,交(或的延伸线)于点.试猜想:线段,和之间的数目关系,并就情况(如图2)说明原因 .( 3)若点与重合(如图3),,且.①求的度数;②设,,,试证明:.【答案】( 1)证明看法析;(2)猜想:,原因看法析;( 3)①;②证明见分析 .【分析】【剖析】( 1)依据平行线的判断,获取,,证明.即可证明.( 2)过点作的平行线交的延伸线于点,证明≌获取.证明四边形是平行四边形,即可获取.( 3)①设,,依据三角形的内角和列出方程,求解即可 .②延伸至,使,连结,证明.依据相像三角形的性质获取,即可证明 .【解答】( 1)∵,,,∴,,∴,,,∴.∴.( 2)猜想:,原因以下:过点作的平行线交的延伸线于点,则,∵,∴,又,.∴≌∴∵,∴,∴四边形是平行四边形,∴.( 3)①设,∵,,∴,又,即,∴,即.②延伸至,使,连结,∵,.∴,∵,∴,∴,而,∴.∴,∴.∵,,,∴,∴.【评论】考察平行四边形的判断与性质,全等三角形的判断与性质,相像三角形的判断与性质,综合性比较强,对学生综合能力要求较高.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年浙江省舟山市中考数学试卷及解析一、选择题(本题有10小题,每题3分,共30分。
请选出各题中唯一的正确选项,不选、多选、错选,均不得分)1.(3分)下列几何体中,俯视图为三角形的是()A. B.C.D.2.(3分)2018年5月25日,中国探月工程的“鹊桥号”中继星成功运行于地月拉格朗日L2点,它距离地球约1500000km,数1500000用科学记数法表示为()A.15×105 B.1.5×106C.0.15×107D.1.5×1053.(3分)2018年1~4月我国新能源乘用车的月销量情况如图所示,则下列说法错误的是()A.1月份销量为2.2万辆B.从2月到3月的月销量增长最快C.4月份销量比3月份增加了1万辆D.1~4月新能源乘用车销量逐月增加4.(3分)不等式1﹣x≥2的解在数轴上表示正确的是()A.B.C.D.5.(3分)将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是()A.B.C. D.6.(3分)用反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是()A.点在圆内B.点在圆上C.点在圆心上D.点在圆上或圆内7.(3分)欧几里得的《原本》记载,形如x2+ax=b2的方程的图解法是:画Rt△ABC,使∠ACB=90°,BC=,AC=b,再在斜边AB上截取BD=.则该方程的一个正根是()A.AC的长 B.AD的长 C.BC的长D.CD的长8.(3分)用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是()A. B.C.D.9.(3分)如图,点C在反比例函数y=(x>0)的图象上,过点C的直线与x 轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,则k的值为()A.1 B.2 C.3 D.410.(3分)某届世界杯的小组比赛规则:四个球队进行单循环比赛(每两队赛一场),胜一场得3分,平一场得1分,负一场得0分,某小组比赛结束后,甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,则与乙打平的球队是()A.甲B.甲与丁C.丙D.丙与丁二、填空题(本题有6小题,每题4分,共24分)11.(4分)分解因式:m2﹣3m=.12.(4分)如图,直线l1∥l2∥l3,直线AC交l1,l2,l3于点A,B,C;直线DF 交l1,l2,l3于点D,E,F,已知=,则=.13.(4分)小明和小红玩抛硬币游戏,连续抛两次,小明说:“如果两次都是正面,那么你赢;如果两次是一正一反,则我嬴.”小红赢的概率是,据此判断该游戏(填“公平”或“不公平”).14.(4分)如图,量角器的0度刻度线为AB,将一矩形直尺与量角器部分重叠,使直尺一边与量角器相切于点C,直尺另一边交量角器于点A,D,量得AD=10cm,点D在量角器上的读数为60°,则该直尺的宽度为cm.15.(4分)甲、乙两个机器人检测零件,甲比乙每小时多检测20个,甲检测300个比乙检测200个所用的时间少10%,若设甲每小时检测x个,则根据题意,可列出方程:.16.(4分)如图,在矩形ABCD中,AB=4,AD=2,点E在CD上,DE=1,点F 是边AB上一动点,以EF为斜边作Rt△EFP.若点P在矩形ABCD的边上,且这样的直角三角形恰好有两个,则AF的值是.三、解答题(本题有8小题,第17~19题每题6分,第20,21题每题8分,第22,23题每题10分,第24题12分,共66分)17.(6分)(1)计算:2(﹣1)+|﹣3|﹣(﹣1)0;(2)化简并求值()•,其中a=1,b=2.18.(6分)用消元法解方程组时,两位同学的解法如下:解法一:由①﹣②,得3x=3.解法二:由②得,3x+(x﹣3y)=2,③把①代入③,得3x+5=2.(1)反思:上述两个解题过程中有无计算错误?若有误,请在错误处打“ד.(2)请选择一种你喜欢的方法,完成解答.19.(6分)已知:在△ABC中,AB=AC,D为AC的中点,DE⊥AB,DF⊥BC,垂足分别为点E,F,且DE=DF.求证:△ABC是等边三角形.20.(8分)某厂为了检验甲、乙两车间生产的同一款新产品的合格情况(尺寸范围为176mm~185mm的产品为合格),随机各抽取了20个样品进行检测,过程如下:收集数据(单位:mm)甲车间:168,175,180,185,172,189,185,182,185,174,192,180,185,178,173,185,169,187,176,180.乙车间:186,180,189,183,176,173,178,167,180,175,178,182,180,179,185,180,184,182,180,183.整理数据:分析数据:应用数据:(1)计算甲车间样品的合格率.(2)估计乙车间生产的1000个该款新产品中合格产品有多少个?(3)结合上述数据信息,请判断哪个车间生产的新产品更好,并说明理由.21.(8分)小红帮弟弟荡秋千(如图1),秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图2所示.(1)根据函数的定义,请判断变量h是否为关于t的函数?(2)结合图象回答:①当t=0.7s时,h的值是多少?并说明它的实际意义.②秋千摆动第一个来回需多少时间?22.(10分)如图1,滑动调节式遮阳伞的立柱AC垂直于地面AB,P为立柱上的滑动调节点,伞体的截面示意图为△PDE,F为PD的中点,AC=2.8m,PD=2m,CF=1m,∠DPE=20°,当点P位于初始位置P0时,点D与C重合(图2).根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳.(1)上午10:00时,太阳光线与地面的夹角为65°(图3),为使遮阳效果最佳,点P需从P0上调多少距离?(结果精确到0.1m)(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点P 在(1)的基础上还需上调多少距离?(结果精确到0.1m)(参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,≈1.41,≈1.73)23.(10分)已知,点M为二次函数y=﹣(x﹣b)2+4b+1图象的顶点,直线y=mx+5分别交x轴正半轴,y轴于点A,B.(1)判断顶点M是否在直线y=4x+1上,并说明理由.(2)如图1,若二次函数图象也经过点A,B,且mx+5>﹣(x﹣b)2+4b+1,根据图象,写出x的取值范围.(3)如图2,点A坐标为(5,0),点M在△AOB内,若点C(,y1),D(,y2)都在二次函数图象上,试比较y1与y2的大小.24.(12分)我们定义:如果一个三角形一条边上的高等于这条边,那么这个三角形叫做“等高底”三角形,这条边叫做这个三角形的“等底”.(1)概念理解:如图1,在△ABC中,AC=6,BC=3,∠ACB=30°,试判断△ABC是否是”等高底”三角形,请说明理由.(2)问题探究:如图2,△ABC是“等高底”三角形,BC是”等底”,作△ABC关于BC所在直线的对称图形得到△A'BC,连结AA′交直线BC于点D.若点B是△AA′C的重心,求的值.(3)应用拓展:如图3,已知l1∥l2,l1与l2之间的距离为2.“等高底”△ABC的“等底”BC在直线l1上,点A在直线l2上,有一边的长是BC的倍.将△ABC绕点C按顺时针方向旋转45°得到△A'B'C,A′C所在直线交l2于点D.求CD的值.2018年浙江省舟山市中考数学试卷参考答案与试题解析一、选择题(本题有10小题,每题3分,共30分。
请选出各题中唯一的正确选项,不选、多选、错选,均不得分)1.【解答】解:A、俯视图是圆,故A不符合题意;B、俯视图是矩形,故B不符合题意;C、俯视图是三角形,故C符合题意;D、俯视图是四边形,故D不符合题意;故选:C.2.【解答】解:1500000=1.5×106,故选:B.3.【解答】解:由图可得,1月份销量为2.2万辆,故选项A正确,从2月到3月的月销量增长最快,故选项B正确,4月份销量比3月份增加了4.3﹣3.3=1万辆,故选项C正确,1~2月新能源乘用车销量减少,2~4月新能源乘用车销量逐月增加,故选项D 错误,故选:D.4.【解答】解:不等式1﹣x≥2,解得:x≤﹣1,表示在数轴上,如图所示:故选:A.5.【解答】解:由于得到的图形的中间是正方形,且顶点在原来的正方形的对角线上,故选:A.6.【解答】解:反证法证明时,假设结论“点在圆外”不成立,那么点与圆的位置关系只能是:点在圆上或圆内.故选:D.7.【解答】解:欧几里得的《原本》记载,形如x2+ax=b2的方程的图解法是:画Rt△ABC,使∠ACB=90°,BC=,AC=b,再在斜边AB上截取BD=.则该方程的一个正根是AD的长,故选:B.8.【解答】解:A、作图根据由作图可知,AC⊥BD,且平分BD,即对角线平分且垂直的四边形是菱形,正确;B、由作图可知AB=BC,AD=AB,即四边相等的四边形是菱形,正确;C、由作图可知AB=DC,AD=BC,只能得出ABCD是平行四边形,错误;D、由作图可知对角线AC平分对角,可以得出是菱形,正确;故选:C.9.【解答】解:设点A的坐标为(a,0),∵过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,∴点C(﹣a,),∴点B的坐标为(0,),∴=1,解得,k=4,故选:D.10.【解答】解:∵甲、乙、丙、丁四队分别获得第一、二、三、四名,各队的总得分恰好是四个连续奇数,∴甲得分为7分,2胜1平,乙得分5分,1胜2平,丙得分3分,1胜0平,丁得分1分,0胜1平,∵甲、乙都没有输球,∴甲一定与乙平,∵丙得分3分,1胜0平,乙得分5分,1胜2平,∴与乙打平的球队是甲与丁.故选:B.二、填空题(本题有6小题,每题4分,共24分)11.【解答】解:m2﹣3m=m(m﹣3).故答案为:m(m﹣3).12.【解答】解:∵=,∴=2,∵l1∥l2∥l3,∴==2,故答案为:2.13.【解答】解:所有可能出现的结果如下表所示:因为抛两枚硬币,所有机会均等的结果为:正正,正反,反正,反反,所以出现两个正面的概率为,一正一反的概率为=,因为二者概率不等,所以游戏不公平.故答案为:,不公平.14.【解答】解:连接OC,∵直尺一边与量角器相切于点C,∴OC⊥AD,∵AD=10,∠DOB=60°,∴∠DAO=30°,∴OE=,OA=,∴CE=OC﹣OE=OA﹣OE=,故答案为:15.【解答】解:设设甲每小时检测x个,则乙每小时检测(x﹣20)个,根据题意得,=(1﹣10%),故答案为=×(1﹣10%).16.【解答】解:∵△EFP是直角三角形,且点P在矩形ABCD的边上,∴P是以EF为直径的圆O与矩形ABCD的交点,①当AF=0时,如图1,此时点P有两个,一个与D重合,一个交在边AB上;②当⊙O与AD相切时,设与AD边的切点为P,如图2,此时△EFP是直角三角形,点P只有一个,当⊙O与BC相切时,如图4,连接OP,此时构成三个直角三角形,则OP⊥BC,设AF=x,则BF=P1C=4﹣x,EP1=x﹣1,∵OP∥EC,OE=OF,∴OG=EP1=,∴⊙O的半径为:OF=OP=,在Rt△OGF中,由勾股定理得:OF2=OG2+GF2,∴,解得:x=,∴当1<AF<时,这样的直角三角形恰好有两个,③当AF=4,即F与B重合时,这样的直角三角形恰好有两个,如图5,综上所述,则AF的值是:0或1<AF或4.故答案为:0或1<AF或4.三、解答题(本题有8小题,第17~19题每题6分,第20,21题每题8分,第22,23题每题10分,第24题12分,共66分)17.【解答】解:(1)原式=4﹣2+3﹣1=4;(2)原式=•=a﹣b;当a=1,b=2时,原式=1﹣2=﹣1.18.【解答】解:(1)解法一中的解题过程有错误,由①﹣②,得3x=3“×”,应为由①﹣②,得﹣3x=3;(2)由①﹣②,得﹣3x=3,解得x=﹣1,把x=﹣1代入①,得﹣1﹣3y=5,解得y=﹣2.故原方程组的解是.19.【解答】证明:∵DE⊥AB,DF⊥BC,垂足分别为点E,F,∴∠AED=∠CFD=90°,∵D为AC的中点,∴AD=DC,在Rt△ADE和Rt△CDF中,,∴Rt△ADE≌Rt△CDF,∴∠A=∠C,∴BA=BC,∵AB=AC,∴AB=BC=AC,∴△ABC是等边三角形.20.【解答】解:(1)甲车间样品的合格率为:×100%=55%;(2)∵乙车间样品的合格产品数为:20﹣(1+2+2)=15(个),∴乙车间样品的合格率为:×100%=75%,∴乙车间的合格产品数为:1000×75%=750(个);(3)①乙车间合格率比甲车间高,所以乙车间生产的新产品更好;②甲、乙平均数相等,且均在合格范围内,而乙的方差小于甲的方差,说明乙比较稳定,所以乙车间生产的新产品更好.21.【解答】解:(1)由图象可知,对于每一个摆动时间t,h都有唯一确定的值与其对应,∴变量h是关于t的函数;(2)①由函数图象可知,当t=0.7s时,h=0.5m,它的实际意义是秋千摆动0.7s时,离地面的高度是0.5m;②由图象可知,秋千摆动第一个来回需2.8s.22.【解答】解:(1)如图2中,当P位于初始位置时,CP0=2m,如图3中,上午10:00时,太阳光线与地面的夹角为65°,上调的距离为P0P1.∵∠1=90°,∠CAB=90°,∠ABE=65°,∴∠AP1E=115°,∴∠CP1E=65°,∵∠DP1E=20°,∴∠CP1F=45°,∵CF=P1F=1m,∴∠C=∠CP1F=45°,∴△CP1F是等腰直角三角形,∴P1C=m,∴P0P1=CP0﹣P1C=2﹣≈0.6m,即为使遮阳效果最佳,点P需从P0上调0.6m.(2)如图4中,中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点P调到P2处.∵P2E∥AB,∴∠CP2E=∠CAB=90°,∵∠DP2E=20°,∴∠CP2F=70°,作FG⊥AC于G,则CP2=2CG=1×cos70°≈0.68m,∴P1P2=CP1﹣CP2=﹣0.68≈0.7m,即点P在(1)的基础上还需上调0.7m.23.【解答】解:(1)点M为二次函数y=﹣(x﹣b)2+4b+1图象的顶点,∴M的坐标是(b,4b+1),把x=b代入y=4x+1,得y=4b+1,∴点M在直线y=4x+1上;(2)如图1,直线y=mx+5交y轴于点B,∴B点坐标为(0,5)又B在抛物线上,∴5=﹣(0﹣b)2+4b+1=5,解得b=2,二次函数的解析是为y=﹣(x﹣2)2+9,当y=0时,﹣(x﹣2)2+9=0,解得x1=5,x2=﹣1,∴A(5,0).由图象,得当mx+5>﹣(x﹣b)2+4b+1时,x的取值范围是x<0或x>5;(3)如图2,∵直线y=4x+1与直线AB交于点E,与y轴交于F,A(5,0),B(0,5)得直线AB的解析式为y=﹣x+5,联立EF,AB得方程组,解得,∴点E(,),F(0,1).点M在△AOB内,1<4b+1<∴0<b<.当点C,D关于抛物线的对称轴对称时,b﹣=﹣b,∴b=,且二次函数图象开口向下,顶点M在直线y=4x+1上,综上:①当0<b<时,y1>y2,②当b=时,y1=y2,③当<b<时,y1<y2.24.【解答】解:(1)△ABC是“等高底”三角形;理由:如图1,过A作AD⊥BC于D,则△ADC是直角三角形,∠ADC=90°,∵∠ACB=30°,AC=6,∴AD=AC=3,∴AD=BC=3,即△ABC是“等高底”三角形;(2)如图2,∵△ABC是“等高底”三角形,BC是“等底”,∴AD=BC,∵△ABC关于BC所在直线的对称图形是△A'BC,∴∠ADC=90°,∵点B是△AA′C的重心,∴BC=2BD,设BD=x,则AD=BC=2x,CD=3x,由勾股定理得AC=x,∴==;(3)①当AB=BC时,Ⅰ.如图3,作AE⊥BC于E,DF⊥AC于F,∵“等高底”△ABC的“等底”为BC,l1∥l2,l1与l2之间的距离为2,AB=BC,∴BC=AE=2,AB=2,∴BE=2,即EC=4,∴AC=2,∵△ABC绕点C按顺时针方向旋转45°得到△A'B'C,∴∠DCF=45°,设DF=CF=x,∵l1∥l2,∴∠ACE=∠DAF,∴==,即AF=2x,∴AC=3x=2,∴x=,CD=x=.Ⅱ.如图4,此时△ABC等腰直角三角形,∵△ABC绕点C按顺时针方向旋转45°得到△A'B'C,∴△ACD是等腰直角三角形,∴CD=AC=2.②当AC=BC时,Ⅰ.如图5,此时△ABC是等腰直角三角形,∵△ABC绕点C按顺时针方向旋转45°得到△A'B'C,∴A'C⊥l1,∴CD=AB=BC=2;Ⅱ.如图6,作AE⊥BC于E,则AE=BC,∴AC=BC=AE,∴∠ACE=45°,∴△ABC绕点C按顺时针方向旋转45°,得到△A'B'C时,点A'在直线l1上,∴A'C∥l2,即直线A'C与l2无交点,综上所述,CD的值为,2,2.。
