勾股定理第一课时PPT课件
合集下载
初中数学《勾股定理》课件

(图中每个小方格代表一个单位面积)
你是怎样得到正方形c 的面积。
P
Q CR
P
Q CR
用了“补”的方法
用了“(1)你能求出正方形R的面积吗?
C A
(2)在图1-2中,正方 形A,B,C中各含有多 少个小方格?它们的面 积各是多少?
B
图1-1
C A
B
图1-2
(3)你能发现图1-1中 三个正方形A,B,C的 面积之间有什么关系吗? 图1-2中呢?
小明妈妈买了一部29英寸(74厘米)的 电视机.小明量了电视机的屏幕后,发现屏幕 只有58厘米长和46厘米宽,他觉得一定是售 货员搞错了.你同意他的想法吗?你能解释这 是为什么吗?
1、小明家住在18层的高楼,一天,他与妈妈去买竹竿。
买最 长的 吧!
快点回家, 好用它凉衣
服。
糟糕,太 长了,放 不进去。
国我家国之是一。最早早在三了千解多勾年前股,定理的 国国家家之之一。一早。在早三千在多三年前千,多年前,周 朝国家数之学一。家早商在高三千就多提年前出,,将一根直 尺国家折之成一。一早个在直三千角多,年前如,果勾等于三, 股国家等之于一。四早,在那三千么多弦年前就,等于五,即 “国家勾之三一。、早股在四三千、多弦年前五,”,它被记 载国家于之我一。国早古在代三千著多名年前的,数学著作 《国家周之髀一。算早经在》三千中多。年前
SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积
C A
B
C
图1-1 A
(1)你能用三角 形的边长表示正方 形的面积吗?
(2)你能发现直 角三角形三边长度 之间存在什么关系 吗?与同伴进行交 流。
B
直角三角形两直角边的
勾股定理(第1课时)精选教学PPT课件

“你走吧。”他说。 她简直不敢相信自己的耳朵。 “快走,不要让我后悔,也许我一分钟之后就后悔了!” 她下了车,走了几步,居然又回头看了他一眼。她永远不知道,是她那个家常电话救了她,那个电话,唤醒了劫匪心中最后仅存的善良,那仅有的一点善良,救了她的命! 她刚走到安全地带,便听到一声枪响,回过头去,她看到他倒在方向盘上。
b
a
证明结y论=0得到定理
勾股定理:
如果直角三角形两直角边分别 为a、b,斜边为c,那么
a2 b2 c2
即 直角三角形两直角边 的平方和等于斜边的平方。
ac
b
勾
弦
股
勾 股
在中国古代,人们把弯曲成直角的手臂的上半部分称为 "勾",下半部分称为"股"。我国古代学者把直角三角形 较短的直角边称为“勾”,较长的直角边称为“股”, 斜边称为“弦”.
清晨,当欢快的小鸟把我从睡中唤醒,我推开窗户,放眼蓝蓝的天,绿绿的草,晶莹的露珠,清清爽爽的早晨,我感恩上天又给予我一个美好的一天。 入夜,夜幕中的天空繁星点点,我打开日记,用笨拙的笔描画着一天的生活感受,月光展露着温柔的笑容,四周笼罩着夜的温馨,我充满了感恩,感谢大地赋予的安宁。
朋友相聚,酒甜歌美,情浓意深,我感恩上苍,给了我这么多的好朋友,我享受着朋友的温暖,生活的香醇,如歌的友情。 走出家门,我走向自然。放眼花红草绿,我感恩大自然的无尽美好,感恩上天的无私给予,感恩大地的宽容浩博。生活的每一天,我都充满着感恩情怀,我学会了宽容,学会了承接,学会了付出,学会了感动,懂得了回报。用微笑去对待每一天,用微笑去对待世界,对待人生,对待朋友,对待困难。所以,每天,我都有一个好心情,我幸福的生活着每一天。
1 = (a2+2ab+b2)
b
a
证明结y论=0得到定理
勾股定理:
如果直角三角形两直角边分别 为a、b,斜边为c,那么
a2 b2 c2
即 直角三角形两直角边 的平方和等于斜边的平方。
ac
b
勾
弦
股
勾 股
在中国古代,人们把弯曲成直角的手臂的上半部分称为 "勾",下半部分称为"股"。我国古代学者把直角三角形 较短的直角边称为“勾”,较长的直角边称为“股”, 斜边称为“弦”.
清晨,当欢快的小鸟把我从睡中唤醒,我推开窗户,放眼蓝蓝的天,绿绿的草,晶莹的露珠,清清爽爽的早晨,我感恩上天又给予我一个美好的一天。 入夜,夜幕中的天空繁星点点,我打开日记,用笨拙的笔描画着一天的生活感受,月光展露着温柔的笑容,四周笼罩着夜的温馨,我充满了感恩,感谢大地赋予的安宁。
朋友相聚,酒甜歌美,情浓意深,我感恩上苍,给了我这么多的好朋友,我享受着朋友的温暖,生活的香醇,如歌的友情。 走出家门,我走向自然。放眼花红草绿,我感恩大自然的无尽美好,感恩上天的无私给予,感恩大地的宽容浩博。生活的每一天,我都充满着感恩情怀,我学会了宽容,学会了承接,学会了付出,学会了感动,懂得了回报。用微笑去对待每一天,用微笑去对待世界,对待人生,对待朋友,对待困难。所以,每天,我都有一个好心情,我幸福的生活着每一天。
1 = (a2+2ab+b2)
北师大版八年级数学上册1.1 第1课时 勾股定理的认识 课件(共23张PPT)

探究新知
1.在纸上画若干个直角三角形,分别测量它们的
三条边,看看三边长的平方之间有怎么样的关系?
c
a
b
直角三角形的两直角边的平方和等于斜边的平方,这就是
著名的“勾股定理”。
如果直角三角形的两条直角边为a、b,斜边为c,那么有
a2+b2=c2.
数学小知识
我国古代称直角三角形的较短的直角边为勾,较长的直角
求 的长.
解:因为 ⊥ ,
所以 ∠ = ∠ = 90∘ .
在 Rt △ 中, 2 = 2 − 2 = 102 − 82 = 36 ,
所以 = 6 .
设 = = ,则 = − 6 .
在 Rt △ 中, 2 = 2 + 2 ,
所以 △ =
1
2
1
2
⋅ = × 25 × 12 = 150 .
6. 如图,直线 上有三个正方形 , , .若 , 的面积分别
为 5 和 11 ,则 的面积为( C )
A. 4
B. 6
C. 16
D. 55
7. 如图,在 △ 中, = , = 10 , ⊥ ,垂足为 , = 8 .
(2) 已知 = 12 , = 16 ,求 .
【解】在 Rt △ 中, ∠ = 90∘ , = 12 , = 16 ,
所以 2 = 2 + 2 = 122 + 162 = 400 .
所以 = 20 .
例2 如图,在 △ 中, ⊥ 于点 ,且 + = 32 ,
因为 ∠ = 90∘ ,所以 2 + 2 = 2 .
《勾股定理》PPT(第1课时)

由上面的例子,我们猜想:
命题1 如果直角三角形的两条直角边长分别为a,b,斜边 长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
ac
b
课程讲授
1 勾股定理
下面让我们跟着以前的数学家们用拼图法来证明这一猜想.
c b a
b-a
证明:∵S大正方形=c2, S小正方形=(b-a)2,
∴S大正方形=4S三角形+S小正方形,
课程讲授 2 勾股定理与图形面积
归纳:与直角三角形三边相连的正方形、半圆及 正多边形、圆都具有相同的结论:两直角边上图 形面积的和等于斜边上图形的面积.本例考查了 勾股定理及半圆面积的求法,解答此类题目的关 键是仔细观察所给图形,面积与边长、直径有平 方关系,就很容易联想到勾股定理.
课程讲授Biblioteka 2 勾股定理与图形面积定有a2+b2=c2.
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
课程讲授
1 勾股定理
几何语言: ∵在Rt△ABC中 ,∠C=90°,
B ac
∟
∴a2+b2=c2(勾股定理).
C
勾股定理揭示了直角三角形三边之间的关系.
bA
课程讲授 1 勾股定理
例 在Rt△ABC中,∠C=90°,AB=10 cm, BC=8 cm,求AC的长.
(1)正方形P的面积是 1 平方厘米; (2)正方形Q的面积是 1 平方厘米; (3)正方形R的面积是 2 平方厘米.
AR P
CQ B
上面三个正方形的面积之间有什么关系? SP+SQ=SR
(图中每一格代表一平方厘米)
课程讲授 1 勾股定理
直角三角形ABC三边长度之间存在什么关系吗? SP=AC2 SQ=BC2 SR=AB2 AC2+BC2=AB2
命题1 如果直角三角形的两条直角边长分别为a,b,斜边 长为c,那么a2+b2=c2.两直角边的平方和等于斜边的平方.
ac
b
课程讲授
1 勾股定理
下面让我们跟着以前的数学家们用拼图法来证明这一猜想.
c b a
b-a
证明:∵S大正方形=c2, S小正方形=(b-a)2,
∴S大正方形=4S三角形+S小正方形,
课程讲授 2 勾股定理与图形面积
归纳:与直角三角形三边相连的正方形、半圆及 正多边形、圆都具有相同的结论:两直角边上图 形面积的和等于斜边上图形的面积.本例考查了 勾股定理及半圆面积的求法,解答此类题目的关 键是仔细观察所给图形,面积与边长、直径有平 方关系,就很容易联想到勾股定理.
课程讲授Biblioteka 2 勾股定理与图形面积定有a2+b2=c2.
勾股定理:直角三角形两直角边的平方和等于斜边的平方.
课程讲授
1 勾股定理
几何语言: ∵在Rt△ABC中 ,∠C=90°,
B ac
∟
∴a2+b2=c2(勾股定理).
C
勾股定理揭示了直角三角形三边之间的关系.
bA
课程讲授 1 勾股定理
例 在Rt△ABC中,∠C=90°,AB=10 cm, BC=8 cm,求AC的长.
(1)正方形P的面积是 1 平方厘米; (2)正方形Q的面积是 1 平方厘米; (3)正方形R的面积是 2 平方厘米.
AR P
CQ B
上面三个正方形的面积之间有什么关系? SP+SQ=SR
(图中每一格代表一平方厘米)
课程讲授 1 勾股定理
直角三角形ABC三边长度之间存在什么关系吗? SP=AC2 SQ=BC2 SR=AB2 AC2+BC2=AB2
《探索勾股定理》勾股定理PPT课件(第1课时)

解:利用勾股定理 a2 + b2 = c2 可以得到c²=100, c=10m
巩固新知
1.求下列直角三角形中未知边的长:
常见整数的平方 (大于10)
12
112 = 121 242 = 576
8
17
5
122 = 144 252 = 625 132 = 169 302 = 900
x
142 = 196 402 =
历史课件: . /kejian/lishi/
c
数是根据圆形和方形的数学道理计算得来的。 圆来自方,而方来自直角三角形,直角三角形是根 据乘法九九表算出来的。如果将一线段折成三段围 成直角三角形,一直角边(勾)为三,另外一直角
边(股)为四,则斜边(弦)就是五。
勾股定理是关于什么图形的定理?
答:关于直角三角形三边的关系
解:∵在Rt△ADC中,AD=12,AC=13(已知), ∴由勾股定理,得CD2=AC2-AD2=132-122=52, ∵CD=5.BC=14(已知), ∴BD=14-5=Hale Waihona Puke . 在Rt△ABD中,由勾股定理,得
AB2=AD2+BD2=122+92=152, ∴AB=15.
课堂小结
如果直角三角形两直角边长分别为a,b,
《周髀算经》曾记载记录着商高和周公的一段对话。
我早就听说您是擅长数 学的人,请问古代伏羲测量天文 制定历法,可没有登天的台阶,又 不能测量大地的尺寸,这数据是
怎么来的呢?
ppt模板: . /moban/
ppt素材: . /sucai/
ppt背景: . /beijing/
ppt图表: . /tubiao/
(2)△ABC的a=6,b=8,则c=10.
巩固新知
1.求下列直角三角形中未知边的长:
常见整数的平方 (大于10)
12
112 = 121 242 = 576
8
17
5
122 = 144 252 = 625 132 = 169 302 = 900
x
142 = 196 402 =
历史课件: . /kejian/lishi/
c
数是根据圆形和方形的数学道理计算得来的。 圆来自方,而方来自直角三角形,直角三角形是根 据乘法九九表算出来的。如果将一线段折成三段围 成直角三角形,一直角边(勾)为三,另外一直角
边(股)为四,则斜边(弦)就是五。
勾股定理是关于什么图形的定理?
答:关于直角三角形三边的关系
解:∵在Rt△ADC中,AD=12,AC=13(已知), ∴由勾股定理,得CD2=AC2-AD2=132-122=52, ∵CD=5.BC=14(已知), ∴BD=14-5=Hale Waihona Puke . 在Rt△ABD中,由勾股定理,得
AB2=AD2+BD2=122+92=152, ∴AB=15.
课堂小结
如果直角三角形两直角边长分别为a,b,
《周髀算经》曾记载记录着商高和周公的一段对话。
我早就听说您是擅长数 学的人,请问古代伏羲测量天文 制定历法,可没有登天的台阶,又 不能测量大地的尺寸,这数据是
怎么来的呢?
ppt模板: . /moban/
ppt素材: . /sucai/
ppt背景: . /beijing/
ppt图表: . /tubiao/
(2)△ABC的a=6,b=8,则c=10.
《勾股定理》PPT优质课件(第1课时)

A. 3
B.3
C. 5
D.5
E
课堂检测
基础巩固题
1. 若一个直角三角形的两直角边长分别为9和12,则斜边的
长为( C)
A.13
B.17
C. 15
D.18
2.若一个直角三角形的斜边长为17,一条直角边长为15,则
另一直角边长为( A )
A.8
B.40
C.50
D.36
3.在Rt△ABC中,∠C=90°,若a︰b=3︰4,c=100,则 a= _6_0___,b = __8_0___.
课堂检测
4.如图,所有的四边形都是正方形,所有的三角形都是直角三角 形,其中最大的正方形的边长为7cm,则正方形A,B,C,D的面 积之和为_____4_9_____cm2 .
C D
B A
7cm
课堂检测
能力提升题
在Rt△ABC中,AB=4,AC=3,求BC的长.
解:本题斜边不确定,需分类讨论:
当AB为斜边时,如图,BC 42 32 7;
形,拼成一个新的正方形.
探究新知 剪、拼过程展示:
b
a ca
朱实
b 朱实 黄实朱实
c 〓b
ba
朱实
a
M a P bb
N
探究新知 “赵爽弦图”
c
朱实
b
朱实
黄实 朱实
a
朱实
证明:∵S大正方形=c2, S小正方形=(b-a)2,
∴S大正方形=4·S三角形+S小正方形,
探究新知
毕达哥拉斯证法:请先用手中的四个全等的直角三角形按图 示进行拼图,然后分析其面积关系后证明吧.
因此设a=x,c=2x,根据勾股定理建立方程得 (2x)2-x2=152,
1勾股定理(第1课时)(教学PPT课件(华师大版))28张
正方形中小方格的个数,你有什么猜想?
1955年希腊发行的一枚纪念邮票.
讲授新课
知识点一 直角三角形三边的关系
视察正方形瓷砖铺成的地面.
(1)正方形P的面积是
1
(2)正方形Q的面积是
1
平方厘米;
(3)正方形R的面积是
2
平方厘米.
平方厘米;
上面三个正方形的面积之间有什么关系?
等腰直角三角形ABC三边长度之间存在什么关系吗?
程.
b
a
b
a
c
c
b
c
c
a
a
b
讲授新课
证明:大正方形的面积=(a+b)2.
四个个全等的直角三角形和小正方形的面积
1
2
2
之和= 4 ab c 2ab c .
2
b
由题可知(a+b)2=2ab+c2,
a
c
化简可得a2+b2=c2.
我们利用拼图的方法,将形的问题
与数的问题结合起来,再进行整式
A的面积
B的面积
C的面积
左图
4
9
13
右图
16
9
25
结论:以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
SA+SB=SC
讲授新课
猜想:两直角边a、b与斜边 c 之间的关系?
A
a
B b
c
a2+b2=c2
C
讲授新课
概念总结
由上面的探索可以发现:对于任意的直角三角形,如果它的两
数学(华东师大版)
八年级 上册
第14章 勾股定理
1955年希腊发行的一枚纪念邮票.
讲授新课
知识点一 直角三角形三边的关系
视察正方形瓷砖铺成的地面.
(1)正方形P的面积是
1
(2)正方形Q的面积是
1
平方厘米;
(3)正方形R的面积是
2
平方厘米.
平方厘米;
上面三个正方形的面积之间有什么关系?
等腰直角三角形ABC三边长度之间存在什么关系吗?
程.
b
a
b
a
c
c
b
c
c
a
a
b
讲授新课
证明:大正方形的面积=(a+b)2.
四个个全等的直角三角形和小正方形的面积
1
2
2
之和= 4 ab c 2ab c .
2
b
由题可知(a+b)2=2ab+c2,
a
c
化简可得a2+b2=c2.
我们利用拼图的方法,将形的问题
与数的问题结合起来,再进行整式
A的面积
B的面积
C的面积
左图
4
9
13
右图
16
9
25
结论:以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
SA+SB=SC
讲授新课
猜想:两直角边a、b与斜边 c 之间的关系?
A
a
B b
c
a2+b2=c2
C
讲授新课
概念总结
由上面的探索可以发现:对于任意的直角三角形,如果它的两
数学(华东师大版)
八年级 上册
第14章 勾股定理
冀教版初中八年级数学上册17-3勾股定理第一课时勾股定理课件

11.(2024江苏扬州邗江期末,16,★★☆)如图,在Rt△ABC中,
AC=4,AB=5,∠C=90°,BD平分∠ABC交AC于点D,则DC的长
3
是2.
解析 在Rt△ABC中,AC=4,AB=5,∠C=90°,∴BC=
A=B2 =3A,C如2图,过52 D 作42 DE⊥AB于点E,∵BD平
分∠ABC,DC⊥BC,∴DC=DE,设DC=DE=x,∵S△BCD+S△ABD=S△ABC,
2
2ab+b2-2ab=a2+b2,∵中间小正方形的边长为c,∴小正方形的
面积为c2,∴a2+b2=c2,∴甲能利用面积验证勾股定理.乙中直
角梯形的面积为 (a =b)(aa2+b) b12+ab1,两个直角三角形
2
22
的面积和为2× 1 ab=ab,则中间等腰直角三角形的面积为1 a2+
2
2
1 b2+ab-ab=1 a12+ b2,∵中间等腰直角三角形的两条直角边
7.(2024四川成都龙泉驿期末)如图,△ABC中,AB=AC,BD⊥AC于 点D,∠BDF=∠BAF=∠C,BD=3,CD=1. (1)求证:∠CBD=∠EDA. (2)求AB的长.
解析 (1)证明:∵BD⊥AC, ∴∠C+∠CBD=∠EDA+∠BDF=90°, ∵∠BDF=∠C,∴∠CBD=∠EDA. (2)设AD=x,则AB=AC=AD+CD=x+1, ∵BD=3,AD2+BD2=AB2,∴x2+32=(x+1)2, 解得x=4,∴AB=x+1=5.
∴1 BC·DC+1 AB·DE1=222解33
北师大版八年级数学上册《1.1.1勾股定理》教学课件(共19张PPT)

例1 高为2.5 m的木梯,架在高为2.4 m的墙上(如图),
这时梯脚与墙的距离是多少?
A
解:在Rt△ABC中,根据勾股定理,得:
BC2=AB2-AC2=2.52-2.42=0.49,
所以BC=0.7.
即梯脚与墙的距离是0.7 m.
C
B
例2 求斜边长为17 cm、一条直角边长为15 cm的直角三 角形的另一边长.
正方形C的面积应该怎么计算呢?
C A
B
图①
➢ 分“割”成若干个直角边为整数的三角形 SC=12×2×3×4+1×1=13;
➢ 把C“补”成边长为5的正方形 SC=5×5-12×2×3×4=13.
观察:
C A
B
图①
正方形A中含有__4__个小正方形,即A的 面积是___4__. 正方形B中含有__9__个小正方形,即B的 面积是___9__. 正方形C中含有_1_3__个小正方形,即C的 面积是__1_3__.
第一章 勾股定理
1.1 探索勾股定理
第1课时 勾股定理
学习目标
1.经历探索勾股定理的过程,了解勾股定理的探 究方法;
2.掌握勾股定理,并能运用勾股定理解决一些简 单问题.
新知引入
一个直角三角形的两条直角边长分别是3和4,你 知道它的第三边长吗?
实际上,利用勾股定理我们可以很容易地解决这个问题. 勾股定理是一个古老的定理,人类很早就发现了这个定理.
观察:
A'
C'
B'
图②
正方形A'中含有__1_6_个小正方形,即 A'的面积是__1_6__.
正方形B'中含有__9__个小正方形,即 B'的面积是__9___.
正方形C'中含有__2_5_个小正方形,即 C'的面积是__2_5__.
苏科版初中八年级数学上册3-1勾股定理第一课时勾股定理课件

圆的面积S2= 9 π,以BC为直径的半圆的面积S3=25 π,S△ABC=6,
8
8
∴S阴影=S1+S2+S△ABC-S3=6,故选A.
13.(2023江苏南京中考,5,★☆☆)我国南宋数学家秦九韶的 著作《数书九章》中有一道问题:“问沙田一段,有三斜,其 小斜一十三里,中斜一十四里,大斜一十五里.里法三百步,欲 知为田几何?”问题大意:在△ABC中,AB=13里,BC=14里,AC =15里,则△ABC的面积是 ( C ) A.80平方里 B.82平方里 C.84平方里 D.86平方里
解析 (1)证明:∵BD⊥AC, ∴∠C+∠CBD=90°=∠EDA+∠BDF, ∵∠BDF=∠C,∴∠CBD=∠EDA. (2)设AD=x,则AB=AC=AD+CD=x+1, ∵BD=3,AD2+BD2=AB2,∴x2+32=(x+1)2, 解得x=4,∴AB=x+1=5.
能力提升全练
11.(情境题·中华优秀传统文化)(2023江苏苏州姑苏期中,5,★ ★☆)勾股定理是人类最伟大的科学发现之一,在我国古算书 《周髀算经》中早有记载.如图1,以直角三角形的各边为边 分别向外作正方形,再把较小的两个正方形按如图2所示的 方式放置在最大正方形内.若知道图中阴影部分的面积,则一 定能求出 ( C )
8.(2022江苏盐城校级期末)若一个直角三角形的两边长分别 为4和5,则第三条边长的平方为 9或41 . 解析 当5为直角边长时,第三条边长的平方为42+52=41;当5 为斜边长时,第三条边长的平方为52-42=9.故答案为9或41.
9.如图,在由边长为1的小正方形组成的网格中,A、B、C均 在格点上,求AB2-CA2的值.
(精选幻灯片)勾股定理ppt课件

2 2 22
“总统证法”. 比较上面二式得 c2=a2+b2
16
1.求下列图中表示边的未知数x、y、z的值.
81 144
144 169
z
625 576
①
②
③
17
做一做:
A
625
P
C
B
400
P的面积 =___2_2__5________ AB=_2__5_______ BC=__2_0_______
b c
a2+b2=c2吗?
• 1881年,伽菲尔 德就任美国第二
A b 1 E aB ∵ S梯形ABCD= 2 a+b2
十任总统.后来, 1
人们为了纪念他 对勾股定理直观、 简捷、易懂、明
= (a2+2ab+b2) 2
又∵ S梯形 ABCD=S
AED+S
EBC+S
CED
了的证明,就把 这一证法称为
1 1 11 = ab+ ba+ c2= (2ab+c2)
33
34
C A
(2)在图2-2中,正 方形A,B,C中各含 有多少个小方格?它 们的面积各是多少?
B C
图2-1
A
(3)你能发现图2-1 中三个正方形A,B, C的面积之间有什么
B 图2-2
关系吗?
(图中每个小方格代表一个单位面积) SA+SB=SC
即:两条直角边上的正方形面积之和等于
斜边上的正方形的面积
3
s1 s2
s3
返 拼回 图 4
合作 & 交S流1+☞S2=S3
a等²+腰a直²=角c三²角形两直角边
“总统证法”. 比较上面二式得 c2=a2+b2
16
1.求下列图中表示边的未知数x、y、z的值.
81 144
144 169
z
625 576
①
②
③
17
做一做:
A
625
P
C
B
400
P的面积 =___2_2__5________ AB=_2__5_______ BC=__2_0_______
b c
a2+b2=c2吗?
• 1881年,伽菲尔 德就任美国第二
A b 1 E aB ∵ S梯形ABCD= 2 a+b2
十任总统.后来, 1
人们为了纪念他 对勾股定理直观、 简捷、易懂、明
= (a2+2ab+b2) 2
又∵ S梯形 ABCD=S
AED+S
EBC+S
CED
了的证明,就把 这一证法称为
1 1 11 = ab+ ba+ c2= (2ab+c2)
33
34
C A
(2)在图2-2中,正 方形A,B,C中各含 有多少个小方格?它 们的面积各是多少?
B C
图2-1
A
(3)你能发现图2-1 中三个正方形A,B, C的面积之间有什么
B 图2-2
关系吗?
(图中每个小方格代表一个单位面积) SA+SB=SC
即:两条直角边上的正方形面积之和等于
斜边上的正方形的面积
3
s1 s2
s3
返 拼回 图 4
合作 & 交S流1+☞S2=S3
a等²+腰a直²=角c三²角形两直角边
17.1勾股定理(第1课时)课件(共23张PPT)

让我们一起再探究:等腰直角三角形三边关系
C A B 9 C A B 图2-2 4 9 4 18 8
图2-1
(图中每个小方格代表一个单位面积)
C A B 图2-1 A B
S正方形c
C
1 4 3318 2
图2-2
(图中每个小方格代表一个单位面积)
(单位面积)
分“割”成若干个直 角边为整数的三角形
弦 勾
股
图1-1
漂亮的勾股树
活动 2
相传2500年前,毕达哥拉斯有一次 在朋友家里做客时,发现朋友家用砖铺 成的地面中反映了直角三角形三边的某 种数量关系.
我们也来观察右 图中的地面,看看有 什么发现?
数学家毕达哥拉斯的发现:
A
B
C
A、B、C的面积有什么关系? SA+SB=SC 直角三角形三边有什么关系? 两直边的平方和等于斜边的平方
设:直角三角形的三边长分别是a、b、c
猜想:两直角边a、b与斜边c 之间的关系? A a B b
Sa+Sb=Sc
c
C
2 2 2 a +b =c
b
a
c b (a+b )2
证 明 二
a
c
c
1 = c 4 ab 2
2
a2 + b2 + 2ab = c2+2ab
b a
c
b
a
可得: a2 + b2 = c2
C A B 图2-1 A B
S正方形c
C
1 6 2
2
1 8(单位面积)
图2-2
(图中每个小方格代表一个单位面积)
把C“补” 成边长为6的 正方形面积的一半
八年级数学《勾股定理》第一课时课件

2
c a
=2ab+b2-2ab+a2
b
=a2+b2
∴a2+b2=c2
c a
b
c a
b
c a
b
我探索、我验证!
大正方形的面积可以表示为 (a+b)2 ;
也可以表示为
c2 +4• ab
2
c a
b
c a
b
c a
b
c a
b
∵
(a+b)2
=
c2
+4•
ab 2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
这就是本届大会 会徽的图案.
这个图案被称为“赵爽弦 图”, 是我国汉代数学家赵 爽在证明勾股定理时用到的.
你听说过勾股定理吗?
我操作 ,我猜想!
请同学们以四人一小组合作完成下列问题,其中 每组选两名同学动手操作,另两名同学负责监督整个 操作过程确保准确无误,最后每组派一名同学代表本 组发言。
(1)分别在方格纸上作两个直角三角形,使其两直角 边分别是3厘米和4厘米,5厘米和12厘米。
勾股定理 (毕达哥拉斯定理)
直角三角形两直角边的平方 和等于斜边的平方.
弦c b股
┏
勾a
a2+b2=c2
走进勾股世界
两千两多千多年年前前,,古古希希腊有腊个有哥拉个毕达哥拉斯 学斯学派派,,他他们们首首先发先现发了勾现股了定勾理,股因定此 理,因此在 国在国外外人人们们通通常常称勾称股勾定理股为定毕理达哥为拉毕斯 达哥拉斯定 理定理。。为为了了纪纪念念毕达毕哥达拉斯哥学拉派斯,1学95派5 ,1955年 希年希腊腊曾曾经经发发行行了一了枚一纪念枚票纪。念邮票。
c a
=2ab+b2-2ab+a2
b
=a2+b2
∴a2+b2=c2
c a
b
c a
b
c a
b
我探索、我验证!
大正方形的面积可以表示为 (a+b)2 ;
也可以表示为
c2 +4• ab
2
c a
b
c a
b
c a
b
c a
b
∵
(a+b)2
=
c2
+4•
ab 2
a2+2ab+b2 = c2 +2ab
∴a2+b2=c2
这就是本届大会 会徽的图案.
这个图案被称为“赵爽弦 图”, 是我国汉代数学家赵 爽在证明勾股定理时用到的.
你听说过勾股定理吗?
我操作 ,我猜想!
请同学们以四人一小组合作完成下列问题,其中 每组选两名同学动手操作,另两名同学负责监督整个 操作过程确保准确无误,最后每组派一名同学代表本 组发言。
(1)分别在方格纸上作两个直角三角形,使其两直角 边分别是3厘米和4厘米,5厘米和12厘米。
勾股定理 (毕达哥拉斯定理)
直角三角形两直角边的平方 和等于斜边的平方.
弦c b股
┏
勾a
a2+b2=c2
走进勾股世界
两千两多千多年年前前,,古古希希腊有腊个有哥拉个毕达哥拉斯 学斯学派派,,他他们们首首先发先现发了勾现股了定勾理,股因定此 理,因此在 国在国外外人人们们通通常常称勾称股勾定理股为定毕理达哥为拉毕斯 达哥拉斯定 理定理。。为为了了纪纪念念毕达毕哥达拉斯哥学拉派斯,1学95派5 ,1955年 希年希腊腊曾曾经经发发行行了一了枚一纪念枚票纪。念邮票。
第1课时勾股定理微课ppt课件
如图我国古代证明该命题 的“赵爽弦图”.
赵爽指出:按弦图,又可以
勾股相乘为朱实二,倍之为
朱实四.以勾股之差自相乘为 中黄实.加差实,亦成弦实.
赵爽弦图
思考 你是如何理解的?你会证明吗?
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的
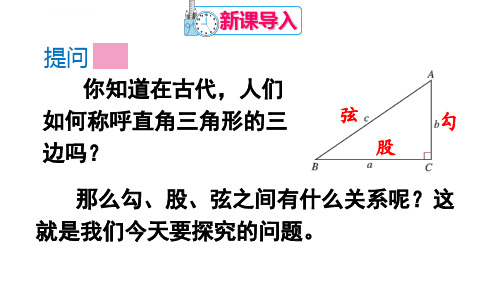
如何称呼直角三角形的三 边吗?
弦 股
勾
那么勾、股、弦之间有什么关系呢?这 就是我们今天要探究的问题。
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
C'
A面、积B/格、C的9面积有25什么关3系4 ? SA+SB=SC
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
思考
等腰直角三角形三条边长度 之间有怎样的特殊关系?
小结
等腰直角三角形斜边的平 方等于两直角边的平方和.
证明
赵爽弦图
小正方形的面积= (a-b)2
=c2-4×
1 2
ab
即c2=a2+b2.
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
赵爽指出:按弦图,又可以
勾股相乘为朱实二,倍之为
朱实四.以勾股之差自相乘为 中黄实.加差实,亦成弦实.
赵爽弦图
思考 你是如何理解的?你会证明吗?
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的
如何称呼直角三角形的三 边吗?
弦 股
勾
那么勾、股、弦之间有什么关系呢?这 就是我们今天要探究的问题。
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
C'
A面、积B/格、C的9面积有25什么关3系4 ? SA+SB=SC
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
思考
等腰直角三角形三条边长度 之间有怎样的特殊关系?
小结
等腰直角三角形斜边的平 方等于两直角边的平方和.
证明
赵爽弦图
小正方形的面积= (a-b)2
=c2-4×
1 2
ab
即c2=a2+b2.
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
浙教版数学八上2.7探索勾股定理(1) 课件(共23张PPT)

C
A
A
a
图1
a
C
B
图2
合作学习
大正方形的面积:c²
小正方形面积:(b-a)²
阴影部分面积:4× ab
1
2
它们之间的关系是: c 4 ab (b a )
2
2
化简得: a2+b2=c2
直角三角形三边有下面的关系:
直角三角形两条直角边的平方和等于斜边的平方
讲解新知
勾股定理: 直角形三角形两条直角边的平方和等于斜边的平方.
2.勾股定理
3.勾股定理的应用
等,则E站应建在距A站______km处.
10
即时演练
解:∵C、D两村到E站距离相等,∴CE=DE,
在Rt△DAE和Rt△CBE中,DE2=AD2+AE2,CE2=BE2+BC2,
∴AD2+AE2=BE2+BC2.
设AE为x,则BE=25-x,
将BC=10,DA=15代入关系式为x2+152=(25-x)2+102,
A
∴AB=130(mm)
答:两孔中心A,B之间的距离
90
B
C
40
为130mm
160
即时演练
m
铁路上A、B两站(视为直线上两点)相距25km,C、D为
两村庄(视为两个点),DA⊥AB于A,CB⊥AB于B(如
图),已知DA=15km,CB=10km,现在要在铁路AB上建
设一个土特产品收购站E,使得C、D两村到E站的距离相
∴S△ABC= ×BC×AC=6,
∴AC=4(cm).
∵BC2+AC2=AB2,
1.1勾股定理_1PPT课件(沪科版)

2.勾股定理的适用条件: 直角三角形,它反应了直角三角形三边的关系,
即已知直角三角形两边长可求第三边长.对于非直 角三角形问题,可根据图形特征构造直角三角形.
3.由勾股定理的基本关系式: a2+b2=c2可得到一些变形关系式: c2=a2+b2=(a+b)2-2ab= (a-b)2 + 2ab ; a2=c2-b2=(c+b)(c-b)等.
3和4,则第三边长为( D )
A.5
B. 7 C. 5 D.5或 7
知识点 2 勾股定理与图形面积
知2-讲
1.命题:如果直角三角形的两条直角边长分别为a, b,斜边长为c,那么a2+b2=c2.
2.常用证法:利用拼图法,通过求面积来验证;这 种方法以数形转换为指点思想、图形拼补为手段, 以各部分面积之间的关系为根据而到达目的.
知2-讲
(1)如图①,△DEF为直角三角形,正方形 P的
面积为9,正方形Q的面积为15,则正方形
M的面积为________;
知2-讲
(2)如图②,分别以直角三角形ABC的三边长为直径 向三角形外作三个半圆,则这三个半圆形的面积 之间的关系式是________; (用图中字母表示)
知2-讲
(3)如图③,如果直角三角形两直角边的长分别为3 和4,分别以直角三角形的三边长为直径作半圆, 请你利用(2)中得出的结论求阴影部分的面积.
知1-导
探究 在行距、列
距都是1的方格网
中,任意作出几
个 以格点为顶点
的直角三角形,
分别以三角形的各边为正方形的一边,向形外作正方形,
如图.并以 S1, S2与S3分别表示几个正方形的面积.
视察图(1),并填写:
视察图(2),并填写:
知1-导
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AB = AC2 BC2 5.4122.162 4.96(米)
答:梯子上端A到墙的底端B的距离AB长约4.96米。
试一试:
1、如图:一个高3 米,宽4 米的大门,需在相对角
的顶点间加一个加固木板,则木板的长为 ( C )
A.3 米 B.4 米 C.5米 D.6米
3
4
试一试:
2、隔湖有两点A、B,从与BA方向成直
角 的BC方向上的点C测得CA=13米,CB=12
米,则AB为
(A)
A.5米 B.12米 C.10米 D.13米
A
13
?
C 12 B
试一试:
3、一个直角三角形的三边长为三个连续
偶数,则它的三边长分别为
( B)
A 2、4、6
B 6、8、10
C 4、6、8
D 8、10、12
试一试:
4、求下列2个三角形中的第三条边的长。
a =
B
c b
a
A
D
c2
证法(三) 总统证法
a
伽菲尔德的证明方法.1881年, 伽菲尔德就任美国第二十任总统后, 人们为了纪念他对勾股定理的证明, 就称这一证法称为“总统”证法。
∟
bc
½(a + b)(b + a) = ½c2 + 2(½ab) ½a2 + ab + ½b2 = ½c2 + ab
a2 + b2 = c2
同学们,我们也来 观察图中的地面, 看看你能发现什么? 是否和大哲学家有 同样的发现呢?
你能发 现图中 的等腰 直角三 角形有 什么性 质吗?
A
B
C
观察 & 发现
C A
B
(1)观察图形
正方形A中含有 __9_个小方格即A的 面积是位面积--9----
正方形B中含有 个小方格,即B的 面积是__9 个单位 面积---9---
正方形C中含 有18 个小方格, 即C的面积是_1_8__ 个单位面积。
是不是所有的直角三角形都有两直边的平方和等于斜边的平方
B
A C
A的面 B的面积 C的面 积(单位 (单位长 积(单位 长度) 度) 长度)
图2 4 9 13
图2
C
图3 9 25 34
A
A、B、 C面积 关系
sA+sB=sC
B 图3
3、学了本节课后我们有什么感想?
很多的数学结论存在于平常的生活中,需要我们用数学 的眼光去观察、思考、发现,这节课我们还受到了数学文化 辉煌历史的教育。
即直角三角形两直角边的平方和等于斜边的平方.
a2 c2 c2
+ -
b2 b2 a2
=c2
=a2 =b2
勾a
弦
c
股b
在西方又称毕达哥拉斯定理!
通过探究我们得到这样的结论 a
c
如果直角三角形的两直角边长分 别为a、b,斜边为c,那么a2+b2=c2. b
这个命题如何证明呢?
试一试,用直角边分别为a b,斜边为c的直角三角
a
c b
图1
ca b
图2
证明:如图1 S大正方形=2ab+c2
S大正方形=(a+b)2
即(a+b)2=2ab+c2 ∴a2+b2=c2 第二种证法
证明:如图2
S大正方形=c2 S大正方形=2ab+(a-b)2
2ab+(a-b)2 =c2
∴a2+
b a2+ b2
D
C
B
A
2、 蚂蚁沿图中的折线从A点爬到D点,一共
爬了多少厘米?(小方格的边长为1厘米)
A
G
B
E
C
F
D
回顾与思考
1、本节课我们经历了怎样的过程?
经历了从实际问题引入数学问题然后发现定理,再到探 索定理,最后学会验证定理及应用定理解决实际问题的过程。
2、本节课我们学到了什么?
通过本节课的学习我们不但知道了著名的勾股定理,还 知道从特殊到一般的探索方法及借助于图形的面积来探索、 验证数学结论的数形结合思想。
直角三 两直角边的平方和
角形三 边关系
等于斜边的平方
勾 股
在中国古代,人们把弯曲成直角的手臂的上半部分称为 "勾",下半部分称为"股"。我国古代学者把直角三角形 较短的直角边称为“勾”,较长的直角边称为“股”, 斜边称为“弦”.
勾股定理
如果直角三角形两直角边分别为a,b,斜边
为c,那么 a2 + b2 = c2
形能拼成哪些图形?
ba
a bc
c bc a
a
我们用下面的图形的来证明直角三角形的三边关系
a2+b2=c2
a
证明:S大正方形=a2+b2+2ab
bc
S大正方形=2ab+c2 ∵S大正方形= S大正方形
a bc
∴a2+b2+2ab =2ab+c2 ∴a2+b2=c2 毕达哥拉斯证法 经过证明被确认为正确的命题叫做 定理.我们把它称为勾股定理.
18.1.1 勾股定理
相传2500年前,古希腊著名数学家毕达哥拉斯 从朋友家的地砖铺成的地面上找到了答案,同学们 看看图中有没有等腰直角三角形,从中你能找到答 案吗?
A
B
C
A
B
C
A、B、C的面积有什么关系? 等腰直角三角形三边有什么 特殊关系? 以等腰直角三角形两直角边为边长的小正方形的面积 的和,等于以斜边为边长的正方形的面积.即SA+SB=SC 两直边的平方和等于斜边的平方
c=? b=2
a=1
c=17
a=15
b=?
已知△ABC中,∠C=Rt ∠,AB=c,
BC=a,AC=b.
B
⑴如果a=12,c=13,求b;
a
c
⑵如果c=34, a∶b=8∶15,
求a,b.
C┓ b
A
考一考:
1、 在我国古代数学著作 《九章算术》中记载了一道 有趣的问题,这个问题的意 思是:有一个水池,水面是 一个边长为10尺的正方形,在 水池的中央有一根新生的芦 苇,它高出水面1尺,如果把 这根芦苇垂直拉向岸边,它 的顶端恰好到达岸边的水面, 请问这个水池的深度和这根 芦苇的长度各是多少?
∟
c a
b
你还有其他证明 方法吗?
想一想:
1、已知:a=3, b=4,求c 2、已知: c =10,a=6,求b
c
ba
3、已知: c =13,a=5,求阴影总分面积
4 、小明妈妈买了一部29英寸
c
(74厘米)的电视机.小明量了电 a
视机的屏幕后,发现屏幕只有58
厘米长和46厘米宽,他觉得一定
是售货员搞错了.你同意他的想法
吗?你能解释这是为什么吗? 46厘米
58厘米
5、如图将长为5.41米的梯子AC斜靠在墙上,BC长
为2.16米,求梯子上端A到墙的底端B的距离AB(精确
到0.01米)
分析:先把实际问题转化成数学问题。
已知:AC = 5.41 , BC = 2.16 且 ∠B =
求:AB的长。
90º
解:在Rt⊿ABC中,∠ABC = 90º , BC = 2.16 , CA = 5.41 根据勾股定理得:
答:梯子上端A到墙的底端B的距离AB长约4.96米。
试一试:
1、如图:一个高3 米,宽4 米的大门,需在相对角
的顶点间加一个加固木板,则木板的长为 ( C )
A.3 米 B.4 米 C.5米 D.6米
3
4
试一试:
2、隔湖有两点A、B,从与BA方向成直
角 的BC方向上的点C测得CA=13米,CB=12
米,则AB为
(A)
A.5米 B.12米 C.10米 D.13米
A
13
?
C 12 B
试一试:
3、一个直角三角形的三边长为三个连续
偶数,则它的三边长分别为
( B)
A 2、4、6
B 6、8、10
C 4、6、8
D 8、10、12
试一试:
4、求下列2个三角形中的第三条边的长。
a =
B
c b
a
A
D
c2
证法(三) 总统证法
a
伽菲尔德的证明方法.1881年, 伽菲尔德就任美国第二十任总统后, 人们为了纪念他对勾股定理的证明, 就称这一证法称为“总统”证法。
∟
bc
½(a + b)(b + a) = ½c2 + 2(½ab) ½a2 + ab + ½b2 = ½c2 + ab
a2 + b2 = c2
同学们,我们也来 观察图中的地面, 看看你能发现什么? 是否和大哲学家有 同样的发现呢?
你能发 现图中 的等腰 直角三 角形有 什么性 质吗?
A
B
C
观察 & 发现
C A
B
(1)观察图形
正方形A中含有 __9_个小方格即A的 面积是位面积--9----
正方形B中含有 个小方格,即B的 面积是__9 个单位 面积---9---
正方形C中含 有18 个小方格, 即C的面积是_1_8__ 个单位面积。
是不是所有的直角三角形都有两直边的平方和等于斜边的平方
B
A C
A的面 B的面积 C的面 积(单位 (单位长 积(单位 长度) 度) 长度)
图2 4 9 13
图2
C
图3 9 25 34
A
A、B、 C面积 关系
sA+sB=sC
B 图3
3、学了本节课后我们有什么感想?
很多的数学结论存在于平常的生活中,需要我们用数学 的眼光去观察、思考、发现,这节课我们还受到了数学文化 辉煌历史的教育。
即直角三角形两直角边的平方和等于斜边的平方.
a2 c2 c2
+ -
b2 b2 a2
=c2
=a2 =b2
勾a
弦
c
股b
在西方又称毕达哥拉斯定理!
通过探究我们得到这样的结论 a
c
如果直角三角形的两直角边长分 别为a、b,斜边为c,那么a2+b2=c2. b
这个命题如何证明呢?
试一试,用直角边分别为a b,斜边为c的直角三角
a
c b
图1
ca b
图2
证明:如图1 S大正方形=2ab+c2
S大正方形=(a+b)2
即(a+b)2=2ab+c2 ∴a2+b2=c2 第二种证法
证明:如图2
S大正方形=c2 S大正方形=2ab+(a-b)2
2ab+(a-b)2 =c2
∴a2+
b a2+ b2
D
C
B
A
2、 蚂蚁沿图中的折线从A点爬到D点,一共
爬了多少厘米?(小方格的边长为1厘米)
A
G
B
E
C
F
D
回顾与思考
1、本节课我们经历了怎样的过程?
经历了从实际问题引入数学问题然后发现定理,再到探 索定理,最后学会验证定理及应用定理解决实际问题的过程。
2、本节课我们学到了什么?
通过本节课的学习我们不但知道了著名的勾股定理,还 知道从特殊到一般的探索方法及借助于图形的面积来探索、 验证数学结论的数形结合思想。
直角三 两直角边的平方和
角形三 边关系
等于斜边的平方
勾 股
在中国古代,人们把弯曲成直角的手臂的上半部分称为 "勾",下半部分称为"股"。我国古代学者把直角三角形 较短的直角边称为“勾”,较长的直角边称为“股”, 斜边称为“弦”.
勾股定理
如果直角三角形两直角边分别为a,b,斜边
为c,那么 a2 + b2 = c2
形能拼成哪些图形?
ba
a bc
c bc a
a
我们用下面的图形的来证明直角三角形的三边关系
a2+b2=c2
a
证明:S大正方形=a2+b2+2ab
bc
S大正方形=2ab+c2 ∵S大正方形= S大正方形
a bc
∴a2+b2+2ab =2ab+c2 ∴a2+b2=c2 毕达哥拉斯证法 经过证明被确认为正确的命题叫做 定理.我们把它称为勾股定理.
18.1.1 勾股定理
相传2500年前,古希腊著名数学家毕达哥拉斯 从朋友家的地砖铺成的地面上找到了答案,同学们 看看图中有没有等腰直角三角形,从中你能找到答 案吗?
A
B
C
A
B
C
A、B、C的面积有什么关系? 等腰直角三角形三边有什么 特殊关系? 以等腰直角三角形两直角边为边长的小正方形的面积 的和,等于以斜边为边长的正方形的面积.即SA+SB=SC 两直边的平方和等于斜边的平方
c=? b=2
a=1
c=17
a=15
b=?
已知△ABC中,∠C=Rt ∠,AB=c,
BC=a,AC=b.
B
⑴如果a=12,c=13,求b;
a
c
⑵如果c=34, a∶b=8∶15,
求a,b.
C┓ b
A
考一考:
1、 在我国古代数学著作 《九章算术》中记载了一道 有趣的问题,这个问题的意 思是:有一个水池,水面是 一个边长为10尺的正方形,在 水池的中央有一根新生的芦 苇,它高出水面1尺,如果把 这根芦苇垂直拉向岸边,它 的顶端恰好到达岸边的水面, 请问这个水池的深度和这根 芦苇的长度各是多少?
∟
c a
b
你还有其他证明 方法吗?
想一想:
1、已知:a=3, b=4,求c 2、已知: c =10,a=6,求b
c
ba
3、已知: c =13,a=5,求阴影总分面积
4 、小明妈妈买了一部29英寸
c
(74厘米)的电视机.小明量了电 a
视机的屏幕后,发现屏幕只有58
厘米长和46厘米宽,他觉得一定
是售货员搞错了.你同意他的想法
吗?你能解释这是为什么吗? 46厘米
58厘米
5、如图将长为5.41米的梯子AC斜靠在墙上,BC长
为2.16米,求梯子上端A到墙的底端B的距离AB(精确
到0.01米)
分析:先把实际问题转化成数学问题。
已知:AC = 5.41 , BC = 2.16 且 ∠B =
求:AB的长。
90º
解:在Rt⊿ABC中,∠ABC = 90º , BC = 2.16 , CA = 5.41 根据勾股定理得:
