实验七 分布滞后模型与自回归模型及格兰杰因果关系检验综述
九章分布滞后和自回归模型-资料

例如人们获得后通常不会立即全部花掉,而是 会在以后一个阶段分次花费,因此收入对人们 消费的影响往往有时间滞后和持续的影响。
滞后效应对经济问题的影响非常重要。要准确 把握经济关系,特别是长期动态关系,避免预 测和决策偏差,必须重视这种滞后效应。
第九章 分布滞后和自回归模型
前言
前面各章基本上没有区别所用的数据究竟是时 间序列数据还是截面数据。但这两类数据在计 量经济分析中还是有明显差异的。
时间序列数据是经济运动动态过程的数量记录, 包含不同于横截面数据的特殊信息,可以进行 动态计量分析,但时间序列数据的内在联系也 可能给计量经济分析带来问题和困难。
考伊克方法形式上是针对无限分布滞后模型: Y t 0 X t 1 X t 1 2 X t 2 t 但由于一般来说随着滞后期的增加滞后效应总
是不断减小,滞后期很大的项非常接近0。因 此无限分布滞后模型与滞后长度较长的有限分 布滞后模型并没有很大差别,考伊克方法也可 处理有限分布滞后模型,特别是滞后长度较长 的有限分布滞后模型。
一般来说,常见的滞后参数变化模式的 m在1到4之间。
确定了滞后参数多项式以后,将这些多 项式代入分布滞后模型进行变换。
以m=2的情况为例。
把i a0a1ia2i2代入前述分布滞后模
型,可得:
K
Yt (a0a1ia2i2)Xtit
i0
K
滞后效应可以直接通过滞后作用的描述来反映。 例如若某地消费者平均来说在获得20000元收
入后,会在当年消费掉8000元,下一年消费 6000元,再下一年又消费4000元,余下2000 元储蓄起来以备不时之需,那么意味着当年收 入一般对当年消费会产生40%的作用,对下年 消费会产生30%的作用,对再下年消费则有 20%的作用。
第七章_分布滞后模型与自回归模型总结

段时间才能显示出来。只有经过一段时间以后,支出对利率
的反应增强,投资、进出口和消费才会不断上升,货币政 策才最终促使GDP增加。通常,货币扩张对GDP影响的最 高点可能是在政策实施以后的一到两年间达到。
思考
在现实经济活动中,滞后现象是普遍存
在的,这就要求我们在做经济分析时应该考
虑时滞的影响。
怎样才能把这类时间上滞后的经济关系
纳入计量经济模型呢?
第 七 章 分布滞后模型与自回归模型
本章主要讨论:
●滞后效应与滞后变量模型 ●分布滞后模型的估计 ●自回归模型的构建 ●自回归模型的估计
第一节 滞后效应与滞后变量模型
本节基本内容:
●经济活动中的滞后现象 ●滞后效应产生的原因 ●滞后变量模型
一、滞后变量模型
通常把这种过去时期的,具有滞后作用的变量 叫做滞后变量(Lagged Variable),含有滞后变量 的模型称为滞后变量模型。 滞后变量模型考虑了时间因素的作用,使静态 分析的问题有可能成为动态分析。含有滞后解释变 量的模型,又称动态模型(Dynamical Model)。
第一步,阿尔蒙变换
对于分布滞后模型
Yt i X t i t
i 0 s
取: 2 m i 0 1i 2i mi i 0,1, 2, , s ; m s
此式称为阿尔蒙多项式变换(图7.2)。
将阿尔蒙多项式变换代入分布滞后模型并整理, 模型变为如下形式 其中
有限期的分布滞后模型,OLS会遇到如下问题:
1、没有先验准则确定滞后期长度; 2、如果滞后期较长,将缺乏足够的自由度进行 估计和检验; 3、同名变量滞后值之间可能存在高度线性相关, 即模型存在高度的多重共线性。
第七章分布滞后模型与自回归模型

然后分别估计如下经验加权模型。
19
回归分析结果整理如下 模型一: Yˆt 66.60404 1.071502 Z1t
(3.6633) (50.9191) R2 0.994248 DW 1.440858
F 2592
模型二: Yˆt = -133.1988 +1.3667 Z2t
(-5.029) (37.35852) R2 = 0.989367 DW = 1.042935
33
库伊克变换的缺陷
1.它假定无限滞后分布呈几何递减滞后结构。 这种假定对某些经济变量可能不适用,如固定资 产投资对总产出影响的滞后结构就不是这种类型。 2.库伊克模型的随机扰动项形如
ut* = ut - λut-1
说明新模型的随机扰动项存在一阶自相关,且与 解释变量相关。
34
3.将随机变量作为解释变量引入了模型,不一 定符合基本假定。 4.库伊克变换是纯粹的数学运算结果,缺乏经 济理论依据。 这些缺陷,特别是第二个缺陷,将给模型的参 数估计带来定困难。
则库伊克模型(7.10)式变为 Yt = α* + β0* X t + β1*Yt-1 + ut*
这是一个一阶自回归模型。
(7.12)
32
库伊克变换的优点
1.以一个滞后被解释变量代替了大量的滞后解 释变量,使模型结构得到极大简化,最大限度 地保证了自由度,解决了滞后长度难以确定的 问题; 2.滞后一期的被解释变量与 X t 的线性相关程 度将低于 X的各滞后值之间的相关程度,从而 在很大程度上缓解了多重共线性。
38
用数学式子表示就是
X
* t
=
X
* t -1
+
γ(
实验8分布滞后模型与自回归模型.docx

计量经济学上机操作 8实验八 分布滞后模型与自回归模型及格兰杰因果关系检验一 实验目的:掌握分布滞后模型与自回归模型的估计与应用,掌握格兰杰因果关系检验方法,熟 悉EViews 的基本操作。
二 实验要求:应用教材P168例子522案例,利用阿尔蒙法做有限分布滞后模型的估计;应用教材P173例子5.2.3案例做分布滞后模型与自回归模型的估计;应用教材 P176例子5.2.4案例额做格兰杰因果关系检验。
三实验原理:普通最小二乘法、阿尔蒙法、格兰杰因果关系检验、 DW 检验、LM 检验。
四预备知识:最小二乘法估计的原理、t 检验、拟合优度检验、阿尔蒙法、多项式近似。
五实验步骤【案例1】分布滞后模型与阿尔蒙法为了研究|1975――2002年期间中国电力基本建设投资与发电量的关系,我们可以对教材 P168例5.2.2采用经验加权法估计分布滞后模型。
尽管经验加权法具有一些优点, 但是设置权数的主观随意性较大,要求分析者对实际问题的特征有比较透彻的了解。
1建立工作工作文件并录入数据,如图8.1.图8.12模型估计与检验为了测算电力行业固定资产投资与发电量增长之间的变动关系,我们拟建立如下双对数线性模 型:slnY t = a +刀6 In Xt-i+ 他,i=0由于无法预知电力行业基本建设投资对发电量影响的时间滞后期,需要取不同的时间滞后期进 行试算。
经过试算发现,在「2阶阿尔蒙多项式变换下,滞后期数取到第 7期估计结果的经验意义 比较合理(即应该参数前面为正号,而且通过 t 检验,AIC,SC 值达到最小)。
针对所研究的问题,为 了进行比较分析,我们给出以下几个分布滞后模型无约束限制的估计结果,如表T 8.1所示(例如, 在2阶阿尔蒙多项式变换下,滞后期数取到第7期的估计结果由图8.2得到)。
表8.1多个无约束限制的分布滞后模型估计结果图8.2图8.35 2 0.9 94123-3.364143 -3.166666 无 6 2 0.9 94648-3.520954 -3.32258 有 7 2 0.9 94404-3.555819-3.356862 有 8 2 0.9 93686-3.525502 -3.326355 有 9 2 0.9 92580-3.464352-3.265523 有 10 20.991531-3.445304-3.247444无从表8.1可以看出,滞后变量参数有经济意义的只有(3,2), (6,2),(7,2),(8,2) ,(9,2)五个模型。
计量经济学-分布滞后模型与自回归模型

分布滞后模型与自回归模型实验目的:设定模型,按照一定的处理方法估计模型参数,并解释模型的经济意义,探测模型扰动项的一阶自相关性。
实验要求:(1)设定模型t tu tXY ++=βα*运用局部调整假定(其中Yt*为预期最佳值)。
(2)设定模型e X Yu tttβα=*运用局部调整假定(其中Yt*为预期最佳值)。
(3)设定模型u X Yttt++=*βα运用自适应预期假定(其中Xt*为预期值)。
(4)运用阿尔蒙多项式变换法,估计分布滞后模型u XX Yt t tt++⋯+++=-X4-t 411βββα实验原理:最小二乘估计 实验步骤:一、在局部调整假定下,先估计回归模型:*1*1*0*t t t t u Y X Y +++=-ββα得到以下回归结果:Dependent Variable: YMethod: Least Squares Date: 11/16/10 Time: 19:39 Sample (adjusted): 1981 2001 Included observations: 21 after adjustmentsVariable Coefficien t Std. Error t-StatisticProb. C -15.10403 4.729450 -3.193613 0.0050 X 0.629273 0.097819 6.433031 0.0000 Y(-1) 0.271676 0.114858 2.365315 0.0294R-squared 0.987125 Mean dependent var109.2167 Adjusted R-squared 0.985695 S.D. dependent var 51.78550 S.E. of regression 6.193728 Akaike info criterion 6.616515 Sum squared resid 690.5208 Schwarz criterion 6.765733 Log likelihood -66.47341 F-statistic 690.0561 Durbin-Watson stat 1.518595 Prob(F-statistic)0.000000t Y ^=-15.10403+0.629273Xt+0.271676Yt 1-(4.729450)(0.097819) (0.114858) t=(-3.193613)(6.433031)(2.365315)R2=0.9871252R -=0.985695F=690.0561 DW=1.518595由局部调整模型的参数关系,有:α*=δα,δββ=*0,δβ-=1*1,u u t t δ=*将上述估计结果代入得到:βδ*11-==1-0.271676=0.728324δαα*==-20.738064δββ*0==0.864001故局部调整模型的估计结果为:=Yt* -20.738064+0.864001X t模型的经济意义:该地区的销售额每增加一亿元,其预期最佳固定资产投资将增加0.864001亿元。
第六章分布滞后模型与自回归模型分析

第六章分布滞后模型与自回归模型分析分布滞后模型(Distributed Lag Models)和自回归模型(Autoregressive Models)是常用于时间序列分析的两种方法。
本章将分别介绍这两种模型以及其在经济学和社会科学领域中的应用。
分布滞后模型是一种广义的线性回归模型,用于分析变量之间的滞后效应。
它的基本形式可以表示为:Yt = α + β1Xt + β2Xt-1 + ... + βpXt-p + et其中,Yt是被解释变量,Xt是解释变量,β1到βp是与解释变量相关的系数,et是误差项。
模型中的滞后项Xt-1到Xt-p表示X在当前时间以及过去的一段时间内对Y的影响。
分布滞后模型可以用来研究两个或多个变量之间的滞后效应,并帮助研究者了解这些变量之间的动态关系。
分布滞后模型在经济学和社会科学领域中有广泛的应用。
例如,在宏观经济学中,可以用分布滞后模型来研究货币政策对经济增长的长期影响。
在健康经济学中,可以用分布滞后模型来研究疫苗接种对流行病传播的影响。
在社会学研究中,可以用分布滞后模型来研究教育程度对就业机会的影响。
自回归模型是一种基于时间序列的统计模型,用于预测一个变量在时间上的变化。
它的基本形式可以表示为:Yt = α + φ1Yt-1 + φ2Yt-2 + ... + φpYt-p + et其中,Yt是被预测的变量,φ1到φp是自回归系数,et是误差项。
自回归模型假设当前时间的值与过去时间的值有关,并且根据过去时间的值来预测未来时间的值。
自回归模型可以帮助研究者预测变量的趋势和周期性,并提供关于未来值的信息。
自回归模型在经济学和社会科学领域中也有广泛的应用。
例如,在金融学中,可以用自回归模型来预测股票价格的变化。
在气象学中,可以用自回归模型来预测天气变化。
在市场研究中,可以用自回归模型来预测产品销售量。
总之,分布滞后模型和自回归模型是两种常用的时间序列分析方法。
它们可以帮助研究者了解变量之间的滞后效应和趋势,并用于预测未来值。
计量经济学课件:第七章分布滞后模型与自回归模型.doc

第七章 分布滞后模型与自回归模型第一节 分布滞后模型与自回归模型的基本概念一、问题的提出1、滞后效应的出现。
(1)在经济学分析中,研究消费函数,人们的消费行为不仅要受到当期收入的影响(绝对收入假设),还要受到前期收入的影响,甚至要受到前期消费的影响(相对收入假设)。
(2)研究投资问题,由于投资周期的原因,本年度投资的形成,与上年度,甚至再上年度的投资形成有关。
(3)运用经济政策调控宏观经济运行,经济政策的实施所产生的政策效果是一个逐步波及的扩散过程。
用计量经济学模型研究这类问题,怎样度量变量的滞后影响?怎样估计有滞后变量的模型?对于上述消费的情况,设C 表示消费,Y 表示收入,则123141t t t t t C Y Y C u ββββ--=++++对于上述投资的情况,设I 表示投资,Y 表示收入,则12314253t t t t t t I Y I I I u ααααα---=+++++2、静态计量经济学模型向动态计量经济学模型的扩展。
什么为“动态计量经济学模型”?二、产生滞后效应的原因1、心理预期因素的作用。
2、技术因素的作用。
3、制度因素的作用。
上述原因的结果表现为经济现象中的“惯性作用”。
二、滞后变量模型的类型1、分布滞后模型。
如果模型中没有滞后的被解释变量,即01122t t t t s t s t Y X X X X u αββββ---=++++++L则模型为分布滞后模型。
由于s 可以是有限数,也可以是无限数,则分布滞后模型可分为有限分布滞后模型和无限分布滞后模型。
在分布滞后模型中,有关系数的解释如下:⑴乘数(又称倍数)的解释。
该概念首先由英国的卡恩提出(R.F.Kahn ,1931)。
所谓乘数是指,在一个模型体系里,外生变量变化一个单位,对内生变量产生的影响程度。
据此进行的经济分析称为乘数分析或乘数效应分析。
如投资乘数,是指在边际消费倾向一定的情况下,投资变动对收入带来的影响,亦即增加一笔投资,可以引起收入倍数的增加。
格兰杰因果关系检验-资料

检验结果
从2阶滞后期开始,检验模型都拒绝了“X不是Y的格兰杰原因”的假 设,而不拒绝“Y不是X的原因”的假设。
滞后阶数为2或3时,两类检验模型都不存在序列相关性。 由赤池信息准则,发现滞后2阶检验模型拥有较小的AIC值。 可判断:可支配收入X是居民消费支出Y的格兰杰原因,而不是相反, 即国民收入的增加更大程度地影响着消费的增加。
从检验模型随机干扰项1阶序列相关的LM检验看,以Y为被解释变量 的模型的LM=0.897,对应的伴随概率P= 0.343,表明在5%的显著性水平 下,该检验模型不存在序列相关性;但是,以X为被解释变量的模型的 LM=11.37,对应的伴随概率P= 0.001,表明在5%的显著性水平下,该检 验模型存在严重的序列相关性。
3、例
检验1978~2019年间实际可支配收入(X)与居 民实际消费总支出(Y)之间的因果关系。
数据
选择Granger检验
选择检验的序列
确定滞后阶数(1阶)
检验结果
由相伴概率知,在5%的显著性水平下,既拒绝“X不是Y的格兰杰原 因”的假设,也拒绝“Y不是X的格兰杰原因”的假设。因此,从1阶滞后 的情况看,可支配收入X的增长与居民消费支出Y增长互为格兰杰原因 。
–如果双方的过去行为在相互影响着对方的当前行为, 存在双向关系。
• 向量自回归分布滞后模型可以用于变量间关系 的检验。
2、格兰杰因果关系检验
m
Yt iXti iYti 1t
i1
i1
m
m
Xt iYti iXti 2t
i1
i1
格兰杰因果关系检验 Granger Test of Causality
1、原理
• 自回归分布滞后模型揭示:某变量的变化受其 自身及其他变量过去行为的影响。
九章分布滞后和自回归模型-资料

思路是:假设分布滞后模型中的未知参 数 k 都有相同的符号,并按照几何级数
k 0k衰减。其中 01。
这种k 0k函数有以下基本特点:
(1) k 不变号; (2) k 是k的减函数;
(3)越小,衰减速度越快,称为衰减率
(4)长期乘数有限。
图9.2 考伊克方法参数衰减模式
有时反映滞后期长度的K也是未知的,也 需要通过分析确定。
这种模型正是分析判断滞后效应的存在性及其 模式,研究经济行为、经济关系中滞后作用的 基本模型,称为“分布滞后模型” 。
理论上可以考虑有无限多滞后项的分布滞后模 型:C t c 0 c 1 I t c 2 I t 1 c 3 I t 2 t 这种分布滞后模型通常称为“无限分布滞后模
(二)分布滞后模型
已知存在滞后效应以及滞后效应的时间 长度和结构时,对滞后作用的分析预测 是比较简单的。
但现实中的问题常常是只知道可能存在 滞后效应,滞后效应是否确实存在,滞 后效应的持续长度,及其结构模式都是 未知的。
例如消费滞后效应问题可能是:
C t c 0 c 1 It c 2 It 1 c 3 It 2 t
但分布滞后模型主要用来研究经济变量作用的 时间滞后效应、长期影响,以及经济变量之间 的动态影响关系,可用于评价经济政策的中长 期效果,属于动态计量分析的范畴。
二、分布滞后模型参数估计
用分布滞后模型研究滞后效应,进行预测分析 和评估政策效果之前,先要估计模型中的未知 参数。
分布滞后模型形式上与一般的多元线性回归相 似,但因为引进多个滞后变量和滞后期长度难 以确定,分布滞后模型的参数估计与一般多元 线性回归模型有所不同。
该模型仍然含有无限多项,但其中的参 数已经只有3个了。只要我们再把模型滞 后一期得:
分布滞后及格兰杰因果检验

实验9 分布滞后模型与自回归模型及格兰杰因果关系检验一实验目的:掌握分布滞后模型与自回归模型的估计与应用,掌握格兰杰因果关系检验方法,熟悉Eviews的基本操作。
二实验要求:应用教材P168例题5.2.2案例,做有限分布滞后模型的估计;应用教材P176例题5.2.4案例,做格兰杰因果关系检验。
三实验原理:普通最小二乘法、阿尔蒙法、格兰杰因果关系检验、LM检验。
四预备知识:普通最小二乘法估计的原理、t检验、拟合优度检验、阿尔蒙法、多项式近似。
五实验内容:(1) 1975~2002年中国电力行业基本建设投资X和发电量Y的相关数据如下表所示。
(数据见第5章EXCEL表格)。
假定电力行业基本建设投资对发电量增长有一个分布滞后效应,使用7期滞后和2次多项式去估计此分布滞后模型;(2) 检验人均可支配收入和居民消费的格兰杰因果关系,使用直至4期为止的滞后并评述你的结果。
(数据见EXCEL例题2.6.2)六实验步骤:6.1 建立工作文件并录入数据如图1所示图 16.2 使用7期滞后2次多项式估计模型在工作文件中,点击Quick\Estimate Equation…,然后在弹出的对话框中输入:log(Y) C PDL(log(X),7,2),点击OK,如图2所示,运行得到如图3所示的回归分析结果。
其中,“PDL指令”表示进行多项式分布滞后(Ploynamial Distributed Lags)模型的估计,X为滞后序列名,7表示滞后长度,2表示多项式次数。
图2由图3中的数据,我们得到估计结果如下:2100061.00199.00244.07095.6ˆln t t t t W W W Y +-+= (157.96) (1.73) (-5.08) (2.13)9952.02=R 9944.02=R 6087.0..=W D 最后得到的分布滞后模型估计式为:(1.80) (2.33) (1.02) (0.77)(1.73) (5.30) (11.75) (6.32) (157.96) 7654321ln 043.0ln 020.0ln 0092.0ln 0107.0ln 0244.0ln 0505.0ln 08875.0ln 1393.07095.6ˆln -------++++++++=t t t t t t t t t X X X X X X X X Y图 3图3所示输出结果的上半部分格式与一般的回归方程相同,给出了模型参数估计值、t 检验统计量值及对应的概率值,以及模型的其他统计量。
第七章分布滞后模型与自回归

第 七 章
分布滞后模型与自回归模型
引子: 货币政策效应的时滞
在宏观经济的调控中,货币政策的传导不是瞬间的,其效应的 发挥有一定的传导过程: 投资 消费 货币供给
GDP
进出口
一般价格
时间滞后
需要思考的问题:
在现实经济活动中,经济变量之间的关系不一定是 瞬间的,解释变量与被解释变量的因果联系不可能在短 时间内完成,在这一过程中通常都存在时间滞后,也就 是说解释变量需要通过一段时间才能完全作用于被解释
i 0
s
s
i 0
s
i 0
am i m X t i ut
i 0
s
可令
Z0t X t i
i 0
Z1t iX t i
i 0
Z 2 t i X t i
2 i 0
s
Z st i s X t i
i 0
s
注意:原模型有S+1个解释变量 变换后模型只有m+1个解释变量
因为
(2)不变滞后结构
假定:权数为常数,即 Zt wX t wX t 1 wX t s 或 例如: W=1/4,1/4,1/4,1/4
Z t X t X t 1 X t s
(3)倒V形滞后结构
假定:滞后变量的权数先递增后递减,权数两头小中间大 例如 1 1 2 1 1
变量。这种滞后现象普遍存在,就要求我们在做经济分
析时应该考虑时滞的影响。
怎样才能把这类时间上滞后的经济关系纳入计量经
济模型呢?
本 章 内 容:
此前讨论的模型变量间的关系是同时(瞬时、静态)的, 实际不一定是这样。要反映不同时期变量之间的关系,需 要引入滞后变量,使静态模型成为动态模型。 从时间关系上看: 变量间瞬时关系
计量经济学第九章分布滞后和自回归模型

自回归模型的理论导出
适应性预期(Adaptive expectation)模型
在某些实际问题中,因变量 Yt 并不取决于解释变量的当
前实际值
X
t
,而取决于X
t
的“预期水平”或“长期均衡水X
* t
平” 。
例如,家庭本期消费水平,取决于本期收入的预期值;
❖ 为了解决滞后长度不确定的困难,可以依次估计滞 后效应变量的一期滞后、二期滞后…当发现滞后变 量(加入的最多期滞后)的回归系数在统计上开始 变得不显著,或至少有一个变量的系数改变符号 (由正变负或由负变正)时,就不再增加滞后期, 把此前一个模型作为分布滞后模型的形式,相应参 数估计作为模型的参数估计。
市场上某种商品供求量,决定于本期该商品价格的均衡值。
因此,适应性预期模型最初表现形式是
Yt
0
1
X
* t
t
由于预期变量是不可实际观测的,往往作如下 适应性预期假定:
X
* t
X* t 1
(Xt
X
* t 1
)
其中:r为预期系数(coefficient of expectation), 0r 1。
该式的经济含义为:“经济行为者将根据过去的 经验修改他们的预期”,即本期预期值的形成是一 个逐步调整过程,本期预期值的增量是本期实际值 与前一期预期值之差的一部分,其比例为r 。
这个假定还可写成:
X
* t
X t
(1
)
X
* t 1
将
X
* t
X t
(1
)
X
* t 1
代入
自回归与分布滞后模型

Yt C 0.4xt 0.3xt 1 0.2xt 2 ut
其中Y是消费量,X是收入
(17.1.1)
更一般的,我们可以写成:
Yt 0 xt 1xt 1 2 xt 2
β
k xt k ut
(17.1.2)
0 表示随着X一个单位的变化, Y均值的同期变化,
• 其中 Y = 对货币(实际现金余额)的需求 * X • =均衡、最优、预期的长期或正常利率 u t =误差项 •
• 方程(17.5.1) 设想,货币需求是预期(预测意义的)利 率的函数.
• 由于预期变量 X 不可直接观测,我们对预期的形成做如 下的设想: (17.5.2) • 其中 为 0 1 ,称期望系数(coefficient of expectation)。假设(17.5.2) 称适应性预期(adaptive expectation)或累进式期望(progressive expectation) 或错误中学习假设(error learning hypothesis). • (17.5.2) 表明:人们每期都按变量的现期值 X t与前期期 望值 X t 1* 之间的差距的一个分数 去修改期望值。 .
• 表达式证明
t 1 )/(1- ) 1 长期反应 ( 0 t期反应 0 / (1 ) 2
1 ln 2 2 t ln ln ln
平均滞后 • 假设所有的β
k
都是正的,则平均滞后有相关滞后的加权平均。扼要地 说,它是滞后加权平均时间。(类似于投资学中的久期) 考伊克模型:平均滞后=
*
• 将 (17.5.3) 代入 (17.5.1), 我们得到:
Yt 0 1 X t 1 X t 1 ut
实验七 分布滞后模型与自回归模型及格兰杰因果关系检验综述
实验七分布滞后模型与自回归模型及格兰杰因果关系检验实验目的:掌握分布滞后模型与自回归模型的估计与应用,掌握格兰杰因果关系检验方法,熟悉EViews的基本操作。
实验要求:应用教材P186第6题进行实验。
实验原理:普通最小二乘法、阿尔蒙法、格兰杰因果关系检验、DW检验、LM 检验。
预备知识:最小二乘法估计的原理、t检验、拟合优度检验、阿尔蒙法、多项式近似。
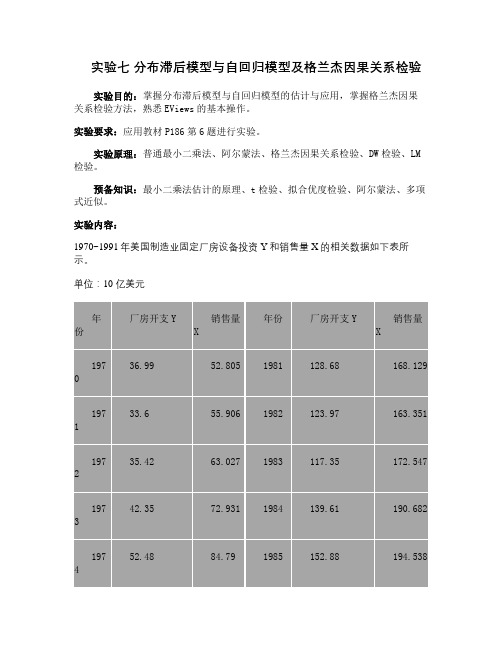
实验内容:1970~1991年美国制造业固定厂房设备投资Y和销售量X的相关数据如下表所示。
单位:10 亿美元(1)假定销售量对厂房设备支出有一个分布滞后效应,试用4期滞后和2次多项式去估计此分布滞后模型;(2)检验销量与厂房设备支出的格兰杰因果关系,使用直至6期为止的滞后并评述你的结果。
实验步骤(1 设要估计的分布滞后模型为根据阿尔蒙变换,令则原模型变形为或其中,在Eviews软件下,可通过选择Quick\Generate Series…,在出现的Generate Series by Eq…窗口分别输入“Z0=X+X(-1+X(-2+X(-3+X(-4”、“Z1=X(-1+2*X(-2+3*X(-3+4*X(-4”、“Z2=X(-1+4*X(-2+9*X(-3+16*X(-4”,生成三个序列Z0、Z1、Z2;然后作Y关于Z0、Z1、Z2的OLS回归,估计结果如图1.1所示。
图1.1由此可计算出原分布滞后模型的参数估计值:也可在Eviews软件中选择“Quick\Estimate Equation”后,在现的对话窗口中输入“Y C PDL(X,4,2)”,得如图1.2所示的估计结果。
图1.2 图1.3由图1.3可知,两种方法所求得的参数是相同的,而第二种方法比起第一种要简便得多。
(2)在Eviews软件下,选择“Quick\Group Statistics\Granger Causality Test”,在出现的Series List窗口中输入“Y X”,点击OK按钮,并在新出现的Lag Speci…窗口中输入滞后期数,点击OK按钮即出现检验结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验七分布滞后模型与自回归模型及格兰杰因果关系检验
实验目的:掌握分布滞后模型与自回归模型的估计与应用,掌握格兰杰因果关系检验方法,熟悉EViews的基本操作。
实验要求:应用教材P186第6题进行实验。
实验原理:普通最小二乘法、阿尔蒙法、格兰杰因果关系检验、DW检验、LM 检验。
预备知识:最小二乘法估计的原理、t检验、拟合优度检验、阿尔蒙法、多项式近似。
实验内容:
1970~1991年美国制造业固定厂房设备投资Y和销售量X的相关数据如下表所示。
单位:10 亿美元
(1)假定销售量对厂房设备支出有一个分布滞后效应,试用4期滞后和2次多项式去估计此分布滞后模型;
(2)检验销量与厂房设备支出的格兰杰因果关系,使用直至6期为止的滞后并评述你的结果。
实验步骤
(1 设要估计的分布滞后模型为
根据阿尔蒙变换,令
则原模型变形为
或
其中,
在Eviews软件下,可通过选择Quick\Generate Series…,在出现的Generate Series by Eq…窗口分别输入“Z0=X+X(-1+X(-2+X(-3+X(-4”、“Z1=X(-1+2*X(-2+3*X(-
3+4*X(-4”、“Z2=X(-1+4*X(-2+9*X(-3+16*X(-4”,生成三个序列Z0、Z1、Z2;然后作Y关于Z0、Z1、Z2的OLS回归,估计结果如图1.1所示。
图1.1
由此可计算出原分布滞后模型的参数估计值:
也可在Eviews软件中选择“Quick\Estimate Equation”后,在现的对话窗口中输入“Y C PDL(X,4,2)”,得如图1.2所示的估计结果。
图1.2 图1.3
由图1.3可知,两种方法所求得的参数是相同的,而第二种方法比起第一种要简便得多。
(2)在Eviews软件下,选择“Quick\Group Statistics\Granger Causality Test”,在出现的Series List窗口中输入“Y X”,点击OK按钮,并在新出现的Lag Speci…窗口中输入滞后期数,点击OK按钮即出现检验结果。
图2.1
图2.1显示,当取滞后阶数为2期时,格兰杰因果关系检验既拒绝了X不是Y的格兰杰原因的假设,也拒绝了Y不是X的格兰杰原因的假设,表明两变量互为因果。
下表列出了从1期直到6期滞后的格兰杰因果关系检验结果。
1 X does not Granger Cause
Y
Y does not Granger Cause
X 21 31.9061
23.8339
2.3E-05
0.00012
6. 840
5.991
2 X does not Granger Cause
Y
Y does not Granger Cause
X 20 18.4684
13.1653
9.0E-05
0.00050
6.805
6.003
3 X does not Granger Cause
Y
Y does not Granger Cause
X 19 6.16196
7.19029
0.00887
0.00509
6.938
6.125
4 X does not Granger Cause
Y
Y does not Granger Cause
X 18 3.71761
4.44678
0.04719
0.02946
7.132
6.329
5 X does not Granger Cause
Y
Y does not Granger Cause
X 17 2.28854
2.77297
0.17124
0.12327
7.370
6.559
6 X does not Granger Cause 16 1.06068 0.52324 7.537
Y
3.07209 0.19255 5.890
Y does not Granger Cause
X
从表中可以看出,随着滞后期的增加,Y与X的格兰杰因果关系有所变化。
在不超过4期滞后的检验中,拒绝了两者没有互为因果关系的假设,即可以说两者互为因果关系;而滞后期为5和6的检验结果又表明,不拒绝两者不是互为因果关系的假设。
然后通过对不同滞后期数的模型进行回归,可以求得相应的AIC值。
在格兰杰因果检验所得的窗口中点击Proc\Make Vector Autoregession…,在弹出窗口中的Lag Intervals for Endogenous栏中输入1 n,就可以得到相应的滞后n期的回归模型,其中滞后1期如图2.2所示
图2.2
从而得到上表中最后一列给出了每组检验模型的AIC值。
从中可以看出,第一组与第二组估计AIC值都相对较小,而两者之间AIC值却互有高低。
不过由于两者的结论都是一样的,都认为X,Y两者互为因果关系。
因此我们可以以此为依据,认为两者是互为因果关系的。
