中考数学动点问题(含答案)
中考数学动点问题(含答案)

中考数学之动点问题一、选择题:1. 如图,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停顿,设点P运动的路程为*,△ABP的面积为y,如果y关于*的函数图象如图2所示,则△ABC的面积是〔〕A、10B、16C、18D、20二、填空题:1. 如上右图,C为线段AE上一动点〔不与点A,E重合〕,在AE同侧分别作正三角形ABC和正三角形CDE、AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°.恒成立的结论有_______________________〔把你认为正确的序号都填上〕。
三、解答题:1.〔2008年大连〕如图12,直角梯形ABCD中,AB∥CD,∠A = 90°,CD = 3,AD = 4,tan B = 2,过点C作CH⊥AB,垂足为H.点P为线段AD上一动点,直线PM∥AB,交BC、C H于点M、Q.以PM为斜边向右作等腰Rt△PMN,直线MN交直线AB于点E,直线PN交直线A B于点F.设PD的长为*,EF的长为y.⑴求PM的长(用*表示);⑵求y与*的函数关系式及自变量*的取值范围(图13为备用图);⑶当点E在线段AH上时,求*的取值范围(图14为备用图).2.〔2008年福建宁德〕如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时0<x<,△DCQ的8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为*秒()8面积为y1平方厘米,△PCQ的面积为y2平方厘米.⑴求y1与*的函数关系,并在图2中画出y1的图象;⑵如图2,y2的图象是抛物线的一局部,其顶点坐标是〔4,12〕,求点P的速度及AC的长;⑶在图2中,点G是*轴正半轴上一点〔0<OG<6=,过G作EF垂直于*轴,分别交y1、y2于点E、F.①说出线段EF的长在图1中所表示的实际意义;②当0<*<6时,求线段EF长的最大值.3.〔2008年白银〕如图,在平面直角坐标系中,四边形OABC 是矩形,点B 的坐标为〔4,3〕.平行于对角线AC 的直线m 从原点O 出发,沿*轴正方向以每秒1个单位长度的速度运动,设直线m 与矩形OABC 的两边..分别交于点M 、N ,直线m 运动的时间为t 〔秒〕. (1) 点A 的坐标是__________,点C 的坐标是__________; (2) 当t=秒或秒时,MN=21AC ; (3) 设△OMN 的面积为S ,求S 与t 的函数关系式;(4) 探求(3)中得到的函数S 有没有最大值?假设有,求出最大值;假设没有,要说明理由.参考答案一、选择 A二、填空:〔1〕〔2〕〔3〕〔5〕 三、解答: 2、解:⑴∵CD CQ S DCQ ⋅⋅=∆21,CD =3,CQ =*, ∴x y 231=. 图象如下图.⑵方法一:CP CQ S PCQ ⋅⋅=∆21,CP =8k -*k ,CQ =*, ∴()kx kx x kx k y 42182122+-=⋅-⨯=.∵抛物线顶点坐标是〔4,12〕,∴12444212=⋅+⋅-k k . 解得23=k .图1C Q → B图2则点P 的速度每秒23厘米,AC =12厘米. 方法二:观察图象知,当*=4时,△PCQ 面积为12. 此时PC =AC -AP =8k -4k =4k ,CQ =4.∴由CP CQ S PCQ ⋅⋅=∆21,得 12244=⨯k .解得23=k . 则点P 的速度每秒23厘米,AC =12厘米.方法三:设y 2的图象所在抛物线的解析式是c bx ax y ++=2. ∵图象过〔0,0〕,〔4,12〕,〔8,0〕,∴⎪⎩⎪⎨⎧=++=++=.0864124160c b a c b a c ,, 解得 ⎪⎪⎩⎪⎪⎨⎧==-=.0643c b a ,, ∴x x y 64322+-=. ①∵CP CQ S PCQ ⋅⋅=∆21,CP =8k -*k ,CQ =*,∴kx kx y 42122+-=. ②比拟①②得23=k .则点P 的速度每秒23厘米,AC =12厘米.⑶①观察图象,知线段的长EF =y 2-y 1,表示△PCQ 与△DCQ 的面积差〔或△PDQ 面积〕. ②由⑵得 x x y 64322+-=.〔方法二,x x x x y 643232382122+-=⋅⎪⎭⎫ ⎝⎛-⨯⨯=〕∵EF =y 2-y 1, ∴EF =x x x x x 29432364322+-=-+-, ∵二次项系数小于0,∴在60<x<范围,当3=x 时,427=EF 最大. 3、解:(1)〔4,0〕,〔0,3〕; 2分 (2) 2,6; 4分 (3) 当0<t ≤4时,OM =t .由△OMN ∽△OAC ,得OCONOA OM =, ∴ ON =t 43,S=283t . 6分 当4<t <8时,如图,∵ OD =t ,∴ AD = t-4. 方法一:由△DAM ∽△AOC ,可得AM =)4(43-t ,∴ BM =6-t 43. 7分 由△BMN ∽△BAC ,可得BN =BM 34=8-t ,∴ CN =t-4. 8分S=矩形OABC 的面积-Rt △OAM 的面积- Rt △MBN 的面积- Rt △NCO 的面积=12-)4(23-t -21〔8-t 〕〔6-t 43〕-)4(23-t =t t 3832+-. ·························· 10分方法二:易知四边形ADNC 是平行四边形,∴ CN =AD =t-4,BN =8-t .7分 由△BMN ∽△BAC ,可得BM =BN 43=6-t 43,∴ AM =)4(43-t .8分 以下同方法一. (4) 有最大值.方法一: 当0<t ≤4时,∵ 抛物线S=283t 的开口向上,在对称轴t=0的右边, S 随t 的增大而增大, ∴ 当t=4时,S 可取到最大值2483⨯=6; 11分当4<t <8时, ∵ 抛物线S=t t 3832+-的开口向下,它的顶点是〔4,6〕,∴ S <6. 综上,当t=4时,S 有最大值6. 12分 方法二:∵ S=22304833488t t t t t ⎧<⎪⎪⎨⎪-+<<⎪⎩,≤,∴ 当0<t <8时,画出S 与t 的函数关系图像,如下图. 11分显然,当t=4时,S有最大值6. 12分说明:只有当第〔3〕问解答正确时,第〔4〕问只答复"有最大值〞无其它步骤,可给1分;否则,不给分.。
(中考数学)动点问题专题训练(含答案)

中考专题训练 动点问题例1. 如图, 在ABC ∆中,AB AC =,AD BC ⊥于点D ,10BC cm =,8AD cm =. 点P 从点B 出发, 在线段BC 上以每秒3cm 的速度向点C 匀速运动, 与此同时, 垂直于AD 的直线m 从底边BC 出发, 以每秒2cm 的速度沿DA 方向匀速平移, 分别交AB 、AC 、AD 于E 、F 、H ,当点P 到达点C 时, 点P 与直线m 同时停止运动, 设运动时间为t 秒(0)t >.(1) 当2t =时, 连接DE 、DF ,求证: 四边形AEDF 为菱形;(2) 在整个运动过程中, 所形成的PEF ∆的面积存在最大值, 当PEF ∆的面积最大时, 求线段BP 的长;(3) 是否存在某一时刻t ,使PEF ∆为直角三角形?若存在, 请求出此时刻t 的值;若不存在, 请说明理由 .【解答】(1) 证明: 当2t =时,4DH AH ==,则H 为AD 的中点, 如答图 1 所示 . 又EF AD ⊥ ,EF ∴为AD 的垂直平分线,AE DE ∴=,AF DF =.AB AC = ,AD BC ⊥于点D ,AD BC ∴⊥,B C ∠=∠.//EF BC ∴,AEF B ∴∠=∠,AFE C ∠=∠,AEF AFE ∴∠=∠,AE AF ∴=,AE AF DE DF ∴===,即四边形AEDF 为菱形 .(2) 解: 如答图 2 所示, 由 (1) 知//EF BC ,AEF ABC ∴∆∆∽, ∴EF AH BC AD =,即82108EF t -=,解得:5102EF t =-. 221155510(10)210(2)10(0)222223PEF S EF DH t t t t t t ∆==-=-+=--+<< , ∴当2t =秒时,PEF S ∆存在最大值, 最大值为210cm ,此时36BP t cm ==.(3) 解: 存在 . 理由如下:①若点E 为直角顶点, 如答图 3①所示,此时//PE AD ,2PE DH t ==,3BP t =.//PE AD ,∴PE BP AD BD =,即2385t t =,此比例式不成立, 故此种情形不存在; ②若点F 为直角顶点如答图 3②所示,此时//PF AD ,2PF DH t ==,3BP t =,103CP t =-.//PF AD ,∴PF CP AD CD =,即210385t t -=,解得4017t =;③若点P 为直角顶点,如答图③所示 .过点E 作EM BC ⊥于点M ,过点F 作FN BC ⊥于点N ,则2EM FN DH t ===,////EM FN AD .//EM AD ,∴EM BM AD BD =,即285t BM =,解得54BM t =, 57344PM BP BM t t t ∴=-=-=. 在Rt EMP ∆中, 由勾股定理得:2222227113(2)()416PE EM PM t t t =+=+=. //FN AD ,∴FN CN AD CD =,即285t CN =,解得54CN t =, 5171031044PN BC BP CN t t t ∴=--=--=-. 在Rt FNP ∆中, 由勾股定理得:22222217353(2)(10)85100416PF FN PN t t t t =+=+-=-+. 在Rt PEF ∆中, 由勾股定理得:222EF PE PF =+, 即:2225113353(10)()(85100)21616t t t t -=+-+ 化简得:21833508t t -=, 解得:280183t =或0t =(舍 去) 280183t ∴=. 综上所述, 当4017t =秒或280183t =秒时,PEF ∆为直角三角形 .例2. 如图, 在同一平面上, 两块斜边相等的直角三角板Rt ABC ∆和Rt ADC ∆拼在一起,使斜边AC 完全重合, 且顶点B ,D 分别在AC 的两旁,90ABC ADC ∠=∠=︒,30CAD ∠=︒,4AB BC cm ==(1) 填空:AD = )cm ,DC = ()cm(2) 点M ,N 分别从A 点,C 点同时以每秒1cm 的速度等速出发, 且分别在AD ,CB 上沿A D →,C B →方向运动, 当N 点运动到B 点时,M 、N 两点同时停止运动, 连接MN ,求当M 、N 点运动了x 秒时, 点N 到AD 的距离 (用 含x 的式子表示)(3) 在 (2) 的条件下, 取DC 中点P ,连接MP ,NP ,设PMN ∆的面积为2()y cm ,在整个运动过程中,PMN ∆的面积y 存在最大值, 请求出y 的最大值 .(参考数据sin 75︒=sin15︒=【解答】解: (1)90ABC ∠=︒ ,4AB BC cm ==,AC ∴===,90ADC ∠=︒ ,30CAD ∠=︒,12DC AC ∴==,AD ∴==;故答案为:,;(2) 过点N 作NE AD ⊥于E ,作NF DC ⊥,交DC 的延长线于F ,如图所示:则NE DF =,90ABC ADC ∠=∠=︒ ,AB BC =,30CAD ∠=︒,45ACB ∴∠=︒,60ACD ∠=︒,180456075NCF ∴∠=︒-︒-︒=︒,15FNC ∠=︒,sinFC FNCNC ∠=,NC x=,FC x∴=,NE DF x∴==+,∴点N到ADx+;(3)sinFN NCFNC ∠=,FN x∴=,P为DC的中点,PD CP∴==PF x∴=PMN∴∆的面积y=梯形MDFN的面积PMD-∆的面积PNF-∆的面积111)) 222x x x x=+-+--+2x x=+,即y是x的二次函数,0<,y∴有最大值,当x==时,y=.例3. 如图,BD 是正方形ABCD 的对角线,2BC =,边BC 在其所在的直线上平移, 将通过平移得到的线段记为PQ ,连接PA 、QD ,并过点Q 作QO BD ⊥,垂足为O ,连接OA 、OP .(1) 请直接写出线段BC 在平移过程中, 四边形APQD 是什么四边形?(2) 请判断OA 、OP 之间的数量关系和位置关系, 并加以证明;(3) 在平移变换过程中, 设OPB y S ∆=,(02)BP x x =……,求y 与x 之间的函数关系式,并求出y 的最大值 .【解答】(1) 四边形APQD 为平行四边形;(2)OA OP =,OA OP ⊥,理由如下:四边形ABCD 是正方形,AB BC PQ ∴==,45ABO OBQ ∠=∠=︒,OQ BD ⊥ ,45PQO ∴∠=︒,45ABO OBQ PQO ∴∠=∠=∠=︒,OB OQ ∴=,在AOB ∆和OPQ ∆中,AB PQABO PQO BO QO=⎧⎪∠=∠⎨⎪=⎩()AOB POQ SAS ∴∆≅∆,OA OP ∴=,AOB POQ ∠=∠,90AOP BOQ ∴∠=∠=︒,OA OP ∴⊥;(3) 如图, 过O 作OE BC ⊥于E .①如图 1 ,当P 点在B 点右侧时,则2BQ x =+,22x OE +=, 1222x y x +∴=⨯,即211(1)44y x =+-, 又02x ……,∴当2x =时,y 有最大值为 2 ;②如图 2 ,当P 点在B 点左侧时,则2BQ x =-,22x OE -=, 1222x y x -∴=⨯ ,即211(1)44y x =--+, 又02x ……,∴当1x =时,y 有最大值为14; 综上所述,∴当2x =时,y 有最大值为 2 .例4. 如图, 在平面直角坐标系中,O 为原点, 四边形ABCO 是矩形, 点A ,C 的坐标分别是(0,2)A 和C ,0),点D 是对角线AC 上一动点 (不 与A ,C 重合) ,连结BD ,作DE DB ⊥,交x 轴于点E ,以线段DE ,DB 为邻边作矩形BDEF .(1) 填空: 点B 的坐标为 ;(2) 是否存在这样的点D ,使得DEC ∆是等腰三角形?若存在, 请求出AD 的长度;若不存在, 请说明理由;(3)①求证:DE DB =; ②设AD x =,矩形BDEF 的面积为y ,求y 关于x 的函数关系式 (可 利用①的结论) ,并求出y 的最小值 .【解答】解: (1) 四边形AOCB 是矩形,2BC OA ∴==,OC AB ==90BCO BAO ∠=∠=︒,B ∴2).故答案为2).(2) 存在 . 理由如下:2OA = ,OC =,tan AO ACO OC ∠== , 30ACO ∴∠=︒,60ACB ∠=︒①如图 1 中, 当E 在线段CO 上时,DEC ∆是等腰三角形, 观察图象可知, 只有ED EC =,30DCE EDC ∴∠=∠=︒,60DBC BCD ∴∠=∠=︒,DBC ∴∆是等边三角形,2DC BC ∴==,在Rt AOC ∆中,30ACO ∠=︒ ,2OA =,24AC AO ∴==,422AD AC CD ∴=-=-=.∴当2AD =时,DEC ∆是等腰三角形 .②如图 2 中, 当E 在OC 的延长线上时,DCE ∆是等腰三角形, 只有CD CE =,15DBC DEC CDE ∠=∠=∠=︒,75ABD ADB ∴∠=∠=︒,AB AD ∴==,综上所述, 满足条件的AD 的值为 2 或(3)①如图 1 ,过点D 作MN AB ⊥交AB 于M ,交OC 于N ,(0,2)A 和C ,0),∴直线AC 的解析式为2y x =+,设(,2)D a +,2DN ∴=+,BM a =90BDE ∠=︒ ,90BDM NDE ∴∠+∠=︒,90BDM DBM ∠+∠=︒,DBM EDN ∴∠=∠,90BMD DNE ∠=∠=︒ ,BMD DNE ∴∆∆∽,∴DE DN BD BM ===②如图 2 中, 作DH AB ⊥于H .在Rt ADH ∆中,AD x = ,30DAH ACO ∠=∠=︒,1122DH AD x ∴==,AH x ==,BH x ∴=, 在Rt BDH ∆中,BD ==,DE ∴==, ∴矩形BDEF的面积为22612)y x x ==-+,即2y x =-+,23)y x ∴=-+,0>,3x ∴=时,y .例5. 已知Rt OAB ∆,90OAB ∠=︒,30ABO ∠=︒,斜边4OB =,将Rt OAB ∆绕点O 顺时针旋转60︒,如图 1 ,连接BC .(1) 填空:OBC ∠= 60 ︒;(2) 如图 1 ,连接AC ,作OP AC ⊥,垂足为P ,求OP 的长度;(3) 如图 2 ,点M ,N 同时从点O 出发, 在OCB ∆边上运动,M 沿O C B →→路径匀速运动,N 沿O B C →→路径匀速运动, 当两点相遇时运动停止, 已知点M 的运动速度为 1.5 单位/秒, 点N 的运动速度为 1 单位/秒, 设运动时间为x 秒,OMN ∆的面积为y ,求当x 为何值时y 取得最大值?最大值为多少?【解答】解: (1) 由旋转性质可知:OB OC =,60BOC ∠=︒,OBC ∴∆是等边三角形,60OBC ∴∠=︒.故答案为 60 .(2) 如图 1 中,4OB = ,30ABO ∠=︒,122OA OB ∴==,AB ==11222AOC S OA AB ∆∴==⨯⨯=BOC ∆ 是等边三角形,60OBC ∴∠=︒,90ABC ABO OBC ∠=∠+∠=︒,AC ∴==2AOC S OP AC ∆∴===.(3)①当803x <…时,M 在OC 上运动,N 在OB 上运动,此时过点N 作NE OC ⊥且交OC 于点E .则sin 60NE ON x =︒= ,11 1.522OMN S OM NE x x ∆∴==⨯ ,2y x ∴=.83x ∴=时,y 有最大值, 最大值=. ②当843x <…时,M 在BC 上运动,N 在OB 上运动 .作MH OB ⊥于H . 则8 1.5BM x =-,sin 60 1.5)MH BM x =︒=- ,212y ON MH x ∴=⨯⨯=+.当83x =时,y 取最大值,y < ③当4 4.8x <…时,M 、N 都在BC 上运动, 作OG BC ⊥于G .12 2.5MN x =-,OG AB ==,12y MN OG ∴== ,当4x =时,y 有最大值, 最大值=,综上所述,y 有最大值, .。
中考数学总复习《动点问题》专项提升训练(带答案)

中考数学总复习《动点问题》专项提升训练(带答案)学校:___________班级:___________姓名:___________考号:___________例题1.如图,在菱形ABCD中,∠A=60°,AB=4,动点M,N同时从A点出发,点M以每秒2个单位长度沿折线A﹣B﹣C向终点C运动;点N以每秒1个单位长度沿线段AD向终点D运动,当其中一点运动至终点时,另一点随之停止运动.设运动时间为x秒,△AMN的面积为y个平方单位,则下列正确表示y与x函数关系的图象是()A B C D解:连接BD,过B作BE⊥AD于E,当0≤x<2时,点M在AB上在菱形ABCD中,∠A=60°,AB=4∴AB=AD∴△ABD是等边三角形∴AE=ED=12AD=2,BE=√3AE=2√3∵AM=2x,AN=x∴AMAN=ABAE=2∵∠A=∠A∴△AMN∽△ABE∴∠ANM=∠AEB=90°∴MN=√AM2−AN2=√3xx×√3x=√32x2∴y=12当2≤x≤4时,点M在BC上y=12AN⋅BE=12x×2√3=√3x综上所述,当0≤x<2时的函数图象是开口向上的抛物线的一部分,当2≤x≤4时,函数图象是直线的一部分故选:A.2.如图1,矩形ABCD中,点E为BC的中点,点P沿BC从点B运动到点C,设B,P两点间的距离为x,P A﹣PE=y,图2是点P运动时y随x变化的关系图象,则BC=.解:由函数图象知:当x=0,即P在B点时,BA﹣BE=1.利用两点之间线段最短,得到P A﹣PE≤AE.∴y的最大值为AE∴AE=5.在Rt△ABE中,由勾股定理得:BA2+BE2=AE2=25设BE的长度为t则AB=t+1∴(t+1)2+t2=25即:t2+t﹣12=0∴(t+4)(t﹣3)=0解得t=﹣4或t=3由于t>0∴t=3∴AB=t+2=3+2=5,AD=BC=3×2=6.故答案为:6.3.如图①,在△ABC中,AB=AC,AD⊥BC于点D(BD>AD),动点P从B点出发,沿折线BA→AC方向运动,运动到点C停止,设点P的运动路程为x,△BPD的面积为y,y与x的函数图象如图②,则BC的长为.解:由题意得:AB+AC=2√13,△ABD的面积=3∵AB=AC∴AB=AC=√13∵AD⊥BC∴∠ADB=90°,BC=2BD∴AD2+BD2=AB2∴AD2+BD2=13∵△ABD的面积=3∴12AD•BD=3∴AD•BD=6∴(AD+BD)2=AD2+2BD•AD+BD2=13+2×6=25∴AD+BD=5或AD+BD=﹣5(舍去)∵AD2+BD2=AB2∴BD2+(5﹣BD)2=13∴BD=2或BD=3当BD=2时,AD=5﹣BD=3(舍去)当BD=3时,AD=5﹣BD=2∴BC=2BD=6故答案为:6.4.如图,在平面直角坐标系中,菱形AOCB的边OC在x轴上,∠AOC=60°,OC的长是一元二次方程x2﹣4x﹣12=0的根,过点C作x轴的垂线,交对角线OB于点D,直线AD分别交x轴和y 轴于点F和点E,动点M从点O以每秒1个单位长度的速度沿OD向终点D运动,动点N从点F 以每秒2个单位长度的速度沿FE向终点E运动.两点同时出发,设运动时间为t秒.(1)求直线AD的解析式;(2)连接MN,求△MDN的面积S与运动时间t的函数关系式;(3)点N在运动的过程中,在坐标平面内是否存在一点Q,使得以A,C,N,Q为顶点的四边形是矩形.若存在,直接写出点Q的坐标,若不存在,说明理由.(1)解:解方程x2﹣4x﹣12=0得:x1=6,x2=﹣2∴OC=6∵四边形AOCB是菱形,∠AOC=60°∴OA=OC=6,∠BOC=1∠AOC=30°2∴CD=OC•tan30°=6×√3=2√33∴D(6,2√3)过点A作AH⊥OC于H∵∠AOH=60°OA=3,AH=OA•sin60°=6×√32=3√3∴OH=12∴A(3,3√3)设直线AD的解析式为y=kx+b(k≠0)代入A(3,3√3),D(6,2√3)得:{3k+b=3√36k+b=2√3解得:{k=−√3 3b=4√3∴直线AD的解析式为y=−√33x+4√3;(2)解:由(1)知在Rt△COD中,CD=2√3,∠DOC=30°∴OD=2CD=4√3,∠EOD=90°﹣∠DOC=90°﹣30°=60°∵直线y=−√33x+4√3与y轴交于点E∴OE=4√3∴OE=OD∴△EOD是等边三角形∴∠OED=∠EDO=∠BDF=60°,ED=OD=4√3∴∠OFE=30°=∠DOF∴DO=DF=4√3①当点N在DF上,即0≤t≤2√3时由题意得:DM=OD−OM=4√3−t,DN=4√3−2t过点N作NP⊥OB于P则NP=DN×sin∠PDN=DN×sin60°=(4√3−2t)×√32=6−√3t∴S=12DM×NP=12(4√3−t)×(6−√3t)=√32t2﹣9t+12√3;②当点N在DE上,即2√3<t≤4√3时由题意得:DM=OD﹣OM=√3−t,DN=2t﹣4√3过点N作NT⊥OB于T则NT =DN •sin ∠NDT =DN •sin60°=(2t ﹣4√3)×√32=√3t −6 ∴S =12DM ⋅NT =12(4√3−t)(√3t −6)=−√32t 2+9t −12√3; 综上,S ={√32t 2−9t +12√3(0≤t ≤2√3)−√32t 2+9t −12√3(2√3<t ≤4√3);(3)解:存在,分情况讨论:①如图,当AN 是直角边时,则CN ⊥EF ,过点N 作NK ⊥CF 于K∵∠NFC =30° OE =4√3 ∴∠NCK =60° OF =√3OE =12 ∴CF =12﹣6=6 ∴CN =12CF =3∴CK =CN ×cos60°=3×12=32 NK =CN ×sin60°=3×√32=3√32 ∴将点N 向左平移32个单位长度,再向下平移3√32个单位长度得到点C ∴将点A 向左平移32个单位长度,再向下平移3√32个单位长度得到点Q∵A(3,3√3) ∴Q (32,3√32); ②如图,当AN 是对角线时,则∠ACN =90°,过点N 作NL ⊥CF 于L∵OA =OC ,∠AOC =60° ∴△AOC 是等边三角形 ∴∠ACO =60°∴∠NCF=180°﹣60°﹣90°=30°=∠NFC∴CL=FL=12CF=3∴NL=CL•tan30°=3×√33=√3∴将点C向右平移3个单位长度,再向上平移√3个单位长度得到点N ∴将点A向右平移3个单位长度,再向上平移√3个单位长度得到点Q ∵A(3,3√3)∴Q(6,4√3);∴存在一点Q,使得以A,C,N,Q为顶点的四边形是矩形,点Q的坐标是(32,3√32)或(6,4√3).练习题1.如图1,在Rt△ABC中,动点P从A点运动到B点再到C点后停止,速度为2单位/s,其中BP 长与运动时间t(单位:s)的关系如图2,则AC的长为()A.15√52B.√427C.17D.5√32.如图1,正方形ABCD的边长为4,E为CD边的中点.动点P从点A出发沿AB→BC匀速运动,运动到点C时停止.设点P的运动路程为x,线段PE的长为y,y与x的函数图象如图2所示,则点M的坐标为()A.(4,2√3)B.(4,4)C.(4,2√5)D.(4,5)3.如图,在正方形ABCD中,AB=4,动点M,N分别从点A,B同时出发,沿射线AB,射线BC 的方向匀速运动,且速度的大小相等,连接DM,MN,ND.设点M运动的路程为x(0≤x≤4),△DMN的面积为S,下列图象中能反映S与x之间函数关系的是()A B C D4.如图,在边长为4的菱形ABCD中,∠A=60°,点P从点A出发,沿路线A→B→C→D运动.设P点经过的路程为x,以点A,D,P为顶点的三角形的面积为y,则下列图象能反映y与x的函数关系的是()A B C D5.如图,四边形ABCD中,已知AB∥CD,AB与CD之间的距离为4,AD=5,CD=3,∠ABC=45°,点P,Q同时由A点出发,分别沿边AB,折线ADCB向终点B方向移动,在移动过程中始终保持PQ⊥AB,已知点P的移动速度为每秒1个单位长度,设点P的移动时间为x秒,△APQ 的面积为y,则能反映y与x之间函数关系的图象是()A B C D6.如图(1),在平面直角坐标系中,矩形ABCD在第一象限,且BC∥x轴,直线y=2x+1沿x轴正方向平移,在平移过程中,直线被矩形ABCD截得的线段长为a,直线在x轴上平移的距离为b,a、b间的函数关系图象如图(2)所示,那么矩形ABCD的面积为.7.如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P是平面内一个动点,且AP=3,Q 为BP的中点,在P点运动过程中,设线段CQ的长度为m,则m的取值范围是.8.如图1,E为矩形ABCD的边AD上一点,点P从点B出发沿折线BE﹣ED﹣DC运动到点C停止,点Q从点B出发沿BC运动到点C停止,它们运动的速度都是1cm/s.若点P、点Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(cm2),已知y与t之间的函数图象如图2所示.=48cm2;③当14<t<22时,y 给出下列结论:①当0<t≤10时,△BPQ是等腰三角形;②S△ABE=110﹣5t;④在运动过程中,使得△ABP是等腰三角形的P点一共有3个;⑤△BPQ与△ABE相似时,t=14.5.其中正确结论的序号是.9.如图,在平面直角坐标系中,点A的坐标为(9,0),点C的坐标为(0,3),以OA,OC为边作矩形OABC.动点E,F分别从点O,B同时出发,以每秒1个单位长度的速度沿OA,BC向终点A,C移动.当移动时间为4秒时,求AC•EF的值.10.在平面直角坐标系中,O为原点,菱形ABCD的顶点A(√3,0),B(0,1),D(2√3,1),矩形EFGH的顶点E(0,12),F(−√3,12),H(0,32).(1)填空:如图①,点C的坐标为点G的坐标为;(2)将矩形EFGH沿水平方向向右平移,得到矩形E′FG′H′,点E,F,G,H的对应点分别为E′,F′,G′,H′,设EE′=t,矩形E′F′G′H′与菱形ABCD重叠部分的面积为S.①如图②,当边E′F′与AB相交于点M、边G′H′与BC相交于点N,且矩形E′F′G′H′与菱形ABCD重叠部分为五边形时,试用含有t的式子表示S,并直接写出t的取值范围;②当2√33≤t≤11√34时,求S的取值范围(直接写出结果即可).11.已知正方形ABCD与正方形AEFG,正方形AEFG绕点A旋转一周.(1)如图①,连接BG、CF,求CFBG的值;(2)当正方形AEFG旋转至图②位置时,连接CF、BE,分别取CF、BE的中点M、N,连接MN、试探究:MN与BE的关系,并说明理由;(3)连接BE、BF,分别取BE、BF的中点N、Q,连接QN,AE=6,请直接写出线段QN扫过的面积.12.已知四边形ABCD是边长为1的正方形,点E是射线BC上的动点,以AE为直角边在直线BC 的上方作等腰直角三角形AEF,∠AEF=90°,设BE=m.(1)如图,若点E在线段BC上运动,EF交CD于点P,AF交CD于点Q,连接CF 时,求线段CF的长;①当m=13②在△PQE中,设边QE上的高为h,请用含m的代数式表示h,并求h的最大值;(2)设过BC的中点且垂直于BC的直线被等腰直角三角形AEF截得的线段长为y,请直接写出y 与m的关系式.参考答案1.C.2.C.3.A.4.A.5.B.6.8.7.72≤m≤132.8.①③⑤.9.30.10.(1)(√3,2)(−√3,32);(2)当2√33≤t≤11√34时,则√316≤S≤√3.11.(1)√2;(2)BE=2MN MN⊥BE (3)9π.12.(1)①√23;②h=﹣m2+m=﹣(m−12)2+14,∴m=12时,h最大值是14;(2)y={1−12m−1−m2(1+m)+m2(0≤m≤12) 1+m22m2+2m(m>12).。
中考数学压轴专题动点问题解析版

1..如图,在平面直角坐标系中,点C的坐标为(0,4),动点A以每秒1个单位长的速度,从点O出发沿x轴的正方向运动,M是线段AC的中点.将线段AM以点A 为中心,沿顺时针方向旋转,得到线段AB.过点B作x轴的垂线,垂足为E,过点C作y轴的垂线,交直线BE于点D.运动时间为t秒.(1)当点B及点D重合时,求t的值;(2)设△BCD的面积为S,当t为何值时,S25=?4(3)连接MB,当MB∥OA时,如果抛物线2=-的顶点y ax10ax在△ABM内部(不包括边),求a的取值范围.3,抛物线2.如图,⊙C的内接△AOB中,AB=AO=4,tan∠AOB=42=+经过点A(4,0)及点(-2,6)y ax bx(1)求抛物线的函数解析式.(2)直线m及⊙C相切于点A交y轴于点D,动点P在线段OB 上,从点O出发向点B运动;同时动点Q在线段DA上,从点D出发向点A运动,点P的速度为每秒1个单位长,点Q的速度为每秒2个单位长,当PQ⊥AD时,求运动时间t的值(3)点R在抛物线位于x轴下方部分的图象上,当△ROB面积最大时,求点R的坐标.3.如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=1,A(3,0),D(﹣1,0),E(0,33).(1)求抛物线的解析式及顶点B的坐标;(2)求证:CB是△ABE外接圆的切线;(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形及△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE及△ABE重叠部分的面积为s,求s及t之间的函数关系式,并指出t的取值范围.4.已知,如图,在平面直角坐标系中,点A坐标为(-2,0),点B坐标为(0,2 ),点E为线段AB上的动点(点E不及点A,B 重合),以E为顶点作∠OET=45°,射线ET交线段OB于点F,C 为y轴正半轴上一点,且OC=AB,抛物线y=2-x2+mx+n的图象经过A,C两点.(1)求此抛物线的函数表达式;(2)求证:∠BEF=∠AOE;(3)当△EOF为等腰三角形时,求此时点E的坐标;(4)在(3)的条件下,当直线EF交x轴于点D,P为(1)中抛物线上一动点,直线PE交x轴于点G,在直线EF上方的抛物线上是否存在一点P,使得△EPF的面积是△EDG面积的(122+)倍.若存在,请直接..写出点P的坐标;若不存在,请说明理由.温馨提示:考生可以根据题意,在备用图中补充图形,以便作答.5.如图,直线AB交x轴于点B(4,0),交y轴于点A(0,4),直线D M⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°.(1)直接写出直线AB的解析式;(2)求点D的坐标;(3)若点P是线段MB上的动点,过点P作x轴的垂线,交AB 于点F,交过O、D、B三点的抛物线于点E,连接CE.是否存在点P,使△BPF及△FCE相似?若存在,请求出点P的坐标;若不存在,请说明理由.6.(10分)(2019•常州)如图,一次函数y=﹣x+4的图象及x 轴、y轴分别相交于点A、B,过点A作x轴的垂线l,点P为直线l上的动点,点Q为直线AB及△OAP外接圆的交点,点P、Q 及点A都不重合.(1)写出点A的坐标;(2)当点P在直线l上运动时,是否存在点P使得△OQB及△APQ 全等?如果存在,求出点P的坐标;如果不存在,请说明理由.(3)若点M在直线l上,且∠POM=90°,记△OAP外接圆和△OAM 外接圆的面积分别是S1、S2,求的值.7.(10分)(2019•常州)如图,反比例函数y=的图象及一次函数y=x 的图象交于点A 、B ,点B 的横坐标是4.点P 是第一象限内反比例函数图象上的动点,且在直线AB 的上方.(1)若点P 的坐标是(1,4),直接写出k 的值和△PAB 的面积;(2)设直线PA 、PB 及x 轴分别交于点M 、N ,求证:△PMN 是等腰三角形;(3)设点Q 是反比例函数图象上位于P 、B 之间的动点(及点P 、B 不重合),连接AQ 、BQ ,比较∠PAQ 及∠PBQ 的大小,并说明理由.1.【答案】解:(1)∵CAO BAE 90∠+∠=︒,∴CAO ABE ∠=∠。
2024辽宁中考数学二轮专题训练 题型七 坐标系中的几何动点问题 (含答案)

2024辽宁中考数学二轮专题训练题型七坐标系中的几何动点问题典例精讲例1如图,平面直角坐标系中,O 是坐标原点,直线y =kx +15(k ≠0)经过点C (3,6),与x 轴交于点A ,与y 轴交于点B.线段CD 平行于x 轴,交直线y =34x 于点D ,连接OC ,AD .例1题图(1)填空:k =________.点A 的坐标是(________,________);【思维教练】将C (3,6)代入y =kx +15即可求k ,将y =0代入新的一次函数解析式,求出A 点坐标.(2)求证:四边形OADC 是平行四边形;【思维教练】因为CD ∥OA ,所以要证明四边形OADC 是平行四边形,可以证明CD =OA ,将C 点纵坐标代入到y =34x 中,求出D 点坐标,从而求出CD 的长,与OA 比较.(3)动点P从点O出发,沿对角线OD以每秒1个单位长度的速度向点D运动,直到点D为止;动点Q同时从点D出发,沿对角线DO以每秒1个单位长度的速度向点O运动,直到点O为止.设两个点的运动时间均为t秒.①当t=1时,△CPQ的面积是________.②当点P,Q运动至四边形CPAQ为矩形时,请直接写出此时t的值.【思维教练】①可求出PQ的长,以及C点到OD的距离.②因为四边形OADC是平行四边形,所以考虑利用判定依据:对角线相等且互相平分的四边形是矩形.证明AC与PQ互相平分,当PQ=AC时,四边形CPAQ为矩形.例2如图,在平面直角坐标系中,△AOB的顶点O是坐标原点,点A的坐标为(4,4),点B的坐标为(6,0),动点P从O开始以每秒1个单位长度的速度沿y轴正方向运动,设运动的时间为t秒(0<t<4),过点P作PN∥x轴,分别交AO,AB于点M,N.例2题图备用图(1)填空:AO的长为________,AB的长为________;【思维教练】要求AO,AB的长,已知点A,B的坐标,利用两点间距离公式求解即可;(2)当t=1时,求点N的坐标;【思维教练】要求t=1时,点N的坐标,可知点N在AB上,利用待定系数法求出直线AB 的解析式即可求解;(3)请直接写出MN的长为________(用含t的代数式表示);【思维教练】要求MN的长,可先求出PN,PM,即点N,M的横坐标即可;(4)点E是线段MN上一动点(点E不与点M,N重合),△AOE和△ABE的面积分别表示为S1和S2,当t=43时,请直接写出S1·S2(即S1与S2的积)的最大值为________.【思维教练】要求△AOE和△ABE的面积之积的最大值,先表示出△AOE和△ABE的面积,当t=43时,可得MN的值,设EM=m,构建二次函数,利用二次函数的性质即可解决问题.针对训练1.如图,在平面直角坐标系中,直线l1:y=43x+83与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B.(1)求直线l2的表达式;(2)点P是直线l2上的一个动点,过点P作EF⊥x轴于点E,交直线l1于点F,①若PF=AB,求点P的坐标.②过点P作PQ⊥l1于点Q,若PQ=2PE,请直接写出点P的坐标.第1题图2.如图,在平面直角坐标系内,点A、B在x轴上,点C在y轴上,∠ACB=90°,AB=10,AC=8,点Q在边AB上,且AQ=2,过点Q作QR⊥AB,垂足为Q,QR交折线AC-CB 于点R(如图①),当点Q以每秒2个单位向终点B移动时,点P同时从点A出发,以每秒6个单位的速度沿AB-BC-CA移动,设移动时间为t秒(如图②).(1)BQ=________;(用含t的代数式表示)(2)求△BCQ的面积S与t的函数关系式;(3)t的值为________秒时,直线QR经过点P;(4)当点P在边AB上运动时,以PQ为边在AB上方所作的正方形PQMN在Rt△ABC内部,此时t的取值范围是________.第2题图参考答案典例精讲例1(1)解:-3,(5,0);【解法提示】将点C (3,6)代入y =kx +15(k ≠0),得6=3k +15.解得k =-3.∴y =-3x +15.当y =0时,0=-3x +15.解得x =5.∴A (5,0).(2)证明:∵CD ∥x 轴,C (3,6),∴CD ∥OA ,y C =y D =6.令y =34x =6,解得x =8.∴D (8,6).∵C (3,6),∴CD =8-3=5.∵A (5,0),∴OA =5.∴OA =CD .∴四边形OADC 是平行四边形;(3)解:①12;【解法提示】如解图①,过C 作CH ⊥OD 于H ,∵D (8,6),∴OD =82+62=10.∵四边形OADC 为平行四边形,∴OD 平分四边形OADC 的面积.∴S 四边形OADC =2S △COD ,即OA ·y C =2·12OD ·CH ,即5·6=2·12×10·CH .解得CH =3.而PQ =OD -OP -DQ =8.∴S △CPQ =12PQ ·CH =12×8×3=12.②5+10或5-10;【解法提示】如解图②,设OD 与AC 相交于M .∵四边形OADC 为平行四边形,∴OM =DM ,AM =CM .∵OP =DQ =t ,所以PM =QM .当PQ =AC 时,四边形CPAQ 为矩形.∵A (5,0),C (3,6),∴AC =(5-3)2+62=210.|PQ |=|10-2t |,∴10-2t =210,或2t -10=210.∴t =5-10或t =5+10时,四边形CPAQ 为矩形.例1题解图①例1题解图②例2解:(1)42,25;【解法提示】∵A (4,4),B (6,0),∴AO =42+42=42,AB =(6-4)2+42=2 5.(2)设直线AB 的解析式为y =kx +b (k ≠0),将A (4,4),B (6,0)代入得,4k +b =46k +b =0,k =-2b =12,∴直线AB 的解析式为y =-2x +12,由题意得,点N 的纵坐标为1,令y =1,则1=-2x +12,∴x =112,∴N (112,1);(3)12-3t 2;【解法提示】当0<t <4时,令y =t ,代入y =-2x +12,得x =12-t 2,∴N (12-t 2,t ),∵∠AOB =∠AOP =45°,∠OPM =90°,∴OP =PM =t ,∴MN =PN -PM =12-t 2-t =12-3t 2.(4)16.【解法提示】如解图,当t =43时,MN =12-3×432=4,设EM =m ,则EN =4-m .由题意得,S 1·S 2=12×m ×4×12×(4-m )×4=-4m 2+16m =-4(m -2)2+16,∵-4<0,∴m =2时,S 1·S 2有最大值,最大值为16.例2题解图针对训练1.解:(1)由题知点C (1,m )在直线l 1上,∴将点C (1,m )代入y =43x +83,得m =43+83=4,故C (1,4),设直线l 2的表达式为y =kx +b (k ≠0),代入A 、C 点坐标,=k +b=3k +b =-2=6,∴直线l 2的表达式为y =-2x +6;(2)设点P 的坐标为(n ,-2n +6),则点E 的坐标为(n ,0),点F 的坐标为(n ,43n +83),在y =43x +83中,令y =0,得0=43x +83,解得x =-2,∴B (-2,0),∴AB =3-(-2)=5,若点P 在F 上方,则-2n +6-(43n +83)=5,解得n =-12,即P (-12,7);若点P 在F 下方,则43n +83-(-2n +6)=5,解得n =52,即P (52,1),综上所述,若PF =AB ,点P 的坐标为(-12,7)或(52,1);②点P 的坐标为(73,43)或(5,-4).【解法提示】设点P 的坐标为(n ,-2n +6),如解图,设直线l 1与y 轴交于点D ,设PQ 交x 轴于点M ,交y 轴于点N ,由题知PQ ⊥l 1于点Q ,∴∠DBO +∠NMO =90°,又∵∠BDO +∠DBO =90°,∴∠NMO =∠BDO ,又∵∠BOD =∠MON =90°,∴△BOD ∽△NOM ,∴OB OD =ON OM,设直线PQ 的表达式为y =k 1x +b 1(k 1≠0),则OM =-b 1k 1,ON =b 1,由题知OB =2,OD =83,∴283=b 1-b 1k 1,解得k 1=-34,∴直线PQ 的表达式为y =-34x +b 1,将点P (n ,-2n +b )代入直线PQ 表达式得-2n +6=-34n +b 1,解得b 1=-54n +6,∴直线PQ 的表达式为y =-34x -54n +6①,又∵直线l 1:y =43x +83②,联立①②,解得Q 点坐标为(-35n +85,-45n +245),∴PQ 2=[n -(-35n +85)]2+[(-2n +6)-(-45n +245)]2=4(n -1)2,(2PE )2=4PE 2=4(-2n +6)2,∵PQ =2PE ,∴4(n -1)2=4(-2n +6)2,解得n =73或n =5,故P (73,43或(5,-4).第1题解图2.解:(1)8-2t ;【解法提示】由题意得AQ =2+2t ,AB =10,∴BQ =AB -AQ =8-2t .(2)在Rt △ABC 中,AB =10,AC =8,根据勾股定理得:BC =6,∵12AC ·BC =12AB ·CO ,即12×6×8=12×10·CO ,∴CO =245,则S △BCQ =12QB ·CO =125(8-2t )=-245t +965(0≤t ≤4);(3)0.5或2.5;【解法提示】①当点Q 、P 均在AB 上时,AP =6t ,AQ =2+2t ,可得:AP =AQ ,即6t =2+2t ,解得t =0.5;②当P 在BC 上时,P 与R 重合,如解图①,第2题解图①∵∠PQB =∠ACB =90°,∠B =∠B ,∴△BPQ ∽△BAC ,∴BP BA =BQ BC,又∵BP =6t -10,AB =10,BQ =8-2t ,BC =6,∴6t -1010=8-2t 6,即6(6t -10)=10(8-2t ),解得t =2.5;③当点P 在AC 上不存在QR 经过点P ,综上,当t =0.5或2.5时,直线QR 经过点P .(4)417<t <2318且t ≠0.5.【解法提示】当点P 在点Q 的左侧时,若点N 落在AC 上,如解图②:第2题解图②∵AP =6t ,AQ =2+2t ,∴PQ =AQ -AP =2+2t -6t =2-4t ,∵四边形PQMN 是正方形,∴PN =PQ =2-4t ,∵∠APN =∠ACB =90°,∠A =∠A ,∴△APN ∽△ACB ,∴PN CB =AP AC ,即2-4t 6=6t 8,解得t =417;当点P 在点Q 的右侧时,若点N 落在BC 上,如解图③,第2题解图③由题意得:BP =10-6t ,PN =PQ =4t -2,∵∠BPN =∠BCA =90°,∠B =∠B ,∴△BPN ∽△BCA ,∴BP BC =PN CA ,即10-6t 6=4t -28,整理得:8(10-6t )=6(4t -2),解得t =2318,∵t =0.5时,点P 与点Q 重合,∴417<t <2318且t ≠0.5时,正方形PQMN 在Rt △ABC 内部.。
2023中考数学-压轴专题训练之动点问题(含答案)

中考数学 压轴专题训练之动点问题1. 如图1,在平面直角坐标系中,四边形OABC 各顶点的坐标分别为O (0,0),A (3,33),B (9,53),C (14,0).动点P 与Q 同时从O 点出发,运动时间为t 秒,点P 沿OC 方向以1单位长度/秒的速度向点C 运动,点Q 沿折线OA -AB -BC 运动,在OA ,AB ,BC 上运动的速度分别为3,3,52(单位长度/秒).当P ,Q 中的一点到达C 点时,两点同时停止运动. (1)求AB 所在直线的函数表达式.(2)如图2,当点Q 在AB 上运动时,求△CPQ 的面积S 关于t 的函数表达式及S 的最大值.(3)在P ,Q 的运动过程中,若线段PQ 的垂直平分线经过四边形OABC 的顶点,求相应的t 值.图1 图21. 【答案】【思维教练】(1)设一次函数解析式,将已知点A 、B 的坐标值代入求解即可;(2)S△CPQ=12·CP ·Q y ,CP =14-t ,点Q 在AB 上,Q y 即为当x =t 时的y 值,代入化简得出S 与t 的函数关系式,化为顶点式得出最值;(3)垂直平分线过顶点需以时间为临界点分情况讨论,当Q 在OA 上时,过点C ;当Q 在AB 上时,过点A ;当Q 在BC 上时,过点C 和点B ,再列方程并求解.解图1解:(1)把A(3,33),B(9,53)代入y =kx +b , 得⎩⎪⎨⎪⎧3k +b =33,9k +b =53,解得⎩⎨⎧k =33,b =23,∴y=33x+23;(3分)(2)在△PQC中,PC=14-t,∵OA=32+(33)2=6且Q在OA上速度为3单位长度/s,AB=62+(23)2=43且Q点在AB上的速度为3单位长度/s,∴Q在OA上时的横坐标为t,Q在AB上时的横坐标为32 t,PC边上的高线长为33t+2 3.(6分)所以S=12(14-t)(32t+23)=-34t2+532t+143(2≤t≤6).当t=5时,S有最大值为8134.(7分)解图2(3)①当0<t≤2时,线段PQ的中垂线经过点C(如解图1).可得方程(332t)2+(14-32t)2=(14-t)2.解得t1=74,t2=0(舍去),此时t=74.(8分)解图3②当2<t≤6时,线段PQ的中垂线经过点A(如解图2).可得方程(33)2+(t-3)2=[3(t-2)]2.解得t1=3+572,∵t2=3-572(舍去),此时t=3+572.③当6<t≤10时,(1)线段PQ的中垂线经过点C(如解图3).可得方程14-t=25-52t,解得t=223.(10分)解图4(2)线段PQ的中垂线经过点B(如解图4).可得方程(53)2+(t-9)2=[52(t-6)]2.解得t1=38+2027,t2=38-2027(舍去).此时t=38+2027.(11分)综上所述,t的值为74,3+572,223,38+2027.(12分)【难点突破】解决本题的关键点在于对PQ的垂直平分线过四边形顶点的情况进行分类讨论,在不同阶段列方程求解.2. 如图,抛物线y=-x2+bx+c与x轴交于A,B两点(A在B的左侧),与y轴交于点N,过A点的直线l:y=kx+n与y轴交于点C,与抛物线y=-x2+bx+c的另一个交点为D,已知A(-1,0),D(5,-6),P点为抛物线y=-x2+bx+c上一动点(不与A,D重合).(1)求抛物线和直线l的解析式;(2)当点P在直线l上方的抛物线上时,过P点作PE∥x轴交直线l于点E,作PF∥y轴交直线l于点F,求PE+PF的最大值;(3)设M为直线l上的点,探究是否存在点M,使得以点N,C,M,P为顶点的四边形为平行四边形.若存在,求出点M的坐标;若不存在,请说明理由.2. 【答案】[分析] (1)将点A,D的坐标分别代入直线表达式、抛物线的表达式,即可求解;(2)设出P点坐标,用参数表示PE,PF的长,利用二次函数求最值的方法.求解;(3)分NC是平行四边形的一条边或NC是平行四边形的对角线两种情况,分别求解即可.解:(1)将点A,D的坐标代入y=kx+n得:解得:故直线l的表达式为y=-x-1.将点A,D的坐标代入抛物线表达式,得解得故抛物线的表达式为:y=-x2+3x+4.(2)∵直线l的表达式为y=-x-1,∴C(0,-1),则直线l与x轴的夹角为45°,即∠OAC=45°,∵PE∥x轴,∴∠PEF=∠OAC=45°.又∵PF∥y轴,∴∠EPF=90°,∴∠EFP=45°.则PE=PF.设点P坐标为(x,-x2+3x+4),则点F(x,-x-1),∴PE+PF=2PF=2(-x2+3x+4+x+1)=-2(x-2)2+18,∵-2<0,∴当x=2时,PE+PF有最大值,其最大值为18.(3)由题意知N(0,4),C(0,-1),∴NC=5,①当NC是平行四边形的一条边时,有NC∥PM,NC=PM.设点P坐标为(x,-x2+3x+4),则点M的坐标为(x,-x-1),∴|y M-y P|=5,即|-x2+3x+4+x+1|=5,解得x=2±或x=0或x=4(舍去x=0),则点M坐标为(2+,-3-)或(2-,-3+)或(4,-5);②当NC是平行四边形的对角线时,线段NC与PM互相平分.由题意,NC的中点坐标为0,,设点P坐标为(m,-m2+3m+4),则点M(n',-n'-1),∴0==,解得:n'=0或-4(舍去n'=0),故点M(-4,3).综上所述,存在点M,使得以N,C,M,P为顶点的四边形为平行四边形,点M 的坐标分别为:(2+,-3-),(2-,-3+),(4,-5),(-4,3).3. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c经过A(-2, -4 )、O(0, 0)、B(2, 0)三点.(1)求抛物线y=ax2+bx+c的解析式;(2)若点M 是该抛物线对称轴上的一点,求AM +OM 的最小值.3. 【答案】(1)212y x x =-+。
人教版九年级数学中考动点问题专项练习及参考答案

人教版九年级数学中考动点问题专项练习例题1. 抛物线223y x x =-++与x 轴相交于A 、B 两点(点A 在B 的左侧),与y轴相交于点C ,顶点为D .⑴ 直接写出A 、B 、C 三点的坐标和抛物线的对称轴;⑵ 连接BC ,与抛物线的对称轴交于点E ,点P 为线段BC 上的一个动点,过点P 作PF DE ∥交抛物线于点F ,设点P 的横坐标为;① 用含m 的代数式表示线段PF 的长,并求出当m 为何值时,四边形PEDF 为平行四边形?② 设BCF ∆的面积为S ,求S 与m 的函数关系式. 【答案】⑴()10A -,,()30B ,,()03C ,.抛物线的对称轴是:1x =.⑵①设直线BC 的函数关系式为:y kx b =+. 把()()3003B C ,,,分别代入得:303.k b b +=⎧⎨=⎩,解得:13k b =-=,. 所以直线BC 的函数关系式为:3y x =-+. 当1x =时,132y =-+=,∴()12E ,. 当x m =时,3y m =-+, ∴()3P m m -+,.在223y x x =-++中,当1x =时,4y =. ∴()14D ,当x m =时,223y m m =-++∴()223F m m m -++,.∴线段422DE =-=,线段()222333PF m m m m m =-++--+=-+. ∵PF DE ∥∴当PF ED =时,四边形PEDF 为平行四边形. 由232m m -+=解得:1221m m ==,.(不合题意,舍去). 因此,当2m =时,四边形PEDF 为平行四边形.②设直线PF 与x 轴交于点M ,由()30B ,,()00O ,,可得:3OB OM MB =+=. ∵BPF CPE S S S ∆∆=+.即()11112222S PF BM PF OM PF BM OM PF OB =⋅+⋅=⋅+=⋅.∴()()221393303222S m m m m m =⨯-+=-+≤≤.例题2. 如图,已知抛物线(1)2)0y a x a =-+≠经过点(2)A -,0,抛物线的顶点为D ,过O 作射线OM AD ∥.过顶点D 平行于x 轴的直线交射线OM 于点C ,B 在x 轴正半轴上,连结BC .(1)求该抛物线的解析式; (2)若动点P 从点O 出发,以每秒1个长度单位的速度沿射线OM 运动,设点P 运动的时间为()t s .问当t 为何值时,四边形DAOP 分别为平行四边形?直角梯形?等腰梯形?(3)若OC OB =,动点P 和动点Q 分别从点O 和点B 同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC 和BO 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t ()s ,连接PQ ,当t 为何值时,四边形BCPQ 的面积最小?并求出最小值及此时PQ 的长.【答案】(1)∵抛物线2(1))0y a x a =-+≠经过点()20A -,,∴09a =+a =∴二次函数的解析式为:2y =+(2)∵D 为抛物线的顶点∴(1D 过D 作DN OB ⊥于N ,则DN =,3AN =,∴6AD ==∴60DAO ∠=︒∵OM AD ∥①当AD OP =时,四边形DAOP 是平行四边形 ∴6OP =∴()6t s =②当DP OM ⊥时,四边形DAOP 是直角梯形 过O 作OH AD ⊥于H ,2AO =,则1AH =(如果没求出60DAO ∠=°可由Rt Rt OHA DNA △∽△求1AH =) ∴5OP DH ==,()5t s =③当PD OA =时,四边形DAOP 是等腰梯形 ∴2624OP AD AH =-=-=∴()4t s =综上所述:当6t =、5、4时,对应四边形分别是平行四边形、直角梯形、等腰梯形.(3)由(2)及已知,60OC OB COB OCB =∠=,,°△是等边三角形 则62OB OC AD OP t BQ t =====,,,∴()6203OQ t t =-<< 过P 作PE OQ ⊥于E,则PE =∴113322263(62)BCPQ t S t -=⨯⨯⨯-⨯=233633228t ⎛⎫-+⎪⎝⎭ 当32t =时,BCPQ S 的面积最小值为6338 ∴此时33324OQ OP OE ==,=,∴39334443PE QE ===- ∴222233933442PE QE PQ ⎛⎫⎛⎫+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭=例题3. 已知⊙O 的半径为3,⊙P 与⊙O 相切于点A ,经过点A 的直线与⊙O 、⊙P 分别交于点B 、C ,cos ∠BAO =13.设⊙P 的半径为x ,线段OC 的长为y .(1)求AB 的长;(2)如图1,当⊙P 与⊙O 外切时,求y 与x 之间的函数关系式,并写出函数的定义域;(3)当∠OCA =∠OPC 时,求⊙P 的半径.图1 【答案】(1)如图2,作OE ⊥AB ,垂足为E ,由垂径定理,得AB =2AE .在Rt △AOE 中,cos ∠BAO =13AE AO =,AO =3,所以AE =1.所以AB =2.(2)如图2,作CH ⊥AP ,垂足为H . 由△OAB ∽△P AC ,得AO AP AB AC =.所以32x AC =.所以23AC x =. 在Rt △ACH 中,由cos ∠CAH =13,得1322AH AC CH==. 所以1239AH AC x ==,224239CH AC x ==. 在Rt △OCH 中,由OC 2=OH 2+CH 2,得222422()(3)99y x x =++. 整理,得23649813y x x =++.定义域为x >0.图2 图3(3)①如图3,当⊙P 与⊙O 外切时,如果∠OCA =∠OPC ,那么△OCA ∽△OPC .因此OA OCOC OP =.所以2OC OA OP =⋅. 解方程236493(3)813x x x ++=+,得154x =.此时⊙P 的半径为154.②如图4,图5,当⊙P 与⊙O 内切时,同样的△OAB ∽△P AC ,23AC x =. 如图5,图6,如果∠OCA =∠OPC ,那么△ACO ∽△APC .所以AO ACAC AP =.因此2AC AO AP =⋅. 解方程22()33x x =,得274x =.此时⊙P 的半径为274.图4 图5 图6例题4. 如图1,在平面直角坐标系中,O为坐标原点,点A的坐标为(0,4),点B 的坐标为(4,0),点C的坐标为(-4,0),点P在射线AB上运动,连结CP与y轴交于点D,连结BD.过P、D、B三点作⊙Q,与y轴的另一个交点为E,延长DQ交⊙Q于F,连结EF、BF.(1)求直线AB的函数解析式;(2)当点P在线段AB(不包括A、B两点)上时.①求证:∠BDE=∠ADP;②设DE=x,DF=y,请求出y关于x的函数解析式;(3)请你探究:点P在运动过程中,是否存在以B、D、F为顶点的直角三角形,满足两条直角边之比为2∶1?如果存在,求出此时点P的坐标;如果不存在,请说明理由.图1【答案】(1)直线AB的函数解析式为y=-x+4.(2)①如图2,∠BDE=∠CDE=∠ADP;②如图3,∠ADP=∠DEP+∠DPE,如图4,∠BDE=∠DBP+∠A,因为∠DEP=∠DBP,所以∠DPE=∠A=45°.所以∠DFE=∠DPE=45°.因此△DEF是等腰直角三角形.于是得到2y x=.图2 图3 图4(3)①如图5,当BD∶BF=2∶1时,P(2,2).思路如下:由△DMB∽△BNF,知122BN DM==.设OD=2m,FN=m,由DE=EF,可得2m+2=4-m.解得23m=.因此4(0,)3D.再由直线CD与直线AB求得交点P(2,2).②如图6,当BD∶BF=1∶2时,P(8,-4).思路同上.图5 图6例题5. 在Rt △ABC 中,∠C =90°,AC =6,53sin =B ,⊙B 的半径长为1,⊙B 交边CB 于点P ,点O 是边AB 上的动点.(1)如图1,将⊙B 绕点P 旋转180°得到⊙M ,请判断⊙M 与直线AB 的位置关系;(2)如图2,在(1)的条件下,当△OMP 是等腰三角形时,求OA 的长; (3)如图3,点N 是边BC 上的动点,如果以NB 为半径的⊙N 和以OA 为半径的⊙O 外切,设NB =y ,OA =x ,求y 关于x 的函数关系式及定义域.图1 图2 图3【答案】(1) 在Rt △ABC 中,AC =6,53sin =B ,所以AB =10,BC =8.过点M 作MD ⊥AB ,垂足为D .在Rt △BMD 中,BM =2,3sin 5MD B BM==,所以65MD =.因此MD >MP ,⊙M 与直线AB 相离. 图4(2)①如图4,MO ≥MD >MP ,因此不存在MO =MP 的情况.②如图5,当PM =PO 时,又因为PB =PO ,因此△BOM 是直角三角形.在Rt △BOM 中,BM =2,4cos 5BO B BM==,所以85BO =.此时425OA =.③如图6,当OM =OP 时,设底边MP 对应的高为OE .在Rt △BOE 中,BE =32,4cos 5BE B BO==,所以158BO =.此时658OA =.图5 图6(3)如图7,过点N 作NF ⊥AB ,垂足为F .联结ON . 当两圆外切时,半径和等于圆心距,所以ON =x +y .在Rt △BNF 中,BN =y ,3sin 5B =,4cos 5B =,所以35NF y =,45BF y =.在Rt △ONF 中,4105OF AB AO BF x y =--=--,由勾股定理得ON 2=OF 2+NF 2. 于是得到22243()(10)()55x y x y y +=--+.整理,得2505040x y x -=+.定义域为0<x <5.图7 图8例题6. 如图1,甲、乙两人分别从A 、B 两点同时出发,点O 为坐标原点.甲沿AO 方向、乙沿BO 方向均以每小时4千米的速度行走,t 小时后,甲到达M 点,乙到达N 点.(1)请说明甲、乙两人到达点O 前,MN 与AB 不可能平行;(2)当t 为何值时,△OMN ∽△OBA ?(3)甲、乙两人之间的距离为MN 的长.设s =MN 2,求s 与t 之间的函数关系式,并求甲、乙两人之间距离的最小值. 图1【答案】 (1)当M 、N 都在O 右侧时,24122OM t t OA-==-,642163ON t t OB-==-,所以OM ON OAOB≠.因此MN 与AB 不平行.(2)①如图2,当M 、N 都在O 右侧时,∠OMN >∠B ,不可能△OMN ∽△OBA .②如图3,当M 在O 左侧、N 在O 右侧时,∠MON >∠BOA ,不可能△OMN ∽△OBA .③如图4,当M 、N 都在O 左侧时,如果△OMN ∽△OBA ,那么ON OA OMOB=.所以462426t t -=-.解得t =2.图2 图3 图4(3)①如图2,24OM t =-,12OH t =-,2)MH t =-.(64)(12)52NH ON OH t t t =-=---=-.②如图3,42OM t =-,21OH t =-,1)MH t =-.(64)(21)52NH ON OH t t t =+=-+-=-.③如图4,42OM t =-,21OH t =-,1)MH t =-.(21)(46)52NH OH ON t t t =-=---=-.综合①、②、③,s 222MN MH NH ==+22221)(52)16322816(1)12t t t t t ⎤=-+-=-+=-+⎦. 所以当t =1时,甲、乙两人的最小距离为12千米.例题7. 已知点 (1,3)在函数ky x=(0x >)的图像上,矩形ABCD 的边BC 在x 轴上,E 是对角线BD 的中点,函数ky x=(0x >)的图像经过A 、E 两点,若45ABD ∠=︒,求E 点的坐标.【解析】点(1,3)在函数k y x=的图像上,3k =.又E 也在函数k y x =的图像上,故设E 点的坐标为(m ,3m). 过E 点作EF x ⊥轴于F ,则3EF m=. 又E 是对角线BD 的中点,62AB CD EF m===. 故A 点的纵坐标为6m ,代入3y x =中,得A 点坐标为 (2m ,6m). 因此22m mBF OF OB m =-=-=.由45ABD ∠=︒,得45EBF ∠=︒,BF EF =. 即有32m m=.解得m =而0m >,故m =则E 点坐标为【答案】例题8. 如图,11POA ∆、212PA A ∆都是等腰直角三角形,点1P 、2P 在函数4y x=(0x >)的图像上,斜边1OA 、12A A 、都在x 轴上,求点2A 的坐标.【解析】分别过点1P 、2P 做x 轴的垂线,根据题意易得1PC OC =,21P D A D =,14PC OC ⋅=,24P D OD ⋅=,得2OA =,所以2A(0).【答案】2A(0).例题9. 如图所示,()()111222P x y P x y ,,,,……,()n n n P x y ,在函数()90y x x=>的图象上,11OP A ∆,212P A A ∆,323P A A ∆,…,1n n n P A A -∆,…都是等腰直角三角形,斜边1121n n OA A A A A -,,…,都在x 轴上,则12n y y y +++=…______________.【解析】由已知易得()133P ,,则13y =,点2P 横坐标为26y +, 那么可得()2269y y +=,解得23y =,同理点3P横坐标为3y,那么可得()339y y =,解得3y =依此类推,n P的纵坐标为n y =∴1233n y y y +++=+++……【答案】例题10. 如图,P 是函数12y x=(0x >)图象上一点,直线1y x =-+交x 轴于点A ,交y 轴于点B ,PM Ox ⊥轴于M ,交AB 于E ,PN Oy ⊥轴于N ,交AB 于F.求AF BE ⋅的值.【解析】设点P (x ,y ),过点E 、F 分别作x 轴的垂线,21AF BE xy ⋅==. 【答案】1例题11. 已知:在矩形AOBC 中,4OB =,3OA =.分别以OB OA ,所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系.F 是边BC 上的一个动点(不与BC ,重合),过F 点的反比例函数(0)ky k x=>的图象与AC 边交于点E .(1)求证:AOE △与BOF △的面积相等; (2)记OEF ECF S S S =-△△,求当k 为何值时,S 有最大值,最大值为多少?(3)请探索:是否存在这样的点F ,使得将CEF △沿EF 对折后,C 点恰好落在OB 上?若存在,求出点F 的坐标;若不存在,请说明理由.【答案】(1)证明:设11()E x y ,,22()F x y ,,AOE △与FOB △的面积分别为1S ,2S ,由题意得11k y x =,22k y x =. ∴1111122S x y k ==,2221122S x y k ==.∴12S S =,即AOE △与FOB △的面积相等.(2)由题意知:E F ,两点坐标分别为33k E ⎛⎫ ⎪⎝⎭,,44k F ⎛⎫ ⎪⎝⎭,, ∴11121222EOF AOE BOF ECF ECF ECF AOBC S S S S S k k S k S =---=---=--△△△△△△矩形∴2112S k k =-+. 当161212k =-=⎛⎫⨯- ⎪⎝⎭时,S 有最大值.131412S -==⎛⎫⨯- ⎪⎝⎭最大值.(3)解:设存在这样的点F ,将沿EF 对折后,C 点恰好落在OB 边上的M 点,过点E 作EN OB ⊥,垂足为N .由题意得:3EN AO ==,143EM EC k ==-,134MF CF k ==-,∵90EMN FMB FMB MFB ∠+∠=∠+∠= ∴EMN MFB ∠=∠.又∵90ENM MBF ∠=∠=, ∴ENM MBF △∽△. ∴EN EM MB MF= ∴11414312311331412k k MB k k ⎛⎫-- ⎪⎝⎭==⎛⎫-- ⎪⎝⎭ ∴94MB =.222MB BF MF +=,解得218k =.∴21432k BF ==∴存在符合条件的点F ,它的坐标为21432⎛⎫⎪⎝⎭,.例题12. 如图,点()1A m m +,,()31B m m +-,都在反比例函数ky x=的图象上. (1)求m k ,的值;(2)如果M 为x 轴上一点,N 为y 轴上一点, 以点A B M N ,,,为顶点的四边形是平行四边形,试求直线MN 的函数表达式.【解析】(1)由题意可知,()()()131m m m m +=+-.解,得3m =.∴()()3462A B ,,,;∴4312k =⨯=.(2)存在两种情况,如图:①当M 点在x 轴的正半轴上,N 点在y 轴的正半轴上时,设1M 点坐标为()10x ,,1N 点坐标为()10y ,. ∵ 四边形11AN M B 为平行四边形,∴线段11N M 可看作由线段AB 向左平移3个单位,再向下平移2个单位得到的(也可看作向下平移2个单位,再向左平移3个单位得到的).由(1)知A 坐标为(3,4),B 坐标为(6,2),∴1N 点坐标为042(,-),即102N (,); 1M 点坐标为(6-3,0),即1M (3,0).设直线11M N 的函数表达式为12y k x =+,把30x y ==,代入,解得123k =-. ∴ 直线11M N 的函数表达式为223y x =-+.②当M 点在x 轴的负半轴上,N 点在y 轴的负半轴上时,设2M 点坐标为20x (,),2N 点坐标为20y (,).∵11221122AB N M AB M N AB N M AB M N ∥,∥,=,=,∴1221122N M M N N M M N ∥,=. ∴线段22M N 与线段11N M 关于原点O 成中心对称. ∴2M 点坐标为(-3,0),2N 点坐标为(0,-2).设直线22M N 的函数表达式为22y k x =-,把30x y =-=,代入,解得223k =-,∴ 直线M 2N 2的函数表达式为223y x =--.所以,直线MN 的函数表达式为223y x =-+或223y x =--.【答案】(1)3m =,12k =;(2)223y x =-+或223y x =--。
中考数学高频考点《动点综合问题》专项测试卷-带答案

中考数学高频考点《动点综合问题》专项测试卷-带答案(16道)一、单选题1.(2023·辽宁盘锦·统考中考真题)如图,在平面直角坐标系中 菱形ABCD 的顶点A 在y 轴的正半轴上 顶点B C 在x 轴的正半轴上 (3D ()1,1P --.点M 在菱形的边AD 和DC 上运动(不与点A C 重合) 过点M 作MN y ∥轴 与菱形的另一边交于点N 连接PM PN 设点M 的横坐标为x PMN 的面积为y ,则下列图象能正确反映y 与x 之间函数关系的是( )A .B .C .D .2.(2023·江苏·统考中考真题)折返跑是一种跑步的形式.如图,在一定距离的两个标志物① ①之间 从①开始 沿直线跑至①处 用手碰到①后立即转身沿直线跑至①处 用手碰到①后继续转身跑至①处 循环进行 全程无需绕过标志物.小华练习了一次250m ⨯的折返跑 用时18s 在整个过程中 他的速度大小v (m/s )随时间t (s )变化的图像可能是( )A .B .C .D .3.(2023·江苏南通·统考中考真题)如图,ABC 中 90C ∠=︒ 15AC = 20BC =.点D 从点A 出发沿折线A C B --运动到点B 停止 过点D 作DE AB ⊥ 垂足为E .设点D 运动的路径长为x BDE △的面积为y 若y 与x 的对应关系如图所示,则a b -的值为( )A .54B .52C .50D .484.(2023·辽宁鞍山·统考中考真题)如图,在矩形ABCD 中 对角线,AC BD 交于点O 4AB = 43BC = 垂直于BC 的直线MN 从AB 出发 沿BC 3 当直线MN 与CD 重合时停止运动 运动过程中MN 分别交矩形的对角线,AC BD 于点E F 以EF 为边在MN 左侧作正方形EFGH 设正方形EFGH 与AOB 重叠部分的面积为S 直线MN 的运动时间为t s ,则下列图象能大致反映S 与t 之间函数关系的是( )A .B .C .D .5.(2023·辽宁锦州·统考中考真题)如图,在Rt ABC △中 90ACB ∠=︒ 3AC = 4BC = 在DEF 中 5DE DF == 8EF = BC 与EF 在同一条直线上 点C 与点E 重合.ABC 以每秒1个单位长度的速度沿线段EF 所在直线向右匀速运动 当点B 运动到点F 时 ABC 停止运动.设运动时间为t 秒 ABC 与DEF 重叠部分的面积为S ,则下列图象能大致反映S 与t 之间函数关系的是( )A .B .C .D .6.(2023·辽宁·统考中考真题)如图,60MAN ∠=︒ 在射线AM AN 上分别截取6AC AB == 连接BC MAN ∠的平分线交BC 于点D 点E 为线段AB 上的动点 作EF AM ⊥交AM 于点F 作EG AM ∥交射线AD 于点G 过点G 作GH AM ⊥于点H 点E 沿AB 方向运动 当点E 与点B 重合时停止运动.设点E 运动的路程为x 四边形EFHG 与ABC 重叠部分的面积为S ,则能大致反映S 与x 之间函数关系的图象是( )A .B .C .D .7.(2023·黑龙江大庆·统考中考真题)如图1 在平行四边形ABCD 中 120ABC ∠=︒ 已知点P 在边AB 上 以1m/s 的速度从点A 向点B 运动 点Q 在边BC 上 3m /s 的速度从点B 向点C 运动.若点P Q 同时出发 当点P 到达点B 时 点Q 恰好到达点C 处 此时两点都停止运动.图2是BPQ 的面积()2m y 与点P的运动时间()s t 之间的函数关系图象(点M 为图象的最高点),则平行四边形ABCD 的面积为( )A .212mB .23mC .224mD .2243m8.(2023·辽宁·统考中考真题)如图,在Rt ABC △中 90ACB ∠=︒ 30A ∠=︒ 3cm AB =.动点P 从点A 出发 以1cm/s 的速度沿射线AB 匀速运动 到点B 停止运动 同时动点Q 从点A 出发 3cm/s 的速度沿射线AC 匀速运动.当点P 停止运动时 点Q 也随之停止运动.在PQ 的右侧以PQ 为边作菱形PQMN 点N 在射线AB .设点P 的运动时间为()s x 菱形PQMN 与ABC 的重叠部分的面积为()2cm y ,则能大致反映y 与x 之间函数关系的图象是( )A .B .C.D.9.(2023·湖北鄂州·统考中考真题)如图,在平面直角坐标系中O为原点35OA OB==点C为平面内一动点32BC=连接AC点M是线段AC上的一点且满足:1:2CM MA=.当线段OM取最大值时点M的坐标是()A.36,55⎛⎫⎪⎝⎭B.365,555C.612,55⎛⎫⎪⎝⎭D.6125,55510.(2023·广东深圳·统考中考真题)如图1 在Rt ABC△中动点P从A点运动到B点再到C点后停止速度为2单位/s 其中BP长与运动时间t(单位:s)的关系如图2,则AC的长为()A155B427C.17D.5311.(2023·黑龙江绥化·统考中考真题)如图,在菱形ABCD中60A∠=︒4AB=动点M N同时从A 点出发点M以每秒2个单位长度沿折线A B C--向终点C运动点N以每秒1个单位长度沿线段AD向终点D运动当其中一点运动至终点时另一点随之停止运动.设运动时间为x秒AMN的面积为y个平方单位,则下列正确表示y与x函数关系的图象是()A .B .C .D .12.(2023·黑龙江齐齐哈尔·统考中考真题)如图,在正方形ABCD 中 4AB = 动点M N 分别从点A B 同时出发 沿射线AB 射线BC 的方向匀速运动 且速度的大小相等 连接DM MN ND .设点M 运动的路程为()04x x ≤≤ DMN 的面积为S 下列图像中能反映S 与x 之间函数关系的是( )A .B .C.D.13.(2023·河南·统考中考真题)如图1 点P从等边三角形ABC的顶点A出发沿直线运动到三角形内部一点再从该点沿直线运动到顶点B.设点P运动的路程为x PByPC图2是点P运动时y随x变化的关系图象,则等边三角形ABC的边长为()A.6B.3C.43D.23二解答题14.(2023·四川绵阳·统考中考真题)如图,已知①ABC中①C=90° 点M从点C出发沿CB方向以1cm/s 的速度匀速运动到达点B停止运动在点M的运动过程中过点M作直线MN交AC于点N且保持①NMC=45° 再过点N作AC的垂线交AB于点F连接MF将①MNF关于直线NF对称后得到①ENF已知AC=8cm BC=4cm设点M运动时间为t(s)①ENF与①ANF重叠部分的面积为y(cm2).(1)在点M的运动过程中能否使得四边形MNEF为正方形?如果能求出相应的t值如果不能说明理由(2)求y关于t的函数解析式及相应t的取值范围(3)当y取最大值时求sin①NEF的值.AB=点O是对角线AC的中点动点P 15.(2023·吉林·统考中考真题)如图,在正方形ABCD中4cmQ分别从点A B同时出发点P以1cm/s的速度沿边AB向终点B匀速运动点Q以2cm/s的速度沿折线-向终点D匀速运动.连接PO并延长交边CD于点M连接QO并延长交折线DA ABBC CD-于点N连接PQ QM MN NP得到四边形PQMN.设点P的运动时间为x(s)(04<<)四边形PQMN的x面积为y(2cm)(1)BP的长为__________cm CM的长为_________cm.(用含x的代数式表示)(2)求y关于x的函数解析式并写出自变量x的取值范围.(3)当四边形PQMN是轴对称图形时直接写出x的值.三 填空题16.(2023·陕西·统考中考真题)如图,在矩形ABCD 中 3AB = 4BC =.点E 在边AD 上 且3ED = M N 分别是边AB BC 上的动点 且BM BN = P 是线段CE 上的动点 连接PM PN .若4PM PN +=.则线段PC 的长为 .参考答案一、单选题1.(2023·辽宁盘锦·统考中考真题)如图,在平面直角坐标系中 菱形ABCD 的顶点A 在y 轴的正半轴上 顶点B C 在x 轴的正半轴上 (3D ()1,1P --.点M 在菱形的边AD 和DC 上运动(不与点A C 重合) 过点M 作MN y ∥轴 与菱形的另一边交于点N 连接PM PN 设点M 的横坐标为x PMN 的面积为y ,则下列图象能正确反映y 与x 之间函数关系的是( )A .B .C .D .【答案】A【分析】先根据菱形的性质求出各点坐标 分M 的横坐标x 在01 12 23~之间三个阶段 用含x 的代数式表示出PMN 的底和高 进而求出分段函数的解析式 根据解析式判断图象即可. 【详解】解:菱形ABCD 的顶点A 在y 轴的正半轴上 顶点B C 在x 轴的正半轴上 ∴2AB AD == 3OA =∴()2222231OB AB OA --= ∴123OC OB BC =+=+=∴(3A ()10B , ()3,0C 设直线AB 的解析式为y kx b =+ 将(3A ()10B ,代入 得: 03k b b +=⎧⎪⎨=⎪⎩ 解得33k b ⎧=-⎪⎨=⎪⎩ ∴直线AB 的解析式为33y x =-MN y ∥轴∴N 的横坐标为x(1)当M 的横坐标x 在01之间时 点N 在线段AB 上 PMN 中MN 上的高为1x + ∴(,33N x x ∴(3333MN x x -+∴()()2113313122PMNS MN x x x x =⋅+=⋅+= ∴该段图象为开口向上的抛物线(2)当M 的横坐标x 在12之间时 点N 在线段BC 上 PMN 中3MN = MN 上的高为1x + ∴()()113313122PMNS MN x x x =⋅+=+=∴该段图象为直线(3)当M 的横坐标x 在23~之间时 点N 在线段BC 上 PMN 中MN 上的高为1x + 由(3D ()3,0C 可得直线CD 的解析式为333y x =-+∴(,333M x x + (),0N x ∴333MN x =-+ ∴()(()21133313331322PMN S MN x x x x =⋅+=-+⋅+=++ ∴该段图象为开口向下的抛物线观察四个选项可知 只有选项A 满足条件故选A .【点睛】本题考查动点问题的函数图象 涉及坐标与图形 菱形的性质 二次函数 一次函数的应用等知识点 解题的关键是分段求出函数解析式.2.(2023·江苏·统考中考真题)折返跑是一种跑步的形式.如图,在一定距离的两个标志物① ①之间 从①开始 沿直线跑至①处 用手碰到①后立即转身沿直线跑至①处 用手碰到①后继续转身跑至①处 循环进行 全程无需绕过标志物.小华练习了一次250m ⨯的折返跑 用时18s 在整个过程中 他的速度大小v (m/s )随时间t (s )变化的图像可能是( )A .B .C .D .【答案】D【分析】根据速度与时间的关系即可得出答案.【详解】解:刚开始速度随时间的增大而增大 匀速跑一段时间后减速到① 然后再加速再匀速到① 由于体力原因 应该第一个50米速度快 用的时间少 第二个50米速度慢 用的时间多故他的速度大小v (m/s )随时间t (s )变化的图像可能是D .故选:D .【点睛】本题主要考查函数的图象 要根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件 结合实际意义得出正确的结论.3.(2023·江苏南通·统考中考真题)如图,ABC 中 90C ∠=︒ 15AC = 20BC =.点D 从点A 出发沿折线A C B --运动到点B 停止 过点D 作DE AB ⊥ 垂足为E .设点D 运动的路径长为x BDE △的面积为y 若y 与x 的对应关系如图所示,则a b -的值为( )A .54B .52C .50D .48【答案】B 【分析】根据点D 运动的路径长为x 在图中表示出来 设,25AE z BE z ==- 在直角三角形中 找到等量关系 求出未知数的值 得到BDE △的值.【详解】解:当10x =时 由题意可知10,5AD CD ==在Rt CDB △中 由勾股定理得22222520425BD CD BC =+=+=设,25AE z BE z ==-222(25)50625BE z z z ∴=-=-+在Rt ADE △中 由勾股定理得2222100DE AD AE z =-=-在Rt DEB △中 由勾股定理得222BD DE BE =+即2242510050625z z z =-+-+解得6z =6,19DE BE ∴==1198762BDE a S ∴==⨯⨯=当25x =时 由题意可知 10CD BD ==设,25BE q AE q ==-222(25)62550AE q q q =-=-+在Rt CDA △中 由勾股定理得222221510325AD AC CD =+=+=在Rt BDE △中由勾股定理得2222100DB BD BE q =-=-Rt DEA 中 由勾股定理得222AD DE AE =+即2232510062550q q q =-+-+解得8q =6DE ∴=168242BDE b S ∴==⨯⨯= 762452a b ∴-=-=.故选:B .【点睛】本题主要考查勾股定理 根据勾股定理列出等式是解题的关键 运用了数形结合的思想解题. 4.(2023·辽宁鞍山·统考中考真题)如图,在矩形ABCD 中 对角线,AC BD 交于点O 4AB = 43BC = 垂直于BC 的直线MN 从AB 出发 沿BC 3 当直线MN 与CD 重合时停止运动 运动过程中MN 分别交矩形的对角线,AC BD 于点E F 以EF 为边在MN 左侧作正方形EFGH 设正方形EFGH 与AOB 重叠部分的面积为S 直线MN 的运动时间为t s ,则下列图象能大致反映S 与t 之间函数关系的是( )A .B .C .D .【答案】B【分析】求出MN 在O 点左侧时的两段图象 即可得出结论.【详解】解:当MN 在O 点左侧 即:2t <时:①当正方形EFGH 的边GH 在AOB 的外部时 重叠部分为矩形 如图:设,HE FG 分别交AB 于点,I K①垂直于BC 的直线MN 从AB 出发 沿BC 3 ①3IE FK t ==①在矩形ABCD 中 4AB =43BC =①228AC AB BC =+=①4OA OB AB ===①ABO 为等边三角形①60OAB OBA ∠=∠=︒①tan60AI BK IE t ==÷︒=①42IK t =- ①()23422343S IK IE t t t t =⋅=-=-+ 图象为开口向下的一段抛物线①当正方形EFGH 的边GH 在AOB 的内部时 与AOB 重叠部分即为正方形EFGH 如图:由①可知:42EF IK t ==-①()242S t =- 图象是一段开口向上的抛物线当MN 过点O 时 即2t =时 ,E F 重合 此时 0S =综上:满足题意的只有B 选项故选B .【点睛】本题考查动点的函数图象问题.解题的关键是确定动点的位置 利用数形结合和分类讨论的思想进行求解.5.(2023·辽宁锦州·统考中考真题)如图,在Rt ABC △中 90ACB ∠=︒ 3AC = 4BC = 在DEF 中 5DE DF == 8EF = BC 与EF 在同一条直线上 点C 与点E 重合.ABC 以每秒1个单位长度的速度沿线段EF 所在直线向右匀速运动 当点B 运动到点F 时 ABC 停止运动.设运动时间为t 秒 ABC 与DEF 重叠部分的面积为S ,则下列图象能大致反映S 与t 之间函数关系的是( )A .B .C .D .【答案】A【分析】分04t ≤< 48t ≤< 812t ≤<三种情况 分别求出函数解析即可判断.【详解】解:过点D 作DH CB ⊥于H①5DE DF == 8EF = ①142EH FH EF === ①223DH DE EH =-当04t ≤<时如图,重叠部分为EPQ △ 此时EQ t = PQ DH ∥①EPQ EDH ∽ ①PQ EQ DH EH= 即34PQ t = ①34PQ t = ①2133248S t t t =⨯= 当48t ≤<时如图,重叠部分为四边形PQC B '' 此时BB CC t ''== PB DE '∥①12B F BC CF BB t ''=+-=- 8FC t '=-①PB DE '∥①PB F DCF '∽ ①2PB F DCF S B F SCF ''⎛⎫= ⎪⎝⎭又183122DCFS =⨯⨯=①212128PB F S t '-⎛⎫= ⎪⎝⎭ ①()231216PB F S t '=-①DH BC ⊥ 90A B C '''∠=︒①A C DH ''∥①C QF HFD '∽①2C QF HFD S C F S HF ''⎛⎫= ⎪⎝⎭ 即2814432C QF S t '-⎛⎫= ⎪⎝⎭⨯⨯ ①()2388C QF S t '=-①()()22233331283168162PB F C QF S S S t t t t ''=-=---=-++当 812t ≤<时如图,重叠部分为四边形PFB ' 此时BB CC t ''== PB DE '∥①12B F BC CF BB t ''=+-=-①PB DE '∥①PB F DCF '∽①2PB F DCF S B F S CF ''⎛⎫= ⎪⎝⎭ 即212128PB FS t '-⎛⎫= ⎪⎝⎭①()231216PB F S S t '==-综上 ()()()()22230483334816231281216t t S t t t t t ⎧≤<⎪⎪⎪=-++≤<⎨⎪⎪-≤<⎪⎩①符合题意的函数图象是选项A .故选:A .【点睛】此题结合图像平移时面积的变化规律 考查二次函数相关知识根据平移点的特点列出函数表达式是关键 有一定难度.6.(2023·辽宁·统考中考真题)如图,60MAN ∠=︒ 在射线AM AN 上分别截取6AC AB == 连接BC MAN ∠的平分线交BC 于点D 点E 为线段AB 上的动点 作EF AM ⊥交AM 于点F 作EG AM ∥交射线AD 于点G 过点G 作GH AM ⊥于点H 点E 沿AB 方向运动 当点E 与点B 重合时停止运动.设点E 运动的路程为x 四边形EFHG 与ABC 重叠部分的面积为S ,则能大致反映S 与x 之间函数关系的图象是( )A .B .C .D .【答案】A【分析】分三种情况分别求出S 与x 的函数关系式 根据函数的类型与其图象的对应关系进行判断即可.【详解】解:①60MAN ∠=︒ 6AC AB ==①ABC 是边长为6的正三角形①AD 平分MAN ∠①30MAD NAD ∠=∠=︒ AD BC ⊥ 3CD DB ==①当矩形EFGH 全部在ABC 之中 即由图1到图2 此时03x <≤①EG AC ∥①30MAD AGE ∠=∠=︒①30NAD AGE ∠=∠=︒①AE EG x ==在Rt AEF 中 60EAF ∠=︒ ①33EF AE =①23S = ①如图3时 当AE AF GE AF AF CF AC +=+=+= 则162x x += 解得4x = 由图2到图3 此时34x <≤如图4 记BC EG 的交点为Q ,则EQB △是正三角形①6EQ EB BQ x ===-①()626GQ x x x =--=- 而60PQG ∠=︒ ①)3326PG QG x ==-①PQG EFHG S S S =-矩形())231263262x x =-⨯-- 233123183x =+- ①如图6时 6x = 由图3到图6 此时46x <≤如图5 同理EKB △是正三角形①6EK KB EB x ===- 162FC AC AF x =-=- 3EF x = ①EKCF S S =梯形1136622x x ⎛⎫=-+- ⎪⎝⎭ 23333x x =+ 因此三段函数的都是二次函数关系 其中第1段是开口向上 第2段 第3段是开口向下的抛物线 故选:A .【点睛】本题考查动点问题的函数图象 求出各种情况下S 与x 的函数关系式是正确解答的前提 理解各种函数所对应的图象的形状是解决问题的关键.7.(2023·黑龙江大庆·统考中考真题)如图1 在平行四边形ABCD 中 120ABC ∠=︒ 已知点P 在边AB 上 以1m/s 的速度从点A 向点B 运动 点Q 在边BC 上 3m /s 的速度从点B 向点C 运动.若点P Q 同时出发 当点P 到达点B 时 点Q 恰好到达点C 处 此时两点都停止运动.图2是BPQ 的面积()2m y 与点P的运动时间()s t 之间的函数关系图象(点M 为图象的最高点),则平行四边形ABCD 的面积为( )A .212mB .23mC .224mD .2243m【答案】C【分析】根据题意可得:3BC = 3AP t BQ t ==, 设m AB a =,则3m BC a = 作PE BC ⊥交CB 的延长线于点E 作AF BC ⊥交CB 的延长线于点F ,则可得33m AF AB == ))333m PE PB AB PA a t =-=- 从而得到22334216PBQa St a ⎛⎫=--+ ⎪⎝⎭ 根据PBQS的最大值为3求出a 的值 从而得到4m 43m 23m AB BC AF ===,, 最后由平行四边形的面积公式进行计算即可得到答案.【详解】解:根据题意可得:3BC = 3AP t BQ t ==, 设m AB a =,则3m BC a =作PE BC ⊥交CB 的延长线于点E 作AF BC ⊥交CB 的延长线于点F120ABC ∠=︒ 60ABF ∴∠=︒33m AF AB ∴== ))333m PE AB PA a t ==-=- )2221133333322444216PBQa SBQ PE t a t t at t a ⎛⎫∴=⋅⋅=-=-+=--+ ⎪⎝⎭ 由图象可得PBQS 的最大值为323316a ∴=解得:4a =或4a =-(舍去) 4a ∴=4m 43m 23m AB BC AF ∴===,,∴平行四边形ABCD 的面积为:2432324m BC AF ⋅=故选:C .【点睛】本题主要考查了平行四边形的性质 解直角三角形 二次函数的图象与性质 熟练掌握平行四边形的性质 二次函数的图象与性质 添加适当的辅助线构造直角三角形 是解题的关键.8.(2023·辽宁·统考中考真题)如图,在Rt ABC △中 90ACB ∠=︒ 30A ∠=︒ 3cm AB =.动点P 从点A 出发 以1cm/s 的速度沿射线AB 匀速运动 到点B 停止运动 同时动点Q 从点A 出发 3cm/s 的速度沿射线AC 匀速运动.当点P 停止运动时 点Q 也随之停止运动.在PQ 的右侧以PQ 为边作菱形PQMN 点N 在射线AB .设点P 的运动时间为()s x菱形PQMN 与ABC 的重叠部分的面积为()2cm y ,则能大致反映y 与x 之间函数关系的图象是( )A .B .C .D .【答案】A【分析】先证明菱形PQMN 是边长为x 一个角为60︒的菱形 找到临界点 分情况讨论 即可求解. 【详解】解:作PD AC ⊥于点D 作⊥QE AB 于点E由题意得AP x = 3AQ x = ①3cos30AD AP =⋅︒= ①12AD DQ AQ ==①PD 是线段AQ 的垂直平分线 ①30PQA A ∠=∠=︒①60QPE ∠=︒ PQ AP x == ①132QE AQ x == PQ PN MN QM x ==== 当点M 运动到直线BC 上时此时 BMN 是等边三角形 ①113AP PN BN AB ==== 1x = 当点Q N 运动到与点C B 、重合时①1322AP PN AB === 32x = 当点P 运动到与点B 重合时 ①3AP AB == 3x = ①当01x <≤时 233y x x ==当312x <≤时 如图,作FG AB ⊥于点G 交QM 于点R则32BN FN FB x ===- 33FM MS FS x ===- )333FR x =- ①())2231373939333332y x x -⋅--=+当332x <<时 如图,作HI AB ⊥于点I则3BP PH HB x ===- )33HI x =- ①())21333393332y x x =⋅--= 综上 y 与x 之间函数关系的图象分为三段 当01x <≤时 是开口向上的一段抛物线 当312x <≤时 是开口向下的一段抛物线 当332x <≤时 是开口向上的一段抛物线 只有选项A 符合题意 故选:A .【点睛】本题主要考查了动点问题的函数的图象 二次函数的图形的性质 等边三角形的性质 菱形的性质 三角形的面积公式 利用分类讨论的思想方法解答和熟练掌握抛物线的性质是解题的关键.9.(2023·湖北鄂州·统考中考真题)如图,在平面直角坐标系中 O 为原点 35OA OB == 点C 为平面内一动点 32BC =连接AC 点M 是线段AC 上的一点 且满足:1:2CM MA =.当线段OM 取最大值时 点M 的坐标是( )A .36,55⎛⎫ ⎪⎝⎭B .365,555C .612,55⎛⎫⎪⎝⎭D .6125,555 【答案】D【分析】由题意可得点C 在以点B 为圆心32为半径的OB 上 在x 轴的负半轴上取点350D ⎛⎫ ⎪ ⎪⎝⎭连接BD 分别过C M 作CF OA ⊥ ME OA ⊥ 垂足为F E 先证OAM DAC ∽ 得23OM OA CD AD == 从而当CD 取得最大值时 OM 取得最大值 结合图形可知当D B C 三点共线 且点B 在线段DC 上时 CD 取得最大值 然后分别证BDO CDF ∽ AEM AFC ∽ 利用相似三角形的性质即可求解.【详解】解:①点C 为平面内一动点 32BC = ①点C 在以点B 为圆心32为半径的OB 上 在x 轴的负半轴上取点350D ⎛⎫⎪ ⎪⎝⎭连接BD 分别过C M 作CF OA ⊥ ME OA ⊥ 垂足为F E①35OA OB ==①AD OD OA =+=95①23OA AD = ①:1:2CM MA = ①23OA CMAD AC==①OAM DAC ∠∠= ①OAM DAC ∽ ①23OM OA CD AD == ①当CD 取得最大值时 OM 取得最大值 结合图形可知当D B C 三点共线 且点B 在线段DC 上时CD 取得最大值①35OA OB == OD =35①BD =()222235153522OB OD ⎛⎫++ ⎪ ⎪⎝⎭①9CD BC BD =+= ①23OM CD = ①6OM =①y 轴x ⊥轴 CF OA ⊥ ①90DOB DFC ∠∠==︒ ①BDO CDF ∠∠= ①BDO CDF ∽①OB BDCF CD=153529=解得185CF =同理可得 AEM AFC ∽①23ME AM CF AC ==23185= 解得125ME =①22221256565OE OM ME ⎛⎫=-- ⎪ ⎪⎝⎭①当线段OM 取最大值时 点M 的坐标是65125⎝⎭,故选D .【点睛】本题主要考查了勾股定理 相似三角形的判定及性质 圆的一般概念以及坐标与图形 熟练掌握相似三角形的判定及性质是解题的关键.10.(2023·广东深圳·统考中考真题)如图1 在Rt ABC △中 动点P 从A 点运动到B 点再到C 点后停止 速度为2单位/s 其中BP 长与运动时间t (单位:s )的关系如图2,则AC 的长为( )A 155B 427C .17D .53【答案】C【分析】根据图象可知0=t 时 点P 与点A 重合 得到15AB = 进而求出点P 从点A 运动到点B 所需的时间 进而得到点P 从点B 运动到点C 的时间 求出BC 的长 再利用勾股定理求出AC 即可. 【详解】解:由图象可知:0=t 时 点P 与点A 重合 ①15AB =①点P 从点A 运动到点B 所需的时间为1527.5s ÷= ①点P 从点B 运动到点C 的时间为11.57.54s -= ①248BC =⨯=在Rt ABC △中:2217AC AB BC += 故选C .【点睛】本题考查动点的函数图象 勾股定理.从函数图象中有效的获取信息 求出,AB BC 的长 是解题的关键.11.(2023·黑龙江绥化·统考中考真题)如图,在菱形ABCD 中 60A ∠=︒ 4AB = 动点M N 同时从A 点出发 点M 以每秒2个单位长度沿折线A B C --向终点C 运动 点N 以每秒1个单位长度沿线段AD 向终点D 运动 当其中一点运动至终点时 另一点随之停止运动.设运动时间为x 秒 AMN 的面积为y 个平方单位,则下列正确表示y 与x 函数关系的图象是( )A .B .C .D .【答案】A【分析】连接BD 过点B 作BE AD ⊥于点E 根据已知条件得出ABD △是等边三角形 进而证明AMN ABE ∽得出90ANM AEB ∠=∠=︒ 当04t <<时 M 在AB 上 当48t ≤<时 M 在BC 上 根据三角形的面积公式得到函数关系式【详解】解:如图所示 连接BD 过点B 作BE AD ⊥于点E 当04t <<时 M 在AB 上菱形ABCD 中 60A ∠=︒ 4AB = ①AB AD =,则ABD △是等边三角形 ①122AE ED AD === 33BE AE =①2,AM x AN x ==①2AM ABAN AE== 又A A ∠=∠ ①AMN ABE ∽ ①90ANM AEB ∠=∠=︒ ①223MN AM AN x - ①21332y x x x =当48t ≤<时 M 在BC 上①1123322y AN BE x x =⨯=⨯ 综上所述 04t <<时的函数图象是开口向上的抛物线的一部分 当48t ≤<时 函数图象是直线的一部分 故选:A .【点睛】本题考查了动点问题的函数图象 二次函数图象的性质 一次函数图象的性质 菱形的性质 勾股定理 等边三角形的性质与判定 相似三角形的性质与判定 熟练掌握以上知识是解题的关键. 12.(2023·黑龙江齐齐哈尔·统考中考真题)如图,在正方形ABCD 中 4AB = 动点M N 分别从点A B 同时出发 沿射线AB 射线BC 的方向匀速运动 且速度的大小相等 连接DM MN ND .设点M 运动的路程为()04x x ≤≤ DMN 的面积为S 下列图像中能反映S 与x 之间函数关系的是( )A .B .C .D .【答案】A【分析】先根据ADMDCNBMNABCD S S S SS=---正方形 求出S 与x 之间函数关系式 再判断即可得出结论.【详解】解:ADMDCNBMNABCD S S SSS=---正方形1114444(4)(4)222x x x x =⨯-⨯-⨯---21282x x =-+ 21(2)62x =-+ 故S 与x 之间函数关系为二次函数 图像开口向上 2x =时 函数有最小值6 故选:A .【点睛】本题考查了正方形的性质 二次函数的图像与性质 本题的关键是求出S 与x 之间函数关系式 再判断S 与x 之间函数类型.13.(2023·河南·统考中考真题)如图1 点P 从等边三角形ABC 的顶点A 出发 沿直线运动到三角形内部一点 再从该点沿直线运动到顶点B .设点P 运动的路程为x PBy PC= 图2是点P 运动时y 随x 变化的关系图象,则等边三角形ABC 的边长为( )A .6B .3C .43D .23【答案】A【分析】如图,令点P 从顶点A 出发 沿直线运动到三角形内部一点O 再从点O 沿直线运动到顶点B .结合图象可知 当点P 在AO 上运动时 PB PC = 23AO = 易知30BAO CAO ∠=∠=︒ 当点P 在OB 上运动时 可知点P 到达点B 时的路程为3 可知23AO OB == 过点O 作OD AB ⊥ 解直角三角形可得cos303AD AO =⋅︒= 进而可求得等边三角形ABC 的边长.【详解】解:如图,令点P 从顶点A 出发 沿直线运动到三角形内部一点O 再从点O 沿直线运动到顶点B .结合图象可知 当点P 在AO 上运动时1PB PC= ①PB PC = 3AO =又①ABC 为等边三角形①60BAC ∠=︒ AB AC =①()SSS APB APC △≌△①BAO CAO ∠=∠①30BAO CAO ∠=∠=︒ 当点P 在OB 上运动时 可知点P 到达点B 时的路程为43①3OB = 即23AO OB ==①30BAO ABO ∠=∠=︒过点O 作OD AB ⊥①AD BD =,则cos303AD AO =⋅︒=①6AB AD BD =+=即:等边三角形ABC 的边长为6故选:A .【点睛】本题考查了动点问题的函数图象 解决本题的关键是综合利用图象和图形给出的条件.2二 解答题14.(2023·四川绵阳·统考中考真题)如图,已知①ABC 中 ①C =90° 点M 从点C 出发沿CB 方向以1cm /s的速度匀速运动 到达点B 停止运动 在点M 的运动过程中 过点M 作直线MN 交AC 于点N 且保持①NMC =45° 再过点N 作AC 的垂线交AB 于点F 连接MF 将①MNF 关于直线NF 对称后得到①ENF 已知AC =8cm BC =4cm 设点M 运动时间为t (s ) ①ENF 与①ANF 重叠部分的面积为y (cm 2).(1)在点M 的运动过程中 能否使得四边形MNEF 为正方形?如果能 求出相应的t 值 如果不能 说明理由(2)求y 关于t 的函数解析式及相应t 的取值范围(3)当y 取最大值时 求sin ①NEF 的值.【答案】(1)85(2)⎪⎪⎩⎪⎪⎨⎧≤≤+-<<+-=)42(31643121)20(24122t t t t t t y (3310 【详解】试题分析:(1)由已知得出CN =CM =t FN ①BC 得出AN =8﹣t 由平行线证出①ANF ①①ACB 得出对应边成比例求出NF =12AN =12(8﹣t ) 由对称的性质得出①ENF =①MNF =①NMC =45° MN =NE OE =OM =CN =t 由正方形的性质得出OE =ON =FN 得出方程 解方程即可(2)分两种情况:①当0<t ≤2时 由三角形面积得出2124y t t =-+ ①当2<t ≤4时 作GH ①NF 于H 由(1)得:NF =12(8﹣t ) GH =NH GH =2FH 得出GH =23NF =13(8﹣t ) 由三角形面积得出21(8)12y t =-(2<t ≤4) (3)当点E 在AB 边上时 y 取最大值 连接EM ,则EF =BF EM =2CN =2CM =2t EM =2BM 得出方程 解方程求出CN =CM =2 AN =6 得出BM =2 NF =12AN =3 因此EM =2BM =4 作FD ①NE 于D由勾股定理求出EB 22EM BM +=25 求出EF =12EB 5 由等腰直角三角形的性质和勾股定理得出DF 的长 在Rt①DEF 中 由三角函数定义即可求出sin①NEF 的值.试题解析:解:(1)能使得四边形MNEF 为正方形 理由如下:连接ME 交NF 于O 如图1所示:①①C =90° ①NMC =45° NF ①AC ①CN =CM =t FN ①BC ①AN =8﹣t ①ANF ①①ACB ①84AN AC NF BC == =2 ①NF =12AN =12(8﹣t ) 由对称的性质得:①ENF =①MNF =①NMC =45° MN =NE OE =OM =CN =t ①四边形MNEF 是正方形 ①OE =ON =FN ①t =12×12(8﹣t ) 解得:t =85即在点M 的运动过程中 能使得四边形MNEF 为正方形 t 的值为85(2)分两种情况:①当0<t ≤2时 y =12×12(8﹣t )×t =2124t t -+ 即2124y t t =-+(0<t ≤2) ①当2<t ≤4时 如图2所示:作GH ①NF 于H 由(1)得:NF =12(8﹣t ) GH =NH GH =2FH ①GH =23NF =13(8﹣t ) ①y =12NF ′GH =12×12(8﹣t )×13(8﹣t )=21(8)12t - 即21(8)12y t =-(2<t ≤4) 综上所述:⎪⎪⎩⎪⎪⎨⎧≤≤+-<<+-=)42(31643121)20(24122t t t t t t y .(3)当点E 在AB 边上时 y 取最大值 连接EM 如图3所示:则EF =BF EM =2CN =2CM =2t EM =2BM ①BM =4﹣t ①2t =2(4﹣t ) 解得:t =2 ①CN =CM =2 AN =6 ①BM =4﹣2=2 NF =12AN =3 ①EM =2BM =4 作FD ①NE 于D ,则EB 22EM BM +2242+=5 ①DNF 是等腰直角三角形①EF =12EB 5 DF =22 NF 32 在Rt①DEF 中 sin①NEF =DF EF 3225310【点睛】本题是四边形综合题目 考查了正方形的判定与性质 相似三角形的判定与性质 勾股定理 三角函数 三角形面积的计算 等腰直角三角形的判定与性质等知识 本题综合性强 有一定难度. 15.(2023·吉林·统考中考真题)如图,在正方形ABCD 中 4cm AB = 点O 是对角线AC 的中点 动点P Q 分别从点A B 同时出发 点P 以1cm/s 的速度沿边AB 向终点B 匀速运动 点Q 以2cm/s 的速度沿折线BC CD -向终点D 匀速运动.连接PO 并延长交边CD 于点M 连接QO 并延长交折线DA AB -于点N 连接PQ QM MN NP 得到四边形PQMN .设点P 的运动时间为x (s )(04x <<) 四边形PQMN 的面积为y (2cm )(1)BP 的长为__________cm CM 的长为_________cm .(用含x 的代数式表示)(2)求y 关于x 的函数解析式 并写出自变量x 的取值范围.(3)当四边形PQMN 是轴对称图形时 直接写出x 的值.【答案】(1)()4x - x(2)()()2412160241624x x x y x x ⎧-+<≤⎪=⎨-+<≤⎪⎩(3)43x =或83x = 【分析】(1)根据正方形中心对称的性质得出,OM OP OQ ON == 可得四边形PQMN 是平行四边形 证明ANP CQM ≌即可(2)分02x <≤ 24x <≤两种情况分别画出图形 根据正方形的面积 以及平行四边形的性质即可求解 (3)根据(2)的图形 分类讨论即可求解.【详解】(1)解:依题意 1AP x x =⨯=()cm ,则()4PB AB AP x cm =-=-①四边形ABCD 是正方形①,90AD BC DAB DCB ∠=∠=︒∥①点O 是正方形对角线AC 的中点①,OM OP OQ ON ==,则四边形PQMN 是平行四边形①MQ PN = MQ NP ∥①PNQ MQN ∠=∠又AD BC ∥①ANQ CQN ∠=∠①ANP MQC ∠=∠在,ANP CQM 中ANP MQC NAP QCM NP MQ ∠=∠⎧⎪∠=∠⎨⎪=⎩①ANP CQM ≌①()cm MC AP x ==故答案为:()4x - x .(2)解:当02x <≤时 点Q 在BC 上由(1)可得ANP CQM ≌同理可得PBQ MDN ≌①4,2,PB x QB x MC x =-== 42QC x =-则222MCQ BPQ y AB S S =--()()164242x x x x =--⨯--241216x x =-+当24x <≤时 如图所示则AP x = 224AN CQ x CB x ==-=-()244PN AP AN x x x =-=--=-+①()44416y x x =-+⨯=-+综上所述 ()()2412160241624x x x y x x ⎧-+<≤⎪=⎨-+<≤⎪⎩(3)依题意 ①如图,当四边形PQMN 是矩形时 此时90PQM ∠=︒①90PQB CQM ∠+∠=︒①90BPQ PQB ∠+∠=︒①BPQ CQM ∠=∠又B BCD ∠=∠①~BPQ CQM ①BP BQ CQ CM= 即4242x x x x-=- 解得:43x =当四边形PQMN 是菱形时,则PQ MQ =①()()()22224242x x x x -+=+-解得:0x =(舍去)①如图所示 当PB CQ =时 四边形PQMN 是轴对称图形424x x -=- 解得83x = 当四边形PQMN 是菱形时,则4PN PQ == 即44x -+= 解得:0x =(舍去)综上所述 当四边形PQMN 是轴对称图形时 43x =或83x =. 【点睛】本题考查了正方形的性质 动点问题 全等三角形的性质与判定 矩形的性质 平行四边形的性质与判定 菱形的性质 轴对称图形 熟练掌握以上知识是解题的关键.三 填空题16.(2023·陕西·统考中考真题)如图,在矩形ABCD 中 3AB = 4BC =.点E 在边AD 上 且3ED = M N 分别是边AB BC 上的动点 且BM BN = P 是线段CE 上的动点 连接PM PN .若4PM PN +=.则线段PC 的长为 .。
2024年中考数学高频压轴题训练——圆-动点问题及参考答案
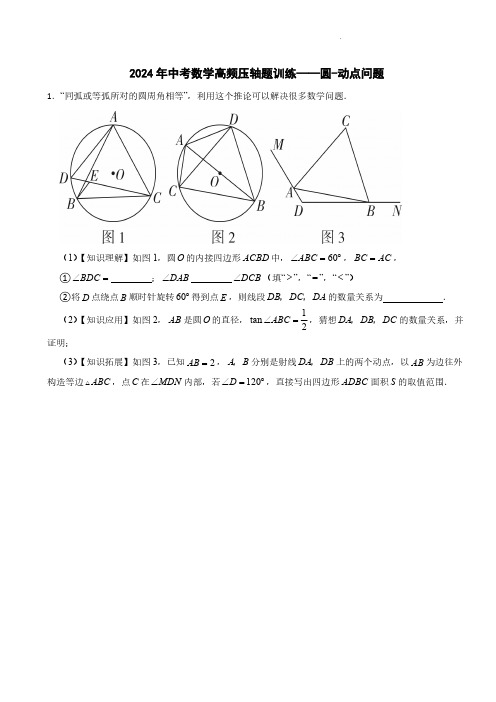
2024年中考数学高频压轴题训练——圆-动点问题1.“同弧或等弧所对的圆周角相等”,利用这个推论可以解决很多数学问题.(1)【知识理解】如图1,圆O 的内接四边形ACBD 中,60ABC ∠=︒,BC AC =,①BDC ∠=;DAB ∠DCB ∠(填“>”,“=”,“<”)②将D 点绕点B 顺时针旋转60︒得到点E ,则线段DB DC DA ,,的数量关系为.(2)【知识应用】如图2,AB 是圆O 的直径,1tan 2ABC ∠=,猜想DA DB DC ,,的数量关系,并证明;(3)【知识拓展】如图3,已知2AB =,A B ,分别是射线DA DB ,上的两个动点,以AB 为边往外构造等边ABC ,点C 在MDN ∠内部,若120D ∠=︒,直接写出四边形ADBC 面积S 的取值范围.2.如图1,对于PMN 的顶点P 及其对边MN 上的一点Q ,给出如下定义:以P 为圆心,PQ 为半径的圆与直线MN 的公共点都在线段MN 上,则称点Q 为PMN 关于点P 的内联点.在平面直角坐标系xOy 中:(1)如图2,已知点(70)A ,,点B 在直线1y x =+上.①若点(34)B ,,点(30)C ,,则在点O ,C ,A 中,点是AOB 关于点B 的内联点;②若AOB 关于点B 的内联点存在,求点B 纵坐标n 的取值范围;(2)已知点(20)D ,,点(42)E ,,将点D 绕原点O 旋转得到点F .若EOF 关于点E 的内联点存在,直接写出点F 横坐标m 的取值范围.3.在平面直角坐标系xOy 中,O 的半径为1,对于点A 和线段BC ,给出如下定义:若将线段BC 绕点A 旋转可以得到O 的弦B C ''(B C '',分别是B C ,的对应点),则称线段BC 是O 的以点A 为中心的“关联线段”.(1)如图,点112233A B C B C B C ,,,,,,的横、纵坐标都是整数.在线段112233B C B C B C ,,中,O 的以点A 为中心的“关联线段”是;(2)ABC 是边长为1的等边三角形,点()0A t ,,其中0t ≠.若BC 是O 的以点A 为中心的“关联线段”,求t 的值;(3)在ABC 中,12AB AC ==,.若BC 是O 的以点A 为中心的“关联线段”,直接写出OA 的最小值和最大值,以及相应的BC 长.4.已知:点C 为⊙O 的直径AB 上一动点,过点C 作CD ⊥AB ,交⊙O 于点D 和点E ,连接AD 、BD ,∠DBA 的角平分线交⊙O 于点F .(1)若DF =BD ,求证:GD =GB ;(2)若AB =2cm ,在(1)的条件下,求DG 的值;(3)若∠ADB 的角平分线DM 交⊙O 于点M ,交AB 于点N .当点C 与点O 重合时,AD BD DM+=;据此猜想,当点C 在AB (不含端点)运动过程中,AD BD DM +的值是否发生改变?若不变,请求其值;若改变,请说明理由.5.在平面直角坐标系xOy 中,O 的半径为1,对于ABC 和直线l 给出如下定义:若ABC 的一条边关于直线l 的对称线段PQ 是O 的弦,则称ABC 是O 的关于直线l 的“关联三角形”,直线l 是“关联轴”.(1)如图1,若ABC 是O 的关于直线l 的“关联三角形”,请画出ABC 与O 的“关联轴”(至少画两条);(2)若ABC 中,点A 坐标为(23),,点B 坐标为(41),,点C 在直线3y x =-+的图像上,存在“关联轴l ”使ABC 是O 的关联三角形,求点C 横坐标的取值范围;(3)已知A ,将点A 向上平移2个单位得到点M ,以M 为圆心MA 为半径画圆,B ,C 为M 上的两点,且2AB =(点B 在点A 右侧),若ABC 与O 的关联轴至少有两条,直接写出OC 的最小值和最大值,以及OC 最大时AC 的长.6.如图,在⊙O 中,AB 为弦,CD 为直径,且AB ⊥CD ,垂足为E ,P 为 AC 上的动点(不与端点重合),连接PD .(1)求证:∠APD =∠BPD ;(2)利用尺规在PD 上找到点I ,使得I 到AB 、AP 的距离相等,连接AD (保留作图痕迹,不写作法).求证:∠AIP+∠DAI =180°;(3)在(2)的条件下,连接IC 、IE ,若∠APB =60°,试问:在P 点的移动过程中,IC IE 是否为定值?若是,请求出这个值;若不是,请说明理由.7.在平面直角坐标系xOy 中,已知线段AB 和点P ,给出如下定义:若PA PB =且点P 不在线段AB 上,则称点P 是线段AB 的等腰顶点.特别地,当90APB ∠≥︒时,则称点P 是线段AB 的非锐角等腰顶点.(1)已知点(20)A ,,(42)B ,.①在点(40)C ,,(31)D ,,(15)E -,,(05)F ,中,是线段AB 的等腰顶点的是▲;②若点P 在直线3(0)y kx k =+≠上,且点P 是线段AB 的非锐角等腰顶点,求k 的取值范围;(2)直线33y x =-+与x 轴交于点M ,与y 轴交于点N .⊙P 的圆心为(0)P t ,,半径为,若⊙P 上存在线段MN 的等腰顶点,请直接写出t 的取值范围.8.在平面直角坐标系xOy中,⊙O的半径为1,T(0,t)为y轴上一点,P为平面上一点.给出如下定义:若在⊙O上存在一点Q,使得△TQP是等腰直角三角形,且∠TQP=90°,则称点P为⊙O的“等直点”,△TQP为⊙O的“等直三角形”.如图,点A,B,C,D的横、纵坐标都是整数.(1)当t=2时,在点A,B,C,D中,⊙O的“等直点”是;(2)当t=3时,若△TQP是⊙O“等直三角形”,且点P,Q都在第一象限,求CPOQ的值.9.综合与实践动手操作利用正方形纸片的折叠开展数学活动.探究体会在正方形折叠过程中,图形与线段的变化及其蕴含的数学思想方法.如图1,点E 为正方形ABCD 的AB 边上的一个动点,3AB =,将正方形ABCD 对折,使点A 与点B 重合,点C 与点D 重合,折痕为MN .思考探索(1)将正方形ABCD 展平后沿过点C 的直线CE 折叠,使点B 的对应点B '落在MN 上,折痕为EC ,连接DB ',如图2.①点B '在以点E 为圆心,的长为半径的圆上;②B M '=;③DB C ' 为三角形,请证明你的结论.(2)拓展延伸当3AB AE =时,正方形ABCD 沿过点E 的直线l (不过点B )折叠后,点B 的对应点B '落在正方形ABCD 内部或边上.①ABB ' 面积的最大值为;②连接AB ',点P 为AE 的中点,点Q 在AB '上,连接PQ AQP AB E ∠=∠',,则2B C PQ '+的最小值为.10.在平面直角坐标系xOy 中,过⊙T (半径为r )外一点P 引它的一条切线,切点为Q ,若0<PQ≤2r ,则称点P 为⊙T 的伴随点.(1)当⊙O 的半径为1时,①在点A(4,0),B(0,),C(1,)中,⊙O 的伴随点是▲;②点D 在直线y =x+3上,且点D 是⊙O 的伴随点,求点D 的横坐标d 的取值范围;(2)⊙M 的圆心为M(m ,0),半径为2,直线y =2x ﹣2与x 轴,y 轴分别交于点E ,F .若线段EF 上的所有点都是⊙M 的伴随点,直接写出m 的取值范围.11.定义:在平面直角坐标系xOy 中,点P 为图形M 上一点,点Q 为图形N 上一点.若存在OP OQ =,则称图形M 与图形N 关于原点O “平衡”.(1)如图,已知⊙A 是以()1,0为圆心,2为半径的圆,点()1,0C -,()2,1D -,()3,2E .①在点C ,D ,E 中,与⊙A 关于原点O “平衡”的点是;②点H 为直线y x =-上一点,若点H 与⊙A 关于原点O “平衡”,点H 的横坐标的取值范围为:;(2)如图,已知图形G 是以原点O 为中心,边长为2的正方形.⊙K 的圆心在x 轴上,半径为2.若⊙K 与图形G 关于原点O “平衡”,请直接写出圆心K 的横坐标的取值范围.12.阅读下列材料,并按要求解答相关问题:【思考发现】根据直径所对的圆周角是直角,我们可以推出“如果一条定边所对的角始终为直角,那么所有满足条件的直角顶点组成的图形是以定边为直径的圆或圆弧(直径的两个端点除外)”这一正确的结论.如图1,若AB 是一条定线段,且90APB ∠=︒,则所有满足条件的直角顶点P 组成的图形是定边AB 为直径的O (直径两端点A 、B 除外)(1)已知:如图2,四边形ABCD 是边长为8的正方形,点E 从点B 出发向点C 运动,同时点F 从点C 出发以相同的速度向点D 运动,连接AE ,BF 相交于点P .①当点E 从点B 运动到点C 的过程中,APB ∠的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请直接写出APB ∠的度数.②当点E 从点B 运动到点C 的过程中,点P 运动的路径是()A .线段;B .弧;C .半圆;D .圆③点P 运动的路经长是▲.(2)已知:如图3,在图2的条件下,连接CP ,请直接写出E 、F 运动过程中,CP 的最小值.13.对于平面内的图形1G 和图形2G ,记平面内一点P 到图形1G 上各点的最短距离为1d ,点P 到图形2G 上各点的最短距离为2d ,若12d d =,就称点P 是图形1G 和图形2G 的一个“等距点”.在平面直角坐标系xOy 中,已知点()60A ,,(0B .(1)在()30R ,,()20S ,,(1T 三点中,点A 和点B 的等距点是;(2)已知直线2y =-.①若点A 和直线2y =-的等距点在x 轴上,则该等距点的坐标为▲;②若直线y a =上存在点A 直线2y =-的等距点,求实数a 的取值范围;(3)记直线AB 为直线1l ,直线2l :33y x =-,以原点O 为圆心作半径为r 的O .若O 上有m 个直线1l 和直线2l 的等距点,以及n 个直线1l 和y 轴的等距点(0m ≠,0n ≠),求m n ≠时,求r 的取值范围.14.如图,平面上存在点P 、点M 与线段AB .若线段AB 上存在一点Q ,使得点M 在以PQ 为直径的圆上,则称点M 为点P 与线段AB 的共圆点.已知点P (0,1),点A (﹣2,﹣1),点B (2,﹣1).(1)在点O (0,0),C (﹣2,1),D (3,0)中,可以成为点P 与线段AB 的共圆点的是;(2)点K 为x 轴上一点,若点K 为点P 与线段AB 的共圆点,请求出点K 横坐标x K 的取值范围;(3)已知点M (m ,﹣1),若直线y =12x +3上存在点P 与线段AM 的共圆点,请直接写出m 的取值范围.15.如图,在ABC 中,AB BC =,30CAB ∠=︒,8AC =,半径为2的O 从点A 开始(如图1)沿直线AB 向右滚动,滚动时始终与直线AB 相切(切点为D ),当O 与ABC 只有一个公共点时滚动停止,作OG AC ⊥于点G .(1)图1中,O 在AC 边上截得的弦长AE =;(2)当圆心落在AC 上时,如图2,判断BC 与O 的位置关系,并说明理由.(3)在O 滚动过程中,线段OG 的长度随之变化,设AD x =,OG y =,求出y 与x 的函数关系式,并直接写出x 的取值范围.16.在平面直角坐标系xOy 中,给出如下定义:若点P 在图形M 上,点Q 在图形N 上,称线段PQ 长度的最小值为图形M ,N 的“近距离”,记为d(M ,N),特别地,若图形M ,N 有公共点,规定d(M ,N)=0.已知:如图,点A(2-,0),B(0,.(1)如果⊙O 的半径为2,那么d(A ,⊙O)=,d(B ,⊙O)=.(2)如果⊙O 的半径为r ,且d (⊙O ,线段AB )=0,求r 的取值范围;(3)如果C(m ,0)是x 轴上的动点,⊙C 的半径为1,使d (⊙C ,线段AB )<1,直接写出m 的取值范围.17.在平面直角坐标系xOy 中,对于点()P m n ,,我们称直线y mx n =+为点P 的关联直线.例如,点()24P ,的关联直线为24y x =+.(1)已知点()12A ,.①点A 的关联直线为;②若O 与点A 的关联直线相切,则O 的半径为;(2)已知点()02C ,,点()0.D d ,点M 为直线CD 上的动点.①当2d =时,求点O 到点M 的关联直线的距离的最大值;②以()11T -,为圆心,3为半径作.T 在点M 运动过程中,当点M 的关联直线与T 交于E ,F 两点时,EF 的最小值为4,请直接写出d 的值.18.在平面直角坐标系xOy 中,给定圆C 和点P ,若过点P 最多可以作出k 条不同的直线,且这些直线被圆C 所截得的线段长度为正整数,则称点P 关于圆C 的特征值为.k 已知圆O 的半径为2,(1)若点M 的坐标为()11,,则经过点M 的直线被圆O 截得的弦长的最小值为,点M 关于圆O 的特征值为;(2)直线y x b =+分别与x ,y 轴交于点A ,B ,若线段AB 上总存在关于圆O 的特征值为4的点,求b 的取值范围;(3)点T 是x 轴正半轴上一点,圆T 的半径为1,点R ,S 分别在圆O 与圆T 上,点R 关于圆T 的特征值记为r ,点S 关于圆O 的特征值记为.s 当点T 在x 轴正轴上运动时,若存在点R ,S ,使得3r s +=,直接写出点T 的横坐标t 的取值范围.答案解析部分1.【答案】(1)60︒;=;DC DB DA=+(2)解:在AB 上取一点E ,使ADE BDC ∠=∠,如图所示:∵AB 是圆O 的直径,1tan 2ABC ∠=,∴1tan 2AC ABC BC BC =∠⋅=,∴在Rt ACB 中,52AB BC ==,∵ BD BD =,∴DAB DCB ∠=∠,∵ADE BDC ∠=∠,∴ADE CDB ∽,∴ADAECD CB =,∴AD CB CD AE ⋅=⋅,∵ AD AD =,∴DBA DCA ∠=∠,∵ADE CDE CDB CDE ∠-∠=∠-∠,即ADC BDE ∠=∠,∴BDE CDA ∽,∴BDBECD AC =,∴BD AC CD BE ⋅=⋅,∴()AD CB AC BD CD AE CD BE CD AE BE CD AB⋅+⋅=⋅+⋅=⋅+=⋅,∴AB CD AC DB AD BC ⋅=⋅+⋅,∴122BC CD BC DB AD BC ⋅=⋅+⋅,∴5122CD DB AD ⋅=⋅+,∴5122CD DB AD =+,即2DB AD =+,故答案为:2DB AD =+.(3)解:∵A B ,分别是射线DA DB ,上的两个动点,120D ∠=︒,ABC 是等边三角形,∴四边形ADBC 的两个对角180ADB ACB ∠+∠=︒,∴构造四边形ADBC 的外接圆,∴根据四边形外接圆的性质可得:当点A 和点D 重合时,四边形ADBC 面积S 最小;当CD AB ⊥时,四边形ADBC 面积S 最大,①当点A 和点D 重合时,四边形ADBC 面积S 最小,∵CBD 时等边三角形,且2AB =,∴60CBD ∠=︒,2AB BD BC ===∴1sin 602CBD S BC BD =⋅⋅⋅= ,②当CD AB ⊥时,四边形ADBC 面积S 最大,∵CBD 时等边三角形,且2AB =,∴30ACD ∠=︒,2AC =,∴tan 233AD ACD AC =∠⋅==,∴11232322233ADC S AD DC =⋅⋅=⨯= ,∴23ADC ADBC S S == 四边形;433S <≤.2.【答案】(1)解:①O ,C ②当点B 的坐标为(0,1)时,如图,此时以BO 为半径的B 与线段OA 相切于点O ,∴点O 是OAB 关于点B 的内联点;当点B 移动到在y 轴左侧时,作图发现B 与x 轴有相交,且有一个交点不在线段OA 上,∴不再有OAB 关于点B 的内联点;当点B 的坐标为(7,8)时,以BA 为半径的B 与x 轴相切于点A ,∴点A 是OAB 关于点B 的内联点;当点B 直线x=7的右侧时,以BA 为半径的B 与x 轴相交,且有一个交点不在线段OA 上∴不再有OAB 关于点B 的内联点;综上所述,若AOB 关于点B 的内联点存在,求点B 纵坐标n 的取值范围为18n ≤≤;(2)80m 555m -≤≤≤≤或3.【答案】(1)22B C (2)解:由题意可得:当BC 是O 的以点A 为中心的“关联线段”时,则有AB C '' 是等边三角形,且边长也为1,当点A 在y 轴的正半轴上时,如图所示:设B C ''与y 轴的交点为D ,连接OB ',易得B C y ''⊥轴,∴12B D DC ''==,∴32OD ==,32==,∴OA =,∴t =;当点A 在y 轴的正半轴上时,如图所示:同理可得此时的OA =,∴t =;(3)当1min OA =时,此时BC =;当2max OA =时,此时2BC =.4.【答案】(1)证明:∵CD ⊥直径AB ,∴ BDBE =,∵DF =BD ,∴ DFBD =,∴ BEDF =,∴∠1=∠2,∴DG =BG(2)解:∠DBA 的角平分线交⊙O 于点F ,∴∠2=∠3,由(1)知,∠1=∠2,∴∠1=∠2=∠3,∵∠BCD =90°,∴∠1+∠2+∠3=90°,∴∠1=∠2=∠3=30°,∵AB 是⊙O 的直径,∴∠ADB =90°,∴∠4=90°﹣∠2﹣∠3=30°,∵AB =2,∴BD =1,在Rt △BCD 中,∠1=30°,∴BC =12BD =12,在Rt △BCG 中,∠3=30°,∴CG ==6,∴BG =2CG =33,由(1)知,DG =BG =33(3)5.【答案】(1)解:如图1,作BM ⊥x 轴,垂足为M ,根据题意AB=AE=EF=BF=,且∠EFO=∠BFM=45°,∴∠EFB=90°,∴四边形ABFE 是正方形,∴边AE ,BF 的中点所在直线就是ABC 与O 的一条“关联轴”;∵O 的半径为1,∴,且∠EFG=90°,∴四边形EFGH 是正方形,∵∠EFG+∠EFB=180°,∴B 、F 、G 三点共线,∴直线EF 是ABC 与O 的一条“关联轴”.(2)解:如图2,根据A (2,3),B (4,1),C (4,1),计算2=,故AB 不能落在圆的内部;过点A 作AN ⊥y 轴,垂足为N ,则AN=2,等于圆的直径,存在“关联轴l ”使ABC 是O 的关联三角形,此时0C x =;作点B 关于x 轴的对称点P ,此时BP=2,等于圆的直径,存在“关联轴l ”使ABC 是O 的关联三角形,此时4C x =,综上所述,点C 横坐标的范围是04C x ≤≤.(3)解:OC 的最小值为2-;OC 最大,根据勾股定理,AC=4.6.【答案】(1)证明:∵直径CD ⊥弦AB ,∴ AD BD=,∴∠APD=∠BPD ;(2)解:如图,作∠BAP 的平分线,交PD 于I ,证:∵AI 平分∠BAP ,∴∠PAI=∠BAI ,∴∠AID=∠APD+∠PAI=∠APD+BAI ,∵ AD BD=,∴∠DAB=∠APD ,∴∠DAI=∠DAB+∠BAI=∠APD+∠BAI ,∴∠AID=∠DAI ,∵∠AIP+∠DAI=180°,∴∠AIP+∠DAI=180°;(3)解:如图2,连接BI ,AC ,OA ,OB ,∵AI 平分∠BAP ,PD 平分∠APB ,∴BI 平分∠ABP ,∠BAI=12∠BAP ,∴∠ABI=12∠ABP ,∵∠APB=60°,∴∠PAB+∠PBA=120°,∴∠BAI+∠ABI=12(∠BAP+∠ABP )=60°,∴∠AIB=120°,∴点I 的运动轨迹是 AB ,∴DI=DA ,∵∠AOB=2∠APB=120°,∵AD ⊥AB ,∴ AD BD=,∴∠AOB=∠BOD=60°,∵OA=OD ,∴△AOD 是等边三角形,∴AD=AO ,∵CD 是⊙O 的直径,∴∠DAC=90°,∵CD ⊥AB ,∴∠AED=90°,∴∠AED=∠CAD ,∵∠ADC=∠ADE ,∴△ADE ∽△CDA ,∴AD DE CD AD=,∴AD 2=DE•CD ,∵DI′=DI=AD ,∴DI 2=DE•CD ,∵∠I′DE 是公共角,∴△DIE ∽△DCI ,∴2IC CD IE DI==.7.【答案】(1)解:①C(4,0),E(-1,5);②(Ⅰ)当点(40),在直线3y kx =+上时,430k +=,34k =-;(Ⅱ)当点(31),在直线3y kx =+上时,331k +=,23k =-;(Ⅲ)当点(22),在直线3y kx =+上时,232k +=,12k =-;结合图象可得3142k -≤≤-且23k ≠-;(2)解:直线333y x =-+与x 轴的交点M 坐标为()30,,与y 轴交点N 的坐标为(03,,∴tan 3NMO ∠=,∴30NMO ∠=︒,如图,作出线段MN 的垂直平分线,如图为两个临界情况:,利用待定系数法求得MN 垂直平分线解析式为y =,∴(0R -,,12230ORQ P RQ ∠=∠=︒,∴1112PR PQ ==,2222P R P Q ==,∴(10P ,(20P -,,∴t -≤<.8.【答案】(1)A 、B 、D(2)解:如图,依题意作⊙O 的“等直三角形”△TQP∴TQ=PQ ,∠TQP=90°过Q 点作MH //x 轴,交y 轴于M 点,过点P 作PH ⊥MH 于H 点∴∠TMQ=∠QHP=90°∴∠TQM+∠MTQ=∠TQM+∠HQP=90°∴∠MTQ=∠HQP∴△TMQ ≌△QHP (AAS )∴TM=QH ,MQ=HP设Q (x ,y )∴HM=MQ+QH=MQ+TM=x+3-y ,PH=MQ=x∴P (x-y+3,x+y )∵C (3,0)∴∵∴CP OQ .9.【答案】(1)BE ;3332-;等边;证明:B′D=BC CD ==,∴△DB'C 为等边三角形(2)310.【答案】(1)B ,C ;解:②如图2中,设点D 的坐标为(3)d d +,当过点D 的切线长为22r =时,OD ==由两点之间的距离公式得:OD =解得1221d d =-=-,结合图象可知,点D 的横坐标d 的取值范围是21d -≤≤-;(2)解:对于22y x =-当0y =时,220x -=,解得1x =,则点E 的坐标为(10)E ,当0x =时,2y =-,则点F 的坐标为(02)F -,⊙M 的半径为2,⊙M 的圆心为(0)M m ,24r ∴=,OM m=由题意,由以下两种情况:如图3-1中,点M 在点E 的右侧设FT 是⊙M 的切线则有两个临界位置:4FT =和点E 对应的切线长为0当4FT =时,则4OM m FT ===当点E 对应的切线长为0,即2EM =12EM m ∴=-=解得3m =结合图象得,当34m <≤时,线段EF 上的所有点都是⊙M 的伴随点②如图3-2和3-3中,点M 在点E 的左侧则有如下两个临界位置:如图3-2,设ET 是⊙M 的切线,连接MT ,则90MTE ∠=︒当4ET =时,2222245EM MT ET =+=+此时15m -=解得15m =-如图3-3,当⊙M 在直线EF 的左侧与EF 相切时,设切点为T ,连接MT∵(10)(02)E F -,,,∴12OE OF ==,∴22125EF =+=∵EF 是切线∴EF MT⊥∴90MTE FOE ∠=∠=︒∵MET FEO∠=∠∴MTE FOE~ ∴EM MTEF OF =,即22=解得EM =,即1m -=解得1m =-结合图象得,当11m -≤<-时,线段EF 上的所有点都是⊙M 的伴随点综上,m 的取值范围是11m -≤<-或34m <≤.11.【答案】(1)点C 、D ;22H x -≤≤-或22H x ≤≤(2)解: 图形G 是以原点O 为中心,边长为2的正方形,∴原点O 到正方形的最短距离是1d =,最长距离是d =,⊙K 与图形G 关于原点O “平衡”,∴原点O 到⊙K 上一点的距离1d ≤≤,⊙K 的圆心在x 轴上,半径为2,∴当⊙K 在x 轴正半轴时,圆心K 的横坐标的取值范围为:22x -≤≤+,当⊙K 在x 轴负半轴时,圆心K 的横坐标的取值范围为:22x --≤≤,综上所述,圆心K 的横坐标的取值范围22x -≤≤+或22x --≤≤.12.【答案】(1)解:①90°;②B ;③2π(2)解:413.【答案】(1)S(2,0)(2)解:①(4,0)或(8,0);②如图,设直线y a =上的点Q 为点A 和直线2y =-的等距点,连接QA ,过点Q 作直线2y =-的垂线,垂足为点C .点Q 为点A 和直线2y =-的等距点,QA QC ∴=.22QA QC ∴=.点Q 在直线y a =上,∴可设点Q 的坐标为()Q x a ,.()()22262x a a ∴-+=--⎡⎤⎣⎦.整理得2123240x x a -+-=.由题意得关于x 的方程2123240x x a -+-=有实数根.()()()212413241610a a ∴∆=--⨯⨯-=+≥.解得1a ≥-.(3)解:如图.直线l 1和直线l 2的等距点在直线l 3:33y x =-+上,直线l 1和y 轴的等距点在直线4l y =+:或33y x =+上,点O 与l 4的距离为32,点O 与l 3的距离为,点O 与l 5的距离为3,当r <时,n=0不符合题意,当r=时,m=2,n=0,符合题意,当<r <3时,m=n=2,不符合题意,当r≥3时,m=2,n=3或4,符合题意,综上所述,r=或r≥3.14.【答案】(1)C(2)解:∵P (0,1),点A (﹣2,﹣1),点B (2,﹣1).∴AP =BP ==2,如图2,分别以PA 、PB 为直径作圆,交x 轴于点K 1、K 2、K 3、K 4,∵OP=OG=1,OE∥AB,∴PE=AE=,∴OE=12AG=1,∴K1(﹣1﹣,0),k2(1﹣,0),k3(﹣1,0),k4(1+,0),∵点K为点P与线段AB的共圆点,∴﹣1﹣≤x k≤1﹣或﹣1≤x k≤1+(3)解:分两种情况:①如图3,当M在点A的左侧时,Q为线段AM上一动点,以PQ为直径的圆E与直线y=12x+3相切于点F,连接EF,则EF⊥FH,当x=0时,y=3,当y=0时,y=12x+3=0,x=﹣6,∴ON=3,OH=6,∵tan∠EHF=ON EFOH FH=36=12,设EF=a,则FH=2a,EH=a,∴OE=6﹣a,Rt △OEP 中,OP =1,EP =a ,由勾股定理得:EP 2=OP 2+OE 2,∴2221(6)a =+-,解得:a =2+(舍去)或2,∴QG =2OE =2(6﹣a )=﹣3+2,∴m≤3﹣2;②如图4,当M 在点A 的右侧时,Q 为线段AM 上一动点,以PQ 为直径的圆E 与直线y =12x+3相切于点F ,连接EF ,则EF ⊥FH ,同理得QG =3+2,∴m≥3+2,综上,m 的取值范围是m≤3﹣2或m≥3+215.【答案】(1)2(2)解:BC 与O 相切;理由:如图2,过点O 作OH BC ⊥于H ,连接OD ,∵O 与AB 相切于D ,∴OD AB ⊥,在Rt AOD 中,30BAC ∠=︒,∴24OA OD ==,∵8AC =,∴4OC =,在ABC 中,AB BC =,∴30C BAC ∠=∠=︒,在Rt OHC 中,30C ∠=︒,∴122OH OC OD ===,∴BC 与O 相切,(3)解:①当点O 在AC 的左侧时,连接OD 交AC 于F ,如备用图1,∵O 与AB 相切于D ,∴OD AB ⊥,∵OG AC ⊥,∴30FOG BAC ∠=∠=︒,在Rt FDA 中,tan FD BAC AD ∠=,∴tan 3FD AD BAC x =⋅∠=,∴23OF x =-,在Rt FOG 中,331cos 2322y OG OF FOG ⎛⎫==⋅∠=-⨯-+ ⎪ ⎪⎝⎭,即12y x =-+,此时x 的取值范围为0x ≤≤;②当点O 在AC 的右侧时,连接DO 并延长交AC 于F ,如备用图2,同①的方法得,33FD x =,∴23OF x =-,∵FD AB ⊥,∴90BAC AFD ∠+∠=︒,∴30FOG BAC ∠=∠=︒,在Rt FOG 中,331cos 2322y OG OF FOG x x ⎛⎫==⋅∠=-⨯- ⎪⎪⎝⎭,即12y x =-,此时x 的取值范围为1433x ≤≤.16.【答案】(1)0;2-(2)解:过点O 作OD ⊥AB 于点D ,∵点A(2-,0),B(0,.∴2OA OB ==,,∴4AB ==,∵1122OA OB AB OD ⋅=⋅,∴112422OD ⨯⨯=⨯⨯∴DO =,∵d (⊙O ,线段AB )=0,∴当⊙O 的半径等于OD 时最小,当⊙O 的半径等于OB 时最大,∴r r ≤≤(3)43423m -<<-17.【答案】(1)2y x =+(2)解:①当2d =时,()20D ,,设直线CD 的解析式为:y kx b =+,()02C ,,202k b b +=⎧∴⎨=⎩,解得:12k b =-⎧⎨=⎩,∴直线CD 的解析式为:y x =-+,设点M 的坐标为()2m m -+,,∴点M 的关联直线为:()212y mx m m x =-+=-+,∴点M 的关联直线经过定点()12N ,,如图2,过点O 作直线2y mx m =--+的垂线,垂足为H ,连接ON ,ON OH ∴≥,∴当点H与点N重合时,OH最大,即点O到点M的关联直线的距离最大,∴点O到点M=;2 d=②或2 3-18.【答案】(1);3(2)解:设点G是O的特征值为4的点,∴经过一点G且弦长为4(最长弦)的直线有1条,弦长为3的直线有2条,弦长为2的直线有且只有1条, 经过点G的直线被O截得的弦长的最小值为2,=,∴关于O的特征值为4的所有点都在以O为半径的圆周上,直线y x b=+分别与x,y轴交于点A、B,()0A b∴-,,()B b,,OA OB b∴==,45OBH∴∠=︒,当0b>时,线段AB与以O为半径的圆相切时,点G特征值为4,设切点为为H,连接OH,则OH=,OB∴==,b∴=,设以O 为半径的圆与y 轴正半轴的交点记为1B ,则1OB =,当线段AB 与以O 1B 时,可得b =,b ≤≤同理可求当0b <时,b ≤≤,综上,b b b ≤≤-≤(3)当372122t -≤≤+时,存在点R ,S ,使得3r s +=。
中考数学动点问题专题练习(含答案)

动点专题一、应用勾股定理建立函数解析式例1(2000年·上海)如图1,在半径为6,圆心角为90°的扇形OAB 的弧AB 上,有一个动点P,PH ⊥O A,垂足为H,△OPH 的重心为G .(1)当点P在弧AB 上运动时,线段GO 、GP 、GH 中,有无长度保持不变的线段?如果有,请指出这样的线段,并求出相应的长度.(2)设P Hx =,GP y =,求y 关于x 的函数解析式,并写出函数的定义域(即自变量x 的取值范围).(3)如果△PG H是等腰三角形,试求出线段PH 的长.二、应用比例式建立函数解析式例2(2006年·山东)如图2,在△ABC 中,AB=AC =1,点D,E在直线B C上运动.设BD=,x CE=y . (1)如果∠B AC=30°,∠DA E=105°,试确定y 与x 之间的函数解析式;(2)如果∠B AC的度数为α,∠DAE 的度数为β,当α,β满足怎样的关系式时,(1)中y 与x 之间的函数解析式还成立?试说明理由.AEDCB 图2H M NG PO A B 图1 x yC三、应用求图形面积的方法建立函数关系式例4(2004年·上海)如图,在△A BC中,∠BAC =90°,AB=AC =22,⊙A 的半径为1.若点O在BC 边上运动(与点B 、C 不重合),设BO=x ,△AOC 的面积为y .(1)求y 关于x 的函数解析式,并写出函数的定义域.(2)以点O 为圆心,BO 长为半径作圆O,求当⊙O 与⊙A相切时, △AO C的面积.一、以动态几何为主线的压轴题 (一)点动问题.1.(09年徐汇区)如图,ABC ∆中,10==AC AB ,12=BC ,点D 在边BC 上,且4=BD ,以点D 为顶点作B EDF ∠=∠,分别交边AB 于点E ,交射线CA 于点F . (1)当6=AE 时,求AF 的长;(2)当以点C 为圆心CF 长为半径的⊙C 和以点A 为圆心AE 长为半径的⊙A 相切时,求BE 的长; (3)当以边AC 为直径的⊙O 与线段DE 相切时,求BE的长.AB C O 图8HAB CDEOlA ′(二)线动问题2,在矩形A BCD 中,AB =3,点O 在对角线A C上,直线l过点O ,且与AC 垂直交AD于点E .(1)若直线l 过点B,把△ABE 沿直线l 翻折,点A 与矩形A BCD的对称中心A '重合,求BC 的长; (2)若直线l 与AB 相交于点F,且AO=41AC,设AD 的长为x ,五边形BCDEF 的面积为S.①求S 关于x 的函数关系式,并指出x 的取值范围;②探索:是否存在这样的x ,以A 为圆心,以-x 43长为半径的圆与直线l 相切,若存在,请求出x 的值;若不存在,请说明理由.(三)面动问题3.如图,在ABC ∆中,6,5===BC AC AB ,D 、E 分别是边AB 、AC 上的两个动点(D 不与A 、B 重合),且保持BC DE ∥,以DE 为边,在点A 的异侧作正方形DEFG .(1)试求ABC ∆的面积;(2)当边FG 与BC 重合时,求正方形DEFG 的边长; (3)设x AD =,ABC ∆与正方形DEFG 重叠部分的面积为y ,试求y 关于x 的函数关系式,并写出定义域;(4)当BDG ∆是等腰三角形时,请直接写出AD 的长.解决动态几何问题的常见方法有:C一、 特殊探路,一般推证例2:(2004年广州市中考题第11题)如图,⊙O 1和⊙O2内切于A,⊙O1的半径为3,⊙O2的半径为2,点P为⊙O1上的任一点(与点A 不重合),直线PA 交⊙O2于点C,PB 切⊙O2于点B ,则PCBP的值为(A)2 (B)3 (C)23(D)26二、 动手实践,操作确认例4(2003年广州市中考试题)在⊙O中,C 为弧AB 的中点,D 为弧A C上任一点(与A 、C 不重合),则(A)A C+CB=AD+DB (B) A C+C B<AD+DB(C) AC+CB >A D+D B (D) AC+C B与AD+DB 的大小关系不确定例5:如图,过两同心圆的小圆上任一点C 分别作小圆的直径CA 和非直径的弦CD ,延长CA 和C D与大圆分别交于点B 、E,则下列结论中正确的是( * ) (A)AB DE = (B )AB DE >(C)AB DE <(D )AB DE ,的大小不确定三、 建立联系,计算说明例6:如图,正方形ABCD 的边长为4,点M在边DC 上,且DM=1,N为对角线A C上任意一点,则DN +MN 的最小值为 .BMND CBA以圆为载体的动点问题中,AC=5,BC=12,∠ACB=90°,P是AB边上的动点(与点A、B不重例1.在Rt ABC合),Q是BC边上的动点(与点B、C不重合),当PQ与AC不平行时,△CPQ可能为直角三角形吗?若有可能,请求出线段CQ的长的取值范围;若不可能,请说明理由。
中考数学总复习《(特殊)平行四边形的动点问题》专题训练(附答案)

中考数学总复习《(特殊)平行四边形的动点问题》专题训练(附答案)学校:___________班级:___________姓名:___________考号:___________1.已知,矩形ABCD 中,AB =4cm ,BC =8cm ,AC 的垂直平分线EF 分别交AD 、BC 于点E 、F ,垂足为O .(1)如图1,连接AF 、CE .求证四边形AFCE 为菱形,并求AF 的长;(2)如图2,动点P 、Q 分别从A 、C 两点同时出发,沿△AFB 和△CDE 各边匀速运动一周.即点P 自A →F →B →A 停止,点Q 自C →D →E →C 停止.在运动过程中,①已知点P 的速度为每秒5cm ,点Q 的速度为每秒4cm ,运动时间为t 秒,当A 、C 、P 、Q 四点为顶点的四边形是平行四边形时,求t 的值.②若点P 、Q 的运动路程分别为a 、b (单位:cm ,ab ≠0),已知A 、C 、P 、Q 四点为顶点的四边形是平行四边形,求a 与b 满足的数量关系式.2.(1)如图1,点P 为矩形ABCD 对角线BD 上一点,过点P 作//EF BC ,分别交AB 、CD 于点E 、F .若2BE =,PF=6,AEP △的面积为1S ,CFP 的面积为2S ,则12S S +=________;(2)如图2,点P 为ABCD 内一点(点P 不在BD 上),点E 、F 、G 、H 分别为各边的中点.设四边形AEPH 的面积为1S ,四边形PFCG 的面积为2S (其中21S S >),求PBD △的面积(用含1S 、S的代数式表示);2(3)如图3,点P为ABCD内一点(点P不在BD上)过点P作//EF AD,HG//AB与各边分别相交于点E、F、G、H设四边形AEPH的面积为1S,四边形PGCF的面积为2S(其中21),S S求PBD△的面积(用含1S、2S的代数式表示);(4)如图4 点A B C D把O四等分.请你在圆内选一点P(点P不在AC BD 上)设PB PC BC围成的封闭图形的面积为1S PA PD AD围成的封闭图形的面积为2S PBD△的面积为3S PAC△的面积为4S.根据你选的点P的位置直接写出一个含有1S2S3S4S的等式(写出一种情况即可).3.已知直线y=x+4与x轴y轴分别交于A B两点∠ABC=60°BC与x轴交于点C.(1)试确定直线BC的解析式.(2)若动点P从A点出发沿AC向点C运动(不与A C重合)同时动点Q从C点出发沿CBA向点A运动(不与C A重合) 动点P的运动速度是每秒1个单位长度动点Q的运动速度是每秒2个单位长度.设△APQ的面积为S P点的运动时间为t秒求S与t的函数关系式并写出自变量的取值范围.(3)在(2)的条件下当△APQ的面积最大时y轴上有一点M 平面内是否存在一点N 使以A Q M N为顶点的四边形为菱形?若存在请直接写出N点的坐标;若不存在请说明理由.4.如图在等腰梯形ABCD中AB∥DC AB=8cm CD=2cm AD=6cm.点P 从点A出发以2cm/s的速度沿AB向终点B运动;点Q从点C出发以1cm/s的速度沿CD DA向终点A运动(P Q两点中有一个点运动到终点时所有运动即终止).设P Q同时出发并运动了t秒.(1)当PQ将梯形ABCD分成两个直角梯形时求t的值;(2)试问是否存在这样的t 使四边形PBCQ的面积是梯形ABCD面积的一半?若存在求出这样的t的值若不存在请说明理由.5.如图在平面直角坐标系中以坐标原点O为圆心2为半径画⊙O P是⊙O上一动点且P在第一象限内过点P作⊙O的切线与轴相交于点A与轴相交于点B.(1)点P在运动时线段AB的长度也在发生变化请写出线段AB长度的最小值并说明理由;(2)在⊙O上是否存在一点Q使得以Q O A P为顶点的四边形时平行四边形?若存在请求出Q点的坐标;若不存在请说明理由.6.如图已知长方形ABCD中AD=6cm AB=4cm 点E为AD的中点.若点P在线段AB上以1cm/s的速度由点A向点B运动同时点Q在线段BC上由点B向点C运动.(1)若点Q的运动速度与点P的运动速度相等经过1秒后△AEP与△BPQ是否全等请说明理由并判断此时线段PE和线段PQ的位置关系;(2)若点Q的运动速度与点P的运动速度相等运动时间为t秒设△PEQ的面积为Scm2请用t的代数式表示S;(3)若点Q的运动速度与点P的运动速度不相等当点Q的运动速度为多少时能够使△AEP与△BPQ全等?7.如图长方形ABCD中5cm,8cm==现有一动点P从A出发以2cm/s的速度沿AB BC----返回到点A停止设点P运动的时间为t秒.长方形的边A B C D At=时BP=___________cm;(1)当2(2)当t为何值时连接,,△是等腰三角形;CP DP CDP(3)Q为AD边上的点且6DQ=P与Q不重合当t为何值时以长方形的两个顶点及点P为顶点的三角形与DCQ全等.8.如图平行四边形ABCD中6cmB∠︒G是CD的中点E是BC==60AB=8cm边AD上的动点EG的延长线与BC的延长线交于点F连接CE DF.(1)求证:四边形CEDF是平行四边形;(2)①AE=______时四边形CEDF是矩形;②AE=______时四边形CEDF是菱形.9.在平面直角坐标系中点A在第一象限AB⊥x轴于点B AC⊥y轴于点C已知点B(b0)C(0 c)其中b c满足|b﹣8|6+-=0.c(1)直接写出点A坐标.(2)如图2 点D从点O出发以每秒1个单位的速度沿y轴正方向运动同时点E从点A出发以每秒2个单位的速度沿射线BA运动过点E作GE⊥y轴于点G设运动时间为t 秒当S四边形AEGC<S△DEG时求t的取值范围.(3)如图3 将线段BC平移使点B的对应点M恰好落在y轴负半轴上点C的对应点为N连接BN交y轴于点P当OM=4OP时求点M的坐标.10.如图在平面直角坐标系中点A B的坐标分别是(﹣4 0)(0 8)动点P从点O出发沿x轴正方向以每秒1个单位的速度运动同时动点C从点B出发沿12.在四边形ABCD中//,90,10cm,8cm∠=︒===点P从点A出发沿折线AB CD BCD AB AD BCABCD方向以3cm/s的速度匀速运动;点Q从点D出发沿线段DC方向以2cm/s的速度匀速运动.已知两点同时出发当一个点到达终点时另一点也停止运动设运动时间为()s t.(1)求CD的长;(2)当四边形PBQD为平行四边形时求四边形PBQD的周长;(3)在点P Q的运动过程中是否存在某一时刻使得BPQ的面积为220cm若存在请求出所有满足条件的t的值;若不存在请说明理由.13.在平面直角坐标系中矩形OABC的边OA任x轴上OC在y轴上B(4 3)点M从点A开始以每秒1个单位长度的速度沿AB→BC→CO运动设△AOM的面积为S 点M运动的时间为t.(1)当0<t<3时AM=当7<t<10时OM=;(用t的代数式表示)(2)当△AOM为等腰三角形时t=;(3)当7<t<10时求S关于t的函数关系式;(4)当S=4时求t的值.14.如图1 在平面直角坐标系中正方形OABC的边长为6 点A C分别在x y 正半轴上点B在第一象限.点P是x正半轴上的一动点且OP=t连结PC将线段PC绕点P顺时针旋转90度至PQ连结CQ取CQ中点M.(1)当t=2时求Q与M的坐标;(2)如图2 连结AM以AM AP为邻边构造平行四边形APNM.记平行四边形APNM 的面积为S.①用含t的代数式表示S(0<t<6).②当N落在△CPQ的直角边上时求∠CPA的度数;(3)在(2)的条件下连结AQ记△AMQ的面积为S'若S=S'则t=(直接写出答案).15.如图平面直角坐标系中矩形OABC的顶点B的坐标为(7 5)顶点A C 分别在x轴y轴上点D的坐标为(0 1)过点D的直线与矩形OABC的边BC交于点G 且点G不与点C重合以DG为一边作菱形DEFG 点E在矩形OABC的边OA 上设直线DG的函数表达式为y=kx+b(1)当CG=OD时求直线DG的函数表达式;(2)当点E的坐标为(5 0)时求直线DG的函数表达式;(3)连接BF 设△FBG的面积为S CG的长为a 请直接写出S与a的函数表达式及自变量a 的取值范围.16.如图 在四边形ABCD 中 //AD BC 3AD = 5DC = 42AB = 45B ∠=︒ 动点M 从点B 出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从点C 出发沿线段CD 以每秒1个单位长度的速度向终点D 运动 设运动的时间为s t .(1)求BC 的长.(2)当//MN AB 时 求t 的值(3)试探究:t 为何值时 MNC ∆为等腰三角形?参考答案:1.(1)证明:∵四边形ABCD 是矩形∴AD ∥BC∴∠CAD =∠ACB ∠AEF =∠CFE∵EF 垂直平分AC 垂足为O∴OA =OC∴△AOE ≌△COF∴OE =OF∴四边形AFCE 为平行四边形又∵EF ⊥AC∴四边形AFCE 为菱形设菱形的边长AF =CF =x cm 则BF =(8﹣x )cm在Rt △ABF 中 AB =4cm由勾股定理得42+(8﹣x )2=x 2解得x =5iii )如图3 当P 点在AB 上 Q 点在CD 上时 AP =CQ 即12﹣a =b 得a +b =12. 综上所述 a 与b 满足的数量关系式是a +b =12(ab ≠0).2.(1)过P 点作AB∥MN∵S 矩形AEPM +S 矩形DFPM =S 矩形CFPN +S 矩形DFPM =S 矩形ABCD -S 矩形BEPN又∵11,,22AEP CFP AEPM CFPN SS S S ==矩形矩形 ∴1==26=62AEP CFP S S ⨯⨯, ∴1212.S S +=(2)如图 连接PA PC在APB △中 因为点E 是AB 中点可设APE BPE S S a ==同理 ,,BPF CPF CPG DFG DPH APH S S b S S c S S d ======所以APE APH CPF AEPH PFCG CPG S S SS a b d S S c =+++=++++四边形四边形 BPE BPF DPH DPH EDFP HPGD S S S S S S a b c d +=+++=+++四边形四边形.所以12EBFP HPGD AEPH PFCG S S S S S S +++=+四边形四边形四边形四边形所以1212ABD ABCD SS S S ==+ 所以1DPH APH S S S a ==-. ()()()1121121PBD ABD BPE PDH S S S S S S S S a S a S S =-++=+-++-=-.(3)易证四边形EBGP 四边形HPFD 是平行四边形.EBP SHPD S .()()121211122222ABD ABCD EBF HPD EBP HPD SS S S S S S S S S ==+++=+++ ()()12112FBD ABD EBP HPD S S S S S S S =-++=-. (4)试题解析:(1)由已知得A 点坐标(﹣4﹐0) B 点坐标(0﹐43﹚ ∵OB=3OA ∴∠BAO=60° ∵∠ABC=60° ∴△ABC 是等边三角形 ∵O C=OA=4 ∴C 点坐标﹙4 0﹚ 设直线BC 解析式为y kx b =+∴ ∴直线BC 的解析式为343y x =-+; ﹙2﹚当P 点在AO 之间运动时 作QH⊥x 轴 ∵QH CQ OB CB= ∴2843QH t = ∴QH=3t ∴S △APQ =AP•QH=132t t ⋅=232t ﹙0<t≤4﹚ 同理可得S △APQ =t·﹙833t -﹚=23432t t -+﹙4≤t<8﹚∴223(04)2{343?(48)2t t S t t t <≤=-+≤<; (3)存在 如图当Q 与B 重合时 四边形AMNQ 为菱形 此时N 坐标为(4 0) 其它类似还有(﹣4 8)或(﹣4 ﹣8)或(﹣4 ).4.(1)53(2)存在 使四边形PBCQ 的面积是梯形ABCD 面积的一半.(1)过D 作DE⊥AB 于E 过C 作CF⊥AB 于F 通过Rt ADE Rt BCF ∆≅∆ 得AE BF = 若四边形APQD 是直角梯形 则四边形DEPQ 为矩形 通过AP AE EP =+ 代入t 值 即可求解(2)假设当时 通过点Q 在CD 上或在AD 上 两种情况进行讨论求解5.(1)线段AB 长度的最小值为4理由如下:连接OP如图② 设四边形APQO 为平行四边形因为OQ PA ∥ 90APO ︒∠=所以90POQ ︒∠= 又因为OP OQ =所以45PQO ︒∠= 因为PQ OA ∥所以PQ y ⊥轴.设PQ y ⊥轴于点H在Rt △OHQ 中 根据2,45OQ HQO ︒=∠= 得Q 点坐标为(2,2-)所以符合条件的点Q 的坐标为(2,2-)或(2,2-).6.(1)∵长方形ABCD∴∠A =∠B =90°∵点E 为AD 的中点 AD =6cm∴AE =3cm又∵P 和Q 的速度相等可得出AP =BQ =1cm BP =3 ∴AE =BP在△AEP 和△BQP 中∴y=xy 3=4-y⎧⎨⎩ 解得:x=1y=1⎧⎨⎩ (舍去). 综上所述,点Q 的运动速度为32cm /s 时能使两三角形全等.7.(1)1(2)54t =或4或232 (3) 3.5t = 5.5或10(1)解:动点P 的速度是2cm/s∴当2t =时 224AP =⨯=∵5cm AB =∴BP =1cm ;(2)解:①当点P 在AB 上时 CDP △是等腰三角形∴PD CP =在长方形ABCD 中 ,90AD BC A B =∠=∠=︒∴()HL DAP CBP ≌∴AP BP =∴1522AP AB ==∵动点P 的速度是2cm/s∵90D5DP CD == 2AB CB CD t ++=∴要使一个三角形与DCQ 全等①当点P运动到1P时16△≌△DCQ CDPCP DQ==此时1∴点P的路程为:1527AB BP+=+=∴72 3.5t=÷=;②当点P运动到2P时26△≌△CDQ ABPBP DQ==此时2∴点P的路程为:25611+=+=AB BP∴112 5.5t=÷=③当点P运动到3P时35△≌△CDQ BAP==此时3AP DQ∴点P的路程为:3585220AB BC CD DP+++=+++=∴20210t=÷=④当点P运动到4P时即P与Q重合时46△≌△CDQ CDPDP DQ==此时4∴点P的路程为:4585624+++=+++=AB BC CD DPt=÷=此结果舍去不符合题意∴24212综上所述t的值可以是: 3.5t= 5.5或10.8.(1)四边形ABCD是平行四边形∥∴BC AD∴∠=∠FCG EDGG是CD的中点∴=CG DG△中在CFG△和DEGCFG∴≅(ASA)DEGFG EG∴=又CG DG=∴四边形CEDF是平行四边形.2)①当5AE=如图过60B∠=12BM∴=5AE=DE AD∴=在MBA△BM DEB=⎧⎪∠=∠⎨⎪(SAS)MBA EDC∴≅CED AMB∴∠=∠四边形CEDF是平行四边形∴平行四边形CEDF②当2AE cm =时 四边形CEDF 是菱形 理由如下:四边形ABCD 是平行四边形8AD ∴= 6CD AB == 60CDE B ∠=∠=︒2AE =6DE AD AE ∴=-=DE CD ∴=CDE ∴∆是等边三角形CE DE ∴=四边形CEDF 是平行四边形∴平行四边形CEDF 是菱形故答案为:2;9.(1)解:∵|b ﹣8|6c +-=0∴b -8=0 c -6=0∴b =8 c =6∵B (b 0) C (0 c )∴B (8 0) C (0 6)又∵AB ⊥x 轴 AC ⊥y 轴∴A (8 6);(2)∵AB ⊥x 轴 AC ⊥y 轴 GE ⊥y 轴∴四边形AEGC 是矩形设运动时间为t 秒∴OD =t AE =2t DG =6+2t-t =6+t∴S 四边形AEGC =8×2t =16t S △DEG =12×(6+t )×8=4t +242∵OM=4OP∴-m=-4×62m解得m=-12综上所述m的值为-4或-12.10.(1)∵点A B的坐标分别是(﹣4 0)(0 8)∴OA=4 OB=8∵点C运动到线段OB的中点∴OC=BC=12OB=4∵动点C从点B出发沿射线BO方向以每秒2个单位的速度运动∴2t=4解之:t=2;∵PE=OA=4 动点P从点O出发沿x轴正方向以每秒1个单位的速度运动∴OE=OP+PE=t+4=2+4=6∴点E(6 0)(2)证明:∵四边形PCOD是平行四边形∴OC=PD OC∥PD当点C在y轴的负半轴上时③如果点M在DE上时24163(3)22t tt--=++解得423t=+④当N在CE上时28(3)8214tt tt-⋅++-=-+解得12t=综上分析可得满足条件的t的值为:t1=28﹣16 3t2=2 t3=4+2 3t4=12.11.(1) ()30D,,()1,3E;(2)933022933222572222t tS t tt t⎧⎛⎫-+≤≤⎪⎪⎝⎭⎪⎪⎛⎫=-<≤⎨ ⎪⎝⎭⎪⎪⎛⎫-≤⎪ ⎪⎝⎭⎩<(3)198s解:(1)3922y x=-+当y=0时39=022x-+则x=3 即点()30D,当y=3时39=322x-+则x=1 故点()1,3E故:()30D,,()1,3E;(2)如图1 ①当点P在OD段时此时0≤t<32119()2223233S PD OC t t=⨯⨯=⨯-⨯=-+;②当点P在点D时此时t=32此时三角形不存在0S=;''6ADP BEP S S -=-30232t t ⎛⎫≤≤ ⎪⎝⎭⎫<≤⎪;即当点P 在边AB 上运动 且PD PE +的值最小时 运动时间t 为198s . 12.(1)16cm ;(2)(8813)cm +;(3)53t =秒或395秒 解:(1)如图1过A 作AM DC ⊥于M在四边形ABCD 中 //AB CD 90BCD ∠=︒//AM BC ∴∴四边形AMCB 是矩形10AB AD cm == 8BC cm =8AM BC cm ∴== 10CM AB cm ==在Rt AMD ∆中 由勾股定理得:6DM cm =10616CD DM CM cm cm cm =+=+=;(2)如图2当四边形PBQD 是平行四边形时 PB DQ =即1032t t -=解得2t =此时4DQ = 12CQ = 22413BQ BC CQ =+=所以()28813PBQD C BQ DQ =+=+;1003t 14(102BPQ BP BC ==解得53t =;P 在BC 上时 63t1(32BP CQ t =此方程没有实数解;CD 上时:在点Q 的右侧54(34PQ BC =6< 不合题意若P 在Q 的左侧 如图6 即3485t <14(534)202BPQ S PQ BC t ∆==-= 解得395t =; 综上所述 当53t =秒或395秒时 BPQ ∆的面积为220cm . 13.(1)t 10-t ;(2)5;(3)S =20-2t ;(4)2或8. 解:(1)当0<t <3时 点M 在线段AB 上 即AM =t 当7<t <10时 点M 在线段OC 上 OM =10-t故填:t 10-t ;(2)∵四边形ABCO 是矩形 B (4 3)∴OA =BC =4 AB =OC =3∵△AOM 为等腰三角形∴只有当MA =MO 此时点M 在线段BC 上 CM =BM =2 ∴t =3+2=5故填:5;(3)∵当7<t <10时 点M 在线段OC 上∴114(10)20222S OA OM t t =⋅⋅=⨯⨯-=-;(4)①当点M 在线段AB 上时 4=12×4t 解得t =2;②当点M 在线段BC 上时 S =6 不符合题意;当点M 在线段OC 上时 4=20-2t 解得t =8.∴OD =OP +PD =8∴Q (8 2)∵M 是CQ 的中点 C (0 6)∴M (4 4);(2)①∵△COP ≌△PDQ∴OP =OQ =t OC =PD =6∴OD =t +6∴Q (t +6 t )∵C (0 6)∴M (62t + 62t +) 当0<t <6时 S =AP ×y M =(6﹣t )×62t +=2362t -; ②分两种情况:a 当N 在PC 上时 连接OB PM 如图2﹣1所示:∵点M 的横 纵坐标相等∴点M 在对角线BD 上∵四边形OABC 是正方形∴OC =OA ∠COM =∠AOM∴∠MPA =12(180°﹣45°)=67.5° ∴∠CPA =67.5﹣45=22.5°;综上所述 当点N 在△CPQ 的直角边上时 ∠CPA 的度数为112.5°或22.5°;(3)过点M 作MH ⊥x 轴于点H 过点Q 作QG ⊥x 轴于点G∵AMQ AHM AGQ MHGQ S S S S =--△△△梯形∴S '=12(62t ++t )•62t +﹣12(6﹣62t +)•62t +﹣12t •t =3t ①当0<t <6时 即点AP 在点A 左侧时 如图3所示:∵S =S '∴2362t -=3t 解得:t =﹣3+35 或t =﹣3﹣35(舍去);②当t >6时 即点P 在点A 右侧时 如图4所示:S =AP ×y M =(t ﹣6)×62t +=2362t - ∵S =S '将D (0 1)G (10 5)代入y=kx+b 得:1105b k b =⎧⎪⎨+=⎪⎩解得:21051k b ⎧=⎪⎨⎪=⎩∴当CG=OD 时 直线DG 的函数表达式为y=2105x+1.(3)设DG 交x 轴于点P 过点F 作FM⊥x 轴于点M 延长MF 交BC 于点N 如图所示.∵DG∥EF∴∠FEM=∠GPO.∵BC∥OA∴∠DGC=∠GPO=∠FEM.在△DCG 和△FME 中90DCG FME DGC FEMDG FE⎧∠=∠=⎪∠=∠⎨⎪=⎩ ∴△DCG≌△FME(AAS )∴FM=DC=4.∵MN⊥x 轴∴四边形OMNC 为矩形在Rt△CDH 中 由勾股定理可得: HC=22543-=∴BC=BK+KH+HC=4+3+3=10;(2)如图② 过D 作DG∥AB 交BC 于G 点 则四边形ADGB 为平行四边形 ∴BG=AD=3∴GC=BC−BC=10−3=7由题意得 当M N 运动t 秒后 CN=t CM=10−2t∵AB∥DG MN∥AB∴DG∥MN∴∠NMC=∠DGC又∵∠C=∠C∴△MNC ~△GDC∴CN CM CD CG=, ∴10257tt -=解得t=5017; (3)第一种情况:当NC=MC 时 如图③22∵∠C=∠C∠MFC=∠DHC=90°∴△MFC~△DHC∴FC MCHC DC=即:1 102253tt-=解得:t=6017;综上所述当t=103t=258或t=6017时△MNC为等腰三角形.。
中考数学总复习《与相似有关的动点问题》集锦(含答案)

与相似有关的动点问题一 、解答题1.如图,在梯形ABCD中,=3,5,45oAD BC AD DC AB B ==∠=∥,.动点M 从B点出发沿线段BC 以每秒2个单位长度的速度向终点C 运动;动点N 同时从C 点出发沿线段CD 以每秒1个单位长度的速度向终点D 运动,设运动的时间为t 秒. (1)求BC 的长;(2)当MN AB ∥时,求t 的值;(3)试探究:t 为何值时,MNC △为等腰三角形.2.如图,在矩形ABCD 中,126AB BC ==,,点P 沿AB 边从点A 开始向点B 以2/秒的速度移动,点Q 沿DA 边以1/秒的速度从点D 开始移动,如果P Q ,同时出发,用t (秒)表示移动的时间(06)t ≤≤. ⑴ 当t 为何值时,QAP ∆为等腰直角三角形?⑵ 求四边形QAPC 面积,提出一个与计算结果相关的正确结论. ⑶ 当t 为何值时,以点Q A P ,,为顶点的三角形与ABC ∆相似.3.如图,矩形ABCD 中,3AD =厘米,AB a =厘米(3a >).动点M N ,同时从B 点出发,分别沿B A →,B C →运动,速度是1厘米/秒.过M 作直线垂直于AB ,分别交AN ,CD 于P Q ,.当点N 到达终点C 时,点M 也随之停止运动.设运动时间为t 秒.⑴若4a =厘米,1t =秒,则PM =______厘米;MBQPD CBA⑵若5a =厘米,求时间t ,使PNB PAD △∽△,并求出它们的相似比; ⑶若在运动过程中,存在某时刻使梯形PMBN 与梯形PQDA 的面积相等,求a 的取值范围;⑷是否存在这样的矩形:在运动过程中,存在某时刻使梯形PMBN ,梯形PQDA ,梯形PQCN 的面积都相等?若存在,求a 的值;若不存在,请说明理由.4.ABC ∆中,90C ∠=︒,60A ∠=︒,2cm AC =.长为1cm 的线段MN 在ABC ∆的边AB上沿AB 方向以1cm/s 的速度向点B 运动(运动前点M 与点A 重合).过M N ,分别作AB 的垂线交直角边于P ,Q 两点,线段MN 运动的时间为ts . (1)若AMP ∆的面积为y ,写出y 与t 的函数关系式(写出自变量t 的取值范围);(2)线段MN 运动过程中,四边形MNQP 有可能成为矩形吗?若有可能,求出此时的值;若不可能,说明理由;(3)t 为何值时,以C ,P ,Q 为顶点的三角形与ABC ∆相似?5.如图,ABC ∆中,39085AC C BC AB ∠=︒==,,,点P 从B 出发,沿BC 方向以2/s 的速度移动,点Q 从C 出发,沿CA 方向也以1/s 的速度移动,若P Q ,分别从B C ,出发,经过多少时间CPQ ∆与CBA ∆相似?P N NMQDC BAQPMDCBAt N M QPBAC QPCBA与相似有关的动点问题答案解析一 、解答题1.(1)过,A D 两点向BC 边做垂线,根据勾股定理可求得:10BC =.(2)过D 点作DG AB ∥交AB 于G 点,如图1,则3,7,BG AD GC MN DG ===∥ 当,M N 运动t 秒时,,102CN t CM t ==-由MNC GDC △∽△得CN CMCD CG=,即10257t t -=,解得:5017t =. (3)当NC MC =时,如图2,则102t t =-,解得:103t =. 当MN NC =时,如图3,过点N 作NE MC ⊥于E ,过点D 作,DH BC ⊥于H ,由NEC DHC △∽△,得NC CE DC HC =,即553t t -=,解得:258t =. 当MN MC =时,如图4,过点M 作MF CN ⊥于F ,则1122FC NC t ==,由MFC DHC △∽△,得FC MC HC DC =,即1102335tt -=,解得:607t =.综上所述当t=103或258或6017时MNC △为等腰三角形 2.⑴ 当QAP ∆为等腰直角三角形时,AP AQ =,∴26t t =-,2t =⑵11(6)12263622QAC APC QAPC S S S t t ∆∆=+=-⨯+⨯⨯=四边形,即四边形QAPC 的面积为定值. ⑶分2种情况 ①当APQ BAC ∆∆∽时,2AP BA AQ BC ==,即226tt =-,解得3t =. 图4图3图2图1DABC FN MH H E M ND GCBAND BAN MGDCBA② 当AQP BAC ∆∆∽时,2AQ BA AP BC ==,即622t t -=,解得65t =. 综上当3t =或65时,以点Q A P ,,为顶点的三角形与ABC ∆相似. 3.⑴ 34PM =,⑵ 2t =,使PNB PAD △∽△,相似比为3:2 ⑶ ∵PM AB CB AB AMP ABC ∠=∠⊥,⊥,,AMP ABC △∽△,∴PM AM BN AB =即PM a t t a -=,∵()t a t PM a-=, ∵(1)3t a QM a-=-当梯形PMBN 与梯形PQDA 的面积相等,即()()22QP AD DQ MP BN BM++=()33(1)()22t a t t a a t t t a a -⎛⎫⎛⎫-+--+ ⎪ ⎪⎝⎭⎝⎭==化简得66a t a =+, ∵3t ≤,∴636aa+≤,则6a ≤,∴36a <≤, ⑷ ∵36a <≤时,梯形PMBN 与梯形PQDA 的面积相等 ∴梯形PQCN 的面积与梯形PMBN 的面积相等即可,则CN PM = ∴()3t a t t a-=-,把66at a=+代入,解之得a =±a = 所以,存在a,当a =PMBN 与梯形PQDA 的面积、梯形PQCN 的面积相等.4.⑴当点P 在AC 上时,∵AM t =,∴tg60PM AM =⋅︒=.∴()21012y t t =≤≤. 当点P 在BC上时,)tan304PM BM t =⋅︒=-.)()214132y t t t =-=≤≤. ⑵∵2AC =,∴4AB =.∴413BN AB AM MN t t =--=--=-.∴)tan303QN BN t =⋅︒-.由条件知,若四边形MNQP 为矩形,需PM QN =)3t =-, ∴34t =.∴当34t s =时,四边形MNQP 为矩形.⑶ 由⑵知,当34t s =时,四边形MNQP 为矩形,此时PQ AB ∥, ∴PQC ABC ∆∆∽.除此之外,当30CPQ B ∠=∠=︒时,QPC ABC ∆∆∽,此时tan 30CQ CP =︒ ∵1cos602AM AP =︒=,∴22AP AM t ==.∴22CP t =-.∵cos30BN BQ =︒=,∴)3BQ t ==-.又∵BC =,∴)3CQ t =-=.∵322t =-12t =.∴当12t s =或34s 时,以C P Q ,,为顶点的三角形与ABC ∆相似. 5.∵39085AC C BC AB ∠=︒==,,,设35AC k AB k ==,, ∴222AC BC AB +=,即222(3)8(5)k k +=,解得2k =(负值已舍去) ∴6AC =设经过s t 后CPQ ∆与CBA ∆相似.此时282BP t PC t CQ t ==-=,, 本题需分两种情况: ⑴ 当CAB CQP ∆∆∽时,CQ CP CA CB =,即8268t t-=,解得 2.4t = ⑵ 当CAB CPQ ∆∆∽时,CQ CP CB CA =,即8286t t -=,解得3211t =.32 11秒时,CPQ∆与CBA∆相似综上,当 2.4t=秒或。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中考数学之 动点问题一、选择题:1. 如图,在矩形ABCD 中,动点P 从点B 出发,沿BC 、CD 、DA 运动至点A 停止,设点P 运动的路程为x ,△ABP 的面积为y ,如果y 关于x 的函数图象如图2所示,则△ABC 的面积是( )94xyOPDA 、10B 、16C 、18D 、20二、填空题:1. 如上右图,C 为线段AE 上一动点(不与点A ,E 重合),在AE 同侧分别作正三角形ABC 和正三角形CDE 、AD 与BE 交于点O ,AD 与BC 交于点P ,BE 与CD 交于点Q ,连结PQ.以下五个结论:①AD=BE ;②PQ ∥AE ;③AP=BQ ;④DE=DP ;⑤∠AOB=60°.恒成立的结论有_______________________(把你认为正确的序号都填上)。
三、解答题:1.(2008年大连)如图12,直角梯形ABCD 中,AB ∥CD ,∠A = 90°,CD = 3,AD = 4,tan B = 2,过点C 作CH ⊥AB ,垂足为H .点P 为线段AD 上一动点,直线PM ∥AB ,交BC 、C H 于点M 、Q .以PM 为斜边向右作等腰Rt △PMN ,直线MN 交直线AB 于点E ,直线PN 交直线A B 于点F .设PD 的长为x ,EF 的长为y .⑴求PM 的长(用x 表示);⑵求y 与x 的函数关系式及自变量x 的取值范围(图13为备用图); ⑶当点E 在线段AH 上时,求x 的取值范围(图14为备用图).Q POBED CA图 13图 14图 12AHBCDA HBCDHM QP DCBA2.(2008年福建宁德)如图1,在Rt △ABC 中,∠C =90°,BC =8厘米,点D 在AC 上,CD =3厘米.点P 、Q 分别由A 、C 两点同时出发,点P 沿AC 方向向点C 匀速移动,速度为每秒k 厘米,行完AC 全程用时8秒;点Q 沿CB 方向向点B 匀速移动,速度为每秒1厘米.设运动的时间为x 秒()80<x<,△DCQ 的面积为y 1平方厘米,△PCQ 的面积为y 2平方厘米. ⑴求y 1与x 的函数关系,并在图2中画出y 1的图象;⑵如图2,y 2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P 的速度及AC 的长;⑶在图2中,点G 是x 轴正半轴上一点(0<OG <6=,过G 作EF 垂直于x 轴,分别交y 1、y 2于点E 、F . ①说出线段EF 的长在图1中所表示的实际意义; ②当0<x <6时,求线段EF 长的最大值.3.(2008年白银)如图,在平面直角坐标系中,四边形OABC 是矩形,点B 的坐标为(4,3).平行于对角线AC 的直线m 从原点O 出发,沿x 轴正方向以每秒1个单位长度的速度运动,设直线m 与矩形OABC 的两边..分别交于点M 、N ,直线m 运动的时间为t (秒). (1) 点A 的坐标是__________,点C 的坐标是__________; (2) 当t= 秒或 秒时,MN=21AC ; (3) 设△OMN 的面积为S ,求S 与t 的函数关系式;(4) 探求(3)中得到的函数S 有没有最大值?若有,求出最大值;若没有,要说明理由.图1C Q → BDAP ↓ 图2G 2 4 6 8 10 1210 86 4 2 yOx参考答案一、选择 A二、填空:(1)(2)(3)(5) 三、解答:2、解:⑴∵CD CQ S DCQ ⋅⋅=∆21,CD =3,CQ =x , ∴x y 231=. 图象如图所示.⑵方法一:CP CQ S PCQ ⋅⋅=∆21,CP =8k -xk ,CQ =x , ∴()kx kx x kx k y 42182122+-=⋅-⨯=.∵抛物线顶点坐标是(4,12),∴12444212=⋅+⋅-k k . 解得23=k .则点P 的速度每秒23厘米,AC =12厘米.方法二:观察图象知,当x=4时,△PCQ 面积为12. 此时PC =AC -AP =8k -4k =4k ,CQ =4.∴由CP CQ S PCQ ⋅⋅=∆21,得 12244=⨯k .解得23=k .则点P 的速度每秒23厘米,AC =12厘米.方法三:设y 2的图象所在抛物线的解析式是c bx ax y ++=2.∵图象过(0,0),(4,12),(8,0),∴⎪⎩⎪⎨⎧=++=++=.0864124160c b a c b a c ,, 解得 ⎪⎪⎩⎪⎪⎨⎧==-=.0643c b a ,, ∴x x y 64322+-=. ①∵CP CQ S PCQ ⋅⋅=∆21,CP =8k -xk ,CQ =x ,∴kx kx y 42122+-=. ②比较①②得23=k .则点P 的速度每秒23厘米,AC =12厘米.⑶①观察图象,知线段的长EF =y 2-y 1,表示△PCQ 与△DCQ 的面积差(或△PDQ 面积). ②由⑵得 x x y 64322+-=.(方法二,x x x x y 643232382122+-=⋅⎪⎭⎫ ⎝⎛-⨯⨯=)∵EF =y 2-y 1, ∴EF =x x x x x 29432364322+-=-+-,∵二次项系数小于0,∴在60<x<范围,当3=x 时,427=EF 最大. 3、解:(1)(4,0),(0,3); ···················· 2分 (2) 2,6; ····························· 4分 (3) 当0<t ≤4时,OM =t . 由△OMN ∽△OAC ,得OCONOA OM =, ∴ ON =t 43,S=283t . ·········· 6分 当4<t <8时,如图,∵ OD =t ,∴ AD = t-4. 方法一:由△DAM ∽△AOC ,可得AM =)4(43-t ,∴ BM =6-t 43. ········ 7分 由△BMN ∽△BAC ,可得BN =BM 34=8-t ,∴ CN =t-4. ········· 8分S=矩形OABC 的面积-Rt △OAM 的面积- Rt △MBN 的面积- Rt △NCO 的面积=12-)4(23-t -21(8-t )(6-t 43)-)4(23-t =t t 3832+-. ·························· 10分方法二:易知四边形ADNC 是平行四边形,∴ CN =AD =t-4,BN =8-t . ·········· 7分 由△BMN ∽△BAC ,可得BM =BN 43=6-t 43,∴ AM =)4(43-t . ····· 8分 以下同方法一. (4) 有最大值.方法一: 当0<t ≤4时,∵ 抛物线S=283t 的开口向上,在对称轴t=0的右边, S 随t 的增大而增大, ∴ 当t=4时,S 可取到最大值2483⨯=6; ············· 11分当4<t <8时, ∵ 抛物线S=t t 3832+-的开口向下,它的顶点是(4,6),∴ S <6. 综上,当t=4时,S 有最大值6. ···················· 12分 方法二:∵ S=22304833488t t t t t ⎧<⎪⎪⎨⎪-+<<⎪⎩,≤,∴ 当0<t <8时,画出S 与t 的函数关系图像,如图所示. ········ 11分 显然,当t=4时,S 有最大值6. ··················· 12分说明:只有当第(3)问解答正确时,第(4)问只回答“有最大值”无其它步骤,可给1分;否则,不给分.。
