中考数学-中考数学热点专题动点问题精品

合集下载

中考动点问题经典题型归类总结附答案

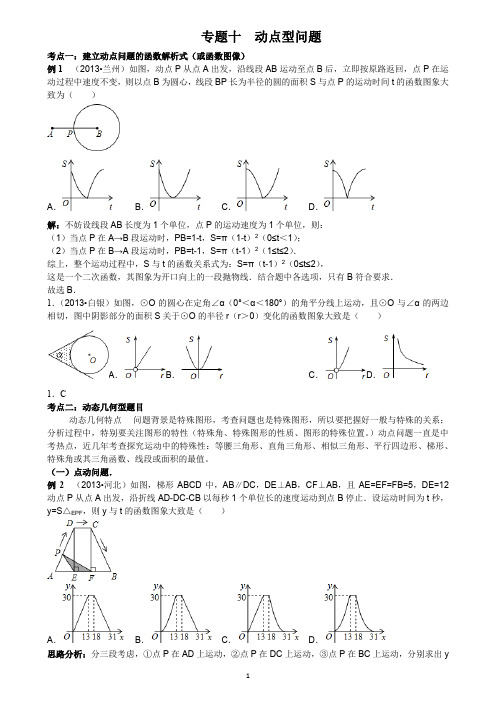
专题十动点型问题考点一：建立动点问题的函数解析式（或函数图像）例1 （2013•兰州）如图，动点P从点A出发，沿线段AB运动至点B后，立即按原路返回，点P在运动过程中速度不变，则以点B为圆心，线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为（）A．B．C．D．解：不妨设线段AB长度为1个单位，点P的运动速度为1个单位，则：（1）当点P在A→B段运动时，PB=1-t，S=π（1-t）2（0≤t＜1）；（2）当点P在B→A段运动时，PB=t-1，S=π（t-1）2（1≤t≤2）．综上，整个运动过程中，S与t的函数关系式为：S=π（t-1）2（0≤t≤2），这是一个二次函数，其图象为开口向上的一段抛物线．结合题中各选项，只有B符合要求．故选B．1．（2013•白银）如图，⊙O的圆心在定角∠α（0°＜α＜180°）的角平分线上运动，且⊙O与∠α的两边相切，图中阴影部分的面积S关于⊙O的半径r（r＞0）变化的函数图象大致是（）A．B．C．D．1．C考点二：动态几何型题目动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

）动点问题一直是中考热点，近几年考查探究运动中的特殊性：等腰三角形、直角三角形、相似三角形、平行四边形、梯形、特殊角或其三角函数、线段或面积的最值。

（一）点动问题．例2 （2013•河北）如图，梯形ABCD中，AB∥DC，DE⊥AB，CF⊥AB，且AE=EF=FB=5，DE=12动点P从点A出发，沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止．设运动时间为t秒，y=S△EPF，则y与t的函数图象大致是（）A．B．C．D．思路分析：分三段考虑，①点P在AD上运动，②点P在DC上运动，③点P在BC上运动，分别求出y与t 的函数表达式，继而可得出函数图象．解：在Rt △ADE 中，AD=2213AE DE +=，在Rt △CFB 中，BC=2213BF CF +=，①点P 在AD 上运动：对应训练2．（2013•北京）如图，点P 是以O 为圆心，AB 为直径的半圆上的动点，AB=2．设弦AP 的长为x ，△APO 的面积为y ，则下列图象中，能表示y 与x 的函数关系的图象大致是（）A ．B ．C ．D ．2．A（二）线动问题例3 （2013•荆门）如右图所示，已知等腰梯形ABCD ，AD ∥BC ，若动直线l 垂直于BC ，且向右平移，设扫过的阴影部分的面积为S ，BP 为x ，则S 关于x 的函数图象大致是（）A．B．C．D．解：①当直线l经过BA段时，阴影部分的面积越来越大，并且增大的速度越来越快；②直线l经过DC段时，阴影部分的面积越来越大，并且增大的速度保持不变；③直线l经过DC段时，阴影部分的面积越来越大，并且增大的速度越来越小；结合选项可得，A选项的图象符合．故选A．对应训练3．（2013•永州）如图所示，在矩形ABCD中，垂直于对角线BD的直线l，从点B开始沿着线段BD匀速平移到D．设直线l被矩形所截线段EF的长度为y，运动时间为t，则y关于t的函数的大致图象是（）A．B．C．D．3．A（三）面动问题例4 （2013•牡丹江）如图所示：边长分别为1和2的两个正方形，其中一边在同一水平线上，小正方形沿该水平线自左向右匀速穿过大正方形，设穿过的时间为t，大正方形内去掉小正方形后的面积为s，那么s与t的大致图象应为（）A．B．C．D．解：根据题意，设小正方形运动的速度为V，分三个阶段；①小正方形向右未完全穿入大正方形，S=2×2-Vt×1=4-Vt，②小正方形穿入大正方形但未穿出大正方形，S=2×2-1×1=3，③小正方形穿出大正方形，S=Vt×1，分析选项可得，A符合；故选A．对应训练4．（2013•衡阳）如图所示，半径为1的圆和边长为3的正方形在同一水平线上，圆沿该水平线从左向右匀速穿过正方形，设穿过时间为t，正方形除去圆部分的面积为S（阴影部分），则S与t的大致图象为（）A．B．C．D．4．A究：当t为何值时，△QMN为等腰三角形？请直接写出t的值．（4）△QMN 为等腰三角形的情形有两种，需要分类讨论，避免漏解．解：（1）∵C （7，4），AB ∥CD ，∴D （0，4）．∵sin ∠DAB=22， ∴∠DAB=45°，∴OA=OD=4，∴A （-4，0）．设直线l 的解析式为：y=kx+b ，则有4-40b k b =⎧⎨+=⎩，解得：k=1，b=4，∴y=x+4．∴点A 坐标为（-4，0），直线l 的解析式为：y=x+4．（2）在点P 、Q 运动的过程中：①当0＜t≤1时，如答图1所示：过点C 作CF ⊥x 轴于点F ，则CF=4，BF=3，由勾股定理得BC=5．过点Q 作QE ⊥x 轴于点E ，则BE=BQ•cos ∠CBF=5t•35=3t ． ∴PE=PB -BE=（14-2t ）-3t=14-5t ，S=12PM•PE=12×2t×（14-5t ）=-5t 2+14t ； ②当1＜t≤2时，如答图2所示：过点C、Q分别作x轴的垂线，垂足分别为F，E，则CQ=5t-5，PE=AF-AP-EF=11-2t-（5t-5）=16-7t，S=12PM•PE=12×2t×（16-7t）=-7t2+16t；③当点M与点Q相遇时，DM+CQ=CD=7，即（2t-4）+（5t-5）=7，解得t=167．当2＜t＜167时，如答图3所示：MQ=CD-DM-CQ=7-（2t-4）-（5t-5）=16-7t，S=12PM•MQ=12×4×（16-7t）=-14t+32．（3）①当0＜t≤1时，S=-5t2+14t=-5（t-75）2+495，∵a=-5＜0，抛物线开口向下，对称轴为直线t=75，∴当0＜t≤1时，S随t的增大而增大，∴当t=1时，S有最大值，最大值为9；②当1＜t≤2时，S=-7t2+16t=-7（t-87）2+647，∵a=-7＜0，抛物线开口向下，对称轴为直线t=87，∴当t=87时，S有最大值，最大值为647；③当2＜t＜167时，S=-14t+32∵k=-14＜0，∴S随t的增大而减小．又∵当t=2时，S=4；当t=167时，S=0，∴0＜S＜4．综上所述，当t=87时，S有最大值，最大值为647．（4）△QMN为等腰三角形，有两种情形：①如答图4所示，点M在线段CD上，MQ=CD-DM-CQ=7-（2t-4）-（5t-5）=16-7t，MN=DM=2t-4，由MN=MQ，得16-7t=2t-4，解得t=209；②如答图5所示，当点M运动到C点，同时当Q刚好运动至终点D，此时△QMN为等腰三角形，t=125．故当t=209或t=125时，△QMN为等腰三角形．对应训练5．（2013•长春）如图①，在▱ABCD中，AB=13，BC=50，BC边上的高为12．点P从点B出发，沿B-A-D-A 运动，沿B-A运动时的速度为每秒13个单位长度，沿A-D-A运动时的速度为每秒8个单位长度．点Q从点B出发沿BC方向运动，速度为每秒5个单位长度．P、Q两点同时出发，当点Q到达点C时，P、Q 两点同时停止运动．设点P的运动时间为t（秒）．连结PQ．（1）当点P沿A-D-A运动时，求AP的长（用含t的代数式表示）．（2）连结AQ，在点P沿B-A-D运动过程中，当点P与点B、点A不重合时，记△APQ的面积为S．求S与t之间的函数关系式．（3）过点Q作QR∥AB，交AD于点R，连结BR，如图②．在点P沿B-A-D运动过程中，当线段PQ 扫过的图形（阴影部分）被线段BR分成面积相等的两部分时t的值．（4）设点C、D关于直线PQ的对称点分别为C′、D′，直接写出C′D′∥BC时t的值．5．解：（1）当点P沿A-D运动时，AP=8（t-1）=8t-8．当0＜t＜1时，如图①．作过点Q作QE⊥AB于点E．S△ABQ=12AB•QE=12BQ×12，4当0＜t≤1时，如图③．∵S △BPM =S △BQM ，∴PM=QM ．∵AB ∥QR ，∴∠PBM=∠QRM ，∠BPM=∠MQR ，在△BPM 和△RQM 中PBM QRMBPM MQR PM QM∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△BPM ≌△RQM ．∴BP=RQ ，∵RQ=AB ，∴BP=AB∴13t=13，解得：t=1当1＜t≤83时，如图④．∵BR 平分阴影部分面积，∴P 与点R 重合．34∵S△ABR=S△QBR，∴S△ABR＜S四边形BQPR．∴BR不能把四边形ABQP分成面积相等的两部分．综上所述，当t=1或83时，线段PQ扫过的图形（阴影部分）被线段BR分成面积相等的两部分．（4）如图⑥，当P在A-D之间或D-A之间时，C′D′在BC上方且C′D′∥BC时，∴∠C′OQ=∠OQC．∵△C′OQ≌△COQ，∴∠C′OQ=∠COQ，∴∠CQO=∠COQ，∴QC=OC，∴50-5t=50-8（t-1）+13，或50-5t=8（t-1）-50+13，解得：t=7或t=95 13．当P在A-D之间或D-A之间，C′D′在BC下方且C′D′∥BC时，如图⑦．同理由菱形的性质可以得出：OD=PD，∴50-5t+13=8（t-1）-50，解得：t=121 13．∴当t=7，t=9513，t=12113时，点C、D关于直线PQ的对称点分别为C′、D′，且C′D′∥BC．中考真题演练一、选择题1．（2013•新疆）如图，Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，D为BC的中点，若动点E 以1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E点的运动时间为t秒（0≤t＜6），连接DE，当△BDE是直角三角形时，t的值为（）A．2B．2.5或3.5C．3.5或4.5D．2或3.5或4.51．D2．（2013•安徽）图1所示矩形ABCD中，BC=x，CD=y，y与x满足的反比例函数关系如图2所示，等腰直角三角形AEF的斜边EF过C点，M为EF的中点，则下列结论正确的是（）A．当x=3时，EC＜EMB．当y=9时，EC＞EMC．当x增大时，EC•CF的值增大D．当y增大时，BE•DF的值不变2．D3．（2013•盘锦）如图，将边长为4的正方形ABCD的一边BC与直角边分别是2和4的Rt△GEF的一边GF重合．正方形ABCD以每秒1个单位长度的速度沿GE向右匀速运动，当点A和点E重合时正方形停止运动．设正方形的运动时间为t秒，正方形ABCD与Rt△GEF重叠部分面积为s，则s关于t的函数图象为（）A．B．C．D．3．B4．（2013•龙岩）如图，在平面直角坐标系xOy中，A（0，2），B（0，6），动点C在直线y=x上．若以A、B、C三点为顶点的三角形是等腰三角形，则点C的个数是（）A．2B．3C．4D．54．B5．（2013•武汉）如图，E，F是正方形ABCD的边AD上两个动点，满足AE=DF．连接CF交BD于点G，连接BE交AG于点H．若正方形的边长为2，则线段DH长度的最小值是．516、如图，在等腰Rt△ABC中，∠C=90°，AC=8，F是AB边上的中点，点D，E分别在AC，BC边上运动，且保持AD=CE．连接DE，DF，EF．在此运动变化的过程中，下列结论：①△DFE是等腰直角三角形；②四边形CDFE不可能为正方形，③DE长度的最小值为4；④四边形CDFE的面积保持不变；⑤△CDE面积的最大值为8．其中正确的结论是（）A、①②③B、①④⑤（3）若⊙P与线段QC只有一个交点，请直接写出t的取值范围．6．解：（1）∵A（8，0），B（0，6），8．（2013•宜昌）半径为2cm的与⊙O边长为2cm的正方形ABCD在水平直线l的同侧，⊙O与l相切于点F，DC在l上．（1）过点B作的一条切线BE，E为切点．①填空：如图1，当点A在⊙O上时，∠EBA的度数是；②如图2，当E，A，D三点在同一直线上时，求线段OA的长；（2）以正方形ABCD的边AD与OF重合的位置为初始位置，向左移动正方形（图3），至边BC与OF 重合时结束移动，M，N分别是边BC，AD与⊙O的公共点，求扇形MON的面积的范围．7．解：（1）①∵半径为2cm的与⊙O边长为2cm的正方形ABCD在水平直线l的同侧，当点A在⊙O如图，过O 点作OK ⊥MN 于K ，∴∠MON=2∠NOK ，MN=2NK ，在Rt △ONK 中，sin ∠NOK=2NK NK ON =， ∴∠NOK 随NK 的增大而增大，∴∠MON 随MN 的增大而增大，∴当MN 最大时∠MON 最大，当MN 最小时∠MON 最小，①当N ，M ，A 分别与D ，B ，O 重合时，MN 最大，MN=BD ，∠MON=∠BOD=90°，S 扇形MON 最大=π（cm 2），②当MN=DC=2时，MN 最小，∴ON=MN=OM ，∴∠NOM=60°，S 扇形MON 最小=23π（cm 2）， ∴23π≤S 扇形MON ≤π．故答案为：30°．9．（2013•重庆）已知：如图①，在平行四边形ABCD 中，AB=12，BC=6，AD ⊥BD ．以AD 为斜边在平8．解：（1）∵四边形ABCD是平行四边形，∴AD=BC=6．在Rt△ADE中，AD=6，∠EAD=30°，∴AE=AD•cos30°=33，DE=AD•sin30°=3，∴△AED的周长为：6+33+3=9+33．（2）在△AED向右平移的过程中：（I）当0≤t≤1.5时，如答图1所示，此时重叠部分为△D0NK．∵DD0=2t，∴ND0=DD0•sin30°=t，NK=ND0•tan30°=3t，∴S=S△D0NK=12ND0•NK=12t•3t=32t2；（II）当1.5＜t≤4.5时，如答图2所示，此时重叠部分为四边形D0E0KN．∵AA0=2t，∴A0B=AB-AA0=12-2t，∴A0N=12A0B=6-t，NK=A0N•tan30°=33（6-t）．∴S=S四边形D0E0KN=S△ADE-S△A0NK=12×3×33-12×（6-t）×33（6-t）=-36t2+23t-332；（III）当4.5＜t≤6时，如答图3所示，此时重叠部分为五边形D0IJKN．∵AA 0=2t，∴A0B=AB-AA0=12-2t=D0C，∴A0N=12A0B=6-t，D0N=6-（6-t）=t，BN=A0B•cos30°=3（6-t）；易知CI=BJ=A0B=D0C=12-2t，∴BI=BC-CI=2t-6，S=S梯形BND0I-S△BKJ=12[t+（2t-6）]• 3（6-t）-12•（12-2t）•33（12-2t）=-1336t2+203t-423．综上所述，S与t之间的函数关系式为：S=2223(0 1.5)2333-23-(1.5 4.5)62133-203-423(4.56)6t tS t t tt t t⎧≤≤⎪⎪⎪⎪=+<≤⎨⎪⎪+<≤⎪⎪⎩．（3）存在α，使△BPQ为等腰三角形．理由如下：经探究，得△BPQ∽△B1QC，故当△BPQ为等腰三角形时，△B1QC也为等腰三角形．（I）当QB=QP时（如答图4），则QB1=QC，∴∠B1CQ=∠B1=30°，即∠BCB1=30°，∴α=30°；（II）当BQ=BP时，则B1Q=B1C，若点Q在线段B1E1的延长线上时（如答图5），∵∠B1=30°，∴∠B1CQ=∠B1QC=75°，即∠BCB1=75°，∴α=75°．10．（2013•吉林）如图，在Rt△ABC中，∠ACB=90°，AC=6cm，BC=8cm．点D、E、F分别是边AB、（2）在点P 从点F 运动到点D 的过程中，某一时刻，点P 落在MQ 上，求此时BQ 的长度；（3）当点P 在线段FD 上运动时，求y 与x 之间的函数关系式．11．解：（1）当点P 运动到点F 时，∵F 为AC 的中点，AC=6cm ，∴AF=FC=3cm ，∵P 和Q 的运动速度都是1cm/s ，∴BQ=AF=3cm ，∴CQ=8cm -3cm=5cm ，故答案为：5．（2）设在点P 从点F 运动到点D 的过程中，点P 落在MQ 上，如图1，则t+t -3=8，t=112， BQ 的长度为112×1=112（cm ）；（3）∵D 、E 、F 分别是AB 、BC 、AC 的中点，∴DE=12AC=12×6=3， DF=12BC=12×8=4， ∵MQ ⊥BC ，∴∠BQM=∠C=90°，∵∠QBM=∠CBA ，∴△MBQ ∽△ABC ，∴BQ MQ BC AC=， ∴86x MQ =，MQ=34x，分为三种情况：①当3≤x＜4时，重叠部分图形为平行四边形，如图2，y=PN•PD=34x（7-x）即y=-34x2+214x；②当4≤x＜112时，重叠部分为矩形，如图3，y=3[（8-X）-（X-3））]即y=-6x+33；③当112≤x≤7时，重叠部分图形为矩形，如图4，y=3[（x-3）-（8-x）]即y=6x-33．213．解：（1）如图，2如图2，由（1）知：抛物线的对称轴l为x=4，因为A、B两点关于l对称，连接CB交l于点P，则AP=BP，所以AP+CP=BC的值最小∵B（6，0），C（0，2）（3）如图3，连接ME ，∵CE 是⊙M 的切线∴ME ⊥CE ，∠CEM=90°由题意，得OC=ME=2，∠ODC=∠MDE ∵在△COD 与△MED 中COA DEMODC MD EOC ME∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△COD ≌△MED （AAS ），∴OD=DE ，DC=DM设OD=x 则CD=DM=OM -OD=4-x 则RT △COD 中，OD 2+OC 2=CD 2， ∴x 2+22=（4-x ）2∴x=32，∴D （32，0）设直线CE 的解析式为y=kx+b ∵直线CE 过C （0，2），D （32，0）两点，则3022k b b ⎧+=⎪⎨⎪=⎩，解得：432k b ⎧=-⎪⎨⎪=⎩。

九年级中考压轴——动点问题集锦

九年级中考压轴——动点问题集锦1、已知等边三角形ABC的边长为4厘米，长为1厘米的线段MN在△ABC的边AB上沿AB方向以1厘米/秒的速度向B点运动。

过点M、N分别作AB边的垂线，与△ABC的其它边交于P、Q两点，线段MN运动的时间为t秒。

1) 当四边形MNQP为矩形时，有MN=QP，即MN在运动t秒后，线段QP的长度为3+t。

因为三角形ABC是等边三角形，所以三角形ABC的高等于边长的一半，即2根号3.因此，四边形MNQP的面积为2根号3*t平方+2t。

2) 四边形MNQP的面积为S，运动时间为t。

因为三角形ABC是等边三角形，所以三角形ABC的高等于边长的一半，即2根号3.因此，四边形MNQP的高为2根号3.由于四边形MNQP是矩形，所以MN=QP=3+t，PQ=2根号3.因此，S=PQ*MN=2根号3*(3+t)。

函数关系式为S=2根号3*t+6根号3，t的取值范围为t≥0.2、在梯形ABCD中，AD∥BC，AD=3，DC=5，AB=42，∠B=45度。

动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动；动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动。

设运动的时间为t 秒。

1) 因为三角形ABD和三角形CBD相似，所以BD=AB-AD=39.由于三角形BCD是直角三角形，所以BC=BD/根号2=39/根号2.2) 当MN∥AB时，由于三角形BMD和三角形BAC相似，所以BD/AB=MD/MN，即39/42=2t/(3+t)，解XXX13秒。

3) 当△MNC为等腰三角形时，由于三角形MNC和三角形ABD相似，所以CN/AD=MN/BD，即CN/3=(3+t)/39，XXX13秒。

3、在平面直角坐标系中，四边形OABC是梯形，OA∥BC，点A的坐标为(6，0)，点B的坐标为(4，3)，点C在y轴的正半轴上。

动点M在OA上运动，从O点出发到A点；动点N在AB上运动，从A点出发到B点。

(中考数学)动点问题专题训练(含答案)

中考专题训练动点问题例1. 如图，在ABC ∆中，AB AC =，AD BC ⊥于点D ，10BC cm =，8AD cm =．点P 从点B 出发，在线段BC 上以每秒3cm 的速度向点C 匀速运动，与此同时，垂直于AD 的直线m 从底边BC 出发，以每秒2cm 的速度沿DA 方向匀速平移，分别交AB 、AC 、AD 于E 、F 、H ，当点P 到达点C 时，点P 与直线m 同时停止运动，设运动时间为t 秒(0)t >．（1）当2t =时，连接DE 、DF ，求证：四边形AEDF 为菱形；（2）在整个运动过程中，所形成的PEF ∆的面积存在最大值，当PEF ∆的面积最大时，求线段BP 的长；（3）是否存在某一时刻t ，使PEF ∆为直角三角形？若存在，请求出此时刻t 的值；若不存在，请说明理由．【解答】（1）证明：当2t =时，4DH AH ==，则H 为AD 的中点，如答图 1 所示．又EF AD ⊥ ，EF ∴为AD 的垂直平分线，AE DE ∴=，AF DF =．AB AC = ，AD BC ⊥于点D ，AD BC ∴⊥，B C ∠=∠．//EF BC ∴，AEF B ∴∠=∠，AFE C ∠=∠，AEF AFE ∴∠=∠，AE AF ∴=，AE AF DE DF ∴===，即四边形AEDF 为菱形．（2）解：如答图 2 所示，由（1）知//EF BC ，AEF ABC ∴∆∆∽， ∴EF AH BC AD =，即82108EF t -=，解得：5102EF t =-． 221155510(10)210(2)10(0)222223PEF S EF DH t t t t t t ∆==-=-+=--+<< ， ∴当2t =秒时，PEF S ∆存在最大值，最大值为210cm ，此时36BP t cm ==．（3）解：存在．理由如下：①若点E 为直角顶点，如答图 3①所示，此时//PE AD ，2PE DH t ==，3BP t =．//PE AD ，∴PE BP AD BD =，即2385t t =，此比例式不成立，故此种情形不存在； ②若点F 为直角顶点如答图 3②所示，此时//PF AD ，2PF DH t ==，3BP t =，103CP t =-．//PF AD ，∴PF CP AD CD =，即210385t t -=，解得4017t =；③若点P 为直角顶点，如答图③所示．过点E 作EM BC ⊥于点M ，过点F 作FN BC ⊥于点N ，则2EM FN DH t ===，////EM FN AD ．//EM AD ，∴EM BM AD BD =，即285t BM =，解得54BM t =， 57344PM BP BM t t t ∴=-=-=．在Rt EMP ∆中，由勾股定理得：2222227113(2)()416PE EM PM t t t =+=+=． //FN AD ，∴FN CN AD CD =，即285t CN =，解得54CN t =， 5171031044PN BC BP CN t t t ∴=--=--=-．在Rt FNP ∆中，由勾股定理得：22222217353(2)(10)85100416PF FN PN t t t t =+=+-=-+．在Rt PEF ∆中，由勾股定理得：222EF PE PF =+，即：2225113353(10)()(85100)21616t t t t -=+-+ 化简得：21833508t t -=，解得：280183t =或0t =（舍去） 280183t ∴=．综上所述，当4017t =秒或280183t =秒时，PEF ∆为直角三角形．例2. 如图，在同一平面上，两块斜边相等的直角三角板Rt ABC ∆和Rt ADC ∆拼在一起，使斜边AC 完全重合，且顶点B ，D 分别在AC 的两旁，90ABC ADC ∠=∠=︒，30CAD ∠=︒，4AB BC cm ==（1）填空：AD =　)cm ，DC = ()cm（2）点M ，N 分别从A 点，C 点同时以每秒1cm 的速度等速出发，且分别在AD ，CB 上沿A D →，C B →方向运动，当N 点运动到B 点时，M 、N 两点同时停止运动，连接MN ，求当M 、N 点运动了x 秒时，点N 到AD 的距离（用含x 的式子表示）（3）在（2）的条件下，取DC 中点P ，连接MP ，NP ，设PMN ∆的面积为2()y cm ，在整个运动过程中，PMN ∆的面积y 存在最大值，请求出y 的最大值．（参考数据sin 75︒=sin15︒=【解答】解：（1）90ABC ∠=︒ ，4AB BC cm ==，AC ∴===，90ADC ∠=︒ ，30CAD ∠=︒，12DC AC ∴==，AD ∴==；故答案为：，；（2）过点N 作NE AD ⊥于E ，作NF DC ⊥，交DC 的延长线于F ，如图所示：则NE DF =，90ABC ADC ∠=∠=︒ ，AB BC =，30CAD ∠=︒，45ACB ∴∠=︒，60ACD ∠=︒，180456075NCF ∴∠=︒-︒-︒=︒，15FNC ∠=︒，sinFC FNCNC ∠=，NC x=，FC x∴=，NE DF x∴==+，∴点N到ADx+；（3）sinFN NCFNC ∠=，FN x∴=，P为DC的中点，PD CP∴==PF x∴=PMN∴∆的面积y=梯形MDFN的面积PMD-∆的面积PNF-∆的面积111)) 222x x x x=+-+--+2x x=+，即y是x的二次函数，0<，y∴有最大值，当x==时，y=．例3. 如图，BD 是正方形ABCD 的对角线，2BC =，边BC 在其所在的直线上平移，将通过平移得到的线段记为PQ ，连接PA 、QD ，并过点Q 作QO BD ⊥，垂足为O ，连接OA 、OP ．（1）请直接写出线段BC 在平移过程中，四边形APQD 是什么四边形？（2）请判断OA 、OP 之间的数量关系和位置关系，并加以证明；（3）在平移变换过程中，设OPB y S ∆=，(02)BP x x =……，求y 与x 之间的函数关系式，并求出y 的最大值．【解答】（1）四边形APQD 为平行四边形；（2）OA OP =，OA OP ⊥，理由如下：四边形ABCD 是正方形，AB BC PQ ∴==，45ABO OBQ ∠=∠=︒，OQ BD ⊥ ，45PQO ∴∠=︒，45ABO OBQ PQO ∴∠=∠=∠=︒，OB OQ ∴=，在AOB ∆和OPQ ∆中，AB PQABO PQO BO QO=⎧⎪∠=∠⎨⎪=⎩()AOB POQ SAS ∴∆≅∆，OA OP ∴=，AOB POQ ∠=∠，90AOP BOQ ∴∠=∠=︒，OA OP ∴⊥；（3）如图，过O 作OE BC ⊥于E ．①如图 1 ，当P 点在B 点右侧时，则2BQ x =+，22x OE +=， 1222x y x +∴=⨯，即211(1)44y x =+-，又02x ……，∴当2x =时，y 有最大值为 2 ；②如图 2 ，当P 点在B 点左侧时，则2BQ x =-，22x OE -=， 1222x y x -∴=⨯ ，即211(1)44y x =--+，又02x ……，∴当1x =时，y 有最大值为14；综上所述，∴当2x =时，y 有最大值为 2 ．例4. 如图，在平面直角坐标系中，O 为原点，四边形ABCO 是矩形，点A ，C 的坐标分别是(0,2)A 和C ，0)，点D 是对角线AC 上一动点（不与A ，C 重合），连结BD ，作DE DB ⊥，交x 轴于点E ，以线段DE ，DB 为邻边作矩形BDEF ．（1）填空：点B 的坐标为；（2）是否存在这样的点D ，使得DEC ∆是等腰三角形？若存在，请求出AD 的长度；若不存在，请说明理由；（3）①求证：DE DB =； ②设AD x =，矩形BDEF 的面积为y ，求y 关于x 的函数关系式（可利用①的结论），并求出y 的最小值．【解答】解：（1）四边形AOCB 是矩形，2BC OA ∴==，OC AB ==90BCO BAO ∠=∠=︒，B ∴2)．故答案为2)．（2）存在．理由如下：2OA = ，OC =，tan AO ACO OC ∠== ， 30ACO ∴∠=︒，60ACB ∠=︒①如图 1 中，当E 在线段CO 上时，DEC ∆是等腰三角形，观察图象可知，只有ED EC =，30DCE EDC ∴∠=∠=︒，60DBC BCD ∴∠=∠=︒，DBC ∴∆是等边三角形，2DC BC ∴==，在Rt AOC ∆中，30ACO ∠=︒ ，2OA =，24AC AO ∴==，422AD AC CD ∴=-=-=．∴当2AD =时，DEC ∆是等腰三角形．②如图 2 中，当E 在OC 的延长线上时，DCE ∆是等腰三角形，只有CD CE =，15DBC DEC CDE ∠=∠=∠=︒，75ABD ADB ∴∠=∠=︒，AB AD ∴==，综上所述，满足条件的AD 的值为 2 或（3）①如图 1 ，过点D 作MN AB ⊥交AB 于M ，交OC 于N ，(0,2)A 和C ，0)，∴直线AC 的解析式为2y x =+，设(,2)D a +，2DN ∴=+，BM a =90BDE ∠=︒ ，90BDM NDE ∴∠+∠=︒，90BDM DBM ∠+∠=︒，DBM EDN ∴∠=∠，90BMD DNE ∠=∠=︒ ，BMD DNE ∴∆∆∽，∴DE DN BD BM ===②如图 2 中，作DH AB ⊥于H ．在Rt ADH ∆中，AD x = ，30DAH ACO ∠=∠=︒，1122DH AD x ∴==，AH x ==，BH x ∴=，在Rt BDH ∆中，BD ==，DE ∴==， ∴矩形BDEF的面积为22612)y x x ==-+，即2y x =-+，23)y x ∴=-+，0>，3x ∴=时，y ．例5. 已知Rt OAB ∆，90OAB ∠=︒，30ABO ∠=︒，斜边4OB =，将Rt OAB ∆绕点O 顺时针旋转60︒，如图 1 ，连接BC ．（1）填空：OBC ∠= 60 ︒；（2）如图 1 ，连接AC ，作OP AC ⊥，垂足为P ，求OP 的长度；（3）如图 2 ，点M ，N 同时从点O 出发，在OCB ∆边上运动，M 沿O C B →→路径匀速运动，N 沿O B C →→路径匀速运动，当两点相遇时运动停止，已知点M 的运动速度为 1.5 单位/秒，点N 的运动速度为 1 单位/秒，设运动时间为x 秒，OMN ∆的面积为y ，求当x 为何值时y 取得最大值？最大值为多少？【解答】解：（1）由旋转性质可知：OB OC =，60BOC ∠=︒，OBC ∴∆是等边三角形，60OBC ∴∠=︒．故答案为 60 ．（2）如图 1 中，4OB = ，30ABO ∠=︒，122OA OB ∴==，AB ==11222AOC S OA AB ∆∴==⨯⨯=BOC ∆ 是等边三角形，60OBC ∴∠=︒，90ABC ABO OBC ∠=∠+∠=︒，AC ∴==2AOC S OP AC ∆∴===．（3）①当803x <…时，M 在OC 上运动，N 在OB 上运动，此时过点N 作NE OC ⊥且交OC 于点E ．则sin 60NE ON x =︒= ，11 1.522OMN S OM NE x x ∆∴==⨯ ，2y x ∴=．83x ∴=时，y 有最大值，最大值=． ②当843x <…时，M 在BC 上运动，N 在OB 上运动．作MH OB ⊥于H ．则8 1.5BM x =-，sin 60 1.5)MH BM x =︒=- ，212y ON MH x ∴=⨯⨯=+．当83x =时，y 取最大值，y < ③当4 4.8x <…时，M 、N 都在BC 上运动，作OG BC ⊥于G ．12 2.5MN x =-，OG AB ==，12y MN OG ∴== ，当4x =时，y 有最大值，最大值=，综上所述，y 有最大值，．。

初中动点题经典例题

动点问题
初中数学中，动点问题是一个经常出现的重要考点。

以下是一些经典的例题：
1. 例题一：
A、B两车相向而行，A车的速度是60 km/h，B车的速度是40 km/h，他们相距300 km，请问他们多长时间能相遇？
2. 例题二：
甲、乙两人同时从相距120 km的两地相向而行，甲每小时行50 km，乙每小时行60 km。

请问几小时后他们相遇？
3. 例题三：
甲、乙两辆汽车同时从同地出发，相向行驶。

已知甲汽车的速度是50 km/h，乙汽车比甲车晚出发30分钟，乙车的速度是60 km/h。

请问几小时后他们相遇？
4. 例题四：
小明从家出发，向东骑自行车匀速行驶20 km/h，行驶2小时后，他改为向南行驶，以同样的速度继续行驶。

请问他最终离家有多远？
这些例题涉及到动点问题中的相遇、相交等概念，考察学生对速度、时间、距离之间关系的理解和运用能力。

解答这些问题需要学生能够根据题目提供的信息确定各个点的位置和变化趋势，并建立方程或方程组解决问题。

练习这些例题可以帮助学生熟悉动点问题的解题思路和方法，提高数学问题应用能力和逻辑思维能力。

九年级中考数学动点问题精选汇编(含答案)

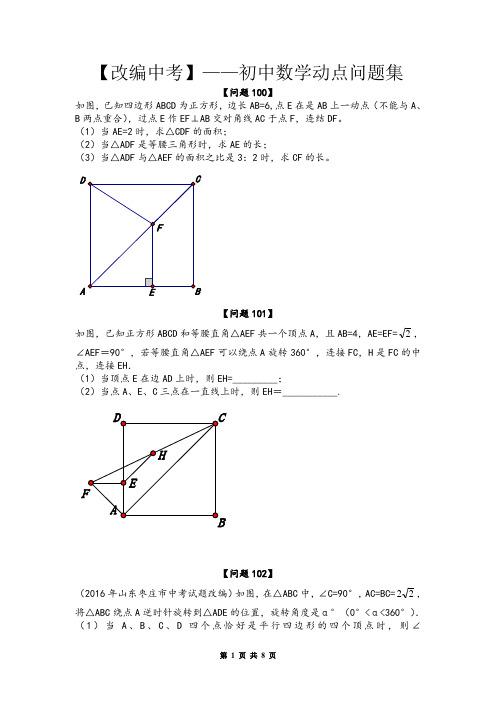
【改编中考】——初中数学动点问题集【问题100】如图，已知四边形ABCD 为正方形，边长AB=6,点E 在是AB 上一动点（不能与A 、B 两点重合），过点E 作EF ⊥AB 交对角线AC 于点F ，连结DF 。

（1）当AE=2时，求△CDF 的面积；（2）当△ADF 是等腰三角形时，求AE 的长；（3）当△ADF 与△AEF 的面积之比是3：2时，求CF 的长。

D A【问题101】如图，已知正方形ABCD 和等腰直角△AEF 共一个顶点A ，且AB=4，AE=EF=2，∠AEF ＝90°，若等腰直角△AEF 可以绕点A 旋转360°，连接FC ，H 是FC 的中点，连接EH ．（1）当顶点E 在边AD 上时，则EH=_________；（2）当点A 、E 、C 三点在一直线上时，则EH ＝___________.【问题102】（2016年山东枣庄市中考试题改编）如图，在△ABC 中，∠C=90°，AC=BC=22，将△ABC 绕点A 逆时针旋转到△ADE 的位置，旋转角度是α°（0°<α<360°）．（1）当A 、B 、C 、D 四个点恰好是平行四边形的四个顶点时，则∠BAD=____________°（2）当△ABE是等边三角形时，则BD＝________;E【问题103】在矩形ABCD中，AB=4 , BC=34，点P是直线BC一动点，若将△ABP沿AP折叠，使点B落在平面上的点E处，连结AE、PE。

（1）当A、E、C三点在一直线上时，则BP＝__________;（2）当P、E、D三点在一直线上时，则BP＝__________.【问题104】如图，四边形ABCD为菱形，且BD=AB=4,点P为对角线BD上的一个动点，作∠PAQ＝60°交CB的延长线于Q点，连结PQ．（1）求证△APQ是等边三角形；（2）求四边形AQBP面积；（3）且△APQ的面积是33，则BP=__________.Q【问题105】如图，在正方形ABCD中，AB=22，E、F是射线AC上两点，且∠EDF=45°，将△ADE绕点D逆时针旋转90°后，得到△DCP，连接FP.（1）求证：△DEF≅△DPF；（2）若CF=1，求AE的长.A【问题106】如图，两个等腰直角△ABC和△CDE，AC=BC=22，CD=CE＝2，∠ACB=∠DCE=90°,现把等腰直角△CDE绕直角顶点C旋转一周，连结AE和BD相交于点O.（1）求证：AE=BD，AE⊥BD（2）当B、D、E三点在一直线上时，则AE＝___________.A【问题107】如图，在菱形ABCD 中，对角线AC 与BD 相交于点O ，AB=34，∠BAD=60°.点E是边AB 上的一动点（不能与A 、B 两点重合），过点E 作EF ⊥AD 于点F ，作EG ∥AD 交AC 于点G ，过点G 作GH ⊥ AD 交AD （或AD 的延长线）于点H ，得到矩形EFHG.（1）求EG EF=______;（2）当DH=3时，则矩形EFHG 的面积是________.A【问题108】如图，在△ABC 中，AB=AC=32，D 是直线BC 边上一动点，以AD 为边作等腰△ADE ，使AE=AD ，若∠BAC+∠DAE ＝180°，设∠BAC=m °（1）∠ABC+∠ADE=______°；（2）当m=90°时，求证：BD=CE ；（3）当m=120°时，若A 、C 、D 、E 四个点构成平行四边形时，求它的面积。

中考数学压轴题专题-动点综合问题

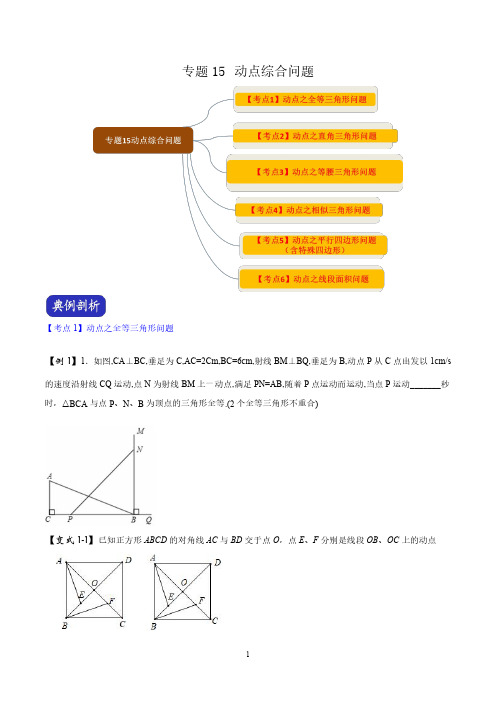
专题15动点综合问题【考点1】动点之全等三角形问题【例1】1．如图,CA⊥BC,垂足为C,AC=2Cm,BC=6cm,射线BM⊥BQ,垂足为B,动点P从C点出发以1cm/s 的速度沿射线CQ运动,点N为射线BM上一动点,满足PN=AB,随着P点运动而运动,当点P运动_______秒时，△BCA与点P、N、B为顶点的三角形全等.(2个全等三角形不重合)【变式1-1】已知正方形ABCD的对角线AC与BD交于点O，点E、F分别是线段OB、OC上的动点（1）如果动点E 、F 满足BE ＝OF （如图），且AE ⊥BF 时，问点E 在什么位置？并证明你的结论；（2）如果动点E 、F 满足BE ＝CF （如图），写出所有以点E 或F 为顶点的全等三角形（不得添加辅助线）．【变式1-2】如图①，将长方形纸片沿对角线剪成两个全等的直角三角形ABC 、EDF ，其中AB ＝8cm ，BC ＝6cm ，AC ＝10cm ．现将△ABC 和△EDF 按如图②的方式摆放（点A 与点D 、点B 与点E 分别重合）．动点P 从点A 出发，沿AC 以2cm /s 的速度向点C 匀速移动；同时，动点Q 从点E 出发，沿射线ED 以acm /s （0＜a ＜3）的速度匀速移动，连接PQ 、CQ 、FQ ，设移动时间为ts （0≤t ≤5）．（1）当t ＝2时，S △AQF ＝3S △BQC ，则a ＝；（2）当以P 、C 、Q 为顶点的三角形与△BQC 全等时，求a 的值；（3）如图③，在动点P 、Q 出发的同时，△ABC 也以3cm /s 的速度沿射线ED 匀速移动，当以A 、P 、Q 为顶点的三角形与△EFQ 全等时，求a 与t 的值．【考点2】动点之直角三角形问题【例2】如图，在四边形纸片ABCD 中，//AB CD ，60A ∠=︒，30B ∠=︒，2CD =，4BC =，点E 是AB 边上的动点，点F 是折线A D C --上的动点，将纸片ABCD 沿直线EF 折叠，使点A 的对应点A '落在AB 边上，连接A C '，若A BC ' 是直角三角形，则AE 的长为________．【变式2-1】（2019·辽宁中考模拟）如图，已知二次函数y ＝ax 2+bx+4的图象与x 轴交于点A(4，0)和点D(﹣1，0)，与y 轴交于点C ，过点C 作BC 平行于x 轴交抛物线于点B ，连接AC(1)求这个二次函数的表达式；(2)点M 从点O 出发以每秒2个单位长度的速度向点A 运动；点N 从点B 同时出发，以每秒1个单位长度的速度向点C 运动，其中一个动点到达终点时，另一个动点也随之停动，过点N 作NQ 垂直于BC 交AC 于点Q ，连结MQ.①求△AQM 的面积S 与运动时间t 之间的函数关系式，写出自变量的取值范围；当t 为何值时，S 有最大值，并求出S 的最大值；②是否存在点M ，使得△AQM 为直角三角形？若存在，求出点M 的坐标；若不存在，说明理由．【变式2-2】如图，在矩形OAHC 中，8,12OC OA ==，B 为CH 中点，连接AB .动点M 从点O 出发沿OA 边向点A 运动，动点N 从点A 出发沿AB 边向点B 运动，两个动点同时出发，速度都是每秒1个单位长度，连接,,CM CN MN ，设运动时间为t （秒）(010)t <<.则t =_____时，CMN ∆为直角三角形【考点3】动点之等腰三角形问题【例3】如图，AB 是⊙O 的直径，BC 是弦，10cm AB =，6cm BC =．若点P 是直径AB 上一动点，当PBC 是等腰三角形时，AP =__________cm ．【变式3-1】如图①，已知正方形ABCD 边长为2，点P 是AD 边上的一个动点，点A 关于直线BP 的对称点是点Q ，连结PQ 、DQ 、CQ 、BQ .设AP=x.（1）当1x =时，求BP 长；（2）如图②，若PQ 的延长线交CD 边于E ，并且90CQD ∠=o ，求证：CEQ ∆为等腰三角形；（3）若点P 是射线AD 上的一个动点，则当CDQ ∆为等腰三角形时，求x 的值.【变式3-2】（2019·河南中考模拟）如图，抛物线y=ax 2+bx+3交y 轴于点A ，交x 轴于点B （-3，0）和点C （1，0），顶点为点M ．（1）求抛物线的解析式；（2）如图，点E 为x 轴上一动点，若△AME 的周长最小，请求出点E 的坐标；（3）点F 为直线AB 上一个动点，点P 为抛物线上一个动点，若△BFP 为等腰直角三角形，请直接写出点P 的坐标．【变式3-3】（2019·广西中考真题）已知抛物线2y mx =和直线y x b =-+都经过点()2,4M -，点O 为坐标原点，点P 为抛物线上的动点，直线y x b =-+与x 轴、y 轴分别交于A B 、两点．（1）求m b 、的值；（2）当PAM ∆是以AM 为底边的等腰三角形时，求点P 的坐标；（3）满足（2）的条件时，求sin BOP ∠的值．【考点4】动点之相似三角形问题【例4】如图，AD∥BC，∠ABC=90°，AB=8，AD=3，BC=4，点P为AB边上一动点，若△PAD与△PBC 是相似三角形，求AP的长．【变式4-1】已知：如图，在平面直角坐标系中，△ABC是直角三角形，∠ACB＝90°，点A，C的坐标分别为A（﹣3，0），C（1，0），BC＝3 4AC（1）求过点A，B的直线的函数表达式；（2）在x轴上找一点D，连接DB，使得△ADB与△ABC相似（不包括全等），并求点D的坐标；（3）在（2）的条件下，如P，Q分别是AB和AD上的动点，连接PQ，设AP＝DQ＝m，问是否存在这样的m，使得△APQ与△ADB相似？如存在，请求出m的值；如不存在，请说明理由．【变式4-2】如图，正方形ABCD，点P为射线DC上的一个动点，点Q为AB的中点，连接PQ，DQ，过点P作PE⊥DQ于点E．（1）请找出图中一对相似三角形，并证明；（2）若AB＝4，以点P，E，Q为顶点的三角形与△ADQ相似，试求出DP的长．【考点5】动点之平行四边形问题（含特殊四边形）【例5】如图，抛物线23y ax bx =++与x 轴交于(3,0),(1,0)A B -两点，与y 轴交于点C ．（1）求抛物线的解析式；（2）点P 是抛物线上的动点，且满足2PAO PCO S S ∆∆=，求出P 点的坐标；（3）连接BC ，点E 是x 轴一动点，点F 是抛物线上一动点，若以B 、C 、E 、F 为顶点的四边形是平行四边形时，请直接写出点F 的坐标．备用图【变式5-1】（2019·江西中考真题）在图1，2，3中，已知，，点为线段上的动点，连接，以为边向上作菱形，且．（1）如图1，当点与点重合时，________°；（2）如图2，连接．①填空：_________（填“>”，“<”，“=”）；②求证：点在的平分线上；（3）如图3，连接，，并延长交的延长线于点，当四边形是平行四边形时，求的值．【变式5-2】（2019·湖南中考真题）如图，二次函数213y x bx c =-++的图象过原点，与x 轴的另一个交点为()8,0（1）求该二次函数的解析式；（2）在x轴上方作x轴的平行线1y m=，交二次函数图象于A、B两点，过A、B两点分别作x轴的垂线，垂足分别为点D、点C．当矩形ABCD为正方形时，求m的值；（3）在（2）的条件下，动点P从点A出发沿射线AB以每秒1个单位长度匀速运动，同时动点Q以相同的速度从点A出发沿线段AD匀速运动，到达点D时立即原速返回，当动点Q返回到点A时，P、Q两点同时停止运动，设运动时间为t秒（0t>）．过点P向x轴作垂线，交抛物线于点E，交直线AC于点F，问：以A、E、F、Q四点为顶点构成的四边形能否是平行四边形．若能，请求出t的值；若不能，请说明理由．【变式5-3】．如图，在平面直角坐标系中，AOB∆的顶点O是坐标原点，点A坐标为()1,3，A、B两点关于直线y x=对称，反比例函数()0ky xx=>图象经过点A，点P是直线y x=上一动点.（1）B点的坐标为______；（2）若点C是反比例函数图象上一点，是否存在这样的点C，使得以A、B、C、P四点为顶点的四边形是平行四边形？若存在，求出点C坐标；若不存在，请说明理由；（3）若点Q 是线段OP 上一点（O 不与O 、P 重合），当四边形AOBP 为菱形时，过点Q 分别作直线OA 和直线AP 的垂线，垂足分别为E 、F ，当QE QF QB ++的值最小时，求出Q 点坐标.【考点6】动点之线段面积问题【例6】如图，在平面直角坐标系中，平行四边形如图放置，将此平行四边形绕点O 顺时针旋转90°得到平行四边形．抛物线经过点A 、C 、A′三点．（1）求A 、A′、C 三点的坐标；（2）求平行四边形和平行四边形重叠部分的面积；（3）点M 是第一象限内抛物线上的一动点，问点M 在何处时，的面积最大？最大面积是多少？并写出此时M 的坐标．【变式6-1】（1）发现：如图1，点A 为线段BC 外一动点，且BC =α，AB b =(0)a b >>，当点A 位于时，线段AC 的长取得最大值，最大值为（用含,a b 的式子表示）；（2）应用：如图2，点A 为线段BC 外一动点，4BC =，2AC =，以AB 为边作等边ABD ∆，连接CD ，求线段CD 的最大值；（3）拓展：如图3，线段3AB =，点P 为线段AB 外一动点，且2AP =，PM PB =，90BPM ∠=︒，求线段AM 长的最大值及此时PBM ∆的面积．【变式6-2】如图，矩形ABCD 中，3,4AD AB ==，点P 是对角线AC 上一动点（不与A C 、重合），连接PB ，过点P 作PE PB ⊥，交射线DC 于点E ，以线段,PE PB 为邻边作矩形BPEF ，过点P 作GH CD ⊥。

中考数学复习专题动点综合问题含中考真题解析

中考数学复习专题动点综合问题含中考真题解析 The document was prepared on January 2, 2021专题36 动点综合问题解读考点知识点名师点晴动点问题中的特殊图形等腰三角形与直角三角形利用等腰三角形或直角三角形的特殊性质求解动点问题相似问题利用相似三角形的对应边成比例、对应角相等求解动点问题动点问题中的计算问题动点问题的最值与定值问题理解最值或定值问题的求法动点问题的面积问题结合面积的计算方法来解决动点问题动点问题的函一次函数或二次函数的图象结合函数的图象解决动点问题数图象问题2年中考【2015年题组】1．（2015牡丹江）在平面直角坐标系中，点P（x，0）是x轴上一动点，它与坐标原点O的距离为y，则y关于x的函数图象大致是（）A．B．C．D．【答案】A．考点：动点问题的函数图象．2．（2015盐城）如图，在边长为2的正方形ABCD中剪去一个边长为1的小正方形CEFG，动点P从点A出发，沿A→D→E→F→G→B的路线绕多边形的边匀速运动到点B时停止（不含点A和点B），则△ABP的面积S 随着时间t变化的函数图象大致是（）A． B． C．D．【答案】B．【解析】试题分析：当点P在AD上时，△ABP的底AB不变，高增大，所以△ABP 的面积S随着时间t的增大而增大；当点P在DE上时，△ABP的底AB不变，高不变，所以△ABP的面积S不变；当点P在EF上时，△ABP的底AB不变，高减小，所以△ABP的面积S随着时间t的减小；当点P在FG上时，△ABP的底AB不变，高不变，所以△ABP的面积S不变；当点P在GB上时，△ABP的底AB不变，高减小，所以△ABP的面积S随着时间t的减小；故选B．考点：1．动点问题的函数图象；2．分段函数；3．分类讨论；4．压轴题．3．（2015资阳）如图，AD、BC是⊙O的两条互相垂直的直径，点P从点O出发，沿O→C→D→O的路线匀速运动．设∠APB=y（单位：度），那么y与点P运动的时间x（单位：秒）的关系图是（）A． B．C． D．【答案】B．考点：1．动点问题的函数图象；2．分段函数．4．（2015广元）如图，矩形ABCD中，AB=3，BC=4，点P从A点出发．按A→B→C的方向在AB和BC上移动．记PA=x，点D到直线PA的距离为y，则y关于x的函数大致图象是（）A． B． C． D．【答案】D．【解析】考点：1．动点问题的函数图象；2．压轴题；3．动点型；4．分段函数．5．（2015荆州）如图，正方形ABCD的边长为3cm，动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动，到达A点停止运动；另一动点Q同时从B点出发，以1cm/s的速度沿着边BA向A点运动，到达A点停止运动．设P点运动时间为x（s），△BPQ的面积为y（cm2），则y关于x的函数图象是（）A． B． C．D．【答案】C．【解析】试题分析：由题意可得BQ=x．①0≤x≤1时，P点在BC边上，BP=3x，则△BPQ的面积=12BPBQ，解y=123xx=232x；故A选项错误；②1＜x≤2时，P点在CD边上，则△BPQ的面积=12BQBC，解y=12x3=32x；故B选项错误；③2＜x≤3时，P点在AD边上，AP=9﹣3x，则△BPQ的面积=12APBQ，解y=12（9﹣3x）x=29322x x；故D选项错误．故选C．考点：1．动点问题的函数图象；2．分段函数．6．（2015邵阳）如图，在等腰△ABC中，直线l垂直底边BC，现将直线l沿线段BC从B点匀速平移至C点，直线l与△ABC的边相交于E、F两点．设线段EF的长度为y，平移时间为t，则下图中能较好反映y与t 的函数关系的图象是（）A． B． C．D．【答案】B．考点：1．动点问题的函数图象；2．数形结合．7．（2015河池）我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”．如图，直线l ：43y kx =+与x 轴、y 轴分别交于A 、B ，∠OAB=30°，点P 在x 轴上，⊙P 与l 相切，当P 在线段OA 上运动时，使得⊙P 成为整圆的点P 个数是（）A ．6B ．8C ．10D ．12【答案】A ．考点：1．切线的性质；2．一次函数图象上点的坐标特征；3．新定义；4．动点型；5．综合题．8．（2015乐山）如图，已知直线334y x =-与x 轴、y 轴分别交于A 、B 两点，P 是以C （0，1）为圆心，1为半径的圆上一动点，连结PA 、PB ．则△PAB 面积的最大值是（）A ．8B ．12C ．212D ．172【答案】C ．【解析】试题分析：∵直线334y x =-与x 轴、y 轴分别交于A 、B 两点，∴A 点的坐标为（4，0），B 点的坐标为（0，﹣3），34120x y --=，即OA=4，OB=3，由勾股定理得：AB=5，∴点C （0，1）到直线34120x y --=的距离是223041234⨯-⨯-+=165，∴圆C 上点到直线334y x =-的最大距离是1615+=215，∴△PAB 面积的最大值是121525⨯⨯=212，故选C ．考点：1．圆的综合题；2．最值问题；3．动点型．9．（2015庆阳）如图，定点A （﹣2，0），动点B 在直线y x =上运动，当线段AB 最短时，点B 的坐标为．【答案】（﹣1，﹣1）．考点：1．一次函数图象上点的坐标特征；2．垂线段最短；3．动点型；4．最值问题；5．综合题．10．（2015三明）如图，在△ABC中，∠ACB=90°，AB=5，BC=3，P是AB边上的动点（不与点B重合），将△BCP沿CP所在的直线翻折，得到△B′CP，连接B′A，则B′A长度的最小值是______ ．【答案】1．考点：1．翻折变换（折叠问题）；2．动点型；3．最值问题；4．综合题．．11．（2015凉山州）菱形ABCD在平面直角坐标系中的位置如图所示，顶点B（2，0），∠DOB=60°，点P是对角线OC上一个动点，E（0，﹣1），当EP+BP最短时，点P的坐标为．【答案】（233-，23-）．【解析】试题分析：连接ED ，如图，∵点B 的对称点是点D ，∴DP=BP，∴ED 即为EP+BP 最短，∵四边形ABCD 是菱形，顶点B （2，0），∠DOB=60°，∴点D 的坐标为（13点C 的坐标为（33OC 的解析式为：3y x =，∵点E 的坐标为（﹣1，0），∴可得直线ED 的解析式为：(13)1y x =+-，∵点P 是直线OC 和直线ED 的交点，∴点P 的坐标为方程组33(13)1y x y x ⎧=⎪⎨⎪=-⎩的解，解方程组得：23323x y ⎧=⎪⎨=-⎪⎩，所以点P 的坐标为（233，23-故答案为：（33，23-）．考点：1．菱形的性质；2．坐标与图形性质；3．轴对称-最短路线问题；4．动点型；5．压轴题；6．综合题．12．（2015咸宁）如图，已知正方形ABCD 的边长为2，E 是边BC 上的动点，BF⊥AE 交CD 于点F ，垂足为G ，连结CG ．下列说法：①AG＞GE ；②AE=BF；③点G 运动的路径长为π；④CG 的最小值为51-．其中正确的说法是．（把你认为正确的说法的序号都填上）【答案】②④．由于OC 和OG 的长度是一定的，因此当O 、G 、C 在同一条直线上时，CG 取最小值，22OB BC +14+5CG 的最小值为OC ﹣51，故④正确；综上所述，正确的结论有②④．故答案为：②④．考点：1．四边形综合题；2．综合题；3．动点型；4．压轴题．13．（2015江西省）如图，在△ABC中，AB=BC=4，AO=BO，P是射线CO 上的一个动点，∠AOC=60°，则当△PAB为直角三角形时，AP的长为．【答案】23或27或2．图（3）中，∠APB=90°，∵AO=BO，∠APB=90°，∴PO=AO=BO=2，又∠AOC=60°，∴△APO是等边三角形，∴AP=2；故答案为：23或27或2．考点：1．勾股定理；2．含30度角的直角三角形；3．直角三角形斜边上的中线；4．分类讨论；5．动点型；6．综合题；7．压轴题。

中考数学高频考点《动点综合问题》专项测试卷-带答案

中考数学高频考点《动点综合问题》专项测试卷-带答案（16道）一、单选题1．（2023·辽宁盘锦·统考中考真题）如图，在平面直角坐标系中菱形ABCD 的顶点A 在y 轴的正半轴上顶点B C 在x 轴的正半轴上 (3D ()1,1P --．点M 在菱形的边AD 和DC 上运动（不与点A C 重合）过点M 作MN y ∥轴与菱形的另一边交于点N 连接PM PN 设点M 的横坐标为x PMN 的面积为y ，则下列图象能正确反映y 与x 之间函数关系的是（）A ．B ．C ．D ．2．（2023·江苏·统考中考真题）折返跑是一种跑步的形式．如图，在一定距离的两个标志物① ①之间从①开始沿直线跑至①处用手碰到①后立即转身沿直线跑至①处用手碰到①后继续转身跑至①处循环进行全程无需绕过标志物．小华练习了一次250m ⨯的折返跑用时18s 在整个过程中他的速度大小v （m/s ）随时间t （s ）变化的图像可能是（）A ．B ．C ．D ．3．（2023·江苏南通·统考中考真题）如图，ABC 中 90C ∠=︒ 15AC = 20BC =．点D 从点A 出发沿折线A C B --运动到点B 停止过点D 作DE AB ⊥ 垂足为E ．设点D 运动的路径长为x BDE △的面积为y 若y 与x 的对应关系如图所示，则a b -的值为（）A ．54B ．52C ．50D ．484．（2023·辽宁鞍山·统考中考真题）如图，在矩形ABCD 中对角线,AC BD 交于点O 4AB = 43BC = 垂直于BC 的直线MN 从AB 出发沿BC 3 当直线MN 与CD 重合时停止运动运动过程中MN 分别交矩形的对角线,AC BD 于点E F 以EF 为边在MN 左侧作正方形EFGH 设正方形EFGH 与AOB 重叠部分的面积为S 直线MN 的运动时间为t s ，则下列图象能大致反映S 与t 之间函数关系的是（）A ．B ．C ．D ．5．（2023·辽宁锦州·统考中考真题）如图，在Rt ABC △中 90ACB ∠=︒ 3AC = 4BC = 在DEF 中 5DE DF == 8EF = BC 与EF 在同一条直线上点C 与点E 重合．ABC 以每秒1个单位长度的速度沿线段EF 所在直线向右匀速运动当点B 运动到点F 时 ABC 停止运动．设运动时间为t 秒 ABC 与DEF 重叠部分的面积为S ，则下列图象能大致反映S 与t 之间函数关系的是（）A ．B ．C ．D ．6．（2023·辽宁·统考中考真题）如图，60MAN ∠=︒ 在射线AM AN 上分别截取6AC AB == 连接BC MAN ∠的平分线交BC 于点D 点E 为线段AB 上的动点作EF AM ⊥交AM 于点F 作EG AM ∥交射线AD 于点G 过点G 作GH AM ⊥于点H 点E 沿AB 方向运动当点E 与点B 重合时停止运动．设点E 运动的路程为x 四边形EFHG 与ABC 重叠部分的面积为S ，则能大致反映S 与x 之间函数关系的图象是（）A ．B ．C ．D ．7．（2023·黑龙江大庆·统考中考真题）如图1 在平行四边形ABCD 中 120ABC ∠=︒ 已知点P 在边AB 上以1m/s 的速度从点A 向点B 运动点Q 在边BC 上 3m /s 的速度从点B 向点C 运动．若点P Q 同时出发当点P 到达点B 时点Q 恰好到达点C 处此时两点都停止运动．图2是BPQ 的面积()2m y 与点P的运动时间()s t 之间的函数关系图象（点M 为图象的最高点），则平行四边形ABCD 的面积为（）A ．212mB ．23mC ．224mD ．2243m8．（2023·辽宁·统考中考真题）如图，在Rt ABC △中 90ACB ∠=︒ 30A ∠=︒ 3cm AB =．动点P 从点A 出发以1cm/s 的速度沿射线AB 匀速运动到点B 停止运动同时动点Q 从点A 出发 3cm/s 的速度沿射线AC 匀速运动．当点P 停止运动时点Q 也随之停止运动．在PQ 的右侧以PQ 为边作菱形PQMN 点N 在射线AB ．设点P 的运动时间为()s x 菱形PQMN 与ABC 的重叠部分的面积为()2cm y ，则能大致反映y 与x 之间函数关系的图象是（）A ．B ．C．D．9．（2023·湖北鄂州·统考中考真题）如图，在平面直角坐标系中O为原点35OA OB==点C为平面内一动点32BC=连接AC点M是线段AC上的一点且满足:1:2CM MA=．当线段OM取最大值时点M的坐标是（）A．36,55⎛⎫⎪⎝⎭B．365,555C．612,55⎛⎫⎪⎝⎭D．6125,55510．（2023·广东深圳·统考中考真题）如图1 在Rt ABC△中动点P从A点运动到B点再到C点后停止速度为2单位/s 其中BP长与运动时间t（单位：s）的关系如图2，则AC的长为（）A155B427C．17D．5311．（2023·黑龙江绥化·统考中考真题）如图，在菱形ABCD中60A∠=︒4AB=动点M N同时从A 点出发点M以每秒2个单位长度沿折线A B C--向终点C运动点N以每秒1个单位长度沿线段AD向终点D运动当其中一点运动至终点时另一点随之停止运动．设运动时间为x秒AMN的面积为y个平方单位，则下列正确表示y与x函数关系的图象是（）A ．B ．C ．D ．12．（2023·黑龙江齐齐哈尔·统考中考真题）如图，在正方形ABCD 中 4AB = 动点M N 分别从点A B 同时出发沿射线AB 射线BC 的方向匀速运动且速度的大小相等连接DM MN ND ．设点M 运动的路程为()04x x ≤≤ DMN 的面积为S 下列图像中能反映S 与x 之间函数关系的是（）A ．B ．C．D．13．（2023·河南·统考中考真题）如图1 点P从等边三角形ABC的顶点A出发沿直线运动到三角形内部一点再从该点沿直线运动到顶点B．设点P运动的路程为x PByPC图2是点P运动时y随x变化的关系图象，则等边三角形ABC的边长为（）A．6B．3C．43D．23二解答题14．（2023·四川绵阳·统考中考真题）如图，已知①ABC中①C=90° 点M从点C出发沿CB方向以1cm/s 的速度匀速运动到达点B停止运动在点M的运动过程中过点M作直线MN交AC于点N且保持①NMC=45° 再过点N作AC的垂线交AB于点F连接MF将①MNF关于直线NF对称后得到①ENF已知AC=8cm BC=4cm设点M运动时间为t（s）①ENF与①ANF重叠部分的面积为y（cm2）．（1）在点M的运动过程中能否使得四边形MNEF为正方形？如果能求出相应的t值如果不能说明理由（2）求y关于t的函数解析式及相应t的取值范围（3）当y取最大值时求sin①NEF的值．AB=点O是对角线AC的中点动点P 15．（2023·吉林·统考中考真题）如图，在正方形ABCD中4cmQ分别从点A B同时出发点P以1cm/s的速度沿边AB向终点B匀速运动点Q以2cm/s的速度沿折线-向终点D匀速运动．连接PO并延长交边CD于点M连接QO并延长交折线DA ABBC CD-于点N连接PQ QM MN NP得到四边形PQMN．设点P的运动时间为x（s）（04<<）四边形PQMN的x面积为y（2cm）(1)BP的长为__________cm CM的长为_________cm．（用含x的代数式表示）(2)求y关于x的函数解析式并写出自变量x的取值范围．(3)当四边形PQMN是轴对称图形时直接写出x的值．三填空题16．（2023·陕西·统考中考真题）如图，在矩形ABCD 中 3AB = 4BC =．点E 在边AD 上且3ED = M N 分别是边AB BC 上的动点且BM BN = P 是线段CE 上的动点连接PM PN ．若4PM PN +=．则线段PC 的长为．参考答案一、单选题1．（2023·辽宁盘锦·统考中考真题）如图，在平面直角坐标系中菱形ABCD 的顶点A 在y 轴的正半轴上顶点B C 在x 轴的正半轴上 (3D ()1,1P --．点M 在菱形的边AD 和DC 上运动（不与点A C 重合）过点M 作MN y ∥轴与菱形的另一边交于点N 连接PM PN 设点M 的横坐标为x PMN 的面积为y ，则下列图象能正确反映y 与x 之间函数关系的是（）A ．B ．C ．D ．【答案】A【分析】先根据菱形的性质求出各点坐标分M 的横坐标x 在01 12 23~之间三个阶段用含x 的代数式表示出PMN 的底和高进而求出分段函数的解析式根据解析式判断图象即可．【详解】解：菱形ABCD 的顶点A 在y 轴的正半轴上顶点B C 在x 轴的正半轴上 ∴2AB AD == 3OA =∴()2222231OB AB OA --= ∴123OC OB BC =+=+=∴(3A ()10B , ()3,0C 设直线AB 的解析式为y kx b =+ 将(3A ()10B ,代入得： 03k b b +=⎧⎪⎨=⎪⎩ 解得33k b ⎧=-⎪⎨=⎪⎩ ∴直线AB 的解析式为33y x =-MN y ∥轴∴N 的横坐标为x（1）当M 的横坐标x 在01之间时点N 在线段AB 上 PMN 中MN 上的高为1x + ∴(,33N x x ∴(3333MN x x -+∴()()2113313122PMNS MN x x x x =⋅+=⋅+= ∴该段图象为开口向上的抛物线（2）当M 的横坐标x 在12之间时点N 在线段BC 上 PMN 中3MN = MN 上的高为1x + ∴()()113313122PMNS MN x x x =⋅+=+=∴该段图象为直线（3）当M 的横坐标x 在23~之间时点N 在线段BC 上 PMN 中MN 上的高为1x + 由(3D ()3,0C 可得直线CD 的解析式为333y x =-+∴(,333M x x + (),0N x ∴333MN x =-+ ∴()(()21133313331322PMN S MN x x x x =⋅+=-+⋅+=++ ∴该段图象为开口向下的抛物线观察四个选项可知只有选项A 满足条件故选A ．【点睛】本题考查动点问题的函数图象涉及坐标与图形菱形的性质二次函数一次函数的应用等知识点解题的关键是分段求出函数解析式．2．（2023·江苏·统考中考真题）折返跑是一种跑步的形式．如图，在一定距离的两个标志物① ①之间从①开始沿直线跑至①处用手碰到①后立即转身沿直线跑至①处用手碰到①后继续转身跑至①处循环进行全程无需绕过标志物．小华练习了一次250m ⨯的折返跑用时18s 在整个过程中他的速度大小v （m/s ）随时间t （s ）变化的图像可能是（）A ．B ．C ．D ．【答案】D【分析】根据速度与时间的关系即可得出答案．【详解】解：刚开始速度随时间的增大而增大匀速跑一段时间后减速到① 然后再加速再匀速到① 由于体力原因应该第一个50米速度快用的时间少第二个50米速度慢用的时间多故他的速度大小v （m/s ）随时间t （s ）变化的图像可能是D ．故选：D ．【点睛】本题主要考查函数的图象要根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件结合实际意义得出正确的结论．3．（2023·江苏南通·统考中考真题）如图，ABC 中 90C ∠=︒ 15AC = 20BC =．点D 从点A 出发沿折线A C B --运动到点B 停止过点D 作DE AB ⊥ 垂足为E ．设点D 运动的路径长为x BDE △的面积为y 若y 与x 的对应关系如图所示，则a b -的值为（）A ．54B ．52C ．50D ．48【答案】B 【分析】根据点D 运动的路径长为x 在图中表示出来设,25AE z BE z ==- 在直角三角形中找到等量关系求出未知数的值得到BDE △的值．【详解】解：当10x =时由题意可知10,5AD CD ==在Rt CDB △中由勾股定理得22222520425BD CD BC =+=+=设,25AE z BE z ==-222(25)50625BE z z z ∴=-=-+在Rt ADE △中由勾股定理得2222100DE AD AE z =-=-在Rt DEB △中由勾股定理得222BD DE BE =+即2242510050625z z z =-+-+解得6z =6,19DE BE ∴==1198762BDE a S ∴==⨯⨯=当25x =时由题意可知 10CD BD ==设,25BE q AE q ==-222(25)62550AE q q q =-=-+在Rt CDA △中由勾股定理得222221510325AD AC CD =+=+=在Rt BDE △中由勾股定理得2222100DB BD BE q =-=-Rt DEA 中由勾股定理得222AD DE AE =+即2232510062550q q q =-+-+解得8q =6DE ∴=168242BDE b S ∴==⨯⨯= 762452a b ∴-=-=．故选：B ．【点睛】本题主要考查勾股定理根据勾股定理列出等式是解题的关键运用了数形结合的思想解题． 4．（2023·辽宁鞍山·统考中考真题）如图，在矩形ABCD 中对角线,AC BD 交于点O 4AB = 43BC = 垂直于BC 的直线MN 从AB 出发沿BC 3 当直线MN 与CD 重合时停止运动运动过程中MN 分别交矩形的对角线,AC BD 于点E F 以EF 为边在MN 左侧作正方形EFGH 设正方形EFGH 与AOB 重叠部分的面积为S 直线MN 的运动时间为t s ，则下列图象能大致反映S 与t 之间函数关系的是（）A ．B ．C ．D ．【答案】B【分析】求出MN 在O 点左侧时的两段图象即可得出结论．【详解】解：当MN 在O 点左侧即：2t <时：①当正方形EFGH 的边GH 在AOB 的外部时重叠部分为矩形如图：设,HE FG 分别交AB 于点,I K①垂直于BC 的直线MN 从AB 出发沿BC 3 ①3IE FK t ==①在矩形ABCD 中 4AB =43BC =①228AC AB BC =+=①4OA OB AB ===①ABO 为等边三角形①60OAB OBA ∠=∠=︒①tan60AI BK IE t ==÷︒=①42IK t =- ①()23422343S IK IE t t t t =⋅=-=-+ 图象为开口向下的一段抛物线①当正方形EFGH 的边GH 在AOB 的内部时与AOB 重叠部分即为正方形EFGH 如图：由①可知：42EF IK t ==-①()242S t =- 图象是一段开口向上的抛物线当MN 过点O 时即2t =时 ,E F 重合此时 0S =综上：满足题意的只有B 选项故选B ．【点睛】本题考查动点的函数图象问题．解题的关键是确定动点的位置利用数形结合和分类讨论的思想进行求解．5．（2023·辽宁锦州·统考中考真题）如图，在Rt ABC △中 90ACB ∠=︒ 3AC = 4BC = 在DEF 中 5DE DF == 8EF = BC 与EF 在同一条直线上点C 与点E 重合．ABC 以每秒1个单位长度的速度沿线段EF 所在直线向右匀速运动当点B 运动到点F 时 ABC 停止运动．设运动时间为t 秒 ABC 与DEF 重叠部分的面积为S ，则下列图象能大致反映S 与t 之间函数关系的是（）A ．B ．C ．D ．【答案】A【分析】分04t ≤< 48t ≤< 812t ≤<三种情况分别求出函数解析即可判断．【详解】解：过点D 作DH CB ⊥于H①5DE DF == 8EF = ①142EH FH EF === ①223DH DE EH =-当04t ≤<时如图，重叠部分为EPQ △ 此时EQ t = PQ DH ∥①EPQ EDH ∽ ①PQ EQ DH EH= 即34PQ t = ①34PQ t = ①2133248S t t t =⨯= 当48t ≤<时如图，重叠部分为四边形PQC B '' 此时BB CC t ''== PB DE '∥①12B F BC CF BB t ''=+-=- 8FC t '=-①PB DE '∥①PB F DCF '∽ ①2PB F DCF S B F SCF ''⎛⎫= ⎪⎝⎭又183122DCFS =⨯⨯=①212128PB F S t '-⎛⎫= ⎪⎝⎭ ①()231216PB F S t '=-①DH BC ⊥ 90A B C '''∠=︒①A C DH ''∥①C QF HFD '∽①2C QF HFD S C F S HF ''⎛⎫= ⎪⎝⎭ 即2814432C QF S t '-⎛⎫= ⎪⎝⎭⨯⨯ ①()2388C QF S t '=-①()()22233331283168162PB F C QF S S S t t t t ''=-=---=-++当 812t ≤<时如图，重叠部分为四边形PFB ' 此时BB CC t ''== PB DE '∥①12B F BC CF BB t ''=+-=-①PB DE '∥①PB F DCF '∽①2PB F DCF S B F S CF ''⎛⎫= ⎪⎝⎭ 即212128PB FS t '-⎛⎫= ⎪⎝⎭①()231216PB F S S t '==-综上 ()()()()22230483334816231281216t t S t t t t t ⎧≤<⎪⎪⎪=-++≤<⎨⎪⎪-≤<⎪⎩①符合题意的函数图象是选项A ．故选：A ．【点睛】此题结合图像平移时面积的变化规律考查二次函数相关知识根据平移点的特点列出函数表达式是关键有一定难度．6．（2023·辽宁·统考中考真题）如图，60MAN ∠=︒ 在射线AM AN 上分别截取6AC AB == 连接BC MAN ∠的平分线交BC 于点D 点E 为线段AB 上的动点作EF AM ⊥交AM 于点F 作EG AM ∥交射线AD 于点G 过点G 作GH AM ⊥于点H 点E 沿AB 方向运动当点E 与点B 重合时停止运动．设点E 运动的路程为x 四边形EFHG 与ABC 重叠部分的面积为S ，则能大致反映S 与x 之间函数关系的图象是（）A ．B ．C ．D ．【答案】A【分析】分三种情况分别求出S 与x 的函数关系式根据函数的类型与其图象的对应关系进行判断即可．【详解】解：①60MAN ∠=︒ 6AC AB ==①ABC 是边长为6的正三角形①AD 平分MAN ∠①30MAD NAD ∠=∠=︒ AD BC ⊥ 3CD DB ==①当矩形EFGH 全部在ABC 之中即由图1到图2 此时03x <≤①EG AC ∥①30MAD AGE ∠=∠=︒①30NAD AGE ∠=∠=︒①AE EG x ==在Rt AEF 中 60EAF ∠=︒ ①33EF AE =①23S = ①如图3时当AE AF GE AF AF CF AC +=+=+= 则162x x += 解得4x = 由图2到图3 此时34x <≤如图4 记BC EG 的交点为Q ，则EQB △是正三角形①6EQ EB BQ x ===-①()626GQ x x x =--=- 而60PQG ∠=︒ ①)3326PG QG x ==-①PQG EFHG S S S =-矩形())231263262x x =-⨯-- 233123183x =+- ①如图6时 6x = 由图3到图6 此时46x <≤如图5 同理EKB △是正三角形①6EK KB EB x ===- 162FC AC AF x =-=- 3EF x = ①EKCF S S =梯形1136622x x ⎛⎫=-+- ⎪⎝⎭ 23333x x =+ 因此三段函数的都是二次函数关系其中第1段是开口向上第2段第3段是开口向下的抛物线故选：A ．【点睛】本题考查动点问题的函数图象求出各种情况下S 与x 的函数关系式是正确解答的前提理解各种函数所对应的图象的形状是解决问题的关键．7．（2023·黑龙江大庆·统考中考真题）如图1 在平行四边形ABCD 中 120ABC ∠=︒ 已知点P 在边AB 上以1m/s 的速度从点A 向点B 运动点Q 在边BC 上 3m /s 的速度从点B 向点C 运动．若点P Q 同时出发当点P 到达点B 时点Q 恰好到达点C 处此时两点都停止运动．图2是BPQ 的面积()2m y 与点P的运动时间()s t 之间的函数关系图象（点M 为图象的最高点），则平行四边形ABCD 的面积为（）A ．212mB ．23mC ．224mD ．2243m【答案】C【分析】根据题意可得：3BC = 3AP t BQ t ==，设m AB a =，则3m BC a = 作PE BC ⊥交CB 的延长线于点E 作AF BC ⊥交CB 的延长线于点F ，则可得33m AF AB == ))333m PE PB AB PA a t =-=- 从而得到22334216PBQa St a ⎛⎫=--+ ⎪⎝⎭ 根据PBQS的最大值为3求出a 的值从而得到4m 43m 23m AB BC AF ===，，最后由平行四边形的面积公式进行计算即可得到答案．【详解】解：根据题意可得：3BC = 3AP t BQ t ==，设m AB a =，则3m BC a =作PE BC ⊥交CB 的延长线于点E 作AF BC ⊥交CB 的延长线于点F120ABC ∠=︒ 60ABF ∴∠=︒33m AF AB ∴== ))333m PE AB PA a t ==-=- )2221133333322444216PBQa SBQ PE t a t t at t a ⎛⎫∴=⋅⋅=-=-+=--+ ⎪⎝⎭ 由图象可得PBQS 的最大值为323316a ∴=解得：4a =或4a =-（舍去） 4a ∴=4m 43m 23m AB BC AF ∴===，，∴平行四边形ABCD 的面积为：2432324m BC AF ⋅=故选：C ．【点睛】本题主要考查了平行四边形的性质解直角三角形二次函数的图象与性质熟练掌握平行四边形的性质二次函数的图象与性质添加适当的辅助线构造直角三角形是解题的关键．8．（2023·辽宁·统考中考真题）如图，在Rt ABC △中 90ACB ∠=︒ 30A ∠=︒ 3cm AB =．动点P 从点A 出发以1cm/s 的速度沿射线AB 匀速运动到点B 停止运动同时动点Q 从点A 出发 3cm/s 的速度沿射线AC 匀速运动．当点P 停止运动时点Q 也随之停止运动．在PQ 的右侧以PQ 为边作菱形PQMN 点N 在射线AB ．设点P 的运动时间为()s x菱形PQMN 与ABC 的重叠部分的面积为()2cm y ，则能大致反映y 与x 之间函数关系的图象是（）A ．B ．C ．D ．【答案】A【分析】先证明菱形PQMN 是边长为x 一个角为60︒的菱形找到临界点分情况讨论即可求解．【详解】解：作PD AC ⊥于点D 作⊥QE AB 于点E由题意得AP x = 3AQ x = ①3cos30AD AP =⋅︒= ①12AD DQ AQ ==①PD 是线段AQ 的垂直平分线 ①30PQA A ∠=∠=︒①60QPE ∠=︒ PQ AP x == ①132QE AQ x == PQ PN MN QM x ==== 当点M 运动到直线BC 上时此时 BMN 是等边三角形 ①113AP PN BN AB ==== 1x = 当点Q N 运动到与点C B 、重合时①1322AP PN AB === 32x = 当点P 运动到与点B 重合时 ①3AP AB == 3x = ①当01x <≤时 233y x x ==当312x <≤时如图，作FG AB ⊥于点G 交QM 于点R则32BN FN FB x ===- 33FM MS FS x ===- )333FR x =- ①())2231373939333332y x x -⋅--=+当332x <<时如图，作HI AB ⊥于点I则3BP PH HB x ===- )33HI x =- ①())21333393332y x x =⋅--= 综上 y 与x 之间函数关系的图象分为三段当01x <≤时是开口向上的一段抛物线当312x <≤时是开口向下的一段抛物线当332x <≤时是开口向上的一段抛物线只有选项A 符合题意故选：A ．【点睛】本题主要考查了动点问题的函数的图象二次函数的图形的性质等边三角形的性质菱形的性质三角形的面积公式利用分类讨论的思想方法解答和熟练掌握抛物线的性质是解题的关键．9．（2023·湖北鄂州·统考中考真题）如图，在平面直角坐标系中 O 为原点 35OA OB == 点C 为平面内一动点 32BC =连接AC 点M 是线段AC 上的一点且满足:1:2CM MA =．当线段OM 取最大值时点M 的坐标是（）A ．36,55⎛⎫ ⎪⎝⎭B ．365,555C ．612,55⎛⎫⎪⎝⎭D ．6125,555 【答案】D【分析】由题意可得点C 在以点B 为圆心32为半径的OB 上在x 轴的负半轴上取点350D ⎛⎫ ⎪ ⎪⎝⎭连接BD 分别过C M 作CF OA ⊥ ME OA ⊥ 垂足为F E 先证OAM DAC ∽ 得23OM OA CD AD == 从而当CD 取得最大值时 OM 取得最大值结合图形可知当D B C 三点共线且点B 在线段DC 上时 CD 取得最大值然后分别证BDO CDF ∽ AEM AFC ∽ 利用相似三角形的性质即可求解．【详解】解：①点C 为平面内一动点 32BC = ①点C 在以点B 为圆心32为半径的OB 上在x 轴的负半轴上取点350D ⎛⎫⎪ ⎪⎝⎭连接BD 分别过C M 作CF OA ⊥ ME OA ⊥ 垂足为F E①35OA OB ==①AD OD OA =+=95①23OA AD = ①:1:2CM MA = ①23OA CMAD AC==①OAM DAC ∠∠= ①OAM DAC ∽ ①23OM OA CD AD == ①当CD 取得最大值时 OM 取得最大值结合图形可知当D B C 三点共线且点B 在线段DC 上时CD 取得最大值①35OA OB == OD =35①BD =()222235153522OB OD ⎛⎫++ ⎪ ⎪⎝⎭①9CD BC BD =+= ①23OM CD = ①6OM =①y 轴x ⊥轴 CF OA ⊥ ①90DOB DFC ∠∠==︒ ①BDO CDF ∠∠= ①BDO CDF ∽①OB BDCF CD=153529=解得185CF =同理可得 AEM AFC ∽①23ME AM CF AC ==23185= 解得125ME =①22221256565OE OM ME ⎛⎫=-- ⎪ ⎪⎝⎭①当线段OM 取最大值时点M 的坐标是65125⎝⎭，故选D ．【点睛】本题主要考查了勾股定理相似三角形的判定及性质圆的一般概念以及坐标与图形熟练掌握相似三角形的判定及性质是解题的关键．10．（2023·广东深圳·统考中考真题）如图1 在Rt ABC △中动点P 从A 点运动到B 点再到C 点后停止速度为2单位/s 其中BP 长与运动时间t （单位：s ）的关系如图2，则AC 的长为（）A 155B 427C ．17D ．53【答案】C【分析】根据图象可知0=t 时点P 与点A 重合得到15AB = 进而求出点P 从点A 运动到点B 所需的时间进而得到点P 从点B 运动到点C 的时间求出BC 的长再利用勾股定理求出AC 即可．【详解】解：由图象可知：0=t 时点P 与点A 重合 ①15AB =①点P 从点A 运动到点B 所需的时间为1527.5s ÷= ①点P 从点B 运动到点C 的时间为11.57.54s -= ①248BC =⨯=在Rt ABC △中：2217AC AB BC += 故选C ．【点睛】本题考查动点的函数图象勾股定理．从函数图象中有效的获取信息求出,AB BC 的长是解题的关键．11．（2023·黑龙江绥化·统考中考真题）如图，在菱形ABCD 中 60A ∠=︒ 4AB = 动点M N 同时从A 点出发点M 以每秒2个单位长度沿折线A B C --向终点C 运动点N 以每秒1个单位长度沿线段AD 向终点D 运动当其中一点运动至终点时另一点随之停止运动．设运动时间为x 秒 AMN 的面积为y 个平方单位，则下列正确表示y 与x 函数关系的图象是（）A ．B ．C ．D ．【答案】A【分析】连接BD 过点B 作BE AD ⊥于点E 根据已知条件得出ABD △是等边三角形进而证明AMN ABE ∽得出90ANM AEB ∠=∠=︒ 当04t <<时 M 在AB 上当48t ≤<时 M 在BC 上根据三角形的面积公式得到函数关系式【详解】解：如图所示连接BD 过点B 作BE AD ⊥于点E 当04t <<时 M 在AB 上菱形ABCD 中 60A ∠=︒ 4AB = ①AB AD =，则ABD △是等边三角形 ①122AE ED AD === 33BE AE =①2,AM x AN x ==①2AM ABAN AE== 又A A ∠=∠ ①AMN ABE ∽ ①90ANM AEB ∠=∠=︒ ①223MN AM AN x - ①21332y x x x =当48t ≤<时 M 在BC 上①1123322y AN BE x x =⨯=⨯ 综上所述 04t <<时的函数图象是开口向上的抛物线的一部分当48t ≤<时函数图象是直线的一部分故选：A ．【点睛】本题考查了动点问题的函数图象二次函数图象的性质一次函数图象的性质菱形的性质勾股定理等边三角形的性质与判定相似三角形的性质与判定熟练掌握以上知识是解题的关键． 12．（2023·黑龙江齐齐哈尔·统考中考真题）如图，在正方形ABCD 中 4AB = 动点M N 分别从点A B 同时出发沿射线AB 射线BC 的方向匀速运动且速度的大小相等连接DM MN ND ．设点M 运动的路程为()04x x ≤≤ DMN 的面积为S 下列图像中能反映S 与x 之间函数关系的是（）A ．B ．C ．D ．【答案】A【分析】先根据ADMDCNBMNABCD S S S SS=---正方形求出S 与x 之间函数关系式再判断即可得出结论．【详解】解：ADMDCNBMNABCD S S SSS=---正方形1114444(4)(4)222x x x x =⨯-⨯-⨯---21282x x =-+ 21(2)62x =-+ 故S 与x 之间函数关系为二次函数图像开口向上 2x =时函数有最小值6 故选：A ．【点睛】本题考查了正方形的性质二次函数的图像与性质本题的关键是求出S 与x 之间函数关系式再判断S 与x 之间函数类型．13．（2023·河南·统考中考真题）如图1 点P 从等边三角形ABC 的顶点A 出发沿直线运动到三角形内部一点再从该点沿直线运动到顶点B ．设点P 运动的路程为x PBy PC= 图2是点P 运动时y 随x 变化的关系图象，则等边三角形ABC 的边长为（）A ．6B ．3C ．43D ．23【答案】A【分析】如图，令点P 从顶点A 出发沿直线运动到三角形内部一点O 再从点O 沿直线运动到顶点B ．结合图象可知当点P 在AO 上运动时 PB PC = 23AO = 易知30BAO CAO ∠=∠=︒ 当点P 在OB 上运动时可知点P 到达点B 时的路程为3 可知23AO OB == 过点O 作OD AB ⊥ 解直角三角形可得cos303AD AO =⋅︒= 进而可求得等边三角形ABC 的边长．【详解】解：如图，令点P 从顶点A 出发沿直线运动到三角形内部一点O 再从点O 沿直线运动到顶点B ．结合图象可知当点P 在AO 上运动时1PB PC= ①PB PC = 3AO =又①ABC 为等边三角形①60BAC ∠=︒ AB AC =①()SSS APB APC △≌△①BAO CAO ∠=∠①30BAO CAO ∠=∠=︒ 当点P 在OB 上运动时可知点P 到达点B 时的路程为43①3OB = 即23AO OB ==①30BAO ABO ∠=∠=︒过点O 作OD AB ⊥①AD BD =，则cos303AD AO =⋅︒=①6AB AD BD =+=即：等边三角形ABC 的边长为6故选：A ．【点睛】本题考查了动点问题的函数图象解决本题的关键是综合利用图象和图形给出的条件．2二解答题14．（2023·四川绵阳·统考中考真题）如图，已知①ABC 中 ①C =90° 点M 从点C 出发沿CB 方向以1cm /s的速度匀速运动到达点B 停止运动在点M 的运动过程中过点M 作直线MN 交AC 于点N 且保持①NMC =45° 再过点N 作AC 的垂线交AB 于点F 连接MF 将①MNF 关于直线NF 对称后得到①ENF 已知AC =8cm BC =4cm 设点M 运动时间为t （s ） ①ENF 与①ANF 重叠部分的面积为y （cm 2）．（1）在点M 的运动过程中能否使得四边形MNEF 为正方形？如果能求出相应的t 值如果不能说明理由（2）求y 关于t 的函数解析式及相应t 的取值范围（3）当y 取最大值时求sin ①NEF 的值．【答案】（1）85（2）⎪⎪⎩⎪⎪⎨⎧≤≤+-<<+-=)42(31643121)20(24122t t t t t t y （3310 【详解】试题分析：（1）由已知得出CN =CM =t FN ①BC 得出AN =8﹣t 由平行线证出①ANF ①①ACB 得出对应边成比例求出NF =12AN =12（8﹣t ）由对称的性质得出①ENF =①MNF =①NMC =45° MN =NE OE =OM =CN =t 由正方形的性质得出OE =ON =FN 得出方程解方程即可（2）分两种情况：①当0＜t ≤2时由三角形面积得出2124y t t =-+ ①当2＜t ≤4时作GH ①NF 于H 由（1）得：NF =12（8﹣t ） GH =NH GH =2FH 得出GH =23NF =13（8﹣t ）由三角形面积得出21(8)12y t =-（2＜t ≤4）（3）当点E 在AB 边上时 y 取最大值连接EM ，则EF =BF EM =2CN =2CM =2t EM =2BM 得出方程解方程求出CN =CM =2 AN =6 得出BM =2 NF =12AN =3 因此EM =2BM =4 作FD ①NE 于D由勾股定理求出EB 22EM BM +=25 求出EF =12EB 5 由等腰直角三角形的性质和勾股定理得出DF 的长在Rt①DEF 中由三角函数定义即可求出sin①NEF 的值．试题解析：解：（1）能使得四边形MNEF 为正方形理由如下：连接ME 交NF 于O 如图1所示：①①C =90° ①NMC =45° NF ①AC ①CN =CM =t FN ①BC ①AN =8﹣t ①ANF ①①ACB ①84AN AC NF BC == =2 ①NF =12AN =12（8﹣t ）由对称的性质得：①ENF =①MNF =①NMC =45° MN =NE OE =OM =CN =t ①四边形MNEF 是正方形 ①OE =ON =FN ①t =12×12（8﹣t ）解得：t =85即在点M 的运动过程中能使得四边形MNEF 为正方形 t 的值为85（2）分两种情况：①当0＜t ≤2时 y =12×12（8﹣t ）×t =2124t t -+ 即2124y t t =-+（0＜t ≤2） ①当2＜t ≤4时如图2所示：作GH ①NF 于H 由（1）得：NF =12（8﹣t ） GH =NH GH =2FH ①GH =23NF =13（8﹣t ） ①y =12NF ′GH =12×12（8﹣t ）×13（8﹣t ）=21(8)12t - 即21(8)12y t =-（2＜t ≤4）综上所述：⎪⎪⎩⎪⎪⎨⎧≤≤+-<<+-=)42(31643121)20(24122t t t t t t y ．（3）当点E 在AB 边上时 y 取最大值连接EM 如图3所示：则EF =BF EM =2CN =2CM =2t EM =2BM ①BM =4﹣t ①2t =2（4﹣t ）解得：t =2 ①CN =CM =2 AN =6 ①BM =4﹣2=2 NF =12AN =3 ①EM =2BM =4 作FD ①NE 于D ，则EB 22EM BM +2242+=5 ①DNF 是等腰直角三角形①EF =12EB 5 DF =22 NF 32 在Rt①DEF 中 sin①NEF =DF EF 3225310【点睛】本题是四边形综合题目考查了正方形的判定与性质相似三角形的判定与性质勾股定理三角函数三角形面积的计算等腰直角三角形的判定与性质等知识本题综合性强有一定难度． 15．（2023·吉林·统考中考真题）如图，在正方形ABCD 中 4cm AB = 点O 是对角线AC 的中点动点P Q 分别从点A B 同时出发点P 以1cm/s 的速度沿边AB 向终点B 匀速运动点Q 以2cm/s 的速度沿折线BC CD -向终点D 匀速运动．连接PO 并延长交边CD 于点M 连接QO 并延长交折线DA AB -于点N 连接PQ QM MN NP 得到四边形PQMN ．设点P 的运动时间为x （s ）（04x <<）四边形PQMN 的面积为y （2cm ）(1)BP 的长为__________cm CM 的长为_________cm ．（用含x 的代数式表示）(2)求y 关于x 的函数解析式并写出自变量x 的取值范围．(3)当四边形PQMN 是轴对称图形时直接写出x 的值．【答案】(1)()4x - x(2)()()2412160241624x x x y x x ⎧-+<≤⎪=⎨-+<≤⎪⎩(3)43x =或83x = 【分析】（1）根据正方形中心对称的性质得出,OM OP OQ ON == 可得四边形PQMN 是平行四边形证明ANP CQM ≌即可（2）分02x <≤ 24x <≤两种情况分别画出图形根据正方形的面积以及平行四边形的性质即可求解（3）根据（2）的图形分类讨论即可求解．【详解】（1）解：依题意 1AP x x =⨯=()cm ，则()4PB AB AP x cm =-=-①四边形ABCD 是正方形①,90AD BC DAB DCB ∠=∠=︒∥①点O 是正方形对角线AC 的中点①,OM OP OQ ON ==，则四边形PQMN 是平行四边形①MQ PN = MQ NP ∥①PNQ MQN ∠=∠又AD BC ∥①ANQ CQN ∠=∠①ANP MQC ∠=∠在,ANP CQM 中ANP MQC NAP QCM NP MQ ∠=∠⎧⎪∠=∠⎨⎪=⎩①ANP CQM ≌①()cm MC AP x ==故答案为：()4x - x ．（2）解：当02x <≤时点Q 在BC 上由（1）可得ANP CQM ≌同理可得PBQ MDN ≌①4,2,PB x QB x MC x =-== 42QC x =-则222MCQ BPQ y AB S S =--()()164242x x x x =--⨯--241216x x =-+当24x <≤时如图所示则AP x = 224AN CQ x CB x ==-=-()244PN AP AN x x x =-=--=-+①()44416y x x =-+⨯=-+综上所述 ()()2412160241624x x x y x x ⎧-+<≤⎪=⎨-+<≤⎪⎩（3）依题意 ①如图，当四边形PQMN 是矩形时此时90PQM ∠=︒①90PQB CQM ∠+∠=︒①90BPQ PQB ∠+∠=︒①BPQ CQM ∠=∠又B BCD ∠=∠①~BPQ CQM ①BP BQ CQ CM= 即4242x x x x-=- 解得：43x =当四边形PQMN 是菱形时，则PQ MQ =①()()()22224242x x x x -+=+-解得：0x =（舍去）①如图所示当PB CQ =时四边形PQMN 是轴对称图形424x x -=- 解得83x = 当四边形PQMN 是菱形时，则4PN PQ == 即44x -+= 解得：0x =（舍去）综上所述当四边形PQMN 是轴对称图形时 43x =或83x =．【点睛】本题考查了正方形的性质动点问题全等三角形的性质与判定矩形的性质平行四边形的性质与判定菱形的性质轴对称图形熟练掌握以上知识是解题的关键．三填空题16．（2023·陕西·统考中考真题）如图，在矩形ABCD 中 3AB = 4BC =．点E 在边AD 上且3ED = M N 分别是边AB BC 上的动点且BM BN = P 是线段CE 上的动点连接PM PN ．若4PM PN +=．则线段PC 的长为．。

中考数学专题复习动点型问题(含详细参考答案)

专题十动点型问题一、中考专题诠释所谓“动点型问题”是指题设图形中存在一个或多个动点,它们在线段、射线或弧线上运动的一类开放性题目.解决这类问题的关键是动中求静,灵活运用有关数学知识解决问题.“动点型问题”题型繁多、题意创新，考察学生的分析问题、解决问题的能力，内容包括空间观念、应用意识、推理能力等，是近几年中考题的热点和难点。

二、解题策略和解法精讲解决动点问题的关键是“动中求静”.从变换的角度和运动变化来研究三角形、四边形、函数图像等图形，通过“对称、动点的运动”等研究手段和方法，来探索与发现图形性质及图形变化，在解题过程中渗透空间观念和合情推理。

在动点的运动过程中观察图形的变化情况，理解图形在不同位置的情况，做好计算推理的过程。

在变化中找到不变的性质是解决数学“动点”探究题的基本思路,这也是动态几何数学问题中最核心的数学本质。

三、中考考点精讲考点一：建立动点问题的函数解析式（或函数图像）函数揭示了运动变化过程中量与量之间的变化规律,是初中数学的重要内容.动点问题反映的是一种函数思想,由于某一个点或某图形的有条件地运动变化,引起未知量与已知量间的一种变化关系,这种变化关系就是动点问题中的函数关系.例1（2013•兰州）如图，动点P从点A出发，沿线段AB运动至点B后，立即按原路返回，点P在运动过程中速度不变，则以点B为圆心，线段BP长为半径的圆的面积S与点P的运动时间t的函数图象大致为（）A．B．C．D．思路分析：分析动点P的运动过程，采用定量分析手段，求出S与t的函数关系式，根据关系式可以得出结论．解：不妨设线段AB长度为1个单位，点P的运动速度为1个单位，则：（1）当点P在A→B段运动时，PB=1-t，S=π（1-t）2（0≤t＜1）；（2）当点P在B→A段运动时，PB=t-1，S=π（t-1）2（1≤t≤2）．综上，整个运动过程中，S与t的函数关系式为：S=π（t-1）2（0≤t≤2），这是一个二次函数，其图象为开口向上的一段抛物线．结合题中各选项，只有B符合要求．故选B．点评：本题结合动点问题考查了二次函数的图象．解题过程中求出了函数关系式，这是定量的分析方法，适用于本题，如果仅仅用定性分析方法则难以作出正确选择．对应训练1．（2013•白银）如图，⊙O的圆心在定角∠α（0°＜α＜180°）的角平分线上运动，且⊙O.与∠α 的两边相切，图中阴影部分的面积 S 关于⊙O 的半径 r （r ＞0）变化的函数图象大致是（）A ．B ．C ．D ． 1．C考点二：动态几何型题目点动、线动、形动构成的问题称之为动态几何问题 . 它主要以几何图形为载体，运动变化为主线，集多个知识点为一体，集多种解题思想于一题 . 这类题综合性强，能力要求高，它能全面的考查学生的实践操作能力，空间想象能力以及分析问题和解决问题的能力动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

2024年中考数学高频压轴题训练——圆-动点问题及参考答案

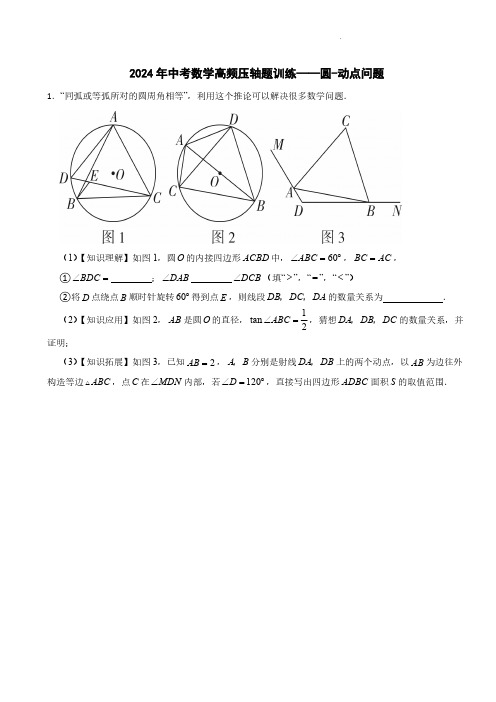
2024年中考数学高频压轴题训练——圆-动点问题1．“同弧或等弧所对的圆周角相等”，利用这个推论可以解决很多数学问题．（1）【知识理解】如图1，圆O 的内接四边形ACBD 中，60ABC ∠=︒，BC AC =，①BDC ∠=；DAB ∠DCB ∠（填“>”，“=”，“<”）②将D 点绕点B 顺时针旋转60︒得到点E ，则线段DB DC DA ，，的数量关系为．（2）【知识应用】如图2，AB 是圆O 的直径，1tan 2ABC ∠=，猜想DA DB DC ，，的数量关系，并证明；（3）【知识拓展】如图3，已知2AB =，A B ，分别是射线DA DB ，上的两个动点，以AB 为边往外构造等边ABC ，点C 在MDN ∠内部，若120D ∠=︒，直接写出四边形ADBC 面积S 的取值范围．2．如图1，对于PMN 的顶点P 及其对边MN 上的一点Q ，给出如下定义：以P 为圆心，PQ 为半径的圆与直线MN 的公共点都在线段MN 上，则称点Q 为PMN 关于点P 的内联点．在平面直角坐标系xOy 中：（1）如图2，已知点(70)A ，，点B 在直线1y x =+上．①若点(34)B ，，点(30)C ，，则在点O ，C ，A 中，点是AOB 关于点B 的内联点；②若AOB 关于点B 的内联点存在，求点B 纵坐标n 的取值范围；（2）已知点(20)D ，，点(42)E ，，将点D 绕原点O 旋转得到点F ．若EOF 关于点E 的内联点存在，直接写出点F 横坐标m 的取值范围．3．在平面直角坐标系xOy 中，O 的半径为1，对于点A 和线段BC ，给出如下定义：若将线段BC 绕点A 旋转可以得到O 的弦B C ''（B C ''，分别是B C ，的对应点），则称线段BC 是O 的以点A 为中心的“关联线段”．（1）如图，点112233A B C B C B C ，，，，，，的横､纵坐标都是整数．在线段112233B C B C B C ，，中，O 的以点A 为中心的“关联线段”是；（2）ABC 是边长为1的等边三角形，点()0A t ，，其中0t ≠．若BC 是O 的以点A 为中心的“关联线段”，求t 的值；（3）在ABC 中，12AB AC ==，．若BC 是O 的以点A 为中心的“关联线段”，直接写出OA 的最小值和最大值，以及相应的BC 长．4．已知：点C 为⊙O 的直径AB 上一动点，过点C 作CD ⊥AB ，交⊙O 于点D 和点E ，连接AD 、BD ，∠DBA 的角平分线交⊙O 于点F ．（1）若DF ＝BD ，求证：GD ＝GB ；（2）若AB ＝2cm ，在（1）的条件下，求DG 的值；（3）若∠ADB 的角平分线DM 交⊙O 于点M ，交AB 于点N ．当点C 与点O 重合时，AD BD DM+＝；据此猜想，当点C 在AB （不含端点）运动过程中，AD BD DM +的值是否发生改变？若不变，请求其值；若改变，请说明理由．5．在平面直角坐标系xOy 中，O 的半径为1，对于ABC 和直线l 给出如下定义：若ABC 的一条边关于直线l 的对称线段PQ 是O 的弦，则称ABC 是O 的关于直线l 的“关联三角形”，直线l 是“关联轴”．（1）如图1，若ABC 是O 的关于直线l 的“关联三角形”，请画出ABC 与O 的“关联轴”（至少画两条）；（2）若ABC 中，点A 坐标为(23)，，点B 坐标为(41)，，点C 在直线3y x =-+的图像上，存在“关联轴l ”使ABC 是O 的关联三角形，求点C 横坐标的取值范围；（3）已知A ，将点A 向上平移2个单位得到点M ，以M 为圆心MA 为半径画圆，B ，C 为M 上的两点，且2AB =（点B 在点A 右侧），若ABC 与O 的关联轴至少有两条，直接写出OC 的最小值和最大值，以及OC 最大时AC 的长．6．如图，在⊙O 中，AB 为弦，CD 为直径，且AB ⊥CD ，垂足为E ，P 为 AC 上的动点（不与端点重合），连接PD ．（1）求证：∠APD ＝∠BPD ；（2）利用尺规在PD 上找到点I ，使得I 到AB 、AP 的距离相等，连接AD （保留作图痕迹，不写作法）．求证：∠AIP+∠DAI ＝180°；（3）在（2）的条件下，连接IC 、IE ，若∠APB ＝60°，试问：在P 点的移动过程中，IC IE 是否为定值？若是，请求出这个值；若不是，请说明理由．7．在平面直角坐标系xOy 中，已知线段AB 和点P ，给出如下定义：若PA PB =且点P 不在线段AB 上，则称点P 是线段AB 的等腰顶点．特别地，当90APB ∠≥︒时，则称点P 是线段AB 的非锐角等腰顶点．（1）已知点(20)A ，，(42)B ，．①在点(40)C ，，(31)D ，，(15)E -，，(05)F ，中，是线段AB 的等腰顶点的是▲；②若点P 在直线3(0)y kx k =+≠上，且点P 是线段AB 的非锐角等腰顶点，求k 的取值范围；（2）直线33y x =-+与x 轴交于点M ，与y 轴交于点N ．⊙P 的圆心为(0)P t ，，半径为，若⊙P 上存在线段MN 的等腰顶点，请直接写出t 的取值范围．8．在平面直角坐标系xOy中，⊙O的半径为1，T（0，t）为y轴上一点，P为平面上一点．给出如下定义：若在⊙O上存在一点Q，使得△TQP是等腰直角三角形，且∠TQP＝90°，则称点P为⊙O的“等直点”，△TQP为⊙O的“等直三角形”．如图，点A，B，C，D的横、纵坐标都是整数．（1）当t＝2时，在点A，B，C，D中，⊙O的“等直点”是；（2）当t＝3时，若△TQP是⊙O“等直三角形”，且点P，Q都在第一象限，求CPOQ的值．9．综合与实践动手操作利用正方形纸片的折叠开展数学活动．探究体会在正方形折叠过程中，图形与线段的变化及其蕴含的数学思想方法．如图1，点E 为正方形ABCD 的AB 边上的一个动点，3AB =，将正方形ABCD 对折，使点A 与点B 重合，点C 与点D 重合，折痕为MN ．思考探索（1）将正方形ABCD 展平后沿过点C 的直线CE 折叠，使点B 的对应点B '落在MN 上，折痕为EC ，连接DB '，如图2．①点B '在以点E 为圆心，的长为半径的圆上；②B M '=；③DB C ' 为三角形，请证明你的结论．（2）拓展延伸当3AB AE =时，正方形ABCD 沿过点E 的直线l （不过点B ）折叠后，点B 的对应点B '落在正方形ABCD 内部或边上．①ABB ' 面积的最大值为；②连接AB '，点P 为AE 的中点，点Q 在AB '上，连接PQ AQP AB E ∠=∠'，，则2B C PQ '+的最小值为．10．在平面直角坐标系xOy 中，过⊙T （半径为r ）外一点P 引它的一条切线，切点为Q ，若0＜PQ≤2r ，则称点P 为⊙T 的伴随点．（1）当⊙O 的半径为1时，①在点A(4，0)，B(0，)，C(1，)中，⊙O 的伴随点是▲；②点D 在直线y ＝x+3上，且点D 是⊙O 的伴随点，求点D 的横坐标d 的取值范围；（2）⊙M 的圆心为M(m ，0)，半径为2，直线y ＝2x ﹣2与x 轴，y 轴分别交于点E ，F ．若线段EF 上的所有点都是⊙M 的伴随点，直接写出m 的取值范围．11．定义：在平面直角坐标系xOy 中，点P 为图形M 上一点，点Q 为图形N 上一点．若存在OP OQ =，则称图形M 与图形N 关于原点O “平衡”．（1）如图，已知⊙A 是以()1,0为圆心，2为半径的圆，点()1,0C -，()2,1D -，()3,2E ．①在点C ，D ，E 中，与⊙A 关于原点O “平衡”的点是；②点H 为直线y x =-上一点，若点H 与⊙A 关于原点O “平衡”，点H 的横坐标的取值范围为：；（2）如图，已知图形G 是以原点O 为中心，边长为2的正方形．⊙K 的圆心在x 轴上，半径为2．若⊙K 与图形G 关于原点O “平衡”，请直接写出圆心K 的横坐标的取值范围．12．阅读下列材料，并按要求解答相关问题：【思考发现】根据直径所对的圆周角是直角，我们可以推出“如果一条定边所对的角始终为直角，那么所有满足条件的直角顶点组成的图形是以定边为直径的圆或圆弧（直径的两个端点除外）”这一正确的结论．如图1，若AB 是一条定线段，且90APB ∠=︒，则所有满足条件的直角顶点P 组成的图形是定边AB 为直径的O （直径两端点A 、B 除外）（1）已知：如图2，四边形ABCD 是边长为8的正方形，点E 从点B 出发向点C 运动，同时点F 从点C 出发以相同的速度向点D 运动，连接AE ，BF 相交于点P ．①当点E 从点B 运动到点C 的过程中，APB ∠的大小是否发生变化？若发生变化，请说明理由；若不发生变化，请直接写出APB ∠的度数．②当点E 从点B 运动到点C 的过程中，点P 运动的路径是（）A ．线段；B ．弧；C ．半圆；D ．圆③点P 运动的路经长是▲．（2）已知：如图3，在图2的条件下，连接CP ，请直接写出E 、F 运动过程中，CP 的最小值．13．对于平面内的图形1G 和图形2G ，记平面内一点P 到图形1G 上各点的最短距离为1d ，点P 到图形2G 上各点的最短距离为2d ，若12d d =，就称点P 是图形1G 和图形2G 的一个“等距点”．在平面直角坐标系xOy 中，已知点()60A ，，(0B ．（1）在()30R ，，()20S ，，(1T 三点中，点A 和点B 的等距点是；（2）已知直线2y =-．①若点A 和直线2y =-的等距点在x 轴上，则该等距点的坐标为▲；②若直线y a =上存在点A 直线2y =-的等距点，求实数a 的取值范围；（3）记直线AB 为直线1l ，直线2l ：33y x =-，以原点O 为圆心作半径为r 的O ．若O 上有m 个直线1l 和直线2l 的等距点，以及n 个直线1l 和y 轴的等距点（0m ≠，0n ≠），求m n ≠时，求r 的取值范围．14．如图，平面上存在点P 、点M 与线段AB ．若线段AB 上存在一点Q ，使得点M 在以PQ 为直径的圆上，则称点M 为点P 与线段AB 的共圆点．已知点P （0，1），点A （﹣2，﹣1），点B （2，﹣1）．（1）在点O （0，0），C （﹣2，1），D （3，0）中，可以成为点P 与线段AB 的共圆点的是；（2）点K 为x 轴上一点，若点K 为点P 与线段AB 的共圆点，请求出点K 横坐标x K 的取值范围；（3）已知点M （m ，﹣1），若直线y ＝12x +3上存在点P 与线段AM 的共圆点，请直接写出m 的取值范围．15．如图，在ABC 中，AB BC =，30CAB ∠=︒，8AC =，半径为2的O 从点A 开始（如图1）沿直线AB 向右滚动，滚动时始终与直线AB 相切（切点为D ），当O 与ABC 只有一个公共点时滚动停止，作OG AC ⊥于点G ．（1）图1中，O 在AC 边上截得的弦长AE =；（2）当圆心落在AC 上时，如图2，判断BC 与O 的位置关系，并说明理由．（3）在O 滚动过程中，线段OG 的长度随之变化，设AD x =，OG y =，求出y 与x 的函数关系式，并直接写出x 的取值范围．16．在平面直角坐标系xOy 中，给出如下定义：若点P 在图形M 上，点Q 在图形N 上，称线段PQ 长度的最小值为图形M ，N 的“近距离”，记为d(M ，N)，特别地，若图形M ，N 有公共点，规定d(M ，N)＝0．已知：如图，点A(2-，0)，B(0，．（1）如果⊙O 的半径为2，那么d(A ，⊙O)＝，d(B ，⊙O)＝．（2）如果⊙O 的半径为r ，且d （⊙O ，线段AB ）=0，求r 的取值范围；（3）如果C(m ，0)是x 轴上的动点，⊙C 的半径为1，使d （⊙C ，线段AB ）<1，直接写出m 的取值范围．17．在平面直角坐标系xOy 中，对于点()P m n ，，我们称直线y mx n =+为点P 的关联直线.例如，点()24P ，的关联直线为24y x =+．（1）已知点()12A ，．①点A 的关联直线为；②若O 与点A 的关联直线相切，则O 的半径为；（2）已知点()02C ，，点()0.D d ，点M 为直线CD 上的动点．①当2d =时，求点O 到点M 的关联直线的距离的最大值；②以()11T -，为圆心，3为半径作.T 在点M 运动过程中，当点M 的关联直线与T 交于E ，F 两点时，EF 的最小值为4，请直接写出d 的值．18．在平面直角坐标系xOy 中，给定圆C 和点P ，若过点P 最多可以作出k 条不同的直线，且这些直线被圆C 所截得的线段长度为正整数，则称点P 关于圆C 的特征值为.k 已知圆O 的半径为2，（1）若点M 的坐标为()11，，则经过点M 的直线被圆O 截得的弦长的最小值为，点M 关于圆O 的特征值为；（2）直线y x b =+分别与x ，y 轴交于点A ，B ，若线段AB 上总存在关于圆O 的特征值为4的点，求b 的取值范围；（3）点T 是x 轴正半轴上一点，圆T 的半径为1，点R ，S 分别在圆O 与圆T 上，点R 关于圆T 的特征值记为r ，点S 关于圆O 的特征值记为.s 当点T 在x 轴正轴上运动时，若存在点R ，S ，使得3r s +=，直接写出点T 的横坐标t 的取值范围．答案解析部分1．【答案】（1）60︒；=；DC DB DA=+（2）解：在AB 上取一点E ，使ADE BDC ∠=∠，如图所示：∵AB 是圆O 的直径，1tan 2ABC ∠=，∴1tan 2AC ABC BC BC =∠⋅=，∴在Rt ACB 中，52AB BC ==，∵ BD BD =，∴DAB DCB ∠=∠，∵ADE BDC ∠=∠，∴ADE CDB ∽，∴ADAECD CB =，∴AD CB CD AE ⋅=⋅，∵ AD AD =，∴DBA DCA ∠=∠，∵ADE CDE CDB CDE ∠-∠=∠-∠，即ADC BDE ∠=∠，∴BDE CDA ∽，∴BDBECD AC =，∴BD AC CD BE ⋅=⋅，∴()AD CB AC BD CD AE CD BE CD AE BE CD AB⋅+⋅=⋅+⋅=⋅+=⋅，∴AB CD AC DB AD BC ⋅=⋅+⋅，∴122BC CD BC DB AD BC ⋅=⋅+⋅，∴5122CD DB AD ⋅=⋅+，∴5122CD DB AD =+，即2DB AD =+，故答案为：2DB AD =+．（3）解：∵A B ，分别是射线DA DB ，上的两个动点，120D ∠=︒，ABC 是等边三角形，∴四边形ADBC 的两个对角180ADB ACB ∠+∠=︒，∴构造四边形ADBC 的外接圆，∴根据四边形外接圆的性质可得：当点A 和点D 重合时，四边形ADBC 面积S 最小；当CD AB ⊥时，四边形ADBC 面积S 最大，①当点A 和点D 重合时，四边形ADBC 面积S 最小，∵CBD 时等边三角形，且2AB =，∴60CBD ∠=︒，2AB BD BC ===∴1sin 602CBD S BC BD =⋅⋅⋅= ，②当CD AB ⊥时，四边形ADBC 面积S 最大，∵CBD 时等边三角形，且2AB =，∴30ACD ∠=︒，2AC =，∴tan 233AD ACD AC =∠⋅==，∴11232322233ADC S AD DC =⋅⋅=⨯= ，∴23ADC ADBC S S == 四边形；433S <≤．2．【答案】（1）解：①O ，C ②当点B 的坐标为（0，1）时，如图，此时以BO 为半径的B 与线段OA 相切于点O ，∴点O 是OAB 关于点B 的内联点；当点B 移动到在y 轴左侧时，作图发现B 与x 轴有相交，且有一个交点不在线段OA 上，∴不再有OAB 关于点B 的内联点；当点B 的坐标为（7，8）时，以BA 为半径的B 与x 轴相切于点A ，∴点A 是OAB 关于点B 的内联点；当点B 直线x=7的右侧时，以BA 为半径的B 与x 轴相交，且有一个交点不在线段OA 上∴不再有OAB 关于点B 的内联点；综上所述，若AOB 关于点B 的内联点存在，求点B 纵坐标n 的取值范围为18n ≤≤；（2）80m 555m -≤≤≤≤或3．【答案】（1）22B C （2）解：由题意可得：当BC 是O 的以点A 为中心的“关联线段”时，则有AB C '' 是等边三角形，且边长也为1，当点A 在y 轴的正半轴上时，如图所示：设B C ''与y 轴的交点为D ，连接OB '，易得B C y ''⊥轴，∴12B D DC ''==，∴32OD ==，32==，∴OA =，∴t =；当点A 在y 轴的正半轴上时，如图所示：同理可得此时的OA =，∴t =；（3）当1min OA =时，此时BC =；当2max OA =时，此时2BC =．4．【答案】（1）证明：∵CD ⊥直径AB ，∴ BDBE =，∵DF ＝BD ，∴ DFBD =，∴ BEDF =，∴∠1＝∠2，∴DG ＝BG（2）解：∠DBA 的角平分线交⊙O 于点F ，∴∠2＝∠3，由（1）知，∠1＝∠2，∴∠1＝∠2＝∠3，∵∠BCD ＝90°，∴∠1+∠2+∠3＝90°，∴∠1＝∠2＝∠3＝30°，∵AB 是⊙O 的直径，∴∠ADB ＝90°，∴∠4＝90°﹣∠2﹣∠3＝30°，∵AB ＝2，∴BD ＝1，在Rt △BCD 中，∠1＝30°，∴BC ＝12BD ＝12，在Rt △BCG 中，∠3＝30°，∴CG ＝＝6，∴BG ＝2CG ＝33，由（1）知，DG ＝BG ＝33（3）5．【答案】（1）解：如图1，作BM ⊥x 轴，垂足为M ，根据题意AB=AE=EF=BF=，且∠EFO=∠BFM=45°，∴∠EFB=90°，∴四边形ABFE 是正方形，∴边AE ，BF 的中点所在直线就是ABC 与O 的一条“关联轴”；∵O 的半径为1，∴，且∠EFG=90°，∴四边形EFGH 是正方形，∵∠EFG+∠EFB=180°，∴B 、F 、G 三点共线，∴直线EF 是ABC 与O 的一条“关联轴”．（2）解：如图2，根据A （2，3），B （4，1），C （4，1），计算2=，故AB 不能落在圆的内部；过点A 作AN ⊥y 轴，垂足为N ，则AN=2，等于圆的直径，存在“关联轴l ”使ABC 是O 的关联三角形，此时0C x =；作点B 关于x 轴的对称点P ，此时BP=2，等于圆的直径，存在“关联轴l ”使ABC 是O 的关联三角形，此时4C x =，综上所述，点C 横坐标的范围是04C x ≤≤．（3）解：OC 的最小值为2-；OC 最大，根据勾股定理，AC=4.6．【答案】（1）证明：∵直径CD ⊥弦AB ，∴ AD BD=，∴∠APD=∠BPD ；（2）解：如图，作∠BAP 的平分线，交PD 于I ，证：∵AI 平分∠BAP ，∴∠PAI=∠BAI ，∴∠AID=∠APD+∠PAI=∠APD+BAI ，∵ AD BD=，∴∠DAB=∠APD ，∴∠DAI=∠DAB+∠BAI=∠APD+∠BAI ，∴∠AID=∠DAI ，∵∠AIP+∠DAI=180°，∴∠AIP+∠DAI=180°；（3）解：如图2，连接BI ，AC ，OA ，OB ，∵AI 平分∠BAP ，PD 平分∠APB ，∴BI 平分∠ABP ，∠BAI=12∠BAP ，∴∠ABI=12∠ABP ，∵∠APB=60°，∴∠PAB+∠PBA=120°，∴∠BAI+∠ABI=12（∠BAP+∠ABP ）=60°，∴∠AIB=120°，∴点I 的运动轨迹是 AB ，∴DI=DA ，∵∠AOB=2∠APB=120°，∵AD ⊥AB ，∴ AD BD=，∴∠AOB=∠BOD=60°，∵OA=OD ，∴△AOD 是等边三角形，∴AD=AO ，∵CD 是⊙O 的直径，∴∠DAC=90°，∵CD ⊥AB ，∴∠AED=90°，∴∠AED=∠CAD ，∵∠ADC=∠ADE ，∴△ADE ∽△CDA ，∴AD DE CD AD=，∴AD 2=DE•CD ，∵DI′=DI=AD ，∴DI 2=DE•CD ，∵∠I′DE 是公共角，∴△DIE ∽△DCI ，∴2IC CD IE DI==．7．【答案】（1）解：①C(4，0)，E(-1，5)；②（Ⅰ）当点(40)，在直线3y kx =+上时，430k +=，34k =-；（Ⅱ）当点(31)，在直线3y kx =+上时，331k +=，23k =-；（Ⅲ）当点(22)，在直线3y kx =+上时，232k +=，12k =-；结合图象可得3142k -≤≤-且23k ≠-；（2）解：直线333y x =-+与x 轴的交点M 坐标为()30，，与y 轴交点N 的坐标为(03，，∴tan 3NMO ∠=，∴30NMO ∠=︒，如图，作出线段MN 的垂直平分线，如图为两个临界情况：，利用待定系数法求得MN 垂直平分线解析式为y =，∴(0R -，，12230ORQ P RQ ∠=∠=︒，∴1112PR PQ ==，2222P R P Q ==，∴(10P ，(20P -，，∴t -≤<．8．【答案】（1）A 、B 、D（2）解：如图，依题意作⊙O 的“等直三角形”△TQP∴TQ=PQ ，∠TQP=90°过Q 点作MH //x 轴，交y 轴于M 点，过点P 作PH ⊥MH 于H 点∴∠TMQ=∠QHP=90°∴∠TQM+∠MTQ=∠TQM+∠HQP=90°∴∠MTQ=∠HQP∴△TMQ ≌△QHP （AAS ）∴TM=QH ，MQ=HP设Q （x ，y ）∴HM=MQ+QH=MQ+TM=x+3-y ，PH=MQ=x∴P （x-y+3，x+y ）∵C （3，0）∴∵∴CP OQ ．9．【答案】（1）BE ；3332-；等边；证明：B′D=BC CD ==，∴△DB'C 为等边三角形（2）310．【答案】（1）B ，C ；解：②如图2中，设点D 的坐标为(3)d d +，当过点D 的切线长为22r =时，OD ==由两点之间的距离公式得：OD =解得1221d d =-=-，结合图象可知，点D 的横坐标d 的取值范围是21d -≤≤-；（2）解：对于22y x =-当0y =时，220x -=，解得1x =，则点E 的坐标为(10)E ，当0x =时，2y =-，则点F 的坐标为(02)F -，⊙M 的半径为2，⊙M 的圆心为(0)M m ，24r ∴=，OM m=由题意，由以下两种情况：如图3-1中，点M 在点E 的右侧设FT 是⊙M 的切线则有两个临界位置：4FT =和点E 对应的切线长为0当4FT =时，则4OM m FT ===当点E 对应的切线长为0，即2EM =12EM m ∴=-=解得3m =结合图象得，当34m <≤时，线段EF 上的所有点都是⊙M 的伴随点②如图3-2和3-3中，点M 在点E 的左侧则有如下两个临界位置：如图3-2，设ET 是⊙M 的切线，连接MT ，则90MTE ∠=︒当4ET =时，2222245EM MT ET =+=+此时15m -=解得15m =-如图3-3，当⊙M 在直线EF 的左侧与EF 相切时，设切点为T ，连接MT∵(10)(02)E F -，，，∴12OE OF ==，∴22125EF =+=∵EF 是切线∴EF MT⊥∴90MTE FOE ∠=∠=︒∵MET FEO∠=∠∴MTE FOE~ ∴EM MTEF OF =，即22=解得EM =，即1m -=解得1m =-结合图象得，当11m -≤<-时，线段EF 上的所有点都是⊙M 的伴随点综上，m 的取值范围是11m -≤<-或34m <≤．11．【答案】（1）点C 、D ；22H x -≤≤-或22H x ≤≤（2）解：图形G 是以原点O 为中心，边长为2的正方形，∴原点O 到正方形的最短距离是1d =，最长距离是d =，⊙K 与图形G 关于原点O “平衡”，∴原点O 到⊙K 上一点的距离1d ≤≤，⊙K 的圆心在x 轴上，半径为2，∴当⊙K 在x 轴正半轴时，圆心K 的横坐标的取值范围为：22x -≤≤+，当⊙K 在x 轴负半轴时，圆心K 的横坐标的取值范围为：22x --≤≤，综上所述，圆心K 的横坐标的取值范围22x -≤≤+或22x --≤≤．12．【答案】（1）解：①90°；②B ；③2π（2）解：413．【答案】（1）S(2，0)（2）解：①（4，0）或（8，0）；②如图，设直线y a =上的点Q 为点A 和直线2y =-的等距点，连接QA ，过点Q 作直线2y =-的垂线，垂足为点C ．点Q 为点A 和直线2y =-的等距点，QA QC ∴=．22QA QC ∴=．点Q 在直线y a =上，∴可设点Q 的坐标为()Q x a ，．()()22262x a a ∴-+=--⎡⎤⎣⎦．整理得2123240x x a -+-=．由题意得关于x 的方程2123240x x a -+-=有实数根．()()()212413241610a a ∴∆=--⨯⨯-=+≥．解得1a ≥-．（3）解：如图．直线l 1和直线l 2的等距点在直线l 3：33y x =-+上，直线l 1和y 轴的等距点在直线4l y =+：或33y x =+上，点O 与l 4的距离为32，点O 与l 3的距离为，点O 与l 5的距离为3，当r ＜时，n=0不符合题意，当r=时，m=2，n=0，符合题意，当＜r ＜3时，m=n=2，不符合题意，当r≥3时，m=2，n=3或4，符合题意，综上所述，r=或r≥3.14．【答案】（1）C（2）解：∵P （0，1），点A （﹣2，﹣1），点B （2，﹣1）．∴AP ＝BP ＝＝2，如图2，分别以PA 、PB 为直径作圆，交x 轴于点K 1、K 2、K 3、K 4，∵OP＝OG＝1，OE∥AB，∴PE＝AE＝，∴OE＝12AG＝1，∴K1（﹣1﹣，0），k2（1﹣，0），k3（﹣1，0），k4（1+，0），∵点K为点P与线段AB的共圆点，∴﹣1﹣≤x k≤1﹣或﹣1≤x k≤1+（3）解：分两种情况：①如图3，当M在点A的左侧时，Q为线段AM上一动点，以PQ为直径的圆E与直线y＝12x+3相切于点F，连接EF，则EF⊥FH，当x＝0时，y＝3，当y＝0时，y＝12x+3＝0，x＝﹣6，∴ON＝3，OH＝6，∵tan∠EHF＝ON EFOH FH＝36＝12，设EF＝a，则FH＝2a，EH＝a，∴OE＝6﹣a，Rt △OEP 中，OP ＝1，EP ＝a ，由勾股定理得：EP 2＝OP 2+OE 2，∴2221(6)a =+-，解得：a ＝2+（舍去）或2，∴QG ＝2OE ＝2（6﹣a ）＝﹣3+2，∴m≤3﹣2；②如图4，当M 在点A 的右侧时，Q 为线段AM 上一动点，以PQ 为直径的圆E 与直线y ＝12x+3相切于点F ，连接EF ，则EF ⊥FH ，同理得QG ＝3+2，∴m≥3+2，综上，m 的取值范围是m≤3﹣2或m≥3+215．【答案】（1）2（2）解：BC 与O 相切；理由：如图2，过点O 作OH BC ⊥于H ，连接OD ，∵O 与AB 相切于D ，∴OD AB ⊥，在Rt AOD 中，30BAC ∠=︒，∴24OA OD ==，∵8AC =，∴4OC =，在ABC 中，AB BC =，∴30C BAC ∠=∠=︒，在Rt OHC 中，30C ∠=︒，∴122OH OC OD ===，∴BC 与O 相切，（3）解：①当点O 在AC 的左侧时，连接OD 交AC 于F ，如备用图1，∵O 与AB 相切于D ，∴OD AB ⊥，∵OG AC ⊥，∴30FOG BAC ∠=∠=︒，在Rt FDA 中，tan FD BAC AD ∠=，∴tan 3FD AD BAC x =⋅∠=，∴23OF x =-，在Rt FOG 中，331cos 2322y OG OF FOG ⎛⎫==⋅∠=-⨯-+ ⎪ ⎪⎝⎭，即12y x =-+，此时x 的取值范围为0x ≤≤；②当点O 在AC 的右侧时，连接DO 并延长交AC 于F ，如备用图2，同①的方法得，33FD x =，∴23OF x =-，∵FD AB ⊥，∴90BAC AFD ∠+∠=︒，∴30FOG BAC ∠=∠=︒，在Rt FOG 中，331cos 2322y OG OF FOG x x ⎛⎫==⋅∠=-⨯- ⎪⎪⎝⎭，即12y x =-，此时x 的取值范围为1433x ≤≤．16．【答案】（1）0；2-（2）解：过点O 作OD ⊥AB 于点D ，∵点A(2-，0)，B(0，．∴2OA OB ==，，∴4AB ==，∵1122OA OB AB OD ⋅=⋅，∴112422OD ⨯⨯=⨯⨯∴DO =，∵d （⊙O ，线段AB ）=0，∴当⊙O 的半径等于OD 时最小，当⊙O 的半径等于OB 时最大，∴r r ≤≤（3）43423m -<<-17．【答案】（1）2y x =+（2）解：①当2d =时，()20D ，，设直线CD 的解析式为：y kx b =+，()02C ，，202k b b +=⎧∴⎨=⎩，解得：12k b =-⎧⎨=⎩，∴直线CD 的解析式为：y x =-+，设点M 的坐标为()2m m -+，，∴点M 的关联直线为：()212y mx m m x =-+=-+，∴点M 的关联直线经过定点()12N ，，如图2，过点O 作直线2y mx m =--+的垂线，垂足为H ，连接ON ，ON OH ∴≥，∴当点H与点N重合时，OH最大，即点O到点M的关联直线的距离最大，∴点O到点M=；2 d=②或2 3-18．【答案】（1）；3（2）解：设点G是O的特征值为4的点，∴经过一点G且弦长为4(最长弦)的直线有1条，弦长为3的直线有2条，弦长为2的直线有且只有1条，经过点G的直线被O截得的弦长的最小值为2，=，∴关于O的特征值为4的所有点都在以O为半径的圆周上，直线y x b=+分别与x，y轴交于点A、B，()0A b∴-，，()B b，，OA OB b∴==，45OBH∴∠=︒，当0b>时，线段AB与以O为半径的圆相切时，点G特征值为4，设切点为为H，连接OH，则OH=，OB∴==，b∴=，设以O 为半径的圆与y 轴正半轴的交点记为1B ，则1OB =，当线段AB 与以O 1B 时，可得b =，b ≤≤同理可求当0b <时，b ≤≤，综上，b b b ≤≤-≤（3）当372122t -≤≤+时，存在点R ，S ，使得3r s +=。

(完整版)初中数学动点问题归纳

BB动点问题题型方法归纳动态几何特点----问题背景是特殊图形，考查问题也是特殊图形，所以要把握好一般与特殊的关系；分析过程中，特别要关注图形的特性（特殊角、特殊图形的性质、图形的特殊位置。

下面就此问题的常见题型作简单介绍，解题方法、关键给以点拨。

一、三角形边上动点1、（2009年齐齐哈尔市）直线364y x =-+与坐标轴分别交于A B 、两点，动点P Q 、同时从O 点出发，同时到达A 点，运动停止．点Q 沿线段OA 运动，速度为每秒1个单位长度，点P 沿路线O →B →A 运动．（1）直接写出A B 、两点的坐标；（2）设点Q 的运动时间为t 秒，OPQ △的面积为S ，求出S 与t 之间的函数关系式；（3）当485S =时，求出点P 的坐标，并直接写出以点O P Q 、、为顶点的平行四边形的第四个顶点M 的坐标．解：1、A （8，0） B （0，6）2、当0＜t ＜3时，S=t2当3＜t ＜8时，S=3／8(8-t)t提示：第（2）问按点P 到拐点B 所有时间分段分类；第（3）问是分类讨论：已知三定点O 、P 、Q ，探究第四点构成平行四边形时按已知线段身份不同分类-----①OP 为边、OQ 为边，②OP 为边、OQ 为对角线，③OP 为对角线、OQ 为边。

然后画出各类的图形，根据图形性质求顶点坐标。

2、（2009年衡阳市）如图，AB 是⊙O 的直径，弦BC=2cm ， ∠ABC=60º．（1）求⊙O 的直径；（2）若D 是AB 延长线上一点，连结CD ，当BD 长为多少时，CD 与⊙O 相切；（3）若动点E 以2cm/s 的速度从A 点出发沿着AB 方向运动，同时动点F 以1cm/s 的速度从B 点出发沿BC 方向运动，设运动时间为)20)((<<t s t ，连结EF ，当t 为何值时，△BEF 为直角三角形．注意：第（3）问按直角位置分类讨论3、（2009重庆綦江）如图，已知抛物线(1)20)y a x a =-+≠经过点(2)A -，0，抛物线的顶点为D ，过O 作射线OM AD ∥．过顶点D 平行于x 轴的直线交射线OM 于点C ，B 在x 轴正半轴上，连结BC ．（1）求该抛物线的解析式；（2）若动点P 从点O 出发，以每秒1个长度单位的速度沿射线OM 运动，设点P 运动的时间为()t s ．问当t 为何值时，四边形DAOP 分别为平行四边形？直角梯形？等腰梯形？（3）若OC OB =，动点P 和动点Q 分别从点O 和点B 同时出发，分别以每秒1单位和2个长度单位的速度沿OC 和BO 之停止运动．设它们的运动的时间为t ()s ，连接PQ ，当t 为何值时，四边形BCPQ 的面积最小？并求出最小值及此时PQ 的长．注意：发现并充分运用特殊角∠DAB=60°当△OPQ 面积最大时，四边形BCPQ 的面积最小。

中考数学综合题专题【动点综合型问题一】专题解析

中考数学综合题专题【动点综合型问题一】专题解析1．（北京模拟）已知抛物线y ＝－x2＋2x ＋m －2与y 轴交于点A （0，2m －7），与直线y ＝2x 交于点B 、C （B 在C 的右侧）．（1）求抛物线的解析式；（2）设抛物线的顶点为E ，在抛物线的对称轴上是否存在一点F ，使得∠BFE ＝∠CFE ，若存在，求出点F 的坐标，若不存在，说明理由；（3）动点P 、Q 同时从原点出发，分别以每秒 5 个单位长度、每秒25个单位长度的速度沿射线OC 运动，以PQ 为斜边在直线BC 的上方作直角三角形PMQ （直角边分别平行于坐标轴），设运动时间为t 秒．若△PMQ 与抛物线y ＝－x2＋2x ＋m －2有公共点，求t 的取值范围．解：（1）把点A （0，2m －7）代入y ＝－x2＋2x ＋m －2，得m ＝5∴抛物线的解析式为y ＝－x2＋2x ＋3（2）由⎩⎪⎨⎪⎧y ＝－x2＋2x ＋3y ＝2x 解得⎩⎨⎧x 1＝3y 1＝23 ⎩⎨⎧x 2＝－3y 2＝－23∴B （3，23），C （－3，－23） ∵y ＝－x2＋2x ＋3＝－(x －1)2＋4∴抛物线的对称轴为x ＝1设F （1，y ）∵∠BFE ＝∠CFE ，∴tan ∠BFE ＝tan ∠CFE 当点F 在点B 上方时，3－1y －23＝3＋1y ＋23解得y ＝6，∴F （1，6）当点F 在点B 下方时，3－123－y＝3＋1－y －23解得y ＝6（舍去）∴满足条件的点F 的坐标是F （1，6）（3）由题意，OP ＝5t ，OQ ＝25t ，∴PQ ＝5t ∵P 、Q 在直线直线y ＝2x 上∴设P （x ，2x ），则Q （2x ，4x ）（x＜0）∴x 2＋4x 2＝5t ，∴x ＝－t∴P （－t ，－2t ），Q （－2t ，－4t ）∴M （－2t ，－2t ）当M （－2t ，－2t ）在抛物线上时，有－2t ＝－4t2－4t ＋3解得t ＝13－14（舍去负值）当P （－t ，－2t ）在抛物线上时，有－2t ＝－t2－2t ＋3 解得t ＝3（舍去负值）∴t 的取值范围是：13－14≤t≤ 32．（北京模拟）在平面直角坐标系中，抛物线y 1＝ax2＋3x ＋c 经过原点及点A （1，2），与x 轴相交于另一点B ．（1）求抛物线y 1的解析式及B 点坐标；（2）若将抛物线y 1以x ＝3为对称轴向右翻折后，得到一条新的抛物线y 2，已知抛物线y 2与x 轴交于两点，其中右边的交点为C 点．动点P 从O 点出发，沿线段OC 向C 点运动，过P 点作x 轴的垂线，交直线OA 于D 点，以PD 为边在PD 的右侧作正方形PDEF ． ①当点E 落在抛物线y 1上时，求OP 的长；②若点P 的运动速度为每秒1个单位长度，同时线段OC 上另一点Q 从C 点出发向O 点运动，速度为每秒2个单位长度，当Q 点到达O 点时P 、Q 两点停止运动．过Q 点作x 轴的垂线，与直线AC 交于G 点，以QG 为边在QG 的左侧作正方形QGMN ．当这两个正方形分别有一条边恰好落在同一条直线上时，求t 的值．（正方形在x 轴上的边除外）解：（1）∵抛物线y 1＝ax2＋3x ＋c 经过原点及点A （1，2） ∴⎩⎪⎨⎪⎧c ＝2a ＋3＋c ＝2 解得⎩⎪⎨⎪⎧a ＝－1c ＝0 ∴抛物线y 1的解析式为y 1＝－x2＋3x令y 1＝0，得－x2＋3x ＝0，解得x 1＝0，x 2＝3∴B （3，0）（2）①由题意，可得C （6，0）过A 作AH ⊥x 轴于H ，设OP ＝a可得△ODP ∽△OAH ，∴DPOP＝AHOH＝2∴DP ＝2OP ＝2a∵正方形PDEF ，∴E （3a ，2a ）∵E （3a ，2a ）在抛物线y 1＝－x2＋3x 上∴2a ＝－9a2＋9a ，解得a 1＝0（舍去），a 2＝79∴OP 的长为79②设直线AC 的解析式为y ＝kx ＋b ∴⎩⎪⎨⎪⎧2＝k ＋b 0＝6k ＋b 解得k ＝－2 5 ，b ＝12 5∴直线AC 的解析式为y ＝－2 5 x ＋125由题意，OP ＝t ，PF ＝2t ，QC ＝2t ，GQ ＝ 45t 当EF 与MN 重合时，则OF ＋CN ＝6∴3t ＋2t ＋ 4 5 t ＝6，∴t ＝3029当EF 与GQ 重合时，则OF ＋QC ＝6∴3t ＋2t ＝6，∴t ＝65当DP 与MN 重合时，则OP ＋CN ＝6∴t ＋2t ＋ 4 5 t ＝6，∴t ＝3019当DP 与GQ 重合时，则OP ＋CQ ＝6∴t ＋2t ＝6，∴t ＝23．（北京模拟）如图，在平面直角坐标系中，抛物线y ＝ax2＋bx ＋4经过A （－3，0）、B （4，0）两点，且与y 轴交于点C ，点D 在x 轴的负半轴上，且BD ＝BC ．动点P 从点A 出发，沿线段AB 以每秒1个单位长度的速度向点B 移动，同时动点Q 从点C 出发，沿线段CA 以某一速度向点A 移动．（1）求该抛物线的解析式；（2）若经过t 秒的移动，线段PQ 被CD 垂直平分，求此时t 的值；（3）该抛物线的对称轴上是否存在一点M ，使MQ ＋MA 的值最小？若存在，求出点M 的坐标；若不存在，请说明理由．解：（1）∵抛物线y ＝ax2＋bx ＋4经过A （－3，0）、B （4，0）两点 ∴⎩⎪⎨⎪⎧9a －3b ＋4＝016a ＋4b ＋4＝0 解得a ＝－1 3 ，b ＝1 3∴所求抛物线的解析式为y ＝－ 1 3 x 2＋ 13x ＋4 （2）连接DQ ，依题意知AP ＝t∵抛物线y ＝－ 1 3 x 2＋ 13x ＋4与y 轴交于点C∴C （0，4）又A （－3，0，B （4，0）可得AC ＝5，BC ＝42，AB ＝7∵BD ＝BC ，∴AD ＝AB －BD ＝7－42∵CD 垂直平分PQ ，∴QD ＝DP ，∠CDQ ＝∠CDP ∵BD ＝BC ，∴∠DCB ＝∠CDB ∴∠CDQ ＝∠DCB ，∴DQ ∥BC∴△ADQ ∽△ABC ，∴ADAB＝DQBC∴ADAB＝DPBC，∴7－427＝DP42解得DP ＝42－32 7 ，∴AP ＝AD ＋DP ＝177∴线段PQ 被CD 垂直平分时，t 的值为177（3）设抛物线y ＝－ 1 3 x 2＋ 1 3 x ＋4的对称轴x ＝ 12与x 轴交于点E由于点A 、B 关于对称轴x ＝ 12对称，连接BQ 交对称轴于点M 则MQ ＋MA ＝MQ ＋MB ，即MQ ＋MA ＝BQ 当BQ ⊥AC 时，BQ 最小，此时∠EBM ＝∠ACO∴tan ∠EBM ＝tan ∠ACO ＝34∴ ME BE ＝ 3 4 ，即 ME 4－ 1 2＝ 34 ，解得ME ＝21 8∴M （1 2，21 8）∴在抛物线的对称轴上存在一点M （1 2，218），使得MQ ＋MA 的值最小4．（北京模拟）如图，在Rt △ABC 中，∠C ＝90°，AC ＝6，BC ＝8．动点P 从点A 出发，沿AC →CB →BA 边运动，点P 在AC 、CB 、BA 边上运动的速度分别为每秒3、4、5个单位．直线l 从与AC 重合的位置开始，以每秒 43个单位的速度沿CB 方向移动，移动过程中保持l ∥AC ，且分别与CB 、AB 边交于点E 、F ．点P 与直线l 同时出发，设运动的时间为t 秒，当点P 第一次回到点A 时，点P 和直线l 同时停止运动．（1）当t ＝_________秒时，点P 与点E 重合；当t ＝_________秒时，点P 与点F 重合；（2）当点P 在AC 边上运动时，将△PEF 绕点E 逆时针旋转，使得点P 的对应点P′ 落在EF 上，点F 的对应点为F′ ，当EF′⊥AB 时，求t 的值；（3）作点P 关于直线EF 的对称点Q ，在运动过程中，若形成的四边形PEQF 为菱形，求t 的值；（4）在整个运动过程中，设△PEF 的面积为S ，直接写出S 关于t 的函数关系式及S 的最大值．解：（1）3；4.5提示：在Rt △ABC 中，∠C ＝90°，AC ＝6，BC ＝8∴AB ＝6 2＋82＝10，∴sin B ＝ACAB ＝ 3 5 ，cos B ＝BCAB ＝ 4 5 ，tan B ＝ACBC ＝34当点P 与点E 重合时，点P 在CB 边上，CP ＝CE∵AC ＝6，点P 在AC 、CB 边上运动的速度分别为每秒3、4个单位 ∴点P 在AC 边上运动的时间为2秒，CP ＝4(t －2)∵CE＝43t，∴4(t－2)＝43t，解得t＝3当点P与点F重合时，点P在BA边上，BP＝BF∵AC＝6，BC＝8，点P在AC、CB、BA边上运动的速度分别为每秒3、4、5个单位∴点P在AC、CB边上运动的时间共为4秒，BF＝BP＝5(t－4)∵CE＝43t，∴BE＝8－4 3t在Rt△BEF中，BEBF＝cos B∴8－43t5(t－4)＝45，解得t＝4.5（2）由题意，∠PEF＝∠MEN∵EF∥AC，∠C＝90°，∴∠BEF＝90°，∠CPE＝∠PEF ∵EN⊥AB，∴∠B＝∠MEN∴∠CPE＝∠B，∴tan∠CPE＝tan B∵tan∠CPE＝CECP，tan B＝ACBC＝34∴CECP＝34，∴CP＝43CE∵AP＝3t（0＜t＜2），CE＝43t，∴CP＝6－3t∴6－3t＝43×43t，解得t＝5443（3）连接PQ交EF于O∵P、Q关于直线EF对称，∴EF垂直平分PQ若四边形PEQF为菱形，则OE＝OF＝1 2EF①当点P在AC边上运动时易知四边形POEC为矩形，∴OE＝PC ∴PC＝12EF∵CE＝43t，∴BE＝8－43t，EF＝BE·tan B＝34(8－43t)＝6－t∴6－3t＝12(6－t)，解得t＝6 5②当点P在CB边上运动时，P、E、Q三点共线，不存在四边形PEQF③当点P在BA边上运动时，则点P在点B、F之间∵BE＝8－43t，∴BF＝BEcos B＝54(8－43t)＝10－53t∵BP＝5(t－4)，∴PF＝BF－BP＝10－53t－5(t－4)＝30－20 3t∵∠POF＝∠BEF＝90°，∴PO∥BE，∴∠OPF＝∠B在Rt△POF中，OFPF＝sin B∴12(6－t)30－203t＝35，解得t＝307∴当t ＝6 5或t ＝307时，四边形PEQF 为菱形（4）S ＝⎩⎪⎪⎨⎪⎪⎧－23t 2＋4t （0≤t≤2）4 3t2－12t ＋24（2＜t≤3）－43t2＋12t －24（3＜t≤4）83t2－28t ＋72（4＜t≤4.5）－8 3t2＋28t －72（4.5＜t≤6）S 的最大值为1635．（北京模拟）在等腰梯形ABCD 中，AB ∥CD ，AB ＝10，CD ＝6，AD ＝BC ＝4．点P 从点B 出发，沿线段BA 向点A 匀速运动，速度为每秒2个单位，过点P 作直线BC 的垂线PE ，垂足为E ．设点P 的运动时间为t （秒）．（1）∠A ＝___________°；（2）将△PBE 沿直线PE 翻折，得到△PB′E ，记△PB′E 与梯形ABCD 重叠部分的面积为S ，求S 与t 之间的函数关系式，并求出S 的最大值；（3）在整个运动过程中，是否存在以点D 、P 、B′为顶点的三角形为直角三角形或等腰三角形？若存在，求出t 的值；若不存在，请说明理由．解：（1）60°（2）∵∠A ＝∠B ＝60°，PB ＝PB′ ∴△PB′B 是等边三角形∴PB ＝PB′＝BB′＝2t ，BE ＝B′E ＝t ，PE ＝3t 当0＜t ≤2时S ＝S △PB′E＝1 2 B′E ·PE ＝ 1 2 t ·3t ＝ 32t2 当2＜t≤4时S ＝S △PB′E － S △FB′C ＝ 3 2 t2－ 3 4 ( 2t －4 )2＝－ 32t2＋43t －4 3 当4＜t≤5时设PB′、PE 分别交DC 于点G 、H ，作GK ⊥PH 于K ∵△PB′B 是等边三角形，∴∠B′PB ＝60°＝∠A ∴PG ∥AD ，又DG ∥AP ∴四边形APGD 是平行四边形∴PG ＝AD ＝4∵AB ∥CD ，∴∠GHP ＝∠BPH∵∠GPH ＝∠BPH ＝12∠B′PB ＝30°∴∠GHP ＝∠GPH ＝30°，∴PG ＝GH ＝4∴GK ＝12PG ＝2，PK ＝KH ＝PG ·cos30°＝2 3∴PH ＝2PK ＝4 3∴S ＝S △PGH＝1 2 PH ·GK ＝12×43×2＝4 3 综上得，S 与t 之间的函数关系式为：S ＝⎩⎪⎨⎪⎧32t 2（0＜t≤2）－32t 2＋43t －43（2＜t≤4）43（4＜t≤5）（3）①若∠DPB′＝90° ∵∠B′PB ＝60°，∴∠DPA ＝30° 又∠A ＝60°，∴∠ADP ＝90° ∴AP ＝2AD ，∴10－2t ＝8，∴t ＝1 若∠PDB′＝90°作DM ⊥AB 于M ，DN ⊥B′B 于N则AM ＝2，DM ＝23，NC ＝3，DN ＝3 3PM ＝|10－2－2t |＝|8－2t | NB′＝|3＋4－2t |＝|7－2t |DP 2＝DM 2＋PM 2＝(23 )2＋( 8－2t )2＝( 8－2t)2＋12 DB′ 2＝DN 2＋NB′＝( 33 )2＋( 7－2t )2＝( 7－2t)2＋27∵DP 2＋DB′ 2＝B′P 2∴(8－2t )2＋12＋( 7－2t )2＋27＝( 2t)2解得t 1＝15＋73 2＞5（舍去），t 2＝15－732若∠DB′P ＝90°，则DB′ 2＋B′P 2＝DP 2 ∴(7－2t )2＋27＋( 2t )2＝( 8－2t)2＋12解得t 1＝－1（舍去），t 2＝0（舍去）∴存在以点D 、P 、B′为顶点的三角形为直角三角形，此时t ＝1或t ＝15－732②若DP ＝B′P ，则(8－2t )2＋12＝( 2t)2解得t ＝198若B′D ＝B′P ，则( 7－2t )2＋27＝( 2t)2解得t ＝197若DP ＝DB′，则( 8－2t )2＋12＝( 7－2t)2＋27 解得t ＝0（舍去）∴存在以点D 、P 、B′为顶点的三角形为等腰三角形，此时t ＝19 8或t ＝1976．（北京模拟）已知二次函数y ＝－ 33mx 2＋3mx －2的图象与x 轴交于点A （23，0）、点B ，与y 轴交于点C ．（1）求点B 坐标；（2）点P 从点C 出发以每秒1个单位的速度沿线段CO 向O 点运动，到达点O 后停止运动，过点P 作PQ ∥AC 交OA 于点Q ，将四边形PQAC 沿PQ 翻折，得到四边形PQA′C′，设点P 的运动时间为t ．①当t 为何值时，点A′恰好落在二次函数y ＝－33mx2＋3mx －2图象的对称轴上；②设四边形PQA′C′落在第一象限内的图形面积为S ，求S 关于t 的函数关系式，并求出S 的最大值．解：（1）将A （2 3，0）代入y ＝－ 33mx2＋3mx －2得0＝－ 3 3 m ×( 2 3 )2＋3m ×2 3－2，解得m ＝33∴y ＝－ 13x2＋3x －2令y ＝0，得－ 13x2＋3x －2＝0，解得：x 1＝3，x 2＝2 3∴B（3，0）（2）①由y ＝－13x2＋3x －2，令x ＝0，得y ＝－2∴C （0，－2）∵y ＝－1 3 x 2＋3x －2＝－ 1 3 ( x － 323 )2＋14∴二次函数图象的对称轴为直线x ＝ 323过A′作A′H ⊥OA 于H在Rt △AOC 中，∵OC ＝2，OA ＝2 3 ∴∠OAC ＝30°，∠OCA ＝60°∴∠PQA ＝150°，∠A′QH ＝60°，AQ ＝A′Q ＝2QH ∵点A′在二次函数图象的对称轴上∴⎩⎪⎨⎪⎧OQ ＋QH ＝3 23OQ ＋2QH ＝23解得QH ＝32∴AQ ＝3，CP ＝1 ∴t ＝1②分两种情况：ⅰ）当0＜t≤1时，四边形PQA′C′ 落在第一象限内的图形为等腰三角形QA′DDQ ＝A′Q ＝3tA′H ＝AQ ·sin60°＝3t ·3 2＝32tS＝S△A′DQ＝12·3t·32t＝334t2∵当0＜t≤1时，S随t的增大而增大∴当t＝1时，S有最大值334ⅱ）当1＜t＜2时，四边形PQA′C′落在第一象限内的图形为四边形EOQA′S四边形EOQA′＝S梯形PQA′C′－S△OPQ－S△PC′E＝[23－32(2－t)2]－32(2－t)2－34t2＝－534t2＋43t－2 3∵－534t2＋43t－23＝－534(t－85)2＋635且1＜85＜2，∴当t＝85时，S有最大值635∵635＞334，∴S的最大值是6357．（北京模拟）已知梯形ABCD中，AD∥BC，∠A＝120°，E是AB的中点，过E点作射线EF∥BC，交CD于点G，AB、AD的长恰好是方程x2－4x＋a2＋2a＋5＝0的两个相等实数根，动点P、Q分别从点A、E出发，点P以每秒1个单位长度的速度沿AB由A向B运动，点Q以每秒2个单位长度的速度沿EF由E向F运动，设点P、Q运动的时间为t（秒）．（1）求线段AB、AD的长；（2）当t＞1时，求△DPQ的面积S与时间t之间的函数关系式；（3）是否存在△DPQ是直角三角形的情况，如果存在，求出时间t；如果不存在，请说明理由．解：（1）由题意，△＝42－4(a2＋2a＋5)＝－4(a＋1)2＝0∴a＝－1原方程可化为x2－4＋4＝0，解得∴x1＝x2＝2∴AB＝AD＝ 2 （2）作AH⊥BC于H，交EG于O，DK⊥EF于K，PM⊥DA交DA的延长线于M∵AD∥BC，∠A＝120°，AB＝AD＝2∴∠B＝60°，AH＝ 3∵E是AB中点，且EF∥BC，∴AO＝DK＝32∵AP＝t，∴PM＝32t∵t＞1，∴点P在点E下方延长FE交PM于S，设DP与EF交于点N则PS＝32t－32∵AD∥BC，EF∥BC，∴EF∥AD∴EN AD＝PEPA，∴EN2＝t－1t∴EN＝2(t－1)t，∴QN＝2t－2(t－1)t∴S＝12(2t－2(t－1)t)(32t－32＋32)＝32t2－32t＋32即S＝32t2－32t＋32（t＞1）（3）由题意，AM＝12t，∴DM＝2＋12t∴DP2＝DM2＋PM2＝(2＋12t)2＋(32t)2＝t2＋2t＋4又DQ2＝DK2＋KQ2＝(32)2＋(2t－12－2)2＝4t2－10t＋7PQ2＝PS2＋SQ2＝(32t－32)2＋(2t＋t－12)2＝7t2－4t＋1①若∠PDQ＝90°，则DP2＋DQ2＝PQ2∴t2＋2t＋4＋4t2－10t＋7＝7t2－4t＋1 解得t＝6－1（舍去负值）②若∠DPQ＝90°，则PD2＋PQ2＝DQ2∴t2＋2t＋4＋7t2－4t＋1＝4t2－10t＋7解得t＝62－1（舍去负值）③若∠DQP＝90°，则DQ2＋PQ2＝PD2∴4t2－10t＋7＋7t2－4t＋1＝t2＋2t＋4解得t＝4±6 5综上所述，存在△DPQ是直角三角形的情况，此时t＝6－1，t＝62－1，t＝4±658．（天津模拟）如图，在平面直角坐标系中，直y＝－x＋42交x轴于点A，交y轴于点B．在线段OA上有一动点P，以每秒2个单位长度的速度由点O向点A匀速运动，以OP 为边作正方形OPQM交y轴于点M，连接QA和QB，并从QA和QB的中点C和D向AB 作垂线，垂足分别为点F和点E．设P点运动的时间为t秒，四边形CDEF的面积为S1，正方形OPQM与四边形CDEF重叠部分的面积为S2．（1）直接写出A点和B点坐标及t的取值范围；（2）当t＝1时，求S1的值；（3）试求S2与t的函数关系式（4）直接写出在整个运动过程中，点C和点D所走过的路程之和．解：（1）A（42，0）、B（0，42），0≤t≤4（2）过Q作QH⊥AB于H∵C、D分别是QA和QB的中点∴CD∥AB，CD＝12AB＝12×42×2＝4∵CF⊥AB，DE⊥AB，∴CF∥DE∴四边形CDEF是平行四边形又∵CF⊥AB，∴四边形CDEF是矩形∵CF⊥AB，QH⊥AB，∴CF∥QH又∵C是QA中点，∴CF＝12QH连接OQ∵正方形OPQM，∴∠1＝∠2，OP＝PQ＝QM＝MO∵OA＝OB，∴PA＝MB∴Rt△QPA≌Rt△QMB，∴QA＝QB，∠PQA＝∠MQB∵QH⊥AB，∴∠3＝∠4∴∠1＋∠MQB＋∠3＝180°，∴O、Q、H三点共线∴QH＝OH－OQ∵t＝1，点P的运动速度为每秒2个单位长度∴OP＝2，∴OQ＝2又∵OA＝42，∴OH＝4∴QH＝OH－OQ＝4－2＝2，∴CF＝1∴S1＝CD·CF＝4×1＝4（3）当点Q落在AB上时，OQ⊥AB，△QOA是等腰直角三角形∴t＝22÷2＝2当0≤t≤2时，S2＝0当点E落在QM上，点F落在PQ上时，△CFK和△DEG都是等腰直角三角形过C作CT⊥PQ于T则CT＝12AP＝12(42－2t)＝22(4－t)∴CF＝2CT＝4－t连接OQ，分别交AB、CD于N、R则ON＝22OA＝22×42＝4∵OP＝2t，∴OQ＝2t，∴QN＝2t－4∴CF＝12QN＝t－2∴4－t＝t－2，∴t＝3当2＜t≤3时，重叠部分为等腰梯形GHIK △QGK和△QHI都是等腰直角三角形∵QN＝2t－4，RN＝CF＝t－2，∴QR＝t－2 ∴GK＝2QR＝2t－4，HI＝2QN＝4t－8∴S 2＝1 2 (GK ＋HI)·RN ＝12(2t －4＋4t －8)(t －2)＝3(t －2)2 当3＜t≤4时，重叠部分为六边形GHEFIK易知Rt △CIK ≌Rt △DHG ，∴GH ＝KI ＝2CT ＝2(4－t)∴S 2＝S 矩形CDEF－2S △CIK＝CD ·CF －KI ·CT＝4(t －2)－2(4－t)·22(4－t)＝－t 2＋12t －24综上得S 2关于t 的函数关系式为：S 2＝⎩⎪⎨⎪⎧0（0≤t≤2）3(t －2 )2（2＜t≤3）－t 2＋12t －24（3＜t≤4）（4）8提示：点C 和点D 走过的路程分别为以OP 为边的正方形的对角线的一半9．（上海模拟）如图，正方形ABCD 中，AB ＝5，点E 是BC 延长线上一点，CE ＝BC ，连接BD ．动点M 从B 出发，以每秒2个单位长度的速度沿BD 向D 运动；动点N 从E 出发，以每秒2个单位长度的速度沿EB 向B 运动，两点同时出发，当其中一点到达终点后另一点也停止运动．设运动时间为t 秒，过M 作BD 的垂线MP 交BE 于P ．（1）当PN ＝2时，求运动时间t ；（2）是否存在这样的t ，使△MPN 为等腰三角形？若存在，求出t 的值；若不存在，请说明理由；（3）设△MPN 与△BCD 重叠部分的面积为S ，直接写出S 与t 的函数关系式和函数的定义域．解：（1）∵正方形ABCD ，∴∠DBC ＝45° ∵MP ⊥DB ，∴△BMP 是等腰直角三角形 ∵BM ＝2t ，∴BP ＝2BM ＝2t 又PN ＝2，NE ＝2t当0＜t＜2.5时，BP ＋PN ＋NE ＝BE∴2t ＋2＋2t ＝10，∴t ＝2当2.5＜t＜5时，BP －PN ＋NE ＝BE∴2t －2＋2t ＝10，∴t ＝3（2）过M 作MH ⊥BC 于H则△NQC ∽△NMH ，∴QCCN＝MHHN∴QC5－2t＝t10－t －2t，∴QC ＝5t －2t 210－3t令QC ＝y ，则y ＝5t －2t 210－3t整理得2t 2－(3y ＋5)t ＋10y ＝0∵t 为实数，∴[－(3y ＋5)]2－4×2×10y≥0即9y 2－50y ＋25≥0，解得y≥5（舍去）或y≤59∴线段QC 长度的最大值为59（3）当0＜t＜2.5时∵∠MPN ＝∠DBC ＋∠BMP ＝45°＋90°＝135° ∴∠MPN 为钝角，∴MN＞MP ，MN＞PN若PM ＝PN ，则2t ＝10－4t解得t ＝57(4－2) 当2.5＜t＜5时∵∠MNP ＞∠MBP ＝∠MPB ，∴MP＞MN 若MN ＝PN ，则∠PMN ＝∠MPN ＝45°∴∠MNP ＝90°，即MN ⊥BP ∴BN ＝NP ，BP ＝2BN ∴2t ＝2(10－2t)，解得t ＝103若PM ＝PN∵PN ＝BP －BN ＝BP －(BE －NE)＝BP ＋NE －BE∴2t ＝2t ＋2t －10，解得t ＝57(4＋2)∴当t ＝ 5 7 ( 4－2 )，t ＝ 10 3 ，t ＝ 57( 4＋2)时，△MPN 为等腰三角形（4）S ＝⎩⎨⎧ 8t 3－50t 2＋75t20－6t（0＜t＜2.5）5t － 252（2.5＜t＜5）10．（重庆模拟）如图，已知△ABC 是等边三角形，点O 是AC 的中点，OB ＝12，动点P 在线段AB 上从点A 向点B 以每秒3个单位的速度运动，设运动时间为t 秒．以点P 为顶点，作等边△PMN ，点M ，N 在直线OB 上，取OB 的中点D ，以OD 为边在△AOB 内部作如图所示的矩形ODEF ，点E 在线段AB 上．（1）求当等边△PMN 的顶点M 运动到与点O 重合时t 的值；（2）求等边△PMN 的边长（用含t 的代数式表示）；（3）设等边△PMN 和矩形ODEF 重叠部分的面积为S ，请直接写出S 与t 的函数关系式及自变量t 的取值范围；（4）点P 在运动过程中，是否存在点M ，使得△EFM 是等腰三角形？若存在，求出对应的t 的值；若不存在，请说明理由．解：（1）当点M 与点O 重合时∵△ABC 、△PMN 是等边三角形，O 为AC 中点 ∴∠AOP ＝30°，∠APO ＝90°∵OB ＝12，∴AO ＝43＝2AP ＝23t 解得t ＝2∴当t ＝2时，点M 与点O 重合（2）由题设知∠ABM ＝30°，AB ＝83，AP ＝3t ∴PB ＝83－3t ，PM ＝PB ·tan30°＝8－t 即等边△PMN 的边长为8－t（3）S ＝⎩⎪⎨⎪⎧23t ＋63（0≤t≤1）－23t2＋63t ＋43（1＜t≤2）－32t2＋103（2＜t≤4）23t2－203t ＋503（4＜t≤5）0（5＜t≤8）提示：①当0≤t≤1时，PM 经过线段AF设PM 交AF 于点J ，PN 交EF 于点G ，则重叠部分为直角梯形FONG ∵AP ＝3t ，∴AJ ＝23t ，JO ＝43－23t MO ＝4－2t ，ON ＝8－t －(4－2t)＝4＋t作GH ⊥ON 于H则GH ＝FO ＝23，HN ＝2，FG ＝OH ＝4＋t －2＝2＋t∴S ＝S 梯形FONG＝12(FG ＋ON)·FO＝ 12( 2＋t ＋4＋t)·23＝23t ＋6 3 ②当1＜t≤2时，PM 经过线段FO设PM 交EF 于点I ，则重叠部分为五边形IJONG FJ ＝AJ －AF ＝23t －23，FI ＝2t －2∴S ＝S 梯形FONG －S △FIJ ＝23t ＋63－ 12( 23t －23 )( 2t －2) ＝－23t 2＋63t ＋4 3③当2＜t≤4时，PN 经过线段ED设PN 交ED 于点K ，则重叠部分为五边形IMDKG ∵AP ＝3t ，∴PE ＝43－3t ∴IG ＝GE ＝4－t ，EK ＝43－3t∴KD ＝23－( 43－3t)＝3t －23，DN ＝t －2∴S ＝S 梯形IMNG－S △KDN＝1 2 (4－t ＋8－t)·23－12(3t －23)(t －2)＝－32t 2＋10 3④当4＜t≤5时，PM 经过线段ED设PM 交ED 于点R ，则重叠部分为△RMD ∵AP ＝3t ，∴EP ＝3t －4 3∴ER＝2EP＝23t－8 3∴RD＝23－(23t－83)＝103－23t MD＝10－2t∴S＝S△RMD＝12(10－2t)(103－23t)＝23t2－203t＋50 3⑤当5＜t≤8时，S＝0（4）∵MN＝BN＝PN＝8－t，∴MB＝16－2t①若FM＝EM，则M为OD中点∴OM＝3∵OM＋MB＝OB，∴3＋16－2t＝12∴t＝3.5②若FM＝FE＝6，则OM＝62－(23)2＝2 6∵OM＋MB＝OB，∴26＋16－2t＝12∴t＝2＋ 6③若EF＝EM＝6，点M在OD或DB上则DM＝62－(23)2＝2 6∴DB＋DM＝MB或者DB－DM＝MB∴6＋26＝16－2t或6－26＝16－2t∴t＝5－6或t＝5＋ 6综上所述，当t＝3.5、2＋6、5－6、5＋6时，△MEF是等腰三角形11．（浙江某校自主招生）如图，正方形OABC的顶点O在坐标原点，且OA边和AB边所在直线的解析式分别为y＝34x和y＝－43x＋253．（1）求正方形OABC的边长；（2）现有动点P、Q分别从C、A同时出发，点P沿线段CB向终点B运动，速度为每秒1个单位，点Q沿折线A→O→C向终点C运动，速度为每秒k个单位，设运动时间为2秒．当k为何值时，将△CPQ沿它的一边翻折，使得翻折前后的两个三角形组成的四边形为菱形？（3）若正方形以每秒53个单位的速度沿射线AO下滑，直至顶点B落在x轴上时停止下滑．设正方形在x轴下方部分的面积为S，求S关于滑行时间t的函数关系式，并写出相应自变量t的取值范围．解：（1）联立⎩⎨⎧y ＝ 3 4x y ＝－ 4 3 x ＋25 3解得⎩⎪⎨⎪⎧x ＝4y ＝3∴A （4，3），∴OA ＝4 2＋32＝5∴正方形OABC 的边长为5（2）要使△CPQ 沿它的一边翻折，翻折前后的两个三角形组成的四边形为菱形，根据轴对称的性质，只需△CPQ 为等腰三角形即可当t ＝2秒时∵点P 的速度为每秒1个单位，∴CP ＝2 分两种情况：①当点Q 在OA 上时，∵PQ ≥BA ＞PC ，∴只存在一点Q ，使QC ＝QP作QN ⊥CP 于N ，则CN ＝12CP ＝OQ ＝1∴QA ＝5－1＝4，∴k ＝ 42＝2②当点Q 在OC 上时，同理只存在一点Q ，使CP ＝CQ ＝2∴OQ ＋OA ＝10－2＝8，∴k ＝ 82＝4综上所述，当t ＝2秒时，以所得的等腰三角形CPQ 沿底边翻折，翻折后得到菱形的k 值为2或4 （3）①当点A 运动到点O 时，t ＝3 当0＜t≤3时，设O′C′ 交x 轴于点D则tan ∠DOO′＝ 3 4 ，即 DO′ OO′ ＝ DO′5 3t＝ 3 4 ，∴DO′＝ 54t∴S ＝ 1 2 DO′·OO′＝ 1 2 ·5 4 t ·5 3 t ＝ 25 24t 2②当点C 运动到x 轴上时，t ＝( 5× 4 3)÷53＝4 当3＜t≤4时，设A′B′ 交x 轴于点E∵A′O ＝ 5 3 t －5，∴A′E ＝ 3 4 A′O ＝5t －154∴S ＝ 1 2 ( A′E ＋O′D )·A′O′＝ 1 2 ( 5t －15 4 ＋ 5 4 t )·5＝50t －75 8③当点B 运动到x 轴上时，t ＝( 5＋5× 4 3)÷53＝7 当4＜t≤7时，设B′C′ 交x 轴于点F∵A′E ＝ 5t －15 4 ，∴B′E ＝5－ 5t －15 4 ＝35－5t4∴B′F ＝ 4 3 B′E ＝35－5t3∴S ＝5 2－ 1 2 · 35－5t 4 · 35－5t 3 ＝－ 25 24 t 2＋ 175 12 t －62524综上所述，S 关于滑行时间t 的函数关系式为：数学专题之【动点综合型问题】精品解析———————————————————————————————————————S ＝ ⎩⎪⎨⎪⎧2524t 2（0＜t≤3）50t －758（3＜t≤4）－25 24t2＋175 12t －625 24（4＜t≤7）12．（浙江某校自主招生）如图，正方形ABCD 的边长为8cm ，动点P 从点A 出发沿AB 边以1cm /秒的速度向点B 匀速移动（点P 不与点A 、B 重合），动点Q 从点B 出发沿折线BC －CD 以2cm /秒的速度匀速移动．点P 、Q 同时出发，当点P 停止时，点Q 也随之停止．连接AQ 交BD 于点E ．设点P 运动时间为t （秒）．（1）当点Q 在线段BC 上运动时，点P 出发多少时间后，∠BEP ＝∠BEQ ？（2）设△APE 的面积为S （cm 2），求S 关于t 的函数关系式，并写出t 的取值范围；（3）当4＜t ＜8时，求△APE 的面积为S 的变化范围．解（1）AP ＝x cm ，BQ ＝2x cm∵∠BEP ＝∠BEQ ，BE ＝BE ，∠PBE ＝∠QBE ＝45° ∴△PBE ≌△QBE ，∴PB ＝BQ即8－x ＝2x ，∴x ＝83∴点P 出发83秒后，∠BEP ＝∠BEQ（2）①当0＜x≤4时，点Q 在BC 上，作EN ⊥AB 于N ，EM ⊥BC 于M∵AD ∥BC ，∴ AE EQ ＝ ADBQ ＝ 8 2x ＝4x即 AE EQ ＝ 4 x ，∴ AEAQ ＝4 x ＋4∴ NE BQ ＝ AE AQ ，∴NE ＝ AE ·BQAQ ＝8x x ＋4∴S ＝ 1 2 AP ·NE ＝ 1 2 x · 8x x ＋4 ＝4x2x ＋4即S ＝ 4x2x ＋4（0＜x≤4）②当4＜x＜8时，点Q 在CD 上，作QF ⊥AB 于F ，交BD 于H 则 AE EQ ＝ ADHQ ＝ 8 16－2x ＝4 8－x即 AE EQ ＝ 4 8－x ，∴ AEAQ ＝ 4 8－x ＋4 ＝4 12－x作EN ⊥AB 于N ，则 NE FQ ＝AEAQ∴NE ＝ AE ·FQFQ ＝32 12－x∴S ＝1 2 AP ·NE ＝ 1 2 x ·32 12－x ＝16x 12－x即S ＝ 16x12－x（4＜x＜8）（3）当4＜x ＜8时，由S ＝ 16x 12－x ，得x ＝12S16＋S∵4＜x ＜8，∴4＜ 12S16＋S＜8∵S＞0，∴16＋S＞0，∴4(16＋S)＜12S＜8(16＋S) 解得8＜S＜3213．（浙江模拟）如图，菱形ABCD 的边长为6且∠DAB ＝60°，以点A 为原点、边AB 所在直线为x 轴且顶点D 在第一象限建立平面直角坐标系．动点P 从点D 出发沿折线D －C －B 向终点B 以每秒2个单位的速度运动，同时动点Q 从点A 出发沿x 轴负半轴以每秒1个单位的速度运动，当点P 到达终点时停止运动．设运动时间为t ，直线PQ 交边AD 于点E ．（1）求出经过A 、D 、C 三点的抛物线解析式；（2）是否存在时刻t ，使得PQ ⊥BD ？若存在，求出t 值，若不存在，请说明理由；（3）设AE 长为y ，试求y 与t 之间的函数关系式；（4）若F 、G 为DC 边上两点，且点DF ＝FG ＝1，试在对角线DB 上找一点M 、抛物线对称轴上找一点N ，使得四边形FMNG 周长最小并求出周长最小值．解：（1）由题意得：D （3，33）、C （9，33）设经过A 、D 、C 三点的抛物线解析式为y ＝ax2＋bx 把D 、C 两点坐标代入上式，得： ⎩⎨⎧9a ＋3b ＝3381a ＋9b ＝33解得：a ＝－3 9 ，b ＝43 3∴抛物线的解析式为：y ＝－3 9 x2＋433x （2）连接AC∵四边形ABCD 是菱形，∴AC ⊥BD 若PQ ⊥BD ，则PQ ∥AC 当点P 在DC 上时∵PC ∥AQ ，PQ ∥AC ，∴四边形PQAC 是平行四边形 ∴PC ＝AQ ，即6－2t ＝t,∴t ＝2当点P 在CB 上时，PQ 与AC 相交，此时不存在符合要求的t 值（3）①当点P 在DC 上，即0≤t≤3时∵DP ∥AQ ，∴△DEP ∽△AEQ ∴DEy＝DPAQ＝2tt＝2，∴y ＝13AD ＝2②当点P 在CB 上，即3＜t≤6时∵AE ∥BP ，∴△QEA ∽△QPB∴AEBP＝QAQB，即y12－2t＝t6＋t∴y ＝12－2t6＋t综上所述，y 与t 之间的函数关系式为： y ＝⎩⎪⎨⎪⎧2 （0≤t≤3）12－2t6＋t（3＜t≤6）（4）作点F 关于直线BD 的对称点F′，由菱形对称性知F′ 在DA 上，且DF′＝DF ＝1作点G 关于抛物线对称轴的对称点G′，易求DG′＝4连接F′G′ 交DB 于点M 、交对称轴于点N ，则点M 、N 即为所求的两点过F′ 作F′H ⊥DG′ 于H ，可得HD ＝1 2 ，F′H ＝ 3 2 ，HG′＝92∴F′G′＝F′H 2＋HG′ 2＝21∴四边形FMNG 周长最小值为F′G′＋FG ＝21＋114．（浙江模拟）如图，直线y ＝－x ＋5和直线y ＝kx －4交于点C （3，m ），两直线分别交y 轴于点A 和点B ，一平行于y 轴的直线l 从点C 出发水平向左平移，速度为每秒1个单位，运动时间为t ，且分别交AC 、BC 于点P 、Q ，以PQ 为一边向左侧作正方形PQDE ．（1）求m 和k 的值；（2）当t 为何值时，正方形的边DE 刚好在y 轴上？（3）当直线l 从点C 出发开始运动的同时，点M 也同时在线段AB 上由点A 向点B 以每秒4个单位的速度运动，问点M 从进入正方形PQDE 到离开正方形持续的时间有多长？解：（1）把C （3，m ）代入y ＝－x ＋5得m ＝2 ∴C （3，2），代入y ＝kx －4得k ＝2 （2）由题意，点P 横坐标为3－t当x ＝3－t 时，y ＝－x ＋5＝t ＋2，∴P （3－t ，t ＋2） ∵PQ ∥y 轴，∴点Q 横坐标为3－t当x ＝3－t 时，y ＝2x －4＝2－2t ，∴Q （3－t ，2－2t ） ∴PQ ＝t ＋2－(2－2t)＝3t∵正方形PQDE ，∴PQ ＝PE当正方形的边DE刚好在y轴上时，3t＝3－t，∴t＝3 4（3）∵直线y＝－x＋5交y轴于点A，∴A（0，5）∴点M坐标为（0，5－4t）当点M和点P的纵坐标相等时，5－4t＝t＋2，∴t＝3 5∵3 5＜34，∴点M进入正方形PQDE时，t＝34当点M和点Q的纵坐标相等时，5－4t＝2－2t，∴t＝3 2∴点M从进入正方形PQDE到离开正方形持续的时间为：t＝32－34＝3415．（浙江模拟）如图，在平面直角坐标系中，O为坐标原点，Rt△OAB的直角边OA在x 轴的正半轴上，点B坐标为（3，1），以OB所在直线为对称轴将△OAB作轴对称变换得△OCB．动点P从点O出发，沿线段OA向点A运动，动点Q从点C出发，沿线段CO向点O运动．P、Q两点同时出发，速度都为每秒1个单位长度．设点P运动的时间为t（秒）．（1）求∠AOC的度数；（2）记四边形BCQP的面积为S（平方单位），求S与t之间的函数关系式；（3）设PQ与OB交于点M．①当△OMQ为等腰三角形时，求t的值．②探究线段OM长度的最大值，说明理由．解：（1）∵点B坐标为（3，1），∴OA＝3，AB＝1∴在Rt△OAB中，tan∠AOB＝ABOA＝13＝33∴∠AOB＝30°∵将△OAB作轴对称变换得△OCB∴△OCB≌△OAB，∴∠COB＝∠AOB＝30°∴∠AOC＝60°（2）∵OP＝CQ＝t，AB＝1，OC＝OA＝ 3 ∴AP＝OQ＝3－t∴S＝2S△OAB－S△OPQ－S△PAB＝OA·AB－12OP·OQ·sin∠AOC－12PA·AB＝3×1－12×t×(3－t)×32－12×(3－t)×1＝34t2－14t＋32（3）①若△OMQ为等腰三角形，则可能有三种情况：（i）若OM＝MQ，则∠MQO＝∠MOQ＝30°∵∠AOC＝60°，∴∠OPQ＝90°∴OP＝12OQ，即t＝12(3－t)解得：t＝3 3（ii）若OM＝OQ，则∠OMQ＝∠OQM＝75°∵∠AOC＝60°，∴∠OPQ＝45°过点Q作QD⊥OA于D，则QD＝DP即32(3－t)＝t－12(3－t)解得：t＝1（iii）若MQ＝OQ，则∠OMQ＝∠MOQ＝∠MOP 得PQ∥OA，显然不符合题意②分别过点P、Q作OB的垂线，垂足分别为E、F ∵OP＝t，OQ＝3－t，∠MOP＝∠MOQ＝30°∴S△OPQ＝S△OPM＋S△OOM＝12OM·PE＋12OM·QF＝14OM·OP＋14OM·OQ＝14OM(OP＋OQ)＝14OM(t＋3－t)＝34OM过点Q作QG⊥OA于G则S△OPQ＝12OP·QG＝12OP·OQ·sin60°＝34t(3－t)＝－34(t2－3t)∴34OM＝－34(t2－3t)∴OM＝－(t2－3t)＝－(t－32)2＋3 4∴当t＝32时，线段OM的长度取得最大值3416．（浙江模拟）已知直线y＝43x＋4与x轴、y轴分别相交于点A、B，点C从O点出发沿射线OA以每秒1个单位长度的速度匀速运动，同时点D从A点出发沿AB以每秒1个单位长度的速度向B点匀速运动，当点D到达B点时C、D都停止运动．点E是CD的中点，直线EF⊥CD交y轴于点F，点E′与E点关于y轴对称．点C、D的运动时间为t（秒）．（1）当t＝________秒时，点F经过原点O；（2）设四边形BDCO的面积为S，求S与t的函数关系式；（3）当直线EF与△AOB的一边垂直时，求t的值；（4）以CD为一边，在CD的右侧作菱形CDMN，其中DM∥x轴．当点N在直线E′F左侧时，直接写出菱形CDMN与△EFE′重叠部分为轴对称图形时t的取值范围．解：（1）5 2提示：∵直线y＝43x＋4与x轴、y轴分别相交于点A、B∴A（－3，0），B（0，4），∴AO＝3，BO＝4 ∴AB＝AO2＋BO2＝32＋42＝5当点F经过原点时，连接OD由题意，EF是CD的垂直平分线∴OD＝OC＝t∵AD＝t，∴AD＝OD，∴∠DAO＝∠DOA∵∠DBO＋∠DAO＝90°，∠DOB＋∠DOA＝90°∴∠DBO＝∠DOB，∴OD＝BD∴AD＝BD，∴AD＝12AB＝5 2（2）∵AO＝3，BO＝4，AB＝5∴sin∠BAO＝BOAB＝45，cos∠BAO＝AOAB＝35过D作DH⊥AC于H当0≤t≤3时∵CO＝t，AD＝t，∴AC＝3－t，DH＝AD·sin∠BAO＝45t∴S＝S△ABO－S△ADC＝12×3×4－12·(3－t)·45t＝25t2－65t＋6当3＜t≤5时，AC＝t－3∴S＝S△ABO＋S△ADC＝12×3×4＋12·(t－3)·45t＝25t2－65t＋6综合得S与t的函数关系式为：S＝25t2－65t＋6（0≤t≤5）（3）当EF⊥BO时∵EF⊥CD，∴CD∥BO，∴∠ACD＝90°在Rt△ADC中，ACAD＝cos∠BAO∴3－tt＝35，∴t＝158当EF⊥AB时∵EF⊥CD，∴直线CD与直线AB重合∴点C与点A重合，∴t＝3（4）t＝54或t＝154提示：①当0＜t＜158，且重叠部分为等腰梯形PEQM时则∠PEQ＝∠MQE∵菱形CDMN，∴CD∥MN∴∠MQE＝∠CEQ，∴∠PEQ＝∠CEQ∵EF⊥CD，即∠CEF＝90°，∴∠CEQ＝45°∴∠ACD＝∠CEQ＝45°过D作DH⊥AC于H，则△DHC是等腰直角三角形∴DH＝HC，∴45t＝3－t－35t，∴t＝54②当158＜t＜5，且重叠部分为等腰梯形EHNK时同理可得∠CHE＝45°连接DH∵EF垂直平分CD，∴CH＝DH，∠DHE＝∠CHE＝45°∴∠DHC＝90°，∴DH＝45t而CH＝CO－HO＝CO－(AO－AH)＝t－(3－3 5t)∴t－(3－35t)＝45t，∴t＝15417．（浙江模拟）如图1，矩形ABCD中，AB＝21，AD＝12，E是CD边上的一点，DE＝16，M是BC边的中点，动点P从点A出发，沿边AB以每秒1个单位长度的速度向终点B运动．设动点P的运动时间是t秒．（1）求线段AE的长；（2）当△ADE与△PBM相似时，求t的值；（3）如图2，连接EP，过点P作PH⊥AE于H．①当EP平分四边形PMEH的面积时，求t的值；②以PE为对称轴作线段BC的轴对称图形B′C′，当线段B′C′与线段AE有公共点时，写出t的取值范围（直接写出答案）．解：（1）∵ABCD是矩形，∴∠D＝90°∴AE＝AD2＋DE2＝122＋162＝20（2）∵∠D＝∠B＝90°∴△ADE与△PBM相似时，有两种情况：当∠DAE＝∠PMB时，有DEPB＝ADBM即1621－t＝126，解得t＝13当∠DAE＝∠BPM时，有DEBM＝ADPB即166＝1221－t，解得t＝332（3）①由题意得：S△EHP＝S△EMP∵DC∥AB，∴∠DEA＝∠HAP又∵∠D＝∠AHP＝90°，∴△ADE∽△PHA∴AH DE＝PHAD＝APAE，即AH16＝PH12＝t20∴AH＝45t，PH＝35t，EH＝20－45t∴S△EHP＝12×35t×(20－45t)∵DC＝21，DE＝16，∴EC＝5 ∴S△EMP＝S梯形EPBC－S△ECM－S△PBM＝12(5＋21－t)×12－12×5×6－12×(21－t)×6∴1 2×35t×(20－45t)＝12(5＋21－t)×12－12×5×6－12×(21－t)×6解得t＝75±5174∵0＜t＜21，∴t＝75－5174②14011≤t≤20提示：当点B′落在线段AE上时连接B′P、EB，∵B′C′和BC关于PE对称∴B′P＝BP＝21－t，B′E＝BE＝BC2＋EC2＝122＋52＝13 ∴AB′＝AE－B′E＝20－13＝7，B′H＝AH－AB′＝45t－7在Rt△B′HP中，B′H2＋PH2＝B′P2∴(45t－7)2＋(35t)2＝(21－t)2，解得t＝14011当点C′落在线段AE上时连接C′P、CP，∵B′C′和BC关于PE对称C′P2＝CP2＝122＋(21－t)2，C′E＝CE＝5∴AC′＝AE－C′E＝20－5＝15，C′H＝AH－AC′＝45t－15 在Rt△C′HP中，C′H2＋PH2＝C′P2∴(45t－15)2＋(35t)2＝122＋(21－t)2，解得t＝2018．（浙江模拟）如图，抛物线与x轴交于A（6，0）、B（19，0）两点，与y轴交于点C（0，8），直线CD∥x轴交抛物线于另一点D．动点P、Q分别从C、D两点同时出发，速度均为每秒1个单位，点P向射线DC方向运动，点Q向射线BD方向运动，设P、Q运动的时间为t（秒），AQ交CD于E．（1）求抛物线的解析式；（2）求△APQ的面积S与t的函数关系式；（3）连接BE．是否存在某一时刻t，使得∠AEB＝∠BDC？若存在，求出t的值；若不存在，请说明理由．解：（1）∵抛物线与x轴交于A（6，0）、B（19，0）两点∴设抛物线的解析式为y＝a(x－6)(x－19)∵抛物线与y轴交于点C（0，8）∴8＝a(0－6)(0－19)，∴a＝457∴y＝457(x－6)(x－19)（2）作PF⊥x轴于F，QG⊥x轴于G，DH⊥x轴于H，∵CD∥x轴，∴PF＝DH＝OC＝8当y＝8时，457(x－6)(x－19)＝8解得x1＝0，x2＝25∴D（25，8），OH＝CD＝25∵B（19，0），∴BH＝25－19＝6 ∴BD＝BH2＋DH2＝62＋82＝10∵△BDH∽△BQG，∴BDBQ＝DHQG＝BHBG∴1010＋t＝8QG＝6BG∴QG＝45t＋8，BG＝35t＋6∴FG＝t＋19＋35t＋6＝85t＋25，AG＝35t＋19∴S＝S梯形PFGQ－S△PAF－S△QAG＝12(PF＋QG)·FG－12AF·PF－12AG·QG＝12(8＋45t＋8)(85t＋25)－12(t＋6)·8－12(35t＋19)(45t＋8)＝25t2＋445t＋100（3）∵AC＝BD＝10，∴四边形ABDC是等腰梯形∴∠ACD＝∠BDC若∠AEB＝∠BDC，则∠AEC＋∠BED＝∠BED＋∠EBD ∴∠AEC＝∠EBD，∴△AEC∽△EBD∴AC ED＝CEDB，即10ED＝25－ED10解得ED＝5或ED＝20（＞AB，舍去）∵△QED∽△QAB，∴EDAB＝QD QB即513＝tt＋10，∴t＝254∴存在某一时刻t，使得∠AEB＝∠BDC，t＝25 419．（浙江模拟）如图，抛物线y＝ax2＋bx＋c（a＞0）交x轴于A、B两点（A在B的左侧），交y 轴于C 点，已知B 点坐标为（8，0），tan ∠ABC ＝12，△ABC 的面积为8．（1）求抛物线的解析式；（2）直线EF （EF ∥x 轴，且分别交y 轴、线段CB 于E 、F 两点）从C 点开始，以每秒1个单位的速度向下运动，与x 轴重合时停止运动；同时动点P 从B 点出发沿线段BO 以每秒2个单位的速度向终点O 运动，连接FP ，设运动时间为t 秒．是否存在t 的值，使以P 、B 、F 为顶点的三角形与△ABC 相似？若存在，求出t 的值；若不存在，请说明理由；（3）在（2）的条件下，连接AC 交EF 于点G ．当t 为何值时，A 、P 、F 、G 所围成的图形是平行四边形、等腰梯形和等腰直角三角形．解：（1）∵B （8，0），∴OB ＝8 ∵OC OB＝tan ∠ABC ＝12，∴OC ＝4，∴C （0，4）∵S △ABC ＝8，∴ 12AB ·OC ＝8∴AB ＝4，∴OA ＝4，∴A （4，0）把A 、B 、C 三点坐标代入y ＝ax2＋bx ＋c ，得 ⎩⎪⎨⎪⎧16a ＋4b ＋c ＝064a ＋8b ＋c ＝0c ＝4解得a ＝1 8 ，b ＝－ 32，c ＝4 ∴抛物线的解析式为y ＝ 1 8 x 2－ 32x ＋4 （2）存在∵AB ＝OC ＝4，OB ＝8，∴AC ＝42，BC ＝4 5由题意，BP ＝2t ，BF ＝45－5t若△PBF ∽△ABC ，则PBAB＝BFBC即2t4＝45－5t45，∴t ＝4 3若△FBP ∽△ABC ，则 BF AB ＝BPBC即 45－5t 4＝ 2t45，∴t ＝20 7∴当t ＝4 3或t ＝207时，以P 、B 、F 为顶点的三角形与△ABC 相似（3）t ＝43时，A 、P 、F 、G 所围成的图形是平行四边形 t ＝2时，A 、P 、F 、G 所围成的图形是等腰梯形 t ＝245时，A 、P 、F 、G 所围成的图形是等腰直角三角形20．（浙江模拟）已知：如图，在平面直角坐标系中，△ABC为等腰三角形，直线AC的解析式为y＝－2x＋6，将△AOC沿直线AC折叠，点O落在平面内的点E处，直线AE交x轴于点D．（1）求直线AD解析式；（2）动点P从点B出发，以每秒1个单位的速度沿x轴正方向匀速运动，点Q是射线CE 上的点，且∠PAQ＝∠BAC．设点P运动时间为t秒，△POQ的面积为S，求S与t之间的函数关系式；（3）在（2）的条件下，直线CE上是否存在一点F，使以点F、A、D、P为顶点的四边形是平行四边形？若存在，求出t值及Q点坐标；若不存在，请说明理由．解：（1）∵直线AC解析式为y＝－2x＋6∴A（0，6），C（3，0），∴OA＝6，OC＝3由题意，∠AEC＝∠AOC＝90°，AE＝AO＝6，CE＝CO＝3设CD＝x，则OD＝x＋3易证△CED∽△AOD，∵AO＝2CE∴OD＝2DE，即DE＝x＋32在Rt△CED中，32＋(x＋32)2＝x2解得x＝5（舍去负值），∴CD＝5∴OD＝8，D（8，0）设直线AD解析式为y＝kx＋6，则有：8k＋6＝0，∴k＝－3 4∴y＝－34x＋6（2）①当P在线段BO上时，即0＜t＜3时∵∠PAQ＝∠BAC，∴∠BAP＝∠CAQ又∵∠ABP＝∠ACQ＝∠ACO，AB＝AC∴△ABP≌△ACQ，∴BP＝CQ＝t，OP＝3－t作QH⊥OD于H，则QH＝CQ·sin∠ECD＝4 5t∴S＝12OP·QH＝12(3－t)·45t＝－25t2＋65t即S＝－25t2＋65t②当P在x轴正半轴上时，即t＞3时同①可得：BP＝CQ＝t，OP＝t－3∴S＝12OP·QH＝12(t－3)·45t＝25t2－65t。