第七章船舶推进轴系的扭转振动与控制
船舶推进器轴承系统设计中的振动与噪音控制技术研究

船舶推进器轴承系统设计中的振动与噪音控制技术研究摘要:船舶推进器轴承系统设计中的振动与噪音控制技术是船舶工程中的关键问题之一。
本文针对这一问题展开研究,分析了船舶推进器轴承系统存在的振动与噪音问题,包括其对船舶性能和船员舒适度的影响。
随后,提出了一系列振动与噪音控制技术,包括结构优化、材料选择、减振措施等方面的方法。
通过实验验证和理论分析,证明了这些控制技术在减少船舶推进器轴承系统振动与噪音方面的有效性和可行性。
总结了研究结果,并对未来研究方向进行展望,为船舶推进器轴承系统设计中的振动与噪音控制提供了理论和实践指导。
关键词:船舶推进器;轴承系统;振动控制;噪音控制;船舶工程引言:船舶作为重要的海上交通工具,其推进器轴承系统的设计与性能关系着船舶的安全、舒适性和效率。
然而,推进器轴承系统常常面临振动与噪音问题,这不仅影响了船舶的正常运行,还影响了船员的工作环境和航行体验。
因此,针对船舶推进器轴承系统设计中的振动与噪音控制技术展开研究具有重要意义。
一、船舶推进器轴承系统振动与噪音问题分析在船舶工程中,推进器轴承系统的振动与噪音问题是一个备受关注的重要议题。
振动与噪音不仅影响船舶的性能和运行效率,还直接影响到船员的工作环境和航行体验。
因此,深入分析船舶推进器轴承系统的振动与噪音问题是至关重要的。
振动问题是船舶推进器轴承系统中的一大挑战。
推进器在运行过程中产生的振动会传递到轴承系统中,导致轴承的振动增加。
这种振动不仅会影响轴承的正常运行,还可能引发轴承故障和损坏,从而影响船舶的安全性和可靠性。
此外,振动还会影响到船舶其他部件的运行,进而影响整个船舶的性能和稳定性。
噪音问题也是船舶推进器轴承系统中需要解决的关键问题之一。
推进器在运行时会产生噪音,这种噪音不仅会扰乱船员的工作和休息,还会影响到船舶周围环境的安静与和谐。
特别是在船舶进行长时间航行或在靠近居民区域航行时,噪音问题更是需要重视和解决的。
除了以上问题外,船舶推进器轴承系统的振动与噪音还会影响到船舶的舒适性。
船舶柴油机的轴系扭转振动的分析与研究

船舶柴油机的轴系扭转振动的分析与研究作者:田浩鹏来源:《中国科技纵横》2013年第15期【摘要】本文通过一些国内因轴系扭转振动而引起的断轴断桨的事故实例,来分析引起轴系扭转振动的主要原因,分析扭振主要特性,并提取一些减振和防振的基本控制措施。
【关键词】船舶柴油机轴系扭振危害分析措施在现代船舶机械工程中,船舶柴油机轴系扭转振动已经成为一个很普遍的问题,它是引起船舶动力装置故障的一个很常见的原因,国内外因轴系扭转而引起的断轴断桨的事故也屡见不鲜,随着科学水平的提高和航运业的发展,人们越来越重视船舶柴油机组的轴系扭转振动,我国《长江水系钢质船舶建造规范》和《钢质海船入级与建造规范》(简称《钢规》)和也均规定了在设计和制造船舶过程中,必须要向船级社呈报柴油机组的轴系扭转振动测量和计算报告,以此来表明轴系扭转振动的有关测量特性指标均在“规范”的允许范围内。
1 船舶柴油机轴系扭转振动现象简介凡具有弹性与惯性的物体,在外力作用下都能产生振动现象。
它在机械,建筑,电工,土木等工程中非常普遍的存在着。
振动是一种周期性的运动,在许多场合下以谐振的形式出现的,船舶振动按其特点和形式可分为三种,船体振动,机械设备及仪器仪表振动,和轴系振动。
船舶柴油机轴系振动按其形式可分为三种:扭转振动,纵向振动,横向振动。
柴油机扭转振动主要是由气缸内燃气压力周期性变化引起的,它的主要表现是轴系上各质点围绕轴系的旋转方向来回不停的扭摆,各轴段产生不相同的扭角。
纵向振动主要是由螺旋桨周期性的推力所引起的。
横向振动主要是由转抽的不平衡,如螺旋桨的悬重以及伴流不均匀产生的推力不均匀等的力的合成。
船舶由于振动引起的危害不但可以产生噪音,严重影响旅客和船员休息,还会造成仪器和仪表的损害,严重的时候甚至出现船体裂缝断轴断桨等海损事故,直接影响船舶的航行安全。
而在船舶柴油机轴系的三种振动中,产生危害最大的便是扭转振动,因扭转振动而引起的海损事故也最多,因此对扭转振动的研究也最多。
船舶推进轴系扭转振动减振研究

第1 9卷
第 4期
中 国 修 船
C NA S PR AI HI HI EP R
V0 . 9 1 1 No 4 . Au . 0 6 g20
20 0 6年 8月
船舶 推进 轴 系扭 转 振 动 减 振 研 究
张建 阳
( 州 市港航 管理局 ,浙 江 杭 州 杭 30 1 ) 10 4
2 调 频 方 法
要改变扭转振动系统的固有频率 ,必须对计算 模型进行修正 ,若不改变模型的结构 ,只能改变某 些计算参数如转动惯量、刚度。通常情况下 ,很难 改变柴油机和螺旋桨 的转 动惯 量 ( 除了少部分柴
角,就能充分发挥其高弹性联轴器 的调频作用。不 同型号的弹性联轴器刚度不尽相同,选用合适的刚
摘要:结合具体实例探讨了改变轴系某些参数对其 固有频率的影响,得 出减振调频的主要方 法和规律。针对某轴 系实例 ,运用减振调频 的具体方法对初始计算结果进行分析 ,对参数进行修
正 ,最 终达到 规 范的要 求 ,消 除 了扭振 故 障 的威胁 。
关键词:推 进 轴 系;扭 转振 动 ;减 振
调整飞轮转动惯量是最常用的调频方法 ,柴油
机制造厂通常会备有不同转动惯量的飞轮供用户选 择。通过具体的分析计算 ,在设计阶段选择合适的
飞轮能够影响系统的扭振特性 ,避免强共振造成破
坏。
22 调 整弹 性联 轴器 刚度 .
如果能将节点调整到弹性联轴器的橡胶上 ,使
橡 胶 承受最 大 的扭振 力矩 ,内 、外 环产 生最 大扭 转
度 对 系统扭 振特 性有 较 大影 响 。
内河某船舶推进轴系 ,主机为 4冲程 8 缸高速 柴油机 ,额定功率 2 4 W,额定转速 60r i, 0k 9 0 m d /
船舶推进轴系多体动力学和扭振特性

船舶推进轴系多体动力学和扭振特性作为一种运输工具和工程装备,船舶的推进轴系(Propulsion Shafting System)是其重要部件之一。
它负责将主机发出的动力通过螺旋桨传递到水中,从而推进船体。
然而,船舶推进轴系也存在着一些复杂的多体动力学和扭振特性,下面将详细介绍。
首先,船舶推进轴系的多体动力学特性是其一大特点。
它由多个组件组成,包括主机、机械传动系统、支承系统、螺旋桨和水动力等。
这些组件之间通过连接件进行连接,形成了一个整体运动系统。
在船舶行驶时,推进轴系的振动会影响到整个船体的运动,因此必须对其进行研究和优化。
其次,船舶推进轴系的扭振特性也是一个重要的研究方向。
由于在运行过程中受到的载荷和运动状态不断变化,船舶推进轴系会产生扭转和振动。
这种扭振会导致推进轴系的一些部件受到应力的过大或过小,从而影响到其功能和使用寿命。
因此,研究和分析推进轴系的扭振特性以及应力分布是非常重要的。
为了更好地控制和优化船舶推进轴系的多体动力学和扭振特性,需要采用一些有效的技术手段。
首先,对推进轴系进行系统的结构设计和优化,采用合适的材料和加强节点,能够大大降低其产生不必要的振动。
其次,通过合理的支承系统、减振器和动平衡等技术手段,能够有效地减小推进轴系的振动和扭振幅值。
此外,利用先进的数值仿真方法,能够更加准确地预测和优化推进轴系的性能和振动特性。
总之,船舶推进轴系的多体动力学和扭振特性是船舶设计和运行中需要考虑的重要问题。
针对这些问题,需要采用一些有效的技术手段和数值仿真方法,实现对推进轴系振动和扭振特性的控制和优化。
作为船舶推进系统的重要组成部分之一,船舶推进轴系的性能数据也是非常重要的。
下面将列出一些相关的数据并进行分析。
1. 推进轴系的重量和尺寸。
推进轴系的重量和尺寸直接影响推进轴系的动力学和扭振特性以及整个船体的运行效率。
一般来说,大型船舶的推进轴系比小型船舶的推进轴系更为复杂,同时更需要关注推进轴系的重量和尺寸。
《船舶推进系统振动》课程教学大纲.doc

《船舶推进系统振动》课程教学大纲_、课程基本信息1、课程代码:NA4182、课程名称(中/英文):船舶推进系统振动/Vibration of propulsion system onboard3、学时/学分:34/24、先修课程:《数学物理方法》、《船舶动力装置》、《工程力学》5、面向对象:轮机工程6、开课院(系)、教研室:船舶海洋与建筑工程学院船舶与海洋工程系轮机工程专业7、教材、教学参考书:《动力机械振动与噪声学》,陈端石,赵玫,周海亭,上海交通大学出版社,1996《船舶推进轴系振动》,陈之炎,上海交通大学出版社,1987二、课程性质和任务《船舶推进系统振动》是轮机工程本科学习的一门重要课程,它主要介绍了船舶主推进系统的各类振动(包括柴油机振动,轴系的横振、纵振、回旋振动以及扭转振动等)现象的产生,物理建模和数学分析,以及相应的控制手段。
船舶主推进系统的振动对于船舶动力系统的设计及维护都有着十分重要的影响。
剧烈的振动不仅会影响到船舶的正常航行,严重的甚至会引起轴系及设备的疲劳损坏。
本课程的主要任务就是让轮机工程的学生对船舶推进系统振动的产生及危害有较为全面地认识,掌握研究推进系统振动的基本建模及分析方法,以及学会基本的船舶推进系统振动控制方法,从而培养学生用系统化的研究方法解决实际问题的能力。
三、教学内容和基本要求本课程的教学内容来自《动力机械振动与噪声学》,其基本内容和要求如下:第一章绪论要求掌握机械振动基本概念及分类,机械振动问题分类,简谐振动及周期振动的谐波分析,声波及噪声的物理特征。
第二章离散系统的振动微分方程要求掌握离散化力学模型,单自由度及多自由度振动微分方程。
第三章自由振动要求掌握无阻尼系统振动特性,粘性阻尼系统阻尼特性及多自由度系统特性分析。
第四章受迫振动要求通过二阶非齐次线性微分方程的解掌握单自由度系统和多自由度系统的幅频响应与相频响应特性。
第五章离散系统振动理论在动力机械中的应用要求掌握识别自然频率的共振法、确定阻尼比的半功率带宽法以及隔振器的设计原理。
船舶推进轴系的扭转振动与控制
当量轴段长 6)轴系中有弹性联轴器或气胎离合器时,应把它们的主、从动
部分分为两集中质量 7)轴系中有液力偶合器时为界,分成两个独立的扭振系统 8)被发动机拖动的机械,转动惯量大的也要作一集中质量
二、多质量系统无阻尼简谐振动计算
等,振幅不同,惯量大的振幅小,惯量小 的振幅大,且振动方向永远相反。
振型图
A1
e12 O
A1
单结 A2
e12
e23
单结
A1
A2
双结
取A1=1,A2=-I1/I2, O为结点,振幅为0, 应力最大,双质量 只有一个结点。
A2
三质量系统有两个
自振频率,单结或
双结,即两个结点。
A3 A3
n个质量就有n-1个 振型,n-1个自振 频率。
(
2 n
2)2
4n 2 2
2 n
2
Asin(t )
A
h
h
1
(
2 n
2)2
4n 2
2
2 n
[1 ( n
)2 ]2
n2
4
2 n
(
n
)2
h
பைடு நூலகம்
2 n
M I
Ie
Me
Ast
静振幅
放大系数
m A Ast
1
f ( , )
[1 ( )2 ]2 ( )2
n
n
n
讨论:
1)
0
n
m 1
有因
IK
次
eK,K+1
AK
n2
Uk,,k+1=(AK+1-AK)/ eK,K+1
船舶轴系的振动与控制分析船舶专业毕业设计毕业论文

船舶轴系的振动与控制分析摘要本文主要进行船舶轴系振动的模态分析(固有频率与固有振型),通过MATLAB 平台实现了船舶轴系纵向振动模态计算的通用程序,并且分别应用该通用程序与ANSYS中的模态分析计算了船舶轴系扭转振动与纵向振动(给定轴系)的模态,并对所计算的结果进行了对比与分析。
同时,本文也介绍了船舶轴系强迫振动的计算以及船舶轴系振动的控制分析。
本文以船舶推进轴系的振动为研究对象,查阅了国内外大量文献,首先介绍了船舶推进轴系振动的分类,接着以一种通俗的方式阐述了各种振动的机理。
其次论述了轴系振动计算的几种常用的方法:霍尔兹法、传递矩阵法与有限元法。
接着论证了传递矩阵法的可用性,以及在什么情况下使用该方法可以达到所需的精度要求。
然后通过MATLAB平台实现了船舶轴系振动(包括扭转振动与纵向振动)的通用程序。
紧随其后,使用该程序计算了一个扭转振动与纵向振动的实例,再后来使用ANSYS对同样的例子进行了计算分析,通过比对,证实了通过MATLAB平台实现的通用程序计算的结果是令人满意的。
随后介绍了轴系的强迫振动及计算强迫振动的传递矩阵法,并给出了该方法的一个简单的算例,之后介绍了避振的几种思路。
最后对研究成果和有关问题进行了总结,对研究中的不足作了说明,对今后的工作做出了展望。
关键词:纵向振动,传递矩阵法,有限元法,通用程序,强迫振动Analysis of Vibration and ControlOn Ship ShaftingAbstractThis paper is mainly researching the vibration characteristics on ship shafting (natural frequencies and mode shapes). Through the platform of MATLAB, we get the general program which can calculate the mode of the longitudinal vibration and torsional vibration on ship shafting, and using this general program, an instance is calculated. ANSYS is applied to, too. And then both of the calculated results were compared and analyzed. At the same time, the paper also describes the calculation of the forced oscillation of ship shafting and the analysis of ship shaft vibration control.In this paper, viewing vibration of ship propulsion shafting as the research object, I consulted relevant data at home and abroad. First, I have introduced the classification of ship propulsion shafting vibration, and then described in a easy manner to various vibration mechanism.Next, several commonly used methods to vibration calculations are discussed: the Holzer method, the transfer matrix method and the finite element method.Then the availability of the transfer matrix method is demonstrated, and also is the required precision when we can achieve by the method.After that, through the platform of MATLAB, we get the general program which can calculate the mode of the vibration (including the longitudinal and the torsional vibration) vibration on ship shafting. Then we use the general program to calculate an instance of longitudinal and torsional vibration. And then we use ANSYS to calculate the same example. By comparison, we confirm the results by the general program through MATLAB platform are satisfactory.Then we introduce the forced vibration of ship shafting and the transfer matrix method of the forced vibration, and a simple example is showed, after that we introduce several ideas to avoid vibration.Finally, a summary about the achievement and problems is presented. An explanation of imperfectness in the study and pieces of advisement for the future work is given.Key words: Longitudinal Vibration,Transfer Matrix Method,Finite Element Method,General Program, Forced Vibration目录摘要........................................................................................................................ I ABSTRACT ................................................................................................................. I I 目录 ................................................................................................................ III 一绪论 (1)1.课题研究的目的和意义 (1)2.国内外研究概况 (2)3.本文主要工作 (3)二船舶轴系振动简介 (5)1.纵向振动 (5)2.扭转振动 (6)3.回旋振动 (7)三轴系振动计算方法 (9)1.霍尔兹(Holzer)法 (9)2.传递矩阵法 (11)3.有限元法 (19)四轴系振动通用程序实现 (23)1.船舶轴系的构造 (23)2.轴系振动通用程序实现 (25)3.轴系振动通用程序的应用与检验 (28)五船舶轴系振动的控制 (46)1.船舶轴系的强迫振动 (46)2.船舶轴系强迫振动的传递矩阵法 (46)3.强迫振动算例 (48)4.船舶轴系避振措施 (50)六总结 (52)1.结论 (52)2.设计评价和展望 (52)致谢 (53)附录 (54)参考文献 (62)一绪论1.课题研究的目的和意义声明:本论文中除特殊说明之外出现的所有物理量的单位均为国际制单位,即长度为米,时间为秒,质量为千克等。
船舶推进轴系扭振研究综述

船舶推进轴系扭振研究综述摘要:船舶推进轴系振动特性是船舶动力性能的重要方面。
本文从扭振模型、扭振计算方法、关键因素分析及扭振软件开发四个方面综述了船舶推进轴系扭振的研究现状,对轴系扭振研究具有一定的知道意义。
关键词:扭振模型;扭振方法;扭振关键因素;扭振软件引言船舶推进轴系扭振研究是船舶动力性能研究的重要方面,对于船舶的安全性、舒适性及可靠性具有重要意义,历来都是船舶设计者需要重点考虑的问题。
德国的Geiger于1916年发表了利用机械式盖格尔扭振仪测量轴系扭振的文章,从而使扭振的研究进入了实测和实验阶段,在1921年又提出了用于计算扭振固有频率和固有振型的计算方法——霍尔茨法[1],扭振的研究在20世纪50年代逐渐变得成熟,到了60年代至80年代,随着计算机技术的高速发展,内燃机向着高速率大功率方向发展,扭振变得更加剧烈,事故发生事件层出不穷,促使人们对扭振进行更深一步的研究,主要体现在精密仪器的使用和计算软件精度的提高上,到了20世纪90年代以后,扭振的研究进入了纵深发展期,力学模型的建立更加精确,如Kouji Fujii建立了发动机的曲轴平面模型,利用传递矩阵法求解曲轴的扭转振动及弯曲振动[2],日本的日立zosen公司等五家公司共同设计出一种新的推进轴系,在稳态性、可靠性等方面都有很大的提升,并降低了成本[3]。
本文重点从扭振模型、扭振计算方法、关键因素分析及扭振软件开发四个方面对船舶内燃机轴系扭振近年来的研究进行分类概述,使读者能够更清晰的了解近年来船舶推进轴系扭振研究的最新成果。
1 扭振的研究结构及数学模型从传统的研究来看,轴系模型一般分为两大类:集总参数模型和分布参数模型。
国内外学者又在此基础上从不同角度建立了不同的轴系模型取得了更好的效果。
涂耿伟等利用模型修正法对缩减后的模型作了进一步的修正,大大提高了模型的精度[4];艾维等利用Pro/E建立了实船轴系三维仿真模型,通过动力仿真分析了轴系振动特性,达到了良好的效果[5];张俊红等采用有限元法结合多体动力学方法对某X8170C型柴油机轴系扭振进行了研究,建立了轴系扭振仿真虚拟样机并引入BP神经网络对减振参数进行了优化[6];肖志建建立了数理模型,利用有限元法对船舶推进轴系扭振问题进行分析,取得了不错的效果[7];姜雪洁等建立了轴系的动态计算模型,对不同转速下的轴系的动态响应进行了计算[8]。
船舶轴系扭振产生的原因及对策

船舶轴系扭振产生的原因及对策摘要:近年以来,随着中国现代化进程的发展,为适应中国海洋事业的快速发展时期,综合确保船舶航行安全的同时,相关工作人员也对船舶轴系扭振成因进行了深入的研究,以期对船舶轴系的扭振特性及规律进行相应的完善与总结,严格按照有关规定处理船舶轴系扭转振动问题,尽量减少轴系扭转振动造成的船舶安全事故。
关键词:船舶轴系,扭振,原因及对策,探讨1前言一般来说,振动定律可以直接使用正弦波来表示轴向运动。
扭转振动是在扭矩变化的作用下所发生的周期性运动。
扭矩振动主要发生在输出和扭矩吸收不均匀的机械装置中,如柴油机运行的某些设备或装置、电机压力机、电机泵等等。
就柴油发动机而言,包括减速齿轮之间的碰撞、齿面的点蚀及断裂、连接螺栓的断裂、橡胶接头的撕裂、引擎零件的加速磨损等。
在运行过程中发生的严重事故,对此方面的研究始终在持续,力度也不再不断加大,积累了大量的经验和数据。
人们一直在探索和寻找一种相对简单的近似计算方法,包括轴系怠速振动固有频率和临界转速的计算方法。
最后,它算是处理实际问题逐渐形成的方法。
2船舶轴系扭转振动的概述主动推进装置的扭转振动问题非常重要,值得去好好深入地研究。
通常情况下,当气缸关闭之后,后续的操作才更安全。
然而,一些辅助振荡器的相对振幅矢量不会减小。
相反,共振应力增大,甚至接近或超过允许的扭转应力。
此外,每个圆柱的分解振幅矢量的相对值也会受到不同程度的影响。
了解气缸轴承拆卸后产生较大冲击应力的推力控制,对于避免单个气缸的拆卸事故具有重要的意义。
在柴油机的实际运行过程中,在电梯试验以及运行试验中,不仅要进行单缸停油试验,而且在柴油机发生紧急故障时,必须要密封气缸进行运行。
此外,最大燃烧压力、排气温度调节等平衡性差异以及各种故障往往导致燃烧不良现象。
因此,在计算转向轴系的振动时,必须考虑这种情况。
在细致完成相关工作之后,还要向船公司提供船舶运行中的计算结果和注意事项,以确保船舶在正常运行和气缸密封运行中的正确操作和管理。
水下航行装置推进轴系扭转振动控制系统

水下航行装置推进轴系扭转振动控制系统
江国和;宋福堂
【期刊名称】《振动.测试与诊断》
【年(卷),期】1997(017)001
【摘要】主要讨论以摆盘式活塞发动机为其主机的某水下航装置推进轴系的扭转振动问题。
首先建立了推进轴系的两个扭振模型,并进行了轴系的扭振计算,为了验证模型参数的准确性,对推进轴第进行了脉冲激励试验。
【总页数】5页(P33-37)
【作者】江国和;宋福堂
【作者单位】华东船舶工业学院振动噪声研究所;华东船舶工业学院振动噪声研究所
【正文语种】中文
【中图分类】U664.21
【相关文献】
1.船舶推进轴系扭转振动的仿真与试验研究 [J], 周立彬;陈焕国
2.冰载荷电力推进轴系扭转振动研究 [J], 肖能齐;周瑞平;徐翔;侯之超
3.隔振技术在水下航行器推进轴系振动控制中的应用 [J], 段勇;郭君;周凌波
4.隔振技术在水下航行器推进轴系振动控制中的应用 [J], 段勇;郭君;周凌波;;;
5.船用推进轴系统扭转和横向振动耦合效应 [J], Akile Nese Halilbese;Cong Zhang;Osman Azmi Ozsoysal
因版权原因,仅展示原文概要,查看原文内容请购买。
船舶结构动力学特性研究与振动控制

船舶结构动力学特性研究与振动控制船舶结构动力学是研究船体在运行和负载条件下的振动响应特性以及其对船体结构的影响的学科。
船舶结构动力学的研究对于优化船舶设计、提高船舶结构安全性以及改善乘船体验具有重要意义。
本文将探讨船舶结构动力学的基本概念、研究方法以及振动控制的相关技术。
一、船舶结构动力学的基本概念船舶结构动力学研究的对象是船体结构在水上行驶时所受到的各种外力的作用下的振动响应。
船体结构的振动主要包括弯曲振动、扭转振动和纵向振动等。
这些振动可能导致船体结构的疲劳破坏甚至失效,因此研究船舶结构动力学特性对于确保船舶的结构安全至关重要。
船舶结构动力学的研究对象还包括船舶在水上行驶时的各类动力激励,如波浪、风力和推进系统等。
这些激励会对船体结构产生作用力,引起船体结构的振动。
因此,研究船舶结构动力学的一个重要任务就是确定这些激励的大小、方向和频谱特性。
二、船舶结构动力学研究的方法船舶结构动力学的研究方法主要包括数值模拟、实验测量和理论分析。
数值模拟方法是研究船舶结构动力学的一种重要手段。
通过建立船舶结构动力学的数学模型,采用计算机仿真的方法进行计算分析,可以预测船体结构在不同工况下的振动响应。
数值模拟方法具有较高的灵活性和效率,可以提供大量的参数和分析结果,为后续的优化设计和振动控制提供依据。
实验测量方法是船舶结构动力学研究的另一种重要手段。
通过在实验室或实际船舶上进行测量,获取船舶结构在不同工况下的振动响应数据,可以验证数值模拟的准确性和结果可靠性。
实验测量方法对于获取实际船舶结构动力学特性的数据具有重要意义,为进一步的研究提供依据。
理论分析方法是船舶结构动力学研究的基础。
通过建立适当的数学模型和采用合适的理论方法,对船舶结构的振动特性和响应进行分析和推导,可以揭示船舶结构振动的机理和规律。
理论分析方法对于深入理解船舶结构的振动行为具有重要意义。
三、船舶振动控制的相关技术船舶振动控制是为了降低船体结构的振动响应,提高船舶的结构安全性和舒适性而采用的一系列控制技术。
第七章船舶推进轴系的扭转振动与控制

轴系振动有:扭转振动、回转振动(横振)、纵向振 动。其中以扭转振动为主,当周期性的交变力矩作 用的频率与自振频率相同时,将产生共振。 我国“船规”规定220kW(300HP)以上的船舶都要 申报扭振计算书。 一、扭振的概述 1、轴系扭振的成因及危害 轴系本身具有扭转振动的基本特性:弹性与惯性 轴系承受不均匀的干扰力矩 当扭转振动所产生的应力超过许用值时,会对轴系产 生极大的破坏作用。
i 1 k 1
k质量振动位移 (k 1)质量位移 (k 1, k )轴段变形
对简谐振动 A sin( n t )
2 n A sin( n t ) 2 max n A
A2 A 3 Ak A n
2 A1 e12 n I 1 A1
A2 e23
2 n
I
i 1 2 n
2
i
Ai
Ak 1 ek 1,k
I
i 1 n 1 i 1
k 1
i
Ai
2 An 1 en 1,n n I i Ai n
2 自由段: U n ,n 1 n I i Ai 0 i 1
高速机一般只考虑
k Ak(1) sin(1t 1 ) Ak( 2) sin( 2 t 2 ) Ak( n1) sin( n1t n1 )
取第一质量作为分离体 S1 U 12 0 1 I1
1 2
e12
0
1 2 1 e12 I 1
n=
n-1- n-1,nEn-1,n n,n+1=n-1,n+ n n=0
船舶推进轴系校中对轴系振动影响分析

实际案例分析:结合实际案例,分析轴系振动对船舶推进性能的影响 以及校中方法的优化效果。
未来研究方向:探讨未来在船舶推进轴系校中与轴系振动影响分析 方面的研究方向,为相关领域的研究提供参考。
06
案例分析:船舶推进轴系校中与轴系振动 的实际应用
案例一:某型船的推进轴系校中与振动控制
某型船的推进轴 系校中与振动控 制背景
某型船的推进轴 系校中与振动控 制目的
某型船的推进轴 系校中与振动控 制过程
某型船的推进轴 系校中与振动控 制结果
案例二:某大型船队的推进轴系校中与振动控制实践
案例背景:某大型船队在运营过程中遇到了推进轴系振动问题,需要进行Fra bibliotek中和振动控制。
定期维护与保养:对轴系进行定 期维护和保养,确保轴系的正常 运行和使用寿命。
添加标题
添加标题
添加标题
添加标题
调整轴系振动:根据轴系振动监 测结果,对轴系进行必要的调整, 以降低振动水平。
应急处理措施:在出现紧急情况 时,采取相应的应急处理措施, 以避免事故的发生。
轴系振动的控制效果评估
轴系振动控制方法:介绍船舶推进轴系校中过程中,采用的控制轴系 振动的方法,如优化设计、调整安装等。
03
轴系振动对船舶推进的影响
轴系振动的原因
螺旋桨设计不合理
螺旋桨安装误差
添加标题
添加标题
螺旋桨制造误差
添加标题
添加标题
螺旋桨运行过程中产生的振动
轴系振动对船舶推进性能的影响
• 轴系振动对船舶推进效率的影响 * 振动会降低轴承的润滑效果,增加摩擦阻力 * 振动会导致轴系中的应力分布不均,影响材料性能 * 振动会引发船舶推进 系统中的其他问题,如密封失效、轴承磨损等 • * 振动会降低轴承的润滑效果,增加摩擦阻力 • * 振动会导致轴系中的应力分布不均,影响材料性能 • * 振动会引发船舶推进系统中的其他问题,如密封失效、轴承磨损等
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
e12
2 n
I
1
A1
2
e23
2 n
I i Ai
i 1
Ak
k 1
Ak 1 ek 1,k
2 n
I i Ai
i 1
0
n
m 1
A Ast
2)
m0
n
3) 1
n
n
m 1
此时阻尼对放大系数的影响最大
4) 2 m 1
n
2 n
1 Ie
增大I或e可使n 下降
时共振
n
tg 1 2n
2 n
2
2
小结: 1)系统自振频率仅与结构有关 n 1/(I e)
1 2 n1
A(1) 1
A(2) 1
A(n1) 1
高速机一般只考虑
1, 2, 3
k
A(1) k
sin(1t
1
)
A(2) k
sin(
2t
2
)
A(n1) k
s
in(
n1t
n1 )
取第一质量作为分离体
S1 U12 0
A
h
h
1
(
2 n
2)2
4n 2
2
2 n
[1 ( n
)2 ]2
n2
4
2 n
(
n
)2
h
2 n
M I
Ie
Me
Ast
静振幅
放大系数
m A Ast
1
f ( , )
[1 ( )2 ]2 ( )2
n
n
n
讨论:
1)
s in( 2 t
2 )
n
A(1) n
sin(1t
1)
n
A(2) n
s in( 2 t
2 )
1
A(n1) 1
s in( n1t
n1 )
2
A(n1) 2
s in( n1t
n1 )
n
A(n1) n
s in( n1t
n1 )
1 A1 sin( nt )
2 A2 sin( nt )
A2 I1
A1
I2
2
I1 I2 I1 I 2 e12
两质量均作简谐振动,频率相同,初相位相
等,振幅不同,惯量大的振幅小,惯量小 的振幅大,且振动方向永远相反。
振型图
A1
e12 O
A1
单结 A2
k 1
k k1 ek1,k I ii i 1
k质量振动位移 (k 1)质量位移 (k 1, k)轴段变形
对简谐振动 Asin( nt )
2 n
A s in(
n
t
)
m a x
2 n
A
A2
A3
A1 A2
轴系承受不均匀的干扰力矩
当扭转振动所产生的应力超过许用值时,会对轴系产 生极大的破坏作用。
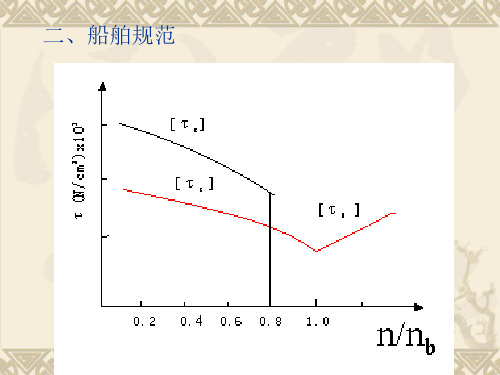
二、船舶规范
三、扭转振动的基本概念 1、扭摆有阻尼的强迫振动 图示的单质量系统,轴只计柔度,不计惯
量,圆盘只计惯量,忽略弹性。 稳太时 S+U+R+T=0
惯性力矩
S I
弹性力矩 阻尼力矩
U
(
2 n
2)2
4n2 2
2 n
2
1 A1ent sin(
1 为自由振动时的解
无阻尼时,即n=0
1 A1 sin( nt 0 )
2 n
n2t
0
2
h
sin(t tg 1 2n )
(
2 n
2)2
4n 2 2
2 n
2
Asin(t )
质量的集中点 3)对于轴系的转动惯量,当轴 ( n段较短时可以忽略或把它平均分
配到飞轮和螺旋桨的质量上 nc 4)齿轮传动时,把主、从动齿轮的转动惯量按传动比合并成一
质量,落点在主动齿轮中心线上 5)两相邻集中质量之间的连接轴,按柔度作为该两质量中心的
当量轴段长 6)轴系中有弹性联轴器或气胎离合器时,应把它们的主、从动
2)强迫振动频率与干扰力矩频率相同, 但由于阻尼存在,共振时,强迫振动的 相位落后于干扰力矩相位/2,并产生动 力放大。
3)减振方法:增加阻尼,改变自振频率及 改变干扰力矩。
2、双质量系统的扭转振动
SS11
U12 S2
0 0
I11
1 2
e12
0
I11 I 22 0
I1
1
1 2
e12
0
取第一、二质量作为分离体
2 1 e12 I1 1
S1 S2 U 23 0
I1 1 I 22
2 3
e23
0
2
3 2 e23 (I11 I 22 ) 2 e23 Iii i 1
e
R C
干扰力矩
T M sint
I C M sin t 0
e
设
2 n
1 I e
2n C I
h M I
2n n h sin t
A1ent sin(
2 n
n2t
0 )
h
sin(t tg 1 2n )
第七章 船舶推进轴系扭转振动及其控制 §4-1 概述
轴系振动有:扭转振动、回转振动(横振)、纵向振 动。其中以扭转振动为主,当周期性的交变力矩作 用的频率与自振频率相同时,将产生共振。
我国“船规”规定220kW(300HP)以上的船舶都要 申报扭振计算书。
一、扭振的概述
1、轴系扭振的成因及危害 轴系本身具有扭转振动的基本特性:弹性与惯性
e12
e23
单结
A1
A2
双结
取A1=1,A2=-I1/I2, O为结点,振幅为0, 应力最大,双质量 只有一个结点。
A2
三质量系统有两个
自振频率,单结或
双结,即两个结点。
A3 A3
n个质量就有n-1个 振型,n-1个自振 频率。
§4-2 推进轴系扭振计算
一、推进轴系的模化 模化原则: 1)以每一曲柄回转平面中心线为单缸运动质量的集中点 2)发动机输出端之后,以具有较大转动惯量部件的中心线作为
部分分为两集中质量 7)轴系中有液力偶合器时为界,分成两个独立的扭振系统 8)被发动机拖动的机械,转动惯量大的也要作一集中质量
二、多质量系统无阻尼简谐振动计算
1
A(1) 1
sin(1t
1)
1
A(2) 1
s in( 2 t
2 )
2
A(
