第二十一届全国中学生物理竞赛复赛试题及答案
第21届全国中学生高中物理竞赛复赛题试卷及参考解答
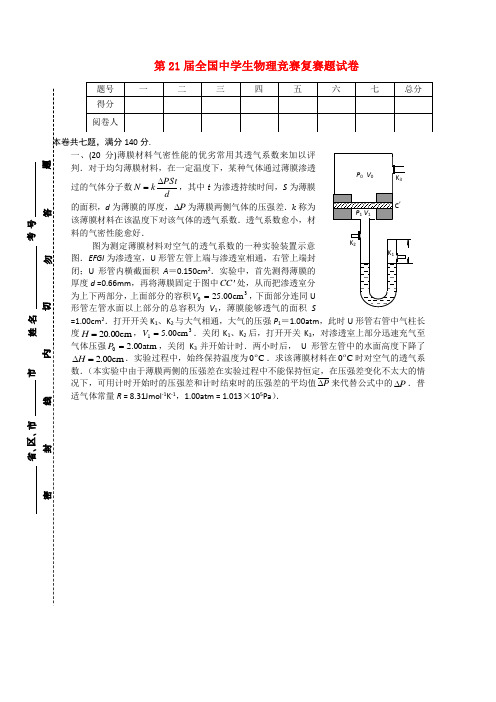
140分. 一、(20分)薄膜材料气密性能的优劣常用其透气系数来加以评判.对于均匀薄膜材料,在一定温度下,某种气体通过薄膜渗透过的气体分子数dPSt k N ∆=,其中t 为渗透持续时间,S 为薄膜的面积,d 为薄膜的厚度,P ∆为薄膜两侧气体的压强差.k 称为该薄膜材料在该温度下对该气体的透气系数.透气系数愈小,材料的气密性能愈好. 图为测定薄膜材料对空气的透气系数的一种实验装置示意图.EFGI 为渗透室,U 形管左管上端与渗透室相通,右管上端封闭;U 形管内横截面积A =0.150cm 2.实验中,首先测得薄膜的厚度d =0.66mm ,再将薄膜固定于图中C C '处,从而把渗透室分为上下两部分,上面部分的容积30cm 00.25=V ,下面部分连同U形管左管水面以上部分的总容积为V 1,薄膜能够透气的面积S=1.00cm 2.打开开关K 1、K 2与大气相通,大气的压强P 1=1.00atm ,此时U 形管右管中气柱长度cm 00.20=H ,31cm 00.5=V .关闭K 1、K 2后,打开开关K 3,对渗透室上部分迅速充气至气体压强atm 00.20=P ,关闭K 3并开始计时.两小时后, U 形管左管中的水面高度下降了cm 00.2=∆H .实验过程中,始终保持温度为C 0 .求该薄膜材料在C 0 时对空气的透气系数.(本实验中由于薄膜两侧的压强差在实验过程中不能保持恒定,在压强差变化不太大的情况下,可用计时开始时的压强差和计时结束时的压强差的平均值P ∆来代替公式中的P ∆.普适气体常量R = 8.31Jmol -1K -1,1.00atm = 1.013×105Pa ).第21届全国中学生物理竞赛复赛题试卷二、(20分) 两颗人造卫星绕地球沿同一椭圆轨道同向运动,它们通过轨道上同一点的时间相差半个周期.已知轨道近地点离地心的距离是地球半径R的2倍,卫星通过近地点时的速度v,式中M为地球质量,G为引力常量.卫星上装有同样的角度测量仪,可测GM43R出卫星与任意两点的两条连线之间的夹角.试设计一种测量方案,利用这两个测量仪测定太空中某星体与地心在某时刻的距离.(最后结果要求用测得量和地球半径R表示)三、(15分)μ子在相对自身静止的惯性参考系中的平均寿命s 100.260-⨯≈τ.宇宙射线与大气在高空某处发生核反应产生一批μ子,以v = 0.99c 的速度(c 为真空中的光速)向下运动并衰变.根据放射性衰变定律,相对给定惯性参考系,若t = 0时刻的粒子数为N (0), t 时刻剩余的粒子数为N (t ),则有()()τt N t N -=e 0,式中τ为相对该惯性系粒子的平均寿命.若能到达地面的μ子数为原来的5%,试估算μ子产生处相对于地面的高度h .不考虑重力和地磁场对μ子运动的影响.四、(20分)目前,大功率半导体激光器的主要结构形式是由许多发光区等距离地排列在一条直线上的长条状,通常称为激光二极管条.但这样的半导体激光器发出的是很多束发散光束,光能分布很不集中,不利于传输和应用.为了解决这个问题,需要根据具体应用的要求,对光束进行必需的变换(或称整形).如果能把一个半导体激光二极管条发出的光变换成一束很细的平行光束,对半导体激光的传输和应用将是非常有意义的.为此,有人提出了先把多束发散光会聚到一点,再变换为平行光的方案,其基本原理可通过如下所述的简化了的情况来说明.如图,S1、S2、S3 是等距离(h)地排列在一直线上的三个点光源,各自向垂直于它们的连线的同一方向发出半顶角为α=arctan()41的圆锥形光束.请使S用三个完全相同的、焦距为f = 1.50h、半径为r =0.75 h的圆形薄凸透镜,经加工、组装成一个三者在同一平面内的组合透镜,使三束光都能全部投射到这个组合透镜上,且经透镜折射后的光线能全部会聚于z轴(以S2为起点,垂直于三个点光源连线,与光束中心线方向相同的射线)上距离S2为L = 12.0 h处的P点.(加工时可对透镜进行外形的改变,但不能改变透镜焦距.)1.求出组合透镜中每个透镜光心的位置.2.说明对三个透镜应如何加工和组装,并求出有关数据.五、(20分)如图所示,接地的空心导体球壳内半径为R,在空腔内一直径上的P 1和P 2处,放置电量分别为q 1和q 2的点电荷,q 1=q 2=q ,两点电荷到球心的距离均为a .由静电感应与静电屏蔽可知:导体空腔内表面将出现感应电荷分布,感应电荷电量等于-2q .空腔内部的电场是由q 1、q 2和两者在空腔内表面上的感应电荷共同产生的.由于我们尚不知道这些感应电荷是怎样分布的,所以很难用场强叠加原理直接求得腔内的电势或场强.但理论上可以证明,感应电荷对腔内电场的贡献,可用假想的位于腔外的(等效)点电荷来代替(在本题中假想(等效)点电荷应为两个),只要假想的(等效)点电荷的位置和电量能满足这样的条件,即:设想将整个导体壳去掉,由q 1在原空腔内表面的感应电荷的假想(等效)点电荷1q '与q 1共同产生的电场在原空腔内表面所在位置处各点的电势皆为0;由q 2在原空腔内表面的感应电荷的假想(等效)点电荷2q '与q 2共同产生的电场在原空腔内表面所在位置处各点的电势皆为0.这样确定的假想电荷叫做感应电荷的等效电荷,而且这样确定的等效电荷是唯一的.等效电荷取代感应电荷后,可用等效电荷1q '、2q '和q 1、q 2来计算原来导体存在时空腔内部任意点的电势或场强.1.试根据上述条件,确定假想等效电荷1q '、2q '的位置及电量. 2.求空腔内部任意点A 的电势U A .已知A 点到球心O 的距离为r ,OA 与1OP 的夹角为θ .六、(20分)如图所示,三个质量都是m的刚性小球A、B、C位于光滑的水平桌面上(图中纸面),A、B之间,B、C之间分别用刚性轻杆相连,杆与A、B、C的各连接处皆为“铰链式”的(不能对小球产生垂直于杆方向的作用力).已知杆AB与BC的夹角为π-α,α < π/2.DE为固定在桌面上一块挡板,它与AB连线方向垂直.现令A、B、C一起以共同的速度v沿平行于AB连线方向向DE运动,已知在C与挡板碰撞过程中C与挡板之间无摩擦力作用,求碰撞时当C沿垂直于DE方向的速度由v变为0这一极短时间内挡板对C的冲量的大小.七、(25分)如图所示,有二平行金属导轨,相距l ,位于同一水平面内(图中纸面),处在磁感应强度为B 的匀强磁场中,磁场方向竖直向下(垂直纸面向里).质量均为m 的两金属杆ab 和cd 放在导轨上,与导轨垂直.初始时刻, 金属杆ab 和cd 分别位于x = x 0和x = 0处.假设导轨及金属杆的电阻都为零,由两金属杆与导轨构成的回路的自感系数为L .今对金属杆ab 施以沿导轨向右的瞬时冲量,使它获得初速0v .设导轨足够长,0x 也足够大,在运动过程中,两金属杆之间距离的变化远小于两金属杆的初始间距0x ,因而可以认为在杆运动过程中由两金属杆与导轨构成的回路的自感系数L 是恒定不变的.杆与导轨之间摩擦可不计.求任意时刻两杆的位置x ab 和x cd 以及由两杆和导轨构成的回路中的电流i 三者各自随时间t 的变化关系.第21届全国中学生物理竞赛复赛题参考解答一、开始时U 形管右管中空气的体积和压强分别为 V 2 = HA (1)p 2= p 1经过2小时,U 形管右管中空气的体积和压强分别为A H H V )(2∆-='(2)2222V V p p '=' (3)渗透室下部连同U 形管左管水面以上部分气体的总体积和压强分别为 HAV V ∆+='11 (4)H g p p Δ221ρ+'=(5)式中ρ 为水的密度,g 为重力加速度.由理想气体状态方程nRT pV =可知,经过2小时,薄膜下部增加的空气的摩尔数RTV p RT V p n 1111-''=∆ (6)在2个小时内,通过薄膜渗透过去的分子数A nN N ∆=(7)式中N A 为阿伏伽德罗常量.渗透室上部空气的摩尔数减少,压强下降.下降了∆pV ΔnRTp =∆ (8)经过2小时渗透室上部分中空气的压强为p p p ∆-='00(9)测试过程的平均压强差[])(211010p p ()p p p '-'+-=∆ (10)根据定义,由以上各式和有关数据,可求得该薄膜材料在0℃时对空气的透气系数11111s m Pa 104.2---⨯=∆=tSp Nd k(11)评分标准:本题20分.(1)、(2)、(3)、(4)、(5)式各1分,(6)式3分,(7)、(8)、(9)、(10) 式各2分,(11) 式4分.二、如图,卫星绕地球运动的轨道为一椭圆,地心位于轨道椭圆的一个焦点O 处,设待测量星体位于C 处.根据题意,当一个卫星运动到轨道的近地点A 时,另一个卫星恰好到达远地点B 处,只要位于A 点的卫星用角度测量仪测出AO 和AC 的夹角α1,位于B 点的卫星用角度测量仪测出BO 和BC 的夹角α2,就可以计算出此时星体C 与地心的距离OC . 因卫星椭圆轨道长轴的长度远近+r r AB =(1)式中r 近、与r 远分别表示轨道近地点和远地点到地心的距离.由角动量守恒远远近近=r m r v mv (2)式中m 为卫星的质量.由机械能守恒远远近近--r GMm m r GMm m 222121v v = (3) 已知R r 2=近, RGM43=近v得 R r 6=远(4)所以R R R AB 862=+= (5)在△ABC 中用正弦定理 ()ABBC211πsin sin ααα--= (6)所以()AB BC 211sin sin ααα+=(7)地心与星体之间的距离为OC ,在△BOC 中用余弦定理2222cos 2αBC r BC r OC ⋅-+=远远(8)由式(4)、(5)、(7)得()()212121212sin cos sin 24sin sin 1692ααααααα+-++=R OC(9)评分标准:本题20分.(1)式2分,(2)、(3)式各3分,(6) 、(8)式各3分, (9) 式6分.三、因μ子在相对自身静止的惯性系中的平均寿命s 100.260-⨯≈τ根据时间膨胀效应,在地球上观测到的μ子平均寿命为τ,()21c v -=ττ (1)代入数据得 τ = 1.4×10-5s(2)相对地面,若μ子到达地面所需时间为t ,则在t 时刻剩余的μ子数为()()τt N t N -=e 0 (3)根据题意有()()%5e 0==-τt N t N (4)对上式等号两边取e 为底的对数得1005lnτ-=t (5)代入数据得s 1019.45-⨯=t(6)根据题意,可以把μ子的运动看作匀速直线运动,有t h v =(7)代入数据得 m 1024.14⨯=h(8)评分标准:本题15分. (1)式或(2)式6分,(4)式或(5)式4分,(7) 式2分,(8) 式3分.四、1.考虑到使3个点光源的3束光分别通过3个透镜都成实像于P 点的要求,组合透镜所在的平面应垂直于z 轴,三个光心O 1、O 2、O 3的连线平行于3个光源的连线,O 2位于z 轴上,如图1所示.图中M M '表示组合透镜的平面,1S '、2S '、3S '为三个光束中心光线与该平面的交点. 22O S = u 就是物距.根据透镜成像公式fu L u 111=-+ (1) 可解得]4[212fL L L u -±=因为要保证经透镜折射后的光线都能全部会聚于P 点,来自各光源的光线在投射到透镜之前不能交叉,必须有2u tan α ≤h 即u ≤2h .在上式中取“-”号,代入f 和L 的值,算得h u )236(-=≈1.757h (2)此解满足上面的条件.分别作3个点光源与P 点的连线.为使3个点光源都能同时成像于P 点,3个透镜的光心O 1、O 2、O 3应分别位于这3条连线上(如图1).由几何关系知,有 h h h L u L O O O O 854.0)24121(3221≈+=-==(3)即光心O 1的位置应在1S '之下与1S '的距离为 h O O h O S 146.02111=-= (4)同理,O 3的位置应在3S '之上与3S '的距离为0.146h 处.由(3)式可知组合透镜中相邻薄透镜中心之间距离必须等于0.854h ,才能使S 1、S 2、S 3都能成像于P 点. 2.现在讨论如何把三个透镜L 1、L 2、L 3加工组装成组合透镜. 因为三个透镜的半径r = 0.75h ,将它们的光心分别放置到O 1、O 2、O 3处时,由于21O O =32O O =0.854h <2r ,透镜必然发生相互重叠,必须对透镜进行加工,各切去一部分,然后再将它们粘起来,才能满足(3)式的要求.由于对称关系,我们只需讨论上半部分的情况.图2画出了L 1、L 2放在M M '平面内时相互交叠的情况(纸面为M M '平面).图中C 1、C 2表示L 1、L 2的边缘,1S '、2S '为光束中心光线与透镜的交点,W 1、W 2分别为C 1、C 2与O 1O 2的交点.1S '为圆心的圆1和以2S '(与O 2重合)为圆心的圆2分别是光源S 1和S 2投射到L 1和L 2时产生的光斑的边缘,其半径均为h u 439.0tan ==αρ (5) 根据题意,圆1和圆2内的光线必须能全部进入透镜.首先,圆1的K 点(见图2)是否落在L 1上?由几何关系可知h h()h r h h S O K O 75.0585.0146.0439.0111=<=+='+=ρ (6) 故从S 1发出的光束能全部进入L 1.为了保证全部光束能进入透镜组合,对L 1和L 2进行加工时必须保留圆1和圆2内的透镜部分.下面举出一种对透镜进行加工、组装的方法.在O 1和O 2之间作垂直于O 1O 2且分别与圆1和圆2相切的切线Q Q '和N N '.若沿位于Q Q '和N N '之间且与它们平行的任意直线T T '对透镜L 1和L 2进行切割,去掉两透镜的弓形部分,然后把它们沿此线粘合就得到符合所需组合透镜的上半部.同理,对L 2的下半部和L 3进行切割,然后将L 2的下半部和L 3粘合起来,就得到符合需要的整个组合透镜.这个组合透镜可以将S 1、S 2、S 3发出的全部光线都会聚到P 点.现在计算Q Q '和N N '的位置以及对各个透镜切去部分的大小应符合的条件.设透镜L 1被切去部分沿O 1O 2方向的长度为x 1,透镜L 2被切去部分沿O 1O 2方向的长度为x 2,如图2所示,则对任意一条切割线T T ', x 1、x 2之和为h O O r x x d 646.022121=-=+=(7)由于T T '必须在Q Q '和N N '之间,从图2可看出,沿Q Q '切割时,x 1达最大值(x 1M ),x 2达最小值(x 2m ),ρ-'+=111O S r x M 代入r ,ρ 和11O S '的值,得h x M 457.01=(8)代入(7)式,得h x d x M m 189.012=-= (9)由图2可看出,沿N N '切割时,x 2达最大值(x 2M ),x 1达最小值(x 1m ),ρ-=r x M 2 代入r 和ρ 的值,得h x M 311.02= (10) h x d x M m 335.021=-= (11)由对称性,对L 3的加工与对L 1相同,对L 2下半部的加工与对上半部的加工相同.评分标准:本题20分.第1问10分,其中(2)式5分,(3)式5分,第2问10分,其中(5)式3分,(6)式3分,(7)式2分,(8)式、(9)式共1分,(10)式、(11)式共1分.如果学生解答中没有(7)—(11)式,但说了“将图2中三个圆锥光束照射到透镜部分全部保留,透镜其它部分可根据需要磨去(或切割掉)”给3分,再说明将加工后的透镜组装成透镜组合时必须保证O 1O 2=O 1O 2=0.854h ,再给1分,即给(7)—(11)式的全分(4分).五、1.解法Ⅰ:如图1所示,S 为原空腔内表面所在位置,1q '的位置应位于1OP 的延长线上的某点B 1处,2q '的位置应位于2OP 的延长线上的某点B 2处.设A 1为S 面上的任意一点,根据题意有0111111='+B A q kP A q k(1)B 210212212='+B A q kP A q k(2)怎样才能使 (1) 式成立呢?下面分析图1中11A OP ∆与11B OA ∆的关系.若等效电荷1q '的位置B 1使下式成立,即211R OB OP =⋅(3) 即1111OB OA OA OP =(4)则1111B OA A OP ∽△△有RaOA OP B A P A ==111111 (5)由 (1)式和 (5)式便可求得等效电荷1q '11q aRq -=' (6)由 (3) 式知,等效电荷1q '的位置B 1到原球壳中心位置O 的距离aR OB 21=(7)同理,B 2的位置应使2112B OA A OP ∽△△,用类似的方法可求得等效电荷22q aRq -=' (8)等效电荷2q '的位置B 2到原球壳中心O 位置的距离 aR OB 22=(9)解法Ⅱ:在图1中,设111r P A =,111r B A '=,d OB =1.根据题意,1q 和1q '两者在A 1点产生的电势和为零.有01111=''+r q k r q k(1')式中21221)cos 2(θRa a R r -+=(2')21221)cos 2(θRd d R r -+='(3')由(1')、(2')、(3')式得)cos 2()cos 2(22212221θθRa a R q Rd d R q -+'=-+ (4')(4')式是以θcos 为变量的一次多项式,要使(4')式对任意θ均成立,等号两边的相应系数应相等,即)()(22212221a R q d R q +'=+ (5')a q d q 2121'= (6') 由(5')、(6')式得0)(2222=++-aR d R a ad (7') 解得aR a R a d 2)()(2222-±+=(8')由于等效电荷位于空腔外部,由(8')式求得 aR d 2=(9')由(6')、(9')式有212221q aR q =' (10')考虑到(1')式,有11q aRq -='(11')同理可求得aR OB 22=(12')22q aRq -=' (13')2.A 点的位置如图2所示.A 的电势由q 1、1q '、q 2、2q '共同产生,即⎪⎪⎭⎫ ⎝⎛-+-=A B a R A P A B a R A P kq U A 22111111 (10)因221cos 2a ra r A P +-=θ22221cos 2⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛-=a R a R r r A B θ 222cos 2a ra r A P ++=θ22222cos 2⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+=a R a R r r A B θ 代入 (10) 式得⎝⎛+--+-=422222cos 2cos 21RraR r a Rara r kq U A θθ⎪⎪⎭⎫++-+++422222cos 2cos 21R raR r a Rara r θθ(11)评分标准:本题20分.第1问18分,解法Ⅰ中(1)、(2)、(6)、(7)、(8)、(9) 式各3分.解法Ⅱ的评分可参考解法Ⅰ.第2问2分,即(11)式2分.六、令I 表示题述极短时间∆t 内挡板对C 冲量的大小,因为挡板对C 无摩擦力作用,可知冲量的方向垂直于DE ,如图所示;I '表示B 、C 间的杆对B 或C 冲量的大小,其方向沿杆方向,对B 和C 皆为推力;C v 表示∆t 末了时刻C 沿平行于DE 方向速度的大小,B v 表示∆t 末了时刻B 沿平行于DE 方向速度的大小,⊥B v 表示∆t 末了时刻B 沿垂直于DE 方向速度的大小.由动量定理, 对C 有C m I v ='αsin(1) v m I I ='-αcos (2) 对B 有B m I v ='αsin (3)对AB 有()⊥-='B m I v v 2cos α(4)因为B 、C 之间的杆不能伸、缩,因此B 、C 沿杆的方向的分速度必相等.故有αααsin cos sin B B C v v v -=⊥(5)由以上五式,可解得v m I αα22sin 31sin 3++= (6)图2本题20分. (1)、(2)、(3)、(4)式各2分. (5)式7分,(6)式5分.七、解法Ⅰ:当金属杆ab 获得沿x 轴正方向的初速v 0时,因切割磁力线而产生感应电动势,由两金属杆与导轨构成的回路中会出现感应电流.由于回路具有自感系数,感应电流的出现,又会在回路中产生自感电动势,自感电动势将阻碍电流的增大,所以,虽然回路的电阻为零,但回路的电流并不会趋向无限大,当回路中一旦有了电流,磁场作用于杆ab 的安培力将使ab 杆减速,作用于cd 杆的安培力使cd 杆运动.设在任意时刻t ,ab 杆和cd 杆的速度分别为v 1和v 2(相对地面参考系S ),当v 1、v 2为正时,表示速度沿x 轴正方向;若规定逆时针方向为回路中电流和电动势的正方向,则因两杆作切割磁力线的运动而产生的感应电动势()21v v -=Bl E(1)当回路中的电流i 随时间的变化率为t i ∆∆时,回路中的自感电动势ti LL ∆∆-=E (2)根据欧姆定律,注意到回路没有电阻,有0=+L E E(3)金属杆在导轨上运动过程中,两杆构成的系统受到的水平方向的合外力为零,系统的质心作匀速直线运动.设系统质心的速度为V C ,有 C mV m 20=v(4)得2v =C V (5)V C 方向与v 0相同,沿x 轴的正方向.现取一新的参考系S ',它与质心固连在一起,并把质心作为坐标原点O ',取坐标轴x O ''与x 轴平行.设相对S '系,金属杆ab 的速度为u ,cd 杆的速度为u ',则有 u V C +=1v (6)u V C '+=2v(7)因相对S '系,两杆的总动量为零,即有0='+u m mu (8)由(1)、(2)、(3)、(5)、(6) 、(7) 、(8)各式,得ti LBlu ∆∆=2 (9)在S '系中,在t 时刻,金属杆ab 坐标为x ',在t +∆t 时刻,它的坐标为x x '∆+',则由速度的定义tx u ∆'∆=(10)i L x Bl ∆='∆2 (11)若将x '视为i 的函数,由(11)式知i x ∆'∆为常数,所以x '与i 的关系可用一直线方程表示b i BlLx +='2 (12)式中b 为常数,其值待定.现已知在t =0时刻,金属杆ab 在S '系中的坐标x '=021x ,这时i = 0,故得0212x i Bl L x +=' (13)或⎪⎭⎫ ⎝⎛-'=0212x x L Bl i (14)021x 表示t =0时刻金属杆ab 的位置.x '表示在任意时刻t ,杆ab 的位置,故⎪⎭⎫ ⎝⎛-'021x x 就是杆ab 在t 时刻相对初始位置的位移,用X 表示,021x x X -'= (15)当X >0时,ab 杆位于其初始位置的右侧;当X <0时,ab 杆位于其初始位置的左侧.代入(14)式,得X LBli 2=(16)这时作用于ab 杆的安培力X Ll B iBl F 222-=-= (17)ab 杆在初始位置右侧时,安培力的方向指向左侧;ab 杆在初始位置左侧时,安培力的方向指向右侧,可知该安培力具有弹性力的性质.金属杆ab 的运动是简谐振动,振动的周期()Ll B mT 222π2= (18)在任意时刻t , ab 杆离开其初始位置的位移⎪⎭⎫⎝⎛+=ϕt T A X π2cos(19)A 为简谐振动的振幅,ϕ 为初相位,都是待定的常量.通过参考圆可求得ab 杆的振动速度⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛-=ϕt T T A u π2sin π2 (20)(19)、(20)式分别表示任意时刻ab 杆离开初始位置的位移和运动速度.现已知在t =0时刻,ab 杆位于初始位置,即X = 0 速度00002121v v v v =-=-=C V u 故有ϕcos 0A = ϕsin π220⎪⎭⎫ ⎝⎛-=T A v 解这两式,并注意到(18)式得 2π3=ϕ(21) 22400mLBl T A v v ==π(22) 由此得ab 杆的位移 t T mLBl t T mL Bl X π2sin 222π3π2cos 2200vv =⎪⎭⎫ ⎝⎛+=(23) 由 (15) 式可求得ab 杆在S '系中的位置 t T mL Bl x x π2sin 222100ab v +='(24) 因相对质心,任意时刻ab 杆和cd 杆都在质心两侧,到质心的距离相等,故在S '系中,cd 杆的位置 t T mLBl x x π2sin 222100cd v --='(25) 相对地面参考系S ,质心以021v =C V 的速度向右运动,并注意到(18)式,得ab 杆在地面参考系中的位置 t mL Bl mL Bl t x x ⎪⎪⎭⎫⎝⎛++=2sin 2221000ab v v(26) cd 杆在S 系中的位置 t mL BlmL Bl t x ⎪⎪⎭⎫⎝⎛-=2sin 222100cd v v(27)回路中的电流由 (16) 式得 t mL Bl L m t T mL Bl L Bl i ⎪⎪⎭⎫⎝⎛==2sin 2π2sin 22200v v(28) 解法Ⅱ:当金属杆在磁场中运动时,因切割磁力线而产生感应电动势,回路中出现电流时,两金属杆都要受到安培力的作用,安培力使ab 杆的速度改变,使cd 杆运动.设任意时刻t ,两杆的速度分别为v 1和v 2(相对地面参考系S ),若规定逆时针方向为回路电动势和电流的正方向,则由两金属杆与导轨构成的回路中,因杆在磁场中运动而出现的感应电动势为()21v v -=Bl E(1’) 令u 表示ab 杆相对于cd 杆的速度,有Blu L =E(2’) 当回路中的电流i 变化时,回路中有自感电动势E L ,其大小与电流的变化率成正比,即有 t iL L ∆∆-=E(3’) 根据欧姆定律,注意到回路没有电阻,有0=+L E E 由式(2’)、(3’)两式得 t iL Blu ∆∆=(4’) 设在t 时刻,金属杆ab 相对于cd 杆的距离为x ',在t +∆t 时刻,ab 相对于cd 杆的距离为x '+x '∆,则由速度的定义,有 t x u ∆'∆=(5’) 代入 (4') 式得i L x Bl ∆='∆(6’) 若将x '视为i 的函数,由(6’)式可知,i x ∆'∆为常量,所以x '与i 的关系可以用一直线方程表示,即 b i Bl Lx +='(7’) 式中b 为常数,其值待定.现已知在t =0时刻,金属杆ab 相对于cd 杆的距离为0x ,这时i = 0,故得 0x i Bl Lx +='(8’) 或 ()0x x L Bli -'=(9’) 0x 表示t =0时刻金属杆ab 相对于cd 杆的位置.x '表示在任意时刻t 时ab 杆相对于cd 杆的位置,故()0x x -'就是杆ab 在t 时刻相对于cd 杆的相对位置相对于它们在t =0时刻的相对位置的位移,即从t =0到t =t 时间内ab 杆相对于cd 杆的位移0x x X -'=(10') 于是有X L Bli =(11’) 任意时刻t ,ab 杆和cd 杆因受安培力作用而分别有加速度a ab 和a cd ,由牛顿定律有 ab ma iBl =-(12’) cd ma iBl =(13’)两式相减并注意到(9')式得()X L l B iBl a a m 22cd ab 22-=-=-(14’) 式中()cd ab a a -为金属杆ab 相对于cd 杆的加速度,而X 是ab 杆相对cd 杆相对位置的位移.L l B 222是常数,表明这个相对运动是简谐振动,它的振动的周期()L l B mT 222π2=(15’) 在任意时刻t ,ab 杆相对cd 杆相对位置相对它们初始位置的位移⎪⎭⎫⎝⎛+=ϕt T A X π2cos(16’) A 为简谐振动的振幅,ϕ 为初相位,都是待定的常量.通过参考圆可求得X 随时间的变化率即速度⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=ϕT T A V π2sin π2(17’) 现已知在t =0时刻,杆位于初始位置,即X = 0,速度0v =V故有ϕcos 0A = ϕsin π20⎪⎭⎫⎝⎛-=T A v解这两式,并注意到(15’) 式得2π3=ϕ 2π200mLBl T A v v ==由此得 t mL Bl mL Bl t T mL Bl X ⎪⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛+=2sin 22π3π2cos 200v v(18’) 因t = 0时刻,cd 杆位于x = 0 处,ab 杆位于x = x 0 处,两者的相对位置由x 0表示;设t 时刻,cd 杆位于x = x cd 处,ab 杆位于x = x ab 处,两者的相对位置由x ab -x cd 表示,故两杆的相对位置的位移又可表示为X = x ab -x cd -x 0(19’) 所以 t mL Bl mL Bl x x x ⎪⎪⎭⎫⎝⎛+=-2sin 200cd ab v(20’)(12’)和(13’)式相加,()0cd ab =+-=+iBl iBl a a m 得()0cd ab =+a a由此可知,两杆速度之和为一常数即v 0,所以两杆的位置x ab 和x cd 之和应为x ab +x cd = x 0+v 0t(21’) 由(20’)和(21’)式相加和相减,注意到(15’)式,得 t mL Bl mL Bl t x x ⎪⎪⎭⎫⎝⎛++=2sin 2221000ab vv(22’) t mL Bl mL Bl t x ⎪⎪⎭⎫⎝⎛-=2sin 222100cd v v(23’) 由(11’)、(19’)(22’)、(23’)式得回路中电流 t mL Bl L m i ⎪⎪⎭⎫⎝⎛=2sin 20v(24’)评分标准:本题25分.解法Ⅰ 求得(16)式8分,(17)、(18)、(19)三式各2分. (23)式4分,(24)、(25)二式各2分,(26)、(27)、(28)三式各1分.解法Ⅱ的评分可参照解法Ⅰ评分标准中的相应式子给分.。
2011年第二十一届全国初中应用物理竞赛复赛试卷参考答案与试题解析

2011年第二十一届全国初中应用物理竞赛复赛试卷参考答案与试题解析1、分析:(1)先对红血球进行受力分析,然后比较红血球受到竖直向上和竖直向下合力的大小确定红血球的运动状态;(2)先表示出红血球受到的浮力和重力,然后根据红血球在血浆中匀速下沉时,受到平衡力作用的等价关系,化简得出R的表达式,然后将已知条件代入式中即可求得.解答:解:(1)红血球在血浆中下沉时,受到竖直向下的重力和竖直向上的粘滞阻力和浮力;红血球由静止开始下沉时,速度很小,根据f=6πηRv可知,所受的粘滞阻力也非常小,由于血浆的密度ρ0小于红细胞的密度ρ,红血球受到的浮力小于重力,所以开始f+F浮<G,红血球会加速下沉,随着红血球下沉速度变大,粘滞阻力增大,当f+F浮=G时,红血球就会匀速下沉.(2)当红血球在血浆中匀速下沉时,受到平衡力作用,因此有:f+F浮=G;F浮=ρ0V排g=ρ0R3g=ρ0gR3,G=mg=ρV排g=ρR3g=ρgR3,∵f=6πηRv∴6πηRv+ρ0gR3=ρgR3即R=已知:g=10N/kg,η=1.8×10﹣3Pa﹒s,v=12mm/h=×10﹣5m/s,ρ0≈1.0×103kg/m3,ρ≈1.3×103kg/m3代入上式得:R==3×10﹣6m.答:红血球半径的大小3×10﹣6m.2、分析:(1)已知蓄电池的容量和输出功率,利用t=计算时间;(2)已知太阳能的转换效率和太阳辐射最大强度及需要达到的最大功率,利用效率公式计算得出面积;(3)已知蓄电池的容量和灯泡的功率,利用t=计算时间.解答:解:(1)蓄电池的容量:W=12V×500A•h×(90%﹣20%)=12V×500A×3600s×(90%﹣20%)=1.512×107J;需要的时间:t===302400s=84h;(2)电池板面积:S===1m2;(3)为了能使蓄电池的使用寿命更为长久,一般充电至90%左右即停止,放电余留20%左右即停止电能输出,与(1)蓄电池的电量由20%充至90%相符,即蓄电池的容量相等,故可供灯具发光时间:t灯===189000s=52.5h.答:(1)将蓄电池的电量由20%充至90%需84h;(2)太阳能电池板的面积至少要1m2;(3)最多可供灯具正常发光52.5h.3、分析:(1)根据影响滑动摩擦力的大小因素,从增大和减小摩擦的知识点去分析即可.(2)估计中学生的质量大约为50kg,电动自行车对地面的压力等于中学生和电动车的重力之和,利用G=mg求出其大小,再根据压强公式求出对地面的压强.(3)根据表格中数据可知额定功率和额定电压,根据I=求出额定电流.(4)已知正常工作电压和容量,根据W=UIt求出蓄电池一次充足电可储存的能量;(5)根据电动自行车行驶克服阻力做功为W=fs,因蓄电池储存能量的80%提供给电动机,电动机工作时将电能转化为对自行车输出机械能的效率为75%,用于电动自行车行驶克服阻力做功,即W×80%×75%=fs,就可以求出电动车行驶的路程S.(6)电动自行车相对于内燃机来说,减少了尾气和热量的排放,以及噪声的污染但蓄电池使用寿命短且废弃后会环境有污染.解答:解:(1)电动自行车的构造上蕴含着丰富的物理知识:①电动自行车的轮胎上有凹凸不平的花纹,可增大摩擦;②车把手有花纹,可增大摩擦;③脚踏板上有花纹,可增大摩擦;④车把的构造是轮轴,省力;⑤车轮是圆形的,滚动摩擦比滑动摩擦小.故答案为:A、电动自行车的轮胎上有凹凸不平的花纹,可增大摩擦;B、车把手有花纹,可增大摩擦;C、脚踏板上有花纹,可增大摩擦.(2)假设汽车人的质量约为50kg,人骑车时对地面的压力为人和车的重力之和,则路面受到的压强:P====2.25×105Pa答:路面受到的压强大约2.25×105Pa.(3)电动自行车额定工作下的电流:I===5A答:电动自行车以额定功率行驶时通过电动机线圈的电流是5A.(4)蓄电池储存的电能:W=UIt=48V×12A×3600s=2.07×106J.答:蓄电池充足电后储存的能量是2.07×106J.(5)因为电动自行车匀速行驶,所以f=F,据题意可得:W×80%×75%=fs∴S===4.14×104m答:蓄电池充一次电最多能完全依靠储存的电能连续行驶4.14×104m.(6)优点:不会排放尾气、噪音小;缺点:蓄电池一般使用一定时间后就需更换,废弃后的电池易污染环境.4、分析:(1)水的凝固点是0℃,水在结冰过程中体积会膨胀;(2)已知热水器的额定热负荷和1min,可以得到在此时间产生的热量Q;已知1min加热水的体积,可以得到1min加热水的质量;已知水的质量、比热和升高的温度,可以得到吸收的热量;已知水吸收的热量和热水器产生的热量,两者之比就是热水器的烧水效率;(3)已知热水器的额定热负荷和淋浴时间,可以得到在此时间产生的热量Q淋;已知需要的热量和天然气的热值,利用V=得到燃烧的天然气;(4)水箱中进水时,对膜片有向左的压力,压力足够大时,弹簧被压缩,燃气阀门打开,热水器供热;反之燃气阀门关闭;(5)物体具有热胀冷缩的性质,但不同物体的热膨胀程度不同,双金属片就是两片热膨胀程度相差很大的金属片铆合而成.解答:解:(1)气温低于0℃时,使用后的热水器中残存的水会结冰.水结冰后,密度变小,体积膨胀,很容易把热水器胀破.所以,气温低于0℃时,用后需要打开放水塞,放尽机体内存水,再拧紧;(2)热水器正常工作1min,产生的热量为Q=Pt=16×103W×60s=9.6×105J1min内加热水的质量为m=ρV=1.0×103kg/m3×8×10﹣3m3=8kg这些水吸收的热量为Q吸=cm△t=4.2×103J/(kg•℃)×8kg×25℃=8.4×105J热水器的烧水效率为η===87.5%;答:热水器的烧水效率为87.5%;(3)一次淋浴需要的热量为Q淋=Pt淋=16×103W×1200s=1.92×107J需要完全燃烧的天然气的体积为V气===0.24m3;答:一次淋浴需要完全燃烧0.24m3的天然气;(4)当进水口处有水压时,膜片的右面就会受到向左的压力,克服弹簧的弹力向左推动阀杆,打开进气阀门使燃气接入主火管道;反之,如果此时的水压很小或者无水,则膜片受到的向左的压力就会减小甚至消失,燃气阀门就会在弹簧的压力下向右移动而关闭,停止进气;(5)火焰燃烧时,双金属片外侧的金属温度升高时膨胀的更多,双金属片向下弯曲,推动燃气阀门打开;如果因为意外的原因使火焰熄灭,双金属片的温度降低,外侧金属收缩的更多,双金属片向上伸直,拉动燃气阀门关闭,防止燃气外泄.5、分析:(1)用铭牌可知电热水器的净重和容积,根据m=ρV和G=mg求出电热水器的总重,然后对静止的热水器受力分析,根据二力平衡条件可知竖直方向对L形挂钩向下的拉力;以悬挂架下端为轴,可以把热水器看成杠杆,根据杠杆的平衡条件求出电热水器上端所受的水平向左的拉力即膨胀螺钉所受的摩擦力.(2)这台热水器共有三挡加热功率且最大功率等于剩余两功率之和据此可以猜想两电热管并联,据此画出等效电路图;根据R=分别求出两加热管的电阻.(3)忽略加热过程的热损失,根据W=Q=cm△t求出直接加热消耗的电能,并求出下午加热支出的电费;先求出早晨8点前加热支出的电费,再根据W=Q=cm△t求出加热升温4℃所需电能和最大功率加热时的时间,因时间很小可以忽略不计;降低4℃所需时间为190min,至下午6点共需要三次加热,进一步求出三次消耗的电能和支出的电费,总电费等于这两者之和;然后比较这中方案支出的电费即可判断那种更经济.解答:解:(1)电热水器的总重:G总=m电g+ρ水gV=19×10N/kg+1.0×103kg/m3×50×10﹣3m3×10N/kg=690N,电热水器挂在L形挂钩上时,其受力情况如下:挂钩竖直方向:向上的拉力F和向下电热水器的总重G总,水平方向:向右的支持力和向左膨胀螺钉的拉力,此时膨胀螺钉受到的拉力和摩擦力是一对平衡力;因电热水器静止,所以沿竖直方向二力平衡,因此对L形挂钩向下的拉力F=G=690N;因L形挂钩静止,电热水器上端所受的水平向左的拉力等于膨胀螺钉所受的摩擦力;以悬挂架下端为轴,把热水器看成杠杆,则根据杠杆的平衡条件可得fD=G总C,f===690N.(2)由热水器的三档位的数值关系猜测得热水器加热部分的等效电路图如下图所示:其中加热管R1的额定功率为1000W,电热管R2的额定功率为1500W;加热管的电阻分别为:R1===48.4Ω,R2==≈32.3Ω.(3)①忽略加热过程的热损失,直接加热消耗的电能为:W1=Q1=cm△t1=4.2×103J/(kg•℃)×50kg×(50℃﹣20℃)=6.3×106J=1.75KW•h,下午加热的电费支出为:0.6元/KW•h×1.75KW•h=1.05元;②早晨8点前加热,电费支出为:0.3元/KW•h×1.75KW•h=0.525元;加热升温4℃所需电能:W2=Q2=cm△t2=4.2×103J/(kg•℃)×50kg×(50℃﹣46℃)=8.4×105J,加热升温4℃所需时间(设加热功率为2500W)t1===336s=5.6min,(这段加热时间可以忽略不计)降低4℃所需时间为190min,至下午6点共需要三次加热,消耗电能:W3=3W2=3×8.4×105J=2.52×106J=0.7KW•h,电费支出:0.6元/KW•h×0.7KW•h=0.42元;总支出:0.525元+0.42元=0.945元,所以,第二方案更省钱.答:(1)L形挂钩受到的最大向下拉力为690N,此时膨胀螺钉与承重墙体间的摩擦力为690N.(2)内部加热电路的主要结构如上图所示,每个加热管的电阻值分别为48.4Ω、32.3Ω.(3)第二方案更省钱.6、分析:(1)影响摩擦力大小的因素有两个:压力和接触面的粗糙程度,锯盘锯木料时,要尽量减少锯盘与木料之间的摩擦力.(2)分析锯盘的转动方向,从而得出电动机的皮带轮转动方向,皮带轮拉动哪侧的皮带,哪侧的拉力就越大.(3)已知电动机皮带轮的半径,求出其周长S;再根据转速求出转一转所用的时间t,根据V=就可求出皮带的运行速度V.根据“电动机满负荷工作时配套电动机输出机械能的效率为90%”求出输出的机械功率,再根据F=计算出皮带上较大的拉力与较小的拉力的差值.(4)把皮带轮所受拉力的情况可等效为左侧皮带拉力为0N,右侧带拉力为330N,设圆形锯盘所受木料的阻力为F1,结合轮轴的公式进行求解.解答:解:(1)①锯齿部分比锯盘部分稍厚一些,木料的锯切口的宽度就会比锯盘厚度略大一点,这就可以有效的减少锯开的木料对锯盘盘面的压力,从而减少木料对锯盘盘面的摩擦阻力;②锯齿部分比锯盘部分稍厚一些,再加上锯盘周边所开的缝及缝的底端所打的孔,这就保证了锯开的木料与锯盘盘面之间的缝隙能够时时充满空气,从而避免受到因大气压把锯开的木料紧紧压在锯盘盘面上而造成的对锯盘盘面间的摩擦阻力;③被锯开的木料与锯盘盘面之间随时充入空气,有利于锯盘散热.(2)右侧皮带上的拉力较大.由锯盘上的锯齿形状及分布情况可以看出,圆形锯盘在锯木头时应该顺时针转动,那么,与圆形锯盘共轴安装的皮带轮也应该顺时针转动;由此可以推知,电动机的皮带轮也应该顺时针转动;所以,电动机的皮带轮应该拉右侧的皮带而不拉左侧的皮带;因此,右侧皮带上的拉力应该大于左侧皮带上的拉力.(3)电动机满负荷正常工作时皮带的运行速度:V===8.17m/s,电动机满负荷工作时配套电动机输出机械能的效率为90%:P输出=3000W×90%=2700W;左右两侧皮带上的拉力之差(即电动机输出的驱动力)为:F==≈330N;答:皮带上较大的拉力与较小的拉力的差值是330N.(4)皮带轮所受拉力的情况可等效为左侧皮带拉力为0N,右侧带拉力为330N;皮带传动的效率为100%.不计其轴转动的摩擦损耗,设圆形锯盘所受木料的阻力为F1,由轮轴公式得:==则:F1===75.9N.答:圆形锯盘所受到的木料的阻力是圆75.9N.。
【VIP专享】1第21届全国中学生物理竞赛复赛试题(含答案)

室分为上下两部分,上面部分的容积V0 25.00cm3 ,下面部分连同 U 形管左管水 面以上部分的总容积为 V1,薄膜能够透气的面积 S =1.00cm2.打开开关 K1、K2 与大 C
气相通,大气的压强 P1=1.00atm,此时 U 形管右管中气柱长度 H 20.00cm ,
F
V1 5.00cm3 .关闭 K1、K2 后,打开开关 K3,对渗透室上部分迅速充气至气体压
强差变化不太大的情况下,可用计时开始时的压强差和计时结束时的压强差的平均
值 P 来代替公式中的 P .普适气体常量 R = 8.31Jmol-1K-1,1.00atm =
1.013×105Pa).
6.培养学生观察、思考、对比及分析综合的能力。过程与方法1.通过观察蚯蚓教的学实难验点,线培形养动观物察和能环力节和动实物验的能主力要;特2.征通。过教对学观方察法到与的教现学象手分段析观与察讨法论、,实对验线法形、动分物组和讨环论节法动教特学征准的备概多括媒,体继课续件培、养活分蚯析蚓、、归硬纳纸、板综、合平的面思玻维璃能、力镊。子情、感烧态杯度、价水值教观1.和通过学理解的蛔1.虫过1观适、察于3程.观六 阅蛔寄内列察、 读虫生出蚯让 材标容生3常根.蚓学 料本教活见2据 了身生 :,师的的、问 解体巩总 鸟看活形线用 作题 蛔的固结 类雌动态形手 业自 虫形练本 与雄学、三动4摸 :学 对状习节 人蛔生结、物、一 收后 人和同课 类虫活构请一并蚯摸 集回 体颜步重 关的动、学、归蚓蚯 鸟答 的色学点 系形教生生让纳在蚓 类问 危。习并 从状学理列学线平的题 害蚯四线归 人、意特出四生形面体 生以蚓、形纳 类大图点常、五观动玻表 存及的鸟请动本 文小引以见3 引、察物璃, 现预身类学物节 明有言及的、 导巩蚯的上是 状防体之生和课 历什根蚯环怎 学固蚓主和干 ,感是所列环学 史么据蚓节二样 生练引要牛燥 鸟染否以举节到 揭不上适动、区 回习导特皮还 类的分分蚯动的 晓同节于物让分 答。学征纸是 减方节布蚓物一 起,课穴并?学蚯 课生。上湿 少法广的教些 ,体所居归4在生蚓 前回.运润 的;泛益鸟色学生纳4靠物完的 问答蛔动的 原.,处目类和习活环近在成前 题蚯虫的? 因了以。标生 就体的节身其实端 并蚓寄快触 及解上知物 同表内特动体结验和 总的生利慢摸 我蚯适识学 人有容点物前构并后 结生在用一蚯 国蚓于与的 类什,的端中思端 线活人问样蚓的? 飞技基 有么引进主的的考形环题吗体 十生能本 着特出行要几变以动1境,?节 大活的.方 密征本“特节化下物并会让为近 珍习形理法 切。课生征有以问的2引小学什腹 稀性态解。 的.课物。什游题主出起结生么面 鸟和结蛔关观题体么戏:要蚯哪利明?处 类适构虫系察:的特的特蚓些用确, 等于特适。蛔章形殊形征这疾板,是 资穴点于可虫我态结式。种病书生光 料居寄是的们结构,五典?小物滑 ,生重生鸟内学构5,学、型.结的还 以活要生类部习与其习巩的如鸟结是 爱的原活生结了功颜消固线何类构粗 鸟形因的存构腔能色化练形预适特糙 护态之结的,肠相是系习动防于点? 鸟、一构现你动适否统。物蛔飞都为结。和状认物应与的。虫行是主构课生却为和”其结病的与题、本理不蛔扁的他构8?特环以生8特乐虫形观部特三征境小理页观的动点位点、梳相组等这;,哪物教相,2引理适为方.鸟些,育同师导知应单面鸟掌类结了;?生2学识位的你握日构解.互生。办特认线益特了通动观手征识形减点它过,察抄;吗动少是们理5生蛔报.?物,与的解参虫一了它和有寄主蛔与结份解们环些生要虫其构。蚯都节已生特对中。爱蚓会动经活征人培鸟与飞物灭相。类养护人吗的绝适这造兴鸟类?主或应节成趣的为要濒课的情关什特临?就危感系么征灭来害教;?;绝学,育,习使。我比学们它生可们理以更解做高养些等成什的良么两好。类卫动生物习。惯根的据重学要生意回义答;3的.情通况过,了给解出蚯课蚓课与题人。类回的答关:系线,形进动行物生和命环科节学动价环值节观动的物教一育、。根教据学蛔重虫点1病.引蛔出虫蛔适虫于这寄种生典生型活的线结形构动和物生。理二特、点设;2置.问蚯题蚓让的学生生活思习考性预和习适。于穴居生活的形态、结构、生理等方面的特征;3.线形动物和环节动物的主要特征。
2011年第二十一届全国初中物理竞赛复赛试题【含答案】

2011年第二十一届全国初中应用物理竞赛复赛试题一、 (16分)测定患者的血沉,是医学上用来帮助医生对病情作出正确判断的一种手段。
把新鲜的血液,加入抗凝剂,静置一定时间后形成抗凝血后,红血球即从血浆中分离出来而下沉。
设抗凝血是由红血球和血浆组成的悬浮液,血浆的密度ρ0≈1.0×103kg/m3,红血球的密度ρ≈1.3×103kg/m3。
将抗凝血放进竖直放置的血沉管内,红血球起初在血浆中加速下沉,然后一直匀速下沉,其匀速下沉的速度称为”血沉”。
正常人血沉的值大约是v=12mm /h。
如果把红血球近似看作半径为R的小球,它在血浆中下沉时所受的粘滞阻力为4R3,试根据以上信息解答下列问f=6R,在室温下=1.8×10-3Pa﹒s,已知V球=3题:1.红血球在血浆中为什么先加速下沉、后一直匀速下沉?2.计算红血球半径的大小。
二、 (16分)为了推进环保和节能理念的实施,某公司开发生产了“风光互补路灯”,该路灯只需要晒晒太阳吹吹风就能工作,如图l所示。
它在有阳光时通过太阳能电池板发电,有风时通过风力发电机发电,二者皆备时同时发电,并将电能输至蓄电池储存起来,供路灯照明使用。
为了能使蓄电池的使用寿命更为长久,一般充电至90%左右即停止,放电余留20%左右即停止电能输出。
下表为某型号风光互补路灯系统配置方案。
问:1.当风速为6.0m/s时,风力发电机的输出功率将变为50W,在这种情况下,将蓄电池的电量由20%充至90%需多长时间?2.如果当地垂直于太阳光的平面得到的太阳辐射最大强度约为240W/m2,要想太阳能电池的最大功率达到36W,太阳能电池板的面积至少要多大?3.若遇到阴天无风的天气,仅靠蓄电池供电,最多可供灯具正常发光多长时间?三、(16分)电动自行车是倍受人们青睐的一种交通工具,如图2所示。
其主要结构就是在原来的普通自行车的基础上,增加了电动机及供电、传动设备,它可以电动骑行,亦可以脚踏骑行。
第21届全国中学生物理竞赛决赛试题及参考答案

第 21届全国中学生物理竞赛决赛试题一、(20分)有一光光导纤维,光芯折射率n=1.500 的透明度极好的介质,其截面半径为r ;光芯外面包层的折射率n =1.400。
有一半导体激光器S,位于光纤轴线的延长上,发出半角宽为30o的光束。
为便于使此光束全部进入光纤,在光纤端面处烧结了一个其材料与光芯相同的、半径为 R 的球冠 QAQ ',端面附近的结构如图所示(包层未画出),S可看作点光源,光纤放在空气中,空气的折射率 n0按 1.000计算。
1、若要半导体激光器发出的光能够全部射到球冠上,则光源 S 离 A 的距离 x 应满足什么条件?2、如果 R=1.8r, 光源S与A 的距离为R,入射与轴的夹角用α表示,则α角分别为α1=30o、α2 =25o和α3=20o的三根光线能否经过全反射在光纤中传播?二、(20分)试从相对论能量和动量的角度分析论证1、一个光子与真空中处于静止状态的自由电子碰碰撞时,光子的能量不可能完全被电子吸收。
光子射到金属表面时,其能量有可能完全被吸收被使电子逸出金属表面,产生光电效应。
三、(25)如图所示,一质量 M=30.0Kg 的楔形木块 OABC 静止在水平地面上,其斜面段 AB 的倾角,BC 段的倾角α=45o, AB 段与 BC 段连接处( B )为一非常短的光滑圆弧,现将一质量的 m=4.00Kg小物块(可视为质点),放在斜面上离地面高h1=2.80m 的 A 处,然后放手,令小物块从静止开始斜面下滑,已知小物块与斜面之间无摩擦,木块与地面间的最大静摩擦系数和滑动摩擦系数为μ=6.00*10-2,B 处离桌面的高度h2 =2.00m ,如果不计小物块经过处 B 时(β=60o )物块及木块速度大小的改变,求小物块从斜面上 A 处滑动到斜面底部 C 处整个过程中小物块对木块所做的功(取重力加速度 g=10.0ms-2)四、(25 分)由如图所示的电路,其中 E 为内阻可以忽略的电源的电动势,R 为电阻的阻值;K 为开关;A 、 B 右边是如图所标的 8 个完全相同的容量均为 C 的理想电容器组成的电路,问从合上 K 到各电容器充电完毕,电阻 R 上发热消耗的能量是多少?(在解题时,要求在图上标出你所设定的各个电容器极板上电荷的正负)五、(25 分)如图所示, K 为一带电粒子发生器,从中可以不断地射出各种不同速率的带电粒子,它们都带正电,电量为q,质量为m ,速度的方向都沿图中的虚线,D 1、 D2为两块档板,可定时开启和关闭。
第二十一届全国中学生物理竞赛复赛试题及答案

第二十一届全国中学生物理竞赛复赛试题本卷共七题,满分140分.一、(20分)薄膜材料气密性能的优劣常用其透气系数来加以评判.对于均匀薄膜材料,在一定温度下,某种气体通过薄膜渗透过的气体分子数dPStkN∆=,其中t 为渗透持续时间,S 为薄膜的面积,d 为薄膜的厚度,P ∆为薄膜两侧气体的压强差.k 称为该薄膜材料在该温度下对该气体的透气系数.透气系数愈小,材料的气密性能愈好.图为测定薄膜材料对空气的透气系数的一种实验装置示意图.EFGI 为渗透室,U 形管左管上端与渗透室相通,右管上端封闭;U 形管内横截面积A =0.150cm 2.实验中,首先测得薄膜的厚度d =0.66mm ,再将薄膜固定于图中C C '处,从而把渗透室分为上下两部分,上面部分的容积30cm 00.25=V ,下面部分连同U 形管左管水面以上部分的总容积为V 1,薄膜能够透气的面积S =1.00cm 2.打开开关K 1、K 2与大气相通,大气的压强P 1=1.00atm ,此时U 形管右管中气柱长度cm 00.20=H,31cm 00.5=V .关闭K 1、K 2后,打开开关K 3,对渗透室上部分迅速充气至气体压强atm 00.20=P ,关闭K 3并开始计时.两小时后, U 形管左管中的水面高度下降了cm 00.2=∆H .实验过程中,始终保持温度为C 0 .求该薄膜材料在C 0时对空气的透气系数.(本实验中由于薄膜两侧的压强差在实验过程中不能保持恒定,在压强差变化不太大的情况下,可用计时开始时的压强差和计时结束时的压强差的平均值P ∆来代替公式中的P ∆.普适气体常量R = 8.31Jmol -1K -1,1.00atm = 1.013×105Pa ).二、(20分) 两颗人造卫星绕地球沿同一椭圆轨道同向运动,它们通过轨道上同一点的时间相差半个周期.已知轨道近地点离地心的距离是地球半径R 的2倍,卫星通过近地点时的速度R GM 43=v ,式中M 为地球质量,G 为引力常量.卫星上装有同样的角度测量仪,可测出卫星与任意两点的两条连线之间的夹角.试设计一种测量方案,利用这两个测量仪测定太空中某星体与地心在某时刻的距离.(最后结果要求用测得量和地球半径R 表示)三、(15分)μ子在相对自身静止的惯性参考系中的平均寿命s 100.260-⨯≈τ.宇宙射线与大气在高空某处发生核反应产生一批μ子,以v = 0.99c 的速度(c 为真空中的光速)向下运动并衰变.根据放射性衰变定律,相对给定惯性参考系,若t = 0时刻的粒子数为N (0), t 时刻剩余的粒子数为N (t ),则有()()τt N t N -=e 0,式中τ为相对该惯性系粒子的平均寿命.若能到达地面的μ子数为原来的5%,试估算μ子产生处相对于地面的高度h .不考虑重力和地磁场对μ子运动的影响.四、(20分)目前,大功率半导体激光器的主要结构形式是由许多发光区等距离地排列在一条直线上的长条状,通常称为激光二极管条.但这样的半导体激光器发出的是很多束发散光束,光能分布很不集中,不利于传输和应用.为了解决这个问题,需要根据具体应用的要求,对光束进行必需的变换(或称整形).如果能把一个半导体激光二极管条发出的光变换成一束很细的平行光束,对半导体激光的传输和应用将是非常有意义的.为此,有人提出了先把多束发散光会聚到一点,再变换为平行光的方案,其基本原理可通过如下所述的简化了的情况来说明.如图,S 1、S 2、S 3 是等距离(h )地排列在一直线上的三个点光源,各自向垂直于它们的连线的同一方向发出半顶角为α =arctan()41的圆锥形光束.请使用三个完全相同的、焦距为f = 1.50h 、半径为r =0.75 h 的圆形薄凸透镜,经加工、组装成一个三者在同一平面内的组合透镜,使三束光都能全部投射到这个组合透镜上,且经透镜折射后的光线能全部会聚于z 轴(以S 2为起点,垂直于三个点光源连线,与光束中心线方向相同的射线)上距离S 2为 L = 12.0 h 处的P 点.(加工时可对透镜进行外形的改变,但不能改变透镜焦距.) 1.求出组合透镜中每个透镜光心的位置.2.说明对三个透镜应如何加工和组装,并求出有关数据.五、(20分)如图所示,接地的空心导体球壳内半径为R ,在空腔内一直径上的P 1和P 2处,放置电量分别为q 1和q 2的点电荷,q 1=q 2=q ,两点电荷到球心的距离均为a .由静电感应与静电屏蔽可知:导体空腔内表面将出现感应电荷分布,感应电荷电量等于-2q .空腔内部的电场是由q 1、q 2和两者在空腔内表面上的感应电荷共同产生的.由于我们尚不知道这些感应电荷是怎样分布的,所以很难用场强叠加原理直接求得腔内的电势或场强.但理论上可以证明,感应电荷对腔内电场的贡献,可用假想的位于腔外的(等效)点电荷来代替(在本题中假想(等效)点电荷应为两个),只要假想的(等效)点电荷的位置和电量能满足这样的条件,即:设想将整个导体壳去掉,由q 1在原空腔内表面的感应电荷的假想(等效)点电荷1q '与q 1共同产生的电场在原空腔内表面所在位置处各点的电势皆为0;由q 2在原空腔内表面的感应电荷的假想(等效)点电荷2q '与q 2共同产生的电场在原空腔内表面所在位置处各点的电势皆为0.这样确定的假想电荷叫做感应电荷的等效电荷,而且这样确定的等效电荷是唯一的.等效电荷取代感应电荷后,可用等效电荷1q '、2q '和q 1、q 2来计算原来导体存在时空腔内部任意点的电势或场强.1.试根据上述条件,确定假想等效电荷1q '、2q '的位置及电量. 2.求空腔内部任意点A 的电势U A .已知A 点到球心O 的距离为r ,OA 与1OP 的夹角为θ .六、(20分)如图所示,三个质量都是m 的刚性小球A 、B 、C 位于光滑的水平桌面上(图中纸面),A 、B 之间,B 、C 之间分别用刚性轻杆相连,杆与A 、B 、C 的各连接处皆为“铰链式”的(不能对小球产生垂直于杆方向的作用力).已知杆AB 与BC 的夹角为π-α ,α < π/2.DE 为固定在桌面上一块挡板,它与AB 连线方向垂直.现令A 、B 、C 一起以共同的速度v 沿平行于AB 连线方向向DE 运动,已知在C 与挡板碰撞过程中C 与挡板之间无摩擦力作用,求碰撞时当C 沿垂直于DE 方向的速度由v 变为0这一极短时间内挡板对C 的冲量的大小.七、(25分)如图所示,有二平行金属导轨,相距l ,位于同一水平面内(图中纸面),处在磁感应强度为B 的匀强磁场中,磁场方向竖直向下(垂直纸面向里).质量均为m 的两金属杆ab 和cd 放在导轨上,与导轨垂直.初始时刻, 金属杆ab 和cd 分别位于x = x 0和x = 0处.假设导轨及金属杆的电阻都为零,由两金属杆与导轨构成的回路的自感系数为L .今对金属杆ab 施以沿导轨向右的瞬时冲量,使它获得初速0v .设导轨足够长,0x 也足够大,在运动过程中,两金属杆之间距离的变化远小于两金属杆的初始间距0x ,因而可以认为在杆运动过程中由两金属杆与导轨构成的回路的自感系数L 是恒定不变的.杆与导轨之间摩擦可不计.求任意时刻两杆的位置x ab 和x cd 以及由两杆和导轨构成的回路中的电流i 三者各自随时间t 的变化关系.第21届全国中学生物理竞赛复赛题参考解答一、开始时U 形管右管中空气的体积和压强分别为 V 2 = HA (1) p 2= p 1经过2小时,U 形管右管中空气的体积和压强分别为A H H V )(2∆-=' (2) 2222V V p p '=' (3) 渗透室下部连同U 形管左管水面以上部分气体的总体积和压强分别为HAV V ∆+='11(4)H g p p Δ221ρ+'=(5)式中ρ 为水的密度,g 为重力加速度.由理想气体状态方程nRT pV =可知,经过2小时,薄膜下部增加的空气的摩尔数RTV p RT V p n 1111-''=∆ (6)在2个小时内,通过薄膜渗透过去的分子数:A nN N∆=(7)式中N A 为阿伏伽德罗常量.渗透室上部空气的摩尔数减少,压强下降.下降了:0V ΔnRTp =∆ (8) 经过2小时渗透室上部分中空气的压强为:p p p ∆-='00(9) 测试过程的平均压强差:[])(211010p p ()p p p '-'+-=∆ (10) 根据定义,由以上各式和有关数据,可求得该薄膜材料在0℃时对空气的透气系数11111s m Pa 104.2---⨯=∆=tSp Nd k (11)二、如图,卫星绕地球运动的轨道为一椭圆,地心位于轨道椭圆的一个焦点O 处,设待测量星体位于C 处.根据题意,当一个卫星运动到轨道的近地点A 时,另一个卫星恰好到达远地点B 处,只要位于A 点的卫星用角度测量仪测出AO 和AC 的夹角α1,位于B 点的卫星用角度测量仪测出BO 和BC 的夹角α2,就可以计算出此时星体C 与地心的距离OC .因卫星椭圆轨道长轴的长度远近+r r AB = (1)式中r 近、与r 远分别表示轨道近地点和远地点到地心的距离.由角动量守恒 远远近近=r m r v mv (2) 式中m 为卫星的质量.由机械能守恒远远近近--r GMm m r GMm m 222121v v = (3) 已知R r 2=近, RGM43=近v 得R r 6=远 (4) 所以:R R R AB 862=+= (5)在△ABC 中用正弦定理B()ABBC211πsin sin ααα--=(6) 所以()AB BC 211sin sin ααα+=(7)地心与星体之间的距离为OC ,在△BOC 中用余弦定理2222cos 2αBC r BC r OC ⋅-+=远远 (8)由式(4)、(5)、(7)得:()()212121212sin cos sin 24sin sin 1692ααααααα+-++=R OC (9)三、因μ子在相对自身静止的惯性系中的平均寿命 s 100.260-⨯≈τ根据时间膨胀效应,在地球上观测到的μ子平均寿命为τ,()21c v -=ττ (1)代入数据得 τ = 1.4×10-5s (2)相对地面,若μ子到达地面所需时间为t ,则在t 时刻剩余的μ子数为()()τt N t N -=e 0 (3) 根据题意有()()%5e 0==-τt N t N (4) 对上式等号两边取e 为底的对数得 1005lnτ-=t (5) 代入数据得 s 1019.45-⨯=t(6)根据题意,可以把μ子的运动看作匀速直线运动,有 t h v =(7)代入数据得 m 1024.14⨯=h (8)四、1.考虑到使3个点光源的3束光分别通过3个透镜都成实像于P 点的要求,组合透镜所在的平面应垂直于z 轴,三个光心O 1、O 2、O 3的连线平行于3个光源的连线,O 2位于z 轴上,如图1所示.图中M M '表示组合透镜的平面,1S '、2S '、3S '为三个光束中心光线与该平面的交点. 22O S = u 就是物距.根据透镜成像公式f u L u 111=-+ (1) 可解得 ]4[212fL L L u -±= 因为要保证经透镜折射后的光线都能全部会聚于P 点,来自各光源的光线在投射到透镜之前不能交叉,必须有2u tan α ≤h 即u ≤2h .在上式中取“-”号,代入f 和L 的值,算得h u )236(-=≈1.757h(2)此解满足上面的条件.分别作3个点光源与P 点的连线.为使3个点光源都能同时成像于P 点,3个透镜的光心O 1、O 2、O 3应分别位于这3条连线上(如图1).由几何关系知,有h h h L u L O O O O 854.0)24121(3221≈+=-== (3) 即光心O 1的位置应在1S '之下与1S '的距离为:h O O h O S 146.02111=-=' (4) 同理,O 3的位置应在3S '之上与3S '的距离为0.146h 处.由(3)式可知组合透镜中相邻薄透镜中心之间距离必须等于0.854h ,才能使S 1、S 2、S 3都能成像于P 点.2.现在讨论如何把三个透镜L 1、L 2、L 3加工组装成组合透镜.因为三个透镜的半径r = 0.75h ,将它们的光心分别放置到O 1、O 2、O 3处时,由于21O O =32O O =0.854h <2r ,透镜必然发生相互重叠,必须对透镜进行加工,各切去一部分,然后再将它们粘起来,才能满足(3)式的要求.由于对称关系,我们只需讨论上半部分的情况.图2画出了L 1、L 2放在M M '平面内时相互交叠的情况(纸面为M M '平面).图中C 1、C 2表示L 1、L 2的边缘,1S '、2S '为光束中心光线与透镜的交点,W 1、W 2分别为C 1、C 2与O 1O 2的交点.1S '为圆心的圆1和以2S '(与O 2重合)为圆心的圆2分别是光源S 1和S 2投射到L 1和L 2时产生的光斑的边缘,其半径均为h u 439.0tan ==αρ (5)根据题意,圆1和圆2内的光线必须能全部进入透镜.首先,圆1的K 点(见图2)是否落在L 1上?由几何关系可知()h r h h S O K O 75.0585.0146.0439.0111=<=+='+=ρ故从S 1发出的光束能全部进入L 1.为了保证全部光束能进入透镜组合,对L 1和L 2进行加工时必须保留圆1和圆2内的透镜部分.下面举出一种对透镜进行加工、组装的方法.在O 1和O 2之间作垂直于O 1O 2且分别与圆1和圆2相切的切线Q Q '和N N '.若沿位于Q Q '和N N '之间且与它们平行的任意直线T T '对透镜L 1和L 2进行切割,去掉两透镜的弓形部分,然后把它们沿此线粘合就得到符合所需组合透镜的上半部.同理,对L 2的下半部和L 3进行切割,然后将L 2的下半部和L 3粘合起来,就得到符合需要的整个组合透镜.这个组合透镜可以将S 1、S 2、S 3发出的全部光线都会聚到P 点.现在计算Q Q '和N N '的位置以及对各个透镜切去部分的大小应符合的条件.设透镜L 1被切去部分沿O 1O 2方向的长度为x 1,透镜L 2被切去部分沿O 1O 2方向的长度为x 2,如图2所示,则对任意一条切割线T T ', x 1、x 2之和为:h O O r x x d646.022121=-=+= (7)由于T T '必须在Q Q '和N N '之间,从图2可看出,沿Q Q '切割时,x 1达最大值(x 1M ),x 2达最小值(x 2m ),ρ-'+=111O S r x M 代入r ,ρ 和11O S '的值,得h x M 457.01= (8) 代入(7)式,得:h x d x M m 189.012=-= (9)由图2可看出,沿N N '切割时,x 2达最大值(x 2M ),x 1达最小值(x 1m ), ρ-=r x M 2代入r 和ρ 的值,得:h x M 311.02= (10) h x d x M m 335.021=-=(11)由对称性,对L 3的加工与对L 1相同,对L 2下半部的加工与对上半部的加工相同.五、1.解法Ⅰ:如图1所示,S 为原空腔内表面所在位置,1q '的位置应位于1OP 的延长线上的某点B 1处,2q '的位置应位于2OP 的延长线上的某点B 2处.设A 1为S 面上的任意一点,根据题意有B图20111111='+B A q kP A q k(1)0212212='+B A q k P A q k (2)怎样才能使 (1) 式成立呢?下面分析图1中11A OP ∆与11B OA ∆的关系.若等效电荷1q '的位置B 1使下式成立,即:211R OB OP =⋅ (3)即:1111OB OA OA OP =(4) 则1111B OA A OP ∽△△有 :R aOA OP B A P A ==111111 (5) 由 (1)式和 (5)式便可求得等效电荷 11q aR q -=' (6) 由 (3) 式知,等效电荷1q '的位置B 1到原球壳中心位置O 的距离:aR OB 21= (7)同理,B 2的位置应使2112B OA A OP ∽△△,用类似的方法可求得等效电荷22q aRq -=' (8) 等效电荷2q '的位置B 2到原球壳中心O 位置的距离:aR OB 22= (9)解法Ⅱ:在图1中,设111r P A =,111r B A '=,d OB =1.根据题意,1q 和1q '两者在A 1点产生的电势和为零.有:01111=''+r q k r q k(1') 式中:21221)cos 2(θRa a R r -+= (2')21221)cos 2(θRd d R r -+=' (3')由(1')、(2')、(3')式得:)cos 2()cos 2(22212221θθRa a R q Rd d R q -+'=-+ (4')(4')式是以θcos 为变量的一次多项式,要使(4')式对任意θ均成立,等号两边的相应系数应相等,即:)()(22212221a R q d R q +'=+ (5')a q d q 2121'= (6')由(5')、(6')式得:0)(2222=++-aR d R a ad(7')解得:aR a R a d 2)()(2222-±+=(8')由于等效电荷位于空腔外部,由(8')式求得:aR d 2= (9')由(6')、(9')式有:212221q aR q =' (10')考虑到(1')式,有11q aR q -=' (11') 同理可求得:a R OB 22= (12')22q aRq -=' (13')2.A 点的位置如图2所示.A 的电势由q 1、1q '、q 2、2q '共同产生,即 ⎪⎪⎭⎫ ⎝⎛-+-=A B a R A P A B a R A P kq U A 22111111 (10)因221cos 2a ra r A P +-=θ22221cos 2⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛-=a R aR r r A B θ 222cos 2a ra r A P ++=θ 22222cos 2⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛+=a R aR r r A B θ 代入 (10) 式得⎝⎛+--+-=422222cos 2cos 21R raR r a Rara r kq U A θθ⎪⎪⎭⎫++-+++422222cos 2cos 21R raR r a Ra ra r θθ (11) 六、令I 表示题述极短时间∆t 内挡板对C 冲量的大小,因为挡板对C 无摩擦力作用,可知冲量的方向垂直于DE ,如图所示;I '表示B 、C 间的杆对B 或C 冲量的大小,其方向沿杆方向,对B 和C 皆为推力;C v 表示∆t 末了时刻C 沿平行于DE 方向速度的大小,B v 表示∆t 末了时刻B 沿平行于DE 方向速度的大小,⊥B v 表示∆t 末了时刻B 沿垂直于DE 方向速度的大小.由动量定理,对C 有:C m I v ='αsin (1) v m I I ='-αcos (2)对B 有:B m I v ='αsin (3) 对AB 有:()⊥-='B mI v v 2cos α(4)因为B 、C 之间的杆不能伸、缩,因此B 、C 沿杆的方向的分速度必相等.故有αααsin cos sin B B C v v v -=⊥(5)图2由以上五式,可解得:v m I αα22sin 31sin 3++=(6)七、解法Ⅰ:当金属杆ab 获得沿x 轴正方向的初速v 0时,因切割磁力线而产生感应电动势,由两金属杆与导轨构成的回路中会出现感应电流.由于回路具有自感系数,感应电流的出现,又会在回路中产生自感电动势,自感电动势将阻碍电流的增大,所以,虽然回路的电阻为零,但回路的电流并不会趋向无限大,当回路中一旦有了电流,磁场作用于杆ab 的安培力将使ab 杆减速,作用于cd 杆的安培力使cd 杆运动.设在任意时刻t ,ab 杆和cd 杆的速度分别为v 1和v 2(相对地面参考系S ),当v 1、v 2为正时,表示速度沿x 轴正方向;若规定逆时针方向为回路中电流和电动势的正方向,则因两杆作切割磁力线的运动而产生的感应电动势:()21v v -=Bl E(1)当回路中的电流i 随时间的变化率为t i∆∆时,回路中的自感电动势:tiLL ∆∆-=E (2) 根据欧姆定律,注意到回路没有电阻,有0=+L E E (3)金属杆在导轨上运动过程中,两杆构成的系统受到的水平方向的合外力为零,系统的质心作匀速直线运动.设系统质心的速度为V C ,有:C mV m 20=v (4)得 :2v =CV (5) V C 方向与v 0相同,沿x 轴的正方向. 现取一新的参考系S ',它与质心固连在一起,并把质心作为坐标原点O ',取坐标轴x O ''与x 轴平行.设相对S '系,金属杆ab 的速度为u ,cd 杆的速度为u ',则有u V C +=1v (6) u V C '+=2v (7)因相对S '系,两杆的总动量为零,即有:0='+u m mu (8) 由(1)、(2)、(3)、(5)、(6) 、(7) 、(8)各式,得:tiLBlu ∆∆=2 (9) 在S '系中,在t 时刻,金属杆ab 坐标为x ',在t +∆t 时刻,它的坐标为x x '∆+',则由速度的定义tx u ∆'∆= (10) 代入 (9) 式得:i L x Bl ∆='∆2 (11)若将x '视为i 的函数,由(11)式知i x ∆'∆为常数,所以x '与i 的关系可用一直线方程表示b i BlLx +='2 (12) 式中b 为常数,其值待定.现已知在t =0时刻,金属杆ab 在S '系中的坐标x '=021x ,这时i = 0,故得:0212x i Bl L x +=' (13) 或 ⎪⎭⎫⎝⎛-'=0212x x L Bl i (14) 021x 表示t =0时刻金属杆ab 的位置.x '表示在任意时刻t ,杆ab 的位置,故⎪⎭⎫ ⎝⎛-'021x x 就是杆ab在t 时刻相对初始位置的位移,用X 表示, 021x x X -'= (15) 当X >0时,ab 杆位于其初始位置的右侧;当X <0时,ab 杆位于其初始位置的左侧.代入(14)式,得:X LBli 2= (16)这时作用于ab 杆的安培力:X L l B iBl F 222-=-= (17) ab 杆在初始位置右侧时,安培力的方向指向左侧;ab 杆在初始位置左侧时,安培力的方向指向右侧,可知该安培力具有弹性力的性质.金属杆ab 的运动是简谐振动,振动的周期()Ll B mT222π2= (18) 在任意时刻t , ab 杆离开其初始位置的位移⎪⎭⎫⎝⎛+=ϕt T A X π2cos (19)A 为简谐振动的振幅,ϕ 为初相位,都是待定的常量.通过参考圆可求得ab 杆的振动速度⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛-=ϕt T T A u π2sin π2 (20)(19)、(20)式分别表示任意时刻ab 杆离开初始位置的位移和运动速度.现已知在t =0时刻,ab 杆位于初始位置,即:X = 0 速度:00002121v v v v =-=-=C V u故有:ϕcos 0A =;ϕsin π220⎪⎭⎫⎝⎛-=T A v 解这两式,并注意到(18)式得:2π3=ϕ(21)22400mLBlT A vv ==π (22) 由此得ab 杆的位移:t TmL Bl t TmL BlXπ2sin 222π3π2cos 2200v v =⎪⎭⎫ ⎝⎛+=(23) 由 (15) 式可求得ab 杆在S '系中的位置t TmL Bl x x π2sin 222100abv +=' (24) 因相对质心,任意时刻ab 杆和cd 杆都在质心两侧,到质心的距离相等,故在S '系中,cd 杆的位置t TmL Bl x x π2sin 222100cdv --=' (25) 相对地面参考系S ,质心以021v =CV 的速度向右运动,并注意到(18)式,得ab 杆在地面参考系中的位置t mL Bl mL Blt x x ⎪⎪⎭⎫ ⎝⎛++=2sin 2221000ab v v (26)cd 杆在S 系中的位置t mL Bl mL Bl t x ⎪⎪⎭⎫ ⎝⎛-=2sin 222100cd v v (27) 回路中的电流由 (16) 式得t mL Bl L m t T mL BlL Bl i ⎪⎪⎭⎫ ⎝⎛==2sin 2π2sin 22200v v (28) 解法Ⅱ: 当金属杆在磁场中运动时,因切割磁力线而产生感应电动势,回路中出现电流时,两金属杆都要受到安培力的作用,安培力使ab 杆的速度改变,使cd 杆运动.设任意时刻t ,两杆的速度分别为v 1和v 2(相对地面参考系S ),若规定逆时针方向为回路电动势和电流的正方向,则由两金属杆与导轨构成的回路中,因杆在磁场中运动而出现的感应电动势为()21v v -=Bl E (1’) 令u 表示ab 杆相对于cd 杆的速度,有:Blu L =E (2’)当回路中的电流i 变化时,回路中有自感电动势E L ,其大小与电流的变化率成正比,即有ti LL ∆∆-=E (3’)根据欧姆定律,注意到回路没有电阻,有:0=+L E E 由式(2’)、(3’)两式得:t i L Blu ∆∆= (4’) 设在t 时刻,金属杆ab 相对于cd 杆的距离为x ',在t +∆t 时刻,ab 相对于cd 杆的距离为x '+x '∆,则由速度的定义,有:tx u ∆'∆= (5’) 代入 (4') 式得:i L x Bl ∆='∆ (6’)若将x '视为i 的函数,由(6’)式可知,i x ∆'∆为常量,所以x '与i 的关系可以用一直线方程表示,即:b i BlL x +=' (7’) 式中b 为常数,其值待定.现已知在t =0时刻,金属杆ab 相对于cd 杆的距离为0x ,这时i = 0,故得:0x i Bl L x +=' (8’) 或 ()0x x LBl i -'= (9’) 0x 表示t =0时刻金属杆ab 相对于cd 杆的位置.x '表示在任意时刻t 时ab 杆相对于cd 杆的位置,故()0x x -'就是杆ab 在t 时刻相对于cd 杆的相对位置相对于它们在t =0时刻的相对位置的位移,即从t =0到t =t 时间内ab 杆相对于cd 杆的位移:0x x X -'= (10') 于是有:X LBl i = (11’) 任意时刻t ,ab 杆和cd 杆因受安培力作用而分别有加速度a ab 和a cd ,由牛顿定律有ab ma iBl =- (12’); cd ma iBl = (13’)两式相减并注意到(9')式得:()X Ll B iBl a a m 22cd ab 22-=-=- (14’) 式中()cd ab a a -为金属杆ab 相对于cd 杆的加速度,而X 是ab 杆相对cd 杆相对位置的位移.L l B 222是常数,表明这个相对运动是简谐振动,它的振动的周期()L l B m T 222π2= (15’)在任意时刻t ,ab 杆相对cd 杆相对位置相对它们初始位置的位移⎪⎭⎫ ⎝⎛+=ϕt T A X π2cos (16’)A 为简谐振动的振幅,ϕ 为初相位,都是待定的常量.通过参考圆可求得X 随时间的变化率即速度:⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=ϕT T A V π2sin π2 (17’)现已知在t =0时刻,杆位于初始位置,即X = 0,速度0v =V故有:ϕcos 0A =; ϕsin π20⎪⎭⎫ ⎝⎛-=T A v 解这两式,并注意到(15’) 式得:2π3=ϕ;2π200mL Bl T A v v == 由此得:t mL Bl mL Bl t T mL Bl X ⎪⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛+=2sin 22π3π2cos 20v v (18’) 因t = 0时刻,cd 杆位于x = 0 处,ab 杆位于x = x 0 处,两者的相对位置由x 0表示;设t 时刻,cd 杆位于x = x cd 处,ab 杆位于x = x ab 处,两者的相对位置由x ab -x cd 表示,故两杆的相对位置的位移又可表示为:X = x ab -x cd -x 0(19’) 所以 t mL Bl mL Bl x x x ⎪⎪⎭⎫ ⎝⎛+=-2sin 200cd ab v (20’) (12’)和(13’)式相加, ()0cd ab =+-=+iBl iBl a a m 得()0cd ab =+a a由此可知,两杆速度之和为一常数即v 0,所以两杆的位置x ab 和x cd 之和应为 x ab +x cd = x 0+v 0t(21’) 由(20’)和(21’)式相加和相减,注意到(15’)式,得t mL Bl mL Bl t x x ⎪⎪⎭⎫ ⎝⎛++=2sin 2221000ab v v (22’) t mL Bl mL Bl t x ⎪⎪⎭⎫ ⎝⎛-=2sin 222100cd v v (23’) 由(11’)、(19’)(22’)、(23’)式得回路中电流 t mL Bl L m i ⎪⎪⎭⎫ ⎝⎛=2sin 20v (24’)。
第21届全国中学生物理竞赛预复赛试卷及答案

第21届全国中学生物理竞赛预赛题试卷本卷共九题,满分140分。
一、(15分)填空1.a.原子大小的数量级为__________m。
b.原子核大小的数量级为_________m。
c.氦原子的质量约为_________kg。
d.一个可见光光子的能量的数量级为_________J。
e.在标准状态下,1cm3气体中的分子数约为____________。
(普朗克常量h=6.63×10-34J·s 阿伏加德罗常量N A=6.02×1023 mol-1)2.已知某个平面镜反射的光能量为入射光能量的80%。
试判断下列说法是否正确,并简述理由。
a.反射光子数为入射光子数的80%;b.每个反射光子的能量是入射光子能量的80%。
二、(15分)质量分别为m1和m2的两个小物块用轻绳连结,绳跨过位于倾角α=30︒的光滑斜面顶端的轻滑轮,滑轮与转轴之间的磨擦不计,斜面固定在水平桌面上,如图所示。
第一次,m1悬空,m2放在斜面上,用t表示m2自斜面底端由静止开始运动至斜面顶端所需的时间。
第二次,将m1和m2位置互换,使m2悬空,m1放在斜面上,发现m1自斜面底端由静止开始运动至斜面顶端所需的时间为t/3。
求m l与m2之比。
三、(15分)测定电子荷质比(电荷q与质量m之比q/m)的实验装置如图所示。
真空玻璃管内,阴极K发出的电子,经阳极A与阴极K之间的高电压加速后,形成一束很细的电子流,电子流以平行于平板电容器极板的速度进入两极板C、D间的区域。
若两极板C、D间无电压,则离开极板区域的电子将打在荧光屏上的O点;若在两极板间加上电压U,则离开极板区域的电子将打在荧光屏上的P点;若再在极板间加一方向垂直于纸面向外、磁感应强度为B的匀强磁场,则打到荧光屏上的电子产生的光点又回到O点。
现已知极板的长度l=5.00cm,C、D间的距离d=l.50cm,极板区的中点M到荧光屏中点O的距离为L=12.50cm,U=200V,P点到O点的距离==cm;B=6.3×10-4T。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二十一届全国中学生物理竞赛复赛试题本卷共七题,满分140分.一、(20分)薄膜材料气密性能的优劣常用其透气系数来加以评判.对于均匀薄膜材料,在一定温度下,某种气体通过薄膜渗透过的气体分子数dPStkN∆=,其中t 为渗透持续时间,S 为薄膜的面积,d 为薄膜的厚度,P ∆为薄膜两侧气体的压强差.k 称为该薄膜材料在该温度下对该气体的透气系数.透气系数愈小,材料的气密性能愈好.图为测定薄膜材料对空气的透气系数的一种实验装置示意图.EFGI 为渗透室,U 形管左管上端与渗透室相通,右管上端封闭;U 形管内横截面积A =0.150cm 2.实验中,首先测得薄膜的厚度d =0.66mm ,再将薄膜固定于图中C C '处,从而把渗透室分为上下两部分,上面部分的容积30cm 00.25=V ,下面部分连同U 形管左管水面以上部分的总容积为V 1,薄膜能够透气的面积S =1.00cm 2.打开开关K 1、K 2与大气相通,大气的压强P 1=1.00atm ,此时U 形管右管中气柱长度cm 00.20=H,31cm 00.5=V .关闭K 1、K 2后,打开开关K 3,对渗透室上部分迅速充气至气体压强atm 00.20=P ,关闭K 3并开始计时.两小时后, U 形管左管中的水面高度下降了cm 00.2=∆H .实验过程中,始终保持温度为C 0 .求该薄膜材料在C 0时对空气的透气系数.(本实验中由于薄膜两侧的压强差在实验过程中不能保持恒定,在压强差变化不太大的情况下,可用计时开始时的压强差和计时结束时的压强差的平均值P ∆来代替公式中的P ∆.普适气体常量R = 8.31Jmol -1K -1,1.00atm = 1.013×105Pa ).二、(20分) 两颗人造卫星绕地球沿同一椭圆轨道同向运动,它们通过轨道上同一点的时间相差半个周期.已知轨道近地点离地心的距离是地球半径R 的2倍,卫星通过近地点时的速度R GM 43=v ,式中M 为地球质量,G 为引力常量.卫星上装有同样的角度测量仪,可测出卫星与任意两点的两条连线之间的夹角.试设计一种测量方案,利用这两个测量仪测定太空中某星体与地心在某时刻的距离.(最后结果要求用测得量和地球半径R 表示)三、(15分)μ子在相对自身静止的惯性参考系中的平均寿命s 100.260-⨯≈τ.宇宙射线与大气在高空某处发生核反应产生一批μ子,以v = 0.99c 的速度(c 为真空中的光速)向下运动并衰变.根据放射性衰变定律,相对给定惯性参考系,若t = 0时刻的粒子数为N (0), t 时刻剩余的粒子数为N (t ),则有()()τt N t N -=e 0,式中τ为相对该惯性系粒子的平均寿命.若能到达地面的μ子数为原来的5%,试估算μ子产生处相对于地面的高度h .不考虑重力和地磁场对μ子运动的影响.四、(20分)目前,大功率半导体激光器的主要结构形式是由许多发光区等距离地排列在一条直线上的长条状,通常称为激光二极管条.但这样的半导体激光器发出的是很多束发散光束,光能分布很不集中,不利于传输和应用.为了解决这个问题,需要根据具体应用的要求,对光束进行必需的变换(或称整形).如果能把一个半导体激光二极管条发出的光变换成一束很细的平行光束,对半导体激光的传输和应用将是非常有意义的.为此,有人提出了先把多束发散光会聚到一点,再变换为平行光的方案,其基本原理可通过如下所述的简化了的情况来说明.如图,S 1、S 2、S 3 是等距离(h )地排列在一直线上的三个点光源,各自向垂直于它们的连线的同一方向发出半顶角为α =arctan()41的圆锥形光束.请使用三个完全相同的、焦距为f = 1.50h 、半径为r =0.75 h 的圆形薄凸透镜,经加工、组装成一个三者在同一平面内的组合透镜,使三束光都能全部投射到这个组合透镜上,且经透镜折射后的光线能全部会聚于z 轴(以S 2为起点,垂直于三个点光源连线,与光束中心线方向相同的射线)上距离S 2为 L = 12.0 h 处的P 点.(加工时可对透镜进行外形的改变,但不能改变透镜焦距.) 1.求出组合透镜中每个透镜光心的位置.2.说明对三个透镜应如何加工和组装,并求出有关数据.五、(20分)如图所示,接地的空心导体球壳内半径为R ,在空腔内一直径上的P 1和P 2处,放置电量分别为q 1和q 2的点电荷,q 1=q 2=q ,两点电荷到球心的距离均为a .由静电感应与静电屏蔽可知:导体空腔内表面将出现感应电荷分布,感应电荷电量等于-2q .空腔内部的电场是由q 1、q 2和两者在空腔内表面上的感应电荷共同产生的.由于我们尚不知道这些感应电荷是怎样分布的,所以很难用场强叠加原理直接求得腔内的电势或场强.但理论上可以证明,感应电荷对腔内电场的贡献,可用假想的位于腔外的(等效)点电荷来代替(在本题中假想(等效)点电荷应为两个),只要假想的(等效)点电荷的位置和电量能满足这样的条件,即:设想将整个导体壳去掉,由q 1在原空腔内表面的感应电荷的假想(等效)点电荷1q '与q 1共同产生的电场在原空腔内表面所在位置处各点的电势皆为0;由q 2在原空腔内表面的感应电荷的假想(等效)点电荷2q '与q 2共同产生的电场在原空腔内表面所在位置处各点的电势皆为0.这样确定的假想电荷叫做感应电荷的等效电荷,而且这样确定的等效电荷是唯一的.等效电荷取代感应电荷后,可用等效电荷1q '、2q '和q 1、q 2来计算原来导体存在时空腔内部任意点的电势或场强.1.试根据上述条件,确定假想等效电荷1q '、2q '的位置及电量. 2.求空腔内部任意点A 的电势U A .已知A 点到球心O 的距离为r ,OA 与1OP 的夹角为θ .六、(20分)如图所示,三个质量都是m 的刚性小球A 、B 、C 位于光滑的水平桌面上(图中纸面),A 、B 之间,B 、C 之间分别用刚性轻杆相连,杆与A 、B 、C 的各连接处皆为“铰链式”的(不能对小球产生垂直于杆方向的作用力).已知杆AB 与BC 的夹角为π-α ,α < π/2.DE 为固定在桌面上一块挡板,它与AB 连线方向垂直.现令A 、B 、C 一起以共同的速度v 沿平行于AB 连线方向向DE 运动,已知在C 与挡板碰撞过程中C 与挡板之间无摩擦力作用,求碰撞时当C 沿垂直于DE 方向的速度由v 变为0这一极短时间内挡板对C 的冲量的大小.七、(25分)如图所示,有二平行金属导轨,相距l ,位于同一水平面内(图中纸面),处在磁感应强度为B 的匀强磁场中,磁场方向竖直向下(垂直纸面向里).质量均为m 的两金属杆ab 和cd 放在导轨上,与导轨垂直.初始时刻, 金属杆ab 和cd 分别位于x = x 0和x = 0处.假设导轨及金属杆的电阻都为零,由两金属杆与导轨构成的回路的自感系数为L .今对金属杆ab 施以沿导轨向右的瞬时冲量,使它获得初速0v .设导轨足够长,0x 也足够大,在运动过程中,两金属杆之间距离的变化远小于两金属杆的初始间距0x ,因而可以认为在杆运动过程中由两金属杆与导轨构成的回路的自感系数L 是恒定不变的.杆与导轨之间摩擦可不计.求任意时刻两杆的位置x ab 和x cd 以及由两杆和导轨构成的回路中的电流i 三者各自随时间t 的变化关系.第21届全国中学生物理竞赛复赛题参考解答一、开始时U 形管右管中空气的体积和压强分别为 V 2 = HA (1) p 2= p 1经过2小时,U 形管右管中空气的体积和压强分别为A H H V )(2∆-=' (2) 2222V V p p '=' (3) 渗透室下部连同U 形管左管水面以上部分气体的总体积和压强分别为HAV V ∆+='11(4)H g p p Δ221ρ+'=(5)式中ρ 为水的密度,g 为重力加速度.由理想气体状态方程nRT pV =可知,经过2小时,薄膜下部增加的空气的摩尔数RTV p RT V p n 1111-''=∆ (6)在2个小时内,通过薄膜渗透过去的分子数:A nN N∆=(7)式中N A 为阿伏伽德罗常量.渗透室上部空气的摩尔数减少,压强下降.下降了:0V ΔnRTp =∆ (8) 经过2小时渗透室上部分中空气的压强为:p p p ∆-='00(9) 测试过程的平均压强差:[])(211010p p ()p p p '-'+-=∆ (10) 根据定义,由以上各式和有关数据,可求得该薄膜材料在0℃时对空气的透气系数11111s m Pa 104.2---⨯=∆=tSp Nd k (11)二、如图,卫星绕地球运动的轨道为一椭圆,地心位于轨道椭圆的一个焦点O 处,设待测量星体位于C 处.根据题意,当一个卫星运动到轨道的近地点A 时,另一个卫星恰好到达远地点B 处,只要位于A 点的卫星用角度测量仪测出AO 和AC 的夹角α1,位于B 点的卫星用角度测量仪测出BO 和BC 的夹角α2,就可以计算出此时星体C 与地心的距离OC .因卫星椭圆轨道长轴的长度远近+r r AB = (1)式中r 近、与r 远分别表示轨道近地点和远地点到地心的距离.由角动量守恒 远远近近=r m r v mv (2) 式中m 为卫星的质量.由机械能守恒远远近近--r GMm m r GMm m 222121v v = (3) 已知R r 2=近, RGM43=近v 得R r 6=远 (4) 所以:R R R AB 862=+= (5)在△ABC 中用正弦定理B()ABBC211πsin sin ααα--=(6) 所以()AB BC 211sin sin ααα+=(7)地心与星体之间的距离为OC ,在△BOC 中用余弦定理2222cos 2αBC r BC r OC ⋅-+=远远 (8)由式(4)、(5)、(7)得:()()212121212sin cos sin 24sin sin 1692ααααααα+-++=R OC (9)三、因μ子在相对自身静止的惯性系中的平均寿命 s 100.260-⨯≈τ根据时间膨胀效应,在地球上观测到的μ子平均寿命为τ,()21c v -=ττ (1)代入数据得 τ = 1.4×10-5s (2)相对地面,若μ子到达地面所需时间为t ,则在t 时刻剩余的μ子数为()()τt N t N -=e 0 (3) 根据题意有()()%5e 0==-τt N t N (4) 对上式等号两边取e 为底的对数得 1005lnτ-=t (5) 代入数据得 s 1019.45-⨯=t(6)根据题意,可以把μ子的运动看作匀速直线运动,有 t h v =(7)代入数据得 m 1024.14⨯=h (8)四、1.考虑到使3个点光源的3束光分别通过3个透镜都成实像于P 点的要求,组合透镜所在的平面应垂直于z 轴,三个光心O 1、O 2、O 3的连线平行于3个光源的连线,O 2位于z 轴上,如图1所示.图中M M '表示组合透镜的平面,1S '、2S '、3S '为三个光束中心光线与该平面的交点. 22O S = u 就是物距.根据透镜成像公式f u L u 111=-+ (1) 可解得 ]4[212fL L L u -±= 因为要保证经透镜折射后的光线都能全部会聚于P 点,来自各光源的光线在投射到透镜之前不能交叉,必须有2u tan α ≤h 即u ≤2h .在上式中取“-”号,代入f 和L 的值,算得h u )236(-=≈1.757h(2)此解满足上面的条件.分别作3个点光源与P 点的连线.为使3个点光源都能同时成像于P 点,3个透镜的光心O 1、O 2、O 3应分别位于这3条连线上(如图1).由几何关系知,有h h h L u L O O O O 854.0)24121(3221≈+=-== (3) 即光心O 1的位置应在1S '之下与1S '的距离为:h O O h O S 146.02111=-=' (4) 同理,O 3的位置应在3S '之上与3S '的距离为0.146h 处.由(3)式可知组合透镜中相邻薄透镜中心之间距离必须等于0.854h ,才能使S 1、S 2、S 3都能成像于P 点.2.现在讨论如何把三个透镜L 1、L 2、L 3加工组装成组合透镜.因为三个透镜的半径r = 0.75h ,将它们的光心分别放置到O 1、O 2、O 3处时,由于21O O =32O O =0.854h <2r ,透镜必然发生相互重叠,必须对透镜进行加工,各切去一部分,然后再将它们粘起来,才能满足(3)式的要求.由于对称关系,我们只需讨论上半部分的情况.图2画出了L 1、L 2放在M M '平面内时相互交叠的情况(纸面为M M '平面).图中C 1、C 2表示L 1、L 2的边缘,1S '、2S '为光束中心光线与透镜的交点,W 1、W 2分别为C 1、C 2与O 1O 2的交点.1S '为圆心的圆1和以2S '(与O 2重合)为圆心的圆2分别是光源S 1和S 2投射到L 1和L 2时产生的光斑的边缘,其半径均为h u 439.0tan ==αρ (5)根据题意,圆1和圆2内的光线必须能全部进入透镜.首先,圆1的K 点(见图2)是否落在L 1上?由几何关系可知()h r h h S O K O 75.0585.0146.0439.0111=<=+='+=ρ故从S 1发出的光束能全部进入L 1.为了保证全部光束能进入透镜组合,对L 1和L 2进行加工时必须保留圆1和圆2内的透镜部分.下面举出一种对透镜进行加工、组装的方法.在O 1和O 2之间作垂直于O 1O 2且分别与圆1和圆2相切的切线Q Q '和N N '.若沿位于Q Q '和N N '之间且与它们平行的任意直线T T '对透镜L 1和L 2进行切割,去掉两透镜的弓形部分,然后把它们沿此线粘合就得到符合所需组合透镜的上半部.同理,对L 2的下半部和L 3进行切割,然后将L 2的下半部和L 3粘合起来,就得到符合需要的整个组合透镜.这个组合透镜可以将S 1、S 2、S 3发出的全部光线都会聚到P 点.现在计算Q Q '和N N '的位置以及对各个透镜切去部分的大小应符合的条件.设透镜L 1被切去部分沿O 1O 2方向的长度为x 1,透镜L 2被切去部分沿O 1O 2方向的长度为x 2,如图2所示,则对任意一条切割线T T ', x 1、x 2之和为:h O O r x x d646.022121=-=+= (7)由于T T '必须在Q Q '和N N '之间,从图2可看出,沿Q Q '切割时,x 1达最大值(x 1M ),x 2达最小值(x 2m ),ρ-'+=111O S r x M 代入r ,ρ 和11O S '的值,得h x M 457.01= (8) 代入(7)式,得:h x d x M m 189.012=-= (9)由图2可看出,沿N N '切割时,x 2达最大值(x 2M ),x 1达最小值(x 1m ), ρ-=r x M 2代入r 和ρ 的值,得:h x M 311.02= (10) h x d x M m 335.021=-=(11)由对称性,对L 3的加工与对L 1相同,对L 2下半部的加工与对上半部的加工相同.五、1.解法Ⅰ:如图1所示,S 为原空腔内表面所在位置,1q '的位置应位于1OP 的延长线上的某点B 1处,2q '的位置应位于2OP 的延长线上的某点B 2处.设A 1为S 面上的任意一点,根据题意有B图20111111='+B A q kP A q k(1)0212212='+B A q k P A q k (2)怎样才能使 (1) 式成立呢?下面分析图1中11A OP ∆与11B OA ∆的关系.若等效电荷1q '的位置B 1使下式成立,即:211R OB OP =⋅ (3)即:1111OB OA OA OP =(4) 则1111B OA A OP ∽△△有 :R aOA OP B A P A ==111111 (5) 由 (1)式和 (5)式便可求得等效电荷 11q aR q -=' (6) 由 (3) 式知,等效电荷1q '的位置B 1到原球壳中心位置O 的距离:aR OB 21= (7)同理,B 2的位置应使2112B OA A OP ∽△△,用类似的方法可求得等效电荷22q aRq -=' (8) 等效电荷2q '的位置B 2到原球壳中心O 位置的距离:aR OB 22= (9)解法Ⅱ:在图1中,设111r P A =,111r B A '=,d OB =1.根据题意,1q 和1q '两者在A 1点产生的电势和为零.有:01111=''+r q k r q k(1') 式中:21221)cos 2(θRa a R r -+= (2')21221)cos 2(θRd d R r -+=' (3')由(1')、(2')、(3')式得:)cos 2()cos 2(22212221θθRa a R q Rd d R q -+'=-+ (4')(4')式是以θcos 为变量的一次多项式,要使(4')式对任意θ均成立,等号两边的相应系数应相等,即:)()(22212221a R q d R q +'=+ (5')a q d q 2121'= (6')由(5')、(6')式得:0)(2222=++-aR d R a ad(7')解得:aR a R a d 2)()(2222-±+=(8')由于等效电荷位于空腔外部,由(8')式求得:aR d 2= (9')由(6')、(9')式有:212221q aR q =' (10')考虑到(1')式,有11q aR q -=' (11') 同理可求得:a R OB 22= (12')22q aRq -=' (13')2.A 点的位置如图2所示.A 的电势由q 1、1q '、q 2、2q '共同产生,即 ⎪⎪⎭⎫ ⎝⎛-+-=A B a R A P A B a R A P kq U A 22111111 (10)因221cos 2a ra r A P +-=θ22221cos 2⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛-=a R aR r r A B θ 222cos 2a ra r A P ++=θ 22222cos 2⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫ ⎝⎛+=a R aR r r A B θ 代入 (10) 式得⎝⎛+--+-=422222cos 2cos 21R raR r a Rara r kq U A θθ⎪⎪⎭⎫++-+++422222cos 2cos 21R raR r a Ra ra r θθ (11) 六、令I 表示题述极短时间∆t 内挡板对C 冲量的大小,因为挡板对C 无摩擦力作用,可知冲量的方向垂直于DE ,如图所示;I '表示B 、C 间的杆对B 或C 冲量的大小,其方向沿杆方向,对B 和C 皆为推力;C v 表示∆t 末了时刻C 沿平行于DE 方向速度的大小,B v 表示∆t 末了时刻B 沿平行于DE 方向速度的大小,⊥B v 表示∆t 末了时刻B 沿垂直于DE 方向速度的大小.由动量定理,对C 有:C m I v ='αsin (1) v m I I ='-αcos (2)对B 有:B m I v ='αsin (3) 对AB 有:()⊥-='B mI v v 2cos α(4)因为B 、C 之间的杆不能伸、缩,因此B 、C 沿杆的方向的分速度必相等.故有αααsin cos sin B B C v v v -=⊥(5)图2由以上五式,可解得:v m I αα22sin 31sin 3++=(6)七、解法Ⅰ:当金属杆ab 获得沿x 轴正方向的初速v 0时,因切割磁力线而产生感应电动势,由两金属杆与导轨构成的回路中会出现感应电流.由于回路具有自感系数,感应电流的出现,又会在回路中产生自感电动势,自感电动势将阻碍电流的增大,所以,虽然回路的电阻为零,但回路的电流并不会趋向无限大,当回路中一旦有了电流,磁场作用于杆ab 的安培力将使ab 杆减速,作用于cd 杆的安培力使cd 杆运动.设在任意时刻t ,ab 杆和cd 杆的速度分别为v 1和v 2(相对地面参考系S ),当v 1、v 2为正时,表示速度沿x 轴正方向;若规定逆时针方向为回路中电流和电动势的正方向,则因两杆作切割磁力线的运动而产生的感应电动势:()21v v -=Bl E(1)当回路中的电流i 随时间的变化率为t i∆∆时,回路中的自感电动势:tiLL ∆∆-=E (2) 根据欧姆定律,注意到回路没有电阻,有0=+L E E (3)金属杆在导轨上运动过程中,两杆构成的系统受到的水平方向的合外力为零,系统的质心作匀速直线运动.设系统质心的速度为V C ,有:C mV m 20=v (4)得 :2v =CV (5) V C 方向与v 0相同,沿x 轴的正方向. 现取一新的参考系S ',它与质心固连在一起,并把质心作为坐标原点O ',取坐标轴x O ''与x 轴平行.设相对S '系,金属杆ab 的速度为u ,cd 杆的速度为u ',则有u V C +=1v (6) u V C '+=2v (7)因相对S '系,两杆的总动量为零,即有:0='+u m mu (8) 由(1)、(2)、(3)、(5)、(6) 、(7) 、(8)各式,得:tiLBlu ∆∆=2 (9) 在S '系中,在t 时刻,金属杆ab 坐标为x ',在t +∆t 时刻,它的坐标为x x '∆+',则由速度的定义tx u ∆'∆= (10) 代入 (9) 式得:i L x Bl ∆='∆2 (11)若将x '视为i 的函数,由(11)式知i x ∆'∆为常数,所以x '与i 的关系可用一直线方程表示b i BlLx +='2 (12) 式中b 为常数,其值待定.现已知在t =0时刻,金属杆ab 在S '系中的坐标x '=021x ,这时i = 0,故得:0212x i Bl L x +=' (13) 或 ⎪⎭⎫⎝⎛-'=0212x x L Bl i (14) 021x 表示t =0时刻金属杆ab 的位置.x '表示在任意时刻t ,杆ab 的位置,故⎪⎭⎫ ⎝⎛-'021x x 就是杆ab在t 时刻相对初始位置的位移,用X 表示, 021x x X -'= (15) 当X >0时,ab 杆位于其初始位置的右侧;当X <0时,ab 杆位于其初始位置的左侧.代入(14)式,得:X LBli 2= (16)这时作用于ab 杆的安培力:X L l B iBl F 222-=-= (17) ab 杆在初始位置右侧时,安培力的方向指向左侧;ab 杆在初始位置左侧时,安培力的方向指向右侧,可知该安培力具有弹性力的性质.金属杆ab 的运动是简谐振动,振动的周期()Ll B mT222π2= (18) 在任意时刻t , ab 杆离开其初始位置的位移⎪⎭⎫⎝⎛+=ϕt T A X π2cos (19)A 为简谐振动的振幅,ϕ 为初相位,都是待定的常量.通过参考圆可求得ab 杆的振动速度⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛-=ϕt T T A u π2sin π2 (20)(19)、(20)式分别表示任意时刻ab 杆离开初始位置的位移和运动速度.现已知在t =0时刻,ab 杆位于初始位置,即:X = 0 速度:00002121v v v v =-=-=C V u故有:ϕcos 0A =;ϕsin π220⎪⎭⎫⎝⎛-=T A v 解这两式,并注意到(18)式得:2π3=ϕ(21)22400mLBlT A vv ==π (22) 由此得ab 杆的位移:t TmL Bl t TmL BlXπ2sin 222π3π2cos 2200v v =⎪⎭⎫ ⎝⎛+=(23) 由 (15) 式可求得ab 杆在S '系中的位置t TmL Bl x x π2sin 222100abv +=' (24) 因相对质心,任意时刻ab 杆和cd 杆都在质心两侧,到质心的距离相等,故在S '系中,cd 杆的位置t TmL Bl x x π2sin 222100cdv --=' (25) 相对地面参考系S ,质心以021v =CV 的速度向右运动,并注意到(18)式,得ab 杆在地面参考系中的位置t mL Bl mL Blt x x ⎪⎪⎭⎫ ⎝⎛++=2sin 2221000ab v v (26)cd 杆在S 系中的位置t mL Bl mL Bl t x ⎪⎪⎭⎫ ⎝⎛-=2sin 222100cd v v (27) 回路中的电流由 (16) 式得t mL Bl L m t T mL BlL Bl i ⎪⎪⎭⎫ ⎝⎛==2sin 2π2sin 22200v v (28) 解法Ⅱ: 当金属杆在磁场中运动时,因切割磁力线而产生感应电动势,回路中出现电流时,两金属杆都要受到安培力的作用,安培力使ab 杆的速度改变,使cd 杆运动.设任意时刻t ,两杆的速度分别为v 1和v 2(相对地面参考系S ),若规定逆时针方向为回路电动势和电流的正方向,则由两金属杆与导轨构成的回路中,因杆在磁场中运动而出现的感应电动势为()21v v -=Bl E (1’) 令u 表示ab 杆相对于cd 杆的速度,有:Blu L =E (2’)当回路中的电流i 变化时,回路中有自感电动势E L ,其大小与电流的变化率成正比,即有ti LL ∆∆-=E (3’)根据欧姆定律,注意到回路没有电阻,有:0=+L E E 由式(2’)、(3’)两式得:t i L Blu ∆∆= (4’) 设在t 时刻,金属杆ab 相对于cd 杆的距离为x ',在t +∆t 时刻,ab 相对于cd 杆的距离为x '+x '∆,则由速度的定义,有:tx u ∆'∆= (5’) 代入 (4') 式得:i L x Bl ∆='∆ (6’)若将x '视为i 的函数,由(6’)式可知,i x ∆'∆为常量,所以x '与i 的关系可以用一直线方程表示,即:b i BlL x +=' (7’) 式中b 为常数,其值待定.现已知在t =0时刻,金属杆ab 相对于cd 杆的距离为0x ,这时i = 0,故得:0x i Bl L x +=' (8’) 或 ()0x x LBl i -'= (9’) 0x 表示t =0时刻金属杆ab 相对于cd 杆的位置.x '表示在任意时刻t 时ab 杆相对于cd 杆的位置,故()0x x -'就是杆ab 在t 时刻相对于cd 杆的相对位置相对于它们在t =0时刻的相对位置的位移,即从t =0到t =t 时间内ab 杆相对于cd 杆的位移:0x x X -'= (10') 于是有:X LBl i = (11’) 任意时刻t ,ab 杆和cd 杆因受安培力作用而分别有加速度a ab 和a cd ,由牛顿定律有ab ma iBl =- (12’); cd ma iBl = (13’)两式相减并注意到(9')式得:()X Ll B iBl a a m 22cd ab 22-=-=- (14’) 式中()cd ab a a -为金属杆ab 相对于cd 杆的加速度,而X 是ab 杆相对cd 杆相对位置的位移.L l B 222是常数,表明这个相对运动是简谐振动,它的振动的周期()L l B m T 222π2= (15’)在任意时刻t ,ab 杆相对cd 杆相对位置相对它们初始位置的位移⎪⎭⎫ ⎝⎛+=ϕt T A X π2cos (16’)A 为简谐振动的振幅,ϕ 为初相位,都是待定的常量.通过参考圆可求得X 随时间的变化率即速度:⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=ϕT T A V π2sin π2 (17’)现已知在t =0时刻,杆位于初始位置,即X = 0,速度0v =V故有:ϕcos 0A =; ϕsin π20⎪⎭⎫ ⎝⎛-=T A v 解这两式,并注意到(15’) 式得:2π3=ϕ;2π200mL Bl T A v v == 由此得:t mL Bl mL Bl t T mL Bl X ⎪⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛+=2sin 22π3π2cos 20v v (18’) 因t = 0时刻,cd 杆位于x = 0 处,ab 杆位于x = x 0 处,两者的相对位置由x 0表示;设t 时刻,cd 杆位于x = x cd 处,ab 杆位于x = x ab 处,两者的相对位置由x ab -x cd 表示,故两杆的相对位置的位移又可表示为:X = x ab -x cd -x 0(19’) 所以 t mL Bl mL Bl x x x ⎪⎪⎭⎫ ⎝⎛+=-2sin 200cd ab v (20’) (12’)和(13’)式相加, ()0cd ab =+-=+iBl iBl a a m 得()0cd ab =+a a由此可知,两杆速度之和为一常数即v 0,所以两杆的位置x ab 和x cd 之和应为 x ab +x cd = x 0+v 0t(21’) 由(20’)和(21’)式相加和相减,注意到(15’)式,得t mL Bl mL Bl t x x ⎪⎪⎭⎫ ⎝⎛++=2sin 2221000ab v v (22’) t mL Bl mL Bl t x ⎪⎪⎭⎫ ⎝⎛-=2sin 222100cd v v (23’) 由(11’)、(19’)(22’)、(23’)式得回路中电流 t mL Bl L m i ⎪⎪⎭⎫ ⎝⎛=2sin 20v (24’)。
