实验四 核衰变的统计规律与放射性测量的实验数据处理
探索核物质的衰变实验步骤

探索核物质的衰变实验步骤核物质的衰变是核能学中的重要研究内容之一。
为了探索核物质的衰变规律,科学家们进行了一系列的实验研究。
本文将介绍探索核物质的衰变实验步骤。
为了使文章易于阅读,我们将按照以下顺序展开叙述:实验目的、实验所需材料、实验步骤及数据处理。
一、实验目的通过实验,探索核物质的衰变规律,了解不同衰变类型的特点及其在实验中的表现,进一步理解核物质的性质。
二、实验所需材料1. 放射性样品:选择具有放射性衰变性质的核物质样品,如放射性同位素。
2. 探测器:可选用放射线探测器、Geiger-Muller管或闪烁体探测器等,以便测量放射性衰变的放射线。
3. 计数器:用于记录和计算衰变事件的次数。
4. 实验设备:包括支架、样品夹持器、闪烁体探测器固定装置等。
5. 安全防护措施:实验室应配备必要的辐射防护设备和个人防护用品。
三、实验步骤1. 样品准备:选取一定数量的放射性样品,并将其放置于样品夹持器中进行固定。
2. 设备安装:将放射线探测器(如闪烁体探测器)固定在样品旁边的支架上,确保其与样品保持一定距离。
3. 数据记录与采集:开启计数器,并将其连接到探测器上,对放射线进行连续计数,记录衰变事件的次数。
4. 实验观测:通过连续观测一定时间段内的衰变事件次数,绘制出衰变事件与时间的关系曲线(即衰变曲线)。
5. 数据处理:根据实验数据,计算出核物质的衰变常数和半衰期等相关参数,并进行分析与讨论。
四、数据处理1. 计算衰变常数:根据衰变曲线的指数衰减形式,采用半对数坐标纸绘制衰变曲线,通过回归分析得到衰变常数。
2. 计算半衰期:利用衰变常数可计算出核物质的半衰期,半衰期是指在衰变曲线上一半原子核衰变所需的时间。
3. 分析与讨论:根据实验得到的衰变常数和半衰期,进行数据分析与讨论,比较不同样品或不同衰变模式下的衰变特点。
通过以上实验步骤和数据处理,我们可以探索核物质的衰变规律,进一步了解核物质的性质,为核能学和相关领域的研究提供实验依据和理论支持。
盖革弥勒计数器及核衰变的统计规律

盖革--弥勒计数器及核衰变的统计规律一.实验目的1. 掌握G-M计数器的工作基础,测定其有关特性,学会使用。
2. 以G-M计数器为测试设备,验证核衰变的统计规律。
3. 学会使用放射性测量结果的误差表示法,学会多次测量结果的误差计算及测试时间的选择。
二.实验仪器盖革--弥勒计数器、放射源、铅室、定标器三.实验原理1. G-M计数器的工作原理G-M计数管有各种不同的结构,本实验选用长圆柱形γ计数管,它们都由圆筒状的阴极和装在轴线上的阳极丝共同密封在玻璃管内组成。
管内充以一定量的惰性气体(氩居多)和少量猝灭气体(为了使一个放射性粒子引起放电后只记一次)。
计数管工作时,在计数管阳极加上直流高压,则在计数管的阳极和阴极(接地)之间形成径向分布的电场。
射线进入管内,与管壁或气体分子相互作用引起管内气体电离,所产生的负离子(实际上即电子)在电场加速下向阳极移动,在到达阳极之前与气体分子发生多次碰撞,打出很多次级电子,这些次级电子也在电场加速下向阳极运动,并在运动过程中与气体分子发生多次碰撞,打出更多次级电子,这样就引起了“雪崩”放电。
在“雪崩”过程中,由于受激原子的退激和正负离子复合产生的光子被猝灭分子吸收。
电子质量小,运动速度快,正离子质量大,运动速度慢,电子到达阳极后,阳极周围形成一层“正离子鞘”,阳极附近的电场随“正离子鞘”的形成而减弱,以致新电子无法增值,放电便终止了。
计数管可看做一个电容器,放电前加了高压,于是在两极上就带有了一定量的电荷,放电过程中在阳极得到一个负电压脉冲。
负脉冲的幅度与电源电压以及电阻R的大小有关,电压高则负脉冲的幅度高;电阻大,脉冲的宽度较大,幅度也较高。
2. G-M计数器的特性1)坪特性——包括起始电压、坪长、坪斜等当射入计数管的粒子数目不变时,改变计数管两极间所加电压值,发现定标器计得的计数率(单位时间内计数)是变化的,曲线中间有一段平坦的部分,所以称其为“坪特性曲线”。
在强度不变的放射源照射下,G-M管的计数率n 随外加电压变化的曲线即坪曲线如图所示。
核衰变与放射性计数的统计规律
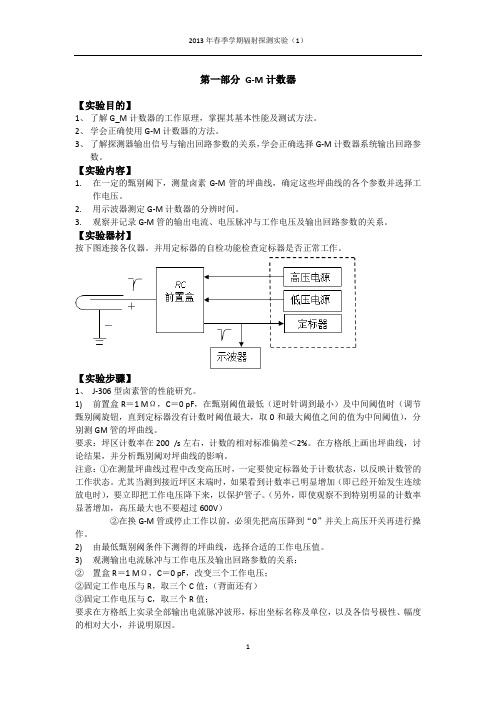
第一部分G-M计数器【实验目的】1、了解G_M计数器的工作原理,掌握其基本性能及测试方法。
2、学会正确使用G-M计数器的方法。
3、了解探测器输出信号与输出回路参数的关系,学会正确选择G-M计数器系统输出回路参数。
【实验内容】1.在一定的甄别阈下,测量卤素G-M管的坪曲线,确定这些坪曲线的各个参数并选择工作电压。
2.用示波器测定G-M计数器的分辨时间。
3.观察并记录G-M管的输出电流、电压脉冲与工作电压及输出回路参数的关系。
【实验器材】按下图连接各仪器。
并用定标器的自检功能检查定标器是否正常工作。
【实验步骤】1、J-306型卤素管的性能研究。
1) 前置盒R=1 MΩ,C=0 pF,在甄别阈值最低(逆时针调到最小)及中间阈值时(调节甄别阈旋钮,直到定标器没有计数时阈值最大,取0和最大阈值之间的值为中间阈值),分别测GM管的坪曲线。
要求:坪区计数率在200 /s左右,计数的相对标准偏差<2%。
在方格纸上画出坪曲线,讨论结果,并分析甄别阈对坪曲线的影响。
注意:①在测量坪曲线过程中改变高压时,一定要使定标器处于计数状态,以反映计数管的工作状态。
尤其当测到接近坪区末端时,如果看到计数率已明显增加(即已经开始发生连续放电时),要立即把工作电压降下来,以保护管子。
(另外,即使观察不到特别明显的计数率显著增加,高压最大也不要超过600V)②在换G-M管或停止工作以前,必须先把高压降到“0”并关上高压开关再进行操作。
2) 由最低甄别阈条件下测得的坪曲线,选择合适的工作电压值。
3) 观测输出电流脉冲与工作电压及输出回路参数的关系:②置盒R=1 MΩ,C=0 pF,改变三个工作电压;②固定工作电压与R,取三个C值;(背面还有)③固定工作电压与C,取三个R值;要求在方格纸上实录全部输出电流脉冲波形,标出坐标名称及单位,以及各信号极性、幅度的相对大小,并说明原因。
注意:①中的三个电压值必须在坪区范围内;为观察到形状较好的电流和电压波形,②、③及以下各步骤中的工作电压可比步骤(2)中选择的工作电压低,具体数值可以取R =1 M Ω,C =0 pF 时,示波器观察电流或电压波形不出现饱和的最大工作电压值。
核衰变的统计规律实验

核衰变的统计规律实验薛佳柳083822一、实验目的1.了解并验证原子核衰变及放射性计数的统计性。
2.了解统计误差的意义,掌握计算统计误差的方法。
3.学习检验测量数据的分布类型的方法。
二、实验原理1. 测量NaI(Tl)闪烁晶体探测器的计数率随工作变化的坪曲线,选定合适的工作电压。
2. 在相同条件下,对某放射源进行重复测量,画出放射性计数的频率直方图并与理论分布曲线作比较。
3. 在相同条件下对本底进行重复测量,画出本底计数的频率分布图,并与理论分布曲线作比较。
4. 用2检验法检验放射性计数的统计分布类型。
三、实验仪器①NaI(Tl)闪烁探测器;②γ放射源(137Cs或60Co);③高压电源、放大器和多道脉冲幅度分析器。
二、实验内容1.放射性测量的随机性和统计性在做重复的放射性测量中,即使保持完全相同的实验条件(例如放射性的半衰期足够长,因此在实验时间内可以认为其强度基本上没有变化;源与计数器的相对位置始终保持不变;每次测量时间不变;测量仪器足够精确,不会产生其它的附加误差等等),每次的测量结果并不完全相同,而是围绕其平均值上下涨落,有时甚至有很大的差别,也就是说物理实验的测量结果具有偶然性,或者说随机性。
物理测量的随机性产生原因不仅在于测量时的偶然误差,而且更是物理现象(当然包括放射性核衰变)本身的随机性质,即——物理量的实际数值时刻围绕着平均值发生微小起伏。
在微观现象领域,特别是在高能物理实验中,物理现象本身的统计性更为突出。
按照量子力学的原理,对处于同一个态的微观粒子,测量同一个可观测的物理量时,即使不存在任何测量误差,各次测量结果也会不同,除非粒子处于这个可观测量的本征态;比如同一种粒子的寿命,其实测值分布在从相当短到相当长的范围内。
另一方面,所谓偶然的东西,是一种有必然性隐藏在里面的形式;我们正是要通过研究其统计分布规律从而找出在随机数据中包含的规律性。
2.核衰变数的统计分布放射性原子核衰变数的统计分布可以根据数理统计分布的理论来推导。
实验一核衰变与放射性计数的统计规律

实验一核衰变与放射性计数的统计规律第一部分 G-M计数器一.实验目的1、了解G-M管的工作原理,掌握其基本性能及其测试方法。
2、学会正确使用G-M管计数装置的方法。
3、了解探测器输出信号与输出回路参数的关系,学会正确选择G-M管计数系统输出回路参量。
二.实验内容1、在一定的甄别阈下,测量卤素G-M管的坪曲线,确定这些坪曲线的各个参量并选择工作电压。
2、用示波器观察法和双源法测定卤素G-M管计数装置的分辨时间。
3、观察并记录G-M计数管的输出电流、电压脉冲与工作电压及输出回路参数的关系。
三.实验原理1、G-M管是一种气体探测器。
当带电粒子射入其灵敏体积时,引起气体原子电离。
电离产生的电子在阳极丝附近的强电场中又引起一系列碰撞电离,即触发“自持放电”。
这一过程产生的电子和正离子向两极漂移时,在外回路产生脉冲信号。
2、从G-M管的工作机制可以看出,入射带电粒子仅仅起一个触发放电的作用,G-M管的输出电流、电压信号的幅度与形状和入射粒子种类与能量无关,只和计数管的几何参量、工作电压以及输出回路参量有关。
在G-M管的使用中,坪特性是其最重要的性能之一。
坪特性是判断管子好坏的主要依据,也是选择管子工作电压的依据。
坪特性曲线就是在一定的实验条件下当入射粒子的注量率不变时,计数管的计数率随工作电压变化的曲线,见图1-1。
图1-1 G-M计数管的坪曲线表征坪特性的参量主要有:起始电压(Vs):即计数管开始计数时的电压。
坪长: B A =V -V 坪长(单位:百伏) (1-1) 这是管子的工作区域,工作电压一般可选在坪区的21~31的范围内。
坪斜:()100% ()2B A B A B A n n n n V V -=⨯+-坪斜(单位:%/百伏) (1-2) 坪斜主要是由假计数引起的,当然它的值越小越好。
当工作电压高于B V 时,曲线急剧上升,表明管子内发生了持续放电,这会大大缩短管子的寿命,因此在使用中必须注意避免这种情况。
实验四 核衰变的统计规律与放射性测量的实验数据处理
实验四 核衰变的统计规律与放射性测量的实验数据处理一、实验目的1、 验证核衰变所服从的统计规律。
2、 熟悉放射性测量误差的表示方法。
3、 了解测量时间对准确度的影响。
4、 学会根据准确度的要求选择测量时间。
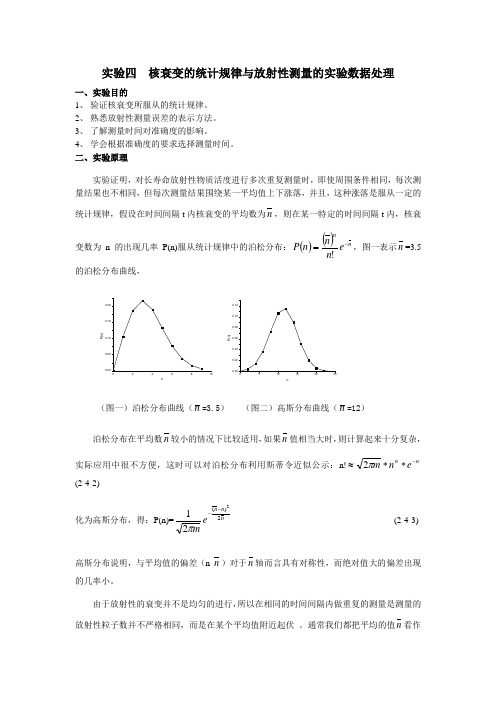
二、实验原理实验证明,对长寿命放射性物质活度进行多次重复测量时,即使周围条件相同,每次测量结果也不相同,但每次测量结果围绕某一平均值上下涨落,并且,这种涨落是服从一定的统计规律,假设在时间间隔t 内核衰变的平均数为n ,则在某一特定的时间间隔t 内,核衰变数为n 的出现几率P(n)服从统计规律中的泊松分布:()()n ne n n n P -=!,图一表示n =3.5的泊松分布曲线,P (n )nP (n )n(图一)泊松分布曲线(n =3.5) (图二)高斯分布曲线(n =12)泊松分布在平均数n 较小的情况下比较适用,如果n 值相当大时,则计算起来十分复杂,实际应用中很不方便,这时可以对泊松分布利用斯蒂令近似公示:n!n n e n m -**≈π2(2-4-2)化为高斯分布,得:P(n)=nn n em2)(221--π (2-4-3)高斯分布说明,与平均值的偏差(n-n )对于n 轴而言具有对称性,而绝对值大的偏差出现的几率小。
由于放射性的衰变并不是均匀的进行,所以在相同的时间间隔内做重复的测量是测量的放射性粒子数并不严格相同,而是在某个平均值附近起伏 。
通常我们都把平均的值n 看作是测量结果的几率值,并用她来表示放射性活度,而把起伏带来的误差叫测量统计误差,习惯上用标准误差n ±来描述。
事实上,测定这种基于无限多次测量而得到的n 是无法完成的,也是没必要的。
因此,实验室里都将一次测量的结果当作平均值,并做类似的处理而记为N N ±,其中N 表示放射性本身,N ±则表示测量误差。
计数的相对标准误差为NN N 1±=±(2-4-4) 它能说明测量的准确度。
放射性计数的统计误差及处理

e 1 1 m 2m ( 1 ) 2 m
利用级数展开式 有
x 2 x3 ln( 1 x) x - 2 3
m 2 1 1 2 ln( 1 ) (m ) [ - ( ) m 2 m 2 m
1 2 1 1 3 2 2m 2m 2m
由以上各式可见,无论是计数或计数率,其 相对误差只取决于总计数,不论是多次( k次), 还是一次测量但时间增加至k 倍,只要总计数相 等,那么结果的精度是相同的。
• 例题. 测样品8min得计数200个,测本底4min得 计数72个。求样品净计数率及误差。 解:
N c N b 200 72 n0 7cpm tc tb 8 4
N 0! n N( N 1 )( N 2 ) ( N n 1 ) N 0 0 0 0 0 (N 0 - n) !n!
( 1 - p)
N0 -n
(e )
-p N0 -n
e
-pN0
因此,得到关于计数的泊松分布
n n N0 m P( n) p n e -pN0 e -m n! n!
n
0
Nc Nb 200 72 ( 2 2 ) 2 2.8cpm 2 tc tb 8 4
n 0 n0 7.2 2.8 ( 7 1 40% )cpm
4. 测量条件的选择
1)测量时间确定 计数率n、测量时间t和相对误差n 三者具有 关系: 2
n nt 1
N
N
N
1 KN
1
N
i
N 3)平均计数率 n 的误差 t 1 Nk 1 n 2N 2 t t k
1 n n n k
盖革-弥勒计数管及核衰变的统计规律实验报告
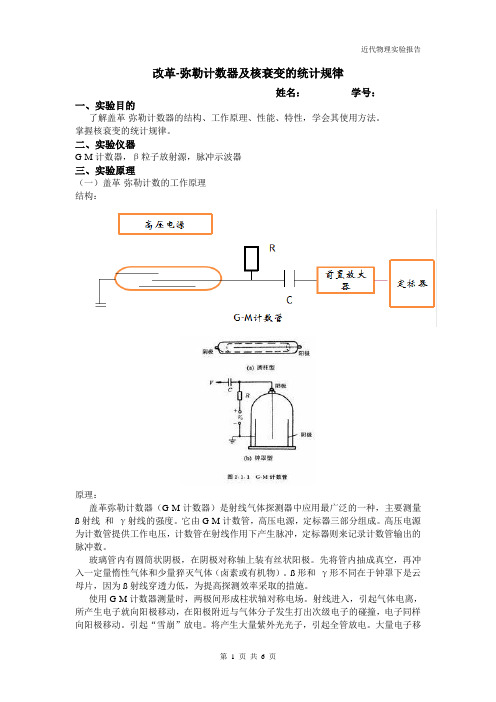
改革-弥勒计数器及核衰变的统计规律姓名:学号:一、实验目的了解盖革-弥勒计数器的结构、工作原理、性能、特性,学会其使用方法。
掌握核衰变的统计规律。
二、实验仪器G-M计数器,β粒子放射源,脉冲示波器三、实验原理(一)盖革-弥勒计数的工作原理结构:原理:盖革弥勒计数器(G-M计数器)是射线气体探测器中应用最广泛的一种,主要测量ß射线和γ射线的强度。
它由G-M计数管,高压电源,定标器三部分组成。
高压电源为计数管提供工作电压,计数管在射线作用下产生脉冲,定标器则来记录计数管输出的脉冲数。
玻璃管内有圆筒状阴极,在阴极对称轴上装有丝状阳极。
先将管内抽成真空,再冲入一定量惰性气体和少量猝灭气体(卤素或有机物)。
ß形和γ形不同在于钟罩下是云母片,因为ß射线穿透力低,为提高探测效率采取的措施。
使用G-M计数器测量时,两极间形成柱状轴对称电场。
射线进入,引起气体电离,所产生电子就向阳极移动,在阳极附近与气体分子发生打出次级电子的碰撞,电子同样向阳极移动。
引起“雪崩”放电。
将产生大量紫外光光子,引起全管放电。
大量电子移动到阳极被中和。
大量正离子由于质量大,移动缓慢,在阳极附近形成正离子鞘。
可将计数器看作电容器,使阳极得到一个负的脉冲。
电源高,波幅大:电阻高,脉冲宽。
(二)计数管的特性开始输出小,计数器示零,电压超过某一值时,定标器开始计数,此时电压Va 为阈电压。
随着脉冲幅度升高,计数率迅速增加,升到Vb 时,只要产生一个离子对,就能引起全管雪崩放电。
进一步升高,只能提高幅度,不能增加个数,直到Vc ,称为坪区。
Vc-Vb 为坪长度。
坪斜]%100[)(2212121每伏特⋅-⋅+-=V V n n n n ε,表示为电压升高1伏计数率的相对增加量。
(三)核衰变的统计规律及测量数据的处理 1、衰变规律:对大量核而言,其衰变遵从统计规律,有衰变定律-λλ0(t)e N =N其中t 表示时间,N0为t=0时刻的放射性核数,N(t)为t 时刻的放射性核数,λ称为衰变常数。
放射性测量数据的处理

一次测量或有限次测量平均值只能是数学期望值近似值,这么就给 测量结果带来了误差。放射性测量这种误差完全是由放射性核衰变 和探测器统计粒子统计性引发,故称为统计误差。
放射性测量数据的处理
6
第6页
第八章 射性测量数据处理与结果表述
✓以被保留数字末位为基准, ✓假如碰到它后面尾数小于5(4以下),则该尾数被舍弃; ✓假如碰到它后面尾数大于5(6以上),则末位数进1; ✓假如尾数恰为5,则要依据被保留数字末位数而定。当末尾数为奇数时,末尾
数进 1;当末尾数为偶数时,尾数5被舍弃。
放射性测量数据的处理
13
第13页
第八章 射性测量数据处理与结果表述
放射性测量数据的处理
16
第16页
第八章 射性测量数据处理与结果表述
2).几个数作乘、除运算: 各数中以有效数字位数最少数为基准,其它各数都凑成比该数多1位有效数字数 参加运算;运算结果取小数位数最少位数。 比如: 13469×34=135×102×34=4590×102=46×104
放射性测量数据的处理
放射性测量数据的处理
放射性测量数据的处理
第1页
第八章 射性测量数据处理与结果表述
➢普通只有经过几个不一样方法测量结果比较; ✓ 或即使是同一个方法,但使用不一样设备,将其测量结果进行比较。 ✓ 一旦找到了系统误差,能够对其进行校正,以降低甚至消除系统误差对测 量结果带来影响。
➢偶然误差也叫随机误差,是由不确定原因引发。
✓ 随机误差出现服从统计分布规律。 ✓ 增加测量次数,能够减小偶然误差。
放射性测量数据的处理
2
第2页
核衰变实验数据分析与处理.

实验数据分析与处理:工作电压的选择:根据坪曲线规律,选择较为平坦时工作电压为880V。
测放射源计数率实验数据分析:实验分析:1. 探测器与放射源的几何位置应保持合理(两者不宜离开太远2.实验中要保证不触碰探测仪,因为本实验是一种强度测量,所以一切有可能影响探测器探测效率的因素都必须严格保持不变,如工作点要保持稳定探测器和源的几何位置也不可以改变。
3.实验数据分析时,软件曾出现提示框显示:“已超出正态分布范围,无法分析”的字样。
打开实验数据后发现实验的第一个数据与之后的数据相去甚远(后面数据均维持在3300~3500范围内,第一个数据为20000+的值,在去除第一个数据后分析实验,软件得以成功分析。
可能由于电压值发生一定变化导致第一个数据出现一定问题,须删除无效数据后进行数据处理。
思考题1.什么是坪曲线?谈谈坪曲线的测量在研究核衰变统计规律实验中的意义? 答:坪曲线是入射粒子的强度不变时,计数器的计数率随工作电压变化的曲线。
测定坪曲线是为了选择一个合适的工作电压,以减少电压漂移对实验的影响.工作点若选在坪区,即使仪器和探头的性能都有变化,也可使总计数率保持稳定。
所以应在曲线较平的部分以及源计数率高本底计数率相对较低处选择工作电压。
2.什么是放射性核衰变的统计性?它服从什么规律?答:放射性原子核衰变的过程是一个相互独立彼此无关的过程,即每一个原子核的衰变是完全独立的,与其他原子核是否衰变无关;因此放射性原子核衰变的测量计数可以看成是一种伯努里试验问题。
其统计分布满足一定的规律性,称此规律性为核衰变的统计性,它服从正态分布。
3.σ的物理意义是什么?以单次测量值N 来表示测量值时,为什么是N N ±?其物理意义又是什么?答:σ的物理意义是在相同条件下作重复测量时,每次测量结果围绕着平均计数值的一个涨落大小。
在实际运算中由于出现概率较大的计数值与平均值N 的偏差不大,我们可以用N 来代N ;因此对于单次测量值N ,可以近似地说在N N ±范围内包含真值的概率是68.3%,这样一来用单次测量值就大体上确定了真值的范围。
4-1.核衰变的统计规律95-103

实验10-2 核衰变的统计规律【实验目的】1.测量NaI(Tl)闪烁探测器的坪曲线,确定合适的工作电压;指导:用闪烁探测器测量强度不变的放射源时,改变光电倍增管的高压,计数率也会随之改变;原因在于任何一种射线在闪烁探测器中产生的脉冲幅度都不会完全一样,输出脉冲的幅度也分布在一定范围内。
尽管如此,只要射线的能量不是特别低而探测器的工作状态又选择得当,绝大部分信号脉冲都会比光电倍增管的噪声脉冲大。
当电压足够高,信号脉冲幅度基本上都超过了仪器的甄别阈而绝大部分噪声的幅度又还比甄别阈小很多时,随着高压的增加计数率的增加就很缓慢了,这时就出现了“坪区”。
在实验中,重要的是向学生说明在许多核物理实验中测量坪曲线的意义何在。
在本实验中,由于高压相对比较稳定,因此我们在实践中发现选取坪曲线较为平坦(计数率随高压漂移变化较小)的工作点和坪曲线较为陡峭的工作点两者的差异不大。
2.了解并验证原子核衰变及放射性计数的统计性;指导:本实验通过反复测量放射源(137Cs 或60Co )在一段时间内强度并作为一个随机事件,取一个样本容量为A 的样本来观察其结果是否符合正态分布。
当然,源的强度本身随时间衰减,但137Cs 的半衰期长达30年,可以近似认为在实验时间内(大约1——2小时)源强不变。
3.了解统计误差的意义,掌握计算统计误差的方法;指导:这一实验需要一定的概率论和数理统计方面的基础,比如二项式分布、泊松分布、正态分布以及样本均值、样本方差、样本方差的无偏估计;学生应该已经学习过相关课程,若没有接受过类似训练,实验讲义的原理部分已经列出了所需知识。
需要说明的是: 鉴于A x x Ai i /)(12∑=-不是方差2S 的无偏估计,)1/()(12--∑=A x x Ai i 才是,因此取)1/()(12--=∑=A x x S Ai ix 作为样本标准差的无偏估计。
(参见任一概率论数理统计教材) 4.学习检验测量数据的分布类型的方法。
利用盖革计数器测量核衰变的统计规律实验报告

所谓“雪崩”电子;在这些碰撞中会产生大量紫外线光子, 这些光子能够进一步地近代物理实验实验报告盖革-弥勒计数器及核衰变的统计规律同组者:****操作人员:*** .号. *******一.实验仪器:G-M 计数器,3粒子放射源,脉冲示波器。
二•实验原理:1. G-M 计数器原理:高压电源定量惰性气体和少量猝灭气体(卤素或有机物)在G-M 阳极半径为a ,阴极半径为b ,则沿着管径向位置为r 处的电场强度为E=V 。
见随着r 减小,电场强度增大,且在阳极附近急剧增大。
2. 脉冲原理:1. )当射线进入G-M 管中使得管中气体电离后,正离子和负离子在管内电场的作用下分别向阴极和阳极移动。
在阳极附近强大的电场作用下,电子获得极大的动能定标器G-M 计数管玻璃管内有圆筒状阴极, 在阴极对称轴上装有丝状阳极。
先将管内抽成真空,再冲入一计数管两极加上电压/In(a/b)可以至于将阳极附近的气体电离。
经过多次碰撞,阳极附近的电子急剧增多,形成了产生第二波的“雪崩”效应,增加电子。
这个电子不断增多的过程成为气体放大。
2. )雪崩过程发生在阳极附近,加上电子的质量远远小于阳离子的质量,因此电子很快被阳极吸收,在管内留下一个由大量阳离子构成的阳离子鞘包围着阳极。
之减小,直到电场强度不足以引起雪崩效应, 这时雪崩效应停止, 阳离子鞘停止生成,G-M 管进入恢复过程。
在电场的作用下,正离子鞘缓慢地向阴极移动,阳极附近的电场也随之恢复,使得与 G-M 管串联的电阻记录下一个电压脉冲。
3.)当阳离子到达阴极时会再次打出光电子, 如果这些电子再次形成离子放电的话,一个入射粒子就将产生多个信号了。
为了避免再次形成雪崩效应, 使得一个入射粒子只产生一个信号,在管内加入少量的卤素气体来吸收这部分电子。
3. 脉冲特性:1. )坪曲线盖革计数器的计数率与电压有“坪”;在 VC 之后,计数率随着电压急速增大。
2. )电源电压越大,负脉冲幅度越大;串联电阻越大,脉冲宽度较宽,幅度也较大。
放射性衰变的规律与计算方法

放射性衰变的规律与计算方法在我们生活的这个世界中,存在着许多神秘而又奇妙的现象,放射性衰变就是其中之一。
放射性衰变是指不稳定的原子核自发地放出射线,转变为另一种原子核的过程。
这一过程不仅在科学研究中具有重要意义,也在许多实际应用中发挥着关键作用,比如医疗、能源和考古等领域。
放射性衰变有着其独特的规律。
首先,它是一个随机的过程。
这意味着我们无法准确预测某个原子核在何时会发生衰变,但在大量原子核的集合中,衰变的发生却遵循着一定的统计规律。
就好像抛硬币,每次抛硬币的结果是正面还是反面是无法预测的,但抛很多次后,正面和反面出现的概率会趋近于相等。
对于放射性衰变来说,也是如此。
放射性衰变的速率通常用半衰期来描述。
半衰期是指放射性原子核数目衰变掉一半所需要的时间。
不同的放射性核素具有不同的半衰期,有的短至几毫秒,有的则长达数十亿年。
例如,碘-131 的半衰期约为 8 天,而铀-238 的半衰期则长达约 45 亿年。
放射性衰变主要有三种类型:α衰变、β衰变和γ衰变。
α衰变是指原子核放出一个α粒子(由两个质子和两个中子组成),从而转变为另一种原子核。
β衰变则分为β⁺衰变和β⁻衰变。
β⁺衰变时,原子核中的一个质子转变为一个中子,并放出一个正电子和一个中微子;β⁻衰变时,原子核中的一个中子转变为一个质子,并放出一个电子和一个反中微子。
γ衰变一般不改变原子核的质子数和中子数,只是原子核从激发态跃迁到基态时放出γ射线。
那么,如何计算放射性衰变呢?这就需要用到一些数学公式和方法。
假设初始时刻放射性原子核的数目为 N₀,经过时间 t 后,剩余的原子核数目为 N,放射性衰变遵循指数衰减规律,可以用以下公式表示:N = N₀ × e^(λt)其中,λ 被称为衰变常数,它与半衰期 T₁/₂的关系为:λ = ln2 /T₁/₂。
通过这个公式,我们就可以计算在任意时刻剩余的放射性原子核的数目。
例如,如果我们知道某种放射性核素的半衰期为 10 天,初始时有1000 个原子核,经过 20 天,剩余的原子核数目是多少呢?首先,我们计算衰变常数λ = ln2 / 10 。
实验一、核衰变与放射性计数的统计规律实验报告

实验一核衰变与放射性计数的统计规律实验报告第一部分G-M计数器一.实验目的1、了解G-M管的工作原理,掌握其基本性能及其测试方法。
2、学会正确使用G-M管计数装置的方法。
3、了解探测器输出信号与输出回路参数的关系,学会正确选择G-M管计数系统输出回路参量。
二.实验内容1、在一定的甄别阈下,测量卤素G-M管的坪曲线,确定这些坪曲线的各个参量并选择工作电压。
2、用示波器观察法和双源法测定卤素G-M管计数装置的分辨时间。
3、观察并记录G-M计数管的输出电流、电压脉冲与工作电压及输出回路参数的关系。
三.实验原理1、G-M管是一种气体探测器。
当带电粒子射入其灵敏体积时,引起气体原子电离。
电离产生的电子在阳极丝附近的强电场中又引起一系列碰撞电离,即触发“自持放电”。
这一过程产生的电子和正离子向两极漂移时,在外回路产生脉冲信号。
2、从G-M管的工作机制可以看出,入射带电粒子仅仅起一个触发放电的作用,G-M管的输出电流、电压信号的幅度与形状和入射粒子种类与能量无关,只和计数管的几何参量、工作电压以及输出回路参量有关。
在G-M管的使用中,坪特性是其最重要的性能之一。
坪特性是判断管子好坏的主要依据,也是选择管子工作电压的依据。
坪特性曲线就是在一定的实验条件下当入射粒子的注量率不变时,计数管的计数率随工作电压变化的曲线,见图1-1。
图1-1 G-M计数管的坪曲线表征坪特性的参量主要有:起始电压(Vs):即计数管开始计数时的电压。
坪长: B A =V -V 坪长(单位:百伏)(1-1) 这是管子的工作区域,工作电压一般可选在坪区的21~31的范围内。
坪斜:()100% ()2B A B A B A n n n n V V -=⨯+-坪斜(单位:%/百伏) (1-2)坪斜主要是由假计数引起的,当然它的值越小越好。
当工作电压高于B V 时,曲线急剧上升,表明管子内发生了持续放电,这会大大缩短管子的寿命,因此在使用中必须注意避免这种情况。
(成都理工大学)放射性衰变涨落统计规律实验报告

放射性衰变涨落统计规律姓名:***同实验人:*** *** ***一、实验目的:1. 了解放射性衰变的统计涨落现象和规律;2. 了解统计误差的概念,掌握计算统计误差的方法; 3. 统计检验放射性衰变涨落的概率分布类型; 4. 学会用列表法和作图法表示实验结果。
二、实验原理简介:放射性现象就是不稳定的核素自发地放出粒子或γ射线,或在轨道电子俘获后放出X 射线,或产生自发裂变的过程。
在不稳定的核素中有天然放射性核素,也有人工放射性核素。
天然放射性核素发生衰变时,会放出α、β、γ 射线。
人工放射性核素还可以辐射出质子或中子等。
放射性自发衰变,一般不受温度、压力的影响,并按一定的指数规律变化。
在放射性测量中我们发现测量条件虽然没有发生变化,而测量结果并不完全一样,即放射源在每单位时间内发生衰变的原子数目是不同的,时多时少,有起有伏,但是它比较集中地在某一范围内波动,而这种现象就是放射性衰变的统计涨落。
出现这种现象的原因在于放射性原子核的衰变是自动发生的,哪一个原子核发生衰变是带有偶然性的,先后顺序并不确定。
“统计”是指对大量数据进行综合评价。
放射性现象的统计特征也需要通过长时间多次测量,采集大量数据(样本)才能观察到。
若测量数据为x ,当采集的样本个数为无穷大(个数很多)时,其数据在平均值x 附近按一定规律分布。
这一规律可以用下式来描述:()()!x xx P x e x -=⋅即泊松分布。
或用高斯正态分布来描述:2()21()2x x xP x exπ---=⋅这里的()P x 是测得计数为x 的概率。
当x 很小时服从泊松分布;当大于10时,泊松分布于高斯分布非常接近。
放射性测量仪器取得的数据,在一般情况下都比较大。
所以常利用高斯分布来描述放射性测量数据。
高斯分布也可以写作:22()()hx x h P x e π--=⋅12h σ=其中()P x 表示观测值x 出现的概率;h 称为“精确度指数”;σ称为“标准误差”。
原子核衰变的统计规律和统计误差 - 复旦大学

0.05
3.841 5.991 7.815 11.07 14.07 16.92 18.31 25.0 31.41 37.65 43.77
布.
2. 实验与分析
装置简图
统计规律的验证
1. 低计数(泊松分布):分别用Tl 和Cs,控制时间,使计数平均值在3~5 之间,取
300 个样本.
下表中左边数据是Tl,右边是Cs
和χ 2 1−α
,若χ2<
χ2 1−α
,就认为数据服从泊松分
χ2 1−α
v
1
2
3
5
7
9
10
15
20
25
30
α
0.50
0.455 1.165 2.366 4.351 6.346 8.343 9.342 14.34 19.34 24.34 29.34
0.10
2.71 4.61 6.25 9.24 12.0 14.684 16.0 22.3 28.4 34.4 40.3
图的形状
从图中可以看出随机变数χ2
所取的值大于某预定值χ12−α
的概率
p(χ2>
χ2 1−α
),令此概
率为α 则
∫ p(χ2>
χ2 1−α
)=
∞ p(χ 2 )d χ 2 = α
χ12−α
实验时要求总次数不少于50.比较时先取一个小概率α (本实验取0.1),称为显著
性水平,查表得χ12−α
的值,比较统计量χ2
9
4/5
0.0133/0.0166
0.0162/0.0152
10
1/3
0.0033/0.0099
0.0067/0.0062
盖革-弥勒计数器及核衰变的统计规律

盖革-弥勒计数器及核衰变的统计规律盖革-弥勒计数器是一种用于测量放射性核素活度的仪器。
它基于核反应速率与放射性核素的活度之间的关系,通过测量辐射计数来估算样品的放射性活度。
本文将探讨盖革-弥勒计数器的工作原理以及核衰变的统计规律。
一、盖革-弥勒计数器的工作原理盖革-弥勒计数器主要由两个部分组成:探头和电子学装置。
探头是由放射性样品和闪烁体组成,通过放射线和闪烁效应将辐射计数转化成可感测的光脉冲。
电子学装置负责对探头输出的信号进行放大、滤波和数字化处理。
当探头接受放射性样品的辐射时,闪烁体被激发并发出光子。
这些光子与光导管中的正电子发生相遇,产生光电效应并产生电子-空穴对。
这些电子会经过倍增器的放大器,产生更多的电子-空穴对,最终形成一个能够被电子学装置记录和分析的电脉冲。
通过校准和标准曲线法,可以将盖革-弥勒计数器的输出辐射计数转化成样品的放射性活度。
在核废料储存和放射性医学诊断等领域中,盖革-弥勒计数器被广泛使用。
二、核衰变的统计规律核衰变是一种随机性过程,每个放射性核素的衰变和放射发生率并不是恒定值。
相反,这些过程遵循一些统计规律,包括:1.指数规律指数规律是最普遍的核衰变统计规律之一。
在这一规律下,放射性核素的活度随时间呈指数下降。
每个放射性核素的半衰期是指其放射性活度减半所需的时间。
每次单个核衰变的发生是一个独立的随机过程,发生的概率在时间上是均匀分布的。
2.泊松分布泊松分布是描述随机事件发生的分布。
在核衰变中,每次放射性衰变是一个随机过程,一个时间点上出现较多的衰变事件比出现较少的衰变事件的概率要小。
这种规律被称为泊松分布。
3.高斯分布高斯分布是另一种随机分布,常常用于描述实验测量误差。
在放射性核素活度的测量中,测量误差会引入高斯分布的误差,并将造成测量值与理论值之间存在一定差异。
结论盖革-弥勒计数器在核科学、医疗和环境监测等领域中起着重要作用。
这种仪器通过电子学装置对辐射计数进行放大和数字化处理,以确定放射性样品的含量和活度。
1放射性衰变涨落的统计规律实验

放射性衰变涨落的统计规律实验一、实验目的1、证放射性衰变的涨落性2、了解统计误差的意义,掌握计算统计误差的方法3、统计检验放射性衰变涨落的概率分布类型4、学会用列表法和作图法表示实验结果二、实验内容1、相同实验条件下,多次重复测量某放射源的计数及测量装置的放射性本底计数2、用列表法和作图法表示实验结果:列出频数、频率统计表和χ2检验表;作放射源和本底计数的频数、频率和累计频率曲线图3、作χ2检验,确定放射源和本底计数的概率分布类型三、FD3013仪器简介:为便携式,操作方便、它适用于地质油矿普查、同位素放射源检测。
也使用于如核电、医院、实验室及废旧钢材等放射性同位素场合的检测。
1、仪器工作原理:γ射线经过外包壳后与探测器NaI(TI)晶体发生作用产生次级电子,它使闪烁体分子电离和激发,退激时发出大量光子荧光(其有各向同性,光谱范围从可见光到紫外光),在闪烁体周围包以反射物质,这样能使光子集中向光电倍增管(由光阴极和若干个打拿极和一个阳极组成)。
闪烁光子经光电倍增管,由于光电效应会产生光电子,这些光电子受极间电场加速和聚焦,打在第一个打拿极上,产生3~6个二次电子,这些二次电子在以后的打拿极上发生同样的倍增FD3013数字γ辐射仪过程,直到最后在阳极上可接收到104~109个电子。
这些电子在阳极负载上形成电压脉冲,通过起阻抗匹配作用的射极跟随器,传送到电压甄别器进行脉冲幅度甄别,当脉冲幅度高于甄别阈40kev时会形成一个计数信号,触发后续计数电路计数(低于甄别阈40kev的脉冲不会引起计数)。
CPM测量:计数选通cpm计数支路(面版上转换按钮置于cpm档),进行64s的计数测量。
测量结束后,计数选通门关闭,给出8秒显示计数。
显示结束后进行监测。
PPM测量:(面版上转换按钮置于ppm档)计数选通ppm计数支路,先进行1s的判测计数。
当计数在0~99时,自动选择16s档的测量时间;计数在100~199时,自动选择4s档的测量时间;计数在200以上时,自动选择2s档的测量时间。
验证原子核衰变的统计规律

1. 实验目的
验证原子核衰变的统计规律
1.1. 学会测量原子核衰变数量的概率分布; 1.2. 学会通过作图法和 χ2 检验法验证原子核衰变数量的分布类型。
2. 实验方法的原理
原子核衰变数量的泊松近似 原子核总数 N0(每组试验次数 n)通常很大,而原子核衰变概率 1-e-λt (事件 A 的发生概率 p)通常很小。例如 1 克 60Co 的原子核总数为 1× 1022 个,60Co 原子核的衰变概率为 4.2× 10-9。此时 t 时间内原子核衰变数量 k 的 分布可用泊松分布 P(N0(1-e-λt))来近似。设 N0(1-e-λt)=M,根据公式(11)易 得, M 恰好为 t 时间内发生衰变的原子核数的统计平均值, 即 k 的期望值。 由公式(8)可得:
2
( f j f j) 2 f j j 1
h
(20)
(20)式中 h 为计数值的分组数量(未分组时即为 xi 的样本数) ,fj 为 每组的实际观测次数,fj'为根据理论分布计算的每组的理论观测次数。每组 理论观测次数的计算方法为:利用(18)式和(19)式计算出每组对应的泊 松分布或正态分布的 f(xi),再乘以总次数。 b)确定自由度 h-l-1,h 为分组数,l 为 fj 的参数数量,泊松分布 l=1, 正态分布 l=2。
5
计数平均值 xi =∑xi /500=96.7
由图知,计数结果满足泊松分布
6
计数值 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四 核衰变的统计规律与放射性测量的实验数据处理一、实验目的1、 验证核衰变所服从的统计规律。
2、 熟悉放射性测量误差的表示方法。
3、 了解测量时间对准确度的影响。
4、 学会根据准确度的要求选择测量时间。
二、实验原理实验证明,对长寿命放射性物质活度进行多次重复测量时,即使周围条件相同,每次测量结果也不相同,但每次测量结果围绕某一平均值上下涨落,并且,这种涨落是服从一定的统计规律,假设在时间间隔t 内核衰变的平均数为n ,则在某一特定的时间间隔t 内,核衰变数为n 的出现几率P(n)服从统计规律中的泊松分布:()()n ne n n n P -=!,图一表示n =3.5的泊松分布曲线,P (n )nP (n )n(图一)泊松分布曲线(n =3.5) (图二)高斯分布曲线(n =12)泊松分布在平均数n 较小的情况下比较适用,如果n 值相当大时,则计算起来十分复杂,实际应用中很不方便,这时可以对泊松分布利用斯蒂令近似公示:n!n n e n m -**≈π2(2-4-2)化为高斯分布,得:P(n)=nn n em2)(221--π (2-4-3)高斯分布说明,与平均值的偏差(n-n )对于n 轴而言具有对称性,而绝对值大的偏差出现的几率小。
由于放射性的衰变并不是均匀的进行,所以在相同的时间间隔内做重复的测量是测量的放射性粒子数并不严格相同,而是在某个平均值附近起伏 。
通常我们都把平均的值n 看作是测量结果的几率值,并用她来表示放射性活度,而把起伏带来的误差叫测量统计误差,习惯上用标准误差n ±来描述。
事实上,测定这种基于无限多次测量而得到的n 是无法完成的,也是没必要的。
因此,实验室里都将一次测量的结果当作平均值,并做类似的处理而记为N N ±,其中N 表示放射性本身,N ±则表示测量误差。
计数的相对标准误差为NN N 1±=±(2-4-4) 它能说明测量的准确度。
当N 大时,相对标准误差小,而准确度高。
反之,则相对误差大,准确度低。
为了得到足够的计数N 以保证准确度,就需要延长放射性的测量时间t 或增加相同测量的次数m 。
根据简单的计算可知,从时间t 内测得的计算结果中算出的计数率的标准误差为t n tN t N ±=±=±2 (2-4-5) 式中N 为t 时间内测得的脉冲数,n 为单位时间内的脉冲数。
可以看出,此误差只有用单位时间测得结果之标准误差n 的t1。
标准误差的意义是指在完全相同的条件下,重复一次测量时,其计数结果有68.3%的几率处在t n n ±之间,有31.7%的几率在tnn ±之外。
计数率的相对标准误差E 用下式表示:ntn t nE 1±=±= (2-4-6) 若相同的实验重复进行了m 次,则平均计数率的标准误差可减小到m1,即等于mtn±。
不过重复测量并不方便,其效果完全可由一次长时间不间断测量代替。
在每次测量的数据里,实际上都包含本底计数。
当被测量的放射性的值和该实验的本底计数处于同一数量级时,计数率的标准误差为:σ==式中c N 为c t 时间内源加本底的计数,b N 为在b t 时间内本底的计数,c n 为源加本底的计数率,b n 为本底的计数率。
考虑了本底后,相对标准误差为:12()c b c bc bn n t t E n n +=±-。
从上式可以看出,测量时间越大,准确度越高。
因此在测量过程中要经常保持较小的本底和较长的测量时间,但过长的测量时间并不利,应选择合理的测量时间。
合理的分配测定源加本底和本底计数的时间,可利用下述公式:c bt t =测量时间和与相对标准误差间的关系如下:c a t =式中a c b n n n =-为放射源的计数率。
当b b n E n 〈时,上式可近似为:21a t n E ≈。
根据放射性活度和对准确度的要求,可算出测量的时间。
三、实验仪器G-M 计数管、定标器、放射源(长寿命)、铅室、有机玻璃架四、实验步骤1. 测量时间对计数率标准误差的影响(1)接好线路(定标器与计数管及电源电路),打开定标器的检验开关,检查进位状况是否正常;(2)将高压调到计数管的工作电压处,然后测本底5min ;(3)将放射源放在计数管下面的适当位置上,使脉冲计数率为1000脉冲/分~5000脉冲/分,然后分别以1min 、5min 、10min 的时间测量源的放射性;(4)将实验结果填入表内,算出每次测量的标准误差,从中得出必要的结论。
2. 重复测量次数对计数率标准误差的影响(1)将放射源放与计数管下面的适当位置上,保持几何条件不变,重复测量5次放射性活度,每次100s ;(2)将数据列入适当的表格内,算出每次测得的计数率的标准误差以及5次平均值的标准误差,从中得出必要的结论,并解释为何5次结果都不相同。
3. 根据放射源的活度和测量的准确度要求选择测量时间(要求相对标准误差为2%)(1)调节放射源和计数管之间的距离,使其计数率为4000脉冲/分~5000脉冲/分。
根据本底与计数率之比相对标准误差值之关系,确定公式,算出测量时间,然后以此时间测量其放射性活度;(2)根据实验数据算出相对标准误差,并与所要求值(2%)相比较。
4. 验证核衰变所服从的统计规律(1)用放射性计数验证高斯分布,时间间隔以2s 计,使其计数在每2s20次左右,测量次数最少在800次以上;(2)根据实验数据,绘出高斯分布曲线; (3)用实验所得平均值根据公式作出高斯分布的理论曲线(与实验曲线绘在同一坐标纸上),比较实验曲线和理论曲线的不同,并讨论原因。
五、实验数据处理按各步骤要求将实验数据列表、作图,并进行结果讨论。
1、 测量时间对计数率标准误差的影响经测量,该实验的本底计数远小于被测量的放射性的值,因此计数率的标准误差计算公式为:=将个数据列表如下:结论:延长测量时间可以减少计数率标准误差。
计数率的标准误差t n ±;平均计数率的误差tn 5±。
结论:相同时间间隔内重复测量时,测量的放射性粒子数并非完全一致,而是在某个值上下 起伏。
这是放射性衰变并不是均匀的产生的。
同时,单次测量的标准偏差也有差别。
但比较5次平均值的标准误差和单次测量的标准误差,发现平均值的标准误差明显小于单次测量的标准误差,这说明增加测量次数可减小计数率的标准误差。
3.根据放射源的活度和测量的准确度要求选择测量时间(要求相对标准误差为2%)本底和放射源的计数率之比为:n b /n a =1.22/125.81=0. 97%<2%,所以测量时间与相对标准误差间的关系式为:21a t n E ≈=20s ,相对标准误差公式为:12()c b c bc bn n t t E n n +=±- 20秒内放射性计数为2420,由上式计算得相对标准误差为±2.06%,相对标准误差稍大于要求的相对标准误差4. 验证核衰变所服从的统计规律 测量次数998 计数 出现次数 实际几率计数 出现次数实际几率12 1 0.001002 50 19 0.019038 13 1 0.00100251 18 0.01803614 1 0.001002 52210.02104215 2 0.002004 53170.01703416 2 0.002004 54140.01402817 5 0.00501 55190.01903818 0 0 56160.01603219 1 0.001002 57140.01402820 0 0 5810.00100221 8 0.008016 59170.01703422 10 0.01002 6060.00601223 13 0.013026 61110.01102224 10 0.01002 6290.00901825 23 0.023046 6390.00901826 21 0.021042 6470.00701427 14 0.014028 6570.00701428 8 0.008016 6640.00400829 22 0.022044 67130.01302630 8 0.008016 6810.00100231 19 0.019038 6950.0050132 23 0.023046 7010.00100233 29 0.029058 7140.00400834 15 0.01503 720035 47 0.047094 7350.0050136 36 0.036072 740037 34 0.034068 750038 6 0.006012 760039 46 0.046092 7710.00100240 21 0.021042 780041 52 0.052104 7910.00100242 31 0.031062 800043 41 0.041082 810044 23 0.023046 8210.00100245 54 0.054108 830046 28 0.028056 8410.00100247 43 0.04308648 10 0.01002P (n )n上图中红线表示标准高斯分布图,黑线为实际高斯分布图,由图可知,高斯分布的理论曲线与实验曲线基本重合,这说明核衰变数n 的出现几率P (n )服从统计规律中的高斯分布。
核衰变数与平均值的偏差()n n -对于n 轴而言具有对称性,绝对值大的偏差出现的几率小。
而两条曲线存在的些许差别表明,实际测量存在误差,n 出现的几率并不是高斯分布理论曲线的完美重现。
六、问题讨论1.试说明为什么测量时间增长时标准误差会减小?=n 不变,t增大,所以标准误差减小。
2.泊松分布和高斯分布说明了核衰变的什么问题?答:它们说明核衰变数与平均值的偏差()n n -对于n 轴而言具有对称性,绝对值大的偏差出现的几率小。
