基于直方图的二值化算法
基于直方图调整和击中击不中变换的弱小目标检测

Ab s t r a c t : I t i s h a r d t o d e t e c t t h e d i m s ma l l t a r g e t wi t h f e w p i x e l s a n d l o w i n t e n s i t y i n he t i ma g e o f c o mp l e x b a c k g r o u n d .
a n d h i t - mi s s t r a n s f o m r i s u s e d t o g e t he t s u s p i c i o u s t a r g e t s . T h e e x p e r i me n t s h o ws ha t t he t me ho t d i s e ic f i e n t i n d e t e c t i小 目 标的检测是当前 国防和军事上的重要研究课题 ,是一类典型的非平稳信号中不确定 信号的检测 问题 ,是信号检测领域的一个重要研究热点。当观测者距离观测 目 标较远时 ,观测 目标即成为
弱小 目标 ,“ 弱”是指其成像的灰度值很低 ,“ 小”是指其成像只有几个像素 , 同时 , 在图像中还存在大小、 灰度与真实 目标类似的类 目标干扰 ,这使得对弱小 目 标的检测变得十分困难。 目 前 ,国内外对弱小 目标的
第4 O 卷第 6 期
2 0 1 3 年 6月
光 电工程
Op t o - El e c t r o ni c Eng i n e e r i n g
自适应二值化公式

自适应二值化公式
自适应二值化是一种图像处理技术,用于将灰度图像转换为二值图像。
根据所使用的具体算法,自适应二值化的公式可能会有所不同。
以下是两种常见的自适应二值化算法的公式:
1. 平均值法(CV_ADAPTIVE_THRESH_MEAN_C):
\(T(x, y) = \text{mean} - C\)
其中,\(T(x, y)\) 是像素点 (x, y) 处的阈值,\(\text{mean}\) 是像素点 (x, y) 所在区域内的平均灰度值,C 是预设的常数参数。
2. 高斯加权法(CV_ADAPTIVE_THRESH_GAUSSIAN_C):
\(T(x, y) = \text{max} - D\)
其中,\(T(x, y)\) 是像素点 (x, y) 处的阈值,\(\text{max}\) 是像素点 (x, y) 所在区域内的最大灰度值,D 是预设的常数参数。
在实际应用中,需要根据具体的图像特性和需求选择合适的自适应二值化算法和参数。
直方图二值化

讲主要内容,观点。
基于直方图分析的车牌二值化应用方法车牌图像二值化在车牌图像识别中是一项关键技术,二值化的结果直接影响到字符分割的精度和识别。
本文,通过分析最大类间方差(Otsu)法和Bernsen法的局限性,提出了基于直方图分析的图像二值化方法。
该方法的准确性测试了8000幅图像,准确度达到99%,只有那些被严重污染的图像或者低分辨率的图像不能被准确的二值化,实验及实地的实验都表明我们的方法有很高的准确度、很高的速度,更好的二值化效果。
已经成功的应用在了识别系统中。
关键词:车牌识别,二值化,阈值确定,直方图分析,图像处理介绍:智能交通系统要完成的功能:比如电子收费,交通管理,安全控制。
车牌识别系统是智能交通实现的一种形式。
主要的任务确定车牌区,图像二值化,字符分割,然后识别。
这些任务相互之间关联紧密。
二值化就是其中的一项关键技术。
它的结果直接影响后面的字符分割与识别。
传统的二值化方法有许多:Otsu’s法和Bernsen's法。
Otsu's法是经典的截止阈值的方法,通过直方图分析确定一个合适的阈值。
如果车牌图像的直方图是双峰的,那么阈值相对容易确定,因为双峰表明,一个峰指的是字符区域,另外一个是背景区域。
直方图的谷被选为二值化的阈值。
但是当车牌图像被噪音污染或者光照强度不够而导致直方图有多个峰或者联合的峰。
那样阈值的确定就麻烦了。
Bernsen法是是个经典的适应阈值确定法,处理不均匀光照图像.但是相当的昂贵有事还会出现()。
两种方法在图像二值化的实际应用中都不理想。
本文,增强二值化的效果,提出了基于直方图分析的实用的图像二值化方法。
中国的车牌有两种:白色字符黑色背景,黑色字符白色背景。
通过判断直方图斜纹的重心偏向高灰度级还是低灰度级来确定车牌类型。
如果偏向低灰度级,则为黑底白字类型。
通过字符区域确定的百分比,我们给出阈值。
实验和实地测试的结果表明,它是一种切实可行的方法,并已在我们的CLPR系统成功应用2.TWO CONVENTIONAL THRESHOLDING METHODS在本节中,有两个传统的阈值确定方法,津市和伯恩森的方法,进行了介绍和它们进行牌照二值化时的局限性进行了分析Otsu’s method最大类间方差的方法同许多截止阈值技术一样,最大类间方差的方法通过直方图分析确定一个合适的图像阈值。
一种基于直方图对二值图像进行处理的方法

一种基于直方图对二值图像进行处理的方法刘跃锋;宋永霞;李松涛【摘要】介绍了利用直方图进行图像特征提取、图像分割、图像边缘检测及图像检索的方法.【期刊名称】《长春工业大学学报(自然科学版)》【年(卷),期】2010(031)005【总页数】5页(P554-558)【关键词】直方图;图像处理;图像分割【作者】刘跃锋;宋永霞;李松涛【作者单位】长春工业大学,计算机科学与工程学院,吉林,长春,130012;长春工业大学,计算机科学与工程学院,吉林,长春,130012;长春工业大学,计算机科学与工程学院,吉林,长春,130012【正文语种】中文【中图分类】TN911.730 引言根据图像的亮度信息并对其进行投影,得到的即为图像的灰度直方图,利用直方图技术对图像进行特征提取、边缘检测、分割等处理,可以得到想要的具有预定效果的图像,方便对其做进一步的处理。
1 灰度直方图简介[1]在一幅数字图像中,若其范围在[0,G]内总共包含有L级灰度,则其直方图定义应为一个离散函数,即:h(rk)=nk,其中rk是区间[0,G]内的第k级亮度,nk是灰度级为rk的图像中的像素数。
对于uint8类图像,G值为255;对于uint16类图像,G值为65535;对于double类图像,G值为1.0。
也就是说,对于uint8或者uint16类图像,G=L-1。
通常会用到归一化直方图,即使用所有元素h(rk)除以像素总数n所得到的图形。
其公式为:在Matlab仿真工具中,可以用imhist(f,b)函数获得图像的直方图。
其中,f为输入图像,b为灰度级的个数。
若要得到归一化的直方图,则需使用函数p=imhist(f,b)/numel(f)得到。
其中,函数numel(f)给出数组f的元素个数。
2 利用直方图对二值图像进行处理图像的分割和边缘检测是图像处理中的一个重要方面[2],对于一幅原始图像,不管要对其进行哪种操作,都要求首先确定整幅图像中有用信息与背景信息的区域,然后才能对该幅图像的有用信息区域进行想要做出的处理,而要达到这个目的,就要用到图像的边缘检测和图像分割技术。
基于直方图分析和OTSU算法的文字图像二值化

s u h s s h o w t h a t i t o f e r s k e y t e c ni h q u e s t o r e d u c e he t l i g h t i n l f u e n c e o f O T S U ,a nd i s o f g e n e r l a s e g me n t a t i o n a p p l i c a b i l i t y .
Bi n a r i z a t i o n o f Te x t I ma g e Ba s e d o n Hi s t o g r a m Ana l y s i s a nd OTS U Al g o r i t h m
W U Da n ,CAI Xi a o — d o n g ,XI E Yu e — f e i ,ZENG We i
计 算
2 0 1 3年第 7期
机
与
现
代
化
总第 2 1 5 期
J I S U A N J I Y U X I A N D A I HU A
文章编号 : 1 0 0 6 - 2 4 7 5 ( 2 0 1 3 ) 0 7 - 0 1 1 7 - 0 3
基 于直 方 图分 析 和 O T S U算 法 的文 字 图像 二值 化
关键词 : 自然 场 景 ; 二值化 ; 直方 图; O T S U
中图分类号 : T P 3 9 1 . 4 1
文献标识码 : A
d o i : 1 0 . 3 9 6 9 / j . i s s n . 1 0 0 6 — 2 4 7 5 . 2 0 1 3 . 0 7 . 0 3 1
Ke y wo r d s :n a t u r a l s c e n e s ;b i n a r i z a t i o n;h i s t o .S c h o o l o f I n f o r ma t i o n a n d C o m mu n i c a t i o n ,G u i l i n U n i v e r s i t y o f E l e c t r o n i c T e c h n o l o g y ,G u i l i n 5 4 1 0 0 4 , C h i n a ;
图像处理中的图像二值化算法

图像处理中的图像二值化算法随着科技的发展,图像处理技术应用越来越广泛。
作为一项基础技术,图像二值化算法在图像处理中扮演着非常关键的角色,它可以将图像分割成黑白两种颜色,也就是将图像中的灰度值转化为0和1,简化了后续的处理流程。
本文将介绍图像二值化算法的基本原理和应用情况。
一、二值化算法的基本原理在图像中,每个像素都有一定的灰度值,在8位灰度图像中,灰度值的范围在0-255之间,其中0是代表黑色,255代表白色。
当我们需要处理一张图片时,如果直接对每一个灰度值进行处理,那么处理的过程就会非常繁琐,因此,我们需要将图像灰度值转化为0和1两种数字进行处理。
常见的二值化算法有全局阈值算法、局部阈值算法、自适应阈值算法、基于梯度算法等。
其中,全局阈值算法是最基本、最简单的一种算法。
它将整张图像分成黑白两个部分,通过将整个图像的像素点的灰度值与一个固定的阈值进行比较,如果像素点的灰度值大于阈值,就将该像素点的灰度值置为1,否则置为0。
使用全局二值化算法的步骤如下:1.将图像读入到内存中;2.将图像转化为灰度图像;3.计算整个图像的平均灰度值,该平均灰度值作为全局阈值;4.将图像中每个像素点的灰度值与该全局阈值进行比较,灰度值大于等于该全局阈值的像素点赋值为255(代表白色),小于该阈值的像素点赋值为0(代表黑色);5.输出处理后的图像。
当然,这种方法的缺点也非常明显,那就是无法适应不同场合下的图像处理需求,处理效果难以保证。
因此,我们需要更为灵活的算法和方法来进行二值化处理。
二、不同类型的二值化算法1.基于直方图的全局阈值法二值化算法中的全局阈值算法通常是将整个图像分成两类像素:一类像素比较暗,另一类像素比较亮。
在直方图中,该分割就是直方图上的两个峰。
我们可以通过直方图分析来确定这个阈值,并将灰度值低于阈值的像素变为黑色,将灰度值高于阈值的像素变为白色。
对于图像I(x,y),它的灰度直方图h(i)可以表示为:h(i) = N(i) / MN (i=0,1,…,L-1)其中N(i)是图像中所有像素灰度值为i的像素数量,MN是总的像素数量,L是灰度级别数量(在8位图像中,L等于256)然后我们需要确定一个阈值T,所有像素点的灰度值小于T的变为黑色,大于等于T的变为白色。
[直方图,图像,方法]基于直方图平移的图像二次分块可逆数据隐藏方法
![[直方图,图像,方法]基于直方图平移的图像二次分块可逆数据隐藏方法](https://img.taocdn.com/s3/m/0a1f56c959eef8c75ebfb357.png)
基于直方图平移的图像二次分块可逆数据隐藏方法摘要:由Ni提出的对像素进行直方图平移进行可逆数据隐藏,一方面在单峰值或双峰值的情况下嵌入容量不够高,另一方面在嵌入数据之后对于图像的保真度也不够好。
在此,基于直方图平移的方式,提出一种改进算法,将图像进行二次划分,增加像素峰值点,提升图片的峰值信噪比。
实验结果表明,该算法不仅可以实现可逆数据隐藏,而且与Ni算法相比,既提升了嵌入容量,也使隐藏后的图像失真更小。
关键词:可逆数据隐藏;直方图平移;像素分块;双向直方图平移;区域再分块0 引言可逆数据隐藏是指在正确提取数据后还能无损地恢复原始图像,通常要满足隐蔽性好和容量高两个特性,被广泛应用于医学、军事、司法、政务等领域。
当前比较受关注的算法是2006年Ni等人提出的基于直方图平移的方法。
该算法是基于图像的直方图来展开。
近年来对于该算法的改进,大多追求容量的最大化。
其改进思路主要有三类:一是通过各类预测算法建立图像预测误差直方图,产生高峰值。
二是通过改变直方图位移水平,增加载荷。
三是在图像中进行多层隐藏,得到多峰值。
四是通过一种自适应的算法让载密信息根据图像特征来动态嵌入。
在实际应用中,对于一些敏感的图像,如医学图像、军事图像等,减少图像失真远比增加负载更重要。
本文的研究就是从提高嵌入容量和降低图像失真的角度对Ni算法进行改进,通过对图像的二次划分,第一次划分将图像划分成若干个大的区域,在这些区域中分别计算其峰值,从而得到较多的峰值点,第二次划分,在第一次划分的若干个大区域中,再一次将区域像素分成很多小像素块,若小像素块中存在当前区域像素的峰值点,就进行直方图平移,嵌人数据,若不存在,就不改变该像素块,以此来降低图像失真。
另外,为了尽量提升嵌入容量,采用双向直方图平移方法,最终可以实现低失真高负载的要求。
1 直方图平移可逆数据隐藏由Ni提出直方图平移可逆数据隐藏算法描述如下:在图1中,左侧为原始图像,右侧为该图像的灰度直方图。
图像处理中的二值化方法对比

图像处理中的二值化方法对比图像处理是一门广泛应用于计算机视觉领域的重要技术。
而二值化是图像处理中常用的一种方法,其能将图像分为黑白两个部分,使得图像中只存在黑白两种颜色的像素点。
在本文中,我将介绍几种常见的二值化方法,并对它们进行对比分析。
1. 阈值二值化方法阈值二值化方法是最简单而直观的一种二值化方法,其通过设置一个固定的阈值,将图像中的像素点的灰度值与该阈值进行比较,大于阈值的像素点设为白色,小于阈值的像素点设为黑色。
这种方法简单易懂,计算速度快,适用于二值化处理较为简单的图像。
2. 自适应阈值二值化方法与阈值二值化方法相比,自适应阈值二值化方法能够根据图像的局部特征自适应地选择最佳阈值。
该方法将图像分割为若干个小块,在每个小块中计算局部的阈值,并将该小块内的像素点进行二值化处理。
这种方法可以有效应对图像中不均匀光照条件的问题,适用于处理具有明暗变化较大的图像。
3. 基于直方图的二值化方法基于直方图的二值化方法是一种基于整幅图像的灰度分布特征进行二值化处理的方法。
该方法通过计算图像的灰度直方图,并选择全局最佳阈值来进行全局二值化处理。
这种方法能够提取图像的全局特征,但对于具有局部噪声的图像效果不佳。
4. 基于聚类的二值化方法基于聚类的二值化方法是一种利用像素点的灰度值进行聚类分析的方法。
该方法通过对图像中的像素点进行聚类分析,将像素点分为前景和背景两类,从而实现二值化处理。
这种方法对于具有复杂纹理和边缘的图像效果较好,但计算复杂度较高。
综上所述,不同的二值化方法各有其优势和适用范围。
在实际应用中,我们应根据具体的图像特征和处理要求选择合适的二值化方法。
例如,对于光照条件较好的图像,阈值二值化方法可以得到较好的效果;对于光照条件不均匀的图像,自适应阈值二值化方法更适合;而对于具有复杂纹理和边缘的图像,基于聚类的二值化方法可能有更好的效果。
总之,图像处理中的二值化方法对比告诉我们,在选择二值化方法时,要充分考虑图像的特征和处理要求,并根据实际情况选择合适的方法。
图像二值化阈值选取常用方法汇总
图像二值化阈值选取常用方法最近在公司搞车牌识别的项目,车牌定位后,发现对车牌区域二值化的好坏直接影响后面字符切分的过程,所以就想把常用阈值选取方法做一个总结。
图像二值化阈值选取常用方法:1.双峰法。
2.P 参数法。
3.最大类间方差法(Otsu 、大津法)。
4.最大熵阈值法。
5.迭代法(最佳阈值法)。
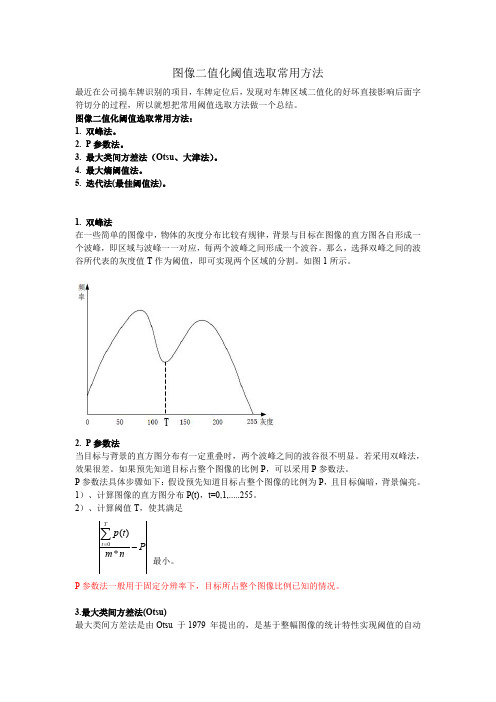
1.双峰法在一些简单的图像中,物体的灰度分布比较有规律,背景与目标在图像的直方图各自形成一个波峰,即区域与波峰一一对应,每两个波峰之间形成一个波谷。
那么,选择双峰之间的波谷所代表的灰度值T 作为阈值,即可实现两个区域的分割。
如图1所示。
2.P 参数法当目标与背景的直方图分布有一定重叠时,两个波峰之间的波谷很不明显。
若采用双峰法,效果很差。
如果预先知道目标占整个图像的比例P ,可以采用P 参数法。
P 参数法具体步骤如下:假设预先知道目标占整个图像的比例为P ,且目标偏暗,背景偏亮。
1)、计算图像的直方图分布P(t),t=0,1,.....255。
2)、计算阈值T ,使其满足0()*Tt p t Pm n =-∑最小。
P 参数法一般用于固定分辨率下,目标所占整个图像比例已知的情况。
3.最大类间方差法(Otsu)最大类间方差法是由Otsu 于1979年提出的,是基于整幅图像的统计特性实现阈值的自动选取的,是全局二值化最杰出的代表。
Otsu 算法的基本思想是用某一假定的灰度值t 将图像的灰度分成两组,当两组的类间方差最大时,此灰度值t 就是图像二值化的最佳阈值。
设图像有L 个灰度值,取值范围在0~L-1,在此范围内选取灰度值T ,将图像分成两组G0和G1,G0包含的像素的灰度值在0~T ,G1的灰度值在T+1~L-1,用N 表示图像像素总数,i n 表示灰度值为i 的像素的个数。
已知:每一个灰度值i 出现的概率为/i i p n N =;假设G0和G1两组像素的个数在整体图像中所占百分比为01ϖϖ、,两组平均灰度值为01μμ、,可得概率:00=T ii p ϖ=∑11011L i i T p ωω-=+==-∑平均灰度值:00T i i ipμ==∑111L ii T i p μ-=+=∑图像总的平均灰度值:0011μϖμϖμ=+类间方差:()()()22200110101()g t ωμμωμμωωμμ=-+-=-最佳阈值为:T=argmax(g(t))使得间类方差最大时所对应的t 值。
基于直方图的迭代式自动阈值分割技术研究

基于直方图的迭代式自动阈值分割技术研究摘要:首先介绍了直方图及其实现,进行了灰度处理,最后对迭代式自动阈值法技术进行了研究,介绍了其核心思想以及算法的实现,完成了图像阈值分割。
关键词:迭代式;自动阈值;图像分割0 引言图像分割是指将一幅图像分解为若干互不交叠的、有意义的、具有相同性质的区域。
分割出来的各区域对某种性质例如灰度、纹理而言具有相似性,区域内部是连通的且没有过多小孔;区域边界是明确的;相邻区域对分割所依据的性质有明显的差异。
图像分割算法一般是基于亮度值的两个基本特性之一:不连续性和相似性。
不连续性的应用途径是基于亮度的不连续变化分割图像,比如图像的边缘。
相似性的主要应用途径是依据事先制定的准则将图像分割为相似的区域。
门限(阈值)处理、区域生长、区域分离和聚合都是这类方法的实例。
本文研究了一种传统的图像分割方法——阈值法,通过迭代方法选取阈值。
由于直方图能够很好地反映图像中目标和背景在灰度特征上的差异等灰度分布特征, 和使用直方图进行阈值化的简单性和直观性, 利用直方图进行图像阈值化一直是图像分割的一个主流。
基于直方图的图像分割主要研究直方图构造和阈值选择两个问题。
1 获取直方图在数字图像处理中,灰度直方图是最简单且最有用的工具,可以说,对图像的分析与观察直到形成一个有效的处理方法,都离不开直方图。
灰度直方图是灰度级的函数,描述的是图像中该灰度级的像素个数或该灰度级像素出现的频率。
有时我们需要知道一幅图中的灰度分布情况,这时就可以采用灰度直方图来表示,即横坐标表示灰度级,纵坐标表示图像中该灰度出现的个数或该灰度级像素出现的频率,它只能反映图像灰度分布的情况,而不能反映图像像素的位置,即所有的空间信息全部丢失。
用来判断一幅图像是否合理的利用了全部被允许的灰度级范围,一般一幅图应该利用全部或几乎去哪不可能的灰度级,否则等于增加了量化间隔,丢失的信息将不能恢复。
下面是获取直方图的算法实现:iMaxGrayValue=0;iMinGrayValue=255;for (i=0;i < lWidth ;i++){for(j=0;j < lHeight ;j++){// 指向源图像倒数第j行,第i个象素的指针lpSrc=(char *)lpDIBBits + lLineBytes * j + i;pixel=(unsigned char)*lpSrc;lHistogram[pixel]++;//修改最大,最小灰度值if(iMinGrayValue > pixel){iMinGrayValue=pixel;}if(iMaxGrayValue < pixel){iMaxGrayValue=pixel;}}}2 基于直方图的灰度处理灰度处理过程只与像素的灰度有关系,与像素的位置无关,假设对横坐标为x,纵坐标为y的像素f(x,y)=g,经过灰度处理,其输出的灰度值为f`(x,y)=T(g)。
大津法实现图像二值化
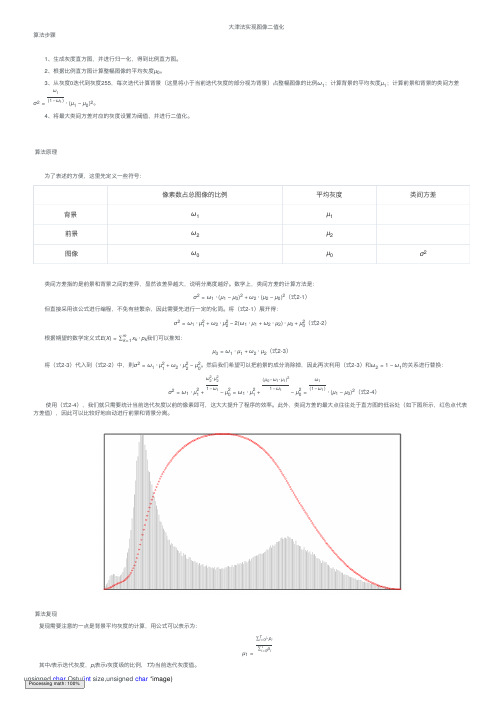
⼤津法实现图像⼆值化算法步骤1、⽣成灰度直⽅图,并进⾏归⼀化,得到⽐例直⽅图。
2、根据⽐例直⽅图计算整幅图像的平均灰度µ0。
3、从灰度0迭代到灰度255,每次迭代计算背景(这⾥将⼩于当前迭代灰度的部分视为背景)占整幅图像的⽐例ω1;计算背景的平均灰度µ1;计算前景和背景的类间⽅差σ2=ω1(1−ω1)·(µ1−µ0)2。
4、将最⼤类间⽅差对应的灰度设置为阈值,并进⾏⼆值化。
算法原理 为了表述的⽅便,这⾥先定义⼀些符号: 类间⽅差指的是前景和背景之间的差异,显然该差异越⼤,说明分离度越好。
数学上,类间⽅差的计算⽅法是:σ2=ω1·(µ1−µ0)2+ω2·(µ2−µ0)2(式2-1) 但直接采⽤该公式进⾏编程,不免有些繁杂,因此需要先进⾏⼀定的化简。
将(式2-1)展开得:σ2=ω1·µ21+ω2·µ22−2(ω1·µ1+ω2·µ2)·µ0+µ20(式2-2) 根据期望的数学定义式E (X )=∑∞k =1x k ·p k 我们可以推知:µ0=ω1·µ1+ω2·µ2(式2-3) 将(式2-3)代⼊到(式2-2)中,则σ2=ω1·µ21+ω2·µ22−µ20。
然后我们希望可以把前景的成分消除掉,因此再次利⽤(式2-3)和ω2=1−ω1的关系进⾏替换: σ2=ω1·µ21+ω22·µ221−ω1−µ20=ω1·µ21+(µ0−ω1·µ1)21−ω1−µ20=ω1(1−ω1)·(µ1−µ0)2(式2-4) 使⽤(式2-4),我们就只需要统计当前迭代灰度以前的像素即可,这⼤⼤提升了程序的效率。
直喷汽油机喷雾图像特征提取方法

直喷汽油机喷雾图像特征提取方法
商微微;任桐慧
【期刊名称】《吉林大学学报(信息科学版)》
【年(卷),期】2017(035)006
【摘要】为解决可视化燃油喷射图像采集系统的喷雾图像对比度低、边界雾化不清晰的问题,提出了一种基于均衡化直方图自适应求取阈值的二值化和图像特征检测算法.该算法根据对比度增强后的喷雾图像的直方图性质,自适应求取二值化阈值,通过自动检测喷嘴位置、喷雾图像最外侧切线以及喷雾最远点位置,确定喷雾贯穿距离和喷雾椎角,然后通过计算得到喷雾图像这两个特征参数,并对喷油全过程采集的25幅图像进行处理.实验结果表明,该方法能较清晰准确地提取喷雾图像轮廓,喷雾贯穿距离和喷雾锥角两个特征参数的变化趋势和理论值具有良好的一致性.【总页数】6页(P617-622)
【作者】商微微;任桐慧
【作者单位】长春大学电子信息工程学院,长春130022;长春光华学院电气信息学院,长春130012
【正文语种】中文
【中图分类】TP751
【相关文献】
1.燃油喷射压力对缸内直喷汽油机喷雾特性的影响 [J], 钱丁超;段加全;刘耀东;王振喜;陈海娥;宫艳峰
2.直喷汽油机喷油器积碳对喷雾落点及喷雾一致性的影响 [J], 张小雨;裴毅强;秦静;王莉;周建伟;李翔;张延峰
3.喷雾落点对直喷汽油机缸内油气混合和湿壁的影响 [J], 桂佳林;陈钰婷;刘丽华;张沛毅;杨万里;王瑞平
4.增压直喷汽油机喷雾及燃烧特性可视化试验研究 [J], 黄彬
5.直喷汽油机多孔喷油器喷雾闪急沸腾特性 [J], 吴坚; 陈泓; 杜家坤; 李钰怀; 占文锋; 林思聪
因版权原因,仅展示原文概要,查看原文内容请购买。
基于直方图凹度分析的印刷网点图二值化算法研究

Ke y wo r d s :b i n a r i z a t i o n;t h r e s h o l d  ̄h i s t o g r a m ;d e r i v a t i o n
v a l u e o f t h e v a l l e y b e t we e n t h e p e a k s o f h i s t o g r a m a s t h e t h r e s h o l d f o r t h e b i n a r i z a t i o n .
Ex p e r i me n t s s h o w t h a t c o mp a r e d wi t h o t h e r me t h o d s ,t h i s me t h o d c a n g e t t h e t h r e s h o l d o f t h e p r i n t d o t i ma g e wi t h a h i g h e r s p e e d a n d a c c u r a c y . As a r e s u l t ,i t h a s a g o o d a p p l i c a t i o n
Re s e a r c h o n pr i n t d o t i ma g e b i na r i z a r a m c o n c a v i t y a na l y s i s Z HE NGS u i ,H Qi , G AOP e n g f e i , WU We i j u n
第3 5卷
第 2 期
光
学
仪
器
Vo 1 . 3 5 ,No . 2 Ap r i 1 ,2 0 1 3
改进二值化算法在QR码识别中的应用

改进二值化算法在QR码识别中的应用随着移动设备的普及,二维码(QR码)已成为了人们生活中不可或缺的一部分。
在QR 码的识别过程中,二值化算法起着重要的作用。
然而,传统的二值化算法在应对一些复杂情况时存在着诸如信息损失、噪点干扰等问题,进而影响QR码的识别效果。
因此,改进二值化算法在QR码识别中的应用,也成为了一个值得关注和研究的课题。
一、QR码的基本原理QR码是一种矩阵型条码,由黑白相间的方块构成。
它的基本原理是利用黑白相间的方块组成一系列的二进制数字,并对数字进行编码,形成一串短码。
通过扫描二维码,就可以读取其中的信息。
QR码可以包含各种类型的数据,例如文字、网址、电话号码等等,具有容量大、读取速度快、易于扫描等优势,因此被广泛应用于各个领域。
二、传统二值化算法存在的问题在QR码的识别过程中,二值化算法扮演了重要角色。
二值化算法是将一副灰度图像转换为黑白二值图像的过程。
它的基本原理是将灰度图像中灰度值高于某个阈值的像素设置为白色,其余像素设置为黑色。
然而,传统的二值化算法在应对一些复杂情况时,存在以下问题:1、信息损失由于传统二值化算法直接将灰度值高于阈值的像素设置为白色,灰度值低于阈值的像素设置为黑色,因此会导致信息的丢失或模糊。
这对于QR码的识别来说,会影响其可靠性和准确性。
2、噪点干扰传统二值化算法容易受到噪点干扰,噪点会使得二值化后的图像出现局部区域差异、毛刺等不连续的情况,进而影响二维码的识别。
三、改进的二值化算法为了解决传统二值化算法存在的问题,我们可以采用经典的Otsu阈值法进行二值化。
Otsu阈值法基于灰度值的直方图,计算出全局的最佳二值化阈值,从而得到更好的二值化效果。
具体步骤包括以下几个方面:1、计算灰度值的直方图将图像中所有像素的灰度值统计成直方图,并将其归一化到0~1范围内。
2、计算全局最佳阈值对于Otsu算法而言,全局最佳阈值为能够使类内方差最小的灰度值。
因此,通过遍历前景和背景的灰度值,计算每一个可能的阈值,然后根据公式计算出每一个阈值下的类内方差。
深度图像的二值化

深度图像的⼆值化3.2 深度图像⼆值化图像⼆值化是图像处理中的⼀项基本技术,也是很多图像处理技术的预处理过程。
在颗粒分析、模式识别技术、光学字符识别(OCR)、医学数据可视化中的切⽚配准等应⽤中,图像⼆值化是它们进⾏数据预处理的重要技术。
由于图像⼆值化过程将会损失原图像的许多有⽤信息,因此在进⾏⼆值化预处理过程中,能否保留原图的主要特征⾮常关键。
在不同的应⽤中,图像⼆值化时阈值的选择是不同的。
因此,⾃适应图像阈值的选取⽅法⾮常值得研究。
研究者对图像⼆值化⽅法进⾏了讨论,在此基础上提出了⼀个新的图像⼆值化算法。
该算法基于数学形态学理论,较好地保留了图像⼆值化时原图的边缘特征。
本⽂主要研究⼆值化及灰度图像⼆值化⽅法。
3.2.1.灰度图像与⼆值图像数字图像是将连续的模拟图像经过离散化处理后得到的计算机能够辨识的点阵图像。
在严格意义上讲,数字图像是经过等距离矩形⽹格采样,对幅度进⾏等间隔量化的⼆维函数。
因此,数字图像实际上就是被量化的⼆维采样数组。
⼀幅数字图像都是由若⼲个数据点组成的,每个数据点称为像素(pixel)。
⽐如⼀幅256×400,就是指该图像是由⽔平⽅向上256列像素和垂直⽅向上400⾏像素组成的矩形图。
每⼀个像素具有⾃⼰的属性,如颜⾊(color)、灰度(grayscale)等,颜⾊和灰度是决定⼀幅图像表现⾥的关键因素。
数字图像⼜可分为彩⾊图像、灰度图像、⼆值图像。
3.2.1.1彩⾊图像彩⾊图像是多光谱图像的⼀种特殊情况,对应于⼈类视觉的三基⾊即红(R)、绿(G)、蓝(B)三个波段,是对⼈眼的光谱量化性质的近似。
彩⾊图像中的每个像素的颜⾊有R、G、B三个分量决定,⽽每个分量有255种值可取,这样⼀个像素点可以有1600多万的颜⾊的变化范围。
⽽灰度图像是R、G、B三个分量相同的⼀种特殊的彩⾊图像,⼀个像素点的变化范围为255种。
图1-1为彩⾊图像。
图1-13.2.1.2灰度图像灰度图像是指只含亮度信息,不含⾊彩信息的图像。
opencv大津法

opencv大津法Opencv大津法,又称Otsu’s方法,是一种基于图像灰度直方图的二值化算法。
该算法是由日本学者大津展之在1979年提出的,被认为是二值化算法中最经典的之一,能够将灰度图像转化为黑白二值图像,使得图像中目标物体背景和噪声的影响被消除,从而有效提取目标物体信息。
Opencv大津法的原理是基于直方图统计特征,从而确定分割阈值。
具体而言,该算法首先计算图像灰度的直方图,统计每种灰度值出现的次数。
然后,对于每一个灰度值i,将图像分割为两部分,即低于i和高于i两个部分,统计两部分的像素数和像素点的平均灰度值。
接着,计算两部分的灰度均值和图像总平均灰度值,根据这些信息,可以计算出两部分的类间方差以及类内方差。
最后,找到使得两部分类间方差最大的灰度值i,即为最佳分割阈值。
大津法在图像处理中广泛应用,特别是在肿瘤检测、面部识别、车牌识别、OCR光学字符识别等领域。
在肿瘤检测中,大津法可以帮助医生准确地识别正常组织和异常组织,从而更好地判断肿瘤是否存在;在OCR光学字符识别中,大津法可以将图像分割为黑白像素点,使得光学字符易于识别。
Opencv大津法具有以下优点:1.准确性高:大津法能够快速准确地确定最佳分割阈值,分割效果较好。
2.算法简单:大津法只需要进行简单的统计操作,算法的步骤简单易懂。
3.适用范围广:大津法适用于各种类型的图像,包括灰度图像、彩色图像等。
4.处理效率高:大津法处理速度快,具有高效性。
总之,Opencv大津法是一种灰度图像处理的经典算法,具有准确性高、算法简单、适用范围广、处理效率高等优点。
在日常生活中,我们可以通过使用Opencv大津法来进行车牌识别、OCR光学字符识别、肿瘤检测等方面的应用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图像二值化的目的是最大限度的将图象中感兴趣的部分保留下来,在很多情况下,也是进行图像分析、特征提取与模式识别之前的必要的图像预处理过程。
这个看似简单的问题,在过去的四十年里受到国内外学者的广泛关注,产生了数以百计的阈值选取方法,但如同其他图像分割算法一样,没有一个现有方法对各种各样的图像都能得到令人满意的结果。
在这些庞大的分类方法中,基于直方图的全局二值算法占有了绝对的市场份额,这些算法都从不同的科学层次提出了各自的实施方案,并且这类方法都有着一些共同的特点:1、简单;2、算法容易实现;3、执行速度快。
本文摘取了若干种这类方法进行了介绍。
一:灰度平局值值法:1、描述:即使用整幅图像的灰度平均值作为二值化的阈值,一般该方法可作为其他方法的初始猜想值。
2、原理:3、实现代码:public static int GetMeanThreshold(int[] HistGram){int Sum = 0, Amount = 0;for (int Y = 0; Y < 256; Y++){Amount += HistGram[Y];Sum += Y * HistGram[Y];}return Sum / Amount;}二、百分比阈值(P-Tile法)1、描述Doyle于1962年提出的P-Tile (即P分位数法)可以说是最古老的一种阈值选取方法。
该方法根据先验概率来设定阈值,使得二值化后的目标或背景像素比例等于先验概率,该方法简单高效,但是对于先验概率难于估计的图像却无能为力。
2、该原理比较简单,直接以代码实现。
/// <summary>/// 百分比阈值/// </summary>/// <param name="HistGram">灰度图像的直方图</param>/// <param name="Tile">背景在图像中所占的面积百分比</param>/// <returns></returns>public static int GetPTileThreshold(int[] HistGram, int Tile = 50){int Y, Amount = 0, Sum = 0;for (Y = 0; Y < 256; Y++) Amount += HistGram[Y]; // 像素总数for (Y = 0; Y < 256; Y++){Sum = Sum + HistGram[Y];if (Sum >= Amount * Tile / 100) return Y;}return -1;}三、基于谷底最小值的阈值1、描述:此方法实用于具有明显双峰直方图的图像,其寻找双峰的谷底作为阈值,但是该方法不一定能获得阈值,对于那些具有平坦的直方图或单峰图像,该方法不合适。
2、实现过程:该函数的实现是一个迭代的过程,每次处理前对直方图数据进行判断,看其是否已经是一个双峰的直方图,如果不是,则对直方图数据进行半径为1(窗口大小为3)的平滑,如果迭代了一定的数量比如1000次后仍未获得一个双峰的直方图,则函数执行失败,如成功获得,则最终阈值取两个双峰之间的谷底值作为阈值。
注意在编码过程中,平滑的处理需要当前像素之前的信息,因此需要对平滑前的数据进行一个备份。
另外,首数据类型精度限制,不应用整形的直方图数据,必须转换为浮点类型数据来进行处理,否则得不到正确的结果。
该算法相关参考论文如下:J. M. S. Prewitt and M. L. Mendelsohn, "The analysis of cell images," innnals of the New York Academy of Sciences, vol. 128, pp. 1035-1053, 1966.C. A. Glasbey, "An analysis of histogram-based thresholding algorithms," CVGIP: Graphical Models and Image Processing, vol. 55, pp. 532-537, 1993.3、实现代码:public static int GetMinimumThreshold(int[] HistGram){int Y, Iter = 0;double[] HistGramC = new double[256]; // 基于精度问题,一定要用浮点数来处理,否则得不到正确的结果double[] HistGramCC = new double[256]; // 求均值的过程会破坏前面的数据,因此需要两份数据for (Y = 0; Y < 256; Y++){HistGramC[Y] = HistGram[Y];HistGramCC[Y] = HistGram[Y];}// 通过三点求均值来平滑直方图while (IsDimodal(HistGramCC) == false)// 判断是否已经是双峰的图像了{HistGramCC[0] = (HistGramC[0] + HistGramC[0] + HistGramC[1]) / 3; // 第一点for (Y = 1; Y < 255; Y++)HistGramCC[Y] = (HistGramC[Y - 1] + HistGramC[Y] + HistGramC[Y + 1]) / 3; // 中间的点HistGramCC[255] = (HistGramC[254] + HistGramC[255] + HistGramC[255]) / 3; // 最后一点System.Buffer.BlockCopy(HistGramCC, 0, HistGramC, 0, 256 * sizeof(double));Iter++;if (Iter >= 1000) return -1;// 直方图无法平滑为双峰的,返回错误代码}// 阈值极为两峰之间的最小值bool Peakfound = false;for (Y = 1; Y < 255; Y++){if (HistGramCC[Y - 1] < HistGramCC[Y] && HistGramCC[Y + 1] < HistGramCC[Y]) Peakfound = true;if (Peakfound == true && HistGramCC[Y - 1] >= HistGramCC[Y] && HistGramCC[Y + 1] >= HistGramCC[Y])return Y - 1;}return -1;}其中IsDimodal函数为判断直方图是否是双峰的函数,代码如下:private static bool IsDimodal(double[] HistGram) // 检测直方图是否为双峰的{// 对直方图的峰进行计数,只有峰数位2才为双峰int Count = 0;for (int Y = 1; Y < 255; Y++){if (HistGram[Y - 1] < HistGram[Y] && HistGram[Y + 1] < HistGram[Y]){Count++;if (Count > 2) return false;}}if (Count == 2)return true;elsereturn false;}4、效果:原图二值图原始直方图平滑后的直方图对于这种有较明显的双峰的图像,该算法还是能取得不错的效果的。
四、基于双峰平均值的阈值1、描述:该算法和基于谷底最小值的阈值方法类似,只是最后一步不是取得双峰之间的谷底值,而是取双峰的平均值作为阈值。
2、参考代码:public static int GetIntermodesThreshold(int[] HistGram){int Y, Iter = 0, Index;double[] HistGramC = new double[256]; // 基于精度问题,一定要用浮点数来处理,否则得不到正确的结果double[] HistGramCC = new double[256]; // 求均值的过程会破坏前面的数据,因此需要两份数据for (Y = 0; Y < 256; Y++){HistGramC[Y] = HistGram[Y];HistGramCC[Y] = HistGram[Y];}// 通过三点求均值来平滑直方图while (IsDimodal(HistGramCC) == false)// 判断是否已经是双峰的图像了{HistGramCC[0] = (HistGramC[0] + HistGramC[0] + HistGramC[1]) / 3; // 第一点for (Y = 1; Y < 255; Y++)HistGramCC[Y] = (HistGramC[Y - 1] + HistGramC[Y] + HistGramC[Y + 1]) / 3; // 中间的点HistGramCC[255] = (HistGramC[254] + HistGramC[255] + HistGramC[255]) / 3; // 最后一点System.Buffer.BlockCopy(HistGramCC, 0, HistGramC, 0, 256 * sizeof(double)); // 备份数据,为下一次迭代做准备Iter++;if (Iter >= 10000) return -1;// 似乎直方图无法平滑为双峰的,返回错误代码}// 阈值为两峰值的平均值int[] Peak = new int[2];for (Y = 1, Index = 0; Y < 255; Y++)if (HistGramCC[Y - 1] < HistGramCC[Y] && HistGramCC[Y + 1] < HistGramCC[Y]) Peak[Index++] = Y - 1;return ((Peak[0] + Peak[1]) / 2);}3、效果:原图二值图原始直方图平滑后的直方图五、迭代最佳阈值1、描述:该算法先假定一个阈值,然后计算在该阈值下的前景和背景的中心值,当前景和背景中心值得平均值和假定的阈值相同时,则迭代中止,并以此值为阈值进行二值化。
