2-3综合测试卷(含答案)
2024-2025学年三年级上册道德与法治第三单元《安全护我成长》综合测试卷(含答案)

人教版三年级上册道德与法治第三单元综合测试卷(安全护我成长)时间:60分钟满分100分题号一二三四五总分得分一、认真填空。
(24分)1.从我们到,可不是一件容易的事情。
2.在养育我们的过程中,更是付出了无数心血。
3.游泳是我们喜爱的一项运动。
4.我们年龄小,还不强,如果防范意识不够,一些的人就会钻空子。
5.如果我们掌握了一些基本的和,就能预防各种事故的发生。
6.如果不小心让身体受到伤害,不仅要承受巨大的痛苦,还要面临生活中的种种和。
7.在陌生人中,有人会像朋友一样关心、爱护、帮助我们,但也有人不怀好意,会危及我们的安全。
二、明辨是非。
(对的打“✓”,错的打“×”)(20分)1.家中不存在危险,危险主要是来自户外。
( ) 2.生命是一切希望的基础。
( ) 3.如发现室内有煤气味,要立即开窗。
( ) 4.体育课有危险,我们尽量少参加。
( ) 5.有人触电了,我们要赶紧把他身上的电线拉开,挽救他的生命。
( ) 6.只要司机遵守交通规则,行人和乘车人没必要遵守交通规则。
( )7.小明在路上遇到歹徒要钱,便在他走后报了警。
( ) 8.只要不影响交通,可以在道路上使用旱冰鞋代步。
( ) 9.不遵守交通规则并不等于就会发生交通事故,所以没必要遵守。
( ) 10.小学生要有礼貌,独自在家有人敲门时要马上开门。
( )三、准确选择。
(把正确答案的序号填在括号里)(18分)1.只有()地生活才能健康成长。
A.幸福B.平安C.安全2.放学路上,有个陌生人免费请你品尝糖果,你应()。
A.拒绝品尝,以免给自己带来危险B.可以少尝点儿3.油锅着火时,正确的灭火方法是()。
A.用水浇B.用锅盖盖灭C.赶快去端油锅4.横过马路时要注意()。
A.遵守交通信号B.快来跑过马路C.没有交警值班时,快速通过5.掌握生活中的一些(),对于安全成长很重要。
A.安全常识B.生活知识C.生活常识6.()目前已成为我国儿童死亡的主要原因。
无锡外国语学校高中数学选修2-3第一章《计数原理》测试卷(包含答案解析)

一、选择题1.重阳节,农历九月初九,谐音是“久”,有长久之意,人们常在此日感恩敬老,是我国民间的传统节日.某校在重阳节当日安排6位学生到两所敬老院开展志愿服务活动,要求每所敬老院至少安排2人,则不同的分配方案数是( ) A .50B .40C .35D .302.()()4221x x x -+-的展开式中x 项的系数为( )A .9-B .5-C .7D .83.从0,1,2,3,…,9中选出三个不同数字组成一个三位数,其中能被3整除的三位数个数为( ) A .252B .216C .162D .2284.电影院一排10个位置,甲、乙、丙三人去看电影,要求他们坐在同一排,那么他们每人左右两边都有空位且甲坐在中间的坐法的种数为( ) A .40B .36C .32D .205.若多项式()210011x x a a x +=++()()91091011a x a x +++++,则9a =( )A .9B .10C .-9D .-106.为深入贯彻实施党中央布置的“精准扶贫”计划,某地方党委政府决定安排5名党员干部到4个贫困村驻村扶贫,每个贫困村至少分配1名党员干部,则不同的分配方案共有( ) A .264种B .480种C .240种D .720种7.某科技小组有四名男生两名女生.现从中选出三名同学参加比赛,其中至少有一名女生入选的不同选法种数为( ) A .36CB .1225C CC .12212424C C C C +D .36A8.从4台甲型和5台乙型电视机中任意取出3台,其中甲型与乙型电视机都要取到,则不同的取法种数为( ) A .40B .50C .60D .709.甲乙和其他2名同学合影留念,站成两排两列,且甲乙两人不在同一排也不在同一列,则这4名同学的站队方法有( ) A .8种B .16种C .32种D .64种10.有5位同学参加青少年科技创新大赛的3个不同项目,要求每位同学参加一个项目且每个项目至少有一位同学,则不同的参加方法种数为( ) A .80 B .120 C .150 D .360 11.现有6位同学站成一排照相,甲乙两同学必须相邻的排法共有多少种?( ) A .720B .360C .240D .12012.式子22223459C C C C ++++=( )A .83B .84C .119D .120二、填空题13.62x x ⎛⎫- ⎪⎝⎭展开式中常数项为________.14.已知()723801238()(21)x m x a a x a x a R x a x m +-=+++++∈,若127a =,则()81ii i a =⋅∑的值为_______.15.已知数列{}n a 共有21项,且11a =, 2115a =,11(1,2,3,,20)k k a a k +-==,则满足条件的不同数列{}n a 有______个. 16.已知集合{}123456,,,,,AB C a a a a a a =,且集合{}123,,A B C a a a =,则集合A 、B 、C 所有可能的情况有__________种.17.在停课不停学期间,某校有四位教师参加三项不同的公益教学活动,每位教师任选一项,则每个项目都有该校教师参加的概率为________(结果用数值表示). 18.计算2222223456C C C C C ++++=______.19.将5名上海世博会的志愿者分配到中国馆、美国馆、英国馆工作,要求每个国家馆至少分配一名志愿者且其中甲、乙两名志愿者不同时在同一个国家馆工作,则不同的分配方案有________种.20.某中学安排,,,A B C D 四支小队去3所不同的高校参观,上午每支小队各参观一所高校,下午A 小队有事返回学校,其余三支小队继续参观.要求每支小队上下午参观的高校不能相同,且每所高校上午和下午均有小队参观,则不同的安排有_____种.三、解答题21.从6名运动员中选出4人参加4100⨯接力赛,分别求满足下列条件的安排方法种数: (1)甲、乙两人都不跑中间两棒; (2)甲、乙二人不都跑中间两棒.22.袋中有相同的5个白球和4个黑球,从中任意摸出3个,求下列事件发生的概率. (1)摸出的全是白球或全是黑球、 (2)摸出的白球个数多于黑球个数.23.我校学生会进行换届选举,共选举出7名学生会委员,其中甲、乙、丙是上一届的委员,现对7名成员进行如下分工.(1)若学生会正、副主席两职位只能由甲、乙、丙三人选两人担任,则有多少种不同的分工方法;(2)若甲不担任学生会主席,乙不能担任组织委员,则有多少种不同的分工方法? 24.设(,)(1)n f x n x =+,*n N ∈. (1)设260126(,6)f x a a x a x a x =++++,求0246a a a a +++的值;(2)求12320192019201920192019232019C C C C +++⋯+的值; (3)*n N ∈,化简01122310144444n n n n n n n n n n C C C C C -----++++.25.已知.(1)若,求及的值;(2)若,求最大的系数;(3)定义,若化简.26.某中学将要举行校园歌手大赛,现有4男3女参加,需要安排他们的出场顺序.(结果..用数字作答.....) (1)如果3个女生都不相邻,那么有多少种不同的出场顺序?(2)如果女生甲在女生乙的前面(可以不相邻),那么有多少种不同的出场顺序? (3)如果3位女生都相邻,且女生甲不在第一个出场,那么有多少种不同的出场顺序?【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【分析】先把6人分成两组,再安排到两所敬老院,由此可得. 【详解】先分组再安排:6人可按3,3分组或2,4分组,然后再安排到敬老院,方法为32266222()50C C A A +⨯=.故选:A 【点睛】关键点点睛:本题考查分组分配问题,涉及到平均分组和不平均分组,平均分组时要除以组数的阶乘.n 个不同元素按12,,,k m m m 分成k 组,若12,,,k m m m 两两不等,则分组数为312112kkmm m m n n m n m m m C C C C ---,若12,,,k m m m 中仅有i 个数相等,则分组数为312112kkm m m m n n m n m m mi iC C C C A---.2.A解析:A 【分析】将()()4221x x x -+-化简为:2444(1)(1)2(1)x x x x x --+--,写出4(1)x -二项展开式的通项公式(4)14(1)rr r r T C x -+=⋅-,即可求得答案.【详解】()()42244421(1)(1)2(1)x x x x x x x x -+---+-=-4(1)x -二项展开式的通项公式(4)14(1)r r r r T C x -+=⋅- 24(1)x x -中不含x 项,无需求解.4(1)x x --中含x 项,即当4r =时(44444)(1)x C xx --⋅⋅=--42(1)x -中含x 项,即当3r =时(43)34328(1)C x x -⋅=-- ∴ ()()4221x x x -+-的展开式中x 项9x -故选:A. 【点睛】本题考查求二项式展开式中常数项,解题关键是掌握二项展开式的通项公式,考查分析能力和计算能力,属基础题.3.D解析:D 【分析】根据题意将10个数字分成三组:即被3除余1的有1,4,7;被3除余2的有2,5,8;被3整除的有3,6,9,0,若要求所得的三位数被3整除,则可以分类讨论:每组自己全排列,每组各选一个,再利用排列与组合的知识求出个数,进而求出答案. 【详解】解:将10个数字分成三组,即被3除余1的有{1,4,7},被3除余2的有{2,5,8},被3整除的有{3,6,9,0}.若要求所得的三位数被3整除,则可以分类讨论:①三个数字均取自第一组{1,4,7}中,或均取自第二组{2,5,8}中,有33212A =个; ②若三个数字均取自第三组{3,6,9,0},则要考虑取出的数字中有无数字0,共有324318A A -=个;③若三组各取一个数字,第三组中不取0,有11133333162C C C A ⋅⋅⋅=个, ④若三组各取一个数字,第三组中取0,有112332236C C A ⋅⋅⋅=个, 这样能被3整除的数共有12+18+162+36228=个. 故选:D. 【点睛】本题考查分类计数原理和排列组合知识,如何分类是关键,属于中档题.4.A解析:A 【分析】根据题意,先排好7个空座位,注意空座位是相同的,其中6个空位符合条件,将3人插入6个空位中,注意甲必须在三人中间,然后再排乙,丙,最后用分步计数原理求解. 【详解】除甲、乙、丙三人的座位外,还有7个座位,它们之间共可形成六个空, 三人从6个空中选三位置坐上去有36C 种坐法, 又甲坐在中间,所以乙、丙有22A 种方法,所以他们每人左右两边都有空位且甲坐在中间的坐法有36C 2240A ⋅=种. 故选:A . 【点睛】本题主要考查排列组合的实际应用,还考查了分析问题的能力,属于中档题.5.D解析:D 【解析】()()9011010019910999991...1[...]nn n x C C x C x a x a C C x C x +=++⇒+=++,()10101a x +=019910101010101010(...)a C C x C x C x ++++,根据已知条件得9x 的系数为0,10x 的系数为19999910101010101010011a a C a C a a C =-⎧⋅+⋅=⎧⇒⇒⎨⎨=⋅=⎩⎩ 故选D. 6.C解析:C 【分析】先从5个党员干部里选2个,再从4个贫困村里选1个接受选出的2个党员,剩下的3名党员分配给3个贫困村,即得解. 【详解】先从5个党员干部里选2个,有25C 种方法,再从4个贫困村里选1个接受选出的2个党员,有14C 种方法,剩下的3名党员分配给3个贫困村,有33A 种方法.所以共有213543240C C A =种方法.故选:C. 【点睛】本题主要考查排列组合的综合应用,意在考查学生对这些知识的理解掌握水平.7.C解析:C 【分析】分只有一名女生入选和有二名女生入选两种情况,结合分步乘法计数原理以及分类加法计数原理,即可得出答案. 【详解】当只有一名女生入选时,先选1名女生,有12C 种,再选2名男生,有24C 种,则根据分步乘法计数原理可知,有1224C C 种当有二名女生入选时,选选2名女生,有22C 种,再选1名男生,有14C 种,则根据分步乘法计数原理可知,有2124C C 种所以从中选出三名同学参加比赛,其中至少有一名女生入选的不同选法种数为12212424C C C C +故选:C 【点睛】本题主要考查了组合的应用,涉及了分步乘法计数原理以及分类加法计数原理的应用,属于中档题.8.D解析:D 【分析】根据题意,可分为2种情况,①取出的3台电视机为:甲型1台与乙型2台,②取出的3台电视机为:甲型2台与乙型1台,结合组合数的公式,即可求解. 【详解】根据题意,可分为2种情况,①取出的3台电视机为:甲型1台与乙型2台,共有124540C C =种不同的取法; ②取出的3台电视机为:甲型2台与乙型1台,共有214530C C =种不同的取法, 由分类计数原理,可得不同的取法共有403070+=种. 故选:D. 【点睛】本题主要考查了分类计数原理,以及组合数公式的应用,其中解答中合理分类,结合组合数的公式求解是解答的关键,着重考查了分析问题和解答问题的能力.9.A解析:A 【分析】根据题意,分3步进行讨论:先在4个位置中任选一个安排甲,再安排乙,最后将剩余的2个人,安排在其余的2个位置,分别求出每一步的情况数目,由分步计数原理计算可得答案. 【详解】根据题意,分3步进行讨论:1、先安排甲,在4个位置中任选一个即可,有14C 4=种选法;2、在与甲所选位置不在同一排也不在同一列只有一个位置,安排乙,即1种选法;3、将剩余的2个人,安排在其余的2个位置,有222A =种安排方法; 则这4名同学的站队方法有4128⨯⨯=种; 故选:A . 【点睛】本题主要考查排列、组合的综合应用,注意要优先分析受到限制的元素,属于中档题.10.C解析:C 【分析】根据题意,分清楚有两种情况,利用公式求得结果. 【详解】根据题意,可知有两种情况,一种是有三位同学去参加同一个项目,一种是有两个项目是两位同学参加,所以不同的参加方法种数为22333535332210310661502C C C A A A ⋅⨯⋅+⋅=⨯+⨯=种, 故选:C. 【点睛】该题考查的是有关排列组合的综合题,涉及到的知识点有分类计数加法计数原理,排列组合综合题,属于中档题目.11.C解析:C 【分析】6名同学排成一排,其中甲、乙两人必须排在一起,这是相邻问题,一般用“捆绑法”.将甲乙两名同学“捆绑”在一起,看成一个元素,再与剩下的4人一起全排列,根据分步计数原理即可得出结果. 【详解】将甲乙“捆绑”在一起看成一个元素,与其余4人一起排列, 而甲和乙之间还有一个排列, 共有5252240A A =. 故选:C. 【点睛】本题考查了排列组合、两个基本原理的应用,相邻问题“捆绑法”求解,属于基础题.12.C解析:C 【分析】根据组合数的计算公式111rr r n n n C C C ++++=,化简运算,即可求解.【详解】由题意,根据组合数的计算公式111rr r n n n C C C ++++=,可得22223459C C C C ++++=32222334591C C C C C +++++-322244591C C C C =++++-32235591011119C C C C =+++-==-=.故选:C. 【点睛】本题主要考查了组合数的化简与运算,其中解答中熟记组合数的运算公式,准确运算是解答的关键,着重考查了计算能力.二、填空题13.240【分析】先求出二项式的展开式的通项公式令的指数等于求出的值即可求得展开式中的常数项【详解】展开式的通项公式令所以的展开式的常数项为故答案为【点睛】本题主要考查二项展开式定理的通项与系数属于简单解析:240 【分析】先求出二项式6x⎛⎝的展开式的通项公式,令x 的指数等于0,求出r 的值,即可求得展开式中的常数项. 【详解】6x⎛- ⎝展开式的通项公式3662166(2),rr r r r r r T C x C x --+⎛==⨯-⨯ ⎝令36342r r -=⇒=,所以6x ⎛ ⎝的展开式的常数项为4462240C ⨯=,故答案为240. 【点睛】本题主要考查二项展开式定理的通项与系数,属于简单题. 二项展开式定理的问题也是高考命题热点之一,关于二项式定理的命题方向比较明确,主要从以下几个方面命题:(1)考查二项展开式的通项公式1C rn r rr n T ab -+=;(可以考查某一项,也可考查某一项的系数)(2)考查各项系数和和各项的二项式系数和;(3)二项展开式定理的应用.14.43【分析】因为的展开通项为:根据求的将所给等式两边求导即可求得的值【详解】的展开通项为:又等式两边求导可得:令得:故答案为:【点睛】本题解题关键是掌握多项式系数的求法和导数基础知识考查了分析能力和解析:43 【分析】因为7(21)x -的展开通项为:777177(2)(1)(1)2rrr rr r r r T C x C x ---+=⋅⋅-⋅-⋅⋅=,根据127a =,求的m ,将所给等式两边求导,即可求得()81i i i a =⋅∑的值.【详解】7(21)x -的展开通项为:777177(2)(1)(1)2r r r rr r r r T C x C x ---+=⋅⋅-⋅-⋅⋅= 又777()(21)(21)(21)x m x x x m x +--+-=∴7661777011(1)2(1)211427a C m C m =⨯-⋅+⨯--+==⋅∴2m =80187(2)(21)x x a a x a x +-=++⋯+等式两边求导可得:762712381(21)(2)7(21)2238x x x a a x a x a x ⋅-++⋅⋅-⋅=+++⋯+6(21)(211428)x x x =--++67128(1627)(21)28x x a a x a x =+-=++⋯+令1x =,得:1282843a a a ++⋯=+∴()8143i i i a =⋅=∑故答案为:43 【点睛】本题解题关键是掌握多项式系数的求法和导数基础知识,考查了分析能力和计算能力,属于中档题.15.【分析】转化条件得或求出满足的个数再利用组合的知识即可得解【详解】或设满足的个数为解得结合组合的应用满足要求的数列有个故答案为:【点睛】本题考查了数列递推公式的应用考查了组合的应用与转化化归思想属于解析:1140【分析】转化条件得11k k a a +-=或11k k a a +-=-,求出满足11k k a a +-=的个数,再利用组合的知识即可得解. 【详解】11k k a a +-=, ∴11k k a a +-=或11k k a a +-=-,设满足11k k a a +-=的个数为x ,()()()211212*********a a a a a a a a -=-+-+⋅⋅⋅+-=, ∴()()20114x x +-⋅-=,解得17x =,结合组合的应用,满足要求的数列有20217301140C C ==个. 故答案为:1140. 【点睛】本题考查了数列递推公式的应用,考查了组合的应用与转化化归思想,属于中档题.16.【分析】由可知集合均含有元素作出韦恩图可知元素可以放在除之外的个区域中每个元素有个选择利用分步乘法计数原理可得结果【详解】如下图所示集合被分为了个区域由可知集合均含有元素则元素可以放在除之外的个区域 解析:216【分析】 由{}123,,AB C a a a =,可知集合A 、B 、C 均含有元素1a 、2a 、3a ,作出韦恩图,可知元素4a 、5a 、6a 可以放在除A B C ⋂⋂之外的6个区域中,每个元素有6个选择,利用分步乘法计数原理可得结果. 【详解】如下图所示,集合A 、B 、C 被分为了7个区域,由{}123,,AB C a a a =,可知集合A 、B 、C 均含有元素1a 、2a 、3a ,则元素4a 、5a 、6a 可以放在除A B C ⋂⋂之外的6个区域中,每个元素有6个选择,由分步乘法计数原理可知,所有可能的情况种数为36216=. 故答案为:216. 【点睛】本题考查排列组合问题,考查分步乘法计数原理的应用,考查运算求解能力,属于中等题.17.【分析】根据题意先求出四位教师参加三项不同的公益教学活动每位教师任选一项的所有情况有种每个项目都有该校教师参加的情况有种即可求得相应的概率【详解】解:由于四位教师参加三项不同的公益教学活动每位教师任解析:49【分析】根据题意,先求出四位教师参加三项不同的公益教学活动,每位教师任选一项的所有情况有43种,每个项目都有该校教师参加的情况有2343C A ⋅种,即可求得相应的概率. 【详解】解:由于四位教师参加三项不同的公益教学活动,每位教师任选一项的情况有:433333⨯⨯⨯=(种),而每个项目都有该校教师参加的情况有:234336C A ⋅=(种), 则每个项目都有该校教师参加的概率为:436439=. 故答案为:49. 【点睛】本题考查概率的计算和分步乘法的计数原理,以及排列组合的应用,考查分析计算能力.18.35【分析】根据组合数的性质计算可得;【详解】解:故答案为:【点睛】本题考查组合数的性质属于中档题解析:35 【分析】根据组合数的性质11mm mn n n C C C -++=计算可得;【详解】解:2222223456C C C C C ++++3222233456C C C C C =++++ 32224456C C C C =+++ 322556C C C =++3266C C =+ 3776535321C ⨯⨯===⨯⨯故答案为:35 【点睛】本题考查组合数的性质,属于中档题.19.114【分析】本题是一个分类计数问题每个国家馆至少分配一名志愿者则有两种不同的情况当按照221安排时共有当按照113安排时有其中包括甲和乙在一个馆里的情况减去不合题意的结果即可【详解】由题意知本题是解析:114 【分析】本题是一个分类计数问题,每个国家馆至少分配一名志愿者,则有两种不同的情况,当按照2,2,1安排时,共有223533902C C A =,当按照1,1,3安排时,有335360C A =,其中包括甲和乙在一个馆里的情况,减去不合题意的结果即可. 【详解】由题意知本题是一个分类计数问题,每个国家馆至少分配一名志愿者,则有两种不同的情况, 每一个馆的人数分别是2,2,1;1,1,3 当按照2,2,1安排时,共有223533902C C A =,当按照1,1,3安排时,有335360C A =, 其中包括甲和乙在一个馆里的情况, 当甲和乙在同一个馆里时,共有234336C A =, ∴满足条件的排列法共有906036114+-=,故答案为:114. 【点睛】本题考查计数原理的应用,解题的关键是先分组再做分配,考查加法原理和乘法原理的实际应用,属于中等题.20.【分析】本题属于分组分配问题可按上午参观时A 是否与其他小队分在一组进行讨论分上下午两步安排参观即可得出答案【详解】若与中的某一支小队分在一组上午有种参观方法下午参观时三支小队不去各自上午参观的高校有解析:【分析】本题属于分组分配问题,可按上午参观时A 是否与其他小队分在一组进行讨论,分上下午两步安排参观,即可得出答案. 【详解】若A 与B 、C 、D 中的某一支小队分在一组,上午有1333C A ⋅种参观方法, 下午参观时B 、C 、D 三支小队不去各自上午参观的高校,有2种方法, 故有1333236C A ⋅⋅=种;若B 、C 、D 中某两支队分在一组,上午有2333C A ⋅种参观方法, 下午再安排时,也有2种方法, 故有2333236C A ⋅⋅=种. 所以一共有363672+=种. 故答案为:72. 【点睛】本题考查考查分组分配问题,注意其中的分类分步,属于中档题.三、解答题21.(1)144(2)336 【分析】(1)第一步,安排中间2个位置,第二步,安排首尾2个位置,利用乘法原理可得结论. (2)利用间接法,任意排法,再去掉甲、乙跑中间的安排方法即可得解; 【详解】解:(1)先选跑中间的两人有24A 种,再从余下的4人中选跑1、4棒的有24A ,则共有2244144A A =种.(2)用间接法:“不都跑”的否定是“都跑”,所以用任意排法46A ,再去掉甲、乙跑中间的安排方法2224A A 种,故满足条件的安排方法有246224336A A A =-种. 【点睛】本题考查计数原理的运用问题,解题的关键是正确分步.注意甲乙都不跑中间,包括了甲乙可能都不上场的情形.22.(1)16(2)2542【分析】(1)从袋中任意摸出3个球有39C 种不同情况,摸出的全是白球有35C 种不同情况,摸出的全是黑球有34C 种不同情况,计算概率得到答案.(2)摸出的3个球都是白球的事件,记为M ;摸出2个白球,1个黑球的事件,记为N .计算概率得到答案. 【详解】(1)设从袋中摸出的3个球全是白球或全是黑球的事件为A , 从袋中任意摸出3个球有39C 种不同情况, 摸出的全是白球有35C 种不同情况, 摸出的全是黑球有34C 种不同情况,因为从袋中任意摸出3个球的所有情况都是等可能的,所以()3354391041846C C P A C ++===. (2)设从袋中摸出的白球个数多于黑球个数的事件为B . 事件B 包含两个基本事件:第一个,摸出的3个球都是白球的事件,记为M ; 第二个,摸出2个白球,1个黑球的事件,记为N .()3539542C P M C ==,()21543940108421C C P N C ===. 所以,()()()51025422142P B P M P N =+=+=. 【点睛】本题考查了概率的计算,意在考查学生的计算能力. 23.(1)720;(2)3720. 【分析】(1)由学生会正、副主席两职位只能由甲乙丙三人中选出两人担任,利用排列、组合计算即可;(2)甲不担任学生会主席,乙不担任组织委员,可用间接法计算,即可求解. 【详解】(1)由题意,学生会正、副主席两职位只能由甲乙丙三人中选出两人担任, 则有225325720C A A =种不同的分工.(2)甲不担任学生会主席,乙不担任组织委员,则有76576523720A A A -+=种不同的分工. 【点睛】本题主要考查了排列、组合及其简单的计数原理的应用,其中解答中认真审题,合理利用排列数、组合数的公式求解是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题.24.(1)32.(2)201820192⨯.(3)54n.【分析】(1)利用赋值法求解,令1x =和1x =-,两式相加可得;(2)利用11k k n n kC nC --=可求;(3)结合式子特点构造(41)n +可求. 【详解】(1)令1x =,得60126264a a a a +++⋯+== ① 令1x =-,得01260a a a a -+-⋯+= ② ①+②得024632a a a a +++=;(2)因为11k k n n kC nC --=所以12320192019201920192019232019C C C C ++++=()12201820182018201820182019C C C C ++++201820192=⨯;(3)01122310144444n n n n n n n n n n C C C C C -----+++⋯++011221144444n n n n nn n nnnC C C CC ---⎡⎤=+++++⎣⎦15(41)44nn=+=. 【点睛】本题主要考查二项式定理的应用,结合组合数的性质,侧重考查数学解题模型的构建能力. 25.(1)(2)(3)【解析】 【分析】(1)由赋值法得到相应的数值;(2)将参数值代入表达式得到其通项公式为,由不等式,可得到,进而得到;(3)按照组合数的展开公式,分组求和即可. 【详解】 (1)若,,令,则, 令,则所以.(2)若,其通项公式为,由不等式解得,且,∴.所以.(3)若,【点睛】本题考查二项式定理的应用,以及组合数公式的相关运算,考查推理能力与计算能力,属于中等题。
统编版2024-2025学年语文五年级上册第一次月考综合测试卷(考查范围:第一、第二单元)(含答案)

2024-2025学年度第一学期五年级语文第一次月考测试卷(考查范围:第一、第二单元)班级:_________________ 姓名:_________________ 成绩:_________________一、看拼音,写词语。
(8分)二、用“√”选择加点字正确的读音或汉字。
(6分)音韵(yún yùn)眼眸(móu mù)挽救(wán wǎn)强迫(qiáng qiǎng)削皮(xiāo xuē)搁置(gē gé)流泻(xiě xiè)铿锵(jiāng kēn)窗(筐框)警(戒诫)等(侍待)(雕碉)堡三、根据句子中划线部分的意思写出二字词语或四字词语。
(6分)1. 我们姐弟第一次尝试种花生,没过几个月,没想到收获了。
()2. 做人要做有用的人,不要做只讲外表好看,而对别人没有好处的人。
()3. 虽然家乡景色很好,但还是有缺陷,村里都是土路,下雨时泥泞不堪,晴天时沙土飞扬。
()4. 不要把别人对你的帮助,视为从道理上讲应当这样。
()5. 面对暴徒的恶性,人们简直是愤怒得头发直竖,把帽子都顶了起来。
()6. 天上的星星真是太多了,没法计算数目。
()四、给句子中的加点词选择正确的解释。
(4分)温和:①指物体具备使人感到暖和的适当温度;②指性情、态度、言语等温柔平和;③指气候不冷不热。
1. 昆明气候温和,夏无酷暑,冬不严寒,四季如春,有“春城”之美称。
()2. 大熊猫性情温和,游客们都喜欢它们。
()姿态:①神情举止,容貌体态;②指物体呈现的样子;③诗文书画意趣的表现;④风俗、气度。
3. 石缝里长出些高高矮矮的树木,苍翠、茂密,姿态不一。
()4. 商场的橱窗里摆放着姿态各异的模特。
()五、按要求写句子。
(8分)1. 白鹭本身不就是一首很优美的歌吗?(改为陈述句)__________________________________________________________________________________2. 弟弟淘气也没人搭理他,他只得乖乖回家。
2022-2023学年四年级英语上册期末综合测试卷(含答案)

2022-2023学年四年级英语上册期末综合测试卷(含答案)一、听力部分(50分)1.(10分)Peter正在听录音,请你帮他把听到的单词选出。
(1)A.angry B.any(2)A.behind B.beside(3)A.cloud B.carrot(4)A.draw B.drink(5)A.his B.her2.(20分)Peter正在听录音,请你选出他所听到的句子代表的图片。
3.(10分)Peter正在询问他朋友的一些情况,请你帮他选出正确的应答语。
(1)A.Good morning,Miss Fang. B.Goodbye,Miss Fang.(2)A.I can write. B.I can draw.(3)A.She is a nurse. B.She is a teacher.(4)A.It's rainy. B.It's cloudy.(5)A.Yes,I have one cousin. B.Yes,I have two cousins.4.(10分)Peter 正在听录音,请你帮他判断下列句子正误,正确的写"T",错误的写"F"。
(1)Her name's Linda.(2)Sally has a red skit.(3)It's on the table.(4)There are two squares.(5)There is a supermarket near my home.二、Peter正在和他的朋友谈论日常生活中的事情,请将他们的谈话内容配对。
(10分)5.(10分)Peter正在和他的朋友谈论日常生活中的事情,请将他们的谈话内容配对。
(1)What would you like? A.Yes,I can.(2)Can you swim? B.It's under the chair.(3)Where is the cat? C.I'd like some orange juice.(4)What does your father do? D.See you,Peter.(5)Goodbye,Kitty. E.He's a bus driver.三、请你帮Peter选择出与下列图片相符的句子。
三年级上册语文第三单元综合测试卷(含答案)

三年级上册语文第三单元综合测试卷考试时间:90分钟满分:100分一、请写出句子中多音字的正确读音,井用它的另一个读音在横线上组词。
(6分)1.这个年轻人通过网络直播挣.( )到了一些钱。
2.一开始几.( )乎没有人看好《流浪地球》这部科幻电影。
3.避免高空抛物和高空坠物伤人的最佳方式是预防和惩处.( )相结合。
二、读句子,根据拼音写字词。
(8分)我梦见自己在巨人国lǚ xíng( ),一位巨人tōu tōu ( ) shēn chū ( )手,拿起粗大的shuǐ guǎn ( )向我喷水,吓得我yǎn lèi ( )直liú( ), pīn mìng ( )呼jiù( )。
三、选择题。
(10分)1.下列加点的多音字读音相同的一项是( )A.喷.泉喷.香喷.火B.答.应回答.答.谢C.处.罚处.分处.理D.挣.钱挣.扎挣.脱2.下面句子中加点词语使用有误的一项是( )A.课堂上,同学们争先恐后....地回答老师的问题。
B.她大吃一惊....,差点儿把饭盘失手落到地上去。
C.我把妈妈最爱的茶杯打碎了,心里七上八下....的。
D.这里的交通四面八方....,人们出行十分方便。
3.下面句子没有语病的一项是( )A.校园里飘扬着五颜六色的红旗。
B.辛勤的啄木鸟医生在给大树捉虫子。
C.联欢会上,我们听到了动听的歌声和优美的舞蹈。
D.我们的语文老师看起来大约三十岁左右。
4.在“猜猜童话人物”比赛中,同学们根据某个主人公的四个特点给出了以下答案,其中正确的一项是( )①她出生在一朵美丽的郁金香花朵里。
②她长得小巧又可爱。
③她是《安徒生童话》中的人物。
④她遇到很多困难,最后被燕子救走。
A.卖火柴的小女孩B.拇指姑娘C.灰姑娘D.小红帽5.把下面的句子插在语段中,应该插在 ( )它哇哇地哭起来了,“哎哟,我的头!”①冬天来了,河上结了厚厚的冰。
②小猴在冰上练习滑冰,不小心摔跤了,头上起了一个大包。
数学三年级下册期末综合试卷测试卷(含答案)

数学三年级下册期末综合试卷测试卷(含答案)一、填空题1.在( )里填上合适的单位。
一本数学书约重250( );一只乒乓球约重3( );小红的身高124( ),体重31( )。
2.某列火车应该在10:30准时到站,结果因大雾而晚点35分钟,这列火车会在( )到站。
3.在估算68×7时,应把68看作______,乘积大约是______。
4.在括号里填上合适的单位。
一辆卡车的载重量是5( )。
一头牛重500( )。
爸爸每天工作8( )。
骑自行车每小时行驶15( ) 5.验算减法时,既可以用被减数减去( ),看是不是等于( )来验算,也可以用差加减数,看是不是等于被减数来验算。
6.640比( )多370,比290多180的数是( )。
7.要使341×□的积是三位数,□里最大能填______,要使积是四位数,□里最小能填______。
8.商场上个月卖出25台电冰箱,卖出的洗衣机比电冰箱多10台,卖出的电视机台数是洗衣机的2倍。
卖出电视机( )台。
二、选择题9.把涂色部分用分数表示出来。
()() ()() ()() 10.40个二年级学生的体重大约是1( )。
A .千米B .千克C .克D .吨 11.秒针走一圈,分针走了( )小格。
A .1B .12C .60 12.115()5+< 6()5266-> 13.下面哪个问题可以用12×4×6解决?( )A .一个玩具熊12元,一包积木6元,买4个玩具熊和1包积木共多少元?B .男生有12人,女生有4人,每人得到6颗糖,共需多少颗糖?C .每小组有12人,每人捐4本书,6个小组共捐多少本书?14.3个15和2个15的和是( )。
A .15B .45C .115.三(3)班有15位同学参加了合唱组,有22位同学参加了书法组,其中有8位同学这两个兴趣小组都参加了,三(3)班至少有( )位同学参加了课外兴趣小组。
2022-2023学年新部编版六年级语文下册第三单元综合能力提升测试卷(附参考答案)

2022-2023学年新部编版六年级语文下册第三单元综合能力提升测试卷一、书写(共10分)1.(本题10分)看拼音,写词语。
cánɡ zài què hūkōnɡ xūbù jīn nuó yíbō nònɡyǐ xuécǎo cónɡhuà bào niàn dāo二、填空题(共15分)2.(本题15分)根据课文内容填空。
(1)洗手的时候,日子从____里过去;吃饭的时候,日子从____里过去;默默时,便从______前过去。
(2)在____的日子里,在千门万户的世界里的我能做什么呢?只有____罢了,只有匆匆罢了。
在八千多日的匆匆里,除____外,又剩些什么呢?过去的日子如____,被____了,如____,被____了。
我留着些什么痕迹呢?我何曾留着_____痕迹呢?这段话选自课文《____》,作者是____,表达了作者________。
文中首尾呼应的句子是:__________三、选择题(共10分)3.(本题2分)下列词语中加点字的读音完全正确的一组是()A.蒸.发(zhēn)蚁.穴(yǐ)绊.倒(bàn)绞.刑(jiǎo)B.空虚.(xū)叹.息(tàn)念叨.(dào)停顿.(dùn)C.亲吻.(wěng)休.止(xiū)时.光(shí)挽.回(mǎn)D.依偎.(wēi)惊惶.(huáng)裸.露(luǒ)徘徊.(huái)4.(本题2分)下列语句不能表现《别了,语文课》中“我”内心情感变化的句子是()A.我拿起一张报纸,单是大字标题就有不少字不认识,不要说报纸的内文了。
B.我张皇地拿出语文书,急急温习今天教过地课文,觉得课文内容饶有趣味。
C.我一连两次默书都得到八十分,张先生每次都鼓励我。
D.我又拿出纸,用笔反复写新学的生字。
【数学】人教版小学六年级数学上 3 第二、三单元达标测试卷(含答案)

人教版小学六年级数学上 3 第二、三单元达标测试卷(含答案)一、 填空。
(4题3分,其余每空1分,共20分) 1.最小的合数的倒数是( ),( )和235互为倒数。
2.学校在公园北偏东40°方向上,也可以说学校在公园( )方向上。
3.若甲城在乙城西偏南30°方向上,则乙城在甲城( )方向上。
4.在里填上“>”“<”或“=”。
910÷4910 712÷58712 89÷1011 1 78÷578×158÷348×34815÷18155.一个数的38是24,这个数的14是( )。
6.( )m 的49是16 m ;48 t 比( )t 多13;30 kg 比( )kg 少16。
7.甲数的15与乙数的16相等,甲数是90,乙数是( )。
8.小敏25小时行了34 km ,她每小时行( ) km ,她行1 km 需要( )小时。
9.甲、乙两车各运4 t 货物,甲车每次运14 t ,乙车每次运这批货物的14,甲车运了( )次,乙车运了( )次。
10.一项工作,甲队每天完成这项工作的18,乙队每天完成这项工作的110。
两队合作( )天完成这项工作的910。
11.玥玥收集了天宫二号图片24张,是欢欢收集的天宫二号图片张数的45,乐乐收集的天宫二号图片张数是欢欢的56,欢欢收集的天宫二号图片有( )张,乐乐收集的天宫二号图片有( )张。
12.修一段铁路,4天修了这条铁路的215,修完剩下的铁路还需要( )天。
二、 判断。
(对的画“√”,错的画“×”)(每题1分,共5分)1.甲在乙东偏南25°方向上,乙就在甲的南偏东25°方向上。
( ) 2.一个分数的倒数一定比这个数小。
( ) 3.一个整数除以一个分数,商一定大于这个整数。
( ) 4.甲数比乙数多15,则乙数比甲数少15。
统编版二年级语文上册期中综合测试卷(含答案)

二年级语文上册期中综合测试卷时间:60分钟分数:100分一、给下列加点字选择正确的读音,打“√”。
(3 分)水分(fēn fèn) 铜号(háo hào) 重新(chóng zhòng)酸甜(sān suān) 丰收(sōu shōu) 神仙(xān xiān)二、读拼音,写词语。
(16分)书会告诉我们:hǎi yáng( )里有水;sōng bǎi( )和shuǐshān ( )都是树木;xióng māo( )和xiǎo gǒu( )都是动物;měi lì( )的chéng shì( )里有很多gāo lóu( )三、反义词对对碰。
(连线)(4分)展现温和结尾仔细开头暴躁粗心消失四、查字典,填表格。
(12 分)要查的字音序音节部首除去部首有几画结构组词给客五、选择合适的词语填空。
(8 分)快活生活1.我们的( )比蜜还甜。
2.同学们在操场上( )地跑来跑去。
非常经常3.丁丁( )喜欢看课外书。
4.丛林里( )有老虎出没。
六、用加点词写句子。
(5分)1. 爸爸的鞋像小船。
(2 分)像2.爸爸一边刮胡子,一边逗露西玩。
(3分)一边,一边。
七、默写下面的古诗及作者,注意不要写错别字,记得加上标点!(10分)登鹳雀楼作者:▢▢▢▢八、课内选文阅读。
(9 分)《小蝌蚪找妈妈》(片段)小蝌蚪游哇游,过了几天,尾巴变短了。
他们游到荷花旁边,看见荷叶上蹲着一只大青蛙,披着碧绿的衣裳,露着雪白的肚皮,鼓着一对大眼睛。
小蝌蚪游过去,叫着:“妈妈,妈妈!”青蛙妈妈低头一看,笑着说:“好孩子,你们已经长成青蛙了,快跳上来吧!”他们后腿一蹬,向前一跳,蹦到了荷叶上。
1.给加点字注音。
(2 分)2.青蛙妈妈长什么样子?(4 分)3.将选文最后一句话中描写小蝌蚪动作的词语画出来。
(3 分)九、课外阅读。
(13 分)保护有益的小动物地球上许许多多的动物都是人类的朋友,它们为大自然做了很多好事,我们可不能伤害它们。
2024年人教版二年级数学上册第三单元综合测试卷(含答案)
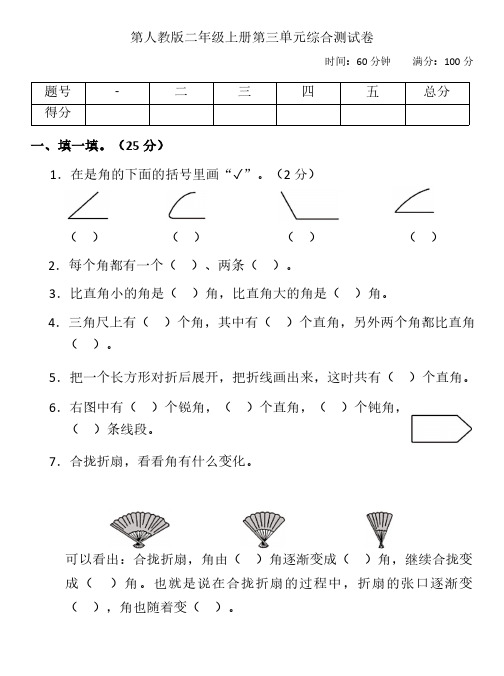
()()()())。
)个钝角,可以看出:合拢折扇,角由()角逐渐变成()角,继续合拢变)角。
也就是说在合拢折扇的过程中,折扇的张口逐渐变8.下面钟面上的时针和分针形成的夹角(较小的角)分别是什么角?并按角的大小排一排。
①②③()角()角()角()>()>()(填序号)二、判断。
(对的打“✓”,错的打“x”)(10分)1.用三角尺中的锐角拼成的角一定是钝角。
()2.判断一个角是锐角还是钝角,可以用三角尺上的直角比一比。
()3.角的两边越长,角越大()4.把一个三角形剪下一个角,还剩2个角。
()5.数学课本封面上的直角和直尺上的直角同样大。
()三、选择。
(将正确答案的序号填在括号里)(12分)1.下列物体中,表面有角的是()。
①②④2.下列各图中,所有的角都是直角的是()。
②③3.下图中,钉在一起的两根木条所形成的角()。
①逐渐减小②逐渐增大③大小不变4.下列说法中错误的是()。
①一个顶点、一条短边和一条长边能组成一个角②一个顶点和两条边能组成一个角③一条边和两个顶点能组成一个角5.下面灯笼杆和灯笼绳形成的三个角中,最大的是(),最小的是()。
①②③四、按要求做题。
(36分)1.数一数下面的图形中各有几个角。
(9分)( )个( )个()个2.填一填。
(9分)(1)七巧板中3号是()形,它里面有()个锐角,()个钝角。
(2)七巧板中5号是()形,它里面有()个直角。
(3)七巧板中三角形有()块,每块有()个锐角,()个钝角,()个直角。
3.按要求剪一剪。
(画线表示你的剪法,只能剪一刀哟)(12分)(1)剩下1个直角。
(2)剩下2个直角。
(3)剩下3个角。
(4)增加2个直角。
4.以下面的点A为顶点画一个任意角,以点B为顶点画一个直角。
(6分)·B·A五、解决问题。
(17分)1.一个有三个角,4个独立的三角形一共有多少个角?(5分)2.一个有多少个直角?2个有多少个直角?(6分)3.数一数下面的车是由哪几种图形组成的,共有几个直角?(6分)答案:。
小学数学三年级下册期末综合试题测试卷(含答案)

小学数学三年级下册期末综合试题测试卷(含答案)一、填空题1.在括号里填上合适的单位。
(1)一个大冬瓜约重6( );一个橙子约重700( )。
(2)一本故事书的封面的面积约是300( );一块黑板的面积约是5( )。
2.下午第一节上课的时间是13:30分,一节课的时间是40分,第一节下课的时间是( )。
3.学校组织三年级150名师生开展游学活动,租了5辆汽车,每辆汽车有36个座位。
每人一个座位,够吗?( )(填够或不够),我是这样估算的:( )。
4.填上合适的单位。
(1)小学生大约每天睡9_____。
(2)犍为距离乐山大约60_____。
(3)一袋大米的质量25_____。
(4)做眼保健操大约需要5_____。
5.45元比( )元多19元。
比198米长42米是( )米。
6.估算638+262时,可以先把638看成( ),把262看成( ),得数大约等于( )。
7.把2、3、5、7四个数分别填入□。
要使积最大□□□×□,要使积最小□□□×□。
8.电影院有9排座位,每排可坐36人,如果坐满,可以坐( )人。
二、选择题9.三年级(1)班参加语文课外小组的有8人,参加数学课外小组的有9人,两个小组都参加的有3人,参加语文、数学课外小组的共有( )人。
10.一批重1吨的货物,运走了600千克,还剩( )千克。
A .300B .400C .500D .1600 11.学校运动会举行短跑比赛,小明用了14秒,小东用了16秒,小斌用了15秒,获得第1名的是( )。
A .小明B .小东C .小斌12.三(2)班所有同学都参加了歌唱或舞蹈兴趣小组,其中参加歌唱兴趣小组的有19人,参加舞蹈兴趣小组的有22人,两个小组都参加的有9人,三(2)班一共有( )人。
13.下面算式中,( )的积大于2000。
A .2996⨯B .3784⨯C .4327⨯14.3个15和2个15的和是( )。
A .15 B .45 C .115.三年级(3)班有31人参加跳绳和足球兴趣小组,其中参加跳绳的有22人,参加足球的有14人,两个组都参加的有( )人。
2020年秋人教版高中物理选修3-2综合测试含答案

绝密★启用前2020年秋人教版高中物理选修3-2综合测试本试卷共100分,考试时间120分钟。
一、单选题(共10小题,每小题4.0分,共40分)1.关于感应电流,下列说法中正确的是()A.只要穿过线圈的磁通量发生变化,线圈中就一定有感应电流B.只要闭合导线做切割磁感线运动,导线中就一定有感应电流C.若闭合电路的一部分导体不做切割磁感线运动,闭合电路中一定没有感应电流D.当穿过闭合电路的磁通量发生变化时,闭合电路中一定有感应电流2.交流发电机在工作时电动势为e=E max sinωt,若将发动机的转速提高一倍,同时将线框所围面积减少一半,其他条件不变,则其电动势变为()A.e′=E max sinB.e′=2E max sinC.e′=E max sin 2ωtD.e′=sin 2ωt3.下列关于磁通量的说法,正确的是()A.只有在匀强磁场中,穿过某一个面的磁通量才等于磁感应强度与该面面积的乘积B.磁通量是矢量,其正负表示方向C.磁通量是形象描述穿过某一个面的磁感线条数的物理量D.磁通量越大,磁通量的变化就越快4.法拉第通过精心设计的一系列实验,发现了电磁感应定律,将历史上认为各自独立的学科“电学”与“磁学”联系起来.在下面几个典型的实验设计思想中,所作的推论后来被实验否定的是() A.既然磁铁可使近旁的铁块带磁,静电荷可使近旁的导体表面感应出电荷,那么静止导线上的稳恒电流也可在近旁静止的线圈中感应出电流B.既然磁铁可在近旁运动的导体中感应出电动势,那么稳恒电流也可在近旁运动的线圈中感应出电流C.既然运动的磁铁可在近旁静止的线圈中感应出电流,那么静止的磁铁也可在近旁运动的导体中感应出电动势D.既然运动的磁铁可在近旁的导体中感应出电动势,那么运动导线上的稳恒电流也可在近旁的线圈中感应出电流5.如图所示,一线圈放在通电螺线管的正中间A处,现向右移动到B处,则在移动过程中通过线圈的磁通量如何变化()A.变大B.变小C.不变D.无法确定6.如图所示,理想变压器的输入端通过灯泡L1与输出电压恒定的正弦交流电源相连,副线圈通过导线与两个相同的灯泡L2和L3相连,开始时开关S处于断开状态.当S闭合后,所有灯泡都能发光,下列说法中正确的有()A.副线圈两端电压不变B.灯泡L1亮度变亮,L2的亮度不变C.副线圈中电流变大,灯泡L1变亮,L2变暗D.因为不知变压器原、副线圈的匝数比,所以L1及L2的亮度变化不能判断7.闭合线圈在匀强磁场中绕垂直于磁场方向的轴做匀速转动,产生的交流电瞬时值的表达式为i=0.2sin 100πt A,从t=0到第一次出现通过线圈的磁通量变化率最大值的时间为()A.sB.sC.sD.s8.如图甲,R0为定值电阻,两金属圆环固定在同一绝缘平面内.左端连接在一周期为T0的正弦交流电源上,经二极管整流后,通过R0的电流i始终向左,其大小按图乙所示规律变化.规定内圆环a端电势高于b端时,ab间的电压uab为正,下列uab-t图象可能正确的是()A. B.C. D.9.如图所示,甲、乙是规格相同的灯泡,接线柱a,b接电压为U的直流电源时,无论电源的正极与哪一个接线柱相连,甲灯均能正常发光,乙灯完全不亮.当a,b接电压的有效值为U的交流电源时,甲灯发出微弱的光,乙灯能正常发光,则下列判断正确的是()A.与甲灯串联的元件x是电容器,与乙灯串联的元件y是电感线圈B.与甲灯串联的元件x是电感线圈,与乙灯串联的元件y是电容器C.与甲灯串联的元件x是二极管,与乙灯串联的元件y是电容器D.与甲灯串联的元件x是电感线圈,与乙灯串联的元件y是二极管10.如图所示,在匀强磁场中,MN、PQ是两条平行的金属导轨,而ab、cd为串接有电流表和电压表的两根金属棒,当两棒以相同速度向右运动时,正确的是()A.电压表有读数,电流表有读数B.电压表无读数,电流表无读数C.电压表有读数,电流表无读数D.电压表无读数,电流表有读数二、多选题(共4小题,每小题5.0分,共20分)11.(多选)如图所示,矩形线圈abcd放在匀强磁场中,ad=bc=l1,ab=cd=l2.从图示位置起该线圈以角速度ω绕不同转轴做匀速转动,则()A.以OO′为转轴时,感应电动势e=Bl1l2ωsinωtB.以O1O1′为转轴时,感应电动势e=Bl1l2ωsinωtC.以OO′为转轴时,感应电动势e=Bl1l2ωcosωtD.以OO′为转轴跟以ab为转轴一样,感应电动势e=Bl1l2ωsin(ωt+)12.(多选)为了监测变电站向外输电情况,要在变电站安装互感器,其接线如图所示,两变压器匝数分别为n1、n2和n3、n4,a和b是交流电表,则()A.n1>n2B.n3>n4C. a为交流电流表,b为交流电压表D. a为交流电压表,b为交流电流表13.(多选)如图所示电路中,L为电感线圈,电阻不计,A、B为两灯泡,则()A.合上S时,A先亮、B后亮B.合上S时,A、B同时亮C.合上S稳定后,A变亮、B熄灭D.断开S时,A熄灭、B重新亮后再熄灭14.(多选)在电磁感应现象中,下列说法中错误的是()A.感应电流的磁场总是阻碍原来磁场的变化B.闭合线框放在变化的磁场中一定能产生感应电流C.闭合线框放在变化的磁场中做切割磁感线运动,一定能产生感应电流D.感应电流的磁场总是跟原来磁场的方向相反三、实验题(共1小题,每小题10.0分,共10分)15.如图甲所示,斯密特触发器可以将连续变化的模拟信号转换为突变的数字信号,当加在它的输入端A的电势逐渐上升到1.6 V,输出端Y会突然从高电平跳到低电平0.25 V,而当输入端A的电势下降到0.8 V时,输出端Y会从低电平跳到高电平3.4 V.如图乙所示是一个温度报警器的简易电路图,R T为热敏电阻,R1为可变电阻(最大阻值为1 kΩ),蜂鸣器工作电压3 ~5 V,热敏电阻的阻值随温度变化如图丙所示,若要求热敏电阻在感测到80 ℃时报警,则R1应调至________ kΩ;若要求热敏电阻在感测到更高的温度时才报警,R1的阻值应________(选填“增大”、“减小”或“不变”).甲乙丙四、计算题(共3小题,每小题10.0分,共30分)16.如图甲所示,两根足够长的平行金属导轨MN、PQ相距为L,导轨平面与水平面夹角为α,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好,金属棒的质量为m,导轨处于匀强磁场中,磁场的方向垂直于导轨平面斜向上,磁感应强度大小为B.金属导轨的上端与开关S,阻值为R1的定值电阻和电阻箱R2相连,不计一切摩擦,不计导轨、金属棒的电阻,重力加速度为g.现在闭合开关S,将金属棒由静止释放.(1)判断金属棒ab中电流的方向;(2)若电阻箱R2接入电路的阻值为0,当金属棒下降高度为h时,速度为v,求此过程中定值电阻上产生的焦耳热Q;(3)当B=0.40 T、L=0.50 m、α=37°时,金属棒能达到的最大速度v m随电阻箱R2阻值的变化关系如图乙所示,取g=10 m/s2,sin 37°=0.60,cos 37°=0.80.求R1的大小和金属棒的质量m.17.如图所示,水平金属导轨AB′、CD通过开关S和电源相连,两导轨间距离为L,匀强磁场垂直金属导轨向里,光滑导体杆ab同导轨接触良好,设电源的电压为E,磁感应强度为B,当开关闭合后,ab杆所能达到的最大速度为多大,此时的反电动势为多大?18.如图所示(俯视),MN和PQ是两根固定在同一水平面上的足够长且电阻不计的平行金属导轨.两导轨间距为L=0.2 m,其间有一个方向垂直水平面竖直向下的匀强磁场B1=5.0 T.导轨上NQ之间接一电阻R1=0.40 Ω,阻值为R2=0.10 Ω的金属杆垂直导轨放置并与导轨始终保持良好接触.两导轨右端通过金属导线分别与电容器C的两极相连.电容器C紧靠着带小孔a(只能容一个粒子通过)的固定绝缘弹性圆筒.圆筒内壁光滑,筒内有垂直水平面竖直向下的匀强磁场B2,O是圆筒的圆心,圆筒的内半径为r=0.40 m.(1)用一个大小恒为10 N,平行于MN水平向左的外力F拉金属杆,使杆从静止开始向左运动,问:当金属杆最终匀速运动时杆的速度大小;(2)当金属杆处于(1)问中的匀速运动状态时,电容器C内紧靠极板且正对a孔的D处有一个带正电的粒子从静止开始经电容器C加速后从a孔垂直磁场B2并正对着圆心O进入筒中,该带电粒子与圆筒壁碰撞四次后恰好又从小孔a射出圆筒.已知粒子的比荷=5×107C/kg,该带电粒子每次与筒壁发生碰撞时电量和能量都不损失,不计粒子重力和空气阻力,则磁感应强度B2多大(结果允许含有三角函数式).答案解析1.【答案】D【解析】如果线圈不闭合,不能形成回路,所以不能产生感应电流,A错误;闭合线圈只有一部分导线做切割磁感线运动时,才会产生感应电流,B、C错误;当穿过闭合电路的磁通量发生变化时,闭合电路中一定有感应电流,D正确.2.【答案】C【解析】电动势的瞬时表达式为e=E max sinωt,而E max=NBSω,当ω加倍而S减半时,E max不变,故C正确.3.【答案】C【解析】在匀强磁场中,如果磁场与平面垂直,则穿过某一个面的磁通量等于磁感应强度与该面面积的乘积,A错;磁通量是标量,B错;磁通量大小与磁通量变化快慢无关,D错.4.【答案】A【解析】电磁感应现象的产生条件是:穿过闭合电路的磁通量发生变化.静止导线上的稳恒电流产生恒定的磁场,静止导线周围的磁通量没有发生变化,近旁静止线圈中不会有感应电流产生,A 错.而B、C、D三项中都会产生电磁感应现象,有感应电动势(或感应电流)产生.5.【答案】B【解析】磁通量有正负之分,所以线圈所在位置有两部分磁通量,内部磁感线和外部磁感线方向不同,向右移动过程中内部磁感线条数不变,外部磁感线条数增多,合磁通量减小,故选B.6.【答案】C【解析】当S接通后,输出功率变大,输出电流变大,变压器的输入功率等于输出功率,所以变压器的输入功率变大,输入电流变大,灯泡L1的电压增大,原线圈电压减小,匝数不变,副线圈电压减小,故A错误;由A可知,灯泡L1变亮,L2变暗,故B、D错误,C正确.7.【答案】C【解析】由瞬时值表达式可知角速度ω=100π,根据周期公式T==s,从t=0到第一次出现通过线圈的磁通量变化率最大值的时间为=s.8.【答案】C【解析】在第一个0.25T0时间内,通过大圆环的电流为顺时针逐渐增加,由楞次定律可判断内环内a端电势高于b端,因电流的变化率逐渐减小故内环的电动势逐渐减小;同理在第0.25T0-0.5T0时间内,通过大圆环的电流为顺时针逐渐减小,由楞次定律可判断内环内a端电势低于b端,因电流的变化率逐渐变大故内环的电动势逐渐变大,故选项C正确.9.【答案】B【解析】由a,b接直流时的现象可知,元件x“通直流”,元件y“隔直流”,由A,B接交流电源时的现象可知,元件x“阻交流”,元件y“通交流”,根据电容器和电感线圈的特点,元件x是电感线圈,元件y是电容器,选项B正确.10.【答案】B【解析】两棒以相同的速度向右运动,回路abdc的磁通量保持不变,所以回路中没有感应电流,故两表均无读数.选项B正确.11.【答案】CD【解析】以O1O1′为轴转动时,磁通量不变,不产生交变电流.无论以OO′为轴还是以ab为轴转动,感应电动势的最大值都是Bl1l2ω.由于是从与磁场平行的面开始计时,产生的是余弦式交变电流,故C、D正确.12.【答案】AD【解析】由电路连接方式可知,左图是电压互感器,把高电压经过变压器降压后测量,所以n1>n2,a为交流电压表,右图为电流互感器,把大电流经过变压器减为小电流再测量,所以n3<n4,b为交流电流表.13.【答案】BCD【解析】合上S时,电路中立即就有了电流,故灯泡A、B同时变亮,但通过线圈的电流增加,线圈会产生自感电动势,故线圈的电流缓慢增加;当电流稳定后,线圈相当于直导线,灯泡B被短路,故开关闭合后,A、B同时亮,但B逐渐熄灭,而A更亮,故A错误,B、C正确;断开S时,A灯立即熄灭,线圈产生自感电动势和灯泡B构成闭合电路,B灯先闪亮后逐渐变暗,故D正确.14.【答案】BCD【解析】由楞次定律可知,感应电流的磁场阻碍的是原磁通量的变化,并不一定与原磁场方向相反,故选项A正确、选项D错误;若闭合线框平行于磁场放置,则无论是磁场变化,还是线框做切割磁感线的运动,穿过闭合线框的磁通量都不变,都不会有感应电流产生.所以选项B、C均错误.故选B、C、D.15.【答案】0.42减小【解析】热敏电阻在80 ℃时的电阻是R T=80 Ω,斯密特触发器输入端A的电势是0.8 V时,输出端Y的电压为3.4 V,这时蜂鸣器开始工作.由串联电路分压特点知:==所以R1=80×Ω=420 Ω=0.42 kΩ由热敏电阻的阻值随温度变化的图象可知,温度升高时,热敏电阻的阻值减小,而斯密特触发器输入端的电压仍保持不变,则电阻R1的阻值应减小.16.【答案】(1)b到a(2)mgh-mv2(3)2.0 Ω0.1 kg【解析】(1)由右手定则可知,金属棒ab中的电流方向为b到a.(2)由能量守恒定律可知,金属棒减小的重力势能等于增加的动能和电路中产生的焦耳热mgh=mv2+Q解得:Q=mgh-mv2(3)设最大速度为v m时,切割磁感线产生的感应电动势E=BLv m由闭合电路欧姆定律得:I=从b端向a端看,金属棒受力如图所示:金属棒达到最大速度时满足mg sinα-BIL=0由以上三式得最大速度:v m=R2+R1图象斜率k=m/(s·Ω)=15 m/(s·Ω),纵截距b=30 m/s则:R1=b=k解得:R1=2.0 Ωm=0.1 kg.17.【答案】最大速度为反电动势为E【解析】ab做加速度减小的加速运动,当速度最大安培力为0,电流为0,则:BLv=E 得:v=,反电动势为E.18.【答案】(1)v=5 m/s(2)①每段轨迹圆弧对应的圆心角为θ=π-=得:B2=tan×10-3T②每段轨迹圆弧对应的圆心角为θ′=π-=,将数据代式得B2′=tan×10-3T.【解析】(1)金属杆先做加速度变小的加速运动,最终以最大速度匀速运动.设杆匀速运动时速度为v,F=B1IL,E=B1LvI=将已知数据代入得:v=5 m/s(2)设杆匀速运动时C两极板间的电压为U,带电粒子进入圆筒的速率为v1.在磁场中作匀速圆周运动的半径为R,由于C与电阻R1并联,据欧姆定律得U=IR1=4.0 V据动能定理有qU=mv带电粒子在磁场中作匀速圆周运动qv1B2=m由于带电粒子与圆筒壁碰撞时无电量和能量损失,那么每次碰撞前后粒子速度大小不变.速度方向总是沿着圆筒半径方向,4个碰撞点与小孔a恰好将圆筒壁五等分,粒子在圆筒内的轨迹具有对称性,由5段相同的圆弧组成,设每段轨迹圆弧对应的圆心角为θ,则由几何关系可得:=tan().有两种情形符合题意(如图所示):①每段轨迹圆弧对应的圆心角为θ=π-=得:B2=tan×10-3T②每段轨迹圆弧对应的圆心角为θ′=π-=.将数据代式得B2′=tan×10-3T.。
语文七上阶段综合测试卷二1-3单元(期中)及答案

阶段综合测试卷二(期中)[第一~三单元]时间:120分钟满分:100分一、积累·运用(28分)1.下列加点字的注音全都正确的一项是(3分)( )A.应和.(hè) 暖和.(hé) 和.泥(huó) 和.弄(huò)B.黄晕.(yūn)头晕.(yūn)晕.车(yūn)酝.酿(yùn)C.蝉蜕.(tuì)盔.甲(kuī)霎.时(shà)俄.而(é)(tìtǎng)确凿.(zuò)搓捻.(niàn)D.睫.毛(jié)倜傥..2.下列句子中加点的成语使用错误的一项是(3分)( )。
A.节日的蓉城张灯结彩,大街上车辆川流不息....,呈现出一片绚丽的景象。
B.五月的西湖,姹紫嫣红....,赢得了听众的阵阵掌声。
C.她演讲时,引经据典....了。
D.虽然这道题比较难,但是在老师的反复讲解下,同学们终于大彻大悟....3.下列句子中没有语病的一项是(3分)( )A.尽管他们怎么造谣、诽谤,铁的事实是改变不了的。
B.我们可以通过有感情地朗读或背诵来深入理解诗人的情感。
C.遭到破坏的生态系统,至少需要三十年的时间才能基本完全恢复。
D.散文是一种最适合抒发作者的主观情感的文学。
4.下列句子组成语段,顺序排列正确的一项是(3分)()①那些经典作品,经过时间的淘汰与筛选,其中有着最伟大的思想、最丰富的内容、最高尚的品格,是人类迄今为止所能达到的巅峰。
②一个人能够获得多大的能量,取得多高的成就,很大程度上取决于这种循环往复的阅读。
③阅读是一种循环往复的过程。
④对于举世公认的中西社科、文学名著,我们自然要尽情揣摩,反复精读,把握其内涵与要旨。
⑤这种循环往复,就是人们常说的精读。
A.④②①③⑤B.③⑤①④②C.②③⑤①④D.③⑤①②④5.名句默写。
(8分)(1)峨眉山月半轮秋, 。
(李白《峨眉山月歌》)(2)遥怜故园菊, 。
三年级上册英语新路径期末综合测试卷2套【含答案】

三年级英语上册期末综合模拟测试卷(一)听力部分(30分)一、听录音,选出你所听到的内容。
(5分)( ) 1. A. lion B. little C. listen( ) 2. A. pink B. please C. purple( ) 3. A. short B. sad C. small( ) 4. A. go to bed B. sit down C. get up( ) 5. A. over there B. look for C. sing a song二、听录音,判断图片与所听内容是(T)否(F)相符。
(10分)1. 2. 3.( ) ( ) ( )4. 5.( ) ( )三、听录音,给下列句子排序。
(5分)Let’s play a game.Nice to meet you.Call me Lele.I’m here.So long.四、听录音,选出你所听到的句子。
(10分)( ) 1. A. What is your name? B. What colour is it? ( ) 2. A. It’s white. B. It’s yellow.( ) 3. A. Who are you? B. Where are you?( ) 4. A. Let’s make a Christmas card. B. Let’s draw a picture. ( ) 5. A. Point to his ear. B. Point to his eye.笔试部分(70分)一、判断下列图片与单词是(T)否(F)对应。
(5分)( ) 1. ( ) 2. ( ) 3.five pear grandpa( ) 4.( ) 5.二、选出与所给单词属于同一类的一项。
(5分)( ) 1. run A. write B. cow C. sister( ) 2. we A. his B. they C. me( ) 3. blue A. foot B. red C. who( ) 4. three A. hand B. he C. ten( ) 5. where A. what B. colour C. let三、英汉词组互译。
人教版二年级数学上册期末 总复习综合测试卷(三)(含答案)
人教版二年级数学上册期末总复习综合测试卷(三)一、单选题1.下图中一共有()根香蕉。
A. 5+4B. 5×4C. 4+4+4+42.下面的图形中有()个角。
A. 5B. 4C. 33.下图中的钢笔长()厘米。
A. 6B. 7C. 84.与8×9-9 的计算结果相同的是()A. 9×9B. 9×7C. 8×85.他们可能在()去图书馆。
A. B. C.二、判断题6.计算5×6和6×5时,都用“五六三十”这句口诀。
()7.直角比钝角大,比锐角小。
()8.8+8+8+6可以用8×4-2来计算。
()9.左图中一共有4条线段。
()三、填空题10.两个乘数都是5,积是________?11.在横线上里填上适当的单位名称。
⑴小林的身高是132________⑵王叔叔的身高是1________70________12.8×5=________,读作________,用口诀________计算。
13.在括号里填上厘米或米。
桌子高约80________床长2________牙刷长约l5________14.________加法算式:________乘法算式:________15.在横线上填上“<”、“>”、“=”。
8×5________8+5 82-35________575×7+5________40 3米+4厘米________7米16.下图中共有________条线段,________个锐角,________个钝角。
17.1小时+30分=________分50厘米+50厘米=________米18.在横线上最大能填几?________×3<22 8×________<65 40>9×________19.用2、5、8三张卡片,可以摆出________个不同的两位数;三个小朋友坐成一排合影,有________种坐法。
2014-2015学年北师大版数学【选修2-3】:第3章《统计案例》综合测试(含答案)

第三章综合测试时间120分钟,满分150分。
一、选择题(本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2014·哈师大附中高二期中)下列说法正确的有几个( ) (1)回归直线过样本点的中心(x -,y -);(2)线性回归方程对应的直线y ^=b ^x +a ^至少经过其样本数据点(x 1,y 1),(x 2,y 2),…,(x n ,y n )中的一个点;(3)在残差图中,残差点分布的带状区域的宽度越宽,其模型拟合的精度越高; (4)在回归分析中,R 2为0.98的模型比R 2为0.80的模型拟合的效果好. A .1 B .2 C .3 D .4[答案] B[解析] 由回归分析的概念知①④正确,②③错误. 2.变量y 对x 的回归方程的意义是( ) A .表示y 与x 之间的函数关系 B .表示y 与x 之间的线性关系 C .反映y 与x 之间的真实关系D .反映y 与x 之间的真实关系达到最大限度的吻合 [答案] D[解析] 用回归方程预测变量y 对x 的不确定关系,反映的不是真实关系,而是真实关系达到最大限度的吻合.3.在列联表中,两个比值( )相差越大,两个分类变量之间的关系越强.( ) A.a a +b 与c c +d B.a c +d 与c a +b C.a a +b 与c b +c D.a b +d 与c a +c[答案] A [解析] a a +b 与c c +d相差越大,说明ad 与bc 相差越大,两个分类变量之间的关系越强.故选A.4.若回归直线方程中的回归系数b =0时,则相关系数r 的值为( )A .1B .-1C .0D .无法确定[答案] C[解析] 若b =0,则∑i =1nx i y i -n x y =0,∴r =0.5.某班主任对全班50名学生进行了作业量多少的调查,数据如下表:A .99%B .95%C .90%D .无充分依据[答案] B[解析] 由表中数据得χ2=50×(18×15-8×9)226×24×27×23≈5.059>3.841,所以约有95%的把握认为两变量之间有关系.6.(2014·淄博市、临淄区学分认定考试)观测两个相关变量,得到如下数据:A.y ^=0.5x -1 B.y ^=x C.y ^=2x +0.3 D.y ^=x +1[答案] B[解析] 因为x -=0,y -=-0.9-2-3.1-3.9-5.1+5+4.1+2.9+2.1+0.910=0,根据回归直线方程必经过样本中心点(x -,y -)可知,回归直线方程过点(0,0),所以选B.7.(2014·枣阳一中、襄州一中、宣城一中、曾都一中高三期中联考)由变量x 与y 相对应的一组数据(1,y 1),(5,y 2),(7,y 3),(13,y 4),(19,y 5)得到的线性回归方程为y ^=2x +45,则y -=( )A .135B .90C .67D .63[答案] D[解析] ∵x -=15(1+5+7+13+19)=9,y -=2x -+45,∴y -=2×9+45=63,故选D.8.为了表示n 个点与相应直线在整体上的接近程度,我们表示它常用( ) A.∑i =1n(y i -y ′i )B.∑i =1n(y ′i -y i )C.∑i =1n(y i -y ′i )2D.∑i =1n(y 2i -y ′2i ) [答案] C[解析] 离差的平方和最小的时候,点均匀分布在直线两侧.9.下表是甲、乙两个班级进行数学考试,按学生考试及格与不及格统计成绩后的2×2列联表:则χ2的值为( ) A .0.559 B .0.456 C .0.443 D .0.4[答案] A[解析] χ2=90(12×36-9×33)245×45×21×69≈0.559.10.给出下列四个命题,其中真命题是( ) A .∀x ∈R ,cos x =sin(x +π3)+sin(x +π6)一定不成立B .今年初某医疗研究所为了检验“达菲(药物)”对甲型H1N1流感病毒是否有抑制作用,把墨西哥的患者数据库中的500名使用达菲的人与另外500名未用达菲的人一段时间内患甲型H1N1流感的疗效记录作比较,提出假设H 0:“达菲不能起到抑制甲型H1N1流感病毒的作用”,利用2×2列联表计算得χ2≈3.918,经查对临界值表知P (χ2≥3.841)≈0.05,说明达菲抑制甲型H1N1流感病毒的有效率为95%C .|a·b|=|a||b|是|λa +μb |=|λ||a |+|μ||b |成立的充要条件D .如图的茎叶图是某班学生一次测验时的成绩;可断定:男生成绩比较集中,整体水平稍高的女生[答案] C二、填空题(本大题共5小题,每小题5分,共25分)11.有下列关系:(1)人的年龄与他(她)拥有的财富之间的关系;(2)曲线上的点与该点的坐标之间的关系;(3)苹果的产量与气候之间的关系;(4)森林中的同一种树木,其断面直径与高度之间的关系;(5)学生与他(她)的学号之间的关系,其中有相关关系的是______.[答案] (3)(4)12.如果χ2的值为8.654,可以认为“A 与B 无关”的可信度是____________. [答案] 1%[解析] ∵8.654>6.635,∴我们认为A 与B 有关的把握为99%,故“A 与B 无关”的可信度为1%. 13.根据下表计算χ2=________.[答案] 1.779[解析] χ2=392×(39×167-157×29)2196×196×68×324≈1.779.14.已知在某种实践运动中获得一组数据:其中不慎将数据y 2y =0.5x +a ,则y 2与a 的近似值为________.[答案] 8,-0.7[解析] 由题意,得x =19.5,y =28.2+y 24.代入∑i =14(x i -x )(y i -y )∑i =14(x i -x )2=0.5中,得y 2≈8.所以y =9.05,a =y -b x ≈9.05-0.5×19.5=-0.7.15.某种产品的业务费支出x (单位:万元)与销售额y (单位:万元)之间有如下对应数据:则变量y 与x [答案] 0.92 [解析] 列表如下:由表中数据计算得x =5,y =50,则相关系数r =1380-5×5×50145-5×52×13500-5×502≈0.92.三、解答题(本大题共6小题,共75分,前4题每题12分,20题13分,21题14分) 16.男性更容易患色盲吗?某机构随机调查了1000人,调查结果如下表(单位:人):[解析] 问题是判断患色盲是否与性别有关,由题目所给数据得到如下列联表(单位:人):由公式计算得χ2=1000×(442×6-514×38)956×44×480×520≈27.139.由于27.139>6.635,所以有99%以上的把握认为患色盲与性别有关.17.下表是随机抽取的8对母女的身高数据,试根据这些数据求出女儿身高y 对母亲身高x 的线性回归方程,并预测母亲身高为165cm 时女儿的身高.由图可知两个变量呈现出近似的线性关系,可以建立女儿身高y 对母亲身高x 的线性回归方程.将数据列成下表.由此可得x =b x ≈-53.191,故y 对x 的线性回归方程为y =-53.191+1.345x .当母亲身高为165cm 时,女儿身高的估计值为 -53.191+1.345×165=168.734≈169(cm).18.(2013·云南玉溪一中高三月考)为考查某种药物预防疾病的效果,进行动物试验,得到如下丢失数据的列联表:2只,未患病数为η,工作人员曾计算过P (ξ=0)=389P (η=0).(1)求出列联表中数据x ,y ,M ,N 的值;(2)求ξ与η的均值(期望)并比较大小,请解释所得结论的实际含义; (3)能够以99%的把握认为药物有效吗? 参考公式:K 2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ).①当K 2≥3.841时有95%的把握认为ξ、η有关联; ②当K 2≥6.635时有99%的把握认为ξ、η有关联. [分析] (1)从已知P (ξ=0)=389P (η=0)出发,结合2×2列联表可求. (2)求出ξ、η的分布列,再利用期望定义式求E (ξ)和E (η)即可. (3)利用公式算出K 2,结合参考数据可以判断. [解析] (1)∵P (ξ=0)=C 220C 250,P (η=0)=C 2xC 250,∴C 220C 250=389×C 2xC 250,∴x =10. ∴y =40,∴M =30,N =70. (2)ξ取值为0,1,2.P (ξ=0)=C 220C 250=38245,P (ξ=1)=C 120C 130C 250=120245,P (ξ=2)=C 230C 250=87245.∴E (ξ)=294245.P (η=0)=C 210C 250=9245.P (η=1)=C 110C 140C 250=80245.P (η=2)=C 240C 250=156245.∴E (η)=392245.∴E (ξ)<E (η),即说明药物有效. (3)∵K 2=100×(800-300)230×70×50×50≈4.76.∵4.76<6.635,∴不能够有99%的把握认为药物有效.19.某商场经营一批进价为30元/台的小商品,在市场试验中发现,此商品的销售单价x (x 取整数)元与日销售量y 台之间有如下关系:(1)画出散点图,并判断(2)求日销售量y 对销售单价x 的线性回归方程;(3)设经营此商品的日销售利润为P 元,根据(2)写出P 关于x 的函数关系式,并预测当销售单位价x 为多少元时,才能获得最大日销售利润.[分析] 两个变量呈现近似的线性关系,可通过公式计算出其线性回归方程,并根据方程求出其预测值.[解析] (1)散点图如图所示,从图中可以看出这些点大致分布在一条直线附近,因此两个变量线性相关.(2)∵x =14×(35+40+45+50)=42.5,y =14×(56+41+28+11)=34,∑i =14x i y i =35×56+40×41+45×28+50×11=5 410,∑i =14x 2i =352+402+452+502=7 350,∴b =∑i =14x i y i -4x ·y ∑i =14x 2i -4x2=5 410-4×42.5×347 350-4×42.52=-370125=-2.96.∴a =y -b x =34-(-2.96)×42.5=159.8.∴y =-2.96x +159.8.(3)依题意有P =(-2.96x +159.8)(x -30) =-2.96x 2+248.6x -4 794,∴当x =248.62×2.96≈42时,P 有最大值,约为426,即预测销售单价为42元时,能获得最大日销售利润.[点评] 该类题属于线性回归线问题,解答本类题目的关键是首先通过散点图(或相关性检验求相关系数r )来分析两变量间的关系是否相关,然后再利用求回归方程的公式求解回归方程,在此基础上,借助回归方程对实际问题进行分析.20.为考察高中生是否喜欢数学课程与性别之间的关系,在某城市的某校高中生中随机抽取300名学生,得到如下列联表:性别与喜欢数学课程列联表么?[解析] 可以有95%的把握认为“性别与喜欢数学课之间有关系”.作出这种判断的依据是独立性检验的基本思想,具体过程如下:分别用a ,b ,c ,d 表示样本中喜欢数学课的男生人数,不喜欢数学课的男生人数,喜欢数学课的女生人数,不喜欢数学课的女生人数.如果性别与是否喜欢数学课有关系,则男生中喜欢数学课的比例a a +b 与女生中喜欢数学课的人数比例c c +d应该相差很多,即|a a +b -cc +d |=|ad -bc (a +b )(c +d )|应很大.将上式等号右边的式子乘以常数(a +b +c +d )(a +b )(c +d )(a +c )(b +d ),然后平方得χ2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d ),其中n =a +b +c +d .因此χ2越大,“性别与喜欢数学课之间有关系”成立的可能性越大.另一方面,假设“性别与喜欢数学课之间没有关系”为事件A ,由于事件A ={χ2>3.841}的概率为P (χ2>3.841)≈0.05,因此事件A 是一个小概率事件.而由样本数据计算得χ2=4.514,这表明小概率事件A 发生.根据假设检验的基本原理,我们应该断定“性别与喜欢数学课之间有关系”成立,并且这种判断出错的可能性约为5%.所以,约有95%的把握认为“性别与喜欢数学课之间有关系”.21.(2014·安徽程集中学期中)电视传媒公司为了解某地区观众对某体育节目的收视情况,随机抽取了100名观众进行调查,其中女性有55名,下面是根据调查结果绘制的观众日均收看该体育节目时间的频率分布直方图:将日均收看该体育节目时间不低于40分钟的观众称为“体育迷”,已知“体育迷”中有10名女性.(1)根据已知条件完成下面的2×2列联表,并据此资料你是否认为“体育迷”与性别有关?(2)迷”中有2名女性,若从“超级体育迷”中任意选取2人,求至少有1名女性观众的概率.附:K2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)[解析](1)体育迷”为25人,从而完成2×2列联表如下:将2×2K2=n(ad-bc)2(a+b)(c+d)(a+c)(b+d)=100×(30×10-45×15)275×25×45×55=10033≈3.030.因为3.030>2.706,所以我们有90名的把握认为“体育迷”与性别有关.(2)由频率分布直方图可知,“超级体育迷”为5人,从而一切可能结果所组成的集合为Ω={(a1,a2),(a1,a3),(a2,a3),(a1,b1),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2)}其中a i表示男性,i=1,2,3,b j表示女性,j=1,2.Ω由10个基本事件组成,而且这些基本事件的出现是等可能的.用A表示“任选2人中,至少有1人是女性”这一事件,则A={(a1,b1),(a1,b2),(a2,b1),(a2,b2),(a3,b1),(a3,b2),(b1,b2)},事件A由7个基本事件组成,因而P(A)=7 10.。
北师大版初中生物七年级上册第2章综合测试试卷-含答案03
第2章综合测试一、单项选择题(共20小题;共60分)1.在我国,种植业同林业、畜牧业、副业和渔业合在一起,称为()A.广义的农业B.信息产业C.工业D.商业2.以鹅颈瓶实验证明细菌不是自然发生的“微生物之父”是()A.奥地利科学家孟德尔B.英国科学家达尔文C.法国科学家巴斯德D.瑞典科学家林奈3.某同学测定花生种子的能量,三次重复实验的数据分别是1244千焦、1249千焦、1248千焦,则该花生的所含能量是()A.1249千焦B.1244千焦C.1248千焦D.1247千焦4.晓白跟妈妈学做面包时,感觉发酵后的面团变轻了。
这是酵母的作用吗?她设计的对照实验应该是()A.甲和乙B.甲和丙C.丙和丁D.乙和丁5.探究“植物对空气湿度的影响”中的实验变量是()A.植被的数量B.裸地C.草地D.灌木丛6.晓玲为探究废旧电池对水质的影响,设计的实验方案如下表:项目对照组实验组加入无污染河水的量/毫升1500①加入7号废旧电池的数量/节不加1放入同种生长状况一致的金鱼的数量/条55该方案中的①应为()A.500B.1000C.1500D.20007.某同学设计了如图实验装置,探究环境对蚯蚓生活的影响,下列有关说法正确的是()A.该实验的变量是光照B.湿土和干土应该从不同的环境中获取C.该实验做一次就可以得出正确结论D.探究的问题是“土壤的潮湿度对蚯蚓生活有影响吗?”8.禽流感是一种急性呼吸道传染病,病死率较高。
为了防控人感染79H N型疾病,某科研机构用发育状况相近的健康小鸡进行了如下实验:编号小鸡数量处理方法实验结果甲组10只不做处理,正常喂养小鸡全部存活乙组10只给小鸡接种活的79H N型禽流感病毒小鸡全部死亡丙组10只给小鸡接种降低活性的79H N型禽流感病毒小鸡全部存活丁组10只给小鸡接种降低活性的79H N型禽流感病毒,两周后,再给它们接种活的79H N型禽流感病毒?下列分析错误的是()A.甲组可以作为对照组,甲、乙对照实验的变量是活的79H N型禽流感病毒B.每组实验选择等量、个体大小和健康状况相近的小鸡,只有接种的物质不同C.每组小鸡数量用10只,而不是用1只,目的是避免实验的偶然性D.丁组实验结果预测:部分小鸡成活,部分小鸡死亡9.以下生物学家与他们的重要成就对应有误的是()A.林奈——显微镜观察细胞B.屠呦呦——提取青蒿素用于治疗疟疾C.袁隆平——培育杂交水稻D.孟德尔——利用豌豆研究遗传规律10.某科研小组为探究山药中的山药多糖对治疗糖尿病的医学价值,召募20至60岁的志愿者分为三组:20位糖尿病患者、20位健康者、20位治疗后血糖含量稳定者,每天只定时服用一定量的山药多糖,结果表明,服用该多糖对糖尿病的治疗及巩固有一定的作用,但由于个体之间的相对差异较大而不能得出明确的结论。
译林版版小学三年级上学期期末英语综合试题测试卷(含答案)

一、单项选择1.—Happy Birthday! ( )—_____A.Happy Birthday! B.Happy New Year! C.Thank you. 2.Look _________ my cap. ( )A.to B.for C.at3.In the book Can I Play? Billy is ____ at last (最后). ( )A.sad B.happy C.tired 4.They ______ look great. ( )A.to B.at C.all 5.—Yellow ______ green? ( )—Yellow, please.A.and B.or C./6.Look at ________ skirt. ( )A.new my B.my new C.I new 7.—Good morning, Miss Li. ( )—__________A.Good afternoon. B.Good morning. C.Hello. 8.Would you like an egg __________ a cake? ( )A.Is B.and C.or 9.—Look at my skirt. ( )—________A.Good afternoon. B.Great!10.This is John. _____ my brother. ( )A.He B.She’s C.He’s 11.—Is Miss Li your _______? ( )—Yes, she is.A.brother B.friend C.father 12.This is John. _________ is my friend. ( )A.He B.She C.I 13.—Good morning! ( )—__________A.Good afternoon. B.Nice to meet you, too. C.Good morning. 14.—What's your mother like? ( )—______A.She is a nurse. B.She has some bread. C.She is friendly. 15.―Good morning, Mr Green. ( )―________A.Good morning. B.Good afternoon. C.Good evening. 16.Look, this is ______ dress. ( )A.she B.I C.my 17.—This is my mother. ( )—______A.Thank you. B.Nice to meet you. C.Great. 18.He’s __________ Mike. ( )A.no B.not C.yes 19.Hello! _______ is my sister Tina. ( )A.He B.She C.she 20.—Would you like a pie? ( )—_______A.Yes, I am. B.No, thank you. C.No. It’s a CD.二、完成句子21.Eat some ____.22.________ (再见), Alice!23.I ________ (是) Tom.24.Tom and Mike are ________________ (我的朋友们).25.__________ (那个) is Yang Ling's T-shirt. It's _________ (绿色的).26.A: What colour is my skirt now?B: It’s _________. (黑色的)27.—Is she Yang Ling?—Yes. S_________ is my friend.28.This is my new .29.No, I'm ________ (不是).30.Touch your ____.31.Would you like _________ _________?32.Eat some _____.33.Look at the (mouth / monkey).34.There are s________ days(天) in a week(周).35.H________ you are.36.We should have an e________ every day.37.(Sh e’s/ He’s) my grandma.38.N________. I’m Wang Bing.39.Frogs are ________ (绿色的).40.This is my ________(mouth / mum).三、阅读理解Hi! I’m Bob. I like animals. Look at my dog. It’s black and white. It has big eyes. This is my bird, Polly. It is three years ol d. It’s very beautiful. I have a small cat. It’s white. She is Mimi. Mimi likes the fish. What about you?41、The dog is _______. ( )A.black B.white C.black and white42、How old is Polly? ( )A.It’s 2 years old.B.It’s 3 years old.C.It’s 4 years old.43、_______ is very beautiful. ( )A.The bird B.The dog C.The giraffe44、Bob has a _______ cat. ( )A.short B.small C.fat45、Mimi likes _______. ( )A.fish B.grapes C.Polly四、阅读理解Hello, I'm Sue. I'm a girl. Now I am six years old. It's my birthday. What's that on the desk? Oh, it is my mother's present. It's a good cake. That's my brother's present---a bag. I like it very much.46、My name is ________. ( )A.Sue B.Lucy C.Tim47、Sue is ________ now. ( )A.nine B.five C.six48、Mother's present is a ________. ( )A.cake B.kite C.bag49、The cake is on the ________. ( )A.chair B.desk C.book50、My brother's present is a ________. ( )A.bag B.pen C.pencil五、阅读理解Hello, I'm Lili. I'm nine. I have a happy family. This is my grandpa. He's a doctor. This is my grandma. She's a nurse. This is my father. He's a policeman. This is my mother, she's an English teacher. This is my little sister. She's two. This is my brother. His name is Mike. Today is Mike's birthday. Look at the birthday cake. There are (有) many candles (蜡烛) on it. How many candles? One candle, two candles, three candles, four candles, five candles, six candles, seven candles, eight candles, nine candles, ten candles, eleven candles, twelve candles. The candles are red. Here is a present for my brother. It's a cat kite. It's yellow and blue. We're happy today.51、Lili is a ____________. ( )A.teacher B.nurse C.pupil52、How old is Mike? ( )A.Nine. B.Twelve. C.Two.53、Lili's father is a ____________. ( )A.policeman B.doctor C.driver54、Mike's present is a ____________. ( )A.cat B.dog kite C.cat kite55、The candles are ____________. ( )A.red B.yellow C.black六、阅读理解Lucy and Bob are students. Lucy is twelve years old. She is from the USA.She likes grapes and apples. She has a bro wn cat. It’s small and fat. Bob is eleven years old. He is from the UK. He likes pears and strawberries. He has a toy car. It’s on the box.56、Bob is _____ years old. ( )A.12 B.11 C.2057、Lucy is from the _____. ( )A.UK B.USA C.UN58、Lucy has a bro wn cat. It’s _____. ( )A.big and fat B.small and thin C.small and fat59、Bob likes _____. ( )A.grapes and apples B.grapes and strawberries C.pears and strawberries60、Bob has a toy car. It’s _____ the box. ( )A.in B.on C.under【参考答案】一、单项选择1.C解析:C【详解】句意:生日快乐!A生日快乐!B新年快乐!C谢谢。
【成才之路】2014-2015学年高中数学(北师大版,选修2-3)综合测试(含答案)

选修2-3综合测试时间120分钟,满分150分。
一、选择题(本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.从单词“equation”中选取5个不同的字母排成一排,含有“qu”(其中“qu”相连且顺序不变)的不同排列共有( )A .120个B .480个C .720个D .840个[答案] B[解析] 第一步,先从除“qu ”之外的另外6个字母中任选3个不同的字母,与“qu ”一起分成一堆,共有C 36种不同的选法;第二步,把“qu ”看作一个字母,与另外3个字母排列,且“qu ”顺序不变,共有A 44种不同的排法,由分步乘法计数原理,共有C 36·A 44=480个不同的排列.故选B.2.(2012·安徽理,7)(x 2+2)(1x 2-1)5的展开式的常数项是( )A .-3B .-2C .2D .3[答案] D[解析] 本题考查了二项式及其展开式中的特定项的问题.第一个因式取x 2,第二个因式取1x 2,得:1×C 15(-1)4=5;第一个因式取2,第二个因式取(-1)5得:2×(-1)5=-2,展开式的常数项是5+(-2)=3.故选D.利用展开式的通项公式求二项式中的特定项是高考考查的重点.3.甲、乙两人从4门课程中各选修2门,则甲、乙所选的课程中至少有1门不相同的选法共有( )A .6种B .12种C .30种D .36种[答案] C[解析] 用间接法求解:第一步:甲从4门课程中选修2门,有C 24种选法. 第二步:乙从4门课程中选修2门,有C 24种选法.根据乘法原理,甲、乙两人从4门课程中各选修2门共有C 24C 24种选法.甲、乙所选的课程完全相同有C 24种选法,所以甲、乙所选的课程中至少有1门不相同的选法共有C 24C 24-C 24=30种.故选C.4.有甲、乙两种钢材,从中各取等量样品检验它们的抗拉强度指标如下:A .期望与方差B .正态分布C .卡方χ2D .概率[答案] A[解析] 检验钢材的抗拉强度,若平均抗拉强度相同,再比较波动情况.故选A. 5.设随机变量ξ服从二项分布ξ~B (n ,p ),则(Dξ)2(Eξ)2等于( )A .p 2B .(1-p )2C .npD .p 2(1-p )[答案] B[解析] 因为ξ~B (n ,p ),(Dξ)2=[np (1-p )]2,(Eξ)2=(np )2,所以(Dξ)2(Eξ)2=[np (1-p )]2(np )2=(1-p )2.故选B.6.随机变量X 的所有等可能取值为1,2,…,n ,若P (X <4)=0.3,则n 的值为( ) A .3 B .4 C .10 D .不能确定[答案] C[解析] 因为P (X <4)=P (X =1)+P (X =2)+P (X =3)=1n +1n +1n =3n =0.3,所以n =10.7.在一次试验中,测得(x ,y )的四组值分别是A (1,2),B (2,3),C (3,4),D (4,5),则y 与x 之间的线性回归方程是( )A .y =x +1B .y =x +2C .y =2x +1D .y =x -1 [答案] A[解析] ∵A ,B ,C ,D 四点共线,都在直线y =x +1上,故选A.8.某校从学生中的10名女生干部与5名男生干部中随机选6名学生干部组成“文明校园督察队”,则组成4女2男的“文明校园督察队”的概率为( )A.C 615A 615B.C 310C 35C 615 C.C 410C 25C 615D.C 410A 25A 615[答案] C[解析] 此题为超几何分布问题,组成4女2男的“文明校园督察队”的概率为C 410C 25C 615.9.为了评价某个电视栏目的改革效果,在改革前后分别从居民点随机抽取了100位居民进行调查,经过计算χ2的观测值χ2=99.9,根据这一数据分析,下列说法正确的是( )A .有99.9%的人认为该栏目优秀B .有99.9%的人认为栏目是否优秀与改革有关C .有99.9%的把握认为电视栏目是否优秀与改革有关系D .以上说法都不对 [答案] C[解析] 当χ2>10.828时有99.9%的把握认为电视栏目是否优秀与改革有关系.故选C. 10.假设每一架飞机的引擎在飞行中出现故障的概率为1-p ,且各引擎是否有故障是独立的,已知4引擎飞机中至少有3个引擎正常运行,飞机就可成功飞行;2引擎飞机要2个引擎全部正常运行,飞机才可成功飞行.要使4引擎飞机比2引擎飞机更安全,则p 的取值范围是( )A.⎝⎛⎭⎫23,1B.⎝⎛⎭⎫13,1 C.⎝⎛⎭⎫0,23 D.⎝⎛⎭⎫0,13 [答案] B[解析] 4引擎飞机成功飞行的概率为C 34p 3(1-p )+p 4,2引擎飞机成功飞行的概率为p 2,要使C 34(1-p )+p 4>p 2,必有13<p <1.故选B. 二、填空题(本大题共5小题,每小题5分,共25分)11.(2014·山东青岛质检)平面内有10个点,其中5个点在一条直线上,此外再没有三点共线,则共可确定______条直线;共可确定________个三角形.[答案] 36;110[解析] 设10个点分别为A 1,A 2,…,A 10,其中A 1,A 2,…,A 5共线,A i (i =1,2,…,5)与A 6、A 7、…、A 10分别确定5条直线,共25条;A 1、A 2、…、A 5确定1条; A 6、A 7、…、A 10确定C 25=10条, 故共可确定36条直线.在A 1,A 2,…,A 5中任取两点,在A 6,A 7,…,A 10中任取一点可构成C 25C 15=50个三角形;在A 1,A 2,…,A 5中任取一点,在A 7,A 7,…,A 10中任取两点可构成C 15C 25=50个三角形;在A 6,A 7,…,A 10中任取3点构成C 35=10个三角形,故共可确定50+50+10=110个三角形.12.(2012·陕西理,12)(a +x )5展开式中x 2的系数为10,则实数a 的值为________. [答案] 1[解析] 本题考查了二项式定理与二项展开式的通项分式.由已知C r 5a5-r ·x r 中r =2,∴C 25a 3=10,a 3=1,∴a =1,准确运用二项展开式的通项公式是解题关键.13.一个袋中装有黑球、白球和红球共n (n ∈N *)个,这些球除颜色外完全相同.已知从袋中任意摸出1个球,得到黑球的概率是25,现从袋中任意摸出2个球.若n =15,且摸出的2个球都是白球的概率是221,设ξ表示摸出的2个球中红球的个数,则随机变量ξ的数学期望Eξ= ________.[答案]815[解析] 设袋中黑球的个数为x (个),记“从袋中任意摸出一个球,得到黑球”为事件A ,则P (A )=x 15=25.∴x =6.设袋中白球的个数为y (个),记“从袋中任意摸出两个球,得到的都是白球”为事件B ,则P (B )=C 2yC 215=221,∴y (y -1)15×14∴y =5或y =-4(舍去)即白球的个数为5(个).∴红球的个数为15-6-5=4(个). ∴随机变量ξ的取值为0,1,2,分布列是ξ的数学期望Eξ=1121×0+44105×1+235×2=815.14.已知X ~N (1.4,0.052),则X 落在区间(1.35,1.45)中的概率为____________.[答案] 0.6826[解析] 因为μ=1.4,σ=0.05,所以X 落在区间(1.35,1.45)中的概率为P (1.4-0.05<X <1.4+0.05)=0.6826.15.若两个分类变量x 与y 的列联表为:则“X 与Y . [答案] 0.01[解析] 由列联表中的数据,得K 2的观测值为K 2=(10+15+40+16)(10×16-15×40)2(10+15)(40+16)(10+40)(15+16)≈7.227>6.635,因为P (K 2≥6.635)≈0.01,所以“X 与Y 有关系”这一结论是错误的概率不超过0.01. 三、解答题(本大题共6小题,共75分,前4题每题12分,20题13分,21题14分) 16.研究某特殊药物有无副作用(比如服用后恶心),给50名患者服用此药,给另外50个患者服用安慰剂,记录每类样本中出现恶心的数目如下表:[解析] 由题意,问题可以归纳为独立检验假设H 1:服该药物(A )与恶心(B )独立.为了检验假设,计算统计量K 2=100×(15×46-4×35)250×50×19×81≈7.86>6.635.故拒绝H 1,即不能认为药物无恶心副作用,也可以说,我们有99%的把握说,该药物与副作用(恶心)有关.17.一厂家向用户提供的一箱产品共10件,其中有2件次品,用户先对产品进行抽检以决定是否接收.抽检规则是这样的:一次取一件产品检查(取出的产品不放回箱子);若前三次没有抽查到次品,则用户接收这箱产品;若前三次中一抽查到次品就立即停止抽检,并且用户拒绝接收这箱产品.(1)求这箱产品被用户接收的概率; (2)记抽检的产品件数为ξ,求ξ的分布列. [解析] (1)设“这箱产品被用户接收”为事件A ,则P (A )=8×7×610×9×8=715.即这箱产品被用户接收的概率为715.(2)ξ的可能取值为1,2,3. P (ξ=1)=210=15.P (ξ=2)=810×29=845.P (ξ=3)=810×79=2845.∴ξ的分布列为:18.已知二项式(x -2x)10的展开式中, (1)求展开式中含x 4项的系数;(2)如果第3r 项和第r +2项的二项式系数相等,试求r 的值. [解析] (1)设第k +1项为T k +1=C k 10x10-k(-2x)k =(-2)k C k 10x 10-32k 令10-32k =4,解得k =4,∴展开式中含x 4项的系数为(-2)C 410=-420.(2)∵第3r 项的二项式系数为C 3r -110,第r +2项的二项式系数为C r +110∴C 3r -110=C r +110,故3r -1=r +1或3r -1+r +1=10,解得r =1.19.(2012·陕西理,20)某银行柜台设有一个服务窗口,假设顾客办理业务所需的时间互相独立,且都是整数分钟,对以往顾客办理业务所需的时间统计结果如下:(1)估计第三个顾客恰好等待4分钟开始办理业务的概率;(2)X 表示至第2分钟末已办理完业务的顾客人数,求X 的分布列及数学期望. [解析] 设Y 表示顾客办理业务所需的时间,用频率估计概率,得Y 的分布列如下:(1)A A对应三种情形:①第一个顾客办理业务所需的时间为1分钟,且第二个顾客办理业务所需的时间为3分钟;②第一个顾客办理业务所需的时间为3分钟,且第二个顾客办理业务所需的时间为1分钟;③第一个和第二个顾客办理业务所需的时间均为2分钟.所以P(A)=P(Y=1)P(Y=3)+P(Y=3)P(Y=1)+P(Y=2)P(Y=2)=0.1×0.3+0.3×0.1+0.4×0.4=0.22.(2)X所有可能的取值为0,1,2.X=0对应第一个顾客办理业务所需的时间超过2分钟,所以P(X=0)=P(Y>2)=0.5;X=1对应第一个顾客办理业务所需的时间为1分钟且第二个顾客办理业务所需的时间超过1分钟,或第一个顾客办理业务所需的时间为2分钟,所以P(X=1)=P(Y=1)P(Y>1)+P(Y=2)=0.1×0.9+0.4=0.49;X=2对应两个顾客办理业务所需的时间均为1分钟,所以P(X=2)=P(Y=1)P(Y=1)=0.1×0.1=0.01;所以X的分布列为E(X)=0×0.5+1×0.49+20.(2014·沈阳市质检)为了研究“教学方式”对教学质量的影响,某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.(1)现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;(2)学校规定:成绩不低于75分的为优秀.请填写下面的2×2列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.(参考公式:K 2=n (ad -bc )(a +b )(c +d )(a +c )(b +d ))[解析] (1)甲班成绩为87分的同学有2个,其他不低于80分的同学有3个“从甲班数学成绩不低于80分的同学中随机抽取两名同学”的一切可能结果组成的基本事件有C 25=10个,“抽到至少有一个87分的同学”所组成的基本事件有C 13C 12+C 22=7个,所以P =710. (2)K 2=40×(6×6-14×14)20×20×20×20=6.4>5.024,因此,我们有97.5%的把握认为成绩优秀与教学方式有关.21.某城市一个交通路口原来只设有红绿灯,平均每年发生交通事故80起,案件的破获率为70%,为了加强该路口的管理,第二年在该路口设置了电子摄像头,该年发生交通事故70起,共破获56起,第三年白天安排了交警执勤,该年发生交通事故60起,共破获了54起.(1)根据以上材料分析,加强管理后的两年该路口的交通状况发生了怎样的变化? (2)试采用独立性检验进行分析,设置电子摄像头对该路口交通肇事案件的破获产生了什么样的影响?设置电子摄像头和交警白天执勤的共同作用对该路口交通肇事案件的破获产生了什么样的影响?[解析] (1)由统计数据可知,没有采取措施之前,案件的发生较多,并且破获率只有70%,安装电子摄像头之后,案件的发生次数有所减少,并且破获率提高到了80%,白天安排交警执勤后,案件的发生次数进一步减少,并且破获率提高到了90%.由此可知,电子摄像头对遏制交通案件的发生起到了一定作用,并且给破案带了一定的帮助,而安排交警执勤对这些的影响更大.(2)根据所提供的数据可以绘制对应的2×2列联表如下:案件的破获率有了明显提高,这说明两种措施对案件的破获都起到了一定的积极作用.先分析电子摄像头对破案的影响的可信度,令a =56,b =24,c =56,d =14,构造随机变量χ2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d )=150×(56×14-24×56)280×70×112×38≈1.974.其中n =a +b +c +d .而查表可知,P (χ2≥1.323)=0.25.且1-0.25=0.75=75%,因此约有75%的把握认为,安装电子摄像头对案件的破获起到了作用.再分析安装电子摄像头及交警执勤的情况,同样令a =56,b =24,c =54,d =6,则 χ2=n (ad -bc )2(a +b )(c +d )(a +c )(b +d )=140×(56×6-24×54)280×60×110×30≈8.145,其中n =a +b +c +d .而查表可知,P (χ2≥6.635)=0.01,且1-0.01=0.99=99%,因此约有99%的把握认为安装电子摄像头及交警执勤对案件的破获起到了作用.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
综合检测(时间:120分钟满分:150分)一、选择题(本大题共12小题,每小题5分,共60分)1.从甲地去乙地有3班火车,从乙地去丙地有2班轮船,甲到丙地再无其他路可走,则从甲地去丙地可选择的旅行方式有()A.5种B.6种C.7种D.8种答案B解析第一步:从甲地去乙地共有3种走法;第二步:从乙地去丙地共有2种走法.由分步乘法计数原理知N=3×2=6(种).2.设(x1,y1),(x2,y2),…,(x n,y n)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的回归直线(如图所示),以下结论中正确的是()A.x和y的相关系数为直线l的斜率B.x和y的相关系数在0到1之间C.当n为偶数时,分布在l两侧的样本点的个数一定相同D.直线l过点(x,y)答案D解析因为相关系数是表示两个变量是否具有线性相关关系的一个值,它的绝对值越接近1,两个变量的线性相关程度越强,所以A,B错误.C中n为偶数时,分布在l两侧的样本点的个数可以不相同,所以C错误.根据回归直线方程一定经过样本点的中心可知D正确.3.袋中装有编号分别为1,2,3,4的4个白球和4个黑球,从中取出3个球,则取出球的编号互不相同的取法种数为()A.32 B.40 C.24 D.56答案A解析装有编号分别为1,2,3,4的4个白球和4个黑球,从中任取3个球,则取出球的编号互不相同,只是分别从有两个球的4个号中选3个球,可以先从4个号中选3个号,再在选出的三个号中二选一,共有C34C12C12C12=32(种)取法.4.设随机变量X 服从二项分布X ~B (n ,p ),则?D ?X ??2?E ?X ??2等于( ) A .p 2 B .(1-p )2 C .1-p D .以上都不对答案 B解析 由题意知,D (X )=np (1-p ),E (X )=np , 则?D ?X ??2?E ?X ??2=n 2p 2?1-p ?2n 2p2=(1-p )2. 5.有三对师徒共6人,站成一排照相,每对师徒相邻的站法共有( ) A .72种 B .54种 C .48种 D .8种 答案 C解析 用捆绑法.A 33A 22A 22A 22=48(种).6.在x (1+x )6的展开式中,含x 3项的系数为( ) A .15 B .20 C .25 D .30 答案 A解析 由题意知含x 3的项为x C 26x 2=C 26x 3=15x 3.7.某校1 000名学生的某次数学考试成绩X 服从正态分布,正态分布密度曲线如图所示,则成绩X 位于区间(51,69]的人数大约是( )A .997B .954C .800D .683答案 D解析 由题图知,X ~N (μ,σ2), 其中,μ=60,σ=9,∴P (μ-σ≤x ≤μ+σ)=P (51<x ≤69)= 6, ∴人数大约为 6×1 000≈683.8.以下四个命题,其中正确的序号是( )①从匀速传递的产品生产流水线上,质检员每20分钟从中抽取一件产品进行某项指标检测,这样的抽样是分层抽样;②两个随机变量相关性越强,则相关系数的绝对值越接近于1 ;③在线性回归方程y ^=+12中,当解释变量x 每增加一个单位时,预报变量y ^平均增加个单位;④对分类变量X 与Y ,它们的随机变量K 2的观测值k 来说,k 越小,“X 与Y 有关系”的把握程度越大.A .②③B .①②C .③④D .②④ 答案 A解析 ①是系统抽样;对于④,随机变量K 2的观测值k 越小,说明两个相关变量有关系的把握程度越小.9.已知变量x 与y 正相关,且由观测数据算得样本平均数x =3,y =,则由该观测数据算得的线性回归方程可能是( ) =+ =2x - =-2x + =-+答案 A解析 因为变量x 和y 正相关,则回归直线的斜率为正,故可以排除选项C 和D.因为样本点的中心在回归直线上,把点(3,的坐标分别代入选项A 和B 中的直线方程进行检验,可以排除B ,故选A.10.甲、乙两队进行排球比赛,现在的情形是甲队只要再赢一局就获冠军,乙队需要再赢2局才能得冠军.若两队胜每局的概率相同,则甲队获得冠军的概率是( ) 答案 D解析 甲获得冠军有两种情况.一是第1场就取胜,这种情况的概率是12,二是第1场失败,第2场取胜,这种情况的概率是12×12=14, 则甲获冠军的概率是12+14=34.11.从1,2,3,4,5中任取2个不同的数,事件A :“取到的2个数之和是偶数”,事件B :“取出的2个数均为偶数”,则P (B |A )等于( ) 答案 A解析 由题意知事件A 包含的基本事件有(1,3),(1,5),(3,5),(2,4),共4个,∴P (A )=4C 25=25.事件B 含有(2,4),共1个基本事件, ∴P (AB )=110, ∴P (B |A )=P ?AB ?P ?A ?=14.12.任意选择四个日期,设X 表示取到的四个日期中星期天的个数,则D (X )等于( )答案 B解析 由题意得X ~B (4,17),所以D (X )=2449.二、填空题(本大题共4个小题,每小题5分,共20分) 13.(x y -y x )4的展开式中x 3y 3的系数为________. 答案 6解析 T k +1=C k 4(x y )4-k (-y x )k =C k 4·x 4-k 2·y 2+k 2·(-1)k , 由已知4-k 2=3,2+k2=3,∴k =2.∴x 3y 3的系数为C 24(-1)2=6.14.已知随机变量X 服从正态分布N (0,σ2),且P (-2≤X ≤0)=,则P (X >2)=________. 答案解析 由已知P (0≤X ≤2)=P (-2≤X ≤0)=, ∴P (X >2)=12×(1--=.15.已知随机变量ξ~B (n ,p ),若E (ξ)=4,η=2ξ+3,D (η)=,则P (ξ=2)=________. 答案 32625解析 由已知np =4,4np (1-p )=, ∴n =5,p =,∴P (ξ=2)=C 25p 2(1-p )3=32625.16.已知离散型随机变量X 的分布列如下表.若E (X )=0,D (X )=1,则a =________,b =________.答案 512 14解析 由题意知,a +b +c =1112,-a +c +16=0, (-1)2×a +12×c +22×112=1, 解得,a =512,b =14.三、解答题(本大题共6小题,共70分)17.(10分)已知f (x )=(1+x )m +(1+x )n (m ,n ∈N *)展开式中x 的系数为19,求f (x )的展开式中x 2的系数的最小值.解 f (x )=1+C 1m x +C 2m x 2+…+C m m x m +1+C 1n x +C 2n x 2+…+C n n x n.由题意知m +n =19,m ,n ∈N *,故x 2项的系数为C 2m +C 2n =m ?m -1?2+n ?n -1?2=⎝⎛⎭⎫m -1922+19×174. 由m ,n ∈N *,根据二次函数的知识知, 当m =9或10时,上式有最小值,也就是当m =9,n =10或m =10,n =9时,x 2项的系数取得最小值,最小值为81. 18.(12分)抛掷一枚骰子(六个面上分别标以数字1,2,3,4,5,6). (1)连续抛掷2次,求向上的数不同的概率; (2)连续抛掷2次,求向上的数之和为6的概率;(3)连续抛掷5次,求恰好出现3次向上的数为奇数的概率. 解 (1)设事件A 表示事件“抛掷2次,向上的数不同”, 则P (A )=6×56×6=56.(2)设事件B 表示事件“抛掷2次,向上的数之和为6”.∵向上的数之和为6的结果有(1,5),(2,4),(3,3),(4,2),(5,1),共5种, ∴P (B )=56×6=536.(3)设事件C 表示事件“抛掷5次,恰好出现3次向上的数为奇数”,∴P (C )=C 35⎝⎛⎭⎫362⎝⎛⎭⎫363=516.19.(12分)生产工艺工程中产品的尺寸偏差X (mm)~N (0,22),如果产品的尺寸与现实的尺寸偏差的绝对值不超过4 mm 的为合格品,求生产5件产品的合格率不小于80%的概率.(精确到解 由题意X ~N (0,22),求得 P (|x |≤4)=P (-4≤X ≤4)= 4.设Y 表示5件产品中合格品个数,则Y ~B (5, 4). ∴P (Y ≥5×=P (Y ≥4)=C 45× 4)4× 6+C 55× 4)5≈ 2+ 9≈.故生产5件产品的合格率不小于80%的概率为.20.(12分)某种产品的广告费支出x 与销售额y (单位:百万元)之间有如下对应数据:x24568y3040605070(1)画出散点图;(2)求线性回归方程;(3)试预测广告费支出为10百万元时,销售额多大解(1)根据表中所列数据可得散点图如下:(2)列出下表,并计算:i12345x i24568y i3040605070x i y i60160300300560因此,x=255=5,y=2505=50,∑i=15x2i=145,∑i=15y2i=13 500,∑i=15x i y i=1 380.于是求得:b^=∑i=15x i y i-5x·y∑i=15x2i·5x2=1 380-5×5×50145-5×5×5=;a^=y-b^x=50-×5=.因此,所求线性回归方程为y^=+.(3)根据上面求得的线性回归方程,当广告费支出为10百万元时,y^=×10+=,即这种产品的销售收入大约为百万元.21.(12分)某饮料公司招聘一名员工,现对其进行一项测试,以便确定工资级别.公司准备了两种不同的饮料共8杯,其颜色完全相同,并且其中4杯为A饮料,另外4杯为B饮料,公司要求此员工一一品尝后,从8杯饮料中选出4杯A饮料.若4杯都选对,则月工资定为3 500元;若4杯选对3杯,则月工资定为2 800元;否则月工资定为2 100元.令X表示此人选对A 饮料的杯数.假设此人对A 和B 两种饮料没有鉴别能力. (1)求X 的分布列; (2)求此员工月工资的均值.解 (1)依题意知X 所有可能取值为0,1,2,3,4,P (X =0)=C 04C 44C 48=170,P (X =1)=C 14C 34C 48=835,P (X =2)=C 24C 24C 48=1835,P (X =3)=C 34C 14C 48=835,P (X =4)=C 44C 04C 48=170.所以X 的分布列为(2)令Y 表示此员工的月工资,则Y 的所有可能取值为2 100,2 800,3 500,则P (Y =3 500)=P (X =4)=170,P (Y =2 800)=P (X =3)=835,P (Y =2 100)=P (X ≤2)=1835+835+170=5370.所以E (Y )=170×3 500+835×2 800+5370×2 100=2 280.所以此员工月工资的均值为2 280元. 22.(12分)随机调查某社区80个人,以研究这一社区居民在20:00~22:00时间段的休闲方式与性别的关系,得到下面的数据表:(1)3人在这一时间段以看书为休闲方式的人数为随机变量X ,求X 的分布列和均值;(2)根据以上数据,能否有99%的把握认为“在20:00~22:00时间段的休闲方式与性别有关系”参考公式:K 2=n ?ad -bc ?2?a +b ??c +d ??a +c ??b +d ?,其中n =a +b +c +d .参考数据:解 (1)依题意,随机变量X 的取值为0,1,2,3,且每个男性在这一时间段以看书为休闲方式的概率P =56.方法一 P (X =0)=C 03⎝⎛⎭⎫163=1216,P (X =1)=C 13⎝⎛⎭⎫162⎝⎛⎭⎫56=572,P (X =2)=C 23⎝⎛⎭⎫16⎝⎛⎭⎫562=2572,P (X =3)=C 33⎝⎛⎭⎫563=125216.故X 的分布列为E (X )=0×1216+1×572+2×2572+3×125216=52.方法二 根据题意可得X ~B ⎝⎛⎭⎫3,56, ∴P (X =k )=C k 3⎝⎛⎭⎫163-k ⎝⎛⎭⎫56k ,k =0,1,2,3,E (X )=np =3×56=52.(2)提出假设H 0:在20:00~22:00时间段的休闲方式与性别无关.根据样本提供的2×2列联表, 得K 2=n ?ad -bc ?2?a +b ??c +d ??a +c ??b +d ?=80×?10×10-10×50?260×20×20×60 =809≈>.∴我们有99%的把握认为“在20:00~22:00时间段的休闲方式与性别有关”.。
