习题解答2讲解
第三版机械制造工艺学第二章习题解答
机械制造工艺学部分习题解答2第二章:机械加工工艺规程设计(第3版P94)2-1何谓机械加工工艺规程?工艺规程在生产中起何作用?概念题,见教材P25.2-2简述机械加工工艺过程卡和工序卡的主要区别以及它们的应用场合?概念题,见教材P25.2-3简述机械加工工艺过程的设计原则、步骤和内容。
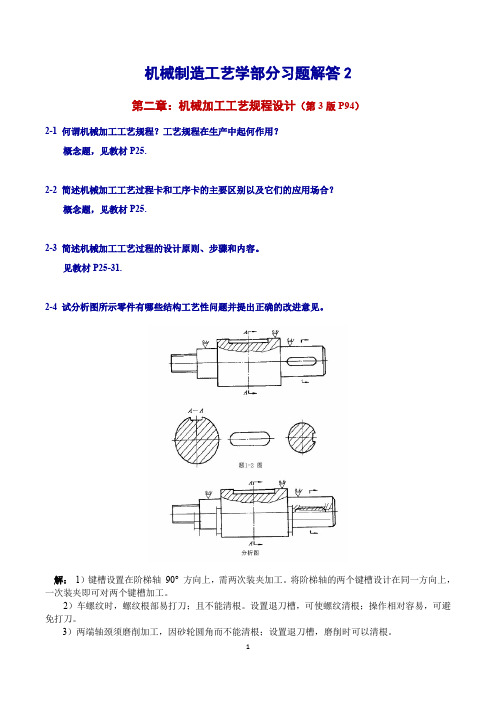
见教材P25-31.2-4试分析图所示零件有哪些结构工艺性问题并提出正确的改进意见。
解:1)键槽设置在阶梯轴90°方向上,需两次装夹加工。
将阶梯轴的两个键槽设计在同一方向上,一次装夹即可对两个键槽加工。
2)车螺纹时,螺纹根部易打刀;且不能清根。
设置退刀槽,可使螺纹清根;操作相对容易,可避免打刀。
3)两端轴颈须磨削加工,因砂轮圆角而不能清根;设置退刀槽,磨削时可以清根。
2-7何谓经济精度?选择加工方法时应考虑的主要问题有哪些?答:(P34)经济精度——在正常加工条件下(采用符合质量标准的设备、工艺装备和标准技术等级的工人,不延长加工时间)所能保证的加工精度和表面粗糙度。
选择加工方法时应考虑(P35):根据零件表面、零件材料和加工精度以及生产率要求,考虑本厂现有的工艺条件,考虑加工经济精度等因素。
2-8在大批量生产条件下,加工一批直径为,长度为58mm的光轴,其表面粗糙度,材料为45钢,试安排其加工路线。
答:粗车——半精车——粗磨——精磨——精密磨削。
2-9图4-71所示箱体零件的两种工艺安排如下:(1)在加工中心上加工:粗、精铣底面;粗、精铣顶面;粗镗、半精镗、精镗Φ80H7孔和60H7孔;粗、精铣两端面。
(2)在流水线上加工:粗刨、半精刨底面,留精刨余量;粗、精铣两端面;粗镗削、半精镗Φ80H7孔和60H7孔,留精镗余量;粗刨、半精刨、精刨顶面;精镗Φ80H7孔和60H7孔;精刨底面。
试分别分析上述两种工艺安排有无问题,若有问题请提出改进意见。
答:(1)应在先加工底面、顶面之后,加工两端面,因为底面、端面是定位表面,定位表面加工之后,再进行镗孔。
数字信号处理第2章习题解答

e
n 0
e
j ( 0 )
n
1 1 e e j (0 )
当 e 1 0
2-9 求 x(n) R5 (n) 的傅里叶变换 解:X (e j )
5 j 2
n
j
x ( n )e j n e j n
1 1 1 z 2
1 1 1 2 1 z z 2 4 1
1 1 1 2 X ( z) 1 z z 2 4 n 1 n z 2 n 0
1 x(n ) u(n ) 2
n
1 1 1 z 2 1 1 z 2 1 1 1 2 z z 2 4 1 2 z 4
解:
1 由x1 ( n ) u( n ) 2
1 z 2
n
1 得 X 1 ( z ) ZT [ x1 ( n )] 1 1 1 z 2 n 1 由x2 ( n ) u( n ) 3 1 得 X 2 ( z ) ZT [ x2 ( n )] 1 1 1 z 3
1 z 3
z3 z 3z 5 1 1 1 1 1 z 1 z z 3 z 2 3 2
1 z 3 2
j x ( n ) X ( e ): 2-7 求以下序列 的频谱
(1) (n n0 )
X ( e j )
n j n ( n n ) e 0
0
1/ 4 Re[ z ]
当 n 1 时, F ( z )在围线c内有一 (n 1)阶极点 z 0 在围线c外有单阶极点 z 1/ 4, 且分母阶次高于分子阶次二阶以上
应用多元统计分析课后习题答案详解北大高惠璇(第二章部分习题解答) (2).ppt

4 3
u1u2
1
2
exp[
1 2
(2u12
u22
2u1u2 )]du1du2
1
2
u12
u1e 2
1
2
u2e
1 2
(
u2
u1
)
2
du2
du1
1
2
u12
u1e 2
1
2
(u2
u1
)e
1 2
(u2
u1
)
2
du2
u1
e
1 2
(
u2
u1
)
2
du2
du1
1
2
u e
2
u12 2
2
x12
22
x1
65
x12
14
x1
49)
1 2
(
x2
x1
7)2
e e dx2
2
1 e
1 2
(
x12
8
x1
16)
2
1
2
e dx
1 2
(
x2
x1
7
)
2
2
1 e
1 2
(
x1
4
)
2
2
X1 ~ N(4,1).
类似地有
f2 (x2 ) f (x1, x2 )dx1
1
e
1 4
(
x2
3)2
X
X X
(1) (2)
~
N
2
p
(1) (2)
,
1 2
2 1
,
其中μ(i) (i=1,2)为p维向量,Σi (i=1,2)为p阶矩阵,
《电机与电气控制技术》第2版 习题解答 第二章 三相异步电动机

《电机与电气控制技术》第2版习题解答第二章三相异步电动机2-1三相异步电动机的旋转磁场是如何产生的?答:在三相异步电动机的定子三相对称绕组中通入三相对称电流,根据三相对称电流的瞬时电流来分析由其产生的磁场,由于三相对称电流其大小、方向随正弦规律变化,由三相对称电流建立的磁场即合成磁极在定子内膛中随一定方向移动。
当正弦交流电流变化一周时,合成磁场在空间旋转了一定角度,随着正弦交流电流不断变化,形成了旋转磁场。
2-2三组异步电动机旋转磁场的转速由什么决定?对于工频下的2、4、6、8、10极的三相异步电动机的同步转速为多少?答:三相异步电动机旋转磁场的转速由电动机定子极对数P交流电源频率f1决定,具体公式为n1=60f1/P。
对于工频下的2、4、6、8、10极的三相异步电动机的同步转速即旋转磁场的转速n1分别为3000r/min、1500r/min、1000r/min、750r/min、600r/min。
2-3试述三相异步电动机的转动原理,并解释“异步”的意义。
答:首先,在三相异步电动机三相定子绕组中通入三相交流电源,流过三相对称电流,在定子内膛中建立三相旋转磁场,开始转子是静止的,由于相对运动,转子导体将切割磁场,在转子导体中产生感应电动势,又由于转子导体是闭合的,将在其内流过转子感应电流,该转子电流与定子磁场相互作用,由左手定则判断电磁力方向,转子将在电磁力作用下依旋转磁场旋转方向旋转。
所谓“异步”是指三相异步电动机转子转速n与定子旋转磁场转速n1之间必须有差别,且n<n1。
2-4旋转磁场的转向由什么决定?如何改变旋转磁场的方向?答:旋转磁场在空间的旋转方向是由三相交流电流相序决定的,若要改变旋转磁场的方向,只需将电动机三相定子绕组与三相交流电源连接的三根导线中的任意两根对调位置即可。
如果来绕组U1接电源L1、V1接L2、W1接L3为正转,要想反转U1仍接L1,但V1接L3、W1接L2即可。
熊金城著的拓扑学部分习题解答II

(3)设 Y 是拓扑空间 X 的一个子空间. A ⊂ Y .证明
① int X ( A) = intY ( A) ∩ int X (Y )
证 先证 int X ( A) ⊂ intY ( A) ∩ int X (Y )
设 a ∈ int X ( A) ,则存在
X
的开集
U
X a
使得
a
∈U
X a
⊂
A ,而
(2)如果Wy 是点 y 在 X 中的一个邻域子基,则Wy Y 是点 y 在 Y 中的一个邻域子基。 证 设 G 是 y 在 Y 中的开邻域,则存在 X 的开集U ,使得 G = U ∩Y .因Wy 是点 y 在 X 中的一个邻域子基,存在 L1, L2 , , Ln ∈Wy ,使得 y ∈ L1 ∩ L2 ∩ ∩ Ln ⊂ U ,于是
Y
i−1 (U ) = U ∩ Y ∈T1 ,即V ∈T1 ,这表明T1 ⊃ T Y .
6. 设 X 和 Y 是 两 个 拓 扑 空 间 . 证 明 映 射 f : X → Y 是 一 个 连 续 映 射 当 且 仅 当 f : X → f ( X ) 是一个连续映射。
证
必要性 设 ( X ,τ1 ) ,(Y ,τ 2 ) ,若 U 是 f ( X ) 的开集,则 ∃G ∈τ 2 ,使得
O ( x,ε ) ⎯ψ≅⎯→ O (0,1) ⎯≅g⎯→
n ,ψ ( y1, y2 ,
,
yn
)
=
1 ε
(
y1
−
x1,
y2
−
x2
,
, yn − xn )
2.如果 Y 是拓扑空间 X 的一个开(闭)子集,则 Y 作为 X 的子空间时特别称为 X 的开(闭)子
系统工程第四版习题解答(2)

系统⼯程第四版习题解答(2)系统⼯程姓名:姚德世专业班级:⼯程管理1107班学号:24系统⼯程第三次作业8、假设每⽉招⼯⼈数MHM和实际需要⼈数RM成⽐例,招⼯⼈员的速率⽅程是:MHM·KL=P*RM·K,请回答以下问题:(1)K和KL的含义是什么?(2)RM是什么变量?(3)MHM、P、RM的量纲是什么?(4)(4)P的实际意义是什么?解:(1)K表⽰现在时间KL表⽰由现在时刻到未来是可的时间间隔(2)RM是速率变量(3)MHM的量纲是KL;P的量纲是RM;RM的量纲是K;(4)P的实际意义是现在之未来的增长速率。
9. 已知如下的部分DYNAMO⽅程:MT·K=MT·J+DT*(MH·JK-MCT·JK),MCT·KL=MT·K/TT·K,TT·K=STT*TEC·K,ME·K=ME·J*DT*(MCT·JK-ML·JK)其中:MT表⽰培训中的⼈员(⼈)、MH表⽰招聘⼈员速率(⼈/⽉)、MCT表⽰⼈员培训速率(⼈/⽉)、TT表⽰培训时间、STT表⽰标准培训时间、TEC表⽰培训有效度、ME表⽰熟练⼈员(⼈),ML表⽰⼈员脱离速率(⼈/⽉)。
请画出对应的SD(程)图。
10. ⾼校的在校本科⽣和教师⼈数(S和T)是按⼀定的⽐例⽽相互增长的。
已知某⾼校现有本科⽣10000名,且每年以SR的幅度增加,每⼀名教师可引起增加本科⽣的速率是1⼈/年。
学校现有教师1500名,每个本科⽣可引起教师增加的速率(TR)是0.05⼈/年。
请⽤SD 模型分析该校未来⼏年的发展规模,要求:(1) 画出因果关系图和流(程)图;(2)写出相应的DYNAMO⽅程;(3)列表对该校未来3~5年的在校本科⽣和教师⼈数进⾏仿真计算;(4)请问该问题能否⽤其它模型⽅法来分析?如何分析?(1)解:(2)、解:L S.K=S.J+SR.JK*DTN S=10000R SR.KL=T.K*TSRC TSR=1L T.K=T.J+TR.JK*DTN T=1500R TR.KL=S.K*STRC STR=0.05(3)解:(4)11.某城市国营和集体服务⽹点的规模可⽤SD来研究。
习题二解答
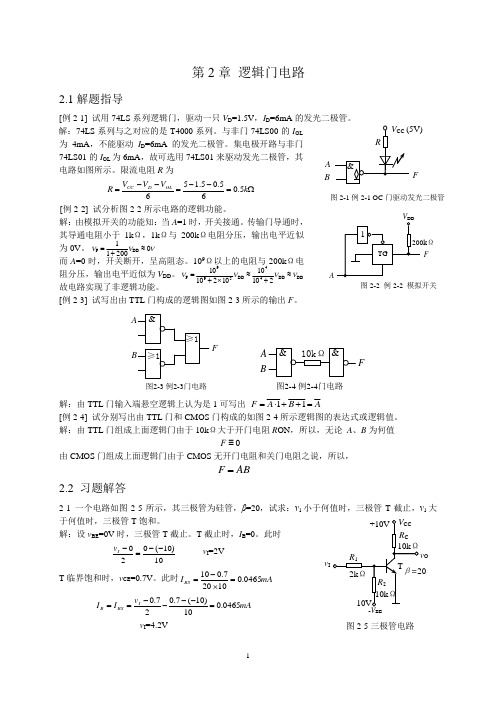
第2章 逻辑门电路2.1解题指导[例2-1] 试用74LS 系列逻辑门,驱动一只V D =1.5V ,I D =6mA 的发光二极管。
解:74LS 系列与之对应的是T4000系列。
与非门74LS00的I OL为4mA ,不能驱动I D =6mA 的发光二极管。
集电极开路与非门74LS01的I OL 为6mA ,故可选用74LS01来驱动发光二极管,其电路如图所示。
限流电阻R 为Ω=--=--=k V V V R OL D CC 5.065.05.156[例2-2] 试分析图2-2所示电路的逻辑功能。
解:由模拟开关的功能知:当A =1时,开关接通。
传输门导通时,其导通电阻小于1k Ω,1k Ω与200k Ω电阻分压,输出电平近似为0V 。
而A =0时,开关断开,呈高阻态。
109Ω以上的电阻与200k Ω电阻分压,输出电平近似为V DD 。
故电路实现了非逻辑功能。
[例2-3] 试写出由TTL 门构成的逻辑图如图2-3所示的输出F 。
&≥1F≥1A B图2-3 例2-3门电路A BF图2-4 例2-4门电路解:由TTL 门输入端悬空逻辑上认为是1可写出 [例2-4] 试分别写出由TTL 门和CMOS 门构成的如图2-4所示逻辑图的表达式或逻辑值。
解:由TTL 门组成上面逻辑门由于10k Ω大于开门电阻R ON ,所以,无论 A 、B 为何值由CMOS 门组成上面逻辑门由于CMOS 无开门电阻和关门电阻之说,所以,2.2 习题解答2-1 一个电路如图2-5所示,其三极管为硅管,β=20,试求:ν1小于何值时,三极管T 截止,ν1大于何值时,三极管T 饱和。
解:设v BE =0V 时,三极管T 截止。
T 截止时,I B =0。
此时 10)10(020--=-I v v I =2VT 临界饱和时,v CE =0.7V 。
此时mA I BS 0465.010207.010=⨯-= mA v I I I BS B 0465.010)10(7.027.0=----==v I=4.2Vv I v O BB 图2-5三极管电路A BF 图2-1例2-1 OC 门驱动发光二极管FA 图2-2 例2-2 模拟开关ΩV V 020011DD F ≈+=DD DD 44DD599F 210101021010V V V V ≈+≈⨯+=AB A F =++⋅=110≡F AB F =上述计算说明v I <2V 时,T 截止;v I >4.2V 时,T 饱和。
高数习题解答(第2章)

第二章 导数与微分习题2.12.设f (x ) 在点x = x 0可导,把下面各题中的字母A 分别用一个关于f ' (x 0)的式子表示出来?(1) A =)()(lim00x f x f x x x x --→(假定f ' (x 0) ≠ 0);(2) A =xx f x x f x x ∆-∆-→)()2(lim000;(3) x 0 = 0,f (0) = 0且A =xx f x )(lim 0→.解:(1) A =0lim→x )()(00x f x f x x --=0lim →x 0)()(1x x x f x f --=)('10x f (2) A =0lim →∆x (-2)xx f x x f ∆--∆-2)()2(00=-2f '(x 0)(3) A =0lim→x x x f )(=0lim →x xx f x x f )()(00-+=f '(x 0) 3.求曲线y = f (x )在点M 处的切线方程: (3) f (x ) = x 2, M(0, 0).解: 因为f ' (x )=2x , 从而f '(0)=0,因此, 所求切线方程为y -0= f '(0)(x -0), 即y =0. 5. 求曲线y = x 3 + x 上的与直线y = 4x 平行的切线.解: 与直线y = 4x 平行的切线的斜率为4. 因此y ' = 3x 2+1 = 4, 从中求出切点的横坐标x =±1. 把它们代入曲线方程y = x 3 + x , 求出切点的纵坐标为2和 -2, 即切点为(1, 2) 和 (-1, -2). 因此, 所求切线方程为: 4x – y -2 = 0 和4x – y +7 = 0. 6.设()⎩⎨⎧≥+<=0,0,sin x b ax x x x f . 讨论a, b 取何值时,f (x )在点x = 0处可导. 解:因为f (x )在x = 0处可导,所以f (x )在x = 0处连续.从而0lim →x (f (x )-f (0))=0, 即lim →x [(ax +b )-b ]=0且 0lim →x [sin x -b ]=0.由此推出b = 0.又,由于f (x )在x = 0处可导,所以下面极限存在且相等lim→x 0)0()(--x f x f =+→0lim x 0)0()(--x f x f =-→0lim x 0)0()(--x f x f .因为+→0lim x 0)0()(--x f x f =+→0lim x xbb ax -+= a ,-→0lim x xb x -sin =-→0lim x x xsin =1(因为b =0) 所以a =1.总之, 当a =1, b =0时f (x )在x = 0处可导. 8. 讨论下列函数在x = 0处的连续性和可导性:(1)y = | sin x |; (2) y = 00,,01sin 2=≠⎪⎩⎪⎨⎧x x xx . 解:(1)因为0lim →x |sin x |-sin0| =0lim →x |sin x | = 0, 所以函数y = |sin x |在x =0处连续.又因为在x =0处的坐导数-→0lim x 0|0sin ||sin |--x x =-→0limx 0|sin |-x x = -1, 在x =0处的右导数 +→0l i m x 0|0s i n ||s i n |--x x =+→0limx 0|sin |-x x =1, 可见左右导数不相等, 所以函数y =|sin x |在x =0处的导数不存在, 即不可导.(2)因为0lim →x x 2sinx 1-0=0lim →x sin x1=0, 所以函数y 在x =0处连续. 又因为0lim →x 01sin 2--x x x =0lim →x x sin x 1=0,所以函数y 在x = 0处可导.习题2.22. 求下列函数的导数: (6) x x x y -=ln ; (8) 21arctan xxy +=. 解: (6) y = x ln x - xy '= ln x + x x1-1= ln x. (8) y =21arctan x x+y '=222222)1()1(2)1(arctan )1(11x x x x x ++--++=4222)1(arctan 2)1(x x x x +++.3. 求下列函数在给定点处的导数: (3) ()ttt f --=11,求()4f '; (4) ()5532x x x f +-=,求()0f '和()2f '. 解: 因为f '(t ) = (t +11) '=2)1(211t t +-=-2)1(21t t +,所以, f '(4) = -361. (4) 因为f '(x ) = 3⨯2)5(1x --+52x ,所以, f '(0) = -253, f '(2) = 157. 习题2.31. 求下列反函数的导数:(2) 22arctan ⎪⎭⎫ ⎝⎛=x y ; (4) 212arcsin t t y +=. 解: (2) y '= 2arctan2x 2)2(121x +=244x +arctan 2x (4) y ' =22)12(11t t +-·222)1(22)1(2t t t t +⋅-+ =2222222)1()1()1(22t t t t ++-- =|1|)1()1(2222t t t -+-= ⎪⎩⎪⎨⎧>+-<+1,121,122222t tt t 2. 求下列复合函数的导数:(2) x x y 22cos cos +=; (4) x y ln ln =; (6) ()22ln a x x y -+=;(8) xx y 2sin =; (10) ()x x y cot csc ln -=; (12) xx y cos =. 解: (2) y '= -sin x 2 2x + 2cos(sin x ) = -2x sin x 2 - sin2x.(4) y ' =x ln 1·x 1=xx ln 1. (6) y ' =221ax x -+·(1+2222ax x -).=222222a x x a x xa x -+-+-=221ax -.(8) y ' =22sin 2cos 2x x x x -⋅=22sin 2cos 2x xx x -.(10) y ' =xx cot csc 1-(-c o txc ss x +c s c 2x ) = csc x.(12) y ' = (e cos x ln x ) '= e cos x ln x (-sin x ln x + cos x ·x 1) = x c os x (-sin x ln x +xxcos ). 习题2.43. 若()x f ''存在,求下列函数y 的二阶导数22d d xy:(1) ()2x f y =; (2) ()[]x f y ln =. 解: (1) y = f (x 2)dxdy= f '(x 2)2x =2xf '(x 2), 22dxy d = 2f '(x 2) + 2xf ''(x 2)2x = 2f '(x 2)+4x 2f ''(x 2). (2) y = ln[f (x )]dx dy =)()('x f x f 22dx d y =)()(')(')()("2x f x f x f x x f -+=)()]('[)(")(22x f x f x f x f -.习题2.52. 求曲线323232a y x =+在点⎪⎪⎭⎫⎝⎛a a 42,42处的切线方程和法线方程. 解: x 32+ y 32= a 32 两端对x 求导得:32x 31-+32y 31-dxdy= 0,从中解出dx dy = - (xy )31, 所以dx dy|)42,42(a a = -1.故所求切线方程为: x + y -22a = 0, 所求法线方程为: x - y = 0. 7. 计算由⎪⎩⎪⎨⎧==ta y ta x 33sin cos 所确定的函数y = y (x )的二阶导数.解: dx dy =)sin (cos 3cos sin 322t t a t t a -⋅⋅= -t t cos sin = - ta n t ,22dx y d = -se c 2t ·)sin (cos 312t t a - =t t a sin cos 314 .习题2.61.x 的值从1=x 变到01.1=x ,试求函数x x y -=22的增量和微分. 解: ∆y = y (1.01) - y (1) = 2(1.01)2-1.01-(2-1) = 0.0302, d y = (4x -1)d x= (4⨯1.01-1) · (1.01-1) = 0.03035. 计算下列函数的近似值: (2) 01.1ln .解: 设f (x ) = ln x , 取x 0 =1, x =1.01. 则∆x = x - x 0 =1.01-1= 0.01. 因为 f '(x )=x1, 从而f '(x 0) =1. 故ln 1.01 = ln x 0 + f '(x 0)∆x = ln 1 + 1·(0.01) = 0.01.总习题21. 利用导数的定义求导数: (2) 设()()1ln ≥<⎩⎨⎧+=x x x xx f ,求()0f '. (3) 设()00>≤⎩⎨⎧+=x x bax e x f x,若函数f (x )在点x = 0处连续且可导,求系数a 和b .解:(2) 因为f -'(x ) =-→0lim x 00--x x = 1, f +'(0) = +→0lim x xx 0)1ln(-+= 1, 故f '(0) =1.(3)由f (x )在x =0处连续,得0lim →x f (x )-f (0) =0, 即+→0lim x (ax +b )-1=-→0lim x e x -1=0. 从中求得b =1.因为f (x )在点x = 0处且可导,所以在点x = 0处左右导数存在且相等, 而f -'(0) =-→0lim x xe x 1-=1, f +'(0) = +→0lim x x ax 1-= a , 故a =1. 总之a =1, b =1.5. 证明题:(1) 设()x f 是可导函数,试证: 若()x f 为偶函数时,则()x f '为奇函数;若()x f 为奇函数时,则()x f '为偶函数.(2) 验证函数22x x y -=满足关系式013=+''y y .证明: (1)因为f (x )为偶函数,所以f (-x ) = f (x ). 因为()x f 是可导函数,可上式两端对x 求导得 -f '(-x ) = f '(x ), 即f '(-x ) = -f '(x ), 这说明了f '(x )为奇函数.当f (x )为奇函数时, f (-x ) = -f (x ). 可上式两端对x 求导得 -f '(-x ) = -f '(x ), 即f '(-x ) = f '(x ), 这说明了f '(x )为为偶函数。
胡寿松自控习题答案 第二章习题解答

(2)
iC 2
=
uC1
+ iC1R R
K 2 x0 = f (x& − x&0 )
消去中间变量 x,可得系统微分方程
f (K1
+
K
2
)
dx0 dt
+
K1K2 x0
=
K1 f
dxi dt
对上式取拉氏变换,并计及初始条件为零,得系统传递函数为
X 0 (s) =
fK1s
X i (s) f (K1 + K2 )s + K1K2
③图 2—57(c):以 x0 的引出点作为辅助点,根据力的平衡原则,可列出如下原始方程:
u0
= (iC
+ iR1 )R2
=
C
duC dt
+
uC R1
R2
=
C
d
(ui −
dt
u0
)
+
ui
− u0 R1
R2
整理得:
CR2
du0 dt
+ C
R2 R1
+ 1u0
= CR2
dui dt
+C
R2 R1ui − u0 = uC1 (1)
iC1
=
C1
duC1 dt
K
=
1
K2
( f1 s + 1)( f 2 s + 1) + f1
K 1
K2
K2
所以图 2-58(a)的电网络与(b)的机械系统有相同的数学模型。 2—4 试分别列写图 2-59 中个无源网络的微分方程式。
解:(a) :列写电压平衡方程:
《理论力学》(范钦珊)习题解答第2篇第46章.doc

(b)第2篇 工程运动学基础第4章 运动分析基础4-1 小环A 套在光滑的钢丝圈上运动,钢丝圈半径为R (如图所示)。
已知小环的初速度为v 0,并且在运动过程中小环的速度和加速度成定角θ,且 0 < θ <2π,试确定小环 A的运动规律。
解:Rv a a 2ns in ==θ,θs in 2R v a =θθt an co s d d 2tR v a tv a ===,⎰⎰=t v v t R v v 02d t an 1d 0θ t v R R v t s v 00t an t an d d -==θθ⎰⎰-=t s t t v R R v s 0000d tan tan d θθtv R R R s 0t an t an ln tan -=θθθ4-2 已知运动方程如下,试画出轨迹曲线、不同瞬时点的 1.⎪⎩⎪⎨⎧-=-=225.1324t t y tt x , 2.⎩⎨⎧==t y t x 2cos 2sin 3解:1.由已知得 3x = 4y (1) ⎩⎨⎧-=-=t y t x3344 t v 55-=⎩⎨⎧-=-=34y x5-=a 为匀减速直线运动,轨迹如图(a ),其v 、a 图像从略。
2.由已知,得2ar cco s 213ar cs i n y x =化简得轨迹方程:2942x y -=(2)轨迹如图(b ),其v 、a 图像从略。
4-3 点作圆周运动,孤坐标的原点在O 点,顺钟向为孤坐标的正方向,运动方程为221Rt s π=,式中s 以厘米计,t 以秒计。
轨迹图形和直角坐标的关系如右图所示。
当点第一次到达y 坐标值最大的位置时,求点的加速度在x 和y 轴上的投影。
解:Rt s v π== ,R v a π== t,222n Rt Rv a π==y 坐标值最大的位置时:R Rt s 2212ππ== ,12=∴tR a a x π==t ,R a y 2π-=4-4 滑块A ,用绳索牵引沿水平导轨滑动,绳的另一端绕在半径为r 的鼓轮上,鼓轮A习题4-1图习题4-2图习题4-3图e e -t (c)e e -t υ (b)R t R +υ (a)习题4-6图以匀角速度ω转动,如图所示。
近世代数习题解答2

近世代数习题解答第二章 群论1 群论1. 全部整数的集合关于一般减法来讲是不是一个群?证 不是一个群,因为不适合结合律.2. 举一个有两个元的群的例子.证 }1,1{-=G 关于一般乘法来讲是一个群.3. 证明, 咱们也能够用条件1,2和下面的条件 ''5,4来作群的概念:'4. G 至少存在一个右单位元e ,能让a ae = 关于G 的任何元a 都成立'5. 关于G 的每一个元a ,在G 里至少存在一个右逆元,1-a 能让 e aa =-1证 (1) 一个右逆元必然是一个左逆元,意思是由e aa=-1得e a a =-1因为由'4G 有元'a 能使e a a =-'1因此))(()('111a a a a e a a ---=e a a a e a a aa a ====----'1'1'11][)]([ 即 e a a =-1(2) 一个右恒等元e 必然也是一个左恒等元,意即 由 a ae = 得 a ea = a ae a a a a aa ea ====--)()(11即 a ea =如此就取得群的第二概念. (3) 证 b ax =可解 取b a x 1-=b be b aa b a a ===--)()(11这就取得群的第一概念.反过来有群的概念取得''5,4是不困难的.2 单位元,逆元,消去律1. 假设群G 的每一个元都适合方程e x =2,那么G 确实是互换群. 证 由条件知G 中的任一元等于它的逆元,因此对G b a ∈,有ba a b ab ab ===---111)(.2. 在一个有限群里阶大于2的元的个数是偶数.证 (1) 先证a 的阶是n 则1-a 的阶也是n .e e a a e a n nn===⇒=---111)()(假设有n m 〈 使e a m =-)(1 即 e a m =-1)(因此 1-=e a m e a m =∴ 这与a 的阶是n 矛盾.a 的阶等于1-a 的阶 (2) a 的阶大于2, 那么1-≠a a 假设 e a a a =⇒=-21 这与a 的阶大于2矛盾(3) b a ≠ 那么 11--≠b a总起来可知阶大于2的元a 与1-a 双双显现,因此有限群里阶大于2的元的个数必然是偶数3. 假定G 是个数一个阶是偶数的有限群,在G 里阶等于2的元的个数必然是奇数.证 依照上题知,有限群G 里的元大于2的个数是偶数;因此阶2≤的元的个数仍是偶数,但阶是1的元只有单位元,因此阶 2≤的元的个数必然是奇数.4. 一个有限群的每一个元的阶都是有限的.证 G a ∈故 G a a a a nm∈ ,,,,,,2由于G 是有限群,因此这些元中至少有两个元相等: nma a = )(n m 〈 故 e amn =-m n -是整数,因此a 的阶不超过它.4 群的同态假定在两个群G 和-G 的一个同态映射之下,-→a a ,a 和-a 的阶是不是必然相同? 证 不必然相同 例如 }231,231,1{i i G +-+-= }1{=-G对一般乘法-G G ,都作成群,且1)(=x φ(那个地址x 是G 的任意元,1是-G 的元)由 φ可知 G ∽-G 但231,231i i --+-的阶都是3. 而1的阶是1.5 变换群1. 假定τ是集合的一个非一一变换,τ会可不能有一个左逆元1-τ,使得εττ=-1?证 咱们的回答是回有的},3,2,1{ =A1τ: 1→1 2τ 1→12→1 2→3 3→2 3→4 4→3 4→5 … …τ显然是一个非一一变换但 εττ=-12. 假定A 是所有实数作成的集合.证明.所有A 的能够写成b a b ax x ,,+→是有理数,0≠a 形式的变换作成一个变换群.那个群是不是一个互换群? 证 (1) :τ b ax x +→:λ d cx x +→:τλ d cb cax d b ax c x ++=++→)( d cb ca +,是有理数 0≠ca 是关闭的.(2) 显然时候结合律(3) 1=a 0=b 那么 :ε x x → (4) :τ b ax + )(1:1ab x a x -+→-τ而 εττ=-1因此组成变换群.又 1τ: 1+→x x :2τ x x 2→ :21ττ )1(2+→x x :12ττ 12+→x x 故1221ττττ≠因此不是互换群.3. 假定S 是一个集合A 的所有变换作成的集合,咱们临时仍用旧符号τ:)('a a a τ=→来讲明一个变换τ.证明,咱们能够用21ττ: )()]([2121a a a ττττ=→来规定一个S 的乘法,那个乘法也适合结合律,而且关于那个乘法来讲ε仍是S 的单位元. 证 :1τ )(1a a τ→ :2τ )(2a a τ→那么:21ττ )()]([2121a a a ττττ=→ 显然也是A 的一个变换. 此刻证那个乘法适合结合律:)]()[(:)(321321a a ττττττ→)]]([[321a τττ= =→)]([:)(321321a a ττττττ)]]([[321a τττ 故 )()(321321ττττττ= 再证ε仍是S 的单位元 :ε )(a a a ε=→ :ετ )()]([a a a ττε=→τ:τε )()]([a a a τετ=→∴ τεετ=4. 证明一个变换群的单位元必然是恒等变换。
电磁场与电磁波课后习题及答案七章习题解答 (2)

《电磁场与电磁波》习题解答 第七章 正弦电磁波求证在无界理想介质内沿任意方向e n (e n 为单位矢量)传播的平面波可写成j()e n r t m βω⋅-=e E E 。
解 E m 为常矢量。
在直角坐标中故 则 而 故可见,已知的()n j e r t m e βω⋅-=E E 满足波动方程 故E 表示沿e n 方向传播的平面波。
试证明:任何椭圆极化波均可分解为两个旋向相反的圆极化波。
:解 表征沿+z 方向传播的椭圆极化波的电场可表示为式中取显然,E 1和E 2分别表示沿+z 方向传播的左旋圆极化波和右旋圆极化波。
在自由空间中,已知电场3(,)10sin()V/my z t t z ωβ=-E e ,试求磁场强度(,)z t H 。
解 以余弦为基准,重新写出已知的电场表示式这是一个沿+z 方向传播的均匀平面波的电场,其初相角为90︒-。
与之相伴的磁场为 均匀平面波的磁场强度H 的振幅为1A/m 3π,以相位常数30rad/m 在空气中沿z -e 方向传播。
当t=0和z=0时,若H 的取向为y -e,试写出E 和H 的表示式,并求出波的频率和波长。
解 以余弦为基准,按题意先写出磁场表示式 与之相伴的电场为由rad/m β=30得波长λ和频率f 分别为 '则磁场和电场分别为一个在空气中沿ye +方向传播的均匀平面波,其磁场强度的瞬时值表示式为(1)求β和在3ms t =时,z H =的位置;(2)写出E 的瞬时表示式。
解(1)781π10πrad /m rad /m 0.105rad /m 31030β==⨯==⨯在t =3ms 时,欲使H z =0,则要求 若取n =0,解得y =。
考虑到波长260mπλβ==,故因此,t =3ms 时,H z =0的位置为(2)电场的瞬时表示式为在自由空间中,某一电磁波的波长为0.2m 。
当该电磁波进入某理想介质后,波长变为0.09m 。
设1r μ=,试求理想介质的相对介电常数r ε以及在该介质中的波速。
《复变函数》第四版习题解答第2章

(2)由于 ∂u = 6x2 , ∂u = 0 , ∂v = 0 , ∂v = 9 y2
∂x
∂y
∂x
∂y
在 z 平面上处处连续,且当且仅当 2x2 = 3y2 ,即 2x ± 3y = 0 时,u,v 才满足 C-R 条件,故
f ( z ) = u + i v = 2x3 + 3y3i 仅在直线 2x ± 3y = 0 上可导,在 z 平面上处处不解析。
解 (1)由于 ∂u = 2x, ∂u = 0, ∂v = 0, ∂v = −1
∂x
∂y ∂x ∂y
在 z 平面上处处连续,且当且仅当 x = − 1 时,u,v 才满足 C-R 条件,故 f (z) = u + i v = x − i y 仅在
2
直线 x = − 1 上可导,在 z 平面上处处不解析。 2
(5)命题假。如函数 f (z) = z Re z = x2 + i xy 仅在点 z=0 处满足 C-R 条件,故 f (z)仅在点 z=0
处可导。
(6)命题真。由 u 是实常数,根据 C-R 方程知 v 也是实常数,故 f (z) 在整个 D 内是常数;
后面同理可得。
7.如果 f (z) = u + i v 是 z 的解析函数,证明:
解
(1)命题假。如函数 f (z) =| z |2 = x 2 + y 2 在 z 平面上处处连续,除了点 z=0 外处处不可导。 (2)命题假,如函数 f (z) =| z |2 在点 z=0 处可导,却在点 z=0 处不解析。
(3)命题假,如果 f (z)在z0点不解析,则z0称为f (z)的奇点。如上例。 (4)命题假,如 f (z) = sin x ch y, g(z) = i cos x sh y , z = (π / 2, 0) 为它们的奇点,但不 是 f (z) + g(z) 的奇点。
《新编基础物理学》 第二章习题解答和分析2

2-19.一质量为0.15kg 的棒球以-1040m s v =⋅的水平速度飞来,被棒打击后,速度与原来方向成1350角,大小为-150m s v =⋅。
如果棒与球的接触时间为0.02s ,求棒对球的平均打击力大小及方向。
分析:通过动量定理求出棒对球在初速方向与垂直初速方向的平均打击力,再合成求平均力及方向。
解:: 10cos135F t mv mv -=︒- ①在和初速度垂直的方向上,由动量定理有: 2cos45F t mv =︒ ②又F =③由①②③带入数据得:624F N =与原方向成F arctan ︒=⎪⎪⎭⎫⎝⎛-15512F F 角2-20. 将一空盒放在秤盘上,并将秤的读数调整到零,然后从高出盒底h 将小钢珠以每秒B 个的速率由静止开始掉入盒内,设每一个小钢珠的质量为m ,若钢珠与盒底碰撞后即静止,试求自钢珠落入盒内起,经过t 秒后秤的读数。
分析:秤的读数是已落在盒里石子的重量与石子下落给秤盘平均冲力之和,平均冲力可由动量定律求得。
解:对在dt 的时间内落下的钢珠,由动量定理:0Fdt -=-所以t 秒后秤的读数为:mgBt +2-21. 两质量均为M 的冰车头尾相接地静止在光滑的水平冰面上,一质量为m 的人从一车跳到另一车上,然后再跳回,试证明,两冰车的末速度之比为()m M +/M 。
分析:系统动量守恒。
解:任意t 时刻,由系统的动量守恒有:12()0Mv M m v -+=所以两冰车的末速度之比: ()M m M v v //21+=2-22. 质量为3.0kg 的木块静止在水平桌面上,质量为5.0g 的子弹沿水平方向射进木块。
两者合在一起,在桌面上滑动25cm 后停止。
木块与桌面的摩擦系数为0.20,试求子弹原来的速度。
分析:由动量守恒、动能定理求解。
解:在子弹沿水平方向射进木块的过程中,由系统的动量守恒有:0()Mv M m v =+①一起在桌面上滑动的过程中,由系统的动能定理有:21()()2M m v M m gl μ+=+ ②由①②带入数据有: 0600/v m s =2-23. 光滑水平平面上有两个物体A 和B ,质量分别为A m 、B m 。
时间序列分析习题解答(2):上课展示的典型题

时间序列分析习题解答(2):上课展⽰的典型题由于本答案由少部分⼈完成,难免存在错误,如有不同意见欢迎在评论区提出。
第⼀题⼀、已知零均值平稳序列{X t}的⾃协⽅差函数为γ0=1,γ±1=ρ,γk=0,|k|≥2.计算{X t}的偏相关系数a1,1,a2,2。
计算最佳线性预测L(X3|X2),L(X3|X2,X1)。
计算预测的均⽅误差E[X3−L(X3|X2)]2,E[X3−L(X3|X2,X1)]2。
证明:ρ应满⾜|ρ|≤1 2。
若ρ=0.4,计算{X t}的谱密度函数,给出{X t}所满⾜的模型。
解:(1)由Yule-Walker⽅程,a1,1=γ1/γ0=ρ,1ρρ1a2,1a2,2=ρ,解得a2,2=−ρ2 1−ρ2.(2)由预测⽅程,有L(X3|X2)=ρX2。
设L(X3|X2,X1)=a2X2+a1X1,则1ρρ1a1a2=ρ,a1=−ρ21−ρ2,a2=ρ1−ρ2.所以L(X3|X2,X1)=−ρ2X1+ρX21−ρ2.(3)预测的均⽅误差是E(X3−ρX2)2=(1+ρ2)γ0−2ργ1=1−ρ2,E X3−−ρ2X1+ρX21−ρ22=(1−ρ2)2+ρ4+ρ2(1−ρ2)2−2ρρ3+ρ(1−ρ2)(1−ρ2)2 =2ρ4−3ρ2+1(1−ρ2)2=1−2ρ21−ρ2.(4)由于{X t}的⾃协⽅差函数1后截尾,所以它是⼀个MA(1)模型,即存在b≤1,⽩噪声εt∼WN(0,σ2)使得X t=εt+bεt−1.于是γ0=(1+b2)σ2=1,γ1=bσ2=ρ,所以ρ(b)=b1+b2,在b∈[−1,1]上ρ(b)是单调的,所以−12≤ρ(−1)≤ρ≤ρ(1)=12.(5)由谱密度反演公式,容易得到[][][][][][]()[][]Processing math: 49%f(λ)=12π[1+0.8cosλ]=12π451+cosλ+14=(2/√5)22π1+12(e iλ)2.所以X t=εt+12εt−1,{εt}∼WN0,45.第⼆题⼆、设零均值平稳序列{X t}的⾃协⽅差函数满⾜γk=187×25|k|,k≠0,k∈Z.当γ0取何值时,该序列为AR(1)序列?说明理由并给出相应的模型。
习题2及解答

习题 21.设p 、q 都是素数,且7p +q ,pq +11也都为素数,求()()22pqp q q p ++的值.【答案】若p 、q 都是奇数,则7p +q 为偶数,它不是素数,故p 、q 中有一个为偶数.情形一 设p 为偶数,则p =2,此时由7p +q 为素数,知q 为奇素数,若q ≠3,则q ≡1或2(mod3) . 若q ≡1 (mod3),则 7p +q =14+q ≡0(mod3), 矛盾;若q ≡2(mod3),则pq +11=2q +11≡4+11≡0(mod3),亦矛盾,所以q =3,此时7p +q =17,pq +11=17,都是素数,故 (p 2+q p )( q 2+p q )=(22+32)( 32+23)=221. 情形二 设q 为偶数,则q =2,同上讨论可知p =3,此时(p 2+q p )( q 2+p q )=(32+23)( 22+32)=221.综上可知,所求的值为221.2.设12345p p p p p <<<<是5个素数,且12345p p p p p ,,,,成等差数列.求5p 的最小值. 【答案】设d 为公差,则p 1,p 1+d ,p 1+2d ,p 1+3d ,p 1+4d 都是素数. 若2d ,即d 为奇数,则p 1+d ,p 1+2d 中有一个为偶数,它不是素数.若3d ,则p 1+d ,p 1+2d ,p 1+3d 中有一个为3的倍数(它们构成模3的一个完系),矛盾. 若5d ,则p 1,p 1+d ,…,p 1+4d 中有一个为5的倍数只能是p 1=5,这时公差d 是6的倍数. 而5,11,17,23,29是5个成等差的素数数列,所以,p 5最小为29.3.对每个正整数n ,用()S n 表示n 在十进制表示下各数码之和.证明:对任意正整数m ,存在正整数n ,使得()()3S n mS n =.【答案】注意到,对任意正整数k ,(1008)k S 个=9,于是,设1008k 个=3n ,则n =336k 个,故S (n )=3k +6,这样,对任意正整数m ,取k =3m -2,就有S (n )=mS (3n ).说明 由S (3n )≡3n (mod9),故要求3|S (n ),进而3|n ,所以在先确定3n 时,要寻找一个9的倍数(例如1002k 个作为3n 就不能满足条件) .另外,在S (2n )与S (n )之间没有上述性质,事实上,可证:S (2n )≤2S (n );S (n )≤5S (2n ).4.求最大的正整数k ,使得存在正整数n ,满足2|31kn+. 【答案】注意到,当n 为偶数时,设n =2m ,有3n =9m ≡1(mod8), 当n =2m +1时,3n =9m ×3≡3(mod8),所以,对任意正整数n ,有3n +1=2或4(mod8), 故k ≤2.又22|31+1,所以,所求k 的最大值为2.5.设n 为正整数.证明:存在十进制表示中只出现数码0和1的正整数m ,使得|n m .【答案】考虑数列 1,11,111,…,111n+个,其中必有两个数对模n 同余(因为任何整数除以n 所得的余数只能为0,1,2,…,n -1,共n 种情况),它们的差(大的减小的)就是符合要求的m .6.设n 为是一个正奇数.证明:存在一个十进制表示中每个数码都是奇数的正整数m ,使得|n m . 【答案】如果(5,n )=1,那么由上题的结论,知存在m =11i 个0j 个,使得n |m ,而n 为奇数,结合5n ,知(n ,10)=1,故n |11i 个.命题获证.如果5|n ,设5α|n ,那么可写n =5α·n 1,其中5n 1.利用2.2节例5的结论,可知存在一个α位的正整数m 1,使得5α|m 1,且m 1的每个数码都是奇数,这时,考虑数m 1, 11m m ,…,111n m m +1个,这里11i m m 个表示i 个m 1连写形成的十进制数(故上面所列的数都是5α的倍数),则存在1≤i <j ≤n 1+1,使得 11j m m 个≡11i m m 个(mod n 1),结合(n 1,10)=1,可知n 1|11j-i m m 个,于是记m =11j-i m m 个,则m 中的每个数码都是奇数,且5α|m ,n 1|m ,而 (5α,n 1)=1, 故5α·n 1|m ,即n |m . 命题获证.7.证明:对每个正整数n ,数19817n⨯+都是合数. 【答案】若n 为偶数,则 19×8n +17≡1×(-1)n +2≡0(mod3);若n ≡1(mod4),写n =4k +1,则19×8n +17=19×642k ×8+17≡6×(-1)2k ×8+4≡0(mod13);若n ≡3(mod4),则 19×8n +17=19×642k +1×8+17≡(-1)×(-1)2k +1×3+2≡0(mod5) . 所以,对任意正整数n ,数19×8n +17是合数.8.Fibonaccia 数列{}n F 定义如下:121F F ==,21n n n F F F ++=+,n =1,2,…. (1)证明:该数列任意连续10项之和是11的倍数;(2)求最小的正整数k ,使得该数列中任意连续k 项之和是12的倍数. 【答案】考虑数列{F n }中每一项除以11(或12)所得的余数. ⑴{F n (mod11)}:1,1,2,3,5,-3,2,-1,1,0,1,1,…,所以{F n (mod11)}是以10为周期的纯周期数列,因此{F n }中任意连续10项之和≡1+1+2+3+5+(-3) +2+ (-1)+1+0=11≡0(mod11), 命题获证.⑵{F n (mod12)}:1,1,2,3,5,-4,1,-3,-2,-5,5,0,1,1,…是以12为周期的纯周期数列.直接验证,可求出满足条件的最小正整数k =36.说明 若k 是满足⑵的最小正整数,而n 是满足⑵的正整数,则k |n (这个结论请读者证明) .因此,找到满足条件的n =36 ({F n (mod12) }的每个周期内各数之和≡4(mod12))后,只需验证36的正因数不合要求,就能断言36是符合条件的最小正整数.9.设整数a 、b 满足:2221|a b +.证明:22441|a b +.【答案】先分别证明:⑴若a 2+b 2≡0(mod3),则a ≡b ≡0(mod3) ; ⑵若a 2+b 2≡0(mod7),则a ≡b ≡0(mod7) .这只需注意到,对任意整数x ,都有x 2≡0或1(mod3), 及 x 2≡0,1,2或4(mod7), 即可证出.现在由21|a 2+b 2可推出21|a ,21|b ,故212|a 2+b 2,所以命题成立.10.正整数a 、b 、c 满足:222c a b ab =++.证明:c 有一个大于5的素因子.【答案】我们分别证明: ⑴若2|c ,则2|a ,2|b ; ⑵若3|c ,则3|a ,3|b ; ⑶若5|c ,则5|a ,5|b . ⑴的证明是平凡的.⑵的证明只需注意到 c 2=a 2+ab +b 2=(a -b ) 2+3ab ,就容易证出. 对于⑶,由条件,知 4c 2=4a 2+4ab +4b 2=3a 2+(a +2b )2, 而对任意整数x ,知 x 2≡0,1,4(mod5), 于是,由 3x 2+y 2≡0 (mod5), 可知 x 2≡y 2≡0 (mod5), 即 x ≡y ≡0 (mod5).因此,由5|c ,知 3a 2+(a +2b )2≡0 (mod5), 故 a ≡a +2b ≡0(mod5), 可得 a ≡b ≡0(mod5), 所以⑶成立.回到原题,当c 是2、3或5的倍数时,c 2=a 2+ab +b 2两边可分别约去22、32或52后,等式的形式保持不变.所以c 有一个大于5的素因子.11.将整数1,2,…,9填入一个3×3的表格,每格一个数,使得每行、每列及每条对角线上各数之和都是9的倍数.(1)证明:该表格中正当中那个方格内的数是3的倍数;(2)给出一个正当中方格内所填数为6的满足条件的放置方法.【答案】⑴设表格中第i 行、第j 列的方格上所填的数为a ij ,1≤i ≤3,1≤j ≤3, 则 a 11+a 22+a 33≡a 13+a 22+a 31≡a 12+a 22+a 32≡a 21+a 22+a 23≡0(mod9), 于是它们求和后,得(a 11+a 12+a 13+a 21+a 22+a 23+a 31+a 32+a 33)+3a 22≡0(mod9), 即 3a 22+(1+2+…+9)≡0(mod9), 故 9|3a 22, 即 3|a 22,从而表格中正当中的格子内所填数为3的倍数. ⑵下表给出的例子是中间格为612.下面的算式给出了一种判别一个数是否为19的倍数的方法:每次去掉该数的最后一位数字,将其两倍与剩下的数相加,依此类推,直到数变为20以内的数为止,若最后一个数为19,则最初的那个数为19的倍数,否则原数不是19的倍数. 6 7 9 4 4 8 6 8 0 2 4 6 8 4 8 7 6 1 2 1 9 4 4 9 7 6 12 4 5 0 9 1 8 4 6 8 16 6 2 4 1 0例如上面判定了67944为19的倍数,而44976不是19的倍数.(1)试证明:上面的判别方法是正确的;(2)请给出判别一个数是否为29的倍数的类似方法. 【答案】一般地,设数10n n a a a -是一个十进制表示下的n +1位数,则若它是19的倍数,那么1011n n a a a -+a 0=10n n a a a -≡0(mod19),故 2011n n a a a -+2a 0≡0(mod19), 即 11n n a a a -+2a 0≡0(mod19),这表明每次操作后的结果都是19的倍数. 另一方面,若 11n n a a a -+2a 0≡0(mod19), 则 1011n n a a a -+20a 0≡0(mod19), 这表明 1011n n a a a -+a 0≡0(mod19),即 10n n a a a -≡0(mod19),所以,每次操作后的结果是19的倍数,则操作前该数也是19的倍数. 所以,题给的判别方法是正确的.对于29而言,类似的判别方法是:每次去掉最后一位,将它的3倍与剩下的数相加,以此类推,直到变为30以内的数为止.若最后的结果为29,则原数是29的倍数,否则原数不是29的倍数.13.能否将2010×2010的方格表的每个方格染成黑色或白色,使得关于表格的中心对称的方格颜色不同,且每行、每列中黑格数与白格数都各占一半? 【答案】不能做到.事实上,若存在满足条件的染色方式,我们在黑格中都写上+1,白格中都写上-1,并依表格的中心所在的两条方格线将表格分为4块,左上角那块中各数之和设为A ,右上角那块为B ,左下角那块为C ,右下角那块为D .由条件,可知A ,B ,C ,D 都是10052个奇数之和,故A ,B ,C ,D 都为奇数,且A =-D ,B =-C (因为关于表格的中心对称的方格不同色),而且A +B =A +C =0(这里用到每行、每列中黑、白格数各占一半).所以,A -C =A +C =0,这要求A =C =0,但A 、C 都是奇数,矛盾.14.标号为1,2,…,100的火柴盒中有一些火柴,如果每次提问允许问其中任意15盒中所有火柴数之和的奇偶性.那么要确定1号盒中火柴数的奇偶性,至少需要提问几次? 【答案】至少需要3次提问.先证“3次提问是足够的” .例如: 第一次为:a 1,a 2,…,a 15;第二次为:a 1,a 2,…,a 8,a 16,a 17,…,a 22; 第三次为:a 1,a 9,a 10,…, a 22.其中a i 表示第i 盒中火柴的数目.这样,3个答案之和的奇偶性与a 1的奇偶性相同(其余每盒在3次提问中恰好出现2次) .因此,经3次提问可确定a 1的奇偶性.再证“至少需要3次提问” .如果提问只有两次,且两次中都出现a 1,那么在两次提问中必有a i 和a j ,使得a i 只在第1次提问中出现,而a j 只在第二次提问中出现,这样同时改变a 1、a i 、 a j 的奇偶性,每次答案是相同的,从而不能确定a 1的奇偶性.如果两次中都不出现a 1,在a 1都不出现时,改变a 1的奇偶性;在a 1只出现一次时,改变a 1与a i (这里a i 是与a 1同时出现的某个火柴盒)的奇偶性,那么两次答案仍是相同的,不能确定a 1的奇偶性. 综上可知,至少需要提问3次.15.求所有的正整数n ,使得可以在一个n ×n 的方格表的每个方格内写上+1或-1,满足:每个标号为+1的方格的相邻格中恰有一个标号是-1,而每个标号为-1的方格的相邻格中恰有一个标号是+1. 【答案】用a ij 表示第i 行、第j 列上的方格内所填的数.如果存在符合要求的填法,那么我们不妨设a 11=1(否则改变表格中所有数的符号再讨论),此时a 21与a 22中恰好有一个为-1,不妨设a 21=-1(否则将表格的第2行与第2列互换后再讨论),则a 12=1,进一步讨论,知a 22=-1,a 13=1,…,可知第1行中的数都是1,第2行中的数都是-1,进而,第3行中的数都是-1,第4行中的数都是1,依此递推,知当且仅当i ≡1(mod3)时,第i 行中的数都是1,而其余每行中的数都是-1.如果,n ≡0(mod3),那么第n 行的数为-1,该行上的每个方格中相邻方格上的书都是-1,不合要求,直接验证可知其余情况都合要求. 所以,当且仅当3n ,n >1时,存在符合要求的填法.16.设12100a a a ,,…,是1,2,…,100的一个排列,令12i i b a a a =++…+,i =1,2,…,100,记i r 为i b 除以100所得的余数.证明:12100r r r ,,…,中至少有11个不同的数.【答案】若r 1,r 2,…,r 100中只有10个不同的数,则对i =1,2,…,99,r i +1-r i 只有102-9=91(这里减去9是因为r i +1=r i 时所得的值都是零)种不同取值.但是在模100的意义下,r i +1-r i 依次为a 2,a 3,…,a 100,共有99种不同的取值,矛盾.所以r 1,r 2,…,r 100中至少有11个不同的值.17.求所有满足下述条件的正整数a 的个数:存在非负数0122001x x x x ,,,…,,使得0xa =200112x x x a a a +++.【答案】若a 是一个满足条件的数,则0x a >1,故a >1.此时,对 0x a =1x a +2x a +…+2001x a 两边模a -1,知 1≡200111++个(mod a -1),所以 a -1|2000.另一方面,若a >1满足a -1|2000,则我们在x 1,x 2,…,x 2001中取a 个数为0,a -1个为1,a -1个为2,…,a -1个为k -1,这里k =20001a -,并取x 0=k ,就有0x a =1x a +2x a +…+2001x a . 所以,当且仅当a >1且a -1|2000时,a 为满足条件的数,这样的a 共有20个.18.设m 、n 为正整数,m >1.证明:()21|mm n -的充要条件是()221|21mn--. 【答案】若m (2m -1)|n ,设n =m (2m -1)k ,则 2n-1=(21)2m m k--1=()()212mmk--1=()21mk -A ,其中 A =()222mmk -+()232mmk -+…+()12mk +1.注意到 2mk -1=()2km -1≡1k -1≡0(mod2m -1), 所以 ()21m -2|2n -1.反过来,若()21m -2|2n -1,我们先证m |n .若否,设n =mq +r ,0<r <m ,则由 2n ≡1(mod2m -1),知 (2m )q ·2 r ≡1(mod2m -1), 故 2 r ≡1(mod2m -1), 但是 1≤2 r -1<2m -1. 所以2m -12 r -1,矛盾.因此m |n .现设n =mq ,则 2n -1=(2m -1)×B ,其中 B =(2m )q -1+(2m )q -2+…+2m +1, 由 (2m -1)2|2n -1, 知 2m -1|B ,又 B =1 q -1+1 q -2+…+1=q (mod 2m -1), 所以 2m -1|q , 从而 m (2m -1)|n . 命题获证.19.设正整数a 、b 互素,p 为奇素数.证明:1p p a b a b p a b ⎛⎫⎪⎝⎭++,=或+. 【答案】记A =p pa b a b ++=a p -1―a p -2b +…―ab p -2+b p -1,结合p 为奇数及b ≡―a (mod a +b ),知A ≡111p p p p a a a ---+++个=pa p -1(mod a +b ).而 (a ,b )=1, 故 (a ,a +b )=1,所以 (a +b ,p pa b a b++)=(a +b ,A )=(a +b ,pa p -1)=(a +b ,p )=1或p .20.求最小的正整数a ,使得对任意整数x ,都有()13565|5139x x ax ++.【答案】由条件,知65|(18+9a )(取x =1),而(9,65)=1,故65|a +2, 即a ≥63.当a =63时,利用Fermat 小定理知:对任意整数x ,都有5x 13+13x 5+9ax ≡13x +9ax ≡(3+(-1)×3)x ≡0(mod5 ); 5x 13+13x 5+9ax ≡5x +9ax ≡(5+9×(-2))x ≡0(mod13 ). 所以 65|5x 13+13x 5+9ax . 综上可知,所求的最小正整数a =63.21.是否存在整数a 、b 、c ,使得方程20ax bx c ++=和()()()21110a x b x c +++++=都有两个整数根?【答案】不存在这样的整数a 、b 、c .事实上,若a 、b 、c 满足条件,我们不妨设a 为偶数(否则用-(a +1)、-(b +1)、-(c +1)代替a 、b 、c 讨论),由条件,结合韦达定理知-b a 与ca都是整数,故b 、c 都是偶数,所以a +1、b +1、c +1都是奇数.此时,对任意整数x ,有(a +1)x 2+(b +1)x +(c +1)≡x 2+x +1=x (x +1)+1≡1(mod2)(最后一步用到x 与x +1中有一个偶数).这表明方程(a +1)x 2+(b +1)x +(c +1)=0没有整数根,矛盾.22.求所有的正整数组(x ,y ,z ,w ),使得x !+y !+z !=w !. 【答案】不妨设x ≤y ≤z <w ,则w ≥z +1,若z ≥3,则w !≥(z +1)·(z !)≥z !+y !+x !, 矛盾,故 z ≤2.若z =1,则x =y =z =1,此时w !=3,不存在这样的w ,故z =2. 此时w ≥3,故 w !≡0(mod3),所以 x !+y !≡1(mod3), 而 x ≤y ≤2, 故只能是 x =y =2, 此时 w =3,故 (x ,y ,z ,w )=(2,2,2,3).23.求满足下述条件的整数数组(a ,b )的组数:0≤a ,b ≤36,且()220mod37a b +=.【答案】注意到,a 2+b 2≡a 2-36b 2(mod37),故由条件知 37|a 2-36b 2, 即 37|(a -6b )(a +6b ),所以 37|a -6b 或37|a +6b .因此,对每个1≤b ≤36,可知恰有两个a (a ≡±6b (mod37)) 满足条件, 而b =0时,由a 2+b 2≡0(mod37)知a =0. 所以,满足条件的(a ,b )共有2×36+1=73(组).24.设m 、n 为正整数,且22|mn m n m ++.证明:m 是一个完全平方数.【答案】有条件可设m 2+n 2+m =kmn ,k 为正整数,这样,关于n 的一元二次方程n 2-kmn +m 2+m =0①有正整数解,故△=(km ) 2-4(m 2+m )=m (k 2m -4m -4)是一个完全平方数.若m 为奇数,则(m ,k 2m -4m -4)=(m ,-4)=1,故由△为完全平方数知m 为完全平方数.若m 为偶数,则由①知n 为偶数 (否则①的左边为奇数,矛盾),故4|n 2,4|kmn ,4|m 2,从而由①知4|m .设m =4m 1,则△=16 m 1(k 2m 1-m 1-1),所以,m 1(k 2m 1-m 1-1)是一个完全平方数,这时(m 1,k 2m 1-m 1-1) =(m 1,-1)=1. 故m 1是完全平方数,所以m =4m 1也是完全平方数,命题获证.25.证明:若正整数n 可以表示为三个正整数的平方和的形式,则2n 也可以表示为三个正整数的平方和的形式.【答案】设n =x 2+y 2+z 2,x ≥y ≥z 为正整数,则n 2=(x 2+y 2+z 2) 2=(x 2+y 2) 2+2(x 2+y 2) z 2+z 4 =(x 2+y 2-z 2) 2+4(x 2+y 2) z 2=(x 2+y 2-z 2) 2+(2xz ) 2+(2yz ) 2.注意到,x 2+y 2-z 2>0,知n 2可表为3个正整数的平方和.26.求所有的正整数n ,使得n 的三次方根等于n 去掉最后三位数字后得到的正整数.【答案】设n =1000x +y ,这里x 为正整数,y 为整数,且0≤y ≤999.依题意知x 3=1000x +y .1000x ≤x 3<1000x +1000=1000(x +1), 故 x 2≥1000,x 3+1≤1000(x +1), 得 x 2≥1000,x 2-x +1≤1000. 所以 32≤x <33, 故 x =32, 这样 y =768, 所以 n =32 768.27.证明:存在无穷多个整数n ,使得数n 、n +1、n +2都可以表示为两个整数(不必不同)的平方和.例如:22000=+,22101=+,22211=+,故n =0即为一个满足条件的整数. 【答案】只需寻找正整数l ,使得l 2-1=x 2+y 2有正整数解.令x =2m 2,y =2m ,及l =2m 2+1,就有l 2-1=x 2+y 2.所以,对任意正整数m ,取 n =(2m 2+1) 2-1=4m 4+4m 2, 则 n =(2m 2) 2+(2m ) 2, n +1=(2m 2+1) 2+02, n +2=(2m 2+1) 2+12.28.求最小的正整数n ,使得在十进制表示下3n 的末三位数字是888. 【答案】由条件,知n 3≡888(mod1000),故n 3≡888(mod8),n 3≡888(mod125), 由前者知n 为偶数,设n =2m ,则m3≡111(mod125),因此m3≡111≡1(mod5) .注意到当m=0,1,2,3,4(mod5)时,对应地m3≡0,1,3,2,4(mod5),所以,由m3≡1(mod5)知m≡1(mod5),可设m=5k+1,这时m3=(5k+1) 3=125k 3+75k2+15k+1≡111(mod125),故75k2+15k≡110(mod125),从而15k2+3k≡22(mod25),既有15k2+3k+3≡0(mod25),故5k2+k+1≡0(mod25) .这要求5k2+k+1≡0(mod25),故5│k+1.可设k+1=5l,得5k2+k+1=5×(5l-1) 2+5l,=125l2-50l+5(l+1)≡0(mod25),故5│l+1.可设l+1=5r,因此n=2m=10k+2=10(5l-1)+2=50l-8=50(5r-1)-8=250r-58.结合n为正整数,可知n≥250-58=192.又1922=7077888符合要求,故满足条件的最小正整数为192.29.设正整数n>1,证明:数21n-既不是完全平方数,也不是完全立方数.【答案】由于n≥2,故2n-1≡-1(mod4),而完全平方数≡0或1(mod4),故2n-1不是完全平方数.另一方面,若存在n>1及正整数x,使得2n-1=x3,则2n=(x+1)(x 2-x+1),由于x 2-x+1=x(x-1)+1,其中x(x-1)为偶数(两个相邻整数中有一个为偶数),故x 2-x+1为奇数,这要求x 2-x+1=1,进而x=1,导出n=1,矛盾.故2n-1不是一个完全平方数.30.设a、b、c a、b、c都是完全平方数.【答案】先证:对任意正整数a a为完全平方数.qp,p、q为正整数,且(p,q)=1,则a=22qp,此时由a为正整数,知p2|q2,但(p,q)=1,故p=1,即a=q2.m,m为整数,则)2=(m2即a+b+m 2-c,n ,n 为正有理数,则 ab =(n 2=n 2-2c ,c =m 可知a ,b 也都是完全平方数.31.已知正整数c 是一个奇合数.证明:存在正整数a ,使得13ca ≤-,且()2218a c -+是一个完全平方数.【答案】通过凑完全平方式来处理.由条件可设c =pq ,3≤p ≤q ,p 、q 都是奇数,现在需要寻找a ,使得(2a -1) 2+8pq 是一个完全平方式,一个自然的取法是:2a -1=2q -p ,则(2a -1)2+8pq =(2q -p ) 2+8pq =(2q +p ) 2,a =12(2q -p +1)=q -12p -≤q -1=c p -1≤3c-1,符合题中的要求.32.设整数a 、b 满足:对任意正整数n ,数2na b •+都是完全平方数.证明:a =0.【答案】若a ≠0,注意到在a <0时,n 充分大后,数2n a +b <0,与2n a +b 为完全平方数矛盾,故a >0.现在设2n a +b ≡x 2n ,x n 为正整数,则对任意正整数n ,有x n <x n +1.由于 4x 2n -x 2n +2=4(2n a +b )-(2n +2a +b )=3b , 故 3│b │=│2x n -x n +2│·│2x n +x n +2│,而 2x n +x n +2随着n 的增大而增大,故只能是│2x n -x n +2│=0, 即 │b │=0,但这时2n a 与2n +1a 都要是完全平方数,这是不可能的,矛盾.所以a =0.33.求不能表示为42的正倍数与一个合数之和的最大正整数.【答案】对任意不能表示为42的正倍数与一个合数之和的正整数n ,考虑n 除以42所得的余数r .若r =0或r 为合数,则n ≤42.下面考虑r =1或r 为素数的情形.若 r ≡1(mod5),则 84+r ≡0(mod5), 此时 n <3×42=126;若 r ≡2(mod5),则 4×42+r ≡0(mod5), 此时 n <5×42=210;若 r ≡3(mod5),则 42+r ≡0(mod5), 此时 n <2×42=84;若 r ≡4(mod5),则 3×42+r ≡0(mod5), 此时 n <4×42=168;若 r ≡0(mod5),则 r =5,此时由于5,47,89,131,173都是素数,故n 最大为215. 综上可知,所求最大正整数为215.34.求一个正整数n ,使得数n ,n +1,…,n +20中每个数都与30030不互素. 【答案】由于30 030=2×3×5×7×11×13,所以若取N =210k ,则N 与N ±r 都与30 030不互素,这里r 为2,3,…,10中的数.现在考虑数N ±1,我们取k ,使得210k ≡1(mod11)且210k ≡-1(mod13),前者要求k ≡1(mod11),设k =11m +1,后者要求 210(11m +1)≡-1(mod13),解得 m ≡4(mod13),所以,令k =45,则所得的21个数9440,9441,…,9460与30 030都不互素,因此取n =9440即可.35.是否存在连续13个正整数,其中每个数都是2、3、5、7、11中的某个数的倍数?连续14个呢?【答案】注意到,114,115,…,126这13个数都是合数,每个数都是2、3、5、7、11中某个数的倍数,因此存在13个符合要求的数.下证:没有连续14个正整数,使得其中每个数都是2、3、5、7、11中某个数的倍数.事实上,若存在这样的14个数,考虑其中的7个奇数,设它们为a ,a +2,…,a +12.由于若两个奇数都是3的倍数,则它们的差至少为6,故这7个奇数中至多有1个数为11的倍数.同样可证这7个奇数中至多有2个数是5的倍数;至多有1个数为7的倍数;至多有1个数为11的倍数.由假设,这7个数都是3、5、7、11中某个数的倍数,故这7个奇数中分别有3个为3的倍数,2个为5的倍数,1个为7的倍数,1个为11的倍数,并且不出现一个数同时是3、5、7、11中某两个数的倍数.但是,这时要求a 、a +6、a +12为3的倍数;a 、a +10或者a +2、a +12中有一组数为5的倍数.必有一个数同为3和5的倍数,矛盾.36.设p 为素数,a 、n 都是正整数,且23p p n a +=.证明:n =1.【答案】当p =2时,a n =13,知a =13,n =1.当p >2时,由p 为素数,可知p 为奇数,此时2p +3 p =(2+3)(2 p -1-2 p -2×3+…-2×3 p -2+3p -1) ,故 5|a n ,即5|a .若n >1,则52|a n ,这时,应有2 p -1-2p -2×3+…-2×3 p -2+3p -1≡0(mod5) .利用3≡-2(mod5),p 为奇数及上式,知2 p -1-2p -2×3+…-2×3 p -2+3p -1≡11112222p p p p p -----++个=p ·2 p -1≡0(mod5), 所以5|p ,而p 为素数,故p =5,这导致a n =25+35=275=52×11,n 只能为1,矛盾.因此n =1.37.圆周上排列着2000个点,在某个点上标上数1,按顺时针方向数两个点,在其上标数2,再数3个点标数3,依此继续,标出数1,2,…,2000.这样,有些点上没有标数,有些点上所标的数不止一个.问:被标上2000的那个点上所标的数中最小的是多少?【答案】等价于求最小的正整数n ,使得1+2+…+n ≡1+2+…+2000(mod2000) . ①即(1)2n n +≡1000(mod2000), 等价于 n (n +1)≡2000(mod4000),这要求 2000|n (n +1) .注意到 (n ,n +1)=1,而 2000=24×53,所以24|n ,53|n +1;或者53|n ,24|n +1;或者n 与n +1中有一个为2000的倍数.分别求得n 最小为624,1375,1999,其中满足①的最小的数为624.所以,被标上2000的那个点上所标的数中最小的那个是624.38.圆周上有800个点,依顺时针方向标号为1,2,…,800,它们将圆周分为800个间隙.现在选定某个点,将其染上红色,然后进行下述操作:如果第k 号点染成了红色,那么依顺时针方向转过k 个间隙,将所到达的点染成红色.问:依此规则,圆周上最多有多少个点被染成了红色?证明你的结论.【答案】等价于求在模800的意义下,数列a ,2a ,22a ,23a ,…中,出现的不同的数的个数的最大值,这里a 在1,2,…,800中取值.注意到,当2n 2m (mod800)时 ,2n a 2m a (mod800)不一定成立;反过来,当2n a 2m a (mod800)成立时,2n 2m (mod800) 一定成立.因此,数列a ,2a ,22a ,…在模800的意义下,不同元素个数的最大值在a =1时可以取到,因此,只需求1,2,22,…在模800的意义下不同元素的个数.由于800=25×52,而n ≥5时有 2n ≡0(mod25),另外{2n (mod25)}为2,4,8,16,7,14,3,6,12,-1,-2,-4,-8,-16,-7,-14,-3,-6,-12,1,…故{2n (mod25)}中恰好有20个不同元素.结合{2n (mod25)}为2,4,8,16,0,0,…,可得{2n (mod800)}中恰好有20+4=24(个)不同的数.所以,圆周上至多有24个点染成了红色.39.设m 为正整数,且()2mod4m ≡.证明:至多存在一对正整数(a ,b ),使得m ab =,且05441a b m <-<++【答案】如果能确定a +b 的值(视m 为常数),那么利用韦达定理的逆定理,可知至多只有一组正整数(a ,b )满足条件.由条件,知(a +b ) 2=(a -b ) 2+4ab 满足1+4m ≤(a +b ) 2<5+4+1m 4m =4+1m 2) 2,即 4+1m a +b 4+1m 2,所以 41411141121m m m a b m m m +++++⎡⎡++++⎪⎣⎣⎩或,若4为整数;或4+1,若4不是整数. 总之,a +b 只能取值于某两个连续正整数.而ab =m ≡2(mod4),可知a 、b 一奇一偶,即a +b 为奇数.这样我们知道a +b 的值唯一确定,命题获证.40.设n 是一个大于10的正整数,且n 的每个数码都为1、3、7或9.证明:n 有一个大于10的素因子.【答案】用反证法,若n 的每个素因子都不大于10,利用条件,知n 为奇数,且n 不是5的倍数,故存在非负整数i 、j ,使得 n =3i ·7j ,考虑3i 与7 j 除以20所得的余数,对i =0,1,2,…, j =0,1,2,…,分别依次有 {3i (mod20)}:1,3,9,7,1,3,…;{7 j (mod20)}:1,7,9,3,1,7,….这两个都是以4为周期循环的数列,因此 3i ·7j ≡ab (mod20),这里a 、b 都为1,3,7或9.分别计算,可知 3i ·7j ≡1,3,7或9 (mod20),这表明,所有形如3i ·7j 的数的十位数字都为偶数,但n 的每一位数字都是1,3,7或9,矛盾. 所以,n 有一个大于10的素因子.41.求所有的素数对(p ,q ),使得|1p qpq p q ++.【答案】由条件可知p ≠q ,利用对称性,不妨设p <q .若p =2,则q q +5≡0(mod q ),知q =5.直接验证,可知(p ,q )=(2,5)符合要求.若p >2,则p ,q 都为奇素数.由条件知p p +1≡0(mod q ),故p 2p ≡1(mod q ),利用Fermat 小定理,有p q -1≡1(mod q ),于是, p (2p ,q -1)≡1(mod q ) . ①注意到,2|(2p ,q -1),而(2p ,q -1) |2p ,故只有下面的两种情形.情形一 (2p ,q -1) =2,则由①知p 2≡1(mod q ),导致q |p +1或q |p -1,这与p ≤q -2矛盾. 情形二 (2p ,q -1) =2p ,则由①知q ≡1(mod p ),于是0≡p p +q q +1=2(mod p ),导致p =2,矛盾.综上可知,满足条件的(p ,q )=(2,5)或(5,2) .42.设()22010f n n n n ⋯=1++++.证明:对任意整数m ,若2≤m ≤2010,则不存在正整数n ,使得()|m f n .【答案】若存在2≤m ≤2010,使得对某个正整数n ,有m |f (n ) .则由于f (1)=2011为素数(这里2011为2011去验证),故n ≠1,此时可写f (n )=201111n n --. 对m 的素因子p ,由m |f (n )知n 2011≡1(mod p ),而由Fermat 小定理知n p -1≡1(mod p ),所以,有 (2011,1)p n -≡1(mod p ).结合 p -1<2011,及2011为素数,可得(2011,p -1)=1,于是n ≡1(mod p ),从而 0≡f (n )≡1+12+…+12010=2011(mod p ),要求 p =2011,这与m ≤2010矛盾.所以命题成立.43.是否存在整数x 、y ,使得2012201120102010442011x y y y -=++?【答案】不存在这样的整数x ,y .若不然,则有x 2012+1=(4y 2010+2011)( y +1) . ①注意到,4y 2010+2011≡3(mod4),这表明①式右边有模4余3的素因子,故存在素数p ,使得p ≡3(mod4), 且 x 2012+1≡0(mod p ) .由于2012为偶数,利用2.3节例2的结论知x 2012+1的每一个奇素因子都≡1(mod4),矛盾.。
《核电子学》习题解答 (2)
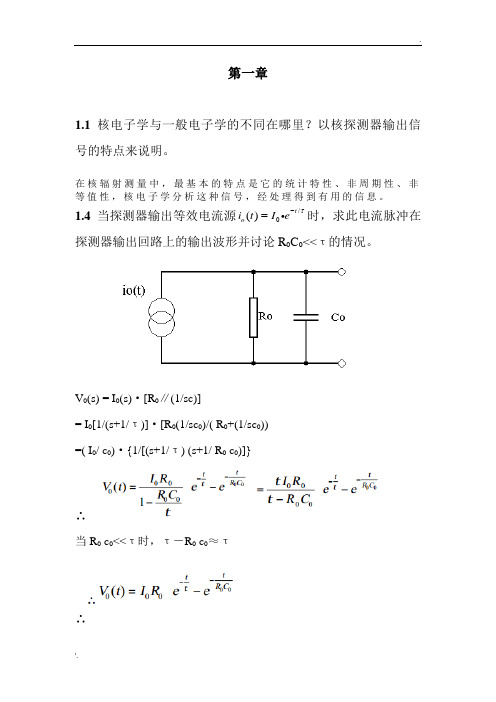
第一章1.1 核电子学与一般电子学的不同在哪里?以核探测器输出信号的特点来说明。
在核辐射测量中,最基本的特点是它的统计特性、非周期性、非等值性,核电子学分析这种信号,经处理得到有用的信息。
1.4 当探测器输出等效电流源/0()t o i t I e τ-=时,求此电流脉冲在探测器输出回路上的输出波形并讨论R 0C 0<<τ的情况。
V 0(s) = I 0(s)·[R 0∥(1/sc)]= I 0[1/(s+1/τ)]·[R 0(1/sc 0)/( R 0+(1/sc 0)) =( I 0/ c 0)·{1/[(s+1/τ) (s+1/ R 0 c 0)]}∴当R 0 c 0<<τ时,τ-R 0 c 0≈τ∴1.5 如图,设,求输出电压V(t)。
1.6 表示系统的噪声性能有哪几种方法?各有什么意义?输入端的噪声电压是否就是等效噪声电压?为什么?ENV ENC ENN ENE η(FWHM)NE不是1.7 设探测器反向漏电流I D =10-8A ,后级电路频宽为1MHz,计算散粒噪声相应的方根值和相对于I D 的比值。
115.6610A -==⨯=35.6610DI -=⨯=1.8 试计算常温下(设T=300K )5M Ω电阻上相应的均方根噪声电压值(同样设频宽为1MHz ),并与1MHz 能量在20pF 电容上的输出幅值作比较。
52.8810V -===⨯∵212E CV =∴0.126V V ==1.9求单个矩形脉冲f (t )通过低通滤波器,RC=T ,RC=5T ,及RC=T/5,时的波形及频谱。
1.10 电路中,若输入电压信号V i(t)=δ(t),求输出电压信号V0(t),并画出波形图,其中A=1为隔离用。
t1.12 设一系统的噪声功率谱密度为2222()//i S a b c ωωω=++,当此噪声通过下图电路后,求A 点与B 点的噪声功率谱密度与噪声均方值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
TTL:晶体管电路
X X
重大通信
学院•何伟
Байду номын сангаас10
【第3章 习题】
3-13. 试分析图P3-6(a)、(b)所示电路的逻辑功能,写出Y的逻辑表达式。图 中的门电路均为CMOS门电路
二极管或门
解:图(a)
图(b)
重大通信 学院•何伟
二极管与门
Y ABC DEF Y ABCDEF
11
重大通信
学院•何伟
14
【第7章 习题】
3/8译码器来选通这8 组
重大通信
学院•何伟
15
【第7章 习题】
7-6. 用PROM实现1位全加器,画出阵列图o
解:
全加器真值表:
重大通信 学院•何伟
全加器阵列图
16
【第9章 习题】
9-2. 图P10-2所示为TTL与非门构成 的积分型单稳态电路,若输入vI为宽度 20 μs的脉冲,画出a、b、d、vo各点的 波形。请考虑为使积分型单稳态电路能 正常工作,对输入脉冲有什么要求o
重大通信
学院•何伟
1
【第3章 习题】
3-2 . 试说明多发射极晶体管的主要作用。 解:多发射极晶体管作为与非门的第一级,其发射结实现对输入信号的与逻辑运算。
重大通信
学院•何伟
2
【第3章 习题】
3-4. 对应图P3-1所示的电路及输入信号波形,画出f1、f2、f3、f4的波形o
重大通信
学院•何伟
3
解:数字器件的输出端不会渐变,输入端可以;
图(b)
2.真值表穷举法
A BY
0 01 0 10 100 111
图(c)
Y AB
重大通信 学院•何伟
Y AB DE AB DE
S G
X (AB)^
(CD)^
非门
3个与非门
8
【第3章 习题】
3-11. 在CMOS门电路中,有时采用图P3-5所示的方法扩展输入端。试分析
图P3-5(a)、(b)所示电路的逻辑功能,写出Y的逻辑表达式。假定VDD=10V,二
缺点: ①电流大、功耗大; ②抗干扰容限低; ③输出电压稳定性差; ④与TTL不兼容。
重大通注信:ECL只有中小规模IC,主要用于高速、超高速的数字系统中,如光设备中。
学院•何伟
7
【第3章 习题】
3-10. 分析图P3-4所示电路的逻辑功能o
解: 图(a) 1.典型电路法
Y A(BC DE) EF(A G)
极管的正向导通电压VD=0.7V。
或非门
二极管与门
X=CDE
X=C+D+E 二极管或门
与非门
解:图(a)
重大通信图(b)
学院•何伟
Y ABCDE 将CMOS与非门输入端扩展到5个输入端
Y A B C D E 将CMOS或非门输入端扩
展到5个输入端
9
【第3章 习题】
都不能完成与的功能? 3-12. 上题中扩展输入端的方法能否用于TTL电路,为什么?
解: 图(a),C、D、E有一端输入为TTL低电平(0.4V)时,硅二极管正 向导通压降0.7V,X处的电平达到0.4+0.7=1.1V。TTL最大输入为0.8V, 本来输入为CDE为低电平,而1.1V在逻辑上相当于1了。不能实现二极管 与门的“入0出0”。所以不行。
图(b),C、D、E均为TTL低电平(0.4V)时,3个硅二极管都截止,但 100k的接地电阻会把X端拉高为逻辑1。实现不了或逻辑的功能。
【第3章 习题】
3-4. 对应图P3-1所示的电路及输入信号波形,画出f1、f2、f3、f4的波形o
解:
NAND2
a
INPUT
VCC
b
INPUT VCC
inst
OUTPUT
f1
b
NOT
NAND2
inst2
OUTPUT
f2
NOT
c
INPUT VCC
inst1
inst3
a
NOR3
b
NOR2
c
inst4
=(64K * 16位)/(8K * 8位) = 16片
需要同时进行位扩展(16位)和字扩展(16位);
单片6264型RAM的位线有8根,扩展到16位需要每次同时选 中两个6264型RAM,因此把16片6264型RAM分为8组,每 组两片;
单片6264型RAM的地址线有13根要扩展到16根,可将高3位 的地址线经3-8译码器输出,用于控制各组的片选,各芯片 的低位地址线并联 ;
【第3章 习题】
3-1. 在TTL门电路中,采用了哪些措施加速清除饱和晶体管的存储电荷,以 提高工作速度?
解:1. T1-T6采用了由双极型三极管和肖特基势垒二极管组成的抗饱和三极管; 2. T5的基级采用了有源泄放回路;3.多发射级三极管改为SBD; 4. 增加了D3、D4,两个SBD,提高了放电速度;
【第3章 习题】
3-15. 试说明下列各种电路中哪些输出端可以并联使用:(1) 具有推拉式输出 端的TTL门电路;(2) TTL电路的OC门。 OC门:集电极开路门
解:(1)不能并联,因为如果一个高,一个低并联,但推拉输出级任何时候都 呈现低阻抗,会有超级大的负载电流流过两个输出级,远超过了正常工作电 流。 (2) 因为是由两个3输入端TTL或非门连接一个二极管与门,则输出低电 平比正常TTL低电平要高,有可能使得低电平大于VIL(MAX),可能无法正常传 递逻辑信号
重大通信
学院•何伟
12
【第7章 习题】
7-4. 具有16位地址码可同时存取8位数据的RAM集成片,其存储容量为多少o 解:64k×8 bit。
= 512kb = 64KB
重大通信
学院•何伟
13
【第7章 习题】
7-5. 用6264型RAM构成一个64k×16位存储器,画出结构示意图o
单片6264容量=8k*8位 所需目标芯片数目n=(目标容量)/(单片6264型RAM的容量)
a
NAND2
OUTPUT
f3
inst7
d
INPUT VCC
inst5
b
NOR3
c
NAND2
d
inst6
b
NOR2
OUTPUT
f4
c
inst9
inst8
重大通信
学院•何伟
4
【第3章 习题】
3-6. 试分析图P3-3所示电路的逻辑功能,列出真值表o
解:(a)图
1.典型电路法
Y AB CD
或非门
重大通信
学院•何伟
5
【第3章 习题】
2.真值表穷举法
Y AB
重大通信
学院•何伟
6
【第3章 习题】
3-7. ECL门电路的主要特点是什么?
解: ECL:发射极耦合逻辑门,是一种非饱和型的高速逻辑电路 ECL电路是由一个差分对管和一对射随器组成的
优点: ①速度快; ②输出电阻很低,带负载能力很强; ③开关噪声很低; ④互补输出,方便使用。
