最小二乘参数辨识方法及应用程序清单
系统辨识之最小二乘法

系统辨识之最小二乘法方法一、最小二乘一次性算法:首先对最小二乘法的一次性辨识算法做简要介绍如下:过程的黑箱模型如图所示:其中u(k)和z(k)分别是过程的输入输出,)(1-z G 描述输入输出关系的模型,成为过程模型。
过程的输入输出关系可以描述成以下最小二乘格式:)()()(k n k h k z T +=θ (1)其中z(k)为系统输出,θ是待辨识的参数,h(k)是观测数据向量,n(k)是均值为0的随机噪声。
利用数据序列{z (k )}和{h (k )}极小化下列准则函数:∑=-=Lk T k h k z J 12])()([)(θθ (2)使J 最小的θ的估计值^θ,成为最小二乘估计值。
具体的对于时不变SISO 动态过程的数学模型为 )()()()()(11k n k u z B k z z A +=-- (3)应该利用过程的输入、输出数据确定)(1-z A 和)(1-Z B 的系数。
对于求解θ的估计值^θ,一般对模型的阶次a n ,b n 已定,且b a n n >;其次将(3)模型写成最小二乘格式)()()(k n k h k z T +=θ (4)式中=------=T n n T b a b a b b b a a a n k u k u n k z k z k h ],,,,,,,[)](,),1(),(,),1([)(2121 θ (5)L k ,,2,1 =因此结合式(4)(5)可以得到一个线性方程组L L L n H Z +=θ (6)其中==T L TL L n n n n L z z z z )](),2(),1([)](),2(),1([ (7)对此可以分析得出,L H 矩阵的行数为),max(b a n n L -,列数b a n n +。
在过程的输入为2n 阶次,噪声为方差为1,均值为0的随机序列,数据长度)(b a n n L +>的情况下,取加权矩阵L Λ为正定的单位矩阵I ,可以得出:L T L L T L z H H H 1^)(-=θ (8)其次,利用在Matlab 中编写M 文件,实现上述算法。
第五章 最小二乘法辨识

服从正态分
❖ 4)有效性
❖ 定理4:假设 (k) 是均值为零,方差为 2I 的正态
白噪声,则最小二乘参数估计量
^
是有效估计
量,即参数估计误差的协方差达到Cramer-Rao不
等式的下界
E (^
^
)(
)T
2E
(
T N
N
) 1
M 1
❖ 其中M为Fisher信息矩阵。
4、适应算法
❖ 随着更多观测数据的处理,递推最小二乘法对线性 定常系统的参数估计并非越来越精确,有时会发现
❖ 现举例说明最小二乘法的估计精度 ❖ 例5.1:设单输入-单输出系统的差分方程为
y(k) a1y(k 1) a2 y(k 2) b1u(k 1) b2u(k 2) (k)
❖ 设 u(k)是幅值为1的伪随机二位式序列,噪声 (k)是 一个方差 2可调的正态分布 N(0, 2 )随机序列。
❖ 为了克服数据饱和现象,可以用降低旧数据影响的 办法来修正算法。而对于时变系统,估计k时刻的 参数最好用k时刻附近的数据估计较准确。否则新 数据所带来的信息将被就数据所淹没。
❖ 几种算法:渐消记忆法,限定记忆法与振荡记忆法
❖ 矩阵求逆引理:设A为 n n 矩阵,B和C为 n m 矩阵,
并且A, A和 BCT I CT都A是1B 非奇异矩阵,则有矩
阵恒等式
A BCT 1 A1 A1B(I CT A1B)1CT A1
❖
令
A
PN1
,B
N 1
,C
T N 1
,根据引理有
PN1
T N 1 N 1
1
❖ 算法中,^ N 为2n+1个存贮单元(ai ,bi ,i 1,2, , n), 而 PN 是 (2n 1) (2n 1)维矩阵,显然,将 N 换成 PN 后,存贮量大为减少(因为n为模型的阶数,一般 远远小于N)
第六章 最小二乘类参数辨识方法

《系统辨识基础》第20讲要点第6章 最小二乘类参数辨识方法6.1 引言最小二乘法是一种最基本的辨识方法,但如果模型的噪声不是白噪声,最小二乘法不一定能给出无偏、一致估计。
以下着重讨论模型噪声是有色噪声时的各种最小二乘辨识方法。
6.2 增广最小二乘法 6.2.1 增广最小二乘原理 考虑如下模型A z z kB z u k N z v k ()()()()()()---=+111式中u (k )和z (k ) 分别为模型输入和输出变量;v (k ) 是均值为零、方差为σv 2的不相关随机噪声或称白噪声;N z ()-1为噪声模型;A z ()-1 和B z ()-1为迟延算子多项式,记作A z a z a z a zB z b z b z b z n n n n a ab b()()--------=++++=+++⎧⎨⎪⎩⎪11122111221 其中n a 和n b 为模型阶次。
为了运用最小二乘原理来辨识这种模型的参数,需要把模型(4-1)式写成最小二乘格式)()()(k v k k z +=θτh这样就必须把噪声模型的参数包含在参数向量θ 中,从而引出增广概念,用来构造模型的参数向量θ和数据向量h(k ),具体的构成形式会因噪声模型的结构不同而不同。
下面是三种不同噪声模型的向量构成方法:① 若N z D z d z d z d z n n dd()()==++++----111221 ,可按下式构成参数向量和数据向量:⎪⎪⎩⎪⎪⎨⎧--------+==--------=∑∑∑===)(ˆ)1(ˆ)()1(ˆ)()1(ˆ)()(ˆ],,,,,,,,[)](ˆ,),1(ˆ),(,),1(),(,),1([)(111111i k v k d i k u k b i k z k a k z k v d d b b a a n k v k v n k u k u n k z k z k db a d b a n i i n i i n i i n n n d b a ττθ h② 若N z C zc zc zc zn n c c()()==++++----11111122,参数向量和数据向量的构成形式为:⎪⎪⎩⎪⎪⎨⎧-----+==----------=∑∑==)()1(ˆ)()1(ˆ)()(ˆ],,,,,,,,[)](ˆ,),1(ˆ),(,),1(),(,),1([)(11111i k u k b i k z k a k z k e c c b b a a n k e k e n k u k u n k z k z k ba cb a n i i n i i n n nc ba ττθ h③ 若N z D z C zd z d z d z c zc zc zn n n n d dc c()()()==++++++++--------111122112211 ,参数向量和数据向量的构成形式为:⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-----+=-----+==------------=∑∑∑∑====)()1(ˆ)()1(ˆ)()(ˆ)(ˆ)1(ˆ)(ˆ)1(ˆ)(ˆ)(ˆ],,,,,,,,,,,[)](ˆ,),1(ˆ),(ˆ,),1(ˆ),(,),1(),(,),1([)(11111111i k u k b i k z k a k z k e i k v k d i k e k c k e k v d d c c b b a a n k v k v n k e k e n k u k u n k z k z k b a dc cc b a n i i n i i n i i n i i n n n nd c b a ττθ h以上这种构成参数向量和数据向量的思想就是所谓的增广原理,它是增广最小二乘法的根本。
Matlab最小二乘系统辨识
Matlab最⼩⼆乘系统辨识原理还是⽐较简单的,不赘述,程序⾥⾯的注释也写的⽐较清楚了%仿真对象:y(k)-1.5y(k-1)+0.7y(k-2)=v(k)+u(k)-0.8u(k-1)%辨识模型:y(k)+a1 y(k-1)+a2 y(k-2)=v(k)+b1 u(k)+b2 u(k-1)%数据长度取n=20000,加权矩阵为I,v(k)是服从正态分布的⽩噪声N(0,1),u(k)=sin(k)%待估计参数K=[a1 a2 a3 a4]';准则函数J(K)=(Yn-HnK)'(Yn-HnK);%将辨识模型写为:y(k)=v(k)+a1 y(k-1)+a2 y(k-2)+b1 u(k)+b2 u(k-1)% =v(k)+KHn%Hn=|y(2) y(1)|% |y(3) y(2)|% |.........|clearclose alldata_length=20002;%% 产⽣⽩噪声和输⼊v=randn(1,data_length);v=v./max(v);u=zeros(1,data_length);for k=1:data_lengthu(k)=sin(k);end%% 获得观测值y=zeros(1,data_length);for k=3:data_lengthy(k)=1.5*y(k-1)-0.7*y(k-2)+v(k)+u(k)-0.8*u(k-1);end%% 构造Hn和Y矩阵Hn=zeros(data_length-2,2);count=1;for k=1:10000Hn(k,2)=y(count);count=count+1;Hn(k,1)=y(count);Hn(k,4)=u(count);Hn(k,3)=u(count+1);end%% 求解参数Y=y(3:data_length)';c1=Hn'*Hn;c2=inv(c1);c3=Hn'*Y;K=c2*c3%% 将辨识得到的参数代⼊,得估计输出y_e=zeros(1,data_length);for k=3:data_lengthy_e(k)=K(1)*y_e(k-1)+K(2)*y_e(k-2)+v(k)+K(3)*u(k)+K(4)*u(k-1);end%% 画出实际输出和辨识输出,进⾏对⽐plot((1:data_length),y');title('实际输出')hold onplot((1:data_length),y_e');title('辨识输出')figuresubplot(2,1,1)plot((1:data_length),y');title('实际输出')subplot(2,1,2)plot((1:data_length),y_e');title('辨识输出')。
递归最小二乘法辨识参数

递归最小二乘法辨识参数递归最小二乘法(Recursive Least Squares, RLS)是一种参数辨识方法,它使用递归算法来求解最小二乘法中的参数。
在许多领域中,例如系统辨识、自适应控制、信号处理等,递归最小二乘法都是一个广泛使用的方法。
递归最小二乘法的基本思想是:通过递归迭代来更新参数估计值,使其逼近最优解。
在递归过程中,每一次迭代时,都会通过当前的测量值来更新参数的估计值,同时保留历史测量值的影响,从而获得更精确的估计值。
具体地说,在递归过程中,首先需要定义一个初始参数向量,然后通过观测数据序列来递归更新参数向量。
假设有一个如下所示的线性关系:y(k) = Φ(k) * θ + v(k)其中,y(k)是被观测到的输出值,Φ(k)是与该输出值相关的输入向量,θ是待辨识的参数向量,v(k)是误差项。
递归最小二乘法的目标就是通过观测数据来估计θ的值。
在递归最小二乘法中,首先需要定义一个初始的参数向量θ0,然后通过数据序列递归地更新θ的值。
每一次迭代时,都会用最新的观测数据来更新参数向量,使得估计值更接近真实值。
具体来说,每次观测到新的数据之后,都会根据当前参数估计值和新的观测值来计算估计误差,并更新参数向量。
具体的迭代步骤如下:1.从数据序列中读取观测值y(k)和输入向量Φ(k);2.计算估计值y(k)hat和估计误差e(k):y(k)hat = Φ(k) * θ(k-1)e(k) = y(k) - y(k)hat3.计算卡尔曼增益K(k)和参数估计值θ(k):K(k) = P(k-1) * Φ(k) / (λ + Φ(k)' * P(k-1) * Φ(k))θ(k) = θ(k-1) + K(k) * e(k)其中,P(k-1)是先前迭代步骤中的误差协方差矩阵,λ是一个小的正数,用于确保逆矩阵的存在性。
需要注意的是,递归最小二乘法的计算量相对较大,因此通常需要对算法进行优化,以提高计算效率和精度。
最小二乘法

最小二乘法一、最小二乘法概述最小二乘法是1795年高斯在预测星体运行轨道最先提出的,它奠定了最小二乘估计理论的基础.到了20世纪60年代瑞典学者Austron 把这个方法用于动态系统的辨识中,在这种辨识方法中,首先给出模型类型,在该类型下确定系统模型的最优参数。
我们可以将所研究的对象按照对其了解的程度分成白箱、灰箱和黑箱。
于其内部结构、 机制只了解一部分,对于其内部运行规律并不十分清楚,这样的研究对象通常称之为 “灰箱”;如果我们对于研究对象的内部结构、 内部机制及运行规律均一无所知的话,则把这样的研究对象称之为“黑箱”。
研究灰箱和黑箱时,将研究的对象看作是一个系统,通过建立该系统的模型,对模型参数进行辨识来确定该系统的运行规律。
对于动态系统辨识的方法有很多,但其中应用最广泛,辨识效果良好的就是最小二乘辨识方法,研究最小二乘法在系统辨识中的应用具有现实的、广泛的意义。
应用最小二乘法对系统模型参数进行辨识的方法有离线辨识和在线辨识两种离线辨识是在采集到系统模型所需全部输入输出数据后,用最小二乘法对数据进行集中处理,从而获得模型参数的估计值;而在线辨识是一种在系统运行过程中进行的递推辨识方法,所应用的数据是实时采集的系统输入输出数据,应用递推算法对参数估计值进行不断修正,以取得更为准确的参数估计值。
假设一个SISO 系统如下图所示:图1 SISO 系统结构图其离散传递函数为:(1)输入输出的关系为:)()()()(1k y k e z G k u =+•- (2)进一步,我们可以得到:)()()()()(11k e z B k u z A k y +⋅=⋅-- (3)其中,扰动量)(k e 为均值为0,不相关的白噪声。
将式(3)写成差分方程的形式:)()()2()1()()2()1()(2121k e n k u b k u b k u b n k y a k y a k y a k y n n +-⋯+-+-+--⋯-----=(4)令T n k u k u k u n k y k y k y k ])()2()1()()2()1([)(-⋯----⋯----=ϕnn n n z a z a z a z b z b z b z A z B z G ---------+⋯++++⋯++==221122111111)()()(][2121n nb b b a a a ⋯⋯=θ则式(4)可以写为:)()()(k e k k y T+=θϕ (5)将上述式子扩展到N 个输入、输出观测值{)(),(k y k u },k=1,2,…,N+n 。
最小二乘法辨识参数
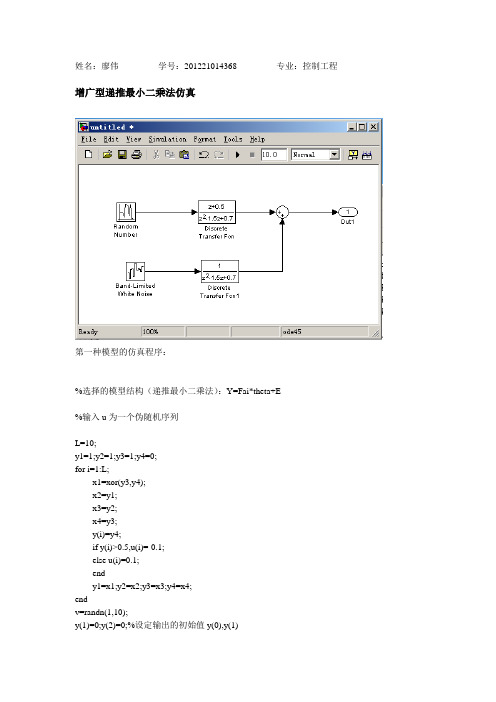
姓名:廖伟学号:201221014368 专业:控制工程增广型递推最小二乘法仿真第一种模型的仿真程序:%选择的模型结构(递推最小二乘法):Y=Fai*theta+E%输入u为一个伪随机序列L=10;y1=1;y2=1;y3=1;y4=0;for i=1:L;x1=xor(y3,y4);x2=y1;x3=y2;x4=y3;y(i)=y4;if y(i)>0.5,u(i)=-0.1;else u(i)=0.1;endy1=x1;y2=x2;y3=x3;y4=x4;endv=randn(1,10);y(1)=0;y(2)=0;%设定输出的初始值y(0),y(1)theta0=[0.01;0;0.01;0;0.01];%给出待辨识参数的初始值P0=10^6*eye(5);%生成初始矩阵7x7的单位阵E=0.00005;%E为递推结束的条件%下面进行递推运算for k=3:10y(k)=1.5*y(k-1)-0.7*y(k-2)+1.0*u(k-1)+0.5*u(k-2)+v(k);%产生输出y Fai1=[-y(k-1) -y(k-2) u(k-1) u(k-2) v(k)]';%生成实测数据组Fai1K1=P0*Fai1/(1+Fai1'*P0*Fai1);theta1=theta0+K1*(y(k)-Fai1'*theta0);e1=theta1-theta0;%e2=e1/theta1;P1=P0-K1*Fai1'*P0;theta0=theta1;%供下次递推使用P0=P1;%供下次递推使用if abs(e1)<E,break;%循环结束条件endendtheta1辨识的参数的最后结果为:theta1 =-1.50000.70001.00000.50001.0000可以从结果看出,辨识的效果很好,基本没有误差。
第二种模型的仿真程序:%选择的模型结构(增广最小二乘法):Y=Fai*theta+E %输入u为一个伪随机序列L=10;y1=1;y2=1;y3=1;y4=0;for i=1:L;x1=xor(y3,y4);x2=y1;x3=y2;x4=y3;y(i)=y4;if y(i)>0.5,u(i)=-0.1;else u(i)=0.1;endy1=x1;y2=x2;y3=x3;y4=x4;endv=randn(1,10);%噪声干扰随机数序列y(1)=0;y(2)=0;%设定输出的初始值y(0),y(1)theta0=[0.01;0;0.01;0;0.01;0;0];%给出待辨识参数的初始值P0=10^6*eye(7);%生成初始矩阵7x7的单位阵E=0.00005;%E为递推结束的条件%下面进行递推运算for k=3:10y(k)=1.5*y(k-1)-0.7*y(k-2)+1.0*u(k-1)+0.5*u(k-2)+v(k)-v(k-1)+0.2*v(k-2);%产生输出y Fai1=[-y(k-1) -y(k-2) u(k-1) u(k-2) v(k) v(k-1) v(k-2)]';%生成实测数据组Fai1K1=P0*Fai1/(1+Fai1'*P0*Fai1);theta1=theta0+K1*(y(k)-Fai1'*theta0);e1=theta1-theta0;%e2=e1/theta1;P1=P0-K1*Fai1'*P0;theta0=theta1;%供下次递推使用P0=P1;%供下次递推使用if abs(e1)<E,break;%循环结束条件endendtheta1辨识的参数最后结果为:-1.50.699990.998890.500191.0001-10.19991从辨识的结果看出,所得结果与真实的模型参数很接近,辨识效果也很好。
python实现一般最小二乘系统辨识方法

python实现⼀般最⼩⼆乘系统辨识⽅法问题:对于⼀个未知参数的系统,往往需要⽤到系统辨识的⽅法,例如对于⼀个单输⼊单输出系统: Z(k)+a1*Z(k-1)+a2*Z(k-2)=b1*U(k-1)+b2*U(k-2)+V(k) 其中:V(k)=c1*v(k)+c2*v(k-1)+c3*v(k-3)输⼊信号采⽤四阶幅值为1的M序列,⾼斯噪声v(k)均值为0,⽅差为0.1。
假设真值为a1=1.6,a2=0.7,b1=1.0,b2=0.4,c1=1.0,c2=1.6,c3=0.7。
需要对以上参数进⾏辨识。
⽅法:⼀般最⼩⼆乘法是系统辨识中最简单的辨识⽅法之⼀,其MATLAB实现⽅法⼗分简单,我发现⽹上⼀⼤把,所以我决定“翻译”⼀个python版的⼀般最⼩⼆乘辨识⽅法供读者参考。
本⽂⽤到的库:import numpy as npimport matplotlib.pyplot as pltfrom operator import xorfrom numpy.linalg import invM序列的产⽣:在python中,M序列的产⽣⽅法与matlab类似,先产⽣随机数,然后采⽤四阶移位寄存器滤波变换,得到我们想要的M序列。
#M序列产⽣L=16#设置M序列周期#定义初始值y=np.zeros(L)u=np.zeros(L)y1=1y2=1y3=1y4=0for i in range(0,L):x1=xor(y3,y4)x2=y1x3=y2x4=y3y[i]=y4if y[i]>0.5:u[i]=-1else:u[i]=1y1=x1y2=x2y3=x3y4=x4plt.figure(num=2)x=np.linspace(0,15,16)plt.bar(x,u,width=0.1)plt.title('输⼊信号M序列')⾼斯分布噪声:这⾥采⽤的是random库中的函数,可以看到,我们设置的均值为0,⽅差为0.1。
第3章最小二乘辨识

u(1)
u(2)
y(n N 1)
y(N)
u(n N)
y(n) y(n y(n
1) N
1)
y(1) u(n 1)
y(2) u(n 2)
y(N) u(n N)
u(1)
第3章 最小二乘法辨识
近代辨识:最小二乘法、极大似然法 辨识对象:以单输入/单输出系统差分方程为模型 辨识内容:系统模型参数和系统模型阶次n 学习内容:各种参数估计算法的推导、特点、
流程、优缺点及适用范围
2019/7/11
1
3.1 基本的最小二乘估计
解决问题:在模型阶次n已知的情况下,根据系统的输入输出数 据,估计出系统差分方程的各项系数。
k n
u(k)u(k 1)
n N 1
u(k n 1)u(k 1)
kn
n N 1
u(k 1)u(k)
k n
n N 1
u2 (k)
k n
n N 1
u(k n 1)u(k)
k n
nN1 u(k 1)u(k n 1)
哪些输入信号{u(k)}的Ru是强对角线占优矩阵?以下输
入信号均能满足Ru正定的要求:
(1)白噪声序列;
(2)伪随机二位式噪声序列;
(3)有色噪声随机信号序列。
工程上常用“伪随机二位式噪声序列”、“有色噪声随机
2019/7/11 信号序列”作为输入信号。
16
4. 最小二乘估计的统计性质
系统辨识—最小二乘法_3

---------------------------------------------------------------最新资料推荐------------------------------------------------------系统辨识—最小二乘法最小二乘法参数辨识 1 引言系统辨识是根据系统的输入输出时间函数来确定描述系统行为的数学模型。
现代控制理论中的一个分支。
通过辨识建立数学模型的目的是估计表征系统行为的重要参数,建立一个能模仿真实系统行为的模型,用当前可测量的系统的输入和输出预测系统输出的未来演变,以及设计控制器。
对系统进行分析的主要问题是根据输入时间函数和系统的特性来确定输出信号。
对系统进行控制的主要问题是根据系统的特性设计控制输入,使输出满足预先规定的要求。
而系统辨识所研究的问题恰好是这些问题的逆问题。
通常,预先给定一个模型类={M}(即给定一类已知结构的模型),一类输入信号 u 和等价准则 J=L(y,yM)(一般情况下,J 是误差函数,是过程输出 y 和模型输出 yM 的一个泛函);然后选择使误差函数J 达到最小的模型,作为辨识所要求的结果。
系统辨识包括两个方面:结构辨识和参数估计。
在实际的辨识过程中,随着使用的方法不同,结构辨识和参数估计这两个方面并不是截然分开的,而是可以交织在一起进行的。
2 系统辨识的目的在提出和解决一个辨识问题时,明确最终使1 / 17用模型的目的是至关重要的。
它对模型类(模型结构)、输入信号和等价准则的选择都有很大的影响。
通过辨识建立数学模型通常有四个目的。
①估计具有特定物理意义的参数有些表征系统行为的重要参数是难以直接测量的,例如在生理、生态、环境、经济等系统中就常有这种情况。
这就需要通过能观测到的输入输出数据,用辨识的方法去估计那些参数。
②仿真仿真的核心是要建立一个能模仿真实系统行为的模型。
用于系统分析的仿真模型要求能真实反映系统的特性。
第五章 最小二乘参数辨识方法 第十二讲

《系统辨识基础》第12讲要点第5章 最小二乘参数辨识方法5.1 辨识方法分类根据不同的辨识原理,参数模型辨识方法可归纳成三类:① 最小二乘类参数辨识方法,其基本思想是通过极小化如下准则函数来估计模型参数:min )()ˆ(ˆ==∑=θθLk k J 12ε其中)(k ε代表模型输出与系统输出的偏差。
典型的方法有最小二乘法、增广最小二乘法、辅助变量法、广义最小二乘法等。
② 梯度校正参数辨识方法,其基本思想是沿着准则函数负梯度方向逐步修正模型参数,使准则函数达到最小,如随机逼近法。
③ 概率密度逼近参数辨识方法,其基本思想是使输出z 的条件概率密度)|(θz p 最大限度地逼近条件0θ下的概率密度)|(0θz p ,即)|()ˆ|(0m a xθθz p z p −−→−。
典型的方法是极大似然法。
5.2 最小二乘法的基本概念● 两种算法形式① 批处理算法:利用一批观测数据,一次计算或经反复迭代,以获得模型参数的估计值。
② 递推算法:在上次模型参数估计值)(ˆ1-k θ的基础上,根据当前获得的数据提出修正,进而获得本次模型参数估计值)(ˆk θ,广泛采用的递推算法形式为() ()()()~()θθk k k k d z k =-+-1K h其中)(ˆk θ表示k 时刻的模型参数估计值,K (k )为算法的增益,h (k -d ) 是由观测数据组成的输入数据向量,d 为整数,)(~k z 表示新息。
● 最小二乘原理定义:设一个随机序列)},,,(),({L k k z 21∈的均值是参数θ 的线性函数θτ)()}({k k z h =E其中h (k )是可测的数据向量,那么利用随机序列的一个实现,使准则函数21])()([)(θθτ∑=-=Lk k k z J h达到极小的参数估计值θˆ称作θ的最小二乘估计。
● 最小二乘原理表明,未知参数估计问题,就是求参数估计值θˆ,使序列的估计值尽可能地接近实际序列,两者的接近程度用实际序列与序列估计值之差的平方和来度量。
第四章最小二乘参数辨识方法及原理

yi Ri vi 或 yi a bt vi
vi yi Ri或vi=yi a bti
第十四页,编辑于星期五:十九点 二十六分。
3利用最小二乘法求模型参数
根据最小二乘的准则有
N
N
J min vi2 [Ri (a bti )]2
i 1
i 1
根据求极值的方法,对上式求导
m
使 w(k) | z(k) y(k) |2 最小 k 1
第十三页,编辑于星期五:十九点 二十六分。
3、最小二乘辨识方法的基本概念
通过试验确定热敏电阻阻值和温度间的关系
t (C)
t1
R ()
R1
t2
t N 1
tN
R2
RN 1
RN
R a bt
• 当测量没有任何误差时,仅需2个测量值。
• 每次测量总是存在随机误差。
k v k aiv k i
i0
(4-5)
n
n
y k ai y k i biu k i (k )
i1
i0
(4-6)
如果u k 也有测量误差,则在 k 中应包含这一测量误差。
第二十三页,编辑于星期五:十九点 二十六分。
现在分别测出个 n N 输出值和输入值:y 1,y 2, ,y n N 及 u 1,u 2, ,u n N 。则可写出N个方程:
4.7 增广矩阵法(ELS/RELS)(增广最小二乘法)
4.8 多阶段最小二乘法(MSLS) 4.9 几种最小二乘类辨识算法的比较
第二页,编辑于星期五:十九点 二十六分。
本章的学习目的
1、掌握最小二乘参数辨识方法的基本原理 2、掌握常用的最小二乘辨识方法 3、熟练应用最小二乘参数辨识方法进行模型参数辨识
(完整)系统辨识—最小二乘法汇总,推荐文档

最小二乘法参数辨识201403027摘要:系统辨识在工程中的应用非常广泛,系统辨识的方法有很多种,最小二乘法是一种应用极其广泛的系统辨识方法.阐述了动态系统模型的建立及其最小二乘法在系统辨识中的应用,并通过实例分析说明了最小二乘法应用于系统辨识中的重要意义.关键词:最小二乘法;系统辨识;动态系统Abstract: System identification in engineering is widely used, system identification methods there are many ways, least squares method is a very wide range of application of system identification method and the least squares method elaborated establish a dynamic system models in System Identification applications and examples analyzed by the least squares method is applied to illustrate the importance of system identification.Keywords: Least Squares; system identification; dynamic system引言随着科学技术的不断发展,人们认识自然、利用自然的能力越来越强,对于未知对象的探索也越来越深入.我们所研究的对象,可以依据对其了解的程度分为三种类型:白箱、灰箱和黑箱.如果我们对于研究对象的内部结构、内部机制了解很深入的话,这样的研究对象通常称之为“白箱”;而有的研究对象,我们对于其内部结构、机制只了解一部分,对于其内部运行规律并不十分清楚,这样的研究对象通常称之为“灰箱”;如果我们对于研究对象的内部结构、内部机制及运行规律均一无所知的话,则把这样的研究对象称之为“黑箱”.研究灰箱和黑箱时,将研究的对象看作是一个系统,通过建立该系统的模型,对模型参数进行辨识来确定该系统的运行规律.对于动态系统辨识的方法有很多,但其中应用最广泛,辨识效果良好的就是最小二乘辨识方法,研究最小二乘法在系统辨识中的应用具有现实的、广泛的意义.1.1 系统辨识简介系统辨识是根据系统的输入输出时间函数来确定描述系统行为的数学模型。
最小二乘法系统辨识

最小二乘法一次完成算法的MATLAB仿真一、二阶系统的最小二乘法一次完成算法的辨识程序及结果程序源代码:clear % 工作间清零u = [-1,1,-1,1,1,1,1,-1,-1,-1,1,-1,-1,1,1]; % 系统辨识的输入信号为一个周期的M序列z = zeros( 1, 16); % 定义输出观测值的长度for k = 3 : 16% 用理想输出值作为观测值z(k) = 1.8*z(k-1) - 0.8*z(k-2) + 1.1*u(k-1) + 0.4*u(k-2);ZL( k, : ) = z(k); % 给样本矩阵ZL赋值Hl = [ -z(k-1), -z(k-2), u(k-1), u(k-2) ]; % 用理想输出值作为观测值HL( k, : ) = Hl;endsubplot(3,1,1) % 画三行一列图形窗口中的第一个图形stem(u) % 画出输入信号u的经线图形subplot(3,1,2) % 画三行一列图形窗口中的第二个图形i=1:1:16; % 横坐标范围是1到16,步长为1% 图形的横坐标是采样时刻i, 纵坐标是输出观测值z, 图形格式为连续曲线plot(i,z)subplot(3,1,3) % 画三行一列图形窗口中的第三个图形stem(z),grid on % 画出输出观测值z的经线图形,并显示坐标网格u,z % 显示输入信号和输出观测信号c1=HL'*HL; % 计算参数并显示c2=inv(c1);c3=HL'*ZL;c=c2*c3a1=c(1), a2=c(2), b1=c(3), b2=c(4) % 从中分离出并显示a1 、a2、b1、b2运算结果如下:u =-1 1 -1 1 1 1 1 -1 -1 -1 1 -1 -1 1 1z =Columns 1 through 90 0 0.7000 0.5600 1.1480 3.1184 6.1947 10.1558 12.6246 Columns 10 through 1613.0997 11.9798 11.7838 10.9270 8.7416 7.6933 8.3546c =-1.80000.80001.10000.4000a1 =-1.8000a2 =0.8000b1 =1.1000b2 =0.4000所画图形如下:二、实际压力系统的最小二乘辨识程序及结果程序源代码:clear % 工作间清零V = [ 54.3, 61.8, 72.4, 88.7, 118.6, 194.0]' % 赋初值V,并显示P = [ 61.2, 49.5, 37.6, 28.4, 19.2, 10.1]' % 赋初值P,并显示% P、V之间的关系:logP=-alpha*logV% +logbeita=[-logV,1][alpha,log(beita)]'=HL*sitafor i = 1 : 6; % 循环变量的取值为从1到6 Z(i) = log( P (i) ); % 赋系统的输出采样值ZL( i, : ) = Z(i); % 给样本矩阵ZL赋值Hl = [ log( V(i) ),1 ]; % 给HL赋值HL( i, : ) = Hlend % 循环结束c1=HL'*HL; % 计算参数并显示c2=inv(c1);c3=HL'*ZL;c4=c2*c3alpha = c4(1) % 为c4的第1个元素beita = exp(c4(2)) % 为以自然数为底的c4的第2个元素的指数运算结果如下:V =54.300061.800072.400088.7000118.6000194.0000P =61.200049.500037.600028.400019.200010.1000HL =3.9945 1.0000HL =3.9945 1.00004.1239 1.0000HL =3.9945 1.00004.1239 1.00004.2822 1.0000HL =3.9945 1.00004.1239 1.00004.2822 1.00004.4853 1.0000HL =3.9945 1.00004.1239 1.00004.2822 1.00004.4853 1.00004.7758 1.0000HL =3.9945 1.00004.1239 1.00004.2822 1.00004.4853 1.00004.7758 1.00005.2679 1.0000 c4 =-1.40429.6786alpha =-1.4042beita =1.5972e+004。
过程辨识-最小二乘类参数

( (
)
)
得 当
(
ˆ = HTΛ z H Λ L H L θWLS L L L
T L
)
正定方程
T H L Λ L H L 是正则矩阵时,有
θˆ
WLS
= H ΛLHL
T L
(
)
−1
T H L Λ L zL
又
∂ J (θ ) ∂θ 2 θˆ
2
T = 2H L Λ L H L
WLS
因为
ΛL
是正定矩阵,故
2
T H L Λ L H L 也是正定矩阵,即
∂ J (θ ) ∂θ 2 θˆ
>0
WLS
ˆ 所以,解 θWLS 使得 J (θ ) θˆWLS = min 并且是唯一的。
称之为加权最小二乘法
若加权矩阵取 则
ΛL = I
T θˆLS = H L H L
(
)
−1
T H L zL
称为最小二乘估计,对应的方法称为最小二乘法。 例 假定模型的形式为 y 据,
过程辨识
-最小二乘类参数辨识方法
引
言
“黑箱”结构
v(k )
N z
( )
−1
n(k )
+
u (k )
G z −1
( )
+
z (k )
图5.1 SISO过程的“黑箱”结构
过程模型:
Gz
( )
−1
Bz = = −1 Az 1 + a1 z −1 + a2 z − 2 + ⋯ + ana z − na
( ) ( )
根据输入输出数据,极小化J,求参数a,b,使得J=min。 这就是所谓的最小二乘问题。
最小二乘法在系统辨识中的应用(包含相关的三种算法)

2008级硕士研究生《系统建模理论》试卷已知一个三阶线性离散系统的输入、输出数据,共有40个采样值,试分别用:最小二乘法(LS )、递推最小二乘法(RLS )、广义最小二乘法(GLS )进行参数估计,给出相应的数学模型,并阐述相应的辨识原理。
k 1 2 3 4 5 6 7 8 9 10 u (k ) 0.8251 0.0988 0.4628 -0.9168 2.2325 0.0777 2.3654 0.3476 1.1473 -1.9035 y (k ) 1.5333 -1.0680 1.0666 -0.5284 -0.5835 3.1471 -3.7185 6.2149 -6.3026 7.2705k 11 12 13 14 15 16 17 18 19 20 u (k ) -0.9229 1.6400 -0.8410 0.7599 -0.4739 -0.1784 -1.7760 -1.6722 1.2959 -0.0591 y (k ) -9.0552 8.1735 -5.9004 3.9870 -2.2486 0.9525 -0.5325 -1.5227 0.4200 1.0786k 21 22 23 24 25 26 27 28 29 30 u (k ) -1.0576 -1.0071 1.1342 -0.0740 0.6759 0.5221 0.9954 0.5271 -1.7656 0.4936 y (k ) -1.5579 0.6640 -1.4222 2.6444 -2.9572 3.6340 -3.1281 3.8334 -3.2542 1.1568k 31 32 33 34 35 36 37 38 39 40 u (k ) 1.4810 0.9591 -3.1293 -0.3604 -0.4251 0.4185 -0.6728 -0.0027 2.1145 1.1157 y (k ) 0.0615 0.9120 -0.0692 -3.2731 3.7486 -4.3194 4.7230 -5.2781 5.1507 -2.7235一、最小二乘法(LS )1、数学模型设时不变SISO 动态过程的数学模型为)()()()()(11k n k u z B k z z A +=-- (1.1.1)其中,)(k u 为过程的输入量,)(k z 为过程的输出量,)(k n 是噪声,多项式)(1-z A 和)(1-z B 为:⎪⎩⎪⎨⎧+++=++++=--------nb n n n zb z b z b z B z a z a z a z A b a a 2211122111)(1)( 在本题中,a n =b n =3.即⎩⎨⎧++=+++=--------33221113322111)(1)(z b z b z b z B z a z a z a z A 将此模型写成最小二乘格式)()()(k n k k z +=θh τ (1.1.2) 其中,)(k z 是过程的输出量;)(k τh 是可观测的数据向量;)(k n 是均值为零的随机噪声。
系统辨识-最小二乘法

5.3 Matlab源程序:%最小二乘估计clearu=[ 1.147 0.201 -0.787 -1.589 -1.052 0.866 1.152 1.573 0.6260.433 -0.985 0.810 -0.044 0.947 -1.474 -0.719 -0.086 -1.099 1.4501.151 0.485 1.633 0.043 1.326 1.706 -0.340 0.890 0.144 1.177-0.390];n=normrnd(0, sqrt(0.1), 1, 31); %方差为0.1z=zeros(1,30);for k=3:31z(k)=-1.642*z(k-1)-0.715*z(k-2)+0.39*u(k-1)+0.35*u(k-2)+n(k)+1.642*n(k-1)+0.715 *n(k-2);endh0=[-z(2) -z(1) u(2) u(1)]';HLT=[h0,zeros(4,28)];for k=3:30h1=[-z(k) -z(k-1) u(k) u(k-1)]';HLT(:,k-1)=h1;endHL=HLT';y=[z(3);z(4);z(5);z(6);z(7);z(8);z(9);z(10);z(11);z(12);z(13);z(14);z(15);z(16) ;z(17);z(18);z(19);z(20);z(21);z(22);z(23);z(24);z(25);z(26);z(27);z(28);z(29); z(30);z(31)];%求出FAIc1=HL'*HL;c2=inv(c1);c3=HL'*y;c=c2*c3;%display('方差=0.1时,最小二乘法估计辨识参数θ如下:');a1=c(1)a2=c(2)b1=c(3)b2=c(4)%递推最小二乘法估计clearu=[ 1.147 0.201 -0.787 -1.589 -1.052 0.866 1.152 1.573 0.6260.433 -0.985 0.810 -0.044 0.947 -1.474 -0.719 -0.086 -1.099 1.4501.151 0.485 1.633 0.043 1.326 1.706 -0.340 0.890 0.144 1.177-0.390];z(2)=0;z(1)=0;n=normrnd(0, sqrt(0.1), 1, 31); %方差为0.1for k=3:31z(k)=-1.642*z(k-1)-0.715*z(k-2)+0.39*u(k-1)+0.35*u(k-2)+n(k)+1.642*n(k-1)+0.715 *n(k-2);endc0=[0.001 0.001 0.001 0.001]'; %直接给出被辨识参数的初始值,即一个充分小的实向量p0=10^6*eye(4,4); %直接给出初始状态P0,即一个充分大的实数单位矩阵E=0.000000005; %取相对误差E=0.000000005c=[c0,zeros(4,30)]; %被辨识参数矩阵的初始值及大小e=zeros(4,30); %相对误差的初始值及大小for k=3:30; %开始求Kh1=[-z(k-1),-z(k-2),u(k-1),u(k-2)]';x=h1'*p0*h1+1; x1=inv(x); %开始求K(k)k1=p0*h1*x1;%求出K的值d1=z(k)-h1'*c0; c1=c0+k1*d1; %求被辨识参数ce1=c1-c0; %求参数当前值与上一次的值的差值e2=e1./c0; %求参数的相对变化e(:,k)=e2; %把当前相对变化的列向量加入误差矩阵的最后一列c0=c1; %新获得的参数作为下一次递推的旧参数c(:,k)=c1; %把辨识参数c 列向量加入辨识参数矩阵的最后一列p1=p0-k1*k1'*[h1'*p0*h1+1]; %求出 p(k)的值p0=p1; %给下次用if e2<=Ebreak; %如果参数收敛情况满足要求,终止计算endend%display('方差为0. 1递推最小二乘法辨识后的结果是:');a1=c(1,:);a2=c(2,:);b1=c(3,:);b2=c(4,:);%display('a1,a2,b1,b2经过递推最小二乘法辨识的结果是:');for i=3:31;if(c(1,i)==0)q1=c(1,i-1);break;endendfor i=3:31;if(c(2,i)==0)q2=c(2,i-1);break;endendfor i=3:31;if(c(3,i)==0)q3=c(3,i-1);break;endendfor i=3:31;if(c(4,i)==0)q4=c(4,i-1);break;endenda1=q1a2=q2b1=q3b2=q4%辅助变量递推最小二乘法估计clearna=2;nb=2;siitt=[1.642 0.715 0.39 0.35]';siit0=0.001*eye(na+nb,1);p=10^6*eye(na+nb);siit(:,1)=siit0;y(2)=0;y(1)=0;x(1)=0;x(2)=0;j=0;u=[ 1.147 0.201 -0.787 -1.589 -1.052 0.866 1.152 1.573 0.6260.433 -0.985 0.810 -0.044 0.947 -1.474 -0.719 -0.086 -1.099 1.4501.151 0.485 1.633 0.043 1.326 1.706 -0.340 0.890 0.144 1.177-0.390];n=normrnd(0, sqrt(0.1), 1, 31); %方差为0.1for k=3:31;h=[-y(k-1),-y(k-2),u(k-1),u(k-2)]';y(k)=h'*siitt+n(k)+1.642*n(k-1)+0.715*n(k-2);hx=[-x(k-1),-x(k-2),u(k-1),u(k-2)]';kk=p*hx/(h'*p*hx+1);p=[eye(na+nb)-kk*h']*p;siit(:,k-1)=siit0+kk*[y(k)-h'*siit0];x(k)=hx'*siit(:,k-1);j=j+(y(k)-h'*[1.642 0.715 0.39 0.35]')^2;e=max(abs((siit(:,k-1)-siit0)./siit0));ess(:,k-2)=siit(:,k-1)-siitt;siit0=siit(:,k-1);enda1=siit0(1)a2=siit0(2)b1=siit0(3)b2=siit0(4)clear%广义最小二乘估计clear;nn = normrnd(0,sqrt(0.1),1,31)'; %方差为0.1uk=[1.147 0.201 -0.787 -1.589 -1.052 0.866 1.152 1.573 0.626 0.433 -0.958 0.810 -0.044 0.947 -1.474 -0.719 -0.086 -1.099 1.450 1.151 0.485 1.633 0.043 1.326 1.706 -0.340 0.890 1.144 1.177 -0.390];yk(1)=0;yk(2)=0;for i=1:29;yk(i+2)=-1.642*yk(i+1)-0.715*yk(i)+0.39*uk(i+1)+0.35*uk(i)+nn(i+2)+1.642*nn(i+1 )+0.715*nn(i);end;for i=1:29;A(i,:)=[-yk(i+1) -yk(i) uk(i+1) uk(i)];endsiit=inv(A'*A)*A'*(yk(3:31)+nn(2:30)')';e(1)=yk(1);e(2)=yk(2)+siit(1)*yk(1)-siit(3)*uk(1);for i=3:31;e(i)=yk(i)+siit(1)*yk(i-1)+siit(2)*yk(i-2)-siit(3)*uk(i-1)-siit(4)*uk(i-2); endfor i=1:29;fai(i,:)=[-e(i+1) -e(i)];endf=inv(fai'*fai)*fai'*e(3:31)';for i=3:31;yk(i)=yk(i)+f(1)*yk(i-1)+f(2)*yk(i-2);endyk(2)=yk(2)+f(1)*yk(1);for i=3:30;uk(i)=uk(i)+f(1)*uk(i-1)+f(2)*uk(i-2);enduk(2)=uk(2)+f(1)*uk(1);for j=1:30for i=1:29;A(i,:)=[-yk(i+1) -yk(i) uk(i+1) uk(i)];endsiit=inv(A'*A)*A'*yk(3:31)';e(1)=yk(1);e(2)=yk(2)+siit(1)*(yk(1))-siit(3)*uk(1);for i=3:31;e(i)=yk(i)+siit(1)*(yk(i-1))+siit(2)*(yk(i-2))-siit(3)*uk(i-1)-siit(4)*uk(i-2); endfor i=1:29;fai(i,:)=[-e(i+1) -e(i)];endf=inv(fai'*fai)*fai'*e(3:31)';k1(j)=f(1);k2(j)=f(2);for i=3:31;yk(i)=yk(i)+f(1)*(yk(i-1))+f(2)*(yk(i-2));endyk(2)=yk(2)+f(1)*yk(1);for i=3:30uk(i)=uk(i)+f(1)*uk(i-1)+f(2)*uk(i-2);enduk(2)=uk(2)+f(1)*uk(1);endsiit'%增广矩阵估计参数clearu=[ 1.147 0.201 -0.787 -1.589 -1.052 0.866 1.152 1.573 0.6260.433 -0.985 0.810 -0.044 0.947 -1.474 -0.719 -0.086 -1.099 1.4501.151 0.485 1.633 0.043 1.326 1.706 -0.340 0.890 0.144 1.177-0.390];n=normrnd(0, sqrt(0.1), 1, 31); %方差为0.1z=zeros(7,30);zs=zeros(7,30);zm=zeros(7,30);zmd=zeros(7,30);%输出采样、不考虑噪声时系统输出、不考虑噪声时模型输出、模型输出矩阵的大小z(2)=0;z(1)=0;zs(2)=0;zs(1)=0;zm(2)=0;zm(1)=0;zmd(2)=0;zmd(1)=0;%给输出采样、不考虑噪声时系统输出、不考虑噪声时模型输出、模型输出赋初值for k=3:31z(k)=-1.642*z(k-1)-0.715*z(k-2)+0.39*u(k-1)+0.35*u(k-2)+n(k)+1.642*n(k-1)+0.715 *n(k-2);endc0=[0.001 0.001 0.001 0.001]'; %直接给出被辨识参数的初始值,即一个充分小的实向量p0=10^6*eye(4,4); %直接给出初始状态P0,即一个充分大的实数单位矩阵E=0.000000005; %取相对误差E=0.000000005c=[c0,zeros(4,30)]; %被辨识参数矩阵的初始值及大小e=zeros(4,30); %相对误差的初始值及大小for k=3:30; %开始求Kh1=[-z(k-1),-z(k-2),u(k-1),u(k-2)]';x=h1'*p0*h1+1; x1=inv(x); %开始求K(k)k1=p0*h1*x1;%求出K的值d1=z(k)-h1'*c0; c1=c0+k1*d1; %求被辨识参数czs(k)=-1.642*z(k-1)-0.715*z(k-2)+0.39*u(k-1)+0.35*u(k-2);%系统在M序列的输入下不考虑扰动时的输出响应zm(k)=[-z(k-1),-z(k-2),u(k-1),u(k-2)]*[c1(1);c1(2);c1(3);c1(4)];%模型在输入下不考虑扰动时的的输出响应zmd(k)=h1'*c1;%模型在输入下的的输出响应e1=c1-c0;e2=e1./c0; %求参数的相对变化e(:,k)=e2; %把当前相对变化的列向量加入误差矩阵的最后一列c0=c1; %新获得的参数作为下一次递推的旧参数c(:,k)=c1; %把辨识参数c 列向量加入辨识参数矩阵的最后一列p1=p0-k1*k1'*[h1'*p0*h1+1]; %求出 p(k)的值p0=p1; %给下次用if e2<=Ebreak; %如果参数收敛情况满足要求,终止计算endend%display('方差为0. 1递推最小二乘法辨识后的结果是:');a1=c(1,:);a2=c(2,:);b1=c(3,:);b2=c(4,:);%display('a1,a2,b1,b2经过递推最小二乘法辨识的结果是:');for i=3:31;if(c(1,i)==0)q1=c(1,i-1);break;endendfor i=3:31;if(c(2,i)==0)q2=c(2,i-1);break;endendfor i=3:31;if(c(3,i)==0)q3=c(3,i-1);break;endendfor i=3:31;if(c(4,i)==0)q4=c(4,i-1);break;endenda1=q1a2=q2b1=q3b2=q4%用夏氏偏差修正法估计参数clear;u=[ 1.147 0.201 -0.787 -1.589 -1.052 0.866 1.152 1.573 0.6260.433 -0.985 0.810 -0.044 0.947 -1.474 -0.719 -0.086 -1.099 1.4501.151 0.485 1.633 0.043 1.326 1.706 -0.340 0.890 0.144 1.177-0.390];n=normrnd(0, sqrt(0.1), 1, 31); %方差为0.1z=zeros(1,30);for k=3:31z(k)=-1.642*z(k-1)-0.715*z(k-2)+0.39*u(k-1)+0.35*u(k-2)+n(k)+1.642*n(k-1)+0.715 *n(k-2);endh0=[-z(2) -z(1) u(2) u(1)]';HLT=[h0,zeros(4,28)];for k=3:30h1=[-z(k) -z(k-1) u(k) u(k-1)]';HLT(:,k-1)=h1;endHL=HLT';y=[z(3);z(4);z(5);z(6);z(7);z(8);z(9);z(10);z(11);z(12);z(13);z(14);z(15);z(16) ;z(17);z(18);z(19);z(20);z(21);z(22);z(23);z(24);z(25);z(26);z(27);z(28);z(29); z(30);z(31)];%求出FAIc1=HL'*HL;c2=inv(c1);c3=HL'*y;c=c2*c3;fai1_xiashi=HL;siit1_ls_guzhi=c;ka_ma=inv(fai1_xiashi'*fai1_xiashi)*fai1_xiashi';M_xiashi=eye(29)-fai1_xiashi*ka_ma;siit_N0_xshi=siit1_ls_guzhi;siit_bxs=[10,10,10,10]';for n=1:30e=zeros(29,1);e(3)=y(5)+siit_N0_xshi(1,1)*y(4)+siit_N0_xshi(2,1)*y(3)-siit_N0_xshi(3,1)*u(4)-siit_N0_xshi(4,1)*u(3);e(4)=y(6)+siit_N0_xshi(1,1)*y(5)+siit_N0_xshi(2,1)*y(4)-siit_N0_xshi(3,1)*u(5)-siit_N0_xshi(4,1)*u(4);e(5:29) = y(5:29) - fai1_xiashi(5:29,:) * siit_N0_xshi;ou_mei_ka=zeros(29,1);for i=1:29ou_mei_ka(i,:)=-e(i);endD_xiashi=ou_mei_ka'*M_xiashi*ou_mei_ka;f_xiashi=inv(D_xiashi)*ou_mei_ka'*M_xiashi*y(1:29);siit_b=ka_ma*ou_mei_ka*f_xiashi;siit_xiashi=siit1_ls_guzhi-siit_b;if norm(siit_b-siit_bxs)/norm(siit_bxs)<0.0001break ;endsiit_N0_xshi=siit_xiashi;siit_bxs=siit_b;endsiit1_xiashi=siit_xiashi;%display('利用夏氏修正法得出的辨识结果:');a1=siit1_xiashi(1)a2=siit1_xiashi(2)b1=siit1_xiashi(3)b2=siit1_xiashi(4)。
最小二乘参数辨识方法及应用程序清单

第3章最小二乘参数辨识方法及应用程序清单一、二、3.3 加权最小二乘算法程序3:最小二乘参数辨识程序clear all%清理工作间变量close all%关闭所有图形clc%清屏z(1)=440,z(2)=430,z(3)=420,z(4)=380,z(5)=370,z(6)=360,z(7)=320,z(8)=310,z(9)=300,z(10)=260,z(11)=250,z(12 )=240,z(13)=220,z(14)=210,z(15)=170,z(16)=160;u(1)=3,u(2)=2.7,u(3)=2.4,u(4)=2.1,u(5)=2.0,u(6)=1.9,u(7)=1.6,u(8)=1.54,u(9)=1.48,u(10)=1.2,u(11)=1.14,u(12)=1 .08,u(13)=0.95,u(14)=0.9,u(15)=0.7,u(16)=0.6;HL=[-z(1) u(1);-z(2) u(2);-z(3) u(3);-z(4) u(4);-z(5) u(5);-z(6) u(6); -z(7) u(7); -z(8) u(8);-z(9) u(9); -z(10) u(10);-z(11) u(11);-z(12) u(12);-z(13) u(13);-z(14) u(14)] %给样本矩阵HL赋值ZL=[z(3);z(4);z(5);z(6);z(7);z(8);z(9);z(10);z(11);z(12);z(13);z(14);z(15);z(16)]% 给样本矩阵zL赋值%calculating parameters%计算参数c1=HL'*HL; c2=inv(c1); c3=HL'*ZL; c=c2*c3 %计算并显示%DISPLAY PARAMETERSa2=c(1), b2=c(2)三、3.4 递推最小二乘算法程序4:递推最小二乘参数辨识程序clear all%清理工作间变量close all%关闭所有图形clc%清屏%%%%%%%%%%%%%%%%%%%%%%%%%% 产生白噪声的程序%%%%%%%%%%%%%%%%%%%%%%%%%%%%A=6;x0=1;M=255;for k=1:10000x2=A*x0;x1=mod (x2,M);v1=x1/256;v(:,k)=(v1-0.5)*2;x0=x1;v0=v1;endnum=v;k1=k;% num=zeros(1,1000);% randn('seed',100);% num=randn(1,1000);% 白噪声程序结束%%%%%%%%%%%%% M序列产生程序%%%L=15;% M序列的周期y1=1;y2=1;y3=1;y4=0;%四个移位积存器的输出初始值for i=1:L;%开始循环,长度为Lx1=xor(y3,y4);%第一个移位积存器的输入是第3个与第4个移位积存器的输出的“或”x2=y1;%第二个移位积存器的输入是第3个移位积存器的输出x3=y2;%第三个移位积存器的输入是第2个移位积存器的输出x4=y3;%第四个移位积存器的输入是第3个移位积存器的输出y(i)=y4;%取出第四个移位积存器幅值为"0"和"1"的输出信号,if y(i)>0.5,u(i)=-1;%如果M序列的值为"1"时,辨识的输入信号取“-0.03”else u(i)=1;%当M序列的值为"0"时,辨识的输入信号取“0.03”end%小循环结束y1=x1;y2=x2;y3=x3;y4=x4;%为下一次的输入信号做准备end%大循环结束,产生输入信号ufigure(1);%第1个图形stem(u),grid on%以径的形式显示出输入信号并给图形加上网格%%%% M序列产生程序程序结束%%%%%%% 递推最小二乘辨识程序%%%%%lamt=1;z(2)=0;z(1)=0;%取z的前两个初始值为零for k=3:15;%循环变量从3到15z(k)=-1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2)+0*num(1,k);%给出理想的辨识输出采样信号end%RLS递推最小二乘辨识c0=[0.001 0.001 0.001 0.001]';%直接给出被辨识参数的初始值,即一个充分小的实向量p0=10^3*eye(4,4);%直接给出初始状态P0,即一个充分大的实数单位矩阵E=0.000000005;%相对误差E=0.000000005c=[c0,zeros(4,14)];%被辨识参数矩阵的初始值及大小e=zeros(4,15);%相对误差的初始值及大小for k=3:15; %开始求Kh1=[-z(k-1),-z(k-2),u(k-1),u(k-2)]';x=h1'*p0*h1+1*lamt;x1=inv(x); %开始求K(k)k1=p0*h1*x1;%求出K的值d1=z(k)-h1'*c0;c1=c0+k1*d1;%求被辨识参数c% p1=p0-k1*k1'*(h1'*p0*h1+1);%求出p(k)的值p1=1/lamt*(eye(4)-k1*h1')*p0;e1=c1-c0;%求参数当前值与上一次的值的差值e2=e1./c0;%求参数的相对变化e(:,k)=e2; %把当前相对变化的列向量加入误差矩阵的最后一列c(:,k)=c1;%把辨识参数c 列向量加入辨识参数矩阵的最后一列c0=c1;%新获得的参数作为下一次递推的旧参数p0=p1;%给下次用if e2<=Ebreak;%若参数收敛满足要求,终止计算end%小循环结束end%大循环结束%%% 最小二乘辨识程序结束%%%%%%%%% 辨识结果显示程序%%%%%c%显示被辨识参数e%显示辨识结果的收敛情况%分离参数a1=c(1,:); a2=c(2,:); b1=c(3,:); b2=c(4,:);ea1=e(1,:); ea2=e(2,:); eb1=e(3,:); eb2=e(4,:);figure(2);%第2个图形i=1:15;%横坐标从1到15plot(i,a1,'r',i,a2,'b',i,b1,'k',i,b2,'g') %画出a1,a2,b1,b2的各次辨识结果title('递推最小二乘参数辨识')%图形标题figure(3); %第3个图形i=1:15; %横坐标从1到15plot(i,ea1,'r',i,ea2,'b',i,eb1,'k',i,eb2,'g') %画出a1,a2,b1,b2的各次辨识结果的收敛情况title('辨识精度') %图形标题%%% 辨识结果显示程序结束%%四、3.5 增广最小二乘辨识算法及原理程序5:增广递推最小二乘参数辨识程序clear all%清理工作间变量close all%关闭所有图形clc%清屏%%%% M序列、噪声信号产生及其显示程序%%%%L=60;%四位移位积存器产生的M序列的周期y1=1;y2=1;y3=1;y4=0;%四个移位积存器的输出初始值for i=1:L;x1=xor(y3,y4);%第一个移位积存器的输入信号x2=y1;%第二个移位积存器的输入信号x3=y2;%第三个移位积存器的输入信号x4=y3;%第四个移位积存器的输入信号y(i)=y4;%第四个移位积存器的输出信号,幅值"0"和"1"if y(i)>0.5,u(i)=-1;%M序列的值为"1"时,辨识的输入信号取“-1”else u(i)=1;%M序列的值为"0"时,辨识的输入信号取“1”endy1=x1;y2=x2;y3=x3;y4=x4;%为下一次的输入信号作准备endfigure(1);%画第一个图形subplot(2,1,1); %画第一个图形的第一个子图stem(u),grid on%画出M序列输入信号v=randn(1,60); %产生一组60个正态分布的随机噪声subplot(2,1,2); %画第一个图形的第二个子图plot(v),grid on;%画出随机噪声信号R=corrcoef(u,v);%计算输入信号与随机噪声信号的相关系数r=R(1,2);%取出互相关系数u%显示输入型号v%显示噪声型号。
系统辨识—最小二乘法

最小二乘法参数辨识1 引言系统辨识是根据系统的输入输出时间函数来确定描述系统行为的数学模型。
现代控制理论中的一个分支。
通过辨识建立数学模型的目的是估计表征系统行为的重要参数,建立一个能模仿真实系统行为的模型,用当前可测量的系统的输入和输出预测系统输出的未来演变,以及设计控制器。
对系统进行分析的主要问题是根据输入时间函数和系统的特性来确定输出信号。
对系统进行控制的主要问题是根据系统的特性设计控制输入,使输出满足预先规定的要求。
而系统辨识所研究的问题恰好是这些问题的逆问题。
通常,预先给定一个模型类μ={M}(即给定一类已知结构的模型),一类输入信号u和等价准则J=L(y,yM)(一般情况下,J是误差函数,是过程输出y和模型输出yM的一个泛函);然后选择使误差函数J达到最小的模型,作为辨识所要求的结果。
系统辨识包括两个方面:结构辨识和参数估计。
在实际的辨识过程中,随着使用的方法不同,结构辨识和参数估计这两个方面并不是截然分开的,而是可以交织在一起进行的。
2 系统辨识的目的在提出和解决一个辨识问题时,明确最终使用模型的目的是至关重要的。
它对模型类(模型结构)、输入信号和等价准则的选择都有很大的影响。
通过辨识建立数学模型通常有四个目的。
①估计具有特定物理意义的参数有些表征系统行为的重要参数是难以直接测量的,例如在生理、生态、环境、经济等系统中就常有这种情况。
这就需要通过能观测到的输入输出数据,用辨识的方法去估计那些参数。
②仿真仿真的核心是要建立一个能模仿真实系统行为的模型。
用于系统分析的仿真模型要求能真实反映系统的特性。
用于系统设计的仿真,则强调设计参数能正确地符合它本身的物理意义。
③预测这是辨识的一个重要应用方面,其目的是用迄今为止系统的可测量的输入和输出去预测系统输出的未来的演变。
例如最常见的气象预报,洪水预报,其他如太阳黑子预报,市场价格的预测,河流污染物含量的预测等。
预测模型辨识的等价准则主要是使预测误差平方和最小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第3章最小二乘参数辨识方法及应用程序清单一、3.2.2节利用最小二乘法求取模型参数的程序二、3.3 加权最小二乘算法程序3:最小二乘参数辨识程序clear all%清理工作间变量close all%关闭所有图形clc%清屏z(1)=440,z(2)=430,z(3)=420,z(4)=380,z(5)=370,z(6)=360,z(7)=320,z(8)=310,z(9)=300,z(10)=260,z(11)=250,z(12 )=240,z(13)=220,z(14)=210,z(15)=170,z(16)=160;u(1)=3,u(2)=2.7,u(3)=2.4,u(4)=2.1,u(5)=2.0,u(6)=1.9,u(7)=1.6,u(8)=1.54,u(9)=1.48,u(10)=1.2,u(11)=1.14,u(12)=1 .08,u(13)=0.95,u(14)=0.9,u(15)=0.7,u(16)=0.6;HL=[-z(1) u(1);-z(2) u(2);-z(3) u(3);-z(4) u(4);-z(5) u(5);-z(6) u(6); -z(7) u(7); -z(8) u(8);-z(9) u(9); -z(10) u(10);-z(11) u(11);-z(12) u(12);-z(13) u(13);-z(14) u(14)] %给样本矩阵HL赋值ZL=[z(3);z(4);z(5);z(6);z(7);z(8);z(9);z(10);z(11);z(12);z(13);z(14);z(15);z(16)]% 给样本矩阵zL赋值%calculating parameters%计算参数c1=HL'*HL; c2=inv(c1); c3=HL'*ZL; c=c2*c3 %计算并显示%DISPLAY PARAMETERSa2=c(1), b2=c(2)三、3.4 递推最小二乘算法程序4:递推最小二乘参数辨识程序clear all%清理工作间变量close all%关闭所有图形clc%清屏%%%%%%%%%%%%%%%%%%%%%%%%%% 产生白噪声的程序%%%%%%%%%%%%%%%%%%%%%%%%%%%%A=6;x0=1;M=255;for k=1:10000x2=A*x0;x1=mod (x2,M);v1=x1/256;v(:,k)=(v1-0.5)*2;x0=x1;v0=v1;endnum=v;k1=k;% num=zeros(1,1000);% randn('seed',100);% num=randn(1,1000);% 白噪声程序结束%%%%%%%%%%%%% M序列产生程序%%%L=15;% M序列的周期y1=1;y2=1;y3=1;y4=0;%四个移位积存器的输出初始值for i=1:L;%开始循环,长度为Lx1=xor(y3,y4);%第一个移位积存器的输入是第3个与第4个移位积存器的输出的“或”x2=y1;%第二个移位积存器的输入是第3个移位积存器的输出x3=y2;%第三个移位积存器的输入是第2个移位积存器的输出x4=y3;%第四个移位积存器的输入是第3个移位积存器的输出y(i)=y4;%取出第四个移位积存器幅值为"0"和"1"的输出信号,if y(i)>0.5,u(i)=-1;%如果M序列的值为"1"时,辨识的输入信号取“-0.03”else u(i)=1;%当M序列的值为"0"时,辨识的输入信号取“0.03”end%小循环结束y1=x1;y2=x2;y3=x3;y4=x4;%为下一次的输入信号做准备end%大循环结束,产生输入信号ufigure(1);%第1个图形stem(u),grid on%以径的形式显示出输入信号并给图形加上网格%%%% M序列产生程序程序结束%%%%%%% 递推最小二乘辨识程序%%%%%lamt=1;z(2)=0;z(1)=0;%取z的前两个初始值为零for k=3:15;%循环变量从3到15z(k)=-1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2)+0*num(1,k);%给出理想的辨识输出采样信号end%RLS递推最小二乘辨识c0=[0.001 0.001 0.001 0.001]';%直接给出被辨识参数的初始值,即一个充分小的实向量p0=10^3*eye(4,4);%直接给出初始状态P0,即一个充分大的实数单位矩阵E=0.000000005;%相对误差E=0.000000005c=[c0,zeros(4,14)];%被辨识参数矩阵的初始值及大小e=zeros(4,15);%相对误差的初始值及大小for k=3:15; %开始求Kh1=[-z(k-1),-z(k-2),u(k-1),u(k-2)]';x=h1'*p0*h1+1*lamt;x1=inv(x); %开始求K(k)k1=p0*h1*x1;%求出K的值d1=z(k)-h1'*c0;c1=c0+k1*d1;%求被辨识参数c% p1=p0-k1*k1'*(h1'*p0*h1+1);%求出p(k)的值p1=1/lamt*(eye(4)-k1*h1')*p0;e1=c1-c0;%求参数当前值与上一次的值的差值e2=e1./c0;%求参数的相对变化e(:,k)=e2; %把当前相对变化的列向量加入误差矩阵的最后一列c(:,k)=c1;%把辨识参数c 列向量加入辨识参数矩阵的最后一列c0=c1;%新获得的参数作为下一次递推的旧参数p0=p1;%给下次用if e2<=Ebreak;%若参数收敛满足要求,终止计算end%小循环结束end%大循环结束%%% 最小二乘辨识程序结束%%%%%%%%% 辨识结果显示程序%%%%%c%显示被辨识参数e%显示辨识结果的收敛情况%分离参数a1=c(1,:); a2=c(2,:); b1=c(3,:); b2=c(4,:);ea1=e(1,:); ea2=e(2,:); eb1=e(3,:); eb2=e(4,:);figure(2);%第2个图形i=1:15;%横坐标从1到15plot(i,a1,'r',i,a2,'b',i,b1,'k',i,b2,'g') %画出a1,a2,b1,b2的各次辨识结果title('递推最小二乘参数辨识')%图形标题figure(3); %第3个图形i=1:15; %横坐标从1到15plot(i,ea1,'r',i,ea2,'b',i,eb1,'k',i,eb2,'g') %画出a1,a2,b1,b2的各次辨识结果的收敛情况title('辨识精度') %图形标题%%% 辨识结果显示程序结束%%四、3.5 增广最小二乘辨识算法及原理程序5:增广递推最小二乘参数辨识程序clear all%清理工作间变量close all%关闭所有图形clc%清屏%%%% M序列、噪声信号产生及其显示程序%%%%L=60;%四位移位积存器产生的M序列的周期y1=1;y2=1;y3=1;y4=0;%四个移位积存器的输出初始值for i=1:L;x1=xor(y3,y4);%第一个移位积存器的输入信号x2=y1;%第二个移位积存器的输入信号x3=y2;%第三个移位积存器的输入信号x4=y3;%第四个移位积存器的输入信号y(i)=y4;%第四个移位积存器的输出信号,幅值"0"和"1"if y(i)>0.5,u(i)=-1;%M序列的值为"1"时,辨识的输入信号取“-1”else u(i)=1;%M序列的值为"0"时,辨识的输入信号取“1”endy1=x1;y2=x2;y3=x3;y4=x4;%为下一次的输入信号作准备endfigure(1);%画第一个图形subplot(2,1,1); %画第一个图形的第一个子图stem(u),grid on%画出M序列输入信号v=randn(1,60); %产生一组60个正态分布的随机噪声subplot(2,1,2); %画第一个图形的第二个子图plot(v),grid on;%画出随机噪声信号R=corrcoef(u,v);%计算输入信号与随机噪声信号的相关系数r=R(1,2);%取出互相关系数u%显示输入型号v%显示噪声型号%%%% M序列、噪声信号产生及其显示程序结束%%%%%% 增广递推最小二乘辨识程序%%%%%%%%%%%z=zeros(7,60);zs=zeros(7,60);zm=zeros(7,60);zmd=zeros(7,60);%输出采样、不考虑噪声时系统输出、不考虑噪声时模型输出、模型输出矩阵的大小z(2)=0;z(1)=0;zs(2)=0;zs(1)=0;zm(2)=0;zm(1)=0;zmd(2)=0;zmd(1)=0;%给输出采样、不考虑噪声时系统输出、不考虑噪声时模型输出、模型输出赋初值%增广递推最小二乘辨识c0=[0.001 0.001 0.001 0.001 0.001 0.001 0.001]';%直接给出被辨识参数的初始值,即一个充分小的实向量p0=10^6*eye(7,7);%直接给出初始状态P0,即一个充分大的实数单位矩阵E=5.0e-15;%取相对误差Ec=[c0,zeros(7,59)];%被辨识参数矩阵的初始值及大小e=zeros(7,60);%相对误差的初始值及大小for k=3:60; %开始求Kz(k)=-1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2)+1.2*v(k)-v(k-1)+0.2*v(k-2);%系统在M序列输入下的输出采样信号h1=[-z(k-1),-z(k-2),u(k-1),u(k-2),v(k),v(k-1),v(k-2)]';%为求K(k)作准备x=h1'*p0*h1+1;x1=inv(x);k1=p0*h1*x1; %Kd1=z(k)-h1'*c0;c1=c0+k1*d1;%辨识参数czs(k)=-1.5*z(k-1)-0.7*z(k-2)+u(k-1)+0.5*u(k-2);%系统在M序列的输入下不考虑扰动时的输出响应zm(k)=[-z(k-1),-z(k-2),u(k-1),u(k-2)]*[c1(1);c1(2);c1(3);c1(4)];%模型在M序列的输入下不考虑扰动时的的输出响应zmd(k)=h1'*c1;%模型在M序列的输入下的的输出响应e1=c1-c0;e2=e1./c0; %求参数的相对变化e(:,k)=e2;c0=c1;%给下一次用c(:,k)=c1;%把辨识参数c 列向量加入辨识参数矩阵p1=p0-k1*k1'*[h1'*p0*h1+1];%find p(k)p0=p1;%给下次用if e2<=E break;%若收敛情况满足要求,终止计算end%判断结束end%循环结束c, e, %显示被辨识参数及参数收敛情况z,zmd %显示输出采样值、系统实际输出值、模型输出值%分离变量a1=c(1,:); a2=c(2,:); b1=c(3,:); b2=c(4,:);%分离出a1、a2、b1、b2d1=c(5,:); d2=c(6,:); d3=c(7,:); %分离出d1、d2、d3ea1=e(1,:); ea2=e(2,:); eb1=e(3,:); eb2=e(4,:); %分离出a1、a2、b1、b2的收敛情况ed1=e(5,:); ed2=e(6,:); ed3=e(7,:); %分离出d1 、d2 、d3的收敛情况figure(2);%画第二个图形i=1:60;plot(i,a1,'r',i,a2,'b',i,b1,'k',i,b2,'y',i,d1,'g',i,d2,'c',i,d3,'m')%画出各个被辨识参数title('递推增广最小二乘辨识方法')%标题figure(3);%画出第三个图形i=1:60;plot(i,ea1,'r',i,ea2,'b',i,eb1,'k',i,eb2,'y',i,ed1,'g',i,ed2,'c',i,ed2,'m')%画出各个参数收敛情况title('辨识误差')%标题。
