高等代数第三章线性方程组知识点复习与相关练习
高等代数课件北大版第三章线性方程组

定义:将线性方程 组中的每一行进行 加减、倍乘等操作, 使得方程组简化
作用:将增广矩阵 化为阶梯形矩阵, 便于求解线性方程 组
步骤:对增广矩阵 进行初等行变换, 得到阶梯形矩阵
注意事项:变换过 程中需保持矩阵的 行列式不变,避免 出现错误结果
矩阵的逆法
定义:如果矩阵A存在逆矩阵,则称A为可逆矩阵 性质:可逆矩阵的行列式不为0 计算方法:通过行初等变换将矩阵变为单位矩阵,得到逆矩阵 应用:解线性方程组的重要工具之一
束优化问题等。
线性方程组在其他领域的应用
物理学中的应用:描述物理现象和规律,如牛顿第二定律、万有引力定律等。 经济学中的应用:分析经济问题,如供需关系、生产成本等。 计算机科学中的应用:解决优化问题、机器学习算法等。 统计学中的应用:处理数据分析和预测问题,如回归分析、主成分分析等。
线性方程组的扩展知识
添加标题
逆矩阵的计算方法:通过高斯消元法或拉普拉斯展开式等方法计算行列式|A|,然后通过|A|*|A^(1)|=1计算逆矩阵A^(-1)。
添加标题
逆矩阵的应用:在解线性方程组、求矩阵的秩、计算行列式、求向量空间的一组基等方面都有应用。
线性方程组的通解与特解的关系
通解与特解的定义
通解与特解的关系
通解与特解的求解方法
线性方程组在计算机科学中的应用
线性方程组在计算机图形学中 的应用:用于计算光照、纹理 映射和渲染等。
线性方程组在计算机视觉中的 应用:用于图像处理、特征提
取和目标检测等。
线性方程组在机器学习中的应 用:用于训练和优化模型,如 线性回归和逻辑回归。
线性方程组在人工智能领域的 应用:用于优化算法、求解约
通解与特解的应用
感谢您的耐心观看
高等代数第三章线性方程组复习

12,,,,,,,,A m m m m k k k k αα++=如果存在不全为零的数线性相关否则称向量组如果向量组A 中有一个向量可由其他向量线性表出,否则,线性无线性相关,等价于存在I,使得ai 可由a1….ai-1线性表出3.线性相关性的判断:线性相关的充分必要条件是1212222,,),(,,,),,,,)n n nm a a a a a a α=齐次线性方程组1222200m m a a x a x a x a x +++++=+++=11121121222212),(...,(,,,)n n m m m nm a a a a a αα==就是线性表示的一组不全为零的系数。
,,)m k 等价于系数行列式等于零,等价于秩n(矩阵的行列式不等于0,等价于有非零解等价于系数矩阵的秩小于未知量的个数补充:线性组合与线性表出1)定义:若有数域P中的数K1 K2….Ks,使向量a=K1b1+…..+Ksbs,则a称为向量组b1 ….bn的一个线性组合,或称a可由该向量组线性表出2)定理:判断一向量是否可由一向量组线性表出,,m α,,m α为系数矩阵列向量,以常数项列向量的线性方程组有解,表示的一组系数。
且任一个解就是线性线性表示的充要条件是:二向量组的极大无关组的定义及求法向量组的等价:. 向量组的等价都可以由向量组3-9:如果向量组中的每一个向量12:,,,mA ααα2,,s ββ线性表示,那么就称向量组A 可以由向量组B 线性表示。
也可以由向量组A 线性与向量组B 等价。
),2,1(m i =向量组的极大无关组的定义及求法2,,s α与是两个向量组,如果12,,,t βββ必线性相关。
,,s α,,s α12,,,t βββ线性表示;可以由向量组即多由少线性表出,则多线性相关。
2,,s α与是两个向量组,如果,,s α12,,,t βββ线性表示;可以由向量组12,,,t βββ线性无关2,,,s αα个n 维向量一定线性相关;n 维向量一定线性相关;.相同个数向量组包含等价的线性无关的向量(推论连续应用两次即可得到上述结论),,rα中任何向量,,r α线性无关。
第三章习题与复习题(线性方程组)---高等代数
x2x2x0
123
2xxx0
123
3xxx0
123
的解,求的值.
5.已知线性方程组
x2xx2x0
1234
xcxcx
234
0
xcxx
124
0
的基础解系由两个解向量构成,求c的值与该方程组的通解.
6.设
123
A
132
21t
211
B是3阶非零矩阵,且AB=O,求t的值.
(D)若n维向量组1,2,⋯,m(m≥2)线性无关,则对于任意不全为零的数k1,k2,⋯,km
一定有
k11k22
k
m
m
7.已知向量组1,2,3线性无关,向量可由1,2,3线性表示,向量不能由1,2,3
线性表示,则对任意常数k,必有().
(A)1,2,3,k线性无关
(B)1,2,3,k线性相关
(C)1,2,3,k线性无关
(B),,,
12233441
(C),,,
12233441
(D),,,
12233441
5.对任意实数a,b,c下列向量组线性无关的是().
(A) (a,1, 2),(2,b,3),(0, 0, 0)
(B) (b,1, 1),(1,a,3),(2, 3,c),(a,0,c)
(C) (1,a,1, 1),(1,b,1, 0),(1,c,0, 0)
当满足时,
1,2,3线性无关.
8.已知向量组
1111
0112
,,
,
1234
23t24
351t9
线性相关,则t满足.
3.设向量组1,2,3线性无关,则当参数l, m满足时,l21,m32,13也线性无关.
高等代数第3章线性方程组

3.1 消元法
线性方程组
3.1.1 高斯消元法及矩阵表示 3.1.2 矩阵表示 3.1.3 一般情形
3.1.1 高斯消元法
分析:用消元法解下列方程组的过程. 分析:用消元法解下列方程组的过程. 引例 求解线性方程组
2 x1 − x2 − x3 + x4 = 2, x + x − 2 x + x = 4, 1 2 3 4 4 x1 − 6 x2 + 2 x3 − 2 x4 = 4, 3 x1 + 6 x2 − 9 x3 + 7 x4 = 9,
1 2
3
4 1 2
3
3
4
↔4 −23
4
用“回代”的方法求出解: 回代”的方法求出解:
x1 = x3 + 4 x2 = x3 + 3 其中 为任意取值 . 其中x3 于是解得 x = −3 4
或令x3 = c , 方程组的解可记作
x1 = c + 4 x = c + 3 2 x3 = c x 4 = −3
阶 矩 : 行 梯 阵
(1)元素全为0的行全在下方; 元素全为0的行全在下方; 行的第一个非0元素的 (2)对于非零行,第i+1行的第一个非 元素的 对于非零行, 行的第一个非 列标大于第i行的第一个非 行的第一个非0元素的列标 列标大于第 行的第一个非 元素的列标
1 0 0 0 1 −2 1 4 1 −1 1 0 0 0 1 − 3 0 0 0 0
3.1.3 一般情形
a11 x1 + a12 x 2 + L + a1n x n = b1 a x + a x +L+ a x = b 21 1 22 2 2n n 2 线性方程组 LLLLLLLLLLLL a m 1 x1 + a m 2 x 2 + L + a mn x n = bm
线性代数第三章习题与答案(东大绝版)

第三章 习题与答案 习题 A1.求向量123(4,1,3,2),(1,2,3,2),(16,9,1,3)T T T=--=-=-ααα的线性组合12335.+-ααα 解 12341161293535331223⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪+-=+- ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭ααα1251613109491512561037⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪⎪ ⎪ ⎪=+-= ⎪ ⎪ ⎪ ⎪--- ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭⎝⎭. 2.从以下方程中求向量α1233()2()5()-++=+αααααα,其中123(2,5,1,3),(10,1,5,10),(4,1,1,1).TT T ===-ααα 解 由方程得1233322550-++--=αααααα,1232104651112632532515118310124⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=+-=+-= ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭αααα故1234⎛⎫ ⎪ ⎪= ⎪ ⎪⎝⎭α,即(1,2,3,4)T =α.3.求证:向量组12i s α,α,,α,α 中的任一向量i α可以由这个向量组线性表出. 证 120010(1,2,,)i i s i s =+++++= ααααα4.证明: 包含零向量的向量组线性相关.证 设向量组为1211α,α,,α,0,α,,αi i s -+ ,则有12110α0αα00α0α0,0i i s k k -++++++++=≠而0,0,,0,,0,,0k 不全为0,故向量组线性相关.5.设有m 个向量12α,α,,αm ,证明: 若αα()i j i j =≠,则向量组12α,α,,αm 线性相关. 证 显然有1210α0αα0α()α0α0,0i i j m k k k +++++++-++=≠ , 而0,,0,,0,,0,,0,,0k k - 不全为0.故向量组线性相关.6.判断下列向量组的线性相关性(1) (1,1,0),(0,1,1,),(3,0,0,); (2) (2,0),(0,-1);(3) (-4,-5,2,6),(2,-2,1,3),(6,-3,3,9),(4,-1,5,6);(4) (1,0,0,2,5),(0,1,0,3,4),(0,0,1,4,7),(2,-3,4,11,12).解 (1)设有三个数123,,k k k ,使123(1,1,0)(0,1,1,) (3,0,0,)=(0,0,0)k k k ++则有方程组131223000k k k k k +=⎧⎪+=⎨⎪=⎩,因为系数行列式10311030010D =≠.方程组仅有零解,所以三个向量线性无关. (2)设有两个数12,k k 使12(2,0)(0,-1)=(0,0)k k + 则有方程组12200k k =⎧⎨-=⎩,由此解得120k k ==,所以两个向量线性无关.另外,也可由其分量不成比例看出两个向量线性无关. (3)设有四个数1234,,,k k k k ,使1234(-4,-5,2,6)(2,-2,1,3)(6,-3,3,9)(4,-1,5,6)=(0,0,0,0)k k k k +++,则有方程组1234123412341234426405230235063960k k k k k k k k k k k k k k k k +++=⎧⎪----=⎪⎨+++=⎪⎪+++=⎩,其系数行列式42645231021356396D ----==,所以方程组有非零解,向量组线性相关.(4) 设有四个数1234,,,k k k k ,使1234(1,0,0,2,5)(0,1,0,3,4)(0,0,1,4,7)(2,-3,4,11,12)=(0,0,0,0)k k k k +++则有方程组14243412341234203040234110547120k k k k k k k k k k k k k k +=⎧⎪-=⎪⎪+=⎨⎪+++=⎪⎪+++=⎩由前三个方程得1424342,3,4k k k k k k =-==-,代入第五个方程得4140k -=, 即40k =,从而1230k k k ===,所以向量组线性无关.7.设123α,α,α线性无关,证明:122331αα,αα,αα+++也线性无关. 证 设有三个数123,,k k k ,使()()()112223331αααααα0k k k +++++=, 则()()()131122233ααα0k k k k k k +++++=,因123α,α,α线性无关,故13122300k k k k k k +=⎧⎪+=⎨⎪+=⎩,因系数行列式10111020011D ==≠,所以只有1230k k k ===, 由此知122331αα,αα,αα+++线性无关.8.设12α,α,,αn 线性无关,问向量组122311αα,αα,,αα,ααn n n -++++ 是线性相关,还是线性无关?并给出证明. 解 设有n 个数12,,,,n k k k 使()()()()112223111αααααααα0n n n n n k k k k --++++++++= ,则得方程组1122310000n n n k k k k k k k k -+=⎧⎪+=⎪⎪+=⎨⎪⎪+=⎪⎩ 其系数行列式11000011100000110001(1),000110000011n n D +==+-可见,当n 为奇数时,20n D =≠,方程组仅有零解,向量组线性无关, 当n 为偶数时,0n D =,方程组有非零解,向量组线性相关.9.设12α(,,,)(1,2,,)i i i in a a a i n == ,证明:向量组12α,α,,αn 线性相关的充分必要条件是det()0ij a =.证 必要性:设12α,α,,αn 线性相关,则存在不全为0的n 个数12,,,,n k k k 使1122ααα0n n k k k +++= ,即有方程组()11121211212222112200*0n n n nn n nn n a k a k a k a k a k a k a k a k a k +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩ 该方程组有非零解,故系数行列式0n D =,即det()0ij a =,充分性: 对于方程组(*)当det()0ij a =时,系数行列式0n D =,所以有非零解,即存在不全为0的12,,,,n k k k 使1122ααα0n n k k k +++= 成立,故12α,α,,αn 线性相关.10.设12α,α,,αn 是一组n 维向量.已知n 维标准单位向量组12e ,e ,,e n 能由它们线性表出,证明: 12α,α,,αn 线性无关.证 设12α(,,,)(1,2,,)i i i in a a a i n == ,则有1122αe e e ,i i i in n a a a =+++可见12α,α,,αn 也能由12e ,e ,,e n 线性表出,从而两个向量组等价. 因为12e ,e ,,e n 线性无关,所以12α,α,,αn 也线性无关.11.设12α,α,,αn 是一组n 维向量.证明:它们线性无关的充分必要条件是:任一n 维向量都可由它们线性表出.证 必要性:设12α,α,,αn 线性无关,β为任一n 维向量,则12α,α,,αn ,β必线性相关.(个数大于维数),因此β可由12α,α,,αn 线性表出.充分性:设任一n 维向量β都可由12α,α,,αn 线性表出.因此12α,α,,αn 与12e ,e ,,e n 等价,从而12α,α,,αn 线性无关.12.判断下列向量是否线性相关,并求出一个极大线性无关组.(1)123α(1,2,1,4),α(9,100,10,4),α(2,4,2,8);T T T =-==--- (2) 123α(1,1,0),α(0,2,0),α(0,0,3);T T T ===(3) 1234α(1,2,1,3),α(4,1,5,6),α(1,3,4,7),α(2,1,1,0);T T T T ==---=---=- 解 (1)19221004A 1102448-⎛⎫ ⎪-⎪= ⎪- ⎪-⎝⎭ 192082001900320-⎛⎫ ⎪ ⎪→ ⎪ ⎪-⎝⎭192010000000-⎛⎫ ⎪ ⎪→ ⎪ ⎪⎝⎭102010000000-⎛⎫⎪ ⎪→⎪ ⎪⎝⎭, 向量组的秩为2, 12α,α为一个极大线性无关组.(2) 100A 120003⎛⎫ ⎪= ⎪ ⎪⎝⎭100020003⎛⎫ ⎪→ ⎪ ⎪⎝⎭向量组的秩为3, 123α,α,α为一个极大线性无关组.(3) 14122131A 15413670⎛⎫ ⎪--⎪= ⎪--- ⎪--⎝⎭141209530953018106⎛⎫ ⎪--- ⎪→ ⎪--- ⎪---⎝⎭1412095300000000⎛⎫ ⎪--- ⎪→ ⎪ ⎪⎝⎭向量组的秩为2, 12α,α为一个极大线性无关组.13.求一个秩是4的方阵,它的两个行向量是(1,0,3,0,0),(1,1,0,0,0)--. 解 所求方阵可写成1030011000A 001000001000000⎛⎫ ⎪-- ⎪ ⎪= ⎪ ⎪ ⎪⎝⎭,则1030001300A 00100000100000⎛⎫⎪- ⎪⎪→⎪⎪ ⎪⎝⎭显然(A)4R =.14.已知12α,α,,αs 的秩为r ,证明: 12α,α,,αs 中任意r 个线性无关的向量都构成它的一个极大线性无关组.证 设12α,α,,α,r i i i 为12α,α,,αs 中任意r 个线性无关的向量,因为向量组的秩为r ,故1212α,α,,α,α,(,,)r i i i i r i i i i ≠ 线性相关.可见12α,α,,αs 中的每个向量都可由12α,α,,α,r i i i 线性表出.因此, 12α,α,,α,r i i i 是12α,α,,αs 的一个极大线性无关组.15.用初等变换化下列矩阵为阶梯形,并判断其秩.(1)001010100⎛⎫ ⎪ ⎪ ⎪⎝⎭; (2)1234110215610-⎛⎫ ⎪- ⎪ ⎪⎝⎭;(3)023*********-⎛⎫ ⎪- ⎪ ⎪--⎝⎭;(4)1725314353759413254759413420253248⎛⎫⎪⎪⎪⎪⎝⎭.解 (1) 001010100⎛⎫ ⎪ ⎪ ⎪⎝⎭131********r r ↔⎛⎫ ⎪→ ⎪ ⎪⎝⎭,秩为3.(2) 1234110215610-⎛⎫ ⎪- ⎪ ⎪⎝⎭2131123403360336r r r r+-⎛⎫ ⎪→ ⎪ ⎪⎝⎭32123403360000r r -⎛⎫ ⎪→ ⎪ ⎪⎝⎭,秩为2.(3)023*********-⎛⎫ ⎪- ⎪⎪--⎝⎭12011203430471r r ---⎛⎫⎪→- ⎪ ⎪--⎝⎭213134011200130039r r r r ++--⎛⎫ ⎪→-- ⎪ ⎪--⎝⎭323011*********r r ---⎛⎫⎪→-- ⎪ ⎪⎝⎭, 秩为2.(4)1725314353759413254759413420253248⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭213143317253143201330153015r r r r r r ---⎛⎫ ⎪ ⎪→ ⎪ ⎪⎝⎭433217253143201310020000r r r r --⎛⎫⎪⎪→⎪ ⎪⎝⎭1310022013172531430000r r ↔⎛⎫ ⎪⎪→ ⎪ ⎪⎝⎭2131217100200110253190000r r r r --⎛⎫ ⎪- ⎪→ ⎪ ⎪⎝⎭23100202531900110000r r ↔⎛⎫⎪ ⎪→ ⎪- ⎪⎝⎭,秩为3. 16.证明: 两个矩阵和的秩不超过这两个矩阵秩的和,即 (A B)(A)(B)R R R +≤+.证 设1A (α,,α),(A),n R r == 1α,,αr 为一个极大线性无关组,1B (β,,β),(B),n R s == 1β,,βs 为一个极大线性无关组, 1A B (r ,,r )n += .因为1r ,,r n 可由1α,,αn ,1β,,βn 线性表出,从而也可由1α,,αr ,1β,,βs 线性表出.故()1A B (r ,,r )n R R +=≤ ()11α,,α,β,,βr s R r s =+=(A)(B)R R +.17.设A 与B 可乘,且AB 0=,证明: (A)(B)A R R +≤的列数. 证法一 设A 为m n ⨯矩阵,B 为n l ⨯矩阵 由AB 0=,有11111111n l m mn n nl m n n l a a b b a a b b ⨯⨯⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭ 0000m l⨯⎛⎫ ⎪= ⎪ ⎪⎝⎭ 比较等式两边对应元素,有111111111100n n m mn n a b a b a b a b ++=⎧⎪⎨⎪++=⎩,11121211220,0n n m mn n a b a b a b a b ++=⎧⎪⎨⎪++=⎩ ,11111100l n nl m lmn nl a b a b a b a b ++=⎧⎪⎨⎪++=⎩ . 可见B 的列向量组为上述l 个齐次线性方程组的解向量,因此有 (B)(A)R n R ≤-, 移项得(A)(B)R R n +≤(A 的列数).证法二 设A 为m n ⨯矩阵,B 为n l ⨯矩阵, 12(A),(B)R r R r ==,因为1(A)R r =,则A 的标准形可写成1E 000r ⎛⎫⎪⎝⎭,即存在可逆阵P,Q 使得 PAQ 1E 000r ⎛⎫=⎪⎝⎭.又设()111B Q B B r m n r m ⨯--⨯⎛⎫= ⎪ ⎪⎝⎭, 则10(AB)(PAB)(PAQQ B)R R R -===,但()111111B E 0B PAQQ B Q B B 000r m r r m n r m ⨯⨯---⨯⎛⎫⎛⎫⎛⎫=== ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 可见11(B )(PAQQ B)0r m R R -⨯==,又因为12(Q B)(B)R R r -==,所以()12(B )n r m R r -⨯=,而()1B n r m -⨯共1n r -行,因此12n r r -≥,即12r r n +≤或(A)(B)R R n +≤.习题 B1.证明: 12α,α,,αs (其中1α0≠)线性相关的充要条件是至少有一个α(1)i i s <≤可被121α,α,,αi - 线性表出.证 必要性:设12α,α,,αs 线性相关(1α0≠),则存在不全为0的s 个数12,,,s k k k 使1122ααα0s s k k k +++= ,设i k 是12,,,s k k k 中最后一个不为零的数,即0i k ≠,而10i s k k +=== ,则1122ααα0i i k k k +++= ,因为1α0≠,所以1i >,即1i s <≤,(否则120,0s k k k ≠=== 则1α0k =不能成立),于是1111αααi i i i ik k k k --=--- ,即αi 可由121α,α,,αi - 线性表出.充分性:如果1111αααi i i k k --=++ ,则11111ααα0αα0i i i i s k k --+++-+++= ,而11,,,1,0,,0i k k -- 不全为0,所以12α,α,,αs 线性相关.2.证明:一个向量组的任一线性无关组都可扩充为一个极大线性无关组. 证 设有向量组12α,α,,αn 秩为s ,12α,α,,αr i i i 是它的任意一个线性无关组,如果r s =,则它就是12α,α,,αn 的一个极大线性无关组.如果r s <,则12α,α,,αn 的其余向量中一定可以选出向量1αr i +,使12α,α,,αr i i i ,1αr i +线性无关(否则与12α,α,,αn 秩s r >矛盾),只要1r s +<,重复上述过程,直到r i s +=时为止.这样121α,α,,α,α,,αr r s i i i i i + 就是由12α,α,,αr i i i 扩充成的一个极大线性无关组.3.已知两向量组有相同的秩,且其中之一可被另一个线性表出,证明:这两个向量组等价. 证 设12A :α,α,,α;s 12B:β,β,,βt 为两个秩为r 的向量组, 1212α,α,,α;β,β,,βr r 分别为A,B 极大线性无关组,设B 可由A 线性表出,则有()()1212β,β,,βα,α,,αTr r K = ,其中K 为组合系数构成的r 阶方阵,因为1212α,α,,α;β,β,,βr r 线性无关,所以K 可逆,()()11212α,α,,αβ,β,,βr r K -= ,从而12α,α,,αr 可由12β,β,,βr 线性表出,从而可由12β,β,,βt 线性表出,又12α,α,,αs 可由12α,α,,αr 线性表出,所以12α,α,,αs 可由12β,β,,βt 线性表出,即A 可由B 线性表出,因此向量组A ,B 等价.4.设向量组12α,α,,αs 的秩为r ,在其中任取m 个向量12α,α,,αm i i i ,证明:{}12α,α,,αm i i i R r m s ≥+- .证 设12α,α,,αm i i i 的秩为t ,从它的一个极大线性无关组(含t 个向量)可扩充为12α,α,,αs 的一个极大线性无关组(含r 个向量),所扩充向量的个数为r t -个.但12α,α,,αs 中除了12α,α,,αm i i i 外,还有s m -个向量,故r t s m -≤-,即t r m s ≥+-.5.设n m ⨯阶矩阵A 的秩为r ,证明:存在秩为r 的n r ⨯阶矩阵P 及秩为r 的r m ⨯阶矩阵Q ,使A PQ =.证 因(A)R r =,故可经有限次初等行变换和初等列变换化为标准形,即存在m 阶可逆阵F 和n 阶可逆阵G ,使得 E 0GAF 00r ⎛⎫=⎪⎝⎭,即11E 0A GF ,00r--⎛⎫= ⎪⎝⎭记111212122G G G ,G G -⎛⎫= ⎪⎝⎭111212122F F F F F -⎛⎫= ⎪⎝⎭,其中1111G ,F 均为r 阶方阵,则111211121121222122G G F F E0E 0A G F GG F F 0000rr--⎛⎫⎛⎫⎛⎫⎛⎫== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭111112212122G 0F F G 0F F ⎛⎫⎛⎫ ⎪⎪⎝⎭⎝⎭=1111111221212122G F G F G F G F ⎛⎫ ⎪⎝⎭()11112121G F F G ⎛⎫= ⎪⎝⎭, 记1121G P G ⎛⎫=⎪⎝⎭,则P 为n r ⨯矩阵且(P )R r =(因1G -可逆,故其前r 列线性无关), ()1121Q F F =,则Q 为r m ⨯矩阵且(Q)R r =(因1F -可逆,故其前r 列线性无关),而A PQ =.。
线性代数 第3章 主要学习内容

求解线性方程组 首先要判断线性 方程组是否有解
若无解则结束
若有解则利用高斯消 元法化简方程组并求 得全体未知数的取值
实际上,高斯消元法通过对线性方程 组进行行变换,将其转化为三角形方 程组,然后再通过回代法求解出未知 数的值,由以下例题加以说明。
3.1 高斯消元法求解线性方程组
例1.《九章算术》第八章中介绍“方程术”的案例为:
方程组(3-11)的解为:
3.3 高斯消元法求逆矩阵
思考:可逆矩阵的乘积矩阵是否可逆?
3.3 高斯消元法求逆矩阵
解:由题意 根据例8的结果知
3.3 高斯消元法求逆矩阵
3.3 高斯消元法求逆矩阵
3.3 高斯消元法求逆矩阵
回顾与小结
1.逆矩阵的定义; 2.用逆矩阵的定义求方阵的逆矩阵; 3.用高斯消元法求方阵的逆矩阵。
“今有上禾三秉,中禾二秉,下禾一秉,实三十九斗;上禾二秉,中禾三秉,下禾一秉, 实三十四斗;上禾一秉,中禾二秉,下禾三秉,实二十六斗.问上、中、下禾实一秉各几何?”
将其翻译过来就是:现有上等谷子3捆,中等谷子2捆,下等谷子1捆,果实共计39斗; 上等谷子2捆,中等谷子3捆,下等谷子1捆,果实共计34斗;上等谷子1捆,中等谷子2捆, 下等谷子3捆,果实共计26斗,问上等、中等、下等谷子1捆分别是几斗?
3.1 高斯消元法求解线性方程组
解:利用高斯消元法从上往下消元依次为:
求解线性方程组首先要 判断线性方程组是否有 解,若无解则结束;若 有解,则利用高斯消元 法化简方程组并求得全 体未知数的取值
3.1 高斯消元法求解线性方程组
例3 求解线性方程组
3.1 高斯消元法求解线性方程组
解:利用高斯消元法从上往下消元依次为:
高等代数北大版第三章线性方程组知识总结

第三章线性方程组( * * * )一、复习指导:线性方程组这一章节是一个十分重要的章节,在这一章节中,有三大考点:1.极大线性无关组2.判断非齐次线性方程解的个数3.求齐次/非齐次线性方程的基础解系。
除此之外,本章节所有涉及到的知识点都要仔细看,不能够忽略掉任何一个细小的知识点。
二、考点精讲:(一)线性相关性1.定义线性相关性是描述向量组内在关系的概念,它是讨论向量组α1, α2,…,αs 中有没有向量可以用其它的s-1个向量线性表示的问题.设α1,α2,…,αs 是n维向量组,如果存在不全为0的一组数c1,c2,…,c s使得c1α1+c2α2+…+c sαs=0,则说α1,α2,…,αs 线性相关,否则(即要使得c1α1+c2α2+…+c sαs=0,必须c1,c2,…,c s全为0)就说它们线性无关.于是, α1,α2,…,αs “线性相关还是无关”也就是向量方程x1α1+ x2α2+…+x sαs=0“有没有非零解”,也就是以(α1,α2,…,αs )为系数矩阵的齐次线性方程组有无非零解.当向量组中只有一个向量(s=1)时,它相关(无关)就是它是(不是)零向量.两个向量的相关就是它们的对应分量成比例.2.性质①当向量的个数s大于维数n时, α1, α2,…,αs 一定线性相关.如果向量的个数s等于维数n,则 α1, α2,…,αn线性相关⇔| α1, α2,…,αn|=0.②线性无关向量组的每个部分组都无关(从而每个向量都不是零向量).③如果α1,α2,…,αs 线性无关,而α1,α2,…,αs ,β线性相关,则β可用α1,α2,…,αs 线性表示.④如果β可用α1,α2,…,αs 线性表示,则表示方式唯一⇔α1,α2,…,αs 线性无关.⑤如果β1,β2,…,βt可以用α1,α2,…,αs 线性表示,并且t>s,则β1,β2,…,βt线性相关.推论如果两个线性无关的向量组互相等价,则它们包含的向量个数相等.3.向量组的极大线性无关组和秩(1定义向量组的秩是刻画向量组相关“程度”的一个数量概念.它表明向量组可以有多大(指包含向量的个数)的线性无关的部分组.设α1,α2,…,αs 是n维向量组,(I)是它的一个部分组.如果① (I) 线性无关.② (I) 再扩大就线性相关.就称(I)为α1,α2,…,αs 的一个极大无关组.条件②可换为:任何αI都可用(I) 线性表示,也就是(I) 与α1,α2,…,αs 等价.当α1,α2,…,αs 不全为零向量时,它就存在极大无关组,并且任意两个极大无关组都等价,从而包含的向量个数相等.如果α1,α2,…,αs 不全为零向量,则把它的极大无关组中所包含向量的个数(是一个正整数)称为α1,α2,…,αs 的秩,记作r(α1,α2,…,αs).如果α1,α2,…,αs 全是零向量,则规定r(α1,α2,…,αs)=0.由定义得出: 如果r(α1,α2,…,αs)=k,则i) α1,α2,…,αs 的一个部分组如果含有多于k 个向量,则它一定的相关.ii) α1,α2,…,αs 的每个含有k 个向量的线性无关部分组一定是极大无关组.(二)线性方程组1.线性方程组的基本概念方程组⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++.0,0,0221122221211212111n mn m m n n n n x a x a x a x a x a x a x a x a x a (I ),称(I )为n 元齐次线性方程组。
线性代数课后习题详细解答 (袁晖坪版)第三章 线性方程组

1 r3 ×( − ) 6 r2 + 3 r3 r1 − r3
r1 − r2
r2 − 2 r1 r3 − 2 r1
4 ⎧ x1 = − x4 , 4 ⎧ ⎪ 3 ⎪ x1 + 3 x4 = 0, ⎪ ⎪ ⎪ x = − x4 , 得 ⎨ x2 + x4 = 0, ,所以 ⎨ 2 ( x4为自由未知量) ,令 x4 =k ,得原方程组 2 ⎪ ⎪ x = −2 − x4 2 ⎪ x3 + x4 = −2; ⎪ 3 3 3 ⎩ ⎪x = x ⎩ 4 4 4 ⎧ ⎪ x1 = − 3 k , ⎪ ⎪ x = −k , 得通解为: ⎨ 2 (k ∈ R) 2 ⎪ x = −2 − k ⎪ 3 3 ⎪x = k ⎩ 4
11 1 ⎧ ⎪ x1 = 5 + k1 + 5 k 2 , ⎪ ⎪ x2 = k1 , 得原方程组得通解为: ⎨ (k1 , k2 ∈ R) ⎪x = 2 + 2 k ⎪ 3 5 5 2 ⎪x = k ⎩ 4 2 (5) 由方程组的增广矩阵: 1 1 1 1 0⎞ 2 −5 r 1 ⎛1 ⎛1 1 1 1 1 0⎞ r ⎜ ⎟ r3 − r2 ⎜ ⎟ A = ( A, β ) = ⎜ 3 2 1 1 −3 0 ⎟ → ⎜ 0 −1 −2 −2 −6 0 ⎟ ⎜ 5 4 −3 3 −1 0 ⎟ ⎜ 0 0 −6 0 0 0 ⎟ ⎝ ⎠ ⎝ ⎠
1 2 3 1⎞ 1 1 −4 1 ⎟ ⎟ 得 r ( A) ≠ r ( A) ,因此原方程组 0 −6 −3 10 ⎟ ⎟ 0 0 0 3⎠
无解。 ⎛ 1 −2 3 −4 4 ⎞ ⎜ 0 1 −1 1 −3 ⎟ ⎟ (3) 由方程组的增广矩阵 A = ( A, β ) = ⎜ ⎜1 3 0 1 1 ⎟ ⎜ ⎟ ⎝ 0 −7 3 1 −3 ⎠
第三章习题与复习题(线性方程组)---高等代数

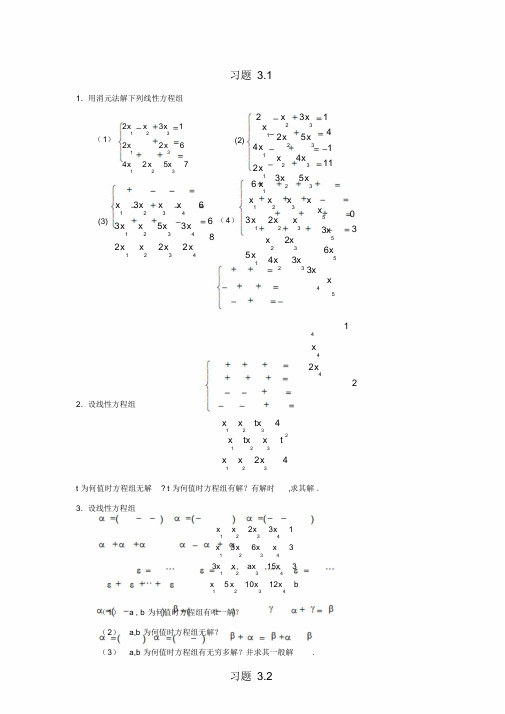
习题3.11.用消元法解下列线性方程组(1)123131232312 264257x x x x x x x x -+=⎧⎪+=⎨⎪++=⎩ (2)⎪⎪⎩⎪⎪⎨⎧=+--=+-=+-=+-115361424524132321321321321x x x x x x x x x x x x(3)⎪⎩⎪⎨⎧=-++=-+-=--+8222635363432143214321x x x x x x x x x x x x (4) ⎪⎪⎩⎪⎪⎨⎧=-+++=+++=-+++=++++233453622032315432154325432154321x x x x x x x x x x x x x x x x x x x 2.设线性方程组1232123123424x x tx x tx x t x x x ++=⎧⎪-++=⎨⎪-+=-⎩ t 为何值时方程组无解? t 为何值时方程组有解?有解时,求其解. 3.设线性方程组1234123412341234231363315351012x x x x x x x x x x ax x x x x x b+++=⎧⎪+++=⎪⎨--+=⎪⎪--+=⎩ (1) a , b 为何值时方程组有唯一解? (2) a, b 为何值时方程组无解?(3) a , b 为何值时方程组有无穷多解?并求其一般解.习题3.21.设()()()1231,1,1,22,1,0,11,2,0,2ααα=--=-=--,, ,求 (1) 321ααα++ (2) 321532ααα+- 1211222. (1,0,,0) (0,1,,0)(0,0,,1),.n n n n a a a εεεεεε===+++设 维向量 , ,, 求()()3. 2 02,1 3 1,124αβγαγβ=-=-+=设2,,,4,2, ,,,求向量 ,使.4.设()()122,0,13,1,1αα==-, 满足 12234βαβα+=+ ,求 β .5.342112231231,.αβαβαβ+=+=-设(,,,), (,,,),求习题3.31. 判断向量 β 能否由向量1α,2α,3α,4α 线性表示,若可以,求出表达式. ()()()()()1234(1) 1,1,1,1 ,1,1,1,11,1,1,11,1,1,11,1,3,1βαααα=--==--=--=-,,, ()()()()()1,1,1,11,1,1,11,1,1,11,1,1,1,1,1,2,1 )2(4321--=--=--===ααααβ,,, ()()()()()3,0,1,37,1,1,40,1,0,17,3,1,23,1,3,4 )3(4321---==-==--=ααααβ,,, 1231231232. 120347110,,,011234(1) , , ,,;(2) , , ,,,;(3) , b a a b a b a b αααββαααβααα⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭设取何值时不能由线性表示取何值时能由唯一线性表示写出该表达式取何值123, ,,,βααα时能由线性表示且表达式不唯一写出全体表达式.3.判断下列向量组的线性相关性.⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=70241202152101014 )1(4321αααα,,,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=2131012021013312 )2(4321αααα,,,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=652111113211 )3(321ααα,,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=14044121302101130112 )4(4321αααα,,,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=7932 ,4354327697656324 )5(54321ααααα,,,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=7023120233631121 )6(4321αααα,,,⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=431003801053001 )7(321ααα,,12344. 12341234 12341234a a a a αααα+⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪+ ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪+ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭设向量组,,, 12341234(1) , ,,,;2 , ,,,.a a αααααααα为何值时线性相关()为何值时线性无关5.讨论向量组12310112,,21425111a b ααα⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭的线性相关性. 6.已知向量组1,,,,i n ααα线性无关,证明1,,,,(0)i n k k ααα≠线性无关.7.已知向量组12,,,n ααα线性无关, 1121212,,,,n n βαβααβααα==+=+++证明: 12,,,n βββ线性无关.8.设12,,,n ααα线性无关,nnn n n n nn n n a a a a a a a a a αααβαααβαααβ+++=+++=+++=22112222121212121111证明:n βββ,,,21 线性无关的充要条件是行列式D = n n n n nna a a a a a a a a 111212122212≠ 09.已知向量组m ααα,,,21 线性无关,设111322211,,,,ααβααβααβααβ+=+=+=+=--m m m m m证明:(1) 当m 为偶数时, m βββ,,,21 线性相关;(2)当m 为奇数时, m βββ,,,21 线性无关.习题3.41.求下列向量组的秩与一个极大线性无关组.(1)12344212 312101308αααα-⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪==-== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,,, (2)1234511005 2112, 153223ααααα⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪===== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,,,(3)123450********* , 0111111011ααααα-⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪ ⎪===== ⎪ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,,, 2.求下列向量组的秩与一个极大无关组并将其余向量用求出的极大无关组线性表示.(1)12342104113410100124αααα⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,,,(2)123452313712024 , 3283023743ααααα--⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪ ⎪===== ⎪ ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,,, (3)123452183723075, 3258010320ααααα⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪ ⎪===== ⎪ ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭,,,3.求向量组123411312000121135a b αααα⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭⎝⎭,,,的秩和一个极大无关组.4.设A 、B 均为m × n 阶矩阵,证明:R (A + B )≤ R (A )+ R (B ) 5.设向量组m ααα,,,21 ( m > 1 )的秩为r ,m m m m βαααβαααβααα-=+++=+++=+++,,,123213121证明:向量组m βββ,,,21 的秩为r .6.设A 为n × m 阶矩阵,B 为m × n 阶矩阵,且n > m ,证明 AB = 0 .习题3.51.求下列齐次线性方程组的一个基础解系并用它表出通解. (1) 123413412313424303 07 730x x x x x x x x x x x x x -+-=⎧⎪+-=⎪⎨++=⎪⎪+-=⎩ (2) 12345123451234512345202 +230322025220x x x x x x x x x x x x x x x x x x x x -+-+=⎧⎪-+-=⎪⎨--+-=⎪⎪-+-+=⎩2.设线性方程组123123123232082021430x x x x x x x x x λλλ---=⎧⎪-+--=⎨⎪+++=⎩()()()问λ为何值时, 该方程组有非零解?并求出它的全部解.3.设n 阶方阵A 的每行元素之和都为零,且R (A )= n -1 ,求方程组A X = 0的通解. 4.已知3阶非零矩阵B 的每个列向量都是线性方程组1231231232202030x x x x x x x x x λ+-=⎧⎪-+=⎨⎪+-=⎩ 的解, 求λ的值. 5.已知线性方程组12342341242200 0x x x x x cx cx x cx x +++=⎧⎪++=⎨⎪++=⎩ 的基础解系由两个解向量构成,求c 的值与该方程组的通解. 6.设12313221211A t ⎛⎫⎪-⎪= ⎪⎪--⎝⎭B 是3阶非零矩阵,且AB=O , 求t 的值.习题3.61.解下列线性方程组(在有无穷多解时求出其结构式通解). (1)12312312312323424538213496x x x x x x x x x x x x ++=⎧⎪-+=-⎪⎨+-=⎪⎪-+=-⎩(2)1234124123401 222461x x x x x x x x x x x --+=⎧⎪⎪--=⎨⎪--+=-⎪⎩2.已知线性方程组1231231232123(2)320x x x x x a x x ax x ++=⎧⎪+++=⎨⎪+-=⎩ 无解,求a 的值.3.参数λμ,取何值时,线性方程组123412341234230327162x x x x x x x x x x x x λμ+-+=⎧⎪+++=⎨⎪---=⎩ 有解、无解?4. 参数a , b 为何值时,线性方程组12345123452345123451323 22635433x x x x x x x x x x a x x x x x x x x x b ++++=⎧⎪+++-=⎪⎨+++=⎪⎪+++-=⎩有解、无解?在有解时,求其解.5. 参数a , b 为何值时,线性方程组1231231234324ax x x x bx x x bx x ++=⎧⎪++=⎨⎪++=⎩ 无解、有唯一解、有无穷多解?在有解时,求其解.6.向量123,,γγγ是四元非齐次线性方程组AX β=的解向量,()2R A =且 121321γγ⎛⎫ ⎪ ⎪+= ⎪ ⎪⎝⎭ ,231102γγ⎛⎫ ⎪ ⎪+= ⎪ ⎪-⎝⎭,132110γγ⎛⎫⎪ ⎪+= ⎪ ⎪⎝⎭求线性方程组AX β=的通解. 7.设线性方程组23112131231222322313233323142434x a x a x a x a x a x a x a x a x a x a x a x a ⎧++=⎪++=⎪⎨++=⎪⎪++=⎩ (1)若1234,,,a a a a 互不相同,证明方程组无解;(2)若1324,(0)a a k a a k k ====-≠,证明方程组有解,并求其通解.8.证明线性方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=-=-=-=-=-515454343232121a x x ax x a x x a x x a x x 有解的充分必要条件是∑=51i i a = 0 ,并在有解时求其通解.9.设非齐次线性方程组A X = β 的解向量12,,,s γγγ,证明(1) 线性组合1122s s k k k γγγ+++是A X = β 的解的充分必要条件是k 1 + k 2 + … + k s = 1;(2)线性组合1122s s k k k γγγ+++是A X = 0 的解的充分必要条件是k 1 + k 2 + … + k s = 0.习题三 (A)一、填空题1.设123111111λααλαλ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,,当λ满足 时, 123ααα,,线性相关; 当λ满足 时, 123ααα,,线性无关. 2.已知向量组123411110112,23243519t t αααα⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪+ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭,, 线性相关, 则t 满足 .3.设向量组123ααα,,线性无关,则当参数l, m 满足 时,213213l m αααααα---,,也线性无关.4. 已知123ααα,,线性无关,若12123123242m m αααααααα+-++-,,也线性无关, 则m .5.设向量组123(, 0, )(, ,0)(0, , )a c b c a b ααα===,,线性无关, 则a , b , c 满足 . 6. 设向量组1234(2,1,1,1)(2,1,,)(3,2,1,),(4,3,2,1)a a a αααα====,,线性相关,且1a ≠, 则 a = .7. 当k = 时, 向量 ()Tk k 2,,0=β 可由向量组()T k 1,1,11+=α ,()()T T k k +=+=1,1,11,1,132αα, 线性表示且表示方法不唯一.()()()1231,2,1,1,2,0,,0,0,4,5,22, t t ααα=-==--=8.已知的秩为 则 .9. 设A = ⎪⎪⎪⎭⎫ ⎝⎛--11334221t , B 为3阶非零矩阵, 且A B = O , 则t = .10. 设B 为3阶非零矩阵,且B 的每个列向量都是方程组 ⎪⎩⎪⎨⎧=-+=+-=++030202321321321x x x x x x kx x x 的解,则k= ,B = .11. 设123,,ααα是齐次线性方程组AX = 0 的一个基础解系, 则当参数a 满足 时,122331a αααααα+++,,也是该方程组的基础解系.12. 已知向量组1234,,,αααα的秩为3, 且1234,,,αααα可由向量组123,,βββ线性表示, 则向量组123,,βββ必线性 .二、单项选择题1. 已知1143α⎛⎫ ⎪= ⎪ ⎪⎝⎭,221t α⎛⎫ ⎪= ⎪ ⎪-⎝⎭,3231α-⎛⎫⎪= ⎪ ⎪⎝⎭线性相关, 则t =( ) .(A ) 2 (B) -2 (C ) 3 (D ) –3 2.已知向量组1234αααα,,,线性无关, 则向量组( )线性无关.12233441122334411223344112233441A αααααααααααααααααααααααααααααααα+++++++-----++--() ,,,(B ) ,,,(C ) ,,,(D ) ,,,3. 对任意实数a , b , c 下列向量组线性无关的是( ).(A) (a , 1, 2), (2, b , 3), (0, 0, 0)(B) (b , 1, 1), (1, a , 3), (2, 3, c ), (a , 0, c ) (C) (1, a , 1, 1), (1, b , 1, 0), (1, c , 0, 0) (D) (1, 1, 1, a ), (2, 2, 2, b ), (0, 0, 0, c )4.若向量组 α , β , γ 线性无关, α , β , δ 线性相关, 则( ).(A ) α 必可由 β , γ , δ 线性表示 (B ) β 必不可由 α , γ , δ 线性表示 (C ) δ 必可由 α , β , γ 线性表示 (D ) δ 必不可由 α , β , γ 线性表示 5. 设同维向量组12121::,rr r mA B αααααααα+,,,,,,,,则下列说法正确的是( ). (A) A 组与B 组的线性相关性相同 (B) 当A 组线性无关时, B 组也线性无关 (C) 当B 组线性相关时, A 组也线性相关 (D) 当A 组线性相关时, B 组也线性相关 6. 下列说法正确的是( ). (A) 若1α,2α线性相关,1β ,2β线性相关, 则11βα+,22βα+一定线性相关(B) 若1α,2α 线性无关, β为任一向量, 则βα+1,βα+2一定线性无关(C) 若1α,2α ,…,m α( m ≥ 2 )线性相关, 则其中任何一个向量都可由其余向量线性表示 (D) 若n 维向量组1α,2α,… ,m α( m ≥ 2 )线性无关,则对于任意不全为零的数k 1, k 2 ,… , k m 一定有 θααα≠+++m m k k k 22117.已知向量组123ααα,,线性无关, 向量β可由123ααα,,线性表示, 向量γ不能由123ααα,,线性表示, 则对任意常数k , 必有( ).(A) 123,,, k αααβγ+线性无关 (B) 123,,, k αααβγ+线性相关 (C) 123,,, k αααβγ+线性无关 (D) 123,,, k αααβγ+线性相关8. 一个向量组的极大线性无关组( ). (A ) 个数唯一 (B) 个数不唯一(C ) 所含向量个数唯一 (D ) 所含向量个数不唯一9.已知任一n 维向量均可由n ααα,,,21 线性表示, 则n ααα,,,21 ( ).(A) 线性相关 (B) 秩等于n(C) 秩小于n (D) 秩不能确定10. 已知21346639A t ⎛⎫ ⎪= ⎪ ⎪⎝⎭, B 为三阶非零矩阵且AB =O ,则( ).(A)当t = 2时,B 的秩必为1 (B)当t = 2时,B 的秩必为2 (C)当t ≠2时,B 的秩必为1 (D)当t ≠ 2时,B 的秩必为211.设非齐次线性方程组A X = B 中未知量个数为n , 方程个数为m , 系数矩阵A 的秩为r ,则 ( ) .(A ) r = m 时,方程组A X = B 有解 (B) r = n 时,方程组A X = B 有唯一解 (C ) m = n 时,方程组A X = B 有唯一解 (D ) r < n 时,方程组A X = B 有无穷多解12.n 元线性方程组AX=B 有唯一解的充分必要条件是( ).(A ) 导出组AX=0仅有零解 (B ) A 为方阵,且∣A ∣≠0(C ) R(A) = n(D ) 系数矩阵A 的列向量组线性无关,且常数项向量B 可由A 的列向量组线性表示13.设A 是n 阶矩阵, α 是n 维列向量,若R ⎪⎪⎭⎫⎝⎛0TAαα = R (A ) ,则线性方程组 ( ).(A ) A X = α 必有无穷多解(B ) A X = α 必有唯一解 (C ) ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫⎝⎛y X A T0αα = 0仅有零解 (D ) ⎪⎪⎭⎫⎝⎛⎪⎪⎭⎫ ⎝⎛y X A T0αα = 0必有非零解 14.将齐次线性方程组⎪⎩⎪⎨⎧=++=++=++0003213213221x x x x x x x x x λλλλ的系数矩阵记为A , 若存在3阶矩阵B ≠ O使得AB =O , 则 ( ) .(A ) λ = -2且 B = 0 (B ) λ = -2且 B ≠ 0 (C ) λ = 1且 B = 0 (D ) λ = 1且 B ≠ 0 15. 已知123,,ααα是非齐次线性方程组AX=b 的3个解, 则下列( )不是导出组 AX = 0的解.(A) 1232ααα+- (B) 121()3αα- (C) 132αα- (D)311()2αα- 16. 已知123,,ααα是非齐次线性方程组AX=b 的3个解,则下列( )是AX = b 的解. (A) 1232ααα+- (B) 123ααα+- (C) 132αα- (D)311()2αα- 17. 已知123ααα,,是4元非齐次线性方程组AX=b 的3个不同的解且R (A ) =3,则下列( )是导出组AX = 0的基础解系.(A) 12312,ααααα+-- (B) 12αα- (C) 13αα+ (D) 3121,αααα--(B)1.设12312300111a b αααβββ⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭1011=,=,010012011=,=,1221求a , b 的值,使向量组123ααα,,与向量组123βββ,,等价.122.,,,.r t t t r n ≤设是互不相同的数,21(1,,,,) (1,2,,)n i i i i t t t i r α-==证明:线性无关.3. ,, , 0. , , , a b c a b c abc αβγαβγθαβαγβγ++=≠设向量,,及数满足且证明和均与等价.4.设向量组123411321326,1511031p p αααα--⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,,(1)p 为何值时,1234,αααα,,线性无关, 并在此时将向量()4,1,6,10Tβ=用该向量组线性表示;(2)p 为何值时,1234,αααα,,线性相关,并在此时求出该向量组的秩和一个极大无关组. 5.求向量组1231111121111k k ααα⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪=== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,,的秩和一个极大无关组.6.,,A m n B n m m n AB E B ⨯⨯<=设为矩阵,为矩阵,且若证明的列向量组线性无关. 7.已知向量组123967ααα⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭13=2,=0,-31与1232110a b βββ⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭0=1,=,-1具有相同的秩且3β可由123ααα,,线性表示,求a , b 的值. 8.已知3阶矩阵B O ≠且B 的列向量都是线性方程组12312312320200x x x x x x ax x x +-=⎧⎪-+=⎨⎪+-=⎩ 的解.(1) 求a 的值; (2) 证明0B =. 9. 已知线性方程组⎪⎩⎪⎨⎧=++=++=++000322212321321x c x b x a cx bx ax x x x ,(1) 当a , b , c 满足何种关系时,方程组仅有零解?(2)当a , b , c 满足何种关系时,方程组有无穷多组解?求出其通解. 10. 两个齐次线性方程组⎪⎪⎩⎪⎪⎨⎧=++=++=++⎪⎪⎩⎪⎪⎨⎧=++=++=++00000011212111111121211111n tn t n n n n n mn m n n n n x b x b x b x b x b x b x a x a x a x a x a x a 与 的系数矩阵A 与B 的秩都小于n /2. 证明:这两个方程组必有相同的非零解. 11. 设12s ααα,,,为某齐次线性方程组的一个基础解系, 11122,t t βαα=+21223,t t βαα=+ 12112,,,s s t t t t βαα=+其中为任意常数. 问当12,t t 满足什么条件时, 12s βββ,,,也为该方程组的一个基础解系.12.设四元齐次线性方程组(Ⅰ)为 ⎩⎨⎧=-++=-+020324321321x x x x x x x , 且已知另一四元齐次线性方程组(Ⅱ)的一个基础解系为 T T a a )(,)(8,4,2,11,2,1,221+-=+-=αα(1) 求方程组(Ⅰ)的一个基础解系; (2) a 为何值时,(Ⅰ)与(Ⅱ)有非零公共解?在有非零公共解时, 求出全部非零公共解.13.设 r n -γγγγ,,,,210 为非齐次线性方程组A X = β 的n - r +1个线性无关的解向量,其中r = R (A ).证明:00201,,,γγγγγγ----r n 是其导出组AX = 0的一个基础解系. 14.若线性方程组n n n n n nn n n a x a x b a x a x b a x a x b ++=⎧⎪++=⎪⎨⎪⎪++=⎩111112112211 的系数矩阵的秩等于矩阵B =1111110n n nnn na ab a a b b b ⎛⎫⎪⎪ ⎪ ⎪ ⎪⎝⎭的秩. 证明此方程组有解.12312315. 4, ()3, ,,,2200,20028.AX B R A αααααα==⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭设元非齐次线性方程组已知为方程组的解其中求该方程组的通解16. 设线性方程组Ⅰ: 123123212302040x x x x x ax x x a x ++=⎧⎪++=⎨⎪++=⎩Ⅱ: 123 21x x x a ++=-有公共解, 求a 的值及所有公共解.。
高等代数线性方程组练习题

第三章 线性方程组练习题一、 填空题1. 如果一个线性方程组的系数矩阵的秩为r ,则增广矩阵的秩取值可能为__________.2. 非齐次线性方程组1212222n n x x x a x x x b +++=⎧⎨+++=⎩有解的充要条件是__________.3. 齐次线性方程组12340x x x x +++=的基础解系是____________________.4. 若矩阵A 中有一个r 级子式不为零,则()R A __________.5. 已知向量组123(1,4,3),(2,,1),(2,3,1)k ααα==-=-线性相关,则参数k =__________.6. 齐次线性方程组111122121122221122000n n n n n n nn n a x a x a x a x a x a x a x a x a x +++=⎧⎪+++=⎪⎨⎪⎪+++=⎩ (*)只有零解的充要条件有______________________________________________________ _(至少写两个).7.非齐次线性方程组AZ b =(A 为m n ⨯矩阵)有唯一解的的充分必要条件是____________。
8. 1n +个n 维向量,组成的向量组为线性 ____________ 向量组。
9.设向量组321,,ααα线性无关,则常数,l m 满足____________时,向量组312312,,αααααα---m l 线性无关。
10.设n 阶矩阵A 的各行元素之和均为零,且()1r A n =-则0Ax = 的通解为________。
11.若向量组321,,ααα线性无关,则向量组312312,,αααααα+++____________。
12.已知四元非齐次线性方程组,()3Ax b r A ==,321,,ηηη是它的三个解向量,其中T T )3,1,0,1(,)2,0,2,1(3221=+=+ηηηη,则齐次线性方程组0Ax =的通解为____________-________________________。
高等代数考研复习[线性方程组]
![高等代数考研复习[线性方程组]](https://img.taocdn.com/s3/m/41e8a4094b73f242336c5fb3.png)
, n ) A, 且1 , 2 ,
, n
线性无关,则 1 , 2 ,
矩阵A可逆.
, n 线性无关的充分必要条件为
(2)若 1 , 2 ,
, n无关,且( 1, 2 , , s ) (1, 2 , , n ) B, , s 线性无关的充
(即B为列满秩).
1, 2 , , s
若 是
的互不相等的解,则 的基础解系 1 , 2 , 3 , 4 A* 0. Asn X 不存在 b 仅含有一个非零解向量 A X 0
sn
B) A) 含两个无关解向量
含三个无关解向量
D)
C)
例4 设 A, B 为n阶方阵,齐次方程组 AX 0 与 BX 0 的
例6 设0 是非齐次方程组 Asn X b 的一个解向量,而
1 , 2 , m 是齐次方程组 AX 0 的基础解系,令
1 0, 2 1 0,
1, 2 , 1)证明:
, m1 m .
, m1 线性无关;
2)方程组 Asn X b 的任一解 都可由它们线性表示.
高等代数考研复习
2014年 8月
第三章 线性方程组
线性方程组是高等代数学的最基本内容之一,它
在数学各分支及其他许多领域被广泛应用。本章 主要分三个部分复习,分别是 :
(1)向量组的相关性 (2) 线性方程组有解判别定理 (3)线性方程组解的结构
1. 向量组的相关性
(1)向量组的线性表示
则称向量组 1 , 2 ,
b)线性相关与线性无关的判别:设 1 , 2 ,
, s 是一 xs s 0
组n维向量,若向量方程组 x11 x2 2
高等代数III知识点整理

高等代数III知识点整理●相似标准型●多项式矩阵●定义●\boldsymbol{A}(\lambda)=\begin{pmatrix}a_{11}(\lambda)&a_{12}(\lambda)&\cdots&a_{1n}(\lambda)\\a_{21}(\lambda)&a_{22}(\lambda)&\cdots&a_{2n}(\lambda)\\\vdots&\vdots&&\vdots\\a_{m1}(\lambda)&a_{m2}(\lambda)&\cdots&a_{mn}(\lambda)\end{pmatrix}●初等\lambda-矩阵●一类P_{ij}ij行互换●二类P_{i}(c)i行乘以常数c●三类T_{ij}(f(\lambda))i行乘以f(\lambda)加到j行●矩阵多项式形式●M(\lambda)=M_m\lambda^m+M_{m-1}\lambda^{m-1}+\cdots+M_0●定理●带余除法:\begin{gathered}\boldsymbol{M}(\lambda) =\left(\lambda\boldsymbol{I}-\boldsymbol{B}\right)\boldsymbol{Q}\left(\lambda\right)+\boldsymbol{R}, \\\boldsymbol{N}(\lambda) =\boldsymbol{S}(\lambda)(\lambda\boldsymbol{I}-\boldsymbol{B})+\boldsymbol{T}. \end{gathered}●\boldsymbol{A}与\boldsymbol{B}相似\Leftrightarrow \lambda\boldsymbol{I}-\boldsymbol{A}与\lambda\boldsymbol{I}-\boldsymbol{B}相抵●矩阵的法式●定理●非零\boldsymbol{A}(\lambda)一定相抵于\boldsymbol{B}(\lambda)=[b_{ij}(\lambda)]_{n\times n}且有b_{11}(\lambda)|b_{ij}(\lambda)●\boldsymbol{A}(\lambda)相抵于\text{diag}\{d_1(\lambda),\cdots,d_r(\lambda);0,\cdots,0\}且有d_i(\lambda)|d_{i+1}(\lambda),i=1,2,\cdots,r-1●n阶可逆\lambda-矩阵可表示为有限个初等\lambda-矩阵的积●特征矩阵\lambda\boldsymbol{I}-\boldsymbol{A}一定相抵于\text{diag}\{1,\cdots,1,d_1(\lambda),\cdots,d_m(\lambda)\}且有d_i(\lambda)|d_{i+1}(\lambda),i=1,2,\cdots,m-1●定义●法式/相抵标准型●\text{diag}\{d_1(\lambda),\cdots,d_r(\lambda);0,\cdots,0\}●d_i(\lambda)|d_{i+1}(\lambda),i=1,2,\cdots,r-1●不变因子●定义●k阶行列式因子所有k阶子式的最大公因子(非零);若子式都为0,规定行列式因子为0●D_i(\lambda)\mid D_{i+1}(\lambda),i=1,2,\cdots,r-1D_{1}(\lambda),D_{2}(\lambda),\cdots,D_{r}(\lambda)是{A}(\lambda) 的非零行列式因子●g_1(\lambda)=D_1(\lambda),g_2(\lambda)=D_2(\lambda)/D_1(\lambda),\cdots,g_r(\lambda)=D_r(\lambda)/D_{r-1}(\lambda)为{A}(\lambda) 的不变因子●定理●相抵的\lambda-矩阵有相同的行列式因子,从而有相同的不变因子●推论●法式和不变因子相互唯一确定●相抵\Leftrightarrow有相同的法式●初等变换不改变法式●相似\Leftrightarrow特征矩阵有相同行列式因子/不变因子●A与B在\mathbb{F}上相似的充分必要条件是在\mathbb{K}上相似\mathbb{F}\sube \mathbb{K}●有理标准型●Frobenius块●\boldsymbol{F}=\left(\begin{array}{ccccc}0 & 1 & 0 & \cdots & 0 \\0 & 0 & 1 &\cdots & 0 \\\vdots & \vdots & \vdots & & \vdots \\0 & 0 & 0 & \cdots & 1 \\-a_{r} & -a_{r-1} & -a_{r-2} & \cdots & -a_{1}\end{array}\right)●行列式因子为1, \cdots, 1, f(\lambda)r-1 个 1, f(\lambda)=\lambda^{r}+a_{1} \lambda^{r-1}+\cdots+a_{r}●\boldsymbol{F}的极小多项式等于f(\lambda)●定义●\boldsymbol{A} 的不变因子组为1, \cdots, 1, d_{1}(\lambda), \cdots,d_{k}(\lambda)●deg d_i(\lambda)=m_i●\boldsymbol{F}=\left(\begin{array}{cccc}\boldsymbol{F}_{1} & & & \\&\boldsymbol{F}_{2} & & \\& & \ddots & \\& & &\boldsymbol{F}_{k}\end{array}\right)●\boldsymbol{F}_{i}的阶为m_i,为Frobenius块,最后一行的系数为d_i({\lambda})除最高项的系数的负值组成●A相似于F●定理●\boldsymbol{A} 的极小多项式m(\lambda)=d_{k}(\lambda)\boldsymbol{A} 的不变因子组为1, \cdots, 1, d_{1}(\lambda), \cdots,d_{k}(\lambda)●初等因子●定义●非常数不变因子分解●\begin{aligned}d_{1}(\lambda)= & p_{1}(\lambda)^{e_{11}}p_{2}(\lambda)^{e_{12}} \cdots p_{t}(\lambda)^{e_{1 t}} \\d_{2}(\lambda)=& p_{1}(\lambda)^{e_{21}} p_{2}(\lambda)^{e_{22}} \cdotsp_{t}(\lambda)^{e_{2 t}} \\& \cdots \cdots \cdots \cdots \\d_{k}(\lambda)= &p_{1}(\lambda)^{e_{k 1}} p_{2}(\lambda)^{e_{k 2}} \cdotsp_{t}(\lambda)^{e_{k t}}\end{aligned}●e_{ij}>0时,p_i(\lambda)^{e_{ij}}为初等因子●定理●不变因子和初等因子组可互相唯一确定●Jordan 标准型●Jordan 块●定义●\boldsymbol{J}=\left(\begin{array}{ccccc}\lambda_{0} & 1 & & & \\&\lambda_{0} & 1 & & \\& & \ddots & \ddots & \\& & & \ddots & 1 \\& & && \lambda_{0}\end{array}\right)●初等因子为(\lambda-\lambda_0)^r●定理●A特征矩阵相似于\lambda-对角阵,则A的初等因子组等于对角阵的准素因子组●Jordan 块对角阵的初等因子组等于各个Jordan块的初等因子●初等因子组可对应一个Jordan 标准型●复数域上的线性变换\varphi必存在一组基使表示矩阵为Jordan标准型●复矩阵可对角化等价条件●极小多项式无重根●初等因子为一次●复数域上的线性变换\varphi可对角化\Leftrightarrow极小多项式无重根\Leftrightarrow初等因子为一次●复数域上的线性变换\varphi可对角化,在不变子空间上的限制也可对角化●复数域上的线性变换\varphi可对角化⇔在每个不变子空间V_i的限制可对角化V=V_{1} \oplus V_{2} \oplus \cdots \oplus V_{k}●特征值在\mathbb{K}上,则矩阵在\mathbb{K}上相似于Jordan标准型●Jordan 标准型的应用●度数与重数●特征值\lambda_i的度数等于\lambda_i的Jordan块的个数●特征值\lambda_i的重数等于\lambda_i的Jordan块的阶数之和●循环子空间●定义●\boldsymbol{\psi} 是线性变换. 若存在 \boldsymbol{\alpha} \in r 维子空间V_{0} , 使\left\{\boldsymbol{\alpha},\boldsymbol{\psi}(\boldsymbol{\alpha}), \cdots, \boldsymbol{\psi}^{r-1}(\boldsymbol{\alpha})\right\}构成 V_{0}的一组基且\boldsymbol{\psi}^{r}(\boldsymbol{\alpha})=\mathbf{0} , 则称 V_{0} 为关于线性变换 \boldsymbol{\psi} 的循环子空间●\lambda_i是线性变换\varphi的特征值,对应的某个Jordan块子空间V_i是(\lambda_iI_V-\varphi)的循环子空间(\lambda_iI_V-\varphi)^{r_i}=0●\lambda_i是线性变换\varphi的特征值,对应的全部Jordan块子空间V_i是(\lambda_iI_V-\varphi)的循环子空间(\lambda_i的根子空间)(\lambda_iI_V-\varphi)^n=0,\max\{r_i\}也可●用初等因子\{(\lambda-\lambda_i)^{r_i}\}将V分解为维数为r_i的循环子空间V_i的直和●根子空间●定义●\lambda_i是线性变换\varphi的特征值,对应的全部Jordan块子空间R(\lambda_i)是\lambda_i的根子空间R(\lambda_i)=\{v\in V|(\lambda_iI_V-\varphi)^n(v)=0\}●V可分解为R(\lambda_i)的直和,维数为重数●Jordan-Chevalley 分解定理●可对角阵A,B满足AB=BA,则可同时对角化●分解定理:A=B+C满足下列性质●B可对角化●C为幂零阵●BC=CB●B,C可用A的多项式表示●分解唯一前三条说明●矩阵函数●定理●复幂级数收敛条件●f(X)收敛\Leftrightarrow f(P^{-1}XP)收敛且f(P^{-1}XP)=P^{-1}f(X)P任一可逆阵P成立●X= diag\{X_i\},f(X)收敛\Leftrightarrow f(X_i)收敛●X为Jordan 块,f(z)的收敛半径为r,\lambda_0<r\Rightarrow f(X)收敛●特征值判断收敛●\lambda=\max\{\lambda_i\},f(z)的收敛半径为r●\lambda>r,f(X)发散●\lambda<r,f(X)收敛●\lambda=r,f(X)收敛\Leftrightarrow f^{(k)}(\lambda_i)收敛对每个特征值\lambda_i,k=0,1,\cdots,r_i-1成立●收敛矩阵f(A)特征值为f(\lambda_i)●矩阵函数●指数函数●\mathrm{e}^{A}=\boldsymbol{I}+\frac{1}{1 !} A+\frac{1}{2 !}A^{2}+\frac{1}{3 !} A^{3}+\cdots●AB=BA\Rightarrow e^{A+B}=e^A e^B●正弦函数●\sin \boldsymbol{A}=\boldsymbol{A}-\frac{1}{3 !}\boldsymbol{A}^{3}+\frac{1}{5 !} \boldsymbol{A}^{5}-\frac{1}{7 !}\boldsymbol{A}^{7}+\cdots●余弦函数●\cos \boldsymbol{A}=\boldsymbol{I}-\frac{1}{2 !}\boldsymbol{A}^{2}+\frac{1}{4 !} \boldsymbol{A}^{4}-\frac{1}{6 !}\boldsymbol{A}^{6}+\cdots●特征值的模长都小于 1●\ln (I+A)=A-\frac{1}{2} A^{2}+\frac{1}{3} A^{3}-\frac{1}{4}A^{4}+\cdots●二次型●n元二次函数能化为只有二次项的形式●对称阵和二次型可互相唯一表示●合同●定义●存在非异阵C,使得B=C'AC●等价关系●合同变换●第一类对换i行与j行,再对换i列与j列●第二类非零常数k乘以第i行,再乘以第j列●第三类第i行乘以k加到第j行,再将第i列乘以k加到第j列●定理●必存在非异阵C,使得C'AC的(1,1)元素不为0●必存在非异阵C,使得C'AC为对角阵●二次型化简●配方法●初等变换法●实二次型●惯性定理●对角化的合同二次型正系数个数相同●规范标准型●系数仅为0,1,-1●合同不变量●秩●正惯性指数●负惯性指数●符号差(+)-(-)●定理●秩与符号差(或正负惯性指数)是实对称阵的合同全系不变量●复二次型只有秩为合同全系不变量●定义●对任意非零向量\alpha●正定型与正定矩阵:\alpha'A\alpha>0●负定型与负定矩阵:\alpha'A\alpha <0●半正定型与半正定矩阵:\alpha'A\alpha\geq 0●半负定型与半负定矩阵:\alpha'A\alpha\leq 0●否则为不定型●正定型充要条件1●正定型\Leftrightarrow正惯性指数等于n●负定型\Leftrightarrow负惯性指数等于n●半正定型\Leftrightarrow正惯性指数等于r●半负定型\Leftrightarrow负惯性指数等于r●正定型充要条件2●合同对应规范标准型●正定型充要条件3●n个顺序主子式全大于0●Hermite 型●定义●f\left(x_{1}, x_{2}, \cdots, x_{n}\right)=\sum\limits_{j=1}^{n}\sum\limits_{i=1}^{n} a_{i j} \bar{x}_{i} x_{j}●矩阵形式:f\left(x_{1}, x_{2}, \cdots, x_{n}\right)=\bar{x}'Ax\bar{A}'=A●系数变元为复数但值为实数●复相合●存在非异阵C,使得B=\bar{C}'AC●正定Hermite型●对非零复数向量函数值总大于0●定理●A为Hermite阵,必存在非异阵C,使得\bar{C}'AC是实对角阵●惯性定理成立●正定Hermite矩阵\Leftrightarrow n个顺序主子式全大于0。
《高等代数》第三章习题及答案

习题3.1计算下列行列式:①5312--+a a ②212313121+----a a a解 ①5312--+a a =(a+2)(a-5)+3=a 2-3a-7②212313121+----a a a =(a-1)(a-1)(a+2)-3-12+2(a-1)-3(a-1)+6(a+2)= a 3+2a习题3.2求从大到小的n 阶排列(n n-1 … 2 1)的逆序数. 解 τ(n n-1 … 2 1)=(n-1)+(n-2)+…+1+0=2)1(-n n 习题3.31.在6阶行列式中,项a 23a 31a 42a 56a 14a 65和项a 32a 43a 14a 51a 66a 25应各带有什么符号?解 因为a 23a 31a 42a 56a 14a 65=a 14a 23a 31a 42a 56a 65,而τ(4 3 1 2 6 5)=3+2+0+0+1+0=6,所以项a 23a 31a 42a 56a 14a 65带有正号.又因为项a 32a 43a 14a 51a 66a 25=a 14a 25a 32a 43a 51a 66,而τ(4 5 2 3 1 6)=3+3+1+1+0+0=8,所以项a 32a 43a 14a 51a 66a 25带有正号. 2.计算:000400010002000300050000 解 因为a 15a 24a 33a 42a 51的逆序数为τ(5 4 3 2 1)=5×4/2=10,带有正号,所以000400010002000300050000=5×3×2×1×4=120 习题3.4计算:6217213424435431014327427246-解 6217213424435431014327427246-=6211003424431001014327100246-=100×621134244*********1246-=-294×105习题3.51.计算下列行列式:①1723621431524021----- ②6234352724135342------解 ①1723621431524021-----=1374310294111120001------=137410291111-----=-726②6234352724135342------=1035732130010313410------=0105731331310---- =05723133710----=-5×72337--=-1002. 计算下列n 阶行列式(n ≥2):①ab ba b a b a 000000000000 ②1210010010011110-n a a a③n n n n x x x x x x a a a a x a 1322113211000000000-----+④111)()1()()1()()1(111n a a a n a a a n a a a n n n n n n --------- 解 ① n n a b b a b a b a ⨯000000000000=)1()1(00000000000-⨯-⨯n n a b a b a b a a+)1()1(1000000000000)1(-⨯-+⨯-n n n b a b b ab b=a n+(-1)n+1b n② D n =1210010*********-n a a a=a n-1×D n-1+(-1)n+1×)1)(1(2100000000001111---n n n a a= a n-1D n-1+(-1)n+1×(-1)1+(n-1)×)2)(2(232100000000----n n n n a a a a=a n-1D n-1-a 1a 2…a n-2=a n-1(a n-2D n-2-a 1a 2…a n-3)-a 1a 2…a n-2 =a n-1a n-2D n-2-a n-1a 1a 2…a n-3-a 1a 2…a n-2 …= a n-1a n-2…a 2D 2-a n-1a n-2…a 3a 1-…-a n-1a n-2a 1a 2…a n-4-a n-1a 1a 2…a n-3-a 1a 2…a n-2= a n-1a n-2…a 21110a -a n-1a n-2…a 3a 1-…-a n-1a n-2a 1a 2…a n-4-a n-1a 1a 2…a n-3-a 1a 2…a n-2=-a n-1a n-2…a 2-a n-1a n-2…a 3a 1-…-a n-1a n-2a 1a 2…a n-4-a n-1a 1a 2…a n-3-a 1a 2…a n-2 =-∑---11211)...(n i in a a a a ③ D n =nn n n x x x x x x a a a a x a 1322113211000000000-----+=112111...)1()1(---++-⨯-n n n n n n D x x x x a =a n x 1x 2…x n-1+x n D n-1=a n x 1x 2…x n-1+x n (a n-1x 1x 2…x n-2+x n-1D n-2) =a n x 1x 2…x n-1+x n a n-1x 1x 2…x n-2+x n x n-1D n-2 …=a n x 1x 2…x n-1+x n a n-1x 1x 2…x n-2+…+x n x n-1…x 4a 3x 1x 2+x n x n-1…x 4x 3D 2=a n x 1x 2...x n-1+x n a n-1x 1x 2...x n-2+...+x n x n-1...x 4a 3x 1x 2+x n x n-1...x 4x 3[(a 1+x 1)x 2+a 2x 1] =)( (1)1121121∑=+--+ni n i i i n n x x a xx x x x x x④D n+1=111)()1()()1()()1(111n a a a n a a a n a a a n n n nn n ---------=nn n n n n n n a a a n a a a n a a a )1()1()()1()()1(111)1(1112)1(----------+=)1()]}1([)2)(1)]{(()2)(1[()1(2)1(---------+ n n n n=2!3!...n!3.计算下列n 阶行列式(n ≥1):①n a a a a ++++1111111111111111321②ax x x x x a x x x x a x a x x x x x a x n n nn ----- 321321321321解 ① D n =na a a a ++++1111111111111111321=na a a a +++++++11110111*********11321=1111111111111111321a a a ++++na a a a111011101110111321+++ =110010010321a a a +1-n n D a =a n D n-1-a 1a 2…a n-1=a n (a n-1D n-2-a 1a 2…a n-2)-a 1a 2…a n-1 =a n a n-1D n-2-a n a 1a 2…a n-2-a 1a 2…a n-1 =n ni n i i a a a a a aa 211111)(+∑=+-=⎪⎪⎭⎫ ⎝⎛+∑=ni i n a a a a 12111 (a i ≠0) ②D n =a x x x x x a x x x x a x a x x x x x a x n n n n -----321321321321=ax x x x x a x x x x a x a x x x x x a x n n n n -+-+--+- 321321321321000=n n n n x x x x x a x x x x a x a x x x x x a x 321321321321----+ax x x a x x x a x a x x x x a x -----321321321321000 =x n (-a)n-1(x 1+x 2+…+x n )+(-a)n4.证明:n 阶行列式yz z x y y x z xzz zz y y x z z yy y x z yy y y x nn ----=)()( 其中z ≠y .解 D n =xzz zzy y x z z yy y x z x y zx00--=(x-z)D n-1-(y-x))1()1(-⨯-n n x zz zy y x zy y y z=(x-z)D n-1-(y-x)z)1()1(111-⨯-n n x z z y y x y yy=(x-z)D n-1-(y-x)z)1()1(10010001-⨯-----n n y x yz y z y x=(x-z)D n-1-(y-x)z(x-y)n-2=(x-z)D n-1+z(x-y)n-1即有D n =(x-z)D n-1+z(x-y)n-1(1)又D n =xzz zy y x z yy y x x z yy y y y x--=(x-y)D n-1-(z-x))1()1(-⨯-n n x zz zy y x zy y y y=(x-y)D n-1-(z-x)y)1()1(1111-⨯-n n x z z z yy x z=(x-y)D n-1-(z-x)y)1()1(001111-⨯-----n n z x z y z y z x=(x-y)D n-1-(z-x)y(x-z)n-2即有D n =(x-y)D n-1+y(x-z)n-1(2) 联立式(1)和式(2)得yz z x y y x z xzz zzy y x z z yy y x z yy y y x nn ----=)()( 习题3.61.设A,B,P ∈Mat n ×n (F),并且P 是可逆的,证明:如果B=P -1AP ,则|B|=|A|.证 因为|P -1||P|=1,所以|B|=|P -1AP|=|P -1||A||P|=|A|. 2*.仿照例3.6.1,试用分块初等变换,证明定理3.6.1. 证 设A ,B 都是n ×n 矩阵,则nE BA -0=B A B A A E B n n n n=-=--+)1(0)1(另一方面,对nE BA -0的第2行小块矩阵乘以A 加到第一行上去,有nE BA -0=AB E BAB n=0所以B A AB =.习题3.71.求下列矩阵的伴随矩阵和逆矩阵①⎪⎪⎭⎫⎝⎛--1112 ②⎪⎪⎪⎭⎫ ⎝⎛--325436752解 ①设原矩阵为A ,则A 11=-1,A 21=-1,A 12=1,A 22=2,伴随矩阵A *=⎪⎪⎭⎫⎝⎛--2111,|A|=-2+1=-1,所以,A -1=⎪⎪⎭⎫ ⎝⎛---211111=⎪⎪⎭⎫ ⎝⎛--2111②设原矩阵为A ,则A 11=3243--=-9+8=-1,A 21=3275---=-(-15+14)=1,A 31=4375=20-21=-1,A 12=3546--=38,A 22=3572-=-41,A 32=4672-=34, A 13=2536-=-27,A 23=2552--=29,A 33=3652=-24伴随矩阵A *=⎪⎪⎪⎭⎫ ⎝⎛-----242927344138111,|A|=-18-84+100-105+16+90=-1,所以,A -1=⎪⎪⎪⎭⎫ ⎝⎛------24292734413811111=⎪⎪⎪⎭⎫ ⎝⎛----2429273441381112.证明:上三角形矩阵是可逆矩阵的充分必要条件是:它的主对角线元全不为零.证 因为矩阵可逆的充分必要条件是它的行列式不为零,而上三角形矩阵的行列式等于它的主对角线上所有元的乘积,所以上三角形矩阵的行列式不为零的充分必要条件是:它的主对角线元全不为零,故上三角形矩阵可逆矩阵的充分必要条件是:它的主对角线元全不为零.3.设A 是n ×n 矩阵.证明:A 是可逆的,当且仅当A *也是可逆的.证 因为 AA *=|A|E ,两边取行列式得|A||A *|=|A|n.若A 可逆,则A 的行列式|A|≠0,从而有|A *|=|A|n-1≠0,所以A *可逆.反之,若A *可逆,设A *的逆阵为(A *)-1.用反证法,假设A 不可逆,则A 的行列式|A|=0,所以AA *=|A|E=0,对AA *=0两边同时右乘(A *)-1,得A=0,从而A 的任一n-1阶子式必为零,故A *=0,这与A *可逆相矛盾,因此A 可逆. 4.证明定理3.7.2的推论1.推论1的描述:设A 是分块对角矩阵,A=diag(A 1,A 2,…,A s ),证明:A 可逆当且仅当A 1,A 2,…,A s 均可逆,并且A -1=diag(A 1-1,A 2-1,…,A s -1).证 A 可逆,当且仅当A 的行列式|A|≠0,而|A|=|A 1||A 2|…|A s |,所以|A|≠0当且仅当|A 1|,|A 2|,…,|A s |都不为零,即A 1,A 2,…,A s 均可逆.令B=diag(A 1-1,A 2-1,…,A s -1),则有AB=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛S A A A21⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---11211s A A A =⎪⎪⎪⎪⎪⎭⎫⎝⎛S E E E21=E 故A -1=diag(A 1-1,A 2-1,…,A s -1).4.设A=⎪⎪⎪⎭⎫⎝⎛333231232221131211a a aa a a a a a 是实矩阵(实数域上的矩阵),且a 33=-1.证明:如果A 的每一个元都等于它的代数余子式,则|A|=1.证 如果A 的每一个元都等于它的代数余子式,则A 的伴随矩阵A *=⎪⎪⎪⎭⎫ ⎝⎛332313322212312111a a a a a a a a a =A T .所以|A *|=|A|,又AA *=|A|E ,两边取行列式得|A|2=|A|3. 由a 33=-1,得AA *=⎪⎪⎪⎭⎫ ⎝⎛333231232221131211a a aa a a a a a ⎪⎪⎪⎭⎫ ⎝⎛332313322212312111a a a a a a a a a =⎪⎪⎪⎭⎫ ⎝⎛-12313322212312111a a a a a a a a ⎪⎪⎪⎭⎫⎝⎛-12313322212312111a a a a a a a a =⎪⎪⎪⎭⎫ ⎝⎛++1232231a a =⎪⎪⎪⎭⎫ ⎝⎛||000||000||A A A比较最后一个等式两端第3行3列的元素知|A|=a 312+a 322+1≠0,对|A|2=|A|3两边同时除以|A|2得|A|=1.6.设A=(a ij )是n ×n 可逆矩阵,有两个线性方程组(Ⅰ)⎪⎪⎪⎩⎪⎪⎪⎨⎧=+++=+++=+++=+++u x c x c x c bx a x a x a b x a x a x a b x a x a x a n n nn nn n n n n n n (221122112222212111212111)(Ⅱ)⎪⎪⎪⎩⎪⎪⎪⎨⎧=+++=+++=+++=+++vx b x b x b cx a x a x a c x a x a x a c x a x a x a n n nn nn n n n n n n (221122112222211211221111)如果(Ⅰ)有解.证明:当且仅当u =v 时,(Ⅱ)有解.证 设方程组(Ⅰ)的解为x 1*, x 2*,…, x n *,代入方程组(Ⅰ)得(Ⅲ)⎪⎪⎪⎩⎪⎪⎪⎨⎧=+++=+++=+++=+++ux c x c x c bx a x a x a b x a x a x a b x a x a x a n n n n n nnn n n n n **2*1**2*12*2*22*211*1*12*11................................................ (212)12121 当u =v 时,因为 A=(a ij )是n ×n 可逆矩阵,A 的行列式不等于零,根据克莱姆法则,方程组(Ⅱ)的前n 个方程作为一个线性方程组,它有唯一解,记该解为x 1**, x 2**,…, x n **,代入方程组(Ⅱ)的前n 个方程中得(Ⅳ)⎪⎪⎪⎩⎪⎪⎪⎨⎧=+++=+++=+++=+++----nnn n n n nn n n n n c x a x a x a cx a x a x a c x a x a x a c x a x a x a n n nn ****2**11**1**12**112**2**22**121**1**21**11......................................................21212121 对等式组(Ⅳ)中第1个等式的两端同时乘以x 1*,第2个等式的两端同时乘以 x 2*,…, 第n个等式的两端同时乘以 x n *,然后将n 各等式的左边全部相加,也将右边全部相加,并利用(Ⅲ)式,可得b 1x 1**+b 2x 2**+…+b n x n **=c 1x 1*+ c 2x 2*+…+ c n x n *=u由u =v ,得b 1x 1**+b 2x 2**+…+b n x n **=u即x 1**, x 2**,…, x n **也满足(Ⅱ)中最后一个方程.所以方程组(Ⅱ)有解.反之,若方程组(Ⅱ)有解,设其解为x 1**, x 2**,…, x n **,代入(Ⅱ)得到(Ⅴ)⎪⎪⎪⎩⎪⎪⎪⎨⎧=+++=+++=+++=+++-vx b x b x b cx a x a x a c x a x a x a c x a x a x a n n n n n n nn n n n n ****2**11****2**12**2**22**121**1**21**11......................................................21212121 对等式组(Ⅲ)中第1个等式的两端同时乘以x 1**,第2个等式的两端同时乘以 x 2**,…,第n 个等式的两端同时乘以 x n **,然后将n 各等式的左边全部相加,也将右边全部相加,并利用(Ⅴ)式,可得c 1x 1*+c 2x 2*+…+c n x n *=b 1x 1**+ b 2x 2**+…+ b n x n **将上式左端与(Ⅴ)式中最后一个等式比较,将上式右端与(Ⅲ)式中最后一个等式比较,得 u =v .7.设A 是n ×n 矩阵.证明:|A *|=|A|n-1证 因为AA *=|A|E ,两边取行列式得 |A||A *|=|A|n .如果|A|≠0,两边除以|A|,得|A *|=|A|n-1如果|A|=0,也可写成|A *|=|A|n-1,总之,有|A *|=|A|n-1成立.。
《高等代数1》复习练习题(三)——第三章 线性方程组(参考解答)

《高等代数1》复习练习题(三)——第三章线性方程组(解答)(供2017级数学与应用数学专业使用)一、填空题1、设23(,2,1),(2,3,0),(1,1,1)T T T k ααα1==-=-,则当1k =-时,向量组321,,ααα线性相关. 2、设矩阵⎪⎪⎪⎭⎫⎝⎛-=403212221A ,向量(,1,1)Ta α=,已知向量组,A αα线性相关,则1a =-.3、设向量组123(,0,),(,,0),(0,,)T T T a c b c a b ααα===线性相关,则,,a b c 必满足关系式 abc=0 .4、线性方程组121232343414,,,x x a x x a x x a x x a -=-=-=-=有解的充分必要条件是_____________.5、设33⨯矩阵A 的秩()1r A =,23(1,1,2),(2,0,1),(1,2,3)T T T ααα1===是线性方程组AX β=的三个特解,则对应导出组0AX =的基础解系是121323,αααααα---中任意两个向量.6、设33⨯矩阵A 的秩()2r A =,A 的各行元素之和均为零,则齐次线性方程组0AX =的通解是(1,1,1)T k .7、若齐次线性方程组⎪⎩⎪⎨⎧=++=++=++000321321321x x x x x x x x x λλ有非零解,则=λ1.8、设齐次线性方程组12312312300x x x x kx x kx x x ++=⎧⎪++=⎨⎪++=⎩只有零解,则k 应满足的条件是1k ≠.9、.齐次线性方程组1231231232302340x x x x ax bx x x x ++=⎧⎪++=⎨⎪++=⎩有非零解,当且仅当,a b 满足关系式1(1)2a b =+.10、若线性方程组b AX =有解,且秩()A r =,则秩()A =r .二、选择题 1、设12,,,s ααα均为n 维向量,下列结论不正确的是 ( B ).(A)若对任意一组不全为零的数12,,,s k k k ,都有1122+++≠s s k k k ααα0,则12,,,s ααα线性无关.(B)若12,,,s ααα线性相关,则对任意一组不全为零的数12,,,s k k k ,都有1122+++=s s k k k ααα0.(C)向量组12,,,s ααα线性无关的充分必要条件是此向量组的秩为s . (D)向量组12,,,s ααα线性无关的必要条件是其中任意两个向量线性无关.2、设向量组123(,2,1),(2,,0),(1,1,1)TTTt t ααα===-线性无关,则( D ).(A )3t ≠-且2t ≠. (B )3t =或2t =-. (C )3t =-或2t =. (D )3t ≠且2t ≠-.3、设向量T T T T )4,0,1,1(,)1,3,0,2(,)5,1,2,0(,)2,2,1,1(4321=-===αααα,则向量组4321,,,αααα的秩等于( C ).(A)1. (B) 2. (C)3. (D)4. 4、设12,,,m ααα是一n 维向量组,它的秩12(,,,)=<m r r m ααα,则下面说法不正确的是( A ).(A)向量组12,,,m ααα中任意一个向量都能由其余向量线性表出.(B)向量组12,,,m ααα线性相关.(C)向量组12,,,m ααα与其任一极大无关组等价.(D)向量组12,,,m ααα中任意r 个线性无关的向量都构成其极大无关组.5、设0=AX 是非齐次方程组AX β=所对应的导出组,则下列结论正确的是 ( D ).(A)若0=AX 仅有零解,则AX β=有唯一解.(B)若0=AX 有非零解,则AX β=有无穷多解. (C)若AX β=有无穷多解,则0=AX 仅有零解. (D)若AX β=有无穷多解,则0=AX 有非零解.6、若A 是n 阶方阵,β是n 维非零向量,且齐次线性方程组0=AX 有非零解,则下列结论中不会发生的是( B ).(A)AX β=无解. (B)AX β=有唯一解. (C)AX β=有无穷多解. (D)()r A n <.7、非齐次线性方程组AX β=中未知量个数为n ,方程个数为m ,()r A r =,则 ( A )(A)r m =时,AX β=有解. (B)r n =时,AX β=有唯一解. (C)m n =时,AX β=有唯一解. (D)r n <时,AX β=有无穷多解. 8、设A 为m n ⨯矩阵,且()1r A n =-,12,αα是非齐次线性方程组AX β=的两个不同的解向量,k 为任意常数,则0AX =的通解为( A ).(A )12()k αα-; (B )12()k αα+; (C )1k α; (D )2k α. 9、设12,,,s ααα均为n 维向量,下列结论正确的是( B ) .(A) 若1122s s k k k ααα+++=0,则12,,,s ααα线性相关.(B) 若对任意一组不全为零的数12,,,s k k k ,都有1122s s k k k ααα+++≠0,则12,,,s ααα线性无关.(C) 若12,,,s ααα线性相关,则对任意一组不全为零的数12,,,s k k k ,都有1122s s k k k ααα+++=0.(D) 若12000s ααα+++=0,则12,,,s ααα线性无关.三、判断题 1、如果当120n k k k ===≠时,11220n n k k k ααα+++=,则向量组12,,,nααα线性相关. ( √ )2、如果12(,,,),1,2,,i i i in a a a i s α==线性相关,则向量组1212(,,,,,,,),1,2,,i i i in i i im a a a b b b i s β==也线性相关.( X )3、若123,,,αααβ线性相关,则β可由向量组123,,ααα线性表出.( X )4、若β不能由向量组123,,ααα线性表出,则123,,,αααβ线性无关.( X )5、若向量12,,,s ααα线性相关,则其中每一个向量皆可由其余向量线性.( X )6、非齐次线性方程组的两个解的和不再是它的解. ( √ )7、方程个数小于未知量个数的线性方程组必有无穷多个解. ( X )8、设12,αα线性相关,12,ββ也线性相关,则1122,αβαβ++线性相关. ( X )9、若线性方程组AX β=有无穷多个解,则0AX =一定有非零解. ( √ ) 10、若线性方程组0AX =有非零解,则AX β=一定有无穷多解.( X ) 四、计算题1、求向量组1234(1,1,2,4),(0,3,1,2),(3,0,7,14),(1,1,2,0),T T T T αααα=-===-5(2,1,5,6)T α=的秩及一个极大线性无关组,并用极大线性无关组线性表示其余向量.解:对以12345,,,,ααααα为列的矩阵作行初等变换化为阶梯形矩阵.1234510312103121301103303(,,,,)21725011014214060224210312131203303011010000000011000440000010301011010001100000ααααα⎛⎫⎛⎫ ⎪ ⎪--⎪ ⎪=→⎪ ⎪⎪⎪--⎝⎭⎝⎭⎛⎫⎛⎫⎪⎪ ⎪ ⎪→→ ⎪ ⎪ ⎪⎪--⎝⎭⎝⎭⎛⎫⎪⎪→ ⎪⎪⎝⎭所以,向量组12345,,,,ααααα的秩是3,124,,ααα是其一个极大线性无关组,且31251243,ααααααα=+=++.2、已知向量组123(0,1,1),(,3,1),(,1,0)T TT a b βββ=-==与向量组123(1,2,3),(2,1,1),(3,0,1)T TT ααα=-=-=具有相同的秩,且3β可由123,,ααα线性表出,求,a b .解:令1231231233(,,),(,,),(,,,)A B A αααβββαααβ===则由条件可知,A 与B ,A 与A 由相同的秩.因为1233123123(,,,)2101036123110051031231231000105103510510300015b b A b b b b b b b b αααβ⎛⎫⎛⎫⎪ ⎪==→--- ⎪ ⎪⎪ ⎪--⎝⎭⎝⎭⎛⎫⎛⎫⎪ ⎪ ⎪⎪→-→ ⎪⎪⎪⎪- ⎪⎝⎭⎝⎭12300004(,,)131041041110110110110041004a b a b a b B a b βββ⎛⎫-⎪⎛⎫⎛⎫⎪ ⎪ ⎪==→→ ⎪⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭ ⎪⎝⎭⎛⎫⎪- ⎪→ ⎪ ⎪- ⎪⎝⎭所以,2=秩A =秩B =秩A ,于是10,1045a b b -=-=,故20,5a b ==. 3、设四元非齐次线性方程组=AX β的系数矩阵A 的秩为2,已知它的三个解向量为123,,ηηη,其中123(4,3,2,1),(1,3,5,1),(2,6,3,2)===-T T T ηηη,求该方程组的通解.解:因为123,,ηηη是=AX β的解,所以12(3,0,3,0)T ηη-=-,13(6,3,1,1)T ηη-=---是0AX =的解,且1213,ηηηη--线性无关.又因为()2r A =,所以0AX =的基础解系含有两个解向量,于是1213,ηηηη--是0AX =的一个基础解系.故=AX β的通解是1112213()()c c ηηηηη+-+-(12,c c F ∈)4、设向量1234,,,αααα是齐次线性方程组0AX =的一个基础解系,若112223334441,,,t t t t βααβααβααβαα=+=+=+=+,试问:当实数t 满足什么关系时,1234,,,ββββ也是0AX =的一个基础解系?解:因为1234,,,αααα是0AX =的基础解系,所以1234,,,αααα的线性组合1234,,,ββββ也是0AX =的解. 因此,当1234,,,ββββ线性无关时,1234,,,ββββ也是0AX =的一个基础解系.因为12341234100100(,,,)(,,,)010001t t t t ββββαααα⎛⎫⎪⎪= ⎪⎪⎝⎭所以,1234,,,ββββ线性无关⇔1234||0ββββ≠⇔410010010010001ttt tt=-≠⇔1t ≠±.故当1t ≠±时,1234,,,ββββ也是0AX =的一个基础解系.5、设3阶非零矩阵A 的每一个列向量都是方程组1231231232020330x x x x x ax x x x +-=⎧⎪-+=⎨⎪+ -=⎩的解,求常数a 和行列式A .解:设123(,,)A βββ=,其中123,,βββ是A 的列向量,则123,,βββ不全为零,且是已知方程组的解,于是已知方程组由非零解,从而其系数矩阵行列式为零,即11211221034120313023a a a ---=-+=-+=--所以12a =. 设已知方程组的系数矩阵为B ,则B O ≠,且123123(,,)(,,)(0,0,0)BA B B B B O ββββββ====若||0A ≠,则A 可逆,从而111()()B BE B AA BA A OA O ---=====,矛盾,所以||0A =.6、讨论常数a 为何值时,线性方程组123123123112ax x x x ax x x x ax ++=⎧⎪++=⎨⎪+ +=-⎩无解、有唯一解、有无穷多解?在有无穷多解的情况下,求出其全部解.解:对线性方程组的增广矩阵作行初等变换得22111011120024211101130113112112112112011300(2)(1)2(2)a a a a a a a A a a a a aa a a a a a a a a ⎛⎫⎛⎫--+--+⎛⎫⎪ ⎪ ⎪=→--→-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭⎝⎭-⎛⎫ ⎪→-- ⎪ ⎪+-+⎝⎭1)当1a =时,秩1A =≠秩2A =,方程组无解. 2)当1,2a ≠-时,秩3A ==秩A ,方程组有唯一解. 3)当2a =-时,秩2A ==秩3A <,方程组有无穷多解:13231,1x x x x =+=+(3x 是自由未知量)7、已知方程组⎪⎩⎪⎨⎧=-=+++=+--330)1(31432321321x ax x a x x x x x ,问a 为何值时,此方程组:(1)有唯一解;(2)无解;(3)有无穷多解?在有无穷多解的情况下,试用其导出组的基础解系表出全部解.解:对线性方程组的增广矩阵作行初等变换得21411141114111310012101210330330233112012100(3)(1)3A a a a a a a a a a a a a a ------⎛⎫⎛⎫⎛⎫ ⎪ ⎪⎪=+→-+→-+ ⎪ ⎪ ⎪⎪ ⎪ ⎪--+-+⎝⎭⎝⎭⎝⎭-⎛⎫⎪→-+ ⎪ ⎪+-+⎝⎭1)当1,3a ≠-时,秩3A ==秩A ,方程组有唯一解.2)当1a =时,秩2A =≠秩3A =,方程组无解.3)当3a =-时,秩2A ==秩3A <,方程组有无穷多解:132314,1x x x x =-+=--(3x 是自由未知量)8、讨论常数,a b 为何值时,线性方程组1231231234324ax x x x bx x x bx x ++=⎧⎪++=⎨⎪+ +=⎩无解、有唯一解、有无穷多解?在有无穷多解的情况下,求出其全部解.解:对线性方程组的增广矩阵作行初等变换得1140114301142113113101212140010010114210121012011420014200(1)142a ab a a a a A bb b b b a a a a ab b b ab b a b ab -----⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪=→→ ⎪ ⎪ ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭--⎛⎫⎛⎫⎪ ⎪→→-- ⎪ ⎪⎪ ⎪--+--+⎝⎭⎝⎭1)当11,2a b =≠或0b =时,秩2A =≠秩3A =,方程组无解.2)当1,0a b ≠≠时,秩3A ==秩A ,方程组有唯一解. 3)当11,2a b ==时,秩2A ==秩3A <,方程组有无穷多解: 1322,2x x x =-=(3x 是自由未知量)9、对于线性方程组123123123322x x x x x x x x x λλλλ++=-⎧⎪++=-⎨⎪++=-⎩(1)λ取何值时,方程组无解、有唯一解、有无穷多解;(2)在方程组有无穷多解时,试用其对应齐次线性方程组的基础解系表示方程组通解.解:对线性方程组的增广矩阵作行初等变换得2211301133112011011211200233112011001101120(2)(1)3(1)A λλλλλλλλλλλλλλλλλλλλλλ⎛⎫----⎛⎫⎪ ⎪=-→-- ⎪ ⎪ ⎪ ⎪--⎝⎭⎝⎭⎛⎫----⎛⎫ ⎪ ⎪→--→-- ⎪ ⎪ ⎪ ⎪--+--⎝⎭⎝⎭(1)1)当2λ=-时,秩2A =≠秩3A =,方程组无解. 2)当1,2λ≠-时,秩3A ==秩A ,方程组有唯一解. 3)当1λ=时,秩1A ==秩3A <,方程组有无穷多解.(2)在方程组有无穷多解时,与原方程组同解方程组为1232x x x ++=-,令230x x ==,得特解0(2,0,0)γ=-.与原方程组同解方程组对应的齐次线性方程组同解方程组为1230x x x ++=,所以对应的齐次线性方程组的基础解系为12(1,1,0),(1,0,1)ηη=-=-.所以原方程组的通解为:01122k k γγηη=++(12,k k 是任意数). 五、证明题1、设向量组123,,ααα线性无关,证明向量组12αα+,23αα+,31αα+也线性无关.证明:设112223331()()()0k k k αααααα+++++=则131122233()()()0k k k k k k ααα+++++=因为123,,ααα线性无关,所以131223000k k k k k k +=⎧⎪+=⎨⎪+=⎩解得1230k k k ===,故122331,,αααααα+++线性无关.2、证明向量组12233441,,,αααααααα++++线性相关. 证明:设112223334441()()()()0k k k k αααααααα+++++++=则141122233344()()()()0k k k k k k k k αααα+++++++=考虑齐次线性方程组141223340000k k k k k k k k +=⎧⎪+=⎪⎨+=⎪⎪+=⎩其系数行列式1001100110110011001111001100110010011=-=-=所以齐次线性方程组有非零解. 于是存在不全为零的数1234,,,k k k k ,使得112223334441()()()()0k k k k αααααααα+++++++=成立,故12233441,,,αααααααα++++线性相关.3、设向量组123,,ααα线性无关,证明向量组1223312,2,32αααααα---也线性无关.证明:设112223331(2)(2)(32)0k k k αααααα-+-+-=则131122233(22)()(23)0k k k k k k ααα-+-++-+=因为123,,ααα线性无关,所以1312232200230k k k k k k -=⎧⎪-+=⎨⎪-+=⎩解得1230k k k ===,故1223312,2,32αααααα---线性无关.4、设向量组123,,ααα线性无关,证明向量组123123,2322,αααααα++-+123355ααα+-线性相关.证明:设112321233123()(2322)(355)0k k k ααααααααα+++-+++-=则123112321233(23)(35)(225)0k k k k k k k k k ααα+++-+++-=因为123,,ααα线性无关,所以1231231232303502250k k k k k k k k k ++=⎧⎪-+=⎨⎪+-=⎩ 解得1323192,95k k k k =-=,取35k =,得1219,2k k =-=使得 112321233123()(2322)(355)0k k k ααααααααα+++-+++-=故123123123,2322,355ααααααααα++-++-线性相关.5、已知向量组1234,,,αααα线性无关,证明向量组12233441,,,αααααααα+++-也线性无关.证明:设112223334441()()()()0k k k k αααααααα++++++-=则141122233344()()()()0k k k k k k k k αααα-++++++=因为1234,,,αααα线性无关,所以141223340000k k k k k k k k -=⎧⎪+=⎪⎨+=⎪⎪+=⎩解得12340k k k k ====,故12233441,,,αααααααα+++-线性无关.6、设12,,,s ααα均为n 维列向量,A 是n n ⨯矩阵,试证明: (1)若12,,,s ααα线性相关,则12,,,s A A A ααα也线性相关;(2)若A 可逆,且12,,,s A A A ααα线性相关,则12,,,s ααα也线性相关.证明:(1)因为12,,,s ααα线性相关,所以存在不全为零的数12,,,s k k k ,使得1122440k k k ααα+++=从而有11221122()00s s s s k A k A k A A k k k A αααααα+++=+++==故12,,,s A A A ααα线性相关.(2)因为12,,,s A A A ααα线性相关,所以存在不全为零的数12,,,s k k k ,使得1122440k A k A k A ααα+++=从而有11221122()0s s s s A k k k k A k A k A αααααα+++=+++=由A 可逆,得1122440k k k ααα+++=.故12,,,s ααα线性相关.7、已知向量组123,,ααα与122331,,αααααα+++ (1)证明123,,ααα与122331,,αααααα+++等价;(2)证明123,,ααα线性相关的充分必要条件是122331,,αααααα+++线性相关.证明:(1)首先,122331,,αααααα+++显然可由123,,ααα线性表示. 其次,由1122331212233131223311[()()()]21[()()()]21[()()()]2ααααααααααααααααααααα⎧=+-+++⎪⎪⎪=+++-+⎨⎪⎪=-+++++⎪⎩可知,123,,ααα可由122331,,αααααα+++线性表示. 故123,,ααα与122331,,αααααα+++等价.8、已知非齐次线性方程组123423423412340221(3)21321x x x x x x x x a x x x x x bx + + +=⎧⎪ ++=⎪⎨ - +--=-⎪⎪+ ++=-⎩ 有3个线性无关的解,证明:系数矩阵A 的秩等于2,并求,a b 的值及方程组的通解.证明:设123ξξξ,,是方程组的3个线性无关解,则1213ξξξξ--,是导出组0AX =的两个解.若1213()()0k l ξξξξ-+-=,则有123()0k l k l ξξξ+--=,于是由123ξξξ,,线性无关可得0k l ==,所以1213ξξξξ--,是导出组0AX =的两个线性无关解,因此,0AX =的基础解系所含向量个数不少于2,即有4()2A -≥秩. 所以有()2A ≤秩.因为系数矩阵111101220132321A a b ⎛⎫ ⎪⎪= ⎪--- ⎪⎝⎭,有一个2阶子式111001=≠,所以有()A ≤2秩,故()=2A 秩.对增广矩阵A 做行初等变换,有313242311110111100122101221=013210132132110123111110012210010000010r r r r r r A a a b b a b -++⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪−−−→ ⎪ ⎪-------- ⎪ ⎪-----⎝⎭⎝⎭⎛⎫⎪⎪−−−→ ⎪- ⎪-⎝⎭于是由()=2A 秩,有1010a b -=⎧⎨-=⎩,即11a b =⎧⎨=⎩.因此有31324212311110111100122101221=012210122132111012211111010111012210122100000000000000000000r r r r r r r r A -++-⎛⎫⎛⎫⎪ ⎪⎪ ⎪−−−→⎪⎪--------⎪ ⎪-----⎝⎭⎝⎭---⎛⎫⎛⎫⎪⎪⎪ ⎪−−−→−−−→ ⎪ ⎪⎪⎪⎝⎭⎝⎭故方程组的通解为1342341122x x x x x x =-++⎧⎨=--⎩.9、设12,,,n ααα均为n 维线性无关列向量,A 是n n ⨯矩阵,试证明:12,,,n A A A ααα线性无关⇔A 可逆.证明:(⇒)因为12n ααα,,,线性无关,所以以12n ααα,,,为列的n n ⨯矩阵12()n B ααα=可逆.因为12,,,n A A A ααα线性无关,所以矩阵1212()()n n C A A A A AB αααααα===可逆,从而1A CB -=可逆.(⇐)若有数12n k k k ,,,,使得11220s n k A k A k A ααα+++=则有1122()0n n A k k k ααα+++=由A 可逆可得11220s n k k k ααα+++=因为12,,,n ααα线性无关.所以120n k k k ====,故12,,,nA A A ααα线性无关.。
高教线性代数第三章 线性方程组课后习题答案

第三章 线性方程组1. 用消元法解下列线性方程组:123412345123451234512345354132211)234321x x x x x x x x x x x x x x x x x x x x x x x x ++-=⎧⎪++-+=-⎪⎪-+--=⎨⎪-++-=⎪⎪++-+=-⎩124512345123451234523213322)23452799616225x x x x x x x x x x x x x x x x x x x +-+=⎧⎪--+-=⎪⎨-+-+=⎪⎪-+-+=⎩ 1234234124234234433)31733x x x x x x x x x x x x x -+-=⎧⎪-+=-⎪⎨+++=⎪⎪-++=-⎩123412341234123434570233204)411131607230x x x x x x x x x x x x x x x x +-+=⎧⎪-+-=⎪⎨+-+=⎪⎪-++=-⎩123412341234123421322325)521234x x x x x x x x x x x x x x x x +-+=⎧⎪-+-=⎪⎨+-+=-⎪⎪-+-=⎩12341234123412341232313216)23122215522x x x x x x x x x x x x x x x x x x x ++-=⎧⎪++-=⎪⎪+++=⎨⎪++-=⎪⎪++=⎩ 解 1)对方程组得增广矩阵作行初等变换,有135401135401132211003212121113054312141113074512121111014812--⎡⎤⎡⎤⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥⎢⎥→------⎢⎥⎢⎥-----⎢⎥⎢⎥⎢⎥⎢⎥-----⎣⎦⎣⎦102101100101003212000212002000002000000000000000011100010100--⎡⎤⎡⎤⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥→→--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦因为()()45rank A rank B ==<,所以方程组有无穷多解,其同解方程组为1445324122200x x x x x x x -=⎧⎪+=-⎪⎨-=⎪⎪-+=⎩,解得123451022x k x k x x k x k=+⎧⎪=⎪⎪=⎨⎪=⎪⎪=--⎩ 其中k 为任意常数。
高等代数第三章习题.ppt

7
线性方程组
定理7 线性方程组有解的充分必要条件是 的系数矩阵与增广矩阵的秩相等,即
向量组的秩 的性质
1)一个向量组线性无关的充要条件是 它的秩与它所含向量个数相同; 一个向量组线性相关的充要条件是
它的秩<它所含向量个数. 2)等价向量组必有相同的秩. 反之,有相同的秩的两个向量组不一定等价.
3)若向量组 1 , 2 ,
, s 可经向量组 1 , 2 , , s } 秩 { 1 , 2 ,
1)一向量组线性相关的充要条件是其中至少有一
个向量可由其余向量线性表出.
2) 若向量组A : 1 , 2 , , s线性相关, 则向量组B :
1 , 2 ,
, s , s 1也线性相关.反言之, 若向量
组B线性无关, 则向量组A也线性无关.
部分相关->整体相关 (整体无关->部分无关)
第三章 线性方程组-习题课
1.线性组合
定义
给定向量组A : 1 , 2 , , k s ,向量
, s 对于任何一组 k s s
实数k1 , k2 ,
k11 k2 2
称为向量组A的一个线性组合
2.线性表出
给定向量组A : 1 , 2 , 实数k1 , k2 , , ks , 使 k s s , , s和向量b, 如果存在一组 b k11 k2 2 向量组A : 1 , 2 ,
推论1 齐次线性方程组
( ) 有非零解 系数矩阵 A (aij )nn 的行列式 A =0 R( A) n . ( )只有零解 A 0 R( A) n.
aij x j 0( i 1, 2, j 1
n
, n) ( )
高等代数(北大版)第3章习题参考答案

第三章 线性方程组1. 用消元法解下列线性方程组:123412345123451234512345354132211)234321x x x x x x x x x x x x x x x x x x x x x x x x ++-=⎧⎪++-+=-⎪⎪-+--=⎨⎪-++-=⎪⎪++-+=-⎩ 124512345123451234523213322)23452799616225x x x x x x x x x x x x x x x x x x x +-+=⎧⎪--+-=⎪⎨-+-+=⎪⎪-+-+=⎩ 1234234124234234433)31733x x x x x x x x x x x x x -+-=⎧⎪-+=-⎪⎨+++=⎪⎪-++=-⎩ 123412341234123434570233204)411131607230x x x x x x x x x x x x x x x x +-+=⎧⎪-+-=⎪⎨+-+=⎪⎪-++=-⎩ 123412341234123421322325)521234x x x x x x x x x x x x x x x x +-+=⎧⎪-+-=⎪⎨+-+=-⎪⎪-+-=⎩ 12341234123412341232313216)23122215522x x x x x x x x x x x x x x x x x x x ++-=⎧⎪++-=⎪⎪+++=⎨⎪++-=⎪⎪++=⎩ 解 1)对方程组得增广矩阵作行初等变换,有135401135401132211003212121113054312141113074512121111014812--⎡⎤⎡⎤⎢⎥⎢⎥----⎢⎥⎢⎥⎢⎥⎢⎥→------⎢⎥⎢⎥-----⎢⎥⎢⎥⎢⎥⎢⎥-----⎣⎦⎣⎦10210110010100321200021200200000200000000000000001110010000--⎡⎤⎡⎤⎢⎥⎢⎥---⎢⎥⎢⎥⎢⎥⎢⎥→→--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦因为()()45rank A rank B ==<,所以方程组有无穷多解,其同解方程组为1415324122200x x x x x x x -=⎧⎪+=-⎪⎨-=⎪⎪-+=⎩, 解得123451022x k x k x x k x k=+⎧⎪=⎪⎪=⎨⎪=⎪⎪=--⎩ 其中k 为任意常数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章线性方程组
3.1主要方法
3.1.1线性相关性的判别
线性关系:
α1,α2,···,αs线性无关⇐⇒α1,α2,···,αs不线性相关
⇐⇒不存在不全为零的数k1,k2,···,k s使成立k1α1+k2α2+···+k sαs=0
⇐⇒若k1,k2,···,k s不全为零,则k1α1+k2α2+···+k sαs=0
⇐⇒若k1α1+k2α2+···+k sαs=0,则k1=k2=···=k s=0.
因此,判断向量组α1,α2,···,αs是否线性相关的方法:令
k1α1+k2α2+···+k sαs=0,
若k1,k2,···,k s有非零解,则α1,α2,···,αs线性相关;若k1,k2,···,k s只有零解,则α1,α2,···,αs无关。
3.1.2求矩阵与向量组的秩的方法
求矩阵秩的方法:
A初等行变换
−−−−−−→B(阶梯形矩阵)
则r(A)=r(B)=B的非零行的行数.
求向量组的秩的方法:
以α1,α2,···,αs为列做成矩阵A,
A=(αT
1,αT
2
,···,αT
s
)初等行变换
−−−−−−→B(阶梯形矩阵)
则
•r(α1,α2,···,αs)=r(A)=r(B)=B的非零行的行数.
•若B的非零行的第一个非零元分别位于i1,i2,···,i r,则αi
1,αi
2
,···,αi
r
就是α1,α2,···,αs
的一个极大线性无关组。
3.1.2解s×n线性方程组
第一步:¯A初等行变换
−−−−−−→¯B(阶梯形矩阵或者行简化阶梯形矩阵)
第二步:由¯B判断有无解
•若r(A)=r(¯A),则方程组无解
•若r(A)=r(¯A)=r,方程组有解,此时
第三步:判断解的个数并求解
•若r=n,则方程组有唯一解,则¯B求出其解即可;
•若r<n,则方程组有无穷多解,此时由¯B求出方程组的一个特解γ0,与导出组的一个基础解系η1,η2,···,ηn−r,则方程组的全部解可表示为:
γ=γ0+k1η1+k2η2+···+k n−rηn−r.
3.2相关练习
一、填空题
1向量组α1,α2,···,αs称为线性相关,如果.
2一个向量组的一个部分组称为一个极大线性无关组,如果
3等价向量组的秩.
4n×n矩阵A的行列式为零的充要条件是.
5一矩阵的秩为r的充要条件是矩阵中有一个,
同时.
6线性方程组有解的充要条件是.
7齐次线性方程组的一组解η1,η2,···,ηt称为它的一个基础解系,如果
8线性方程组有唯一解的充要条件是它的导出线性方程组.
9如果向量组α1,α2,···,αs的秩为r,那么α1,α2,···,αs中任意r个的向量,都构成它的一个极大无关组。
二、计算题与解答
1求向量组α1=(1,1,1,1),α2=(2,1,3,−1),α3=(1,2,0,1),α4=(1,1,−3,0),α5=(2,3,1,2),的一个极大无关组与秩。
2求向量组α1=(1,−1,2,4),α2=(0,3,1,2),α3=(3,0,7,14),α4=(1,−1,2,0),α5=(2,2,5,6),的一个极大线性无关组与秩。
3设线性方程组为
x1+x2+x3+x4+x5=1,
4x1+3x2+2x3+2x4−2x5=a, 2x1+3x2+4x3+4x4+8x5=5, x2+2x3+2x4+6x5=3, 5x1+4x2+3x3+3x4−x5=b.
1)当a,b取什么值时,方程组有解。
2)有解的情形,求解的结构式(要求必须求出方程组的一个特解及其导出组的一个基础解系).
4设线性方程组为
x1+x2−x3+3x4−5x5=0,
x1+2x2−4x3+5x4−9x5=−1, 2x1+x2+x3+4x4−6x5=a, 4x1+1x2+5x3+6x4−8x5=b.
1)当a,b取什么值时,方程组有解。
2)有解的情形,求解的结构式(要求必须求出方程组的一个特解及其导出组的一个基础解系).
5设向量组α1,α2,···,αs线性无关,问向量组α1+α2,α2+α3,···,αs−1+αs,αs+α1是否线性相关,并证明你的结论。
三、证明
1证明:如果向量组α1,α2,···,αr线性无关,而α1,α2,···,αr,β线性相关,则向量β可以由α1,α2,···,αr线性表出,且表示法唯一。
2设η0是线性方程组的一个解,η1,η2,···,ηt是它的导出组的一个基础解系,令
γ1=η0,γ2=η1+η0,···,γt+1=ηt+η0.
证明:线性方程组的任一个解γ都可表成
γ=u1γ1+u2γ2+···+u t+1γt+1
其中u1+u2+···+u t+1=1.
3设α1,α2,···,αn是一组线性无关的向量,βi=∑n
j=1
a ijαj(i=1,2,···,n),令A=(a ij).证明:
β1,β1,···,βn线性相关的充要条件是|A|=0
4证明:一个向量组的任何一个线性无关组都可以扩充成一极大线性无关组.
5设向量组α1,α2,···,αm线性无关,向量组而β,α1,α2,···,αm,(β=0)线性相关,证明:向量组β,α1,α2,···,αm中有且仅有一个向量αj(1≤j≤m)可以由它前面的向量β,α1,α2,···,αj−1线性表出.
6设A是一个m×n齐次线性方程组的系数矩阵,向量(a1,a2,···,a n)是该齐次线性方程组的一个非零解,证明
1)若A的任何列向量均非零,则a1,a2,···,a n中至少有两个非零;
2)若A的任何两个列向量线性无关,则a1,a2,···,a n中至少有三个非零.。
