Matlab解热传导方程代码
导热方程求解matlab

使用差分方法求解下面的热传导方程2(,)4(,)0100.2t xx T x t T x t x t =<<<<初值条件:2(,0)44T x x x =-边值条件:(0,)0(1,)0T t T t ==使用差分公式1,,1,222(,)2(,)(,)2(,)()i j i j i j i j i j i j xx i j T x h t T x t T x h t T T T T x t O h h h -+--++-+=+≈,1,(,)(,)(,)()i j i j i j i jt i j T x t k T x t T T T x t O k k k ++--=+≈上面两式带入原热传导方程,1,1,,1,22i j i ji j i j i jT T T T T k h +-+--+= 令224k r h=,化简上式的 ,1,1,1,(12)()i j i j i j i j T r T r T T +-+=-++ix jt j编程MATLAB 程序,运行结果如下x t Tfunction mypdesolutionc=1;xspan=[0 1];tspan=[0 0.2];ngrid=[100 10];f=@(x)4*x-4*x.^2;g1=@(t)0;g2=@(t)0;[T,x,t]=rechuandao(c,f,g1,g2,xspan,tspan,ngrid);[x,t]=meshgrid(x,t);mesh(x,t,T);xlabel('x')ylabel('t')zlabel('T')function [U,x,t]=rechuandao(c,f,g1,g2,xspan,tspan,ngrid)% 热传导方程:% Ut(x,t)=c^2*Uxx(x,t) a<x<b ts<t<tf% 初值条件:% u(x,0)=f(x)% 边值条件:% u(a,t)=g1(t)% u(b,t)=g2(t)%% 参数说明% c:方程中的系数% f:初值条件% g1,g2:边值条件% xspan=[a,b]:x的取值范围% tspan=[ts,tf]:t的取值范围% ngrid=[n,m]:网格数量,m为x网格点数量,n为t的网格点数量% U:方程的数值解% x,t:x和t的网格点n=ngrid(1);m=ngrid(2);h=range(xspan)/(m-1);x=linspace(xspan(1),xspan(2),m);k=range(tspan)/(n-1);t=linspace(tspan(1),tspan(2),n);r=c^2*k/h^2;if r>0.5error('为了保证算法的收敛,请增大步长h或减小步长k!')ends=1-2*r;U=zeros(ngrid);% 边界条件U(:,1)=g1(t);U(:,m)=g2(t);% 初值条件U(1,:)=f(x);% 差分计算for j=2:nfor i=2:m-1U(j,i)=s*U(j-1,i)+r*(U(j-1,i-1)+U(j-1,i+1));endend。
热传导模型方程matlab

热传导模型方程引言热传导模型方程是描述热传导过程的数学模型,它在物理学、工程学等领域中有着广泛的应用。
该方程可以用来求解物体内部的温度分布以及热量的传输过程。
本文将重点介绍热传导模型方程在Matlab中的实现方法及应用。
热传导模型方程热传导模型方程是一种偏微分方程,用于描述物体内部温度分布随时间的变化。
它的一般形式如下:∂u/∂t = κ∇²u其中,u是温度分布函数,t是时间,κ是热传导率,∇²是拉普拉斯算子。
离散化处理为了在计算机中求解热传导模型方程,我们需要对其进行离散化处理。
通常,我们将物体分成若干个小区域,每个小区域的温度可以看作是一个离散节点。
然后,我们利用数值差分方法将偏微分方程转化为差分方程。
最常用的数值差分方法是有限差分法,其中最简单的方法是二阶中心差分法。
二阶中心差分法二阶中心差分法是一种常用的数值差分方法,它能够较为准确地近似热传导模型方程。
该方法利用了节点的前后两个时间步长的温度值和空间步长的温度梯度。
具体来说,对于一个二维网格,节点(i, j)的二阶中心差分近似可以表示为:(∂u/∂t)(i, j) ≈ (u(i+1, j) - 2u(i, j) + u(i-1, j))/(Δx²) + (u(i, j+1) - 2u(i, j) + u(i, j-1))/(Δy²)其中,Δx和Δy分别是空间步长。
Matlab实现在Matlab中,我们可以通过编写代码来求解热传导模型方程。
下面是实现该方程的一个示例代码:% 定义初始条件和边界条件N = 50; % 网格节点数L = 1; % 系统尺寸T = 1; % 总时间dx = L/N;dt = dx^2/4;x = linspace(0, L, N+1);y = linspace(0, L, N+1);[X, Y] = meshgrid(x, y);u = sin(pi*X).*sin(pi*Y); % 初始温度分布% 迭代求解热传导模型方程for t = 0:dt:Tu_new = u + dt*(del2(u)/dx^2);u = u_new;end% 可视化温度分布surf(X, Y, u)xlabel('x')ylabel('y')zlabel('Temperature')在上面的代码中,我们首先定义了初始条件和边界条件,然后利用循环迭代的方式求解热传导模型方程。
matlab傅里叶谱方法求解热传导方程

文章标题:深度解析matlab傅里叶谱方法求解热传导方程在工程学和科学领域中,热传导方程是一个非常重要的偏微分方程,描述了物体内部温度分布随时间的变化。
而傅里叶谱方法是一种常用的数值求解方法,能够高效地对热传导方程进行求解。
本文将深入探讨matlab傅里叶谱方法在求解热传导方程中的应用,以及该方法在实际工程中的意义。
1. 热传导方程的基本概念热传导方程是描述物体内部温度分布随时间演化的方程。
一维情况下,热传导方程可以表示为:$$\frac{\partial u}{\partial t} = \alpha \frac{\partial^2 u}{\partialx^2}$$其中,$u(x,t)$是位置$x$和时间$t$的温度分布函数,$\alpha$是热扩散系数。
对于二维、三维情况,热传导方程的形式也可以相应拓展。
2. matlab傅里叶谱方法的基本原理傅里叶谱方法是一种基于傅里叶级数展开的数值求解方法。
它的基本思想是将热传导方程通过傅里叶变换转化为频域上的方程,再通过离散化的方式进行求解。
在matlab中,可以利用快速傅里叶变换(FFT)来高效地实现傅里叶谱方法。
该方法的优点是高精度、高效率,并且适用于多维情况。
3. matlab傅里叶谱方法的具体实现在matlab中,可以通过编写相应的程序来实现对热传导方程的求解。
首先需要将热传导方程进行离散化,得到一个离散的时间和空间网格。
然后利用傅里叶变换将热传导方程转化为频域上的方程,通过FFT算法高效地求解。
最后再利用逆傅里叶变换将频域上的解转化为时域的解。
通过这一系列步骤,就可以在matlab中实现对热传导方程的高效求解。
4. 实际工程中的应用与意义matlab傅里叶谱方法在实际工程中有着广泛的应用与意义。
例如在材料科学中,可以利用该方法对材料的热传导特性进行建模和仿真。
在电子工程领域,也可以利用该方法对电路元件的热特性进行分析和优化。
另外,在生物医学工程中,对人体组织的热传导特性进行研究也可以借助matlab傅里叶谱方法来实现。
Matlab解热传导方程代码

Sample MATLAB codes1.%Newton Cooling Lawclear; close all; clc;h = 1;T(1) = 10; %T(0)error = 1;TOL = 1e-6;k = 0;dt = 1/10;while error > TOL,k = k+1;T(k+1) = h*(1-T(k))*dt+T(k);error = abs(T(k+1)-T(k));endt = linspace(0,dt*(k+1),k+1);plot(t,T),hold on, plot(t,1,'r-.')xlabel('Time'),ylabel('Temperature'),title(['T_0 = ',num2str(T(1)), ', T_\infty = 1']), legend('Cooling Trend','Steady State')2.%Boltzman Cooling Lawclear; close all; clc;h = 1;T(1) = 10; %T(0)error = 1;TOL = 1e-6;k = 0;dt = 1/10000;while error > TOL,k = k+1;T(k+1) = h*(1-(T(k))^4)*dt+T(k);error = abs(T(k+1)-T(k));endt = linspace(0,dt*(k+1),k+1);plot(t,T),hold on, plot(t,1,'r-.')xlabel('Time'),ylabel('Temperature'),title(['T_0 = ',num2str(T(1)), ', T_\infty = 1']), legend('Cooling Trend','Steady State')3.%Fourier Heat conductionclear; close all; clc;h = 1;n = 11;T = ones(n,1); Told = T;T(1) = 1; %Left boundaryT(n) = 10; %Right boundaryx = linspace(0,1,n);dx = x(2)-x(1);dt = dx^2/3; %cfl conditionerror = 1;TOL = 1e-6;k = 0;while error > TOL,Told = T;k = k+1;for i = 2:n-1T(i) = dt*(Told(i+1)-2*Told(i)+Told(i-1))/dx^2+Told(i);enderror = max(abs(T-Told));if mod(k,5)==0, out(k,:) = T; endendplot(x,out)xlabel('x'),ylabel('Temperature'),title(['Fourier Heat Conduction']),%legend('Cooling Trend','Steady State')4. 2D Heat Equation%2D Heat Equation.clear; close all; clcn = 10; %grid has n - 2 interior points per dimension (overlapping)x = linspace(0,1,n); dx = x(2)-x(1); y = x; dy = dx;TOL = 1e-6;T = zeros(n);T(1,1:n) = 10; %TOPT(n,1:n) = 1; %BOTTOMT(1:n,1) = 1; %LEFTT(1:n,n) = 1; %RIGHTdt = dx^2/4;error = 1; k = 0;while error > TOLk = k+1;Told = T;for i = 2:n-1for j = 2:n-1T(i,j) = dt*((Told(i+1,j)-2*Told(i,j)+Told(i-1,j))/dx^2 ... + (Told(i,j+1)-2*Told(i,j)+Told(i,j-1))/dy^2) ... + Told(i,j);endenderror = max(max(abs(Told-T)));endsubplot(2,1,1),contour(x,y,T),title('Temperature (Steady State)'),xlabel('x'),ylabel('y'),colorbar subplot(2,1,2),pcolor(x,y,T),shading interp,title('Temperature (Steady State)'),xlabel('x'),ylabel('y'),colorbar5. Wave Translation%Oscillations - translation left and rightclear; close all; clc;for c = [1 -1]cc = 0;n = 261;x = linspace(0,13,n);u = zeros(n,1);u(121:141) = sin(pi*x(121:141));dx = x(2)-x(1);dt = dx;error = 1;TOL = 1e-6;k = 0;while k < 110uold = u;k = k+1;for i = 2:n-1if c == 1, u(i) = dt*c*(uold(i+1)-uold(i))/dx+uold(i); end%c = 1if c == -1, u(i) = dt*c*(uold(i)-uold(i-1))/dx+uold(i); end%c = -1 enderror = max(abs(u-uold));if mod(k,10)==0, cc = cc+1; out(cc,:) = u;endendif c == 1subplot(2,1,1),for hh = 1:ccplot(x,out(hh,:)+hh),hold on,endu = zeros(n,1);u(121:141) = sin(pi*x(121:141)); plot(x,u)xlabel('u(x)'),ylabel('Time'),title('Translation to the Left')elseif c == -1subplot(2,1,2),for hh = 1:ccplot(x,out(hh,:)+hh),hold on,endu = zeros(n,1);u(121:141) = sin(pi*x(121:141)); plot(x,u)xlabel('u(x)'),ylabel('Time'),title('Translation to the Right')endend6.%wave equationclear; close all; clc;c = 1;n = 21;x = linspace(0,1,n);dx = 1/(n-1);dt = dx;u(:,1) = sin(pi*x);u(1,2) = 0;for i = 2:n-1u(i,2) = 0.5*(dt^2*c^2*(u(i+1,1)-2*u(i,1)+u(i-1,1))/dx^2+2*u(i,1));endu(n,2) = 0;error = 1; k = 1;while k < 100k = k+1;u(1,k+1) = 0;for i = 2:n-1u(i,k+1) = dt^2*c^2*(u(i+1,k)-2*u(i,k)+u(i-1,k))/dx^2+2*u(i,k)-u(i,k-1);endu(n,k+1) = 0;endplot(x,u), xlabel('x'),ylabel('y')如有侵权请联系告知删除,感谢你们的配合!。
matlab偏微分方程

matlab偏微分方程Matlab可以用于求解偏微分方程(PDE)。
以下是一些示例:1. 热传导方程热传导方程描述了温度随时间和空间的变化,由以下方程给出:$\frac{\partial T}{\partial t} = \alpha \frac{\partial^2 T}{\partialx^2}$在Matlab中,可以使用“pdepe”函数来求解这个问题。
具体来说,需要指定初始条件和边界条件,并设置物理参数。
2. 波动方程波动方程描述了波的传播,由以下方程给出:$\frac{\partial^2 u}{\partial t^2} = c^2 \frac{\partial^2 u}{\partialx^2}$在Matlab中,可以使用“pdepe”函数来求解这个问题。
需要指定初始条件和边界条件,并设置物理参数。
3. Navier-Stokes方程Navier-Stokes方程描述了流体的运动,由以下方程给出:$\frac{\partial u}{\partial t} + u \cdot \nabla u = -\frac{1}{\rho}\nabla p + \nu \nabla^2 u$在Matlab中,可以使用PDE工具箱进行求解。
需要指定初始条件、边界条件和物理参数。
4. Schrödinger方程Schrödinger方程描述了量子力学中的波函数演化,由以下方程给出:$i \hbar \frac{\partial \psi}{\partial t} = -\frac{\hbar^2}{2m}\nabla^2 \psi + V(x) \psi$在Matlab中,可以使用PDE工具箱或ODE工具箱进行求解。
需要指定初始条件、边界条件和物理参数。
以上仅是部分示例,Matlab还可以用于求解其他类型的偏微分方程。
matlab求解一维带内热源传热问题

matlab 求解一维带内热源传热问题解一维带有内部热源的传热问题通常涉及到热传导方程的求解。
热传导方程描述了温度场随时间和空间的变化。
一维热传导方程通常写作:22()T T Q x t xα∂∂=+∂∂ 其中:• T 是温度,• t 是时间,• x 是空间坐标,• α 是热扩散系数,• Q(x) 是热源。
解这个方程需要适当的边界条件和初始条件。
为了简化问题,我们可以考虑一个稳态(0T t∂=∂)情况。
以下是使用 MATLAB 求解一维带有内部热源的传热问题的简单示例代码:% 参数设置L = 1; % 区域长度alpha = 0.01; % 热扩散系数Q = @(x) 1; % 内部热源% 空间离散化N = 100; % 离散网格数x = linspace(0, L, N);% 热传导方程T = zeros(1, N);T(1) = 0; % 初始条件T(N) = 100; % 边界条件% 离散格式求解dx = x(2) - x(1);dt = 0.01;num_steps = 1000;for step = 1:num_stepsfor i = 2:N-1T(i) = T(i) + alpha * dt / dx^2 * (T(i+1) - 2*T(i) + T(i-1)) + Q(x(i)) * dt;endend% 结果可视化plot(x, T);xlabel('空间坐标');ylabel('温度');title('一维带内部热源传热问题');请注意,这是一个简化的例子,具体的问题可能需要更多的考虑,例如更精确的数值方法、不同的边界条件和初始条件、更复杂的热源分布等。
这个示例主要用于演示MATLAB 中解决这类问题的基本方法。
利用matlab程序解决热传导问题

哈佛大学能源与环境学院课程作业报告作业名称:传热学大作业——利用matlab程序解决热传导问题院系:能源与环境学院专业:建筑环境与设备工程学号:姓名:盖茨比2015年6月8日一、题目及要求1.原始题目及要求2.各节点的离散化的代数方程3.源程序4.不同初值时的收敛快慢5.上下边界的热流量(λ=1W/(m℃))6.计算结果的等温线图7.计算小结题目:已知条件如下图所示:二、各节点的离散化的代数方程各温度节点的代数方程ta=(300+b+e)/4 ; tb=(200+a+c+f)/4; tc=(200+b+d+g)/4; td=(2*c+200+h)/4 te=(100+a+f+i)/4; tf=(b+e+g+j)/4; tg=(c+f+h+k)/4 ; th=(2*g+d+l)/4ti=(100+e+m+j)/4; tj=(f+i+k+n)/4; tk=(g+j+l+o)/4; tl=(2*k+h+q)/4tm=(2*i+300+n)/24; tn=(2*j+m+p+200)/24; to=(2*k+p+n+200)/24; tp=(l+o+100)/12 三、源程序【G-S迭代程序】【方法一】函数文件为:function [y,n]=gauseidel(A,b,x0,eps)D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);G=(D-L)\U;f=(D-L)\b;y=G*x0+f;n=1;while norm(y-x0)>=epsx0=y;y=G*x0+f;n=n+1;end命令文件为:A=[4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0,0;-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0;0,-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0;0,0,-2,4,0,0,0,-1,0,0,0,0,0,0,0,0;-1,0,0,0,4,-1,0,0,-1,0,0,0,0,0,0,0;0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0,0;0,0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0;0,0,0,-1,0,0,-2,4,0,0,0,-1,0,0,0,0;0,0,0,0,-1,0,-1,0,4,0,0,0,-1,0,0,0;0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0,0;0,0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0;0,0,0,0,0,0,0,-1,0,0,-2,4,0,0,0,-1;0,0,0,0,0,0,0,0,-2,0,0,0,24,-1,0,0;0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1,0;0,0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1;0,0,0,0,0,0,0,0,0,0,0,-1,0,0,-1,12];b=[300,200,200,200,100,0,0,0,100,0,0,0,300,200,200,100]';[x,n]=gauseidel(A,b,[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]',1.0e-6) xx=1:1:4;yy=xx;[X,Y]=meshgrid(xx,yy);Z=reshape(x,4,4);Z=Z'contour(X,Y,Z,30)Z =139.6088 150.3312 153.0517 153.5639108.1040 108.6641 108.3119 108.1523 84.1429 67.9096 63.3793 62.4214 20.1557 15.4521 14.8744 14.7746 【方法2】>> t=zeros(5,5);t(1,1)=100;t(1,2)=100;t(1,3)=100;t(1,4)=100;t(1,5)=100;t(2,1)=200;t(3,1)=200;t(4,1)=200;t(5,1)=200;for i=1:10t(2,2)=(300+t(3,2)+t(2,3))/4 ;t(3,2)=(200+t(2,2)+t(4,2)+t(3,3))/4;t(4,2)=(200+t(3,2)+t(5,2)+t(4,3))/4;t(5,2)=(2*t(4,2)+200+t(5,3))/4;t(2,3)=(100+t(2,2)+t(3,3)+t(2,4))/4;t(3,3)=(t(3,2)+t(2,3)+t(4,3)+t(3,4))/4; t(4,3)=(t(4,2)+t(3,3)+t(5,3)+t(4,4))/4; t(5,3)=(2*t(4,3)+t(5,2)+t(5,4))/4;t(2,4)=(100+t(2,3)+t(2,5)+t(3,4))/4;t(3,4)=(t(3,3)+t(2,4)+t(4,4)+t(3,5))/4;t(4,4)=(t(4,3)+t(4,5)+t(3,4)+t(5,4))/4;t(5,4)=(2*t(4,4)+t(5,3)+t(5,5))/4;t(2,5)=(2*t(2,4)+300+t(3,5))/24;t(3,5)=(2*t(3,4)+t(2,5)+t(4,5)+200)/24;t(4,5)=(2*t(4,4)+t(3,5)+t(5,5)+200)/24;t(5,5)=(t(5,4)+t(4,5)+100)/12;t'endcontour(t',50);ans =100.0000 200.0000 200.0000 200.0000 200.0000 100.0000 136.8905 146.9674 149.8587 150.7444 100.0000 102.3012 103.2880 103.8632 104.3496 100.0000 70.6264 61.9465 59.8018 59.6008 100.0000 19.0033 14.8903 14.5393 14.5117【Jacobi迭代程序】函数文件为:function [y,n]=jacobi(A,b,x0,eps)D=diag(diag(A));L=-tril(A,-1);U=-triu(A,1);B=D\(L+U);f=D\b;y=B*x0+f;n=1;while norm(y-x0)>=epsx0=y;y=B*x0+f;n=n+1;end命令文件为:A=[4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0,0;-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0,0; 0,-1,4,-1,0,0,-1,0,0,0,0,0,0,0,0,0; 0,0,-2,4,0,0,0,-1,0,0,0,0,0,0,0,0;-1,0,0,0,4,-1,0,0,-1,0,0,0,0,0,0,0; 0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0,0; 0,0,-1,0,0,-1,4,-1,0,0,-1,0,0,0,0,0;0,0,0,-1,0,0,-2,4,0,0,0,-1,0,0,0,0;0,0,0,0,-1,0,-1,0,4,0,0,0,-1,0,0,0;0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0,0;0,0,0,0,0,0,-1,0,0,-1,4,-1,0,0,-1,0;0,0,0,0,0,0,0,-1,0,0,-2,4,0,0,0,-1;0,0,0,0,0,0,0,0,-2,0,0,0,24,-1,0,0;0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1,0;0,0,0,0,0,0,0,0,0,0,-2,0,0,-1,24,-1;0,0,0,0,0,0,0,0,0,0,0,-1,0,0,-1,12];b=[300,200,200,200,100,0,0,0,100,0,0,0,300,200,200,100]'; [x,n]=jacobi(A,b,[0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0]',1.0e-6); xx=1:1:4;yy=xx;[X,Y]=meshgrid(xx,yy);Z=reshape(x,4,4);Z=Z'contour(X,Y,Z,30)n =97Z =139.6088 150.3312 153.0517 153.5639108.1040 108.6641 108.3119 108.152384.1429 67.9096 63.3793 62.421420.1557 15.4521 14.8744 14.7746四、不同初值时的收敛快慢1、[方法1]在Gauss 迭代和Jacobi 迭代中,本程序应用的收敛条件均为norm(y-x0)>=eps ,即使前后所求误差达到e 的-6次方时,跳出循环得出结果。
二维热传导方程 matlab

二维热传导方程是描述二维热传导过程的数学模型,它在工程、物理、地球科学等领域都有重要应用。
在实际工程问题中,我们经常需要求解二维热传导方程,以预测物体表面的温度分布、热量传递速率等参数。
Matlab是一个强大的数学软件,通过Matlab我们可以很方便地求解二维热传导方程,并得到预期的结果。
一、二维热传导方程的基本形式二维热传导方程可以用偏微分方程的形式表示为:∂u/∂t = k(∂²u/∂x² + ∂²u/∂y²)其中,u(x, y, t)是温度分布随时间和空间的变化,k是热传导系数。
二、Matlab中求解二维热传导方程的方法在Matlab中,我们可以采用有限差分法(finite difference method)求解二维热传导方程。
有限差分法将偏微分方程离散化,转化为代数方程组,然后通过迭代求解得到数值解。
具体步骤如下:1. 离散化空间和时间变量,将连续的空间区域和时间区间分割成若干个小区间。
2. 利用二阶中心差分格式对二维热传导方程进行离散化,得到代数方程组。
3. 利用Matlab中的矩阵运算和迭代方法,求解代数方程组,得到数值解。
三、Matlab代码示例下面是一个简单的Matlab代码示例,用于求解二维热传导方程:```matlab定义参数和初始条件Lx = 1; Ly = 1; 区域大小Nx = 100; Ny = 100; 离散化网格数T = 1; 总时间Nt = 100; 时间步数k = 1; 热传导系数dx = Lx/Nx; dy = Ly/Ny;dt = T/Nt;x = 0:dx:Lx; y = 0:dy:Ly;[X, Y] = meshgrid(x, y);u = sin(pi*X).*sin(pi*Y); 初始温度分布迭代求解for n = 1:Ntun = u;for i = 2:Nx-1for j = 2:Ny-1u(i, j) = un(i, j) + k*dt/dx^2*(un(i+1, j)-2*un(i, j)+un(i-1, j)) + k*dt/dy^2*(un(i, j+1)-2*un(i, j)+un(i, j-1));endendend可视化结果figure;surf(X, Y, u);xlabel('x'); ylabel('y'); zlabel('Temperature');```以上代码首先定义了区域大小、离散化网格数、总时间、热传导系数等参数,然后利用有限差分法进行迭代求解,最后利用Matlab绘制了温度分布的三维图像。
二维 热传导方程 matlab

二维热传导方程在实际工程问题中有着广泛的应用。
热传导方程描述了热量在空间和时间中的传播规律,而二维热传导方程则特指热量在二维平面上的传播情况。
在工程领域,我们经常需要利用数值方法来求解二维热传导方程,而MATLAB作为一款强大的工程计算软件,提供了丰富的工具和函数来进行热传导方程的数值求解。
让我们回顾一下二维热传导方程的基本形式,它通常可以表示为:\[ \frac{\partial u}{\partial t} = \alpha \left( \frac{\partial^2u}{\partial x^2} + \frac{\partial^2 u}{\partial y^2} \right) \]其中,\( u(x, y, t) \) 是温度场的分布,\( \alpha \) 是热扩散系数。
这个偏微分方程描述了温度场随时间和空间的演化规律,是研究热传导问题的基本方程之一。
在实际工程中,我们经常需要利用数值方法求解二维热传导方程,特别是在复杂几何结构和边界条件下。
MATLAB提供了丰富的数值求解工具,最常用的是有限差分法。
有限差分法将空间离散化为网格,用差分格式逼近偏微分方程,然后利用迭代方法求解离散化的代数方程组,得到温度场的数值解。
为了使用MATLAB进行二维热传导方程的数值求解,我们需要进行以下基本步骤:1. 网格划分:将求解区域进行网格划分,确定空间离散化的步长。
2. 边界条件处理:根据实际问题确定边界条件,例如固定温度、热通量等。
3. 数值格式选取:选择合适的差分格式逼近偏微分方程,通常采用显式或隐式格式。
4. 迭代求解:利用MATLAB提供的迭代方法,求解离散化后的代数方程组,得到温度场的数值解。
在实际工程中,二维热传导方程的数值求解往往涉及到复杂的边界条件、材料参数、热源分布等。
我们需要对MATLAB的数值求解工具有深入的理解和熟练的应用,才能准确地模拟和分析实际问题。
在我看来,二维热传导方程的数值求解是工程领域中非常重要的课题之一。
热传导模型方程matlab

热传导模型方程matlab热传导模型方程可以用 MATLAB 求解,具体步骤如下:1. 导入 MATLAB 环境,新建一个 MATLAB 文件。
2. 定义热传导模型的参数,如物体的热传导系数、接触面积等。
3. 定义物体的温度分布,可以使用 MATLAB 的函数生成随机数来模拟温度分布。
4. 定义物体内部的热量传输过程,可以使用 MATLAB 的函数来计算热传导的过程。
5. 求解热传导模型的结果,可以使用 MATLAB 的积分函数来计算热量的传输速率。
6. 可视化结果,可以使用 MATLAB 的绘图函数来绘制温度分布曲线和热量传输速率曲线。
具体求解过程可以参考以下 MATLAB 代码示例:```matlab% 创建 MATLAB 文件f = @(t,y) [-y(2); y(1)]; % 定义物体的温度分布函数A = 1; % 定义接触面积k = 0.1; % 定义物体的热传导系数t0 = 0; % 定义物体初始温度t1 = 1; % 定义物体目标温度tstep = 0.1; % 定义温度变化率y0 = A*rand(1,1000); % 定义物体内部的温度分布y = f(t,y0); % 计算物体内部的温度分布t = t0:tstep:t1; % 定义时间序列Q = zeros(length(t),1); % 定义热量传输速率for i=1:length(t)y = y(1:end-1); % 将时间序列中的前一部分代入热传导模型 Q(i) = -k*sum(y(2:end),2); % 计算热量传输速率y = y(2:end); % 将时间序列中的后一部分代入热传导模型Q(i) = -k*sum(y(2:end),2); % 计算热量传输速率endQ = Q/length(t); % 将热量传输速率进行归一化处理plot(t,y,"o",t,Q); % 绘制温度分布和热量传输速率曲线title("热传导模型方程"); % 添加标题xlabel("时间"); % 添加 x 轴标签ylabel("温度分布"); % 添加 y 轴标签```上述 MATLAB 代码可以求解热传导模型方程,并可视化结果。
一维非稳态导热方程求解(附Matlab程序)
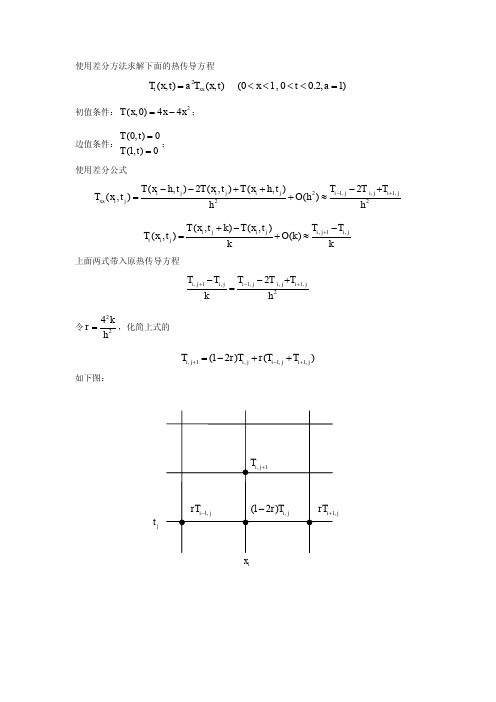
%%%%%%本文来自互联网%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
初值条件: T ( x, 0) 4 x 4 x ;
2
(0 x 1, 0 t 0.2, a 1)
边值条件:
T (0, t ) 0 ; T (1, t ) 0
使用差分公式
Txx ( xi , t j )
T ( xi h, t j ) 2T ( xi , t j ) T ( xi h, t j ) h2 Tt ( xi , t j ) T ( xi , t j k ) T ( xi , t j ) k
O( h 2 )
Ti 1, j 2T i , j Ti 1, j h2
O( k )
Ti , j 1 Ti , j k
上面两式带入原热传导方程
Ti , j 1 Ti , j k 42 k 令 r 2 ,化简上式的 h
Ti 1, j 2T i , j Ti 1, j h2
% 边值条件: % u(a,t)=g1(t) % u(b,t)=g2(t) % % 参数说明 % c:方程中的系数 % f:初值条件 % g1,g2:边值条件 % xspan=[a,b]: x 的取值范围 % tspan=[ts,tf]:t 的取值范围 % ngrid=[n,m]:网格数量, m 为 x 网格点数量, n 为 t 的网格点数量 % U:方程的数值解 % x,t: x 和 t 的网格点 n=ngrid(1); m=ngrid(2); h=range(xspan)/(m-1); x=linspace(xspan(1),xspan(2),m); k=range(tspan)/(n-1); t=linspace(tspan(1),tspan(2),n); r=c^2*k/h^2; if r>0.5 error('为了保证算法的收敛,请增大步长 h 或减小步长 k!') end s=1-2*r; U=zeros(ngrid); % 边界条件 U(:,1)=g1(t); U(:,m)=g2(t); % 初值条件 U(1,:)=f(x); % 差分计算 for j=2:n for i=2:m-1 U(j,i)=s*U(j-1,i)+r*(U(j-1,i-1)+U(j-1,i+1)); end end
matlab一维非稳态导热 -回复

matlab一维非稳态导热-回复Matlab是一种常用的科学计算软件,广泛应用于工程、物理、数学等领域。
在热传导研究中,非稳态导热问题是一个重要课题。
本文将以Matlab 为工具,介绍一维非稳态导热问题的求解方法。
首先,我们需要了解非稳态导热问题的基本概念。
非稳态导热问题是指热传导过程中温度场随时间的变化,即瞬态问题。
一维非稳态导热问题可以用下面的热传导方程描述:∂T/∂t = α∂²T/∂x²其中,T是温度,t是时间,x是空间坐标,α是热扩散系数。
为了求解上面的偏微分方程,我们需要确定边界条件和初始条件。
假设热导体的两端为x=0和x=L,边界条件可以是温度固定、热流固定或边界绝热(无热量流入或流出)。
初始条件是指在t=0时刻的温度场分布。
首先,我们需要定义问题的参数,包括热扩散系数α、热导体的长度L、时间范围tspan等等。
在Matlab中,可以使用类似下面的语句进行定义:alpha = 0.1; 热扩散系数L = 1; 热导体长度tspan = [0 10]; 时间范围接下来,我们需要定义初始条件和边界条件。
假设在t=0时刻,热导体的温度分布是一个高斯函数,可以使用下面的语句定义初始条件:x = linspace(0, L, 100); 在空间范围内生成100个均匀分布的点T0 = exp(-(x-L/2).^2); 初始温度分布对于边界条件,我们可以选择温度固定的情况,即热导体的两端温度为固定值T1和T2。
可以使用下面的语句定义边界条件:T1 = 1; 左端温度T2 = 0; 右端温度然后,我们可以使用Matlab的pdepe函数来求解一维非稳态导热问题。
pdepe函数是用于求解偏微分方程组的函数,其中包含了默认的边界条件和初始条件设置。
可以使用下面的语句进行求解:sol = pdepe(0,pdefun,icfun,bcfun,x,tspan);在上面的语句中,pdefun是一个用于计算偏微分方程右端项的函数句柄,icfun是一个用于计算初始条件的函数句柄,bcfun是一个用于计算边界条件的函数句柄。
谱元法 matlab代码

t = 0:dt:T; %时间向量
%定义谱元网格
x = linபைடு நூலகம்pace(0,L,N)';
X = ChebyshevNodes(N+1);
X = [X -L; L X]; %扩展谱元网格到[-L, L]
X = X/L; %归一化谱元网格
%定义初始条件和边界条件
u0 = sin(pi*x); %初始条件
谱元法(Spectral Element Method, SEM)是一种高效的数值计算方法,用于求解偏微分方程。以下是一个简单的 MATLAB 代码示例,用于求解一维热传导方程。
%定义网格参数
N = 100; %网格点数
L = 1.0; %计算区域长度
h = L/N; %网格步长
%定义时间参数
T = 1.0; %计算时间
u_left = u0; %左边界条件
u_right = u0; %右边界条件
%定义离散化算子和求解矩阵
Dx = -I*(X/h).^2; %一阶离散化算子
D2x = -I*(X/h).^4; %二阶离散化算子
F = [D2x -2*Dx + I*Dt2]; %求解矩阵
%时间循环求解
u = u0;
for k = 1:length(t)-1
F\u'; %解矩阵方程求解下一个时间层解
u = [u; u']; %更新解向量
end
%可视化结果
plot(x, real(u));
xlabel('x');
ylabel('u');
在上述代码中,我们首先定义了网格参数和时间参数。然后,我们使用 Chebyshev 多项式定义了谱元网格,并扩展到整个计算区域。接下来,我们定义了初始条件和边界条件,并离散化了一阶和二阶导数算子。最后,我们使用时间循环求解方程,并可视化结果。
matlab练习程序(差分法解一维热传导方程)

matlab练习程序(差分法解⼀维热传导⽅程)差分法计算⼀维热传导⽅程是计算偏微分⽅程数值解的⼀个经典例⼦。
热传导⽅程也是⼀种抛物型偏微分⽅程。
⼀维热传导⽅程如下:该⽅程的解析解为:通过对⽐解析解和数值解,我们能够知道数值解的是否正确。
下⾯根据微分写出差分形式:整理得:已知⽹格平⾯三条边的边界条件,根据上⾯递推公式,不断递推就能计算出每个⽹格的值。
matlab代码如下:clear all;close all;clc;t = 0.03; %时间范围,计算到0.03秒x = 1; %空间范围,0-1⽶m = 320; %时间⽅向分320个格⼦n = 64; %空间⽅向分64个格⼦ht = t/(m-1); %时间步长dthx = x/(n-1); %空间步长dxu = zeros(m,n);%设置边界条件i=2:n-1;xx = (i-1)*x/(n-1);u(1,2:n-1) = sin(4*pi*xx);u(:,1) = 0;u(:,end) = 0;%根据推导的差分公式计算for i=1:m-1for j=2:n-1u(i+1,j) = ht*(u(i,j+1)+u(i,j-1)-2*u(i,j))/hx^2 + u(i,j);endend%画出数值解[x,t] = meshgrid(0:x/(n-1):1,0:0.03/(m-1):0.03);mesh(x,t,u)%画出解析解u1 = exp(-(4*pi)^2*t).*sin(4*pi*x);figure;mesh(x,t,u1);%数值解与解析解的差figure;mesh(abs(u-u1));数值解:解析解:两种解的差的绝对值:。
MATLAB编辑一维热传导方程的模拟程序之欧阳家百创编

求解下列热传导问题:欧阳家百(2021.03.07)程序:function heat_conduction() %一维齐次热传导方程options={'空间杆长L','空间点数N' ,'时间点数M','扩散系数alfa','稳定条件的值lambda(取值必须小于0.5)',};topic='seting';lines=1;def={'1','100','1000','1','0.5'};h=inputdlg(options,topic,lines,def);L=eval(h{1});N=eval(h{2});M=eval(h{3});alfa=eval(h{4});lambda=eval(h{5});%lambda的值必须小于0.5%***************************************************h=L/N;%空间步长z=0:h:L;z=z';tao=lambda*h^2/alfa;%时间步长tm=M*tao;%热传导的总时间tmt=0:tao:tm;%计算初值和边值T=zeros(N+1,M+1);Ti=init_fun(z);To=border_funo(t);Te=border_fune(t);T(:,1)=Ti;T(1,:)=To;T(N+1,:)=Te;%用差分法求出温度T与杆长L、时间t的关系for k=1:Mm=2;while m<=NT(m,k+1)=lambda*(T(m+1,k)+T(m-1,k))+(-2*lambda+1)*T(m,k); m=m+1;end;end;%设置立体网格for i=1:M+1X(:,i)=z;end;for j=1:N+1Y(j,:)=t;mesh(X,Y,T);view([1 -1 1]);xlabel('Z');ylabel('t');zlabel('T');function y=init_fun(z)%初值条件y=1-z.^2;returnfunction y=border_funo(t)%z=0的边界条件y=1+t.*0;returnfunction y=border_fune(t)%z=L的边界条件y=t*.0;return运行情况:按“run”运行时,弹出窗口将图中相关数据更改为:点击图框中的“OK”,在“command window”中输出结果为:。
matlab二维热传导方程

matlab二维热传导方程
二维热传导方程描述了在二维空间中热量如何随时间传播。
假设我们有一个矩形区域,比如一个金属板,该区域的温度随时间变化。
热传导方程可以用来描述这个过程。
在Matlab中,我们可以使用偏微分方程来解决二维热传导方程。
二维热传导方程通常写成以下的偏微分方程形式:
∂u/∂t = α(∂^2u/∂x^2 + ∂^2u/∂y^2)。
其中,u是温度的函数,t是时间,x和y是空间坐标,α是热扩散系数。
在Matlab中,我们可以使用偏微分方程的求解器来解决这个方程。
我们需要定义边界条件和初始条件,并且将偏微分方程转化为离散形式,然后使用Matlab中的函数比如pdepe来求解。
我们也可以使用有限差分法或者有限元法来解决这个方程。
另外,我们也可以使用Matlab中的热传导方程的数值求解工具箱来解决这个问题。
这个工具箱提供了一些方便的函数和工具来解
决热传导方程,比如heat2d和thermalmodel等函数。
总之,在Matlab中,我们有多种方法来解决二维热传导方程,可以根据具体情况选择合适的方法来求解这个方程。
希望这些信息对你有所帮助。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Sample MATLAB codes
1.
%Newton Cooling Law
clear; close all; clc;
h = 1;
T(1) = 10; %T(0)
error = 1;
TOL = 1e-6;
k = 0;
dt = 1/10;
while error > TOL,
k = k+1;
T(k+1) = h*(1-T(k))*dt+T(k);
error = abs(T(k+1)-T(k));
end
t = linspace(0,dt*(k+1),k+1);
plot(t,T),hold on, plot(t,1,'r-.')
xlabel('Time'),ylabel('Temperature'),
title(['T_0 = ',num2str(T(1)), ', T_\infty = 1']), legend('Cooling Trend','Steady State')
2.
%Boltzman Cooling Law
clear; close all; clc;
h = 1;
T(1) = 10; %T(0)
error = 1;
TOL = 1e-6;
k = 0;
dt = 1/10000;
while error > TOL,
k = k+1;
T(k+1) = h*(1-(T(k))^4)*dt+T(k);
error = abs(T(k+1)-T(k));
end
t = linspace(0,dt*(k+1),k+1);
plot(t,T),hold on, plot(t,1,'r-.')
xlabel('Time'),ylabel('Temperature'),
title(['T_0 = ',num2str(T(1)), ', T_\infty = 1']), legend('Cooling Trend','Steady State')
3.
%Fourier Heat conduction
clear; close all; clc;
h = 1;
n = 11;
T = ones(n,1); Told = T;
T(1) = 1; %Left boundary
T(n) = 10; %Right boundary
x = linspace(0,1,n);
dx = x(2)-x(1);
dt = dx^2/3; %cfl condition
error = 1;
TOL = 1e-6;
k = 0;
while error > TOL,
Told = T;
k = k+1;
for i = 2:n-1
T(i) = dt*(Told(i+1)-2*Told(i)+Told(i-1))/dx^2+Told(i);
end
error = max(abs(T-Told));
if mod(k,5)==0, out(k,:) = T; end
end
plot(x,out)
xlabel('x'),ylabel('Temperature'),
title(['Fourier Heat Conduction']),
%legend('Cooling Trend','Steady State')
4. 2D Heat Equation
%2D Heat Equation.
clear; close all; clc
n = 10; %grid has n - 2 interior points per dimension (overlapping)
x = linspace(0,1,n); dx = x(2)-x(1); y = x; dy = dx;
TOL = 1e-6;
T = zeros(n);
T(1,1:n) = 10; %TOP
T(n,1:n) = 1; %BOTTOM
T(1:n,1) = 1; %LEFT
T(1:n,n) = 1; %RIGHT
dt = dx^2/4;
error = 1; k = 0;
while error > TOL
k = k+1;
Told = T;
for i = 2:n-1
for j = 2:n-1
T(i,j) = dt*((Told(i+1,j)-2*Told(i,j)+Told(i-1,j))/dx^2 ... + (Told(i,j+1)-2*Told(i,j)+Told(i,j-1))/dy^2) ...
+ Told(i,j);
end
end
error = max(max(abs(Told-T)));
end
subplot(2,1,1),contour(x,y,T),
title('Temperature (Steady State)'),xlabel('x'),ylabel('y'),colorbar subplot(2,1,2),pcolor(x,y,T),shading interp,
title('Temperature (Steady State)'),xlabel('x'),ylabel('y'),colorbar
5. Wave Translation
%Oscillations - translation left and right
clear; close all; clc;
for c = [1 -1]
cc = 0;
n = 261;
x = linspace(0,13,n);
u = zeros(n,1);
u(121:141) = sin(pi*x(121:141));
dx = x(2)-x(1);
dt = dx;
error = 1;
TOL = 1e-6;
k = 0;
while k < 110
uold = u;
k = k+1;
for i = 2:n-1
if c == 1, u(i) = dt*c*(uold(i+1)-uold(i))/dx+uold(i); end%c = 1
if c == -1, u(i) = dt*c*(uold(i)-uold(i-1))/dx+uold(i); end%c = -1 end
error = max(abs(u-uold));
if mod(k,10)==0, cc = cc+1; out(cc,:) = u;
end
end
if c == 1
subplot(2,1,1),
for hh = 1:cc
plot(x,out(hh,:)+hh),hold on,
end
u = zeros(n,1);
u(121:141) = sin(pi*x(121:141)); plot(x,u)
xlabel('u(x)'),ylabel('Time'),
title('Translation to the Left')
elseif c == -1
subplot(2,1,2),
for hh = 1:cc
plot(x,out(hh,:)+hh),hold on,
end
u = zeros(n,1);
u(121:141) = sin(pi*x(121:141)); plot(x,u)
xlabel('u(x)'),ylabel('Time'),
title('Translation to the Right')
end
end
6.
%wave equation
clear; close all; clc;
c = 1;
n = 21;
x = linspace(0,1,n);
dx = 1/(n-1);
dt = dx;
u(:,1) = sin(pi*x);
u(1,2) = 0;
for i = 2:n-1
u(i,2) = 0.5*(dt^2*c^2*(u(i+1,1)-2*u(i,1)+u(i-1,1))/dx^2+2*u(i,1));
end
u(n,2) = 0;
error = 1; k = 1;
while k < 100
k = k+1;
u(1,k+1) = 0;
for i = 2:n-1
u(i,k+1) = dt^2*c^2*(u(i+1,k)-2*u(i,k)+u(i-1,k))/dx^2+2*u(i,k)-u(i,k-1);
end
u(n,k+1) = 0;
end
plot(x,u), xlabel('x'),ylabel('y')。
