循环队列
循环队列及链队列的基本操作 头歌

循环队列及链队列的基本操作1. 循环队列的基本概念和原理循环队列是一种常见的数据结构,它具有队列的特点,即先进先出(FIFO)。
与普通队列相比,循环队列的特点在于它可以充分利用数组的空间,解决了普通队列在出队操作时需要频繁搬移数据的问题。
循环队列的基本原理是使用环形数组来实现队列的存储和操作,通过头指针和尾指针的移动,实现队列的入队和出队操作。
2. 循环队列的基本操作2.1 入队操作:将元素插入队列的尾部,并更新尾指针的位置。
2.2 出队操作:从队列的头部取出元素,并更新头指针的位置。
2.3 判空操作:当头指针和尾指针重合时,队列为空。
2.4 判满操作:当尾指针的下一个位置与头指针重合时,队列为满。
3. 链队列的基本概念和原理链队列是另一种常见的队列实现方式,与循环队列不同的是,链队列使用链表来存储队列元素。
链队列的基本原理是使用链表的头节点和尾节点来实现队列的操作,通过指针的移动,实现入队和出队操作。
4. 链队列的基本操作4.1 入队操作:将元素插入队列的尾部,并更新尾节点的位置。
4.2 出队操作:从队列的头部取出元素,并更新头节点的位置。
4.3 判空操作:当头节点和尾节点指向同一个节点时,队列为空。
4.4 遍历操作:通过指针的遍历,可以获取队列中的所有元素。
5. 总结和回顾通过对循环队列和链队列的基本概念、原理和操作进行分析,我们可以看出它们都是用于实现队列功能的数据结构,但在不同的场景下有着不同的优势和应用。
循环队列适合于对空间有限且需要频繁进行入队和出队操作的场景,而链队列适合于对空间要求宽松、对操作有一定顺序要求的场景。
6. 个人观点和理解在实际编程中,循环队列和链队列都有着各自的优点和局限性,需要根据具体的场景和需求来选择合适的队列实现方式。
在使用循环队列时,需要注意头尾指针的移动,避免产生死循环和队列溢出的问题;而在使用链队列时,需要考虑对节点的动态分配和释放,避免产生内存泄漏和指针错乱的问题。
循环队列是什么结构

循环队列是什么结构引言:在计算机科学领域中,队列是一种简单而常见的数据结构,它按照先进先出(FIFO)的原则管理数据。
循环队列是队列的一种特殊形式,将队列的首尾连接起来,形成一个环。
本文将详细介绍循环队列的定义、实现和应用。
一、循环队列的定义循环队列是一种通过环形缓冲区实现的线性数据结构,具有固定大小。
它包含一个数组,用于存储数据元素,以及两个指针front和rear,分别指向队列的头部和尾部。
特点:1. 队列为空时,front和rear指向同一个位置;2. 队列满时,front和rear指向相邻位置;3. 队列长度为数组的长度减1。
二、循环队列的实现1. 初始化:创建一个空数组,并将front和rear指针初始化为0。
2. 入队操作:将元素插入rear指针指向的位置,然后将rear指针右移一位。
如果rear指针超过数组边界,则将rear指针重置为0。
3. 出队操作:将front指针指向的元素返回,并将front指针右移一位。
如果front指针超过数组边界,则将front指针重置为0。
4. 队列判空:如果front和rear指向同一个位置,则队列为空。
5. 队列判满:如果rear指针的下一个位置是front指针,则队列为满。
三、循环队列的优势相比于普通队列,循环队列具有以下几个优势:1. 优化了空间利用:循环队列通过环形缓冲区的方式实现,充分利用了数据存储空间,避免了普通队列数组一旦填满就无法再存入元素的问题。
2. 提高了入队和出队的效率:循环队列通过指针的移动实现元素的插入和删除,无需移动整个队列,并且时间复杂度为O(1),相比于普通队列的O(n)效率更高。
3. 简化了队列的操作:循环队列可以自动调整指针的位置,无需移动整个队列,更加简洁高效。
四、循环队列的应用循环队列在实际应用中具有广泛的用途,下面列举了其中几个常见的应用场景:1. 生产者消费者模型:循环队列可以用来实现线程间的数据传递,生产者线程将数据入队,消费者线程从队列中取出数据进行处理。
简要叙述循环队列的数据结构

简要叙述循环队列的数据结构循环队列是一种基于数组实现的队列数据结构,它具有队列的所有特性,同时还具有循环的特性。
循环队列的主要思想是将队列的头尾相连,形成一个环状结构,这样可以充分利用数组空间,避免了数组满时的浪费。
循环队列的实现需要两个指针:front 和rear。
front 指向队列的头部,rear 指向队列的尾部。
当队列为空时,front 和rear 指向同一个位置。
当队列满时,rear 指向的位置是最后一个元素的下一个位置,而 front 指向的位置不变。
这样,当 rear 指向数组的最后一个位置时,如果还有元素要入队,就会循环回到数组的第一个位置,形成一个环状结构。
循环队列的主要操作包括入队和出队。
入队操作需要将元素插入到队列的尾部,即将元素放到 rear 指向的位置,然后将 rear 指针向后移动一位。
如果队列已满,则无法插入元素。
出队操作需要将队列的头部元素删除,并将 front 指针向后移动一位。
如果队列为空,则无法执行出队操作。
循环队列的优点是可以充分利用数组空间,避免了数组满时的浪费。
同时,由于循环队列的头尾相连,可以在一定程度上提高队列的效率。
循环队列的缺点是实现比较复杂,需要考虑队列满和队列空的情况,同时需要注意指针的移动。
在实际应用中,循环队列常用于缓存、任务队列等场景。
例如,在多线程编程中,可以使用循环队列来实现任务队列,将需要执行的任务放入队列中,然后由线程池中的线程来执行任务。
在网络编程中,可以使用循环队列来实现消息队列,将需要发送或接收的消息放入队列中,然后由网络线程来处理消息。
总之,循环队列是一种非常实用的数据结构,可以在一定程度上提高队列的效率,同时充分利用数组空间,避免了数组满时的浪费。
在实际应用中,循环队列有着广泛的应用场景,是一种非常重要的数据结构。
循环队列出队操作语句

循环队列出队操作语句循环队列的出队操作就像从魔法盒子里取宝贝,你永远不知道下一个出来的会是啥惊喜。
”出处:计算机编程领域常见操作。
意思是在循环队列中进行出队操作时,无法预先确定取出的元素具体是什么。
例子:我和小伙伴一起做编程作业,他正为不知道怎么处理数据发愁呢。
我就说:“试试循环队列的出队操作呀,这就像从魔法盒子里取宝贝,说不定下一个出来的就是你要的答案呢。
”“哇塞,循环队列出队,那感觉就像在抽奖,紧张又刺激。
”出处:编程操作之一。
意思是出队操作带有不确定性,和抽奖类似。
例子:“我在调试程序,心里七上八下的。
旁边的同学说:“你别慌呀,试试循环队列出队,那感觉就像在抽奖,紧张又刺激,说不定就成了呢。
”“循环队列出队,简直就是打开神秘宝箱,谁知道会蹦出啥玩意儿。
”出处:编程用语。
意思是出队的结果不可预测。
例子:我跟室友讨论项目,室友一脸茫然。
我说:“要不试试循环队列出队,简直就是打开神秘宝箱,谁知道会蹦出啥玩意儿,说不定能解决咱的问题呢。
”“嘿哟,循环队列出队操作,就跟开盲盒似的,充满期待。
”出处:编程知识。
意思是和开盲盒一样充满未知的期待。
例子:我在编程课上犯难,同桌说:“别愁啦,用循环队列出队操作呀,嘿哟,就跟开盲盒似的,充满期待,说不定有惊喜。
”“循环队列出队,那可不就是在探索未知宝藏嘛,刺激得很。
”出处:编程技巧。
意思是出队如同探索未知的宝藏。
例子:我和小组同学为项目绞尽脑汁。
我说:“咱试试循环队列出队呗,那可不就是在探索未知宝藏嘛,刺激得很,说不定能找到关键线索。
”“哇哦,循环队列出队,跟挖掘神秘宝藏的过程一样,让人兴奋。
”出处:编程操作方法。
意思是出队过程充满惊喜。
例子:我们在讨论编程方案,有人没头绪。
我说:“试试循环队列出队呀,哇哦,跟挖掘神秘宝藏的过程一样,让人兴奋,说不定有意外收获。
”“循环队列出队,就好像在开启神秘大门,不知道后面有啥惊喜。
”出处:编程概念。
意思是出队操作带来未知的结果。
循环队列实验报告心得与体会

循环队列实验报告心得与体会循环队列是数据结构中一个非常经典的概念,相对于其他队列结构,循环队列可以优化存储空间的使用,减少空间的浪费。
循环队列的操作也比较高效,能够快速执行入队和出队操作。
本次实验,我们对循环队列结构进行了深入的了解与实践,更深刻地认识到了数据结构的重要性。
在实验中,我们首先对循环队列的基本概念进行了学习,通过查阅相关资料和教材,我们了解到循环队列是一种环形的特殊队列,其队尾指针在达到数组的末尾时,再从数组的第一个位置开始存储数据,如此循环下去。
这样一来,就可以充分利用数组中的元素,减少不必要的空间浪费,提高队列结构的空间利用率。
在深入了解循环队列的概念之后,我们开始实现循环队列的基本操作,包括入队、出队、判空、判满等。
通过实现这些基础操作,我们更加熟悉了循环队列的内部结构和操作流程,同时也掌握了程序设计中的一些基本思路和技巧。
在实验过程中,我们还注意到了循环队列一些常见的问题和局限性。
当队列元素数量达到数组大小时,会出现队列满的情况,此时需要进行特殊处理。
由于循环队列是基于数组实现的,所以其大小是固定的,不能动态调整,这也是循环队列的一个缺陷。
在实验结束后,我们对循环队列的性能进行了一些简单分析。
通过测试,我们发现循环队列在入队和出队操作的时间复杂度都是O(1),即不受元素数量的影响,具有较高的效率。
这进一步证明了循环队列是一种高效的数据结构。
本次实验让我们深入了解了循环队列的内部结构和基本操作,也发现了循环队列存在的问题和局限性。
通过这次实验的实践,我们进一步理解了数据结构的重要性,同时也锻炼了自己的程序设计能力和思维能力。
除了实现循环队列的基本操作,我们还对循环队列进行了扩展,添加了一些实用的操作,比如获取队列长度、获取队首和队尾元素等。
这些操作虽然不是必要的,但是在实际的应用中却非常实用,可以方便我们处理队列中的元素。
我们在实验中还掌握了一些编程技巧和调试工具,来提高程序的效率和可靠性。
头歌循环队列的基本操作

头歌循环队列的基本操作头歌循环队列是一种基于数组实现的队列数据结构,它可以实现基本的入队、出队、判空、判满等操作。
下面是对头歌循环队列的基本操作进行详细介绍。
1. 初始化操作头歌循环队列需要初始化队列的容量和头尾指针,一般将队列的容量设置为数组的长度减1,头尾指针初始化为0。
2. 入队操作头歌循环队列的入队操作是将元素插入到队尾的操作。
首先需要判断队列是否已满,即判断队列的头指针和尾指针相遇的位置是否为数组的首位置。
如果队列已满,则插入失败,否则将元素插入到队尾,并更新尾指针。
3. 出队操作头歌循环队列的出队操作是将队头元素删除的操作。
首先需要判断队列是否为空,即判断头指针和尾指针是否相等。
如果队列为空,则删除失败,否则将队头元素删除,并更新头指针。
4. 判空操作头歌循环队列的判空操作即判断队列是否为空。
当头指针和尾指针相等时,队列为空,返回true;否则,队列不为空,返回false。
5. 判满操作头歌循环队列的判满操作即判断队列是否已满。
当尾指针的下一个位置(即尾指针+1)与头指针相遇时,队列已满,返回true;否则,队列未满,返回false。
6. 获取队头元素操作头歌循环队列可以通过头指针获取队头元素,即数组中头指针的位置的元素。
7. 获取队尾元素操作头歌循环队列可以通过尾指针获取队尾元素,即数组中尾指针的位置的元素。
8. 获取队列长度操作头歌循环队列的长度可以通过尾指针和头指针之间的距离计算得出,即`(尾指针 - 头指针 + 队列长度) % 队列长度`。
9. 扩容操作当头歌循环队列的容量不足以插入更多的元素时,可以进行扩容操作。
扩容操作需要重新创建一个更大容量的数组,并将原有的数据复制到新数组中,然后更新队列的容量、头指针和尾指针。
以上就是头歌循环队列的基本操作。
通过这些操作,我们可以实现对队列的基本操作,使其具备按照先进先出的原则存储和访问数据的功能。
头歌循环队列的实现原理相对简单,但是需要特别注意指针的更新和边界条件的处理,以确保队列的正确性和效率。
8584 循环队列的基本操作

8584 循环队列的基本操作
循环队列是一种常见的数据结构,它可以有效地处理排队问题。
在循环队列中,队列的元素是排成一条线的,队首和队尾相连。
队列
的长度是固定的,一旦队列满了,就不能再插入元素。
循环队列的基本操作包括创建队列、队列的入队和出队、判断队
列是否为空或已满等。
创建队列时需要指定队列的长度和数组大小,
而入队和出队操作则是向队列的尾部(队尾)添加元素和从队首删除
元素。
当队列为空时,即队尾和队首指针相同时,出队操作不可用。
当队列已满时,入队操作将无法添加更多元素。
在循环队列的实现中,我们需要使用一个数组来存储队列中的元素。
因为循环队列的队首和队尾指针是相连的,所以我们可以使用取
模操作来实现队列的循环。
这样,当队首或队尾指针到达数组末尾时,它会自动回到数组开头。
循环队列的实现是相对比较简单的,但是在使用时需要注意以下
几个问题:
1. 队列的长度必须是固定的,一旦创建后不能改变。
2. 队列长度为n,则数组大小应该为n+1,因为队列中有一个空
位置没有使用。
3. 为了避免队列中元素混乱,应该尽可能地利用数组中的空位置。
4. 创建队列后,队列指针要初始化为0。
综上所述,循环队列是一种高效的数据结构,它可以很好地解决排队问题。
在实现循环队列时,需要注意队列长度的固定、数组大小的确认、队列的指针初始化等细节问题。
如果我们能够合理地使用循环队列,就能够更加高效地解决掉队列问题。
循环队列 经典题目

循环队列经典题目循环队列是一种常见的数据结构,它具有固定大小的缓冲区,可以在其中存储元素,并且在达到缓冲区的最大容量时,新元素会覆盖最早添加的元素,形成循环的效果。
下面我将回答一些经典的与循环队列相关的问题。
1. 什么是循环队列?循环队列是一种环形的队列,它使用数组实现,通过循环利用数组空间来实现队列的基本操作。
循环队列有一个固定的大小,当队列满时,新元素会覆盖最早添加的元素。
2. 循环队列的基本操作有哪些?循环队列的基本操作包括入队(enqueue)、出队(dequeue)、获取队首元素(front)、判空(isEmpty)和判满(isFull)等。
入队操作将元素添加到队列尾部,出队操作将队首元素移除并返回,获取队首元素操作返回队首元素,判空操作检查队列是否为空,判满操作检查队列是否已满。
3. 循环队列与普通队列有何区别?循环队列与普通队列最大的区别在于循环队列可以循环利用数组空间,而普通队列在队尾添加元素后,可能会出现队首有空间但无法添加新元素的情况。
循环队列通过维护队首和队尾指针,可以实现循环添加和删除元素,提高了空间的利用率。
4. 如何实现循环队列?循环队列可以通过数组来实现,需要维护队首和队尾指针,以及数组来存储元素。
在入队和出队操作时,需要更新队首和队尾指针的位置,并且考虑循环利用数组空间的情况。
另外,需要考虑循环队列的空间复杂度和时间复杂度,确保操作的高效性。
5. 给出一个经典的循环队列问题?一个经典的循环队列问题是设计一个循环队列,实现入队、出队、获取队首元素和判满等基本操作,并且保证循环队列的空间利用率高、操作高效。
这个问题涉及到循环队列的实现细节和基本操作的正确性,需要考虑边界情况和异常情况。
以上是关于循环队列的一些经典问题的回答,希望能够帮助到你。
如果你还有其他问题,欢迎随时提出。
循环队列的基本运算实现

① 运算规则不同,线性表为随机存取,而栈是只允 许在一端进行插入和删除运算,因而是后进先出 表LIFO;队列是只允许在一端进行插入、另一端 进行删除运算,因而是先进先出表FIFO。
② 用途不同,线性表比较通用;堆栈用于函数调用、 递归和简化设计等;队列用于离散事件模拟、多 道作业处理和简化设计等。
循环队列的操作演示flash
队空:front==rear 队满:front==rear
初始状态
rear
J6
J5 5
4
0
J4
3
1
2
front
队空、队满无法判断:
1.另外设一个标志以区别 2.少用一个元素空间:
队空:front==rear 队满:(rear+1)%M==front
5
4
0
3
1
2
front rear
循环队列的基本运算实现
1)进队列算法 (1)检查队列是否已满,若队满,则溢出错误; (2)将新元素赋给队尾指针所指单元; (3)将队尾指针后移一个位置(即加1)。 2)出队列算法 (1)检查队列是否为空,若队空,则下溢错误; (2)取队首元素的值。 (3)将队首指针后移一个位置(即加1);
3.4.2 链队列
3.4.1 队列的定义
队列(Queue)也是一种运算受限的线性 表。它只允许在表的一端进行插入,而 在另一端进行删除。允许删除的一端称 为队头(front),允许插入的一端称为队 尾(rear)。
队列的修改是依先进先出的原则进行的。
队列的基本运算
1.初始化队列 InitQueue(&Q) 将队列Q设置成一个空队列。
front
J6
J
J4 2 J8
循环队列入队操作公式

循环队列入队操作公式循环队列是一种常见的数据结构,在很多编程和算法相关的场景中都会用到。
要说这循环队列入队操作公式,那咱们得好好说道说道。
我记得之前有一次给学生们讲这个知识点的时候,有个小家伙一直皱着眉头,满脸困惑。
我就问他:“咋啦,没听懂?”他怯生生地说:“老师,这也太复杂了,我感觉脑子都转不过来了。
”我笑了笑,心想,得换个法子让他们明白。
循环队列啊,就像是一个环形的跑道。
想象一下,一群小朋友在这个环形跑道上排队跑步。
跑道上能站的位置是有限的,就像循环队列的存储空间是有限的一样。
那循环队列入队操作公式到底是啥呢?简单来说,就是要找到一个合适的位置把新元素放进去。
这就需要考虑队列的当前状态,比如队头和队尾的位置。
假设我们的循环队列长度为n,队头指针为front,队尾指针为rear。
当 rear 不等于 front 时,如果 rear 再往后移一位就会超过队列的末尾,那么此时 rear 就应该回到队列的开头,也就是 rear = (rear + 1) % n 。
这就好比小朋友在跑道上跑,跑到尽头就得回到起点重新跑。
咱们再深入一点说,入队操作的时候还得判断队列是不是满了。
如果 (rear + 1) % n == front ,那就说明队列满了,不能再入队了。
不然新元素就没地方站啦,就像跑道上已经挤满了小朋友,再也塞不下一个人了。
为了让学生们更好地理解,我在黑板上画了个大大的环形跑道,标上了 front 和 rear 的位置,然后拿着小粉笔,一步一步地演示入队的过程。
“同学们,看这里,假如现在 rear 在这儿,front 在这儿,我们要入队一个新元素,rear 就得这样移动……”我一边说一边比划着,学生们的眼睛紧紧地盯着黑板,慢慢地,他们的表情从迷茫变得清晰起来。
那个一开始困惑的小家伙,眼睛突然亮了起来,大声说:“老师,我懂啦!”那一刻,我心里别提多高兴了。
总之,循环队列入队操作公式虽然看起来有点复杂,但只要我们把它想象成那个环形跑道上的小朋友排队,理解起来也就没那么难啦。
判断循环队列为满或空的方法

判断循环队列为满或空的方法嘿,咱今儿就来唠唠判断循环队列为满或空的那些事儿!你说这循环队列啊,就好像是个特别的小世界。
想象一下,循环队列就像是一个首尾相接的圈圈跑道,元素们在里面排着队跑呢。
那怎么知道这个跑道是满了还是空的呀?咱先说说为空的情况。
这就好比跑道上一个人都没有,那不是空的是啥呀!要是咱设定的头指针和尾指针指向同一个位置,那不就说明里面啥都没有嘛。
这多简单呀,就像你一眼看过去,啥都没有,那就是空啦!那满的情况呢,这可得动点小脑筋了。
就好像跑道上已经密密麻麻站满了人,没有一点儿空隙了。
咱可以通过一些巧妙的办法来判断呀。
比如说,规定尾指针再往前走一步就会回到头指针的位置,这时候不就意味着满了嘛。
举个例子哈,就像一个装糖果的小盒子,要是你不停地往里面放糖果,放到最后一颗糖果放进去的时候,盒子刚刚好满了,再放就放不下啦。
循环队列也是这个道理呀。
你想想看,要是没有这些方法,那可就乱套啦。
一会儿以为满了,一会儿又以为空了,那不就闹笑话了嘛。
所以说呀,这些方法就像是我们的小助手,能帮我们准确地判断循环队列的状态呢。
判断循环队列为满或空,这可不是随随便便就能搞定的事儿,得认真对待呀。
就像我们走路,得看清路才能走得稳当。
这方法就像是我们的眼睛,让我们能清楚地知道循环队列现在是个啥情况。
有时候我就想啊,这计算机的世界还真奇妙,这么个小小的循环队列都有这么多门道。
我们得像探索宝藏一样,一点点去发现其中的奥秘。
哎呀,说了这么多,总结起来就是,判断循环队列为满或空,得有合适的方法,得仔细观察,得用心去体会。
这样我们才能准确地掌握循环队列的情况,让它更好地为我们服务呀!你说是不是这个理儿?。
循环队列的基本操作

循环队列的基本操作循环队列是一种基于数组实现的队列,通过利用数组的循环利用,实现了队列的基本操作。
循环队列主要包括初始化、入队、出队、判空、判满和获取队列长度等操作。
1.初始化循环队列:2.入队操作:入队操作是将元素添加到队列尾部,首先需要判断队列是否已满。
如果队列已满,则入队失败,如果队列未满,则将元素添加到队尾,并将队尾指针rear后移一位。
如果队尾指针已经到达数组末尾,则将队尾指针rear重新设置为0,实现循环利用。
3.出队操作:出队操作是将队头元素删除,并返回该元素的值。
首先需要判断队列是否为空。
如果队列为空,则出队失败,如果队列不为空,则将队头元素返回,并将队头指针front后移一位。
如果队头指针已经到达数组末尾,则将队头指针front重新设置为0。
4.判空操作:判空操作是判断队列是否为空。
当队头指针和队尾指针相等时,队列为空。
5.判满操作:判满操作是判断队列是否已满。
当队尾指针后移一位后,与队头指针相等时,队列已满。
6.获取队列长度:获取队列长度操作是获取循环队列中元素的个数。
循环队列的长度等于rear指针减去front指针,如果rear指针小于front指针,需要加上数组的长度,以实现考虑循环利用后的队列长度。
下面是一个循环队列的基本操作的实现示例:```Pythonclass CircularQueue:def __init__(self, size):self.size = size + 1self.queue = [None] * self.sizeself.front = 0self.rear = 0def enqueue(self, item):if (self.rear + 1) % self.size == self.front:return "Queue is full"self.queue[self.rear] = itemself.rear = (self.rear + 1) % self.sizedef dequeue(self):if self.front == self.rear:return "Queue is empty"item = self.queue[self.front]self.front = (self.front + 1) % self.sizereturn itemdef is_empty(self):return self.front == self.reardef is_full(self):return (self.rear + 1) % self.size == self.frontdef get_length(self):if self.rear >= self.front:return self.rear - self.frontelse:return self.rear - self.front + self.size```循环队列是一种常用的队列实现方式,在实际编程中应用广泛。
队列的顺序存储(循环队列)
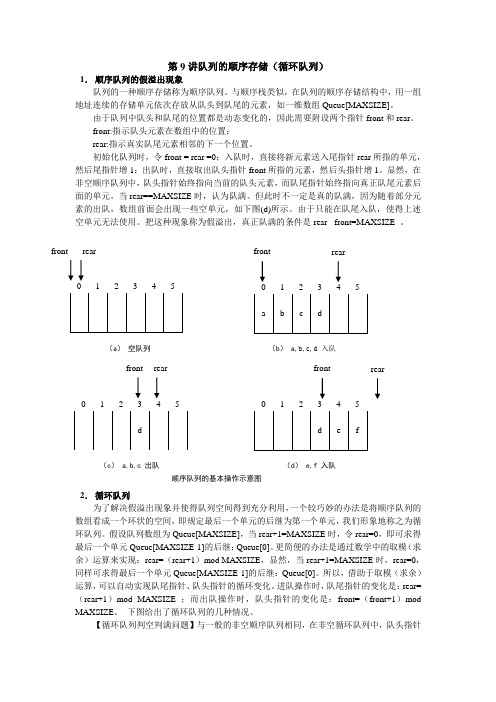
第9讲队列的顺序存储(循环队列)1. 顺序队列的假溢出现象队列的一种顺序存储称为顺序队列。
与顺序栈类似,在队列的顺序存储结构中,用一组地址连续的存储单元依次存放从队头到队尾的元素,如一维数组Queue[MAXSIZE]。
由于队列中队头和队尾的位置都是动态变化的,因此需要附设两个指针front 和rear 。
front:指示队头元素在数组中的位置;rear:指示真实队尾元素相邻的下一个位置。
初始化队列时,令front = rear =0;入队时,直接将新元素送入尾指针rear 所指的单元,然后尾指针增1;出队时,直接取出队头指针front 所指的元素,然后头指针增1。
显然,在非空顺序队列中,队头指针始终指向当前的队头元素,而队尾指针始终指向真正队尾元素后面的单元。
当rear==MAXSIZE 时,认为队满。
但此时不一定是真的队满,因为随着部分元素的出队,数组前面会出现一些空单元,如下图(d)所示。
由于只能在队尾入队,使得上述空单元无法使用。
把这种现象称为假溢出,真正队满的条件是rear - front=MAXSIZE 。
2. 循环队列为了解决假溢出现象并使得队列空间得到充分利用,一个较巧妙的办法是将顺序队列的数组看成一个环状的空间,即规定最后一个单元的后继为第一个单元,我们形象地称之为循环队列。
假设队列数组为Queue[MAXSIZE],当rear+1=MAXSIZE 时,令rear=0,即可求得最后一个单元Queue[MAXSIZE-1]的后继:Queue[0]。
更简便的办法是通过数学中的取模(求余)运算来实现:rear=(rear+1)mod MAXSIZE ,显然,当rear+1=MAXSIZE 时,rear=0,同样可求得最后一个单元Queue[MAXSIZE-1]的后继:Queue[0]。
所以,借助于取模(求余)运算,可以自动实现队尾指针、队头指针的循环变化。
进队操作时,队尾指针的变化是:rear=(rear+1)mod MAXSIZE ;而出队操作时,队头指针的变化是:front=(front+1)mod MAXSIZE 。
循环队列的初始化条件

循环队列的初始化条件
循环队列是一种特殊的队列数据结构,它可以充分利用数组的空间,实现循环使用队列的效果。
循环队列的初始化需要满足一些条件,才能确保循环队列能够正常工作。
首先,循环队列需要使用一个数组作为存储空间,数组的长度需要事先确定。
循环队列的初始化条件之一是队列的最大长度,也就是数组的大小,这是必需的。
其次,循环队列需要使用两个指针来表示队首和队尾,分别指向数组中的元素。
队首指针初始值为0,队尾指针初始值为-1, 这是我们的第二个循环队列初始化条件。
其三,循环队列的初始状态必须为空,也就是队列中没有任何元素。
为了实现这个条件,我们需要在初始化时将队首和队尾指针进行重置。
因此,循环队列的初始化条件包括:队列的最大长度、队首指针的初始值为0,队尾指针的初始值为-1和队列为空。
只有在满足这些条件之后,循环队列才能正
常地进行插入和删除操作,从而实现数据的高效存储和处理。
循环队列的使用

循环队列的使用
你们有没有坐过那种小火车?大家排着队,一个接着一个上车,等小火车绕一圈回来,后面的小朋友又接着排队上车,这就有点像我们今天要讲的循环队列。
想象一下,学校要举办运动会,每个班级的小朋友都要参加接力比赛。
那在比赛前,大家是不是得排队等着上场?这时候,排队的方式就有点像一个队列。
每个小朋友都站在自己的位置上,前面的小朋友跑出去后,后面的小朋友就往前一步,准备接着跑。
可是,循环队列又有点不一样。
比如说,有一个神奇的魔法小盒子,这个小盒子只能装5个小玩具。
我们把小玩具一个一个地放进盒子里,放满了5个后,要是还想再放新的玩具,怎么办?这时候,循环队列的奇妙就出现!
就好像盒子有魔法一样,它会把最早放进去的那个小玩具拿出来,然后再把新的小玩具放进去。
就好像排队坐小火车,小火车的座位是有限的,坐满了一圈后,第一排的小朋友下车了,后面的小朋友就可以坐到他们的位置上。
再比如说,家里有一个小小的书架,只能放10本书。
当我们把10本书都放满了,又买了新的书回来,那怎么办?我们可以把最开始放上去的那本书拿下来,然后把新书放上去。
这也是一种循环队列的感觉,就像一个循环,不停地更新里面的东西。
在生活中,循环队列还有很多用处。
比如电脑里的一些程序,它们处理信息的时候,也会用到类似循环队列的方法。
就像我们玩游戏的时候,游戏里的角色排队出现,出现了一轮后,又会按照顺序再出现一轮,这也是循环队列在起作用。
现在你们是不是对循环队列有点了解?其实它就在我们身边,只要我们细心观察,就能发现很多这样有趣的小秘密!。
无锁循环队列原理

无锁循环队列原理今天咱们来聊聊一个超有趣的数据结构——无锁循环队列。
这就像是一场数据们的排队游戏,而且是不需要锁来维持秩序的超酷玩法呢!想象一下,有好多好多的数据,就像一群小朋友,要排队做游戏。
普通的队列就像是小朋友们规规矩矩地排成一条直线,一个接一个。
但是无锁循环队列可不一样哦。
它是一个环形的队伍,就像小朋友们手拉手围成一个圈。
这个圈呢,有个头有个尾。
数据们就从尾部进入这个圈圈,然后从头部出去,就像小朋友们从队伍的后面加入,然后从前面离开去玩游戏一样。
那为啥叫无锁呢?这可就很厉害了。
你知道吗,在很多数据结构里,当多个程序或者线程要对同一个队列进行操作的时候,就像好多小朋友同时想加入队伍或者离开队伍,很容易乱套的。
就好比大家都抢着第一个位置,或者同时想从一个地方进出。
这时候通常会用一把锁,就像一个小警察一样,说“一个一个来”。
但是无锁循环队列不需要这个小警察。
它是怎么做到的呢?这里面有一些很巧妙的小技巧。
比如说,它会用一些原子操作。
原子操作就像是超级小的、不可分割的动作。
就好像小朋友们有一种神奇的约定,每次只能一个人做一个小动作,而且这个动作一定能顺利完成,不会被别人打断。
比如有个原子操作是比较并交换(CAS),这就像是小朋友们在加入队伍的时候,先看看这个位置是不是空的,如果是空的,就迅速把自己放进去,而且这个过程是一气呵成的,别人不能在这个中间捣乱。
无锁循环队列的环形结构也很关键哦。
因为是环形的,所以它可以循环利用空间。
就像小朋友们围成的圈,只要有一个小朋友离开前面的位置,后面的小朋友就可以补上去。
这样就不会浪费空间啦。
而且在判断队列满和空的时候也有独特的方法。
如果头和尾碰到一起了,可能是队列空了,因为没有小朋友在队伍里了;但如果尾快要追上头了,那可能就是队列满了,就像这个圈圈快要被小朋友们挤满了。
这个无锁循环队列在很多地方都超级有用呢。
比如说在多线程编程里,就像好多小机器人同时工作。
每个小机器人可能都要往这个队列里放东西或者取东西。
循环队列元素个数的计算方法

循环队列元素个数的计算方法循环队列是一种特殊的队列,它优化了普通队列在删除元素时需要移动大量元素的问题。
通过循环队列的特定设计,可以在固定长度的数组中,实现对队列元素的循环使用。
循环队列有两个指针,一个是队头指针front,指向队列的第一个元素,一个是队尾指针rear,指向队列最后一个元素的下一个位置。
当队列为空时,front和rear指向同一个位置。
在循环队列中,元素个数的计算方法是通过队头指针front和队尾指针rear的位置关系来计算的。
一、队列为空时当队列为空时,front和rear指向同一个位置,即front == rear。
此时队列中没有任何元素,元素个数为0。
二、队列非空时当队列非空时,有以下两种情况:1. rear > front:队列中的元素是连续存储的,rear指针位于front指针之后。
此时元素个数为rear - front。
2. rear < front:队列中的元素被分为两部分,一部分在数组的末尾,另一部分在数组的开头,形成了环形。
此时元素个数为rear + (队列长度 - front)。
综上所述,循环队列元素个数的计算方法如下:1. 如果front == rear,队列为空,元素个数为0。
2. 如果rear > front,元素个数为rear - front。
3. 如果rear < front,元素个数为rear + (队列长度 - front)。
需要注意的是,计算元素个数时,应该对队列长度取余数,即rear 和front相对于队列长度的余数,以处理rear和front超出队列长度的情况。
例如,假设循环队列的长度为N,队列中有5个元素,front指针为2,rear指针为71. 元素个数计算:rear - front = 7 - 2 = 52. 假设队列的长度为8,队列中有5个元素,front指针为6,rear 指针为3元素个数计算:rear + (队列长度 - front) = 3 + (8 - 6) = 5以上就是循环队列元素个数的计算方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、实验目的
1. 理解并掌握队列的逻辑结构和顺序存储结构,了解循环队列的特点;
2. 掌握循环队列中基本操作的相关算法;
3. 编程实现相关算法;
4. 学会利用循环队列解决实际问题。
二、实验条件
Visual C++。
三、实验原理及相关知识
1. 循环队列存储结构描述
#define MAXSIZE 100 //最大队列长度
typedef struct
{
QElemType *base; //存储空间基址
int front; //头指针
int rear; //尾指针
}SqQueue;
2. 基本操作的算法描述
设下标为index,队列长度为m,则下一个下标的累进循环计算公式为:
index_next = ( index+1 ) % m。
实验中涉及的三个关键操作时循环队列中求队列长度、入队和出队操作。
(1) 求长度
所谓求队列长度,即技术队列中元素的个数。
算法思想:根据循环队列的结构特征,可以用公式(Q.rear-Q.front+ MAXSIZE)%MAXSIZE直接计算出队列的长度。
算法描述
Status QueueLength(SqQueue Q)
{
return ( ( Q.rear-Q.front+ MAXSIZE) %MAXSIZE);
}//QueueLength
(2) 入队
入队运算实际上相当于顺序表中的插入运算,所不同的是这里只能在队尾插入元素。
算法思想:①将元素e插入循环队列中队尾元素的下一个存储空间
②修改队尾指针,根据循环累计公式计算出其新位置
算法描述
Status EnQueue(SqQueue &Q, QElemType e)
{
if ( ( Q.rear + 1 ) % MAXSIZE == Q.front )
return ERROR; //队列满
Q.base[Q.rear] = e;
Q.rear = ( Q.rear + 1 ) % MAXSIZE;
return OK;
}// EnQueue
(3) 出队
出队运算实际上相当于顺序表中的删除运算,所不同的是这里只能在队头删除元素。
算法思想:修改队头指针,根据循环累计公式计算出其新位置
算法描述
Status DeQueue(SqQueue &Q, QElemType &e)
{
if (Q.rear == Q.front ) return ERROR; //队列为空
e = Q.base[Q.front];
Q.front = ( Q.front + 1 ) % MAXSIZE;
return OK;
}// DeQueue
四、实验步骤
1. 使用C语言实现循环队列的初始化、计算长度、入队、出队和遍历算法
2. 用顺序存储方式构造一个循环队列Q,并输出构造好的队列和该队列的长度
3. 在第1步所构造的队列Q中将元素e入队,并将更新后的队列Q输出
4. 在第2步更新后所得到的队列Q中将队头元素出队,用变量e返回该元素,并将更新后的队列Q 输出
五、思考题及其它
1. 使用循环队列实现输出杨辉三角的前N行
2. 如何使用循环队列解决“猴子选大王“问题
【参考程序】
#include "stdio.h"
#include "malloc.h"
#define OK 1
#define ERROR 0
#define MAXQSIZE 10 /*最大队列长度+1*/
typedef int QElemType;
typedef struct {
QElemType *base;
int front;
int rear;
} SqQueue;
int InitQueue(SqQueue *Q){
Q->base=(QElemType *)malloc(MAXQSIZE*sizeof(QElemType));
if(!Q->base) return ERROR;
Q->front = Q->rear = 0;
return OK;
}
int EnQueue(SqQueue *Q,QElemType e) {
if( (Q->rear+1)%MAXQSIZE==Q->front ) // 队列满
return ERROR;
Q->base[Q->rear]=e;
Q->rear=(Q->rear+1)%MAXQSIZE ;
return OK;
}
int DeQueue(SqQueue *Q, QElemType *e){
if(Q->front == Q->rear) // 队列空
return ERROR;
*e=Q->base[Q->front];
Q->front=(Q->front+1)%MAXQSIZE;
return OK;
}
int QueueLength(SqQueue Q){
return (Q.rear-Q.front+MAXQSIZE)%MAXQSIZE;
}
void QueueTraverse(SqQueue Q){ /*从队头到队尾依次打印队列Q中每个元素*/ int i,k;
k=QueueLength(Q);
for(i=1;i<=k;i++){
printf("%d ",Q.base[Q.front]);
Q.front=(Q.front+1)%MAXQSIZE;
}
}
void main()
{
int n,e,i;SqQueue q;
InitQueue(&q); //初始化循环队列
printf("该循环队列最多可存放%d个元素\n",MAXQSIZE-1);
printf("请输入数据元素的个数n \n");
scanf("%d",&n);
printf("\n请输入%d个整数\n",n);
/*创建队列*/
for(i=1;i<=n;i++){
scanf("%d",&e);
EnQueue(&q, e); //入队
}
printf("q=");
QueueTraverse(q); //输出循环队列q的内容
fflush(stdin);//刷新缓冲区
printf("\n请输入入队元素e\n");
scanf("%d",&e);
EnQueue(&q, e); //入队
printf("q=");
QueueTraverse(q); //输出循环队列q的内容
fflush(stdin);//刷新缓冲区
printf("\n执行出队操作\n");
DeQueue(&q, &e); //出队
printf("出队元素是%d\n",e);//输出出队元素值printf("q=");
QueueTraverse(q); //输出循环队列q的内容}。
