第三章 2-正则表达式
《编译原理》第3章

NFA到相应的DFA的构造的基本思路是: DFA的每 一个状态对应NFA的一组状态. DFA使用它的状 态去记录在NFA读入一个输入符号后可能达到的 所有状态.
NFA M所能接受的符号串的全体记为L(M)
结论:
上一个符号串集V是正规的,当且仅当存 在一个上的不确定的有穷自动机M,使得 V=L(M)。
DFA是NFA的特例.对每个NFA N一定存在一个DFA M,使得 L(M)=L(N)。对每个NFA N存在着与之 等价的DFA M。 有一种算法,将NFA转换成接受同样语言的DFA.这 种算法称为子集法. 与某一NFA等价的DFA不唯一.
0
1
S P
Z
{P} {}
{P}
{S,Z} {Z}
{P}
• δ为S * 到S的子集(2 S)的一种映射
• 从NFA的矩阵表示中可以看出,表项通常是一状态的集合, 而在DFA的矩阵表示中,表项是一个状态
∑*上的符号串t被NFA M接受:
• 对于Σ*中的任何一个串t,若存在一条从某一初态 结点到某一终态结点的道路,且这条道路上所有 弧的标记字依序连接成的串(不理采那些标记为ε 的弧)等于t,则称t可为NFA M所识别(读出或接 受)。 • 若M的某些结点既是初态结点又是终态结点;或 者存在一条从某个初态结点到某个终态结点的道 路,其上所有弧的标记均为ε,那么空字ε可为M所 接受。
其中: δ(S,0)={P}
δ(S,1)={S,Z} δ(Z,0)={P} δ(Z,1)={P} δ(P,1)={Z} • 状态图表示
1 1 S 0 0,1 Z
P
1
• 矩阵表示
状态 输入
δ(S,0)={P} δ(S,1)={S,Z} δ(Z,0)={P} δ(Z,1)={P} δ(P,1)={Z}
Perl编程中的正则表达式和数据分析技巧

Perl编程中的正则表达式和数据分析技巧第一章:概述Perl编程是一种通用的编程语言,被广泛应用于Web开发、系统管理、网络编程等领域。
正则表达式是Perl编程中的常用工具,用于处理字符串数据。
数据分析是现代计算机科学中的一个重要领域,也是Perl编程中的重点之一。
本文将重点介绍Perl编程中的正则表达式和数据分析技巧。
第二章:正则表达式正则表达式是一种用于匹配字符串的模式,可以用于搜索、替换和分析文本等操作。
在Perl编程中,正则表达式被广泛应用于文本处理和字符串操作。
2.1 正则表达式语法Perl编程中的正则表达式语法与其他编程语言的正则表达式语法有些不同。
基本的正则表达式语法包括元字符、转义字符和字符集等。
2.2 正则表达式函数Perl编程中常用的正则表达式函数包括正则匹配函数、正则替换函数和正则赋值函数等。
这些函数可以用于实现文本搜索、替换、过滤等操作。
第三章:数据分析数据分析是一种从数据中提取信息、研究数据特征和关联的技术,是现代计算机科学中的一个重要领域。
在Perl编程中,数据分析被广泛应用于数据挖掘、数据可视化和机器学习等领域。
3.1 数据处理函数Perl编程中常用的数据处理函数包括排序函数、过滤函数和聚合函数等。
这些函数可以用于对数据进行排序、筛选和统计等操作。
3.2 数据可视化技巧数据可视化是将数据转化为图形化展示的技术,能够帮助人们更好地理解数据。
在Perl编程中,常用的数据可视化技巧包括使用图表、色彩和图形效果等,可以使用Perl模块如Chart::Plot、Cairo和GD等来实现。
3.3 机器学习技术机器学习是一种能够自动从数据中学习和优化模型的技术,已在机器翻译、推荐系统和自然语言处理等领域得到广泛应用。
在Perl编程中,常用的机器学习技术包括决策树、支持向量机和神经网络等。
第四章:案例分析为了更好地说明Perl编程中的正则表达式和数据分析技巧的应用,本章介绍两个具体的案例。
正则表达式知识详解

正则表达式知识详解一、什么是正则表达式?1.定义:正则表达式(regular expression)描述了一种字符串匹配的模式,可以用来检查一个串是否含有某种子串、将匹配的子串做替换或者从某个串中取出符合某个条件的子串等。
构造正则表达式的方法和创建数学表达式的方法一样。
也就是用多种元字符与运算符可以将小的表达式结合在一起来创建更大的表达式。
正则表达式的组件可以是单个的字符、字符集合、字符范围、字符间的选择或者所有这些组件的任意组合。
2.组成:正则表达式是由普通字符(例如字符 a 到 z)以及特殊字符(称为"元字符")组成的文字模式。
模式描述在搜索文本时要匹配的一个或多个字符串。
正则表达式作为一个模板,将某个字符模式与所搜索的字符串进行匹配。
3.何时使用:验证——从头到尾完整匹配!查找——只要部分匹配即可!二、正则表达式的基本语法和规则1.备选字符集:规定某*一位字符*可用的备选字符的集合语法:[可选字符列表]强调:1. 无论备选字符集包含多少字符,只能选1个2. 必须选1个!比如:6位数字的密码[0123456789][0123456789][0123456789][0123456789][012 3456789][0123456789]简化:1. 当备选字符连续时,可用-表示范围的区间比如:[0123456789]-->[0-9][0-9][0-9][0-9][0-9][0-9][0-9][a-z]-->1位小写字母[A-Z]-->1位大写字母[A-Za-z]-->1位字母,大小写都行[0-9a-zA-Z]-->1位字母或数字都行反选:[^不能选的字符列表]比如:[^47] 强调:^作“除了”使用时,只能放在开头2. 预定义字符集:为常用的字符集专门提供的简化写法!“\d”-->[0-9]-->1位数字“\w”-->[0-9a-zA-Z_]-->1位字母,数字或_“\s”-->1位空字符:匹配任何空白字符,包括空格、制表符、换页符等等。
正则表达式

(abc)*
仅包含任意个abc的 字符串
abc、abca bcabc
a、abca ma、abc
m+(abc) 以至少1个m开头,后 m、mabc、 * 接任意个abc的字符 mabcabc 串 m+abc?
?
以至少1个m开头,后 mab、mabc、ab、abc、 接ab或abc的字符串 mmmab、mm mabcc abc
3
正则表达式概念及发展史(续)
之后一段时间,人们发现可以将这一工作成果应用于其他方面。Ken Thom pson就把这一成果应用于计算搜索算法的一些早期研究,Ken Thompson 是 Unix的主要发明人,也就是大名鼎鼎的Unix之父。Unix之父将此符号系 统引入编辑器QED,然后是Unix上的编辑器ed,并最终引入grep。 在最近的六十年中,正则表达式逐渐从模糊而深奥的数学概念,发展成为 在计算机各类工具和软件包 应用中的主要功能。不仅仅众多UNIX工具支 持正则表达式,近二十年来,在WINDOW的阵营下,正则表达式的思想和 应用在大部分 Windows 开发者工具包中得到支持和嵌入应用! 从正则式在Microsoft Visual Basic 6 或 Microsoft VBScript到.NET Fram ework中的探索和发展,WINDOWS系列产品对正则表达式的支持发展到无 与伦比的高度,目前几乎所有 Microsoft 开发者和所有.NET语言都可以使 用正则表达式! 简言之,一个正则表达式,就是用某种模式去匹配一类字符串的一个公式。
\d \D
匹配单个数字字 \d{3}(\d)? 包含3个或4个数字的 符,相当于[0-9] 字符串 匹配单个非数字 字符,相当于[^ 0-9] 匹配单个数字、 大小写字母和汉 字字符 \D(\d)* 以单个非数字字符开 头,后接任意个数字 字符串
编译原理第三章练习题答案

编译原理第三章练习题答案编译原理第三章练习题答案编译原理是计算机科学中的重要课程之一,它研究的是将高级语言程序转化为机器语言的过程。
在编译原理的学习过程中,练习题是提高理解和应用能力的重要途径。
本文将为大家提供编译原理第三章的练习题答案,希望能够对大家的学习有所帮助。
1. 什么是词法分析?请简要描述词法分析的过程。
词法分析是编译过程中的第一个阶段,它的主要任务是将源程序中的字符序列划分为有意义的词素(token)序列。
词法分析的过程包括以下几个步骤:1)扫描:从源程序中读取字符序列,并将其转化为内部表示形式。
2)识别:根据预先定义的词法规则,将字符序列划分为不同的词素。
3)分类:将识别出的词素进行分类,如关键字、标识符、常量等。
4)输出:将分类后的词素输出给语法分析器进行进一步处理。
2. 什么是正则表达式?请给出一个简单的正则表达式示例。
正则表达式是一种用于描述字符串模式的工具,它由一系列字符和操作符组成。
正则表达式可以用于词法分析中的词法规则定义。
以下是一个简单的正则表达式示例:[a-z]+该正则表达式表示匹配一个或多个小写字母。
3. 请简要描述DFA和NFA的区别。
DFA(Deterministic Finite Automaton)和NFA(Nondeterministic Finite Automaton)是有限状态自动机的两种形式。
它们在词法分析中常用于构建词法分析器。
DFA是一种确定性有限状态自动机,它的状态转换是确定的,每个输入符号只能对应一个状态转换。
相比之下,NFA是一种非确定性有限状态自动机,它的状态转换是非确定的,每个输入符号可以对应多个状态转换。
4. 请简要描述词法分析器的实现过程。
词法分析器的实现过程包括以下几个步骤:1)定义词法规则:根据编程语言的语法规范,定义词法规则,如关键字、标识符、常量等。
2)构建正则表达式:根据词法规则,使用正则表达式描述不同类型的词素。
3)构建有限状态自动机:根据正则表达式,构建DFA或NFA来识别词素。
正则表达式基本语法

正则表达式基本语法1、正则表达式的作⽤ 正则表达式是很繁琐的,但也相当有⽤。
学会正则表达式,可以让你做很多⼯作时都成倍地提⾼效率。
正则表达式的作⽤可以概括为三个⽅⾯测试字符串内模式、替换⽂本、基于模式匹配从字符串中提取⼦字符串。
它的应⽤领域也相当⼴泛,C#, java, python等等语⾔中都有应⽤。
这⾥主要说明python中的正则表达式。
2、正则表达式语法 正则表达式是由普通字符(如a-z)以及特殊字符(“元字符")组成的⽂字模式。
模式描述在搜索⽂本时要匹配的⼀个或多个字符串。
正则表达式作为⼀个模板,将字符串模式与搜索资源进⾏匹配。
构造正则表达式的⽅法实际上跟构造数学公式相似。
即⽤多种元字符与运算符将⼩的表达式结合在⼀起来创建更⼤的表达式。
正则表达式的组建可以是单个字符、字符集合、字符范围、字符间的选择或者所有这些组建的任意组合。
3、字符种类 字符⼀般分为普通字符、⾮打印字符、特殊字符、限定符、定位符等。
1)普通字符:包括没有显⽰指定为元字符的所有可打印和不可打印字符。
这包括所有⼤写和⼩写字母,所有数字、所有标点符号和⼀些其他符号。
2)⾮打印字符,如下表所⽰:字符概述\cx匹配由x指明的控制字符。
如\cM匹配⼀个Control-M1或者回车符。
X值必须为A-Z或a-z之⼀。
否则,将c是为⼀个原义的’c’字符。
\f匹配⼀个换页符。
等价于\x0c和\cL。
\n匹配⼀个换⾏符。
等价于\x0d和\cJ。
\r匹配⼀个回车符。
等价于\x0d和\cM。
\s匹配任何空⽩字符,包括空格、制表符、换页符等等。
等价于[\f\v\r\t\v]\S匹配任何空⽩字符。
等价于[^\f\v\r\t\v]。
\t匹配⼀个制表符。
等价于\x09和\cl。
\v匹配垂直制表符。
等价于\x0b和\cK。
3)特殊字符,有特殊含义的字符。
如要匹配这些元素需要在字符前⾯加转义符,即反斜杠字符(\)。
4)限定符:⽤来指定正则表达式的⼀个给定组件必须要出现多少次才能满⾜匹配。
《易语言“正则表达式”教程》

《易语⾔“正则表达式”教程》”与字符串”匹配时,匹配的结果是:成功;匹配到的内容是”整个字符串,表达式中的”将与字符串中最后⼀个《易语⾔“正则表达式”教程》本⽂改编⾃多个⽂档,因此如有雷同,不是巧合。
“正则表达式”的应⽤范围越来越⼴,有了这个强⼤的⼯具,我们可以做很多事情,如搜索⼀句话中某个特定的数据,屏蔽掉⼀些⾮法贴⼦的发⾔,⽹页中匹配特定数据,代码编辑框中字符的⾼亮等等,这都可以⽤正则表达式来完成。
本书分为四个部分。
第⼀部分介绍了易语⾔的正则表达式⽀持库,在这⾥,⼤家可以了解第⼀个正则表达式的易语⾔程序写法,以及⼀个通⽤的⼩⼯具的制作。
第⼆部分介绍了正则表达式的基本语法,⼤家可以⽤上述的⼩⼯具进⾏试验。
第三部分介绍了⽤易语⾔写的正则表达式⼯具的使⽤⽅法。
这些⼯具是由易语⾔⽤户提供的,有的⼯具还带有易语⾔源码。
他们是:monkeycz、零点飞越、寻梦。
第四部分介绍了正则表达式的⾼级技巧。
⽬录《易语⾔“正则表达式”教程》 1⽬录 1第⼀章易语⾔正则表达式⼊门 3⼀.与DOS下的通配符类似 3⼆.初步了解正则表达式的规定 3三.⼀个速查列表 4四.正则表达式⽀持库的命令 54.1第1个正则表达式程序 54.2第2个正则表达式例程 74.3第3个例程 84.4⼀个⼩型的正则⼯具 9第⼆章揭开正则表达式的神秘⾯纱 11引⾔ 12⼀.正则表达式规则 121.1普通字符 121.2简单的转义字符 131.3能够与“多种字符”匹配的表达式 141.4⾃定义能够匹配“多种字符”的表达式 16 1.5修饰匹配次数的特殊符号 171.6其他⼀些代表抽象意义的特殊符号 20⼆.正则表达式中的⼀些⾼级规则 212.1匹配次数中的贪婪与⾮贪婪 212.2反向引⽤\1,\2 (23)2.3预搜索,不匹配;反向预搜索,不匹配 24三.其他通⽤规则 25四.其他提⽰ 27第三章正则表达式⼯具与实例 28⼀.正则表达式⽀持库 291.1“正则表达式”数据类型 291.2“搜索结果”数据类型 30⼆.正则表达式实⽤⼯具 302.1⼀个成品⼯具 302.2易语⾔写的⼯具 33三.应⽤实例 343.1实例1 343.2实例2 363.3实例3 373.4实例4 37第四章正则表达式话题 38引⾔ 38⼀.表达式的递归匹配 381.1匹配未知层次的嵌套 381.2匹配有限层次的嵌套 39⼆.⾮贪婪匹配的效率 402.1效率陷阱的产⽣ 402.2效率陷阱的避免 41附录: 42⼀.17种常⽤正则表达式 42第⼀章易语⾔正则表达式⼊门⼀.与DOS下的通配符类似其实,所谓的“正则表达式”,是⼤家⼀直在使⽤的,记得吗?在搜索⽂件时,会使⽤⼀种威⼒巨⼤的武器——DOS通配符——“?”和“”。
三章(续一)正则表达式与右线性文法

College of Computer Science & Technology, BUPT
6
语言的闭包(closure)运算
语言 L 的闭包 L* = wn w L n0 , 其中wn 为w 的 n 次连接 或 L* = L0 L1 L2 … = i 0 Li , 其中 L0 = , L1 = L, L2 = LL, … 举例
先证L L1∪ L2:
在G中,由G的定义,对于任意,意味着或者(按G1的产生式),或者(按 G2的产生式) 即文法G的每个句子或由G1产生,或由G2产生。 ∴ L(G) L(G1)∪ L(G2)
再证 L1∪ L2 L:
S1
G1=> +ω
设有ω∈L1∪ L2,则存在推导
或 S2
G2=> +ω
College of Computer Science & Technology, BUPT 4
语言的联合、并(union)运算
两个语言 L 和 M 的联合、并
L M = w w L w M
举例
设 L = 001,10,111 , M = , 001, 则 L M = , 10, 001, 111
如何根据文法,求出正则表达式呢?求联立方程
College of Computer Science & Technology, BUPT
14
四、从右线性文法导出正则式
求解规则R:
设x αx+β,α∈T*,β∈T*, x∈N 则x的解为 x=α*β 证明: x αx+β 表示x有两个生成式: x αx 和 x β, 生成的语言为(β,αβ,ααβ,αααβ, …), 显然该 语言可用正则式α*β表示。 书p78, 例2 书p79, 例3
正则表达式(正则表达式括号的作用)

正则表达式(正则表达式括号的作⽤)正则表达式之前学习的时候,因为很久没怎么⽤,或者⽤的时候直接找⽹上现成的,所以都基本忘的差不多了。
所以这篇⽂章即是笔记,也让⾃⼰再重新学习⼀遍正则表达式。
其实平时在操作⼀些字符串的时候,⽤正则的机会还是挺多的,之前没怎么重视正则,这是⼀个错误。
写完这篇⽂章后,发觉⼯作中很多地⽅都可以⽤到正则,⽽且⽤起来其实还是挺爽的。
正则表达式作⽤ 正则表达式,⼜称规则表达式,它可以通过⼀些设定的规则来匹配⼀些字符串,是⼀个强⼤的字符串匹配⼯具。
正则表达式⽅法基本语法,正则声明js中,正则的声明有两种⽅式1. 直接量语法:1var reg = /d+/g/2. 创建RegExp对象的语法1var reg = new RegExp("\\d+", "g");这两种声明⽅式其实还是有区别的,平时的话我⽐较喜欢第⼀种,⽅便⼀点,如果需要给正则表达式传递参数的话,那么只能⽤第⼆种创建RegExp的形式格式:var pattern = new RegExp('regexp','modifier');regexp:匹配的模式,也就是上⽂指的正则规则。
modifier: 正则实例的修饰符,可选值有:i : 表⽰区分⼤⼩写字母匹配。
m :表⽰多⾏匹配。
g : 表⽰全局匹配。
传参的形式如下:我们⽤构造函数来⽣成正则表达式1var re = new RegExp("^\\d+$","gim");这⾥需要注意,反斜杠需要转义,所以,直接声明量中的语法为\d,这⾥需要为\\d那么,给它加变量,就和我们前⾯写的给字符串加变量⼀样了。
1 2var v = "bl";var re =new RegExp("^\\d+" + v + "$","gim"); // re为/^\d+bl$/gim⽀持正则的STRING对象⽅法1. search ⽅法作⽤:该⽅法⽤于检索字符串中指定的⼦字符串,或检索与正则表达式相匹配的字符串基本语法:stringObject.search(regexp);返回值:该字符串中第⼀个与regexp对象相匹配的⼦串的起始位置。
正则表达式入门教程

正则表达式入门教程以下内容经正则表达式学习网授权≈正则表达式是什么?≈在使用电脑进行各种文字处理的时候,我们有时需要查找和匹配一些特殊的字符串,如邮箱地址、验证用户输入的密码是否包含了大小写字母和数字,查找HTML源文档中的所有web地址等等,这时我们就可以使用到正则表达式。
正则表达式本身是一个“字符串”,通过这个“字符串”去描述字符组成规则。
如abbb、abbbb、abbbbb这三个字符串包都是以a字母开头a后面有一个b字母,而且b字母重复了3到5次。
用正则表达式来描述就是ab{3,5},b{3,5}表示b字符重复3到5次。
如果我们想匹配ababab这样的字符串,ab重复了3次,用正则表达式表示就是(ab){3},圆括号()是正则表达式中的分组。
大家如果想亲自感受正则表达式的使用效果,可以打开正则表达式测试系统。
如以上实例所展示的,正则表达式为人们提供了一种简单易用的字符处理工具。
它在目前主流的文字处理软件中都提供了良好的支持(不仅是编程软件,还有文字处理软件Uedit32、EditPlus,网页采集软件火车头等等),它具有很强的通用性,学好它,我们可以达一变应万变的效果。
≈正则表达式详解≈像{},()这种在正则表达式中,具有特殊含义的字符称为元字符(metacharacter)。
元字符是组成正则表达式的基本元素,在正则表达式经常使用的元字符不是很多,概念容易理解。
大家只要花30来分钟学完我们的教程基本上就可以完全掌握。
为了您能更快速的掌握正则表达式,我们为您推荐一款方便的正则表达式在线测试工具“RegExr”,(RegExr由免费提供)。
保留字符匹配字符本身匹配字符数量匹配字符位置分组匹配表达式选项保留字符(返回目录)在正则表达式中,有一些字符在正则表达式中具有特殊含义被称保留字符,如*表示前一个元素可以重复零次或多次,要匹配“*”字符本身使用\*,半角句号.匹配除了换行符外的所有字符,要匹配“.”使用\.。
正则表达式介绍

正则表达式介绍正则表达式是一种强大的文本处理工具,它用于匹配、查找和替换文本中的模式。
它是一种特殊的语法,可以用于描述字符串的结构和内容。
在日常工作中,我们经常需要处理各种各样的文本数据,比如文本文件、数据库中的数据、网页中的内容等。
而正则表达式正是将这些文本数据进行有效处理的利器。
正则表达式的语法非常丰富,包含了大量的元字符和语法规则。
下面我们就来介绍一些常见的元字符和语法规则。
元字符元字符是正则表达式中的基本单位,它用于表示某种特殊的文本字符或字符集。
下面是一些常见的元字符:1. . :用于匹配任意一个字符,除了换行符(\n)。
2. ^ :用于匹配字符串的开头。
3. $ :用于匹配字符串的结尾。
4. * :用于匹配前面的字符出现0次或多次。
5. + :用于匹配前面的字符出现1次或多次。
6. ? :用于匹配前面的字符出现0次或1次。
7. | :用于表示或者的关系。
语法规则除了元字符之外,正则表达式还包含了许多语法规则。
下面是一些常见的语法规则:1. 字符集:方括号([])内表示要匹配的字符集,可以使用连字符(-)表示范围。
比如[0-9]表示匹配0到9之间的任意数字。
2. 分组:用小括号()来把多个元字符组合起来,形成一个整体。
比如(ab)+表示匹配一个或多个连续的"ab"。
3. 反向引用:用反斜杠(\)加数字来引用前面的分组。
比如(\w)\1表示匹配出现两次的任意单词字符。
4. 贪婪/非贪婪:在元字符后面加上问号(?)可以实现非贪婪模式。
比如.*?表示匹配尽可能少的任意字符。
5. 零宽度断言:用于限定匹配的位置,但不会消耗任何字符。
比如正向预查(?=)表示必须跟着某个模式,但不包含该模式;负向预查(?!)表示必须不跟着某个模式。
应用实例下面我们通过一些实例来演示正则表达式的应用:1. 匹配手机号码:^(13\d|14[579]|15[^4\D]|17[^49\D]|18\d)\d{8}$2. 匹配IP地址:^([01]?\d\d?|2[0-4]\d|25[0-5])\.([01]?\d\d?|2[0-4]\d|25[0-5])\.([01]?\d\d?|2[0-4]\d|25[0-5])\.([01]?\d\d?|2[0-4]\d|25[0-5])$3. 匹配邮箱地址:^\w+([-+.]\w+)*@\w+([-.]\w+)*\.\w+([-.]\w+)*$4. 匹配HTML标签:<(?:"[^"]*"['"]*|'[^']*'['"]*|[^'">])+>结语正则表达式是一个非常强大的工具,可以用于各种各样的文本处理任务。
Sigil正则表达式入门

实用标准文档Sigil 正则表达式入门 正则表达式,是一种用特殊符号表示文字的方法,主要用在查找和替换方面。
下面的例子可以让你知道正则表达式是干什么用的。
在一个文本中,有这样的一些内容:序章 第一章 ABCDEF 第二章 GHIJKL 第三章 ………… 终章这种内容我们都很熟悉,你有没有想过,用什么办法可以把这些内容一次过 查找出来呢?为了简化,我们先来看这个部分。
第一章 第二章 第三章可以看到,这些内容有着极高的相似性,由“第”,“章”开头和结尾,中 间有着一些数字。
如果我们能用一个什么符号来代表中间的所有字,比如一个圆 点“.”,不就可以用这样的方式来查找出所有这样的内容了吗。
第.章很早之前,就有人发明了一套完整的方案,让我们可以用各种不同的符号来 达到这种目的,那就是我们将要了解的正则表达式。
正则表达式作为一种描述字符的方案,在大量软件、编程语言中都有所运用, 而在这些不同的平台上,正则表达式的使用方式又往往会有或多或少的差异,在 某个平台上管用的表达式,换个地方可能就要改改才能正确运行。
那么在这篇文 章里,我们主要是讲 Sigil 中的正则表达式,至于推广应用,就要靠大家去查找 资料了。
1. 元字符我们前面提到,正则表达式一个重要作用就是用特别的符号来代表一类字符, 而这些符号就叫做“元字符”。
这些元字符在大多数环境下都是通用的。
注意,元字符中所有符号都是半角符号,也就是通常说的英文符号。
文案大全实用标准文档以下是一些常见的元字符,实际上还有更多。
这些元字符都经过测试,在 Sigil 下有效。
符号 意义 说明任意.一个最简单的元字符,匹配任意字符,但不包括换行符“\n”。
字符把元字符改变为普通字符,或者把某些普通字符转变为元\转义 字符。
比如,“\.”就是代表普通的点号,不代表其他字符。
半角空格、制表符等空白字符。
在 Sigil 中还能匹配到换\s空白 字符行符“\n”和空白行,使用要注意。
正则表达式语法或者符号语法

正则表达式语法或者符号语法正则表达式是一种用于匹配字符串的模式,通常用于文本搜索、替换和验证等操作。
它是由一些特殊字符和元字符组成的语法,用于描述字符串的结构和模式。
正则表达式的基本符号包括:1. 点号(.):匹配任意单个字符,除了换行符。
2. 加号(+):匹配前面的子表达式一次或多次。
3. 星号(*):匹配前面的子表达式零次或多次。
4. 问号(?):匹配前面的子表达式零次或一次。
5. 方括号([]):定义一个字符集合,匹配其中的任意一个字符。
6. 大括号({}):定义一个重复次数的范围,匹配指定次数的前面的子表达式。
7. 圆括号(()):将多个表达式组合成一个整体,用于分组或优先级控制。
8. 竖线(|):表示逻辑“或”,匹配左右两边的任意一个表达式。
9. 反斜杠(\):转义特殊字符,使其失去特殊含义。
10. 插入符号(^):匹配字符串的开头。
11. $符号:匹配字符串的结尾。
12. 百分号(%):匹配任意数量的非换行字符。
13. 数字符号(\d):匹配任意数字字符,等同于[0-9]。
14. 字母符号(\w):匹配任意字母、数字或下划线字符,等同于[A-Za-z0-9_]。
15. 空白符号(\s):匹配任意空白字符,包括空格、制表符、换行符等。
16. 非空白符号(\S):匹配任意非空白字符。
17. 单词边界符号(b):匹配单词的边界,即字母、数字或下划线字符与非字母、非数字、非下划线字符之间的边界。
18. Unicode属性符号(p{Property}):匹配Unicode属性,如汉字、字母等。
以上是正则表达式的一些基本符号,通过这些符号的组合可以构建出复杂的模式来匹配各种字符串。
以下是一些常用的正则表达式语法:1. 字符匹配:直接使用字符进行匹配,例如`a`可以匹配字符"a",`abc`可以匹配字符串"abc"。
2. 点号通配符:`.`可以匹配任何单个字符(除换行符外),`\.`可以匹配实际的点号字符。
正则表达式用法详解

正则表达式⽤法详解正则表达式之基本概念在我们写页⾯时,往往需要对表单的数据⽐如账号、⾝份证号等进⾏验证,⽽最有效的、⽤的最多的便是使⽤正则表达式来验证。
那什么是正则表达式呢?正则表达式(Regular Expression)是⽤于描述⼀组字符串特征的模式,⽤来匹配特定的字符串。
它的应⽤⾮常⼴泛,特别是在字符串处理⽅⾯。
其常见的应⽤如下:验证字符串,即验证给定的字符串或⼦字符串是否符合指定的特征,例如,验证是否是合法的邮件地址、验证是否是合法的HTTP地址等等。
查找字符串,从给定的⽂本当中查找符合指定特征的字符串,这样⽐查找固定字符串更加灵活。
替换字符串,即查找到符合某特征的字符串之后将之替换。
提取字符串,即从给定的字符串中提取符合指定特征的⼦字符串。
第⼀部分:正则表达式之⼯具正所谓⼯欲善其事必先利其器! 所以我们需要知道下⾯⼏个主要的⼯具:第⼆部分:正则表达式之元字符正则表达式中元字符恐怕是我们听得最多的了。
元字符(Metacharacter)是⼀类⾮常特殊的字符,它能够匹配⼀个位置或者字符集合中的⼀个字符。
如.、\w等都是元字符。
刚刚说到,元字符既可以匹配位置,也可以匹配字符,那么我们就可以通过此来将元字符分为匹配位置的元字符和匹配字符的元字符。
A匹配位置的元字符---^、$、\b即匹配位置的元字符只有^(脱字符号)、$(美元符号)和\b这三个字符。
分别匹配⾏的开始、⾏的结尾以及单词的开始或结尾。
它们匹配的都只是位置。
1.^匹配⾏的开始位置如^zzw匹配的是以"zzw"为⾏开头的"zzw"(注意:我这⾥想要表达的是:尽管加了⼀个^,它匹配的仍是字符串,⽽不是⼀整⾏!),如果zzw不是作为⾏开头的字符串,则它不会被匹配。
2.$匹配⾏的结尾位置如zzw$匹配的是以"zzw"为⾏结尾的"zzw"(同样,这⾥$只是匹配的⼀个位置,那个位置是零宽度,⽽不是⼀整⾏),如果zzw不是作为⾏的结尾,那么它不会被匹配。
形式语言3

4. 正则表达式运算符的优先级 括号>星>连接>并
例 01*+1和0(1*+1)表示的语言
8
§2 正则表达式与正则语言的等价关系 1. 将正则语言转化为正则表达式 (1) 定理 设A是任一给定的DFA,则存在正 则表达式R,使得L(R)=L(A)。 证: 设A = (Q,Σ,δ, q1, F) ,且
b) 下面证明L(M)=L(G). 对于任一w L(G), 设对应的推导为:
S v1Av1v2B … v1v2…vn-1C v1v2…vn,
这在M中恰对应于从S出发,途经A,B,C,最后到达终态f 的一条道路w,故w L(M) 。
反过来,对于任一w L(M) ,则w是M中从S出发, 最后到达终态f的一条道路。设此路途经的中间结点中属 于V的依次为A1,A2,…,Am, 则根据M的构造过程知,必有 相应的G的一个推导:
2. 将正则表达式转化为自动机 因为正则表达式中涉及的运算只有并、
连接、星号,故只需分别考虑这三种情形 的转化。
一个字母c或或的表达式的自动机 是容易构造的。故只需考虑已知两台自动 机A1,A2, 如何构造相关的新自动机A。
17
(1) 并( L(A) = L(A1)∪L(A2) )
……
….
…
F1 …
L1L2= {w * :w有奇数个0 }.
3
(3) 语言L的闭包星号L* L*是连接L中任意有限个(包括0个,1个)字符串
所得的集合。 记L0={ }, Lk为LL…L(k个L的连接),易知 L* L0 L1 L2 ... Ln ....
例 设L={a,b}, 则 L*={ , a, b, ab, ba, aa, bb, abb, bab, bba,
Sigil正则表达式入门

Sigil正则表达式入门正则表达式,是一种用特殊符号表示文字的方法,主要用在查找和替换方面。
下面的例子可以让你知道正则表达式是干什么用的。
在一个文本中,有这样的一些容:这种容我们都很熟悉,你有没有想过,用什么办法可以把这些容一次过查找出来呢?为了简化,我们先来看这个部分。
可以看到,这些容有着极高的相似性,由“第”,“章”开头和结尾,中间有着一些数字。
如果我们能用一个什么符号来代表中间的所有字,比如一个圆点“.”,不就可以用这样的方式来查找出所有这样的容了吗。
很早之前,就有人发明了一套完整的方案,让我们可以用各种不同的符号来达到这种目的,那就是我们将要了解的正则表达式。
正则表达式作为一种描述字符的方案,在大量软件、编程语言中都有所运用,而在这些不同的平台上,正则表达式的使用方式又往往会有或多或少的差异,在某个平台上管用的表达式,换个地方可能就要改改才能正确运行。
那么在这篇文章里,我们主要是讲Sigil中的正则表达式,至于推广应用,就要靠大家去查找资料了。
1. 元字符我们前面提到,正则表达式一个重要作用就是用特别的符号来代表一类字符,而这些符号就叫做“元字符”。
这些元字符在大多数环境下都是通用的。
注意,元字符中所有符号都是半角符号,也就是通常说的英文符号。
以下是一些常见的元字符,实际上还有更多。
这些元字符都经过测试,在2. 常用正则表达式在这一部分,我们回来看一些很常用的正则表达式,这些表达式往往是更复杂表达式的组成部分。
2.1 所有字符匹配所有容。
“.”代表一个字符,“*”代表任意多个,因此“.*”代表“所有字符”。
比如表示<div>标签的所有容,可以依次匹配到下列各项但不能跨行,这样是匹配不到的。
如果要跨行,需要使用“(?s)”。
2.2 空白行匹配空白行的典型写法。
可以匹配无容的行,只有空格的行,只有制表符的行或者空格和制表符混合排列的行。
[]中包括的分别是空格“ ”,制表符“\t”和全角空格“”。
正则表达式的概念和应用

正则表达式的概念和应用正则表达式是一种文本模式,用于描述字符串的特定格式。
通过它,可以匹配到符合特定规则的字符串,并进行各种操作,如字符串替换、查找等。
正则表达式常用于编程语言中,如Python、Java等。
一、基本概念1. 字符集:由一组字符组成的集合,可以用中括号[]表示。
比如[abc]表示匹配a、b、c中的任意一个字符。
2. 元字符:正则表达式中的特殊字符,有特定的含义,如"."表示匹配任意单个字符,"^"表示匹配字符串的开头,"$"表示匹配字符串的结尾。
3. 量词:表示匹配的次数,如"*"表示匹配任意个数(0或多个),"+"表示至少匹配一个,"?"表示匹配0或1个,"{n}"表示匹配n个,"{n,m}"表示匹配n到m个。
4. 分组:使用小括号()表示,可以将同一规则的内容进行分组,方便进行操作和引用。
二、常见应用1. 匹配数字:用\d表示匹配任意一个数字,用\w匹配任意一个字母、数字或下划线,用\s匹配任意空白符。
2. 匹配邮箱:使用正则表达式可以匹配邮箱格式是否正确,如^[a-zA-Z0-9_-]+@[a-zA-Z0-9_-]+(\.[a-zA-Z0-9_-]+)+$可以匹配正确的邮箱格式。
3. 替换字符串:我们可以使用正则表达式进行字符串的替换操作,如将字符串中的所有空格替换为下划线,可以使用\s替换为_。
4. 查找关键字:如果需要在大量文本中查找特定关键字,使用正则表达式可以更方便和快捷,如使用正则表达式(?i)KeyWord可以忽略大小写进行查找。
5. URL匹配:在爬虫开发中,可以使用正则表达式匹配特定的URL格式,用于爬取网站内容。
6. 数据清洗:在进行数据清洗时,使用正则表达式可以更轻松地对数据进行处理和提取。
总之,正则表达式在编程中的应用十分广泛,可以用于字符串匹配、替换、查找等各种操作,对于使用者来说是非常有用的工具。
最全的常用正则表达式大全

最全的常⽤正则表达式⼤全⼀、校验数字的表达式1 数字:^[0-9]*$2 n位的数字:^\d{n}$3 ⾄少n位的数字:^\d{n,}$4 m-n位的数字:^\d{m,n}$5 零和⾮零开头的数字:^(0|[1-9][0-9]*)$6 ⾮零开头的最多带两位⼩数的数字:^([1-9][0-9]*)+(.[0-9]{1,2})?$7 带1-2位⼩数的正数或负数:^(\-)?\d+(\.\d{1,2})?$8 正数、负数、和⼩数:^(\-|\+)?\d+(\.\d+)?$9 有两位⼩数的正实数:^[0-9]+(.[0-9]{2})?$10 有1~3位⼩数的正实数:^[0-9]+(.[0-9]{1,3})?$11 ⾮零的正整数:^[1-9]\d*$ 或 ^([1-9][0-9]*){1,3}$ 或 ^\+?[1-9][0-9]*$12 ⾮零的负整数:^\-[1-9][]0-9"*$ 或 ^-[1-9]\d*$13 ⾮负整数:^\d+$ 或 ^[1-9]\d*|0$14 ⾮正整数:^-[1-9]\d*|0$ 或 ^((-\d+)|(0+))$15 ⾮负浮点数:^\d+(\.\d+)?$ 或 ^[1-9]\d*\.\d*|0\.\d*[1-9]\d*|0?\.0+|0$16 ⾮正浮点数:^((-\d+(\.\d+)?)|(0+(\.0+)?))$ 或 ^(-([1-9]\d*\.\d*|0\.\d*[1-9]\d*))|0?\.0+|0$17 正浮点数:^[1-9]\d*\.\d*|0\.\d*[1-9]\d*$ 或 ^(([0-9]+\.[0-9]*[1-9][0-9]*)|([0-9]*[1-9][0-9]*\.[0-9]+)|([0-9]*[1-9][0-9]*))$18 负浮点数:^-([1-9]\d*\.\d*|0\.\d*[1-9]\d*)$ 或 ^(-(([0-9]+\.[0-9]*[1-9][0-9]*)|([0-9]*[1-9][0-9]*\.[0-9]+)|([0-9]*[1-9][0-9]*)))$19 浮点数:^(-?\d+)(\.\d+)?$ 或 ^-?([1-9]\d*\.\d*|0\.\d*[1-9]\d*|0?\.0+|0)$⼆、校验字符的表达式1 汉字:^[\u4e00-\u9fa5]{0,}$2 英⽂和数字:^[A-Za-z0-9]+$ 或 ^[A-Za-z0-9]{4,40}$3 长度为3-20的所有字符:^.{3,20}$4 由26个英⽂字母组成的字符串:^[A-Za-z]+$5 由26个⼤写英⽂字母组成的字符串:^[A-Z]+$6 由26个⼩写英⽂字母组成的字符串:^[a-z]+$7 由数字和26个英⽂字母组成的字符串:^[A-Za-z0-9]+$8 由数字、26个英⽂字母或者下划线组成的字符串:^\w+$ 或 ^\w{3,20}$9 中⽂、英⽂、数字包括下划线:^[\u4E00-\u9FA5A-Za-z0-9_]+$10 中⽂、英⽂、数字但不包括下划线等符号:^[\u4E00-\u9FA5A-Za-z0-9]+$ 或 ^[\u4E00-\u9FA5A-Za-z0-9]{2,20}$11 可以输⼊含有^%&',;=?$\"等字符:[^%&',;=?$\x22]+12 禁⽌输⼊含有~的字符:[^~\x22]+三、特殊需求表达式1 Email地址:^\w+([-+.]\w+)*@\w+([-.]\w+)*\.\w+([-.]\w+)*$2 域名:[a-zA-Z0-9][-a-zA-Z0-9]{0,62}(/.[a-zA-Z0-9][-a-zA-Z0-9]{0,62})+/.?3 InternetURL:[a-zA-z]+://[^\s]* 或 ^http://([\w-]+\.)+[\w-]+(/[\w-./?%&=]*)?$4 ⼿机号码:^(13[0-9]|14[5|7]|15[0|1|2|3|5|6|7|8|9]|18[0|1|2|3|5|6|7|8|9])\d{8}$5 电话号码("XXX-XXXXXXX"、"XXXX-XXXXXXXX"、"XXX-XXXXXXX"、"XXX-XXXXXXXX"、"XXXXXXX"和"XXXXXXXX):^(\(\d{3,4}-)|\d{3.4}-)?\d{7,8}$6 国内电话号码(0511-*******、021-********):\d{3}-\d{8}|\d{4}-\d{7}7 ⾝份证号(15位、18位数字):^\d{15}|\d{18}$8 短⾝份证号码(数字、字母x结尾):^([0-9]){7,18}(x|X)?$ 或 ^\d{8,18}|[0-9x]{8,18}|[0-9X]{8,18}?$9 帐号是否合法(字母开头,允许5-16字节,允许字母数字下划线):^[a-zA-Z][a-zA-Z0-9_]{4,15}$10 密码(以字母开头,长度在6~18之间,只能包含字母、数字和下划线):^[a-zA-Z]\w{5,17}$11 强密码(必须包含⼤⼩写字母和数字的组合,不能使⽤特殊字符,长度在8-10之间):^(?=.*\d)(?=.*[a-z])(?=.*[A-Z]).{8,10}$12 ⽇期格式:^\d{4}-\d{1,2}-\d{1,2}13 ⼀年的12个⽉(01~09和1~12):^(0?[1-9]|1[0-2])$14 ⼀个⽉的31天(01~09和1~31):^((0?[1-9])|((1|2)[0-9])|30|31)$15 钱的输⼊格式:16 1.有四种钱的表⽰形式我们可以接受:"10000.00" 和 "10,000.00", 和没有 "分" 的 "10000" 和 "10,000":^[1-9][0-9]*$17 2.这表⽰任意⼀个不以0开头的数字,但是,这也意味着⼀个字符"0"不通过,所以我们采⽤下⾯的形式:^(0|[1-9][0-9]*)$18 3.⼀个0或者⼀个不以0开头的数字.我们还可以允许开头有⼀个负号:^(0|-?[1-9][0-9]*)$19 4.这表⽰⼀个0或者⼀个可能为负的开头不为0的数字.让⽤户以0开头好了.把负号的也去掉,因为钱总不能是负的吧.下⾯我们要加的是说明可能的⼩数部分:^[0-9]+(.[0-9]+)?$20 5.必须说明的是,⼩数点后⾯⾄少应该有1位数,所以"10."是不通过的,但是 "10" 和 "10.2" 是通过的:^[0-9]+(.[0-9]{2})?$21 6.这样我们规定⼩数点后⾯必须有两位,如果你认为太苛刻了,可以这样:^[0-9]+(.[0-9]{1,2})?$22 7.这样就允许⽤户只写⼀位⼩数.下⾯我们该考虑数字中的逗号了,我们可以这样:^[0-9]{1,3}(,[0-9]{3})*(.[0-9]{1,2})?$23 8.1到3个数字,后⾯跟着任意个逗号+3个数字,逗号成为可选,⽽不是必须:^([0-9]+|[0-9]{1,3}(,[0-9]{3})*)(.[0-9]{1,2})?$24 备注:这就是最终结果了,别忘了"+"可以⽤"*"替代如果你觉得空字符串也可以接受的话(奇怪,为什么?)最后,别忘了在⽤函数时去掉去掉那个反斜杠,⼀般的错误都在这⾥25 xml⽂件:^([a-zA-Z]+-?)+[a-zA-Z0-9]+\\.[x|X][m|M][l|L]$26 中⽂字符的正则表达式:[\u4e00-\u9fa5]27 双字节字符:[^\x00-\xff] (包括汉字在内,可以⽤来计算字符串的长度(⼀个双字节字符长度计2,ASCII字符计1))28 空⽩⾏的正则表达式:\n\s*\r (可以⽤来删除空⽩⾏)29 HTML标记的正则表达式:<(\S*?)[^>]*>.*?</\1>|<.*? /> (⽹上流传的版本太糟糕,上⾯这个也仅仅能部分,对于复杂的嵌套标记依旧⽆能为⼒)30 ⾸尾空⽩字符的正则表达式:^\s*|\s*$或(^\s*)|(\s*$) (可以⽤来删除⾏⾸⾏尾的空⽩字符(包括空格、制表符、换页符等等),⾮常有⽤的表达式)31 腾讯QQ号:[1-9][0-9]{4,} (腾讯QQ号从10000开始)32 中国邮政编码:[1-9]\d{5}(?!\d) (中国邮政编码为6位数字) 33 IP地址:\d+\.\d+\.\d+\.\d+ (提取IP地址时有⽤) 34 IP地址:((?:(?:25[0-5]|2[0-4]\\d|[01]?\\d?\\d)\\.){3}(?:25[0-5]|2[0-4]\\d|[01]?\\d?\\d))20个正则表达式必知(能让你少写1,000⾏代码)正则表达式(regular expression)描述了⼀种字符串匹配的模式,可以⽤来检查⼀个串是否含有某种⼦串、将匹配的⼦串做替换或者从某个串中取出符合某个条件的⼦串等。
正则表达式
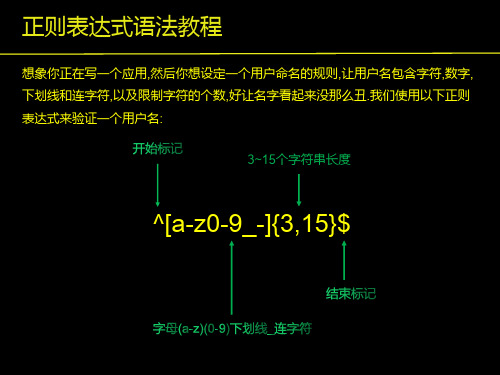
正则表达式语法教程
2.6 | 或运算符
或运算符就表示或, 用作判断条件. 例如 (T|t)he|car 匹配 (T|t)he 或 car.
"(T|t)he|car" => The car is parked in the garage.
描述 匹配num个大括号之前的字符 (n <= num <= m). 字符集, 匹配与 xyz 完全相等的字符串. 或运算符,匹配符号前或后的字符. 转义字符,用于匹配一些保留的字符 [ ] ( ) { } . * + ? ^ $ \ | 从开始行开始匹配. 从末端开始匹配.
正则表达式语法教程
2.1 点运算符
正则表达式语法教程
2.4 {}号
在正则表达式中 {} 是一个量词, 常用来一个或一组字符可以重复出现的次数. 例如, 表达式 [0-9]{2,3} 匹配最少 2 位最多 3 位 0~9 的数字.
"[0-9]{2,3}" => The number was 9.9997 but we rounded it off to 10.0.
"[a-z]*" => The car parked in the garage #21.
*字符和.字符搭配可以匹配所有的字符.*.*和表示匹配空格的符号\s连起来 用, 如表达式\s*cat\s*匹配0或更多个空格开头和0或更多个空格结尾的cat 字符串.
"\s*cat\s*" => The fat cat sat on the concatenation.
常用正则表达式

常用正则表达式正则表达式是一种用于查找和替换文本字符串的强大工具,它能够有效地检测和处理字符串中的模式。
它们被广泛应用于编程语言、文本编辑器、网页开发器和其他软件工具中,以满足各种应用的需求。
正则表达式的出现使得我们可以快速查找和替换字符串中的特定模式。
它们可以简化搜索、提取、编辑和替换文本的工作,从而大大提高工作效率。
本文将针对正则表达式,深入讨论它的语法、用法和常见问题,并总结一些常用的正则表达式。
一、正则表达式语法正则表达式使用一种特殊的语法结构来表达文本字符串的模式,称为“正则表达式语法”。
语法结构由普通字符和“元字符”两部分组成,其中元字符用于指示文本字符串的模式,普通字符表示要查找的文本字符串。
正则表达式语法是由以下几个原则组成的:(1)普通字符。
普通字符会被原样匹配。
例如,在正则表达式中输入字符“a”将仅匹配文本中的“a”字符;(2)元字符。
元字符用于描述文本字符串的模式。
它们是正则表达式语法中最重要的部分,常用的元字符有“*”、“+”、“?”、“()”等符号;(3)字符组(Character Class)。
字符组用于指定一个字符集合,可以搜索任何在该字符集合中的字符,例如“[0-9]”将搜索任何数字;(4)字符范围(Character Ranges)。
字符范围用于指定一个连续的字符集合,例如“a-z”将搜索所有小写字母;(5)量词(Quantifiers)。
量词用于指定字符出现的次数,例如“*”表示字符可以出现任意次数,“+”表示字符至少要出现一次;(6)分组(Groups)。
分组可以将一个模式的不同部分分开,例如“(abc)”将abc分成三个模式;(7)反义(Anchors)。
反义用于指定非指定字符的模式,例如“^”表示任何非数字的字符;(8)转义(Escapes)。
转义符可以将特殊字符转换为普通字符,例如“”将使“”变为普通字符。
二、正则表达式用法正则表达式可以用于各种文本处理任务,如搜索、提取、编辑和替换等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正则表达式→字符串集的映射。 正则表达式→字符串集的映射。
的定义及其含义如下: 则RΣ 的定义及其含义如下:
■ ■ ■ ■ 其中L( L(∅ ∅是正则表达式,即∅∈RΣ 。其中L(∅)={ }。 是正则表达式, ∅∈R 是正则表达式, λ∈R 其中L( L(λ λ 是正则表达式 , 即 λ∈ RΣ 。 其中 L(λ)={ λ }。 其中L(c)={c} L(c)={c}。 c∈Σ是正则表达式,即c∈RΣ。其中L(c)={c}。 ∈Σ是正则表达式, 是正则表达式 A和B是正则表达式,即A ∈RΣ,B ∈RΣ ,则有 是正则表达式, ( A ) ∈ R Σ, A | B ∈ R Σ, A B A* ∈ R Σ, ∈ R Σ, L( (A) ) = L(A) L(A)∪ L( A | B ) = L(A)∪L(B) L( A B ) L( A*) = L(A)L(B) = L(A)*
(A|B)*≠ A*|B* (A·B)* ≠ A*·B*
2011-1-5 CS_Dept. GDCC Hjj
| 的可交换性 | 的可结合性
连接的可结合性 连接的可分配性 连接的可分配性 幂的等价性 λ是连接的恒等元素
(A|B)* = (A*|B*)*
13 /29
程序设计语言中单词的 正则表达式定义
1) 2) 3)
A|B AB A*
2011-1-5
CS_Dept. GDCC Hjj
17 /29
课堂练习2 课堂练习2
假定字母表∑={0, 1},如何用正则表达式描述 下述语言(字符串集)? 1) ?={w|w中恰好有一个1} 2) ?= {w|w是由任意个0和1组成的字符串} 3) ?={w|w中至少有一个1} 4) ?={w|w含有子串001} 5) ?={w|w的长度是3的整数倍} 6) ?={w|w的开始符号和结束符号相同}
数字
整数Int=[1整数Int=[1-9]Digit*|0 Int 实数real Int. real= 实数real=Int.Int
+|特殊符号 +|-|…
正则表达式的局限性
正则表达式不能用于描述配对或嵌套的结 正则表达式不能用于描述配对或嵌套的结 不能用于描述配对 构 正则表达式不能用于描述重复串 正则表达式不能用于描述重复串 的串}无法用正则表 例:{w c w | w是a和b的串 无法用正则表 是 和 的串 达式表示(保证两边w是相同的 是相同的)。 达式表示(保证两边 是相同的)。
3.3 正则表达式
广东商学院信息学院 胡建军
正则表达式
描述程序设计语言中单词的一种简单而 且数学化的工具。 且数学化的工具。 表示符号串的构成模式 正则表达式r定义了一个符号串集合r 正则表达式r定义了一个符号串集合rs, 内的每个符号串都与r rs内的每个符号串都与r所定义的模式相 匹配, 称为由r生成的语言L(r) 匹配,rs称为由r生成的语言L(r) 正则表达式中出现的所有符号构成的集 合为该正则表达式的字母表 字母表, 合为该正则表达式的字母表,用Σ表示
2011-1-5 CS_Dept. GDCC Hjj
10 /29
正则表达式例
∑={ a,b }. 正则表达式e 正则表达式e 1. ab* L(e) 上所有以a 1. ∑上所有以a为首后跟任意多 包括0 个(包括0个)b的字符串集 上所有以a 2. ∑上所有以a为首的字符串集
2. a(a|b)*
正则表达式的性质
正则表达式的应用
程序设计语言中的基本元素-单字 程序设计语言中的基本元素 单字(token) 单字 的描述和判读。 的描述和判读。 在涉及文本的应用领域里。 在涉及文本Байду номын сангаас应用领域里。
2011-1-5
CS_Dept. GDCC Hjj
16 /29
课堂练习1 课堂练习1
正则运算:
设∑={a,b,…,z},A={good,bad},B={boy,girl}, 求:
符号串的方幂: 符号串的方幂: 是符号串的集合 则称A 的集合, 设A是符号串的集合,则称Ai为符号 串集A的方幂,其中i是非负整数。 串集A的方幂,其中i是非负整数。 ={λ A0 ={λ} A1 = A , A2 = A A AA......A(k个 AK = AA......A(k个) 符号串集合的正闭包: 符号串集合的正闭包: A+ =A1 ∪ A2 ∪A3 ...... 符号串集合的星闭包: 符号串集合的星闭包: A* =A0 ∪ A1 ∪ A2 ∪A3 ...... A* = A+ ∪ A0 = A+ ∪ {λ}
扩充的正则表达式
一次或多次重复: 一次或多次重复: A+ 任何符号: 任何符号:“…”在字母表中任何符号.|.|.|. ”在字母表中任何符号.|.|.|. 符号范围: [0[a [A符号范围: [0-9] [a-z] [A-Z] 不在给定范围内的符号: ~(a|b|c) a|b|c)或 不在给定范围内的符号: ~(a|b|c)或[^ a] 可选: (+| 可有可无,即有和无两种情况) 可选: (+|-)? (可有可无,即有和无两种情况) L( A+) = L(A)+ 例:A+∈RΣ, A?∈ RΣ , L( A ?)= L(A) ∪{λ} ? λ 枚举[abc] ∈ RΣ , L([abc] )_=(a|b|c) 枚举 [0-9a-z]=[0-9]|[a-z]=(0|1|2…9)|[a-z]
20 /29
正则定义
如要为一个或多个数字序列写一个正则表 达式,则可写作: 达式,则可写作: 0|1|2|…|9)(0|1|2| |9)(0|1|2|…9) (0|1|2|…|9)(0|1|2|…9)* 或写作 digit digit* 其中 digit= 0|1|2| |9就是名字 0|1|2|…|9 |9就是名字 digit的正则定义,表示为: 的正则定义,表示为: 0|1|2|…|9 digit 0|1|2| |9
正则定义
如要为一个或多个数字序列写一个正则表 达式,则可写作: 达式,则可写作: 0|1|2|…|9)(0|1|2| |9)(0|1|2|…9) (0|1|2|…|9)(0|1|2|…9)* 或写作 digit digit* 其中 digit= 0|1|2| |9就是名字 0|1|2|…|9 |9就是名字 digit的正则定义,表示为: 的正则定义,表示为: 0|1|2|…|9 digit 0|1|2| |9
正则表达式
主要内容: 主要内容: 基本概念 正则表达式定义及一些性质 扩充的正则表达式及程序设计语言中 单词的定义 正则表达式的局限性。 正则表达式的局限性。 正则定义
正则表达式(正规式) 正则表达式(正规式)
基本概念: 基本概念: 字母表:非空有限集, 其元素称为符号或字母. 字母表:非空有限集,∑,其元素称为符号或字母. 符号串:符号的有限序列,也称为‘ 符号串:符号的有限序列,也称为‘字’。λ或ε表示 空串 空串集{ 不同于空集∅ 空串集{λ}不同于空集∅ 。 符号串长度:符号串中字符的个数.| .|β 符号串长度:符号串中字符的个数.|β| 符号串连接: 都是符号串, αβ为符号串的连接 符号串连接:α和β都是符号串,则αβ为符号串的连接 特别有: 特别有:λβ = βλ = β 符号串集的乘积:A和B是符号串的集合,则称 符号串集的乘积: 是符号串的集合, AB={αβ α∈A αβ| AB={αβ| α∈A,β ∈B} 特别有: A=A∅=A,其中∅表示空集。 特别有:∅A=A∅=A,其中∅表示空集。
连接的可结合性 连接的可分配性 连接的可分配性 幂的等价性 λ是连接的恒等元素
(A|B)* (A*|B*)*
正则表达式的性质
A | B = B | A A | (B | C) =(A | B )| C A (B C) =(A B )C A (B | C) =A B | A C (A | B ) C =A C | B C A** =A* Aλ=λA=A λ=λA=A
2011-1-5
CS_Dept. GDCC Hjj
6 /29
正则表达式及其一些性质
书上: 书上:
RE
∑为给定的字母表,则每个Σ上的正则表达 为给定的字母表,则每个Σ上的正则表达 式将定义Σ上的一个字符串集 字符串集。 表示∑ 式将定义Σ上的一个字符串集。 用RΣ表示∑ 上的正则表达式 表示R 上的正则表达式,用L(RΣ)表示RΣ所表示的字 符串集合(正则表达式的集合,语言, 符串集合(正则表达式的集合,语言,正规 集) 。 函数L 即:函数L表示
CS_Dept. GDCC Hjj
2011-1-5
23 /29
正则表达式的缩写形式
一个或多个实例 一元后缀算符“+”,表示“一个或多个实 例” 例:a+表示一个或多个a的所有串的集合。 r*=r +|λ r +=r r* 零个或一个实例 一元后缀算符“?” 表示“零个或一个实 例” 例: (r)? 表示 L(r) ∪|λ| | 2011-1-5 字符组 24 /29 CS_Dept. GDCC Hjj
A | B = B | A A | (B | C) =(A | B )| C A (B C) =(A B )C A (B | C) =A B | A C (A | B ) C =A C | B C A** =A* Aλ=λA=A λ=λA=A
(A|B)* (A·B)* A*|B* A*·B*
| 的可交换性 | 的可结合性
Begin= 保留字 如 Begin=begin 标识符
letter=[aletter=[a-z,A-Z] digit=[0 digit=[0-9] identifier=letter(letter|digit letter|digit) identifier=letter(letter|digit)*
